| Issue |
A&A
Volume 535, November 2011
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117167 | |
| Published online | 18 November 2011 | |
Binary-induced magnetic activity?⋆
Time-series echelle spectroscopy and photometry of HD 123351 = CZ CVn
1 Leibniz Institute for Astrophysics Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany ,
e-mail: Kstrassmeier@aip.de
2 Konkoly Observatory, 1525 Budapest, PO Box 67, Hungary
e-mail: olah@konkoly.hu
3
Department of Physics, Brandon University, Brandon, Manitoba R7A 6A9, Canada
e-mail: rice@BrandonU.ca
Received: 2 May 2011
Accepted: 20 July 2011
Context. Multi-wavelength time-series observations with high cadence and long duration are needed to resolve and understand the many variations of magnetically active late-type stars, which is an approach often used to observe the Sun.
Aims. We present a first and detailed study of the bright and active K0IV-III star HD 123351.
Methods. We acquired a total of 955 high-resolution STELLA echelle spectra during the years 2006–2010 and a total of 2260 photometric VIC data points during 1998–2010. These data are complemented by some spectra from CFHT and KPNO.
Results. The star is found to be a single-lined spectroscopic binary with a period of 147.8919 ± 0.0003 days and a large eccentricity of e = 0.8086 ± 0.0001. The rms of the orbital solution is just 47 m s-1, making it the most precise orbit ever obtained for an active binary system. The rotation period is constrained from long-term photometry to be 58.32 ± 0.01 days. It shows that HD 123351 is a very asynchronous rotator, rotating five times slower than the expected pseudo-synchronous value. Two spotted regions persisted throughout the 12 years of our observations. We interpret them as active longitudes on a differentially rotating surface with a ΔP/P of 0.076. Four years of Hα, Ca ii H&K and He i D3 monitoring identifies the same main periodicity as the photometry but dynamic spectra also indicate that there is an intermittent dependence on the orbital period, in particular for Ca ii H&K in 2008. Line-profile inversions of a pair of Zeeman sensitive/insensitive iron lines yield an average surface magnetic-flux density of 542 ± 72 G. The time series for 2008 is modulated by the stellar rotation as well as the orbital motion, such that the magnetic flux is generally weaker during times of periastron and that the chromospheric emissions vary in anti-phase with the magnetic flux. We also identify a broad and asymmetric lithium line profile and measure an abundance of log n(Li) = 1.70 ± 0.05. The star’s position in the H-R diagram indicates a mass of 1.2 ± 0.1 M⊙ and an age of 6–7 Gyr.
Conclusions. We interpret the anti-phase relation of the magnetic flux with the chromospheric emissions as evidence that there are two magnetic fields present at the same time, a localized surface magnetic field associated with spots and a global field that is oriented towards the (low-mass) secondary component. We suggest that the inter-binary field is responsible for the magnetic-flux dilution at periastron. It is also likely to be responsible for the unexpected slow and asynchronous rotation of the primary star.
Key words: stars: late-type / stars: activity / stars: magnetic field / starspots / stars: individual: HD 123351
© ESO, 2011
1. Introduction
Cool main-sequence stars in binaries appear to be magnetically very active when the orbital period is as short as a few days. Evolved components in binaries are suspected to display photospheric spots and strong chromospheric emission at significantly longer periods, say, 20 days. This has been generally interpreted as meaning that there is a stellar dynamo that needs a convective envelope with a long-enough turn-over time and short-enough rotation to function efficiently (Durney & Latour 1978). The existence of active longitudes in tidally interacting binaries is part of the proof of this concept (see, e.g., Berdyugina 2007). The observational evidence is less clear for stars in a binary where the rotation and the orbital revolution is not synchronized or, even more complex, if having additionally a highly eccentric orbit (Hall 1991; Strassmeier 2001). A binary system with an active component and all of above properties, in particular with a high eccentricity, may allow us to prove or disprove the speculation that a dynamo would operate more efficiently at periastron when the stars are closest, as would be the case for a dynamo influenced by tidal forces (e.g. Schrijver & Zwaan 1991). Such a binary system is presented and analyzed in the present paper.
The star HD 123351 (α = 14h06m26s, δ = 3050′47′′ [2000], 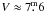 ) was found to exhibit strong Ca ii H&K emission as part of the Vienna-KPNO Doppler imaging candidate survey (Strassmeier et al. 2000). The survey spectra allowed us to determine Ca ii H&K and Hα emission-line fluxes, a projected rotational velocity of 5.2 ± 2 km s-1, a logarithmic lithium abundance of 1.9, and provided two radial velocities 160 days apart that basically agreed within their errors and thus were implied that we had observed a single star. To our knowledge there had been no evidence in the literature that the star is a spectroscopic or a visual binary despite of its relative brightness. Our new data in the present paper indicate the star is a single-lined spectroscopic binary with a very eccentric orbit.
) was found to exhibit strong Ca ii H&K emission as part of the Vienna-KPNO Doppler imaging candidate survey (Strassmeier et al. 2000). The survey spectra allowed us to determine Ca ii H&K and Hα emission-line fluxes, a projected rotational velocity of 5.2 ± 2 km s-1, a logarithmic lithium abundance of 1.9, and provided two radial velocities 160 days apart that basically agreed within their errors and thus were implied that we had observed a single star. To our knowledge there had been no evidence in the literature that the star is a spectroscopic or a visual binary despite of its relative brightness. Our new data in the present paper indicate the star is a single-lined spectroscopic binary with a very eccentric orbit.
The light variability appears to have been first detected by the Hipparcos satellite which led Kazarovets et al. (1999) to include HD 123351 (HIP 68904) in the 74th name list of variable stars as CZ CVn. Simbad identifies it as a “pulsating star” with evidence neither for nor against it. The Hipparcos light curve was analyzed a few years later by Koen & Eyer (2002), who found a photometric period of 59.4 days with an amplitude of 0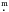 028. A year earlier we had published our first three years of Automatic Photoelectric Telescope (APT) VI data from 1998–2000 (in a paper on APT data reduction by Granzer et al. 2001) that also clearly showed the ≈60-day periodicity.
028. A year earlier we had published our first three years of Automatic Photoelectric Telescope (APT) VI data from 1998–2000 (in a paper on APT data reduction by Granzer et al. 2001) that also clearly showed the ≈60-day periodicity.
The star was detected as an X-ray and EUV source by EUVE and ROSAT with count rates of 0.88 and 0.021, respectively (Lampton et al. 1997). It is listed in the ROSAT all-sky survey (Schwope et al. 2000) and identified in the Hamburg/RASS bright source identification catalogue (Zickgraf et al. 2003). A study of the X-ray selected Seyfert galaxies by Vaughan et al. (2001) listed HD 123351 in their Galactic sample with a Galactic column density of 1.25 × 1020 cm-2. A study of the local kinematics of K and M giants with Coravel/Hipparcos/Tycho data (Famaey et al. 2005) included HD 123351 but did not provide a new radial-velocity measurement. The new Pulkova radial-velocity catalog of HIP stars lists HD 123351 with a single measurement of −11.2 ± 0.8 km s-1 (Gontcharov 2006).
Therefore, the star appeared to be an interesting and rather bright chromospherically active star and deserved a more detailed study. In this paper, we present and analyze an extensive time-series database consisting of high-resolution echelle spectra obtained as part of the science demonstration of the first of our two robotic STELLA telescopes in Tenerife, complemented by some previous KPNO and CFHT spectra, and 12 years of photometric monitoring with our APT in southern Arizona. In Sect. 2, we describe our data. In Sect. 3, we focus on the recovery of the star’s basic astrophysical parameters such as the rotational period, the orbital elements, stellar mass, radius and age, lithium abundance, Rossby number, and evolutionary status in general. Section 4 presents the time-series analysis of the photometric and spectroscopic data in order to reconstruct the stellar surface structure as a function of rotational and orbital phase. Section 5 is an attempt to gather the various results together. Our summary and conclusions are presented in Sect. 6.
 |
Fig. 1 The long-term brightness variations of HD 123351. The top panel shows our twelve years of V-band photometry (dots), the lower panel plots the corresponding V − I color index. The lines are the seasonal fits of the two-spot models from Sect. 4. These models are plotted here as spherical projections at four different phases (from top to bottom, 0°, 90°, 180°, 270°). The gray scale indicates the spot temperature. Note the rotational modulation with a period of ≈ 60 d and a long-term variation in both V and V − I in the sense that the star appears redder when fainter. |
2. Observations
2.1. APT photometry since 1998
High-precision photometry of HD 123351 was obtained with the former University of Vienna 0.75 m twin automatic photoelectric telescopes (APTs) at Fairborn Observatory in southern Arizona (Strassmeier et al. 1997; Granzer et al. 2001). The T7-APT Amadeus was used since JD 2 450 900. It achieved an external precision of 3.2 mmag in Johnson-Cousins VIC. A total of 2260 V and IC data points were obtained until the end of the observing season 2010 and are presented in this paper in Fig. 1. The integration time was 10 sec in V and IC. All measurements were done differentially with respect to HD 123929 (G8, V = 7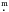 27, B − V = 0.85, Oja 1985; VT = 7
27, B − V = 0.85, Oja 1985; VT = 7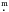 360, B − V = 0
360, B − V = 0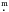 835, Høg et al. 2000). The check star was HD 123533 (K0). Both stars appear constant to within the telescope’s internal precision. The APT data were transformed to absolute values with nightly observations of up to 60 standard stars. For further details of the observing procedure and the APT data reduction in general, we refer to Granzer et al. (2001).
835, Høg et al. 2000). The check star was HD 123533 (K0). Both stars appear constant to within the telescope’s internal precision. The APT data were transformed to absolute values with nightly observations of up to 60 standard stars. For further details of the observing procedure and the APT data reduction in general, we refer to Granzer et al. (2001).
2.2. STELLA/SES spectroscopy in 2006–2010
High-resolution time-series spectroscopy was obtained with the STELLA Echelle Spectrograph (SES) at the robotic 1.2-m STELLA-I telescope in Tenerife, Spain (Strassmeier et al. 2004, 2010a). A total of 955 echelle spectra were acquired over the course of four years. The SES is a fiber-fed white-pupil echelle spectrograph with a fixed wavelength format of 388–882 nm. Despite increasing inter-order gaps in the red, it records the range 390–720 nm continuously. The instrument is located in a dedicated room on a stabilized optical bench and is fed by a 12-m long 50 μm Ceram-Optec fibre, corresponding to an entrance aperture of 1.7′′ on the sky. This fiber enables a two-pixel resolution of R = 55000. The spectrograph’s heart is a 31 lines per mm R2 grating. Two off-axis parabolic collimators, one folding mirror, and a prism as a cross disperser transport the light into the f/2.7 kata-dioptric camera with a 20 cm corrector and a 40 cm spherical mirror. The CCD is currently an E2V 42-40 2048 × 2048 13.5 μm-pixel device. Its quantum efficiency is 90% at 650nm, and 65% at 400 and 800 nm, respectively. Together with a second-generation CUO controller, the read-out noise is 3–4 electrons rms at 200 kbyte/s. A closed cycle cooler keeps the detector cooled to −130C.
Spectroscopic and photometric observing logs.
Integrations on HD 123351 were set to exposure times of between 3600 s and 1200 s and achieved a signal-to-noise ratio (S/N) of between 200:1 to 50:1 per resolution element, respectively, depending on weather conditions. One spectrum on almost every clear night was obtained between June 25, 2006 and June 22, 2010. Numerous radial velocity standards and stellar comparison targets were also observed with the same set-up. Earlier data in 2006 and during March–October 2007 had to be shifted by +280 m s-1 because of a fiber misalignment problem. The time-series velocities are plotted in Fig. 2. The best rms radial-velocity precision over the three years of observation was 30 m s-1. The time series also included nightly flat-field exposures, bias readouts, and Th-Ar comparison-lamp exposures. For details of the echelle data reduction, we refer to Ritter & Washuettl (2004) and Weber et al. (2008) and our previous paper on HD 1 (Strassmeier et al. 2010c). The data log is summarized in Table 1.
2.3. KPNO/CF spectroscopy in 1998 and 2000
Twenty KPNO observations were obtained with the 0.9-m coudé feed (CF) telescope in April 1998 and in March 2000 (Table 1). The F3KB 3k-CCD was used together with grating A, the long collimator and a 280 μm slit. This configuration allowed a resolving power of R ≈ 28 000 at a dispersion of 4.81 km s-1/pixel. The wavelength coverage was 30 nm and the spectra were centered at 649 nm. The exposure time was 1200 s resulting in an average S/N of 100:1.
All KPNO spectra were reduced and extracted using the Interactive Reduction and Analysis Facility (IRAF) provided by NOAO. More details of the standard coudé-spectra reduction procedure were given in previous papers, e.g. by Weber & Strassmeier (1998).
2.4. CFHT/Gecko spectroscopy in 2000
Three very high-resolution lithium spectra were obtained consecutively on one night at CFHT with Gecko and an order-sorting filter in the 9th order at HJD 2,451,687.75. A fourth integration of 900 s was taken centered at 644 nm at 2 451 683.73. Equipped with the CAFE fiber feed module Gecko provided a spectral resolution of 120 000. CAFE feeds light through a 27 m-long 100 μm Ceram-Optec fiber to a four-slice Bowen-Walraven image slicer before it enters the collimator. In combination with the 4600 × 2048 13.5 μm-pixel EEV1 CCD, it gives a 10 nm wavelength coverage centered at 671 nm. An integration time of 600 s per exposure gave a peak S/N of 300:1 per resolution element. For a brief description of the data reduction, we refer to the paper by Strassmeier & Rice (2003). The data log summary is given in Table 1.
 |
Fig. 2 Radial velocities of HD 123351. a) Phased STELLA radial velocities with the orbital period of 147.8919 d. Dots are the observations and the line is the orbital fit to the spot-corrected elements in Table 2. b) Top panel: the four years of monitoring. Such data sampling is made possible with robotic telescopes. The line is again the orbital solution from Table 2 (column “Spot corrected”). Lower panel: residuals after removal of the orbital fit. The modulation is due to stellar rotation and the insert shows a DFT periodogram with the strongest peak at 61.0 ± 1.1 d, in agreement with the photometric period. The full amplitude varied over the years between 400 m s-1 in 2007 and 100 m s-1 in 2009, indicating the variable asymmetry of the spot distribution. The line is a Blackman-function fit to the data. |
3. Stellar parameters of HD 123351
3.1. Orbital elements
Radial velocities of the STELLA spectra were determined from an order-by-order cross correlation with a synthetic G8 template computed from a Kurucz (1993) atmosphere. Only the central 19 echelle orders are used, providing a wavelength range of ≈ 150 nm. The coudé spectra from KPNO and CFHT were analyzed similarly but using the IRAF cross-correlation program fxcor together with various reference-star spectra. All velocities are corrected for the solar-system’s barycenter (the full data are given in machine readable format in the electronic attachment). The gravitational redshift is expected to be 133 m s-1 according to the mass and radius in Table 3 but was not corrected for.
For the orbital solution with non-zero eccentricity we use the prescription from Danby & Burkardt (1983) to calculate the eccentric anomaly. The elements are solved for by using the general least-square fitting algorithm MPFIT (Markwardt 2009). More details about the orbit computation are discussed in Weber & Strassmeier (2011) and we refer the reader to this paper. Owing to unclear zero-point differences between the three data sets, and the different set ups, we include the earlier velocities from KPNO and CFHT only for the period determination. An SB1 solution of all velocities, but with zero weight given to the KPNO and CFHT data, resulted in an eccentricity of 0.809 ± 0.001 and a period of 147.890 d. We note that all previous KPNO and CFHT velocities fell into the phase range 0.1–0.8 where almost no velocity variations because of the high eccentricity. From these spectra alone, one could conclude that the star has a constant radial velocity, as actually done by Strassmeier et al. (2000). For the initial orbital solution, a total of 955 STELLA radial velocities were used. The standard error in an observation of unit weight was 73 m s-1, which is the best so far achieved for an orbit of a chromospherically active star (e.g. Fekel et al. 1999; Griffin 2009; Torres et al. 2009). However, this rms includes the modulation due to the asynchronously rotating spotted surface. Table 2 (left column) lists the orbital elements from the unaltered initial data. In Sect. 3.2, we refine the orbit by removing the starspot jitter from the radial velocity data and then achieve a standard error of 47 m s-1 close to the measuring error of approximately 30 m s-1. Figure 2a plots the spot-corrected radial velocities along with the orbital fit, Fig. 2b (top panel) shows the unaltered original data. The difference cannot be seen by eye.
Spectroscopic orbital elements.
We note that the low mass function, together with our inability to see a secondary star in our spectra, suggests that the orbit has a low inclinationwith respect to the sky. If we assume at least a 2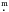 5 brightness difference between the secondary and the primary at red and blue wavelengths, the secondary cannot be of earlier spectral type than G2(V). Adopting its mass as m2 = 1.0 M⊙, the observed f(m) = 0.0113 provides a lower limit to the inclination of almost 22°. A more likely secondary would be a red dwarf of mass m2 ≈ 0.5 M⊙, which suggests a more likely inclination of ≈ 40° and a minimum separation of ≈ 2 × 107 km (≈5 stellar radii) during periastron.
5 brightness difference between the secondary and the primary at red and blue wavelengths, the secondary cannot be of earlier spectral type than G2(V). Adopting its mass as m2 = 1.0 M⊙, the observed f(m) = 0.0113 provides a lower limit to the inclination of almost 22°. A more likely secondary would be a red dwarf of mass m2 ≈ 0.5 M⊙, which suggests a more likely inclination of ≈ 40° and a minimum separation of ≈ 2 × 107 km (≈5 stellar radii) during periastron.
3.2. Rotational parameters
The photometric data have high amplitude, both short-term and long-term, variations. The short-term variations are clearly due to rotational modulation, while the long-term variation is likely due to some sort of multi-periodic spot cycle.
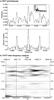 |
Fig. 3 Periodograms from HD 123351 photometry. a) Discrete Fourier transform (DFT) periodogram from the pre-whitened V-band data (top panel). The twelve-year average period is 61.9 d (0.01616 c/d). The bottom panel is the corresponding window function. The insert in the top panel shows the entire search range. b) Two-dimensional short-term Fourier transform (STFT) analysis. The power distribution in the time-frequency plane is shown as a gray scale (black means highest power, white no power). It shows that the photometric period reached values between a maximum of 62.0 d and a minimum of 57.3 d. Around 2 453 000 (2002–2005), a bimodal distribution was recovered. Note that the excess power in the lower left corner is due to the length of the data vector and is artificial. |
A photometric period of ≈ 60 d is obtained with a very high level of confidence, which we interpret to be close to the true stellar rotation period. This value is based on a one-dimensional discrete Fourier transform (DFT) analysis of the VIC-band data. The best-fit twelve-year average period is 61.9 ± 0.4 d from a Gaussian fit to the V and IC-band DFT peaks (the results from V data are shown in Fig. 3a). However, other significant peaks show up at slightly higher frequencies even in the pre-whitened data. Repeating the analysis for three data subsets by splitting the entire time series into three parts of similar length, we get periods of 61.4 d for the first (1998–2001), 62.0 and 57.3 d for the second (2002–2005), and 59.2 d for the third (2006–2010) part of the data set, identifying the variable and sometimes even two significant periods. The typical error is 0.7 d. For spotted stars, this is a sign of surface differential rotation, i.e., spots modulate the light with different periods when they appear at different latitudes on the stellar surface. It also means that we cannot simply interpret the photometric period to be the rotational period of the star. Seasonal changes occur when spots disappear after a certain (life)time but others appear, possibly cyclically as on the Sun, and possibly at different latitudes. If either the cycle is short enough or the database of sufficiently long duration and the sampling dense enough, it allows us in principle to determine the amount of differential rotation (e.g. Oláh et al. 2003). Its sign, however, could only be determined from simultaneous Doppler imaging.
To confirm the above-mentioned period splitting, and pinpoint its onset and duration, we performed a two-dimensional time-frequency analysis with the program package Time-Frequency Analysis (TiFrAn) (Kolláth & Csubry 2006). The time-frequency analysis is conventionally applied to continuous datasets, whereas our observations are gapped. Thus, the yearly interruptions are filled with straight lines, which do not alter our main results but may produce spurious features. More details about the procedure can be found in Kolláth & Oláh (2009). We chose the short-term Fourier transform (STFT) but also compared the results with those obtained using the Choi-Williams and the pseudo-Wigner kernel. The resulting patterns of periods are identical to those of the above DFT analysis to a very high degree. Figure 3b shows the frequency distribution over the 12 years of data from the STFT analysis. The continuous variability, and the splitting of the rotational period, is clearly visible. The splitting started in 2003 and lasted until 2005. The 2004 observing season is the one where the light curve shape became double-humped and the V and IC amplitudes reached their smallest value in our entire time series. At the same time, the photometry appeared bluest, indicating, together with the low amplitudes, that the spot coverage had reached a minimum.
The coadded R = 120000 CFHT spectrum with S/N = 500 in the wavelength range 638–646 nm was measured for spectral-line broadening. We followed the recipe of Fekel (1997) and found a best-fit vsini value of 1.8 ± 0.7 km s-1, adopting a typical radial-tangential macroturbulence for a K subgiant/giant of 3 km s-1. We note that such a low vsini cannot be resolved by our spectra and thus formally constitutes only an upper limit. Together with Pphtm ≈ Prot ≈ 60 d and the assumption that the rotational axis is perpendicular to the orbital plane, we infer that the minimum stellar radius is Rsini ≈ 2.1 ± 0.8 R⊙.
3.3. Rotation induced radial-velocity variations
Today’s high-precision radial-velocity surveys of stars with exoplanets may record the rotation of the host star if it has dark spots just large enough to mimic a “transit” (Saar & Donahue 1997). Such rotational modulation was first detected in active pre-main sequence stars with large cool spots (e.g. Stelzer et al. 2003) but also in an active main-sequence star (Huber et al. 2009). Amplitudes of 2 km s-1 were detected for the extremely active T Tauri star LkCa 19 (Huerta et al. 2008), while a flare on the M-dwarf CN Leo introduced radial velocity jitter of several tens of m s-1 (Reiners 2009). We found radial velocity variations with an amplitude of 270 m s-1 for the single, active giant 31 Com with a period in agreement with the photometric period from MOST satellite data (Strassmeier et al. 2010b).
HD 123351 exhibits radial-velocity modulations that are even visible by eye in the plot of the residuals in Fig. 2b after the removal of the orbital variation. The peak-to-peak amplitude varied across the range 300–400 m s-1 in 2007 and was 100 m s-1 in early 2009. The simulations of Hatzes (2002) suggested that spots induce a radial-velocity amplitude of at least hundred m s-1 for even low-activity stars. His relationship of velocity amplitude δv in m s-1 with spot coverage A in per cent and line broadening vsini in km s-1 (δv = (8.6vsini − 1.6)A0.9) would suggest a variable spot coverage in the range of A ≈ 9−42% for HD 123351. This is incorrect by a factor of three when compared to the more detailed simulations by Desort et al. (2007), who found 3−12%, mostly because these authors took into account the spot temperature. However, this difference is of no relevance here because we only wish to make an order-of-magnitude estimate. Makarov et al. (2009) extended these analytical relations to astrometry. We performed a DFT analysis of the radial-velocity residuals shown in Fig. 2b and found the best-fit period to be 61.0 ± 1.1 days, in agreement with the photometric period.
The rotation of the spotted stellar surface introduces systematic jitter into the radial velocity curve. However, this jitter is unevenly distributed across one orbital revolution because of the asynchronous stellar rotation. We note that the residual radial-velocity curve appeared even quintuple humped in 2008, just as the light curve appeared double humped at the same time. We remove the starspot jitter from the original data and then repeat the determination of the orbital elements from Sect. 3.1. This is achieved by convolving the residuals in Fig. 2b with a smoothing function (Blackman function) and then subtracting it from the radial-velocity data. The largest values that were added to or removed from the data were + 100 m s-1 and − 200 m s-1, respectively. The revised orbital elements are given in the column “Spot corrected” in Table 2.
Summary of astrophysical data of HD 123351.
The effect of the applied procedure on the orbital elements is also demonstrated in Table 2. We note that the elements did not change much, i.e. the corrected solution is largely within the errors of the uncorrected solution. Typically, the error per element became smaller by a factor 2–3. This is what is expected if the jitter due to rotational modulation spreads equally, or nearly equally, around a mean radial velocity. For our long-term observations, this is indeed the case because the phased orbital radial-velocity curve is sampled in total by 25 stellar rotations (for each orbital revolution we have 2.5 stellar rotations). Because the starspot distribution changes with time, we do not just correct with a harmonic sinusoidal of period Prot and fixed amplitude but with the actual residuals of the rotationally modulated radial velocity.
3.4. Luminosity, radius, metallicity, mass, and age
Figure 4 compares the position of HD 123351 in the H-R diagram with theoretical evolutionary tracks. We note that the revised Hipparcos parallax of 10.22 ± 0.67 mas (van Leeuwen 2007) corresponds now to a distance of 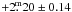 pc, which is different by +1.7 pc from the original data reduction. At this distance, it is only moderately affected by interstellar extinction. We adopted the mean extinction value from Henry et al. (2000) for the absolute magnitude calculation (AV = 0.8 mag kpc-1 and E(B − V) = AV/3.3). The brightest recorded V magnitude of 7
pc, which is different by +1.7 pc from the original data reduction. At this distance, it is only moderately affected by interstellar extinction. We adopted the mean extinction value from Henry et al. (2000) for the absolute magnitude calculation (AV = 0.8 mag kpc-1 and E(B − V) = AV/3.3). The brightest recorded V magnitude of 7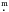 235 converts into an absolute visual magnitude of MV =
235 converts into an absolute visual magnitude of MV = 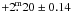 . Its dereddened B − V based on the Tycho color (1
. Its dereddened B − V based on the Tycho color (1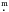 029 ± 0.01) is 1
029 ± 0.01) is 1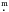 00. This can be converted to a Teff of ≈ 4840 K with the transformation of Flower (1996). The bolometric magnitude of HD 123351 is +1
00. This can be converted to a Teff of ≈ 4840 K with the transformation of Flower (1996). The bolometric magnitude of HD 123351 is +1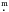 78 obtained with a solar bolometric magnitude of +4
78 obtained with a solar bolometric magnitude of +4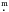 75 and a bolometric correction (B.C.) of − 0.42 (Flower 1996). The ± 70 K uncertainty in Teff (see next paragraph) corresponds to an uncertainty in the B.C. of ± 0.04 and the star’s luminosity becomes 15.4
75 and a bolometric correction (B.C.) of − 0.42 (Flower 1996). The ± 70 K uncertainty in Teff (see next paragraph) corresponds to an uncertainty in the B.C. of ± 0.04 and the star’s luminosity becomes 15.4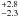 L⊙. These errors are still driven by the error in the parallax rather than in the effective temperature ( ± 70 K). The Stefan-Boltzmann law gives a stellar radius of 5.74
L⊙. These errors are still driven by the error in the parallax rather than in the effective temperature ( ± 70 K). The Stefan-Boltzmann law gives a stellar radius of 5.74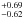 R⊙, which is appropriate for a K0 subgiant/giant. The minimum radius inferred from vsini and Prot in Sect. 3.2 of 2.1 ± 0.8 R⊙ suggests a minimum inclination of as low as i ≈ 23.
R⊙, which is appropriate for a K0 subgiant/giant. The minimum radius inferred from vsini and Prot in Sect. 3.2 of 2.1 ± 0.8 R⊙ suggests a minimum inclination of as low as i ≈ 23.
Our SES spectra are used to refine the effective temperature, gravity, and metallicity. We employ the spectrum-synthesis technique and the numerical tools described in Allende-Prieto et al. (2004) with a grid of synthetic ATLAS-9 spectra tailored to the stellar parameters of HD 123351. Five spectral orders around 600 nm were chosen and the result per spectral order combined on the basis of a weighted least-squares minimization. The average and the standard deviations then constitute our final values and their internal precisions. We found Teff = 4780 ± 70 K, log g = 3.25 ± 0.30, and [Fe/H] = 0.00 ± 0.08 with a prefixed value for the microturbulence of 2 km s-1 and a total line broadening of 3.80 km s-1.
 |
Fig. 4 The position of HD 123351 (dot) in the theoretical H-R diagram (log L/L⊙ vs. log T in K). Shown are evolutionary tracks for masses of 1.1–2.5 M⊙, solar metallicity, and core overshooting (dotted lines; Pietrinferni et al. 2004). The best-fit model track (full line) suggests a mass for HD 123351 of 1.2 ± 0.1 M⊙. The insert is a zoomed image of the box around the observed location indicating the nominal ages of the 1.2-M⊙ track (again the full line) and a 1.1-M⊙, 1.3-M⊙, and 1.5-M⊙ track (dotted lines), respectively. This suggests a most-likely age of HD 123351 of 6–7 Gyr. |
These values are compared with theoretical evolutionary tracks in Fig. 4. We selected post main-sequence tracks from the grid of Pietrinferni et al. (2004). All tracks are for solar metallicity and core overshooting. The HD 123351 position suggests a most likely mass of 1.2 ± 0.1 M⊙. We note that the models without core overshooting would increase the mass by about 0.1 M⊙ and decrease the age by ≈ 1 Gyr. The star appears on the ascent of the red-giant branch (RGB) at an age of approximately 6–7 Gyr. The 12C14N lines around 800.35 nm are clearly detectable with a combined equivalent width of 96 mÅ. However, the equivalent width of the 13C14N line at 800.46 nm is at ≈2.5 mÅ very weak and probably below our detection limit but provides a lower limit to 12C/13C of ≈ 40, in agreement with the expectation that small 12C/13C ratios (around 10–15) are only found in giants that have evolved up to or beyond the RGB (e.g. Allende Prieto et al. 2004). At this point we recall the findings of radius and temperature inconsistencies for active low-mass eclipsing binaries with model computations (e.g. Morales et al. 2009, 2010). Oversized stars with a temperature deficit caused by chromospheric activity could alter the true stellar position in the H-R diagram, thus affect the mass and age estimate.
3.5. Lithium abundance
We employ the averaged R = 120000 CFHT spectrum for the measurement of the Li equivalent width (Fig. 5). This spectrum has a peak S/N of almost 500:1. A Gaussian fit gives an equivalent width of the combined 670.78 nm line (6Li+7Li) of 90 ± 3 mÅ (the error is an estimate inferred from the spread in the values from the three individual spectra and the quality of the Gaussian fit). Subtraction of a reference spectrum with presumably no lithium (16 Vir in Fig. 5) removes a contribution of 16 mÅ from the nearby Fe i+V i blend. The remaining 74 mÅ converts into an abundance of log n(Li) = 1.70 (log n(H) ≡ 12) with Teff = 4780 K and log g = 3.0 from the NLTE tables in Pavlenko & Magazzú (1996). Its uncertainties produced by the measuring error and the error of ± 70 K in Teff and ± 0.3 in log g, combine to ≈ 0.05 dex.
 |
Fig. 5 Lithium 670.8-nm region in the spectrum of HD 123351. Shown are three consecutive R = 120000 spectra obtained at CFHT in May 2000 at orbital phase 0 |
The very low rotational broadening of vsini = 1.8 km s-1 enables a detailed line-profile modeling of the 6Li/ 7Li isotope ratio. As this is a complex synthesis based on a three-dimensional, radiative hydrodynamics simulation, we refer to a forthcoming paper by Steffen et al. (in prep.). Not much is known about this ratio in magnetically active stars (see, e.g., Balachandran et al. 2000) but it plays an important role in constraining or even excluding some mixing mechanisms and determining the likelihood of extra lithium production. HD 123351 shows a moderately strong but broader than expected Li i line at 670.8 nm (see Fig. 5). The line strength is weaker than to the nearby Fe i lines at 671.03 nm and 670.51 nm, i.e. 0.76 compared to 0.68 and 0.67, respectively, but the equivalent width is larger by more than 20%. A weak excited Li feature at 610.36 nm is also present but strongly blended with the nearby double Fe i line and appears rather uncertain for a quantitative analysis. We measure an equivalent width of 8 ± 4 mÅ from a double Gaussian fit, close to the detection limit of, say, 3–5 mÅ. Therefore, we refrain from modelling this line.
3.6. Rossby number and dynamo activity
The Rossby number, Ro = Prot/τc, is widely used as an indicator of the existence and efficiency of a dynamo process. While the rotation period can be observed very accurately, the convective turn-over time, τc, remains an elusive parameter. It describes the ratio of a characteristic length of convection to a characteristic velocity, ℓ/u, and is either determined theoretically (e.g. Kim & Demarque 1996) or semi-empirically (e.g. Pizzolato et al. 2003). We determine τc with the differential-rotation code of Küker & Stix (2001) as a function of depth based on a description of the pressure scale height, Hp, and the classical mixing length, α. The characteristic convective length is then defined as ℓ = α Hp, with α = 2. In the case of a fast rotator, the convective heat flux is no longer aligned with the temperature gradient and tilts towards the rotational axis. It then creates a horizontal heat flux from the equator to the poles (meridionally circulated) that, together with the Reynolds stress, maintains differential rotation. Figure 6 shows the turn-over time for HD 123351 plotted versus the fractional stellar radius. The depth of the convection zone is predicted from the MESA1 code (Paxton et al. 2010) to be 90% of the stellar radius. The average turn-over time is around 40 d. It would give a Rossby number of ≈ 1.4 and, according to the dynamo criterium of Durney & Latour (1978), be insufficient to operate an effective dynamo, in contradiction with the observations. If we determine the Rossby number using the convective turnover time at the base of the stellar convection zone, i.e. Ro ≈ 0.73 with τc ≈ 80 d, it agrees with the dynamo criterium. This may indicate that the dynamo of HD 123351 is indeed located at the base of the convection zone, as in the Sun.
 |
Fig. 6 Convective turn-over times, τc, in seconds as a function of depth in the convection zone of HD 123351. Note that the turn-around of the curve below a fractional radius of ≈ 0.35 strongly depends on the adopted stellar model and could be an artefact. τc spans between a maximum of 80 d near the bottom of the convection zone and 10 d near the surface. |
3.7. Chromospheric activity
We measure an average equivalent width of the He i D3-line of 39 mÅ with an estimated error of 5 mÅ, which is comparable to the measurements for most active G and K dwarfs in the sample of Saar et al. (1997). The detection of the He i D3-line at 587.56 nm indicates the presence of non-thermal heating processes on HD 123351, since the line cannot be excited at photospheric temperatures. It is thus a comparably “pure” indicator of chromospheric magnetic activity because of the absence of photospheric contamination present in most other optical activity diagnostics, e.g. Ca ii H&K and Hα. However, the comparable weakness of the line makes it more likely to be affected by a limited S/N ratio.
Besides He i D3, both Ca ii features, the H&K doublet, and the infrared triplet, appear as moderately-strong central emission lines, while Hα appears as a filled-in absorption line with an equivalent width of 850 mÅ. Absolute Ca ii H&K emission-line fluxes for HD 123351 are determined with the method of Linsky et al. (1979) as adapted and applied, e.g., in Strassmeier et al. (1990). It is based on the measurement of the relative flux in a 5.0-nm bandpass centered at 395.0 nm, and the relative flux in the two emission lines, defined by the blue and red emission-line footpoints, respectively. Absolute fluxes are then determined using the Barnes-Evans relation (Barnes & Evans 1976) and the measured value of the star’s Johnson V − R color. Following the recipes in Hall (1996), the relative fluxes convert into absolute chromospheric emission-line fluxes of, on average, 1.6 × 106 erg cm-2 s-1 for the sum of the Ca ii H and K lines, 1.4 × 106 erg cm-2 s-1 for Hα and 8 × 105 erg cm-2 s-1 for the sum of the Ca ii infrared-triplet lines. These are values typical of RS CVn stars and indicative of a magnetically active atmosphere.
Seasonal average spot parameters 1998–2009.
 |
Fig. 7 Results from the photometric spot modeling. a) The reconstructed spot longitudes expressed in stellar rotations versus time. Filled gray points refer to spot 1, open circles to spot 2. These values were obtained based on the initial photometric period of 61.9 d and after shifting full seasons by an integer rotation such that the resulting long-term migration is brought into agreement with the seasonal migration (the latter is indicated by the short lines). The two lines are linear regression fits and their slopes indicate the true rotation period of 58.32 d. b) Top panel: spot longitudes versus time based on the 58.32-d period. Filled gray points refer to spot 1, open circles to spot 2 as in panel a). The pluses indicate the longitudinal separation of the two spots and show a fairly constant value of 150° ± 17°. Bottom panel: the reconstructed fractional spot area versus time. In both panels, seasonal average values are additionally plotted. |
4. Time-series analysis
4.1. The location and evolution of photospheric spots
The spot longitude, which is the most stable and well-determined parameter, arises directly from the light-curve shape and marks the presumed spot concentration. The longitude difference between the spots can depict systematic surface patterns. When the spots are very close, then a single, elongated spotted region probably causes the light variation that then appears quasi-sinusoidal. On the other hand, double-humped light curves indicate spotted regions on the two hemispheres of the star separated by nearly 180°. We perform a more detailed light-curve fitting with our time-series spot-modelling code SpotModeL. The strengths and shortcomings of the code were described in detail in Ribárik et al. (2003). The program reconstructs the position, size, and temperature of up to three cool spots by minimizing the fit residuals with the help of the Levenberg-Marquardt algorithm as formulated in Press et al. (2002). Free parameters are the spot radii, the temperature relative to the (fixed) photospheric temperature, and their longitudes and latitudes. In the present application, we solve for the V and IC light curves simultaneously. Figure 1 illustrates the fits along with a graphic presentation of the resulting two spot models.
We first proceed with the determination of the spot temperatures and the best-fit spot latitudes. For this initial step, we assume the average photometric period (61.9 days) to be the rotational period. Average spot temperatures are obtained by a simultaneous two-spot fit of the seasonal V and IC light curves. The seasonal light curves usually span three stellar rotations with significant changes in the light-curve shape in V and in IC. Spot latitudes are kept as a free parameter in this initial step. We note that these spot latitudes are strongly model dependent. Here we assume two circular spots. The average rms of the fits to V − IC implies spot temperatures precise to roughly ± 100 K, with a span of 20–180 K for the various seasons. Any seasonal change below this threshold is deemed unrealistic from our data. The grand average spot temperature over the 12 years was 3620 K (rms of 250 K), i.e. cooler than the unspotted photosphere by 1160 K. With the exception of years 2000 and 2009, all seasonal rms values are below or around 100 K, i.e. 1.4 to 8 times smaller than the 250 K from the grand average, thus considered real differences. In a second step, we again applied SpotModeL but now to the V and IC light curves in the time domain and with the spot temperatures and spot latitudes kept fixed to the corresponding average seasonal values listed in Table 4. In that table, ℓ denotes the spot longitude, b the spot latitude (positive in the dominating hemisphere), A the fractional spot coverage in per cent of the total sphere, Tspot the spot temperature, and σfit the squared sum of the residuals in V and I in mmag. Labels 1 and 2 denote spots 1 and 2, respectively.
The next step included the revision of the rotational period. This was done by determining the slope of the longitudinal spot migration in the longitude versus (vs.) time diagram for each spot and during each observing season. Then, the seasonally averaged longitude of each spot, or spot group, was allowed to be shifted by an integer rotation such that the resulting long-term migration was brought into the best-possible agreement with the seasonal migration (Fig. 7a). This was achieved for a slope of − 0.38 deg/d for spot 1 and − 0.39 for spot 2, corresponding to a new period of 58.32 days. As a comparison, the seasonal average slopes were − 0.32 and − 0.35 for spots 1 and 2, respectively. The slight difference between the two spots is due to spot 1 appearing at a slightly longer longitude than expected in 2000 and by spot 2 being at a markedly shorter longitude than expected in 2007. We tend to ignore the difference and adopt the average slope as the true rotation period of the star. We then applied SpotModeL again in the time domain but with the rotation period fixed to 58.32 days. This led to the refined spot parameters in Table 4. We emphasize that our spot solutions, although precise and consistent, are not a detailed accurate representation of the real stellar surface because of the assumption of circular spots and the mathematically non-unique fit (see Savanov & Strassmeier 2008) but serve as a qualitative surface map for further discussions.
Figure 7b shows the migration of the spot longitudes and the spot size together with the (longitudinal) separation of the two spotted regions based on a period of 58.32 days. We note that in all cases only two spots were needed to fit the light curves to within their observational errors. We interpret them as active longitudes that appear to migrate in both directions with respect to the average photometric period but with more-or-less constant longitudinal separation. There is a short-term rapid migration of individual spots (appearing as jumps in Fig. 7b, top panel), e.g. of spot 1 between 1999 and 2000. This migration during the observing season 2000 was paralleled with a systematic increase in its area by ≈ 40% as well as a decay in the area of spot 2 by even a factor of three from an almost equal area at the beginning of 2000 to almost disappearance at the end. During 2000–2004, the separation between the spots increased and reached a maximum separation in 2004 when indeed a double-humped light curve was observed. The rapid migration of spot 1 around 2005 caused the two spots to become closer and after that the separation increased again, reaching an equal maximum in 2008 as in 2004. From the time-frequency analysis in Fig. 3b, we find that around 2004, i.e. when the spot longitude separation was the largest, the photometric period had split into two distinct values (62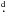 0 and 57
0 and 57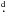 3). This suggests that in reality the two spotted regions were at different latitudes on a differentially rotating surface with ΔP/P ≈ 0.076 as a lower limit, albeit a short-term, fast, spot-morphology change could not be excluded as an alternative explanation. We note that the sign of the differential rotation cannot be reconstructed because of the inherent lack of a reliable latitude determination from one-dimensional photometry. We note again that the longitudinal separation of the two spots remained nearly constant during the 12 years of observations (150° ± 17°). This suggests that the two spots, or spotted regions, have a common origin inside the star and are not just two independent flux tube rings. However, we see no evidence of a periodic flip flop of the active longitudes, as found for many other spotted stars with long-term photometric coverage (e.g. Korhonen & Järvinen 2007). Only in 1999 and in 2002 was spot 2 larger than spot 1.
3). This suggests that in reality the two spotted regions were at different latitudes on a differentially rotating surface with ΔP/P ≈ 0.076 as a lower limit, albeit a short-term, fast, spot-morphology change could not be excluded as an alternative explanation. We note that the sign of the differential rotation cannot be reconstructed because of the inherent lack of a reliable latitude determination from one-dimensional photometry. We note again that the longitudinal separation of the two spots remained nearly constant during the 12 years of observations (150° ± 17°). This suggests that the two spots, or spotted regions, have a common origin inside the star and are not just two independent flux tube rings. However, we see no evidence of a periodic flip flop of the active longitudes, as found for many other spotted stars with long-term photometric coverage (e.g. Korhonen & Järvinen 2007). Only in 1999 and in 2002 was spot 2 larger than spot 1.
4.2. Modulation of chromospheric tracers
Our STELLA spectra contain a number of chromospheric activity tracers, most notably Hα and Ca ii H&K. With a total time span of four consecutive years, 2006–2010, and a sampling of the order of one spectrum per (clear) night, the spectra are suitable for searching a modulation as short as a fraction of the star’s rotational period. Table 5 summarizes the results.
Balmer Hα. The spectra were first re-normalized to optimize the continuum setting in the echelle order that contains the Hα line. We computed a median spectrum from the total of 955 spectra and then iteratively shifted the individual spectra in intensity and wavelength by minimizing the scatter on both sides ± 0.3nm around the Hα line. Figure 8a is a time series plot of the Hα-line profiles for the entire time series together with a dynamic plot of its residual spectra after removing the median line profile. We then determined the relative 0.1-nm flux centered on the Hα laboratory wavelength and subjected this to a period search with a discrete Fourier analysis. This search revealed the strongest peak for a period of 58.7 ± 0.2 d, in agreement with the 58.32-days obtained from our photometric analysis (note that DFT errors are internal errors). After prewhitening with this period, two more periods become significant, one around 90 d and another at the orbital period of 147 d. Because 1/147 + 1/90 ≈ 1/58, we conclude that the ≈ 90-day peak is an alias and that we see very weak modulation of Hα also with the orbital period. The latter is only marginally significant though with an amplitude of around one standard deviation. The two panels in Fig. 9b show plots of the line-core emission phased with the rotational period and the orbital period, respectively.
Summary of period determinations.
 |
Fig. 8 Modulation of chromospheric activity tracers during the years 2007–2010. The two top rows show Hαa), the two bottom rows show Ca ii H&K (b). The left panels are overplots of all line profiles for 2007–2010 (in panel b) only the K-line is shown), while the bright lines indicate the median profiles, respectively. The right hand panels are the dynamic spectra phased with the photometric rotational period (top) and the orbital period (bottom) and the zero points from Table 2. The color scale indicates the relative emission-line flux with respect to the median profile. The two dashed, horizontal lines show ± vsini, and the chain of points in the very bottom of the graphs represents the phase coverage (one dot is one spectrum). It appears that both activity tracers display a clear modulation with the rotational period, with a tendency to cluster around a time of periastron at phase 1.0, and maintained that behavior for the entire duration of our observations. |
Ca IIH&K. We construct relative Ca ii H&K emission-line fluxes based on the measurement of the flux in a 5.0-nm bandpass centered at 395.0 nm, F50, and a 0.1-nm flux in the two emission lines, FH and FK, respectively. The sum of the emission-line fluxes with respect to the 5.0-nm flux, (FH + FK)/F50, as well as the ratios of each of the two emission lines are then subjected to a period search similar to Hα. Figure 8b shows dynamic spectra of both emission-line profiles with a pattern in agreement with Hα, albeit a bit “cleaner”. The S/N is lower by a factor of two relative to Hα because of the lower efficiency of the SES at blue wavelengths and the star being fainter in the blue by one magnitude. Nevertheless, the periodogram from the four-year data set reveals a clear peak at a period of 63 ± 5 days, which is in moderate but formal agreement with the periods from Hα and the optical photometry. Surprisingly, the 90-day alias and the 147-day peaks are more evident in Ca ii H&K than in Hα, although less well-defined for the combined data in 2007–2010 than for observing season 2008 shown in Fig. 9c. It indicates variations from year to year. The two panels in Fig. 9c are phase plots of the relative emission-line flux (relative to the median profile) with the rotational and the orbital period, respectively. It shows a ≈ 1-σ drop in flux during periastron passage at around phase 0 or 1.
He ID3. For this indicator, we chose to simply fit a Gaussian to its line profile and then use the Gaussian’s peak residual intensity for the period search. Another approach, similar to measuring the equivalent widths directly between two defined points in the continuum, did not ensure in the same homogeneity of the results. This is mostly because the line is rather weak and narrow with a full-width at the continuum level of about 0.014 nm, with the red line wing blended by a nearby Fe i line (587.630 nm). As we do not resolve the line width, a Gaussian fit appears to be an acceptable compromise. A Lomb-Scargle periodogram (e.g. Lomb 1976) of the Gaussian-fit residual intensities from all epochs combined gives a well-defined peak with a period of 60.68 ± 0.15 d, i.e. very close to the expected rotational period of the star. A weighted wavelet transform analysis (Foster 1996), i.e. without a re-sampling of the data along the time axis as for the Lomb method, shows that this period is present during all seasons. However, it is always 10–15σ longer than the true rotation period from spot migration. The orbital period does not appear as clearly as the rotational period. This is partly because of the shorter exposure time that had been required resolve the rapid change in the radial velocity during periastron introducing phase-dependent scatter. Figure 9d shows the residual intensity of the line core, again phased with the 58.32-d rotational period and the orbital period, respectively.
 |
Fig. 9 Residual variations for the observing season 2008. a) V-band light curve, b) Hα-core flux, c) relative Ca ii H&K emission-line flux, and d) He i D3 absorption line depth. The left column shows the data phased with the rotational period of 58.32 d, the right column with the orbital period of 147.89 d, both with respect to a time of periastron passage. Units are as in Fig. 8. We note the sharp decline in Ca ii H&K flux around periastron in 2008. For better visibility we plot the phases twice. |
4.3. Magnetic analysis
A single STELLA/SES spectrum provides a mean S/N of about 125, too low for a direct magnetic analysis. However, this can be compensated for by our having 273 well-sampled spectra in 2008 alone. This time sampling of each individual spectral line profile can be used in a principal component analysis (PCA; Bishop 1995) approach to boost the S/N of a particular line by a factor of more than five. It also allows us to search for phase-dependent variations in the Zeeman-sensitive spectral line profiles. To differentiate the small excess line-broadening caused by a surface magnetic field from other line-broadening mechanisms such as thermal effects, micro- and macroturbulence or atomic-line parameter variation, e.g. of the oscillator strengths, we need to use a sophisticated line-profile inversion technique. Examples of this method that is based on radiative transfer in magnetic atmospheres has for a long time been applied to various active cool stars (e.g., Saar et al. 1986; Valenti et al. 1995; Ruedi et al. 1997; Anderson et al. 2010).
4.3.1. Signal-to-noise ratio enhancement
A straightforward statistical method that can be readily applied to individual line profiles is the technique of PCA. The application of PCA in the present work is twofold. Firstly, it provides a simple means of detecting the dominant variations in the data set by building the sample covariance matrix of the time-sampled measurements for each individual spectral line profile of interest. This is done in the following separately for the two spectral lines Fe i 617.3 nm and FeI i 624.0 nm. Calculating its eigenvalues and eigenprofiles allows us to capture the dominant (energy) variances in the leading eigenprofiles (principal components). The second motivation for using PCA is its noise-filtering capability. By retaining only the leading components in the data, one can obtain a significant reduction in noise without compromising the basic physical content in the line profile. Details of the application procedure to Stokes profiles were described in Carroll et al. (2007) and Martínez et al. (2008). We note that the PCA analysis in this work differs from these studies in that we build the covariance matrix over the time domain, i.e. for a particular wavelength (target line) many line profiles measured over time are used rather than many spectral lines with different wavelength at a certain time. Applying PCA to our STELLA spectra and reconstructing the individual line profiles with just a small number of principal components (three eigenprofiles), we reached a formal S/N of 650, i.e. an enhancement of approximately a factor of five with respect to the original data.
4.3.2. Magnetic flux density inversion
Our aim is to obtain the magnetic-flux density over the respective visible surface of the star. The magnetic flux density, or loosely called magnetic flux, is described by the product B.f, the magnetic field strength B times the surface filling factor f. In the present work no attempt is made to distinguish these two quantities, our main goal being to provide an estimate of the magnetic flux and its time variation. All inversions are performed under the common assumption that the magnetic field is homogeneously distributed over the surface and radially aligned.
We follow the analysis of Ruedi et al. (1997) and choose the Zeeman-sensitive line Fe i 617.3 (effective Landé factor geff = 2.50) and the Zeeman-insensitive line Fe i 624.0 (geff = 1.00) for a simultaneous analysis of the two lines. This iron line pair has the advantage of being of similar strength and having the same excitation potential (χe = 2.22 eV) so that their response to temperature variations can be expected to be similar. Owing to the temperature inhomogeneities across the stellar surface of HD 123351, a simultaneous inversion of this line pair is expected to reduce the cross-talk between temperature-related broadening and magnetic-field effects. All spectral line blends found in the VALD database (Piskunov et al. 1995) with a line depth of more than 0.02 within a 0.03 nm range about the line center of both iron lines are taken into account.
The flux inversion is done with a variant of our Zeeman-Doppler imaging code iMap (Carroll et al. 2007). The forward module of this code consists of an LTE polarized radiative-transfer computation with the DELO integration method and is described in more detail in Carroll et al. (2008) to which we refer for more details and references. In addition to the magnetic flux density B.f, we consider the effective temperature of the atmospheric model as a free parameter. The atmospheres are Kurucz (1993) ATLAS-9 models. Spectral lines are calculated in the L-S coupling regime and atomic line parameters are taken from VALD, except for the logarithmic oscillator strength, which is determined by an initial inversion fit of the average spectral line profile. Assuming the oscillator strength as a free parameter follows the argument of Basri & Marcy (1988) and Ruedi et al. (1997) that solar values are inappropriate for the analysis of different stellar types. The optimization procedure relies again on the Levenberg-Marquardt algorithm.
The underlying stellar model used in the inversion consists of a segmented surface with a 5 × 5 resolution. Each segment obtains the magnetic flux density and the effective temperature of the model atmosphere. During the disk-integration process, the atmospheric model with its depth stratification of the temperature and pressure is adjusted according to the line-of-sight angle to account for limb-darkening in the flux profiles. In total, the inversion solves for the following six free parameters for both spectral lines simultaneously; the magnetic flux density B.f, the effective temperature, the microturbulence, the radial-tangential macroturbulence with equal radial and tangential components, an instrumental broadening modeled with a Gaussian velocity distribution, and the oscillator strength. The rotational velocity and the iron abundance are taken from the pre-analysis in Sect. 3 as they are not expected to be modulated.
 |
Fig. 10 Inversion fits to the averaged line profiles for the observing season 2008. Panel a) shows the Zeeman-sensitive Fe i 6173 line (effective Landé factor geff = 2.50), panel b) shows the Zeeman-insensitive Fe i 6240 line (geff = 1.00). The dots are the PCA-enhanced observations, the lines are the inversion fits with a total of six free parameters. The respective lower panels show the residuals enhanced by a factor of ten. The average magnetic flux density is 542 ± 72 G. |
4.3.3. Results from the inversion
We concentrate on the data set obtained in the year 2008, as was the most finely sampled. Selecting only the highest S/N spectra still gives a database of 273 spectral line profiles for each of the above iron lines. In the first step, we only invert the average line profiles (zeroth eigenprofile) that determine the global surface-averaged values of B.f and the other free parameters. This gives a first hint on the average strength of this field. In addition, we can determine the other free parameters and then keep them fixed for the following analysis of the individual line profiles.
From Fig. 10, we see that the fits to the averaged line profiles are extremely precise and consistent with the low noise level and a reduced χ2 error of 1.12 for the Fe i 617.3 line, and 1.58 for the Fe i 624.0 line. The obtained (logarithmic) oscillator strengths are –2.78 for the Fe i-617.3 line, and –3.18 for the Fe i-624.0 line. Micro- and macroturbulence were found to be 1.15 km s-1 and 3.9 km s-1, respectively, and the average effective temperature to 4830 K (with a peak-to-valley variation of 60 K). The inferred magnetic flux density was 542 G with a formal error of 72 G calculated from the covariance matrix (see Carroll et al. 2007). We emphasize that the continuum depression caused by a slightly reduced effective temperature related in turn to a non-zero spot-filling factor, is implicitly solved for in our inversion. If we plot the effective temperature of each line pair versus rotational (or orbital) phase, it shows plots similar to those in Figs. 11a and b. This is expected if the magnetic flux density stems from localized regions rather than from a global network. An indication of the reality of the magnetic field broadening is obtained from a number of inversions without a magnetic field. In all of these zero-field cases, the quality of the fits (χ2 of 1.74 and 1.92 for the two lines, respectively) were unable to reach that of the magnetic case. This is also obvious in the projected χ2 landscape, which shows that the zero-field case is far beyond the 5-σ region of the χ2 minimum with a magnetic field. Therefore, we consider our magnetic-flux result as significant.
 |
Fig. 11 Magnetic flux variation for the observing season 2008. a) Phase plot with the stellar rotation period of 58.32 d, b) phase plot with the orbital period of 147.89 d, and c) Lomb-Scargle periodogram from the 273 individual spectral line inversions. The two strongest peaks in the periodogram agree with the rotational and the orbital periods, respectively. The strongest peak refers to a period of 58.7 d, the second strongest peak to 144.3 d. Note again that we plot the phases twice for clearer visibility. |
The next step in our analysis is to invert the 273 individual line profiles of our iron-line pair to search for a systematic periodic behavior. Figure 11 shows the results and indicates a clear rotational dependence on the magnetic flux, as well as a (weaker) dependence on the orbital phase. The individual formal errors in the retrieved magnetic flux values are between 55 and 80 G, depending on the initial S/N. We note again that by performing a simultaneous inversion of the two iron lines with both having a similar temperature response but a different magnetic response, we reduce the crosstalk of temperature effects and its possible misinterpretation in the inversion process. A Lomb-Scargle periodogram (Fig. 11c) indeed indicates a pronounced peak above a 0.01% false-alarm probability at 58.7 d with an uncertainty of 4.3 d determined from a Monte Carlo resampling. A second significant peak, but not quite with as high a probability as the first peak, shows a periodicity of 144.3 d with an uncertainty of 8.9 d. The distribution of the summed squared errors for each line-profile fit versus phase does not indicate any systematic distribution, suggesting that the inversion was not fooled by a systematic, residual surface-temperature variation. As in Fig. 9 for the chromospheric indicators, we plot the magnetic flux densities over the rotational and orbital phase in Figs. 11a, b.
5. Discussion
5.1. Circularization and synchronization
Tidal interaction between stars can couple their spin to their orbital angular momentum such that dissipation of tidal energy causes a binary to circularize its orbit (e.g. Zahn 1989 and earlier papers; Tassoul & Tassoul 1996). Observational results indicate that most active binaries have circular orbits with synchronized rotation and a spin axis perpendicular to the orbital plane (e.g. Fekel & Eitter 1989). Other systems with weaker tidal interactions may not be currently old enough to have reached complete synchronization or circularization. However, these conditions may occur once tidal interactions have operated long enough or after a system evolved to a state in which tidal interactions are enhanced. For late-type stars with convective envelopes, Zahn (1989) investigated the effects of the equilibrium tide on synchronization and circularization, while Tassoul (1988) explored the theory of geometrical distortions that cause large-scale hydrodynamic currents. Although these two theories disagree significantly on absolute timescales, both predict that synchronization should occur before circularization.
HD 123351 is neither synchronized nor circularized. Its large orbital eccentricity suggests a pseudo-synchronous rotation period of ≈ 12 d according to the tidal-friction theory of Hut (1981), which is just 8% of the orbital period. With a 58.3-d rotation period, the star appears to be a strongly asynchronous and slow rotator. Since all convective stars likely undergo some sort of differential surface rotation, one would expect a certain range of rotation periods if derived from photometric spot activity because spots could appear at various stellar latitudes. For comparison, the (strong) solar differential rotation allows a spread of rotation periods of ≈ 10%. Comparable results are found for other active stars based on Doppler imaging (e.g. Barnes et al. 2005; Strassmeier 2009). However, the difference between the observed photometric period and the pseudo-synchronous rotation period for HD 123351 is more than 500% and could not be explained by differential surface rotation.
Therefore, we ask what caused a cool star to fail to reach equilibrium in terms of its spin and orbital angular momentum after 6–7 Gyr? Although not in disagreement with the prediction that synchronization shall occur before circularization, the Tassoul and Zahn mechanisms predict vastly different timescales for HD 123351. While the original Zahn (1989) equations predict synchronization and circularization well beyond the age of the universe, the Tassoul (1988) equations predict synchronization after ≈ 200 000 years and circularization after ≈ 3 Gyr. Both can obviously be excluded because of the measurements derived from the observations. Additional mechanisms were proposed to account for the strong tidal coupling required by the observations of circularization of binary systems in open clusters of various age (Ogilvie & Lin 2007), but we refer to the refutation of Tassoul’s hydrodynamical mechanism by the proper accounting of an Ekman layer by Rieutord & Zahn (1997). In the case of HD 123351, the orbital and rotational frequencies today imply that inertial oscillations (waves) might have neen excited in the star leading to an average tidal dissipation approximately 10–100 times that predicted by Zahn’s theory. Such inertial waves are not described in the traditional approximations and correspondingly reduce the estimated synchronization and circularization times. Because non-linearities are expected for eccentric binaries and for components older than the Sun, no simple prediction of Ogilvie & Lin (2007) is possible for HD 123351, but in general brings the theory closer to the observation.
5.2. Inter-binary activity?
The assumption of an inter-binary magnetic field that could transfer orbital to spin momentum and vice versa may indeed be inaccurate for intervals longer than purely gravitationally and hydrodynamically predicted timescales. It is well known that inter-binary magnetic fields focus the accretion stream in cataclysmic variables (CV) containing a magnetic white dwarf (e.g. Warner & Woudt 2002), as well as some Algol systems (e.g. Richards 2007). Reconnection processes within these fields may also act as the source of inter-binary flares, suggested e.g. for the RS CVn binary system HR 5110 (Graffagnino et al. 1995). The field lines in general provide a channel for the exchange of charged particles between the two stellar components. Its principal existence on a geometrically shorter scale is nicely demonstrated by the Jupiter-Io system (e.g. Su 2009). However, the closest distance between the two components in the HD 123351 binary system ( ≈ 5 R ⋆ ) is still larger than for the aforementioned CV and Algol binaries, thus the expected field density may be insufficient for inter-binary flares. No such superflare was detected in our data. Coronal mass ejections may however still exist, which would have had an effect on the evolution of the spin and orbital angular momentum of the star but remains speculative.
5.3. Orbital-induced magnetic activity?
In a very eccentric close binary similar to HD 123351, we might have the rare possibility of exploring a hypothetical efficiency increase and decrease of a stellar dynamo when the two components are closest and farthest, respectively, assuming e.g. that some sort of extra convective mixing couples the dynamo action to tidal forces. Glebocki & Stawikowski (1977, 1988) found some relation between chromospheric Ca ii emissions and the orbital parameters of late-type giants and suggested that tidal forces are somehow responsible for the enhanced chromospheric activity. In contrast, Basri (1987) ruled out tidal coupling as an explanation of the increased activity in binaries. Schrijver & Zwaan (1991) argued that in a synchronized close binary the relevant axis for rotational effects is through the center of gravity of the binary system and thereby could affect the stellar dynamo in such a way that it produces enhanced magnetic activity relative to single stars. Zaqarashvili et al. (2002) assumed that the deviation from a spherical shape of a binary component due to tidal interaction excites a fundamental pulsation mode that then amplifies the torsional waves in the interior magnetic field and eventually causes greater surface activity. It has been found that (extra-solar) planets can induce chromospheric and coronal activity in the form of a hot spot (Shkolnik et al. 2003), although not all stars with close-in planets are prone to these star-planet interactions (e.g. Fares et al. 2010). Lanza (2008, 2009) argued that a flux rope between the host star’s coronal magnetic field and the planet’s magnetosphere experiences a decrease in relative helicity and reacts with an energy release from the flux rope’s footpoint(s). His model predicts a greater prominence activity for stars with planets than without, caused by the accumulation of matter evaporated from the planet. A very similar picture may be adopted for binaries such as HD 123351 that have a low-mass dwarf star as a companion instead of a close-in hot Jupiter.
Our Ca ii H&K and He i data indeed indicate a correspondence of magnetic activity with orbital periastron, at least during observing season 2008. No clear relation was seen for the observing seasons 2007 and 2009. However, this may be caused by some bias because the season 2008 was the one with the highest data quality and finest data sampling, both of which are needed to detect such a correspondence. Furthermore, the modulation amplitudes were always small and on the order of the annual rms. But the detection is quite surprising because Hα does not show a similar correspondence at all, which is the opposite of what we would expect if there is prominence activity (e.g. Mackay et al. 2010; Frasca et al. 2008). Our magnetic-flux analysis also revealed evidence of a weak orbital-phase coherence in 2008 and thus strengthens the Ca ii and He i detections. The B.f orbital variation is in phase with the variation in both Ca ii and He i in the sense that lower chromospheric emission is seen when the (photospheric) magnetic flux density is lower, with their respective minima coinciding with a time when the two binary components are closest in distance, i.e. at periastron. The orbitally phased V-band light curve in Fig. 9a is completely out of phase, as expected because it is purely photospheric in origin. The comparison of the chromospheric emissions with the magnetic flux density is more puzzling when plotted with the rotational period. Then, B.f varies exactly in anti-phase with all three chromospheric lines, in particular also with Hα (compare the left columns in Fig. 9bcd with Fig. 11a), which is unexpected. The rotationally phased V-light curve appears nicely in phase with B.f and in anti phase with the chromospheric lines, as expected if chromospheric plages are superposed on photospheric spots as in the Sun. In summary, we take the anti-phase relation of the magnetic flux with the chromospheric emissions as evidence that there are two magnetic fields present at the same time, a localized surface magnetic field associated with spots and a global field that is oriented towards the secondary component such as an inter-binary field. We have no already developed model to combine all of this but conclude that the B-component that we measure in B.f possibly stems from a mixture of bright plage-like regions and dark spots, both with different respective filling factors (f), but the former also caused by the interaction with the secondary star.
The overall amplitude of the radial-velocity residuals shown in Fig. 2b suggests that the star was more asymmetrically spotted in 2007 than in 2008, albeit the V-light curves showed approximately the same amplitudes and shapes. In 2007, the Hα-core flux indeed showed the most pronounced variations ( ≈ 4σ) of all seasons when phased with the rotation period but again basically just a scatter plot when phased with the orbital period (not shown). This indicates that Hα responds to the same surface inhomogeneities as seen in the other lines or the photometry. It encourages us to believe that the Hα-profile variations of HD 123351 originate predominantly from near the stellar surface and have no detectable circumstellar (absorption) component, as would be expected for coronal prominence activity. We note that we did not apply a correction for the photospheric contribution to Hα but did all time-series analysis from residual line profiles after subtraction of a median profile.
6. Summary and conclusions
We have obtained a four-year-long, phase-resolved, spectral database of the active star HD 123351 using our new robotic telescope facility STELLA in Tenerife. These data are complemented with 12 years of photometric monitoring with our automatic photometric telescope Amadeus in Arizona. Our summary and conclusions are as follows:
-
We have discovered HD 123351 to be asingle-lined spectroscopic binary with a period of147.8919 d and an orbital eccentricity of 0.809.
-
The STELLA Echelle Spectrograph enabled the most precise (and presumably also most accurate) orbit determination of any active binary so far in the literature with an rms of the residuals of just 47 m s-1.
-
A period of ≈ 60 d was obtained from 12 years of Amadeus VI-band photometry and has been converted into a true rotation period of 58.32 d from a linear fit to the two dominant spot-migration curves. The period difference from the two spots in 2004 suggests a lower limit to the surface differential rotation of ΔP/P of 0.076, which is roughly half the solar value.
-
The global rotation period of HD 123351 was also recovered from the orbital radial-velocity residuals.
-
A spectrum synthesis yielded average stellar atmospheric parameters of Teff = 4780 ± 70 K, log g = 3.25 ± 0.30, and [Fe/H] = 0.00 ± 0.08. The Hipparcos parallax in combination with evolutionary tracks suggests a mass of 1.2 ± 0.1 M⊙ and an age of 6–7 Gyr, consistent with the measured 12C/13C ratio of ≈ 40.
-
The lithium abundance of log n = 1.70 appears higher than expected for that age but the line also appears broader than expected for the vsini of 1.8 ± 0.7 km s-1. We suspect that its asymmetry is partly due to a significant contribution from the 6Li isotope.
-
From an application of the Küker-Stix differential-rotation code to a MESA stellar model with matching parameters of HD 123351, we obtain a convective turn-over time that spans between a maximum of 80 d near the bottom of the convection zone to 10 d near the surface. This implies an average Rossby number greater than unity.
-
Our light-curve analysis has reconstructed two persistent spotted regions with a nearly constant longitudinal separation of 150° ± 17° over the course of 12 years. The spot temperatures were on average 1160 K lower than the effective temperature covering between 5–10% of the entire surface. The photometry showed no signs of a flip flop nor of flares.
-
Chromospheric emission-line fluxes of ≈ 106 erg cm-2 s-1 were measured for Ca ii H&K, Hα, and the Ca ii infrared triplet. The detection of the He i D3-line at 587.56 nm also indicated the presence of non-thermal heating processes.
-
Time-series analysis of above chromospheric activity indicators yielded a clear modulation with the stellar rotation period but also provided evidence of a modulation with the orbital period, albeit less well-defined.
-
We measured the Zeeman broadening from a pair of iron lines and obtained an average surface magnetic flux density of 542 ± 72 G. A time-series analysis of the data from 2008 yielded again a clear modulation with the rotation period and a weak modulation with the orbital period in the sense that a lower magnetic flux was seen at times near periastron.
-
It remains unclear why the magnetic flux varies exactly in anti-phase with the chromospheric emissions if plotted versus the rotational period, and is lowest near periastron when plotted versus the orbital period. The measured magnetic flux possibly stems not only from cool photospheric spots but also from bright plage-like regions.
-
We postulate an inter-binary magnetic field and tentatively conclude that it is responsible for the flux dilution at periastron. It is also possibly responsible for the unexpected slow and asynchronous rotation of the primary star.
Acknowledgments
STELLA was made possible by funding through the State of Brandenburg (MWFK) and the German Federal Ministry of Education and Research (BMBF). The facility is a collaboration of the AIP in Brandenburg with the IAC in Tenerife. We thank all engineers and technicians involved, in particular Manfred Woche and Emil Popow and his team, and Ignacio del Rosario and Miguel Serra from the IAC Tenerife day-time crew. We also thank M. Küker for computing the convective turn-over times for us. K.O. thanks Z. Kollath for useful discussions and acknowledges support from the Hungarian research grant OTKA K-081421. Finally, we thank the referee, Dr. Antonio Lanza, for a very constructive report that helped to improve the paper considerably.
References
- Allende-Prieto, C. 2004, AN 325, 604 [Google Scholar]
- Allen de Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, R. I., Reiners, A., & Solanki, S. K. 2010, A&A, 522, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balachandran, S. C., Fekel, F. C., Henry, G. W., & Uitenbroek, H. 2000, ApJ, 542, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, E. S., Evans, D. S., & Laing, J. D. 1967, R. Obs. Bull., 130 [Google Scholar]
- Barnes, T. G., & Evans, D. S. 1976, MNRAS, 174, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. R., Collier-Cameron, A., Donati, J.-F., et al. 2005, MNRAS, 357, L1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Basri, G. 1987, ApJ, 316, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Basri, G., & Marcy, G. W. 1988, ApJ, 330, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 2007, Highlights of Astronomy, 14, 275 [NASA ADS] [Google Scholar]
- Bishop, C. M. 1995, Neural Networks for Pattern Recognition (Oxford University Press) [Google Scholar]
- Carroll, T. A., Kopf, M., Ilyin, I., & Strassmeier, K. G. 2007, AN, 328, 1043 [Google Scholar]
- Carroll, T. A., Kopf, M., & Strassmeier, K. G. 2008, A&A, 488, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danby, J. M. A., & Burkardt, T. M. 1983, Celestial Mechanics, 31, 95 [Google Scholar]
- Desort, M., Lagrange, A.-M., Galland, F., Udry, S., & Mayor, M. 2007, A&A, 473, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durney, B. R., & Latour, J. 1978, Geophys. Ap. Fluid Dyn., 9, 241 [Google Scholar]
- Famaey, B., Jorissen, A., Luri, X., et al. 2005, A&A, 430, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fares, R., Donati, J.-F., Moutou, C., et al. 2010, MNRAS, 406, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C. 1997, PASP, 109, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C., & Eitter, J. J. 1989, AJ, 97, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C., Strassmeier, K. G., Washuettl, A., & Weber, M. 1999, A&AS, 137, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, G. 1996, AJ, 112, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Frasca, A., Kövári, Zs., Strassmeier, K. G., & Biazzo, K. 2008, A&A, 481, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gleboki, R., & Stawikowski, A. 1977, Acta Astron., 27, 225 [NASA ADS] [Google Scholar]
- Gleboki, R., & Stawikowski, A. 1988, A&A, 189, 199 [NASA ADS] [Google Scholar]
- Gontcharov, G. A. 2006, Astron. Lett., 32, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Graffagnino, V. G., Wonnacott, D., & Schaeidt, S. 1995, MNRAS, 275, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Granzer, T., Reegen, P., & Strassmeier, K. G. 2001, AN, 322, 325 [Google Scholar]
- Griffin, R. F. 2009, Observatory, 209, 317 [Google Scholar]
- Hall, D. S. 1991, ApJ, 309, L83 [Google Scholar]
- Hall. J. C. 1996, PASP, 108, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P. 2002, AN, 323, 392 [Google Scholar]
- Henry, G. W., Fekel, F. C., Henry, S. M., & Hall, D. S. 2000, ApJS, 130, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Huber, K. F., Wolter, U., Czesla, S., et al. 2009, A&A, 501, 715 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huerta, M., Johns-Krull, C. M., Prato, L., Hartigan, P., & Jaffe, D. T. 2008, ApJ, 678, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Kazarovets, E. V., Samus, N. N., Durlevich, O. V., et al. 1999, IBVS, 4659 [Google Scholar]
- Kim, Y.-C., & Demarque, P. 1996, ApJ, 457, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., & Eyer, L. 2002, MNRAS, 331, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Kolláth, Z., & Csubry, Z. 2006, MmSAI, 77, 109 [NASA ADS] [Google Scholar]
- Kolláth, Z., & Oláh, K. 2009, A&A, 501, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korhonen, H., Järvinen, S. 2007, in Binary Stars as Critical Tools & Tests in Contemporary Astrophysics, Cambridge University Press, ed. W. I. Hartkopf, E. F. Guinan, & P. Harmanec, IAU Symp., 240, 453 [Google Scholar]
- Küker, M., & Stix, M. 2001, A&A, 366, 668 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1993, ATLAS-9, CD-ROM #13 [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, NSO Atlas No. 1, Solar flux atlas from 296 to 1300 nm [Google Scholar]
- Lampton, M., Lieu, R., Schmitt, J. H. M. M., et al. 1997, ApJS, 108, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F. 2008, A&A, 487, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F. 2009, A&A, 505, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L., McClintock, W., Robertson, R. M., & Worden, S. P. 1979, ApJS, 41, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Makarov, V. V., Beichman, C. A., Catanzarite, J. H., et al. 2009, ApJ, 707, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, ed. D. A. Bohlender, D. Durand, & P. Dowler, ASPC Ser., 411, 251 [Google Scholar]
- Martínez González, M. J., Asensio Ramos, A., Carroll, T. A., et al. 2008, A&A, 486, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morales, J. C., Torres, G., Marschall, L. A., & Brehm, W. 2009, ApJ, 707, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Morales, J. C., Gallardo, J., Ribas, I., et al. 2010, ApJ, 718, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2007, ApJ, 661, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Oja, T. 1985, A&AS, 61, 331 [NASA ADS] [Google Scholar]
- Oláh, K., Jurcsik, J., & Strassmeier, K. G. 2003, A&A, 410, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlenko, Ya. V., & Magazzú, A. 1996, A&A, 311, 961 [NASA ADS] [Google Scholar]
- Paxton, W., et al. 2010, Modules for Experiments in Stellar Astrophysics (MESA), http://mesa.sourceforge.ne [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical Recipes, 2nd ed. (Cambridge: Cambridge University Press) [Google Scholar]
- Reiners, A. 2009, A&A, 498, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribárik, G., Oláh, K., & Strassmeier, K. G. 2003, AN, 324, 202 [Google Scholar]
- Richards, T. 2007, in W. I. Hartkopf, E. F. Guinan, & P. Harmanec, Binary Stars as Critical Tools & Tests in Contemporary Astrophysics (Cambridge University Press), IAU Symp., 240, 160 [Google Scholar]
- Rieutord, M., & Zahn, J.-P. 1997, ApJ, 474, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, A., & Washuettl, A. 2004, AN, 325, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Ruedi, I., Solanki, S. K., Mathys, G., & Saar, S. H. 1997, A&A, 318, 429 [NASA ADS] [Google Scholar]
- Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., Linsky, J. L., & Beckers, J. M. 1986, ApJ, 302, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., Huovelin, J., Osten, R. A., & Shcherbakov, A. G. 1997, A&A, 326, 741 [NASA ADS] [Google Scholar]
- Savanov, I. S., & Strassmeier, K. G. 2008, AN, 329, 364 [Google Scholar]
- Scarfe, C. D., Batten, A. H., & Fletcher, J. M. 1990, Publ. Dominion Astron. Obs. Victoria, 18, 21 [Google Scholar]
- Schrijvers, C. J., & Zwaan, C. 1991, A&A, 251, 183 [NASA ADS] [Google Scholar]
- Schwope, A. D., Hasinger, G., Lehmann, I., et al. 2000, AN, 321, 1 [NASA ADS] [Google Scholar]
- Shkolnik, E., Walker, G. A. H., & Bohlender, D. A. 2003, ApJ, 597, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Stelzer, B., Fernández, M., Costa, V. M., et al. 2003, A&A, 411, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G. 2001, in Binary Stars: Selected Topics on Observations and Physical Processes, Lecture Notes in Physics, ed. F. C. Lázaro, & M. J. Arévalo, 563, 48 [Google Scholar]
- Strassmeier, K. G. 2009, A&AR, 17, 251 [Google Scholar]
- Strassmeier, K. G., & Rice, J. B. 2003, A&A, 399, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Fekel, F. C., Bopp, B. W., Dempsey, R. C., & Henry, G. W. 1990, ApJS, 72, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Boyd, L. J., Epand, D. H., & Granzer, T. 1997, PASP, 109, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Washuettl, A., Granzer, T., Scheck, M., & Weber, M. 2000, A&AS, 142, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Granzer, T., Weber, M., et al. 2004, AN, 325, 527 [Google Scholar]
- Strassmeier, K. G., Granzer, T., Weber, M., et al. 2010a, Adv. Astr., 19 [Google Scholar]
- Strassmeier, K. G., Granzer, T., Kopf, M., et al. 2010b, A&A, 520, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Weber, M., Granzer, T., & Dall, T. H. 2010c, AN, 331, 368 [NASA ADS] [Google Scholar]
- Su, Y.-J. 2009, in Cosmic Magnetic Fields: from Planets, to Stars to Galaxies, ed. K. G. Strassmeier, A. G. Kosovichev, & J. E. Beckman (Cambridge University Press), IAU Symp., 273, 271 [Google Scholar]
- Tassoul, J.-L. 1988, ApJ, 324, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, J.-L., & Tassoul, M. 1996, Fund. Cosm. Phys., 16, 377 [Google Scholar]
- Torres, G., Claret, A., & Young, P. A. 2009, ApJ, 700, 1349 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., Marcy, G. W., & Basri, G. 1995, ApJ, 439, 939 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., Malkan, M. A., & Goad, M. R. 2001, MNRAS, 327, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B., & Woudt, P. A. 2002, MNRAS, 335, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M., & Strassmeier, K. G. 1998, A&A, 330, 1029 [NASA ADS] [Google Scholar]
- Weber, M., & Strassmeier, K. G. 2011, A&A, 531, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weber, M., Granzer, T., Strassmeier, K. G., & Woche, M. 2008, Proc. SPIE, 7019, 70190 [Google Scholar]
- Zahn, J.-P. 1989, A&A, 220, 112 [NASA ADS] [Google Scholar]
- Zaqarashvili, T., Javakhishvili, G., & Belvedere, G. 2002, ApJ, 579, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Zickgraf, F.-J., Engels, D., Hagen, H.-J., Reimers, D., & Voges, W. 2003, A&A, 406, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The long-term brightness variations of HD 123351. The top panel shows our twelve years of V-band photometry (dots), the lower panel plots the corresponding V − I color index. The lines are the seasonal fits of the two-spot models from Sect. 4. These models are plotted here as spherical projections at four different phases (from top to bottom, 0°, 90°, 180°, 270°). The gray scale indicates the spot temperature. Note the rotational modulation with a period of ≈ 60 d and a long-term variation in both V and V − I in the sense that the star appears redder when fainter. |
| In the text | |
 |
Fig. 2 Radial velocities of HD 123351. a) Phased STELLA radial velocities with the orbital period of 147.8919 d. Dots are the observations and the line is the orbital fit to the spot-corrected elements in Table 2. b) Top panel: the four years of monitoring. Such data sampling is made possible with robotic telescopes. The line is again the orbital solution from Table 2 (column “Spot corrected”). Lower panel: residuals after removal of the orbital fit. The modulation is due to stellar rotation and the insert shows a DFT periodogram with the strongest peak at 61.0 ± 1.1 d, in agreement with the photometric period. The full amplitude varied over the years between 400 m s-1 in 2007 and 100 m s-1 in 2009, indicating the variable asymmetry of the spot distribution. The line is a Blackman-function fit to the data. |
| In the text | |
 |
Fig. 3 Periodograms from HD 123351 photometry. a) Discrete Fourier transform (DFT) periodogram from the pre-whitened V-band data (top panel). The twelve-year average period is 61.9 d (0.01616 c/d). The bottom panel is the corresponding window function. The insert in the top panel shows the entire search range. b) Two-dimensional short-term Fourier transform (STFT) analysis. The power distribution in the time-frequency plane is shown as a gray scale (black means highest power, white no power). It shows that the photometric period reached values between a maximum of 62.0 d and a minimum of 57.3 d. Around 2 453 000 (2002–2005), a bimodal distribution was recovered. Note that the excess power in the lower left corner is due to the length of the data vector and is artificial. |
| In the text | |
 |
Fig. 4 The position of HD 123351 (dot) in the theoretical H-R diagram (log L/L⊙ vs. log T in K). Shown are evolutionary tracks for masses of 1.1–2.5 M⊙, solar metallicity, and core overshooting (dotted lines; Pietrinferni et al. 2004). The best-fit model track (full line) suggests a mass for HD 123351 of 1.2 ± 0.1 M⊙. The insert is a zoomed image of the box around the observed location indicating the nominal ages of the 1.2-M⊙ track (again the full line) and a 1.1-M⊙, 1.3-M⊙, and 1.5-M⊙ track (dotted lines), respectively. This suggests a most-likely age of HD 123351 of 6–7 Gyr. |
| In the text | |
 |
Fig. 5 Lithium 670.8-nm region in the spectrum of HD 123351. Shown are three consecutive R = 120000 spectra obtained at CFHT in May 2000 at orbital phase 0 |
| In the text | |
 |
Fig. 6 Convective turn-over times, τc, in seconds as a function of depth in the convection zone of HD 123351. Note that the turn-around of the curve below a fractional radius of ≈ 0.35 strongly depends on the adopted stellar model and could be an artefact. τc spans between a maximum of 80 d near the bottom of the convection zone and 10 d near the surface. |
| In the text | |
 |
Fig. 7 Results from the photometric spot modeling. a) The reconstructed spot longitudes expressed in stellar rotations versus time. Filled gray points refer to spot 1, open circles to spot 2. These values were obtained based on the initial photometric period of 61.9 d and after shifting full seasons by an integer rotation such that the resulting long-term migration is brought into agreement with the seasonal migration (the latter is indicated by the short lines). The two lines are linear regression fits and their slopes indicate the true rotation period of 58.32 d. b) Top panel: spot longitudes versus time based on the 58.32-d period. Filled gray points refer to spot 1, open circles to spot 2 as in panel a). The pluses indicate the longitudinal separation of the two spots and show a fairly constant value of 150° ± 17°. Bottom panel: the reconstructed fractional spot area versus time. In both panels, seasonal average values are additionally plotted. |
| In the text | |
 |
Fig. 8 Modulation of chromospheric activity tracers during the years 2007–2010. The two top rows show Hαa), the two bottom rows show Ca ii H&K (b). The left panels are overplots of all line profiles for 2007–2010 (in panel b) only the K-line is shown), while the bright lines indicate the median profiles, respectively. The right hand panels are the dynamic spectra phased with the photometric rotational period (top) and the orbital period (bottom) and the zero points from Table 2. The color scale indicates the relative emission-line flux with respect to the median profile. The two dashed, horizontal lines show ± vsini, and the chain of points in the very bottom of the graphs represents the phase coverage (one dot is one spectrum). It appears that both activity tracers display a clear modulation with the rotational period, with a tendency to cluster around a time of periastron at phase 1.0, and maintained that behavior for the entire duration of our observations. |
| In the text | |
 |
Fig. 9 Residual variations for the observing season 2008. a) V-band light curve, b) Hα-core flux, c) relative Ca ii H&K emission-line flux, and d) He i D3 absorption line depth. The left column shows the data phased with the rotational period of 58.32 d, the right column with the orbital period of 147.89 d, both with respect to a time of periastron passage. Units are as in Fig. 8. We note the sharp decline in Ca ii H&K flux around periastron in 2008. For better visibility we plot the phases twice. |
| In the text | |
 |
Fig. 10 Inversion fits to the averaged line profiles for the observing season 2008. Panel a) shows the Zeeman-sensitive Fe i 6173 line (effective Landé factor geff = 2.50), panel b) shows the Zeeman-insensitive Fe i 6240 line (geff = 1.00). The dots are the PCA-enhanced observations, the lines are the inversion fits with a total of six free parameters. The respective lower panels show the residuals enhanced by a factor of ten. The average magnetic flux density is 542 ± 72 G. |
| In the text | |
 |
Fig. 11 Magnetic flux variation for the observing season 2008. a) Phase plot with the stellar rotation period of 58.32 d, b) phase plot with the orbital period of 147.89 d, and c) Lomb-Scargle periodogram from the 273 individual spectral line inversions. The two strongest peaks in the periodogram agree with the rotational and the orbital periods, respectively. The strongest peak refers to a period of 58.7 d, the second strongest peak to 144.3 d. Note again that we plot the phases twice for clearer visibility. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.