| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201116834 | |
| Published online | 13 July 2011 | |
Filaments and the magnetic configuration
I. Observation of the solar case
UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
e-mail: nadege.meunier@obs.ujf-grenoble.fr
Received: 5 March 2011
Accepted: 5 May 2011
Context. The emission of Ca and Hα is correlated for the Sun, but this does not seem to be true for other stars. We previously demonstrated that this lack of correlation could be due to the presence of filaments.
Aims. We aim to establish a link between the activity level, the magnetic configuration, and the number of filaments, and therefore with observables of other stars that the Sun.
Methods. We studied the relationship between the filaments and the magnetic configuration using a large scale approach on MDI/SOHO magnetograms and a large sample of filaments. We validated the reconstruction of synthetic time series of filament surface coverage representative of the magnetic configuration, and then apply it to observations over a full solar cycle.
Results. We derived quantitative criteria that relates the presence of filaments to the properties at polarity inversion lines, hereafter PIL, magnetic field gradient, and unipolar areas on the solar surface (size and distance to these areas). We also observed that the number of PIL pixels is anti-correlated with the activity level, and the increase in filament surface coverage is due to the modification of the PIL pixel properties. We reconstructed synthetic time series of filaments that are in good agreement with observations.
Conclusions. This work validates our method, which will later be applied to solar and stellar simulations.
Key words: Sun: chromosphere / Sun: activity / Sun: filaments, prominences / Sun: magnetic topology / stars: activity / stars: chromospheres
© ESO, 2011
1. Introduction
Meunier & Delfosse (2009) showed that a lack of correlation between the Ca and Hα emission of the Sun (i.e. a slight departure from a correlation of 1) as well as for other stars may be due to the presence of filaments. Filaments are structures of cool dense plasma in the solar corona that appear as dark features in Hα but whose contrast is very low when observed in the Ca lines (hereafter Ca refers to the Ca II H and K lines). A sun-like spatio-temporal distribution of filaments and active regions implied a correlation not below −0.4. However, Cincunegui et al. (2007) observed a few stars with correlation close to −1. Our objective is therefore to study magnetic configurations that would differ sufficiently from the solar one to allow for these anti-correlations.
To produce such a model, it is important to understand the relation between the magnetic configuration and the filaments. It is well-known that filaments tend to be located on polarity inversion lines (hereafter PIL), as shown by Babcock & Babcock (1955) and Martres et al. (1966) for example. The PIL divides the regions of positive and negative magnetic flux, and they can be defined on smoothed magnetograms as zero flux lines (Durrant 2002). On stars other than the Sun, magnetic activity can be characterized in several ways. Chromospheric activity is usually characterized by an index derived from spectroscopic observations in the Ca II H and K lines (e.g. Baliunas et al. 1995). Photometry also provides information about the activity level, being sensitive to the residual contributions between bright plages (and network) and dark spots (e.g. Radick et al. 1998; Lockwood et al. 2007). In a few cases, the global magnetic configuration can be obtained using Zeeman-Doppler spectropolarimetry (e.g. Donati & Collier Cameron 1997), which has only been applied to a small amount of stars so far but future applications of which promise to cover the HR diagram. However, these indicators are related to spots and plages, not filaments. We therefore wish to establish a relationship between available observables for other stars and the possible presence of filaments.
The present work aims to answer the following questions. Is the number of PIL pixels representative of the filament surface coverage? Given a magnetic field map, can we predict the number of filaments that would exist, at least statistically, and over which timescales would such a prediction be correct? Is the general activity level – for example determined by the average flux over the surface, in absolute value – sufficient to predict a filament surface coverage? What determine the percentage of the PIL occupied by filaments at a given time? Our objective is therefore to 1/ more clearly understand the link between the filaments and the magnetic configuration using this large-scale approach and a large sample of filaments, 2/ validate the reconstruction of synthetic time series of filaments coverage from the magnetic configuration, 3/ apply this reconstruction to observations of the full solar cycle, 4/ and apply it in addition to simulations of both the Sun and other stars. In this paper, we are interested in the three first questions, in order to test, calibrate and validate our method. The fourth question will be the subject of a future paper.
The outline of this paper is as follows. We review in Sect. 2 our current knowledge of this association between filaments and PIL. In Sect. 3, we present the data analysis: the filament determination, the PIL determination, and the computation of complementary variables for further analysis (for example, the proximity to unipolar regions). In Sect. 4, we first analyse the properties of filaments, especially in terms of their distance to the PIL, and we then provide a detailed study of the properties of PIL pixels, which we find depends on their association with filaments. We emphasize the possible solar cycle variations of these properties. Following this characterization, we devise a method to reproduce the observed filament surface coverage as a function of variables derived from the magnetic maps. We also reproduce Hα and Ca emissions to establish a comparison with our previous work Meunier & Delfosse (2009). In Sect. 5, we then apply this method to a long time series of magnetograms covering a solar cycle, for which we derive a synthetic surface coverage of filaments and the corresponding correlation between the Hα and Ca emission.
2. Filaments and the magnetic configuration
To extrapolate our analysis to other stars, we first need to devise and test a way of linking stellar observables and filaments in the solar case. We now briefly review previous studies that can help us to establish this relationship.
Duvall et al. (1977) qualitatively studied the association between the filaments and the PIL. More recently, Durrant (2002) derived the distance between polar filaments and the PIL as a function of the spatial smoothing applied to the magnetograms (see also Durrant et al. 2001; McCloughan & Durrant 2002) and found the agreement to depend on the proximity to active regions. They also studied the relationship between the distance to the PIL and the filament height, as projection effects could lead to a significant departure from the PIL for high filaments. Ipson et al. (2005) then studied various spatial smoothings (with standard deviations up to 30 arcsec) and identified a sample of 551 filaments in 14 images. They also studied the relationship with their height. The distance between PIL and filaments peaks at ~10 arcsec (~7 Mm), although that is also the size of their bin, and most values are smaller than 18 arcsec (13 Mm). Ipson et al. (2009) also applied this approach to a few images. There have therefore been a few studies of the relation between the filaments and the distance to the PIL, either on a small sample of filaments or specific filaments (polar filaments).
Furthermore, most PIL locations are not associated with a filament. According to the review by Martin (1990) for example, there are several necessary conditions to form filaments, i.e. the presence of coronal loops connecting the opposite polarities on each side of the PIL, the existence of long-term converging flows associated with patches of opposite polarities towards the PIL (see also Roudier et al. 2008, for their role in filament eruption) and cancellation of these patches close to the PIL. Martin (1998) confirms these conditions, in addition to conditions related to small-scale flows, chirality, and quadrupolar configurations. Models of the formation of filaments have been developed to take these conditions into account (e.g. Mackay et al. 2008). Filament channels, defined as regions of the chromosphere where the fibrils are aligned with the PIL, are necessary conditions for the formation of filaments. There are however few observations of their formation (e.g. Gaizauskas et al. 1997, 2001), and it is not clearly understood why they form all over the Sun (see for example the review by Mackay et al. 2010). They also point out that the precise localization of the filament formation along the PIL is still an open question. For quiet Sun filaments (in which we are mostly interested in this paper), Mackay et al. (2010) show that the dominant role is probably played by converging flows leading to flux cancellation and reconnexion (see also Mackay 2005, for the role played by these converging motions). Unfortunately, these criteria cannot be applied to single magnetograms and are too complex to be useful for other stars. That filaments form in very different magnetic environments on the Sun also increases the complexity of the problem.
Therefore, even if we know that filaments are closely related to the magnetic configuration and are associated with PIL, no study in the literature provides a deep enough understanding to allow us to predict how the surface can be covered by filaments at a given time, given a global magnetic configuration, as for example represented by a certain distribution of the magnetic flux over the surface. We therefore seek other criteria that would be easy to apply to single magnetograms (next section). Shelke & Pande (1983); Maksimov & Ermakova (1985), and Maksimov & Prokopiev (1995) found that the magnetic field gradient normal to the PIL had to be smaller than a threshold for the PIL to be associated with a filament. The threshold however depends on the spatial resolution of the magnetograms (Maksimov & Prokopiev 1995). In our work, we also consider the unipolar patches close to the PIL and their distance to the PIL.
3. Data analysis
3.1. Filaments and Hα spectroheliograms
Filaments are extracted from the 676 Hα Meudon spectroheliograms as described in Meunier & Delfosse (2009): centre-to-limb correction, determination of an intensity threshold from intensity distributions, thresholding and thinning algorithm, and structure extraction from the segmented images. We use images between 1996 May 5 and 2002 September 21 (this covers the period between the minimum and the maximum of cycle 23). In this paper, we consider all filaments detected within 0.85 R⊙ of the disk center. This is necessary to avoid uncertain identifications of filaments close to the limb due to the strong limb-darkening contribution (see also next section). We are mostly interested in the surface covered by filaments, hence our analysis is less complex than the one performed by Fuller et al. (2005); Ipson et al. (2005); Bernasconi et al. (2005); Aboudarham et al. (2008), or Scholl & Habbal (2008), as we do not attempt for example to reconstitute the whole filament skeleton (including matching smaller pieces of a single filaments) nor to track them in time. This leads to 8602 filaments (or elements of filaments in a few cases).
 |
Fig. 1 Upper left panel: example of a full sun magnetogram during a low activity period, with PIL pixels superimposed (solid line) and filaments (red patches). The dotted circle indicates a distance of 0.85 R⊙. Upper right panel: for the same magnetogram, positive polarity (white) and negative polarity (black) unipolar areas (see text for more details) are superimposed on the PIL (dotted line). The gray circle indicates the position of the limb. Lower panels: same as upper panels but for a high activity period. |
3.2. Magnetogram analysis
The polarity inversion line (PIL) is determined from magnetograms, which provide the line-of-sight magnetic field. We select magnetograms obtained by MDI/SOHO (Scherrer et al. 1995) close in time to the Hα spectroheliograms (Δt < 1 day), the latter allowing us to derive the filament coverage. We analyse only pixels that are closer than 0.85 R⊙ from disk the center. In addition to the limit related to the identification of filaments, strong projection effects as well as the presence of noise in MDI magnetograms far from disk center affect the determination of the polarity inversion line. We use the following method to determine the PIL pixels. We first smooth the magnetograms with a gaussian filter of FWHM 44 Mm (i.e. about 60 arcsec on average, which represents a good compromise between the different values studied by Durrant 2002). On the resulting map, we identify the pixels for which both negative and positive polarity adjacent pixels exist. We then perform a thinning operation in order to keep the skeleton only. This results in a number of pixel Npil, which is normalized according to the mean solar radius over our series. Two examples, taken during low and high activity periods, are illustrated in Fig. 1 (left panels).
Variables derived from the magnetogram and Hα spectroheliogram analysis.
 |
Fig. 2 Upper panel: surface distribution of filaments (ppm of the solar hemisphere). Middle panel: distribution of the average distance from filament to PIL |
Average filaments properties (see Table 1 for definitions and units).
To characterize more reliably the local conditions, we analyse unipolar areas defined as regions above 3 G on the smoothed map. For each PIL pixel, we compute the distance to the closest positive polarity unipolar region and retrieve the size of that region. We do the same for the negative polarity area (see Fig. 1, right panels). In the following, we average the positive and negative polarity values for each PIL pixel, which provide, for each PIL pixel, a distance Duni (in Mm) and a size Auni (hereafter in fractions of the solar hemisphere), where Duni is measured between the PIL and the closest pixels belonging to the unipolar area. These variables help us to characterize each PIL pixel. We also derive from the smoothed map a local gradient in the magnetic field (in G/m), ∇Bpil. Table 1 summarizes the definition of these parameters.
3.3. Relation between the filaments and the magnetograms
Finally, each map of filaments (derived from the Hα spectroheliograms) is remapped onto the magnetogram, correcting for the rotation and image size and position. For each PIL pixel, we compute the closest distance to a filament pixel, hereafter Dfil. Similarly, for each filament, we determine its closest distance to the PIL, Dpil (i.e. the distance bewteen the edge of the filament to the closest PIL pixel), as well as this distance averaged over all filament pixels, 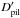 . Table 1 summarizes the definition of all parameters used.
. Table 1 summarizes the definition of all parameters used.
4. Filaments and the magnetic configuration
4.1. Filament properties
4.1.1. Average properties
Figure 2 shows the size distribution for our 8602 filaments. The average value is around 300 ppm (part per million of the solar hemisphere). Most filaments are superimposed1 on the PIL (63.5%), and 96% are located within 30 Mm of the PIL. We therefore confirm the close association between filaments and the PIL, which has been known for a long time (Babcock & Babcock 1955; Martres et al. 1966). For comparison, when considering all pixels on the disk (and averaging over the cycle), only 50% are within a distance to the PIL of 30 Mm. Figure 2 also shows the distribution of the distances between the filaments and the PIL, which in some ways is similar to that of Ipson et al. (2005), in particular a maximum of the 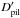 distribution around 5 Mm. Finally, the lower panel of Fig. 2 shows the distribution of the magnetic field (in absolute value) averaged over each filament. Unsurprisingly most filaments correspond to a very low magnetic flux, as they are located close to the PIL. We note that the noise level of these magnetograms is about 15 G, which is close to the minimum value in this plot. In the following, our criteria for determining whether a filament is associated with a PIL will be the distance Dpil < 30 Mm, which allows us to recover 96% of our whole sample of filaments. This distance is close to the supergranulation scale, and may be related to the role played by the converging motions represented by supergranules in the filament evolution (Roudier et al. 2008).
distribution around 5 Mm. Finally, the lower panel of Fig. 2 shows the distribution of the magnetic field (in absolute value) averaged over each filament. Unsurprisingly most filaments correspond to a very low magnetic flux, as they are located close to the PIL. We note that the noise level of these magnetograms is about 15 G, which is close to the minimum value in this plot. In the following, our criteria for determining whether a filament is associated with a PIL will be the distance Dpil < 30 Mm, which allows us to recover 96% of our whole sample of filaments. This distance is close to the supergranulation scale, and may be related to the role played by the converging motions represented by supergranules in the filament evolution (Roudier et al. 2008).
Average PIL pixels properties (see Table 1 for definitions and units).
Table 2 shows the properties of the PIL pixels closest to the filaments (one PIL pixel for each filament), for various filament categories (first column) depending on their distance to the PIL. These variables are related to the global magnetic configuration. The unipolar areas closer to the PIL have an average size Auni of the order of 4% of a solar hemisphere, which corresponds to ~122 000 Mm2 (or a radius of 196 Mm assuming circular shapes), and they are located at ~25 Mm from the PIL (which is also close to the supergranulation scale). The gradient ∇Bpil is in the range 0.30–0.34 G/Mm. We do not observe any significant variation with the distance to the PIL (but see next section).
 |
Fig. 3 Panel A): average magnetic flux over the disk (daily values) versus time (years), in ppm of the solar hemisphere. Dots in red correspond to the time series studied in Sect. 4 (days for which we know the filament coverage) and dots in black correspond to the full time series studied in Sect. 5 (study of the magnetograms only). Panel B): same for the number of PIL pixels. Panel C): same for the average Auni. Panel D): same for the average Duni. Panel E): same for the average ∇Bpil. Panel F): same for the Ca plage filling factor (from Meunier & Delfosse 2009). Panel G): same for the surface coverage of the filaments, in ppm of the solar hemisphere. Panel H): same for the percentage of occupied PIL pixels, corresponding to PIL pixels that are at a distance smaller than 30 Mm from a filament. |
 |
Fig. 4 Upper right panel: number of PIL pixels versus Auni, for all pixels (solid line) and for pixels associated with a filament (dashed line). Lower right panel: percentage of occupied PIL pixels (i.e. Dfil < 30 Mm) versus Auni (solid line). The horizontal dahsed line shows the average percentage, and the dotted line the 5% level. Middle panels: same for Duni. Right panels: same for ∇Bpil. |
Finally, we find that Auni and Duni do not exhibit any significant trend with the size of the filament, although there is a small deficit of small Duni for large filaments. On the other hand, the gradient ∇Bpil decreases on average as the size increases (by about a factor of two between the smallest and the largest filaments): this decrease is mostly due to the presence of a long tail in the distribution of ∇Bpil values toward there being large gradients for small filaments. Finally, 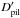 increases strongly (by a factor of three on average) between the smallest and the largest filaments, because of a strong deficit in small
increases strongly (by a factor of three on average) between the smallest and the largest filaments, because of a strong deficit in small 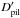 for large filaments, showing that the distance to the PIL may be related to the height of filaments, owing to projection effects (Durrant 2002; Ipson et al. 2005). This means that the selection of filaments superimposed on the PIL is probably slightly biased toward smaller filaments.
for large filaments, showing that the distance to the PIL may be related to the height of filaments, owing to projection effects (Durrant 2002; Ipson et al. 2005). This means that the selection of filaments superimposed on the PIL is probably slightly biased toward smaller filaments.
4.1.2. Temporal variations
We now consider the temporal variations in the filament properties. We define a low activity period (first 163 days of our time series) and a high activity period (the 513 last days of our time series). The average number of filaments is about 8.3/day during the low activity period and 14.1/day during the high activity period. Figure 3 (panel G) shows the surface coverage of the filament over time (one value per day), which should be compared with the variation in the total magnetic flux (panel A, red dots). The two series are correlated, but only weakly (correlation of 0.31), probably because of the large small-scale dispersion of filaments. In conclusion, there are more filaments (and a wider filament surface coverage when considering the whole disk) during cycle maximum, as well as a larger dispersion in the filament number on short timescales.
However, we do not observe any significant variation in the filament properties (size and distance to PIL Dpil) versus time. On the other hand, the properties of the PIL pixels associated with filaments (the closest pixel for each filament) vary over the solar cycle: the average Auni corresponding to PIL pixels associated with filaments is smaller at cycle minimum (0.012) than at cycle maximum (0.045) by a factor of almost four, while Duni is larger at cycle minimum by about a factor of two and ∇Bpil is smaller during cycle minimum. We later discuss (Sect. 4.2.2) the implication of these variations. Owing to the limit at 0.85 R⊙ (see Sect. 3), the most polar unipolar zones (corresponding to the polar crown filaments) may be missing.
4.2. PIL analysis
In the previous section we studied the properties of the PIL pixels closest to filaments. We now consider all PIL pixels identified on the magnetograms, and study their properties. In particular, we compare the properties of those associated with filaments with the properties of all PIL pixels.
4.2.1. Average properties
Table 3 shows the number of PIL pixels in each category, i.e. depending whether they are associated with a filament. Out of the almost five million PIL pixels for the whole data set (about 7045 on average per day), only 2.2% are superimposed on a filament. However, when using the distance criteria derived from the filament analysis described in the previous section, we find that 11% of the PIL pixels have a filament within 30 Mm, and 16% have a filament within 50 Mm, which therefore accounts for almost all filaments (see Table 2). For comparison, 6% of all disk pixels (over the whole cycle) are at a distance of within 30 Mm from a filament (compared to 11% for PIL pixels).
As shown in Table 3, the PIL pixels associated with filaments have quite different properties on average from the rest of the pixels. While the average Auni for all PIL pixels is about 0.026 (i.e. 79 000 Mm2), it is larger for PIL pixels associated with filaments (between 0.037 and 0.042 depending on the category). On the other hand, Duni is larger (about 47 Mm) for all PIL pixels (i.e. dominated by the pixels not associated with a filament), and smaller (of the order of or below 30 Mm) when there is a filament nearby. Therefore, PIL pixels associated with filaments tend to be closer to unipolar area, which are also larger than average. We therefore note a general anti-correlation between Auni and Duni (correlation of − 0.37). The gradient ∇Bpil is smaller when the pixel is associated with a filament.
Figure 4 shows the number of pixels as a function of the three variables Auni, Duni, and ∇Bpil, for all PIL pixels and for occupied PIL pixels (defined as pixels that are at a distance Dfil smaller than 30 Mm from a filament). The lower panels show the percentage of occupied pixels for each bin, indicating that some conditions on the PIL pixels are more likely to produce filaments than others. The strong percentage at low Auni is not however significant, as it corresponds to a very small number of pixels. PIL pixels close to a large unipolar region are more likely to be associated with a filament: for Auni > 0.02 the percentage is above average (11%). It is above 5% for Auni > 0.002. As for Duni, the highest efficiency is reached around 10 Mm, and the percentage of occupation is above average for Duni between 3 and 40 Mm. The ∇Bpil peak efficiency is about 0.3 G/Mm, with an efficiency above average for values between 0.1 and 1 G/Mm. Shelke & Pande (1983); Maksimov & Ermakova (1985), and Maksimov & Prokopiev (1995) showed that the gradient had to be smaller than a certain threshold to have a filament, which also implies that a small gradient is associated with a filament. As shown in Table 3, smaller gradients are associated with filaments, but the size distribution does not show a clear cutoff. However, the percentage is significantly below 3 G/Mm, although there are still PIL pixels associated with filaments above that value. These correspond to very small values of Duni (below 2.5 Mm) and relatively large Auni, which are both probably associated with active regions. The distribution does not drop as much on the small gradient side, because for very small gradients the percentage is still around 5%. On the other hand, a strong Auni and a small Duni (more likely to be associated with filaments) are naturally associated with a larger gradient, as shown in Fig. 5 (see also Table 4 showing the average values during the periods of low and high activity). For large Auni, the tail of the distribution of ∇Bpil towards large values is stronger. As Duni decreases, the distribution of ∇Bpil shifts toward smaller values. This means that there must be a trade off, as on the other hand large gradients do not have a large efficiency. This also explains the low correlation (0.18) between Auni and ∇Bpil. Finally, the peak percentage is similar for all three variables (about 20%), so at this stage all parameters seem important, and the gradient is not a sufficient parameter to describe the conditions that would be best to allow the formation of filaments.
Average PIL pixels properties for two periods (see Table 1 for definitions and units).
To summarize, we have derived the following properties:
-
we confirm the proximity of filaments to PIL, with a characteristic distance of 30 Mm;
-
PIL pixels associated with filaments are close to large unipolar regions (i.e. small Duni and large Auni);
-
independently of the unipolar size and distances, the PIL pixels associated with filaments correspond to relatively low magnetic field gradients ∇Bpil, with a peak of the distribution around 0.3 G/Mm for our data;
-
the peak efficiency is 20%.
4.2.2. Temporal variation of the parameters
We now consider the temporal variations between cycle minimum and cycle maximum, i.e. covering the full range of activity levels. We analyse the variation in the PIL pixels properties associated with filaments over that period.
First of all, Fig. 3 shows that the number of PIL pixels Npil decreases as the activity level increases, while the percentage of occupied pixels (at a distance to a filament smaller than 30 Mm) increases. The decrease in Npil is caused by no large unipolar regions being produced by the decay of active regions at low activity level, but instead many small unipolar regions, as illustrated in Fig. 1: this leads to a large total length of PIL. As we observe a larger number of filaments at cycle maximum, it is therefore logical to observe a strong increase in the proportion of occupied pixels. Our interpretation is confirmed by the plots in the lower panels of Fig. 3: Auni is indeed increasing as the activity level increases and Duni decreases. As filaments are associated with larger Auni and smaller Duni, it is also consistent with the larger proportion of occupied pixels at cycle maximum, as the conditions necessary to form filaments are more adequate for a larger proportion of the PIL pixels.
 |
Fig. 5 Upper panel: number of pixels versus ∇Bpil for three Auni ranges: Auni > 0.1 (solid line), 0.01 < Auni < 0.1 (dashed line), and Auni < 0.01 (dotted line). The vertical lines represent the corresponding ∇Bpil averages. Lower panel: same for three Duni ranges: Duni < 3 Mm (solid line), 3 < Duni < 40 Mm (dashed line), Duni > 40 Mm (dotted line). |
 |
Fig. 6 Upper panel: Auni versus time (Julian days minus t0 = 2 450 000) for all PIL pixels (solid line), pixels superimposed on filaments (dashed line), pixels at distances of smaller than 30 Mm from a filament (dotted line), pixels at distance smaller than 50 Mm from a filament (dashed-dotted line). Averages are computed over 1 year periods. The minimum activity period correspond to the left of the curves, and the maximum activity period to the right. Middle panel: same for Duni. Lower panel: same for ∇Bpil. |
 |
Fig. 7 Upper panel: number of PIL pixels for various Auni bins during periods of low activity (solid line) and high activity (dashed line). Middle panel: number of PIL pixels at a distance smaller than 30 Mm from a filament for various Auni bins, during periods of low activity (solid line) and high activity (dashed line). The dotted line represents the expected numbers for the high activity period, when using the number of PIL pixels during the high activity period and the proportion of occupied pixels during the low activity period. Lower panel: percentage of occupied PIL pixels (distance smaller than 30 Mm from a filament) during periods of low activity (solid line) and high activity (dashed line). |
Figure 6 shows the variation in Auni, Duni, and ∇Bpil, with time for various categories of PIL pixels. Auni is always increasing and Duni always decreasing, either for all pixels or for occupied pixels (for distances to filaments smaller than 30 Mm). Values are averaged over one year bins. It should be kept in mind that the distributions are far from being gaussian distributions. Furthermore, at all times, Auni is larger for pixels associated with filaments and Duni is smaller, but the closer the filament is to the PIL the stronger the difference from the global average is. The behaviour of ∇Bpil is a little more complex. ∇Bpil always increases with time for occupied pixels, but not as much as for the whole data set: ∇Bpil for occupied pixels is below average (as seen previously) only during the period of high activity. It is the opposite during the quiet period. The reason is probably the difference with the Auni variation, as there is a need for large Auni and small gradients to produce a filament, but large values of Auni are generally associated with large gradients. This may constrain the number of filaments at a given time.
4.2.3. Parameter distributions and percentages of occupied pixels
If the conditions vary over time, then we naturally expect the global percentage of occupied pixels to vary accordingly. The top panel of Fig. 7 indeed shows that the PIL properties vary over time, with there being a larger proportion of PIL pixels with large Auni. What is not illustrated here is that there is also a larger proportion of small Duni pixels at cycle maximum, and a drop in the number of pixels with large Duni, as well as a strong increase in large ∇Bpil values at cycle maximum. The resulting distribution of Auni for occupied pixels is therefore different for the two periods (middle panel). We assume for a moment that the percentage of occupied pixels versus Auni does not vary, and consider the solar minimum values. If we apply these percentages to the number of PIL pixels at cycle maximum, we obtain the dotted curves in the middle panel of Fig. 7. This curve is quite close to the observed number of occupied PIL pixels at cycle maximum, showing that the modification of the general PIL property distribution accounts for most of the variation. The same result can be observed for the other two variables (Duni and ∇Bpil).
The remaining difference is caused by a slight variation in the fraction of occupied pixels versus Auni for example, and an increase in efficiency for smaller Auni at cycle maximum (see lower panel of Fig. 7). This may be because we have considered the three criteria independently: if Auni seems to play the dominant role on the filament presence, it is necessary to consider the three parameters together to understand second order effects. In the Auni domain where the percentage is larger than average for example, it does not vary by more than a factor of 1.5 for example between low and high activity periods. A variation of a factor of 2 between the two periods is observed only for small percentages, below 5%. On the other hand, the percentage of occupation for the other two variables varies by a larger amount. We consider for example the variation in the mean values of the three variables between low and high activity periods for Auni in the range [10-3–3 × 10-3]: the percentage of occupied pixels increases from 3.6 to 6.5%, Duni decreases from 78 to 43 Mm, and ∇Bpil increases from 0.08 from 1.13. For Duni, the peak of the percentage of occupied pixels shifts toward larger values when the activity level increases: during the high activity period, the efficiency is multiplied by ~1.5–2 for Duni between 15 and 50 Mm, leading to larger than average values for additional values of Duni compared to the low activity period (i.e. between 30 and 50 Mm). If we consider for example the pixels for which Duni is in the range 20–25 Mm, for which the percentage of occupation changes significantly with time (factor of two), the gradient ∇Bpil remains stable, while Auni increases by a factor of three, which may be due to a larger impact of Auni. Similarly, the peak efficiency for ∇Bpil shifts toward low gradients, by a strong factor as well.
To summarize, we have derived the following conclusions:
-
Auni seems to play a dominant role in the presence of filaments. This is interesting because the surface of unipolar region will have an impact on chromospheric index and therefore may be related to a stellar observable (see Fig. 3 for a plot of the plage filling factor in the chromosphere);
-
the other parameters Duni and ∇Bpil also play a role, but the most efficient conditions according to these criteria seem to vary along the solar cycle, maybe in correlation with the Auni conditions.
4.2.4. Dispersion in the number of filaments versus time
Finally, the large dispersion in the number of filaments at small temporal scales (see for example the upper left panel of Fig. 3) shows that it will probably be difficult to reproduce exactly the surface coverage of filaments at these scales. Periodograms of the filament surface coverage time series show that the peak corresponding to the rotation for example is not as obvious as for other variables (for example the total magnetic flux), as there is a lot of power on all short timescales. We also attempted to study the cross-correlation function between the filling-factor time series and for example the average flux, in order to see whether some systematic effects caused by a time lag, could be observed, but no variation was significant. This may be because even if there is a delay between the emergence of the magnetic flux in active regions and the formation of these filaments, that these delays cover a wide range of values of between a few days and a month (see for example the review by Mackay et al. 2010). We therefore expect our reconstruction to be valid only statistically on short timescales.
 |
Fig. 8 Upper panel: percentage of occupied pixels (distance to a filament smaller than 30 Mm) versus the number of PIL pixels. Each dot corresponds to a daily value. The solid line is a second degree polynomial fit on the 676 points. Lower panel: filament coverage (in ppm of the solar hemisphere) versus the number of occupied pixels (distance to a filament smaller than 30 Mm). The solid line is a second degree polynomial fit to the 676 points. |
 |
Fig. 9 Upper panel: observed filament coverage (in ppm of the solar hemisphere) versus the average flux. Middle panel: same for reconstructed filament coverage |
4.3. Synthetic filament series
In addition to characterizing more clearly the relation between the filaments and the PIL pixels, we also wish to be able at least statistically, to reconstruct the surface covered by filaments for a given magnetic configuration. We now use the results obtained in the previous sections to build and test several ways of analysing this time series, for which we know how many filaments were actually observed. Given the larger dispersion in the observed surface coverage on short timescales, we do not reproduce the signal precisely, but at least wish to be able to reconstruct a signal with similar properties. In both methods, we assume that we are able to characterize the magnetic configuration as studied previously, i.e. by defining the PIL pixels and the unipolar area, as well as the magnetic flux.
4.3.1. First method
Our first recipe is the simplest. We consider the relationship between the percentage of occupied pixels (here we use the criteria filaments closer than 30 Mm) versus the number of PIL pixels, as illustrated in Fig. 8 (upper panel). We model this relation using a second degree polynomial. From this relation and a number of PIL pixels, we can reconstruct the number of occupied pixels. We then need to normalize this number of occupied pixels with the observed filament coverage Sfil, as illustrated in the lower panel. We also model this relation with a second degree polynomial. This allows us to compute a surface coverage, which is analysed with either time or average magnetic flux2. When using only these two relations, we obtain a very small dispersion, much smaller than the observed one. For example, the correlation between the observed Sfil and the average flux is only about 0.31, while in this simulation the correlation would be 0.72. We therefore add an additional noise component that depends on the number of PIL pixels: the use of a white noise is justified because we observe power on all short timescales in the periodogram. For temporal bins of 200 days, we compute the rms of Sfil, and then make a linear fit to these rms versus the average Npil in each bin. The resulting reconstructed filament coverage  is shown in Fig. 9 (middle panel) versus the average flux. The correlation between the two time series (filament coverage and magnetic flux) is 0.32, as for the observation. The dispersion in Sfil and
is shown in Fig. 9 (middle panel) versus the average flux. The correlation between the two time series (filament coverage and magnetic flux) is 0.32, as for the observation. The dispersion in Sfil and  is similar, and the average filament surface coverage is about 0.0044 for
is similar, and the average filament surface coverage is about 0.0044 for  and 0.0048 for Sfil during the low activity period, and, respectively, 0.0081 and 0.0080 during the high activity period. This provides very good agreement between our simulation and observations.
and 0.0048 for Sfil during the low activity period, and, respectively, 0.0081 and 0.0080 during the high activity period. This provides very good agreement between our simulation and observations.
4.3.2. Second method
Alternatively, we can take into account that all PIL pixels are not equivalent, as some of them are more likely to be associated with filaments. This method is therefore more realistic than the previous one, although when applied to stellar cases we have to assume properties similar to the solar ones, since the efficiency depends on Auni and Duni. We chose not to introduce the magnetic field gradient at this stage as it is correlated with Duni. For a given Auni and Duni, we know the probability of each pixel being occupied by a filament, because this equals the fraction of occupied pixels for such Auni and Duni values. We then multiply this probability with the number of PIL pixels in that Auni and Duni bin, and then sum the values over all Auni and Duni bins to obtain a total number of occupied pixels. Figure 9 (lower panel) shows the resulting time series  . The correlation between the two time series (filament coverage and magnetic flux) is 0.40 (of the same order as the observation). As in the previous method, the agreement with observation is very good (similar dispersion, similar average levels during the low and high activity periods).
. The correlation between the two time series (filament coverage and magnetic flux) is 0.40 (of the same order as the observation). As in the previous method, the agreement with observation is very good (similar dispersion, similar average levels during the low and high activity periods).
 |
Fig. 10 Upper panel: observed Hα emission versus the observed Ca emission. Middle panel: same for reconstructed emissions (first method, see text). Lower panel: same for reconstructed emissions (second method, see text). |
4.4. Synthetic Ca and Hα emissions series
We define synthetic Ca and Hα emission as in Meunier & Delfosse (2009)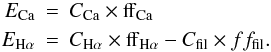 We use the contrast values determined in Meunier & Delfosse (2009), i.e. CCa = 0.20 (plage contrast in Ca), CHα = 0.13 (plage contrast in Hα), and Cfil = 0.30 (filament contrast in Hα). The filling factors for plages in both Ca (ffCa) and Hα (ffHα) and for filaments (fffil) is either the observed one (in this section only, for validation of the reconstructed one) or a reconstructed one. The reconstructed filling factor for filaments is derived from the previous section (Sfil for the observed time series,
We use the contrast values determined in Meunier & Delfosse (2009), i.e. CCa = 0.20 (plage contrast in Ca), CHα = 0.13 (plage contrast in Hα), and Cfil = 0.30 (filament contrast in Hα). The filling factors for plages in both Ca (ffCa) and Hα (ffHα) and for filaments (fffil) is either the observed one (in this section only, for validation of the reconstructed one) or a reconstructed one. The reconstructed filling factor for filaments is derived from the previous section (Sfil for the observed time series,  and
and  for the reconstructed ones). We derive ffCa from the magnetograms. Following Schrijver (2001), we derive a calcium map as | B | 0.6, smooth it, and then apply a threshold that provides a filling factor normalized to the observations. We then derive ffHα from ffCa using a polynomial fit to the observations made in Meunier & Delfosse (2009) over 1690 daily values
for the reconstructed ones). We derive ffCa from the magnetograms. Following Schrijver (2001), we derive a calcium map as | B | 0.6, smooth it, and then apply a threshold that provides a filling factor normalized to the observations. We then derive ffHα from ffCa using a polynomial fit to the observations made in Meunier & Delfosse (2009) over 1690 daily values
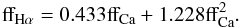 Figure 10 shows the results for the observation, compared to the two reconstructions of the emissions (one for each filament reconstruction). The correlation between the two temporal series ffHα and ffCa is 0.74 for the observation, i.e. slightly different from the 0.80 value of Meunier & Delfosse (2009) because here we consider a significantly shorter time series (which does not give the same weight to all phases of the solar cycle), while it is 0.80 for the first simulation and 0.81 for the second simulation. The reconstruction therefore tends to slightly overestimate the correlation. This is probably due to the necessary uncertainty when dealing with the dispersion in the filament surface coverage. In the next section, we use both methods.
Figure 10 shows the results for the observation, compared to the two reconstructions of the emissions (one for each filament reconstruction). The correlation between the two temporal series ffHα and ffCa is 0.74 for the observation, i.e. slightly different from the 0.80 value of Meunier & Delfosse (2009) because here we consider a significantly shorter time series (which does not give the same weight to all phases of the solar cycle), while it is 0.80 for the first simulation and 0.81 for the second simulation. The reconstruction therefore tends to slightly overestimate the correlation. This is probably due to the necessary uncertainty when dealing with the dispersion in the filament surface coverage. In the next section, we use both methods.
5. Analysis of magnetograms over the cycle
We analyse 3594 magnetograms covering a full solar cycle, between April 1996 and October 2007. In the previous section, we estimated the corresponding number of filaments, whereas here we study only the magnetograms. We therefore derive the parameters studied before to characterize the magnetic configuration and then apply our method (Sects. 4.3 and 4.4) to estimate the number of filaments over time.
 |
Fig. 11 Upper panel: number of PIL pixels versus the average magnetic flux (daily values), for the complete solar cycle. Middle panel: same as for the average Auni. Lower panel: same as for the average Duni. |
 |
Fig. 12 Upper left panel: average number of PIL pixels versus the average flux, for the ascending phase of the cycle (diamonds) and the descending phase of the cycle (stars). Upper right panel: same for Auni. Middle left panel: same for Duni. Middle right panel: same for ∇Bpil. Lower left panel: same for Meudon filament coverage, versus the Wolf number (from Meunier & Delfosse 2009). Lower right panel: same for Mackay et al. (2008) external filaments versus the Wolf number. |
5.1. PIL pixels
We analyse the magnetograms as described in the previous section (Sect. 2.2), and determine for each day the PIL pixels (leading to the daily number of PIL pixels Npil) and for each of them Auni and Duni. The results are shown in Fig. 3 (black dots). As observed before, the number of PIL pixels is anticorrelated with the magnetic flux on the disk (correlation of −0.68), although it has a smaller dispersion at cycle maximum and a larger dispersion at cycle minimum. The daily Auni time series are correlated with the magnetic flux (correlation of 0.74), with a similar dispersion, while Duni is anticorrelated with a smaller dispersion (correlation of −0.85). Figure 11 also shows Npil versus the average magnetic flux. We observe a saturation at high magnetic fluxes (typically above 30 G, corresponding to the lowest value observed during cycle maximum): despite the correlation, the number of PIL pixels does not continue to decrease at high magnetic fluxes. That same saturation is observed for Duni. It does not prevent the formation of a larger amount of filaments, as Auni can have larger values during cycle maximum (Fig. 11).
There is a general good correlation between the mean flux, Npil, Auni, Duni, and ∇Bpil. However, if we average over bins of 180 days for example, and plot these last four variables versus the mean flux, we observe a different behaviour between the ascending phase of the cycle and the descending phase of the cycle, except for the gradient, as shown in Fig. 12. During the descending phase, Npil does not increase as fast as expected if it were symmetric. Similarly, Auni does not decrease as fast as expected either. Because large values of Auni are associated with more filaments, this could mean that the number of filaments should not decrease as fast as expected during the descending phase. On the other hand, Duni increases faster than expected during the descending phase of the cycle, which could mean that we expect the number of filament to decrease more rapidly. Auni and Duni therefore seem to oppose each other. Mackay et al. (2008) counted the number of external filaments during four phases of the cycle four measurements and found that there are a smaller number of filaments during the descending phase of the cycle than for the ascending phase, for a similar activity level. The surface coverage determined from Meudon data by Meunier et al. (2008) provides similar results (although the descending phase does not correspond to the same cycle, so the comparison must be made with care). This means that the values of Duni also have a significant effect on the filament number. This is a second order effect, but it is interesting to understand more clearly the respective roles of the various parameters.
 |
Fig. 13 Upper panel: reconstructed filament filling factor Sfil versus time (years), representing daily values, for the complete solar cycle, for method 1. Middle panel: same for ECa. Lower panel: same for EHα. |
5.2. Synthetic time series
We now use the methods tested in the previous section to compile a synthetic time series of the filament coverages  and
and  , as well as the Ca and Hα filling factors for plages (derived from the magnetograms). This provides a synthetic time series for both the Ca emission ECa and the Hα emission EHα. The results are shown in Fig. 13 for method 1. The correlation between these two types of emission is 0.82, in very good agreement with the observation (it is 0.81 for the second method). The comparison of the reconstructed Ca emission with actual observations of the emission in the Ca II K line obtained at Sacramento Peak Observatory3 show that they are well correlated, with a correlation of 0.9. This good agreement with observation shows that the reconstructed Ca emission derived from magnetograms is reliable, a reliability that is necessary for our future work on stellar activity. Figure 14 also shows the reconstructed filament coverage averaged over time and compared to the results of the two previous sections (for which we knew the filament coverage), and both includes the observed time series and illustrates the very good quality of the reconstruction for long timescales.
, as well as the Ca and Hα filling factors for plages (derived from the magnetograms). This provides a synthetic time series for both the Ca emission ECa and the Hα emission EHα. The results are shown in Fig. 13 for method 1. The correlation between these two types of emission is 0.82, in very good agreement with the observation (it is 0.81 for the second method). The comparison of the reconstructed Ca emission with actual observations of the emission in the Ca II K line obtained at Sacramento Peak Observatory3 show that they are well correlated, with a correlation of 0.9. This good agreement with observation shows that the reconstructed Ca emission derived from magnetograms is reliable, a reliability that is necessary for our future work on stellar activity. Figure 14 also shows the reconstructed filament coverage averaged over time and compared to the results of the two previous sections (for which we knew the filament coverage), and both includes the observed time series and illustrates the very good quality of the reconstruction for long timescales.
 |
Fig. 14 Surface coverage of filaments versus time (years), for bins of 100 days: reconstruction for the complete cycle (solid line), reconstruction for the short period (dotted line), observed (dashed line). |
6. Conclusion
Our statistical analysis of a large number of filaments have confirmed that most filaments are associated with PIL pixels within ~30 Mm, with a peak distribution arount 5 Mm. They are also associated with a very low magnetic flux. We have also found that there are more filaments during cycle maximum, as found by Mackay et al. (2008) for external filaments, i.e. filaments that are formed between two bipoles. Their properties do not vary significantly with time, although the size and distance of unipolar region close to the PIL do vary. A detailed analysis of all PIL pixels has shown that 11% of them are associated with a filament (within 30 Mm). These particular pixels are associated with larger unipolar regions (above 2% of the solar hemisphere), which are also closer than average (between 3 and 40 Mm) and associated with a moderate magnetic field gradient (between 0.1 and 1 G/Mm on the smoothed maps). We do not observe a clear cut off, as filaments also exist for large gradients, but the efficiency declines significantly around a few G/Mm (in agreement with Maksimov & Prokopiev 1995, for example), although the smallest values of the gradient are also inconsistent with the presence of a filament. Because larger unipolar regions and small distances are naturally associated with large gradients, there is a trade off between these two constraints. We observe that the number of PIL pixels is anti-correlated with the activity level, and the increase in filament coverage at high activity levels is mostly due to the modification of the PIL pixel properties, while the variation in efficiency for given conditions accounts for only a small part of the variation. Among the three parameters we studied (size and distance of unipolar region from the PIL, magnetic field gradient), the size of the unipolar regions seems to be more important than the other two.
We used these results to derive two methods to reconstruct a time series of filament coverage from magnetograms, one using only the number of PIL pixels and the activity level, the other including the variation in efficiency as a function of the size and distance of the unipolar regions. Both methods give good results for long-term variations. Because of the very large small-scale variation in the number of filaments, these can however only be built statistically. This approach also allowed us to build synthetic time series of Ca and Hα emission, which provided satisfactory results. We then applied this method to the full solar cycle.
Our reconstruction has been shown to provide reliable results. In a future paper, we will develop a model of the magnetic activity over the solar cycle. We will validate our simulation of Sun by applying a technique similar to that described in the present paper, and then apply it to stellar simulations in order to explore in more detail the possible range of variation in Ca and Hα emission depending on the presence of active regions and filaments for the first time. Our approach could later be extended to other activity proxies using various emission lines, or to spectral irradiance observed in different broadband filters, because correlations and anticorrelations with solar activity may be present (Harder et al. 2009).
Our approach presented here has not taken into account parameters such as the orientation of the magnetic field (which can be inferred from vector magnetograms) or the local flows, which probably play an important role (e.g. van Ballegooijen 2008). These cannot however be determined from single magnetograms. A further step could be to use the magnetograms to extrapolate the magnetic field in the corona (e.g. Aulanier & Demoulin 1998; Aulanier et al. 1998) and use this important information as an additional criteria. Filaments indeed form in highly non-potential magnetic field configurations associated with strong magnetic shears (Mackay et al. 2010). This method could also be applied to simulated maps of the magnetic field. This was however beyond the scope of this paper. It would also be useful to consider the horizontal flows, although they are not available on a very large data set. Observations made by the Solar Dynamics Observatory starting in 2010 could be a key to such an analysis, allowing the determination of these horizontal flows for the full disk as well as the measurement of the vector magnetic field.
When computed directly from the absolute value of the magnetic field over the disk, this provides a good idea of the global activity level, see panel A of Fig. 3.
K3 intensity, http://nsosp.nso.edu/data/cak_mon.html
Acknowledgments
SOHO is a mission of international cooperation between the European Space Agency (ESA) and NASA. The Meudon spectroheliograms have been retrieved from the database BASS2000. We thank J. Aboudarham for informations on these data. Ca II K observations used in Sect. 5 have been provided by the Sacramento Peak Observatory.
References
- Aboudarham, J., Scholl, I., Fuller, N., et al. 2008, Ann. Geophys., 26, 243 [Google Scholar]
- Aulanier, G., & Demoulin, P. 1998, A&A, 329, 1125 [NASA ADS] [Google Scholar]
- Aulanier, G., Demoulin, P., van Driel-Gesztelyi, L., Mein, P., & Deforest, C. 1998, A&A, 335, 309 [NASA ADS] [Google Scholar]
- Babcock, H. W., & Babcock, H. D. 1955, ApJ, 121, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Bernasconi, P. N., Rust, D. M., & Hakim, D. 2005, Sol. Phys., 228, 97 [Google Scholar]
- Cincunegui, C., Díaz, R. F., & Mauas, P. J. D. 2007, A&A, 469, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Durrant, C. J. 2002, Sol. Phys., 211, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Durrant, C. J., Kress, J. M., & Wilson, P. R. 2001, Sol. Phys., 201, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, Jr., T. L., Wilcox, J. M., Svalgaard, L., Scherrer, P. H., & McIntosh, P. S. 1977, Sol. Phys., 55, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, N., Aboudarham, J., & Bentley, R. D. 2005, Sol. Phys., 227, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gaizauskas, V., Zirker, J. B., Sweetland, C., & Kovacs, A. 1997, ApJ, 479, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Gaizauskas, V., Mackay, D. H., & Harvey, K. L. 2001, ApJ, 558, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Harder, J. W., Fontenla, J. M., Pilewskie, P., Richard, E. C., & Woods, T. N. 2009, Geophys. Res. Lett., 36, L07801 [Google Scholar]
- Ipson, S. S., Zharkova, V. V., Zharkov, S., et al. 2005, Sol. Phys., 228, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Ipson, S., Zharkova, V., Zharkov, S., et al. 2009, Adv. Space Res., 43, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Henry, G. W., et al. 2007, ApJS, 171, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H. 2005, in Large-scale Structures and their Role in Solar Activity, ed. K. Sankarasubramanian, M. Penn, & A. Pevtsov, ASP Conf. Ser., 346, 177 [Google Scholar]
- Mackay, D. H., Gaizauskas, V., & Yeates, A. R. 2008, Sol. Phys., 248, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Maksimov, V. P., & Ermakova, L. V. 1985, SvA, 29, 323 [NASA ADS] [Google Scholar]
- Maksimov, V. P., & Prokopiev, A. A. 1995, Astron. Nachr., 316, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, S. F. 1990, in Dynamics of Quiescent Prominences (Berlin: Springer Verlag), ed. V. Ruzdjak, & E. Tandberg-Hanssen, Lect. Notes Phys., 363, IAU Colloq., 117, 1 [Google Scholar]
- Martin, S. F. 1998, Sol. Phys., 182, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Martres, M. J., Michard, R., & Soru-Iscovici. 1966, Ann. Astrophys., 29, 249 [NASA ADS] [Google Scholar]
- McCloughan, J., & Durrant, C. J. 2002, Sol. Phys., 211, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Meunier, N., & Delfosse, X. 2009, A&A, 501, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Roudier, T., & Rieutord, M. 2008, A&A, 488, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Radick, R. R., Lockwood, G. W., Skiff, B. A., & Baliunas, S. L. 1998, ApJS, 118, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Roudier, T., Švanda, M., Meunier, N., et al. 2008, A&A, 480, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Scholl, I. F., & Habbal, S. R. 2008, Sol. Phys., 248, 425 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Schrijver, C. J. 2001, ApJ, 547, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Shelke, R. N., & Pande, M. C. 1983, BASI, 11, 327 [NASA ADS] [Google Scholar]
- van Ballegooijen, A. A. 2008, in Subsurface and Atmospheric Influences on Solar Activity, ed. R. Howe, R. W. Komm, K. S. Balasubramaniam, & G. J. D. Petrie, ASP Conf. Ser., 383, 191 [Google Scholar]
All Tables
Average PIL pixels properties for two periods (see Table 1 for definitions and units).
All Figures
 |
Fig. 1 Upper left panel: example of a full sun magnetogram during a low activity period, with PIL pixels superimposed (solid line) and filaments (red patches). The dotted circle indicates a distance of 0.85 R⊙. Upper right panel: for the same magnetogram, positive polarity (white) and negative polarity (black) unipolar areas (see text for more details) are superimposed on the PIL (dotted line). The gray circle indicates the position of the limb. Lower panels: same as upper panels but for a high activity period. |
| In the text | |
 |
Fig. 2 Upper panel: surface distribution of filaments (ppm of the solar hemisphere). Middle panel: distribution of the average distance from filament to PIL |
| In the text | |
 |
Fig. 3 Panel A): average magnetic flux over the disk (daily values) versus time (years), in ppm of the solar hemisphere. Dots in red correspond to the time series studied in Sect. 4 (days for which we know the filament coverage) and dots in black correspond to the full time series studied in Sect. 5 (study of the magnetograms only). Panel B): same for the number of PIL pixels. Panel C): same for the average Auni. Panel D): same for the average Duni. Panel E): same for the average ∇Bpil. Panel F): same for the Ca plage filling factor (from Meunier & Delfosse 2009). Panel G): same for the surface coverage of the filaments, in ppm of the solar hemisphere. Panel H): same for the percentage of occupied PIL pixels, corresponding to PIL pixels that are at a distance smaller than 30 Mm from a filament. |
| In the text | |
 |
Fig. 4 Upper right panel: number of PIL pixels versus Auni, for all pixels (solid line) and for pixels associated with a filament (dashed line). Lower right panel: percentage of occupied PIL pixels (i.e. Dfil < 30 Mm) versus Auni (solid line). The horizontal dahsed line shows the average percentage, and the dotted line the 5% level. Middle panels: same for Duni. Right panels: same for ∇Bpil. |
| In the text | |
 |
Fig. 5 Upper panel: number of pixels versus ∇Bpil for three Auni ranges: Auni > 0.1 (solid line), 0.01 < Auni < 0.1 (dashed line), and Auni < 0.01 (dotted line). The vertical lines represent the corresponding ∇Bpil averages. Lower panel: same for three Duni ranges: Duni < 3 Mm (solid line), 3 < Duni < 40 Mm (dashed line), Duni > 40 Mm (dotted line). |
| In the text | |
 |
Fig. 6 Upper panel: Auni versus time (Julian days minus t0 = 2 450 000) for all PIL pixels (solid line), pixels superimposed on filaments (dashed line), pixels at distances of smaller than 30 Mm from a filament (dotted line), pixels at distance smaller than 50 Mm from a filament (dashed-dotted line). Averages are computed over 1 year periods. The minimum activity period correspond to the left of the curves, and the maximum activity period to the right. Middle panel: same for Duni. Lower panel: same for ∇Bpil. |
| In the text | |
 |
Fig. 7 Upper panel: number of PIL pixels for various Auni bins during periods of low activity (solid line) and high activity (dashed line). Middle panel: number of PIL pixels at a distance smaller than 30 Mm from a filament for various Auni bins, during periods of low activity (solid line) and high activity (dashed line). The dotted line represents the expected numbers for the high activity period, when using the number of PIL pixels during the high activity period and the proportion of occupied pixels during the low activity period. Lower panel: percentage of occupied PIL pixels (distance smaller than 30 Mm from a filament) during periods of low activity (solid line) and high activity (dashed line). |
| In the text | |
 |
Fig. 8 Upper panel: percentage of occupied pixels (distance to a filament smaller than 30 Mm) versus the number of PIL pixels. Each dot corresponds to a daily value. The solid line is a second degree polynomial fit on the 676 points. Lower panel: filament coverage (in ppm of the solar hemisphere) versus the number of occupied pixels (distance to a filament smaller than 30 Mm). The solid line is a second degree polynomial fit to the 676 points. |
| In the text | |
 |
Fig. 9 Upper panel: observed filament coverage (in ppm of the solar hemisphere) versus the average flux. Middle panel: same for reconstructed filament coverage |
| In the text | |
 |
Fig. 10 Upper panel: observed Hα emission versus the observed Ca emission. Middle panel: same for reconstructed emissions (first method, see text). Lower panel: same for reconstructed emissions (second method, see text). |
| In the text | |
 |
Fig. 11 Upper panel: number of PIL pixels versus the average magnetic flux (daily values), for the complete solar cycle. Middle panel: same as for the average Auni. Lower panel: same as for the average Duni. |
| In the text | |
 |
Fig. 12 Upper left panel: average number of PIL pixels versus the average flux, for the ascending phase of the cycle (diamonds) and the descending phase of the cycle (stars). Upper right panel: same for Auni. Middle left panel: same for Duni. Middle right panel: same for ∇Bpil. Lower left panel: same for Meudon filament coverage, versus the Wolf number (from Meunier & Delfosse 2009). Lower right panel: same for Mackay et al. (2008) external filaments versus the Wolf number. |
| In the text | |
 |
Fig. 13 Upper panel: reconstructed filament filling factor Sfil versus time (years), representing daily values, for the complete solar cycle, for method 1. Middle panel: same for ECa. Lower panel: same for EHα. |
| In the text | |
 |
Fig. 14 Surface coverage of filaments versus time (years), for bins of 100 days: reconstruction for the complete cycle (solid line), reconstruction for the short period (dotted line), observed (dashed line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


