| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A145 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015672 | |
| Published online | 09 August 2011 | |
The effect of environment on star forming galaxies at redshift
I. First insight from PACS
1 Max-Planck-Institut für Extraterrestrische Physik (MPE), Postfach 1312, 85741 Garching, Germany
e-mail: popesso@mpe.mpg.de
2 Dipartimento di Astronomia, Università di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
3 INAF – Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
4 Herschel Science Centre, Spain
5 ESO, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
6 Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU/Service d’Astrophysique, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
7 Instituto de Astrofísica de Canarias, 38205 La Laguna, Spain
8 Dipartimento di Astronomia, Università di Bologna, via Ranzani 1, 40127 Bologna, Italy
9 INAF – Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
Received: 1 September 2010
Accepted: 6 April 2011
We use deep 70, 100 and 160 μm observations taken with PACS, the Photodetector Array Camera and Spectrometer on board of Herschel, as part of the PACS Evolutionary Probe (PEP) guaranteed time, to study the relation between star formation rate and environment at redshift ~ 1 in the GOODS-S and GOODS-N fields. We use the SDSS spectroscopic catalog to build the local analog and study the evolution of the star formation activity dependence on the environment. At z ~ 1 we observe a reversal of the relation between star formation rate and local density, confirming the results based on Spitzer 24 μm data. However, due to the high accuracy provided by PACS in measuring the star formation rate also for AGN hosts, we identify in this class of objects the cause for the reversal of the density–SFR relation. Indeed, AGN hosts favor high stellar masses, dense regions and high star formation rates. Without the AGN contribution the relation flattens consistently with respect to the local analog in the same range of star formation rates. As in the local universe, the specific star formation rate anti-correlates with the density. This is due to mass segregation both at high and low redshift. The contribution of AGN hosts does not affect this anti-correlation, since AGN hosts exhibit the same specific star formation rate as star forming galaxies at the same mass. The same global trends and AGN contribution is observed once the relations are studied per morphological type. We study the specific star formation rate vs. stellar mass relation in three density regimes. Our data provides an indication that at M/M⊙ > 1011 the mean specific star formation rate tends to be higher at higher density, while the opposite trend is observed in the local SDSS star forming sample.
Key words: galaxies: evolution / galaxies: star formation / infrared: galaxies
© ESO, 2011
1. Introduction
One of the most fundamental correlations between the properties of galaxies in the local Universe is the so-called morphology (color) − density relation. This relation, quantified for the first time by Dressler (1980), shows that blue, star-forming, disk-dominated galaxies reside in lower density regions of the Universe than red, inactive elliptical galaxies. The physical origin of the morphology density relation is still a subject of debate. Much of the argument centers on whether the relation arises early on during the formation of the object, or whether it is caused by density-driven evolution. Given the tight link between galaxy morphology, colors and instantaneous star formation rate (SFR), an alternative way to tackle this issue is to analyze the density–SFR relation. To shed light on how the environment affects the galaxy properties, these relations have to be studied at high redshift, when the galaxy formation processes are still undergoing.
The existence and the behavior of the density–SFR relation at redshift ~ 1 is still matter of debate. Kovac et al. (2010) show that galaxy star-formation and color transformation rates are higher in the groups than in lower density regions at z ~ 1. Elbaz et al. (2007) and Cooper et al. (2008) observe the reversal of the density–SFR relation at z ~ 1 in the GOODS and the DEEP2 fields, respectively, using a spectroscopically defined density parameter. Caputi et al. (2009) analyze the close environment, on 1 Mpc scales, of luminous infrared galaxies (LIRGs, LIR = 1011 − 1012 L⊙) and ultra-luminous infrared galaxies (ULIRGs, LIR > 1012 L⊙) in the zCOSMOS dataset (Lilly et al. 2007), finding that LIRGs at 0.6 < z < 1 are more often found in overdense environment, while ULIRGs prefer underdense regions. On the other hand, Feruglio et al. (2010), using photometric redshifts to define the local galaxy density, find no dependence of the SFR and LIRG fraction on environment. The scenario is made even more complicated by the interplay of mass and density. Indeed, Scodeggio et al. (2009) reveals that already at z ~ 1 mass and galaxy density are coupled with the most massive galaxies segregated in the most dense environment. Therefore, the evidence for a clear density-SFR trend could be due to the different contribution of massive and less massive galaxies favoring different density regimes. A first attempt to disentangle the mass-driven and the environment driven evolution is provided by Peng et al. (2010), based on the zCOSMOS and SDSS data. They argue that two distinct processes are operating to affect the galaxy star formation activity, “mass-quenching” and “environment-quenching”.
A different approach to this issue is to study the SFR of galaxies directly in high dense regions like clusters and groups. A rather long list of cluster-related environmental processes can affect the SFRs of galaxies. Some processes mainly affect the gaseous content of a galaxy, such as the ram-pressure stripping (Gunn & Gott 1972; Kenney et al. 2004; van Gorkom 2004), re-accretion of the stripped gas (Vollmer et al. 2001), turbulence and viscosity (e.g. Quilis et al. 2001), and starvation/strangulation (Larson et al. 1980). Gravitational processes, which affect both the gaseous and the stellar properties of a galaxy, range from low-velocity tidal interactions and mergers (e.g. Mamon 1996; Barnes & Hernquist 1996; Conselice 2006), to high-velocity interactions between galaxies and/or clusters (Moore et al. 1998, 1999; Struck 1999; Mihos 2004). Several of these processes can affect the galaxy properties both by quenching or enhancing the star formation activity. At low redshift it is well recognized that the star formation is suppressed in groups and clusters. The surrounding regions of groups and clusters have been identified as the most likely environment where the star formation in accreted galaxies is quenched (e.g. Abraham et al. 1996; Balogh et al. 1999; Pimbblet et al. 2002). Indeed, passive spirals (i.e. spiral morphology but no star formation), which are considered objects in a transition phase to an early type morphology, tend to be found in this kind of intermediate density regions (e.g. Goto et al. 2003). The situation seems to change towards higher redshift. At intermediate redshift, Kodama et al. (2001) performed a wide-field imaging of the CL0939 cluster at z = 0.41 and discovered that the color distribution changes dramatically at the intermediate-density environment which corresponds to groups/filaments. A very similar result was reported by Tanaka et al. (2005) for the surrounding regions of higher redshift clusters, CL0016 at z = 0.55. Studies of clusters at redshift z ~ 0.8 (Koyama et al. 2008) show that star-forming activity is enhanced in the intermediate-density cluster infalling region between low-density general field and the high-density cluster core. More recent studies of forming clusters (Tran et al. 2010; Hilton et al. 2010) show that towards higher redshift, z ~ 1.4−1.6, enhanced star formation rates are observed also in the cluster core. However, these studies do not compare cluster and field galaxy star formation activity at the same redshift. Thus, it is not clear whether this enhancement of the cluster galaxy star formation activity is part of a global enhancement at the peak of the SFR density at z − 1.5 − 2 (Madau et al. 1996) or is due to a real reversal of the density − SFR relation.
In this work we use PACS data to study the relation between the galaxy SFR and the environment at redshift ~1. In order to disentangle the mass segregation from the environmental effects, we dissect in mass bins the instantaneous galaxy density–SFR relation and in density bins the specific SFR-stellar mass relation. To achieve this goal we need deep IR (dominating the bolometric luminosity at high SFR) data to get a reliable estimate of the SFR. We also require a highly complete spectroscopic coverage to estimate the local galaxy density. Thanks to the observations carried with PACS (Photodetector Array and Camera Spectrometer, Poglitsch et al. 2010; Pilbratt et al. 2010) as part of the PACS Evolutionary Probe (PEP) GT Program, we are able to meet these requirements. Indeed, PACS with PEP provides at the moment the deepest far-infrared survey at 70, 100 and 160 μm of the GOODS fields, for which an extremely rich multiwavelength dataset and extremely highly complete spectroscopic catalog are available. Moreover, the GOODS fields show the presence of several intermediate density regions, such as groups and filaments, at z ~ 1, where the enhancement of the star formation activity should be found. We use also the SDSS DR7 spectroscopic catalog to relate the Hα based SFR to the local galaxy density at z ~ 0 in order to evaluate the evolution of the density − SFR relation. The paper is organized as follows. In Sect. 1 we describe the data and the sample selection. In Sect. 2 we describe the methods applied to estimate the galaxy properties. In Sect. 3 we provide our results about the relation of the SFR and the local environment at redshift ~1. In Sect. 4 we provide the evolutionary analysis of the density–SFR relation. In Sect. 5 we list our conclusions.
We adopt ΩΛ = 0.73, Ωm = 0.27 and H0 = 75 km s-1 Mpc-1 throughout this paper.
2. Data and sample selection
2.1. PACS data
In this work we use the PACS data of the PACS Evolutionary Probe (PEP) guaranteed time observations collected in the GOODS-N and GOODS-S fields. The GOODS-N 30 h observations were carried out in medium speed (20′′/s) scan map mode at 100 and 160 μm during the science demonstration phase of the Herschel mission. The GOODS-S 113 h observations were taken in medium speed scan map mode at 70, 100 and 160 μm in December/January (2009 − 2010). Data have been processed through the standard PACS data reduction pipeline in the Hipe environment (Ott et al. 2006), with the addition of some custom procedures aimed at removal of instrument artifacts.
Glitch removal is based on the Multiresolution Median Transform, a method developed by Starck & Murthag (1998) for the detection of faint sources in ISOCAM data. The method relies on the evidence that signal due to a real source and a glitch, respectively, shows different signatures in the pixel time-line. These features are identified using a multiscale transform separating the various frequencies of the signal. Once the glitch components are identified, they are replaced by interpolated value in the pixel time-line.
PACS photometer observation exhibit 1/f noise (see Lutz et al., in prep., for a more detailed explanation). In oder to remove the bulk of the noise we apply a “running-box” median filter to the pixel time-line. The source positions are masked in order to avoid source flux subtraction. The source mask is created by masking all pixels with S/N above a given threshold in a preliminary map. The source mask is optimized by iterating the procedure.
The blue channel (70 and 100 μm) data show clear interference patterns which are not ascribable to the 1/f noise. In order to remove those features, the individual scan legs of each observation have been visually checked and flagged when needed.
Before the map reconstruction, offsets and errors in the pointing accuracy of the Herschel satellite have been corrected by re-centering the data on a grid of known 24 μm sources. Scan legs of different scan directions and repetition numbers have been projected in separate maps. The 24 μm sources were then stacked in the individual maps to compute the average Δx and Δy offsets to be applied to the given set of scan legs.
The map reconstruction was done via a drizzle method (Fruchter & Hook 2002). Given the high data redundancy in the GOODS fields, we chose a very small drop size (pixfrac = 1/8 with a final output pixel scale of 2′′ at 70 and 100 μm and 3′′ at 160 μm) to reduce the correlated noise in the final map (see Fruchter & Hook 2002, for a detailed discussion). The individual maps were then coadded, weighting pixel contributions by the effective exposure. The final error map is derived as the standard deviation of the weighted mean in each map pixel. Due to the map projection and residual 1/f noise, the output pixels show partial correlation. A correlation correction factor is calculated in different subareas of the final map under the assumption that it depends only on relative pixel positions. The correlation turned out to be rather uniform across the final map. Thus, a mean correlated noise correction factor is used in our noise estimation.
The Point Spread Function (PSF) were extracted from the final science maps, and have a FWHM of ~ 7.1, ~7.5 and ~11 arcsec in the 70, 100 μm and 160 μm bands, respectively. The aperture correction is based on the calibration observation of the Vesta asteroid. Particular care was taken in calibrating the derived flux densities to account for the known flux overestimation in the used Hipe version by factors 1.02, 1.09 and 1.29 at 70, 100 μm and 160 μm, respectively as described in the PACS scan map release note PICC-ME-TN-035. As outlined in the note, the absolute flux accuracy is within 10% at 70 and 100 μm and better than 20% at 160 μm.
PACS catalogs were created using two different approaches: a blind extraction using the Starfinder PSF-fitting code (Diolaiti et al. 2000) and a guided extraction using 24 μm priors. Flux reliability, incompleteness and spurious source fraction were estimated and tested via Monte Carlo simulations. We created 500 images of the individual fields by adding ~20 artificial sources each for a total of 10 000 sources. Input and output fluxes are consistent within a few percent. The completeness is defined as the fraction of sources detected with photometric accuracy of at least 50% (Papovich et al. 2004). Spurious sources are defined as those detected at 3σ flux level and with an input flux lower than 3σ. The GOODS-N observations reach the 3σ level at ~3.0 mJy and ~5.7 mJy at 100 and 160 μm, respectively. The observations in GOODS-S reach the 3σ limit at ~1.2, 1.2, 2.4 mJy at 70, 100, 160 μm, respectively. In order to test our results against biases, we performed the analysis with both catalogs to compare the results. The use of different catalogs does not lead to any significant difference. Thus, hereafter we show only the results based on the 24 μm prior catalog. The final catalog comprises all PACS detections down to the 3σ level. We reach a completeness level of ~70% at the 5σ level and of 35% at the 3σ level. The spurious contamination is about 10%.
2.2. Auxiliary data
The PACS catalogs are matched to highly reliable multiwavelength catalogs in both fields. For GOODS-N the PEP Team created a PSF-matched database adopting the Grazian et al. (2006, ConvPhot) approach, including UV (GALEX), optical (HST), near-infrared (FLAMINGOS) and infrared (Spitzer IRAC and MIPS) data, which includes also the spectroscopic redshifts collected by Barger et al. (2008). We include in the catalog also the X-ray rest-frame luminosity of Alexander et al. (2003) based on the Chandra 2 Ms observations of GOODS-N. For GOODS-S we use the second version of the PSF-matched GOODS-MUSIC catalog (Santini et al. 2009), which provides U band (2.2 ESO and VLT-VIMOS), optical (HST), near-infrared (VLT-ISAAC) and infrared (Spitzer IRAC and MIPS) data. We matched the GOODS-MUSIC catalog to the GOODS-S spectroscopic redshift master catalog of Balestra et al. (2010) after removal of multiple entries for the same source. The GOODS-MUSIC catalog is matched also to the Luo et al. (2008) X-ray catalog based on the 2 Ms observation of GOODS-S.
2.3. The sample selection
For the purpose of the paper we need to define two different catalogs: the star forming galaxy sample and the galaxy sample to use for building the density field around each star forming galaxy. In this section we describe how we select the star forming galaxy sample at high and low redshift.
2.3.1. Star forming galaxies at z ~ 1
The PACS GOODS-N and GOODS-S observations are quite different in terms of depth. The GOODS-S maps are twice as deep as the GOODS-N data. In order to harmonize the two datasets without loosing in depth, we complement the PACS data with MIPS 24 μm data, which reach the 3σ level at ~25 μJy in both fields (Elbaz et al. 2007). This solves also any incompleteness issue of the GOODS-N and GOODS-S PACS samples between the 3 and 5σ flux levels. Given the need for spectroscopic redshifts to reliably estimate the local galaxy density, we use a subsample of the combined PACS+MIPS sample with high quality spectroscopic redshift. The analysis of the spectroscopic completeness shows that this is above ~60% in any flux bin down to 80 μJy for both GOODS-N and GOODS-S PACS sample. Below 80 μJy the spectroscopic completeness per flux bin in the 24 μm sample drops down quickly to ~35%. Thus, we apply a 80 μJy cut in the 24 μm sample. To ensure mass completeness we apply an additional cut at [4.5 μm] < 23 mag (Mancini et al. 2009).
We chose the redshift range 0.7 < z < 1.1 in order to sample the two main large scale structures in the fields: a low mass cluster (M ~ 1014 M⊙) at z = 0.736 (Popesso et al. 2009) in GOODS-S and a big group at z = 1.016 (Elbaz et al. 2007) in GOODS-N. Figure 1 shows the PACS+MIPS sources identified by our selection criteria in the M/M⊙ − LIR plane. The horizontal and vertical lines shows the M/M⊙ = 8 × 109 and LIR/L⊙ = 1011 cuts corresponding to our selection criteria at 0.7 < z < 1.1. The mass limit is estimated as described in Rodighiero et al. (2010): we computed the mass-completeness thresholds as a function of redshift for our IRAC 4.5 μm-selected sample (mag 4.5 μm < 23.0, AB), derived from synthetic stellar population models as described in Mancini et al. (2009). We used a variety of galaxy models from the templates of Bruzual & Charlot (2003), with a Salpeter IMF, and different ages, and dust extinction parameters (E(B − V)). We decided to adopt the most conservative mass-completeness limit, above which even the oldest (2 Gyr) and highly extincted (E(B − V) = 0.8) star-forming galaxy population would be entirely recovered. The filled points in the figure refer to galaxies with spectroscopic redshift. The spectroscopic completeness is fairly uniform in both mass and LIR bins. Red circles identify PACS detections, which dominate the LIR bright end. In addition, the cut at LIR/L⊙ = 1011 nicely separates the star forming and passive galaxies at the high mass end.
 |
Fig. 1 Bolometric IR luminosity – stellar mass relation. Empty circles in the figure are MIPS 24 μm detections without spectroscopic information. Filled circles in the figure are MIPS 24 μm detections with spectroscopic information. Red circles identify MIPS sources with PACS detection. The horizontal and vertical lines shows the M/M⊙ = 8 × 109 and LIR/L⊙ = 1011 cuts corresponding to our selection criteria at 0.7 < z < 1.1. |
 |
Fig. 2 LIR,24 μm/LIR,PACS ratio versus LIR,24 μm obtained using the CE01 method, in the left panel. LIR,24 μm/LIR,PACS ratio versus the M/M⊙ using the CE01 method, in the central panel. LIR,24 μm/LIR,PACS ratio versus the LIR,24 μm obtained using the R10 method, in the right panel. In all panels empty circles are normal star forming galaxies in our sample with both a MIPS 24 μm and PACS 100 or 160 μm detection. Filled points are low luminosity obscured AGNs with both a MIPS 24 μm and PACS 100 or 160 μm detection. The point with error bar is the result of the stacking analysis in the GOODS-N 160 μm map of the obscured AGNs of our sample with only MIPS detection. |
We identify also 60 X-ray detected sources in our sample, 40 in GOODS-N and 20 in GOODS-S. 49 of these sources are identified as AGN following the criteria of Brusa et al. (2009). 3 out of 49 AGNs are broad line AGNs. We exclude those sources from our sample since in those cases the AGN contribution dominates the SED at optical and IRAC wavelengths, thus, not allowing a reliable estimate of the host galaxy stellar mass (see Merloni et al. 2010). The dominant AGN contribution at MIR wavelength prevents also a reliable estimate of the host galaxy star formation rate. The remaining 46 AGNs are classified as obscured AGNs, the dominant population in the GOODS fields as outlined in Alexander et al. (2003) and Luo et al. (2008). These sources are all at luminosities below that of typical QSOs (LX > 1044 erg s-1). Moderate-luminosity AGN (LX ~ 1043 erg s-1) have been shown to be ideal laboratories for the study of their host galaxies due to their low optical brightness which in many cases is due to their nuclear obscuration (Tozzi et al. 2006; Mainieri et al. 2007). In particular, as shown in Merloni et al. (2010), an obscured AGN contributes in a negligible way to the host galaxy SED at shorter wavelengths, thus allowing a reliable estimate of the host galaxy stellar mass. 22 out of the 46 obscured AGNs in GOODS fields have only a 24 μm detection. MIR wavelength can be affected by the AGN contribution and can provide overestimated estimates of the instantaneous star formation rate. Instead, the rest-frame far infrared seems to be dominated by the host (Netzer et al. 2007; Lutz et al. 2010). In order to check whether the MIR flux provides a reliable estimate of the host galaxy star formation rate, we compare the LIR extrapolated from the 24 μm flux versus the LIR given by the PACS FIR flux, for the sources which have both detections. Figure 2 shows the ratio LIR,24 μm/LIR,PACS versus the LIR,24 μm. The trend of the relation is discussed in the next session, but we point out here that, with the exclusion of the broad lines AGNs, the remaining sources lie on the same relation and show the same scatter as the normal star forming galaxies. To check the reliability of the 24 μm extrapolation, we stacked in the GOODS-N 160 μm map the 17 AGNs without PACS detection. The mean flux is then converted into LIR by using the empirical L160 μm − LIR relation found in our dataset. The stacked point gives a ratio LIR,24 μm/LIR,PACS of 1 and it is consistent within 1σ with the relation obtained with the individual detections. We conclude that in the redshift range of interest LIR extrapolated from the 24 μm flux can provide a reliable estimate of the host galaxy star formation rate.
After the exclusion of broad line AGNs, we are left with 326 sources, of which 185 are PACS sources.
2.3.2. The z ~ 0 counterpart: the Sloan star forming galaxy sample
The local galaxy sample is drawn from the SDSS DR7 spectroscopic database (Abazajian et al. 2009). The spectroscopic component of the SDSS survey is carried out using two fiber-fed double spectrographs, covering the wavelength range 3800 − 9200 Å, over 4098 pixels. They have a resolution varying between 1850 and 2200, and together they are fed by 640 fibers, each with an entrance diameter of 3 arcsec. The fibers are manually plugged into plates inserted into the focal plane; the mapping of fibers to plates is carried out by a tiling algorithm (Blanton et al. 2003a,b) that optimizes observing efficiency in the presence of large-scale structure.
Using the selection criteria of Yasuda et al. (2001) we identify 813 287 unique galaxies in the SDSS galaxy spectroscopic sample. We match this sample to the catalog provided by the MPA-JHU DR7 release of spectrum measurements1. This catalog provides stellar mass estimates based on Kauffmann et al. (2003) and Salim et al. (2007). The star formation rate and specific star formation rate are based on Brinchman et al. (2004, hereafter B04, we refer to this work for further detail of the SFR and sSFR estimation). The current version of the catalog provides mainly Hα-derived SFR. An estimate of the SFR is provided also for galaxies without emission lines. This estimate is based on D4000 index. Since no calibration is provided for this indicator, we limit our sample to the galaxies with emission lines and Hα-derived SFR. The total SFR and sSFR is obtained by correcting the fiber estimates. The extinction correction is based on the Hα/Hβ ratio. The aperture corrections are done by fitting the photometry of the outer regions of the galaxies with models and should remove the systematic overestimate of total SFR in certain classes of galaxies identified by Salim et al. (2007). B04 divide the galaxy sample into several classes on the basis of the BPT diagram (Baldwin et al. 1981). The following galaxy categories are identified: star-forming galaxies, low S/N star forming galaxies, composite galaxies, AGNs, and unclassifiable objects. Since the AGN contribution to the Hα flux can lead to a SFR overestimation, we exclude this class of objects from the sample. Moreover, we limit our sample to the galaxies classified as star forming and low S/N star forming. We exclude the unclassifiable objects, which, according to B04 are galaxies with extremely low S/N or absent Hα emission and with very uncertain SFR estimate.
We select a subsample of galaxies in the redshift slice 0.01 < z < 0.1 and with the same stellar mass cut used for the high redshift sample, M/M⊙ = 8 × 109, for a total number of 97 244 star forming galaxies.
3. Galaxy properties estimate
3.1. The local galaxy density parameter
To reconstruct the density field around each star forming galaxy in the GOODS-N and GOODS-S fields we use all galaxies with spectroscopic redshift in the range 0.7−1.1 and with zAB < 23 mag to ensure a rather high spectroscopic completeness level (Popesso et al. 2009).
 |
Fig. 3 Distribution of the completeness parameter calculated around each source. The solid line shows the histogram of the completeness parameter based on a galaxy sample selected with an apparent magnitude cut at zAB < 23 mag. The dashed histogram shows the distribution of the completeness parameter based on a galaxy sample selected with an absolute magnitude cut at zAB < −21.35 mag. |
We compute the projected local galaxy density, Σ, by counting all galaxies located inside a radius of 0.75 Mpc and within a fixed velocity interval of Δv = 3000 km s-1, 3 times the typical velocity dispersion of massive clusters (σv ~ 1000 km s-1), around each galaxy. The key ingredient for building a reliable density field is a very high and spatially uniform spectroscopic coverage. For this purpose we measure the spectroscopic completeness around each source as the ratio between the number of objects with spectroscopic redshift and the number of all sources with and without redshift, at zAB < 23 mag in the cylinder along the line of sight of the considered source and with a radius corresponding to 0.75 Mpc at the redshift of the considered source. As shown in Fig. 3, the distribution of the completeness parameter is very narrow with a rms of 0.04 around the median value of 77%. This ensures that the spectroscopic coverage of the fields is very high and rather uniform. However, number densities measured within an apparent magnitude limit exhibit a strong redshift bias. Indeed, an apparent magnitude limit samples different regions of the rest frame luminosity function (LF) at different redshifts: the lower the redshift, the larger the region of the LF sampled, thus the larger the number of galaxies measured within the cylinder. For this reason, we prefer to measure the number densities at an absolute magnitude cut. We set the cut to the absolute magnitude corresponding to zAB = 23 at the highest redshift of our sample, z = 1.1, which is zAB = −21.35. The local galaxy density and the local completeness in this case are estimated as described above with the difference that galaxies are counted down to the m(z) = −21.35 + 5log (dl) + 5log (h) + k(z) + 25, where z is the redshift of the reference star forming galaxy at the center, dl is its distance luminosity and k(z) is the k correction with respect to z = 1.1. The k correction is estimated through the Kcorrect code of Blanton et al. (2007, version 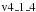 ). The distribution of the completeness parameter is as narrow as the one obtained with the apparent magnitude cut, with a somewhat higher peak at 80% ± 0.05, as shown in Fig. 3 (dashed histogram). Thus, our absolute magnitude cut ensures the highest completeness level up to the highest redshift of our sample without biasing the density parameter. We use our local completeness measure to correct the local galaxy density to retrieve the actual density field. This is done under the assumption that the incompleteness in the cylinder along the line of sight around each galaxy is the same as in the portion of the same cylinder within Δv = 3000 km s-1 from the redshift of the galaxy.
). The distribution of the completeness parameter is as narrow as the one obtained with the apparent magnitude cut, with a somewhat higher peak at 80% ± 0.05, as shown in Fig. 3 (dashed histogram). Thus, our absolute magnitude cut ensures the highest completeness level up to the highest redshift of our sample without biasing the density parameter. We use our local completeness measure to correct the local galaxy density to retrieve the actual density field. This is done under the assumption that the incompleteness in the cylinder along the line of sight around each galaxy is the same as in the portion of the same cylinder within Δv = 3000 km s-1 from the redshift of the galaxy.
 |
Fig. 4 Comparison of the density parameter calculated assuming 80% incompleteness and corrected for that (Σ(output)) versus the actual value (Σ(input)) in a light-cone of the Millennium simulation (Springel et al. 2005). |
The reliability of the method is also tested on a sample of simulated galaxies in lightcones built from the Millenium simulation (Kitzbichler & White 2007; Springel et al. 2005) in the same redshift range considered in this analysis and at MB < −20.75 mag, corresponding to our absolute magnitude cut at z ~ 1. We assume a mean spectroscopic completeness of 80% and extract randomly a corresponding percentage of galaxies in the lightcone. We apply our method to estimate the projected local galaxy density and compare with the actual value in Fig. 4. The corrected projected local galaxy density based on 80% completeness and the real density lie on average on the 1 to 1 line. The errors in the figure are estimated through a jackknife technique. According to the mock catalog result, the average uncertainty in our density estimate is about 15%, with a maximum of ~23% at the minimum density and a minimum of ~7% at the maximum density. This shows that using our approach we trace reliably the actual density field.
We compared this local density estimator with similar methods. Elbaz et al. (2007) vary the redshift interval in order to sample the same comoving value, 90 Mpc3, around each galaxy. Instead, as in Poggianti et al. (2010) we use proper quantities. This is motivated by the fact that, in order to study the dependence of galaxy properties on the density of the local environment, what matters are gravitational and vicinity effects, and therefore proper distances between galaxies. However, given the narrow redshift slice considered here, we see that our estimates of the surface and volume densities are consistent within the errors with the quantities derived at a fixed comoving volume. Our approach is also consistent with the method of Elbaz et al. (2007) once we use the same apparent magnitude cut as in that work. However, the two estimates diverge when we use our absolute magnitude limits, since the Elbaz et al. (2007) method shows the redshift bias discussed above. Elbaz et al. (2007) use also volume densities to study the SFR-environment relation. However, we use here only the projected galaxy local density.
We compare our method also to the Nth nearest neighbor density estimator (Dressler 1980; Capak et al. 2007; Guzzo et al. 2007; Postman et al. 2005). According to this method, the projected density around each galaxy is derived from the distance to the Nth neighbor, r, which define a circular area whose surface density is Σ = N/πr2. We found that the two density estimators similarly trace the same large scale structures. In order to compare with similar works based on accurate photometric redshifts, we use the accurate GOODS-S phot-z to define a photometrically defined projected local galaxy density. To compare to Feruglio et al. (2010) we use the 10th nearest neighbor density estimator by adopting the same absolute magnitude limit used above and a velocity interval equal to 3 × σz(1 + z), where σz is the accuracy of the photometric redshift (σz = 0.01 at z < 1.1 and zAB < 23, similar to the one used in Feruglio et al. 2010). We find that the two different definitions of the projected local galaxy density agree with a very large scatter. The photometrically defined projected local galaxy density can trace very high density regimes, however it is not able to separate intermediate and low density regimes.
We use a subsample of the whole SDSS DR7 galaxy spectroscopic sample described above, with spectroscopic redshift in the slice 0.01 − 0.1 (~350 000 galaxies), to build the density field around each star forming galaxy at low redshift. In order to study the evolution of the density–SFR relation, we derive the projected local number density of the SDSS galaxies in the same way, within 0.75 Mpc and Δv = 3000 km s-1. Our absolute magnitude cut in the z band corresponds to MB = −20.75 at redshift ~ 1. According to the B band rest frame luminosity function estimated at 0.75 < z < 1 in Zucca et al. (2009), this cut is equal to M∗ + 0.42, where M∗ is the characteristic magnitude of the best-fit Schechter function. In order to sample the same luminosity range in the low redshift sample, we use as absolute magnitude cut MB = M∗(z = 0.1) + 0.42 = −20.3 mag, where M∗(z = 0.1) = −20.73 mag is the characteristic magnitude of the Schechter function fitted to the rest frame B band LF at 0.1 < z < 0.35 in Zucca et al. (2009). The B band is obtained from the SDSS g band by using the Kcorrect code of Blanton et al. (2007)
In order to obtain an estimate of the completeness correction for the SDSS star forming sample, we perform the same analysis applied to the high redshift sample to a subsample of SDSS galaxies in a region of 10 × 10 deg2, which includes several clusters at the redshift considered here. We use the mean value of the completeness level to correct the local galaxy density and we use the dispersion of the completeness distribution as error associated to this correction. As shown if Fig. 5, the mean completeness level is 85% ± 0.07. As already shown in Popesso et al. (2005), the completeness level drops down to ~70% only in the very central region of the massive clusters within ~0.1 Mpc, due to the so called “fiber-fiber collision” problem: fibers cannot be placed closer than 55 arcsec. Given the very large volume used for the estimate of the local galaxy density, the higher central incompleteness level does not affect significantly our density estimates.
 |
Fig. 5 Distribution of the completeness parameter calculated around each source in a SDSS subsample in a area of 10 × 10 deg2. |
3.2. Stellar masses and star formation rates
Stellar masses and the total infrared luminosity (LIR) of each PACS source are derived according to the method described in Rodighiero et al. (2010, and 2007), through a fitting of the whole spectral energy distribution (SED) of each source. The stellar mass is derived by fitting the UV-5.8 μm broad band photometric data with the Bruzual & Charlot (2003) stellar population synthesis models, assuming a Salpeter IMF and a Calzetti extinction law, and by fixing the redshift at the available spectroscopic redshift. For GOODS-S the stellar masses are available from Santini et al. (2009) and are calculated with the same stellar population synthesis models and recipes (Rodighiero et al. 2010; and Santini et al. 2009, for further details).
 |
Fig. 6 Density–SFR relation. We show the relation obtained by including the low luminosity obscured AGNs (left panel) and the relation obtained after removing the AGNs from the sample (middle panel). In these panels the shaded regions show the global relations at M/M⊙ > 8 × 109, empty triangles show the relation obtained in the low mass sample (8 × 109 < M/M⊙ < 5 × 1010), stars show the relation obtained in the high mass sample (M/M⊙ > 5 × 1010). The right panel show the comparison of the global relations obtained by inclusion (pink area) and excluding (purple area) the AGNs in the sample. |
The LIR is derived in a similar way by fitting the optical-FIR SED with a library of local templates, including the library from Polletta et al. (2007) and few additional modified templates with colder FIR emission (see Gruppioni et al. 2010, for more details) at a given redshift. We compute LIR by integrating the best-fit SEDs in the [8 − 1000] μm rest-frame range. The use of the whole SED allows to obtain a more accurate and reliable estimate the K correction (Rodighiero et al. 2010). For the sources with 24 μm detection only, the fit is performed from optical up to MIR wavelength only (hereafter R10 method). For comparison with previous works we calculate also LIR extrapolated from the 24 μm flux via the Chary & Elbaz (2001) method (hereafter CE01). To check for consistency, we compare the LIR estimate provided by the MIR (LIR,24 μm) only and the LIR based on the FIR fluxes (LIR,PACS), for sources with both 24 μm and PACS detections. Figure 2 shows the LIR,24 μm/LIR,PACS ratio versus the LIR,24 μm for the R10 and CE01 methods. In both cases we see a positive correlation, confirmed by a Spearman test at more than 7σ level. There is a clear bias, whereby at lower LIR,24 μm the bolometric LIR is on average underestimated with respect to the FIR based estimate. The CE01 method produces a similar bias also versus the stellar mass as shown in the right-hand panel of Fig. 2, which we do not find in the R10 results. However, the R10 LIR,24 μm/LIR,PACS vs. LIR,24 μm relation is steeper and tighter, possibly indicating a somewhat stronger bias. Thus, we use the CE01 LIR,24 μm as estimate of the LIR for the sources with only MIPS detection. As already outlined in the previous section, the X-ray detected AGNs follow the same trend as the normal star forming galaxies. We perform a fit of the data with and without the AGNs and we get consistent best fit lines. Before combining PACS detected and MIPS only detected sources, we correct the CE01 estimate LIR,24 μm by using the best fit obtained in the LIR,24 μm/LIR,PACS vs. LIR,24 μm relation.
The star formation rate is derived from the total infrared luminosity LIR according to the Kennicutt law (1998). We checked that above LIR/L⊙ > 1011, as in our selection, the contribution of the uncorrected for extinction UV luminosity is negligible (on average ~ 3%, much less than the mean 10% accuracy of our SFR estimate).
4. Star formation activity and environment at z ~ 1
4.1. The density–SFR relation
We build the density–SFR relation to check which is the typical environment of star forming galaxies at any given star formation rate. Thus, our approach is to derive the mean density of the star forming galaxies per SFR bin. This approach is less sensitive to selection effects due to spectroscopic incompleteness. Indeed, the spectroscopic coverage of the GOODS fields is spatially rather uniform, as pointed out in the previous section. Instead, taking the average SFR per density bin is more prone to biases because of the non uniform sampling of the LIR luminosity function through the spectroscopic selection function. We associate an error to the mean density per SFR bin through a jackknife technique. As done in Elbaz et al. (2007), if ntot is the number of galaxies within a selected SFR interval, we randomly extract njackknife galaxies from this sample and computed their mean density. This process is repeated 500 times. The error bar on the typical density for a given SFR bin is equal to the root mean square of the 500 measurements of the density divided by the square root of ntot/njackknife. We checked that the error bar was robust by trying several values for Njackknife. In the highest SFR bins, where the number of galaxies gets small, we use the dispersion around mean density in the SFR bin divided by the square root of the number of galaxies in the bin. This technique is applied also to the study of the density–sSFR and sSFR–stellar mass relation in the following sections.
In order to disentangle the environment from the mass effect, we perform this analysis in two bins of stellar masses with a cut at 5 × 1010 M⊙. The density–SFR relation is different in the two mass bins. A 2-dimensional Kolmogorov-Smirnoff test shows that the probability that the two distributions are drawn from the same parent population is 1.6 × 10-4. A Spearman test performed on the high mass sample gives a positive density-SFR correlation at the 3σ confidence level (mean relation shown by stars in the left panel of Fig. 6). The same test applied to the low mass sample, shows, instead, that SFR and density do not correlate (mean relation shown by empty triangles in the left panel of Fig. 6). In addition, as expected due to mass segregation, star forming galaxies in the low mass bin lie in lower densities regimes with respect to the systems of higher mass.
To check if the positive correlation observed in the high mass bin is due to a residual mass segregation effect, we check through a KS test that the mass distribution is the same in all SFR bins. According to the KS statistics the probability that the mass distributions of galaxies in different SFR bins are drawn from the same parent distribution is 85% in the worst case. We conclude that the the rising of the density–SFR relation in the high mass bin is due to an environmental effect. The density–SFR relation estimated in the whole sample gives a 3.5σ positive correlation (shaded pink area in Fig. 6). We ascribe the correlation to the fact that massive galaxies are dominating at high star formation rates.
Before comparing the redshift ~1 density–SFR relation with the local reference, we have first to remove the AGN from the sample. Indeed, we exclude the AGN from the low redshift SDSS star forming sample since the AGN contribution to the Hα emission can lead to a strong overestimation of the star formation rate. Once the AGN host galaxies are removed from the sample, the observed correlations become less significant and flatter, as shown in the middle panel of Fig. 6. The Spearman test gives a much higher probability of no correlation both in the high mass bin and in the global relation (~20%). We also point out that the AGN with only MIPS detection lie all at low luminosities (the first three SFR bins in the density–SFR relation). Their removal do not affect at all the relation, meaning that even if the 12 μm rest frame flux can be biased by the AGN contribution towards higher LIR, this bias is not affecting our relation.
 |
Fig. 7 Fraction of AGN hosts in our sample of star forming galaxies as a function of density (panel a)) and stellar mass (panel b)), star formation rate (panel c)) and specific star formation rate (panel d)). |
 |
Fig. 8 Density–SFR relation obtained using only 24 μm derived SFR. The filled points show the relation obtained with 24 μm only derived SFR with the AGN contribution, the empty stars show the same without AGN contribution. The positive correlation does not disappear after removing the AGN when 24 μm derived SFR are used. The shaded regions show the density–SFR relations estimated with PACS+MIPS data: pink region is the density–SFR relation with the AGN contribution, the violet region is the same without AGN contribution. |
The effect due to the AGN removal is to remove massive galaxies at high density. Indeed, the AGN fraction in our sample is a rising function of density and mass and star formation rate (Fig. 7). This result is in agreement with previous results obtained at low redshift and based on obscured AGNs (Kauffmann et al. 2003) and radio-loud (Best et al. 2005) AGN in the SDSS. More recently Silverman et al. (2009) find in the COSMOS field a similar trend at z ~ 0.5, but with a fraction of AGN 5 times smaller. The discrepancy is likely due to to the fact that the deep 2 Ms Chandra observations of the GOODS fields allow to sample a larger portion of the LX luminosity function at the steep faint-end with respect to the shallower XMM survey of the COSMOS field.
In order to test whether removing massive galaxies irrespective of the AGN presence can destroy the density-SFR correlation in the same way, we performed a MonteCarlo simulation by randomly removing a million times massive galaxies from our sample in the same number of the AGNs and performing the Spearman test on the remaining galaxies. Only in 0.5% of the cases removing massive galaxies leads to the same or lower probability of correlation as removing the AGN. The probability is somewhat higher (1.5%) is we remove randomly chosen galaxies irrespective of the mass. As additional test we removed for a million times randomly chosen galaxies in the same number and with the same mass distribution of the AGN in our sample. Similarly, we find that in 1.6% of the cases, the Spearman test gives the same or lower probability of correlation as removing the AGN. In addition, the higher the AGN fraction left in the sample, the higher the correlation probability. Thus we consider AGN host galaxies as a good candidate to cause the reversal of the density–SFR relation in our sample.
Once the AGN hosts are removed from the high redshift star forming galaxy sample as in the low redshift sample, the agreement between the behavior of the density–SFR relation at z ~ 1 and z ~ 0.1 is remarkable. Indeed, as shown in Fig. 9, although in a much larger SFR range, we do not observe any correlation in the SDSS star forming sample as confirmed by the Spearman test. The mean relation is shown by filled points in Fig. 9. Once we split the SDSS sample in two mass bins as we do for the z ~ 1 galaxies, we observe the same mass segregation effect, e.g. the higher the mass, the higher the mean density. We do not observe any correlation in any mass bin similarly to the z ~ 1 galaxies without AGN hosts. We do not compare here the absolute value of the local density of star forming galaxies at z ~ 1 and z ~ 0.1, because the density parameter is not estimated exactly in the same comoving volume.
 |
Fig. 9 Density–SFR relation in the local SDSS star forming sample. Filled points show the global relations at M/M⊙ > 8 × 109, empty triangles show the relation obtained in the low mass sample (8 × 109 < M/M⊙ < 5 × 1010), stars show the relation obtained in the high mass sample (M/M⊙ > 5 × 1010). |
The comparison of our density–SFR relation with analogous results in the literature is not straightforward. Indeed, all previous works use a different approach to derive the same relation: they estimate the mean SFR per density bin. This is equivalent to study the galaxy type mix per density regime rather than investigate which is the typical environment of galaxy with a given instantaneous star formation rate. However, qualitatively we find a good agreement with Elbaz et al. (2007) and Cooper et al. (2008) if AGN hosts are kept in our analysis. The density − SFR relation obtained after removing the AGN contribution is much flatter than in Elbaz et al. (2007). Indeed, as shown in Fig. 8, when we use 24 μm only derived SFR, the density–SFR relation is steeper than the one based on PACS data if AGN are kept in the sample. In addition, the removal of AGN from the sample does not destroy the correlation as observed in the relation obtained with PACS derived SFR. This is confirmed by a Spearman test, which gives a positive correlation at 3.5σ level even after removing the AGN. This can be explained by the bias observed in the 24 μm only derived LIR in Fig. 2. The same comparison is not possible with Cooper et al. (2008) because they cannot identify and remove AGN in the DEEP2 sample. We find a better agreement with Feruglio et al. (2010) who exclude AGN from the analysis and find a flat relation.
 |
Fig. 10 Density–sSFR relation. We show the relation obtained by including the low luminosity obscured AGNs (left panel) and the relation obtained after removing the AGNs from the sample (middle panel). In these panels the shaded regions show the global relations at M/M⊙ > 8 × 109, empty triangles show the relation obtained in the low mass sample (8 × 109 < M/M⊙ < 5 × 1010), stars show the relation obtained in the high mass sample (M/M⊙ > 5 × 1010). The right panel shows the comparison of the global relations obtained by inclusion (pink area) and excluding (purple area) the AGNs in the sample. |
4.2. The density–sSFR relation
We analyze here the density-specific SFR (sSFR = SFR/M⊙) relation. Due to the known anti-correlation between the sSFR and the galaxy stellar mass (Elbaz et al. 2007; Rodighiero et al. 2010), binning in stellar mass implies a selection in sSFR. We show the result also for the low and high mass samples (same stellar mass cut as in the previous analysis) separately, to analyse the different contributions to the global density–sSFR relation. The mean relation is shown in the left panel of Fig. 10 (shaded region). The Spearman test reveals a negative correlation with probability of no correlation P(rS) = 0.23%. The analysis of the contributions from the different mass samples reveals that: a) in the high mass bin sSFR and density marginally correlate (90% confidence level according a the Spearman test, empty stars in left panel of Fig. 10), as already found in the same mass bin by Elbaz et al. (2007); b) at lower stellar masses there is no correlation (empty triangles in left panel of Fig. 10); c) due to mass segregation, high mass systems lie generally in dense regions while low mass systems prefer low density environments; d) the high mass systems dominate the low sSFR end; e) the low mass systems dominate the high sSFR bins. This mass segregation leads to a global density-sSFR anti-correlation.
The removal of AGN hosts from the sample does not affect significantly the result. Indeed, as shown in the panel d) of Fig. 7, the AGN fraction is relatively constant at any sSFR. Thus the effect of removing AGNs is to reduce the number of galaxies populating any sSFR bin and consequently to enlarge the error bars. This directly implies that the level of star formation activity of AGN hosts is consistent with the star formation level of star forming galaxies at the same mass.
 |
Fig. 11 Density–sSFR relation in the local SDSS star forming sample. Filled points show the global relations at M/M⊙ > 8 × 109, empty triangles show the relation obtained in the low mass sample (8 × 109 < M/M⊙ < 5 × 1010), stars show the relation obtained in the high mass sample (M/M⊙ > 5 × 1010). |
The anti-correlation observed in the star forming sample at z ~ 1 is consistent with the behavior observed at z ~ 0, as shown in Fig. 11. The local star forming sample show the same mean anticorrelation (filled points in Fig. 11) as confirmed by the Spearman test. Differently from the high redshift case, we observe a significant anti-correlation also in the high (stars) and low mass bins (triangles). However, this can still be due to mass segregation since a Spearman test reveals a very significant (>15σ) positive correlation between mass and local density in the individual mass bins.
For the same reasons described in the previous section, the comparison of our relations with the previous work is not straightforward. Nonetheless, as already outlined, we can reproduce the marginal positive correlation observed by Elbaz et al. (2007) between sSFR and density in the high mass bin. We ascribe this marginal correlation to the AGN contribution. We find good agreement with Cooper et al. (2008) who observe a global density-sSFR anti-correlation. We find partial agreement with Feruglio et al. (2010) who do not find any relation in fixed stellar mass bins. However, they do not provide a definitive result about the combination of the contributions of the different mass bins to the global sSFR-mass relation.
 |
Fig. 12 The left panel shows the density–SFR relation per morphological type. Black points refer to early type galaxies, magenta points refer to late type galaxies, and red points to galaxies with disturbed morphology. The central panel shows the same relation without the contribution of AGN hosts. The left panel shows the density–sSFR relation per morphological type. The symbols have the same meaning in all panels. The shaded regions in all panels shows the global trend of the considered relation. |
 |
Fig. 13 sSFR-stellar mass relation in three density bins (left panel). The green circles identify AGN hosts. The solid line shows the best fit to the relation. The shaded purple region is the relation obtained via stacking in Rodighiero et al. (2010) based on a IRAC selected sample. The right panel shows the best fit parameters (filled points, normalization in the top panel, slope in the bottom panel) as a function of the bin mean density. The empty points show the best fit parameters obtained after excluding the AGN hosts. |
4.3. The morphological analysis
In this section we analyse the previous relation per morphological type in order to link the galaxy SFR (sSFR) and environment to the galaxy morphology. The morphological classification is performed by visual inspection of all objects in our sample. We identify 5 morphological types: 49 spheroidal, 71 bulge dominated objects, 73 disk dominated spirals, 97 irregulars, 34 interacting galaxies. We exclude two objects that turn out to be stars. In order to have enough statistics, we group the spheroidals and the bulge dominated galaxies as early type galaxies, and the irregulars and interacting objects as galaxies with disturbed morphology. Thus, early type galaxies account for 37% of the sample, late type galaxies for 22% and galaxies with disturbed morphology for the remaining 41%. Figure 12 shows the density–SFR relation (left panel) for the different morphological types. According to the Spearman test none of the three considered morphological types shows a significant correlation. The mean density slightly increases from the late to the early types. Below 50 M⊙ yr-1 the late type and irregular galaxies are dominating. As a consequence the mean density is low around 2.6 ± 0.4 Mpc-1. Above that threshold the galaxies are almost equally distributed in the three morphological types. This brings the mean density at 3.9 ± 0.5 Mpc-1 above 50 M⊙ yr-1. This shows that the morphology-density relation is already in place among LIRGs at redshift ~1 and how the morphological type mix relates to the reversal of the density–SFR relation. As for the global relation, the removal of the AGN hosts from the sample leads to a flattening of the density–SFR relation for any morphological type, as shown in the central panel of Fig. 12. A Spearman test confirms that there is no correlation for all morphological types. This is also confirmed by the large error bars in the figure.
The right panel of Fig. 12 shows the density–sSFR relation per morphological type. All three galaxy types follow the global relation. We do not show the effect of the AGN removal because, as for the global relation, the trend remains unchanged while the error bars increase due to the lower statistics.
4.4. The sSFR–stellar mass relation
In order to gain more insight into the relation between galaxy SFR and environmental conditions we study also the sSFR − stellar mass relation in three density bins, to isolate low, intermediate and high density regimes. Each bin contains at least 100 sources. In order to control the selection effects, we compare our relation with the relation of Rodighiero et al. (2010) based on the stacking of an IRAC selected sample. As shown in Fig. 13 the R010 relation (left panel, shaded region) is consistent with our relation. As expected, we slightly overestimate the sSFR-mass relation at the low mass end due to our 1011 L/L⊙ luminosity cut. We find a rather significant difference (at the 3σ level) rising from low to high density regimes. The discrepancy is confirmed by a 2-dimensional Kolmogorov-Smirnoff test showing that the mutual sSFR and stellar mass distributions have a probability of 6 × 10-3 to be drawn from the same parent distribution from the lowest to the highest density bin. Partly this is due to mass segregation. Indeed a unidimensional KS test applied to the stellar mass distribution between the lowest and highest density bins, shows with high significance that they are not drawn from the same parent distribution. The same test applied to the sSFR gives a somewhat higher probability, 20%. The left panel of Fig. 13 shows the sSFR-mass relation in the three density bin. We fit the best fit line by linear regression in the log-log space and show the best fit parameters as a function of the mean density in the central panel. The errors are estimated through a jackknife technique. We see a clear trend of the relation which is flattening towards higher local density. The removal of AGN hosts does not change the trend. This is due to the fact that the AGN fraction is equally distributed at all sSFR (panel d of Fig. 7). So removing the AGN hosts mainly enlarges the error bars due to the lower statistics. Figure 14 shows the same analysis applied to the SDSS local star forming sample. We observe a change in the sSFR-mass relation as a function of the local density. This was already pointed out in Kauffmann et al. (2004), although they consider all SDSS galaxies and not only star forming systems as in this work. The effect is visible only at the high mass end of the relation, M/M⊙ > 1011, whereby the higher the density the lower the mean sSFR of the star forming galaxies. We point out that Peng et al. (2010) studies the same relation using SDSS galaxies without reporting any environmental effect. However, we also point out that Peng et al. (2010) consider a much larger range of stellar masses, from 107 to 1012 M/M⊙. As shown in Fig. 14, below 1011 M/M⊙, we do not observe a deviation as a function of density with respect to the mean relation (shaded region). Although they do not dominate in mass, low mass galaxies surely dominate in number with respect to massive galaxies and determine statistically the slope of the relation. Thus, a linear fit to the sSFR-mass relation in the log-log space, as done in Peng et al. (2010), provides slopes consistent in any density regime.
 |
Fig. 14 sSFR-stellar mass relation per density bin in the local SDSS star forming sample. The shaded region is the mean relation based on the full star forming sample. The relations are color-coded as a function of density as explained in the figure. |
Figure 15 shows the direct comparison of the density dependence of the sSFR-mass relation at low and high redshift. The figure shows the residuals Δ(log (sSFR)) of the sSFR-mass relation per density bin with respect to the mean relation in the local SDSS star forming sample (left panel) and in the high redshift star forming sample (right panel). The deviation from the mean relation at the high mass end is clear at z ~ 0.1 (left panel) and, although much less significant (2.5σ effect), still visible in the z ~ 1 case (right panel). As indicated by the arrows, we find an indication that the effect is going in opposite direction at high redshift with respect to the local analog. To explain this reversal of tendency, we look at the sSFR-mass relation per morphological type in the three density bins at z ~ 1. However, this analysis, due to the poor statistics of the current high z sample, can provide only an indication. As shown in Fig. 16, we observe a marginal increase of the mean sSFR of massive (M/M⊙ > 5 × 1011) early type galaxies from the low density to the high density bin. This figure is equivalent to the right panel of Fig. 12 limited to the high mass bin. Late type and irregular galaxies do not exhibit any variation of the mean sSFR as a function of density given the current accuracy. The fraction of massive early type galaxies varies from ~20% in the low density regime to ~40% at the highest density at the expenses of the late type galaxy fraction which decreases from 40% to 20%, while the fraction of irregular galaxies remains constant. The tilt of the sSFR-mass relation at high density could be due to the presence of a larger number of massive and highly star forming early type galaxies. We point out that this is in agreement with the marginal increase of the density–sSFR relation observed in the high mass bin in the left panel of Fig. 10. However, to confirm this indication we need a dataset with much higher statistics. In addition, the picture proposed here is partial because we can not check what is the role of the star forming galaxies with early-type morphology in the local SDSS star forming sample. Indeed the visual morphological classification applied to the high z star forming sample is just unfeasible for the large Sloan sample. The detailed study of the sSFR-mass relation as a function of the morphological type and environemnt in an homogeneous way and on a dataset with much higher statistics is the aim of another paper of this series.
 |
Fig. 15 Residual Δ(sSFR) as a function of mass and density with respect to the mean sSFR-mass relation of the local SDSS star forming sample (left panel) and of the z ~ 1 star forming sample (right panel). The points are color-coded as a function of local density as explained in the panels. |
5. Discussion
The main structures sampled by our high density regimes are two clusters in formation: a low mass cluster at z = 0.73 at the center of two long filaments in the GOODS-S region, and two merging groups at z = 1.016 in GOODS-N. Recently, Fadda et al. (2008) conducted a very wide field MIR observation with Spitzer MIPS which covers two filaments around the Abell 1763 cluster (z = 0.23), and found that the fraction of starburst galaxies is more than twice larger in the filaments than in the inner region or outer fields of the clusters. The enhancement of star-forming activity in filaments is also suggested in nearby clusters in optical studies (e.g. Porter & Raychaudhury 2007; Porter et al. 2008). Tzanavaris et al. (2010) find also an enhanced sSFR in members of gas rich Hickson compact groups (HGC) harboring mainly spirals and irregulars with respect to gas poor groups dominated by ellipticals and S0 galaxies. Following Verdes-Montenegro et al. (2001) they argue that S/I and E/S0 HGC galaxies may constitute two distinct subclasses, consistent with being the two extremes of a possible evolutionary sequence progressing from the S/I high-sSFR subclass to the E/S0 low-SSFR one. Initially, loose groups contract to a more compact configuration (Barton et al. 1998). At this stage, most of the H I is found in galaxy disks, which constitute the prevailing morphological type. As the effects of tidal interactions gain in importance with time, an increasing fraction of the group H I mass is stripped from the interstellar medium of member galaxies and forms tidal tails, bridges, and intergalactic structures. At this stage old, gas poor groups host quiescent elliptical and S0 galaxies. This scenario is also in agreement with the more recent findings of Hwang et al. (2010) based on the cross-correlation of the SDSS galaxy catalog and IRAS faint source catalog. They find that the star formation activity in LIRGs and ULIRGs is triggered by galaxy galaxy interaction. Moreover, the star formation activity is boosted when the interaction happens between gas rich galaxies, while it is suppressed when a gas-rich galaxy encounter an early type gas poor system.
 |
Fig. 16 Mean sSFR per density bin in the high mass bin (M/M⊙ > 5 × 1010) and per morphological type. The color coding as function of morphology is shown in the figure. |
Tran et al. (2009) analyses the star formation activity of a super galaxy group at z ~ 0.37. The system is merging to form a galaxy cluster comparable in mass to Coma. The super-group has a significantly higher fraction of dusty star-forming members than the massive cluster at the same redshift. The star forming galaxy population of the super-group is composed of luminous (MB < −20.5) and relatively low mass (1010 < M/M⊙ < 4 × 1010) members with late type morphology. Most of these members are outside the cluster core. Similarly, Vulcani et al. (2010) find that the median SFR of groups at 0.4 < z < 0.8 is comparable to the median SFR of field galaxies, while in cluster SF galaxies they observe a much lower star formation activity.
A similar scenario is confirmed at redshift z ~ 0.8 by Koyama et al. (2008). They find that star-forming activity is enhanced in the intermediate-density cluster infalling region between low-density general field and the high-density cluster core. They argue that the infalling galaxies would experience close interactions among themselves, even before they experience any significant influence of the gravitational potential of the cluster, and that of its ICM, on their rate of star formation. Particularly for galaxies falling along crowded filaments into a cluster, the local density of galaxies would already have begun to increase rapidly, and it could be appreciable at distances as large as twice the virial radius. Therefore, the most likely cause for enhanced star formation in the cluster infall region and groups is most likely due to galaxy-galaxy harassment, which is a rapidly acting process, working efficiently in crowded environments. Moving towards the center of the cluster, the infalling galaxies experience ram pressure stripping by the hot ICM and galaxy strangulation that quench the star formation rate. At higher redshift, z ~ 1.4−1.6, Tran et al. (2010) and Hilton et al. (2010) observe enhanced star formation rates towards the cluster core and not only in the infalling region. This would suggest that at that epoch the processes quenching the star formation rate in the cluster highest density region did not yet take place or are not yet fully efficient.
Putting our results in the context, all tends to be consistent with the scenario described above. Indeed, we do observe segregation of highly star forming galaxies, though AGN hosts, in the group density regime. In addition, the dynamical analysis of the structures considered here show that they are all groups with substructures, long filamentary structures and probably experiencing merging (Popesso et al., in prep.). Thus, we are probably observing systems similar to the supergroup of Tran et al. (2009) at z ~ 0.37 with a confirmed enhanced star formation activity in the infalling regions. However, our estimate of the galaxy local density is not accurate enough to distinguish between the infalling and virial regions. Thus, we can not confirm whether the reversal of the density–SFR relation still holds in the group core or whether it is dominated by the infalling systems. In addition, our data provides an indication for a reversal of tendency at the high mass end of the sSFR-mass relation with respect to z ~ 0.1, possibly due to early type galaxies. This could indicate that we are whitnessing the formation of massive systems (M/M⊙ > 1011) with early type morphology in the dense regions where they are usually segregated, as also observed at z ~ 1.4−1.6 (Tran et al. 2010; Hilton et al. 2010). To have a clearer picture, a more detailed study of the members of the structures contained in our sample is needed and it is the aim of a second paper.
6. Summary and conclusions
In order to build a clean catalog of star forming galaxies at redshift ~ 1, we complement the PACS catalogs in the GOODS fields with MIPS 24 μm sources to cope with the different depth and incompletness levels in the GOODS-N and GOODS-S PACS observations. Applying additional cuts at 4.5 μm and at 24 μm we build a catalog complete in stellar mass down to 8 × 109 M⊙ and LIR = 1011 L⊙ with an average spectroscopic completeness of 80% and above 60% in any flux bin. We identify X-ray detected AGNs and exclude broad line AGNs for which we can not obtain either a reliable estimate of the host stellar mass or star formation rate. We keep in the sample low luminosity obscured AGNs for which we obtain reliable estimates of the host galaxy properties. In order to build a reference sample of star forming galaxies at z ~ 0, we use the SDSS DR7 spectroscopic sample toghether with the SFR, stellar mass and classification of the MPA-JHU spectroscopic catalog. We estimate the density parameter at high and low redshift in a homogeneous way. The density parameter is based on spectroscopic redshift information to properly identify low, intermediate and high density regimes.
We list here our findings:
-
we analyse the density–SFR relation at redshift ~1 in two mass bins. We observe a reversal of the density–SFR relation, as previously found by Elbaz et al. (2007) and Cooper et al. (2008) for galaxies at masses M/M⊙ > 5 × 1010. At lower masses the SFR and the density do not correlate.
-
Thanks to the high accuracy provided by PACS in measuring the star formation rate also for AGN hosts (we have PACS detection for the 50% most luminous AGN in the sample), we indentify in this class of objects the cause for the reversal of the global density–SFR relation at M/M⊙ > 8 × 109. This was not previously seen by works based only Spitzer 24 μm data, which can be biased towards higher bolometric infrared luminosities by the AGN contribution (Elbaz et al. 2007) and works based on optical data which suffer even more by this bias (Cooper et al. 2008).
-
Our data reveals that the fraction of AGN in the sample is rising towards high masses, high densities and high SFR. Thus, removing AGN from the sample is equivalent to removing an increasing fraction of the most star forming systems towards high densities, which causes the steepening of the density − SFR relation to disappear.
-
Once AGN hosts are removed from the sample, as done for the local SDSS star forming sample based on optical data, the qualitative behavior of the density–SFR relation is consistent between high and low redshift.
-
We observe a clear density-sSFR anti-correlation which is due to the different contribution of massive and less massive galaxies, thus, to mass segregation. Removing the AGN hosts from the sample does not affect significantly the anti-correlation, since they are equally distributed in any bin of sSFR, thus, they have the same mean sSFR of star forming galaxies at the same mass.
-
The same trends and AGN effect are observed even when galaxies are separated in different morphological types.
-
We observe an indication for a reversal of tendency at the high mass end of the sSFR-mass relation with respect to the z ~ 0.1 relation. At M/M⊙ > 1011 the mean specific star formation rate tends to be higher at higher density, while the opposite trend is observed in the local SDSS star forming sample.
Acknowledgments
PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KUL, CSL, IMEC (Belgium); CEA, OAMP (France); MPIA (Germany); IFSI, OAP/AOT, OAA/CAISMI, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI (Italy), and CICYT/MCYT (Spain). We would like to thank the anonymous referee for the useful comments which significantly helped in improving the paper.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Abraham, R. G., Smecker-Hane, T. A., Hutchings, J. B., et al. 1996, ApJ, 471, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M., Bauer, F. E., Brandt, W. N., et al. 2003, AJ, 126, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balogh, M. L., Morris, S. L., Yee, H. K. C., Carlberg, R. G., & Ellingson, E. 1999, ApJ, 527, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M., Eke, V., Miller, C., et al. 2004, MNRAS, 348, 1355 [Google Scholar]
- Barger, A. J., Cowie, L. L., & Wang, W.-H. 2008, ApJ, 689, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E., & Hernquist, L. 1996, ApJ, 471, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Kauffmann, G., Heckman, T. M., et al. 2005, MNRAS, 362, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bethermin, M., Dole, H., Beelen, A., et al. 2010, Cat, 35129078 [Google Scholar]
- Blanton, M. R., Hogg, D. W., Bahcall, N. A., et al. 2003a, ApJ, 592, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Lin, H., Lupton, R. H., et al. 2003b, AJ, 125, 2276 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, AIPC, 736, 117 [NASA ADS] [Google Scholar]
- Brusa, M., Fiore, F., Santini, P., et al. 2009, A&A, 507, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Abraha, R. G., Ellis, R. S., et al. 2007, ApJS, 172, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Caputi, K., Kovac, K., Bolzonella, M., et al. 2009, ApJ, 691,91 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Guzzo, L., Franceschini, A., et al. 2007, ApJS, 172, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2006, ApJ, 638, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Weiner, B. J., et al. 2008, MNRAS, 383, 1058 [Google Scholar]
- Cucciati, O., Iovino, A., Marinoni, C., et al. 2006, A&A, 458, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diolaiti, E., Bendinelli, O., Bonaccini, D., et al. 2000, A&AS, 147, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 531 [Google Scholar]
- Goto, T., Okamura, S., Sekiguchi, M., et al. 2003, PASJ, 55, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Pozzi, F., Andreani, P., et al. 2010, A&A, 518, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., & Gott, J. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Cassata, P., Finoguenov, A., et al. 2007, ApJS, 172, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fadda, D., Biviano, A., Marleau, F. R., et al. 2008, ApJ, 672, 9 [Google Scholar]
- Feruglio, C., Aussel, H., Le Floc’h, E., et al. 2010, ApJ, 721, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., & Hook, R. N. 2002, PASP, 114, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Haines, C. P., Gargiulo, A., La Barbera, F., et al. 2007, MNRAS, 381, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Hilton, M., Lloyd-Davies, Ed., Stanford, S. A., et al. 2010, ApJ, 718, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, 353, 713 [Google Scholar]
- Kenney, J. D. P., van Gorkom, J. H., & Vollmer, B. 2004, AJ, 127, 3361 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. Jr 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzbichler, M. G., & White, S. D. M. 2007, MNRAS, 376, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kodama, T., Smail, I., Nakata, F., Okamura, S., & Bower, R. G. 2001, ApJ, 562, L9 [Google Scholar]
- Kovac, C., Lilly, S. J., Knobel, C., et al. 2010, ApJ, 718, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, Y., Kodama, T., Shimasaku, K., et al. 2008, MNRAS, 391, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., Tinsley, B. M., & Caldwell, C. N. 1980, ApJ, 237, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Bauer, F. E., Brandt, W. N., et al. 2008, ApJS, 179, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Mainieri, V., Rafferty, D., et al. 2010, ApJ, 712, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Ferguson, H. C., Dickinson, M. E., et al. 1996, MNRAS, 283, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Mainieri, V., Tozzi, P., Gilli, R., et al. 2007, ASPC, 380, 151 [NASA ADS] [Google Scholar]
- Mamon, G. A. 1996, in The Dynamics of Groups and Clusters of Galaxies and Links to Cosmology, ed. H. de Vega, & N. Sanchez (Singapore: World Scientific), 95 [Google Scholar]
- Mancini, C., Matute, I., Cimatti, A., et al. 2009, A&A, 500, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merloni, A., Bongiorno, A., Bolzonella, M., et al. 2010, ApJ, 708, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C. 2004, in Clusters of Galaxies: Probes of Cosmological Structure and Galaxy Evolution, ed. J. S. Mulchaey, A. Dressler, & A. Oemler (Cambridge: Cambridge Univ. Press), 278 [Google Scholar]
- Moore, B., Lake, G., & Katz, N. 1998, ApJ, 495, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Lake, G., Quinn, T., & Stadel, J. 1999, MNRAS, 304, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H., Lutz, D., Schweitzer, M., et al. 2007, ApJ, 666, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Oemler, A. 1974, ApJ, 194, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Papovich, C., Dole, H., Egami, E., et al. 2004, ApJS, 154, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y., Lilly, S. J., Kovac, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pimbblet, K. A., Smail, I., Kodama, T., et al. 2002, MNRAS, 331, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Aragon-Salamanca, A., Zaritsky, D., et al. 2009, ApJ, 693, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., De Lucia, G., Varela, J., et al. 2010, MNRAS, 405, 995 [NASA ADS] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, 1005, 1487 [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, 663, 81 [Google Scholar]
- Popesso, P., Biviano, A., Böhringer, H., et al. 2005, A&A, 433, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Dickinson, M., Nonino, M., et al. 2009, A&A, 494, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postman, M., Franx, M., Cross, N. J. G., et al. 2005, ApJ, 623, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Quilis, V., Moore, B., & Bower, R. 2000, Science, 288, 5471 [Google Scholar]
- Rodighiero, G., Cimatti, A., Franceschini A., et al. 2007, A&A, 470, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodighiero, G., Cimatti, A., Gruppioni, C., et al. 2010, A&A, 518, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Fontana, A., Grazian, A., et al. 2009, A&A, 504, 571 [Google Scholar]
- Scodeggio, M., Vergani, D., Cucciati, O., et al. 2009, A&A, 501, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silverman, J. D., Lamareille, F., Maier, C., et al. 2009, ApJ, 696, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Starck, J.-L., & Murtagh, F. 1998, PASP, 110, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Struck, C. 1999, Phys. Rep., 321, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Kodama, T., Arimoto, N., et al. 2005, MNRAS, 362, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Tasca, L. A. M., Kneib, J.-P., Iovino, A., et al. 2009, A&A, 503, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tozzi, P., Gilli, R., Mainieri, V., et al. 2006, A&A, 451, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tran, K., Saintonge, A., Moustakas, J., et al. 2009, 705, 809 [Google Scholar]
- Tran, K., Papovich, C. J., Saintonge, A., et al. 2010, ApJ, 719, 126 [Google Scholar]
- Tzanavaris, P., Hornschemeier, A. E., Gallagher, S. C., et al. 2010, ApJ, 716, 556 [NASA ADS] [CrossRef] [Google Scholar]
- van Gorkom, J. H. 2004, in Clusters of Galaxies: Probes of Cosmological Structure and Galaxy Evolution, ed. J. S. Mulchaey, A. Dressler, & A. Oemler (Cambridge: Cambridge Univ. Press), 306 [Google Scholar]
- Vulcani, B., Poggianti, B. M., Finn, R. A., et al. 2010, ApJ, 710, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., et al. 2010, ApJ, 713, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Willmer, C. N. A., Faber, S. M., Koo, D. C., et al. 2006, ApJ, 647, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Yasuda, N., Fukugita, M., Narayanan, V. K., et al. 2001, AJ, 122, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Bardelli, S., Bolzonella, M., et al. 2009, 508, 1217 [Google Scholar]
All Figures
 |
Fig. 1 Bolometric IR luminosity – stellar mass relation. Empty circles in the figure are MIPS 24 μm detections without spectroscopic information. Filled circles in the figure are MIPS 24 μm detections with spectroscopic information. Red circles identify MIPS sources with PACS detection. The horizontal and vertical lines shows the M/M⊙ = 8 × 109 and LIR/L⊙ = 1011 cuts corresponding to our selection criteria at 0.7 < z < 1.1. |
| In the text | |
 |
Fig. 2 LIR,24 μm/LIR,PACS ratio versus LIR,24 μm obtained using the CE01 method, in the left panel. LIR,24 μm/LIR,PACS ratio versus the M/M⊙ using the CE01 method, in the central panel. LIR,24 μm/LIR,PACS ratio versus the LIR,24 μm obtained using the R10 method, in the right panel. In all panels empty circles are normal star forming galaxies in our sample with both a MIPS 24 μm and PACS 100 or 160 μm detection. Filled points are low luminosity obscured AGNs with both a MIPS 24 μm and PACS 100 or 160 μm detection. The point with error bar is the result of the stacking analysis in the GOODS-N 160 μm map of the obscured AGNs of our sample with only MIPS detection. |
| In the text | |
 |
Fig. 3 Distribution of the completeness parameter calculated around each source. The solid line shows the histogram of the completeness parameter based on a galaxy sample selected with an apparent magnitude cut at zAB < 23 mag. The dashed histogram shows the distribution of the completeness parameter based on a galaxy sample selected with an absolute magnitude cut at zAB < −21.35 mag. |
| In the text | |
 |
Fig. 4 Comparison of the density parameter calculated assuming 80% incompleteness and corrected for that (Σ(output)) versus the actual value (Σ(input)) in a light-cone of the Millennium simulation (Springel et al. 2005). |
| In the text | |
 |
Fig. 5 Distribution of the completeness parameter calculated around each source in a SDSS subsample in a area of 10 × 10 deg2. |
| In the text | |
 |
Fig. 6 Density–SFR relation. We show the relation obtained by including the low luminosity obscured AGNs (left panel) and the relation obtained after removing the AGNs from the sample (middle panel). In these panels the shaded regions show the global relations at M/M⊙ > 8 × 109, empty triangles show the relation obtained in the low mass sample (8 × 109 < M/M⊙ < 5 × 1010), stars show the relation obtained in the high mass sample (M/M⊙ > 5 × 1010). The right panel show the comparison of the global relations obtained by inclusion (pink area) and excluding (purple area) the AGNs in the sample. |
| In the text | |
 |
Fig. 7 Fraction of AGN hosts in our sample of star forming galaxies as a function of density (panel a)) and stellar mass (panel b)), star formation rate (panel c)) and specific star formation rate (panel d)). |
| In the text | |
 |
Fig. 8 Density–SFR relation obtained using only 24 μm derived SFR. The filled points show the relation obtained with 24 μm only derived SFR with the AGN contribution, the empty stars show the same without AGN contribution. The positive correlation does not disappear after removing the AGN when 24 μm derived SFR are used. The shaded regions show the density–SFR relations estimated with PACS+MIPS data: pink region is the density–SFR relation with the AGN contribution, the violet region is the same without AGN contribution. |
| In the text | |
 |
Fig. 9 Density–SFR relation in the local SDSS star forming sample. Filled points show the global relations at M/M⊙ > 8 × 109, empty triangles show the relation obtained in the low mass sample (8 × 109 < M/M⊙ < 5 × 1010), stars show the relation obtained in the high mass sample (M/M⊙ > 5 × 1010). |
| In the text | |
 |
Fig. 10 Density–sSFR relation. We show the relation obtained by including the low luminosity obscured AGNs (left panel) and the relation obtained after removing the AGNs from the sample (middle panel). In these panels the shaded regions show the global relations at M/M⊙ > 8 × 109, empty triangles show the relation obtained in the low mass sample (8 × 109 < M/M⊙ < 5 × 1010), stars show the relation obtained in the high mass sample (M/M⊙ > 5 × 1010). The right panel shows the comparison of the global relations obtained by inclusion (pink area) and excluding (purple area) the AGNs in the sample. |
| In the text | |
 |
Fig. 11 Density–sSFR relation in the local SDSS star forming sample. Filled points show the global relations at M/M⊙ > 8 × 109, empty triangles show the relation obtained in the low mass sample (8 × 109 < M/M⊙ < 5 × 1010), stars show the relation obtained in the high mass sample (M/M⊙ > 5 × 1010). |
| In the text | |
 |
Fig. 12 The left panel shows the density–SFR relation per morphological type. Black points refer to early type galaxies, magenta points refer to late type galaxies, and red points to galaxies with disturbed morphology. The central panel shows the same relation without the contribution of AGN hosts. The left panel shows the density–sSFR relation per morphological type. The symbols have the same meaning in all panels. The shaded regions in all panels shows the global trend of the considered relation. |
| In the text | |
 |
Fig. 13 sSFR-stellar mass relation in three density bins (left panel). The green circles identify AGN hosts. The solid line shows the best fit to the relation. The shaded purple region is the relation obtained via stacking in Rodighiero et al. (2010) based on a IRAC selected sample. The right panel shows the best fit parameters (filled points, normalization in the top panel, slope in the bottom panel) as a function of the bin mean density. The empty points show the best fit parameters obtained after excluding the AGN hosts. |
| In the text | |
 |
Fig. 14 sSFR-stellar mass relation per density bin in the local SDSS star forming sample. The shaded region is the mean relation based on the full star forming sample. The relations are color-coded as a function of density as explained in the figure. |
| In the text | |
 |
Fig. 15 Residual Δ(sSFR) as a function of mass and density with respect to the mean sSFR-mass relation of the local SDSS star forming sample (left panel) and of the z ~ 1 star forming sample (right panel). The points are color-coded as a function of local density as explained in the panels. |
| In the text | |
 |
Fig. 16 Mean sSFR per density bin in the high mass bin (M/M⊙ > 5 × 1010) and per morphological type. The color coding as function of morphology is shown in the figure. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


