| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201016206 | |
| Published online | 23 March 2011 | |
The star cluster – field star connection in nearby spiral galaxies
II. Field star and cluster formation histories and their relation⋆
Astronomical Institute, University of Utrecht, Princetonplein 5, 3584 CC Utrecht, The Netherlands
e-mail: e.silvavilla@uu.nl; s.s.larsen@uu.nl
Received: 25 November 2010
Accepted: 8 January 2011
Context. Recent studies have started to cast doubt on the assumption that most stars are formed in clusters. Observational studies of field stars and star cluster systems in nearby galaxies can lead to better constraints on the fraction of stars forming in clusters. Ultimately this may lead to a better understanding of star formation in galaxies, and galaxy evolution in general.
Aims. We aim to constrain the amount of star formation happening in long-lived clusters for four galaxies through the homogeneous, simultaneous study of field stars and star clusters.
Methods. Using HST/ACS and HST/WFPC2 images of the galaxies NGC 45, NGC 1313, NGC 5236, and NGC 7793, we estimate star formation histories by means of the synthetic CMD method. Masses and ages of star clusters are estimated using simple stellar population model fitting. Comparing observed and modeled luminosity functions, we estimate cluster formation rates. By randomly sampling the stellar initial mass function (SIMF), we construct artificial star clusters and quantify how stochastic effects influence cluster detection, integrated colors, and age estimates.
Results. Star formation rates appear to be constant over the past 107 − 108 years within the fields covered by our observations. The number of clusters identified per galaxy varies, with a few detected massive clusters (M ≥ 105 M⊙) and a few older than 1 Gyr. Among our sample of galaxies, NGC 5236 and NGC 1313 show high star and cluster formation rates, while NGC 7793 and NGC 45 show lower values. We find that stochastic sampling of the SIMF has a strong impact on the estimation of ages, colors, and completeness for clusters with masses ≤ 103 − 104 M⊙, while the effect is less pronounced for high masses. Stochasticity also makes size measurements highly uncertain at young ages (τ ≲ 108 yr), making it difficult to distinguish between clusters and stars based on sizes.
Conclusions. The ratio of star formation happening in clusters (Γ) compared to the global star formation appears to vary for different galaxies. We find similar values to previous studies (Γ ≈ 2%–10%), but we find no obvious relation between Γ and the star formation rate density (ΣSFR) within the range probed here (ΣSFR ~ 10-3 − 10-2 M⊙ yr-1 kpc-2). The Γ values do, however, appear to correlate with the specific U-band luminosity (TL(U), the fraction of total light coming from clusters compared to the total U-band light of the galaxy).
Key words: galaxies: individual: NGC 5236 / galaxies: individual: NGC 7793 / galaxies: individual: NGC 1313 / galaxies: individual: NGC 45 / galaxies: star formation / galaxies: photometry
Full Table 10 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/529/A25
© ESO, 2011
1. Introduction
It is often assumed that stars can be formed either in the field of a galaxy as single stars or in a group of stars (cluster) that formed from the same molecular cloud at the same time. However this view has been recently questioned by Bressert et al. (2010), who challenged the idea that field and cluster formation are actually distinct modes of star formation.
Owing to dynamical and stellar evolution, clusters disrupt (Spitzer 1987) and the stars become members of the field stellar population. While it is commonly assumed that most (if not all) stars formed in clusters (e.g. Lada & Lada 2003; Porras et al. 2003, in the solar neighborhood), the amount of star formation happening in those clusters that remain bound beyond the embedded phase is still uncertain. In any case, if clusters are to be used as tracers of galactic star formation histories, it is of key importance to understand what fraction of star formation is happening in long-lived clusters and whether or not this fraction correlates with other host galaxy parameters. Following Bastian (2008), we refer to this fraction as Γ.
Estimating Γ is not straightforward. Apart from differences arising at the time of formation, cluster disruption will also affect the detected number of clusters of a given age (τ). Lada & Lada (2003) estimate that between 70% to 90% of the stars in the solar neighborhood form in embedded star clusters, while only 4–7% of these clusters survive for more than about 100 Myr. Similarly, Lamers & Gieles (2008) estimate an “infant mortality” rate of 50% to 95%, based on a comparison of the surface density of open clusters and the star formation rate near the Sun. By studying the UV flux in and out of clusters in the galaxy NGC 1313, Pellerin et al. (2007) suggest that over 75% (between 75% and 90%) of the flux is produced by stars in the field, concluding that the large number of B-type stars in the field of the galaxy could be a consequence of the (high) infant mortality of clusters. For the Small Magellanic Cloud, Gieles & Bastian (2008) estimate that optically visible, bound clusters account for 2%–4% of the star formation, while Gieles (2010) estimates this fraction to be in the range 5%–18% for the spiral galaxies M74, M51, and M101. However, most of these studies could not distinguish between scenarios in which a large fraction of stars initially form in clusters that rapidly dissolve or whether there is a genuine “field” mode of star formation. Studying the Antennae galaxy, Fall (2004) estimates that 20% (and possibly all) stars were formed in clusters. Using a larger sample of galaxies, Goddard et al. (2010) find a power-law relation (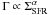 ) between the fraction of stars forming in clusters that survive long enough to be optically visible and the star formation rate density of the galaxy (ΣSFR). Their data set covers different types of galaxies, from irregulars (i.e. LMC, SMC, and NGC 1569) to grand design spirals (i.e. NGC 5236). The ΣSFR of these galaxies vary from 7 × 10-3 to ~700 × 10-3 M⊙ yr-1 Kpc-2. Their Γ vs. ΣSFR relation, however, is based on somewhat heterogenous data with different mass- and age ranges, which do not come from the same observations (see details in Sect. 4 of Goddard et al. 2010), although the authors do attempt to homogenize the sample by normalizing the cluster samples to a common mass limit.
) between the fraction of stars forming in clusters that survive long enough to be optically visible and the star formation rate density of the galaxy (ΣSFR). Their data set covers different types of galaxies, from irregulars (i.e. LMC, SMC, and NGC 1569) to grand design spirals (i.e. NGC 5236). The ΣSFR of these galaxies vary from 7 × 10-3 to ~700 × 10-3 M⊙ yr-1 Kpc-2. Their Γ vs. ΣSFR relation, however, is based on somewhat heterogenous data with different mass- and age ranges, which do not come from the same observations (see details in Sect. 4 of Goddard et al. 2010), although the authors do attempt to homogenize the sample by normalizing the cluster samples to a common mass limit.
The actual definition of the phase called infant mortality is somewhat ambiguous in the literature. Early disruption due to rapid gas expulsion may only take a few Myrs, but the term has also been used to describe mass-independent disruption, meaning that clusters lifetime is independent of mass over a much longer time span. In the latter case, the “infant mortality rate” (IMR) refers to the fraction of clusters that are disrupted per decade of age. We prefer to simply use the term “mass-independent” disruption (MID) in this case. For MID, the IMR is related to the slope a of the age distribution, dN/dτ ∝ τa of a mass limited cluster sample as a = log (1 − IMR) (Whitmore et al. 2007). For example, de Grijs & Goodwin (2008) found that for the SMC the IMR is close to 30% (between 3−160 Myr), while the logarithmic age distribution of clusters in the Antennae galaxies is about flat (a ≈ −1), indicating an IMR close to 90% (Fall 2004), assuming that the star formation rate has been about constant over the past few 108 years. On theoretical grounds, the time scale for the (gradual) cluster disruption is expected to be mass-dependent, owing to tidal shocks and evaporation that follows early gas expulsion (e.g. Gieles et al. 2006), assuming there is no strong relation between cluster mass and radius. In this description, the dissolution time tdis of a cluster scales with cluster mass as tdis = t4(M/104 M⊙)γ, where t4 is the lifetime of a 104 M⊙ cluster (see Boutloukos & Lamers 2003; Lamers et al. 2005). The time scale on which clusters dissolve may also depend on external factors, such as the tidal field strength, density of molecular gas, passages near/through giant molecular clouds, or through spiral arms, etc. (see e.g. Gieles et al. 2006, 2007). This scenario attempts to compile in one single formula all the possible processes that affect cluster disruption. See Lamers (2009) for a description of the different models for cluster dissolution.
Determining the extent to which cluster dissolution is a mass-dependent process has turned out to be difficult. Estimations of cluster parameters based on observations are affected by stochastic effects, degeneracies, and observational uncertainties. For example, Maíz Apellániz (2009) used Monte Carlo simulations to estimate how stochastic effects coming from the random sampling of the stellar initial mass function influence the determination of ages and masses, which are derived from broadband photometry. Piskunov et al. (2009) show how the consideration of the discreteness of the stellar initial mass function (IMF) can explain features observed in the color-age relation and can improve the fit between models and observations. They conclude that the large number of red outliers can be explained as a systematic offset coming from the difference between discrete- and continuous-IMF at low masses (Mc = 102 M⊙) and young ages (log(τ) [yr ] ~ 7), reaching up to ~0.5 mag, and decreases down to ~0.04 mag at higher masses (Mc = 106 M⊙).
To estimate field star formation histories, a different approach is needed than for clusters, because ages cannot in general be determined directly for individual stars. Tosi et al. (1991) presented a method that takes incompleteness, resolution, depth, and observational errors (among other parameters) into account to construct a synthetic color-magnitude diagram (CMD), which can be used to estimate the star formation history by comparison with observations . This method has been developed further by other authors in the past years, e.g. Dolphin (1997) and Harris & Zaritsky (2001), and has been used for a large number of galaxies, e.g. SMC, LMC (Harris & Zaritsky 2004, 2009), M 31 (Brown et al. 2008), NGC 1313 (Larsen et al. 2007). In this series of papers, we make use of this method to estimate the field star formation rates of our target galaxies, which we then compare with cluster formation rates to estimate Γ.
In Silva-Villa & Larsen (2010, hereafter Paper I), we presented the tools needed to study and constrain the Γ value of our set of galaxies, and used NGC 4395 as a testbed galaxy. As the second paper in a series, this paper aims to estimate Γ in different environments and compare it with previous work (e.g. Gieles 2010; Goddard et al. 2010), using the complete set of galaxies. To this end, we took advantage of the superb spatial resolution of the Hubble Space Telescope (HST) and used images of the galaxies NGC 5236, NGC 7793, NGC 1313, and NGC 45, which are nearby, face-on spiral galaxies that differ in their current star formation rates and morphology. These galaxies are near enough (≈ 4 Mpc) to allow us to disentangle the cluster system from the field stars, making it possible to estimate cluster and star formation histories separately and simultaneously from the same data.
Galaxy parameters.
Journal of the observations.
The paper is structured as follows. In Sect. 2, we present a short overview of previous work on our target galaxies, related to the present study. The basic reduction and characteristics of the observations are described in Sect. 3. In Sect. 4 we present the photometry procedures applied to the data and describe how completeness tests were carried out. We also discuss the effect of stochastic sampling of the stellar IMF on integrated cluster properties. In Sect. 5 we present the results of the estimation of ages and masses of clusters, as well as the field star formation histories. We also estimate the cluster formation rates and use these to determine Γ values. In Sect. 6 we discuss our results and finally, we summarize and conclude our work in Sect. 7.
2. Dataset overview
In this paper we describe results for the remaining four galaxies in our HST/ACS sample: NGC 5236, NGC 7793, NGC 1313, and NGC 45. These four galaxies share the properties of being face-on, nearby spirals; however, they differ in their morphology, star, and cluster formation histories. We present the basic properties of each galaxy in Table 1.
Larsen & Richtler (1999) studied cluster populations in a set of 21 galaxies, including the four included here. Using ground-based multiband (UBVRI and Hα) observations they estimated the total number of young massive clusters in each galaxy, using a magnitude limit of MV ≤ − 8.5. In a further work, Larsen & Richtler (2000) estimated the star formation rate density (ΣSFR) and the specific U-band luminosity, TL(U) = 100 × L(clusters,U)/L(galaxy,U), for each galaxy. The TL(U) was found to correlate with ΣSFR. Taking TL(U) as a proxy for the cluster formation efficiency, these data thus suggested an increase in the cluster formation efficiency with ΣSFR. It is worth noting here that the ΣSFR values were derived by normalizing the total star formation rates, obtained from IRAS far-infrared fluxes, to the optical galaxy diameters obtained from the RC3 catalog. Therefore, while these numbers were useful for studying trends and correlations, they should not be taken as reliable absolute values.
More recent estimates of ΣSFR have been made by Chandar et al. (2010b) for the galaxies NGC 5236 and NGC 7793, where they found similar values to Larsen & Richtler (2000). Harris et al. (2001) present a photometric observation of clusters in the center (inner 300 pc) of NGC 5236. Harris et al. find a large number of young and massive clusters, consistent with a burst of star formation that began around 10 Myr ago, but note that the apparent absence of older clusters might also be due to rapid disruption. Chandar et al. (2010c) used the new Wide Field Camera 3 (WFC3) on HST to analyze the cluster system of NGC 5236. They find that luminosity functions and age distributions are consistent with previous work on galaxies of different morphological types (e.g. Fall 2004). Mora et al. (2007, 2009) studied the cluster system for the same set of galaxies used in this work, based on the same HST images. They present detailed estimates of the sizes, ages, and masses for the clusters detected. Mora et al. conclude that the age distributions are consistent with a ~ 80% MID per decade in age up to 1 Gyr, but could not make a distinction between different models (MDD vs. MID) of cluster disruption. In the galaxy NGC 45 they found a large number of old globular clusters, of which 8 were spectroscopically confirmed to be ancient and metal-poor (Mora et al. 2008).
3. Observation and data reduction
The five galaxies studied in this series of papers were selected for detailed observations with the Advanced Camera for Surveys (ACS) and Wide Field Planetary Camera 2 (WPFC2) onboard HST from the work of Larsen & Richtler (1999, 2000). The two instruments have a resolution of 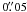 and
and 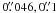 for ACS and WFPC2 (PC,WFs), respectively. At the distance of our galaxies (~4 Mpc) the ACS pixel scale corresponds to ~ 1 pc.
for ACS and WFPC2 (PC,WFs), respectively. At the distance of our galaxies (~4 Mpc) the ACS pixel scale corresponds to ~ 1 pc.
 |
Fig. 1 Galaxies studied in this paper. Top left: NGC 5236; top right: NGC 7793; bottom left: NGC 1313; and bottom right: NGC 45. Red lines represent the pointings covered by the HST/ACS, while the blue lines represent the pointings of the HST/WFPC2. Images were taken from the DSS archive using Aladin software. |
Besides NGC 1313, which has three different fields observed, the rest of the galaxies were covered using two pointings (see Fig. 1). The bands used for the observations were F336W(~U), F435W(~B), F555W(~V), and F814W(~I), with the exposure times listed in Table 2. The standard STScI pipeline was used for the initial data processing. ACS images were drizzled using the multidrizzle task (Koekemoer et al. 2002) in the STSDAS package in IRAF using the default parameters, but disabling the automatic sky subtraction. WFPC2 images were combined and corrected for cosmic rays using the crrej task using the default parameters.
Object detection for field stars and star clusters was performed on an average B, V, and I image, using daofind in IRAF for the stars and SExtractor V2.5.0 (Bertin & Arnouts 1996) for the clusters. Coordinate transformations between ACS and WFPC2 used IRAF. For details we refer to Paper I.
4. Photometry
We review here the procedures for carrying out photometry on our data, however, for details, we refer to Paper I. Due to the crowding we performed PSF photometry for field stars, while we used aperture photometry for the star clusters.
 |
Fig. 2 Hess diagram for the field stars of the observed galaxies. The dashed white line represents the 50% completeness curve. Red lines enclose the fitted areas used to estimate the SFH (see Sect. 5). |
4.1. Field stars
With a set of bona-fide stars visually selected in our images, measuring their FWHM with imexam, we constructed our point-spread function (PSF) using the PSF task in DAOPHOT. This procedure was followed in the same manner for each band (i.e., B,V, and I). The PSF stars were selected individually in each band, in order to appear bright and isolated. PSF photometry was done with DAOPHOT in IRAF.
HST zeropoints1 were applied to the PSF magnitudes after applying aperture corrections (see Sect. 4.3). The zeropoints used in this work are ZPB = 25.767, ZPV = 25.727 and ZPI = 25.520 mag. Typical errors of our photometry do not change dramatically from the ones in Paper I (see its Fig. 2).
Number of clusters detected per field, per galaxy.
Having magnitudes for our field stars, Hess diagrams were constructed and are depicted in Fig. 2 (each panel presents all fields combined for each galaxy). The total number of stars varies among the galaxies, all having some tens of thousands. Various phases of stellar evolution can be identified in the Hess diagrams:
-
main sequence and possible blue He-core burning stars atV − I ~ 0 and − 2 ≤ V ≤ − 8;
-
red He core burning stars at 1.2 ≤ V − I ≤ 2.5 and −2.5 ≤ V ≤ −6.5;
-
RGB/AGB stars, near the detection limit at 1 ≤ V − I ≤ 3 and −0.5 ≤ V ≤ −2.5.
The same features were observed for NGC 4395 in Paper I.
Overplotted in Fig. 2 are the 50% completeness lines (see Sect. 4.5 for details of the completeness analysis). Also, red lines enclose the fitted areas that will be used in Sect. 5 to estimate the star formation histories of the galaxies. These areas were selected to cover regions that were clearly over the 50% completeness and represent stars in different stages of evolution (e.g. main sequence, red He core burning).
4.2. Star clusters
To detect the cluster candidates we used SExtractor with a detection criterion of six connected pixels and a threshold of 10 sigma above the background level. The total numbers of objects detected in each galaxy are listed in the second column of Table 3. For these objects aperture photometry was performed using an aperture radius of six pixels on our ACS pointings, corresponding to about two half-light radii for a typical star cluster. We used a sky annulus with five pixels width and an inner radius of eight pixels. For the WFPC2 images, the apertures used cover the same area. There is a possibility of having close-neighbor objects that contaminate the photometry, whether inside either of the aperture radii or the sky annulus. Sizes were measured using the ISHAPE task in the BAOLAB package (Larsen 1999).
As mentioned in Paper I, three criteria were used to produce catalogs of cluster candidates from the initial SExtractor output.
-
1.
Size: candidates must satisfyFWHMSExtractor ≥ 2.7 pixels and FWHMishape ≥ 0.7 pixels. These are rather conservative size cuts that may eliminate some of the most compact clusters, but reduce the risk of contamination from other sources.
-
2.
Color: candidates must satisfy V − I ≤ 1.5.
-
3.
Magnitude: candidates must be brighter than mV = 23 (MV brighter than −4.6 to −5.4, depending on the galaxy distance).
Since the WFPC2 fields only cover about half the area of the ACS fields, some objects will only have three-band photometry (BVI), while others will have all four colors. Objects that satisfy the three criteria listed above are considered as star cluster candidates in the rest of the paper. However, as found in many previous studies, there is no unique combination of objective criteria that can lead to a successful detection of bona-fide clusters and no false detections. Our cluster candidates were therefore visually inspected to determine whether they resemble star clusters. Based on this, we classified the cluster candidates into three categories: accepted, Suspected, and Rejected. Figure 3 presents some examples of each category. In this figure, the first row presents the Accepted objects, which are clearly extended objects with normal measured sizes and magnitudes. The second row presents the Suspected objects, where the size/magnitude measurements may be affected by crowding, where the shape appears irregular, or where the contrast against the background is not strong. The last (third) row presents examples of the Rejected objects.
 |
Fig. 3 Examples of objects that were accepted (first row), suspected (second row), and rejected (third row) after visual inspection. Stamps are from the first field observed in NGC 7793 and have sizes of 100 × 100 pixels. |
Table 3 summarizes the total number of objects detected that have size measurements (2nd column), the total number of objects with three-band photometry and have sizes over the limits imposed (3rd column), the total number of accepted objects with three- and four band photometry (4th and 5th columns), the total number of suspected objects with three- and four band photometry (6th and 7th columns), and the total number of rejected objects (8th column). Shaded areas are the total numbers per galaxy.
Figure 4 shows two-color diagrams for accepted plus suspected clusters with four band photometry (all the fields combined per galaxy), corrected for foreground extinction with the values presented in Table 1. Overplotted is a theoretical track that a cluster will follow between 4 Myr and 1 Gyr using Galev models (Anders & Fritze-v. Alvensleben 2003), assuming LMC metallicity and no extinction. We see that the clusters generally tend to align with the model sequence, but with significant scatter around it. Below we investigate to what extent this scatter may come from stochastic color variations due to random sampling of the stellar IMF.
 |
Fig. 4 Two-color diagrams for the clusters with four band photometry. The red line represents the theoretical path a cluster will follow using GALEV models, assuming LMC metallicity and no extinction. Accepted+ Suspected clusters are presented. |
4.3. Completeness
Completeness analysis was carried out separately for field stars and star clusters to account for both populations.
4.3.1. Field stars
As in Paper I, we created artificial stars using the PSF obtained in Sect. 4.1. In the magnitude range between 20 to 28, every 0.5 mag, we generated 5 images and passed each one through the photometry procedures, using the exact same parameters as are used for the original photometry. A total of 528 stars were added to each image, with a separation of 100 pixels (we did not take subpixels shifts into account). The images were created using mksynth in BAOLab (Larsen 1999) and added to the science images using imarith in IRAF. To quantify the dependency of completeness functions on color, we made use of the near 1:1 relation between the B − V and V − I colors of stars (see Paper I for details).
Based on our analysis, we found 50% completeness limits for each galaxy and for each band, as shown in Table 4.
50% completeness limits for field stars.
4.3.2. Star clusters
In order to quantify completeness limits we added artificial clusters of different ages and masses to our images. We created artificial clusters using a stochastic approach. Assuming a Kroupa IMF (Kroupa 2002) in the mass range 0.01 to 100 M⊙, a total cluster mass of M = [103,104,105 ] M⊙, and a cluster age range between τ = [107,109.5 ] yr (with 0.5 dex steps), we randomly sampled stars from the IMF until the total mass of the stars reached the total mass assumed for the cluster. Positions were assigned by randomly sampling a King profile (King 1962). There is a possible pitfall regarding the mass of the last star sampled, because it could overcome the total input (assumed) mass. We kept the last star, even if the total mass is higher than assumed. This problem affects low-mass clusters more than high-mass clusters. With the ages and masses for the stars, we then interpolated in isochrones (of LMC-like metallicity) from the Padova group (Marigo et al. 2008) and assigned magnitudes to each star. For all the artificial clusters, an FWHM = 2.7 pixels was assumed (corresponding to a Reff ≈ 4 pc). Figure 5 shows stamps of artificial clusters of different ages and masses, using an average (B, V, and I) image of the galaxy NGC 7793 as an example.
 |
Fig. 5 Stochastic clusters created to estimate the completeness in NGC 7793 (average B, V, and I image, first field). From top to bottom, rows represent masses of log(M) [M⊙] = [3, 4, 5] . From left to right, columns represent ages of log(τ)[yr] = [7, 8, 9]. Each images has a size of 100 × 100 pixels. |
For each combination of age and mass, a total of 100 randomly generated clusters were added to the science images using a square grid. The artificial images with clusters were created using mksynth in BAOLab (Larsen 1999) and added to the science images using imarith in IRAF. Following the same procedure used for the cluster photometry, an average BVI image was created for each field. SExtractor was then run on this average image, using the same parameters as in Sect. 4.2. SExtractor returns a file with coordinates, measured FWHM and other information. To save computational time, owing to the large amount of objects that SExtractor could detect, we removed all the original objects (science objects detected previously) from the list and kept the ones that are not in the original image. This new coordinate file was passed to ishape in BAOLab to compute PSF-corrected sizes. We used the coordinate file to run photometry, again with the same procedures and parameters as for the science photometry. Having B, V, I photometry done, size cuts were applied and the output file was matched with the input coordinate file to evaluate how many of the added artificial objects were recovered successfully.
 |
Fig. 6 Completeness curves for stochastic clusters with ages log(τ)[yr] = [7, 7.5,8, 8.5, 9, 9.5] and masses of log(M) [M⊙] = [3,4,5] for the four galaxies. All clusters have an input FWHM = 2.7 pixels. Red lines represent the number of detections without applying any size criteria (right column). Blue lines are the number of detections after applying the size criteria of FWHMishape ≥ 0.2 pixels, used in Mora et al. (2007, 2009) (middle column). Black lines are the number of detections after applying the size criteria used in this work (FWHMishape ≥ 0.7 pixels) (left column). The legend is in units of solar masses (M⊙). The symbols over the lines represent an age step (i.e. 0.5 dex) starting from the left. |
Figure 6 shows the output (mV) average magnitude of the recovered clusters versus the fraction recovered for the three masses and six ages assumed in each galaxy. For the masses log(M)[M⊙ ] = [3, 4, 5 ] as an illustrative example, Fig. 6 shows the total number of objects detected applying three different size criteria: (1.) FWHMishape > 0, i.e. no size cut used to select the clusters; (2.) FWHMishape ≥ 0.2, same size cut used by Mora et al. (2007, 2009); and (3.) FWHMishape ≥ 0.7, the size cut used in this paper. Each line is for a given cluster mass, while each symbol belonging to a line represents the time steps assumed, i.e., τ = [107,109.5 ] yr (with 0.5 dex step). From this test we conclude that
-
1.
High-mass clusters (log(M) [M⊙ ] = 5), at any age, are easily recognized byour procedures, regardless of the size criteria used.
-
2.
For decreasing cluster mass, clusters of old ages drop out of the sample, and for log(τ)[yr] ≥ 8.5 our completeness is less than 50% for masses below log(M)[M⊙] = 4.
-
3.
The completeness depends on the mass, on the size used to classify an object as extended or not extended, and on age. Decreasing the size threshold would increase the completeness somewhat for low-mass, young objects, but could introduce additional contamination.
-
4.
Stochasticity affects young star clusters (log(τ)[yr] ≤ 7.5) more dramatically.
At the very young ages in Fig. 6 the completeness drops below 100% at all masses. This can be understood from Fig. 7, which shows the histograms for the FWHM of the detected objects measured with ishape for log(M) [M⊙ ] = [3, 4, 5 ] and log(τ)[yr] = [7, 8, 9], using the results from NGC 7793 as an example. The figure shows that at high masses and old ages, the recovered sizes are on average similar to the input values, with some spread. However, at younger ages and/or lower masses, the measured sizes are systematically less than the input values. In these cases, the light profiles can be dominated by a single or a few bright stars, while for high masses and/or old ages, the light profiles are much smoother and better fit by the assumed analytic profiles. At young ages and low masses, this bias in the size measurements leads to a decrease in the completeness fraction as more clusters fall below the size cut.
 |
Fig. 7 Histograms of measured FWHMs for the stochastic clusters in NGC 7793 created for the completeness analysis. From top to bottom, rows represent masses of log(M) [M⊙] = [3, 4, 5] . From left to right, columns represent ages of log(τ)[yr] = [7, 8, 9]. Legends are in logarithmic mass and age units. The red dashed line represents an FWHM = 0.7 pixels, as assumed in Sect. 4.3.2, while the blue dash-dotted line represents the input FWHM = 2.7 pixels. |
4.4. Aperture corrections
Aperture corrections were estimated separately for star and clusters. We applied the same procedures as in Paper I. For field stars, our PSF-fitting magnitudes were corrected to a nominal aperture radius of 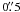 , following standard procedures. From this nominal value to infinity, we applied the corrections in Sirianni et al. (2005).
, following standard procedures. From this nominal value to infinity, we applied the corrections in Sirianni et al. (2005).
For star clusters, aperture corrections were applied following the equations in Mora et al. (2009), which give a relation between the FWHM of the objects and the aperture corrections. The photometric parameters (and data set) used in our work are the same as the ones used by Mora et al. (2009), allowing us to use their equations. This set of equations apply corrections to a nominal radius of 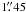 . We adopted the values in Sirianni et al. (2005) to correct from there on, although the corrections to infinity are minor (~97% of the total energy is encircled within
. We adopted the values in Sirianni et al. (2005) to correct from there on, although the corrections to infinity are minor (~97% of the total energy is encircled within  ).
).
4.5. How do stochastic effects influence star cluster photometry?
 |
Fig. 8 Stochastic effects on colors and ages of clusters. First row: two color diagrams for a stochastic sample of clusters with different masses and different ages. The dashed line represents Padova 2008 SSP models of solar-like metallicity. Second row: U − B color evolution. Third row: V − I color evolution. Fourth row: density plot to make a comparison between input and output ages. The red line represents the 1:1 relation, not a fit to the data. |
The classical approach used to estimate masses and ages of unresolved star clusters in the extragalactic field is based on the use of multi-band integrated colors and comparison of these with SSP models. Anders et al. (2004) show that it is necessary to have at least four-band photometry to be able to break degeneracies (e.g. age-metallicity). However, standard SSP models assume a continuously populated stellar initial mass function (SIMF), while clusters consist of a finite number of stars. For unresolved clusters, the random sampling of the SIMF can strongly affect integrated properties such as cluster colors, magnitudes, and parameters (ages, masses) derived from them (Cerviño & Luridiana 2006; Maíz Apellániz 2009; Popescu & Hanson 2010a,b). A promising attempt to take the stochastic color fluctuations into account when deriving ages and masses has been made by Fouesneau & Lançon (2010), based on a Bayesian approach.
Here we do not attempt to offer any solution to the SIMF sampling problem, but we quantify its effects that are related to our study. To that aim, we created clusters by randomly sampling the SIMF and assigning magnitudes to individual stars in the same bands used for our photometry (i.e. U, B, V, and I). In addition to its impact on cluster detection and classification, as described in the previous section, we also investigated how stochastic SIMF sampling affects the two-color diagrams and ages.
We used the same recipe as in Sect. 4.3.2 to create artificial clusters. Assuming a range of ages between 106.6 Myr and 109.5 yr and total masses of M = [102,103,104,105,106 ] M⊙, we created 100 clusters every 0.1 dex in age. The top row in Fig. 8 shows the two-color diagrams for each one of the total masses, together with an solar-metallicity Padova SSP model (Marigo et al. 2008). The evolution of the colors U − B and V − I with time are shown in the second and third rows, and the comparison of input (assumed) and output (estimated) ages using AnalySED (Anders et al. 2004) are in the bottom row. The colors indicate the input ages.
Many features are observed here. (1) For high masses (log(Mass) [M⊙] = [5,6]), the stochastically sampled clusters form narrow sequences in the color–color and color-age diagrams, in agreement with Cerviño & Luridiana (2006). (2) At intermediate masses, i.e., log(Mass) [M⊙ ] = [3,4] , which are typical of the cluster masses observed in extragalactic works, the scatter increases strongly. The scatter observed in the two-color diagrams for this mass range is similar to what is seen in our observed two-color diagrams. (3) For very low masses (log(Mass) [M⊙ ] = [2 ] ), the scatter again decreases but the model colors now deviate strongly from the SSP colors. This is because such clusters have a very low probability of hosting a luminous (but rare and short-lived) post-main sequence star, while the SSP models assume that the colors are an average over all stages of stellar evolution (see Piskunov et al. 2009). (4) For ages log(τ) ≲ 8 and intermediate masses (log(Mass)[M⊙ ] = [3,4 ] ), the color distribution actually becomes bimodal, as observed by Popescu & Hanson (2010a,b). The blue “peak” in the color distribution is due to clusters without red supergiants, while the presence of even a single red supergiant shifts the colors into the other peak. (5) The bottom row shows that age estimates are completely dominated by stochastic effects for low-mass clusters (log(Mass) [M⊙ ] = [2,3 ] ). For higher masses the ages are more accurately recovered, even if a small scatter is observed compared to the 1:1 relation, especially at ages of a few tens of Myr where the light is strongly dominated by red supergiant stars.
Based on these results it is clear that photometry and the ages estimated from broad band photometry can be heavily affected by the stochastic effects introduced by SIMF sampling, as also shown by Maíz Apellániz (2009). We conclude that low-mass clusters (M ≤ 103M⊙) are very strongly affected, reaching age differences up to log(agein)-log(ageout) ≈ 2.5 dex, for clusters with log(τ)[yr] ≤ 8.5, while for high-mass clusters (M ≥ 104 M⊙), this effect gradually diminishes, an effect that is clearly visible as gaps in Fig. 8 (last row). Another important effect is observed as a deviation from the 1:1 red line observed for the low-mass clusters, which indicate that the estimated age (Ageout) is again wrongly recovered, even at old ages (1 Gyr). One should be aware of the risk that low-mass, young clusters may erroneously be assigned old ages. When using SSP models to convert their luminosities to masses, based on such wrong age estimates, such objects might be assigned erroneously high masses, thus making it into an observed sample (e.g. Popescu & Hanson 2010b).
It is important to mention that the SSP models used do not take the binarity or rotation of massive stars into account (see e.g. Maeder & Meynet 2008; Eldridge & Stanway 2009). Also, different isochrone assumptions and the techniques used to perform the fit to the ages and masses can be affecting the results (see e.g. Scheepmaker et al. 2009; de Grijs et al. 2005). The tests presented in this paper are only intended to address the stochastic sampling effects, and we only rely on Padova isochrones. A more detailed study must be made to better account for other effects (e.g. by binaries, rotation, etc.).
 |
Fig. 9 Fitted Hess diagrams for the sample studied. Red lines are the boxes used for the fit and the 50% completeness, same as Fig. 2. |
 |
Fig. 10 Star formation rate densities for the data set. Each line represent an assumption for the binarity (see text for details). |
5. Results
In the next sections we estimate the field star formation histories (SFHs) for each galaxy and determine the ages and masses of the cluster candidates. We then estimate the cluster formation efficiencies, Γ.
5.1. Field star formation histories
To estimate the SFHs, we used the synthetic CMD method. We implemented this method using an IDL-based program that was introduced and tested in Paper I. For a description of the program we refer the reader to that paper, but here we summarize the basic functionality.
The synthetic CMD method (Tosi et al. 1991) takes advantage of the power supplied by the CMDs. The method uses a group of isochrones, together with assumptions about the SIMF, metallicity, distance, extinction, and binarity, to reproduce an observed CMD. Photometric errors and completeness functions (both being treated as magnitude dependent parameters by our program) are also taken into account. The program searches for the combination of isochrones that best matches the observed CMD, thereby estimating the SFH.
The parameters used to estimate the SFH of the galaxies are: a Hess diagram with a resolution of 200 × 200 pixels is created, using a Gaussian kernel with a standard deviation of 0.02 mag along the color axis. The matching is done within the rectangular boxes depicted in Fig. 2, using the V − I vs. V color combination, Padova 2008 isochrones (Marigo et al. 2008) and a Kroupa (2002) IMF in the mass range 0.1 to 100 M⊙. The assumed distance moduli, foreground extinctions, and metallicities are given in Table 1, while the photometric errors and completeness for each galaxy were determined in Sect. 4. The program also includes a simplified treatment of binaries, in which binary evolution is ignored, but the effect of unresolved binaries on the CMD are modeled. To account for binarity we used three different assumptions for the binary fraction (f) and mass ratio (q): (1) f = 0.0 and q = 0.0, (2.) f = 0.5 and q = [0.1,0.9] (assuming a flat distribution), and (3.) f = 1 and q = 1. These three assumptions are the same ones as used in Paper I.
Figures 9 shows the best-fit Hess diagrams. Comparing with the observed Hess diagrams (Fig. 2), we see that the fits are far from perfect. In particular, all the model Hess diagrams show a clear separation between the blue core He burning (“blue loop”) stars and the main sequence, while this is not obvious in most of the observed diagrams. This might be partly due to some variation in the internal extinction, which has not been included in our modeling. To infer the SFHs of our sample, we combined all the fields (per galaxy) and passed to our program. The star formation rates, normalized to unit area, are shown in Fig. 10 and the average values are listed in Table 5 for ages between 10 and 100 Myr. In this age range, our data are less affected by incompleteness. Previous estimates of the ΣSFR done by Larsen & Richtler (2000) and Chandar et al. (2010b) are included in Table 5. We see that NGC 5236 and NGC 1313 have higher ΣSFR values than NGC 7793 and NGC 45, in agreement with the previous estimates. Within the uncertainties (see Paper I), we do not see any significant trends in the SFRs between 107 and 108 years. While our estimate of ΣSFR agrees very well with the others for NGC 5236, there are significant differences for some of the other galaxies, most notably for NGC 4395. It should be kept in mind that the ΣSFR values derived here are for our specific ACS fields, while the others are averages over whole galaxies over a rather large outer diameter. It is therefore not very surprising that our new estimates tend to be higher.
Estimates of the star formation rates.
5.2. Cluster ages and masses
To determine the ages and masses of the clusters we used the program AnalySED (Anders et al. 2004). Using GALEV SSP models (Schulz et al. 2002), AnalySED compares the observed spectral energy distributions with a library of models to find the best fit. We used GALEV models based on a Kroupa IMF (Kroupa 2002) in the mass range 0.1 to 100 M⊙, Padova isochrones (Girardi et al. 2002), and different metallicities, depending on the galaxy.
 |
Fig. 11 Age-mass distributions for the cluster systems. Blue dashed lines represent the magnitude cut at mv = 23. Red boxes will be used to create the age and mass distributions. Left column present the distribution for the Accepted sample, while the right column present the suspected sample of clusters (see Sect. 4.2). Red dash-dotted line in the right column denotes the mass 104 M⊙ for comparison. |
Based on our analysis of uncertainties due to stochasticity, we applied a mass criterion to the cluster samples in addition to the three selection criteria defined in Sect. 4. We require clusters in our sample to be more massive than 1000 M⊙; however, we remind the reader that ages are only reliable for masses greater than 104 M⊙ (for ages τ ≤ 1 Gyr). The magnitude limit, MV ~ −, is generally below our 50% detection limit based on the stochasticity test.
Figure 11 shows the age-mass diagrams for clusters that satisfy the four criteria for the accepted and suspected samples separated. Overall, we observe that the suspected clusters are below 104 M⊙ (right column in the figure). We see that the number of clusters in NGC 45 is small, compared with the other three galaxies. To first order, this appears to be consistent with the overall low star formation rate derived for this galaxy. Clusters in all four galaxies display a range in age and mass, but most are younger than 1 Gyr and have masses below 105 M⊙, with few exceptions. We cannot exclude, however, that the sample contains some older clusters that have been assigned too young ages. In particular, relatively metal-poor old globulars would not be fit well by the models used here. Our sample includes two of the eight spectroscopically confirmed old globular clusters in NGC 45 from Mora et al. (2008). From these we find ages of 0.04 and 0.8 Gyr, while Mora et al. find spectroscopic average ages of 4.5 and 6.5 Gyr but consistent with ages as old as 10 Gyr. This confirms the suspicion that some of the clusters in our sample might be older, metal-poor globulars with misassigned ages.
Our catalogs of the cluster candidates are available online. Table 10 shows a few example lines to illustrate the format and the information contained in the catalogs.
5.3. Cluster disruption and formation efficiencies
Although we have derived masses and ages for our cluster candidates, some additional steps are necessary before we can use this information to derive cluster formation rates. In Paper I we used a Schechter (Schechter 1976) mass function (M ⋆ = 2 × 105 M⊙) to extrapolate below the (age-dependent) mass limit and in this way we estimated the total mass in clusters with ages between 107 and 108 years for NGC 4395. This approach ignores any effects of disruption but is still useful for relative comparisons. We therefore first apply the same approach to the four galaxies in this paper. Completeness limits were estimated by plotting the luminosity functions and identifying the point where they start to deviate significantly from a smooth power law. This occurs at the following absolute magnitudes: MV = −6.2 for NGC 5236, MV = −5.7 for NGC 7793, MV = −6.8 for NGC 1313, and MV = −5.9 for NGC 45. After estimating the mass in clusters with 107 < τ/yr < 108 down to a limit of 10 M⊙ and dividing by the age interval (see Paper I for details), the resulting CFRs were normalized to the area of the full ACS fields (a factor of ~ 2.27 more) for comparison with the field star formation rates. The resulting CFRs are listed in the second column of Table 8 (CFRP1).
Especially for NGC 45, the CFRs derived in this way are highly uncertain owing to the small number of clusters that have four-band photometry. Better statistics can be obtained by only using the three-band photometry in the ACS frames, but at the cost of having no age information for individual clusters. However, CFRs may still be estimated by comparing the observed luminosity functions (LFs) with scaled model LFs (Gieles 2010). If the CFR is assumed constant and assumptions made about the initial cluster mass function (Ψ) and disruption parameters, the LF can be modeled as follows (Eq. (7) in Larsen 2009): ![\begin{eqnarray} \frac{{\rm d}N}{{\rm d}L} & = & \int_{\tau_{\rm min}}^{\tau_{\rm max}} \Psi_{\rm i}[M_{\rm i}(L,\tau)] \times \frac{{\rm d}M_{\rm i}}{{\rm d}M_{\rm c}}\times \Upsilon_{\rm c}(\tau) \times {\rm CFR} \nonumber \\ & & \ \ \ \ \ \ \ \ \ \ \ \ \ \times f_{\rm surv}(\tau) \ {\rm d}\tau \ , \label{eq:dndl} \end{eqnarray}](/articles/aa/full_html/2011/05/aa16206-10/aa16206-10-eq183.png) (1)where Ψi [Mi(L,τ) ] is the initial mass function; Υc(τ) is the mass-to-light ratio, which is only dependent on time in order to be able to compute it from classical SSP models; CFR is assumed constant over time; and fsurv(τ) is the number of clusters that survive after applying MID; Mi and Mc are the initial and current masses of a cluster with luminosity L and age τ, and these are related through the assumed secular disruption law (Lamers et al. 2005). The description of MID adopted here assumes that a constant fraction of the cluster population is removed per logarithmic age bin, as opposed to a constant fraction of the mass of each individual cluster. If Ψi is a uniform power law, this makes no difference. However, if the MID stem from gradual mass loss from individual clusters, any features in Ψi (such as the cut-off mass for the Schechter function) will be shifted downwards with time, whereas only the normalization of Ψi will change with time for constant number loss.
(1)where Ψi [Mi(L,τ) ] is the initial mass function; Υc(τ) is the mass-to-light ratio, which is only dependent on time in order to be able to compute it from classical SSP models; CFR is assumed constant over time; and fsurv(τ) is the number of clusters that survive after applying MID; Mi and Mc are the initial and current masses of a cluster with luminosity L and age τ, and these are related through the assumed secular disruption law (Lamers et al. 2005). The description of MID adopted here assumes that a constant fraction of the cluster population is removed per logarithmic age bin, as opposed to a constant fraction of the mass of each individual cluster. If Ψi is a uniform power law, this makes no difference. However, if the MID stem from gradual mass loss from individual clusters, any features in Ψi (such as the cut-off mass for the Schechter function) will be shifted downwards with time, whereas only the normalization of Ψi will change with time for constant number loss.
 |
Fig. 12 Age distributions for clusters in the galaxies NGC 5236, NGC 7793, and NGC 1313 in the mass range 104 to 105 M⊙. Black lines represent the distributions for galaxies. Red lines represent the best fit. Upper panel are the ADs only using the clusters classified as accepted. The lower panel are the ADs for the clusters classified as accepted plus suspected. |
In order to apply Eq. (1), some constraints on cluster disruption are necessary. Models and empirical constraints on cluster disruption have been discussed in recent years by different authors (e.g. Boutloukos & Lamers 2003; Lamers et al. 2005; Whitmore et al. 2007; Larsen 2009; Zhang & Fall 1999; Fall 2004,among others), and Fall et al. (2009) for different types of galaxies such as the LMC, SMC, Milky Way, M83, or Antennae. Given that it is currently uncertain to what extent MID or MDD dominates the cluster disruption, we carried out our analysis for both scenarios.
Slopes for the age distributions for the accepted and the accepted+suspected samples.
Figure 12 shows the age distributions (ADs) for clusters with masses between 104 and 105 M⊙ for the galaxies NGC 1313, NGC 5236, and NGC 7793. NGC 45 has too few clusters to derive meaningful ADs. We show fits for both the Accepted and Accepted + Suspected samples. The slopes of the age distributions, obtained by carrying out fits of the form log (dN/dt) = a × log (τ) + b to the data in Fig. 12, are given in Table 6. There are no large differences between the slopes derived for the Accepted and Accepted + Suspected sample. Figure 11 shows that most of the clusters in the suspected sample have masses below our limit of log (M) [M⊙] = 4.0, explaining the similarity of the age distributions above this limit.
As a consistency check for the slope of the age distributions, we performed a maximum likelihood fit to the data, assuming a power-law relation and using the power-law index as a free parameter. Using the accepted and accepted plus suspected sample of clusters, we estimated the slope of the age distributions using the same age and mass ranges as shown in Fig. 12 (i.e. ages between 4 Myr up to 1 Gyr and masses between 104 and 105 M⊙). The results obtained are presented in Table 7. The derived slopes agree very well with those in Table 6, within the errors.
Using clusters with ages between 106.6 ≤ τ ≤ 108 yr and a mass 104 ≤ M ≤ 105 M⊙ we checked for (possible) variations over the slope of the age distributions. The best fit for these slopes in the new age interval are −0.17 ± 0.39, −0.38 ± 2.34, and 0.78 ± 0.43 using the accepted sample, and −0.39 ± 0.31, 0.05 ± 0.91, and 0.59 ± 0.91 using the accepted plus suspected sample, for the galaxies NGC 5236, NGC 7793, and NGC 1313 respectively. The new slopes are to be flatter than the values for the whole age range, showing even positive values; however, in most of the cases, the error is larger than the estimation itself. The possibility of having shallower slopes indicate that there is a possible curvature of the age distribution of star cluster systems, which is not consistent with a (simple) power law.
Slopes for the age distributions for the accepted and the accepted+suspected samples based on the maximum likelihood fit.
The slopes found here are, however, somewhat shallower than the value of a = −0.9 ± 0.2 found for NGC 5236 by Chandar et al. (2010c). If interpreted within the MID scenario, the slopes derived here correspond to MID disruption rates of 41%, 81%, and 77% per decade in age if we use the accepted sample, and 45%, 62%, and 73% if we use the sample of accepted plus suspected objects, for the galaxies NGC 5236, NGC 7793, and NGC 1313, respectively. A weighted average of the slopes for the Accepted samples leads to a mean slope of ⟨ a ⟩ = −0.42 ± 0.07 and an MID disruption rate of (62 ± 6)% per decade in age. We use this mean weighted value for all the galaxies in our sample, including NGC 45 and NGC 4395 where the numbers of detected clusters are too low to allow us to estimate the slopes of the age distributions independently.
It is worth comparing our age distributions with those of Mora et al. (2009). Their slopes were considerably steeper than those found here, but this is partly because Mora et al. worked with magnitude-limited samples, while our age distributions are for mass-limited samples. When taking this into account, Mora et al. found that their data were consistent with MID disruption rates of 75%–85% per dex, still somewhat higher than the values found here. We note that the stochastic effects, combined with our relatively conservative size cuts, likely cause us to underestimate the number of objects in the youngest bins. This might account for some of the flattening of the age distributions in the youngest bins that is also seen in Fig. 12 for NGC 1313 and NGC 5236. For this reason our estimates of the slopes and disruption rates might also be considered lower limits. The less strict size cut used by Mora et al. (FWHM = 0.2 pixels instead of our 0.7 pixels) would cause them to detect more compact, young objects, but also possibly ones with increased contamination. Finally, since visual selection was part of the sample selection in both our work and the one of Mora et al., this will also lead to differences in the final samples.
A key difference between the MID and MDD models is that, while the former predicts no change in the shape of the mass distribution with age, the latter predicts a flattening at low masses. In order to test whether we can distinguish between the two scenarios, model mass distributions (MD, number of objects, per mass bin, per linear age bin) were computed for different age intervals using a relation analogous to Eq. (1), but integrating over τ for fixed M rather than fixed L. These model MDs were then compared with the observed MDs in the same age intervals. For the MDD scenario we assumed γ = 0.62 and a disruption time of t4 = 1 × 109 yr (Lamers et al. 2005). No infant mortality was included in the MDD models (i.e. fsurv = 1 at all ages). The MID models used the IMR obtained above (62%), which is active in the age range 5 Myr to 1 Gyr, and t4 was set to infinity, making the models independent of mass. We compared the model MDs with our observations, dividing our cluster samples into the following age and mass bins: log(M)[M⊙ ] = [3.0, 3.5, 4.0, 4.5, 5.0] and log(τ)[yr] = [6.6, 7.5, 8.0, 8.5, 9.0] (shown in Fig. 11).
 |
Fig. 13 Mass-independent models. Left column: MDs observed (black symbols) and predicted models (red lines). Right column: luminosity function observed (black horizontal lines), predicted models (red horizontal lines), and theoretical model (dash-dotted line). Vertical straight lines represent the limits used for the fit of the LFs. |
 |
Fig. 14 Mass-dependent models. Left column: MDs observed (black symbols) and predicted models (red lines). Right column: luminosity function observed (black horizontal lines), predicted models (red horizontal lines), and theoretical model (dash-dotted line). Vertical straight lines represent the limits used for the fit of the LFs. |
 |
Fig. 15 LFs for the five galaxies in our sample. We used MDD and MID theoretical models in left and right columns, respectively. Vertical lines are the limits of the fit. Red horizontal lines represent the binned theoretical values, while black horizontal lines represent observations. Errors are Poissoninan. Dashed-dotted line is the theoretical LF not binned. |
 |
Fig. 16 Relation between Γ and ΣSFR using average values of Γ for the models MDD and MID. Rhombs symbols and line represents the Goddard et al. (2010) data and black star symbols represent our set of galaxies. |
In Figs. 13 and 14 we compare the observed and predicted MD and LF for MID and MDD models. The best fits were defined by scaling the model LFs to match the observed ones, where the observed LFs were created using variable binning with ten objects per bin for NGC 1313 and NGC 5236 (following Maíz Apellániz 2009) and five objects per bin for NGC 45, NGC 4395, and NGC 7793. Errors were assumed to be Poissonian. Also shown is the reduced χ2 for each galaxy. Based on these figures, it is difficult to distinguish between the MID and MDD scenarios, mostly because of the limited dynamical range of the data and the poor statistics.
Our final estimates of the CFRs come from the LFs for clusters with 3-band photometry in all five galaxies in our sample, using model LFs computed for both MDD and MID disruption. The observed LFs were created in the same way as described above, using variable binning. We used the magnitude ranges up to the brightest cluster in the sample and the lower limit was set at the completeness limits estimated above (see vertical lines in Fig. 15). The CFRs are listed in Table 7 for the 4- and 3 band photometry. The CFRs for the four-band photometry have been scaled to the size of the ACS fields. The observed LFs and the best-fitting models are shown in Fig. 15, where MID and MDD models have been tested for the five galaxies in our sample. The CFRs inferred from the fits in Fig. 15 only include the accepted clusters. If we include the “suspected” objects then the CFRs increase by 52%, 62%, 30%, 4%, and 25% for NGC 5236, NGC 7793, NGC 1313, NGC 45 and NGC 4395, respectively, for the MDD scenario. Similar changes occur for MID. Furthermore, if we exclude the known ancient GCs in NGC 45 (Mora et al. 2008) from the sample, the Γ value for this galaxy decreases by ~ 20%. Taken together, this then makes NGC 45 less of an outlier in Fig. 16 and in general shifts the data points upwards.
Estimates of the cluster formation rates.
Estimations of Γ and comparison with Goddard et al. (2010) results.
 |
Fig. 17 Relation between TL(U) and Γ using the models MDD and MID. The values for Γ using the Accepted+Suspected sample are also included. |
Having estimated the SFRs and CFRs, we are now able to calculate Γ. Table 9 lists the Γ values corresponding to the different estimates of the CFR. As an additional consistency check, we also include a direct comparison of the fraction of light coming from clusters and from field stars, using the magnitude range between mV = 23 and mV = 18. This is not a direct measure of Γ, but is still useful for checking any trends. The Γ values derived from the LF fitting are generally a few percent, with the values derived from MDD models about 48% smaller (or less) than those derived for the MID models. We computed the mean value for each model and the respective standard error of the mean (columns 5th and 8th in Table 9).
Catalogs of the cluster candidates.
Continued.
6. Discussion
In Fig. 16 we compare our Γ vs. ΣSFR measurements with the data in Goddard et al. (2010) (rhombs). We cannot confirm whether a correlation is present within the range of ΣSFR values probed by our data, but overall our Γ values are similar to those found by Goddard et al. in this range of ΣSFR or slightly lower. However, following the methods of Goddard et al., Adamo et al. (2011) estimated values for Γ in the two blue compact galaxies ESO 185 and Haro 11. The results from Adamo et al. are in good agreement with the power law proposed by Goddard et al. (2010).
According to Larsen & Richtler (2000), the five galaxies span a significant range in specific U-band luminosity. From Table 9 and Fig. 17, we see that galaxies with high Γ values generally tend to also have high TL(U) values. One exception to this is NGC 45, which has a rather high Γ for its TL(U). The TL(U) value for this galaxy is, however, based on only two clusters, hence subject to very large uncertainty. Nevertheless, the high Γ value for NGC 45 is also somewhat puzzling given that it has the lowest ΣSFR. This may suggest that there is not a simple relation between Γ and ΣSFR. In this context, it is also interesting that this galaxy has a large number of ancient GCs for its luminosity, yielding an unusually high globular cluster specific frequency for a late-type (Sd) galaxy (Mora et al. 2009).
Our measurements of Γ values in the range ~ 2–10% are consistent with other recent estimates of the fraction of stars forming in bound clusters. It should be kept in mind that this number is not necessarily an indicator of “clustered” vs. “isolated” star formation, since some stars may form in embedded clusters that dissolve or expand on short enough time scales to drop out of our sample.
There is a correlation between TL(U) and Γ, as shown in Fig. 17. We estimated values for Γ using the accepted+suspected samples for the three-band photometry and for MDD and MID models as presented in the figure. The galaxy NGC 45 deviates from the apparent relation. Two things must be noted. (1) The inclusion of the suspected sample does not change the trend observed dramatically, although the increases in the CFRs is reflected in the new Γ estimations, and (2) CFR estimates based on different disruption models follow the same trend.
Estimates of the actual “infant mortality rate” are hard to make unless the embedded phase is probed directly, something which is difficult in external galaxies. For NGC 1313, Pellerin et al. (2007) find that the IMR is a very efficient process for the dissolution of star clusters in this galaxy (IMR = 90%) based on UV fluxes in and out of clusters. Our estimate of a Γ value of 3%–5% for NGC 1313 indicates that ≳ 95% of star formation in this galaxy happens outside clusters that are detected in our sample, in reasonable agreement with the Pellerin et al. estimate. However, it is also clear that cluster dissolution is a continuous process, and systems that are probed at older ages are generally expected to show a lower fraction of stars in clusters.
A proper account of dissolution effects could, in principle, be used to correct measurements of Γ at different ages to a common reference (say, 10 Myr), but current uncertainties in the disruption process makes this difficult to apply in practice. As a case in point, Chandar et al. (2010a) estimate a mass-independent disruption rate of 80%–90% per decade in age for NGC 5236, a value that is significantly higher than our estimate ~ 40% (~62% is our estimated weighted average). These differences underscore that the definition of cluster samples (especially in star-forming galaxies) is subject to strong selection effects, many of which are age dependent and thus likely to affect the age distributions. One example is the size cuts, which can easily cause a bias against young objects where stochastic SIMF sampling leads to underestimated sizes even for masses of ~ 104 M⊙. Furthermore, there may also be a physical relation between cluster size and age (e.g. Elson et al. 1989; Barmby et al. 2009; Mackey & Gilmore 2003a,b), compounding this problem.
When using young clusters (τ less than 100 Myr) we observed that the slope of the age distribution gets shallower, indicating a possible curvature or deviation from a power-law relation and showing values for the age distributions different from previous estimations. However, these results are based on a sample that is strongly affected by very few of clusters.
7. Summary and conclusions
Using HST observations of the galaxies NGC 45, NGC 1313, NGC 4395, NGC 5236, and NGC 7793, we studied their populations of star clusters and field stars separately with the aim of constraining the quantity Γ, i.e. the ratio of stars forming in bound clusters and the “field”. We have been following the basic approach described in Paper I, i.e. comparing synthetic and observed color-magnitude diagrams (for the field stars) and SED model fitting (for the star clusters), to get the formation histories of stars and clusters.
We tested how stochastic effects induced by the SIMF influence photometry and the estimation of ages and how the completeness limits are affected. We conclude that massive clusters (log(Mass)[M⊙] ≥ 5]) are easily detected (with the parameters used in this work) at any age, while the detection of clusters with masses below ~104 M⊙ can be strongly affected by stochasticity. Our tests thus show that completeness functions do not just depend on magnitude, but also on age and size. It would be desirable to find better classification methods than a simple size cut to determine what is, and what is not, a cluster.
We estimated star formation histories and found that NGC 5236 and NGC 1313 have the highest star formation rates, while NGC 7793, NGC 4395, and NGC 45 have lower SFRs. Within the uncertainties, we do not see significant variations within the past 100 Myr.
Comparing observed and modeled mass- and and luminosity distributions for the cluster populations in different galaxies, we find that we cannot distinguish between different disruption models (mass dependent vs. mass independent). We compared model luminosity functions for each disruption scenario with observed LFs and derived CFRs for the cluster systems. From our measurements of the CFRs and SFRs we derived the ratio of the two, Γ, as an indication of the formation efficiency of clusters that remain identifiable until at least 107 years. We find Γ values in the range ~ 2–10%, with no clear correlation with ΣSFR within the (limited) range probed by our data. However, our measurements are roughly consistent with those of Goddard et al. (2010), who find a relation between ΣSFR and Γ for a sample of galaxies spanning a wider range in ΣSFR (but more heterogeneous data).
A general difficulty in this type of work is to identify a reliable sample of bona-fide clusters. Comparison with previous work suggests that the cluster samples, although covering the same galaxies, are significantly affected by the criteria used to classify clusters over the images. This results in different estimates of cluster system parameters, such as those related to the disruption law. Accurate estimates of these parameters are also hampered by the relatively poor statistics that result from having only patchy coverage of large, nearby galaxies in typical HST imaging programs.
Acknowledgments
We would like to thank the referee for comments that helped to improve this article. We would like to thank Morgan Fouesneau for catching an error in Fig. 8. This work was supported by an NWO VIDI grant to S.L.
References
- Adamo, A., Ostlin, G., Zackrisson, E., & Hayes, M. 2011, MNRAS, accepted [arXiv:1101.1968] [Google Scholar]
- Anders, P., & Fritze-v. Alvensleben, U. 2003, A&A, 401, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, P., Bissantz, N., Fritze-v. Alvensleben, U., & de Grijs, R. 2004, MNRAS, 347, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Barmby, P., Perina, S., Bellazzini, M., et al. 2009, AJ, 138, 1667 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N. 2008, MNRAS, 390, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boutloukos, S. G., & Lamers, H. J. G. L. M. 2003, MNRAS, 338, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Ryan-Weber, E., Kennicutt, R. C., & Goddard, Q. 2009, ApJ, 695, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Bressert, E., Bastian, N., Gutermuth, R., et al. 2010, MNRAS, 409, L53 [Google Scholar]
- Brown, T. M., Beaton, R., Chiba, M., et al. 2008, ApJ, 685, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Cerviño, M., & Luridiana, V. 2006, A&A, 451, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandar, R., Fall, S. M., & Whitmore, B. C. 2010a, ApJ, 711, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Chandar, R., Whitmore, B. C., Kim, H., et al. 2010b, ApJ, 719, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Chandar, R., Whitmore, B. C., Kim, H., et al. 2010c, ApJ, 719, 966 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., & Goodwin, S. P. 2008, MNRAS, 383, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., Anders, P., Lamers, H. J. G. L. M., et al. 2005, MNRAS, 359, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Dolphin, A. 1997, New Astron., 2, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2009, MNRAS, 400, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Elson, R. A. W., Freeman, K. C., & Lauer, T. R. 1989, ApJ, 347, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M. 2004, in The Formation and Evolution of Massive Young Star Clusters, ed. H. J. G. L. M. Lamers, L. J. Smith, & A. Nota, ASP Conf. Ser., 322, 399 [Google Scholar]
- Fall, S. M., Chandar, R., & Whitmore, B. C. 2009, ApJ, 704, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Fouesneau, M., & Lançon, A. 2010, A&A, 521, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieles, M. 2010, in Astronomical Society of the Pacific Conference Series, ed. B. Smith, J. Higdon, S. Higdon, & N. Bastian, ASP Conf. Ser., 423, 123 [Google Scholar]
- Gieles, M., & Bastian, N. 2008, A&A, 482, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieles, M., Portegies Zwart, S. F., Baumgardt, H., et al. 2006, MNRAS, 371, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Gieles, M., Athanassoula, E., & Portegies Zwart, S. F. 2007, MNRAS, 376, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goddard, Q. E., Bastian, N., & Kennicutt, R. C. 2010, MNRAS, 405, 857 [NASA ADS] [Google Scholar]
- Harris, J., & Zaritsky, D. 2001, ApJS, 136, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J., & Zaritsky, D. 2004, AJ, 127, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J., & Zaritsky, D. 2009, AJ, 138, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J., Calzetti, D., Gallagher,, III J. S., Conselice, C. J., & Smith, D. A. 2001, AJ, 122, 3046 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Fruchter, A. S., Hook, R. N., & Hack, W. 2002, in The 2002 HST Calibration Workshop : Hubble after the Installation of the ACS and the NICMOS Cooling System, ed. S. Arribas, A. Koekemoer, & B. Whitmore, 337 [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M. 2009, Ap&SS, 132 [Google Scholar]
- Lamers, H. J. G. L. M., & Gieles, M. 2008, in Mass Loss from Stars and the Evolution of Stellar Clusters, ed. A. de Koter, L. J. Smith, & L. B. F. M. Waters, ASP Conf. Ser., 388, 367 [Google Scholar]
- Lamers, H. J. G. L. M., Gieles, M., Bastian, N., et al. 2005, A&A, 441, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsen, S. S. 1999, A&AS, 139, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsen, S. S. 2009, A&A, 503, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsen, S. S., & Richtler, T. 1999, A&A, 345, 59 [NASA ADS] [Google Scholar]
- Larsen, S. S., & Richtler, T. 2000, A&A, 354, 836 [NASA ADS] [Google Scholar]
- Larsen, S. S., Mora, M. D., Brodie, J. P., & Richtler, T. 2007, in IAU Symp. 241, ed. A. Vazdekis & R. F. Peletier, 435 [Google Scholar]
- Mackey, A. D., & Gilmore, G. F. 2003a, MNRAS, 338, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, A. D., & Gilmore, G. F. 2003b, MNRAS, 338, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2008, in Mass Loss from Stars and the Evolution of Stellar Clusters, ed. A. de Koter, L. J. Smith, & L. B. F. M. Waters, ASP Conf. Ser., 388, 3 [Google Scholar]
- Maíz Apellániz, J. 2009, ApJ, 699, 1938 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mora, M. D., Larsen, S. S., & Kissler-Patig, M. 2007, A&A, 464, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mora, M. D., Larsen, S. S., & Kissler-Patig, M. 2008, A&A, 489, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mora, M. D., Larsen, S. S., Kissler-Patig, M., Brodie, J. P., & Richtler, T. 2009, A&A, 501, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pellerin, A., Meyer, M., Harris, J., & Calzetti, D. 2007, ApJ, 658, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, A. E., Kharchenko, N. V., Schilbach, E., et al. 2009, A&A, 507, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, B., & Hanson, M. M. 2010a, ApJ, 724, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Popescu, B., & Hanson, M. M. 2010b, ApJ, 713, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Porras, A., Christopher, M., Allen, L., et al. 2003, AJ, 126, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Scheepmaker, R. A., Lamers, H. J. G. L. M., Anders, P., & Larsen, S. S. 2009, A&A, 494, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, J., Fritze-v. Alvensleben, U., Möller, C. S., & Fricke, K. J. 2002, A&A, 392, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silva-Villa, E., & Larsen, S. S. 2010, A&A, 516, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sirianni, M., Jee, M. J., Benítez, N., et al. 2005, PASP, 117, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1987, Dynamical evolution of globular clusters, ed. L. Spitzer [Google Scholar]
- Tosi, M., Greggio, L., Marconi, G., & Focardi, P. 1991, AJ, 102, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, J. R., & Roy, J. 1997, MNRAS, 288, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Whitmore, B. C., Chandar, R., & Fall, S. M. 2007, AJ, 133, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Kennicutt, Jr., R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., & Fall, S. M. 1999, ApJ, 527, L81 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
Slopes for the age distributions for the accepted and the accepted+suspected samples.
Slopes for the age distributions for the accepted and the accepted+suspected samples based on the maximum likelihood fit.
All Figures
 |
Fig. 1 Galaxies studied in this paper. Top left: NGC 5236; top right: NGC 7793; bottom left: NGC 1313; and bottom right: NGC 45. Red lines represent the pointings covered by the HST/ACS, while the blue lines represent the pointings of the HST/WFPC2. Images were taken from the DSS archive using Aladin software. |
| In the text | |
 |
Fig. 2 Hess diagram for the field stars of the observed galaxies. The dashed white line represents the 50% completeness curve. Red lines enclose the fitted areas used to estimate the SFH (see Sect. 5). |
| In the text | |
 |
Fig. 3 Examples of objects that were accepted (first row), suspected (second row), and rejected (third row) after visual inspection. Stamps are from the first field observed in NGC 7793 and have sizes of 100 × 100 pixels. |
| In the text | |
 |
Fig. 4 Two-color diagrams for the clusters with four band photometry. The red line represents the theoretical path a cluster will follow using GALEV models, assuming LMC metallicity and no extinction. Accepted+ Suspected clusters are presented. |
| In the text | |
 |
Fig. 5 Stochastic clusters created to estimate the completeness in NGC 7793 (average B, V, and I image, first field). From top to bottom, rows represent masses of log(M) [M⊙] = [3, 4, 5] . From left to right, columns represent ages of log(τ)[yr] = [7, 8, 9]. Each images has a size of 100 × 100 pixels. |
| In the text | |
 |
Fig. 6 Completeness curves for stochastic clusters with ages log(τ)[yr] = [7, 7.5,8, 8.5, 9, 9.5] and masses of log(M) [M⊙] = [3,4,5] for the four galaxies. All clusters have an input FWHM = 2.7 pixels. Red lines represent the number of detections without applying any size criteria (right column). Blue lines are the number of detections after applying the size criteria of FWHMishape ≥ 0.2 pixels, used in Mora et al. (2007, 2009) (middle column). Black lines are the number of detections after applying the size criteria used in this work (FWHMishape ≥ 0.7 pixels) (left column). The legend is in units of solar masses (M⊙). The symbols over the lines represent an age step (i.e. 0.5 dex) starting from the left. |
| In the text | |
 |
Fig. 7 Histograms of measured FWHMs for the stochastic clusters in NGC 7793 created for the completeness analysis. From top to bottom, rows represent masses of log(M) [M⊙] = [3, 4, 5] . From left to right, columns represent ages of log(τ)[yr] = [7, 8, 9]. Legends are in logarithmic mass and age units. The red dashed line represents an FWHM = 0.7 pixels, as assumed in Sect. 4.3.2, while the blue dash-dotted line represents the input FWHM = 2.7 pixels. |
| In the text | |
 |
Fig. 8 Stochastic effects on colors and ages of clusters. First row: two color diagrams for a stochastic sample of clusters with different masses and different ages. The dashed line represents Padova 2008 SSP models of solar-like metallicity. Second row: U − B color evolution. Third row: V − I color evolution. Fourth row: density plot to make a comparison between input and output ages. The red line represents the 1:1 relation, not a fit to the data. |
| In the text | |
 |
Fig. 9 Fitted Hess diagrams for the sample studied. Red lines are the boxes used for the fit and the 50% completeness, same as Fig. 2. |
| In the text | |
 |
Fig. 10 Star formation rate densities for the data set. Each line represent an assumption for the binarity (see text for details). |
| In the text | |
 |
Fig. 11 Age-mass distributions for the cluster systems. Blue dashed lines represent the magnitude cut at mv = 23. Red boxes will be used to create the age and mass distributions. Left column present the distribution for the Accepted sample, while the right column present the suspected sample of clusters (see Sect. 4.2). Red dash-dotted line in the right column denotes the mass 104 M⊙ for comparison. |
| In the text | |
 |
Fig. 12 Age distributions for clusters in the galaxies NGC 5236, NGC 7793, and NGC 1313 in the mass range 104 to 105 M⊙. Black lines represent the distributions for galaxies. Red lines represent the best fit. Upper panel are the ADs only using the clusters classified as accepted. The lower panel are the ADs for the clusters classified as accepted plus suspected. |
| In the text | |
 |
Fig. 13 Mass-independent models. Left column: MDs observed (black symbols) and predicted models (red lines). Right column: luminosity function observed (black horizontal lines), predicted models (red horizontal lines), and theoretical model (dash-dotted line). Vertical straight lines represent the limits used for the fit of the LFs. |
| In the text | |
 |
Fig. 14 Mass-dependent models. Left column: MDs observed (black symbols) and predicted models (red lines). Right column: luminosity function observed (black horizontal lines), predicted models (red horizontal lines), and theoretical model (dash-dotted line). Vertical straight lines represent the limits used for the fit of the LFs. |
| In the text | |
 |
Fig. 15 LFs for the five galaxies in our sample. We used MDD and MID theoretical models in left and right columns, respectively. Vertical lines are the limits of the fit. Red horizontal lines represent the binned theoretical values, while black horizontal lines represent observations. Errors are Poissoninan. Dashed-dotted line is the theoretical LF not binned. |
| In the text | |
 |
Fig. 16 Relation between Γ and ΣSFR using average values of Γ for the models MDD and MID. Rhombs symbols and line represents the Goddard et al. (2010) data and black star symbols represent our set of galaxies. |
| In the text | |
 |
Fig. 17 Relation between TL(U) and Γ using the models MDD and MID. The values for Γ using the Accepted+Suspected sample are also included. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


