| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015997 | |
| Published online | 01 April 2011 | |
Horizontal branch evolution, metallicity, and sdB stars⋆
1
LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
2
Département de Physique, Université de Montréal, Montréal, PQ, H3C 3J7, Canada
e-mail: michaudg@astro.umontreal.ca; jacques.richer@umontreal.ca
3
Université Montpellier II, GRAAL, CNRS, UMR 5024, place Eugène Bataillon, 34095 Montpellier, France
e-mail: Olivier.Richard@univ-montp2.fr
Received: 25 October 2010
Accepted: 8 February 2011
Context. Abundance anomalies have been observed in field sdB stars and in nearly all horizontal branch (HB) stars of globular clusters with Teff > 11 000 K, whatever be the cluster metallicity.
Aims. We aim to determine the abundance variations that are expected in sdB stars and in HB stars of metallicities Z ≥ 10-4 and investigate what the observed abundances teach us about hydrodynamical processes competing with atomic diffusion.
Methods. Complete stellar evolution models, including the effects of atomic diffusion and radiative acceleration, have been computed from the zero age main-sequence for metallicities of Z0 = 0.0001, 0.001, 0.004 and 0.02. On the HB the masses were selected to cover the Teff interval from 7000 to 37 000 K. Some 60 evolutionary HB models were calculated. The calculations of surface abundance anomalies during the horizontal branch depend on one parameter, the surface mixed mass.
Results. For sdB stars with Teff < 37 000 K and for HB stars with Teff > 11 000 K in all observed clusters, independent of metallicity, we found that most observed abundance anomalies (even up to ~ × 200) were compatible, within error bars, with expected abundances. A mixed mass of ~10-7 M⊙ was determined by comparison with observations.
Conclusions. Observations of globular cluster HB stars with Teff > 11 000 K and of sdB stars with Teff < 37 000 K suggest that most observed abundance anomalies can be explained by element separation driven by radiative acceleration occuring at a mass fraction of ~10-7 M⊙. Mass loss or turbulence appear to limit the separation between 10-7 M⊙ and the surface.
Key words: stars: evolution / stars: horizontal-branch / stars: abundances / stars: Population II / subdwarfs
Appendices are only available in electronic form at http://www.aanda.org
© ESO, 2011
1. Astrophysical context
Large abundance anomalies have been observed on the horizontal branch (HB) of NGC 6752, NGC 1904, NGC 2808, M 15, and M 13 (Behr et al. 1999, 2000; Behr 2003; Moehler et al. 2000; Fabbian et al. 2005; Pace et al. 2006): whereas those stars cooler than about 11 000 K have the same composition as giants, those hotter than 11 000 K usually have larger abundances of some metals by large factors. This occurs in all clusters with sufficiently blue HB stars irrespective of their metallicity as defined by their giant branch stars.
Field sdOB stars are observed to have large abundance anomalies compared with Pop I stars (for a review see Heber 2009). They were already recognized by Sargent & Searle (1968) to have a surface composition different from the one with which they formed. While cool (Teff < 104 K) field Pop II stars have low Z, the sdBs1 which must come from the red giants often have iron peak abundances that are solar or even larger. While sdBs correspond to the blue end of the HB, the hotter sdO stars are apparently a mixed bag of post HB stars and other highly evolved evolutionary stages. Spectroscopically, sdOs have much more diverse characteristics than sdBs. In this paper we extend the Teff coverage of evolutionary models to sdBs, but not to sdOs.
In preceding papers (Michaud et al. 2007; Michaud et al. 2008) the evolution of a Pop II star2 with Z0 = 10-4 was followed from the zero age main-sequence to the middle of the HB and comparisons were made with observed abundance anomalies in M 15. The overabundances are explained by atomic diffusion driven by radiative accelerations in stars with Teff > 11 000 K, and the sudden break in anomalies at 11 000 K was shown to be related to observed rotation velocities (Quievy et al. 2009). Given the relatively large observational error bars, the anomalies appeared compatible with a simple diffusion model involving only one parameter, the mass of the outer region mixed by turbulence. It was determined by Michaud et al. (2008) to be about 10-7 M∗.
Extending these calculations to higher metallicities allows a comparison with field sdOB stars. While these have the disadvantage that their original metallicity is unknown, some of them are much closer than any globular cluster, and their surface composition can consequently be determined more precisely than that of corresponding HB stars of clusters. This opens the possibility of further constraining the process competing with atomic diffusion in causing abundance anomalies.
According to Morrison et al. (2009) and Kinman et al. (2009), inner halo stars have a mean [Fe/H] = −1.6 and almost all have [Fe/H] < −0.8. Presumably most field sdB stars have a similar range of original metallicities. It is then useful to determine to what extent the surface abundances of sdBs should be affected by the various metallicities they may have formed with. Carrying calculations with different metallicities allows not only comparisons with globular clusters whose giant branch shows various metallicities, but also to analyze potential causes of the abundance range observed in field sdBs.
Among previous work relevant to this paper, radiative accelerations of metals and He in sdBs were calculated by Bergeron et al. (1988) and Michaud et al. (1989). The calculations of grad(He) were for stars of 40 000 K or more. The role of He diffusion for the structure of sdBs has been investigated by Hu et al. (2009) and Hu et al. (2010), but without the important contribution of metal diffusion with radiative accelerations.
The sdBs correspond to the highest Teff HB stars observed in globular clusters. Why did they lose more mass above the He-burning core than the cooler HB stars? A number of more or less complicated scenarios have been suggested for them. Here we assume a simple scenario and determine what anomalies would, in this scenario, be expected on the surface. We do not claim to exclude more complicated ones, but consider it useful to determine if surface abundances can be understood in a simple scenario, assuming nature chose that way.
In this paper, the evolution is carried out with models evolved with atomic diffusion from the zero age main-sequence and through the Red Giant Branch, as described in Michaud et al. (2010). During the HB, it is continued with a surface mixed zone with enough turbulence to force abundance homogeneity. The mass of this mixed zone is kept constant. Abundance anomalies depend on its extent, which is determined by a comparison with observations (see Sect. 3.2). In general the calculated anomalies also depend on the original metallicity of the star. For globular clusters this is fixed by the metallicity of the giants of the cluster. This approach is different from that of Charpinet et al. (1997) and Fontaine et al. (2003) in that these authors assumed the abundances in the exterior regions to be such that gravity and radiative accelerations were at equilibrium. This led to a parameter-free determination of abundances, which is a function of Teff only. Their model has considerable success in explaining observations and pulsation properties. However, can the assumed equilibrium always be reached during evolution on the HB? Is there a sufficient Fe reservoir to fill the region of the Fe opacity bump? Does a mixing process modify it? Observations suggest a range of abundances for some species in sdBs at a given Teff.
After a very brief description of the calculations (Sect. 2), the internal structure is analyzed (Sect. 3), contrasting that of 14 000 and 30 100 K stars; the resulting surface abundances are discussed and compared with observations in Sect. 4, insisting on the metallicity dependence of clusters, which leads us to continue with field sdB stars (Sect. 4.4). After a summary of the main results (Sect. 5.1), the potential role of mass loss (Sect. 5.2) and μ gradient inversion (Sect. 5.3) are mentioned. While this paper is concerned with the role of stellar evolution for surface abundances, it is concluded by a brief discussion of the need to test the models using asterosismology (Sect. 5.4).
2. Calculations
Stellar evolution models were calculated from the zero age main-sequence to the HB as described in Michaud et al. (2007). Using opacity spectra from Iglesias & Rogers (1996), all aspects of atomic diffusion transport are treated in detail from first principles. These models are called models with diffusion in Michaud et al. (2007).
 |
Fig. 1 Turbulent diffusion coefficient in a 0.50 M⊙ model. The left axis is for the diffusion coefficient and the right axis for the Fe mass fraction. The coefficient is anchored at a mass ΔM0 = 10-7.5 M⊙. The vertical dashed line is at ΔM0. The Fe mass fraction, X(Fe), is nearly constant from the surface down to ΔM = 10-7 M⊙, which corresponds to Fe being mixed down to approximately 3 × ΔM0. |
 |
Fig. 2 HR diagram (left) for all calculated models with a mixed mass ~10-7 M⊙. Each segment represents the evolution of one model whose mass is color-coded using a simple formula. The metallicity (Z0) of each series of models is indicated at the left of the sequence. The dotted part represents the first 10 Myr of HB evolution, while the solid line represents the rest of the calculated HB evolution, ususally an additional 27 Myr. In the right panel, g vs. Teff diagram of a subset of the calculations (those with Teff > 20 000 K) corresponding to the observations of Geier et al. 2010. This panel contains data (gray and red dots as defined in the text) from their Fig. 2. |
During the HB, the surface convection zone includes very little mass for Teff ≥ 10 000 K. To carry out HB evolution, it was found necessary to keep a small surface zone mixed. A simple turbulent diffusion coefficient (see Fig. 1), similar to those used for AmFm stars of the main-sequence, was used to mix the exterior region during HB evolution. Turbulence was assumed sufficiently large to completely mix the regions between superficial convection zones; this mixing is expected from the results of numerical simulations (Kupka & Montgomery 2002; Freytag & Steffen 2004). Below the deepest surface convection zone, the turbulent diffusion coefficient was assumed to obey a simple algebraic dependence on density, which is given in most calculations presented here by 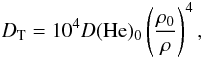 (1)where D(He)0 is the atomic diffusion coefficient of He3 at some reference depth. For most calculations in Michaud et al. (2008), the turbulent diffusion coefficient was anchored at a given constant temperature, T0. Then
(1)where D(He)0 is the atomic diffusion coefficient of He3 at some reference depth. For most calculations in Michaud et al. (2008), the turbulent diffusion coefficient was anchored at a given constant temperature, T0. Then 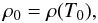 (2)and Eq. (2) is given by the stellar model. That density varies during evolution. While a given ρ0 or T0 during the evolution of one star of a given mass on the HB approximately occurs at a constant value of ΔM ≡ M∗ − Mr, the latter changes considerably between cool and hot HB and especially hot sdB stars. For this paper, most calculations were carried out with
(2)and Eq. (2) is given by the stellar model. That density varies during evolution. While a given ρ0 or T0 during the evolution of one star of a given mass on the HB approximately occurs at a constant value of ΔM ≡ M∗ − Mr, the latter changes considerably between cool and hot HB and especially hot sdB stars. For this paper, most calculations were carried out with  (3)and Eq. (3) is given by the current stellar model. In words, in the calculations reported in this paper, ρ0 of Eq. (1) is the density at which ΔM = ΔM0 in the evolutionary model. For ΔM0 = 10-7.5 M⊙ the concentration of most species is constant for ΔM ≲ 10-7.0 M⊙ when the assumed turbulent coefficient is 104 × the He diffusion coefficient at ΔM0 and varying as ρ-4. As one increases ΔM0, one defines a one parameter family of models. As may be seen from Fig. 1, turbulence decreases very rapidly inward; using this turbulence is equivalent to mixing a certain mass4. The exact mass over which concentration is kept uniform by turbulence depends on the driving terms in the atomic diffusion equation and so varies slightly with atomic species. As may be seen from Fig. 1, it is 3 × ΔM0 for Fe, but it is 10 × ΔM0 for He (not shown). For log (ΔM0/ M⊙) = −7.5 these models are labeled dM–7.5D10K-4.
(3)and Eq. (3) is given by the current stellar model. In words, in the calculations reported in this paper, ρ0 of Eq. (1) is the density at which ΔM = ΔM0 in the evolutionary model. For ΔM0 = 10-7.5 M⊙ the concentration of most species is constant for ΔM ≲ 10-7.0 M⊙ when the assumed turbulent coefficient is 104 × the He diffusion coefficient at ΔM0 and varying as ρ-4. As one increases ΔM0, one defines a one parameter family of models. As may be seen from Fig. 1, turbulence decreases very rapidly inward; using this turbulence is equivalent to mixing a certain mass4. The exact mass over which concentration is kept uniform by turbulence depends on the driving terms in the atomic diffusion equation and so varies slightly with atomic species. As may be seen from Fig. 1, it is 3 × ΔM0 for Fe, but it is 10 × ΔM0 for He (not shown). For log (ΔM0/ M⊙) = −7.5 these models are labeled dM–7.5D10K-4.
3. Abundance anomalies and internal concentration variations
Calculations were carried out for metallicities of Z0 = 0.02, 0.004, 0.001 and 0.0001. Corresponding tracks in the HR diagrams and in the log g-Teff plane are shown in Fig. 2. The time evolution of L, Teff, of surface abundances of He, Ca, Cr, and Fe, and of other variables of interest may be found as an appendix (Appendix B) for all models.
In the right panel of Fig. 2 we compare the data from Fig. 2 of Geier et al. (2010) with the g vs. Teff covered by our models5. These cover the range of most stars in that paper for Teff < 36 000 K. There are some lower-gravity stars that have gravities more than a factor of 2 lower than those of our models; they are identified using a different color (red). According to Fig. 1 of Charpinet et al. (2000), they should correspond to the end of the HB phase, which is not treated in our models. When we compare the results with Figs. 3 and 4 of Geier et al. (2010) and Fig. 1 of Geier et al. (2008), we will usually identify them separately. Evolution was stopped when the He mass fraction dropped below ~ 60% in the star center (after around 32 Myr on the HB), because the algorithm used to calculate diffusion velocities requires the presence of either He or H. For technical reasons eliminating this limitation requires the rewriting of major sections of the code and this is outside the scope of this paper. For a few models the calculations were stopped after less than 32 Myr (see Appendix B) because of convergence problems.
 |
Fig. 3 Mass within and above the He II, He I, and H convection zones as a function of Teff. The H convection zone is separate from the He I convection zone in only a few models. For stars hotter than 22 000 K, the temperature at the bottom of the convection zone is less than a factor of 2 higher than Teff and is probably not precisely determined by interior models; it is not shown. The color code is the same as in Fig. 2. |
The mass in the surface convection zone is usually one of the most important stellar model properties for atomic diffusion because it is thoroughly mixed and separation generally occurs below. The bottom of the He II, He I, and H convection zones are shown in Fig. 3. The bottom of the He II convection zone does not depend significantly on metallicity in so far as the points define a single line (for instance, at low Teff, the magenta stars are on the same line as the blue stars). Just as occurs on the main-sequence of Pop II stars (see Fig. 1 of Richard et al. 2005), the mass in and above the surface convection zone depends nearly only on Teff, which effectively defines the depth of the surface convection zone. Calculated models cooler than 22 000 K are shown with metallicities ranging from Z0 = 0.0001 to 0.02. For stars hotter than 22 000 K, the temperature at the bottom of the convection zone is less than a factor of 2 higher than Teff, and this outer structure is probably not precisely determined by interior models. We decided not to show the mass above that Teff. The mass mixed by turbulence, ~10-7 M⊙ in this paper (see Sect. 3.2), is always larger than the mass in the surface convection zones. The latter then does not play a major role.
3.1. A 30 100 K sdB vs. a 14 000 K HB star
In Fig. 4, are compared the internal concentrations in a 30 100 K HB (0.51 M⊙; right panel) with those in a 14 000 K HB star (0.59 M⊙; left panel). Both started with the same metallicity (Z0 = 0.0001) and have spent the same time on the HB, 25 Myr. Given that they both started with Z0 = 0.0001, the two have similar Fe peak surface overabundances (a factor of ~ 200 overabundance from the original abundance of the star), but very different He, N, Ne, Na, Mg, Al, and Si surface abundances (compare the black curves in the right and left panels of Fig. 5). However, the lower temperature model has a radius 5.4 times larger than that of the hotter model. The hotter model is shown, in the small central inset, on the radius scale of the cooler one. The central region (defined as the region where 12C has been produced by He burning) of the two models is quite similar. By comparing the central region of the inset with the central region of the left panel, one notices that the various concentrations are about the same at approximately the same radius and inner mass (that is as a function of mr, the mass within radius r) in both models. However, while abundance variations caused by nuclear reactions extend over the inner 50% of the radius in the hotter model, they extend only over the inner 10% of the radius in the cooler model. Furthermore the central region corresponds to different fractions of the stellar mass of the two models: it is the inner 99% by mass of the 0.51 M⊙ star, but it corresponds to the inner 85% by mass of the 0.59 M⊙ model. The difference originates in the different peeling applied to the red giant to obtain the different Teff of the two models: 14% more mass has been removed from the red giant to obtain the 30 100 K model than to the cooler model. Indeed approximately the same inner mass is affected by nuclear reactions in both models, and the structure of the central core is similar in both. However, the envelope has quite a different structure, because it extends much farther in the higher mass model. Abundance variations caused by diffusion are seen to extend over the outer 40% by radius for many species in both models so that, as a function of the fractional radius as used in Fig. 4, the outer region (log ΔM/M∗ < −5) has many similarities in the two. However, between log ΔM/M∗ = −5 and the central region, the concentration variations are quite different. Furthermore, even when the fractional radius is about the same in the two models, the thickness in physical distances differs by the scale factor of 5.4.
 |
Fig. 4 Color-intensity coded concentrations in two HB stars of the same metallicity after 25 Myr on the HB. Left panel with a Teff of 14 000 K (0.59 M⊙) and right panel of 30 100 K (0.51 M⊙). The radial coordinate is the radius and its scale is linear, but the logarithmic value of the mass coordinate above a number of points, log ΔM/M∗, is shown on the left of the horizontal black line. The concentration scale is given in the right insert. Small circles near the top of the left panel mark the extent of the surface convection zone, while similar circles near the center of both models mark the central convection zone. The small inset in between the two panels shows the high Teff star, that is the right panel, on the radius scale of the low Teff star, that is the left panel. For −7 < log ΔM/M∗ < − 4 the concentration is quite different for many species. It is surprisingly so for C and O for log ΔM/M∗ > − 2. See the text. A black-and-white version of this figure may be found in Fig. A.1. |
 |
Fig. 5 Comparison of surface abundances expected in 14 000 (black line, left panel) and 30 100 K (black line, right panel) HB stars with Z0 = 0.0001, whose interior is shown in Fig. 4. In the left panel, to facilatate a comparison with the turbulence model used by Michaud et al. (2008, see the text for details), the red curve is taken from the left panel of their Fig. 11 and the data for B203 from Behr (2003). In the right panel the other curves correspond to stars of original metallicities of Z0 = 0.001, 0.004, and 0.02 and the data for Feige 48 are from O’Toole & Heber (2006). Gray is used for data points of atomic species, which are not included in our calculations because they are not in OPAL opacities. |
In Fig. 5 the black curves represent the surface abundances of the two stars of Fig. 4: left panel, 0.59 M⊙ model; right panel, 0.51 M⊙ model. The right panel also contains results for models of higher metallicities than used in Fig. 4; the original metallicities range up to Z0 = 0.02. The surprise is the similarity of the surface Fe abundance: it is nearly solar in both the left and right panels and for all curves of the right panel; this corresponds to a factor of 1 to 200 overabundance from the original abundance of the star, depending on the original metallicity. The Fe abundance seems to be determined by saturation of grad(Fe) where the separation occurs. One may relate them to the grad(Fe) at the bottom of the mixed zone for the turbulence model used. The black curves in the left and right panels are quite similar from Ca to Ni, but differ strongly from C to K. This figure will be further discussed in Sect. 4.
3.2. Determining the mixed mass
In Fig. 6, are shown the internal distributions of Fe and Ni in four models of the same mass and original metallicity, but with different turbulence. The original Fe mass fraction at the beginning of HB evolution was ~10-4.1 throughout the star with only small variations left over by red giant evolution (see Michaud et al. 2010). The grad(Fe) has clearly defined peaks at around log ΔM/M⊙ = −7.5 and at around log ΔM/M⊙ = −5 (these may also be seen in Fig. 3 of Michaud et al. 2008). In between these peaks grad(Fe) remains slightly larger than gravity, allowing a limited Fe flux to be pushed toward the surface and creating a small underabundance over the interval −5 < log ΔM/M⊙ < −4, the iron from that mass interval being pushed toward the surface. Between log ΔM/M⊙ = −5 and slightly below the bottom of the mixed zone, the Fe abundance is determined by the requirement of flux conservation. Immediately below the mixed zone, a Fe gradient develops to satisfy the diffusion equation as grad(Fe), the Fe abundance in the mixed zone and the Fe flux coming from below evolve. The largest turbulence shown is labeled by log ΔM0/ M⊙ = −7.5; it is used for most calculations and leads to about solar surface Fe abundance. The surface Fe abundance is mainly determined by the value of grad(Fe) immediately below the mass mixed by turbulence. Because at log T ~ 5.4, grad(Fe) is larger than g even at solar Fe concentrations, mixing only from the surface to log ΔM/M⊙ = −8.6 (or log T ~ 5.4) leads to larger X(Fe) than observed. One needs to mix farther inward, to log ΔM/M⊙ ~ − 7 for surface Fe abundances to be about solar. This in practice is what fixes the mixed zone for the models presented in this paper, so that the mass in the mixed zone was fixed by the Fe abundance in sdBs. It was then used for all sdB and HB calculations with Teff from 7000 to 35 000 K. A mixed mass a factor of 10 smaller would clearly lead to unacceptably large Fe abundances, while a factor of three larger is marginally excluded.
 |
Fig. 6 Internal distribution of Fe and Ni together with their relation to grad(Fe) and grad(Ni) in a 0.5 M⊙ model with Z0 = 0.001 for four turbulence strengths, each anchored at a fixed ΔM0 (see Eqs. (1) and (3)), identified in the upper panel. The solutions labeled −7.5, −8 and −9 are after 32 Myr on the HB, while the solution labeled − 10 is after 7 Myr. The lower panel gives κR as a function of log ΔM/M⊙. A local maximum of grad(Fe) and of κR occurs for log ΔM/M⊙ between − 10 and − 9 and corresponds to log T ~ 5.5. When the iron abundance becomes rapidly much higher than solar in contradiction with observations of sdB stars. The function 1/μ0 is shown (solid lines) for each model in the panel above that for κR. In the same panel, the function 1/μ0eff is shown by dotted lines. It is defined in Sect. 5.3. |
In the third panel, is shown 1/μ0, where μ0 is the reduced mass per nucleus, that is excluding electrons. When , it has a local maximum interior to the Fe accumulation. It is caused by the accumulation of metals pushed upward by grad. The local maximum is very small for . There still is an accumulation of metals in this case above log ΔM/M⊙ = −6.0, but its effect in increasing μ0 is largely canceled, for , by the decrease of the He concentration. It was verified (not shown) that for turbulence with , there was no μ0 inversion related to metal overabundances for metallicities of Z0 = 0.0001, 0.001 and 0.02 and, in each case, in both a star of 30 000 K and of 15 000 K. The case shown in Fig. 6 is the one with the largest effect among all those verified.
3.3. Radiative accelerations and interior mass fractions
Radiative accelerations are shown at ~25 Myr after ZAHB in Fig. 7, in the left panel for various metallicities, while in the right panel they are shown at various Teffs for a metallicity of Z0 = 0.001. The grads clearly vary more with Teff at a given metallicity than with metallicity at a given Teff. The change with metallicity is mainly due to saturation of the lines, which causes a general reduction of grad as metallicity is increased; also as metallicity is increased, T increases at a given and a given ionization state shifts toward the surface. As Teff increases however, the radiative flux increases with Teff4 and furthermore, gravity increases by orders of magnitude, strongly affecting the ionization equilibrium at a given within the star. As seen in the figure, a given grad maximum migrates toward the surface as Teff increases.
In the right panel of Fig. 7 one notices large scatter for grad(P) in the Teff = 10 700 K model. We verified by an analysis of the spectra used to calculate grad(P) that very few lines contribute to it in the Teff = 10 700 K model. At , where the grad(P) curve is most irregular, a single line contributes at least 30% of the value and five lines, the following 30%. Given that these are calculated in opacity sampling, this leads to the observed fluctuations. For more details, see the discussion of grad(Li) in Richer & Michaud (2005) and in Sect. 3 of Vick et al. (2010). Because of the uncertainties in grad(P), the corresponding curve for X(P) is not shown in Fig. 8. The grads only matter where turbulence does not force homogenization, so only for . No large glitches owing to improper sampling occur for any of the other cases shown for . Abundance variations as seen in Fig. 8 do lead to variations in grads, however. In the same model, for instance, the Ca abundance minimum below the mixed zone is partly responsible for the grad(Ca) peak at the same place. The large overabundance of Ni in the mixed region of the Teff = 10 700 and 15 000 K models is mainly responsible for the rapid variation of grad(Ni) there.
 |
Fig. 7 Radiative accelerations for a subset of the included species in models with turbulence anchored at a fixed ΔM0 = 10-7.5 M⊙, after approximately 25 Myr on the HB. Dotted lines represent gravity. Left panel: in models with Teff ~ 31 000 K and metallicities of Z0 = 0.0001, 0.001, 0.004 and 0.02, (masses from 0.51 to 0.47 M⊙) from top to bottom. Right panel: with Z0 = 0.001 and various masses corresponding, from bottom to top, to Teffs of 10 700, 15 000, 20 000, 25 000, and 30 400 K. |
 |
Fig. 8 Abundance profiles corresponding to the grads of Fig. 7. The abundance at the right of each small panel still approximately equals the starting abundance, while that at the left is the surface abundance after 23 Myr of HB evolution. |
In the left panel of Fig. 8 one sees that the surface abundances at 25 Myr increase as the starting abundances increase. However, saturation plays a role for all species shown: the range in surface abundances is smaller than the range of starting abundances. Saturation is most evident for Si and Fe, whose surface abundances differ by at most a factor of 3, while starting abundances covered a range of 200, which is still visible in the deeper layers. In the right panel of Fig. 8 one sees a much less regular behavior. The starting abundances were the same for all models, as is still evident from the deeper layers, at . The surface abundance of Si is smallest in the coolest model, but the surface abundance of Ni is largest in the coolest model. Iron peak elements have a similar behavior with Teff. Lower mass nuclei vary much more differently (compare Al and Ca for instance), as could be expected from the behavior of grads on the right panel of Fig. 7. The shape of the surface abundance curve as a function of Z, the nuclear charge number, is then expected to vary with Teff.
4. Comparison with observations
4.1. Metallicity, Teff, and age dependence
Before comparing our results with observed abundance patterns of individual stars, it is useful to evaluate the dependence of the calculated abundances on the original metallicity, Teff, and age.
If one observes a star of 30 000 K, how sensitive are its surface abundances to the original stellar metallicity? In the right panel of Fig. 5 the surface abundances at 25 Myr after ZAHB are shown in four stars of original metallicity ranging from Z0 = 0.0001 to 0.02. They were chosen to have Teff as close as possible to 30 000 K, because Teff is usually the better determined quantity. This imposed different masses, which range from 0.47 to 0.51 M⊙. While the original abundances vary by a factor of 200, the final ones vary by at most a factor of 30 and for Fe and Ni by a factor of about 3. The largest differences are for species around Ca and Ne. Generally a star that starts with a larger metallicity ends up with larger abundances of metals, but there are a few exceptions, such as P and S in the Z0 = 0.004 and 0.02 models. This must be caused by a competition for photons with, for instance, Fe (see Fig. 4 of Richer et al. 1998). Helium is most underabundant in the higher Z0 stars.
Comparing the right and left panels of Fig. 5 shows that a factor of 2 difference in Teff for stars originally with Z0 = 0.0001 does not change the expected Fe peak abundances considerably, but it does lead to large differences for atomic elements with masses equal to or smaller than that of Ca. While a peak occurs for N in the higher Teff model, it occurs for P in the lower Teff one. The differences can reach 1–2 orders of magnitude. But for smaller Teff differences, the abundance variations tend to be relatively small (see Fig. 9). Phosphorus is most sensitive, its abundance variation reaching a factor of 5 between 11 500 and 14 000 K (however see also Sect. 3.3). But for Fe and Ni an uncertainty of 2500 K hardly affects the expected surface abundances even though they are more than a factor of 100 overabundant. By comparing the left and right panels of Fig. 10, one notes that a relatively small Teff change (~3000 K) can lead, in a cluster with Z0 = 0.001, to significant abundance variations for species between Si and Ti. For heavier iron peak elements, the variations are much smaller.
Examples of age dependence are shown in Fig. 10. The abundance variations are rapid for the first 5 Myr, but much smaller between 10 and 30 Myr for all species whose abundance increases. The variations are much more regular for species with A < 10, which become underabundant. In a population of stars of various unknown HB ages, one consequently expects most stars to have at least the overabundance attained after the first 5 Myr. See also Figs. B.1 to B.4.
 |
Fig. 9 Surface abundances expected for models with turbulence anchored at , Z0 ~ 0.0001 and three slightly different masses, or equivalenty Teff. Observations for star B315 of M 15 with Teff ~ 13 000 K are from Behr (2003). These are the same observations as used in the right panel of Fig. 11 of Michaud et al. (2008). The turbulence models are different, however. The agreement is equivalent. |
4.2. Low-metallicity clusters
In Michaud et al. (2008) one turbulence model anchored at a fixed T was shown to reproduce abundance anomalies observed on the HB of M 15 from 11 000 to 15 000 K. A single turbulence model was used for all HB stars of that cluster. For this paper, we tried using the same model for HB stars of higher metallicities and for sdBs of higher Teff, but it was found not to reproduce all observations. We then searched for a model anchored at a fixed , that is at a fixed fraction of M⊙. It is a priori not clear how the different turbulence models (given by the difference between Eqs. (2) and (3) during evolution) should affect surface abundances. It was first verified that one obtains with turbulence anchored at , as good an agreement between observations and calculations as shown in Figs. 9 to 12 of Michaud et al. (2008) by comparing the detailed abundances for two stars of M 15 and by comparing the Fe abundance for all stars as a function of Teff.
Results obtained with both turbulence models are compared in the left panel of Fig. 5 with observations of the Teff ~ 14 000 K star B203, from Behr (2003). For all calculated species, the surface abundances calculated with both turbulences are within a factor of 3 of each other except for S, where the agreement with observations is better with the model of this paper. Note that for iron peak elements the abundances are more than 100 × the original abundances.
 |
Fig. 10 Comparison of abundance patterns with models of metallicity [Fe/H] = −1.3 and with turbulence anchored at . Left panel: surface abundances expected at six HB ages, from 0.0 to 31 Myr, for a 0.55 M⊙ model compared with observations for WF4–3085, a star of M 13 with Teff ~ 14 000 K, from Behr (2003). Right panel: surface abundances at five HB ages, from 0.0 to 16 Myr, for a 0.58 M⊙ model compared with observations of the Teff = 12 000 K star 469 of NGC 1904 from Fabbian et al. (2005). |
 |
Fig. 11 Left panel: surface concentration of Fe as a function of Teff in clusters (M 15, M 68 and M 92) from Behr (2003) with original Fe concentration ~ −2.3. Models are shown for this metallicity. Each color-coded segment represents the evolution of the surface Fe concentration. The line is solid for the time interval from 10 to 30 Myr after ZAHB, but dotted from 0 to 10 Myr. Bottom part: rotation velocities; three stars have their rotation velocities and [Fe/H] in red to facilitate their identification. Right panel: field stars also from Behr (2003). The distribution of metallicity for the cooler field stars gives an indication of the original metallicity distribution for the hotter field stars as well as for sdBs. |
In Fig. 9 observations (Behr 2003) of star B315 of M 15 (Teff ~ 13 000 K) are compared with calculations with turbulence anchored at for stars of slightly different masses or Teff. Two observed values are shown for Mg, the upper one for Mg I and the lower one for Mg II. The agreement may be compared with that obtained in the right panel of Fig. 11 of Michaud et al. (2008). At least from their effect on surface composition, the two turbulence models are seen to be equivalent for B315.
A third comparison with previous results may be made by comparing Fig. 9 of Michaud et al. (2008) with the left panel of Fig. 11, where observed Fe abundances in the clusters M 15, M 68 and M 92 are compared with our calculations over the Teff interval from 7000 to 15 000 K. Lines represent the Fe surface abundance evolution during the first 30 Myr of HB evolution. They are color-coded as a function of the mass of the model, the first 10 Myr, dotted, the following 20 Myr, solid. Given the slope of the solid lines, the Fe abundance may continue to increase by a factor of 1.5–2 during the following 60 Myr. The calculated abundances then agree with observed abundances from 11 000 to 15 000 K. The stars with Teff < 11 000 K are influenced by rotation as shown by Quievy et al. (2009). The comparison with observations is extended to more clusters of low metallicity than considered by Michaud et al. (2008). Few stars hotter than 11 000 K are added, but there are three rapidly rotating ones; they follow the pattern explained by Quievy et al. (2009) and are shown in red. When compared with the results of Fig. 9 of Michaud et al. (2008), those of Fig. 11 vary less as Teff increases from 11 000 to 16 000 K. There is a hint that this agrees better with observations, though the error bars are too large to allow a firm claim.
The model used here for all calculations reproduces observations as well as that used in Michaud et al. (2008). As will be verified in Sect. 4.4, fitting observed anomalies of stars over a large Teff interval requires mixing to involve a given mass, approximately the same independent of metallicity and Teff.
 |
Fig. 12 Left panel: surface concentration of Fe as a function of Teff in clusters (M 3, M 13 NGC 288) from Behr (2003) with original Fe concentration between − 2.3 and − 1.3 dex the solar one. Models are shown for those two metallicities. Each color-coded segment represents the evolution of the surface Fe concentration. The line is solid for the time interval from 10 to 30 Myr after ZAHB, but dotted from 0 to 10 Myr. Right panel: surface concentrations of Fe as a function of Teff in the cluster NGC 2808 from Pace et al. (2006). The color-coding is defined in footnote (5). For most models the spanned time interval is approximately 30 Myr. |
4.3. Intermediate-metallicity globular clusters
For intermediate-metallicity clusters, comparisons are made in Fig. 10 with patterns of anomalies for two stars in clusters6 (M 13 and NGC 1904) and in Fig. 12 for observations of Fe as a function of Teff in M 3, M 13, NGC 288 and NGC 2898.
The expected patterns at six HB ages in a 0.55 M⊙ model with original [Fe/H] = −1.3 are compared in the left panel of Fig. 10 with WF4-3085 from the cluster M 13 (Behr 2003). According to Table 1 of that paper, the cluster iron abundance is [Fe/H] = −1.54. In the right panel, comparisons are also made of models with original [Fe/H] = −1.3 with star 469 of the cluster NGC 1904 (M 79) (Fabbian et al. 2005) which has [Fe/H] = −1.59 according to Kraft & Ivans (2003). Because according to Fig. 5 results are not too sensitive to metallicity (see also Fig. 13), this comparison is accurate enough given that models with original [Fe/H] = −1.55 were not available. In WF4-3085 the abundances are well reproduced by models of 10 Myr or more. In 469, they are well reproduced by models of 5 Myr or more. Given error bars, all species heavier than Mg are well reproduced in both. One may argue about P in WF4-3085, which is claimed to be overabundant by a factor of 500, while the model gives a factor of 50 overabundance. The main difficulty is with He however, which is observed to be underabundant by a much larger factor than models predict. On the one hand this observation is probably difficult, because these are relatively cool stars where the He abundance is more difficult to determine. On the other hand, He is largely neutral in the atmosphere, which may enhance additional effects of diffusion there. These will be further discussed in Sect. 5.1.
 |
Fig. 13 Surface abundances expected at 25 Myr for models with turbulence anchored at calculated with Z0 = 0.0001, 0.001, 0.004 and 0.02. Observations are for PG0101+039 from Blanchette et al. (2008). |
 |
Fig. 14 Surface concentrations of Fe as a function of Teff in sdB stars. Models were calculated with original concentrations of [Fe/H] = −2.3, −1.3, −0.4 and 0.0. Models span the Teff interval from 20 000 to 37 000 K and the mass interval from 0.47 to 0.52 M⊙. The lines give the surface abundance variation for each calculated model. They are color-coded as a function of the mass of the model, which may be read by zooming on the figure in the electronic version; solid lines for the time interval from 10 to 32 Myr after ZAHB and dotted from 0 to 10 Myr. The dotted line starts at the original abundance of the model. For most models the spanned time interval is approximately 32 Myr. Note that most models starting with a solar metallicity have very short tracks. Observations (circles) are from Geier et al. (2008), Geier et al. (2010) and Geier (2010, priv. commun.). Inverted triangles are upper limits. The stars in red in Fig. 2 are also in red in this figure. The bottom part of the figure gives the rotation velocities and the error bars on Teff. |
In the right panel of Fig. 12, the models with [Fe/H] = − 0.7 and [Fe/H] = − 1.3 are compared with observations of NGC 2808 from Pace et al. (2006). The [Fe/H] = −1.14 determined by Carretta et al. (2004) agrees within error bars with the [Fe/H] of the cooler HB stars (below 12 000 K) and is bracketed by tracks for models with [Fe/H] − 1.3 and − 0.7. By zooming in on the figure, the origin (zero age HB) of each track may be clearly seen. The break between HB stars with the same Fe abundance as giants and those with an overabundance by a factor of ~ 20 occurs slightly above 12 000 K, which is ~ 1000 K hotter than in the three clusters M 3, M 13, and NGC 288 in the left panel whose original [Fe/H] are bracketed by tracks for [Fe/H] = −2.3 and − 1.3. In Fig. 4 of Quievy et al. (2009), the Teff interval from 10 000 to 12 000 K is the interval over which anomalies are expected in only a fraction of the stars. In M 3, M 13, and NGC 288 (left panel), all stars with Teff > 11 000 K rotate slowly and have [Fe/H] within the range expected over most of the lifetime of a cluster with the original metallicity of the cluster. The cooler stars have sufficiently large rotation velocities for no anomalies to be expected7. Because we do not know the rotation velocities of the NGC 2808 stars between 11 000 and 12 000 K, we do not know if the 1000 K difference in the Teff of the break in abundances is significant. One may then say that the run of Fe abundances in BHB stars shown in Fig. 12 from 11 000 K to 17 000 K is well represented by calculations with a single value for the mixed mass of about 10-7 M⊙.
Finally the advantage of using clusters over field stars may be inferred from the right panel of Fig. 11. There, the stars with Teff < 11 000 K give an indication of the original Fe distribution in the field. No information is available on the original Fe abundance of individual stars with Teff > 11 000 K, however. Consequently the link with rotation is more difficult to establish. According to Fig. 4 of Quievy et al. (2009), the 13 500 and 15 000 K stars with rotation velocities of 30–40 km s-1 may or may not rotate fast enough for atomic diffusion to be affected, depending on whether meridional circulation penetrates into the surface convection zone or not. Because both stars may have a solar metallicity to start with, little can be inferred from their relatively large rotation velocities. The other field stars with large metallicity all have very small rotation velocities, as was the case in clusters.
4.4. Field sdB stars
For sdB stars, neither the age nor the metallicity are known. Anomaly patterns are compared with observations for two stars with models of four different original metallicities. Comparisons are made with sdBs of Teff ~ 31 000 K using data from O’Toole & Heber (2006) (Feige 48, see right panel of Fig. 5) and Teff ~ 30 000 K in Fig. 13 using data from Blanchette et al. (2008) for PG0101+039. We decided to compare with models of 25 Myr, whose surface abundances are representative of a significant fraction of the evolutionary span. For Feige 48 (Fig. 5), 14 of the 17 species that were both calculated (with original [Fe/H] between −0.7 and −1.3 or Z0 between 0.001 and 0.004) and observed agree reasonably well. For PG0101+039 (Fig. 13), 15 species are both calculated and observed, and 12 agree reasonably well with either of the two lower metallicity models. The agreement is not perfect however, but this is perhaps not too surprising given the uncertainty of the age.
Once neither age nor original metallicity are known, perhaps as useful information is obtained by comparing an ensemble of models spanning the metallicity, mass and age intervals of a large number of stars. Models of four metallicities are used with ages spanning the first 32 Myr of HB evolution and a mass interval leading to the observed Teff interval of 20 000 to 37 000 K. This Teff interval corresponds to that of a recent survey of the chemical composition of sdB stars, whose preliminary results are published in Geier et al. (2008) and Geier et al. (2010) with additional private communications to us from Dr Geier. In Fig. 14, observations of X(Fe) are the gray (or red) circles with triangles being upper limits. The long dashed gray lines define the interval where observations are found. They are similarly defined for other elements from the observations and are shown in order to constrain the observed abundance interval in Figs. 15 and 16. The rotation velocities are shown on the lower panel of Fig. 14. They are all smaller than 10 km s-1, which is too small to interfere with atomic diffusion at those Teff according to Quievy et al. (2009). The uncertainty on Teff is also shown in that panel.
Comparisons are made as a function of Teff using observations from Geier et al. (2008) and Geier et al. (2010) in Fig. 15 for Ne, Mg, Al, Si, P, S, Ar, K, Ca,Ti, Cr, and Fe and in Fig. 16 for He and CNO. These are the species for which observations are reported by Geier et al. (2010), and which are also present in the OPAL opacity calculations. An indication of the limits of the domain of observed points is given by the long dashed gray lines, which are defined for Fe in Fig. 14. For most atomic species, the lower broken gray line corresponds to as many upper limits as data points. We refer the reader to the original publication of the data.
In all three figures, for each model and each chemical species the abundance is indicated by a curve originating at the original abundance, dotted for the first 10 Myr and solid until the end of the calculation, usually around 32 Myr. The various colors distinguish masses (see footnote 5). The masses are indicated at the end of each colored curve in Fig. 14 and may be read more easily by zooming in the electronic version. In doing the comparison between observations and calculations, one should take into account that the calculations covered the first 32 Myr of the HB evolution. Because the HB evolution probably lasts three times longer, the colored lines should often be extended by a factor of 2, or perhaps 3 when no saturation is involved. When saturation is important, the lines can be much shorter however as is seen for many models that originally had the solar abundance (these are easily identified because their dotted line starts at the solid horizontal gray line in Fig. 15).
 |
Fig. 15 Surface abundances for atomic species from Ne to Fe. Iron is also in Fig. 14 where is found a detailed caption. The domain of observed values is bounded by long dashed broken gray lines which are also shown for Fe in Fig. 14. The domain of abundances often extends below the lower curve because many measurements are upper limits (see Geier et al. 2008, 2010). The solid horizontal gray line is the solar abundance. Note that individual panels span 7 orders of magnitude in abundances. |
For Fe (Fig. 14) the calculated values cover the range of observed Fe abundances at all Teff’s especially when the expected extension of the curves to the end of the HB evolution is taken into account. The concentration of Fe abundances between solar and 10 times below solar is to be expected given the expected original distribution of Fe abundances as seen in the right panel of Fig. 11. A number of upper limits were measured (the gray triangles) and can be accounted for by the early evolution of stars starting with very small original Fe abundances. Even those, however, end up spending most of their HB evolution within the main interval of the observations. The objects represented by red circles are also compatible with the results presented here even though they have a smaller gravity and so are probably more evolved than the models (see Fig. 2).
The comparison between calculated and observed abundances for elements from Ne to Fe is shown in Fig. 15. Iron is repeated to allow evaluating the effect of representing observations as lying between the two long dashed gray lines of each panel. But the lower bound frequently appears to correspond to the smallest abundance that can be detected because it generally corresponds to the data points defined as upper limits by Geier et al. (2008) and Geier et al. (2010). The reader will benefit from looking at the original data. In two cases, Si and S, observed abundances cover the same interval as the simulations’ starting abundances (the dotted lines originate within or very close to the gray lines). In both cases they remain within those bounds. For Si, the small observed Teff dependence is obtained, while for S, the observed slight increase around 35 000 K is not reproduced. In four cases (K, Ca, Ti and Cr) the observed abundances are 4 to 5 orders of magnitude larger than the original abundances in the more metal poor original models. Taking into consideration the number of upper limits in the observations and that only the first third of HB evolution is covered by the lines, the agreement is generally good. One property that is not reproduced is the apparent increase in observed abundance above 33 000 K for K and Cr. For P and Ar the observed values are compatible with observations except for Teff > 33 000 K; however for P there are mainly upper limits.
For C and N, (see Fig. 16) there seems to be strong disagreement for Teff > 33 000 K, while at lower Teff, there is agreement for C, while N is on average perhaps three times more abundant than expected. This could be related to some nuclear effects. On the other hand, calculated O seems generally compatible with observations.
 |
Fig. 16 Surface concentration of He as a function of Teff in sdB stars. See the caption of Fig. 14 for the definition of the curves. Observations (circles) are from Geier et al. (2008), Geier et al. (2010) and Geier (2010, priv. commun.). The stars in red in Fig. 2 are also in red in this figure. The lines for He were stopped between X(He) = 0.001 and 0.0001 because the evaluation of the surface He abundance becomes inaccurate for smaller values. |
Our calculations of the surface He abundance compared with observations in Fig. 16 are constrained by a limitation of our code, because in our calculation algorithm X(He) is obtained by subtraction8. Consequently the lines for He were stopped between X(He) = 0.001 and 0.0001 because the evaluation of the surface He abundance becomes inaccurate for smaller values when Y ≪ Z. One has the surprising result that observations of X(He) agree with calculations in the stars with Teff > 29 000 K, but not cooler. The agreement for stars with Teff ~ 30 000 K is reinforced by the detailed comparisons shown in Figs. 5 and 13. In the higher Teff stars, the observed abundance range is easily covered once one takes into account that calculations cover only the first third of the HB life span. While still helping at lower Teff, this is not sufficient to explain the absence of stars with an underabundance smaller than a factor of 0.1, nor the presence of stars underabundant by a factor of 10-4. This reinforces the problem with He abundance in globular cluster stars (see Fig. 10) and is discussed in Sect. 5.1.
5. Conclusion and general discussion
Stellar models have been evolved over the first 32 Myr of HB evolution for masses leading to the Teff interval of 8000 to 37 000 K and for metallicities ranging from Z0 = 10-4 to 0.02. A total of some 60 models were evolved. They all started from the evolution, from the zero age main-sequence to the He flash, of 0.8 to 1.0 M⊙ models of metallicities from Z0 = 10-4 to 0.02 described in Michaud et al. (2010, see in particular their Sect. 2). They corrrespond to the metallicities of the various globular clusters whose horizontal branch was studied. They also cover the metallicity (right panel of Fig. 11) and Teff intervals (right panel of Fig. 2) of field sdB stars.
5.1. The main results
One remarkable observational property of both field sdB stars (studied here up to 37 000 K) and cluster HB stars with Teff > 11 000 K is that their Fe abundance is relatively close to solar whatever the metallicity of the cluster and independent of the unknown original Fe abundance in the case of sdB stars. In the calculations described above for field stars, the original metallicity was varied from Z0 = 0.0001 to Z0 = 0.02. In globular clusters, the original abundances for the calculations are those of giants of the cluster. As long as HB stars have their outer 10-7 M⊙ mixed, it has been shown to follow naturally from the stellar evolution with atomic diffusion that the final Fe abundance ended within a factor of ten interval nearly independent of Teff (see Sect. 4 and in particular Figs. 11, 12 and 14). Overabundances of Fe by factors of up to 100 are implied. Reducing the mixed mass by a factor of ten or more leads to unacceptably large Fe abundances (see Sect. 3.2 and Fig. 6). The well observed Fe abundance consequently constrains the mixed zone in stellar evolution models9. Is this mixing compatible with observation of other atomic species?
Detailed comparisons were carried out for a number of sdBs and cluster stars in which the abundance of many elements were determined. In all cases the comparison between observations and model calculations led to acceptable results (see Sect. 4 and Figs. 5, 9, 10, and 13). Approximately 12 of 15 elements agree reasonably in each case. This is obtained without any adjustment because the only adjustable parameter was fixed by the Fe abundance. This is true in globular clusters, whose original [Fe/H] varies from − 2.3 to − 0.7, as well as in field sdB stars. For these, a comparison with a large sample of field stars covering a large age and original metallicity interval was also carried out with general agreement (see Figs. 15 and 16).
The calculated surface abundance of He agrees with that observed in the sdB stars shown in Figs. 5 and 13 and also for Teff > 25 000 K in Fig. 16, but there appears to be a large discrepancy in the cooler stars and in particular those HB stars shown in Fig. 10 and the left panel of Fig. 5. In the latter cases, Teff is low enough that He is not ionized in the atmosphere. The neutral He atomic diffusion coefficient is ~ × 100 larger than the ionized one (Michaud et al. 1978). Additional element separation could be occuring in the stellar atmosphere for He because its settling velocity there is enhanced by its being neutral. There is observational evidence for such stratification of Fe (Khalack et al. 2007, 2010; LeBlanc et al. 2009, 2010). Other species, for which grad in the atmosphere would happen to be very large, could also be affected by separation in the atmosphere if the mixing there is not very strong. The evolutionary models described in this paper may then not tell the whole story. In real stars, there could be additional abundance variations between the surface and the bottom of the mixed mass of some 10-7 M⊙.
Since in particular gravity varies by two orders of magnitude over that Teff interval on the HB, the similarity of observed abundances is quite surprising. It is clearly linked to the saturation of radiative accelerations.
The agreement between the observations over the whole HB and the expected abundance anomalies from the evolution calculations leaves little doubt that radiative accelerations are the main cause of abundance anomalies on the HB.
5.2. Turbulence or mass loss
In this paper it was found that if the outer 10-7 M⊙ was mixed10 by turbulence, most observed abundance anomalies followed. However as soon as an adjustable parameter has an effect on the results, one must remain cautious and, in spite of the observational support described above, one must question if the physical process assumed to do the mixing is the only one possible or if there exist alternatives. In the only stellar evolution calculations we know of where mixing (or homogeneity) was not assumed for the outer region, it has been shown by Vick et al. (2010) that abundance anomalies observed on AmFm stars could be reproduced as well by a model that assumes mass loss as by the model where turbulence is in competition with atomic diffusion (Richer et al. 2000; Talon et al. 2006). They found that the velocity corresponding to the mass loss rate had to equal the atomic diffusion velocity at the stellar mass fraction where the mixed zone ends in the turbulence model. This occurs here at 10-7 M⊙. Presumably the same would be true in HB stars. Instead of turbulence, mass loss could play a role to reduce anomalies. One may evaluate the required mass loss rate by equating the corresponding velocity to the He settling velocity at 10-7 M⊙ using the expression 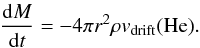 (4)It was found to equal 3–5 × 10-14 M⊙/yr at log ΔM/M∗ = −7, in a model with Teff ~ 30 000 K. A ten times smaller mass loss rate has been suggested before to explain in particular observations of Si in sdB stars (Michaud et al. 1985). The calculations included only the outer 10-5 M⊙ and the separation occured right in the atmosphere. Both the mass loss rates and the timescales of the calculations were smaller. A complete stellar evolution calculation including mass loss instead of turbulence as the mixing process seems justified for HB stars, along the lines investigated by Vick et al. (2010) for main-sequence stars.
(4)It was found to equal 3–5 × 10-14 M⊙/yr at log ΔM/M∗ = −7, in a model with Teff ~ 30 000 K. A ten times smaller mass loss rate has been suggested before to explain in particular observations of Si in sdB stars (Michaud et al. 1985). The calculations included only the outer 10-5 M⊙ and the separation occured right in the atmosphere. Both the mass loss rates and the timescales of the calculations were smaller. A complete stellar evolution calculation including mass loss instead of turbulence as the mixing process seems justified for HB stars, along the lines investigated by Vick et al. (2010) for main-sequence stars.
5.3. μ gradient inversions
It was shown in Sect. 3.2 that when the mixed mass is smaller than 10-7 M⊙, an inversion of the mean molecular weight often occurs (see Fig. 6). It has been suggested in a similar context by Théado et al. (2009) that such a μ0 inversion is unstable and should lead to mixing. It is tempting to conclude that this μ0 inversion is the cause of the mixing implied by observations. However, their analysis does not include the effect of grad on the instability. Since the radiative accelerations are the cause of the μ0 inversion, their role in the analysis of the hydrodynamical instability could be important. The metals that are supported by grads do not contribute to the increase of the weight of the material. So one may wish to consider an effective μ0 for which supported metals contribute negatively. Intuitively, one may assume that if the function ![\begin{equation} \mu_{0\mathrm{eff}} = \frac{\sum N(A_i) A_i m_{\rm p} [g-\gr(A_i)]} {\sum N(A_i) m_{\rm p} g} \label{eq:muoeff} \end{equation}](/articles/aa/full_html/2011/05/aa15997-10/aa15997-10-eq141.png) (5)does not decrease inward where μ0 decreases inward because of grads (which cause some metal abundances to increase outward), then grads may maintain stability. This function μ0eff is shown (inverted) by the dotted curves (see Fig. 6). Contrary to 1/μ0, 1/μ0eff increases outward where the Fe and Ni abundances increase outward. It seems to us that one should not conclude that a μ0 inversion caused by grads on metals immediately leads to an instability; further work is needed to investigate the nature of the μ inversion instability in the presence of radiative accelerations.
(5)does not decrease inward where μ0 decreases inward because of grads (which cause some metal abundances to increase outward), then grads may maintain stability. This function μ0eff is shown (inverted) by the dotted curves (see Fig. 6). Contrary to 1/μ0, 1/μ0eff increases outward where the Fe and Ni abundances increase outward. It seems to us that one should not conclude that a μ0 inversion caused by grads on metals immediately leads to an instability; further work is needed to investigate the nature of the μ inversion instability in the presence of radiative accelerations.
5.4. Asterosismology
In their groundbreaking work, Charpinet et al. (1996) have established that the Fe abundance expected to follow from atomic diffusion in the envelope of sdB stars should lead to pulsations. This was observationnally confirmed (Kilkenny et al. 1997). See also the reviews of Charpinet et al. (2001) and Fontaine et al. (2008). Their approach has the advantage to involve no adjustable parameter since they assume equilibrium between grad and gravity in the driving region for the pulsations. This implies that mass loss and turbulence have a negligible effect. It is however not established if in sdBs with small original metallicity there is enough Fe to sufficiently fill the region where the driving occurs. As noted in the conclusion to the tenth sdB for which a detailed asterosismic analysis had yielded the mass (Randall et al. 2009), a more accurate fit to the asterosismic data requires evolutionary models of sdB stars. The approach to equilibrium in the driving region was studied by Fontaine et al. (2006) starting from a solar Fe abundance. They showed using static models that the Fe abundance became able to drive pulsations within 105 yrs. These works are based on a detailed analysis of the structure of the outer regions of these stars.
Our results cleary show that from whatever Fe abundance sdB stars start with, a sdB star model with the outer 10-7 M⊙ mixed ends up with a solar Fe abundance in a fraction of the HB lifetime of 100 Myr. This could be used as a starting abundance for the calculations of Fontaine et al. (2006) mentioned above. Indeed, the curve labeled − 9 in Fig. 6 shows that after 32 Myr, starting from a metallicity 20 times below solar, the complete evolutionary models calculated here with OPAL data have accumulated approximately the same Fe abundance as shown in Fig. 1 of Fontaine et al. (2006) at the same age for a model starting with a solar abundance. According to Fig. 14, models starting with a Fe abundance 200 times below solar end up with three times less Fe after 32 Myr, but according to Figs. 1 and 3 of Fontaine et al. (2006) this is still sufficient to excite the spectrum.
More recently, using an analysis of the Fe abundance required to cause observed pulsations in sdBs, Charpinet et al. (2009) conclude that if Fe is the sole atomic species responsible for the pulsation of sdB stars, the Fe abundance needs to be log NFe/NH ~ −4.09 and −3.75 at Teff = 29 580 and 35 050 K respectively in the driving region. This is larger than the observed Fe abundance and suggests that some separation needs to occur between the driving region and the surface. However, from Fig. 8, Ni is easily a factor of 3 more overabundant than Fe, and it may contribute significantly to driving the pulsations as suggested by Jeffery & Saio (2007), just as it contributes significantly to iron convection zones in Pop. I stars (see Fig. 4 of Richard et al. 2001).
The models described in this paper clearly need to be tested by calculating their pulsation spectra. When models with mass loss become available (see Sect. 5.2), asterosismology could help decide which is the main mechanism competing with atomic diffusion driven by grad’s. This is outside the scope of the present paper, however.
Online material
Appendix A: Black-and-white version of Fig. 4
 |
Fig. A.1 Black-and-white version of Fig. 4. Gray-coded concentrations in two HB stars of the same metallicity after 25 Myr on the HB. Left panel with a Teff of 14 000 K (0.59 M⊙) and right panel of 30 100 K (0.51 M⊙). The scale of the radius is linear, but the logarithmic value of the mass coordinate above a number of points, log ΔM/M∗, is shown to the left of the horizontal black line. The concentration scale is given in the right insert. Small circles near the top of the left panel mark the extent of the surface convection zone, while similar circles near the center of both models mark the central convection zone. The small inset in between the two panels shows the high Teff star on the radius scale of the low Teff star. For −7 < log ΔM/M∗ < −4 the concentration is quite different for many species. It is surprisingly so for C and O for log ΔM/M∗ > −2. |
Appendix B: Properties of evolutionary models
Some of the properties of all evolutionary models calculated, grouped by metallicity. All models in Figs. B.1 to B.4 were calculated with a turbulent diffusion coefficient given by Eqs. (1) and (3) with ΔM0 = 10-7.5 M⊙. See Sect. 2.
 |
Fig. B.1 Models with Z0 = 0.0001. The curves are identified in the figure by the mass of the HB model. The color code is the same as used for the left panel of Fig. 2 and is defined in footnote [5]. Zero age HB is defined as the moment when X(12C) reaches 0.04. In the figures the curves are not all very precisely aligned to that value. X0(surfFe) identifies the Fe mass fraction in the original main-sequence model, similarly for the other species. |
Models illustrated in this article, with their ZAHB characteristics.
We use the expression HB stars for horizontal branch stars in clusters, and sdB stars for those in the field. In practice, because calculations are always done for a given metallicity, they are always made for cluster stars, in apparent contradiction to that rule when comparisons are made with field stars.
In this series of papers, the relative values of the α elements are increased following VandenBerg et al. (2000). Models are labeled according to their original Z0 value calculated before the α correction. See also Table 1 of Richard et al. (2002). This correction was not applied in the Z0 = 0.02 models.
The values of D(He)0 actually used in this formula were always obtained – for programming convenience – from the simple analytical approximation D(He) = 3.3 × 10-15T2.5/ [4ρln(1 + 1.125 × 10-16T3/ρ)] (in cgs units) for He in trace amount in an ionized hydrogen plasma. These can differ significantly from the more accurate values used elsewhere in the code.
Richer et al. (2000) found that using 2 or 3 instead of 4 as the exponent for ρ in Eq. (1) only changed the mixed mass corresponding to ΔM0. Talon et al. (2006) found moreover that distinguishing between different turbulence models required an accuracy of 0.03 dex, which is beyond the accuracy of current abundance determinations (see their Sect. 5).
We use color codes that depend on the envelope mass, that is on log 10(M∗ − MHecore)/M⊙. This expression is used to define an index referring to 16 predefined colors. The same code is used for all figures involving stars with Teff > 20 000 K. Another code is used when only stars with Teff < 20 000 K are present.
Variations in the abundances of Na and O, but not of Fe, as a function of Teff have recently been observed on the HB of M 4 (Marino et al. 2010). However, this is for cooler stars than the Fe abundance variations discussed here and in M 4, the O and Na abundance variations are probably caused by nuclear reactions. It would be of interest to verify the rotation velocities of the hotter stars in M 4, given the correlations seen in Fig. 11.
For an interesting correlation between [Fe/H], Teff and rotation in HB and sdB stars see Fig. 8 of Cortés et al. (2009).
If instead of using Eq. (3) one used Eq. (2) so that turbulence were fixed at a given T0, the mixed mass would vary by more than 3 orders of magnitude between stars of Teff = 12 000 and 30 000 K. We verified that starting with Z0 = 0.001, a 12 000 K HB star would develop solar surface Fe abundance, while a 30 000 K star would develop a Fe abundance 50 times solar. This would lead to completely unacceptable changes in relative surface abundances when taking sdBs and HB stars of clusters into account (see Figs. 12 and 14 for observed surface Fe abundances and also Fig. 6 for the effect of a change of the mixed mass by 2.5 orders of magnitude).
Acknowledgments
We thank Drs Ulrich Heber and Stephan Geier for very kindly communicating to us their data in tabular form. We thank an anonymous referee for a very careful reading of the manuscript and for numerous constructive remarks. This research was partially supported at the Université de Montréal by NSERC. We thank the Réseau québécois de calcul de haute performance (RQCHP) for providing us with the computational resources required for this work.
References
- Behr, B. B. 2003, ApJS, 149, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Behr, B. B., Cohen, J. G., McCarthy, J. K., & Djorgovski, S. G. 1999, ApJ, 517, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Behr, B. B., Cohen, J. G., & McCarthy, J. K. 2000, ApJ, 531, L37 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bergeron, P., Wesemael, F., Michaud, G., & Fontaine, G. 1988, ApJ, 332, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchette, J.-P., Chayer, P., Wesemael, F., et al. 2008, ApJ, 678, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., & Cacciari, C. 2004, ApJ, 610, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 1996, ApJ, 471, L103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 1997, ApJ, 483, L123 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 2000, ApJS, 131, 223 [Google Scholar]
- Charpinet, S., Fontaine, G., & Brassard, P. 2001, PASP, 113, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Charpinet, S., Fontaine, G., & Brassard, P. 2009, A&A, 493, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortés, C., Silva, J. R. P., Recio-Blanco, A., et al. 2009, ApJ, 704, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Fabbian, D., Recio-Blanco, A., Gratton, R. G., & Piotto, G. 2005, A&A, 434, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., et al. 2003, ApJ, 597, 518 [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., & Chayer, P. 2006, Mem. Soc. Astron. Ital., 77, 49 [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., et al. 2008, in Hot Subdwarf Stars and Related Objects, ed. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 231 [Google Scholar]
- Freytag, B., & Steffen, M. 2004, in The A-Star Puzzle, ed. J. Zverko, J. Ziznovsky, S. J. Adelman, & W. W. Weiss, IAU Symp., 224, 139 [Google Scholar]
- Geier, S., Heber, U., & Napiwotzki, R. 2008, ASP Conf. Ser., 392, 159 [NASA ADS] [Google Scholar]
- Geier, S., Heber, U., Edelmann, H., Morales-Rueda, L., & Napiwotzki, R. 2010, Ap&SS, 329, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, H., Nelemans, G., Aerts, C., & Dupret, M. 2009, A&A, 508, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, H., Glebbeek, E., Thoul, A. A., et al. 2010, A&A, 511, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffery, C. S., & Saio, H. 2007, MNRAS, 378, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Khalack, V. R., LeBlanc, F., Bohlender, D., Wade, G. A., & Behr, B. B. 2007, A&A, 466, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khalack, V., LeBlanc, F., & Behr, B. B. 2010, MNRAS, 407, 1767 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Koen, C., O’Donoghue, D., & Stobie, R. S. 1997, MNRAS, 285, 640 [Google Scholar]
- Kinman, T. D., Morrison, H. L., & Brown, W. R. 2009, AJ, 137, 3198 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P., & Ivans, I. I. 2003, PASP, 115, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., & Montgomery, M. H. 2002, MNRAS, 330, L6 [NASA ADS] [CrossRef] [Google Scholar]
- LeBlanc, F., Monin, D., Hui-Bon-Hoa, A., & Hauschildt, P. H. 2009, A&A, 495, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- LeBlanc, F., Hui-Bon-Hoa, A., & Khalack, V. R. 2010, MNRAS, 409, 1606 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, A. F., Villanova, S., Milone, A. P., et al. 2011, ApJ, 730, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Martel, A., & Ratel, A. 1978, ApJ, 226, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Bergeron, P., Wesemael, F., & Fontaine, G. 1985, ApJ, 299, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Bergeron, P., Heber, U., & Wesemael, F. 1989, ApJ, 338, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Richer, J., & Richard, O. 2007, ApJ, 670, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Richer, J., & Richard, O. 2008, ApJ, 675, 1223 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Richer, J., & Richard, O. 2010, A&A, 510, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moehler, S., Sweigart, A. V., Landsman, W. B., & Heber, U. 2000, A&A, 360, 120 [NASA ADS] [Google Scholar]
- Morrison, H. L., Helmi, A., Sun, J., et al. 2009, ApJ, 694, 130 [NASA ADS] [CrossRef] [Google Scholar]
- O’Toole, S. J., & Heber, U. 2006, A&A, 452, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pace, G., Recio-Blanco, A., Piotto, G., & Momany, Y. 2006, A&A, 452, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quievy, D., Charbonneau, P., Michaud, G., & Richer, J. 2009, A&A, 500, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randall, S. K., van Grootel, V., Fontaine, G., Charpinet, S., & Brassard, P. 2009, A&A, 507, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2001, ApJ, 558, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, O., Michaud, G., Richer, J., et al. 2002, ApJ, 568, 979 [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2005, ApJ, 619, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Richer, J., Michaud, G., Rogers, F., et al. 1998, ApJ, 492, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Richer, J., Michaud, G., & Turcotte, S. 2000, ApJ, 529, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Richer, J., & Michaud, G. 2005, in Proc. Element Stratification in Stars: 40 Years of Atomic Diffusion. Meeting in Honour of Georges Michaud, held on June 6–10, in Château de Mons, France, ed. G. Alecian, O. Richard, & S. Vauclair, EAS Pub. Ser., 17, 53 [Google Scholar]
- Sargent, W. L. W., & Searle, L. 1968, ApJ, 152, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Talon, S., Richard, O., & Michaud, G. 2006, ApJ, 645, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Théado, S., Vauclair, S., Alecian, G., & LeBlanc, F. 2009, ApJ, 704, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., Swenson, F. J., Rogers, F. J., Iglesias, C. A., & Alexander, D. R. 2000, ApJ, 532, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Vick, M., Michaud, G., Richer, J., & Richard, O. 2010, A&A, 521, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Turbulent diffusion coefficient in a 0.50 M⊙ model. The left axis is for the diffusion coefficient and the right axis for the Fe mass fraction. The coefficient is anchored at a mass ΔM0 = 10-7.5 M⊙. The vertical dashed line is at ΔM0. The Fe mass fraction, X(Fe), is nearly constant from the surface down to ΔM = 10-7 M⊙, which corresponds to Fe being mixed down to approximately 3 × ΔM0. |
| In the text | |
 |
Fig. 2 HR diagram (left) for all calculated models with a mixed mass ~10-7 M⊙. Each segment represents the evolution of one model whose mass is color-coded using a simple formula. The metallicity (Z0) of each series of models is indicated at the left of the sequence. The dotted part represents the first 10 Myr of HB evolution, while the solid line represents the rest of the calculated HB evolution, ususally an additional 27 Myr. In the right panel, g vs. Teff diagram of a subset of the calculations (those with Teff > 20 000 K) corresponding to the observations of Geier et al. 2010. This panel contains data (gray and red dots as defined in the text) from their Fig. 2. |
| In the text | |
 |
Fig. 3 Mass within and above the He II, He I, and H convection zones as a function of Teff. The H convection zone is separate from the He I convection zone in only a few models. For stars hotter than 22 000 K, the temperature at the bottom of the convection zone is less than a factor of 2 higher than Teff and is probably not precisely determined by interior models; it is not shown. The color code is the same as in Fig. 2. |
| In the text | |
 |
Fig. 4 Color-intensity coded concentrations in two HB stars of the same metallicity after 25 Myr on the HB. Left panel with a Teff of 14 000 K (0.59 M⊙) and right panel of 30 100 K (0.51 M⊙). The radial coordinate is the radius and its scale is linear, but the logarithmic value of the mass coordinate above a number of points, log ΔM/M∗, is shown on the left of the horizontal black line. The concentration scale is given in the right insert. Small circles near the top of the left panel mark the extent of the surface convection zone, while similar circles near the center of both models mark the central convection zone. The small inset in between the two panels shows the high Teff star, that is the right panel, on the radius scale of the low Teff star, that is the left panel. For −7 < log ΔM/M∗ < − 4 the concentration is quite different for many species. It is surprisingly so for C and O for log ΔM/M∗ > − 2. See the text. A black-and-white version of this figure may be found in Fig. A.1. |
| In the text | |
 |
Fig. 5 Comparison of surface abundances expected in 14 000 (black line, left panel) and 30 100 K (black line, right panel) HB stars with Z0 = 0.0001, whose interior is shown in Fig. 4. In the left panel, to facilatate a comparison with the turbulence model used by Michaud et al. (2008, see the text for details), the red curve is taken from the left panel of their Fig. 11 and the data for B203 from Behr (2003). In the right panel the other curves correspond to stars of original metallicities of Z0 = 0.001, 0.004, and 0.02 and the data for Feige 48 are from O’Toole & Heber (2006). Gray is used for data points of atomic species, which are not included in our calculations because they are not in OPAL opacities. |
| In the text | |
 |
Fig. 6 Internal distribution of Fe and Ni together with their relation to grad(Fe) and grad(Ni) in a 0.5 M⊙ model with Z0 = 0.001 for four turbulence strengths, each anchored at a fixed ΔM0 (see Eqs. (1) and (3)), identified in the upper panel. The solutions labeled −7.5, −8 and −9 are after 32 Myr on the HB, while the solution labeled − 10 is after 7 Myr. The lower panel gives κR as a function of log ΔM/M⊙. A local maximum of grad(Fe) and of κR occurs for log ΔM/M⊙ between − 10 and − 9 and corresponds to log T ~ 5.5. When the iron abundance becomes rapidly much higher than solar in contradiction with observations of sdB stars. The function 1/μ0 is shown (solid lines) for each model in the panel above that for κR. In the same panel, the function 1/μ0eff is shown by dotted lines. It is defined in Sect. 5.3. |
| In the text | |
 |
Fig. 7 Radiative accelerations for a subset of the included species in models with turbulence anchored at a fixed ΔM0 = 10-7.5 M⊙, after approximately 25 Myr on the HB. Dotted lines represent gravity. Left panel: in models with Teff ~ 31 000 K and metallicities of Z0 = 0.0001, 0.001, 0.004 and 0.02, (masses from 0.51 to 0.47 M⊙) from top to bottom. Right panel: with Z0 = 0.001 and various masses corresponding, from bottom to top, to Teffs of 10 700, 15 000, 20 000, 25 000, and 30 400 K. |
| In the text | |
 |
Fig. 8 Abundance profiles corresponding to the grads of Fig. 7. The abundance at the right of each small panel still approximately equals the starting abundance, while that at the left is the surface abundance after 23 Myr of HB evolution. |
| In the text | |
 |
Fig. 9 Surface abundances expected for models with turbulence anchored at , Z0 ~ 0.0001 and three slightly different masses, or equivalenty Teff. Observations for star B315 of M 15 with Teff ~ 13 000 K are from Behr (2003). These are the same observations as used in the right panel of Fig. 11 of Michaud et al. (2008). The turbulence models are different, however. The agreement is equivalent. |
| In the text | |
 |
Fig. 10 Comparison of abundance patterns with models of metallicity [Fe/H] = −1.3 and with turbulence anchored at . Left panel: surface abundances expected at six HB ages, from 0.0 to 31 Myr, for a 0.55 M⊙ model compared with observations for WF4–3085, a star of M 13 with Teff ~ 14 000 K, from Behr (2003). Right panel: surface abundances at five HB ages, from 0.0 to 16 Myr, for a 0.58 M⊙ model compared with observations of the Teff = 12 000 K star 469 of NGC 1904 from Fabbian et al. (2005). |
| In the text | |
 |
Fig. 11 Left panel: surface concentration of Fe as a function of Teff in clusters (M 15, M 68 and M 92) from Behr (2003) with original Fe concentration ~ −2.3. Models are shown for this metallicity. Each color-coded segment represents the evolution of the surface Fe concentration. The line is solid for the time interval from 10 to 30 Myr after ZAHB, but dotted from 0 to 10 Myr. Bottom part: rotation velocities; three stars have their rotation velocities and [Fe/H] in red to facilitate their identification. Right panel: field stars also from Behr (2003). The distribution of metallicity for the cooler field stars gives an indication of the original metallicity distribution for the hotter field stars as well as for sdBs. |
| In the text | |
 |
Fig. 12 Left panel: surface concentration of Fe as a function of Teff in clusters (M 3, M 13 NGC 288) from Behr (2003) with original Fe concentration between − 2.3 and − 1.3 dex the solar one. Models are shown for those two metallicities. Each color-coded segment represents the evolution of the surface Fe concentration. The line is solid for the time interval from 10 to 30 Myr after ZAHB, but dotted from 0 to 10 Myr. Right panel: surface concentrations of Fe as a function of Teff in the cluster NGC 2808 from Pace et al. (2006). The color-coding is defined in footnote (5). For most models the spanned time interval is approximately 30 Myr. |
| In the text | |
 |
Fig. 13 Surface abundances expected at 25 Myr for models with turbulence anchored at calculated with Z0 = 0.0001, 0.001, 0.004 and 0.02. Observations are for PG0101+039 from Blanchette et al. (2008). |
| In the text | |
 |
Fig. 14 Surface concentrations of Fe as a function of Teff in sdB stars. Models were calculated with original concentrations of [Fe/H] = −2.3, −1.3, −0.4 and 0.0. Models span the Teff interval from 20 000 to 37 000 K and the mass interval from 0.47 to 0.52 M⊙. The lines give the surface abundance variation for each calculated model. They are color-coded as a function of the mass of the model, which may be read by zooming on the figure in the electronic version; solid lines for the time interval from 10 to 32 Myr after ZAHB and dotted from 0 to 10 Myr. The dotted line starts at the original abundance of the model. For most models the spanned time interval is approximately 32 Myr. Note that most models starting with a solar metallicity have very short tracks. Observations (circles) are from Geier et al. (2008), Geier et al. (2010) and Geier (2010, priv. commun.). Inverted triangles are upper limits. The stars in red in Fig. 2 are also in red in this figure. The bottom part of the figure gives the rotation velocities and the error bars on Teff. |
| In the text | |
 |
Fig. 15 Surface abundances for atomic species from Ne to Fe. Iron is also in Fig. 14 where is found a detailed caption. The domain of observed values is bounded by long dashed broken gray lines which are also shown for Fe in Fig. 14. The domain of abundances often extends below the lower curve because many measurements are upper limits (see Geier et al. 2008, 2010). The solid horizontal gray line is the solar abundance. Note that individual panels span 7 orders of magnitude in abundances. |
| In the text | |
 |
Fig. 16 Surface concentration of He as a function of Teff in sdB stars. See the caption of Fig. 14 for the definition of the curves. Observations (circles) are from Geier et al. (2008), Geier et al. (2010) and Geier (2010, priv. commun.). The stars in red in Fig. 2 are also in red in this figure. The lines for He were stopped between X(He) = 0.001 and 0.0001 because the evaluation of the surface He abundance becomes inaccurate for smaller values. |
| In the text | |
 |
Fig. A.1 Black-and-white version of Fig. 4. Gray-coded concentrations in two HB stars of the same metallicity after 25 Myr on the HB. Left panel with a Teff of 14 000 K (0.59 M⊙) and right panel of 30 100 K (0.51 M⊙). The scale of the radius is linear, but the logarithmic value of the mass coordinate above a number of points, log ΔM/M∗, is shown to the left of the horizontal black line. The concentration scale is given in the right insert. Small circles near the top of the left panel mark the extent of the surface convection zone, while similar circles near the center of both models mark the central convection zone. The small inset in between the two panels shows the high Teff star on the radius scale of the low Teff star. For −7 < log ΔM/M∗ < −4 the concentration is quite different for many species. It is surprisingly so for C and O for log ΔM/M∗ > −2. |
| In the text | |
 |
Fig. B.1 Models with Z0 = 0.0001. The curves are identified in the figure by the mass of the HB model. The color code is the same as used for the left panel of Fig. 2 and is defined in footnote [5]. Zero age HB is defined as the moment when X(12C) reaches 0.04. In the figures the curves are not all very precisely aligned to that value. X0(surfFe) identifies the Fe mass fraction in the original main-sequence model, similarly for the other species. |
| In the text | |
 |
Fig. B.2 Models with Z0 = 0.001. See caption of Fig. B.1. |
| In the text | |
 |
Fig. B.3 Models with Z0 = 0.004. See caption of Fig. B.1. |
| In the text | |
 |
Fig. B.4 Models with Z0 = 0.02. See caption of Fig. B.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


