| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014507 | |
| Published online | 01 December 2010 | |
A low frequency study of PSRs B1133+16, B1112+50, and B0031−07
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, Bonn, Germany
e-mail: ramesh@mpifr-bonn.mpg.de
2
Sterrenkunde Instituut Anton Pannenkoek, University of
Amsterdam, Kruislaan
403, Amsterdam,
The Netherlands
3
Jodrell Bank Centre for Astrophysics, School of Physics and
Astronomy, The University of Manchester, Manchester
M13 9PL,
UK
e-mail: Ben.Stappers@manchester.ac.uk
4
Netherlands Institute for Radio Astronomy (ASTRON),
Postbus 2, 7990 AA, Dwingeloo, The Netherlands
e-mail: serylak@astron.nl
Received:
26
March
2010
Accepted:
18
August
2010
We use the low frequency (110–180 MHz) capabilities of the Westerbork Synthesis Radio Telescope (WSRT) to characterise a large collection of single pulses from three low magnetic field pulsars. Using the Pulsar Machine II (PuMa-II) to acquire and coherently dedisperse the pulsar signals, we examine whether the bright pulses observed in these pulsars are related to the classical giant pulse emission. Giant pulses are reported from PSR B1112+50 and bright pulses from the PSRs B1133+16 and B0031−07. These pulsars also exhibit large intensity modulations observed as rapid changes in the single pulse intensity. Evidence of global magnetospheric effects is provided by our detection of bright double pulses in PSRs B0031−07 and B1133+16. Using the multi-frequency observations, we accurately determine the dispersion measures (4.844 ± 0.002 for B1133+16 and 9.1750 ± 0.0001 for B1112+50), derive the radio emission height in PSR B1133+16 and report on the properties of subpulse drift modes in these pulsars. We also find that these pulsars show a much larger intensity modulation at low sky frequencies resulting in narrow and bright emissions.
Key words: stars: neutron
© ESO, 2010
1. Introduction
Most radio pulsars are characterised by a stable average pulse profile at a given sky frequency. The average profiles are formed by integrating all pulses emitted by the star over a given time. The pulsed emission from the star is observed as individual pulses that carry detailed information about the physics of the pulsar radio emission. These pulses can only be directly detected in a fewer than a third of the known radio pulsars, mainly because of their weak nature. One of the remarkable features of the single pulse emission is the occurrence of intense pulses called giant pulses, which are defined as pulses with energy greater than 10 times the average pulse energy. Furthermore, the giant pulses are very narrow compared to the width of average pulsed emission and result in a pulse intensity distribution described by a power law. For example, in the radio emission of the young Crab pulsar, the giant-pulse widths are found to be narrower than 0.4 ns, implying a high brightness temperature of ~1041 K (Hankins & Eilek 2007), and the single pulse flux distribution follows a power law with slope −3.3 (Lundgren et al. 1995). Another example is the emission of single bright pulses from the young Crab-like pulsar, PSR B0540−69 located in the Large Magellanic Cloud; the pulsar is visible at radio wavelengths only by virtue of the star’s intense giant pulse emission (Johnston & Romani 2003). Similar bright and narrow pulses were reported in the emission of very old millisecond pulsars such as PSR B1937+21 (Cognard et al. 1996) and B1821-24 (Romani & Johnston 2001). Concerted giant pulse searches in these older and short period pulsars have revealed more giant pulse sources e.g., PSRs J1823-3021A and J0218+4232 (Knight et al. 2005, 2006b). The only common feature of these pulsars is a strong magnetic field (BLC ~ 105 G) at the velocity of light cylinder, which is the limiting radius where the velocity of the co-rotating plasma and magnetic field lines is less than the speed of light.
However, some studies propose giant pulse-like emission in pulsars with a low magnetic field at the light cylinder e.g., BLC in the 4−100 G range. For instance, the bright single pulse emission from PSRs B0031−07, J1752+2359, and B1112+50 at 40 and 111 MHz (Kuzmin & Ershov 2004; Ershov & Kuzmin 2005, 2003). Kramer et al. (2003) also report bright pulses from PSR B1133+16 at 5 GHz. If these bright pulses are similar to the classical giant pulses, this questions the requirement of a high value of BLC to produce giant radio pulse emission. After the initial discovery, a detailed statistical analysis of the bright pulses in these low BLC pulsars has not been attempted, unlike the extensive studies of the giant pulses from the young pulsars and the millisecond pulsars (Lundgren et al. 1995; Kinkhabwala & Thorsett 2000; Knight 2007; Knight et al. 2006a).
The pulsars in this study also exhibit other interesting single pulse behaviour: PSRs B1133+16, B0031−07, and B1112+50 show drifting subpulses (Backer 1973; Taylor et al. 1975; Wright et al. 1986) and nulling (Herfindal & Rankin 2007; Ritchings 1976; Wright et al. 1986; Vivekanand 1995). PSR B1133+16 also shows narrow emission features called microstructure (Hankins 1972; Cordes et al. 1990; Lange et al. 1998).
Observation details and telescope parameters.
Radio pulsars in general show a negative spectrum (Slee et al. 1986) and a low frequency spectral turnover (Kuzmin et al. 1978; Malofeev et al. 1994). This implies that pulsars are brighter at low sky frequencies, although the sky temperature also increases, contributing significantly to the system temperature. Moreover, microstructure and drifting subpulses can be more easily studied at low frequencies when sufficient telescope sensitivity is available (Cordes et al. 1990). Motivated by the possible presence of giant pulses and a rich single pulse behaviour in the pulsars considered here and the availability of the Low Frequency Front Ends (LFFEs) at the WSRT, we undertook this study in the 110−180 MHz frequency range. The flexible baseband recorder PuMa-II (Karuppusamy et al. 2008) and full coherent dedispersion, permitted a detailed single pulse study with high sensitivity and relatively high time resolution. Although these pulsars have been studied at low sky frequencies before, we are able with our system to observe for much longer and across a far wider frequency range. Our long observations are useful in determining the flux distribution and the occurrence rates of bright pulses. Furthermore, the wide frequency coverage permits the computation of the pulsar spectra in this band.
The rest of the paper is organised as follows. The observations, the pulsar fluxes, and spectra are described in Sects. 2 and 3. We present our revised values of the dispersion measure (DM) of two pulsars based on the narrow giant pulses in Sects. 5 and 4. The single pulse intensity, energy distributions, and microstructure are the subjects of discussion in Sects. 6 and 7. We proceed with the pulse drift analysis in Sect. 8, which is followed by our discussion and conclusions.
2. Observations and data reduction
The pulsars were observed with the WSRT on three different days between June−November 2008 in the 110−180 MHz range (see Table 1). The design of the WSRT backend systems allows the selection of a maximum of eight different radio bands within the frequency range of the front end receiver. Eight 2.5 MHz-wide bands tuned to various sky frequencies (see Table 1) were chosen for this study since these bands showed comparatively little radio frequency interference (RFI). The signals were recorded and processed using the PuMa-II instrument. When possible, the observations were carried out in the early hours of the day to reduce the effect of RFI. Despite our careful choice of the frequency bands and observing times, these observations were still susceptible to RFI because of (1) strong in-band RFI in the passband of the LFFE electronic amplifiers (2) the presence of the automatic gain control (AGC) in the WSRT’s signal chain and (3) the 2-bit system design. Therefore, the data were subjected to an extensive RFI cleaning procedure by a combination of automated algorithms and visual examination.
The WSRT was operated in the tied-array mode by adding signals from 13 telescopes each 25-m in diameter. The analogue signals from the individual telescopes were digitally sampled at 2-bit resolution and a fixed rate of 40 MHz. The 2-bit data were then coherently added in a dedicated hardware unit to produce the 6-bit tied-array data. Coherent addition improved the signal-to-noise ratio (S/N) by a factor of 13. The summed data was then read into PuMa-II as 8-bit numbers, downsampled by a factor of 8 in realtime, and written to disk. Single pulses were generated from the coherently dedispersed baseband data using the dispersion measure in the catalog and based on a polynomial determined by the TEMPO software (Taylor & Weisberg 1989).
The open-source DSPSR1 software package was used to form a 64-channel software filterbank simultaneously at the dedispersion stage in each 2.5 MHz band, and the resulting frequency-time cubes were written to the disk as single pulses. The original time resolution of 2.5 μs and the formation of a 64-channel synthetic filterbank permitted 2048 samples to be extracted across the pulse period of the three pulsars observed and resulted in the final time resolutions in Col. 9 of Table 1. The large number of frequency channels was later used to correct for the residual dispersion smearing, since the DMs in the catalog had either changed or were not sufficiently accurate and it also aided the removal of narrow band RFI in the signal. Extensive use of the PSRCHIVE package (Hotan et al. 2004) was made in the computation of the total intensity, signal-to-noise ratio, and visual inspection of the single pulses for RFI. Pulse stacks were formed by stacking individual pulse intensities one above the other according to their phases. When required, the signal was flux calibrated using the off-pulse radiometer noise. With the computed fluxes in each band, various statistical analyses of the data was performed.
3. Low frequency flux
3.1. Radio frequency interference
The data was cleaned of interference using various cleaning strategies for the three purposes of estimation of mean flux density, fluctuation analysis, and single pulse flux estimates. For the mean pulse flux computation, the pulses that showed excessive noise, negative drop outs, and large intensity peaks in the off-pulse region were removed. The single pulses were combined to create pulse stacks that were then examined for the second time as time-phase plots; impulsive interference missed by the automated algorithm was then identified and removed. The remaining pulses were then averaged over the period of integration to compute the average pulse profile. The number of pulses removed in this method was accounted for in the time term of Eq. (1) before the profile was flux calibrated. From the calibrated profiles, the spectral indices were derived.
For the fluctuation analysis, the pulses were first gated to contain at least three times the width of the average pulse profile at the lowest observed frequency. The gated pulse stack was then subjected to the two-pass RFI cleaning procedure explained above. Pulse stacks were inspected by eye and pulses that showed a saturation in the off-pulse phases were replaced by zeros. This procedure was repeated until a visually clean image was seen in the time-phase plane.
The single pulse statistics were computed using only the single pulses from one of the eight bands observed. RFI was cleaned from the dedispersed single pulses by visually examining the frequency-phase images within 30° of the pulse longitude. For these comparatively long period pulsars, retaining a narrow phase range of the pulse period has the advantage of being less sensitive to impulsive RFI affecting other pulse longitudes. Only pulses that showed the required dispersion were retained. An interactive plot utility was developed to examine the frequency-phase images of the large S/N pulses.
3.2. Flux calibration
Calibrating pulsar fluxes at low sky frequencies at the WSRT is difficult for three reasons. First the main contribution to the system noise Tsys, is from the sky temperature Tsky which in turn depends on the position of the pulsar on the sky. Second, the aperture efficiency of the LFFE’s at the WSRT is poorly constrained and thirdly, the presence of RFI introduces errors into the flux measurements of the calibrators and the pulsars. The system parameters (telescope gain and system temperature) were derived from continuum observations of the calibrator source 3C 196 made shortly before these measurements. From these measurements, the aperture efficiency is estimated to be ~30% translating to an effective telescope collecting area of 1500 m2. A constant value Tsys in the entire 110−180 MHz is used, since the Galactic synchrotron foreground varying with frequency as ν-2.6 is almost removed by the frequency-dependent amplitude gains of the LFFEs. The system temperatures derived in this manner are shown in Table 1. Assuming a frequency scaling of ν-2.6, the sky temperature estimated from the 408 MHz continuum maps of Haslam et al. (1981) in the direction of these pulsars is consistent to within 20% of the system temperatures listed in Table 1.
Once the telescope gain and system temperature had been established, the off-pulse noise
in flux units was computed using the radiometer equation (Dicke 1946) that can be expressed as 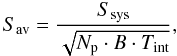 (1)where
Ssys = Tsys/G
is the system equivalent flux density in Jy, Np the number of
polarisations summed, and Tint the equivalent integration
time. The pulse profile was then flux calibrated by multiplying by
Sav. Integrating the fluxes in all phase bins and dividing
by the total number of bins then resulted in the mean continuum flux density of the
pulsar. While this method is not as accurate as the absolute flux measurements based on
noise generators, this is the only option in a synthesis telescope such as the WSRT for
non-imaging observations; it also yields fluxes comparable to those reported elsewhere.
(1)where
Ssys = Tsys/G
is the system equivalent flux density in Jy, Np the number of
polarisations summed, and Tint the equivalent integration
time. The pulse profile was then flux calibrated by multiplying by
Sav. Integrating the fluxes in all phase bins and dividing
by the total number of bins then resulted in the mean continuum flux density of the
pulsar. While this method is not as accurate as the absolute flux measurements based on
noise generators, this is the only option in a synthesis telescope such as the WSRT for
non-imaging observations; it also yields fluxes comparable to those reported elsewhere.
In our method of detecting the pulsars, the dedispersed signal was written to disk as single pulses. Following the formation of total intensities, diagnostic plots of peak S/N against the phase of the peaks were made. Any pulsed emission could then be seen as clustering of data points near the nominal emission phase and the corresponding pulses were visually examined. Combining the single pulses in time after removing the RFI afflicted pulses produced the average emission profiles. Thus, this method is sensitive to any pulsed emission above the noise floor.
 |
Fig. 1 Average pulse profiles of the three pulsars. The profile changes with sky frequency is clearly evident. The profile for PSR B1133+16 at 163.5 MHz is not shown because it was too corrupted by RFI. The profiles are shown at 809, 580, 460 μs time resolution for PSRs B1112+50, B1133+16 and B0031−07 respectively. All profiles are normalised by the maximum flux density in the band and are aligned at the phase of maximum intensity in each band. Profiles at 116.75 and 130 MHz have comparatively more noise because up to ~15% of pulses were removed to reject RFI. |
3.3. Profile evolution
The average pulse profiles in all recorded bands for the three detected pulsars are displayed in Fig. 1. PSR B1112+50 displayed 10% peak widths W10 = 35.5−38.8 ms in this frequency range. This can be compared to W10 = 35.0 ms at 405 MHz (Lorimer et al. 1995). The single component in the average emission of PSR B1112+50 at these frequencies and at 328 MHz (Weltevrede et al. 2006a) evolves to a two-component average emission profile at 1400 MHz (Wright et al. 1986).
PSR B0031−07 shows W10 = 120.2−155.1 ms, while Lorimer et al. (1995) report a value of 104.5 ms at 405 MHz. The trailing edge in the average profile of PSR B0031−07 shows a gradual decrease in steepness with frequency. We rule out scattering in the ISM as a possible cause of this decrease because that would manifest itself as pulse broadening by a factor of ~5 in the 110−180 MHz band considered here, which is clearly not seen (e.g. Fig. 1). However, this change in slope is indicative of the emergence of a second emission component at even lower frequencies e.g at 40 and 62 MHz (Izvekova et al. 1993) and represents almost the opposite behaviour of the average emission profile in PSR B1112+50. Another contribution to the slope of the trailing part of the average emission profile in PSR B0031−07 could be the vertically drifting subpulses, which is discussed in Sect. 8. The characteristic age of PSRs B1112+50 and B0031−07 is 10 Myr and 36 Myr, respectively. The general expectation of a narrower pulse profile for older pulsars is not valid with respect to these pulsars, as the impact angle of the observer’s line of sight to the emission beams from the pulsars may not be equal.
PSR B1133+16 displays a profile width of W10 = 44.0−48.1 ms compared to 41.8 ms at 405 MHz (Lorimer et al. 1995). The component separation of the average profile decreases with frequency and this phenomenon was successfully explained by the radius-to-frequency mapping in the pulsar magnetosphere (Cordes 1978). The average profile also shows a double emission component, with a pronounced bridge emission that rises from 14% to 25% of the peak flux density at our lowest and highest frequencies, respectively. The second component in the average emission profile also reduces from 90% to 70% of the leading component intensity with increasing frequency. These variations clearly probe different parts of the emission beam. Nowakowski (1996) assumed a model in which the pulsar beam consists of two concentric emission cones to explain the observed two-component emission profile and the increasing bridge emission with frequency. However, this model is unable to explain why multiple emission components are not visible at higher frequencies. Polarisation observations of this pulsar over a range of frequencies would offer further insights into the emission geometry. As discussed later in this work and by Kardashev et al. (1982), the emission height of various radio frequencies in the magnetosphere of the pulsar can be derived using the frequency dependence of the component separation. Our analysis shows that a ν−0.30 ± 0.02 relation is valid for the component separation in the frequency range considered here and is slightly steeper than the ν-0.24 and ν-0.26 scaling laws derived by Backer (1972) and Sieber et al. (1975), respectively.
3.4. Radio spectrum
The observations presented here span a reasonably wide frequency range and we use the flux of the pulsar in each of the recorded bands to compute the pulsar spectra. The pulsar flux used here is the mean continuum flux density of these sources, computed from the flux-calibrated pulse profiles. The functional form of the radio spectrum of the pulsars was assumed to follow S(ν) ∝ να, where S(ν) is the pulsar flux at frequency ν and α is the spectral index. The parameter α was estimated using a least squares fitting procedure and the result is displayed in Fig. 2 and Table 2 for the three pulsars. To account for the effect of RFI and possible errors in telescope parameters, a 10% uncertainty in the estimation of the pulsar flux density in each band is considered, which dominates other errors in S/N estimates because all pulsars are strongly detected.
 |
Fig. 2 Spectra for three pulsars in the frequency range 100−200 MHz. Errors bars correspond to a 10% uncertainty in the pulsar flux estimation. The best fit power law curves are also displayed. For PSR B1133+16, a broken power-law provides a closer fit to the measured fluxes. The flux in the RFI-affected band centred at 163.5 MHz is not included for PSR B1133+16. |
We now consider the effects of scintillation on the estimation of the spectral indices. The length of these observations are between 5 and 9 h (see Table 1) and may be susceptible to scintillation effects on these timescales. Diffractive scintillation does not influence our results here as we now demonstrate. The frequency-phase plots displayed in Fig. 3 shows that the intensity modulation induced by this type of scintillation is confined to a few channels. To help validate this, the diffractive scintillation bandwidth and time were derived from values published in other work (see Table 2), using ΔνDISS ∝ ν4.4 and ΔtDISS ∝ ν1.2 scaling laws. From the foregoing discussion, it is clear that the observed and derived diffractive scintillation bandwidth is narrow for these pulsars at low frequencies and that we average over many “scintiles” with the wide band used here. The effects of the refractive scintillation should also be considered for these long observations, and this timescale is derived as outlined in Stinebring & Condon (1990) and listed in Table 2. Hence, it is clear that the diffractive scintillation does not affect the results derived here. The refractive scintillation may affect the these long observations, but are accounted for in the 10% uncertainty in flux estimation considered here. The derived timescale Tr shows that refractive scintillation, if there is any, affects only the spectral index estimation for PSR B1112+50.
Measured and derived parameters of three pulsars.
 |
Fig. 3 Narrow bright pulses from the three pulsars detected at all eight sky frequencies. The total intensity displayed in the top panels is computed by summing the signal in the 8 bands. The lower panels show a dedispersed pulse as a frequency-phase plot. The abscissa in these plots correspond to the pulse phase at 116.75 MHz. Some residual RFI is visible as low-level intensity modulating the entire pulse phase in the frequency-phase plots of all three pulsars. |
PSR B1112+50 shows a slightly positive spectral index and we find a value of α = 1.12 ± 0.46. Even though this pulsar is the weaker of the three pulsars, it is detected with high significance, as is clearly evident from Fig. 1. The somewhat poor fit to the pulsar spectra in these observations is not caused by fluxes corrugated by diffractive scintillation for the reasons explained above and may have its origins in the residual RFI and/or refractive scintillation. The results presented here imply that the spectra turns over at a frequency higher than 180 MHz.
For PSR B1133+16, the middle panel of Fig. 2 can be
compared to Fig. 4e in Deshpande & Radhakrishnan
(1992), which extends down to 34.5 MHz. Their figure can be interpreted as
indicating a spectral turnover in our frequency range. With this consideration, the
spectrum was modelled by a two component power-law defined as  (2)where, νb is the
break frequency, C1 is a constant, and normalisation yields
(2)where, νb is the
break frequency, C1 is a constant, and normalisation yields
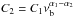 . The values of break frequency of
139.75 MHz with spectral indices α1 = 2.33 ± 2.55
and α2 = −3.81 ± 2.24 were derived from the best fits to the
data. The effect of scintillation gives rise to “scintiles” with typical widths of
≤ 40 KHz, which tend to average out within each 2.5 MHz band and do not contribute to the
intensity variations in the 110−180 MHz frequency range. Combined with the 75% error in
400 mJy at 151 MHz (Sieber 1973) and 900 mJy at
111 MHz (Fig. 3 in Malofeev et al. 1994), we
conclude that our results are consistent with those reported previously.
. The values of break frequency of
139.75 MHz with spectral indices α1 = 2.33 ± 2.55
and α2 = −3.81 ± 2.24 were derived from the best fits to the
data. The effect of scintillation gives rise to “scintiles” with typical widths of
≤ 40 KHz, which tend to average out within each 2.5 MHz band and do not contribute to the
intensity variations in the 110−180 MHz frequency range. Combined with the 75% error in
400 mJy at 151 MHz (Sieber 1973) and 900 mJy at
111 MHz (Fig. 3 in Malofeev et al. 1994), we
conclude that our results are consistent with those reported previously.
We find a relatively flat spectrum for PSR B0031−07 with an index of α = 0.71 ± 0.45. As for the other two pulsars, B0031−07 has partially resolved scintillation (see Fig. 3) at these frequencies that do not contribute to the estimated fluxes. For sky frequencies ν ≤ 1 GHz, Malofeev et al. (1994) find that the spectral index of this pulsar is α = −1.2 ± 0.26. Considering the two data points below ν = 100 MHz and the error limits in Malofeev et al. (1994), the spectral index derived here is consistent with their work. The trend seen in the spectra of this pulsar implies that the spectra turns over at a frequency higher than 180 MHz.
4. Bright single pulses
Several bright pulses were detected from all three pulsars and examples are shown in Fig. 3. These pulses are very narrow and often less than 1 ms in width. In general, giant pulses are characterised by their widths, the phase of the pulses with respect to the average emission profile, and the pulse energy (Knight 2007). The classical giant pulses are also found to be broadband, for example in B1937+21 Δν/ν ~ 0.2 (Popov & Stappers 2003), where ν and Δν are the observation frequency and bandwidth. In this study, we find similar bright, broadband bursts from the pulsars studied, although they are not as energetic as the classical giant pulse emitters.
Brightness temperature of single pulses.
The implied brightness temperature of the single pulses can be computed from (pp. 79; Lorimer & Kramer 2005), 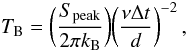 (3)where Speak is the
peak pulse flux, kB is the Boltzmann’s constant,
d is the distance to the pulsar, ν the sky frequency and
Δt is the pulse width. Using Δt values from Table 1 and the known distances for these pulsars, the computed
brightness temperatures are listed in Table 3.
(3)where Speak is the
peak pulse flux, kB is the Boltzmann’s constant,
d is the distance to the pulsar, ν the sky frequency and
Δt is the pulse width. Using Δt values from Table 1 and the known distances for these pulsars, the computed
brightness temperatures are listed in Table 3.
While the brightness temperatures of these pulses are several orders of magnitude lower than the 1035−1040 K seen in typical giant pulses from the Crab pulsar or PSR B9137+21, the large values of TB do point to a coherent emission mechanism for these pulses. From the frequency-phase plots in Fig. 3, these bright pulses clearly represent broadband emission, with Δν/ν = 0.3, and can be compared to the value of 0.1 and 0.2 for the Crab pulsar and PSR B1937+21 at 1400 MHz. The scintiles in all three pulsars are also visible in this figure, though they are more evident in PSRs B1133+16 and B0031−07. Therefore these bright pulses are not due to the occasional focussing effects brought about by scintillation. The similarities between the bright pulses found here and the classical giant pulses are indicative of high energy counterparts as in the Crab pulsar and PSR B1937+21.
5. Dispersion measure variations
Pulsar dispersion measures are normally estimated from multi-frequency multi-epoch timing observations (Phillips & Wolszczan 1992; Backer et al. 1993). However, in some pulsars the absence of an appropriate fiducial point in the average emission profile introduces errors in the estimated DM values. Ahuja et al. (2005) used cross-correlation of the pulse profiles at two different frequencies of observation to partially overcome this problem. These authors also point out that an alternative means of estimating the DM is to use multi-frequency simultaneous observation of the pulsar, and use a fiducial point in the average emission profile to align the profiles at the two frequencies. Our detection of single, narrow, and bright pulses at low sky frequencies provides in an excellent reference to align the pulses and hence compute the DM very accurately for these low DM pulsars. The frequency resolution of 64 channels across each 2.5 MHz band gives a total of 512 channels in the 110−180 MHz range, which permits the accurate determination of the quadratic dispersion curve. We generally started with the catalog DM, which was varied until a peak S/N in the combined pulse profile was attained. The frequency-phase plots were then visually inspected for the pulse alignment using the new value of DM. To compute the change in the DM at the epoch of our observations, the dispersion smearing caused by the use of an incorrect DM within a single frequency channel was considered negligible.
From their multi-year timing data, Hobbs et al. (2004) find DM = 4.864 cm-3pc for PSR B1133+16 corresponding to the epoch MJD 46407 and also determine d(DM)/dt ≈ −0.0008 cm-3 pc yr-1. Our analysis shows that the DM has changed to 4.844 ± 0.002 cm-3pc at epoch MJD 54793 from our reference value of 4.871 cm-3pc at epoch MJD 41665. The error estimate comes from the DM uncertainty caused by the misalignment of a broadband pulse by one phase bin across the 110−180 MHz band. The total DM change, ΔDM, found here is consistent with the predictions of Hobbs et al. (2004). The somewhat high yearly rate of change in the DM of this pulsar probably arises from its large proper motion ~630 km s-1. The ΔDM = 0.0265 cm-3 pc corresponds to a 0.5% change in DM and failing to correct for this change leads to the peak flux of the bright pulses being underestimated by ~3%.
For PSR B1112+50, we find that the DM increased from 9.16 cm-3pc at an epoch MJD 50899 to 9.1750 ± 0.0001 cm-3pc at epoch of MJD 54795 resulting in ΔDM = 0.015 cm-3pc. The error in our DM value is derived from the pulse misalignment by one phase bin in a 2.5 MHz band at 147.5 MHz. We again refer to Hobbs et al. (2004) for DM estimates of this pulsar, where they find DM = 9.195 cm-3 pc and a yearly rate of d(DM)/dt = −0.004 cm-3 pc yr-1. These values are inconsistent with the rate of −0.0014 cm-3 pc yr-1 derived from our analysis. One reason for this discrepancy could be the difference between the high frequency observations at 408−1600 MHz used in the work of Hobbs et al. (2004) and the much lower frequencies used in our study which are more sensitive to DM changes. The second reason could be that a single value of d(DM)/dt is insufficient implying that higher order terms of the DM time derivative may be necessary to accurately model the DM variations.
We do not detect a change in the DM of PSR B0031−07 from the reference DM value of 10.89 cm-3 pc. The narrow and bright single pulses have no discernible errors when the signal is dedispersed with this DM. However, the pulsar’s DM of 10.89 cm-3 pc is inconsistent with the value of 11.29 cm-3 pc at this epoch expected from the −0.007 cm-3 pc yr-1 listed in Hobbs et al. (2004). Moreover, in the studies of Taylor et al. (1993), Kuzmin & Ershov (2004), and Smits et al. (2007), the authors use a DM of 10.89 cm-3 pc, which implies that the DM of the pulsar has not changed since 1993. Therefore both the DM value and the rate of DM change for this pulsar in Hobbs et al. (2004) may be incorrect.
6. Single pulse analyses
 |
Fig. 4 Single bright pulses and the integrated pulse profiles at 156 MHz for the three pulsars. The flux scale on the left ordinate corresponds to the peak flux of the single pulses and the scale on the right ordinate axis corresponds to the average pulse profile. The phase displayed here is different from that of Fig. 3 due to the signal being dedispered to a different central frequency. Peak flux densities of the single pulses are shown as crosses. Only pulses ≥20σ are shown in these plots which represent a low flux cut-off in the fluxes of single pulses. |
Our long observations resulted in the detection of a large number of pulses and are shown in Table 1. Robust statistics can be obtained by computing the distribution of single pulse energies E and peak intensities Sp. A scatter plot of the peak fluxes and the average emission profile for the three pulsars are shown in Fig. 4. The 2.5 MHz band at 156 MHz was chosen out of the eight bands for further study because it showed comparatively less RFI. We note that after an exhaustive RFI search and removal, all eight bands show similar trends.
The presence of narrow bright pulses was evident when the data was examined visually in the RFI cleaning stage. These unusual emission entities should be evident in the single pulse energy and flux distributions. For example, giant pulses in the emission of the Crab pulsar should result in a power law in the pulse flux distribution (Lundgren et al. 1995). For the three pulsars considered here, the distribution of the pulse flux and energy are shown in Figs. 5 and 6, respectively. The pulse energy was computed by summing the emission in a window of width equal to the average emission profile. The single-pulse peak flux was computed using the product of the peak S/N and Sav (Eq. (1)).
 |
Fig. 5 Pulse energy distribution for the three pulsars. The abscissa shows pulse energy normalised to the mean pulse energy. Dark and light grey lines correspond to the on-pulse and off-pulse energy distributions. The clear peak at zero energy is introduced by the RFI affected pulses replaced by zeros. |
 |
Fig. 6 Plot of the peak flux distribution of the single pulses for the three pulsars. The dashed line shows 10 × Sav,peak for each pulsar. |
6.1. PSR B1112+50
The top panel of Fig. 4 shows that this pulsar emits bright pulses. Some of these pulses show considerable structure, with narrow subpulses separated by a few milliseconds. These pulses have a slight preference to the trailing phase of the average pulse profile, although a clear phase relationship is not evident. This is similar to the giant pulse-like emission from this pulsar reported by Ershov & Kuzmin (2003). Figure 5 shows the pulse energy distribution and the bright pulses with energies greater than 10 × ⟨ E ⟩ comprise the trailing part of the distribution. An indication of the null emission in this pulsar is visible from the slight turn-over in the pulse energy distribution near 3 × ⟨ E ⟩ , which is similar to the offpulse energy distribution. Our data is consistent with the ≥60% nulling fraction at 1412 MHz (Wright et al. 1986) and at 408 MHz (Ritchings 1976). If the null emissions are accounted for with this nulling fraction, then ⟨ E ⟩ increases by 60%. This causes a decrease in the energy of bright pulses in the 10−13 × ⟨ E ⟩ range. The pulse flux distribution also displays a shallow power-law like tail in the peak flux distribution (top panel in Fig. 6) produced by the occasional bright pulses in this pulsar.
6.2. PSR B1133+16
Kramer et al. (2003) reported bright pulses from this pulsar at a frequency of 5 GHz but not at 1.4 GHz. We detected bright, narrow pulses in all eight bands in the range 110−180 MHz with peak fluxes greater than 10 times the peak of average flux density as seen in the middle panel of Fig. 6. The pulse energy distribution shown in the middle panel of Fig. 5 can be qualitatively approximated by a power law. The distribution does not exhibit pulses with energies >10 × ⟨ E ⟩ , which is the normal working definition of giant pulses (Cognard et al. 1996). From the middle panel in Fig. 4, a preference for the bright pulses to fall on the inner edge of the two components is evident. Some of these bright pulses contain two distinct and narrow subpulses. Bright pulses from this pulsar at 327 MHz were also noted by Herfindal & Rankin (2007). The turn-over in the pulse energy distribution ~1.0 × ⟨ E ⟩ is indicative of a bimodal distribution, and hence of nulling. The pulsar shows a ~20% null fraction at 327 MHz (Herfindal & Rankin 2007), but at our frequency we are unable to identify the null distribution because we were limited by the system sensitivity.
6.3. PSR B0031−07
Kuzmin & Ershov (2004) reported giant pulses from PSR B0031−07. Our observations reveal that the bright and spiky pulses do not satisfy the 10 × ⟨ E ⟩ criterion but are easily greater than 10 × Sav,peak, as seen in Figs. 4 and 6. Figure 4 also reveals the emission of bright pulses on the leading edge of the average pulse profile. The work of Ershov & Kuzmin (2005) (see their Table 1) suggests that the bright pulses in this pulsar have a steep spectral index. We also draw the reader’s attention to Fig. 4 of Kuzmin & Ershov (2004), where the authors report the detection of “double giants” in this pulsar at 40 and 111 MHz. These pulses were detected in our observations, as seen in the rightmost panel of Fig. 3. These bright subpulses with two distinct peaks show structure spanning a few milliseconds implying that they are not microstructure in the emission. As with PSR B1133+16, a turn-over in the pulsar energy distribution ~1.5 × ⟨ E ⟩ is indicative of null emission.
7. Microstructure
Several single pulses from both PSR B1133+16 and B0031−07 show pulse structures
considerably narrower than the width of the average pulsed emission. The presence of pulses
with microstructure became evident when several thousand pulses were examined in the process
of cleaning RFI from the data. To quantify the microstructure, the autocorrelation function
(ACF) (Cordes et al. 1990) of the single pulses and
their averages were computed. The discrete ACF is defined by 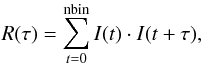 (4)where I(t) is
the intensity of the pulsar. Figure 7 shows
R(τ) for a single pulse and the averaged ACF of several
pulses.
(4)where I(t) is
the intensity of the pulsar. Figure 7 shows
R(τ) for a single pulse and the averaged ACF of several
pulses.
 |
Fig. 7 Intensity autocorrelation functions (ACF) of pulses with structure for two pulsars. The uppermost panels present example pulses. The autocorrelations displayed in the middle panel correspond to the pulses above them. The two bottom panels display the averaged ACFs for 120 and 132 pulses for PSRs B0031−07 and B1133+16 respectively. The averaged ACF’s for two bands centred on 116.75 MHz and 173.25 MHz (dashed line) are shown. |
For PSR B1112+50, the single pulses were quite narrow, devoid of any feature that can be recognised as microstructure. Therefore, this pulsar is not considered any further in this section. The separation between the two main emission components can be clearly seen for B1133+16 and is the feature at correlation lag ~30 ms. The ACF for the pulse shown in the uppermost panel exhibits the periodicity of microstructure (i.e., the local maxima near correlation lag 5 ms in the middle panel of Fig. 7). It is known that PSR B1133+16 shows structure down to ~8 μs and a characteristic intensity fluctuation of the order of ~575−663 μs in the 111−196 MHz range (Hankins 1972). Our final resolution of 580 μs was sufficient neither to resolve narrower structures nor to permit us to estimate the persistent quasi-periodic intensity variations in the averaged ACF.
In the case of PSR B0031−07, single pulses display narrow bursty features. However, the single pulse ACF in the right middle panel of Fig. 7 shows no characteristic variations implying that the pulse consists of non-periodic microstructure. These nonperiodic features were also found in PSR B0950+08 (Lange et al. 1998). The average subpulse separation is seen in the averaged ACFs and is visible at ~55 ms for PSR B0031−07. Expressed in pulse longitude, this is 20°, which is also the value of P2 found in Sect. 8. For the average ACF’s displayed in the two lowest panels of Fig. 7, the pulses chosen are detected simultaneously in the two bands. The slight shift of local maxima to the left cannot be measured with high significance, implying that the subpulse separation decreases with frequency as can be seen by comparing the subpulse properties at 328 and 1380 MHz in Weltevrede et al. (2006a) and Weltevrede et al. (2007). The slight break at ~10 ms in the ACF of the single pulse represents the width of microstructure in the pulsar. The reason for the lack of a prominent characteristic timescale in the microstructure of PSR B0031−07 may be our coarse time resolution.
8. Fluctuation spectra
Since the three pulsars under discussion display bright and bursty emission, it is natural to expect considerable pulse-to-pulse variation. In some pulsars (eg. PSRs B0809+74, B1944+17), drifting and persistent microstructure were detected leading Cordes et al. (1990) to suggest that these two phenomena are correlated. Moreover, PSRs B1133+16 and B0031−07 show drifting subpulses at other frequencies. To ascertain the drifting behaviour at these frequencies, we undertook sub-pulse drift analysis.
To perform the analysis presented in this section, the pulse stacks were subjected to a pulse drift analysis based on the longitude-resolved modulation index (LRMI), longitude-resolved fluctuation spectrum (LRFS), and two-dimensional fluctuation spectrum (2DFS) (Edwards & Stappers 2002; Weltevrede et al. 2006a). The sliding two-dimensional fluctuation spectrum (S2DFS) was also computed to identify the onset of the various drift modes (Serylak et al. 2009). The resulting plots from the LRMI, LRFS, and 2DFS analysis are shown in Fig. 8. In this plot, only LRMI values that are detected with a significance of more than 6σ are shown (top panel; Fig. 8). In the LRFS and 2DFS plots, drifting subpulses produce regions of enhanced brightness called “features”. The vertical drift rate P3 and the horizontal separation P2 of the subpulses are defined to be the centroid of a rectangular region in the 2DFS containing the features (Eq. (6); Weltevrede et al. 2006a). The sign of P2 denotes the direction of the drift, i.e., whether subpulses drift towards the leading (negative) or trailing (positive) edge of the pulsar’s average profile, respectively. In what follows, the S2DFS analysis results are discussed only for PSR B0031−07. The analysis of PSRs B1133+16 and B1112+50 using the S2DFS technique provided results that are comparable to those obtained from the 2DFS method alone.
The results presented in this section are for the 2.5 MHz band centred on 156 MHz, as in the previous section. In the RFI cleaning procedure discussed in Sect. 3.1, fewer than 2% of the pulses were replaced by zero, and therefore the effect is considered small enough to be neglected. The drift analysis was performed on all eight bands, and the results presented here are representative of the other bands. Within the 110−180 MHz range, there are no noteworthy changes in drift features. The modulation index was also in general agreement with the results found in the band reported here but are higher than the values reported in previous high frequency studies (see Table 4).
Drift analysis results for three pulsars.
 |
Fig. 8 Plots of the fluctuation analysis for the PSRs B1112+50, B1133+16, and B0031−07. The average pulse profile, and the longitude-resolved modulation index (LRMI) are shown in the uppermost panels. The panels directly below the average pulse profile present the longitude-resolved fluctuation spectrum (LRFS). The two-dimensional fluctuation spectra (2DFS) are shown in the third and fourth rows. For PSR B1133+16, the 2DFS plots are shown separately corresponding to the two components of the average pulse profile. The panels on the left and bottom of the LRFS and 2DFS images contain the vertically and horizontally integrated spectra, respectively. |
8.1. PSR B1112+50
This pulsar shows a broad, non-specific vertical drift feature as seen in the panels on
the left in Fig. 8. Wright et al. (1986) reported the presence of three different drift modes in
this pulsar and that the dominant mode in the trailing part of the average pulse profile
showed a periodicity of
P3 ~ 6P0. At 328 MHz, Weltevrede et al. (2007) report that
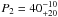 degrees and a
P3 = 9 ± 5P0. We detect
degrees and a
P3 = 9 ± 5P0. We detect
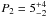 degrees and subpulse modulation of
P3 = 6 ± 3P0. We also note a
greater amount of power in the entire range of P3 centred
around P0/P2 = 0. While the
P3 found here is consistent with values reported elsewhere
within the errors, the discrepancy between the P2 results
reported by Weltevrede et al. (2007) and our own
can be explained by the higher S/N of individual pulses
in our observations. This results in a more prominent feature in the spectrum and less
convolution with the higher power in the entire range of P3
centered around P0/P2 = 0.
degrees and subpulse modulation of
P3 = 6 ± 3P0. We also note a
greater amount of power in the entire range of P3 centred
around P0/P2 = 0. While the
P3 found here is consistent with values reported elsewhere
within the errors, the discrepancy between the P2 results
reported by Weltevrede et al. (2007) and our own
can be explained by the higher S/N of individual pulses
in our observations. This results in a more prominent feature in the spectrum and less
convolution with the higher power in the entire range of P3
centered around P0/P2 = 0.
It is possible that only the prominent drift mode active at 1412 MHz (mode 2 of Wright et al. 1986) is also active at this frequency. The support for this comes from the similarity of the average profile at our frequency to the average profile computed from 193 pulses containing drift mode 2 in Wright et al. (1986). In their work, the profile computed from 176 pulses in mode 1 displays a prominent double peak. From the LRMI plot, the modulation index m ~ 3.5 is quite high at this frequency. Combined with the values reported elsewhere (see Table 4), this indicates that the pulse-to-pulse intensity variations increase with decreasing frequency. This again suggests that the large amplitude pulses are more common in this pulsar at lower sky frequencies. The LRFS shows an excess near P0/P3 ~ 0 owing to the large nulling fraction of ~60% in the emission of this pulsar (Ritchings 1976), which can be also seen in Fig. 5. However, this can only be indicative of nulling because some contribution to the excess seen comes from the zeros introduced by the RFI cleaning procedure. Therefore, these plots cannot be used to measure the pulsar’s nulling fraction.
8.2. PSR B1133+16
The results of the analysis presented here confirms the presence of the long-period
feature P3 ~ 30 at this frequency, which was previously
reported at frequencies greater than 300 MHz (Weltevrede
et al. 2006a; Herfindal & Rankin
2007). In Fig. 8 (middle panel), the
horizontal component of the drift feature, P2 is very weak and
consistent with no ordered horizontal separation of the subpulses. The feature near
P0/P3 = 0.18 is present in both
components of the pulse profile and the LRMI plot shows the presence of a significant
modulation in the bridge emission region. We find
P3 = 30 ± 5P0 for the leading
component and 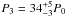 for the trailing component. Apart from the
aforementioned P3 feature, the LRFS shows a non-ordered
feature that modulates the emission throughout the entire stretch of the analysed pulse
sequence. This is also evident from the elevated baseline of the collapsed spectra shown
in the side panels of Fig. 8. The excess power seen
near P0/P3 = 0 is due to the
combination of null emission and the pulses replaced by zeros in the process of cleaning
RFI, though as in PSR B1112+50 this cannot be measured reliably from this analysis.
for the trailing component. Apart from the
aforementioned P3 feature, the LRFS shows a non-ordered
feature that modulates the emission throughout the entire stretch of the analysed pulse
sequence. This is also evident from the elevated baseline of the collapsed spectra shown
in the side panels of Fig. 8. The excess power seen
near P0/P3 = 0 is due to the
combination of null emission and the pulses replaced by zeros in the process of cleaning
RFI, though as in PSR B1112+50 this cannot be measured reliably from this analysis.
8.3. PSR B0031−07
The three different drift modes in this pulsar were first reported by Huguenin et al. (1970) of which two are clearly visible in our analysis (Fig. 8, right-hand panel). The very low frequency feature at P0/P3 ~ 0.02 comes from the nulls present in the pulse stack. The nulls are a combination of the null emission and the zeros introduced by RFI cleaning procedure. We detect this feature in all the eight observed bands. The feature seen at P0/P3 = 0.15 denotes the prominent drift mode “B” that introduces harmonics and hence appears as the feature seen at P0/P3 = 0.3. The other feature seen at P0/P3 = 0.08 is the drift mode “A”, which can be identified with regular upward drifting bands in the pulse stack. The drift mode “C” is not seen in the 2DFS spectrum. We used the S2DFS method to analyze the occurrence rate of different drift modes. While modes “A” and “B” were clearly detected in the S2DFS output, mode “C” remained undetected. The mode “C” has a low occurrence rate and is active only for ~2.6% of the observation time at 327 MHz (Vivekanand & Joshi 1997). However, Smits et al. (2005) detect this mode marginally at 328 MHz but not at 4.85 GHz, indicating a steeper spectral index for the drift mode. Therefore, other than susceptibility to RFI and lower sensitivity, it is unclear why this mode is not detected at these frequencies.
9. Discussion
The long observations reported in this paper provide good sensitivity to persistent weak features in the average emission of the pulsars. We were thus able to test the hypothesis of interpulse emission in PSR B1112+50 proposed by Wright et al. (1986) at 1400 MHz. Based on the outer gap emission model then proposed, these authors recommend the use of observations at low sky frequencies to detect the inter pulse, as the model predicts large fanbeams. Our deep exposures at low sky frequencies shows no evidence of inter-pulse emission with an upper limit of 3.5 mJy at 156 MHz (see Fig. 1), which is <0.6% of the main pulse peak flux. The non-detection of an interpulse in this pulsar is unsurprising given that only ~1.5% of the 1847 known pulsars possess an interpulse emission component (Weltevrede & Johnston 2008). Examination of polarimetric profiles at 400 and 608 MHz from the Jodrell Bank Observatory archives shows that the position angle swing is too shallow, which would result in a large impact angle to the observed radio beam. Our observations and the indication from past polarisation studies shows that if the neutron star has a dipolar magnetic field, PSR B1112+50 is not an orthogonal rotator. Consequently, the alternate magnetic pole never sweeps across our line of sight.
The pulsar spectral indices found in this study indicate a turn-over near 180 MHz. Michel (1978) modelled the pulsar emission as consisting of a coherent part and an incoherent synchrotron component. This model also predicts a spectral index of −8/3 and a spectral turn-over below 100 MHz based on the finite energy of the injected particles, and that the radiation is dominated by incoherent emission mechanisms. However, this contrasts with the presence of bright pulses and clear single pulses near the putative turnover frequency implying that the radiation is still of a coherent nature. The simulations of Gil & Kijak (1992), which assume that the pulsar radiation is produced by emission cones, clearly illustrate that the estimated intensity is very sensitive to the viewing geometry. If the radiation originates quite high in the magnetosphere (as at low sky frequencies), it is possible that the viewing geometry changes quite rapidly. This in turn can give rise to the observed pulse flux near the spectral turn-over resulting in spectra that does not vary smoothly. Detailed polarisation studies at these frequencies can be used to test whether the observed frequency dependence of the pulse flux has its origins in the viewing geometry, although the pulse shape is quite stable. In summary, past studies have been inconclusive on the value of spectral index for PSRs B1133+16 and B0031−07 at low sky frequencies. The results presented in this work suggest a spectral turn-over near ~140 MHz for PSR B1133+16 and above 180 MHz for PSRs B0031−07 and B1112+50.
As pointed out by other authors, the discrepancies in pulsar DMs stem from the difficulty in aligning multi-frequency pulse profiles and the choice of a fiducial point in the average profile (Hobbs et al. 2004; Ahuja et al. 2007). The narrow bright pulses at low sky frequencies in the pulsars studied in this work have permitted a very accurate estimation of the DM. We note that scatter broadening of the emitted pulses can limit the accuracy of the DMs estimated by both other methods and ourselves. This can be another source of the DM discrepancies. Because of the broad band nature of the pulsar emission mechanism, we cannot rule out the claim that some pulsars may have slightly different values of DM in different parts of the frequency spectrum (Kardashev et al. 1982). However, with the S/N in this work we do not measure any deviation from the ν2 dependence of the interstellar medium contribution to dispersion in the 110−180 MHz band. Simultaneous broad-band observations with the existing instruments and LOFAR can address these outstanding questions effectively.
The analyses of the single pulse energy distributions revealed that only PSR B1112+50 exhibits pulses of energy ≥10 × ⟨ E ⟩ . The presence of null emissions in these pulsars leads to an underestimate of the average pulse energy. Therefore, this is an important consideration when interpreting pulse energy distributions for pulsars that exhibit the nulling phenomena. The width and intensity of the bright pulses in this study are quite similar to those of the normal giant pulses suggesting that they are caused by similar emission mechanisms. Sources of classical giant pulses display a phase correlation between the giant pulses and the high energy non-thermal X-ray emission, as in the Crab pulsar (Lundgren et al. 1995), PSR B1937+21 (Cusumano et al. 2003), and in other millisecond pulsars (Knight et al. 2006a). However, these are energetic pulsars with large values of BLC. It is known that PSR B1133+16 shows X-ray emission (Kargaltsev et al. 2006), which the authors claim contains both thermal and non-thermal components. With their coarse time resolution of 3.2 s and low photon counts, these authors were unable to detect any X-ray pulsations. However, the non-thermal high energy emission may be related to the bright pulses observed in our work. For PSRs B1112+50 and B0031−07, a deep search in the archival X-Ray data might reveal any correlation that might exist. The bright double-pulses reported in this work and by Kuzmin & Ershov (2004) are indicative of a global magnetospheric phenomena, despite the different physical locations of the emitting regions. However, it could also be that drifting occasionally brings these two regions into our line of sight resulting in the double pulses. Detailed analysis of these double pulses will provide insight into the phenomena that might be active over the whole magnetosphere.
The preference of the bright pulse emission to occur at the phase coincident with the peak in the average emission profile is a feature common to all pulsars in this study. This argues that these pulses are preferentially emitted further away from the last open magnetic line in the magnetosphere, in contrast to pulsars such as PSR B1937+21 (Kinkhabwala & Thorsett 2000). The bright pulses in B0031−07 are more frequent and bright at even lower sky frequencies when we compare our results in the 110−180 MHz range with those found by Ershov & Kuzmin (2005) at 40 MHz. This is also valid for the other two pulsars studied here – bright pulses are more common in these pulsars at lower frequencies. This finding contrasts with the models of Petrova (2004) in which the bright and narrow pulses at high frequencies were explained by inverse Compton scattering of low frequency radio photons. Simultaneous multi-wavelength radio observations might help to resolve this issue.
In the pulsar models proposed by Ruderman & Sutherland (1975), the radio waves are emitted tangentially to the diverging magnetic field lines by the relativistic electron-positron pairs. In this model, the width of the observed average profile is then defined by the last open magnetic field lines. Furthermore, the model predicts that the emitted radio frequencies ν follows a ν ∝ r−3/2 relation, where r is the radial distance from the centre of the star. This leads to the lower frequencies being emitted higher in the magnetosphere than the high frequency radio waves, giving rise to a radius-to-frequency mapping (RFM). Our observations show a decrease in the component separation in the average pulse profile of PSR B1133+16 with frequency, which scales as ν-0.3. After correcting for the residual DM smearing, the retardation and abberation time delays predicted by the RFM model can be measured from the 116 and 173 MHz average profiles. Using a method similar to Cordes (1978), we find a lower limit of 5.6 × 105 m for the height of 116 MHz radio emission. Depending on the methods used, previously measured emission heights were <105.0−105.8 m and <104.7−105.8 m for the radio emission in the 40−1400 MHz range (Cordes 1978; Matese & Whitmire 1980). The upper limit in these works corresponds to the 40 MHz radiation emitted at radius r < 105.8 = 6.3 × 105 m. Therefore, the derived emission height of 5.6 × 105 m for the 116 MHz radiation is consistent with the former results. For the other two pulsars, a reduction in the profile width is visible in Fig. 1. The lack of a reliable fiducial point in the average profiles of these two pulsars prevents a robust estimate being made of the retardation and abberation time delays, hence estimate of emission heights.
The drift analysis revealed the large modulation index in all three pulsars at this frequency, which are similar to that of the Crab pulsar (m = 5 to 8) as found by Weltevrede et al. (2006a) and Weltevrede et al. (2007) at 1380 and 382 MHz, respectively. Combined with the values in their work, the modulation index of the pulsars considered here increases with decreasing frequency indicating the prevalence of bright and spiky emission. From their observations in the 341−4850 MHz range, Kramer et al. (2003) report giant pulses in PSR B1133+16 at 4850 MHz, with a majority of them occurring at the phase of the leading component of the average emission profile. They also report individual pulses at 1412 MHz that can be distinguished clearly from the noise, but have less than 10 times the average pulse energy. Furthermore, these pulses were contemporaneous with the giant pulse emission at 4850 MHz. If the pulses we detect are related to those found at 4850 MHz, then this raises the question of why the mechanism responsible for the bright pulses is not active at 1412 MHz. A possible reason is the unusual spectral behaviour of these bright pulses. Alternatively, the average emission may have a greater contribution from the normal pulses at 1412 MHz than at 4850 MHz or at 116 MHz. Simultaneous observations spanning even wider frequencies than Kramer et al. (2003) could help us to answer this question.
We note that the slopes at the edges of the average emission profiles seen in PSRs B1112+50 and B0031−07 are indicative of the direction of the dominant drift mode. These pulsars were also identified as drifters by Weltevrede et al. (2007). From their work, it can also be seen that several pulsars exhibiting coherent drifting indicate that one of the leading or trailing edges of the average emission profiles is steeper than the other (e.g. B2012+51, B2310+42, B2016+28 etc.).
10. Conclusions
The main conclusion that can be drawn from the pulse energy distributions for PSRs B1133+16 and B0031−07 is that they show a power-law like form in the frequency range observed here. PSR B1112+50 displays a pulse energy distribution with a somewhat steeper power law as a result of several pulses with energy ≥10 × ⟨ E ⟩ . Even though the pulses detected are much narrower than the average pulse profile, these characteristics alone do not qualify these pulsars as giant pulse emitters in the classical sense. However, a single pulse analysis for these pulsars does reveal large modulation indices, suggesting that they are similar to the “spiky” emission observed in the low frequency observations of B0656+14 (Weltevrede et al. 2006c). Extending this argument, this emission may be related to the RRAT-like emissions (Weltevrede et al. 2006b).
In this work, the spectrum of three pulsars in the 110−180 MHz range have been derived. PSR B1133+16 has been found to exhibit a spectral break in this range, while the spectra of PSRs B1112+50 and B0031−07 display spectra peak at frequencies higher than 180 MHz. From our detections of narrow and bright pulses, we reported DM changes for PSRs B1112+50 and B1133+16, but no change in the DM of PSR B0031−07. We have detected microstructure in PSRs B1133+16 and B0031−07, although with our sensitivity we are unable to measure the characteristic intensity variation timescales. In a drift analysis of the single pulses in PSR B0031−07, two of the three drift modes were detected. The modulation indices computed from the pulse stacks of all three pulsars have values larger than those at higher frequencies. This shows the presence of strong pulse to pulse intensity variations and probably arises from the combination of drifting subpulses, single bright pulses and emission nulls. While it remains unclear whether these pulsars emit giant pulses, the emission does change considerably as one moves to lower radio frequencies.
Acknowledgments
We acknowledge the use of European Pulsar Data network, the ATNF pulsar catalogue for this work and the SAO/NASA Astronomical Data System maintained by Harvard-Smithsonian Center for Astrophysics. The WSRT is operated by ASTRON/NWO. We thank the observers in setting up the observations. The PuMa-II instrument and RK were funded by Nederlands Onderzoekschool Voor Astronomie (NOVA). M.S. is supported by the EU Framework 6 Marie Curie Early Stage Training programme under contract number MEST-CT-2005-19669 (ESTRELA). R.K. thanks Priya for help in certain aspects of data analysis. We thank the anonymous referee for comments which improved this manuscript.
References
- Ahuja, A. L., Gupta, Y., Mitra, D., & Kembhavi, A. K. 2005, MNRAS, 357, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Ahuja, A. L., Mitra, D., & Gupta, Y. 2007, MNRAS, 377, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Backer, D. C. 1972, ApJ, 174, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Backer, D. C. 1973, ApJ, 182, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Backer, D. C., Hama, S., Hook, S. V., & Foster, R. S. 1993, ApJ, 404, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Brisken, W. F., Benson, J. M., Goss, W. M., & Thorsett, S. E. 2002, ApJ, 571, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Brisken, W. F., Vlemmings, W. H. T., et al. 2009, ApJ, 698, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Cognard, I., Shrauner, J. A., Taylor, J. H., & Thorsett, S. E. 1996, ApJ, 457, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M. 1978, ApJ, 222, 1006 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cordes, J. M., & Rickett, B. J. 1998, ApJ, 507, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., Weisberg, J. M., & Hankins, T. H. 1990, ApJ, 100, 1882 [Google Scholar]
- Cusumano, G., Hermsen, W., Kramer, M., et al. 2003, A&A, 410, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deshpande, A. A., & Radhakrishnan, V. 1992, JA&A, 13, 151 [Google Scholar]
- Dicke, R. H. 1946, Rev. Sci. Instrum., 17, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, R. T., & Stappers, B. W. 2002, A&A, 393, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ershov, A. A., & Kuzmin, A. D. 2003, SvA, 29, 91 [Google Scholar]
- Ershov, A. A., & Kuzmin, A. D. 2005, A&A, 443, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil, J., & Kijak, J. 1992, A&A, 256, 477 [NASA ADS] [Google Scholar]
- Hankins, T. H. 1972, ApJ, 177, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Hankins, T. H., & Eilek, J. A. 2007, ApJ, 670, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Haslam, C. G. T., Klein, U., Salter, C. J., et al. 1981, A&A, 100, 209 [NASA ADS] [Google Scholar]
- Herfindal, J. L., & Rankin, J. M. 2007, MNRAS, 380, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Faulkner, A., Stairs, I. H., et al. 2004, MNRAS, 352, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- Hotan, A. W., van Straten, W., & Manchester, R. N. 2004, PASA, 21, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Huguenin, G. R., Taylor, J. H., & Troland, T. H. 1970, ApJ, 162, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Izvekova, V. A., Kuz’min, A. D., Lyne, A. G., Shitov, Y. P., & Graham Smith, F. 1993, MNRAS, 261, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, S., & Romani, R. 2003, ApJ, 590, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Kardashev, N. S., Nikolaev, N. I., Novikov, A. I., et al. 1982, A&A, 109, 340 [NASA ADS] [Google Scholar]
- Kargaltsev, O., Pavlov, G. G., & Garmire, G. P. 2006, ApJ, 636, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Karuppusamy, R., Stappers, B., & van Straten, W. 2008, PASP, 120, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Kinkhabwala, A., & Thorsett, S. E. 2000, ApJ, 535, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, H. S. 2007, MNRAS, 378, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, H. S., Bailes, M., Manchester, R. N., & Ord, S. M. 2005, ApJ, 625, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, H. S., Bailes, M., Manchester, R. N., & Ord, S. M. 2006a, ApJ, 653, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, H. S., Bailes, M., Manchester, R. N., Ord, S. M., & Jacoby, B. A. 2006b, ApJ, 640, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, M., Karastergiou, A., Gupta, Y., et al. 2003, A&A, 407, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuzmin, A. D., & Ershov, A. A. 2004, A&A, 427, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuzmin, A. D., Malofeev, V. M., Shitov, Y. P., et al. 1978, MNRAS, 185, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Lange, C., Kramer, M., Wielebinski, R., & Jessner, A. 1998, A&A, 332, 111 [NASA ADS] [Google Scholar]
- Lorimer, D. R., & Kramer, M. 2005, Handbook of Pulsar Astronomy (Cambridge University Press) [Google Scholar]
- Lorimer, D. R., Yates, J. A., Lyne, A. G., & Gould, D. M. 1995, MNRAS, 273, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Lundgren, S. C., Cordes, J. M., Ulmer, M., et al. 1995, ApJ, 453, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Malofeev, V. M., Gil, J. A., Jessner, A., et al. 1994, A&A, 285, 201 [NASA ADS] [Google Scholar]
- Matese, J. J., & Whitmire, D. P. 1980, ApJ, 235, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, F. C. 1978, ApJ, 220, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Nowakowski, L. A. 1996, ApJ, 457, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Petrova, S. A. 2004, A&A, 424, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, J. A., & Wolszczan, A. 1992, ApJ, 385, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Popov, M. V., & Stappers, B. 2003, Astron. Rep., 47, 660 [Google Scholar]
- Ritchings, R. T. 1976, MNRAS, 176, 249 [NASA ADS] [Google Scholar]
- Romani, R., & Johnston, S. 2001, ApJ, 557, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. A., & Sutherland, P. G. 1975, ApJ, 196, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serylak, M., Stappers, B. W., & Weltevrede, P. 2009, A&A, 506, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sieber, W. 1973, A&A, 28, 237 [NASA ADS] [Google Scholar]
- Sieber, W., Reinecke, R., & Wielebinski, R. 1975, A&A, 38, 169 [NASA ADS] [Google Scholar]
- Slee, O. B., Alurkar, S. K., & Bobra, A. D. 1986, Aust. J. Phys., 39, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Smits, J. M., Mitra, D., & Kuijpers, J. 2005, A&A, 440, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smits, J. M., Mitra, D., Stappers, B. W., et al. 2007, A&A, 465, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stinebring, D. R., & Condon, J. J. 1990, ApJ, 352, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J. H., & Cordes, J. M. 1993, ApJ, 411, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J. H., & Weisberg, J. M. 1989, ApJ, 345, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J. H., Manchester, R. N., & Huguenin, G. R. 1975, ApJ, 195, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J. H., Manchester, R. N., & Lyne, A. G. 1993, ApJS, 88, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Vivekanand, M. 1995, MNRAS, 274, 785 [NASA ADS] [Google Scholar]
- Vivekanand, M., & Joshi, V. 1997, ApJ, 477, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Weltevrede, P., & Johnston, S. 2008, MNRAS, 387, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Weltevrede, P., Edwards, R. T., & Stappers, B. W. 2006a, A&A, 445, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weltevrede, P., Stappers, B. W., Rankin, J. M., & Wright, G. A. E. 2006b, ApJ, 645, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Weltevrede, P., Wright, G. A. E., Stappers, B. W., & Rankin, J. M. 2006c, A&A, 458, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weltevrede, P., Stappers, B. W., & Edwards, R. T. 2007, A&A, 469, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, G. A. E., Sieber, W., & Wolszczan, A. 1986, A&A, 160, 402 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Average pulse profiles of the three pulsars. The profile changes with sky frequency is clearly evident. The profile for PSR B1133+16 at 163.5 MHz is not shown because it was too corrupted by RFI. The profiles are shown at 809, 580, 460 μs time resolution for PSRs B1112+50, B1133+16 and B0031−07 respectively. All profiles are normalised by the maximum flux density in the band and are aligned at the phase of maximum intensity in each band. Profiles at 116.75 and 130 MHz have comparatively more noise because up to ~15% of pulses were removed to reject RFI. |
| In the text | |
 |
Fig. 2 Spectra for three pulsars in the frequency range 100−200 MHz. Errors bars correspond to a 10% uncertainty in the pulsar flux estimation. The best fit power law curves are also displayed. For PSR B1133+16, a broken power-law provides a closer fit to the measured fluxes. The flux in the RFI-affected band centred at 163.5 MHz is not included for PSR B1133+16. |
| In the text | |
 |
Fig. 3 Narrow bright pulses from the three pulsars detected at all eight sky frequencies. The total intensity displayed in the top panels is computed by summing the signal in the 8 bands. The lower panels show a dedispersed pulse as a frequency-phase plot. The abscissa in these plots correspond to the pulse phase at 116.75 MHz. Some residual RFI is visible as low-level intensity modulating the entire pulse phase in the frequency-phase plots of all three pulsars. |
| In the text | |
 |
Fig. 4 Single bright pulses and the integrated pulse profiles at 156 MHz for the three pulsars. The flux scale on the left ordinate corresponds to the peak flux of the single pulses and the scale on the right ordinate axis corresponds to the average pulse profile. The phase displayed here is different from that of Fig. 3 due to the signal being dedispered to a different central frequency. Peak flux densities of the single pulses are shown as crosses. Only pulses ≥20σ are shown in these plots which represent a low flux cut-off in the fluxes of single pulses. |
| In the text | |
 |
Fig. 5 Pulse energy distribution for the three pulsars. The abscissa shows pulse energy normalised to the mean pulse energy. Dark and light grey lines correspond to the on-pulse and off-pulse energy distributions. The clear peak at zero energy is introduced by the RFI affected pulses replaced by zeros. |
| In the text | |
 |
Fig. 6 Plot of the peak flux distribution of the single pulses for the three pulsars. The dashed line shows 10 × Sav,peak for each pulsar. |
| In the text | |
 |
Fig. 7 Intensity autocorrelation functions (ACF) of pulses with structure for two pulsars. The uppermost panels present example pulses. The autocorrelations displayed in the middle panel correspond to the pulses above them. The two bottom panels display the averaged ACFs for 120 and 132 pulses for PSRs B0031−07 and B1133+16 respectively. The averaged ACF’s for two bands centred on 116.75 MHz and 173.25 MHz (dashed line) are shown. |
| In the text | |
 |
Fig. 8 Plots of the fluctuation analysis for the PSRs B1112+50, B1133+16, and B0031−07. The average pulse profile, and the longitude-resolved modulation index (LRMI) are shown in the uppermost panels. The panels directly below the average pulse profile present the longitude-resolved fluctuation spectrum (LRFS). The two-dimensional fluctuation spectra (2DFS) are shown in the third and fourth rows. For PSR B1133+16, the 2DFS plots are shown separately corresponding to the two components of the average pulse profile. The panels on the left and bottom of the LRFS and 2DFS images contain the vertically and horizontally integrated spectra, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


