EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 524 (December 2010) A&A, 524 (2010) A43 Full HTML
Free Access
Issue
A&A
Volume 524, December 2010
Article Number A43
Number of page(s) 12
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201015191
Published online 22 November 2010

© ESO, 2010

1. Introduction

Blazars are active galactic nuclei whose extreme properties are thought to be owing to their relativistic jets pointing toward us. BL Lacertae, the prototype of the “BL Lac objects” blazar class, has been the target of many campaigns by the whole earth blazar telescope (WEBT) collaboration1 since 1999. The tens of thousands of optical-to-radio data collected by the WEBT allowed us to study its multiwavelength flux variability, colour behaviour, and the correlations among flux variations in different bands, and revealed a possible periodicity of the radio outbursts. The results have been published by Villata et al. (2002), Ravasio et al. (2002), Böttcher et al. (2003), Villata et al. (2004b), Villata et al. (2004a), Bach et al. (2006), Papadakis et al. (2007), Villata et al. (2009b), Larionov et al. (2010).

In a recent paper, Raiteri et al. (2009) analysed the multiwavelength data from the 2007–2008 WEBT campaign, including three pointings by XMM-Newton. The XMM-Newton data revealed a UV excess, which was interpreted to be due to thermal emission from the accretion disc, as well as a spectral curvature in the X-ray band. The authors constructed spectral energy distributions (SEDs) of BL Lacertae corresponding to various epochs where the source was in different brightness states, using both their own data and data from the literature. They applied the inhomogeneous, rotating helical jet model by Villata & Raiteri (1999, see also Raiteri et al. 1999; Raiteri et al. 2003; Ostorero et al. 2004 to fit the SEDs, and suggested that the broad-band spectral properties of BL Lacertae may result from the combination of two synchrotron emission components with their self inverse-Compton emission, plus a thermal component from the disc. Subsequently, Capetti et al. (2010) analysed optical spectra acquired in the same period with the 3.56 m telescopio nazionale galileo (TNG). They found a broad Hα emission line, with luminosity of  ~4 × 1041   ergs-1 and FWHM of  ~4600 km s-1, even brighter than that found in 1995–1997 by Vermeulen et al. (1995) and Corbett et al. (1996, 2000). This favours the hypothesis that the UV excess is caused by thermal emission from the accretion disc, the most likely source of ionising photons for the broad line region. The multiwavelength data available for the Raiteri et al. (2009) analysis lacked simultaneous information in the γ-ray band, so that the inverse-Compton spectral region was poorly constrained. But in 2008 the Fermi satellite was able to detect BL Lacertae (Abdo et al. 2010a), even if in a low state compared to the past detections by the compton gamma ray observatory2 (CGRO, Hartman et al. 1999; Bloom et al. 1997). In the same period, observations in the UV and X-ray bands were performed by Swift, while in the optical, near-IR, mm and cm radio bands the source was monitored by the GLAST-AGILE Support Program (GASP) of the WEBT. This offered the unique opportunity to study the source emission over a very extended spectral range. The results of this further investigation effort on BL Lacertae are presented in this paper.

2. GASP observations

The GASP was born in 2007 as a WEBT project, with the aim of monitoring a list of 28 γ-ray loud blazars in the optical, near-IR, mm, and cm radio bands during the γ-ray observations of the AGILE3 and Fermi4 (formerly GLAST) satellites (see e.g. Villata et al. 2008, 2009a). Data are collected periodically by the WEBT President, who checks the consistency of the various datasets. The GASP light curves are then available for multiwavelength studies, mostly in the framework of the GASP collaboration with the AGILE and Fermi research teams. The GASP data presented in this paper were taken at the observatories listed in Table 1.

Table 1

List of optical, near-IR, and mm–cm radio observatories contributing data to this work.

The optical data were calibrated with respect to a common choice of reference stars in the same field of the source (Bertaud et al. 1969 in U and B bands; Fiorucci & Tosti 1996 in V, R, and I). The source photometry was evaluated from a circular region with an 8 arcsec aperture radius, while the background was taken in a surrounding annulus with 10 and 16 arcsec radii. In this way the measure is essentially seeing-independent and all datasets are affected by the same contamination from the light of the host galaxy. Raiteri et al. (2009) estimated that with the above prescriptions the contamination amounts to about 60% of the host total flux density, which is 0.36, 1.30, 2.89, 4.23, 5.90, 11.83, 13.97, and 10.62 mJy in the U, B, V, R, I, J, H, and K bands, respectively. When converting magnitudes into flux densities, we corrected for the Galactic extinction according to the Cardelli et al. (1989) laws, using RV = 3.1, the standard value for the diffuse interstellar medium, and AB = 1.42 (from Schlegel et al. 1998). We adopted the absolute fluxes by Bessell et al. (1998).

thumbnail Fig. 1

R-band light curve by the GASP collaboration from February 2008 to February 2009. Data are not corrected for the host galaxy contamination or Galactic extinction. The participating observatories are marked with different symbols and colours. The total number of data points is indicated in the upper right.

thumbnail Fig. 2

June–November 2008 light curves of BL Lacertae from UV to near-IR after correction for the host galaxy contribution, but not for the Galactic extinction. Data taken by the GASP-WEBT collaboration are plotted as blue circles, UVOT data as red triangles. The UVOT u, b, and v light curves have been shifted to match the ground-based U, B, and V ones (see text for details).

Figure 1 shows the best-sampled total R-band light curve from February 2008 to February 2009 built with GASP data, which are not corrected for the host galaxy contribution here. A noticeable flare was observed at the beginning of the period, in 2008 February–March; afterwards both the average brightness level and the variability amplitude decreased. However, the source remained active, its brightness oscillating by several tenths of magnitude on a few-day time scale. This is not an unusual behaviour for BL Lacertae (see e.g. Raiteri et al. 2009, who reported on a 0.9 mag brightening in 24 h).

Optical data at other wavelengths as well as near-IR data are shown in Fig. 2 for the period June–November 2008 (the UV data displayed in the figure are presented in Sect. 3). The host galaxy contribution has been subtracted to distinguish the behaviour of the active nucleus. This reveals that the brightness evolution follows the same trend in the various bands, but magnitude variations are more pronounced at higher frequencies, which is a common feature of BL Lac objects. For example, the brightness increase following the almost symmetric dip around JD ~ 2454681 involved a variation of 0.79, 0.64, 0.57, and 0.54 mag in  ~5 days in the B, V, R, and I bands, respectively. We notice that the source redshift is z = 0.0686 (Vermeulen et al. 1995) and hence the broad Hα emission line enters the tails of the R and I passbands. However, referring to Capetti et al. (2010), one can estimate that its flux contribution is only a few thousandths of that of the continuum. Hence, the presence of the line cannot affect the variability in these bands, at least when the source brightness is at these levels. Another interesting example of fast variability is the rise of  ~0.9 mag in 4 days, from JD = 2454752.3 to 2454756.3, in the R band, which unfortunately was not observed in other bands.

Radio flux densities at cm–mm wavelengths are displayed in Fig. 3 together with de-reddened and host-galaxy subtracted R-band optical flux densities. The former are complemented by data from the VLA/VLBA polarization calibration database5 (PCD). The flux variation amplitude appears to decrease from the highest to the lowest frequencies, as usual. One interesting feature is the fast radio flare that is visible in the 37 GHz light curve at JD ~ 2454760, because it occurred simultaneously with an optical flare. The correlation between optical and radio flux variations in BL Lacertae has been the subject of several studies, and most of them found a correlation with a long time delay (a few months) of the radio after the optical flux changes (see e.g. Hufnagel & Bregman 1992; Tornikoski et al. 1994b; Clements et al. 1995; Villata et al. 2004a; Bach et al. 2006; Villata et al. 2009b). However, simultaneous variations have already been found (Tornikoski et al. 1994a). The 37 GHz data we are dealing with are affected by large uncertainties due to unfavourable weather conditions; but an increase of the radio flux is visible also at 43, 22, and 14.5 GHz, giving strength to the possibility that these events are correlated. We also notice that there is neither a contemporaneous nor a delayed clear radio counterpart to the optical flare observed at the beginning of the period (JD ~ 2454520). Yet, one would have expected to see it in the high-frequency radio light curves. A better sampling in the mm wavelength range perhaps would have helped to understand whether the variability mechanism responsible for this flare affected the optical emission region only or if it extended also to the radio domain.

thumbnail Fig. 3

Optical flux densities (R band, top panel), after correction for Galactic extinction and host galaxy contamination, compared to radio flux densities at different frequencies. Blue circles represent GASP data; red diamonds indicate data from the VLA/VLBA PCD. The vertical green line corresponds to the XMM-Newton pointing of May 16–17; the yellow strip highlights the period of Swift observations, from 2008 August 20 to October 2.

3. Swift observations

The Swift satellite observed BL Lacertae in 2008 August, September, and October, for a total of 24 pointings. In particular, from August 20 to September 9 a daily sampling was obtained.

3.1. UVOT data

The Ultraviolet/Optical Telescope (UVOT; Roming et al. 2005) onboard the Swift spacecraft acquires data in the optical v, b, and u bands, as well as in the UV filters uvw1, uvm2, and uvw2 (Poole et al. 2008).

We reduced the BL Lacertae data with the HEAsoft package version 6.7, with CALDB updated at the end of November 2009. Source counts were extracted from a circular region with a radius of 5 arcsec, while background counts were estimated in a neighbouring source-free region. When multiple exposures in the same filter were present during an observing epoch, we first processed each frame separately with the task uvotmaghist and then binned the results. These values were compared with those obtained by first summing the frames acquired in the same band with uvotimsum, and then performing the aperture photometry with the task uvotsource. We verified that the two methods are equivalent.

The final UVOT light curves are shown in Fig. 2. We subtracted the host galaxy contribution, taking into account that with the 5 arcsec aperture radius we used for the photometry, about 50% of the host flux was included. We adopted the host galaxy flux densities given by Raiteri et al. (2009, see also Sect. 2; these authors also discussed that the host contribution can be considered negligible in the UV.

The comparison between the UVOT u, b, and v data and the U, B, and V data taken by the GASP observers reveals that an offset is present between the space light curves and the ground-based ones. We estimated mean offsets U−u = 0.2, B−b = 0.1, and V−v = −0.05. The UVOT light curves shown in Fig. 2 have been shifted accordingly. Taking into account that the average UVOT colour indices of BL Lacertae are u−b ~ −0.4 and b−v ~ 0.8, the above offsets disagree with those derived by Poole et al. (2008) for the objects on which they based their photometric calibration of UVOT, i.e. Pickles stars and GRB models. Indeed, these objects have a different spectral shape, so that the Poole et al. (2008) calibrations may not hold for BL Lacertae.

The UVOT data confirm the variability trend traced by the ground-based ones, extending it to UV frequencies. This indicates that the variability mechanism affecting the near-IR–optical emission, which is dominated by beamed synchrotron radiation, can also produce flux changes in the UV, where a contribution from the synchrotron emission is thus expected, besides a possible contribution from thermal disc radiation.

thumbnail Fig. 4

Top: observed spectrum of BL Lacertae in the optical-UV band. Red diamonds refer to the mean UVOT spectrum resulting from 16 epochs analysed in this paper. Blue circles represent the average spectrum obtained from the three observations of the OM instrument onboard XMM-Newton in 2007–2008 (Raiteri et al. 2009), normalised to the mean UVOT spectrum in the v band. The solid line is the log-parabolic fit used in the calibration procedure. Bottom: optical-UV SEDs of BL Lacertae. Blue circles and red diamonds are derived from the OM and UVOT average spectra shown in the top panel by using standard prescriptions to obtain dereddened flux densities. Black squares represent the mean UVOT SED after recalibration as explained in the text. In both panels the filter labels are centred on the standard UVOT λeff (Poole et al. 2008).

The derivation of the source intrinsic flux densities for further analysis (see Sect. 5) requires some attention. In their paper on the photometric calibration of UVOT, Poole et al. (2008) give effective wavelengths of 5402, 4329, 3501, 2634, 2231, and 2030 Å for the v, b, u, uvw1, uvm2, and uvw2 filters, respectively, but warn that the λeff of the UV filters will be longer for very red spectra. Moreover, they provide count-rate-to-flux conversion factors for both Pickles stars and GRB models, but in the UV bands their validity range is limited to b−v = 0.1 and b−v = 0.03, respectively, while BL Lacertae has b−v ~ 0.8.

In order to attenuate possible calibration problems, we thus calculated both the effective wavelengths λeff and count-rate-to-flux conversion factors CF for the UVOT filters by folding the BL Lacertae spectrum with their effective areas (see Poole et al. 2008). We first built a composite observed spectrum of BL Lacertae by combining a mean OM spectrum (obtained from the three XMM-Newton pointings of 2007–2008, Raiteri et al. 2009) with an average UVOT spectrum (resulting from 16 UVOT observing epochs analysed in this paper). To compensate for the different brightness state, we increased the OM flux densities by  ~6% so that the two spectra match in the V band. The composite spectrum is shown in Fig. 4 (top panel), together with its log-parabolic fit that we used in the folding procedure. The resulting effective wavelengths (see Eq. (8) in Poole et al. 2008) are: 5439, 4381, 3500, 2776, 2295, and 2225 Å for the v, b, u, uvw1, uvm2, and uvw2 filters, respectively, showing a clear shift towards longer wavelengths in the ultraviolet. As for the count-rate-to-flux conversion factors, we obtained 2.60, 1.47, 1.65, 4.31, 8.54, and 6.72 × 10-16ergcm-2s-1   Å-1 from the v to the uvw2 band, respectively. These new CF differ from those given by Poole et al. (2008) for the GRB models by  ≲ 1%, with the only exceptions of CF(uvw1) and CF(uvw2), which are now 8% larger6.

The new λeff would produce a decrease of extinction in the uvw1 and uvm2 bands with respect to those given by Poole et al. (2008), and an increase in the uvw2 band. Indeed, the Galactic mean extinction curve shows a dramatic bump peaking at λ ~ 2175   Å owing to absorption by graphite dust. Actually, an accurate evaluation of extinction in this critical frequency range requires that the Cardelli et al. (1989) law is folded with the filter’s effective area and BL Lacertae spectrum, similarly to what was done above for the λeff and CF: 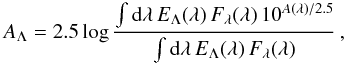(1)where AΛ is the extinction in the Λ band, EΛ is the effective area of that band, and Fλ is the source flux density. The result is a Galactic extinction of 1.10, 1.44, 1.74, 2.40, 3.04, and 2.92 mag from the v to the uvw2 band, respectively.

We verified the stability of our results by iterating the procedure with the recalibrated UVOT flux densities and λeff. The bottom panel of Fig. 4 shows the mean SED obtained after recalibration of the UVOT data according to our procedure. For comparison, we also show the OM and UVOT SEDs derived from the average spectra shown in the top panel, for which the amount of Galactic extinction was calculated from the Cardelli et al. (1989) law at the standard λeff. Notice that the recalibration process has shifted λeff(uvw2) redward so much that it overlaps with the standard λeff(uvm2). This is because of the noticeable red tail of the uvw2 filter (Poole et al. 2008) as well as to the red BL Lacertae spectrum. Recalibration has solved the uvw1-dip problem, which is a common feature of UVOT SEDs for a number of blazars at different redshifts (see e.g. Villata et al. 2008; Raiteri et al. 2008; D’Ammando et al. 2009). Moreover, it seems to confirm the UV excess claimed by Raiteri et al. (2009) that was ascribed to thermal emission from the accretion disc, even if this excess may be less pronounced than indicated by the OM data. Our analysis highlights the importance of calculating the amount of extinction in the critical UV bands, close to the 2175 Å bump, by folding the Galactic mean extinction law through the effective area curves and source spectrum. In any case, as pointed out by Fitzpatrick & Massa (2007), one has to keep in mind that the use of an average dereddening curve implies a significant error owing to the scatter of Galactic extinction curves.

3.2. XRT data

The X-ray Telescope (XRT; Burrows et al. 2005) data were processed with version 0.12.3 of the xrtpipeline task contained in the FTOOLS package, applying standard screening criteria. Inspection of the light curves revealed that the count rate was low, from 0.15 to 0.24 counts s-1, so that observations were performed in photon counting mode, and no correction for pile-up was necessary. Source and background spectra were extracted with xselect from a circular region of 20 pixel (47 arcsec) radius centred on the source and from a surrounding annulus of 30 and 50 pixel radii, respectively. We used version 011 of the response matrix available in the HEASARC calibration database (CALDB), and calculated the ancillary response file with xrtmkarf, using the exposure map created by xrtpipeline. The source spectra were binned with grppha to have a minimum of 20 counts in each bin, and they were finally analysed with version 12.5.1 of the Xspec task, using the energy channels greater than 0.3 keV.

Spectral analysis was performed for each observation following Raiteri et al. (2009): we first fitted a single power law with free absorption7, and then fixed the Galactic absorption to NH = 3.4 × 1021   cm-2, which takes into account both atomic and molecular column density. Statistics is not good enough to evaluate if a double power law model can improve the fit. The results of spectral fitting on XRT data are reported in Table 2 for all observations with an exposure longer than 3 ks; Col. 1 gives the date and start time of the observation; Col. 2 its duration; Col. 3 the hydrogen column; Col. 4 the power law photon index; Col. 5 the 1 keV flux density; Col. 6 the χ2/ν (and degrees of freedom). One spectrum (August 29) is shown in Fig. 5.

Fits with free absorption resulted in a very variable NH, which is unlikely to correspond to a real change of absorption. The average and median values are 3.46 and 3.44 × 1021   cm-2, respectively, confirming that the value assumed for the Galactic absorption is quite reasonable. Hence, we favoured the second model, whose χ2/ν is usually smaller than in the NH-free case, and that produces results with smaller errors (because of one degree of freedom more). In only two cases (August 23 and September 2) a double power law model with absorption fixed to the Galactic value clearly improved the fit.

The photon index Γ ranges from 1.92 to 2.25, indicating a spectrum that oscillates from moderately hard to moderately soft. The average value is 2.07, with standard deviation of 0.08. To understand whether these spectral changes correspond to real variations or are owing to noise, we recall the definition of the mean fractional variation 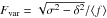(Peterson 2001), which is commonly used to characterise variability. Here  ⟨ f ⟩  is the mean value of the variable we are analysing, σ2 its variance, and δ2 the mean square uncertainty. In our case, σ2 = 0.006 is smaller than δ2 = 0.011, so that the result is imaginary; thus we conclude that the variations are consistent with noise rather than source variability.

The 1 keV flux density varies between 1.34 and 2.24   μJy, with a mean value of 1.75 and standard deviation of 0.24. In this case Fvar = 0.11, and the variations can be considered reliable.

Table 2

Spectral fitting to the XRT data from Swift observations in 2008.

Multiwavelength light curves of BL Lacertae in the period around the Swift observations are shown in Fig. 6. The source behaviour at 1 keV differs from the common trend characterising the UV, optical, and near-IR bands. In particular, the X-ray flux peaks when the near-IR–UV fluxes reach a minimum. However, there are also similarities, like the flux increase at the beginning of the common observing period, and the final decrease. This may indicate that the 1 keV flux behaviour sometimes is related to the brightness changes that occur at lower wavelengths, while in other cases another variability mechanism prevails. Indeed, according to Raiteri et al. (2009) this frequency domain receives the variable contribution of two different emission components (see also Sect. 5).

4. XMM-Newton observations

The X-ray multi-mirror mission (XMM) - Newton satellite observed the source during revolution 1545, on 2008 May 16–17, with a total exposure of  ~134   ks. Data were processed with the science analysis system (SAS) package version 9.0.

4.1. OM data

The Optical Monitor (OM; Mason et al. 2001) onboard XMM-Newton is a 30-cm telescope carrying six optical/UV filters, and two grisms. BL Lacertae observations in May 2008 consisted of 10 subsequent exposures in UVW1, followed by 9 in UVM2, and then 8 in UVW2. All exposures were  ~4000   s long. We used the SAS task omichain to reduce the data and the tasks omsource and omphotom to derive the source magnitude. The error on the aperture photometry is 0.03, 0.04, and 0.09 mag for the UVW1, UVM2, and UVW2 filters, respectively. The resulting light curves are shown in Fig. 7; average magnitudes are UVW1 = 15.45, UVM2 = 16.25, and UVW2 = 16.54.

To obtain flux densities for further analysis, OM magnitudes were corrected for the Galactic extinction calculated according to the Cardelli et al. (1989, see Sect. 2 laws at the effective wavelengths of the OM filters (2910, 2310, and 2120 Å for the UVW1, UVM2, and UVW2 filters, respectively). Conversion of de-reddened magnitudes into flux densities was done with respect to Vega.

4.2. EPIC data

The European Photon Imaging Camera (EPIC) onboard XMM-Newton includes three detectors: MOS1, MOS2 (Turner et al. 2001), and pn (Strüder et al. 2001). All instruments were used with a thin filter. The two MOS cameras observed in small-window imaging mode, while pn was used in timing mode.

We followed the standard prescription to reduce the data, including filtering of high background periods with a threshold of 0.35 counts s-1 for MOS, but with a stricter threshold of 0.1 counts s-1 for pn.

For both MOS1 and MOS2, we created a filtered sky image, and extracted the source counts from a 50 arcsec radius circular region, while background was evaluated in a circle on an external CCD. As for pn, we extracted the source counts from a strip between RAWX=35 and 39, and the background from two strips at columns 24–28 and 48–52. To get the most reliable and best calibrated events, we used the FLAG==0 selection expression and kept only single and double events (PATTERN < =4). We verified that pile-up effects were not affecting the MOS data with the epatplot task.

Through the grppha task of the FTOOL package we binned the source spectra to have a minimum of 25 counts in each bin and then analysed them together by means of the Xspec task of the XANADU package. Only spectral bins corresponding to energies between 0.3 and 10 keV for MOS1 and MOS2 and in the range 0.5–10 keV for pn were considered, because they have both a better calibration and a higher signal-to-noise ratio.

The three EPIC spectra were analysed together by first fitting a single power law with free absorption, and then fixing the Galactic absorption to NH = 3.4 × 1021   cm-2. We also tried a double power law with the same Galactic absorption. The results are shown in Table 3 (see also Fig. 8). In agreement with Raiteri et al. (2009), the χ2/ν suggests that a single power law with Galactic absorption of NH = 3.4 × 1021   cm-2 does not represent a good fit to the data. As for the other two fits, the double power law seems to better fit the data, which is also confirmed by a very low F-test probability of  ~6.8 × 10-16. This implies a strong spectral curvature.

To check for possible flux variations, we extracted X-ray light curves from the same source and background regions defined for the spectra, with the same selection expressions. We considered only the events in the time intervals free from high background and belonging to the 0.3–10 keV energy range for MOS1 and MOS2, and 0.5–10 keV for pn. The source counts were corrected for the background and then binned in one hour intervals. The results are shown in Fig. 7, which also displays the behaviour of the background to check the reliability of the flux variations. The background increased significantly only in the last 6 h. Just before, at JD ~ 2454604.05, there is a small flare clearly visible in all three light curves. Mean source rates for the whole period are 1.63, 0.61, and 0.64 counts s-1 for pn, MOS1, and MOS2, respectively, with standard deviations of 0.15, 0.04, and 0.03 counts s-1. This means fractional variations Fvar of 7%, 6%, and 4%, which do not change significantly if we exclude the last 6 h. Hence, we can conclude that the X-ray flux of BL Lacertae is mildly variable on an hour time scale.

thumbnail Fig. 5

Swift-XRT spectrum of BL Lacertae on 2008 August 29. The bottom panel shows the deviations of the observed data from the folded model (a single power law with fixed absorption) in units of standard deviations.
thumbnail Fig. 6

Details of the multiwavelength behaviour of BL Lacertae in the period around the Swift observations. The X-ray flux density (at 1 keV, top) is compared to that in the UV (uvw1 band), optical (R band), near-IR (K band), and radio (37 GHz, bottom) frequency range.

thumbnail Fig. 7

UV and X-ray light curves obtained by the OM and EPIC instruments onboard XMM-Newton on 2008 May 16–17. Black, red, and blue filled circles represent UVW1, UVM2, and UVW2 magnitudes, respectively. Arrows mark the data points used for the SED shown in Fig. 9. Green diamonds, black squares, and red triangles refer to pn (0.5–10 keV), MOS1 (0.3–10 keV), and MOS2 (0.3–10 keV) count rates, respectively. Plus signs show the corresponding backgrounds. In all panels horizontal dashed lines indicate average values and dotted lines represent standard deviations from the mean.

5. Modelling the SED

Figure 9 shows the broad-band SED of BL Lacertae in different brightness states. The SED corresponding to 2008 May 16–17 includes the XMM-Newton UV and X-ray data analysed in Sect. 4. In order to avoid offsets caused by source variability, the OM spectrum was constructed with the last UVW1 data point, the first UVM2 (which is close to the last UVM2), and the first UVW2 datum of the corresponding light curves (see Fig. 7). These data indicate a hard UV spectrum. Two SEDs in the figure refer to the Swift observations of 2008 August 25 and 30, which were chosen among those analysed in Sect. 3 because of the different spectral slope in the X-ray band. The low-frequency part of these three SEDs is built with GASP optical and radio data (see Sect. 2); for August 30 near-IR data were also available. The strong source variability in the optical band requires that the optical (and near-IR) data are simultaneous with the satellite observations. In the radio bands flux variations are slower, so that we used data taken within 2–3 days from the satellite ones, when simultaneous data were not available. Near-IR, optical, and UV data were corrected for the Galactic extinction; the near-IR and optical data were also corrected for the contribution of the host galaxy (see Sect. 2). In August 2008 the Fermi γ-ray satellite detected BL Lacertae; the Fermi data we plotted in Fig. 9 were derived from Abdo et al. (2010a).

The August 2008 SEDs indicate a faint, synchrotron-dominated state of the source that we fitted with the rotating helical jet model by Villata & Raiteri (1999, see also Raiteri et al. 1999; Raiteri et al. 2003; Ostorero et al. 2004. This model has been used by Raiteri et al. (2009) to fit the broad-band SED of BL Lacertae in December 2007–January 2008. Their main finding was that the BL Lacertae broad-band SED cannot be explained by a single synchrotron component plus its self inverse-Compton emission. Indeed, the very strong historical X-ray variability requires an additional synchrotron (plus self inverse-Compton) component. Moreover, the UV excess suggests thermal contribution from the accretion disc (see Sect. 3.1). The SED analysed by Raiteri et al. (2009) lacked simultaneous γ-ray data, which made it impossible to constrain the inverse-Compton emission of the high-energy component. The 2008 August SED in Fig. 9 now offers us the possibility to perform a more detailed analysis.

Table 3

Spectral fitting to the EPIC (pn+MOS1+MOS2) data from the XMM-Newton observations of 2008 May 16–17.

thumbnail Fig. 8

EPIC spectrum of BL Lacertae on 2008 May 16–17; black squares, red triangles, and green diamonds represent MOS1, MOS2, and pn data, respectively. The bottom panel shows the deviations of the observed data from the folded model (a double power law with fixed absorption) in units of standard deviations.

In addition, we also display in Fig. 9 the broad-band SED corresponding to the big outburst of July 1997, which showed a considerable inverse-Compton dominance. The X-ray spectra plotted in the figure are the result of the combined analysis of the ASCA and RXTE data by Tanihata et al. (2000). Because of the very strong variability of the source in that period, the authors distinguished between a low state, which was well fitted by a single power law model, and a flare state, for which the best fit was obtained with a double power law model. This last fit resulted in a very strong spectral curvature8. In July 1997 observations in the γ-ray band were performed by CGRO. The data from the EGRET instrument onboard CGRO in Fig. 9 were taken from Bloom et al. (1997), while those from the OSSE detector were derived from the high energy astrophysics science archive research center9 (HEASARC). The low-frequency information is from the WEBT archive; the range of optical flux variation in the period is indicated. This outburst state of the source was fitted with the same rotating helical model that we used to fit the faint state of 2008.

In performing the model fits our aim was to see whether it was possible to reproduce the high and low states by changing the geometrical configuration only. Moreover, we took into account the results by Larionov et al. (2010), who explained the long-term BL Lacertae optical and near-IR variability in terms of variations of the Doppler boosting factor due to changes of the viewing angle of the emitting region.

The resulting model parameters are reported in Table 4, while the corresponding fits are shown in Fig. 9. We also included blackbody radiation from an accretion disc with a luminosity of 5 × 1044   ergs-1 and a temperature of  ~16000 K. The low-energy (radio-to-optical and related inverse-Compton) emission component comes from a helix portion with a pitch angle ζ = 2°, covering an angle a = 180°. The maximum Lorentz factor of the relativistic electrons is log γmax(0) = 3.7, while the bulk Lorentz factor of the plasma in the jet is Γ = 7. The high-energy (UV–X-ray and related inverse-Compton) emission component comes from a helix portion with a pitch angle ζ = 8°, covering an angle a = 360°. The maximum Lorentz factor of the relativistic electrons is log γmax(0) = 3.8, while the bulk Lorentz factor is Γ = 13. These parameters, as well as those defining the power laws according to which the maximum and minimum emitted frequencies and the flux densities decrease with distance from the jet apex, are maintained fixed. The difference between the fits to the 1997 and 2008 SEDs is only due to a variation of the orientation of the jet emitting regions, through only two geometric parameters: the angle between the helix axis and the line of sight ψ and the rotation angle φ. The outburst state requires a better alignment of the emitting regions with the line of sight, which implies ψ approaching the helix pitch angle, and smaller rotation angles φ.

thumbnail Fig. 9

Broad-band SEDs of BL Lacertae in August 2008 (blue) and July 1997 (red). The 2008 SED is built with UV and X-ray data from two epochs of Swift observations (Sect. 3), 2008 August 25 and 30, together with simultaneous optical-to-radio data from the GASP-WEBT collaboration, and contemporaneous γ-ray data from Fermi (from Abdo et al. 2010a). The 1997 SED includes EGRET data from Bloom et al. (1997), OSSE data from the HEASARC archive, ASCA+RXTE spectra from Tanihata et al. (2000), while low-frequency data are from the WEBT archive. Solid lines represent model fits; we distinguish the low-energy emission component (dotted lines) from the high-energy one (dashed lines); the contribution by an accretion disc of  ~16000 K and 5 × 1044   ergs-1 is marked with a dotted-dashed line. We also show in black the SED corresponding to the XMM-Newton observations of May 2008 (Sect. 4); both the single power law with free absorption and double power law with Galactic absorption fits to the EPIC spectra are displayed.

Table 4

Main parameters of the helical jet model for the fit to both the 2008 faint-state SED and the 1997 outburst-state SED.

6. Discussion

The satisfactory fits that we obtained in the previous section for both the outburst and faint states of BL Lacertae give strength to our interpretation of the source SED in terms of two synchrotron plus self inverse-Compton emission components. In the SED, the synchrotron peak of the low-energy component falls in the near-IR band, and its inverse-Compton reaches a maximum in the 1–50 MeV energy range. The synchrotron and inverse-Compton peaks of the high-energy component occur in the far-UV-soft-X-ray band and in the energy range 0.2–5 GeV, respectively. Whether these two components come from two distinct helices or from different regions inside the same helical jet is not clear. We consider it more likely that there is a unique jet, where the high-energy component comes from a region closer to the emitting jet apex than the low-energy one. We notice that a double synchrotron component is not an unusual interpretation for the blazar emission properties, as it has been proposed also for Mkn 421 (Donnarumma et al. 2009) and 3C 454.3 (Ogle et al. 2010).

Moreover, the fits show that the whole range of BL Lacertae multiwavelength variability can be interpreted in terms of orientation effects. Although the rotating helical jet model we have adopted in the previous section is not a physically complete model, but more a phenomenological approach, it has the advantage of taking into account variations of the orientation of the emitting regions with respect to the line of sight, with consequent changes of the Doppler beaming factor. This is an aspect that is usually neglected by theoretical models of blazar emission, which explain flux and spectral changes uniquely in terms of energetic processes inside the jet.

Our interpretation is in line with previous results. Marscher et al. (2008) analysed the evolution of the BL Lacertae optical polarization during 2005, and suggested that the plasma flows along helical streamlines. According to Villata et al. (2009b), the long-term optical and radio behaviour of BL Lacertae suggests a scenario where the emitting plasma flows along a rotating helical path in a curved jet. This rotating helical structure could be caused by orbital motion in a binary black hole system, coupled with the interaction of the plasma jet with the surrounding medium. Indeed, the binary black hole scenario could explain the periodicity observed in the radio light curves of BL Lacertae (Villata et al. 2004a, 2009b), the discovery of a precessing jet nozzle with the VLBA (Stirling et al. 2003), and possibly the parsec-to-kiloparsec jet misalignment (see e.g. Kharb et al. 2010). Moreover, the analysis of the BL Lacertae spectral evolution in 2000–2008 by Larionov et al. (2010) favoured a picture where the optical and near-IR flux and colour variability can be explained by a variable viewing angle of the emitting region. These authors also suggested that a fractal helical structure may be at the origin of the different time scales of variability.

The values of the angles ζ = 2° and ψ = 4.5–5°, as well as the Lorentz factor Γ = 7 adopted in the model fits for the low-energy component, agree very well with the corresponding values of Larionov et al. (2010), thus supporting the common interpretation. The helix pitch angle ζ = 8° found for the high-energy component indicates that this inner jet helical region would be more twisted than the outer, lower-energy one. In practice, our model results indicate a helical jet whose axis is bent between the X-ray and optical regions by about 2° (see the values of ψ in Table 4) and that is more wrapped near the apex and then tends to relax with a decreasing pitch angle. The different orientations assumed by such a jet in 2008 and 1997 are sketched in Fig. 10, where all the angles are strongly increased for clarity.

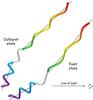thumbnail Fig. 10

Sketch of our helical jet model during both the 2008 faint state and the 1997 outburst state. The angle between the jet axis and the line of sight, ψ, has been multiplied by a factor 10 with respect to the values given in Table 4 for clarity. We distinguish the inner region, emitting the high-energy synchrotron plus self inverse-Compton component (purple-blue) from the outer zone, where the low-energy emission component is produced (green-yellow-red).

The thermal emission component that we added to the helical jet model is justified by the UV excess found in the OM data from XMM-Newton, and (though with less evidence) in the UVOT data from Swift. As discussed in the present paper and in Raiteri et al. (2009), the amount of this excess strongly depends on both the Galactic extinction and instrument calibration, but it is not easy to cancel it out completely. In any case, Capetti et al. (2010) showed that after twelve years from the first detection of the Hα broad emission line by Vermeulen et al. (1995) and Corbett et al. (1996, see also Corbett et al. 2000, the Hα line is still there, even more luminous than before. This suggests that a disc is also there to photoionise the broad line region.

Photons coming from the disc or broad line region could then enter the jet, and be inverse-Compton scattered, giving rise to other high-energy emission components that are sometimes invoked to account for the SED properties of blazars. In particular, the 1997 outburst state has previously been interpreted by Madejski et al. (1999) in terms of three emission components: synchrotron, synchrotron self-Compton, and Comptonisation of the broad emission line flux. Similar results were obtained by Böttcher & Bloom (2000) and by Ravasio et al. (2002). Our “geometrical” interpretation does not require these external-Compton emission components, which are not expected to contribute if the jet emission regions are parsecs away from the central black hole (see e.g. Sikora et al. 2008; Marscher et al. 2010; Abdo et al. 2010b).

6

Notice that our CF(uvw1) corresponds to that given by Poole et al. (2008) for the Pickles stars.

7

We adopted the Tuebingen-Boulder ISM absorption model (Wilms et al. 2000).

8

We notice that Tanihata et al. (2000) adopted a Galactic total absorption of NH = 4.6 × 1021   cm-2.

Acknowledgments

We acknowledge Ann E. Wehrle for useful comments. This research has made use of NASA’s Astrophysics Data System. The Torino and Palermo teams acknowledge financial support by the Italian Space Agency through contract ASI-INAF I/088/06/0 for the Study of High-Energy Astrophysics. The Abastumani Observatory team acknowledges financial support by the Georgian National Science Foundation through grant GNSF/ST08/4-404. St. Petersburg University team acknowledges support from Russian RFBR foundation via grant 09-02-00092. AZT-24 observations are made within an agreement between Pulkovo, Rome and Teramo observatories. This work was partly supported by the Taiwan National Science Council grant No. 96-2811-M-008-033. This paper is partly based on observations carried out at the

German-Spanish Calar Alto Observatory, which is jointly operated by the MPIA and the IAA-CSIC. Acquisition of the MAPCAT data is supported in part by the Spanish Ministry of Science and Innovation and the Regional Government of Andalucía through grants AYA2007-67626-C03-03 and P09-FQM-4784, respectively. The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica. The BU team acknowledges financial support by NASA through Fermi Guest Investigator grants NNX08AV65G and NNX08AV61G and by the NSF through grant AST-0907893. The Metsähovi team acknowledges the support from the Academy of Finland to our observing projects (numbers 212656, 210338, and others).

References

  1. Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010a, ApJ, 716, 30 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Nature, 463, 919 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  3. Bach, U., Villata, M., Raiteri, C. M., et al. 2006, A&A, 456, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bertaud, C., Dumortier, B., Veron, P., et al. 1969, A&A, 3, 436 [NASA ADS] [Google Scholar]
  5. Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
  6. Bloom, S. D., Bertsch, D. L., Hartman, R. C., et al. 1997, ApJ, 490, L145 [NASA ADS] [CrossRef] [Google Scholar]
  7. Böttcher, M., & Bloom, S. D. 2000, AJ, 119, 469 [NASA ADS] [CrossRef] [Google Scholar]
  8. Böttcher, M., Marscher, A. P., Ravasio, M., et al. 2003, ApJ, 596, 847 [NASA ADS] [CrossRef] [Google Scholar]
  9. Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
  10. Capetti, A., Raiteri, C. M., & Buttiglione, S. 2010, A&A, 516, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
  12. Clements, S. D., Smith, A. G., Aller, H. D., & Aller, M. F. 1995, AJ, 110, 529 [NASA ADS] [CrossRef] [Google Scholar]
  13. Corbett, E. A., Robinson, A., Axon, D. J., & Hough, J. H. 2000, MNRAS, 311, 485 [NASA ADS] [CrossRef] [Google Scholar]
  14. Corbett, E. A., Robinson, A., Axon, D. J., et al. 1996, MNRAS, 281, 737 [NASA ADS] [Google Scholar]
  15. D’Ammando, F., Pucella, G., Raiteri, C. M., et al. 2009, A&A, 508, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Donnarumma, I., Vittorini, V., Vercellone, S., et al. 2009, ApJ, 691, L13 [Google Scholar]
  17. Fiorucci, M., & Tosti, G. 1996, A&AS, 116, 403 [Google Scholar]
  18. Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Hartman, R. C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hufnagel, B. R., & Bregman, J. N. 1992, ApJ, 386, 473 [NASA ADS] [CrossRef] [Google Scholar]
  21. Kharb, P., Lister, M. L., & Cooper, N. J. 2010, ApJ, 710, 764 [NASA ADS] [CrossRef] [Google Scholar]
  22. Larionov, V. M., Villata, M., & Raiteri, C. M. 2010, A&A, 510, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Madejski, G. M., Sikora, M., Jaffe, T., et al. 1999, ApJ, 521, 145 [NASA ADS] [CrossRef] [Google Scholar]
  24. Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  25. Marscher, A. P., Jorstad, S. G., Larionov, V. M., et al. 2010, ApJ, 710, L126 [NASA ADS] [CrossRef] [Google Scholar]
  26. Mason, K. O., Breeveld, A., Much, R., et al. 2001, A&A, 365, L36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Ogle, P. M., Wehrle, A. E., Balonek, T., & Gurwell, M. A. 2010 [arXiv:1003.3642] [Google Scholar]
  28. Ostorero, L., Villata, M., & Raiteri, C. M. 2004, A&A, 419, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Papadakis, I. E., Villata, M., & Raiteri, C. M. 2007, A&A, 470, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Peterson, B. M. 2001, in Advanced Lectures on the Starburst-AGN Connection, ed. I. Aretxaga, D. Kunth, & R. Mújica (Singapore: World Scientific), 3 [Google Scholar]
  31. Poole, T. S., Breeveld, A. A., Page, M. J., et al. 2008, MNRAS, 383, 627 [NASA ADS] [CrossRef] [Google Scholar]
  32. Raiteri, C. M., Villata, M., Tosti, G., et al. 1999, A&A, 352, 19 [NASA ADS] [Google Scholar]
  33. Raiteri, C. M., Villata, M., Tosti, G., et al. 2003, A&A, 402, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Raiteri, C. M., Villata, M., Chen, W. P., et al. 2008, A&A, 485, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Raiteri, C. M., Villata, M., Capetti, A., et al. 2009, A&A, 507, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Ravasio, M., Tagliaferri, G., Ghisellini, G., et al. 2002, A&A, 383, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
  38. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  39. Sikora, M., Moderski, R., & Madejski, G. M. 2008, ApJ, 675, 71 [NASA ADS] [CrossRef] [Google Scholar]
  40. Stirling, A. M., Cawthorne, T. V., Stevens, J. A., et al. 2003, MNRAS, 341, 405 [NASA ADS] [CrossRef] [Google Scholar]
  41. Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Tanihata, C., Takahashi, T., Kataoka, J., et al. 2000, ApJ, 543, 124 [NASA ADS] [CrossRef] [Google Scholar]
  43. Tornikoski, M., Valtaoja, E., Teräsranta, H., & Okyudo, M. 1994a, A&A, 286, 80 [NASA ADS] [Google Scholar]
  44. Tornikoski, M., Valtaoja, E., Teräsranta, H., et al. 1994b, A&A, 289, 673 [NASA ADS] [Google Scholar]
  45. Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Vermeulen, R. C., Ogle, P. M., Tran, H. D., et al. 1995, ApJ, 452, L5 [NASA ADS] [CrossRef] [Google Scholar]
  47. Villata, M., & Raiteri, C. M. 1999, A&A, 347, 30 [NASA ADS] [Google Scholar]
  48. Villata, M., Raiteri, C. M., Kurtanidze, O. M., et al. 2002, A&A, 390, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Villata, M., Raiteri, C. M., Aller, H. D., et al. 2004a, A&A, 424, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Villata, M., Raiteri, C. M., Kurtanidze, O. M., et al. 2004b, A&A, 421, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Villata, M., Raiteri, C. M., Larionov, V. M., et al. 2008, A&A, 481, L79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Villata, M., Raiteri, C. M., Gurwell, M. A., et al. 2009a, A&A, 504, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Villata, M., Raiteri, C. M., Larionov, V. M., et al. 2009b, A&A, 501, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

List of optical, near-IR, and mm–cm radio observatories contributing data to this work.

In the text
Table 2

Spectral fitting to the XRT data from Swift observations in 2008.

In the text
Table 3

Spectral fitting to the EPIC (pn+MOS1+MOS2) data from the XMM-Newton observations of 2008 May 16–17.

In the text
Table 4

Main parameters of the helical jet model for the fit to both the 2008 faint-state SED and the 1997 outburst-state SED.

In the text

All Figures

thumbnail Fig. 1

R-band light curve by the GASP collaboration from February 2008 to February 2009. Data are not corrected for the host galaxy contamination or Galactic extinction. The participating observatories are marked with different symbols and colours. The total number of data points is indicated in the upper right.
In the text
thumbnail Fig. 2

June–November 2008 light curves of BL Lacertae from UV to near-IR after correction for the host galaxy contribution, but not for the Galactic extinction. Data taken by the GASP-WEBT collaboration are plotted as blue circles, UVOT data as red triangles. The UVOT u, b, and v light curves have been shifted to match the ground-based U, B, and V ones (see text for details).

In the text
thumbnail Fig. 3

Optical flux densities (R band, top panel), after correction for Galactic extinction and host galaxy contamination, compared to radio flux densities at different frequencies. Blue circles represent GASP data; red diamonds indicate data from the VLA/VLBA PCD. The vertical green line corresponds to the XMM-Newton pointing of May 16–17; the yellow strip highlights the period of Swift observations, from 2008 August 20 to October 2.
In the text
thumbnail Fig. 4

Top: observed spectrum of BL Lacertae in the optical-UV band. Red diamonds refer to the mean UVOT spectrum resulting from 16 epochs analysed in this paper. Blue circles represent the average spectrum obtained from the three observations of the OM instrument onboard XMM-Newton in 2007–2008 (Raiteri et al. 2009), normalised to the mean UVOT spectrum in the v band. The solid line is the log-parabolic fit used in the calibration procedure. Bottom: optical-UV SEDs of BL Lacertae. Blue circles and red diamonds are derived from the OM and UVOT average spectra shown in the top panel by using standard prescriptions to obtain dereddened flux densities. Black squares represent the mean UVOT SED after recalibration as explained in the text. In both panels the filter labels are centred on the standard UVOT λeff (Poole et al. 2008).
In the text
thumbnail Fig. 5

Swift-XRT spectrum of BL Lacertae on 2008 August 29. The bottom panel shows the deviations of the observed data from the folded model (a single power law with fixed absorption) in units of standard deviations.
In the text
thumbnail Fig. 6

Details of the multiwavelength behaviour of BL Lacertae in the period around the Swift observations. The X-ray flux density (at 1 keV, top) is compared to that in the UV (uvw1 band), optical (R band), near-IR (K band), and radio (37 GHz, bottom) frequency range.
In the text
thumbnail Fig. 7

UV and X-ray light curves obtained by the OM and EPIC instruments onboard XMM-Newton on 2008 May 16–17. Black, red, and blue filled circles represent UVW1, UVM2, and UVW2 magnitudes, respectively. Arrows mark the data points used for the SED shown in Fig. 9. Green diamonds, black squares, and red triangles refer to pn (0.5–10 keV), MOS1 (0.3–10 keV), and MOS2 (0.3–10 keV) count rates, respectively. Plus signs show the corresponding backgrounds. In all panels horizontal dashed lines indicate average values and dotted lines represent standard deviations from the mean.
In the text
thumbnail Fig. 8

EPIC spectrum of BL Lacertae on 2008 May 16–17; black squares, red triangles, and green diamonds represent MOS1, MOS2, and pn data, respectively. The bottom panel shows the deviations of the observed data from the folded model (a double power law with fixed absorption) in units of standard deviations.
In the text
thumbnail Fig. 9

Broad-band SEDs of BL Lacertae in August 2008 (blue) and July 1997 (red). The 2008 SED is built with UV and X-ray data from two epochs of Swift observations (Sect. 3), 2008 August 25 and 30, together with simultaneous optical-to-radio data from the GASP-WEBT collaboration, and contemporaneous γ-ray data from Fermi (from Abdo et al. 2010a). The 1997 SED includes EGRET data from Bloom et al. (1997), OSSE data from the HEASARC archive, ASCA+RXTE spectra from Tanihata et al. (2000), while low-frequency data are from the WEBT archive. Solid lines represent model fits; we distinguish the low-energy emission component (dotted lines) from the high-energy one (dashed lines); the contribution by an accretion disc of  ~16000 K and 5 × 1044   ergs-1 is marked with a dotted-dashed line. We also show in black the SED corresponding to the XMM-Newton observations of May 2008 (Sect. 4); both the single power law with free absorption and double power law with Galactic absorption fits to the EPIC spectra are displayed.
In the text
thumbnail Fig. 10

Sketch of our helical jet model during both the 2008 faint state and the 1997 outburst state. The angle between the jet axis and the line of sight, ψ, has been multiplied by a factor 10 with respect to the values given in Table 4 for clarity. We distinguish the inner region, emitting the high-energy synchrotron plus self inverse-Compton component (purple-blue) from the outer zone, where the low-energy emission component is produced (green-yellow-red).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.