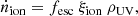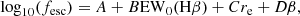EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 685 (May 2024) A&A, 685 (2024) A3 Full HTML
Open Access
Issue
A&A
Volume 685, May 2024
Article Number A3
Number of page(s) 15
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202347884
Published online 30 April 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The Epoch of Reionization (EoR) is a period in the history of the Universe, occurring roughly during its first billion years, when the hydrogen in the intergalactic medium (IGM) transitioned from a nearly completely neutral to a nearly completely ionized state. This transition was driven by the Lyman continuum (LyC; λ < 912 Å) radiation emitted by the first luminous sources that formed in the early Universe. However, these sources, i.e. the so-called cosmic reionizers, remain elusive: star-forming galaxies can only account for the photon budget to complete reionization if a substantial fraction of the ultraviolet (UV) photons produced by their stellar populations escape from the galaxies’ interstellar medium (ISM) and circumgalactic medium (CGM). As a result of the density of star-forming galaxies in the EoR, an average LyC escape fraction (fesc) of 10% across all galaxies is needed (e.g., Yung et al. 2020a,b; Finkelstein et al. 2019; Robertson et al. 2015) to maintain the Universe being ionized by z = 6, and match the Thomson optical depth of electron scattering in the cosmic microwave background (CMB; Planck Collaboration VI 2020). At z ≥ 4.5, however, it is impossible to detect the LyC photons escaping from galaxies, since they are absorbed and scattered by the IGM along the line of sight (Inoue et al. 2014), and the LyC can only be detected at low and intermediate redshift (e.g., Flury et al. 2022; Izotov et al. 2016a,b, 2018a, b; Wang et al. 2019; Steidel et al. 2018; Fletcher et al. 2019; Vanzella et al. 2018, 2020; Marques-Chaves et al. 2021, 2022). To overcome this problem, key properties of the ISM and conditions that facilitate LyC photons escape (the so-called indirect indicators) at lower redshifts have been identified (see Flury et al. 2022, for a review) and used to infer the average fesc of the cosmic reionizers (e.g., Jung et al. 2023; Mascia et al. 2023; Roy et al. 2023; Saxena et al. 2023).

The relative importance of massive and low-mass galaxies in driving reionization is still a matter of great debate as it is intrinsically related to the timeline and topology of reionization. It is expected that reionization starts earlier, and perhaps proceeds in a spatially more homogeneous manner, when faint and low-mass galaxies with a higher fesc dominate ionizing photon budgets over bright galaxies (e.g., Ferrara & Loeb 2013; Finkelstein et al. 2019; Dayal et al. 2020). Conversely, a relatively delayed reionization process is predicted when the contributions from faint galaxies (M1500 ≥ −18) are subdominant to that from brighter systems (Robertson et al. 2015; Naidu et al. 2020). While both types of galaxies are likely to contribute to the ionizing budget, the balance and interplay between them remain uncertain.

To understand the role of faint and bright sources, we need to determine what their relative contribution is to the total ionizing emissivity (ṅion), that is, the number of ionizing photons emitted per unit time and comoving volume (see Robertson 2022, for a detailed review) which is commonly expressed as

n ˙ ion = f esc ξ ion ρ UV , $$ \begin{aligned} \dot{n}_{\rm ion} = f_{\rm esc} \ \xi _{\rm ion} \ \rho _{\rm UV}, \end{aligned} $$(1)

in which ξion is the ionizing photon production efficiency, that is, the number of produced ionizing photons per UV luminosity density, the ρUV is the integral of the UV luminosity function (the number of galaxies per UV luminosity per comoving volume), and fesc is the fraction of ionizing photons that reaches the IGM.

In the above equation, the ρUV of galaxies is relatively well constrained up to z ∼ 10 (e.g., Bouwens et al. 2015, 2021; Donnan et al. 2023). We know that many factors influence the photon production efficiency, including the initial mass function, the stellar metallicity, the evolution of individual stars, and possible stellar binary interactions (e.g., Zackrisson et al. 2011, 2013, 2017; Eldridge et al. 2017; Stanway & Eldridge 2018, 2019). A commonly accepted value is log ξion = 25.3, but many recent observations at intermediate and high redshifts (e.g., Matthee et al. 2017; Izotov et al. 2017; Nakajima et al. 2018; Shivaei et al. 2018; Lam et al. 2019; Bouwens et al. 2016; Stark et al. 2015, 2017; Atek et al. 2022; Castellano et al. 2022, 2023). Yung et al. (2020b) have demonstrated that ξion can vary quite widely as a function of galaxy properties, and a fixed value is just not sufficient to properly capture the scatter in a large population of galaxies. With the James Webb Space Telescope (JWST), we are now able to measure ξion from the rest-frame optical lines (e.g., Schaerer et al. 2016; Shivaei et al. 2018; Chevallard et al. 2013; Tang et al. 2019), instead of adapting the same value for the entire galaxy population. The only remaining big uncertainty in the emissivity equation is thus the escape fraction and how it varies with stellar mass or M1500 (which depends on many effects including age, dust attenuation constraints, metallicity, etc.), which is the subject of this work.

In Mascia et al. (2023; M23 hereafter), we have shown that at the end of reionization (4.5 ≤ z ≤ 8), star-forming galaxies are often compact (UV half-light radius re ≃ 0.2 − 0.5 kpc), and with blue UV slopes (median β = −2.08). Moreover, the analyzed sources present properties (in terms of the [O III]λλ4959, 5007/[O II]λ3727 line ratios, O32 hereafter, Hβ rest-frame equivalent widths, EW0(Hβ), UV-β slopes, re, and ΣSFR) consistent with those of low-z galaxies with measured fesc larger than 0.05. These results suggested that the average low-mass galaxies around the EoR have physical and spectroscopic properties consistent with moderate escape of ionizing photons (fesc = 0.1 − 0.2), resulting in a dominance of low-mass, faint galaxies during cosmic reionization. The results of M23 may clarify the role of faint galaxies during reionization, but they were based on a very limited sample of sources. For this work, we used the JWST/Near InfraRed Spectrograph (NIRSpec) and Near InfraRed Camera (NIRCam) observations from the Cosmic Evolution Early Release Science (CEERS) survey of a much larger sample of high redshift galaxies to probe their role as cosmic reionizers during the EoR and put the conclusions of M23 on firmer grounds.

This paper is organized as follows: we present the dataset in Sect. 2. We characterize the selected sample in Sect. 3, and compare the physical and spectroscopic properties with models in Sect. 4. In Sect. 5 we estimate the total ionizing budget from our sample and discuss our results, while in Sect. 6 we summarize our key conclusions. Throughout this work, we assume a flat Λ cold dark matter cosmology with H0 = 67.7 km s−1 Mpc−1 and Ωm = 0.307 (Planck Collaboration VI 2020) and the Chabrier (2003) initial mass function. All magnitudes are expressed in the AB system (Oke & Gunn 1983).

2. Data

2.1. CEERS-JWST data

We used JWST/NIRSpec observations from the Cosmic Evolution Early Release Science survey (CEERS; ERS 1345, PI: S. Finkelstein) in the CANDELS Extended Groth Strip (EGS) field (Grogin et al. 2011; Koekemoer et al. 2011). The final list of targets selected for spectroscopic observations during the CEERS program and the way in which targets have been prioritized will be presented in Finkelstein et al. (in prep., see also Finkelstein et al. 2022a,b), while the NIRSpec data will be described in Arrabal Haro et al. (in prep.), see also Arrabal Haro et al. (2023). We also use the CEERS NIRCam imaging in six broadband filters (F115W, F150W, F200W, F277W, F356W and F444W) and one medium-band filter (F410M) over 10 pointings. Details on imaging data reduction and analysis are presented in Bagley et al. (2023; see also Finkelstein et al. 2022a,b).

In this section, we provide a brief summary, highlighting the most relevant points and explaining the methods we used to study the properties of the galaxies of our sample.

The focus of this study is on all sources at 6 ≤ z ≤ 9. We selected all the sources with a photometric redshift higher than 5 that have a NIRSpec spectrum obtained either with the three medium-resolution (R ≈ 1000) grating spectral configurations (G140M/F100LP, G235M/F170LP and G395M/F290LP), which, together, cover wavelengths between 0.7 and 5.1 μm, or with the PRISM/CLEAR configuration, which provides continuous wavelength coverage of 0.6−5.3 μm with spectral resolution ranging from R ∼ 30 to 300.

We visually examined all these spectra for detectable optical lines and measured the systemic redshifts of 70 sources in the chosen range, using the Hβ, [O III]λλ4959, 5007, and (when present) Hα lines. The best redshift solution was determined by fitting single Gaussian functions to the strongest emission lines and combining the centroids of the fits. In 66 cases, the [O II]λλ3727, 3729, [O III] and/or Hβ were detected and their line fluxes were measured. For the remaining 4 cases, the redshifts were obtained by fitting the Hα line alone, so they are formally included in our sample but they can not be used for further analysis since this is the only line present in the spectra. For this part of our analysis, we use MPFIT1 (Markwardt 2009). We note that with the PRISM’s resolution of R > 140 at λ > 3.4 μm, we are able to discern Hβ from [O III], and resolve the [O III] doublet but we do not resolve the Hα + [N II] doublet.

All CEERS MSA IDs, coordinates, and spectroscopic redshifts are reported in Table A.1, along with their spectroscopic and physical properties, whose determination is described in the next sections. Some of the sources presented in this work have been already identified and analyzed in previous works, specifically Jung et al. (2023; MSA IDs: 686, 689, 698), Fujimoto et al. (2023; MSA IDs: 2, 3, 4, 7, 20, 23, 24), Arrabal Haro et al. (2023; MSA IDs: 80025, 80083), Larson et al. (2023; MSA ID: 1019), and Tang et al. (2023; MSA IDs: 3, 23, 24, 44, 407, 498, 499, 686, 689, 698, 717, 1019, 1023, 1025, 1027, 1029, 1038, 1102, 1143, 1149, 1163).

2.2. Data from other programs

Several additional public sources are used to expand our EoR sample. In M23, we examined a sample of sources observed from the GLASS-ERS program (PID 1324, PI: T. Treu) using three high-resolution (R ∼ 2000 − 3000) spectral configurations (G140H/F100LP, G235H/F170LP, and G395H/F290LP). For the purpose of this work we specifically selected the 7 sources at zspec > 6 (GLASS-JWST IDs: 10000, 10021, 100001, 100003, 100005, 150008, 400009), along with 2 additional sources at zspec > 6 from a DDT program (PID 2756, PI: W. Chen), which were obtained using the PRISM/CLEAR configuration (DDT IDs: 10025, 100004). All these sources are located in the Abell 2744 cluster field.

From the spectroscopic redshift catalog by Noirot et al. (2023), we selected four more sources from the Early Release Observations (ERO) program on the galaxy cluster SMACS J0723.3−7327 at zspec > 6 (ERO IDs: 4590, 5144, 6355, 10612). These spectra were acquired with medium resolution spectral configurations (G235M and G395M). The properties we use in this work were derived from Trussler et al. (2023) and Schaerer et al. (2022). For all the above sources, IDs, coordinates, spectroscopic redshifts, spectroscopic, and physical properties are reported in Table A.2.

3. Method

3.1. Measurements of physical parameters

We measured the physical parameters of the CEERS sample as described in Santini et al. (2023), by fitting synthetic stellar templates with ZPHOT (Fontana et al. 2000) to the seven-band NIRCam photometry (Finkelstein et al. 2023, for the sources marked with * in Table A.1) and the released HST photometry (Stefanon et al. 2017). Specifically we measured the stellar masses M⋆, obs, the observed absolute UV magnitudes at 1500 Å (M1500, obs), the dust reddening E(B − V) and the ages. We adopted Bruzual & Charlot (2003) models and assumed delayed exponentially declining star formation histories – SFH(t) ∝ (t2/τ)⋅exp(−t/τ) – with τ ranging from 0.1 to 7 Gyr. The age ranges from 10 Myr to the age of the Universe at each galaxy redshift, while metallicity can assume values of 0.02, 0.2 or 1 times Solar metallicity. For the dust attenuation, we used the Calzetti et al. (2000) law with E(B − V) which can assume values ranging from 0, 0.03, 0.06, 0.1, 0.15, and from 0.2 to 1.1 in step of 0.1. We computed 1σ uncertainties on the physical parameters by retaining, for each object, the minimum and maximum fitted masses among all the solutions with a probability P(χ2) > 32% of being correct, fixing the redshift to the best-fit value. In Fig. 1 we present the M1500, obs distribution of the CEERS sources in our sample, which ranges from −22 to −18 AB mag. For reference, we also show the distribution of the M1500 for the GLASS and ERO sources we are considering in this work.

thumbnail Fig. 1.

M1500 distribution for the analyzed sources at 6 ≤ z ≤ 9 (gray: total sample; red and blue are respectively the GLASS sample and the ERO sample from Mascia et al. 2023; Noirot et al. 2023).

3.2. Dust correction and emission line flux measurements

We measured the total flux of each detected line (Balmer lines, [O II], and [O III]) with a single Gaussian fit. From the flux measurement we subtracted a constant continuum emission, which is estimated from a wavelength region adjacent (±160 Å) to the emission line. When the continuum was not well constrained (signal-to-noise ratio S/N < 2) from the fit, we estimated it subtracting the line contribution to the F444W photometry, following Fujimoto et al. (2023). When the S/N of [O II], [O III], or Hβ was less than 2, we set 2σ as an upper limit.

Prior to carrying out a quantitative analysis, it is necessary to consider corrections for dust reddening. For 28 galaxies, Hα and Hβ are both available and we calculated the correction for dust extinction on the basis of the Balmer decrement, assuming a Calzetti et al. (1994) extinction law and an intrinsic ratio Hα/Hβ = 2.86 (see e.g., Domínguez et al. 2013; Kashino et al. 2013; Price et al. 2014), which is valid for an electron temperature of 10 000 K. The nebular E(B − V) determined from the Balmer decrement are in agreement with the stellar reddening determined from the SED fitting. Therefore for the 38 sources in the sample without Hα, we converted their stellar E(B − V)SED to nebular E(B − V) following Calzetti et al. (2000) and applied the nebular corrections derived from these values.

With the dust corrected spectra, we calculated the O32 line ratios and the [O III] and/or Hβ rest-frame EWs. We list all these values in Table A.1. Within the errors, our measurements are consistent with those from previous works for sources in common (Jung et al. 2023; Fujimoto et al. 2023; Arrabal Haro et al. 2023; Tang et al. 2023).

3.3. UV-β slopes

We measured the UV-β slope of our galaxies from the NIRCam photometry and/or the previously available HST photometry (Stefanon et al. 2017), with the approach detailed in Calabrò et al. (2021). We considered all the photometric bands whose entire bandwidths are between 1216 and 3000 Å rest frame. The former limit is set to exclude the Lyα line and Ly-break, while the latter limit is slightly larger than that adopted in Calabrò et al. (2021) to ensure that we can use more bands.

We then fitted the selected photometry with a single power-law of the form f(λ) ∝ λβ (Calzetti et al. 1994; Meurer et al. 1999). In practice, we fit the available photometric bands amongst HST F125W, F140W, F160W and JWST-NIRCam F115W, F150W or F200W depending on the exact redshift of the sources. This choice allows us to uniformly probe the spectral range between 1500 and 3000 Å for most of the galaxies. We measured the β and associated uncertainty for each source using a Monte Carlo (MC) simulation. For each band, we randomly sampled the flux within 1σ for a total of n = 1000 times. The results provided a MC sampling of β from which we calculated the mean and standard deviation of β for each galaxy. Two of the sources in our sample did not have the necessary data, so we were able to estimate the β slopes only for 64 galaxies. The results on β with associated errors are reported in Table A.1. We note that for 5 sources different β slopes are published in literature (Jung et al. 2023; Arrabal Haro et al. 2023), but they were estimated from SED fitting or from the spectra. For 4 out of 5, our values are consistent with the published ones within the uncertainties.

In Fig. 2 we show the relation between our measured β slope values and M1500 and the observed trend at z = 7 from Bouwens et al. (2014). We also plot the β values as function of M1500 for the GLASS and ERO sample. Our results are consistent with the best fit relation from Bouwens et al. (2014) although with a large scatter. We must notice that the galaxies with the bluer slopes (with values around −3) that most deviate from the relation also have the largest uncertainties. Overall we confirm the existence of a broad correlation between β and UV magnitude at z ∼ 7 (e.g., Wilkins et al. 2011; Finkelstein et al. 2012; Bouwens et al. 2014; Nanayakkara et al. 2023). Our average β value at z ∼ 7, ⟨β⟩= − 2.17 ± 0.47, is in good agreement with Dunlop et al. (2013; ⟨β⟩= − 2.1 ± 0.2 at z ∼ 7).

thumbnail Fig. 2.

β vs. M1500. Black triangles represent the CEERS sources with β slope obtained fitting 3 or 2 photometric bands. Red dots are for the GLASS sample, and blue squares are for the ERO sample. The green line shows the relation at z ∼ 7 derived from HST data by Bouwens et al. (2014). Dashed portions indicate the extrapolation of the relation in our range of M1500. The Spearman rank correlation coefficient for the correlation between β and M1500 is 0.36, with a p-value of 0.02.

3.4. UV half-light radii

We measure the re of each galaxy in the rest-frame UV using the python software GALIGHT2 (Ding et al. 2020), which adopts a forward-modeling technique to fit a model to the observed luminosity profile of a source. We assume that the galaxies are well represented by a Sersic profile (Sersic 1968). In the fitting process, we constrain the axial ratio q to the range 0.1 − 1, and we fix the Sersic index n to 1, which is suitable for star-forming galaxies and also adopted by Yang et al. (2022a) and Morishita et al. (2018). This latter choice is consistent with the median value that we find for a subset of sources with higher S/N for which the fit converges to a finite n and re when leaving all the parameters free (see also Mc Grath et al., in prep.). The uncertainties on the sizes were estimated following Yang et al. (2022a) and re-scaled to the S/N from the photometry. The results obtained with GALIGHT are robust, as shown by previous works (e.g., Kawinwanichakij et al. 2021), and in agreement with those estimated using traditional softwares such as GALFIT (Peng et al. 2002).

For 50 galaxies, we used the NIRCam photometry to measure re in the F150W band (except for ID:542, for which the size is measured in F200W to improve the fit precision), corresponding to the UV rest-frame of the galaxies. For 19 galaxies where only the HST photometry was available, we measured re using the F160W filter, which has the highest S/N. 14 sources have profile resolutions that are likely unresolved, so we place an upper limit (see Calabrò et al., in prep.). In cases where additional sources are present in the same cutout of a galaxy, we masked them or fitted them with additional Sersic profiles. We list all these measurements in in Table A.1. To determine the minimum size measurable in the F150W band, we followed a similar approach to that recently adopted by Akins et al. (2023) in the F444W band. In brief, we performed a set of simulations by creating mock F150W images of galaxies (as observed by CEERS) with a Sersic profile, different magnitudes (from 25 to 28), and different intrinsic sizes from 0.005″ to 0.1″, in steps of 0.005. We then applied PSF fitting with GALFIT, considering unresolved a source if it is undetected (S/N < 2) in the residual image. This procedure yields a minimum measurable size of 0.025″ (that is, ∼123 pc at redshift 8), which we adopt in this work as a lower limit. We will describe these simulations in more detail in Calabrò et al. (in prep.).

As for the galaxies taken from previous works, for the M23 sample re was measured in the F115W band; for the ERO sample, F200W was considered for the sources at z > 7, and F150W for the galaxy ID:5144 at z = 6.381 (Trussler et al. 2023). Typical sizes of our galaxies range from 0.1 to 2 kpc and are consistent with rest-frame UV re measured during reionization by recent works (Morishita et al. 2023; Yang et al. 2022a; Shibuya et al. 2015). In Fig. 3 we show the relation between our measured re and M1500. Apart for a few outliers, we recover the well known magnitude-size relation: although with a large scatter, our results are consistent with the relation found at z ∼ 7 derived from HST data by Shibuya et al. (2015), and the relation at z ∼ 6 − 7 from Yang et al. (2022b) based on photometrically selected galaxies lensed by six foreground Hubble Frontier Fields (HFF) clusters. We note that most potential cosmic reionizers should have very small UV rest-frame dimensions (≤0.4 kpc), indicating highly concentrated star formation as for example found by Flury et al. (2022) and in a few intermediate redshift leakers such as Ion1 (Ji et al. 2020) and Ion2 (de Barros et al. 2016).

thumbnail Fig. 3.

Rest-frame UV re vs. M1500. Symbols are the same as in Fig. 2. The green line shows the relation derived from HST data by Shibuya et al. (2015) at z ∼ 7, the blue line shows the size-luminosity relation at z ∼ 6 − 7 from Yang et al. (2022b). The Spearman rank correlation coefficient for the correlation between re and M1500 is −0.33, with a p-value of 0.003.

3.5. AGN contamination

While we recognize that AGN may also play some role in reionization, for example, Madau & Haardt (2015) and Smith et al. (2018, 2020), a concern with our current dataset is that any AGN identified here may constitute too small a sample, and might be too heterogeneous to properly evaluate their role in reionization. Therefore we exclude them in the current work, in order for us to provide the most robust measurements of the contribution of galaxies (non-AGN) to reionization, while the role of AGN is deferred to future studies with more suitable samples. We first visually examined all spectra to see if there were any broad lines in them. Then, we employed the optical rest-frame spectroscopic diagnostics to distinguish between star-forming galaxies and AGNs. Most of our sources from the CEERS program have redshifts higher than 6.7 (7.07), so their Hα and [N II] emission lines cannot be identified due to the long-wavelength limit of NIRSpec G395M at z ≥ 6.7, and z ≥ 7.07 for the PRISM. In any case, at lower redshift Hα + [N II] cannot be resolved with the PRISM. For this reason, we employed the mass-excitation (MEx) diagram (Juneau et al. 2011, 2014) with the division line identified by Coil et al. (2015) for z = 2.3 galaxies and AGN from the MOSDEF survey, as already done in M23. According to the visual inspection and the position of our sources in the MEx diagram, we conclude that our sample contains one AGN (ID: 1019) and 69 star-forming galaxies. The AGN at z = 8.679 was already identified and discussed by Larson et al. (2023).

4. Results

4.1. Evaluating fesc

Assuming that the mechanisms that drive the escape of LyC photons are the same at all redshifts and depend only on the physical properties of the sources, several authors have recently attempted to derive empirical relations between fesc values and other observable and/or physical properties that can be measured also at high redshift. In particular, Lin et al. (2024) have applied the relation with the β slope derived by Chisholm et al. (2022), which is empirical but based on measurements from z ∼ 0.3 galaxies, while Saxena et al. (2023) applied the relation predicted from cosmological simulations by Choustikov et al. (2023), which relies on the β slope, the E(B − V), the Hβ line luminosity, the M1500, the R23, and the O32.

In M23 we presented our own empirical relation calibrated on the Flury et al. (2022) low-redshift Lyman Continuum survey (LzLCS) sample, between fesc and β slope, re, and logO32 (Eq. (1) in M23). It is based on the weighted least squares linear regression model, as it proved to be the model that minimizes the mean square error (MSE) most effectively. Due to the fact that O32 and EW0(Hβ) exhibit a very tight correlation (Spearman correlation between them > 0.9), in M23 we used only one of the two values. However, since in some cases Hβ is measurable while O32 is not, here we also present an alternative relation using re, β, and the EW0(Hβ). This relation can be used when it is not possible to derive O32 due to a lack of one of the two lines. This new relation has the following form:

log 10 ( f esc ) = A + B EW 0 ( H β ) + C r e + D β , $$ \begin{aligned} \log _{10}(f_{\rm esc}) = A + B \mathrm{EW}_0(\mathrm{H}\beta ) + C r_{\rm e} + D \beta , \end{aligned} $$(2)

with A = −1.92 [−2.46,   − 1.75], B = 0.0026 [0.0019,  0.0035], C = −0.94 [−1.14,   − 0.67], D = −0.42 [−0.59,   − 0.33], where the values between the parentheses are in the 95th percentile distribution. In Appendix B we present an analysis of the residuals between the measured fesc values for the LzLCS sample and those predicted using both relations.

Using either Eq. (1) in M23 or Eq. (2), we predicted the fesc value for the CEERS 65 star-forming galaxies, in addition to the GLASS+DDT and ERO sources for which we have the β slopes. As already mentioned, the UV half-light radius of 1 source from the CEERS sample could not be determined due to the inability to achieve a good fit of the profile. Moreover, in 2 cases, the β slope could not be measured. Since these quantities appear in both of the proposed equations, we were unable to estimate fesc for 3 sources of the CEERS sample. For the remaining sources, we used the M23 equation in 49 cases in which O32 is measured accurately or it is a limit but Hβ is not evaluated, and the Eq. (2) for the other 13 cases. In total, we predict an fesc value for 74 sources from the three samples. Given the uncertainty both on the coefficients of the relations and on the quantities on which fesc depends, we estimate the fesc errors using n = 1000 MC simulations varying both the coefficients and the individual properties within their uncertainty. The results provide an fesc distribution from which we determine the mean fesc and the standard deviation for each galaxy, which is taken as the uncertainty. In Fig. 4 we show two examples of the probability distribution function (PDF) of the fesc values resulting from the above Monte Carlo runs, for a galaxy with modest inferred mean fesc (0.05) and one with a high inferred mean fesc (0.24). In Table A.1, we report the mean fesc and the standard deviation for the CEERS galaxies, in Table A.2, we report the same values for the GLASS and ERO sources.

thumbnail Fig. 4.

PDFs of the fesc values for two sources from the CEERS sample (MSA IDs: 390 and 80925). The considered fesc of the source, which is the mean fesc of the distribution, is shown in red. Given the non-normal distribution of the fesc values, we have included the 16th and 84th percentiles (red dashed lines) to measure the confidence interval.

In Fig. 5 we present the distribution of the inferred mean fesc values. Most of our galaxies have modest inferred fesc, of the order of 0.10 or below. The average fesc for our sample (with the standard error of the mean) is 0.13 ± 0.02. This value is affected by the high fesc (0.3 − 0.5) inferred for a handful of sources. The median in this case is a more representative value and it is equal to 0.08 ± 0.02. To evaluate the impact of using the mean fesc for each galaxy instead of the full PDF (which is not gaussian but more lognormal), we produced the same distribution shown in Fig. 5, this time stacking the individual PDF of all galaxies. The resulting distribution is essentially unchanged: computing the mean and median values they are respectively 0.11 and 0.08, confirming that our results are robust. To compute errors for each bin, we generated 100 PDFs, similar to the one illustrated in Fig. 4, for each galaxy. For each iteration, a value was randomly selected from these PDFs to construct the distribution of the inferred fesc values. The error on each bin is defined as the standard deviation of all values within that bin across the 100 obtained histograms.

thumbnail Fig. 5.

Predicted fesc distribution for the analyzed sources at 6 ≤ z ≤ 9 (gray: CEERS sample; red and blue are respectively the GLASS sample and the ERO sample). The mean fesc of the sample is shown in yellow, the median fesc is presented in orange.

4.2. fesc dependencies

In Fig. 6, left panel, we plot the predicted fesc values vs. the stellar mass M*. We show average binned values (using a running average) with the shaded area indicating the 1σ uncertainty. We find that low-mass galaxies tend to have slightly higher escape fractions, although the relation is rather scattered. For comparison we also plot the prediction by Rosdahl et al. (2022) based on SPHINX cosmological radiation-hydrodynamical simulations of reionization. Their simulated values of fesc are generally lower than our predictions, well below 0.1 during most of the EoR, although they also find the same dependence on total stellar mass. We also compare our results with Lewis et al. (2023), which used RAMSES-CUDATON radiation-hydrodynamical simulations, and Ma et al. (2020), whose results are based on FIRE high-resolution hydro-dynamical simulations.

thumbnail Fig. 6.

Left: predicted fesc vs. stellar mass (log10M⋆). Symbols are the same as in Fig. 2. To enhance the clarity of the plots, we have colored the entire sample in black. The green line shows the running average for our sample, while the red one is the prediction at z = 6 − 8 from Rosdahl et al. (2022). Right: predicted fesc vs. halo mass (log10Mh) estimated with Behroozi et al. (2019) conversion. The magenta and orange lines are the models from Ocvirk et al. (2021), the violet one is the prediction from Lewis et al. (2023), the line ones are the predictions from Bremer & Dayal (2023), and the blue line is the prediction from Ma et al. (2020).

Since most simulations predict fesc vs. halo mass Mh relations, we converted our stellar masses M* into halo masses Mh following the relation as a function of redshift derived by Behroozi et al. (2019). We plot the Mh vs. the predicted fesc values in Fig. 6, right panel. We compare our results to the prediction by Rosdahl et al. (2022; see above) and to those obtained by Ocvirk et al. (2021) and Lewis et al. (2023) using RAMSES-CUDATON simulations. These simulations aim at reproducing the observed Lyα opacity distribution. Their predicted fesc are ∼1 for very low-mass galaxies and drop at Mh ≥ ×109.5 M⊙. We plot both the fiducial and “permissive” model of Ocvirk et al. (2021), where this second one allows a more permissive recipe for SF also above the temperature of T* = 2 × 104 K. In Lewis et al. (2023) the fiducial model of Ocvirk et al. (2021) is extended through the inclusion of a physical model for dust production, coupled to the radiative transfer module. Finally we plot the predictions by Bremer & Dayal (2023) that are based on DELPHI simulations at z = 5 and z = 10. In this work, reionization starts at z ∼ 16, is complete at z = 5.67 and it is dominated by faint, low-mass galaxies with Mh ≤ 107.8 M⊙ at z ∼ 15 that show fesc up to 0.7.

Most of the above models predict a very rapid increase of fesc with decreasing halo mass, below Mh ≃ 1010 M⊙, a range which we barely sample with our observations, and a very low almost null fesc for the more massive halos, at odds with our inferences. In the range of halo mass observed, simulations are more than 1σ away from our inferred fesc.

The strong discrepancy between the fesc values we derive from NIRSpec data and the model predictions could be due to a number of aspects:

  • It may be that simulations do not adequately capture the bursty nature of star formation. It has been shown that Supernova (SN) feedback plays a critical role in creating regions with higher transparency for LyC escape. As a consequence in the models there is a positive correlation between fesc and the SFR measured over the last 10 million years (Rosdahl et al. 2022). This suggests that bursty star formation contributes to higher fesc values. However accurately quantifying the burstiness of star formation observationally, and comparing it to a simulation’s burstiness is a difficult task. For instance, it has been suggested that Hα/FUV fluxes for could help quantifying SFR burstiness observationally (Sparre et al. 2017), but this requires a fairly sophisticated post-treatment of simulations, and is very sensitive to the details of star formation, feedback (SN and radiative) and ISM modelling. Other probes of burstiness have been and will be proposed (Sun et al. 2023), and may offer avenues of progress on this topic. Nonetheless, the dominant mechanism for LyC escape remains uncertain. Recent observations of Lyman Continuum Emitters (LCEs) indicate that extreme radiative feedback can clear out gas and contribute to LyC escape (Komarova et al. 2021; Mainali et al. 2022). Furthermore, observations of Haro 11 suggest that both SNe and ionizing radiation can play significant roles in LyC escape (Menacho et al. 2019). A compelling argument is presented by Flury et al. (2022), who show that fesc correlates more strongly with Hβ star formation rates (SFRs) than with UV SFRs. This suggests that radiative feedback might be more influential than burstiness and/or SNe in the context of LyC escape. The intricate interplay between bursty star formation, SN feedback, and radiative processes in LyC escape mechanisms underscores the complexity of this phenomenon.

  • Another potential reason for the large discrepancy could be the description of the thermodynamical state of the shock-heated multi phase CGM (van de Voort et al. 2015). For example, in a case in which a clumpy CGM is composed of hot, highly ionized gas surrounding cold dense clumps, if the cold phase is sufficiently dense and the hot phase has high pressure, the clumps may have a small cross-section: with a small total covering fraction, a high fesc value could be observed. Insufficient spatial resolution in this case would imply artificially larger clumps, leading to a higher covering fraction and reducing the fesc. The complexity of this behavior is being explored in simulations (Gronke & Oh 2020). Observationally, patchiness has been studied in Saldana-Lopez et al. (2022, 2023), Gazagnes et al. (2020), with absorption line measurements from z ∼ 0.3 up to z ∼ 2 − 4 that suggest the existence of low gas-column-density channels in the interstellar medium, which enables the escape of ionizing photons. We note that the zoomed-in simulations of Ma et al. (2020) present some of the highest average escape fraction in our mass range. The authors claim that this has to do with the very high spatial resolution achieved in their work, even higher than SPHINX simulations, allowing LyC to escape through low density channels. We note that it may also be a result of enhanced feedback prescriptions compared to other works. Indeed, their simulations include continuous feedback from both OB and AGB stars’ winds, on top of the discrete supernova feedback usually implemented. This additional, pre-SN feedback may also play a role in increasing their escape fractions.

  • Finally, in the previous section we have already discussed that the relations that we have used to infer the fesc for galaxies in the EoR have been derived and tested using the LzLCs sample that is located at low redshift (z = 0.2 − 0.4). Therefore its applicability to the CEERS sample (6 ≤ z ≤ 9) is not straightforward. The large discrepancy with simulations might be due to an overestimate of the fesc in the EoR.

The permissive model of Ocvirk et al. (2021) has average fesc high enough to be comparable to our values. This can be attributed to the permissive run’s unique characteristic of permitting star formation in cells with temperatures potentially exceeding 2 × 104 K. These higher temperatures inherently lead to greater ionization and increased transparency compared to the fiducial run and hence to larger values of fesc. Interestingly, this model is not the one favored by Ocvirk et al. (2021) as it leads to an overionization of the Lyman-α forest characterized by unrealistically low Lyman-α IGM opacities. Our results align with the predictions of Ma et al. (2020) simulations, emphasizing the importance of high resolution in better resolving LyC escape through galaxies. However, as stated before, the absence of radiation-hydrodynamics coupling in their simulations introduces a further layer of complexity that may influence escape fractions.

In Fig. 7 we plot our predicted average fesc values vs. the UV magnitude M1500. We note that Eq. (2) and the M23 relation have been derived on the LzLCS which only contains galaxies brighter than M1500 ≃ −18.5. Therefore for our few faintest objects using the above equations might be an incorrect extrapolation. Our average fesc is almost constant within the observed magnitude range, although we point out that we might start to be biased at the faintest luminosities (especially for objects with faint emission lines and hence small fesc) due to the spectroscopic flux limit of the CEERS survey. In the same figure we also show the predicted fesc vs. M1500 relationship by Lin et al. (2024), who analyzed 3 galaxies at z ≥ 8 behind the cluster RX J2129.4+0009. They developed an empirical model based on the LzLCS program, which first defines for a given galaxy a probability of being a LyC-leaker based on M1500, O32 and β and then infers the fesc values from the β slope following Chisholm et al. (2022). In their restrained scenario, they note a consistent rise in the average escape fraction until M1500 = −16, reaching a peak at intermediate UV magnitudes (−18.5 < M1500 < −16), followed by a decline toward the faint UV magnitude end. While there are no sufficient observations of faint galaxies to study this trend, simulations predict a similar pattern (e.g., Rosdahl et al. 2022; Ma et al. 2020), for which the decrease for lower mass and fainter objects is linked to inefficient star formation and increased susceptibility to stellar feedback. As a final comparison, we plot the results by Matthee et al. (2022) who produced a semi-empirical model based on constraints on the escape fractions of bright LAEs at z ∼ 2. These authors find that fesc peaks between −19 ≤ M1500 ≤ −20 and then decreases very rapidly at fainter magnitudes (the so-called reionization by the oligarchs). At magnitudes brighter than M1500 = 19 our average results are consistent with theirs, within the uncertainties, but we do not observe the strong decrease at fainter magnitudes.

thumbnail Fig. 7.

Predicted fesc vs. M1500. Symbols are the same as in Fig. 6. The green line shows the running average for our sample, the pink one refers to Matthee et al. (2022) and the yellow one to Lin et al. (2024).

4.3. Redshift evolution

In Fig. 8 we plot our predicted fesc vs. the redshift. We also plot the sources from M23 at redshift lower than 6 which were derived with the same method. The average fesc in the three redshift bins, 5 ≤ z < 6, 6 ≤ z < 7 and 7 ≤ z ≤ 9, are respectively equal to 0.11 ± 0.07, 0.12 ± 0.08 and 0.14 ± 0.08. The associated error represents the standard deviation of the mean value within each redshift bin. We therefore observe a slight increase of the average fesc with redshift, although statistically not significant. A similar trend would be observed using the median values. We also show the predicted fesc as function of redshift from Rosdahl et al. (2022), derived from Fig. 6 of their paper at a median M1500 = −19. As previously discussed, their fesc values are generally lower than ours, but they predict a slow increase of the fesc with redshift which is very similar to what we observe. Finally, we also present a comparison between our predicted fesc values and the prediction from Finkelstein et al. (2019) within the UV magnitude range of −16 to −20. This model also predicts lower escape fractions compared to our inferred values, and a similar almost flat trend as a function of redshift.

thumbnail Fig. 8.

Predicted fesc as a function of redshift. Symbols are the same as in Fig. 6. The magenta points are the average fesc values of our sample at z = 6.5 and z = 8. The green dots are the M23 sources, while the green point is the average fesc value at z = 5.1. The blue hexagons represent the Lyα emitters from Saxena et al. (2023). The red line is the prediction at fixed M1500 = −19 from Rosdahl et al. (2022), the orange line is the prediction from Finkelstein et al. (2019) for sources with M1500 between −20 and −16.

In the same plot we also show the sample of Lyα emitters at z = 6 − 8 from the JWST Advanced Deep Extragalactic Survey (JADES) presented in Saxena et al. (2023), which span the same M1500 range as our sources. They predict the fesc using an equation proposed by the Choustikov et al. (2023), based on the SPHINX simulations which uses six observed galaxies’ properties to infer the angle-averaged (and not sight-line dependent) fesc. We see that non-Lyα emitters and Lyα emitters at the same redshift and in the same UV magnitude range do not show significant differences in the predicted fesc, although determined using two different and independent methods. This might be a first indication that in the EoR, when the visibility of Lyα emission is increasingly suppressed by neutral IGM, the Lyα line emerging from the galaxies is not a good indicator of the LyC photons’ escape and therefore other indirect indicators are needed. Further investigation of this important issue is in progress and will be presented in follow up paper.

4.4. Extreme LyC emitters

We analyzed, in more details, the 16 sources from our final sample that show an fesc higher than 0.2. The majority of them show an intense O32 or high EW(Hβ) coupled with small re or very blue β slope. We highlight the fact that an extremely blue β is a very good predictor of a high fesc: 10 out of 17 sources with β > −2.5 have a predicted fesc > 0.2. Indeed Chisholm et al. (2022) identified the β slope as one of the best indirect indicators. However this condition does not seem necessary, since there are several sources that have more average β slopes (that is, of the order of −2) but for which we predict high fesc because they are both extremely compact and have a high O32 or high EW(Hβ). Similarly of the 8 unresolved sources for which we are able to infer fesc, 5 are extreme leakers (fesc > 0.2). However we have some leakers with re larger than 0.5 kpc. Overall, there is not one single property that stands out as more important (e.g., Flury et al. 2022; Saxena et al. 2022). This reinforces the idea that more than one indicator is needed to correctly pinpoint the entire population of LyC emitters. The wide range of ISM and physical properties of the extreme LCE could imply that there could be multiple independent mechanisms and/or conditions that make a galaxy a strong leaker, with no one dominating. For some galaxies it could be the low absorption by neutral gas and dust, for others it could be the presence of cleared channels (e.g., due to a high ΣSFR or previous AGN activity). Last but not least, line of sight effects are probably also very important (e.g., Dijkstra et al. 2016; Zackrisson et al. 2017; Chisholm et al. 2022).

4.5. Ionizing photon production efficiency

Direct constraints on ξion can be obtained from the measurement of Balmer emission lines luminosity after correcting for dust attenuation (e.g., Schaerer et al. 2016; Shivaei et al. 2018) or from modelling the contribution of these optical emission lines to the broad band measurements when spectroscopic observations are not available (e.g., Bouwens et al. 2016). Unfortunately, the Hα line is outside the observed range of most of our galaxies (see Sect. 3.2) and the Hβ line is also missing from some sources: in addition, there are still some calibration uncertainties on NIRSpec absolute flux (and therefore luminosity). Chevallard et al. (2013) showed that log ξion can be measured by using EW([O III]λλ4959, 5007) (see also Tang et al. 2019). The [O III] lines are clearly detected for all sources, and in addition the EW measurements have less calibration uncertainty compared to the flux. We calculated the log ξion values from EW([O III]) following the Eq. (3) from Chevallard et al. (2018). We obtain an average ⟨log ξion⟩ = 25.27 ± 0.51, which is consistent with predictions from physical models (Yung et al. 2020b; Wilkins et al. 2016) and slightly lower than other measurements at the EoR. For example, Saxena et al. (2023), Simmonds et al. (2023) estimated log ξion from Hα luminosity, finding respectively average values of 25.56 and 25.44 although their samples included Lyα emitters whose photon production efficiency is generally higher, while Castellano et al. (2022), Prieto-Lyon et al. (2023), Endsley et al. (2023), using SED fitting, obtain an average value of log ξion of 25.14, 25.33, 25.7 respectively. In Fig. 9 we show the distribution of ξion for our sample. We do not find any correlation with the β slope: our best fit is consistent with the average value also shown in the figure. At variance with this, Prieto-Lyon et al. (2023) find a slight dependence on this property for galaxies at z = 3 − 7, in the sense that bluer star-forming sources tend to have higher photon production efficiencies (see also Castellano et al. 2023). We also do not find any dependence of ξion on M1500 in accordance to what found by Prieto-Lyon et al. (2023), Endsley et al. (2023). We note that the recent results by Atek et al. (2023) indicate a higher ξion for much fainter galaxies (MUV ≥ −17) during the EoR.

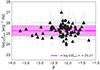thumbnail Fig. 9.

log ξion vs. β. Symbols are the same as in Fig. 6. The magenta line shows the mean log ξion for our sample. The Spearman rank correlation coefficient for the correlation between log ξion and β is 0.05, with a p-value of 0.63 indicating no correlation between the two quantities.

5. The ionizing photon production of bright and faint sources

Having derived predictions for fesc and ξion for our large sample of galaxies in the EoR, our goal is now to solve Eq. (1) and determine the relative contribution of galaxies as a function of M1500, to establish which sources contributed most to the total ionizing photon production rate at these epochs. We consider: (1) ρUV from the luminosity function (LF) of Bouwens et al. (2021) at our median redshift ⟨z⟩∼7.2. The best-fit α slope that characterizes the faint-end of the UV-LF is −2.06 ± 0.03; (2) fesc as a function of M1500 from the values derived in Fig. 7 between M1500 −22 and −18 (i.e. the range covered by our observations); we use a fixed value of 0.10 at fainter magnitudes, where we have only few sources, and a value of 0.05 at magnitudes brighter than −22, where we do not have any observed source in our sample; (3) ⟨log ξion⟩ = 25.27, which does not vary with M1500, as found in Sect. 4.5. We assume a low luminosity cut at M1500 = −13 and a high luminosity cut of M1500 = −23 (as in Robertson et al. 2015).

To estimate the total ṅion we proceeded as follows: we first discretized the M1500 range over [−13, −23] in bins of width 1 mag. For each of these intervals we calculated ρUV in the considered magnitude bin and multiplied it by the appropriate ξion and fesc. We then summed these values to estimate the total ṅion. The total integrated ionizing emissivity at z = 8 and z = 6 are respectively ṅion = 50.50 ± 0.38 and 50.75 ± 0.35 s−1 Mpc−3, consistent with the canonical threshold needed to maintain the Universe ionized at z = 7 (e.g., Madau et al. 1999; Gnedin & Madau 2022) and in the range of previous determination (Finkelstein et al. 2019; Bouwens et al. 2015; Robertson et al. 2015).

We then derive the fraction of the total ṅion that is provided by galaxies in each magnitude bin: the results are shown in Fig. 10 and indicate that the galaxies that we can currently characterize with JWST observations are contributing to only a fraction of the total ionizing budget, i.e. less than 35% of the total. We would therefore need to push our observations at 2−3 mag deeper to characterize the bulk of the cosmic ionizers. We note however than in previous studies (e.g., Finkelstein et al. 2019; Robertson et al. 2015) the fraction of ionizing photons from faint galaxies was even more prominent, with the extreme faint end of the luminosity function dominating the ionizing emissivity (e.g., see Fig. 8 of Finkelstein et al. 2019). We also show how the results would vary by changing the faint end fesc to a values of 0.05 and 0.15 respectively (right top panels of Fig. 10) and by changing the faint end slope of the UV-ρUV within the 5σ uncertainties [ − 1.94, −2.27]. We see that the contribution of JWST sources with M1500 < −18 to the integrated ionizing emissivity becomes 40% if we assume a very small fesc for the faintest galaxies, or an extremely flat LFUV at the faint end, but it is never dominant even in these extreme cases.

thumbnail Fig. 10.

Left: the ṅion fraction of galaxies at 6 ≤ z ≤ 9 as function of the M1500. Triangles represent the ṅion obtained from the predicted fesc as a function of M1500 in each bin. Bars represent the extrapolated value, i.e. the ṅion fraction derived assuming that for M1500 > −18 a fesc value constant and equal to 0.10, and for M1500 < −22 a fesc value constant and equal to 0.05. Right: in yellow we show the ṅion fraction of galaxies at 6 ≤ z ≤ 9 as function of M1500 changing, respectively, from the top left to the bottom right, the fesc values at the faint-end (0.05 and 0.15) and the α parameter of the ρUV (−1.94 and −2.27). The original result is also shown with the same symbols as in the figure from the left.

6. Summary and conclusions

In this paper, we have presented an analysis of 70 spectroscopically confirmed star-forming galaxies at 6 ≤ z ≤ 9 from the CEERS survey, combined with 12 sources with public data from other JWST early campaigns. Assuming that the mechanisms that facilitate the escape of LyC photons from galaxies remain consistent across all cosmic epochs, we estimated the fesc of the observed sources employing two empirical relations based on the most promising indirect indicators of this emission identified at z ∼ 0.3, which are also measurable during the EoR. Using the mean inferred fesc as function of MUV and the photon production efficiency derived from the [O III] emission line, we have then evaluated the relative role of faint and galaxies and their contribution to the process of reionization. Our main results are the following:

  • The majority of our sources show modest fesc values, with a mean fesc of 0.13 ± 0.02, and an even lower median of 0.08 ± 0.02. Just 20% of galaxies have fesc > 0.2: the majority of these extreme LyC emitters show an intense O32 or high EW(Hβ) coupled with small re or very blue β slope. As expected there is no single property that stands out as the best indirect indicator of a high LyC escape.

  • The predicted fesc has a modest dependence on the total stellar mass M⋆ with low-mass galaxies tending to have higher mean fesc although the trend is scattered. The relation with M1500 is less well characterized and there is not a significant dependence.

  • There is a strong discrepancy between our inferred fesc and those predicted by most cosmological hydrodynamical simulations of reionization, which consistently infer much lower fesc values for galaxies in the same mass range as the one explored by the JWST observations. We discuss potential causes for the discrepancy such as the failure of simulations to fully account for the bursty nature of star formation, or the limited resolution. Alternatively using relations derived from low-redshift samples to infer fesc for galaxies in the EoR might not be correct and could lead to an overestimate of the fesc values.

  • The average predicted fesc have at most a modest increase with redshift from z = 5 to z = 8 raising from 0.11 to 0.14.

  • The predicted fesc during the EoR does not show a clear dependence on the presence of Lyα emission. This is actually expected since in the EoR the Lyα emission is modulated also by the IGM opacity in the local surroundings and not just by the galaxies properties as at low redshift.

  • With the inferred values of fesc and ξion we derive a total ionizing emissivity ṅion = 50.50 ± 0.38 and 50.75 ± 0.35 s−1 Mpc−3 at redshift 8 and 6 respectively, i.e. comparable to the threshold needed to maintain the Universe ionized. Sources brighter than M1500 = −18, which are those we can currently characterize with JWST observations, only contribute less than 35% to the total ionizing emissivity.

The findings of this study provide crucial insights into the reionization epoch, primarily focusing on the characterization of relatively bright sources and indicating that galaxies significantly fainter and less massive than those observed by the initial JWST programs, could potentially play a dominant role in the reionization process. To study significantly large samples of such faint galaxies, ultra-deep observations of galaxy cluster fields will be needed since lensing becomes a necessary tool, as in the recent work by Atek et al. (2023) which reaches galaxies as faint as MUV = −15. In addition further work on the LyC indirect indicators will be needed to validate the fundamental assumption that the physical mechanisms and conditions that facilitate the escape of Lyman continuum photons remain the same over cosmic time. In particular, future work should be aimed at assembling a solid reference sample of Lyman continuum emitting galaxies, analogous in size to the LzLCS survey, but at z = 3 − 4, i.e. the highest redshift where a direct detection of LyC photons is possible and which is much closer in time to the epoch of reionization. If our derived relations to infer fesc were still valid at z = 3 − 4, then we could be much more confident that they can be also applied in the EoR.

Acknowledgments

We thank the anonymous referee for a careful and constructive evaluation of our manuscript. This work is based on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with program JWST-ERS-01345. We thank H. Katz, J. Rosdahl and M. Trebitsch for insightful discussions around escape fractions in numerical simulations in the literature. We acknowledge support from the INAF Large Grant 2022 “Extragalactic Surveys with JWST” (PI: Pentericci). We acknowledge support from the PRIN 2022 MUR project 2022CB3PJ3 – First Light And Galaxy aSsembly (FLAGS) funded by the European Union – Next Generation EU. P.G.P.-G. and L.C. acknowledge support from Spanish Ministerio de Ciencia e Innovación MCIN/AEI/10.13039/501100011033 through grant PGC2018-093499-B-I00. L.C. acknowledges financial support from the Comunidad de Madrid under Atracción de Talento grant 2018-T2/TIC-11612. J.S.W.L. acknowledges support from the DFG via the Heidelberg Cluster of Excellence STRUCTURES in the framework of Germany’s Excellence Strategy (grant EXC2181/1 – 390900948).

References

  1. Akins, H. B., Casey, C. M., Allen, N., et al. 2023, ApJ, submitted [arXiv:2304.12347] [Google Scholar]
  2. Arrabal Haro, P., Dickinson, M., Finkelstein, S. L., et al. 2023, ApJ, 951, L22 [NASA ADS] [CrossRef] [Google Scholar]
  3. Atek, H., Furtak, L. J., Oesch, P., et al. 2022, MNRAS, 511, 4464 [CrossRef] [Google Scholar]
  4. Atek, H., Labbé, I., Furtak, L. J., et al. 2023, ArXiv e-prints [arXiv:2308.08540] [Google Scholar]
  5. Bagley, M. B., Finkelstein, S. L., Koekemoer, A. M., et al. 2023, ApJ, 946, L12 [NASA ADS] [CrossRef] [Google Scholar]
  6. Behroozi, P., Wechsler, R. H., Hearin, A. P., & Conroy, C. 2019, MNRAS, 488, 3143 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2014, ApJ, 793, 115 [Google Scholar]
  8. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [Google Scholar]
  9. Bouwens, R. J., Smit, R., Labbé, I., et al. 2016, ApJ, 831, 176 [Google Scholar]
  10. Bouwens, R. J., Oesch, P. A., Stefanon, M., et al. 2021, AJ, 162, 47 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bremer, J., & Dayal, P. 2023, MNRAS, 524, 118 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  13. Calabrò, A., Castellano, M., Pentericci, L., et al. 2021, A&A, 646, A39 [EDP Sciences] [Google Scholar]
  14. Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [Google Scholar]
  15. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  16. Castellano, M., Pentericci, L., Cupani, G., et al. 2022, A&A, 662, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Castellano, M., Belfiori, D., Pentericci, L., et al. 2023, A&A, 675, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  19. Chevallard, J., Charlot, S., Wandelt, B., & Wild, V. 2013, MNRAS, 432, 2061 [CrossRef] [Google Scholar]
  20. Chevallard, J., Charlot, S., Senchyna, P., et al. 2018, MNRAS, 479, 3264 [Google Scholar]
  21. Chisholm, J., Saldana-Lopez, A., Flury, S., et al. 2022, MNRAS, 517, 5104 [CrossRef] [Google Scholar]
  22. Choustikov, N., Katz, H., Saxena, A., et al. 2023, ArXiv e-prints [arXiv:2304.08526] [Google Scholar]
  23. Coil, A. L., Aird, J., Reddy, N., et al. 2015, ApJ, 801, 35 [Google Scholar]
  24. Dayal, P., Volonteri, M., Choudhury, T. R., et al. 2020, MNRAS, 495, 3065 [Google Scholar]
  25. de Barros, S., Vanzella, E., Amorín, R., et al. 2016, A&A, 585, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Dijkstra, M., Gronke, M., & Venkatesan, A. 2016, ApJ, 828, 71 [Google Scholar]
  27. Ding, X., Silverman, J., Treu, T., et al. 2020, ApJ, 888, 37 [NASA ADS] [CrossRef] [Google Scholar]
  28. Domínguez, A., Siana, B., Henry, A. L., et al. 2013, ApJ, 763, 145 [CrossRef] [Google Scholar]
  29. Donnan, C. T., McLeod, D. J., Dunlop, J. S., et al. 2023, MNRAS, 518, 6011 [Google Scholar]
  30. Dunlop, J. S., Rogers, A. B., McLure, R. J., et al. 2013, MNRAS, 432, 3520 [NASA ADS] [CrossRef] [Google Scholar]
  31. Eldridge, J. J., Stanway, E. R., Xiao, L., et al. 2017, PASA, 34, e058 [Google Scholar]
  32. Endsley, R., Stark, D. P., Whitler, L., et al. 2023, MNRAS, 524, 2312 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ferrara, A., & Loeb, A. 2013, MNRAS, 431, 2826 [NASA ADS] [CrossRef] [Google Scholar]
  34. Finkelstein, S. L., Papovich, C., Salmon, B., et al. 2012, ApJ, 756, 164 [NASA ADS] [CrossRef] [Google Scholar]
  35. Finkelstein, S. L., D’Aloisio, A., Paardekooper, J.-P., et al. 2019, ApJ, 879, 36 [Google Scholar]
  36. Finkelstein, S. L., Bagley, M., Song, M., et al. 2022a, ApJ, 928, 52 [CrossRef] [Google Scholar]
  37. Finkelstein, S. L., Bagley, M. B., Haro, P. A., et al. 2022b, ApJ, 940, L55 [NASA ADS] [CrossRef] [Google Scholar]
  38. Finkelstein, S. L., Bagley, M. B., Ferguson, H. C., et al. 2023, ApJ, 946, L13 [NASA ADS] [CrossRef] [Google Scholar]
  39. Fletcher, T. J., Tang, M., Robertson, B. E., et al. 2019, ApJ, 878, 87 [Google Scholar]
  40. Flury, S. R., Jaskot, A. E., Ferguson, H. C., et al. 2022, ApJS, 260, 1 [NASA ADS] [CrossRef] [Google Scholar]
  41. Fontana, A., D’Odorico, S., Poli, F., et al. 2000, AJ, 120, 2206 [NASA ADS] [CrossRef] [Google Scholar]
  42. Fujimoto, S., Haro, P. A., Dickinson, M., et al. 2023, ApJ, 949, L25 [NASA ADS] [CrossRef] [Google Scholar]
  43. Gazagnes, S., Chisholm, J., Schaerer, D., Verhamme, A., & Izotov, Y. 2020, A&A, 639, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Gnedin, N. Y., & Madau, P. 2022, Liv. Rev. Comput. Astrophys., 8, 3 [CrossRef] [Google Scholar]
  45. Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
  46. Gronke, M., & Oh, S. P. 2020, MNRAS, 494, L27 [Google Scholar]
  47. Inoue, A. K., Shimizu, I., Iwata, I., & Tanaka, M. 2014, MNRAS, 442, 1805 [NASA ADS] [CrossRef] [Google Scholar]
  48. Izotov, Y. I., Orlitová, I., Schaerer, D., et al. 2016a, Nature, 529, 178 [Google Scholar]
  49. Izotov, Y. I., Schaerer, D., Thuan, T. X., et al. 2016b, MNRAS, 461, 3683 [Google Scholar]
  50. Izotov, Y. I., Guseva, N. G., Fricke, K. J., Henkel, C., & Schaerer, D. 2017, MNRAS, 467, 4118 [NASA ADS] [CrossRef] [Google Scholar]
  51. Izotov, Y. I., Schaerer, D., Worseck, G., et al. 2018a, MNRAS, 474, 4514 [Google Scholar]
  52. Izotov, Y. I., Worseck, G., Schaerer, D., et al. 2018b, MNRAS, 478, 4851 [Google Scholar]
  53. Ji, Z., Giavalisco, M., Vanzella, E., et al. 2020, ApJ, 888, 109 [Google Scholar]
  54. Juneau, S., Dickinson, M., Alexander, D. M., & Salim, S. 2011, ApJ, 736, 104 [Google Scholar]
  55. Juneau, S., Bournaud, F., Charlot, S., et al. 2014, ApJ, 788, 88 [NASA ADS] [CrossRef] [Google Scholar]
  56. Jung, I., Finkelstein, S. L., Arrabal Haro, P., et al. 2023, ApJ, submitted [arXiv:2304.05385] [Google Scholar]
  57. Kashino, D., Silverman, J. D., Rodighiero, G., et al. 2013, ApJ, 777, L8 [Google Scholar]
  58. Kawinwanichakij, L., Silverman, J. D., Ding, X., et al. 2021, ApJ, 921, 38 [NASA ADS] [CrossRef] [Google Scholar]
  59. Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
  60. Komarova, L., Oey, M. S., Krumholz, M. R., et al. 2021, ApJ, 920, L46 [NASA ADS] [CrossRef] [Google Scholar]
  61. Lam, D., Bouwens, R. J., Labbé, I., et al. 2019, A&A, 627, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Larson, R. L., Finkelstein, S. L., Kocevski, D. D., et al. 2023, ApJ, 953, L29 [NASA ADS] [CrossRef] [Google Scholar]
  63. Lewis, J. S. W., Ocvirk, P., Dubois, Y., et al. 2023, MNRAS, 519, 5987 [CrossRef] [Google Scholar]
  64. Lin, Y.-H., Scarlata, C., Williams, H., et al. 2024, MNRAS, 527, 4173 [Google Scholar]
  65. Ma, X., Quataert, E., Wetzel, A., et al. 2020, MNRAS, 498, 2001 [Google Scholar]
  66. Madau, P., & Haardt, F. 2015, ApJ, 813, L8 [Google Scholar]
  67. Madau, P., Haardt, F., & Rees, M. J. 1999, ApJ, 514, 648 [CrossRef] [Google Scholar]
  68. Mainali, R., Rigby, J. R., Chisholm, J., et al. 2022, ApJ, 940, 160 [NASA ADS] [CrossRef] [Google Scholar]
  69. Markwardt, C. B. 2009, ASP Conf. Ser., 411, 251 [Google Scholar]
  70. Marques-Chaves, R., Schaerer, D., Álvarez-Márquez, J., et al. 2021, MNRAS, 507, 524 [NASA ADS] [CrossRef] [Google Scholar]
  71. Marques-Chaves, R., Schaerer, D., Álvarez-Márquez, J., et al. 2022, MNRAS, 517, 2972 [CrossRef] [Google Scholar]
  72. Mascia, S., Pentericci, L., Calabrò, A., et al. 2023, A&A, 672, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Matthee, J., Sobral, D., Best, P., et al. 2017, MNRAS, 465, 3637 [NASA ADS] [CrossRef] [Google Scholar]
  74. Matthee, J., Naidu, R. P., Pezzulli, G., et al. 2022, MNRAS, 512, 5960 [NASA ADS] [CrossRef] [Google Scholar]
  75. Menacho, V., Östlin, G., Bik, A., et al. 2019, MNRAS, 487, 3183 [CrossRef] [Google Scholar]
  76. Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [Google Scholar]
  77. Morishita, T., Trenti, M., Stiavelli, M., et al. 2018, ApJ, 867, 150 [NASA ADS] [CrossRef] [Google Scholar]
  78. Morishita, T., Stiavelli, M., Chary, R. R., et al. 2023, ApJ, accepted [arXiv:2308.05018] [Google Scholar]
  79. Naidu, R. P., Tacchella, S., Mason, C. A., et al. 2020, ApJ, 892, 109 [NASA ADS] [CrossRef] [Google Scholar]
  80. Nakajima, K., Fletcher, T., Ellis, R. S., Robertson, B. E., & Iwata, I. 2018, MNRAS, 477, 2098 [NASA ADS] [CrossRef] [Google Scholar]
  81. Nanayakkara, T., Glazebrook, K., Jacobs, C., et al. 2023, ApJ, 947, L26 [NASA ADS] [CrossRef] [Google Scholar]
  82. Noirot, G., Desprez, G., Asada, Y., et al. 2023, MNRAS, 525, 1867 [NASA ADS] [CrossRef] [Google Scholar]
  83. Ocvirk, P., Lewis, J. S. W., Gillet, N., et al. 2021, MNRAS, 507, 6108 [NASA ADS] [CrossRef] [Google Scholar]
  84. Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
  85. Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]
  86. Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Price, S. H., Kriek, M., Brammer, G. B., et al. 2014, ApJ, 788, 86 [NASA ADS] [CrossRef] [Google Scholar]
  88. Prieto-Lyon, G., Strait, V., Mason, C. A., et al. 2023, A&A, 672, A186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Robertson, B. E. 2022, ARA&A, 60, 121 [NASA ADS] [CrossRef] [Google Scholar]
  90. Robertson, B. E., Ellis, R. S., Furlanetto, S. R., & Dunlop, J. S. 2015, ApJ, 802, L19 [Google Scholar]
  91. Rosdahl, J., Blaizot, J., Katz, H., et al. 2022, MNRAS, 515, 2386 [CrossRef] [Google Scholar]
  92. Roy, N., Henry, A., Treu, T., et al. 2023, ApJ, 952, L14 [NASA ADS] [CrossRef] [Google Scholar]
  93. Saldana-Lopez, A., Schaerer, D., Chisholm, J., et al. 2022, A&A, 663, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Saldana-Lopez, A., Schaerer, D., Chisholm, J., et al. 2023, MNRAS, 522, 6295 [NASA ADS] [CrossRef] [Google Scholar]
  95. Santini, P., Fontana, A., Castellano, M., et al. 2023, ApJ, 942, L27 [NASA ADS] [CrossRef] [Google Scholar]
  96. Saxena, A., Cryer, E., Ellis, R. S., et al. 2022, MNRAS, 517, 1098 [Google Scholar]
  97. Saxena, A., Bunker, A. J., Jones, G. C., et al. 2023, A&A, accepted [arXiv:2306.04536] [Google Scholar]
  98. Schaerer, D., Izotov, Y. I., Verhamme, A., et al. 2016, A&A, 591, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Schaerer, D., Izotov, Y. I., Worseck, G., et al. 2022, A&A, 658, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Sersic, J. L. 1968, Atlas de Galaxias Australes (Cordoba: Observatorio Astronomico) [Google Scholar]
  101. Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [Google Scholar]
  102. Shivaei, I., Reddy, N. A., Siana, B., et al. 2018, ApJ, 855, 42 [Google Scholar]
  103. Simmonds, C., Tacchella, S., Maseda, M. V., et al. 2023, MNRAS, 523, 5468 [NASA ADS] [CrossRef] [Google Scholar]
  104. Smith, B. M., Windhorst, R. A., Jansen, R. A., et al. 2018, ApJ, 853, 191 [NASA ADS] [CrossRef] [Google Scholar]
  105. Smith, B. M., Windhorst, R. A., Cohen, S. H., et al. 2020, ApJ, 897, 41 [NASA ADS] [CrossRef] [Google Scholar]
  106. Sparre, M., Hayward, C. C., Feldmann, R., et al. 2017, MNRAS, 466, 88 [NASA ADS] [CrossRef] [Google Scholar]
  107. Stanway, E. R., & Eldridge, J. J. 2018, MNRAS, 479, 75 [NASA ADS] [CrossRef] [Google Scholar]
  108. Stanway, E. R., & Eldridge, J. J. 2019, A&A, 621, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Stark, D. P., Walth, G., Charlot, S., et al. 2015, MNRAS, 454, 1393 [Google Scholar]
  110. Stark, D. P., Ellis, R. S., Charlot, S., et al. 2017, MNRAS, 464, 469 [NASA ADS] [CrossRef] [Google Scholar]
  111. Stefanon, M., Yan, H., Mobasher, B., et al. 2017, ApJS, 229, 32 [NASA ADS] [CrossRef] [Google Scholar]
  112. Steidel, C. C., Bogosavljević, M., Shapley, A. E., et al. 2018, ApJ, 869, 123 [Google Scholar]
  113. Sun, G., Lidz, A., Faisst, A. L., & Faucher-Giguère, C. A. 2023, MNRAS, 524, 2395 [CrossRef] [Google Scholar]
  114. Tang, M., Stark, D. P., Chevallard, J., & Charlot, S. 2019, MNRAS, 489, 2572 [NASA ADS] [CrossRef] [Google Scholar]
  115. Tang, M., Stark, D. P., Chen, Z., et al. 2023, MNRAS, accepted [arXiv:2301.07072] [Google Scholar]
  116. Trussler, J. A. A., Adams, N. J., Conselice, C. J., et al. 2023, MNRAS, 523, 3423 [NASA ADS] [CrossRef] [Google Scholar]
  117. van de Voort, F., Davis, T. A., Kereš, D., et al. 2015, MNRAS, 451, 3269 [Google Scholar]
  118. Vanzella, E., Nonino, M., Cupani, G., et al. 2018, MNRAS, 476, L15 [Google Scholar]
  119. Vanzella, E., Caminha, G. B., Calura, F., et al. 2020, MNRAS, 491, 1093 [Google Scholar]
  120. Wang, B., Heckman, T. M., Leitherer, C., et al. 2019, ApJ, 885, 57 [NASA ADS] [CrossRef] [Google Scholar]
  121. Wilkins, S. M., Bunker, A. J., Stanway, E., Lorenzoni, S., & Caruana, J. 2011, MNRAS, 417, 717 [NASA ADS] [CrossRef] [Google Scholar]
  122. Wilkins, S. M., Feng, Y., Di-Matteo, T., et al. 2016, MNRAS, 458, L6 [NASA ADS] [CrossRef] [Google Scholar]
  123. Yang, L., Morishita, T., Leethochawalit, N., et al. 2022a, ApJ, 938, L17 [NASA ADS] [CrossRef] [Google Scholar]
  124. Yang, L., Leethochawalit, N., Treu, T., et al. 2022b, MNRAS, 514, 1148 [NASA ADS] [CrossRef] [Google Scholar]
  125. Yung, L. Y. A., Somerville, R. S., Finkelstein, S. L., et al. 2020a, MNRAS, 496, 4574 [NASA ADS] [CrossRef] [Google Scholar]
  126. Yung, L. Y. A., Somerville, R. S., Popping, G., & Finkelstein, S. L. 2020b, MNRAS, 494, 1002 [NASA ADS] [CrossRef] [Google Scholar]
  127. Zackrisson, E., Rydberg, C.-E., Schaerer, D., Östlin, G., & Tuli, M. 2011, ApJ, 740, 13 [NASA ADS] [CrossRef] [Google Scholar]
  128. Zackrisson, E., Inoue, A. K., & Jensen, H. 2013, ApJ, 777, 39 [NASA ADS] [CrossRef] [Google Scholar]
  129. Zackrisson, E., Binggeli, C., Finlator, K., et al. 2017, ApJ, 836, 78 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Properties of the sources

This appendix comprises a sequence of tables detailing the properties of the sources included in this study.

Table A.1.

Physical and spectroscopic properties for the CEERS sample.

Table A.2.

Physical and spectroscopic properties of non-CEERS galaxies.

Appendix B: An analysis on the empirical relation calibrated on the LzLCS sample

To accurately assess the reliability of the empirical relation calibrated on the LzLCS presented in two versions (Eq. 1 in M23 and Eq. (2) of this study) for estimating the fesc values using indirect indicators, we examined the distribution of the residuals which are defined as the difference between the measured values and the values estimated by our relation. In Figure B.1, we plot the residuals obtained using both versions of our relation plotted against the real values, in logarithmic scale. To assess the correlation quantitatively, we conducted an ANOVA test on the two residual distributions, yielding a p-value of 0.96. It is evident that the two relations exhibit statistical equivalence, as their residual distributions are identical. We can also see that our relation tends to underestimate the fesc values for fesc > 0.1 and overestimate them for fesc below 0.01. This outcome is a direct consequence of the initial sample, which is predominantly composed of sources with modest fesc, around 0.02-0.05.

thumbnail Fig. B.1.

Left: The difference between the measured values and the values estimated by the M23 empirical relation. Right: Same for the values estimated using for Eq. (2) of this paper.

All Tables

Table A.1.

Physical and spectroscopic properties for the CEERS sample.

In the text
Table A.2.

Physical and spectroscopic properties of non-CEERS galaxies.

In the text

All Figures

thumbnail Fig. 1.

M1500 distribution for the analyzed sources at 6 ≤ z ≤ 9 (gray: total sample; red and blue are respectively the GLASS sample and the ERO sample from Mascia et al. 2023; Noirot et al. 2023).
In the text
thumbnail Fig. 2.

β vs. M1500. Black triangles represent the CEERS sources with β slope obtained fitting 3 or 2 photometric bands. Red dots are for the GLASS sample, and blue squares are for the ERO sample. The green line shows the relation at z ∼ 7 derived from HST data by Bouwens et al. (2014). Dashed portions indicate the extrapolation of the relation in our range of M1500. The Spearman rank correlation coefficient for the correlation between β and M1500 is 0.36, with a p-value of 0.02.
In the text
thumbnail Fig. 3.

Rest-frame UV re vs. M1500. Symbols are the same as in Fig. 2. The green line shows the relation derived from HST data by Shibuya et al. (2015) at z ∼ 7, the blue line shows the size-luminosity relation at z ∼ 6 − 7 from Yang et al. (2022b). The Spearman rank correlation coefficient for the correlation between re and M1500 is −0.33, with a p-value of 0.003.
In the text
thumbnail Fig. 4.

PDFs of the fesc values for two sources from the CEERS sample (MSA IDs: 390 and 80925). The considered fesc of the source, which is the mean fesc of the distribution, is shown in red. Given the non-normal distribution of the fesc values, we have included the 16th and 84th percentiles (red dashed lines) to measure the confidence interval.
In the text
thumbnail Fig. 5.

Predicted fesc distribution for the analyzed sources at 6 ≤ z ≤ 9 (gray: CEERS sample; red and blue are respectively the GLASS sample and the ERO sample). The mean fesc of the sample is shown in yellow, the median fesc is presented in orange.
In the text
thumbnail Fig. 6.

Left: predicted fesc vs. stellar mass (log10M⋆). Symbols are the same as in Fig. 2. To enhance the clarity of the plots, we have colored the entire sample in black. The green line shows the running average for our sample, while the red one is the prediction at z = 6 − 8 from Rosdahl et al. (2022). Right: predicted fesc vs. halo mass (log10Mh) estimated with Behroozi et al. (2019) conversion. The magenta and orange lines are the models from Ocvirk et al. (2021), the violet one is the prediction from Lewis et al. (2023), the line ones are the predictions from Bremer & Dayal (2023), and the blue line is the prediction from Ma et al. (2020).
In the text
thumbnail Fig. 7.

Predicted fesc vs. M1500. Symbols are the same as in Fig. 6. The green line shows the running average for our sample, the pink one refers to Matthee et al. (2022) and the yellow one to Lin et al. (2024).
In the text
thumbnail Fig. 8.

Predicted fesc as a function of redshift. Symbols are the same as in Fig. 6. The magenta points are the average fesc values of our sample at z = 6.5 and z = 8. The green dots are the M23 sources, while the green point is the average fesc value at z = 5.1. The blue hexagons represent the Lyα emitters from Saxena et al. (2023). The red line is the prediction at fixed M1500 = −19 from Rosdahl et al. (2022), the orange line is the prediction from Finkelstein et al. (2019) for sources with M1500 between −20 and −16.
In the text
thumbnail Fig. 9.

log ξion vs. β. Symbols are the same as in Fig. 6. The magenta line shows the mean log ξion for our sample. The Spearman rank correlation coefficient for the correlation between log ξion and β is 0.05, with a p-value of 0.63 indicating no correlation between the two quantities.
In the text
thumbnail Fig. 10.

Left: the ṅion fraction of galaxies at 6 ≤ z ≤ 9 as function of the M1500. Triangles represent the ṅion obtained from the predicted fesc as a function of M1500 in each bin. Bars represent the extrapolated value, i.e. the ṅion fraction derived assuming that for M1500 > −18 a fesc value constant and equal to 0.10, and for M1500 < −22 a fesc value constant and equal to 0.05. Right: in yellow we show the ṅion fraction of galaxies at 6 ≤ z ≤ 9 as function of M1500 changing, respectively, from the top left to the bottom right, the fesc values at the faint-end (0.05 and 0.15) and the α parameter of the ρUV (−1.94 and −2.27). The original result is also shown with the same symbols as in the figure from the left.
In the text
thumbnail Fig. B.1.

Left: The difference between the measured values and the values estimated by the M23 empirical relation. Right: Same for the values estimated using for Eq. (2) of this paper.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.