| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 33 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201424388 | |
| Published online | 24 December 2014 | |
Online material
Appendix A: Spitzer/IRAC data reduction
We downloaded all the basic calibrated data (BCD) and corrected BCD (CBCD) products, which were provided by the Spitzer Science Center through their standard data processing pipeline version S18.18.0. Data obtained from S18.18.0 need to be corrected in the 5.8 and 8.0 μm bands due to an error in calibration, so they have been multiplied by 0.968 and 0.973, respectively, following the prescriptions given in the web page4. For each raw image, the pipeline produces a flux-calibrated image (BCD), where all well-understood instrumental signatures (e.g., muxbleed) are removed (and including dark-subtraction and flat-fielding). The pipeline also attempts to systematically find all saturated point sources in the images and fit them using an appropriate PSF that is matched to the unsaturated wings of the source. A dedicated software module replaces the saturated point source with an unsaturated point source that has the correct flux density of the point source. We checked that this works quite well on the short-exposure frames but not on the long-exposure ones. Another pipeline module performs artefact correction (stray light, saturation, muxstripe, column pulldown and banding) on the BCD files, creating “corrected” BCD (CBCD) files. For details, see the on-line instrument handbook5.
The observations were performed in high dynamic range (HDR) mode, i.e., two images were taken at each position, a short exposure one (0.4 s) and a long exposure one (10.4 s). This allows one to also obtain photometry for bright sources avoiding saturation. The observed area was covered by using the IRAC mapping mode, with a grid of 10 × 8 positions in “array” coordinates, spaced by 260″ (i.e., slightly less than the detector size) in both directions defined by the detector axes. The selected dithering mode was “cycling”, with a scale factor “medium” and a number of positions equal to 5, i.e., for each grid position, 5 pairs (the short- and long-exposure integration) of dithered images were taken, randomly distributed up to a maximum distance of 119 pixels and with a median distance of 53 pixels. Therefore, most of the points in the mosaic result from the overlap of up to five images, although small areas can be covered by more than 5 images (where the dithered patterns of adjacent grid positions overlap) and few smaller areas may be covered by less than 5 images.
Mosaicking and co-adding of all frames were carried out by using MOPEX version 18.4.9, yielding a pair of larger images (short- and long-exposure) per band with a pixel size ![]() (about half the native pixel size). We used a dual-outlier rejection strategy with conservative settings and experimented different values of the parameter RThreshold. The long-exposure CBCD frames at 5.8 and 8.0 μm displayed intense stripes associated with bright sources, absent in the corresponding BCD frames. We found out that these are features caused by the artefact-mitigation pipeline. Consequently, we constructed the long-exposure 5.8 and 8.0 μm images using the BCD files rather than the CBCD ones. On the other hand, as for the short-exposure mosaics, only a few CBCDs at 8.0 μm were found heavily affected by the problem and replaced by the corresponding BCDs. In all other cases we used the CBCDs.
(about half the native pixel size). We used a dual-outlier rejection strategy with conservative settings and experimented different values of the parameter RThreshold. The long-exposure CBCD frames at 5.8 and 8.0 μm displayed intense stripes associated with bright sources, absent in the corresponding BCD frames. We found out that these are features caused by the artefact-mitigation pipeline. Consequently, we constructed the long-exposure 5.8 and 8.0 μm images using the BCD files rather than the CBCD ones. On the other hand, as for the short-exposure mosaics, only a few CBCDs at 8.0 μm were found heavily affected by the problem and replaced by the corresponding BCDs. In all other cases we used the CBCDs.
Appendix B: Spitzer/IRAC photometry
We checked that any artefact had been removed efficiently from the final mosaicked images, except for the bandwidth effect in the long-exposure 5.8 and 8.0 μm ones. This gives rise to ghosts associated with the brightest sources. However, the corresponding artefacts were clearly recognisable and removed from the final point-source photometry. Some optical banding, as well, due to internal radiation scattering in the arrays, is present in the long-exposur 5.8 and 8.0 μm images yielding a small faint halo around the brightest areas. Being a diffuse structure, however, it is not expected to affect the final photometry significantly.
 |
Fig. B.1
Magnitude–colour diagrams showing the magnitude in the various IRAC bands of the sources from the sample obtained in this work (black dots) as a function of [4.5] – [8.0]. Panels on the same row display, from top to bottom, the measurements for these sources in the 3.6, 4.5, 5.8, and 8.0 μm bands, respectively. In the left column panels, the sources from our sample are overlaid with those from GLIMPSE II (red dots). The green dots in the right column panels are those remaining from our photometry list after removal of sources contaminated by PAH emission. Only objects detected in all four bands with photometric errors <0.3 mag are plotted. |
| Open with DEXTER | |
 |
Fig. B.2
Magnitude–colour diagrams showing the magnitude of all sources from the sample obtained in this work (black dots) only detected in the first three wavelength IRAC bands (i.e., 3.6, 4.5 and 5.8 μm). Panels on the same row display, from top to bottom, the measurements for these sources in the 3.6, 4.5, and 5.8 μm bands, respectively, plotted as a function of [4.5] – [5.8]. In the left column panels, they are overlaid with all sources from GLIMPSE II (red dots) at least detected in the three shorter wavelength bands. The green dots in the right column panels are the sources remaining from our photometry list after removal of those contaminated by PAH emission. Only objects with photometric errors <0.3 mag in the three shorter wavelength bands are plotted. |
| Open with DEXTER | |
 |
Fig. B.3
Magnitude–colour diagrams showing the magnitudes of all sources from the sample obtained in this work (black dots) only detected in the two shorter wavelength IRAC bands (i.e., 3.6 and 4.5μm). Panels on the same row display, from top to bottom, the measurements for these sources in the 3.6 and 4.5μm band, respectively, plotted as a function of [3.6] – [4.5]. On the left column panels, they are overlaid with all sources from GLIMPSE II (red dots) at least detected in the two shorter wavelength bands. Only objects with photometric errors <0.3 mag in the two shorter wavelength bands are plotted. |
| Open with DEXTER | |
Photometry was performed both on the short-exposure images and on the long-exposure ones. In each band, we set a saturation limit to the long-exposure mosaic, conservatively derived by estimating the saturation limit in a single BCD following the IRAC instrument handbook. The measured fluxes were converted into magnitudes by using the zero magnitude flux densities given in Table 4.1 of the IRAC instrument handbook (also given in Reach et al. 2005). The errors were calculated by using Eq. (7) of Reach et al. (2005), i.e., neglecting electronic noise. We discarded a number of residual false detections by visual inspection of the images, while others were subsequently removed by operating a colour-based selection during the analysis.
Short- and long-exposure photometry were matched in each band, adding the bright sources from the former to the faint sources from the latter according to the following criterion. We estimated a magnitude threshold for each band by requiring both that the average signal to noise ratio at the shorter exposure time was high enough, and that its corresponding flux was well below the single BCD saturation limit set at the longer exposure time. The sources with flux above the threshold were then taken from the short-exposure photometry, whereas those with flux below it were taken from the long-exposure photometry. The chosen thresholds are [3.6] = 10.5, [4.5] = 10, [5.8] = 8 and [8.0] = 8.5.
 |
Fig. B.4
Number of sources per magnitude bins of 0.5 mag, from our database (black line) and the GLIMPSE sample (red line). The boxes in each row refer to the band indicated on the upper left corner. For the diagrams on the left column we used the sources detected in all four IRAC bands with photometric errors <0.3 mag, whereas for those on the right column we used all sources detected in at least the corresponding band (with photometric errors <0.3 mag in that band). |
| Open with DEXTER | |
We cross-checked the photometry from the long- and short-exposure mosaics in each band I by computing the difference in magnitude of all sources retrieved in both of them (with photometric uncertainties less than 0.3 mag). We plotted the histogram of the difference Δm between long- and short-exposure measurements in bins of 0.5 [I]-magnitudes, sampling the sources over two different image test areas. One area was chosen well inside the large ring-like structure (hence with little diffuse emission) and the other one inside the G353.2+0.9 projected area (with the most intense diffuse emission). For brighter magnitude bins, the histograms appear to peak at values that are within 0.05 mag from 0 (with a trend of the long-exposure measurements to be brighter) following distributions resembling Gaussian curves. However, when moving towards fainter magnitudes, the distributions become less peaked, their width increases, and a wing develops on the side where long-exposure measurements are brighter than short-exposure ones. The dispersion around the peak is always narrower than the typical photometric error inside each magnitude bin, This flatter distribution in the faint bins is more evident towards the test area with large diffuse emission, although it does not seem to be correlated with the presence of diffuse emission. This may be due either to the short-exposure photometry being nearer to its sensitivity limit, and/or to a better sampling of the sky around point-sources for longer exposures (i.e., better signal-to-noise). In addition, the distributions for the 8.0 μm band do not exhibit the wing and are narrower than in the other bands. It appears that we used a DAOFIND finding threshold larger at 8.0 μm than in the other bands, in units of one sigma of effective noise, leading to a smaller overlap between short and long exposures.
Whatever caused this trend in the distributions of magnitude difference, the difference between long- and short-exposures is of no concern at all at bright magnitudes (where the final photometry is taken from the short-exposure mosaics), while we assume that anyway the fainter fluxes are better characterised in the long-exposure mosaics (yielding higher signal to noise ratios).
A few sources (much less than 1% of the total) exhibit large differences between short- and long-exposure magnitudes (larger than 2–3 times the width of the Δm distribution). In most cases, either they fall on some artefacts in one of the two mosaics or they are residual cosmic rays passing the outlier rejection stage of MOPEX. These sources were either removed or were assigned a photometric estimate from the image unaffected by the artefact. This further confirms that residual contamination from artefacts or cosmic rays is very low, well below ~1% of the total sample in each band.
Another consistency test that we performed consisted in comparing the photometry from this work with that from the GLIMPSE survey. We retrieved all sources from the GLIMPSE II (epoch 1) archive within 30′ from RA = 17h25m and Dec = −34°18′. The area covered by our data is smaller than that and lies well inside the 30′ radius. In the magnitude-colour diagrams of Fig. B.1 showing magnitudes vs. [4.5] – [8.0], we have overlaid (left column) the GLIMPSE datapoints (red) and those from this work (black). We have selected only objects detected in all four bands with photometric errors <0.3 mag from the two samples. It appears that the two photometry lists as a whole are consistent with each other, apart for a large group of sources with [4.5] – [8.0] >2 much more numerous in our sample. These are sources contaminated by PAH emission arising in the bright filaments that cross the region (see Appendix D). When these objects are filtered out as explained in Appendix D, the remaining ones (green dots, in the right column boxes) are distributed in the mag-colour diagram like the GLIMPSE datapoints.
We repeated the same test by selecting all sources from our database with detections only in the first three bands (3.6, 4.5 and 5.8 μm). In the magnitude–colour diagrams of Fig. B.2 their magnitudes are plotted vs. [4.5] – [5.8]. We have overlaid these (in black) with (boxes in the left column) the GLIMPSE datapoints with detections in at least the first three bands (red). We have selected only objects with photometric errors <0.3 mag in the three shorter wavelength bands from the two samples. In this case the two photometric lists appear to be consistent, as well, apart from a slight excess of red sources in our sample with respect to the GLIMPSE sample. By removing all sources contaminated by PAH emission as explained in Appendix D and plotting the remaining ones (green dots, boxes in the right column), the excess of red sources disappears, confirming its origin. We note that the brightest sources in our sample with detection only in the first three bands have a magnitude ~10 in all bands. Since stars have colours ~0 mag in all IRAC bands, this indicates that the sources with detections only in the three shorter wavelength bands are mostly stars too faint to be detected at 8.0 μm, where the sensitivity is [8.0] ~ 10 − 12 (see bottom row of Fig. B.1).
Finally, in Fig. B.3 we plot magnitudes vs. [3.6] – [4.5] for all sources from our database with detections only in the first two bands and photometric errors <0.3 mag (black dots). These are overlaid (boxes in the left column) with datapoints from the GLIMPSE sample with detection in at least the first two bands (red dots). The two photometric lists appear again to be consistent with each other. The brightest sources from our database are a bit fainter than those in Fig. B.2, suggesting that sources detected only in the first two bands are again mostly stars too faint to be detected in the two longer wavelength bands.
One striking thing that appears clearly from Figs. B.1–B.3 is that the sensitivity limits of our photometry are about the same as those of the GLIMPSE photometry. Nevertheless, our photometry does result from images integrated at least for 10.4 s and, on average, corresponding to a total exposure time of 52 s. On the other hand, the GLIMPSE II (epoch 1) photometry is produced using two images per position with exposure times 1.2 s each. This property of the limiting sensitivities is demonstrated in Fig B.4, comparing histograms of number of sources grouped in 0.5 mag magnitude bins from our sample (black) and the GLIMPSE one (red). For the diagrams on the left column, we have used only the sources detected in all four bands with photometric errors <0.3 mag, whereas for the diagrams on the right column we have used all sources detected in at least one wavelength band (with photometric errors <0.3 mag in that band). In any case, the distributions from the two samples are about equal, except for the different number of sources retrieved (as said the selected GLIMPSE field is larger than the target one). Both exhibit an increase in the number of sources starting from low magnitudes, a turn off roughly at the same magnitude, and a steep decrease. This clearly indicates that the completeness limit (and the sensitivity limit) in each band is roughly the same for the two samples.
We noticed a similar effect when comparing our short- and long-exposure photometry. The latter is about one magnitude (1.5 mag at 5.8 μm) deeper than the former, although the sensitivity values listed in the IRAC handbook would suggest a difference of at least 3–4 mag. This means that our photometry is limited by a source of noise that does not depend on the integration time. This can only be confusion due to the large number of sources in the field, given that we are observing along a line of sight close to the Galactic Centre. This is confirmed by Ramírez et al. (2008) who, in their IRAC survey of the Galactic Centre, found that their photometry is limited by confusion, as well. Using images with average total integration time of 6 s, they quote completeness limits which are even less than those we can infer from Fig. B.4 for the GLIMPSE sample (with 2.4 s total exposure time). The histograms of number of sources vs. magnitude that they show, exhibit the same abrupt turn-off at the faint end as ours. Furthermore, Fang et al. (2012) achieve only slightly better sensitivities compared to GLIMPSE using IRAC images of NGC 6357 of 10.4 s exposure time. Therefore, we can conclude that our photometry is limited by source confusion.
Appendix C: Completeness of Spitzer photometry
The photometric completeness in a band (i.e., the capability of retrieving most of the sources up to a given magnitude in a field) mainly depends on the sensitivity of the observations in that band. Because the sensitivity attained in the four IRAC bands is different, the completeness limit is fainter in the first two bands and gets brighter by requiring simultaneous detection in more than one band. To study the effect, we constructed histograms of the magnitude distribution, in bins 0.5 mag wide, adopting several different selection criteria. All histograms display an increase in the number of sources N with increasing magnitude up to a peak, and a subsequent decrease due to loss of completeness. A few examples are shown for all bands in Fig. C.1. In the following, by “good” detection we will mean one with a photometric error <0.3 mag. In addition, by “completeness degree” we will mean the fraction of sources of a given magnitude (irrespective of their nature) that are retrieved in the field.
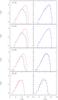 |
Fig. C.1
Number of sources retrieved in the I band vs. [I] in bins of 0.5 mag. The boxes in each row refer to the Spitzer/IRAC band I indicated on the upper left corner of the left-hand box. Upper two rows: in the left column, we compare the I-band sources detected in all IRAC bands with photometric errors <0.3 mag (black line), and the sources detected in at least the first two IRAC bands with photometric errors <0.3 mag (red line); in the right column, we compare all sources detected in at least the first two IRAC bands, with photometric errors either <0.3 mag in both bands (black line), or <0.3 mag in at least the considered band I (blue line). Lower two rows: in the left column, we compare the I-band sources detected in all IRAC bands, with photometric errors either <0.3 mag in all bands (black line), or <0.3 mag in at least the considered band I (red line); in the right column, we compare the I-band sources detected in all IRAC bands, with photometric errors <0.3 mag in at least the considered band I (black line), and the sources detected in at least the considered band I with photometric errors <0.3 mag (blue line). |
| Open with DEXTER | |
To derive the completeness degree as a function of magnitude, we first compared the histograms obtained in each IRAC band from the following two samples of sources (see the left column in Fig. C.1). The first sample (S1) contains all the sources retrieved in a band I with simultaneous good detections in all 4 bands. The second sample (S2) contains all the sources retrieved in a band I with good detections in I and in at least one adjacent band. Hence, different samples S2 can be obtained depending on the choice of the adjacent band (e.g., we used 3.6 and 4.5μm for each of these two bands, 5.8 and 4.5μm for the 5.8μm band, and 5.8 and 8.0μm for the 8.0μm band). Hereafter, we will refer to the distribution of magnitude [I] for samples S1 and S2 as S1[I] and S2[I], respectively. At their peak, the distribution of S1[3.6] and S1[4.5] are a factor ~0.6–0.7 of that of S2[3.6] and S2[4.5], respectively. This ratio increases to >0.8 one magnitude below (i.e., brighter than) the peak.
The distributions of S1[8.0] and S2[8.0] (not shown) are qualitatively similar, although the ratio S1[8.0] to S2[8.0] is ~0.72 one magnitude below the peak of S1[8.0]. However, such a comparison is less significant than for other bands, given that most of the sources without a detection in any of the first two bands are probably just blobs of diffuse emission rather than stellar objects.
Based on the histograms of the magnitude distribution for sources with good detections in at least two bands (i.e., S2[I]), we conservatively estimate that the 80% completeness limits of each sample S2 lie roughly one magnitude below its distribution peak (set CL0). E.g., [3.6] = 12.25, and [4.5] = 12.25. Therefore, based on the above assumption, we can derive ~80% completeness limits for sources with good detections in all IRAC bands (set CL1): [3.6] = 10.25, [4.5] = 9.75, [5.8] = 9.25, and [8.0] = 8.75. These are obtained simply by measuring the magnitude at which the ratio of the distribution S1[I] to S2[I] is ~0.8, considering that this usually occurs more than one magnitude below the peak of S2[I] (hence where S2[I] has been assumed to be almost complete).
Estimated completeness limits.
The same exercise, but replacing the samples S1 with other samples obtained by requiring that the selected sources are detected in at least the first three bands with photometric errors <0.3 mag (S1a), yields the following 80% completeness limits (set CL2): [3.6] = 11.75, [4.5] = 11.5, and [5.8] = 10.25.
Requiring that all the sources in a given band be also detected in other bands with photometric errors <0.3 mag can be quite a demanding prescription, causing otherwise good detections in that band to be removed because the detection in just another band has an error >0.3 mag. We checked that this is only a minor problem by noting the following. The histograms of the magnitude distribution obtained by selecting I-band sources detected in all four bands, but requiring good detections in all bands for one histogram (S1[I]) and at least in the I band for the other (S4[I]), both peak at the same magnitude, irrespectively of I. The ratio S1[I] to S4[I] slightly decreases with increasing magnitudes down to >80% at the peak. The same is found by selecting I-band sources detected in the first three bands, but either requiring good detections in all three bands (S1a[I]) or at least in the I band (sample S6[I]). In this case, the ratio of the distribution S1a[I] to S6[I] is >75% at the peak. For I = 3.6 and I = 4.5μm bands, we compared the histograms of I-band sources with good detections in at least the first two bands (S2[I]) and I-band sources detected in at least the first two bands but with good detection in at least the I band (sample S8[I]). These histograms (see the two upper rows in the right column of Fig. C.1 are very similar each other, with ratio of distribution S2[I] to S8[I] > 95% at the peak. By replacing the distribution S8[I] with those of sources with at least a good detection in one of the first two bands (S8[3.6] ∪ S8[4.5]), the ratio decreases to > 86% at the histogram peaks. Therefore, the effect of requiring good detections in at least the first two bands should imply a completeness limit not too different from that in each single lower-wavelength band.
The lower two rows of Fig. C.1 show that 5.6 and 8.0 μm-band sources with at least a good detection in the considered band, peak at slightly lower magnitudes than the corresponding sub-sample obtained by requiring a good detection in all bands. As said, we believe that most of the sources in the two upper-wavelength bands without simultaneous detections in the first two bands are mostly blobs of diffuse emission or even artefacts. So the statistics of all detections (multiple as well as single) in those bands is very likely to be biased.
Finally, we expect quite different completeness limits in areas without and with diffuse emission. To test this, we repeated all experiments described above but by selecting 1) only sources contained in an area with at most faint diffuse emission, i.e., inside the large ring; and 2) only sources inside the area containing G353.2+0.9. There is no difference in the histogram peak locations for the sets CL0, CL1, and CL2, at 3.6 and 4.5μm, between the complete samples discussed above and those of the sources inside the ring. On the other hand, the peaks of the histograms for 5.8 and 8.0μm sources inside the ring shift to larger magnitudes. This is probably because the crowding of sources far from diffuse emission areas is much less severe in the two longer wavelength IRAC bands. Apparently, in the first two bands the total (i.e., with sources from the whole field) samples are dominated by sources not falling towards diffuse emission, hence by crowding effects.
As far as sources inside the area containing G353.2+0.9 are concerned, the peaks of the histograms shift to lower magnitudes for sets CL0, CL1, and CL2, as expected, excluding CL1 at 3.6 and 4.5 μm whose peaks are one magnitude above (i.e., fainter than) those of the total samples. We suspect that this is due to the chance associations of faint sources in the first two bands and blobs of diffuse emission in the two upper-wavelength bands, artificially increasing the detection efficiency when requiring good detections in all bands. In any case, the source statistics is quite poor. Thus, we believe that only the estimates from CL0 (i.e., from the first two bands) are reliable in areas of intense diffuse emission.
The derived completeness limits (at a 70–80% level) for different detection requirements and areas in the images are listed in Table C.1.
Appendix D: Contamination of YSOs due to other red sources in the Spitzer photometry
Figure B.1 clearly shows a prominent group of sources with [4.5] – [8.0] > 2 in our sample, much more numerous than in the GLIMPSE sample. This is better evidenced in Fig. D.1, by plotting [3.6] and [8.0] vs. [5.8] – [8.0] for sources detected in all four bands and having photometric errors <0.3 mag. The [4.5] vs. [5.8] – [8.0] plot (not shown) is similar to the [3.6] vs. [5.8] – [8.0] one, whereas the [5.8] vs. [5.8] – [8.0] plot (not shown) is similar to the [8.0] vs. [5.8] – [8.0] one. A population of red sources centred at [5.8] – [8.0] ~1.7–1.8 is quite easily identified. These sources appear to be faint at 3.6 and 4.5 μm (<10 mag), but bright at 5.8 and 8.0 μm (>10 mag). On the other hand, the group of sources centred at [5.8] – [8.0] ~ 0 are mostly stars.
|
Fig. D.1
Magnitude vs. [5.8] – [8.0] in the 3.6 μm (left) and 8.0 μm (right) bands for all sources in our sample with detections in all four bands and photometric errors <0.3 mag (black dots). Overlaid (green dots), all remaining sources after removal of the various contaminants as explained in the text. |
|
| Open with DEXTER | |
|
Fig. D.2
[3.6] – [4.5] vs. [5.8] – [8.0] (left) and [4.5] – [5.8] vs. [5.8] – [8.0] (right) for all sources in our sample detected in all four bands with photometric errors <0.3 mag (black dots). Overlaid (green dots), all remaining sources after removal of the various contaminants as explained in the text. |
|
| Open with DEXTER | |
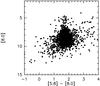 |
Fig. D.3
[8.0] vs. [5.8] – [8.0] for all sources in our sample only detected at 5.8 and 8.0 μm. |
| Open with DEXTER | |
 |
Fig. D.4
IRAC colour–colour diagrams. Top panel, [3.6] – [4.5] vs. [5.8] – [8.0] for sources detected in all four bands and with photometric errors <0.3 mag. Bottom panel, [3.6] – [4.5] vs. [4.5] – [5.8] for the same sources as above, plus those only detected in the three shorter wavelength bands (with photometric errors <0.3 mag). The two samples have been cleaned of contaminants as explained in the text. Following the prescriptions of Gutermuth et al. (2009) for their identification, Class I sources are in red and Class II sources in blue. Stars are marked as black dots. A reddening corresponding to AV = 20 mag (according to Indebetouw et al. 2005) is marked by an arrow. In the top panel, the regions occupied by Stage I and Stage II sources (Robitaille et al. 2006) are also outlined. |
| Open with DEXTER | |
Plotting the position of the sources with [5.8] – [8.0] > 1 on each of the IRAC images, we found that almost all appear to concentrate towards the filaments and areas of diffuse emission, whereas sources with [5.8] – [8.0] < 1 are anti-correlated with those areas. This suggests that most of the red sources are likely to be sources contaminated by PAH emission rather than actual intrinsically red objects. In fact, Zavagno et al. (2006) found that analogous filaments in RCW 79 have colours [3.6] – [4.5] ~0.1 and [5.8] – [8.0] ~ 1.8. The same average colours can be derived from Fig. D.2 for the red sources in our sample. These red sources probably arise due to random association of faint sources in the two shorter wavelength bands and bright blobs of diffuse emission in the two longer wavelength bands. All these blobs are bright, because of both the lower sensitivity and saturation problems towards those areas. Figure D.2 (right panel) shows well this datapoint population, whose colour [5.8] – [8.0] is remarkably constant (~1.7–1.8 mag) whereas [4.5] – [5.8] spreads between ~1 and ~4. In other words, there is a sort of break between the emission at 3.6 and 4.5 μm ([3.6] – [4.5] ~ 0) and that at 5.8 and 8.0 μm ([5.8] – [8.0] ~1.7–1.8 mag), which points to a random association rather than intrinsically red objects, as well.
A plot of [8.0] vs. [5.8] – [8.0] is shown in Fig. D.3 for sources only detected at 5.8 and 8.0μm; again, they are mostly concentrated at [5.8] – [8.0] ~1.7–1.8 and are distributed like the red sources in Fig. B.1. Spatially, they concentrate towards filaments and diffuse emission areas, as well. If they had counterparts in the two lower wavelengths, they would correspond to even redder sources (so red to remain undetected at those wavelengths because lying below the sensitivity limits) than those with detections in all four bands. Consequently, it is more plausible that the objects exhibiting [5.8] – [8.0] ~1.7–1.8 are mostly blobs of diffuse emission.
To understand why this population of red sources is scarcely represented in the GLIMPSE survey (see Fig. B.1), we plotted the position of all GLIMPSE sources detected in all four bands with photometric errors <0.3 mag. Unlike the red sources in our sample, few objects fall towards the filaments and Hii regions. Therefore, the analogues of our red sources were filtered out of the GLIMPSE database because of their adopted selection criteria.
To remove the identified PAH-contaminants, we used the prescriptions given by Gutermuth et al. (2009). We also removed all other possible contaminants following Gutermuth et al. (2009), i.e., AGNs, star forming galaxies and unresolved shock emission. This is a conservative choice, since we are observing through the Galactic plane and contamination due to galaxies should be negligible. As can be seen in Figs. B.1 through D.2 (green dots), the PAH contaminants appear to have been removed quite satisfactorily. On the other hand, for sources only detected in the first three bands, we applied the criterion for PAH-contamination but not the others, which require a knowledge of the flux at 8.0 μm as well.
The final efficiency of the cleaning process can be checked by plotting the colours of Class I and Class II sources (see Fig. D.4), identified after removal of contaminants by using the colour criteria of Gutermuth et al. (2009). In the top panel of Fig. D.4, the regions occupied by Stage I and Stage II sources (following the scheme proposed by Robitaille et al. 2006, who slightly modified the original classification scheme resulting in Class I and II sources) are also outlined. By following the colour criteria of Allen et al. (2004), we would have obtained similar results for Class I and Class II sources. The colour–colour diagram showing [3.6] – [4.5] vs. [5.8] – [8.0] is very similar to that obtained by Fang et al. (2012), although a look at their Fig. 5a shows the effects of the different classification criteria they adopted.
Appendix E: Multi-wavelength classification of YSOs in the SofI field
The evolutionary stages of the cluster members can be derived by using either NIR/MIR colours or their association with X-ray emission. Nevertheless, different methods definitely suffer from different selection effects and this has to be accounted for when comparing the obtained results.
In this paper, we adopted several classification schemes based on: JHKs, [3.6][4.5][5.8][8.0], [3.6][4.5][5.8], JH(HKs)[4.5] colours, X-ray emission. All these indicators allow us to identify the embedded protostar population, the classical T Tauri population and the weak-line T Tauri population out of the whole cluster stellar population. However, when computing number ratios we have to check for any difference in completeness that might arise because of the different sensitivities attained in each band.
To derive these differences, we reasonably assume that our Ks image is the most sensitive of all available bands, either SofI or IRAC. On the one hand, many Ks sources are missed in J and H because of extinction. On the other hand, the observations in the IRAC 3.6 and 4.5 μm bands are less extincted, but not as deep as Ks and with a worse spatial resolution. Therefore, Ks can be considered as our reference band. Consequently, we can compute the maximum Ks for which at least 80% of the Ks sources are also detected i) in the JH bands; ii) in the 4.5 μm bands AND either in the JH bands or in at least the H band; iii) in all four IRAC bands and iv) in the first three IRAC bands. We will refer to the derived Ks in each case as the “80% completeness limit” throughout this section. We constructed the Ks luminosity functions for all these classes (i–iv) of sources and compared them with the Ks luminosity function of the sources at least detected in the Ks band, both for the northern and the southern part of the SofI field. We only counted sources with photometric uncertainty <0.3 mag in every band considered. The luminosity functions are compared in Fig. E.1. For detections in three and four IRAC bands, we discarded sources with IRAC colours typical of PAH contamination (see Appendix D). We found however that this is important only for sources with good detections in 4 IRAC bands located in the northern field, as expected because of the contaminating diffuse emission from the Hii region. The 80% completeness limits are indicated with vertical dotted lines in Fig. E.1. They are also listed in Table E.1.
 |
Fig. E.1
Number of Ks sources per magnitude in bins of 0.5 mag (dashed line) compared with (full line): the number of Ks sources with also good detections both at J and Ha), northern field; f) southern field; the number of Ks sources with also good detections either at both J and H or at least at H, and in the IRAC 4.5 μm band b), northern field; g) southern field; the number of Ks sources with also good detections in all four IRAC bands c), northern field; h) southern field; the number of Ks sources with also good detections in the first three IRAC bands d), northern field; i) southern field; the number of Ks sources that exhibits an X-ray emission e), northern field; j) southern field. We only took into account sources with photometric uncertainty <0.3 mag in all the considered bands. In addition, the samples plotted in panels c), d), h), i), have been rid of sources with colours indicating PAH contamination as explained in Appendix D. On the upper left corner of each box, a xN tag indicates whether the histograms plotted have been multiplied by a constant N to expand the scale. The vertical dotted lines mark the Ks values at which ~80% of the Ks sources are still retrieved when requiring simultaneous valid detections in other bands. |
| Open with DEXTER | |
Ks values at which 80% of Ks sources are still retrieved when also detected in other bands.
We note that the 80% completeness limit significantly varies from case to case, depending on the colours used and the area of the field. For example, a lot of Ks sources are missed particularly in the northern SofI field when requiring valid detections in all four IRAC bands. This is due to the problems suffered by the two upper wavelength IRAC bands in the regions of diffuse emission outlined in the text. We also note that the JHKs colours mostly tend to filter out embedded stars, young PMS stars and protostars, whereas IRAC colours mostly tend to filter out unreddened stars. Thus, we can hope to obtain a better 80% completeness limit by combining Ks sources for which at least one of the colours from i) to iv) is available. However, as shown in the 6th column of Table E.1, this only happens in the northern SofI field.
The bottom row in Fig. E.1 shows the luminosity function of Ks sources that also exhibit an X-ray emission. Given that not all Ks sources (particularly field stars, unlike T Tauri stars) have detectable X-ray emission, this luminosity function cannot be directly compared with the one of all sources with a valid Ks detection. In the southern field, the luminosity function exhibits a fast increase up to Ks ~ 13. This suggests that all Ks sources emitting X-rays are roughly complete down to that limit. On the other hand, in the northern field the luminosity function is much less steep; if this were mainly due to an increased difficulty in retrieving sources in the northern area of the Ks image, lots of X-ray sources without a NIR counterpart should be detected. Only 5 X-ray sources are actually detected without a NIR counterpart there. So, the flatter X-source Ks luminosity function in the north may arise due to either a decrease in the probability of detecting X-ray emission from embedded cluster members, or a greater Ks magnitude spread of cluster members caused by variable extinction. Therefore, it is difficult to estimate a Ks completeness limit for X-ray emitting sources in this case; it may lie in the range 11–13 mag. However, we note that for strongly variable extinction (as expected when moving from south to north) this would not correspond to a particular mass limit.
Appendix F: Individual NIR sources towards Pismis 24
 |
Fig. F.1
J − H vs. H − Ks for NIR sources towards the five areas (or subclusters) selected in the SofI field of view. Sources with a JHKs colour excess (and H − Ks< 1) are marked by blue squares, sources with a JH(HKs) [4.5] colour excess (and H − Ks< 1) are marked by red squares, other sources are marked by black squares (small squares for H − Ks ≥ 1). The main sequence locus is also drawn in each diagram, along with reddening (dashed lines with crosses every AV = 10 mag). The sources discussed in the text are labelled, as well. |
| Open with DEXTER | |
The nature of the most massive stars in each subcluster of Pis24 core can be better investigated by considering the corresponding J − H vs. H − Ks (Fig. F.1) and Ks vs. H − Ks diagrams (Fig. F.2). Clearly, all the O-type stars lie towards the south-eastern part of subcluster core C, whereas the other star concentrations are more reminiscent of the small embedded young clusters where typically intermediate-mass stars form. Core SW: it is the only subcluster, apart from core C SE, with a possible earlier-than-B0 star. Our NIR source # 578 is, in fact, bright enough and exhibits a clear JHKs colour excess, suggesting it is a massive young star. H II region: the most massive star towards the Hii region, our NIR source # 998, is a B2 star located on the western part of the bar. The other bright (Ks ~ 10.22) star is located just west of the elephant trunk but is probably a background giant. The star at the tip of the elephant trunk (IRS4 of Felli et al. 1990) is a B0–B4 star with a JHKs colour excess. IRS7 and IRS8 of Felli et al. (1990) also exhibit a JHKs colour excess, but appear to be less massive than IRS4. We found that IRS1 and IRS2 were misplaced by Felli et al. (1990): by comparing their Fig. 4 with our Fig. 2 it can easily be verified that these two sources lie ~15″ further south than the bar (in their Fig. 7), i.e., towards the north-western part of subcluster core C and not in the bar. In addition, Figs. F.2 and F.1 clearly show that they are probably background giants. Core C (NW): the most massive star is a B1–B2 star, our NIR source # 962. It is located near the border between the two parts of subcluster core C, and it could be associated with C SE rather than the C NW. Core NE: it is the only core region hosting an IRAC-retrieved Class I source (with Ks< 13.5), namely our NIR source # 702, which has a characteristic colour excess in the J − H vs. H − Ks diagram (Fig. F.1), as well.
 |
Fig. F.2
Ks vs. H − Ks for NIR sources towards the five areas (or subclusters) selected in the SofI field of view. Sources with a JHKs colour excess (and H − Ks< 1) are marked by blue squares, sources with a JH(HKs) [4.5] colour excess (and H − Ks< 1) are marked by red squares, other sources are marked by black squares (small squares for H − Ks ≥ 1). The ZAMS is also drawn in each diagram, whereas an arrow in the first box from left marks an extinction AV = 20 mag. The sources discussed in the text are labelled, as well. |
| Open with DEXTER | |
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


