| Issue |
A&A
Volume 697, May 2025
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 12 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202452617 | |
| Published online | 07 May 2025 | |
Diffusive versus non-diffusive paths to interstellar hydrogen peroxide
A machine-learning-based molecular-dynamics study
1
Department of Physical Chemistry, University of Chemistry and Technology,
Technická 5,
16628
Prague 6,
Czech Republic
2
Departamento de Astrofísica Molecular, Instituto de Física Fundamental (IFF-CSIC),
C/ Serrano 121,
28006
Madrid,
Spain
3
Institute for Theoretical Chemistry, University of Stuttgart,
Pfaffenwaldring 55,
70569
Stuttgart,
Germany
★ Corresponding authors: petr.slavicek@vscht.cz; german.molpeceres@iff.csic.es
Received:
15
October
2024
Accepted:
8
March
2025
Context. Radical chemical reactions on cosmic dust grains play a crucial role in forming various chemical species. Among different radicals, the hydroxyl (OH) is one of the most important, with a rather specific chemistry.
Aims. The goal of this work is to simulate the recombination dynamics of hydroxyl radicals and the subsequent formation of hydrogen peroxide (H2O2).
Methods. We employed neural-network potentials trained on ONIOM(QM/QM) data, combining multi-reference (CASPT2) and density functional theory calculations. This approach allowed us to model the recombination of hydroxyl radicals on ice surfaces with high computational efficiency and accuracy.
Results. Our simulations reveal that the initial position of the radicals plays a decisive role in determining recombination probability. We found that the formation of a hydrogen bond between radicals competes with the formation of hydrogen peroxide, reducing the recombination efficiency, which is contrary to what was expected. This competition reduces the recombination probability for radicals that are initially formed approximately 3 Å apart. Recombination probabilities also depend on the kinetic energy of the added radicals, with values around 0.33 for thermal radicals and a wide range of values between 0.33 and 1.00 for suprathermal OH radicals.
Conclusions. Based on our calculations, we provide recommendations for introducing OH radical recombination into kinetic astrochemical models, differentiating between thermal and suprathermal radicals. The recombination behaviour varies significantly between these two cases: while thermal radicals are sometimes trapped in hydrogen-bonded minima, the case of suprathermal radicals varies with the added energy. Our most important conclusion is that OH radical recombination probability cannot be assumed to be 1.0 for a wide variety of cases.
Key words: astrochemistry / molecular data / methods: laboratory: molecular / methods: numerical / ISM: molecules
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The formation of interstellar water, which is actually amorphous solid water (ASW), is a subject that has sparked a lot of interest over the years, (see for example Van Dishoeck et al. 2013). While our understanding of the water formation process has evolved, the conclusions obtained in the early models (Tielens 1982) are consistent with current experimental (Ioppolo et al. 2008; Oba et al. 2009; Romanzin et al. 2011; Dulieu et al. 2010; Ioppolo et al. 2010; Lamberts et al. 2014) and theoretical understanding (Cuppen et al. 2010; Lamberts et al. 2013, 2014; Meisner et al. 2017; Molpeceres et al. 2019). Essentially, there is a large body of evidence showing that ASW forms atop interstellar dust grains through reactions where the hydroxyl radical (OH) takes a protagonist role through the O-atom reaction network (see for example Fig. 17 of Van Dishoeck et al. 2013); namely:
![$\[\mathrm{O} \xrightarrow{\mathrm{H}} \mathrm{OH} \xrightarrow{\mathrm{H}} \mathrm{H}_2 \mathrm{O},\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq1.png) (1)
(1)
![$\[\mathrm{H}_2+\mathrm{OH} \longrightarrow \mathrm{H}_2 \mathrm{O},\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq2.png) (2)
(2)
![$\[\mathrm{O}_3+\mathrm{H} \longrightarrow \mathrm{OH}+\mathrm{O}_2 \xrightarrow{\mathrm{H}} \mathrm{H}_2 \mathrm{O},\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq3.png) (3)
(3)
![$\[\mathrm{OH}+\mathrm{OH} \longrightarrow \mathrm{H}_2 \mathrm{O}+\mathrm{O},\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq4.png) (4)
(4)
![$\[\mathrm{OH}+\mathrm{OH} \longrightarrow \mathrm{H}_2 \mathrm{O}_2 \xrightarrow{\mathrm{H}} \mathrm{H}_2 \mathrm{O}+\mathrm{H}_2.\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq5.png) (5)
(5)
In addition to the above, the chemistry of O2 also plays a role in the formation of H2O without the need for OH radicals:
![$\[\mathrm{O}_2 \xrightarrow{\mathrm{H}} \mathrm{HO}_2 \xrightarrow{\mathrm{H}} \mathrm{H}_2 \mathrm{O}_2 \xrightarrow{\mathrm{H}} \mathrm{H}_2 \mathrm{O}+\mathrm{H}_2.\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq6.png) (6)
(6)
In diffuse and translucent clouds, or in photo-processed regions in a broad sense, water ice is subjected to energetic chemistry (see for example Öberg 2016), where the main dissociation channel is
![$\[\mathrm{H}_2 \mathrm{O}+\mathrm{h} \nu \longrightarrow \mathrm{OH}+\mathrm{H},\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq7.png) (7)
(7)
leading again to the OH radical.
In view of what is presented above, the immediate conclusion is that ASW in photo-processed regions is constantly formed and destroyed, with OH radicals present in every reactive or energetic event. Considering that H2O ice is ubiquitously detected in infrared observations of interstellar ices (Öberg et al. 2011; Boogert et al. 2015; McClure et al. 2023; Dartois et al. 2024), it is implied that either H2O formation rates surpass destruction ones or formation and destruction are in a pseudoequilibrium. The most obvious “reconstruction” pathway involves the OH + H ⟶ H2O recombination (rightmost reaction in Eq. (1)). However, it is expected that the nascent H atom will either desorb or diffuse farther from the reaction partner due to the excess energy of the fragmentation, which greatly surpasses the meager binding energy of H on H2O (Hama et al. 2012). An additional reconstruction pathway was studied by Redondo et al. (2020) recently. In their study, Redondo et al. (2020) showed the viability of Reaction (4) using theoretical methods and finding the process viable. This study was performed on the triplet potential energy surface (PES), meaning that both OH radicals have parallel spins at the time of encountering. The same reaction in the singlet state produces, as a byproduct 1O, an excited state that puts into question whether such a route has low or no barriers and is exothermic. In fact, the expected product of the 2 OH recombination in the singlet state (leftmost reaction in Eq. (5)) is the production of hydrogen peroxide (H2O2) that is directly linked with H2O via a H-abstraction reaction (Lamberts et al. 2016). We present Reaction (5) again because it is the chemical process that we simulated in this work:
![$\[\mathrm{OH}+\mathrm{OH} \longrightarrow \mathrm{H}_2 \mathrm{O}_2.\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq8.png) (8)
(8)
Both triplet and singlet channels for the OH + OH reaction are possible in the UV-irradiated icy dust grain, with the triplet one being statistically favoured. While the triplet channel is easily investigated owing to the kinetic barriers associated with this route, the singlet channel is less straightforward as it is assumed to readily produce H2O2 upon encountering a 1.00 branching ratio. Nevertheless, the strong interaction between OH and H2O (Miyazaki et al. 2020; Tsuge & Watanabe 2021) can actually lower this branching ratio, making 2 OH adsorption favourable over reaction for certain OH-OH orientations, similarly to what was found for a wide collection of radicals on ASW (Enrique-Romero et al. 2022).
Neutral-neutral two-body reactions, a term encompassing the aforementioned radical-radical recombinations, can mechanistically proceed in several ways in interstellar dust grains. Without any input of external energy, that is under strictly thermal conditions, the rate of the reaction depends on the diffusion of the participating reactants in addition to the activation barriers or lack thereof. Therefore, adsorbates that are not mobile on the surface will hardly react, leaving only a handful of radicals and molecules, for example, the H, N, and O atoms, or CO molecules (Hama et al. 2012; Minissale et al. 2016; Furuya et al. 2022) to diffuse and react at 10 K. However, the presence of complex organic molecules (COMs) not explainable by reactions with the above-mentioned species in very cold prestellar cores (Bacmann et al. 2012; Jiménez-Serra et al. 2016; Scibelli & Shirley 2020) used to constitute a challenge for astrochemical models. Energetic processes, initiated by cosmic rays (Shingledecker et al. 2018), photons (Mullikin et al. 2021), or chemical reactions (Jin & Garrod 2020), have emerged as viable alternatives to explain the mobility of otherwise immobile species, at least in H2O ice (see Molpeceres et al. 2024, for results on other ices). Considering the main dissociation channel of H2O (Reaction 7) by photons and cosmic rays, in addition to the prevalence of OH radicals in hydrogenation reactions, for example O + H ⟶ OH makes OH radicals arguably the most abundant radical produced by energetic mechanisms. In fact, with a null mobility at 10 K (Miyazaki et al. 2022) Ishibashi et al. (2021) experimentally showed that suprathermal OH radicals are able to react on an ASW surface.
In this work, we aim to deepen our knowledge of the chemistry of suprathermal OH radicals by focusing on a detailed study of Reaction (8) using molecular dynamics (MD) simulations driven by machine-learned interatomic potentials (MLIPs)1. Following our previous study for the hydrogenation of the phosphorus atom (Molpeceres et al. 2023), here we increased the complexity of our system and studied the formation of a polyatomic molecule (H2O2) from the recombination of two OH radicals. We focused on the singlet PES that leads to the molecule of interest. From an astrochemical point of view, our goal is to enhance the description of energetic chemistry in the early stages of the star formation cycle, with a strong focus on the reformation of the ASW ice mantle after interaction with energetic photons.
The techniques of ab initio simulations are becoming widely used in astrochemistry, as they provide insight into processes that are difficult to access experimentally (Wiesenfeld et al. 2018). MD simulations are typically conducted using density functional theory (DFT) as the computational framework, with key stationary points often benchmarked using coupled cluster methods for higher accuracy. However, single-reference methods such as DFT and coupled clusters can encounter significant limitations when orbital degeneracies arise, such as in the modelling of excited states, multiple radicals, or homolytic bond cleavage (Cramer 2002). In such cases, multi-reference methods are essential. Among these, the complete active space self-consistent field (CASSCF) method is widely employed, as it effectively captures static electron correlation. To achieve quantitative accuracy, however, the inclusion of dynamic correlation is critical. In this work, we addressed this by employing a perturbation correction to CASSCF, leading to the complete active space with second-order perturbation theory (CASPT2) approach.
Our paper is structured as follows. In Sect. 2 we introduce our theoretical and structural models for the MLIP and surface slabs. Section 3 is dedicated to an exhaustive description of all the factors that influence Reaction (8) on ASW. Following this theoretical description, our results are put into an astrophysical context in Sect. 4, including a summary of our findings, recommendations to include these results in astrochemical models, and their impact on our current understanding of interstellar H2O formation and suprathermal chemistry. We conclude with a brief summary of the work in Sect. 5.
2 Methodology
We investigated the recombination dynamics of two hydroxyl radicals on a water surface. Such a task requires long simulations (from tens to hundreds of picoseconds) and a large system to cover both the reacting radicals and the surface of water ice. For that, we constructed a reactive machine-learning force field, enabling us to simulate (maximum) nanosecond trajectories with hundreds of molecules.
2.1 Construction of the training set: Description of the ground-truth method for our MLIP potential
The most time-consuming part of MLIP production is choosing and labelling training-set data points. Data-set structures in our case were mainly 20–30 molecule clusters of water with two hydroxyl radicals, and less than 10% of the set were geometries of pure water clusters (see Table 1). As a reference method to calculate energies and forces of the data set, a combination of two methods was used first was the state-averaged complete active space (SA4-CASPT2(6,4)/6-31+G(d,p)) (Werner 1996; Celani & Werner 2000) averaging four lowest singlet electronic states and the second was Perdew-Burke-Ernzerhof functional (PBE(D3BJ)/def2-SVP) (Perdew et al. 1996; Grimme et al. 2010) was used. The active space in the CASPT2 calculations composed of six electrons and one virtual orbital proved to be the best choice considering the smoothness of the PES along the inter-radical distance, which was the key parameter for our calculations. Smaller or slightly larger active spaces showed discontinuities in the rigid scans of PES along the inter-radical distance, which made the 6,4 active space the optimal choice, as shown in Fig. 2. The CASPT2 calculations were performed using the Molpro 2012.1.11 package (Werner et al. 2012, 2020, 2024), and the DFT calculations were done using the ORCA 5.0.3 code (Neese et al. 2020). In the training set, both OH radicals were described using the multi-reference CASPT2 method. Water molecules were described at the PBE level, because calculating the whole system at the CASPT2 level would be computationally intractable. Both theoretical treatments were combined in a QM/QM manner using the subtractive ONIOM (Our own N-layered Integrated molecular Orbital and Molecular mechanics) embedding scheme (Svensson et al. 1996) with the electrostatic effects of the outer region on the CASPT2 core region’s wave function treated by adding CHELPG (CHarges from ELectrostatic Potentials using a Grid-based method) charges (Breneman & Wiberg 1990) of water atoms as point charges in the CASPT2 calculation. Energies and gradients from both the multi-reference and the DFT calculations were then subtracted using our own script, completing the simplest ONIOM scheme. This approach combines computational feasibility with accuracy, putting the focus on a good description of the radical-radical interactions. It is important to indicate that the DFT part of the QM/QM embedding was simulated using a broken-symmetry wave function.
A sampling of the configuration space for the MLIP training set was done using several exploratory MD simulations, similarly as in our previous works (Molpeceres et al. 2020, 2021, 2023). Sampling simulations in the canonical ensemble (NVT; that is keeping the number of particles, volume, and system temperature constant) were performed at 300 K, using Nosé–Hoover chains of four thermostats, to sample interactions of the OH radical with the water surface. MD was simulated using the in-house code ABIN (Hollas et al. 2018). Because hydroxyl radicals bind strongly with H2O and their actual diffusion, even at 300 K, is beyond our simulation timescales, we performed steering dynamics interfacing the ABIN code (Hollas et al. 2018) with the PLUMED library (Bonomi et al. 2019; Tribello et al. 2014; Bonomi et al. 2009), ensuring a sufficient configurational sampling. Additionally, remaining non-sampled spots in the OH-OH distance interval were then recovered via an a posteriori umbrella sampling (Torrie & Valleau 1977). After obtaining all the training points, we randomly divided them as follows: 75% for training, 10% for the validation set, and 15% for the test set in our MLIP protocol.
 |
Fig. 1 Initial and final geometry of one recombination trajectory; unbound radicals on the left and hydrogen peroxide on the right. |
Types and quantity of clusters in the training set.
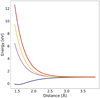 |
Fig. 2 Rigid scan of PES of all four states included in the CASPT2 calculations with active space 6,4. |
2.2 Training of the model
The MLIP was obtained using the Gaussian-Moment Neural Network (GMNN) code (Zaverkin & Kästner 2020; Zaverkin et al. 2021). A neural network with two hidden layers and 512 nodes each was trained on a data set containing 39 205 geometries, electronic energies, and atomic forces. Three independent MLIPs were trained simultaneously on 75% of the data set in the training set and 10% in the validation set. Training was done for 1500 epochs on Nvidia GeForce RTX 3090 GPU. A cut-off radius of 5.5 Å was used for Gaussian moments’ descriptors. The usage of an ensemble of models allows us to determine the uncertainty of the predicted forces during our simulation from the disagreement of trained models. We achieved a mean absolute error in forces under 0.5 kcal mol−1 Å−1 for the training and validation set as well as for the test set, which was previously unknown to the neural network.
Apart from evaluation on a predefined test set, we performed an optimisation test. The calculation was done on a randomly sampled cluster of 20 molecules in order to to compute it efficiently with not only our model, but also with the reference method. In Fig. 3 an energy curve during optimisation is presented to show how well the model performs in this manner. The predicted energy tracks the reference optimisation curve very well, with only minor deviations from the reference values. This test again shows good performance in the prediction of the shape of the reference PES.
Finally, we conducted in-depth testing of the inter-radical potential, given our main goal was to study the recombination of radicals. In order to test the interaction of radicals along the reaction coordinate, we used steering MD. The simulation started with H2O2 formed on a cluster surface, and a moving artificial potential was added to separate oxygen atoms and form radicals at the end of the simulation. This way, the radicals were sampled at distances between the bond length of about 1.5 Å and a potential cut-off radius of 5.5 Å. In Fig. 4 the force uncertainty by the MLIP in the trajectory consistently stays below the 1 kcal/mol/Å threshold. This performance exceeded our expectations and attests to the accuracy of our potential. Further validation tests of the potential are gathered in Appendix A.
 |
Fig. 3 Performance of model in structure optimisation calculation compared to reference QM/QM method. |
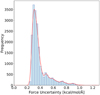 |
Fig. 4 Force uncertainty tracked along trajectory of MD steering dynamics to determine the performance along the reaction coordinate. Uncertainty was computed from the ensemble of three models and was tracked throughout the simulation. |
2.3 Creation of surface slabs
Our simulations are run on the surface of a spherical amorphous water cluster. We prepared a cluster of 500 water molecules with two OH radicals on the surface. We began the construction of the cluster by randomly positioning 500 water molecules in a spherical volume of approximately 1.00 g cm−3 density. From this cluster, we initially ran a molecular-dynamics trajectory at 300 K for 500 ps to generate different cluster conformations. The geometry of the system was sampled every 250 fs after an equilibration period of 50 ps. For every sampled water cluster, we deposited OH radicals on its surface by randomly positioning them in the proximity of the water cluster. The distance between the two radicals was preset to a specific value in the interval from 2.0 to 5.5 Å (see Sect. 3), the inter-radical distance being one of the sampled magnitudes in our study (see Sect. 3). Before the production run of MD, clusters were thermalised at 10 K for the duration of 20 ps. The distance between radicals was constrained for the whole time in order to keep the randomised sampling of the inter-radical distance between 2.0 and 5.5 Å.
2.4 Calculating potential of mean force
To determine the range of attractive forces between the radicals, understand the dynamics of the system, and estimate ideal conditions for our production calculations, we performed a long simulation using the metadynamics approach (Huber et al. 1994; Laio & Parrinello 2002). For this purpose, a long trajectory was run with a time step of 0.5 fs and a total simulation time of 2.5 ns with the starting positions corresponding to already formed H2O2 on the surface of a water cluster containing 500 molecules. We were adding bias potentials to the distance of oxygen atoms. The potential was added every 1000 steps (500 fs) in the form of a Gaussian function with a height of 1 kJ mol−1 and width of 0.1 Å. An additional strong wall potential was placed at a value of 6.0 Å of the distance of radical (just slightly higher than our training cut-off (see above)), to prevent them from separating further. This simulation was set up with the PLUMED program (Bonomi et al. 2019; Tribello et al. 2014; Bonomi et al. 2009), which was also used to reconstruct the free energy surface from the simulation at a temperature of 10 K.
2.5 Generation of initial conditions for production trajectories
We performed a set of MD trajectories to study the recombination of hydroxyl radicals on a water surface using the MLIP. For every geometry from the initial equilibrated position (see above), a total of five trajectories were performed with different momenta given to the OH radicals, one with initial velocities extracted from the previous NVT equilibration at 10 K and another four trajectories associated with the different extra momenta added to one of the hydroxyl radicals to mimic the production of suprathermal OH radical by different mechanisms, for example through chemical reactions or the photodissociation of a H2O molecule. The list of added energies is {0.1, 0.3, 0.5, and 1.0} eV. The energy was added by appropriate scaling of the velocity vector from the initial velocities. To prevent radical evaporation by this added energy, only the projection of the velocity vector to the surface tangent and the cluster surface was prolonged. Trajectories were simulated for 500 ps or preemptively terminated after a recombination occurred (to save computational resources). These simulations were performed in the NVE regime, so the reactivity would not be influenced by the artificial thermostat. MD using the MLIP were performed using the Atomic Simulation Environment (ASE) (Larsen et al. 2017; Bahn & Jacobsen 2002). An example trajectory is shown in Figure 1 with two snapshots of the start and end geometries.
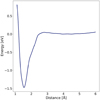 |
Fig. 5 Potential of mean force for inter-radical distance, showing the free energy curve obtained from the metadynamics simulation. |
2.6 Motion of hydroxyl radical
Finally, simulations similar to those shown in Sect. 2.5 (that is NVE on a 10 K water surface) were performed to study the motion of only a single OH radical. In this case, apart from simulations with added kinetic energy (of 0.1, 0.3, 0.5, or 1.0 eV), we performed a single NVT simulation with a constant temperature of 10 K using the ASE, with the latter serving as a blank (no mobility; see Sect. 3.3). The goal of such simulation was to observe the motion of OH without the influence of a second radical and possible recombination.
3 Results
The main purpose of this work is to determine recombination probabilities for Reaction (8) with respect to the initial position of the two radicals, and their initial kinetic energy. Such information allows us to discuss the influence of diffusive processes versus the influence of formation routes of the hydroxyl radical. After introducing the energy surface in the first section of the results, we focused on the dynamics of the reaction OH + OH ⟶ H2O2 (Reaction 8) in the second section; finally, we investigated the motion of OH radical on the surface of water.
3.1 Potential of mean force
To determine the range and shape of the inter-radical potential for OH radicals, a free energy surface (FES) was reconstructed from bias potentials added in a long metadynamics simulation. The free energy curve for inter-radical distance is presented in Fig. 5. The inter-radical potential is very attractive up to a distance of 2.5 Å where the FES curve quickly flattens and changes only minimally for greater distances. It ought to be mentioned that full convergence was not achieved, given the size of the system and therefore very large conformational space. With that in mind, we look at this figure in a qualitative manner. Nevertheless, we can convincingly say that radicals have to approach each other to a distance closer than 2.5 Å in order to be trapped in the deepest potential well, the H2O2 molecule. The well depth of the potential does not allow radicals to dissociate without additional energy provided by photoexcitation or similar processes. We can observe a small barrier at the distance of 2.8 Å with a height of 0.05 eV, roughly equivalent to the thermal energy of 600 K. The nature of this barrier is difficult to identify, as it is somewhat low with regard to diffusion barriers arising from the HO–H2O H-bond breaking with the surface, and it is associated with barriers of around 1600 K Miyazaki et al. (2022). Besides diffusion the barrier could originate from the OH...OH complex that we found in our dynamical calculations (see Sect. 3.2). The low inter-radical distances make us think that the latter is a more likely explanation. In either case, it is important to clarify what the FES represents. Our FES is a reconstruction over a limited time (2.5 ns) of all possible events occurring in that time lapse in a metadynamics run. In other words, the FES shows a balance between the barrierless reaction and the process with a barrier. Because the OH...OH complex will, in many cases, lead to a barrierless recombination, the contribution of the activated processes in the FES is weighed down when barrierless paths are found. We emphasise, however, that finding a barrier in the FES does not mean that Reaction (8) has an intrinsic barrier by itself, but rather that some reactive orientations on an ASW do have a barrier, depending on the position on the ASW.
We can see the curve rising at the largest distance of 6 Å again. This is, however, just an artefact of the repulsive wall, which was placed at 6.5 Å to prevent the radicals from separating further in the metadynamics simulation. The potential should be basically flat for larger distances, where the influence of the second radical disappears.
3.2 Recombination reaction
3.2.1 Influence of the initial position
We investigated the OH recombination probability as a function of the initial distance of radicals. The results are shown in Fig. 6. In the top left panel, we see that the recombination probability in general decreases with growing initial distance, thus supporting the expected outcome of the close radicals having a better chance of recombining. Even at the closest distance of 2.5 Å, there is a finite probability of the radicals avoiding recombination; this is due to an unfavorable direction of initial velocities. With higher added kinetic energies, it is reasonable to assume that some trajectories will leave the reactive potential because the added energy is sufficient to overcome the attractive potential. This is especially true when the velocity vector is pointing in the opposite direction to recombination. However, even when no kinetic energy is added to either of the two OH radicals, we observe some trajectories where there is no recombination. This seems counterintuitive at first, since the energy gradient is supposed to be high and pointing towards the minimum energy H2O2 situation. A careful inspection of these few outliers reveals the presence of hydrogen-bonded OH...OH strong pairs that are key in the recombination efficiencies and dynamics. These situations are central to our discussion and are investigated in more detail later in the text. Here, it suffices to indicate that the presence of these complexes at distances of ~2.5 Å is rare (Fig. 7), which correlates with the high (yet not of unity) recombination probability at short distances. No dissociation of H2O2 ever occurs once the molecule is formed, which was expected considering the depth of the minimum listed in Table 2.
Continuing with other starting energies, for the case of no additional energy, we observe no recombination above 5 Å (within the simulation time). Recombination takes place when radicals are trapped in the inter-radical attractive potential; radicals either have to approach one another by diffusion, or, at a shorter distance, they slip to the preferred binding site on the surface when they were initially in an unfavorable position. This line of thinking inevitably leads to the assumption that the closer the radicals, the higher the probability of recombination. However, if we look closely at the separate plots of the trajectories with different amounts of kinetic energy added to the radicals, we observe a minimum in the probability at around 3 Å for the cases where 0, 0.1, and 0.3 eV of kinetic energy were added. This minimum seems counter-intuitive as we would expect that the closer the radicals are, the higher the probability of recombination. As we note above, if we suppose a diffusive nature of this process it should lead to a continual decrease with energy; thus, this minimum suggests a more complex mechanism of the whole process.
Our results clearly evince that inter-radical distance is an important factor for the probability of recombination, but it is not the only feature that defines whether radicals recombine or not. Because of that, additional structural features such as radical orientation were analysed. A possible explanation for the minima in Fig. 6 can therefore be inferred from Fig. 7, which shows endpoints of each trajectory in the 2D plot of distance between radicals (distance of oxygen atoms) and collective variable CV1. This is defined as
![$\[\mathrm{CV}_1=\min \left(d_{\mathrm{O}(1) \mathrm{H}(2)}, d_{\mathrm{O}(2) \mathrm{H}(1)}\right),\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq9.png) (9)
(9)
where dO(1)H(2) is the distance of oxygen from the first radical and hydrogen from the second radical, and dO(2)H(1) for oxygen from the second radicals and hydrogen from the first. Thus, CV1 represents the shortest OH distance of the non-bonded atoms in the studied radicals. From the position in this 2D plane, we can analyse not only the proximity of the radicals but also the orientation of H atoms on them. In the upper part of Fig. 7, we see how in some of the trajectories that diffuse away, larger interradical distances are dominated by trajectories with higher added kinetic energy. This is obviously related to the ease of moving at larger distances for radicals with higher energy. In the bottom panel of Fig. 7, we present a zoomed-in view of the region in the top panel, focusing on the short and medium inter-radical ranges. At these ranges, we can identify two major clusters: one with the O-O distance around 1.4 Å and a CV1 of around 1.7 Å, which represents H2O2; and one showing the O-O distance around 3 Å and CV1 around 2 Å and representing radicals forming a hydrogen bond in the singlet state. Such clustering of final conformations in our simulations suggests the mechanism of the recombination and explains the minima present in Fig. 6 as we anticipated above. Visualisations of system geometry showing these conformations can be found in Fig. 8. Hydrogen bonding apparently plays a role of competitive minimum on the PES, in which radicals can be trapped at very low temperatures. Many trajectories with the initial radical distance around 3 Å fell in this local minimum and stayed there until the end of the simulation, with not enough energy available to escape the minimum. The depth of this minimum was estimated to be about 0.21 eV (see Table 2) at the CASPT2 level in the gas phase, without considering the effect of the environment. This minimum correlates well with what was found for trajectories with 0.5 and 1.0 eV of added kinetic energy, where the radicals have enough energy to escape hydrogen bonding, even though they visit the H-bonded minimum. It should be noted that radicals lose their energy as time progresses by dissipation into the water surface.
As previously mentioned, the calculated FES shows a small barrier (of 0.05 eV) in the 2.5–3.0 Å range. We cannot confidently indicate the origin of this barrier, but is likely associated with the transition between the H-bond minima and the H2O2 potential well. Again, we remind the reader that we present an averaged barrier, and therefore it is different from a barrier of a single reactive trajectory, which could happen both barrierlessly or with a barrier much higher than the one in Fig. 5. Finally, although we explained the minimum in recombination probability (Fig. 6) for energies {0.0, 0.1, 0.3} as caused by the H-bond minimum, the large error bars make it difficult to provide a quantitative estimation of its depth. Despite the error bars, we are certain of the presence of a local minimum for recombination probabilities in Fig. 6. The presence of the non-bonded dimer minimum in the CASPT2 gas-phase calculations, summed to the presence of such a minimum for multiple added energies and the visual inspection of the trajectories (Fig. 8), indicates that the OH...OH minimum is the reason for this local minimum. More trajectories would be necessary to quantitatively estimate its depth. However, it would require a number of trajectories beyond our current computational reach. Nevertheless, the disappearance of this feature at higher added energies reinforces our explanation.
 |
Fig. 6 Recombination probability as a function of initial distance of OH radicals. The first top-left plot presents the results for all the energies combined. The following graphs present the datasets for different added energy individually, with the error bars included in the plots. Error bars represent the Jeffreys Bayesian interval generated by Python library statsmodels (Seabold & Perktold 2010). |
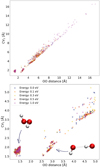 |
Fig. 7 Plot of final geometries of all trajectories. The upper plot shows all endpoints of trajectories in the 2D graph of CV1 and O-O distance; the lower plot presents data from the same trajectories with a zoomed-in view of H-bonding and hydrogen-peroxide conformers. |
Depth of minima on PES for small complexes in the gas phase with respect to the separated radicals.
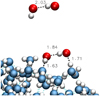 |
Fig. 8 Gas-phase (top) and surface (bottom) minimal geometries showing the OH...OH hydrogen-bonded complex in competition with Reaction (8). Minima were obtained at the CASPT2 level for the gas phase and with MLIP for the large cluster. |
3.2.2 Effect of the binding energy
We also explored the influence of the binding energy of OH in the recombination probability. We calculated binding energy as the difference between the energy of the whole cluster and a sum of a cluster without radical and one with separated radicals. Therefore, the positive value of energy corresponds to spontaneous binding with the surface. It should be noted that sampling of binding sites on the surface was affected by constraints during equilibration of the dynamics. As the main focus was on sampling the inter-radical distance. The sole presence of the second radical in proximity results in higher values of the binding energy (in some cases) than what would be expected for a single OH on the water surface. This is especially true in cases where the two OH are close together (for example binding energies close to 1.0 eV). In general, we can conclude that, for these reasons, the presented binding energies are higher than the binding energy of one OH radical on a water surface. In previous studies of an OH radical, the binding energy of a single hydroxyl radical were found to be 0.06–0.74 eV (Tsuge & Watanabe 2021; Miyazaki et al. 2020). Figure 9 shows the dependence of the recombination probability on the binding energy. As already stated, due to the interaction of OH radicals, higher binding energies correlate with shorter distances between the two OH radicals, so the isolated effect of the binding site is difficult to capture. Due to the sampling process, the error bars in Fig. 9 are quite large for some values of binding energy. A detailed discussion of the effect of binding energy would therefore require a separate study. Nevertheless, we are able to see that there is no major effect of binding energy, as the graphs in Fig. 9 do not show any clear trend. In general, because (at least in this work) the binding energy serves as a proxy for the proximity of the radicals, it can be said that the recombination probability depends mostly on the distance factor. This is also supported by the behaviour of radicals with added kinetic energy, where there is an apparently lower recombination probability. This is shown in Fig. 9 and is simple to rationalise, as radicals with more kinetic energy are more likely to separate and escape the recombination, independently of the binding energy.
 |
Fig. 9 Recombination probability of hydroxyl radicals as function of binding energy of OH radical. The binding energy of the more weakly bound radical is shown on the x-axis. The first top left plot presents the results for all the energies combined. The following graphs present the datasets for different amounts of added energy individually, with the error bars included in the plots. Error bars represent Jeffreys Bayesian interval generated by Python library statsmodels (Seabold & Perktold 2010). |
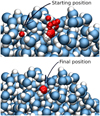 |
Fig. 10 Visualisation of dynamics of OH radical on water surface after addition of 1.0 eV of additional translation energy. In the upper part of the picture, we can see all positions of the OH radical during the MD simulation. In the lower part, positions from the last nanosecond of the simulation are visualised. |
3.3 Motion of radicals on ice surface
For an even deeper understanding of the process, the populations of the conformers (OH...OH, H2O2) in time are plotted in Fig. 11. The population dramatically changes during the first few picoseconds. Higher kinetic energy in the radicals leads to faster stabilisation of population levels. Extending the simulation further would not provide any qualitative change, given the low mobility of OH radicals on the cluster surface, which can be concluded both from the stabilisation of populations in Fig. 11 and from the visualisation in Fig. 10. On the upper part of the visualisation, we can see that at the beginning of the simulation there is a transfer of the thermally excited radical from one position on the surface to another, but after the additional energy dissipates there is essentially no change in position and the radical stays at the same binding site (the lower part of Fig. 10). In Fig. 11 we observe differences in the behaviour of low- and high-energy radicals. For the added energy of 0.01 eV, we observe an increase in the population of H-bonded radicals and then a decrease of the population until stabilisation at around 5 ps. This phenomenon is also observed for other values of added energy, but, as we see in the lower part of Fig. 11, it is not present for the 1.0 eV. In this highly energetic case, the radicals are not as often trapped and the population of H-bonded radicals behaves similarly to the population of radicals in a non-specific position. Furthermore, as previously noted, separation is more effective for radicals with higher energy levels, but as the additional translation energy will be dissipated to the water surface, the radicals essentially freeze on the surface. This is supported by data in Fig. 12, where distributions of kinetic energy at the start and at the end of the simulation are shown. We can see that even thermally excited radicals have very low kinetic energy at the end of the simulation. Therefore, radicals after 500 ps move very little, regardless of the added kinetic energy at time zero.
4 Discussion and context of our results for astrochemical-rate-equation models
Our results show that, despite the a priori expectation that radical-radical coupling in Reaction (8) would have a unity probability of recombination, this was never the case in our simulations, even in the attractive region of the potential (free energy in our simulations). For thermalised radicals (added energy = 0.0 eV) there are two reasons for this observation, one specific to the OH + OH pair and another one that is general for any reaction on interstellar ices. Beginning with the latter, which is important at intermediate and long inter-radical distances, we attribute it to the presence of the water ice that brings diffusion barriers to an otherwise barrierless approach. This is essentially the same conclusion that, for example, Enrique-Romero et al. (2022) reached using static quantum-chemical calculations. The specific reason as to why OH + OH does not have a unity recombination probability is the formation of the OH...OH hydrogen-bond complex, which precludes reaction. However, contrary to the first case, where the barriers or lack thereof are a consequence of the interaction with the ice, the formation of the OH...OH complex is also found in the gas phase (see Fig. 8); that is, it is not a consequence of the adsorbate ice interaction.
It is worth discussing what the presence of these occasional barriers and alternative minima entail for astrochemical models. Our reconstructed FES for the inter-radical distance shows that diffusion barriers are averaged out, making them absent or very small in the total reconstructed profile. This does not mean that they do not exist; our interpretation is that they are simply not kinetic barriers intrinsic to the OH + OH reactive event. Thermal two-body reactions in astrochemical models follow a Langmuir-Hinshelwood formalism (Hasegawa & Herbst 1993):
![$\[k_{\mathrm{t}}=\alpha \kappa_{i j}\left(\frac{1}{\tau(i)}+\frac{1}{\tau(j)}\right) \frac{1}{N_{\text {Site}} n_{\text {Dust}}},\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq10.png) (10)
(10)
where α is the branching ratio of the reaction, 1/τ(i)+1/τ(j) is the term dedicated to diffusion with τ(x) representing times for a single diffusion step, and 1/NSitenDust is a term accounting for the number of binding sites (NSite) and number density of dust grains (nDust). In reactions with competing processes such as diffusion or desorption, κij are obtained from the competition relation (Chang et al. 2007):
![$\[\kappa=\frac{k_{\text {reac }}}{k_{\text {reac }}+k_{\text {diff }}+k_{\text {des }}},\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq11.png) (11)
(11)
where kreac, kdiff, and kdes are the rate constants for reaction, diffusion, and desorption (in the last two cases of the two possible reactants). In particular, kreac takes the form of
![$\[k_{\text {reac }}=\nu ~\exp \left(-2(\gamma / \hbar)(2 \mu \beta)^{1 / 2}\right),\]$](/articles/aa/full_html/2025/05/aa52617-24/aa52617-24-eq12.png) (12)
(12)
with β and γ being the variable parameters and ν a term accounting for the characteristic frequency of the adsorbates, which in many models is simply the maximum of the characteristic frequencies of the two reactants; μ is the reduced mass. The two parameters have different meanings, with β representing the reaction activation energy and γ corresponding to the barrier width of the reaction, assuming a rectangular barrier for quantum tunneling. When β=0 (barrierless), κ is made equal to unity (that is κ=1.0), effectively making the reaction depend solely on the diffusion terms and α. In the context of the reaction studied in this work, it is reasonable to wonder what the best way of including our recombination probabilities in models is. There are two possibilities. First, we can vary α, which could be taken directly from Fig. 6. Second, we can vary β, whose value must be taken from the transition state of the OH + OH ⟶ H2O2 reaction (not computed in this work). The latter approach can clearly generate misleading results, at least in the context of Reaction (8); this is because it introduces an exponential term for every single reaction event, while our simulations clearly show that the probability of recombination is non-zero in Fig. 6. This should indeed be the case if an intrinsic barrier is present, because such a barrier could not be overcome in the short term of the MD simulations. The approach of linearly weighting Eq. (10) by varying α is much more physically sound, at least at low temperatures up to 40 K, where the OH radical can slowly diffuse on ASW (Miyazaki et al. 2022). However, what the value for α should be in these cases remains to be determined from the different distances that we sampled in Fig. 6. With this in mind, it is clear that the recombination rate does depend on the origin of the radicals, not only through their initial energy, but also through their starting position, which is a key factor to take into account when setting the value of α. We think that the values of 3 Å, just before the effective barrier (see Fig. 5), are an excellent compromise in order not to double count diffusion. Thus, α for Reaction (8) in a thermal regime is 0.33 (also gathered in Table 3). When the temperature increases, it is more difficult to recommend a particular scheme, as emerging barriers could be overcome thermally. In those cases, the best compromise is likely to set α=1.0 as usual. At this stage of research, the arguments and recommendations given in this paragraph can only be applied to Eq. (8). Although we think they must be general to any interstellar grain reaction on ASW with both barrierless and non-barrierless channels depending on the orientation, we do not have a sufficiently large body of evidence to confirm it, so we postpone the study of more reactions to future works.
The second case to be discussed is the case of suprathermal OH, whose rate constant does not have any diffusion terms. While several formalisms are available (Shingledecker et al. 2018; Jin & Garrod 2020), we can generally consider that all reactions are effectively barrierless, making the rate constant essentially proportional to the branching ratio, α, kt ∝ α. We note that in reality, this is only true if the amount of energy is enough to submerge otherwise emerged barriers, as we recently discussed in del Valle et al. (2024). However, the recombination probability derived for suprathermal OH is not unique, as it depends on the added energy of the OH radical (Figs. 6 and 9). The inclusion of this heterogeneity in models is complex as it requires treating species differently depending on the added energy, which is a continuous function. Alternatively, an average value could serve as a compromise, assuming the distribution of translational energies upon excitation follows a certain distribution. The latter solution also has flaws, since different excitation mechanisms, chemicals, photons, and cosmic rays, do not have similar energy distributions. Moreover, our sampled cases reach their maxima at an added energy of 1.0 eV, which is reasonable for simulating a fraction of the energy deposited by photons, but a lower bound for cosmic-ray initiated chemistry (Shingledecker et al. 2018), for example, and an upper bound for chemically activated reactions. Despite the uncertainties, we think that a value of α=1.0 for radiolysis is reasonable. We rationalise this choice on the basis of the lack of plateau in the rightmost bottom panel of Fig. 6, meaning that the H-bonded complex will not be formed and the lower recombination probability is a consequence of diffusion out of the reaction site, something already considered in the models and not intrinsic to the reaction event. For lower energy processes, a value between 0.40 and 0.62 could be used; this is based on the same observations that – at intermediate added energies – the plateau in recombination probabilities still appears, indicating the formation of an H-bond complex. As in the thermal case, the study of more systems with this methodology will allow us to determine whether Reaction (8) can be extrapolated to any suprathermal reaction in the interstellar medium (ISM), although we anticipate that in the case of Reaction (8), the presence of the vdW complex shown in Fig. 8 makes this a particular case.
Lastly, we discuss the effect of the different spin states in astrochemical models as the OH + OH reactants can also appear in the triplet state, as stated in the introduction (Redondo et al. 2020). To properly weigh the contribution of the different spin states of a reaction, one should weigh the branching ratios. The population of the relative spin states of two interacting radicals can, however, strongly change in time. If we analyse the gas-phase case, the weighting factor for a reaction can be obtained from the ratio of spin multiplicities of each channel (M). For the reaction studied in this work, OH + OH ⟶ H2O2, M1 = 1, whereas for the competing channel, OH + OH ⟶ H2O + 3O, M2 = 3. The weighting factor for OH + OH ⟶ H2O2 is therefore 1 / (1 + 3) = 0.25 and for OH + OH ⟶ H2O + 3O it is 0.75. Looking now at the reactions on the surface, the non-diffusive reaction should essentially behave as in the case of the gas phase, because the timescale for the reaction (around picoseconds; see for example Shingledecker et al. 2018) is probably too low for intersystem crossing to occur. In the case of a diffusive reaction (thermal regime), the situation can be much more complicated. At 10 K, with the diffusion of OH being effectively null, the rate for any reaction will be insignificant. At temperatures close to the diffusion temperature of the OH radical, 36 K (Miyazaki et al. 2022), the situation is much more complex. In the singlet state, the radicals would move on the potential of mean force given by a Boltzmann weighting of the multiple potentials. This potential would effectively be very similar to the lowest energy potential, as done in our simulations. The possibility of intersystem crossing might not be negligible for longer timescales, thus enhancing the total recombination rate. Our recommendation is, in the absence of non-adiabatic simulations (beyond the scope of this work), to keep using the quotient of spin multiplicities, but recognise the potential source of uncertainty. However, we advocate for an increasingly more complex treatment of different spin channels in surface astrochemistry. Finally, these correction factors can be incorporated in models by multiplying α, such as those collated in Table 3.
 |
Fig. 11 Populations of H-bonding and hydrogen-peroxide conformers in time for trajectories with 0.1 eV of added kinetic energy (upper plot) and 1.0 eV of added kinetic energy (lower plot). |
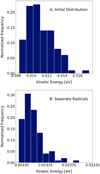 |
Fig. 12 Distribution of kinetic energy for trajectories with 0.5 eV added. The upper plot shows kinetic energy for initial conditions, and the lower one gives averaged kinetic energy during the last 250 fs of MD trajectories. |
Recommended values of α for Reaction (8).
5 Conclusions
The study explored the recombination dynamics of hydroxyl OH radicals on ASW surfaces using MD simulations driven by MLIPs. This reaction had not been theoretically described on water surfaces before, largely due to the significant methodological challenges that were overcome in this work through the use of novel computational techniques. As far as we know, this is the first study to employ neural networks trained on hybrid, multi-reference/DFT data for MD. Although multi-reference data labelling requires extensive data points and specialised expertise, it emerged as the best compromise between accuracy and feasibility for simulating radical reactions. The methodology presented in this study sets the foundation for future non-adiabatic simulations in large systems.
Our findings describe the mechanism of hydroxyl radical recombination and highlight the significance of the local minimum of hydrogen-bonded radicals, which plays a crucial role as a competitive product for thermal OH radicals. At low temperatures, this hydrogen-bonding minimum reduces the probability of recombination for radicals starting at a distance larger than 3 Å. This effect is only partially overcome when additional energy is introduced to the OH radicals. Radicals with higher initial kinetic energy were also less likely to recombine due to their greater ability to separate and move across the surface. Regarding the influence of binding energy, our study demonstrates that the initial inter-radical distance has a greater effect on recombination probability than the binding energy itself. However, binding energies and inter-radical distances are correlated and weighting specific contributions is difficult.
We consider the recombination reaction essentially barrierless, with the barrier being (or not being) present based on the character of the surface and the initial motion of the radicals on it. In the total reconstructed profile, such diffusion barriers are averaged out. Based on these results, we recommend adjusting the branching ratio parameter (α) in Eq. (10) in astrochemical models for both thermal and suprathermal reactions. For thermal reactions, a value of α ≈ 0.33 is suggested, while for suprathermal processes, a value closer to 1.0 is more appropriate, topping α at 1.0 for radiolytic processes. These recommendations pave the way for more refined astrochemical models that can better simulate the complex chemistry occurring on interstellar dust grains.
Data availability
Molecular structures and corresponding energies and forces can be accessed online2. Further information can be requested by contacting the corresponding authors.
Acknowledgements
J.P. and P.S. were supported by the Czech Science Foundation (EXPRO project no. 21-26601X), by the grant of Specific university research – No. A2_FCHI_2023_011 from UCT Prague and supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:90254). J.P. is a student of the International Max Planck Research School “Quantum Dynamics and Control”. G.M acknowledges the support of the grant RYC2022-035442-I funded by MCIU/AEI/10.13039/501100011033 and ESF+. G.M. also received support from project 20245AT016 (Proyectos Intramurales CSIC). We acknowledge the computational resources provided by bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster), the DRAGO computer cluster managed by SGAI-CSIC, and the Galician Supercomputing Center (CESGA). The supercomputer Finis-Terrae III and its permanent data storage system have been funded by the Spanish Ministry of Science and Innovation, the Galician Government and the European Regional Development Fund (ERDF).
Appendix A Consistency tests between the machine learned potential and the reference ab initio method
To check the quality of MLIP used for the simulations, we employed several tests. Firstly, we determined the mean absolute error (MAE) and root-mean-square error (RMSE) on the data in our test set. The test data were sampled from the original data set same as the training and validation set but were never seen by the model during the training phase. The MEA for forces was 0.44 kcal/mol/Å and the RMSE was 0.83 kcal/mol/Å. These values are averaged over all 3 models, which were trained simultaneously, their average was also used for all production calculations. Figure A.1 shows the performance of the calculated forces against the reference force computed by QM/QM(CASPT2(6,4/6-31+G(d,p) + PBE(D3BJ)/def2-SVP). Apart from few outliers, the data lie on the diagonal and therefore confirm the quality and usability of our model. Outlying geometries can be predicted during the production runs with uncertainty computed from the ensemble of models.
An important process in simulations on cluster surfaces is the evaporation of molecules from the cluster surface. To test our model with respect to this process, we produced trajectories with one radical impacting a cluster surface. Such geometries were added to the data set for small clusters. To estimate the performance in this manner, we present Fig. A.2 in which reference vs predicted forces are presented for a data set of geometries from impacting trajectories similar to those in the original data set. In principle, such trajectories represent clusters with one of the radicals at different distances from the cluster surface up the cutoff 5.5 Å where no interaction with the surface is present. With all data points lying on the diagonal, we concluded that our model is performing well with regard to interaction with the surface.
The uncertainty of force prediction was tracked along the MD simulations to avoid artificial results coming from possible prediction failure. In Fig. A.3 force uncertainty during NVE MD simulation is presented. The model performs very well, with the force uncertainty not exceeding 0.6 kcal/mol/Å. Such performance is way below the threshold of 1 kcal/mol/Å which is often considered a threshold for chemical accuracy.
The produced models performed well in all proposed tests and were therefore used for production calculations. We also note, that the fact of training multiple models allowed for checking the performance in any further calculations.
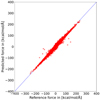 |
Fig. A.1 Analysis of reference vs predicted forces for geometries from test set (part of original data set which was previously unseen by the model). The blue diagonal line is the function y = x and therefore represents perfect agreement of reference and prediction. |
 |
Fig. A.2 Analysis of reference vs predicted forces for geometries produced by MD of OH radical impacting on water cluster. The blue diagonal line is the function y = x and therefore represents perfect agreement of reference and prediction. |
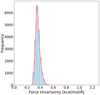 |
Fig. A.3 Force uncertainty tracked along the MD trajectory of relaxed MD of radicals moving on the cluster surface. Uncertainty was computed from the ensemble of 3 models and was tracked during the whole time of the simulation. |
Appendix B Supplementary analysis of performed MD trajectories
To address expected questions and provide additional support for our data, we present supplementary graphics analyzing the MD trajectories central to this study. In Fig. B.1 we present graphics similar to those in Fig. 5 from the results section. In this case, a Gaussian function with a height 10 times smaller was used to sample the observed barrier more cautiously. The presence of the barrier was also confirmed in this calculation; however, fully converging this simulation with higher accuracy would require an impractical amount of computational time. Therefore, we focus on presenting Fig. 5 in the results section, as it provides more robust conclusions.
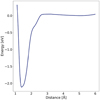 |
Fig. B.1 Potential of mean force from metadynamics using smaller (0.001 eV) height of Gaussian functions. |
References
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bahn, S. R., & Jacobsen, K. W. 2002, Comput. Sci. Eng., 4, 56 [Google Scholar]
- Bonomi, M., Branduardi, D., Bussi, G., et al. 2009, Comput. Phys. Comm., 180, 1961 [Google Scholar]
- Bonomi, M., Bussi, G., Camilloni, C., et al. 2019, Nat. Methods, 16, 670 [Google Scholar]
- Boogert, A. C., Gerakines, P. A., & Whittet, D. C. 2015, Annu. Rev. Astron. Astrophys., 53, 541 [CrossRef] [Google Scholar]
- Breneman, C. M., & Wiberg, K. B. 1990, J. Comp. Chem., 11, 361 [Google Scholar]
- Celani, P., & Werner, H.-J. 2000, JCP, 112, 5546 [Google Scholar]
- Chang, Q., Cuppen, H. M., & Herbst, E. 2007, A&A, 469, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cramer, C. J. 2002, Essentials of Computational Chemistry : Theories and Models (West Sussex, England; New York : John Wiley) [Google Scholar]
- Cuppen, H. M., Ioppolo, S., Romanzin, C., & Linnartz, H. 2010, PCCP, 12, 12077 [CrossRef] [Google Scholar]
- Dartois, E., Noble, J. A., Caselli, P., et al. 2024, Nat. Astron., 8, 359 [NASA ADS] [CrossRef] [Google Scholar]
- del Valle, J. C., Redondo, P., Kästner, J., & Molpeceres, G. 2024, ApJ, 974, 129 [Google Scholar]
- Dulieu, F., Amiaud, L., Congiu, E., et al. 2010, A&A, 512, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enrique-Romero, J., Rimola, A., Ceccarelli, C., et al. 2022, ApJS, 259, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Furuya, K., Hama, T., Oba, Y., et al. 2022, ApJ, 933, L16 [CrossRef] [Google Scholar]
- Grimme, S., Antony, J., Ehrlich, S., & Krieg, H. 2010, JCP, 132, 154104 [Google Scholar]
- Hama, T., Kuwahata, K., Watanabe, N., et al. 2012, ApJ, 757, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 263, 589 [Google Scholar]
- Hollas, D., Suchan, J., Ončák, M., & Slavíček, P. 2018, https://doi.org/10.5281/zenodo.1228463 [Google Scholar]
- Huber, T., Torda, A. E., & van Gunsteren, W. F. 1994, J. Comp. Aided Mol. Des., 8, 695 [Google Scholar]
- Ioppolo, S., Cuppen, H. M., Romanzin, C., van Dishoeck, E. F., & Linnartz, H. 2008, ApJ, 686, 1474 [NASA ADS] [CrossRef] [Google Scholar]
- Ioppolo, S., Cuppen, H. M., Romanzin, C., van Dishoeck, E. F., & Linnartz, H. 2010, PCCP, 12, 12065 [NASA ADS] [CrossRef] [Google Scholar]
- Ishibashi, A., Hidaka, H., Oba, Y., Kouchi, A., & Watanabe, N. 2021, ApJ, 921, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ, 830, L6 [Google Scholar]
- Jin, M., & Garrod, R. T. 2020, ApJS, 249, 26 [Google Scholar]
- Laio, A., & Parrinello, M. 2002, Proc. Natl. Acad. Sci., 99, 12562 [Google Scholar]
- Lamberts, T., Cuppen, H. M., Ioppolo, S., & Linnartz, H. 2013, PCCP, 15, 8287 [NASA ADS] [CrossRef] [Google Scholar]
- Lamberts, T., Cuppen, H. M., Fedoseev, G., et al. 2014, A&A, 570, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamberts, T., Samanta, P. K., Köhn, A., & Kästner, J. 2016, PCCP, 18, 33021 [Google Scholar]
- Larsen, A. H., Mortensen, J. J., Blomqvist, J., et al. 2017, J. Phys.: Condens. Matter, 29, 273002 [CrossRef] [PubMed] [Google Scholar]
- McClure, M. K., Rocha, W. R. M., Pontoppidan, K. M., et al. 2023, Nat. Astron., 7, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Meisner, J., Lamberts, T., & Kästner, J. 2017, ACS Earth Space Chem., 1, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Minissale, M., Congiu, E., & Dulieu, F. 2016, A&A, 585, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyazaki, A., Watanabe, N., Sameera, W. M. C., et al. 2020, PRA, 102, 052822 [Google Scholar]
- Miyazaki, A., Tsuge, M., Hidaka, H., Nakai, Y., & Watanabe, N. 2022, ApJ, 940, L2 [Google Scholar]
- Molpeceres, G., Rimola, A., Ceccarelli, C., et al. 2019, MNRAS, 482, 5389 [NASA ADS] [CrossRef] [Google Scholar]
- Molpeceres, G., Zaverkin, V., & Kästner, J. 2020, MNRAS, 499, 1373 [Google Scholar]
- Molpeceres, G., Zaverkin, V., Watanabe, N., & Kastner, J. 2021, A&A, 648, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molpeceres, G., Zaverkin, V., Furuya, K., Aikawa, Y., & Kästner, J. 2023, A&A, 673, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molpeceres, G., Furuya, K., & Aikawa, Y. 2024, A&A, 688, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mullikin, E., Anderson, H., O’Hern, N., et al. 2021, ApJ, 910, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Neese, F., Wennmohs, F., Becker, U., & Riplinger, C. 2020, JCP, 152, 224108 [Google Scholar]
- Oba, Y., Miyauchi, N., Hidaka, H., et al. 2009, ApJ, 701, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I. 2016, Chem. Rev., 116, 9631 [Google Scholar]
- Öberg, K. I., Boogert, A. C., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [CrossRef] [Google Scholar]
- Perdew, J. P., Burke, K., & Ernzerhof, M. 1996, PRL, 77, 3865 [Google Scholar]
- Redondo, P., Pauzat, F., Ellinger, Y., & Markovits, A. 2020, A&A, 638, A125 [EDP Sciences] [Google Scholar]
- Romanzin, C., Ioppolo, S., Cuppen, H. M., Van Dishoeck, E. F., & Linnartz, H. 2011, JCP, 134, 084504 [Google Scholar]
- Scibelli, S., & Shirley, Y. 2020, ApJ, 891, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Seabold, S., & Perktold, J. 2010, 9th Py. Sci. Conf. [Google Scholar]
- Shingledecker, C. N., Tennis, J., Gal, R. L., & Herbst, E. 2018, ApJ, 861, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Svensson, M., Humbel, S., Froese, R. D. J., et al. 1996, J. Phys. Chem., 100, 19357 [Google Scholar]
- Tielens, A.G.G.M, & Hagen, W. 1982, A&A, 114, 245 [Google Scholar]
- Torrie, G., & Valleau, J. 1977, J. Comp. Phys., 23, 187 [Google Scholar]
- Tribello, G. A., Bonomi, M., Branduardi, D., Camilloni, C., & Bussi, G. 2014, Comput. Phys. Comm., 185, 604 [Google Scholar]
- Tsuge, M., & Watanabe, N. 2021, Acc. Chem. Res., 54, 471 [CrossRef] [Google Scholar]
- Van Dishoeck, E. F., Herbst, E., & Neufeld, D. A. 2013, Chem. Rev., 113, 9043 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J. 1996, Mol. Phys., 89, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., & Schütz, M. 2012, WIREs Comp. Mol. Sci., 2, 242 [Google Scholar]
- Werner, H.-J., Knowles, P. J., Manby, F. R., et al. 2020, JCP, 152, 144107 [Google Scholar]
- Werner, H.-J., Knowles, P. J., Celani, P., et al. 2024, MOLPRO, 2012.1.11, a package of ab initio programs, see www.molpro.net [Google Scholar]
- Wiesenfeld, L., Oomens, J., & Cheung, A. S. C. 2018, PCCP, 20, 5341 [Google Scholar]
- Zaverkin, V., & Kästner, J. 2020, J. Chem. Theory Comp., 16, 5410 [Google Scholar]
- Zaverkin, V., Holzmüller, D., Steinwart, I., & Kästner, J. 2021, J. Chem. Theory Comp., 17, 6658 [CrossRef] [Google Scholar]
A possible competitive reaction could be OH + OH ⟶ H2O + O in the singlet channel. However, this reaction is endothermic in the gas phase by 1.5 eV at the ground level of the theory considered in this work (CASPT2(6,4)/6-31+G(d,p); see Sect. 2).
All Tables
Depth of minima on PES for small complexes in the gas phase with respect to the separated radicals.
All Figures
 |
Fig. 1 Initial and final geometry of one recombination trajectory; unbound radicals on the left and hydrogen peroxide on the right. |
| In the text | |
 |
Fig. 2 Rigid scan of PES of all four states included in the CASPT2 calculations with active space 6,4. |
| In the text | |
 |
Fig. 3 Performance of model in structure optimisation calculation compared to reference QM/QM method. |
| In the text | |
 |
Fig. 4 Force uncertainty tracked along trajectory of MD steering dynamics to determine the performance along the reaction coordinate. Uncertainty was computed from the ensemble of three models and was tracked throughout the simulation. |
| In the text | |
 |
Fig. 5 Potential of mean force for inter-radical distance, showing the free energy curve obtained from the metadynamics simulation. |
| In the text | |
 |
Fig. 6 Recombination probability as a function of initial distance of OH radicals. The first top-left plot presents the results for all the energies combined. The following graphs present the datasets for different added energy individually, with the error bars included in the plots. Error bars represent the Jeffreys Bayesian interval generated by Python library statsmodels (Seabold & Perktold 2010). |
| In the text | |
 |
Fig. 7 Plot of final geometries of all trajectories. The upper plot shows all endpoints of trajectories in the 2D graph of CV1 and O-O distance; the lower plot presents data from the same trajectories with a zoomed-in view of H-bonding and hydrogen-peroxide conformers. |
| In the text | |
 |
Fig. 8 Gas-phase (top) and surface (bottom) minimal geometries showing the OH...OH hydrogen-bonded complex in competition with Reaction (8). Minima were obtained at the CASPT2 level for the gas phase and with MLIP for the large cluster. |
| In the text | |
 |
Fig. 9 Recombination probability of hydroxyl radicals as function of binding energy of OH radical. The binding energy of the more weakly bound radical is shown on the x-axis. The first top left plot presents the results for all the energies combined. The following graphs present the datasets for different amounts of added energy individually, with the error bars included in the plots. Error bars represent Jeffreys Bayesian interval generated by Python library statsmodels (Seabold & Perktold 2010). |
| In the text | |
 |
Fig. 10 Visualisation of dynamics of OH radical on water surface after addition of 1.0 eV of additional translation energy. In the upper part of the picture, we can see all positions of the OH radical during the MD simulation. In the lower part, positions from the last nanosecond of the simulation are visualised. |
| In the text | |
 |
Fig. 11 Populations of H-bonding and hydrogen-peroxide conformers in time for trajectories with 0.1 eV of added kinetic energy (upper plot) and 1.0 eV of added kinetic energy (lower plot). |
| In the text | |
 |
Fig. 12 Distribution of kinetic energy for trajectories with 0.5 eV added. The upper plot shows kinetic energy for initial conditions, and the lower one gives averaged kinetic energy during the last 250 fs of MD trajectories. |
| In the text | |
 |
Fig. A.1 Analysis of reference vs predicted forces for geometries from test set (part of original data set which was previously unseen by the model). The blue diagonal line is the function y = x and therefore represents perfect agreement of reference and prediction. |
| In the text | |
 |
Fig. A.2 Analysis of reference vs predicted forces for geometries produced by MD of OH radical impacting on water cluster. The blue diagonal line is the function y = x and therefore represents perfect agreement of reference and prediction. |
| In the text | |
 |
Fig. A.3 Force uncertainty tracked along the MD trajectory of relaxed MD of radicals moving on the cluster surface. Uncertainty was computed from the ensemble of 3 models and was tracked during the whole time of the simulation. |
| In the text | |
 |
Fig. B.1 Potential of mean force from metadynamics using smaller (0.001 eV) height of Gaussian functions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


