| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202451030 | |
| Published online | 04 October 2024 | |
Multi-iron subpopulations in Liller 1 from high-resolution H-band spectroscopy★
1
INAF, Osservatorio di Astrofisica e Scienza dello Spazio di Bologna,
Via Gobetti 93/3,
40129
Bologna,
Italy
2
Department of Physics and Astronomy, UCLA,
430 Portola Plaza,
Box 951547,
Los Angeles,
CA
90095-1547,
USA
3
Dipartimento di Fisica e Astronomia, Università degli Studi di Bologna,
Via Gobetti 93/2,
40129
Bologna,
Italy
★★ Corresponding author; cristiano.fanelli@inaf.it
Received:
7
June
2024
Accepted:
21
August
2024
We present a high-resolution chemical study of a representative sample of 21 luminous giant stars in Liller 1, a complex stellar system in the Galactic bulge, based on H-band spectra acquired with the Near-Infrared Spectrograph at KeckII. In this sample, we found fifteen stars with a subsolar iron abundance and enhanced [α/Fe] and [Al/Fe], likely older, having formed early and quickly from gas mainly enriched by type II supernovae, and six stars with supersolar iron and roughly solar-scaled [α/Fe] and [Al/Fe], likely younger, having formed at later epochs from gas also enriched by type Ia supernovae. Moreover, both subpopulations show enhanced [N/Fe], as in the bulge field, approximately solar-scaled [V/Fe], and depletion of [C/Fe] and 12C/13C with respect to the solar values, indicating the occurrence of significant mixing in the stellar interiors of these evolved stars. Our study also reveals that the subsolar subpopulation shows some structuring, and the presence of a third subcomponent with iron content and intermediate [α/Fe] enhancement, in between that of the metal-poor and metal-rich main subpopulations, has been statistically assessed, providing the chemical signature of both an extended star formation with multiple bursts and some self-enrichment.
Key words: techniques: spectroscopic / stars: abundances / stars: late-type / Galaxy: bulge / Galaxy: stellar content / infrared: stars
Based on observations collected at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California, and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation.
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Star clusters in the Galactic bulge are usually ~ 12 Gyr-old stellar systems with masses in the 104 ≲ M/M⊙ ≲ 106 range and with overall evolutionary and chemical properties typical of genuine globular clusters, that is, single-age and single-iron populations with some spread in the light element abundances (see e.g. Carretta et al. 2009, 2010; Caloi & D’Antona 2011; Milone et al. 2017; Villanova et al. 2019; Cadelano et al. 2023, and references therein). Notable exceptions are Terzan 5 and Liller 1, two stellar systems in the bulge with present-day masses exceeding 106 M⊙ (Lanzoni et al. 2010; Ferraro et al. 2021) that host stellar subpopulations with a significant spread in age and metallicity. In particular, they both host a main stellar component older in age (11–12 Gyr) and with an α-enhanced chemical mixture and subsolar iron abundance (−1.0 < [Fe/H] < 0 in Terzan 5, and −0.5 < [Fe/H] < 0 in Liller 1), cohabiting with one or more stellar populations that are supersolar, approximately solar-scaled alpha, and significantly younger, with an age of 4–5 Gyr in Terzan 5, and 6–8 Gyr and 1–3 Gyr in Liller 1 (Ferraro et al. 2009, 2016, 2021; Origlia et al. 2011, 2013, 2019; Massari et al. 2014; Dalessandro et al. 2022; Crociati et al. 2023; Alvarez Garay et al. 2024). In recent years, a number of scenarios for the formation and evolution of these peculiar systems have been proposed, although none can reasonably explain all of the chemical, kinematic, and evolutionary properties derived thus far from the state-of-the-art photometric and spectroscopic observations mentioned above. In particular, an extragalactic origin of Terzan 5 and Liller 1 (see e.g., Brown et al. 2018; Alfaro-Cuello et al. 2019; Taylor et al. 2022) has almost been discarded based on kinematic (see Massari et al. 2015, 2019; Baumgardt et al. 2019) and age-metallicity (see e.g. Pfeffer et al. 2021, and references therein) considerations, which instead favor an in situ formation and evolution within the Galactic bulge. The metallic-ity also makes it unlikely that Liller 1 and Terzan 5 formed in a halo, metal-poor Galactic environment (Moreno et al. 2022). Furthermore, scenarios that foresee the merger of two globulars (Khoperskov et al. 2018; Mastrobuono-Battisti et al. 2019; Pfeffer et al. 2021) cannot account for the multi-age subpopulations of Terzan 5 and Liller 1, while the accretion of a giant molecular cloud by a genuine globular cluster (McKenzie & Bekki 2018; Bastian & Pfeffer 2022) seems at variance with the observed iron distributions, which show multiple peaks, and, at least in Liller 1, also provides evidence of an underlying continuous star formation (Dalessandro et al. 2022). Considering that an in situ bulge formation best accounts for the observed kinematics and metallicity of Liller 1 and Terzan 5, in order to simultaneously explain their multi-age and multi-iron distributions as well as their complex chemistry, our group made the hypothesis that these systems could be fossil fragments of the pristine clumps of stars and gas that could have contributed to forming the early bulge (e.g., Immeli et al. 2004; Elmegreen et al. 2008, and references therein). These fragments could have survived complete disruption and evolved as independent stellar systems within the bulge, possibly self-enriching (Romano et al. 2023) and experiencing multiple events of star formation (Dalessandro et al. 2022).
This paper presents a detailed chemical study of the Liller 1 stellar populations based on high-spectral-resolution (R≈25 000) spectroscopic observations with the Near-Infrared Spectrograph (NIRSpec) at KeckII in the H band, thus complementing the study by Alvarez Garay et al. (2024, hereafter AG24) based on medium-resolution spectroscopy (R≈8000) in the near-IR (NIR) J, H, and K bands with X-shooter at the Very Large Telescope (VLT). NIR observations are critical to studying the stellar populations in Liller 1, due to its huge absolute and differential reddening (Pallanca et al. 2021) that makes observations in the optical difficult or even impossible. We present the observations and spectral analysis, including target selection and membership assessment via proper motions (PMs), in Sect. 2, results for the radial velocities (RVs) and chemical abundances in Sect. 3, and discussion of the chemical constraints on the formation and evolution of Liller 1 in Sect. 4. We then draw our conclusions in Sect. 5.
2 Observations and spectral analysis
We acquired high-resolution spectra of 22 giant stars toward Liller 1 with the NIRSpec echelle spectrograph (McLean et al. 1998) at Keck II. Observations were made in 2012 on April 28, and in 2013 on May 13 and June 17. We used the NIRSpec-5 setting to enable observations in the H band and a 0.43″ slit width that provided an overall spectral resolution of R = 25 000. Data reduction was performed using the REDSPEC IDL-based package developed at the UCLA IR Laboratory. Each spectrum was sky-subtracted using nod pairs, corrected for flat field, and calibrated in wavelength using arc lamps. An O-star spectrum observed the same night was used to identify and remove telluric features. The signal-to-noise ratio per resolution element of the final spectra was always ≥40.
Table 1 lists the observed target stars and their coordinates and J and K magnitudes from our compilation of NIR photometry (Valenti et al. 2010; Ferraro et al. 2021) and from the VISTA Variables in the Via Lactea (VVV, Minniti et al. 2010). Nine stars are in common with AG24. Before proceeding with the spectral analysis, we first checked the membership of the observed stars using the Gaia Data Release 3 (DR3) PMs (Gaia Collaboration 2016, 2023), which show a distribution peaked at µαcosδ = −5.403, µδ = −7.431 mas yr−1 (see Vasiliev & Baumgardt 2021) and with a dispersion σPM ~ 0.5 mas yr−1 in the direction of Liller 1 (see also AG24). Hence, by assuming that all of the stars with PMs within 3 × σPM of the systemic value belong to the system, we conclude that 21 spectroscopic targets are likely members of Liller 1, and that only star #57 is a field interloper (see Figure 1). As such, the latter was excluded from the subsequent spectral analysis. The position of the 21 members stars in the NIR color-magnitude diagram (CMD), and on the plane of the sky with respect to the center of the system, is shown in Figure 2. All of the observed stars are luminous giants located in the innermost 2 arcmin.
The surface temperature (Teff) and gravity (log g) of the spectroscopic targets were estimated photometrically from the projection of each star onto the closest isochrone in the CMD. Two isochrones (Bressan et al. 2012) properly matching the older and metal-poor, and the younger and metal-rich, components of Liller 1 were considered: one with an age of 12 Gyr and a metallicity [Fe/H] = −0.3, and the other with an age of 2 Gyr and a metallicity [Fe/H] = +0.3. The comparison was done in the differential-reddening-corrected CMD, adopting a distance modulus (m-M)0=14.65 and an average color excess E(B-V)=4.52 (see Pallanca et al. 2021; Ferraro et al. 2021). To proceed, we first projected all of the stars on the isochrone with an age of 12 Gyr and a metallicity of −0.3, representative of the bulk of the Liller 1 population, deriving corresponding Teff and log(𝑔) values. We then used synthetic spectra with these stellar parameters to derive a first estimate of the metallicity. For the stars found to have a different metallicity, we repeated the procedure, projecting them onto the younger, metal-rich isochrone and deriving new estimates for Teff and log(𝑔), and then metallicity. The resulting values of Teff and log 𝑔 were then fine-tuned by requiring the simultaneous fit of the observed OH and CO molecular lines and bandheads. Low temperatures (in the 3300–3700 K range, with uncertainties of ±100 K) and surface gravities log 𝑔 = 0.5 ± 0.3 dex were estimated. The adopted uncertainties of ± 100 K and ±0.3 dex for the derived temperatures and gravities, respectively, also account for some possible degeneracy in identifying of the best-fit isochrone. In addition, for all of the observed stars, a microturbulence velocity of 2 ± 0.3 km s−1, which is typical of bulge giant stars with similar temperatures and metallicities, was safely adopted.
The synthetic spectra used to measure the RVs and chemical abundances of the target stars were computed by adopting the list of atomic lines from the VALD3 compilation (Ryabchikova & Pakhomov 2015), molecular lines from the website of B. Plez1, MARCS models atmospheres (Gustafsson et al. 2008), and the radiative transfer code TURBOSPECTRUM (Alvarez & Plez 1998; Plez 2012). We generated multiple grids of synthetic spectra, with fixed stellar parameters (appropriate to each star), and varying the metallicity from −1.0 dex to +0.5 dex, in steps of 0.1 dex, with both solar-scaled and some enhancement of [α/Fe] and [N/Fe] and corresponding depletion of [C/Fe] for a proper computation of the molecular equilibria. Solar-scaled [X/Fe] values were adopted for the other elements. For optimal matching of the observed line profile broadening, the synthetic spectra were convoluted with a Gaussian function at R≈25 000 spectral resolution and resampled in pixels of ≈0.2 Å, as the NIRSpec spectra. This instrumental broadening amounts to 12 km s−1, which is dominant with respect to any possible intrinsic broadening due, for example, to macroturbulence and rotation, which typically do not exceed 10 km s−1 in giant stars.
Observed stars in Liller 1.
 |
Fig. 1 Gaia DR3 PMs referred to the systemic values of Liller 1 (from Vasiliev & Baumgardt 2021), for the stars with a magnitude comparable to that of the spectroscopic targets (G < 19) and located within 2 arcmin of the center of the system (gray dots), where the 22 spec-troscopic targets (color-filled circles and squares) are also located. The red-filled circles and blue-filled squares are likely member stars of Liller 1, belonging to the metal-poor and metal-rich subpopulations, respectively (see Sect. 3.2). The typical error bars for the spectroscopic targets are reported in the bottom-right corner. The large dashed circle has a radius equal to three times the PM dispersion of Liller 1 (see text). The spectroscopic target located beyond the dashed circle (star #57, marked as a black-filled circle) is likely a Galactic field interloper and was excluded from the chemical analysis. |
3 Results
3.1 Radial velocities
The RVs of the 21 member stars were measured by means of cross-correlation between the observed and the synthetic spectra. The resulting values (see Table 2) range between 45 and 110 km s−1, with uncertainties smaller than 1 km s−1, and are (within 1 km s−1) fully consistent with the measurements quoted by AG24 for the nine stars in common. The sample has a mean value of 68.8±3.1 km s−1, which is in very good agreement with the average RVs quoted in Crociati et al. (2023, 67.9±0.8 km s−1) and in AG24 (66.6±2.7 km s−1). The measured RV dispersion is 14.1 ±2.2 km s−1, consistent with the line-of-sight velocity dispersion of ≈13 km s−1 measured at about 100″ from the center of Liller 1 by Baumgardt & Hilker (2018)2. All 21 of the stars have RVs within 3σ of the systemic value, thus confirming their membership based on the PMs.
3.2 Chemical abundances and abundance ratios
The chemical abundances of Fe, CNO, Ca, Si, Mg, Ti, Al, and V were determined via spectral synthesis around each line of interest. For each measured star and chemical element, Table 2 lists the average abundance (if two or more lines are used) and corresponding error, that is, the standard deviation divided by the square root of the number of lines used, or a conservative value of 0.1 dex if only one line is used. While chemical abundances of Fe, Ca, Si, Mg, Ti, Al, and V were determined from atomic lines, those of N and O were derived from CN and OH molecular transitions and those of 12C and13 C from the second overtone CO molecular bandheads. Indeed, as discussed in Fanelli et al. (2021, and references therein), reliable C abundances from CO can be determined from individual roto-vibrational transitions and/or from the bandheads.
At the low effective temperatures of these targets, the estimated uncertainties on the stellar parameters (see previous section) have an overall impact of approximately 0.10–0.15 dex on the derived abundances. However, it is worth mentioning that this global uncertainty can be regarded as mostly systematic, thus being essentially canceled out when computing abundance ratios, as well as when abundance differences among the Liller 1 stars are considered.
Nine targets in our NIRSpec sample are in common with the AG24 study. The abundance differences for the chemical elements in common are symmetrically distributed around the zero value, typically well within 0.1 dex and comparable to the measurement errors (see Figure 3). The average differences are always within 0.05 dex, indicating that the two sets of abundance measurements can be merged without introducing major systematic biases.
The distribution of the inferred [Fe/H] values for the 21 likely member stars of Liller 1 is shown in Figure 4 (left panel). It shows a major, subsolar component counting 15 stars at an average [Fe/H]=−0.29 ± 0.03 and a 1 σ dispersion of 0.13 ± 0.02 (which exceeds the measurement errors), and a supersolar one with an average [Fe/H]=+0.27 ± 0.02 and 1σ = 0.05 ± 0.01, comprising six stars. Interestingly, this bimodal distribution is fully consistent with that found by Crociati et al. (2023) and AG24, and it agrees with the prediction obtained from the reconstructed star formation history of the system (Dalessandro et al. 2022). The stars belonging to the two components are highlighted with different shapes and colors (red-filled circles and blue-filled squares for the sub- and supersolar components, respectively) in all of the figures.
Concerning the other chemical elements measured in the NIRSpec spectra, Fig. 5 displays their [X/Fe] abundance ratios as a function of [Fe/H]. The metal-poor subpopulation shows some enhanced (on average by a factor of 2–3) [O/Fe], [Mg/Fe], [Al/Fe], [Si/Fe], [Ca/Fe], and [Ti/Fe], while the super-solar component has approximately solar-scaled values. Interestingly, the few stars with intermediate iron content (in the −0.2<[Fe/H]<+0.2 dex range) also show somewhat intermediate enhancement in [O/Fe], [Mg/Fe], [Si/Fe], [Ca/Fe], and [Ti/Fe], in between the main metal-poor and metal-rich subcomponents. The rather clear separation between the α-enhanced, metal-poor population and the solar-scaled, metal-rich population can be appreciated in the right panel of Fig. 4, which shows the average [<O,Si,Mg>/Fe] distribution for the observed stars. Irrespective of their iron content, all of the stars show enhancement of [N/Fe] up to a factor of about six, and approximately solar-scaled [V/Fe] values with small scatters. [C/Fe] is depleted with respect to the solar-scaled value in all of the stars, but at subsolar [Fe/H] the scatter is significantly larger than at [Fe/H] > 0, with an overall 1σ dispersion exceeding 0.2 dex. We did not find any hint of Mg–Al or C–N anticorrelations, confirming the results of AG24 on the lack of chemical anomalies among light elements, and also similar to what Origlia et al. (2011) found in Terzan 5.
Figure 6 shows the distributions of 12C/13C as a function of [Fe/H] (left panel) and [C/N] (right panel). Low 12C/13C isotopic ratios (in the 5–15 range) with an average value of ~10 were measured regardless of the star iron content. [C/N] values below −0.5 dex and as low as −1.4 dex were obtained, with significantly larger scatter among the metal-poor than the metal-rich stars, thus reflecting the [C/Fe] distribution. The inferred low [C/Fe] and 12C/13 C abundance ratios are the typical signature that mixing and extra-mixing processes occurred in the stellar interiors during the post-main-sequence evolution (see, e.g., Charbonnel 1995; Denissenkov & Weiss 1996; Cavallo et al. 1998; Boothroyd & Sackmann 1999).
The abundance ratio distributions obtained in this work fully match those of AG24 for the chemical elements in common. Hence, we can merge the two datasets, obtaining a global sample counting 39 stars, for which abundances of Fe, C, O, Mg, Al, Si, Ca, Ti, and V and the 12C/13C isotopic ratio are available.
 |
Fig. 2 Lilleг 1 K, J-K CMD (left panel, gray dots) with, highlighted, the metal-poor (red-filled circles) and metal-rich (blue-filled squares) likely member stars, for which we measured chemical abundances (see Sect. 3.2), and distribution of these stars on the plane of the sky with respect to its center, marked with the black cross and located at RA=263.°3523333, Dec=−33.°3895556 (right panel). The dashed black circles have radii equal to 10, 20, and 30 times the core radius rc = 5.″39 (Saracino et al. 2015). |
IDs, Teff, RVs, and chemical abundances for the observed stars in Liller 1.
 |
Fig. 3 Abundance differences between this work and AG24 for the stars and chemical elements in common. Gray dots refer to the measurements obtained for each individual star, while the black-filled circles represent the average differences along with their associated errors. The dashed horizontal line marks the zero difference. |
 |
Fig. 4 Distribution of the [Fe/H] and [<O,Mg,Si>/Fe] abundance measurements (left and right panels, respectively) obtained in the present work from the analysis of NIRSpec spectra alone (top panel), and in combination with the AG24 sample (bottom panels). |
4 A third, metal-intermediate component
The histograms shown in Fig. 4 and the distributions of [<O,Mg,Si>/Fe] plotted in Fig. 5 suggest the possible presence of multiple (>2) components, although the low number statistics remains a somewhat limiting factor. To explore this hypothesis more quantitatively, we analyzed the [<O,Mg,Si>/Fe] versus [Fe/H] distribution of the 39 stars in the merged sample (this work and AG24) by means of two different statistical methods (see e.g., the scikit-learn3 library), namely K-means clustering and the Gaussian mixture model (GMM). The expectation-maximization algorithm was used to improve the fit to the data by iteratively varying the model parameters.
K-means is an unsupervised clustering algorithm that provides the optimal number of components from the inertia parameter I defined as
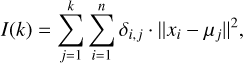
where k is the total number of j-th components, n the total number of i data points, µj the corresponding centroid, xi the 2D coordinate of each i-th data point, δi,j a δ function that assesses the membership of the i-th point to the j-th component, and ‖xi − µj‖ the Euclidean distance. The optimal number of components is defined by the "elbow" in the inertia versus k diagram, at which the inertia and its derivative sharply level off. Figure 7 shows the inferred K-means optimal solution for the [<O,Mg,Si>/Fe] versus [Fe/H] distribution of Liller 1. We explored solutions with a total number of components between one and six, and find that the optimal number is k=3. Although the distribution of the two variables ([<O,Mg,Si>/Fe] and [Fe/H]) separately is well reproduced, the model was unable to properly describe the 2D distribution of the stars in the diagram because they are not uniformly and spherically distributed (see the bottom panel of Fig. 7).
This suggests that an alternative approach (such as the GMM) that allows an observed distribution to be broken down into a given number of Gaussian components with their own mean, variance, and rotation parameters is more appropriate. As figures of merit for the selection of the best-fit solution with the GMM, we employed the Bayesian information criterion (BIC) and the Akaike information criterion (AIC). The BIC and the AIC are statistical methods that balance model complexity against fitting to the data. The BIC is defined as 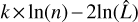 , while the AIC is defined as
, while the AIC is defined as 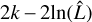 , where k is the number of parameters, n the sample size, and
, where k is the number of parameters, n the sample size, and 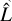 the maximum likelihood of the model. The BIC increases with the number of model parameters and, logarithmically, with the sample size, while it decreases logarithmically with the maximum likelihood of the model. The AIC has no direct dependence on the sample size and depends primarily on the maximum likelihood of the model. The best-fit model is the one that minimizes both the BIC and AIC.
the maximum likelihood of the model. The BIC increases with the number of model parameters and, logarithmically, with the sample size, while it decreases logarithmically with the maximum likelihood of the model. The AIC has no direct dependence on the sample size and depends primarily on the maximum likelihood of the model. The best-fit model is the one that minimizes both the BIC and AIC.
We explored different solutions, varying the number of Gaussian components from one to six. The best fit to the data was obtained with three components, as indicated by both the BIC and AIC parameters in the upper panel of Figure 8. The bottom panel of the same figure shows the GMM optimal solution for the considered distribution, and Table 3 summarizes the parameters of the best-fit model. In order to evaluate the statistical significance of the three-component model with respect to the two-component model, we also computed the p-value using a likelihood-ratio test and a chi-squared distribution with one degree of freedom. We find a p-value of ≈0.01, indicating that the three-component model has high statistical significance and is therefore the most appropriate for describing the observed distribution.
We finally investigated, on a statistical basis, the distribution of the global sample of 39 stars in the spatial and velocity planes. We applied a GMM to determine the optimal number of Gaussian components to fit the RA-Dec and RV-PM 2D distributions. Both the BIC and AIC increase with the number of Gaussian components used to fit the data, thus indicating that the best-fitting model is a single Gaussian. Fig. 9 shows the spatial and kinematic distributions of the 39 stars that are likely members of Liller 1, color-coded according to their metal content, and the 1, 2, and 3 σ contour levels from the GMM analysis. This test indicates that the 39 stars have spatial and velocity distributions consistent with being members of the same stellar system.
 |
Fig. 5 Behavior of [C/Fe], [N/Fe], [O/Fe], [Mg/Fe], [Al/Fe], [Si/Fe], [Ca/Fe], [Ti/Fe], and [V/Fe] as a function of [Fe/H] for the metal-poor (red-filled circles) and metal-rich (blue-filled squares) subpopulations of Liller 1. The gray dots represent the stars of AG24 not in common with the NIRSpec sample. The typical error bars are reported in the left corner of each panel. The dashed vertical and horizontal lines denote the corresponding zero [Fe/H] and [X/Fe] values. |
 |
Fig. 6 12C/13C isotopic ratio as a function of [Fe/H] (left panels) and [C/N] (right panel). Typical error bars are reported in the bottom-right corner of each panel. Symbols are as in Fig. 5. |
Liller 1 components (metal-poor, metal-intermediate, and metal-rich) as derived from a GMM decomposition of the observed [<O,Mg,Si>/Fe] vs. [Fe/H] distribution.
 |
Fig. 7 K-means clustering solution for the [<O,Mg,Si>/Fe] vs. [Fe/H] distribution of Liller 1. Bottom panel: distribution for the observed 39 stars (black-filled circles) and best-fit solution with three Gaussian components and 1, 2, and 3 σ contours, where σ is the standard deviation. Top panel: inertia parameter I(k) (red-filled circles and solid line) and its derivative (red triangles and dashed line) as a function of K, the total number of components. |
5 Discussion and conclusions
This paper presents a high-resolution spectroscopic study in the H band of a significant sample of giant stars (21 objects), members of the bulge stellar system Liller 1 according to their 3D kinematics, that follows the pioneering work by Origlia et al. (2002) and the studies of Crociati et al. (2023) (AG24) at lower spectral resolution. In particular, the nine stars in common between this study and AG24 have allowed us to properly cross-check the inferred abundances for the chemical elements in common and to conclude that they are fully consistent within the errors. By merging the two samples, chemical abundances of Fe, C, O, Mg, Al, Si, Ca, Ti, and V are thus available for the 39 stars that are likely members of Liller 1.
Our statistical analysis of the [α/Fe] versus [Fe/H] distribution was performed on a significantly larger sample of stars (30% larger) compared to the AG24 sample. This analysis led to the first chemical detection of a minor, third subcomponent. This subcomponent has somewhat intermediate [Fe/H] and [α/Fe] abundance ratios, which lie between the values characterizing the two main subpopulations. The first subpopulation is characterized by subsolar iron and [α/Fe] enhancement, likely formed at an early epoch from gas enriched by type II supernovae, while the second subpopulation, with supersolar iron and solar-scaled [α/Fe], likely formed at much later epochs from gas enriched by type Ia supernovae on a longer timescale and is more centrally concentrated. The three subcomponents have similar kinematic properties, consistent with belonging to the same stellar system.
Although more statistics are needed to firmly establish whether this third component is truly a distinct subpopulation or a pronounced tail toward higher metallicities within the main, metal-poor subpopulation, this finding represents an important piece in the puzzle of the origin of Liller 1. It provides the observational signature that this stellar system cannot be explained as the simple merging of two genuine globulars (Khoperskov et al. 2018; Mastrobuono-Battisti et al. 2019; Pfeffer et al. 2021) or by a genuine globular accreting a giant molecular cloud (McKenzie & Bekki 2018; Bastian & Pfeffer 2022), since its age, metallicity, and [α/Fe] distributions are by far more complex and characterized by multiple episodes of star formation likely accompanied by some degree of self-enrichment.
High-resolution spectroscopy of an additional large sample of giant stars is currently ongoing at the ESO/VLT with the spectrograph CRIRES+ in the context of the Bulge Cluster Origin (BulCO) survey, a Large Program specifically aimed at settling the origin of the most massive stellar clusters in the Galactic bulge. This sample will provide larger-scale statistics on the distribution, especially in the least-populated region of the [α/Fe]-[Fe/H] diagram around solar metallicity, thus finally constraining the details of the complex star formation and chemical evolution history of this fascinating stellar system.
 |
Fig. 8 GMM solution for the [<0,Mg,Si>/Fe] vs. [Fe/H] distribution of Liller 1. Bottom panel: distribution for the observed 39 stars (black-filled circles) and best-fit solution with three Gaussian components and 1, 2, and 3 σ contours, where σ is the standard deviation of each component. Top panel: BIC (red-filled circles) and AIC (big, green triangles) parameters as a function of the total number of Gaussian components. |
 |
Fig. 9 Spatial (in the RA and Dec plane referred to the system center, left panel) and kinematic (in the RV-PM plane referred to the systemic velocities, right panel) distributions of the 39 stars that are likely members of Liller 1, color-coded according to their metal content: red (metal-poor), green (metal-intermediate), and blue (metal-rich). The 1, 2, and 3 σ contour levels from the GMM analysis are also plotted. |
Acknowledgements
CF and LO acknowledge the financial support by INAF within the VLT-MOONS project. CF would like to thank R. Pascale for useful discussions. This work is part of the project Cosmic-Lab at the Physics and Astronomy Department "A. Righi" of the Bologna University (http://www.cosmic-lab.eu/Cosmic-Lab/Home.html).
References
- Alfaro-Cuello, M., Kacharov, N., Neumayer, N., et al. 2019, ApJ, 886, 57 [Google Scholar]
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Alvarez Garay, D. A., Fanelli, C., Origlia, L., et al. 2024, A&A, 686, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bastian, N., & Pfeffer, J. 2022, MNRAS, 509, 614 [Google Scholar]
- Baumgardt, H., & Hilker, M. 2018, MNRAS, 478, 1520 [Google Scholar]
- Baumgardt, H., Hilker, M., Sollima, A., & Bellini, A. 2019, MNRAS, 482, 5138 [Google Scholar]
- Boothroyd, A. I., & Sackmann, I. J. 1999, ApJ, 510, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, G., Gnedin, O. Y., & Li, H. 2018, ApJ, 864, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Cadelano, M., Pallanca, C., Dalessandro, E., et al. 2023, A&A, 679, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caloi, V., & D’Antona, F. 2011, MNRAS, 417, 228 [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavallo, R. M., Sweigart, A. V., & Bell, R. A. 1998, ApJ, 492, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonnel, C. 1995, ApJ, 453, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Crociati, C., Valenti, E., Ferraro, F. R., et al. 2023, ApJ, 951, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Dalessandro, E., Crociati, C., Cignoni, M., et al. 2022, ApJ, 940, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., & Weiss, A. 1996, A&A, 308, 773 [NASA ADS] [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Fanelli, C., Origlia, L., Oliva, E., et al. 2021, A&A, 645, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferraro, F. R., Dalessandro, E., Mucciarelli, A., et al. 2009, Nature, 462, 483 [Google Scholar]
- Ferraro, F. R., Massari, D., Dalessandro, E., et al. 2016, ApJ, 828, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Pallanca, C., Lanzoni, B., et al. 2021, Nat. Astron., 5, 311 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Immeli, A., Samland, M., Gerhard, O., & Westera, P. 2004, A&A, 413, 547 [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Mastrobuono-Battisti, A., Di Matteo, P., & Haywood, M. 2018, A&A, 620, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanzoni, B., Ferraro, F. R., Dalessandro, E., et al. 2010, ApJ, 717, 653 [Google Scholar]
- Magg, E., Bergemann, M., Serenelli, A., et al. 2022, A&A, 661, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massari, D., Mucciarelli, A., Ferraro, F. R., et al. 2014, ApJ, 795, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Massari, D., Dalessandro, E., Ferraro, F. R., et al. 2015, ApJ, 810, 69 [CrossRef] [Google Scholar]
- Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mastrobuono-Battisti, A., Khoperskov, S., Di Matteo, P., & Haywood, M. 2019, A&A, 622, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKenzie, M., & Bekki, K. 2018, MNRAS, 479, 3126 [CrossRef] [Google Scholar]
- McLean, I. S., Becklin, E. E., Bendiksen, O., et al. 1998, SPIE Conf. Ser., 3354, 566 [NASA ADS] [Google Scholar]
- Milone, A. P., Piotto, G., Renzini, A., et al. 2017, MNRAS, 464, 3636 [Google Scholar]
- Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New A, 15, 433 [Google Scholar]
- Moreno, E., Fernández-Trincado, J. G., Pérez-Villegas, A., Chaves-Velasquez, L., & Schuster, W. J. 2022, MNRAS, 510, 5945 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Rich, R. M., & Castro, S. 2002, AJ, 123, 1559 [Google Scholar]
- Origlia, L., Rich, R. M., Ferraro, F. R., et al. 2011, ApJ, 726, L20 [CrossRef] [Google Scholar]
- Origlia, L., Massari, D., Rich, R. M., et al. 2013, ApJ, 779, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Mucciarelli, A., Fiorentino, G., et al. 2019, ApJ, 871, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Pallanca, C., Ferraro, F. R., Lanzoni, B., et al. 2021, ApJ, 917, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Pfeffer, J., Lardo, C., Bastian, N., Saracino, S., & Kamann, S. 2021, MNRAS, 500, 2514 [Google Scholar]
- Plez, B. 2012, Turbospectrum: Code for spectral synthesis, Astrophysics Source Code Library [record ascl:1205.004] [Google Scholar]
- Romano, D., Ferraro, F. R., Origlia, L., et al. 2023, ApJ, 951, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabchikova, T., & Pakhomov, Y. 2015, Baltic Astron., 24, 453 [NASA ADS] [Google Scholar]
- Saracino, S., Dalessandro, E., Ferraro, F. R., et al. 2015, ApJ, 806, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, D. J., Mason, A. C., Schiavon, R. P., et al. 2022, MNRAS, 513, 3429 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, E., Ferraro, F. R., & Origlia, L. 2010, MNRAS, 402, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Vasiliev, E., & Baumgardt, H. 2021, MNRAS, 505, 5978 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Monaco, L., Geisler, D., et al. 2019, ApJ, 882, 174 [NASA ADS] [CrossRef] [Google Scholar]
Fundamental parameters of Galactic globular clusters https://people.smp.uq.edu.au/HolgerBaumgardt/globular/
All Tables
Liller 1 components (metal-poor, metal-intermediate, and metal-rich) as derived from a GMM decomposition of the observed [<O,Mg,Si>/Fe] vs. [Fe/H] distribution.
All Figures
 |
Fig. 1 Gaia DR3 PMs referred to the systemic values of Liller 1 (from Vasiliev & Baumgardt 2021), for the stars with a magnitude comparable to that of the spectroscopic targets (G < 19) and located within 2 arcmin of the center of the system (gray dots), where the 22 spec-troscopic targets (color-filled circles and squares) are also located. The red-filled circles and blue-filled squares are likely member stars of Liller 1, belonging to the metal-poor and metal-rich subpopulations, respectively (see Sect. 3.2). The typical error bars for the spectroscopic targets are reported in the bottom-right corner. The large dashed circle has a radius equal to three times the PM dispersion of Liller 1 (see text). The spectroscopic target located beyond the dashed circle (star #57, marked as a black-filled circle) is likely a Galactic field interloper and was excluded from the chemical analysis. |
| In the text | |
 |
Fig. 2 Lilleг 1 K, J-K CMD (left panel, gray dots) with, highlighted, the metal-poor (red-filled circles) and metal-rich (blue-filled squares) likely member stars, for which we measured chemical abundances (see Sect. 3.2), and distribution of these stars on the plane of the sky with respect to its center, marked with the black cross and located at RA=263.°3523333, Dec=−33.°3895556 (right panel). The dashed black circles have radii equal to 10, 20, and 30 times the core radius rc = 5.″39 (Saracino et al. 2015). |
| In the text | |
 |
Fig. 3 Abundance differences between this work and AG24 for the stars and chemical elements in common. Gray dots refer to the measurements obtained for each individual star, while the black-filled circles represent the average differences along with their associated errors. The dashed horizontal line marks the zero difference. |
| In the text | |
 |
Fig. 4 Distribution of the [Fe/H] and [<O,Mg,Si>/Fe] abundance measurements (left and right panels, respectively) obtained in the present work from the analysis of NIRSpec spectra alone (top panel), and in combination with the AG24 sample (bottom panels). |
| In the text | |
 |
Fig. 5 Behavior of [C/Fe], [N/Fe], [O/Fe], [Mg/Fe], [Al/Fe], [Si/Fe], [Ca/Fe], [Ti/Fe], and [V/Fe] as a function of [Fe/H] for the metal-poor (red-filled circles) and metal-rich (blue-filled squares) subpopulations of Liller 1. The gray dots represent the stars of AG24 not in common with the NIRSpec sample. The typical error bars are reported in the left corner of each panel. The dashed vertical and horizontal lines denote the corresponding zero [Fe/H] and [X/Fe] values. |
| In the text | |
 |
Fig. 6 12C/13C isotopic ratio as a function of [Fe/H] (left panels) and [C/N] (right panel). Typical error bars are reported in the bottom-right corner of each panel. Symbols are as in Fig. 5. |
| In the text | |
 |
Fig. 7 K-means clustering solution for the [<O,Mg,Si>/Fe] vs. [Fe/H] distribution of Liller 1. Bottom panel: distribution for the observed 39 stars (black-filled circles) and best-fit solution with three Gaussian components and 1, 2, and 3 σ contours, where σ is the standard deviation. Top panel: inertia parameter I(k) (red-filled circles and solid line) and its derivative (red triangles and dashed line) as a function of K, the total number of components. |
| In the text | |
 |
Fig. 8 GMM solution for the [<0,Mg,Si>/Fe] vs. [Fe/H] distribution of Liller 1. Bottom panel: distribution for the observed 39 stars (black-filled circles) and best-fit solution with three Gaussian components and 1, 2, and 3 σ contours, where σ is the standard deviation of each component. Top panel: BIC (red-filled circles) and AIC (big, green triangles) parameters as a function of the total number of Gaussian components. |
| In the text | |
 |
Fig. 9 Spatial (in the RA and Dec plane referred to the system center, left panel) and kinematic (in the RV-PM plane referred to the systemic velocities, right panel) distributions of the 39 stars that are likely members of Liller 1, color-coded according to their metal content: red (metal-poor), green (metal-intermediate), and blue (metal-rich). The 1, 2, and 3 σ contour levels from the GMM analysis are also plotted. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


