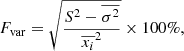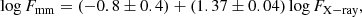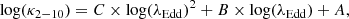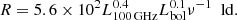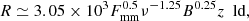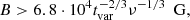| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A232 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202450133 | |
| Published online | 10 October 2024 | |
Joint ALMA/X-ray monitoring of the radio-quiet type 1 active galactic nucleus IC 4329A
1
Instituto de Estudios Astrofísicos, Facultad de Ingeniería y Ciencias, Universidad Diego Portales, Santiago 8370191, Chile
2
Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing 100871, China
3
Joint ALMA Observatory, Avenida Alonso de Cordova 3107, Vitacura, Santiago 7630355, Chile
4
INAF – Astronomical Observatory of Rome, Via Frascati 33, 00040 Monte Porzio Catone, Italy
5
Department of Space, Earth and Environment, Chalmers University of Technology, SE-412 96 Gothenburg, Sweden
6
RIKEN Cluster for Pioneering Research, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan
7
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory, 43992 Onsala, Sweden
8
X-Ray Astrophysics Laboratory, NASA Goddard Space Flight Center, Code 662, Greenbelt, MD 20771, USA
9
Yale Center for Astronomy & Astrophysics, 52 Hillhouse Avenue, New Haven, CT 06511, USA
10
Instituto de Astrofísica and Centro de Astroingeniería, Facultad de Física, Pontificia Universidad Católica de Chile, Campus San Joaquín, Av. Vicuña Mackenna 4860, Macul, Santiago 7820436, Chile
11
Millennium Institute of Astrophysics, Nuncio Monseñor Sótero Sanz 100, Of 104 Providencia, Santiago, Chile
12
Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, Colorado 80301, USA
13
NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
14
Department of Astronomy, School of Physics, Peking University, Beijing 100871, China
15
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
16
MIT Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, Cambridge, MD 02139, USA
17
Eureka Scientific, 2452 Delmer Street Suite 100, Oakland, CA 94602-3017, USA
18
Department of Physics and Astronomy, West Virginia University, P.O. Box 6315 Morgantown, WV 26506, USA
19
Center for Research and Exploration in Space Science and Technology, NASA/GSFC, Greenbelt, MD 20771, USA
20
Department of Astronomy, University of Maryland, College Park, MD 20742, USA
21
Joint Space-Science Institute, University of Maryland, College Park, MD 20742, USA
22
Department of Astronomy, University of Geneva, ch. d’Écogia 16, CH-1290 Versoix, Switzerland
23
National Radio Astronomy Observatory, Charlottesville, VA 22903, USA
24
Department of Astronomy, University of Florida, Gainesville, FL 32611, USA
25
Department of Astronomy, University of Virginia, Charlottesville, VA 22904, USA
26
Department of Physics and Astronomy, Texas A&M University, College Station, TX 77845, USA
27
Department of Physics, Southern Methodist University, 3215 Daniel Ave., Dallas, TX 75205, USA
28
Physics Department, Tor Vergata University of Rome, Via della Ricerca Scientifica 1, 00133 Rome, Italy
29
INFN – Rome Tor Vergata, Via della Ricerca Scientifica 1, 00133 Rome, Italy
30
School of Physics and Astronomy, Tel Aviv University, Tel Aviv 69978, Israel
Received:
26
March
2024
Accepted:
12
July
2024
The origin of a compact millimeter (mm, 100–250 GHz) emission in radio-quiet active galactic nuclei (RQ AGN) remains debated. Recent studies propose a connection with self-absorbed synchrotron emission from the accretion disk X-ray corona. We present the first joint ALMA (∼100 GHz) and X-ray (NICER/XMM-Newton/Swift; 2–10 keV) observations of the unobscured RQ AGN, IC 4329A (z = 0.016). The time-averaged mm-to-X-ray flux ratio aligns with recently established trends for larger samples, but with a tighter scatter (∼0.1 dex) compared to previous studies. However, there is no significant correlation on timescales of less than 20 days. The compact mm emission exhibits a spectral index of −0.23 ± 0.18, remains unresolved with a 13 pc upper limit, and shows no jet signatures. Notably, the mm flux density varies significantly (by factor of 3) within four days, exceeding the contemporaneous X-ray variability and showing the largest mm variations ever detected in RQ AGN over daily timescales. The high amplitude variability rules out scenarios of heated dust and thermal free–free emission, pointing toward a synchrotron origin for the mm radiation in a source of ∼1 light day (∼120 gravitational radii) size. While the exact source is not yet certain, an X-ray corona scenario emerges as the most plausible compared to a scaled-down jet or outflow-driven shocks.
Key words: galaxies: individual: IC 4329A / submillimeter: galaxies / X-rays: galaxies
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Most active galactic nuclei (AGN) do not show bright radio structures associated with powerful relativistic jets launched from regions close to the accreting supermassive black hole (SMBH). However, these radio-quiet (RQ) sources exhibit faint radio emissions, often appearing in compact, parsec-scale regions that remain unresolved even with VLBA observations (e.g., Alhosani et al. 2022; Chen et al. 2024; Wang et al. 2023). While in radio-loud AGN the emission is known to be dominated by nonthermal synchrotron radiation from jets, the origin of compact radio emissions in RQ AGN is still a subject of debate. Various hypotheses have been proposed, including small-scale jets, nuclear star formation regions, thermal free–free radiation, and the magnetized corona of the accretion disk (see Panessa et al. 2019, for a review). Among these explanations, the accretion disk corona is one of the most favored. This arises from the RQ AGN following the radio/X-ray relation L5 GHz/L0.2 − 20 keV ∼ 10−5 (Laor & Behar 2008) previously discovered for the coronally active stars (Guedel & Benz 1993), where the corona is magnetically heated, similarly to what is expected for AGN (e.g., Merloni & Fabian 2001a,b). In this scenario, the population of high-energy electrons upscattering UV/optical seed photons into X-ray energies also produces optically thick synchrotron radio emission, while moving in the coronal magnetic field. Under certain assumptions, the synchrotron emission of the structure with an approximately X-ray corona size can be self-absorbed at frequencies lower than ∼100–300 GHz (i.e., millimeter-wave band, mm), where the contribution from cold dust emission is minimal. Recent theoretical calculations (e.g., Raginski & Laor 2016; Inoue & Doi 2018) also predict that coronal emission can peak at 100–200 GHz, producing flat synchrotron emission up to 300 GHz. Flux densities at 100 GHz have been measured for a few dozen AGN and consistently exceed extrapolations from low-frequency power-law slopes (e.g., Behar et al. 2015, 2018; Inoue & Doi 2018), confirming the presence of a compact optically thick core.
Recent research has further supported the connection between mm and X-ray luminosity: while Behar et al. (2018) found only a tentative correlation between 100 GHz and 2–10 keV luminosity for 34 AGN with a large scatter1 (∼0.5 dex) likely caused by the sample heterogeneity and low angular resolution (≳1″), a recent high spatial resolution study of a sample of 98 AGN with ALMA (Kawamuro et al. 2022, 2023) measured a highly significant linear correlation between the time-averaged hard X-ray (14–150 keV) and the instantaneous mm (230 GHz) luminosity with a ∼0.36 dex scatter. Notably, higher spatial resolution (1–23 pc) 100 GHz ALMA observations of nearby hard X-ray-selected AGN have shown that the correlation between X-ray and mm emission (Ricci et al. 2023) has a low scatter of 0.22 dex. However, to unequivocally establish the common origin of mm and X-ray flux by the electrons in the X-ray corona, it would be crucial to detect their correlated variability. Detecting correlated variability would also significantly contribute to our understanding of the X-ray origin, providing evidence that the magnetic field plays an important role in relativistic particle acceleration and corona heating (Merloni & Fabian 2001a,b). Currently, only two observational campaigns (Behar et al. 2020; Petrucci et al. 2023) have been conducted, using IRAM (with ∼17–28″ resolution) and NOEMA (∼1″) at 100 GHz, and they found no definitive evidence of correlated variability (see Sect. 4.2). In this context, subarcsecond observations with ALMA can play a crucial role, due to its sensitivity and angular resolution, in localizing the compact source of the mm emission.
For this paper we studied the X-ray and mm variability of the nearby RQ AGN IC 4329A (z = 0.016) using, for the first time, ALMA observations with angular resolution < 0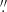 1. Previous high-resolution (0
1. Previous high-resolution (0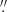 16–0
16–0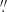 4) ALMA observations have shown that IC 4329A exhibits relatively bright (∼8 mJy) compact emission at 100 GHz, showing an excess compared to lower frequencies (Inoue & Doi 2018), which can be attributed to self-absorbed synchrotron radiation. Additionally, IC 4329A stands out as the brightest unobscured AGN in the southern sky (F2 − 10 keV ∼ 10−10
erg cm−2 s−1, Ricci et al. 2017), showing significant variability in the X-ray band (from ∼8 × 10−11
erg cm−2 s−1 to ∼2 × 10−9
erg cm−2 s−1 in 2–10 keV band on timescales as short as several hours; see Tortosa et al. 2024, for details). All these characteristics, in both the X-ray and mm band, make IC 4329A the best target for the search for correlated X-ray/mm variability. In 2021, IC 4329A was the focus of an extensive observational campaign, with 45 X-ray observations carried out by XMM-Newton, NuSTAR, NICER, and Swift and ten ALMA observations over ten consecutive days. The analysis of these high-quality XMM-Newton and NuSTAR observations was described in Tortosa et al. (2024). In the present article, we report the analysis of the X-ray and mm variability on timescales of days, with the goal of investigating the correlation between these two bands. Throughout the paper we use the standard cosmological parameters (H0 = 70 km s−1 Mpc−1, Ωm = 0.3, ΩΛ = 0.7).
4) ALMA observations have shown that IC 4329A exhibits relatively bright (∼8 mJy) compact emission at 100 GHz, showing an excess compared to lower frequencies (Inoue & Doi 2018), which can be attributed to self-absorbed synchrotron radiation. Additionally, IC 4329A stands out as the brightest unobscured AGN in the southern sky (F2 − 10 keV ∼ 10−10
erg cm−2 s−1, Ricci et al. 2017), showing significant variability in the X-ray band (from ∼8 × 10−11
erg cm−2 s−1 to ∼2 × 10−9
erg cm−2 s−1 in 2–10 keV band on timescales as short as several hours; see Tortosa et al. 2024, for details). All these characteristics, in both the X-ray and mm band, make IC 4329A the best target for the search for correlated X-ray/mm variability. In 2021, IC 4329A was the focus of an extensive observational campaign, with 45 X-ray observations carried out by XMM-Newton, NuSTAR, NICER, and Swift and ten ALMA observations over ten consecutive days. The analysis of these high-quality XMM-Newton and NuSTAR observations was described in Tortosa et al. (2024). In the present article, we report the analysis of the X-ray and mm variability on timescales of days, with the goal of investigating the correlation between these two bands. Throughout the paper we use the standard cosmological parameters (H0 = 70 km s−1 Mpc−1, Ωm = 0.3, ΩΛ = 0.7).
2. Observations and data reduction
2.1. X-ray
2.1.1. XMM-Newton
IC 4329A was observed once per day for ten consecutive days (from 2021 August 10 to 2021 August 19, P.I. C. Ricci) by the X-ray Multi-Mirror Mission (XMM-Newton, Jansen et al. 2001) during XMM-Newton AO 19. The European Photon Imaging Camera (EPIC) instruments were operated in the small window and thin filter mode. Observation 0862090401 was not included in the analysis since, due to a problem in the ground segment, the EPIC exposure was lost.
The EPIC event lists are extracted with the EPPROC (pn) and EMPROC (MOS) tools of the standard System Analysis Software (SAS v.18.0.0; Gabriel et al. 2004). The latest calibration files, available in January 2023, were used. The choice of optimal time cuts for the flaring particle background was performed by visually inspecting light curves created in the energy range 10–12 keV (EPIC-pn) with PATTERN = 0 (single events). For the choice of source and background extraction radii, we identified point-like sources in each target field of view running the meta-task edetect-chain on the 0.5–2 keV energy band EPIC images and performed an iterative process that maximizes the signal-to-noise ratio (S/N), as in Piconcelli et al. (2004). The resulting optimal source extraction radius was 30″, and the background spectra were extracted from source-free circular regions with radii of ∼50″ for each observation. Response matrices and auxiliary response files were generated using the SAS tools RMFGEN and ARFGEN, respectively. EPIC-pn spectra were binned to oversample the instrumental energy resolution by a factor larger than three and to have no less than 20 counts in each background-subtracted spectral channel. No significant pile-up affected the EPIC data, as indicated by the SAS task EPATPLOT.
2.1.2. NICER
Data reduction of the 21 NICER (Gendreau et al. 2012; Arzoumanian et al. 2014; Gendreau et al. 2016) observations (PI: C. Ricci) of our campaign was performed following the same procedure reported in Ricci et al. (2021).
2.1.3. Swift
A total of 12 observations from the X-ray telescope (XRT, Burrows et al. 2005) on board the Neil Gehrels Swift Observatory (Gehrels et al. 2004) (PI: C. Ricci) were used here. We performed the Swift/XRT data analysis using the XRTPIPELINE following the standard guidelines (Evans et al. 2009).
2.2. Millimeter wave band
The ALMA band-3 observations were taken over ten consecutive days from August 28 to September 6, 2021 (Project code 2019.1.01181.S; PI C. Ricci), in four channels of 1.985 GHz bandwidth with the central frequencies ν = 90.52, 92.42, 102.52, and 104.48 GHz. Most observations were taken within three hours from the NICER observations. Data were processed using CASA version 6.1.1.15 and the ALMA Pipeline version 2020.1.0.40 (Hunter et al. 2023). The spectral setup is in time-division mode (TDM) around 100 GHz, as our aim was to detect the continuum emission of IC 4329A. Our monitoring campaign was scheduled during the ALMA long baseline configuration (C43-9/10) with the longest baseline of 13.8 km. For each observing session, the on-source time was about eight minutes. As a result, the typical beam size is between 0″.04 and 0″.09 (i.e., ∼13 and ∼29 pc). According to the ALMA proposer’s guide, the statistical flux error for band-3 observations is 5%. By analyzing the flux measurements of the phase calibrator J1351-2912 and the check source J1352-2745, we derived consistent results. Therefore, we applied the 5% error to our analysis.
For an insight into the spectral variability of IC 4329A, we derived the spectral index using the fluxes measured by the four spectral windows from the ten epochs of observations. This analysis assumes that the spectral slope of the flux calibrator J1337-1257 and the phase calibrator were stable during our campaign. The ALMA calibration shows that the variation of the spectral index for the flux calibrator is within 2% during our campaign.
3. Results
The X-ray (2–10 keV) and mm (100 GHz) light curves of IC 4329A obtained are illustrated in Fig. 1. We note that the error bars are shown in the figure, but are typically smaller than the symbols. In both wavebands, the observations were carried out with a daily cadence. The X-ray light curve, obtained with XMM-Newton, NICER, and Swift, spanning 40 days, is shown in the top panel of Fig. 1. Contemporaneous ALMA 100 GHz observations were carried out over ten days (bottom panel). In the following, we examine the behavior of both light curves.
 |
Fig. 1. X-ray and mm-band light curves. From top to bottom: X-ray (2–10 keV) flux with fitted power-law model, 2–10 keV flux deviations from the long-term trend, and 3 mm (97.5 GHz) flux density. The interval of the contemporaneous X-ray and mm observations is marked with a gray region. All data are listed in Appendix A. |
3.1. X-ray variability
During our campaign, the X-ray (2–10 keV) flux of IC 4329A showed significant variability on timescales of days. To quantify the intensity of the variability taking into account the measurement uncertainties, we calculated the fractional variability of the light curve Fvar (Vaughan et al. 2003),
where S2 is the sample variance, 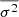 is the mean square error, and
is the mean square error, and 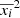 is the square mean of the data. For the X-ray data, FvarX − ray = (17.5 ± 0.5)%, while the intraday variations are less than 5% (see Tortosa et al. 2024). Due to the focus of the work on the variability of the longer (daily) timescale, we ignored the intraday variations in the analysis.
is the square mean of the data. For the X-ray data, FvarX − ray = (17.5 ± 0.5)%, while the intraday variations are less than 5% (see Tortosa et al. 2024). Due to the focus of the work on the variability of the longer (daily) timescale, we ignored the intraday variations in the analysis.
During our monitoring campaign, the X-ray flux steadily increased (top panel of Fig. 1), following a long-term trend of ∼10−12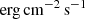 per day. Once this trend is subtracted (middle panel of Fig. 1), the X-ray light curve shows variations on a timescale of several days. Although the nature of the variability in AGN is stochastic, the observed fluctuations in the X-ray flux relative to the average may suggest the presence of regular oscillations. To investigate the periodicity of these variations, we calculated the Lomb-Scargle periodogram (Lomb 1976; Scargle 1982) used for the analysis of unevenly sampled data employing a least-squares fitting procedure. The periodogram revealed two possible variability periods of 14.4 ± 0.9 and 4.5 ± 0.1 days. However, when the light curve is irregular and evolves over time, wavelet analysis (Morlet 1983) is more efficient than the periodogram. Unlike the Fourier transform, whose kernel is not time-localized, wavelet analysis dissects the data series into distinct frequency components and examines each segment with corresponding temporal resolution. Therefore, the wavelet analysis provides both variability frequency (or period) and its evolution during the observations. For IC 4329A, the result of the wavelet transformation of the X-ray flux variability with the subtracted trend is illustrated in Fig. 2. Here, the original epochs are interpolated to the regular grid using the spline extrapolation. The wavelet analysis revealed two variation periods corresponding to the periodogram result: 4.5 ± 0.8 and 14.9 ± 2.5 days. The period of 14.9 ± 2.5 days is stable during the observations, but is greater than one-third of the monitoring period and is located out of the cone of influence (see details in Torrence & Compo 1998) in the area where the analysis may be affected by data limitations (such as the finite duration of observations) and edge effects, and thus it may be an artifact. The period of 4.5 ± 0.8 days is less stable, but can potentially reveal quasi-periodic oscillations in the AGN. Nevertheless, the estimated periods characterize only the observed segment of the light curve, the overall behavior of which can be entirely stochastic.
per day. Once this trend is subtracted (middle panel of Fig. 1), the X-ray light curve shows variations on a timescale of several days. Although the nature of the variability in AGN is stochastic, the observed fluctuations in the X-ray flux relative to the average may suggest the presence of regular oscillations. To investigate the periodicity of these variations, we calculated the Lomb-Scargle periodogram (Lomb 1976; Scargle 1982) used for the analysis of unevenly sampled data employing a least-squares fitting procedure. The periodogram revealed two possible variability periods of 14.4 ± 0.9 and 4.5 ± 0.1 days. However, when the light curve is irregular and evolves over time, wavelet analysis (Morlet 1983) is more efficient than the periodogram. Unlike the Fourier transform, whose kernel is not time-localized, wavelet analysis dissects the data series into distinct frequency components and examines each segment with corresponding temporal resolution. Therefore, the wavelet analysis provides both variability frequency (or period) and its evolution during the observations. For IC 4329A, the result of the wavelet transformation of the X-ray flux variability with the subtracted trend is illustrated in Fig. 2. Here, the original epochs are interpolated to the regular grid using the spline extrapolation. The wavelet analysis revealed two variation periods corresponding to the periodogram result: 4.5 ± 0.8 and 14.9 ± 2.5 days. The period of 14.9 ± 2.5 days is stable during the observations, but is greater than one-third of the monitoring period and is located out of the cone of influence (see details in Torrence & Compo 1998) in the area where the analysis may be affected by data limitations (such as the finite duration of observations) and edge effects, and thus it may be an artifact. The period of 4.5 ± 0.8 days is less stable, but can potentially reveal quasi-periodic oscillations in the AGN. Nevertheless, the estimated periods characterize only the observed segment of the light curve, the overall behavior of which can be entirely stochastic.
 |
Fig. 2. Wavelet analysis of the X-ray variability with the trend subtracted and the data interpolated on the regular grid. Left: Magnitude of the wavelet transform. The 95% confidence level is given in white contours. The cone of influence is given as the solid black line; the region out of the cone in the darker color shows less reliable periods that may be affected by edge effects (see text for details). Right: Wavelet transform profiles in gray and their median value in black indicate the variability periods of 14.9 and 4.5 days. The dashed lines correspond to the maxima of the Lomb-Scargle periodogram. |
3.2. Millimeter variability
In the mm band, IC 4329A showed very strong variability during the ten-day observational campaign: the flux changed significantly, up to a factor of 2.6 between maximum and minimum, with the day-to-day variations reaching a factor of ∼1.5. The observed variability is clearly independent of the beam size. The fractional variability for the mm data calculated using Eq. (1) is two times higher than in the X-rays: 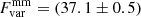 %, including ALMA calibration uncertainties of ∼5%. It is interesting that
%, including ALMA calibration uncertainties of ∼5%. It is interesting that 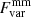 was found to be significantly larger than
was found to be significantly larger than 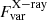 . Even during the same period of ten days, corresponding to the simultaneous X-ray/ALMA observations,
. Even during the same period of ten days, corresponding to the simultaneous X-ray/ALMA observations, 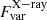 was only 18.5%. Additionally, we examined the very short time variability within each epoch of ALMA observations. Each observation of the object lasted ∼15 minutes, which we divided into two segments and analyzed separately. However, no changes were found within the 5% flux uncertainties.
was only 18.5%. Additionally, we examined the very short time variability within each epoch of ALMA observations. Each observation of the object lasted ∼15 minutes, which we divided into two segments and analyzed separately. However, no changes were found within the 5% flux uncertainties.
As ALMA observations were performed at frequencies ν = 90.52, 92.42, 102.52, and 104.48 GHz, this could provide us with insight into the spectral variability of IC 4329A. Assuming a power-law spectrum (Fmm ∝ να) for each epoch, we calculated the spectral slope α. We found an average spectral slope −0.23 with σ = 0.18, with neither significant temporal variations nor correlation with the flux changes.
The light curves of IC 4329A in different frequencies are shown in Fig. 3 (upper panel). The variability pattern is the same for all wavebands. For comparison, we illustrated the variations of the spectral slope α in the bottom panel of Fig. 3 that did not show a correlation with the flux. Additionally, we examined the difference (Δ) between the lower and higher frequencies, Δ = (F91 − F103)/F103 × 100%, where F91 is the mean flux between 90.52 and 92.42 GHz, and F103 is the mean flux between 102.52 and 104.48 GHz. We found that Δ varied between ∼6% (during the first flare) and ∼0% (before the second flare). Similarly to α, this parameter showed no correlation with the flux and did not exhibit statistically significant variations at the 95% confidence level, according to the Kolmogorov–Smirnov test.
 |
Fig. 3. Variability of the mm flux and slope during the campaign. Upper panel: mm light curve in four different frequencies: 90.52, 92.42, 102.52, and 104.48 GHz, shown in different colors and symbols. Bottom panel: Variations in the mm spectral slope. The gray dashed line corresponds to the median spectral slope −0.23. |
The exceptional resolution and sensitivity of ALMA allowed us to resolve a faint diffuse structure to the east of the central bright source in the continuum maps of IC 4329A (Fig. 4). Notably, this structure is observed throughout the entire campaign, though due to beam size and shape, it is clearly distinguishable in only five of the ten epochs. We measured the flux of this diffuse spot whenever possible and found that it is consistent, within the uncertainties in all epochs, with a flux density of ∼0.6 mJy. Given that this value is about six times lower than the flux emitted by the bright variable core even at its minimum, we ignored the contribution of this constant fainter elongated structure to the mm flux.
 |
Fig. 4. ALMA image of IC 4329A (median band 3) 9/3/2021. Beam size is 0 |
3.3. X-ray–millimeter correlation
To quantitatively investigate a possible correlation and time delay between the X-ray and mm light curves, we applied several approaches commonly used in reverberation mapping campaigns (e.g., the SDSS-RM project; see Shen et al. 2024). Hereafter, positive time lags correspond to the X-ray flux variability preceding the mm flux. For the analysis, we used the full X-ray and mm light curves without trend subtraction. One of the most commonly used approaches to look for correlated variability is the interpolated cross-correlation function (CCF), which involves the linear interpolation of unevenly sampled light curves. Its modernized version PyMCCF (Gaskell & Sparke 1986; Oknyanskii 1993; Peterson et al. 1998; Oknyansky & Oknyansky 2022) optimizes interpolation to reduce noise occurring from interpolation errors, which minimizes the number of interpolated points used. The result of the PyMCCF analysis is shown as a gray curve in Fig. 5. The calculated CCF shows two peaks corresponding to time delays of 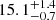 and
and 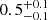 days (vertical dashed lines). The errors are estimated by calculating the 84.13th (+1σ) and 15.87th (−1σ) percentiles of a dataset.
days (vertical dashed lines). The errors are estimated by calculating the 84.13th (+1σ) and 15.87th (−1σ) percentiles of a dataset.
 |
Fig. 5. Results of the cross-correlation analysis of X-ray and mm data. The posterior distribution of the time lag provided by JAVELIN is illustrated by the red histogram. Two peaks at τ1 = −11.5 days (for the mm flux preceding the X-ray flux) and τ2 = 15.5 days are shown as vertical dashed lines. The result of PyMCCF is in gray with the 0.5-day time lag shown as a vertical dashed line. |
It has been shown that CCF-based methods can be less stable and efficient when the observational cadence is irregular (Li et al. 2019). This is the reason why tools such as JAVELIN (Zu et al. 2016; Yu et al. 2020) have been widely used. JAVELIN constructs a model of the flux variability utilizing the damped random walk (DRW), extracting posterior distributions for critical DRW parameters through MCMC sampling. Another iteration of MCMC allows JAVELIN to determine the posterior time delay distribution between the light curves comparing the constructed models. Applying the JAVELIN analysis to the IC 4329A data, we found two peaks in the posterior distribution of the time lag (see the histogram of 105 sampling iterations in Fig. 5), which are not identical to those identified by PyMCCF. We found two possible cases: a negative time lag τ1 = −11.5 ± 0.2 days and a positive time lag τ2 = 15.5 ± 0.9 days. The posterior distribution shows a larger and narrower peak at −11.5 days; however, the mm light curve shifted to −11.5 days does not fully overlap the X-ray light curve, so τ1 comes partially from the modeled variability behavior. In addition, the JAVELIN analysis generally provides a constraint on the width of a top-hat function. This quantity could be used to have an insight into the size of the structure responding to variable emission. However, for our dataset, we found no peak in the distribution of this parameter.
We also used the PyROA tool (Donnan et al. 2021) based on an approach similar to JAVELIN; the main difference is that the variability is described using a running optimal average. However, it appeared that for the given data series the PyROA code provides unstable results, dependent on the initial parameters of the model, and no clear estimation of a time lag can be obtained.
Generalizing the results obtained by various methods, we obtain three possible time delays: −11.5, 0.5, and 15.5 days. We note that 15 and 11 days are longer than the duration of the ALMA campaign, and 0.5 days is less than the cadence of the observations. Thus, the data is distorted by windowing and aliasing effects. While we will continue to analyze the light curves considering all three time lags, their reliability is questionable. Therefore, we will prioritize τ = 0.
4. Discussion
4.1. Evolution of mm/X-ray ratio and intrinsic scatter
Recently, for a volume-limited sample of radio-quiet hard X-ray selected AGN, Ricci et al. (2023) found a tight correlation between the observed X-ray (2–10 keV) and mm (100 GHz) emission, described by
where the fluxes are given in units of erg s−1 cm−2, with a scatter of 0.22 dex. From this correlation, the typical ratio of the 100 GHz continuum to the 2–10 keV emission is log(Fmm/FX − ray) = − 4.63 ± 0.06. In addition, a significant correlation between 230 GHz and 14–150 keV luminosities for 98 AGN was found by Kawamuro et al. (2022) with a scatter of ∼0.36 dex. In both cases, nonsimultaneous X-ray and mm observations were used, and thus the scatter observed in these correlations can be (at least partly) due to the intrinsic variability of the AGN. To investigate intrinsic scatter in the correlation, we studied the variations of the mm–to–X-ray ratio in our IC 4329A data given in the left column of panels 1 and 2 in Fig. 6. We note that while the original X-ray and mm data were obtained with a minor time difference of a few hours, sometimes the data points cannot be compared with each other unambiguously. Therefore, we interpolated the X-ray data to match the ALMA epochs. The evolution of log(Fmm/FX − ray) over time during the simultaneous mm and X-ray monitoring is shown in Fig. 6 (panel 3, left column). The scatter was estimated in two different ways. The first value, σ, was calculated relative to the time-averaged value of the flux ratio, which was found to be log(Fmm/FX − ray)≈ − 4.4, and is shown in black in panel 3 in Fig. 6. The second estimate, σ′, is calculated relative to the flux ratio expected from Eq. (2), using the mean X-ray flux log(Fmm/FX − ray)≈ − 4.5. Although σ′ is not the mathematically correct scatter, we present this value in red in panel 3 to highlight the deviation from Ricci et al. (2023), without further physical interpretation. The average observed ratio is in good agreement with the expected X-ray/100 GHz correlation. We estimate the scatters as σ = 0.11 dex and σ′ = 0.13 dex, respectively.
 |
Fig. 6. Variations of the mm/X-ray ratio during our observational campaign. The X-ray light curves shifted to the three time lags, τ = 0, −11.5, and +15.5 days (from left to right), are shown in panel (1), and the mm light curve is in panel (2). The ratio log(Fmm/FX − ray), where the X-ray light curve was interpolated to the ALMA epochs, is given in panel (3) for each of the time lags; the black dash-dotted line is the median value, and the red solid line corresponds to the relation between the 100 GHz and 2–10 keV fluxes from Ricci et al. (2023) with the 1σ scatter given by the dashed red lines. The IC 4329A epoch-to-epoch scatter (σ) is also presented in the figure: the scatter relative to the median is shown in black, while that relative to the predicted value is in red. Panel (4) contains the same values as panel (3), but as a function of the Eddington ratio λEdd. The color of the circles gives the date of the observation. |
The scatter σ is about two times smaller than that reported by Ricci et al. (2023). We can assume that the latter consists of two independent contributions: the nonsimultaneity of the observations, σns, and the intrinsic variability of the sources, σint. In this case the total value is the quadrature sum, 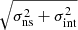 . In our observations of IC 4329A, the observed scatter should be solely due to intrinsic effects. This suggests that nonsimultaneous observations can introduce a significant contribution to the scatter in the mm/X-ray correlation, about 75%, due to the long-term variability of AGN, as discussed in Kawamuro et al. (2022).
. In our observations of IC 4329A, the observed scatter should be solely due to intrinsic effects. This suggests that nonsimultaneous observations can introduce a significant contribution to the scatter in the mm/X-ray correlation, about 75%, due to the long-term variability of AGN, as discussed in Kawamuro et al. (2022).
Since we have found a possible time delay between the mm and X-ray light curves, in Fig. 6 we show the mm/X-ray ratio both for the zero time lag and two more cases: τ = −11.5 and 15.5 days (middle and right column, respectively). In panel 1 the X-ray light curve is shifted according to the different τ; the unshifted mm light curve is in panel 2. We found that the scatter of the mm/X-ray ratio (panel 3) changes when we correct the light curves for the possible time shift. For τ = +15.5, the scatter relative to the median ratio log(Fmm/FX − ray) = − 4.3 is the same as for τ = 0: σ = 0.11 dex. However, the value σ′ is twice as large, 0.24 dex. It is also worth noting that the mm/X-ray ratio calculated using Eq. (2) is slightly lower compared to the cases of τ = 0 and τ = −11.5, as it was calculated using the median X-ray flux from panel 1. For τ = −11.5 days, the scatter becomes very small (σ = 0.05), and the median ratio coincides with that predicted by the correlation. The values of scatter calculated as the standard deviation relative to the mm/X-ray average and the value predicted from mm/X-ray correlation from Ricci et al. (2023) are illustrated in Fig. 6 for each time lag.
Together with the evolution of the mm/X-ray ratio in time, we also studied its variation with the Eddington ratio (λEdd). To calculate λEdd, we used the SMBH mass recently estimated for IC 4329A by reverberation mapping 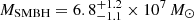 (Bentz et al. 2023), while the bolometric luminosity was calculated from the X-ray flux in the 2–10 keV range. We considered a comoving distance D = 69.3 Mpc (Koss et al. 2022). It can be shown that the 2–10 keV bolometric correction (κ2 − 10) is primarily a function of the Eddington ratio (Gupta et al., in prep.), and follows
(Bentz et al. 2023), while the bolometric luminosity was calculated from the X-ray flux in the 2–10 keV range. We considered a comoving distance D = 69.3 Mpc (Koss et al. 2022). It can be shown that the 2–10 keV bolometric correction (κ2 − 10) is primarily a function of the Eddington ratio (Gupta et al., in prep.), and follows
where C = 0.054 ± 0.034, B = 0.309 ± 0.095 and A = 1.538 ± 0.063. Using this approach we found that during joint ALMA/X-ray monitoring, the Eddington ratio changes from log(λEdd) = − 1.01 to −0.73 with a median value log(λEdd) = − 0.89 for τ = 0. The median bolometric correction is κ2 − 10 = 20.2. Although the κ2 − 10 could be tentative due to the large intrinsic dispersion, the obtained value of the bolometric correction is very close to the commonly used value κ = 20 from Vasudevan & Fabian (2009). In panel 4 of Fig. 6 we illustrate the relation between the mm/X-ray ratio and the Eddington ratio. The figure does not show a clear correlation between the mm/X-ray ratio and λEdd for the three different time lags.
It is important to note that while our calculated time delays show lower scatters compared to previous studies, we did not observe a clear correlation between X-ray and mm emission over the campaign duration, which is not surprising given the short duration of ALMA observations and coarse sampling. This suggests that unstable processes might dominate on the scale of days, leading to varied flux behaviors. The discovered tentative characteristic timescales selected by the periodogram and wavelet analysis also do not shed light on this correlation: the observed mm flares are spaced eight days apart, while the most probable (if any) X-ray oscillations occur with a five-day period. Despite the roughly constant flux ratio between mm and X-rays, it seems that different processes influence their variability on short timescales. With longer ALMA observations, we could better understand this flux correlation.
4.2. Comparison with other millimeter/X-ray monitoring campaigns
Simultaneous mm and X-ray studies of the variability of RQ AGN are still scarce, and only two such monitoring campaigns have been carried out. The first of these was dedicated to the RQ Seyfert 1 NGC 7469 located at the same distance as IC 4329A (z = 0.016) and having lower mass MSMBH ≈ 9.1 × 106 M⊙ (Peterson et al. 2014). This object was known for a significant variability at 95 GHz, by a factor of two within four to five days, as found in Combined Array for Research in Millimeter-wave Astronomy (CARMA) observations by Baldi et al. (2015). Later, Behar et al. (2020) provided the simultaneous mm/X-ray monitoring of NGC 7469. The observations were taken in the 0.3–10 keV range with Swift/XRT and in the mm band at 95 and 143 GHz frequencies with the Institut de Radioastronomie Millimetrique (IRAM) 30 m single-dish radio telescope. This monitoring lasted longer than our campaign (∼70 days in X-rays, of which ∼50 days of contemporaneous mm and X-ray observations) with a cadence of one to two days, but both the typical mm uncertainties (∼0.8 mJy) and beam sizes (∼17–28″) are considerably larger than those of our ALMA observations. Although Behar et al. (2020) stated a marginal correspondence of the measured mm flux with earlier observations with a smaller beam size ∼2.2″ at CARMA interferometer (Baldi et al. 2015), the mm/X-ray ratio observed for NGC 7469 is unexpectedly high: log(F95GHz/F2 − 10keV)≈ − 3.5, which could be, at least in part, explained by the low resolution of both the IRAM and CARMA data. The scatter associated with variability (σ = 0.12) appears consistent with that found for the current dataset from IC 4329A.
While Behar et al. (2020) provides a comprehensive analysis of the X-ray and mm variability in NGC 7469, we are reanalyzing these data using the same approaches applied to our IC 4329A data. This ensures a homogeneous analysis of the two datasets for a more accurate comparison. Using the wavelet analysis, we do not find any evidence of a periodicity in the X-ray light curve of NGC 7469. With regard to the time delay between X-ray and mm emission in the simultaneous NGC 7469 observations, Behar et al. (2020) cautiously stated that the mm variability appears to precede the X-ray flux by ∼14 days. We repeated the correlation analysis of NGC 7469 data using the same tools as described in Sect. 3.3. The PyROA and PyMCCF methods did not reveal any time lag, while the analysis done with the JAVELIN code confirmed the −14-day time lag. Moreover, we also discovered two more peaks in the posterior distribution, corresponding to 4.1 and 13.8 days. The correlation peaks at −14 and 13.8 days showed an amplitude approximately seven times lower than the peak at 4.1 days. Thus, as in the case of IC 4329A, we cannot clearly determine the presence and magnitude of the time delay between mm and X-rays. While in NGC 7469 this uncertainty could result from insufficient observational accuracy, a similar outcome for IC 4329A indicates that in both cases the relation between the bands is intricate, and shorter timescales of the variability need to be probed.
Behar et al. (2020) also examined the X-ray hardness ratios as a proxy of possible changes in the level of photo-electric absorption, which could give rise to the observed X-ray variability. However, neither the harder-when-dimmer trend, predicted by Behar et al. (2020) following Mehdipour et al. (2017), nor a significant correlation between mm flux and hardness ratio was observed in NGC 7469. Following Behar et al. (2020), we calculated the hardness ratio in terms of count rates for the NICER data for IC 4329A: HR = (H − S)/(H + S), where H is the count rate (count s−1) in the hard band (2.0–10.0 keV), and S is the count rate in the soft band (0.3–2.0 keV). We found that the HR does not vary significantly, and it does not show any correlation with the mm flux or mm spectral index changes.
A second simultaneous mm/X-ray campaign of an RQ AGN was recently reported by Petrucci et al. (2023) for MCG+08−11−11 (z = 0.02), a Seyfert 1 galaxy with a black hole mass comparable to that in IC 4329A, MSMBH ≈ 2.8 × 107 M⊙. The variability in the 3–10 keV X-ray band obtained by XMM-Newton and the 100 GHz flux inferred by NOEMA were studied on timescales of 14 hours. Both fluxes showed slight increases, corresponding to ∼1.06 times and ∼1.19 times for the mm and X-ray flux, respectively, but no correlated variability was found. Similarly to the NGC 7469 data, the mm/X-ray ratio is significantly higher than the mean value found for nearby AGN by Ricci et al. (2023): log(F100 GHz/F2 − 10 keV)≈ − 3.4 with σ = 0.12. Moreover, the mm/X-ray ratio previously measured in Behar et al. (2018) with comparable angular resolution in mm also appeared to be an order of magnitude higher than Ricci et al. (2023) predicted, yet the mm flux was 2.4 times lower (∼7.5 mJy instead of ∼18.3 mJy). It is likely that such a high mm/X-ray ratio is due to the relatively low resolution of the mm observations (∼1″ according to the data archive), for which other components emitting in mm may contribute to the measured flux. Therefore, the observed mm variability might be more contaminated by nonvariable extended emission. This highlights the critical importance of utilizing ALMA, not only to achieve higher accuracy of the flux measurement (two times better than the NOEMA data for MCG+08−11−11 and 50 times better than the IRAM data for NGC 7469), but also to isolate the flux coming from the compact structure in the core thanks to the < 0 1 resolution.
1 resolution.
Interestingly, the simultaneous monitoring campaigns presented in Behar et al. (2020) and Petrucci et al. (2023), as well as our results for IC 4329A, although they have different measured mm/X-ray ratios, showed a similar scatter in the variations of this ratio (∼0.12 dex). In all cases, this scatter is a factor of ∼2 lower than that found by Ricci et al. (2023) for the nonsimultaneous mm and X-ray data. Thus, we can argue that ∼75% of the scatter in Ricci et al. (2023) is due to the nonsimultaneity of the mm and X-ray observations, while the remaining ∼25% of the scatter could be intrinsic, and associated with the different physical drivers of variability on the short (daily) timescale, or due to the possible time lag between X-rays and mm. However, unlike in the IC 4329A monitoring, a smaller scatter in the NGC 7469 and MCG+08−11−11 observations may also be related to the contribution from extended nonvariable mm radiation, which is why a direct comparison of the scatters is not entirely correct. This once again shows the importance of using high spatial resolution mm observations.
While no clear evidence of correlated mm/X-ray variability was found for NGC 7469 and MCG+08−11−11, the two AGN showed significant variations in both bands during the monitoring campaigns: 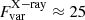 % and
% and 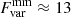 % for NGC 7469 (with the maximum amplitude of a factor of 2 between days), and
% for NGC 7469 (with the maximum amplitude of a factor of 2 between days), and 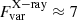 % and
% and 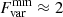 %2 for MCG+08−11−11. In both cases, the X-ray fractional variability was larger than that in the mm band. However, our data for IC 4329A showed the opposite:
%2 for MCG+08−11−11. In both cases, the X-ray fractional variability was larger than that in the mm band. However, our data for IC 4329A showed the opposite: 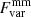 is approximately twice as large as
is approximately twice as large as 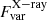 . The mm flux of IC 4329A also showed a significant flare, during which the flux increased by a factor of ∼3 within four to five days, which was not observed before in other RQ AGN. A similar finding was recently reported by Michiyama et al. (2024) for the RQ AGN GRS 1734-292, an unexpected source of GeV emission. ALMA observations at 100 GHz with ∼0
. The mm flux of IC 4329A also showed a significant flare, during which the flux increased by a factor of ∼3 within four to five days, which was not observed before in other RQ AGN. A similar finding was recently reported by Michiyama et al. (2024) for the RQ AGN GRS 1734-292, an unexpected source of GeV emission. ALMA observations at 100 GHz with ∼0 2 resolution revealed the 1.6 times flux change in four days. The amount of data showing mm variability is still limited, so it is challenging to define whether the observed variations of IC 4329A and other RQ AGN are a specific characteristic of the source or are typical, but not observed in the existing mm observations of NGC 7469 and MCG+08−11−11 for some reason. In any case, it is evident that further high spatial resolution variability studies in the mm band are necessary to identify, at the very least, the characteristics of mm variability in RQ AGN.
2 resolution revealed the 1.6 times flux change in four days. The amount of data showing mm variability is still limited, so it is challenging to define whether the observed variations of IC 4329A and other RQ AGN are a specific characteristic of the source or are typical, but not observed in the existing mm observations of NGC 7469 and MCG+08−11−11 for some reason. In any case, it is evident that further high spatial resolution variability studies in the mm band are necessary to identify, at the very least, the characteristics of mm variability in RQ AGN.
4.3. Extended millimeter structure
As discussed in Sect. 3.2 and shown in Fig. 4, high spatial resolution ALMA observations of IC 4329A revealed a distant structure in addition to the bright variable unresolved core in the observed mm region. Our observations show that the flux of the extended mm structure is constant at ∼0.6 mJy within the errors during the ten-day campaign. Since the bright variable core and the faint extended structure are clearly resolved in the ALMA maps, the linear distance between them projected onto the celestial plane is on the order of 10 pc.
Given the edge-on orientation of the host galaxy of IC 4329A, the observed emission may be non-nuclear while appearing projected onto the circumnuclear region. In such a scenario it might originate in structures unrelated to the AGN, such as HII regions or supernova remnants. Nonetheless, the mm observations from the literature suggest that none of them can yield substantial flux. The anticipated flux from HII regions at redshift z = 0.016 is merely a few μJy when scaling data from Sabbatini & Cavaliere (2005). Similarly, the expected flux from recent supernovae is < μJy, as derived from the SN 1987A (Lakićević et al. 2011) and Cas A (Wright et al. 1999; Loinard et al. 2003) data. Therefore, a non-AGN origin of the extended structure is not plausible.
The extended structure is possibly associated with the radio jet of IC 4329A, which is detected at lower frequencies (see Inoue & Doi 2018). The VLA images with a resolution of 1 5 × 0
5 × 0 9 at 1.5 GHz and 1
9 at 1.5 GHz and 1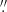 3 × 1
3 × 1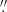 2 at 4.9 GHz from Unger et al. (1987) revealed a bright radio flux. However, the jet extends ∼6″ to the west, 180° opposite to our current mm band observations. Moreover, according to Inoue & Doi (2018), the expected mm emission from the jet is considerably higher. Extrapolating from the radio data yields a flux density of ∼3.3 mJy at 100 GHz, which is five times higher than the observed emission. It is intriguing that we detect no evidence of a jet structure in the mm band to the west of the core. This suggests that the mm emission from the jet is either concentrated in a very compact and confined region within the unresolved central component, or it could indicate that the jet structure at mm wavelengths differs significantly from that observed at lower frequencies, so extrapolating the mm flux of the jet from radio emission may not be straightforward.
2 at 4.9 GHz from Unger et al. (1987) revealed a bright radio flux. However, the jet extends ∼6″ to the west, 180° opposite to our current mm band observations. Moreover, according to Inoue & Doi (2018), the expected mm emission from the jet is considerably higher. Extrapolating from the radio data yields a flux density of ∼3.3 mJy at 100 GHz, which is five times higher than the observed emission. It is intriguing that we detect no evidence of a jet structure in the mm band to the west of the core. This suggests that the mm emission from the jet is either concentrated in a very compact and confined region within the unresolved central component, or it could indicate that the jet structure at mm wavelengths differs significantly from that observed at lower frequencies, so extrapolating the mm flux of the jet from radio emission may not be straightforward.
It turned out that the observed flux in the extended mm structure closely matches the expected emission from the photoionized gas in the ionization cone of the narrow-line region. In this region, mm emission is anticipated as a result of free–free emission (see Panessa et al. 2019; Baskin & Laor 2021). Previous studies of IC 4329A have identified features of the ionization cone, which align with the extended low-frequency radio jet observed in VLA data (Colbert et al. 1996; Thomas et al. 2017). Following Baskin & Laor (2021), we estimated the mm flux using the relation log νL100 GHz = log L[OIII] − 3.36, where the [OIII] flux F[OIII] = 2.34 ⋅ 10−13 and the intrinsic reddening factor 9.5 are from Bentz et al. (2023). We find the apparent flux F100 GHz ≈ 1 mJy. To provide a conclusive assessment, checking the spectral slope is essential. As the structure is relatively faint, evaluating its spectral parameters at a single epoch was challenging. Therefore, we combined all ten epochs of ALMA observations at each frequency into unified datasets. The analysis of these data revealed a spectral slope of the extended structure to be −1.1 ± 0.4, indicative of synchrotron rather than free-free emission. These findings hinder our ability to definitively determine the origin of this structure, emphasizing the necessity for further mm observations.
4.4. Millimeter variability and its origin
One of the key findings of the monitoring is the remarkable variability exhibited by the compact mm source in IC 4329A. Previous studies lacked mm monitoring data for IC 4329A, with only limited ALMA observations. Imanishi et al. (2016) reported a continuum flux of 13.0 mJy at 260 GHz with a 1 × 0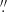 5 beam in April 2014. Subsequent observations in October 2016 published by Inoue & Doi (2018) across the 90.5–231 GHz range revealed a frequency-dependent flux, ranging from 8 to ∼5 mJy, with spatial resolution between 0
5 beam in April 2014. Subsequent observations in October 2016 published by Inoue & Doi (2018) across the 90.5–231 GHz range revealed a frequency-dependent flux, ranging from 8 to ∼5 mJy, with spatial resolution between 0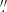 45 and 0
45 and 0 14. Thus, during the ten days of our ALMA monitoring, we captured the full historical range of flux variations, with a flux change of 2.6 within just four to five days.
14. Thus, during the ten days of our ALMA monitoring, we captured the full historical range of flux variations, with a flux change of 2.6 within just four to five days.
The observed mm changes are quite surprising. Traditionally, the largest amplitude of variability in nonblazar AGN on timescales of less than a month has been observed in the X-ray range, as demonstrated by numerous multiwavelength variability campaigns (e.g., Edelson et al. 2000, 2015). However, during our campaign, IC 4329A exhibited more variability in the mm band than in X-rays, as discussed in our comparison of Fvar in Sect. 4.2. In the optical band, IC 4329A also exhibits no significant variations: long-term V-band observations showed only 1.5 times the variability (Bentz et al. 2023), and no intranight changes were detected in recent high-cadence photometric monitoring3. Based on the factor of ∼3 variability, we can rule out two of the most stable mechanisms of the mm origin: thermal dust and free–free emission.
The dust contribution in IC 4329A is constrained to be at least two orders of magnitude lower than the observed flux at 100 GHz (Fig. 6), less than 1.6 × 10−2 mJy (Inoue & Doi 2018). More importantly, the observed mm spectral slope of ∼ − 0.2 is inconsistent with the dust scenario, where a spectral index of ∼3.5 would be expected (e.g., Mullaney et al. 2011). The estimated brightness temperature Tb from the mm flux density following Eq. (1.34) from Wilson et al. (2013): Tb ≈ 200 ± 100 K is also higher than predicted from the SED fitting by Mehdipour & Costantini (2018).
In some AGN, such as NGC 1068, a significant fraction of mm emission is described by the free–free emission coming from the winds or X-ray-heated disk gas (Gallimore et al. 2004; Inoue et al. 2020). While the observed spectral slope in IC 4329A is consistent with that expected for free–free processes, the flux density and its rapid variations exclude this mechanism. Laor & Behar (2008) demonstrated that the contribution of thermal free–free emission from hot X-ray plasma in the corona is negligible. The free–free emission can originate from the dusty torus in AGN. The torus size measured in IC 4329A is on the order of a few hundred light days (ld; 0.15–0.19 pc Kishimoto et al. 2011; GRAVITY Collaboration 2023), and as Baskin & Laor (2021) suggested, the expected variations of the free–free emission originating there should occur on a yearly timescale rather than within days.
Therefore, the preferable mm emission mechanism is nonthermal synchrotron produced in a compact region: since the flux changed by more than 3σ from one day to another, we can assume the mm source size is smaller than 1 ld (∼0.0008 pc). The observed nearly flat spectrum with a slope of −0.23 suggests that the observed frequency is near the turnover between optically thick (α = 2.5) and optically thin (α < −0.5) regime. Below, we discuss the estimation of the synchrotron source size and the emission origin.
4.5. Synchrotron emission
In Sect. 4.4 we estimate the mm emitter size as ∼1 ld. This estimation aligns perfectly with the optically thick synchrotron source size derived under the assumption of equipartition between magnetic energy density and photon energy density, as introduced by Laor & Behar (2008):
Here L100 GHz is the mm luminosity in units of 1030 erg s−1 Hz−1, Lbol is the bolometric luminosity in units of 1030 erg s−1, and ν is the observed frequency in GHz. Using the bolometric luminosity calculated in Sect. 4.1 we obtain the source size 1.0 ± 0.1 ld. In the more common case, the physical size of a self-absorbed synchrotron source R is the function of the radio flux density and the magnetic field strength B (Laor & Behar 2008; Petrucci et al. 2023),
where Fmm is in mJy and z is the source redshift. In Fig. 7 we present this relation as the R–B diagram. The mm flux of IC 4329A varied within the range of ∼3–10 mJy. Assuming the emission region size does not exceed 1 ld, we estimate the constraint on the permissible maximum magnetic field strength of 200 G for the minimum flux. The minimum magnetic field value can be estimated following Laor & Behar (2008), assuming that synchrotron cooling dominates over other cooling processes. Thus,
where tvar day is the variability timescale in seconds. We obtained the limiting value Blim = 7.5 G, leading to R > 0.4 ld for the minimum flux. These constraints significantly limit the permissible parameter space of the mm emitter. In particular, if the source flux is 10 mJy, its size must lie within 0.8–1 ld, and the magnetic field must range between 7.5–18 G. We caution that there is additional uncertainty to these numbers as the source is not deep in the optically thick regime at 100 GHz (as the observed spectral slope is −0.23), but this should still provide a valid zero-order estimate of the emitter size and magnetic field.
 |
Fig. 7. Dependence of the mm flux density at 100 GHz on the source size and magnetic field strength for z = 0.016. The dashed horizontal line illustrates the region of source sizes ≥1 ld. The dashed vertical line delineates the range where the magnetic field ≤Blim. The region between the refined values of R and B for the optically thick synchrotron regime and the observed flux of IC 4329A is highlighted in yellow. |
Further, we discuss several possible synchrotron mechanisms of mm emission origin following Kawamuro et al. (2022). Here we address a more detailed modeling that does not require the assumption of an optically thick spectrum.
4.5.1. Synchrotron emission from outflow-driven shocks
One of the possible explanations for the tight mm/X-ray correlation observed in RQ AGN is synchrotron emission from electrons accelerated in the shock produced by an AGN outflow colliding with the surrounding interstellar medium. Kawamuro et al. (2022) showed that the expected conversion of the kinetic energy of the outflow into synchrotron emission of the relativistic particles (Nims et al. 2015) is consistent with the results found, specifically in the case of AGN with ultrafast X-ray outflows.
The kinetic energy of the outflow is derived from the bolometric luminosity of the AGN, and it is anticipated that more luminous AGN expel more energetic outflows (see Kawamuro et al. 2022, for references). Thus, a correlation between the mm/X-ray ratio and the Eddington ratio is expected. Kawamuro et al. (2022) reported the absence of such a correlation for the AGN sample. In IC 4329A, where the ultra-fast outflow was found (Tombesi et al. 2012; Tortosa et al. 2024), we also did not find any relation between the mm/X-ray ratio and λEdd for either τ = 0 or −11.5 days. Nevertheless, in the case of τ = +15.5 days, a faint correlation can be assumed with the Pearson coefficient of ∼0.65 (see Fig. 6). However, +15.5-day time lag seems inconsistent, as Tombesi et al. (2012) and Tortosa et al. (2024) discovered the outflow location in the range of 1.5–12 ld from the core. Moreover, 1.5–12 ld scales of the outflow exceed the expected size of the mm source and, as we show later, should produce optically thin emission at 100 GHz (see details in Sect. 4.5.3).
4.5.2. Synchrotron emission from jet
Kawamuro et al. (2022) investigated the potential contribution of the jet to the mm emission and found no discernible difference between type 1 and type 2 AGN, suggesting that the jet does not dominate the mm band. However, in IC 4329A, the jet still appears to contribute. As previously noted, extrapolating data from Inoue & Doi (2018) yielded a mm flux from the jet at 100 GHz of ∼3.3 mJy. Interestingly, the source flux has never been observed below this value, implying a significant contribution from the jet in the flux minimum.
However, the jet is unlikely to contribute to the mm variability significantly. The main argument here is that the observed radio jet in IC 4329A exhibits a spectral slope of approximately −0.59 ± 0.09 (in the 1.4–43.3 GHz range, Inoue & Doi 2018). The spectral slope of the mm emission is much flatter and never exhibits a spectral index as negative as the jet component. Furthermore, there is no indication that the spectral slope becomes more negative as the flux increases (see Fig. 3). Additionally, the daily scale variability seems inconsistent with the activity of the radio jet with the typical scale exceeding several kpc. However, it is worth noting that rapid variability may originate from a compact jet even in nonblazar AGN (e.g., Smith & Sartori 2023), and thus this requires additional study. These findings suggest that the contribution of the jet to the mm emission is limited and possibly exhibits slower changes compared to the observed mm variability.
At present, the jet scenario is not favored. However, determining the exact contribution of the jet to the mm flux and whether this contribution is variable remains an intriguing open question, necessitating simultaneous observations at lower radio frequencies and in the mm band.
4.5.3. Synchrotron emission from X-ray corona
As shown by Behar et al. (2018), the mm excess observed in many RQ AGN cannot be extrapolated from the radio data. In Sect. 4.5.2 we demonstrate that, in the case of IC 4329A, the minimum of the flux aligns well with the radio observations. However, this cannot fully account for the observed variability and the mm excess in IC 4329A during its maximum.
Inoue & Doi (2014) proposed a scenario in which nonthermal relativistic electrons produce mm emission in the magnetized X-ray corona. The model was further investigated by Inoue & Doi (2018), predicting that synchrotron emission peaks in the mm band, at ∼100–300 GHz or even lower (as in the case of, e.g., NGC 985), due to synchrotron self-absorption (SSA). The SSA scenario was also preferred by Kawamuro et al. (2022, see their Fig. 25). For IC 4329A, we found a flatter spectral slope than the average of the sample in Kawamuro et al. (2022) (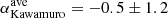 ), which can be explained by the lower central frequency of these observations (100 GHz instead of 230 GHz), where SSA is higher and the emission is more optically thick.
), which can be explained by the lower central frequency of these observations (100 GHz instead of 230 GHz), where SSA is higher and the emission is more optically thick.
In this scenario, synchrotron emissivity is a function of the electron spectrum and the magnetic field strength and size of the corona. Thus, to produce the observed rapid variability on timescales of days, fast changes in the physical properties of the corona are required. To explore this in greater detail, we introduced a corona emission model based on Inoue & Doi (2018) and Margalit & Quataert (2021) (see details in del Palacio et al., in prep.). This model has several parameters to characterize the coronal properties and the nonthermal electron distribution in it. Specifically, the parameters include the temperature, electron density, size of the corona, the fraction of energy in the magnetic field and nonthermal electrons, and the spectral index of the relativistic electron energy distribution. Most of these parameters affect the SED in a similar way, increasing both the peak frequency and the peak flux (due to increasing SSA opacity and synchrotron emissivity). The only parameter that increases the flux while decreasing the peak frequency is the size of the corona, with a larger size yielding a more diluted (and thus transparent) electron population. As usually done, we parameterize the size as Rc = rcRg, where Rg ∝ MSMBH is the gravitational radius. Thus, if the flux varies and the spectral index remains flat, the size must change. Otherwise, the emission would get a more positive spectral index when it is brighter, which is not observed (Fig. 3).
To reduce the number of free parameters, we link the magnetic field strength to the nonthermal electron population by adopting a scaling between the energy density in the magnetic fields and in nonthermal electrons, namely ηB = UB/Unt, e = 40. This is motivated by the fact that the heating source of the corona is assumed to be related to magnetic reconnection events. We then allow the parameters rc and δ = Unt, e/Uth, e (fraction of the energy in nonthermal electrons with respect to the thermal electrons) to vary, while we fix the remaining parameters of the corona, kT = 200 keV, τT = 0.43, and p = 2.5 (relativistic electron distribution); we also parameterize the dust emission as a modified blackbody spectrum (Sν ∝ ν2 + β for ν ≤ ντ = 1 and Sν ∝ ν2 for ν > ντ = 1) with fixed parameters β = 1.6 and ντ = 1 = 800 GHz, and also fix the spectral index of the diffuse synchrotron emission to α = −0.6. We note that the diffuse components are very poorly constrained due to the lack of observations with comparable resolution at other frequencies. Given that low-resolution observations probe larger volumes in the galaxy, and thus capture more emission, the fluxes from archival low-resolution observations (Inoue & Doi 2018, and references therein) represent strict upper limits to the flux coming from the inner region probed by the high-resolution ALMA observations. In Fig. 8 we present the SED fitting of IC 4329A during two days that show the highest variability. We obtain that the corona expanded from rc ≈ 179 ± 54 (Rc ≈ 0.7 ld) during the minimum (MJD 59461.4) to rc ≈ 368 ± 60 (Rc ≈ 1.4 ld) during the maximum (MJD 59464.3) with the magnetic field strength decreasing from 10.4 to 7.5 G and the fraction of nonthermal electrons remaining constant (log δ ≈ −2.6 ± 0.2). The change in the size of the corona of ∼0.7 ld in three days would require a very fast expansion velocity of ∼0.2 c, which could be consistent with the outflowing corona scenario (e.g., Kylafis et al. 2023). A similar conclusion was reached by Ingram et al. (2023), who also favored an outflowing corona interpretation in IC 4329A based on IXPE data.
 |
Fig. 8. Multifrequency SED fitting of IC 4329A during the flux minimum and maximum. The black points represent the high-resolution ALMA data (this work), whereas the red arrows are the fluxes from low-resolution radio and infrared observations (Inoue & Doi 2018, and references therein), which in the context of the fitting procedure represent strict upper limits to the total flux coming from the nuclear region probed by ALMA. The different emission components in the model and their 1σ confidence intervals are marked, together with the total emission. The coronal component dominates the 100 GHz emission, and the diffuse synchrotron and dust emission components are poorly constrained. The bottom subpanels show the fitting residuals. |
In summary, our preferred scenario attributes the mm variability and tight X-ray/mm ratio to a compact X-ray corona. However, in this scenario, as well as in the jet and outflow scenarios, no time lag is expected. The 11.5-day and 15.5-day time lags pose challenges as we struggle to envision how the source could accumulate and later reradiate energy in mm or X-rays within such time frames. Treating these time lags as light travel times is not a satisfactory explanation as it would require the sources to be separated by a distance approximately equivalent to the broad-line region (BLR), which is about 16 ld (Bentz et al. 2023). Within our current understanding of the mm source, a zero time lag (τ = 0) seems to be more plausible.
Additionally, none of the discussed mechanisms accounts for the five-day timescale variations observed in X-rays and their absence in mm. The distinct variability patterns over several days hint at the potential for common X-ray and mm variability on longer timescales (weeks), while the daily timescale variations suggest differences in short-term processes between X-rays and mm, possibly involving distinct electron populations. Furthermore, investigating X-ray variability showing local periodic changes independently holds interest, given that X-rays are generally known for stochastic variability. However, comparing X-ray periods with known timescales in IC 4329A fails to provide insights into their physical origin.
5. Conclusions
We observed the RQ unobscured type 1 AGN IC 4329A to investigate the origin and properties of the compact mm emission in RQ AGN. The source was observed daily for 40 days in the 2–10 keV X-ray band using XMM-Newton, Swift, and NICER. Within this campaign, we contemporaneously obtained ten epochs of high-resolution mm observations with daily cadence using ALMA at ∼100 GHz frequency. Unlike previous contemporaneous mm/X-ray campaigns (Behar et al. 2020; Petrucci et al. 2023), the outstanding capabilities of ALMA enabled us to isolate the compact mm emission from the potential contributions of other components of the active galaxy and to observe the surprising behavior of the mm emission in the RQ AGN.
The recent results of the tight mm/X-ray correlation in RQ AGN by Ricci et al. (2023) and Kawamuro et al. (2022) suggested the common origin of the mm and X-ray emission most likely in the X-ray corona. Thus, we expected to discover a correlated behavior of both fluxes on a daily timescale. However, we did not find statistically robust evidence of the correlated variability, and distinct variability patterns were observed in each band. Our findings can be summarized as follows:
-
The observed ratio between X-ray (2–10 keV) and mm (100 GHz) aligns with the tight correlation reported in Kawamuro et al. (2022), Ricci et al. (2023). Moreover, our simultaneous observations indicate a reduced scatter in this ratio, measuring ∼0.1 dex instead of the 0.22 dex (Ricci et al. 2023). This suggests that ∼75% of the previously observed scatter is due to the nonsimultaneity of the observations, while the rest may arise from intrinsic processes in the AGN.
-
During the ten-day campaign, the compact mm emission exhibited significant variability by a factor of three within four to five days, with an amplitude surprisingly larger than in X-rays. This rules out the heated dust and thermal free–free emission origin, indicating a synchrotron origin for the mm radiation. The in-band spectral slope −0.23 ± 0.18 suggests that the observed emission is close to the SSA turnover frequency. The SED fitting modeling suggests a source size of ∼1 ld (∼120 gravitational radii), consistent with size estimations from the variability timescale, and a magnetic field strength of ∼5–7 G. The observed variability and spectral indices require the emitter size to change in time.
-
The combined analysis of the 40-day X-ray (2–10 keV) and ten-day mm (100 GHz) light curves suggests no reliable time lag. Additionally, the tentative oscillations on the five-day timescale observed in X-rays at the 95% confidence level are not evident in the mm variability.
-
The high resolution of ALMA (up to ∼0
 05) allowed us to resolve the variable bright core together with the faint and nonvariable mm structure 10 pc from the nucleus. The measured flux and the position of the nonvariable component indicate that its emission likely originates in the ionization cone of the narrow-line region; however, the estimated spectral slope −1.1 ± 0.4 contradicts it and suggests the synchrotron nature of the structure.
05) allowed us to resolve the variable bright core together with the faint and nonvariable mm structure 10 pc from the nucleus. The measured flux and the position of the nonvariable component indicate that its emission likely originates in the ionization cone of the narrow-line region; however, the estimated spectral slope −1.1 ± 0.4 contradicts it and suggests the synchrotron nature of the structure.
The evidence (flux density, flat/negative spectral index, daily variability) strongly suggests that the observed mm radiation has a nonthermal synchrotron nature and originates from a compact source. This is closely consistent with the idea that, as suggested by Inoue & Doi (2014) and mm/X-ray correlations, the mm emission is produced in a compact X-ray corona. Future simultaneous radio, mm, and X-ray observations, possibly covering more ALMA bands and longer timescales, as well as mm polarization observations, will help to elucidate the physical processes in the compact mm emitting region observed in RQ AGNs.
The observations were obtained on April 3 and 4 with the 1m telescope of the SPECULOOS Southern Observatory (Jehin et al. 2018). During each night, we carried out nonstop nine-hour observations with a one-minute cadence in the g-sdss band. The estimated magnitude of the source in a 4″ aperture is 15.12±0.02 mag, with no host-galaxy subtraction.
Acknowledgments
We are grateful to the ALMA, NICER and XMM-Newton teams for their invaluable help in coordinating the joint mm/ALMA observations. We sincerely thank Ari Laor for the comments and fruitful discussion. SdP thanks Chentao Yang for his contributions to the model fitting code. ES acknowledges ANID BASAL project FB210003 and Gemini ANID ASTRO21-0003. CR acknowledges support from Fondecyt Regular grant 1230345 and ANID BASAL project FB210003. SdP and SA gratefully acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 789410, PI: S. Aalto). AT acknowledges financial support from the Bando Ricerca Fondamentale INAF 2022 Large Grant ‘Toward a holistic view of the Titans: multi-band observations of z > 6 QSOs powered by greedy supermassive black holes’. TK is grateful for support from RIKEN Special Postdoctoral Researcher Program and is supported by JSPS KAKENHI Grant number JP23K13153. We gratefully acknowledge funding for this work by ANID through the Millennium Science Initiative Program - ICN12_009 (FEB), CATA-BASAL - FB210003 (FEB), and FONDECYT Regular - 1200495 (FEB). LCH was supported by the National Science Foundation of China (11991052, 12011540375, 12233001), the National Key R&D Program of China (2022YFF0503401), and the China Manned Space Project (CMS-CSST-2021-A04, CMS-CSST-2021-A06). The material is based upon work supported by NASA under award number 80GSFC21M0002 (ML). FT acknowledges funding from the European Union - Next Generation EU, PRIN/MUR 2022 (2022K9N5B4). The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
References
- Alhosani, A., Gelfand, J. D., Zaw, I., et al. 2022, ApJ, 936, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Arzoumanian, Z., Gendreau, K. C., Baker, C. L., et al. 2014, SPIE Conf. Ser., 9144, 914420 [Google Scholar]
- Baldi, R. D., Behar, E., Laor, A., & Horesh, A. 2015, MNRAS, 454, 4277 [Google Scholar]
- Baskin, A., & Laor, A. 2021, MNRAS, 508, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Behar, E., Baldi, R. D., Laor, A., et al. 2015, MNRAS, 451, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Behar, E., Vogel, S., Baldi, R. D., Smith, K. L., & Mushotzky, R. F. 2018, MNRAS, 478, 399 [CrossRef] [Google Scholar]
- Behar, E., Kaspi, S., Paubert, G., et al. 2020, MNRAS, 491, 3523 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Onken, C. A., Street, R., & Valluri, M. 2023, ApJ, 944, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [Google Scholar]
- Chen, S., Kharb, P., Silpa, S., et al. 2024, ApJ, 963, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Colbert, E. J. M., Baum, S. A., Gallimore, J. F., et al. 1996, ApJS, 105, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Donnan, F. R., Horne, K., & Hernández Santisteban, J. V. 2021, MNRAS, 508, 5449 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Koratkar, A., Nandra, K., et al. 2000, ApJ, 534, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Gelbord, J. M., Horne, K., et al. 2015, ApJ, 806, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [Google Scholar]
- Gabriel, C., Denby, M., Fyfe, D. J., et al. 2004, ASP Conf. Ser., 314, 759 [Google Scholar]
- Gallimore, J. F., Baum, S. A., & O’Dea, C. P. 2004, ApJ, 613, 794 [Google Scholar]
- Gaskell, C. M., & Sparke, L. S. 1986, ApJ, 305, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [Google Scholar]
- Gendreau, K. C., Arzoumanian, Z., & Okajima, T. 2012, SPIE Conf. Ser., 8443, 844313 [Google Scholar]
- Gendreau, K. C., Arzoumanian, Z., Adkins, P. W., et al. 2016, SPIE Conf. Ser., 9905, 99051H [NASA ADS] [Google Scholar]
- GRAVITY Collaboration (Amorim, A., et al.) 2023, A&A, 669, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guedel, M., & Benz, A. O. 1993, ApJ, 405, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, T. R., Indebetouw, R., Brogan, C. L., et al. 2023, PASP, 135, 074501 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., Nakanishi, K., & Izumi, T. 2016, AJ, 152, 218 [Google Scholar]
- Ingram, A., Ewing, M., Marinucci, A., et al. 2023, MNRAS, 525, 5437 [CrossRef] [Google Scholar]
- Inoue, Y., & Doi, A. 2014, PASJ, 66, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, Y., & Doi, A. 2018, ApJ, 869, 114 [Google Scholar]
- Inoue, Y., Khangulyan, D., & Doi, A. 2020, ApJ, 891, L33 [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2018, Messenger, 174, 2 [NASA ADS] [Google Scholar]
- Kawamuro, T., Ricci, C., Imanishi, M., et al. 2022, ApJ, 938, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamuro, T., Ricci, C., Mushotzky, R. F., et al. 2023, ApJS, 269, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Antonucci, R., et al. 2011, A&A, 527, A121 [CrossRef] [EDP Sciences] [Google Scholar]
- Koss, M. J., Ricci, C., Trakhtenbrot, B., et al. 2022, ApJS, 261, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kylafis, N. D., Reig, P., & Tsouros, A. 2023, A&A, 679, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lakićević, M., van Loon, J. T., Patat, F., Staveley-Smith, L., & Zanardo, G. 2011, A&A, 532, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laor, A., & Behar, E. 2008, MNRAS, 390, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Li, I.-H. J., Shen, Y., Brandt, W. N., et al. 2019, ApJ, 884, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Lequeux, J., Tilanus, R. P. T., & Lagage, P. O. 2003, Rev. Mex. Astron. Astrofis. Conf. Ser., 15, 267 [NASA ADS] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Margalit, B., & Quataert, E. 2021, ApJ, 923, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Mehdipour, M., & Costantini, E. 2018, A&A, 619, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mehdipour, M., Kaastra, J. S., Kriss, G. A., et al. 2017, A&A, 607, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merloni, A., & Fabian, A. C. 2001a, MNRAS, 328, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., & Fabian, A. C. 2001b, MNRAS, 321, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Michiyama, T., Inoue, Y., Doi, A., et al. 2024, ApJ, 965, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Morlet, J. 1983, Sampling Theory and Wave Propagation (Springer Berlin Heidelberg), 233 [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Goulding, A. D., & Hickox, R. C. 2011, MNRAS, 414, 1082 [Google Scholar]
- Nims, J., Quataert, E., & Faucher-Giguère, C.-A. 2015, MNRAS, 447, 3612 [NASA ADS] [CrossRef] [Google Scholar]
- Oknyanskii, V. L. 1993, Astron. Lett., 19, 416 [NASA ADS] [Google Scholar]
- Oknyansky, V., & Oknyansky, R. 2022, Astrophysics Source Code Library [record ascl:2212.007] [Google Scholar]
- Panessa, F., Baldi, R. D., Laor, A., et al. 2019, Nat. Astron., 3, 387 [Google Scholar]
- Peterson, B. M., Wanders, I., Horne, K., et al. 1998, PASP, 110, 660 [Google Scholar]
- Peterson, B. M., Grier, C. J., Horne, K., et al. 2014, ApJ, 795, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P. O., Piétu, V., Behar, E., et al. 2023, A&A, 678, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2004, MNRAS, 351, 161 [Google Scholar]
- Raginski, I., & Laor, A. 2016, MNRAS, 459, 2082 [CrossRef] [Google Scholar]
- Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017, ApJS, 233, 17 [Google Scholar]
- Ricci, C., Loewenstein, M., Kara, E., et al. 2021, ApJS, 255, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Chang, C.-S., Kawamuro, T., et al. 2023, ApJ, 952, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbatini, L., Cavaliere, F., dall’Oglio, G., et al. 2005, A&A, 439, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Shen, Y., Grier, C. J., Horne, K., et al. 2024, ApJS, 272, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. L., & Sartori, L. F. 2023, ApJ, 958, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, A. D., Dopita, M. A., Shastri, P., et al. 2017, ApJS, 232, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., & Braito, V. 2012, MNRAS, 422, L1 [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, BAMS, 79, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Tortosa, A., Ricci, C., Shablovinskaia, E., et al. 2024, A&A, 687, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unger, S. W., Lawrence, A., Wilson, A. S., Elvis, M., & Wright, A. E. 1987, MNRAS, 228, 521 [NASA ADS] [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2009, MNRAS, 392, 1124 [CrossRef] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [Google Scholar]
- Wang, A., An, T., Zhang, Y., et al. 2023, MNRAS, 525, 6064 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., Rohlfs, K., & Hüttemeister, S. 2013, Tools of Radio Astronomy (Berlin: Springer Berlin Heidelberg) [Google Scholar]
- Wright, M., Dickel, J., Koralesky, B., & Rudnick, L. 1999, ApJ, 518, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Z., Kochanek, C. S., Peterson, B. M., et al. 2020, MNRAS, 491, 6045 [CrossRef] [Google Scholar]
- Zu, Y., Kochanek, C. S., Kozłowski, S., & Peterson, B. M. 2016, ApJ, 819, 122 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Data
ALMA data.
X-ray data in 2–10 keV range (except NICER epoch marked with the asterisk, where the data is given for 0.7–7 keV range).
All Tables
X-ray data in 2–10 keV range (except NICER epoch marked with the asterisk, where the data is given for 0.7–7 keV range).
All Figures
 |
Fig. 1. X-ray and mm-band light curves. From top to bottom: X-ray (2–10 keV) flux with fitted power-law model, 2–10 keV flux deviations from the long-term trend, and 3 mm (97.5 GHz) flux density. The interval of the contemporaneous X-ray and mm observations is marked with a gray region. All data are listed in Appendix A. |
| In the text | |
 |
Fig. 2. Wavelet analysis of the X-ray variability with the trend subtracted and the data interpolated on the regular grid. Left: Magnitude of the wavelet transform. The 95% confidence level is given in white contours. The cone of influence is given as the solid black line; the region out of the cone in the darker color shows less reliable periods that may be affected by edge effects (see text for details). Right: Wavelet transform profiles in gray and their median value in black indicate the variability periods of 14.9 and 4.5 days. The dashed lines correspond to the maxima of the Lomb-Scargle periodogram. |
| In the text | |
 |
Fig. 3. Variability of the mm flux and slope during the campaign. Upper panel: mm light curve in four different frequencies: 90.52, 92.42, 102.52, and 104.48 GHz, shown in different colors and symbols. Bottom panel: Variations in the mm spectral slope. The gray dashed line corresponds to the median spectral slope −0.23. |
| In the text | |
 |
Fig. 4. ALMA image of IC 4329A (median band 3) 9/3/2021. Beam size is 0 |
| In the text | |
 |
Fig. 5. Results of the cross-correlation analysis of X-ray and mm data. The posterior distribution of the time lag provided by JAVELIN is illustrated by the red histogram. Two peaks at τ1 = −11.5 days (for the mm flux preceding the X-ray flux) and τ2 = 15.5 days are shown as vertical dashed lines. The result of PyMCCF is in gray with the 0.5-day time lag shown as a vertical dashed line. |
| In the text | |
 |
Fig. 6. Variations of the mm/X-ray ratio during our observational campaign. The X-ray light curves shifted to the three time lags, τ = 0, −11.5, and +15.5 days (from left to right), are shown in panel (1), and the mm light curve is in panel (2). The ratio log(Fmm/FX − ray), where the X-ray light curve was interpolated to the ALMA epochs, is given in panel (3) for each of the time lags; the black dash-dotted line is the median value, and the red solid line corresponds to the relation between the 100 GHz and 2–10 keV fluxes from Ricci et al. (2023) with the 1σ scatter given by the dashed red lines. The IC 4329A epoch-to-epoch scatter (σ) is also presented in the figure: the scatter relative to the median is shown in black, while that relative to the predicted value is in red. Panel (4) contains the same values as panel (3), but as a function of the Eddington ratio λEdd. The color of the circles gives the date of the observation. |
| In the text | |
 |
Fig. 7. Dependence of the mm flux density at 100 GHz on the source size and magnetic field strength for z = 0.016. The dashed horizontal line illustrates the region of source sizes ≥1 ld. The dashed vertical line delineates the range where the magnetic field ≤Blim. The region between the refined values of R and B for the optically thick synchrotron regime and the observed flux of IC 4329A is highlighted in yellow. |
| In the text | |
 |
Fig. 8. Multifrequency SED fitting of IC 4329A during the flux minimum and maximum. The black points represent the high-resolution ALMA data (this work), whereas the red arrows are the fluxes from low-resolution radio and infrared observations (Inoue & Doi 2018, and references therein), which in the context of the fitting procedure represent strict upper limits to the total flux coming from the nuclear region probed by ALMA. The different emission components in the model and their 1σ confidence intervals are marked, together with the total emission. The coronal component dominates the 100 GHz emission, and the diffuse synchrotron and dust emission components are poorly constrained. The bottom subpanels show the fitting residuals. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.