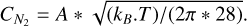| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A165 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202244583 | |
| Published online | 04 October 2024 | |
Reanalysis of the Huygens GCMS dataset
I. High-resolution methane vertical profile in the atmosphere of Titan
1
LATMOS-IPSL, CNRS, Sorbonne Université, UVSQ,
Guyancourt,
France
2
LESIA, Observatoire de Paris, Université PSL, Sorbonne Université, Université Paris Cité, CNRS,
Meudon,
France
3
Department of Earth and Planetary Sciences, Johns Hopkins University,
Baltimore,
MD,
USA
4
NASA Goddard Space Flight Center,
Greenbelt,
USA
5
Max-Planck-Institut für Sonnensystemforschung,
Göttingen,
Germany
★ Corresponding author; thomas.gautier@latmos.ipsl.fr
Received:
22
July
2022
Accepted:
22
August
2024
Context. More than 15 years after its landing on the surface of Titan, the data returned by the Huygens probe remain the only available in situ information on Titan’s lower atmosphere and its methane content.
Aims. In this work, we present a reanalysis of the Huygens probe data obtained by the Gas Chromatograph Mass Spectrometer (GCMS) instrument on board Huygens. GCMS measured the atmospheric composition almost continuously during the Huygens probe descent by acquiring mass spectra between 145 km of altitude and Titan’s surface. We first focus on the recollection, reconstruction, and recalibration of the GCMS dataset to facilitate similar future work.
Methods. We then reevaluate the methane vertical profile in Titan’s lower atmosphere by applying novel mass spectra data-treatment methods to this dataset.
Results. In addition to finding a slightly lower methane mixing ratio than those previously reported using GCMS measurements above the Huygens probe landing site, our work has revealed several kilometric to subkilometric-scale oscillations in the methane vertical profile below 30 km of altitude.
Conclusions. We discuss several hypotheses that could explain these features, such as multiple layers of optically thin clouds or local convection cells, and strongly encourage the reanalysis of other Huygens datasets to further investigate these variations in the methane mixing ratio.
Key words: methods: data analysis / space vehicles / space vehicles: instruments / planets and satellites: atmospheres / planets and satellites: composition / planets and satellites: individual: Titan
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Methane (CH4) is the second most abundant gas in Titan’s atmosphere, with an atmospheric mixing ratio of a few percent, and plays a crucial role in both its physics and chemistry. In the upper atmosphere, its photoionization and photodissociation are key processes in initiating some of the most complex organic chemistry occurring in the Solar System. In the stratosphere and troposphere, methane has a major effect on the thermal radiative balance of the atmosphere and its dynamics (e.g., Battalio & Lora 2021; Mitchell et al. 2006; Rafkin et al. 2022). Methane is also essential to the presence of an active hydrocarbon cycle at the surface of Titan, similar to Earth’s water cycle, which involves the formation of methane clouds, precipitation, and surface liquid hydrocarbon reservoirs (Hörst 2017; Lunine & Atreya 2008). The atmospheric lifetime of methane (~ 10 million years) in the atmosphere, mainly driven by photolysis, implies the presence of subsurface or other sources that sustain its current atmospheric concentration. Analyzing the CH4 mixing ratio in the atmosphere, especially in the lower layers, may therefore be key to understanding the distribution of methane at the surface and subsurface of Titan (Lora & Ádámkovics 2017). The methane ionospheric mixing ratio was measured by the Cassini Ion and Neutral Mass Spectrometer (INMS) instrument to be approximately 2% at around 1050 km (Cui et al. 2009; Waite 2005; Magee et al. 2009; Coutelier et al. 2024). In the stratosphere, using data from the Cassini Composite Infrared Spectrometer (CIRS), Lellouch et al. (2014) studied the latitudinal and seasonal evolution of the CH4 mixing ratio, finding the methane mixing ratio to be 0.95 ± 0.06% around 175 km above the equator but without a detailed vertical resolution. A recent reanalysis of Cassini Visible and Infrared Mapping Spectrometer (VIMS) data was performed by Rannou et al. (2021), leading to a new estimate of the CH4 mixing ratio of 1.15% at 175 km above the equator (Flyby T53, Apr 2009).
Aside from these measurements at relatively high altitude above Titan’s surface, the source of information most heavily used so far for the methane profile comes from the measurements performed by the Huygens probe during its descent through Titan’s atmosphere. Using an updated line list for methane, Rey et al. (2018) reanalyzed data from the Descent Imager Spectral Radiometer (DISR) instrument on board the Huygens probe that landed on Titan in January 2005. These authors found a methane mixing ratio of 1.0% at 110 km and of around 1.4–1.5% below 60 km of altitude. Using the same DISR data recorded in the last 30 m of Huygens descent above Titan’s surface, Jacquemart et al. (2008) and Schröder & Keller (2008) found a methane mixing ratio of5.1 ± 0.8% and 4.5 ± 0.5%, respectively. A summary of previously reported methane measurements in Titan’s atmosphere can be found in Table 1.
The Gas Chromatograph Mass Spectrometer (GCMS) instrument on board Huygens performed vertically resolved sampling of the atmosphere (Niemann et al. 2005, 2010). The accuracy of these measurements is of crucial importance to our understanding of Titan’s atmospheric composition and dynamics, as even a slight variation of methane mixing ratios in the troposphere and the deep stratosphere can induce dramatic variation in retrieval from other instruments or even theoretical or dynamical models. The GCMS data were examined shortly after landing by the original GCMS team (Niemann et al. 2005) and were reevaluated further in 2010 following additional laboratory calibrations (Niemann et al. 2010).
Recent advances in mass spectrometry data treatment (Gautier et al. 2020) have been successfully applied to reanalyze space-based mass spectrometry data obtained by the INMS instrument, which is very similar in design to GCMS (Serigano et al. 2020, 2022), and by the COmetary SAmpling and Composition (COSAC) instrument on board the Philae lander, which investigated the surface of comet 67P/Churyumov-Gerasimenko (Leseigneur et al. 2022). This led us to conduct the reanalysis of Huygens/GCMS data presented here. In addition, during our analysis, it became clear that the archived GCMS data suffered major issues, the extent of which is sufficient to prevent possible future investigations using this dataset. An example of these issues refers to the post-flight calibration data acquired in the laboratory. These data were actively used for the 2010 reanalysis paper. To the best of our knowledge, these data have not been archived and may be lost.
The aims of the present work are therefore two-fold. First, we aim to present a reanalysis of the GCMS data using up-to-date mass-spectrum-deconvolution methods, mainly focusing on the methane vertical profile. Second, we aim to provide as many details as we have been able to ascertain (or not) on the instrument operations and data processing to help any further investigation of this unique dataset.
Reported methane mole fractions at different altitudes in Titan’s atmosphere, for similar latitude and season to those sampled by Huygens.
2 Methods
2.1 The GCMS instrument on board Huygens
The GCMS instrument was a gas chromatograph coupled to a mass spectrometer designed to sample Titan’s atmosphere during Huygens descent and precisely measure its composition (Niemann 2002). The instrument included four possible analytical strategies:
The first type of data returned by GCMS was used to determine the atmospheric composition by direct sampling of the atmosphere. In this configuration, atmospheric gas entered the instrument through the GCMS inlet in contact with the atmosphere and was then directed through either one of two capillary leaks (called L1 and L2) toward the ion source of the mass spectrometer. Both rare gas analyses and atmospheric direct sampling were performed using GCMS Ion source number 1. The present work focuses on the data acquired using this mode.
The second strategy was to precisely analyze the mixing ratios of key components of the atmosphere using gas chromatography-mass spectrometry. For this analytical pathway, atmospheric gases were to be trapped and accumulated in a sampling loop before being injected into the gas chromatograph and detected by the mass spectrometer. While no publication on this dataset has ever been published, data from this mode are available in the Planetary Data System (PDS) and confirm that the instrument performed nominally for these measurements using Ion Sources 3 and 4 (see Sect. 2.3.1 and later description for the ion sources). However, the science data related to this subsystem had very low signal-to-noise ratio (S/N) and its investigation was inconclusive. A definitive answer is missing, but the low S/N may have been due to an underestimation of the sampling loop size as part of the instrument design in order to achieve detectable signals in the mass spectrometer.
The third analytical goal of GCMS was to provide accurate determinations of rare-gas abundances and isotopic ratios. This science objective was achieved using a rare-gas enrichment cell before injection into the mass spectrometer, as presented in Niemann et al. (2010).
Finally, GCMS also aimed at determining the composition of Titan’s aerosols by coupling with the Aerosols Collector and Pyrolyzer (ACP) experiment. Results of this experiment, obtained using GCMS Ion source number 2, can be found in Israël et al. (2005).
Detailed description of the instrument and its nominal modes can be found in Niemann (2002) and Niemann et al. (2010). In the present paper, we therefore discuss parameters for which no information was easily accessible or presented discrepancies that could affect the measurements.
2.2 Descent dataset and raw count correction
Data used in this work were retrieved from the Huygens archive deposited in the Atmosphere Node of the Planetary Data System. We used the level 2 GCMS data archived in the HP-SSA-GCMS-3-FCO-DESCENT-V1.0.2 file. Description of GCMS data levels can also be found in the documentation attached to this archive. We note that some level 3 data exist under the archive HP-SSA-GCMS-3-FCO-DESCENT-V1.2. While the PDS documentation states that the V.1.2 archive has not been reviewed, we find that data archived in it do not appear to have been processed to Stage 3, and are identified as Stage 2 data in the filenames themselves. A byte-by-byte comparison of the content of the HP-SSA-GCMS-3-FCO/DESCENT-V1.0 folder and the HP-SSA-GCMS-3-FCO/DESCENT-V1.2 one reveals that they are exactly identical, and that stage 3 data used by Niemann et al. in their 2010 paper have likely been lost. We also highlight the fact that the folder named “Prelaunch_calibration” in the PDS archive contains only very limited information regarding the experiments performed in 1996. Specifically, it contains an excerpt from a laboratory notebook mentioning laboratory calibrations on several gas mixtures but not the data themselves. Thanks to E. Raaen, we were able to retrieve the corresponding data from archived compact disks located at NASA Goddard Space Flight Center. Unfortunately, the accompanying information regarding both the instrument configuration and the exact composition of the gas mixture injected were too limited to allow us to use these to obtain species-specific calibration factors.
We therefore proceeded with the 1.0.2 version and recalibrated the data ourselves. The exact file used for the present work (GCMS_1US_STG2) is the direct atmospheric sampling performed during the descent of Huygens and can be found in the 20050114_DESCENT folder of the aforementioned archive. This file regroups the direct atmospheric sampling performed with a 70 eV electron energy and using both capillary leaks of interest for this work. L1 was used from the beginning of GCMS measurements at 09:10:58.6 (~146 km altitude) until 9:39:27.7 (66.9 km altitude) and L2 from 09:46:22.4 (56.4 km) until reaching the surface at 11:38:10 and for all subsequent measurements at the surface until the end of the recorded data at 12:47:27. In this file, data with a time stamp lying between 9:39:27.7 and 09:46:22.4 correspond to data obtained through a different sampling and used in particular for the rare-gas analyses and whose interpretation is beyond the scope of this work.
This dataset includes around 1600 full mass spectra (i.e., unit step values of mass-to-charge ratios from 2 to 141 acquired with a resolution of 100) recorded during the descent and an additional 450 obtained while Huygens was resting at the surface of Titan. We removed the background contribution due to residual gas in the instrument by subtracting from all subsequent data the mass spectra acquired by GCMS at the very beginning of the sequence before the opening of the atmospheric inlet. Due to relatively low pressure inducing low signal at high altitude and in order to enhance the S/N, Niemann et al. (2005, 2010) used an averaged vertical stacking. In their 2010 paper, these latter authors stated that approximately 50 sample points were used. However, we find that obtaining the average values presented in Table 1 of Niemann et al. (2010) for time, altitude, pressure, and temperature can only be done using variable bin sizes. Even if indeed 50 sample points were used on average, we find that the bin size used in this paper varies from 8 to 60 consecutive spectra. Figure A.4 of the Appendix1 presents the bin size used by Niemann et al. (2010) as a function of altitude as we were able to reconstruct them. This resulted in a vertical resolution varying from ~5 km at high altitude to ~1.5 km below 15 km. For the present work, we chose to use two different stacking methods. From 146 km to 30 km altitude, data were binned to a kilometer resolution, corresponding to an average of 5–10 consecutive mass spectra. Such binning improves the S/N and allows us to limit the computing time for the Monte-Carlo inversion. The corresponding mass spectra were therefore analyzed after binning. On the other hand, in the lower troposphere, the increase in atmospheric density leads to sufficient S/N to detect short-scale variations. We kept the native GCMS sampling resolution, typically a measurement every 30 to 100 m, and inverted all mass spectra recorded below 30 km. To minimize variations due to noise, retrieved mixing ratios were subsequently smoothed using their ten-point moving median values.
Regarding instrument parameters, Niemann et al. (2010) state a maximum ion source operating pressure of 1.10−4 hPa and a pressure in the mass filter of always below 1.10−6 hPa, ensuring that the mass spectrometer was properly operating within its nominal working conditions. It should however be noted that the origin of this information remains unclear to us, as we found no information regarding the existence of pressure gauges in the ion sources or the mass filter in the archived GCMS documentation, nor its corresponding data in the archived House-Keeping data.
Following the method described in Niemann et al. (2010), raw count rates of up to 7.106 cps were corrected for pulse pile-up following equation 1:
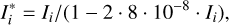 (1)
(1)
where Ii is the measured count rate on channel i and Ii* is the corrected one. The exponential value was determined by Niemann et al. (2010) empirically using cruise checkout on background gases.
This correction is only valid for count rates of up to 7.106 cps, which is within the range of the measured signal for all m/z ratios (at every moment) except for m/z 28, which is due to the high density of molecular nitrogen in Titan’s atmosphere. For altitudes where the signal at m/z 28 went higher than 7.106 cps, the signal saturated and another correction was needed. Niemann et al. (2010) determined the ratio between m/z 14, which is due to N+ and  , and m/z 28, which is due to
, and m/z 28, which is due to  at high altitudes, before counter saturation, and reconstructed the signal at m/z 28 where it saturates, using a factor applied on the m/z 14 intensity as a proxy. We used a similar yet slightly different approach. To reconstruct m/z 28 intensities at high pressure, we did not use the signal due to the N+ fragment, but rather the one due to 15N14N+. We thus used the m/z 29/28 ratio, which was also determined from high-altitude presaturation measurements, instead of using the m/z 14/28 ratio. The reason for this choice comes from the fact that both methods assume that most of the signal of the minor peak chosen to correct m/z 28 is only due to molecular nitrogen contribution. While this is true to first order given the dominance of N2 in Titan’s atmosphere, in electron ionization (EI) mass spectrometry and at GCMS resolution neither m/z 14 nor m/z 29 is unique to molecular nitrogen. m/z 14 has a significant contribution from methane due to the
at high altitudes, before counter saturation, and reconstructed the signal at m/z 28 where it saturates, using a factor applied on the m/z 14 intensity as a proxy. We used a similar yet slightly different approach. To reconstruct m/z 28 intensities at high pressure, we did not use the signal due to the N+ fragment, but rather the one due to 15N14N+. We thus used the m/z 29/28 ratio, which was also determined from high-altitude presaturation measurements, instead of using the m/z 14/28 ratio. The reason for this choice comes from the fact that both methods assume that most of the signal of the minor peak chosen to correct m/z 28 is only due to molecular nitrogen contribution. While this is true to first order given the dominance of N2 in Titan’s atmosphere, in electron ionization (EI) mass spectrometry and at GCMS resolution neither m/z 14 nor m/z 29 is unique to molecular nitrogen. m/z 14 has a significant contribution from methane due to the 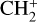 fragment, while m/z 29 includes contributions from several higher order hydrocarbons through the C2H5+ fragment. A correction based on m/z 14, even taking into account a baseline contribution of methane to m/z 14, is more prone to uncertainties than one using m/z 29. As methane is the second most important constituent of Titan’s atmosphere, any variation of its mixing ratio with altitude would affect the m/z 14 to 28 ratio and thus the reconstructed m/z 28 intensities. On the other hand, the m/z 29 to 28 ratio is impacted by parameters of much less importance: at the sensitivity of GCMS, the 15N14N to 14N14N ratio is not expected to be altitude dependent in the low atmosphere, and the concentrations of higher order hydrocarbons are several orders of magnitude below that of methane.
fragment, while m/z 29 includes contributions from several higher order hydrocarbons through the C2H5+ fragment. A correction based on m/z 14, even taking into account a baseline contribution of methane to m/z 14, is more prone to uncertainties than one using m/z 29. As methane is the second most important constituent of Titan’s atmosphere, any variation of its mixing ratio with altitude would affect the m/z 14 to 28 ratio and thus the reconstructed m/z 28 intensities. On the other hand, the m/z 29 to 28 ratio is impacted by parameters of much less importance: at the sensitivity of GCMS, the 15N14N to 14N14N ratio is not expected to be altitude dependent in the low atmosphere, and the concentrations of higher order hydrocarbons are several orders of magnitude below that of methane.
A comparison of both correction methods is given in Figure A.1 available with the appendix and archived data on Zenodo. Please refer to the data availability section for the link to the repository. Figure 1 shows the ratio of m/z 16 to m/z 28 as a first-order proxy for the methane mixing ratio throughout Huygens descent. Blue dots represent the raw counts and black dots the corrected counts using m/z 29 as a proxy. The sudden saturation of m/z 28 at an altitude of 75 km corresponds to the failure of Ion Source (IS) number 5, which incidentally induced a voltage bias on the rest of the instrument, including the measurement performed using IS1 discussed here. Between the altitudes of 65 km and 56 km, the GCMS instrument performed measurements using different sequences, sampling, and ion sources than the atmospheric sniffing with IS1. As a consequence, the corresponding data acquired between altitudes of 76 km and 55 km were excluded from the subsequent data treatment presented in this work.
 |
Fig. 1 m/z 16 to m/z 28 count ratios in GCMS data versus altitude recorded during Huygens descent. Black dots correspond to raw counts archived in level 2 data requiring no correction. Blue dots correspond to raw counts for which a correction is required and red dots correspond to corrected counts using m/z 29 as a proxy when m/z 28 saturates. We note that the very sharp increase in counts at altitude 0 corresponds to outgassing after Huygens’s touchdown and GCMS continued recording atmospheric mass spectra for a couple of hours after the touchdown (not shown here). A comparison between the two correction methods using either m/z 14 or 29 as a proxy is given in Figure A.1. |
Archived level 2 data were also improved by incorporating calibrated altitude, atmospheric pressure, and ambient temperature for each GCMS run. These data were extracted from the consolidated archive of the Huygens Atmospheric Structure Instrument (HASI) also archived on the Planetary Data System Atmospheres Node in the volume HP-SSA-HASI-2–3-4-MISSION-V1.1.
The file used (HASI_L4_ATMO_PROFILE_DESCEN.TAB) is located in the /data/hphasi_0001/DATA/PROFILES folder. Altitudes were correlated between GCMS and HASI data using Huygens internal time stamps. As GCMS and HASI had different sampling rates, for a given GCMS time stamp a linear interpolation was done between the two closest bracketing HASI stamps in order to determine the corresponding sampling altitude, temperature, and pressure for each GCMS sampling.
This linear interpolation was applied on data recorded between 09:11:23.072 and 11:38:09.713 for which both datasets overlap. For the few GCMS data recorded before 09:11:23.072, no corresponding time stamps are given in the HASI dataset and approximate altitude, pressure, and temperature were calculated using linear extrapolation. For GCMS data recorded at the surface, that is, after 11:38:09.713, the pressure and temperature values in the created GCMS file correspond to the latest recording HASI value before touchdown, of 1466.31 mbar and 93.5 K, respectively. The level 3 data reconstructed from all these corrections are in the repository archived with the appendix of the present paper (See data availability section).
2.3 Signal processing and mass spectra inversion
In addition to the raw count measurement correction, in order to retrieve atmospheric mixing ratios from the measured signal, one must take into account all possible sources of alteration of the gas composition during its transmission between the entrance of atmospheric gases into the GCMS inlet and the instrument detector. While the absolute values of subsystem transmission efficiencies affect the signal sensitivity, for mixing ratio determination we only need to take into account processes that can induce differential transmission for separate species and/or masses. Following statements by the original GCMS team, the quadrupole mass spectrometer transfer function and the detector efficiency function are assumed to be flat (Niemann 2002; Niemann et al. 2010). We note that this may be a strong assumption, as most quadrupole mass spectrometers do not present a flat transmission curve but rather a log-normal slowly decaying at high masses. If it were discovered that the GCMS quadrupole transfer function was not flat, this would imply the following: (1) Any differences between our results and those of Niemann et al. 2010 could not originate from this assumption because we both use the exact same assumption; and (2) this could alter the retrieve mixing ratio of certain species. Without knowledge of the exact transfer function, it is near impossible to know exactly which species would be affected and the extent of the uncertainties. However, the quadrupole transfer function should follow a log-normal law, whose maximum is generally tuned to the species of interest and whose profile is tuned to be as flat as possible on the largest possible range (see e.g., Franz et al. 2014, 2017; Mahaffy et al. 2012 for the tuning strategy of the SAM instrument on the Curiosity rover). GCMS used an adaptative tuning across the mass range (Niemann 2002), therefore minimizing the uncertainties on species with relatively close masses and thus on the methane/nitrogen ratio. It is however possible that the mole fractions of species beyond the scope of this paper and far out of this mass range (typically below m/z 10, such as H2 or above m/z 60, such as C6H6) could be slightly underestimated due to this phenomenon.
2.3.1 Sampling
In direct sampling mode, atmospheric gases penetrated the Huygens probe through the GCMS inlet, which was located near the apex of the probe fairing (see Figure 2 in Niemann et al. 2010).
Figure 2 presents a schematic diagram of the different possible gas flow paths in the instrument. The one representing the direct atmospheric sniffing mode discussed in this work is highlighted in red. From the inlet to the precapillary area, atmospheric gases flow through large tubing, which we can assume to not induce mass and/or species differential transmission. A small portion of the gas then leaked through two capillary leaks (depending on the altitude) to the mass spectrometer ionization source number 1 (IS1). Unfortunately, the exact properties of these leaks remain unknown, besides the following statement from (Niemann 2002): “Typically, seven capillaries per leak are used with inside diameters ranging from 2 µm to 20 µm for the largest”. Due to the conductance of these leaks, Niemann et al. (2010) concluded that gas transfer through them occurred in a transitional regime, meaning that a mass dependence transmission efficiency for the gas is to be expected at this stage. Such mass-dependent induced fractionation must thus be corrected for in order to retrieve the atmospheric composition. To do this, Niemann et al. (2010) used laboratory calibration on the spare instrument measured for N2, CH4, and H2. Unfortunately, the papers published by the original team do not provide the calibration factors, these calibration data have not been archived, and our efforts to locate them have been unsuccessful. Using the recalibrated level 3 data and Equations (2) and (3) of Niemann et al. (2010) and the retrieved methane mole fraction presented in their Table 1, we were able to retro-engineer the value of the C f16,28 empirical calibration coefficient through the entire Huygens descent. Results are presented in Figure A.5. The dashed red line represents the value of our analytical calibration factor obtained as described in Section 2. On this figure, we can see that even if the empirical calibration does vary with pressure and thus altitude, the effect is quite limited and shows no clear trend. Moreover, when propagating the uncertainties associated with the mass 16 to 28 ratio and the methane mixing ratio, we find that the analytical proxy we use in our work fits within the uncertainties of the empirical calibration. This agreement between the coefficient coming from the GCMS flight data inversion and our simple analytical model is quite comforting in regards to our retrieved values. We note that the slightly lower value in our analytical calibration factor, on average, compared to the empirical one from Niemann et al. (2010) could be a further explanation as to why our retrieved mixing ratios are on the lower end of their error bars. Given the uncertainties in the Cf16,28 retrieved, and the fact that such retrieval would be impossible for any other trace species in the GCMS data (while our approach would remain valid), we decided to continue using the same analytical approach for the methane inversion. However, we warn the reader that the differences in absolute methane mixing ratio with Niemann et al. (2010) values could originate from this. It is also unclear as to whether or not a calibration factor was applied to the mixing ratios provided in Niemann et al. (2010) for rare gases, and if so, which one.
In order to account for possible sampling and transfer fractionation, we decided to use an analytical correction. While this is less accurate than laboratory calibration, especially for hydrogen given its potential retro-diffusion through the capillaries due to its low molecular weight, it has the advantage of being applicable to any species based on its intrinsic properties. As stated above, if we assume no fractionation until the capillary leaks, the only correction to take into account is the correction due to the gas flow in the transitional regime either through L1 or through L2.
The transitional regime can be expressed as a linear combination of laminar flow and molecular flow. While the laminar flow rate depends on the pressure difference between the sampling area and the ion source, as well as on the mean density and viscosity of the gas, it does not depend on the molecular mass of individual species and thus does not induce fractionation of the sampled gas. On the other hand, the molecular flow component is species dependent and thus induces a fractionation of the gas mixture that needs to be corrected in order to retrieve the atmospheric mixing ratios. The conductance (in m3 s−1) of a given species j through a capillary via molecular flow can be expressed as
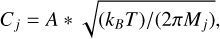 (2)
(2)
where A is a cross-section constant (in m2) depending on the pumping efficiency and capillary diameters and lengths, kB is the Boltzmann constant, T is the temperature of the gas, and Mj is the molecular mass of species j. As the concentration [j]incom of a given species j arriving in the ion source is proportional to its atmospheric concentration [j]atmo multiplied by the conductance, and given that we are only concerned with the relative transmission for different species, the absolute values of A and T are irrelevant, and we can express the molecular ratio of a species j relative to molecular nitrogen, as
![${[j]_{incom{\rm{ }}}}/{\left[ {{N_2}} \right]_{incom{\rm{ }}}} = \left( {{{[j]}_{atmo{\rm{ }}}}/{{\left[ {{N_2}} \right]}_{atmo{\rm{ }}}}} \right)*\left( {{C_j}/{C_{{N_2}}}} \right),$](/articles/aa/full_html/2024/10/aa44583-22/aa44583-22-eq6.png) (3)
(3)
This gives a relation between atmospheric composition and molecular ratio for the gas entering the ion source of
![$\matrix{ {{{[j]}_{atmo{\rm{}}}}/{{\left[ {{N_2}} \right]}_{atmo{\rm{}}}} = \left( {{{[j]}_{incom}}/{{\left[ {{N_2}} \right]}_{incom{\rm{}}}}} \right) * \left( {{C_{{N_2}}}/{C_j}} \right)} \cr { = \sqrt {{M_j}/28} * \left( {{{[j]}_{incom{\rm{}}}}/\left( {{{\left[ {{N_2}} \right]}_{incom}}} \right)} \right.} \cr } .$](/articles/aa/full_html/2024/10/aa44583-22/aa44583-22-eq8.png) (5)
(5)
 |
Fig. 2 Schematic representation of gas flow in the GCMS instrument. Flow path for measurements discussed in this paper are highlighted in red. Highlighted in the blue box are the L1 and L2 capillary arrays, main source of possible gas fractionation between Titan’s atmosphere and the detector. Adapted from Niemann (2002). |
2.3.2 Ionization, transmission, and detection efficiency
Once in IS1, incoming neutral molecules are ionized by EI through interaction with a 70 eV electron beam emitted by a tungsten/rhenium filament. With EI, depending on the conformation of the molecules and the energy of the electrons, each different species j has different ionization cross-sections, 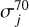 . This induces a second molecule-dependent fractionation process that must be corrected during the data processing.
. This induces a second molecule-dependent fractionation process that must be corrected during the data processing.
For a species j, and considering the sum of all fragments coming from j, the concentration of ions exiting the ion source and transmitted to the detector, [j]ion is proportional to [j]incom, the concentration of molecules of species j entering the ionization source multiplied by 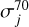 . Assuming a flat function for the quadrupole transmission and detector efficiency as specified in Niemann (2002) and Niemann et al. (2010), the molecular ratios at the exit of the ion source correspond to the mixing ratio detected during the GCMS measurement. The measured ratio relative to N2 can thus be expressed as
. Assuming a flat function for the quadrupole transmission and detector efficiency as specified in Niemann (2002) and Niemann et al. (2010), the molecular ratios at the exit of the ion source correspond to the mixing ratio detected during the GCMS measurement. The measured ratio relative to N2 can thus be expressed as
![${[j]_{measured{\rm{}}}}/{\left[ {{N_2}} \right]_{measured{\rm{}}}} = {[j]_{incom}}/{\left[ {{N_2}} \right]_{incom.{\rm{}}}} \cdot \left( {\sigma _j^{70}} \right)/\left( {\sigma _{{N_2}}^{70}} \right){\rm{.}}$](/articles/aa/full_html/2024/10/aa44583-22/aa44583-22-eq11.png) (6)
(6)
Combining equations (5) and (6), the atmospheric mixing ratio can be recalculated from the measured one as
![${[j]_{atmo{\rm{}}}}/{\left[ {{N_2}} \right]_{atmo}} = {[j]_{measured{\rm{}}}}/{\left[ {{N_2}} \right]_{measured{\rm{}}}} * \sigma _{{N_2}}^{70}/\sigma _j^{70} * \sqrt {{M_j}/28} {\rm{}}{\rm{.}}$](/articles/aa/full_html/2024/10/aa44583-22/aa44583-22-eq12.png) (7)
(7)
For a few species, experimental values for 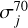 can be found in the literature. It can also be calculated empirically using Fitch and Sauter formula (Fitch & Sauter 1983) or through quantum chemistry calculation using for example a Binary-Encounter-Dipole (BED) or a Binary-Encounter Bethe (BEB) model (Hwang et al. 1996; Kim & Rudd 1994). Again, in the present work, as we are only concerned with the relative mixing ratios, the absolute values of the cross sections are of no importance and we favored self-consistency for the source of values in order to minimize uncertainties. All fragmentation cross-section values used and reported in Table A.2 were therefore obtained using the BEB calculation provided by the National Institute of Standards and Technology (NIST) Electron-Impact Cross Section Database (Hwang et al. 1996; Kim & Rudd 1994). We strongly encourage instrumental teams developing future mass spectrometers for space exploration to perform laboratory calibrations on the flight model before delivery. Such calibrations would altogether eliminate the need for analytical calibration factors, including the ionization cross-section one.
can be found in the literature. It can also be calculated empirically using Fitch and Sauter formula (Fitch & Sauter 1983) or through quantum chemistry calculation using for example a Binary-Encounter-Dipole (BED) or a Binary-Encounter Bethe (BEB) model (Hwang et al. 1996; Kim & Rudd 1994). Again, in the present work, as we are only concerned with the relative mixing ratios, the absolute values of the cross sections are of no importance and we favored self-consistency for the source of values in order to minimize uncertainties. All fragmentation cross-section values used and reported in Table A.2 were therefore obtained using the BEB calculation provided by the National Institute of Standards and Technology (NIST) Electron-Impact Cross Section Database (Hwang et al. 1996; Kim & Rudd 1994). We strongly encourage instrumental teams developing future mass spectrometers for space exploration to perform laboratory calibrations on the flight model before delivery. Such calibrations would altogether eliminate the need for analytical calibration factors, including the ionization cross-section one.
We note, however, that species-specific calibrations (i.e., a combination of ionization, sampling, and possibly detection calibration) can induce larger uncertainties in the mixing ratio retrievals. For example, Magee et al. (2009) studied the effect of these species-specific calibrations on the methane mixing ratio retrieved from Cassini-INMS measurements compared to the one from Cui et al. (2008). While both used laboratory calibrations, their retrieved mixing ratios vary by up to 20%. While the situation seems even more dire in the case of GCMS given the lack of proper calibrations, the Monte Carlo-based inversion method we use (see Section 2.3.4) allows us to mitigate this effect. A single inversion of the mass spectra and the calculation of the mixing ratios using equation (7) of our manuscript yields uncertainties on the methane mixing ratio directly proportional to uncertainties on their species-specific calibration, that is, on the order of 20%, similarly to the results of Magee et al. (2009) and Cui et al. (2008) on INMS. However, because we do Monte Carlo (MC) sampling and inversion 100 000 times, we can access the histogram of the retrieved methane concentration in all simulations (Gautier et al. 2020). As such, our retrieval does not consist of a single value with associated uncertainties, but results in a probability density function, where each point is associated with uncertainties (here 20%, coming from the species-specific calibration). Now, as both the general distribution and the individual one of a single bin each follow a Poisson distribution, where variance is equal to the mean of the distribution, the uncertainty propagation associated to the methane ratio, [CH4], simply becomes roughly equal to ![$\sqrt {\left[ {{\rm{C}}{{\rm{H}}_4}} \right]} $](/articles/aa/full_html/2024/10/aa44583-22/aa44583-22-eq14.png) .
.
Regarding potential species-dependent efficiency in the detector, the empirical values from the missing calibration files are lost and we find no perfect workaround and as such did not include an additional correction factor. However, the following points must be considered: (1) The detector effect related to dead-time and the saturation effect is taken into account in our level 3 recalibration. (2) The electron multiplier detector efficiency is much more sensitive to the energy of the incoming ions than to their mass. Its correction could thus be critical for instruments such as INMS in open-source mode but is much less so for GCMS, where all ions coming to the detector have the same energy. (3) The detector effect has a lesser impact on sensitivity and thus retrieval than the ionization cross-section, as stated in Niemann et al. (2010); or see for example Fig. 12 in Gasc et al. (2017) comparing the total detection sensitivity to the ionization cross-section for the ROSINA instrument on board Rosetta.
2.3.3 Fragmentation and species preselection
Another phenomenon occurring in the ion source that heavily affects the data treatment is the fragmentation of the molecules through dissociative ionization processes (McLafferty & Tureček 1993). This fragmentation results in each different species having a characteristic fingerprint fragmentation pattern. At the resolution of the GCMS instrument, the signal collected within a nominal mass unit thus represents the sum of the fingerprints of all the molecules present in the sample, weighted by their relative concentrations. If fragmentation patterns of molecules of interest are perfectly known, it is then possible to inverse the mass spectrum to retrieve the molecular mixing ratios in the sample using least square fitting on the measured mass signal and a custom-built fragmentation database for candidate molecules (Gautier et al. 2020). The initial fragmentation database used in this work is presented in Table A.2.
In the present work, we focus on the mixing ratio of methane and its vertical profile. We thus chose to use a very limited database of ten species, which includes H2, CH4, N2, Ne, C2H2, C2H4, C2H6, HCN, Ar, and CO2. While this approach prevents the identification of species of high molecular weight, it allows accurate determination of mixing ratios for nitrogen and methane by focusing the deconvolution on ions with m/z of up to 45. A similar approach was successfully implemented by Serigano et al. (2020) to investigate INMS results obtained in Saturn’s atmosphere during the Cassini Grand Finale. The work presented here focuses on the methane vertical profile and an investigation of trace species will be presented in part II of this series (Das et al. 2024). It should be noted that our investigation on trace species raised serious questions regarding the representativeness of GCMS measurements for atmospheric trace species, as most if not all trace species detected by GCMS may have originated from evolved aerosols heated in the instrument (Das et al. 2024).
2.3.4 Mass spectrum inversion using Monte Carlo sampling
While the masses of the fragments and general pattern aspects are usually well known for organic molecules, the branching ratios of the dissociative processes, and thus the relative intensities of the peaks in the pattern, are much more uncertain. These branching ratios are strongly dependent on the geometry of the interaction between the incoming neutral molecules and the electron beams and are therefore instrument dependent and subject to high uncertainties. Mass spectrometry databases for EI spectra typically provide fragmentation patterns with 20% uncertainties on the peak intensities, but these uncertainties could be much higher for minor peaks (Linstrom et al. 2019; Serigano et al. 2020; Valdez et al. 2018). For complex mixtures, such as Titan’s atmosphere, these high uncertainties on fragmentation pattern rapidly result in severely under-constrained mathematical inversions, rendering the retrieval of mixing ratios in the sample impossible.
To overcome this issue, we used the method developed in Gautier et al. (2020) that introduced MC sampling on the fragmentation pattern intensities in order to solve the loosely bound problem not once but several hundred thousand times.
This method allows the retrieval of the probability density functions of mixing ratios for species analyzed by Huygens in Titan’s atmosphere. Details on the deconvolution algorithm used can be found in Gautier et al. (2020). For the present work, MC sampling of the fragmentation database was performed 100 000 times and all fragments were sampled using a uniform distribution with a ±30% deviation of their intensities from the nominal database reported in Table A.2. As mentioned above, in electron ionization mass spectrometry the relative intensity of peaks can vary widely and there is no consensus on the potential variability of fragment intensity, even in fields that rely on it (see e.g., the discussion in Davidson et al. 2018 for forensics science). We thus chose to apply the recommendation of the American Society for Mass Spectrometry of a “fit for purpose” approach and allowed a 30% possible deviation, which allows us to encompass the vast majority of uncertainties related to fragmentation pattern for light molecules, which is similar to approach we used previously to interpret INMS data obtained during Cassini Grand Finale (Serigano et al. 2022). These sampling parameters have been validated for the deconvolution of mass spectra of similar complexity obtained at the surface of comet 67P/Churyumov-Gerasimenko Leseigneur et al. (2022). The least square fitting algorithm was set with a lower boundary value of zero for all species in order to prevent unrealistic non-negative solutions, and no upper boundary values were used. Figure 3 summarizes the calibration pipeline applied to GCMS data in order to retrieve atmospheric mixing ratios from the measured signal.
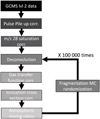 |
Fig. 3 Schematic representation of the data workflow from retrieved GCMS level 2 data on the PDS to atmospheric mixing ratios. |
3 Results and discussion
The set of retrieved methane mole fractions for the entire atmospheric column can be found in Table A.1. Figure 4 presents the maximum of the probability density function for the methane mixing ratio as a function of altitude between 147 km altitude and the surface of Titan at a kilometric vertical resolution. The black points represent our estimate of the CH4 mixing ratio with its associated error bars and blue diamonds are the mole fraction reported by Niemann et al. (2010). An example of the retrieved contribution of methane and nitrogen to the mass spectra (here at 130 km of altitude) is given in the insert of this figure. Regarding the methane profile, at first glance, the values retrieved with our method are consistent with those provided by the original team, although a few discrepancies are visible when looking in greater detail. While GCMS measurements started at an altitude of around 147 km , Niemann et al. (2010) did not provide any values above 140 km. As visible in Figure 4, a slight trend of a decreasing CH4 mixing ratio with altitude is visible in our data between 140 and 147 km. This trend appears to be very regular and hard to explain given our current knowledge of Titan’s atmosphere, suggesting a possible instrumental artifact following the inlet gas flow opening.
From 140 km down to 76 km, while the values retrieved Niemann et al. (2010) are always within our distribution, the peak of the probability density function is systematically lower than their mean values by 0.1–0.2%. While this is likely due to the fact that our retrieval accounts more precisely for secondary contributions from other species, we cannot exclude that this systematic shift toward lower values could be due to the fact that our analytical calibration factors do not include pressure and mole fraction dependence, as opposed to the empirical ones used in Niemann et al. (2010).
Niemann et al. (2010) excluded altitudes of between 45 km and 76 km from their reported methane mixing ratio values while we only exclude them between 55 km and 76 km. Between 45 and 55 km, a clear trend is visible, with the methane mixing ratio increasing with altitude. However, the data at these altitudes should be taken with slightly more caution than the rest of the dataset given the instrumental issues between 76 km and 55 km discussed above. In particular, it is not clear how an instrumental memory effect in the methane mass channels related to ion pump malfunction above 45 km could have affected these measurements. As at that time there was no other reason to suspect a methane enrichment at these altitudes, we believe the original GCMS team may have excluded these data for this reason.
While an instrumental issue remains the most likely explanation for this methane variation, we also see reasons that justify keeping it in the dataset for follow-up work to decide whether this effect is real or not. The first reason is that, between 30 and 45 km, our retrieved mixing ratios are clearly above those obtained by Niemann et al. (2010), and an upward trend is visible in the methane profile as early as 35 km in altitude, where the data are much more robust. Such a trend would point toward an actual enrichment of Titan’s atmosphere in methane somewhere above 55 km in altitude, with the methane mixing ratio then slowly decreasing until 35 km before trending again positively at lower altitude following a wet adiabat until around 10 km in altitude. A second justification for keeping this variation in the dataset is that, if present, such an enriched methane layer would be consistent with the predictions of Global Climate Model simulations of Titan’s atmosphere of an influx of methane above the equator of Titan at around 70 km due to mid-latitude evaporation of methane (Rannou et al. 2021). Interestingly, this altitude range also corresponds to a change in the optical properties of aerosols modeled at around 55 km to explain the data returned by the DISR instrument (Doose et al. 2016). The observed increase in the aerosol extinction coefficient occurs over an altitude span of 10 to 20 km and could have been induced by an increased methane adsorption triggered by higher atmospheric methane concentration.
For the lower atmosphere, given the accuracy of our retrieval method, we do not need vertical binning and obtain a higher vertical resolution for the methane profile. The high-resolution vertical profile of methane below 30 km is reported in Figure 5, where multiple phenomena can be observed. First, we note that our high-vertical-resolution CH4 mixing ratios are in agreement with the values and associated uncertainties given in Niemann et al. (2010). We also note that our most likely retrieved methane mixing ratio is systematically lower than the one previously reported in Niemann et al. (2010).
This fact is due to the differences in the retrieval philosophy between the two methods. For Niemann et al. (2010), the methane mole fraction is computed using information at m/z 14, 16, and 28 (equations (2) and (3) in their paper), thus assuming that the contribution at m/z 16 is entirely from CH4. With our deconvolution method, we take into account the entire fragmentation patterns of methane (m/z 12–17) and nitrogen (m/z 14, 28, 29) as well as higher order hydrocarbons. Although CH4 remains the main contributor to the peaks at m/z 12 to 16, a small, albeit non-negligible, fraction of the signal is contributed by heavier hydrocarbons, thus reducing the retrieved methane mixing ratio compared to using the 16/28 ratio and explaining its overestimation in Niemann et al. (2010).
The high vertical resolution of the measurement also unveils many features in the methane vertical profile. Indeed, it is clear from Figure 5 that the methane vertical profile in Titan’s troposphere is not a smooth regular profile but presents many subkilometer-scale structures, indicating an active and dynamic atmosphere.
We investigated several potential origins, natural or instrumental, for these oscillations in the methane profile:
No correlation was found with known instrumental effects. In particular, the vertical distribution of the structures does not present a periodicity that could, for example, be due to the spin or oscillation of Huygens.
No correlation was found with pressure and temperature recording by HASI. However, the variation of the CH4 mixing ratio in these structures is typically less than 10−3 of the signal intensity at these altitudes. If such variation were to have existed in the P or T profile, it is unlikely that HASI would have had the sensitivity to detect it (M. Fulchignoni, private communication).
Subsequently, the lack of well-defined periodicity and strong variations in the pressure and temperature profile tends to exclude the presence of gravity waves to explain such structure.
Such structures could correspond to local saturation of the methane profile. This would imply the presence of many optically thin high-altitude tropospheric clouds. Such cloud may be correlated with the thin condensation layer detected by DISR at 21 km in altitude (Doose et al. 2016; Tomasko et al. 2005). This hypothesis also correlates with the detection of a stationary mid-latitude cloud system using remote sensing observations by Ádámkovics et al. (2010) who observed several clouds between 13 and 37 km in altitude in 2006 and 2007.
Such fluctuations in the methane profile could also be indicative of small-scale convective cells in the troposphere probed by Huygens. This hypothesis would be particularly consistent with the observation of high-altitude gravity waves by HASI during Huygens descent toward Titan (Fulchignoni et al. 2005). While Titan’s equatorial regions do not present strong orographic gradients that could easily induce such gravity waves, the presence of tropospheric convective structure can initiate such high-altitude gravity waves (Barth & Rafkin 2007; Spiga 2011).
Another point, noted already by the original Huygens team, is the apparent saturation of the CH4 mixing ratio at low altitude, which has been interpreted as the presence of a methane cloud at around 7 km altitude (Niemann et al. 2005, 2010), and the presence of distinct planetary boundary layers below 2 km visible in the HASI profile (Charnay & Lebonnois 2012). Figure 6 presents a close up of Figure 5 below 5 km with our retrieved mixing ratio (black), values from Niemann et al. (2010) (blue diamonds), and the altitude of the three boundary layers A, B, and C identified in Charnay & Lebonnois (2012) at 300 m, 800 m, and 2 km, respectively. In Fig. 6, layers B and C are not especially remarkable in the methane profile. On the contrary, layer A corresponds perfectly to the altitude below which the methane mixing ratio is perfectly stable, in accordance with a well-mixed diurnal boundary layer below 300 m, as suggested by Charnay & Lebonnois (2012).
Figure 7 presents the methane relative humidity below 10 km, which corresponds to the ratio between methane partial pressure and methane vapor pressure. Methane partial pressure was calculated from our retrieved mixing ratio and the pressure measured by HASI at the corresponding altitude. Methane vapor pressure was calculated from the temperature measured by HASI using the Antoine Equation and parameters A, B, and C of 3.9895, 443.028, and −0.49, respectively, from Prydz & Goodwin (1972). Using the nominal HASI temperature results in the plain black line in Figure 7. Atreya et al. (2006), using parameters for the Antoine equation from Ziegler (1959) and the Niemann et al. (2005) methane mixing ratio, found that an adjustment of the HASI temperature by −1.3 K was necessary to reach saturation of methane at 8 km. Using this −1.3 K offset on HASI temperature data results in the dashed line in Figure 7. With our retrieved mixing ratio and parameters, we find that a methane saturation at 7.9 km would require an adjustment of the temperature measured by HASI of −1.6 K. We also confirm that even at high vertical resolution, the vertical profile of methane humidity below this layer decreases almost linearly until reaching 55% at the surface (using the HASI temperature minus 1.6 K; or 47% using the nominal HASI temperature profile). This is consistent with a drizzle evaporation as suggested by Tokano et al. (2006).
 |
Fig. 4 Retrieved methane mixing ratio through the lower atmosphere. Black dots: retrieved maximum probabilities for the CH4 mixing ratio as a function of altitude; associated error bars correspond to 1σ uncertainties assuming a Gaussian profile for the methane mixing ratio probability density function. Blue diamonds are the methane mixing ratio reported in Niemann et al. (2010). Data were stacked to a kilo-metric resolution before deconvolution. Insert shows the deconvolution for a typical mass spectrum recorded by Huygens at high altitude (here 130 km). Black bars are the measured signal and blue, orange, and green bars show the contribution of hydrogen, methane, and molecular nitrogen, respectively. Peaks at m/z 2, 12, and 13 are slightly underfitted to the contribution of higher order hydrocarbons to the signal, which is not shown here. |
 |
Fig. 5 High resolution vertical profile of methane below 30 km. Black dots represent the median of 100 000 deconvolutions and grey bars their 1 − σ deviations. As the main source of uncertainties comes from the seeding fractionation pattern and not the retrieval method, error bars should be understood as systematic errors. This means that for example if a more accurate measurement was to confirm a given value to be lower than the mean reported value here, this would be valid for all the other altitudes as well. Blue diamonds and bars represent methane mixing ratios reported by Niemann et al. (2010) and their standard deviation, respectively. |
 |
Fig. 6 Close up of the high-resolution profile of methane in the lower troposphere below 5 km. Black dots represent our median retrieved values with their associated error bars. Blue diamonds and bars represent methane mixing ratios reported by Niemann et al. (2010) and their standard deviation, respectively. Red horizontal dashed lines labeled A, B, and C represent the altitude of the boundary layers identified in Charnay & Lebonnois (2012) at 300 m, 800 m, and 2 km, respectively. |
 |
Fig. 7 Methane relative humidity below 10 km. The three humidity profiles are calculated using the nominal HASI temperature (plain line), the HASI temperature shifted by −1.3 K (dotted line), and the HASI temperature shifted by −1.6 K (dashed line), respectively. |
4 Conclusions
Huygens GCMS measurements provide a unique insight into Titan’s atmospheric composition. This data set is likely to remain the sole in situ source of information on the troposphere and lower stratosphere of Titan for the foreseeable future, as the Dragonfly mission planned to reach Titan by 2034 will focus on the composition of Titan’s surface and organics and near-surface atmosphere Barnes et al. (2021). It is therefore of prime importance to leverage every bit of information on the atmosphere of Titan that may be present in the Huygens data. In this paper, we re-examined part of the GCMS dataset using novel tools for the treatment of mass spectra in order to reevaluate the methane content of Titan’s lower atmosphere. We obtained the methane profile between 145 km and 30 km in altitude along Huygens’ descent trajectory at a kilometric vertical resolution, and at a subkilometric vertical resolution between 30 km in altitude and Huygens’ landing site.
Our retrieved methane mixing ratio is in general agreement with that of Niemann et al. (2010). This does not allow us to reconcile the GCMS-derived methane mole fraction with those obtained from remote sensing. Given that remote sensing observations were carried out in similar seasons but on different dates compared to the Huygens landing on January 14 2005, it is possible that a solution to this inconsistency may be related to short-timescale variations of the methane mole fraction in the lower stratosphere, similarly to the observation of methane cloud variability in the troposphere. Our main findings can be summarized as follows:
We find a slightly lower average mixing ratio for methane, and decreased uncertainties, compared to Niemann et al. (2010). However, this decrease is not sufficient at high altitude (above 80 km) to reconcile the GCMS-derived methane mole fraction with those obtained from remote sensing. Given that remote-sensing observations were carried out in similar seasons but on different dates compared to the Huygens landing on January 14 2005, perhaps a solution to this inconsistency is to look for short-timescale variations of the methane mole fraction in the lower stratosphere, similarly to the observation of methane cloud variability in the troposphere;
Our results suggest the possible presence of an atmospheric layer enriched in methane somewhere between 75 and 50 km in altitude. Although we cannot draw any definitive conclusions as to its existence because of the specificities of GCMS sampling and analyses within the 75−55 km altitude range, this layer could be indicated by the CH4 mole fraction decreasing with altitude in the 55−40 km range where we recollected reliable data. We emphasize that an instrumental origin for this methane enrichment remains thus far the most likely hypothesis. While being even harder to decipher than the dataset presented in this paper, the measurements performed by GCMS between 75 and 55 km in altitude, specifically chromatographic runs and the enrichment/rare gas cell experiments, may bear supplementary information able to confirm or rule out the existence of this layer;
We find clear evidence for short-scale vertical variation in the tropospheric methane mixing ratio. Here again we cannot yet draw conclusions that offer a definitive explanation for their presence, but these features could be indicative of optically thin clouds and/or local convection cells at the time and place of the Huygens landing. No evidence for thin cloud layers was found in DISR data (Doose et al. 2016), and Barth & Rafkin (2007) found that although Titan’s atmosphere could produce convective methane cloud at mid to high latitudes, the methane humidity at the Huygens landing site may have been too low to induce large-scale convective clouds. However, Tokano et al. (2006), based on the atmospheric pressure and temperature profile, suggested the possible presence of optically thin ice clouds in the troposphere. The study of Huygens’ motion during its descent also pointed toward the presence of turbulent layers Lorenz et al. (2007), which would be consistent with our findings regarding the vertical profile of methane. Future investigation of the surface methane content and humidity, either with existing data or with Dragonfly, the next mission to fly to Titan, which will arrive at approximately the same time of year and in a similar location to Huygens, may provide further elements with which to investigate the variation of the methane profile in the troposphere. In particular, the Dragonfly mission will carry a methane humidity sensor as part of the Dragmet suite (Barnes et al. 2021; Lorenz et al. 2018). This instrument will allow monitoring of the surface methane humidity while Dragonfly is landed, providing key information on the diurnal variations of the methane cycle. When Dragonfly will be airborne, flight operations will of course be of the highest priority in terms of energy conservation. However, any inflight operation of the Dragmet sensor would bring highly valuable information regarding the currently debated altitude of the planetary boundary layer (Charnay & Lebonnois 2012) and would strongly enhance our understanding of the methane cycle on Titan. In addition, if Dragonfly can perform these in-flight measurements, the methane humidity sensor would have the vertical resolution sufficient to confirm the subkilometric features in the methane profile presented here and could be used to investigate their temporal variation, providing unprecedented access to local convection phenomena.
In addition to these conclusions regarding methane in Titan’s atmosphere, by recollecting every piece of information available on the GCMS measurements, we provide a set of calibrated GCMS data (see data availability section). We believe this set to be readily usable by anyone interested in Titan’s lower atmosphere composition, without having to perform the same data-mining protocols. The lesson learned from our archived-data-treatment project can also benefit ongoing or future space exploration missions carrying a mass spectrometer. In particular, the full interpretation of data returned by such instruments requires extensive calibration data – which would have drastically reduced the uncertainties of our retrieval for GCMS – and, equally importantly, the proper archiving of not only the flight data but also of any calibration file and documentation relevant to the instrument. Beyond the data themselves, the tools we developed to analyze complex mass spectra could be useful for the treatment of data returned by future space-flight mass spectrometers, such as the Dragonfly Mass Spectrometer (DraMS) instrument.
We also hope that the evidence we provide of previously unnoticed phenomena affecting the second most important atmospheric component of Titan will emulate similar reanalysis of other data sets returned by the Huygens probe, such as those from the HASI and the DISR instruments.
Data availability
The GCMS level 2 data used in this work were retrieved from the NASA PDS, Atmosphere node, and can be found at: https://atmos.nmsu.edu/PDS/data/PDS4/Huygens/hpgcms_bundle/
Appendix A containing supplementary data and Figures, level 3 GCMS data produced during this work and retrieved methane mole fractions at all altitudes have been archived on Zenodo and can be found at: https://zenodo.org/doi/1S.5281/zenodo.13384793
Acknowledgements
We are truly grateful to the numerous people who supported, encouraged and guided us through the lengthy effort this project represents. We wish to thank in particular E. Raaen, for sharing any bits of information he could found from the original team, and P. Rannou, B. Bézard, E. Lellouch, M. Fulchignoni, J.-P. Lebreton and many other for the fruitful discussions we had regarding the Huygens mission and data interpretation. The data analyzed here is archived in the Planetary Data System, atmospheres node. We also extend our thanks and acknowledgement to the following programs who funded us throughout this work: the NASA Cassini Data Analysis Program under CDAP16 2–0087 to T.G., M.G.T., J.S and S.M.H.; the NASA’s Planetary Science Division Internal Scientist Funding Program through the Fundamental Laboratory Research (FlaRe) work package to M.G.T.; the NASA Cassini Data Analysis Program Grants 80NSSC19K0903 to J.S. and S.M.H.; the Programme National de Planétologie (PNP) of CNRS/INSU co-funded by CNES; and the Agence Nationale de la Recherche under the grant ANR-20-CE49–0004–01 to T.G., C.S., K.D. and M.C.
References
- Ádámkovics, M., Barnes, J. W., Hartung, M., & de Pater, I. 2010, Icarus, 208, 868 [CrossRef] [Google Scholar]
- Atreya, S. K., Adams, E. Y., Niemann, H. B., et al. 2006, Planet. Space Sci., 54, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. W., Turtle, E. P., Trainer, M. G., et al. 2021, Planet. Sci. J., 2, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Barth, E. L., & Rafkin, S. C. 2007, Geophys. Res. Lett., 34, L03203 [NASA ADS] [Google Scholar]
- Battalio, J. M., & Lora, J. M. 2021, Geophys. Res. Lett., 48, e2021GL094244 [NASA ADS] [CrossRef] [Google Scholar]
- Charnay, B., & Lebonnois, S. 2012, Nat. Geosci., 5, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Coutelier, M., Gautier, T., Das, K., Serigano, J., & Trainer, M. G. 2024, A&A, submitted [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cui, J., Yelle, R. V., & Volk, K. 2008, J. Geophys. Res., 113, E10004 [Google Scholar]
- Cui, J., Yelle, R. R., Vuitton, V., et al. 2009, Icarus, 200, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Das, K., Gautier, T., Szopa, C., et al. 2024, A&A, submitted [Google Scholar]
- Davidson, J. T., Lum, B. J., Nano, G., & Jackson, G. P. 2018, Forensic Chem., 10, 15 [CrossRef] [Google Scholar]
- Doose, L. R., Karkoschka, E., Tomasko, M. G., & Anderson, C. M. 2016, Icarus, 270, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Fitch, W. L., & Sauter, A. D. 1983, Analyt. Chem., 55, 832 [CrossRef] [Google Scholar]
- Franz, H. B., Trainer, M. G., Wong, M. H., et al. 2014, Planet. Space Sci., 96, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Franz, H. B., Trainer, M. G., Malespin, C. A., et al. 2017, Planet. Space Sci., 138, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Fulchignoni, M., Ferri, F., Angrilli, F., et al. 2005, Nature, 438, 785 [CrossRef] [Google Scholar]
- Gasc, S., Altwegg, K., Fiethe, B., et al. 2017, Planet. Space Sci., 135, 64 [Google Scholar]
- Gautier, T., Serigano, J., Bourgalais, J., Hörst, S. M., & Trainer, M. G. 2020, Rapid Commun. Mass Spectrom., 34, e8684 [CrossRef] [Google Scholar]
- Hwang, W., Kim, Y., & Rudd, M. E. 1996, J. Chem. Phys., 104, 2956 [NASA ADS] [CrossRef] [Google Scholar]
- Hörst, S. M. 2017, J. Geophys. Res. Planets, 122, 432 [CrossRef] [Google Scholar]
- Israël, G., Szopa, C., Raulin, F., et al. 2005, Nature, 438, 796 [CrossRef] [Google Scholar]
- Jacquemart, D., Lellouch, E., Bézard, B., et al. 2008, Planet. Space Sci., 56, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y.-K., & Rudd, M. E. 1994, Phys. Rev. A, 50, 3954 [NASA ADS] [CrossRef] [Google Scholar]
- Lellouch, E., Bézard, B., Flasar, F. M., et al. 2014, Icarus, 231, 323 [CrossRef] [Google Scholar]
- Leseigneur, G., Bredehöft, J. H., Gautier, T., et al. 2022, Angew. Chem. Int. Ed., 87, e202200116 [Google Scholar]
- Linstrom, P. J. et al. 2019, in WebBook de Chimie NIST, Base de Données Standard de Référence NIST Numéro 69 (Gaityhersurbg, MD) [Google Scholar]
- Lora, J. M., & Ádámkovics, M. 2017, Icarus, 286, 270 [CrossRef] [Google Scholar]
- Lorenz, R. D., Zarnecki, J. C., Towner, M. C., et al. 2007, Planet. Space Sci., 55, 1936 [NASA ADS] [CrossRef] [Google Scholar]
- Lorenz, R. D., Turtle, E. P., Barnes, J. W., et al. 2018, Johns Hopkins APL Technical Digest, 34 [Google Scholar]
- Lunine, J. I., & Atreya, S. K. 2008, Nat. Geosci., 1, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Magee, B. A., Waite, J. H., Mandt, K. E., et al. 2009, Planet. Space Sci., 57, 1895 [NASA ADS] [CrossRef] [Google Scholar]
- Mahaffy, P. R., Webster, C. R., Cabane, M., et al. 2012, Space Sci. Rev., 170, 401 [CrossRef] [Google Scholar]
- McLafferty, F. W., & Turecek, F. 1993, Interpretation of Mass Spectra (University Science Books), 371 [Google Scholar]
- Mitchell, J. L., Pierrehumbert, R. T., Frierson, D. M., & Caballero, R. 2006, Proc. Natl. Acad. Sci. U.S.A., 103, 18421 [NASA ADS] [CrossRef] [Google Scholar]
- Niemann, H. 2002, Space Sci. Rev., 104, 553 [CrossRef] [Google Scholar]
- Niemann, H. B., Atreya, S. K., Bauer, S. J., et al. 2005, Nature, 438, 779 [Google Scholar]
- Niemann, H. B., Atreya, S. K., Demick, J. E., et al. 2010, J. Geophys. Res., 115, E12006 [Google Scholar]
- Prydz, R., & Goodwin, R. D. 1972, J. Chem. Thermodyn., 4, 127 [Google Scholar]
- Rafkin, S. C., Lora, J. M., Soto, A., & Battalio, J. M. 2022, Icarus, 373, 114755 [CrossRef] [Google Scholar]
- Rannou, P., Coutelier, M., Rivière, E., et al. 2021, ApJ, 922, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Rey, M., Nikitin, A. V., Bézard, B., et al. 2018, Icarus, 303, 114 [Google Scholar]
- Schröder, S. E., & Keller, H. U. 2008, Planet. Space Sci., 56, 753 [CrossRef] [Google Scholar]
- Serigano, J., Hörst, S. M., He, C., et al. 2020, J. Geophys. Res. Planets, 125, e2020JE006427 [CrossRef] [Google Scholar]
- Serigano, J., Hörst, S. M., He, C., et al. 2022, J. Geophys. Res. Planets, 127, e2022JE007238 [CrossRef] [Google Scholar]
- Spiga, A. 2011, Planet. Space Sci., 59, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Tokano, T., McKay, C. P., Neubauer, F. M., et al. 2006, Nature, 442, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Tomasko, M. G., Archinal, B., Becker, T., et al. 2005, Nature, 438, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Valdez, C. A., Leif, R. N., Hok, S., & Alcaraz, A. 2018, J. Mass Spectrom., 53, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Waite, J. H. 2005, Science, 308, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Waite, J. H., Young, D. T., Cravens, T. E., et al. 2007, Science, 316, 870 [CrossRef] [Google Scholar]
- Ziegler, W.T., 1959, National Bureau of Standards, Technical Note 4, NIST Pubs https://doi.org/10.6028/NBS.TN.4 [Google Scholar]
All Tables
Reported methane mole fractions at different altitudes in Titan’s atmosphere, for similar latitude and season to those sampled by Huygens.
All Figures
 |
Fig. 1 m/z 16 to m/z 28 count ratios in GCMS data versus altitude recorded during Huygens descent. Black dots correspond to raw counts archived in level 2 data requiring no correction. Blue dots correspond to raw counts for which a correction is required and red dots correspond to corrected counts using m/z 29 as a proxy when m/z 28 saturates. We note that the very sharp increase in counts at altitude 0 corresponds to outgassing after Huygens’s touchdown and GCMS continued recording atmospheric mass spectra for a couple of hours after the touchdown (not shown here). A comparison between the two correction methods using either m/z 14 or 29 as a proxy is given in Figure A.1. |
| In the text | |
 |
Fig. 2 Schematic representation of gas flow in the GCMS instrument. Flow path for measurements discussed in this paper are highlighted in red. Highlighted in the blue box are the L1 and L2 capillary arrays, main source of possible gas fractionation between Titan’s atmosphere and the detector. Adapted from Niemann (2002). |
| In the text | |
 |
Fig. 3 Schematic representation of the data workflow from retrieved GCMS level 2 data on the PDS to atmospheric mixing ratios. |
| In the text | |
 |
Fig. 4 Retrieved methane mixing ratio through the lower atmosphere. Black dots: retrieved maximum probabilities for the CH4 mixing ratio as a function of altitude; associated error bars correspond to 1σ uncertainties assuming a Gaussian profile for the methane mixing ratio probability density function. Blue diamonds are the methane mixing ratio reported in Niemann et al. (2010). Data were stacked to a kilo-metric resolution before deconvolution. Insert shows the deconvolution for a typical mass spectrum recorded by Huygens at high altitude (here 130 km). Black bars are the measured signal and blue, orange, and green bars show the contribution of hydrogen, methane, and molecular nitrogen, respectively. Peaks at m/z 2, 12, and 13 are slightly underfitted to the contribution of higher order hydrocarbons to the signal, which is not shown here. |
| In the text | |
 |
Fig. 5 High resolution vertical profile of methane below 30 km. Black dots represent the median of 100 000 deconvolutions and grey bars their 1 − σ deviations. As the main source of uncertainties comes from the seeding fractionation pattern and not the retrieval method, error bars should be understood as systematic errors. This means that for example if a more accurate measurement was to confirm a given value to be lower than the mean reported value here, this would be valid for all the other altitudes as well. Blue diamonds and bars represent methane mixing ratios reported by Niemann et al. (2010) and their standard deviation, respectively. |
| In the text | |
 |
Fig. 6 Close up of the high-resolution profile of methane in the lower troposphere below 5 km. Black dots represent our median retrieved values with their associated error bars. Blue diamonds and bars represent methane mixing ratios reported by Niemann et al. (2010) and their standard deviation, respectively. Red horizontal dashed lines labeled A, B, and C represent the altitude of the boundary layers identified in Charnay & Lebonnois (2012) at 300 m, 800 m, and 2 km, respectively. |
| In the text | |
 |
Fig. 7 Methane relative humidity below 10 km. The three humidity profiles are calculated using the nominal HASI temperature (plain line), the HASI temperature shifted by −1.3 K (dotted line), and the HASI temperature shifted by −1.6 K (dashed line), respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.