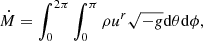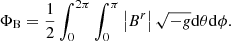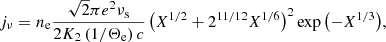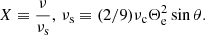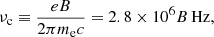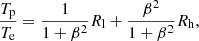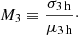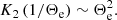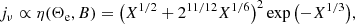| Issue |
A&A
Volume 688, August 2024
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 15 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202449681 | |
| Published online | 06 August 2024 | |
Dynamics and emission properties of flux ropes from two-temperature GRMHD simulations with multiple magnetic loops
1
Tsung-Dao Lee Institute, Shanghai Jiao Tong University, Shengrong Road 520, Shanghai 201210, PR China
e-mail: hongxuan_jiang@sjtu.edu.cn; mizuno@sjtu.edu.cn
2
School of Physics and Astronomy, Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai 200240, PR China
3
Institut für Theoretische Physik, Goethe-Universität Frankfurt, Max-von-Laue-Straße 1, 60438 Frankfurt am Main, Germany
4
Research Center for Astronomy, Academy of Athens, Soranou Efessiou 4, 11527 Athens, Greece
5
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
6
Institut für Theoretische Physik und Astrophysik, Universität Würzburg, Emil-Fischer-Str. 31, 97074 Würzburg, Germany
7
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received:
21
February
2024
Accepted:
26
April
2024
Context. Flux ropes erupting in the vicinity of a black hole are thought to be a potential model for the flares observed in Sagittarius A*.
Aims. In this study, we examine the radiative properties of flux ropes that emerged in the vicinity of a black hole.
Methods. We performed three-dimensional two-temperature general relativistic magnetohydrodynamic (GRMHD) simulations of magnetized accretion flows with alternating multiple magnetic loops and general relativistic radiation transfer (GRRT) calculations. In the GRMHD simulations, we implemented two different sizes of initial magnetic loops.
Results. In the small loop case, magnetic dissipation leads to a weaker excitement of magneto-rotational instability inside the torus, which generates a lower accretion rate compared to the large loop case. However, the small loop case generates more flux ropes due to frequent reconnection by magnetic loops with different polarities. By calculating the thermal synchrotron emission, we found that the variability of light curves and the emitting region are tightly related. At 230 GHz and higher, the emission from the flux ropes is relatively stronger compared to the background, which is responsible for the filamentary structure in the images. At lower frequencies (e.g., 43 GHz), emission comes from more extended regions, which have a less filamentary structure in the image.
Conclusions. Our study shows that self-consistent electron temperature models are essential for the calculation of thermal synchrotron radiation and the morphology of the GRRT images. Flux ropes contribute considerable emission at frequencies ≳230 GHz.
Key words: accretion, accretion disks / black hole physics / magnetic reconnection / magnetohydrodynamics (MHD) / radiation mechanisms: thermal / radiative transfer
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The supermassive black hole (SMBH) in our galaxy, Sagittarius A* (Sgr A*), is one of the most mysterious objects. Despite many extensive research efforts to comprehend the physics of Sgr A*, there are still many open questions (e.g., Frank et al. 2002; Genzel et al. 2010; Morris et al. 2012). Recent Event Horizon Telescope (EHT) observations have made significant progress in understanding its basic properties (Event Horizon Telescope Collaboration 2022a,b,c,d,e). The EHT observations of Sgr A* have been tested with various astrophysical models. However, none of the models have passed all observational constraints (Event Horizon Telescope Collaboration 2022e). Nonetheless, the EHT model constraint prefers magnetically arrested disk (MAD) models over standard and normal evolution (SANE) flow models and other accretion flow models, including tilted disks (Liska et al. 2018) and stellar-wind-fed models (Ressler et al. 2020). Both Sgr A* and M 87 are categorized as low-luminosity active galactic nuclei (LLAGNs) (e.g., Yuan & Narayan 2014; Ho 2008). Their accretion rates are far below the Eddington rate (Ho 2009; Marrone et al. 2007). Many recent models have indicated that the accretion flows around the SMBH in M 87 (M 87*) are possibly also in a MAD state (Event Horizon Telescope Collaboration 2019; Cruz-Osorio et al. 2021; Yuan et al. 2022). However, though the accretion rates of the two SMBHs are similar, the physical properties of the accretion flow of Sgr A* are still not perfectly understood yet.
The observed hot spot in Sgr A* is another unsolved problem (GRAVITY Collaboration 2020b; Lin et al. 2023; Jiang et al. 2023). GRAVITY Collaboration (2018) detected orbital motions of a hot spot near the innermost stable circular orbit of Sgr A* at near-infrared (NIR) frequency. Their modeling shows a hot spot orbiting at a few gravitational radii away from the horizon, consistent with the observed flare activities (GRAVITY Collaboration 2020b). Flares in Sgr A* are observed at both sub-millimeter and NIR frequencies (e.g., Do et al. 2019). During flares, the NIR flux increases several times from the magnitude of the quiescent state. The NIR flux distribution suggests the total emission of Sgr A* is a combination of a quiescent state and sporadic flares (GRAVITY Collaboration 2020a). Polarization information of the hot spots of Sgr A* is provided by EHT-ALMA observation (Wielgus et al. 2022), and the hot spots seem to be consistent with the vertical magnetic flux rope from the magnetically arrested region in accretion flows (e.g., Dexter et al. 2020; Porth et al. 2021; Scepi et al. 2022). In particular, Dexter et al. (2020) has reported a clockwise rotating hot-spot motion in MAD flow around Sgr A* through GRMHD simulations. Furthermore, EHT observations suggest a small line of sight inclination angle (Event Horizon Telescope Collaboration 2019), which has also been recommended by Von Fellenberg et al. (2023) based on light curve fitting of the flares. These MAD models suggest the flaring events are strongly related to the flux eruptions, which are located in the equatorial plane. However, polarimetric tomography suggests the orbital motion of the flare is in a low-inclination orbital plane (Levis et al. 2024). Plasmoid chains and flux ropes, typically generated in the jet sheath, exhibit a low inclination angle (Nathanail et al. 2020, 2022a; Jiang et al. 2023; Aimar et al. 2023; El Mellah et al. 2023). Considering this, we propose that the plasmoid chain model offers a more plausible explanation for the observed flares.
The formation of the plasmoids in the accretion flow has been proven to be a plausible scenario in GRMHD simulations of magnetized accretion flows with multi-loop magnetic configurations (Nathanail et al. 2020; Jiang et al. 2023). In these simulations, highly turbulent accretion flow and frequent reconnection events occur due to merging magnetic loops. Plasmoid chains are also seen in the jet sheath in the 3D general relativistic particle-in-cell (GRPIC) simulations of El Mellah et al. (2023). Due to the frequent reconnection from the merging magnetic loops, non-steady jets with low power are generated along with large numbers of plasmoids (for detail, see Nathanail et al. 2020, 2022a; Chashkina et al. 2021; Jiang et al. 2023). In our previous 2D GRMHD simulations of magnetized accretion flows with multiple magnetic loops (Jiang et al. 2023), plasmoid chains were generated mainly via the reconnection of a magnetic field with opposite polarity. In 2D, we only observed purely poloidal plasmoid chains due to underlying axisymmetric conditions. Recently, Nathanail et al. (2022a) suggested that the plasmoid chains have three-dimensional structures. Accordingly, self-consistent evolution of the toroidal component of the magnetic field becomes important, which requires 3D simulations. We expect to observe the filamentary structure, which may be instrumental in explaining the flaring activities. Unfortunately, it cannot be fully resolved in our simulations due to the resolution limit. Although the plasmoid chains in this work are not fully resolved, the two-temperature sub-grid models partially address this issue by providing a more accurate calculation of electron temperature. Consequently, we can study the emission properties of these structures more precisely.
The presence of a mean-field dynamo in the accretion disk can change the initial magnetic configuration and make it easier to get alternating polarities of the magnetic field (Del Zanna et al. 2022; Mattia & Fendt 2020, 2022). However, previous simulations (Mizuno et al. 2021) have revealed that the alternating polarities generated within the MAD do not significantly impact the formation of a strong jet. This limitation may arise from the finite numerical resolution, which weakens the amplification of the magnetic field by the dynamo process. Consequently, an additional dynamo term becomes necessary (e.g., Mattia & Fendt 2020, 2022; Zhou 2024). Even when the numerical resolution is sufficiently high, a strong persistent jet exists in the MAD regime (Ripperda et al. 2022). To achieve a sufficiently weak jet and promote frequent reconnection within the jet sheath, a multiple magnetic loop configuration remains essential, implying distinct polarities of plasma injection into the torus.
Previous simulations have only examined accretion flow in single-fluid approximation, which cannot produce self-consistent radiative signatures (Jiang et al. 2023). Calculation of self-consistent synchrotron emissions from electrons in radiatively inefficient accretion flow (RIAF) requires a two-temperature framework (Ressler et al. 2015). In our previous study, we used two-temperature GRMHD simulations of magnetized accretion flow with multiple loops to investigate electron temperature distributions, drawing on the electron heating prescriptions of Rowan et al. (2017), Kawazura et al. (2019). Our findings revealed that the temperature distributions of plasmoids and the current sheet around black holes differ significantly when compared to the parameterized electron-to-ion temperature ratio prescription with two-temperature calculations (Jiang et al. 2023). We have also shown that the flaring activity in Sgr A* is likely related to the unique features of plasmoids formed in various magnetic field configurations. Following these findings, we extend our previous work with this study.
We performed two-temperature 3D GRMHD simulations of magnetized accretion flows with multiple magnetic loops. In our investigations, the accretion flow formed from multi-loop configurations is mostly in the SANE regime. Although MAD models are more favored for the observations of Sgr A*, many SANE models also pass the EHT tests (Event Horizon Telescope Collaboration 2022e). Moreover, none of the MAD or SANE models used in the EHT analysis (with a single-loop magnetic field) can meet the light curve’s variability requirement (Event Horizon Telescope Collaboration 2022e). This suggests that neither the single-loop SANE models nor the MAD models are appropriate to explain all the observation features of Sgr A*. Thus, new accretion flow models are required to better understand the accretion flow of Sgr A*.
The results of multiple magnetic loops show unique features, including frequent magnetic reconnections with a relatively higher accreting magnetic flux than a normal SANE torus (Fromm et al. 2022). Therefore, we studied the dynamics of the accretion flows from different sizes of magnetic loops in order to investigate the possible applications for Sgr A*. Subsequently, we tried to understand the radiation properties of the accretion flows by performing GRRT calculations of thermal synchrotron emission. Through a comparative analysis of the GRRT calculations and the emissivity distribution calculated from GRMHD data, we investigated the properties of emitting regions across various observing frequencies. In particular, we explored the time variability and the formation of hot spots.
The rest of the paper is organized as follows: In Sect. 2, we describe our simulation setup, which includes the initial condition and magnetic field configurations used in this study. In Sect. 3, we discuss our findings from our GRMHD simulations and post-processed GRRT calculations. We provide our conclusions in Sect. 4.
2. Numerical method
The numerical methods employed for the GRMHD simulation of this study are identical to those utilized in previous work (Mizuno et al. 2021; Jiang et al. 2023). For the sake of completeness, we only describe the basic information here. The BHAC code is used to perform the 3D GRMHD simulations, which solve the 3 + 1 form of ideal GRMHD equations in geometric units (G = M = c = 1 and  are included in the magnetic field; Porth et al. 2017; Olivares et al. 2019). The simulations are performed in Kerr spacetime, and the self-gravity of matter is also neglected.
are included in the magnetic field; Porth et al. 2017; Olivares et al. 2019). The simulations are performed in Kerr spacetime, and the self-gravity of matter is also neglected.
The simulations are initiated from a rotation-supported hydrodynamic equilibrium torus following (Fishbone & Moncrief 1976). To avoid repetition, we do not show the explicit expressions for the initial quantities here. Instead, we only show the initial torus parameters, which are rin = 20 rg and rmax = 40 rg, where rg = GM/c2 is the gravitational radius and M is the mass of the black hole. The constant adiabatic index Γ = 4/3 is used (Rezzolla & Zanotti 2013). In our study, we consider a black hole with a spin parameter of a = 0.9375. The torus mass is assumed to be negligible compared to that of the black hole, resulting in a spacetime described by the static Kerr metric. Two percent of a random perturbation is applied to the gas pressure within the torus to excite the magneto-rotational instability (MRI). This instability generates turbulence in the accretion disk.
A pure poloidal magnetic field configuration is considered as an initial condition for the magnetic fields, which is set up with an initial vector potential:
where N = 3 is used in all cases and λ is a the wavelength of the magnetic configuration in the radial direction. The value of Aϕ is determined by setting the minimum of plasma βmin = 100, where β ≡ pg/pmag. pg is the gas pressure and pmag = b2/2 is the magnetic pressure, where b2 = bμbμ and bμ is the four-magnetic field. Figure 1 demonstrates the initial density distribution with the multiple poloidal magnetic loops (black lines). The solid and dashed contours represent different polarities of the poloidal magnetic loops. In Fig. 1, we present the initial magnetic field configuration (black lines) of case M80a3D with an initial density distribution (color map) as an illustration of the alternating multi-loop magnetic configuration. In the case of M20a3D, each loop length becomes shorter, but the torus structure does not change.
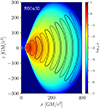 |
Fig. 1. Initial torus profile of logarithmic density (color) and magnetic field configuration (black contours). The dashed contours represent positive polarity, while solid ones are the opposite. |
In this work, we adopted the parameters of the two representative cases from our 2D simulations (Jiang et al. 2023), that is, the cases of M20a and M80a, to perform 3D simulations, which we label as M20a3D and M80a3D. We remind the readers that models M20a3D and M80a3D correspond to the cases with λ = 20 and λ = 80, respectively.
We also adopted two electron heating prescriptions: turbulence heating and magnetic reconnection heating. The turbulence electron heating model was originally prescribed with damping of MHD turbulence, which is given by Kawazura et al. (2019)
where
Subsequently, for the reconnection heating prescription, we adopted a fitting function measured by PIC simulations, which is given by Rowan et al. (2017):
where βmax = 1/4σh, σh = b2/ρh is magnetization as defined according to the fluid specific enthalpy h = 1 + Γgpg/(Γg − 1). Applying the turbulence and reconnection electron heating prescriptions simultaneously, we stored the electron entropy from the two models separately and obtained the electron temperatures from the two heating models. The benefit of this method is that it avoids the non-linear effect in the GRMHD simulations and allows us to directly compare the different electron heating models in the same GRMHD data.
We set the outer boundary of the simulations at r = 2500 rg. The simulations were performed in spherical Modified Kerr-Schild coordinates (see Porth et al. 2017) with an effective grid resolution of 384 × 192 × 192 and including the entire 2π azimuthal domain with three static mesh refinement levels. The simulation models M20a3D and M80a3D were evolved up to t = 15 000 M and 20 000 M, respectively. These simulation times are enough for both models to reach a quasi-steady state.
To obtain synthetic images from GRMHD simulations, a GRRT calculation is performed with the BHOSS code (Younsi et al. 2012, 2020) in post-process. The GRRT equations are solved along the geodesics and integrated through 3D GRMHD data. The resultant images, light curves, and spectra are obtained at a given viewing angle i and observing frequency ν as seen by a distant observer. In this work, all the GRRT post-processed calculations used the same viewing angle, i = 30°, which is adapted from Event Horizon Telescope Collaboration (2022e). In the GRRT calculations, a threshold on the magnetization σ = b2/ρ was imposed in order to limit the emission regions in the high-magnetized domain because the high magnetization region in the GRMHD simulations may be affected by the floor treatment and thus rendered unreliable. In this work, we only consider the region with σ < 1. We also adopted the fast light approximation, which neglects the propagation time of light. We also used Sgr A* as the target for the GRRT calculation. It has a mass M• = 4.5 × 106 M⊙ and a distance DSgrA = 8.5 × 103 pc from Earth. The field of view (FOV) is 160 μ as with a resolution of 1000 × 1000 pixels. For the calculation of electron temperature, we used both the two-temperature model and the parameterized R-β model. The accretion rate was normalized at 230 GHz, with an averaged flux of 2.4 Jy. We mainly discuss the property of the emission at sub-millimeter frequency, which is dominated by a thermal component. Therefore, only thermal synchrotron is considered in this work (e.g., Najafi-Ziyazi et al. 2024).
3. Results
3.1. Dynamics of accretion flow
To explore the dynamics of accretion flows in 3D GRMHD simulations of magnetized accretion flows with multiple poloidal loops, we employed the definition from Porth et al. (2019) to compute the mass accretion rate evaluated at the event horizon,
and we calculated the magnetic flux rate measured at the event horizon as
Figure 2 shows the time evolution of the mass accretion rate Ṁ and the normalized magnetic flux rate 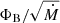 for M20a3D (black) and M80a3D (blue). Due to the slower evolution of the bigger magnetic loop in the case of M80a3D, we simulated it up to 20 000 M to study the long-term evolution of accretion dynamics. The accretion flow of M20a3D loses its initial magnetic configuration and enters a non-linear evolution phase after 5000 M. Thus, we simulated it up to 15 000 M only.
for M20a3D (black) and M80a3D (blue). Due to the slower evolution of the bigger magnetic loop in the case of M80a3D, we simulated it up to 20 000 M to study the long-term evolution of accretion dynamics. The accretion flow of M20a3D loses its initial magnetic configuration and enters a non-linear evolution phase after 5000 M. Thus, we simulated it up to 15 000 M only.
 |
Fig. 2. Time evolution of (a) mass accretion rate (Ṁ) and (b) magnetic flux rate ( |
In general, the dynamics of the accretion flow of M20a3D are similar to those in the 2D cases shown in Jiang et al. (2023) (Model M20a). When the simulation reaches the quasi-steady phase (10 000–15 000 M), it does not have a persistent jet. A similar phenomenon has been observed in the smaller torus simulations in Nathanail et al. (2022b). In 3D simulations, the accretion flow becomes turbulent in the ϕ direction due to the interchange instabilities (see Begelman et al. 2022), which is absent in 2D simulations. The initially ordered magnetic loops are mixed up before accreting onto the horizon. The magnetic dissipation due to the multiple loops inside the torus reduces the development of magnetorotational instability (MRI). It weakens the poloidal magnetic field inside the torus, which leads to a lower accretion rate at the event horizon (see the black curve in Fig. 2a). The average value of the accretion rate for the case M20a3D (Ṁ ∼ 10−1) is roughly two orders of magnitude lower than that of the simulations with a single loop, as reported by Mizuno et al. (2021; Ṁ ≲ 10; see Model a = 0.94 and a = 0). However, when the initial magnetic loop size becomes larger, we observed a magnitude higher accretion rate from M80a3D compared to M20a3D. In contrast to the findings from the single-loop simulation (Mizuno et al. 2021), we observe a significantly reduced magnetic flux in both the M20a3D and M80a3D cases. The initial configuration of the magnetic loops depends on the density structure of the torus (see Eq. (1)). The strength of each magnetic loop becomes weaker in a larger radius. Despite the presence of relatively larger magnetic loops in the case of M80a3D, there are at least four magnetic field loops with alternating polarities that hold magnetic energy exceeding 10% of the maximum magnetic energy in the torus. Similarly, for M20a3D, there are over ten loops with magnetic energy significant enough within the torus. The dynamics of these loops mainly contribute to the overall characteristics of the accretion flow. More small-scale magnetic fields are generated in M80a3D compared to the single-loop simulation in Mizuno et al. (2021). This leads to roughly half of the magnetic flux in the single-loop case and fails to generate a fully MAD accretion flow. However, due to less magnetic dissipation in M80a3D, MRI is better resolved, leading to a higher accretion rate than in M20a3D, which has an accretion rate closer to the single-loop cases (e.g., Mizuno et al. 2021).
To understand the accretion dynamics, we present the time (between t = 10 000 M to 15 000 M) and azimuthally averaged distribution of density (log10(ρ)), magnetization (log10(σ)), and plasma beta (log10(β)) for both cases in Fig. 3. The solid and dashed lines in panels (a)–(c) represent the boundaries of the Bernoulli parameter −hut = 1 and magnetization σ = 1, respectively. We also present the time evolution of average MRI quality factors Q(r, θ, ϕ) of M20a3D and M80a3D in Figs. 3d and e. The quality factors are spatially averaged in the high-density torus region (i.e., r < 50 rg, 60° < θ < 120°). In the density distributions of the two cases in Fig. 3a, M20a3D has a larger gravitationally bounded region (see the solid lines) and smaller disk region as compared to M80a3D. The initial magnetic configuration with larger loops produces a less chaotic magnetic field and magnetic dissipation by reconnection inside the torus (Jiang et al. 2023). Therefore, we observed a stronger jet and a lower plasma β (stronger magnetic field) in the case of M80a3D compared to M20a3D (see Fig. 3, panels b and c). The different strengths of the leftover magnetic field after the merger of the magnetic loops generated different magnitudes of MRI. In Fig. 3, panels (d) and (e), we observed that all MRI quality factors are higher than eight, which means MRI is fully resolved (Hawley et al. 2011; Porth et al. 2019). However, slightly lower MRI quality factors were observed in M20a3D than in M80a3D, which is caused by the globally weaker magnetic field in the torus. This also resulted in different accretion rates in both models (Fig. 2), and due to that, M20a3D forms a narrower high-density equatorial region compared to M80a3D.
 |
Fig. 3. Distribution of time (between t = 10 000 M to 15 000 M) and azimuthal averaged (a) density ρ, (b) magnetization σ, and (c) plasma beta for 3D GRMHD simulations with multi-loops in different loop length (left: λ = 20, M20a3D and right: λ = 80, M80a3D). The solid and dashed contours in each panel represent the Bernoulli parameter −hut = 1 and magnetization σ = 1, respectively. Lower panels (d) and (e) show the evolution of averaged MRI quality factors of M20a3D and M80a3D. |
In Fig. 4, we show the distribution of the toroidal component of the magnetic field (Bϕ) along with the poloidal magnetic field lines. In both cases, we observed the formation of opposite polarity islands (indicated by red regions inside the blue region and vice versa). These are the results of active MRI in the accretion flow. We observed a stronger toroidal component of the magnetic field close to the horizon for M80a3D compared to M20a3D. The strong magnetic field in case M80a3D aids in the formation of a stronger jet in M80a3D as compared to M20a3D (see Fig. 3b).
 |
Fig. 4. Distributions of the toroidal component of the magnetic field for M20a3D (left) and M80a3D (right). The streamlines show the poloidal magnetic field lines. |
3.2. Radiative property
In this section, we study the radiative signatures of the multi-loop magnetic field configuration in the accretion flows. Radiative signatures of the single-loop magnetic field configuration in accretion flows have been studied extensively in the two-temperature and in R-β considerations for electron temperature (e.g., Mościbrodzka et al. 2016; Mizuno et al. 2021; Fromm et al. 2022). In multi-loop cases, more frequent reconnection generates more turbulent accretion flow and intermittent strength in jets. In this section, we investigate these radiative properties in detail and study their observational implications.
In this paper, we only consider thermal synchrotron emission to investigate the radiative property of the accretion flow. We calculated emissivity following Leung et al. (2011), which introduces an approximate expression of the thermal synchrotron emission. The explicit expression can be written as follows:
where
In the above equation, Θe = kBTe/mec2 is the dimensionless electron temperature, kB is the Boltzmann constant, Te is the electron temperature in the CGS unit, K2 is the modified Bessel function of the second kind, and νc is the electron cyclotron frequency, which is given by
where the symbols have their usual meaning, viz., e is the electronic charge, me is the electronic mass, the magnetic field strength 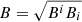 , and Bi is the Eulerian three-magnetic field.
, and Bi is the Eulerian three-magnetic field.
In our calculations, we used the R-β prescription as well as two-temperature models to calculate the electron temperature in the accretion flow. In the R-β prescription, the electron temperature is calculated from the proton temperature as follows Mościbrodzka et al. (2016):
where Rl and Rh are two dimensionless parameters. In our work, we fixed Rl = 1 and used two different values for Rh (1 and 160) to compare with the two-temperature electron heating models.
In Fig. 5, we show the light curves of the case M80a3D at 230 GHz during the initial phase of the evolution. The black, blue, red, and green lines correspond to the light curves calculated for turbulence heating, reconnection heating, and the R-β model with Rh = 1 and Rh = 160, respectively. During the early phase of the evolution, accretion happens only due to the first magnetic loop inside the torus (simulation time t = 3000 − 4000 M), which is quite similar to the single-loop simulations. During this phase, the light curves of different electron heating models and R-β models show similar behavior, albeit with small variations. That is because the reconnection between the poloidal field lines with different polarities starts only after t ≳ 4000 M. This result agrees with Mizuno et al. (2021) due to the similarity of the magnetic field configuration. However, when the follow-up loops with different polarities accrete onto the horizon, the behavior of the light curves from different electron heating models varies. During the period that is t ≳ 4000 M, we observed strong magnetic reconnection between the first and second loops, which releases a large amount of magnetic energy and contributes to increasing the luminosity.
 |
Fig. 5. Evolution of light curves at 230 GHz for the case of M80a3D with different heating models and R-β models. The black solid line represents the light curve from the turbulence heating model. The blue solid line is the reconnection heating one. The red and dark-green lines represent the R-β models with Rh equals 1 and 160, respectively. |
Figure 6 shows the light curves in different electron heating models at the later simulation time for M80a3D and M20a3D. The behavior of the light curves from the various electron temperature models shows significant differences from the ones at the earlier simulation time shown in Fig. 5. In Fig. 6. We observed that the global trend of the light curve for the R-β models and the two-temperature models is similar, which roughly follows the trend of the mass accretion rate. However, the detailed structure of the light curves for each electron heating model is different. The turbulence heating model is closer to the result of the Rh = 160 case, while reconnection heating is closer to the Rh = 1 case. The two different values of Rh in the R-β model represent two extreme conditions of the electron heating prescriptions. The effect of the different Rh values is mainly seen on the estimated electron temperature of the high plasma β region. A higher Rh value gives a lower temperature in the disk. Therefore, in that case, we observed less radiation from the disk as compared to the lower Rh value case. If the turbulence and frequent reconnection do not happen, the difference of the 230 GHz light curves in the two-temperature and the R-β models is expected to be minimal, as seen in the initial simulation time (Fig. 5) and previous single-loop simulations (Mizuno et al. 2021).
 |
Fig. 6. Panels (a) and (b) are the light curves of 4 different electron heating models for the case M80a3D, which is the same as Fig. 5 but in different times. Panel (c) is for the case M20a3D. In each panel, the gray solid line is the corresponding accretion rate during each period. |
To understand the variability of the four different models for both cases, in Fig. 7, we show the standard deviations of light curves at 230 GHz for different electron heating models and R-β models at different time periods. The first two sections of Fig. 7 correspond to the case M80a3D but at different periods of time, t = 5000 − 10 000 M, and t = 15 000 − 20 000 M. The rightmost section of Fig. 7 corresponds to the case M20a3D in the period of t = 10 000 − 15 000 M. In general, the R-β model with Rh = 160 shows the highest standard deviation, suggesting it is the most variable case among the four models. On the contrary, the light curve for Rh = 1 is the least variable model. By comparing in Figs. 6a and b, we observed that due to the continuous merging of the magnetic field loops, the variability reduces with simulation time. It is reflected in Fig. 7 that all models have a lower standard deviations at a later simulation time. Similarly, by comparing in Figs. 6c and a, we found that for case M80a3D, the variability of the light curves is larger than that of case M20a3D due to the larger and stronger magnetic field loops in the initial torus. In Fig. 7, case M20a3D has a smaller average standard deviation than that of the case M80a3D.
 |
Fig. 7. Standard deviation of the light curves of different electron heating models. The error bar represents the standard deviation of the light curves. Black dots show the deviation of case M80a3D during 5000–10 000 M, red dots are 15 000–20 000 M, and blue dots show the data of case M20a3D during 10 000–15 000 M. |
Other than the standard deviation in the light curves, in Event Horizon Telescope Collaboration (2022e), a modulation index M3 with a duration of 3 h was utilized to quantify the light curve variation. The modulation index M3 is defined as the ratio between the standard deviation σ3 h and the mean value μ3 h calculated over a time bin lasting approximately 3 h from the light curve:
It offers quantitative measurement of the light curve variability. Historical M3 observation data suggests M3 ≲ 0.1. However, most of the simulation models in Event Horizon Telescope Collaboration (2022e) failed to match this constraint. The M3 distribution from the light curves of four different electron heating models of the cases M80a3D and M20a3D is presented in Fig. 8. Similar to Fig. 7, the turbulence model shows a distribution similar to the R-β model with Rh = 160. The R-β model with Rh = 1 and the reconnection heating model have a lower variability. In particular, the R-β model with Rh = 1 presents a value (∼0.06) similar to that of a historical observation of Sgr A*.
 |
Fig. 8. Probability distribution function of the M3 of the light curves generated from M20a3D (a) and M80a3D (b). The probability distribution functions have been normalized by setting the peak value to one. The black and red lines represent the cases with different Rh values from the R-β model. The blue and yellow lines are from turbulence and reconnection models, respectively. |
The difference among the light curves from the two electron heating models suggests that the dominant emitting region is not the same for different models. This emitting region is determined by the electron temperature distribution. We discuss the emitting regions in detail in the subsequent sections.
3.3. GRRT images at the flaring state
3.3.1. Emitting region at 230 GHz
In the previous section, we demonstrated the distinct features of light curves for different electron heating models, which could be essential to understanding the variability observed in Sgr A* (Event Horizon Telescope Collaboration 2022d). The dynamics and the dominant emitting region of the accretion flow are related to the variability of the observed light curves. In this section, we investigate the connection between the GRRT images from different electron heating models and the corresponding emissivity distributions in the GRMHD simulations.
As shown in Fig. 4, the case M20a3D generates more turbulence in the accretion flows and has more reconnections than in M80a3D, which leads to the eruption of more flux ropes (Čemeljić et al. 2022). We expected to relate the flux ropes to the flaring events as seen in Sgr A*. To study the properties of the flux ropes and their connection to the observed flaring events, our discussion in the following sections is focused on case M20a3D.
In the first row of Fig. 9, we show snapshot GRRT images at 230 GHz for the four different electron heating models of the case M20a3D at t = 12 240 M. Images from the two different electron heating models (turbulence and reconnection) are presented in panels (a) and (b), respectively. The turbulence model creates a more extended filamentary structure in the GRRT image than the reconnection model. We show the snapshot GRRT images from the R-β model with Rh = 160 and 1 in panels (c) and (d), respectively. The Rh = 160 case shows a very compact GRRT image, while the Rh = 1 one has the most extended emission among the four models.
 |
Fig. 9. GRRT images and corresponding emissivity and electron temperature distributions. First row: GRRT snapshot images for Sgr A* with inclination angle i = 30° at t = 12 240 M from (a) the turbulence heating model, (b) reconnection heating model, (c) R-β model with Rh = 160, and (d) R-β model with Rh = 1. Second row: Corresponding 230 GHz emissivity (left) and electron temperature (right) distributions. The solid white contours in panels (e)–(h) represent the edge of the torus, which is the ρ = 0.01 contour. The dashed contour represents the high magnetization region with σ > 1, which is cutoff in GRRT post-process. |
The differences in the GRRT images seen in Fig. 9 are due to the different electron temperature distributions of the models. To understand the variation, in the second row of Fig. 9, we present the corresponding distributions of azimuthally averaged emissivity and electron temperature for different electron heating models of GRRT images. In general, the two-temperature models (turbulence and magnetic reconnection heating) agree with each other qualitatively in both distributions of electron temperature and emissivity. The difference, however, comes from the more extended emission in the sheath region of the turbulence model, which is the source of the more extended filament structure in the GRRT image. The emission for the reconnection heating model is more concentrated from the disk near the equatorial plane.
The electron temperature distributions of the R-β model vary depending on the values of Rh. For the case where Rh = 160, the contribution from the disk is very low (see Fig. 9g). Therefore, similar to the turbulence heating model, the emission at 230 GHz mainly comes from the sheath region. The case of Rh = 1 provides a more extended emission due to a higher disk temperature (see Fig. 9h), which corresponds to the large and extended diffuse emission in the GRRT image seen in Fig. 9d. A further detailed comparison of electron temperature distribution for different electron heating models is discussed in Appendix A.
The emission from the jet sheath is interesting to study, as most of the plasmoid chain (Jiang et al. 2023; Nathanail et al. 2020) and flux ropes (Čemeljić et al. 2022) are generated there. A similar phenomenon was also observed in the GRPIC simulation in El Mellah et al. (2023). In general, the flux ropes contain a relatively more ordered magnetic field as well as a higher density and electron temperature. In Fig. 10, we show the 3D distribution of electron temperature from the turbulence heating model for the case M20a3D at t = 12 240 M. The volume rendering of electron temperature is shown in orange and purple colors. It clearly shows the filamentary structure (red and purple) in the sheath region, which is a flux rope and contains ordered bundles of magnetic field lines (indicated in yellow magnetic lines). The red and black background in Fig. 10 shows the distribution of the toroidal component magnetic field. Flux ropes emerge near the horizon within the jet sheath region through magnetic reconnection, eventually forming a helical structure. We considered a similar mechanism for the formation of the plasmoid chain seen in the 2D high-resolution simulation (e.g., Jiang et al. 2023). In Fig. 10, we observed a relatively strong magnetic field at the edge of a torus with different polarities, which causes strong reconnection. Due to the low numerical resolution of our 3D simulations, as compared to that in 2D simulations, the tearing instability was not able to develop. Therefore, we did not see any clear evidence of the development of plasmoids in our 3D simulations. If we had performed the 3D simulations with a very high numerical resolution, the plasmoid chains would have been seen (Ripperda et al. 2022). Unfortunately, due to the limitations of our numerical resources, we could not perform such super-high-resolution simulations. Based on the same forming machenism and location in the simulations, we think a reasonable conjecture is that the flux ropes observed in Fig. 10 would be unresolved plasmoid chains.
 |
Fig. 10. Volume rendering of the 3D distribution of electron temperature (yellow to black) and toroidal component of the magnetic field (red to black) from the turbulence heating model at 12 240 M for M20a3D. The white arrows mark the direction of the poloidal magnetic field. Yellow tubes represent the magnetic lines. The size of the box is 10 rg. |
3.3.2. Filamentary structure and flux ropes
In the last section, we presented the filamentary structures in GRRT images obtained from the turbulence heating model. This emission originates from emerging flux ropes. To establish this correlation rigorously, we deeply investigate the interplay between emissivity and electron temperature. According to Eq. (7), thermal synchrotron emission jν is proportional to the electron number density ne, which is related to density ρ in the simulations. From Fig. 9, the funnel region near the pole has a high electron temperature. However, due to the low density, the contribution to the emission from the funnel region is small.
Under the ultra-relativistic condition (Θe ≫ 1), we have (Leung et al. 2011):
Different electron heating models give different distributions of electron temperature. Thus, we focused on the dependency of the electron temperature on emissivity. Leaving other parameters such as electron number density, ne, and magnetic field strength, B, constant, we rewrote Eq. (7) as follows:
where 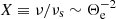 . Here we define η as a coefficient proportional to emissivity. From Eqs. (8) and (9), the relation between emissivity jν and electron temperature Θe is only influenced by the observing frequency ν and the local magnetic field B (see also Event Horizon Telescope Collaboration 2022e). Figure 11 shows the emissivity coefficient as a function of electron temperature in different magnetic field strengths and frequencies. This helped us understand the relationship between emissivity and electron temperature, and it indicates that the strength of the local magnetic field is very sensitive to emissivity.
. Here we define η as a coefficient proportional to emissivity. From Eqs. (8) and (9), the relation between emissivity jν and electron temperature Θe is only influenced by the observing frequency ν and the local magnetic field B (see also Event Horizon Telescope Collaboration 2022e). Figure 11 shows the emissivity coefficient as a function of electron temperature in different magnetic field strengths and frequencies. This helped us understand the relationship between emissivity and electron temperature, and it indicates that the strength of the local magnetic field is very sensitive to emissivity.
 |
Fig. 11. Distribution of emissivity coefficient η as a function of electron temperature. Solid lines represent the frequency of 230 GHz with different local magnetic field strengths. The purple dash-dotted, red dashed, and dotted lines represent the emissivity coefficient of the 46 GHz, 86 GHz, and NIR frequencies, respectively, with typical magnetic fields in flux rope (B = 0.05). |
To obtain the strength of the magnetic field inside flux ropes, we measured it at the regions with high electron temperature (Θe > 10; obtained from the turbulence heating model) and high density (ρ > 0.001) in the case of M20a3D at t = 12 240 M. The histogram of the magnetic field strength distribution is presented in Fig. 12. It indicates that inside the flux ropes, the magnetic field is relatively stronger than in other regions. In most of the regions, the magnetic field strength is B = 10−1.3 ≈ 0.05 in the simulation code unit. Applying the typical value of the magnetic field strength in the flux ropes, we present the relation between the emissivity under different observing frequencies and electron temperatures in Fig. 11. At any frequency or magnetic field strength, emissivity and electron temperature are in positive correlation before the electron temperature reaches its peak value. After the peak, their relationship becomes negatively correlated. However, the position of the peak value of the emissivity depends on the observing frequency and local magnetic field strength.
 |
Fig. 12. Histogram of magnetic field strength distribution in the flaring region. The magnetic field is in code units. We measured the magnetic field strength at the high electron temperature (Θe > 10) and high density (ρ > 0.001) region at t = 12 240 M of the turbulence heating model of case M20a3D. |
At 230 GHz, a stronger magnetic field makes the peak move to a lower electron temperature. This change explains the suppression of the emission from the funnel region, which has a high electron temperature and high magnetic fields. The electron temperature of the filamentary structure seen in Fig. 10 is about Θe = 10 − 100, which corresponds to the high emissivity region at 230 GHz from Fig. 11 when using a typical magnetic field, B = 0.05, in the code unit. Accordingly, we observed a clear filamentary structure in the GRRT images for the turbulence heating model (see Fig. 9a) in the 230 GHz image.
Figure 13 displays the GRRT images computed from the same snapshot used in Fig. 10 at different frequencies (43 GHz and 138 THz). At the lower frequency, the image has a peak at a lower electron temperature (see the dotted line in Fig. 11). Assuming optically thin emission, the lower frequency GRRT image has less filamentary structure due to the weaker emission from the high electron temperature flux ropes. At higher frequencies, such as NIR (138 THz), the peak of the emissivity coefficient occurs when Θe > 1000 since the maximum electron temperature is usually ∼1000, which is always positively correlated with Θe (see dashed line of Fig. 11). As a result, the region with the highest electron temperature dominates the emission at 138 THz. From the lower (43 GHz) to the higher frequencies (NIR), emission becomes more compact due to less contribution from outer accretion flows, and this leads to an enhancement of the contribution of emission from flux ropes and shows more filament structure at a higher frequency.
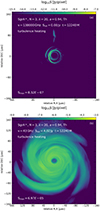 |
Fig. 13. GRRT images at NIR and 43 GHz. Panels (a) and (b) present the NIR and 43 GHz GRRT image from the turbulence model at t = 12 240 M. |
To understand the detailed differences between the emissions from the turbulence and reconnection heating models, we plotted a pixel-by-pixel comparison of the electron temperature between the models for M20a3D at t = 12 240 M (Fig. 14). In the figure, one can see the asymmetry between the left and right halves. It corresponds to the asymmetric structure of the accretion flow in the azimuthal direction related to the existence of the flux rope. Figure 14 indicates that the turbulence heating model has a higher electron temperature in the jet and sheath than in the reconnection heating model. On the other hand, the electron temperature for the reconnection heating model is higher than that of the turbulence heating model in the high-density disk region. Considering the similar mass accretion rates (turbulence model: Ṁtur = 2.19 × 10−8 M⊙ yr−1; reconnection model: Ṁrec = 1.19 × 10−8 M⊙ yr−1), the difference of Θe is the key component for the significantly higher flux at 138 THz from the turbulence heating model compared to the reconnection heating model (see Fig. 15), which has a lower maximum electron temperature inside the flux ropes. Although the torus electron temperature is higher in the reconnection model, it is still lower than the electron temperature of the flux ropes in the turbulence model.
 |
Fig. 14. Distribution of the relative difference between the electron temperature distribution given by the turbulence model and the reconnection model for M20a3D at t = 12 240 M. |
3.3.3. Emitting region at NIR frequency
Since the mass accretion rates of different models are calibrated at 230 GHz, the average NIR flux varies among the models. The light curves of M20a3D with different electron heating models are presented in Fig. 151. Unlike the situation at 230 GHz, the two-temperature models have less similarity with the parameterized R-β models. The reconnection heating model has a significantly lower flux (by about a magnitude) than other models, while the R-β model with Rh = 1 has the highest flux. The turbulence heating model still shows some similarity with the R-β model with Rh = 160. Focusing on the two periods with frequent flaring activities at t = 12 000 − 13 000 M and t = 14 000 − 15 000 M in Fig. 15, the light curve of the turbulence heating model shows a more spiked structure than that in the R-β model with either of the Rh values discussed here. Less variation but stronger emission is seen in the R-β model with Rh = 1. Such light curves in the four different models are caused by the different emitting regions at the NIR frequency. Since the emission at NIR frequencies is dominated by non-thermal emission, the peaks of the light curves observed in Fig. 15 are one to two orders of magnitude lower than the observed value for Sgr A* (5–25 mJy) (GRAVITY Collaboration 2020a). Accordingly, consideration of non-thermal emission is required to explain observed NIR emission (Yusef-Zadeh et al. 2006; Dodds-Eden et al. 2010; Witzel et al. 2021; Zhao et al. 2023). We will investigate this subject in a future work.
Although the non-thermal component is not included in this work, the thermal NIR emission property is nonetheless of interest. The NIR light curves are strongly related to the regions with very high electron temperatures (Θe ≳ 100). The maximum electron temperature is roughly Θe ∼ 500 in all models. According to the relationship in Fig. 11, with a fixed magnetic field strength, the thermal synchrotron emission increases with electron temperature until Θe ≲ 1000. Therefore, at the NIR frequency, the thermal synchrotron emission mainly comes from the high electron temperature regions. As Jiang et al. (2023) suggested, the R-β model is not able to reflect the detailed structure of the high-temperature plasmoids and current sheet. In this 3D simulation result, a more detailed structure is revealed by the two-temperature electron heating models (see Fig. 9). To determine the emitting region at NIR frequency, we plotted the NIR emissivity distributions of turbulence and reconnection models in averaged ϕ and θ directions, respectively, at t = 12 240 M (Fig. 16). In the turbulence heating model, NIR emission mainly comes from the sheath region. On the other hand, in the reconnection heating model, the weaker NIR emission originates mainly from the torus. When comparing with Figs. 16b and c, we observed a bright spiral-like structure in the θ-averaged figures, which is contributed by the flux rope. The turbulence model generates a higher and more extended high emissivity region than that of the reconnection model, leading to a higher flux.
 |
Fig. 16. NIR emissivity and electron temperature distributions. Panel (a) is the azimuthally averaged NIR emissivity distributions from turbulence (left) and reconnection (right) electron heating models. Panels (b) and (c) are the zenith averaged NIR emissivity distributions of turbulence and the reconnection heating model, respectively. |
Since the flux ropes have an important contribution at the NIR frequency, which can be a potential source for the observed NIR flares (e.g., GRAVITY Collaboration 2023), a low-inclination orbital plane is suggested for the 3D orbit of the flares (Levis et al. 2024). The fact that the orbital motion of the flares is located in the equatorial plane (inclination angle ∼90°) conflicts with the MAD model (e.g., Scepi et al. 2022; Dexter et al. 2020; Porth et al. 2021). From our simulations, we observed that most flux ropes are located in the sheath region, have a relatively small inclination angle ∼30°, and are highly variable. The orbiting timescale of the flux ropes is ∼50 M. In most cases, they can only last roughly one orbital period before becoming too weak to be observed. Therefore, the duration of the NIR flares is also roughly 10–100 M, as seen in Fig. 16. The frequent energy release in these regions gives rise to the highly variable light curve in the turbulence heating model. Because the dominant emitting region for this model is the flux ropes (see Fig. 16b), the dynamics of the high-temperature plasma directly influence the behavior of light curves.
4. Conclusions
We have performed 3D two-temperature GRMHD simulations of magnetized accretion flows onto a rotating black hole with multiple magnetic loops. We used two different initial magnetic loop sizes (λ = 20, 80). For the electron heating prescription, we applied turbulence and reconnection heating models. We also included the parameterized R-β model for comparison with the two-temperature electron heating models. A summary of our results is presented below.
-
The simulations show that the initial magnetic loop size affects the strength of the magnetic dissipation and the MRI inside the torus. A smaller loop size results in stronger dissipation and a weaker MRI, while a larger loop size leads to a partial transition from the SANE to the MAD flow model. This finding is consistent with our previous 2D simulations (Jiang et al. 2023). However, in 3D, the transition is not fully observed due to the magnetic field being insufficient to quench the accretion.
-
When the first loop reaches the horizon, the flow resembles that of the simulations with a single loop in Mizuno et al. (2021). The light curves at 230 GHz from different electron heating models are also similar, regardless of whether they use two-temperature GRMHD or parameterized R-β models. However, when the different polarities of a magnetic loop accrete, a large amount of reconnection happens, and a highly turbulent accretion flow is generated.
-
After the accretion flow is fully turbulent, the light curves from the different electron heating models show distinct differences. The turbulence heating model and the R-β model with Rh = 160 show more variability than the reconnection heating model and the model with Rh = 1 because the two former models have strong emissions from the sheath region, where the accretion flow is more variable due to the frequent reconnection events. On the other hand, the reconnection heating model and the R-β model with Rh = 1 have more emission from the equatorial plane with less turbulence. Thus, the variability of light curves from different electron heating models in the multi-loop simulations reflects the dynamics of the emitting regions.
-
Electron temperature has a direct impact on thermal emissivity, which is also related to the observing frequency. At higher frequencies, most of the emissions come from regions with high electron temperatures, such as erupting flux ropes. The flux ropes have a high density and a high electron temperature, and they are more variable than the accretion flow in the equatorial plane. Therefore, they are responsible for the filamentary structure seen in the GRRT images and the light curve variability at high frequencies, such as NIR. However, at lower frequencies (e.g., 43 GHz), a less distinct filamentary structure is observed than at 230 GHz and NIR.
-
In comparison to the two electron heating models, the turbulence heating model shows more variance in the distribution of electron temperature. It provides a higher electron temperature in the jet and flux ropes but a lower temperature than the reconnection model in the accretion disk. This result is also observed in our 2D simulations (Jiang et al. 2023). The global distribution of electron temperature still matches the R-β model. However, the difference comes from small-scale regions.
This paper is focused on the 3D GRMHD dynamics and thermal synchrotron emission from the multi-loop magnetic field configuration. The accretion flow from multiple magnetic loop configurations does not show clear features of the MAD state, which is more favored for Sgr A*, as suggested by EHT observation (Event Horizon Telescope Collaboration 2022e). However, none of the models (irrespective of being SANE or MAD) pass all the constraints from the EHT observations. Most of them failed to satisfy the variability constraint. Considering the flaring activities of Sgr A*, we tried to use the accretion flow generated from a multi-loop magnetic configuration to explain it. We observed reconnection events in the jet sheath, which we find to be related to the observed flares. However, with only thermal emission, the magnitude is not strong enough to compare with NIR observations. A study considering non-thermal emissions from flux ropes will be implemented in our next work, and we plan to investigate its contribution to the NIR flux. Another possible reason for the underestimated NIR emission may originate from the limited resolution of our 3D simulations. Because of the low resolution, tearing instability as well as plasmoids are not well resolved, leading possible underestimation the electron temperature in these regions. This indicates that higher resolution simulations are required to resolve the flaring events of Sgr A*. More comparisons with observations, such as of visibility amplitude morphology and M-ring fits, are required to determine the applicability of the simulations of multi-loop configurations to the Sgr A*. Besides the effects from plasma, althernative theory of gravity may also have observable impacts to the flaring activities (Jiang et al. 2024a,b), which will be investigate in our future work.
In this work, flux ropes with relatively ordered magnetic fields were observed and proven to contribute to the total flux when observing frequencies increase. This finding suggests that relatively higher polarized emission will be observed from these flux ropes. We will investigate the flux ropes via polarized GRRT calculations in our next work.
Acknowledgments
The authors gratefully acknowledge insightful discussions with Dr. Xi Lin from Shanghai Astronomical Observatory. This research is supported by the National Natural Science Foundation of China (Grant No. 12273022), the Shanghai Municipality orientation program of Basic Research for International Scientists (Grant No. 22JC1410600), and the National Key R&D Program of China (No. 2023YFE0101200). Z.Y. acknowledges support from a UKRI Stephen Hawking Fellowship. C.M.F. is supported by the DFG research grant “Jet physics on horizon scales and beyond” (Grant No. 443220636). The simulations were performed on TDLI-Astro, Pi2.0, and Siyuan Mark-I at Shanghai Jiao Tong University.
References
- Aimar, N., Dmytriiev, A., Vincent, F. H., et al. 2023, A&A, 672, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Begelman, M. C., Scepi, N., & Dexter, J. 2022, MNRAS, 511, 2040 [NASA ADS] [CrossRef] [Google Scholar]
- Chashkina, A., Bromberg, O., & Levinson, A. 2021, MNRAS, 508, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Cruz-Osorio, A., Fromm, C. M., Mizuno, Y., et al. 2021, Nat. Astron., 6, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, L., Tomei, N., Franceschetti, K., Bugli, M., & Bucciantini, N. 2022, Fluids, 7, 1 [Google Scholar]
- Dexter, J., Tchekhovskoy, A., Jiménez-Rosales, A., et al. 2020, MNRAS, 497, 4999 [Google Scholar]
- Do, T., Witzel, G., Gautam, A. K., et al. 2019, ApJ, 882, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Dodds-Eden, K., Sharma, P., Quataert, E., et al. 2010, ApJ, 725, 450 [NASA ADS] [CrossRef] [Google Scholar]
- El Mellah, I., Cerutti, B., & Crinquand, B. 2023, A&A, 677, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L5 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022a, ApJ, 930, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022b, ApJ, 930, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022c, ApJ, 930, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022d, ApJ, 930, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022e, ApJ, 930, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Fishbone, L. G., & Moncrief, V. 1976, ApJ, 207, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics: Third Edition (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Fromm, C. M., Cruz-Osorio, A., Mizuno, Y., et al. 2022, A&A, 660, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, Rev. Mod. Phys., 82, 3121 [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 618, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2020a, A&A, 638, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Bauböck, M., et al.) 2020b, A&A, 635, A143 [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2023, A&A, 677, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hawley, J. F., Guan, X., & Krolik, J. H. 2011, ApJ, 738, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C. 2008, ARA&A, 46, 475 [Google Scholar]
- Ho, L. C. 2009, ApJ, 699, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, H.-X., Mizuno, Y., Fromm, C. M., & Nathanail, A. 2023, MNRAS, 522, 2307 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, H.-X., Dihingia, I. K., Liu, C., Mizuno, Y., & Zhu, T. 2024a, JCAP, 2024, 101 [CrossRef] [Google Scholar]
- Jiang, H.-X., Liu, C., Dihingia, I. K., et al. 2024b, JCAP, 2024, 059 [CrossRef] [Google Scholar]
- Kawazura, Y., Barnes, M., & Schekochihin, A. A. 2019, Proc. Natl. Acad. Sci. USA, 116, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, P. K., Gammie, C. F., & Noble, S. C. 2011, ApJ, 737, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Levis, A., Chael, A. A., Bouman, K. L., Wielgus, M., & Srinivasan, P. P. 2024, Nat. Astron., 8, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, X., Li, Y.-P., & Yuan, F. 2023, MNRAS, 520, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Liska, M., Hesp, C., Tchekhovskoy, A., et al. 2018, MNRAS, 474, L81 [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2007, ApJ, 654, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Mattia, G., & Fendt, C. 2020, ApJ, 900, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Mattia, G., & Fendt, C. 2022, ApJ, 935, 22 [CrossRef] [Google Scholar]
- Mizuno, Y., Fromm, C. M., Younsi, Z., et al. 2021, MNRAS, 506, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M. R., Meyer, L., & Ghez, A. M. 2012, Res. Astron. Astrophys., 12, 995 [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [Google Scholar]
- Najafi-Ziyazi, M., Davelaar, J., Mizuno, Y., & Porth, O. 2024, MNRAS, 531, 3961 [NASA ADS] [CrossRef] [Google Scholar]
- Nathanail, A., Fromm, C. M., Porth, O., et al. 2020, MNRAS, 495, 1549 [Google Scholar]
- Nathanail, A., Mpisketzis, V., Porth, O., Fromm, C. M., & Rezzolla, L. 2022a, MNRAS, 513, 4267 [NASA ADS] [CrossRef] [Google Scholar]
- Nathanail, A., Dhang, P., & Fromm, C. M. 2022b, MNRAS, 513, 5204 [NASA ADS] [CrossRef] [Google Scholar]
- Olivares, H., Porth, O., Davelaar, J., et al. 2019, A&A, 629, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porth, O., Olivares, H., Mizuno, Y., et al. 2017, Comput. Astrophys. Cosmol., 4, 1 [Google Scholar]
- Porth, O., Chatterjee, K., Narayan, R., et al. 2019, ApJ, 243, 26 [NASA ADS] [Google Scholar]
- Porth, O., Mizuno, Y., Younsi, Z., & Fromm, C. M. 2021, MNRAS, 502, 2023 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., Tchekhovskoy, A., Quataert, E., Chandra, M., & Gammie, C. F. 2015, MNRAS, 454, 1848 [Google Scholar]
- Ressler, S. M., White, C. J., Quataert, E., & Stone, J. M. 2020, ApJ, 896, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., & Zanotti, O. 2013, Relativistic Hydrodynamics (Oxford University Press) [CrossRef] [Google Scholar]
- Ripperda, B., Liska, M., Chatterjee, K., et al. 2022, ApJ, 924, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan, M. E., Sironi, L., & Narayan, R. 2017, ApJ, 850, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Scepi, N., Dexter, J., & Begelman, M. C. 2022, MNRAS, 511, 3536 [NASA ADS] [CrossRef] [Google Scholar]
- Čemeljić, M., Yang, H., Yuan, F., & Shang, H. 2022, ApJ, 933, 55 [CrossRef] [Google Scholar]
- Von Fellenberg, S. D., Witzel, G., Bauböck, M., et al. 2023, A&A, 669, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wielgus, M., Moscibrodzka, M., Vos, J., et al. 2022, A&A, 665, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witzel, G., Martinez, G., Willner, S. P., et al. 2021, ApJ, 917, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Younsi, Z., Wu, K., & Fuerst, S. V. 2012, A&A, 545, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Younsi, Z., Porth, O., Mizuno, Y., Fromm, C. M., & Olivares, H. 2020, in Perseus in Sicily: From Black Hole to Cluster Outskirts, eds. K. Asada, E. de Gouveia Dal Pino, M. Giroletti, H. Nagai, & R. Nemmen, 342, 9 [Google Scholar]
- Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Wang, H., & Yang, H. 2022, ApJ, 924, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Wardle, M., Roberts, D. A., et al. 2006, Am. Astron. Soc. Meet. Abstr., 209, 112.07 [NASA ADS] [Google Scholar]
- Zhao, S.-S., Huang, L., Lu, R.-S., & Shen, Z. 2023, MNRAS, 519, 340 [Google Scholar]
- Zhou, H. 2024, MNRAS, 527, 3018 [Google Scholar]
Appendix A: Electron temperature profile
The electron distribution of the two-temperature models implies a more complicated relationship between Te/Tp and plasma β. Therefore, we plot the Te/Tp − β relations from the time and azimuthal averaged data of the cases M80a3D and M20a3D in Fig. A.1. In the jet regions of both two-temperature models, the existence of points with Te/Tp > 1 indicates that the electron temperature is dominant in some regions. The Te/Tp ratio scatters at the low β region, implying the simple R-β model may not describe the underlying physics in this region. For the weak magnetic field region (i.e., high plasma β), both two-temperature models converge at the same value in M20a3D (see the lower panel of Fig. A.1). However, at β ∼ 10, a higher Te/Tp is observed in the reconnection heating model, corresponding to the bluish part of the disk region of Fig. 14. A similar phenomenon has been observed in our previous 2D simulations (see Jiang et al. (2023)).
 |
Fig. A.1. Te/Tp − β diagram of the average of collapse data from 15, 000 to 20,000 M of M80a3D (a) and from 10, 000 to 15,000 M of case M20a3D (b). Different colors mark the jet and disk components as well as the turbulence and reconnection heating models. The jet and disk are divided with criteria of magnetization σ > 1. The red and blue lines represent the R-β model with Rh = 1 and 160, respectively. |
All Figures
 |
Fig. 1. Initial torus profile of logarithmic density (color) and magnetic field configuration (black contours). The dashed contours represent positive polarity, while solid ones are the opposite. |
| In the text | |
 |
Fig. 2. Time evolution of (a) mass accretion rate (Ṁ) and (b) magnetic flux rate ( |
| In the text | |
 |
Fig. 3. Distribution of time (between t = 10 000 M to 15 000 M) and azimuthal averaged (a) density ρ, (b) magnetization σ, and (c) plasma beta for 3D GRMHD simulations with multi-loops in different loop length (left: λ = 20, M20a3D and right: λ = 80, M80a3D). The solid and dashed contours in each panel represent the Bernoulli parameter −hut = 1 and magnetization σ = 1, respectively. Lower panels (d) and (e) show the evolution of averaged MRI quality factors of M20a3D and M80a3D. |
| In the text | |
 |
Fig. 4. Distributions of the toroidal component of the magnetic field for M20a3D (left) and M80a3D (right). The streamlines show the poloidal magnetic field lines. |
| In the text | |
 |
Fig. 5. Evolution of light curves at 230 GHz for the case of M80a3D with different heating models and R-β models. The black solid line represents the light curve from the turbulence heating model. The blue solid line is the reconnection heating one. The red and dark-green lines represent the R-β models with Rh equals 1 and 160, respectively. |
| In the text | |
 |
Fig. 6. Panels (a) and (b) are the light curves of 4 different electron heating models for the case M80a3D, which is the same as Fig. 5 but in different times. Panel (c) is for the case M20a3D. In each panel, the gray solid line is the corresponding accretion rate during each period. |
| In the text | |
 |
Fig. 7. Standard deviation of the light curves of different electron heating models. The error bar represents the standard deviation of the light curves. Black dots show the deviation of case M80a3D during 5000–10 000 M, red dots are 15 000–20 000 M, and blue dots show the data of case M20a3D during 10 000–15 000 M. |
| In the text | |
 |
Fig. 8. Probability distribution function of the M3 of the light curves generated from M20a3D (a) and M80a3D (b). The probability distribution functions have been normalized by setting the peak value to one. The black and red lines represent the cases with different Rh values from the R-β model. The blue and yellow lines are from turbulence and reconnection models, respectively. |
| In the text | |
 |
Fig. 9. GRRT images and corresponding emissivity and electron temperature distributions. First row: GRRT snapshot images for Sgr A* with inclination angle i = 30° at t = 12 240 M from (a) the turbulence heating model, (b) reconnection heating model, (c) R-β model with Rh = 160, and (d) R-β model with Rh = 1. Second row: Corresponding 230 GHz emissivity (left) and electron temperature (right) distributions. The solid white contours in panels (e)–(h) represent the edge of the torus, which is the ρ = 0.01 contour. The dashed contour represents the high magnetization region with σ > 1, which is cutoff in GRRT post-process. |
| In the text | |
 |
Fig. 10. Volume rendering of the 3D distribution of electron temperature (yellow to black) and toroidal component of the magnetic field (red to black) from the turbulence heating model at 12 240 M for M20a3D. The white arrows mark the direction of the poloidal magnetic field. Yellow tubes represent the magnetic lines. The size of the box is 10 rg. |
| In the text | |
 |
Fig. 11. Distribution of emissivity coefficient η as a function of electron temperature. Solid lines represent the frequency of 230 GHz with different local magnetic field strengths. The purple dash-dotted, red dashed, and dotted lines represent the emissivity coefficient of the 46 GHz, 86 GHz, and NIR frequencies, respectively, with typical magnetic fields in flux rope (B = 0.05). |
| In the text | |
 |
Fig. 12. Histogram of magnetic field strength distribution in the flaring region. The magnetic field is in code units. We measured the magnetic field strength at the high electron temperature (Θe > 10) and high density (ρ > 0.001) region at t = 12 240 M of the turbulence heating model of case M20a3D. |
| In the text | |
 |
Fig. 13. GRRT images at NIR and 43 GHz. Panels (a) and (b) present the NIR and 43 GHz GRRT image from the turbulence model at t = 12 240 M. |
| In the text | |
 |
Fig. 14. Distribution of the relative difference between the electron temperature distribution given by the turbulence model and the reconnection model for M20a3D at t = 12 240 M. |
| In the text | |
 |
Fig. 15. Same as Fig. 6 but at NIR frequency. |
| In the text | |
 |
Fig. 16. NIR emissivity and electron temperature distributions. Panel (a) is the azimuthally averaged NIR emissivity distributions from turbulence (left) and reconnection (right) electron heating models. Panels (b) and (c) are the zenith averaged NIR emissivity distributions of turbulence and the reconnection heating model, respectively. |
| In the text | |
 |
Fig. A.1. Te/Tp − β diagram of the average of collapse data from 15, 000 to 20,000 M of M80a3D (a) and from 10, 000 to 15,000 M of case M20a3D (b). Different colors mark the jet and disk components as well as the turbulence and reconnection heating models. The jet and disk are divided with criteria of magnetization σ > 1. The red and blue lines represent the R-β model with Rh = 1 and 160, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



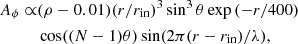
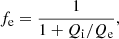
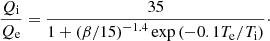
![$$ \begin{aligned} f_{\rm e} = \frac{1}{2} \exp \left[\frac{-(1-\beta /\beta _{\rm max})}{0.8+\sigma _{\rm h}^{0.5}}\right], \end{aligned} $$](/articles/aa/full_html/2024/08/aa49681-24/aa49681-24-eq5.gif)