EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 686 (June 2024) A&A, 686 (2024) A49 Full HTML
Open Access
Issue
A&A
Volume 686, June 2024
Article Number A49
Number of page(s) 13
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202449152
Published online 28 May 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The diffuse interstellar medium is known to host a rich polyatomic chemistry despite the low densities of a few tens to a few hundreds of molecules per cubic centimeter (Snow & McCall 2006), and the ubiquitous illumination by far-UV radiation. The moderate reddening E(B–V) ~ 0.1 mag at which milllimeter-wave absorption is indeed observed from HCO+ and other species, just above the threshold for H2 formation (Liszt et al. 2018a,b), ensures that UV radiation permeates the material, making photodissociation the main destruction routes for neutral molecules. In those conditions, carbon is largely ionized, consistent with the small observed CO and CI column densities (Liszt & Gerin 2023). Therefore, the electron fraction is high and the gas is warm, with mean kinetic temperatures ~75 K determined in H2 at UV wavelengths (Shull et al. 2021), and decreasing to ~35–50 K in the slightly denser material absorbing in C2 (Sonnentrucker et al. 2007). Despite this, the relative abundances of many molecules observed in both diffuse and cold dark molecular clouds are strikingly similar (Liszt & Lucas 1995).

Given the low densities, collisional excitation is weak and the internal energy level population is mainly controlled by the cosmic microwave background (CMB) radiation (e.g., Liszt & Pety 2016). Absorption lines from low-lying levels are easily detected with a high signal-to-noise against background continuum sources, whether stars in the UV-optical domain or quasars at radio frequencies, and the derivation of molecular column densities is straightforward. With the exception of CO, the weak excitation is confirmed by observing molecular emission around even the most strongly absorbed background sources (Lucas & Liszt 1996).

Despite having demonstrated the richness of the chemistry in diffuse molecular gas, our understanding of it is largely conceptual, along the lines that turbulence in the interstellar medium must somehow speed up the formation of HCO+ that subsequently recombines at thermal rates to form CO, or HCS+ to form CS, and presumably HCNH+ to form CN, HNC, and HCN (Godard et al. 2014; Lesaffre et al. 2020; Gong et al. 2023a). No model exists to explain, in detail, the series of polyatomic hydrocarbons C2H, 1 − C3H, c − C3H, C3H+, l − C3H2, and c − C3H2, or the widespread CH3CN (Liszt et al. 2018a)

One of the most perplexing molecules in diffuse gas is indeed formaldehyde, one of the first interstellar molecules detected at radio wavelengths. The early H2CO detection along sight lines with AV = 1 mag (Nash 1990) was not predicted by gas phase models. The presence of outer envelopes of nearby dark clouds along the sight lines was advocated by Federman & Allen (1991) because active grain surface chemistry could be forming enough H2CO. But the accumulated evidence from observations of H2CO and other species convincingly showed that the detected absorption toward quasars is produced in the diffuse molecular gas (Liszt & Lucas 1995).

H2CO has two spin symmetry states, the para states with even Ka values and the ortho states with odd Ka values and three times higher spin degeneracy. Since only reactive collisions destroying formaldehyde can change the nuclear-spin symmetry in the gas phase, the ortho-to-para ratio should be determined at formation and bear the mark of the responsible chemical (gas- or solid-phase) process. Laboratory experiments have shown that the ortho-to-para ratio of H2O desorbed from interstellar ices is the statistical value and high-temperature local thermodynamic equilibrium (LTE) limit of three (Hama et al. 2018; Putaud et al. 2019; Dupuy et al. 2021), which should also apply to the ortho-to-para ratio of H2CO and c-C3H2, which have the same type of ortho and para symmetry states as H2O. Yocum et al. (2023) have indeed shown that the ortho-to-para ratio of formaldehyde that desorbed from UV-irradiated cold CH3OH ices is consistent with the statistical value of three, and independent of the ice temperature. Alternatively, the gas-phase formation chemistry accounting for the nuclear-spin statistics of H2 predicts an ortho-to-para ratio between two and three for H2CO (Faure et al., in prep.). Deviations from an ortho-to-para ratio of three have been observed in the interstellar medium for H2CO (Guzmán et al. 2011) and other species such as NH2, NH3, and H2O (Persson et al. 2016; Faure et al. 2013, 2019) and were attributed to nuclear-spin gas-phase formation chemistry.

In this paper we present new λ2 mm observations of ortho and para formaldehyde absorption along the sight line toward NRAO150, which we interpret in conjunction with an analysis of the excitation of carbon monosulfide (CS) based on new observations of the J = 3−2 line. We also report observations of cyclopropenilydene (c-C3H2) lines in the 2 mm spectral window. The observations and detected species are described in Sect. 2, and the sight line toward NRAO150 is presented in Sect. 3. Section 4 presents the implication for the density structure along the sightline to NRAO150. In Sect. 5 we discuss the derived column densities and abundances, and in Sects. 6 and 7 the implication for the diffuse interstellar chemistry. The conclusions are laid out in Sect. 8.

2 Observations

Observations have been performed with the NOEMA interferometer in March 2022 toward NRAO150 (B0355+508). The channel spacing of 62.5 kHz was used, corresponding to a velocity resolution of 0.13 km s-1 at 145 GHz. Side band separating receivers were used allowing simultaneous observations of the lower and upper side bands. To improve the sensitivity, the same frequency was observed in both the horizontal and vertical polarization. Two frequency tunings have been observed to obtain a continuous frequency coverage between 128.4 and 136.1 GHz in the lower side band and between 143.9 and 151.5 GHz in the upper side band. Observations were performed in excellent weather conditions. The data have been processed with the GILDAS software. The spectra were obtained at the peak of the continuum emission and normalized by the value of the continuum. The noise levels were determined by subtracting a base line in signal-free spectral regions and reach about 0.3% for all spectral bands. The detected absorption features are shown in Fig. 1 together with previously observed lines toward the same source as listed in Table 1. The parameters of the newly detected lines are displayed in Table 2. The spectra show the previously detected velocity components. Each absorption spectrum was fitted with five Gaussian velocity components, except for CS where a four Gaussian component fit is enough. Table 3 lists the resulting centroid velocities, Full Widths at Half Maximum (FWHM) and opacities.

Table 1

References for the ancillary data.

3 The sightline toward NRAO150

The sightline toward NRAO150 is known to exhibit a complex structure, with five main velocity components as illustrated in Fig. 1. At low galactic latitude (l, b = 150.3772°,−1.6037°), the path through the Galactic disk is long, with most of the extinction located at a distance of about 1 kpc and a total reddening of E(𝑔−r) ~ 1.2 mag (AV ~ 4.5 mag ) according to the 3D dust distribution established from the Panstarrs and Gaia data (Green et al. 2019). The five features detected in HCO+ absorption have comparable integrated opacities, hence comparable HCO+ and H2 column densities, N(HCO+) ~ 1.2 × 1012 cm-2 and N(H2) ~ 4 × 1020 cm-2, corresponding to AV ~ 0.8 mag each (Lucas & Liszt 1996) for a total column density integrated in these five velocity components of N(H2) = 2.1 × 1021 cm-2. By comparing HI absorption and emission spectra toward this source, Liszt & Lucas (2000) have derived the atomic hydrogen column density in the velocity range between −20 and 0 kms-1, N(HI) = 4.56 × 1021cm-2. The mean fraction of hydrogen in molecular form along the line of sight is therefore about 0.5. Taken together, these five absorption features contribute most of the extinction toward NRAO150.

Pety et al. (2008) extensively studied the environment of this sight line combining observations with the IRAM 30 m single dish telescope and the PdBI interferometer. The CO column densities of each velocity component remain moderate, as expected for diffuse gas where the free gas phase carbon is either C+ for the broader and fainter velocity components, or on the verge of recombining to C and CO for the strong, narrow velocity components, at −17 and −10 km s-1, where the CO column density gets larger than 1016cm-2. The CO emission profiles show strong spatial variations with the achieved angular resolution. Pety et al. (2008) show that overall spatial variations in the strongly CO emitting gas have Poisson statistics with rms fluctuations about equal to the mean emission level in the line wings and much of the line cores. The brightest emission peaks reach the brightness temperature of 13 K and the ratio between the CO(2−1) and CO(1−0) is about 0.7. It is remarkable that the CO emission line profile converges toward the CO absorption profile only when observed at the highest angular resolution of 6″. At lower angular resolution, the CO profiles are broader and more similar to those of HCO+. The variations of the CO emission are explained by the presence of density fluctuations along the line of sight,

that affect the CO abundance and excitation, hence introducing variations in the line profile. As the fraction of hydrogen in molecular form is mostly sensitive to the total gas column, the variations of the molecular hydrogen column density are expected to be much less than those of an individual molecule (Shull et al. 2021; Liszt & Gerin 2023).

Araya et al. (2014) confirmed the variation of the −10.4 km s-1 absorption feature with time in the ground state o-H2CO (11,0 − 11,1) line at 4.8 GHz. They interpreted this as a slow increase in the path length with time when the sight line crosses a denser filament close to its edge. They determined a filament radius of 2 × 104 au for a density of n(H2) = 104 cm-3, consistent with the CO emission maps (Pety et al. 2008). The detection of absorption lines from excited levels of CS, c-C3H2, and H2CO allows to reconsider the density determinations of the different velocity components.

thumbnail Fig. 1

Absorption lines detected toward NRAO 150. The left panel shows previous detections including the o-H2CO (11,0–11,1) line at 4.8 GHz and the o-c-C3H2 (11,0–10,1) line at 18 GHz observed at the VLA (Liszt & Lucas 1995; Liszt et al. 2012), and the CS (2–1) (98 GHz), o-c-C3H2 (21,2–10,1)(85.3 GHz), CCH(1, 3/2, 2–0,1/2,1) (87.3 GHz), and HCO+(1–0) (89.2 GHz) lines (Liszt & Lucas 1995; Lucas & Liszt 1994, 1996, 2000, 2002) observed with the PdBI. The right panel presents the new observations including the o-H2CO(21,1–10,2), o-H213CO(21,1–10,2), and p-H2CO (20,2–10,1) lines, the CS (3–2), C34S(3–2) lines, and the c-C3H2 transitions listed in Table 2. All displayed spectra have been normalized by the continuum strength. Vertical offsets have been used for clarity.
Table 2

Detected lines.

Table 3

Properties of the velocity components.

4 Modeling the molecule excitation

We used the RADEX code (van der Tak et al. 2007) to study the excitation conditions. The references for the collision rate coefficients are given in Table 4. We included collisions with ortho and para H2, electrons and Helium to represent the diffuse and translucent gas where atomic neutral and ionized carbon are the main reservoirs of gas phase carbon, up to the regions where CO dominates the carbon budget. All calculations were performed using the default value for the escape probability formulation, a uniform sphere. Changing for a different geometry, for instance a plane-parallel slab, leads to similar conclusions but introduces changes of the derived densities by ~30%. Changing the hypotheses on the electron fraction, H2 ortho-to-para ratio or kinetic temperature also have an impact on the derived densities. We therefore have not attempted to obtain a precise determination of the density, but we chose to bracket the acceptable interval of the molecular hydrogen density, given the restricted set of hypotheses.

In the RADEX calculations, we did not include atomic hydrogen as a collision partner as no such data are currently available for the considered molecules. Daniel et al. (2015) have shown in the case of water vapor, that the rate coefficients with atomic hydrogen can be larger or smaller than those for H2, but they are usually similar in magnitude, at least for the dominant transitions with the highest values of the cross sections. The cross sections with H cannot be easily extrapolated from those with either He or H2 as a collision partner in the case of H2O. for the considered diffuse and translucent clouds, especially for the narrow velocity components that have the highest abundance of molecular species including CO, molecular hydrogen is expected to dominate the hydrogen budget. To complete the picture of molecule excitation in diffuse and translucent gas, cross sections with H would be interesting, especially for regions where atomic hydrogen is dominant. We assume the electrons are thermalized at the kinetic temperature of the gas as the time scales for thermalization by interactions with electrons or neutrals are shorter than one year in the considered conditions (Tielens 2012).

We considered five cases for the kinetic temperature, 10, 15, 20, 30, and 60 K to bracket the possible range of conditions along this sight line which is expected to be similar to the C2 clouds investigated by Fan et al. (2024), and varied the electron fraction x(e) between 2 × 10-6 and 2 × 10-4 to probe the transition between diffuse and translucent gas. Ten values of the molecular hydrogen density have been considered, 200, 300, 500, 1000, 1500, 2000, 2500, 3000, 5000, and 10 000 cm-3.

thumbnail Fig. 2

Variation of the predicted opacities of the CS (2–1) (filled symbols) and CS (3–2) (starred symbols) transitions as a function of the molecular hydrogen density in the diffuse and translucent cloud conditions computed with RADEX using the column densities and FWHM listed in Table 3. The colors show the kinetic temperature from 10 to 60 K, and the H2 ortho-to-para ratio scales with the kinetic temperature. The symbol shapes indicate the electron fraction as follows for the CS (2–1) line: lower than 2 × 10-5 filled triangles, between 2 × 10-5 and 10-4, small filled squares, and filled circles for 2 × 10-4. A similar progression is used for the CS (3–2) line, lower than 2 × 10-5 crosses, between 2 × 10-5 and 10-4, small stars, and 8-branch stars for 2 × 10-4. The measured opacities for the four detected velocity components are shown with the dashed and dotted gray areas, from top to bottom: −17.2 km s-1, −10.3 km s-1, −8.5 km s-1 and −4 km s-1.
Table 4

References for rate coefficients.

4.1 CS excitation

The calculations were performed using the molecular parameters derived from the observed line profiles, the peak opacity, velocity dispersion, and column density. For this last parameter, we used the excitation temperature listed in Table 3, to take into account the slight deviation from the excitation by the CMB for the narrow velocity components at −17 and −10 km s-1. We computed the H2 ortho-to-para ratio at thermal equilibrium for the kinetic temperature of the medium. Figure 2 presents the calculations of CS excitation for the four main velocity components. It displays the variations of the peak opacity of the CS (2−1) and CS (3−2) lines as a function of the molecular hydrogen density, for five values of the kinetic temperature and six values of the electron fraction. Each velocity component is displayed in a different box, from top to bottom, −17.2 , −10.3, −8.5, and −4 km s-1. The measured opacities for these four velocity components are shown with dashed and dotted gray areas. As listed in Table 3 the strongest velocity components at −17.2 km s-1 and −10.3 km s-1 show narrow and deep absorption features in the two CS transitions, τ ~ 1 and FWHM ~ 0.4 km s-1. The detection of a significant opacity of the J = 3 − 2 transition implies a relatively high H2 density of n(H2) ~ 2500 cm-3 for these two velocity components. As indicated by the H2CO excitation described below, these two velocity components have a moderate electron fraction, x(e) < 10-4, and the CS excitation is mainly dependent on the gas density and temperature. The faint components at −8.5 and −4 km s-1 exhibit broader profiles (τ ~ 0.1 and FWHM ~ 1.5 km s-1) and a lower level of excitation as compared to the main components. For these two velocity components, the low CS (3−2) opacities are consistent with the typical densities encountered in diffuse and translucent clouds, n(H2) ≤ 500 cm-3 and any electron fraction. At such densities, the excitation temperature of CS, as that of other high-dipole moment species is very close to the temperature of the CMB.

4.2 H2CO excitation

We also performed excitation calculations for ortho and para formaldehyde, using the extended set of physical conditions with five values of the kinetic temperatures, six values of the electron fraction, and five values of the H2 ortho-to-para ratio, opr = 3 × 10-5, 3 × 10-4, 0.03, 0.3 and 3 for the five values of the kinetic temperature. We choose a value for the o-H2CO column density, 2.2 × 1012 cm-2, and line width (0.5 km s-1) corresponding to the measured column density in the −17 km s-1 velocity component. The calculations have been done for different values of the volume density, but we only show the results for n(H2) = 103 cm-3 in Fig. 3, a value intermediate between the density of the broad and the narrow velocity components. The behavior is qualitatively similar for other densities in the range of the densities encountered in the clouds along this line of sight. To illustrate the general behavior of the excitation of the rotational lines of formaldehyde, and provide information for future observations, we have included in the calculations two low energy lines of ortho and para formaldehyde that can be easily observed with ground based millimeter telescopes, the 21,2−11,1 line of o- H2CO at 140 GHz, and the ground state 10,1−00,0 transition of p- H2CO at 72 GHz. The extensive set of calculations is presented in Appendix A.

The 11,0−11,1 transition of H2CO at 4.8 GHz is particularly sensitive to the physical conditions. In the cold envelopes of molecular clouds, it can have an excitation temperature lower than the CMB because of specific propensity rules for the collision of o- H2CO with H2 molecules (Troscompt et al. 2009). The effect depends on the ortho-to-para ratio of H2, since collisions with o-H2 are more efficient at exciting this transition leading to a smaller range of physical conditions where the transition is cooled when using collisions with ortho and para H2, than when using collisions with p-H2 only. Collisions with electrons can also have an important effect for the diffuse regions we probe, as noted previously by Kutner et al. (1971) and by Turner (1993). These authors used crude approximate analytical formulations for the collisional cross sections with electrons. New cross sections have therefore been computed here using the Born dipole theory which works well for dipolar transitions in molecules with large dipoles (the H2CO dipole is 2.3 D). Rate coefficients were then obtained by integrating the cross sections over Maxwell-Boltzmann distributions of the electron velocity for kinetic temperatures in the range 10–300 K. This dataset will be made available through the Excitation of Molecules and Atoms for Astrophysics (EMAA) database1.

Figure 3 presents the results for three transitions of o-H2CO, the 11,0−11,1 line at 4.8 GHz, together with the two strong transitions which relate to the levels involved in the 4.8 GHz line, the 21,2−11,1 line at 140 GHz (not observed in this work), and the 21,1−11,0 line at 150 GHz which was observed at NOEMA. Over most of the covered set of physical conditions, the excitation temperature of the latter two lines remain close to the CMB, except for the highest values of the density and electron fraction, and the opacity is almost constant. Figure A.2 shows the variation of the excitation temperature with the molecular gas density. The excitation temperature and opacity show a small dependence on the kinetic temperature and H2 ortho-to-para ratio with a higher excitation temperature at higher kinetic temperatures and opr. At low values of the electron fraction (x(e) < 3 × 10-5), a small asymmetry between the 2mm lines appears with slightly higher values for the 140 GHz line opacity and slightly lower values for the 150 GHz line opacity as compared with the same set of parameters and a higher electron fraction. This effect is a consequence of the strong cooling of the excitation temperature of the 4.8 GHz line which is predicted to be significantly lower than the CMB, that is to say overcooled. For the chosen column density, density and line width, the overcooling of the 4.8 GHz line is present up to an electron fraction of about 6 × 10-5 depending on the kinetic temperature and H2 opr. As illustrated in Fig. 3 (top left and top right panels) and Fig. A.2, regions with lower electron densities, lower opr and higher kinetic temperatures seem to be favorable for the overcooling phenomenon within the range of parameters covered. The opacity of the 11,0−11,1 transition is strongly affected by its excitation conditions : the region with overcooling is associated with a significant opacity while the opacity decreases when the excitation temperature increases above the CMB. This strong sensitivity of the 4.8 GHz line excitation temperature to the local physical conditions, for a given value of the molecular column density, may qualitatively explain the higher rate of variations of the line profile with time toward quasar sight lines, as compared with other species (Araya et al. 2014). Indeed, a variation of the electron fraction, which could be combined with a variation of the local density, or the kinetic temperature, or of the H2CO column density when the line of sight is crossing a filamentary structure could explain the detected trend in the H2CO profile toward NRAO150 (Araya et al. 2014), and the absence of significant variation in other species such as HCO+ (Liszt & Lucas 2000). The sensitivity of the line profile to the excitation conditions implies that, for a given H2CO column density, regions with a moderate electron fraction will be more easily detected because the line opacity with be higher. Such regions will appear more prominently in the 4.8 GHz line profile than regions with a high electron fraction. By contrast, the 2 mm lines are mostly sensitive to the molecular column density and do not determine the physical conditions. These lines are therefore more appropriate for studying the formaldehyde column density and abundance.

According to the excitation calculations shown in Fig. A.3, the 145 GHz p-H2CO line optical depth should be less affected by electrons than the 150 GHz o-H2CO line (compare Figs. 3 and A.3). We list in Table 5 the ratios of integrated opacities of the discussed H2CO lines with respect to the measurement of the strong component at −10 km s-1. The high level of agreement between the line ratios in the two mm-wave lines indicates that the −10 km s-1 line optical depth has not been strongly affected by electrons. The 10% difference between the mm-lines at −17 km s-1 indicates a higher electron density at −17 km s-1 than at −10 km s-1 but less than at −14, −8 or −4 km s-1. The intrinsic column density ratio N(v = −17)/N(v = −10) might then be given by the ratio of the p-H2CO column density and be about 1/1.72 (see Table 5). Using the excitation calculations, we conclude that the electron fraction in the two narrow components is about x(e) ~ 1−3 × 10-5, a value consistent with the CS calculations, noting that the electron fraction is higher in the −17 km s-1 component. The electron fraction of the broad components must be significantly higher since these components are much less prominent at 4.8 GHz than at 150 GHz. In particular the comparison of the spectra traced in blue on the left and right panels of Fig. 1 shows that the velocity components at −13.8 and −4.2 kms-1 are not detected and that at −8.4 is barely seen.

In the range of densities and electron fraction derived from the CS and o-H2CO excitation analysis, the excitation temperature of the 2 mm lines remain close to the CMB and does not exceed 3 K. Similar calculations for p-H2CO lead to the same conclusion. Hence the derivation of the formaldehyde column densities from the integrated opacities is straightforward using the simple assumption that the molecules are thermalized with the CMB.

thumbnail Fig. 3

Variation of the excitation temperature and opacity with the electron fraction, kinetic temperature, and H2 ortho-to-para ratio for the 11,0−11,1 line at 4.8 GHz (top left), and zoom on the region with excitation temperature lower than the CMB indicated by a dotted box (top right). The 21,2−11,1 line at 140 GHz is shown in the bottom left panel and the 21,1−11,0 line at 150 GHz in the bottom right panel. The difference between the excitation temperature and the CMB is plotted to illustrate the change of regime of the 11,0−11,1 transition at 4.8 GHz, and a different scale is used for the 140 GHz and 150 GHz lines. Different symbols show the values of the H2 ortho-to-para ratio between 3 × 10-5 and 3, their color and size indicate the kinetic temperature between 10 and 60 K. The column density of o-H2CO is 2.2 × 1012 cm-2, the H2 density is set to 103 cm-3, and the FWHM is 0.5 km s-1. The 21,2−11,1 line at 140 GHz has not been observed in this work.

4.3 c-C3H2 excitation

Excitation calculations are reported in Appendix A and illustrated in Fig. A.4. Given the high dipole moment of this molecule, 3.27 Debye (Lovas et al. 1992) and the good corre-spondance of the line profiles with those of CCH and HCO+ with no narrow and deep features, it is expected that the excitation temperature of its millimeter rotational lines is close to the CMB. Excitation calculations with RADEX confirm the hypothesis.

Table 5

Ratios of integrated optical depth to the integrated optical depth of the −10 km s-1 velocity component.

5 Molecular column densities

We used the information on the excitation conditions to derive the column densities for the five main velocity components. They are listed in the last column of Table 3 with the assumed excitation temperature. The new data confirm the previous results (Liszt & Lucas 1995) but provide better determinations due to the increased sensitivity of NOEMA as compared with the Plateau de Bure Interferometer. The new data also provide contraints on the molecular gas density and electron fraction for the velocity components. Table 6 summarizes the abundances relative to H2 of the studied molecules, CS, H2CO, and c-C3H2, and the ortho-to-para ratio for the latter two species for each velocity component separately. For all velocity components, we use the HCO+ integrated opacity to determine the H2 column density assuming the fixed abundance relative to H2, [HCO+] = 3 × 10-9 (Gerin et al. 2019). Abundances of the rare isotopologues H213CO and C34S are also listed for the velocity components where these species are detected.

The CS abundances are four times higher in the narrow, higher density velocity components than in the more diffuse components, reaching ~10-8, a similar or even higher abundance than in nearby molecular clouds, 10-9.5 to 10-7.5 (Tafalla et al. 2021; Rodríguez-Baras et al. 2021). In those velocity components C34S is detected and the [CS]/[C34S] abundance ratio is 22 ± 5, consistent with the sulfur isotopic ratios in the solar neighborhood, 22 (Wilson & Rood 1994; Yan et al. 2023). The large increase of the CS abundance indicates a more efficient formation mechanism at the higher densities encountered in the narrow velocity components. Even in the low density components the CS abundance remains above 10-9, a significant level for such highly illuminated and low density conditions.

For formaldehyde, the ortho-to-para ratio is consistent with the statistical value of three in all velocity components. Formaldehyde abundances are also higher in the velocity components associated with higher gas densities but the variation is not as pronounced as that of CS, from ~2.5 × 10-9 in the low density components up to ~6.7 × 10-9 in the two higher density components, which represents an increase of a factor of 2.7. The same range of increase of the abundance has been seen for CO (Liszt & Lucas 1998) although the strongest component in H2CO and in CO are different. This increase of the abundance implies that the chemistry is somewhat more efficient at producing H2CO in the higher density velocity components than for the low density components. o-H213CO is detected in the strongest narrow velocity component near −10 km s-1. The corresponding 12C/13C ratio is 61 ± 12 indicating that o- H2CO is not heavily fractionated, contrasting with CO along the same sightline where 12CO/13CO = 25 (Liszt & Lucas 1998) for this particular velocity component. The full range of the 12CO/13CO abundance ratio extends from 15 to 33 for the five velocity components. CO and H2CO therefore seem to have different chemical pathways.

The c-C3H2 abundance relative to H2 does not vary much across the five velocity components with a possible trend of higher values for the more diffuse, lower density components with broader profiles. The mean abundance of ortho c-C3H2 is 1.8 ± 1 × 10-9. As for H2CO, the ortho-to-para ratio is generally consistent with the statistical value of three. The derived abundance toward NRAO150 is comparable with the abundance detected in the Horsehead photodissociation region, 1.3 × 10-9 (Pety et al. 2012) and the mean abundance of o-C3H2 in diffuse clouds, 1.4 ± 0.7 × 10-9 (Lucas & Liszt 2000). By comparison, the abundance of ortho c-C3H2 is ~4.5 × 10-9 in the TMC-1 dark cloud (Cernicharo et al. 2021) and ~5 × 10-9 in L483 (Agúndez et al. 2019). There are few measurements of the ortho-to-para ratio but for TMC-1, it seems consistent with three (Cernicharo et al. 2021). The abundance of c-C3H2 therefore increases by a factor of ~3 in dark and dense clouds as compared with UV-illuminated diffuse and translucent clouds. While the increase in CS and H2CO abundance is already seen in the two moderately dense components along the line of sight to NRAO150, these components do not stand out in c-C3H2. The chemical changes seem therefore to require a more pronounced modification of the environment, such as higher densities and extinctions than those encountered along this particular line of sight.

6 Comparison of the H2CO abundance and excitation in other regions

Large-scale maps of the formaldehyde 4.8 GHz line have been obtained toward molecular clouds and complexes. Extended absorption is detected in this line, which remains optically thin. The high latitude molecular cloud MBM40 has been studied by Monaci et al. (2023) in HI,12CO(1−0), 13CO(1−0), and 4.8 GHz o-H2CO among other lines. The o-H2CO line is detected in absorption and its profile is similar to that of 13CO (1−0) and narrower than that of 12CO and HCO+(1−0). Gong et al. (2023b) present large-scale maps of the o-H2CO line at 4.8 GHz toward the Cygnus star forming molecular complex. The line is detected in absorption over very large scales, indicating an excitation temperature lower than the CMB. As for MBM40, the 11,0−10,1 integrated opacity is well correlated with the 13CO(1−0) emission. This behavior can be explained by our excitation calculations since the opacity of the o-H2CO line is stronger for the denser and lower electron fraction regions which are associated with narrower line profiles. Absorption at 4.8 GHz preferentially selects the regions along the line of sight with a low electron fraction and a relatively low H2 opr. Gong et al. (2023b) performed RADEX excitation calculations to evaluate the behavior of the 4.8 GHz line and to derive the o-H2CO column densities, using collision cross sections with ortho and para H2, but a single value of the ortho-to-para ratio and a limited range of kinetic temperatures. As neither the influence of the H2 opr nor the role of electron excitation was included, the derived column densities may have been under-estimated, leading to a significantly lower abundance relative to H2 than that we derived, 7 × 10−10 as compared with 2−8 × 10−9.

7 Chemistry

The analysis of the excitation conditions shows that the different velocity components have somewhat different densities, ranging from a few hundred cm-3 for the broad velocity components at −13, −8 and −4 km s-1, up to ~2500 cm-3 for the narrow components at −17 and −10 km s-1. H2CO is present in all velocity components, with a higher abundance relative to H2 in the higher density velocity components. At the moderate extinction along this sightline (Av = 4.5 mag in total and 0.8 mag for each velocity component), grains are expected to stay bare with little condensation of water ice, especially in the low density, diffuse components. The most likely chemical formation mechanism of formaldehyde is therefore the gas-phase reaction: O + CH3 → H + H2CO with a rate of about ~1.1 × 10-10 cm3s-1 at 300 K in the KIDA data base2 (Wakelam et al. 2012). This reaction has been evaluated in the framework of combustion and atmospheric chemistry (Baulch et al. 2005; Atkinson et al. 2006). Ramal-Olmedo et al. (2021) performed theoretical calculations on the reactions forming formaldehyde in interstellar clouds. They showed that the reaction between O and CH3 can be effective in diffuse cloud conditions. Other reactions may also contribute to the production of gas phase formaldehyde, involving O, O2, or OH, and hydrocarbons as reactants, as well as dissociative recombination reactions of complex organic ions with electrons. Formaldehyde is destroyed by photons, cosmic rays and reactions with atoms and ions, notably C and C+. Because most of the gas phase oxygen is expected to be neutral and atomic in diffuse clouds, this chemistry may constrain the abundance of the methyl radical CH3 if the reaction rate is known with a reasonable precision, of a factor of two or better. The observed increase by a factor 2.5 of the H2CO abundance with the density is qualitatively consistent with a gas phase production route, since the formation rate of formaldehyde by reactive collisions increases more rapidly with the molecular hydrogen density than its destruction rate by photons or cosmic rays. Hence the formaldehyde abundance may be higher in denser gas, for a given molecular hydrogen column density and extinction. Quantitative models are needed to fully test the formation and destruction processes of formaldehyde and how its relative abundance scales with the molecular hydrogen density and electron fraction.

Table 6

Column densities, abundances, and ortho-to-para ratios.

8 Conclusions

We presented new observations of the sight line toward NRAO150 with the NOEMA interferometer. The detected absorption lines from H2CO, CS, and c-C3H2 were combined with existing data at lower frequencies, and used to constrain the physical conditions along this sight line and the chemical mechanisms forming H2CO. Cross sections for the collisional excitation of o-H2CO and p-H2CO with electrons have been computed allowing a detailed analysis of their excitation in diffuse and translucent cloud conditions, with a focus on the behavior of the 11,0−11,1 transition of H2CO at 4.8 GHz. These cross sections are available in the EMAA data base. Cross sections for the collisional excitation of CS and H2CO with atomic hydrogen are missing and could be of interest for the study of these molecules in the most diffuse regions.

  • The excitation of the 11,0−11,1 transition of H2CO at 4.8 GHz is sensitive to the electron fraction, in addition to the kinetic temperature and ortho-to-para ratio of H2. This line therefore does not provide by itself a measurement of the H2CO column density. Combined with observations of the higher frequency rotational lines of H2CO at 3mm or 2mm, this line can be used as a diagnostic of the electron fraction and H2 ortho-to-para ratio.

  • The narrow components at −17 and −10 km s-1 correspond to moderately dense gas, n(H2) ~ 2500 cm-3, at the transition from C+ to C and CO, with an electron fraction of ~3 × 10-5 where the neutral carbon atom is the main bearer of carbon.

  • The broad components at −13, −8, and 4 km s-1 correspond to low density gas (n(H2) < 500 cm-3), with a high electron fraction (~10-4), where C+ is the dominant reservoir of carbon.

  • The CS abundance increases by a factor of four in the narrow velocity components and reaches 10-8 .

  • The abundance of H2CO increases by a factor of 2.5, from 2.5 × 10-9 to 6.5 × 10-9, from the low density to the moderate density components.

  • The abundance of c-C3H2 is equivalent in all velocity component [c-C3H2] = 1.8 × 10-9.

  • We derive ortho-to-para ratios of 3, the statistical value for all components detected in H2CO and in c-C3H2.

  • We derived the isotopic ratios [ H2CO ]/[ H213CO ]=61±12$\left[ {{{\rm{H}}_2}{\rm{CO}}} \right]/\left[ {{\rm{H}}_2^{13}{\rm{CO}}} \right] = 61 \pm 12$ and [CS]/[C34S] = 24 ± 6 in the narrow velocity components.

Acknowledgements

This work is based on observations carried out under project number W21AB with the IRAM NOEMA Interferometer. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). We thank the IRAM staff, for help in the preparation and reduction of the observations and for the high quality of the NOEMA observations. This research has made use of spectroscopic and collisional data from the EMAA database (https://emaa.osug.fr and https://dx.doi.org/10.17178/EMAA). EMAA is supported by the Observatoire des Sciences de l’Univers de Grenoble (OSUG). This work was supported by the program “Physique et Chimie du Milieu Interstellaire (PCMI)” funded by Centre National de la Recherche Scientifique (CNRS) and Centre National d’Etudes Spatiales (CNES). The National Radio Astronomy Observatory is operated by Associated Universities, Inc. under a cooperative agreement with the National Science Foundation.

Appendix A RADEX calculations

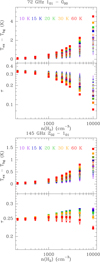thumbnail Fig. A.1

Variation of the predicted excitation temperature (top) and opacity (bottom) for the two lowest lines of p-H2CO. The top panel shows the 10,1 − 00,0 line at 72 GHz, and the bottom panel shows the 20,2 − 10,1 line at 145 GHz. The p-H2CO column density is set to 7.3 × 1011 cm-2, the line FWHM is 0.5 km s-1. The kinetic temperature varies from 10 K to 60 K. The H2 ortho-to-para ratio varies with the kinetic temperature. The symbol sizes and shapes indicate the electron fraction : empty triangles for 2 × 10-6, starred triangles for 10-5, filled triangles for 3 × 10-5, empty squares for 6 × 10-5, starred squares for 10-4, and filled squares for 2 × 10-4. Larger symbols are used for larger values of the electron fraction. The 10,1 − 00,0 line at 72 GHz has not been observed in this work.

In this appendix we present more extensive calculations of o-H2CO and p-H2CO excitation using the new set of cross sections including electron excitation.

Fig. A.2 and Fig. A.1 present the variation of the excitation temperature and opacity of the low energy transitions of o-H2CO and p-H2CO. The grid covers the same parameter space as the CS calculations, five values for the kinetic temperature, 10, 15, 20, 30, and 60 K, ten values for the molecular hydrogen density, 200, 300, 500, 1000, 1500, 2000, 2500, 3000, 5000, and 10000 cm-3, and six values for the electron fraction, 2 × 10-6, 10-5, 3 × 10-5, 6 × 10-5, 10-4, and 2 × 10-4. The chosen range encompasses the low electron fraction values where electron excitation is negligible and the high electron fraction values where electron excitation plays a significant role. The chosen column densities are identical as those discussed in Fig.3 and Fig. A.3, namely N(o-H2CO)= 2.2× 1012 cm-2 and N(p-H2CO)= 7.3 × 1011 cm-2, and the FWHM is set at ∆V = 0.5 km s-1.

The behavior of the 11,0 − 11,1 line is very different from that of the other low energy transitions of either o-H2CO or p-H2CO, which involve levels with a larger difference of energies and frequencies larger than 70 GHz. For those transitions, the excitation temperature is always higher than the CMB, and a higher excitation is mainly governed by the higher values of the density and/or the kinetic temperature. The electrons provide an additional source of excitation for high values of the electron fraction, typically above an electron fraction of ~3 × 10-5, corresponding to the transition region between the three main carbon reservoirs, C+, C and CO. The excitation temperature of the 11,0 − 11,1 line takes values lower than the CMB when the electron fraction is low to moderate, and stays below ~5 × 10-5 for the range of parameters covered here. The excitation temperatures lower than the CMB are also favored by higher values of the kinetic temperature and low values of the H2 ortho-to-para ratio as shown in Fig 3. Variations of the excitation temperature are associated to variations of the corresponding line opacity for a given column density. Even when the line is detected in absorption, the range of excitation temperature and corresponding opacities is significant, and may reach a factor of four. Therefore, column density determinations based on the 11,0− 11,1 line at 4.8 GHz should be based on an accurate knowledge of the physical conditions along the line of sight, including the electron fraction and kinetic temperature.

Figure A.3 presents the variation of the p-H2CO lines with the electron fraction and H2 ortho-to-para ratio in the same way as Fig. 3 for o-H2CO. The molecular hydrogen density is fixed at n(H2)=103 cm-3, the p-H2CO column density is N(p-H2CO)= 7.3 × 1011 cm-2, and the line width is ∆V = 0.5 km s-1. The excitation of the p-H2CO line is similar to that of the 2 mm lines of o-H2CO and exhibits a simple variation with the electron fraction, H2 density, opr, and gas kinetic temperature. For diffuse and translucent clouds with moderate densities, the excitation temperature of the two lines remains within 0.5 K from the CMB for H2 densities lower than ~2000 cm-3. The derivation of p-H2CO column densities from integrated opacities is therefore straightforward even when few informations on the physical conditions along the line of sight are accessible.

Figure A.4 shows RADEX calculation for ortho c-C3H2, using a total column density of 1012 cm-2 and a line FWHM of 0.6 km s-1. These calculations use collisional cross sections with para H2 and He only (Ben Khalifa et al. 2019). The effect of collisional excitation is more pronounced for the lowest frequency transition, the 11,0− 10,1 line at 18 GHz, than for the other lines at higher frequencies. For these lines, the CMB is the main source of excitation up to densities larger than about 2000 cm−3, as expected for such a high dipole moment species.

thumbnail Fig. A.2

Variation of the predicted excitation temperature (top) and opacity (bottom) for the three lowest lines of o-H2CO. The left panel shows the 11,0 − 11,1 line at 4.8 GHz, the middle panel shows the 21,2 − 11,1 line at 140 GHz, and the right panel the 21.1 − 11,1 line at 150 GHz. The o-H2CO column density is set to 2.2 × 1012 cm−2, the line FWHM is 0.5 km s−1. The kinetic temperature varies from 10 K to 60 K. The H2 ortho-to-para ratio increases with the kinetic temperature. The symbol sizes and shapes indicate the electron fraction : empty triangles for 2 × 10−6, starred triangles for 10−5, filled triangles for 3 × 10−5, empty squares for 6 × 10−5, starred squares for 10−4, and filled squares for 2 × 10−4. Larger symbols are used for larger values of the electron fraction. The 21,2 − 11,1 line at 140 GHz has not been observed in this work.
thumbnail Fig. A.3

Variation of the excitation temperature and opacity for the l0,1 − 00,0 line at 72 GHz (left), and the 20,2 − 10,1 line at 145 GHz (right) with the electron fraction, kinetic temperature, and H2 ortho-to-para ratio. The difference between the excitation temperature and the CMB is plotted. Different symbols show the values of the H2 ortho-to-para ratio between 3 × 10-5 and 3, their color and size indicate the kinetic temperature between 10 K and 60 K. The column density of p-H2CO is 7.3 × 1011 cm-2, the H2 density is set to 103 cm-3, and the line FWHM is 0.5 km s-1. The 10,1 − 00,0 line at 72 GHz has not been observed in this work.
thumbnail Fig. A.4

Variation of the opacity and excitation temperature of the four detected lines of ortho c-C3H3, as a function of the H2 density and kinetic temperature. The calculations used collision cross sections with He from Ben Khalifa et al. (2019), and their scaled version for para H2. Stars show the values for the 11,0 − 10,1 line at 18 GHz, filled squares for the 21,2 − 10,1 line at 85 GHz, filled triangles for the 31,2 − 22,1 line at 145 GHz, and empty hexagons for the 41,4 − 30,3 line at 150 GHz. The left panel presents the line opacities and the right panel the difference between the excitation temperature and the CMB. The adopted column density is 1012 cm−2 and the line FWHM is 0.6 km s−1.

References

  1. Agúndez, M., Marcelino, N., Cernicharo, J., Roueff, E., & Tafalla, M. 2019, A&A, 625, A147 [Google Scholar]
  2. Araya, E. D., Dieter-Conklin, N., Goss, W. M., & Andreev, N. 2014, ApJ, 784, 129 [CrossRef] [Google Scholar]
  3. Atkinson, R., Baulch, D. L., Cox, R. A., et al. 2006, Atmos. Chem. Phys., 6, 3625 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baulch, D. L., Bowman, C. T., Cobos, C. J., et al. 2005, J. Phys. Chem. Ref. Data, 34, 757 [Google Scholar]
  5. Ben Khalifa, M., Sahnoun, E., Wiesenfeld, L., et al. 2019, Phys. Chem. Chem. Phys. Incorporating Faraday Transac., 21, 1443 [Google Scholar]
  6. Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021, A&A, 649, L15 [EDP Sciences] [Google Scholar]
  7. Daniel, F., Faure, A., Dagdigian, P. J., et al. 2015, MNRAS, 446, 2312 [NASA ADS] [CrossRef] [Google Scholar]
  8. Denis-Alpizar, O., Stoecklin, T., Guilloteau, S., & Dutrey, A. 2018, MNRAS, 478, 1811 [Google Scholar]
  9. Dupuy, R., Bertin, M., Féraud, G., et al. 2021, Phys. Rev. Lett., 126, 156001 [NASA ADS] [CrossRef] [Google Scholar]
  10. Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectr., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
  11. Fan, H., Rocha, C. M. R., Cordiner, M., et al. 2024, A&A, 681, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Faure, A., Hily-Blant, P., Le Gal, R., Rist, C., & Pineau des Forêts, G. 2013, ApJ, 770, L2 [NASA ADS] [CrossRef] [Google Scholar]
  13. Faure, A., Hily-Blant, P., Rist, C., et al. 2019, MNRAS, 487, 3392 [Google Scholar]
  14. Federman, S. R., & Allen, M. 1991, ApJ, 375, 157 [NASA ADS] [CrossRef] [Google Scholar]
  15. Gerin, M., Liszt, H., Neufeld, D., et al. 2019, A&A, 622, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Godard, B., Falgarone, E., & Pineau des Forêts, G. 2014, A&A, 570, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Gong, Y., Du, F. J., Henkel, C., et al. 2023a, A&A, 679, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Gong, Y., Ortiz-León, G. N., Rugel, M. R., et al. 2023b, A&A, 678, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Green, S. 1991, ApJS, 76, 979 [NASA ADS] [CrossRef] [Google Scholar]
  20. Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
  21. Guzmán, V., Pety, J., Goicoechea, J. R., Gerin, M., & Roueff, E. 2011, A&A, 534, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Hama, T., Kouchi, A., & Watanabe, N. 2018, ApJ, 857, L13 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kutner, M., Thaddeus, P., Jefferts, K. B., Penzias, A. A., & Wilson, R. W. 1971, ApJ, 164, L49 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lesaffre, P., Todorov, P., Levrier, F., et al. 2020, MNRAS, 495, 816 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lique, F., & Spielfiedel, A. 2007, A&A, 462, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Liszt, H., & Gerin, M. 2023, ApJ, 943, 172 [NASA ADS] [CrossRef] [Google Scholar]
  27. Liszt, H., & Lucas, R. 1995, A&A, 299, 847 [Google Scholar]
  28. Liszt, H. S., & Lucas, R. 1998, A&A, 339, 561 [NASA ADS] [Google Scholar]
  29. Liszt, H., & Lucas, R. 2000, A&A, 355, 333 [NASA ADS] [Google Scholar]
  30. Liszt, H., & Lucas, R. 2001, A&A, 370, 576 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Liszt, H. S., & Pety, J. 2016, ApJ, 823, 124 [NASA ADS] [CrossRef] [Google Scholar]
  32. Liszt, H., Sonnentrucker, P., Cordiner, M., & Gerin, M. 2012, ApJ, 753, L28 [NASA ADS] [CrossRef] [Google Scholar]
  33. Liszt, H., Gerin, M., Beasley, A., & Pety, J. 2018a, ApJ, 856, 151 [Google Scholar]
  34. Liszt, H., Gerin, M., & Grenier, I. 2018b, A&A, 617, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Lovas, F. J., Suenram, R. D., Ogata, T., & Yamamoto, S. 1992, ApJ, 399, 325 [CrossRef] [Google Scholar]
  36. Lucas, R., & Liszt, H. 1994, A&A, 282, L5 [Google Scholar]
  37. Lucas, R., & Liszt, H. 1996, A&A, 307, 237 [NASA ADS] [Google Scholar]
  38. Lucas, R., & Liszt, H. S. 2000, A&A, 358, 1069 [NASA ADS] [Google Scholar]
  39. Lucas, R., & Liszt, H. S. 2002, A&A, 384, 1054 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Monaci, M., Magnani, L., Shore, S. N., Olofsson, H., & Joy, M. R. 2023, A&A, 676, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struc., 742, 215 [Google Scholar]
  42. Nash, A. G. 1990, ApJS, 72, 303 [NASA ADS] [CrossRef] [Google Scholar]
  43. Persson, C. M., Olofsson, A. O. H., Le Gal, R., et al. 2016, A&A, 586, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Pety, J., Lucas, R., & Liszt, H. S. 2008, A&A, 489, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Pety, J., Gratier, P., Guzmán, V., et al. 2012, A&A, 548, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Putaud, T., Michaut, X., Le Petit, F., Roueff, E., & Lis, D. C. 2019, A&A, 632, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Ramal-Olmedo, J. C., Menor-Salván, C. A., & Fortenberry, R. C. 2021, A&A, 656, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Rodríguez-Baras, M., Fuente, A., Riviére-Marichalar, P., et al. 2021, A&A, 648, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Shull, J. M., Danforth, C. W., & Anderson, K. L. 2021, ApJ, 911, 55 [NASA ADS] [CrossRef] [Google Scholar]
  50. Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [Google Scholar]
  51. Sonnentrucker, P., Welty, D. E., Thorburn, J. A., & York, D. G. 2007, ApJS, 168, 58 [NASA ADS] [CrossRef] [Google Scholar]
  52. Tafalla, M., Usero, A., & Hacar, A. 2021, A&A, 646, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Tielens, A. G. G. M. 2012, The Physics and Chemistry of the Interstellar Medium (Cambridge: Cambridge University Press) [Google Scholar]
  54. Troscompt, N., Faure, A., Maret, S., et al. 2009, A&A, 506, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Turner, B. E. 1993, ApJ, 410, 140 [NASA ADS] [CrossRef] [Google Scholar]
  56. van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Varambhia, H. N., Faure, A., Graupner, K., Field, T. A., & Tennyson, J. 2010, MNRAS, 403, 1409 [NASA ADS] [CrossRef] [Google Scholar]
  58. Wakelam, V., Herbst, E., Loison, J. C., et al. 2012, ApJS, 199, 21 [Google Scholar]
  59. Wiesenfeld, L., & Faure, A. 2013, MNRAS, 432, 2573 [NASA ADS] [CrossRef] [Google Scholar]
  60. Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [Google Scholar]
  61. Yan, Y. T., Henkel, C., Kobayashi, C., et al. 2023, A&A, 670, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Yocum, K. M., Wilkins, O. H., Bardwell, J. C., Milam, S. N., & Gerakines, P. A. 2023, ApJ, 958, L41 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

References for the ancillary data.

In the text
Table 2

Detected lines.

In the text
Table 3

Properties of the velocity components.

In the text
Table 4

References for rate coefficients.

In the text
Table 5

Ratios of integrated optical depth to the integrated optical depth of the −10 km s-1 velocity component.

In the text
Table 6

Column densities, abundances, and ortho-to-para ratios.

In the text

All Figures

thumbnail Fig. 1

Absorption lines detected toward NRAO 150. The left panel shows previous detections including the o-H2CO (11,0–11,1) line at 4.8 GHz and the o-c-C3H2 (11,0–10,1) line at 18 GHz observed at the VLA (Liszt & Lucas 1995; Liszt et al. 2012), and the CS (2–1) (98 GHz), o-c-C3H2 (21,2–10,1)(85.3 GHz), CCH(1, 3/2, 2–0,1/2,1) (87.3 GHz), and HCO+(1–0) (89.2 GHz) lines (Liszt & Lucas 1995; Lucas & Liszt 1994, 1996, 2000, 2002) observed with the PdBI. The right panel presents the new observations including the o-H2CO(21,1–10,2), o-H213CO(21,1–10,2), and p-H2CO (20,2–10,1) lines, the CS (3–2), C34S(3–2) lines, and the c-C3H2 transitions listed in Table 2. All displayed spectra have been normalized by the continuum strength. Vertical offsets have been used for clarity.
In the text
thumbnail Fig. 2

Variation of the predicted opacities of the CS (2–1) (filled symbols) and CS (3–2) (starred symbols) transitions as a function of the molecular hydrogen density in the diffuse and translucent cloud conditions computed with RADEX using the column densities and FWHM listed in Table 3. The colors show the kinetic temperature from 10 to 60 K, and the H2 ortho-to-para ratio scales with the kinetic temperature. The symbol shapes indicate the electron fraction as follows for the CS (2–1) line: lower than 2 × 10-5 filled triangles, between 2 × 10-5 and 10-4, small filled squares, and filled circles for 2 × 10-4. A similar progression is used for the CS (3–2) line, lower than 2 × 10-5 crosses, between 2 × 10-5 and 10-4, small stars, and 8-branch stars for 2 × 10-4. The measured opacities for the four detected velocity components are shown with the dashed and dotted gray areas, from top to bottom: −17.2 km s-1, −10.3 km s-1, −8.5 km s-1 and −4 km s-1.
In the text
thumbnail Fig. 3

Variation of the excitation temperature and opacity with the electron fraction, kinetic temperature, and H2 ortho-to-para ratio for the 11,0−11,1 line at 4.8 GHz (top left), and zoom on the region with excitation temperature lower than the CMB indicated by a dotted box (top right). The 21,2−11,1 line at 140 GHz is shown in the bottom left panel and the 21,1−11,0 line at 150 GHz in the bottom right panel. The difference between the excitation temperature and the CMB is plotted to illustrate the change of regime of the 11,0−11,1 transition at 4.8 GHz, and a different scale is used for the 140 GHz and 150 GHz lines. Different symbols show the values of the H2 ortho-to-para ratio between 3 × 10-5 and 3, their color and size indicate the kinetic temperature between 10 and 60 K. The column density of o-H2CO is 2.2 × 1012 cm-2, the H2 density is set to 103 cm-3, and the FWHM is 0.5 km s-1. The 21,2−11,1 line at 140 GHz has not been observed in this work.
In the text
thumbnail Fig. A.1

Variation of the predicted excitation temperature (top) and opacity (bottom) for the two lowest lines of p-H2CO. The top panel shows the 10,1 − 00,0 line at 72 GHz, and the bottom panel shows the 20,2 − 10,1 line at 145 GHz. The p-H2CO column density is set to 7.3 × 1011 cm-2, the line FWHM is 0.5 km s-1. The kinetic temperature varies from 10 K to 60 K. The H2 ortho-to-para ratio varies with the kinetic temperature. The symbol sizes and shapes indicate the electron fraction : empty triangles for 2 × 10-6, starred triangles for 10-5, filled triangles for 3 × 10-5, empty squares for 6 × 10-5, starred squares for 10-4, and filled squares for 2 × 10-4. Larger symbols are used for larger values of the electron fraction. The 10,1 − 00,0 line at 72 GHz has not been observed in this work.
In the text
thumbnail Fig. A.2

Variation of the predicted excitation temperature (top) and opacity (bottom) for the three lowest lines of o-H2CO. The left panel shows the 11,0 − 11,1 line at 4.8 GHz, the middle panel shows the 21,2 − 11,1 line at 140 GHz, and the right panel the 21.1 − 11,1 line at 150 GHz. The o-H2CO column density is set to 2.2 × 1012 cm−2, the line FWHM is 0.5 km s−1. The kinetic temperature varies from 10 K to 60 K. The H2 ortho-to-para ratio increases with the kinetic temperature. The symbol sizes and shapes indicate the electron fraction : empty triangles for 2 × 10−6, starred triangles for 10−5, filled triangles for 3 × 10−5, empty squares for 6 × 10−5, starred squares for 10−4, and filled squares for 2 × 10−4. Larger symbols are used for larger values of the electron fraction. The 21,2 − 11,1 line at 140 GHz has not been observed in this work.
In the text
thumbnail Fig. A.3

Variation of the excitation temperature and opacity for the l0,1 − 00,0 line at 72 GHz (left), and the 20,2 − 10,1 line at 145 GHz (right) with the electron fraction, kinetic temperature, and H2 ortho-to-para ratio. The difference between the excitation temperature and the CMB is plotted. Different symbols show the values of the H2 ortho-to-para ratio between 3 × 10-5 and 3, their color and size indicate the kinetic temperature between 10 K and 60 K. The column density of p-H2CO is 7.3 × 1011 cm-2, the H2 density is set to 103 cm-3, and the line FWHM is 0.5 km s-1. The 10,1 − 00,0 line at 72 GHz has not been observed in this work.
In the text
thumbnail Fig. A.4

Variation of the opacity and excitation temperature of the four detected lines of ortho c-C3H3, as a function of the H2 density and kinetic temperature. The calculations used collision cross sections with He from Ben Khalifa et al. (2019), and their scaled version for para H2. Stars show the values for the 11,0 − 10,1 line at 18 GHz, filled squares for the 21,2 − 10,1 line at 85 GHz, filled triangles for the 31,2 − 22,1 line at 145 GHz, and empty hexagons for the 41,4 − 30,3 line at 150 GHz. The left panel presents the line opacities and the right panel the difference between the excitation temperature and the CMB. The adopted column density is 1012 cm−2 and the line FWHM is 0.6 km s−1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.