EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 685 (May 2024) A&A, 685 (2024) A130 Full HTML
Open Access
Issue
A&A
Volume 685, May 2024
Article Number A130
Number of page(s) 40
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/202347273
Published online 17 May 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

An extensive census of quasars (QSOs) is fundamental to many cosmological studies. Specifically, in cases where these QSOs exhibit multiple images, strongly lensed QSOs enable the estimation of the Hubble constant H0 directly from time delay measurements (e.g. Refsdal 1964; Courbin et al. 2005; Millon et al. 2020; Suyu et al. 2017; Chen et al. 2019; Wong et al. 2020). In addition to many other astrophysical and cosmological applications, these sources are also used for detailed studies of dark matter halos and their substructures (e.g. Nierenberg et al. 2017; Li et al. 2017; Diaz Rivero et al. 2018; Gilman et al. 2020b,a, 2021; Nierenberg et al. 2020; Minor et al. 2021), and for constraining the dark energy equation of state (e.g. Linder 2004, 2011; Oguri et al. 2012; Xia et al. 2017; Liu et al. 2019; Wang et al. 2022). All lensed QSOs discussed in this work are strongly lensed by definition.

Detecting lenses has been historically challenging because (i) most lensed QSOs are distant and hence faint and (ii) broad sky coverage and high angular resolution are required as the angular separations between the lensed images are small. Moreover, chance projection can create astrometric configurations and even broad-band photometry similar to those expected from lensed QSOs such that a reliable confirmation requires spectroscopic measurements of the QSO images and the lensing galaxy. Due to these difficulties, the number of confirmed lensed QSOs has been low for decades. The European Space Agency (ESA) Gaia mission (Gaia Collaboration 2016) and its data releases, particularly since Data Release 2 (Gaia Collaboration 2018, 2021, 2023b), have been dramatically improving this situation.

Although Gaia was primarily designed to study the Milky Way through astrometry at the micro-arcsecond level, it produces an all-sky survey including millions of galaxies and QSOs (Robin et al. 2012; Krone-Martins et al. 2013, 2022; de Souza et al. 2014; de Bruijne et al. 2015; Gaia Collaboration 2023a; Ducourant et al. 2023). In their work, de Souza et al. (2014) and de Bruijne et al. (2015) define downlink criteria. The sources can be used to create a homogeneous, magnitude-limited survey of lensed QSOs down to image separations of ~0.18″. This is comparable to the angular resolution of the NASA-ESA Hubble Space Telescope (HST), but Gaia measurements have all-sky coverage. During this decade, the recently launched ESA-NASA Euclid space mission (Laureijs et al. 2011) will also be surveying ~ 14 000 square degrees at comparable angular resolutions, providing deep and high-resolution images in multiple bands for the first time at such large scales (Euclid Collaboration 2022). This is expected to revolutionise strong lensing studies by enabling almost direct confirmation of thousands of lensed QSOs (e.g. Treu et al. 2022), and complementing Gaia’s µas astrometry with deep and precise photometry.

Conservative estimates of the number of lensed QSOs detectable by Gaia in standard ΛCDM (Λ cold dark matter) cosmology (Λ = 0.7, Ωm = 0.3) suggest that ~3 000 multiply imaged QSOs could be detected by Gaia of which >250 would have ≥3 images and the rest are doublets (Surdej et al. 2002; Finet & Surdej 2016). Gaia could then lead to a ten-fold increase in the number of lensed QSOs resulting in a homogeneous survey providing precise astrometry for all lensed images. Such a census is being built by the astronomical community, which continuously scans the Gaia data releases for follow-up spectroscopic confirmation (e.g. Krone-Martins et al. 2018, 2019; Ducourant et al. 2018; Agnello et al. 2018; Lemon et al. 2018, 2019, 2023; Delchambre et al. 2019; Stern et al. 2021; Desira et al. 2022). This endeavour is already resulting in a unique and statistically significant sample of lenses that will be used to study the evolution of the population of the deflecting galaxies and to constrain cosmological parameters, including the value of H0 that is currently under significant tension (e.g. Verde et al. 2019; Di Valentino et al. 2021).

Current Gaia Data Releases are still incomplete at the lowest angular separations (e.g. Arenou et al. 2017, 2018; Fabricius et al. 2021; Torra et al. 2021), as expected for early mission products. This has led some known lensed images to lack Gaia counterparts (see, e.g. Ducourant et al. 2018). And this has slowed the identification of new lenses since most lensed QSOs that have yet to be discovered are probably angularly small. Thus, within the Gaia Data Processing and Analysis Consortium, we developed a dedicated processing chain to analyse the environment of QSOs and produce a catalogue of sources and clusters, including new lens candidates for further studies and confirmation by the community. The major goals of this work are to make this focused Gaia data available to the community, to present the new data, and to call the attention of the community to the possibility of using this data to study currently known lensed QSOs and to discover new lensed QSOs while also providing a first, non-exhaustive, candidate list.

Finally, new astrophysical cases can emerge from the large lens samples expected. For instance, because the QSO is unique and point-like, but the images are seen through different parts of the lensing object, we can use the colours and magnitudes to study the obscuring dust in the line of sight. Cosmic dust reddens light but not always in the same way. Let AV designate the V band absorption and B − V the colour of an object. When there is reddening, we define the excess B − V as E(B − V) = (B − V) − (B − V)0 where (B − V)0 is the intrinsic colour of the object. Milky Way dust shows a pattern where AV ≈ 3.1 E(B − V) but the dust absorption spectrum is not identical for all galaxies (e.g. Gordon et al. 2003). Gaia provides much of this information, so using a large sample, as should come out of this work, we can reconstruct and study dust at cosmological distances via the AV/E(B − V) ratio, possibly inferring the existence of major dust features in the Universe (e.g. as done in Lallement et al. 2018; Green et al. 2019; Leike et al. 2021, 2022, for features in our galaxy), a new method to the best of our knowledge.

This paper is organised as follows. Section 2 presents the list of QSOs and QSOs candidates used as inputs to GravLens. Section 3 describes how the GravLens algorithm clusters transits (individual detections) mapping transits to sources along with some remaining issues. Section 4 describes the resulting catalogue, the field contents, and the new sources. Afterward, in Sect. 5, we present the methods developed to create lens scores and a list of candidates. Finally, we present our conclusions in Sect. 6.

2 The list of QSOs

Our processing starts from an input list of QSOs. Since gravitational lenses are rare, with less than ~80 lensed QSOs with four images – quads hereafter – known today (Stern et al. 2021), we want to make this input list of QSOs for the GravLens processing as complete as possible to maximise our chances of detecting new lenses. Therefore we tolerate moderate stellar or galaxy contamination in this input list.

We merged some major catalogues of QSOs and candidate active galactic nuclei (AGN) published before 2022. These include the data releases 6.4, 7.0, 7.1b, 7.4c, 7.5, 7.5b of the Milliquas catalogue (Flesch 2021, 2019), the R90 and C75 selections of the AllWISE catalogue (Assef et al. 2018), the catalogue of AGN candidates from (Shu et al. 2019), a selection of sources from Klioner et al. 2021 (priv. comm.), a subset of the Gaia DR3 quasar_candidates table (Gaia Collaboration 2023a), and additional QSOs whose morphology was analysed by Ducourant et al. (2023). Most of these catalogues contain stellar contaminants.

The catalogues were cross-matched using a search radius of 3″ and we only kept a single entry. The data priority follows the order listed above such that if a source is found in Milliquas 7.4c and 7.1b, only Milliquas 7.4c will be recorded. The compilation contains ~24 million total sources, of which ~5 million are matched to a Gaia DR3 source.

Sources that are clearly stellar were eliminated by applying a weak astrometric filter rejecting proper motions larger than 14 mas/yr or parallaxes larger than 6 mas. This filter was derived from the astrometric properties of the multiply imaged QSOs by gravitational lensing (Ducourant et al. 2018) and is intentionally not severe because most QSOs are in the faint luminosity regime of Gaia where the astrometry is less accurate and the potential presence of a surrounding host galaxy can perturb the astrometry of the central nucleus. We also filtered out objects brighter than G = 14 magnitudes and excluded sources with colours compatible with stellar sources: (GBP − G) > 1 & (G − GRP) > 0.8 & G < 20 (see Gaia Collaboration 2023a, Fig. 37). We thus discarded ~ 21000 sources judged stellar. The small number of discarded sources indicates that possibly some sort of astrometric filtering had already been performed in the construction of the original catalogues. Finally, sources in the direction of the Magellanic clouds, of other large galaxies, or of major globular clusters (Harris 2010) were removed.

The final list of QSOs and candidates contains 3 760480 sources with an entry in Gaia DR3 and we refer to the list as the QSOs or the QSO catalogue. The original catalogue name (e.g. Milliquas 7.4c) for each source is stored in lens_catalogue_name.

The sky distribution of the QSOs in our input list is shown in Fig. 1 in galactic coordinates. The sky coverage of each of the merged catalogues is heterogeneous, as is the resulting compiled list. Most (81%) of the sources have a G magnitude fainter than 19.5 mag, as seen in Fig. 2. Figure 2 also shows the Gaia colour GBP − GRP, the W1–W2 colour from catWISE (Eisenhardt et al. 2020), and the redshift distribution when available from Milliquas (~900 000 sources). The redshift distribution peaks at ɀ ~ 1.4 and extends to ɀ ~ 6 for a small number of sources.

thumbnail Fig. 1

Sky distribution in galactic coordinates of the QSOs included in the input list. The cell of this map is approximately 0.2 deg2, and the colour indicates the number of sources in each cell on a logarithmic scale.

3 How GravLens searches for sources near QSOs

The all-sky coverage and ~180 mas angular resolution make Gaia an exceptional instrument to search for lenses. Most currently known lenses have image separations ≫1″ (e.g. Ducourant et al. 2018)1. Nevertheless, the expected distribution of lenses should peak at smaller separations, ≲1″, making most of them quasi-undetectable from the ground (e.g. Finet & Surdej 2016). Unfortunately, the Gaia DR2 and Gaia DR3 are incomplete at separations ≤ 2″ (e.g. Arenou et al. 2017, 2018; Fabricius et al. 2021; Torra et al. 2021). This results from a severe selection on the astrometric and photometric quality indicators of the sources that are published in these Data Releases.

The primary goal of GravLens is to detect secondary sources near QSOs and QSO candidates, and derive their mean astrometry and raw photometry. In this context, each source that is detected in a field centred on the coordinates of a QSO is named component. The ensemble of all the components in a field is named multiplets. The field centred on a QSO is designated by quasar.

3.1 The adopted Gaia data

The instruments and focal plane of the satellite are welldescribed in Gaia Collaboration (2016). Unlike most Gaia data processing chains that assign transits to a single source exploiting the Gaia cross-match (Torra et al. 2021), GravLens manipulates upstream data and allows a finer clustering to separate adjacent sources. The data adopted by GravLens comes from the pre-processing step of Gaia treatment which is referred to as Image Parameter Determination (IPD, Fabricius et al. 2016). The purpose of IPD is to transform the raw spacecraft telemetry into basic astrometric and photometric measures for the Sky Mapper (SM) and Astrometric Field (AF) windows. Our input data is the Gaia DR3 IPD outputs (flux and positions). These epoch positions are not the high-precision one-dimensional Gaia astrometry, but approximate 2D positions with a resolution of about one charge-coupled device (CCD) pixel. GravLens uses the positions (right ascension and declination) of each transit, the fluxes in the G-band measured in SM and AF windows, and a rough on-board estimation of the G magnitude done in the Gaia Video Processing Unit (VPU, de Bruijne et al. 2015; Fabricius et al. 2016)2. GravLens identifies by itself all Gaia transits within 6″ of each QSO, without relying on the Gaia standard cross-matching since at this stage of the data processing, the Gaia cross-match is not yet known. The Gaia cross-match might subsequently identify more additional sources in the field at the later processing stages, but this is not included in GravLens.

thumbnail Fig. 2

Distributions of (a) Gaia G magnitudes (phot_g_mean_mag) from the Gaia DR3 gaia_source table, (b) GBP − GRP colours (phot_bp_mean_mag − phot_rp_mean_mag), (c) W1–W2 colours (from catWISE), (d) redshifts (from Milliquas) of the QSOs and candidates from the input list.

3.2 The GravLens clustering algorithm

GravLens uses the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm (Ester et al. 1996) for unsupervised clustering3. Without indicating the number of clusters, as required, for example, for K-Means algorithms, it identifies groups of connected points and outliers. The principle of DBSCAN is to build a neighbourhood graph by connecting points (which here are individual detections in right ascension and declination) if their distance is smaller than a certain ϵ. Here, we adopt ϵ = 100 mas, a value chosen empirically that is within the PSF width of Gaia, thus corresponding to an angular distance that the instrument cannot physically resolve into individual sources. The angular distances between the points are calculated using the haversine formula (e.g. de Mendoza y Ríos 1795).

While there are non-connected points within ϵ, the algorithm tries to connect them, and thus the graph grows. Otherwise, the set of connected points remains as is. When at least minPts = 3 (empirically chosen) points are connected, a cluster is formed (called a component); otherwise, the points are considered outliers. All Gaia transits associated with an entry of the QSO catalogue are then either outliers or within components (clusters). Once the clustering is complete, a sigma-clipping filter based on the positions and the magnitude is applied to the components, using 3σ as the threshold. The GravLens processing of the QSOs has produced a catalogue of ~4.7 million components.

As an example of GravLens results, Fig. 3 illustrates the application of the clustering algorithm on the well-known lens Einstein cross G2237+0305 (Huchra et al. 1985). Five components are found by GravLens, corresponding to the four images of the QSO, and to the lensing galaxy that is also clearly detected.

thumbnail Fig. 3

GravLens results for the Einstein cross G2237+0305 (DR3Gaia224030.229+032130.03 in our output). The black dots represent the five components and the blue crosses, red diamonds, green crosses, and pink dots represent the four images of the QSO. The yellow triangles show the Gaia transits on the deflecting galaxy. The information is in the ra_obs, dec_obs fields of the lens_candidates and lens_outlier tables.

3.3 Clustering issues

The GravLens algorithm is efficient and, in most lensing configurations reaches an optimal solution. However, occasionally, it converges to sub-optimal solutions. Figure 4 illustrates some examples of known issues.

We show in Fig. 4a the known quadruply imaged lens (Krone-Martins et al. 2018; Wertz et al. 2019), that corresponds to the multiplet DR3Gaia113100.075-441959.69. Gaia DR3 identifies four distinct sources with their own source_id. In the figure, all Gaia detections are plotted, and the two known components in the top left were merged by GravLens, which only outputs three components. The two components are connected by detections closer than 100 mas, which causes the method to group the two sources; this is a major drawback of DBSCAN. The central point, identified as an outlier, could even bring some physical information about the lens. The end user of the tables of this Focused Product Release (FPR) should be aware that useful information may be present in the table of outliers.

We show another example of a clustering issue in Fig. 4b. This figure corresponds to the source DR3Gaia235007.548+365434.45. This source is a known doubly image QSO, but GravLens identified only one of its components. The component is 2.9″ away from the QSO and the individual detections at the QSO position were labelled as outliers. Therefore, the information is not completely lost, but present in the lens_outlier table. Five transits are near the QSO but the distance between the transits is >ϵ = 100 mas so they are not considered to be a component. The astrometry may have been perturbed by the deflecting galaxy and the Gaia DR3 astrometry is unreliable, presenting errors of ~17 mas.

We illustrate the case of a large planetary nebula (IC 351) decomposed into many components in Fig. 4c. This figure represents the source DR3Gaia034732.982+350248.6. There are 3508 Gaia observations in this field. GravLens found 120 components with 2768 detections, and 740 outliers. This example highlights one of the causes of the large number of components in certain fields when an extended object is decomposed.

Figure 4d shows another odd example of a large number of detections (DR3Gaia082523.532+241524.53). In this case, the central source is a very bright object (magnitude ~ 9.7). GravLens detects 136 components in radial spokes from the central source, based on 2481 observations, of which 1424 are considered outliers. A halo of outliers is present around this source.

3.4 Post-processing

After the GravLens processing, we perform a post-processing stage. The post-processing can handle specific situations and flag problematic sources or sources to be discarded. In particular, we observed an excess of doublets separated by less than 300 mas and with ≤5 observations of one of the components. A small fraction of these are probably real sources but the majority of them result from the excessive decomposition of single sources into doublets by the clustering algorithm. The postprocessing gathered these nearby components into single sources for ~200 000 doublets.

The post-processing aims at raising flags to indicate problematic multiplets or multiplets which are clearly not lensed QSOs. The flags are raised at the QSO level flag and/or at the component level component_flag.

The flag is a two-bit binary flag. The first bit is set to one if the maximum difference of magnitude within the multiplet is larger than 5 mag which indicates that it is very improbable that this is a lensed QSO. The second bit is set to one if there are more outliers than clustered observations, such as could be the case for a galaxy and other extended objects, see, e.g. Fig. 4c.

The component_flag is also a two-bit binary flag. The first bit is set to one if the standard deviation in right ascension or declination of a component is larger than 100 mas. A point source should yield σRA,Dec ≈ 60 mas, at the order of the uncertainty of the RA/Dec of the SM position. The second bit is set to one if the standard deviation of the raw mean magnitude is larger than 0.4 mag. In both cases, component_flag points to unusually high measurement uncertainty, possibly resulting from a bright nearby source or several very nearby sources which are considered a single component. There are 4 444 145 components with both flags set to 00, indicating no alert is raised. This represents 93% of all components.

4 The catalogue of sources around QSOs

GravLens has analysed 183 368 062 transits matched to the 3 760480 QSOs from our list during the first 3yr of Gaia operations. It attributed 171 545 519 transits to components and rejected 11 822 543 as outliers. GravLens did not converge in 448 cases. Within 6″ of the 3 760 032 QSOs, 4 760 920 sources were found (see Table 1), including the QSOs.

These results are included in the lens_candidates table. The data model of the catalogue is presented in Appendix A. Additional information can be found in the table lens_catalogue_name (see Sect. 2). The individual observations of each component and the outliers are found in the lens_observation and lens_outlier tables4.

thumbnail Fig. 4

Examples of known issues. Black dots are the mean positions of the components, red points correspond to individual observations no matter the component and grey dots are outliers. In (c), a planetary nebula (IC 351) that unduly entered in the QSO catalogue is decomposed by the algorithm into numerous sources. as well as in (d) for the halo of a bright star.

4.1 General properties

The distribution of the main properties of the components published in the lens_candidates table is given in Fig. 5. The number of sources detected in the fields of the QSOs along with the number of components in the fields is given in Table 1.

The vast majority of the QSOs (87%) have no neighbour within 6″ and 9% are doublets. There are ~ 159 000 multiplets with more than two components (4%). The search for quadruply imaged QSOs will therefore focus on this sample of multiplets. There are ~9000 multiplets containing a large number of components (>10). They generally correspond to large galaxies decomposed in many sources as seen in Sect. 3.3.

The distribution of magnitudes follows that of the QSOs in the input list (see Fig. 2). This distribution reflects the fact that the majority of the sources in our catalogue are not multiply-imaged.

Components have a median of 36 observations, ranging from three to 630 observations, and are time-resolved. Sources with a very low number of observations should be considered with caution and generally correspond to the faintest sources detected.

thumbnail Fig. 5

Distributions of components’ main features provided in the lens_candidates table - (a) number of components found in the fields analysed, (b) mean G magnitude of the components of all fields. (c) number of observations of the components. (d) standard deviation of mean coordinates (ra_component, dec_component) and (e) standard deviation of mean G magnitude.
Table 1

Source counts in the lens_candidates table according to the number of components in the field.

4.2 Astrometry and photometry

GravLens astrometry and photometry are meant to complement the information from the current Gaia Data Releases, especially for the sources that are not present in the latter. GravLens magnitudes and fluxes use uncalibrated onboard magnitudes, for instance. For many GravLens sources not published in Gaia DR3 the measurements are poor, as these sources are usually faint. The mean standard deviations are 62 mas and 57 mas, respectively, for right ascension and declination and 0.15 mag for the magnitudes.

The GravLens and Gaia DR3 positions and magnitudes for common sources are compared in Fig. 6. A slight asymmetry is present in RA and Dec, with (RAGL − RADR3) ≈ −1.33mas and DecGL − DecDR3 ≈ −5.4 mas, with dispersions of ~13 mas.

The GravLens magnitudes agree well with Gaia magnitudes with a mean difference of −0.06 mag and a standard deviation of 0.15 mag. Around G = 12 ± 0.5 mag, the GravLens magnitudes are slightly higher. This is a well-known effect of the uncalibrated onboard magnitudes (Riello et al. 2018), and for Gaia DR3 magnitudes ≳21, the GravLens magnitudes are quite dispersed and generally lower (i.e. the magnitudes can be overestimating the true brightness of the source).

The astrometry and photometry of the GravLens components are based on the Gaia onboard detections. These data should be much improved in solutions published in future Data Releases when the individual components are properly handled.

4.3 New sources not in Gaia DR3

There are ~10500 Gaia DR3 sources in the vicinity of analysed QSOs (6″) that are not among the GravLens components, representing less than 0.2% of all GravLens components. Meanwhile, there are 306 970 new sources that are not in Gaia DR3 among the 4 760 920 GravLens components. About ~200 000 new sources are either bright with g_mag_component<17.5 mag or in crowded fields with n_components>20 (Fig. 7). The bright new sources correspond to problems illustrated in Figs. 4c and d. They are generally flagged either at the quasar level (flag) or at the component level (component_flag) (see Sect. 3.4 for a description of the flags). After this process, ~103 000 new sources remain which are not flagged and believed to be bona-fide sources.

4.4 Known lenses

We first compare the GravLens results to known lenses. The GravLens catalogue includes ~450 known or candidate lenses published in the literature, 76 with four images (quads) and the rest being doublets. For 67 quads out of the 76 quads, GravLens complements the existing measures from Gaia DR3 by measuring one or more additional components or the deflecting galaxy. In total GravLens measured 1293 components in the fields of known lenses while 1 207 are present in Gaia DR3. The 86 newly detected components in the fields of known lenses are mostly faint real components lying around lenses with a previously small number of Gaia DR3 counterparts.

We show two examples in Fig. 8. This figure shows images from the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS, Chambers et al. 2016) of two known lenses: the Einstein cross G2237+0305 (Huchra et al. 1985) where GravLens detects all four images of the QSO and the deflecting galaxy while Gaia DR3 only contains two entries, and 2MASSJ13102005-1714579 (Lucey et al. 2018) where GravLens detects the four images of the QSO and two central deflecting galaxies that had no entry in Gaia DR3.

Some of the presently known lensed QSOs have been targeted by the HST, and new structures can be found in the HST source catalogue version 3 (Whitmore et al. 2016). However, of the 476 known lenses, only 69 have space-borne measurements from the HST catalogue.

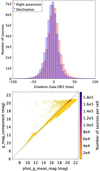thumbnail Fig. 6

Comparison between coordinates and magnitudes from GravLens and Gaia DR3. Top: comparison of the coordinates (ra, dec) derived by GravLens and by Gaia DR3. ∆ra includes the cos(dec) factor. Bottom: comparison of GravLens magnitudes (table lens_candidates field g_mag_component) with Gaia DR3 magnitudes (table gaiadr3.gaia_source field phot_g_mean_mag).
thumbnail Fig. 7

Density plot of the magnitudes of the GravLens components not present in Gaia DR3 along with the number of components in the multiplet. Coulour scale is logarithmic.

5 Search for new lenses

To look for new lenses and help guiding the users of this FPR, we developed two methods using artificial intelligence: an outlier scoring algorithm (Sect. 5.1) and the application of Extremely Randomised Trees (Delchambre et al. 2019, and Sect. 5.2). When Gaia spectra are available, we also make use of this information, and in Sect. 5.3 we explain the method that compares the mean spectra obtained by Gaia slitless spectrophotometer (i.e. BP and RP-spectra) using chi-squares and Wasserstein distances. High-scoring multiplets are then visually inspected.

5.1 The Hesiod score for the input list of QSOs

Only a small fraction of components near QSOs are expected to be QSO images. So, analysing the QSOs from the list presented in Sect. 2 to identify good lens candidates can be seen as an outlier detection or a one-class classification problem. Accordingly, we can use these techniques to produce a lens score.

In these methods, distances, densities, and, in some instances, labelled data are used to train to identify a class called the positive class (see, e.g. Elkan & Noto 2008). The supervised or semi-supervised training assumes (a) that the learning method has access to a reliable subset of positive examples such as spectroscopically confirmed lenses and (b) that the data contains positive and unknown examples (i.e. new lenses and other objects).

To increase the reliability of the scores, photometric and astrometric indicators from the Gaia DR3 data (Gaia Collaboration 2023a) and public unWISE data (Lang 2014) were calculated based on sources within 6″ of each QSO. Missing data patterns appear when sources lack Gaia DR3 or unWISE data or when there is no unWISE counterpart for a Gaia source. Missing data is a serious problem that prevents the adoption of many approaches readily available in the literature (e.g. Bekker & Davis 2020). So, to produce a score in this situation, we developed a simple heuristic method that we call HESIOD for Heuristical Ensemble Splitting Imputation and Organization of Data that can be applied to large datasets as it is embarrassingly parallel.

HESIOD assumes that the dataset can be described by a single matrix D of n rows by d columns. Each row corresponds to an astronomical source, and each column corresponds to a physical parameter (e.g. astrometric and photometric measurements from Gaia and unWISE, maximum and minimum angular distances and colour differences between sources, etc.). D can be incomplete in that not all elements Dij are filled (i.e. data for one or more column j can be missing in any row i). The binary vector c ∈ {0, 1}n encodes the class of the ith row (ith source); ci = 1 if the source belongs to the positive class, here equivalent to a known lens, and ci = 0 if the class is unknown. Only k components of the vector c are equal to one, with k ≪ n. HESIOD is a method ℋ to estimate a vector o ∈ Rn |0 ≤ oi ≤ 1, ∀i ∈ [1, n], from D and c (i.e. ℋ(D, c) → o), such that o contains a score oi for all n rows (sources) of D to indicate if the ith source can belong to a different class than the positive class (the lenses). HESIOD thus starts with the known lenses c and ends with a new real-valued vector o. The vector o is initially an outlier score, that is, a score for the source not being a lens, which we complement (i.e. 1 − o) to obtain a lens score.

Informally, HESIOD solves this problem by creating ensembles of smaller problems that are easier to solve. It has two steps, an initial 'inner' phase followed by an 'outer' phase, as in UPMASK (Krone-Martins & Moitinho 2014). The inner phase randomly splits the matrix D into a set of m smaller p × d sub-matrices {Sj|∀j ∈ [1, m]}, without replacement. This corresponds to random partitions of the catalogue into random samplings of sources (keeping all the associated data). Then, an imputation method 𝒥 solves the less complex imputation problem for each sub-matrix 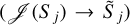(J(Sj)→S˜j)$\left( {{\cal J}\left( {{S_j}} \right) \to {{\tilde S}_j}} \right)$. Afterward, a 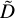D˜${\tilde D}$ matrix is reassembled from the results of the imputations on the S sub-matrices, and multiple outlier or one-class classification methods 𝒞 produce scores from 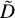D˜${\tilde D}$ and the vector c, resulting in the matrix 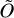O˜${\tilde O}$ containing the scores for each source (i.e. 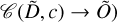C(D˜,c)→O˜)$C(\tilde D,c) \to \tilde O)$.

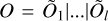The outer phase of HESIOD executes the inner phase q times, resulting in a set of matrices { O˜l∣∀l∈[1,q] }$\left\{ {{{\tilde O}_l}\mid \forall l \in [1,q]} \right\}$. This ensures diversity in the imputation process due to the random splitting of D. Then it runs the final scoring method 𝒪 over the matrix O, where O=O˜1|…|O˜l$O = {{\tilde O}_1}| \ldots |{{\tilde O}_l}$ (i.e. this matrix is the concatenation of the individual matrices resulting from the q runs of the inner phase), producing a final score for each source (i.e. 𝒪(O) → o), where o is a score for the source to be an outlier (i.e. not a lens), and 1 − o is the HESIOD score.

Since here the positive class is composed of lenses, which corresponds to a small number of rows of the total dataset D, all known lenses are concatenated with each sub-matrix S. This is important to avoid significantly biasing the imputation process against the lenses.

The HESIOD results depend on the choice of the ensembles of methods used for imputation 𝒥 and classifications 𝒞 and 𝒪. In this work, we adopted different methods based on ensembles of decision trees. We adopted miceRanger (Wilson 2021) for the imputation 𝒥. This is a version of the Multiple Imputation by Chained Equations method (van Buuren 2007) that uses a random forest regression for individual imputations (Stekhoven & Bühlmann 2011), as in Ducourant et al. (2017). For the outlier scoring 𝒞 we use three types of ensembles of decision trees as there is usually no optimal method for all problems (e.g. Wolpert 1996; Wolpert & Macready 1997; Cortes 2021): the classic Isolation Forest method (Liu et al. 2008), SciForests (Liu et al. 2010), and Fair-Cut Forests (Cortes 2019). The final outlier score 𝒪 also uses Fair-Cut Forests. The resulting distribution of the HESIOD scores is presented in Fig. 9. Known lenses were iteratively used during the training, so it is expected that their scores would peak at high values, which indeed happens. The results on all 319 296 sources for which the method produced results show a central peak indicating more uncertain sources and two sharp peaks at the low and high score extremes.

The HESIOD method seems effective in the present lens candidate scoring application since it was designed to deal with large datasets with missing data and, moreover, to consider a parameter space constructed from combinations of the measurements of all sources around the analysed QSO. The parameter space (i.e. columns of the matrix D) is constructed from summary information about distributions of the measurements of all sources around the QSO, such as minimum and maximum differences in colour in all possible Gaia DR3, unWISE, Gaia-unWISE W1 and W2 bands, astrometric errors, angular distances, between the images, as well as global properties of the parameter distributions as the minimum, mean and maximum astrometric and photometric errors, astrometric excess noise, Renormalised Unit Weight Error (RUWE), BPRP excesses and signal to noise ratios (e.g. fluxes, positions, proper motions and parallaxes over their errors) for all sources. As such, the HESIOD score is assigned for the entire candidate system, composed of multiple Gaia DR3 sources. This parameter space also enables HESIOD to deal with more challenging lensing cases. For instance, although gravitational lenses are achromatic, one or more of the QSO images can be superposed with parts of the lensing galaxy, and in the most extreme cases, the lensing galaxy can be completely unresolved and mixed with one or more images due to finite spatial resolution. In such cases, property gradients (such as colour, and astrometry) could be expected to exist within the candidate system, and HESIOD can deal with such non-textbook lensing cases as long as there are similar examples among the positive class sample in D.

thumbnail Fig. 8

Pan-STARRS images (Chambers et al. 2016) of two known gravitational lenses with an indication of GravLens components in black (filled circles) and entry in Gaia DR3 in red (squares). Left: the Einstein cross (G2237+0305). Right: 2MASSJ13102005-1714579. The central sources in 2MASSJ13102005-1714579 encompass two lensing galaxies recovered as GravLens components.
thumbnail Fig. 9

Distribution of the HESIOD score for the 319 296 QSOs for which it was computed. We note that the left axis corresponds to all the QSOs and is represented in logarithmic scale, while the right axis corresponds to the known lenses and is represented in linear scale.

5.2 Extremely Randomised Trees

Another technique for identifying strong gravitational lenses assumes that multiplets whose positions and magnitudes can be modelled by a singular isothermal ellipsoid in the presence of an external shear (Kormann et al. 1994, hereafter SIEγ lens model) are good lens candidates. Whereas doublets do not yield a sufficient number of constraints to properly assess if their component positions and magnitudes can be reproduced through a SIEγ lens model, those composed of three or four images do. Classical lens modelling tools, such as those from Keeton (2001) or Birrer et al. (2015), are based on a sampling of log-posterior distributions, which efficiently provide estimates of the lens model parameters along with a thorough estimate of their uncertainties. As we are not interested in those parameters but only in the ability they reproduce the multiplet positions and fluxes, we choose to simulate the relative positions and magnitudes of quadruple lenses using a SIEγ lens model, then simulate random multiplets and train a supervised machine learning model to identify the simulated lenses from the random multiplets.

For this purpose, we use an updated version of the method described in Delchambre et al. (2019), which is based on Extremely Randomised Trees (Geurts et al. 2006, hereafter ERT). The training used 112784 simulated quadruple lenses drawn from a SIEγ model. The simulations use random values of the ellipticity and shear drawn from the distributions provided in Petit et al. (2023) and in Holder & Schechter (2003), respectively. A Gaussian noise with a standard deviation of 0.3 mag was also added to the simulated magnitudes in order to deal with the imperfection of the SIEγ lens model (galaxy substructures, micro-lensing, time delays, …), see Delchambre et al. (2019, Sect. 3.2) for details. We also simulated a similar number of random multiplets using G magnitudes drawn from the empirical Gaia DR3 distribution. Cross-validation tests, where 20% of our simulations are kept as a test set and 80% of our simulations are used for training, show that 90.4% of our simulated lenses are recovered by the method if four images are present while 0.7% of the random multiplets are falsely classified as lenses. These numbers become 90.3% and 12.5% if triplets are considered5. When only three out of the four lensed images are observed, we do not know – a priori – which lensed image is not detected (not necessarily the faintest). We test the four possibilities and keep the highest score. Similarly, if a multiplet is composed of more than three components, we consider all combinations of three and four components out of this multiplet. This allows us to identify quadruply imaged QSOs having a contaminating star or (lensing) galaxy in their vicinity.

Figure 10 shows the ERT scores, Pert, for all combinations of three and four images of the GravLens multiplets. We can see that 20/24 (83%) of the known lenses have Pert > 0.8 if four components are available, while only 0.75% of the combinations of four components from the GravLens multiplets have Pert > 0.8.

Regarding the combinations of three components, 91/117 (78%) of the combinations from known lenses have Pert > 0.8 compared to 22.7% of all multiplets. This is in good agreement with the identification performance estimated from cross-validation tests. The differences for three components are mostly explained by the fact that we keep the maximal score out of the four ERT models (and explains the peak at Pert ≈ 0.95 in the bottom panel of Fig. 10). Misclassified lenses can either be due to the inability of the SIEγ model to reproduce the observed fluxes or positions of the lens (e.g. if two lensing galaxies are present), to extreme values of the eccentricity or shear (i.e. not covered by our simulations) or to microlensing (see Delchambre et al. 2019, for further discussions).

5.3 Comparison of mean BP/RP spectra

The most secure way of identifying strong gravitational lenses is to compare the spectral energy distributions (SEDs) of their images. Indeed, as the background QSO is unique and the lensing phenomenon achromatic, all of the lensed images should have similar SEDs (except for any absorption by the deflecting galaxy; intervening gas and lens time delays). Gaia provides epoch spectro-photometry in the blue (300–700 nm, resp. BP) and in the red (600–1100 nm, resp. RP) part of the optical domain (Gaia Collaboration 2016), and hence should be a very powerful tool to identify lenses. Gaia’s spectral resolution of R = λ/∆λ ≤ 100 with a full width at half maximum between 10 nm and 40 nm (Montegriffo et al. 2023), can however hardly differentiate strongly lensed QSOs from QSO pairs, although both have important applications in cosmology (see Mannucci et al. 2022, for examples).

To compare components of a GravLens multiplet, we use the Gaia epoch BP/RP spectra associated with each of the components since we cluster components at the transit level. Each of these epoch spectra has 60 fluxes, associated uncertainties, and pixel positions in the along-scan (AL) direction. Pixel positions are converted into wavelength positions using dedicated dispersion functions6. The spectra are not sampled on the same pixel scale due to the geometric and flux calibrations that minimise the discrepancies between otherwise similar spectra but acquired over different CCD rows, CCD columns, or TDI gates (see De Angeli et al. 2023, for details). We resample the epoch spectra on a uniform pixel grid with xBP = {13, 13.5,…, 36} in BP and xRP = {13, 13.5,…, 49} in RP. These cover the wavelength regions 394–690 nm in BP and 638–1022 nm in RP. For each x ∈ xBP or x ∈ xRP, we first isolate epoch BP or RP fluxes falling in the pixel range [x − 0.5, x + 0.5] and reject those for which the distance to the median flux in this range is larger than 7.5σ.

We then fitted a line to the remaining fluxes and take its value at x as the value of the resampled flux, along with its associated uncertainty. Since the resampling bins overlap, correlations exist between the noise on the resampled fluxes that should be taken in account. During resampling, we estimate the total fluxes of each component, FBP and FRP; their signal-to-noise ratio, S/NBP and S/NRP; and a mean chi-square for the fit of the lines to the epoch fluxes in each of the resampling bin, 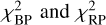χBP2 and χRP2$\chi _{{\rm{BP}}}^2{\rm{and}}\chi _{{\rm{RP}}}^2$. High 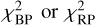χBP2 and χRP2$\chi _{{\rm{BP}}}^2{\rm{and}}\chi _{{\rm{RP}}}^2$ are indicative of the inability of our resampling to fully model the variance seen in the epoch spectra. This could be due to multiple effects, such as blended sources, unfiltered cosmic rays, border effects, and high intrinsic variability of the sources, to cite a few examples. The procedure is illustrated in Fig. 11 for the case of the known lens GraL J065904.1+162909 (Delchambre et al. 2019; Stern et al. 2021).

The resampled spectra of N components are compared using the method described in the appendices of Gaia Collaboration (2023a)7. If fi is the resampled BP or RP spectrum of the ith component of the multiplet, then we aim to find a mean vector, m, and linear coefficients, si, that minimise the reduced chi-square defined by χv2=1v∑​i=1N‖ Wi[ fi−msi ]2 ‖$\chi _v^2 = {1 \over v}\mathop {{{\mathop \sum \nolimits^ }^}}\limits_{i = 1}^N {W_i}{\left[ {{f_i} - m{s_i}} \right]^2}$(1)

where v are degrees of freedom of the problem and Wi is the inverse of the Cholesky decomposition of the covariance matrix associated with fi, Ci, such that 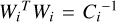WiTWi=Ci−1$W_i^T{W_i} = C_i^{ - 1}$. Absorption of QSO light by the lens affects the colour of the lensed images so Eq. (1) was evaluated separately for BP and RP before producing a single reduced chi-square. Multiplets composed of components having similar spectra thus have 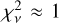χv2≈1$\chi _v^2 \approx 1$. Finally, to ease the comparison of the 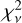χv2$\chi _v^2$, we use the well-known cubic root transformation (Wilson & Hilferty 1931), 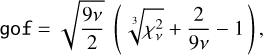gof=9v2(χv23+29v−1),${\rm{gof}} = \sqrt {{{9v} \over 2}} \left( {\root 3 \of {\chi _v^2} + {2 \over {9v}} - 1} \right),$(2)

which approximately follows a standard Gaussian distribution that is independent of the degrees of freedom, v, once is large (here the mode of v is equal to 118).

We complement this chi-square approach by a comparison based on the Wasserstein distance (Kantorovich 1942, 2006), which is potentially more robust to outliers. Intuitively, the Wasserstein distance corresponds to the minimal 'effort', or optimal transport cost (e.g. Villani 2003, 2016; Peyré & Cuturi 2019), that is needed in order to convert a pile of earth into another pile, hence the reason why it is often called the earth mover’s distance. Given two sets of epoch spectra, f and g, and their linear interpolations in pixel space, f (x) and g(x), we define the 1-Wasserstein distance between f and g as 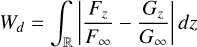Wd=∫ℝ| FzF∞−GzG∞ |dz${W_d} = \int_ {\left| {{{{F_z}} \over {{F_\infty }}} - {{{G_z}} \over {{G_\infty }}}} \right|dz} $(3)

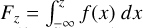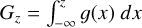where Fz=∫​−∞zf(x) dx${F_z} = \mathop \smallint \nolimits^ _{ - \infty }^zf(x)dx$ and Gz=∫​−∞zg(x) dx${G_z} = \mathop \smallint \nolimits^ _{ - \infty }^zg(x)dx$. Two components with similar SEDs then have Wd ≪ 1. No resampling is needed here and we do not use the uncertainties on the epoch spectra as the comparison is done on the overall shape of the epoch spectra only.

thumbnail Fig. 10

Distribution of the ERT scores for the 56 398 multiplets (24 known lenses) composed of at least four components (top) and 134 656 multiplets (45 known lenses) composed of at least three components (bottom). If multiplets are composed of more than three or four components, respectively, then all combinations of three and four components are considered for computing the ERT scores.

5.4 Selection of the lens candidates

Focusing on providing a first non-exhaustive list of lens candidates based on the Gaia FPR data, we applied the methods described above to the 491504 multiplets with less than seven components (Table 1) to provide scores quantifying if a multiplet is likely to be a strongly lensed QSO. As the scoring methods have different limitations, not all scores are available for all multiplets. The selection of the most promising candidates is done by isolating regions in the space defined by the parameters: Pert score; minimal HESIOD score 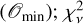(Omin);χv2$\left( {{{\cal O}_{\min }}} \right);\chi _v^2$; gof and Wd, with the addition of the galactic latitude, b; maximal separation between pair of components; G magnitudes; S/NXP; integrated flux FXP and mean resampling chi-square, ;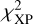χXP2$\chi _{{\rm{XP}}}^2$. Instead of performing cuts manually, we use machine learning to compute a combined score, Scomb, that reflects the similarities between the multiplets and the set of known lenses. To do so, we use a cross-validation procedure where we split the set of 1 957 559 combinations of 2–6 components from the 491 504 multiplets into 100 subsets of approximately equal size. For each subset, we run a Random Forest classifier (Breiman 2001) built on the set of known lenses and on the combinations from the 99 other subsets. The combinations from these 99 subsets that are closer than 10″ from one of the combinations in the selected subset are discarded, as the combinations from multiplets share input parameters (e.g. G magnitudes, S/NXP, …). Figure 12 shows the distribution of the combined score for all the 1 957 559 combinations. The 869 combinations at Scomb > 0.9 correspond to combinations from known lenses. As the known lenses are always included in the Random Forest training sample, these will automatically have Scomb ≈ 1. Most of the combinations, however, have Scomb ≪ 1, and sorting by this score can drastically reduce the number of combinations the user has to explore. The set of known lenses is limited in number, and thus the score combination is naturally biased due to the lack of coverage of the parameter space. Thus, it is expected that some yet-to-be-discovered lenses may have low S comb values. We hence encourage users of this FPR to explore alternative selections.

The scores and discriminators we use to isolate the lens candidates are provided in Table 2. We concentrate our search on multiplets having Scomb > 0.01 but also consider each of the discriminators from Table 2 separately. Finally, for deeper cleaning, we cross-match the GravLens components with the Gaia DR3 in order to obtain information on proper motions, parallaxes, redshifts, and source classification; and with the CatWlSE2020 catalogue (Marocco et al. 2021) to obtain W1–W2 colours. The use of these two public catalogues allows us to discard some obvious contaminants with large proper motions, large parallaxes, or low W1–W2 colours as well, as to select interesting candidates based on components with nearly equal redshifts or magnification biases (Turner 1980).

We finally selected 1307 candidates from Table 2 using loose cuts on our discriminators so as to favour completeness. This selection consists in a compilation of various subsets that were independently drawn by the main authors of this paper and is consequently very heterogeneous. These candidates however share some common characteristics: |b| > 5°, W1–W2> 0.275, maximal component separation< 6.5″, gof < 3, Wd < 6 and Scomb > 0.01; although not all candidates satisfy all these characteristics at the same time. These candidates were then visually ranked from A to D, where A corresponds to the most promising candidates, where the lensing hypothesis is the most probable. Out of these candidates, 621 were ruled out (ranked D) because of one or more components exhibiting very large proper motions, large parallaxes, low W1–W2 WISE colours, or because they are spectroscopically confirmed as stars, nearby galaxies, or AGN. 305 candidates are given a rank of C, because the visual inspection tends to support the stars, QSO+star or QSO+galaxy hypothesis, or fortuitous alignment of QSOs. 332 candidates have interesting lens-like features and are classified as plausible candidates (rank B). Rank A is further subdivided into two subcategories: A+ if all components have similar spectra, image(s) that support the lensing hypothesis while exhibiting a potential deflector and are ranked A− otherwise. Rank B candidates are similarly split into B+ and B−, depending of the degree of confidence we put on the observed lens-like features. The 381 candidates A and B are presented in Table 3 (available at the CDS), highlighting the 49 candidates ranked A (see also Appendix B). The rank A candidates have angular sizes from 1.03″ to 5.97″, reaching minimal image separations of 0.41″.

We note that depending on the involved redshifts, lensing galaxies, and image separations, the lensing galaxies can be hard to detect from the currently available ground-based imaging surveys. Thus, good candidates for lensed QSOs can present no detectable lensing galaxy based on stamps from current ground-based survey archives, such as PS1. However, the lensing galaxy can later be identified in higher resolution and/or deeper images or via absorption lines directly in spatially unresolved, slit-based, follow-up spectra. Moreover, some effects can effectively bias the eye-detection of the lensing galaxy: first, we use a default colour scale to display Dark Energy Spectroscopic Instrument Legacy Surveys (DESi) and PanSTARRS images in Appendix B, while sharper cuts or a more detailed inspection of the individual 𝑔, r, i, z,y images can reveal hints of a lensing galaxy in several cases (e.g. DR3Gaia014718.509-465709.04 or DR3Gaia020209.884-431922.09). Secondly, for more compact lenses, the lensing galaxy is often blended with the lensed images, and the HESIOD method then reports a high score, likely due to a blue-red colour gradient in the system that does not appear immediately by the eye (e.g. DR3Gaia115352.588-252027.70).

thumbnail Fig. 11

Epoch and resampled BP and RP spectra of the first and third components of the quadruple lens system GraL J065904.1+162909 (Delchambre et al. 2019; Stern et al. 2021), corresponding to the GravLens multiplet DR3Gaia065903.826+162907.83. Points are the epoch BP/RP spectra of each of the components (blue for BP, red for RP) while solid lines are the resampled BP/RP spectra, as described in Sect. 5.3. We also provide the additional parameters derived during the resampling phase: mean resampling chi-square (χXP2)$\left( {\chi _{{\rm{XP}}}^2} \right)$, integrated flux (FXP) and signal-to-noise ratio (S/NXP) where XP stands for BP or RP. Both component spectra show strong Lyα and CIV emission lines that allow us to unambiguously identify this multiplet as a lensed QSO.
thumbnail Fig. 12

Distribution of the combined score, Scomb.
Table 2

Extract of the table containing 1957559 combinations of 2–6 components out of the 501 385 multiplets including the scores calculated in this work.

6 Conclusions

The Gaia satellite has all-sky coverage with an angular resolution of ~0.18″. This is unprecedented for an astronomical survey operating in optical wavelengths. In this article we describe the Gaia Focused Product Release (FPR) aimed at detecting strongly lensed QSOs and the results of the DPAC GravLens processing.

We developed novel methods to analyse the Gaia detections near QSOs and produce a list of secondary sources that complement the current Gaia Data Releases. The methods produce a series of scores that can guide the user in the selection of promising new lensed QSO candidates.

A list of 3760480 QSO candidates from well-known catalogues (Sect. 2) was input to our GravLens pipeline. GravLens uses the DBSCAN unsupervised clustering algorithm to produce a list of sources within a 6″ radius of each QSO. It identifies clusters of Gaia detections, referred to as components, around the QSO and labels anomalous ones as outliers. A list of point sources with mean positions, fluxes, and magnitudes of the components are computed and stored in the table lens_candidates. GravLens has analysed 183 368 062 transits around QSOs obtained during the first 3yr of Gaia operations, and produced a catalogue of 4 760 920 sources of which ~ 103 000 are new sources complementing those from Gaia DR3. 87% of the QSOs were identified as single sources, while 501385 resulted in multiplets (doublets or more).

We developed scoring methods to guide the selection of the best candidates for new lenses of different types, quads, and doubles. Two of these are the HESIOD score (Sect. 5.1), an outlier detection algorithm, and an Extremely Randomised Tree algorithm (ERT, Sect. 5.2). These methods use astrometric and photometric data. When available, Gaia spectrophotometry was used to ascertain whether a component was a probable image of the QSO (Sect. 5.3). The outlier detection methods were trained on real data from a set of known lenses, while the ERT method was trained on a large number (~105) of simulated lenses. The methods are complementary as the ERT score works best for quads and triplets, whereas HESIOD is particularly effective for doublets. The scores accompany this Focused Product Release.

Finally, we use our scores complemented by visual inspection to derive a refined, non-exhaustive, list of 381 lensed QSO candidates, each with assigned quality grades. Among these candidates, 49 are particularly promising.

The spatial resolution and all-sky coverage make Gaia data a treasure for lensing studies. This Focused Product Release provides a first list of new lens candidates and data beyond the Gaia DR3 to establish an all-sky catalogue of multiply-imaged QSOs at the full Gaia angular resolution. We anticipate that the data products from this FPR and the upcoming Gaia Data Releases can contribute to various realms of cosmology. After identification and confirmation of lensed QSOs through spectroscopic analysis, these lenses can help to progress on the elusive topics of dark matter and dark energy, and potentially offer insights into the tension surrounding the determination of the Hubble constant.

Table 3

Most promising 49 lens candidates out of the 381 selected in this work.

Acknowledgements

We thank the anonymous referee for providing valuable comments that helped improve this paper. This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia. The full acknowledgments are available in Appendix C.

Appendix A Catalogue data model

The data model of the catalogue of sources in the vicinity of QSOs is described in Table A.1.

Table A.1

lens_candidates table that presents the content of the table of all sources found in the fields of the QSOs analysed. For more information about the data model please refer to https://gaia.esac.esa.int/dpacsvn/DPAC/docs/ReleaseDocumentation/FPR/FPR_master.pdf

Appendix B Lens candidates

This section compares the resampled spectra of the components from some of the most promising lens candidates in Table 3 and displays the associated Dark Energy Survey (Dey et al. 2019) or Pan-STARRS1 (Chambers et al. 2016) images. Candidates composed of three components either have spectra for two components only (DR3Gaia021120.383+210749.64) or we decided to discard one of the spectrum for clarity purpose. The discarded spectrum is either the faintest (DR3Gaia031013.747+352414.86 and DR3Gaia210752.320-161131.67) or the most contaminated (DR3Gaia172201.867+201920.75 and DR3Gaia175323.439+144702.74). None of these discarded spectra allows to rule out the lensing hypothesis.

thumbnail Fig. B.1

Comparison of the resampled spectra of the DR3Gaia010120.807-494324.36 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.2

Comparison of the resampled spectra of the DR3Gaia014718.509-465709.04 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.3

Comparison of the resampled spectra of the DR3Gaia015426.227-440213.66 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.4

Comparison of the resampled spectra of the DR3Gaia015739.213-683707.60 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.5

Comparison of the resampled spectra of the DR3Gaia020209.884-431922.09 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.6

Comparison of the resampled spectra of the DR3Gaia020501.994-323348.59 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.7

Comparison of the resampled spectra of the DR3Gaia021120.383+210749.64 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.8

Comparison of the resampled spectra of the DR3Gaia031013.747+352414.86 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.9

Comparison of the resampled spectra of the DR3Gaia033001.688-441335.60 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.10

Comparison of the resampled spectra of the DR3Gaia044652.260-310219.85 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.11

Comparison of the resampled spectra of the DR3Gaia045755.331+124238.67 multiplet (Left) and associated Pan-STARRSl image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.12

Comparison of the resampled spectra of the DR3Gaia050613.596-253047.45 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.13

Comparison of the resampled spectra of the DR3Gaia055409.442-234754.13 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.14

Comparison of the resampled spectra of the DR3Gaia060216.151-433540.97 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.15

Comparison of the resampled spectra of the DR3Gaia070020.352+132813.68 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.16

Comparison of the resampled spectra of the DR3Gaia092321.265-020554.21 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.17

Comparison of the resampled spectra of the DR3Gaia105221.613-195238.39 multiplet (Left) and associated Pan-STARRSl image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.18

Comparison of the resampled spectra of the DR3Gaia110527.117-391343.61 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.19

Comparison of the resampled spectra of the DR3Gaia111221.158-201111.55 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.20

Comparison of the resampled spectra of the DR3Gaia114934.110-172651.95 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.21

Comparison of the resampled spectra of the DR3Gaia115352.588-252027.70 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.22

Comparison of the resampled spectra of the DR3Gaia121504.295-200556.84 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.23

Comparison of the resampled spectra of the DR3Gaia124708.184-092332.50 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.24

Comparison of the resampled spectra of the DR3Gaia125238.119-270906.98 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.25

Comparison of the resampled spectra of the DR3Gaia133741.153-132524.24 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.26

Comparison of the resampled spectra of the DR3Gaia134839.786+002343.29 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.27

Comparison of the resampled spectra of the DR3Gaia150826.916+670544.68 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.28

Comparison of the resampled spectra of the DR3Gaia151030.678-791857.87 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.29

Comparison of the resampled spectra of the DR3Gaial5l723.117-241848.13 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.30

Comparison of the resampled spectra of the DR3Gaia160508.549+024739.44 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.31

Comparison of the resampled spectra of the DR3Gaia161135.764+515346.43 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.32

Comparison of the resampled spectra of the DR3Gaia170842.333+064614.31 multiplet (Left) and associated Pan-STARRSl image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.33

Comparison of the resampled spectra of the DR3Gaia172201.867+201920.75 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.34

Comparison of the resampled spectra of the DR3Gaia173144.453+250232.26 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.35

Comparison of the resampled spectra of the DR3Gaia175323.439+144702.74 multiplet (Left) and associated Pan-STARRSl image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.36

Comparison of the resampled spectra of the DR3Gaia190007.256-624734.16 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0" × 15.0", north is up and east is left. Component 2 is presumably a contaminating source.
thumbnail Fig. B.37

Comparison of the resampled spectra of the DR3Gaia193647.137-320217.79 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.38

Comparison of the resampled spectra of the DR3Gaia201951.245-062931.96 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.39

Comparison of the resampled spectra of the DR3Gaia202042.974-265023.86 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.40

Comparison of the resampled spectra of the DR3Gaia202627.737+161850.69 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.41

Comparison of the resampled spectra of the DR3Gaia202710.607+060438.30 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.42

Comparison of the resampled spectra of the DR3Gaia204449.725-040357.87 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0" × 15.0", north is up and east is left.
thumbnail Fig. B.43

Comparison of the resampled spectra of the DR3Gaia210752.320-161131.67 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.44

Comparison of the resampled spectra of the DR3Gaia220231.754-800425.40 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.45

Comparison of the resampled spectra of the DR3Gaia221540.110-520404.66 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.46

Comparison of the resampled spectra of the DR3Gaia222638.124-521519.18 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.47

Comparison of the resampled spectra of the DR3Gaia230405.819-802805.72 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
thumbnail Fig. B.48

Comparison of the resampled spectra of the DR3Gaia235506.238-455335.44 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.

Appendix C Acknowledgements

We thank the anonymous referee for providing valuable comments that helped improve this paper.

This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia.

The Gaia mission and data processing have financially been supported by, in alphabetical order by country:

  • the Algerian Centre de Recherche en Astronomie, Astro-physique et Géophysique of Bouzareah Observatory;

  • the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (FWF) Hertha Firnberg Programme through grants T359, P20046, and P23737;

  • the BELgian federal Science Policy Office (BEL-SPO) through various PROgramme de Développement d’Expériences scientifiques (PRODEX) grants of the European Space Agency (ESA), the Research Foundation Flanders (Fonds Wetenschappelijk Onderzoek) through grant VS.091.16N, the Fonds de la Recherche Scientifique (FNRS), and the Research Council of Katholieke Univer-siteit (KU) Leuven through grant C16/18/005 (Pushing AsteRoseismology to the next level with TESS, GaiA, and the Sloan Digital Sky SurvEy – PARADISE);

  • the Brazil-France exchange programmes Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) and Coordenação de Aperfeicoamento de Pessoal de Nível Superior (CAPES) – Comité Français d’Evaluation de la Coopération Universitaire et Scientifique avec le Brésil (COFECUB);

  • the Chilean Agencia Nacional de Investigación y Desar-rollo (ANID) through Fondo Nacional de Desarrollo Cientí-fico y Tecnológico (FONDECYT) Regular Project 1210992 (L. Chemin);

  • the National Natural Science Foundation of China (NSFC) through grants 11573054, 11703065, and 12173069, the China Scholarship Council through grant 201806040200, and the Natural Science Foundation of Shanghai through grant 21ZR1474100;

  • the Tenure Track Pilot Programme of the Croatian Science Foundation and the École Polytechnique Fédérale de Lausanne and the project TTP-2018-07-1171 'Mining the Variable Sky', with the funds of the Croatian-Swiss Research Programme;

  • the Czech-Republic Ministry of Education, Youth, and Sports through grant LG 15010 and INTER-EXCELLENCE grant LTAUSA18093, and the Czech Space Office through ESA PECS contract 98058;

  • the Danish Ministry of Science;

  • the Estonian Ministry of Education and Research through grant IUT40-1;

  • the European Commission’s Sixth Framework Programme through the European Leadership in Space Astrometry (ELSA) Marie Curie Research Training Network (MRTN-CT-2006-033481), through Marie Curie project PIOF-GA-2009-255267 (Space AsteroSeismology & RR Lyrae stars, SAS-RRL), and through a Marie Curie Transfer-of-Knowledge (ToK) fellowship (MTKD-CT-2004-014188); the European Commission’s Seventh Framework Programme through grant FP7-606740 (FP7-SPACE-2013-1) for the Gaia European Network for Improved data User Services (GENIUS) and through grant 264895 for the Gaia Research for European Astronomy Training (GREAT-ITN) network;

  • the European Cooperation in Science and Technology (COST) through COST Action CA18104 'Revealing the Milky Way with Gaia (MW-Gaia)';

  • the European Research Council (ERC) through grants 320360, 647208, and 834148 and through the European Union’s Horizon 2020 research and innovation and excellent science programmes through Marie Skłodowska-Curie grants 687378 (Small Bodies: Near and Far), 682115 (Using the Magellanic Clouds to Understand the Interaction of Galaxies), 695099 (A sub-percent distance scale from binaries and Cepheids - CepBin), 716155 (Structured ACCREtion Disks - SACCRED), 745617 (Our Galaxy at full HD -Gal-HD), 895174 (The build-up and fate of self-gravitating systems in the Universe), 951549 (Sub-percent calibration of the extragalactic distance scale in the era of big surveys – UniverScale), 101004214 (Innovative Scientific Data Exploration and Exploitation Applications for Space Sciences – EXPLORE), 101004719 (OPTICON-RadioNET Pilot), 101055318 (The 3D motion of the Interstellar Medium with ESO and ESA telescopes – ISM-FLOW), and 101063193 (Evolutionary Mechanisms in the Milky waY; the Gaia Data Release 3 revolution – EMMY);

  • the European Science Foundation (ESF), in the framework of the Gaia Research for European Astronomy Training Research Network Programme (GREAT-ESF);

  • the European Space Agency (ESA) in the framework of the Gaia project, through the Plan for European Cooperating States (PECS) programme through contracts C98090 and 4000106398/12/NL/KML for Hungary, through contract 4000115263/15/NL/IB for Germany, through PROgramme de Développement d'Expériences scientifiques (PRODEX) grants 4000132054 for Hungary and through contract 4000132226/20/ES/CM;

  • the Academy of Finland through grants 299543, 307157, 325805, 328654, 336546, and 345115 and the Magnus Ehrn-rooth Foundation;

  • the French Centre National d'Études Spatiales (CNES), the Agence Nationale de la Recherche (ANR) through grant ANR-10-IDEX-0001-02 for the 'Investissements d'avenir' programme, through grant ANR-15-CE31-0007 for project 'Modelling the Milky Way in the Gaia era' (MOD4Gaia), through grant ANR-14-CE33-0014-01 for project 'The Milky Way disc formation in the Gaia era' (ARCHEOGAL), through grant ANR-15-CE31-0012-01 for project 'Unlocking the potential of Cepheids as primary distance calibrators’ (UnlockCepheids), through grant ANR-19-CE31-0017 for project 'Secular evolution of galaxies’ (SEGAL), and through grant ANR-18-CE31-0006 for project 'Galactic Dark Matter' (GaDaMa), the Centre National de la Recherche Scientifique (CNRS) and its SNO Gaia of the Institut des Sciences de l'Univers (INSU), its Programmes Nationaux: Cosmologie et Galaxies (PNCG), Gravitation Références Astronomie Métrologie (PNGRAM), Planétolo-gie (PNP), Physique et Chimie du Milieu Interstellaire (PCMI), and Physique Stellaire (PNPS), supported by INSU along with the Institut National de Physique (INP) and the Institut National de Physique nucléaire et de Physique des Particules (IN2P3), and co-funded by CNES; the 'Action Fédératrice Gaia’ of the Observatoire de Paris, and the Région de Franche-Comté;

  • the German Aerospace Agency (Deutsches Zentrum für Luft- und Raumfahrt e.V., DLR) through grants 50QG0501, 50QG0601, 50QG0602, 50QG0701, 50QG0901, 50QG1001, 50QG1101, 50QG1401, 50QG1402, 50QG1403, 50QG1404, 50QG1904, 50QG2101, 50QG2102, and 50QG2202, and the Centre for Information Services and High Performance Computing (ZIH) at the Technische Universität Dresden for generous allocations of computer time;

  • the Hungarian Academy of Sciences through the János Bolyai Research Scholarship (G. Marton and Z. Nagy), the Lendület Programme grants LP2014-17 and LP2018-7 and the Hungarian National Research, Development, and Innovation Office (NKFIH) through grant KKP-137523 ('Seis-moLab');

  • the Science Foundation Ireland (SFI) through a Royal Society – SFI University Research Fellowship (M. Fraser);

  • the Israel Ministry of Science and Technology through grant 3-18143 and the Israel Science Foundation (ISF) through grant 1404/22;

  • the Agenzia Spaziale Italiana (ASI) through contracts I/037/08/0, I/058/10/0, 2014-025-R.0, 2014-025-R.1.2015, and 2018-24-HH.0 and its addendum 2018-24-HH.1-2022 to the Italian Istituto Nazionale di Astrofisica (INAF), contract 2014-049-R.0/1/2, 2022-14-HH.0 to INAF for the Space Science Data Centre (SSDC, formerly known as the ASI Science Data Center, ASDC), contracts I/008/10/0, 2013/030/I.0, 2013-030-I.0.1-2015, and 2016-17-I.0 to the Aerospace Logistics Technology Engineering Company (ALTEC S.p.A.), INAF, and the Italian Ministry of Education, University, and Research (Ministero dell'Istruzione, dell'Università e della Ricerca) through the Premiale project 'MIning The Cosmos Big Data and Innovative Italian Technology for Frontier Astrophysics and Cosmology' (MITiC);

  • the Netherlands Organisation for Scientific Research (NWO) through grant NWO-M-614.061.414, through a VICI grant (A. Helmi), and through a Spinoza prize (A. Helmi), and the Netherlands Research School for Astronomy (NOVA);

  • the Polish National Science Centre through HAR-MONIA grant 2018/30/M/ST9/00311 and DAINA grant 2017/27/L/ST9/03221 and the Ministry of Science and Higher Education (MNiSW) through grant DIR/WK/2018/12;

  • the Portuguese Fundação para a Ciência e a Tecnologia (FCT) through national funds, grants 2022.06962.PTDC and 2022.03993.PTDC, and work contract DL 57/2016/CP1364/CT0006, grants UIDB/04434/2020 and UIDP/04434/2020 for the Instituto de Astrofisica e Ciências do Espaço (IA), grants UIDB/00408/2020 and UIDP/00408/2020 for LASIGE, and grants UIDB/00099/2020 and UIDP/00099/2020 for the Centro de Astrofisica e Gravitação (CENTRA);

  • the Slovenian Research Agency through grant P1-0188;

  • the Spanish Ministry of Economy (MINECO/FEDER, UE), the Spanish Ministry of Science and Innovation (MCIN), the Spanish Ministry of Education, Culture, and Sports, and the Spanish Government through grants BES-2016-078499, BES-2017-083126, BES-C-2017-0085, ESP2016-80079-C2-1-R, FPU16/03827, RTI2018-095076-B-C22, PID2021-122842OB-C22, PDC2021-121059-C22, and TIN2015-65316-P ('Computation de Altas Prestaciones VII'), the Juan de la Cierva Incorporación Programme (FJCI-2015-2671 and IJC2019-04862-I for F. Anders), the Severo Ochoa Centre of Excellence Programme (SEV2015-0493) and MCIN/AEI/10.13039/501100011033/ EU FEDER and Next Generation EU/PRTR (PRTR- C17.I1); the European Union through European Regional Development Fund 'A way of making Europe' through grants PID2021-122842OB-C21, PID2021-125451NA-I00, CNS2022-13523 and RTI2018-095076-B-C21, the Institute of Cosmos Sciences University of Barcelona (ICCUB, Unidad de Excelencia 'Mar a de Maeztu') through grant CEX2019-000918-M, the University of Barcelona’s official doctoral programme for the development of an R+D+i project through an Ajuts de Personal Investigador en For-mació (APIF) grant, the Spanish Virtual Observatory project funded by MCIN/AEI/10.13039/501100011033/ through grant PID2020-112949GB-I00; the Centro de Investigación en Tecnolog as de la Información y las Comunicaciones (CITIC), funded by the Xunta de Galicia through the collaboration agreement to reinforce CIGUS research centers, research consolidation grant ED431B 2021/36 and scholarships from Xunta de Galicia and the EU – ESF ED481A-2019/155 and ED481A 2021/296; the Red Española de Supercomputación (RES) computer resources at MareNostrum, the Barcelona Supercomputing Centre -Centro Nacional de Supercomputación (BSC-CNS) through activities AECT-2017-2-0002, AECT-2017-3-0006, AECT-2018-1-0017, AECT-2018-2-0013, AECT-2018-3-0011, AECT-2019-1-0010, AECT-2019-2-0014, AECT-2019-3-0003, AECT-2020-1-0004, and DATA-2020-1-0010, the Departament d'Innovació, Universitats i Empresa de la Generalitat de Catalunya through grant 2014-SGR-1051 for project 'Models de Programació i Entorns d'Execució Parallels’ (MPEXPAR), and Ramon y Cajal Fellowships RYC2018-025968-I, RYC2021-031683-I and RYC2021-033762-I, funded by MICIN/AEI/10.13039/501100011033 and by the European Union NextGenerationEU/PRTR and the European Science Foundation ('Investing in your future'); the Port d'Informació Cientifica (PIC), through a collaboration between the Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT) and the Institut de F sica d'Altes Energies (IFAE), supported by the call for grants for Scientific and Technical Equipment 2021 of the State Program for Knowledge Generation and Scientific and Technological Strengthening of the R+D+i System, financed by MCIN/AEI/ 10.13039/501100011033 and the EU NextGeneration/PRTR (Hadoop Cluster for the comprehensive management of massive scientific data, reference EQC2021-007479-P);

  • the Swedish National Space Agency (SNSA/Rymdstyrelsen);

  • the Swiss State Secretariat for Education, Research, and Innovation through the Swiss Activités Nationales Com-plémentaires and the Swiss National Science Foundation through an Eccellenza Professorial Fellowship (award PCEFP2_194638 for R. Anderson);

  • the United Kingdom Particle Physics and Astronomy Research Council (PPARC), the United Kingdom Science and Technology Facilities Council (STFC), and the United Kingdom Space Agency (UKSA) through the following grants to the University of Bristol, Brunel University London, the Open University, the University of Cambridge, the University of Edinburgh, the University of Leicester, the Mullard Space Sciences Laboratory of University College London, and the United Kingdom Rutherford Apple-ton Laboratory (RAL): PP/D006503/1, PP/D006511/1, PP/D006546/1, PP/D006570/1, PP/D006791/1, ST/ I000852/1, ST/J005045/1, ST/K00056X/1, ST/K000209/1, ST/K000756/1, ST/K000578/1, ST/L002388/1, ST/ L006553/1, ST/L006561/1, ST/N000595/1, ST/N000641/1, ST/N000978/1, ST/N001117/1, ST/S000089/1, ST/S000976/1, ST/S000984/1, ST/S001123/1, ST/S001948/1, ST/S001980/1, ST/S002103/1, ST/V000969/1, ST/W002469/1, ST/W002493/1, ST/W002671/1, ST/W002809/1, EP/V520342/1, ST/X00158X/1, ST/X001601/1, ST/X001636/1, ST/X001687/1, ST/X002667/1, ST/X002683/1 and ST/X002969/1.

    The Gaia project and data processing have made use of:

  • the Set of Identifications, Measurements, and Bibliography for Astronomical Data (SIMBAD, Wenger et al. 2000), the 'Aladin sky atlas’ (Bonnarel et al. 2000; Boch & Fernique 2014), and the VizieR catalogue access tool (Ochsenbein et al. 2000), all operated at the Centre de Données astronomiques de Strasbourg (CDS);

  • the National Aeronautics and Space Administration (NASA) Astrophysics Data System (ADS);

  • the SPace ENVironment Information System (SPENVIS), initiated by the Space Environment and Effects Section (TEC-EES) of ESA and developed by the Belgian Institute for Space Aeronomy (BIRA-IASB) under ESA contract through ESA’s General Support Technologies Programme (GSTP), administered by the BELgian federal Science Policy Office (BELSPO);

  • the software products TOPCAT, STIL, and STILTS (Taylor 2005, 2006);

  • Matplotlib (Hunter 2007);

  • IPython (Pérez & Granger 2007);

  • Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration et al. 2018);

  • R (R Core Team 2013);

  • the HEALPix package (Górski et al. 2005, http://healpix.sourceforge.net/);

  • Vaex (Breddels & Veljanoski 2018);

  • the HIPPARCOS-2 catalogue (van Leeuwen 2007). The HIP-PARCOS and Tycho catalogues were constructed under the responsibility of large scientific teams collaborating with ESA. The Consortia Leaders were Lennart Lindegren (Lund, Sweden: NDAC) and Jean Kovalevsky (Grasse, France: FAST), together responsible for the HIPPARCOS Catalogue; Erik Høg (Copenhagen, Denmark: TDAC) responsible for the Tycho Catalogue; and Catherine Turon (Meudon, France: INCA) responsible for the HIPPARCOS Input Catalogue (HIC);

  • the Tycho-2 catalogue (Høg et al. 2000), the construction of which was supported by the Velux Foundation of 1981 and the Danish Space Board;

  • The Tycho double star catalogue (TDSC, Fabricius et al. 2002), based on observations made with the ESA HIPPAR-COSastrometry satellite, as supported by the Danish Space Board and the United States Naval Observatory through their double-star programme;

  • data products from the Two Micron All Sky Survey (2MASS, Skrutskie et al. 2006), which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center (IPAC) / California Institute of Technology, funded by the National Aeronautics and Space Administration (NASA) and the National Science Foundation (NSF) of the USA;

  • the ninth data release of the AAVSO Photometric All-Sky Survey (APASS, Henden et al. 2016), funded by the Robert Martin Ayers Sciences Fund;

  • the first data release of the Pan-STARRS survey (Chambers et al. 2016; Magnier et al. 2020a; Waters et al. 2020; Flewelling et al. 2020; Magnier et al. 2020b,c). The Pan-STARRS1 Surveys (PS1) and the PS1 public science archive have been made possible through contributions by the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, The Johns Hopkins University, Durham University, the University of Edinburgh, the Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration (NASA) through grant NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the National Science Foundation through grant AST-1238877, the University of Maryland, Eotvos Lorand University (ELTE), the Los Alamos National Laboratory, and the Gordon and Betty Moore Foundation;

  • the second release of the Guide Star Catalogue (GSC2.3, Lasker et al. 2008). The Guide Star Catalogue II is a joint project of the Space Telescope Science Institute (STScI) and the Osservatorio Astrofisico di Torino (OATo). STScI is operated by the Association of Universities for Research in Astronomy (AURA), for the National Aeronautics and Space Administration (NASA) under contract NAS5-26555. OATo is operated by the Italian National Institute for Astrophysics (INAF). Additional support was provided by the European Southern Observatory (ESO), the Space Telescope European Coordinating Facility (STECF), the International GEMINI project, and the European Space Agency (ESA) Astrophysics Division (nowadays SCI-S);

  • the eXtended, Large (XL) version of the catalogue of Positions and Proper Motions (PPM-XL, Roeser et al. 2010);

  • data products from the Wide-field Infrared Survey Explorer (WISE), which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, and NEO-WISE, which is a project of the Jet Propulsion Laboratory/California Institute of Technology. WISE and NEO-WISE are funded by the National Aeronautics and Space Administration (NASA);

  • the first data release of the United States Naval Observatory (USNO) Robotic Astrometric Telescope (URAT-1, Zacharias et al. 2015);

  • the fourth data release of the United States Naval Observatory (USNO) CCD Astrograph Catalogue (UCAC-4, Zacharias et al. 2013);

  • the sixth and final data release of the Radial Velocity Experiment (RAVE DR6, Steinmetz et al. 2020a,b). Funding for RAVE has been provided by the Leibniz Institute for Astrophysics Potsdam (AIP), the Australian Astronomical Observatory, the Australian National University, the Australian Research Council, the French National Research Agency, the German Research Foundation (SPP 1177 and SFB 881), the European Research Council (ERC-StG 240271 Galac-tica), the Istituto Nazionale di Astrofisica at Padova, the Johns Hopkins University, the National Science Foundation of the USA (AST-0908326), the W.M. Keck foundation, the Macquarie University, the Netherlands Research School for Astronomy, the Natural Sciences and Engineering Research Council of Canada, the Slovenian Research Agency, the Swiss National Science Foundation, the Science & Technology Facilities Council of the UK, Opticon, Strasbourg Observatory, and the Universities of Basel, Groningen, Heidelberg, and Sydney. The RAVE website is at https://www.rave-survey.org/;

  • the first data release of the Large sky Area Multi-Object Fibre Spectroscopic Telescope (LAMOST DR1, Luo et al. 2015);

  • the K2 Ecliptic Plane Input Catalogue (EPIC, Huber et al. 2016);

  • the ninth data release of the Sloan Digitial Sky Survey (SDSS DR9, Ahn et al. 2012). Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the United States Department of Energy Office of Science. The SDSS-III website is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofísica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University;

  • the thirteenth release of the Sloan Digital Sky Survey (SDSS DR13, Albareti et al. 2017). Funding for SDSS-IV has been provided by the Alfred P. Sloan Foundation, the United States Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is https://www.sdss.org/. SDSS-IV is managed by the Astrophys-ical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU) / University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional / MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University;

  • the second release of the SkyMapper catalogue (SkyMap-per DR2, Onken et al. 2019, Digital Object Identifier 10.25914/5ce60d31ce759). The national facility capability for SkyMapper has been funded through grant LE130100104 from the Australian Research Council (ARC) Linkage Infrastructure, Equipment, and Facilities (LIEF) programme, awarded to the University of Sydney, the Australian National University, Swinburne University of Technology, the University of Queensland, the University of Western Australia, the University of Melbourne, Curtin University of Technology, Monash University, and the Australian Astronomical Observatory. SkyMapper is owned and operated by The Australian National University’s Research School of Astronomy and Astrophysics. The survey data were processed and provided by the SkyMapper Team at the Australian National University. The SkyMapper node of the All-Sky Virtual Observatory (ASVO) is hosted at the National Computational Infrastructure (NCI). Development and support the SkyMapper node of the ASVO has been funded in part by Astronomy Australia Limited (AAL) and the Australian Government through the Commonwealth’s Education Investment Fund (EIF) and National Collaborative Research Infrastructure Strategy (NCRIS), particularly the National eResearch Collaboration Tools and Resources (NeCTAR) and the Australian National Data Service Projects (ANDS);

  • the Gaia-ESO Public Spectroscopic Survey (GES, Gilmore et al. 2022; Randich et al. 2022). The Gaia-ESO Survey is based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 188.B-3002. Public data releases are available through the ESO Science Portal. The project has received funding from the Leverhulme Trust (project RPG-2012-541), the European Research Council (project ERC-2012-AdG 320360-Gaia-ESO-MW), and the Istituto Nazionale di Astrofisica, INAF (2012: CRA 1.05.01.09.16; 2013: CRA 1.05.06.02.07).

The GBOT programme (GBOT) uses observations collected at (i) the European Organisation for Astronomical Research in the Southern Hemisphere (ESO) with the VLT Survey Telescope (VST), under ESO programmes 092.B-0165, 093.B-0236, 094.B-0181, 095.B-0046, 096.B-0162, 097.B-0304, 098.B-0030, 099.B-0034, 0100.B-0131, 0101.B-0156, 0102.B-0174, 0103.B-0165, 0104.B-0081, 0106.20ZA.001 (OmegaCam), 0106.20ZA.002 (FORS2), 0108.21YF; and under INAF programs 110.256C, 112.266Q; and (ii) the Liverpool Telescope, which is operated on the island of La Palma by Liverpool John Moores University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias with financial support from the United Kingdom Science and Technology Facilities Council, and (iii) telescopes of the Las Cumbres Observatory Global Telescope Network.

In addition to the currently active DPAC (and ESA science) authors of the peer-reviewed papers accompanying the data release, there are large numbers of former DPAC members who made significant contributions to the (preparations of the) data processing. In addition to the DPAC consortium, past and present, there are numerous people, mostly in ESA and in industry, who have made or continue to make essential contributions to Gaia, for instance those employed in science and mission operations or in the design, manufacturing, integration, and testing of the spacecraft and its modules, subsystems, and units. Many of those will remain unnamed yet spent countless hours, occasionally during nights, weekends, and public holidays, in cold offices and dark clean rooms. They are acknowledged in the Gaia Documentation.

References

  1. Agnello, A., Lin, H., Kuropatkin, N., et al. 2018, MNRAS, 479, 4345 [Google Scholar]
  2. Ahn, C. P., Alexandroff, R., Allende Prieto, C., et al. 2012, ApJS, 203, 21 [Google Scholar]
  3. Albareti, F. D., Allende Prieto, C., Almeida, A., et al. 2017, ApJS, 233, 25 [Google Scholar]
  4. Arenou, F., Luri, X., Babusiaux, C., et al. 2017, A&A, 599, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Arenou, F., Luri, X., Babusiaux, C., et al. 2018, A&A, 616, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Assef, R. J., Stern, D., Noirot, G., et al. 2018, ApJS, 234, 23 [Google Scholar]
  7. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  8. Bekker, J., & Davis, J. 2020, Mach. Learn., 109, 719 [CrossRef] [Google Scholar]
  9. Birrer, S., Amara, A., & Refregier, A. 2015, ApJ, 813, 102 [Google Scholar]
  10. Boch, T., & Fernique, P. 2014, in ASP Conf. Ser., 485, Astronomical Data Analysis Software and Systems XXIII, eds. N. Manset, & P. Forshay, 277 [Google Scholar]
  11. Bonnarel, F., Fernique, P., Bienaymé, O., et al. 2000, A&AS, 143, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Breddels, M. A., & Veljanoski, J. 2018, A&A, 618, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Breiman, L. 2001, Mach. Learn., 45, 5 [Google Scholar]
  14. Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints, [arXiv: 1612.05560] [Google Scholar]
  15. Chen, G. C. F., Fassnacht, C. D., Suyu, S. H., et al. 2019, MNRAS, 490, 1743 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cortes, D. 2019, ArXiv e-prints, [arXiv: 1911.06646] [Google Scholar]
  17. Cortes, D. 2021, ArXiv e-prints, [arXiv:2110.13402] [Google Scholar]
  18. Courbin, F., Eigenbrod, A., Vuissoz, C., Meylan, G., & Magain, P. 2005, in Gravitational Lensing Impact on Cosmology, 225, ed. Y. Mellier & G. Meylan, IAU Symp., 225, 297 [NASA ADS] [Google Scholar]
  19. De Angeli, F., Weiler, M., Montegriffo, P., et al. 2023, A&A, 674, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. de Bruijne, J. H. J., Allen, M., Azaz, S., et al. 2015, A&A, 576, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Delchambre, L., Krone-Martins, A., Wertz, O., et al. 2019, A&A, 622, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. de Mendoza y Ríos, J. 1795, Memoria sobre algunos metodos nuevos de calcular la longitud por las distancias lunares y explicaciones prácticas de una teoría para la solución de otros problemas de navegación (Imp. Real de Madrid) [Google Scholar]
  23. Desira, C., Shu, Y., Auger, M. W., et al. 2022, MNRAS, 509, 738 [Google Scholar]
  24. de Souza, R. E., Krone-Martins, A., dos Anjos, S., Ducourant, C., & Teixeira, R. 2014, A&A, 568, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Dey, A., Schlegel, D. J., Lang, D., et al. 2019, AJ, 157, 168 [Google Scholar]
  26. Diaz Rivero, A., Cyr-Racine, F.-Y., & Dvorkin, C. 2018, Phys. Rev. D, 97, 023001 [CrossRef] [Google Scholar]
  27. Di Valentino, E., Mena, O., Pan, S., et al. 2021, Class. Quant. Grav., 38, 153001 [NASA ADS] [CrossRef] [Google Scholar]
  28. Ducourant, C., Teixeira, R., Krone-Martins, A., et al. 2017, A&A, 597, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Ducourant, C., Wertz, O., Krone-Martins, A., et al. 2018, A&A, 618, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Ducourant, C., Krone-Martins, A., Galluccio, L., et al. 2023, A&A, 674, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Eisenhardt, P. R. M., Marocco, F., Fowler, J. W., et al. 2020, ApJS, 247, 69 [Google Scholar]
  32. Elkan, C., & Noto, K. 2008, in Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’08 (New York, NY, USA: Association for Computing Machinery), 213 [CrossRef] [Google Scholar]
  33. Ester, M., Kriegel, H.-P., Sander, J., & Xu, X. 1996, in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, KDD’96 (AAAI Press), 226 [Google Scholar]
  34. Euclid Collaboration (Scaramella, R., et al.) 2022, A&A, 662, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Fabricius, C., Høg, E., Makarov, V. V., et al. 2002, A&A, 384, 180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Fabricius, C., Bastian, U., Portell, J., et al. 2016, A&A, 595, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Fabricius, C., Luri, X., Arenou, F., et al. 2021, A&A, 649, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Finet, F., & Surdej, J. 2016, A&A, 590, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Flesch, E. W. 2019, ArXiv e-prints, [arXiv:1912.05614] [Google Scholar]
  40. Flesch, E. W. 2021, ArXiv e-prints, [arXiv:2185.12985] [Google Scholar]
  41. Flewelling, H. A., Magnier, E. A., Chambers, K. C., et al. 2020, ApJS, 251, 7 [Google Scholar]
  42. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Gaia Collaboration (Bailer-Jones, C. A. L., et al.) 2023a, A&A, 674, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Geurts, P., Ernst, D., & Wehenkel, L. 2006, Mach. Learn., 63, 3 [Google Scholar]
  48. Gilman, D., Birrer, S., Nierenberg, A., et al. 2020a, MNRAS, 491, 6077 [NASA ADS] [CrossRef] [Google Scholar]
  49. Gilman, D., Du, X., Benson, A., et al. 2020b, MNRAS, 492, L12 [NASA ADS] [CrossRef] [Google Scholar]
  50. Gilman, D., Bovy, J., Treu, T., et al. 2021, MNRAS, 507, 2432 [NASA ADS] [CrossRef] [Google Scholar]
  51. Gilmore, G., Randich, S., Worley, C. C., et al. 2022, A&A, 666, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [Google Scholar]
  53. Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
  54. Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
  55. Harris, W. E. 2010, ArXiv e-prints, [arXiv:1812.3224] [Google Scholar]
  56. Henden, A. A., Templeton, M., Terrell, D., et al. 2016, VizieR Online Data Catalogue: II/336 [Google Scholar]
  57. Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, A27 [NASA ADS] [Google Scholar]
  58. Holder, G. P., & Schechter, P. L. 2003, ApJ, 589, 688 [Google Scholar]
  59. Huber, D., Bryson, S. T., Haas, M. R., et al. 2016, ApJS, 224, 2 [Google Scholar]
  60. Huchra, J., Gorenstein, M., Kent, S., et al. 1985, AJ, 90, 691 [NASA ADS] [CrossRef] [Google Scholar]
  61. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  62. Kantorovich, L. V. 1942, Dokl. Akad. Nauk SSSR, 37, 227 [Google Scholar]
  63. Kantorovich, L. V. 2006, J. Math. Sci. (Engl. Transl.), 133, 1381 [CrossRef] [Google Scholar]
  64. Keeton, C. R. 2001, ArXiv e-prints [arXiv:astro-ph/0102341] [Google Scholar]
  65. Kormann, R., Schneider, P., & Bartelmann, M. 1994, A&A, 284, 285 [NASA ADS] [Google Scholar]
  66. Krone-Martins, A., & Moitinho, A. 2014, A&A, 561, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Krone-Martins, A., Ducourant, C., Teixeira, R., et al. 2013, A&A, 556, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Krone-Martins, A., Delchambre, L., Wertz, O., et al. 2018, A&A, 616, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Krone-Martins, A., Graham, M. J., Stern, D., et al. 2019, ArXiv e-prints, [arXiv:1912.08977] [Google Scholar]
  70. Krone-Martins, A., Gravras, P., Ducourant, C., et al. 2022, A&A, submitted [Google Scholar]
  71. Lallement, R., Capitanio, L., Ruiz-Dern, L., et al. 2018, A&A, 616, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Lang, D. 2014, AJ, 147, 108 [Google Scholar]
  73. Lasker, B. M., Lattanzi, M. G., McLean, B. J., et al. 2008, AJ, 136, 735 [Google Scholar]
  74. Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints, [arXiv:1110.3193] [Google Scholar]
  75. Leike, R., Celli, S., Krone-Martins, A., et al. 2021, Nat. Astron., 5, 832 [NASA ADS] [CrossRef] [Google Scholar]
  76. Leike, R. H., Edenhofer, G., Knollmüller, J., et al. 2022, ArXiv e-prints, [arXiv:2204.11715] [Google Scholar]
  77. Lemon, C. A., Auger, M. W., McMahon, R. G., & Ostrovski, F. 2018, MNRAS, 479, 5060 [Google Scholar]
  78. Lemon, C. A., Auger, M. W., & McMahon, R. G. 2019, MNRAS, 483, 4242 [NASA ADS] [CrossRef] [Google Scholar]
  79. Lemon, C., Anguita, T., Auger-Williams, M. W., et al. 2023, MNRAS, 520, 3305 [NASA ADS] [CrossRef] [Google Scholar]
  80. Li, R., Frenk, C. S., Cole, S., Wang, Q., & Gao, L. 2017, MNRAS, 468, 1426 [NASA ADS] [CrossRef] [Google Scholar]
  81. Linder, E. V. 2004, Phys. Rev. D, 70, 043534 [NASA ADS] [CrossRef] [Google Scholar]
  82. Linder, E. V. 2011, Phys. Rev. D, 84, 123529 [NASA ADS] [CrossRef] [Google Scholar]
  83. Liu, F. T., Ting, K. M., & Zhou, Z.-H. 2008, in 2008 Eighth IEEE International Conference on Data Mining, 413 [CrossRef] [Google Scholar]
  84. Liu, F. T., Ting, K. M., & Zhou, Z.-H. 2010, in Machine Learning and Knowledge Discovery in Databases, eds. J. L. Balcázar, F. Bonchi, A. Gionis, & M. Sebag (Berlin, Heidelberg: Springer), 274 [Google Scholar]
  85. Liu, B., Li, Z., & Zhu, Z.-H. 2019, MNRAS, 487, 1980 [NASA ADS] [CrossRef] [Google Scholar]
  86. Lucey, J. R., Schechter, P. L., Smith, R. J., & Anguita, T. 2018, MNRAS, 476, 927 [NASA ADS] [CrossRef] [Google Scholar]
  87. Luo, A. L., Zhao, Y.-H., Zhao, G., et al. 2015, Res. Astron. Astrophys., 15, 1095 [Google Scholar]
  88. Magnier, E. A., Chambers, K. C., Flewelling, H. A., et al. 2020a, ApJS, 251, 3 [NASA ADS] [CrossRef] [Google Scholar]
  89. Magnier, E. A., Schlafly, E. F., Finkbeiner, D. P., et al. 2020b, ApJS, 251, 6 [NASA ADS] [CrossRef] [Google Scholar]
  90. Magnier, E. A., Sweeney, W. E., Chambers, K. C., et al. 2020c, ApJS, 251, 5 [NASA ADS] [CrossRef] [Google Scholar]
  91. Mannucci, F., Pancino, E., Belfiore, F., et al. 2022, Nat. Astron., 6, 1185 [NASA ADS] [CrossRef] [Google Scholar]
  92. Marocco, F., Eisenhardt, P. R. M., Fowler, J. W., et al. 2021, ApJS, 253, 8 [Google Scholar]
  93. Millon, M., Courbin, F., Bonvin, V., et al. 2020, A&A, 640, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Minor, Q., Kaplinghat, M., Chan, T. H., & Simon, E. 2021, MNRAS, 507, 1202 [NASA ADS] [CrossRef] [Google Scholar]
  95. Montegriffo, P., De Angeli, F., Andrae, R., et al. 2023, A&A, 674, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Nierenberg, A. M., Treu, T., Brammer, G., et al. 2017, MNRAS, 471, 2224 [NASA ADS] [CrossRef] [Google Scholar]
  97. Nierenberg, A. M., Gilman, D., Treu, T., et al. 2020, MNRAS, 492, 5314 [Google Scholar]
  98. Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Oguri, M., Inada, N., Strauss, M. A., et al. 2012, AJ, 143, 120 [NASA ADS] [CrossRef] [Google Scholar]
  100. Onken, C. A., Wolf, C., Bessell, M. S., et al. 2019, PASA, 36, e033 [Google Scholar]
  101. Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
  102. Petit, Q., Ducourant, C., Slezak, E., Sluse, D., & Delchambre, L. 2023, A&A, 669, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Peyré, G. & Cuturi, M. 2019, Found. Trends Mach. Learn., 51, 1 [Google Scholar]
  104. Randich, S., Gilmore, G., Magrini, L., et al. 2022, A&A, 666, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. R Core Team 2013, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria [Google Scholar]
  106. Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
  107. Riello, M., De Angeli, F., Evans, D. W., et al. 2018, A&A, 616, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Robin, A. C., Luri, X., Reylé, C., et al. 2012, A&A, 543, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Roeser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [Google Scholar]
  110. Shu, Y., Koposov, S. E., Evans, N. W., et al. 2019, MNRAS, 489, 4741 [Google Scholar]
  111. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  112. Steinmetz, M., Guiglion, G., McMillan, P. J., et al. 2020a, AJ, 160, 83 [NASA ADS] [CrossRef] [Google Scholar]
  113. Steinmetz, M., MatijeviC, G., Enke, H., et al. 2020b, AJ, 160, 82 [NASA ADS] [CrossRef] [Google Scholar]
  114. Stekhoven, D. J., & Bühlmann, P. 2011, Bioinformatics, 28, 112 [Google Scholar]
  115. Stern, D., Djorgovski, S. G., Krone-Martins, A., et al. 2021, ApJ, 921, 42 [NASA ADS] [CrossRef] [Google Scholar]
  116. Surdej, J., Claeskens, J.-F., & Smette, A. 2002, Gaia Relativity and Reference Frame WG meeting [Google Scholar]
  117. Suyu, S. H., Bonvin, V., Courbin, F., et al. 2017, MNRAS, 468, 2590 [Google Scholar]
  118. Taylor, M. B. 2005, in ASP Conf. Ser., 347, Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, 29 [NASA ADS] [Google Scholar]
  119. Taylor, M. B. 2006, in ASP Conf. Ser., 351, Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, 666 [NASA ADS] [Google Scholar]
  120. Torra, F., Castañeda, J., Fabricius, C., et al. 2021, A&A, 649, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  121. Treu, T., Suyu, S. H., & Marshall, P. J. 2022, A&A Rev., 30, 8 [NASA ADS] [CrossRef] [Google Scholar]
  122. Turner, E. L. 1980, ApJ, 242, L135 [NASA ADS] [CrossRef] [Google Scholar]
  123. van Buuren, S. 2007, Stat. Methods Med. Res., 16, 219 [CrossRef] [Google Scholar]
  124. van Leeuwen, F. 2007, A&A, 474, 653 [CrossRef] [EDP Sciences] [Google Scholar]
  125. Verde, L., Treu, T., & Riess, A. G. 2019, Nat. Astron., 3, 891 [Google Scholar]
  126. Villani, C. 2003, Topics in Optimal Transportation, Graduate Studies in Mathematics Series (American Mathematical Society) [CrossRef] [Google Scholar]
  127. Villani, C. 2016, Optimal Transport: Old and New, Grundlehren der mathematischen Wissenschaften (Berlin Heidelberg: Springer) [Google Scholar]
  128. Wang, L.-F., Zhang, J.-H., He, D.-Z., Zhang, J.-F., & Zhang, X. 2022, MNRAS, 514, 1433 [NASA ADS] [CrossRef] [Google Scholar]
  129. Waters, C. Z., Magnier, E. A., Price, P. A., et al. 2020, ApJS, 251, 4 [NASA ADS] [CrossRef] [Google Scholar]
  130. Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Wertz, O., Stern, D., Krone-Martins, A., et al. 2019, A&A, 628, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  132. Whitmore, B. C., Allam, S. S., Budavári, T., et al. 2016, AJ, 151, 134 [NASA ADS] [CrossRef] [Google Scholar]
  133. Wilson, S. 2021, miceRanger: Multiple Imputation by Chained Equations with Random Forests, R package version 1.5.0, https://cran.r-project.org/web/packages/miceRanger/index.html [Google Scholar]
  134. Wilson, E. B., & Hilferty, M. M. 1931, PNAS, 17, 684 [CrossRef] [Google Scholar]
  135. Wolpert, D. H. 1996, Neural Comput., 8, 1341 [CrossRef] [Google Scholar]
  136. Wolpert, D., & Macready, W. 1997, IEEE Trans. Evol. Comput., 1, 67 [CrossRef] [Google Scholar]
  137. Wong, K. C., Suyu, S. H., Chen, G. C. F., et al. 2020, MNRAS, 498, 1420 [Google Scholar]
  138. Xia, J.-Q., Yu, H., Wang, G.-J., et al. 2017, ApJ, 834, 75 [CrossRef] [Google Scholar]
  139. Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [Google Scholar]
  140. Zacharias, N., Finch, C., Subasavage, J., et al. 2015, AJ, 150, 101 [Google Scholar]
2

The resolution of the onboard estimation of the G magnitude is 0.015625 mag.

3

We used the software implementation from the Apache Commons Math library v.3.6.1.

4

See https://gea.esac.esa.int/archive/documentation/FPR/ for a detailed description of all tables and fields.

5

The areas under the receiver operating characteristic curve are equal to 0.9958 and 0.9554 for the cases of four images and three images, respectively

7

The Octave-Matlab source code is publicly available at https://github.com/ldelchambre/gls_mean

All Tables

Table 1

Source counts in the lens_candidates table according to the number of components in the field.

In the text
Table 2

Extract of the table containing 1957559 combinations of 2–6 components out of the 501 385 multiplets including the scores calculated in this work.

In the text
Table 3

Most promising 49 lens candidates out of the 381 selected in this work.

In the text
Table A.1

lens_candidates table that presents the content of the table of all sources found in the fields of the QSOs analysed. For more information about the data model please refer to https://gaia.esac.esa.int/dpacsvn/DPAC/docs/ReleaseDocumentation/FPR/FPR_master.pdf

In the text

All Figures

thumbnail Fig. 1

Sky distribution in galactic coordinates of the QSOs included in the input list. The cell of this map is approximately 0.2 deg2, and the colour indicates the number of sources in each cell on a logarithmic scale.
In the text
thumbnail Fig. 2

Distributions of (a) Gaia G magnitudes (phot_g_mean_mag) from the Gaia DR3 gaia_source table, (b) GBP − GRP colours (phot_bp_mean_mag − phot_rp_mean_mag), (c) W1–W2 colours (from catWISE), (d) redshifts (from Milliquas) of the QSOs and candidates from the input list.
In the text
thumbnail Fig. 3

GravLens results for the Einstein cross G2237+0305 (DR3Gaia224030.229+032130.03 in our output). The black dots represent the five components and the blue crosses, red diamonds, green crosses, and pink dots represent the four images of the QSO. The yellow triangles show the Gaia transits on the deflecting galaxy. The information is in the ra_obs, dec_obs fields of the lens_candidates and lens_outlier tables.
In the text
thumbnail Fig. 4

Examples of known issues. Black dots are the mean positions of the components, red points correspond to individual observations no matter the component and grey dots are outliers. In (c), a planetary nebula (IC 351) that unduly entered in the QSO catalogue is decomposed by the algorithm into numerous sources. as well as in (d) for the halo of a bright star.
In the text
thumbnail Fig. 5

Distributions of components’ main features provided in the lens_candidates table - (a) number of components found in the fields analysed, (b) mean G magnitude of the components of all fields. (c) number of observations of the components. (d) standard deviation of mean coordinates (ra_component, dec_component) and (e) standard deviation of mean G magnitude.
In the text
thumbnail Fig. 6

Comparison between coordinates and magnitudes from GravLens and Gaia DR3. Top: comparison of the coordinates (ra, dec) derived by GravLens and by Gaia DR3. ∆ra includes the cos(dec) factor. Bottom: comparison of GravLens magnitudes (table lens_candidates field g_mag_component) with Gaia DR3 magnitudes (table gaiadr3.gaia_source field phot_g_mean_mag).
In the text
thumbnail Fig. 7

Density plot of the magnitudes of the GravLens components not present in Gaia DR3 along with the number of components in the multiplet. Coulour scale is logarithmic.
In the text
thumbnail Fig. 8

Pan-STARRS images (Chambers et al. 2016) of two known gravitational lenses with an indication of GravLens components in black (filled circles) and entry in Gaia DR3 in red (squares). Left: the Einstein cross (G2237+0305). Right: 2MASSJ13102005-1714579. The central sources in 2MASSJ13102005-1714579 encompass two lensing galaxies recovered as GravLens components.
In the text
thumbnail Fig. 9

Distribution of the HESIOD score for the 319 296 QSOs for which it was computed. We note that the left axis corresponds to all the QSOs and is represented in logarithmic scale, while the right axis corresponds to the known lenses and is represented in linear scale.
In the text
thumbnail Fig. 10

Distribution of the ERT scores for the 56 398 multiplets (24 known lenses) composed of at least four components (top) and 134 656 multiplets (45 known lenses) composed of at least three components (bottom). If multiplets are composed of more than three or four components, respectively, then all combinations of three and four components are considered for computing the ERT scores.
In the text
thumbnail Fig. 11

Epoch and resampled BP and RP spectra of the first and third components of the quadruple lens system GraL J065904.1+162909 (Delchambre et al. 2019; Stern et al. 2021), corresponding to the GravLens multiplet DR3Gaia065903.826+162907.83. Points are the epoch BP/RP spectra of each of the components (blue for BP, red for RP) while solid lines are the resampled BP/RP spectra, as described in Sect. 5.3. We also provide the additional parameters derived during the resampling phase: mean resampling chi-square (χXP2)$\left( {\chi _{{\rm{XP}}}^2} \right)$, integrated flux (FXP) and signal-to-noise ratio (S/NXP) where XP stands for BP or RP. Both component spectra show strong Lyα and CIV emission lines that allow us to unambiguously identify this multiplet as a lensed QSO.
In the text
thumbnail Fig. 12

Distribution of the combined score, Scomb.
In the text
thumbnail Fig. B.1

Comparison of the resampled spectra of the DR3Gaia010120.807-494324.36 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.2

Comparison of the resampled spectra of the DR3Gaia014718.509-465709.04 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.3

Comparison of the resampled spectra of the DR3Gaia015426.227-440213.66 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.4

Comparison of the resampled spectra of the DR3Gaia015739.213-683707.60 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.5

Comparison of the resampled spectra of the DR3Gaia020209.884-431922.09 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.6

Comparison of the resampled spectra of the DR3Gaia020501.994-323348.59 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.7

Comparison of the resampled spectra of the DR3Gaia021120.383+210749.64 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.8

Comparison of the resampled spectra of the DR3Gaia031013.747+352414.86 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.9

Comparison of the resampled spectra of the DR3Gaia033001.688-441335.60 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.10

Comparison of the resampled spectra of the DR3Gaia044652.260-310219.85 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.11

Comparison of the resampled spectra of the DR3Gaia045755.331+124238.67 multiplet (Left) and associated Pan-STARRSl image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.12

Comparison of the resampled spectra of the DR3Gaia050613.596-253047.45 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.13

Comparison of the resampled spectra of the DR3Gaia055409.442-234754.13 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.14

Comparison of the resampled spectra of the DR3Gaia060216.151-433540.97 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.15

Comparison of the resampled spectra of the DR3Gaia070020.352+132813.68 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.16

Comparison of the resampled spectra of the DR3Gaia092321.265-020554.21 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.17

Comparison of the resampled spectra of the DR3Gaia105221.613-195238.39 multiplet (Left) and associated Pan-STARRSl image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.18

Comparison of the resampled spectra of the DR3Gaia110527.117-391343.61 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.19

Comparison of the resampled spectra of the DR3Gaia111221.158-201111.55 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.20

Comparison of the resampled spectra of the DR3Gaia114934.110-172651.95 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.21

Comparison of the resampled spectra of the DR3Gaia115352.588-252027.70 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.22

Comparison of the resampled spectra of the DR3Gaia121504.295-200556.84 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.23

Comparison of the resampled spectra of the DR3Gaia124708.184-092332.50 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.24

Comparison of the resampled spectra of the DR3Gaia125238.119-270906.98 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.25

Comparison of the resampled spectra of the DR3Gaia133741.153-132524.24 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.26

Comparison of the resampled spectra of the DR3Gaia134839.786+002343.29 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.27

Comparison of the resampled spectra of the DR3Gaia150826.916+670544.68 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.28

Comparison of the resampled spectra of the DR3Gaia151030.678-791857.87 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.29

Comparison of the resampled spectra of the DR3Gaial5l723.117-241848.13 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.30

Comparison of the resampled spectra of the DR3Gaia160508.549+024739.44 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.31

Comparison of the resampled spectra of the DR3Gaia161135.764+515346.43 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.32

Comparison of the resampled spectra of the DR3Gaia170842.333+064614.31 multiplet (Left) and associated Pan-STARRSl image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.33

Comparison of the resampled spectra of the DR3Gaia172201.867+201920.75 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.34

Comparison of the resampled spectra of the DR3Gaia173144.453+250232.26 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.35

Comparison of the resampled spectra of the DR3Gaia175323.439+144702.74 multiplet (Left) and associated Pan-STARRSl image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.36

Comparison of the resampled spectra of the DR3Gaia190007.256-624734.16 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0" × 15.0", north is up and east is left. Component 2 is presumably a contaminating source.
In the text
thumbnail Fig. B.37

Comparison of the resampled spectra of the DR3Gaia193647.137-320217.79 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.38

Comparison of the resampled spectra of the DR3Gaia201951.245-062931.96 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.39

Comparison of the resampled spectra of the DR3Gaia202042.974-265023.86 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.40

Comparison of the resampled spectra of the DR3Gaia202627.737+161850.69 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.41

Comparison of the resampled spectra of the DR3Gaia202710.607+060438.30 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.42

Comparison of the resampled spectra of the DR3Gaia204449.725-040357.87 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0" × 15.0", north is up and east is left.
In the text
thumbnail Fig. B.43

Comparison of the resampled spectra of the DR3Gaia210752.320-161131.67 multiplet (Left) and associated Pan-STARRS1 image (Right) (Chambers et al. 2016). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.44

Comparison of the resampled spectra of the DR3Gaia220231.754-800425.40 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.45

Comparison of the resampled spectra of the DR3Gaia221540.110-520404.66 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.46

Comparison of the resampled spectra of the DR3Gaia222638.124-521519.18 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.47

Comparison of the resampled spectra of the DR3Gaia230405.819-802805.72 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text
thumbnail Fig. B.48

Comparison of the resampled spectra of the DR3Gaia235506.238-455335.44 multiplet (Left) and associated Dark Energy Survey image (Right) (Dey et al. 2019). Blue dots correspond to the GravLens components. The cutout size is 15.0″ × 15.0″, north is up and east is left.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.