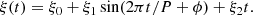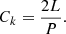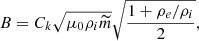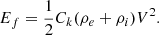EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 685 (May 2024) A&A, 685 (2024) A36 Full HTML
Issue
A&A
Volume 685, May 2024
Solar Orbiter First Results (Nominal Mission Phase)
Article Number A36
Number of page(s) 11
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202346670
Published online 01 May 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The outer layers of the solar atmosphere maintain temperatures that are greater than those in the solar photosphere. To maintain the million-degree temperature of the solar corona, heating should balance the strong radiative losses. The energy flux needed to equipoise the energy losses in the quiet-Sun, coronal holes, and active region is ∼300 W m−2, ∼800 W m−2, and 104 W m−2 (Withbroe & Noyes 1977). One of the proposed heating mechanisms of energy transfer in the solar atmosphere is magnetohydrodynamic (MHD) waves (De Moortel & Browning 2015; Arregui 2015; Van Doorsselaere et al. 2020; Banerjee et al. 2021). The transverse displacements of coronal structures in extreme-ultraviolet (EUV) images are interpreted as the standing (Schrijver et al. 1999; Aschwanden et al. 1999) and propagating kink modes of MHD waves (McIntosh et al. 2011; Thurgood et al. 2014; Weberg et al. 2018; Morton et al. 2019). Since kink oscillations are ubiquitous in the solar atmosphere (Anfinogentov et al. 2015), they are candidates for coronal heating (Van Doorsselaere et al. 2020).

Standing kink oscillations have been categorized into two distinct regimes. The amplitude of the oscillations, that are excited by low coronal eruptions such as jets, flares, and coronal mass ejections (Nakariakov et al. 1999; White & Verwichte 2012; Goddard et al. 2016; Sarkar et al. 2016), decays with time, and they are defined as decaying oscillations. Many active-region loops have been observed to oscillate with no apparent decay in amplitude for a few periods. These are known as decayless oscillations (Tian et al. 2012; Wang et al. 2012; Anfinogentov et al. 2013; Zhong et al. 2022a). The generation of decayless oscillations is the subject of ongoing debate, but evidence from modelling and numerical simulations suggests that these oscillations can be triggered by quasi-steady flows acting as footpoint drivers (Nakariakov et al. 2016; Karampelas & Van Doorsselaere 2020). Furthermore, the excitation of these oscillations due to periodic footpoint drivers has been explored in numerical simulations (Karampelas et al. 2017, 2019; Guo et al. 2019; Shi et al. 2021). Recently, Karampelas & Van Doorsselaere (2021) investigated the origin of decayless waves through vortex shedding, while Afanasyev et al. (2020) demonstrated that the observational signature of decayless oscillations could also be reproduced by random footpoint driving. The decayless kink oscillations have been studied for active regions (Anfinogentov et al. 2013, 2015; Nisticò et al. 2013; Anfinogentov & Nakariakov 2019) and quiescent loops (Duckenfield et al. 2018) (for a detailed review on kink oscillations, see Nakariakov et al. 2021).

In the past, several attempts have been made to investigate whether transverse waves carry sufficient energy to heat different regions of the solar atmosphere. Several studies have reported transverse waves in the solar atmosphere and estimated the energy fluxes by measuring the non-thermal line broadening of the transition region and coronal emission lines (Hassler et al. 1990; Banerjee et al. 1998; Hahn & Savin 2013). These authors advocated that the energy fluxes estimated using the non-thermal line widths are sufficient to heat the solar corona and accelerate solar wind (Hassler et al. 1990; Banerjee et al. 1998; Hahn & Savin 2013). Doppler velocity fluctuations, which are direct signatures of transverse waves, observed from the Coronal Multi-Channel Polarimeter (CoMP; Tomczyk et al. 2008), were found to be surprisingly small, which indicated that these waves do not provide sufficient energy to heat the active regions (Tomczyk et al. 2007). It was later found that the large line-of-sight integration in the CoMP data leads to the underestimation of the wave amplitudes that were estimated using Doppler velocity fluctuations (McIntosh & De Pontieu 2012; Pant et al. 2019).

The observations of the chromosphere and transition region reveal that kink waves with significant energies to support the energy losses are omnipresent (De Pontieu et al. 2007; Morton et al. 2012; Tian et al. 2014). The High Resolution Coronal Imager (Hi-C; Kobayashi et al. 2014) observations of active regions indicated that coronal loops contain only little energy that might support heating (Morton & McLaughlin 2013). The study of transverse motions in fine-scale structures in active region moss revealed that kink waves have a higher energy in the lower layers of the atmosphere than in the corona (Morton & McLaughlin 2014). These fine-scale structures were not well resolved by the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on board the Solar Dynamic Observatory (SDO; Pesnell et al. 2012). MHD waves play an important role in accelerating the solar wind. The large-scale structures in coronal holes have been explored widely in this context and are seen to exhibit transverse motions (McIntosh et al. 2011; Thurgood et al. 2014; Morton et al. 2015, 2019; Weberg et al. 2020). The energy flux of kink waves in open field structures in coronal holes is computed to be lower than required for solar wind acceleration (Thurgood et al. 2014; Morton et al. 2015; Weberg et al. 2018).

Transverse standing waves have been analysed in quiet-Sun loops as well. Duckenfield et al. (2018) found two periods in decayless oscillation in a large quiet-Sun loop. The quiet Sun and coronal holes, when seen in X-ray and EUV images, are permeated by small-scale loops and coronal bright points (CBPs) (Golub et al. 1976; Alipour & Safari 2015). Recently, Gao et al. (2022) analysed decayless kink oscillations in CBPs using AIA. The study indicated that decayless oscillations are common in CBPs. The average loop length in their study was ∼23 mm. The resolution of AIA does not allow us to detect low-amplitude transverse oscillations in CBPs, and therefore, the motion magnification technique was applied to enhance the oscillations. Gao et al. (2022) showed that the energy flux in kink waves in CBPs is not enough to support the radiative losses.

The high resolution and cadence of the Extreme Ultraviolet Imager (EUI; Rochus et al. 2020) on board Solar Orbiter (Müller et al. 2020) has enabled us to probe the dynamics of small-scale coronal loops, whose signatures in AIA are largely unclear (Mandal et al. 2021a). Petrova et al. (2023) performed a case study of two short-period decayless oscillations in the quiet-Sun region using EUI. The estimated loop lengths were ∼5–10 mm. Although these oscillations were observed in the quiet Sun, the energy flux of the wave was calculated to be approximately of a magnitude to balance even active region energy losses. Li & Long (2023) conducted a statistical analysis of 111 small-scale active region loops with an average length of ∼15 mm. The analysis identified short periods of oscillations ranging from ∼11 to 185 s, with energy fluxes spanning from ∼7 to 9220 W m−2. The findings of Li & Long (2023) revealed that the median wave energy flux of these oscillations is considerably lower than the energy required to heat the active region corona. Additionally, the authors found a strong correlation between the loop length and period. Although several studies of transverse oscillations in the polar region for large-scale structures exist, the kink waves in small loops rooted in coronal holes and in the quiet Sun have not been examined extensively. We present a statistical investigation of the oscillation properties of small coronal loops (of ∼10 mm) that are rooted in the coronal holes and quiet regions of the solar corona using high-resolution observations from EUI. The paper is structured as follows: Sect. 2 presents the datasets. Section 3 describes the technique we used. The results and discussions are presented in Sect. 4, followed by Sect. 5, which concludes the work.

2. Observation and data

The observational datasets we used in this study were obtained from the High Resolution Imager (HRIEUV) telescope of EUI on board Solar Orbiter. HRIEUV observes the corona at 174 Å which is attributed to Fe IX and Fe X ions, and it captures the coronal dynamics of plasma at a temperature of ∼1mK. It has a field of view (FOV) of ∼17′× 17′with a plate scale of 0.492″ pixel−1.

The level 2 images were obtained from the EUI data release 5.0 (Mampaey et al. 2022) and 4.0 (Auchère et al. 2021). The EUI images are affected by spacecraft jitter, which we corrected for, and the images were aligned by applying the cross-correlation technique, as suggested in Mandal et al. (2022).

Figures 1a–c show snapshots of the FOV of the Sun observed by HRIEUV for three different datasets. These snapshots show many small-scale loops. The green boxes outline the loops for which oscillations are observed. These images also show large-scale polar coronal holes and plumes. The datasets are focused on the quiet Sun and polar regions, with cadences suitable for observing short-period kink oscillations. Details of the datasets we used to identify the loops and build the statistics are described in Table 1.

thumbnail Fig. 1.

Description of events. Panels a, b, and c represent the context images of the three datasets. The green boxes show examples of the selected loops for which oscillations are detected. The other loops we studied appear at different times and are not shown here. A magnified view of the loops in the green boxes for each upper panel is shown in the lower panels. The red lines in panels d–i depict the position of the artificial slits we used to generate the x − t maps. The blue crosses in each panel show the approximate position of the footpoints. Details of the dataset are provided in Table 1. An animation related to this figure is accessible online.

Table 1.

Datasets used in this study.

We selected several small-scale loops for our study and found 42 oscillating events in 40 coronal loops. These small-scale loops appear to be dynamic when investigated using animation, and many loops appear and disappear during the time interval of the datasets. The properties of some of these loops are similar to active region fine-scale loops because they possess drifting motions (Li & Long 2023).

3. Analysis

Figures 1d–i show the small-scale loops outlined by green boxes corresponding to the upper panels a, b, and c. We placed slits approximately perpendicular to the loop axis. They are shown by red lines in each panel. These slits are 5 pixels wide and were used to generate distance-time (x − t) maps. The intensity was averaged over the width of the slits to increase the signal-to-noise ratio (White & Verwichte 2012; Nisticò et al. 2013).

Figure 2 shows the x − t maps of slits S1 to S6 as displayed in Figs. 1d–i. The x − t maps reveal transverse oscillations. These x − t maps indicate only a part of the slit to show the oscillations better. The noise in relatively dimly illuminated areas such as coronal holes and the quiet Sun (Fig. 1) is dominated by the sensor read-out noise, in particular, the photon shot noise. This can be seen as salt-and-pepper noise in the subfields in Figs. 1d–i. In order to optimise the telemetry, the images were Poisson recoded (Nicula et al. 2005) and compressed by a JP2000-based compression scheme (WICOM, Rochus et al. 2020) before transmission. During high-cadence HRIEUV observations, this process is commanded in a high-quality mode such that artefacts are entirely insignificant. The absence of obvious horizontal streaks in Fig. 2, other than the expected solar features under study, also confirms that possibly remaining fixed noise patterns are negligible after the dark and flat corrections. We thus approximated the uncertainty in the intensity, I, in DN, using the following formula (Petrova et al. 2023)

σ DN 2 = σ readout 2 + σ photon 2 . $$ \begin{aligned} \sigma _{\mathrm{DN}}^{2} = \sigma _{\mathrm{readout}}^{2}+\sigma _{\mathrm{photon}}^{2}. \end{aligned} $$(1)

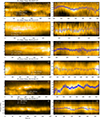thumbnail Fig. 2.

Overview of x − t maps. Panels a–f show the x − t maps produced for slits S1 to S6 indicated in Figs. 1d–i. The red curves depict the best fit for the oscillations. The error bars represent standard errors on the centre position of the loop. The amplitude, ξ1, and period, P, of the oscillation, along with the propagated errors, are written close to the fitted oscillations. A few x − t maps show only part of the slits so that the oscillations are better visible. Panels g–l show the fitted oscillations along with the error bars for the position of the loop. These correspond to the x − t maps shown in panels a–f. The dashed curves show the overplotted best-fit model. The chi-square values for the fits are also provided.

σreadout denotes the readout noise of the HRIEUV detector, estimated to be 2 DN. Additionally, the variance in the photon noise(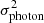 σ photon 2 $ \sigma_{\mathrm{photon}}^{2} $) is determined by the product of the gain factor, g (with a value of 6.85 DN/photon, Petrova et al. 2023), and the intensity, I. Subsequently, the obtained uncertainty values were employed as errors in intensities to fit a Gaussian function perpendicular to the oscillating structure at each time slice. The Gaussian fitting provides the centre of the oscillating structure at a particular time. To obtain the parameter of oscillations, we fit these centres using a sinusoidal function with a linear trend.

ξ ( t ) = ξ 0 + ξ 1 sin ( 2 π t / P + ϕ ) + ξ 2 t . $$ \begin{aligned} \xi (t) = \xi _{0}+\xi _{1} \sin (2\pi t/P+\phi )+\xi _{2}t. \end{aligned} $$(2)

where ξ1 represents the oscillation amplitude, P is the oscillation period, ϕ is the phase, and ξ0 and ξ2 are constants. We implemented the same techniques for calculating oscillation parameters in the 42 oscillations, and 6 are shown in Fig. 2. The best-fit functions are shown as red curves. The error bars shown in Fig. 2 are the standard errors on the centre position of the loop, obtained after fitting the Gaussian at each time slice. The amplitude and period obtained after fitting, along with the values of propagated errors, are indicated in the x − t maps. We did not use any automatic method to fit the oscillations as performed in previous statistical studies (Thurgood et al. 2014; Weberg et al. 2018, 2020). The velocity amplitude of these oscillations was estimated using the relation V = 2πξ1/P. We computed the uncertainty in velocity amplitude by 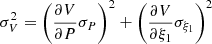σ V 2 = ( ∂ V ∂ P σ P ) 2 + ( ∂ V ∂ ξ 1 σ ξ 1 ) 2 $ \sigma_{V}^2 = \left(\frac{\partial V}{\partial P}\sigma_{P} \right)^{2} + \left(\frac{\partial V}{\partial \xi_{1}}\sigma_{\xi_{1}} \right)^{2} $. The loop length was approximated by measuring the distance between footpoints, assuming a semicircular loop model. We calculated the loop length using the relation L = πD/2, where D is the distance between the loop footpoints. We assumed the uncertainty in the loop lengths to be 40% (discussed in Sect. 4.5). The details of the oscillation parameters are provided in Table 2.

Table 2.

Details of the oscillating loop and oscillation parameters.

4. Results and discussion

4.1. Distribution of the parameters

We estimated the oscillation amplitude, ξ1, the period, P, the loop length, L, and the velocity amplitude V for oscillations captured using x − t maps and plotted their distribution. Figure 3 shows the histograms of these parameters. The loop lengths vary from 3 to 23 mm with a mean of 9.1 ± 4.3 mm. Previous studies of decayless oscillations in active-region loops estimated loop lengths of a few hundred megameters (Anfinogentov et al. 2013, 2015). The study of kink oscillations in CBPs estimated a loop length in the range of 14–42 mm (Gao et al. 2022). The loop length of the few loops we estimated here overlaps with the recent length measurement of active and quiet region loops using EUI (Petrova et al. 2023; Li & Long 2023). The average loop length in this analysis is shorter than in previous statistical studies using AIA because the resolution of EUI is high. The oscillation period lies between 28 to 272s, with a mean of 140 ± 64 s. Around 90% of the oscillations have periods greater than 60s, which is similar to previously estimated periods for coronal loops (Anfinogentov et al. 2015; Nechaeva et al. 2019; Gao et al. 2022; Zhong et al. 2022b). Ten percent of the oscillation periods range from 28 to 60s, analogously to the decayless oscillations detected in small loops (Petrova et al. 2023; Li & Long 2023). The displacement amplitudes are in the range of 35 to 358 km, with an average value of 134±72 km. The average displacement amplitude is comparable to the estimated oscillation amplitude in active region coronal loops (Anfinogentov et al. 2015; Li & Long 2023). In contrast, it is larger than the estimated amplitudes for CBPs (Gao et al. 2022). When we consider a similar amount of energy flux in both scenarios, a greater displacement amplitude is required in smaller loops. The velocity amplitudes are between 2.1 to 16.4 km s−1, with a mean of 6.6 ± 3.1 km s−1. The velocity amplitudes found in oscillations in CBPs, fine structures in active region moss, and in large-scale coronal loops are lower than 10 km s−1 (Anfinogentov et al. 2013; Morton & McLaughlin 2013, 2014; Nakariakov et al. 2016; Gao et al. 2022), whereas ∼15% of the oscillations in our study have velocity amplitudes larger than 10 km s−1.

thumbnail Fig. 3.

Distribution of the oscillation parameters. The estimated parameter values are displayed as histograms, showing the distribution of (a) the loop length, (b) the period, (c) the displacement amplitude, and (d) the velocity amplitude. These histograms illustrate the range of values for each parameter. The average and standard deviation are provided in the respective panels. The plots also include the standard error in the mean and the standard deviation.

The mean period, amplitude, and velocity amplitude calculated in the statistical analysis of propagating kink waves in coronal plumes using AIA are greater than the estimated average of these quantities in the current work (Thurgood et al. 2014; Morton et al. 2015; Weberg et al. 2018, 2020). Morton et al. (2019) examined propagating waves in the fine-scale structure within the quiet Sun using EUV images. The mean of the period and velocity amplitudes are larger than those computed in this work. Furthermore, the velocity amplitudes of propagating waves were estimated by McIntosh et al. (2011) to be in the range of 20–25 km s−1 in quiet regions and coronal holes, which is higher than the velocity amplitudes measured in this study.

4.2. Correlation between different parameters

Figure 4 shows the scatter plots between the estimated parameters, described in Sect. 3. The linear Pearson correlation coefficients, along with their standard errors, are also provided in the plots. The kink speed of an oscillating coronal loop will be proportional to loop length (L) and inverse of the period (P) (Edwin & Roberts 1983). For a close range of kink speeds, the period is therefore approximately proportional to the loop length, as observed in the analysis of decayless oscillations of active region coronal loops with lengths of several hundred megameters (Anfinogentov et al. 2015).

thumbnail Fig. 4.

Relations between parameters. Panels a–f show the scatter plots between the four estimated parameters loop length, period, displacement amplitude, and velocity amplitude. The linear Pearson correlation coefficient, along with standard errors, is also provided in each panel.

We found no significant correlation between the loop length and the period of oscillations (Fig. 4a). Gao et al. (2022) did not observe a significant correlation between the loop length and period in their study and suggested that these oscillations could be driven at the footpoints and can have periods similar to the driver, which can also be a possible reason for the poor correlation in our study. Recently, Li & Long (2023) observed short-period oscillations in coronal loops with a mean length of ∼15 mm. They found a strong correlation (0.98) between the loop length and the period.

We found no correlation of the loop length with the displacement and velocity amplitudes. Moreover, our study indicated a correlation of 0.52 between the displacement amplitude and the period, as shown in the lower left panel of Fig. 4. It is possible that the correlation between the displacement amplitude and the period also depends on the sample and is therefore a selection effect. There may not necessarily be a physical relation between these two parameters. We find a negative correlation between the velocity amplitude and the period, as reported in Gao et al. (2022). The positive correlation between the displacement and the velocity amplitude and the negative correlation between the period and the velocity amplitude might arise because they are directly related.

Figure 5 presents the variation in the period with the loop length in our work, combined with various studies of decayless oscillations compiled from Wang et al. (2012), Nisticò et al. (2013), Anfinogentov et al. (2013, 2015), Duckenfield et al. (2018), Anfinogentov & Nakariakov (2019), Mandal et al. (2021b), Zhong et al. (2022a,b), Petrova et al. (2023), Gao et al. (2022), Li & Long (2023). The black line provides the least-squares fit to these data points with a slope of 1.16 ± 0.05. The uncertainty in the measurement of the loop length (see Van Doorsselaere et al. 2007; Berghmans et al. 2021) might affect the correlation between the loop length and the period in our study. However, it is unlikely to cause a significant shift in the direction of the length axis for the current work, preventing them from being aligned with the L versus P relation seen for longer loops (see Fig. 5).

thumbnail Fig. 5.

Scaling between the loop length and the period. The figure shows the variation in the loop length vs. the period of the decayless oscillations analysed in previous studies (Wang et al. 2012; Nisticò et al. 2013; Anfinogentov et al. 2013, 2015; Duckenfield et al. 2018; Anfinogentov & Nakariakov 2019; Mandal et al. 2021b; Zhong et al. 2022a,b; Petrova et al. 2023; Gao et al. 2022; Li & Long 2023). The red points represent the results of the current work. The black lines represent the best fit for the datasets.

Figure 6 shows the variation in the loop length and the period only for loops found in the quiet Sun and coronal holes that were studied in Gao et al. (2022), Petrova et al. (2023), and this work. We assumed an uncertainty of 20% in the loop length estimation for loops studied in Gao et al. (2022). The red data points were obtained in this study, which indicates that the average loop length is shorter than in previous statistical studies. The dependence of the oscillation period on the loop length suggests that the shorter loops will have short periods (Anfinogentov et al. 2015; Goddard et al. 2016; Zhong et al. 2022b; Li & Long 2023). However, several long-period oscillations are observed in CBPs with an average loop length of ∼23 mm (Gao et al. 2022). We also find many oscillations with longer periods in loops with a mean length of ∼10 mm (see Fig. 5). We find almost no correlation between the loop length and the period obtained in this work. However, when we consider loops embedded in the quiet Sun and coronal holes, the cross-correlation coefficient is improved to be 0.47 ± 0.12, which is greater and more significant than the correlation coefficient obtained in the present study. It should be noted that the properties of loops that are embedded in the quiet Sun and coronal holes can be different because they form in different magnetic field configurations. However, the difference between the populations of small loops in the quiet Sun and coronal holes and its effect on the oscillations is not yet clear.

thumbnail Fig. 6.

Variation in the loop length vs. period for the small loops embedded in the quiet Sun and coronal holes. This figure displays the relation of the loop length and the period of the current work combined with Gao et al. (2022), and Petrova et al. (2023). The cross-correlation coefficients combining the studies are provided. The black lines represent the best fit for the datasets.

4.3. Phase lag analysis

To understand whether the observed waves are standing or propagating, we positioned multiple slits along each loop in the sample. We examined the oscillation detected at different slits to capture any significant phase shift. These loops are characterized by their small size, short duration, and highly dynamic nature. Due to the dynamic behaviour of these loops, it is challenging to accurately place the slits and identify a reliable oscillation pattern at the footpoints. Additionally, the loops are not clearly distinguishable from the background at different locations along their length, making it difficult to capture oscillations in each part of the loop. We find that approximately 50% of the loops did not exhibit any noticeable phase shift in the oscillations captured at different positions of the loop. For the remaining loops, no distinct oscillation signatures were detected at slits far from the apex. Nevertheless, no phase shift was obtained close to the apex of these loops.

Figure 7 shows two loops along with the oscillation signatures at two artificial slits. Figures 7a and c depict the oscillations profiles at slit positions S0 (red) and S1 (blue), shown in Figs. 7b and d. These oscillation profiles were obtained after fitting the x − t maps of these slits. The x − t maps used for phase analysis are unsharp masked to minimise the effect of the variable background and to better detect the oscillations. S1 (Fig. 7b) is situated between the loop top and right footpoint, and the amplitude of the oscillation for S1 is smaller than the amplitude in S0. Figures 7a and c show that no significant phase shift is present between oscillations at S0 and S1. The phase lags for these oscillation time-series are 0 ± 0.1 s and 0 ± 0.03 s. The uncertainty in the phase lag is calculated by fitting a Gaussian profile near the maximum phase lag.

thumbnail Fig. 7.

Phase lag analysis of the oscillations. The figure presents the multi-slit analysis for the two loops shown in panels b and d. S0 and S1 are two slits that were placed at different positions of the loops. Panels a and c show the fitted oscillation profile from slits S0 and S1 indicated in panels b and d. The oscillations detected in S0 and S1 show no significant phase shift.

We detected transverse oscillations lasting for ∼1.5–5 cycles at multiple slits at different loop positions. If the loops are not stable for a longer duration, then oscillations cannot be detected for several cycles. Thirty-two (∼75%) of the detected oscillations were found to occur with cycles equal to or greater than two. It is not possible to identify the decay in amplitude for oscillations with fewer than two cycles because the decay time of the decaying oscillations is mostly greater than two cycles. However, oscillations with cycles equal to or greater than two exhibit no apparent decay in amplitude.

4.4. Possible wave modes

4.4.1. Standing wave

Unlike the decayless oscillations observed in larger loops, which demonstrate a linear relation between the loop length and the period, which is indicative of a standing wave mode (Anfinogentov et al. 2013, 2015), our study revealed no strong correlation between the loop length and the period. This suggests that the nature of these waves may differ from the expected standing-wave behaviour. We focused our attention exclusively on small loops located in the quiet Sun and coronal holes, as depicted in Fig. 6, which include Gao et al. (2022), Petrova et al. (2023), and this study. In this subset, we found a correlation coefficient of 0.47 between the loop length and the period, which is notably higher than the correlation observed in this study alone. However, even with this improvement, the correlation is still insufficient to firmly support the interpretation of a standing-wave behaviour.

In addition, in limited studies of coronal loops, the oscillations measured at different slit positions showed an in-phase behaviour, indicating a standing-mode interpretation (Anfinogentov et al. 2015). Nonetheless, when we consider the phase lag obtained in this study, they may be indicating a standing-wave interpretation. However, as the loop length and period showed no strong correlation, it is not possible to conclude that these waves are standing.

4.4.2. Propagating wave

The absence of a significant correlation between the loop length and the period in this study can be considered to mean a wave mode other than a standing wave. A scenario of a fast-propagating wave appears to be a possibility. When we assume that the speeds of fast-propagating waves range from 500–600 km s−1 and the imaging cadences are 3s and 5s (Table 1), then the slits need to be at least several megameters apart to detect the propagation of waves. Because the loop half-length (apex to footpoint) is of comparable size, it will in most cases, be hard to identify the propagating waves. Because it takes a considerable amount of time for a wave to traverse the entire length of large stable loops, the measurement of the phase shift between oscillations at various slit positions is not restricted by the observational cadence of EUV imagers such as AIA. It is difficult to eliminate the possibility of propagating waves completely, but it is equally challenging to prove their existence in the current analysis. Consequently, it is not feasible to assert with absolute certainty whether these waves are standing or propagating.

4.5. Coronal seismology and the estimation of the energy flux

As discussed in the previous section, the wave mode of these waves is uncertain, and a standing nature is a possibility. The calculations and estimates provided in this section hold true under the assumption that the oscillations are indeed standing.

For a standing wave, the kink speed (Ck) can be calculated as

C k = 2 L P . $$ \begin{aligned} C_{k} = \frac{2L}{P}. \end{aligned} $$

We assumed that the observed oscillations are fundamental modes. Figure 8a shows the distribution of the kink speed. The kink speed has a range of 27–630 km s−1 with an average of 164 ± 123 km s−1. The estimated kink speed for most loops is lower than that of active region loops (Anfinogentov & Nakariakov 2019), but comparable to the kink speeds in CBPs. Using the internal and external intensities ratio, Gao et al. (2022) showed that the internal Alfvén speed is correlated to the loop length with a correlation coefficient of 0.63. Although we did not estimate the internal and external intensities, the kink speed and loop length show a correlation of 0.55 in our study. This supports the idea that the Alfvén speed increases with height and is higher for larger loops.

thumbnail Fig. 8.

Results from coronal seismology. The figure shows the histograms of the kink speeds, Ck, and magnetic field strength, B, obtained using the estimated oscillation parameters. The mean value of the distribution is also provided.

The magnetic field strength, B, can be estimated using the following relation:

B = C k μ 0 ρ i m ∼ 1 + ρ e / ρ i 2 , $$ \begin{aligned} B = C_{k}\sqrt{\mu _{0}\rho _{i}\widetilde{m}}\sqrt{\frac{1+\rho _{e}/\rho _{i}}{2}}, \end{aligned} $$

where ρi and ρe are the internal and external plasma density, and μ0 and 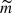m ∼ $ \widetilde{m} $ denote the magnetic permeability in vacuum and the mean molecular weight. We took ρi = 109 cm−3 and a density contrast, ρe/ρi = 1/3 to calculate the magnetic field (Gao et al. 2022; Petrova et al. 2023; Li & Long 2023). Figure 8b shows the distribution of estimated magnetic field strengths. The average value of the magnetic field is 2.1 ± 1.5 G, with a range of 0.34–8 G. These loops are embedded in the quiet Sun and coronal holes, and most of the loops have a magnetic field strength lower than 4 G. These estimates of the magnetic fields are lower than previous estimates using seismology for loop lengths of a few hundred megameters in an active region (Nisticò et al. 2013). The potential field extrapolation of photospheric magnetograms for x-ray bright points shows that several loops with a length of ∼10 mm have a magnetic field strength greater than 10 G (Mondal et al. 2023). However, the average value of the magnetic field obtained here is similar to quiet-Sun magnetic fields calculated using magnetoseismology of propagating kink waves (Yang et al. 2020). West et al. (2011) found a magnetic field strength of 0.7 ± 0.7 G in the quiet-Sun region by performing coronal seismology using EIT waves. The underestimation of the loop length could result in a lower kink speed. The underestimation of the loop length can be about 10% for loops of a few hundred megameters (Mackay et al. 2000; Van Doorsselaere et al. 2007). The analysis of campfire loops with a loop length of ∼3–4 mm indicated that this underestimation could increase up to ∼40–50% as it is possible that the part of the loop that is embedded in the chromosphere and photosphere is not observed in 174 Å emission (Berghmans et al. 2021). It must be noted that even when we add a 50% error in length, the average value of the kink speed would be 245 km s−1, which remains smaller than those observed in the coronal heights. Because the kink speed depends on the internal and external Alfvén speeds, it might be possible that these structures have quite different density contrasts and/or magnetic fields compared to large-scale coronal loops.

The energy flux carried by the observed kink waves can be estimated by the following expression (Van Doorsselaere et al. 2014; Petrova et al. 2023):

E f = 1 2 C k ( ρ e + ρ i ) V 2 . $$ \begin{aligned} E_{f} = \frac{1}{2} C_{k} (\rho _{e}+\rho _{i}) V^{2} . \end{aligned} $$

Using the distribution of Ck and V, and considering the values of the internal plasma density and density contrast, we find a broad range of the energy flux, 0.6–313 W m−2. The mean and median of the energy flux distribution are 19 and 6 W m−2, respectively. The energy flux of 313 W m−2 is obtained for the period of 28 s with a displacement amplitude of ∼73 km. This suggests that short-period oscillations have a high energy flux in the quiet Sun and coronal holes. Petrova et al. (2023) analysed two short-period oscillations of ∼14 and 30 s in the quiet-Sun region. The wave energy fluxes calculated for these oscillations were 1.9 and 6.5 kW m−2, but in this work, we find much lower values for the energy flux. This potentially means that high-energy flux events such as in Petrova et al. (2023) are not so common in the quiet Sun. We thoroughly examined each small-scale loop in the datasets and observed these oscillations on only a few occasions. Within the limited duration of the observation and the limited field of view of data, we were unable to find the oscillations to be omnipresent like for the propagating waves in the CoMP. Gao et al. (2022) presented long-period low-energy decayless waves in bright points. In our study, we find both short-period and long-period oscillations. Figure 5 shows that our study has revealed periods and loop lengths that were absent in Gao et al. (2022) and Petrova et al. (2023). Although the maximum energy flux we estimated is sufficient to heat the quiet corona (Withbroe & Noyes 1977), the mean and median energy fluxes indicate that decayless waves with high-energy fluxes are not prevalent in the quiet Sun and coronal holes.

5. Summary and conclusion

We performed the statistical analysis of decayless kink oscillations in small loops using high-resolution observation from the HRIEUV telescopes of EUI. The oscillating loops have lengths of about 10 mm, and they are dynamic in nature. The average loop length in this study is shorter than in previous statistical studies of decayless kink oscillations in coronal loops. The analysed loops have a mean oscillation period and displacement amplitude of 140s and 134 km, respectively. The analysis we carried out to identify wave modes suggests the potential presence of standing waves. Nonetheless, the identification of propagating waves with the datasets used here proves to be a challenging endeavour. Moreover, the absence of a significant correlation between the loop length and period precludes their categorisation as standing-wave modes. The available evidence currently does not suffice to draw a definitive conclusion of whether these waves are standing or propagating. Further insights into the nature of these waves can be gained through numerical simulations of transverse oscillations in small loops and additional studies focusing on the same phenomenon. The kink speed, magnetic field, and energy flux of these waves were calculated considering that standing waves are one possibility. The estimation of the kink speed shows a range of ∼27–630 km s−1, which is lower than the kink speed found in loops of several hundred megameters in active regions. We estimated the magnetic field strength, which indicated lower values than were obtained in active region loops. The energy flux estimation provided a range of ∼0.6–313 W m−2. We find that the energy flux of most oscillations is insufficient to compensate for the radiative losses in the quiet corona and coronal holes. This indicates that transverse oscillations with high-energy flux in the quiet Sun and coronal holes may not be prevalent. In conclusion, if the waves identified in this study are standing, it implies that the transverse waves in small loops, immersed in coronal holes and quiet corona, cannot provide significant energy to balance the radiative losses and accelerate the solar wind.

Movie

Movie 1 associated with Fig. 1 (small_scale_loops_oscl) Access here

Acknowledgments

A.K.S is supported by funds of the Council of Scientific & Industrial Research (CSIR), India, under file no. 09/079(2872)/2021-EMR-I. V.P. is supported by SERB start-up research grant (File no. SRG/2022/001687). A.K.S. acknowledges Krishna Prasad Sayamanthula and Ritesh Patel for their thoughtful discussions. A. N. Z. thanks the Belgian Federal Science Policy Office (BELSPO) for the provision of financial support in the framework of the PRODEX Programme of the European Space Agency (ESA) under contract number 4000136424. T.V.D. was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 724326), the C1 grant TRACEspace of Internal Funds KU Leuven, and a Senior Research Project (G088021N) of the FWO Vlaanderen. Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. The EUI instrument was built by CSL, IAS, MPS, MSSL/UCL, PMOD/WRC, ROB, LCF/IO with funding from the Belgian Federal Science Policy Office (BELSPO/PRODEX PEA 4000112292 and 4000134088); the Centre National d’Études Spatiales (CNES); the UK Space Agency (UKSA); the Bundesministerium für Wirtschaft und Energie (BMWi) through the Deutsches Zentrum für Luft- und Raumfahrt (DLR); and the Swiss Space Office (SSO).

References

  1. Afanasyev, A. N., Van Doorsselaere, T., & Nakariakov, V. M. 2020, A&A, 633, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Alipour, N., & Safari, H. 2015, ApJ, 807, 175 [NASA ADS] [CrossRef] [Google Scholar]
  3. Anfinogentov, S. A., & Nakariakov, V. M. 2019, ApJ, 884, L40 [CrossRef] [Google Scholar]
  4. Anfinogentov, S., Nisticò, G., & Nakariakov, V. M. 2013, A&A, 560, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Anfinogentov, S. A., Nakariakov, V. M., & Nisticò, G. 2015, A&A, 583, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Arregui, I. 2015, Philos. Trans. R. Soc. London Ser. A, 373, 20140261 [Google Scholar]
  7. Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [Google Scholar]
  8. Auchère, F., Mampaey, B., Verbeeck, F., et al. 2021, SolO/EUI Data Release 4.0 2021–12 (Royal Observatory of Belgium (ROB)) [Google Scholar]
  9. Banerjee, D., Teriaca, L., Doyle, J. G., & Wilhelm, K. 1998, A&A, 339, 208 [Google Scholar]
  10. Banerjee, D., Krishna Prasad, S., Pant, V., et al. 2021, Space Sci. Rev., 217, 76 [NASA ADS] [CrossRef] [Google Scholar]
  11. Berghmans, D., Auchère, F., Long, D. M., et al. 2021, A&A, 656, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. De Moortel, I., & Browning, P. 2015, Philos. Trans. R. Soc. London Ser. A, 373, 20140269 [NASA ADS] [Google Scholar]
  13. De Pontieu, B., McIntosh, S. W., Carlsson, M., et al. 2007, Science, 318, 1574 [Google Scholar]
  14. Duckenfield, T., Anfinogentov, S. A., Pascoe, D. J., & Nakariakov, V. M. 2018, ApJ, 854, L5 [Google Scholar]
  15. Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [Google Scholar]
  16. Gao, Y., Tian, H., Van Doorsselaere, T., & Chen, Y. 2022, ApJ, 930, 55 [NASA ADS] [CrossRef] [Google Scholar]
  17. Goddard, C. R., Nisticò, G., Nakariakov, V. M., & Zimovets, I. V. 2016, A&A, 585, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Golub, L., Krieger, A. S., & Vaiana, G. S. 1976, Sol. Phys., 49, 79 [NASA ADS] [CrossRef] [Google Scholar]
  19. Guo, M., Van Doorsselaere, T., Karampelas, K., et al. 2019, ApJ, 870, 55 [Google Scholar]
  20. Hahn, M., & Savin, D. W. 2013, ApJ, 776, 78 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hassler, D. M., Rottman, G. J., Shoub, E. C., & Holzer, T. E. 1990, ApJ, 348, L77 [CrossRef] [Google Scholar]
  22. Karampelas, K., & Van Doorsselaere, T. 2020, ApJ, 897, L35 [Google Scholar]
  23. Karampelas, K., & Van Doorsselaere, T. 2021, ApJ, 908, L7 [NASA ADS] [CrossRef] [Google Scholar]
  24. Karampelas, K., Van Doorsselaere, T., & Antolin, P. 2017, A&A, 604, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Karampelas, K., Van Doorsselaere, T., Pascoe, D. J., Guo, M., & Antolin, P. 2019, Front. Astron. Space Sci., 6, 38 [Google Scholar]
  26. Kobayashi, K., Cirtain, J., Winebarger, A. R., et al. 2014, Sol. Phys., 289, 4393 [Google Scholar]
  27. Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
  28. Li, D., & Long, D. M. 2023, ApJ, 944, 8 [NASA ADS] [CrossRef] [Google Scholar]
  29. Mackay, D. H., Galsgaard, K., Priest, E. R., & Foley, C. R. 2000, Sol. Phys., 193, 93 [CrossRef] [Google Scholar]
  30. Mampaey, B., Verbeeck, F., Stegen, K., et al. 2022, in SolO/EUI Data Release 5.0 2022–04 (Royal Observatory of Belgium (ROB)) [Google Scholar]
  31. Mandal, S., Peter, H., Chitta, L. P., et al. 2021a, A&A, 656, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Mandal, S., Tian, H., & Peter, H. 2021b, A&A, 652, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Mandal, S., Chitta, L. P., Antolin, P., et al. 2022, A&A, 666, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. McIntosh, S. W., & De Pontieu, B. 2012, ApJ, 761, 138 [NASA ADS] [CrossRef] [Google Scholar]
  35. McIntosh, S. W., de Pontieu, B., Carlsson, M., et al. 2011, Nature, 475, 477 [Google Scholar]
  36. Mondal, B., Klimchuk, J. A., Vadawale, S. V., et al. 2023, ApJ, 945, 37 [NASA ADS] [CrossRef] [Google Scholar]
  37. Morton, R. J., & McLaughlin, J. A. 2013, A&A, 553, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Morton, R. J., & McLaughlin, J. A. 2014, ApJ, 789, 105 [NASA ADS] [CrossRef] [Google Scholar]
  39. Morton, R. J., Verth, G., Jess, D. B., et al. 2012, Nat. Commun., 3, 1315 [Google Scholar]
  40. Morton, R. J., Tomczyk, S., & Pinto, R. 2015, Nat. Commun., 6, 7813 [Google Scholar]
  41. Morton, R. J., Weberg, M. J., & McLaughlin, J. A. 2019, Nat. Astron., 3, 223 [Google Scholar]
  42. Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
  43. Nakariakov, V. M., Anfinogentov, S. A., Nisticò, G., & Lee, D. H. 2016, A&A, 591, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Nakariakov, V. M., Anfinogentov, S. A., Antolin, P., et al. 2021, Space Sci. Rev., 217, 73 [NASA ADS] [CrossRef] [Google Scholar]
  45. Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [Google Scholar]
  46. Nechaeva, A., Zimovets, I. V., Nakariakov, V. M., & Goddard, C. R. 2019, ApJS, 241, 31 [NASA ADS] [CrossRef] [Google Scholar]
  47. Nicula, B., Berghmans, D., & Hochedez, J.-F. 2005, Sol. Phys., 228, 253 [NASA ADS] [CrossRef] [Google Scholar]
  48. Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Pant, V., Magyar, N., Van Doorsselaere, T., & Morton, R. J. 2019, ApJ, 881, 95 [NASA ADS] [CrossRef] [Google Scholar]
  50. Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
  51. Petrova, E., Magyar, N., Van Doorsselaere, T., & Berghmans, D. 2023, ApJ, 946, 36 [CrossRef] [Google Scholar]
  52. Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Sarkar, S., Pant, V., Srivastava, A. K., & Banerjee, D. 2016, Sol. Phys., 291, 3269 [CrossRef] [Google Scholar]
  54. Schrijver, C. J., Title, A. M., Berger, T. E., et al. 1999, Sol. Phys., 187, 261 [NASA ADS] [CrossRef] [Google Scholar]
  55. Shi, M., Van Doorsselaere, T., Guo, M., et al. 2021, ApJ, 908, 233 [Google Scholar]
  56. Thurgood, J. O., Morton, R. J., & McLaughlin, J. A. 2014, ApJ, 790, L2 [Google Scholar]
  57. Tian, H., McIntosh, S. W., Wang, T., et al. 2012, ApJ, 759, 144 [Google Scholar]
  58. Tian, H., DeLuca, E. E., Cranmer, S. R., et al. 2014, Science, 346, 1255711 [Google Scholar]
  59. Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 [Google Scholar]
  60. Tomczyk, S., Card, G. L., Darnell, T., et al. 2008, Sol. Phys., 247, 411 [Google Scholar]
  61. Van Doorsselaere, T., Andries, J., & Poedts, S. 2007, A&A, 471, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Van Doorsselaere, T., Gijsen, S. E., Andries, J., & Verth, G. 2014, ApJ, 795, 18 [NASA ADS] [CrossRef] [Google Scholar]
  63. Van Doorsselaere, T., Srivastava, A. K., Antolin, P., et al. 2020, Space Sci. Rev., 216, 140 [Google Scholar]
  64. Wang, T., Ofman, L., Davila, J. M., & Su, Y. 2012, ApJ, 751, L27 [Google Scholar]
  65. Weberg, M. J., Morton, R. J., & McLaughlin, J. A. 2018, ApJ, 852, 57 [Google Scholar]
  66. Weberg, M. J., Morton, R. J., & McLaughlin, J. A. 2020, ApJ, 894, 79 [NASA ADS] [CrossRef] [Google Scholar]
  67. West, M. J., Zhukov, A. N., Dolla, L., & Rodriguez, L. 2011, ApJ, 730, 122 [Google Scholar]
  68. White, R. S., & Verwichte, E. 2012, A&A, 537, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Withbroe, G. L., & Noyes, R. W. 1977, ARA&A, 15, 363 [Google Scholar]
  70. Yang, Z., Tian, H., Tomczyk, S., et al. 2020, Sci. Chin. E Technol. Sci., 63, 2357 [CrossRef] [Google Scholar]
  71. Zhong, S., Nakariakov, V. M., Kolotkov, D. Y., & Anfinogentov, S. A. 2022a, MNRAS, 513, 1834 [NASA ADS] [CrossRef] [Google Scholar]
  72. Zhong, S., Nakariakov, V. M., Kolotkov, D. Y., Verbeeck, C., & Berghmans, D. 2022b, MNRAS, 516, 5989 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Datasets used in this study.

In the text
Table 2.

Details of the oscillating loop and oscillation parameters.

In the text

All Figures

thumbnail Fig. 1.

Description of events. Panels a, b, and c represent the context images of the three datasets. The green boxes show examples of the selected loops for which oscillations are detected. The other loops we studied appear at different times and are not shown here. A magnified view of the loops in the green boxes for each upper panel is shown in the lower panels. The red lines in panels d–i depict the position of the artificial slits we used to generate the x − t maps. The blue crosses in each panel show the approximate position of the footpoints. Details of the dataset are provided in Table 1. An animation related to this figure is accessible online.
In the text
thumbnail Fig. 2.

Overview of x − t maps. Panels a–f show the x − t maps produced for slits S1 to S6 indicated in Figs. 1d–i. The red curves depict the best fit for the oscillations. The error bars represent standard errors on the centre position of the loop. The amplitude, ξ1, and period, P, of the oscillation, along with the propagated errors, are written close to the fitted oscillations. A few x − t maps show only part of the slits so that the oscillations are better visible. Panels g–l show the fitted oscillations along with the error bars for the position of the loop. These correspond to the x − t maps shown in panels a–f. The dashed curves show the overplotted best-fit model. The chi-square values for the fits are also provided.
In the text
thumbnail Fig. 3.

Distribution of the oscillation parameters. The estimated parameter values are displayed as histograms, showing the distribution of (a) the loop length, (b) the period, (c) the displacement amplitude, and (d) the velocity amplitude. These histograms illustrate the range of values for each parameter. The average and standard deviation are provided in the respective panels. The plots also include the standard error in the mean and the standard deviation.
In the text
thumbnail Fig. 4.

Relations between parameters. Panels a–f show the scatter plots between the four estimated parameters loop length, period, displacement amplitude, and velocity amplitude. The linear Pearson correlation coefficient, along with standard errors, is also provided in each panel.
In the text
thumbnail Fig. 5.

Scaling between the loop length and the period. The figure shows the variation in the loop length vs. the period of the decayless oscillations analysed in previous studies (Wang et al. 2012; Nisticò et al. 2013; Anfinogentov et al. 2013, 2015; Duckenfield et al. 2018; Anfinogentov & Nakariakov 2019; Mandal et al. 2021b; Zhong et al. 2022a,b; Petrova et al. 2023; Gao et al. 2022; Li & Long 2023). The red points represent the results of the current work. The black lines represent the best fit for the datasets.
In the text
thumbnail Fig. 6.

Variation in the loop length vs. period for the small loops embedded in the quiet Sun and coronal holes. This figure displays the relation of the loop length and the period of the current work combined with Gao et al. (2022), and Petrova et al. (2023). The cross-correlation coefficients combining the studies are provided. The black lines represent the best fit for the datasets.
In the text
thumbnail Fig. 7.

Phase lag analysis of the oscillations. The figure presents the multi-slit analysis for the two loops shown in panels b and d. S0 and S1 are two slits that were placed at different positions of the loops. Panels a and c show the fitted oscillation profile from slits S0 and S1 indicated in panels b and d. The oscillations detected in S0 and S1 show no significant phase shift.
In the text
thumbnail Fig. 8.

Results from coronal seismology. The figure shows the histograms of the kink speeds, Ck, and magnetic field strength, B, obtained using the estimated oscillation parameters. The mean value of the distribution is also provided.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.