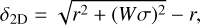| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A192 | |
| Number of page(s) | 32 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202348687 | |
| Published online | 24 April 2024 | |
FARGOCPT: 2D Multiphysics code for simulating disk interactions with stars, planets, and particles★
1
Institut für Theoretische Astrophysik, Zentrum für Astronomie (ZAH), Universität Heidelberg,
Albert-Ueberle-Str. 2,
69120
Heidelberg,
Germany
e-mail: rometsch@uni-heidelberg.de
2
Institut für Astronomie und Astrophysik, Universität Tübingen,
Auf der Morgenstelle 10,
72076
Tübingen,
Germany
3
Fakultät für Physik, Universität Duisburg-Essen,
Lotharstraße 1,
47057
Duisburg,
Germany
4
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
5
Universitäts-Sternwarte, Fakultät für Physik, Ludwig-Maximilians-Universität München,
Scheinerstr. 1,
81679
München,
Germany
Received:
21
November
2023
Accepted:
29
January
2024
Context. Planet-disk interactions play a crucial role in the understanding of planet formation and disk evolution. There are multiple numerical tools available to simulate these interactions, including the commonly used FARGO code and its variants. Many of the codes have been extended over time to include additional physical processes, with a focus on their accurate modeling.
Aims. We introduce FARGOCPT, an updated version of FARGO that incorporates other previous enhancements to the code, to provide a simulation environment tailored to studies of the interactions between stars, planets, and disks. It is meant to ensure an accurate representation of planet systems, hydrodynamics, and dust dynamics, with a focus on usability.
Methods. The radiation-hydrodynamics part of FARGOCPT uses a second-order upwind scheme in 2D polar coordinates, supporting multiple equations of state, radiation transport, heating and cooling, and self-gravity. Shocks are considered using artificial viscosity. The integration of the N-body system is achieved by leveraging the REBOUND code. The dust module utilizes massless tracer particles, adapted to drag laws for the Stokes and Epstein regimes. Moreover, FARGOCPT provides mechanisms to simulate accretion onto stars and planets.
Results. The code has been tested in practice in the context of multiple studies. Additionally, it comes with an automated test suite for checking the physics modules. It is available online.
Conclusions. FARGOCPT offers a unique set of simulation capabilities within the current landscape of publicly available planet-disk interaction simulation tools. Its structured interface and underlying technical updates are intended to assist researchers in ongoing explorations of planet formation.
Key words: hydrodynamics / methods: numerical / protoplanetary disks / planet–disk interactions / binaries: close / novae, cataclysmic variables
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Planet migration is a crucial component of our understanding of planet formation. Besides analytical or semi-analytical calculations, one way to study it is via hydrodynamic calculations coupled with gravitational N-body simulations. Specifically, in the context of planet formation, the shape of the hydrodynamic object resembles a thin, flared disk. The computer program FARGO (Masset 2000) is meant to simulate these protoplane-tary disks by numerically solving the hydrodynamics equations on a staggered grid using a second-order upwind scheme. It includes a special algorithm, with the same name, which can relax the time step constraint by making use of the axial symmetry of the disk flow, thereby reducing the computational cost of simulations. The specific form of the hydrodynamic equations solved by the program is stated later in Sect. 2.
Because FARGO is tailored to the study of protoplane-tary disks, the code uses a cylindrical grid, reflecting the major symmetry of the system. One main assumption used in the code is that the simulated disks are thin in the sense that their vertical extent is small compared to the radial distance from the central star. This is the justification for approximating the three-dimensional (3D) disk with a two-dimensional (2D) representation. Using this approximation significantly reduces the required time for simulations of protoplanetary disks and enables the long-term study of these systems. In its original form, the code employed the (locally) isothermal assumption, in which the temperature is assumed to be fixed in time and only dependent on the distance from the central start. This allows for the energy equation to be solved analytically, while additionally reducing the computational cost of the simulation.
Over the past two decades, studies have shown that additional effects play an important role in the evolution of protoplanetary disks and their interaction with embedded planets (for overviews, see Kley & Nelson 2012; Baruteau et al. 2014; Paardekooper et al. 2023). The relevant physical processes include the heating and cooling of the gas (e.g., Baruteau & Masset 2008a; Kley & Crida 2008; Paardekooper & Papaloizou 2008; Lega et al. 2014; Masset 2017), self-gravity (e.g., Pierens & Huré 2005; Baruteau & Masset 2008b), and radiation transport (e.g., Morohoshi & Tanaka 2003; Paardekooper & Mellema 2006). We have added all of these effects to our version of the FARGO code and made them fully controllable from the input file and verified their correctness through extensive testing. We also extended the number of physical quantities that are evaluated during the simulation and written to output files.
While there are multiple options to run planet-disk interaction simulations including the aforementioned effects, we have recognized a need for a simulation code that is not only able to simulate the relevant physical processes accurately, but is also easy to use. This is especially important for students and researchers who are not experts in modifying and compiling C/C++ or FORTRAN codes in a typical Linux environment. These skills can pose a significant hurdle when running simulations.
The primary aim behind publishing this code is to provide a comprehensive simulation tool for planet-disk interactions that remains accessible and useful to both students and more senior researchers. To this end, the testing suite for the physical modules is fully automated with pass-fail tests so it can be run after every future modification of the code to ensure that it is still working as intended.
On the physics side, a significant enhancement is the incorporation of radiation physics. Furthermore, the introduction of a particle module enables in-depth studies on the impact of embedded planet systems on the structure and dust distribution of planet-forming disks, a task that is currently often performed to model disk observations. We also added cooling and mass inflow functions and an updated equation of state specifically tailored to study cataclysmic variable systems. Additionally, the code can simulate the disk centered around any combination of N-body objects. This enables, for instance, simulations of cir-cumbinary disks in the center of mass-frame or simulations of a circumsecondary disk in a binary star system.
Simulation programs for planet-disk interaction can, broadly speaking be organized into two main categories: Lagrangian and Eulerian methods. Lagrangian methods trace the dynamics of the disk by following the motion of a large number of particles. The most common example of this is the Smoothed Particle Hydrodynamics (SPH) method with a prominent example being the PHANTOM code (Price et al. 2018).
The Eulerian methods solve the hydrodynamics equations on a grid, which can either be fixed or dynamic. In this category, again, we can distinguish between two main approaches used in astrophysics: methods that require artificial viscosity and Godunov methods (Woodward & Colella 1984). Either of these methods can be implemented as a finite-volume or finite-difference method. Godunov methods solve the Riemann problem at the cell interfaces to compute the fluxes through the interfaces. This approach allows for an accurate treatment of shocks and an approximate treatment of smooth flows. Prominent examples include the PLUTO code Mignone et al. (2007) and the Athena++ code (Stone et al. 2020).
Schemes based on artificial viscosity can be derived as a finite-difference scheme from Taylor series expansions of the Euler equations (Woodward & Colella 1984). This technique assumes that the solution is smooth, which is not the case at discontinuities such as shocks. It approximates shocks by smearing out discontinuities into smooth regions of strong gradients via artificial viscosity. The ZEUS code (Stone & Norman 1992) and the FARGO code (which is based on the ZEUS code) are prominent examples of this approach. While these codes were classified as finite-difference schemes, they employed a staggered grid and implemented their advection step by splitting the domain into cells and computing the fluxes through the cell interfaces. The cell as a basic geometrical unit and the sharing of fluxes among adjacent cells, which ensures the conservation of the advected quantities to machine-precision by construction, warrant the classification of the advection scheme as “finite-volume” (Anderson et al. 2020). We lean towards this classification because it rests on an intrinsic property of the scheme. However, the crucial distinction seems to be the one between Godunov methods and methods that require artificial viscosity and the FARGO code family falls into the latter category.
While Godunov methods are (formally) more accurate when handling discontinuities such as shocks, the artificial viscosity methods are better at modeling smooth flows and, in practice, they are often more robust and easier to use. Both approaches have their advantages and disadvantages and the choice of which method to use depends on the specific problem at hand. For a specific example, see Ziampras et al. (2023b) who used both PLUTO and FARGO3D to investigate the buoyancy waves in the coorbital region of small-mass planets.
The original FARGO code was introduced by Masset (2000). Based on this code, other groups developed their version of the FARGO code. Examples include FARGO2D1D (Crida et al. 2007), GFARGO (Regály et al. 2012; Masset 2015), FARGOCA (Lega et al. 2014), FARGO_THORIN (Chrenko et al. 2017), the official successor FARGO3D (Benítez-Llambay & Masset 2016), as well as FARGOADSG (Baruteau & Masset 2008a,b; Baruteau & Zhu 2016), which is the predecessor of our code.
In this work, we present FARGOCPT, the FARGO version developed by members of the Computational Physics group at the University of Tübingen since 2012. Publications from this group, using the code, include Müller & Kley (2012, 2013), Picogna & Kley (2015), Rometsch et al. (2020, 2021), and Jordan et al. (2021).
Furthermore, we present novel approaches for handling challenging aspects of planet-disk interaction simulations. We introduce a new method for handling the indirect term suitable for simulations centered on individual stars in binary systems (Sect. 3.5), a local viscosity stabilizer for use in the context of cataclysmic variables (Sect. 3.9.2), and a correction for dust diffusion treated by stochastic kicks (Sect. 3.12.2).
This document is structured as follows. First, the physical problem at hand is sketched out in Sect. 2. Then, the newly introduced physics modules are described in Sect. 3. Software engineering and usability aspects of the code are discussed in Sect. 4. Finally, we present our conclusions in Sect. 5 with a discussion of the code. The appendix includes a presentation of various test cases included in the automatic test suite.
2 Physical system
The FARGOCPT code is a computer program that numerically solves the vertically integrated radiation-hydrodynamics equations in the one-temperature approximation coupled with an N-body system. They are expressed as:
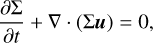 (1)
(1)
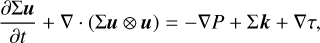 (2)
(2)
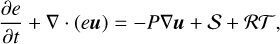 (3)
(3)
with the surface density, 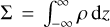 , as the vertically integrated gas volume density, ρ, the gas velocity, u, the vertically integrated internal energy density, e = Σє, with the specific internal energy, є, the vertically integrated pressure,
, as the vertically integrated gas volume density, ρ, the gas velocity, u, the vertically integrated internal energy density, e = Σє, with the specific internal energy, є, the vertically integrated pressure, 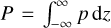 , accelerations, k, due to external forces (e.g., due to gravity), the viscous stress tensor, τ, and heat sinks and sources, S (see Sect. 3.8). The last term represents the radiation transport:
, accelerations, k, due to external forces (e.g., due to gravity), the viscous stress tensor, τ, and heat sinks and sources, S (see Sect. 3.8). The last term represents the radiation transport:
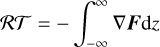 (4)
(4)
with the radiation flux, F, in three dimensions. In the code, the vertical component of the radiation flux is split off and treated with an effective model, see Sect. 3.8. The code handles radiation hydrodynamics using the one-temperature approach which is discussed in more detail in Sect. 3.8.5.
In polar coordinates (r, ϕ), to which the code is tailored, the equations are expressed as (e.g., Masset 2002):
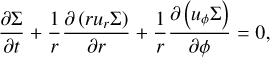 (5)
(5)
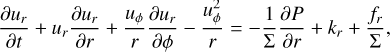 (6)
(6)
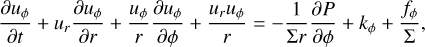 (7)
(7)
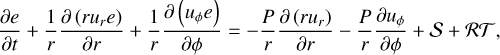 (8)
(8)
where ƒr and ƒϕ are the radial and azimuthal forces per unit area due to viscosity (see Eqs. (82) and (83)). For a rotating coordinate system, we follow the conservative formulation of Kley (1998) and add the respective terms to the two momentum equations.
The left-hand sides of these equations are the transport step and the right-hand sides are the source terms. Following the scheme of the ZEUS code (Stone & Norman 1992), the transport step is solved by a finite-volume method based on an upwind scheme with a second-order slope limiter (van Leer 1977) and the code can make use of the FARGO algorithm (Masset 2000) to speed up the simulation. The source terms are updated as described in Sect. 3.1 using first-order Euler steps or implicit updates. The definitions for the heating and cooling term, S, and the radiation transport term, 𝓡𝒯, are given in Sect. 3.8.
The external accelerations k are due to the gravitational forces from the star(s) and planets, correction terms in case of a non-inertial frame, and the self-gravity of the disk:
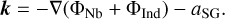 (9)
(9)
The interaction of the disk with the N-body objects is considered via the gravitational potential, as expressed in Eq. (15). Self-gravity of the gas is considered as an acceleration (see Sect. 3.7).
The N-body objects feel the gravitational acceleration a exerted by the gas. This is computed by summation of the smoothed gravitational acceleration over all grid cells. We refer to Sect. 3.6 for formulas and details about the smoothing. Because the simulation can be run in a non-inertial frame of reference, the correction terms are applied as detailed in Sect. 3.5.
Finally, FARGOCPT features a particle module based on Lagrangian super-particles, where a single particle might represent any number of physical dust particles or solid bodies. The particles feel the gravity from the N-bodies and interact with the gas through a gas-drag law. Additionally, the dust diffusion was modeled to consider the effects of gas turbulence. The particle module is described in detail in Sect. 3.12. The next section describes the various physics modules that were added to the code.
3 Improvements of the physics modules
We built upon the original FARGO code by Masset (2000) and its improved version FARGOADSG. It already included treatment of the energy equation (Baruteau & Masset 2008a), self-gravity (Baruteau & Masset 2008b), and a Lagrangian particle module (Baruteau & Zhu 2016). We advanced these modules, added new physics modules, and added features to improve the usability of the code. For a detailed description of the FARGOADSG code, and with it of the underlying hydrodynamics part of the code presented here, we recommend Chap. 3 of Baruteau (2008). This section starts with outlining the order of operations in the operator splitting approach and then describes the various new features and changes.
3.1 Order of operations and interaction of subsystems
This section details the order in which the physical processes are considered during one iteration in the code and how they interact. For the update step, we used the sequential operator splitting (also known as Lie-Trotter splitting) where possible, meaning that we always use the most up-to-date quantities from the previous operators when applying the current operator. This is the simplest and oldest splitting scheme and has better accuracy than applying all operators using the quantities at the beginning of the step. This scheme is known as additive splitting (e.g., Geiser et al. 2017). Each time step starts with accretion onto the planets. Conceptually, this is the same as performing planet accretion at the end of the time step, except for the first and last iteration of the simulation.
Then, the code computes the gravitational forces between the N-body objects and the gas, between the N-body objects and the dust particles, and the self-gravity of the disk. At this stage, the indirect term, namely, the corrections for the non-inertial frame, is computed and added to the gravitational interaction. These are then applied to the subsystems by updating the velocities of the N-body objects, updating the acceleration of the dust particles, and updating the potential of the gas. Experience shows that for the interaction between N-body and gas the positions of the N-body objects have to be at the same time as the gas. From this point on, the N-body system and the particle system evolve independently in time until the end of the time step.
The gas velocities are first updated by the self-gravity acceleration and then by the N-body gravity potential, the pressure gradient, and, in the case of the radial update, also the centrifugal acceleration. At this step, the code updates the internal energy of the gas with compression heating. It is important to perform the energy update at this step before the viscosity is applied to avoid instabilities. Then, the code sequentially updates the velocities and the internal energy further by artificial viscosity, viscosity (both of which depend on the gas velocities), as well as heating and cooling terms. The heating and cooling steps are applied simultaneously for numerical stability. Finally, the internal energy is updated by radiation transport. Once all the forces and source terms were applied, the transport step is conducted. Boundary conditions and the wave-damping zone are applied at the appropriate sub-steps throughout the hydrodynamics step.
A detailed diagram of the order of the operations during each time step and the interactions between the subsystems is shown in Fig. 1. The diagram illustrates how each of the subsystems is advanced in time and between which sub-steps information is exchanged between the subsystems. The next paragraphs guide through the diagram starting from the top, explaining the meaning of the differently shaped patches, arrows, and lines. Each of the three subsystems is colored differently: the N-body system is shown in green, the hydrodynamics in blue, and the dust particles in orange. A colored patch represents the “state” of a subsystem. Elliptical patches indicate the initial state at the beginning of a time step, parallelograms indicate the intermediate states and colored rectangles with rounded corners indicate the final state at the end of the time step. Each state is labeled with variable names. The respective subscript indicates the sub-step during the operator splitting. For example, the energy is updated from en, first to ea, then to eb and after additional steps finally to en+1. These variables will be used in Sect. 3.8 to refer to the sub-steps. A variable printed in bold text indicates that the variable was changed by the last operation.
A white rectangle with rounded corners indicates an “intermediate calculation”, the result of which is subsequently used in multiple operations. For example, the calculation of the indirect term is used in all three subsystems. Finally, the rectangles with bars on the sides indicate an “operation” that changes the state of a system.
Double lines trace the change of a subsystem throughout the time step. Lines with arrows attached at the end emerge from a state patch or an intermediate calculation and end in an operation or intermediate calculation patch. The large rectangle with bars shaded in grey at the right side of the diagram illustrates the sub-steps involved in the hydrodynamics part of the simulation. Except for the irradiation operation which requires the position of the N-bodies, this part of the simulation is independent of the N-body system.
The shaded rectangle with rounded corners in the upper third of the diagram illustrates the various gravitational interactions between the subsystems. The information indicated by arrows that end at the borders of this patch can be applied in any of the contained intermediate calculations.
The operations are ordered from the top to bottom in the order they are applied during the time step. This means that an operation or a state is generally only influenced by states above it or at the same level. Please follow the arrows to get a sense of the order of operations.
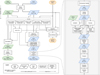 |
Fig. 1 Order of operations in the operator splitting scheme showing the evolution of the N-body, hydro, and particle subsystems throughout one iteration step. Single-line arrows mean that the originating object is used in the calculation of the destination. Double lines indicated the evolution of one of the subsystems from the initial state (ellipse) over intermediate states (parallelogram) to the final state (round shape). Each rectangle with rounded corners is a computation of an intermediate quantity using the state of the subsystem to which it is connected. The rectangles with bars on the sides indicate an operation that changes the state of a system. The variables that were changed by an operation are indicated in boldface in the intermediate states. |
Possible cases for the disk gravity.
3.2 N-body module
The original FARGO code includes a Runge-Kutta fifth-order N-body integrator, which was used with the same time step as the hydro simulations. This could lead to some situations in which the time step was too large for the N-body simulation, for instance, during close encounters in simulations of multiple migrating planets. Instead of implementing our N-body code with adaptive time-stepping, we incorporated the well-established and well-tested REBOUND code (Rein & Liu 2012) with its 15th order IAS15 integrator (Rein & Spiegel 2015) into FARGOCPT. REBOUND is called during every integration step of the hydro system to advance the N-body system for the length of the CFL time step. During this time, multiple N-body steps might be performed as needed. The interaction with the gas is incorporated by adding Δt a to the velocities of the bodies before the N-body integration.
We changed the central object from an implicit object, which was assumed to be of mass 1 in code units placed at the origin, to a moving point mass. It is now treated exactly like any other N-body object, notably including gravitational smoothing, which was not applied to the star before. This solves an inconsistency between the interaction of disk and planets and of the disk and star. This is necessary as the smoothing simulates the effect of the disk being stratified in the vertical direction and makes the potential behave more like it would in 3D (Müller et al. 2012).
Changing the star from being an implicit object to an explicit one, we changed all the relevant equations, which now include the mass of the central object and the distance to it.
3.3 Gravitational interactions
The dominant physical interaction between planets and a disk is gravity. In principle, any object that has mass causes a gravitational acceleration on any other object. In our simulation, N-body objects are considered to have a mass and particles are considered to be massless. The gas disk can be configured in one of three states. First, it can be massless and not accelerate the N-bodies. Second, the disk can massive, accelerate the N-bodies, the particles and itself (self-gravity included). Third, it can massive, accelerate the N-bodies, but not itself or the particles (self-gravity ignored).
The first two cases are consistent whereas the third case is inconsistent. However, it is a commonly used approximation. The reason for this is that the computation of the (self)gravity of the gas disk is computationally expensive.
In the third case, when the forces on the N-bodies due to the gas are computed using the full surface density, the N-bodies feel the full mass of the disk interior to their orbit, while gas on the same orbit does not feel this mass. Consequently, their respective equilibrium state angular velocities differ which causes a non-physical shift in resonance locations and, thus, in the torque and migration rate experienced by the planets (Baruteau & Masset 2008b). This mismatch can be alleviated by simply subtracting the azimuthal average of the surface density in the calculation of the force. This is done in the code in the case that self-gravity is disabled.
Our code does not support a configuration in which only one of the N-bodies feels the disk, such as a situation in which the planet feels the disk but the star does not. This is done intentionally to avoid nonphysical systems. Likewise, the indirect term caused by the disk is always included if the disk has mass (cases 2 and 3).
Whether the disk is considered to have mass is configured by the “DiskFeedback” option. If this is set to “yes”, the disk is considered to have mass and vice-versa. The three cases and the value of the code parameters are summarized in Table 1.
3.4 Coordinate center
Because the star is treated like any other N-body object and it is able to move, we need to define the coordinate center of the hydro domain. In principle, we can choose an arbitrary reference point. However, because the N-body system dominates the gravity, we choose the center of mass of any combination of N-bodies as the coordinate center.
With the N-body objects located at ri, with i = 1,2,…, Np, the coordinate center, R, can now be set as:
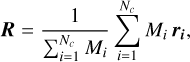 (10)
(10)
where Nc is the number of point masses whose center of mass is chosen to be the coordinate center. For example, Nc = Np selects the full N-body system as a reference, Nc = 1 selects the primary as a center and Nc = 2 selects a stellar binary or the center of mass of a star-planet system.
The center of mass of the full N-body system is likely the most desirable of such choices because it can be an inertial frame that does not require considering fictitious forces. This eliminates the need for an extra acceleration term to correct for the non-inertial frame, the so-called indirect term, which can be the source of numerical instabilities. At least it eliminates the need for the indirect term resulting from the N-body system, which generally dominates the indirect term, although contributions from the disk gravity might still need to be considered. One application is the simulation of circumbinary disks, in which the natural coordinate center is the center of mass of the binary stars.
3.5 Shift-based indirect term
The correction forces needed because of a non-inertial frame are typically called the indirect term in the context of planet-disk interaction simulations. Based on the definition of the coordinate center in Eq. (10), the corresponding acceleration can formally be written as:
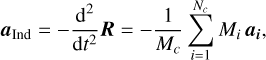 (11)
(11)
where we used 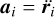 , defined
, defined 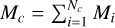 , and assumed that the derivatives of the masses are negligible. The individual ai should include all accelerations from forces acting on a specific N-body , including gravity from all sources, other N-bodies or the disk.
, and assumed that the derivatives of the masses are negligible. The individual ai should include all accelerations from forces acting on a specific N-body , including gravity from all sources, other N-bodies or the disk.
Usually, this correction term is evaluated at the start of a time step, yielding a vector 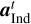 . As outlined in Sect. 2, this is then added to the velocities of the N-bodies as a sort of Euler step
. As outlined in Sect. 2, this is then added to the velocities of the N-bodies as a sort of Euler step 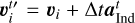 before integration of the N-body system. For the disk, the indirect term is applied through the potential. This update is first-order in time. As long as the magnitude of the indirect term is small compared to direct gravity, this choice appears to be good enough.
before integration of the N-body system. For the disk, the indirect term is applied through the potential. This update is first-order in time. As long as the magnitude of the indirect term is small compared to direct gravity, this choice appears to be good enough.
Using an Euler step as above is not sufficient in simulations in which the indirect term becomes stronger than the direct gravity. This can be the case in simulations of circumbinary disks centered on one of the stars that are useful for the study of cir-cumstellar disks in binary star systems. In such simulations, the disk can become unstable with the Euler method.
As a solution, we compute the indirect term as the average acceleration felt by the coordinate center during the whole time step. The average acceleration is computed from the actual shift needed to keep the coordinate center put. Therefore we call this method the “shift-based indirect term”. In our code, this is achieved by making a copy of the N-body system after the N-body velocities have been updated by disk gravity, integrating the copy in time and computing the net acceleration from the velocities as:
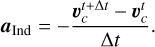 (12)
(12)
where 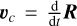 is the velocity of the coordinate center. The code then discards the N-body system copy, applies this indirect term to the N-body, hydro, and particle systems, and integrates them. In this way, the acceleration of the center and the indirect term cancel out and the system stays put much better compared to the old method. The computation of the acceleration is handled this way because the IASl5 integrator is a predictor-corrector scheme that does not produce an effective acceleration that would be accessible from the outside. Using the acceleration from an explicit Runge-Kutta scheme would produce the same results.
is the velocity of the coordinate center. The code then discards the N-body system copy, applies this indirect term to the N-body, hydro, and particle systems, and integrates them. In this way, the acceleration of the center and the indirect term cancel out and the system stays put much better compared to the old method. The computation of the acceleration is handled this way because the IASl5 integrator is a predictor-corrector scheme that does not produce an effective acceleration that would be accessible from the outside. Using the acceleration from an explicit Runge-Kutta scheme would produce the same results.
We tested, both, the old and the shift-based indirect term implementations and could not find any discernable difference in the dynamics of systems with embedded planets as massive as 10 Jupiter masses around a solar mass star. However, the shift-based indirect term enables simulations of circumbinary disks centered on one of the stars which was previously not possible. Even resolved simulations of circumsecondary disks (centered on the secondary star) when the latter is less massive than the primary star are possible. For the impact of this new scheme on the simulation of circumbinary disks, we refer to Jordan et al. (in prep.).
3.6 Gravity and smoothing
For modeling the gravity, we used the common scale-height-dependent smoothing approach. This approach accounts for the fact that a gas cell in 2D, which represents a vertically extended disk, experiences a weaker gravitational pull from an N-body object compared to the same cell for a truly razor-thin 2D disk (Müller et al. 2012). The potential due to a point mass, k, with mass, Mk, at a distance, dik, from the center of a cell, i, is then given by:
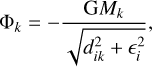 (13)
(13)
where G is the gravitational constant, dij is the distance between the point mass and the cell, and єi = αsmHi is the smoothing length with the smoothing parameter, αsm, and the cell scale height, Hi. According to Müller et al. (2012), αsm should be between 0.6 and 0.7 to accurately describe gravitational forces and torques, which is why we apply it to all N-bodies, even the central star. Masset (2002) found that a factor of 0.76 most closely reproduces type I migration rates of 3D simulations. We note that єi has to be evaluated with the scale height at the location of the cell, not the location of the N-body object (Müller et al. 2012).
When the gravity of planets inside the disk is also considered for computing the scale height (Sect. 3.11), the scale height and the smoothing length in Eq. (13) become smaller in the vicinity of the planet. There, the smoothing can then become too small such that numerical instabilities occur.
To remedy this issue, we added an additional smoothing adapted from Klahr & Kley (2006). We found this to be a necessity when simulating binaries where one component enters the simulation domain due to an eccentric orbit or small inner domain radius. It is applied as a factor to the potential in Eq. (13) and is given by:
![${\rm{\Phi }}_k^{{\rm{sm}}} = {{\rm{\Phi }}_k}\left\{ {\matrix{ {\left[ {{{\left( {{{{s_{ik}}} \over {{_i}}}} \right)}^4} - 2{{\left( {{{{s_{ik}}} \over {{_i}}}} \right)}^3} + 2\left( {{{{s_{ik}}} \over {{_i}}}} \right)} \right]\,\,\,\,\,{\rm{if}}{s_{ik}} < {d_{{\rm{sm}},k}}} \cr {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{otherwise;}}} \cr } } \right.$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq21.png) (14)
(14)
where 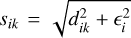 is the є-smoothed distance and dsm,k is another smoothing length, separate from єi. This smoothing is purely numerically motivated and guarantees numerical stability close to the planet. It has no effect outside dsm,k. The smoothing length, dsm,k, is a fraction of the Roche radius, RRoche, which is the distance from the point mass to its L1 point with respect to point mass, k = 1. For the case that the mass of the N-body particles changes, for example, with planet accretion, we compute RRoche using one Newton-Raphson iteration to calculate the dimensionless Roche radius, starting from its value during the last iteration. For low planet masses, RRoche reduces to the Hill radius.
is the є-smoothed distance and dsm,k is another smoothing length, separate from єi. This smoothing is purely numerically motivated and guarantees numerical stability close to the planet. It has no effect outside dsm,k. The smoothing length, dsm,k, is a fraction of the Roche radius, RRoche, which is the distance from the point mass to its L1 point with respect to point mass, k = 1. For the case that the mass of the N-body particles changes, for example, with planet accretion, we compute RRoche using one Newton-Raphson iteration to calculate the dimensionless Roche radius, starting from its value during the last iteration. For low planet masses, RRoche reduces to the Hill radius.
In many Fargo code variants, the gravity of the central star is not smoothed. However, the smoothing is required because the disk is vertically extended. The gravitational potential of the central star should therefore also be smoothed, otherwise, it is overestimated. This results in a deviation of order 10−4 for the azimuthal velocity compared to a non-smoothed stellar potential. Although this deviation is small, we believe that the stellar potential should be smoothed for consistency. A downside of this choice is that there exists no known analytical solution for the equilibrium state of a disk around a central star with a smoothed potential.
The full N-body system with NNB members then has the total potential:
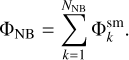 (15)
(15)
Having covered how the point masses affect the gas, the following paragraphs describe how the planets are affected by the gas. For a given point mass, k, at position, rk, the gravitational acceleration exerted onto the point mass by the disk is:
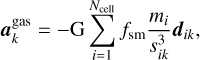 (16)
(16)
where dik = rk − ri is the distance vector between the planet and the cell, mi is the mass of a grid-cell, i, and sik is the smoothed distance between the cell and the point mass. It is given by 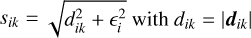 .
.
Again, the acceleration includes єi to account for the finite vertical extent of the disk. The same coefficient is used for the potential. The additional factor is the analog to Eq. (14) and is given by:
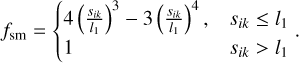 (17)
(17)
We note that the interaction is not symmetric. The acceleration of N-body objects due to the gas is computed using direct summation while the gravitational potential in Eq. (15) enters into the momentum expressions in Eqs. (6) and (7) via a numerical differentiation. Because we computed the smoothing length using the scale height at the location of the cell (as we argue should be done on physical grounds, e.g., Müller et al. 2012), the differentiation causes extra terms that depend on the smoothing length.
To alleviate this issue, we implemented computing the acceleration of the gas due to the N-body objects by direct summation, which has negligible computational overhead. In this way, the interaction is fully symmetric and no additional terms are introduced. As of now, we are unaware of how much this asymmetry affects the results of simulations of planet–disk interaction and the issue is left for future work.
3.7 Self-gravity
Calculating the gravitational potential of a thin (2D) disk is a complex task. Indeed, it requires the vertical averaging of Poisson’s equation, which in general is not feasible. Due to this limitation, in thin disk simulations, we often resort to a Plummer potential approximation for the gas, taking the following form:
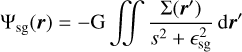 (18)
(18)
with s = ‖r − r'‖, the gravitational constant, G, and a smoothing length, єsg. Contrary to a common belief, the role of this smoothing length is not to avoid numerical divergences at the singularity, s = 0. While it indeed fulfills this function, its main purpose is to account for the vertical stratification of the disk. In other terms, it permits gathering the combined effects of all disk vertical layers in the midplane. Without such a smoothing length, the magnitude of the self-gravity (SG) acceleration would be overestimated. In this context, many smoothing-lengths have been proposed but the most widely used is the one proposed by Müller et al. (2012). Based on an analytic approach, they suggested that the softening should be proportional to the gas scale height, ϵsg = 1.2Hg, to correctly capture SG at large distances.
Direct computation of the potential according to Eq. (18) is prohibitive since it requires N2 operations. Fortunately, assuming a logarithmic spacing in the radial direction and a constant disk aspect ratio, h = H/r = const., the potential can be recast as a convolution product, which can be efficiently computed in order N log(N) operations (Binney & Tremaine 1987) thanks to fast Fourier methods (Frigo & Johnson 2005). Such a method was implemented for the SG accelerations by Baruteau (2008). We use the same method and the module used in FARGOCPT is based on the implementation in FargoADSG (Baruteau & Masset 2008b).
The traditional choice for the smoothing length is  where B is a constant. This choice, however, has two drawbacks. First, it breaks the r − r′ symmetry of the gravitational interaction, which violates Newton’s third law of motion. As a consequence, a nonphysical acceleration in the radial direction is manifested (Baruteau 2008). Second, even if the choice of B = 1.2 h minimizes the errors at large distances (Müller et al. 2012) this, nonetheless, results in SG underestimation at small distances, independent of the value of B (Rendon Restrepo & Barge 2023). This underestimation can quench gravitational collapse.
where B is a constant. This choice, however, has two drawbacks. First, it breaks the r − r′ symmetry of the gravitational interaction, which violates Newton’s third law of motion. As a consequence, a nonphysical acceleration in the radial direction is manifested (Baruteau 2008). Second, even if the choice of B = 1.2 h minimizes the errors at large distances (Müller et al. 2012) this, nonetheless, results in SG underestimation at small distances, independent of the value of B (Rendon Restrepo & Barge 2023). This underestimation can quench gravitational collapse.
FARGOCPT includes two improvements to alleviate those problems. The asymmetry problem can be alleviated by choosing a smoothing length that fulfills the symmetry requirement 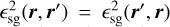 . Additionally, it can be shown that the Fourier scheme is still applicable for a more general form of the smoothing length
. Additionally, it can be shown that the Fourier scheme is still applicable for a more general form of the smoothing length 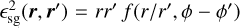 This is fulfilled if the smoothing length is a Laurent series in the ratio
This is fulfilled if the smoothing length is a Laurent series in the ratio 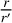 and a Fourier series in ϕ − ϕ' (which additionally captures the 2π periodicity in ϕ). Testing has shown, that the azimuthal dependence is negligible, so we only consider the constant term from the Fourier series. Furthermore, the radial dependence is only weak, so we only consider the first two terms of the Laurent series. This leads to the following form of the smoothing length:
and a Fourier series in ϕ − ϕ' (which additionally captures the 2π periodicity in ϕ). Testing has shown, that the azimuthal dependence is negligible, so we only consider the constant term from the Fourier series. Furthermore, the radial dependence is only weak, so we only consider the first two terms of the Laurent series. This leads to the following form of the smoothing length:
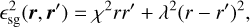 (19)
(19)
with two positively defined coefficients χ and λ. These two parameters depend on the aspect ratio h and can be precom-puted for a given grid size by numerically minimizing the error between the 2D approximation and the full 3D summation of the gravitational acceleration. This requires specifying the vertical stratification of the disk. Assuming that the gravity from the central object is negligible compared to the disk SG, the vertical stratification is a Spitzer profile:
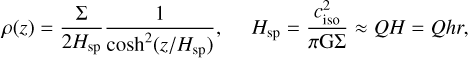 (20)
(20)
with the Toomre parameter
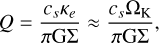 (21)
(21)
with the epicycle frequency κe. Furthermore assuming a grid with rmax/rmin = 250/20, the fit formula for the coefficients are χ(h) = −0.7543h2 + 0.6472h and 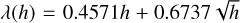 . This is the formula used in FARGOCPT. For grids with substantially different ratios of outer to inner boundary radius, the minimization procedure has to be repeated and the constants changed. This smoothing length leads to a symmetric self-gravity force and has reduced errors for both small and large distances.
. This is the formula used in FARGOCPT. For grids with substantially different ratios of outer to inner boundary radius, the minimization procedure has to be repeated and the constants changed. This smoothing length leads to a symmetric self-gravity force and has reduced errors for both small and large distances.
In the case of a non-constant aspect ratio, we use the mass-averaged aspect ratio which is recomputed after several time-steps. An additional benefit of the symmetric formulation is improved conservation of angular momentum by way of removing the self-acceleration present when using the old smoothing length.
In the limit of weak self-gravity, Q ≥ 20, Rendon Restrepo & Barge (2023) corrected the underestimation of SG at small distances introducing a space-dependent smoothing length, which matches the exact 3D SG force with an accuracy of 0.5%. However, they did not correct the symmetry issue. Despite, this oversight they showed that their correction can lead to the gravitational collapse of a dust clump trapped inside a gaseous vortex (Rendon Restrepo & Gressel 2023) or maintain a fragment bound by gravity (Rendon Restrepo et al. 2022). In their latest work, (Rendon Restrepo et al., in prep.) found the exact kernel for all SG regimes which makes the use of a smoothing length obsolete:
![$K = {1 \over {\sqrt \pi }}{\left\langle H \right\rangle ^{ - 2}}{d \over 8}\exp \left( {{{{d^2}} \over 8}} \right)\left[ {{K_1}\left( {{{{d^2}} \over 8}} \right) - {K_0}\left( {{{{d^2}} \over 8}} \right)} \right],$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq36.png) (22)
(22)
where K0 and K1 are modified Bessel functions of the second kind, 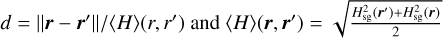 with Hsg defined in Eq. (23). This Kernel remains compatible with the aforementioned convolution product and fast Fourier methods. Although it is computationally expensive to compute the kernel using Bessel functions, it can be precomputed for locally isothermal simulations, thus, it has to be computed only once. For radiative simulations in which the aspect ratio changes, it can be updated only every so often making the method computationally feasible. Finally, this solution shares the properties of the solution presented above making the SG acceleration symmetric and removing the self-acceleration.
with Hsg defined in Eq. (23). This Kernel remains compatible with the aforementioned convolution product and fast Fourier methods. Although it is computationally expensive to compute the kernel using Bessel functions, it can be precomputed for locally isothermal simulations, thus, it has to be computed only once. For radiative simulations in which the aspect ratio changes, it can be updated only every so often making the method computationally feasible. Finally, this solution shares the properties of the solution presented above making the SG acceleration symmetric and removing the self-acceleration.
When considering SG, the balance between vertical gravity and pressure that sets the scale height needs to include the SG component as well. This effect can be included in the standard vertical density stratification ρ(z) = Σ/(2πH) exp (−1/2(z/H)2) to good approximation by adjusting the definition of the scale height (Bertin & Lodato 1999, see their Appendix A). In the case that the SG option is turned on, the standard scale height is replaced by:
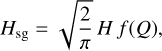 (23)
(23)
![${f(Q) = {\pi \over {4Q}}\left[ {\sqrt {1 + {{8{Q^2}} \over \pi }} - 1} \right],}$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq39.png) (24)
(24)
with the Toomre Q parameter from Eq. (21). In the code, we multiply the result of the standard scale height computation by the factor 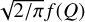 . The epicycle frequency κe in the Toomre parameter in Eq. (21) is calculated as
. The epicycle frequency κe in the Toomre parameter in Eq. (21) is calculated as 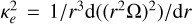 (e.g., Binney & Tremaine 1987) with the angular velocity of the gas Ω.
(e.g., Binney & Tremaine 1987) with the angular velocity of the gas Ω.
For simulations of collapse in self-gravitating disks, we added the OpenSimplex algorithm to our code to initialize noise in the density distribution. The noise is intended to break the axial symmetry of the disk and thereby help gravitational instabilities to develop.
3.8 Energy equation and radiative processes
The original FARGO (Masset 2000) code did not include treatment of the energy equation. This was added in various later incarnations of the FARGO code, including FargoADSG (Baruteau & Masset 2008a) on which this code is based. In this section, we outline the procedure of how the energy update is performed in FARGOCPT. Refer to the grey box on the right in Fig. 1 for a visual representation. The subscripts of the variables in this section refer to the ones in Fig. 1, intended to help the reader in locating the sub-steps.
The energy update step due to compression or expansion, shock heating, viscosity, irradiation, and radiative cooling or β-cooling is implemented using operator splitting. Our scheme consists of a mix of implicit update steps.
In principle, we perform the energy update on the sum of internal energy density e and the radiation energy density erad = aT4, thus assuming a perfect coupling between the ideal and the photon gas, the so-called one-temperature approximation (see Sect. 3.8.5 for more detail). Separately, these quantities change according to:
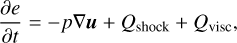 (25)
(25)
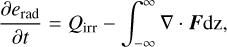 (26)
(26)
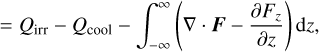 (27)
(27)
with the 3D radiation energy flux F, viscous heating Qvisc, shock-heating as captured by artificial viscosity Qshock, irradiation Qirr, and radiative losses at the disk surfaces 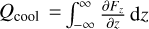 . Note, that the vertical cooling part Qcool is split off from the integral over ∇ • F.
. Note, that the vertical cooling part Qcool is split off from the integral over ∇ • F.
In principle, the total energy update is then:
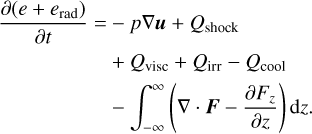 (28)
(28)
We split this update into three main parts applied in the following order. The first line represents shock heating and compression heating (see Sect. 3.8.1), the second line represents heating and cooling (see Sect. 3.8.2), and the third line represents the radiation transport (see Sect. 3.8.5).
The following subsections review the details of this process.
3.8.1 Compression heating and shock heating
The pressure term is updated first following D’Angelo et al. (2003) with an implicit step using an exponential decay ensuring stability (see their Eq. (24)). The update is expressed as:
![${e_b} = {e_a}\exp \left[ { - (\gamma - 1){\rm{\Delta }}t\nabla \cdot {u_n}} \right],$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq47.png) (29)
(29)
with the adiabatic index, γ. As a next step, shock heating is treated in the form of heating from artificial viscosity:
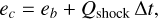 (30)
(30)
with Qshock being the right-hand-side of Eq. (88) where Σ = Σa and u = ub.
3.8.2 Heating and cooling
This step considers the update due to viscosity, irradiation, and cooling. The relevant part from Eq. (28) is
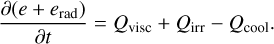 (31)
(31)
To arrive at the expression for this update step, we first insert explicit expressions for the two energies. The internal energy density is e = ρcVT with the specific heat capacity 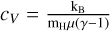 , where kB is the Boltzmann constant, mH is the mass of a hydrogen atom, and µ is the mean molecular weight. The radiation energy density is given by
, where kB is the Boltzmann constant, mH is the mass of a hydrogen atom, and µ is the mean molecular weight. The radiation energy density is given by 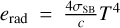 with the Stefan-Boltzmann constant σSB and the speed of light c. Then, we use a first-order discretization for the time derivative and rearrange it according to the time index of T. Finally, we convert to an expression for the internal energy e arriving at:
with the Stefan-Boltzmann constant σSB and the speed of light c. Then, we use a first-order discretization for the time derivative and rearrange it according to the time index of T. Finally, we convert to an expression for the internal energy e arriving at:
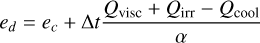 (32)
(32)
This implicit energy update is stable in our testing. The heating and cooling rates are calculated as described in the following sections. Each of the terms is optional and can be configured by the user. Cooling rates are discussed in Sects. 3.8.3 and 3.8.4, irradiation is discussed in Sect. 3.8.6. and viscous heating is discussed in Sect. 3.9.
3.8.3 Radiative Cooling
For radiative cooling, we take the same approach as (Müller & Kley 2012) where energy can escape through the disk surfaces and the energy transport from the disk midplane to the surfaces is modeled using an effective opacity. The associated cooling term is
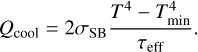 (34)
(34)
The minimum temperature Tmin, defaulting to 4 K, is set to take into account that the disk does not cool towards a zero Kelvin region but rather towards a cold environment slightly warmer than the cosmic microwave background. This can be important in the outer regions of the disk and effectively sets a temperature floor. For the effective opacity we used (Hubeny 1990; Müller & Kley 2012; D’Angelo & Marzari 2012):
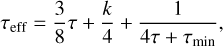 (35)
(35)
where k = 2 for an irradiated disk and 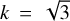 for a non-irradiated disk (D’Angelo & Marzari 2012),
for a non-irradiated disk (D’Angelo & Marzari 2012),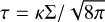 is the optical depth calculated from the Rosseland mean opacity k, and τmin = 0.01 is a floor value to capture optically very thin cases in which line opacities become dominant (Hubeny 1990).
is the optical depth calculated from the Rosseland mean opacity k, and τmin = 0.01 is a floor value to capture optically very thin cases in which line opacities become dominant (Hubeny 1990).
There are three options to compute the opacity in the code: lin (Lin & Papaloizou 1985), bell (Bell & Lin 1994), and constant for a constant opacity. For the first two, see Müller & Kley (2012) for more details. Additional opacity laws can be easily implemented by expanding the code by a function that returns the opacity κ(ρ, T) as a function of the temperature and volume density.
In case of β-cooling (Gammie 2001), we have:
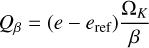 (36)
(36)
is added to Qcool where eref is the reference energy to which the energy is relaxed. This reference can either be the initial value or prescribed by a locally isothermal temperature profile. We note that β-cooling is a misnomer as it is not exclusively a cooling process but rather a relaxation process towards a reference state. If the temperature is lower than in the reference state, the energy is increased, that is, heating occurs.
3.8.4 S-curve cooling
For the specific case of simulating cataclysmic variables, we also included the option to compute Qcool according to Ichikawa & Osaki (1992) and Kimura et al. (2020). Their model splits the cooling function into a cold, radiative branch and a hot, convec-tive branch. They used opacities based on Cox & Stewart (1969) and a vertical radiative flux, namely, the radiative loss from one surface of the disk, of:
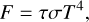 (37)
(37)
for the optically thin regime to derive the radiative flux of the cold branch:
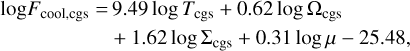 (38)
(38)
where the subscript cgs indicates the value of the respective quantity in cgs units. The cold branch is valid for temperatures, T < TA, where TA is the temperature at which:
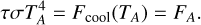 (39)
(39)
The radiative flux of the hot branch is derived by assuming that disk quantities do not vary in the vertical direction (one-zone model) for an optically thick disk:
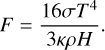 (40)
(40)
Using Kramer’s law for the opacity of ionized gas, the radiative flux can be approximated as:
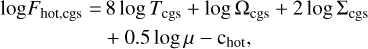 (41)
(41)
where the constant chot = 25.49 was used in Ichikawa & Osaki (1992) and chot = 23.405 in Kimura et al. (2020). The difference between the two constants is that the first leads to weaker cooling compared to the latter. The hot branch is valid for temperatures T > TB, where TB is the temperature at which:
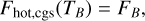 (42)
(42)
where log FB = max(K, log FA) with (based on Fig. 3 in Mineshige & Osaki 1983)
![$K = 11 + 0.4\log \left[ {{{2 \times {{10}^{10}}} \over {{r_{{\rm{cm}}}}}}} \right].$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq65.png) (43)
(43)
The radiative flux in the intermediate branch is given by an interpolation between the cold and hot branches:
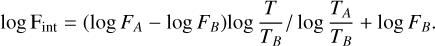 (44)
(44)
The cooling term is then given by 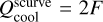 due to the radiation from both sides of the disk where F is the radiative flux pieced together from the cool, intermediate, and hot branches as described above. These prescriptions were developed for the conditions inside an accretion disk, and we found that it leads to numerical issues when applied to the low-density regions outside a truncated disk. We therefore opted to modulate the radiative flux with a square root function for densities below Σthresh < 2 g cm−2 and a square function for temperatures below Tthresh < 1200K:
due to the radiation from both sides of the disk where F is the radiative flux pieced together from the cool, intermediate, and hot branches as described above. These prescriptions were developed for the conditions inside an accretion disk, and we found that it leads to numerical issues when applied to the low-density regions outside a truncated disk. We therefore opted to modulate the radiative flux with a square root function for densities below Σthresh < 2 g cm−2 and a square function for temperatures below Tthresh < 1200K:
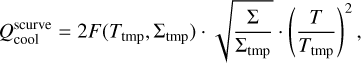 (45)
(45)
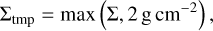 (46)
(46)
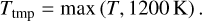 (47)
(47)
3.8.5 In-plane radiation transport using FLD
The last term in Eqs. (3) and (28), the in-plane radiation transport, is treated using the flux-limited diffusion (FLD) approach (Levermore & Pomraning 1981; Levermore 1984). The method allows us to treat radiation transport as a diffusion process, both, in the optically thick and optically thin regime. Our implementation builds upon Kley (1989), Kley & Crida (2008), Müller (2013) and uses the successive over-relaxation (SOR) method to solve the linear equation system involved in the implicit energy update.
In principle, the process of radiation transport is described by the evolution of a two-component gas consisting of an ideal gas and a photon gas which have thermal energy densities e = egas and erad, respectively (Mihalas & Mihalas 1984). In the flux-limited diffusion approximation, their coupled evolution is given by (Kley 1989; Commerçon et al. 2011; Kolb et al. 2013):
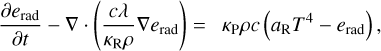 (48)
(48)
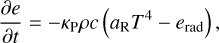 (49)
(49)
where λ is the flux limiter. We use the flux limiter presented in Kley (1989, see this reference for alternatives) which is given by:
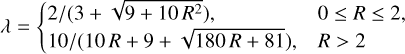 (50)
(50)
with the dimensionless quantity
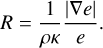 (51)
(51)
In FARGOCPT, we use the one-temperature approximation, meaning that we assume that the photon gas and the ideal gas instantaneously equilibrate their temperatures, Tgas = T and Trad. This approximation allows us to reduce Eqs. (48) and (49) into a single equation for the total thermal energy, e + erad. We further assume that erad is negligible against e (and the same for their time derivatives) yielding:
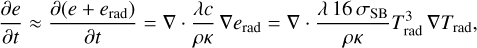 (52)
(52)
where we used 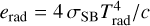 . To see that erad is indeed negligible against e, we assume that the gas is a perfect gas and consider the ratio of energy densities:
. To see that erad is indeed negligible against e, we assume that the gas is a perfect gas and consider the ratio of energy densities:
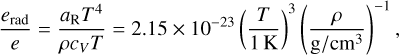 (53)
(53)
where we used µ = 2.35 and γ = 1.4. Assuming further a minimum mass solar nebula (MMSN; Hayashi 1981) density with Σ(r) = 1700 g/cm2 (r/au)−3/2, the ratio becomes:
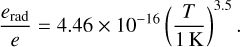 (54)
(54)
The dependence on the radius cancels out in the calculation of ρ from Σ because of the specific exponent of −3/2 of the MMSN. Now, we can see that erad/e ranges from 4.7 × 10−9 at T = 100 K to 1.6 × 10−4 at T = 2000 K. Thus, the approximation is justified in the context of planet-forming disks.
Then, we again make use of the assumption that the gas and the photon gas equilibrate their temperatures instantaneously, namely, T = Trad, and use the fact that ρ can be considered constant during the radiation transport part of the operator splitting scheme. Furthermore, we assume the opacity k to be constant during the radiation transport step, although in principle it depends on T. Equation (52) can then be recast into an equation for T yielding:
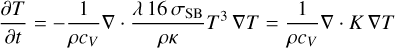 (55)
(55)
with 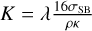 . This diffusion equation is then discretized and the resulting linear equation system is solved using the SOR method resulting in an updated temperature T'. Details of the discretization and implementation of the SOR solver can be found in Appendix 1 of Müller (2013). Finally, we assume that the gas is a perfect gas and update its internal energy density by using the new temperature,
. This diffusion equation is then discretized and the resulting linear equation system is solved using the SOR method resulting in an updated temperature T'. Details of the discretization and implementation of the SOR solver can be found in Appendix 1 of Müller (2013). Finally, we assume that the gas is a perfect gas and update its internal energy density by using the new temperature,
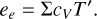 (56)
(56)
Here, ee is an energy surface density again (also see Fig. 1), as opposed to the energy volume densities in the rest of the section above.
We note that our implementation uses the 3D formulation. Other implementations of midplane radiation transport (also the one described in Müller 2013) use the surface density instead and have to introduce a factor 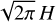 (sometimes also chosen as 2H) to link the surface density to the volume density which depends on the vertical stratification of the disk. However, if we assume ρ (or equivalently H) to be constant throughout the radiative transport step, this factor cancels out in the end and the two approaches are equivalent. For the sake of simplicity, we use the 3D version and assume that all horizontal radiation transport is confined to the midplane. Before the radiation transport step, we compute
(sometimes also chosen as 2H) to link the surface density to the volume density which depends on the vertical stratification of the disk. However, if we assume ρ (or equivalently H) to be constant throughout the radiative transport step, this factor cancels out in the end and the two approaches are equivalent. For the sake of simplicity, we use the 3D version and assume that all horizontal radiation transport is confined to the midplane. Before the radiation transport step, we compute 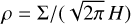
The FLD implementation is tested with two separate tests. The first test, presented in Appendix D.8, shows a test for the physical part in which a disk equilibrates to two different temperatures enforced at the inner and outer boundaries. The second test, presented in Appendix D.9, shows a test for the SOR diffusion solver which compares the numerical results of a 2D diffusion process against the available analytical solution. We note that the current implementation of the FLD module only considers a perfect gas so it should not be used together with the non-constant adiabatic index (see Sect. 3.8.7) without further testing or modifications.
3.8.6 Irradiation
The irradiation term is computed as the sum of the irradiation from all N-body objects. This allows for simulations in which planets or a secondary star irradiate the disk. An N-body object is considered to be irradiating, if it is assigned a temperature and radius in the config file.
For each single source with index k, the heating rate due to irradiation is computed following Menou & Goodman (2004) and D’Angelo & Marzari (2012) as:
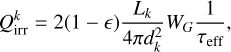 (57)
(57)
with the disk albedo є which is set to 1 /2, the luminosity of the source, Lk, the distance to the source, dk, and the effective optical depth, τeff. The luminosity is calculated as 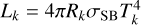 with the radius, Rk, and the temperature, Tk, of the source, and the effective opacity, τeff, as given in Eq. (35). The remaining factor WG is a geometrical factor that accounts for the disk geometry in the case of a central star (Chiang & Goldreich 1997) and includes terms for close to the source (first term) and far from the source (second term). It is given by:
with the radius, Rk, and the temperature, Tk, of the source, and the effective opacity, τeff, as given in Eq. (35). The remaining factor WG is a geometrical factor that accounts for the disk geometry in the case of a central star (Chiang & Goldreich 1997) and includes terms for close to the source (first term) and far from the source (second term). It is given by:
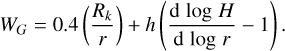 (58)
(58)
We assume the flaring of the disk, 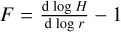 , is constant in time and has the value of the free parameter specified for the initial conditions. Properly accounting for the disk geometry would require ray-tracing from all sources to all grid cells which is computationally expensive. Finally, the total irradiation heating rate is given by:
, is constant in time and has the value of the free parameter specified for the initial conditions. Properly accounting for the disk geometry would require ray-tracing from all sources to all grid cells which is computationally expensive. Finally, the total irradiation heating rate is given by:
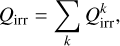 (59)
(59)
where the sum runs over all irradiating objects.
3.8.7 Non-constant adiabatic Index
In astrophysics, it is very common to treat matter as ideal gas, for which the following equation, also known as the ideal gas law, holds:
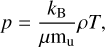 (60)
(60)
with the pressure p, the Boltzmann constant, kB, the mean molecular weight, µ, the density, ρ, the temperature, T, and the atomic mass unit mu. In the case of an ideal gas, the assumption is that there are no interactions between the gas particles and the pressure is only exerted by interactions with the boundary of a volume, containing the gas. This is very often a good approximation, especially in the case of accretion disks where densities are low.
A further assumption that is commonly made is that of a perfect gas, for which the pressure and sound speed are related to ρ and T by the same constant adiabatic index:
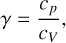 (61)
(61)
which is the ratio of the specific heat capacity at constant pressure with the one at constant volume, with γ = 5/3 for a monatomic gas and γ = 7/5 for a diatomic gas (e.g., Vaidya et al. 2015). The pressure and sound speed of a perfect gas are:
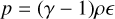 (62)
(62)
The assumption of a perfect gas is a good approximation at 300 ≲ T ≲ 1000–2000 K, with some density dependence (see Fig. 1 of D’Angelo & Bodenheimer 2013). At lower or higher temperatures, contributions by rotational and vibrational degrees of freedom, or changes in the chemical composition such as the dissociation and ionization of hydrogen, would need to be taken into account. Confusingly, the perfect gas is often referred to as the ideal gas in the literature.
In the following, we outline the case of a general ideal gas in which the single constant adiabatic index is replaced with two other quantities. Hence, in Eqs. (62) and (63) the constant γ will be replaced by the effective adiabatic index γeff and the first adiabatic exponent Γ1, respectively.
With these changes, the equation of state can account for the dissociation and ionization processes of hydrogen, as well as rotational and translational degrees of freedom at lower temperatures. Such an equation of state was already implemented in PLUTO by Vaidya et al. (2015) which serves as a basis for the changes in our code. In the PLUTO code, this equation of state is called the “PVTE” equation of state which stands for pressure-volume-temperature-energy. We adopted the same name for the equation of state in FARGOCPT.
We start by writing the total internal energy density ρє of an ideal gas as a summation of several contributions:
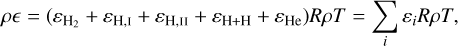 (64)
(64)
with R = kB/mH. These contributions are given by (compare Table 1 from Vaidya et al. 2015):
![$\eqalign{ & {\varepsilon _{{\rm{H}},{\rm{I}}}} = {3 \over 2}X(1 + x)y\left( {{\rm{translational energy for hydrogen}}} \right), \cr & {\varepsilon _{{\rm{He}}}} = {3 \over 8}Y\left( {{\rm{translational energy for helium}}} \right), \cr & {\varepsilon _{{\rm{H}} + {\rm{H}}}} = 4.48{\rm{eVXy}}/\left( {2{k_B}T} \right)\left( \matrix{ {\rm{dissociation energy for}} \hfill \cr {\rm{molecular hydrogen}} \hfill \cr} \right), \cr & {\varepsilon _{{\rm{H}},{\rm{II}}}} = 13.6{\rm{eV}}Xxy/\left( {{k_B}T} \right)\left( \matrix{ {\rm{ionization energy for}} \hfill \cr {\rm{atomic hydrogen}} \hfill \cr} \right), \cr & {\varepsilon _{{{\rm{H}}_2}}} = {{X(1 - y)} \over 2}\left[ {{3 \over 2} + {T \over {{\zeta _v}}}{{{\rm{d}}{\zeta _v}} \over {{\rm{d}}T}} + {T \over {{\zeta _r}}}{{{\rm{d}}{\zeta _r}} \over {{\rm{d}}T}}} \right]\left( \matrix{ {\rm{internal}} \hfill \cr {\rm{energy for molecular hydrogen}} \hfill \cr} \right), \cr} $](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq94.png)
where X (defaulting to 0.75 in the code) and Y = 1 − X are the hydrogen and helium mass fractions and y and x are the hydrogen dissociation and ionization fractions, defined as:
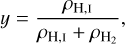 (65)
(65)
ζv and ζr are the partition functions of vibration and rotation of the hydrogen molecule and are described in D’Angelo & Bodenheimer (2013). If we assume local thermodynamic equilibrium, then y and x can be computed by using the following two Saha equations:
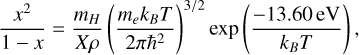 (67)
(67)
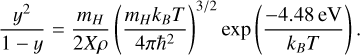 (68)
(68)
After applying the ideal gas law and inserting Eq. (64), the pressure-internal energy relation becomes:
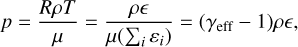 (69)
(69)
where 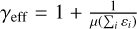 is the effective adiabatic index and µ is the mean molecular weight, given by:
is the effective adiabatic index and µ is the mean molecular weight, given by:
![$\mu = 4[2X(1 + y + 2xy) + Y].$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq101.png) (70)
(70)
Now, by using the relation from Eq. (69) an equation for the temperature can be derived:
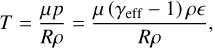 (71)
(71)
which can be solved for a given internal energy and density as a root-finding problem:
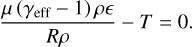 (72)
(72)
The sound speed is given by:
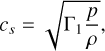 (73)
(73)
where Γ1 is the first adiabatic exponent, which is defined as:
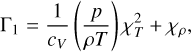 (74)
(74)
where the temperature and density exponents are defined by:
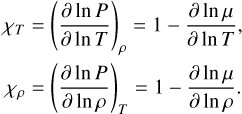 (75)
(75)
Since the computational effort to compute γeff, Γ1, and µ for every cell at every time step is very high, we precompute them to create lookup tables. During the simulation, the values of γeff, Γ1, and µ are interpolated from the lookup tables for given densities and internal energies. How these tables can be implemented is also explained in Vaidya et al. (2015).
As our code is 2D, we require the scale height to compute the densities used for reading the adiabatic indices from the lookup table. To compute the scale height, our method requires the adiabatic indices. This results in a cyclic dependency. We found that this is not an issue, as successive time-steps naturally act as an iterative solver for this problem. We additionally always compute the scale height twice, before and after updating the adiabatic indices and we perform this iteration twice per time step. We tested our implementation using the shock tube test. Because there is no analytical solution for the shock tube test with non-constant adiabatic indices, we compared our results against results generated with the PLUTO code. The test is shown in Fig. D.3 under the label ‘PVTE’ and we find good agreement between our implementation and the implementation by Vaidya et al. (2015).
3.9 Viscosity
Viscosity is implemented as an operator splitting step (see Fig. 1 for its context). The full viscous stress tensor reads (see, e.g., Shu 1992):
![${\sigma _{ij}} = 2\mu \left[ {{1 \over 2}\left( {{{\partial {u_i}} \over {\partial {x_j}}} + {{\partial {u_j}} \over {\partial {x_i}}}} \right) - {{{\delta _{ij}}} \over 3}\nabla \cdot u} \right] + \zeta {\delta _{ij}}\nabla \cdot u,$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq107.png) (76)
(76)
where i, j ∈ {1,2} indicate the spatial directions, µ and ζ are the shear and bulk viscosity, respectively, and δij is the Kronecker δ. The shear viscosity is given by µ = vΣ with the kinematic viscosity denoted by v. In our case, ζ is neglected, although artificial viscosity (see Sect. 3.9.1) reintroduces a bulk viscosity. The kinematic viscosity is either given by a constant value or the α-prescription (Shakura & Sunyaev 1973) for which:
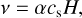 (77)
(77)
with the disk scale height, H.
The relevant elements in polar coordinates of the viscous stress tensor are:
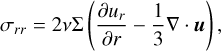 (78)
(78)
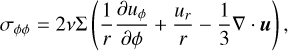 (79)
(79)
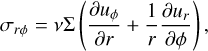 (80)
(80)
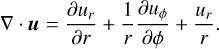 (81)
(81)
The momentum update is then performed according to Kley (1999; see also D’Angelo et al. 2002) as:
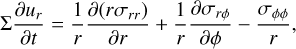 (82)
(82)
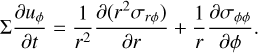 (83)
(83)
Finally, the energy update due to viscosity (D’Angelo et al. 2003) is given by:
![${{\partial e} \over {\partial t}} = {{{Q_{{\rm{visc}}}}} \over {\Delta t}} = {1 \over {2v{\rm{\Sigma }}}}\left[ {\sigma _{rr}^2 + 2\sigma _{r\phi }^2 + \sigma _{\phi \phi }^2} \right] + {{2v{\rm{\Sigma }}} \over 9}{(\nabla \cdot u)^2},$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq115.png) (84)
(84)
where Qvisc is to be used in the energy update in Eq. (32).
3.9.1 Tscharnuter and Winkler artificial viscosity
The role of artificial viscosity is to handle (discontinuous) shock fronts in finite-difference schemes. This is achieved by smoothing the shock front over several grid cells by adding a bulk viscosity term. Tscharnuter & Winkler (1979) raised concerns about the formulation of artificial viscosity introduced by Von Neumann & Richtmyer (1950), as it can produce artificial pressure even if there are no shocks (e.g., Bodenheimer et al. 2006, Sect. 6.1.4). Tscharnuter & Winkler (1979) then proposed a tensor artificial viscosity, analogous to the viscous stress tensor, that is independent of the coordinate system and frame of reference. For our implementation of this artificial viscosity, we follow Stone & Norman (1992, Appendix B) who added two additional constraints on the artificial viscosity: the artificial viscosity constant must be the same in all directions and the off-diagonal elements of the tensor must be zero to prevent artificial angular momentum transport. We note that there is also an artificial viscosity described in the main text of Stone & Norman (1992), sometimes referred to as the “Stone and Norman” artificial viscosity, which does not have these properties and is only applicable in Cartesian coordinates. Nonetheless, it is sometimes used in cylindrical and spherical coordinates.
In our case, we use the version suited for curve-linear coordinates and the artificial viscosity pressure tensor is given by:
![${\bf{Q}} = \left\{ {\matrix{ {{l^2}{\rm{\Sigma }}(\nabla \cdot u)\left[ {\nabla \otimes u - {1 \over 3}(\nabla \cdot u){\bf{I}}} \right]\,\,\,\,\,{\rm{if}}\nabla \cdot {\bf{u}} < 0} \cr {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{otherwise}}} \cr } ,} \right.$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq116.png) (85)
(85)
where l = q Δx is the distance over which shocks are smoothed with the dimensionless parameter q near unity and the cells size Δx. It is given by Δx = max(Δxa, Δxb) where a and b indicate the grid of cell centers and interfaces, respectively. The contribution to the momentum equation is:
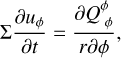 (86)
(86)
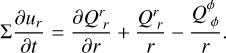 (87)
(87)
Finally, the shock heating caused by the artificial viscosity is given by:
![$\matrix{ {{{\partial e} \over {\partial t}} = - {l^2}{\rm{\Sigma }}(\nabla \cdot u){1 \over 3}\left[ {{{\left( {{{\partial {u_r}} \over {\partial r}}} \right)}^2} + {{\left( {{{\partial {u_\phi }} \over {r\partial \phi }} + {{{u_r}} \over r}} \right)}^2}} \right.} \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{\left( {{{\partial {u_\phi }} \over {r\partial \phi }} + {{{u_r}} \over r} - {{\partial {u_r}} \over {\partial r}}} \right)}^2}} \right].} \cr } $](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq119.png) (88)
(88)
To ensure the stability of these updates, we use a CFL constraint analogous to the one in (Stone & Norman 1992, see their Sect. 4.6):
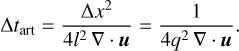 (89)
(89)
3.9.2 Local viscosity stabilizer
We found numerical instabilities in simulations of disks in close binary systems. In these systems, the disk is truncated by tidal forces (e.g., Artymowicz & Lubow 1994). At this truncation radius, the strong density gradients can cause numerical instabilities in the viscosity update step which drastically reduces the time step.
To prevent these instabilities, we designed a damping method that checks whether the viscosity update is too large and unstable and then reduces the update to a stable size. This method has the advantage that it is a local per-cell update that can be dropped into the existing code with only one modification to the update step. An alternative solution would be to implement a full implicit viscosity update step based on solving a linear system of equations which would have required substantial changes to our code in the viscosity update step. Furthermore, this implicit update would be computationally more expensive whereas the overhead of the local damping method is negligible. Because the instability is numerical and confined to only a small region, we argue that the damping method is a valid solution.
For our method, we interpret the viscosity update as a diffusion process. As we are only looking at a single cell, we treat the velocities of the neighboring cells as constant. We then can write the velocity update due to viscosity in the form of:
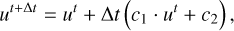 (90)
(90)
where in the nomenclature of Fig. 1, ut+Δt = ud and ut = uc. The analytical solution to this equation is an exponential relaxation to the equilibrium velocity of 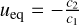 When the explicit update overshoots the equilibrium velocity, the method becomes unstable. One option to avoid the instability is to add Δt • c1 > −1 to the CFL criteria but this effectively freezes the simulation. Instead, the code can now be configured to:
When the explicit update overshoots the equilibrium velocity, the method becomes unstable. One option to avoid the instability is to add Δt • c1 > −1 to the CFL criteria but this effectively freezes the simulation. Instead, the code can now be configured to:
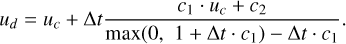 (91)
(91)
for the velocity update due to viscosity (see Sect. 3.9). For Δt • c1 > −1, the update reverts to Eq. (90), while for Δt • c1 < −1, the new velocity is set to the equilibrium velocity, ueq.
Compared to the other solution for overly large time steps (which typically allow for overshooting), we argue that an exponential decay to the equilibrium velocity is a physically more plausible choice. However, we should keep in mind that this method violates angular momentum conservation. In our tests, we found that only a few, low-density cells are unstable that have little influence on the whole simulation.
In Fig. 2, we show two simulations of a cataclysmic variable during a super-outburst, with the only difference being the stabilizing method turned on (blue line) or off (red line). The top and bottom panels show the time evolution of luminosity and mass-weighted eccentricity, respectively. The numerical instabilities that are dominating the luminosity (red line) are prevented by this method. Yet, the overall time evolution of the eccentricity is similar. Using the eccentricity as a proxy for the dynamical evolution of the disk, we can conclude that the stabilizing method only has a negligible impact on the physics.
 |
Fig. 2 Luminosity and mass-weighted eccentricity during a super-outburst in a cataclysmic variable system with and without our viscosity stabilizer. The simulation without the stabilizer required 3.8 times more time-steps during the shown time frame. |
3.10 CFL criterion for heating and cooling
A heating and cooling time step criterion was added similar to the cooling CFL criteria used in the PLUTO code (Mignone et al. 2007). We found the additional CFL criteria beneficial to simulations of disks in close binaries that have truncated disks with strong density gradients (Wehner et al., in prep.). The time step must be smaller than:
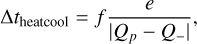 (92)
(92)
where f is a fudge factor to set the maximum energy change per time step. We found that a factor of f = 10 by trial-and-error to improve stability while not impacting the overall time step too much.
3.11 Scale-height dependent on all point masses
The scale height is determined by the balance between vertical gravity and pressure forces. Realistically, the gravity of all N-body objects, including planets, should contribute to the gravitational force. Including these contributions, the scale height can be computed as (Günther et al. 2004):
![$H = {\left[ {\mathop {\mathop \sum \nolimits^ }\limits_{{N_b}}^i {1 \over {H_i^2}}} \right]^{ - 1/2}},\quad {H_i} = {{c_s^{{\rm{iso}}}} \over {{{\rm{\Omega }}_{{\rm{K}},i}}}},$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq125.png) (93)
(93)
where 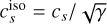 is the isothermal sound speed and ΩK,i is the Keplerian frequency with respect to the ith N-body object.
is the isothermal sound speed and ΩK,i is the Keplerian frequency with respect to the ith N-body object.
For the computation of self-gravity presented in Sect. 3.7, we need a value for the aspect ratio. In the case that the full N-body system influences the scale height, we compute the aspect ratio in an analog way:
![$h = {\left[ {\mathop {\mathop \sum \nolimits^ }\limits_{{N_b}}^i {1 \over {h_i^2}}} \right]^{ - 1/2}},\quad {h_i} = {{c_s^{{\rm{iso}}}} \over {{\upsilon _{{\rm{K}},i}}}}.$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq127.png) (94)
(94)
3.12 Particle system
FARGOCPT can simulate solid particles of any size in a proto-planetary disk. A collection of solid particles is represented as Lagrangian super-particles. This means that a bunch of identical physical particles, with the same size and same density, are represented by one super-particle. These super-particles are then evolved in the simulation according to the forces acting on them: a drag force due to the gas and gravity from the N-body objects and the disk if self-gravity of the gas is enabled.
These super-particles do not react back on the gas. As such, the mass of each super-particle can be changed freely even after the simulation. The number of super-particles determines how well the dynamics of solid particles are resolved or sampled in the simulation. The first implementation of these Lagrangian super-particles in FARGOCPT was used in Picogna & Kley (2015).
The particle system is synchronized to the N-body and hydro simulation once every iteration, namely, at time tn, and then integrated for a time equal to the time step resulting from the CFL criterion Δt , that is, until tn+1 = tn + Δt . The code supports two different integrators for particle motion. The first one is an implicit exponential midpoint integrator as described in Mignone et al. (2019, Appendix B.2.1) that combines two regimes of particle sizes ranging from micrometer-sized dust (St ≪ 1) to meter-sized boulders (St ≥ 1). The second choice is an explicit fifth order Runge-Kutta integrator with adaptive time stepping (Cash & Karp 1990) to integrate very large particles with St ≫ 1 such as planetesimals.
In both integrators, the integration step can be performed in polar coordinates while the explicit integrator also supports Cartesian coordinates. The polar formulation conserves angular momentum better in the case of circular particle orbits. We found, however, that as soon as the orbits become eccentric, this advantage disappears.
3.12.1 Drag force
The friction force for the gas drag is calculated as a smooth interpolation between the Epstein and Stokes regimes. We use a model that follows Picogna et al. (2018) but with the Epstein drag calculated according to Woitke & Helling (2003).
The drag model depends on three dimensionless numbers: Knudsen number Kn, Mach number Ma, and Reynolds number Re. Those are given by:
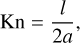 (95)
(95)
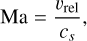 (96)
(96)
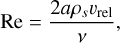 (97)
(97)
where a is the radius of the solid particle, l is the mean free path of the gas molecules, cs is the sound speed, ρs is the material density of the particle, vrel is the relative velocity between the particle and the gas, and v is the kinematic viscosity coefficient of the gas. We note that the latter is different from the kinematic viscosity coefficient used to model turbulent accretion with the α model.
The mean free path of the gas molecules is given by (Haghighipour & Boss 2003):
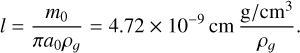 (98)
(98)
with a0 = 1.5 × 10−8 cm, assuming the gas consists primarily of H2 molecules, and the mass volume density of the gas ρg. The kinematic viscosity coefficient is given by:
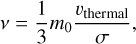 (99)
(99)
with the thermal velocity 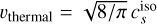 and the collisional cross-section between the gas molecules
and the collisional cross-section between the gas molecules 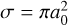 .
.
The drag force Fdrag, a particle in the disk is subjected to, is related to the stopping time tstop via:
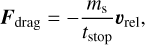 (100)
(100)
with the mass of a solid particle ms. The stopping time is given by:
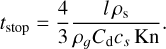 (101)
(101)
The total drag coefficient results from a quadratic interpolation between the free molecular flow (Epstein) and viscous regime (Stokes) and is given by (Woitke & Helling 2003, see their Eq. (18)):
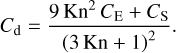 (102)
(102)
The Epstein drag coefficient is a smooth interpolation of the sub-and supersonic regimes of the Stokes drag (Woitke & Helling 2003, see their Eq. (13)):
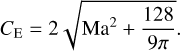 (103)
(103)
The Stokes drag coefficient is given by (Eq. (15) in Woitke & Helling 2003):
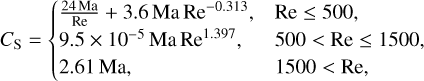 (104)
(104)
We note that the expressions here differ from the ones in Picogna et al. (2018) and Woitke & Helling (2003) because ours are formulated for computing tstop in Eq. (101), while the others are formulated for computing Fdrag directly. In Appendix D.6, we present a test of the radial dust drift velocity resulting from the gas drag.
3.12.2 Dust diffusion
Simulating dust with Stokes numbers around unity requires treating dust diffusion due to unresolved small-scale turbulent motion of the gas. Otherwise, this dust accumulates nonphysically in a single point at a pressure maximum, such as the centers of large-scale vortices. Our code includes dust diffusion modeled with stochastic kicks in analogy to Charnoz et al. (2011). In this model, the Lagrangian super-particles receive a kick at every time step. The kick is only applied in the radial direction such that:
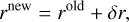 (105)
(105)
and the azimuthal velocity is corrected to conserve angular momentum:
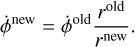 (106)
(106)
The correction of the azimuthal velocity is required to avoid a nonphysical drift due to the changed angular momentum.
where we the symbols carry the same meaning as in Charnoz et al. (2011, see their Eq. (17)). 〈δr〉 = ΔtDd/ρgδρg/δr is the mean and σ2 = 2DdΔt is the variance of a random Gaussian variable, W is a standard normal random variable, and δ2D is an additional displacement to take into account the second dimension, namely, the diffusion in the ϕ direction. The dust diffusion coefficient is Dd = v/Sc = αcsH/Sc with the Schmidt number, Sc = (1 + St2)2/(1 + 4St2) (Youdin & Lithwick 2007). The factor ΔtΩK takes into account the time correlation in the kicks due to the gas turbulence (see Sect. 2.7 in Charnoz et al. 2011).
can be derived by a geometrical argument taking into account the diffusive spread in the azimuthal direction. We consider a dust particle on a circular orbit that is displaced by a turbulent kick in the azimuthal direction. Its final location will be radially further out from where it started, independent of whether it was kicked in the direction of the orbit or opposite to it. This positive radial change is taken into account by δ2D.
To save computational costs, we use the same standard random number, W, in Eq. (107) and in Eq. (108). This introduces correlations between two contributions to the kick. However, the factor Wσ is a small number compared to the relevant length scales and the 2D correction is quadratic in Wσ which can be seen by a Taylor expansion of Eq. (108): 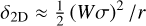 . Additionally, the direction of the radial kick and the 2D correction are not correlated, because the latter is always positive. Thus the effect of the correlations should be negligible.
. Additionally, the direction of the radial kick and the 2D correction are not correlated, because the latter is always positive. Thus the effect of the correlations should be negligible.
To our knowledge, this correction has not been used before when kicks were only applied in the radial direction. However, we found it to be necessary to match the solutions of the radial advection-diffusion equation, see Appendix D.5.
For generating the random numbers for these steps, we added the small non-cryptographic random generator by Bob Jenkins (JSF) which is fast and well-tested. The implementation of the generator as well as tests are shown in O’Neill (2018).
A test of this procedure is presented in Appendix D.6 in the form of a comparison of simulations of the spread of a thin dust ring simulated in FARGOCPT against a solution of the radial advection-diffusion equation. We find excellent agreement between the two approaches.
3.13 Accretion onto point masses
When accretion is enabled, mass is removed from the disk and added to the N-body object. The mass is removed from the vicinity of the N-body object similar to Kley (1999) with a fixed half-emptying time. The momentum of the accreted mass is added to the N-body object. The radius around the N-body object from which mass is removed, Racc, is given by a fraction of the Roche lobe radius RRoche, which we calculate as described in Sect. 3.6. The accretion radius is given by:
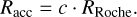 (109)
(109)
For a cell with mass mi and distance di to the accreting object, the rate of mass removal is given by:
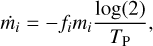 (110)
(110)
where ƒi is the accretion fraction for cell i. Close to the planet, it is higher and decreases with distance. We use a simple two-step function such that:
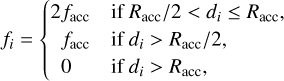 (111)
(111)
with the accretion parameter, ƒacc, which can be chosen individually for each N-body object. ƒi is additionally limited by the mass in the cell mi such that ƒi = min(ƒi , (mi - AiΣfloor)TP/(log(2)Δt)), where Ai is the area of cell i and Σfloor is the density floor. This scheme effectively takes away mass from the cells with a half-emptying time of TP/ƒi. Summation over the cells in the vicinity of the body yields the accretion rate and momentum transfer onto it:
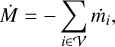 (112)
(112)
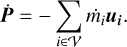 (113)
(113)
where 𝓥 is the set of indices of cells that are located within Racc of the accreting object.
For accretion onto binary stars from a circumbinary disk, we can use a more sophisticated model of accretion. Assume that, within the cavity of the circumbinary disk, both stars are surrounded by their own disks which are tidally truncated, keeping them small. Assume further that within these disks the accretion happens according to a simple 1D viscous accretion-disk model and that the stars accrete at the same rate as the mass flows through these disks. Then, the accretion rate onto the stars is given by (Lynden-Bell & Pringle 1974):
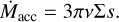 (114)
(114)
The free parameter s accounts for the increase in accretion close to an object due to gas friction at the boundary layer. The idea is analogous to the viscous inflow boundary condition (Sect. 3.14.2). For our purposes, we assume v and Σ to be constant and equal to the average values within Racc.
With this model of accretion, we can modify the scheme above in such a way that the rate of mass removed from the disk in the vicinity of the object is equal to the 1D viscous accretion rate given by Eq. (114). To achieve this, we choose ƒi such, that
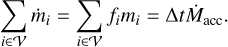 (115)
(115)
Again, we want ƒ(d) to vary with the distance d to the accreting object and we want ƒ(d) to be zero for d > Racc. Now, instead of a step function, we choose a smooth power law function for ƒ(d) such that
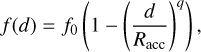 (116)
(116)
with the understanding that ƒ(d > Racc) = 0. With this choice, the physical model from above, and assuming q > 0, we find:
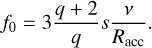 (117)
(117)
In the code, we use q = 1 . This enables the physically motivated computation of an accretion rate onto a secondary star which is located within the computational domain.
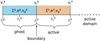 |
Fig. 3 Schematic of the location of the quantities for the boundary conditions. The first active cell is shown in beige and the ghost cells are in blue. The ghost cells are not updated by the source terms and transport steps. Their values are used to apply the boundary conditions. |
3.14 Boundary conditions
This section describes the boundary conditions (BCs) that are implemented in the code. We start by stating the most basic BCs and then describe the more complex ones. In the code, BCs are applied by setting the value of Σ, e, uϕ in the center of the ghost cells and ur on its two interfaces.
The nomenclature used in this section is as follows. The superscripts a and g denote the last cell in the active domain and the ghost cell, respectively. The location of the cell centers are ra and rg. Additionally, the superscript b denotes the boundary at Rmin and Rmax. The locations of the interfaces are 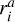 for the interface between the first and second active cell,
for the interface between the first and second active cell, 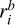 for the boundary interface, and
for the boundary interface, and 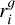 for the interface of the ghost cell facing away from the active domain. Values in the center of the ghost cells are Σg, eg and
for the interface of the ghost cell facing away from the active domain. Values in the center of the ghost cells are Σg, eg and 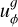 . The two values on the ghost cell interfaces are
. The two values on the ghost cell interfaces are 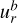 , at the interface between the active domain and the ghost cell and
, at the interface between the active domain and the ghost cell and 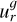 . The values in the first cell of the active domain are Σa, ea,
. The values in the first cell of the active domain are Σa, ea, 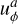 and the radial velocity at the interface between the first and second active cell is
and the radial velocity at the interface between the first and second active cell is 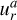 . See Fig. 3 for a schematic of the location of these quantities.
. See Fig. 3 for a schematic of the location of these quantities.
In the code, BCs can either be set for each variable individually or for all variables at once. We call the latter case a composite BC. Here, we start by introducing the individual BCs.
Boundary conditions available on all variables of x ∈ {Σ, e, ur, uϕ}.
3.14.1 Boundary conditions applicable to all variables
Several BCs are available for each variable. These are summarized in Table 2.
The “zero-gradient” BC enforces a radial derivative of zero at the boundary. It copies the value from the last active cell into the ghost cell for cell-centered variables and from the last active cell interface into the ghost cell interface for interface variables.
The “disk model” BC is used to set the boundaries according to a specific disk model. The code currently supports a power law disk as a model. The functions xdm(r) specify the disk model for each variable x. An example is the surface density Σdm(r) = Σ0(r/r0)−p.
Another choice to set the boundaries to a specific model is the “reference” BC. In this case, the reference values xref(r) are loaded from a special simulation snapshot. The same snapshot is used for the damping zones (see Sect. 3.14.6). This snapshot is generated at the beginning of the simulation and contains the initial conditions by default. To specify a custom model, the user can run the simulation for zero time steps (using the -N 0 command line flag) and then replace the reference values with the desired arbitrary model using an external tool. Then, the simulation can be continued from snapshot number 0.
3.14.2 Radial velocity boundary conditions
Several BCs apply only to the radial velocity ur, see Table 3. They are mostly connected to the flow through the boundary.
By mirroring the flow, we can simulate a “reflective” boundary. This is achieved by setting the radial velocity to zero on the boundary and to the negative value of the radial velocity in the last active cell at the other interface of the ghost cell. This keeps mass from flowing out of the domain but also reflects waves back into the domain and can cause wave interference patterns and instabilities in the worst case. Usually, the reflective boundary is used together with damping zones (see Sect. 3.14.6) to prevent these issues.
The opposite behavior is achieved by the “outflow” BC. It lets mass flow out of the domain but does not allow mass to flow into the domain. This is achieved by using a zero-gradient condition if the velocity vector is pointing outwards at the boundary and by setting the radial velocity to zero otherwise. Pointing outwards means that the radial velocity is positive at the outer boundary and negative at the inner boundary. Despite being an outflow condition for mass, this prescription can still reflect waves back into the domain, but it is less of an issue as the boundary tends to form an empty area between the disk and the boundary.
At the inner boundary, it can be advantageous to more closely control the flow through the boundary to model a certain accretion rate onto the star. There are currently two options to influence this flow. The first option is the “viscous outflow” BC. This BC assumes a steady-state accretion disk at the inner boundary. Then, analogous to the viscous accretion model presented in Sect. 3.13, the accretion rate through the boundary is given by (Lynden-Bell & Pringle 1974):
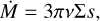 (118)
(118)
with the free parameter s for which 5 is a suitable value for accretion onto a solar-type star (Pierens & Nelson 2008). The BC is implemented by setting the radial velocity at the boundary 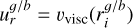 with the viscous inflow speed:
with the viscous inflow speed:
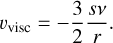 (119)
(119)
Another choice is to set the radial velocity to a fraction of the Keplerian velocity at the inner boundary. This is done by the “Keplerian” BC for the radial direction. It sets the radial velocity to the negative of the fraction of the Keplerian velocity at the inner boundary. This BC can also be applied at the outer boundary.
Boundary conditions for the radial velocity, ur.
Boundary conditions for the azimuthal velocity uϕ.
3.14.3 Azimuthal velocity boundary conditions
Table 4 summarizes the BCs that are available for the azimuthal velocity. The most basic condition is the “Keplerian” BC which sets the azimuthal velocity to a fraction of the Keplerian velocity at the boundary, corrected for the frame rotation. The fraction can be chosen to be sub- or super-Keplerian to reflect additional pressure support or other effects. It can be used to model boundary layers where the disk connects to the star. Then the fraction is chosen such that uϕ is the surface rotation velocity of the star.
Depending on the flow close to the boundary, the Keplerian or any of the basic BCs might lead to shear at the boundary. This results in torques at the boundary which might be nonphys-ical or undesirable. To avoid this, we can use the “zero-shear” BC which removes the shear at the boundary by scaling the azimuthal velocity in the last active cell to the ghost cell such that both have the same angular velocity.
Finally, the code supports the “balanced” BC which sets the azimuthal velocity such that the centrifugal force is in equilibrium with all other forces. This is especially useful for equilibrium disk models, see also Appendix B. In addition to the gravity of the central object, this takes into account pressure, the quadrupole moment from a central binary, smoothing, and self-gravity. It is expressed as:
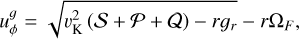 (120)
(120)
where gr is the radial component of the self-gravity acceleration (see Sect. 3.7) and 𝓟, S, and 𝑄 represent pressure, smoothing, and quadrupole moment, respectively, and the last term accounts for the rotating frame. This equation can be derived (see Appendix B) from the radial force balance starting from the radial momentum conservation Eq. (6).
Usually, the term S equals 1 in other instances of this formula in the literature. However, when the gravitational potential (Eq. (13)) is differentiated to calculate the external forces acting on the disk, additional terms that depend on the smoothing length appear, because the smoothing length depends on the location in the disk. These terms are accounted for in the centrifugal balance by:
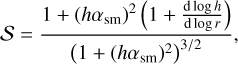 (121)
(121)
where αsm is the smoothing parameter (see Sect. 3.6). See Appendix B for more detail. The pressure term is as usual given by (e.g., Baruteau 2008, Eq. (3.4)):
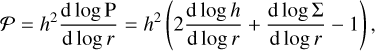 (122)
(122)
where where the last equality follows from 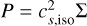 and cs,iso = h vK. For simulations of circumbinary disks, it can be advantageous to account for the quadrupole term of the gravitation potential of the binary. The inclusion of this term can be turned on by the user. The term reads (Muñoz et al. 2019, Eq. (23)):
and cs,iso = h vK. For simulations of circumbinary disks, it can be advantageous to account for the quadrupole term of the gravitation potential of the binary. The inclusion of this term can be turned on by the user. The term reads (Muñoz et al. 2019, Eq. (23)):
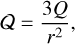 (123)
(123)
with the quadrupole moment of the binary (Muñoz et al. 2019, Eq. (24)):
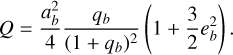 (124)
(124)
Here, ab is the binary separation, qb is the binary mass ratio qb, and eb is the binary eccentricity.
3.14.4 Radiative transfer boundary conditions
The radiative transfer module solves a diffusion equation. In the azimuthal boundary, the periodicity is built in, but on the radial boundaries, a BC is required. If the module is enabled, the user must specify such conditions. The BC is applied right before the SOR solver is called.
There are three options available. First, a “zero-gradient” conditions for the diffusion coefficient K (see Eq. (52)). Second, a “zero-flux” condition which sets the diffusion coefficient to zero at the boundary 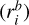 . Third, an “outflow” condition which allows for the flux to leave the domain, implemented by setting T = Tfloor in the ghost cell.
. Third, an “outflow” condition which allows for the flux to leave the domain, implemented by setting T = Tfloor in the ghost cell.
Composite boundaries and their descriptions
3.14.5 Composite boundary conditions
The BCs presented above apply to single variables. This subsection introduces the composite BCs, collections of BCs which apply to the variables, Σ, e, and ur. The BC for uϕ still needs to be set individually, except for the “reference” case.
The “outflow”, “reflecting”, and “zero-gradient” composite BCs are simply shorthands to set the individual BCs as described in Table 5. These BCs reflect what is commonly used in other codes.
The “center of mass” BC is intended for the special case of simulating infinite circumbinary disks in the center of one of the stars. It enforces the initial power law profile for density and temperature, the equilibrium for azimuthal velocity according to Eq. (120), and the viscous speed for the radial velocity at the boundary and the outer damping region with respect to the center of mass of the N-body system instead of the coordinate center. In a second step, the gas velocities are transformed from polar to cartesian coordinates, shifted by the velocity of the coordinate center and transformed back to polar coordinates in the frame of the central object.
For simulations of cataclysmic variables, we implemented a “Roche lobe overflow” BC that models the mass flow through the L1 point between binary stars when one of the stars is overflowing its Roche lobe. While the function is implemented generally, it only works as intended if the primary is at the coordinate center and the outer edge of the domain has the size of the Lagrangian L1 point.
We compute the width of the mass stream using the approximate function in Warner (2003) Sect. 2.4.1 which is a simplified version of the isothermal model for a Roche lobe overflow from Meyer & Meyer-Hofmeister (1983):
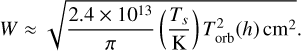 (125)
(125)
We then select the cell in the outer boundary, which is closest to the secondary and smooth the mass stream with a Gaussian profile over three times its width. We found that the initial stream width and temperature are of little importance as it quickly reaches a new equilibrium upon entering the simulation domain and that the width is mostly determined by the grid resolution.
The initial radial velocity of the stream is computed, the same as in Kley et al. (2008), as a small fraction binary’s orbital frequency:
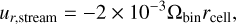 (126)
(126)
however, again, the exact value of ur,stream does not make a difference as long it is small compared to the orbital velocity. for this localized infall condition, the described boundary values are set inside the transport step to ensure the chosen mass flux. We note that the Roche lobe overflow condition is only applied to the cells within the width of the stream. The rest of the ghost cells are unaffected. Thus, when using the Roche lobe overflow BC, additional individual BCs have to be specified for all variables. A demonstration of the “Roche lobe overflow” BC is presented in Fig. 4. Note that is up to the user to ensure that the outer boundary is located at the Lagrangian L1 point.
 |
Fig. 4 Logarithmic density plot of a simulation with the “Roche lobe overflow” boundary condition showing the stream of material emerging from the L1 point. The green line indicates the Roche lobe of the binary system and the grey circle is the outer boundary of the simulation domain. Outside the small region around the Lagrangian L1 point the boundary condition is set to “outflow”. |
3.14.6 Damping zones
FARGOCPT supports damping zones (DZ) at the inner and outer boundary as presented in de Val-Borro et al. (2006). The DZs are used to damp waves that are reflected at the boundaries. We choose to use the words “damping zone” instead of “damping boundary condition” because they are, strictly speaking, not a boundary condition in the context of partial differential equations. They behave more akin to a heat bath in thermodynamics.
The DZs are implemented as an exponential relaxation of any of the quantities X ∈ {Σ, e, ur, uϕ}. The damping is given by:
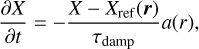 (127)
(127)
with the damping timescale τdamp and the damping function, a(r).
The reference value, Xref, is saved as a separate snapshot at the beginning of the simulation and by default contains the initial values. It can also be manually changed by the user to support arbitrary damping fields in 2D. Other choices for Xref include 0, the azimuthal average of the ring, or for the case of inner radial velocity, the viscous speed according to Eq. (119). This relaxation step is applied at the end of each time step as the last update of the hydro system, see Fig. 1.
The regions of the DZs are defined by two separate parameters cdi and cdo for the inner and outer zone, respectively. The inner damping zone reaches from Rmin to Rdi = cdiRmin and the outer damping zone reaches from Rdo = cdoRmax to Rmax.
The damping timescale τdamp is given by:
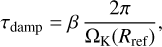 (128)
(128)
where β is a free parameter to configure the damping strength. The reference radius, Rref, can be chosen by the user for each zone separately and defaults to inner and outer boundary radius.
The damping function a(r) is used to smoothly reduce the damping from one at the boundary to zero towards the active computational domain. We use a second-order polynomial with the condition that its first derivative vanishes at the transition from the damping zone to the active domain located at Rdi/do. This is fulfilled by the choice of:
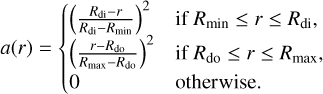 (129)
(129)
The update step is discretized using the analytical solution of Eq. (127) to avoid overshooting and is given by:
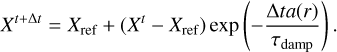 (130)
(130)
The DZ can be enabled for each quantity and in each zone individually. We note that the DZ creates and removes mass, energy and momentum in the simulation domain and, thus, breaks conservation of these quantities. The change of mass due to the DZ can be monitored.
4 Software features
4.1 Hybrid parallelization
FARGOCPT has been parallelized using a hybrid MPI + OpenMP approach. This is currently the most efficient way to make use of the underlying CPU and memory structure of most supercomputers. A scaling test can be found in Appendix A which shows that the code reasonably scales at least up to 500 CPU cores.
Modern computers often have multiple NUMA (non-uniform memory access) nodes per processor package. As a result, a specific CPU core can access a part of the system memory with lower latency than the rest of the memory. Because hydrodynamics simulations rely heavily on memory access, it is important to instruct the operating system to take this into account.
This is automatically attempted by default when using the launcher (see Sect. 4.3), but can be done manually and the automatic mapping should be checked. In practice, one MPI process is launched per NUMA node and OpenMP threads are launched as many as there are cores per NUMA node. It is usually worthwhile to tune the execution settings (number of processes and threads) to the architecture of the computer used to run the simulation. To find out the number of NUMA nodes and cores per NUMA node on a Linux system, one can use the lstopo or lscpu utilities. For consumer PCs, one might need to enable a setting in the bios for the operating system to be aware of the NUMA topology.
4.2 Interactivity via signals
Planet-disk interaction simulations with any of the available codes typically run in a non-interactive mode, and only provide feedback through logs and monitor files once a predefined time step has been covered by the simulation. For example, in the case that the CFL time step tends to zero, this can lead to simulations freezing without any indication of the cause.
To address issues such as frozen simulations, we have introduced UNIX signal handling with three signals. One can interact with the simulation using the kill command, for example, using kill -SIGUSR1 <fargo pid>.
SIGUSR1 allows users to request a status report, including current simulation time and details on CFL time step constraints, aiding in identifying freeze causes. SIGUSR2 enables immediate stack trace printing, useful in development for locating algorithmic issues or runtime issues, for instance, when a cluster filesystem hangs. Finally, SIGTERM allows for a graceful shutdown, saving a snapshot for later resumption, beneficial in cluster environments or when simulations must be paused due to resource sharing.
4.3 Usability
We aimed to make using the code as straightforward as possible to encourage students to perform numerical experiments. This includes changes to the command line interface as well as the restructuring of the config files discussed later in Sect. 4.6.
The command line interface traditionally included the selection of a mode, either to start or restart a simulation and the specification of the path to a config file. A common task is to restart an existing simulation to extend it after its initially targeted time was reached or after the allocated wall time on a shared computing resource has elapsed.
Traditionally, this required specifying the output number of the snapshot that was last written to disk. In our experience, this manual task can be error-prone, sometimes resulting in the loss of parts of the simulation data. We added the “automatic” mode, which starts the simulation if no simulation output has been written yet and restarts the simulation from the latest snapshot present. This has proven to essentially eliminate errors during routine restarting of simulations, saving duplicate spending of computational resources.
Furthermore, the compiled executable is launched through a Python launcher to handle the setup for parallel execution. This launcher guesses an appropriate selection of the OpenMP thread and MPI process numbers under several different workload managers and MPI implementations. Again, this is aimed to enable straightforward access to the code without specific knowledge about OpenMP and MPI, which can initially be a substantial hurdle. Experienced users can skip this launcher, write their own or manually specify the parameters, to achieve a potentially more optimal configuration.
Installing all required libraries and compiling the code can be a substantial hurdle, especially for someone not familiar with Linux operating systems. To this end, we made FARGOCPT seamlessly available inside the virtual computers provided by GitHub called “codespaces”1. Using this service, one can start a virtual machine with the code ready to go from within the FARGOCPT GitHub repository2 with the click of a button. Then one can get familiar with or use the code with the integrated Jupyter notebooks, all in the browser and without needing to use the command line or compile the code. Although these codespaces have runtime restrictions, the freely available resources are enough, at the time of writing, for learning to use the code, prototyping setups and even low-resolution scientific simulations. When this free service should no longer be available, the FARGOCPT code can still be used in a similar fashion using the docker container provided in the GitHub repository.
4.4 Python interface
We created a Python module that comes with the code to facilitate starting the code from within a Jupyter Notebook or Python scripts, loading data from output directories and creating an interactive overview plot. It comes with a command line interface that can be used to start simulations with an automatically determined suitable CPU allocation and to inspect output data.
The GitHub repository of the code includes multiple Jupyter notebooks with example cases that illustrate how to build and use the code. Additionally, there are examples of how to load and visualize the output data and some common simulation scenarios.
4.5 C++ port and code restructuring
FargoADSG (Baruteau 2008) was converted from a C code to a C++ object-oriented by Müller et al. (2012). Notably, the data structure was converted to be object-oriented, a data class holding a number of other structures for the storage of physical quantities defined on a polar grid. Functionalities of these classes include the tracking of units with pre- and post-hooks for input and output.
Later, functionally separate parts of the code were split up (into C++ namespaces). Examples include software aspects such as the parsing and storage of parameters, units and output, and physics modules such as the N-body system, boundary conditions or radiative transport. This was done to highlight the structure of the code to make it easier to maintain and extend, and to make it easier to understand for new users.
4.6 Config files
Config files have been changed from a custom flavor of the ini file format to the well-defined and documented yaml format. The advantage of this is twofold. First, the config files can be easily processed and generated using scripts, for example, with any of the yaml packages in the Python ecosystem. This can help avoid errors in preparing simulations for parameter studies. Along the same lines, the parsing of the config files in the actual C++ simulation code is off-loaded to an existing and tested library which can handle and report syntax errors in the config files and handle type conversions. The latter two are examples in which the authors experienced time-consuming errors with other codes in the past.
Second, yaml supports structured data which enables setting the parameters and initial conditions of the N-body objects within the config file. This change removes the column-based and unchecked planet file in favor of a structured entry in the main configuration file.
An aspect that sets FARGOCPT apart from other versions of the code is that the config file is the only place that is changed to configure the simulations. No compile time parameters are used. In our opinion, this makes the code easier to use for first-time users.
4.7 Output format
Originally, all simulation output files were stored in one single output folder for all snapshots. Depending on the simulation, several thousand snapshots can be written to disk resulting in several thousand to several tens of thousands of files in a single folder. This makes working with these simulations cumbersome because simply listing the contents of this output directory can take multiple tens of seconds on cluster file systems which are optimized for parallel throughput rather than metadata access.
Furthermore, extracting a single snapshot from a simulation directory included the error-prone manual extraction of various state variables from different text files.
In FARGO-like codes, time series data is usually written to tab-separated-value text files. However, the contents of the columns are often not described, neither the content of a column nor its unit. This lack of description of the data is made worse by the fact that the structure of these files can change between different versions of the same code or be modified by the user to track any quantity of interest that is not already present in the standard output leading to confusion and necessitating the knowledge of which particular version of the code was used to generate a particular set out output data. While we generally encourage saving which exact version of the code was used (e.g., the git commit id), even storing the source code of the simulation with the output data, reading the values from a text file should not necessitate the study of the accompanying source code.
In addition, the input files for the simulation were required to infer the unit system used in the simulation because the base units of length, mass and time can be set in the configuration file. Hence, the outputs were not self-descriptive.
We remedied these issues with the following changes. The output directory was restructured such that each snapshot was saved into a separate directory within the snapshot subdirectory. Such a directory contains all binary data about density, energy and velocity fields, all scalar quantities such as the time, the rotation angle of the frame and intermediate integration variables and all information about the state of the N-body and particle systems. Additionally, a copy of the input file is saved for each snapshot to save the history of parameters should they change during a restart.
Additionally, yaml info files are written to the output directory containing information about the units used in the simulation and the quantities that were written as parts of the snapshots to unambiguously specify the physical quantities. This grounds these code units on a physical scale. A rescaling of the results can still be done as long as the set of physical assumptions allow it.
The files containing time series data are now collected in one single sub-directory called monitor. Each such text file includes a header that describes the content of each column in the text file and specifies its unit in a string readable by the astropy Python library in an automated fashion.
Furthermore, the output directory now contains an empty text file with the name fargocpt_output_vx_y, where x_y specifies the major and minor version of the code. This helps with the automation of postprocessing when multiple versions of the same code or even different codes are used in a single project.
4.8 Unit system
Because we carry out numerical simulations of physical processes, we necessarily need to choose a system of units. This unit system, often called “code units”, can be specified using two or four parameters in the config file. The base length L0 and the base mass M0 are required and the base time T0 and the base temperature Θ0 are optional. If the base time T0 is not chosen explicitly, it is computed such that G = 1 in code units. This is equivalent to one Keplerian orbit at distance L0 around an object of mass M0 having a period of 2π, thus:
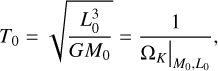 (131)
(131)
with the gravitational constant G and the Keplerian angular velocity, 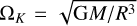 . If the temperature unit is not specified, it is calculated such that the specific gas constant
. If the temperature unit is not specified, it is calculated such that the specific gas constant 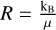 is unity in code units, thus:
is unity in code units, thus:
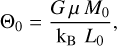 (132)
(132)
with the mean molecular weight µ and the Boltzmann constant kB. Internally, all calculations are carried out and all output is written in the code unit system 𝒰 = (L0, M0, T0, Θ0).
In the config file, the user can specify physical parameters either as a number without units, in which case they are interpreted to be in code units, or they can be specified with a number and a unit symbol. This number and unit are then automatically converted to code units. As an example, consider a unit system with L0 = 1 au and M0 = 1M⊙. The reference surface density, Σ0, which has the key Sigma0 in the config file can then either be specified in code units using
Sigma0: 1e-5,
in which case, 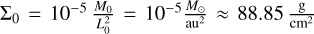 . Alternatively, the same could be specified using:
. Alternatively, the same could be specified using:
Sigma0: 88.85 g/cm2.
The formerversionis more informative in simulations of a scale-free problem while the latter version is more informative in simulations aimedatsimulating existing protoplanetary disksys-tems. This flexibility in terms of units combines the usefulness of a unit system adapted to the physical problem at hand (code units) with the necessity to specify certain physical parameters in physical units, such as parameters inferred from observations or experiments. We hope that this feature helps to avoid common conversion errors in setting up simulations.
The implementation of the unit parsing is based on the C++ units runtime library (LLNL 2022). All conversions are performed in the initialization step, so variables during the actual simulations do not carry any units.
Unit symbols supported in the config file are specified by the LLNL (2022) library3, they include all SI units with prefixes, and the convenience units: au, solMass, solRadius, jupiterMass, jupiterRadius, earthMass, and earthRadius. Usually, most unit strings that work with the Python astropy package also work here. Furthermore, combinations of powers of units are supported, as in the example above.
In addition to the definition of units, (LLNL 2022) is also the source for the definition of physical constant4, namely the gravitational constant, G, the Boltzmann constant, kB, the atomic mass units u, the Planck constant, h, and the speed of light, c. These are based on the 2019 redefinition of the SI units5 and the NIST 2018 CODATA6 physical constants table.
Automated test cases and references to their descriptions in Appendix D.
4.9 Test suite
Having a test suite is crucial to illustrate that the code is working as intended and that the various physical modules of the code actually provide approximations to the underlying equations. This is an essential part of any simulation code.
FARGOCPT comes with an automatic test suite. The test suite can be run by executing the run_tests.sh script within the tests directory. This automatically executes multiple test cases and compares the results to reference data or theoretical expectations. The result of the test is then either “passed” or “failed”. Each test case therefore includes threshold values for deviations from the reference data. The test suite is designed to be run on a local computer in a matter of minutes and does not require a supercomputer. This makes testing the code base relatively straightforward and cheap. Currently, the automatic tests include tests for most of the major physical modules. The tests are are listed in Table 6. See Appendix D for more details.
5 Discussion
5.1 Leapfrog-like scheme
In addition to the integration schedule presented in Fig. 1, we also implemented a leapfrog-like schedule presented in Appendix C. This scheme performs the source term step twice with half of the time step size and the transport step once with the full time step size. The transport step is performed in between the two source term steps.
This allows for larger simulation time steps by relaxing the CFL criteria of the source step but it also becomes more expensive because the source term is evaluated twice. This is prohibitive when self-gravity or radiative transport is enabled.
Without these enabled, the scheme still runs around 7% slower than the Euler scheme.
While in theory, a leapfrog scheme has higher accuracy than an Euler scheme, and it is advantageous to conduct the transport step less often and with larger time steps due to numerical diffusion, we found that the benefits are negligible for typical planet disk interaction simulations. We found the leapfrog scheme only to be beneficial for simulations where the source terms dominate the numerical errors and not the transport step, for instance, in test simulations of an equilibrium disk. An example of such a simulation is the heating and cooling test presented in Appendix D.3. In this model, the transport step is effectively only an advection along the azimuthal direction, which is trivial in the polar coordinate system.
Because of these reasons, we see no benefit in using the leapfrog scheme as implemented in the current version of the code over the default scheme for typical planet-disk interaction simulations. The operator splitting scheme we use is formally only accurate up to first-order in time (worst case). Therefore, we suspect that more substantial improvements to accuracy can be made by implementing higher-order time stepping such as a second-order Runge-Kutta scheme. This is left for future work.
5.2 Considering why another FARGO code would be useful
FARGOCPT is another addition to the family of FARGO codes. This raises the question of why the community needs another FARGO code when FARGO3D or FARGOCA exist which even support 3D simulations. Our answer to this question is twofold. First, to the knowledge of the authors, the collection of physics modules implemented in FARGOCPT is unique compared to other publicly available versions of codes for the study of planet–disk interaction. At present, the FARGOCPT code includes different equations of state, viscous heating and irradiation, local β-cooling, cooling through the disk surfaces, midplane energy transport, self-gravity, high-order N-body integration, accretion onto N-body objects, and a particle module which includes gas drag laws for a wide range of particle sizes and dust diffusion, all while making use of the FARGO speedup. For example, the public version of FARGO3D does not support self-gravity, while FARGOADSG and Athena++ do not support radiation transport. Both are processes that are important in current problems of planet–disk interaction (e.g., Ziampras et al. 2023a) and protoplanetary disks (e.g., Rendon Restrepo & Barge 2022). FARGOCPT also includes many of the typically used effective models for planet–disk interaction, such as β-cooling. While these effective models can be implemented in other codes with relative ease by an experienced programmer, these implementations still have to be manually validated by the user. Hence, having a tested implementation is nearly always preferable (Wilson et al. 2012), even if they are only taken as a starting point and modified for a specific problem.
Second, we believe that the code presented here is easier to use, understand and modify than other versions of FARGO. This is especially important for students who are new to the field and want to perform numerical experiments. We anticipate that this will lead to a more efficient learning process and a more efficient use of the time of the students. Additionally, features such as the support for physical units in the config files and a self-contained output reduce the chance of human error in the simulation workflow. This leads to a more efficient use of the attention of the user to the physical model behind the simulation and the scientific problem at hand.
Furthermore, we are not aware of any other hydrodynamics code for the study of planet-disk interactions that can be used in the browser. This property can make FARGOCPT a valuable tool for teaching and learning about planet-disk interactions. Indeed, it was already successfully used to teach hydrodynamics and planet migration at the SPP 1992 summer school on planet formation in Rauenberg, Germany, in August of 2023.
5.3 Future development
As with any software project, many possible improvements can be made to the code base. Here, we outline some of the potential improvements that we believe might be worthwhile to be incorporated into future iterations of the code:
More general self-gravity solver. One of the foundational assumptions of our current self-gravity module is that the aspect ratio needs to be assumed constant for the Fourier Method to work. This limits the accuracy of simulations with the combination of self-gravity and radiation physics, the latter of which generally leads to a non-uniform aspect ratio. Removing this limitation would, for example, allow for more accurate studies of gravitational collapse within the disk, which includes a balance between pressure, built up by compression heating and reduced by radiation transport, and self-gravity. This could be achieved using tree-based or multigrid methods.
Higher-order time-stepping. By integrating higher-order time-stepping techniques, we can potentially achieve better temporal resolution and improved simulation stability, thus ensuring more accurate representations of physical systems over time. The groundwork for such a change has already been laid in the leapfrog-like scheme presented in Appendix C and a second-order Runge-Kutta scheme could be implemented in a similar fashion.
Matrix solvers for heating, cooling and viscosity. Currently, the heating and cooling terms, as well as the viscosity update rely on either a simple implicit but local update step and the viscosity update uses a simple explicit update step (see Sect. 2 for resulting issues). These updates can be replaced by fully implicit updates which rely on a matrix or linear system solver to increase accuracy and stability (see also Sect. 3.9.2). To this end, the SOR linear system solver used in the flux-limited diffusion model could be adapted to the heating, cooling and viscosity update steps.
Irradiation Using Ray-tracing. For studying scenarios such as accretion onto planets, where the impact of radiation sources can dominate the local evolution, introducing a ray-tracing mechanism for irradiation can be beneficial. Currently, the irradiation is computed using a simple distance-based approximation, formally only valid for a single star in the center of a flaring disk. While it is computationally expensive, ray tracing can provide a more precise depiction of the dynamics of the disk when it is heated by accreting planets including influences of shadows.
In this paper, we introduce FARGOCPT, a new and publicly available7 version of the FARGO code. We present the new and improved physics modules, such as radiation physics, self-gravity, and the particle module, and the new features of the code, such as the hybrid parallelization, the Python interface, and the new test suite. The paper is intended as a reference for students and researchers who want to use the code and as a starting point for future development of this and other FARGO-like codes. We hope that the code will be useful for the community and that it will be used to study the complex and fascinating physics of planet-disk interactions and protoplanetary disks.
Acknowledgements
TR and LJ would like to express their gratitude to Alex Ziampras for the numerous insightful and productive discussions and Gabriel-Dominique Marleau for helpful comments on the thermodynamics aspects of the manuscript. T.R., G.P., W.K. and C.D. acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG) research group FOR 2634 “Planet Formation Witnesses and Probes: Transition Disks” under grants DU 414/22-1, and KL 650/29-1, 650/29-2, 650/30-1, and 650/30-2. SRR acknowledges funding from the European Union (ERC, Epoch-of-Taurus, 101043302). Views and opinions expressed are however those of the authors only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. The authors acknowledge support by the High Performance and Cloud Computing Group at the Zentrum für Datenverarbeitung of the University of Tübingen, the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant INST37/935-z1 FUGG. Plots in this paper were made using the Python library matplotlib (Hunter 2007).
Appendix A Parallel scaling
This section presents the scaling of the code with the number of cores used in the simulation. The scaling was measured on the Tübingen compute cluster BINAC on 1 to 16 nodes with 28 cores each of an Intel Xeon E5-2630v4 CPU connected via an InfiniBand network.
The test was performed using a locally isothermal disk with an embedded Saturn-mass planet and a grid size of Nr × Nϕ = 1024 × 2048. The strong scaling speed-up, namely, the time required for a constant workload (same grid size) divided by the number of cores, is nearly perfect up to 224 cores, see Fig. A.1.
For 112 cores, there appears to be a super-linear speed-up. The code is parallelized by dividing the disk up into radial sub-domains, each assigned to an MPI process (one for each NUMA node used). Each subdomain consists of several consecutive rings. These domains are then processed by several OpenMP threads (7 in the case of this test). The case of 112 cores might be a sweet spot where the CPU cache is utilized more efficiently for this specific size of the subdomain, resulting in the super-linear speed up. For higher core counts, the speed-up declines, which might be due to the increased communication overhead or because the grid size is not large enough to keep the cores busy.
 |
Fig. A.1 Speedup factor with number of cores on the Tübingen compute cluster BINAC. |
Appendix B Simulations of equilibrium disks
To simulate a steady-state accretion disk, we prescribe the densities and velocities of a locally isothermal model at the outer boundary with an additional wave-killing zone where we damp to only the velocities of the isothermal mode. To achieve a steady state, we need to consider all forces in the centrifugal balance.
The model disk is described by the following equations. The scale height is given by:
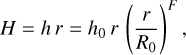 (B.1)
(B.1)
where r is the distance to the central star, F is the flaring index, and R0 the radius where h = h0. The surface density is:
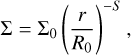 (B.2)
(B.2)
with the free parameter, S. The sound speed is:
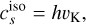 (B.3)
(B.3)
where vK and ΩK denote the Keplerian orbital velocity and frequency. Assuming an perfect equation of state, the pressure is:
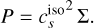 (B.4)
(B.4)
The gravitational interaction between the central star and the disk is computed using a smoothed gravitational potential of a point mass:
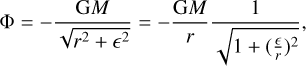 (B.5)
(B.5)
with the smoothing length, ϵ = αsmH. Note that this smoothing length also has a radial dependence. Its radial derivative is given by:
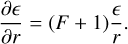 (B.6)
(B.6)
With that in mind, we can compute the radial derivative of the smoothed potential:
 (B.7)
(B.7)
where we identify the second term on the r.h.s as the effect of the gravitational force due to smoothing.
Following is a derivation of the equilibrium azimuthal velocity of the disk. Assume, that the disk is axially symmetric and in a steady state, thus, in the radial momentum equation Eq. (6) we have ∂/∂t = 0 and ∂/∂ϕ = 0. Additionally, assume, that ur is much smaller than uϕ and that radial changes of ur are small, so ur∂ur/∂r can be neglected. Furthermore, assume that viscous effects can be neglected, fr = 0. Equation (6) is then reduced to:
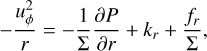 (B.8)
(B.8)
We now assume that the gravitational forces are the only external force, kr = −∂Φ/∂r + gr, with the gravitational potential due to point masses, Φ, and the radial acceleration due to the gravity of the disk, gr. Then, multiply by −r to arrive at:
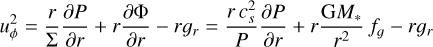 (B.9)
(B.9)
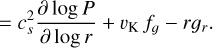 (B.10)
(B.10)
In the second step, we used 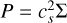 and factored out the squared Keplerian velocity,
and factored out the squared Keplerian velocity, 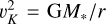 , from the gravitational potential term. The new factor fg contains the information about the spatial dependence of the smoothing length and of higher multi-pole moments of the gravitational potential (for the quadrupole term see Eq. (123)). For a non-smoothed gravitational potential of a point mass or one with a smoothing length without spacial dependence fg = 1 . Typically, fg is close to unity. Now we divide by r2, take the square root, and use cs = h vK to obtain the angular velocity,
, from the gravitational potential term. The new factor fg contains the information about the spatial dependence of the smoothing length and of higher multi-pole moments of the gravitational potential (for the quadrupole term see Eq. (123)). For a non-smoothed gravitational potential of a point mass or one with a smoothing length without spacial dependence fg = 1 . Typically, fg is close to unity. Now we divide by r2, take the square root, and use cs = h vK to obtain the angular velocity,
![${\rm{\Omega }} = \sqrt {{{\rm{\Omega }}_{\rm{K}}}\left[ {{h^2}{{\partial \log P} \over {\partial \log r}} + {f_g}} \right] - r{g_r}} .$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq202.png) (B.11)
(B.11)
Finally, we insert the expressions for h (Eq. (B.1)) and Σ (Eq. (B.2)), and differentiate the smoothed gravitational potential (see Eq. (B.7)) to obtain:
![${\rm{\Omega }} = \sqrt {{\rm{\Omega }}_{\rm{K}}^2\left[ {(2F - S - 1){h^2} + {{1 + (F + 1){h^2}\alpha _{{\rm{sm}}}^2} \over {{{\left( {1 + {h^2}\alpha _{{\rm{sm}}}^2} \right)}^{(3/2)}}}} + Q} \right] - {{{g_r}} \over r}} .$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq203.png) (B.12)
(B.12)
The second term in square brackets would be equal to 1 if the effect of the gravitational smoothing is neglected and the formula would then be the common solution for a pressure-supported disk.
The quadrupole term, 𝑄, (see Eq. (123)) is only needed for a disk around binary stars. In this case, the approximation used for computing the quadrupole term is linearly independent of the other contribution to the centrifugal balance Eq. (B.8). Therefore the contribution of the quadrupole moment can simply be added to the term inside the square brackets.
The radial velocity in a steady-state viscous accretion disk is given by (e.g., Lodato 2008):
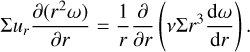 (B.13)
(B.13)
where v is given by the α-viscosity (Shakura & Sunyaev 1973) prescription:
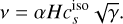 (B.14)
(B.14)
Here, α is the viscosity parameter. While analytical solutions exist to Eq. (B.13), we found them to be impractical and chose to solve the equation numerically for ur, using a five-point stencil derivative (Sauer 2012, p. 250) to generate a lookup table that is evaluated with linear interpolation. To ensure that the in-falling mass rate has the exact prescribed value the density must only be created at the outer boundary. Beware of using the wave-damping zones at the same time, because they can also create mass.
Appendix C Leapfrog-like scheme
We implemented a leapfrog-like scheme for the time-stepping, trying to solve a numeric instability that arose in the simulation of circum-binary disk simulations. It increases the accuracy of the source terms step by splitting it into two halves, one before and one after the transport step. This corresponds to a kick-drift-kick leapfrog scheme known from N-body integrators.
During testing, we found that the biggest source of errors is in the transport step and improving the source terms step brings little improvement in most cases. The gas feedback on the N-body system is already accurate with a single kick because the hydro time step is significantly smaller than the N-body time step would allow. The scheme only noticeably improves the accuracy of the code for simulations where the transport step is not important, such as the heating and cooling test presented in Appendix. D.3. There, the simulation benefits from the higher temporal resolution of the source terms step. However, this scenario would be identical to using a smaller time step for the whole simulation. The rough outline of this scheme is that a kick-drift-kick scheme is used for the gas (when identifying the source terms as kick and transport as drift) and a drift-kick-drift scheme for the N-body system.
First, we advance the N-body system and the dust particles by half a time step from t0 to t0 + 1 /2dt and use them at this position to update their velocities and compute their interaction with the gas. We then apply the source terms with half a time step and perform the transport step with a full time step. After transport, we compute the second half of the source terms and N-body-gas interactions and with the fully updated velocities evolve the N-body system and gas particles to the full time step. The steps in the scheme are as follows:
advance N-body by Δt/2 to t + Δt/2
update N-body velocities by Δt/2 from disk feedback
advance particles to t + Δt/2 from interactions with N-body and gas
gas source terms with Δt/2
gas transport gas by Δt
update N-body velocities by Δt/2 from disk feedback
gas source terms with Δt/2
advance particles to t + Δt from interactions with N-body and gas
advance N-body with previously calculated accelerations by Δt/2 to t + Δt
The N-body advance steps include accretion onto the N-body objects. Ultimately, we found that the benefits of using this scheme are only minor. The transport step is the largest source of error except in artificial test cases where the source terms are the only relevant part of the simulation.
The only noteworthy difference we could find is that the scheme needs fewer hydro steps compared to the default scheme because the CFL conditions for the source terms can be relaxed. This can lead to less numerical diffusion but at slightly longer runtimes. For example, for a typical simulation of a circum-stellar disk in a close binary, the leapfrog scheme needed 25% fewer iterations compared to the default scheme at 5% increased runtime.
Appendix D Test suite
This section describes some of the tests that are included in the test suite of FARGOCPT. The test suite can be run by executing the run_tests.sh script within the tests directory. For a list of the tests, please refer to Sect. 4.9.
Appendix D.1 Steady-state accretion test
To test our boundary conditions (BCs), we initialize an infinite disk with a constant mass flow rate throughout the whole domain. We use a simple locally isothermal model without any gravitational potential smoothing 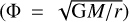 to simplify the equations in Sect. B. Using
to simplify the equations in Sect. B. Using 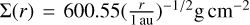 , h = 0.05, α = 10−3, F = 0 around a 1M⊙ star should result in Ṁ = 10−8M⊙/yr. At the outer edge, we set the surface density and velocities of the model in the ghost cells and damp to the velocities of the model near the boundaries (from 100 to 64 au, with a damping time factor of β = 3, see Eq. (128)). By only setting the density in the ghost cells and not damping to it, we keep precise control over the amount of mass flowing into the domain. In Fig. D.1 we showcase the model on a domain from 1 to 100 au and Nr × Nϕ = 192 × 270 resolution (square cells), the plot is taken after a time of 5 • 105 orbits at r = 1. At the outer boundary, our inflow condition deviates from the analytical model by 3% for the mass flow rate and 0.4% for the surface density. At the inner boundary, a simple open boundary (blue line in Fig. D.1) leads to a larger radial velocity (and thereby mass flow rate) than the viscous speeds. This causes the disk to be drained of mass inwards to outwards. Setting a no torque condition for the azimuthal velocity (dΩ/dr = 0, orange line) increases the radial velocity and mass drain at the inner boundary. We do not recommend this option, as it has also caused problems in other simulations. When we damp the radial velocity and surface density to the initial values from 1 to 2 au (green line), the mass rate is constant throughout the whole domain, except the few cells at the inner boundary; but those are well within the damping zone and do not affect the inner domain.
, h = 0.05, α = 10−3, F = 0 around a 1M⊙ star should result in Ṁ = 10−8M⊙/yr. At the outer edge, we set the surface density and velocities of the model in the ghost cells and damp to the velocities of the model near the boundaries (from 100 to 64 au, with a damping time factor of β = 3, see Eq. (128)). By only setting the density in the ghost cells and not damping to it, we keep precise control over the amount of mass flowing into the domain. In Fig. D.1 we showcase the model on a domain from 1 to 100 au and Nr × Nϕ = 192 × 270 resolution (square cells), the plot is taken after a time of 5 • 105 orbits at r = 1. At the outer boundary, our inflow condition deviates from the analytical model by 3% for the mass flow rate and 0.4% for the surface density. At the inner boundary, a simple open boundary (blue line in Fig. D.1) leads to a larger radial velocity (and thereby mass flow rate) than the viscous speeds. This causes the disk to be drained of mass inwards to outwards. Setting a no torque condition for the azimuthal velocity (dΩ/dr = 0, orange line) increases the radial velocity and mass drain at the inner boundary. We do not recommend this option, as it has also caused problems in other simulations. When we damp the radial velocity and surface density to the initial values from 1 to 2 au (green line), the mass rate is constant throughout the whole domain, except the few cells at the inner boundary; but those are well within the damping zone and do not affect the inner domain.
In Fig. D.2 we test our viscous outflow boundary (see Sect. 3.14.2) and our viscous accretion function (see Sect. 3.13), each with a viscous enhancement factor of s = 1 . The viscous accretion function removes mass from 1 to 5 au, which is not measured in the mass flow rate inside the domain, the mass piles up near the inner boundary due to the reflective BCs used. Note that the accretion function is not intended as a BC but for accreting objects inside the simulation domain. Both functions keep the surface density and mass flow rate relatively close to the analytical model inside the domain. These functions utilize the viscosity of the gas to remove mass from the domain. Other mechanisms can drive accretion but are not measured by our α viscosity, such as angular momentum transfer by spirals due to a massive planet. These have to be accounted for in the accretion enhancement factor s. This factor is an approximation for the increased accretion due to shearing at the boundary layer between the disk and the star (compare eq. 46 in Lodato (2008)):
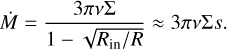 (D.1)
(D.1)
Using the viscous outflow condition allows us to change the influence on the disk from a reflective-like boundary 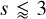 to an open like boundary
to an open like boundary 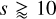 . A value of s = 5 was found to be suitable for accretion on a star with Jupiter-type companion Pierens & Nelson (2008).
. A value of s = 5 was found to be suitable for accretion on a star with Jupiter-type companion Pierens & Nelson (2008).
Generally, all our tests show deviations from the analytical solution, which we suspect is due to the numerical errors when the equations are solved on the grid. Even small discrepancies in the velocity on the grid and analytical solution can then lead to larger density pile-ups that we find in our tests. To test this, we repeated our viscous inflow simulation with half the resolution (Nr × Nϕ = 96 × 135), which is the green line in Fig. D.2. This run shows slightly larger errors in the mass flow rate and significantly larger errors in the density profile close to the inner boundary.
Appendix D.2 Shock tube
We added the Sod shock tube test by Sod (1978) to our code, see Fig. D.3, which is a classic test for the transport step, updated due to pressure forces and artificial viscosity. The test is split into two parts, the first part is the classical shock tube with a perfect gas, meaning that the adiabatic index for the sound speed and pressure are equal and constant and the second part is for an ideal gas with the caloric equation of state (PVTE) by Vaidya et al. (2015). For these tests, we approximate a Cartesian grid by spacing the radial cells arithmetically between Rmin = 1000 and Rmax = 1001 . As the setup is axisymmetric and the viscosity is zero, there is no interaction due to the azimuthal dimension. All units are set to 1 for this test. For the classical shock tube, we follow Stone & Norman (1992) and initialize the right half of the domain with Σ0 = 1 and e0 = 2.5 and the left half with Σ0 = 0.125 and e = 0.25. How to analytically solve the setup at t > 0 is described in Hawley et al. (1984). The analytical solution as well as the results from our code with 100 cells for different combinations of integrator schemes and artificial viscosity is shown in Fig D.3. For space reasons, we only show the results for the densities. The full results can be viewed by executing the Python script of the test case in our code. All four combinations of integration schemes and artificial viscosity reproduce the analytical solution and converge to it for higher resolutions without meaningful differences in quality and performance.
 |
Fig. D.1 Outflow boundary removes more mass than supplied by the disk. The figure shows the accretion rate through the disk and surface density for different choices of boundary conditions. The top and bottom panels show the mass per unit of time flowing through a ring of a given radius and the ratio of surface density to its initial value, respectively. |
 |
Fig. D.2 Viscous accretion through and at the inner boundary for different resolutions and methods. The panels are analogous to Fig. D.1. The dip in mass flow rate for the blue line in the inner region is due to the method removing mass from the domain and thus disturbing the equilibrium state. |
We used the same initial conditions for the caloric equation of state shock tube test. But in this case, the units used are important and there is no known analytical solution. We copied the units from the shock tube test in Vaidya et al. (2015) and used it as a reference to our results. Both, the setup and the units are supplied with the official PLUTO code inside the HD test problems and 1000 radial cells are used. The results are shown as the second set of lines in Fig. D.3 where our FARGO run used the TW artificial viscosity and the standard integration scheme and agrees with the PLUTO results.
 |
Fig. D.3 Gas surface densities of the shock tube test with 100 cells for different combinations of artificial viscosity and integration schemes as well as for the caloric equation of state (PVTE) by Vaidya et al. (2015) with 1000 cells. The simulation time is t = 0.228 in both cases. The top and bottom panels show the surface density and the deviations from the reference case respectively, respectively. |
Appendix D.3 Heating and cooling test
To evaluate our viscous heating and radiative cooling modules, we used the setup and model presented in D’Angelo et al. (2003), see their Sect. 3.1. The model simplifies the radiative cooling module such that an analytical formula for the density and temperature profile for a disk in hydrostatic equilibrium can be derived. The formula for the effective opacity in (35) is changed to:
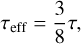 (D.2)
(D.2)
with τ = 1 /2κΣ. The opacity of the material in the disk is computed as:
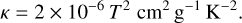 (D.3)
(D.3)
The kinematic viscosity is set to a constant v = 5 × 1016 cm2 s−1. The setup consists of a central star M = 1M⊙ and a domain ranging from 1 to 20 au with reflective boundaries. To reach the equilibrium state faster, the radial velocities at the boundaries are damped to zero. The initial surface density and temperature are set as constant Σ = 197 g cm−2 and T = 352 K. The simulation is then evolved to 104 orbital periods at r = 1 au. The expected equilibrium profiles for this specific setup are given by (D’Angelo et al. 2003):
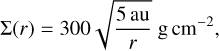 (D.4)
(D.4)
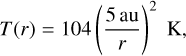 (D.5)
(D.5)
and are plotted alongside the results from our code in Fig. D.4. Apart from deviations at the boundaries, the theoretical profiles are reproduced by the code well.
 |
Fig. D.4 Gas surface density and temperature profile in the hydrostatic equilibrium for the model from D’Angelo et al. (2003) together with the expected theoretical profiles. |
Appendix D.4 Viscous spreading ring test
The viscous spreading ring is suited to test the ability of the code to transport angular momentum due to the radial shearing inside disks. A pressure-less ring is initialized and then evolved in time. Such a setup has been studied and solved analytically by Lust (1952); Pringle (1981) among others. A gas ring of mass m at radius R0 from the central star evolves in terms of dimensionless radius x = R/R0 and time 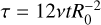 as:
as:
![${\rm{\Sigma }}(x,\tau ) = {m \over {\pi R_0^2}}{\tau ^{ - 1}}{x^{ - 1/4}}\exp \left[ { - \left( {1 + {x^2}} \right)/\tau } \right]{I_{1/4}}(2x/\tau ),$](/articles/aa/full_html/2024/04/aa48687-23/aa48687-23-eq216.png) (D.6)
(D.6)
where I1/4 is the modified Bessel function of the first kind. The ring is also subject to a viscous instability developing on top of the ring (Speith & Kley 2003). We initialized a spreading ring according to (D.6) at τ0 = 0.16 in a setup where GMc = R0 = 1 on a logarithmic grid with Nr × Nϕ = 512 × 256 in a domain ranging from 0.2 to 1.8 with a constant kinematic viscosity of v = 4.77 • 10−5. Figure D.5 shows the azimuthally averaged surface density at τ = 439.82 and it agrees well with the analytical model from (D.6). There are clear deviations from the analytical model close to the inner boundary, which is due to the strict outflow boundaries used in the simulation. The viscous instability becomes visible as density waves when taking a slice along the x axis (magenta line). This instability was studied numerically in detail by Joseph et al. (2023), where it was found that it should always develop as a one-armed trailing spiral spanning the whole domain.
Appendix D.5 Dust diffusion test
This section presents the test case for the dust diffusion module. We compare our stochastic implementation against a numerical solution of the 1D advection-diffusion equation. The setup is inspired by the test case in Charnoz et al. (2011, see their Eq. (28) for the 1D advection-diffusion equation). We tried to exactly replicate their setup as described in their Sect. 3.3 with the goal of replicating their Fig. 5. However, using the parameters available in their text and using educated guesses for the remaining model parameters we could not match the curves in their Figure. Thus, we changed our reference to a 1D simulation with the DISKLAB code developed by Cornelis Dullemond and Til Birnstiel which can be used to solve the 1D advection-diffusion equation using an implicit method. The comparison of the dust surface density calculated from the dust particle location histogram with the surface density from the DISKLAB simulation is shown in Fig. D.6. The dust surface density is normalized such that the total dust mass equals 1. There is an excellent agreement between the results of the two approaches.
 |
Fig. D.5 Viscous spreading ring test from Speith & Kley (2003) on a logarithmic grid Nr × Nϕ= 512 × 256. The ring is initialized with Σ(x, τ = 0.016) (black line) and then evolved to τ = 439.82. The vertical dashed cyan line marks the position of the initial ring at time τ = 0. The blue line is the azimuthal averaged surface density, which matches the analytical formula (red line) well. The viscous instability can be seen as waves in a density slice along the x axis (magenta line). |
Notably, the 2D correction from Eq. (108) to account for kicks in the azimuthal direction is needed to match the results from the advection-diffusion equation.
The parameters for the setup are as follows. The simulation tracks 10.000 particles with a physical particle size of 10−5 cm and a material density of 2.65 g/cm2 on their orbit around a 0.5 solar-mass star. Turbulence is parameterized by a viscous α = 0.01. The surface density of the gas follows Σ(r) = 20g/cm2 (r/1au)−1. At r = 10au, where the particles are initially launched on circular orbits, the Stokes number is St = 2.08 × 10−5. The grid spans from 1 au to 40 au with 1235 radial cells spaces logarithmically and 726 equally spaced azimuthal cells. The time step is fixed at 0.1 in code units which corresponds to 5.81 days.
Appendix D.6 Dust drift test
This test repeats the test from Picogna & Kley (2015) Appendix C.1, first suggested by Zhu et al. (2014), by comparing the dust drift velocity of individual particles with different stokes numbers to an analytical prediction.
The equilibrium radial dust drift velocity is expected to be (Picogna & Kley 2015, Eq. (C.1)):
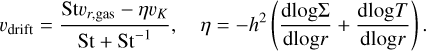 (D.7)
(D.7)
In this case, the gas is not evolved and its radial velocity ur,gas is kept zero in the whole domain, such that only the second term contributes to the drift velocity. Note that this definition of η follows from Nakagawa et al. (1986) Eq. (1) for a locally isothermal disk by correcting for a missing ‘/’ in their formula, such that 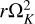 is in the denominator.
is in the denominator.
 |
Fig. D.6 Dust diffusion test. Comparison of dust diffusion with Lagrangian super-particles in FARGOCPT with numerical integration of the 1D advection-diffusion equation using an implicit method. |
 |
Fig. D.7 Results of the dust drift test. The top and bottom panel shows the value and deviation from the theoretical prediction of the drift speed as a function of the Stokes number, respectively. The large deviations for Stokes numbers around and larger than unity are due to oscillations in the integration. See Fig. D.8. |
The resulting comparison of particle drift velocities is compared to the analytical predictions for the exponential midpoint integrator in Fig. D.7. The time evolution of these velocities is shown in Fig. D.8 where the oscillations of the velocity around the mean value can be observed for particles with St > 1 , in line with the findings of Picogna & Kley (2015) Fig. C.2 and Zhu et al. (2014) Fig. 23.
The simulation models a protoplanetary disk around a 1M⊙ star, with an initial surface density of Σ(r) = 88.872 g/cm2 (r/1au)−1 at r = 1 au. The disk, with zero explicit viscosity and a constant aspect ratio of h = 0.05, extends from 0. 5 au to 3 au, and is governed by an isothermal equation of state. Dust particles with material density 2.65 g/cm3 and sizes from 10−8 to 102 m are initialized on circular orbits at r = 1 au.
Appendix D.7 Planet torque
This test case evaluates the torque exerted onto a low-mass planet by the disk. We compare the torque from a simulation to the theoretical expression for the linear Lindblad torque from Paardekooper et al. (2011, their Eq. (14)). The torque, ΓL, is given by:
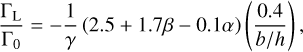 (D.8)
(D.8)
with the adiabatic index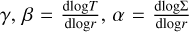 , aspect ratio h, and the smoothing length factor b = rsm/r. The torque normalization is
, aspect ratio h, and the smoothing length factor b = rsm/r. The torque normalization is 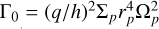 , with the planet-to-star mass ratio q, the surface density at the planet location Σp, the planetary orbital radius rp and the planetary orbital angular velocity Ωp.
, with the planet-to-star mass ratio q, the surface density at the planet location Σp, the planetary orbital radius rp and the planetary orbital angular velocity Ωp.
 |
Fig. D.8 Selected dust particle trajectories from the dust drift test. The panel shows the drift velocity as a function of time with the particle size and Stokes number encoded by color. The black lines show the expected value from Eq. (D.7). For larger dust particles with Stokes equal or greater than unity, oscillations occur due to the integration method. The particles represented by the red and purple lines leave the domain at the inner boundary during the simulation. |
 |
Fig. D.9 Torque of a small mass planet compared to theoretical prediction. The torque needs some time to build while the initially smooth disk adjusts to the presence of the planet. |
Figure D.9 shows a comparison of the torque as measured in two simulations and the theoretical prediction. One simulation calculates the torques for a planet that is on a fixed orbit, while in the other simulation, the planet is allowed to move. For the fixed planet, the resulting torque is overestimated while the torque for the moving planet oscillates around the expected value.
We note that the boundary conditions can have a substantial impact on the torque in this test. Here, reflective boundary conditions in combination with wave-damping zones towards the inner and outer boundaries had to be used.
 |
Fig. D.10 Equilibration of a radial temperature profile due to radiation transport in the midplane with a constant opacity. This is used to test the FLD module. The panels show, from top to bottom, the radial temperature profile, the deviation from the equilibrium solution, and the azimuthally integrated flux through a ring at the respective radius, normalized by the equilibrium flux. Time is indicated by the color of the lines. |
The simulation features a 2 • 10−5 M⊙ planet at r = 1 au around a 1 M⊙ star. The locally isothermal disk is initialized with Σ(r) = 0.000376(r/1au)–1.5 = 3340.84g/cm2 (r/1au)–1.5 with zero explicit viscosity and a constant aspect ratio of h = 0.05. The resolution is such that the scale height is resolved by 6 cells at the location of the planet which corresponds to 219 x 753 cells.
Appendix D.8 Flux-limited-diffusion test
This section describes the test of the flux-limited diffusion (FLD) module. This test is a simple 1D diffusion test with constant opacity and two different temperatures at the inner and outer boundaries.
Figure D.10 shows the results of this test. The panels show, from top to bottom, the radial temperature profile, the deviation from the equilibrium solution, and the azimuthally integrated flux through a ring at the respective radius, normalized by the equilibrium flux. Time is indicated by the color of the lines. The azimuthally integrated flux is expected to be constant for an equilibrium disk.
The numerical criterion for passing this test is that the maximum deviation from the equilibrium solution is smaller than 0.1 inside of r < 9.5 au. The numerical solution shows boundary effects, because of which the pass criterion is relatively loose. Please see the center panel of Fig. D.10 for the radial profile and time evolution of the deviation.
Appendix D.9 Diffusion equation solver test
This test is aimed at the 2D diffusion part of the FLD solver and tests the solution of the diffusion equation with a constant diffusion coefficient. The diffusion equation with a constant coefficient,
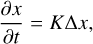 (D.9)
(D.9)
has an analytical solution in 2D in the form of a Gaussian profile with a prefactor containing the time. We use this analytical solution both as an initial condition and as the solution to compare. In this test, we treat the temperature as an arbitrary variable and manually set the diffusion coefficient to a constant value. The usual schedule for the time stepping is ignored and the initial condition is loaded from a file at the start of the diffusion test and the result is written out directly after the test. We perform a specified number of iterations with a fixed time step.
With an infinite domain and a δ distribution as an initial condition, the analytical solution in two dimensions is:
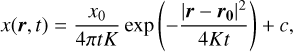 (D.10)
(D.10)
where c is a constant offset.
We use a domain size of r ϵ {0.01,2} cm with 1000 uniformly spaced radial cells and 1500 azimuthal cells, a constant diffusion coefficient of K = 1 cm2/s, the center of the Gaussian profile r0 = (1 cm, 0), an offset c = 0.1, and an initial time of t0 = 10−3 s. We then evolve the diffusion equation until t = 2 × 10−3 s, with 10 steps of Δt = 10−4 s.
A radial cut through the center of the Gaussian profiles and the deviation from the analytical solution is shown in Fig. D.11. The top panel shows the radial cut minus the offset and the bottom panel shows the relative deviation from the analytical solution.
The criterion for passing the test is that the integrated absolute deviation: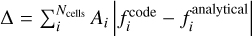 , with the cell area Ai is smaller than the threshold of 4 × 10−2 at the given resolution.
, with the cell area Ai is smaller than the threshold of 4 × 10−2 at the given resolution.
There are deviations from the analytical solution at the center of the numerical solution. It tends to be slightly higher than the analytical solution. We suspect that this is due to boundary effects. Increasing the resolution helps to reduce the deviation at the center, but it stays up to the resolution of 1000 radial and 1500 azimuthal cells, for which δ = 1.5 × 10−2. For runtime reasons, the resolution for the test suite is chosen lower at 100 times 150 cells, for which δ = 3.73 × 10−2 and the threshold is chosen just above this value at 4 × 10−2.
Appendix D.10 Self-gravity solver test
This test is aimed at verifying the self-gravity solver based on the Fourier method, as described in Sect. 3.7. It is separated into two parts: a test of the solver in the radial direction and one in the azimuthal direction. We test the implementation with the symmetric smoothing length given in Eq. (19).
As a comparison, we recompute the gravitational acceleration from the surface density by direct summation according to:
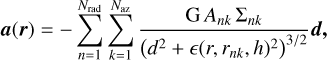 (D.11)
(D.11)
where d = rnk − r, d = |d|, and Ank is the cell area. The quantities with subscript are the cell center values loaded from the simulation output. These recomputed values are then compared to the output from the Fourier-method-based SG solver in the code.
 |
Fig. D.11 2D diffusion of the analytical solution to the diffusion equation with constant diffusion coefficient. The top panel shows radial cuts through the center of the 2D distributions: the initial condition and the analytical and numerical solutions. The bottom panel shows the relative deviation between the numerical and the analytical solution. |
In both cases, the test is performed on a 2D grid with Nrad × Naz = 128 × 256 cells, with a logarithmic radial grid spanning from 1 to 12.5 au.
For the radial test, the surface density is axisymmetric and given by Σ(r) = 200 g/cm2 (r/ 1au)−1 and the aspect ratio is constant throughout the disk with h = 0.05. Fig. D.12 shows the radial acceleration of the disk due to the self-gravity of the disk. The top panel shows the radial SG acceleration as a function of radius for the direct summation,  , and the Fourier method,
, and the Fourier method, 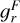 . The bottom panel shows their relative difference,
. The bottom panel shows their relative difference, 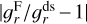 , and absolute difference,
, and absolute difference, 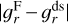 . The two methods agree well which illustrates that the Fourier method works as intended. The relative difference is below 0.0014 for r > 2 au. This value is used as a threshold in the pass-fail test. We exclude the zone inwards of 2 au because the acceleration has a crossing of zero there which enlarges the relative difference at this location.
. The two methods agree well which illustrates that the Fourier method works as intended. The relative difference is below 0.0014 for r > 2 au. This value is used as a threshold in the pass-fail test. We exclude the zone inwards of 2 au because the acceleration has a crossing of zero there which enlarges the relative difference at this location.
For the azimuthal case, we initialize the surface density with two Gaussian peaks at r0 = 4 au at two different azimuths:
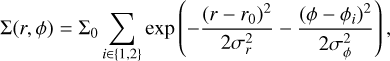 (D.12)
(D.12)
with σr = 1 au, σϕ = 0.3 rad, ϕ1 = π, ϕ2 = π/2 and Σ0 = 50 g/cm2.
Fig. D.13 shows the azimuthal acceleration due to the self-gravity of the disk as a function of azimuth at r = 4 au. In this case, the match is even better than in the radial case and relative deviations are constant and smaller.
The difference between the radial and azimuthal direction might stem from a subtle difference in the implementation of the Fourier-based SG solver. A property of this solver is that it implicitly treats all directions as periodic. In the azimuthal direction, our simulation grid is periodic which makes the Fourier method directly applicable. In the radial direction, however, a trick has to be used and the grid needs to be enlarged at the outer radial boundary to twice the size with cells containing zero density. We suspect that this trick causes the radial acceleration to be less accurate than the azimuthal acceleration.
 |
Fig. D.12 Comparison of the radial SG acceleration against results from direct summation. The top and bottom panels show the radial SG acceleration as a function of radius obtained with the Fourier method (code) and direct summation, and the relative and absolute differences between both curves, respectively. The horizontal gray line marks the zero value of acceleration and the vertical gray line indicates the crossing of zero. |
 |
Fig. D.13 Same as Fig. D.12, but showing the azimuthal SG acceleration as a function of azimuth at r = 4 au. |
References
- Anderson, D. A., Tannehill, J. C., & Pletcher, R. H. 2020, Computational Fluid Mechanics and Heat Transfer, 4th edn., Computational and Physical Processes in Mechanics and Thermal Sciences (Boca Raton, FL: CRC Press) [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [Google Scholar]
- Baruteau, C. 2008, PhD thesis, Observatoire de Paris [Google Scholar]
- Baruteau, C., & Masset, F. 2008a, ApJ, 672, 1054 [CrossRef] [Google Scholar]
- Baruteau, C., & Masset, F. 2008b, ApJ, 678, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., & Zhu, Z. 2016, MNRAS, 458, 3927 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., Crida, A., Paardekooper, S. J., et al. 2014, Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (University of Arizona Press), 667 [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Benitez-Llambay, P., & Masset, F. 2016, ApJS, 223, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, G., & Lodato, G. 1999, A&A, 350, 694 [NASA ADS] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton University Press) [Google Scholar]
- Bodenheimer, P., Laughlin, G., Rozyczka, M., et al. 2006, Numerical Methods in Astrophysics: An Introduction, Series in Astronomy and Astrophysics (Taylor & Francis) [Google Scholar]
- Cash, J. R., & Karp, A. H. 1990, ACM Trans. Math. Softw., 16, 201 [CrossRef] [Google Scholar]
- Charnoz, S., Fouchet, L., Aleon, J., & Moreira, M. 2011, ApJ, 737, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [Google Scholar]
- Chrenko, O., Brož, M., & Lambrechts, M. 2017, A&A, 606, A114 [Google Scholar]
- Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., & Chabrier, G. 2011, A&A, 529, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, A. N., & Stewart, J. N. 1969, Nauchnye Informatsii, 15, 1 [NASA ADS] [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2007, A&A, 461, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., & Marzari, F. 2012, ApJ, 757, 50 [CrossRef] [Google Scholar]
- D’Angelo, G., & Bodenheimer, P. 2013, ApJ, 778, 77 [Google Scholar]
- D’Angelo, G., Henning, T., & Kley, W. 2002, A&A, 385, 647 [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., Henning, T., & Kley, W. 2003, ApJ, 599, 548 [CrossRef] [Google Scholar]
- de Val-Borro, M., Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370, 529 [Google Scholar]
- Frigo, M., & Johnson, S. G. 2005, Proc. IEEE, 93, 216 [Google Scholar]
- Gammie, C. F. 2001, ApJ, 553, 174 [Google Scholar]
- Geiser, J., Hueso, J. L., & Martinez, E. 2017, J. Comput. Appl. Math., 309, 359 [CrossRef] [Google Scholar]
- Günther, R., Schäfer, C., & Kley, W. 2004, A&A, 423, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haghighipour, N., & Boss, A. P. 2003, ApJ, 583, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Smarr, L. L., & Wilson, J. R. 1984, ApJ, 277, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Progr. Theor. Phys. Suppl., 70, 35 [Google Scholar]
- Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ichikawa, S., & Osaki, Y. 1992, PASJ, 44, 15 [NASA ADS] [Google Scholar]
- Jordan, L. M., Kley, W., Picogna, G., & Marzari, F. 2021, A&A, 654, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joseph, J., Ziampras, A., Jordan, L., Turpin, G. A., & Nelson, R. P. 2023, A&A, 678, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kimura, M., Osaki, Y., Kato, T., & Mineshige, S. 2020, PASJ, 72, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H., & Kley, W. 2006, A&A, 445, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W. 1989, A&A, 208, 98 [NASA ADS] [Google Scholar]
- Kley, W. 1998, A&A, 338, L37 [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [Google Scholar]
- Kley, W., Papaloizou, J. C. B., & Ogilvie, G. I. 2008, A&A, 487, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolb, S. M., Stute, M., Kley, W., & Mignone, A. 2013, A&A, 559, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lega, E., Crida, A., Bitsch, B., & Morbidelli, A. 2014, MNRAS, 440, 683 [Google Scholar]
- Levermore, C. D. 1984, J. Quant. Spec. Radiat. Transf., 31, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1985, On the Dynamical Origin of the Solar System (University of Arizona Press) [Google Scholar]
- LLNL 2022, Units C++ runtime library, https://github.com/LLNL [Google Scholar]
- Lodato, G. 2008, New Astron. Rev, 52, 21 [CrossRef] [Google Scholar]
- Lust, R. 1952, Zeitsch. Naturfor. A, 7, 87 [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. 2002, A&A, 387, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. 2015, Astrophysics Source Code Library [record ascl:1509.008] [Google Scholar]
- Masset, F. 2017, MNRAS, 472, 4204 [NASA ADS] [CrossRef] [Google Scholar]
- Menou, K., & Goodman, J. 2004, ApJ, 606, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, F., & Meyer-Hofmeister, E. 1983, A&A, 121, 29 [NASA ADS] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Flock, M., & Vaidya, B. 2019, ApJS, 244, 38 [Google Scholar]
- Mihalas, D., & Mihalas, B. W. 1984, Foundations of Radiation Hydrodynamics (Oxford University Press) [Google Scholar]
- Mineshige, S., & Osaki, Y. 1983, PASJ, 35, 377 [NASA ADS] [Google Scholar]
- Morohoshi, K., & Tanaka, H. 2003, MNRAS, 346, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz, D. J., Miranda, R., & Lai, D. 2019, ApJ, 871, 84 [CrossRef] [Google Scholar]
- Müller, T. W. A. 2013, Dissertation, Universität Tubingen [Google Scholar]
- Müller, T. W. A., & Kley, W. 2012, A&A, 539, A18 [Google Scholar]
- Müller, T. W. A., & Kley, W. 2013, A&A, 560, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. W. A., Kley, W., & Meru, F. 2012, A&A, 541, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986, Icarus, 67, 375 [Google Scholar]
- O’Neill, M. 2018, Bob Jenkins’s Small PRNG Passes PractRand (And More!), https://www.pcg-random.org/posts/bob-jenkins-small-prng-passes-practrand.html [Google Scholar]
- Paardekooper, S. J., & Mellema, G. 2006, A&A, 459, L17 [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S. J., & Papaloizou, J. C. B. 2008, A&A, 485, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S., Dong, R., Duffell, P., et al. 2023, Astron. Soc. Pac., 534, 685 [NASA ADS] [Google Scholar]
- Picogna, G., & Kley, W. 2015, A&A, 584, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Picogna, G., Stoll, M. H. R., & Kley, W. 2018, A&A, 616, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierens, A., & Huré, J. M. 2005, A&A, 433, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierens, A., & Nelson, R. P. 2008, A&A, 482, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price, D. J., Wurster, J., Tricco, T. S., et al. 2018, PASA, 35, e031 [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Regály, Z., Juhász, A., Sándor, Z., & Dullemond, C. P. 2012, MNRAS, 419, 1701 [Google Scholar]
- Rein, H., & Liu, S.-F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Spiegel, D. S. 2015, MNRAS, 446, 1424 [Google Scholar]
- Rendon Restrepo, S., & Barge, P. 2022, A&A, 666, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rendon Restrepo, S., & Barge, P. 2023, A&A, 675, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rendon Restrepo, S., & Gressel, O. 2023, 2D simulations of dust trapping by self-gravitating vortices, Protostars and Planets VII, poster PF-07-003 [Google Scholar]
- Rendon Restrepo, S., Barge, P., & Vavrik, R. 2022, arXiv e-prints [arXiv:2207.04252] [Google Scholar]
- Rometsch, T., Rodenkirch, P. J., Kley, W., & Dullemond, C. P. 2020, A&A, 643, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rometsch, T., Ziampras, A., Kley, W., & Bethune, W. 2021, A&A, 656, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sauer, T. 2012, Numerical Analysis (Pearson Education) [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
- Shu, F. H. 1992, The Physics of Astrophysics, II: Gas Dynamics (University Science Books) [Google Scholar]
- Sod, G. A. 1978, J. Comput. Phys., 27, 1 [CrossRef] [MathSciNet] [Google Scholar]
- Speith, R., & Kley, W. 2003, A&A, 399, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Stone, J. M., Tomida, K., White, C. J., & Felker, K. G. 2020, ApJS, 249, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Tscharnuter, W. M., & Winkler, K. H. A. 1979, Comput. Phys. Commun., 18, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Vaidya, B., Mignone, A., Bodo, G., & Massaglia, S. 2015, A&A, 580, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leer, B. 1977, J. Comput. Phys., 23, 276 [Google Scholar]
- Von Neumann, J., & Richtmyer, R. D. 1950, J. Appl. Phys., 21, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 2003, Cataclysmic Variable Stars (Cambridge University Press) [Google Scholar]
- Wilson, G., Aruliah, D. A., Titus Brown, C., et al. 2012, arXiv e-prints [arXiv:1210.0530] [Google Scholar]
- Woitke, P., & Helling, C. 2003, A&A, 399, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woodward, P., & Colella, P. 1984, J. Comput. Phys., 54, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Stone, J. M., Rafikov, R. R., & Bai, X.-n. 2014, ApJ, 785, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Ziampras, A., Nelson, R. P., & Rafikov, R. R. 2023a, MNRAS, 524, 3930 [NASA ADS] [CrossRef] [Google Scholar]
- Ziampras, A., Paardekooper, S.-J., & Nelson, R. P. 2023b, MNRAS, 525, 5893 [CrossRef] [Google Scholar]
See https://units.readthedocs.io/en/latest/user-guide/from_string.html for more details.
Available at https://github.com/rometsch/fargocpt.
All Tables
All Figures
 |
Fig. 1 Order of operations in the operator splitting scheme showing the evolution of the N-body, hydro, and particle subsystems throughout one iteration step. Single-line arrows mean that the originating object is used in the calculation of the destination. Double lines indicated the evolution of one of the subsystems from the initial state (ellipse) over intermediate states (parallelogram) to the final state (round shape). Each rectangle with rounded corners is a computation of an intermediate quantity using the state of the subsystem to which it is connected. The rectangles with bars on the sides indicate an operation that changes the state of a system. The variables that were changed by an operation are indicated in boldface in the intermediate states. |
| In the text | |
 |
Fig. 2 Luminosity and mass-weighted eccentricity during a super-outburst in a cataclysmic variable system with and without our viscosity stabilizer. The simulation without the stabilizer required 3.8 times more time-steps during the shown time frame. |
| In the text | |
 |
Fig. 3 Schematic of the location of the quantities for the boundary conditions. The first active cell is shown in beige and the ghost cells are in blue. The ghost cells are not updated by the source terms and transport steps. Their values are used to apply the boundary conditions. |
| In the text | |
 |
Fig. 4 Logarithmic density plot of a simulation with the “Roche lobe overflow” boundary condition showing the stream of material emerging from the L1 point. The green line indicates the Roche lobe of the binary system and the grey circle is the outer boundary of the simulation domain. Outside the small region around the Lagrangian L1 point the boundary condition is set to “outflow”. |
| In the text | |
 |
Fig. A.1 Speedup factor with number of cores on the Tübingen compute cluster BINAC. |
| In the text | |
 |
Fig. D.1 Outflow boundary removes more mass than supplied by the disk. The figure shows the accretion rate through the disk and surface density for different choices of boundary conditions. The top and bottom panels show the mass per unit of time flowing through a ring of a given radius and the ratio of surface density to its initial value, respectively. |
| In the text | |
 |
Fig. D.2 Viscous accretion through and at the inner boundary for different resolutions and methods. The panels are analogous to Fig. D.1. The dip in mass flow rate for the blue line in the inner region is due to the method removing mass from the domain and thus disturbing the equilibrium state. |
| In the text | |
 |
Fig. D.3 Gas surface densities of the shock tube test with 100 cells for different combinations of artificial viscosity and integration schemes as well as for the caloric equation of state (PVTE) by Vaidya et al. (2015) with 1000 cells. The simulation time is t = 0.228 in both cases. The top and bottom panels show the surface density and the deviations from the reference case respectively, respectively. |
| In the text | |
 |
Fig. D.4 Gas surface density and temperature profile in the hydrostatic equilibrium for the model from D’Angelo et al. (2003) together with the expected theoretical profiles. |
| In the text | |
 |
Fig. D.5 Viscous spreading ring test from Speith & Kley (2003) on a logarithmic grid Nr × Nϕ= 512 × 256. The ring is initialized with Σ(x, τ = 0.016) (black line) and then evolved to τ = 439.82. The vertical dashed cyan line marks the position of the initial ring at time τ = 0. The blue line is the azimuthal averaged surface density, which matches the analytical formula (red line) well. The viscous instability can be seen as waves in a density slice along the x axis (magenta line). |
| In the text | |
 |
Fig. D.6 Dust diffusion test. Comparison of dust diffusion with Lagrangian super-particles in FARGOCPT with numerical integration of the 1D advection-diffusion equation using an implicit method. |
| In the text | |
 |
Fig. D.7 Results of the dust drift test. The top and bottom panel shows the value and deviation from the theoretical prediction of the drift speed as a function of the Stokes number, respectively. The large deviations for Stokes numbers around and larger than unity are due to oscillations in the integration. See Fig. D.8. |
| In the text | |
 |
Fig. D.8 Selected dust particle trajectories from the dust drift test. The panel shows the drift velocity as a function of time with the particle size and Stokes number encoded by color. The black lines show the expected value from Eq. (D.7). For larger dust particles with Stokes equal or greater than unity, oscillations occur due to the integration method. The particles represented by the red and purple lines leave the domain at the inner boundary during the simulation. |
| In the text | |
 |
Fig. D.9 Torque of a small mass planet compared to theoretical prediction. The torque needs some time to build while the initially smooth disk adjusts to the presence of the planet. |
| In the text | |
 |
Fig. D.10 Equilibration of a radial temperature profile due to radiation transport in the midplane with a constant opacity. This is used to test the FLD module. The panels show, from top to bottom, the radial temperature profile, the deviation from the equilibrium solution, and the azimuthally integrated flux through a ring at the respective radius, normalized by the equilibrium flux. Time is indicated by the color of the lines. |
| In the text | |
 |
Fig. D.11 2D diffusion of the analytical solution to the diffusion equation with constant diffusion coefficient. The top panel shows radial cuts through the center of the 2D distributions: the initial condition and the analytical and numerical solutions. The bottom panel shows the relative deviation between the numerical and the analytical solution. |
| In the text | |
 |
Fig. D.12 Comparison of the radial SG acceleration against results from direct summation. The top and bottom panels show the radial SG acceleration as a function of radius obtained with the Fourier method (code) and direct summation, and the relative and absolute differences between both curves, respectively. The horizontal gray line marks the zero value of acceleration and the vertical gray line indicates the crossing of zero. |
| In the text | |
 |
Fig. D.13 Same as Fig. D.12, but showing the azimuthal SG acceleration as a function of azimuth at r = 4 au. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.