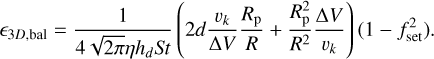| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A199 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348923 | |
| Published online | 24 April 2024 | |
Growth and evolution of low-mass planets in pressure bumps
Laboratoire d’astrophysique de Bordeaux, Univ. Bordeaux, CNRS,
B18N, allée Geoffroy Saint-Hilaire,
33615
Pessac,
France
e-mail: arnaud.pierens@u-bordeaux.fr
Received:
12
December
2023
Accepted:
5
February
2024
Observations of protoplanetary disks have revealed dust rings that are likely due to the presence of pressure bumps in the disk. Because these structures tend to trap drifting pebbles, it has been proposed that pressure bumps may play an important role in the planet formation process. In this paper, we investigate the orbital evolution of a 0.1 M⊕ protoplanet embedded in a pressure bump using 2D hydrodynamical simulations of protoplanetary disks consisting of gas and pebbles. We examine the role of thermal forces generated by the pebble accretion-induced heat release, taking into account the feedback between the luminosity and the eccentricity. We also study the effect of the pebble-scattered flow on the planet’s orbital evolution. Due to the accumulation of pebbles at the pressure bump, the planet’s accretion luminosity is high enough to induce significant eccentricity growth through thermal forces. Accretion luminosity is also responsible for vortex formation at the planet’s position through baroclinic effects, which cause the planet to escape from the dust ring if dust feedback on the gas is neglected. Including the effect of the dust feedback leads to weaker vortices, which enable the planet to remain close to the pressure maximum on an eccentric orbit. Simulations in which the planet mass is allowed to increase as a consequence of pebble accretion result in the formation of giant planet cores with masses in the range of 5–20 M⊕ over ~2 × 104 yr. This occurs for moderate values of the Stokes number, St ≈ 0.01, such that the pebble drift velocity is not too high and the dust ring mass not too small. Our results suggest that pressure bumps mays be preferred locations for the formation of giant planets, but this requires a moderate level of grain growth within the disk.
Key words: methods: numerical / planets and satellites: formation / planet–disk interactions
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In the standard scenario for planet formation, millimeter-sized dust grows from the coagulation of micron-sized grains (Dullemond & Dominik 2005). However, further growth of particles in the millimeter-size range is limited because of the bouncing (Zsom et al. 2010) and fragmentation (Blum & Wurm 2008) barriers. An emerging picture to bypass these growth barriers is that 100-km sized planetesimals form directly through the streaming instability (SI; Youdin & Goodman 2005; Johansen et al. 2009; Simon et al. 2016), as particles with Stokes number (or dimensionless stopping time) St ~ 0.001–0.1 directly concentrate into clumps or filaments under the action of gas drag, and these become gravitationally unstable to form ~100–1000 km-sized bodies. Planetesimals can subsequently grow very efficiently by capturing inward drifting pebbles (Johansen & Lacerda 2010; Lambrechts & Johansen 2012), namely solids with a Stokes number, St ~ 0.01–1, that are marginally coupled to the gas, leading eventually to the formation of giant planet cores within 1 Myr (Lambrechts & Johansen 2014).
The conditions for triggering the SI, and the efficiency of pebble accretion, are however sensitive to the level of turbulence operating in the disk. Small particles are lofted away from the midplane by turbulent mixing such that the local dust-to-gas ratio, and hence the growth rate of the SI, are reduced. One possibility to counteract the effect of turbulence in the disk is to invoke the presence of pressure bumps in the disk, where the radial drift of dust particles can be stopped, leading subsequently to an enhancement in the dust-to-gas ratio.
Pressure bumps may be associated with ringed structures, which have been observed with ALMA in a variety of protoplanetary disks (ALMA Partnership 2015; Andrews et al. 2018). Although there is no current consensus, possible mechanisms that might be able to explain these features include: the presence of planets that can open gaps in the disk (Dipierro et al. 2015; Dong et al. 2017), zonal flows (Flock et al. 2015), snow lines (Zhang et al. 2015), large-scale instabilities (Lorén-Aguilar & Bate 2015), spontaneous ring formation through radial drift plus dust coagulation (Gonzalez et al. 2017), and dust-driven viscous ring instability (Dullemond & Penzlin 2018). Whenever the physical origin of pressure bumps takes place, recent work suggests that planetesimals could indeed be formed at such locations as a result of the SI (Carrera et al. 2021; Xu & Bai 2022), at least if the protoplanetary disk can form grains larger than 1mm (Carrera et al. 2021).
Planetesimals formed at pressure bumps are expected to grow efficiently though pebble accretion. It has been shown that the gravitational potential energy release associated with pebble accretion can significantly impact its orbital evolution in the disk (Benítez-Llambay et al. 2015). Accretion heating makes gas streamlines outflowing from the Hill sphere form two under-dense lobes – one leading and one following the planet – that exert a torque on the planet. Because the orbital velocity of gas is slightly sub-Keplerian, the lobe located behind the planet tends to be less dense than the one located ahead of the planet, resulting in a net positive torque that has been referred to as the “heating torque”. Due to the locally enhanced dust-to-gas ratio at the pressure bump, the heating torque could potentially be strong, as well as the torque induced by scattered pebble flow (Benítez-Llambay & Pessah 2018). It cannot be excluded that a planet’s orbital evolution would even be dominated by these processes, since the classical Lindblad and corotation torques arising from the interaction with the gas disk tend to counteract each other in the vicinity of the pressure bump (Masset et al. 2006). Of course, this would be true, provided that the equilibrium planet position set by the Lindblad and corotation torques lies within the pebble ring; otherwise, the pebble accretion rate onto the planet would be very small (Morbidelli 2020). The effect of thermal torques on the migration of Mars-to super-Earth-sized planets in the vicinity of a pressure bump was recently investigated by Chrenko & Chametla (2023). These authors found that thermal forces can cause low-mass planets to escape the pressure bump. This arises because thermal forces make the planet eccentricity grow, which subsequently quenches the corotation torque responsible for the migration trap.
In this paper, we use 2D hydrodynamical simulations to examine the orbital evolution of a protoplanet forming at a pressure bump and whose mass increases as a result of pebble accretion. Torques induced by the pebble-scattered flow are taken into account and the pebble accretion rate is determined self-consistently using the formulae of Liu & Ormel (2018) and Ormel & Liu (2018) for the pebble accretion efficiency. This is an important issue as the latter depends on the planet eccentricity, while the planet eccentricity growth rate through thermal forces is regulated by the accretion rate. Hence, the positive feedback that exists between the planet luminosity and eccentricity (Velasco Romero et al. 2022) is also considered in our study. The aim of this paper is twofold: first, we identify the main physical processes that drive the planet’s orbital evolution at a pressure bump. Second, we study whether giant planet cores can form at a pressure bump under realistic conditions for the accretion and migration of the planet.
This paper is organized as follows. In Sects. 2 and 3, we present the physical model and the numerical setup. In Sect. 4, we discuss the results of our simulations. Finally, we draw our conclusions in Sect. 5.
2 The physical model
2.1 Gas equations
We solve the hydrodynamical equations for the gas component in polar coordinates (r, φ) (radial, azimuthal), with the origin of the frame located at the central star. The governing equations are the continuity equation, which is given by
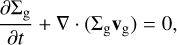 (1)
(1)
the Navier-Stokes equation, which is given by
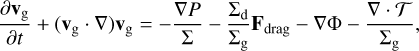 (2)
(2)
and the energy equation, which is described in Sect. 2.1.2. In Eq. (2), ∑g and ∑d are the gas and pebble surface densities, respectively, vg is the gas velocity, Fdrag describes the frictional drag force between the gas and the dust (see Sect. 2.2), P is the gas pressure, and 𝒯 the viscous stress tensor (e.g., Nelson et al. 2000).
2.1.1 Gravitational potential
In Eq. (2), the gravitational potential, Φ, includes the contributions from the star, the planet, and the indirect term. In this work, the gravitational influence of the planet on the gas disk was modeled using a vertically averaged expression for the gravitational potential, Φp (Müller et al. 2012; Chrenko et al. 2017):
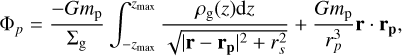 (3)
(3)
where mp is the planet mass, rs is a softening length that is employed to avoid divergence of the gravitational potential at the planet’s location, r is the vector pointing to the location in the disk, and rp is the vector pointing to the planet. In the previous equation, the second term corresponds to the acceleration experienced by the center of the reference frame due to the presence of the planet. The integral in Eq. (3) was computed by dividing the interval [0, ɀmax] into Nɀ = l0 equal intervals with ɀmαx = 3H, where H is the disk scale height, and assuming hydrostatic equilibrium in the vertical direction such that the mass density of the gas, ρg(ɀ), is given by
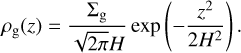 (4)
(4)
This averaging procedure allows us to use a smoothing length, rs, which is similar to the characteristic grid cell at rp and which is set to rs = 0.01 H in this work. This is much smaller than the value for the softening parameter that is classically adopted in 2D simulations, which is chosen to be on the order of H to mimic the gravitational potential of a vertically extended 3D disk. It has been shown, however, to lead to torques experienced by the planet that can significantly differ from the full 3D case (Müller et al. 2012).
The indirect term, Φind, arising from the fact that the frame centered on the central star is not inertial, is given by (e.g., Nelson et al. 2000)
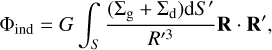 (5)
(5)
where S is the surface of the simulation domain.
2.1.2 Energy equation
In addition to the continuity equation and momentum equation, we solved an energy equation that includes the effect of viscous heating, stellar irradiation, and radiative cooling. It reads:
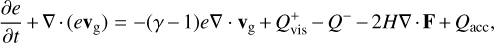 (6)
(6)
where e is the thermal energy density and γ the adiabatic index, which was set to γ = 1.4. In the previous equation, 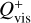 is the viscous heating term, and
is the viscous heating term, and 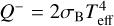 is the local radiative cooling from the disk surfaces, where σB is the Stephan-Boltzmann constant and Teff the effective temperature, which is given by (Menou & Goodman 2004)
is the local radiative cooling from the disk surfaces, where σB is the Stephan-Boltzmann constant and Teff the effective temperature, which is given by (Menou & Goodman 2004)
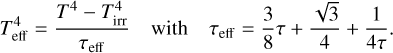 (7)
(7)
Here, T is the midplane temperature and τ = κ∑g /2 is the vertical optical depth, where κ is the Rosseland mean opacity, which is taken from Bell & Lin (1994). Tirr is the irradiation temperature, which is computed from the irradiation flux (Menou & Goodman 2004),
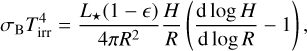 (8)
(8)
where ϵ = 1/2 is the disk albedo, L★ is the stellar luminosity, which is set to L★ = 1.43 L⊙, and where the factor, d log H/d log R, is set to be d log H/d log R = 9/7 (Chiang & Goldreich 1997). This implies that self-shadowing effects are not taken into account in this study.
In Eq. (6), F is the radiative flux that is treated in the flux-limited diffusion approach and that reads (e.g., Kley & Crida 2008):
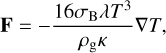 (9)
(9)
where λ is a flux-limiter (e.g., Kley 1989). Finally, Qacc = Lacc/S is the accretion heating term, with S the cell area and Lacc the luminosity of the accreting embryo (see Sect. 2.3).
2.2 Dust equations
The solid component was treated as a pressureless fluid whose equations for the conservation of mass and momentum are given by
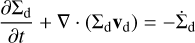 (10)
(10)
where vd is the dust velocity, ts is the particle stopping time, Dv is the turbulent (viscous) dust diffusion coefficient, and 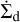 represents the local dust density decrease resulting from pebble accretion (see Sect. 2.3).
represents the local dust density decrease resulting from pebble accretion (see Sect. 2.3).
2.2.1 Drag force between gas and dust
In Eq. (11), the drag force resulting from the interaction with the gaseous disk is given by
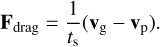 (12)
(12)
In the following, we parameterize the stopping time, ts, through the Stokes number, St = tsΩ, with Ω the Keplerian frequency. We note that in the well-coupled regime, ts is related to the particle size, sd, through
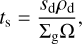 (13)
(13)
where ρd is the particle internal density. With respect to our previous work, in which we employed a model of dust evolution with a single representative, we here adopted instead a fixed particle Stokes number, for which we considered values of St = 0.001, 0.01, 0.05.
2.2.2 Dust diffusion
Tominaga et al. (2019) show that introducing a diffusion term as a source term in the continuity equation for the dust can violate the conservation of the total angular momentum of the dusty disk. To bypass this issue, Klahr & Schreiber (2021) implemented the diffusion flux in the momentum equation for the dust rather than in the continuity equation. As a consequence, we modeled dust diffusion arising from the residual turbulence in the disk by including a diffusion pressure term within the dust momentum equation and corresponding to the last source term in Eq. (11). The corresponding dust diffusion coefficient is given by
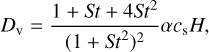 (14)
(14)
with α the viscous stress parameter (Shakura & Sunyaev 1973).
2.3 Planets
2.3.1 Accretion luminosity
We considered luminous planets that can release heat in the disk as a consequence of pebble accretion. The planet’s luminosity is related to the pebble accretion rate onto the planet, Ṁp, through the relation
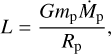 (15)
(15)
where Rp is the physical radius of the planet, which was calculated assuming a material density of 2 g cm−3. Defining the pebble accretion efficiency as ϵ = Ṁp/Ṁpeb where Ṁpeb is the inward mass flux of pebbles, it has been shown that ϵ depends mainly on η, St, α, and on the planet’s eccentricity, ep. Liu & Ormel (2018) and Ormel & Liu (2018) have derived prescriptions to calculate e as a function of these parameters (see Appendix A) and we employed these to self-consistently determine the value of the planet luminosity. Thermal forces arising from heat release in the disk are indeed expected to make the planet’s eccentricity increase, and consequently impact the pebble accretion efficiency. As has been noted by Velasco Romero et al. (2022), there exists a feedback loop between the eccentricity growth driven by thermal forces and the luminosity that tends to increase with eccentricity, at least in the regime where the eccentricity remains smaller than the disk aspect ratio.
2.3.2 Accretion procedure
In our simulations, the pebble accretion rate onto the planet was therefore based on the prescription of Liu & Ormel (2018) and is given by Ṁp = ϵṀpeb. To make sure that the latter was indeed smaller to what the disk could provide, we followed Crida & Bitsch (2017) and calculated the maximum expected accretion rate, ṀK, using Kley (1999)’s recipe. At each time step, the total mass of pebbles located within 0.5 of the accretion radius, Racc, of the planet was added to the planet’s mass, at such a rate that half of the total pebble mass within 0.5 Racc was accreted by the planet over an orbital period. The effective pebble accretion rate onto the planet is then given by
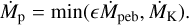 (16)
(16)
The accretion of solids is accompanied by a reduction in the local gas surface density within the accretion radius of the planet according to the determined value for the accretion rate. This process is implemented as a the source term in the dust continuity equation (see Eq. (10)). We also note that the angular momentum contained within the removed material was not added to the planet’s angular momentum.
3 Numerical simulations
3.1 Numerical method
Simulations were performed using the GENESIS (de Val-Borro et al. 2006) code, which solves the equations governing the disk evolution on a polar grid (R, φ) using an advection scheme based on the monotonic transport algorithm (van Leer 1977). It uses the FARGO algorithm (Masset 2000) to avoid time step limitation due to the Keplerian velocity at the inner edge of the disk, and was recently extended to follow the evolution of a solid component that is modeled assuming a pressureless fluid. Momentum exchange between the particles and the gas was handled by employing the semi-analytical scheme presented in Stoyanovskaya et al. (2018). This approach enables the consideration of arbitrary solid concentrations and values for the Stokes number, and is therefore very well suited for looking for solutions of non-stationary problems. Tests of the numerical method to handle the momentum transfer between gas and dust were presented in Pierens et al. (2019) and the code was recently used to study the nonlinear evolution of the secular gravitational instability (Pierens 2021).
The computational domain was covered by NR = 1572 radial grid cells, uniformly distributed between Rin = 0.55 and Rout = 1.6, and Nϕ = 3072 azimuthal grid cells. The numerical resolution was chosen so that (i) the amplitude of the dust torques was converged (see Sect. 4.1.2) and (ii) the thermal disturbance in the vicinity of the planet was resolved by ~5 grid cells (see Sect. 4.1.3). The computational units that we adopted were such that the unit of mass was the central mass, M★ = 1, and was assumed to be equivalent to one Solar mass, the gravitational constant was G = 1, and the distance, R = 1, in the computational domain was set to 5.2 AU. In the following, this corresponds also to the initial semimajor axis, R0, of migrating planets so that when presenting the simulation results, time will be expressed in orbital periods at R = R0.
3.2 Initial and boundary conditions
The initial disk aspect ratio, h, was set assuming that stellar heating dominates over viscous heating and corresponded to that expected for a purely passive disk, h ∝ (R/R0)2/7 (Chiang & Goldreich 1997). For a constant mass flow through the disk, Ṁ, this implies an initial gas surface density, ∑BG = ∑0(R/R0)−15/14 (Bitsch et al. 2014), where Σ0 = 6 × 10−4 is the surface density at R = R0. Superimposed on this background surface density, we set up a Gaussian bump by employing the following profile for the α viscous stress parameter:
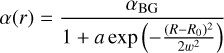 (17)
(17)
where αBG is the background value for which we considered values in the range [10−5, 10−3] and a = 0.5 is the amplitude of the pressure bump. Hence, the initial surface density profile is given by
![${{\rm{\Sigma }}_{\rm{g}}}(R) = {{\rm{\Sigma }}_{{\rm{BG}}}}\left[ {1 + a\exp \left( { - {{{{\left( {R - {R_0}} \right)}^2}} \over {2{w^2}}}} \right)} \right].$](/articles/aa/full_html/2024/04/aa48923-23/aa48923-23-eq21.png) (18)
(18)
The dust surface density was initialized assuming a constant dust-to-gas ratio, Z = 0.01.
Our simulations were split into two steps. We first evolved the gas and pebble disks until a quasi-stationary state was achieved, namely until the gas and solid mass fluxes became constant throughout the disk, and then used the relaxed hydrodynamical quantities as initial conditions for runs with embedded planets. In that case, we made use of wave-killing zones in the intervals R ∊ [0.55, 0.6] and R ∊ [1.55, 1.6], where each variable, f, was relaxed toward its initial value, f0, using the prescription of de Val-Borro et al. (2006):
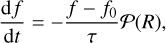 (19)
(19)
where τ is the damping timescale, which was set to 0.1 of the orbital period, and 𝒫(R) is a parabolic function that varies between 1 and 0 from the edge of the domain to the inner edge of the damping zone.
 |
Fig. 1 Pebble surface density, Σp, gas surface density, Σg, and gas pressure as a function of radius for the fiducial run, with St = 0.01 and α = 10−4. |
4 Results
4.1 A reference run
In the following, we focus on a fiducial model that has St = 0.01 and α = 10−4. The model was evolved for 5 × 105 orbits prior to inserting the planet, which is typically the time required to reach a quasi-stationary configuration. The dust and gas surface densities and pressure radial profiles at equilibrium are shown in Fig. 1. As was expected, dust trapping at the pressure bump leads to the formation of a ring whose mass is ~15 M⊕. We also see that the pressure and gas surface density maxima are slightly shifted because of the use of a non-constant sound speed. The pressure maximum is indeed located at R ≈ 0.984, whereas the surface density maximum is found to be at R ≈ 0.988.
At Time = 5 × 105, we inserted a 0.1 M⊕ core that initially evolved on a nearly circular orbit with an initial semimajor axis, ap = 1, and an eccentricity, ep = 10−4, and we examined its orbital evolution within the pressure bump. In order to highlight the physical processes that control the dynamics of an embryo formed at a pressure bump, we adopted a step-by-step procedure. We first performed a simulation in which we assumed that the protoplanet feels only the effects of the gas torques. Next, we studied the impact of taking into account the torques resulting from the scattered pebble flow (Benítez-Llambay & Pessah 2018). Then, we performed an additional run with accretion heating included. Finally, we performed full calculations in which each of the aforementioned processes were taken into account. The results of this multistep procedure are shown in Fig. 2, where we plot for each run the planet’s semimajor axis and eccentricity as a function of time.
 |
Fig. 2 Planet semimajor axis and eccentricity as a function of time for the fiducial run, with St = 0.01 and α = 10−4, and in cases where a 0.1 M⊕ protoplanet is allowed to evolve under the effect of gas torques, pebble scattering, pebble accretion, and dust feedback. |
4.1.1 Orbital evolution under the effect of gas torques only
We first focused on the situation where only the effects of the gas torques were considered. The total gas torque, Γ, exerted on the planet is given by
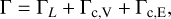 (20)
(20)
where ΓL, Γc,V, and Γc,E are the Lindblad torque, vortensity-driven corotation torque, and entropy-related corotation torque, respectively. Following Morbidelli (2020), these components can be written as
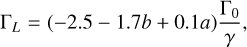 (21)
(21)
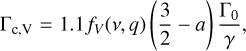 (22)
(22)
where a, b are the power law indexes of the surface density and temperature profiles, respectively, and ξ = b − (γ − 1)a is the exponent of the entropy profile, ƒV and fE are saturation functions that depend on the planet’s mass ratio, q = mp/M★, disk viscosity, v, and thermal diffusivity, χ, and that can be computed using the classical Paardekooper et al. (2011) formulae. In the previous equations, Γ0 is the nominal torque, which is given by
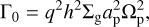 (24)
(24)
with Ωp the planet angular velocity. When only the contribution from the gas torques is taken into account, Fig. 2 shows that the planet becomes trapped near the surface density maximum at a radial location, rp ≈ 0.995. Following Morbidelli (2020) and defining the location of the trap relative to the pressure bump as δω2/r0, this would correspond to δ ≈ 6. It is worth noticing that the planet trap is located slightly beyond the surface density maximum, in a region where the surface density gradient is <0. Although the vortensity-related corotation torque is not expected to be very strong at this location, the (total) corotation torque may still counterbalance the Lindblad torque, provided that the contribution from the entropy-related corotation torque is >0 and unsaturated near the pressure bump. To demonstrate that this is indeed the case, ΓL, Γc,V, and Γc,E are represented as a function of radius in Fig. 3. Consistently with the results of our simulations, we see that the total torque is expected to cancel outside of the location of the maximum gas density. From Fig. 3, this is clearly a consequence of the strong entropy-related corotation torque, which is indeed >0 in the vicinity of the pressure bump and which acts in concert with Γc,V to counteract the effect of the Lindblad torque. In the case in which the entropy-related corotation torque was saturated, however, we would expect the trap to be located in a region with a positive surface density gradient, since a strong vortensity-related corotation torque would be required to cancel out the Lindblad torque.
Strickly speaking, the total torque exerted on the planet should also include a contribution from the cold thermal torque (Lega et al. 2014; Masset 2017). The latter originates from dense lobes forming on each side of the orbit and is given by
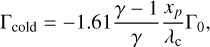 (25)
(25)
where xp = ηh2rp is the distance to corotation, η = α/3 + β/6 + 1/2, and 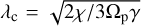 is the typical size of the lobes forming on either side of the orbit. The dashed blue line in Fig. 3 shows that the cold thermal torque has a negligible effect on the location of the planet trap. It is interesting to note that inside the pressure bump η < 0 such that the cold thermal torque can become positive there.
is the typical size of the lobes forming on either side of the orbit. The dashed blue line in Fig. 3 shows that the cold thermal torque has a negligible effect on the location of the planet trap. It is interesting to note that inside the pressure bump η < 0 such that the cold thermal torque can become positive there.
 |
Fig. 3 Torque profile of the fiducial simulation, with St = 0.01 and α = 10−4, at a point in time when migration is halted. Overplotted are the contributions from the Lindblad torque, ΓL, vortensity-related corotation torque, Γc,V, and entropy-related corotation torque, Γc,V. The dashed line shows the total torque in the case where the cold torque, Γcold, is taken into account. |
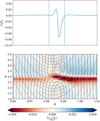 |
Fig. 4 Top panel: pebble torque profile for St = 0.01 and α = 10−4 in the situation where the planet can evolve under the effect of gas plus pebble torques. Bottom panel: pebble surface density perturbation and streamlines (blue) for the same run. The orange lines correspond to streamlines obtained in the absence of a pressure bump. |
4.1.2 Effect of taking into account dust torques
Previous work has emphasized the ability of a low-mass planet to develop an asymmetric dust distribution in its vicinity that is responsible for a dust torque exerted on the planet (Benítez-Llambay & Pessah 2018). It has been shown that this dust torque can potentially be strong and can even reverse inward planetary migration for cores with masses ≲ 10 M⊕ (Guilera et al. 2023). Here, we examine how dust torques impact the planet trap concept mentioned in the previous section, and how they affect the trap location. We note in passing that the numerical setup adopted in this work leads to a resolution of 6 × 10−4 rp at the planet’s position, similar to that used in the simulations of Benítez-Llambay & Pessah (2018) and Regály (2020). It has been demonstrated by these authors that such a resolution is sufficient to properly capture the dust dynamics in the vicinity of the planet (e.g., Regály (2020).
Figure 2 shows that a planet trap is still effective when taking into account dust torques. The main difference is that the location of the trap is slightly shifted inward, which suggests negative dust torques. This is confirmed by examining the dust torque density, which is shown as a function of radius in the upper panel of Fig. 4. Inspecting the time evolution of the dust torques also reveals that they tend to counterbalance the positive gas torques at equilibrium. For St = 0.01 and mp = 0.1 M⊕, a negative dust torque is in agreement with the results of Benítez-Llambay & Pessah (2018, see their Fig. 2). However, whereas Benítez-Llambay & Pessah (2018) found that small planets feel a negative torque due to an overdensity behind the planet that competes with an overdensity located in front of the planet, here the origin of the negative torque exerted on the planet is found to be different. This is illustrated in the bottom panel of Fig. 4 where we display the relative dust density perturbation near the planet. An overdense region behind the planet can indeed be observed but a density depletion located in front of the planet also contributes to the negative dust torque acting on the planet.
In the bottom panel of Fig. 4, the overplotted blue streamlines also show possible horseshoe dynamics in the presence of a pressure bump, which would give rise to a dust corotation torque acting on the planet. After executing their U-turn, pebbles migrating from the outer disk to the inner one can drift back outside of the planet’s orbit as a result of the change in the pressure gradient sign, leading to the formation of a corotation region. In the absence of pressure bump, we see that pebbles also execute U-turns as they approach the planet but the bended trajectories (orange lines in Fig. 4) are not due to horseshoe dynamics and occur simply because we employed a reference frame corotating with the embryo (Morbidelli & Nesvorny 2012).
By analogy with the classical corotation torque in a gas disk, we expect a dust corotation torque to be established, provided that χτ < 1, where χτ is the ratio between the time, τf, for a pebble to move across the radial extent, xs, of the (dust) corotation region due to the dust radial inflow and the libration timescale, τlib:
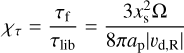 (26)
(26)
where xs is estimated to be xs ≈ 5 × 10−3ap and |υd,R| ≈ 6 × 10−4apΩ. This gives χτ ≈ 0.5 such that we indeed expect the dust corotation torque to be unsaturated.
4.1.3 Impact of pebble accretion
In this section, we study the impact of taking into account pebble accretion onto the core, which was modeled in our simulations using the procedure described in Sect. 2.3.2. As the planet accretes pebbles, the release of potential energy heats the disk locally, leading to the formation of two underdense lobes (Benítez-Llambay et al. 2015) that exert thermal forces onto the planet. Since our aim is to examine the effect of each physical process on the planet’s orbital evolution, torques resulting from pebble scattering and whose effect has been discussed in the previous section are not included here. In addition, the mass removed during the pebble accretion process has not been added to the planet’s mass for the time being.
Under standard conditions, namely in disks where η > 0, the torque resulting from accretion heat is positive. It has been shown that the net thermal torque, due to the contributions from the cold (negative) plus heating (positive) torques, is >0, provided that the planet’s luminosity exceeds a critical value, Lc, given by (Masset 2017)
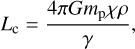 (27)
(27)
where χ is the thermal diffusion coefficient and ρ the gas density. A planet with a super-critical luminosity tends to undergo not only outward migration but also eccentricity growth (Fromenteau & Masset 2019), until the planet’s eccentricity saturates to a value close to the disk aspect ratio (Velasco Romero et al. 2022).
For a 0.1 M⊕ planet forming at a pressure bump, the planet luminosity relative to Lc is plotted as a function of time in Fig. 5. Initially, L/Lc ≈ 3 such that growth in eccentricity with time is expected. Referring back to Fig. 2, this is indeed what is observed in the case with pebble accretion only (green line). Linear theory predicts that this eccentricity growth should be exponential as long as it is much smaller than the thermal length scale, λc (Masset 2017), whereas for a given value of the planet’s luminosity, the eccentricity tends to increase linearly with time once ep ≫ λ (Cornejo et al. 2023). This is referred to as the headwind-dominated regime, where the two-lobes feature is replaced by a hot trail (Chrenko et al. 2017). Here, λ ≈ 0.0015 ap such that the episode of rapid eccentricity growth that can be seen at Time ≈3 × 103 is likely to arise in the headwind-dominated regime. This is a consequence of two effects. First, it results from the feedback loop between the eccentricity of the planet and its luminosity. The pebble accretion efficiency increases with the planet’s eccentricity, while at the same time the thermal forces that cause eccentricity growth strengthen as the planet becomes more luminous. Second, the η parameter is continuously increasing in absolute value as the planet migrates outward, resulting in a higher pebble flux. Although the semimajor axis evolution rate is much smaller than that of the eccentricity, the important increase in luminosity that is generated by both effects causes the brief period of fast outward migration that can also be observed at Time ≈3 × 103. As the eccentricity reaches ep ~ h at later times, the contribution from thermal forces to the semimajor axis evolution becomes negligible (Pierens 2023), while both the resonant (Papaloizou & Larwood 2000) and corotation (Fendyke & Nelson 2014) torques become quenched as well. This leads to a final evolution outcome with the planet able to evolve on a fixed eccentric orbit. Here, the planet’s eccentricity at a steady state is found to be ep ~ 0.04 while ap ~ 1 .025, such that the planet is located just outside of the dust ring.
 |
Fig. 5 Accretion luminosity as a function of time for the fiducial run, with St = 0.01, α = 10−4 and pebble accretion included. For luminosities higher than the critical value, Lc, growth in the planet’s eccentricity occurs as a result of thermal forces. |
4.1.4 Combining pebble accretion and torques from the pebble-scattered flow
This situation is represented by the red line in Fig. 2 and resulted in a different mode of evolution. Here, the planet is found to escape from the ring, migrating inward in the pebble-depleted region and maintaining a small eccentricity due to its small accretion luminosity. The continuous inward migration that is observed is clearly related to the significant increase in eccentricity that arises at early times. The large eccentricity that is reached, ep ~ 0.06, quenches not only the corotation (Fendyke & Nelson 2014) but also the thermal torques (Pierens 2023), which are both positive. In order to get an insight into the physical origin of the eccentricity growth, we show in the two upper panels of Fig. 6 the gas and dust surface densities when the planet eccentricity begins to increase. The gas surface density reveals a vortex forming at the radial location of the planet, which is confirmed by inspecting the vortensity distribution in the third panel of Fig. 6. This is consistent with the recent results of Cummins et al. (2022), who find that including the thermal feedback on the gas resulting from the accretion luminosity tends to lead to the formation of an anticyclonic vortex. Consistently with Cummins et al. (2022), we also find that the vortex is formed at the location of the planet, as is suggested by the Time = 6 panel. It is important to note that vortex formation is also observed in the simulations corresponding to the previous situation in which only pebble accretion was included, although it had no impact on the planet orbital evolution because dust torques were not included in this run. This implies that the initial eccentricity growth that occurs is due to interactions of the planet with the dust component of the vortex rather than with its gas component. We checked by inspecting the time evolution of the theoretical change in ep due to the gas and dust components that this is indeed the case. Previous studies have also reported the plausibility of a planet undergoing significant eccentricity growth due to its interaction with a dusty vortex (Pierens et al. 2019; Hsieh & Lin 2020). For instance, Hsieh & Lin (2020) find that the eccentricity induced by a dusty vortex is ep ~ 0.03 in disks with metallicity Z = 0.3, whereas ep ~ 0.1 in disk with Z ≥ 0.5. Since the planet here is located in a pressure with a dust-to-gas ratio ≈1, a maximum eccentricity of ep ≈ 0.06 is therefore compatible with these estimations.
4.1.5 Effect of dust feedback
Due to the large solid abundance within the ring, an important issue that needs to be examined is the effect of dust feedback on the gas. Compared to the previous case where it was discarded, including dust feedback (purple line in Fig. 2) enables the planet to remain trapped near the pressure maximum, at a location similar to that found in the situation where only torques due to pebble scattering were considered (orange line in Fig. 2). As first glance this is surprising since it has been shown that by altering the gas azimuthal velocity, dust feedback tends to lead to meso-scale instabilities (Pierens et al. 2019; Huang et al. 2020; Hsieh & Lin 2020), which can subsequently excite the planet’s eccentricity. This is especially true in the case where vortices are formed as a result of the Rossby wave instability (RWI) associated with an extremum in the potential vorticity. Here, however, the source of vorticity is a baroclinic instability associated with the embryo accretion luminosity (Owen & Kollmeier 2017) rather than the RWI. In this case, it is plausible that vortices suffer drag instabilities while they collect dust, as has been demonstrated by past studies (Fu et al. 2014; Crnkovic-Rubsamen et al. 2015; Surville & Mayer 2019). Our results are consistent with this scenario, since we find that including the effect of dust feedback leads to weaker vortices. This can be clearly observed by comparing Figs. 6 and 7, in which we show the density and vorticity distributions when including dust feedback. An additional difference is that the amplitude of the hot trail is higher when dust feedback is included. Given that it is responsible for driving its eccentricity, this causes the planet to reach a maximum value, ep ~ h, much earlier in comparison with the situation discussed in Sect. 4.1.3 in which the effect of the dust feedback on the gas was not included. The effect of the thermal torque on the semi-major axis also weakens more rapidly, with the consequence that the main contribution to the dust torque becomes dust scattering. At equilibrium, the planet eccentricity is therefore driven by thermal forces, whereas the semimajor axis evolution is driven by dust scattering.
 |
Fig. 6 Top panel: gas surface density perturbation at different times for the run with St = 0.01, α = 10−4, and pebble accretion included. Gas heating due to pebble accretion leads to vortex formation at the planet’s position. Middle panel: pebble surface density perturbation. Bottom panel: contours of the normalized vorticity for the same run. |
4.2 Taking into account the change in planet mass due to pebble accretion
We now discuss the results of more realistic simulations in which planets are truly allowed to accrete pebbles and increase in mass. In that case, Fig. 8 reveals the important role played by dust feedback on the orbital and mass evolution of the planet. When this effect is discarded, the evolution is similar to that described in Sect. 4.1.4, involving rapid escape from the pressure bump due to vortex formation at the planet position. Because pebbles accumulate at the pressure maximum, planet growth is mostly stalled as it migrates inward in such a way that the maximum mass of the growing embyo is only ≈0.2 M⊕. When the effect of dust feedback on the gas is included, however, the growth of the planet is also found to stop, but at a much higher mass of ≈20 M⊕. This demonstrates that the growth of giant planet cores at pressure bumps is plausible and can happen on a relatively short timescale. Again, the early evolution in that case proceeds similarly to what has been described in Sect. 4.1.5, with the planet trapped at the zero-torque radius set by gas torques and pebble scattering. Because this location is close to the pressure maximum, this allows the planet to accrete at a higher rate and to rapidly reach a mass at which gap opening can occur. Not surprisingly, the gap opening process is accompanied by vortex formation, as can be seen in Fig. 9 in which we show the gas density and vorticity at two different times. At Time = 1000, several vortices form at the inner edge of the gap carved by the planet at R ~ 0.9. Given that the planet has semimajor axis ap ≈ 1 and eccentricity ep ~ 0.1 at that time, this implies significant planet-vortex interactions when the planet is at the pericenter. This cause the planet to subsequently undergo an episode of rapid inward migration (Lin & Papaloizou 2010; Wafflard-Fernandez & Baruteau 2020) and escape from the pressure bump. From this point onward, pebble accretion is stopped due to (i) the very low density of pebbles in the inner disk while the planet continuously migrates inward and (ii) the halting of pebble flux at the gap created by the planet.
 |
Fig. 8 Planet mass, semimajor axis, and eccentricity as a function of time for runs in which the planet grows as a result of pebble accretion. |
 |
Fig. 9 Top panel: gas surface density perturbation at different times for the run in which the planet is allowed to grow, and with the effect of dust feedback on the gas included. Bottom panel: contours of the normalized vorticity at the same times. |
4.3 Varying the α viscosity
In the left panel of Fig. 10, we present the time evolution of planet mass, semimajor axis, and eccentricity for three different values of the α viscosity. Here, dust torques have been taken into account, as well as the effect of dust feedback on the gas. Clearly, the value of the viscosity has a major impact on the planetary growth process. For α = 10−3, pebble accretion is slow at first because of the larger width of the pressure bump (see Fig. 11), resulting in weaker dust trapping. This also occurs because gas diffusivity tends to hinder eccentricity growth, especially for smaller planetary masses (Chametla & Masset 2021). As pebble accretion efficiency scales with planet eccentricity, pebble accretion is therefore expected to be less efficient for high values of gas diffusivity.
One might expect that the planet would grow more rapidly in the run with α = 10−5. However, this is not observed in our simulations, as the planet mass saturates to mp ≈ 0.5 M⊕, whereas it reaches mp ≈ 20 M⊕ when α = 10−2. Although not shown here, we find that this is due to the vortices forming in the vicinity of the planet. These vortices generate spiral waves that propagate outward and dissipate. For α = 10−5, this leads to the formation of a secondary pressure bump that can trap pebbles drifting from the outer disk, with the consequence that the planetary growth process is stopped.
4.4 Varying the Stokes number
We now turn our attention to the dependence of our results on the Stokes number. The pressure bump profiles in a quasi-steady state are shown for different values of St in the bottom panel of Fig. 11, whereas the corresponding time evolution of the planet mass, semimajor axis, and eccentricity are presented in the right panel of Fig. 10. Compared to the case with St = 0.01, the mass growth rate is significantly reduced for St = 0.001. Here, this is simply a consequence of the less pronounced density peak for this value of the Stokes number. In the absence of a pressure bump, we would indeed have expected a higher accretion rate, as St = 0.001 pebbles are more coupled to the gas and drift more slowly, such that they have a higher probability of being accreted by the planet (Velasco Romero et al. 2022).
The smaller pebble accretion rate found for St = 0.1 (relative to St = 0.01) is due to both a larger drift velocity and the narrower dust ring. Provided that the width of the dust ring is small enough, we indeed find that the planet can eventually evolve outside of the dust ring over one orbital period due to its finite eccentricity. To demonstrate that this is indeed the case, we show in Fig. 12 the accretion rate onto the planet over a few orbits. For St = 0.01, the accretion rate oscillates with a period corresponding to half of the planet’s orbital period, whereas for St = 0.1, the oscillation period corresponds to that of the planet. In particular, the accretion rate is at its maximum when the planet is at the pericenter, whereas it takes small values at the apocenter. This corresponds to a situation in which it temporarily escapes from the dust ring. For St = 0.01, such large variations in the pebble accretion rate are not observed, simply because the dust ring is wider in that case.
Similarly to the case St = 0.01, the planet mass is also found to saturate for St = 0.1, but at a somewhat smaller value, mp ≈ 5 M⊕. Here, pebble accretion is stopped once the planet mass becomes high enough to significantly modify the pebble disk structure. From this time, the amplitude of the density peak is smaller, which, combined with the significant value for the planet eccentricity, ep ~ 0.05−0.1, leads to a drastic reduction in the pebble accretion rate. This is consistent with the results of Liu & Ormel (2018), who find for similar parameters, ep ~ 0.05−0.1 and St = 0.1, a very small pebble accretion efficiency (see their Fig. 5).
 |
Fig. 10 Left: planet mass, semimajor axis, and eccentricity as a function of time for runs in which the planet grows as a result of pebble accretion and for different values of the α viscosity and for St = 0.01. Right: same, but for different values of the Stokes number and for α = 10−4. |
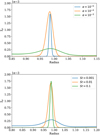 |
Fig. 11 Top: pebble surface density, ∑p, profile for different values of the α viscosity. Bottom: pebble surface density, ∑p, profile for different values of the Stokes number, St. |
 |
Fig. 12 Accretion rate onto the planet over a few orbits for the runs with St = 0.1 and St = 0.01. |
5 Conclusions
In this paper, we studied the orbital evolution of low-mass planets embedded in pressure bumps. Due to their ability to trap drifting pebbles, pressure bumps have been considered as favored locations for planetesimal formation through the SI. We performed 2D, two-fluid hydrodynamical simulations in which a Gaussian pressure bump was modeled by adjusting the viscosity profile of the disk. The planet has an initial mass of 0.1 M⊕ and can grow by accreting pebbles from the dust ring, with a pebble accretion efficiency that was calculated using the prescription of Liu & Ormel (2018). Heat release resulting from pebble accretion was taken into account, such that the planet is subject to thermal torques. We also took into account the feedback between the eccentricity and the luminosity, as well as the torques resulting from the pebble-scattered flow (Benítez-Llambay & Pessah 2018).
We find evidence for the existence of a dust corotation torque, resulting from the change in the dust streamlines at the pressure bump. This additional corotation torque can slightly alter the location of the planet trap, in comparison with the situation where only gas torques are considered. We also find that, due to the significant pebble surface density at the bump’s location, the accretion luminosity of a 0.1 M⊕ protoplanet can easily exceed the critical luminosity above which eccentricity growth is expected as a result of thermal forces. Eccentricity growth causes both Lindblad and corotation torques to weaken, and the planet ultimately ends up moving just outside of the dust ring, on an eccentric orbit with ep ≈ h, where h is the disk aspect ratio. Thermal feedback onto gas also leads to the formation of an anticyclonic vortex at the planet’s location, consistent with the results of Cummins et al. (2022). This vortex can subsequently capture drifting pebbles and we find that the interaction with the dusty vortex can make the planet escape from the pressure bump when dust feedback is not accounted for. Including the effect of dust feedback on the gas, however, weakens the dusty vortex, which enables the planet to achieve a stable, eccentric orbit close to the gas pressure maximum.
Simulations in which the planet’s mass was allowed to increase as a consequence of pebble accretion resulted in the formation of giant planet cores with masses in the range of 5–20 M⊕, depending on the values for the Stokes number, St, and α viscosity. Pebble accretion is particularly efficient at the pressure bump for St = 0.01 and α = 10−4. For smaller values of St the mass of the dust ring is simply too small to enable strong pebble accretion, whereas for higher St, pebble accretion efficiency decreases due to a larger drift velocity. Moreover, we find in that case that the planet can temporarily evolve outside of the dust ring as it approaches its pericenter, resulting in a reduced accretion rate.
In protoplanetary disks with α ≳ 10−4, the planet’s luminosity tends to decrease below the critical luminosity (Velasco Romero et al. 2022), thereby preventing eccentricity growth through thermal forces and consequently efficient pebble accretion. Similarly, for α ≲ 10−5, the planet achieves a maximum mass of just ≈0.5 M⊕, due to the formation of strong vortices that tend to create a secondary pressure bump outside the planet’s orbit and where the pebble flux is halted.
One main limitation here is that we only performed 2D simulations and future work should adopt a more realistic 3D setup. It has indeed been shown that the streamlines outflowing from the Hill sphere may be significantly distorted in 3D (Chrenko & Lambrechts 2019) such that we expect significant differences in the heating torque magnitude between 2D and 3D.
Acknowledgments
Computer time for this study was provided by the computing facilities MCIA (Mésocentre de Calcul Intensif Aquitain) of the Université de Bordeaux and by HPC resources of Cines under the allocation A0150406957 made by GENCI (Grand Equipement National de Calcul Intensif). S.N.R. acknowledges funding from the French Programme National de Planétologie (PNP), and in the framework of the Investments for the Future programme IdEx, Université de Bordeaux/RRI ORIGINS. Data availability: The data underlying this article will be shared on reasonable request to the corresponding author.
Appendix A Pebble accretion efficiency of eccentric planets
In this section, we give the prescriptions of Liu & Ormel (2018) and Ormel & Liu (2018) for the pebble accretion efficiency of eccentric planets, which we used in our simulations. The pebble accretion efficiency of the 2D settling regime is given by
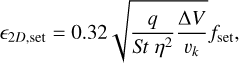 (A.1)
(A.1)
where vk is the Keplerian velocity and ∆V the pebble-embryo relative velocity, which is given by
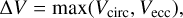 (A.2)
(A.2)
Moreover, in Eq. A.1, the transition function is given by
![${f_{{\rm{set}}}} = \exp \left[ { - 0.5{{\Delta V} \over {V_ * ^2}}} \right] \times {{{V_ * }} \over {\sqrt {V_ * ^2 + 0.33\sigma _{pz}^2} }},$](/articles/aa/full_html/2024/04/aa48923-23/aa48923-23-eq36.png) (A.5)
(A.5)
where V* is the transition velocity,
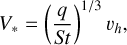 (A.6)
(A.6)
and σpɀ is the vertical turbulent velocity (Youdin & Lithwick 2007),
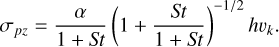 (A.7)
(A.7)
The pebble accretion in the 3D settling regime is given by
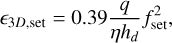 (A.8)
(A.8)
with hd the pebble disk aspect ratio (Youdin & Lithwick 2007),
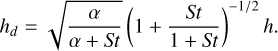 (A.9)
(A.9)
In this regime, the accretion radius, Racc, is given by
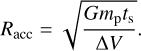 (A.10)
(A.10)
Finally, the accretion efficiency in the 2D and 3D ballistic regimes, respectively, is given by
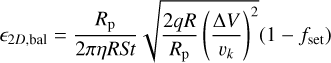 (A.11)
(A.11)
In the ballistic regime, Racc reads:
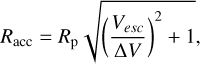 (A.13)
(A.13)
where 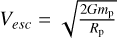 is the escape velocity.
is the escape velocity.
The expression that we employed to calculate the pebble accretion efficiency in our calculations is given by
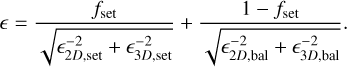 (A.14)
(A.14)
References
- ALMA Partnership (Brogan, C. L., et al.) 2015, ApJ, 808, L3 [Google Scholar]
- Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez-Llambay, P., & Pessah, M. E. 2018, ApJ, 855, L28 [Google Scholar]
- Benítez-Llambay, P., Masset, F., Koenigsberger, G., et al. 2015, Nature, 520, 63 [CrossRef] [Google Scholar]
- Bitsch, B., Morbidelli, A., Lega, E., et al. 2014, A&A, 564, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [Google Scholar]
- Carrera, D., & Simon, J. B. 2022, ApJ, 933, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, D., Simon, J. B., Li, R., et al. 2021, AJ, 161, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Chametla, R. O., & Masset, F. S. 2021, MNRAS, 501, 24 [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [Google Scholar]
- Chrenko, O. & Chametla, R. O. 2023, MNRAS, 524, 2705 [NASA ADS] [CrossRef] [Google Scholar]
- Chrenko, O., & Lambrechts, M. 2019, A&A, 626, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chrenko, O., Brož, M., & Lambrechts, M. 2017, A&A, 606, A114 [Google Scholar]
- Cornejo, S., Masset, F. S., Chametla, R. O., et al. 2023, MNRAS, 522, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Crida, A., & Bitsch, B. 2017, Icarus, 285, 145 [Google Scholar]
- Crnkovic-Rubsamen, I., Zhu, Z., & Stone, J. M. 2015, MNRAS, 450, 4285 [NASA ADS] [CrossRef] [Google Scholar]
- Cummins, D. P., Owen, J. E., & Booth, R. A. 2022, MNRAS, 515, 1276 [NASA ADS] [CrossRef] [Google Scholar]
- de Val-Borro, M., Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370, 529 [Google Scholar]
- Dipierro, G., Price, D., Laibe, G., et al. 2015, MNRAS, 453, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, R., Li, S., Chiang, E., et al. 2017, ApJ, 843, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Penzlin, A. B. T. 2018, A&A, 609, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fendyke, S. M., & Nelson, R. P. 2014, MNRAS, 437, 96 [Google Scholar]
- Flock, M., Ruge, J. P., Dzyurkevich, N., et al. 2015, A&A, 574, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromenteau, S., & Masset, F. S. 2019, MNRAS, 485, 5035 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, W., Li, H., Lubow, S., et al. 2014, ApJ, 795, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, J.-F., Laibe, G., & Maddison, S. T. 2017, MNRAS, 467, 1984 [NASA ADS] [Google Scholar]
- Guilera, O. M., Benitez-Llambay, P., Miller Bertolami, M. M., et al. 2023, ApJ, 953, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, H.-F., & Lin, M.-K. 2020, MNRAS, 497, 2425 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, P., Li, H., Isella, A., et al. 2020, ApJ, 893, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
- Johansen, A., Youdin, A., & Mac Low, M.-M. 2009, ApJ, 704, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W. 1989, A&A, 208, 98 [NASA ADS] [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klahr, H., & Schreiber, A. 2021, ApJ, 911, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lega, E., Crida, A., Bitsch, B., et al. 2014, MNRAS, 440, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, M.-K., & Papaloizou, J. C. B. 2010, MNRAS, 405, 1473 [NASA ADS] [Google Scholar]
- Liu, B., & Ormel, C. W. 2018, A&A, 615, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorén-Aguilar, P., & Bate, M. R. 2015, MNRAS, 453, L78 [CrossRef] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S. 2017, MNRAS, 472, 4204 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., Morbidelli, A., Crida, A., et al. 2006, ApJ, 642, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Menou, K., & Goodman, J. 2004, ApJ, 606, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A. 2020, A&A, 638, A1 [Google Scholar]
- Morbidelli, A., & Nesvorny, D. 2012, A&A, 546, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. W. A., Kley, W., & Meru, F. 2012, A&A, 541, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, R. P., Papaloizou, J. C. B., Masset, F., et al. 2000, MNRAS, 318, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Liu, B. 2018, A&A, 615, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., & Kollmeier, J. A. 2017, MNRAS, 467, 3379 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Larwood, J. D. 2000, MNRAS, 315, 823 [Google Scholar]
- Pierens, A. 2021, MNRAS, 504, 4522 [CrossRef] [Google Scholar]
- Pierens, A. 2023, MNRAS, 520, 3286 [NASA ADS] [CrossRef] [Google Scholar]
- Pierens, A., Lin, M.-K., & Raymond, S. N. 2019, MNRAS, 488, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Regály, Z. 2020, MNRAS, 497, 5540 [CrossRef] [Google Scholar]
- Shakura, N. I. & Sunyaev, R. A. 1973, A&A, 24, 337 [Google Scholar]
- Simon, J. B., Armitage, P. J., Li, R., & Youdin, A. N. 2016, ApJ, 822, 55 [Google Scholar]
- Stoyanovskaya, O. P., Vorobyov, E. I., & Snytnikov, V. N. 2018, Astron. Rep., 62, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Surville, C. & Mayer, L. 2019, ApJ, 883, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Tominaga, R. T., Takahashi, S. Z., & Inutsuka, S.-i. 2019, ApJ, 881, 53 [NASA ADS] [CrossRef] [Google Scholar]
- van Leer, B. 1977, J. Comput. Phys., 23, 276 [Google Scholar]
- Velasco Romero, D. A., Masset, F. S., & Teyssier, R. 2022, MNRAS, 509, 5622 [Google Scholar]
- Wafflard-Fernandez, G., & Baruteau, C. 2020, MNRAS, 493, 5892 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Z., & Bai, X.-N. 2022, ApJ, 937, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
- Youdin, A. N. & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Blake, G. A., & Bergin, E. A. 2015, ApJ, 806, L7 [Google Scholar]
- Zsom, A., Ormel, C. W., Güttler, C., et al. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Pebble surface density, Σp, gas surface density, Σg, and gas pressure as a function of radius for the fiducial run, with St = 0.01 and α = 10−4. |
| In the text | |
 |
Fig. 2 Planet semimajor axis and eccentricity as a function of time for the fiducial run, with St = 0.01 and α = 10−4, and in cases where a 0.1 M⊕ protoplanet is allowed to evolve under the effect of gas torques, pebble scattering, pebble accretion, and dust feedback. |
| In the text | |
 |
Fig. 3 Torque profile of the fiducial simulation, with St = 0.01 and α = 10−4, at a point in time when migration is halted. Overplotted are the contributions from the Lindblad torque, ΓL, vortensity-related corotation torque, Γc,V, and entropy-related corotation torque, Γc,V. The dashed line shows the total torque in the case where the cold torque, Γcold, is taken into account. |
| In the text | |
 |
Fig. 4 Top panel: pebble torque profile for St = 0.01 and α = 10−4 in the situation where the planet can evolve under the effect of gas plus pebble torques. Bottom panel: pebble surface density perturbation and streamlines (blue) for the same run. The orange lines correspond to streamlines obtained in the absence of a pressure bump. |
| In the text | |
 |
Fig. 5 Accretion luminosity as a function of time for the fiducial run, with St = 0.01, α = 10−4 and pebble accretion included. For luminosities higher than the critical value, Lc, growth in the planet’s eccentricity occurs as a result of thermal forces. |
| In the text | |
 |
Fig. 6 Top panel: gas surface density perturbation at different times for the run with St = 0.01, α = 10−4, and pebble accretion included. Gas heating due to pebble accretion leads to vortex formation at the planet’s position. Middle panel: pebble surface density perturbation. Bottom panel: contours of the normalized vorticity for the same run. |
| In the text | |
 |
Fig. 7 Same as Fig. 6 but with the effect of dust feedback on the gas included. |
| In the text | |
 |
Fig. 8 Planet mass, semimajor axis, and eccentricity as a function of time for runs in which the planet grows as a result of pebble accretion. |
| In the text | |
 |
Fig. 9 Top panel: gas surface density perturbation at different times for the run in which the planet is allowed to grow, and with the effect of dust feedback on the gas included. Bottom panel: contours of the normalized vorticity at the same times. |
| In the text | |
 |
Fig. 10 Left: planet mass, semimajor axis, and eccentricity as a function of time for runs in which the planet grows as a result of pebble accretion and for different values of the α viscosity and for St = 0.01. Right: same, but for different values of the Stokes number and for α = 10−4. |
| In the text | |
 |
Fig. 11 Top: pebble surface density, ∑p, profile for different values of the α viscosity. Bottom: pebble surface density, ∑p, profile for different values of the Stokes number, St. |
| In the text | |
 |
Fig. 12 Accretion rate onto the planet over a few orbits for the runs with St = 0.1 and St = 0.01. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



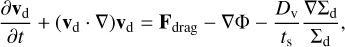
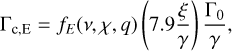
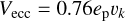
![${V_{{\rm{circ}}}} = {\left[ {1 + 5.7\left( {{{qSt} \over {{\eta ^3}}}} \right)} \right]^{ - 1}} + 0.52{(qSt)^{1/3}}{\upsilon _k}.$](/articles/aa/full_html/2024/04/aa48923-23/aa48923-23-eq35.png)