| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A191 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348028 | |
| Published online | 23 April 2024 | |
Uranus’s complex internal structure★
Department of Astrophysics, University of Zurich,
Winterthurerstrasse 190,
8057
Zurich,
Switzerland
e-mail: benno.neuenschwander@outlook.com
Received:
20
September
2023
Accepted:
18
January
2024
Context. Uranus’s bulk composition remains unknown. Although there are clear indications that Uranus’s interior is not fully convec-tive, and therefore has a non-adiabatic temperature profile, many interior models continue to assume an adiabatic interior.
Aims. In this paper we present a new method for interpreting empirical structure models in terms of composition and for identifying non-convective regions. We also explore how the uncertainty in Uranus’s rotation period and winds affects the inferred composition and temperature profile.
Methods. We used Uranus’s density profiles from previous work in which the density is represented by up to three polytropes.
Results. Using our new method, we find that these empirical models imply that Uranus’s interior includes non-adiabatic regions. This leads to significantly hotter internal temperatures, which can reach several tens of thousands of kelvins, and higher bulk heavy-element abundances (up to 1 M⊕) compared to standard adiabatic models. We find that the assumed rotation period strongly affects the inferred composition, while the winds have a negligible effect. Although solutions with only H–He and rock are possible, we find that the maximum water-to-rock ratio in Uranus for our models ranges between 2.6 and 21. This is significantly lower compared to standard adiabatic models.
Conclusions. We conclude that it is important to include non-adiabatic regions in Uranus structure models as they significantly affect the inferred temperature profile and, therefore, the inferred bulk heavy-element abundance. In addition, we suggest that to decrease the uncertainty in Uranus’s bulk composition, it is of great value to measure Uranus’s gravitational field and determine its rotation period.
Key words: planets and satellites: composition / planets and satellites: gaseous planets / planets and satellites: individual: Uranus / planets and satellites: interiors
Data for all models are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/684/A191
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Determining the composition, material distribution, and temperature profile within a giant planet is crucial to understanding its formation and evolution. Therefore, much effort has been made to investigate and understand the internal structure of Jupiter (e.g., Hubbard 1968; Militzer et al. 2016), Saturn (e.g., Zharkov & Gudkova 1991; Movshovitz et al. 2020; Militzer & Hubbard 2023), Uranus, and Neptune (e.g., Podolak et al. 1991; Helled et al. 2011; Nettelmann et al. 2013). In early work, the interior structure of gaseous planets was assumed to be convective or convective within layers (e.g., the core, mantle, or envelope). This implies that the entropy throughout the planet or layer is constant and that the temperature profile follows an adiabat that is usually fixed by the planet’s known surface properties (typically at 1 bar). The reason this method was (and still is) so widespread is its simplicity: for each model with an assumed constant composition of either the entire planet or within its layers, the planet’s temperature profile and bulk composition are uniquely determined.
However, recent studies have indicated that the assumption of a fully convective planet is inappropriate and that all the outer planets in the Solar System show evidence of nonhomogeneous regions (Wahl et al. 2017; Nettelmann et al. 2021; Miguel et al. 2022; Mankovich & Fuller 2021; Stanley & Bloxham 2004). An indication that Uranus has a non-adiabatic interior is its flux.
Uranus’s flux is nearly in equilibrium with the solar one (Pearl et al. 1990), and such a low flux is inconsistent with an adiabatic cooling, as it would have taken Uranus much longer than the age of the Solar System to cool down to its present state (Fortney & Nettelmann 2010). Uranus’s low flux could be a result of a thermal boundary that prevents the underlying heat from escaping, leading to a hotter interior (Nettelmann et al. 2016; Scheibe et al. 2019, 2021), layered convection (Leconte & Chabrier 2013), composition gradients (Vazan & Helled 2020), or a frozen core (Stixrude et al. 2021). Another possibility is that Uranus experienced an extreme event, such as a giant impact, which led to a rapid cooling. This would suggest that Uranus’s interior is in fact cold (Helled & Fortney 2020). While the origin of Uranus’s flux is still unknown, it seems more likely that its low heat flux is a result of a non-adiabatic interior. Numerical dynamo models also indicate the existence of non-convective regions within Uranus and Neptune (e.g., Stanley & Bloxham 2004, 2006; Soderlund et al. 2013). Finally, formation models of Uranus and Neptune imply that the formation process led to a deep interior with composition gradients that can be sustained for gigayears (e.g., Valletta & Helled 2020; Vazan & Helled 2020; Helled 2023).
Although there are several methods that describe the behavior of non-adiabatic regions (see, e.g., Leconte & Chabrier 2013), modeling a non-adiabatic planet poses several difficulties. First, it is unclear where the non-adiabatic regions are located and how extended they are. Second, even if the size and extent of a non-adiabatic region are known, its exact characteristics may still be unknown. For example, it can be unclear whether a region is fully Schwarzschild-stable or if double-diffusive convection can occur (see Leconte & Chabrier 2013).
A way to avoid both the simplified assumption of a fully adi-abatic planet and the modeling issues of a non-adiabatic planet is to use empirical structure models. In this case, the density profile can be represented by, for example, a high-order polynomial (e.g., Helled et al. 2011; Movshovitz et al. 2020) or polytropes (e.g., Horedt & Hubbard 1983; Neuenschwander et al. 2021), or it can be produced on a random basis (e.g., Podolak et al. 2022). Such models determine the density distribution within the planet without a direct link to the physical composition. Empirical structure models can also describe nonstandard solutions that include composition gradients and other non-adiabatic regions.
By design, empirical structure models do not infer the planetary composition or temperature profile, which makes them difficult to interpret and compare to “physical” models (e.g., models based on physical equations of state).
However, given an adequate temperature profile, empirical models can be interpreted in terms of composition. In this study, we present a new method for interpreting empirical structure models and determining the planetary temperature profile and composition using physical equations of state (EoS) of hydrogen, helium water, rock (SiO2), and iron. The method is designed to detect and account for composition gradients and non-convective regions. The inferred temperature profiles are consistent with the density-pressure profiles determined by empirical models.
We applied this method to various empirical structure models of Uranus and inferred its temperature and composition profiles. We then compared these non-adiabatic models to existing adiabatic Uranus solutions and quantified their differences.
This paper is structured as follows: in Sect. 2 we explain the newly developed method that we used to infer the temperature and composition profiles of empirical structure models of Uranus. In Sect. 3, we present our findings, which are followed by a summary and conclusions in Sect. 4.
2 Method
Here, we describe how we inferred the temperature profile and then interpreted the planetary composition of the density profiles inferred from the empirical structure models presented in Neuenschwander & Helled (2022).
We used our newly developed method to investigate the effect of the depth of the winds and the rotation period on Uranus’s temperature profile, its bulk composition (including its water-to-rock ratio), and the size and location of non-convective regions.
2.1 Models: Empirical density profiles
The empirical structure models presented in Neuenschwander & Helled (2022) are based on up to three polytropes. A polytrope relates the pressure, P, with the density, ρ:
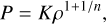 (1)
(1)
where K (polytropic constant) and n (polytropic index) are free parameters. The three polytropes are arranged piece-wise. This means that each polytropic relation holds only for a specific radial region of the planet. The radii, where the transition from one to the next polytropic relation occurs, are referred to as “transition radii”. At these transition radii, density discontinuities can (but do not have to) occur.
The free parameters (Ki and ni (for i = 1,2,3) and transition radii) were chosen such that the resulting density profile fits Uranus’s total mass, M, equatorial radius, a, rotation rate, ω, and gravitational harmonics, J2 and J4. The computation of the gravitational field is achieved with fourth-order theory of figures that calculates the hydrostatic equilibrium of the planet (Zharkov & Trubitsyn 1970, 1975; Zharkov et al. 1978; Hubbard et al. 2014; Nettelmann 2017; Nettelmann et al. 2021). For this calculation, we used 4096 radially equally spaced computational layers for the density profiles. To speed up the calculation while maintaining the desired precision, the planet’s equipotential shape was calculated every 32th layer while using a spline interpolated for intermediate layers. More information about, for example, the model calculation method or model parameters can be found in Neuenschwander et al. (2021) and Neuenschwander & Helled (2022).
Only J2 and J4 have been measured for Uranus, and their values have relatively large uncertainties. The depth of Uranus’s zonal winds also remains unknown, although maximum depths of ~1100 km (Kaspi et al. 2013) and ~500–750 km (Soyuer et al. 2023) have been estimated. Although Uranus’s winds are likely relatively shallow (Soyuer et al. 2020), they still contribute to the measured gravitational field. The rotation period of Uranus is not well understood either (Helled et al. 2010). There are different techniques to estimate the bulk rotation period of Uranus and Neptune: one method is to measure periodicities in the radio signal and the magnetic field of the planet (Desch et al. 1986). A complementary approach is to minimize the dynamical heights on the surface (see Helled et al. 2010 and references therein). However, these different estimation methods disagree on the order of ~40 min (see Helled et al. 2010 and references therein for more details). Neuenschwander & Helled (2022) showed that both the uncertainty in the depth of Uranus’s winds and the large uncertainty in its rotation period affect the internal structure models.
If Uranus’s winds are not shallow, we must consider the correction of the winds to the gravitational moments. We therefore also present models with the zonal winds penetrating to a depth of 1100 km. We followed Kaspi et al. (2013) and subtracted the expected dynamical contribution from the measured value 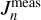 . In this case, the measured gravitational coefficients
. In this case, the measured gravitational coefficients 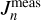 can be split into a static
can be split into a static 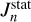 and a dynamic part
and a dynamic part 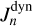 where
where 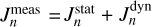 . In principle, Uranus’s winds perturb both its second and fourth gravitational harmonics (J2 and J4). For simplicity, we followed Kaspi et al. (2013) and only considered the wind effects in
. In principle, Uranus’s winds perturb both its second and fourth gravitational harmonics (J2 and J4). For simplicity, we followed Kaspi et al. (2013) and only considered the wind effects in 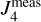 (i.e.,
(i.e., 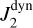 ). However, the effect of deep winds on J2 could also affect the density profile and should be considered. We plan to investigate this topic in future research. The empirical models that include the wind contribution are discussed in Neuenschwander & Helled (2022). Figure 1 presents the density profiles (taken from Neuenschwander & Helled 2022) that we used in this study. For comparison, we also present other published density profiles from Nettelmann et al. (2013), Vazan & Helled (2020), and Helled et al. (2011). Blue-colored models are models based on the rotation period as measured by the Voyager 2 mission (hereafter PV = 17.24 h) and green models are based on the rotation period as evaluated by Helled et al. (2010; hereafter PH = 16.57 h). Models colored in red account for winds that penetrate to a depth of 1,100 km and, finally, the yellow-colored models represent a “high-density core” (i.e., high central density) solutions.
). However, the effect of deep winds on J2 could also affect the density profile and should be considered. We plan to investigate this topic in future research. The empirical models that include the wind contribution are discussed in Neuenschwander & Helled (2022). Figure 1 presents the density profiles (taken from Neuenschwander & Helled 2022) that we used in this study. For comparison, we also present other published density profiles from Nettelmann et al. (2013), Vazan & Helled (2020), and Helled et al. (2011). Blue-colored models are models based on the rotation period as measured by the Voyager 2 mission (hereafter PV = 17.24 h) and green models are based on the rotation period as evaluated by Helled et al. (2010; hereafter PH = 16.57 h). Models colored in red account for winds that penetrate to a depth of 1,100 km and, finally, the yellow-colored models represent a “high-density core” (i.e., high central density) solutions.
As discussed in Neuenschwander et al. (2021) for Jupiter, the polytropic-based solutions of Uranus published in Neuenschwander & Helled (2022) tend to overestimate its surface density. As the affected region contains only a tiny fraction of the total planetary mass, its effect on the internal structure model and therefore the published results were negligible. However, since the composition interpretation algorithm is a top-down algorithm, as discussed below, it is sensitive to the outer-density profile: An over-dense surface and/or atmospheric region could lead to unrealistically high heavy-element fractions in this region. This, in turn, could prevent the algorithm from converging to solutions below the over-dense region as, by design, the metallicity cannot decrease with depth. To avoid this situation, and to obtain more realistic results, the over-dense region has been replaced beforehand with an adiabatic atmosphere model from Hueso et al. (2020). This substitution only affects the outermost region (r ≳ 0.99) of Uranus with pressures up to P ≈ 150–250 bar. The affected mass is only ∽0.002 M⊕, which corresponds to ∽0.015% of Uranus’s total mass.
Below this region and up to a pressure of ≃10 000 bar, we sometimes encounter situations in the models’ convective region wherein the density is lower than expected from a uniform composition. These instances can then lead to violent large-scale convection that would need special treatment. However, the involved mass is less than 1% and the regions with violent large-scale convection only affects the bulk heavy-elements abundance by around ∽0.01% in mass. Therefore, its effect has been neglected in this study.
However, it should be acknowledged that empirical models based on three piece-wise arranged polytropes might be insufficient to accurately represent the atmosphere of Uranus. Adding a fourth polytrope to represent the atmosphere can resolve this issue (Morf et al., in prep.).
 |
Fig. 1 Empirical density profiles from Neuenschwander & Helled (2022) we considered in this study. Also shown are published density profiles of Uranus. The blue curves show Uranus models that use the rotation period estimated by the Voyager 2 mission, while the green curves show models that use the rotation period proposed by Helled et al. (2010). The red curves show models with 1100 km deep winds, and the yellow curves correspond to solutions with high central densities. |
2.2 The algorithm for inferring the temperature profile
There are several ways to obtain a suitable temperature profile of an (empirical) model, given its density and pressure profile (see, e.g., Helled et al. 2011; Podolak et al. 2019, 2022). However, these methods often assume that the planet is fully convective, and apply an adiabatic temperature profile. This assumption may lead to temperature profiles that are not consistent with the composition. If, for example, the empirical density profile predicts a (local) composition gradient, an adiabatic temperature profile fails to describe this region adequately.
Below, we describe our method for inferring the temperature profile for a given empirical structure model using physical EoS in a self-consistent manner: For each model, the method explained in Sect. 2.1 yields the density-pressure profile (ρ(r), P(r)) but no information about the temperature T(r) or composition profile in the interior. There are several approaches to overcoming this issue, which always rely on a physical equation of state. For example, the equation of state could describe P(ρ, T, C), where C = (X, Y, Z) parametrizes the dependence on the composition, and X, Y, Z are the hydrogen, helium, and heavy-element mass fractions. If the hydrogen-helium ratio is held constant at the protosolar ratio, then the composition dependence is parametrized by the single value Z, since X + Y + Z = 1. The problem, however, is that without knowing the temperature, the composition cannot be uniquely determined. This is because the equation P(r) = P(ρ(r), T(r), Z(r)) provides a single constraint, but has two unknowns.
One solution is to assume that the temperature follows a particular adiabat, which means that the temperature profile is known and therefore the composition can be inferred without any ambiguity (e.g., Helled et al. 2011). However, these solutions are not self-consistent and can result in adiabatic (and therefore convective) regions with an inhomogeneous composition. Another approach is to use non-adiabatic temperature gradients. This was done by Podolak et al. (2019), who used radiative (e.g., Kippenhahn et al. 2013) and semi-convective (Leconte & Chabrier 2012) temperature gradients to construct non-adiabatic temperature profiles.
Here, we used a different approach: In order to be independent of a prescribed temperature gradient, we developed a top-down algorithm (starting from well-defined planetary surface values) that finds convective and non-convective regions in the interior. Our equation of state is an updated version that was developed for planetary evolution models (Müller et al. 2020; Müller & Helled 2021) and combines the Chabrier & Debras (2021) equation of state for hydrogen and helium with the “quotidian EoS” heavy-element EoS for H2O, SiO2, and Fe (More et al. 1988; Vazan et al. 2013). The algorithm works as follows: At the P0 = 1 bar surface of Uranus, the temperature T0 and density ρ0 are known. We assumed that the surface composition only consists of an ideally mixed protosolar ratio of hydrogen and helium, together with one heavy element. We used the ideal-mixing approximation and hence 1/ρ(P, T) = X/ρX(P, T) + Y/ρY(P, T) + Z/ρZ(P, T), where ρX,Y,Z are the hydrogen, helium and heavy-element densities at the given pressure and temperature. Using (ρ0, P0, T0) we can then determine the composition (X0, Y0, Z0) from the EoS. This allows us to also calculate the surface entropy S0(P0, T0, Z0). Then we moved downward into the planet to the next (computational) layer that is at a higher pressure P1 and density ρ1. Using these two values, we checked whether the layer is convective as follows: If the layer is convec-tive, the composition and entropy should stay constant: Z1 = Z0 and S1 = S0. Using (ρ1, P1, Z1 = Z0), we calculated the entropy S1 with the equation of state and compare it to the surface value S0. If S1 = S0, the layer is indeed convective, T1 follows the adiabat, and therefore all required variables (T1, Z1, S1) are determined.
If S1 ≠ S0, the region is not convective and therefore there is potentially a composition gradient such that Z1 > Z0 (i.e., we force Zi+1 ≥ Zi). In this case, we searched for the temperature T1 and composition Z1 that lead to a marginally Ledoux-stable state. In other words, we equalized the Ledoux criterion (see Eq. (2)) and solved it to obtain T1 and Z1. The equalized Ledoux criterion (Ledoux 1947) is
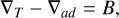 (2)
(2)
where 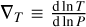 is the temperature gradient,
is the temperature gradient, 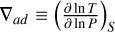 the adiabatic temperature gradient and B is the composition term. B can be written as (see, e.g., Paxton et al. 2013)
the adiabatic temperature gradient and B is the composition term. B can be written as (see, e.g., Paxton et al. 2013)
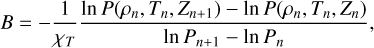 (3)
(3)
where the subscript n denotes the (computational) layer the quantity is assigned to and 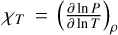 . We note that it is not guaranteed that there is always a (T1, Z1) tuple that equates the Ledoux criterion. Given, for example, the temperature TLD and metallicity ZLD that equates Eq. (2) for layer “1.” This solution is rejected if either the temperature or metallicity is smaller than the one of the layer above (TLD < T0 and/or ZLD < Z0). In this case, out of all the possible solutions in (T1, Z1), we chose the solution that first minimizes |T0 − T1 |, then minimizes |Z0 − Z1 |, and finally minimizes |S0 − S1 |. In these situations, T1 and Z1 are chosen such that they minimize the change in T, Z, and S (in this order). Again, this yields all required variables (T1, Z1, S1) and ensures that the temperature gradient is minimized. This approach can lead to regions in the planet that are of positive static stability (i.e., are stable against convection).
. We note that it is not guaranteed that there is always a (T1, Z1) tuple that equates the Ledoux criterion. Given, for example, the temperature TLD and metallicity ZLD that equates Eq. (2) for layer “1.” This solution is rejected if either the temperature or metallicity is smaller than the one of the layer above (TLD < T0 and/or ZLD < Z0). In this case, out of all the possible solutions in (T1, Z1), we chose the solution that first minimizes |T0 − T1 |, then minimizes |Z0 − Z1 |, and finally minimizes |S0 − S1 |. In these situations, T1 and Z1 are chosen such that they minimize the change in T, Z, and S (in this order). Again, this yields all required variables (T1, Z1, S1) and ensures that the temperature gradient is minimized. This approach can lead to regions in the planet that are of positive static stability (i.e., are stable against convection).
Then, the algorithm moves to the next layer, continuing with the same evaluation method described above until the center of the planet is reached. Typically, we analyzed the composition of ∽1200 computational layers per model. The central temperature is allowed to go up to Tmax < 30 000 K. We note that this generous limit also includes the most extreme models of (see Vazan & Helled 2020). Convective and non-convective regions are marked as each layer is evaluated and are highlighted or marked in all the relevant figures. By following this procedure, we ensured that the composition and potential composition gradients are always consistent with the temperature profile. Furthermore, convective regions are detected and accounted for in an unbiased manner. We note that the detection of non-convective regions depends solely on the combination of pressure, density and the used EoS.
 |
Fig. 2 Temperature profiles (solid black curve), heavy-element mass fractions (dashed curves), and density profiles (dotted purple curve) of various solutions. In the upper row, the heavy elements are represented by pure rock (dashed brown line) only. The lower row shows more “physical” solutions in which the heavy elements are represented by water (dashed blue curve), rock (dashed brown curve), and, if necessary, iron (dashed gray curve). The gray-shaded radial area marks the convective regions. On the other hand, the blue-shaded radial area marks the non-convective and nonhomogeneous region. The dashed blue, brown, and gray lines show the radial mass fraction of water, rock, and iron, respectively. |
3 Results
We introduce non-adiabatic models that are based on empirical structure models in Sect. 3.1. We next compare the effects of non-adiabatic regions on the planetary temperature profile and composition with pure adiabatic models in Sect. 3.2. We also explore how the rotation period of Uranus influences the inferred temperature profile and bulk composition in Sect. 3.3. In Sect. 3.3.3 we show high-density core solutions of Uranus. Then we discuss the water-to-rock ratio of Uranus in Sect. 3.4. Finally, in Sect. 3.5, we investigate whether wind dynamics affect Uranus’s inferred internal structure.
3.1 Non-adiabatic models
We analyzed the 16 different density profiles presented in Fig. 1 and calculated their temperature profile, the material distribution, and the bulk composition. We could clearly identify non-adiabatic regions in the planetary interior.
Figure 2 shows the temperature profiles of a diverse subset covering the diversity of all solutions. It should be noted that in this paper we plot various variables against the normalized radius. Figure C.1 shows how Uranus’s normalized radius compares to its mass. The gray-shaded radial region in Fig. 2 is convective, while the blue-shaded radial region is non-convective. The top row shows models consisting only of a protosolar mixture of hydrogen and helium, with rock as the heavy element. The density of each model is represented by the purple curve (see also Fig. E.2). In the bottom row, models are based on a protosolar H–He mixture together with water, rock, and iron as heavy elements. We note that iron is only needed when the central densities are high (bottom row, most right panel).
All the models have non-convective regions covering between 40% and 80% of the planet’s radius. The exact size depends on the model, but the inferred structure is always similar: Uranus consists of an convective layer that begins at its surface and can extend down to r ≈ 0.4. Underneath the convec-tive region, a non-convective region with a composition gradient extends down to the core. Again, the exact characteristics of the composition gradient are model-dependent. Given the relative size of the non-convective region and its incorporated mass, this region has a non-negligible effect on the planet’s temperature profile and bulk composition (see Sect. 3.2). We get very diverse solutions in terms of central temperature and metallicity. The core’s temperature varies between 7500 and 28 000 K, while the bulk heavy-element abundance ranges between 11.6 and 14.4 (see Tables 1 and 2 for more details).
Figure 3 illustrates the resulting structure, composition and temperature of Uranus based on our non-adiabatic models. The internal structure of Uranus in panel (i) is based on a mixture of protosolar H–He, water, and rock. The structure models in panel (v) corresponds to high central density models (see Sect. 3.3.3) that require iron to be present in the core. Otherwise, it has the same composition as the structure models in panel (i). The sketches also show the composition gradient in the non-convective region. Panel (i): starting at around r ≈ 0.8 the water mass fraction increases up to its maximum around r ≈ 0.4–0.5. After that, it is successively replaced by rock until it reaches the center of the planet. Panel (v): starting at around r ≈ 0.56–0.75 rock increases its mass fraction in the water-rock mixture continuously up to around r ≈ 0.15–0.21. After this point, water is replaced by iron, which successively increases its mass fraction in the rock-iron mixture down to the planet’s center. A detailed discussion and comparison of the various panels are provided in Sects. 3.3.1, 3.3.2, and 3.3.3, respectively.
Key parameters for all evaluated models consisting of a mixture of H–He and rock.
Key parameters for all evaluated models consisting of H–He, water, rock, and potentially iron.
 |
Fig. 3 Sketches of Uranus’s interior structure. The left side of each panel shows the composition, and the right side illustrates the temperature. Cold regions are colored in blue, hot regions in yellow. The protosolar H–He mixture is colored in light blue, water in dark blue, rock in orange, and iron (bottom panel) in gray. Composition gradients are illustrated by a color gradient of the two mixed materials. The dashed curve marks the boundary between the convective and non-convective regions. Mass fractions of water, rock, and iron are indicated with Zw, Zr, and ZFe. The subscript “c” stands for “central” and “cb” for “core boundary.” Panel (i) represents Uranus with Pv, while panel (ii) corresponds to Uranus with PH. Panels (iii) and (iv) illustrate Uranus’s interior structure with pure rock as the heavy element, based on different rotation periods: Pv in panel (iii) or PH in panel (iv). Panel (v) represents Uranus with a high density core. |
 |
Fig. 4 Solution space of temperature profiles of all evaluated models presented in Fig. 1. The solid blue curve marks the mean temperature, and the blue-shaded region marks the 2-sigma uncertainty. For comparison, published adiabatic temperature profiles of Nettelmann et al. (2013) and Podolak et al. (2019) are included. |
3.2 Adiabatic versus non-adiabatic interiors
Here we investigate how non-adiabatic regions within Uranus affect its temperature profile, bulk heavy-element abundance, and heavy-element distribution.
For this, we extracted various adiabatic temperature profiles from published models and, if necessary, linearly extrapolated them to match the required pressures.
Figure 4 shows the solution space of our non-adiabatic temperature profiles together with published adiabatic temperature profiles. We included the adiabatic temperature profiles “U1” from Nettelmann et al. (2013, denoted as “Nettelmann+13 orig.”) and “P19+N13 cold” and “P19+H10 cold” from Podolak et al. (2019). We note that Podolak et al. (2019) interpreted the composition of Uranus and Neptune using the density profiles from Helled et al. (2011) and Nettelmann et al. (2013). For each model, they calculated two temperature profiles, one that follows an adi-abat and a second one that accounts for non-adiabatic regions. For the latter they applied the formalism of Leconte & Chabrier (2012) to obtain a non-adiabatic temperature profile. Both temperature profiles are then used to infer the composition of each model. We refer to the adiabatic models published in Podolak et al. (2019) as “Podolak+19 cold” and to the non-adiabatic models as “Podolak+19 hot.” Accordingly, we refer to their adia-batic and non-adiabatic composition interpretation of models by Nettelmann et al. (2013) by “P19+N13 cold” and “P19+N13 hot”, respectively. The same is true for models of Helled et al. (2011): “P19+H10 cold” and “P19+H10 hot.” Figure 4 clearly shows that non-adiabatic models have significantly hotter interiors compared to adiabatic models. This is expected as most of Uranus’s interior is stable and heat dissipates much more slowly in these non-convective regions, which then trap primordial heat and stay hot for a longer time, leading to hotter present-day interiors.
We used the external adiabatic temperature profiles described above together with the non-adiabatic model “U-4” (denoted as “Vazan4”) from Vazan & Helled (2020) to infer the composition of an arbitrary dense core model using a protoso-lar H–He mixture, together with water, rock and iron as heavy elements. A simpler comparison with only rock as the heavy element is provided in Appendix A. We also applied our method to infer the non-adiabatic temperature profile and composition of the same model. This allows us to compare the inferred composition of adiabatic and non-adiabatic temperature profiles against each other.
Figure 5 shows an example of the inferred distribution of H–He, water, rock and iron using our method (solid curves). For comparison, we also present the composition distributions evaluated with published adiabatic (P19+N13 cold and Nettelmann+13 orig.) and non-adiabatic (Vazan4) temperature profiles. We note, however, that these external temperature profiles are not consistent with the empirical P(r) and ρ(r) from the model and therefore could lead to nonphysical solutions. Since we mostly observe a nonphysical behavior in the outermost regions (upper ∼10% in radius), these regions are excluded. Excluding the upper most ∼10% does not change the results to any significant extent, since the associated mass is only about ∼1% of the planet’s mass.
The adiabatic structure model assumes that the composition is homogeneously mixed throughout the planet. However, the adiabatic temperature profiles (P19+N13 cold and Nettelmann+13 orig.) suggest that there is a composition gradient, meaning that the composition changes with depth. This is a contradiction, and it shows that neither of the adiabatic temperature profiles agrees with the structure model.
We find that different adiabatic temperature profiles have little impact on the distribution of the heavy elements and the bulk heavy-elements abundance. For P19+N13 cold, we obtain 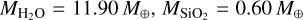 and MFe = 0.38 M⊕, while for Nettelmann+13, we obtain
and MFe = 0.38 M⊕, while for Nettelmann+13, we obtain 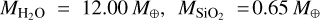 and MFe = 0.40 M⊕. The differences are around 0.1 M⊕. However, when we compare the adiabatic P19+N13 cold to the non-adiabatic Vazan4 (
and MFe = 0.40 M⊕. The differences are around 0.1 M⊕. However, when we compare the adiabatic P19+N13 cold to the non-adiabatic Vazan4 (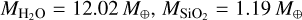 and MFe = 0.47 M⊕), we see larger differences of up to ∼0.8 M⊕.
and MFe = 0.47 M⊕), we see larger differences of up to ∼0.8 M⊕.
This result is expected because in general, the density of material decreases with increasing temperature. Therefore, a hot region with a given density can store more heavy elements than the same region with a cooler temperature.
Uranus’s deep interior is expected to be composed of refractory materials where the density is less sensitive to temperature. Therefore, although the inferred composition is not expected to be very sensitive to an increase in temperature, we find a difference of 0.5 M⊕ for the inferred bulk heavy-element abundance for the non-adiabatic models, and a difference in the rock-to-water ratio on the order of 50%, compared to non-adiabatic models. While Nettelmann (2017) inferred for an adiabatic model a water-to-rock ratio of 19–35, our non-adiabatic models predict a water-to-rock ratio between 7 and 15 (for more information, see Sect. 3.4).
We conclude that different adiabatic temperatures do not alter the resulting bulk heavy-element abundance in a significant way. However, the hotter non-adiabatic temperatures can significantly affect the bulk heavy-element abundance and definitely need to be accounted for. The non-adiabatic regions also significantly affect the planetary long-term evolution (Vazan & Helled 2020; Scheibe et al. 2019, 2021). Therefore, a precise description of the non-adiabatic regions within Uranus is key to constrain its formation and evolution path. For these reasons, it is crucial that internal structure models of Uranus take into account non-convective regions.
 |
Fig. 5 Mass fractions of a dense core model evaluated with different temperature profiles. The yellow curves mark the mass fraction of the protosolar H–He mixture. The blue, brown, and gray curves mark the heavy-element mass fraction of water, rock, and iron, respectively. The solid lines mark the mass fractions as evaluated by our method. Mass fractions obtained with the adiabatic temperature profiles P19+N13 cold and Nettelmann+13 orig. are shown with dashed and dotted curves, respectively. Finally, the mass fractions based on the non-adiabatic temperature of Vazan4 are presented with dash-dotted curves. The gray and blue shaded area indicates the convective and non-convective regions, respectively, as identified by our algorithm. |
3.3 Effect of the rotation period on the composition
In Neuenschwander & Helled (2022; see Sect. 3.2.1), we explored the sensitivity of the inferred density profile to the assumed planetary rotation period. It was concluded that the mean central density for a faster rotating Uranus (with PH) is 13% higher than for a Uranus with PV.
In this section, we investigate the effect of different rotation periods on the temperature profile, the distribution and total amount of heavy elements, and the water-to-rock ratio. We chose a subset of models presented in Neuenschwander & Helled (2022). Although this subset does not cover the entire solution space (shown in the bottom-left panel of Fig. 2 of Neuenschwander & Helled 2022), it still represents its mean density.
3.3.1 Pure rock
To explore the effect of different rotation periods on the inferred composition and temperature profile in isolation, we first interpreted Uranus’s models in the simplest way, where the heavy elements are represented solely by rock, together with H–He at a protosolar ratio. This oversimplified assumed composition is clearly unrealistic but has the advantage that no assumptions on the ratios between various heavy elements need to be made. This assumption allows us to isolate the effect of the assumed rotation rate on the inferred composition. In the next subsection, a more realistic model is used. Figure 6 shows the temperature profile (left panel) and heavy-element distribution (right panel) of Uranus models using PH (orange) and PV (blue). We find that models with PH can exhibit significantly hotter interiors that are more enriched with heavy elements. This result is in agreement with Nettelmann et al. (2013). Core temperatures over 15 000 K are only found in a Uranus with PH. Furthermore, models based on PH have an increased bulk heavy-elements abundance of around ~5% (or 0.6 M⊕). As shown in Table 1 the bulk heavy-elements abundance increases from 11.6–11.9 M⊕ (for PV) to 11.9–12.2 M⊕ (for PH). Finally, the rotation period affects the size of the convective region within the planet: for Uranus models with PV, ~ 25% of the planet is convective, while models with PH have convective regions that can cover up to ~60% of the planetary radius. The size of the convective region within Uranus can lead to a significantly different cooling history (Scheibe et al. 2021). Therefore, an accurate measurement of the rotation period of Uranus is key to constrain its formation and evolution path.
Figure 3 (panels (iii) and (iv)) shows sketches of Uranus’s structure and temperature for the two different rotation periods. Although qualitatively similar, there are differences in the heavy-element mass fraction, temperature, and size of the convective region.
 |
Fig. 6 Temperature (left panel) and metallicity (right panel) profiles of Uranus models with different rotation periods. Different orange and blue shades are used to make individual models traceable across the two panels. The dotted (solid) part of each curve corresponds to convective (non-convective) regions. |
3.3.2 Water and rock
To investigate the effect of the rotation period on a more realistic configuration, we allowed Uranus to consist of H–He, water, and rock. We interpreted the same models as in the previous section. Since the internal structure of Uranus is now more complex, the bulk composition is derived as follows.
We assumed that Uranus’s atmosphere consists of a mixture of H–He and water. In the non-convective region, the water mass fraction begins to steadily increase toward the center until it reaches 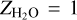 (and hence X = Y = 0). The H–He mixture is then replaced by rock, which increases (in the presence of a composition gradient) toward the planetary center, while the water fraction decreases (to assure
(and hence X = Y = 0). The H–He mixture is then replaced by rock, which increases (in the presence of a composition gradient) toward the planetary center, while the water fraction decreases (to assure 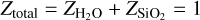 ).
).
Figure 7 shows the distribution of the H–He, water, and rock mass fraction for a selection of models with PV (left panel) and PH (right panel). The main findings are similar: We find that models with PV have higher bulk heavy-element abundances and higher mass fractions of denser material (i.e., rock). This in turn affects the overall water-to-rock ratio (see Sect. 3.4). Again, models with PV have a larger convective region in Uranus’s atmosphere and mantle (by 35%). Finally, Uranus’s interiors with a core temperature >10 000 K are found for Uranus models with the faster rotation period (PH). The higher central temperature found for Uranus models with PH is a consequence of the higher bulk heavy-elements abundance (and lower water-to-rock ratio; see Table 2).
The inclusion of water as a heavy-element affects the inferred bulk composition of Uranus. The H–He bulk abundance is roughly halved (below ~1.25 M⊕) in comparison to the pure rock solution (~2–3 M⊕; see Tables 1 and 2). This is because, in the pure rock scenario, the H–He mixture mixes with rock down to the planetary center. In the case where the heavy elements are represented by water and rock, the H–He mixture gets substituted relatively quickly by water.
Figure 7 shows that similar to the pure rock solutions, the convective region is larger for the faster-rotating Uranus with PH. However, in comparison with the pure rock solutions, the transition radius between the convective atmosphere and the non-convective deeper interior is, independent of the rotation period, farther out. This indicates that a more physical interior of Uranus is largely non-convective. This result has important implications for Uranus evolution models.
Figure 3 (panels (i) and (ii)) presents Uranus’s internal composition and temperature when both water and rock are included. We note that panels (i) and (ii) represent a Uranus with PV and PH, respectively. As for pure rock, the convective atmosphere is dominated by H–He. This is followed by a composition change around r ≈ 0.88 where water becomes the dominant constituent (at least in terms of mass). In the non-convective region, the water mass fraction steadily increases until a pure-water1 region is reached. After this point, the rock mass fraction keeps increasing toward the planetary center. Interestingly, the transition to a rock-rich layer occurs farther out for Uranus models with PH. It should be noted that recent studies suggest that water and rock could be miscible in Uranus’s deep interior (Kovačević et al. 2022; Pan et al. 2023; see also our Sect. 3.4). If this is correct, the deep interior of Uranus is expected to be even more rock-rich. It is therefore clear that improved knowledge of rock-water mixtures is required.
 |
Fig. 7 Radial mass fractions of the H–He mixture, water, and rock of Uranus models using PV (left panel) and PH (right panel). The solid, dashed, and dotted curves show the mass fraction of different models. In the left panel, the solid and dashed curves show the most extreme models in terms of rock and water mass fractions, whereas the dotted curves mark an in-between model. The gray- and blue-colored areas mark the average of the convective and non-convective regions of the presented models. |
3.3.3 High central densities and the inclusion of iron
So far, our Uranus models only consist of H–He where the heavy elements are represented by water and rock. This mixture is more appropriate for models where the central densities are relatively low (< ρcore ≈ 7000 kg m−3). For models with high central densities (see the orange curves in Fig. 1) Uranus’s central density exceeds the density of pure rock under the inferred pressure and (calculated) temperature. For these models, the inclusion of a denser material is needed; we used iron. We note that in Uranus, iron is only needed for densities above ~7000 – 8500 kg m−3 where the exact number depends on the actual pressure and temperature.
Figure 8 shows the distribution of H–He, water, rock, and iron for three Uranus models with high central densities. We note that iron replaces water at the point where the water-rock mixture is no longer dense enough to match the planetary density profile. The inferred bulk abundance of iron in these models is rather small and is between 0.22 and 0.7 M⊕. In this analysis, high central density models have the lowest water-to-rock ratio (as low as 2.6) and exhibit the lowest central entropy.
Figure 3 (panel (v)) shows the structure of a high central density model. It consists of a convective and metal-poor atmosphere above a convective water-rich layer. Below the convective region, water is gradually replaced by rock down to the core-envelope boundary. The non-convective “core” (innermost region) consists of rock and iron, where the mass fraction of iron is steadily increasing up to the planetary center. The transition into the non-convective region occurs deeper in the planet compared to solutions with only water and rock as heavy elements. This effect, however, is not necessarily a direct consequence of including iron as a heavy element. Rather, it arises directly from the density profile, which is different for models with a high central density. Since more mass is concentrated in the innermost region, the mantle and/or envelope of the planet are less massive. This leads to a flatter density gradient in the mantle, which, at least partially, does not have to be described by a material gradient.
 |
Fig. 8 Mass fractions of three high central density models. The different models are represented by the different lines (solid, dashed, and dotted). |
3.4 Water-to-rock ratio
Knowledge about the water-to-rock ratio in Uranus is crucial for constraining Uranus’s formation history. The water-to-rock ratio of Uranus (and Neptune) is unknown. Since Uranus has probably formed outside the water-ice-line, condensed water ice is expected to be abundant. On the other hand objects near Uranus (and Neptune), for example Kuiper belt objects, are found to be rock-rich (e.g., Malamud & Prialnik 2015; Bierson & Nimmo 2019). Also, the Pluto system is rock-dominated (Stern et al. 2018, and references therein), as well as other Kuiper belt dwarf planets and comets (Podolak et al. 2022, and references therein). As a result, Uranus might also be rock-dominated in composition (e.g., Teanby et al. 2020). Although it has been shown that Uranus’s measured properties can be reproduced even with an internal structure without any water (e.g., Helled et al. 2011), typically, structure models predict that Uranus is water-dominated in composition. For example, Nettelmann et al. (2013) infer a water-to-rock ratio of 19–35 for Uranus.
Below, we determine the water-to-rock ratios from our models and show that although our method prefers water over rock, the inferred water-to-rock ratio can be significantly lower compared to previous studies. In Sect. 3.3, we show that the water-to-rock ratio of Uranus depends on its rotation period. For Uranus models with PV, the water-to-rock ratio is between 7 and 15, whereas for Uranus models with PH it is between 5 and 6. Due to the higher metallicity of the models with PH, the transition to rock starts farther out in the planet (around r ≈ 0.5– 0.61 instead of r ≈ 0.41–0.51). This increases (lowers) the total amount of rock (water) and leads to a decreased water-to-rock ratio. It should be noted, however, that these water-to-rock ratios mark an upper bound. The way the planetary composition is inferred is biased toward a high water content because the heavy elements are represented exclusively by water until the model density exceeds the density of pure water, and only at that point rock is added. In reality, both water and rock are expected to be mixed in the outer regions of Uranus, which would decrease the water-to-rock ratio. Previous studies support that scenario by demonstrating that water and rock are miscible in conditions that exist in Uranus (e.g., Kim et al. 2021; Soubiran et al. 2017; Pan et al. 2023). Also, other molecules (such as CO or MgO) could be present that might perturb the overall water-to-rock ratio.
Finally, it is important to keep in mind that we can represent Uranus’s interior without the presence of water at all, and its density profile can be reproduced by a mixture of H–He and rock (see Sect. 3.3.1). We note that in the compact core solution, in principle, water, rock and iron could coexist in the core. This is however, not very likely, and also corresponds to a very small mass. Therefore, our estimates to the water-to-rock ratios could be taken as upper bounds.
 |
Fig. 9 Temperature (left panel) and metallicity (right panel) profiles of Uranus models with and without 1100 km deep winds. Different orange and blue shades are used to make individual models traceable across the two panels. The dotted and solid part of each curve corresponds to an convective and a non-convective region, respectively. |
3.5 The effect of winds on the inferred composition
In Neuenschwander & Helled (2022) we showed that winds penetrating to 1100 km in Uranus can affect Uranus’s density. In this section we investigate how such winds affect the inferred planetary temperature profile and bulk composition. We compared the inferred composition of five models that have no winds with four models that include the dynamics contribution (winds going down to 1100 km). This subset does not cover the entire parameter space of solutions but is a fair representation of the various models. Figure 9 shows the temperature (left panel) and metal-licity (right panel) profiles of Uranus models with (orange) and without (blue) winds. The figure suggests that both the temperature and the metallicity profile are not affected by the winds up to some minor shifts in the central region where rc ≲ 0.4. (incorporates roughly one-fourth of the planet’s mass). While we find that winds can lead to higher central metallicity, the bulk heavy-element abundance remains the same (around 11.5–12 M⊕ for both models; see Table 1). This suggests that the higher metal-licity in the core region of models with winds is at least partially compensated by a lower metallicity in the mantle (around r -0.4–0.8, incorporating ∼2/3 of the planetary mass). Furthermore, the higher central metallicities go along with a smaller core entropy. Finally, the transition radius between the convective and non-convective regions is not affected in a systematic way. We conclude that winds going down to ∼1100 km have only a minor effect on Uranus’s inferred composition.
4 Summary and conclusion
We present a new method for interpreting the composition of Uranus from empirical models using a physical EoS. This method detects potential composition gradients and non-convective regions. The resulting composition and temperature profiles are fully consistent with the pressure-density profiles from the empirical models. We explore the thermal profile and composition distribution in Uranus using various density profiles and show that Uranus is expected to have a large non-convective region. This non-convective region can significantly affect the temperature profile and the distribution of heavy elements in Uranus. We next explored how the rotation period and the wind depth of the planet influence the inferred composition and water-to-rock ratio. A comparison between our findings and previous studies is also presented. Our key conclusions can be summarized as follows:
The interpretation of the empirical structure models of Uranus presented by Neuenschwander & Helled (2022), which are based on empirical density profiles, suggests that Uranus’s interior includes non-convective regions. Uranus is found to have a convective region in its atmosphere, and potentially mantle, on top of a non-convective inner region, which is stable. The transition between the convective and non-convective region is highly model-dependent and can vary between ~40% and ~85% of Uranus’s radius;
The existence of non-adiabatic regions leads to much higher central temperatures in comparison to adiabatic models. This in turn leads to a higher inferred bulk heavy-elements abundance in Uranus (up to ~10%);
Different rotation periods affect the internal structure and composition of Uranus. A faster rotation period leads to hotter interiors (higher than 10000 K for PH), a higher bulk heavy-element abundance (+ ~ 0.5 M⊕), a lower water-to-rock ratio (5–6 compared to 7–15), and a larger convective region (+ ~ 35%); Therefore, an accurate determination of the rotation rate is required;
Winds penetrating to ~1000 km have only a minor effect on Uranus’s inferred bulk heavy-element abundance. However, they can change the heavy-element distribution and mildly affect the temperature profile.
Our study clearly shows that the consideration of non-adiabatic regions in Uranus significantly affects the inferred determined internal temperatures and planetary composition. This in turn has crucial implications for our understanding of Uranus’s formation and evolution histories. The fact that in all the models we considered a non-adiabatic interior has been inferred also has implications for exoplanet science. Since Uranus is an intermediate-mass planet, a planetary type that is very abundant in the galaxy, its characterization can be used to characterize exoplanets. In particular, our work suggests that non-adiabatic interiors must be included for exoplanetary characterization, and this can substantially affect the inferred composition of exo-planets. Finally, our study highlights the importance of a future mission to Uranus. We argue that measuring Uranus’s rotation period is crucial since the uncertainty in the rotation period affects the inferred temperature, composition, and structure of the planet. In addition, measuring Uranus’s gravitational field with high accuracy would further constrain the possible density profiles and would put stricter limits on the depth of the winds. This would constrain Uranus’s bulk composition and internal structure and therefore improve our understanding of Uranus’s formation and evolution.
Acknowledgements
We thank Naor Movshovitz and Morris Podolak for many fruitful discussions. We also thank an anonymous referee for valuable comments that helped to improve the paper. Finally, we acknowledge support from the Swiss National Science Foundation (SNSF) under grant 200020_2l5634.
Appendix A Adiabatic versus non-adiabatic (pure rock)
For a simpler comparison we analyzed a model with only “rock” as heavy element. Figure A.1 shows the external temperature profiles (left panel) and the corresponding heavy elements distribution (right panel).
 |
Fig. A.1 Temperature (left panel) and metallicity (right panel) of a single profile of Uranus evaluated with different temperature profiles. The heavy elements are represented by pure rock. P19+N13 cold, P19+H10 cold and Nettelmann+13 orig. are adiabatic temperature models, while P19+H10 hot and Vazan4 are non-adiabatic temperature models. |
It is clear from the figure that the non-adiabatic temperature profiles are hotter in comparison to the adiabatic ones. Therefore, P19+H10 hot has a hotter interior than P19+H10 cold. The same is true for the non-adiabatic solution of Vazan4 or this work, both of which are crucially hotter than pure adiabatic solutions. This is expected as heat is transported much more slowly in non-adiabatic regions, which then stay hot for a longer time, leading to hotter interiors.
For each temperature, a composition profile is obtained (right panel of Fig. A.1. The outermost region (r>0.9) of the density profile clearly cannot be represented by any of the external temperature profiles. One reason could be that these external temperature profiles themselves are inferred by an assumed composition. Applying these temperature profiles to a different composition or density can cause unphysical behavior. This effect is even more pronounced in low temperature and pressure regimes such as the atmosphere. Below r~0.9, the pressure and temperature are large enough to diminish this behavior. We note that for further analysis the uppermost ~10% of the planet are neglected. This does not change the results to any significant extent, since the mass associated with these uppermost ~10% is only about ~1% of the planet’s mass.
It becomes clear from the figure that small differences in the temperature profile do not affect both, the total amount or distribution of heavy elements in a significant way. In fact, the difference in the bulk heavy-elements abundance of P19+N13 cold (10.7 M⊕) and Nettelmann+13 orig. (10.9 M⊕) is smaller than 2%. This is expected as the applied equation of states are not strongly temperature-dependent in large parts of the planet. However, larger temperature differences, for example those between the adiabatic P19+N13 cold and non-adiabatic Vazan4 (bulk heavy-elements abundance of 11.7 M⊕), affect the bulk heavy-elements abundance in the order of ~9%. This result is to be expected, as in general the density of material decreases with increasing temperature. Therefore, a hot region with a given density can store more heavy elements than the same region with a cooler temperature. We conclude that different adiabatic temperatures do not significantly alter the amount and distribution of heavy elements. However, the large temperature differences that may arise between adiabatic and non-adiabatic models are significant. We conclude that non-adiabatic temperature models change the planetary composition in a non-negligible way and that future studies have to account for the possible existence of non-convective regions.
Appendix B Comparison with published interior models
In this section we compare our models to several published adi-abatic and non-adiabatic models of Uranus. Figure 1 already compares our density distributions with results from Helled et al. (2011), Nettelmann et al. (2013), and Vazan & Helled (2020). Although we included different density profiles, some of the published models are not exactly covered with our sample. A potential explanation to that could be differences in the J2 and J4 values and their uncertainties. Uranus’s gravitational harmonics were updated in 2014 Jacobson (2014) and, naturally, were not yet taken into account in the studies of Helled et al. (2011) and Net-telmann et al. (2013). Furthermore, the non-adiabatic solutions of Vazan & Helled (2020) are calculated by evolution models and therefore do not reproduce Uranus’s gravity field.
 |
Fig. B.1 Temperature-Pressure dependence of all evaluated models (note color code). For comparison, adiabatic and non-adiabatic solutions of published work are included. |
Figure B.1 collects all the temperature profiles of this work as well as published results including adiabatic and non-adiabatic models. It is clear from the figure that our models first follow very closely an adiabat (similar to Nettelmann et al. (2013) and Podolak+19 cold). At ~100 bar, the composition (and therefore also the adiabat) begins to change. This happens because, as discussed above, at this pressure the adiabatic atmosphere model from Hueso et al. (2020) ends and, from this point to the center of the planet, the density is described by the corresponding polytropic relation, while at ~104 bar, Uranus’s interior clearly becomes non-adiabatic. We note the flattening of the curves at very high pressures. At this depth, the temperature has little effect on the EoS used, since they are mainly pressure-dependent and only slightly temperature-dependent. It is clear that the non-adiabatic models lead to hotter deep interiors. This is crucial to consider in Uranus studies since it affects Uranus’s cooling efficiency, and therefore its evolution history.
Appendix C Relation between radius and mass
There are at least two widely used approaches for presenting the density, pressure, or temperature profile. The first is to plot the quantity against the planetary radius, the second way is to plot it against the planetary mass. Of course, both approaches have their justification as well as individual strengths and weaknesses. In the end, the approach chosen may come down to an individual’s preference.
In this paper we mostly plot quantities such as the density, temperature, and mass fractions against the normalized radius. However, for people that think more in terms of mass, we provide here the conversion of planetary radius and mass for all models. Figure C.1 illustrates the dependence between the planetary radius and accumulated mass of the analyzed models in this paper.
 |
Fig. C.1 Relation between the accumulated planetary mass and normalized radius of the analyzed Uranus models. Note that small kinks may arise due to density discontinuities. |
Appendix D Bulk heavy-element abundance versus central temperature
Figure D.1 shows how Uranus’s bulk heavy-element abundance depends on its central temperature. Models with different rotation periods and compositions are treated separately. Exact numbers depend on the chosen set of models; however, the general trend persists. Higher central temperatures lead to a higher bulk heavy-element abundance of Uranus. This finding is well known but the figure does quantify the effect and shows first-order trends.
 |
Fig. D.1 How Uranus’s total bulk heavy-element abundance depends on its central temperature. Each set of models is plotted separately (see legend). For each set, a dashed trend line is calculated and drawn in the corresponding color. |
Appendix E Supplementary material
Figure E.1 collects all models that consist of pure rock and compares them in terms of temperature (left panel) and metallicity (right panel) with published solutions. Figure E.2 shows for each panel in Fig. 2 its appropriate density profile. For better illustration, the transition region around r ≈ 0.9 is shown enlarged.
 |
Fig. E.1 Comparison of our models with published results. The left (right) panel compares our models to the gray-shaded solutions of Nettelmann et al. (2013) and Podolak et al. (2019) in terms of temperature (metallicity). The convective and non-convective regions of each model are indicated by dotted and solid parts in each curve, respectively. All our models presented here consist of a protosolar H–He mixture and pure rock as heavy elements. |
References
- Bierson, C. J., & Nimmo, F. 2019, Icarus, 326, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Debras, F. 2021, ApJ, 917, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Desch, M. D., Connerney, J. E. P., & Kaiser, M. L. 1986, Nature, 322, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., & Nettelmann, N. 2010, Space Sci. Rev., 152, 423 [CrossRef] [Google Scholar]
- Helled, R. 2023, A&A, 675, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helled, R., & Fortney, J. J. 2020, Philos. Trans. Roy. Soc. Lond. A, 378, 20190474 [NASA ADS] [Google Scholar]
- Helled, R., Anderson, J. D., & Schubert, G. 2010, Icarus, 210, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Helled, R., Anderson, J. D., Podolak, M., & Schubert, G. 2011, ApJ, 726, 15 [Google Scholar]
- Horedt, G. P., & Hubbard, W. B. 1983, Moon Planets, 29, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B. 1968, ApJ, 152, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., Schubert, G., Kong, D., & Zhang, K. 2014, Icarus, 242, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Hueso, R., Guillot, T., & Sanchez-Lavega, A. 2020, Philos. Trans. Roy. Soc. A: Math. Phys. Eng. Sci., 378, 20190476 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, R. A. 2014, AJ, 148, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, Y., Showman, A. P., Hubbard, W. B., Aharonson, O., & Helled, R. 2013, Nature, 497, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, T., Chariton, S., Prakapenka, V., et al. 2021, Nat. Astron., 5, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution (Springer Berlin Heidelberg) [Google Scholar]
- Kovačević, T., Gonzalez-Cataldo, F., Stewart, S. T., & Militzer, B. 2022, Sci. Rep., 12, 13055 [CrossRef] [Google Scholar]
- Leconte, J., & Chabrier, G. 2012, A&A, 540, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leconte, J., & Chabrier, G. 2013, Nat. Geosci., 6, 347 [Google Scholar]
- Ledoux, P. 1947, ApJ, 105, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Malamud, U., & Prialnik, D. 2015, Icarus, 246, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Mankovich, C. R., & Fuller, J. 2021, Nat. Astron., 5, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Miguel, Y., Bazot, M., Guillot, T., et al. 2022, A&A, 662, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Militzer, B., & Hubbard, W. B. 2023, Planet. Sci. J., 4, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Militzer, B., Soubiran, F., Wahl, S. M., & Hubbard, W. 2016, J. Geophys. Res. (Planets), 121, 1552 [NASA ADS] [CrossRef] [Google Scholar]
- More, R. M., Warren, K. H., Young, D. A., & Zimmerman, G. B. 1988, Phys. Fluids, 31, 3059 [NASA ADS] [CrossRef] [Google Scholar]
- Movshovitz, N., Fortney, J. J., Mankovich, C., Thorngren, D., & Helled, R. 2020, ApJ, 891, 109 [Google Scholar]
- Müller, S., & Helled, R. 2021, MNRAS, 507, 2094 [CrossRef] [Google Scholar]
- Müller, S., Helled, R., & Cumming, A. 2020, A&A, 638, A121 [Google Scholar]
- Nettelmann, N. 2017, A&A, 606, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nettelmann, N., Helled, R., Fortney, J., & Redmer, R. 2013, Planet. Space Sci., 77, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Nettelmann, N., Wang, K., Fortney, J. J., et al. 2016, Icarus, 275, 107 [Google Scholar]
- Nettelmann, N., Movshovitz, N., Ni, D., et al. 2021, Planet. Sci. J., 2, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Neuenschwander, B. A., & Helled, R. 2022, MNRAS, 512, 3124 [CrossRef] [Google Scholar]
- Neuenschwander, B. A., Helled, R., Movshovitz, N., & Fortney, J. J. 2021, ApJ, 910, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, S., Huang, T., Vazan, A., et al. 2023, Nat. Commun., 14, 1165 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Pearl, J. C., Conrath, B. J., Hanel, R. A., Pirraglia, J. A., & Coustenis, A. 1990, Icarus, 84, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Podolak, M., Hubbard, W. B., & Stevenson, D. J. 1991, in Uranus, eds. J. T. Bergstralh, E. D. Miner, & M. S. Matthews, 29 [Google Scholar]
- Podolak, M., Helled, R., & Schubert, G. 2019, MNRAS, 487, 2653 [NASA ADS] [CrossRef] [Google Scholar]
- Podolak, J. I., Malamud, U., & Podolak, M. 2022, Icarus, 382, 115017 [NASA ADS] [CrossRef] [Google Scholar]
- Scheibe, L., Nettelmann, N., & Redmer, R. 2019, A&A, 632, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scheibe, L., Nettelmann, N., & Redmer, R. 2021, A&A, 650, A200 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soderlund, K. M., Heimpel, M. H., King, E. M., & Aurnou, J. M. 2013, Icarus, 224, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, F., Militzer, B., Driver, K. P., & Zhang, S. 2017, Phys. Plasmas, 24, 041401 [NASA ADS] [CrossRef] [Google Scholar]
- Soyuer, D., Soubiran, F., & Helled, R. 2020, MNRAS, 498, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Soyuer, D., Neuenschwander, B., & Helled, R. 2023, AJ, 165, 27 [CrossRef] [Google Scholar]
- Stanley, S., & Bloxham, J. 2004, Nature, 428, 151 [CrossRef] [Google Scholar]
- Stanley, S., & Bloxham, J. 2006, Icarus, 184, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, S. A., Grundy, W. M., McKinnon, W. B., Weaver, H. A., & Young, L. A. 2018, ArA&A, 56, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Stixrude, L., Baroni, S., & Grasselli, F. 2021, Planet. Sci. J., 2, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Teanby, N. A., Irwin, P. G. J., Moses, J. I., & Helled, R. 2020, Philos. Trans. Roy. Soc. A: Math. Phys. Eng. Sci., 378, 20190489 [NASA ADS] [CrossRef] [Google Scholar]
- Valletta, C., & Helled, R. 2020, ApJ, 900, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., & Helled, R. 2020, A&A, 633, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazan, A., Kovetz, A., Podolak, M., & Helled, R. 2013, MNRAS, 434, 3283 [NASA ADS] [CrossRef] [Google Scholar]
- Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [CrossRef] [Google Scholar]
- Zharkov, V. N., & Gudkova, T. V. 1991, Ann. Geophys., 9, 357 [Google Scholar]
- Zharkov, V. N., & Trubitsyn, V. P. 1970, Soviet Ast., 13, 981 [NASA ADS] [Google Scholar]
- Zharkov, V. N., & Trubitsyn, V. P. 1975, Soviet Ast., 19, 366 [NASA ADS] [Google Scholar]
- Zharkov, V. N., Hubbard, W., & Trubicyn, V. 1978, in Astronomy and Astrophysics Series, Physics of planetary interiors (Tucson-Arizona: Pachart), 6 [Google Scholar]
All Tables
Key parameters for all evaluated models consisting of a mixture of H–He and rock.
Key parameters for all evaluated models consisting of H–He, water, rock, and potentially iron.
All Figures
 |
Fig. 1 Empirical density profiles from Neuenschwander & Helled (2022) we considered in this study. Also shown are published density profiles of Uranus. The blue curves show Uranus models that use the rotation period estimated by the Voyager 2 mission, while the green curves show models that use the rotation period proposed by Helled et al. (2010). The red curves show models with 1100 km deep winds, and the yellow curves correspond to solutions with high central densities. |
| In the text | |
 |
Fig. 2 Temperature profiles (solid black curve), heavy-element mass fractions (dashed curves), and density profiles (dotted purple curve) of various solutions. In the upper row, the heavy elements are represented by pure rock (dashed brown line) only. The lower row shows more “physical” solutions in which the heavy elements are represented by water (dashed blue curve), rock (dashed brown curve), and, if necessary, iron (dashed gray curve). The gray-shaded radial area marks the convective regions. On the other hand, the blue-shaded radial area marks the non-convective and nonhomogeneous region. The dashed blue, brown, and gray lines show the radial mass fraction of water, rock, and iron, respectively. |
| In the text | |
 |
Fig. 3 Sketches of Uranus’s interior structure. The left side of each panel shows the composition, and the right side illustrates the temperature. Cold regions are colored in blue, hot regions in yellow. The protosolar H–He mixture is colored in light blue, water in dark blue, rock in orange, and iron (bottom panel) in gray. Composition gradients are illustrated by a color gradient of the two mixed materials. The dashed curve marks the boundary between the convective and non-convective regions. Mass fractions of water, rock, and iron are indicated with Zw, Zr, and ZFe. The subscript “c” stands for “central” and “cb” for “core boundary.” Panel (i) represents Uranus with Pv, while panel (ii) corresponds to Uranus with PH. Panels (iii) and (iv) illustrate Uranus’s interior structure with pure rock as the heavy element, based on different rotation periods: Pv in panel (iii) or PH in panel (iv). Panel (v) represents Uranus with a high density core. |
| In the text | |
 |
Fig. 4 Solution space of temperature profiles of all evaluated models presented in Fig. 1. The solid blue curve marks the mean temperature, and the blue-shaded region marks the 2-sigma uncertainty. For comparison, published adiabatic temperature profiles of Nettelmann et al. (2013) and Podolak et al. (2019) are included. |
| In the text | |
 |
Fig. 5 Mass fractions of a dense core model evaluated with different temperature profiles. The yellow curves mark the mass fraction of the protosolar H–He mixture. The blue, brown, and gray curves mark the heavy-element mass fraction of water, rock, and iron, respectively. The solid lines mark the mass fractions as evaluated by our method. Mass fractions obtained with the adiabatic temperature profiles P19+N13 cold and Nettelmann+13 orig. are shown with dashed and dotted curves, respectively. Finally, the mass fractions based on the non-adiabatic temperature of Vazan4 are presented with dash-dotted curves. The gray and blue shaded area indicates the convective and non-convective regions, respectively, as identified by our algorithm. |
| In the text | |
 |
Fig. 6 Temperature (left panel) and metallicity (right panel) profiles of Uranus models with different rotation periods. Different orange and blue shades are used to make individual models traceable across the two panels. The dotted (solid) part of each curve corresponds to convective (non-convective) regions. |
| In the text | |
 |
Fig. 7 Radial mass fractions of the H–He mixture, water, and rock of Uranus models using PV (left panel) and PH (right panel). The solid, dashed, and dotted curves show the mass fraction of different models. In the left panel, the solid and dashed curves show the most extreme models in terms of rock and water mass fractions, whereas the dotted curves mark an in-between model. The gray- and blue-colored areas mark the average of the convective and non-convective regions of the presented models. |
| In the text | |
 |
Fig. 8 Mass fractions of three high central density models. The different models are represented by the different lines (solid, dashed, and dotted). |
| In the text | |
 |
Fig. 9 Temperature (left panel) and metallicity (right panel) profiles of Uranus models with and without 1100 km deep winds. Different orange and blue shades are used to make individual models traceable across the two panels. The dotted and solid part of each curve corresponds to an convective and a non-convective region, respectively. |
| In the text | |
 |
Fig. A.1 Temperature (left panel) and metallicity (right panel) of a single profile of Uranus evaluated with different temperature profiles. The heavy elements are represented by pure rock. P19+N13 cold, P19+H10 cold and Nettelmann+13 orig. are adiabatic temperature models, while P19+H10 hot and Vazan4 are non-adiabatic temperature models. |
| In the text | |
 |
Fig. B.1 Temperature-Pressure dependence of all evaluated models (note color code). For comparison, adiabatic and non-adiabatic solutions of published work are included. |
| In the text | |
 |
Fig. C.1 Relation between the accumulated planetary mass and normalized radius of the analyzed Uranus models. Note that small kinks may arise due to density discontinuities. |
| In the text | |
 |
Fig. D.1 How Uranus’s total bulk heavy-element abundance depends on its central temperature. Each set of models is plotted separately (see legend). For each set, a dashed trend line is calculated and drawn in the corresponding color. |
| In the text | |
 |
Fig. E.1 Comparison of our models with published results. The left (right) panel compares our models to the gray-shaded solutions of Nettelmann et al. (2013) and Podolak et al. (2019) in terms of temperature (metallicity). The convective and non-convective regions of each model are indicated by dotted and solid parts in each curve, respectively. All our models presented here consist of a protosolar H–He mixture and pure rock as heavy elements. |
| In the text | |
 |
Fig. E.2 Density profiles of each model shown in Fig. 2 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


