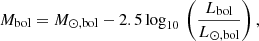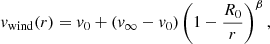EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A154 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A154
Number of page(s) 12
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202348142
Published online 15 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Type II supernovae (SNe II1) are the result of the explosion of massive stars (≳9 M⊙) that have retained a hydrogen-rich envelope at the end of their evolution. SNe II are characterised by prominent hydrogen lines in their spectra (Minkowski 1941; Filippenko 1997) and they are the most common type of core-collapse SNe (Shivvers et al. 2017). Direct detections of progenitors in pre-explosion images provide strong evidence for red supergiant (RSG) stars as SN II progenitors (e.g. Van Dyk et al. 2012; Smartt 2015).

Hydrogen-rich SNe are sub-classified based on their photometric and/or spectral characteristics. Some of these objects show prevalent narrow emission lines in their spectra and luminous light curves (Schlegel 1990; Arcavi 2017). These events are referred to as type IIn SNe. The characteristics of this subgroup are attributed to the interaction of the SN ejecta with a pre-existing dense circumstellar material (CSM). This CSM is the result of a high mass-loss rate during the last stage of the progenitor evolution.

A significant fraction of SNe II also show narrow emission features, disappearing within hours to days after explosion (Bruch et al. 2021), thus suggesting that the spatial extension of the CSM is small and that the progenitor experienced enhanced mass loss shortly before core collapse (e.g. Yaron et al. 2017). The SN shock wave breaks out from the progenitor surface emitting high-energy photons that excite and ionise the CSM; moreover, the continuous interaction between the shock wave and the CSM converts kinetic energy into radiation that also ionises the material outwards from the shock front. The narrow emission features are a consequence of the recombination of the slow-expanding ionised CSM (Khazov et al. 2016; Dessart et al. 2017; Smith 2017).

SN 2023ixf is a SN II (Perley et al. 2023) discovered on 2023 May 19 17:27:15.00 UT in the galaxy M 101 (Itagaki 2023). The proximity to this object allowed several detections of the progenitor candidate in pre-explosion images taken with the Hubble Space Telescope, the Spitzer Space Telescope, and ground-based telescopes. The analysis of these images results in a variable RSG candidate obscured by dust, whose luminosity is consistent with the evolution of a star with an initial mass of MZAMS = 10−15 M⊙ (Szalai & Dyk 2023; Pledger & Shara 2023; Kilpatrick et al. 2023; Jencson et al. 2023; Xiang et al. 2024; Neustadt et al. 2024). At the same time, the analysis of the progenitor variability implies an initially more massive star of MZAMS = 20 ± 4 M⊙ (Soraisam et al. 2023), while the study of the stellar populations in the vicinity of the site of explosion of SN 2023ixf infers a progenitor initial mass of MZAMS = 17−19 M⊙ (Niu et al. 2023). The progenitor could not be detected in X-rays and ultraviolet (UV) pre-explosion images (Kong 2023; Matsunaga et al. 2023; Basu et al. 2023). Pre-explosion observations disfavour the presence of outbursts in the last ∼20 yr (Jencson et al. 2023; Dong et al. 2023; Neustadt et al. 2024), although a low-luminosity outburst might not alter the dust optical depth enough to become detectable (Hiramatsu et al. 2023; Neustadt et al. 2024). Additionally, light-curve modelling infers a progenitor initial mass of MZAMS = 12 M⊙ (Bersten et al. 2024).

After the discovery, intensive photometric, spectroscopic, and polarimetric follows-up were carried out (e.g. Hosseinzadeh et al. 2023; Grefenstette et al. 2023; Teja et al. 2023; Vasylyev et al. 2023). Early-time spectra show narrow emission features during the first week after discovery, which indicate the presence of a dense CSM (Sutaria & Ray 2023; Yamanaka et al. 2023; Teja et al. 2023; Jacobson-Galán et al. 2023; Bostroem et al. 2023; Smith et al. 2023; Hiramatsu et al. 2023).

In the present paper, we attempt to estimate the physical properties of the CSM surrounding the progenitor of SN 2023ixf by modelling the early-time bolometric light curve and evolution of the expansion velocity. We note that the characteristics of the wind producing the CSM has to be consistent not only with the aforementioned observables of SN 2023ixf but also with the epoch of disappearance of the narrow emission features and the absence of outbursts – at least – during the last ∼20 yr before explosion.

There are only a small number of objects observed as early and intensively as SN 2023ixf; therefore, it is a great opportunity to calculate and analyse the early bolometric light curve of a SN II. The early follow-up of SN 2023ixf allowed us to calculate the bolometric light curve before the maximum luminosity, during the rise to peak. This is of particular interest given that this has only been observed in a small number of previously discovered SNe II. Given the exceptional temporal and wavelength coverage of SN 2023ixf observations, the analysis of this early phase can provide important information about the shock wave emergence. In addition, the calculation of the early-time bolometric light curve allows us to estimate bolometric corrections (BCs) and to extend the calibrations of BC against optical colours previously established in the literature (Martinez et al. 2022a) to earlier epochs.

In this work, we adopted a Cepheid-based distance of 6.85 ± 0.15 Mpc (Riess et al. 2022). For the explosion epoch, there are various constraints thanks to the large number of non-detections close to the discovery date. We adopted MJD 60082.75 as the explosion date, following the analysis of Hosseinzadeh et al. (2023) and the non-detections by Mao et al. (2023). The Milky Way reddening in the direction of SN 2023ixf is E(B − V)MW = 0.008 mag (Schlafly & Finkbeiner 2011), while we adopted a host-galaxy reddening of E(B − V)host = 0.031 mag based on the equivalent widths of Na I lines (Lundquist et al. 2023, see also Smith et al. 2023). We considered a Galactic extinction law from Cardelli et al. (1989) with RV = 3.1.

The present paper is organised as follows. Section 2 describes the methodology to calculate the bolometric light curve of SN 2023ixf. Section 3 inspects the currently available calibrations for BCs versus optical colours and presents an extension of the calibrations previously found by Martinez et al. (2022a) by including SN 2023ixf in the analysis. Section 4 presents the modelling to the early-time bolometric light curve of SN 2023ixf and the derived physical properties of the CSM. In Sect. 5, we discuss the scenario that produces the CSM and compare with the results from the literature. We provide our concluding remarks in Sect. 6.

2. Bolometric light curve

The main goal of this work is to derive physical properties for the mass-loss history of the progenitor of SN 2023ixf near core collapse, based on comparing models with early-time observations (< 19 days). The models are computed using a 1D code that simulates the explosion of the SN and calculates bolometric luminosities, among other observables (Bersten et al. 2011, see Sect. 4 for additional details). Therefore, in a first stage, we estimated bolometric luminosities for SN 2023ixf.

SN 2023ixf has been monitored since shortly after its discovery with an exceptional cadence and wavelength coverage. In order to estimate bolometric luminosities, we collected publicly-available multi-band photometric data from the literature and additional photometry reported through The Astronomer’s Telegrams2 and TNS Astronotes3 services. Specifically, we gathered UV, optical (UBVu′g′r′i′z′ filters) and near-infrared (NIR, JHKs filters) magnitudes from Teja et al. (2023), and optical photometry (BVRIg′r′i′) from Balam & Kendurkar (2023), D’Avanzo et al. (2023), Fowler et al. (2023), Kendurkar & Balam (2023), Sgro et al. (2023), and Vannini (2023a,b,c). The UV data presented in Teja et al. (2023) correspond to UVW2, UVM2, and UVW1 filters from the Ultraviolet Optical Telescope (Roming et al. 2005) on board the Swift Observatory (Gehrels et al. 2004). The entire data set covers from 0.3 to 19 days after explosion, which allow us to analyse the early SN emission and to estimate the physical properties of the CSM.

The estimation of the bolometric luminosities was performed in the same manner as in Martinez et al. (2022a). This method consists in the integration of the observed fluxes, which in the present study represents the spectral energy distribution (SED) of SN 2023ixf from mid-UV – when available – to NIR wavelengths. In addition, the calculation method assumes that the SN emits as a black body at the unobserved wavelengths (see details below).

The early-time photometry of SN 2023ixf is characterised by a high cadence of observations. However, magnitude values are not always available at a given epoch for all the observed bands, which are necessary to produce reliable black-body fits to the observed SED. We obtained a complete set of magnitudes at each observed epoch performing loess non-parametric regressions using the ALR code4 described in Rodríguez et al. (2019). Observed UVW2 and UVM2 light curves have a small number of observations, therefore, these light curves were not interpolated. Extrapolations were not allowed for any band.

Having photometric measurements or interpolated magnitudes in all observed bands at each epoch of observation (with the exception of UVW2 and UVM2), we proceeded with the bolometric luminosity estimation method. We transformed magnitudes into monochromatic fluxes at the mean wavelength of the filter using the transmission functions provided by the SVO filter service (Rodrigo et al. 2012; Rodrigo & Solano 2020), taking into account that the collected data are available in different photometric systems. The monochromatic fluxes were then integrated using the trapezoidal method and the observed flux was estimated at each epoch of observation.

To estimate the unobserved flux at shorter and longer wavelengths we assumed that the SN emission in those regimes is well described by a black-body model. At early times, this assumption is mostly correct. As the SN ejecta expands and cools, the UV emission starts to depart from a black-body model as a consequence of the increasing line blanketing produced by iron-group elements. However, with our collected data set, we note that black-body models are still consistent with the observed UV emission at least up to ∼15 days from explosion (after this epoch there are no available observations at UV bands). Therefore, it is not necessary to remove the bluest bands from the black-body fitting as it is, in general, for later observations (see e.g. Bersten & Hamuy 2009; Faran et al. 2018; Martinez et al. 2022a). Black-body fits were carried out only for observational epochs with at least four data points.

Once we found a black-body model that fits the observed SED, the extrapolated flux at longer wavelengths is simply the emission of the black-body model between the reddest observed band and infinity (known as the IR correction). At the same time, the extrapolated flux at shorter wavelengths is the emission of the black-body model between the bluest observed band and zero wavelength (known as the UV correction). The sum of the observed flux and the extrapolated fluxes from the black-body model equates the bolometric flux.

To take the magnitude uncertainties into account, we calculated the bolometric flux via a Monte Carlo procedure. For each of the two thousand simulations, we randomly sampled broadband magnitudes assuming a Gaussian distribution centred at the magnitude value with a standard deviation equal to the magnitude uncertainty. Then, the observed flux was integrated, the best-fitting black-body model was found, and the IR and UV corrections were estimated. The mean bolometric flux of the two thousand simulations was calculated and taken as the bolometric flux. We took the standard deviation of the distribution as the uncertainty of the luminosity. This procedure was repeated at every epoch of observation. Finally, the bolometric flux was transformed into luminosity using the distance to the SN. The bolometric light curve was calculated from 1.9 to 18.9 days after explosion.

Figure 1 shows the resulting bolometric light curve for SN 2023ixf. In addition, this figure shows the pseudo-bolometric light curve for SN 2023ixf, which is defined as the integration of the observed flux in the optical and NIR regimes. At early times, the differences between both light curves are significant. This behaviour indicates the great contribution of the UV to the bolometric flux at these epochs. Moreover, the absence of the UV flux erases the luminosity peak. Therefore, if the photometric coverage is limited to optical and redder bands, or the unobserved flux in the UV is not taken into account, the peak in the bolometric light curve is lost. Eventually, the differences become smaller because the SN ejecta cools and the UV emission decreases, while the SN emission in the optical increases.

thumbnail Fig. 1.

Early bolometric light curve for SN 2023ixf (blue dots). The dashed line represents the pseudo-bolometric light curve. The inset plot shows the first week of evolution of the bolometric luminosity. In this plot, the pink triangles are the bolometric luminosities when observed UV data are not taken into account in the calculation method. In most cases the error bars are smaller than the dot size.

The early bolometric light curve of SN 2023ixf consists of a rapid rise time of 3.47 days to maximum at log Lbol = 45.5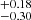 (Mbol = −25.08 ± 0.54 mag). This is the first time – to our knowledge – that such a detailed rise to maximum and sharp peak are observed in bolometric luminosities, having a large wavelength coverage and using similar techniques. At the epoch of maximum luminosity, the black-body model fits observed fluxes in the following bands: UVOT-B, B, g, UVOT-V, V, r, i, z, J, H, and K; resulting in a black body with a temperature of ∼1.3 × 105 K. Recently, while our study was on the revision stage, a study appeared on the archive: Zimmerman et al. (2023), who also presented bolometric light curve calculations for SN 2023ixf. While the time of maximum bolometric luminosity estimated by Zimmerman et al. (2023) agrees very well with our estimation, their maximum luminosity is much lower. Given that Zimmerman et al. (2023) used a larger wavelength coverage to compute the luminosity at maximum light, we note that our estimation of the maximum luminosity might be magnified due to an overestimation of the extrapolation to shorter wavelengths. After peak, the luminosity drops ∼2.3 dex in the following 1.5 days. Then, the luminosity starts a slower decline, at least up to day 19 post-explosion.

During the luminosity rise, SN 2023ixf shows different slopes to reach the maximum luminosity (see Fig. 1). First, the luminosity increases almost linearly up to 2.2 days post-explosion. Then, the luminosity starts a slower rise up to day 2.9. Finally, the light curve rises up to maximum with a single slope – much steeper than in earlier times – from day 2.9. This epoch matches with the last epoch of observation – before maximum – having Swift data in the UV. Specifically, before maximum luminosity, the UVW1-band light curve is available until 2.9 days post-explosion, while only a single data point in the UVM2 band was obtained.

In order to test the influence of the available UV data on the rise to maximum luminosity, we calculated the early bolometric light curve for SN 2023ixf again, but this time neglecting the Swift data in the UV regime, both from the black-body fitting procedure and the integration of the observed SED. This is shown in the inset plot of Fig. 1 as pink triangles (only the first three days are shown given that these are the epochs with most UV observations). This process results in a bolometric light curve without the slope changes mentioned above, and with lower luminosities before day 2.9 post-explosion. The lower luminosities are obtained because the Swift data in the UV (mostly in the UVW1 band) are more luminous than the predicted flux from black-body models at the mean wavelength of the UVW1 filter, when the UVW1 data are neglected from the calculation. This means that black-body fits ignoring the available UV data underestimate the UV extrapolation. Therefore, the observed UVW1 data produce black-body models that peak at shorter wavelengths (i.e. hotter black-body models), causing larger UV corrections and higher temperatures during this time interval (see Fig. 2).

thumbnail Fig. 2.

Evolution in time of black-body fit parameters for SN 2023ixf: temperature (red dots) and radius (green diamonds).

Figure 2 shows the black-body parameters obtained from the fits. Before the luminosity peak, the temperature shows values between log T ∼ 4.3−4.4, while the radius increase by a factor of ∼2. Then, the temperature suddenly increases to a value of log T ∼ 5.1 in less than 0.5 days, coincident with the maximum luminosity. At the same time, the black-body radius takes smaller values. This increase in temperature coincides with the blueward evolution of the (U − V) colour and the transition to higher ionisation states of some lines visible in early-time spectra, which may indicate the observation of the delayed shock breakout inside a dense CSM (Hiramatsu et al. 2023). After the luminosity peak, the black-body temperature (radius) decreases (increases) almost monotonically.

3. Bolometric corrections

In Sect. 2, we estimated bolometric luminosities for SN 2023ixf through direct integration of the observed flux (covering UV, optical, and NIR bands) and assuming that the SN emits as a black body at shorter and longer – unobserved – wavelengths. This is the most accurate method to estimate bolometric luminosities when extensive wavelength coverage is available. The use of bolometric corrections to convert broadband magnitudes into bolometric magnitudes is a more frequent technique when the photometric coverage is limited only to optical filters. From the work of Bersten & Hamuy (2009), where the authors developed calibrations between BCs and optical colours, several other studies have analysed these relations (e.g. Lyman et al. 2014; Pejcha & Prieto 2015). More recently, Martinez et al. (2022a) presented updated calibrations of BC against optical colours using the most homogeneous and largest sample of SN II bolometric light curves.

The unprecedented early-time bolometric light curve of SN 2023ixf, characterised by a high cadence of observations and the wide wavelength coverage of the broadband data, allows us to examine the calibrations of bolometric corrections versus colour found in the literature (Sect. 3.1) and to extend previous calibrations to bluer colours (i.e. to earlier times, Sect. 3.2).

3.1. Testing calibrations of bolometric corrections

In this section, we compare the bolometric light curve of SN 2023ixf estimated in Sect. 2 with those constructed employing the calibrations of bolometric corrections from the literature. Specifically, we compare with the calibrations from Bersten & Hamuy (2009), Lyman et al. (2014), Pritchard et al. (2014), Pejcha & Prieto (2015), and Martinez et al. (2022a). Figure 3 shows the results of the analysis. Each panel also shows the colour curves used for the calculation. The details of the comparison are found below.

thumbnail Fig. 3.

Bolometric light curve for SN 2023ixf calculated from the integration of the observed flux plus black-body extrapolations (thick grey line, referred to as “SED integration”) in comparison with those calculated from calibrations of bolometric corrections versus colours found in the literature: Martinez et al. (2022a; top-left panel), Lyman et al. (2014; top-right panel), Bersten & Hamuy (2009), Pejcha & Prieto (2015), and Pritchard et al. (2014; bottom-left panel). The bottom-right panel shows bolometric light curves using the calibrations by Martinez et al. (2022a) when larger validity ranges of colours are allowed.

Martinez et al. (2022a) presented calibrations of BCs versus (B − V), (g − r), and (g − i) colours, with the latter two colour indices showing the smallest dispersions. These BC calibrations are distinguished according to the phase in which the SN is found. For the comparison, we utilised the calibrations that corresponds to the “cooling phase”, since these are the most appropriate for our data set. In addition, these calibrations were performed with photometric data points in the natural system of the Swope telescope at Las Campanas Observatory (Contreras et al. 2010). Therefore, we first converted our data into the corresponding photometric system. Vega magnitudes were transformed into AB system using the conversion values published in Blanton & Roweis (2007). We then used the magnitude offsets from Krisciunas et al. (2017) to convert AB magnitudes into the natural system of the Swope telescope. At that moment, the calibrations of BCs were applied.

We find good agreements between the bolometric light curve calculated in Sect. 2 (referred to as “SED integration” in Fig. 3), and those calculated using the BC calibrations from Martinez et al. (2022a; Fig. 3, top-left panel). The bolometric light curve constructed with the BC calibration against (g − r) produces the most similar light curve to that observed. At the same time, the predicted bolometric luminosities using the calibration versus (g − i) are slightly brighter than those estimated using the (g − r) colour index. The bolometric light curve using the BC calibration against (B − V) agrees well between days 6 and 10. After day 10 the predicted bolometric luminosities overestimate the observations. We note that earlier estimations are not possible because the colour values are bluer than the validity ranges of the calibrations (see below for predicted bolometric luminosities if the validity colour ranges are not considered).

The top-right panel of Fig. 3 compares our bolometric light curve and those predicted using the BC calibrations for the cooling phase from Lyman et al. (2014). These authors constructed calibrations for several colour indices. However, we show comparisons only to calibrations using (B − V), (g − r), and (g − i) given that the other colour indices present a small number of data points. The bolometric light curve computed using BC calibrations versus (B − V) shows good agreement with our, with the exception of the data points between 7 and 10 days post-explosion. At those epochs, the predicted luminosities underestimate our estimation by ∼0.1 dex. The predicted bolometric light curves using (g − r) and (g − i) colours show similar behaviours. In both cases, the luminosity is underestimated, especially during the first 5 days post-explosion. For the (g − i) colour, the rise to maximum is much smoother than the calculated with our procedure, similar to the behaviour of the pseudo-bolometric light curve (see Fig. 1).

The bottom-left panel of Fig. 3 shows a comparison with several other calibrations found in the literature. We chose to compare with the BC calibrations versus (B − V) from Bersten & Hamuy (2009) and Pejcha & Prieto (2015). The other BC calibrations from these latter two papers cannot be well compared due to the small number of data points for the colours involved ((B − I) and (V − I) in the case of Bersten & Hamuy 2009 and (B − R) and (B − I) for Pejcha & Prieto 2015). The bolometric light curve calculated with the BC calibration from Bersten & Hamuy (2009) present two data points – around days 6.5 and 10.5 post-explosion – much brighter than those using the SED integration method. With the exception of these values, the luminosity agrees well with our estimate. The BC calibration from Pejcha & Prieto (2015) agrees well with our bolometric light curve at some epochs. However, other epochs show a variable behaviour. This behaviour can possibly be explained due to the irregular conduct of the (B − V) colour curve, which could also explain the over-luminous data points in the comparison with the BC calibration from Bersten & Hamuy (2009). Additionally, we compared to the BC calibrations from Pritchard et al. (2014). These calibrations were performed for (U − B) and (B − V) colours using Swift+UVOT filters; therefore, we used the available Swift+UVOT photometry for this comparison. For both BC calibrations, the resulting bolometric light curves are much dimmer than that estimated via SED integration.

Finally, we used the BC calibrations from Martinez et al. (2022a) again, but this time without considering the validity ranges of colours. This means that we extrapolated the calibrations to bluer colours. The predicted bolometric light curves using the extrapolated BC calibrations versus (g − r) and (g − i) shows remarkable good agreement at these early epochs, with the exception of the value around day 6. However, we note the large error bars in the (g − r) and (g − i) colour curves at that epoch, arising predominantly from the g-band magnitude. Surprisingly, the BC calibration versus (B − V) predicts the behaviour of the rise to maximum luminosity and the subsequent drop, although the following data points clearly overestimate the luminosity from the SED integration method. However, as stated before, we note the variable behaviour of the (B − V) colour curve. This analysis shows that the BC calibrations from Martinez et al. (2022a) are a satisfactory method to estimate bolometric luminosities, particularly the calibrations versus (g − r) and (g − i) colours.

3.2. Calibrations of bolometric corrections including SN 2023ixf

In Sect. 3.1, we show that the BC calibrations from Martinez et al. (2022a) adequately reproduce the bolometric light curve of SN 2023ixf. In addition, SN 2023ixf has an unique early-time bolometric light curve, due to the high observational cadence that resolves the rise to maximum luminosity, and the extensive wavelength coverage from UV to NIR. This motivates us to incorporate the early-time data of SN 2023ixf to the BC calibrations from Martinez et al. (2022a) in order to extend the calibrations (corresponding to the “cooling phase”) to bluer colours (i.e. to earlier times).

The BC calibrations from Martinez et al. (2022a) were performed using a sample of 74 SNe II observed by the Carnegie Supernova Project-I (Hamuy et al. 2006) using the facilities of the Las Campanas Observatory. Therefore, we used the same data, in addition to those from SN 2023ixf, to construct new BC calibrations.

First, we converted the bolometric luminosities of SN 2023ixf into bolometric magnitudes. By definition

(1)

where L⊙,bol = 3.845 × 1033 erg s−1 and M⊙,bol = 4.74 mag are the luminosity and the absolute bolometric magnitude of the Sun (Drilling & Landolt 2000). We then calculated the bolometric corrections for SN 2023ixf employing the definition, BCj = mbol − mj, where mj is the extinction-corrected magnitude in the band j of the SN, and mbol is its the bolometric magnitude. Finally, we looked for calibrations between the bolometric corrections and the same three colour indices.

Figure 4 displays the bolometric correction relative to the g band (BCg) as a function of (g − r) and (g − i) colours (top and middle panels, respectively). Figure 4 also includes polynomial fits to the data computed via Markov chain Monte Carlo (MCMC) methods using the python package emcee (Foreman-Mackey et al. 2013). We used third order polynomial fits for the calibrations comprising (g − r) and (g − i) colours. We find good agreement between the polynomial fits and the data, except for the lowest BCg value in both plots (BCg = −2.40 mag). This value corresponds to the epoch when the luminosity peak is taking place.

thumbnail Fig. 4.

Bolometric corrections relative to the g band as a function of (g − r) colour (top panel) and (g − i) colour (middle panel), and relative to the V band as a function of (B − V) colour (bottom panel). SN 2023ixf is presented as blue dots, while pink dots represent the cooling phase of the SNe II in the CSP-I sample (see Martinez et al. 2022a). The dashed lines shows the fit to the data. The errors in the CSP-I SN II data are not plotted for better visualisation.

We also searched for calibrations between the bolometric correction relative to the V band (BCV) as a function of (B − V). This is shown in the bottom panel of Fig. 4. For this case, we utilised a fourth order polynomial to fit the early-time data of SN 2023ixf. We do not find any improvement in the BC calibration versus (B − V) colour with respect to that obtained using the CSP-I SN II data, that is, towards (B − V) values lower than −0.10 mag. The lowest two BCV values (BCV = −5.04 and −4.10 mag) corresponds to the peak time. However, we note that these calibrations should be considered more uncertain for the bluest colours for the following reasons: (1) we are using only one SN II at these colour ranges; and (2) the steep dependence of the BC with colour, which implies that an uncertainty in the colour measurement could produce a considerable error in the estimation of the BC. The coefficients of the polynomial fits and the standard deviation around the fits are presented in Table 1.

Table 1.

Coefficients of the polynomial fits to the bolometric corrections versus optical colours.

4. Modelling

The early-time bolometric light curve of SN 2023ixf allows us to constrain its progenitor mass-loss history by comparing models with observations. Theoretical light curves are calculated using a code that solves the hydrodynamical equations assuming spherical symmetry coupled to the radiation transfer equations in the diffusion approximation (Bersten et al. 2011). The explosion is simulated by injecting energy near the centre of the progenitor star, producing a powerful shock wave that propagates out.

In addition to bolometric light curves, our code calculates expansion velocities at different layers. Therefore, we also compare the expansion velocity at the photospheric layer to the Fe IIλ5169 line velocity, given that this line gives a good estimation of the photospheric velocity (Dessart & Hillier 2005). The omission of the expansion velocities in the fitting procedure can result in solutions that are not consistent with the SN expansion rate (see Martinez et al. 2020). If this is the case, the solution found is spurious. In order to measure expansion velocities of SN 2023ixf, we used public spectra from the WISeREP5 archive (Yaron & Gal-Yam 2012) in those epochs where Fe IIλ5169 profiles started appearing (approximately at 25 days after explosion). We used three spectra uploaded to WISeREP from the Dark Energy Spectroscopic Instrument (DESI; Levi et al. 2019) at the 4m Mayall Telescope at Kitt Peak National Observatory and one spectrum uploaded by TNS, without information about the telescope and instrument listed. We measured the expansion velocities of Fe IIλ5169 in the spectra by fitting a Gaussian to the minimum of the absorption profiles. Additionally, we utilised the relation by Faran et al. (2014) that predicts the photospheric velocity at 50 days post-explosion from Fe II velocity measurements.

Progenitor models at the time of core collapse are needed to initialise the explosion. In this context, we used the public stellar evolution code MESA6 version 22.6.1 (Paxton et al. 2011, 2013, 2015, 2018, 2019; Jermyn et al. 2023) to obtain a non-rotating RSG pre-SN model at solar metallicity (Z⊙ = 0.0142; Asplund et al. 2009) for a star of 15 M⊙ on the main sequence. The choice of this initial mass value was carried out to agree with the progenitor luminosity observed in pre-explosion images (Jencson et al. 2023; Van Dyk et al. 2023; Xiang et al. 2024; Neustadt et al. 2024). The stellar models were evolved from the main sequence to core collapse, defined as the time when any location inside the iron core reaches an infall velocity of 1000 km s−1. During massive-star evolution, mass loss was treated using the “Dutch” wind scheme defined in MESA (Vink et al. 2001; de Jager et al. 1988). Convection was modelled using the mixing-length theory (Böhm-Vitense 1958) adopting a mixing-length parameter αmlt = 2.0. The convective regions were determined using the Ledoux criterion. Semiconvenction was implemented as a diffusive process adopting an efficiency of αsc = 1.0 (Langer et al. 1983). Convective-core overshooting is treated in the step formalism during hydrogen- and helium-core burning adopting overshooting parameters of αos = 0.15 (Martins & Palacios 2013) and 0.03 (Li et al. 2019) pressure scale heights, respectively. For later core-burning stages, we adopted the decreasing exponential approach implemented in MESA to account for convective overshooting with a parameter f = 0.003 (Farmer et al. 2016; Jones et al. 2017). The evolution of the initially 15 M⊙ star with the above evolutionary parameters results in a progenitor model with a final mass of 12.7 M⊙, hydrogen-rich envelope of 8.0 M⊙, and radius of 918 R⊙.

The observation of narrow emission lines in early-time SN spectra result from the presence of a dense and confined CSM surrounding the progenitor star. The CSM formation is thought as a consequence of a high mass-loss rate occurred during the last years to decades before core collapse, although the exact mechanism is unclear. As the SN ejecta interacts with the CSM, kinetic energy of the ejecta is converted to radiation that can ionise the CSM and boost the SN early-time luminosity. Given that the progenitor models computed with MESA do not consider the mass loss producing the CSM we are interested in, we artificially attached a CSM profile to the outer layers of the pre-SN model as usually done in the literature (e.g. Moriya et al. 2011; Morozova et al. 2018; Englert Urrutia et al. 2020).

Before attaching any CSM profile, we computed several models with different explosion energies (Eexp) and compared them to our observations. Particularly, we look for agreement to the observed expansion velocities of SN 2023ixf, since these observables are strongly influenced by the energy of the explosion (for a fixed pre-SN model). We choose an explosion energy of Eexp = 1.25 × 1051 erg for each of our simulations with CSM interaction7. We note that the ejecta mass and the explosion energy are rough estimates because in the present paper we are focused on the properties of the CSM. In Bersten et al. (2024), we analyse the complete evolution of the bolometric light curve and estimate the physical properties of the progenitor and explosion.

In the following we aim to reproduce the early-time bolometric light curve of SN 2023ixf by considering two different scenarios to simulate the CSM formation: steady-state (Sect. 4.1) and accelerated (Sect. 4.2) winds. The nomenclature is based on naming each model according to its initial mass, wind mass-loss rate, radial CSM extension, and velocity law for the wind velocity. For example, m15_w3m3_r12000_beta5 corresponds to a initial mass of MZAMS = 15 M⊙, a mass-loss rate of Ṁ = 3 × 10−3 M⊙ yr−1, a CSM extension of RCSM = 12 000 R⊙, and a velocity law of β = 5. A summary of the presented models is found in Table 2. We note that none of the models presented in this section can reproduce the change in the slope during the rise to maximum, observed in the bolometric light curve before day 2.9 post-explosion (see Sect. 2).

Table 2.

Summary of the initial conditions of the models presented in this work.

We note that the explosion epoch of SN 2023ixf is based on the first detection and last non-detection, while in our models the explosion epoch is defined as the moment when the energy is deposited near the centre of the progenitor star. Given the difference in the definition of “explosion epoch” and that it takes a few days for the shock wave to break out from the CSM, we shifted our models to match the time of maximum luminosity. These shifts were always less than 1 day for the best-fitting models.

4.1. Steady-state winds

The first scenario to survey involves steady-state winds. In this scenario, the CSM density (ρCSM) is represented as ρCSM(r) = Ṁ/(4πvwindr2), where r is the radial coordinate, Ṁ is the wind mass-loss rate and vwind is the velocity of the wind. Throughout the present work, we assume a terminal wind velocity of vwind = 115 km s−1, as measured by Smith et al. (2023).

The top panel of Fig. 5 compares explosion models including CSM-ejecta interaction to observations of SN 2023ixf. In this case, we choose CSM models characterised for their confined radial extent between 2500 and 3000 R⊙ (∼1.7−2.1 × 1014 cm) and high mass-loss rates in the range of 0.3−1.0 M⊙ yr−1. While all of these models reproduce the width of the luminosity peak, model m15_w0.3_r2500 does it better. However, this model underestimates the luminosity after day 6 after explosion. Higher mass-loss rates (models m15_w0.5_r2500 and m15_w1.0_r2500) result in higher peak luminosities. However, these models achieve more luminous light curves after peak than observed, and underestimate the observed luminosities after day 10. A more extended CSM produce higher luminosities after peak, inconsistent with observations.

thumbnail Fig. 5.

Comparison between the bolometric light curve of SN 2023ixf (dots) with models varying the CSM properties (lines), assuming steady-state mass loss. The upper panel involves models with higher mass-loss rates and more confined CSMs than the models shown in the bottom panel. The inset plot compares the photospheric velocities of SN 2023ixf to the same models previously mentioned. For the model nomenclature, see Sect. 4.

The comparison from the top panel of Fig. 5 shows that some parts of the early light curve of SN 2023ixf can be reproduced with the adopted CSM parameters. Potentially, a more detailed study around these parameters could result in better agreements. However, all of these models are inconsistent with the epoch of disappearance of the narrow emission lines in observed spectra. Following Dessart et al. (2017), the narrow lines last as long as the shock is placed within a slow-moving optically thick material (i.e. until the shock goes through the SN photosphere). We checked this epoch in each of our simulations and found values around ∼0.7−1.5 days after explosion, while the observations of SN 2023ixf show interaction lines until 6−7 days post-explosion (Bostroem et al. 2023).

In the following we look for a model that reproduces the epoch when the interaction lines faded, while matching the bolometric light curve and photospheric expansion velocities. The thick blue solid line in the bottom panel of Fig. 5 shows a CSM interaction model for Ṁ = 1.2 × 10−2 M⊙ yr−1 and RCSM = 8000 R⊙ (∼5.5 × 1014 cm). This model is able to reproduce the width of the luminosity peak, post-peak luminosities, photospheric velocities, and the epoch of disappearance of the narrow emission features. However, this model fails to reproduce the peak luminosity. Higher mass-loss rates produce wider peaks and more luminous post-maximum light curves (bottom panel of Fig. 5, dashed line). The opposite effect is expected for lower mass-loss rates. Alternatively, a more confined CSM produce a higher peak luminosity, but lower luminosities post-maximum (bottom panel of Fig. 5, dotted line).

4.2. Accelerated winds

In this section we model SN explosions within a CSM but considering the wind acceleration mechanism previously presented in Moriya et al. (2018). In this scenario, the mass-loss rate is set constant and the CSM density follows the same expression as in Sect. 4.1; however, the wind velocity is no longer constant. As in Moriya et al. (2018), the wind velocity takes the form of a β velocity law given below:

(2)

where v0 is the initial wind velocity (0.1 km s−1), v∞ is the terminal velocity of the wind (115 km s−1, Smith et al. 2023), R0 is the radial coordinate where the CSM is attached, and β is the wind acceleration parameter (see also Lamers & Cassinelli 1999).

We compared the early-time bolometric light curve and photospheric velocity evolution of SN 2023ixf with explosion models assuming different CSM parameters (Ṁ, RCSM, and β). Figure 6 shows some of these models. The thick solid line in Fig. 6 represents the model m15_w3m3_r12000_beta5, that is, with Ṁ = 3 × 10−3 M⊙ yr−1, RCSM = 12 000 R⊙, and β = 5. From all the models we computed, this is the one that best reproduces the observations, even better than those models assuming steady mass loss (see Sect. 4.1). In addition, model m15_w3m3_r12000_beta5 predicts that the narrow emission features should disappear at day 6.5, which is consistent with the observed date (Bostroem et al. 2023).

thumbnail Fig. 6.

Comparison between the bolometric light curve of SN 2023ixf (dots) with models varying CSM properties (lines) assuming wind acceleration. The inset plot compares the photospheric velocities of SN 2023ixf to the same models previously mentioned. For the model nomenclature, see Sect. 4.

Figure 6 also shows models computed with varying CSM properties to notice the sensitivity of the early bolometric light curve with these parameters. Higher mass-loss rates (e.g. model m15_w1m2_r12000_beta5) produce wider peaks and more luminous post-peak light curves, while more confined CSMs (e.g. model m15_w3m3_r7000_beta5) underestimate the post-peak luminosity. Alternatively, a smaller wind acceleration parameter (e.g. model m15_w3m3_r12000_beta2) results in narrower and less luminous peak, while at the same time, less luminous light curves after maximum. This behaviour is due to the different amount of CSM mass near the progenitor surface for varying wind acceleration parameters. A larger β involves more mass near the progenitor surface, and therefore, a larger boost to the luminosity due to conversion of kinetic energy into radiation. We note that the models presented cannot reach the observed maximum luminosity (see Sect. 5).

5. Discussion

In Sect. 4, we inferred physical properties of the CSM around SN 2023ixf via modelling of its early-time bolometric light curve. However, the degeneracy present in SN II light curves with CSM – which means that similar light curves can be obtained from different CSM configurations – may cause invalid results. As pointed out by Dessart & Jacobson-Galán (2023), the epoch when narrow line disappear must be used for constraining more accurately the CSM physical properties. For this reason, we also reproduced the epoch of disappearance of narrow lines.

As an example, if we had not taken this epoch into account in the modelling, we would consider the models with the most confined CSM structures (those between 2500 and 3000 R⊙) as valid. However, these dense and confined CSM configurations would show narrow emission lines only for a short time. Moreover, following Dessart & Jacobson-Galán (2023), more confined CSMs would not show narrow emission lines at all. These CSM structures may produce SNe II as the unusual SN 2020jfo (Utrobin & Chugai 2024), given that this SN does not show narrow, electron-scattering broadened emission lines in early spectra.

Now we discuss the timescales of the mass loss inferred from our models. The first wind mass-loss scenario explored assumes a steady flow from the progenitor. With the assumed wind velocity (vwind = 115 km s−1; Smith et al. 2023), the size of the progenitor, and the extent of the CSM presented in Sect. 4, we looked for an estimate of the time before explosion in which this enhanced mass loss must have started. For the CSM extents between 2500 and 3000 R⊙ (∼1.7−2.1 × 1014 cm) first analysed, we found an enhanced wind that developed over the last 0.3−0.4 yr before explosion8. In addition, for a CSM extension of 8000 R⊙ (∼5.5 × 1014 cm), the enhanced wind should have started ∼1.3 yr before explosion. Adopting a commonly used wind velocity for a “superwind” (50 km s−1), the enhanced mass loss would have developed over the last ∼3 yr. The inferred timescales and mass-loss rates are similar to some values found in the literature for SN 2023ixf (e.g. Jacobson-Galán et al. 2023; Hiramatsu et al. 2023).

Mid-IR Spitzer data in the preceding ∼20 yr before the explosion show variability similar to those pulsating RSGs, but does not show any indication of eruptive mass-loss processes (Szalai & Dyk 2023; Jencson et al. 2023; Kilpatrick et al. 2023; Soraisam et al. 2023). Neustadt et al. (2024) found no evidence of outbursts in optical data taken with the Large Binocular Telescope between ∼1 and 15 yr before the SN. The analysis of pre-explosion optical data from the Zwicky Transient Facility (Bellm et al. 2019; Graham et al. 2019), Asteroid Terrestrial-impact Last Alert System (Tonry et al. 2018; Smith et al. 2020), Distance Less Than 40 Mpc, and All-Sky Automated Survey for Supernovae (Kochanek et al. 2017) surveys during the last 8 yr up to 0.3 days before explosion also found no evidence of precursor activity in the optical (Hiramatsu et al. 2023; Dong et al. 2023; Panjkov et al. 2023). In addition, UV observations from the Galaxy Evolution Explorer and Swift space telescopes did not find pre-explosion outbursts ∼20 yr prior to explosion (Flinner et al. 2023; Panjkov et al. 2023). Therefore, pre-explosion observations indicate a quiescent progenitor in the last ∼20 yr, with no indication of any pre-SN outbursts or large magnitude changes, except for the IR variability similar to pulsating RSGs (although see Hiramatsu et al. 2023; Neustadt et al. 2024 for a discussion of low-luminosity outbursts without major changes in the dust optical depth). The assumption of steady-state winds results in enhanced mass loss shortly before explosion, which does not seem consistent with a quiescent progenitor.

Steady winds assume that the mass-loss rate and wind velocity are constant through the wind. However, the wind is gradually accelerated at the stellar surface until the terminal velocity is reached. This produces an increment of the timescales for the wind development to reach a particular extension. The bolometric light-curve modelling including CSM interaction that takes the wind acceleration into account infer that the enhanced mass loss was launched ∼80 yr prior to the SN. These timescales are related to the final stages of massive-star evolution, although the details of the connection are unknown.

Some mechanisms propose mass loss driven by local radiation-driven instabilities in the outer layers (Suárez-Madrigal et al. 2013), hydrodynamic instabilities at pre-SN stage driven by turbulent convection (Smith & Arnett 2014), common envelope interaction with a close companion (Chevalier 2012), or regular mass transfer to a companion star. Wave heating is an alternative picture to explain pre-SN outbursts (Quataert & Shiode 2012). Internal gravity waves excited by vigorous convection that occurs during late-burning stages in massive stars deposit energy in the stellar envelope, which may be able to inflate the envelope and drive intense mass loss years before core collapse (Shiode & Quataert 2014; Fuller 2017). In this context, hydrodynamical simulations of RSG stars were performed to model the formation of CSM caused by energy deposition in the base of the hydrogen-rich envelope – mimicking the effects of wave heating during late nuclear burning stages – which allowed light-curve modelling for some SNe II without ad hoc prescriptions for the CSM structure (Morozova et al. 2020; Chugai & Utrobin 2022). However, recent studies suggest that wave heating may favour pre-SN outbursts only for specific initial mass ranges (Wu & Fuller 2021, 2022).

As stated in Sect. 4, the code we use to compute SN observables assumes spherical symmetry; however, the aspherical nature of RSG envelopes is known from spectro-interferometric observations (e.g. Arroyo-Torres et al. 2015; Ohnaka et al. 2011). Moreover, some of the proposed mechanisms for severe mass loss during the last evolutionary stages of RSGs could also produce an asymmetric CSM. Particularly, although wave heating may not be the main channel to drive high mass loss (Wu & Fuller 2022), this mechanism may inflate the RSG envelope, trigger Roche-lobe overflow, and produce asymmetric mass loss in binary systems (Smith & Arnett 2014).

Vasylyev et al. (2023) and Smith et al. (2023) suggest an asymmetric CSM around SN 2023ixf based on polarimetric and spectroscopic observations, where the CSM concentrates on the equatorial plane. In this context, the shock front that goes through the CSM will be decelerated, while the shock in other directions will expand freely. Therefore, after some time, the SN ejecta will overrun and hide the interaction signatures (see Smith et al. 2023, for details). In this case, the time of disappearance of the narrow emission lines is given by a different physical effect than that considered in our 1D simulations, leading to misinterpretation of the observations. Therefore, the potential 3D nature of the CSM of SN 2023ixf adds a caveat to our study. This is a challenging scenario to study because it requires 3D radiation hydrodynamics.

Teja et al. (2023) compared the g-band light curve of SN 2023ixf with a grid of models of SN II explosions interacting with an accelerated RSG wind (Moriya et al. 2023). The CSM parameters found in our study are within the ranges of values constrained by Teja et al. (2023), with the exception of the wind-acceleration parameter for which we infer a larger value. However, Teja et al. (2023) infer higher explosion energies (2−5 × 1051 erg), much larger than typical SNe II (e.g. Morozova et al. 2018; Martinez et al. 2020, 2022b) and the predictions from 1D neutrino-powered explosions (Sukhbold et al. 2016). These high values could be because Teja et al. (2023) did not use velocity measurements in their fitting. If expansion velocities are not taken into account in the fitting procedure, it could lead to incorrect determination of the explosion energy (Martinez et al. 2020).

Davies et al. (2022) carried out an analysis where they predict the characteristics of the RSGs at core collapse based on two enhanced mass-loss scenarios: a short outburst lasting a few months and a ‘superwind’ arising from a very high mass-loss rate during the last decades prior to explosion. These authors considered an accelerated wind for the latter scenario. Davies et al. (2022) found that the outburst scenario produces redder colours in a short timescale after the outburst, which would not be consistent with the steady IR variability of the progenitor of SN 2023ixf (e.g. Jencson et al. 2023). Alternatively, the scenario that involves the acceleration of the RSG winds causes redder colours decades prior the SN explosion. Jencson et al. (2023) found that the IR colours of the progenitor of SN 2023ixf are well reproduced by one of the “superwind” models from Davies et al. (2022), which assumes the same wind acceleration mechanism than the one analysed in our work. The discussion provided in this section would imply that the enhanced mass loss started decades before core collapse, supporting the wind acceleration scenario.

Regarding the modelling of the bolometric light curve peak, we note that none of our models can reproduce the maximum luminosity value. This could be related to the simplifications included in our code, as local thermodynamic equilibrium and/or spherical symmetry, among others (see Bersten et al. 2011, for details). On the other hand, our maximum luminosity value could be overestimated. We arrived at this after comparison to the bolometric light curve presented in Zimmerman et al. (2023), who used more comprehensive data set to compute the luminosity at maximum. We note that the models presented match the maximum luminosity estimated by Zimmerman et al. (2023).

6. Summary and conclusions

SN 2023ixf is among the closest SN II in the last decades, which allowed intensive multi-wavelength and high-cadence observations. We used publicly available data to calculate the early (< 19 days post-explosion) bolometric light curve based on the integration of the observed SED (from UV to NIR bands) and black-body extrapolations for the unobserved flux at shorter and longer wavelengths. Thanks to the early monitoring and high cadence of observations, we capture the sudden rise to maximum and the successive fall of the bolometric light curve. This is the first time that this behaviour is observed in bolometric luminosities given the lack of early-time multi-wavelength observations for most SNe II.

The fact that there are a small number of SNe II with detailed calculations of their early bolometric light curve (see e.g. Yaron et al. 2017; Jacobson-Galán et al. 2022 for bolometric light curves after maximum for SN 2013fs and SN 2020tlf, respectively), allowed us to test the currently available calibrations of BC against colours. This analysis provides good agreements for most of these calibrations. Additionally, we included the observations of SN 2023ixf to the recently published calibrations of BC from Martinez et al. (2022a). These calibrations include data of 74 SNe II, but none with observations as early as SN 2023ixf. Therefore, the incorporation of SN 2023ixf to the previously mentioned calibrations allows us to extend them to bluer optical colours, and therefore, to earlier epochs. It would be necessary to include all SNe II with early detections and good photometric coverage in order to analyse the bluest part of these calibrations in detail, and to study a possible general behaviour.

Armed with the bolometric light curve for SN 2023ixf, we have studied the mass-loss history of the progenitor of SN 2023ixf through comparison with hydrodynamical simulations of SN II explosions with CSM interaction. We found that a CSM interaction model that takes the wind acceleration into account with Ṁ = 3 × 10−3 M⊙ yr−1, RCSM = 12 000 R⊙, and β = 5 reproduces the width of the luminosity peak, the post-peak luminosity, and the epoch of disappearance of the interaction lines in the spectra. Our findings indicate an enhanced wind that developed continuously over the last ∼80 yr of the progenitor evolution. This may be consistent with the quiescence of SN 2023ixf in the last 20 yr prior to explosion, favouring the accelerated wind scenario – in connection with the results of Jencson et al. (2023). In Bersten et al. (2024), we analyse the complete bolometric light curve and photospheric velocity evolution of SN 2023ixf and derive the physical properties of the progenitor and explosion, which allow us to have a full description of the nature of SN 2023ixf.

1

Throughout this paper we use the denomination “SNe II” to refer to hydrogen rich core-collapse supernovae excluding type IIn, IIb, and SN 1987A-like events.

7

We note that the inclusion of CSM can alter the photospheric velocities of a SN due to the conversion of kinetic energy into radiation at the shock front. This depends on the adopted physical parameters for the CSM.

8

We note again that these CSM parameters do not reproduce the fading time of the narrow emission lines.

Acknowledgments

We thank the referee for the useful comments that improved the manuscript. L.M. acknowledges support from a CONICET fellowship. L.M. and M.O. acknowledge support from UNRN PI2022 40B1039 grant. This work is partially sponsored by the National Stays Program de la Asociación Argentina de Astronomía. This research has made use of the Spanish Virtual Observatory (https://svo.cab.inta-csic.es) project funded by MCIN/AEI/10.13039/501100011033/ through grant PID2020-112949GB-I00. This work has made use of WISeREP (https://www.wiserep.org). Software: NumPy (Oliphant 2006; Van Der Walt et al. 2011), matplotlib (Hunter 2007), Astropy (Astropy Collaboration 2013, 2018, 2022), SciPy (Virtanen et al. 2020), emcee (Foreman-Mackey et al. 2013), Pandas (McKinney 2010), ipython/jupyter (Perez & Granger 2007), extinction (https://github.com/kbarbary/extinction).

References

  1. Arcavi, I. 2017, in Handbook of Supernovae, eds. A. W. Alsabti, & P. Murdin (Cham: Springer), 239 [CrossRef] [Google Scholar]
  2. Arroyo-Torres, B., Wittkowski, M., Chiavassa, A., et al. 2015, A&A, 575, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  4. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  6. Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
  7. Balam, D. D., & Kendurkar, M. 2023, Transient Name Server AstroNote, 154, 1 [NASA ADS] [Google Scholar]
  8. Basu, J., Barway, S., Anupama, G. C., Teja, R. S., & Dutta, A. 2023, ATel, 16064, 1 [NASA ADS] [Google Scholar]
  9. Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002 [Google Scholar]
  10. Bersten, M. C., & Hamuy, M. 2009, ApJ, 701, 200 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bersten, M. C., Benvenuto, O., & Hamuy, M. 2011, ApJ, 729, 61 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bersten, M. C., Orellana, M., Folatelli, G., et al. 2024, A&A, 681, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
  14. Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
  15. Bostroem, K. A., Pearson, J., Shrestha, M., et al. 2023, ApJ, 956, L5 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bruch, R. J., Gal-Yam, A., Schulze, S., et al. 2021, ApJ, 912, 46 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
  18. Chevalier, R. A. 2012, ApJ, 752, L2 [NASA ADS] [CrossRef] [Google Scholar]
  19. Chugai, N., & Utrobin, V. 2022, Astron. Lett., submitted [arXiv:2205.07749] [Google Scholar]
  20. Contreras, C., Hamuy, M., Phillips, M. M., et al. 2010, AJ, 139, 519 [Google Scholar]
  21. D’Avanzo, P., Bianchetti, N., Bianchessi, M., et al. 2023, Transient Name Server AstroNote, 153, 1 [Google Scholar]
  22. Davies, B., Plez, B., & Petrault, M. 2022, MNRAS, 517, 1483 [NASA ADS] [CrossRef] [Google Scholar]
  23. de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
  24. Dessart, L., & Hillier, D. J. 2005, A&A, 439, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Dessart, L., & Jacobson-Galán, W. V. 2023, A&A, 677, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Dessart, L., Hillier, D. J., & Audit, E. 2017, A&A, 605, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Dong, Y., Sand, D. J., Valenti, S., et al. 2023, ApJ, 957, 28 [NASA ADS] [CrossRef] [Google Scholar]
  28. Drilling, J. S., & Landolt, A. U. 2000, Normal Stars (New York: Springer), 381 [Google Scholar]
  29. Englert Urrutia, B. N., Bersten, M. C., & Cidale, L. S. 2020, Boletin de la Asociacion Argentina de Astronomia La Plata Argentina, 61B, 51 [Google Scholar]
  30. Faran, T., Poznanski, D., Filippenko, A. V., et al. 2014, MNRAS, 442, 844 [NASA ADS] [CrossRef] [Google Scholar]
  31. Faran, T., Nakar, E., & Poznanski, D. 2018, MNRAS, 473, 513 [NASA ADS] [CrossRef] [Google Scholar]
  32. Farmer, R., Fields, C. E., Petermann, I., et al. 2016, ApJS, 227, 22 [NASA ADS] [CrossRef] [Google Scholar]
  33. Filippenko, A. V. 1997, ARA&A, 35, 309 [NASA ADS] [CrossRef] [Google Scholar]
  34. Flinner, N., Tucker, M. A., Beacom, J. F., & Shappee, B. J. 2023, Res. Notes Am. Astron. Soc., 7, 174 [NASA ADS] [Google Scholar]
  35. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  36. Fowler, M., Sienkiewicz, F., & Dussault, M. 2023, Transient Name Server AstroNote, 143, 1 [NASA ADS] [Google Scholar]
  37. Fuller, J. 2017, MNRAS, 470, 1642 [NASA ADS] [CrossRef] [Google Scholar]
  38. Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [Google Scholar]
  39. Graham, M. J., Kulkarni, S. R., Bellm, E. C., et al. 2019, PASP, 131, 078001 [Google Scholar]
  40. Grefenstette, B. W., Brightman, M., Earnshaw, H. P., Harrison, F. A., & Margutti, R. 2023, ApJ, 952, L3 [NASA ADS] [CrossRef] [Google Scholar]
  41. Hamuy, M., Folatelli, G., Morrell, N. I., et al. 2006, PASP, 118, 2 [NASA ADS] [CrossRef] [Google Scholar]
  42. Hiramatsu, D., Tsuna, D., Berger, E., et al. 2023, ApJ, 955, L8 [NASA ADS] [CrossRef] [Google Scholar]
  43. Hosseinzadeh, G., Farah, J., Shrestha, M., et al. 2023, ApJ, 953, L16 [NASA ADS] [CrossRef] [Google Scholar]
  44. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  45. Itagaki, K. 2023, Transient Name Server Discovery Report, 2023-1158, 1 [Google Scholar]
  46. Jacobson-Galán, W. V., Dessart, L., Jones, D. O., et al. 2022, ApJ, 924, 15 [CrossRef] [Google Scholar]
  47. Jacobson-Galán, W. V., Dessart, L., Margutti, R., et al. 2023, ApJ, 954, L42 [CrossRef] [Google Scholar]
  48. Jencson, J. E., Pearson, J., Beasor, E. R., et al. 2023, ApJ, 952, L30 [NASA ADS] [CrossRef] [Google Scholar]
  49. Jermyn, A. S., Bauer, E. B., Schwab, J., et al. 2023, ApJS, 265, 15 [NASA ADS] [CrossRef] [Google Scholar]
  50. Jones, S., Andrassy, R., Sandalski, S., et al. 2017, MNRAS, 465, 2991 [NASA ADS] [CrossRef] [Google Scholar]
  51. Kendurkar, M. R., & Balam, D. D. 2023, Transient Name Server AstroNote, 129, 1 [NASA ADS] [Google Scholar]
  52. Khazov, D., Yaron, O., Gal-Yam, A., et al. 2016, ApJ, 818, 3 [CrossRef] [Google Scholar]
  53. Kilpatrick, C. D., Foley, R. J., Jacobson-Galán, W. V., et al. 2023, ApJ, 952, L23 [NASA ADS] [CrossRef] [Google Scholar]
  54. Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, PASP, 129, 104502 [Google Scholar]
  55. Kong, A. K. H. 2023, ATel, 16051, 1 [NASA ADS] [Google Scholar]
  56. Krisciunas, K., Contreras, C., Burns, C. R., et al. 2017, AJ, 154, 211 [NASA ADS] [CrossRef] [Google Scholar]
  57. Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to Stellar Winds (Cambridge: Cambridge University Press) [Google Scholar]
  58. Langer, N., Fricke, K. J., & Sugimoto, D. 1983, A&A, 126, 207 [NASA ADS] [Google Scholar]
  59. Levi, M., Allen, L. E., Raichoor, A., et al. 2019, BAAS, 51, 57 [NASA ADS] [Google Scholar]
  60. Li, Y., Chen, X.-H., & Chen, H.-L. 2019, ApJ, 870, 77 [NASA ADS] [CrossRef] [Google Scholar]
  61. Lundquist, M., O’Meara, J., & Walawender, J. 2023, Transient Name Server AstroNote, 160, 1 [NASA ADS] [Google Scholar]
  62. Lyman, J. D., Bersier, D., & James, P. A. 2014, MNRAS, 437, 3848 [Google Scholar]
  63. Mao, Y., Zhang, M., Cai, G., et al. 2023, Transient Name Server AstroNote, 130, 1 [NASA ADS] [Google Scholar]
  64. Martinez, L., Bersten, M. C., Anderson, J. P., et al. 2020, A&A, 642, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Martinez, L., Bersten, M. C., Anderson, J. P., et al. 2022a, A&A, 660, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Martinez, L., Bersten, M. C., Anderson, J. P., et al. 2022b, A&A, 660, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Martins, F., & Palacios, A. 2013, A&A, 560, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Matsunaga, K., Uchida, H., Enoto, T., Tsuru, T., & Sato, T. 2023, ATel, 16060, 1 [NASA ADS] [Google Scholar]
  69. McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 56 [Google Scholar]
  70. Minkowski, R. 1941, PASP, 53, 224 [NASA ADS] [CrossRef] [Google Scholar]
  71. Moriya, T., Tominaga, N., Blinnikov, S. I., Baklanov, P. V., & Sorokina, E. I. 2011, MNRAS, 415, 199 [NASA ADS] [CrossRef] [Google Scholar]
  72. Moriya, T. J., Förster, F., Yoon, S.-C., Gräfener, G., & Blinnikov, S. I. 2018, MNRAS, 476, 2840 [Google Scholar]
  73. Moriya, T. J., Subrayan, B. M., Milisavljevic, D., & Blinnikov, S. I. 2023, PASJ, 75, 634 [NASA ADS] [CrossRef] [Google Scholar]
  74. Morozova, V., Piro, A. L., & Valenti, S. 2018, ApJ, 858, 15 [Google Scholar]
  75. Morozova, V., Piro, A. L., Fuller, J., & Van Dyk, S. D. 2020, ApJ, 891, L32 [NASA ADS] [CrossRef] [Google Scholar]
  76. Neustadt, J. M. M., Kochanek, C. S., & Smith, M. R. 2024, MNRAS, 527, 5366 [Google Scholar]
  77. Niu, Z., Sun, N.-C., Maund, J. R., et al. 2023, ApJ, 955, L15 [NASA ADS] [CrossRef] [Google Scholar]
  78. Ohnaka, K., Weigelt, G., Millour, F., et al. 2011, A&A, 529, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Oliphant, T. E. 2006, A Guide to NumPy (USA: Trelgol Publishing), 1 [Google Scholar]
  80. Panjkov, S., Auchettl, K., Shappee, B. J., et al. 2023, PASA, submitted [arXiv:2308.13101] [Google Scholar]
  81. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  82. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  83. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  84. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  85. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  86. Pejcha, O., & Prieto, J. L. 2015, ApJ, 799, 215 [NASA ADS] [CrossRef] [Google Scholar]
  87. Perez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
  88. Perley, D. A., Gal-Yam, A., Irani, I., & Zimmerman, E. 2023, Transient Name Server AstroNote, 119, 1 [NASA ADS] [Google Scholar]
  89. Pledger, J. L., & Shara, M. M. 2023, ApJ, 953, L14 [NASA ADS] [CrossRef] [Google Scholar]
  90. Pritchard, T. A., Roming, P. W. A., Brown, P. J., Bayless, A. J., & Frey, L. H. 2014, ApJ, 787, 157 [NASA ADS] [CrossRef] [Google Scholar]
  91. Quataert, E., & Shiode, J. 2012, MNRAS, 423, L92 [NASA ADS] [CrossRef] [Google Scholar]
  92. Riess, A. G., Yuan, W., Macri, L. M., et al. 2022, ApJ, 934, L7 [NASA ADS] [CrossRef] [Google Scholar]
  93. Rodrigo, C., & Solano, E. 2020, XIV.0 Scientific Meeting (virtual) of the Spanish Astronomical Society, 182 [Google Scholar]
  94. Rodrigo, C., Solano, E., & Bayo, A. 2012, SVO Filter Profile Service Version 1.0, IVOA Working Draft 15 October 2012 [Google Scholar]
  95. Rodríguez, Ó., Pignata, G., Hamuy, M., et al. 2019, MNRAS, 483, 5459 [CrossRef] [Google Scholar]
  96. Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [Google Scholar]
  97. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  98. Schlegel, E. M. 1990, MNRAS, 244, 269 [NASA ADS] [Google Scholar]
  99. Sgro, L. A., Esposito, T. M., Blaclard, G., et al. 2023, Res. Notes Am. Astron. Soc., 7, 141 [Google Scholar]
  100. Shiode, J. H., & Quataert, E. 2014, ApJ, 780, 96 [Google Scholar]
  101. Shivvers, I., Modjaz, M., Zheng, W., et al. 2017, PASP, 129, 054201 [NASA ADS] [CrossRef] [Google Scholar]
  102. Smartt, S. J. 2015, PASA, 32, e016 [NASA ADS] [CrossRef] [Google Scholar]
  103. Smith, N. 2017, in Handbook of Supernovae, eds. A. W. Alsabti, & P. Murdin (Cham: Springer), 403 [Google Scholar]
  104. Smith, N., & Arnett, W. D. 2014, ApJ, 785, 82 [NASA ADS] [CrossRef] [Google Scholar]
  105. Smith, K. W., Smartt, S. J., Young, D. R., et al. 2020, PASP, 132, 085002 [Google Scholar]
  106. Smith, N., Pearson, J., Sand, D. J., et al. 2023, ApJ, 956, 46 [NASA ADS] [CrossRef] [Google Scholar]
  107. Soraisam, M. D., Szalai, T., Van Dyk, S. D., et al. 2023, ApJ, 957, 64 [NASA ADS] [CrossRef] [Google Scholar]
  108. Suárez-Madrigal, A., Krumholz, M., & Ramirez-Ruiz, E. 2013, arXiv e-prints [arXiv:1304.2317] [Google Scholar]
  109. Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H. T. 2016, ApJ, 821, 38 [NASA ADS] [CrossRef] [Google Scholar]
  110. Sutaria, F., & Ray, A. 2023, ATel, 16053, 1 [NASA ADS] [Google Scholar]
  111. Szalai, T., & Dyk, S. V. 2023, ATel, 16042, 1 [NASA ADS] [Google Scholar]
  112. Teja, R. S., Singh, A., Basu, J., et al. 2023, ApJ, 954, L12 [NASA ADS] [CrossRef] [Google Scholar]
  113. Tonry, J. L., Denneau, L., Heinze, A. N., et al. 2018, PASP, 130, 064505 [Google Scholar]
  114. Utrobin, V. P., & Chugai, N. N. 2024, MNRAS, 527, 6227 [Google Scholar]
  115. Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
  116. Van Dyk, S. D., Davidge, T. J., Elias-Rosa, N., et al. 2012, AJ, 143, 19 [NASA ADS] [CrossRef] [Google Scholar]
  117. Van Dyk, S. D., Srinivasan, S., Andrews, J. E., et al. 2023, AAS J., submitted [arXiv:2308.14844] [Google Scholar]
  118. Vannini, J. 2023a, Transient Name Server AstroNote, 141, 1 [NASA ADS] [Google Scholar]
  119. Vannini, J. 2023b, Transient Name Server AstroNote, 156, 1 [NASA ADS] [Google Scholar]
  120. Vannini, J. 2023c, Transient Name Server AstroNote, 161, 1 [NASA ADS] [Google Scholar]
  121. Vasylyev, S. S., Yang, Y., Filippenko, A. V., et al. 2023, ApJ, 955, L37 [NASA ADS] [CrossRef] [Google Scholar]
  122. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
  124. Wu, S., & Fuller, J. 2021, ApJ, 906, 3 [NASA ADS] [CrossRef] [Google Scholar]
  125. Wu, S. C., & Fuller, J. 2022, ApJ, 930, 119 [NASA ADS] [CrossRef] [Google Scholar]
  126. Xiang, D., Mo, J., Wang, L., et al. 2024, Sci. China Phys. Mechan. Astron., 67, 219514 [CrossRef] [Google Scholar]
  127. Yamanaka, M., Fujii, M., & Nagayama, T. 2023, PASJ, 75, L27 [NASA ADS] [CrossRef] [Google Scholar]
  128. Yaron, O., & Gal-Yam, A. 2012, PASP, 124, 668 [Google Scholar]
  129. Yaron, O., Perley, D. A., Gal-Yam, A., et al. 2017, Nat. Phys., 13, 510 [NASA ADS] [CrossRef] [Google Scholar]
  130. Zimmerman, E. A., Irani, I., Chen, P., et al. 2023, arXiv e-prints [arXiv:2310.10727] [Google Scholar]

All Tables

Table 1.

Coefficients of the polynomial fits to the bolometric corrections versus optical colours.

In the text
Table 2.

Summary of the initial conditions of the models presented in this work.

In the text

All Figures

thumbnail Fig. 1.

Early bolometric light curve for SN 2023ixf (blue dots). The dashed line represents the pseudo-bolometric light curve. The inset plot shows the first week of evolution of the bolometric luminosity. In this plot, the pink triangles are the bolometric luminosities when observed UV data are not taken into account in the calculation method. In most cases the error bars are smaller than the dot size.
In the text
thumbnail Fig. 2.

Evolution in time of black-body fit parameters for SN 2023ixf: temperature (red dots) and radius (green diamonds).
In the text
thumbnail Fig. 3.

Bolometric light curve for SN 2023ixf calculated from the integration of the observed flux plus black-body extrapolations (thick grey line, referred to as “SED integration”) in comparison with those calculated from calibrations of bolometric corrections versus colours found in the literature: Martinez et al. (2022a; top-left panel), Lyman et al. (2014; top-right panel), Bersten & Hamuy (2009), Pejcha & Prieto (2015), and Pritchard et al. (2014; bottom-left panel). The bottom-right panel shows bolometric light curves using the calibrations by Martinez et al. (2022a) when larger validity ranges of colours are allowed.
In the text
thumbnail Fig. 4.

Bolometric corrections relative to the g band as a function of (g − r) colour (top panel) and (g − i) colour (middle panel), and relative to the V band as a function of (B − V) colour (bottom panel). SN 2023ixf is presented as blue dots, while pink dots represent the cooling phase of the SNe II in the CSP-I sample (see Martinez et al. 2022a). The dashed lines shows the fit to the data. The errors in the CSP-I SN II data are not plotted for better visualisation.
In the text
thumbnail Fig. 5.

Comparison between the bolometric light curve of SN 2023ixf (dots) with models varying the CSM properties (lines), assuming steady-state mass loss. The upper panel involves models with higher mass-loss rates and more confined CSMs than the models shown in the bottom panel. The inset plot compares the photospheric velocities of SN 2023ixf to the same models previously mentioned. For the model nomenclature, see Sect. 4.
In the text
thumbnail Fig. 6.

Comparison between the bolometric light curve of SN 2023ixf (dots) with models varying CSM properties (lines) assuming wind acceleration. The inset plot compares the photospheric velocities of SN 2023ixf to the same models previously mentioned. For the model nomenclature, see Sect. 4.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.