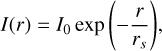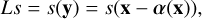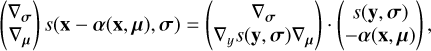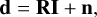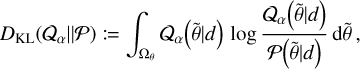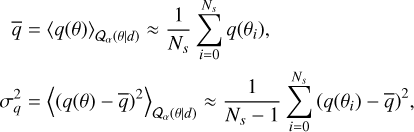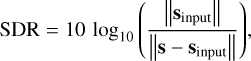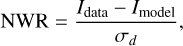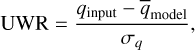| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A146 | |
| Number of page(s) | 19 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202348256 | |
| Published online | 15 February 2024 | |
Introducing LensCharm
A charming Bayesian strong lensing reconstruction framework
1
Ludwig-Maximilians-Universität München,
Geschwister-Scholl-Platz 1,
80539
Munich,
Germany
e-mail: jruestig@posteo.de
2
Max Planck Institute for Astrophysics,
Karl-Schwarzschild-Straße 1,
85748
Garching,
Germany
3
Excellence Cluster ORIGINS,
Boltzmannstraße 2,
85748
Garching,
Germany
4
Technische Universität München,
Boltzmannstraße 3,
85748
Garching,
Germany
Received:
12
October
2023
Accepted:
6
December
2023
Strong gravitational lensing, a phenomenon rooted in the principles of general relativity, grants us a unique window into the distant cosmos by offering a direct probe into dark matter and providing independent constraints on the Hubble constant. These research objectives call for the utmost precision in the estimation of the lens mass and the source brightness distributions. Recent strides in telescope technology promise to provide an abundance of yet undiscovered strong-lensing systems, presenting observations of unprecedented quality. Realizing the full potential of these advancements hinges on achieving the highest fidelity in both source and lens reconstruction. In this study, we introduce LensCharm, a novel Bayesian approach for strong-lensing signal reconstruction. Unlike more prevalent methods, LensCharm enables the nonparametric reconstruction of both the source and lens concurrently, along with their associated uncertainties. We showcase the distinctive strengths of our approach through comprehensive analyses of both real-world and simulated astronomical data, underscoring its superiority in achieving precise reconstructions. We have made LensCharm publicly accessible, envisioning its empowerment of the next generation of astronomical observation reconstructions and cosmological constraints derived from strong gravitational lensing.
Key words: gravitation / gravitational lensing: strong / methods: data analysis / galaxies: high-redshift / dark matter / infrared: galaxies
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Since the path of light is bent by matter, galaxies and galaxy clusters can serve as powerful cosmic telescopes. Harnessing this "gravitational lensing" effect serves three purposes: first, it improves the imaging capabilities of telescopes, making it possible to resolve sources at high redshifts with higher signal-to-noise ratios (S/N; see, e.g., Schneider et al. 2006). The properties of these sources, for instance, their dynamical properties (see Mo et al. 2010), provide a distinctive view into the structure of the early Universe (see, e.g., Rizzo et al. 2020). Second, lensing provides a unique opportunity to investigate the properties of dark matter. Numerical simulations suggest that matter forms hierarchically, where smaller structures merge to from larger halos which serve as hosts for galaxies and galaxy clusters (see, e.g., Springel et al. 2008). The number of subhalos (i.e., the smaller structures inside a halo) strongly depends on the initial velocity dispersion of dark matter (see, e.g., Li et al. 2017). As small-mass subhalos become detectable through the lensing effect (see, e.g., Hezaveh et al. 2016; Chatterjee & Koopmans 2018; Gilman et al. 2019), gravitational lensing could provide a way to distinguish between dark matter models (see, e.g. Vegetti et al. 2014; Hsueh et al. 2020). Finally, the lensing effect can be used to constrain the expansion rate of the Universe through the measurement of the time delay between different multiple images (see, e.g., Fassnacht et al. 2002; Treu & Marshall 2016; Wong et al. 2020)
In the years to come, we anticipate the discovery of new lens-ing systems, which will become observable with unprecedented angular resolution. Notably, the dark energy survey, the legacy survey of space and time conducted by the Vera C. Rubin observatory and the Euclid survey are expected to identify approximately 105 new galaxy-galaxy lens systems (Collett 2015). Additionally, Europe’s Extremely Large Telescope (ELT) and the James Webb Space Telescope (JWST) will be able to observe these systems with an unprecedented angular resolution. Thanks to its exceptional near and mid-infrared imaging capabilities, JWST already offers a unique window into the early Universe (see, e.g., Hsiao et al. 2023). Collectively, observations from JWST and other forthcoming instruments promise to significantly advance our understanding of the early Universe. Moreover, these upcoming observations will enhance our ability to investigate the nature of dark matter, with angular resolution and the S/N being crucial factors for subhalo sensitivity (Despali et al. 2022).
These discoveries crucially depend on the capabilities of lensing models to disentangle and accurately reconstruct the quantities of interest. Specifically, this task involves simultaneously inferring both the lens mass and the source light distribution, while untangling the lensed source light from the light emitted by the lens itself. This is a fundamentally under-constrained problem. Primarily, this is due to the entanglement of the lensed source light with the light from the lens, compounded by the unknown lens mass and source light distribution. To accomplish this decomposition task, lensing models need to rely on prior assumptions, in addition to utilizing the constraints contained in multiple images. In Sect. 2, we present a comprehensive overview of previous models for both for the source light and the lensing mass. When aiming to represent complex light distributions, such as sources in the early Universe, non-parametric models are indispensable. However, nonparametric models depend on regularization, which we go on to formulate in terms of Bayesian prior distributions. Furthermore, the detection of subhalos within the lens mass distribution can only be obtained through models which account for deviations from a simple parametric mass profile. For example, both Vegetti et al. (2012) and Hezaveh et al. (2016) were able to detect a 108.28 M⊙ and 108.98 M⊙ subhalo, respectively, by employing more complex models than a simple parametric profile. In this way, the complexity of lensing models enable the discovery of interesting phenomena. However, handling such complexities presents its own challenges, particularly as models with high number of parameters can be computationally demanding.
To tackle these challenges, this work introduces the strong lensing framework, LensCharm, which focuses on four crucial aspects for resolving the degenerate inverse problem inherent in strong lensing observations, as follows. First, the LensCharm framework applies a probabilistic approach to solve the inverse problem utilizing the NIFTy library (Arras et al. 2019), based on information field theory (Enßlin et al. 2009). Second, LensCharm is able to perform joint inference in high dimensions and is able to obtain an approximate posterior distribution for all parameters. Third, through samples of the posterior distribution, we are able to derive posterior uncertainties for all quantities of interests. Lastly, LensCharm provides the flexibility to model both the lensing mass and the source brightness distribution using parametric, nonparametric, or hybrid models. We have derived these models from physically motivated prior assumptions, ensuring, for example, the positivity of the source brightness distribution. To demonstrate LensCharm’s capabilities, we present its performance in three distinct scenarios. First, we conduct a comparative analysis with the publicly available lensing framework Lenstronomy (Birrer et al. 2015). This comparison demonstrates that LensCharm is able to achieve results that are comparable with state-of-the-art lensing models. Second, we test our framework on a simulated JWST dataset. In this scenario, we illustrate the capability of our hybrid model to accurately capture the source brightness distribution and substructures within the lensing mass. Lastly, we reconstruct the source brightness, mass and lens light distribution of the lensing system SPT0418-47 employing a real observation of JWST. We have made LensCharm publicly available1 to the scientific community to contribute to the advancement of strong lensing research.
The remaining of the paper is structured as follows. Section 2 provides a review on previous lens modeling techniques. In Sect. 3, we describe the components of our lensing framework. This includes the development of parametric, non-parametric, and hybrid models, as well as the relationship between model parameters through the lens equation and the computation of gradients for efficient parameter reconstruction. Section 4 describes how to connect the continuous signal field to the discrete data space. In Sect. 5, we provide a brief overview of our inference strategy, which is centered on variational inference and we detail how posterior estimates for quantities of interest are obtained. Section 6 presents a validation of our strong lens-ing framework using three distinct datasets. Section 7 gives our summary and outlines potential directions for future research.
2 Review of lensing models
In this section, our aim is to provide an overview of strong lensing modeling techniques. We have categorized the models into two distinct sections: one addressing models for the source brightness distribution and the other focusing on models for the lensing mass. We chose these categories as they pertain to independent physical quantities, which warrant separate discussion. In Table 1, we include a comprehensive comparison between the modeling techniques discussed in this section.
2.1 Source model
In the following, we concentrate on models for sources with an extended brightness distribution. Modeling these sources poses greater challenges then modeling point sources. However, their lensed extended emission also provides more constraints for the lens mass distribution.
A straightforward approach to model extended sources is to assume a parametric light distribution. This has the benefit that the projected light distribution can be evaluated analytically, which makes these models very efficient. Additionally, the low dimensionality of the parameter space allows for feasible sampling of the posterior distribution using Markov chain Monte Carlo (MCMC) techniques. A Gaussian function is one example of a simple parametric profile that can be used in this way. Given that the overall light profile of low-redshift late and early-type galaxies (see, e.g., Mo et al. 2010) is well described by the Sérsic profile, this particular profile is also often employed in parametric source reconstructions.
However, according to the theory of structure formation, many sources in the early Universe are expected to exhibit an irregular or asymmetric morphology, which is ascribed to interactions and mergers. These sources become observable through strong lensing, providing an opportunity to test theories of structure formation. Since irregular light distributions are not fully describable by parametric profiles, accurate source light reconstruction has to rely on more complex models. Nonpara-metric models are better suited to tackle complex distributions. These have been first developed on regular grids by Warren & Dye (2003) and have been extended to irregular source grids (see, e.g., Dye & Warren 2005; Vegetti & Koopmans 2009; Nightingale & Dye 2015). A nonparametric model has the flexibility of changing its value at each grid-point, whether it is regular or irregular. Consequently, some sort of regularization is needed. An overview of regularizations in a Bayesian setting is provided in Suyu et al. (2006). In this work, the authors discuss how to obtain smooth source distributions based on zeroth-order, gradient and curvature penalization. Furthermore, Vernardos & Koopmans (2022) have recently shown that more physically motivated regularizations can yield lower residuals in the reconstructions. While nonparametric models are able to reconstruct complex light distributions, they are often optimized by the use of linear inversion techniques. On the one hand, the use of linear inversion has the benefit of being analytically solvable, which effectively reduces the source reconstruction to a matrix application (see, e.g., Vegetti & Koopmans 2009). On the other hand, however, linear inversion can lead to unphysical light distributions, for example, negative flux values.
A different approach to model the source brightness distribution is to employ shapelet functions, which form a complete set of basis functions (Birrer et al. 2015). Since the structural complexity of shapelets increases with their order, they can provide an effective regularization, when only lower order shapelets are included into the modeling. It is often the case that the number of basis functions, their scale, and their center are set by hand, which, in turn, requires the introduction of additional regularization terms (see Tagore & Jackson 2016). Similarly, Galan et al. (2021) explored the possibility of modeling the source brightness distribution with wavelet basis functions, which can yield accurate source reconstructions, particularly with high-resolution data.
A different way to specify prior for the source brightness distribution is to use neural networks (NN), which need to be trained on a very large sample of source brightness distributions. After training, the NN can be used to sample sources, which are able to resemble realistic galaxies (see Holzschuh et al. 2022). Similarly, a NN can be trained to infer the background source distribution when the full pipeline of image production also includes the lens projection (ray-tracing), as demonstrated in Morningstar et al. (2019) and Chianese et al. (2020). These authors have shown that this approach results in more accurate results when compared to a linear source inversion. There are two main drawbacks of using neural networks trained on specific input sources. First, NNs are prone to overfitting, mostly because the training set is usually incomplete or biased. For example, this is the case for early Universe galaxies of which very few direct observations are known and for which simulations produce a wild variety of possible outputs. Second, it is difficult to get an uncertainty quantification of the NN reconstructions.
In a recent work conducted by Karchev et al. (2022), the authors introduced a source model based on Gaussian processes. The benefit of this approach lies in the flexibility of the Gaussian process to accurately capture nonparametric source light distributions, while also offering the ability to obtain uncertainties on the reconstruction. For a review on Gaussian processes, we refer to Rasmussen & Williams (2006). Also, Karchev et al. (2022) utilized a sum of radial basis functions with fixed correlation lengths, termed "layers", for the Gaussian covariance kernel. By adjusting the relative weights of these layers, the authors demonstrated that this model can yield an accurate reconstruction of an input source brightness distribution.
Comparison between different strong lensing codes along with their corresponding modeling techniques.
2.2 Lens model
Models that are used to study the lensing effect of gravitational lens systems, whether that is for galaxy or galaxy-cluster lensing, can be categorized into parametric, nonparametric, and hybrid models. The lensing effect can be formalized in terms of the mass of the lens, but can also be phrased in terms of the lensing potential or its first derivative the deflection angle field, as these quantities are related via Poisson’s equation.
The most widely used mass model is the parametric one (see, e.g., Vegetti & Koopmans 2009; Oguri 2010; Keeton 2011; Kneib et al. 2011; Suyu et al. 2013; Spilker et al. 2016; Birrer & Amara 2018; Nightingale et al. 2018). A multitude of parametric mass models exist and a comprehensive overview of these models can be found in Keeton (2001). The advantages and disadvantages of using parametric models are analogous to those encountered when modeling the source light distribution parametrically. The primary advantage is the efficient MCMC posterior sampling, due to the low dimensionality of the parameter space and the availability of an analytical solution to the deflection angle. However, parametric models have fixed symmetric properties, which can bias the measurement of different quantities of interest, such as H0 (see Cao et al. 2022), when the mass model is too simple to represent the mass distribution of the lens system. This can result in parts of the lens mass' complexity being absorbed by other parts of the model, for example, the external shear component Etherington et al. (2023).
One way to address these challenges is to model deviations from the smooth parametric profile, which can also facilitate the detection of dark-matter substructures. An example of adding complexities to the parametric profile is to incorporate multipole expansion components (see, e.g., Schneider et al. 2006). In a recent analysis by Powell et al. (2022), for example, the authors show that this added complexity is able to improve the reconstruction of very long baseline interferometry data compared to model of a simple parametric profile. Another approach is to introduce corrections to the lensing potential (see, e.g., Koopmans 2005; Vegetti & Koopmans 2009; Suyu et al. 2009). Here, a pixelized, nonparametric lensing potential is added to an initially smooth mass distribution. The lensing potential gets iteratively optimized by adding linear corrections. Once optimized, the lensing potential can be utilized to seed parametric substructure components. This process has been applied to successfully identify dark matter substructures in strong lens-ing systems (see, e.g., Vegetti et al. 2010). In a recent study, Biggio et al. (2023) explore the possibility to capture deviations from a smooth mass model with the help of sparse wavelet basis functions, which they are able to jointly optimized with the parametric profile. In this work, the authors show that they can effectively model higher-order multipole components, substructures and perturbations originating from a Gaussian random field.
A hybrid model for the mass profile of cluster scales is presented in the WSLAP+ algorithm (see Diego et al. 2005). The algorithm employs a combination of parametric and non-parametric models for the mass of the cluster field. Specifically, it assumes a parametric model, such as a Navarro-Frenk-White profile, for the cluster members. The profile of the cluster members can be further fit by a fixed mass-to-light ratio, which reduces the dimensionality of the problem. Additionally, a non-parametric diffuse mass component is modeled using a dis-cretized field, where the values of the diffuse field are associated with self-optimized (multi-resolution) grid points. The deflection angle can be computed from this discretized field using a fixed matrix. In this way, the reconstruction of the strong lensing data, given as image positions, can be formulated as a system of linear equations, analyzable by matrix inversion.
Similarly, the SWUnited algorithm (presented in Bradač et al. 2005) reconstructs the lensing potential nonparametri-cally, namely, the potential is described by a discretized field at potentially non-equidistant grid points (Bradač et al. 2009). The optimal values of the lensing potential are found by minimizing strong and weak lensing constraints, expressed by a χ2 function, in combination with a regularization term, which penalizes small fluctuations of the inferred lensing potential. The deflection angle and the convergence are calculated by finite differences and if values between grid points are needed these are calculated by bi-linear interpolation. The method has recently been re-implemented with improved modeling capabilities, (see Torres-Ballesteros & Castañeda 2022).
Lastly, the LensPerfect algorithm by Coe et al. (2008) reconstructs the deflection angle field nonparametrically by employing radial basis functions. From the Poisson equation follows that the deflection angle field has to be curl-free. This constraint can be used to regularize the model of the deflection angle field. LensPerfect has, for example, been used to model the lensing effect of the galaxy cluster MACS0647, which hosts one of the highest redshift sources observed, Coe et al. (2012).
An interesting approach to nonparametric modeling is presented in Liesenborgs et al. (2006), where the authors made use of a genetic algorithm to model the lens mass. The lens plane is subdivided into a regular grid of pixels, which are, in turn, populated with Plummer spheres representing the mass profile of the lens system. The Plummer spheres are subsequently genetically updated to optimize a figure of merit, where the authors use a distance measure of back-projected strongly lensed image position in the source plane. The algorithm further updates the lens mass by subdividing the pixel in regions with previously found high mass regions. This process is repeated until a predefined stopping criteria is reached.
3 Model
Reconstructing the source and lens brightness distributions and the lens mass distribution from the observed image is the main goal of any strong gravitational lensing analysis. This requires modeling the light coming from the source, s, and the lens components, l. Furthermore, we have to model the distribution of the lensing mass, m, which is often divided into a main lens and substructure components. We also have to model how this distribution deflects the light coming from the source to produce the observed data. In principle, both the brightness and the mass distributions are continuous quantities in space. Unless a parametric form is considered, continuous quantities have an infinite number of degrees of freedom. Therefore, reconstructing them from finite measurement data is an ill-posed problem and further regularization is needed. In Bayesian statistics, additional regularization can be provided by adding prior knowledge. We formulate the lensing reconstruction problem as a Bayesian inference problem and build on information field theory (Enßlin et al. 2009; Enßlin 2019) to provide prior knowledge about the continuous quantities. In this section, we outline our strong lensing model and describe the prior assumptions encoded in each of the above model components.
3.1 Bayesian inference for strong lensing
The posterior distribution, Ƥ(s, l, m| d), represents our knowledge of s, l, m after combining the prior with the constraints from the data d. Mathematically, the posterior is given by:
where Ƥ(s, l, m) is known as the prior distribution and Ƥ(d| s, l, m) as the likelihood. While the prior distribution contains the state of knowledge about the model parameters prior to the obtained data, the likelihood expresses the probability of obtaining the data given s, l, m. In the context of strong lens-ing, the likelihood describes how a foreground mass bends the light of a background source through the lens equation and the measurement process that converts this signal into data, which includes the noise statistics. Finally, Ƥ(d) represents the marginalized likelihood or the Bayesian evidence, which normalizes the posterior distribution. For any complex strong lensing model, we cannot evaluate the posterior distribution analytically. Therefore, we have to rely on numerical algorithms. To approximate the posterior, we use variational inference (VI), which allows for models with many parameters. In Sect. 5, we explain the VI algorithm in detail.
In this work, we model signals as prior distributions in a Bayesian forward-modeling fashion. In particular, we implement our forward models as generative models. A generative model is a transformation 𝑔: Ωξ ↦ Ωs from a latent coordinate frame, Ωξ, to a target coordinate frame, Ωs, in which we want to represent the signal distribution, Ƥ(s). For the sake of simplicity, we choose random variables in the latent space Ωξ to have an a priori standard-normal distribution. The transformation, 𝑔, then has to be chosen in such a way that s is distributed according to Ƥ(s).
3.2 Source models
In the following, we describe how the surface brightness distribution of the background source is modeled in LensCharm. In order to have a physically meaningful source model, we want to encode some astrophysical insights into our prior. First, brightness distributions are strictly positive and can exhibit significant variations over many orders of magnitude. Additionally, in most cases, the source’s brightness profile is localized, meaning that it is mostly centered around a specific location in the field of view. Second, the surface brightness fluctuations of the background source are mostly smooth.
These considerations are encoded in three types of models, from which the user of LensCharm can choose. This includes simple parametric models and more complicated non-parametric models, depending on the amount of features recoverable from the data. We also propose a combined model, where the main features in the source brightness distribution are captured by a parametric model and only deviations from these are learned non-parametrically. In this section, we describe different source models highlighting their advantages and disadvantages.
3.2.1 Parametric source profiles
In LensCharm, we implement some of the most common parametric models used in the literature. In the following, we give a brief description of the currently implemented parametric models. Further custom model can be easily implemented by the user.
The Gaussian profile implements a positive brightness distribution, which follows a two-dimensional (2D) Gaussian distribution with learnable mean and covariance of the form:
where a, b, c are the parameters that control the ellipticity of the Gaussian, (xc, yc) specifies its center and I0 is the central brightness. This model has only very few parameters and may be oversimplified in many cases.
The Sérsic profile has been shown (Sérsic 1963) to adequately approximate the brightness distribution of galaxies, as per:
where Ie is the intensity at the half-light radius, re, while n is called "Sérsic index" and governs the degree of curvature of the profile and q is a parameter that steers the ellipticity of the profile. Additionally, we specify the elliptical radius by:
centered on (xc,yc) and ||·|| indicates the L2 norm. However, given the prevalent strong interactions between galaxies in the early Universe, high-redshift galaxies often display an irregular or clumpy morphology, which cannot be accurately modeled with either a Sérsic or a Gaussian profile.
3.2.2 Nonparametric source profiles
Many astrophysical sources, including spiral arms, star-forming regions, and others, are insufficiently described by parametric models. Therefore, often times we need nonparametric models to account for features that are not present in the parametric models. In this work, we make use of nonparametric models for Gaussian processes developed by Guardiani et al. (2022) and Arras et al. (2022). Alongside the source brightness distribution, the non-parametric models are also able to infer its power spectrum. The power spectrum can be interpreted as a penalization over source fluctuations and can in this way be related to the penalization terms described in Suyu et al. (2006), as the gradient and curvature penalization correspond to an assumed power spectrum of P(k) ∝ k−2 and P(k) ∝ k−4, respectively.
The Matérn-kernel correlated field (MKF) is based on Gaussian processes. Gaussian processes are a powerful tool for nonparametric modeling, and have already been used as a source model by Karchev et al. (2022). They allow complicated source fields to be represented, while still maintaining smoothness between neighboring pixels.
Upon denoting a function f (x) on a domain Ωx with f, we define the Gaussian process as the (Gaussian) distribution P(f) over the space of functions on Ωx
where F = 〈f (x)f (x′)〉P(f) is the covariance of the process that correlates the field values in space. For gravitationally lensed source fields, we can both ensure positivity and smooth logarithmic flux variations, by modeling the logarithm of the source flux s = s(x, y) : = log b(x, y) with a Gaussian process, namely,
In order to infer the correlation structure of the source flux field, we can choose to parametrize the covariance, B. In particular, if we expect the source distribution to be a priori homogeneous and isotropic, we can invoke the Wiener-Khinchin theorem to restrict B to be diagonal in Fourier space. We then introduce field correlations by convolving the latent-space excitations ξ ∈ Ωξ with an amplitude model:
where ℱ denotes the Fourier transform operator and A the spatial correlation kernel expressed in the latent Fourier coordinates. The square of the amplitude model A represents the power spectrum of the process. Specifically, we choose a Matérn form for the correlation kernel, parametrized by:
where a represents the scale of the Matérn-kernel process, k0 the cutoff wavelength, and c the spectral index of the corresponding power spectrum2. We call the field distribution implied by this generative prior Matérn-kernel correlated field. Matérn-like correlation kernels are widely used in Astrophysics and machine learning because of their flexibility. It has been shown that Matérn kernels incorporate Gaussian kernels for a set of specific parameter values and that they can also represent rougher (i.e., less smooth) processes (Stein 1999).
The correlated field model (CFM) is a model that goes beyond the MKF. Parametrizing the Gaussian process prior covariance with a Matérn kernel is often sufficient to model many astrophysical sources. Sometimes though the data carries more information about the power spectrum than what can actually be explained by the set of parameters of the Matérn kernel. This could happen, for example, in the case of high S/N observations or when we get more information about specific source regions (via the lens equation) thanks to multiple images and magnification. In these cases, we aimed to capture the additional information contained in the data by a more flexible nonpara-metric power spectrum. To this end, we used the correlated field model described in Arras et al. (2022). The CFM allowed us to reconstruct the field and its power spectrum jointly from the data. Similarly to the MKF, the generative model for the amplitude of the field correlation structure reads
where γ(log |k|) is an integrated Wiener process. We reconstruct this Wiener process alongside the signal field. The zero mode amplitude A(k = 0) is modeled separately as a lognormal distributed quantity, since the integrated Wiener process γ(log k) is not defined for k = 0. While in the MKF, the source brightness spatial power spectrum is limited to a power-law-asymptotic parametric function, the CFM can capture continuous deviations from this power law.
3.2.3 Nonparametric perturbations of parametric sources
In general (and especially in order to encode our prior assumption of localization of the source brightness distribution), it is useful to use a nonparametric model to describe only the perturbations around a parametric profile. This is the case for two main reasons. The first is that such combination resembles more closely typical astrophysical sources. As previously discussed, the lensing problem is, in fact, highly degenerate. Having a more constrained model for the allowed brightness distributions in the source plane assists in breaking this degeneracy and reconstructing the most typical sources more easily and accurately. In fact, Maresca et al. (2021) highlighted how nonparametric models can often lead to unphysical source disruptions. Having an underlying parametric distribution to constrain the model can help to mitigate these issues. It must be kept in mind that this introduces a weak bias on the type of sources the algorithm will be able to recover. For instance, it will be harder for the algorithm to reconstruct a source composed by two nearby, but well separated galaxies in the source plane if the combined model is composed by a nonparametric perturbation of a single Gaussian profile. Nevertheless, if we suspect that the actual source brightness distribution is multimodal or not well localized, we can include this insight into our prior. In the previous example of the two well-separated galaxies this could be done, for instance, by introducing two Gaussian parametric fields and a nonparametric perturbation field. The second reason relates to optimization purposes. Finding the optimal source and lens configuration that gives rise to the observational data is ultimately a hard optimization problem. The advantage of a combined parametric and nonparametric source model is that a more realistic prior model can improve the inference, reducing the degeneracies in parameter space, while simultaneously having sufficient complexity to model most source distributions accurately.
3.3 Lens mass model
In the following section, we describe our prior models for the lens mass, which bends the source brightness distribution onto the lens plane. To effectively uncover substructures within the lensing system and constrain dark matter, it is imperative to have an accurate and flexible representation of the lens mass. The mass, which is relevant for the lensing signal, is, under the thin-lens assumption, described by the convergence:
which is the surface mass density Σ(χ) scaled by the critical density 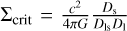 , (see e.g. Meneghetti 2021). The terms D1, Ds, and Dls describe the angular diameter distance between observer and lens, observer and source, and lens and source, respectively.
, (see e.g. Meneghetti 2021). The terms D1, Ds, and Dls describe the angular diameter distance between observer and lens, observer and source, and lens and source, respectively.
In LensCharm, we formulate the lens mass model by directly modeling the convergence field. In fact, it is comparatively simpler to formulate physical prior beliefs for the convergence – as opposed to the lensing potential or the deflection angle field – since many convergence models have been derived from N-body simulations. In particular, we assume that the convergence field is a strictly positive and can exhibit significant variations in magnitude. Furthermore, we assume that in most cases, the convergence profile is localized, and can be modulated by smooth fluctuations. Similar to the light profile, users of LensCharm have the flexibility to model the convergence field in the following ways: employing a parametric model, a non-parametric model, or a hybrid model combining a parametric profile with nonparametric perturbations.
3.3.1 Parametric mass profiles
In LensCharm, we implemented some of the most common parametric models used in the literature. We give a short description of the mass models which we use in the context of this paper. The choice of which parametric model to use and the corresponding priors depend on the observation and need to be adjusted by the user.
The pseudo isothermal ellipsoid (PIE) generalizes the isothermal spheroid (see, e.g., Binney & Tremaine 2011), allowing the profile to be non-singular and elliptical. Its convergence is described by:
where r is an elliptical radius according to Eq. (2), rc is the core radius, and b controls the overall strength of the profile. In the limit of vanishing core radius, the PIE profile falls off with r−1. The PIE has a known analytical solution to the deflection angle (see Kormann et al. 1994). Furthermore, the SLACS survey showed that the PIE’s slope is consistent with measured slope of the mass profile of early-type galaxies (see Auger et al. 2010).
The dual pseudo isothermal ellipsoid (dPIE) extends the PIE by introducing the truncation radius, rt, which leads to a slope approaching r−3 beyond the truncation radius. The convergence profile is given by:
where r is an elliptical radius, see Eq. (2), rc the core radius, rt the truncation radius, and b the lens strength. The dPIE has also a known analytical solution to the deflection angle (see Kormann et al. 1994).
The Navarro-Frenk-White (NFW) profile has been found to well describe the distribution of simulated dark matter halos (see Navarro et al. 1996). When projected into two dimensions, the convergence of the NFW profile is described by
where r is the elliptical radius according to Eq. (2), b = ρsrs/Σcrit the lens strength, which is related to the characteristic density contrast, ρs, the scale radius, rs, and the critical density, Σcrit (see Bartelmann 1996). Furthermore, the profile depends on
In the elliptical case, the NFW profile has no known closed form solution for the deflection angle.
The external shear aims to model the influence of line-of-sight structures and galaxies outside the immediate vicinity of the lensing system (see, e.g., Schneider et al. 2006). The shear model has two parameters: the shear strength, γsh, and its orientation, θsh. Additionally, for its evaluation we also need to provide the shear center, xc, yc, which can be inferred. In the context of this work, we fixed these coordinates to the lensing center.
3.3.2 Nonparametric profiles and perturbations
As recently demonstrated by Cao et al. (2022) and Etherington et al. (2023), parametric profiles might lack the necessary complexity to accurately represent the mass profile of real lens systems and can lead to systematic errors and spurious parameter fits. Moreover, the work of Richardson et al. (2022) shows that dark matter filaments, contributing between 5 and 50 percent of the matter content in the Universe and not associated with any specific dark matter halo, can have a significant influence on the flux ratio signal. To address the challenge of modeling these complex mass profiles, we propose the adoption of a non-parametric convergence model.
As shown in Sect. 3.2, we can incorporate positivity, along with smooth nonparametric fluctuations, using a lognormal Gaussian process with an inferable correlation structure. Moreover, similarly to the source light profile, it can be advantageous to describe the lens mass using a hybrid model, where nonpara-metric perturbations are modeling deviations from a parametric profile. Besides providing the algorithm with the possibility to fit more complex structures, this allows for the inference to be divided into two phases. In the beginning, only the parametric model parameters are optimized for. In a second minimization step, the perturbations are introduced in the model and a joint reconstruction is achieved. This approach bears similarities to the method proposed by Koopmans (2005), which involves the addition of a pixelized nonparametric field to the lensing potential. However, it is important to note structural differences. In our method, we introduce the nonparametric field in the convergence, allowing for the inclusion of prior assumptions. These priors help guiding the inference of the perturbation field by providing a physically motivated regularization. We show in Sect. 6 how these perturbations are able to account for substructures and nonparametric features in the lens mass profiles present in the data. Furthermore, Chatterjee & Koopmans (2018) suggested that perturbations of the lens can be statistically modeled by a Gaussian random field. Importantly, our nonparametric and combined models inherently encompass these perturbations, allowing for the inference of the dark matter field’s power spectrum. Contrary to the multi-stage algorithm proposed in Chatterjee & Koopmans (2018), we have the capability to jointly model the Gaussian random field alongside the parametric profile.
3.4 The deflection angle
In order to infer the mass profile from observational data, we need to link the mass profile to the deflection angle field. The deflection angle field describes how light rays from the background source are mapped through the lens equation onto the lens plane. This field can be computed from the convergence profile using the two dimensional Poisson equation ∇ ⋅ α = 2κ (see, e.g., Meneghetti 2021), which can be solved in Fourier space:
As mentioned in Sect. 3.3.1, some parametric mass profiles have a closed-form solution to the deflection angle. However, in scenarios where such solutions are not available, especially in the nonparametric case, we employ Eq. (8) to calculate the deflection angle field.
3.5 Lens light models
Most galaxy-galaxy lens systems are dominated by a central early-type galaxy (see, e.g., Barnabè et al. 2009), whose light profile is well described by a Sérsic profile. Consequently, in the forthcoming analysis, we adopt a Sérsic profile to model the lens light, whose parameters we infere alongside the lens mass and source. This approach has been shown to lead to more accurate results compared to subtracting it from the data (see, e.g., Nightingale et al. 2018). Furthermore, we have employed an exponential disk profile to model the central component of the elliptical foreground galaxy of SPT0418-47 (see Sect. 6).
The exponential disk models the surface brightness profile of disk galaxies (see, e.g., Mo et al. 2010). The profile is given by:
where r is an elliptical radius, I0 the central brightness, and rs the "scale" length, at which the brightness is e-times smaller then the central brightness. In this way, the exponential disk profile can be interpreted as a Sérsic profile with n = 1.
In the LensCharm framework, users also have the option to employ a more versatile nonparametric light model. However, we defer the exploration of this possibility to future investigations.
3.6 Lensing operator
Under the assumption that the surface brightness is conserved, its mapping from the source to the lens plane can be represented by a linear operation (see, e.g., Meneghetti 2021):
where the surface brightness of the source at a position, s(y), is related to a location in the lens plane, x, through the lens equation, y = x − α(x).
This description is useful to optimize the parameters of the lens mass and the source model efficiently. In order to use efficient first and second order solvers, we need to evaluate the gradient of Eq. (9) with respect to both parameter sets:
where we have denoted the lens mass model parameters by μ and the source ones by σ. Koopmans (2005) has shown how to use a linear approximation to the gradient in order to infer perturbations to the lensing potential. These perturbations have then been used in order to detect and model substructures in multiple lensing systems, (see, e.g., Vegetti et al. 2012). In contrast, with our approach we are able to access the full information contained in the gradient expression in Eq. (10) without having to rely on approximations. This enables us to jointly optimize all relevant parameters of the lensing model, in particular: the source, the lens mass, and its nonparametric perturbations. For this reason, more flexible convergence models could be developed in order to better account, detect, and model substructures.
We implement the mapping of the surface brightness distribution, described by Eq. (9), via bilinear interpolation. For a comparison of different interpolation schemes we refer to Galan et al. (2021). In their work, the authors show that typically multiple positions in the source plane are unconstrained by the data. The flux at these positions can only be constrained by appropriate regularization.
4 Response operator and likelihood
In order to infer the quantities of interests from the data, we need to specify how the continuous signal field is transformed into discrete data space. This measurement process can be described by the combined effect of the detector response R and a statistical model of the measurement noise. The mathematical expression is given by the measurement equation:
where n specifies the noise realization, I is the sky intensity, and d is the data.
4.1 Response operator
The response describes how the sky signal, I, (e.g. astronomical source flux) is transformed by the detector. The response operator can potential model multiple effects and might even depend on the flux of the observed object. In the examples we show in Sect. 6, we have simply approximated the detector response with a point-spread function (PSF), since the focus of this work is to showcase the lens reconstruction model. Yet, developing a more accurate measurement model could also improve reconstruction result, which we leave to future work.
4.2 Likelihood
The likelihood incorporates the noise statistics, as it defines the probability of the data given the signal Ƥ(d| s, l, m, M) in Eq. (1). Since our inference scheme is based on NIFTy, the LensCharm user can choose from a set of likelihoods implemented in the NIFTy package. Within the context of this paper, we only make use of Gaussian likelihoods. Other possible likelihood choices include the Poissonian likelihood, the variable-covariance Gaussian likelihood, and others.
5 Inference
The estimation of the optimal source and lens and their relative perturbation-field configurations given the data is a very degenerate and high-dimensional problem. In particular, for strong lensing we would need to be able to calculate Ƥ(s, l, m| d, M) in Eq. (1). While we address the problem of degeneracy in parameter space with our prior models, we tackle the high-dimensional inference problem using variational inference. This allows us to model the full joint posterior distribution Ƥ(s, l, m| d, M) instead of only relying on conditional inference. For example, a commonly used inference approach for strong lensing observations is to fit the lens light first and then subtract this fit from the data. In a next step, the residual data is modeled to obtain the source light and the lens mass distribution. In contrast, since we have a model for the joint distribution Ƥ(s, l, m| d, M), we can more accurately represent – and, hence, reconstruct – each model component.
In this work, we make use of variational inference. In variational inference, the usually intractable high-dimensional posterior probability distribution of the model parameters Ƥ(θ|d) is approximated by a variational family of distributions Qα(θ|d), parametrized by some variational parameters α. This varia-tional family of distributions is then optimized to match the true posterior by minimizing the Kullback-Leibler divergence:
where Ωθ is the domain of the model parameters. Specifically, we made use of the Metric Gaussian Variational Inference (MGVI; Knollmüller & Enßlin 2020) and geometric Variational Inference (geoVI; Frank et al. 2021) algorithms. In MGVI, the variational family of approximating posterior distributions is Gaussian in a latent-space coordinate system and the covari-ance is approximated with the inverse of the Fisher metric. Furthermore, geoVI extends MGVI by solving the inference optimization problem in a coordinate space in which the metric is approximately Euclidean. This coordinate transformation allows for non-Gaussian approximating posterior distributions in the MGVI latent coordinate space, while being still applicable to very high-dimensional problems as the ones considered in this work. Both MGVI and geoVI allow for samples to be drawn from the approximating posterior distribution Qα(θ|d) and, therefore, to estimate uncertainties and compute posterior expectation values of the signal fields.
For instance, we can evaluate the mean and the standard deviation of any desired quantity, q, by calculating the sample averages:
where Ns is the number of samples drawn. In the context of strong lensing models, which employ a nonparametric source brightness model, the estimation of the uncertainties of the source reconstruction is nontrivial. For example, the outlined procedure of Suyu et al. (2006) assumes fixed lens mass parameters in order to estimate the uncertainties of the source brightness distribution. Within this framework, we must resort to nested sampling or similar techniques in order to obtain the uncertainties of the source reconstruction which result from the uncertainties of the lens mass parameters. It is important to note that such estimations can present significant computational challenges. In contrast, within the LensCharm framework, we can, through sampling the approximating posterior distribution Qα(θ|d), directly estimate the uncertainties. This enables us to efficiently access the correlations between all parameters, in particular, the correlations between the lens parameters and the source brightness distribution.
Finding optimal solutions in high-dimensional problems poses a series of formidable challenges. These encompass increased computational complexity and challenges arising from the large search volume, which grows exponentially with the degrees of freedom. Within the framework we explore in this work, these challenges are partially addressed by the prior probability and the adopted variational inference scheme. Nevertheless, the high-dimensional spaces of non linear problems are often populated by many local optima. geoVI’s sampling strategy helps to escape from some of the local minima arising from a non-Gaussian posterior (see Frank et al. 2021).
To further improve the efficiency and robustness of our inference algorithm, we propose an adaptive inference strategy. In this scheme, we first optimize the parametric profiles and subsequently add the non-parametric perturbations to the model. We test the adequateness of this scheme and find that on the one hand, starting the optimization with the parametric lens mass profile leads to faster and more robust solutions. On the other hand, we do not notice any significant benefit in starting the optimization with reduced complexity for the source model. In the following, we adopt the adaptive optimization for the lens mass model. In this scheme, we initially optimize the parametric model of the lens mass before transitioning to the full hybrid model. Simultaneously, we retain the full complexity of the hybrid model for the source brightness distribution throughout the optimization.
6 Results
In this section, we showcase the capabilities of LensCharm by applying it to different datasets. Specifically, we consider three different examples. In the first, we compare our algorithm with the publicly available Lenstronomy package on a simulated dataset provided with the Lenstronomy pipeline3. In the second, we create a simulated JWST observation with a detectable substructure in the convergence to test our lens mass profile model. Finally, in the third, we reconstruct the source and lens mass distributions of the lens system SPT0418-47 observed with JWST.
6.1 Comparison with Lenstronomy
In this section, we compare our modeling approach to Lenstronomy (Birrer & Amara 2018), a state-of-the-art package for strong lensing. For the comparison, we use a dataset provided in a tutorial in the Lenstronomy package. The tutorial showcases the shapelet basis function reconstruction. The very same reconstruction is used as a paradigmatic example of the Lenstronomy pipeline capabilities in Birrer & Amara (2018).
The data are a synthetic strong lensing observation. This observation has been generated by inputting the source brightness distribution of an image of the NGC 1300 galaxy through the Lenstronomy forward pipeline. The lensed image is convolved with a Gaussian PSF and corrupted by a simulated normally distributed measurement noise.
In the publicly available Lenstronomy reconstruction, the lens mass distribution parameters are not inferred but are set to the values that produced the mock observation. In contrast, we both reconstruct the lens and the source simultaneously. Our source model for this dataset consists of a Gaussian profile with multiplicative MKF perturbations, while for the lens mass model we use a PIE with multiplicative CFM perturbations. We evaluated the data reconstruction quality using the reduced χ2-statistic and estimate the source reconstruction accuracy in terms of the source distortion ratio (SDR), as defined in Joseph et al. (2019)
where a higher SDR signifies a more accurate reconstruction. We display both of these quantities alongside the data and the reconstructions of LensCharm and Lenstronomy in Fig. 1.
The reconstructions of both methods are consistent with the data, as the reduced χ2 is in both cases close to unity. Furthermore, we can analyze the noise-weighted residuals (NWR):
where Idata is the data counts and Imodel is the flux predicted by the model. We find in Fig. 1 that the NWRs are distributed according to a standard normal distribution, as expected. Considering the source brightness distribution, both algorithms yield comparable reconstructions of the large-scale features. Moreover, notably, both reconstructions are able to recover the arcs and the central bulge of the source galaxy. This is reflected by the comparable SDR values for both reconstructions, which is slightly higher for the LensCharm reconstruction. This difference is explained by two features of the reconstructions. First, in the outskirts of the Lenstronomy reconstruction, low-flux fluctuations are sometimes negative. This is not the case in the LensCharm reconstruction, as the prior doesn't allow for negative flux values and the Gaussian profile suppresses the flux in regions of low input brightness. Second, while the Lenstronomy reconstruction is largely smooth, the LensCharm reconstructions show more small-scale features, some of which correspond to the ones in the ground truth input source brightness distribution.
In contrast to the Lenstronomy reconstruction, which keeps the lens parameters fixed during the inference of the source parameters, with LensCharm reconstruction we infer the lens parameters jointly alongside those of the source. Considering the lens mass reconstruction, we find that the CFM perturbations are suppressed. Additionally, we find that the posterior parameters of the PIE model closely match the input parameters that generated the data, as can be viewed in Fig. 2.
In addition to reconstructing the source flux and lens convergence, LensCharm also provides estimates for the associated uncertainties in these parameters. We estimate the accuracy of the uncertainties by examining the uncertainty-weighted residuals (UWRs), given by:
where qįnput is the ground truth of the input quantity of interest, 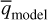 is the estimator of the same quantity obtained from the reconstruction, and σq is its standard deviation. We display a histogram of the UWRs for the source reconstruction in the top right panel of Fig. 1. The UWRs in the source plane provide a quantification of the reliability of the posterior uncertainties expressed by σs. As a matter of fact, as shown in Table 2, approximately 75% of the reconstruction residuals fall within one standard deviation, σs, (for flux values higher than 0.5). However, this fraction decreases for lower flux levels, as expected (see following section). This effect is partly driven by the sharp cut in the input image which generated the data, which is not accurately described by our physically motivated model. Moreover, from the UWR distribution we observe a slight overestimation of the input source flux in the source reconstruction. This overestimation can be attributed to the presence of unphysical negative flux values in the input image, deliberately left unaccounted for by our model. These factors contribute to an increased error budget, subsequently diminishing the precision of the uncertainty estimation. In the following section, we discuss additional aspects concerning the accuracy of the uncertainty estimation.
is the estimator of the same quantity obtained from the reconstruction, and σq is its standard deviation. We display a histogram of the UWRs for the source reconstruction in the top right panel of Fig. 1. The UWRs in the source plane provide a quantification of the reliability of the posterior uncertainties expressed by σs. As a matter of fact, as shown in Table 2, approximately 75% of the reconstruction residuals fall within one standard deviation, σs, (for flux values higher than 0.5). However, this fraction decreases for lower flux levels, as expected (see following section). This effect is partly driven by the sharp cut in the input image which generated the data, which is not accurately described by our physically motivated model. Moreover, from the UWR distribution we observe a slight overestimation of the input source flux in the source reconstruction. This overestimation can be attributed to the presence of unphysical negative flux values in the input image, deliberately left unaccounted for by our model. These factors contribute to an increased error budget, subsequently diminishing the precision of the uncertainty estimation. In the following section, we discuss additional aspects concerning the accuracy of the uncertainty estimation.
 |
Fig. 1 Reconstruction of simulated strong lensing data of NGC 1300 from Birrer & Amara (2018). Top panels: data, distribution of the noise-weighted data residuals for both LensCharm and Lenstronomy where the gray dashed line depicts a standard normal distribution, input source, and distribution of the uncertainty weighted residuals of LensCharm evaluated at reconstructed source flux above 0.5 (from left to right). Middle panels: results of the LensCharm reconstruction: lensed source reconstruction, residuals between the lensed light and the data, source reconstruction, and residuals between the input source and the LensCharm reconstruction (from left to right). Bottom panels: results of the Lenstronomy reconstruction, which follow the same order as the middle panels. |
6.2 Simulated JWST observation
We test our model with a simulated JWST observation. Since actual galaxies are expected to exhibit brightness and mass distributions that diverge from our model, we deliberately chose a source brightness distribution and a lens mass distribution that do not originate from the reconstruction model.
In order to have access to a realistic source brightness distribution, we took a source from the Hubble deep field (HDF) (Beckwith et al. 2006) catalog Rafelski et al. (2015). We performed a deconvolution and denoising procedure on the HDF observation to generate a smooth source brightness distribution, following the process described by O’Riordan et al. (2023). Subsequently, we project the smooth source through the lens mass distribution, which consists of a main deflector and a substructure. The main deflector follows a dPIE profile4, see Eq. (5). The substructure mass, which we place on the arc of the lensed images to ensure detectability, follows a NFW profile, see Eq. (6). We assume a substructure mass of 5 × 1010 M⊙, which is comparable to a substructure mass previously detected in an observation of the Hubble Space Telescope (Vegetti et al. 2010). We calculate the mass according to Duffy’s concentration-mass-relation (Duffy et al. 2008) for a lens at redshift z = 0.4.
We simulate a JWST NIRCam observation of the F200W filter, with a pixel resolution of 0.031 arcsec5. We convolve the lensed source light with the corresponding PSF, which we calculate employing the WebbPSF library (Perrin et al. 2014). Furthermore, we add uncorrelated Gaussian random noise to the image. The standard deviation of the noise of the data, denoted by σd, is determined according to the procedure described in O’Riordan et al. (2019). In this procedure, we calculate the standard deviation according to a predefined S/N. As suggested by O’Riordan et al. (2019), the S/N ranges from [50–500] in real observations. Consequently, we set the S/N to an intermediate value of 200.
Similarly to the previous example, we model the source by a Gaussian profile with multiplicative MKF perturbations. For the lens mass we assume a PIE profile with multiplicative CFM deviations, since we expect that substructures can be better represented with the help of a fully flexible power spectrum.
The results of the reconstruction can be viewed in Fig. 3. We find that the model is able to reconstruct the data up to the noise level, as the chi-squared statistic approaches unity, χ2 = 0.99. From Fig. 4, we can conclude that the reconstruction of both lens and source plane flux is unbiased. The remaining spread between the underlying lensed source flux and its deconvolved reconstruction is within one standard deviation of the noise, σd. Inspecting the source reconstruction, depicted in the first row of Fig. 3, we conclude that the model accurately captures large-scale features of the source, but we also observe subtle discrepancies in small-scale features. These discrepancies are reflected in the spread of the source flux reconstruction for larger flux values, as depicted in the upper panel of Fig. 4. We attribute this phenomenon to the noise in the data and the effect of the PSF, which distributes flux over the kernel’s support, consequently reducing information on finer scales. This increases the influence of the prior on the reconstruction, which favors smoother source brightness distributions, leading to discrepancies where larger fluctuations are present in the input source. The same effect can also be seen in the lens-plane flux comparison (lower panel in Fig. 4). Here the PSF attenuation leads to a decrease of high flux values and an increased spread for lower flux values.
Comparing the reconstructed convergence, depicted in the last row of Fig. 3, to the ground truth we find that the algorithm is able to recover the general shape and large-scale features of the convergence profile. However, when considering the main lens mass profile, we found two regions with significant residuals. First, we notice a difference in the center of the lensing mass. The lens mass is effectively only constrained in regions where the extended source brightness distribution is lensed to. Consequently, broadening the model to regions with low data counts inevitably requires some degree of extrapolation (see, e.g., Nightingale & Dye 2015, for further discussion). In the center, where there are fewer data constraints, only the integrated 2D mass density contributes to the deflection angle. This justifies the larger residuals in the central area, as different mass distributions in this area produce the same lensing signal. This is also confirmed by the higher relative uncertainty. Furthermore, we observe a discrepancy between the ground-truth convergence and its reconstruction in regions larger than the dPIE’s cutoff radius (rb = 1.85). Here, the data does not provide sufficient constraints for the convergence model; hence, the CFM perturbations cannot account for the flatter profile of the PIE model.
Considering the substructure, we find that the CFM perturbations are able to pick up the location of the substructure. On the other hand, the reconstruction of the substructure by the CFM perturbations lead to two types of residuals. First, a residual at the substructure’s central position. Second, there are correlated residuals distributed across the lensing mass field. Notably, these correlated residuals are similar in scale to the reconstructed substructure. These two residuals are related. The localized parametric NFW profile in the synthetic data exhibits a steep increase of mass towards its center, which needs to be modeled by the CFM perturbations. However, the CFM prior favors relatively smooth perturbations and hence it only is able to partly recover this localized substructure. Such model inconsistencies can be leveraged to identify substructures within the lensing mass. For example, by repeating the inference with a model that includes a substructure profile at the indicated by the CFM model fluctuations and then use model comparison (e.g., evidence lower bound) measures to validate the insertion of the substructure. We defer this exploration to future investigation.
When considering the relative uncertainty of the lensed flux (see middle row of Fig. 3), we observe a notable relative uncertainty in the position of the central image. Because the central light component is de-magnified, it becomes challenging to distinguish it from the measurement noise. Furthermore, the position of the central light is highly sensitive to the lensing mass. Consequently, the uncertainty in the lensed light is influenced by the uncertainties in the lens mass parameters, highlighting the capacity of the LensCharm framework to uncover and explore the cross-correlated uncertainties.
Finally, we analyzed the estimated uncertainties by examining the UWRs for the source reconstruction, shown in Fig. 5. We find that the uncertainties accurately represent the difference between input and reconstructed source in regions of high to medium source flux. However, we find that the difference in the uncertainty weighted residuals increases as the lower the source flux values become. In these regions, the data offer fewer constraints, as the lensed source flux cannot be definitely distinguished from the measurement noise. Moreover, we note that the posterior distribution of the source flux reconstruction is non-Gaussian and that VI is known to underestimate uncertainties. For all these reasons, the estimated uncertainties do not closely follow the 68, 95, 99.7-rule for flux contour lines, as shown in Table 3. For instance, we get higher fractions in regions in which the data are more informative and progressively lower fractions in less-informative regions.
 |
Fig. 2 Marginalized posterior distribution of the lens model parameters for the simulated strong lensing data of NGC1300, estimated using 80 samples. The dashed lines depict the input parameters of the lens model used to generate the synthetic data. |
 |
Fig. 3 Reconstruction of simulated strong lensing observation with JWST. Top panels: input source model is depicted next to its reconstruction, which is the mean of the source flux averaged over the approximating posterior. Next, we display the relative uncertainties estimated from posterior samples. Lastly, the residuals between the input and the reconstruction are displayed (described from left to right). Middle panels: simulated JWST data, its reconstruction, relative uncertainty of the reconstruction, and normalized data residuals. Bottom panels: input convergence, its reconstruction, the relative uncertainty of the convergence reconstruction, and the residuals between the input convergence and its reconstruction. |
6.3 JWST observation
We applied our lensing framework to real data, specifically, to a JWST observation of SPT0418-47. The observation was taken as part of the Targeting Extremely Magnified Panchromatic Lensed Arcs and Their Extended Star formation (TEMPLATES)6. SPT0418-47 is a strong lensing system with a lensing galaxy at redshift z = 0.263 and source light at redshift z = 4.2248, as identified by observations by the Atacama Large Millimetre/submillimetre Array (Weiß et al. 2013). A reconstruction by Rizzo et al. (2020) suggested the source to be isolated and dominated by self rotation, whereas an analysis by Peng et al. (2023) revealed, based on H-alpha detection, the source light to be emitted by two companion galaxies. We reconstructed the data of the NIRCam observation in the F356W filter, which makes it possible to resolve the two galaxies, as demonstrated by Cathey et al. (2023).
 |
Fig. 4 Scatter plots for the source and lens flux of the reconstruction depicted in Fig. 3. Top panel: pixel-wise comparison between the input source flux and its reconstruction. Bottom panel: similar pixel-wise comparison between the unconvolved lensed input source flux and its reconstruction. In both panels, the solid black line depicts the one-to-one correspondence between model and input flux. Furthermore, in the bottom panel, the dashed black lines depict the standard deviation of the noise σd. |
 |
Fig. 5 Uncertainty weighted residuals (UWR) for the source reconstruction depicted in Fig. 3. Top panel: UWR alongside contour levels of the reconstructed source flux, indicated by the white lines. Bottom panel: UWR for pixels above the depicted contour line levels. |
6.3.1 Super-resolution, background subtraction, masking, PSF, and noise model
The TEMPLATES program observed SPT0418-47 in the F356W filter with two dithers. Here, we use the information contained in the difference between these two dithers to super-resolve the JWST reconstruction. This can be achieved by using the output of the second JWST pipeline step, which calculates, among other quantities, a world coordinate system for the two shifted observations (see Bushouse 2020). In order to achieve super-resolution, we built our lens plane brightness distribution model on a grid with a finer resolution than the JWST data. While the pixel size of the F365W filter is 0.063 arcsec, we chose a pixel resolution for the model’s lens plane of 0.0315 arcsec. From the world coordinate system, we calculated the fractional shift of the two dithers with respect to the lens plane. Subsequently, we shifted the higher resolved lens brightness reconstruction to the respective data using a Lanczos kernel. The shifted high-resolution image is then convolved with the PSF, which we calculate with the help of the WebbPSF library. Finally, the surface brightness is integrated to the data resolution.
The second JWST pipeline step also includes background subtraction (see Bushouse 2020). However, we noticed a discrepancy in the scales between the two datasets, suggesting that the subtraction step might have not completely worked. To address this issue, we introduce an additional parameter that account for the mean flux for each data set, which we infer alongside the remaining degrees of freedom. These two values, which we assume to be normally distributed around the mean of the two datasets, help compensate for potential errors arising from the background subtraction procedure.
Furthermore, we followed Cathey et al. (2023) and applied masking to two objects located at the coordinates (04:18:39.4, −47:51:52.81) and (04:18:39.6, −47:51:54.76). These two objects are close to the lensed arcs and could potentially be part of the companion galaxies lensed by SPT0418-47. However, we followed the conclusion drawn by Cathey et al. (2023) and consider these objects not to be part of the lensing system. Additionally, since we have taken a larger field-of-view, we masked two objects located well outside the lensing system at the coordinates (04:18:39.9, −47:51:49.65) and (04:18:39.51, −47:51:57.0). The masking step ensures that they are not incorporated into our modeling process.
We assumed that the noise of the data products of the JWST pipeline follows a Gaussian distribution, where the standard deviation is provided by the total error array7, which saves the square root of the quadratic sum of all variances in the pipeline.
 |
Fig. 6 Reconstruction of the JWST NIRCam observation of SPT0418-47 in the F356W filter. Top panels: source reconstruction and its relative uncertainty (left to right). Both these quantities are obtained by sampling the approximating posterior. We depict the caustics with solid lines. The remaining two panels show the data used for the reconstruction, which are the outputs of the second JWST pipeline step. Middle panels: lensed light distribution resolved on the finer pixel grid (we include the critical lines as solid lines), followed by the lens light which is also displayed on the finer pixel grid. The last two middle panels show the sum of the lens light and the lensed source light convolved by the PSF and integrated onto the data resolution. Bottom panels: reconstructed convergence profile, next to its relative uncertainty. The last two bottom panels depict the residuals between the data and the lens plane flux reconstruction, where the white boxes depict the masks used for flux which is unassociated with the lensed light. |
 |
Fig. 7 Zoom-in view of the reconstructed source light and convergence perturbations from the JWST NIRCam observation of SPT0418-47. Left panel: reconstruction of the source light distribution, accompanied by the caustics depicted by the solid lines. Right panel: convergence perturbations through the relative difference between the reconstructed convergence and the parametric (PIE) model. The solid contour lines are the lensed source light distribution contours, cf. Fig. 6. |
6.3.2 Lensing model
In order to reconstruct the source brightness distribution of the lensing system, we employed two Gaussians with MKF perturbations to model the two galaxies in the source plane. In a previous reconstruction, we observed that a single Gaussian with MKF perturbations was able to reconstruct the light distribution of both source galaxies. However, to facilitate a more accurate source reconstruction, we subsequently decided to utilize two Gaussian profiles. We set the prior mean of the center, xc, yc, of the two Gaussians to the estimated central positions of the two source galaxies found in the previous source reconstruction. This ensures a well-informed starting point for our modeling process. Similarly to Cathey et al. (2023), we model the light emitted by the lensing galaxy by a composite model consisting of a Sérsic and an exponential disk component. However, our methodology differs from that of Cathey et al. (2023), who subtract their model’s lensing light profile from the observational data. In our study, we simultaneously optimized the lens light model alongside the lens mass and the source light. This joint optimization strategy is advantageous, as it preserves the noise characteristics of the observational data. Finally, we reconstructed the lens mass by employing the PIE model with CFM perturbations.
6.3.3 Results
The outcome of this reconstruction is shown in Fig. 6. Our algorithm effectively captures the lensed-light emission, as evident from the absence of structural residuals in this area. However, for both datasets, the reduced χ2-statistic falls short of reaching unity. In order to see that these discrepancies do not originate from our data combination strategy, we reconstructed the two NIRCam observations separately. From these reconstructions (both displayed in Figs. A.1 and A.2), we find similar reconstruction statistics and discrepancies. We can attribute these to two possible explanations, which warrant further investigation. First, the lens light model does not completely capture the complexity of the lens as we find substantial residuals at the center. Although we find that the masking the central residuals only reduces the reduced χ2 marginally. Second, the standard deviation derived from the JWST pipeline might underestimate the actual noise level present in the data. This could explain the high value of the reported χ2-statistic. Both these problems could be addressed by a more accurate modeling of the JWST pipeline and a more complex lens light model. However, this inquiry lies beyond the scope of our present paper, which primarily aims to showcase the strong lens modeling capabilities of the LensCharm framework. Therefore, we defer this aspect to future investigations.
Our analysis reveals that the convergence mass profile is closely aligned with the PIE profile. The deviations from the parametric PIE profile are displayed in Fig. 7. We find that the main contribution of these mass deviations is to modify the asymptotic slope of the isothermal profile along different angular directions. Moreover, we notice a moderate perturbation near the lensed arc, which could hint at the presence of a substructure at this location. However, conclusive confirmation or refutation of this hypothesis demands for further investigation. Regarding the source light distribution, also shown in a zoom-in view in Fig. 7, we find good structural agreement with the reconstruction by Cathey et al. (2023), with two main differences. First, the reconstruction by Cathey et al. (2023), which is based on shapelet basis functions, leads to negative flux values, which are not observed in our reconstruction. Second, we find that our reconstruction has sharper features for both source galaxies. From this, can see that one of the galaxies seems to be an edge-on disk galaxy, while the other galaxy’s light profile is more complex and has sharp details. Interestingly, if we compare these features with the reconstruction of the same system made by Cathey et al. (2023) using multiple filters, we find similar details. These independent and morphologically similar reconstructions hint at the validity of both methods. Nevertheless, it is worth noting that LensCharm was in this case able to recover the high resolution details of the source using a much smaller dataset. We defer the study of multifrequency strong lensing observations to future investigations.
7 Conclusions and future works
In this work, we present LensCharm, a novel strong gravitational lensing modeling framework. Within this framework, users can choose to model the lens mass and the source brightness distribution with either a parametric, nonparametric, or a hybrid model. The nonparametric models are based on Gaussian processes, which have been previously applied in the context of strong lensing, for example, by Karchev et al. (2022). We have shown how to incorporate physical insights into LensCharm models and how this can improve the reconstructions. Moreover, the parameters of our models can be reconstructed jointly, as we make use of the probabilistic programming framework NIFTy. Leveraging fast second order solvers and variational inference, we are able to obtain an approximate posterior distribution for our high-dimensional nonparametric models, which takes into account cross-correlations between all model parameters. Furthermore, we can use the approximate posterior distribution resulting from variational inference to obtain uncertainties on quantities of interest, which include the source surface brightness and the convergence profile of the lens. To give a demonstration of LensCharm capabilities, we have applied it to three different strong lensing observations.
First, we have compared our reconstruction to a state-of-the-art lensing framework Lenstronomy. We have shown that we are able to achieve high-resolution reconstructions of the source, while circumventing some problems which can occur with other approaches and that can lead, for instance, to negative reconstructed flux.
We then applied our framework to a simulated JWST observation. Here, we have shown how to jointly reconstruct a realistic source brightness distribution together with the underlying lensing mass distribution. To test the robustness of the pipeline, we have inferred the system using a different lens mass distribution model than the one used to produce the synthetic observation. This mimicks the analysis of a real observation for which the real lens mass distribution is unknown and might deviate from the model. While the proposed hybrid model was able to reconstruct the source with high accuracy, the adopted convergence model was not fully able to reconstruct the substructure to high resolution. To address this problem, LensCharm offers the ability to include new prior models for the convergence. Such an exploration might lead to improved substructure detections, which may enable probes into the nature of dark matter.
Finally, we have applied our algorithm to a real JWST observation obtained from the TEMPLATES program. This reconstruction is to some extent preliminary, as it serves as a proof of concept of the capabilities of LensCharm. A more complete analysis could include multiple filters and a better instrument model, for instance. We defer this work to future investigations. Even though this study is preliminary, our reconstruction framework leads to an image of the source brightness distribution, a companion galaxy system at redshift z = 4.2248 (for source reconstruction comparison see Cathey et al. 2023) of an unprecedented high resolution. LensCharm has been made publicly available8 to enable the next generation of strong gravitational lensing research.
Acknowledgements
M.G. acknowledges financial support from the German Aerospace Center and Federal Ministry of Education and Research through the project Universal Bayesian Imaging Kit – Information Field Theory for Space Instrumentation (Förderkennzeichen 50OO2103). J.R. acknowledges financial support by the German Federal Ministry of Education and Research (BMBF) under grant 05A20W01 (Verbundprojekt D-MeerKAT). P.F. acknowledges funding through the German Federal Ministry of Education and Research for the project ErUM-IFT: Informationsfeldtheorie für Experimente an Großforschungsanlagen (Förderkennzeichen: 05D23EO1). The authors thank Aymeric Galan for the insightful discussions and the anonymous reviewer for the constructive feedback.
Appendix A Single data reconstruction of SPT0418-47 NIRCam observation
As discussed in Section 6.3, when reconstructing the source flux of the SPT0418-47 galaxy system from the two different datasets jointly, we observe that the data residuals are incompatible with the assumed noise statistics. This is summarized by the χ2-statistic values being larger than one. In order to test the hypothesis that these residuals are indeed not a result of an error in combining the two dataset into a single reconstruction, we repeated the reconstruction using only one dataset at the time. We display the independent reconstructions for dataset 1 and dataset 2 in Fig. A.1 and in Fig. A.2, respectively.
We find that the χ2-statistic of the independent reconstructions is close to the value obtained in the combined reconstruction. This hints toward the fact that the pipeline is indeed robust with respect to using both datasets in a joint fashion. Furthermore, we notice a slight difference in the light distribution of one of the companion source galaxies. This discrepancy can be associated with a region in the data that has been partly masked by the JWST pipeline. In combination with the fact that the residual χ2-statistic is far from 1 – even when neglecting the lens light residuals at the center – this difference seems to suggest that the data noise level is underestimated. We leave a more accurate analysis of this mismatch to future investigations.
 |
Fig. A.1 Reconstruction of the JWST NIRCam observation of SPT0418-47 in the F356W filter using only the first data set. Top row: Source reconstruction with its relative uncertainty, both of these quantities are obtained via sampling the approximating posterior. The remaining panel displays the single data used for the reconstruction, which is part of the output of the second JWST pipeline step. Middle panels: Reconstructed lensed light distribution resolved on the finer pixel grid, followed by the lens light which is also displayed on the finer pixel grid. The last panel depicts the summation of the lens and lensed source light convolved by the PSF and integrated onto data resolution. Bottom panels: Reconstructed convergence profile, next to its relative uncertainty. The last bottom panel of the depicts the residuals between the data and the lens plane flux reconstruction, where the white boxes depict the masks used for flux which is unassociated with the lensed light. |
 |
Fig. A.2 Reconstruction of the JWST NIRCam observation of SPT0418-47 in the F356W filter using only the second data set. The panels display the same quantities as in Fig. A.1. |
References
- Arras, P., Baltac, M., Ensslin, T. A., et al. 2019, Astrophysics Source Code Library [record ascl:1903.008] [Google Scholar]
- Arras, P., Frank, P., Haim, P., et al. 2022, Nat. Astron., 6, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Auger, M., Treu, T., Bolton, A., et al. 2010, ApJ, 724, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Barnabè, M., Czoske, O., Koopmans, L. V., et al. 2009, MNRAS, 399, 21 [CrossRef] [Google Scholar]
- Bartelmann, M. 1996, A&A, 313, 697 [NASA ADS] [Google Scholar]
- Beckwith, S. V., Stiavelli, M., Koekemoer, A. M., et al. 2006, AJ, 132, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Biggio, L., Vernardos, G., Galan, A., Peel, A., & Courbin, F. 2023, A&A, 675, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 2011, Galactic Dynamics (Princeton: Princeton University Press), 20 [Google Scholar]
- Birrer, S., & Amara, A. 2018, Phys. Dark Universe, 22, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Birrer, S., Amara, A., & Refregier, A. 2015, ApJ, 813, 102 [Google Scholar]
- Birrer, S., Shajib, A. J., Gilman, D., et al. 2021, J. Open Source Softw., 6, 3283 [NASA ADS] [CrossRef] [Google Scholar]
- Bradač, M., Schneider, P., Lombardi, M., & Erben, T. 2005, A&A, 437, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradač, M., Treu, T., Applegate, D., et al. 2009, ApJ, 706, 1201 [CrossRef] [Google Scholar]
- Broadhurst, T., Benítez, N., Coe, D., et al. 2005, ApJ, 621, 53 [Google Scholar]
- Bushouse, H. 2020, Astronomical Data Analysis Software and Systems XXIX, 527, 583 [NASA ADS] [Google Scholar]
- Cao, X., Li, R., Nightingale, J., et al. 2022, Res. Astron. Astrophys., 22, 025014 [CrossRef] [Google Scholar]
- Cathey, J., Gonzalez, A. H., Lower, S., et al. 2023, AASJ., submitted [arXiv:2307.10115] [Google Scholar]
- Chatterjee, S., & Koopmans, L. V. 2018, MNRAS, 474, 1762 [NASA ADS] [CrossRef] [Google Scholar]
- Chianese, M., Coogan, A., Hofma, P., Otten, S., & Weniger, C. 2020, MNRAS, 496, 381 [Google Scholar]
- Coe, D., Fuselier, E., Benítez, N., et al. 2008, ApJ, 681, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, D., Zitrin, A., Carrasco, M., et al. 2012, ApJ, 762, 32 [Google Scholar]
- Collett, T. E. 2015, ApJ, 811, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Despali, G., Vegetti, S., White, S. D., et al. 2022, MNRAS, 510, 2480 [NASA ADS] [CrossRef] [Google Scholar]
- Diego, J., Protopapas, P., Sandvik, H., & Tegmark, M. 2005, MNRAS, 360, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dalla Vecchia, C. 2008, MNRAS, 390, L64 [Google Scholar]
- Dye, S., & Warren, S. 2005, ApJ, 623, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A. 2019, Ann. Phys., 531, 1800127 [Google Scholar]
- Enßlin, T. A., Frommert, M., & Kitaura, F. S. 2009, Phys. Rev. D, 80, 105005 [Google Scholar]
- Etherington, A., Nightingale, J. W., Massey, R., et al. 2023, MNRAS, submitted [arXiv:2301.05244] [Google Scholar]
- Fassnacht, C., Xanthopoulos, E., Koopmans, L., & Rusin, D. 2002, ApJ, 581, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, P., Leike, R., & Enßlin, T. A. 2021, Entropy, 23, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Galan, A., Peel, A., Joseph, R., Courbin, F., & Starck, J.-L. 2021, A&A, 647, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galan, A., Vernardos, G., Peel, A., Courbin, F., & Starck, J.-L. 2022, A&A, 668, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilman, D., Birrer, S., Treu, T., Nierenberg, A., & Benson, A. 2019, MNRAS, 487, 5721 [NASA ADS] [CrossRef] [Google Scholar]
- Guardiani, M., Frank, P., Kostić, A., et al. 2022, PLOS ONE, 17, 1 [Google Scholar]
- Hezaveh, Y. D., Dalal, N., Marrone, D. P., et al. 2016, ApJ, 823, 37 [Google Scholar]
- Holzschuh, B. J., O’Riordan, C. M., Vegetti, S., Rodriguez-Gomez, V., & Thuerey, N. 2022, MNRAS, 515, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Hsiao, T. Y.-Y., Abdurro’uf, Coe, D., et al. 2023, ApJ, submitted [arXiv:2305.03042] [Google Scholar]
- Hsueh, J.-W., Enzi, W., Vegetti, S., et al. 2020, MNRAS, 492, 3047 [NASA ADS] [CrossRef] [Google Scholar]
- Joseph, R., Courbin, F., Starck, J.-L., & Birrer, S. 2019, A&A, 623, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karchev, K., Coogan, A., & Weniger, C. 2022, MNRAS, 512, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R. 2001, arXiv e-prints [arXiv:0102341v2] [Google Scholar]
- Keeton, C. R. 2011, Astrophysics Source Code Library [record ascl:1102.003] [Google Scholar]
- Kneib, J.-P., Bonnet, H., Golse, G., et al. 2011, Astrophysics Source Code Library [record ascl:1102.004] [Google Scholar]
- Knollmüller, J., & Enßlin, T. A. 2020, arXiv e-prints [arXiv:1901.11033] [Google Scholar]
- Koopmans, L. V. E. 2005, MNRAS, 363, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Kormann, R., Schneider, P., & Bartelmann, M. 1994, A&A, 284, 285 [NASA ADS] [Google Scholar]
- Li, R., Frenk, C. S., Cole, S., Wang, Q., & Gao, L. 2017, MNRAS, 468, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Liesenborgs, J., De Rijcke, S., & Dejonghe, H. 2006, MNRAS, 367, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Maresca, J., Dye, S., & Li, N. 2021, MNRAS, 503, 2229 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M. 2021, Introduction to Gravitational Lensing Meneghetti (Berlin: Springer) [CrossRef] [Google Scholar]
- Mo, H., Van den Bosch, F., & White, S. 2010, Galaxy Formation and Evolution (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Morningstar, W. R., Levasseur, L. P., Hezaveh, Y. D., et al. 2019, ApJ, 883, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Nightingale, J., & Dye, S. 2015, MNRAS, 452, 2940 [NASA ADS] [CrossRef] [Google Scholar]
- Nightingale, J., Dye, S., & Massey, R. J. 2018, MNRAS, 478, 4738 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M. 2010, PASJ, 62, 1017 [NASA ADS] [Google Scholar]
- O’Riordan, C. M., Warren, S. J., & Mortlock, D. J. 2019, MNRAS, 487, 5143 [CrossRef] [Google Scholar]
- O’Riordan, C. M., Despali, G., Vegetti, S., Lovell, M. R., & Moliné, Á. 2023, MNRAS, 521, 2342 [CrossRef] [Google Scholar]
- Peng, B., Vishwas, A., Stacey, G., et al. 2023, ApJ, 944, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Sivaramakrishnan, A., Lajoie, C.-P., et al. 2014, SPIE, 9143, 1174 [Google Scholar]
- Powell, D. M., Vegetti, S., McKean, J. P., et al. 2022, MNRAS, 516, 1808 [NASA ADS] [CrossRef] [Google Scholar]
- Rafelski, M., Teplitz, H. I., Gardner, J. P., et al. 2015, AJ, 150, 31 [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. I. 2006, Gaussian Processes for Machine Learning, Adaptive Computation and Machine Learning (Cambridge: MIT Press) [Google Scholar]
- Richardson, T., Stücker, J., Angulo, R., & Hahn, O. 2022, MNRAS, 511, 6019 [NASA ADS] [CrossRef] [Google Scholar]
- Rizzo, F., Vegetti, S., Powell, D., et al. 2020, Nature, 584, 201 [Google Scholar]
- Saha, P., & Williams, L. L. 1997, MNRAS, 292, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Kochanek, C., & Wambsganss, J. 2006, Gravitational Lensing: Strong, Weak and Micro: Saas-Fee Advanced Course 33 (Berlin: Springer Science & Business Media), 33 [Google Scholar]
- Sérsic, J. L. 1963, Boletin de la Asociacion Argentina de Astronomia La Plata Argentina, 6, 41 [Google Scholar]
- Spilker, J. S., Marrone, D. P., Aravena, M., et al. 2016, ApJ, 826, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Wang, J., Vogelsberger, M., et al. 2008, MNRAS, 391, 1685 [Google Scholar]
- Stein, M. L. 1999, Interpolation of Spatial Data: Some Theory for Kriging (Berlin: Springer Science & Business Media) [CrossRef] [Google Scholar]
- Suyu, S. H., & Halkola, A. 2010, A&A, 524, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suyu, S. H., Marshall, P., Hobson, M., & Blandford, R. 2006, MNRAS, 371, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S., Marshall, P., Blandford, R., et al. 2009, ApJ, 691, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S., Auger, M., Hilbert, S., et al. 2013, ApJ, 766, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Tagore, A. S., & Jackson, N. 2016, MNRAS, 457, 3066 [NASA ADS] [CrossRef] [Google Scholar]
- Torres-Ballesteros, D. A., & Castañeda, L. 2022, MNRAS, 518, 4494 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., & Marshall, P. J. 2016, A&ARv, 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vegetti, S., & Koopmans, L. V. 2009, MNRAS, 392, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Vegetti, S., Koopmans, L. V. E., Bolton, A., Treu, T., & Gavazzi, R. 2010, MNRAS, 408, 1969 [Google Scholar]
- Vegetti, S., Lagattuta, D., McKean, J., et al. 2012, Nature, 481, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Vegetti, S., Koopmans, L., Auger, M., Treu, T., & Bolton, A. 2014, MNRAS, 442, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Vernardos, G., & Koopmans, L. V. 2022, MNRAS, 516, 1347 [CrossRef] [Google Scholar]
- Warren, S., & Dye, S. 2003, ApJ, 590, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Weiß, A., De Breuck, C., Marrone, D., et al. 2013, ApJ, 767, 88 [CrossRef] [Google Scholar]
- Wong, K. C., Suyu, S. H., Chen, G. C., et al. 2020, MNRAS, 498, 1420 [NASA ADS] [CrossRef] [Google Scholar]
For an intuition on how these parameters influence the prior distribution, we refer to https://ift.pages.mpcdf.de/nifty/user/getting_started_4_CorrelatedFields.html
https://jwst-docs.stsci.edu/jwst-near-infrared-camera/nircam-observing-modes/nircam-imaging (last visited 05-09-23).
Early release science program under the program ID 1355, https://www.stsci.edu/jwst/science-execution/program-information?id=1355 (last visited 29-08-2023).
https://jwst-pipeline.readthedocs.io/en/stable/jwst/error_propagation/main.html (last visited 05-09-2023).
All Tables
Comparison between different strong lensing codes along with their corresponding modeling techniques.
All Figures
 |
Fig. 1 Reconstruction of simulated strong lensing data of NGC 1300 from Birrer & Amara (2018). Top panels: data, distribution of the noise-weighted data residuals for both LensCharm and Lenstronomy where the gray dashed line depicts a standard normal distribution, input source, and distribution of the uncertainty weighted residuals of LensCharm evaluated at reconstructed source flux above 0.5 (from left to right). Middle panels: results of the LensCharm reconstruction: lensed source reconstruction, residuals between the lensed light and the data, source reconstruction, and residuals between the input source and the LensCharm reconstruction (from left to right). Bottom panels: results of the Lenstronomy reconstruction, which follow the same order as the middle panels. |
| In the text | |
 |
Fig. 2 Marginalized posterior distribution of the lens model parameters for the simulated strong lensing data of NGC1300, estimated using 80 samples. The dashed lines depict the input parameters of the lens model used to generate the synthetic data. |
| In the text | |
 |
Fig. 3 Reconstruction of simulated strong lensing observation with JWST. Top panels: input source model is depicted next to its reconstruction, which is the mean of the source flux averaged over the approximating posterior. Next, we display the relative uncertainties estimated from posterior samples. Lastly, the residuals between the input and the reconstruction are displayed (described from left to right). Middle panels: simulated JWST data, its reconstruction, relative uncertainty of the reconstruction, and normalized data residuals. Bottom panels: input convergence, its reconstruction, the relative uncertainty of the convergence reconstruction, and the residuals between the input convergence and its reconstruction. |
| In the text | |
 |
Fig. 4 Scatter plots for the source and lens flux of the reconstruction depicted in Fig. 3. Top panel: pixel-wise comparison between the input source flux and its reconstruction. Bottom panel: similar pixel-wise comparison between the unconvolved lensed input source flux and its reconstruction. In both panels, the solid black line depicts the one-to-one correspondence between model and input flux. Furthermore, in the bottom panel, the dashed black lines depict the standard deviation of the noise σd. |
| In the text | |
 |
Fig. 5 Uncertainty weighted residuals (UWR) for the source reconstruction depicted in Fig. 3. Top panel: UWR alongside contour levels of the reconstructed source flux, indicated by the white lines. Bottom panel: UWR for pixels above the depicted contour line levels. |
| In the text | |
 |
Fig. 6 Reconstruction of the JWST NIRCam observation of SPT0418-47 in the F356W filter. Top panels: source reconstruction and its relative uncertainty (left to right). Both these quantities are obtained by sampling the approximating posterior. We depict the caustics with solid lines. The remaining two panels show the data used for the reconstruction, which are the outputs of the second JWST pipeline step. Middle panels: lensed light distribution resolved on the finer pixel grid (we include the critical lines as solid lines), followed by the lens light which is also displayed on the finer pixel grid. The last two middle panels show the sum of the lens light and the lensed source light convolved by the PSF and integrated onto the data resolution. Bottom panels: reconstructed convergence profile, next to its relative uncertainty. The last two bottom panels depict the residuals between the data and the lens plane flux reconstruction, where the white boxes depict the masks used for flux which is unassociated with the lensed light. |
| In the text | |
 |
Fig. 7 Zoom-in view of the reconstructed source light and convergence perturbations from the JWST NIRCam observation of SPT0418-47. Left panel: reconstruction of the source light distribution, accompanied by the caustics depicted by the solid lines. Right panel: convergence perturbations through the relative difference between the reconstructed convergence and the parametric (PIE) model. The solid contour lines are the lensed source light distribution contours, cf. Fig. 6. |
| In the text | |
 |
Fig. A.1 Reconstruction of the JWST NIRCam observation of SPT0418-47 in the F356W filter using only the first data set. Top row: Source reconstruction with its relative uncertainty, both of these quantities are obtained via sampling the approximating posterior. The remaining panel displays the single data used for the reconstruction, which is part of the output of the second JWST pipeline step. Middle panels: Reconstructed lensed light distribution resolved on the finer pixel grid, followed by the lens light which is also displayed on the finer pixel grid. The last panel depicts the summation of the lens and lensed source light convolved by the PSF and integrated onto data resolution. Bottom panels: Reconstructed convergence profile, next to its relative uncertainty. The last bottom panel of the depicts the residuals between the data and the lens plane flux reconstruction, where the white boxes depict the masks used for flux which is unassociated with the lensed light. |
| In the text | |
 |
Fig. A.2 Reconstruction of the JWST NIRCam observation of SPT0418-47 in the F356W filter using only the second data set. The panels display the same quantities as in Fig. A.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



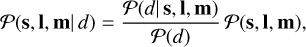
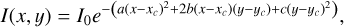
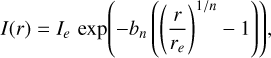
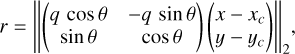
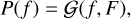
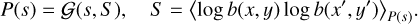
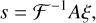
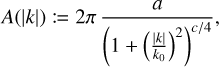
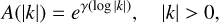
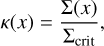
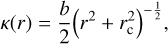
![$\kappa (r) = {b \over 2}\left[ {{{\left( {{r^2} + r_{\rm{c}}^2} \right)}^{ - {1 \over 2}}} - {{\left( {{r^2} + r_{\rm{t}}^2} \right)}^{ - {1 \over 2}}}} \right],$](/articles/aa/full_html/2024/02/aa48256-23/aa48256-23-eq13.png)
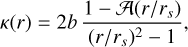

![$\alpha (x) = {{\cal F}^{ - 1}}\left[ {{{ - 2i{\bf{k}}} \over {|{\bf{k}}{|^2}}}{\cal F}[\kappa (x)]} \right].$](/articles/aa/full_html/2024/02/aa48256-23/aa48256-23-eq16.png)