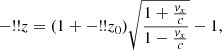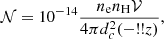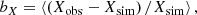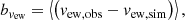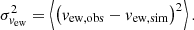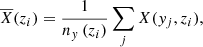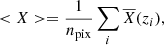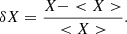| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202347123 | |
| Published online | 07 December 2023 | |
Dynamical properties and detectability of the magneto-thermal instability in the intracluster medium
Institut de Recherche en Astrophysique et Planétologie (IRAP), Université de Toulouse, CNRS, UPS, 31400 Toulouse, France
e-mail: jean.kempf@irap.omp.eu
Received:
8
June
2023
Accepted:
15
September
2023
Context. Amongst the many plasma processes potentially relevant to the dynamics of the intracluster medium (ICM), turbulence driven at observable scales by internal magnetised buoyancy instabilities such as the magneto-thermal instability (MTI) stands out in the outskirts of the ICM, where the background temperature decreases with the radius.
Aims. We characterise the statistical properties of MTI turbulence in the ICM and assess whether such large-scale magnetised plasma dynamics would be detectable with the future X-ray calorimeter X-IFU on board Athena.
Methods. We made use of scaling laws previously derived to phenomenologically estimate the observable turbulent saturation levels and injection length of MTI turbulence for different ICM thermodynamic profiles, and performed a numerical magnetohydrodynamic simulation of the dynamics with Braginskii heat and momentum diffusion. As a prospective exercise, we used the simulation to virtually observe MTI turbulence through the X-IFU.
Results. In bright enough regions amenable to X-ray observations, the MTI drives mild turbulence up to ∼5% and ∼100 km s−1 (root-mean square temperature fluctuation and velocity). However, the measurable integrated temperature fluctuation and line-of-sight velocity fields, the latter being essentially the azimuthal velocity component in cluster haloes, hardly exceed 1% and 10 km s−1, respectively (root-mean square). We show that such moderate signals would be difficult to detect with upcoming X-ray telescopes. We also find that MTI turbulence is anisotropic in the direction of gravity and develops at scales ≳0.2 Mpc. If the fluctuation intensities were to be stronger than the current theoretical estimates, MTI fluctuations would be detectable and their anisotropy discernible with the X-IFU.
Conclusions. Finding direct signatures of magnetised plasma dynamics in the ICM, even at observable scales typical of the fluid MTI, remains challenging. This study only marks a first step in this direction. Several numerical and observational strategies are discussed to make further progress in the future.
Key words: galaxies: clusters: intracluster medium / instabilities / turbulence / magnetohydrodynamics (MHD) / methods: numerical / techniques: imaging spectroscopy
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Galaxy clusters are filled with hot and diffuse gas: kBT ∼ 5 keV, ρ ∼ 10−27 g cm−3. This plasma, usually referred to as the intracluster medium (ICM), radiates in the X-ray through the combined emission of lines and Bremsstrahlung at a very high temperature. It accounts for ∼15% of the total mass of clusters and is in rough hydrostatic equilibrium within its dark matter potential well. Recent observations however suggest that the ICM sustains subsonic turbulence (Zhuravleva et al. 2018; Dupourqué et al. 2023), which could alter the hydrostatic balance and the internal transport of chemicals and energy, and hence shaping the evolution of clusters on cosmological timescales (Zhuravleva et al. 2014). A departure from ideal hydrostatic equilibrium in the ICM could also provide additional non-thermal pressure support (Eckert et al. 2019), biasing the determination of cluster masses through X-ray and Sunyaev-Zeldovich (SZ) measurements (Vazza et al. 2018; Angelinelli et al. 2020). The assessment of such a systematic bias is critical for cosmology since the mass distribution of galaxy clusters is used as a late-universe probe for the cosmological parameters (see the reviews by Allen et al. 2011; Pratt et al. 2019).
The dynamics of the ICM remains observationally poorly constrained. The Soft X-ray Spectrometer (SXS) calorimeter on board the Hitomi satellite made the only direct measurement of a velocity field in the ICM of the Perseus cluster core (Hitomi Collaboration 2016, 2018). The instrument was able to measure velocity gradients and turbulent broadening about 150 km s−1 thanks to both an emission line centroid shift and width measurements, respectively, but only down to the SXS pixel resolution of 20 kpc. So far, putting observational constraints on ICM turbulence below this length scale is exclusively achievable with the detection of ICM thermodynamic perturbations (Hofmann et al. 2016) or thanks to indirect measurements of its kinematics (Simionescu et al. 2019) through measurements of X-ray surface brightness (Churazov et al. 2012; Zhuravleva et al. 2015) and SZ fluctuations (Zeldovich & Sunyaev 1969; Mroczkowski et al. 2019). However, the next generation of spatially resolved X-ray spectroscopy instruments, such as Resolve (Ishisaki et al. 2018) or the X-ray Integral Field Unit (X-IFU; Barret et al. 2016, 2023) on board the future X-ray observatory Athena, and their unprecedented spectral resolution (7 and 2.5 eV below 7 keV, respectively) will push this limit downwards and provide us with an unprecedented opportunity to characterise the ICM dynamics down to the kiloparsec scale for the closest clusters.
The possible sources of turbulence in galaxy clusters are numerous and diversely distributed across the ICM, ranging from active galactic nuclei (AGN) feedback at the centre (Conroy & Ostriker 2008; Gitti et al. 2012) to accretion of infalling baryons on the outer edge (Vazza et al. 2017; Iapichino et al. 2017) and ram-pressure stripping in between (Domainko et al. 2006; Ebeling et al. 2014; Li et al. 2023) for instance. Internal fluid instabilities may also be important in this context. The ICM is stably stratified against thermal convection (Cavagnolo et al. 2009; Ghirardini et al. 2019) according to the usual Schwarzschild criterion on the entropy gradient ∂rlog(Tρ1 − γ) > 0 (Schwarzschild 1906), with γ being the adiabatic index. However, it is magnetised up to B ∼ 1 − 10 μG (Govoni & Feretti 2004; Ferrari et al. 2008; Botteon et al. 2022). ICM plasma is therefore thought to be in a ‘dilute’ regime where the particles’ mean-free path is much larger (a dozen orders of magnitude) than the particles’ Larmor radius. This ordering introduces an anisotropy with respect to the direction of the local magnetic field: heat and momentum collisionally diffuse primarily along the magnetic field lines and barely across them (Braginskii 1965). In these conditions, Balbus (2001, 2000) showed that the sign of the temperature (and no longer the entropy) gradient dictates the stability of the stratified fluid. In particular, a so-called magneto-thermal instability (MTI) is triggered when the background temperature gradient is in the direction of the gravity, and may excite turbulence. This magnetised buoyancy instability is to dilute plasma what classical thermal convection is to usual gas. As seen from XMM-Newton (Leccardi & Molendi 2008) and Chandra (Simionescu et al. 2011) observations (sometimes combined for a SZ analysis, Shitanishi et al. 2018; Ghirardini et al. 2019), all galaxy clusters exhibit a decreasing temperature profile (though as of a certain radius for relaxed clusters) and should therefore be unstable to the MTI, at least in the halo.
Magnetised buoyancy instabilities such as the MTI and its counterpart, the Heat-flux driven Buoyancy Instability (HBI; triggered when the temperature increases with radius, Quataert 2008), have been theorised two decades ago and their potential relevance in the ICM has been largely emphasised since then (Bogdanović et al. 2009; Balbus & Reynolds 2010; McCourt et al. 2012; Parrish et al. 2012b; Kunz et al. 2012; Latter & Kunz 2012; Berlok & Pessah 2016b). For example, they are thought to drive a substantial magnetic field amplification through a dynamo, and thus making them a serious candidate mechanism for cluster magnetisation. Magnetic seeds in galaxy clusters (e.g. stemming from primordial magnetic fields, Durrer & Neronov 2013) would indeed need to grow by several orders of magnitude to match the strength currently observed in neighbour clusters, although strong enough primordial magnetic seeds could also lead up to the present magnetic strengths through compression only (Jedamzik & Pogosian 2020; see Donnert et al. 2018 for a review on magnetic field amplification in galaxy clusters). Such magnetised buoyancy instabilities remain however somewhat speculative since no observational evidence of their presence has ever been detected. An additional complexity stems from the conservation of the adiabatic invariant 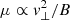 (with v⊥ being the perpendicular component of the particle’s peculiar velocity with respect to the magnetic field B), which drives pressure anisotropy when coupled to changes in magnetic-field strength in high-beta and weakly collisional plasma. Such pressure anisotropies can, when large enough, trigger mirror, firehose, ion-, and electron-cyclotron whistler instabilities (Schekochihin et al. 2005, 2010). The saturation of such micro-scale kinetic instabilities could severely reduce and/or isotropise the heat conductivity (Riquelme et al. 2016; Komarov et al. 2018) and hamper the development of the MTI in the ICM, if not completely annihilate it (Drake et al. 2021); although, recent work by Berlok et al. (2021) tends to show only modest consequences of these micro-instabilities on the MTI saturation.
(with v⊥ being the perpendicular component of the particle’s peculiar velocity with respect to the magnetic field B), which drives pressure anisotropy when coupled to changes in magnetic-field strength in high-beta and weakly collisional plasma. Such pressure anisotropies can, when large enough, trigger mirror, firehose, ion-, and electron-cyclotron whistler instabilities (Schekochihin et al. 2005, 2010). The saturation of such micro-scale kinetic instabilities could severely reduce and/or isotropise the heat conductivity (Riquelme et al. 2016; Komarov et al. 2018) and hamper the development of the MTI in the ICM, if not completely annihilate it (Drake et al. 2021); although, recent work by Berlok et al. (2021) tends to show only modest consequences of these micro-instabilities on the MTI saturation.
Overall, detecting the MTI, if it is present in the ICM and if detectable with future X-ray missions, would be a very interesting step forward, not only from a purely observational perspective to characterise turbulent transport or magnetisation in the ICM, but also from a theoretical and astrophysical plasma physics standpoint. It would open a direct observational window into the physics of dilute and magnetised astrophysical plasmas on large fluid scales, where previous work by Zhuravleva et al. (2019) could only rely on indirect signatures of micro-scale plasma processes such as the enhanced collision rate possibly due to the previously mentioned kinetic instabilities. In that paper, the authors used deep Chandra observations of the Coma cluster to probe the ICM dynamics through X-ray surface brightness fluctuations down to what should be the viscous scale if only Coulomb collisions were responsible of momentum transport. They could not detect any effect of the viscosity at this scale and therefore deduced that the ICM plasma is either subject to enhanced collision rates or to Braginskii anisotropic transport. The interest for such new observational windows goes beyond the ICM because the same plasma regime is also relevant in accretion flows around black holes for instance (Molokov et al. 2007; Sharma et al. 2007). The current study is therefore intended to be a first step towards bridging the gap between theoretical astrophysical plasma studies and future X-ray astronomy observations.
The outline of this paper is as follows. In Sect. 2, we introduce different thermodynamic profile models of the ICM, and we describe the magnetohydrodynamics (MHD) model and the numerical methods used to simulate MTI turbulence, as well as the post-processing pipeline developed to build synthetic observations of the MTI through the X-IFU instrument. We use the X-IFU specifications as defined before the recent design-to-cost exercise (Barret et al. 2016, 2023) as a potential model of a future X-ray spectrometer: it acts as our baseline instrumental configuration throughout this paper. In Sect. 3, we characterise the phenomenological dynamical properties of MTI-driven turbulence expected in the ICM, relying on scaling laws derived recently by Perrone & Latter (2022a,b, respectively PL22a,b hereafter) and on the ICM thermodynamic models previously introduced. The objective of that section is to provide a first estimate of the expected levels of measurable MTI turbulence in the ICM, taking into account various observational effects such as the finite value of the Athena/X-IFU effective collecting area or the cancellation of opposite-sign fluctuations present along the line of sight. In Sect. 4, we present the numerical results from our Braginskii-MHD simulation and discuss the consequences of the discrepancy between numerical and real ICM plasma regimes, and the need for a rescaling of the simulation to perform mock observations. As a prospective exercise that may also prove of interest to theoreticians to fix ideas about the observability of the MTI, we then present two synthetic observations of the MHD simulation scaled in different ways. We qualitatively compare the output velocity and thermodynamic fluctuation fields that can be reconstructed from these observations with the raw input fields from the rescaled simulation. Using one of the two synthetic observations, we observationally constrain the anisotropic nature of the MTI. Our main conclusions are summarised in Sect. 5, where we also stress the caveats or the current work along with its implications for future X-IFU observations. We finally extend the discussion to other sources of anisotropic turbulence in the ICM.
2. Methods and models
In this section, we first present three different thermodynamic profile models of the ICM, which will be used in Sect. 3 to phenomenologically discuss the properties of MTI-driven turbulence in clusters. Based on the expected number of photons from a 2-Ms observation with the X-IFU (which we use as a prospective model of X-ray spectrometer), we also give a criterion to determine an admissible range of radii at which measurement uncertainties due to a lack of photons are expected not to be predominant over the instrumental limitations themselves. We then describe the physical MHD model used to numerically study the development of the MTI up to a state of sustained turbulence. Finally, we present the methods used to build synthetic X-IFU observations of a MHD simulation.
Throughout this work, we assume a universe with a Λ-CDM cosmology and H0 = 70 km s−1Mpc−1, Ωm = 0.3, ΩΛ = 0.7. We set the primordial helium and metal mass abundances to Y = 0.24 and Z = 0.06 respectively. The virial radius R200 is defined as the radius within which the average matter density is 200 times higher that the critical density of the universe ρc = 3H2/(8πG) where H is the Hubble parameter and G the universal gravitational constant. Although this radius varies from a cluster to another, we set it to a standard value of R200 = 1.8 Mpc for all clusters. The symbol −!!z0 (resp. −!!z) denotes the cosmological (resp. cosmological plus Doppler) redshift whereas the letter z always represents a vertical coordinate in Cartesian geometry (in spherical geometry, r is the radial coordinate). v and B respectively stand for the velocity and magnetic field. The unit vector in the direction of the local magnetic field is 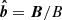 . The pressure, density, temperature and entropy are respectively denoted by p, ρ, T and S = Tρ1 − γ (the adiabatic index γ equals 5/3 for mono-atomic perfect gas). Their respective fluctuations are always preceded by the lower-case Greek δ and expressed in a non-dimensional way:
. The pressure, density, temperature and entropy are respectively denoted by p, ρ, T and S = Tρ1 − γ (the adiabatic index γ equals 5/3 for mono-atomic perfect gas). Their respective fluctuations are always preceded by the lower-case Greek δ and expressed in a non-dimensional way: 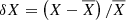 where X is one of the previous thermodynamic quantity and
where X is one of the previous thermodynamic quantity and 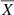 its average at iso-gravity. The letter g stands for the gravity and g0 for its intensity. The thermal diffusivity, the kinematic viscosity and the magnetic resistivity are represented by χ, ν and η respectively. The scale-height of a physical quantity X is HX ≡ (∂r log X)−1. The symbol ⟨ ⋅ ⟩ denotes a spatial average, while the root-mean square of the physical quantity X is defined as
its average at iso-gravity. The letter g stands for the gravity and g0 for its intensity. The thermal diffusivity, the kinematic viscosity and the magnetic resistivity are represented by χ, ν and η respectively. The scale-height of a physical quantity X is HX ≡ (∂r log X)−1. The symbol ⟨ ⋅ ⟩ denotes a spatial average, while the root-mean square of the physical quantity X is defined as 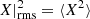 since we systematically assume ⟨X⟩ = 0 for turbulent fluctuations.
since we systematically assume ⟨X⟩ = 0 for turbulent fluctuations.
2.1. Thermodynamic models of ICM
We introduce three different density and temperature profiles that will be later used in Sect. 3 to show that the observable characteristics of MTI-driven turbulence in galaxy clusters are robust against the choice of thermodynamic model. The first density and temperature profiles (in green in Fig. 1) comes from Ghirardini et al. (2019), in which universal thermodynamic profiles are presented for typical cool core (CC) and non-cool core (NCC) galaxy clusters as deduced from a joint X-ray and SZ analysis of a X-COP sample with 12 different clusters. More specifically, we used the functional forms from Sects. 3.2 and 3.4 of their paper along with the best-fit parameters given in their Table 3 for CC galaxy clusters. The reason behind this choice is that dynamically relaxed CC clusters are a priori better suited to detect MTI turbulence than their NCC counterparts whose dynamics at Mpc scales is certainly dictated, or at least polluted, by merger events rather than MHD instabilities. The second profiles (in blue in Fig. 1) are computed from a 1D-spherical model by McCourt et al. (2013), which we have independently reproduced. This model assumes hydrostatic equilibrium of the plasma in a Navarro-Frenk-White gravitational dark matter potential (Navarro et al. 1997) for a type III accretion history (McBride et al. 2009) with a concentration parameter of 5 and no effect of thermal conduction. Finally, as our closest cosmic neighbour, current X-ray missions have dedicated large exposure times to very deep observations of the Perseus cluster (Fabian et al. 2003, 2006), which is a relaxed CC cluster (Simionescu et al. 2011). Perseus-like thermodynamic profiles (in red in Fig. 1) are therefore well suited for this study and we chose them to complete our set of ICM profiles. In practice, we extracted the data corrected for clumping of the Perseus north-west arm, available in Simionescu et al. (2011), and we fitted them with the same functionals as those used in Ghirardini et al. (2019). The detailed form of the three thermodynamic profiles can be found in Appendix A. For the three models, only radii between 0.2 R200 and R200 are considered, as this range ensures that all temperature profiles are decreasing with radius, thus meeting the primary criterion for the MTI to be triggered. The chosen outer radius is equal to the largest radius at which thermodynamic data were available from observation in Simionescu et al. (2011), Ghirardini et al. (2019).
 |
Fig. 1. Density ρ (top) and temperature T (bottom) profiles as a function of radius for three typical ICM models (Ghirardini et al. 2019; McCourt et al. 2013; Simionescu et al. 2011). Only the range with decreasing temperature is shown, until R200. The grey shaded areas highlight radii for which the X-IFU will collect less than two million photons in the 0.2–12 keV energy range during a 2-Ms observation. |
All regions with decreasing temperature are not necessarily bright enough to make their observation in X-ray possible in a reasonable amount of exposure time, even with the large effective collecting area of the Athena/X-IFU (Barret et al. 2016). The plasma emissivity is indeed proportional to the squared density (but also non-trivially depends on the temperature and metallicity; Rybicki & Lightman 1979). Assuming uniform temperature and metallicity fields, the knowledge of the density profile determines the line-of-sight integrated emissivity (i.e. the emission measure Eq. (14)) and therefore the expected number of photons in a certain range of energy for a given exposure time, when combined with the X-IFU effective area. We choose to virtually observe bright enough cluster regions only, which would provide more than 2 × 106 photons in the 0.2 − 12 keV range during a 2-Ms X-IFU observation of a Perseus-like cluster. In our case, it consists in excluding regions beyond 0.6 R200 (grey shaded areas in Fig. 1). Below this threshold (i.e. beyond the latter radius), we consider X-IFU observation impossible because the uncertainties related to the Poisson noise due to a lack of photons certainly exceed the instrumental limitations.
2.2. Numerical MHD model
We now detail the physical numerical MHD model used to study the MTI at saturation. First, the equations and the numerical methods implemented to evolve them are introduced. We then describe the initial hydrostatic equilibrium along with the numerical parameters of our Braginskii-MHD simulation of MTI turbulence.
2.2.1. Equations and numerical methods
The model relies on the usual system of compressible MHD equations in conservative forms, where stratification and non-ideal effects are accounted for; namely magnetic resistivity and anisotropic heat and momentum diffusion. In practice, we use the same equations as in Parrish et al. (2012a) Eqs. (3)–(9) with an additional magnetic resistive term and without the Bremsstrahlung cooling term. This system of equations is closed thanks to the usual equation of state for a perfect gas.
As a consequence of the ICM dilute plasma regime, the transport of heat and momentum is anisotropic with respect to the direction of the local magnetic field. The Braginskii heat flux and viscous stress tensor take the following forms:
where we recall that 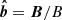 is the unit vector in the direction of the magnetic field.
is the unit vector in the direction of the magnetic field.
These Braginskii-MHD partial differential equations are solved in Cartesian geometry using IDEFIX, a new finite-volume MHD code for astrophysical fluid dynamics (Lesur et al. 2023). Amongst the vast choice of available Riemann-solvers, we selected HLLD associated with a third-order reconstruction scheme which proved to be robust enough. The physical quantities are integrated in time using a third-order Runge-Kutta algorithm. We developed and included two additional physical modules accounting for both the anisotropic heat and momentum diffusions. Standard tests are presented in Appendix B, validating the implementation of the Braginskii operators. All parabolic terms can be integrated explicitly at each time step, but a Runge-Kutta-Legendre (RKL) super time-stepping scheme is also available to speed up this integration. We opted for the latter after making sure that the results we obtained with both RKL and fully explicit integrations were identical for a reduced set of numerical setups.
2.2.2. Simulation configuration and hydrostatic equilibrium
The Braginskii-MHD equations are integrated in a local cubic box of size L = 1.5, with lengths normalised by the sixth of the temperature scale-height HT (i.e. HT/6 = 1 in this setup). The box is thus HT/4 long and spans 25% of the temperature scale-height with 256 points regularly spaced in each direction. Velocities are normalised by the thermal velocity 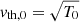 at the bottom of the atmosphere. The magnetic energy is normalised as a kinetic energy and magnetic fields therefore by
at the bottom of the atmosphere. The magnetic energy is normalised as a kinetic energy and magnetic fields therefore by 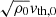 . In these units, times are normalised by t0 = HT/(6vth,0). The simulation is integrated for 100t0 (roughly 8 turnover times, see Sect. 4). The numerical parameters of the setup are the thermal diffusivity χ = 1.5 × 10−2, the Prandtl number Pr = 0.06 and its magnetic counterpart Pm = 4. We also define the magnetic Reynolds number Rm = v|rms/(kiη), where v|rms and ki are respectively the root-mean square velocity and the integral scale that will be determined a posteriori from the simulation.
. In these units, times are normalised by t0 = HT/(6vth,0). The simulation is integrated for 100t0 (roughly 8 turnover times, see Sect. 4). The numerical parameters of the setup are the thermal diffusivity χ = 1.5 × 10−2, the Prandtl number Pr = 0.06 and its magnetic counterpart Pm = 4. We also define the magnetic Reynolds number Rm = v|rms/(kiη), where v|rms and ki are respectively the root-mean square velocity and the integral scale that will be determined a posteriori from the simulation.
In what follows, (ex, ey) is the horizontal plane and −ez the direction of the gravity g = −g0ez. The local model of stratified atmosphere is initialised with the hydrostatic equilibrium from Parrish et al. (2012a):
where T0 and ρ0 are respectively the temperature and density at the bottom of the atmosphere, and α a free non-dimensional parameter controlling the level of stratification. We set α = 2, HT = 6, T0 = ρ0 = 1. All components of the initial velocity field follow a random white noise with an amplitude of 10−4. Both horizontal components of the magnetic field are initialised with an amplitude of 10−5. In the horizontal directions, we chose periodic boundary conditions (BC) for all fields and, in the vertical direction, we implemented a quasi-periodic BC as described by Berlok & Pessah (2016a). This vertical BC allow us to hold both the background hydrostatic equilibria and the background temperature profile all along the simulation, while periodising the velocity, the magnetic field and the thermodynamic perturbations. Thus, we do not need to ‘sandwich’ the MTI-unstable layer between two stable layers with isotropic heat conduction, as usually done in such MTI configurations (PL22b; McCourt et al. 2011; Parrish & Stone 2005).
2.3. Virtual X-IFU observations
We finally sketch how to construct synthetic X-IFU observations from our numerical MHD simulation. The first step is to extract, from a Braginskii-MHD simulation, 3D spatial (x, y, z)-representations of the density, temperature and velocity fields adapted to a mock observation. The procedure is quite technical, and thus described in details in Appendix C.1. The geometrical configuration of the final box is always a parallelepiped rectangle, with equal lengths in the plane of the sky (ey, ez) but elongated along the ex-axis. The latter is assumed to be aligned with the line of sight of the observation and the ez-axis with the cluster’s outward radial direction (see Fig. 2 for an illustrative sketch). Each direction is sampled with 128 different cells, which are therefore not cubic but rather rectangular. Their volume is ℓx × ℓy × ℓz, with ℓy = ℓz < ℓx.
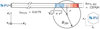 |
Fig. 2. Problem geometry and schematic of statistical fluctuation cancellation for an observation of an ICM at Perseus redshift through the X-IFU, which observes the plane of the sky (ey, ez). The coloured boxes can represent either temperature, density or velocity fluctuations. The colour scale is arbitrary but blue and red tones are of opposite signs, and the more opaque the stronger the fluctuation. The dependency of the fluctuations with y, z is overlooked for clarity. |
Each cell is assumed to radiate in X-ray according to the APEC emission spectrum for collisionally ionised diffuse gas (Smith et al. 2001), with no galactic absorption considered: we checked that taking it into account with the PHABS model and a hydrogen column density of 5 × 1020 cm−2 leads to a decrease in flux only by a factor of two in the 0.2 − 1 keV range and to almost no flux loss beyond 1 keV. A synthetic observation is performed thanks to the E2E simulator SIXTE (Dauser et al. 2019), with a total exposure time of 2 Ms. We refer to this procedure as the forward problem.
Such a virtual observation can be reverse-engineered by fitting the mock spectra in the 0.2 − 12 keV range with the APEC model using the X-ray fitting package XSPEC, after gathering pixels into bins, in order to reconstruct the observed thermodynamic and velocity fields. This procedure is referred to as the inverse problem.
The whole pipeline (sketched in Fig. 3) is somewhat idealised because no background noise, no foreground absorption and no vignetting effects are included. It is however sufficient for the purpose of this exploratory study. More details about the technical work required to solve the forward and inverse problems can be found respectively in Appendices C.2 and C.3.
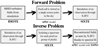 |
Fig. 3. Schematic diagram of the pipeline to build a X-IFU synthetic observation and to reconstruct the physical fields from such an observation: the forward and inverse problems are solved separately. The tool and/or model used at each step is indicated below the respective boxes. |
3. Observational phenomenology of MTI turbulence in the ICM
This section aims at obtaining a first phenomenological estimate of the measurable properties of MTI-driven turbulence in the ICM as a function of the radial coordinate, in terms of both injection length and observable 2D turbulent kinetic and buoyancy potential energies. For this purpose, we make use of the three thermodynamic models presented in Sect. 2.1. Physical quantities in this section are dimensional and either deduced from the local values or from the local scale-heights of the aforementioned thermodynamics models at a given radius. Although those models are global in essence, here they are only used for their local properties (which however vary with radius).
We first introduce the physics of the MTI and of its saturation mechanism. We then present scaling laws for the injection length and for the root-mean square of the 3D velocity and density fluctuation fields of MTI-induced turbulence, theoretically derived by PL22a,b. We finally assess, from an observational point of view, how much the intensity of the measurable 2D fluctuations is affected by the statistical cancellation of 3D fluctuations with opposite signs present along the line of sight. These first results will provide guidance on where to point the X-IFU if we were to detect features of magnetised turbulence induced by the MTI in ICM haloes.
3.1. Physics of the MTI
The simplest MTI-favourable configuration consists in a dynamically negligible horizontal magnetic field threading a plasma layer with temperature gradient and gravity both pointing downwards. When a blob of fluid is subsonically displaced from its initial equilibrium position, it is in pressure equilibrium with its new surrounding but remains thermally connected to its initial neighbours thanks to the dragging of the magnetic field lines. Provided that conduction parallel to the magnetic field is fast enough, the perturbation is then isothermal. A rising blob will then be hotter (and less dense) than the neighbouring fluid and keep rising through buoyancy, triggering the MTI.
There are three ways for this instability to be inhibited, namely through viscous damping, magnetic tension and entropy stratification in a stable atmosphere (with respect to the Schwarzschild criterion), which are specific of short (for the two first effects) and long wavelengths respectively. On scales in between, the MTI can fully develop up to a state of saturated turbulence in the ICM on timescales ∼Gyr, shorter than the Hubble time, with a maximal growth rate 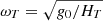 . The MTI way of saturating remains however unclear. PL22a,b argue that the instability saturates in such a way that the energy injected is roughly balanced by anisotropic thermal diffusion at all scales, leading to theoretical scaling laws that they were able to numerically verify for the kinetic and buoyancy potential energies as well as for the injection length. But other authors (Parrish et al. 2012b; McCourt et al. 2013) claim that MTI saturation is best described by a standard convection-like mixing-length theory, which would lead to other dependencies of the kinetic energy on the local or global atmospheric model. It could be that the former saturation mechanism is best suited to describe MTI turbulence on scales smaller than typical ICM scale-heights, while the latter mixing-length theory would describe MTI turbulence on larger scales, with a transition regime occurring in regions where the instability length scale becomes of the order of the temperature scale-height. In this paper, we make intensive use of the scaling laws from PL22a,b, therefore fostering a local approach to MTI turbulence, which we subsequently find to be justified for ICM radii sufficiently small where X-ray emissivity is high enough to make observations possible (see Sect. 3.2); however, global models are needed to eventually settle this debate.
. The MTI way of saturating remains however unclear. PL22a,b argue that the instability saturates in such a way that the energy injected is roughly balanced by anisotropic thermal diffusion at all scales, leading to theoretical scaling laws that they were able to numerically verify for the kinetic and buoyancy potential energies as well as for the injection length. But other authors (Parrish et al. 2012b; McCourt et al. 2013) claim that MTI saturation is best described by a standard convection-like mixing-length theory, which would lead to other dependencies of the kinetic energy on the local or global atmospheric model. It could be that the former saturation mechanism is best suited to describe MTI turbulence on scales smaller than typical ICM scale-heights, while the latter mixing-length theory would describe MTI turbulence on larger scales, with a transition regime occurring in regions where the instability length scale becomes of the order of the temperature scale-height. In this paper, we make intensive use of the scaling laws from PL22a,b, therefore fostering a local approach to MTI turbulence, which we subsequently find to be justified for ICM radii sufficiently small where X-ray emissivity is high enough to make observations possible (see Sect. 3.2); however, global models are needed to eventually settle this debate.
3.2. Length scale of the MTI
The scaling relation derived by PL22a,b for the injection length of MTI-driven turbulence reads:
with N the Brunt-Väisälä frequency of a perfect gas and χ the Spitzer thermal diffusivity1 (Spitzer 1962) respectively defined according to:
where ne is the electron number density. In PL22a,b, Eq. (6) is given without the numerical prefactor but the tabulated data are sufficient to recover it (its value was confirmed by the corresponding author, priv. comm.). As seen in Fig. 4, the MTI injection length is not always small compared to HT, especially beyond 0.6 R200 and this may prevent us from using local models to study MTI dynamics in these regions. We consider that the use of local simulations remains justified to model MTI dynamics at radii below 0.6 R200, as ℓi ≲ 0.5 HT there for the three ICM models. The regions where this criterion is no longer fulfilled are located at large cluster radii, where the previously introduced criterion on the minimal number of photons required for a given exposure time is not met anyway (grey shaded areas in Fig. 1). This further justifies our local approach to MTI turbulence, and the use of the scaling laws from PL22a,b. We note that the expected injection length of MTI-driven turbulence at 0.6 R200 is ∼0.7 Mpc, which is not negligible compared to the injection length typically associated with turbulence driven by mergers, accretion, shocks, etc. In the next subsection, we assess the levels of turbulence induced by the instability.
 |
Fig. 4. Theoretical injection length of turbulence induced by the MTI (top) and the same quantity divided by the local temperature scale-height (bottom) as a function of the radius for three models of ICM. The colour encoding is the same as in Fig. 1. The dash-dotted black line is the X-IFU field of view at Perseus redshift. Again, the grey shaded areas highlight radii at which a X-IFU observation will not provide enough photons. These radii also roughly correspond to regions where the hypothesis of locality for MTI-driven turbulence may break down (and so would the scalings Eqs. (6), (9), and (11)). |
3.3. Turbulence levels of the MTI
To assess the expected levels of turbulence driven by the MTI in the ICM, we use the scaling relations for the root-mean square velocity v|rms and density fluctuations δρ|rms derived in PL22a,b:
While the former relation is provided as such in their paper and dimensionally consistent, the latter is provided without the prefactor, which must be dimensional in this case because of the weaker (to the power 3/4) dependency of the buoyancy potential energy on 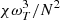 making the right-hand side of Eq. (10) not the dimension of a specific energy. This means that the turbulent saturation of this quantity is controlled by one or several other physical processes as resistivity or viscosity for instance (Perrone, priv. comm.). Such residual dependencies on both the magnetic and the usual Prandtl numbers (Pm = ν/η and Pr = ν/χ respectively) have been numerically highlighted at least in 2D perrone2DPL22a perrone2D. perrone2DPL22a,b Further theoretical and numerical work would be needed to overcome this limitation and to derive the full dependencies. Absent such a fully self-consistent scaling law, we chose to dimensionalise the numerical prefactor, which we determined to be 0.003 thanks to the data available in PL22b, by the root-square of the thermal velocity vth at kBT = 5 keV. This is the easiest way of making this scaling dimensionally consistent without using any MTI-related quantities, which would otherwise introduce unwelcome dependencies of the potential energy on MTI-related parameters that are not seen in the results from PL22a,b. The scaling relation for the buoyancy potential energy finally reads:
making the right-hand side of Eq. (10) not the dimension of a specific energy. This means that the turbulent saturation of this quantity is controlled by one or several other physical processes as resistivity or viscosity for instance (Perrone, priv. comm.). Such residual dependencies on both the magnetic and the usual Prandtl numbers (Pm = ν/η and Pr = ν/χ respectively) have been numerically highlighted at least in 2D perrone2DPL22a perrone2D. perrone2DPL22a,b Further theoretical and numerical work would be needed to overcome this limitation and to derive the full dependencies. Absent such a fully self-consistent scaling law, we chose to dimensionalise the numerical prefactor, which we determined to be 0.003 thanks to the data available in PL22b, by the root-square of the thermal velocity vth at kBT = 5 keV. This is the easiest way of making this scaling dimensionally consistent without using any MTI-related quantities, which would otherwise introduce unwelcome dependencies of the potential energy on MTI-related parameters that are not seen in the results from PL22a,b. The scaling relation for the buoyancy potential energy finally reads:
Equations (9)–(11) translate into moderate values of the root-mean square velocity 𝒪(100 km s−1) (dashed lines on the top plot in Fig. 5) and temperature fluctuations2 𝒪(5%) (full lines on the bottom plot), in the observable regions of interest. According to PL22a,b, the MTI turbulent velocity field at saturation exhibits an anisotropy with respect to the direction of gravity, with the vertical (i.e. radial) component of the velocity being larger than its horizontal (i.e. azimuthal) counterparts. For illustrative purposes, we consider here that the root-mean square of the line-of-sight velocity field (full lines on the top plot in Fig. 5) is smaller than the root-mean square velocity itself by a factor ∼2.5 (this value will be further justified by the simulation in Sect. 4), rather than the usual 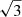 factor for isotropic turbulence. Indeed, X-ray spectrometers like the X-IFU have only access to the line-of-sight velocity because it is deduced from the measurement of the Doppler shift of spectral lines. The relative contribution of the horizontal component of the velocity field to the line-of-sight velocity increases as the X-IFU points further away from the cluster centre, as illustrated in Fig. 2. Indeed, at large ICM radii, the projection of the vertical (i.e. radial) velocity on the line-of-sight direction is weak, especially at locations where the plasma emissivity is high. This geometrical effect has two unfavourable consequences for the possible detection of the MTI. On the one hand, the anisotropy of the kinetic energy components makes the observed line-of-sight velocity, which mostly correlates with the horizontal velocity in cluster haloes, weaker than its purely vertical counterpart and therefore harder to measure. On the other hand, the horizontal velocity does not correlate with density fluctuations; unlike the vertical velocity, due to the convective nature of the instability. Combined together, these two effects might limit the opportunity to detect relevant signatures of the MTI in the ICM. A naive solution to observe the vertical component of the velocity field would be to look at the ICM arbitrarily close to its centre. However, this is not possible since we are aiming at regions with decreasing background temperature in relaxed CC clusters, and central regions are likely more disturbed by AGNs.
factor for isotropic turbulence. Indeed, X-ray spectrometers like the X-IFU have only access to the line-of-sight velocity because it is deduced from the measurement of the Doppler shift of spectral lines. The relative contribution of the horizontal component of the velocity field to the line-of-sight velocity increases as the X-IFU points further away from the cluster centre, as illustrated in Fig. 2. Indeed, at large ICM radii, the projection of the vertical (i.e. radial) velocity on the line-of-sight direction is weak, especially at locations where the plasma emissivity is high. This geometrical effect has two unfavourable consequences for the possible detection of the MTI. On the one hand, the anisotropy of the kinetic energy components makes the observed line-of-sight velocity, which mostly correlates with the horizontal velocity in cluster haloes, weaker than its purely vertical counterpart and therefore harder to measure. On the other hand, the horizontal velocity does not correlate with density fluctuations; unlike the vertical velocity, due to the convective nature of the instability. Combined together, these two effects might limit the opportunity to detect relevant signatures of the MTI in the ICM. A naive solution to observe the vertical component of the velocity field would be to look at the ICM arbitrarily close to its centre. However, this is not possible since we are aiming at regions with decreasing background temperature in relaxed CC clusters, and central regions are likely more disturbed by AGNs.
 |
Fig. 5. Intensity levels of MTI turbulence. Dashed line: root-mean square of the 3D turbulent velocity field as a function of the radius in the ICM. Full line: root-mean square of the 3D turbulent line-of-sight velocity (top) and temperature (bottom) fluctuations. Dotted line: same but for the estimated 2D projected quantities after integration along the line of sight. The dash-dotted black lines are X-IFU detectability limits (determined in Sect. 4) for a typical 2-Ms observation of a Perseus-like cluster at 0.25R200. The colour encoding follows Fig. 1. |
3.4. Observation along the line of sight
The values of the root-mean square fluctuations shown in Fig. 5 (full lines) are for the 3D line-of-sight velocity and the 3D temperature fluctuation fields. However, these 3D fields are not available as such from an observation but their 2D counterparts integrated along the line of sight are because the ICM is optically thin. More precisely, the observed line-of-sight velocity is often assimilated to the emission-weighted velocity (Roncarelli et al. 2018; Cucchetti et al. 2019) and the observed temperature to the spectroscopic temperature (Mazzotta et al. 2004), respectively defined as:
where s is the line-of-sight coordinate (Fig. 2). Accordingly and for later use, we also define the emission measure which tracks the total plasma emissivity:
When observing or integrating along the line of sight, fluctuations with opposite signs will statistically cancel each other, especially when the average size of turbulent eddies is small with respect to the length over which significant emission takes place (which is precisely the length over which the fields should be integrated). We now aim at quantifying the reduction in signal due to this observational effect, illustrated in Fig. 2.
Hints about the behaviour of the root-mean square and dispersion of the emission-weighted velocity and of the second-order velocity structure function after integration along the line of sight can be gained from previous works by Churazov et al. (2012), Zhuravleva et al. (2012), ZuHone et al. (2016), Clerc et al. (2019), and Mohapatra et al. (2022). Many different models have been developed, accounting for the two-dimensionality of the observable fields or the variation of the background thermodynamic fields over the field of view for example. The present phenomenological discussion does not require such sophisticated derivations. So we chose the simplest model, namely the root-mean square velocity along a single line of sight (Eq. (5) from Clerc et al. 2019, which is identical to Eq. (A.9) in Zhuravleva et al. 2012), to infer the decrease in signal due to fluctuation-cancellation along the line of sight. In both equations, the brackets denote an average over independent realisations of a 1D velocity field with the same underlying power spectra. In our case, the assumption made when using this simple model is therefore to assume that the root-mean square of a single realisation of an emission-weighted 2D velocity field is equivalent to the root-mean square of independent realisations of a 1D velocity field, postulating the same underlying power spectra for all processes. Although this hypothesis may not hold in general, we deem the estimates obtained from it sufficiently enlightening as a zeroth-order assessment of the signal reduction due to the cancellation of fluctuations along the line of sight. Using this toy-model for the different density profiles (with the MTI turbulent energy spectra that will be later presented in Sect. 4), we obtain first estimates of the root-mean square emissivity-weighted velocity after integration along the line of sight for MTI-induced turbulence. In the case of temperature fluctuations, the spectroscopic weighting scheme introduces an additional complexity with respect to the simple emissivity weighting. However we checked, thanks to simulated turbulent fields, that the levels of fluctuation-cancellation of temperature fluctuations are similar for both weighting schemes. We therefore use the same toy-model Eq. (5) from Clerc et al. (2019) to anticipate the loss of signal due to the cancellation of fluctuations along the line of sight for both the emissivity-weighted velocity field and the spectroscopic temperature fluctuations. These forecasts are shown as dotted lines in Fig. 5.
The results of this section are well summarised in Fig. 5. The latter overall shows that the root-mean square of the observable spectroscopic temperature fluctuations (dotted lines on the bottom panel) is below the root-mean square of the respective 3D temperature fluctuation field (full lines on the same plot). The only effect responsible for that is the cancellation of opposite-sign fluctuations when observing along the line of sight. The situation is slightly less straightforward in the case of the velocity field. The MTI-driven turbulent 3D velocity field has a pristine root-mean square intensity deduced from Eq. (9) (dashed lines on the top panel in Fig. 5). However, only the line-of-sight component of the velocity field is accessible to an observation. In cluster peripheries, the line of sight is mostly aligned with the azimuthal direction rather than the radial direction (at least wherever the plasma emissivity is higher). As shown in PL22a,b, the MTI saturates in such a way that the vertical component of its velocity field carries most of the total kinetic energy. As a result, the root-mean square of the 3D line-of-sight velocity field (before integration along the line of sight, full lines on the top plot) is ∼2.5 smaller than the pristine root-mean square of the full 3D velocity field (dashed lines on the top plot in Fig. 5). Then, the cancellation of fluctuations along the line of sight brings further down the root-mean square of the emissivity-weighted velocity field (dotted lines on the top panel in Fig. 5). Our analysis suggests that the estimated ratio between the actual root-mean square of a 3D MTI-like fluctuation field and its measurable line-of-sight integrated 2D counterpart ranges from 2.6 to 5.6 according to the density profile used and the ICM radial coordinate. Keeping this phenomenology in mind, we assess in Sect. 4 whether such moderate levels of fluctuations (vew|rms ∼ 10 km s−1,δTs|rms ∼ 0.5% at 0.25R200 in a Perseus-like cluster) would be detectable with our baseline instrumental X-IFU configuration (the corresponding detectability limits are shown in Fig. 5), by modelling the observable ICM magnetised dynamics more quantitatively thanks to a Braginskii-MHD simulation and to X-IFU synthetic observations.
4. Quantitative numerical study with virtual observations
Armed with the previous phenomenological estimates, we now characterise more precisely the statistical properties and the spatial structure of MTI dynamics in the ICM and assess to what extent these characteristics may be recovered from an observation through the X-IFU. For this purpose, we first present diagnostics derived from a local Braginskii-MHD numerical simulation of MTI turbulence. We then discuss the reason why the saturation levels seen in the simulation are not representative of those found in the real ICM by comparing the numerical against ICM plasma regimes, and we rescale the turbulent fluctuation fields of the simulation accordingly. Finally, we perform two X-IFU mock observations of a snapshot of the rescaled MHD simulation in the stage of developed turbulence. We evaluate the quality of the reconstructed fields for each run and we bring to light the inherent anisotropy of MTI-induced turbulence in the second mock observation.
4.1. Simulation of MTI-driven turbulence
The time evolution of key quantities related to the MTI are shown in Fig. 6. In the top panel, the average volume density of the potential, kinetic and magnetic energies during the simulation, respectively defined as 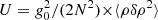 , K = ⟨ρv2⟩/2 and M = ⟨B2⟩/2, are presented. In the linear regime, the MTI displays an exponential growth phase before saturating in a turbulent state. The anisotropy between the vertical and horizontal components of the kinetic energy is quantified by the bias
, K = ⟨ρv2⟩/2 and M = ⟨B2⟩/2, are presented. In the linear regime, the MTI displays an exponential growth phase before saturating in a turbulent state. The anisotropy between the vertical and horizontal components of the kinetic energy is quantified by the bias 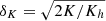 , with Kh = Kx + Ky (bottom panel in Fig. 6), which is higher during the linear growth phase than at saturation, where it settles around 2.5. This is the value we used to convert from v|rms to vlos|rms in Fig. 5 introducing the qualitative phenomenology of MTI observations. This strong anisotropy is a well-known feature of the MTI perrone2D. The instability is indeed driven by the buoyancy and tends to fight its physical origin, namely the temperature gradient. The latter is brought to isothermality via preferentially vertical convection-like fluid motions though the anisotropic conductive heat flux also comes into play in this process. We note that Braginskii-MHD equations with anisotropic viscosity support a fluid version of the firehose instability (Kunz et al. 2012). We do not see such a small-scale instability develop in our simulation, certainly on account of the numerical dissipation at the grid level and of the low magnetic Reynolds number of the simulation.
, with Kh = Kx + Ky (bottom panel in Fig. 6), which is higher during the linear growth phase than at saturation, where it settles around 2.5. This is the value we used to convert from v|rms to vlos|rms in Fig. 5 introducing the qualitative phenomenology of MTI observations. This strong anisotropy is a well-known feature of the MTI perrone2D. The instability is indeed driven by the buoyancy and tends to fight its physical origin, namely the temperature gradient. The latter is brought to isothermality via preferentially vertical convection-like fluid motions though the anisotropic conductive heat flux also comes into play in this process. We note that Braginskii-MHD equations with anisotropic viscosity support a fluid version of the firehose instability (Kunz et al. 2012). We do not see such a small-scale instability develop in our simulation, certainly on account of the numerical dissipation at the grid level and of the low magnetic Reynolds number of the simulation.
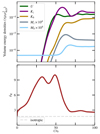 |
Fig. 6. Time evolution of key MTI quantities. Top: potential (in green), vertical (in dark purple), and horizontal (in gold) kinetic energy densities and vertical (in dark blue) and horizontal (in light blue) magnetic energy densities. Bottom: kinetic energy anisotropy |
Although the magnetic field initially grows as a result of the MTI, the magnetic field evolution shows no sign of an exponential kinematic dynamo phase after the MTI saturates because of the value of the magnetic Reynolds number, which is about 5.4 in our simulation. This is below the critical magnetic Reynolds number Rmc = 35 identified by PL22b for the small-scale fluctuation dynamo to initiate a kinematic growth with MTI turbulence. Therefore, the magnetic field strength here never reaches equipartition with the turbulent kinetic energy; unlike in the higher-resolution fiducial run from PL22b which has Rm = 110.
Figure 7 shows key MTI turbulent fields at the very end of the simulation (at t = 100t0): vertical and horizontal snapshots of the velocity and magnetic field norms, and of the fluctuation temperature field. Because the magnetic and velocity fields are divergence-free, the vertical anisotropy related to the different components of the magnetic and kinetic energies reflects into the shape of the turbulent structures which are more elongated along the vertical direction than in the horizontal directions (leftmost and centre slices in Fig. 7). Such an anisotropy is also seen in the temperature fluctuation field (rightmost slices). Another interesting feature of anisotropic heat diffusion is the formation of almost isothermal magnetic field lines with possibly strong temperature gradients across them (rightmost slices in Fig. 7). Observing such temperature fluctuations in the ICM could thus indirectly shed light on the magnetic field geometry, if anisotropic heat flux is active in such plasma.
 |
Fig. 7. Snapshots of MTI turbulent fields at t = 100t0. Top: vertical (x, z) cuts at y = 0.75. Bottom: horizontal (x, y) cuts at z = 0.75. From left to right: norm of the velocity and magnetic fields (in code units) and temperature fluctuations (in % of the background temperature T(z), Eq. (3)). Magnetic field lines are superimposed as black lines on the temperature fluctuations. |
In Fig. 8, we look at the shell-integrated spectral energy volume densities at saturation (at t = 100t0). In the case of the kinetic energy, this quantity is:
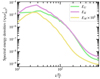 |
Fig. 8. Energy spectra of the potential (green), kinetic (purple) and magnetic (yellow) energy volume densities. |
where 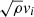 needs to be replaced by Bi for computing the spectra of the magnetic energy. For the potential energy, it is:
needs to be replaced by Bi for computing the spectra of the magnetic energy. For the potential energy, it is:
ℱ is the Fourier transform of the field between brackets and k = kxex + kyey + kzez the wavevector. Taking the Fourier transform of the previous fields is justified here for the x and y coordinates because the BC are periodic in these directions. This is also justified in the vertical z direction here thanks to the quasi-periodic BC which periodises the velocity and magnetic field and, in the case of the thermodynamic fields, their fluctuations rather than the fields themselves. All fields present a typical phenomenological picture of developed turbulence in which energy cascades from larger to smaller scales in spectral space, though on a relatively small range of scales here. The large-scale flow is characterised by the injection scale ℓi, defined as
In the MHD simulation, we have ki ≈ 28L−1, meaning that the injection length is about 22% of the box length. The turnover time ℓi/vrms is therefore ∼13t0.
4.2. Rescaling of the simulation
We aim at making virtual observations at 0.25 R200 in a Perseus-like cluster but the dimensional parallel heat diffusivity used in the simulation χ = 1.5 × 10−2 vth,0HT/6 is roughly two orders of magnitude less than the value expected from the Spitzer diffusivity Eq. (8) at the same radius. We therefore anticipate, from the scaling relation Eq. (9), that the raw dimensional root-mean square velocity in our MHD simulation is one order of magnitude less than what would be found in the ICM. The same argument holds for the potential energy. For instance, Eq. (9) is equal to 14 km s−1 when used with the simulation parameters given in Sect. 2.2.2 and then dimensionalise with the thermal velocity vth,0 of the Perseus cluster at 0.25 R200. But Eq. (9) can also directly be used with the physical parameters deduced from Perseus thermodynamic profiles at the same radius as done in Sect. 3, Fig. 5, in which case we find v|rms ∼ 55 km s−1. Consequently, to make a virtual observation, the fluctuation fields of the simulation first need to be rescaled according to Eqs. (9)–(11) to match the expected intensity of MTI-induced turbulent fluctuations in the realistic ICM diffusion regime. Similarly, the scaling law Eq. (6) predicts the physical injection length of MTI turbulence in the ICM, which is not the one that we see in the simulation (when the lengths are dimensionalised by HT/6) since the simulation is not in the right regime. Equation (6) thus provides a new length scale from which the box size of the MHD simulation can be dimensionalised, by matching the expected physical injection length with the one found in our simulation.
This physically motivated rescaling is always conducted before any synthetic observation is performed in the next section. A peculiar rescaling is fully characterised by the final injection length ℓi and root-mean square of the emission-weighted velocity vew|rms and spectroscopic temperature fluctuations δTs|rms.
4.3. Virtual observations of MTI-induced turbulence with the X-IFU
We now consider the final state (after ∼8 turnover times) of the MHD simulation examined in the previous sections, and virtually observe its rescaled dynamics through the X-IFU according to the methodology described in Sect. 2.3. Solving the forward problem, we obtain a mock observation, which we can then reverse-engineer by solving the inverse problem to reconstruct the emission measure, temperature and velocity fields. In the next sections, we display the maps derived from the synthetic observations. We qualitatively (and quantitatively in the Appendix D) compare them to the respective pristine input data from the rescaled Braginskii-MHD simulation, numerically integrated along the line of sight.
4.3.1. Two synthetic observations
We virtually point the X-IFU at 0.25R200 in a mock galaxy cluster with Perseus-like thermodynamic profiles (ρ ∼ 1.6 × 10−27 g cm−3, T ∼ 6.2 keV, Hρ ∼ 0.3 Mpc, HT ∼ 2.8 Mpc) and at redshift −!!z0 = 0.0179 (the corresponding comoving distance is 77 Mpc). At this cosmological redshift, the field of view of the X-IFU is about fovX − IFU = 120 kpc (see Fig. 4). The mock observation and field reconstruction pipelines are run two times for different input fluctuation fields:
-
In the fiducial observation OBSfid, we take the fluctuation fields from the Braginskii-MHD simulation in the phase of developed turbulence at the very end of the simulation, and rescale their intensities and length scales according to the phenomenological discussion from Sect. 3, Fig. 5. This translates into ℓi ≈ 315 kpc (that is 2.6fovX − IFU), vew|rms ≈ 10 km s−1 and δTs|rms ≈ 0.5%. This run will allow us to formally determine the X-IFU detectability limits that we introduced in the phenomenological discussion from Sect. 3, Fig. 5. We see a posteriori that the fluctuation fields reconstructed from this synthetic observation are too noisy to derive precise physical diagnostics of turbulence. This is why we performed a second virtual observation.
-
Theoretical and observational uncertainties related to the estimates from the phenomenological discussion from Sect. 3 necessarily remain because of all the assumptions that we made. We therefore lead the following formal exercise to better understand what physical information could be deduced from a mock X-IFU observation if the fluctuation fields of the MTI ended up being detectable: we perform a second virtual observation OBScustom, in which the properties of the fluctuation fields are optimally customise. We set ℓi ≈ 84 kpc, vew|rms ≈ 50 km s−1 and δTs|rms ≈ 5%, which ensure that the fluctuation levels are above the X-IFU detectability limits identified in the previous run. OBScustom corresponds to a kind of best-case scenario in which the intensities of the temperature fluctuation and velocity fields are respectively increased by factors of 10 and 5 with respect to the fiducial synthetic observation OBSfid.
In each case, we simulated an observation of 2 Ms. Although such long observations are not currently forecasted with the Athena/X-IFU, we stand by this value for the needs of this formal and prospective exercise. We note that Roncarelli et al. (2018) used similar exposure times. 2 Ms of observation leads to Nph ∼ 15 × 106 photons in the 0.2 − 12 keV range in both cases. Such a total number of photons is quite low given the very large exposure time used, the reason being that we are looking at the cluster periphery where the MTI is expected to grow, rather than its centre as was done, for instance, in Roncarelli et al. (2018) and Cucchetti et al. (2019). Given the small number of photons, pixels need to be gathered into bins using the Voronoi tessellation method (Cappellari & Copin 2003) to obtain satisfying spectral fits. We found that grouping pixels into regions with ∼4 × 104 photons in average was sufficient in this respect. This leads to ∼340 Voronoi regions in total. The extracted spectra are then fitted with the APEC model using the X-ray fitting package XSPEC.
4.3.2. X-IFU maps of integrated and reconstructed quantities
To assess the quality of the 2D fields inferred from a synthetic observation, they should be compared to the actual input 3D physical quantities integrated along the line of sight. We therefore computed the numerical counterparts of the physical quantities Eqs. (12)–(14) from the rescaled MHD simulation on a 2D X-IFU–like grid divided into Voronoi regions:
where i runs over all cells pertaining to a given Voronoi region, therefore summing on cells with close enough position in the sky but possibly very different positions along the line of sight. In the context of subsonic turbulence, we are equally interested in the simulated and observed thermodynamic fluctuations δTs and δEM, whose cumbersome derivation is deferred to Appendix E.
Figure 9 shows X-IFU Voronoi-tesselated maps from the synthetic observation OBSfid, physically motivated by Sect. 3, Fig. 5. The emission measure fluctuation (leftmost maps) and emission-weighted velocity (rightmost maps) fields are partially recovered, although they look very noisy with respect to their respective input maps. In the case of the spectroscopic temperature fluctuations (middle panels), the reconstructed signal is overwhelmed by the observational noise due to both a lack of photons and instrumental limitations. From the quantitative analysis of the biases and standard deviations of the reconstructed output fields with respect to the true input fields presented in Appendix D, we know that the X-IFU detectability limits for a 2-Ms observation at 0.25R200 of the Perseus cluster are about vew|rms,min ∼ 20 km s−1, δT|rms, min ∼ 2%. We note that, even on the ideal input maps from the rescaled MHD simulation (top panels), very few turbulent structures are seen because the MTI injection length at 0.25 R200 in a Perseus-like cluster is 315 kpc, which is 2.6 times larger than the X-IFU field of view.
 |
Fig. 9. Fiducial synthetic observation OBSfid based on the Braginskii-MHD simulation rescaled with the values of Eqs. (6), (9), and (11) at 0.25 R200 in a Perseus-like cluster. From left to right: emission measure fluctuation δEM, spectroscopic temperature fluctuation δTs and emission-weighted velocity vew maps. Top: line-of-sight integrated input fields from the rescaled MHD simulation. Bottom: output fields reconstructed from the synthetic observation OBSfid. The colourbars are set according to the input quantities. The values of the thermodynamic fluctuation fields are given in percents of the average background quantities (see Eq. (E.3)). |
Because of both weak fluctuation intensities and large injection length, OBSfid cannot be used to satisfactorily derive usual physical diagnostics like turbulent spectra or structure functions. We therefore performed the synthetic observation OBScustom with optimally customised parameters to further check our procedures for building mock observation and for reconstructing physical fluctuation fields. We stress that these parameters are not directly motivated by PL22a,b scaling laws. They will however allow us to estimate to which extent the anisotropic structure of MTI turbulence may be constrained with the perturbation fields available from a X-IFU observation. Figure 10 shows that the fluctuation fields reconstructed from OBScustom (for which the root-mean square of the input fluctuation fields now exceed the expected observational noise) are visually well recovered.
 |
Fig. 10. Custom synthetic observation OBScustom (at 0.25 R200 with Perseus density profile), based on the optimally custom-rescaled Braginskii-MHD simulation. From left to right: emission measure fluctuation δEM, spectroscopic temperature fluctuation δTs and emission-weighted velocity vew maps. Top: line-of-sight integrated input fields from the rescaled MHD simulation. Bottom: output fields reconstructed from the synthetic observation OBScustom. The colourbars are set according to the input quantities. The values of the thermodynamic fluctuation fields are in percents of the average background quantities (see Eq. (E.3)). |
Altogether, we now know to which extent the capabilities of the X-IFU would allow us to retrieve, or not, thermodynamic and velocity fluctuations according to their expected intensities. More specifically, the X-IFU detectability thresholds are vew|rms,min ∼ 20 km s−1, δT|rms, min ∼ 2% for a 2-Ms observation of a Perseus-like cluster at 0.25 R200. In the next section, we assess whether a signature of MTI turbulence, namely its anisotropic structure with respect to the direction of the temperature gradient, could be observationally detected if the fluctuation intensities turned out to be higher (by factors of 5–10) than the physical estimates used to scale OBSfid. For this purpose, we use the synthetic observation OBScustom.
4.4. Anisotropic structure functions
We now investigate the detectability of MTI-induced anisotropy in the best-case scenario, represented by the synthetic observation OBScustom. To this end, we introduce the horizontal and vertical second-order structure functions and their ratio:
where X is either δEM or vew, the spatial average runs over the centres c of the Voronoi regions. We set y = z = r in the last equation. We ignore the spectroscopic temperature fluctuations as, in our setup, the physical information they contain is redundant with, and of worse quality than, that found in the emission measure fluctuations. In isotropic turbulence, scalar structure functions does not depend on the particular direction along which they are computed and the quantity ℛX is thus equal to unity at all scales (statistically speaking at least) for any isotropic scalar field X. This ratio provides somehow a measurement of the anisotropic structure of a turbulent field (Rincon 2006). ℛX > 1 indicates that the vertical injection length ℓv is greater than the horizontal injection length ℓh (corresponding to vertically elongated structures) because the second-order horizontal and vertical structure functions 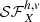 are expected to tend towards 0 for y, z ≪ ℓh, ℓv, towards the same value ⟨X2⟩ when y, z ≫ ℓh, ℓv, and to increase in-between.
are expected to tend towards 0 for y, z ≪ ℓh, ℓv, towards the same value ⟨X2⟩ when y, z ≫ ℓh, ℓv, and to increase in-between.
This new diagnostic is used to characterise the anisotropy of the emission measure fluctuation and emissivity-weighted velocity fields from the best-case synthetic observation OBScustom. All relevant quantities related to this diagnostic are presented in Fig. 11. Dots and stars on the rightmost panels show the ratio ℛX as derived from the input fields of this mock observation (top maps in Fig. 10), and from the reconstructed fields (bottom maps in Fig. 10), on the corresponding Voronoi grid; whereas the horizontal and vertical structure functions 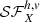 are plotted in the leftmost and centre panels respectively. In all cases but the structure functions of the emission-weighted velocity field, data computed from the input fields of the virtual observation (dots) and from solving the inverse problem (stars) are in broad agreement. This is actually expected when the statistical and systematic errors (gathered into the dispersion σX in this work) are small enough with respect to the quantity X itself, as previously demonstrated by ZuHone et al. (2016), Roncarelli et al. (2018), and Cucchetti et al. (2019) for isotropic second-order structure functions. In the case of the reconstructed emissivity-weighted velocity field from OBScustom, the statistical dispersion σvew with respect to the true input field is of the order of the root-mean square of the true input field. The structure functions computed from the reconstructed emissivity-weighted velocity field (green stars on the leftmost and centre bottom plots in Fig. 11) are therefore uniformly biased with an additional
are plotted in the leftmost and centre panels respectively. In all cases but the structure functions of the emission-weighted velocity field, data computed from the input fields of the virtual observation (dots) and from solving the inverse problem (stars) are in broad agreement. This is actually expected when the statistical and systematic errors (gathered into the dispersion σX in this work) are small enough with respect to the quantity X itself, as previously demonstrated by ZuHone et al. (2016), Roncarelli et al. (2018), and Cucchetti et al. (2019) for isotropic second-order structure functions. In the case of the reconstructed emissivity-weighted velocity field from OBScustom, the statistical dispersion σvew with respect to the true input field is of the order of the root-mean square of the true input field. The structure functions computed from the reconstructed emissivity-weighted velocity field (green stars on the leftmost and centre bottom plots in Fig. 11) are therefore uniformly biased with an additional 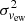 term with respect to the structure functions computed from the true input field (green dots). This effect is independent of the direction in which the structure function is computed, so it does not affect the ratio of the structure functions itself.
term with respect to the structure functions computed from the true input field (green dots). This effect is independent of the direction in which the structure function is computed, so it does not affect the ratio of the structure functions itself.
 |
Fig. 11. Diagnostic tools for probing the anisotropic structure of turbulent fields. From left to right: second-order horizontal and vertical structure functions and their ratios for the emission measure fluctuations (top) and emissivity-weighted velocity (bottom). Full (resp. dashed) lines correspond to the quantities computed from the rescaled MHD simulation on a X-IFU–like (resp. Voronoi) grid with 12 independent MTI turbulent fields. The dots represent the same ratios, but derived from a single rescaled field of the MHD simulation used as input to OBScustom (top maps in Fig. 10). They are naturally noisier than those computed from the statistics of 12 independent fields, but also more anisotropic in average in the case of the emission measure fluctuations. Stars show the ratios as derived from the fields reconstructed from OBScustom (bottom maps in Fig. 10). The y-axis of the leftmost and centre panels showing the structure functions are in arbitrary units but similar for each row, so that the horizontal and vertical structure functions can be directly compared. |
We overall see that the emission measure fluctuation field is relatively anisotropic ℛδEM ≳ 2 while the emission-weighted velocity field is rather isotropic ℛδvew ∼ 1. To check that these specific features are robust against the variance associated with a single realisation of a MTI turbulent field, we accumulated better statistics by computing the same ratios and structure functions (dashed lines in Fig. 11), on the same Voronoi grid, from 3 different snapshots of the simulation at saturation, separated by at least one turnover time. Each snapshot represents, after integration along the line of sight, 4 independent realisations of a MTI turbulent field since ℓi/L ∼ 22% at saturation. We still get ℛδEM ∼ 2. To further check that these specific features does not originate from binning X-IFU pixels into bigger Voronoi regions, we also computed ℛX and 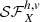 on the original X-IFU grid (full lines in Fig. 11). In this case, the fields from the simulation are first degraded at X-IFU pixel resolution and the average in Eqs. (21) and (22) runs over the centres of X-IFU pixels. Binning pixels into Voronoi regions does not alter the degree of anisotropy seen in the fields, although it slightly changes the shape of the ratio ℛX.
on the original X-IFU grid (full lines in Fig. 11). In this case, the fields from the simulation are first degraded at X-IFU pixel resolution and the average in Eqs. (21) and (22) runs over the centres of X-IFU pixels. Binning pixels into Voronoi regions does not alter the degree of anisotropy seen in the fields, although it slightly changes the shape of the ratio ℛX.
We are therefore able to reliably identify MTI-induced anisotropy in the emission measure fluctuation field with an ideal 2-Ms observation of a Perseus-like cluster at 0.25 R200, if the actual levels of MTI turbulent fluctuations at saturation were to be five to ten times higher than the current theoretical estimates from Sect. 3, Fig. 5. Finally, we note that our technique is broadly applicable to the detection of anisotropic dynamics beyond the case of the MTI.
5. Conclusions and discussion
5.1. Summary and main conclusions
The current work was intended as a first step towards bridging the gap between theoretical astrophysical plasma studies and future X-ray observations with the X-IFU on board the future European X-ray observatory Athena, given the instrumental specifications targeted before the recent design-to-cost exercise (the discussion is extended to present X-ray telescopes later in this section). We characterised the dynamical properties of the MTI, a magnetised buoyancy instability suspected to operate at fluid scales in the ICM (as opposed to micro-scale kinetic instabilities) and conducive to the anisotropic conductive heat flux, and we assessed whether it would be detectable with the X-IFU.
Our main conclusion comes from the combination of the results of Sects. 3 and 4: while the raw physical estimates for MTI fluctuations suggest that they should be detectable, we have shown that several physical and observational factors conspire in a non-trivial, cumulative way to put the actual observational MTI signal close to the X-IFU detectability limits. More specifically, fluctuation fields from a Braginskii-MHD simulation, rescaled in a physically motivated way according to the results of Sect. 3 for a Perseus-like cluster at 0.25 R200, and used as inputs of the 2-Ms synthetic observation OBSfid cannot be satisfactorily recovered (but only marginally so and this was not obvious in the first place). Yet this virtual observation corresponds in many ways to an ideal scenario because of the very large exposure time, as well as the absence of background noise and of any other sources of turbulence but the MTI. Our analysis suggests that MTI-induced turbulence, if it is indeed described by the physical scaling laws of PL22a,b in cluster haloes, would not be detectable in the real ICM, even with the upcoming generation of X-ray spectrometers such as the X-IFU. We identified several effects conspiring to hamper the detectability of MTI turbulence in ICM regions amenable to X-ray observations:
-
The levels of MTI turbulence at saturation, as computed from the scaling laws derived by PL22a,b, are only moderate for radii between 0.2 and 0.6 R200 with v|rms = 𝒪(100 km s−1), δT|rms = 𝒪(5%) for the three different ICM models of thermodynamic profiles.
-
The contribution of the azimuthal (i.e. horizontal) component over the radial (i.e. vertical) component of the velocity field is predominant on the observable line-of-sight velocity in the halo of galaxy clusters, where the MTI can develop. The former is significantly smaller than the latter because of the inherent anisotropy of MTI turbulence with respect to the direction of gravity, the root-mean square of the line-of-sight velocity field is then vlos|rms = 𝒪(50 km s−1). This reduction is stronger than in the case of isotropic turbulence.
-
The root-mean square of the measurable turbulent fluctuations are also lowered because of the statistical cancellation of opposite-sign fluctuations present along the line of sight due to the expected MTI injection scale (∼300 kpc) being smaller than the typical length over which significant emission takes place (≳Mpc). This effect, which has been statistically estimated thanks to Eq. (5) from Clerc et al. (2019), leads to vew|rms = 𝒪(10 km s−1), δT|rms = 𝒪(1%). It is likely to intrinsically limit the ability of current and future X-ray observations to probe small-scale fluctuations of MTI and other types of turbulence, and to measure small-scale spectral energy density below some critical threshold.
-
Finally, there is no robust cross-correlation between the horizontal velocity and the density fluctuations in MTI-induced turbulence, which could otherwise have been exploited if present.
We made some assumptions and used some simplifications when we phenomenologically quantified the observable dynamical properties of the MTI: uncertainties related to the previous estimates necessarily remain. An additional synthetic observation OBScustom was therefore performed to anticipate to what extent the conclusions would differ if the estimations of the observable MTI turbulent levels, as expected from Sect. 3 and Fig. 5, are too weak in reality. We have shown that, when the intensity of the fluctuations is higher than the X-IFU detectability limits, the inherent vertically anisotropic structure of MTI-driven turbulence can be detected in the emission measure fluctuation field as recovered from a 2-Ms observation with the X-IFU. Obviously though, this characteristic is neither a strong observational signature of, nor specific to, the MTI since many other processes could drive anisotropic turbulence in the ICM.
More broadly, our study confirms that directly identifying plasma effects in the internal magnetised dynamics of the ICM remains a difficult observational task given the intrinsic performance of X-ray instrumentation. We further discuss the possible detection of anisotropic MTI dynamics at large fluid scales in Sect. 5.3. Such an enterprise may benefit from the advent of large radio telescopes such as the SKA to combine observations of the ICM dynamics with observations of its magnetic geometry, enabling the use of cross-diagnostics to identify magnetised plasma structures in the ICM.
5.2. Validity of the scaling laws and magnetic feedback
The phenomenological estimates of the measurable length scales and intensities of MTI turbulent fluctuations depicted in Sect. 3 are subservient to the validity of the scaling laws derived in PL22a,b. Though we do believe that these relations hold in regions of galaxy clusters amenable to X-ray observations, on dimensional grounds the scaling for the buoyancy potential energy Eq. (10) is currently incomplete and might be subject to revision before the root-mean square of the density and temperature fluctuations can be self-consistently computed. Furthermore, additional work would be required to determine whether these scaling laws are robust against the development of kinetic instabilities triggered by pressure anisotropy. For instance, a well-known feature of electron-scale instabilities is the reduction and/or isotropisation of the heat flux (Riquelme et al. 2016; Komarov et al. 2018; Drake et al. 2021), which would lower the MTI injection scale according to Eq. (6). The intensity of the MTI thermodynamic and velocity fluctuations would also suffer from such a reduction of the Spitzer conductivity, if we assume Eqs. (9) and (11) to hold as such in the presence of micro-scale kinetic instabilities, thereby further compromising the detection of any relevant MTI signal from an X-IFU observation.
At this stage, it is also relevant to wonder whether (and, if so, how) the structure of MTI turbulence depends on the feedback of the magnetic field on the flow through the Lorentz force when equipartition between magnetic and kinetic energies is reached. This is indeed a difference between the fiducial simulation of PL22b and ours because of the higher viscosity and resistivity we used in our simulation, and which might bias our conclusions on the possible anisotropy of the relevant fluctuation fields. From the PL22b fiducial simulation, it seems that the magnetic feedback tends to make the flow even more anisotropic at equipartition. This peculiarity may, at the same time, lower the intensity of the observable line-of-sight velocity in the outskirts of the ICM, and exacerbate the anisotropy of the density fluctuations, which we were already able to detect with an ideal X-IFU synthetic observation of the Braginskii-MHD simulation yet not at equipartition. In any case, determining whether the MTI drives a dynamo in the ICM requires a clear picture of the ICM effective collisionallity. Such a picture is still currently missing but is under intense theoretical and numerical investigation (Rincon et al. 2016; St-Onge & Kunz 2018; St-Onge et al. 2020; Squire et al. 2019, 2023; Arzamasskiy et al. 2023).
As a final note, we emphasise that the vertical and horizontal injection lengths of MTI-induced turbulence may be subject to different scaling laws, although we assumed Eq. (6) for both. This could also bias the degree of anisotropy of realistic MTI turbulent fields, with respect to those used in this study.
5.3. Future observational strategies
We found that directly detecting features of MTI turbulence in the ICM would be very demanding, even with the X-IFU. Yet what we learnt from trying to do so and what this implies for future observations are worth discussing. A possible observational strategy for the detection of MTI-driven turbulence could be to aim the instrument at the Perseus cluster and build a mosaic of X-IFU maps with a shorter exposure time for each observation. Given the large injection length expected for MTI-driven turbulence, ∼34 Voronoi regions (instead of ∼340 currently) seem enough to satisfactorily map the X-IFU field of view without degrading the spatial resolution of the observed field too much. Assuming the same cumulated exposure time and signal-to-noise ratio requirement, ten observations of 200 ks each would roughly lead to the same total number of Voronoi regions with an average global effective field of view about three times that of X-IFU. The ratio between MTI injection length and such a global field of view would then be about ∼0.9, which is quite close to the ratio of 0.7 used in the virtual observation OSBcustom, partially justifying the approach adopted for prospective purposes in the last synthetic observation, at least in terms of the injection scale (providing similar arguments to justify the boost of the velocity and thermodynamic fluctuations is more challenging, as discussed in Sect. 5.2). In addition, this strategy would offer some flexibility in the choice of the pointing configuration, which could then be optimised for the detection of MTI turbulent features, as explored by ZuHone et al. (2016) with Hitomi in the case of isotropic turbulence.
We have shown that the MTI-driven anisotropy is better inscribed in the emission measure (i.e. density) fluctuations than in the emissivity-weighted velocity field, in the periphery of galaxy clusters at least. The detection of such density perturbations does not require X-ray spectrometers. However, we argue that current XMM-Newton, Chandra, and XRISM observatories would not collect enough photons with a reasonable exposure time to probe the anisotropic dynamics of the faint cluster haloes. The next generation of X-ray telescopes such as the Athena/X-IFU will increase the photon collecting area by a factor ∼10 relative to current X-ray missions. They will therefore provide key observations of dim ICM outskirts, precisely in those regions most favourable to the development of the MTI.
5.4. Competing sources of anisotropic turbulence in the ICM
The MTI is not the only source of anisotropic turbulence in the ICM. We now discuss the role of stable entropy stratification and accretion in this context.
Using idealised high-resolution simulations of compressible or solenoidal stratified turbulence, Mohapatra et al. (2020, 2021) were able to numerically relate the ratio between the root-mean square of the vertical vz|rms and the horizontal vh|rms velocity with the Froude number. The latter is defined as Fr = v|rms/(ℓiN) and compares the timescales associated with the turbulence and with the stratification. Injecting the scaling laws from PL22a,b, we find Fr ≈ 0.15ωT/N for MTI-driven turbulence, which is about ∼0.1 in regions of galaxy clusters amenable to X-IFU observations. This estimation lies right in the range that Mohapatra et al. (2020, 2021) identified as the more susceptible to the effects of stratification. In their simulations, the turbulent forcing is however isotropic (or, in some cases, perpendicular to the direction of gravity): MTI-induced turbulence exhibits a different structure and may not be subject to the exact same physics in the presence of strong entropy stratification. At this stage, it is still unclear whether the stable stratification will isotropise MTI turbulence, in the stratification regime relevant to the ICM (Fr ∼ 0.1), or whether it will stay vertically anisotropic, on account of its convective nature. Some clues can however be gained from our simulation and from the most stratified MTI run in PL22b, which used N ≈ 0.8ωT, Fr ∼ 0.2 and N = ωT, Fr ∼ 0.15, respectively, and are therefore not too far from real ICM stratification regimes. These simulations suggest that the MTI vertical anisotropy remains active despite the strong entropy stratification. Further progress on this question would require additional high-resolution numerical simulations of strongly stratified MTI turbulence, in the regime relevant to the ICM.
On the other hand, Simonte et al. (2022) and Vazza et al. (2018) argue that local simulations of stratified turbulence are too idealised and that, in real clusters, global accretion drives, preferentially, radial turbulence with enough momentum and energy to overcome the effect of the stable stratification. Accretion could thus be another relevant source of vertical anisotropy in the ICM. However, with this turbulent forcing being compressible with Mach numbers ≳0.3, the velocity field is no longer divergence-free and the anisotropy between the radial and azimuthal kinetic energies may reflect less on the structure of the turbulent eddies.
High-resolution global simulations including MTI and other magnetised plasma effects, internal stirring mechanisms, and accretion-driven turbulence are needed to analyse, more precisely, the competition between different sources of turbulence in the ICM and to draw a clearer picture of the ICM internal dynamics in the outskirts of galaxy clusters. Such global MHD simulations could also be virtually observed through the X-IFU, and their internal dynamics reconstructed, to assess what turbulent components dominate and could be identified with a mock observation. Previous larger-scale cosmological style simulations with anisotropic heat conduction failed to shed light on any distinctive MTI flow in cluster peripheries (Ruszkowski et al. 2011). PL22a,b however clearly showed that MTI saturation is very dependent on the level of parallel thermal diffusivity used. Care should therefore be taken to simulate the right anisotropic diffusive regime and to control perpendicular numerical dissipation as much as possible if one wants to detect any MTI flow in such simulations of structure formation.
Acknowledgments
The authors are grateful to CNES for financial support provided by Didier Barret for the internships of J.M.K. during which a major part of this work was conducted. J.M.K. is thankful for the organisation of the SIXTE workshops by the development team, allowing him a smooth start with the software. The work benefited from very fruitful exchanges with Lorenzo Perrone, Henrik Latter, Simon Dupourqué and Alexeï Molin. The authors also thank Geoffroy Lesur for giving them access to a beta version of IDEFIX and for his support in the integration of the Braginskii physical modules. This work was granted access to the HPC resources of CALMIP under allocation 2021/2022-P16006 and the authors thank the associated support team. We are finally grateful for the generous hospitality of the Wolfgang Pauli Institute, Vienna, where preliminary results were discussed during the 2022 Plasma Kinetics workshop.
References
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Angelinelli, M., Vazza, F., Giocoli, C., et al. 2020, MNRAS, 495, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Arzamasskiy, L., Kunz, M. W., Squire, J., Quataert, E., & Schekochihin, A. A. 2023, Phys. Rev. X, 13, 021014 [NASA ADS] [Google Scholar]
- Balbus, S. A. 2000, ApJ, 534, 420 [CrossRef] [Google Scholar]
- Balbus, S. A. 2001, ApJ, 562, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Reynolds, C. S. 2010, ApJ, 720, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Albouys, V., Herder, J.-W. D., et al. 2023, Exp. Astron., 55, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Trong, T. L., Den Herder, J.-W., et al. 2016, Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray (SPIE), 9905, 714 [Google Scholar]
- Berlok, T., & Pessah, M. E. 2016a, ApJ, 833, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Berlok, T., & Pessah, M. E. 2016b, ApJ, 824, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Berlok, T., Quataert, E., Pessah, M. E., & Pfrommer, C. 2021, MNRAS, 504, 3435 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanović, T., Reynolds, C. S., Balbus, S. A., & Parrish, I. J. 2009, ApJ, 704, 211 [CrossRef] [Google Scholar]
- Botteon, A., van Weeren, R. J., Brunetti, G., et al. 2022, Sci. Adv., 8, eabq7623 [NASA ADS] [CrossRef] [Google Scholar]
- Braginskii, S. 1965, Rev. plasma Phys., 1, 205 [NASA ADS] [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [Google Scholar]
- Churazov, E., Vikhlinin, A., Zhuravleva, I., et al. 2012, MNRAS, 421, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Clerc, N., Cucchetti, E., Pointecouteau, E., & Peille, P. 2019, A&A, 629, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conroy, C., & Ostriker, J. P. 2008, ApJ, 681, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Cucchetti, E., Clerc, N., Pointecouteau, E., Peille, P., & Pajot, F. 2019, A&A, 629, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dauser, T., Falkner, S., Lorenz, M., et al. 2019, A&A, 630, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domainko, W., Mair, M., Kapferer, W., et al. 2006, A&A, 452, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donnert, J., Vazza, F., Brüggen, M., & ZuHone, J. 2018, Space Sci. Rev., 214, 122 [Google Scholar]
- Drake, J. F., Pfrommer, C., Reynolds, C. S., et al. 2021, ApJ, 923, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Dupourqué, S., Clerc, N., Pointecouteau, E., et al. 2023, A&A, 673, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durrer, R., & Neronov, A. 2013, A&ARv, 21, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Stephenson, L. N., & Edge, A. C. 2014, ApJ, 781, L40 [Google Scholar]
- Eckert, D., Ghirardini, V., Ettori, S., et al. 2019, A&A, 621, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Sanders, J. S., Allen, S. W., et al. 2003, MNRAS, 344, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Sanders, J. S., Taylor, G. B., et al. 2006, MNRAS, 366, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., & Rephaeli, Y. 2008, Space Sci. Rev., 134, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirardini, V., Eckert, D., Ettori, S., et al. 2019, A&A, 621, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gitti, M., Brighenti, F., & McNamara, B. R. 2012, Adv. Astron., 2012, 950641 [CrossRef] [Google Scholar]
- Govoni, F., & Feretti, L. 2004, Int. J. Mod. Phys. D, 13, 1549 [Google Scholar]
- Hitomi Collaboration (Aharonian, F., et al.) 2016, Nature, 535, 117 [Google Scholar]
- Hitomi Collaboration (Aharonian, F., et al.) 2018, PASJ, 70, 9 [NASA ADS] [Google Scholar]
- Hofmann, F., Sanders, J. S., Nandra, K., Clerc, N., & Gaspari, M. 2016, A&A, 585, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iapichino, L., Federrath, C., & Klessen, R. S. 2017, MNRAS, 469, 3641 [NASA ADS] [CrossRef] [Google Scholar]
- Ishisaki, Y., Ezoe, Y., Yamada, S., et al. 2018, J. Low Temp. Phys., 193, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Jedamzik, K., & Pogosian, L. 2020, Phys. Rev. Lett., 125, 181302 [NASA ADS] [CrossRef] [Google Scholar]
- Komarov, S., Schekochihin, A. A., Churazov, E., & Spitkovsky, A. 2018, J. Plasma Phys., 84, 905840305 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. W., Bogdanović, T., Reynolds, C. S., & Stone, J. M. 2012, ApJ, 754, 122 [CrossRef] [Google Scholar]
- Latter, H. N., & Kunz, M. W. 2012, MNRAS, 423, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Leccardi, A., & Molendi, S. 2008, A&A, 486, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G. R. J., Baghdadi, S., Wafflard-Fernandez, G., et al. 2023, A&A, 677, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, Y., Luo, R., Fossati, M., Sun, M., & Jáchym, P. 2023, MNRAS, 521, 4785 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzotta, P., Rasia, E., Moscardini, L., & Tormen, G. 2004, MNRAS, 354, 10 [NASA ADS] [CrossRef] [Google Scholar]
- McBride, J., Fakhouri, O., & Ma, C.-P. 2009, MNRAS, 398, 1858 [NASA ADS] [CrossRef] [Google Scholar]
- McCourt, M., Parrish, I. J., Sharma, P., & Quataert, E. 2011, MNRAS, 413, 1295 [NASA ADS] [CrossRef] [Google Scholar]
- McCourt, M., Sharma, P., Quataert, E., & Parrish, I. J. 2012, MNRAS, 419, 3319 [NASA ADS] [CrossRef] [Google Scholar]
- McCourt, M., Quataert, E., & Parrish, I. J. 2013, MNRAS, 432, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Mohapatra, R., Federrath, C., & Sharma, P. 2020, MNRAS, 493, 5838 [NASA ADS] [CrossRef] [Google Scholar]
- Mohapatra, R., Federrath, C., & Sharma, P. 2021, MNRAS, 500, 5072 [Google Scholar]
- Mohapatra, R., Jetti, M., Sharma, P., & Federrath, C. 2022, MNRAS, 510, 2327 [NASA ADS] [CrossRef] [Google Scholar]
- Molokov, S., Moreau, R., & Moffatt, H. K. 2007, Magnetohydrodynamics: Historical Evolution and Trends (Dordrecht, The Netherlands: Springer) [CrossRef] [Google Scholar]
- Mroczkowski, T., Nagai, D., Basu, K., et al. 2019, Space Sci. Rev., 215, 17 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Parrish, I. J., & Stone, J. M. 2005, ApJ, 633, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Parrish, I. J., McCourt, M., Quataert, E., & Sharma, P. 2012a, MNRAS, 419, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Parrish, I. J., McCourt, M., Quataert, E., & Sharma, P. 2012b, MNRAS, 422, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Perrone, L. M., & Latter, H. 2022a, MNRAS, 513, 4605 [NASA ADS] [CrossRef] [Google Scholar]
- Perrone, L. M., & Latter, H. 2022b, MNRAS, 513, 4625 [NASA ADS] [CrossRef] [Google Scholar]
- Pratt, G. W., Arnaud, M., Biviano, A., et al. 2019, Space Sci. Rev., 215, 25 [Google Scholar]
- Quataert, E. 2008, ApJ, 673, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Rincon, F. 2006, J. Fluid Mech., 563, 43 [Google Scholar]
- Rincon, F., Califano, F., Schekochihin, A. A., & Valentini, F. 2016, Proc. Nat. Acad. Sci., 113, 3950 [NASA ADS] [CrossRef] [Google Scholar]
- Riquelme, M. A., Quataert, E., & Verscharen, D. 2016, ApJ, 824, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Roncarelli, M., Gaspari, M., Ettori, S., et al. 2018, A&A, 618, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruszkowski, M., Lee, D., Brüggen, M., Parrish, I., & Oh, S. P. 2011, ApJ, 740, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley) [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Kulsrud, R. M., Hammett, G. W., & Sharma, P. 2005, ApJ, 629, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Rincon, F., & Rosin, M. S. 2010, MNRAS, 405, 291 [NASA ADS] [Google Scholar]
- Schwarzschild, K. 1906, Math.-phys. Klasse, 195, 41 [NASA ADS] [Google Scholar]
- Sharma, P., & Hammett, G. W. 2007, J. Comput. Phys., 227, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, P., Quataert, E., Hammett, G. W., & Stone, J. M. 2007, ApJ, 667, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, X., Komatsu, E., Nagai, D., & Lau, E. T. 2016, MNRAS, 455, 2936 [NASA ADS] [CrossRef] [Google Scholar]
- Shitanishi, J. A., Pierpaoli, E., Sayers, J., et al. 2018, MNRAS, 481, 749 [CrossRef] [Google Scholar]
- Simionescu, A., Allen, S. W., Mantz, A., et al. 2011, Science, 331, 1576 [Google Scholar]
- Simionescu, A., ZuHone, J., Zhuravleva, I., et al. 2019, Space Sci. Rev., 215, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Simonte, M., Vazza, F., Brighenti, F., et al. 2022, A&A, 658, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [Google Scholar]
- Spitzer, L. 1962, Physics of Fully Ionized Gases (New York: Interscience) [Google Scholar]
- Squire, J., Schekochihin, A. A., Quataert, E., & Kunz, M. W. 2019, J. Plasma Phys., 85, 905850114 [NASA ADS] [CrossRef] [Google Scholar]
- Squire, J., Kunz, M. W., Arzamasskiy, L., et al. 2023, J. Plasma Phys., 89, 905890417 [NASA ADS] [CrossRef] [Google Scholar]
- St-Onge, D. A., & Kunz, M. W. 2018, ApJ, 863, L25 [CrossRef] [Google Scholar]
- St-Onge, D. A., Kunz, M. W., Squire, J., & Schekochihin, A. A. 2020, J. Plasma Phys., 86, 905860503 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Jones, T. W., Brüggen, M., et al. 2017, MNRAS, 464, 210 [Google Scholar]
- Vazza, F., Angelinelli, M., Jones, T. W., et al. 2018, MNRAS, 481, L120 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [Google Scholar]
- Zeldovich, Y. B., & Sunyaev, R. A. 1969, Ap&SS, 4, 301 [Google Scholar]
- Zhuravleva, I., Churazov, E., Kravtsov, A., & Sunyaev, R. 2012, MNRAS, 422, 2712 [NASA ADS] [CrossRef] [Google Scholar]
- Zhuravleva, I., Churazov, E., Schekochihin, A. A., et al. 2014, Nature, 515, 85 [Google Scholar]
- Zhuravleva, I., Churazov, E., Arévalo, P., et al. 2015, MNRAS, 450, 4184 [NASA ADS] [CrossRef] [Google Scholar]
- Zhuravleva, I., Allen, S. W., Mantz, A., & Werner, N. 2018, ApJ, 865, 53 [CrossRef] [Google Scholar]
- Zhuravleva, I., Churazov, E., Schekochihin, A. A., et al. 2019, Nat. Astron., 3, 832 [Google Scholar]
- ZuHone, J. A., Markevitch, M., & Zhuravleva, I. 2016, ApJ, 817, 110 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Thermodynamic profiles
All thermodynamic profiles presented in Section 2 and used to derive the properties of MTI-induced turbulence in Section 3 can be parametrised as (Vikhlinin et al. 2006; Ghirardini et al. 2019):
with x = r/R500, T500 = 5 keV and where we simply set R500 = 1.1 Mpc for all clusters. All the other quantities are parameters to fit. For the universal thermodynamic profiles from Ghirardini et al. (2019), the best-fit parameter values from that paper for CC clusters are directly used. Fits are performed for Perseus temperature and density profiles (Simionescu et al. 2011), but also for the 1D-spherical accretion model of McCourt et al. (2013) since the data resulting from the numerical integration of this model are not perfectly robust against numerical derivation (which we need to obtain the local scale-height of the different atmospheres). In the case of the density, the fit is not performed on the data but rather on their logarithm, so that the weak tail of the density profiles are well fitted too. The best parameter values are given in Table A.1 for the different profiles. We do not fit the data from the different entropy profiles. Instead, we assume perfect hydrostatic equilibrium to deduce the entropy scale-height from the temperature and density scale-heights:
Set of parameters for the temperature and density profiles of the different thermodynamic models of ICM.
Appendix B: Validation of the Braginskii operators in IDEFIX
We implemented the parabolic operator for anisotropic heat diffusion Eq. (1) with the centred asymmetric scheme described in Sharma & Hammett (2007, Section 2.1), though without harmonic mean nor slope limiter. The Braginskii viscosity Eq. (2) is implemented in a similar way, again without any slope limiter. The implementation of these operators in IDEFIX is validated thanks to the methodology and setups described in Parrish et al. (2012a, Sections 3,4). The linear growth rates of both MTI and
HBI diagonal modes that we numerically measured are compared with the theoretical values expected from the dispersion relation.
For the MTI setup, the tests are run in 2D (ey,ez) at either low or high resolution (642 and 2562, respectively the stars and the dots in Fig. B.1) in a square box of size L = 0.1. Lengths are normalised by the third of the temperature scale-height, velocities and magnetic fields respectively by the thermal velocity vth,0 at the bottom of the atmosphere and by 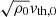 . The atmosphere is initialised according to the hydrostatic equilibrium described by Eqs. (3-5) with α = 1 and HT = 3. We initially seed both components of the velocity field with a fundamental divergence-free diagonal eigenmode ∝exp(σt+i[kyy+kzz]) with an amplitude of 10−4 and where ky = kz = 2π/L. The kinematic viscosity ν is based on the thermal diffusivity through the Prandtl number Pr = {0;0.01;0.06} (respectively the blue, green and red curves and points in Fig. B.1).
. The atmosphere is initialised according to the hydrostatic equilibrium described by Eqs. (3-5) with α = 1 and HT = 3. We initially seed both components of the velocity field with a fundamental divergence-free diagonal eigenmode ∝exp(σt+i[kyy+kzz]) with an amplitude of 10−4 and where ky = kz = 2π/L. The kinematic viscosity ν is based on the thermal diffusivity through the Prandtl number Pr = {0;0.01;0.06} (respectively the blue, green and red curves and points in Fig. B.1).
 |
Fig. B.1. Comparison between the MTI (top) and HBI (bottom) linear growth rates numerically measured and theoretically computed thanks to the dispersion relations. The initial velocity perturbation is a fundamental divergence-free diagonal mode (ky = kz = 2π/L) with amplitude 10−4. Different colour tones are for the different Prandtl numbers. Runs with resolution 642 and 2562 are represented by stars and dots. |
The runs are initialised with a purely horizontal magnetic field By, 0 = 10−5. In this configuration, the dispersion relation is:
Regarding the HBI setup, the runs are performed in a box with L = 0.2, HT = 2 and with the same hydrostatic equilibria as Parrish et al. (2012a) in the corresponding local HBI runs (Section 4.1 in that paper). The magnetic field is initialised vertically with Bz, 0 = 10−5 while the initial velocity field is the same than in the MTI runs. The dispersion relation is then:
We successfully tried other 2D configurations with higher-order harmonic modes as well as 3D setups with the gravity set artificially along the ex- or ey-axis to check that the operators are correctly implemented in all directions.
Appendix C: Building X-IFU mock observations
In this Appendix, we compile technical details about the post-processing observational pipeline. The first subsection is specific to our MHD simulation since it describes how to convert its outputs to a (x, y, z)-spatial representation of the density, temperature and velocity fields suited to mock observations. The second and third subsections are more generic in the sense that they indicate how to solve the forward and inverse problems, once the spatial representation of the different fields has been built.
C.1. Designing boxes adapted to synthetic observations
In this section, we elaborate on how to build, from the Braginskii-MHD simulation, a spatial (x, y, z)-representation of the density ρ, temperature T and velocity vlos adapted to a mock observation through the X-IFU with SIXTE. First, the physical box size L is set by matching the numerical injection length in the simulation with the chosen dimensional integral length of MTI-driven turbulence, which is either picked from Eq. (6) for OBSfid or customised for OBScustom. In the same manner, the fluctuation amplitudes from the MHD simulation at t = 100t0 are rescaled in such a way that their root-mean square match the requested values, deduced from Section 3, Fig. 5 for OBSfid or again custom-picked for OBScustom.
Next, we extract the fluctuation fields of the rescaled MHD simulation in the parallelepiped rectangle extending over the whole box along the line of sight (i.e. the ex-axis), centred on the centre of the box in the (ey,ez) plane and extending over 1.1 × fovX − IFU at least (about 130 kpc at −!!z0 = 0.0179) in this plane. In practice, this translates into a parallelepiped rectangle with 256 × n2 cells from the MHD simulation, where n = ⌈256 × 1.1 × fovX − IFU/L⌉ is the number of extracted cells in one direction ey or ez of the sky plane. But virtually observing an ICM-like resolved and extended X-ray source with SIXTE requires that the field of view of a single observing pixel contains enough individual source points. For instance, in the work of Roncarelli et al. (2018), one X-IFU pixel encompassed ∼8 cells from their simulation. We find that ∼4 simulation cells per X-IFU pixel are enough to properly run our observational pipeline. It is possible that the number of cells extracted from the MHD simulation in a single direction of the sky plane is less than ∼2 per X-IFU pixel, depending on the dimensional injection length chosen to set the size of the simulation box. In such cases (in which both OBScustom and OBSfid lie), the extracted fluctuation fields need to be interpolated on a new grid with 128 cells in each direction, so that ∼4 cells lie in the field of view of one X-IFU pixel as illustrated in Fig. C.1. This is why the final cells with volume ℓx × ℓy × ℓz are no longer cubic but rectangular with ℓy = ℓz < ℓx.
 |
Fig. C.1. Schematic of the different grids used in the observational pipeline. The relative sizes of the grids are consistent with respect to each other: there is almost one cell from the MHD simulation grid (full grey lines, left), after rescaling of the box as in OBScustom, in a X-IFU pixel (black dashed lines, left) and there are ∼4 cells of the finer grid (light blue lines, right), refined from the MHD simulation grid within the dotted red square and used for the synthetic observation, in a pixel of X-IFU. For the sake of clarity, the absolute sizes of the grids are however not to scale. For instance, there should be 3168 pixels in X-IFU’s hexagon (in our baseline instrumental configuration) instead of ∼30 on the schema, in which X-IFU border pixels are not squared whereas they should be as well in reality. |
For both OBSfid and OBScustom, the length L over which the cells are stacked in the line-of-sight direction (which is the physical length of the simulation box) may be smaller than the length scale over which significant emission takes place at 0.25R200 in Perseus. We therefore rescale the integrated emissivity in the box in such a way that it matches the expected value from the integration of the squared density over the full line of sight, that is the total plasma emissivity (i.e. the emission measure) at 0.25R200 in Perseus. This rescaling does not affect the root-mean square of the fluctuations after integration over the full line of sight themselves because the latter is self-consistently computed thanks to the toy-model Eq. (5) in Clerc et al. (2019; dotted lines in Fig. 5), and the amplitude of the fluctuation fields rescaled accordingly.
At this stage, we stress that only the fluctuations of the thermodynamic fields, and not the global (background plus fluctuation) thermodynamic fields, are extracted from the MHD simulation and rescaled. The case of the velocity is different from the case of the thermodynamic fields since there is no bulk motion in the simulation and the field fluctuates around a zero average value. So we still need a proxy for the background temperature and density profiles by which the thermodynamic fluctuations will be weighted before being virtually observed. We chose the following local expression:
with X = T, ρ and where HX is derived from the Perseus thermodynamic profiles presented in 2.1. With this choice, we are actually neglecting the cluster curvature by assuming a purely vertical dependency of the thermodynamic background profiles. With this hypothesis, the error made on the background temperature and density is less than 1% when looking at 0.25R200 of a cluster at Perseus redshift. However this error can grow up to 10% for a similar density profile at −!!z0 ≳ 0.08. At higher redshift, the methodology later described in Appendix E to isolate the fluctuations from the global fields can no longer be used as such, and should be modified to account for the cluster curvature.
C.2. Forward problem
The purpose of the observation simulator SIXTE is essentially to create a photon list from a catalogue of point sources in the sky, according to the specifications of the instrument chosen for the virtual observation. A straightforward way to simulate the mock observation of an extended and resolved astrophysical source is to regard it as a collection of independent point sources More specifically, the initial spatial (x, y, z)-representation of the density, temperature and velocity fields need to be converted to a hybrid (y, z, E)-representation of the ideal spectra as a function of the sky position (y, z), and where the energy variable E ranges uniformly from 0.2 to 12 keV, covering the X-IFU energy range with a 1-eV resolution. Each cell of this spatial representation is given a set of coordinates on the sky plane (ey,ez) according to the position of its centre in the mock cluster (there are 128 cells stacked in the line-of-sight direction ex, all with the same sky coordinates). Its X-ray line and Bremsstrahlung emission is modelled thanks to the APEC emission spectrum for collisionally-ionised diffuse gas (Smith et al. 2001). After summing the spectra along the line of sight ex, we recover a hybrid (y, z, E) representation by placing each integrated spectrum at its corresponding sky position. This catalogue of point sources is the input to the SIXTE simulator, which eventually leads to a mock observation of the ICM. In this process, the important instrumental and geometrical effects taken into account are the PSF, the response function, the detector geometry and its pixel filling-factor (∼97%). Cross-talk and pile-up effects are simulated as well but marginal in our case, hence not accounted for in the post-processing step. More details about the SIXTE software and the response matrices of our baseline instrumental X-IFU configuration can respectively be found in Dauser et al. (2019)3 and in Barret et al. (2016)4. Our setup does not simulate the vignetting. Therefore, the same response function can be used for all group of pixels in the post-processing step regardless of their off-axis position.
The APEC model takes the metal abundance Z, the electron temperature kBT, the redshift −!!z and the norm 𝒩 as parameters. While the temperature is a direct output of the MHD simulation, the chemical abundance is not self-consistently computed and we simply assume a uniform metal abundance Z = 0.3Z⊙ for the modelling of the spectra, with Z⊙ the solar value measured by Anders & Grevesse (1989). The line-of-sight velocity field vlos = vx is encoded in the redshift according to:
with c the speed of light in vacuum. The norm is expressed as:
where ne and nH, the electron and hydrogen number densities, are deduced from the density given the primordial abundances considered, dc(−!!z) is the comoving distance and 𝒱 = ℓxℓyℓz.
C.3. Inverse problem
Solving the inverse problem is to reverse-engineer the virtual observation in order to recover the thermodynamic and velocity fields. We recall that, for each observation, we divide the X-IFU grid into ∼340 Voronoi regions, from which a spectrum is extracted. These spectra are then fitted with the APEC model using the X-ray fitting package XSPEC. The spectral fit is done by minimising the Cash statistic (Cash 1979) and without any a priori knowledge of the fitting parameters but the cluster cosmological redshift −!!z0. Since no vignetting effect is simulated in the forward problem, the same Ancillary Response File (ARF) is used for all Voronoi regions irrespective of their positions. At this step, the pixel filling-factor from the X-IFU must be taken into account in the ARF used for the fit in XSPEC, meaning that the response of all energy channels are 97% of the response from the ARF used by SIXTE to generate the mock observation.
Appendix D: Quantitative analysis of bias and dispersion
The bias and standard deviation of the output fields coming from solving the inverse problem can be quantified, with respect to their input counterparts from the rescaled MHD simulation, by:
where X is either the emission measure EM or the spectroscopic temperature Ts. In the case of the emission-weighted velocity vew, the bias and dispersion are rather defined according to:
< ⋅ > is the spatial average running over all the Voronoi regions. The subscripts obs and sim respectively stand for the observed and true input quantities. All these quantities are tabulated in Table D.1 for the different synthetic observations. We do not necessarily seek to compare the quality of the reconstructed fields between the two different observations since they use different input physical fields anyway. We are rather aiming at validating the post-processing pipeline by checking that there is no significant bias or dispersion of the reconstructed fields with respect to the input quantities, independently for each observation. We are also looking for a quantitative criterion on the input fluctuation fields to predict whether they will be visually well recovered (as in OBScustom, Fig. 10) or not (as in OBSfid, Fig. 9) with a X-IFU observation.
Bias and dispersion of the output fields recovered from virtual observations with respect to their input counterparts from the rescaled MHD simulation.
The first row in Table D.1 shows the biases and standard deviations of the reconstructed fields with respect to the input quantities in the case of OBSfid: both the thermodynamic and velocity fields are very well reconstructed with no significant biases and acceptable dispersions. More quantitatively, we find dispersions σTs ∼ 2%, σvew ∼ 20 km/s for the observed temperature and velocity field. This proves the robustness of our observational post-processing chain. Yet the fluctuation fields reconstructed from this synthetic observation are not necessarily visually satisfactorily retrieved, as seen in Fig. 9. The root-mean square of the input temperature fluctuation and velocity fields after integration along the line of sight δTs|rms ∼ 0.5%, vew|rms ∼ 10 km/s are smaller than the respective standard deviations σTs ∼ 2%, σvew ∼ 20 km/s of the reconstructed temperature and velocity fields with respect to the input quantities. We deduce that having δX|rms ≳ σX, with X = EM, Ts or vew|rms ≳ σvew are necessary (albeit maybe not sufficient) conditions to satisfactorily detect the fluctuation fields from a synthetic observation. In this case, σX can therefore be seen as a detectability threshold due to the inherent noise associated with a X-IFU observation: the fluctuation fields will be detected (i.e. visually well recovered) if their intensities exceed the noise level associated with the observation. This is why, in the phenomenological discussion of Section 3, Fig. 5, we used σTs ∼ 2% and σvew ∼ 20 km/s as the typical X-IFU detectability limits for a 2-Ms observation of the Perseus cluster at 0.25R200. The case of the emission measure needs more caution because this extensive physical quantity is proportional to the squared density: when the root-mean square of the emission-measure and spectroscopic temperature fluctuations are small enough, they relate according to δEM|rms ∼ 2δTs|rms. In the case of the emission measure fluctuation field, the factor two puts the root-mean square δEM|rms ∼ 1% closer to the corresponding detectability limit σEM ∼ 2%. This explains why the emission measure fluctuations are, to some extent, visually better recovered than those of spectroscopic temperature in the case of the mock observation OBSfid (bottom maps in Fig. 9).
The biases and dispersions of the velocity and thermodynamic fields reconstructed from the observation OBScustom are given in the second row of Table D.1. In the case of the thermodynamic fields, they are very similar to those found for the previous mock observation and prove once again the robustness of the reconstruction. However, the output velocity field is slightly biased towards negative values and more dispersed than in the first virtual observation. This is a consequence of the root-mean square of the input velocity field being larger in this synthetic observation: a similar behaviour was seen when the Mach number from an input hydrodynamic simulation was increased in Roncarelli et al. (2018).
Appendix E: Computation of the thermodynamic fluctuations in the Voronoi regions
In this respect, we first derive the average thermodynamic quantity 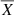 at fixed zi (which represents an iso-gravity line when the cluster curvature is neglected, see Appendix C.1):
at fixed zi (which represents an iso-gravity line when the cluster curvature is neglected, see Appendix C.1):
where X is either the spectroscopic temperature Ts or the emission measure EM. j runs on all the X-IFU pixels of the y-axis at a given vertical position zi on the 2D grid and ny is the number of such pixels (which depends on zi because of X-IFU’s hexagonal shape). The same Voronoi region can therefore be accounted for more than once in the average of a single row. The next step is to compute the average quantity < X> in a single Voronoi region:
where npix is the number of pixels in the Voronoi regions considered and i runs on all those pixels, whose vertical position is zi. We finally obtain the thermodynamic fluctuation δX in a given Voronoi region according to:
We emphasise that this procedure is greatly simplified by the fact that the cluster curvature can be neglected. Ideally, it should return the same fluctuation field that we would get if we were to directly integrate the thermodynamic fluctuations themselves along the line of sight (not weighted by the background quantities, as done for the velocity field actually). We checked whether this procedure is robust or not in this sense for diverse fluctuation fields that we parametrise with different intensities and injection lengths. In the parameter ranges relevant to the present study, we find very little influence of these diverse parameters on the robustness of the method, which proves to be overall satisfying.
All Tables
Set of parameters for the temperature and density profiles of the different thermodynamic models of ICM.
Bias and dispersion of the output fields recovered from virtual observations with respect to their input counterparts from the rescaled MHD simulation.
All Figures
 |
Fig. 1. Density ρ (top) and temperature T (bottom) profiles as a function of radius for three typical ICM models (Ghirardini et al. 2019; McCourt et al. 2013; Simionescu et al. 2011). Only the range with decreasing temperature is shown, until R200. The grey shaded areas highlight radii for which the X-IFU will collect less than two million photons in the 0.2–12 keV energy range during a 2-Ms observation. |
| In the text | |
 |
Fig. 2. Problem geometry and schematic of statistical fluctuation cancellation for an observation of an ICM at Perseus redshift through the X-IFU, which observes the plane of the sky (ey, ez). The coloured boxes can represent either temperature, density or velocity fluctuations. The colour scale is arbitrary but blue and red tones are of opposite signs, and the more opaque the stronger the fluctuation. The dependency of the fluctuations with y, z is overlooked for clarity. |
| In the text | |
 |
Fig. 3. Schematic diagram of the pipeline to build a X-IFU synthetic observation and to reconstruct the physical fields from such an observation: the forward and inverse problems are solved separately. The tool and/or model used at each step is indicated below the respective boxes. |
| In the text | |
 |
Fig. 4. Theoretical injection length of turbulence induced by the MTI (top) and the same quantity divided by the local temperature scale-height (bottom) as a function of the radius for three models of ICM. The colour encoding is the same as in Fig. 1. The dash-dotted black line is the X-IFU field of view at Perseus redshift. Again, the grey shaded areas highlight radii at which a X-IFU observation will not provide enough photons. These radii also roughly correspond to regions where the hypothesis of locality for MTI-driven turbulence may break down (and so would the scalings Eqs. (6), (9), and (11)). |
| In the text | |
 |
Fig. 5. Intensity levels of MTI turbulence. Dashed line: root-mean square of the 3D turbulent velocity field as a function of the radius in the ICM. Full line: root-mean square of the 3D turbulent line-of-sight velocity (top) and temperature (bottom) fluctuations. Dotted line: same but for the estimated 2D projected quantities after integration along the line of sight. The dash-dotted black lines are X-IFU detectability limits (determined in Sect. 4) for a typical 2-Ms observation of a Perseus-like cluster at 0.25R200. The colour encoding follows Fig. 1. |
| In the text | |
 |
Fig. 6. Time evolution of key MTI quantities. Top: potential (in green), vertical (in dark purple), and horizontal (in gold) kinetic energy densities and vertical (in dark blue) and horizontal (in light blue) magnetic energy densities. Bottom: kinetic energy anisotropy |
| In the text | |
 |
Fig. 7. Snapshots of MTI turbulent fields at t = 100t0. Top: vertical (x, z) cuts at y = 0.75. Bottom: horizontal (x, y) cuts at z = 0.75. From left to right: norm of the velocity and magnetic fields (in code units) and temperature fluctuations (in % of the background temperature T(z), Eq. (3)). Magnetic field lines are superimposed as black lines on the temperature fluctuations. |
| In the text | |
 |
Fig. 8. Energy spectra of the potential (green), kinetic (purple) and magnetic (yellow) energy volume densities. |
| In the text | |
 |
Fig. 9. Fiducial synthetic observation OBSfid based on the Braginskii-MHD simulation rescaled with the values of Eqs. (6), (9), and (11) at 0.25 R200 in a Perseus-like cluster. From left to right: emission measure fluctuation δEM, spectroscopic temperature fluctuation δTs and emission-weighted velocity vew maps. Top: line-of-sight integrated input fields from the rescaled MHD simulation. Bottom: output fields reconstructed from the synthetic observation OBSfid. The colourbars are set according to the input quantities. The values of the thermodynamic fluctuation fields are given in percents of the average background quantities (see Eq. (E.3)). |
| In the text | |
 |
Fig. 10. Custom synthetic observation OBScustom (at 0.25 R200 with Perseus density profile), based on the optimally custom-rescaled Braginskii-MHD simulation. From left to right: emission measure fluctuation δEM, spectroscopic temperature fluctuation δTs and emission-weighted velocity vew maps. Top: line-of-sight integrated input fields from the rescaled MHD simulation. Bottom: output fields reconstructed from the synthetic observation OBScustom. The colourbars are set according to the input quantities. The values of the thermodynamic fluctuation fields are in percents of the average background quantities (see Eq. (E.3)). |
| In the text | |
 |
Fig. 11. Diagnostic tools for probing the anisotropic structure of turbulent fields. From left to right: second-order horizontal and vertical structure functions and their ratios for the emission measure fluctuations (top) and emissivity-weighted velocity (bottom). Full (resp. dashed) lines correspond to the quantities computed from the rescaled MHD simulation on a X-IFU–like (resp. Voronoi) grid with 12 independent MTI turbulent fields. The dots represent the same ratios, but derived from a single rescaled field of the MHD simulation used as input to OBScustom (top maps in Fig. 10). They are naturally noisier than those computed from the statistics of 12 independent fields, but also more anisotropic in average in the case of the emission measure fluctuations. Stars show the ratios as derived from the fields reconstructed from OBScustom (bottom maps in Fig. 10). The y-axis of the leftmost and centre panels showing the structure functions are in arbitrary units but similar for each row, so that the horizontal and vertical structure functions can be directly compared. |
| In the text | |
 |
Fig. B.1. Comparison between the MTI (top) and HBI (bottom) linear growth rates numerically measured and theoretically computed thanks to the dispersion relations. The initial velocity perturbation is a fundamental divergence-free diagonal mode (ky = kz = 2π/L) with amplitude 10−4. Different colour tones are for the different Prandtl numbers. Runs with resolution 642 and 2562 are represented by stars and dots. |
| In the text | |
 |
Fig. C.1. Schematic of the different grids used in the observational pipeline. The relative sizes of the grids are consistent with respect to each other: there is almost one cell from the MHD simulation grid (full grey lines, left), after rescaling of the box as in OBScustom, in a X-IFU pixel (black dashed lines, left) and there are ∼4 cells of the finer grid (light blue lines, right), refined from the MHD simulation grid within the dotted red square and used for the synthetic observation, in a pixel of X-IFU. For the sake of clarity, the absolute sizes of the grids are however not to scale. For instance, there should be 3168 pixels in X-IFU’s hexagon (in our baseline instrumental configuration) instead of ∼30 on the schema, in which X-IFU border pixels are not squared whereas they should be as well in reality. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



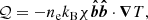
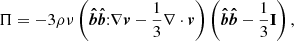
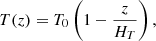
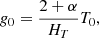
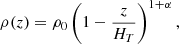
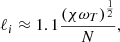
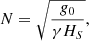
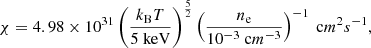
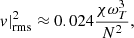
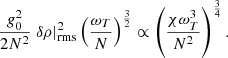
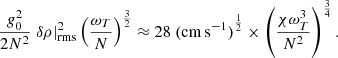
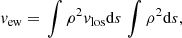
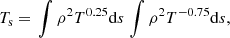
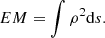
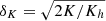
\right|^2, \end{aligned} $$](/articles/aa/full_html/2023/12/aa47123-23/aa47123-23-eq29.gif)
\right|^2. \end{aligned} $$](/articles/aa/full_html/2023/12/aa47123-23/aa47123-23-eq31.gif)
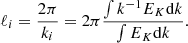
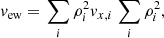
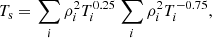
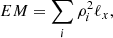
![$$ \begin{aligned} \mathcal{SF} _X^h(y)&= \left\langle \left[X\left(\boldsymbol{c} + y\boldsymbol{e_y}\right) - X\left(\boldsymbol{c}\right)\right]^2\right\rangle ,\end{aligned} $$](/articles/aa/full_html/2023/12/aa47123-23/aa47123-23-eq36.gif)
![$$ \begin{aligned} \mathcal{SF} _X^v(z)&= \left\langle \left[X\left(\boldsymbol{c} + z\boldsymbol{e_z}\right) - X\left(\boldsymbol{c}\right)\right]^2\right\rangle ,\end{aligned} $$](/articles/aa/full_html/2023/12/aa47123-23/aa47123-23-eq37.gif)
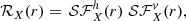
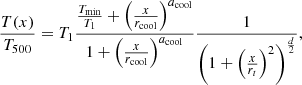
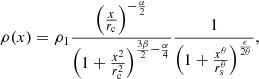
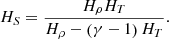
![$$ \begin{aligned} \sigma \left(\sigma +\frac{2}{5} \chi k_y^2 \right) \left[ \sigma + 3 \nu k_y^2 \left( 1 - \frac{k_y^2}{k^2} \right) \right] + \sigma N^2 \frac{k_y^2}{k^2} + \frac{2}{5} \chi \omega _T^2 k_y^2 \frac{k_y^2}{k^2} = 0. \end{aligned} $$](/articles/aa/full_html/2023/12/aa47123-23/aa47123-23-eq47.gif)
![$$ \begin{aligned} \sigma \left(\sigma +\frac{2}{5} \chi k_z^2 \right) \left[ \sigma + 3 \nu k_z^2 \left( 1 - \frac{k_z^2}{k^2} \right) \right] + \sigma N^2 \frac{k_y^2}{k^2} - \frac{2}{5} \chi \omega _T^2 k_z^2 \frac{k_y^2}{k^2} = 0. \end{aligned} $$](/articles/aa/full_html/2023/12/aa47123-23/aa47123-23-eq48.gif)