EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 679 (November 2023) A&A, 679 (2023) A137 Full HTML
Open Access
Issue
A&A
Volume 679, November 2023
Article Number A137
Number of page(s) 14
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202347514
Published online 30 November 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Very massive stars (VMSs), often considered as those stars with an initial mass of greater than 100 M⊙, mostly stimulate interest in Population III and the early Universe. Indeed, early hydrodynamical simulations predicted preferential formation of VMSs for Population III stars (Abel et al. 2002; Bromm et al. 2002). More recent simulations now predict a more significant fragmentation process (Stacy et al. 2010; Clark et al. 2011; Turk et al. 2009), and wide initial mass distributions (Hirano et al. 2014, 2015). Moreover, the initial mass function (IMF) might even be redshift dependent for Population III stars (Hirano et al. 2015) because of the different temperatures of formation sites. However, there is general agreement on a top-heavy primordial IMF (Greif et al. 2011; Stacy & Bromm 2013; Hirano et al. 2014, 2015; Susa et al. 2014; Stacy et al. 2016; Jeřábková et al. 2018; Wollenberg et al. 2020). Population III stars could be a very significant source of ionizing photons, making them interesting candidates for drivers of the reionization of the intergalactic medium (Haehnelt et al. 2001; Faucher-Giguère et al. 2008, 2009; Becker & Bolton 2013; Wise et al. 2014; Sibony et al. 2022). Using the present Population III models, Murphy et al. (2021) showed that including initial masses of up to 500 M⊙ can increase the total number of ionization by 30% compared to the case where the upper mass limit is chosen equal to 120 M⊙. While VMSs have an undeniable impact in the early Universe, their contribution across cosmic time might be underestimated even in higher metallicity environments.

One of the most spectacular observations in the early 1980s was that of the central object R136 of the 30 Doradus Nebulae in the Large Magellanic Cloud (LMC). Cassinelli et al. (1981) showed that R136 could potentially be a ∼2500 M⊙ star according to their spectroscopic analysis. With instruments providing higher spatial resolution, R136 was then shown to be a young cluster composed of stars of far lower masses. The stellar upper mass limit was then found to lie around 150 M⊙ (Weidner & Kroupa 2004; Figer 2005; Oey & Clarke 2005; Koen 2006). Crowther et al. (2010) used new adaptive optics observations combined with more refined non-local thermodynamic equilibrium (non-LTE) atmosphere code to derive the fundamental parameters of these objects. The results of these latter authors show that for four stars in R136, models suggest masses in the range of 165–320 M⊙. This was confirmed by recent studies using new HST data (Bestenlehner et al. 2020; Brands et al. 2022).

Interestingly, VMSs could also be viable candidates to explain the self-enrichment of globular clusters (see Vink 2018). For the last decade, one of the main candidate drivers of this self-enrichment process has been massive AGB stars (D’Ercole et al. 2010) given their slow winds compared to the fast line-driven winds of massive O-stars. Indeed, such fast winds (up to 2000–3000 km s−1) are not able to deposit the enriched material efficiently into the globular clusters as the winds are too fast to be trapped in their potential well. Alternatives such as rotating massive stars (Decressin et al. 2007), massive binaries (de Mink et al. 2009; Vanbeveren et al. 2012), red supergiants (Szécsi et al. 2018), or supermassive stars (SMSs; Denissenkov & Hartwick 2014) have been proposed and are discussed in Bastian & Lardo (2018). Interestingly, SMSs have been proposed as a workaround for the so-called mass–budget problem (Gieles et al. 2018), but the estimated wind velocities of roughly 1000 km s−1 are still too fast compared to the estimated escape velocities (≃500 km s−1) at the center of young globular clusters (Gieles et al. 2018). Vink (2018) then proposed that VMSs, after inflating due to their proximity to the Eddington limit (Ishii et al. 1999; Gräfener et al. 2012; Sanyal et al. 2015), lose mass through slower winds, satisfying conditions on both wind velocity for enrichment and mass budget.

Moreover, VMSs have been shown to have a potentially important impact on chemical enrichment at high metallicity. Indeed, Martinet et al. (2022) showed that the galactic production of the short-lived radioactive isotope 26Al by the wind-driven mass loss of massive stars might be increased by up to 150% when including VMS into a Milky Way-like population, and could then account for a large part of the observed 26Al galactic content.

To explore the evolution of VMSs throughout cosmic history, and as a follow-up to the work done by Yusof et al. (2013), we computed a grid of both rotating and nonrotating VMSs from Population III stars to solar-metallicity stars with GENEC (Eggenberger et al. 2008). In the present work, we take advantage of the improvements made compared to Yusof et al. (2013) models, such as the improvement of angular momentum conservation (Ekström et al. 2012), the use of another convective criterion (Kaiser et al. 2020), a revised overshooting parameter (Martinet et al. 2021), and the introduction in this work of an equation of state accounting for the pair-creation production.

The paper is organized as follows: in Sect. 2, we describe the physical ingredients used to compute the present models for VMSs. The effect of different physics on VMS evolution is discussed in Sect. 3. Comparison with previous models is discussed in Sect. 4. Comparison between our models and observed VMS in the LMC is discussed in Sect. 5. In Sect. 6, we discuss the potential impact of different physics on the final fate of VMSs, and present the main conclusions of this work.

2. Ingredients of the stellar models

The present models were computed with the 1D stellar evolution code GENEC (Eggenberger et al. 2008). These models differ mainly in three points with respect to the physics used in the grids by Ekström et al. (2012) and Yusof et al. (2022). First, we adopted the Ledoux criterion for convection instead of Schwarzschild and an overshoot of 0.2 Hp instead of 0.1 Hp. These changes were made because there are some indications that the Ledoux criterion might be more appropriate for reproducing some observed properties of massive stars (Georgy et al. 2014; Kaiser et al. 2020), and that an increase in the overshoot parameter is needed for stars with masses of greater than 8 M⊙ (Martinet et al. 2021; Scott et al. 2021). The third change is that our VMS models have been computed with an equation of state accounting for electron–positron pair production (Timmes & Swesty 2000). The other ingredients are the same as in Ekström et al. (2012) and Yusof et al. (2022). However, to make the paper more self-consistent, let us reiterate the prescriptions used for rotation and mass loss. We considered here the physics of shellular rotating models as described in Zahn (1992). For the vertical shear diffusion coefficient, we used the expression by Maeder (1997) and the expression of the horizontal shear diffusion coefficient by Zahn (1992).

The radiative mass-loss rate adopted on the main-sequence (MS) is from Vink et al. (2001); the domains not covered by this prescription (see Fig. 1 of Eggenberger et al. 2021) use the de Jager et al. (1988) rates. Gräfener & Hamann (2008) prescriptions are used in their domain of application, while Nugis & Lamers (2000) prescriptions are used everywhere else for the Wolf-Rayet phase1. For consistency, we retained the same prescriptions as for the overall grids published so far, although more recent prescriptions are now available (see the review of Vink 2022, and Fig. 8). In Sect. 6.1, we propose a more in-depth discussion on new mass-loss prescriptions and the relevance of the prescriptions used in this work. The radiative mass-loss-rate correction factor described in Maeder & Meynet (2000) is applied for rotating models. The dependence on metallicity is taken such that Ṁ(Z) = (Z/Z⊙)0.7 Ṁ(Z), except during the red supergiant (RSG) phase, for which no dependence on the metallicity is used. This is done according to van Loon et al. (2005) and Groenewegen (2012a,b), who show that the metallicity dependence appears to be weak for the mass-loss rates of these stars.

We computed stellar models with initial masses of 180, 250, and 300 M⊙ for Z = 0.000, Z = 10−5, Z = 0.006, and Z = 0.014 metallicities, with no rotation and a rotation rate of V/Vc = 0.4, where Vc is the critical velocity2. The nuclear network allows us to follow the abundance variation of 30 isotopes3.

3. The grid of VMS stellar models

Table 1 presents the initial parameters and various physical quantities of the models presented in this paper at different evolutionary stages. We define the beginning of a phase when 1% of the central burning element has been consumed and the end of a phase when the mass fraction of the main fuel at the center is lower than 10−3.

Table 1.

Properties of the stellar models at different stages of their evolution.

Figure 1 presents the Hertzsprung-Russell diagram (HRD) of the higher-metallicity models, at Z = 0.014 and Z = 0.006. The nonrotating models are displayed in solid lines, while the rotating ones are in dashed lines. Starting with the 180 M⊙ at Z = 0.014, we can see that the rotating model evolves more to the blue during the MS because of the rotational mixing; it enters the Wolf-Rayet (WR) phase at a slightly earlier evolutionary stage. The rotating model enters the core He-burning phase at a much higher effective temperature than the nonrotating models. The evolution through the advanced phases is then very similar due to the dominant WR mass loss, with the rotating models at slightly lower luminosity.

thumbnail Fig. 1.

HRD of the nonrotating model (solid lines) and the model rotating at V/Vc = 0.4 (dashed lines) at Z = 0.014 (solar) and Z = 0.006 (LMC). The top, middle, and bottom rows show models with initial masses of 180, 250, and 300 M⊙, respectively. The tracks are color-coded according to their mass-loss rates. The beginning and the end of the burning phases are indicated by circles and crosses, respectively. The beginning of the Wolf-Rayet phase is indicated by a light blue circle.

If we go to a higher initial mass, the evolution is now highly dominated by the greater mass loss, with the rotating models still evolving with slightly lower luminosities. The 300 M⊙ at Z = 0.014 is the perfect example of mass-loss-dominated evolution, where both the nonrotating and the rotating models undergo so much mass loss that their evolution through the HRD is effectively similar.

If we go to lower metallicity, we now have a lower contribution to the mass loss of the line-driven wind. This means that the evolution of VMSs will now be more sensitive to the rotational mixing. Indeed, as we can see for the whole 180–300 M⊙ mass range, the rotating models undergo quasi-chemically homogeneous evolution because of the very strong mixing. Rotating stars reach the WR phase much earlier. This causes the star to undergo a greater amount of mass loss. The He-burning phase of rotating models occurs at much lower luminosities than for the nonrotating models. The same is true for the more advanced phases.

In summary, we can say that at solar metallicity, the tracks of the models of 250 and 300 M⊙ nearly always decrease in luminosity as a result of the very strong mass loss. The effects of rotation become less and less strong when the initial mass increases because of the dominating effect of mass loss. At the metallicity Z = 0.006, as well as for the 180 M⊙ model at solar metallicity, that is, for all the models where the mass losses are weaker, the effects of rotation are important. As is well known, rotating tracks are bluer on the MS phase. The models enter into the WR phase earlier on and therefore reach lower luminosities during the post-MS phases.

Figure 2 shows the HRD of 180 M⊙ nonrotating stellar models at different metallicities. One of the main effects of metallicity on the surface properties is clearly the cooler effective temperature at higher metallicity (see Fig. 2 bottom right panel). Indeed, we can see that the beginning of the H-burning phase, while starting at a roughly similar luminosity, starts at very different Teff. This is mainly due to the fact that the opacity of the outer layers increases with the metallicity. As the gradient of the radiative pressure scales with the opacity, this means that the outer layers receive a stronger radiative support in high-metallicity stars than in low-metallicity ones. This produces stars with larger radii and lower effective temperatures. Moreover, a higher metallicity implies more CNO elements in stars, which in turn implies that lower temperatures are needed to produce a given amount of energy. Lower temperature means that the star needs to contract less to allow nuclear reactions to produce enough energy to compensate the losses at the surface (see Sect. 4.2 in Farrell et al. 2022). This also contributes to making metal-rich stars more extended than metal-poor ones.

thumbnail Fig. 2.

HRD for 180 M⊙ nonrotating models at Z = 0.014, Z = 0.006, Z = 10−5, and Z = 0. The tracks are color-coded according to their current total mass. The MS of the models at Z = 0.014, Z = 0.006, and Z = 10−5 is plotted in dashed gray in the lower right panel for comparison.

The evolution of the first parts of the MS is similar for the metallicities considered in Fig. 2, until the effect of the line-driven wind – which is very sensitive to metallicity – truly begins to take hold. From then, the higher-metallicity models start to evolve to the blue because of the large quantities of mass loss, quickly forming WR stars.

At low metallicity, the star remains more massive, and this has a strong impact on the evolutionary tracks in the HRD. During the MS phase, tracks cover a larger range both in luminosity and effective temperature. After the MS phase, as there is still an important H-rich envelope, the star reaches larger radii.

During the post-core He-burning phases, the low-metallicity models have higher luminosities than the more metal-rich models. This is a consequence of their larger actual masses. Their effective temperature is not reaching values as high as those of the stripped core resulting from the higher-metallicity models. It is interesting to note that these models are very close to the Eddington limit and therefore undergo large mass-loss events for a short time during the advanced phases.

Figure 3 shows the evolution of the surface rotation for a 180 M⊙ star at low metallicities. At these metallicities, the line-driven wind is almost negligible, and therefore the transport of angular momentum from the core spins up the surface. From here, the surface accelerates up to the critical velocity. From this point on, works usually assume that some matter will be lost from the star, forming an equatorial disk (see e.g., Hirschi 2007). Indeed, at the critical velocity, a small additional force is sufficient to launch the matter into Keplerian orbits around the star. The disk may lose mass (see e.g., Krtička et al. 2011). The net result will be a mechanical loss of mass by the star.

thumbnail Fig. 3.

Evolution of the surface angular velocity divided by the critical angular velocity for 180 M⊙ rotating models initially at V/Vc = 0.4 (Ω/Ωcrit ≃ 0.58), for Z = 10−5 and Z = 0. The gray dashed line shows the numerical limit used to trigger the mechanical mass loss.

Numerically, this induces large problems of angular momentum conservation at the surface that are very difficult to overcome when so close to the critical velocity. To manage this problem, we chose to artificially lower the effective velocity needed to trigger this mechanical mass loss to Ωlimit/Ωcrit = 0.8. While the effects of lowering this limit are minimal in this case (≈2% of the total mass is lost by mechanical mass loss) and tremendously help the computation, it can also be partly justified by the uncertainties of the mass-loss processes for very fast rotators. If we consider the case of the Be stars, which are stars that show a decretion disk likely resulting from their high rotation, the velocity at which those stars begin to lose mass is unclear (see the review by Rivinius et al. 2013, and references therein). Indeed, in addition to the centrifugal force, some other forces should be involved to kick the matter into an outward-expanding disk. This may be momentum given by radiation or by pulsations. At the very least, it is likely that stars begin to lose mass well before the critical limit is reached. Therefore, choosing a subcritical velocity here for triggering the mechanical mass loss is not unrealistic. The star remains at the lower limit of the surface rotation for triggering the mechanical mass loss until the end of the MS phase (see Fig. 3). After the MS phase, the star rapidly expands, the surface rotation becomes much lower than the limit and the mechanical mass loss stops. Other processes like line-driven winds or mass loss triggered by the continuum when some outer layers have supra-Eddington luminosities become dominant.

The zero-metallicity model has a similar evolution on the MS to the model with Z = 10−5 because it is not dominated by the line-driven mass loss. However, the Population III model has not been pushed further in its evolution due to numerical problems linked to mechanical mass loss.

3.1. Wolf-Rayet stars from very massive stars

WR stars are classified into different categories according to their spectral features. As we do not predict the output spectra of our models, we cannot use the same spectroscopic criteria here as those used by spectroscopists to classify our models among the different WR subtypes. Here, we adopted different theoretical criteria for WR classification. The WR phase in GENEC is assumed to begin when the model has an effective temperature of higher than 10 000 K and a surface mass fraction of hydrogen 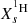X s 1 H $ X^{^1\rm H}_s $ of below 0.3. Assuming the star fulfills these WR conditions:

  • the WNL phase is defined when 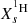X s 1 H $ X^{^1\rm H}_s $ > 10−5;

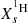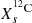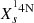  • the WNE phase is defined when both X s 1 H $ X^{^1\rm H}_s $ ≤ 10−5 and the surface mass fraction of carbon X s 12 C $ X^{^{12}\rm C}_s $ is smaller than or equal to that of nitrogen X s 14 N $ X^{^14\rm N}_s $;

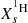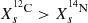  • the WCO phase is defined when X s 1 H $ X^{^1\rm H}_s $ ≤ 10−5 and X s 12 C > X s 14 N $ X^{^{12}\rm C}_s > X^{^{14}\mathrm{N}}_s $;

  • the WO phase is defined when it is a WCO with log(Teff) > 5.25;

  • the WC phase is defined when it is a WCO with log(Teff)≤5.25.

It is important to note that these classification criteria may actually result in differences in classification compared to the ones based on spectroscopy (see Groh et al. 2014). This is why the WO/WC criteria have been defined following the work of Groh et al. (2014).

Figure 4 shows the stacked lifetimes of different spectral phases of massive stars as a percentage of the total lifetime of a given star. The lifetimes are displayed for nonrotating (left panels) and rotating (at V/Vc = 0.4; right panels) models at Z = 0.006 in the upper panels and Z = 0.014 in the lower panels. The Z = 0.006 models below 150 M⊙ are from Eggenberger et al. (2021) and those with Z = 0.014 are from Ekström et al. (2012).

thumbnail Fig. 4.

Stacked lifetimes as a percentage of the total lifetime for O-type stars, RSGs, YSGs, BSGs, and WR types for nonrotating (left) and rotating models (right) at Z = 0.006 (top) and Z = 0.014 (bottom).

Most of the life of a massive star is spent as an O-type MS star (we note that the y-axis begins at 60%). The post-MS O-type star phase represents between 10% and 40% of the total lifetime depending on the initial mass, metallicity, and rotation. In general, this phase covers a larger fraction of the total lifetime when the initial mass, the metallicity, and/or the initial rotation are greater. For example, the whole post O-type MS phase lasts about 27% of the total lifetime of a 250 M⊙ nonrotating Z = 0.006 model. Increasing the metallicity to Z = 0.014 brings that fraction to about 30%. The rotating models at Z = 0.006 and 0.014 still increase that fraction to 35% and 40%, respectively. Except in the case of the nonrotating Z = 0.006 model, where the fractions of the total lifetime spent as a B-type, WNL, and WC are approximately the same, for the other models, the post O-type MS star phase is only divided in two types of stars, either WNL (the longest ones covering about two-thirds of the remaining time) and the WC phase (one-third). This means that statistically, for single stars in a region with a constant star formation rate (e.g., during the last ten million years or so), there is in these last cases twice as great a chance of observing a WNL than a WC.

As is well known from previous models of rotating massive stars (see e.g. Fig. 2 in Georgy et al. 2012), rotational mixing significantly increases the mass of the star that has a chemical composition enriched by H-burning products; hence the longer duration of the WN phase in rotating models than in nonrotating ones.

3.2. Evolution of the core mass and final fate

The CO core mass is an important quantity that affects the advanced stages of massive stars and especially their final fate. This quantity is highly dependent on the initial mass, but also on rotation and mass-loss events.

Figure 5 shows the evolution of the convective core mass of VMSs between the beginning and the end of the He-burning phase for different rotation rates and metallicities. The convective core at the end of He-burning is a good proxy for the CO core mass. The figure also shows the actual total mass of the star at the different evolutionary stages shown on that figure.

thumbnail Fig. 5.

Evolution of the convective core mass of VMSs at the beginning and at the end of the He-burning phase, for nonrotating and V/Vc = 0.4 models at both Z = 0.006 and Z = 0.014. The light gray region corresponds to the total actual mass of the star at the considered evolutionary stage, and is emphasized by a line of the corresponding color.

We see that for the masses considered in Fig. 5, the total mass significantly decreases during the core He-burning phase and causes the convective core to also decrease. We note that at the metallicity Z = 0.006, the total mass of the nonrotating models at the beginning of the core He-burning phase increases with initial mass, and the same is true for the convective core mass. This trend disappears at the end of the core He-burning phase. Typically, the total actual mass of the 300 M⊙ model is smaller than that of the 250 M⊙ one. This is a consequence of the fact that the 300 M⊙ entering into the core He-burning phase with a higher mass loses mass more rapidly than the 250 M⊙ model, allowing the model to lose a larger fraction of its mass by the end of that phase. This reflects the fact that the mass-loss rates increase with the luminosity, which itself increases with the actual mass of the star. There are far fewer differences between the different initial masses for the rotating models; they begin their core He-burning phase with a similar actual mass and lose a similar amount of their mass during that phase. Rotational mixing, as shown above, makes the star enter at an early evolutionary stage in the WR phase. From that stage, the mass loss scales with the luminosity and hence the mass, making the models converge towards similar masses. Indeed, as explained above, by starting with more mass, the high luminosity will produce stronger mass losses, and thus causes the model to reach a similar mass to models starting with a lower mass.

At solar metallicity, the differences between the nonrotating and rotating models are much smaller than at Z = 0.006. The strong winds dominate here, leaving little room for the effects of rotational mixing.

Very often in the literature, the mass of the He core or that of the CO core at the end of He-burning is used to determine whether the star will explode as a PISN or PPISNe (see e.g., Farmer et al. 2019; Costa et al. 2021). As we show here, the convective core mass at the end of He-burning is a good proxy for the CO core mass. In Fig. 6, the CO core mass limits given by Farmer et al. (2019) are indicated. We see that according to this criterion, the only two models that will explode as a pair-instability supernova would be the 250 and 300 M⊙ nonrotating models at Z = 0.006. The inferior mass limit would be 200 M⊙ for entering into the domain of PISNe. The result is different from that of Yusof et al. (2013; see their Fig. 18). These latter authors find that for the nonrotating Z = 0.006 model, the inferior mass limit for the nonrotating models was found to be around 300 M⊙. This is likely due to the absence of models of between 150 and 500 M⊙ in the Yusof et al. (2013) study. Indeed, we see in the present study that the final mass has a peak for an initial mass of around 260 M⊙, and so it is likely that the Yusof et al. (2013) study missed that peak. For rotating models at Z = 0.006, the 250 and 300 M⊙ models are expected to undergo PPISNe.

thumbnail Fig. 6.

Convective core mass at the end of He-burning as a function of the initial mass for nonrotating and rotating stars at Z = 0.006 and Z = 0.014. The models with initial masses lower than 180 M⊙ are from Ekström et al. (2012) for Z = 0.014 and from Eggenberger et al. (2021) for Z = 0.006, and share the same physics, albeit with the differences described in Sect. 2. The range of CO core masses from Farmer et al. (2019) where (P)PISNe can occur is shown as an example to underline the very different potential final fate of VMSs when considering rotation and metallicity effects.

We also note that the models for Z = 0.014 are expected to avoid both the pulsational pair instability phase and pair instability explosions for all the models computed here. Therefore, at least for models up to an initial mass of 300 M⊙. In cases where those models end their lives as black holes engulfing the whole mass that the star has retained until the final core collapse, black hole masses of up to 30–45 M⊙ could be formed. Still higher mass black holes (up to about 60 M⊙) could be formed from the nonrotating Z = 0.006 models if the mass loss induced by the pulsational pair instability were smaller than a few solar masses.

In a paper in preparation, we will present a more in-depth study of the final fate of VMSs where we will study both core mass criteria and an average value for the first adiabatic exponent over the whole mass (see Stothers 1999; Marchant et al. 2019; Costa et al. 2021). We will discuss whether indeed those models that should explode as a (P)PISNe according to the core mass criterion contain a sufficiently large fraction of unstable mass to trigger the explosion mechanism (Martinet et al., in prep.).

4. Comparison with previous models

Figure 7 presents the evolution of a rotating (V/Vc = 0.4) 300 M⊙ model at Z = 0.014 computed with GENEC, from the computations of Yusof et al. (2013), and from this work. The main differences between these two computations mainly come from the improvement to the code, namely the treatment of conservation of angular momentum in the envelope (see Ekström et al. 2012), and the new EOS we introduce to take into account the pair-creation effects. As we also show in Sect. 2, these new VMS models are computed with the Ledoux criterion and an increased overshoot αov = 0.2, while the models of Yusof et al. (2013) are computed with the Schwarzschild criterion and αov = 0.1. The left panel of Fig. 7 shows the HRD of these two models, with the beginning and end of the different burning phases depicted by circles and crosses.

thumbnail Fig. 7.

Comparison with previous models. Left: HRD of a rotating 300 M⊙ at Z = 0.014 from the work of Yusof et al. (2013) and from this work. The beginning of each burning phase (defined as the moment when the central abundance of the element concerned decreases by 1%) and the end of it (defined as the moment when the central abundance is lower than 10−5) are displayed as open circles and crosses, respectively. Right: central temperature as a function of the central density for the same models. A zoom can be seen in the upper left displaying the region where the model starts undergoing pair-creation inside the core, leading the model with the new EOS – which takes this effect into account – to contract and expand rapidly as the pair-creation reduces the radiative pressure.

The beginning of the MS is very similar for both models; however, slight discrepancies appear at the surface during the rest of the MS evolution. This is due to the different treatment of the angular momentum conservation at the surface, combined with the very high mass-loss rates occurring for such massive stars at solar metallicity. The larger overshooting parameter does not induce a meaningful increase in the core size during the MS due to VMS already having very large convective cores. The total mass of both models during most of the MS is similar because mass loss dominates its evolution. However, at the end of the H-burning phase, a large mass loss occurs for both models, leading to larger quantities lost in the Yusof et al. (2013) models. This leads our models to be 40% larger in mass at the end of the MS.

The He-burning phase occurs at higher luminosity and goes through a slight evolution to the red for the model of this work. The leading consequence is that the VMS will undergo slightly larger mass-loss rates during the middle of the He-burning phase when going to the redder part of the HRD. This reduces the difference in the actual mass between our model and that of Yusof et al. (2013) from 40% at the end of the MS phase to 35% at the end of the core He-burning phase. Interestingly, the evolution from the C-burning phase is slightly different, with the Yusof et al. (2013) model continuing to higher effective temperatures while model in this work evolves back to the red. To explain this feature, we need refer to the right panel of Fig. 7 where the central temperature of the star is depicted as a function of the central density. Once again, we see that the central conditions are very similar in early stages, with a slightly higher temperature in the core in the new model (likely due to the larger overshoot parameter). The very interesting features appear at the end of the C-burning phase and are displayed as a zoom in the upper-right part of the diagram. The oscillations of the central conditions are a direct effect of the pair production inside the star. Indeed, while the center is outside of the pair-instability zone, a slightly off-centered part of the core is crossing this instability region. The production of a pair inside these parts of the star results in destabilization of this region of the core4.

5. Comparison with observed VMSs in the LMC

The Tarantula Nebula in the LMC hosts one particular young cluster, known as R136, that itself hosts very high-mass components. Recent work (Bestenlehner et al. 2020; Brands et al. 2022) confirmed these results with new VLT-FLAMES and HST/STIS optic and spectroscopic measurements and provided interesting stellar characteristics to the most massive stars observed. With the new VMS models computed here, we can confront our results with these new observations. We explore here the impact of the physics we have included inside our models on the observables, and compare the results to those provided by the most recent observations.

As we show in the previous section, the evolution of VMSs at high metallicity is dominated by mass loss. The prescriptions used in our models come from both theoretical and empirical results obtained from lower mass O-type stars, and are highly uncertain, especially when getting close to the Eddington limit (see the review of Vink 2022). In Fig. 8, we confront our models with the observed mass-loss rates obtained by Brands et al. (2022) and show their corresponding fit using the prescription proposed by Bestenlehner et al. (2020). The mass-loss rates are plotted as a function of the Eddington parameter (with Γedd, e = 1 being the Eddington limit). The time-averaged mass loss of our models over the main sequence is shown by colored rectangles. The time-averaged mass-loss rates of our nonrotating VMS models with initial masses equal to or above 180 M⊙ are below the fitting line by at most 0.3 dex (a factor two). The contrary is true for our rotating models, which show time-averaged mass-loss rates of at most about 0.3 dex above the fitting line. At the very least, this shows that although we did not account for the most recent developments of the mass-loss rates in the present models, the fact that the nonrotating and rotating models approximately frame the fitting curve by Brands et al. (2022) with differences of at most a factor of 2 is rather encouraging.

thumbnail Fig. 8.

Time-averaged mass-loss rates over the main sequence as a function of the Eddington parameter Γedd, e. The models of 85–120 M⊙ are from Eggenberger et al. (2021), and the models of 180–300 M⊙ are from this work. The observations of Brands et al. (2022) of the R136 components are displayed in gold. The fit they obtained is displayed in purple. The three most massive components of the cluster (R136a1/2/3) are pinpointed by arrows.

Figure 9 presents the HRD of the Tarantula Nebula, a very active star-forming region in the LMC. The compilation of Schneider et al. (2018) is displayed in yellow, while the components of the R136 cluster obtained by Brands et al. (2022) are displayed in magenta. The tracks used here are the Z = 0.006 GENEC tracks from Eggenberger et al. (2021) and the VMS tracks we computed for this work with the new EOS. We can see that this cluster hosts several high-mass components. If we look at the evolution of our VMS models, three stars inside this cluster are above Mini = 200 M⊙ (R136a1/2/3). At first glance, one would favor the nonrotating models for these VMS, covering a large range of effective temperatures on the MS, while the rotating models, as we show in Sect. 3, evolve quasi-chemically homogeneously and stray directly to the bluer part of the HRD (also true for models rotating at V/Vc = 0.2 not shown here), and are therefore apparently incompatible with the observed effective temperatures. However, the problem is more complicated: the VMS undergoes very large mass loss already during the MS, which means that the star is embedded inside a “nebula” of very thick wind. When observing such stars, we are in reality observing this thick wind, and this blurs the determination of the effective temperature of the surface of the star. Indeed, with the wind being much cooler than the surface of the star, we obtain a lower observed effective temperature if we take this effect into account. We computed corrected effective temperatures and find that both nonrotating and rotating models are compatible with the observations (the corrected effective temperatures go down to 35 000 K, which is 6000 K below the lowest limit of the observed Teff of VMS; see the details of how this correction has been computed in Schaller et al. 1992).

thumbnail Fig. 9.

HRD of the Tarantula Nebula from the compilation of Schneider et al. (2018; regrouping results from Ramírez-Agudelo et al. 2017; Sabín-Sanjulián et al. 2014, 2017; McEvoy et al. 2015; Bestenlehner et al. 2014) and the R136 cluster members from the work of Brands et al. (2022). The GENEC tracks are overplotted in gray, with color emphasis on the VMS models computed here, and the ZAMS is drawn in dark gray. The HRD is plotted for nonrotating (left) and rotating (at V/Vc = 0.4; right) models. Their effective temperatures are not corrected for the optical thickness of the wind. The three most massive components of the cluster (R136a1/2/3) are pinpointed by arrows in the right panel.

Figure 10 shows the values of V sin i obtained by Bestenlehner et al. (2020) overplotted over the tracks of VMS models. From the spectroscopic studies, the surface velocities observed do not differentiate the surface velocity from the macro-turbulent velocity. This means that the lower limit of the surface velocity would be when the macro-turbulence is at its maximum. We take the maximum macro-turbulent velocities obtained by Simón-Díaz et al. (2017) for stars close to the Eddington limit to obtain the lower displayed limit. The upper limit is obtained from the angle-of-view effects. The theoretical models (see the continuous lines in Fig. 10) show that the surface velocity decreases rapidly as a function of time as a result of the large amount of angular momentum taken away by stellar winds.

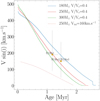thumbnail Fig. 10.

Evolution of the surface velocity of VMS models. An additional model with slower initial rotation rate has been computed for this plot. The observed velocities of the three most massive components of R136 are overplotted (R136a2 and R136a3 have similar velocities obtained). The uncertainties on the velocity are taken from the maximum macro-turbulent velocity observed for stars close to the Eddington limit (Simón-Díaz et al. 2017) for the lower limit, and from the maximum velocities obtained from the angle-of-view effect for the upper limit.

To ensure that the theoretical model goes through the region covered by the error bars given by Bestenlehner et al. (2020) at this stage of the MS, relatively high rotation rates are required already at the ZAMS. In reality, given that – as recalled above – the V sin i value is a lower limit to the true surface velocity, even larger initial rotations than those shown for the models in Fig. 10 could be considered.

A 250 M⊙ model with a lower rotation rate has been computed to show that the mass loss still dominates the surface velocity evolution and would not be able to reproduce the high velocities observed for these VMSs. We might wonder whether or not assuming a solid body rotation – as a model accounting for the impact of an internal magnetic field would need to – would allow us to start from a lower initial rotation rate. This will be explored in the future. However, we can note that despite the fact that we considered nonmagnetic models here, since these stars host a very massive convective core, they have a solid body rotation in any case in a very large part of the star. We therefore suspect that including magnetic fields in our models would have a modest effect here (see discussion in Sect. 6.1).

Figure 11 shows the observed surface enrichment of nitrogen as a function of the observed surface helium, from Brands et al. (2022) and Bestenlehner et al. (2020), respectively. The nonrotating (in solid lines) and the rotating (in dashed lines) VMS models are overplotted. Interestingly, the evolution of nitrogen at the surface is very similar between the nonrotating and rotating models. This is because the models quickly reach (before the surface helium fraction reaches 0.4) the maximum quantity of nitrogen produced from the CNO cycle in these stars. This maximum value depends solely on the initial abundances of CNO. Hence, while the most massive component R136a1 is well reproduced by the models, there is no possibility for these models to explain the very high enrichment value of nitrogen of the two other VMSs (R136a2/a3). Understanding these discrepancies is difficult. A first possibility could be that the initial abundances and in particular the initial content of CNO elements could be different in the different stars. We can see that the Z = 0.014 models are able to reproduce such values due to the larger initial abundances of CNO. Can we imagine that this region can host populations with different metallicities? This would imply, in a self-enrichment scenario, multiple stellar generations born from material differently enriched in metals by previous generations of stars. There are massive young clusters that show evidence for multiple generations of stars, such as the Orion nebula cluster with potentially generations with an age separation of less than 1 Myr (Beccari et al. 2017). The Tarantula nebula is a much more massive star-forming region than Orion, and is even more susceptible to having hosted multiple generations. Interestingly, a scenario where the (re)collapse of the cluster allows the birth of a second generation of stars has been invoked by Domínguez et al. (2022) to explain the observational characteristics of the central region of 30 Doradus. A second possibility to explain the result shown in Fig. 11 is that the error bars have been underestimated. The error bars should be significantly increased to allow tracks at a given fixed metallicity to cross them. This does not appear to be a realistic possibility. Third, we might wonder whether or not the history of the star (e.g., a binary interaction or early merger) could be invoked to explain the discrepancy in nitrogen surface abundances for such similar values of the surface helium abundance. Modeling of the evolution of multiple systems is required to answer such a question.

thumbnail Fig. 11.

Surface enrichment of nitrogen over hydrogen as a function of surface helium. The observed values of [N/H] are from Brands et al. (2022), and the surface helium fraction is from Bestenlehner et al. (2020).

6. Discussion and conclusions

6.1. Impact of changing physical ingredients of the models

Changes of some physical ingredients, such as the criterion for convection, the overshooting, or the expression for the diffusion coefficient in rotating models, and a change of the EOS have non-negligible impacts on the outputs of the stellar models as discussed in Sect. 4, where we performed a comparison with the models by Yusof et al. (2013), which also used GENEC as the stellar evolution code.

For solar metallicity, models are dominated by mass loss, and therefore most of the differences come from the changes in angular momentum conservation and the slightly different evolution in the HRD. While nonrotating models are quite similar, rotating ones lead to final masses of up to 42% larger than previous models. At Z = 0.006, the differences are smaller due to a decrease in the occurrence of mass loss. For the rotating models, the final masses are up to 12% larger than in the models of Yusof et al. (2013).

We might speculate as to the impact of changing the angular momentum transport by considering a more efficient process, such as the one proposed in the Taylor-Spruit (TS) dynamo (Spruit 2002; Maeder & Meynet 2004; Eggenberger et al. 2010). The present VMS rotating models at V/Vc = 0.4 are almost rotating as a solid body at the beginning of the MS due to their very large convective core. This is also the case for slower rotators such as the Z = 0.006 180 M⊙ rotating at V/Vc ≃ 0.2 presented in Fig. 10. The rotation of the envelope and that of the core indeed remain coupled up until the end of the MS for models at Z = 0.006, when the mass loss becomes prevalent. A more efficient transport such as the TS dynamo would not significantly change the rotation profile in that case. For models at Z = 0.014, differential rotation between envelope and core sets in from the middle of the MS due to higher mass-loss rates. In this case, a more efficient transport of angular momentum might produce stars with faster surface rotation.

Very massive stars are highly sensitive to mass loss, especially at high metallicities. We chose for this work to keep the same physical ingredients as those used for all the grids published so far (Ekström et al. 2012; Georgy et al. 2013; Groh et al. 2019; Murphy et al. 2021; Eggenberger et al. 2021; Yusof et al. 2022). Doing so allows us to discuss how varying the initial mass, metallicity, and rotation impact the outputs. While the mass-loss prescription scheme we use here is used in many recent grids for massive stars (see e.g., Fragos et al. 2023; Simaz Bunzel et al. 2023; Jiang et al. 2023; Brinkman et al. 2023; Song & Liu 2023), recent works presented new predictions for mass loss in massive stars (such as Björklund et al. 2023; Gormaz-Matamala et al. 2023; Yang et al. 2023). Björklund et al. (2023) predict that the mass-loss rates of O-stars are lower by about a factor of three than the rates typically used in stellar-evolution calculations; however, differences decrease with increasing luminosity and temperature (i.e., smaller differences for VMSs and their high luminosity). Moreover, these latter authors find that the remaining key uncertainty regarding these predictions concerns unsteady mass loss for very high-luminosity stars close to the Eddington limit, which is a major mass-loss component due to VMSs being very close to the Eddington limit (as we show in Fig. 8). For RSG mass-loss rates, Massey et al. (2023) discussed the relevance of the prescriptions used in this work by comparing the predicted and observed luminosity function of red supergiants, finding good agreement. Still, Yang et al. (2023) present a new prescription for RSG mass-loss rates from a large spectroscopic survey in the Small Magellanic Cloud, finding that it may provide a more accurate relation at the cool and luminous region of the HR diagram at low metallicity compared to previous studies. The mass-loss-rate prescriptions we use at Z = 0.006, although not considering the effects discussed in Bestenlehner et al. (2020), provide a time-averaged mass-loss rate during the main sequence that is underestimated by a factor of up to 2 for the nonrotating models and overestimated by a factor of up to 2 for the rotating models. The scatter is reasonably small when compared to the scatter of the individual mass-loss-rate determinations used to establish the fitting mass-loss-rate prescription. However, it is uncertain how our current prescriptions reproduce the mass-loss rate at solar metallicity, and whether or not we under- or overestimate the quantity of mass lost by solar metallicity VMSs (Bestenlehner et al. 2014; Vink 2022). For the low metallicity case, while they undergo almost no mass loss during the MS, their mass loss close to the Eddington limit is very uncertain and might have an important impact on their evolution in the later stages (Sander & Vink 2020).

Studying the impact of recent mass-loss-rate prescriptions on VMSs is crucial (see Sabhahit et al. 2022, 2023; Higgins et al. 2023), but updating important physics such as chemical mixing and transport of angular momentum is equally necessary. Therefore, new generations of stellar models should not only update the mass-loss rates but also the physics of many other physical ingredients. This is beyond the aim of the present work and will be the topic of future works.

6.2. Synthesis of the main results and future perspectives

We computed a grid of VMSs from Population III to solar metallicity with and without rotation. We showed that the low-metallicity models are highly sensitive to rotation, while the evolution of higher-metallicity models is dominated by mass-loss effects. The mass loss strongly affects surface velocity evolution, quickly at high metallicity, while reaching the critical velocity for low-metallicity models. Our comparison to observed VMSs in the LMC shows that the mass-loss prescriptions used for these nonrotating and rotating models lead to slight under- or over-estimations compared to the observed mass-loss rates. According to the treatment of rotation in our models, observed VMSs need a high initial velocity to be able to account for their observed surface velocity. The surface enrichment of these observed VMSs is difficult to explain with only one initial composition and this suggests the possible existence of multiple populations in the R136 cluster or perhaps a more complex scenario involving multiple star interactions.

The tremendous dependence of the evolution of VMSs on the input physics in the models will clearly have a crucial impact on the final fate and the nature of the remnants that such stars can produce. As shown in multiple studies (Woosley & Heger 2021; Costa et al. 2021; Marchant & Moriya 2020; Farmer et al. 2019), the final fate of VMSs is strongly linked to the CO core mass at the end of He-burning. The present work provides a new illustration of the fact that rotation, mass loss, and other physics inputs play an important role in the CO core mass value, and could be essential to our understanding of the final fate and the maximum mass of the remnants produced by VMSs. A first discussion shows that at a metallicity typical of R136, only the non- or slowly rotating VMS models may produce pair instability supernovae. The most massive black holes that could be formed then are expected to be less massive than about 60 M⊙. In a dedicated follow-up paper, we discuss the impact of the different physics introduced here on the final fate of the stars. Thanks to the addition of an equation of state following the pair production inside the star, we can now track the evolution of the pair-instability inside VMSs. This will allow us to determine, for the whole grid of models, which ones are either undergoing core collapse, pulsational pair-instability supernovae, or direct collapse through pair instability.

1

The Wolf-Rayet phase in GENEC is assumed to begin when the model has an effective temperature of higher than 10 000 K and a surface mass fraction of hydrogen of below 0.3.

2

The critical velocity is the velocity at which the centrifugal force at the equator balances the gravity there. Its expression is taken as indicated by expression (6) in Ekström et al. (2008).

3

These isotopes are 1H, 3, 4He, 12, 13, 14C, 14, 15N, 16, 17, 18O, 18, 19F, 20, 21, 22Ne, 23Na, 24, 25, 26Mg, 26, 27Al, 28Si, 32S, 36Ar, 40Ca, 44Ti, 48Cr, 52Fe, and 56Ni.

4

We note that the models here are always by construction at hydrostatic equilibrium. The oscillation seen here is likely due to the fact that pair-creation removes radiative support and thus triggers contraction. At its turn, contraction leads to larger nuclear energy production, which triggers expansion.

Acknowledgments

S.M. has received support from the SNS project number 200020-205154, the European Union’s Horizon 2020 research and innovation program under grant agreement No. 101008324 (ChETEC-INFRA) and by the Fonds de la Recherche Scientifique (FNRS, Belgium) and the Research Foundation Flanders (FWO, Belgium) under the EOS Project nr O022818F and O000422. G.M., S.E., C.G. and have received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 833925, project STAREX). R.H. acknowledges support from the World Premier International Research Centre Initiative (WPI Initiative, MEXT, Japan), STFC UK, the European Union’s Horizon 2020 research and innovation program under grant agreement No. 101008324 (ChETEC-INFRA) and the IReNA AccelNet Network of Networks, supported by the National Science Foundation under Grant No. OISE-1927130.

References

  1. Abel, T., Bryan, G. L., & Norman, M. L. 2002, Science, 295, 93 [CrossRef] [Google Scholar]
  2. Bastian, N., & Lardo, C. 2018, ARA&A, 56, 83 [Google Scholar]
  3. Beccari, G., Petr-Gotzens, M. G., Boffin, H. M. J., et al. 2017, A&A, 604, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Becker, G. D., & Bolton, J. S. 2013, MNRAS, 436, 1023 [Google Scholar]
  5. Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A&A, 570, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bestenlehner, J. M., Crowther, P. A., Caballero-Nieves, S. M., et al. 2020, MNRAS, 499, 1918 [Google Scholar]
  7. Björklund, R., Sundqvist, J. O., Singh, S. M., Puls, J., & Najarro, F. 2023, A&A, 676, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Brands, S. A., de Koter, A., Bestenlehner, J. M., et al. 2022, A&A, 663, A36 [Google Scholar]
  9. Brinkman, H. E., Doherty, C., Pignatari, M., Pols, O., & Lugaro, M. 2023, ApJ, 951, 110 [CrossRef] [Google Scholar]
  10. Bromm, V., Coppi, P. S., & Larson, R. B. 2002, ApJ, 564, 23 [Google Scholar]
  11. Cassinelli, J. P., Mathis, J. S., & Savage, B. D. 1981, Science, 212, 1497 [NASA ADS] [CrossRef] [Google Scholar]
  12. Clark, P. C., Glover, S. C. O., Klessen, R. S., & Bromm, V. 2011, ApJ, 727, 110 [NASA ADS] [CrossRef] [Google Scholar]
  13. Costa, G., Bressan, A., Mapelli, M., et al. 2021, MNRAS, 501, 4514 [NASA ADS] [CrossRef] [Google Scholar]
  14. Crowther, P. A., Schnurr, O., Hirschi, R., et al. 2010, MNRAS, 408, 731 [Google Scholar]
  15. Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
  17. de Mink, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Denissenkov, P. A., & Hartwick, F. D. A. 2014, MNRAS, 437, L21 [Google Scholar]
  19. D’Ercole, A., D’Antona, F., Ventura, P., Vesperini, E., & McMillan, S. L. W. 2010, MNRAS, 407, 854 [Google Scholar]
  20. Domínguez, R., Pellegrini, E. W., Klessen, R. S., & Rahner, D. 2022, ArXiv e-prints [arXiv:2205.06209] [Google Scholar]
  21. Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [Google Scholar]
  22. Eggenberger, P., Miglio, A., Montalban, J., et al. 2010, A&A, 509, A72 [CrossRef] [EDP Sciences] [Google Scholar]
  23. Eggenberger, P., Ekström, S., Georgy, C., et al. 2021, A&A, 652, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Ekström, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 [Google Scholar]
  25. Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
  26. Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., & Justham, S. 2019, ApJ, 887, 53 [Google Scholar]
  27. Farrell, E., Groh, J. H., Meynet, G., & Eldridge, J. J. 2022, MNRAS, 512, 4116 [NASA ADS] [CrossRef] [Google Scholar]
  28. Faucher-Giguère, C.-A., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008, ApJ, 688, 85 [CrossRef] [Google Scholar]
  29. Faucher-Giguère, C.-A., Lidz, A., Zaldarriaga, M., & Hernquist, L. 2009, ApJ, 703, 1416 [Google Scholar]
  30. Figer, D. F. 2005, Nature, 434, 192 [Google Scholar]
  31. Fragos, T., Andrews, J. J., Bavera, S. S., et al. 2023, ApJS, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]
  32. Georgy, C., Ekström, S., Meynet, G., et al. 2012, A&A, 542, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Georgy, C., Ekström, S., Granada, A., et al. 2013, A&A, 553, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Georgy, C., Saio, H., & Meynet, G. 2014, MNRAS, 439, L6 [Google Scholar]
  35. Gieles, M., Charbonnel, C., Krause, M. G. H., et al. 2018, MNRAS, 478, 2461 [Google Scholar]
  36. Gormaz-Matamala, A. C., Cuadra, J., Meynet, G., & Curé, M. 2023, A&A, 673, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Gräfener, G., & Hamann, W. R. 2008, A&A, 482, 945 [Google Scholar]
  38. Gräfener, G., Owocki, S. P., & Vink, J. S. 2012, A&A, 538, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Greif, T. H., Springel, V., White, S. D. M., et al. 2011, ApJ, 737, 75 [NASA ADS] [CrossRef] [Google Scholar]
  40. Groenewegen, M. A. T. 2012a, A&A, 540, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Groenewegen, M. A. T. 2012b, A&A, 541, C3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Groh, J. H., Meynet, G., Ekström, S., & Georgy, C. 2014, A&A, 564, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Groh, J. H., Ekström, S., Georgy, C., et al. 2019, A&A, 627, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Haehnelt, M. G., Madau, P., Kudritzki, R., & Haardt, F. 2001, ApJ, 549, L151 [NASA ADS] [CrossRef] [Google Scholar]
  45. Higgins, E. R., Vink, J. S., Hirschi, R., Laird, A. M., & Sabhahit, G. N. 2023, MNRAS, 526, 534 [NASA ADS] [CrossRef] [Google Scholar]
  46. Hirano, S., Hosokawa, T., Yoshida, N., et al. 2014, ApJ, 781, 60 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hirano, S., Hosokawa, T., Yoshida, N., Omukai, K., & Yorke, H. W. 2015, MNRAS, 448, 568 [NASA ADS] [CrossRef] [Google Scholar]
  48. Hirschi, R. 2007, A&A, 461, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Ishii, M., Ueno, M., & Kato, M. 1999, PASJ, 51, 417 [NASA ADS] [Google Scholar]
  50. Jeřábková, T., Hasani Zonoozi, A., Kroupa, P., et al. 2018, A&A, 620, A39 [Google Scholar]
  51. Jiang, L., Chen, W.-C., Tauris, T. M., Müller, B., & Li, X.-D. 2023, ApJ, 945, 90 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kaiser, E. A., Hirschi, R., Arnett, W. D., et al. 2020, MNRAS, 496, 1967 [Google Scholar]
  53. Koen, C. 2006, MNRAS, 365, 590 [NASA ADS] [CrossRef] [Google Scholar]
  54. Krtička, J., Owocki, S. P., & Meynet, G. 2011, A&A, 527, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Maeder, A. 1997, A&A, 321, 134 [NASA ADS] [Google Scholar]
  56. Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
  57. Maeder, A., & Meynet, G. 2004, A&A, 422, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Marchant, P., & Moriya, T. J. 2020, A&A, 640, L18 [EDP Sciences] [Google Scholar]
  59. Marchant, P., Renzo, M., Farmer, R., et al. 2019, ApJ, 882, 36 [Google Scholar]
  60. Martinet, S., Meynet, G., Ekström, S., et al. 2021, A&A, 648, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Martinet, S., Meynet, G., Nandal, D., et al. 2022, A&A, 664, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Massey, P., Neugent, K. F., Ekström, S., Georgy, C., & Meynet, G. 2023, ApJ, 942, 69 [NASA ADS] [CrossRef] [Google Scholar]
  63. McEvoy, C. M., Dufton, P. L., Evans, C. J., et al. 2015, A&A, 575, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Murphy, L. J., Groh, J. H., Farrell, E., et al. 2021, MNRAS, 506, 5731 [NASA ADS] [CrossRef] [Google Scholar]
  65. Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
  66. Oey, M. S., & Clarke, C. J. 2005, ApJ, 620, L43 [NASA ADS] [CrossRef] [Google Scholar]
  67. Ramírez-Agudelo, O. H., Sana, H., de Koter, A., et al. 2017, A&A, 600, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
  69. Sabhahit, G. N., Vink, J. S., Higgins, E. R., & Sander, A. A. C. 2022, MNRAS, 514, 3736 [NASA ADS] [CrossRef] [Google Scholar]
  70. Sabhahit, G. N., Vink, J. S., Sander, A. A. C., & Higgins, E. R. 2023, MNRAS, 524, 1529 [NASA ADS] [CrossRef] [Google Scholar]
  71. Sabín-Sanjulián, C., Simón-Díaz, S., Herrero, A., et al. 2014, A&A, 564, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Sabín-Sanjulián, C., Simón-Díaz, S., Herrero, A., et al. 2017, A&A, 601, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Sander, A. A. C., & Vink, J. S. 2020, MNRAS, 499, 873 [Google Scholar]
  74. Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
  76. Schneider, F. R. N., Ramírez-Agudelo, O. H., Tramper, F., et al. 2018, A&A, 618, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Scott, L. J. A., Hirschi, R., Georgy, C., et al. 2021, MNRAS, 503, 4208 [NASA ADS] [CrossRef] [Google Scholar]
  78. Sibony, Y., Liu, B., Simmonds, C., Meynet, G., & Bromm, V. 2022, A&A, 666, A199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Simaz Bunzel, A., García, F., Combi, J. A., & Chaty, S. 2023, A&A, 670, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Simón-Díaz, S., Godart, M., Castro, N., et al. 2017, A&A, 597, A22 [CrossRef] [EDP Sciences] [Google Scholar]
  81. Song, C.-Y., & Liu, T. 2023, ApJ, 952, 156 [CrossRef] [Google Scholar]
  82. Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
  83. Stacy, A., & Bromm, V. 2013, MNRAS, 433, 1094 [NASA ADS] [CrossRef] [Google Scholar]
  84. Stacy, A., Greif, T. H., & Bromm, V. 2010, MNRAS, 403, 45 [NASA ADS] [CrossRef] [Google Scholar]
  85. Stacy, A., Bromm, V., & Lee, A. T. 2016, MNRAS, 462, 1307 [NASA ADS] [CrossRef] [Google Scholar]
  86. Stothers, R. B. 1999, MNRAS, 305, 365 [NASA ADS] [CrossRef] [Google Scholar]
  87. Susa, H., Hasegawa, K., & Tominaga, N. 2014, ApJ, 792, 32 [NASA ADS] [CrossRef] [Google Scholar]
  88. Szécsi, D., Mackey, J., & Langer, N. 2018, A&A, 612, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
  90. Turk, M. J., Abel, T., & O’Shea, B. 2009, Science, 325, 601 [NASA ADS] [CrossRef] [Google Scholar]
  91. Vanbeveren, D., Mennekens, N., & De Greve, J. P. 2012, A&A, 543, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. van Loon, J. T., Cioni, M. R. L., Zijlstra, A. A., & Loup, C. 2005, A&A, 438, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Vink, J. S. 2018, A&A, 615, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Vink, J. S. 2022, ARA&A, 60, 203 [NASA ADS] [CrossRef] [Google Scholar]
  95. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Weidner, C., & Kroupa, P. 2004, MNRAS, 348, 187 [NASA ADS] [CrossRef] [Google Scholar]
  97. Wise, J. H., Demchenko, V. G., Halicek, M. T., et al. 2014, MNRAS, 442, 2560 [NASA ADS] [CrossRef] [Google Scholar]
  98. Wollenberg, K. M. J., Glover, S. C. O., Clark, P. C., & Klessen, R. S. 2020, MNRAS, 494, 1871 [NASA ADS] [CrossRef] [Google Scholar]
  99. Woosley, S. E., & Heger, A. 2021, ApJ, 912, L31 [NASA ADS] [CrossRef] [Google Scholar]
  100. Yang, M., Bonanos, A. Z., Jiang, B., et al. 2023, A&A, 676, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Yusof, N., Hirschi, R., Meynet, G., et al. 2013, MNRAS, 433, 1114 [NASA ADS] [CrossRef] [Google Scholar]
  102. Yusof, N., Hirschi, R., Eggenberger, P., et al. 2022, MNRAS, 511, 2814 [NASA ADS] [CrossRef] [Google Scholar]
  103. Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]

All Tables

Table 1.

Properties of the stellar models at different stages of their evolution.

In the text

All Figures

thumbnail Fig. 1.

HRD of the nonrotating model (solid lines) and the model rotating at V/Vc = 0.4 (dashed lines) at Z = 0.014 (solar) and Z = 0.006 (LMC). The top, middle, and bottom rows show models with initial masses of 180, 250, and 300 M⊙, respectively. The tracks are color-coded according to their mass-loss rates. The beginning and the end of the burning phases are indicated by circles and crosses, respectively. The beginning of the Wolf-Rayet phase is indicated by a light blue circle.
In the text
thumbnail Fig. 2.

HRD for 180 M⊙ nonrotating models at Z = 0.014, Z = 0.006, Z = 10−5, and Z = 0. The tracks are color-coded according to their current total mass. The MS of the models at Z = 0.014, Z = 0.006, and Z = 10−5 is plotted in dashed gray in the lower right panel for comparison.
In the text
thumbnail Fig. 3.

Evolution of the surface angular velocity divided by the critical angular velocity for 180 M⊙ rotating models initially at V/Vc = 0.4 (Ω/Ωcrit ≃ 0.58), for Z = 10−5 and Z = 0. The gray dashed line shows the numerical limit used to trigger the mechanical mass loss.
In the text
thumbnail Fig. 4.

Stacked lifetimes as a percentage of the total lifetime for O-type stars, RSGs, YSGs, BSGs, and WR types for nonrotating (left) and rotating models (right) at Z = 0.006 (top) and Z = 0.014 (bottom).
In the text
thumbnail Fig. 5.

Evolution of the convective core mass of VMSs at the beginning and at the end of the He-burning phase, for nonrotating and V/Vc = 0.4 models at both Z = 0.006 and Z = 0.014. The light gray region corresponds to the total actual mass of the star at the considered evolutionary stage, and is emphasized by a line of the corresponding color.
In the text
thumbnail Fig. 6.

Convective core mass at the end of He-burning as a function of the initial mass for nonrotating and rotating stars at Z = 0.006 and Z = 0.014. The models with initial masses lower than 180 M⊙ are from Ekström et al. (2012) for Z = 0.014 and from Eggenberger et al. (2021) for Z = 0.006, and share the same physics, albeit with the differences described in Sect. 2. The range of CO core masses from Farmer et al. (2019) where (P)PISNe can occur is shown as an example to underline the very different potential final fate of VMSs when considering rotation and metallicity effects.
In the text
thumbnail Fig. 7.

Comparison with previous models. Left: HRD of a rotating 300 M⊙ at Z = 0.014 from the work of Yusof et al. (2013) and from this work. The beginning of each burning phase (defined as the moment when the central abundance of the element concerned decreases by 1%) and the end of it (defined as the moment when the central abundance is lower than 10−5) are displayed as open circles and crosses, respectively. Right: central temperature as a function of the central density for the same models. A zoom can be seen in the upper left displaying the region where the model starts undergoing pair-creation inside the core, leading the model with the new EOS – which takes this effect into account – to contract and expand rapidly as the pair-creation reduces the radiative pressure.
In the text
thumbnail Fig. 8.

Time-averaged mass-loss rates over the main sequence as a function of the Eddington parameter Γedd, e. The models of 85–120 M⊙ are from Eggenberger et al. (2021), and the models of 180–300 M⊙ are from this work. The observations of Brands et al. (2022) of the R136 components are displayed in gold. The fit they obtained is displayed in purple. The three most massive components of the cluster (R136a1/2/3) are pinpointed by arrows.
In the text
thumbnail Fig. 9.

HRD of the Tarantula Nebula from the compilation of Schneider et al. (2018; regrouping results from Ramírez-Agudelo et al. 2017; Sabín-Sanjulián et al. 2014, 2017; McEvoy et al. 2015; Bestenlehner et al. 2014) and the R136 cluster members from the work of Brands et al. (2022). The GENEC tracks are overplotted in gray, with color emphasis on the VMS models computed here, and the ZAMS is drawn in dark gray. The HRD is plotted for nonrotating (left) and rotating (at V/Vc = 0.4; right) models. Their effective temperatures are not corrected for the optical thickness of the wind. The three most massive components of the cluster (R136a1/2/3) are pinpointed by arrows in the right panel.
In the text
thumbnail Fig. 10.

Evolution of the surface velocity of VMS models. An additional model with slower initial rotation rate has been computed for this plot. The observed velocities of the three most massive components of R136 are overplotted (R136a2 and R136a3 have similar velocities obtained). The uncertainties on the velocity are taken from the maximum macro-turbulent velocity observed for stars close to the Eddington limit (Simón-Díaz et al. 2017) for the lower limit, and from the maximum velocities obtained from the angle-of-view effect for the upper limit.
In the text
thumbnail Fig. 11.

Surface enrichment of nitrogen over hydrogen as a function of surface helium. The observed values of [N/H] are from Brands et al. (2022), and the surface helium fraction is from Bestenlehner et al. (2020).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.