| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347366 | |
| Published online | 13 October 2023 | |
KMT-2021-BLG-1547Lb: Giant microlensing planet detected through a signal deformed due to source binarity
1
Department of Physics, Chungbuk National University,
Cheongju
28644,
Republic of Korea
e-mail: cheongho@astroph.chungbuk.ac.kr
2
Center for Astrophysics | Harvard & Smithsonian,
60 Garden St.,
Cambridge, MA
02138,
USA
3
Department of Astronomy, Tsinghua University,
Beijing
100084,
PR China
4
Korea Astronomy and Space Science Institute,
Daejon
34055,
Republic of Korea
5
Korea University of Science and Technology, Korea, (UST),
217 Gajeong-ro,
Yuseong-gu, Daejeon
34113,
Republic of Korea
6
Institute of Natural and Mathematical Science, Massey University,
Auckland
0745,
New Zealand
7
University of Canterbury, Department of Physics and Astronomy,
Private Bag 4800,
Christchurch
8020,
New Zealand
8
Max-Planck-Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg,
Germany
9
Department of Astronomy, Ohio State University,
140 W. 18th Ave.,
Columbus, OH
43210,
USA
10
Department of Particle Physics and Astrophysics, Weizmann Institute of Science,
Rehovot
76100,
Israel
11
School of Space Research, Kyung Hee University, Yongin,
Kyeonggi
17104,
Republic of Korea
12
Klein Karoo Observatory, Calitzdorp, and Bronberg Observatory,
Pretoria,
South Africa
13
Kavli Institute for Astronomy and Astrophysics, Peking University,
Yi He Yuan Road 5, Hai Dian District,
Beijing
100871,
PR China
14
School of Physics and Astronomy, Tel-Aviv University,
Tel-Aviv
6997801,
Israel
15
Department of Physics and Astronomy, Louisiana State University,
Baton Rouge, LA
70803,
USA
16
Institute for Space-Earth Environmental Research, Nagoya University,
Nagoya
464-8601,
Japan
17
Code 667, NASA Goddard Space Flight Center,
Greenbelt, MD
20771,
USA
18
Department of Astronomy, University of Maryland,
College Park, MD
20742,
USA
19
Department of Earth and Planetary Science, Graduate School of Science, The University of Tokyo,
7-3-1 Hongo,
Bunkyo-ku, Tokyo
113-0033,
Japan
20
Instituto de Astrofisica de Canarias,
Via Lâctea s/n,
38205
La Laguna, Tenerife,
Spain
21
Department of Earth and Space Science, Graduate School of Science, Osaka University,
Toyonaka, Osaka
560-0043,
Japan
22
Institute of Astronomy, Graduate School of Science, The University of Tokyo,
2-21-1 Osawa,
Mitaka, Tokyo
181-0015,
Japan
23
Department of Physics, The Catholic University of America,
Washington, DC
20064,
USA
24
Department of Astronomy, Graduate School of Science, The University of Tokyo,
7-3-1 Hongo,
Bunkyo-ku, Tokyo
113-0033,
Japan
25
Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency,
3-1-1 Yoshinodai, Chuo,
Sagamihara, Kanagawa
252-5210,
Japan
26
Sorbonne Université, CNRS, UMR 7095, Institut d’Astrophysique de Paris,
98 bis bd Arago,
75014
Paris,
France
27
Department of Physics, University of Auckland,
Private Bag
92019,
Auckland,
New Zealand
28
University of Canterbury Mt. John Observatory,
PO Box 56,
Lake Tekapo
8770,
New Zealand
Received:
5
July
2023
Accepted:
31
August
2023
Aims. We investigate the previous microlensing data collected by the KMTNet survey in search of anomalous events for which no precise interpretations of the anomalies had been suggested. From this investigation, we find that the anomaly in the lensing light curve of the event KMT-2021-BLG-1547 is approximately described by a binary-lens (2L1S) model with a lens possessing a giant planet, but the model leaves unexplained residuals.
Methods. We investigated the origin of the residuals by testing more sophisticated models that include either an extra lens component (3L1S model) or an extra source star (2L2S model) on top of the 2L1S configuration of the lens system. From these analyses, we find that the residuals from the 2L1S model originate from the existence of a faint companion to the source. The 2L2S solution substantially reduces the residuals and improves the model fit by Δχ2 = 67.1 with respect to the 2L1S solution. The 3L1S solution also improves the fit, but its fit is worse than that of the 2L2S solution by Δχ2 = 24.7.
Results. According to the 2L2S solution, the lens of the event is a planetary system with planet and host masses (Mp/MJ, Mh/M⊙) = (1.47−0.77+0.64, 0.72−0.38+0.32) lying at a distance DL = 5.07−1.50+0.98 kpc, and the source is a binary composed of a subgiant primary of a late G or an early K spectral type and a main-sequence companion of a K spectral type. The event demonstrates the need for sophisticated modeling of unexplained anomalies if one wants to construct a complete microlensing planet sample.
Key words: gravitational lensing: micro / planets and satellites: detection
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The planetary signal in a lensing light curve is mostly described by a 2L1S model, in which the lens comprises two masses – those of the planet and its host – and the source is a single star (Mao & Paczyński 1991; Gould & Loeb 1992). Sometimes a planetary signal cannot be precisely described by the usual 2L1S model for several major reasons.
The first cause of the deviation of a planetary signal from a 2L1S form is the existence of an additional planet. In general, a planet induces two sets of caustics, one of which lies near the position of the planet host (central caustic) and the other lies away from the host (planetary caustic) at the position s – 1/s, where s denotes the position vector of the planet from the host (Griest & Safizadeh 1998; Han 2006). For a lens system that contains multiple planets, the central caustics induced by the individual planets appear in a common region around the planet host, and thus the magnification pattern of the central region deviates from that of a single-planet system (Gaudi et al. 1998) and deforms the planetary signal. There are five known cases of microlensing events with planetary signals deformed by multiple planets: OGLE-2006-BLG-109 (Gaudi et al. 2008; Bennett et al. 2010), OGLE-2012-BLG-0026 (Han et al. 2013; Beaulieu et al. 2016), OGLE-2018-BLG-1011 (Han et al. 2019), OGLE-2019-BLG-0468 (Han et al. 2022d), and KMT-2021-BLG-1077 (Han et al. 2022a).
The second cause of a planetary signal deformation is the binarity of the planet host. Under the lens configuration in which a planet orbits around one component of a wide binary star or around the barycenter of a close binary star, the binary companion induces additional perturbations in the central magnification region, and thus the signal of the planet may deviate from a single-planet form (Lee et al. 2008). There have been five reports of microlensing planets with signals affected by binary companions to the hosts: OGLE-2006-BLG-284 (Bennett et al. 2020), OGLE-2007-BLG-349 (Bennett et al. 2016), OGLE– 2016-BLG-0613 (Han et al. 2017), OGLE-2018-BLG-1700 (Han et al. 2020), and KMT-2020-BLG-0414 (Zang et al. 2021).
A planetary signal can also be deformed by the bina– rity of the source star. If the source is accompanied by a close companion, the perturbation region induced by the planet can be additionally swept by the primary source’s companion star, and this can induce a deformation of the planetary signal. There are three known cases of planetary signals affected by the existence of source companions: MOA-2010-BLG-117 (Bennett et al. 2018), KMT-2018-BLG-1743 (Han et al. 2021a), and KMT-2021-BLG-1898 (Han et al. 2022b).
Firmly identifying the cause of the deformation in a planetary signal is often difficult, as demonstrated in the case of KMT-2021-BLG-0240. For this event, Han et al. (2022c) find that the central anomaly can be explained with either a triple-lens (3L1S) model, in which the lens is composed of three masses – those of two planets and that of their host – or a binary-lens binary-source (2L2S) model, in which the lens is a single-planet system and the source is a binary.
We conducted a systematic investigation of the microlensing data collected in previous seasons by the Korea Microlensing Telescope Network (KMTNet; Kim et al. 2016) survey in search of anomalous lensing events for which no precise interpretations of the anomalies had been suggested. From this investigation, Han et al. (2023a) find that the precise descriptions of the anomalies in the two lensing events OGLE-2018-BLG-0584 and KMT-2018-BLG-2119 required four-body (lens plus source) lensing models, in which both the lens and the source are binaries. Han et al. (2023b) also find that the description of the anomaly that appeared in the lensing event KMT-2021-BLG– 1122 required a different four-body lensing model, in which the lens is a triple stellar system and the source is a single star. In this work, we present the analysis of the lensing event KMT-2021– BLG-1547, for which no lensing solution that precisely described the anomaly appearing in the lensing light curve had been put forward.
This paper is organized as follows. In Sect. 2 we describe the observations of the lensing event, the instruments used for the observations, and the reduction procedure of the data. In Sect. 3 we present the analysis of the observed lensing light curve using three models of the lens-system configurations: 2L1S (in Sect. 3.1), 3L1S (Sect. 3.2), and 2L2S (Sect. 3.3). In Sect. 4 we determine the source of the event and estimate the angular Einstein radius of the lens system. In Sect. 5 we present the physical parameters of the lens system estimated from the Bayesian analysis of the lensing event. In Sect. 6 we summarize the results of our analysis and conclude.
2 Observation and data
The source of the lensing event KMT-2021-BLG-1547 lies toward the Galactic bulge field at the equatorial coordinates (RA, Dec)J2000 = (18:09:35.90, −29:05:02.18), which correspond to the Galactic coordinates (l, b) = (2°.494, −4°.614). The baseline magnitude of the source is Ibase = 19.09, and the extinction toward the field is AI = 0.83. The lensing-induced magnification of the source flux was first found by the KMTNet group on 2021 July 1, which corresponds to the abridged heliocentric Julian date HJD′ = HJD – 2450000 = 9396.5, when the source became brighter than the baseline magnitude by ΔI ~ 0.63 mag. The position of the source corresponds to the KMTNet BLG33 field, toward which observations in a normal survey mode were conducted with a 2.5 h cadence. On 2021 July 7, HJD′ ~ 9402, the event was independently found by the Microlensing Observations in Astrophysics (MOA) survey group (Bond et al. 2001), who referred to the event as MOA-2021-BLG-228. We hereafter designate the event as KMT-2021-BLG-1547 in accordance with the convention of the microlensing community using the event ID reference of the first discovery survey. The KMTNet observations of the event were conducted with the use of three identical 1.6 m telescopes located at three sites of the Southern Hemisphere: the Siding Spring Observatory (SSO) in Australia (KMTA), the Cerro Tololo Interamerican Observatory (CTIO) in Chile (KMTC), and the South African Astronomical Observatory (SAAO) in South Africa (KMTS). The MOA observations were conducted with the 1.8 m telescope of the Mt. John Observatory in New Zealand.
Images containing the source of the event were mostly acquired in the I band for the KMTNet survey and in the customized MOA-R band for the MOA survey. The initial reduction of the images and photometry of the source were done using the pipelines developed by Albrow et al. (2009) and Bond et al. (2001) for the KMTNet and MOA surveys, respectively. For the optimization of the data, the KMTNet data used in the analysis were prepared by re-reducing the images using the updated tender loving care (TLC) algorithms developed by Yang et al. (in prep.). In order to set the scatter of the data to be consistent with the error bars and to set χ2 per degree of freedom (dof) for each data set to unity, we readjusted the error bars of the data resulting from the automatized photometry pipelines using the Yee et al. (2012) routine. For a subset of KMTC images taken in V and I bands, we conducted an additional photometry using the pyDIA code of Albrow (2017) for the source color measurement.
The lensing light curve of KMT-2021-BLG-1547 constructed with the combined KMTNet and MOA data is presented in Fig. 1, in which the lower panel shows the whole view and the upper panel shows the zoomed-in view of the peak region. The light curve peaked at HJD′ = 9407.280 with a very high magnification of Amax ~ 299. Because the peak region of a very high-magnification event is sensitive to planetary signals (Griest & Safizadeh 1998), an alert was issued by the KMTNet HighMagFinder system (Yang et al. 2022) to cover the peak region of the light curve. In response to this alert, the KMTNet group increased its observational cadence to ~0.15 h, which is about 17 times shorter than the cadence of the normal survey mode. Furthermore, the Microlensing Astronomy Probe (MAP) and the Microlensing Follow-Up Network (μFUN) follow-up teams (Zang et al. 2021) carried out follow-up observations of the event around the peak of the lensing light curve using the 1.0 m telescope of Las Cumbres Observatory (LCO) at SAAO and the 0.36 m telescope of Klein Karoo Observatory (KKO) in South Africa. The KKO data were acquired at a very high cadence, and we use a binned data with a 5 min interval. The densely covered peak region, the shaded region in the upper panel of Fig. 1, revealed a clear signature of an anomaly that lasted slightly less than a day. We note that the high-magnification alert was issued at UT 20:15 on 2021 July 10 (HJD′ = 9406.34), which was well before the anomaly was noticed. In Fig. 2, the magnitudes of the data collected from MOA and MAP & μFUN follow-up observations are scaled to the KMTNet system by linearly aligning the source flux to that of the KMTNet data.
 |
Fig. 1 Light curve of the microlensing event KMT-2021-BLG-1547. The lower and upper panels show the whole view and a zoomed-in view around the anomalous region near the peak, respectively. The solid curve drawn over the data point is a 1L1S model obtained by excluding the data around the anomaly region of the light curve. The shaded region in the upper panel represents the duration of intensive observations, and the arrow indicates the position of a weak bump. |
3 Light curve analysis
3.1 2L1S model
The pattern of the anomaly, in which the light curve rapidly rises and falls during a short period of time, likely indicates that a caustic is involved in the pattern of the anomaly. Therefore, we began the analysis by modeling the light curve under a 2L1S interpretation. The modeling was carried out in search of a lensing solution, which indicates a set of the lensing parameters that describes the light curve. Under the approximation of the rectilinear relative motion between the lens and source, a 2L1S lensing light curve is depicted by seven parameters, t0, u0, tE, s, q, α, and ρ. The first three parameters (t0, u0, and tE) describe the lens-source approach, and the individual parameters denote the time of the closest lens-source approach, the lens-source separation (normalized to the angular Einstein radius θE) at t0, and the event timescale defined as the time required for the source to cross θE. The next three parameters (s, q, and α) are related to the binary lens, and they indicate the projected separation (scaled to θE) and mass ratio between the binary-lens components (M1 and M2), and the angle of the source trajectory with respect to the M1–M2 axis, respectively. The last parameter ρ, defined as the ratio of the angular source radius θ* to θE, depicts the parts of the lensing light curve affected by finite-source effects.
The 2L1S modeling was conducted in two stages. In the first stage, we divided the lensing parameters into two categories, and the binary parameters (s, q) in the first category were searched for using a grid approach with multiple starting values of a, and the other parameters were found using a downhill approach based on the Markov chain Monte Carlo method with an adaptive step size Gaussian sampler (Doran & Mueller 2004). We then constructed a Δχ2 map on the s-q parameter plane and identified local minima on the map. In the second stage, we refined the local solutions by allowing all parameters to vary, and then found a global solution by comparing the goodness of the fits of the individual local solutions.
From the 2L1S modeling, we found a pair of solutions with a projected binary-lens separation s < 1 (close solution) and a separation s > 1 (wide solution) resulting from the close-wide degeneracy (Griest & Safizadeh 1998; Dominik 1999; An 2005). The binary parameters are (s, q)close ~ (0.73,2.2 × 10−3) for the close solution, and (s, q)wide ~ (1.37,2.1 × 10−3) for the wide solution. The full lensing parameters of the individual solutions are listed in Table 1 together with the χ2 values of the fits of the models. For both solutions, the estimated very low mass ratio q ~ 2.1 × 10−3 between the lens components indicates that the companion to the lens is a planetary-mass object. The lens-system configuration of the wide 2L1S solution is presented in the inset of the top panel in Fig. 2. The configuration shows that the central anomaly was produced by the source passage very close to lower left cusp of the central caustic induced by a planet. We note that the configuration of the close solution is very similar to that of the wide solution. Although the source did not cross the caustic, it passes within 1.5 source radii of the caustic cusp. Hence, the normalized radius ρ = (1.49 ± 0.03) × 10−3 was precisely measured from the peak part of the light curve deformed by finite-source effects.
We find that the wide solution is preferred over the close solution by Δχ2 = 60.1 despite the two solutions being subject to the close-wide degeneracy. In order to investigate the region of the fit difference, we created a cumulative diagram of  between the two solutions, shown in Fig. 3. The diagram shows that the wide solution yields better fits than than the close solution in the two regions around HJD′ ~ 9407.5 and ~ 9408.8. In the inset of the top panel, we compare the contour maps of lensing magnifications for the close (gray contours) and wide (black contours) solutions. We find that the maps exhibit subtle differences despite the similarity between the caustics of the two solutions. From this difference together with the large number of data points contributing to the degeneracy between the close and wide solutions is lifted.
between the two solutions, shown in Fig. 3. The diagram shows that the wide solution yields better fits than than the close solution in the two regions around HJD′ ~ 9407.5 and ~ 9408.8. In the inset of the top panel, we compare the contour maps of lensing magnifications for the close (gray contours) and wide (black contours) solutions. We find that the maps exhibit subtle differences despite the similarity between the caustics of the two solutions. From this difference together with the large number of data points contributing to the degeneracy between the close and wide solutions is lifted.
Figure 2 shows the model curve (dotted curve in the top panel) and residual of the wide 2L1S solution. The 2L1S model appears to approximately describe the anomaly, but detailed inspection reveals that the model leaves residuals from the model. The most conspicuous residual appears at around the bump centered at tbump ~ 9406.85, while small but systematic negative residuals appear in the KMTA data in the part of the light curve after the bump during 9406.92 ≲ HJD' ≲ 9407.2. The bump in the residual is likely to be of astrophysical origin rather than systematics in the data, because it appears in three different data sets: KMTC, MOA, and KMTA. Despite the fact that 2L1S models that are very similar to ours were circulated around the microlensing community during the season of the event, an analysis of the event has not been published because the residual could not be fully explained with a 2L1S model. In order to explain the residual, we inspected more sophisticated models to check whether the residuals may vanish with other interpretations of the lens system.
Model parameters of the 2L1S solutions.
 |
Fig. 2 Zoomed-in view around the peak region of the KMT-2021-BLG-1547 light curve. The lower three panels show the residuals from the 2L2S (wide), 3L1S (wide), and 2L1S (wide) models. The dotted and solid curves drawn over the data points in the top panel are the models of the 2L1S and 2L2S solutions, respectively. The arrow labeled “tbump” indicates the region that leaves a bump in the residual from the 2L1S model. The two insets in the top panel show the lens-system configurations of the 2L1S and 3L1S models. In each inset, the red figures are the caustics, and the line with an arrow represents the source trajectory. |
 |
Fig. 3 Cumulative diagram of |
3.2 3L1S model
In order to explain the residual from the 2L1S model, we checked a model with a 3L1S configuration by introducing an extra lens component to the binary-lens system. The consideration of an extra lens component M3 requires one to include additional lensing parameters in modeling. These parameters are (s3, q3,ψ), which denote the mass ratio and normalized projected separation between M1 and M3, and the orientation of M3 as measured from the M1–M2 axis, respectively. We use the notations (s2, q2) for the parameters related to M1–M2 pair to distinguish them from those related to M3. Because the 2L1S model approximately described the overall feature of the anomaly, we started searches for the third-body parameters (s3, q3,ψ) via a grid approach by fixing the other lensing parameters as those of the 2L1S solution, and then refined the solution by allowing all parameters to vary. We carried out this procedure two times based on the close and wide 2L1S solutions.
The lensing parameters of the 3L1S solutions found based on the close and wide 2L1S solutions are listed in Table 2. For both solutions, the parameters related to M2 are very similar to those of the 2L1S solutions, and the parameters related to M3 are (s3, q3)close ~ (1.012,1.8 × 10−6) and (s3, q3)wide ~ (1.001,1.5 × 10−6) for the close and wide solutions, respectively. These parameters indicate that the lens would be a two-planet system, in which the second planet has an extremely low planet-to-host mass ratio of order 10−6 and lies very close to the Einstein ring of the planet host. If the signal of the second planet is real, then the measured mass ratio would be the lowest among the microlensing planets that have ever been detected. Similarly to the case of the 2L1S solutions, we find the wide solution yields a better fit than the close solution by Δχ2 = 59.9.
In the inset of the top panel in Fig. 2, we present the lens-system configuration of the wide 3L1S solution. It shows that the second planet induces an additional caustic elongated along the M1–M3 axis, and the source passed through this caustic. This diminishes the residuals at around and after the bump at tbump, as shown in the residual of the wide 3L1S model presented in Fig. 2. We find that the introduction of the second planet improves the model fit by Δχ2 = 42.4 with respect to the 2L1S model.
Model parameters of the 3L1S solutions.
3.3 2L2S model
It is known that a subtle deviation in a planetary signal can arise not only due to an extra companion to the lens but also a companion to the source, as demonstrated in the case of the lensing event OGLE-2019-BLG-0304 (Han et al. 2021b). Therefore, we additionally tested a 2L2S configuration of the lens system, in which an extra source was introduced to the 2L1S system. As in the case of the 3L1S modeling, the introduction of the source companion (S2) to the primary source (S1) requires one to include additional parameters. These parameters are (t0,2, u0,2,ρ2, qF), which represent the time and separation at the moment of the closest S2 approach to the lens, the normalized source radius of S2, and the flux ratio between S1 and S2, respectively. We use the notations (t0,1, u0,1, ρ1) for the parameters related to S1 to distinguish them from the parameters related to S2. In the 2L2S modeling, the solution was found by testing various trajectories of the source companion based on the 2L1S solution considering the locations and amplitudes of the anomaly features that could not be fully explained by the 2L1S model.
In Table 3 we list the lensing parameters of the close and wide 2L2S solutions found based on the close and wide 2L1S solutions, respectively. Between the two solutions, we find that the wide solution yields a better fit than the fit of the close solution by Δχ2 = 19.0. From the comparison of the parameters of the wide solution related to S1, (t0,1, u0,1) = (9407.277, 5.16 × 10−3), with those related to S2, (t0,2, u0,2) = (9407.339,−10.62 × 10−3), we find that the secondary source passed on the opposite side of the primary source with respect to the planet host, trailing the primary with a slightly larger impact parameter than that of the primary source. The flux ratio between the source stars is qF ~ 5.7% for the close solution and ~ 2.6% for the wide solution, indicating that the source companion is much fainter than the primary source. The lens-system configurations of the close and wide 2L2S solutions are presented in the upper and lower panels of Fig. 4, respectively.
We find that the 2L2S solution yields the best fit to the observed light curve among the three sets of tested models. From the comparison of the model fits, we find that the 2L2S solution yields a better fit than the 2L1S and 3L1S solutions by Δχ2 = 67.1 and 24.7, respectively. In Fig. 2, we draw the model curve of the wide 2L2S solution over the data points and present the residuals from the model. From the inspection of the residuals, we find that the residual bump at around tbump vanishes and the negative 2L1S residuals during the period 9406.92 ≲ HJD′ ≲ 9407.2 substantially diminishes. In Fig. 5 we present the cumulative distributions of  (blue curve in the lower panel) and
(blue curve in the lower panel) and  (red curve) to show the region of fit improvement from the 2L1S model. The distributions show that the fit improvement of the 2L2S model occurs throughout the anomaly region, while the improvement of the 3L1S model is mostly confined to the region around tbump.
(red curve) to show the region of fit improvement from the 2L1S model. The distributions show that the fit improvement of the 2L2S model occurs throughout the anomaly region, while the improvement of the 3L1S model is mostly confined to the region around tbump.
Model parameters of the 2L2S solutions.
 |
Fig. 4 Lens-system configurations of the close and wide 2L2S solutions. In each panel, the red figure is the caustic, and the lines with arrows represent the trajectories of the primary (labeled “S1”) and secondary (“S2”) source stars. The small empty circles on the source trajectories indicate the scaled sizes of the source stars. Gray curves encompassing the caustic represent equi-magnification contours. |
 |
Fig. 5 Cumulative χ2 distributions. The blue curve is the distribution of the χ2 difference between the 2L1S and 2L2S solutions, |
4 Source star and Einstein radius
In this section we specify the source stars of the event and estimate the angular Einstein radius of the lens system. The source stars were determined by measuring their de-reddened colors and magnitudes, and the Einstein radius was estimated from the relation
 (1)
(1)
where the angular source radius θ* was deduced from the source type, and the normalized source radius ρ was measured from the modeling. In estimating θE, we used the angular and normalized source radii of the primary source, that is, θE = θ*/ρ1, because the uncertainties of θ*,1 and ρ1 are much smaller than those of the secondary source star.
For the measurements of the de-reddened source color and magnitude, (V – I,I)0, we first estimated the instrumental magnitudes of the source in the I and V bands, (V, I), by regressing the photometric data processed using the pyDIA code with respect to the lensing model. We then assessed the flux values from the primary and secondary source stars, (F1, F2), in each passband as
 (2)
(2)
where Ftot = F1 + F2 is the combined source flux measured from the model regression, and the flux ratio between the binary source stars, qF = F2/F1, is estimated from the modeling. Figure 6 shows the locations of S1 and S2 in the instrumental color-magnitude diagram (CMD) of stars lying near the source constructed from the pyDIA photometry of these stars. The measured instrumental color and magnitude are (V − I,I)1 = (1.574 ± 0.012,19.439 ± 0.005) for the primary source and (V − I,I)2 = (2.179 ± 0.571,23.088 ± 0.130) for the secondary source.
We calibrated the instrumental source color and magnitude with the use of the Yoo et al. (2004) routine, in which the centroid of the red giant clump (RGC), with (V − I,I)RGC = (1.820,15.806) in the instrumental CMD, was used as a reference for calibration. With the measured offsets in color and magnitude of the source from the RGC centroid, Δ(V − I,I) = (V − I,I) − (V − I,I)RGC, we estimated the de-reddened values of the source as
 (3)
(3)
where (V − I,I)RGC,0 = (1.060,14.322) represent the de-reddened color and magnitude of the RGC centroid known from Bensby et al. (2013) and Nataf et al. (2013), respectively. The estimated de-reddened source color and magnitude from this procedure are
 (4)
(4)
respectively. According to the estimated colors and magnitudes, we find that the primary source of the event is a subgiant of a late G or an early K spectral type, and the companion is a main- sequence star of a late K spectral type.
For the estimation of the source radius, we first converted V − I color into V − K color using the Bessell & Brett (1988) relation, and then deduced the source radius from the relation between 0* and (V − K, I) of Kervella et al. (2004). This yields the radii of the primary and secondary source stars of θ*,1 = 0.91 ± 0.06 μas and θ*,2 = 0.30 ± 0.17 μas, respectively. Finally, the Einstein radius was estimated using the relation in Eq. (1) as
 (5)
(5)
and the relative lens-source proper motion was estimated as
 (6)
(6)
The values derived from θ*,2 are consistent with, but significantly less precise than, those above. We inspected the Gaia data archive (Gaia Collaboration 2018) to check the binarity of the source using the value of the Gaia renormalized unit weight error. This value is close to unity for a well-behaved single star solution, and a high value suggests a binarity of stars. From this inspection, we found that the source is not registered in the Gaia archive, and thus it was difficult to check the source binarity based on the Gaia data.
We note that the estimated value of the relative lens-source proper motion may be subject to an additional uncertainty caused by the internal motion of the source induced by the source orbital motion. According to the wide 2L2S solution, the projected separation between the component stars of the binary source, Δθs⊥, in units of the primary source is
![$ {{{\rm{\Delta }}{\theta _{s, \bot }}} \over {{\theta _{ * ,1}}}} = {{{\rm{\Delta }}u} \over {{\rho _1}}} = {{{{\left[ {{\rm{\Delta }}u_0^2 + {{\left( {{{{\rm{\Delta }}{t_0}} \mathord{\left/ {\vphantom {{{\rm{\Delta }}{t_0}} {{t_{\rm{E}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{E}}}}}} \right)}^2}} \right]}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}} \over {{\rho _1}}} \sim 11.1, $](/articles/aa/full_html/2023/10/aa47366-23/aa47366-23-eq15.png) (7)
(7)
where Δu0 = |u0,2 − u0,2| and Δt0 = |t0,2 − t0,1| denote the differences between the impact parameters and closest approach times of the S1 and S2 trajectories, respectively. With θ*,1 ~ 0.91 μas together with the adopted distance to the source of DS = 8 kpc, the projected physical separation between the source stars is
 (8)
(8)
By adopting the primary source mass of Ms,1 = 1 M⊙ and the secondary source mass of Ms,2 = 0.6 M⊙, and assuming a circular face-on orbit, this yields a source orbital period of P ~ 6.65 days. Then the internal velocity of the binary-source system would be  , which corresponds to the internal proper motion,
, which corresponds to the internal proper motion,
 (9)
(9)
This internal proper motion is a non-negligible fraction of the proper motion μ = 11.02 mas yr−1 estimated without considering the internal source motion.
The internal motion of the source can have several effects. First, the normalized source radius of the source companion, ρ2, can be somewhat different from the value that is found from the model fit. The internal proper motion of S2 relative to the center of mass would be ![${\mu _{{\mathop{\rm int}} ,2}} = \left[ {{{{M_{S,1}}} \mathord{\left/ {\vphantom {{{M_{S,1}}} {\left( {{M_{S,1}} + {M_{S,2}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{M_{S,1}} + {M_{S,2}}} \right)}}} \right]{\mu _{{\mathop{\rm int}} }}\~2.2\,{\rm{mas}}\,{\rm{y}}{{\rm{r}}^{ - 1}}$](/articles/aa/full_html/2023/10/aa47366-23/aa47366-23-eq19.png) . Then, ρ2 could be a factor
. Then, ρ2 could be a factor  larger or smaller than what is found in the fit. However, we note that this does not qualitatively affect the result because the uncertainty of ρ2 is already very big. Second, the primary would move relative to the center of mass with a proper motion
larger or smaller than what is found in the fit. However, we note that this does not qualitatively affect the result because the uncertainty of ρ2 is already very big. Second, the primary would move relative to the center of mass with a proper motion ![${\mu _{{\mathop{\rm int}} ,1}} = \left[ {{{{M_2}} \mathord{\left/ {\vphantom {{{M_2}} {\left( {{M_1} + {M_2}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{M_1} + {M_2}} \right)}}} \right]{\mu _{{\mathop{\rm int}} }}\~1.3\,{\rm{mas}}\,{\rm{y}}{{\rm{r}}^{ - 1}}$](/articles/aa/full_html/2023/10/aa47366-23/aa47366-23-eq21.png) , which is about 12% of the value μ = 11.02 mas yr−1 obtained without considering the internal motion. This implies that the estimated proper motion is subject to an additional ~ 12% uncertainty due to internal proper motion, which should be considered when future adaptive optics observations are made.
, which is about 12% of the value μ = 11.02 mas yr−1 obtained without considering the internal motion. This implies that the estimated proper motion is subject to an additional ~ 12% uncertainty due to internal proper motion, which should be considered when future adaptive optics observations are made.
 |
Fig. 6 Locations of the primary and companion stars of the binary source with respect to the RGC in the instrumental CMD of stars located in the neighborhood of the source. |
5 Physical parameters
We estimated the physical parameters of the mass, M, and distance, DL, to the planetary lens system using the measured lensing observables of tE and θE, which are related to the mass and distance to the lens by the relations
 (10)
(10)
respectively. Here k = 4G/(c2AU) ≃ 8.14 mas  and πrel =
and πrel =  represent the relative lens-source parallax. The physical parameters can be uniquely determined with the additional observable of the microlens parallax πE by the relations
represent the relative lens-source parallax. The physical parameters can be uniquely determined with the additional observable of the microlens parallax πE by the relations
 (11)
(11)
(Gould 2000), but πE could not be securely measured for KMT-2021-BLG-1547 because of the relatively short timescale, tE ~ 21 day, of the event. Therefore, we estimate M and DL by conducting a Bayesian analysis based on the measured observables of tE and θE.
The Bayesian analysis was conducted with the use Galaxy and mass-function (MF) models. Based on these models, we produced a large number of artificial lensing events, for which the locations of the lens and source and their relative proper motions were derived from the Galactic model, and the lens mass were derived from the MF model from a Monte Carlo simulation. In this simulation, we used the Jung et al. (2021) Galaxy model and the Jung et al. (2018) MF model. In the Galaxy model, the density profile of disk objects follows the modified double-exponential form presented in second line of Table 3 in Robin et al. (2003), and the bulge profile follows the triaxial model of Han & Gould (1995). The motion of disk objects follows the model originally based on Han & Gould (1995) and modified to reconcile the Robin et al. (2003) disk density profile. The motion of bulge objects is modeled based on the proper motions of stars in the Gaia catalog (Gaia Collaboration 2016, 2018). The MFs of disk and bulge lens objects are constructed by adopting the initial and present-day MFs of Chabrier (2003), respectively. For the individual artificial events, we computed the Einstein timescales and Einstein radii using the relations in Eq. (10), and then constructed the posteriors of the lens mass and distance by imposing a weight  to each event. Here we compute χ2 value as
to each event. Here we compute χ2 value as
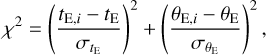 (12)
(12)
where (tE,i, θE,i) are the timescale and Einstein radius of each simulated event, and (tE, θE) and  represent the measured values and their uncertainties, respectively.
represent the measured values and their uncertainties, respectively.
In Fig. 7 we present the Bayesian posteriors of the primary lens mass, distance to the lens and source. In Table 4, we list the estimated values of the host mass Mh, planet mass Mp, distance to the planetary system, and the projected separation between the planet and host,  . We use the median values of the posterior distributions as representative values, and the uncertainties were estimated as the 16 and 84% of the distributions. According to the estimated parameters, the lens is a planetary system, in which a planet with a mass about 50% more massive than the Jupiter of the solar system orbits a host star with a mass about 30% less massive than the sun. The projected planet-host separation a⊥ ~ 4.5 AU is substantially greater than the snow line asnow ~ 2.7(M/M⊙) ~ 1.9 AU of the planetary system, indicating that the planet lies well beyond the snow line of the planetary system. In each posterior distribution, we mark the contributions by the disk (blue curve) and bulge (red curve) lens populations. We find that the relative probabilities for the planet host to be in the disk and bulge are 55 and 45%, respectively
. We use the median values of the posterior distributions as representative values, and the uncertainties were estimated as the 16 and 84% of the distributions. According to the estimated parameters, the lens is a planetary system, in which a planet with a mass about 50% more massive than the Jupiter of the solar system orbits a host star with a mass about 30% less massive than the sun. The projected planet-host separation a⊥ ~ 4.5 AU is substantially greater than the snow line asnow ~ 2.7(M/M⊙) ~ 1.9 AU of the planetary system, indicating that the planet lies well beyond the snow line of the planetary system. In each posterior distribution, we mark the contributions by the disk (blue curve) and bulge (red curve) lens populations. We find that the relative probabilities for the planet host to be in the disk and bulge are 55 and 45%, respectively
 |
Fig. 7 Bayesian posteriors of the primary lens mass and distance to the lens and source. In each panel, the solid vertical line represents the median value, and the two vertical dotted lines indicate the 16 and 84% of the posterior distribution. The blue and red curves represent the contributions from the disk and bulge lens populations, respectively, and black curve is the sum of the two lens populations. |
Physical lens parameters.
6 Summary and discussion
As part of our recent project, we inspected the previous microlensing data collected by the KMTNet survey in search of anomalous lensing events for which no models precisely described the observed anomalies. Following the analyses of the events OGLE-2018-BLG-0584 and KMT-2018-BLG-2119 by Han et al. (2023a) and KMT-2021-BLG-1122 by Han et al. (2023b), we analyzed the event KMT-2021-BLG-1547, for which the anomaly in the lensing light curve could not be precisely described by a usual binary-lens model.
We investigated the origin of the residuals by testing more sophisticated models that included either an extra lens component or an extra source star on top of the 2L1S configuration of the lens system. From these analyses, we find that the residuals from the binary-lens model originated from the existence of a faint companion to the source. The 2L2S solution substantially diminished the residuals and improved the model fit by Δχ2 = 67.1 with respect to the 2L1S solution. The 3L1S solution also improved the fit, but the fit was worse than that of the 2L2S solution by Δχ2 = 24.7.
An important scientific goal of microlensing surveys is to reveal the demographic properties of extrasolar planets, especially those lying in the outer regions of planetary systems. For such studies, it is important to accurately assess the detection efficiency, which is based on a complete planet sample constructed under well-defined detection criteria. If a fraction of planets are missed in this sample because their signals cannot not be fully explained, this would lead to an erroneous estimation of the detection efficiency and, thus, incorrect demographic property results. The event KMT-2021-BLG-1547 demonstrates the need for sophisticated modeling that takes unexplained anomalies into account when attempting to construct a complete microlensing planet sample.
Acknowledgements
Work by C.H. was supported by the grants of National Research Foundation of Korea (2020R1A4A2002885 and 2019R1A2C2085965). This research has made use of the KMTNet system operated by the Korea Astronomy and Space Science Institute (KASI) at three host sites of CTIO in Chile, SAAO in South Africa, and SSO in Australia. Data transfer from the host site to KASI was supported by the Korea Research Environment Open NETwork (KREONET). This research was supported by the Korea Astronomy and Space Science Institute under the R&D program (Project No. 2023-1-832-03) supervised by the Ministry of Science and ICT. The MOA project is supported by JSPS KAKENHI Grant Number JSPS24253004, JSPS26247023, JSPS23340064, JSPS15H00781, JP16H06287, and JP17H02871. J.C.Y., I.G.S., and S.J.C. acknowledge support from NSF Grant No. AST-2108414. Y.S. acknowledges support from NSF Grant No. 2020740. W.Z. acknowledges the support from the Harvard-Smithsonian Center for Astrophysics through the CfA Fellowship. This research uses data obtained through the Telescope Access Program (TAP), which has been funded by the TAP member institutes. W.Z., H.Y., S.M., and W.Z. acknowledge support by the National Natural Science Foundation of China (Grant No. 12133005). C.R. was supported by the Research fellowship of the Alexander von Humboldt Foundation.
References
- Albrow, M. 2017, https://doi.org/10.5281/zenodo.268049 [Google Scholar]
- Albrow, M., Horne, K., Bramich, D. M., et al. 2009, MNRAS, 397, 2099 [Google Scholar]
- An, J. H. 2005, MNRAS, 356, 1409 [Google Scholar]
- Beaulieu, J.-P., Bennett, D. P., Batista, V., et al. 2016, ApJ, 824, 83 [CrossRef] [Google Scholar]
- Bennett, D. P., Rhie, S. H., Nikolaev, S., et al. 2010, ApJ, 713, 837 [Google Scholar]
- Bennett, D. P., Rhie, S. H., Udalski, A., et al. 2016, AJ, 152, 125 [Google Scholar]
- Bennett, D. P., Udalski, A., & Han, C. 2018, AJ, 155, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, D. P., Udalski, A., Bond, I. A., et al. 2020, AJ, 160, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [Google Scholar]
- Bond, I. A., Abe, F., Dodd, R. J., et al. 2001, MNRAS, 327, 868 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Dominik, M. 1999, A&A, 349, 108 [NASA ADS] [Google Scholar]
- Doran, M., & Mueller, C. M. 2004, J. Cosmol. Astropart. Phys., 09, 003 [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A.G.A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaudi, B. S., Naber, R. M., & Sackett, P. D. 1998, ApJ, 502, L33 [CrossRef] [Google Scholar]
- Gaudi, B. S., Bennett, D. P., Udalski, A., et al. 2008, Science, 319, 927 [Google Scholar]
- Gould, A. 2000, ApJ, 542, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., & Loeb, A. 1992, ApJ, 396, 104 [Google Scholar]
- Griest, K., & Safizadeh, N. 1998, ApJ, 500, 37 [Google Scholar]
- Han, C. 2006, ApJ, 638, 1080 [Google Scholar]
- Han, C., & Gould, A. 1995, ApJ, 447, 53 [Google Scholar]
- Han, C., Udalski, A., Choi, J.-Y., et al. 2013, ApJ, 762, L28 [Google Scholar]
- Han, C., Udalski, A., Gould, A., et al. 2017, AJ, 154, 223 [Google Scholar]
- Han, C., Bennett, D. P., Udalski, A., et al. 2019, AJ, 158, 114 [Google Scholar]
- Han, C., Lee, C.-U., Udalski, A., et al. 2020, AJ, 159, 48 [Google Scholar]
- Han, C., Albrow, M. D., Chung, S.-J., et al. 2021a, A&A, 652, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Udalski, A., Lee, C.-U., et al. 2021b, AJ, 162, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., Gould, A., Bond, I. A., et al. 2022a, A&A, 662, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Gould, A., Kim, D., et al. 2022b, A&A, 663, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Kim, D., Yang, H., et al. 2022c, A&A, 664, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Udalski, A., & Lee, C.-U. 2022d, A&A, 658, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Udalski, A., Jung, Y. K., et al. 2023a, A&A, 670, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Jung, Y. K., Gould, A., et al. 2023b, A&A, 672, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jung, Y. K., Udalski, A., Gould, A., et al. 2018, AJ, 155, 219 [Google Scholar]
- Jung, Y. K., Han, C., Udalski, A., et al. 2021, AJ, 161, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 29 [Google Scholar]
- Kim, S.-L., Lee, C.-U., Park, B.-G., et al. 2016, J. Korean Astron. Soc., 49, 37 [Google Scholar]
- Lee, D.-W., Lee, C.-U., Park, B.-G., et al. 2008, ApJ, 672, L623 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S., & Paczynski, B. 1991, ApJ, 374, 37 [Google Scholar]
- Nataf, D. M., Gould, A., Fouqué, P., et al. 2013, ApJ, 769, 88 [Google Scholar]
- Robin, A. C., Reyle, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, H., Zang, W., Gould, A., et al. 2022, MNRAS, 5146, 189 [Google Scholar]
- Yee, J. C., Shvartzvald, Y., Gal-Yam, A., et al. 2012, ApJ, 755, 102 [Google Scholar]
- Yoo, J., DePoy, D.L., Gal-Yam, A., et al. 2004, ApJ, 603, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Zang, W., Han, C., Kondo, I., et al. 2021, Res. Astron. Astrophys., 21, 239 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Light curve of the microlensing event KMT-2021-BLG-1547. The lower and upper panels show the whole view and a zoomed-in view around the anomalous region near the peak, respectively. The solid curve drawn over the data point is a 1L1S model obtained by excluding the data around the anomaly region of the light curve. The shaded region in the upper panel represents the duration of intensive observations, and the arrow indicates the position of a weak bump. |
| In the text | |
 |
Fig. 2 Zoomed-in view around the peak region of the KMT-2021-BLG-1547 light curve. The lower three panels show the residuals from the 2L2S (wide), 3L1S (wide), and 2L1S (wide) models. The dotted and solid curves drawn over the data points in the top panel are the models of the 2L1S and 2L2S solutions, respectively. The arrow labeled “tbump” indicates the region that leaves a bump in the residual from the 2L1S model. The two insets in the top panel show the lens-system configurations of the 2L1S and 3L1S models. In each inset, the red figures are the caustics, and the line with an arrow represents the source trajectory. |
| In the text | |
 |
Fig. 3 Cumulative diagram of |
| In the text | |
 |
Fig. 4 Lens-system configurations of the close and wide 2L2S solutions. In each panel, the red figure is the caustic, and the lines with arrows represent the trajectories of the primary (labeled “S1”) and secondary (“S2”) source stars. The small empty circles on the source trajectories indicate the scaled sizes of the source stars. Gray curves encompassing the caustic represent equi-magnification contours. |
| In the text | |
 |
Fig. 5 Cumulative χ2 distributions. The blue curve is the distribution of the χ2 difference between the 2L1S and 2L2S solutions, |
| In the text | |
 |
Fig. 6 Locations of the primary and companion stars of the binary source with respect to the RGC in the instrumental CMD of stars located in the neighborhood of the source. |
| In the text | |
 |
Fig. 7 Bayesian posteriors of the primary lens mass and distance to the lens and source. In each panel, the solid vertical line represents the median value, and the two vertical dotted lines indicate the 16 and 84% of the posterior distribution. The blue and red curves represent the contributions from the disk and bulge lens populations, respectively, and black curve is the sum of the two lens populations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





