| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348791 | |
| Published online | 30 April 2024 | |
OGLE-2023-BLG-0836L: The sixth microlensing planet in a binary stellar system
1
Department of Physics, Chungbuk National University,
Cheongju
28644,
Republic of Korea
e-mail: cheongho@astroph.chungbuk.ac.kr
2
Astronomical Observatory, University of Warsaw,
Al. Ujazdowskie 4,
00-478
Warszawa,
Poland
3
Korea Astronomy and Space Science Institute,
Daejon
34055,
Republic of Korea
4
Max Planck Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg,
Germany
5
Department of Astronomy, The Ohio State University,
140 W. 18th Ave.,
Columbus,
OH
43210,
USA
6
University of Canterbury, Department of Physics and Astronomy,
Private Bag 4800,
Christchurch
8020,
New Zealand
7
Department of Particle Physics and Astrophysics, Weizmann Institute of Science,
Rehovot
76100,
Israel
8
Center for Astrophysics | Harvard & Smithsonian
60 Garden St.,
Cambridge,
MA
02138,
USA
9
Department of Astronomy and Tsinghua Centre for Astrophysics, Tsinghua University,
Beijing
100084,
PR China
10
School of Space Research, Kyung Hee University,
Yongin,
Kyeonggi
17104,
Republic of Korea
11
Korea University of Science and Technology,
217 Gajeong-ro,
Yuseong-gu,
Daejeon,
34113,
Republic of Korea
12
Department of Physics, University of Warwick,
Gibbet Hill Road,
Coventry
CV4 7AL,
UK
Received:
30
November
2023
Accepted:
12
February
2024
Aims. Light curves of microlensing events occasionally deviate from the smooth and symmetric form of a single-lens single-source event. While most of these anomalous events can be accounted for by employing a binary-lens single-source (2L 1S) or a single-lens binary-source (1L2S) framework, it is established that a small fraction of events remain unexplained by either of these interpretations. We carried out a project in which data collected by high-cadence microlensing surveys were reinvestigated with the aim of uncovering the nature of anomalous lensing events with no proposed 2L 1S or 1L 2S models.
Methods. From the project we found that the anomaly appearing in the lensing event OGLE-2023-BLG-0836 cannot be explained by the usual interpretations, and we conducted a comprehensive analysis of the event. From thorough modeling of the light curve under sophisticated lens-system configurations, we arrived at the conclusion that a triple-mass lens system is imperative to account for the anomalous features observed in the lensing light curve.
Results. From the Bayesian analysis using the measured observables of the event timescale and angular Einstein radius, we determined that the least massive component of the lens has a planetary mass of 4.36−2.18+2.35 MJ. This planet orbits within a stellar binary system composed of two stars with masses 0.71−0.36+0.38 M⊙ and 0.56−0.28+0.30 M⊙. This lensing event signifies the sixth occurrence of a planetary microlensing system in which a planet belongs to a stellar binary system.
Key words: planets and satellites: detection
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The light curve of a microlensing event involving a single lens and a single source (1L1S) is represented by
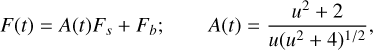 (1)
(1)
where A(t) is the lensing magnification, Fs and Fb denote the respective flux values originating from the source and blended light components, and represents the projected lens-source separation normalized to the angular Einstein radius θE. The lensing magnification varies in time as the lens-source separation changes due to their relative motion as
![$u(t) = {\left[ {u_0^2 + {{{{\left( {t - {t_0}} \right)}^2}} \over {{t_{\rm{E}}}}}} \right]^{1/2}},$](/articles/aa/full_html/2024/05/aa48791-23/aa48791-23-eq5.png) (2)
(2)
where 0 and t0 represent the minimum lens-source separation (scaled to θE) and the corresponding time, and tE is the Einstein timescale. The resulting light curve is characterized by a smooth and symmetric form (Paczynski 1986).
Light curves in microlensing events occasionally exhibit deviations from the standard 1L1S form. These deviations are, in most cases, attributed to two primary factors: the potential binarity of the lens, as described by Mao & Paczynski (1991), and the binarity of the source, as noted by Griest & Hu (1992). In the case of a binary-lens (2L1S) event, the lensing system creates a complex pattern of caustics. These caustics represent specific positions of the source at which the lensing magnification for a point source diverges to infinity. When a source crosses the caustic, a pair of new images are created or disappear, resulting in a complicated lensing light curve that deviates from the 1L1S form. In the case of a binary-source (1L 2S) event, the lensing magnification corresponds to the mean of the magnifications associated with the individual binary source stars, A1 and A2, weighted by the flux contributions of the component source stars, F1 and F2:
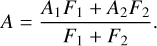 (3)
(3)
As a consequence, the light curve of a 1L2S event displays deviations from the standard 1L1S form.
Since 2016, the Korea Microlensing Telescope Network (KMTNet) has been conducting a microlensing survey with frequent observations of stars located in the direction of the Galactic bulge (Kim et al. 2016). Among about 3000 microlensing events that are annually detected from the survey, about 10% of the events exhibit anomalies in the lensing light curves. While the majority of these anomalous lensing events can be explained by applying a 2L1S or a 1L2S framework, it is known that a small fraction of events defy explanation under either of these interpretations. The challenge in precisely characterizing the peculiarities of these events hints at the necessity for more advanced models to interpret the observed anomalies.
We conducted a project that involved revisiting microlensing data collected by the KMTNet survey. The primary goal of this project was to uncover instances of anomalous lensing events for which the conventional 2L1S or 1L2S models had not been previously proposed. Through this investigation, we identified multiple occurrences that required the application of advanced modeling approaches beyond the standard 2L1S or 1L2S frameworks. Han et al. (2019) found that the anomaly appearing in the light curve of the lensing event OGLE-2018-BLG-1011, which corresponds to KMTNet event KMT-2018-BLG-2122, could be explained with a triple-lens (3L1S) model in which the lens is composed of two giant planets and their host star. Through a detailed analysis of the light curve for the lensing event OGLE-2018-BLG-1700 (KMT-2018-BLG-2330), Han et al. (2020a) identified the triple nature of the lens by decomposing the anomaly into two parts produced by two binary-lens pairs. In one of these binary pairs, the mass ratio of the lens components is approximately q ~ 0.01, while in the other pair the mass ratio is around ~0.3, suggesting that the lens is a planetary system in a binary. Through a careful examination of the central anomaly observed in the lensing curve of the highly magnified event KMT-2019-BLG-1953, Han et al. (2020b) found that the discrepancies from the 2L1S model were significantly reduced when an additional planetary lens companion or a source companion was introduced, although distinguishing these two interpretations was difficult within the precision of the photometric data. In their study, Han et al. (2021a) determined that the anomalous characteristics observed in the lensing light curve of the event KMT-2019-BLG-0797 could be accounted for by a 2L2S model in which both the lens and source are binary systems. By analyzing the event KMT-2019-BLG-1715, for which the lensing light curve exhibited two short-term deviation features from a caustic-crossing 2L1S light curve, Han et al. (2021b) suggested a five-body (lens+source) model, in which one deviation feature was generated by a planetary-mass third body of the lens, and the other feature was generated by a faint source companion, and thus the event is a very complex five-body system composed of three lens masses (planet + two stars) and two source stars. Han et al. (2021c) found that KMT-2018-BLG-1743 is another planetary lensing event occurring on two source stars. In their analysis of the anomalies observed in the lensing event OGLE-2019-BLG-0304 (KMT-2019-BLG-2583), Han et al. (2021d) put forward two rivaling interpretations between a 3L1S and a 2L2S models. The 3L1S model suggests the presence of a planetarymass third body situated near the primary lens of the binary lens system. The 2L2S model proposes the existence of an additional nearby companion to the source. Zang et al. (2021) found that the central anomaly in the lensing light curve of the event KMT-2020-BLG-0414 was produced by a triple-lens system, which consists of an Earth-mass planet and its binary host. Through the investigation of the anomalous lensing event KMT-2021-BLG-1077, Han et al. (2022a) identified that the lens of the event is a multi-planetary system in which two giant planets orbit a very low-mass star. It was found by Han et al. (2022b) that the dual bump anomaly feature in the light curve of the lensing event KMT-2021-BLG-1898 could be explained with a 2L2S model, in which the lens contains a giant planet and the source is a binary composed of a turnoff star and a K-type dwarf. Han et al. (2022c) found that the planetary signal in the lensing light curve of the event KMT-2021-BLG-0240 was deformed either by an extra planetary lens component or by a companion to the source, although the 3L1S and 2L2S interpretations could not be distinguished with the available data. Han et al. (2023a) found that the lensing events OGLE-2018-BLG-0584 and KMT-2018-BLG-2119 were generated by 2L2S lens systems. From the analysis of the lensing event KMT-2021-BLG-1122, Han et al. (2023b) revealed that the anomaly appeared in the light curve was produced by a 3L1S system, which consists of three stars.
In this study, we provide a comprehensive analysis of the microlensing event OGLE-2023-BLG-0836/KMT-2023-BLG-1144, for which no existing model has successfully explained the anomaly observed in the lensing light curve. The anomaly in question presents two distinctive features: a caustic-crossing pattern and a strong cusp-approaching peak. Our investigation has led us to the conclusion that the inclusion of a triple-mass lens system is imperative to adequately account for all the anomalous features in the lensing light curve of the event.
2 Observations and data
The source of the microlensing event OGLE-2023-BLG-0836/KMT-2023-BLG-1144 is positioned in the direction of the Galactic bulge field, with equatorial coordinates (RA, Dec)J2000 = (17:48:44.85, −23:44:29.47), which correspond to the Galactic coordinates (l, b) = (4°.8075, 2°.0912). In this direction, the extinction in the I-band is approximately AI ~ 2.01. The magnification of the source flux caused by lensing was first detected from the Optical Gravitational Lensing Experiment IV (OGLE-IV: Udalski et al. 2015) survey on 28 June 2023, corresponding to the reduced Heliocentric Julian Date (HJD′ ≡ HJD − 2460000 = 123). Five days later, the KMTNet group independently found the event and designated it as KMT-2023-BLG-1144. While we initially recognized the anomalous nature of the event through a systematic analysis of the KMTNet data gathered during the 2023 season, we have chosen to label the event as OGLE-2023-BLG-0836, aligning with the reference ID from the OGLE survey that initially detected the event.
The event observations were conducted using the telescopes operated by individual survey groups. The KMTNet group employs three identical telescopes, each featuring a 1.6-m aperture and a wide-field camera capable of capturing 4 square degrees in a single exposure. In order to ensure continuous coverage of lensing events, the KMTNet telescopes are strategically positioned across the three continents in the southern hemisphere: Siding Spring Observatory in Australia (KMTA), Cerro Tololo Interamerican Observatory in Chile (KMTC), and South African Astronomical Observatory in South Africa (KMTS). Additionally, the OGLE telescope, featuring a 1.3-m aperture and a camera yielding a 1.4 square degree field of view, is located at Las Campanas Observatory in Chile. Images from the KMT-Net and OGLE surveys were mainly obtained in the I-band with the inclusion of some V-band images taken for source color measurement. Observations of the event by the KMTNet and OGLE surveys were done with cadences of an hour and about two days, respectively. Image reduction and photometry for the lensing event were accomplished using automated pipelines tailored to the individual surveys, with those developed by Albrow (2017) for the KMTNet survey and by Woźniak (2000) for the OGLE survey. For the use of optimal data in the analysis, we conducted re-reduction of the KMTNet data using the photometry code developed by Yang (in prep.). Additionally, the error bars of the data were adjusted to ensure consistency with the data scatter, and to set the χ2 value per degree of freedom (d.o.f.) for each data set to unity following the procedure outlined in Yee et al. (2012).
Figure 1 presents the lensing light curve of OGLE-2023-BLG-0836, revealing deviations from the typical smooth and symmetric shape observed in a 1L1S event. These deviations are marked by two primary features. The first is the caustic-crossing feature, which is characterized by a pair of caustic-crossing spikes at HJD′ ~ 115.7 and ~119.6 and a U-shape trough region between the spikes. The second feature is the strong peak, centered at HJD′ ~ 111.3, which is likely to be produced by the source star’s approach to a caustic cusp. The upper panel of Fig. 1 offers a detailed view of this anomalous region. Because caustics in gravitational lensing are formed due to the presence of multiple lensing masses, the caustic-crossing feature indicates that the lens is comprised of multiple masses. Furthermore, the approximate symmetry between the ascending and descending segments of the peak anomaly feature suggests that the feature likely originated from the source’s approach to a cusp of a caustic.
 |
Fig. 1 Lensing light curve of OGLE-2023-BLG-0836. The top panel displays an enlarged view focused on the vicinity of the anomaly. |
3 Lensing light curve analysis
3.1 Binary-lens analysis
Taking into account the potential involvement of the anomaly features with caustics, our analysis commences by modeling the light curve under the interpretation with a 2L1S lens-system configuration. This modeling process is conducted to identify a lensing solution, which comprises a set of lensing parameters that best describe the characteristics of the light curve. Under the approximation of rectilinear relative motion between the lens and source, the light curve of a 2L1S event is defined by seven fundamental lensing parameters. The three initial parameters (t0, u0, tE) characterize the approach of the source to the lens. The next three parameters (s, q, α) provide information about the binary lens system: s denotes the projected separation (scaled to θE) between the lens components M1 and M2; q = M2/M1 represents the mass ratio of these lens components; and α is the source trajectory angle, defined as the angle between the direction of the relative lens-source proper motion vector µ and the M1−M2, axis. The last parameter, ρ, is defined as the ratio of the angular source radius θ* to the Einstein radius (normalized source radius), that is, ρ = θ*/θE, and it characterizes how finite source effects contribute to the deformation of the lensing light curve during caustic crossings.
In our pursuit of the lensing solution, we categorized the lensing parameters into two groups. Within the first group, which pertains to the binary parameters (s, q, α), we conducted a grid-based exploration to determine the values of parameters s and q with multiple initial values of α. The other parameters of the second group were determined by minimizing χ2 through the use of the Markov chain Monte Carlo (MCMC) method, which employs an adaptive step size Gaussian sampler, as described in Doran & Mueller (2004). To assess the presence of degenerate solutions, we examined the ∆χ2 map in the s–q parameter space derived from the grid search. After identifying local solutions, we further refined the lensing parameters of the solutions using a downhill approach. In cases for which the discrepancies in χ2 values among these local solutions were marginal, we presented all of them and investigated the causes of degeneracies.
Despite our comprehensive exploration of the parameter space, we were unable to identify a 2L1S solution capable of sufficiently explaining both the caustic-crossing and cusp-approaching features within the anomaly. This underscores the necessity of employing a more sophisticated model for a comprehensive understanding of the observed anomaly features.
While the 2L1S model cannot simultaneously accommodate both the caustic-crossing and cusp-approaching features, we identified that each anomaly feature can be adequately approximated by a 2L1S model. This is illustrated in Fig. 2, where we present two 2L1S model curves depicting the individual anomaly features. The curve presented in the upper panel represents a 2L1S model derived by fitting the data excluding the observations around the cusp-approaching feature during the time interval 110 ≲ HJD′ ≲ 115, while the curve shown in the lower panel is a model obtained by fitting the data with the exclusion of the data around the caustic feature within the time range 114 ≲ HJD′ ≲ 110. Another example of an anomaly that can be divided into two parts produced by two 2L1S events can be seen in Fig. 2 of Han et al. (2020a). We found a solution with binary parameters (s, q) ~ (0.60, 0.85) from the 2L1S fit to the data excluding the caustic-crossing feature. Similarly, we also identified a solution with (s, q) ~ (1.13, 3.4 × 10−3) from the fit to the data excluding those around the cusp-approaching feature. The full lensing parameters of the pair of 2L1S solutions are presented in Table 1. Regarding the lensing parameters in the model describing the caustic-crossing feature, we note that the mass ratio of the lens components is on the order of 10−3, indicating that the companion is very likely to be a planet-mass object.
Figure 3 displays the lens-system configurations corresponding to the individual 2L1S models presented in Fig. 2. In each panel, the red figure comprising the concave closed curves represents the caustic, and the arrowed line represents the trajectory of the source. The configuration illustrates that the caustic-crossing feature resulted from the source star’s crossing over the planetary caustic induced by a planetary companion. On the other hand, the peak feature of the anomaly was produced by the source star’s close approach to the sharp off-axis cusp of a caustic induced by a binary lens composed of roughly equal masses.
 |
Fig. 2 Division of the anomaly into two parts. The curve presented in the upper panel represents a 2L1S model derived by fitting the data excluding those around the cusp-approaching feature, while the curve in the lower panel is a 2L1S model obtained by fitting the data with the exclusion of the data around caustic-crossing feature. |
Lensing parameters of 2L1S solutions.
3.2 Triple-lens analysis
Bozza (1999) and Han (2001) pointed out that anomalies produced by a triple-lens system, composed of three masses (M1, M2, M3), can often be approximated by combining the anomalies induced by the two binary pairs M1−M2 and M1−M3 through superposition. Then, the fact that the two anomaly features in the peak region of the OGLE-2023-BLG-0836 light curve are well approximated by two 2L 1S models implies the possibility of the lens system being a triple system. Consequently, we proceeded with a modeling approach based on a 3L 1S configuration for the lens system.
The 3L1S configuration corresponds to the case in which an extra lens component, M3, is present in addition to the 2L 1S configuration. Incorporating this supplementary lens component necessitates the addition of extra lensing parameters in the modeling procedure. These parameters consist of (s3, q3, ψ), which respectively stand for the projected separation and mass ratio between M1 and M3, and the orientation angle of M3 as measured from M1−M2 axis. In order to distinguish these parameters describing M3 from those describing M2, we use the notations (s2, q2) to designate the separation and mass ratio between the M1−M2 pair.
The 3L1S modeling was carried out using the following procedure. In the first step, we searched for the tertiary lens parameters (s3, q3, ψ) via a grid approach using the parameters of the 2L 1S model as initial values for the other parameters. In our analysis we used the lensing parameters of the 2L 1S solution depicting the cusp-approaching feature. In the second step we identified local solutions appearing in the s3−q3−ψ parameter space, and then refined the individual solutions by gradually minimizing χ2 of the fit using a downhill approach.
Through the 3L1S modeling, we identified three distinct solutions resulting from the ambiguity in s3. Figure 4 shows the locations of the individual local solutions in the ∆χ2 map on the (log s3, log q3) parameter plane obtained from the grid searches for the tertiary lens parameters. The parameters describing the M1−M2 pair, which lie in the ranges of 0.5 ≲ s2≲ 0.6 and 0.59 ≲ q2 ≲ 0.88, are similar to those of the 2L1S model describing the cusp-approaching feature. Similarly, the parameters describing the M1−M3 pair, which lie in the ranges of 1.11 ≲ s3 ≲ 1.16 and 4.9 × 10−3 ≲ q3 ≲ 5.9 × 10−3, are similar to those of the 2L1S model describing the caustic-crossing feature. We label the individual local solutions as “inner,” “intermediate,” and “outer” for the reason discussed below. In the ∆χ2 map, it appears that there are two local minima with log q values approximately around -2.5. However, during the refinement of the solutions, we found that these two minima converge into a single solution.
In Table 2, we list the full lensing parameters of the three 3L1S solutions together with their χ2 values of the fits and d.o.f. Our analysis reveals a preference for the outer solution, with χ2 differences of 34.0 and 4.2 over the inner and intermediate solutions, respectively. We present the model curve of the outer 3L1S solution in the top panel of Fig. 5 and the residuals from all three 3L1S solutions in the lower panels. It is worth noting that the normalized source radius is measured based on the finite-source constraint, although the measured value carries a substantial uncertainty. The lensing light curve is affected by finite-source effects during the source crossings over the fold caustics induced by the planet and during the approach to the cusp induced by the binary companion. We checked the origin of the ρ constraint by conducting two modeling runs; the first run was done by excluding the two points near the caustic crossings at HJD′ = 115.685 and 119.559, and the second run was conducted by excluding the two KMTC points near the cusp peak at HJD′ = 121.513 and 121.527. From these runs we find that the constraint on ρ comes mainly from the two data points observed during the caustic crossings. In Fig. 6, we plot the relative probability of the normalized source radius estimated from the 3L1S modeling.
The configurations of the lens systems corresponding to the three 3L1S solutions are presented in Fig. 7. In all instances, the triple-lens caustic seems to result from the combination of two separate binary-lens caustics caused by the M1–M2 and M1–M3 pairs. The source first traversed the planetary caustic created by the M1 – M3 pair, giving rise to the caustic-crossing feature. Subsequently, the source moved past the lower tip of the caustic formed by the M1 –M2 pair, leading to the emergence of the cusp-approaching anomaly feature. While the fundamental structures of the three solutions resemble one another, there exist subtle distinctions between them. According to the inner and outer solutions, the source traversed the two folds of the planetary caustic situated in the inner and outer regions between the caustic center and the primary lens, respectively. As we discuss below, the degeneracy between the inner and outer solutions is caused by the inner–outer degeneracy (Gaudi & Gould 1997). In the intermediate solution, the source encountered the inner caustic fold upon entering the caustic, and the outer caustic fold while departing from it. We assigned labels to the individual solutions based on the side of the caustic that the source crossed.
Hwang et al. (2022) and Gould et al. (2022) showed that the planet separations of a pair of solutions resulting from an innerouter degeneracy follow the relation
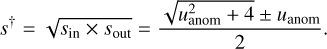 (4)
(4)
Here sin and sout respectively denote the binary separations of the inner and outer solutions; 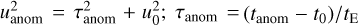 ; and tanom is the time of the anomaly. The symbols “+” and “−” on the right side of the equation apply to the major-image and minor-image perturbations, respectively. In the case of OGLE-2023-BLG-0836, the planet-induced anomaly (i.e., the caustic-crossing feature) was produced by a major-image perturbation, and as a result the sign associated with this event is “+.” In order to investigate the origin of the degeneracy in the separation s3, we checked whether s3 values of the inner and outer solutions follow the relation in Eq. (4). With the lensing parameters (t0, u′0, t′E, tanom, s′in, s′out) = (115.37, 0.22, 46.2, 117.0, 1.435, 1.408), we find that the geometric mean (sin × sout)1/2 ~ 1.124 closely matches the value
; and tanom is the time of the anomaly. The symbols “+” and “−” on the right side of the equation apply to the major-image and minor-image perturbations, respectively. In the case of OGLE-2023-BLG-0836, the planet-induced anomaly (i.e., the caustic-crossing feature) was produced by a major-image perturbation, and as a result the sign associated with this event is “+.” In order to investigate the origin of the degeneracy in the separation s3, we checked whether s3 values of the inner and outer solutions follow the relation in Eq. (4). With the lensing parameters (t0, u′0, t′E, tanom, s′in, s′out) = (115.37, 0.22, 46.2, 117.0, 1.435, 1.408), we find that the geometric mean (sin × sout)1/2 ~ 1.124 closely matches the value ![$\left[ {{{\left( {u_{{\rm{anom}}}^2 + 4} \right)}^{1/2}} + {u_{{\rm{anom}}}}} \right]/2 = 1.119$](/articles/aa/full_html/2024/05/aa48791-23/aa48791-23-eq9.png) . This confirms that the similarity between the model curves of the inner and outer solutions stems from the inner-outer degeneracy. In computing s†, we used the values of the lensing parameters normalized to the Einstein radius corresponding to sum of M1 and M3: (u′0, t′E, s′in, s′out) ≡ (u0f, tE/f, sinf, soutf), where f = (1 + q3)1/2.
. This confirms that the similarity between the model curves of the inner and outer solutions stems from the inner-outer degeneracy. In computing s†, we used the values of the lensing parameters normalized to the Einstein radius corresponding to sum of M1 and M3: (u′0, t′E, s′in, s′out) ≡ (u0f, tE/f, sinf, soutf), where f = (1 + q3)1/2.
After identifying the origin of the degeneracy between the inner and outer solutions, we further investigate the origin of the degeneracy involving the intermediate solution and the other solutions. It is worth noting that Shin et al. (2023) and Han et al. (2024) independently reported the presence of such degeneracies in their respective analyses of the planetary lensing events KMT-2016-BLG-1751 and KMT-2023-BLG-0469. Upon closer examination of the caustic-crossing feature, we found that the degeneracy between the intermediate solution and the other solutions is an accidental one stemming from inadequate caustic coverage. This is depicted in Fig. 8, which provides a detailed view around the caustic-crossing feature. The figure illustrates that the source magnitudes just before the caustic entrance and just after the caustic exit for the inner and outer solutions are remarkably similar, suggesting an inherent degeneracy. On the contrary, the source magnitude just before the caustic entrance for the intermediate solution is approximately 0.1 magnitude brighter than what is expected from the other solutions, indicating that this degeneracy is a chance occurrence. If the light curve in this specific region had been more thoroughly covered, the degeneracy between the intermediate solution and the other solutions could have been lifted. The issue of degeneracies arising due to insufficient coverage of certain parts of caustic-crossing features was explored by Skowron et al. (2018).
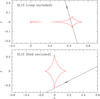 |
Fig. 3 Lens system configurations of the two 2L1S solutions for which the model curves are presented in the corresponding panels of Fig. 2. In each panel, the red figure is the caustic, the line represents the source trajectory, and the arrow on the source trajectory indicates the direction of the source motion. By convention, the abscissa of these 2L1S diagrams is defined by the binary axis of the lens system. |
 |
Fig. 4 ∆χ2 map on the (log s3, log q3) parameter plane. The color-coding is configured to correspond to data points based on their ∆χ2 values: red for ∆χ2 ≤ 12n, yellow for ≤ 22n, green for ≤ 32n, and cyan for ≤ 42n, where n = 4. The three distinct local solutions are marked as inner, intermediate, and outer. The dashed vertical line represents the geometric mean (s3,in × s3,out)1/2 of the planetary separations for the inner and outer solutions. |
Lensing parameters of 3L1S solutions.
 |
Fig. 5 Model curves of the best-fit 3L1S solution (outer solution) and 2L2S solution in the region of the anomaly. The lower four panels present the residuals from the three degenerate 3L1S solutions (inner, intermediate, and outer solutions) and the 2L2S solution. |
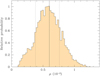 |
Fig. 6 Relative distribution of the normalized source radius. The solid vertical line indicates the median value, and the two dotted lines represent the 1σ ranges of the distribution. |
3.3 Binary-lens binary-source analysis
As illustrated in the lensing event KMT-2021-BLG-0240 (Han et al. 2022c), anomalies arising from a 3L1S system can, on occasion, be confused with anomalies resulting from 2L2S systems. Hence, we conducted a more thorough examination to ascertain whether the observed anomalies in the lensing light curve of OGLE-2023-BLG-0836 could be explained by a 2L2S interpretation.
The 2L2S configuration involves the presence of an additional source alongside the 2L1S configuration. We designate the primary and secondary source stars as S1 and S2, respectively. To account for the additional source, it is necessary to incorporate extra lensing parameters into the modeling process. These additional parameters encompass (t0,2, u0,2, ρ2, qF), which respectively represent the time and separation of the closest approach of S2 to the lens, the normalized source radius of S2, and the flux ratio between S2 and S1. Concurrently, we employ the notations (t0,1, u0,1, ρ1) to define the parameters describing the approach of S1 to the lens. During the modeling process we seek the 2L2S parameters by exploring various trajectories for S2, building upon the 2L1S solution that describes the caustic-crossing feature.
In Table 3, we list the best-fit lensing parameters of the 2L2S solution. The lens-system configuration corresponding to the solution is shown in Fig. 9. In this illustration the paths of the primary and secondary source stars are indicated by black and blue lines, respectively, and they are labeled as S1 and S2. The model curve and residual of the 2L2S solution in the region of the anomaly are presented in Fig. 5, showing that the model approximately describes the anomaly features.
Although the 2L2S model offers an approximate description of the anomaly features, it is found that the model exhibits a less accurate fit to the data when compared to the 3L1S model. This can be seen in Fig. 10, where the cumulative distribution of χ2 difference between the 2L2S and 3L1S solutions, that is, 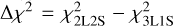 , is presented. From the distribution, it is found that the 2L2S solution yields a poorer fit in the region after the cusp-approaching feature. Overall, it is found that the 2L2S solution is less favorable by ∆χ2 = 31.3 when compared to the 3L 1S solution. As a result, we dismissed the 2L2S interpretation for the anomaly.
, is presented. From the distribution, it is found that the 2L2S solution yields a poorer fit in the region after the cusp-approaching feature. Overall, it is found that the 2L2S solution is less favorable by ∆χ2 = 31.3 when compared to the 3L 1S solution. As a result, we dismissed the 2L2S interpretation for the anomaly.
 |
Fig. 7 Lens-system configurations of the three degenerate 3L1S solutions. For each solution, the lower panel shows the source trajectory, marked by an arrowed line, with respect to the caustic, and the upper panel shows the trajectory with respect to the positions of the lens components, marked by blue dots with labels M1, M1, and M3. The gray curves encompassing the caustic in the lower panels represent equi-magnification contours. The dashed circles in the upper panels represent the Einstein ring. |
 |
Fig. 8 Zoomed-in view around the caustic-crossing feature. Model curves of the three degenerate solutions (outer, intermediate, and inner) are drawn in the top panel, and the residuals from the models are shown in the lower panels. |
Best-fit parameters of 2L2S solution.
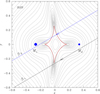 |
Fig. 9 Lens-system configuration of the 2L2S solution. The notations are the same as in Fig. 6, except that there are two source trajectories. The black and blue lines represent the trajectories of the primary and secondary source stars, respectively. |
 |
Fig. 10 Cumulative distribution of χ2 difference between the 2L2S and 3L 1S solutions. The light curve in the upper panel is provided to illustrate the region of disparity in the fit. |
 |
Fig. 11 Positions of the source and red giant clump (RGC) centroid in the instrumental color–magnitude diagram, created by merging observations from KMTC (gray dots) and HST (brown dots). |
4 Source star and angular Einstein radius
In this section, we specify the source star of the lensing event and estimate the angular Einstein radius. The source star is specified by estimating its color and magnitude after being corrected for reddening and extinction. With the angular source radius θ*, deduced from the color and magnitude together with the normalized source radius ρ measured from the modeling, the angular Einstein radius is estimated as
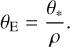 (5)
(5)
Figure 11 shows the location of the source in the instrumental color-magnitude diagram (CMD) of stars lying near the source. The CMD was created by merging two sets of CMDs. One set was generated from the pyDIA photometry (Albrow 2017) of stars in the KMTC image, and the other set pertains to stars in Baade’s window observed using the Hubble Space Telescope (Holtzman et al. 1998). The alignment of these two CMDs was achieved by using the centroids of the red giant clump (RGC) in the individual CMDs. We used the combined CMD because the V-band source magnitude could not be determined even though the I-band magnitude of the source was measured. As a result, the color of the source was estimated as the median value observed in the main-sequence branch of the combined CMD corresponding to the measured I-band magnitude.
To estimate the de-reddened source color and magnitude, denoted as (V − I, I)0, from their corresponding instrumental values, denoted as (V − I, I), we employed the Yoo et al. (2004) method. This method utilizes the RGC centroid, for which its dereddened color and magnitude (V − I, I)RGC,0 = (1.060, 14.308) were established by previous studies (Bensby et al. 2013; Nataf et al. 2013), as a reference point for calibration:
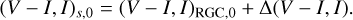 (6)
(6)
Here (V − I, I)RGC represent the instrumental color and magnitude of the RGC centroid, and ∆(V − I, I) = (V − I, I) − (V − I, I)RGC indicate the offsets in color and magnitude between the source and RGC centroid. In Table 4 we list the measured values (V − I, I), (V − I, I)rgc, (V − I, I)rgc,0, and (V − I, I)0. From the estimated de-reddened color and magnitude it is found that the source is a late G-type main-sequence star.
For the estimation of the angular source radius, we first converted the measured V − I color into V − K color using the color-color relation established by Bessell & Brett (1988), and subsequently calculated the angular source radius by applying the relation between V − K and θ* provided by Kervella et al. (2004). The derived value of the angular source radius is
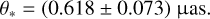 (7)
(7)
This yields the angular Einstein radius and relative lens-source proper motion of
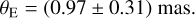 (8)
(8)
respectively. We note that the uncertainties associated with θE and µ are relatively large, primarily stemming from the large uncertainty in ρ.
A degeneracy between two competing interpretations with widely different lensing parameters of (tE, ρ) can occasionally be lifted from the resulting values of the relative lens-source proper motion if one model results in a µ value that is relatively disfavored by the Galactic model. We checked the feasibility of this method by additionally estimating the relative proper motion expected from the 2L2S model. The estimated value of µ2L2S ~ 6.0 mas yr−1, which is similar to the value for the 3L1S model, and is also a very typical value for a Galactic lensing event. Therefore, the constraint from the estimated relative proper motion cannot used to distinguish between the two interpretations.
Source parameters.
5 Physical lens parameters
In this section, we estimate the physical parameters of the lens system. The lens parameters of the mass M and distance DL are constrained by three lensing observables: the event timescale tE, the angular Einstein radius θE, and the microlens parallax πE.
The microlens parallax is defined as the ratio of the relative lens-source parallax πrel to the angular Einstein radius,
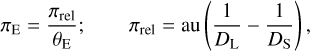 (10)
(10)
where DS denotes the distance to the source. With the measurements of all these observables, the mass and distance to the lens are uniquely determined as
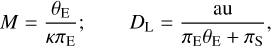 (11)
(11)
where κ = 4G/(c2au) and πS = au/DS denotes the parallax of the source (Gould 2000). For OGLE-2023-BLG-0836 the observables tE and θE were constrained, while the accurate determination of microlens parallax was hindered by limited photometric data precision. Consequently, we estimated M and DL by conducting a Bayesian analysis, leveraging the constraints provided by the measured observables tE and θE together with the priors of the physical and dynamical distributions and mass function of lens objects in the Galaxy.
The Bayesian analysis was initiated by generating a large number of synthetic events through a Monte Carlo simulation. In the simulation, the physical parameters of the lens mass were derived from a model mass function, and the distances to the lens and source as well as the relative proper motion between them were obtained from a Galaxy model. We adopted the mass function model proposed by Jung et al. (2018) and the Galaxy model introduced by Jung et al. (2021). Using physical parameters (Mi, DL,i, DS,i, µi) for each synthetic lensing event, we computed the corresponding lensing observables, specifically the event timescale and angular Einstein radius, according to the following relations:
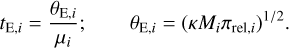 (12)
(12)
Then, the posteriors of the lens mass and distance were subsequently constructed by assigning a weight to each event of
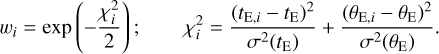 (13)
(13)
Here (tE, θE) represent the measured values of the observables, and [σ(tE), σ(θE)] denote their respective uncertainties.
In Fig. 12, we present the Bayesian posteriors of the primary lens mass M1 and the distances to the lens and source, DL and DS, of OGLE-2023-BLG-0836. In Table 5 we list the masses of the individual lens components (M1, M2, M3), distance to the lens, and the projected separations of the individual lens companions from the primary (a⊥,2, a⊥,3). The physical parameters were derived based on the observables of the outer solution, which provided the best fit to the data. Given the similarity of the observables, the physical parameters derived from the other solutions are similar to the presented values. For each physical parameter, we provide the median of the Bayesian posterior as a representative value and estimate the uncertainty range as the 16% and 84% of the distribution. The least massive component of the lens has a mass M3 ~ 4.4 MJ, which classifies it as a giant planet. The masses of the other lens components M1 ~ 0.71 M⊙ and M2 ~ 0.56 M⊙ correspond to those of mid- and late K-type main-sequence stars. Given that the planetary separation between M1 and M3, a⊥,3 ~ 3.7 au, is not much greater than that between the M1 and M2 binary pair, a⊥,2 ~ 1.9 au, it is likely that the planet orbits both binary components. However, the possibility of the planet orbiting one of the binary components cannot be entirely ruled out because of the projected nature of the separations. The estimated distance to the lens is DL ~ 5.1 kpc, and the probabilities for the lens lying in the disk and bulge are 66% and 34%, respectively.
 |
Fig. 12 Bayesian posteriors of the primary lens mass (M1) and the distances to the lens (DL) and source (DS) of the lensing event OGLE-2023-BLG-0836. Within each panel the event contributions from the disk and bulge lenses are illustrated by blue and red curves, and the black curve represents the combined distribution of the two lens populations. The solid vertical line marks the median value, and the dotted lines indicate the 1σ range of the posterior distribution. |
Physical lens parameters.
6 Summary and conclusion
We conducted an analysis of the peculiar lensing event OGLE-2023-BLG-0836, for which the light curve is characterized by two distinctive anomaly features produced by a caustic crossing and a cusp approach of a source. Despite the comprehensive exploration of the parameter space, we were unable to identify a binary-lens solution capable of sufficiently explaining both features within the anomaly.
From the analysis with a sophisticated model prompted by the fact that each anomaly feature can be approximated by a 2L1S model, we arrived at the conclusion that a triple-mass lens system is necessary to account for the observed anomaly pattern in the lensing light curve. A binary-lens binary-source interpretation could also offer an approximate explanation for the anomaly pattern, but this interpretation was rejected with a high degree of statistical confidence. Through the detailed triple-lens modeling, we identified three distinct solutions resulting from the degeneracy in the separation between the primary and the least massive companion of the lens.
Through a Bayesian analysis using the measured observables of the event timescale and angular Einstein radius, we determined that the least massive component of the lens has a planetary mass of 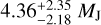 . This planet orbits within a stellar binary system composed of two stars with masses
. This planet orbits within a stellar binary system composed of two stars with masses 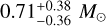 and
and 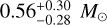 . This lensing event signifies the sixth occurrence of a microlensing planetary system in which a planet belongs to a stellar binary system.
. This lensing event signifies the sixth occurrence of a microlensing planetary system in which a planet belongs to a stellar binary system.
Acknowledgements
Work by C.H. was supported by the grants of National Research Foundation of Korea (2019R1A2C2085965). J.C.Y. and I.-G.S. acknowledge support from U.S. NSF Grant No. AST-2108414. Y.S. acknowledges support from BSF Grant No. 2020740. This research has made use of the KMTNet system operated by the Korea Astronomy and Space Science Institute (KASI) at three host sites of CTIO in Chile, SAAO in South Africa, and SSO in Australia. Data transfer from the host site to KASI was supported by the Korea Research Environment Open NETwork (KREONET). This research was supported by KASI under the R&D program (project no. 2023-1-832-03) supervised by the Ministry of Science and ICT. W. Zang, H.Y., S.M., R.K., J.Z., and W. Zhu acknowledge support by the National Natural Science Foundation of China (Grant No. 12133005). W. Zang acknowledges the support from the Harvard-Smithsonian Center for Astrophysics through the CfA Fellowship. The OGLE has received funding from the National Science Centre, Poland, grant MAESTRO 2014/14/A/ST9/00121 to A.U.
References
- Albrow, M. 2017, https://doi.org/18.5281/zenodo.268849 [Google Scholar]
- Bennett, D. P., Rhie, S. H., Udalski, A. et al. 2016, AJ, 152, 125 [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [Google Scholar]
- Bozza, V. 1999, A&A, 348, 311 [NASA ADS] [Google Scholar]
- Doran, M., & Mueller, C. M. 2004, J. Cosmology Astropart. Phys., 09, 003 [CrossRef] [Google Scholar]
- Gaudi, B. S., & Gould, A. 1997, ApJ, 486, 85 [Google Scholar]
- Gould, A. 2000, ApJ, 542, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., Udalski, A., Shin, I.-G., et al. 2014, Science, 345, 46 [Google Scholar]
- Gould, A., Han, C., Weicheng, Z., et al. 2022, A&A, 664, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griest, K., & Hu, W. 1992, ApJ, 397, 362 [Google Scholar]
- Han, C., Chang, H.-Y., An, J. H., & Chang, K. 2001, MNRAS, 328, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., Udalski, A., Gould, A., et al. 2017, AJ, 154, 223 [Google Scholar]
- Han, C., Bennett, D. P., Udalski, A., et al. 2019, AJ, 158, 114 [Google Scholar]
- Han, C., Lee, C.-U., Udalski, A., et al. 2020a, AJ, 159, 48 [Google Scholar]
- Han, C., Kim, D., Jung Y. K., et al. 2020b, AJ, 160, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., Udalski, A., Lee, C.-U., et al. 2020c, AJ, 162, 203 [Google Scholar]
- Han, C., Lee, C.-U., Ryu, Y.-H., et al. 2021a, A&A, 649, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Udalski, A., Kim, D., et al. 2021b, AJ, 161, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., Albrow, M. D., Chung S.-J., et al. 2021c, A&A, 652, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Udalski, A., Lee, C.-U., et al. 2021d, AJ, 162, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., Gould, A., Bond, I. A., et al. 2022a, A&A, 662, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Gould, A., Kim, D., et al. 2022b, A&A, 663, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Kim, D., Yang, H., et al. 2022c, A&A, 664, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Udalski, A., Jung Y. K., et al. 2023a, A&A, 670, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Jung, Y. K., Gould, A., et al. 2023b, A&A, 672, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Jung, Y. K., Bond, I. A., et al. 2024, A&A, 683, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holtzman, J. A., Watson, A. M., Baum, W. A., et al. 1998, AJ, 115, 1946 [Google Scholar]
- Hwang, K.-H., Zang, W., Gould, A., et al. 2022, AJ, 163, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Jung, Y. K., Udalski, A., Gould, A., et al. 2018, AJ, 155, 219 [Google Scholar]
- Jung, Y. K., Han, C., Udalski, A., et al. 2021, AJ, 161, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 29 [Google Scholar]
- Kim, S.-L., Lee, C.-U., Park, B.-G., et al. 2016, JKAS, 49, 37 [Google Scholar]
- Kuang, R., Zang, W., Jung Y. K., et al. 2022, MNRAS, 516, 1704 [Google Scholar]
- Mao, S., & Paczynski, B., 1991, ApJ, 374, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Gould, A., Fouqué, P., et al. 2013, ApJ, 769, 88 [Google Scholar]
- Paczynski, B. 1986, ApJ, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Poleski, R., Skowron, J., Udalski, A., et al. 2014, ApJ, 795, 42 [Google Scholar]
- Shin, I.-G., Yee, J. C., Zang, W., et al. 2023, AJ, 166, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Skowron, J., Ryu, Y.-H., Hwang, K.-H., et al. 2018, Acta Astron., 68, 43 [Google Scholar]
- Udalski, A., Szymanski, M. K., Szymanski, G., et al. 2015, Acta Astron., 65, 1 [NASA ADS] [Google Scholar]
- Wozniak, P. R. 2000, Acta Astron., 50, 42 [Google Scholar]
- Yee, J. C., Shvartzvald, Y., Gal-Yam, A., et al. 2012, ApJ, 755, 102 [Google Scholar]
- Yoo, J., DePoy, D. L., Gal-Yam, A., et al. 2004, ApJ, 603, 139 [Google Scholar]
- Zang, W., Han, C., Kondo, I., et al. 2021, Res. Astron. Astrophys., 21, 239 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Lensing light curve of OGLE-2023-BLG-0836. The top panel displays an enlarged view focused on the vicinity of the anomaly. |
| In the text | |
 |
Fig. 2 Division of the anomaly into two parts. The curve presented in the upper panel represents a 2L1S model derived by fitting the data excluding those around the cusp-approaching feature, while the curve in the lower panel is a 2L1S model obtained by fitting the data with the exclusion of the data around caustic-crossing feature. |
| In the text | |
 |
Fig. 3 Lens system configurations of the two 2L1S solutions for which the model curves are presented in the corresponding panels of Fig. 2. In each panel, the red figure is the caustic, the line represents the source trajectory, and the arrow on the source trajectory indicates the direction of the source motion. By convention, the abscissa of these 2L1S diagrams is defined by the binary axis of the lens system. |
| In the text | |
 |
Fig. 4 ∆χ2 map on the (log s3, log q3) parameter plane. The color-coding is configured to correspond to data points based on their ∆χ2 values: red for ∆χ2 ≤ 12n, yellow for ≤ 22n, green for ≤ 32n, and cyan for ≤ 42n, where n = 4. The three distinct local solutions are marked as inner, intermediate, and outer. The dashed vertical line represents the geometric mean (s3,in × s3,out)1/2 of the planetary separations for the inner and outer solutions. |
| In the text | |
 |
Fig. 5 Model curves of the best-fit 3L1S solution (outer solution) and 2L2S solution in the region of the anomaly. The lower four panels present the residuals from the three degenerate 3L1S solutions (inner, intermediate, and outer solutions) and the 2L2S solution. |
| In the text | |
 |
Fig. 6 Relative distribution of the normalized source radius. The solid vertical line indicates the median value, and the two dotted lines represent the 1σ ranges of the distribution. |
| In the text | |
 |
Fig. 7 Lens-system configurations of the three degenerate 3L1S solutions. For each solution, the lower panel shows the source trajectory, marked by an arrowed line, with respect to the caustic, and the upper panel shows the trajectory with respect to the positions of the lens components, marked by blue dots with labels M1, M1, and M3. The gray curves encompassing the caustic in the lower panels represent equi-magnification contours. The dashed circles in the upper panels represent the Einstein ring. |
| In the text | |
 |
Fig. 8 Zoomed-in view around the caustic-crossing feature. Model curves of the three degenerate solutions (outer, intermediate, and inner) are drawn in the top panel, and the residuals from the models are shown in the lower panels. |
| In the text | |
 |
Fig. 9 Lens-system configuration of the 2L2S solution. The notations are the same as in Fig. 6, except that there are two source trajectories. The black and blue lines represent the trajectories of the primary and secondary source stars, respectively. |
| In the text | |
 |
Fig. 10 Cumulative distribution of χ2 difference between the 2L2S and 3L 1S solutions. The light curve in the upper panel is provided to illustrate the region of disparity in the fit. |
| In the text | |
 |
Fig. 11 Positions of the source and red giant clump (RGC) centroid in the instrumental color–magnitude diagram, created by merging observations from KMTC (gray dots) and HST (brown dots). |
| In the text | |
 |
Fig. 12 Bayesian posteriors of the primary lens mass (M1) and the distances to the lens (DL) and source (DS) of the lensing event OGLE-2023-BLG-0836. Within each panel the event contributions from the disk and bulge lenses are illustrated by blue and red curves, and the black curve represents the combined distribution of the two lens populations. The solid vertical line marks the median value, and the dotted lines indicate the 1σ range of the posterior distribution. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.