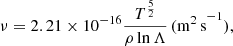| Issue |
A&A
Volume 678, October 2023
Solar Orbiter First Results (Nominal Mission Phase)
|
|
|---|---|---|
| Article Number | L7 | |
| Number of page(s) | 14 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202347313 | |
| Published online | 12 October 2023 | |
Letter to the Editor
Concurrence of a Kelvin-Helmholtz instability and Kármán vortex street in the Sun’s corona⋆
1
Shandong Key Laboratory of Optical Astronomy and Solar-Terrestrial Environment, Institute of Space Sciences, 180 Wenhua Xilu, Weihai, 264209 Shandong, PR China
e-mail: z.huang@sdu.edu.cn; xld@sdu.edu.cn
2
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast, University Road, Belfast, BT7 1NN Northern Ireland, UK
3
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, RH5 6NT Surrey, UK
4
Key Laboratory of Solar Activity and Space Weather, National Space Science Center, Chinese Academy of Sciences, Beijing, 100049
PR China
Received:
29
June
2023
Accepted:
28
September
2023
Context. Instabilities are crucial to understanding the mass transportation and energy transformation in the solar atmosphere. Observations of the concurrence among the Kelvin-Helmholtz instability (KHI) and Kármán vortex street (KVS) in conditions as extreme as the Sun’s corona have yet to be reported.
Aims. We aim to find evidence of a concurrence between the KHI and KVS in the Sun’s corona.
Methods. We analyzed high-resolution data from Extreme Ultraviolet Imager aboard Solar Orbiter and the Atmospheric Imaging Assembly aboard Solar Dynamics Observatory.
Results. Thanks to the high temporal resolution of EUI data, in an interacting region between a jet and coronal plumes, we observed the development of ruffles and breakdown of blobs. The intrinsic parameters of this dynamic system suggest the possibility of both the KHI and KVS occurring in the corona. The observations also show that the coupling of the two instabilities has facilitated the formation of vortices, which may therefore have enhanced the transformation from kinetic energy to thermal energy, as well as mass mixing among systems across magnetic field lines in the Sun’s corona.
Conclusions. The present study reports the very first EUI observations of a concurrence of the KHI and KVS and their coupling in the coronal conditions.
Key words: Sun: corona / Sun: activity / Sun: atmosphere
Movies associated to Figs. C.2 and C.3 are available at https://www.aanda.org.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Kelvin-Helmholtz instability (KHI) that occurs in the interface layer where there is velocity shear (Helmholtz 1868; Thomson 1871) and the Kármán vortex street (KVS), a repeating pattern of swirling vortices developing when a flow interacts with a blunt body (Williamson 1996; Tritton 1977; Matsumoto 1999), are two common forms of instability in fluids. These instabilities can generate vortices or rolls in flows, leading to energy transformation and mass mixing in the direction transverse to the flows (Chandrasekhar 1961; Williamson 1996; Caulfield 2021). Hence, they must be considered in many aspects of engineering and sciences involving fluids, such as meteorology, hydroscience, atmospheric science, space science, and astronomy (Chopra 1964; Williamson & Govardhan 2004; Choi et al. 2008; Berné et al. 2010; Gregg et al. 2018; Masson & Nykyri 2018).
The upper atmosphere of our Sun, the million-degree hot corona, consists of ionised fluids, namely plasma, which is strongly coupled with the magnetic field. The Sun’s corona is characterized by temperatures several hundred times higher than that of the surface below where the heating energy originates and it supplies mass to the solar wind that fill the interplanetary space of our solar system. The question of how energy and mass are pumped to the corona, known as the so-called coronal heating problem, is a long-standing puzzle in the science community. Even though the density of the corona is extremely low, having a pressure of only about ten billionths of the Earth’s atmosphere, instabilities are still thought to take place as mass and energy are transferred from the cool surface to then dissipate in the hot corona (Priest 2014).
Studies have shown that rolls generated by the KHI at the interface layer could develop into turbulence eddies and thus promote dissipation of energy in the corona (Heyvaerts & Priest 1983). The KHI might also result in reconfiguration of magnetic field and release magnetic energy to produce tiny jets in the corona (Sukarmadji et al. 2022). The KHI at the boundary of fast and slow solar winds could effectively heat plasma, with a positive correlation between the sheared speeds and temperatures (Telloni et al. 2022). Observational evidence of the KHI and its significance in energy transformation and mass mixing in the solar atmosphere has been found, for instance, in the transition layer between cold prominence and hot corona (Berger et al. 2010; Ryutova et al. 2010; Yuan et al. 2019), at the flanks of coronal mass ejection (Foullon et al. 2011), and at the boundary of filament embedded in coronal mass ejection (Möstl et al. 2013). The growth of rolls generated by the KHI might be exponential, and observations find a growth rate of 0.06–0.07 for a shearing flow in the corona with a speed difference of about 200 km s−1 (Li et al. 2018).
Numerical experiments suggest that the generation of a KVS in magnetohydrodynamic domain is similar to those of hydrodynamic and aerodynamic conditions (Gruszecki et al. 2010). In a low-beta plasma environment with the magnetic field parallel to the flow, a KVS could occur when the Reynolds number is in the range of 80–180 (Chen et al. 2018). In the coronal condition, a KVS might result in a quasi-periodic horizontal force and that excites the oscillations of plasma trapped in magnetic loops (Nakariakov et al. 2009), from which energy could be transported in the form of waves. Although observations of a KVS in the corona are rare, recent observations of an oscillating plasma flow with a tadpole-like shape in the solar corona could be interpreted as a KVS (Samanta et al. 2019). In other observations, the KVS is also believed to be responsible for the radial and azimuthal oscillations of the halo coronal mass ejection (Lee et al. 2015).
In reality, instabilities in fluid could be complex, in which more than one forms of instability can occur simultaneously (Chandrasekhar 1961). Laboratory experiments have offered a clear picture to support the scenario that the KHI and KVS occur simultaneously (Rajamanickam & Basu 2018). In coronal conditions, numerical experiments (Syntelis & Antolin 2019) have shown that both the KHI and KVS might be able to develop at different location of the same plasma system of coronal mass ejections. Observations of concurrence of the KHI and KVS in conditions as extreme as the corona’s have yet to be reported. This situation has been improving since the launch of Solar Orbiter (SO; Müller 2020) in 2020, which now observes our Sun from locations as close as 0.28 astronomical units (AU) and images the Sun’s corona with unprecedentedly high resolution.
In the solar atmosphere, jets are one of the most common eruptive events and they are persistent phenomena in the chromosphere, transition region, and corona (Shen 2021). Jets in the corona can be observed in X-rays and almost all extreme-ultraviolet (EUV) wave bands (Shibata et al. 1992; Shimojo et al. 1996; Nisticò et al. 2009; Sterling et al. 2015; Huang et al. 2018). They are believed to be transient ejections of materials along the open field or large loops, taking the shape of straight anemone ejections or two-side-loop ejections. They are thought to be results of magnetic reconnection between emerging bipoles and open fields (Yokoyama & Shibata 1995; Shen et al. 2011, 2012; Zhang et al. 2012). In this study, we report on observations of a jet where we have observed a concurrence of the KHI and KVS.
2. Observation
The data used here were taken by the space-borne Extreme Ultraviolet Imager (EUI; Rochus et al. 2020) aboard the Solar Orbiter (SO; Müller 2020) and the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) aboard the Solar Dynamics Observatory (SDO; Pesnell et al. 2012). All the data are publicly available. The SO/EUI data can be found in the official website1. The SDO/AIA data can be obtained from JSOC2. The studied event at the south pole of the Sun was observed on 2021 September 14 from 05:53:02 UT to 06:11:42 UT by EUI. The EUI data were taken in the passband of 174 Å by the High Resolution Imager (HRI) from 05:53:02 UT to 06:11:42 UT. An image taken by the Full Sun Imager (FSI) of EUI at 10:25:30 UT is also used to show the overview of the full Sun. The AIA data taken in the passbands of 304 Å, 171 Å, 193 Å, 211 Å, 335 Å, 94 Å and 131 Å have been exploited, however, the main body of the jet is not visible in the 94 Å passband.
At the time of the observations, SO is 0.59 AU away from the Sun and 0.75 AU from the Earth, while SDO is an Earth-orbiting satellite. The acute angle between Sun-Earth (SDO) line and Sun-SO line is about 48° (see Fig. A.1). The level 2 data of EUI observations are analysed and no further calibration is needed. The level 1 data of AIA observations are downloaded and then calibrated by the standard procedure of aia_prep.pro provided by the instrument team in solarsoft (ssw).
The angular resolution of the EUI data is 0.492″ per pixel and that of the AIA data is 0.6″ per pixel, corresponding to 210 km and 430 km on the Sun, respectively. The cadence of the EUI data is 5 s and that of the AIA data is 12 s.
3. Results
The jet occurs at the south pole of the Sun, where should be dominated by open fields (Cranmer 2009) and forests of coronal plumes are also located (see Figs. 1a and b; Fig. B.1; and the animation online). Please note that the driving and evolution of the jet was already studied by Long et al. (2023). Here, we only give some critical parameters of the jet and more details are given in Long et al. (2023). The jet is initiated at 05:58:42 UT in the EUI observations and about 3.7 min later in the AIA observations due to the difference of the distances of the two satellites to the Sun (see Fig. A.1). A minifilament eruption occurs in prior to the jet, which is in agreement with previous studies (Sterling et al. 2015; Wyper et al. 2017; Wei et al. 2022). The jet consists of a dark core with thin bright shells and has a bright base. The speed of the jet projected on the planes of sky of the EUI observations is about 110 km s−1 (see Fig. 1c) and that of the AIA observations is about 190 km s−1 (see Fig. C.1b). The jet propagates in a direction inclined to the ambient coronal plume with an acute angle of 38.5° (see Fig. 3). Around 06:00:17 UT, it interacts with the coronal plumes and changes its propagating direction (see the animation mov174s_sobel.m4v online). At the same time, the jet flows are brightened and produce multiple insular blobs. The cross-section of the jet is about 980 km at the location where it is about to impact the coronal plume (see Fig. 2). This is considered to be the effective length scale of the interaction between the jet and the coronal plumes (Kaneko et al. 2008).
 |
Fig. 1. Overview of the studied jet as seen by EUI at the extreme ultraviolet passband of 174 Å. (a): full disk of the Sun at 10:25 UT. The jet occurs in the region in the south pole as enclosed by the white square. (b): region of the jet at the time when the jet just contacts the coronal plumes. The trajectory of the upstream of the jet flows is outlined by dashed line in red (S1), and a bright feature can be observed at the top of the jet where the interaction between the jet and the coronal plumes takes place. The square (white dashed lines) encloses the region that is shown in Figs. 4a–f. The dashed line in cyan (SS) marks the location at the downstream of the jet flows from which the variation of radiation is obtained and shown in Fig. 4g. (c): time–distance map of the jet along the cut of S1. The propagation of the jet flows appears as bright streaks on this map. The diamond symbols (with error bars), which mark the largest gradients at the boundary of a bright streak at the corresponding times, follow the propagation of a stream of the flows. The speed of the stream is then derived from the slope of the linear fitting to the diamond symbols (green line) and given as about 110 km s−1. |
 |
Fig. 2. Measurement of the width of the jet at the location in the upstream near the turning point where the jet contacts the coronal plume. (a): region of the jet at the time when the jet comes into contact with the coronal plume on 06:00:32 UT in the EUI 174 Å image. The square (green dashed lines) encloses the region that is shown in Fig. 5. The dashed line in white (‘S’) marks the location in the upstream of the jet near the turning point, from which the intensity distribution is obtained and shown in panel b. (b): intensity distribution (with a base of 800) along the cut of ‘S’. The profile of the distribution is obtained through a Gaussian fit, and the width of the jet is the full width at half maximum of the Gaussian fit and given as 978 km. |
 |
Fig. 3. Growth of the KHI at the boundary of the jet and coronal plumes. (a): jet seen in EUI 174 Å passband before the development of ruffles, while the trajectory of the jet is smooth (the dashed line in blue). The location of coronal plumes is outlined by the dashed line in red (see Appendix B for further information). The acute angle between the upstream of the jet and the plumes is about 38.5°. (b): jet seen in EUI 174 Å passband while the ruffles have developed and the boundary becomes sawtooth (see the dashed line in blue), indicating the occurrence of the KHI. The red arrow points to a ruffle, whose distortions are tracked and given in panel d. (c): edge-enhanced image of that shown in panel b, based on Sobel operator, on which the edges of the jet and the developed ruffles are better seen. (d): growth of the distortions of the ruffle marked in panel b. The ruffle is tracked in five frames of the observations and its distortions (the asteroid symbols with error bars) follow an exponential growth that is 326.2e0.061t, where t is the time in seconds. |
An inspection of the dynamics of the jet shows that ruffles are developed at the boundary between the jet flows and the coronal plume (see Figs. 3a–c). It is clear from the EUI high-resolution observations that the boundary changes from smooth to sawtooth (Fig. 3). We can also observe that the distortions of a ruffle increase with time, starting from about 400 km at 06:00:37 UT to about 1100 km at 06:00:57 UT as derived from the EUI data. The growth of the distortions is exponential with a growth rate of 0.061 (Fig. 3d).
From 06:00:52 UT, bright blobs form in the region at the turning point, move away and detach from the main stream of the flows (Figs. 4a–f and Appendix C). The sizes of these blobs are about 860 km in diameter, which might expand while they are propagating along with the jet flows. These bright blobs appear repeatedly and the variation of the radiance at the downstream of the flows shows a period of about 25 s (Figs. 4g–i). The dynamics of these blobs is similar to alternating vortices produced in the phenomenon of KVS (Williamson 1996).
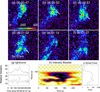 |
Fig. 4. Development of a KVS in the jet flows. (a–f): evolution of the region where the jet interacts with the coronal plumes viewed in EUI 174 Å. These are base-different images, each of which is the difference between the observation at the given time and that at 05:58:52 UT. The white arrows point to and follow a vortex structure that is detaching from the main stream of the jet flows, and the red arrows are tracking another one. (g): light curve (top plot) and detrended light curve (bottom plot) obtained from the location marked as ‘SS’ in Fig. 1b, giving the relative variations of the brightness of the region. The detrended light curve is the difference as given by subtracting the trend (the red line in the top plot) from the original light curve (black line in the top plot). (h): wavelet power map of the detrended light curve shown in panel g, in which a darker color corresponds to a greater power. The white dots denote the periods with maximum power at the corresponding time. The region with confidence level greater than 95% is enclosed by the contours. The cross-hatched region indicates the ranges of periods and times where edge effects become important. (i): global wavelet power summed from panel h, indicating the dominant period at 25 s in the light curve. |
The coupling between the KHI and KVS is also examined with the observations. At the location of KHI ruffles, occasionally small bright points might form just after the distortions reach maxima. The small bright points then move with the jet flows and merge with the other bright points to form a larger bright blob (see Fig. 5 and Appendix C). These dynamics indicates that occurrence of the KHI at the upstream might have promoted the formation of vortices in the KVS.
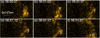 |
Fig. 5. Evolution of a brightening associated with the KHI. These are EUI 174 Å observations showing the difference between the observation at the given time and that at 05:58:52 UT. (a): development of ruffles at the interface between the jet and coronal plumes at 06:00:57 UT. The dashed lines in blue outline the boundary of the distortions of a ruffle. (b–f): evolution of brightening forming at the time when the ruffle reaches its maximum of distortion. The squares in white trace the location of the brightening from 06:01:02 UT to 06:01:27 UT. |
4. Discussion and conclusions
The distortions at the boundary are consistent with observations of a KHI in the corona, as previously reported in a number of studies (Berger et al. 2010; Ryutova et al. 2010; Li et al. 2018; Yuan et al. 2019). These distortions at the boundary between jets and plumes could be the manifestation of the vortex and its growth process caused by the KHI. Their growth rate is at 0.061 (Fig. 3d), which is consistent with the theoretical prediction of the growth rate of the KHI in the corona (Zhou et al. 2019).
The development of the KHI depends on sheared velocity gradient at the boundary layer, which is the velocity component of the jet in parallel to the coronal plume and found to be about 150 km s−1. In theoretical consideration (Priest 2014; Li et al. 2018), the onset of a KHI should meet the condition of Eq. (1),
where k, B, V, and ρ are the wave vector, magnetic strength, velocity, and the mass density, respectively. Subscripts “1” and “2” represent the parameters of the plasmas at one and the other sides of the boundary. In the present case, the jet flows are not in parallel to the coronal plumes, and k is given by the extending direction of the coronal plumes. We could presume that V1 ∥ B1 for the jet, k ∥ V2 ∥ B2 for the coronal plumes and the angle between V1 and V2 is θ, then we can work out the threshold in our case as shown in Eq. (2),
We let ρ1 = 1.67 × 10−11 kg m−3 that is for typical EUV jets in coronal holes (Shen 2021), ρ2 = 1.67 × 10−12 kg m−3 for coronal plumes (Poletto 2015), and B1 = B2 = 2 × 10−4 T that is typical coronal magnetic strength (Yang et al. 2020), |V2| = 0 is the plasma speed along the coronal plumes, and θ = 38.5°, which is the acute angle between the jet and the coronal plumes. Then, we work out that the speed of the jet (|V1|) for the KHI onset should exceed 235 km s−1 (or 184 km s−1 for the component in parallel to the coronal plumes). It should be noticed that this is only a rough estimation for the critical velocity. Such an estimation strongly depends on the plasma parameters of the jet and plumes. For example, the densities of coronal jets (also plumes) could vary from case to case with a factor as large as a magnitude. Although the speed of jet is slightly smaller than the threshold for the KHI onset in a typical coronal condition, the real velocity of the jet is likely larger than the given number; thus, this might allow a KHI to develop. The compressibility of fluids and magnetic component parallel to the speed of fluids could suppress the growth of a KHI (Miura & Pritchett 1982). To estimate the effect of compressibility in the growth of a KHI, we calculated the local sound speed (Cs) in the jet with Eq. (3),
where T is the temperature. By setting the order of temperature (T) in jets at 106 K (Shen 2021), the local sound speed in the jet is 152 km s−1 (smaller than the velocity of jet), and thus the compressibility may suppress the growth of the KHI in this event. In a MHD environment with magnetic field parallel to the flow, the growth of the KHI could be suppressed with large undulations but no over-turning vortices; while in partially ionized plasma, the over-turning vortices could form due to the plasma pressure gradient along the magnetic field and fluids’ compression or expansion (Hillier 2019). As in this case, the plasma environment in corona is viewed as fully ionized plasma, so the ruffles at the boundary could be the undulations caused by a KHI in a MHD environment. For the case of V ∥ B, with an angle θ between k and B1 at 38.5°, the growth rate of the KHI could be about a half of the rate in an unmagnetized case (Miura & Pritchett 1982).
The possibility of the critical layer proposed by Wang & Balmforth (2021) could not be excluded. The baroclinic critical levels appear as singularities when waves propagate through a stratified, horizontal, and sheared flow. Disturbances grow at the critical layers surrounding these levels, which could induce secondary instabilities. These secondary instabilities could roll up into a vortical structure, which then excites new waves forcing new baroclinic critical levels. In this case, it is also possible that the critical layer exists at the boundary between the jet and nearby plumes, which could turn into ruffles at the boundary.
The Reynolds number (Re = VL/ν) and Strouhal number (St = L/(PV)) in the downstream of the flows are two critical parameters in a KVS and can be computed from the speed of the jet (V), the size of the blunt body (L), the period of the breaking-down of the vortexes (P), and the coefficient of kinematic viscosity of the fluid (ν). The coefficient of kinematic viscosity of the coronal plasma (ν) can be obtained from Eq. (4) (Priest 2014),
where T is the temperature, ρ is the density, and lnΛ is the Coulomb logarithm. Using typical parameters for coronal jets, we let T = 106 K, ρ = 1.67 × 10−11 kg m−3 and lnΛ = 20 (Priest 2014), then we can work out: ν = 6.9 × 108 m2 s−1. In the present case, the size of a blunt body, L, is determined by the interaction area between the jet and the coronal plumes and is estimated by the width of the jet in the upstream, namely, L ≈ 980 km; the speed V can be taken as the component that is vertical to the coronal plumes, namely, V = 190 × sin(38.5° ) ≈ 118 km s−1; the period is obtained from the wavelet analysis (Torrence & Compo 1998) to the light curve at the downstream of the flow, given as about 25 s. Then, we can work out: Re ≈ 168 and St ≈ 0.33.
The Strouhal (St) number, which represents the ratio of inertial forces due to the flow to the inertial forces due to the convection, is a robust indicator for the onset of KVS (Samanta et al. 2019). In the numerical experiments of KVS in magnetohydrodynamic conditions similar to the Sun’s corona, the St numbers are found to be in the range of 0.15–0.25 (Gruszecki et al. 2010). In the present event, the St number is estimated to be about 0.33, which is closed to the upper limit reported in the numerical experiments. The actual St number of the present event might be smaller because speed of the jet is taken at its lower limit in the calculation. Reynolds (Re) number, the ratio of inertial forces to viscous forces, is normally in the range of 49–194 to have a steady KVS in hydrodynamics environment (Williamson 1996) and in the range of 80–180 to have a steady KVS in magnetohydrodynamic environment (Chen et al. 2018). The Re number of the present event is estimated to be about 168, which again falls in the regime of a steady KVS. Therefore, it is very likely that the occurrence of a KVS is the causes of the production of bright blobs observed here. However, as the vortices generated by the KVS and those by the KHI have many characteristics in common, we cannot totally rule out the possibility that these bright blobs are caused by secondary instabilities developing along the vortex arms.
To remain consistent with the laboratory experiment (Jukes & Choi 2009), the existence of lift and drag fluctuations due to the KHI could be the factors that amplify the formation of a KVS. In other words, concurrence of the KHI and KVS is more efficient in generating vortices in a flow. The KHI in this event might undergo a nonlinear growth process when it grows to an observable size and the nonlinear growth could lead to vortex shedding in fluids (Rodi 2005). The transformation from ruffles to small bright points could be the results of the nonlinear growth of the KHI. Since the coronal magnetic field is frozen-in the plasma (Priest 2014), it will be complicated by the generations of vortices and allow energy and mass transportation crossing magnetic field lines to take place. Then, the rapid developing vortices could enhance the mass mixing and energy dissipation via Joule heating or internal reconnections (Heyvaerts & Priest 1983; Li et al. 2018; Zhou et al. 2019; Yuan et al. 2019). This explains why the jet becomes bright immediately while it interacts with the coronal plume.
The concurrence of the KHI and KVS observed in this work demonstrates the complexity of instabilities occurring in such extreme conditions as those observed in the hot corona of our Sun. While the occurrence of KHI could promote the formation of vortices in KVS, their concurrence can then speed-up the mass-mixing and energy dissipation in the corona. Therefore, the instabilities and their complex coupling in the magnetohydrodynamic domain are essential to improving our understanding of energy and mass transportation from the cold surface to the hot outer atmosphere of the Sun. These issues are also of significance for other stars in the Universe beyond our Sun. A comprehensive simulation involving both the KHI and KVS in the solar corona is also crucial to obtain a clear picture of such a phenomenon, as our discussion in this work is based on simplified and ideal conditions.
Movies
Movie 1 associated with Fig. C.2 (mov3_aia3) Access here
Movie 2 associated with Fig. C.3 (mov174s_ sobel) Access here
Acknowledgments
We are grateful to the anonymous referee for helping improve the manuscript. Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. The EUI instrument was built by CSL, IAS, MPS, MSSL/UCL, PMOD/WRC, ROB, LCF/IO with funding from the Belgian Federal Science Policy Office (BELSPO/PRODEX PEA 4000134088); the Centre National d’Etudes Spatiales (CNES); the UK Space Agency (UKSA); the Bundesministerium für Wirtschaft und Energie (BMWi) through the Deutsches Zentrum für Luft- und Raumfahrt (DLR); and the Swiss Space Office (SSO). The AIA data are used by courtesy of NASA/SDO, the AIA and HMI teams and JSOC. H.W., Z.H., H.F. and L.X. are supported by the National Key R&D Program of China No. 2021YFA0718600 and National Natural Science Foundation of China (42174201, 42230203, 41974201). D.M.L. is grateful to the Science Technology and Facilities Council for the award of an Ernest Rutherford Fellowship (ST/R003246/1). M.X. acknowledges support from National Natural Science Foundation of China (42074208).
References
- Berger, T. E., Slater, G., Hurlburt, N., et al. 2010, ApJ, 716, 1288 [Google Scholar]
- Berné, O., Marcelino, N., & Cernicharo, J. 2010, Nature, 466, 947 [CrossRef] [Google Scholar]
- Caulfield, C. P. 2021, Ann. Rev. Fluid Mech., 53, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and Hydromagnetic Stability (Oxford: Clarendon) [Google Scholar]
- Chen, L., Xu, S.-J., & Ni, M.-J. 2018, Int. J. Heat Mass Transf., 117, 768 [CrossRef] [Google Scholar]
- Choi, H., Jeon, W.-P., & Kim, J. 2008, Ann. Rev. Fluid Mech., 40, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Chopra, K. P. 1964, Nature, 203, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R. 2009, Liv. Rev. Sol. Phys., 6, 3 [Google Scholar]
- DeForest, C. E., Hoeksema, J. T., Gurman, J. B., et al. 1997, Sol. Phys., 175, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, R., & Guhathakurta, M. 1995, ApJ, 447, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Foullon, C., Verwichte, E., Nakariakov, V. M., Nykyri, K., & Farrugia, C. J. 2011, ApJ, 729, L8 [Google Scholar]
- Gregg, M. C., D’Asaro, E. A., Riley, J. J., & Kunze, E. 2018, Ann. Rev. Marine Sci., 10, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Gruszecki, M., Nakariakov, V. M., van Doorsselaere, T., & Arber, T. D. 2010, Phys. Rev. Lett., 105, 055004 [NASA ADS] [CrossRef] [Google Scholar]
- Helmholtz, H. 1868, Berl. Monatsber., 1868, 215 [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Hillier, A. 2019, Phys. Plasmas, 26, 082902 [Google Scholar]
- Huang, Z., Xia, L., Nelson, C. J., et al. 2018, ApJ, 854, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Jukes, T. N., & Choi, K.-S. 2009, Phys. Rev. Lett., 102, 254501P [NASA ADS] [CrossRef] [Google Scholar]
- Kaneko, S., Nakamura, T., Inada, F., & Kato, M. 2008, Flow Induced Vibrations: Classifications and Lessons from Practical Experiences (Amsterdam: Elsevier), 29 [Google Scholar]
- Lee, H., Moon, Y. J., & Nakariakov, V. M. 2015, ApJ, 803, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Li, X., Zhang, J., Yang, S., Hou, Y., & Erdélyi, R. 2018, Sci. Rep., 8, 8136 [CrossRef] [Google Scholar]
- Long, D. M., Chitta, L. P., Baker, D., et al. 2023, ApJ, 944, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Masson, A., & Nykyri, K. 2018, Space. Sci. Rev., 214, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, M. 1999, J. Fluids Struct., 13, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Miura, A., & Pritchett, P. L. 1982, J. Geophys. Res., 87, 7431 [NASA ADS] [CrossRef] [Google Scholar]
- Möstl, U. V., Temmer, M., & Veronig, A. M. 2013, ApJ, 766, L12 [Google Scholar]
- Müller, D., St Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Nakariakov, V. M., Aschwanden, M. J., & van Doorsselaere, T. 2009, A&A, 502, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Bothmer, V., Patsourakos, S., & Zimbardo, G. 2009, Sol. Phys., 259, 87 [CrossRef] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Poletto, G. 2015, Liv. Rev. Sol. Phys., 12, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. 2014, Magnetohydrodynamics of the Sun (Cambridge: Cambridge University Press) [Google Scholar]
- Pucci, S., Poletto, G., Sterling, A. C., & Romoli, M. 2014, ApJ, 793, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Rajamanickam, K., & Basu, S. 2018, J. Fluid Mech., 853, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodi, W. 2005, Engineering Turbulence Modelling and Experiments 6, 1st edn. (Kidlington: Elsevier Science) [Google Scholar]
- Ryutova, M., Berger, T., Frank, Z., Tarbell, T., & Title, A. 2010, Sol. Phys., 267, 75 [Google Scholar]
- Saito, K. 1965, PASJ, 17, 1 [NASA ADS] [Google Scholar]
- Samanta, T., Tian, H., & Nakariakov, V. M. 2019, Phys. Rev. Lett., 123, 035102 [Google Scholar]
- Shen, Y. 2021, Proc. R. Soc. London Ser. A, 477, 217 [NASA ADS] [Google Scholar]
- Shen, Y., Liu, Y., Su, J., & Ibrahim, A. 2011, ApJ, 735, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Liu, Y., Su, J., & Deng, Y. 2012, ApJ, 745, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, K., Ishido, Y., Acton, L. W., et al. 1992, PASJ, 44, L173 [Google Scholar]
- Shimojo, M., Hashimoto, S., Shibata, K., et al. 1996, PASJ, 48, 123 [Google Scholar]
- Sterling, A. C., Moore, R. L., Falconer, D. A., & Adams, M. 2015, Nature, 523, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Sukarmadji, A. R. C., Antolin, P., & McLaughlin, J. A. 2022, ApJ, 934, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Syntelis, P., & Antolin, P. 2019, ApJ, 884, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Telloni, D., Adhikari, L., Zank, G. P., et al. 2022, ApJ, 929, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Thomson, W. 1871, Phil. Mag., 42, 362 [CrossRef] [Google Scholar]
- Tian, H., McIntosh, S. W., Habbal, S. R., & He, J. 2011, ApJ, 736, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, Bull. Am. Meteorol. Soc., 79, 61 [Google Scholar]
- Tritton, D. J. 1977, Physics of Fluid Dynamics, 1st edn. (Princeton: Van Nostrand) [CrossRef] [Google Scholar]
- Wang, C., & Balmforth, N. J. 2021, J. Fluid Mech., 917, A48 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, H., Huang, Z., Fu, H., et al. 2022, ApJ, 936, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhelm, K., Abbo, L., Auchère, F., et al. 2011, A&A Rev., 19, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Williamson, C. H. K. 1996, Ann. Rev. Fluid Mech., 28, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Williamson, C. H. K., & Govardhan, R. 2004, Ann. Rev. Fluid Mech., 36, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Wyper, P. F., Antiochos, S. K., & DeVore, C. R. 2017, Nature, 544, 452 [Google Scholar]
- Yang, Z., Bethge, C., Tian, H., et al. 2020, Science, 369, 694 [Google Scholar]
- Yokoyama, T., & Shibata, K. 1995, Nature, 375, 42 [Google Scholar]
- Yuan, D., Shen, Y., Liu, Y., et al. 2019, ApJ, 884, L51 [CrossRef] [Google Scholar]
- Zhang, Q. M., Chen, P. F., Guo, Y., Fang, C., & Ding, M. D. 2012, ApJ, 746, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Y., Clark, T. T., Clark, D. S., et al. 2019, Phys. Plasmas, 26, 080901 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Positions of SDO and Solar Orbiter in relative to the Sun
The relative positions of SDO and Solar Orbiter are shown in Fig. A.1.
 |
Fig. A.1. Relative positions among the Sun, the Earth (SDO), and SO on 2021 September 14. The orange circle represents the observed object (the Sun). The red circle represents the position of Solar Orbiter, which is about 0.59 AU away from the Sun. The blue circle represents the position of SDO, which is an Earth-orbiting satellite and is 1 AU away from the Sun. The angle between the Sun-Earth line and the Sun-SO line is about 48°. The sizes of the objects are not in scale. |
Appendix B: Jet interactions with the coronal plume
Coronal plumes are ray-like structures extending from the chromosphere into the high corona (Wilhelm et al. 2011). They are abundant in coronal hole (CH) and the quiet Sun (QS) (Tian et al. 2011). They are a few times to an order of magnitude denser than the ambient corona (Wilhelm et al. 2011). Typically, they are cylindrical features with a base diameter in an order of 3000 km (Saito 1965; Fisher & Guhathakurta 1995; DeForest et al. 1997) and could be detected in visible light, ultraviolet (UV), and extreme-ultraviolet (EUV) (Wilhelm et al. 2011). Coronal plumes are normally associated with coronal bright points and their lifetimes are tens of hours (Pucci et al. 2014). The typical electron temperature of a coronal plume is about 8 × 105 K, which is 1 − 3 × 105 K higher than the ambient corona (Poletto 2015).
The forest of coronal plumes can be clearly seen in the polar regions of the Sun, where coronal holes permanently present. Figure B.1(a) shows a full disk of the Sun taken by AIA at 171 Å passband and Figure B.1(b) shows a zoomed-in view of the south pole in EUI 174 Å at the times when the jet is occurring. The ray-like coronal plumes can be clearly seen in these images.
 |
Fig. B.1. Overview of the region where the jet event occurs as seen in AIA 171 Å and EUI 174 Å. The ray-like coronal plumes can be clearly seen in these large field-of-views. (a): Full disk of the Sun observed by AIA 171 Å passband at 06:04:45 UT. The jet occurs in the region at the south pole as marked by the white square. (b): Zoomed-in view of the south pole in EUI 174 Å passband at 06:00:32 UT. The jet occurs in the region marked by the white square. We note that the difference between the occurring time in the AIA data and that in the EUI data is mainly due to the difference in their distances to the Sun. |
The evolution of the region where the jet takes place is shown in Figure B.2, which gives inversed-color-table images of the region before (05:53:02 UT) and after (06:11:42 UT) the occurrence of the jet. Due to the interaction with the jet flows, the extending of the coronal plumes has significantly changed, which is shown as the dashed lines in red (before interaction) and green (after interaction).
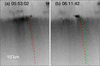 |
Fig. B.2. Evolution of the region where the jet takes place in EUI 174 Å images showing with an inversed-color table. (a): Region seen at 05:53:02 UT (before occurrence of the jet). The extension of the coronal plumes about to contact the jet flow is outlined by the dashed line in red. (b): Region at 06:11:42 UT (after occurrence of the jet). The extension of the coronal plumes at this time is outlined by the dashed line in green. The change of the coronal plumes due to the interaction of the jet can be seen from the their extension at 05:53:02 UT (red line) and that at 06:11:42 UT (green line). |
Appendix C: Evolution of the jet in EUI and AIA observations
The full evolution of the region of interest observed in EUI 174 Å observations is shown in the animation of mov174s_sobel.m4v and that in AIA 304 Å, 171 Å and 193 Å is given in mov3_aia.m4v.
The speeds of the jet can be obtained from the space-time plots. The local maxima of the gradient at the boundary of the bright streak are first obtained, and then the speeds can be achieved by applying a linear fit to these points. Figure C.1 shows the calculation based on the AIA 171 Å observations, in which the diamond symbols are the local maxima of gradient and at each point, the error bar is determined by the distance between the maximum to the location where the intensity (in relative to the background) decrease to its half maximum. The speeds of the jet are found to be 110 km s−1 in EUI 174 Å and 190 km s−1 in AIA 171 Å observations. The width of the jet at the location in the upstream near the turning point where the jet contacts the coronal plume is found to be about 980 km in EUI 174 Å observations (Figure 2). At the turning point, we observe a bright blob which is formed at the turning point (Figure C.2). We can see that the blob appears as compact brightening in the 304 Å passband and more diffused in passbands with greater representative temperatures (e.g., 171 Å and 193 Å). More details on the trigger and evolution of the jet can be found in Long et al. (2023).
 |
Fig. C.1. Dynamics of the jet in the observations of AIA 171 Å passband. (a): Region of the jet at the time when the jet is contacting the coronal plumes on 06:03:45 UT. The trajectory of the upstream of the jet flows is outlined by the dashed line in red (S2). (b): Time-distance map for the jet along the cut of S2. The propagation of the jet flows appears as bright streaks on this map. The diamond symbols (with error bars) mark the largest gradients at the boundary of the a bright streak at the corresponding times to follow the propagation of a stream of the flows. The speed of the stream is then derived from the slope of the linear fitting to the diamond symbols (green line) and given as 190 km s−1. |
 |
Fig. C.2. Evolutions of the jet seen in AIA extreme ultraviolet 304 Å (first column), 171 Å (second column), and 193Å (third column) passbands at and after the time it is contacting the coronal plumes. The white dashed squares follow the bright blob presenting in at the turning point. Associated animation from 06:02:45 UT to 06:09:33 UT could be obtained online. The real-time duration of the animation is 14s. |
The development of ruffles at the interface between the jet and coronal plumes can be clearly seen in the animations (mov174s_sobel.m4v) and the distortions of ruffles are shown in Figure C.3 (a–l). We also observe that the location of the ruffle turns into a brightening after it reaches maximum of distortion (Figure 5). The brightening then moves and merges with the others to form a bright blob (Figure 5), which may be a possible vortex breaking down from the stream of the flows. The size of the bright blob is about 860 km in diameter (Figure C.4).
 |
Fig. C.3. Evolution of the KHI at the boundary of the jet and coronal plumes in the EUI 174 Å observations. (a-c, g-i): Development of ruffles at the interface between the jet and coronal plumes from 06:00:17 UT to 06:00:57 UT. The dashed lines in blue outline the boundary of the distortions of the ruffles, the ruffle marked with red arrow in panel (i) is used for estimating the growth rate of the KHI in Figure 2d in the main text. (d-f, j-l): Development of ruffles at the interface between the jet and coronal plumes from 06:00:17 UT to 06:00:57 UT with a Sobel enhancement. Associated animation from 05:58:52 UT to 06:05:32 UT could be obtained online. The real-time duration of the animation is 16 s. |
 |
Fig. C.4. Measurement of the width of a vortex froming in the jet flow. (a): Different image between observation at 06:01:02 UT and that at 05:58:52 UT, in which the bright blob structure (vortex) is better seen. The dashed line in red (‘S’) cuts through a bright blob, from which the intensity distribution is obtained and shown in panel b. (b): Intensity distribution along the cut of S. The profile of the distribution is obtained through a Gaussian fit, and the width of the jet is determined to be the full width at half maximum of the Gaussian fit and given as 862 km. |
All Figures
 |
Fig. 1. Overview of the studied jet as seen by EUI at the extreme ultraviolet passband of 174 Å. (a): full disk of the Sun at 10:25 UT. The jet occurs in the region in the south pole as enclosed by the white square. (b): region of the jet at the time when the jet just contacts the coronal plumes. The trajectory of the upstream of the jet flows is outlined by dashed line in red (S1), and a bright feature can be observed at the top of the jet where the interaction between the jet and the coronal plumes takes place. The square (white dashed lines) encloses the region that is shown in Figs. 4a–f. The dashed line in cyan (SS) marks the location at the downstream of the jet flows from which the variation of radiation is obtained and shown in Fig. 4g. (c): time–distance map of the jet along the cut of S1. The propagation of the jet flows appears as bright streaks on this map. The diamond symbols (with error bars), which mark the largest gradients at the boundary of a bright streak at the corresponding times, follow the propagation of a stream of the flows. The speed of the stream is then derived from the slope of the linear fitting to the diamond symbols (green line) and given as about 110 km s−1. |
| In the text | |
 |
Fig. 2. Measurement of the width of the jet at the location in the upstream near the turning point where the jet contacts the coronal plume. (a): region of the jet at the time when the jet comes into contact with the coronal plume on 06:00:32 UT in the EUI 174 Å image. The square (green dashed lines) encloses the region that is shown in Fig. 5. The dashed line in white (‘S’) marks the location in the upstream of the jet near the turning point, from which the intensity distribution is obtained and shown in panel b. (b): intensity distribution (with a base of 800) along the cut of ‘S’. The profile of the distribution is obtained through a Gaussian fit, and the width of the jet is the full width at half maximum of the Gaussian fit and given as 978 km. |
| In the text | |
 |
Fig. 3. Growth of the KHI at the boundary of the jet and coronal plumes. (a): jet seen in EUI 174 Å passband before the development of ruffles, while the trajectory of the jet is smooth (the dashed line in blue). The location of coronal plumes is outlined by the dashed line in red (see Appendix B for further information). The acute angle between the upstream of the jet and the plumes is about 38.5°. (b): jet seen in EUI 174 Å passband while the ruffles have developed and the boundary becomes sawtooth (see the dashed line in blue), indicating the occurrence of the KHI. The red arrow points to a ruffle, whose distortions are tracked and given in panel d. (c): edge-enhanced image of that shown in panel b, based on Sobel operator, on which the edges of the jet and the developed ruffles are better seen. (d): growth of the distortions of the ruffle marked in panel b. The ruffle is tracked in five frames of the observations and its distortions (the asteroid symbols with error bars) follow an exponential growth that is 326.2e0.061t, where t is the time in seconds. |
| In the text | |
 |
Fig. 4. Development of a KVS in the jet flows. (a–f): evolution of the region where the jet interacts with the coronal plumes viewed in EUI 174 Å. These are base-different images, each of which is the difference between the observation at the given time and that at 05:58:52 UT. The white arrows point to and follow a vortex structure that is detaching from the main stream of the jet flows, and the red arrows are tracking another one. (g): light curve (top plot) and detrended light curve (bottom plot) obtained from the location marked as ‘SS’ in Fig. 1b, giving the relative variations of the brightness of the region. The detrended light curve is the difference as given by subtracting the trend (the red line in the top plot) from the original light curve (black line in the top plot). (h): wavelet power map of the detrended light curve shown in panel g, in which a darker color corresponds to a greater power. The white dots denote the periods with maximum power at the corresponding time. The region with confidence level greater than 95% is enclosed by the contours. The cross-hatched region indicates the ranges of periods and times where edge effects become important. (i): global wavelet power summed from panel h, indicating the dominant period at 25 s in the light curve. |
| In the text | |
 |
Fig. 5. Evolution of a brightening associated with the KHI. These are EUI 174 Å observations showing the difference between the observation at the given time and that at 05:58:52 UT. (a): development of ruffles at the interface between the jet and coronal plumes at 06:00:57 UT. The dashed lines in blue outline the boundary of the distortions of a ruffle. (b–f): evolution of brightening forming at the time when the ruffle reaches its maximum of distortion. The squares in white trace the location of the brightening from 06:01:02 UT to 06:01:27 UT. |
| In the text | |
 |
Fig. A.1. Relative positions among the Sun, the Earth (SDO), and SO on 2021 September 14. The orange circle represents the observed object (the Sun). The red circle represents the position of Solar Orbiter, which is about 0.59 AU away from the Sun. The blue circle represents the position of SDO, which is an Earth-orbiting satellite and is 1 AU away from the Sun. The angle between the Sun-Earth line and the Sun-SO line is about 48°. The sizes of the objects are not in scale. |
| In the text | |
 |
Fig. B.1. Overview of the region where the jet event occurs as seen in AIA 171 Å and EUI 174 Å. The ray-like coronal plumes can be clearly seen in these large field-of-views. (a): Full disk of the Sun observed by AIA 171 Å passband at 06:04:45 UT. The jet occurs in the region at the south pole as marked by the white square. (b): Zoomed-in view of the south pole in EUI 174 Å passband at 06:00:32 UT. The jet occurs in the region marked by the white square. We note that the difference between the occurring time in the AIA data and that in the EUI data is mainly due to the difference in their distances to the Sun. |
| In the text | |
 |
Fig. B.2. Evolution of the region where the jet takes place in EUI 174 Å images showing with an inversed-color table. (a): Region seen at 05:53:02 UT (before occurrence of the jet). The extension of the coronal plumes about to contact the jet flow is outlined by the dashed line in red. (b): Region at 06:11:42 UT (after occurrence of the jet). The extension of the coronal plumes at this time is outlined by the dashed line in green. The change of the coronal plumes due to the interaction of the jet can be seen from the their extension at 05:53:02 UT (red line) and that at 06:11:42 UT (green line). |
| In the text | |
 |
Fig. C.1. Dynamics of the jet in the observations of AIA 171 Å passband. (a): Region of the jet at the time when the jet is contacting the coronal plumes on 06:03:45 UT. The trajectory of the upstream of the jet flows is outlined by the dashed line in red (S2). (b): Time-distance map for the jet along the cut of S2. The propagation of the jet flows appears as bright streaks on this map. The diamond symbols (with error bars) mark the largest gradients at the boundary of the a bright streak at the corresponding times to follow the propagation of a stream of the flows. The speed of the stream is then derived from the slope of the linear fitting to the diamond symbols (green line) and given as 190 km s−1. |
| In the text | |
 |
Fig. C.2. Evolutions of the jet seen in AIA extreme ultraviolet 304 Å (first column), 171 Å (second column), and 193Å (third column) passbands at and after the time it is contacting the coronal plumes. The white dashed squares follow the bright blob presenting in at the turning point. Associated animation from 06:02:45 UT to 06:09:33 UT could be obtained online. The real-time duration of the animation is 14s. |
| In the text | |
 |
Fig. C.3. Evolution of the KHI at the boundary of the jet and coronal plumes in the EUI 174 Å observations. (a-c, g-i): Development of ruffles at the interface between the jet and coronal plumes from 06:00:17 UT to 06:00:57 UT. The dashed lines in blue outline the boundary of the distortions of the ruffles, the ruffle marked with red arrow in panel (i) is used for estimating the growth rate of the KHI in Figure 2d in the main text. (d-f, j-l): Development of ruffles at the interface between the jet and coronal plumes from 06:00:17 UT to 06:00:57 UT with a Sobel enhancement. Associated animation from 05:58:52 UT to 06:05:32 UT could be obtained online. The real-time duration of the animation is 16 s. |
| In the text | |
 |
Fig. C.4. Measurement of the width of a vortex froming in the jet flow. (a): Different image between observation at 06:01:02 UT and that at 05:58:52 UT, in which the bright blob structure (vortex) is better seen. The dashed line in red (‘S’) cuts through a bright blob, from which the intensity distribution is obtained and shown in panel b. (b): Intensity distribution along the cut of S. The profile of the distribution is obtained through a Gaussian fit, and the width of the jet is determined to be the full width at half maximum of the Gaussian fit and given as 862 km. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} (\boldsymbol{k} \cdot \boldsymbol{V_1} - \boldsymbol{k} \cdot \boldsymbol{V_2})^2 > (\rho _1 + \rho _2)[(\boldsymbol{k}\cdot \boldsymbol{B_1})^2+(\boldsymbol{k}\cdot \boldsymbol{B_2})^2]/(\mu _0\rho _1\rho _2), \end{aligned} $$](/articles/aa/full_html/2023/10/aa47313-23/aa47313-23-eq1.gif)
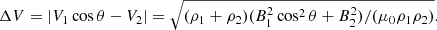
![$$ \begin{aligned} C_{\rm s} = 0.152\sqrt{T/[\mathrm{K}]} \, (\mathrm{km\,s^{-1}}), \end{aligned} $$](/articles/aa/full_html/2023/10/aa47313-23/aa47313-23-eq3.gif)