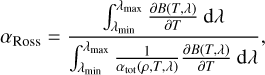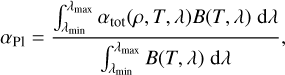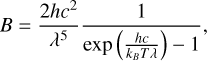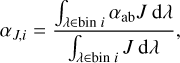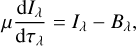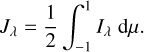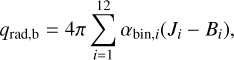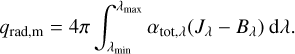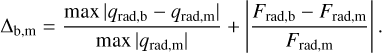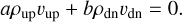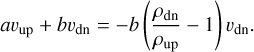| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 22 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202346398 | |
| Published online | 11 September 2023 | |
3D Stagger model atmospheres with FreeEOS
I. Exploring the impact of microphysics on the Sun
1
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University,
Ny Munkegade 120,
8000
Aarhus C, Denmark
e-mail: yixiao.zhou@qq.com
2
Theoretical Astrophysics, Department of Physics and Astronomy, Uppsala University,
Box 516,
751 20
Uppsala, Sweden
e-mail: anish.amarsi@physics.uu.se
3
DARK, Niels Bohr Institute, University of Copenhagen,
Jagtvej 128,
2200
Copenhagen, Denmark
4
Research School of Astronomy and Astrophysics, Australian National University,
Canberra, ACT
2611, Australia
5
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D),
Australia
Received:
13
March
2023
Accepted:
4
July
2023
Three-dimensional radiation-hydrodynamics (3D RHD) simulations of stellar surface convection provide valuable insights into many problems in solar and stellar physics. However, almost all 3D near-surface convection simulations to date are based on solar-scaled chemical compositions, which limits their relevance when applied to stars with peculiar abundance patterns. To overcome this difficulty, we implement the robust and widely used FreeEOS equation of state and our Blue opacity package into the Stagger 3D radiation-magnetohydrodynamics code. We present a new 3D RHD model of the solar atmosphere, and demonstrate that the mean stratification as well as the distributions of key physical quantities are in good agreement with those of the latest Stagger solar model atmosphere. The new model is further validated by comparisons with solar observations. The new model atmospheres reproduce the observed flux spectrum, continuum centre-to-limb variation, and hydrogen line profiles at a satisfactory level, thereby confirming the realism of the model and the underlying input physics. These implementations open the prospect for studying other stars with different α-element abundance, carbon-enhanced metal-poor stars, and population II stars with peculiar chemical compositions using 3D Stagger model atmospheres.
Key words: equation of state / opacity / convection / Sun: granulation / Sun: photosphere / line: formation
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Stellar atmosphere models are indispensable tools for the quantitative interpretation of astronomical observations. For late-type stars, although the majority of theoretical atmosphere models are computed assuming one-dimensional (1D) geometry, hydrostatic equilibrium, and phenomenological theories of convection such as the mixing length theory (MLT, Böhm-Vitense 1958), three-dimensional radiation-hydrodynamical (3D RHD) modelling of stellar atmospheres has become more common in recent years, and activity in this area continues to grow. This is partly driven by more detailed observational data and the rapid growth in computing power. In 3D RHD models, sometimes referred to as near-surface convection simulations, the motion of fluid is computed from first principles by solving the equation of mass and momentum conservation as well as the energy conservation equation coupled with the equation of radiative transfer in 3D space for each time step. Although the current study ignores the effects of magnetic fields, these can be included in the models by adding the induction equation, Ampere’s circuital law, and Ohm’s law to the equation system.
The 3D RHD models have proved to be superior to their 1D counterparts in all aspects and shed light on many problems in stellar physics. The early simulations by, for example, Nordlund (1985) and Stein & Nordlund (1989) provided valuable insight into how convection operates in the near-surface layers of low-mass stars: Rather than distinct and coherent fluid parcels assumed in the MLT, convective regions show finger-like downflows that merge together as they descend from the photosphere before finally reaching the bottom of the simulation domain. Conservation of mass forces the relatively hot material to rise back up through the thin optical surface, forming so-called granules. Detailed solar simulations presented in Stein & Nordlund (1998) further confirmed this picture, and their work demonstrated the excellent agreement between simulation and observation in terms of the granulation pattern.
These ab initio simulations enabled the prediction of various observables in a parameter-free manner. The most remarkable breakthrough brought by 3D RHD models is associated with spectral line profiles: Predicted spectral line broadening, blueshifts, and bisectors agree excellently with observations (Asplund et al. 2000b; Pereira et al. 2013), to a degree that cannot be achieved by 1D models even if free parameters in the latter can be adjusted to fit the measured line profiles. This renders 3D model atmospheres a powerful tool for elemental abundance determinations and lead to a revision of the standard solar chemical composition (Asplund et al. 2005, 2009, 2021; Caffau et al. 2011). Moreover, 3D RHD models perform well in the case of centre-to-limb variations of intensity (Pereira et al. 2013; Kervella et al. 2017), making them useful for deriving limb-darkened stellar radii and effective temperatures from interferometric measurements (White et al. 2018; Karovicova et al. 2020; Rains et al. 2020). Three-dimensional simulations of stellar surface convection have also contributed to the field of helioseismology. Rosenthal et al. (1999) showed that the discrepancy between theoretical and measured solar pressure mode frequencies can be reduced by combining the averaged 3D model with 1D interior model before computing the theoretical oscillation frequency based on such a patched model (see also Ball et al. 2016 and Houdek et al. 2017). The reason for the better agreement is that the convective turbulence is self-consistently described in 3D simulations,which results in more realistic pressure stratification in the near-surface convective layers.
Three-dimensional hydrodynamical simulations of the solar near-surface convective region and solar atmosphere have been carried out by several research groups with independent codes, such as ANTARES (Muthsam et al. 2010), Bifrost (Gudiksen et al. 2011), CO5BOLD (Freytag et al. 2012), MURaM (Vögler et al. 2005), and Stagger (Nordlund & Galsgaard 1995). The Bifrost solar simulation extends from the near-surface convection zone upwards to the corona to investigate processes in the transition region and the solar chromosphere (Carlsson et al. 2016). The magneto-hydrodynamical simulations of the Sun constructed with the MURaM code have provided valuable insights into our understanding of sunspots (Rempel et al. 2009) and the solar small-scale dynamo (Vögler & Schüssler 2007). Reference solar simulations computed with the CO5BOLD, MURaM, and Stagger code were compared in detail by Beeck et al. (2012), who found good quantitative agreement between the three models.
Meanwhile, near-surface convection simulations with CO5BOLD, MURaM, and Stagger were constructed for a variety of stars including warm turn-off stars (Allende Prieto et al. 2002), M-type dwarfs (Ludwig et al. 2006), metal-poor benchmark stars (Collet et al. 2009, 2018), and extremely metal-poor stars (Collet et al. 2006; Lagae et al. 2023). Also, grids of 3D model atmospheres, such as the CIFIST grid (Ludwig et al. 2009b; Bertran de Lis et al. 2022), the Trampedach et al. (2013) grid, and the Stagger grid (Magic et al. 2013a; Rodríguez Díaz et al., in prep.), are now available, and cover a large area of the Hertzsprung-Russell diagram and span a wide metallicity range.
However, most of the 3D model atmospheres to date are constructed based on solar-scaled chemical compositions and a fixed value of abundance enhancement of α elements1. Although this is usually an acceptable approximation for solar-type stars (i.e. F- and G-type dwarfs), the validity of the model atmosphere is in doubt when applied to, for example, relatively metal-rich ([Fe/H] ~ −0.5) halo stars with high α element abundance ([α/Fe] up to ~0.35, see Nissen & Schuster 2010) because α-enhancement is not considered at this metallicity. Neglecting variations in the abundance of individual elements may result in more significant systematic errors when investigating stars with peculiar abundance patterns, such as carbon-enhanced extremely metal-poor stars, whose carbon and oxygen abundance is usually enhanced by at least 1 dex with respect to solar-scaled values (Frebel & Norris 2015).
Therefore, model atmospheres with chemical composition tailored for individual cases are necessary for the aforementioned stars given their importance in revealing the chemical evolution history of the Milky Way and the early Universe. Gallagher et al. (2017) and Steffen et al. (2018) made pioneering efforts in this direction by generating 3D model atmospheres for carbon-enhanced metal-poor stars. To allow realistic Stagger simulations with arbitrary chemical composition, we use an open-source equation-of-state (EOS) code and an opacity package developed in-house (Sect. 2), which form the basis of our new models. As the input physics has changed, the resulting model atmospheres need to be validated before any scientific application. The Sun is a natural test bench for all theoretical stellar models because of the rich observational constraints available. Therefore, in this work, we validate the newly implemented input physics and the resulting 3D solar model atmosphere by comparisons with previously published results in terms of mean structure and horizontal distribution of key quantities (Sect. 3), and by comparing model-predicted quantities with corresponding solar observations (Sect. 4).
Elements included in the FreeEOS calculation and the corresponding solar abundance adopted in this work.
2 Input physics
2.1 Equation of state
FreeEOS is an open-source EOS code by Irwin (2004a, Irwin 2012) for stellar interior and atmosphere conditions. The EOS covers a wide temperature and density range that blankets both the lower atmosphere and the core of low-mass stars. It is widely adopted in stellar evolution codes, such as GARSTEC (Weiss & Schlattl 2008) and MESA (Jermyn et al. 2023), and was recently applied to MURaM magneto-hydrodynamical simulations to study small-scale dynamo in cool stars with different spectral types and metallicities (Bhatia et al. 2022; Witzke et al. 2023). The EOS includes 20 elements (Table 1) as well as H2 and 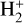 molecules.
molecules.
At each density and temperature (or pressure) pair, chemical equilibrium is computed by adjusting the number density of various species (atoms, ions, and electrons) such that the Helmholtz free energy is minimised, with the charge-neutral condition and particle number conservation (also known as abundance conservation) as constraints. The free-energy minimisation technique is often used in EOS calculations (e.g. Hummer & Mihalas 1988) because when temperature and volume are fixed, the Helmholtz free energy is a minimum at equilibrium. For detailed explanations of the code, we refer readers to the FreeEOS documentations (Irwin 2004a,b)2.
We used the most realistic free-energy model implemented in the FreeEOS (named EOS1) in our calculation. The EOS1 option takes into account all ionisation stages of the 20 included elements, arbitrarily relativistic and degenerate free electrons, higher order Coulomb effects through a Coulomb factor on the first-order Debye-Hückel term, and an occupation probability formulation (similar to the Mihalas et al. 1988 EOS, hereafter MHD EOS) for pressure ionisation. EOS1 yields good agreement with the OPAL EOS (Rogers & Nayfonov 2002) by design. Tests performed by Irwin (2004b) show that the thermodynamical quantities predicted by the FreeEOS EOS1 option differ from those of the OPAL EOS by less than 0.2% for solar conditions.
We adopted two solar abundance mixtures in this work: the Asplund et al. (2009, hereafter AGSS09) and Asplund et al. (2021, AAG21) solar abundance. The input abundances for 20 elements included in the EOS are listed in Table 1. Thermal (gas plus radiation) pressure given by the two sets of abundances differs by about 0.7% in the mass density and temperature area of interest (−10 < log(ρ/[gcm−3]) < −4; 3.5 < log(T/[K]) < 4.5, where ρ and T are mass density and temperature, respectively). The difference is almost entirely due to the different helium abundances adopted in AGSS09 and AAG21. The effect of metals on thermal pressure is negligible. As detailed in Appendix A, key quantities from the FreeEOS with the AGSS09 solar abundance are compared with a modified version of the MHD EOS (Trampedach et al. 2013, the EOS employed in previous Stagger simulations). We find good agreement between the two EOSs, which further validates our FreeEOS results.
With the aforementioned setup and inputs, we generated FreeEOS tables in the format required by the Stagger code. Our EOS tables are based on mass density and internal energy per mass em as independent variables, as internal energy per mass rather than temperature is the fundamental variable in the Stagger code (see Sect. 2 of Nordlund & Galsgaard 1995). Densities and internal energies are equidistant in logarithm space. Density log ρ ranges from −13.9 to 0 log[g cm−3] in steps of 0.05 while log em ranges from 11 to 14 log[ergg−1] in steps of 0.005. The resolution of our EOS table is higher than that previously used in the Stagger code.
The EOS table stores thermal pressure Pther, temperature T, and electron number density ne and their partial derivatives with respect to two independent variables, namely 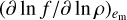 and (∂ ln f /∂ ln em)ρ, where f ∈ {Pther, T, ne}. We note that these thermodynamic derivatives are obtained directly from EOS calculations and the Maxwell relations, and therefore no interpolation is needed.
and (∂ ln f /∂ ln em)ρ, where f ∈ {Pther, T, ne}. We note that these thermodynamic derivatives are obtained directly from EOS calculations and the Maxwell relations, and therefore no interpolation is needed.
2.2 Opacities
2.2.1 The Blue opacity code
We used the Blue code developed by Amarsi et al. (2016, 2018) to calculate total line and continuous monochromatic extinction coefficients at different gas temperatures and densities. The first step in calculating these quantities is to obtain the number density of each species from the EOS. The original EOS implemented in Blue is based on the Saha ionisation equation, albeit with a truncation of ionisation energies to account for non-ideal gas effects. Although valid for studying the relatively cool photospheres of FGK-type stars, a free-energy minimisation approach is expected to be more valid in hotter environments (Hummer & Mihalas 1988). Thus, in the high temperature regime3, we instead fed the number densities from FreeEOS into Blue. For H−, whose number density is not accessible from FreeEOS, we solved the Saha equation (assuming chemical equilibrium between neutral hydrogen and H−) to obtain its number density. It is worth mentioning that FreeEOS handles only 20 elements, whereas 83 elements are included in Blue. Therefore, for the 63 elements that are not incorporated in the FreeEOS, their number densities (including all ionisation states) were set to zero in Blue in this high-temperature regime. Molecular abundances were also set to zero in this limit.
In the low-temperature regime, we instead used the Blue EOS, so as to include the effects of atoms and ions of all 83 elements, as well as of molecules. The code uses molecular partition functions from Barklem & Collet (2016). Atomic and ionic partition functions were calculated using data from the Kurucz online database (Kurucz 1995), including at least three-times ionised species for all the FreeEOS metals except Cl (up to twice ionised), which is sufficient for the temperature range concerned in this work (i.e. log(T/[K]) ≤ 4.5). Our tests show that, below log T = 4.5, the number densities of four-times and higher ionised species are negligible for all 18 FreeEOS metals. In this work, for a given temperature, pressure, and chemical composition, the ionisation energy was truncated prior to the calculation of the partition function (by an amount calculated via the expression in Chapter 10.5 of Thorne et al. 1999).
Given the EOS, Blue calculates total line and continuous monochromatic extinction coefficients using transition cross-sections from various sources. The bound-free and free-free data sources can be found in Table 2. We note that for many of the species listed in Table 2, cross-sections of bound-free transitions were adopted from the Opacity project (TOP) or IRON Project (TIP) online database. These data are exactly the same as those used in the previous generation of Stagger surface convection simulations (Magic et al. 2013a). We took data for bound-bound transitions in atoms, ions, and molecules from the Kurucz online database; we summarise the considered molecular species in Table 3. With the exception of the scattering processes at the end of Table 2, all radiative transitions were treated in true absorption. The line opacities are slightly influenced by the choice of microturbulence; here we set this to 2 km s−1 as was used in the original Stagger grid. In this work, for bound-bound transitions of species other than hydrogen, occupation probabilities w were calculated following Appendix A of Hubeny et al. (1994). Individual bound-bound transitions with monochromatic extinction coefficients αv;m,n were therefore modified as αv;m,n → αv;m,n × wn, where m and n denote the lower and upper levels of the transition. For hydrogen lines and continua, we instead implemented the HBOP module provided by Barklem & Piskunov (2016).
Blue gives continuum and line absorption monochromatic extinction coefficients, which we added to get total absorption coefficients, separated into true absorption (αab) and scattering (αSC). These can also be added together to obtain a total extinction coefficient (αtot). We used these quantities in the opacity binning procedure described in Sect. 2.2.3.
In order to have a smooth transition between the low-and high-temperature regimes, in practice we carried out two separate opacity calculations. Extinction coefficients were computed using the Blue EOS in the low-temperature (3.2 ≤ log T ≤ 4.1) regime, and FreeEOS in the high-temperature (3.9 ≤ log T ≤ 4.5) regime. The overlapping temperature interval log T ∈ [3.9, 4.1] serves as an intermediate bridging region.
Here, we merged extinction coefficients from the two different calculations via
where log T1 and log T2 are the lower and upper boundaries of the bridging region, respectively. The bridging function ƒb equals 0 at the lower boundary, and smoothly increases to 1 at the upper boundary. The term αmg denotes the merged extinction coefficient, which could be monochromatic, or a mean value such as the Rosseland mean.
Data sources for continuum bound-free (bf) and free-free (ff) absorption as well as scattering processes included in the Blue opacity code.
Molecular species and corresponding line list data adopted in the Blue code.
2.2.2 Opacity grids
Using the methods described in Sect. 2.2.1, we constructed grids of monochromatic extinction coefficients for different values of (log T, log ρ) for the AGSS09 and AAG21 solar chemical compositions. The temperature ranged from log T = 3.2 to 4.5 in steps of 0.01 log [K], and the density ranged from log ρ = −13.7 to −1.0 in steps of 0.1 log [g cm−3]. This temperature-density coverage is sufficient for our applications because the surface convection simulations do not reach the low-density upper atmosphere, nor do they extend to the high-temperature stellar interior. It is known that the carbon-to-oxygen ratio has a great impact on the molecular opacity when log T ≲ 3.4 (Marigo et al. 2022). Nevertheless, given that the C/O ratio is very similar in AGSS09 and AAG21, its influence on the opacity is limited, as demonstrated in Fig. 6 of Marigo et al. (2022). However, the different Mg and Fe abundances in the two versions of solar composition is likely to leave imprints on opacities, because these elements are important electron donors (due to their high abundances and relatively low ionisation energies), and influence the H− opacity (Gustafsson et al. 2008, Sect. 6.3). Although Si is another important electron donor, its abundance is identical in AGSS09 and AAG21.
Extinction coefficients were computed at 250000 wavelength points between 50 nm and 50 µm, evenly sampled in logarithmic space to better resolve the ultraviolet. The resolving power is therefore given by λ/Δλ ≈ 36 200. This wavelength resolution is not adequate for resolving all absorption features caused by spectral lines. Nevertheless, in the scenario of stellar atmosphere modelling, the focus is on finding a sufficient wavelength resolution such that the modelled temperature stratification converges rather than resolving all the line features in the opacity calculation (see Plez 2008, Sect. 4 for detailed discussion). In order to verify our selected wavelength resolution, we computed monochromatic extinction coefficients at very high wavelength resolution along (ρ, T) points of the horizontal- and time-averaged sunA09 model (cf. Table 4 and Sect. 3 about the model). The wavelength sampling is uniform in logarithm space, with two million points between 50 nm and 50 µm, corresponding to a wavelength resolution of λ/Δλ ≈ 289 530. We compared the temperature stratification predicted from high-resolution extinction coefficients with that adopted in this work using the 1D stellar atmosphere code ATMO. The ATMO code, described in Magic et al. (2013a) Appendix A, employs the same EOS and opacity table as the Stagger code. At solar effective temperature and surface gravity, we find that 1D temperature structure evaluated from opacities with wavelength resolutions of λ/Δλ ≈ 289 530 and λ/Δλ ≈ 36200 differ by less than 0.1% in the stellar atmosphere, which translates to a less than 5 K error in the optically thin regime. The error estimation implies that given the opacity binning method used in this work (cf. Sect. 2.2.3), our adopted wavelength sampling is sufficient for obtaining a reliable temperature structure.
We compared the Rosseland and Planck mean extinction coefficients with corresponding results from other opacity datasets, and found reasonable agreement in general (cf. Appendix C for quantitative comparisons). The Rosseland mean extinction coefficient was calculated as
and the Planck mean extinction coefficient as
where B is the Planck function,
where c, h, and kB are the speed of light, the Planck constant, and the Boltzmann constant, respectively. Numerically, the integrals in Eqs. (2) and (3) are discretised by the trapezoid rule, with the lower (upper) limit being the shortest (longest) wavelength point computed by Blue, which is λmin = 50 nm (λmax = 50 µm) throughout our calculation. The mean extinction coefficients evaluated in this way, together with continuum extinction coefficients (continuum absorption plus scattering) at 500 nm, are then interpolated to (ρ, T) combinations – which correspond to the EOS (ρ, em) grid – and stored in the EOS table as auxiliary quantities for the post-processing of simulation data (not used by the Stagger code).
Fundamental parameters and basic information about solar simulations presented in this study.
2.2.3 Opacity binning
In radiative hydrodynamical simulations, solving the radiative transfer equation across the 3D simulation domain at every time step and in about ten different directions for a large number of wavelengths is computationally demanding. In order to make the problem computationally feasible, the Stagger code adopts the opacity binning method (also called the multi-group method, Nordlund 1982; Skartlien 2000; Magic et al. 2013a; Collet et al. 2018). With this method, we divide monochromatic opacities into multiple groups based on wavelength and opacity, or more precisely the approximate formation depth in a given model atmosphere. In each group, monochromatic opacities are appropriately averaged and treated as a ’single wavelength’ in the radiative transfer calculation, thereby reducing the workload enormously. We elaborate on our opacity binning procedure below and refer readers to Collet et al. (2018, their Sect. 2.4.2) for more information. A detailed study on different opacity binning approaches and their accuracy can be found in Perdomo García et al. (2023).
Apart from the opacity data, a stellar atmosphere model is required for the binning process. In our implementation, we use the horizontal- and time-averaged 3D model (<3D> model hereinafter), which implies opacity binning is an iterative process as the adopted (3D) model affects the binned opacities, and the latter alters the stratification of the 3D atmosphere model in return. Monochromatic absorption and total extinction coefficients, as well as the Rosseland mean extinction coefficients computed at low and high temperature regions, were first merged as described in Sect. 2.2.2 and were then interpolated to the densities and temperatures of the (3D) model. Subsequently, we calculated the Rosseland optical depth τRoss and monochromatic optical depth τλ according to the interpolated αRoss and αtot,λ, respectively. This is to obtain the Rosseland optical depth where monochromatic optical depth is unity, that is, τRoss(τλ = 1), which indicates the approximate location where flux emerges (also the approximate formation depth of lines). For a given selection of the opacity bins, as demonstrated in Fig. 1, all wavelength points were assigned to an opacity bin based on their wavelength and τRoss(τλ = 1) value. We note that the organisation of opacity bins in Fig. 1 (not the exact location of their boundaries) is the same as that adopted in the 3D solar model of Pereira et al. (2013), which was well tested against various observational constraints.
For each bin, averaged extinction coefficients were computed by integrating over wavelengths that belong to that bin. In the optically thick region, the Rosseland mean, αRoss,i, as defined in Eq. (2) – but integrating over the wavelengths and transitions included in the ith bin – is a good representation of the mean extinction coefficient within that bin.
However, in the optically thin part, the radiative flux cannot be described by the diffusion equation. Inspired by the fact that the divergence of monochromatic radiative flux is proportional to αtot,λ (Jλ − Bλ) in local thermodynamic equilibrium (LTE), where J denotes the monochromatic mean intensity (Eq. (8)), and considering that the absorption processes (characterised by J) are usually stronger than emission processes (characterised by the source function B in LTE) in stellar atmospheres (see e.g. Fig. 5 of Bergemann et al. 2012), we used J as the weighting function in the optically thin part (Nordlund & Dravins 1990; Magic et al. 2013a). Also, scattering was excluded from the extinction coefficient when calculating mean opacities in the optically thin region. This is referred to as the no-scattering-in-streaming-regime approximation. The purpose of this modification is to approximate the temperature structure predicted by surface-convection simulations with continuum scattering processes properly treated in the radiative transfer calculation using simulations with LTE radiative transfer (Collet et al. 2011). Although the inclusion of continuum scattering in the extinction coefficient has little impact on the temperature structure of the 3D solar model (Hayek et al. 2010, Fig. 7), Collet et al. (2011) demonstrated that for metal-poor stars, the no-scattering-in-streaming-regime approximation leads to good agreement with the correct solution where scattering is included in the modelling, whereas using the total extinction coefficient in the optically thin region overheats the stellar atmosphere. In order to be consistent with future non-solar metallicity simulations, the no-scattering-in-streaming-regime approximation is adopted in this work. The same approximation was also used in the construction of the Stagger-grid (Magic et al. 2013a, Sect. 2.1.5). The mean extinction coefficient in the optically thin regime is therefore
where i = 1, 2,…, 12 indicates a specific opacity bin. We note that, as discussed above, scattering is excluded from the integrand. The integration is carried out with the midpoint (or rectangle) method. We verified that the midpoint integration rule is the preferred choice for the opacity binning problem, as it accurately reproduces αJ,i and αRos,i· obtained from monochromatic opacities with high wavelength resolution for all opacity bins. However, higher-order integration methods, such as the trapezoid and Simpson’s rule, will lead to large errors in the mean extinction coefficient for some bins and will result in incorrect temperature structure in the solar atmosphere.
The two types of mean extinction coefficients were blended together with an exponential bridging function to obtain the final combined bin-averaged extinction coefficient, which reads
with αRos,i· being the Rosseland mean extinction coefficient evaluated from wavelengths belonging to bin i and τRoss,i· the optical depth based on αRoss,i.
The bin-averaged extinction coefficients for two selected opacity bins are depicted in Fig. 2. These are typical of opacity bins including optical and near-infrared wavelengths that form around the optical surface, and of opacity bins including ultraviolet wavelengths that form in higher layers. Red solid lines stand for αbin,i· used in this work, whereas black dotted lines represent extinction coefficients calculated from the binning code implemented in Trampedach et al. (2013) with the Trampedach et al. (2014) opacity dataset (see also Appendix C), which corresponds to binned extinction coefficients adopted in previous Stagger simulations. The αbin,i·results from the previous calculation and our new one agree reasonably well for both bin 3 and bin 5. The small difference seen in Fig. 2 is due to different opacity datasets adopted, as the opacity binning procedure is identical between this work and Trampedach et al. (2013).
To get the mean intensity in Eq. (5), we solved the radiative transfer equation in the 1D plane parallel ( 3D) model under the assumption of LTE:
where µ = cos θ represents the polar angle along which the equation is solved, Iλ is the monochromatic intensity, and τλ is the vertical monochromatic optical depth. Integrating Iλ over the polar angle gives the mean intensity,
The 1D LTE radiative transfer problem was solved using a modified Feautrier (1964) technique developed by Nordlund (1982, their Sect. 3.9.1) and Stein & Nordlund (2003, their Sect. 4), which rearranges the Feautrier transport equation and solves for Qλ = (1/2)[Iλ(µ) + Iλ(−µ)] − Bλ in order to improve the numerical accuracy at large optical depths. This is the same numerical technique as is implemented in the 3D radiative transfer solver of the Stagger code. The integration in Eq. (8) was approximated with the Gaussian-Legendre quadrature with five polar angles, which is sufficient for this problem, as increasing the number of µ-angles hardly changes the resulting mean intensity.
Reducing a large number of wavelengths to 12 opacity bins in the radiative transfer calculation is a significant simplification. To examine how accurate the opacity binning method is, we compared the radiative heating (or cooling) rate computed from bin-averaged quantities,
with the monochromatic solution
Here, 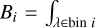 Bλ dλ is the Planck function integrated over a given bin, and Ji, the mean intensity of bin i, was obtained from Eqs. (7) and (8) with source function Bi and optical depth computed via αbin,i·. The heating rate is a crucial outcome of the radiative transfer process because it enters directly into the energy equation, thereby influencing the temperature stratification of the model. The difference in qrad is quantified by max |qrad,b − qrad,m|/max |qrad,m| (Magic et al. 2013a), which is the relative difference at the cooling peak in most cases. In addition to qrad, we examined how well the opacity binning method reproduces the radiative flux, as it determines the effective temperature of the model. The radiative flux (Frad) was calculated by integrating the heating rate from the bottom (stellar interior) to the top (atmosphere) along the (3D) model. Therefore, differences in Frad are a manifestation of differences in qrad. Nevertheless, comparing Frad probes the mean differences in qrad rather than at a particular location. Briefly, we employed a combination of max |qrad,b − qrad,m|/max |qrad,m| and the relative difference in Frad as an indicator of the accuracy of opacity binning:
Bλ dλ is the Planck function integrated over a given bin, and Ji, the mean intensity of bin i, was obtained from Eqs. (7) and (8) with source function Bi and optical depth computed via αbin,i·. The heating rate is a crucial outcome of the radiative transfer process because it enters directly into the energy equation, thereby influencing the temperature stratification of the model. The difference in qrad is quantified by max |qrad,b − qrad,m|/max |qrad,m| (Magic et al. 2013a), which is the relative difference at the cooling peak in most cases. In addition to qrad, we examined how well the opacity binning method reproduces the radiative flux, as it determines the effective temperature of the model. The radiative flux (Frad) was calculated by integrating the heating rate from the bottom (stellar interior) to the top (atmosphere) along the (3D) model. Therefore, differences in Frad are a manifestation of differences in qrad. Nevertheless, comparing Frad probes the mean differences in qrad rather than at a particular location. Briefly, we employed a combination of max |qrad,b − qrad,m|/max |qrad,m| and the relative difference in Frad as an indicator of the accuracy of opacity binning:
As a criterion of the realism of the opacity binning method, Δb,m was used to select the ‘best’ binning configuration for a given model atmosphere and opacity dataset: The ‘best selection’ of opacity bins corresponds to the global minimum of Δb,m. In practice, we iteratively adjusted the location of bin boundaries and computed the corresponding Δb,m. The optimisation problem was tackled with Powell’s method (cf. Press et al. 1992, Sect. 10.5) with the location of bin boundaries as multi-dimensional variables and Δb,m the minimisation target. Our preferred bin selection for model sunA09 (Table 4) obtained from minimising Δb,m is illustrated in Fig. 1. Because Blue monochromatic extinction coefficients for the AGSS09 and AAG21 abundance are close to each other at most wavelengths, the optimised location of bin boundaries for model sunA21 is nearly identical to that of the sunA09 model. We caution that for multi-variable optimisation, it is very challenging to find the global minimum, and therefore our preferred bin selections might represent only the local minimum of Δb,m and may be affected by our initial guess.
A comparison of qrad and Frad between the opacity binning and monochromatic calculation is presented in Fig. 3. In the case of the (3D) sunA09 model, the relative difference of qrad at the cooling peak (in this case the same as max |qrad,b − qrad,m|/max |qrad,m|) is 2.42%, which is of a similar accuracy level to that achieved by Magic et al. (2013a). The relative difference in surface flux (defined as the radiative flux at log τRoss = −4) is 1.49%, which translates to a 0.37% relative difference and ≈21 K absolute difference in effective temperature. Nevertheless, we note that errors in surface flux presented here are merely illustrative. Owing to the non-linear, turbulent nature of 3D surface convection simulations, it is possible that the true error of binning is larger than the estimation based on the (3D) model. True errors in flux can be determined by synthesising the flux spectrum with a 3D model atmosphere and comparing it with observations.
 |
Fig. 1 Rosseland optical depth where monochromatic optical depth is unity – which reflects the strength of opacity – as a function of wavelength computed based on the (3D) sunA09 model (cf. Table 4 and Sect. 3 for basic information about the model and how it is constructed) and Blue opacities assuming the AGSS09 solar abundance. One out of ten points in our wavelength sampling is shown to avoid overcrowding the figure. Grey boxes numbered from 1 to 12 in red define the opacity bins used for the sunA09 simulation. Bins 1–3 divide the ultraviolet wavelength region according to the location where flux emerges; Bins 4, 5, and 9 mainly consist of wavelength points distributed near the continuum-forming layers; Bins 8 and 12 include only wavelengths with strong opacity, which typically correspond to lines. |
 |
Fig. 2 Bin-averaged extinction coefficients (Eq. (6)) as a function of the bin-wise Rosseland optical depth of bins 3 and 5 (as defined in Fig. 1) based on the (3D) sunA09 model. The bin-wise Rosseland optical depth τRoss,i is computed from wavelengths belonging to bin i. Extinction coefficients calculated from the binning code implemented in Trampedach et al. (2013) with the Trampedach et al. (2014) opacity dataset are shown in black dotted lines, whereas red solid lines represent αbin,i used in this work. |
 |
Fig. 3 Radiative heating (or cooling) rate and radiative flux computed based on the (3D) sunA09 model. Left panel: comparison of the radiative heating (or cooling) rate computed from the 12 opacity bins shown in Fig. 1 (red plus mark) with the monochromatic solution using 250 000 wavelengths (black solid line) for the (3D) sunA09 model. The relative difference of qrad at the cooling peak is 2.42%. Right panel: comparison between radiative flux obtained from the opacity binning method and the monochromatic solution. The relative difference of surface flux (defined as the radiative flux at log τRoss = −4) is 1.49%. |
3 Solar atmosphere model
The EOS and opacities described in Sect. 2 were incorporated into the Stagger code as basic input physics for our 3D solar model atmospheres. The Stagger code (Nordlund & Galsgaard 1995; Collet et al. 2018; Stein et al., in prep.) is a radiation-magnetohydrodynamics code that solves the time-dependent equation of mass, momentum, and energy conservation, the magnetic-field induction equation, as well as the radiative transfer equation on a 3D staggered Eulerian mesh. The solar models in this study were constructed without magnetic fields. Radiative energy transport was modelled in LTE. The equation of radiative transfer with the Planck function as source function (Eq. (7)) was solved with a modified Feautrier (1964) technique (Nordlund 1982; Stein & Nordlund 2003) for all mesh points above τRoss = 500 at every time step of the simulation. The frequency dependence of the radiative transfer problem was approximated by the opacity binning method detailed in Sect. 2.2.3, where the layout of 12 opacity bins was optimised individually for each solar model. Spatially, the radiative transfer equation was solved along nine different directions which consists of eight inclined directions, representing the combination of two polar angles and four azimuthal angles, plus the vertical direction. The integration over the polar angle was approximated by the Gauss-Radau quadrature. The radiative heating rate evaluated in this way enters the equation of energy conservation and meanwhile was used to compute the radiative flux and the effective temperature of the model.
The two new 3D solar atmosphere models presented in this work are labelled sunA09 and sunA21. The former adopts the AGSS09 solar chemical composition while the latter uses the recent AAG21 abundance. Both model atmospheres were constructed based on the reference solar effective temperature and surface gravity given by Prša et al. (2016). Their basic configurations are summarised in Table 4. In addition, in the subsequent sections, we present comparisons of these two models with an older Stagger model (i.e. with the same input physics as used in the Stagger-grid) used in previous studies (e.g. Zhou et al. 2019), which we refer to as sunRef hereafter.
The simulation domain is discretised on a Cartesian mesh located around the solar photosphere (with coordinates x, y, z where y denotes the vertical dimension). For both models, the distribution of mesh is identical to that used in sunRef. The horizontal extent of the simulations is 6 Mm × 6 Mm with 240 mesh points evenly distributed in each direction, which is large enough to enclose at least ten granules at any time of the simulation (Magic et al. 2013a). There are 240 mesh points in the vertical direction, where five layers at the top and bottom of the simulation domain are reserved as the so-called ‘ghost-zone’ to ensure that vertical boundary conditions fulfil the six-order numerical differentiation scheme employed in the Stagger code (Nordlund & Galsgaard 1995 Sect. 2.2). The remaining 230 vertical meshes constitute the ‘physical domain’ of the simulation and are equated with the simulation domain further below. The vertical size of our simulations is 3.6 Mm (excluding ghost zones), which extends from 2.7 Mm below the base of the photosphere (the near-surface convection layers) to 0.9 Mm above it (the bottom of the chromosphere). This corresponds roughly to the outer 0.5% of the solar radius. Because the vertical scale of the simulations is very small compared to the solar radius, spherical effects are negligible and the surface gravity can be used in the entire simulation domain. The 230 vertical mesh points are not evenly placed: the finest numerical resolution is applied around the optical surface in order to resolve the steep transition from the optically thick to thin regime (see Magic et al. 2013a, Fig. 2 for an illustration). Given the size of the simulation box, the 2402 × 230 numerical resolution was verified as being adequate for line formation calculations (Asplund et al. 2000a), which is the main application of our models.
The boundaries are periodic in the horizontal directions, while open in the vertical (Collet et al. 2018). At the bottom boundary, outgoing flows (vertical velocities towards the stellar centre) freely carry their entropy fluctuations out of the simulation domain, whereas constant entropy and thermal (gas plus radiation) pressure is enforced for incoming flows. Temporally, our simulations span 200 solar minutes, with one snapshot stored every 30 seconds solar time. All these simulation snapshots were generated after numerical relaxation procedures described in Sect. 2.3 of Magic et al. (2013a).
We note that except for the updates to the input physics, the setup and mesh properties of sunA09 and sunA21 simulations are almost identical to those of sunRef, which is well-tested against other 3D solar atmosphere models and observational constraints (Beeck et al. 2012; Pereira et al. 2013, hereafter P2013)4. To this end, we verify the new atmosphere models by comparing them with model sunRef in Sects. 3.1 and 3.2.
 |
Fig. 4 Averaged temperature profiles for different solar model atmospheres. Left panel: simple horizontal- and time-averaged temperature profiles 〈T〉h as a function of geometric depth. Zero geometric depth corresponds approximately to the optical surface. Relative and absolute differences between the new models and sunRef are shown in the middle and lower parts, respectively. Right panel: the τRoss- and time-averaged temperature 〈T〉τ as a function of Rosseland optical depth (T − τ relation) for models sunA09, sunA21, and sunRef. |
3.1 Spatially and temporally averaged model
Figure 4 shows the mean temperature structure for the two new models as well as model sunRef. The models sunA09 and sunRef are directly comparable, as they are based on the same solar abundance. Here, two different methods were used when averaging over space: the simple horizontal average and the average over layers of constant Rosseland optical depth (τRoss-average). The simple horizontal averaged quantities were obtained by taking the mean value at given vertical geometric depths, which, in practice, are defined by the numerical mesh. The τRoss-average was achieved by first computing the Rosseland optical depth for the entire simulation domain. For an arbitrary physical quantity ƒ, this establishes an ƒ− τRoss relationship at every column of the simulation box. For all columns, the ƒ(τRoss) function was then interpolated to a reference optical depth frame. Taking the mean value for all interpolated ƒ at a particular reference optical depth gives the τRoss-averaged quantity. Spatially averaged quantities were then averaged over the whole time series of the simulation, that is, at every simulation snapshot, in order to obtain the horizontal- and time-averaged model. In this paper, we use symbols 〈…〉h and 〈…〉τ to represent the spatial and temporal averaging over constant vertical geometric depth and Rosseland optical depth, respectively.
We note that there are other ways to average 3D models. However, the focus of this section is to compare the mean structure of new models with the reference model sunRef: We aim neither to compare different averaging methods nor to determine the suitable averaging method for a certain application. We refer the readers to Magic et al. (2013b) for a thorough investigation in this direction.
Comparisons of averaged temperature and density profiles are shown in Figs. 4 and 5, respectively. We can see from the middle and bottom left panels of Fig. 4 that around zero geometric depth, 〈T〉h of sunA09 and sunRef differ by more than 100 K (relative difference of about 3%). This discrepancy arises because the models sunA09 and sunRef (also sunA21) adopt identical geometric depth scales but are computed with different opacities. Therefore, their optical surfaces correspond to slightly different geometric depths. Because of the large temperature gradient in the convective-radiative transition zone, a small mismatch in the placement of the optical surface will cause a considerable temperature difference in the geometric depth scale. To this end, a more sensible approach is to compare the averaged temperature profile based on the optical depth scale. From the right panels of Fig. 4, it is clear that sunA09 and sunRef have similar mean temperature structure in general: their τRoss- and time-averaged temperature differs by less than 25 K above log τRoss —3. The absolute temperature differences reach up to ~100 K at log τRoss = -5. Nevertheless, the highly turbulent outermost layers of the simulation are likely the least realistic given our neglect of magnetic fields.
In Appendix B, we isolate the impact of EOSs on the mean temperature structure of 3D solar models by constructing two nearly identical models that differ solely in their input EOS. We find that using MHD or FreeEOS will lead to ~15 K temperature difference in optically thick layers. However, in most parts of the optically thin regime, averaged temperatures between models with MHD and FreeEOS agree within 5 K, suggesting that temperature differences shown in the right panels of Fig. 4 are primarily attributed to different opacity data and the selection of opacity bins between sunA09 and sunRef. Here we emphasise that a careful selection of opacity bins is of great importance to obtain a reliable temperature structure. From our experience, different binning configurations could affect the averaged temperature profile by more than 50 K in the modelled solar atmosphere. Although the exact number depends on the location of the atmosphere where the temperature difference is measured, the impact of binning configuration is clearly non-negligible, and has a much stronger affect than the EOS, especially in the optically thin region. We note that Collet et al. (2018) modelled the atmosphere of a metal-poor red giant with the opacity binning method and reached the same conclusion that an erroneous selection of bins leads to a temperature discrepancy in the stellar atmosphere of about 100 K (see their Fig. 9).
As shown in Fig. 6, the three solar models give similar mean vertical velocity profiles. Particularly notable is the large upward, mean vertical velocity just below the photosphere, which is a consequence of surface convection. The upflows and downflows that form the observed solar granulation pattern must have the same absolute momentum. We can construct a toy model that assumes all upflows (downflows) have identical density ρup (ρdn) and vertical velocity υup (υdn), leading to an equation for the conservation of momentum,
Here a and b is the fractional area covered by upflows and down-flows the ‘filling factor’), respectively. A simple rearrangement of Eq. (12) gives
The left hand side of Eq. (13) is the mean vertical velocity. Because the density is typically higher in downflows (Stein & Nordlund 1998, Fig. 10), the mean vertical velocity has the same direction as the upflows as depicted in Fig. 6. The magnitude of 〈υy〉h reflects the asymmetry between upflows and downflows. The strongest asymmetry is found in the convective region just below the optical surface, where the vertical velocity fluctuations, represented by 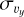 , are also the largest (Fig. 7).
, are also the largest (Fig. 7).
The ratio of turbulent to thermal pressure, which is a proxy for vertical velocity fluctuations, is demonstrated in Fig. 8. Thermal pressures were evaluated from the EOS while turbulent pressures were computed via (Rosenthal et al. 1999, Sect. 3)
where overlines stand for horizontal (but not temporal) averaging. At most vertical layers, the three solar models agree well in terms of 〈Pturb〉h/〈Pther〉h.
For our plane-parallel radiative-hydrodynamical simulations, horizontally averaged fluid properties averaged over sufficiently long stellar time should fulfil the equation of hydrostatic equilibrium (Magic et al. 2013b, Appendix A.2). We check how close the (3D)h models are to hydrostatic equilibrium in Fig. 9, and find that hydrostatic equilibrium is fulfilled at most parts for all three solar simulations. However, we observe deviations from hydrostatic equilibrium in the uppermost layers for all solar models considered, which indicates momentum is not conserved at the top boundary. Nevertheless, the top boundary has little impact on the stratification of the 3D model because of the low density there. Meanwhile, we note that it is the total (thermal plus turbulent) pressure that enters into the equation of hydrostatic equilibrium, as detailed in Magic et al. (2013b).
 |
Fig. 5 Similar to the top and middle panels of Fig. 4, but showing the mean density stratification for different solar simulations. |
 |
Fig. 6 Temporal mean of simple horizontal-averaged (left panel) and τRoss-averaged vertical velocity (right panel) for different solar simulations. Positive velocities correspond to downflows that move towards the stellar interior. |
 |
Fig. 7 Time-averaged standard deviation of vertical velocity in geometric depth scale (left panel) and Rosseland optical depth scale (right panel). This quantity, also called the root-mean-square (rms) of vertical velocity fluctuation, indicates the variation of vertical velocity at a given depth. |
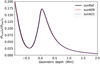 |
Fig. 8 Ratio of simple horizontal- and time-averaged turbulent pressure to thermal pressure. |
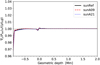 |
Fig. 9 Deviations from hydrostatic equilibrium as a function of vertical geometric depth for (3D)h models. |
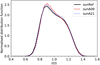 |
Fig. 10 Time-averaged distribution of disc-centre bolometric intensity predicted by the two solar models with new input physics but different chemical compositions, sunA09 (AGSS09 composition) and sunA21 (AAG21 composition), as well as the reference model with unmodified input physics, sunRef (AGSS09 composition). The bolometric intensity is normalised by its mean value 〈I〉, and the distribution function is normalised such that its integration over I/〈I〉 is equal to one. |
3.2 Distribution of intensity and vertical velocity
Checking the mean stratification provides an intuitive overview of 3D models, but meanwhile wipes out fluctuations across the horizontal plane. In this section, we scrutinise the distribution of key simulation properties at selected horizontal planes, which captures the inhomogeneity in the convective motions.
One of the main breakthroughs brought by surface convection simulations is that they reveal how convection operates in the convective-radiative boundary layers of stars. In the photosphere, fluid elements rapidly lose their heat to radiation and become denser than their surroundings. The overdense material is pulled down by negative buoyancy through the optical surface forming the intergranular lanes. Below the surface, conservation of mass forces the warmer, lower-density material to rise back through the optical surface, forming the so-called granules (cf. Nordlund et al. 2009 for detailed description). The distribution of emergent intensity is a direct reflection of the radiation field in granules and intergranular lanes, which originated from upflows and downflows at different heights of the atmosphere.
Here, we compare the disc-centre bolometric intensity distribution of sunA09 and sunA21 with the reference model sunRef. The distribution of bolometric intensity across the simulation domain is shown as a histogram of normalised intensity I/〈I〉, where 〈I〉 is the mean bolometric intensity. In all cases, 30 equidistant bins were assigned between I/〈I〉 = 0.4 and 1.6 for the evaluation of the distribution function. The time-averaged distribution shown in Fig. 10 was obtained by computing the normalised distribution function for every simulation snapshot and then averaging over all snapshots. The intensity distribution of the new solar models agrees well with model sunRef, all showing a bimodal distribution with a primary peak located at I/〈I〉 ≈ 0.9 that corresponds to intergranular lanes, and a secondary peak at a higher intensity I/〈I〉 ≈ 1.1. However, the new models predict slightly higher peaks around I/〈I〉 = 0.9.
The area coverage and the strength of upflows and down-flows is revealed by the distribution of vertical velocities. For each simulation snapshot, vertical velocities at each column were interpolated to τRoss = 2/3 to obtain the velocity distribution in the vicinity of the optical surface5. Averaging over all distribution functions gives the time-averaged velocity distribution shown in Fig. 11. Similar to the case of intensity, the distribution function of vertical velocity appears to be bimodal, where the primary peak corresponds to upflow. It is worth noting that the distribution function confirms the visual impression we get from the right panel of Fig. 11, namely that upflows fill more area in the simulation domain.
4 Comparison with observations
The best way to examine the fidelity of stellar models is to compare model predictions with observables. In this section, we compute the absolute flux spectrum (Sect. 4.1), the centre-to-limb variations (Sect. 4.2), and hydrogen lines (Sect. 4.3) from the new solar model atmospheres. All modelling results are compared with solar observations as well as theoretical predictions presented in P2013, which is based on a well-established solar atmosphere model computed with the Stagger code and the Asplund et al. (2005) abundance. We name this model sunP2013 in order to avoid confusion with model sunRef mentioned in Sect. 3 (see footnote 4).
The spectrum synthesis was carried out using the 3D non-LTE radiative transfer code Balder (Amarsi et al. 2018), a branch of Multi3D (Leenaarts & Carlsson 2009) with updates for example to the formal solver (Amarsi et al. 2016, 2019) and in particular to the EOS and opacities as discussed in Sect. 2.2.1. In this work, identical abundances and opacity data were employed in Balder and the surface convection simulation. The calculations follow what was presented in Amarsi et al. (2018) and employ the same model atom. Previous investigations have indicated that departures from LTE have non-negligible effects on the wings of Balmer lines (particularly Hα, see e.g., Fig. 7 of P2013 and Fig. 4 of Amarsi et al. 2018): In the solar case, Balmer lines computed in non-LTE show weaker wings than in LTE.
4.1 Absolute flux spectrum
The emergent flux spectrum (or spectral energy distribution) plays an important role in stellar physics. Theoretical flux spectra generated from model atmospheres can be applied to, for example: calculate synthetic photometry (Casagrande & VandenBerg 2014; Chiavassa et al. 2018), determine stellar parameters (Vines & Jenkins 2022), and derive interstellar extinctions (Yu et al. 2023). Previous investigations have demonstrated that 3D model atmospheres are able to produce realistic absolute flux spectra for the Sun (Chiavassa et al. 2018; Kučinskas et al. 2018). It is therefore worth checking how our new models perform in this respect.
Here, we first compare the continuum flux spectrum predicted by our new models with that of model sunP2013. Figure 12 shows that except for wavelengths slightly above the Balmer jump (≈364.5 nm), continuum flux spectra computed from the two new models and sunP2013 agree well with each other, indicating that the temperature stratification of the three models are close to each other around the optical surface. The differences redwards of the Balmer jump can be attributed to the treatment of dissolved Rydberg states as implemented in the HBOP module of Barklem & Piskunov (2016), that lead to a smooth decay of the continuous opacity instead of a sharp transition. This is also apparent in the continuum centre-to-limb variation discussed in Sect. 4.2.
Comparing the synthesised continuum flux with observations is challenging owing to the difficulty in deriving the continuum level from irradiance data in the ultraviolet wavelength region (cf. Neckel & Labs 1984, Sect. 5 and P2013, Sect. 4). To this end, we elect to synthesise the absolute flux spectrum by incorporating the information of spectral lines into opacities used in the radiative transfer calculation and comparing with the solar irradiance data of Kurucz (2005) as well as the Solar Irradiance Reference Spectra of Woods et al. (2009). The latter spectra were obtained during the solar minimum in 2008. For both sunA09 and sunA21 models, we computed the theoretical absolute flux spectrum with Balder using identical opacity data employed in our 3D atmosphere modelling. The flux spectrum calculation was carried out from 300 to 1000 nm, at a wavelength resolution of λ/Δλ = 50 000. The absolute flux spectrum obtained in this way is illustrated in the upper panel of Fig. 13 for model sunA09. Nevertheless, the absolute flux spectrum contains a forest of lines, impeding detailed comparison between simulation and observation. Therefore, we heavily smooth both the synthetic and the observed spectra using a 5 nm wavelength bin such that line features in the spectra are smoothed out. Comparing the smoothed absolute spectra examines the temperature structure of the 3D model, which sets the modelled continuum, as well as the overall reliability of our opacity data.
The lower panels of Fig. 13 show the smoothed flux spectra along with the relative difference between the sunA09 and sunA2l simulations and two sets of solar observations. The agreement between (smoothed) synthesised and measured flux is satisfactory above ~450 nm: Fractional differences between modelling and the Kurucz (2005) irradiance are below 3% in general. The difference between modelling and the Woods et al. (2009) spectra is around 3%, which is close to the maximum uncertainty of the measurement (about 3.5% in the optical and near-infrared, see Sect. 3 of Woods et al. 2009). However, notable differences are found below ~400 nm, where the predicted absolute fluxes are systematically larger than observations by more than 10% for both solar irradiance datasets. As discussed in Asplund (2004), Witzke et al. (2021), and Korotin & Kučinskas (2022), we suspect the discrepancy in the blue end of the spectra is due to missing opacities in the ultraviolet. We also note that several solar model atmospheres (both 1D and 3D) all predict higher flux than the measured values below the Balmer jump (Kučinskas et al. 2018; Witzke et al. 2021; Korotin & Kučinskas 2022). Further investigations into the continuum and/or line opacities in the near-ultraviolet region might be needed in order to improve the theoretical-observational consistency in absolute flux within this wavelength range.
 |
Fig. 11 Characteristics of the surface vertical velocity predicted by 3D solar models. Left panel: time-averaged distribution of surface vertical velocity. The histograms were calculated based on 30 equidistant bins between −10 and 10 km s−1, where positive velocities indicate downflow moving towards the stellar interior. The distribution function was normalised in the same way as the bolometric intensity (Fig. 10) so that the total area under it is equal to one. Right panel: spatially resolved surface vertical velocity pattern from one snapshot of the sunA09 simulation. |
 |
Fig. 12 Continuum emergent flux spectra computed from new 3D solar atmosphere models (red dashed line and blue dotted line indicate results from sunA89 and sunA21, respectively). The theoretical result from model sunP20l 3 is also shown in the green dash-dotted line. All fluxes presented here are absolute values at the solar surface. |
4.2 Continuum centre-to-limb variations
The magnitude of stellar surface intensity depends on both wavelength and viewing angle. From the Eddington–Barbier approximation, at a given wavelength, the surface intensity at the stellar limb emerges from a smaller optical depth (lower temperature) than the intensity at the disc centre, and therefore appears darker. A detailed understanding of the limb darkening phenomenon is necessary in order to accurately interpret the light curve of transiting exoplanets (Espinoza & Jordán 2016). Limb-darkening laws are also important for the determination of stellar radii via interferometry: the angular diameter of a star is obtained by fitting the limb-darkened stellar disc model to the visibility curve measured from interferometry (Bigot et al. 2006; White et al. 2013). Limb darkening can be quantified by the ratio of emergent intensity Iλ(µ)/Iλ(µ = 1), with µ = cos θ, where θ is the viewing angle relative to disc centre. In this section, we compute the continuum centre-to-limb variation (CLV) for the new solar models and compare them with the corresponding observations. The continuum CLV reflects the temperature stratification in the continuum-forming regions, and is therefore often used to check the realism of 3D atmosphere models (e.g. Beeck et al. 2012; P2013).
We used Balder to compute theoretical emergent intensities for different wavelengths and angles. The setup of our radiative transfer calculation is detailed in Sect. 4.1. Between 303.3 nm and 1098.9 nm, our theoretical predictions are compared with the observations of Neckel & Labs (1994), where the CLV was measured at multiple continuum wavelengths. Above 1100 nm, the observational data are taken from Pierce et al. (1977). Results from model sunP2013 are also included in Fig. 14 for reference.
Figure 14 reveals a general trend in continuum CLV: it is strong at shorter wavelengths while becoming less pronounced in the near-infrared. For all five angles considered, continuum CLVs predicted by the three 3D model atmospheres are almost indistinguishable at most wavelengths, indicating the temperature gradient between the three models is nearly identical around the optical surface. Below 400 nm, predicted CLVs are systematically weaker (i.e. larger ratios) than those determined from observations. This discrepancy is likely associated with difficulties in determining the continuum level in this wavelength region. The near-ultraviolet regime is abundant in spectral lines. CLVs measured at selected wavelengths with finite band-widths (Neckel & Labs 1994, Sect. 2) might contain lines that have not been unaccounted for, which will affect the measured values. From 400 nm to about 1300 nm, there is excellent agreement between all synthetic continuum CLVs and observations. At longer wavelengths (1400 ≲ λ ≲ 1800 nm) and closer to the limb (µ ≤ 0.5), continuum CLVs predicted by 3D models are systematically stronger than measurements by about 1%. The discrepancy here is smaller for the sunA09 and sunA21 models. Overall, the new solar model atmospheres predict continuum CLVs that match well with measurements, performing even better than the solar model of P2013 in the near-infrared.
 |
Fig. 13 Distribution of the solar absolute emergent flux from 300 to 1000 nm. Upper panel: absolute emergent flux (thin grey line) computed using Balder based on the sunA09 model, at a resolution of λ/Δλ = 50, 000. The smoothed synthetic spectrum using a 5 nm wavelength bin is depicted as a red dashed line (equivalent to the red dashed line in the right panel). Lower left panel: Comparison of smoothed synthetic spectra with the smoothed solar flux of Kurucz (2005, black solid line). All results presented here were smoothed with a 5 nm wavelength bin in order to facilitate comparison between simulations and observations. Relative differences in smoothed absolute flux as a function of wavelength, evaluated through Fλ/Fλ,obs − 1 with Fλ,obs denoting the smoothed measured values, are shown in the bottom right panel for two solar models. Lower right panel: similar to the lower left panel, but the smoothed synthetic spectra are compared with the smoothed Solar Irradiance Reference Spectra of Woods et al. (2009, orange solid line). All fluxes presented here are absolute values at the solar surface. |
 |
Fig. 14 Continuum CLVs at different viewing angles in the optical and near-infrared wavelength range. Observational data (red dots) in the upper left and upper right panel are taken from Neckel & Labs (1994) and Pierce et al. (1977), respectively. Blue and green dashed lines are theoretical results of the sunA09 and sunA21 models computed using Balder. Continuum CLVs predicted by model sunP2013 are shown as black dotted lines (cf. Fig. 3 of P2013). Relative differences between the modelled and measured CLVs are demonstrated in the lower panels, computed via [I(µ)/I(µ = 1)]/[I(µ)/I(µ = 1)]obs − 1, where the subscript ‘obs’ stands for observational data. Only the difference at µ = 0.5 is shown for clarity. |
4.3 Hydrogen line profiles
The spectral lines of hydrogen, in particular the Balmer series, are commonly used to derive the effective temperature for late-type stars owing to their relative insensitivity to the surface gravity and hydrogen abundance (e.g. Fuhrmann et al. 1993; Barklem et al. 2002; Amarsi et al. 2018). These lines feature pronounced pressure-broadened wings that form across the lower atmosphere and the surface convection zone (−2 ≲ log τRoss ≲ 1 , Fig. 2 of Amarsi et al. 2018), while the line cores are formed in the chromosphere. As the wings of Balmer lines (especially Hβ and Hγ) form in relatively deep layers, their shape is affected by the near-surface convection process. Nevertheless, the wings are largely unaffected by Doppler broadening and shifts due to con-vective motions, making them suitable probes of the temperature structure of the stellar atmosphere, including the surface convection zone (Ludwig et al. 2009a). We follow P2013 in comparing our synthetic spectra to solar observations of the Hα, Hβ , and Hγ Balmer lines, as well as the Paβ and Paγ Paschen lines.
The synthesised Balmer and Paschen line profiles are presented in Figs. 15 and 16, together with the normalised solar flux atlases of Kurucz (2005) and Reiners et al. (2016) for comparison. The grey-shaded regions in Fig. 15 are the ‘line masks’ for the Hα, Hβ , and Hγ lines derived in Amarsi et al. (2018). The masks were carefully selected based on theoretical line lists and the observed solar spectrum (cf. Sect. 4.2.1 of Amarsi et al. 2018 for a detailed description) in order to highlight the unblended wavelength sections that reflect only the Balmer lines. This is particularly necessary for a clear identification of the observed Hβ and Hγ lines, as their wavelength regions suffer from severe line blending. The line masks were chosen to bracket the wavelength regions that are sensitive to the effective temperature. For Balmer lines, we inspect how well our theoretical line profiles fit solar observations with the help of these masks.
Results based on the new 3D solar models and ab initio non-LTE radiative transfer calculations are in reasonable agreement with measured normalised fluxes for all of the hydrogen lines considered, indicating that the temperature stratification from the surface convection zone and the lower atmosphere of our new models is realistic. Nevertheless, neither the 3D solar model presented in P2013 nor the new models are able to predict line profiles that perfectly match observations for all Balmer and Paschen lines. For the wings of the Hα line, models sunA09 and sunA21 predict profiles that are almost identical to those predicted by the solar model of P2013, all being smaller than the measured normalised flux. On the other hand, the new solar models give rise to weaker Hβ lines, particularly in the outer wings (≳0.4 nm away from the line core). Although the wavelength region of the Hγ line is heavily blended, we find reasonable agreement between the synthesised and the measured line profiles in the unblended region highlighted by the line masks.
As discussed in P2013, the discrepancy at the Hβ wings is not associated with the single line simplification in our line formation calculations, as including the effect of blends in theoretical calculation hardly changes the overall magnitude of the Hβ wings. The input physics to the 3D atmosphere model is also unlikely the main factor behind this discrepancy, because two sets of 3D solar models with distinct EOS and opacity both failed to perfectly reproduce the observed line profile. In summary, the underlying reason why 3D models underestimate the strength of Hβ wings is currently unknown.
For Paschen lines, the sunA09 and sunA21 models predict stronger wings compared with sunP2013. The new solar models perform better in the case of the Paβ line, achieving good agreement with the observed solar spectrum. Conversely, the Paγ line computed from the new models deviates slightly further from observations compared to model sunP2013, being slightly stronger than seen in observations, especially in the blue wing.
In conclusion, hydrogen lines computed based on the new 3D solar models agree with solar observations in general, with some synthetic lines (Hγ, Paβ ) matching observations at a very satisfactory level, while others (Hα, Hβ, Paγ) demonstrate small deviations. Meanwhile, synthetic lines computed with the sunA09 and sunA21 models are almost indistinguishable in all cases, implying that differences between the alternative versions of the solar chemical composition have little impact on the hydrogen line profile.
 |
Fig. 15 Comparison of the synthesised normalised flux profiles with the Kurucz (2005) normalised solar flux atlas (yellow lines) for the Balmer series Hα (upper panel), Hβ (middle panel), and Hγ (lower panel), where λair is air wavelength. Black dashed and red dash-dotted lines represent synthesised line profiles computed in non-LTE using Balder based on the sunA09 and sunA21 models, respectively. Theoretical results from the sunP2813 model (taken from P2013 Fig. 8) are depicted in blue solid lines. Grey vertical bands indicate the ‘line masks’ derived in Amarsi et al. (2018), which highlights the unblended wavelength sections. Only the wings are shown in the figure because line cores, which are formed in the chromosphere, are of no relevance in this study. |
 |
Fig. 16 Normalised flux profiles for the Paschen lines Paβ (upper panel) and Paγ (lower panel). All theoretical line profiles are computed in non-LTE. For the Paγ line, the measured flux is adopted from Kurucz (2005). However, the observational data of the Paβ line are taken from the IAG solar flux atlas (Reiners et al. 2016) because this wavelength region is not covered by the Kurucz (2005) atlas. |
5 Summary and conclusions
In this work, we constructed new 3D solar atmosphere models with the Stagger code using EOS, opacity, and solar compositions that are different from previous studies. We adopted the FreeEOS, an open-source EOS code based on the minimisation of the Helmholtz free energy. Thermodynamic quantities computed via the EOS were tabulated in a format compatible with the Stagger code. Monochromatic extinction coefficients were computed from the Blue opacity package. In the high-temperature region, opacity calculations were based on FreeEOS for more accurate number densities of all atomic species and better consistency between the EOS and opacity code. Monochromatic extinction coefficients were grouped into 12 different bins to be used in the 3D simulation. Following Collet et al. (2011), we excluded continuum scattering from the extinction coefficient when calculating the mean intensity weighted mean opacities (αJ) in the optically thin part (the no-scattering-in-streaming-regime approximation). For each opacity bin, the mean intensity weighted coefficient and the Rosseland mean extinction coefficient were merged in order to obtain the final bin-averaged extinction coefficients. The opacity binning procedure is identical to that used in previous studies (Magic et al. 2013a; Collet et al. 2018). It is worth noting that, for all models constructed utilising the opacity binning method, the predicted surface flux and effective temperature differ from the monochromatic solution (see Perdomo García et al. 2023 for an in-depth investigation of this problem). For the solar models presented in this work, we carefully optimised the organisation of opacity bins to minimise the error in radiative heating rates and surface flux.
Three-dimensional solar atmosphere models were constructed with a recent version of the Stagger code (Collet et al. 2018), based on the aforementioned input physics and the AGSS09 and AAG21 solar abundance. The simulations were properly relaxed and bottom boundary conditions carefully adjusted such that the effective temperature of the model is as close to the reference solar value as possible. The new models employ identical numerical mesh to those of the sunRef model of Zhou et al. (2019) and AAG21. As this is the first time the FreeEOS and Blue opacity have been implemented in Stagger simulations, and noticing that the mean extinction coefficients given by Blue show recognisable differences from our previous opacity choice (Figs. C.1 and C.2), it is necessary to test the fidelity of the new models. We first checked the mean structure of the new models by comparing the spatial and temporal averaged quantities with those of the sunRef model. We find that our new model agrees well with the sunRef model in terms of mean stratification: for all mean quantities studied, the relative differences are within a few percent in most parts of the atmosphere model. Larger discrepancies appear only in the outermost layers of the simulation, where the realism of the model is more uncertain because of other factors such as the magnetic field. We subsequently examined the distribution of disc-centre bolomet-ric intensity and vertical velocity near the optical surface of the new solar models, which reflects the area coverage and relative strength of upflows and downflows at the solar photosphere. Similar good agreements are achieved between the reference models and our new solar models.
Our new solar model atmospheres are not only compared with model sunRef but are also validated against various observational constraints. We carried out the radiative transfer post-processing of the new 3D models using the Balder code, which employs identical opacity sources to the atmosphere model. The modelled absolute flux spectrum and continuum CLVs were compared with corresponding solar observations as well as results from a well-justified Stagger solar model of P2013 (sunP2013). Although different input physics are used in P2013 and this work, our theoretical results are a good match to observations in both tests, performing even better in terms of continuum CLVs in the near-infrared region. Moreover, we performed detailed non-LTE line formation calculations for five hydrogen lines with Balder. We find that neither of the two new 3D models is able to perfectly reproduce the measured normalised fluxes for all hydrogen lines investigated. Nevertheless, considering the approximations (e.g. opacity binning) employed in the 3D modelling, and also the performance of 1D solar atmosphere models in this problem (see Fig. 8 of P2013), the wings of the synthetic lines predicted by the new 3D models fit reasonably well with the solar flux atlases, accomplishing a similar level of realism to model sunP2813. In summary, the new solar models are able to satisfactorily reproduce observations in all diagnostics, suggesting that these ab initio simulations predict highly realistic temperature stratification at the top of the convective envelope and the lower atmosphere.
We also note that the two new models with different solar abundance have very similar structures and predict nearly identical observables in all cases studied. This finding is in line with expectations, as the AGSS09 and AAG21 solar compositions are not drastically different from each other.
Having passed comprehensive tests against the sunRef model and observations, the validity of the new models as well as their underlying input physics can be confirmed. Therefore, the input physics developed in this work can be applied to the modelling of other stars with confidence. This opens an exciting new path for studying stars with different α-element abundances, carbon-enhanced metal-poor stars, and population II stars with peculiar chemical compositions, which we were previously incapable of modelling because of limitations in input physics: Previous studies on key benchmark metal-poor stars were often based on 3D model atmospheres with solar-scaled chemical composition and a fixed value of α enhancement (e.g. Amarsi et al. 2016; Wang et al. 2022). While this assumption is usually valid, the abundances of certain elements, including carbon, oxygen, and magnesium, have a strong influence on microphysics because of their contribution to either atmospheric opacities or electron density. Neglecting variations in their abundance can lead to undesirable systematic errors (Gallagher et al. 2017; Amarsi et al. 2018). In the future, we plan to construct 3D model atmospheres with varying α enhancement, carbon-to-oxygen ratio, or abundance patterns tailored for individual cases, as more detailed atmosphere models might improve the accuracy of abundance determination, thereby providing insights into the chemical evolution of the Milky Way.
Acknowledgements
The authors would like to thank the anonymous referee for their careful and thorough report that improved the quality of this work. We also thank Åke Nordlund, Martin Asplund and Regner Trampedach for kindly answering many questions regarding EOS, opacities and 3D modelling. Lionel Bigot's help on opacity binning and intensity distribution is greatly appreciated. We are grateful to Regner Trampedach, Åke Nordlund, Jørgen Christensen-Dalsgaard, Cis Lagae, Luisa Rodríguez Díaz, Tiago Pereira and Karin Lind for reading and commenting on this manuscript. We thank also Sven Wedemeyer and Friedrich Kupka for valuable comments and fruitful discussions. Finally, we thank Alan Irwin for making the FreeEOS code publicly available. Y.Z. acknowledges support from the Carlsberg Foundation (grant agreement CF19-0649). AMA gratefully acknowledges support from the Swedish Research Council (VR 2020-03940). Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (grant agreement no.: DNRF106). This research was supported by computational resources provided by the Australian Government through the National Computational Infrastructure (NCI) under the National Computational Merit Allocation Scheme and the ANU Merit Allocation Scheme (project y89). This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:90254).
Appendix A Comparison between MHD and FreeEOS
To validate the results from FreeEOS, we compare key EOS outputs with the corresponding quantities from the (modified version of the) MHD EOS table, which was our adopted EOS in previous simulations (e.g. sunRef mentioned in Sect. 3, the solar model presented in P2013, and the Stagger-grid models of Magic et al. 2013a). Figure A.1 shows comparisons of two of the output parameters – thermal pressure and internal energy per mass. Our comparison adequately covers the parameter space reachable by surface convection simulations of low-mass stars. For reference, the mean structure of the horizontal- and time-averaged 3D solar model is plotted in red in Fig. A.1 to indicate the approximate area of most interest.
As shown in Fig. A.1, the agreement between MHD and FreeEOS is overall excellent, with the relative difference in key thermodynamic quantities being far less than 1% at most in the (ρ, T) range considered. This is reassuring and indicates that our FreeEOS results are reasonable. Meanwhile, differences are found in both comparisons in the high-temperature (log(T/[K]) ≳ 4.5) and high-density (log(ρ/[g/cm3]) ≳ −5) area. As the difference appears in both comparisons at the same region, it is likely that this area is subject to a difference in the general treatment of some physical aspect between the two EOS codes rather than numerical issues. Hummer & Mihalas (1988) implemented a τ-correction (not to be confused with optical depth) in the MHD EOS in order to limit the otherwise diverging, first-order Debye-Hückel term of the Coulomb pressure. In comparison with the OPAL EOS, Trampedach et al. (2006) found the suppression by τ to be too strong and found much better agreement between the two EOSs if it was left out completely. The FreeEOS was written and originally tested with respect to a version of the MHD EOS (and OPAL EOS) including the τ-correction. Moreover, Trampedach et al. (2006) showed the τ-correction to be especially relevant in areas of higher density. As the observed differences lie at high densities, this suggests that the differences are, at least in part, due to the τ-correction still being implemented in the FreeEOS. However, modifying the FreeEOS code and changing the τ-correction implementation is beyond the scope of this work.
 |
Fig. A.1 Comparison of thermodynamic quantities between the MHD and FreeEOS. Left panel: Relative differences between the MHD and FreeEOS in thermal pressure, computed via (Pther,Free– Pther,MHD)/Pther,MHD. Data used in the comparison are generated directly from the corresponding EOS code and based on identical (ρ, T) values, therefore no interpolation is involved in the comparison. The mean structure of our reference 3D solar model atmosphere is over-plotted in the red line, indicating the area of most interest. Both EOSs are computed assuming the same chemical composition, which includes 15 elements with the AGSS09 solar abundance value. Densities and temperatures are in cgs units. Right panel: Relative differences between the MHD and FreeEOS in internal energy per mass. |
Appendix B The effect of EOS on the mean temperature stratification
 |
Fig. B.1 The τRoss- and time-averaged temperature as a function of Rosseland optical depth for sunA09 (identical to the red dashed line in the upper right panel of Fig. 4) and a model constructed with the MHD EOS (black solid line labelled sunA09MEOS). The two solar models are identical in all aspects except that they employ different EOSs. In the middle and bottom panel, the model based on MHD EOS was used as a reference to compute relative and absolute differences. |
To study how different EOSs affect the mean temperature structure of the 3D solar model atmosphere, we compare two 3D models based on FreeEOS (sunA09) and MHD EOS but identical in all other aspects such as opacity data and numerical setup. For both models, their initial simulation snapshot was constructed from the same density and pressure datacube of a relaxed simulation, with respective EOS used to derive initial internal energy and temperature (see also Vitas & Khomenko 2015 Sect. 3). The initial simulation snapshot of the two models underwent identical relaxation processes, after which they were evolved for the same time duration in order to obtain a fair comparison.
Spatial and temporal averaged temperature for the two models, as well as their relative and absolute difference, are demonstrated in Fig. B.1. Using the MHD or FreeEOS could lead to a temperature difference of approximately 15 K around the optical surface and in the near-surface convective region. The impact of EOS on atmospherical temperature structure is smaller than 5 K for τRoss ≲ 0.1. This is in line with the conclusion of Vitas & Khomenko (2015), who investigated the effect of EOS on the temperature structure for 2D MURaM solar near-surface convection simulations and found that different EOSs cause temperature differences of less than 10 K in the atmosphere.
Appendix C Comparing mean opacities
Relative differences between the Rosseland mean extinction coefficient from Blue and that previously adopted in the Stagger code are shown in the left panel of Fig. C.1 for the AGSS09 solar abundance. The latter adopts a comprehensive source of continuum opacities as elaborated in Hayek et al. (2010) and Trampedach et al. (2014), while line opacities are taken from the MARCS package (Gustafsson et al. 2008; Plez 2008). The relative difference in Rosseland mean extinction coefficient is generally below 10% in our area of interest. However, the difference becomes large when log(T/[K]) ≲ 3.3 and log T ≳ 4.2. The underlying reason for this disagreement is not clear. As the two types of opacities are calculated based on different atomic data, partition function, continuum opacity sources and so on, and each factor could lead to the observed difference, investigating the source of the disagreement is beyond the scope of this work. Nevertheless, the areas where a large difference in αRoss is seen have little impact on our modelling at least for the solar case, because (1) temperatures in the simulation domain hardly drop below 2000 K, (2) the Stagger code no longer solves the radiative transfer equation at regions with very high temperature (i.e. regions located well below the photosphere), because the diffusion limit of heat transfer is a good approximation there. We also compared Rosseland mean extinction coefficients given by Blue with the corresponding Ferguson et al. (2005) table and found better agreement at the high-temperature, high-density regime (see the right panel of Fig. C.1).
Because the Rosseland mean extinction coefficient is obtained by integrating  , it mainly reflects the contribution from low-value continuum opacities. The Planck mean extinction coefficient, on the other hand, is dominated by strong line opacities. In Fig. C.2, we compare our Planck mean extinction coefficients at a given density with corresponding data from Ferguson et al. (2005) and Trampedach et al. (2014). Below log T ~ 3.4, the agreement between Blue and Trampedach et al. (2014) is good, but they are both smaller than the Ferguson et al. (2005) result. The cause of this disagreement between Blue and Ferguson et al. (2005) is not clear, but it might be due to different H2O and TiO line lists adopted in Blue and Ferguson et al. (2005, see their Fig. 4). Above log T ~ 3.4, Planck mean extinction coefficients predicted by Blue agree well with Ferguson et al. (2005). However, the disagreement between Blue and Trampedach et al. (2014) within 3.4 ≲ log T ≲ 3.7 is not understood.
, it mainly reflects the contribution from low-value continuum opacities. The Planck mean extinction coefficient, on the other hand, is dominated by strong line opacities. In Fig. C.2, we compare our Planck mean extinction coefficients at a given density with corresponding data from Ferguson et al. (2005) and Trampedach et al. (2014). Below log T ~ 3.4, the agreement between Blue and Trampedach et al. (2014) is good, but they are both smaller than the Ferguson et al. (2005) result. The cause of this disagreement between Blue and Ferguson et al. (2005) is not clear, but it might be due to different H2O and TiO line lists adopted in Blue and Ferguson et al. (2005, see their Fig. 4). Above log T ~ 3.4, Planck mean extinction coefficients predicted by Blue agree well with Ferguson et al. (2005). However, the disagreement between Blue and Trampedach et al. (2014) within 3.4 ≲ log T ≲ 3.7 is not understood.
 |
Fig. C.1 Comparison of Rosseland mean extinction coefficients. Left panel: Relative differences between Rosseland mean extinction coefficients from Blue and those previously adopted in the Stagger code (Hayek et al. 2010; Trampedach et al. 2014), computed via (αRoss, BLUE – αRoss, T14)/αRoss, T14. Blue extinction coefficients are calculated with the internal EOS in Blue (FreeEOS) when log T ≤ 3.9 (log T ≥ 4.1). Results from the two different EOSs are merged in the region where 3.9 < log T < 4.1 (cf. Sect. 2.2.2). The (ρ, T) distribution of the horizontal- and time-averaged reference solar model atmosphere is over-plotted as a thick black line. The grey dotted vertical line crudely marks the temperature limit above which the radiative transfer equation is not solved in the reference solar simulation. Densities and temperatures are in cgs units. Right panel: Relative differences between Rosseland mean extinction coefficients from Blue and those of Ferguson et al. (2005) for the AGSS09 solar composition. The white areas are (ρ, T) combinations not covered by the Ferguson et al. (2005) opacity table. |
 |
Fig. C.2 Comparison between the Planck mean extinction coefficient at log(ρ/[g/cm3]) = −10 from Blue and those from other sources. The green solid line and black dashed line represents Planck mean extinction coefficients from Ferguson et al. (2005, see also their Fig. 12) and Trampedach et al. (2014, the one previously used in the Stagger code), respectively. The blue dash-dotted line is αPl computed using Blue, with 250 000 wavelength points between 50 nm and 50 µm. All calculations are based on the AGSS09 solar chemical composition. |
References
- Allende Prieto, C., Asplund, M., García López, R. J., & Lambert, D. L. 2002, ApJ, 567, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., Lind, K., Asplund, M., Barklem, P. S., & Collet, R. 2016, MNRAS, 463, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., Nordlander, T., Barklem, P. S., et al. 2018, A&A, 615, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amarsi, A. M., Barklem, P. S., Collet, R., Grevesse, N., & Asplund, M. 2019, A&A, 624, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M. 2004, A&A, 417, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Ludwig, H. G., Nordlund, Å., & Stein, R. F. 2000a, A&A, 359, 669 [NASA ADS] [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., Allende Prieto, C., & Stein, R. F. 2000b, A&A, 359, 729 [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. I. Barnes, Thomas, G., & F. N. Bash, Astronomical Society of the Pacific Conference Series, 336, 25 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Amarsi, A. M., & Grevesse, N. 2021, A&A, 653, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ball, W. H., Beeck, B., Cameron, R. H., & Gizon, L. 2016, A&A, 592, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barber, R. J., Tennyson, J., Harris, G. J., & Tolchenov, R. N. 2006, MNRAS, 368, 1087 [Google Scholar]
- Barklem, P., & Piskunov, N. 2016, https://zenodo.org/record/58215 [Google Scholar]
- Barklem, P. S., & Collet, R. 2016, A&A, 588, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Stempels, H. C., Allende Prieto, C., et al. 2002, A&A, 385, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bauschlicher, C. W., Ram, R. S., Bernath, P. F., Parsons, C. G., & Galehouse, D. 2001, J. Chem. Phys., 115, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Beeck, B., Collet, R., Steffen, M., et al. 2012, A&A, 539, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, K. L. 1980, J. Phys. B: At. Mol. Phys., 13, 1859 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, K. L., & Berrington, K. A. 1987, J. Phys. B: At. Mol. Phys., 20, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, K. L., Hibbert, A., & Berrington, K. A. 1988, J. Phys. B: At. Mol. Opt. Phys., 21, 2319 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [Google Scholar]
- Bernath, P. F., & Colin, R. 2009, J. Mol. Spectrosc., 257, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Bertran de Lis, S., Allende Prieto, C., Ludwig, H.G., & Koesterke, L. 2022, A&A, 661, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhatia, T. S., Cameron, R. H., Solanki, S. K., et al. 2022, A&A, 663, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigot, L., Kervella, P., Thévenin, F., & Ségransan, D. 2006, A&A, 446, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Brooke, J. S. A., Bernath, P. F., Schmidt, T. W., & Bacskay, G. B. 2013, J. Quant. Spec. Radiat. Transf., 124, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Brooke, J. S. A., Ram, R. S., Western, C. M., et al. 2014, ApJS, 210, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Ram, R. S., Bernath, P., Sharp, C. M., & Milsom, J. A. 2002, ApJ, 577, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Dulick, M., Bauschlicher, C. W. J., et al. 2005, ApJ, 624, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H. G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [Google Scholar]
- Carlsson, M., Hansteen, V. H., Gudiksen, B. V., Leenaarts, J., & De Pontieu, B. 2016, A&A, 585, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., & VandenBerg, D. A. 2014, MNRAS, 444, 392 [Google Scholar]
- Chiavassa, A., Casagrande, L., Collet, R., et al. 2018, A&A, 611, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collet, R., Asplund, M., & Trampedach, R. 2006, ApJ, 644, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Collet, R., Asplund, M., & Nissen, P. E. 2009, PASA, 26, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Collet, R., Hayek, W., Asplund, M., et al. 2011, A&A, 528, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collet, R., Nordlund, Å., Asplund, M., Hayek, W., & Trampedach, R. 2018, MNRAS, 475, 3369 [NASA ADS] [CrossRef] [Google Scholar]
- Cunto, W., & Mendoza, C. 1992, Rev. Mex. Astron. Astrofis., 23, 107 [NASA ADS] [Google Scholar]
- Cunto, W., Mendoza, C., Ochsenbein, F., & Zeippen, C. J. 1993, A&A, 275, L5 [NASA ADS] [Google Scholar]
- Daily, J. W., Dreyer, C., Abbud-Madrid, A., & Branch, M. C. 2002, J. Mol. Spectrosc., 214, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Dulick, M., Bauschlicher, C. W. J., Burrows, A., et al. 2003, ApJ, 594, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., & Jordán, A. 2016, MNRAS, 457, 3573 [NASA ADS] [CrossRef] [Google Scholar]
- Feautrier, P. 1964, Comp. Rend. Acad. Sci., 258, 3189 [NASA ADS] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [Google Scholar]
- Frebel, A., & Norris, J. E. 2015, ARA&A, 53, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H. G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Gallagher, A. J., Caffau, E., Bonifacio, P., et al. 2017, A&A, 598, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldman, A., Schoenfeld, W. G., Goorvitch, D., et al. 1998, J. Quant. Spec. Radiat. Transf., 59, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayek, W., Asplund, M., Carlsson, M., et al. 2010, A&A, 517, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hodges, J. N., Bittner, D. M., & Bernath, P. F. 2018, ApJ, 855, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Houdek, G., Trampedach, R., Aarslev, M. J., & Christensen-Dalsgaard, J. 2017, MNRAS, 464, L124 [Google Scholar]
- Hubeny, I., Hummer, D. G., & Lanz, T. 1994, A&A, 282, 151 [NASA ADS] [Google Scholar]
- Hummer, D. G. 1988, ApJ, 327, 477 [CrossRef] [Google Scholar]
- Hummer, D. G., & Mihalas, D. 1988, ApJ, 331, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]
- Irwin, A. W. 2004a, unpublished, available at http://freeeos.sourceforge.net/eff_fit.pdf [Google Scholar]
- Irwin, A. W. 2004b, unpublished, available at http://freeeos.sourceforge.net/solution.pdf [Google Scholar]
- Irwin, A. W. 2012, FreeEOS: Equation of State for stellar interiors calculations Astrophysics Source Code Library, [record asc1:1211.002] [Google Scholar]
- Jermyn, A. S., Bauer, E. B., Schwab, J., et al. 2023, ApJS, 265, 15 [NASA ADS] [CrossRef] [Google Scholar]
- John, T. L. 1975, MNRAS, 172, 305 [NASA ADS] [Google Scholar]
- John, T. L. 1995, J. Phys. B: At. Mol. Opt. Phys., 28, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Karovicova, I., White, T. R., Nordlander, T., et al. 2020, A&A, 640, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Bigot, L., Gallenne, A., & Thévenin, F. 2017, A&A, 597, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korotin, S., & Kučinskas, A. 2022, A&A, 657, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1992, Rev. Mex. Astron. Astrofis., 23, 45 [Google Scholar]
- Kurucz, R. L. 1995, in Astrophysical Applications of Powerful New Databases, eds. S. J. Adelman, & W. L. Wiese, Astronomical Society of the Pacific Conference Series, 78, 205 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 189 [Google Scholar]
- Kučinskas, A., Klevas, J., Ludwig, H. G., et al. 2018, A&A, 613, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagae, C., Amarsi, A. M., Rodríguez Díaz, L. F., et al. 2023, A&A, 672, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langhoff, P. W., Sims, J., & Corcoran, C. T. 1974, Phys. Rev. A, 10, 829 [CrossRef] [Google Scholar]
- Lee, H.-W., & Kim, H. I. 2004, MNRAS, 347, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., & Carlsson, M. 2009, in The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, eds. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, Astronomical Society of the Pacific Conference Series, 415, 87 [NASA ADS] [Google Scholar]
- Ludwig, H. G., Allard, F., & Hauschildt, P. H. 2006, A&A, 459, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H. G., Behara, N. T., Steffen, M., & Bonifacio, P. 2009a, A&A, 502, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H. G., Caffau, E., Steffen, M., et al. 2009b, Mem. Soc. Astron. Italiana, 80, 711 [NASA ADS] [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013a, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Collet, R., Hayek, W., & Asplund, M. 2013b, A&A, 560, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Aringer, B., Girardi, L., & Bressan, A. 2022, ApJ, 940, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Masseron, T., Plez, B., Van Eck, S., et al. 2014, A&A, 571, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKemmish, L. K., Yurchenko, S. N., & Tennyson, J. 2016, MNRAS, 463, 771 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, B. M., Stancil, P. C., Sadeghpour, H. R., & Forrey, R. C. 2017, J. Phys. B: At. Mol. Opt. Phys., 50, 114001 [NASA ADS] [CrossRef] [Google Scholar]
- McKemmish, L. K., Masseron, T., Hoeijmakers, H. J., et al. 2019, MNRAS, 488, 2836 [Google Scholar]
- Mihalas, D., Dappen, W., & Hummer, D. G. 1988, ApJ, 331, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Muthsam, H. J., Kupka, F., Löw-Baselli, B., et al. 2010, New Astron., 15, 460 [Google Scholar]
- Neckel, H., & Labs, D. 1984, Sol. Phys., 90, 205 [Google Scholar]
- Neckel, H., & Labs, D. 1994, Sol. Phys., 153, 91 [CrossRef] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, A10 [Google Scholar]
- Nordlund, A. 1982, A&A, 107, 1 [Google Scholar]
- Nordlund, A. 1985, Sol. Phys., 100, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, Å., & Dravins, D. 1990, A&A, 228, 155 [NASA ADS] [Google Scholar]
- Nordlund, Å., & Galsgaard, K. 1995, Tech. rep., Astronomical Observatory, Copenhagen University [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Patrascu, A. T., Yurchenko, S. N., & Tennyson, J. 2015, MNRAS, 449, 3613 [NASA ADS] [CrossRef] [Google Scholar]
- Perdomo García, A., Vitas, N., Khomenko, E., et al. 2023, A&A, 675, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Asplund, M., Collet, R., et al. 2013, A&A, 554, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierce, A. K., Slaughter, C. D., & Weinberger, D. 1977, Sol. Phys., 52, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B. 2008, Phys. Scr. Vol. T, 133, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The Art of Scientific Computing (Cambridge University Press) [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [Google Scholar]
- Rains, A. D., Ireland, M. J., White, T. R., Casagrande, L., & Karovicova, I. 2020, MNRAS, 493, 2377 [Google Scholar]
- Ramsbottom, C. A., Bell, K. L., & Berrington, K. A. 1992, J. Phys. B: At. Mol. Opt. Phys., 25, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Mrotzek, N., Lemke, U., Hinrichs, J., & Reinsch, K. 2016, A&A, 587, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rempel, M., Schüssler, M., Cameron, R. H., & Knölker, M. 2009, Science, 325, 171 [CrossRef] [Google Scholar]
- Rivlin, T., Lodi, L., Yurchenko, S. N., Tennyson, J., & Le Roy, R. J. 2015, MNRAS, 451, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Rosenthal, C. S., Christensen-Dalsgaard, J., Nordlund, Å., Stein, R. F., & Trampedach, R. 1999, A&A, 351, 689 [NASA ADS] [Google Scholar]
- Skartlien, R. 2000, ApJ, 536, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Stancil, P. C. 1994, ApJ, 430, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, M., Gallagher, A. J., Caffau, E., Bonifacio, P., & Ludwig, H. G. 2018, in Rediscovering Our Galaxy, 334, eds. C. Chiappini, I. Minchev, E. Starkenburg, & M. Valentini, 364 [NASA ADS] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1989, ApJ, 342, L95 [Google Scholar]
- Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, Astronomical Society of the Pacific Conference Series, 288, 519 [NASA ADS] [Google Scholar]
- Thomson, J. J. 1912, London Edinb. Dublin Philos. Mag. J. Sci., 23, 449 [CrossRef] [Google Scholar]
- Thorne, A. P., Litzen, U., & Johansson, S. 1999, Spectrophysics: Principles and Applications (Heidelberg: Springer Berlin) [Google Scholar]
- Trampedach, R., Däppen, W., & Baturin, V. A. 2006, ApJ, 646, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Trampedach, R., Asplund, M., Collet, R., Nordlund, Å., & Stein, R. F. 2013, ApJ, 769, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Trampedach, R., Stein, R. F., Christensen-Dalsgaard, J., Nordlund, Å., & Asplund, M. 2014, MNRAS, 442, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Vines, J. I., & Jenkins, J. S. 2022, MNRAS, 513, 2719 [NASA ADS] [CrossRef] [Google Scholar]
- Vitas, N., & Khomenko, E. 2015, Ann. Geophys., 33, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [Google Scholar]
- Wang, E. X., Nordlander, T., Asplund, M., et al. 2022, MNRAS, 509, 1521 [Google Scholar]
- Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [CrossRef] [Google Scholar]
- White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [Google Scholar]
- White, T. R., Huber, D., Mann, A. W., et al. 2018, MNRAS, 477, 4403 [NASA ADS] [CrossRef] [Google Scholar]
- Witzke, V., Shapiro, A. I., Cernetic, M., et al. 2021, A&A, 653, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witzke, V., Duehnen, H. B., Shapiro, A. I., et al. 2023, A&A, 669, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woods, T. N., Chamberlin, P. C., Harder, J. W., et al. 2009, Geophys. Res. Lett., 36, L01101 [NASA ADS] [CrossRef] [Google Scholar]
- Yadin, B., Veness, T., Conti, P., et al. 2012, MNRAS, 425, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, J., Khanna, S., Themessl, N., et al. 2023, ApJS, 264, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., Blissett, A., Asari, U., et al. 2016, MNRAS, 456, 4524 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., Sinden, F., Lodi, L., et al. 2018a, MNRAS, 473, 5324 [NASA ADS] [CrossRef] [Google Scholar]
- Yurchenko, S. N., Williams, H., Leyland, P. C., Lodi, L., & Tennyson, J. 2018b, MNRAS, 479, 1401 [CrossRef] [Google Scholar]
- Zhou, Y., Asplund, M., & Collet, R. 2019, ApJ, 880, 13 [NASA ADS] [CrossRef] [Google Scholar]
In the Stagger grid, the abundances of α process elements O, Ne, Mg, Si, S, Ar and Ca are enhanced by 0.4 dex, [α/Fe] = 0.4, for metal-poor models with [Fe/H] ≤ −1. The notation [A/B] = log(nA/nB) − log(nA/nB)⊙, where nA/nB and (nA/nB)0 represent number density ratios between element A and B in the star and the Sun, respectively.
Available at http://freeeos.sourceforge.net/documentation.html
More precisely, the Stagger solar model atmosphere presented in Beeck et al. (2012) and P2013 is slightly different from the model sunRef: The former two were generated with an older version of the Stagger code and use the Asplund et al. (2005) chemical composition, while the latter adopts the AGSS09 abundance. Nevertheless, these two models are identical in all other aspects and the differences in their photospheric structure are minor.
All Tables
Elements included in the FreeEOS calculation and the corresponding solar abundance adopted in this work.
Data sources for continuum bound-free (bf) and free-free (ff) absorption as well as scattering processes included in the Blue opacity code.
Fundamental parameters and basic information about solar simulations presented in this study.
All Figures
 |
Fig. 1 Rosseland optical depth where monochromatic optical depth is unity – which reflects the strength of opacity – as a function of wavelength computed based on the (3D) sunA09 model (cf. Table 4 and Sect. 3 for basic information about the model and how it is constructed) and Blue opacities assuming the AGSS09 solar abundance. One out of ten points in our wavelength sampling is shown to avoid overcrowding the figure. Grey boxes numbered from 1 to 12 in red define the opacity bins used for the sunA09 simulation. Bins 1–3 divide the ultraviolet wavelength region according to the location where flux emerges; Bins 4, 5, and 9 mainly consist of wavelength points distributed near the continuum-forming layers; Bins 8 and 12 include only wavelengths with strong opacity, which typically correspond to lines. |
| In the text | |
 |
Fig. 2 Bin-averaged extinction coefficients (Eq. (6)) as a function of the bin-wise Rosseland optical depth of bins 3 and 5 (as defined in Fig. 1) based on the (3D) sunA09 model. The bin-wise Rosseland optical depth τRoss,i is computed from wavelengths belonging to bin i. Extinction coefficients calculated from the binning code implemented in Trampedach et al. (2013) with the Trampedach et al. (2014) opacity dataset are shown in black dotted lines, whereas red solid lines represent αbin,i used in this work. |
| In the text | |
 |
Fig. 3 Radiative heating (or cooling) rate and radiative flux computed based on the (3D) sunA09 model. Left panel: comparison of the radiative heating (or cooling) rate computed from the 12 opacity bins shown in Fig. 1 (red plus mark) with the monochromatic solution using 250 000 wavelengths (black solid line) for the (3D) sunA09 model. The relative difference of qrad at the cooling peak is 2.42%. Right panel: comparison between radiative flux obtained from the opacity binning method and the monochromatic solution. The relative difference of surface flux (defined as the radiative flux at log τRoss = −4) is 1.49%. |
| In the text | |
 |
Fig. 4 Averaged temperature profiles for different solar model atmospheres. Left panel: simple horizontal- and time-averaged temperature profiles 〈T〉h as a function of geometric depth. Zero geometric depth corresponds approximately to the optical surface. Relative and absolute differences between the new models and sunRef are shown in the middle and lower parts, respectively. Right panel: the τRoss- and time-averaged temperature 〈T〉τ as a function of Rosseland optical depth (T − τ relation) for models sunA09, sunA21, and sunRef. |
| In the text | |
 |
Fig. 5 Similar to the top and middle panels of Fig. 4, but showing the mean density stratification for different solar simulations. |
| In the text | |
 |
Fig. 6 Temporal mean of simple horizontal-averaged (left panel) and τRoss-averaged vertical velocity (right panel) for different solar simulations. Positive velocities correspond to downflows that move towards the stellar interior. |
| In the text | |
 |
Fig. 7 Time-averaged standard deviation of vertical velocity in geometric depth scale (left panel) and Rosseland optical depth scale (right panel). This quantity, also called the root-mean-square (rms) of vertical velocity fluctuation, indicates the variation of vertical velocity at a given depth. |
| In the text | |
 |
Fig. 8 Ratio of simple horizontal- and time-averaged turbulent pressure to thermal pressure. |
| In the text | |
 |
Fig. 9 Deviations from hydrostatic equilibrium as a function of vertical geometric depth for (3D)h models. |
| In the text | |
 |
Fig. 10 Time-averaged distribution of disc-centre bolometric intensity predicted by the two solar models with new input physics but different chemical compositions, sunA09 (AGSS09 composition) and sunA21 (AAG21 composition), as well as the reference model with unmodified input physics, sunRef (AGSS09 composition). The bolometric intensity is normalised by its mean value 〈I〉, and the distribution function is normalised such that its integration over I/〈I〉 is equal to one. |
| In the text | |
 |
Fig. 11 Characteristics of the surface vertical velocity predicted by 3D solar models. Left panel: time-averaged distribution of surface vertical velocity. The histograms were calculated based on 30 equidistant bins between −10 and 10 km s−1, where positive velocities indicate downflow moving towards the stellar interior. The distribution function was normalised in the same way as the bolometric intensity (Fig. 10) so that the total area under it is equal to one. Right panel: spatially resolved surface vertical velocity pattern from one snapshot of the sunA09 simulation. |
| In the text | |
 |
Fig. 12 Continuum emergent flux spectra computed from new 3D solar atmosphere models (red dashed line and blue dotted line indicate results from sunA89 and sunA21, respectively). The theoretical result from model sunP20l 3 is also shown in the green dash-dotted line. All fluxes presented here are absolute values at the solar surface. |
| In the text | |
 |
Fig. 13 Distribution of the solar absolute emergent flux from 300 to 1000 nm. Upper panel: absolute emergent flux (thin grey line) computed using Balder based on the sunA09 model, at a resolution of λ/Δλ = 50, 000. The smoothed synthetic spectrum using a 5 nm wavelength bin is depicted as a red dashed line (equivalent to the red dashed line in the right panel). Lower left panel: Comparison of smoothed synthetic spectra with the smoothed solar flux of Kurucz (2005, black solid line). All results presented here were smoothed with a 5 nm wavelength bin in order to facilitate comparison between simulations and observations. Relative differences in smoothed absolute flux as a function of wavelength, evaluated through Fλ/Fλ,obs − 1 with Fλ,obs denoting the smoothed measured values, are shown in the bottom right panel for two solar models. Lower right panel: similar to the lower left panel, but the smoothed synthetic spectra are compared with the smoothed Solar Irradiance Reference Spectra of Woods et al. (2009, orange solid line). All fluxes presented here are absolute values at the solar surface. |
| In the text | |
 |
Fig. 14 Continuum CLVs at different viewing angles in the optical and near-infrared wavelength range. Observational data (red dots) in the upper left and upper right panel are taken from Neckel & Labs (1994) and Pierce et al. (1977), respectively. Blue and green dashed lines are theoretical results of the sunA09 and sunA21 models computed using Balder. Continuum CLVs predicted by model sunP2013 are shown as black dotted lines (cf. Fig. 3 of P2013). Relative differences between the modelled and measured CLVs are demonstrated in the lower panels, computed via [I(µ)/I(µ = 1)]/[I(µ)/I(µ = 1)]obs − 1, where the subscript ‘obs’ stands for observational data. Only the difference at µ = 0.5 is shown for clarity. |
| In the text | |
 |
Fig. 15 Comparison of the synthesised normalised flux profiles with the Kurucz (2005) normalised solar flux atlas (yellow lines) for the Balmer series Hα (upper panel), Hβ (middle panel), and Hγ (lower panel), where λair is air wavelength. Black dashed and red dash-dotted lines represent synthesised line profiles computed in non-LTE using Balder based on the sunA09 and sunA21 models, respectively. Theoretical results from the sunP2813 model (taken from P2013 Fig. 8) are depicted in blue solid lines. Grey vertical bands indicate the ‘line masks’ derived in Amarsi et al. (2018), which highlights the unblended wavelength sections. Only the wings are shown in the figure because line cores, which are formed in the chromosphere, are of no relevance in this study. |
| In the text | |
 |
Fig. 16 Normalised flux profiles for the Paschen lines Paβ (upper panel) and Paγ (lower panel). All theoretical line profiles are computed in non-LTE. For the Paγ line, the measured flux is adopted from Kurucz (2005). However, the observational data of the Paβ line are taken from the IAG solar flux atlas (Reiners et al. 2016) because this wavelength region is not covered by the Kurucz (2005) atlas. |
| In the text | |
 |
Fig. A.1 Comparison of thermodynamic quantities between the MHD and FreeEOS. Left panel: Relative differences between the MHD and FreeEOS in thermal pressure, computed via (Pther,Free– Pther,MHD)/Pther,MHD. Data used in the comparison are generated directly from the corresponding EOS code and based on identical (ρ, T) values, therefore no interpolation is involved in the comparison. The mean structure of our reference 3D solar model atmosphere is over-plotted in the red line, indicating the area of most interest. Both EOSs are computed assuming the same chemical composition, which includes 15 elements with the AGSS09 solar abundance value. Densities and temperatures are in cgs units. Right panel: Relative differences between the MHD and FreeEOS in internal energy per mass. |
| In the text | |
 |
Fig. B.1 The τRoss- and time-averaged temperature as a function of Rosseland optical depth for sunA09 (identical to the red dashed line in the upper right panel of Fig. 4) and a model constructed with the MHD EOS (black solid line labelled sunA09MEOS). The two solar models are identical in all aspects except that they employ different EOSs. In the middle and bottom panel, the model based on MHD EOS was used as a reference to compute relative and absolute differences. |
| In the text | |
 |
Fig. C.1 Comparison of Rosseland mean extinction coefficients. Left panel: Relative differences between Rosseland mean extinction coefficients from Blue and those previously adopted in the Stagger code (Hayek et al. 2010; Trampedach et al. 2014), computed via (αRoss, BLUE – αRoss, T14)/αRoss, T14. Blue extinction coefficients are calculated with the internal EOS in Blue (FreeEOS) when log T ≤ 3.9 (log T ≥ 4.1). Results from the two different EOSs are merged in the region where 3.9 < log T < 4.1 (cf. Sect. 2.2.2). The (ρ, T) distribution of the horizontal- and time-averaged reference solar model atmosphere is over-plotted as a thick black line. The grey dotted vertical line crudely marks the temperature limit above which the radiative transfer equation is not solved in the reference solar simulation. Densities and temperatures are in cgs units. Right panel: Relative differences between Rosseland mean extinction coefficients from Blue and those of Ferguson et al. (2005) for the AGSS09 solar composition. The white areas are (ρ, T) combinations not covered by the Ferguson et al. (2005) opacity table. |
| In the text | |
 |
Fig. C.2 Comparison between the Planck mean extinction coefficient at log(ρ/[g/cm3]) = −10 from Blue and those from other sources. The green solid line and black dashed line represents Planck mean extinction coefficients from Ferguson et al. (2005, see also their Fig. 12) and Trampedach et al. (2014, the one previously used in the Stagger code), respectively. The blue dash-dotted line is αPl computed using Blue, with 250 000 wavelength points between 50 nm and 50 µm. All calculations are based on the AGSS09 solar chemical composition. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\matrix{ {{f_{\rm{b}}} = {1 \over 2}\left[ {\sin \,\left( {{{\log \,T - \log \,{T_1}} \over {\log \,{T_2} - \log \,{T_1}}} - {1 \over 2}} \right)\,\pi + 1} \right],} \hfill \cr {{\alpha _{{\rm{mg}}}} = {\alpha _{{\rm{lowT}}}}\left( {1 - {f_{\rm{b}}}} \right) + {\alpha _{{\rm{highT}}}}\,{f_{\rm{b}}},} \hfill \cr } $](/articles/aa/full_html/2023/09/aa46398-23/aa46398-23-eq3.png)