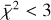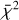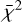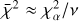EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) A90 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number A90
Number of page(s) 12
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/202245786
Published online 05 April 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The first stars (Population III stars; hereafter ‘Pop III stars’) in our Universe formed directly from Big Bang nucleosynthesis products H, He, and traces of Li. These stars are the source of the first enrichment of the interstellar and intergalactic medium, and they set the stage for the formation of the first galaxies and started the epoch of re-ionisation (Bromm & Yoshida 2011).

Despite their importance, the details of star formation and the resulting initial mass function (IMF) of Pop III stars are still uncertain. Initial studies suggested that the lack of metals in star-forming clouds caused the absence of an efficient cooling mechanism and suppressed the formation of low-mass stars in the early Universe. Hydrodynamic simulations based on cooling by hydrogen molecules predicted stellar masses larger than 100 M⊙ (Bromm & Yoshida 2011). More recent simulations that incorporate longer timescales, higher resolutions, and improved physics, such as sub-sonic turbulence (Clark et al. 2011a), fragmentation of accretion discs (Greif et al. 2011; Clark et al. 2011b), proto-stellar radiation feedback (Hosokawa et al. 2011, 2016; Hirano et al. 2014), multiplicity (Stacy & Bromm 2013), and a combination of these (Susa 2013; Susa et al. 2014; Stacy et al. 2016), allow stars to form with initial masses of several solar masses from ≲ 1 M⊙ up to 1000 M⊙. The lack of direct observations of Pop III stars and expected scarcity of long-lived low-mass (M ≲ 0.8 M⊙) Pop III stars in the galaxy (Hartwig et al. 2015; Magg et al. 2019), however, makes it difficult to directly constrain these predictions.

One way to indirectly study the properties of the first stars is to look at metal-poor second-generation stars (Population II stars; henceforth ‘Pop II stars’). These stars were born from the gas that the Pop III stars enriched. Moreover, studies claim that stars with metallicities of up to [Fe/H] < −3 could, in principle, be formed from a cloud enriched by a single supernova (Tominaga et al. 2007; Nomoto et al. 2013; Keller et al. 2014; Frebel & Norris 2015). Using a semi-analytical model of early universe star formation, Hartwig et al. (2018) found that 40% of stars with −6 ⪅ [Fe/H] ⪅ −4 were enriched by only one nucleosynthesis event (mono-enriched). Therefore, by comparing the chemical compositions of ultra metal-poor stars (UMP; [Fe/H] < −4, Beers & Christlieb 2005) to theoretical yields of first-star core-collapse supernovae, it is, in principle, possible to constrain the explosion properties and IMF of the first stars – at least for single stars, although some questions about asymmetric supernovae and dilution would remain (Ezzeddine et al. 2019; Magg et al. 2020). These types of analyses indicate that the progenitors of Pop II stars typically have stellar masses in the range of 10–100 M⊙ (Lai et al. 2008; Heger & Woosley 2010; Joggerst et al. 2010; Ishigaki et al. 2014,2018; Tominaga et al. 2007,2014; Placco et al. 2015).

A related problem concerns the transition from Pop III star formation to low-mass star formation that follows the currently known IMF peaking at approximately 0.2–0.3 M⊙ (Kroupa 2002; Chabrier 2003; Bastian et al. 2010). Two models have been proposed for this transition to predominantly low-mass star formation: Atomic fine-structure line cooling (Bromm & Loeb 2003) and dust-induced fragmentation (Schneider et al. 2003; Omukai et al. 2005; Ji et al. 2014). Atomic fine-structure line cooling can occur if the gas is enriched beyond critical abundances of C II and O I, often approximated as Zcrit/Z⊙ ~ 10−3.5. On the other hand, dust-induced fragmentation, which requires dust formation in the ejecta from first-star supernovae, can already operate at critical abundances that are a factor of ten to 100 times smaller: Zcrit/Z⊙ ~ 10−5 (Omukai et al. 2005; Schneider et al. 2012a).

In the past decade, multiple large spectroscopic surveys have expanded the available sample of UMP stars, allowing us to make a first classification of these stars (Beers et al. 1985; Beers & Christlieb 2005; Christlieb et al. 2008). One result of this collective work is that the fraction of carbon-enhanced metal-poor (CEMP; [C/Fe] > 0.7; Aoki et al. 2007; Beers & Christlieb 2005) stars increases with decreasing metallicity (Placco et al. 2014; Arentsen et al. 2022). Below [Fe/H] < −4.5, CEMP stars are almost exclusively observed. Due to their carbon-enhanced nature, these stars all obey the critical abundance necessary for atomic line cooling.

There is one notable exception: SDSS J102915.14+172927.9 (hereafter, ‘SDSS J102915+172927’ Caffau et al. 2011). This star has the lowest metal mass fraction Z currently known, in large parts due to a low upper limit on its carbon abundance (i.e. [C/H] ≤ −4.5 Caffau et al. 2012). Its low carbon abundance puts the star below the critical abundance for metal-line cooling, providing support for the dust-induced formation model (Caffau et al. 2012; Schneider et al. 2012b; Klessen et al. 2012).

Inferences about the Pop III progenitors and about the Pop II formation mechanism, however, rely on stellar chemical abundances that are determined via high-resolution spectroscopy. These analyses are strongly sensitive to the approximations employed when modelling the synthetic spectra. The abundance offsets introduced by the simplifying assumptions of one-dimensional (1D) hydrostatic atmospheres and local ther-modynamic equilibrium (LTE) have been shown to be particularly severe at lower metallicities (Amarsi et al. 2016b, 2022; Bergemann et al. 2012, 2019; Ezzeddine et al. 2017).

One source of these discrepancies is that, contrary to 3D simulations, wherein convection arises naturally, in 1D hydrostatic models, convection must be treated in an approximate way, for example, by the mixing-length theory (Böhm-Vitense 1958). In addition, the 1D models cannot make predictions on other intrinsic 3D hydrodynamic effects, such as granulation and cooling by adiabatic expansion. The first 3D models of metal-poor stellar atmospheres showed that the absence of adiabatic cooling in 1D models leads to a severe overestimation of the surface temperature stratification (Stein & Nordlund 1998; Asplund et al. 2005). Hence, in LTE, 3D synthetic spectral lines of neutral species formed in the surface layers of metal-poor stars are often stronger than their 1D counterparts. Equally important, non-LTE effects for minority species subject to overionisation are expected to be larger in the steeper temperature gradients of metal-poor stars (Bergemann et al. 2012). To mitigate the problems without attempting to impose fully consistent 3D non-LTE synthesis, estimates of non-LTE and 3D effects have often been made separately, as is the case for SDSS J102915+172927 (Caffau et al. 2011, 2012). The non-LTE effects, in fact, vary across the surface due to horizontal inhomogeneities (Asplund et al. 2003; Nordlander et al. 2017). Hence, attempting to correct for 3D and non-LTE effects separately often leads to new abundance offsets. Nordlander et al. (2017) already showed that doing a full 3D non-LTE spectral synthesis of SMSS0313-6708, which is the most iron-poor star currently known, can significantly change abundance estimates. The full 3D non-LTE analysis increased the upper limit on the Fe abundance for this star to [Fe/H] < −6.53 as compared to the previous non-LTE upper limit of [Fe/H] < −7.52 computed using averaged 3D (〈3D〉) model atmospheres (Bessell et al. 2015). Additionally, recent work on C and O (Amarsi et al. 2016a), Li (Wang et al. 2021), and Fe (Amarsi et al. 2016b, 2022) have also demonstrated significant 1D LTE-3D non-LTE abundance corrections for metal-poor stars.

In light of recent advancements in the field of modelling 3D atmospheres and 3D non-LTE spectral synthesis, we perform, for the first time, a fully consistent 3D non-LTE abundance analysis of the most metal-poor star SDSS J102915+172927. In Sect. 2, we present the model atmosphere, the radiative transfer, and the model atoms used to produce 3D non-LTE synthetic spectra. The resulting abundances are presented in Sect. 3 and discussed in Sect. 4. Our conclusions given in Sect. 5.

2 Method

2.1 Observational data and stellar parameters

Observational spectra of SDSS J102915+172927 (G = 16.5, Gaia Collaboration 2020) were obtained by the programme 286.D-5045 and principle investigator P. Bonifacio using the Ultraviolet and Visual Echelle Spectrograph (UVES) spectrograph (Dekker et al. 2000) mounted on the Very Large Telescope (VLT). More information about the instrument settings and other details of the observations can be found in Caffau et al. (2012). For this work, we downloaded the reduced science spectra containing 14 individual exposures of 3005 s each from the ESO advanced data product archive1. We found a S/N ratio per pixel of approximately 35 at 650 nm for each individual exposure, which agrees with the values found by Caffau et al. (2012). Each exposure was aligned manually by adding a radial velocity shift such that the cores of the H Balmer lines and the, Ca II-doublet corresponded to the correct central wavelength. Subsequently, co-adding all exposures resulted in the final spectrum with a S/N ratio per pixel of ≈20 in the blue region around 3500 Å, ≈ 70 around the green region 5200 Å, and ≈35 in the red region at 8500 Å of the spectrum.

Caffau et al. (2012) determined the stellar effective temperature (Teff) from the (g – z) colour obtained by Ludwig et al. (2008), resulting in a value of 5811 ± 150 K. For the surface gravity, it was still unclear at the time of the original analysis whether SDSS J102915+172927 is a dwarf or a sub-giant star. Caffau et al. (2012) determined a gravity of log ɡ = 4.0 ± 0.5 dex but did not exclude a higher gravity of ≈4.5 dex. With the release of an improved parallax by Gaia DR2 ϖ = 0.734 ± 0.07 mas, Bonifacio et al. (2018) resolved the gravity issue by comparing metal-poor isochrones from A. Chieffi (priv. comm.) to their newly computed absolute V-magnitude using Gaia DR2 data, concluding that SDSS J102915+172927 is a dwarf star. Sestito et al. (2019) computed Teff = 5764 ± 60 K and log ɡ = 4.7 ± 0.1 dex by fitting MESA isochrones, with [Fe/H] = −4, to observations using astrometric and photometric Gaia DR2 data. The estimated error of using isochrones with a fixed metallicity for stars that are more metal poor than [Fe/H] = −4 is expected to be small and was accounted for by adding an additional error of 0.01 mag to the photometric uncertainties (Sestito et al. 2019). Using the parallax from Gaia DR3 ϖ = 0.648 ± 0.06 mas, Sestito (priv. comm.) arrived at Teff = 5811 ± 51K and log ɡ = 4.68 ± 0.1 dex. This effective temperature compares well to the original derived value, and though the surface gravity is 0.7 dex higher, it corresponds to SDSS J102915+172927 being a dwarf star. In this work, we used the latest values derived by Sestito (priv. comm.) from Gaia DR3 data.

Table 1

Summary of the stellar parameters of SDSS J102915+172927 obtained in previous literature studies and for the hydrodynamic models used in this work.

2.2 Model atmosphere

The tailored 3D ‘box-in-a-star’ model atmosphere was computed for this work by using the radiative-hydrodynamic Stagger code (Nordlund & Galsgaard 1995; Nordlund et al. 2009), which has had more recent improvements thanks to its user community (Magic et al. 2013; Collet et al. 2018). The Stagger code solves the fluid conservation equations (mass, energy, momentum) on a Staggered Eulerian mesh, and radiation is included as heating and cooling terms in the energy conservation equation. The size of the box was chosen such that it contains roughly ten granules and covered the top of the convective zone, the superadiabatic region, the photosphere, and upper layers of the atmosphere. The surface gravity is fixed since the box only represents a small region of the star. The radiative transfer was solved in LTE, where the scattering contribution is included in the total extinction, using an approximate opacity binning method (Nordlund 1982; Skartlien 2000; Ludwig & Steffen 2013; Collet et al. 2018) with 12 bins. Since computing the full monochromatic solution in 3D is computationally unfeasible, all wavelength points were sorted in 12 bins according to their formation depth τRoss(τλ = 1). For each bin, a mean opacity κi containing both continuum and line opacity was computed and subsequently used in the calculation of the mean intensity and radiative heating rate: 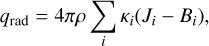(1)

with ρ as density, Ji as the mean intensity for bin i, and Bi as the Planck function at the local gas temperature. More details on the implementation in Stagger can be found in Magic et al. (2013). The equation of state is a customised version from Mihalas et al. (1988) constructed by Trampedach et al. (2013), which includes the following species: H, He, C, N, O, Ne, Na, Mg, Al, Si, S, Ar, K, Ca, Cr, Fe, Ni, H2, and 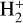. Continuous absorption and scattering coefficients were taken from Hayek et al. (2010) and line opacities from Gustafsson et al. (2008).

Surface gravity, metallicity, bottom boundary entropy, and a fiducial hyper-viscosity parameter are the only free parameters in the Stagger simulations, with effective temperature being an emergent property. As such, the surface gravity was fixed to the value selected in Sect. 2.1, and metallicity was fixed at [Fe/H] = −4 with alpha enhancement [α/Fe] = 0.4, which is typical for stars at these low metallicities (Mashonkina et al. 2017). The bottom boundary entropy was modified iteratively in order to obtain the desired effective temperature of approximately 5811K. The H to He abundance ratio was fixed at solar value, while the other elemental abundance ratios with respect to H were scaled down from their solar values, for example, [C/H] = −4 and [N/H] = −4 using solar abundances from Asplund et al. (2009). A summary of the input and emergent stellar parameters of the computed model are given in Table 1 together with literature estimates. The model itself is set on a 240 × 240 × 240 Cartesian grid that is more spatially refined near the surface to resolve the steep photospheric temperature gradient. Information about the numerical details of the code can be found in Magic et al. (2013) and Collet et al. (2018).

In addition to the tailored 3D model atmosphere, a MARCS atmosphere, interpolated from the MARCS grid (Gustafsson et al. 2008), was used to compute 1D abundances. The 1D plane-parallel atmosphere has a metallicity of [Fe/H] = −4 with α, C, N, and O abundances similar to the Stagger model and a microturbulence of 1 km s−1. The exact value of the microturbulence was relaxed for the post-processing spectrum synthesis described in Sect. 2.3. A comparison between the 1D MARCS and 3D Stagger model is made in Fig. 1, where the temperature stratification of both models is displayed along with the average stratification of the 3D model (〈3D〉). This average was calculated by taking the mean temperature of all vertical cross-sections at each depth point in optical depth space. Figure 1 showcases the impact of adiabatic cooling in 3D metal-poor atmospheric models in the upper atmosphere where the temperature structure differs significantly compared to the 1D model. The 3D model has a steeper temperature gradient at the photosphere. Although the 〈3D〉 model is an improvement over the 1D model, as it accurately describes the temperature stratification of the full 3D model, it loses information on the surface granulation and the accompanying impact on the spectral line formation.

thumbnail Fig. 1

Temperature heat map of the Stagger model with its corresponding average (3D) of all vertical columns over optical depth. The 〈3D〉 model is shown as a red dashed line and the 1D MARCS temperature stratification is shown in blue.

2.3 Spectral modelling

The radiative transfer code Balder was used to compute 1D and 3D non-LTE synthetic line profiles for the elements for which we had suitable atomic models: Si (Amarsi & Asplund 2017), Li (Wang et al. 2021), Ca, Mg (Asplund et al. 2021), Na (Lind et al. 2011), Al (Nordlander & Lind 2017), and Fe (Amarsi et al. 2016b, 2022; Lind et al. 2017). The code itself is based on the original framework of Multi3D (Leenaarts & Carlsson 2009). Amarsi et al. (2016a,b) expanded the original code, in particular by implementing a new opacity package, BLUE; making a change in its angle quadrature; and implementing frequency parallelisation.

The Balder code solves the statistical equilibrium for user-specified trace elements using the multi-level approximate lambda iteration pre-conditioning method of Rybicki & Hummer (1992) on a Cartesian grid. The code assumes that any deviations from LTE do not impact the temperature stratification or the densities of other elements. The equation of state, background, and line opacities were treated by the BLUE package (Amarsi et al. 2016b). The line opacities were pre-computed on a grid of wavelength, density, and temperature. To decrease the computational cost of the 3D calculations, the resolution of the Stagger model was reduced to 60 grid points in the horizontal direction and 101 points in the vertical direction. Nordlander et al. (2017) showed that this mesh reduction impacts the derived abundances by at most 0.03 dex. For the 3D spectral synthesis, we sampled the temporal variation of the atmosphere by computing line strengths from three different snapshots of the Stagger model. These were chosen so as to maximise the difference in Teff and, therefore, the difference in resulting line profiles. Between snapshots, we found mean abundance variations of no more than 0. 02 dex, which is in line with similar work done by Nordlander et al. (2017).

For the other elements that we either did not expect to have large deviations from non-LTE (Ti II; Mallinson et al. 2022) or did not have the atomic and molecular data needed to solve the statistical equilibrium equations (Ni I, CH and NH), we computed the 1D and 3D LTE synthetic spectra using Scate (Hayek et al. 2011). The necessary atomic line data (oscillator strengths, excitation potential, and damping parameters) were taken from Kurucz (2016) for Ti II and Kurucz (2008) for Ni I using the VALD database (Piskunov et al. 1995; Ryabchikova et al. 2015).

A range of synthetic spectra were calculated with varying abundances (Δ = 0.2 dex) for the elements Li I, CH, NH, Na I, Al I, Mg I, Si I, Ca I, Ca II, Ti II, Fe I, and Ni I, which are also listed in Table 3. The equivalent width (Wλ) of these synthetic spectral lines were interpolated to the Wλ measured in the UVES spectrum. The UVES equivalent width was found by fitting one or more, in the case of blended lines, Gaussians to the observed line profiles. An overview of the identified spectral lines and corresponding equivalent widths is given in Table B.1. Caffau et al. (2012) report the equivalent widths for a selection of lines in their Table 4, all of which agree with our values within their error. For the elements with no visible lines in the UVES spectrum (Li, Na, Al, CH, and NH), upper limits were estimated using either Cayrel’s formula (Cayrel 1988; Cayrel et al. 2004, for Li, Na, and Al) or a reduced χ2 statistical test (CH and NH). In the second case, we applied artificial broadening to the synthetic spectra to simulate instrumental broadening with a resolution of 38 000. Further details on the upper limit determination are given in the respective results section of Li (Sect. 3.1) and C (Sect. 3.2).

Spectrum synthesis calculations in 1D contain microturbulent velocity vmic as an extra free broadening parameter to approximate the convective velocity fields. This free parameter is usually determined by flattening the abundances of individual Fe I and Fe II lines as a function of the reduced equivalent width Wλ/λ0. Since we only detected Fe I in the observed spectrum, we computed 1D (non-)LTE Fe I abundances for three different values of microturbulence υmic = 1, 1.5 and 2 km s−1 to obtain a final best-fitting value of υmic = 1.48 ± 0.25 km s−1. The result of this analysis is shown in Fig. 2, where all detected Fe I lines are used to determine vmic. This value is consistent with the empirical analysis performed by Frebel et al. (2013) for a star with log ɡ = 4.7. In all subsequent spectral synthesis computations, a value of υmic = 1.5 km s−1 was used.

The stipulated abundance errors originate from manually placing the continuum and from the noise of the spectrum. The errors were calculated from Cayrel’s formula (Cayrel 1988; Cayrel et al. 2004), which gives an error on the equivalent width that propagates through to the abundance error, with a separate contribution from the continuum placement. In addition, there is an error coming from the uncertainties on Teff, log ɡ, and υmic, which are computed by shifting one stellar parameter at a time in the MARCS atmosphere and performing an abundance analysis as described above. The error is then equal to the abundance offset between the new model and the model with correct stellar parameters. For example, the Mg I abundance increases by 0.08 dex when computed using a MARCS atmosphere with a Teff that is 100 K hotter. The results of these calculations are summarised in Table 2. Finally, the total error becomes: 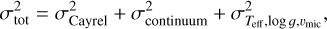(2)

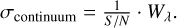
thumbnail Fig. 2

One-dimensional non-LTE Fe I abundances for each visible line in the spectrum interpolated to a microturbulence of υmicro = 1.48 km s−1. The blue line shows the best linear fit through the data, while the red dashed line denotes the mean non-LTE abundance. The black solid line denotes the cut-off in reduced equivalent width between saturated and non-saturated lines: log[Wλ/λ0] < −4.95.
Table 2

One-dimensional (non-)LTE abundance (A(X), see Eq. (3)) sensitivity to the uncertainties on Teff log ɡ, and υmic.

Table 3

Summary of the computed abundances (A(X), see Eq. (3)) and upper limits as well as the 3D plus non-LTE values from Caffau et al. (2012).

3 Results

All abundance results are summarised in Table 3 in the form: 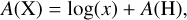(3)

where x is the number fraction of element X and A(H) = 12. Whenever an abundance is converted to the solar normalised abundance, [X/H] = A(X) – A(X)⊙, we used the solar abundances from Asplund et al. (2021).

3.1 Lithium

The Li I line at 6707.6 Å was not detected in the UVES spectrum, so we could only determine an upper limit. We used Cayrel’s formula (Cayrel 1988), similar to Caffau et al. (2012), to determine a 3σ upper limit. The resulting 3D non-LTE upper limit, A(Li) < 1.06 ± 0.05, is slightly higher than the original value, A(Li)Caffau+12 < 0.9, but still well below the Spite plateau, A(Li)Spite ~ 2.2 (Spite & Spite 1982; Sbordone et al. 2010; Meléndez et al. 2010), implying that the star has undergone significant Li depletion, as expected based on its effective temperature.

3.2 Carbon and nitrogen

Both C and N were undetected in the UVES spectrum, but the quality of the spectrum did allow for the calculation of robust upper limits. To obtain these limits, we computed 1D and 3D LTE synthetic spectra of the CH G-band at 4300 Å and the NH-band at 3360 Å for a wide range of abundances, A(C) = 3.6–5.6 and A(N) = 2.4–6.0, in steps of Δ = 0.2 dex. The upper limit was determined using a reduced χ2-statistic where we ‘fitted’ the synthetic spectral bands to the UVES spectrum. The null hypothesis stated that our featureless observed spectrum can be fully described by the synthetic spectrum, meaning that the two are indistinguishable. The upper limit was then defined as the synthetic spectrum with abundance A(C) that does not statistically describe the observed featureless spectrum.

To find the upper limit, we started by masking the blended Ti II and Fe I line in the NH-band and CH-band, respectively, and computed the reduced 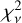for each synthetic spectrum: 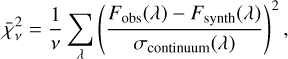(4)

with v as the degrees of freedom equal to the number of wavelength points minus one and σcont = S/N−1. For a significance level of α = 0.05, we looked up the corresponding mean of the χ2-distribution, 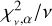(Bognar 2021), where the probability that a randomly chosen χ2 from the distribution function will be greater than 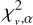is equal to the significance level α. Consequently, the null hypothesis was rejected for the synthetic models that have 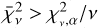either because the synthetic spectrum does not properly model the observed spectrum or due to a statistically improbable excursion of probability (i.e. 5% for out chosen value of α). This means that the upper limit on the CH and NH abundances is equal to the synthetic spectrum for which 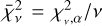, as any model with a higher abundance does not statistically describe the featureless UVES spectrum. A visualisation of the 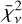values used to determine the upper limits for C and N is shown in Fig. A.1.

Using this method, we increased the upper limit significantly for both molecular bands: A(C) = 4.86 dex and A(N) = 4.65 dex (compared to Caffau et al. 2012: A(C)Caffau = 3.96 dex and A(N)Caffau = 2.83 dex). The corresponding synthetic spectra are shown in Figs. 3 and 4 for N and C, respectively. In addition, the new and old upper limits on C are shown together with a subset of metal-poor stars from the SAGA database (Suda et al. 2008) in Fig. 5.

The large increase of the C and N upper limits can originate from multiple sources, such as changes in surface gravity, differences in spectrum synthesis code, and variations in atmosphere between the original work and this work. In the case of the CH and NH upper limits, however, we believe that the main discrepancy is likely due to a difference in methodology when determining the limits. Caffau et al. (2012) show in their Figs. 6 and 7 the molecular bands for different abundances A(C) = 4.65, 6.00 and A(N) = 3.60, 5.40. From visual inspection, their A(C) = 5.40 spectrum corresponds well to our synthetic spectrum, with A(C) = 5.00, which points towards a ~0.4 dex variation in abundance originating from the difference in surface gravity, atmospheric model, and spectrum synthesis code. We hypothesise that the remaining difference is due to the choice in methodology. The authors of Caffau et al. (2012), however, do not describe how the upper limits were derived, and therefore a more direct comparison could not be made.

thumbnail Fig. 3

UVES spectrum zoomed in on the NH-band at 3360 Å. The synthetic spectrum corresponding to the upper limit derived in this work is shown in blue, the UVES spectrum in black and the upper limit from Caffau et al. (2012) is shown in red. The Ti II at 3361.2 Å was excluded from the χ2-analysis.
thumbnail Fig. 4

CH G-band at 4300 Å. The Fe I at 4307.9 Å was excluded from the χ2-analysis.
thumbnail Fig. 5

Upper limits on [C/Fe] for SDSS J102915+172927. The 1D LTE and 3D LTE results are shown as triangles and squares, respectively, for the original limits (Caffau et al. 2012, red) and the results of this work (blue). For comparison, we show the [C/Fe] abundance for a sample of metal-poor stars from the SAGA database (Suda et al. 2008, black circles) and the cut-off for carbon-enhancement at [C/Fe] = 0.7 (dotted line) from Aoki et al. (2007).

3.3 Sodium and aluminium

No Na or Al absorption features could be identified in the spectrum. We therefore present upper limits for the two elements in this star for the first time at the Na I line at 5891.6 Å and Al I line at 3961.5 Å using the same method as for Li. The resulting 3σ upper limits are shown in Table 3.

3.4 Alpha elements

Magnesium

We measured four Mg I lines that combine to a mean 3D non-LTE abundance of A (Mg) = 3.18 ± 0.05. This finding is marginally consistent with Caffau et al. (2012), A (Mg) = 3.06 ± 0.12. Sitnova et al. (2019) computed a 1D non-LTE value of A(Mg) = 3.17 ± 0.07 using the updated surface gravity of log ɡ = 4.7.

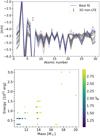thumbnail Fig. 6

Visualisation of the STARFIT fitting analysis for all models with . The top panel shows the 3D non-LTE abundances (red squares) together with all the best-fitting supernovae models (grey lines), and the best fit (blue line). The bottom panel shows the progenitor mass and explosion energy for the same best-fitting models shown in the top panel along with their respective values.
thumbnail Fig. 7

Impact of progenitor mass on the supernova yields as compared to the best-fitting model. Three-dimensional non-LTE abundances from this paper are shown as red squares together with the best-fitting progenitor supernova model in blue and three other models with a higher progenitor mass in grey: M = 50, 70, 100 M⊙, E51 = 0.3 and fmix = 0.25.

Silicon

One Si I line was detected at 3905.5 Å for which we computed a 3D non-LTE abundance of A(Si) = 3.42 ± 0.12. This result is smaller than what was found by Caffau et al. (2012): A(Si) = 3.55 ± 0.1.

Calcium

One Ca I line was detected at 4226 Å along with the Ca II H&K lines and the Ca II triplet at ≈8500 Å. The Ca II H&K and the weakest line of the CaII triplet were discarded due to being blended or too weak for a reliable equivalent width measurement. Using the resulting lines, we were able to recover ionisation balance between CaI and CaII in 3D non-LTE: A(Ca)Ca I – A(Ca)Ca II = 0.01 dex with a mean Ca abundance of A(Ca) = 1.87 ± 0.02.

Caffau et al. (2012) obtained a 3D + non-LTE abundance of A(Ca)Ca I = 1.76 and A(Ca)Ca II = 1.35. Using an updated model atom, Sitnova et al. (2019) computed a 1D non-LTE Ca abundance with stellar parameters similar to those in this work, reporting A(Ca) = 1.82 ± 0.06. However, Sitnova et al. (2019) fixed the Ca I/Ca II ionisation equilibrium to derive the surface gravity.

Titanium

We detected five Ti II lines in the UVES spectrum, and three of them were deemed strong enough to determine a reliable equivalent width. The resulting mean 3D LTE abundance A(Ti) = 0.62 ± 0.06 is +0.55 dex higher than the original value derived by Caffau et al. (2012). A similar increase was seen in the 1D LTE case, as we obtained an abundance that is larger by +0.39 dex. Following Table 2, we can attribute approximately 0.2 dex to the change in surface gravity. The remaining 0.19 dex difference for the 1D LTE abundance cannot be attributed to the different oscillator strengths used in this work, which are higher than the ones reported in Caffau et al. (2012, Table 4), leaving the origin of the discrepancy unknown.

3.5 Iron

The UVES spectrum contains 52 visible Fe I lines but no Fe II lines. For the abundance computation, a cut-off in reduced equivalent width of log[Wλ/λ0] < −4.95 was used to remove lines that did not fall on the linear part of the curve-of-growth (Tielens 1999). The remaining 46 Fe I lines are shown in Fig. 2. For the 1D LTE case, we expected the only differences between our results and those from Caffau et al. (2012), to originate from the change in gravity (Δ log ɡ = +0.7 dex), choice of spectral synthesis codes and model atmospheres employed. We obtained a value of A(Fe) = 2.80 ± 0.15 that is comparable to the value found by Caffau et al. (2012), that is, A(Fe) = 2.87 ± 0.13. This result is reassuring since Fe I is not strongly sensitive to surface gravity (see Table 2).

Our 1D non-LTE abundance, A(Fe) = 3.05 ± 0.13, is comparable within its error to that of Caffau et al. (2012): A(Fe) = 3.00 ± 0.13. In addition, Ezzeddine et al. (2017) recomputed the 1D non-LTE Fe abundance for this star using a surface gravity of log ɡ = 4.0 and obtained a slightly higher value of A(Fe) = 3.23 ± 0.14. They based their analysis only on three Fe I lines however.

From our consistent 3D non-LTE analysis, we derived an abundance of A(Fe) = 3.28 ± 0.13 that is 0.57 dex higher than the 3D LTE plus non-LTE value obtained by Caffau et al. (2012), A(Fe) = 2.71 ± 0.10. We emphasise that Caffau et al. (2012) computed separate 1D non-LTE and 3D LTE abundance corrections and added these corrections together to get a final 3D plus non-LTE abundance. Applying a similar method to our abundances would yield a value of A(Fe)3D+NLTE = 2.97 ± 0.14, which has better agreement with Caffau et al. (2012) but is also significantly lower than the fully consistent 3D non-LTE result. Hence, this work demonstrates again that 3D and non-LTE effects influence each other non-linearly and cannot be simply added together for metal-poor stars.

This result supports the claim by Amarsi et al. (2016b) that metallicities of the most metal-poor stars are often systematically underestimated. This is because for Fe I lines, the non-LTE effects and the 3D effects tend to go in the same direction and can enhance each other in warm metal-poor stars.

3.6 Nickel

We detected nine usable Ni I lines in the UVES spectrum for which we computed a mean 3D LTE abundance of A(Ni) = 1.67 ± 0.14. This value is +0.34 dex higher than the original value. On the other hand, our 1D LTE abundance agrees within +0.03 dex with the value from Caffau et al. (2012): A(Ni) = 1.65 ± 0.14.

4 Discussion

4.1 Supernova yield comparison

We compared our 3D non-LTE abundances with yields of core-collapse supernovae of non-rotating Pop III stars Heger & Woosley (2010) (updated in 2012 for missing low-mass models)2 using the StarFit code (Heger et al., in prep.). Specifically, we used the Python version (0.17.12) of StarFit3 to find the best match between an input abundance pattern and supernova model employing a reduced χ2-algorithm (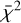) (Heger & Woosley 2010, see their Sect. 7). Upper limits, however, were then treated by StarFit as in Eq. (6) of Magg et al. (2020) – they contribute to 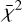in a manner similar to a measurement mismatch if violated and are basically ignored when well fulfilled. The 1D mixing and fallback models (*.S4.*) covers progenitor stars with masses in the 9.6–100 M⊙ range, piston-driven explosion energies of E51 = 0.3–10 (with E51 = 1051 erg), and hydrodynamic mixing fractions of fmix = 0–0.25 (see Heger & Woosley 2010 for details). In addition, the fitting code employs a dilution factor fdil that accounts for mixing of the supernova ejecta with the interstellar medium (Big Bang composition). This free parameter essentially shifts the whole supernova abundance pattern up or down. While Li was excluded from the fitting procedure, C, N, Al, and Na were treated as upper limits. For Na and Al, stricter 1σ upper limits were calculated with Cayrel’s formula (Cayrel 1988; Cayrel et al. 2004) so the limits could be used in the supernova fitting: A(Na)1σ < 1.12 ± 0.15 and A(Na)1σ < 1.54 ± 0.15.

The best-fitting model has a progenitor mass of M = 10.9 M⊙, an explosion energy of E51 = 0.6, and a mixing efficiency of fmix = 0.01, and it matches with 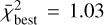. The variance of the best-fitting models (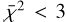) was analysed by selecting the fmix that has the lowest 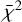for each mass-energy pair. The reasoning is that mixing acts as a free parameter in the 1D explosion models. Moreover, the effect of mixing is small at masses ~10 M⊙ and mainly affects elements with Z > 20 (Ca). The resulting distribution in mass and energy and the corresponding abundance patterns are shown in Fig. 6. We find that only a narrow range of progenitor masses, M = 10–20 M⊙, and explosion energies, E51 = 0.3–3, are able to fit the abundance pattern of SDSS J102915+172927.

The difference between the best fit and yields from models with higher progenitor masses is shown in Fig. 7. At higher masses, the supernova underproduces heavy elements (Ti, Fe, Ni) and overproduces Mg, Si, and Ca, compared to the best-fit model.

Applying the same fitting routine to our 1D LTE abundances resulted in a broader mass, M ≈ 10–30, and energy range, E51 = 0.3–10, for all models with 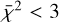. This is explained by the lower 1D LTE Fe abundance that allows models with a higher progenitor mass to achieve good fits. Already in Fig. 7, most supernova yields have noticeably lower Fe abundances than our 3D non-LTE result.

Since the original discovery of SDSS J102915+172927, there have been several papers comparing its abundance pattern to the-oretical yields of Pop III supernovae. The following literature results all used the original abundances from Caffau et al. (2012). Similar to this work, Placco et al. (2015) used the supernova models of Heger & Woosley (2010) to find the best-fitting progenitor mass of M = 10.6 M⊙ with explosion energy E51 = 0.9, which is in agreement with our work. Schneider et al. (2012b) used the Pop III core-collapse supernova models by Limongi & Chieffi (2012) to find a best fit for progenitors with mass M = 20 and 35 M⊙ and explosion energy E51 = 1. Tominaga et al. (2014) compared three core-collapse supernovae models taken from Iwamoto et al. (2005); Tominaga et al. (2007) with varying masses (25 and 40 M⊙) and mixing efficiencies with a sample of metal-poor stars that included SDSS J102915+172927. Their best match is a progenitor star with M = 25 M⊙ without mixing enhancement. Using the same Pop III supernova and hypernova models as Tominaga et al. (2014), Ishigaki et al. (2014) found a better agreement with a hypernova of M = 40 M⊙, E51 = 30, and mixing log f = −0.9. They attributed the obtained explosion energy to the relatively high [Si/Ca] ratio. These papers report a higher progenitor mass and explosion energy than this work. We note, however, that the data sets of Iwamoto et al. (2005) and Tominaga et al. (2007) only cover a comparably limited progenitor mass range. In summary, based on our new analysis and by using the model set of Heger & Woosley (2010), we find that the observed abundance pattern of SDSS J102915+172927 can be well explained by a typical single-star supernova (typical mass range: 10–20 M⊙; typical explosion energy: E51 = 0.3–3) of a compact Pop III star (low mixing, fmix = 0.01, as compared to red supergiants, consistent with the hydrodynamical models of Joggerst et al. 2009).

4.2 Mean alpha abundance

Using our new 3D non-LTE abundances, we computed the mean alpha abundance using a simple mean of [Si/Fe], [Mg/Fe], and [Ca/Fe]. We find that the mean alpha enhancement of SDSS J102915+172927 decreases substantially compared to the original work: (5)

also shown in Fig. 8. The observed change from alpha enhanced ([α/Fe] ~ 0.4) to sub-solar alpha abundance is mainly driven by the relatively large increase in Fe abundance, compared to the alpha elements, when going from 1D LTE to 3D non-LTE. Amarsi et al. (2022) found that for warm metal-poor subgiants ([M/H] = −3), the change in iron abundance, A(Fe I)1DLTE – A(Fe I)3DnonLTE, can be as large as 0.4–0.5 dex. The 3D non-LTE abundance changes for the alpha elements are expected to be smaller. Hence, it is not unrealistic to expect similar shifts in alpha enhancement for other UMP stars, shifting the mean alpha-to-iron ratio of the stars shown in Fig. 8 downwards. This would imply that the yields of Pop III supernovae produced a lower [α/Fe] than previously thought. Verification of this claim, however, would require a consistent 3D non-LTE abundance analysis of extremely metal-poor stars ([Fe/H] < −3).

Our atmospheric models were calculated using alpha elements enhanced by [α/Fe] = +0.4, contrary to our findings that SDSS J102915+172927 has a sub-solar alpha abundance. At these low metallicities, H is expected to be the main electron donor such that small changes in the metal mass fraction are not expected to significantly impact the atmosphere. To test this, we compared two MARCS models (Tef = 5750 K, log ɡ = 4.5, [Fe/H] = −2.5, υmicro = 1 km s−1): one alpha-enhanced model ([α/Fe] = +0.4) and one alpha-normal model ([α/Fe] = +0.0). The temperature stratification of both models differ at most 15 K throughout the atmosphere. Following Table 2, such small changes in temperature would have a negligible impact on the derived abundances.

thumbnail Fig. 8

Similar to Fig. 5 but for the mean [α/Fe] abundance.

4.3 Impact on Pop II star formation theories

In their work, Caffau et al. (2012) concluded that the low-carbon upper limit of SDSS J102915+172927 excluded metal-line cooling as a possible mechanism of its star formation. In addition, the reported total metal mass fraction made SDSS J102915+172927 the most metal-poor star known to date. Using the new 3D non-LTE abundances derived in this work, we make an estimate of the metal mass fraction Z: (6)

where A(i) is the abundance and Aw is the atomic weight of element i. Subsequently, the normalisation X + Y + Z = 1 allowed us to compute the total metal mass fraction Z: (7)

where Y = 0.2477 is the primordial He mass fraction (Peimbert et al. 2007). Using Eq. (7), we computed two estimates of the mass fraction Z: one where we restricted the sum over all elements to the species that Caffau et al. (2012) reported (including upper limits) in order to make a consistent comparison and one where we used the abundances from the best-fitting Pop III supernova model.

In the first case, we included oxygen as [O/Fe] = +0.6 and Sr with the upper limit as derived in Caffau et al. (2012). This resulted in a total metal content of Z ⪅ 1.38 × 10−6 or Z/Z⊙ ⪅ 9.8 × 10−5, which is approximately a factor of two higher than the original estimation ZCaffau+12/Z⊙ = 5 × 10−5. In the second case, by applying the abundances of all species from Li to Zn of the best-fitting supernova model, we obtained a value of ZSNe ≈ 9.1 × 10−7 or ZSNe/Z⊙ ≈ 6.6 × 10−5. Even though this estimate includes more elements, the significantly lower N abundance of the supernova model resulted in an overall lower mass fraction compared to the first case.

Turning to the possibility of low-mass star formation through the mechanism of metal-line cooling, it is theorised (Bromm & Loeb 2003) that this will only occur if there is a sufficient amount of C and O available in the star-forming cloud. Indeed, metal-line cooling is able to produce low-mass stars if the transition discriminant (Bromm & Loeb 2003; Frebel et al. 2007), (8)

is greater than D ≥ Dcrit = −3.5 ± 0.2. Using our new upper limit on C and [O/Fe] = +0.6, we obtained a transition discriminant D ≤ −3.6 ± 0.15 that is marginally comparable to the critical value needed for metal-line cooling, contrary to the original result of Caffau et al. (2011) D ≤ −4.2. Hence, our result cannot exclude neither metal-line cooling nor dust-induced fragmentation as the underlying mechanism in the formation of SDSS J102915+172927.

5 Conclusions

In this work we performed a fully consistent 3D non-LTE abundance analysis of SDSS J102915+172927, which is known as the most metal-poor star. For this purpose, we employed a tailored 3D atmospheric model using improved stellar parameters and up-to-date atomic data to calculate synthetic spectra. The primary outcome is that the resulting Fe abundance is +0.57 dex higher than the original value, showcasing the importance of performing consistent 3D non-LTE calculations for UMP stars.

The increase in metallicity combined with new upper limits on C and N has important implications regarding progenitor Pop III properties and low-mass star formation in the early Universe. First, we find that the upper limit of the total metal content of the star increases by a factor of two. Together with the increased carbon upper limit, we find that the abundances of the star are consistent with formation through metal-line cooling and dust-induced fragmentation. However, observations with higher S/N are necessary to improve the upper limit on C and to draw stronger conclusions. Secondly, our new 3D non-LTE abundances provide stronger constraints on the mass of the progenitor Pop III star as well as on its explosion energy, assuming that SDSS J102915+172927 is mono-enriched, as compared to a 1D LTE analysis. In particular, we find that progenitors with masses in the range of M = 10–20 M⊙ and explosion energies in the range of E51 = 0.3–3 are able to reproduce the abundance pattern. Specifically, the best fit is a Pop III progenitor with mass M = 10.9 M⊙ that exploded with energy E51 = 0.6. These masses and explosion energies are typical for core-collapse supernovae (e.g. Müller 2020), and no hypernova model is required. Lastly, the strong increase in A(Fe) coupled with smaller changes in alpha-element abundances causes the star to change from being alpha enhanced to being a star with sub-solar alpha abundance. Following the conclusion of Nordlander et al. (2017) and in light of upcoming large-scale surveys that will provide dozens of new UMP stars, it is critical for future studies to apply full 3D non-LTE abundance calculations whenever possible.

Acknowledgements

We thank the anonymous referee for their comments, which have improved the manuscript. We gratefully thank Federico Sestito for providing updated stellar parameters for SDSS J102915.14+172927.9 using Gaia DR3 data. This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. CL and KL acknowledge funds from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement no. 852977). KL also acknowledges funds from the Knut and Alice Wallenberg foundation. AMA gratefully acknowledges support from the Swedish Research Council (VR 2020-03940). LFRD acknowledges support from the Carlsberg Foundation (grant agreement CF19-0649). TTH acknowledges support from the Swedish Research Council (VR 2021-05556). Parts of this research were supported by the Australian Research Council (ARC) Centre of Excellence (CoE) for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. AH wad supported, in part, by the ARC CoE for Gravitational Wave Discovery (OzGrave) project number CE170100004 and acknowledges software development support from Astronomy Australia Limited’s ADACS scheme (Project IDs AHeger_2022B, AHeger_2023A). This work is based on data obtained from the ESO Science Archive Facility. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at UPPMAX under project SNIC2022/5-351 and PDC under project PDC-BUS-2022-4, and at the Centre for Scientific Computing, Aarhus: http://phys.au.dk/forskning/cscaa/.

Appendix A 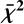values of the upper limit determination

thumbnail Fig. A.1

Overview of the values from the upper limit analysis described in Sect. 3.2. Th top panel corresponds to the different synthetic spectra of CH and the bottom panel to NH. The red star represents the interpolated abundance where , which is also highlighted with a vertical dashed line.

Appendix B Line list

Table B.1

Atomic data for all the spectral lines used in this study.

References

  1. Amarsi, A. M., & Asplund, M. 2017, MNRAS, 464, 264 [Google Scholar]
  2. Amarsi, A. M., Asplund, M., Collet, R., & Leenaarts, J. 2016a, MNRAS, 455, 3735 [NASA ADS] [CrossRef] [Google Scholar]
  3. Amarsi, A. M., Lind, K., Asplund, M., Barklem, P. S., & Collet, R. 2016b, MNRAS, 463, 1518 [NASA ADS] [CrossRef] [Google Scholar]
  4. Amarsi, A. M., Liljegren, S., & Nissen, P. E. 2022, A&A, 668, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Aoki, W., Beers, T. C., Christlieb, N., et al. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] [Google Scholar]
  6. Arentsen, A., Placco, V. M., Lee, Y. S., et al. 2022, MNRAS, 515, 4082 [NASA ADS] [CrossRef] [Google Scholar]
  7. Asplund, M., Carlsson, M., & Botnen, A. V. 2003, A&A, 399, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, Astronomical Society of the Pacific Conference Series, 336, 25 [NASA ADS] [Google Scholar]
  9. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  10. Asplund, M., Amarsi, A. M., & Grevesse, N. 2021, A&A, 653, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bastian, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [Google Scholar]
  12. Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
  13. Beers, T. C., Preston, G. W., & Shectman, S. A. 1985, AJ, 90, 2089 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [Google Scholar]
  15. Bergemann, M., Gallagher, A. J., Eitner, P., et al. 2019, A&A, 631, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bessell, M. S., Collet, R., Keller, S. C., et al. 2015, ApJ, 806, L16 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bognar, M. 2021, Chi-Square Distribution Online Applet, https://homepage.divms.uiowa.edu/~mbognar/applets/chisq.html [Google Scholar]
  18. Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
  19. Bonifacio, P., Caffau, E., Spite, M., et al. 2018, Res. Notes Am. Astron. Soc., 2, 19 [Google Scholar]
  20. Bromm, V., & Loeb, A. 2003, Nature, 425, 812 [NASA ADS] [CrossRef] [Google Scholar]
  21. Bromm, V., & Yoshida, N. 2011, ARA&A, 49, 373 [CrossRef] [Google Scholar]
  22. Caffau, E., Bonifacio, P., François, P., et al. 2011, Nature, 477, 67 [NASA ADS] [CrossRef] [Google Scholar]
  23. Caffau, E., Bonifacio, P., François, P., et al. 2012, A&A, 542, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Cayrel, R. 1988, in The Impact of Very High S/N Spectroscopy on Stellar Physics, 132, eds. G. Cayrel de Strobel, & M. Spite, 345 [NASA ADS] [CrossRef] [Google Scholar]
  25. Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  27. Christlieb, N., Schörck, T., Frebel, A., et al. 2008, A&A, 484, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Clark, P. C., Glover, S. C. O., Klessen, R. S., & Bromm, V. 2011a, ApJ, 727, 110 [NASA ADS] [CrossRef] [Google Scholar]
  29. Clark, P. C., Glover, S. C. O., Smith, R. J., et al. 2011b, Science, 331, 1040 [Google Scholar]
  30. Collet, R., Nordlund, Å., Asplund, M., Hayek, W., & Trampedach, R. 2018, MNRAS, 475, 3369 [NASA ADS] [CrossRef] [Google Scholar]
  31. Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, SPIE Conf. Ser., 4008, 534 [Google Scholar]
  32. Ezzeddine, R., Frebel, A., & Plez, B. 2017, ApJ, 847, 142 [Google Scholar]
  33. Ezzeddine, R., Frebel, A., Roederer, I. U., et al. 2019, ApJ, 876, 97 [NASA ADS] [CrossRef] [Google Scholar]
  34. Frebel, A., & Norris, J. E. 2015, ARA&A, 53, 631 [NASA ADS] [CrossRef] [Google Scholar]
  35. Frebel, A., Johnson, J. L., & Bromm, V. 2007, MNRAS, 380, L40 [NASA ADS] [CrossRef] [Google Scholar]
  36. Frebel, A., Casey, A. R., Jacobson, H. R., & Yu, Q. 2013, ApJ, 769, 57 [NASA ADS] [CrossRef] [Google Scholar]
  37. Gaia Collaboration 2020, VizieR Online Data Catalog: I/350 [Google Scholar]
  38. Greif, T. H., Springel, V., White, S. D. M., et al. 2011, ApJ, 737, 75 [NASA ADS] [CrossRef] [Google Scholar]
  39. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Hartwig, T., Bromm, V., Klessen, R. S., & Glover, S. C. O. 2015, MNRAS, 447, 3892 [NASA ADS] [CrossRef] [Google Scholar]
  41. Hartwig, T., Yoshida, N., Magg, M., et al. 2018, MNRAS, 478, 1795 [CrossRef] [Google Scholar]
  42. Hayek, W., Asplund, M., Carlsson, M., et al. 2010, A&A, 517, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Hayek, W., Asplund, M., Collet, R., & Nordlund, Å. 2011, A&A, 529, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Heger, A., & Woosley, S. E. 2010, ApJ, 724, 341 [Google Scholar]
  45. Hirano, S., Hosokawa, T., Yoshida, N., et al. 2014, ApJ, 781, 60 [NASA ADS] [CrossRef] [Google Scholar]
  46. Hosokawa, T., Omukai, K., Yoshida, N., & Yorke, H.W. 2011, Science, 334, 1250 [CrossRef] [Google Scholar]
  47. Hosokawa, T., Hirano, S., Kuiper, R., et al. 2016, ApJ, 824, 119 [NASA ADS] [CrossRef] [Google Scholar]
  48. Ishigaki, M. N., Tominaga, N., Kobayashi, C., & Nomoto, K. 2014, ApJ, 792, L32 [NASA ADS] [CrossRef] [Google Scholar]
  49. Ishigaki, M. N., Tominaga, N., Kobayashi, C., & Nomoto, K. 2018, ApJ, 857, 46 [Google Scholar]
  50. Iwamoto, N., Umeda, H., Tominaga, N., Nomoto, K., & Maeda, K. 2005, Science, 309, 451 [NASA ADS] [CrossRef] [Google Scholar]
  51. Ji, A. P., Frebel, A., & Bromm, V. 2014, ApJ, 782, 95 [NASA ADS] [CrossRef] [Google Scholar]
  52. Joggerst, C. C., Woosley, S. E., & Heger, A. 2009, ApJ, 693, 1780 [NASA ADS] [CrossRef] [Google Scholar]
  53. Joggerst, C. C., Almgren, A., Bell, J., et al. 2010, ApJ, 709, 11 [NASA ADS] [CrossRef] [Google Scholar]
  54. Keller, S. C., Bessell, M. S., Frebel, A., et al. 2014, Nature, 506, 463 [NASA ADS] [CrossRef] [Google Scholar]
  55. Klessen, R. S., Glover, S. C. O., & Clark, P. C. 2012, MNRAS, 421, 3217 [NASA ADS] [CrossRef] [Google Scholar]
  56. Kroupa, P. 2002, Science, 295, 82 [Google Scholar]
  57. Kurucz, R. L. 2008, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  58. Kurucz, R. L. 2016, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  59. Lai, D. K., Bolte, M., Johnson, J. A., et al. 2008, ApJ, 681, 1524 [NASA ADS] [CrossRef] [Google Scholar]
  60. Leenaarts, J., & Carlsson, M. 2009, in The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, eds. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, Astronomical Society of the Pacific Conference Series, 415, 87 [NASA ADS] [Google Scholar]
  61. Limongi, M., & Chieffi, A. 2012, ApJS, 199, 38 [NASA ADS] [CrossRef] [Google Scholar]
  62. Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Lind, K., Amarsi, A. M., Asplund, M., et al. 2017, MNRAS, 468, 4311 [NASA ADS] [CrossRef] [Google Scholar]
  64. Ludwig, H. G., & Steffen, M. 2013, Mem. Soc. Astron. Ital. Suppl., 24, 53 [Google Scholar]
  65. Ludwig, H. G., Bonifacio, P., Caffau, E., et al. 2008, Physica Scripta T, 133, 014037 [NASA ADS] [CrossRef] [Google Scholar]
  66. Magg, M., Klessen, R. S., Glover, S. C. O., & Li, H. 2019, MNRAS, 487, 486 [CrossRef] [Google Scholar]
  67. Magg, M., Nordlander, T., Glover, S. C. O., et al. 2020, MNRAS, 498, 3703 [Google Scholar]
  68. Magic, Z., Collet, R., Asplund, M., et al. 2013, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Mallinson, J. W. E., Lind, K., Amarsi, A. M., et al. 2022, A&A, 668, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Mashonkina, L., Jablonka, P., Sitnova, T., Pakhomov, Y., & North, P. 2017, A&A, 608, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Meléndez, J., Casagrande, L., Ramírez, I., Asplund, M., & Schuster, W. J. 2010, A&A, 515, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Mihalas, D., Dappen, W., & Hummer, D. G. 1988, ApJ, 331, 815 [NASA ADS] [CrossRef] [Google Scholar]
  73. Müller, B. 2020, Living Rev. Comput. Astrophys., 6, 3 [CrossRef] [Google Scholar]
  74. Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [CrossRef] [Google Scholar]
  75. Nordlander, T., & Lind, K. 2017, A&A, 607, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Nordlander, T., Amarsi, A. M., Lind, K., et al. 2017, A&A, 597, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Nordlund, A. 1982, A&A, 107, 1 [Google Scholar]
  78. Nordlund, A., & Galsgaard, K. 1995, Stagger-Code [Google Scholar]
  79. Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Living Rev. Solar Phys., 6, 2 [CrossRef] [Google Scholar]
  80. Omukai, K., Tsuribe, T., Schneider, R., & Ferrara, A. 2005, ApJ, 626, 627 [NASA ADS] [CrossRef] [Google Scholar]
  81. Peimbert, M., Luridiana, V., & Peimbert, A. 2007, ApJ, 666, 636 [NASA ADS] [CrossRef] [Google Scholar]
  82. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
  83. Placco, V. M., Frebel, A., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 797, 21 [Google Scholar]
  84. Placco, V. M., Frebel, A., Lee, Y. S., et al. 2015, ApJ, 809, 136 [NASA ADS] [CrossRef] [Google Scholar]
  85. Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr, 90, 054005 [Google Scholar]
  86. Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] [Google Scholar]
  87. Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Schneider, R., Ferrara, A., Salvaterra, R., Omukai, K., & Bromm, V. 2003, Nature, 422, 869 [NASA ADS] [CrossRef] [Google Scholar]
  89. Schneider, R., Omukai, K., Bianchi, S., & Valiante, R. 2012a, MNRAS, 419, 1566 [CrossRef] [Google Scholar]
  90. Schneider, R., Omukai, K., Limongi, M., et al. 2012b, MNRAS, 423, L60 [NASA ADS] [CrossRef] [Google Scholar]
  91. Sestito, F., Longeard, N., Martin, N. F., et al. 2019, MNRAS, 484, 2166 [NASA ADS] [CrossRef] [Google Scholar]
  92. Sitnova, T. M., Mashonkina, L. I., Ezzeddine, R., & Frebel, A. 2019, MNRAS, 485, 3527 [NASA ADS] [CrossRef] [Google Scholar]
  93. Skartlien, R. 2000, ApJ, 536, 465 [NASA ADS] [CrossRef] [Google Scholar]
  94. Spite, F., & Spite, M. 1982, A&A, 115, 357 [NASA ADS] [Google Scholar]
  95. Stacy, A., & Bromm, V. 2013, MNRAS, 433, 1094 [NASA ADS] [CrossRef] [Google Scholar]
  96. Stacy, A., Bromm, V., & Lee, A. T. 2016, MNRAS, 462, 1307 [NASA ADS] [CrossRef] [Google Scholar]
  97. Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
  98. Suda, T., Katsuta, Y., Yamada, S., et al. 2008, PASJ, 60, 1159 [NASA ADS] [Google Scholar]
  99. Susa, H. 2013, ApJ, 773, 185 [NASA ADS] [CrossRef] [Google Scholar]
  100. Susa, H., Hasegawa, K., & Tominaga, N. 2014, ApJ, 792, 32 [NASA ADS] [CrossRef] [Google Scholar]
  101. Tielens, A. G. G. M. 1999, Encyclop. Spectrosc. Spectrom., 3, 2199 [CrossRef] [Google Scholar]
  102. Tominaga, N., Umeda, H., & Nomoto, K. 2007, ApJ, 660, 516 [NASA ADS] [CrossRef] [Google Scholar]
  103. Tominaga, N., Iwamoto, N., & Nomoto, K. 2014, ApJ, 785, 98 [NASA ADS] [CrossRef] [Google Scholar]
  104. Trampedach, R., Asplund, M., Collet, R., Nordlund, Å., & Stein, R. F. 2013, ApJ, 769, 18 [NASA ADS] [CrossRef] [Google Scholar]
  105. Wang, E. X., Nordlander, T., Asplund, M., et al. 2021, MNRAS, 500, 2159 [Google Scholar]
2

Data is available at https://starfit.org

3

Data and routines are available at https://pypi.org/project/starfit/

All Tables

Table 1

Summary of the stellar parameters of SDSS J102915+172927 obtained in previous literature studies and for the hydrodynamic models used in this work.

In the text
Table 2

One-dimensional (non-)LTE abundance (A(X), see Eq. (3)) sensitivity to the uncertainties on Teff log ɡ, and υmic.

In the text
Table 3

Summary of the computed abundances (A(X), see Eq. (3)) and upper limits as well as the 3D plus non-LTE values from Caffau et al. (2012).

In the text
Table B.1

Atomic data for all the spectral lines used in this study.

In the text

All Figures

thumbnail Fig. 1

Temperature heat map of the Stagger model with its corresponding average (3D) of all vertical columns over optical depth. The 〈3D〉 model is shown as a red dashed line and the 1D MARCS temperature stratification is shown in blue.
In the text
thumbnail Fig. 2

One-dimensional non-LTE Fe I abundances for each visible line in the spectrum interpolated to a microturbulence of υmicro = 1.48 km s−1. The blue line shows the best linear fit through the data, while the red dashed line denotes the mean non-LTE abundance. The black solid line denotes the cut-off in reduced equivalent width between saturated and non-saturated lines: log[Wλ/λ0] < −4.95.
In the text
thumbnail Fig. 3

UVES spectrum zoomed in on the NH-band at 3360 Å. The synthetic spectrum corresponding to the upper limit derived in this work is shown in blue, the UVES spectrum in black and the upper limit from Caffau et al. (2012) is shown in red. The Ti II at 3361.2 Å was excluded from the χ2-analysis.
In the text
thumbnail Fig. 4

CH G-band at 4300 Å. The Fe I at 4307.9 Å was excluded from the χ2-analysis.
In the text
thumbnail Fig. 5

Upper limits on [C/Fe] for SDSS J102915+172927. The 1D LTE and 3D LTE results are shown as triangles and squares, respectively, for the original limits (Caffau et al. 2012, red) and the results of this work (blue). For comparison, we show the [C/Fe] abundance for a sample of metal-poor stars from the SAGA database (Suda et al. 2008, black circles) and the cut-off for carbon-enhancement at [C/Fe] = 0.7 (dotted line) from Aoki et al. (2007).
In the text
thumbnail Fig. 6

Visualisation of the STARFIT fitting analysis for all models with . The top panel shows the 3D non-LTE abundances (red squares) together with all the best-fitting supernovae models (grey lines), and the best fit (blue line). The bottom panel shows the progenitor mass and explosion energy for the same best-fitting models shown in the top panel along with their respective values.
In the text
thumbnail Fig. 7

Impact of progenitor mass on the supernova yields as compared to the best-fitting model. Three-dimensional non-LTE abundances from this paper are shown as red squares together with the best-fitting progenitor supernova model in blue and three other models with a higher progenitor mass in grey: M = 50, 70, 100 M⊙, E51 = 0.3 and fmix = 0.25.
In the text
thumbnail Fig. 8

Similar to Fig. 5 but for the mean [α/Fe] abundance.
In the text
thumbnail Fig. A.1

Overview of the values from the upper limit analysis described in Sect. 3.2. Th top panel corresponds to the different synthetic spectra of CH and the bottom panel to NH. The red star represents the interpolated abundance where , which is also highlighted with a vertical dashed line.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.