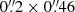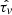EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A88 Full HTML
Highlight
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A88
Number of page(s) 17
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202346159
Published online 11 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Spectroscopically confirming galaxies formed within the first few hundred million years after the Big Bang, and understanding their nature and evolution, represents one of the biggest challenges of modern astrophysics, and one of the main drivers behind the James Webb Space Telescope (JWST). Probing the formation of some of the very first galaxies helps establish the epoch of first light in the Universe, that is to say, the timescales of the formation of the first stars, bringing an end to the so-called cosmic Dark Ages. Deep spectroscopic follow-up with NIRSpec of some of the highest-redshift galaxy candidates has already yielded spectroscopic confirmations via a clear detection of the Lyman break in four galaxies at z > 10 (Curtis-Lake et al. 2023; Robertson et al. 2023).

The onset of the first star formation began the process of re-ionising the intergalactic medium (IGM), although the exact details of this re-ionisation are still uncertain. Observations of Lyman-α emission and absorption provide strong constraints on how and when the diffuse gas in the IGM transitions from neutral to ionised (see Robertson 2022 for a review). An important observation is the decrease in the Lyman-α emission line equivalent width with increasing redshift above z = 6 (Stark et al. 2010; Schenker et al. 2014; Caruana et al. 2014; Jung et al. 2020), consistent with stronger absorption from an increasingly neutral IGM. However, this picture was largely based on moderate-luminosity galaxies. Luminous galaxies at 7.5 < z < 9 often show Lyman-α emission (Zitrin et al. 2015; Oesch et al. 2015; Stark et al. 2017; Larson et al. 2022; Finkelstein et al. 2013; Roberts-Borsani et al. 2016; Jung et al. 2019; Song et al. 2016), a redshift where quasar damping wing studies suggest the IGM is significantly neutral (xHI ∼ 0.5; Greig et al. 2017; Davies et al. 2018; Wang et al. 2020). This indicates that around luminous (and potentially massive) galaxies, Lyman-α escapes more easily, perhaps as a result of ionised bubbles that grew early in overdense regions (Endsley & Stark 2022; Jung et al. 2022; cf. Saxena et al. 2023). Another possible Lyman-α escape mechanism is through resonant scattering, with high velocity neutral gas (perhaps associated with outflows) redshifting the photons to lower frequencies at which they are no longer absorbed by the intervening neutral IGM (Dijkstra 2014; Mason et al. 2018a). Deep spectroscopy with JWST is vastly increasing our knowledge in this area, both by detecting rest-frame optical lines of known Lyman-α emitters to derive systemic redshifts and details of nebular physical conditions, and by detecting Lyman-α further into the re-ionisation epoch than has been possible from the ground (e.g., Tang et al. 2023).

Before the launch of JWST, the most distant galaxy with a tentative but plausible spectroscopic redshift was GN-z11 (Oesch et al. 2016). It was first selected as a likely high-redshift Lyman break candidate through multi-colour imaging with the Hubble Space Telescope (HST; Bouwens et al. 2010; Oesch et al. 2015), and subsequent HST/WFC3 slitless grism spectroscopy revealed a possible Lyman break in the continuum (Oesch et al. 2016), yielding a redshift of zgrism = 11.09. With an apparent H160 magnitude of 26.0 ± 0.1, GN-z11 is remarkably bright, up to three more luminous than the characteristic rest-UV luminosity (L⋆) measured from luminosity functions at z ∼ 6 − 8 (e.g., Finkelstein & Ryan 2015; Bouwens et al. 2015). Using Spitzer/IRAC fluxes, Oesch et al. (2016) estimated its stellar mass to be M⋆ = 109 M⊙, indicating a rapid buildup of stellar mass in the very early Universe.

Through ground-based near-infrared spectroscopy using MOSFIRE on the Keck Telescope, the redshift of GN-z11 was further refined by Jiang et al. (2021) via the possible detection of the [C III]λ1907+ C III]λ1909 doublet, yielding a redshift of z = 10.957. If real, the intense C III] emission line might originate partly due to an active galactic nucleus (AGN) hosted by the galaxy, or due to rapid carbon enrichment (Jiang et al. 2021).

Given the unique nature of this source and the low signal-to-noise ratio (S/N) of existing continuum break and emission line detections of this galaxy, NIRSpec on JWST now offers a chance to confirm its true distance and nature through high S/N detections of multiple rest-UV and optical emission lines as well as its bright continuum. Several diagnostics that rely on the ratios and strengths of rest-UV and optical emission lines can help differentiate between photoionisation due to AGN or star formation alone, and further help characterise the ionisation conditions in the interstellar medium (ISM) of this remarkably luminous distant galaxy.

In this paper we report an unambiguous spectroscopic redshift of z = 10.6034 for GN-z11 using deep NIRSpec observations in the GOODS-North field via the robust detection of several emission lines, including N IV] λ 1486, N III]λλ1747, 1749, [C III]λ1907+ C III]λ1909, [O II] λλ3726, 3729, [Ne III] λλ3869, 3967, Hδ, and Hγ. Although the measured redshift is lower than previously reported in other work, this still places GN-z11 as comfortably the most luminous source currently confirmed at z > 10. This galaxy is given the designation JADES-GN-z10-0 in the JWST Advanced Deep Extragalactic Survey (JADES) spectroscopic database, but for the remainder of this paper we use the more familiar name GN-z11. The photometric properties from our JWST/NIRCam imaging are reported in a companion paper (Tacchella et al. 2023).

The layout of this paper is as follows. In Sect. 2 we describe our JWST/NIRSpec observations of GN-z11 and the data reduction strategies adopted. In Sect. 3 we present the 1D and 2D spectra of GN-z11 and emission line measurements and discuss the inferred physical properties. In Sect. 4 we conclude and summarize our findings. Throughout this work, we assume the Planck 2018 cosmology (Planck Collaboration VI 2020) and the AB magnitude system (Oke & Gunn 1983).

2. Observations

The NIRSpec observations of GN-z11 were taken as part of JADES, a collaboration between the Instrument Science Teams of NIRSpec and NIRCam to study galaxy evolution out to high redshifts through imaging and spectroscopy in the two GOODS fields. The Guaranteed Time Observations presented here are part of programme ID 1181 (P.I.: D. Eisenstein), with spectroscopic targets based on pre-JWST data, largely HST imaging.

Our observations of GN-z11 were taken on UT 5 and 7 February 2023, using NIRSpec (Jakobsen et al. 2022) in its microshutter array (MSA) mode (Ferruit et al. 2022). The MSA comprises four arrays of 365 × 171 independently operable shutters, each covering 98″ × 91″ on the sky. GN-z11 was targeted in four independent MSA configurations. Each configuration acquired 3100 s of integration in each of the medium-resolution G140M/F070LP, G235M/F170LP, and G395M/F290LP grating–filter combinations (with resolving power R ≈ 1000 and combined spectral coverage over 0.7 − 5.3 μm) and 6200 s in the low-resolution PRISM/CLEAR mode (with R ∼ 100 and continuous coverage 0.7 − 5.3 μm). Targets were assigned three shutter slitlets, with the targets nodded into each of the three shutters during the observing sequence to facilitate background subtraction. As GN-z11 was one of our highest priority targets, we ensured that its spectra did not overlap with other targets, even for the gratings (where the spectra are more extended on the detector than the low-dispersion prism). Individual integrations used the NRSIRS2 readout mode with 14 groups (1035 s each) to limit correlated readout noise. In total our integration time was 3.45 h in each of the three gratings, and 6.9 h in the prism.

These observations were processed with algorithms developed by the ESA NIRSpec Science Operations Team and the NIRSpec GTO Team. We refer the reader to Cameron et al. (2023) for more details of the processing. We note that for the G140M/F070LP grating–filter combination we extended the calibration of the spectrum up to 1.84 μm, taking into account the transmission filter throughput beyond the nominal wavelength range of this configuration (0.70 μm–1.27 μm). Since GN-z11 is at z > 10 with no flux at wavelengths below Lyman-α, there is no second order light to overlap with the extended wavelength range of 1.27 μm–1.84 μm. Wavelength-dependent path-loss corrections were made based on the object position within the shutter and modelling the galaxy as a point-like source. GN-z11 is very compact, so this is a good approximation. In all four of the configurations, GN-z11 was located not more than 40% of the illuminated slit width or slit height from the centre along either axis of the 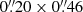0 . ″ 20 × 0 . ″ 46 $ 0{{\overset{\prime\prime}{.}}}20\times 0{{\overset{\prime\prime}{.}}}46 $ slitlet, and Fig. 1 shows the locations of the open areas of the microshutters overlaid on the NIRCam F200W image of GN-z11. Individual calibrated 1D and 2D spectra were combined excluding bad pixels by using an an iterative sigma clipping algorithm at the 3σ level. The wavelength calibration takes into account the position of the galaxy within the slit at each pointing. Before the combination process a spatial median of each exposure is subtracted to remove any residual background. 1D spectral extractions were made from the rectified 2D spectra using box extractions of height 3 and 5 pixels ( 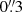0 . ″ 3 $ 0{{\overset{\prime\prime}{.}}}3 $ and 0 . 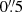″ 5 $ 0{{\overset{\prime\prime}{.}}}5 $, respectively).

thumbnail Fig. 1.

NIRCam F200W image of GN-z11 (see Tacchella et al. 2023) with the NIRSpec microshutters overlaid for the four different pointings. The green rectangles denote the illuminated region of each microshutter ( 0 . ″ 2 × 0 . ″ 46 $ 0{{\overset{\prime\prime}{.}}}2 \times 0{{\overset{\prime\prime}{.}}}46 $). North is up and east to the left, and the image is 1.5 arcsec per side. The flux density units on the colour bar are MJy/sr.

3. Results

Our NIRSpec spectra of GN-z11 show a well-detected continuum in the prism (Fig. 2) where we have S/N > 20 per spectral resolution element at wavelength above Lyman-α and out to ∼3 μm. We also see the continuum at lower S/N in the medium-resolution gratings (Figs. 3 and B.1). A strong spectral break at Lyman-α is observed, with no significant flux at shorter wavelengths. We have robust detections of several emission lines, most of which are seen in both the prism (Fig. 2) and grating (Fig. 3) spectra (Table 1). We also see evidence of interstellar absorption lines, but in this paper we focus on the emission lines properties.

thumbnail Fig. 2.

2D (top) and 1D (bottom) spectra of GN-z11 using the PRISM/CLEAR configuration of NIRSpec. The 1D spectrum has been extracted using a 3-pixel-wide aperture that leads to improved S/N in this highly compact object. Prominent emission lines present in the spectra are marked. The S/N of the continuum is high, and the emission lines are clearly seen in both the 1D and 2D spectra.

thumbnail Fig. 3.

Gallery of the most prominent emission lines seen in the GN-z11 spectrum from the medium resolution (R1000) gratings using a 3-pixel 1D spectral extraction.

Table 1.

Emission line fluxes (in units of ×10−19 erg s−1 cm−2) detected in the prism (R ∼ 100) and grating (R ∼ 1000) spectra.

In the subsections below, we use the spectrum of GN-z11 to infer physical properties. As well as using empirical diagnostics from the emission line fluxes and ratios, we also use the BEAGLE Bayesian spectral energy distribution (SED) fitting code (Chevallard & Charlot 2016) on our full prism spectrum, the exact details and results are presented in Table 2 and in Appendix A.

Table 2.

GN-z11 physical parameters from BEAGLE SED fitting of the prism spectrum.

3.1. Emission lines and redshift determination

The full list of detected lines is given in Table 1. Line wavelengths are measured from the grating spectra because they have higher resolution resulting in less blending and more accurate line centroids. Line fluxes are measured from both the prism and gratings, and we discuss the relative flux calibration between the two in Appendix C. We perform a cubic-spline fit to the continuum in the prism (excluding the emission lines from the fit), and use this to subtract the continuum level in both the prism and the grating spectra (since the continua in the grating spectra have low S/N). We then fit each emission line with a single Gaussian model, except for blended lines (noted in Table 1) where we measure the total flux of the complex. The uncertainty is computed taking into account the Poisson counting statistics and the readout noise. This is preferred to taking the intra-pixel standard deviation in counts in the spectrum, which would underestimate the true noise since the pixels are sub-sampled and interpolated from their native size by the data reduction pipeline and hence the noise is correlated. One emission line, N IV] λ 1486, falls in the spectral coverage of both the G140M and G235M gratings, and we report both measurements in Table 1. The wavelength and flux of this line are consistent between the gratings within the uncertainties.

In determining the redshift from the vacuum rest-frame wavelengths, we exclude Lyman-α (which has a velocity offset; see Sect. 3.3), Mg II (which is only significantly detected in the low-resolution prism) and He Iλ3889 (which is blended with Balmer-8). A weighted fit of the remaining 8 well-detected emission lines (S/N > 5) from the grating spectra give a redshift z = 10.6034 ± 0.0013, where we assume a [C III] λ1907/C III]λ1909 doublet ratio of 1.5 for these spectrally-unresolved lines.

The redshift we measure is considerably lower than the previously reported redshift values of 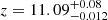z= 11.09 −0.012 +0.08 $ z = 11.09 ^{+0.08}_{-0.012} $ from HST grism (Oesch et al. 2016) and z = 10.957 ± 0.001 from Keck MOSFIRE (Jiang et al. 2021). The 2D HST grism observation shows flux down to the wavelength we measure for the Lyman break (1.41 μm), but due to noise fluctuations their fitted model break was at a longer wavelength of 1.47 μm. The Keck MOSFIRE redshift was based on possible detections of the [C III] λ1907 and C III]λ1909 lines at 2.2797 μm and 2.282 μm respectively, at 2.6σ and 5.3σ. We do not find any significant emission lines at these observed wavelengths in our data, where they would have been detected at 20σ and 40σ for the line fluxes quoted in Jiang et al. (2021). Instead, we do detect C III] but at a shorter wavelength consistent with our measured z = 10.603.

3.2. Is GN-z11 an AGN?

GN-z11 has a compact morphology and the continuum spatial extent in our NIRSpec 2D spectroscopy is barely resolved. In a companion paper, Tacchella et al. (2023) analyse JADES NIRCam imaging data and derive the best size constraint so far, finding an intrinsic half-light radius of only 0.016 ± 0.005″ (64 ± 20 pc). The possibility of a significant point source contribution to the total flux leaves open the question of whether some of the light originates from an AGN. Our data do contain several high ionisation lines, and we wish to explore the excitation mechanism.

We have detected a large number of emission lines of varying ionisation potential in GN-z11. In particular the N IV] λ1486 line (ionisation potential E > 47.5 eV) is often a signature of an AGN, although it has been seen in some high-redshift star forming galaxies (e.g., Fosbury et al. 2003 and McGreer et al. 2018) and it is detected in 6 of 44 galaxies in the low-redshift CLASSY survey (Mingozzi et al. 2022). N IV] λ1486 or N III] λ1748 is seen in 1% of SDSS quasars at 1.7 < z < 4.0 (Jiang et al. 2008). Vanzella et al. (2010) detected N IV] λ1486 in an object at z = 5.6 that may be an AGN, although Raiter et al. (2010) are able to model this spectrum with stars. For GN-z11, the higher ionisation nitrogen line N V (E > 77.5 eV), which is a clear signature of AGN activity, is undetected in the G140M grating (where the 3σ sensitivity is 4 × 10−19 erg cm−2 s−1), and is blended with Lyman-α continuum break at the prism resolution.

We note that in the prism (R ∼ 100) spectrum we see prominent emission features arising from blended He II and [O III] λλ1660, 1666 lines, as well as a P-Cygni type feature from C IV (see Fig. 3), with redshifted emission and blueshifted absorption relative to the systemic redshift. C IV emission with a P-Cygni-like profile is also detected in the grating, along with a low S/N tentative detection (3σ) of He II and [O III] λλ1660, 1666.

The reliable detection of C III] and N III] lines in the grating spectra, however, enables us to investigate rest-UV line ratios that can be compared with predictions from photoionisation models to differentiate between an AGN or a star formation origin (e.g., Feltre et al. 2016). In Fig. 4 we plot the line ratios C III] λ 1909/He IIλ1640 versus C III] λ 1909/C IVλλ1548, 1550, along with predictions from photoionisation models of Feltre et al. (2016) for type 2 AGN, and Gutkin et al. (2016) for star formation. We consider a density range of log10(nH/cm−3) range of 2 − 4, and metallicities in the range Z = 0.001 − 0.002, corresponding to Z/Z⊙ = 0.066 − 0.131 (based on Z⊙ = 0.0152 assumed by Feltre et al. 2016), which is consistent with the gas-phase metallicity inferred from SED fitting using BEAGLE (Appendix A), and the estimates from emission line ratios in Sect. 3.5.

thumbnail Fig. 4.

Measured C III]/He II versus C III]/C IV ratios for GN-z11 shown along with predictions from photoionisation due to AGN (circles) and star formation (stars) from Feltre et al. (2016) and Gutkin et al. (2016) in the range of Z/Z⊙ = 0.066 − 0.131 and gas densities in the range log10(nH)/cm−3 = 2 − 4. Based on the observed line ratios, neither photoionisation from AGN nor star formation alone can conclusively explain the observations, placing GN-z11 right between the model predictions from the two.

We find that neither AGN nor star forming galaxy model predictions are able to conclusively explain the observed line ratios in GN-z11. As previously noted, there is C IV absorption visible in the spectrum, blueshifted from the systemic redshift. However, it is unclear how much of the nebular component of the C IV line flux is being attenuated by this blueshifted absorption as there is not enough S/N in the grating to disentangle the nebular and stellar components of C IV. If a significant amount of nebular C IV emission is also being absorbed, then the data point would move downwards on the y-axis in Fig. 4.

Additionally, using the C III] and He II based diagnostics from Nakajima et al. (2018), we find that the observed strength of C III] emission and the C III]/He II ratio once again lie between photoionisation model predictions due to type-2 AGN and star formation. Nakajima et al. (2018) found a parameter space in their diagnostic plots where both AGN and star-forming models could overlap due to low metallicities and high C/O ratios, which is where the measurements from GN-z11 suggest it could lie. We note that when considering the photoionisation models of Nakajima & Maiolino (2022), the limit on C III]/C IV we derive is compatible with the envelope of expectations from AGN over a range of metallicities.

A ratio of N III]/He II ≈ 3.3 is consistent with photoionisation due to star formation (e.g., Hirschmann et al. 2019), and interestingly, no type 2 AGN scenario in the models of Hirschmann et al. (2019) predicts a N III]/He II ratio greater than 1. Composite models containing contribution from both AGN and star formation can achieve N III]/He II ratios ∼1, but only star formation is favoured at ratios > 1.

Overall, we find that the C III] and N III] emission and their ratios with respect to He II and C IV do not obviously favour photoionisation due to AGN. However, the presence of other rare lines (e.g., N IV]) that have previously been observed in the spectra of AGN makes ruling out the presence of an AGN less obvious (see Übler et al. 2023, for example). Given the expected extreme nature of GN-z11, together with a lack of any observational insights into the expected spectroscopic properties of AGN at z > 10, we are unable to draw definitive conclusions about the dominant source of photoionisation in GN-z11.

Finally, we note that the grating spectra do not show obvious evidence for the presence of a broad component of permitted lines (see Fig. 3), which would be ascribed to the broad line region (BLR) of an AGN. This is not necessarily conclusive proof against the AGN scenario, as the BLR is often obscured along our line of sight in most AGN; however, it is another element consistent with the lack of dominant contribution from an AGN.

3.3. Lyman-α emission

The prism spectrum shows a near-total Gunn-Peterson trough at wavelengths below Lyman-α, consistent with a highly neutral intervening IGM (Gunn & Peterson 1965). Although the spectral break is fairly sharp in wavelength at the low dispersion of the prism, we do see some evidence of a damping wing absorption.

In spectra from the bluest G140M grating, an emission line is seen at 14 132 Å, close to the sharp Lyman break observed with the prism. Taking the systemic redshift of GN-z11 to be z = 10.6034 (see Sect. 3.1), the rest-frame wavelength is 1217.92 Å, consistent with being Lyman-α in emission, but with the line centroid redshifted by 555 ± 32 km s−1 (see Fig. 5). This emission line is seen in all 12 of the individual G140M grating exposures (in each of the three nod positions in the four MSA configurations), and is > 10σ in the combined grating spectrum.

thumbnail Fig. 5.

Velocity offset of the Lyα emission line (blue solid line) compared with the Hγ line (dashed green line). The Lyα line is redshifted by 555 km s−1 compared to the redshift derived from other emission lines in the spectrum.

Figure 6 shows a close-up of the G140M spectral region around Lyman-α. There is zero transmitted flux shortwards of the systemic Lyman-α wavelength. Any such flux would require an ionised bubble around the galaxy, but the lack of such flux rules out an optically thin H II region around GN-z11 (e.g., Mason & Gronke 2020). The redshifted line is well approximated by a Gaussian, without significant asymmetry. We measure a full width half maximum (FWHM) of 566 ± 61 km s−1, which is extended beyond the instrumental line spread function of ≈200 km s−1 (de Graaff et al., in prep.) for a compact source in the G140M grating at this wavelength. Removing the line spread function in quadrature suggests an intrinsic velocity spread of δvFWHM = 530 ± 65 km s−1.

thumbnail Fig. 6.

Zoom in on the Lyα emission line in the G140M 1D (lower) and 2D (upper) spectra. The dashed grey line shows the systemic wavelength of the Lyα transition. The histograms (top left) of the Lyα spatial profile (yellow) and that of the continuum (blue) show the Lyα emission from GN-z11 is more extended towards the south-west (up in the MSA shutter in this view).

In the 2D spectrum of Fig. 6 it is apparent that the Lyman-α emission is more spatially extended than the continuum. Whilst the continuum flux is largely contained within 2 pixels (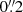 0 . ″ 2 $ 0{{\overset{\prime\prime}{.}}}2 $), as expected based on the small size measured in our NIRCam imaging presented in Tacchella et al. (2023), the Lyman-α emission extends further to the south-west. The Lyman-α extension beyond the continuum is at least 2 pixels, corresponding to an extra 0.8 kpc. We note the Lyman-α could extend further since the MSA shutters are only 5 pixels high, so beyond this region there is self-subtraction, but a visual check of the 2D spectrum without background subtraction did not show Lyman-α in neighbouring shutters. A similar check on the extent of other well-detected lines in the grating spectra ([O II] and Hγ) shows that these lines have the same spatial profile as their nearby continuum.

The fact that Lyman-α is spatially extended is a remarkable result, which may be suggestive of a Lyman-α halo. The presence of such haloes around individual star-forming galaxies has been reported at lower redshifts (e.g., Rauch et al. 2008; Wisotzki et al. 2016; Leclercq et al. 2017; Kusakabe et al. 2022) and we may be seeing the gas in the circum-galactic medium, from Lyman-α fluorescence or shock heating.

Using a 3 pixel (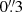 0 . ″ 3 $ 0{{\overset{\prime\prime}{.}}}3 $) extraction aperture, the measured Lyman-α flux is (1.51 ± 0.15)×10−18 erg s−1 cm−2, with a rest-frame equivalent width (with respect to the continuum longwards of the Lyman-α break) of EW0 = 12 Å. Using a larger ‘full-shutter’ extraction aperture of height 5 pixels ( 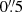0 . ″ 5 $ 0{{\overset{\prime\prime}{.}}}5 $) gives a significantly higher flux of (2.30 ± 0.19)×10−18 erg s−1 cm−2, and the rest-frame equivalent width rises to EW0 = 18 Å. The emission line flux of Lyman-α is about twice that of Hγ (the strongest Balmer line we detect). From Case B recombination and assuming no dust as found from the Balmer line ratio, Lyman-α would have about 50 times the line flux of Hγ, so it appears to be suppressed by about a factor of 26 (i.e. fesc, Lyα = 0.038 ± 0.004), presumably through resonant scattering effects.

The discovery of Lyman-α emission at such high redshifts is remarkable, given the expected highly neutral IGM at this epoch so much earlier than the end of re-ionisation at z ≈ 6 (Fan et al. 2001). However, perhaps this result is not so surprising when one considers the high rate of Lyman-α detection in luminous 7.5 < z < 9 galaxies (Zitrin et al. 2015; Oesch et al. 2015; Stark et al. 2017; Larson et al. 2022; Finkelstein et al. 2013; Roberts-Borsani et al. 2016; Jung et al. 2019; Song et al. 2016) at redshifts prior to complete re-ionisation. GN-z11 is a similarly luminous galaxy with MUV = −21.5 so the effects that make Lyman-α detectable in such galaxies (see Mason et al. 2018a) may be at play for GN-z11.

There are two aspects of our Lyman-α observations that may explain the significant transmission of fesc, Lyα = 0.04. Firstly, the large velocity offset of 555 ± 32 km s−1 and rest-frame equivalent width are similar to those measured in luminous 7.5 < z < 9 galaxies with Lyman-α (Fig. 7; see also Tang et al. 2023). Large velocity offsets are key to the escape of Lyman-α photons from galaxies in a highly-neutral IGM. Since the damping wing of the IGM and proximate H I will absorb photons close to the resonant frequency, photons that escape must resonantly scatter in the wings. Those that scatter far enough to the red may then be able to escape the system without being absorbed (Dijkstra 2014). We note that the infall motion of the neutral gas around galaxies may also play a role (Santos 2004; Sadoun et al. 2017; Weinberger et al. 2019; Park et al. 2021; Smith et al. 2022). If the peculiar velocity of neutral gas near a Lyman-a source is infalling, then even photons redwards of the Lyman-α will be resonantly absorbed, necessitating large velocity offsets of Lyman-α to facilitate its escape.

thumbnail Fig. 7.

Lyman-α velocity offset (ΔvLyα) versus MUV for GN-z11 (star) and other high-redshift galaxies, colour-coded by Lyman-α equivalent width. We overplot data of z > 6 galaxies with ground-based observations from the literature (Cuby et al. 2003; Pentericci et al. 2011, 2016, 2018; Vanzella et al. 2011; Willott et al. 2013, 2015; Maiolino et al. 2015; Oesch et al. 2015; Stark et al. 2015, 2017; Furusawa et al. 2016; Knudsen et al. 2016; Carniani et al. 2017; Laporte et al. 2017; Mainali et al. 2017; Hashimoto et al. 2019; see Endsley et al. 2022 and the Table 4 therein) in circles, and Lyα emitting galaxies at z ∼ 7 − 9 from CEERS NIRSpec observations (Tang et al. 2023) in squares. The prediction of the correlation between the Lyα velocity offset and MUV at z = 7 from Mason et al. (2018b) is shown by the dashed grey line. GN-z11 has properties similar to the Lyα-emitting galaxies at z ∼ 7 − 9.

Additionally, the intense star formation in luminous galaxies will be driving powerful and fast-moving outflows. Outflows on the far side of the galaxy may provide a redshifted medium from which the photons can backscatter to our line of sight with the required velocity offset. In this context, our observation of spatially extended Lyman-α emission to the south-west suggests that if an outflow is present, it would extend in the north-east direction.

3.4. Rest-frame UV properties of GN-z11

From our low-dispersion prism spectra, where we have high S/N detection of the continuum, we measure a UV spectral slope of β = −2.36 ± 0.10 (over the range λrest = 1500 − 2600 Å), consistent with that of β = −2.4 reported from our NIRCam imaging in Tacchella et al. (2023). We measure a luminosity of 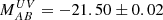M AB UV = − 21.50 ± 0.02 $ M^{UV}_{AB}=-21.50\pm 0.02 $ over the range λrest = 1400 − 1600 Å (adopting a luminosity distance of 113,148.8 Mpc from our chosen cosmology). This corresponds to a luminosity density of 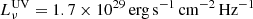L ν UV = 1.7 × 10 29 erg s − 1 cm − 2 Hz − 1 $ L_{\nu}^{\mathrm{UV}}=1.7\times 10^{29}\,\mathrm{erg}\,\mathrm{s}^{-1}\,\mathrm{cm}^{-2}\,\mathrm{Hz}^{-1} $ around λrest = 1500 Å.

The rest-UV will be potentially affected by dust reddening. However, from the prism spectrum, we measure a Balmer line ratio using Hδ/Hγ of 0.53 ± 0.06, which is very close and within the errors of the intrinsic ratio of 0.55 expected in an H II region with electron density ne = 300 cm−3 and temperature Te = 15 000 K, conditions expected in very high-redshift galaxies (e.g., Curti et al. 2023; Katz et al. 2023; Isobe et al. 2023). We note that the wavelength baseline between Hδ and Hγ is short, so does not provide a large lever arm to quantify the dust attenuation accurately, and also that the Hδ/Hγ ratio of the fluxes from our 3-pixel medium grating spectrum is 0.68 ± 0.20, above the case B value of 0.55 but consistent within the errors. Our full-SED BEAGLE fits to the prism spectrum, assuming that this is a star-forming galaxy rather than an AGN, also suggest low attenuation (AV ≈ 0.17, only 70% of which is from dust outside H II regions affecting nebular emission). Therefore, from the observed Balmer decrement and SED fitting we do not measure any considerable dust attenuation or reddening in the spectrum of GN-z11.

We now turn to the production and potential escape of ionising photons in GN-z11. We can potentially constrain the escape fraction of ionising photons (fesc) by looking at how many produce local recombinations (as tracked by the hydrogen Balmer emission lines), compared with the total number produced. Zackrisson et al. (2017) provide tracks of the rest-UV spectral slope (β, which is related to the hardness of the spectrum and hence the production of ionising photons) and the equivalent width of Hβ. Although we do not measure Hβ in GN-z11, as it is beyond our spectral range, we can use the continuum slope we measure (β ≈ −2.4) along with the flux in Hγ and the case B ratio (appropriate if fesc is low) of Hγ/Hβ = 0.468 to estimate log10(EW(Hβ)/Å) = 1.8. From the plots of Zackrisson et al. (2017), this high Hβ equivalent width suggests a low escape fraction of fesc ≲ 0.1. Our BEAGLE SED fits also yield a low 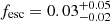f esc = 0 . 03 − 0.02 + 0.05 $ f_{\mathrm{esc}}=0.03^{+0.05}_{-0.02} $. We do not see strong evidence for a ‘reverse Balmer break’ in our NIRSpec spectra, which might be expected from nebular continuum if the escape fraction is indeed low, although in the best-fit BEAGLE SED the reverse Balmer break is small. Conversely, we also see no evidence for a Balmer break that would be indicative of a moderately evolved stellar population. This is consistent with the very young age determined by the BEAGLE SED fitting (t ∼ 19 Myr), with the light in the rest-frame UV and blue wavelengths we probe being completely dominated by a young stellar population.

Additional constraints on fesc could potentially be derived from the presence of Mg IIλλ2795, 2802 emission in the prism spectrum (e.g., Chisholm et al. 2020). The considerable rest-frame equivalent width of 12 Å for Mg II might suggest the presence of ionised channels in the galaxy, potentially facilitating the escape of ionising radiation and Lyman-α. Similar to Lyman-α, the resonant nature of Mg II routinely causes strong absorption by low-ionisation gas, while pure Mg II emission is thought to indicate a porous ISM (Feltre et al. 2018; Henry et al. 2018; Witstok et al. 2021). Following the predicted relationship in Witstok et al. (2021) between the strength of Mg II and the [Ne III] and [O II] lines, we estimate an intrinsic Mg IIλ2795 flux of 3.1 × 10−19 erg s−1 cm−2. This results in a Mg II escape fraction of fesc,Mg II ∼ 60% under the assumption of a typical doublet ratio of F2795/F2802 ≈ 1.7 (which itself depends on fesc,Mg II and the dust content; Chisholm et al. 2020). This is much larger than the estimated Lyman-α escape fraction, and also larger than the fesc inferred above from the equivalent width of the Balmer lines and the BEAGLE SED fitting. However, it has been suggested that Mg II escape could be more sensitive to dust rather than fesc particularly for galaxies in the optically thick regime, which may explain the discrepancy between the escape fractions measured from Balmer emission and Mg II (e.g., Katz et al. 2022).

We now consider the production of ionising photons, under the assumption of a low escape fraction fesc as discussed above, and compare these with the non-ionising UV continuum detected. In case B, f(Hα)/f(Hγ) = 6.11, and 45% of recombinations result in an Hα photon being emitted (Osterbrock & Ferland 2006). We take the observed Hγ line flux to be 1.2 × 10−18 erg s−1 cm−2 from the 5-pixel extraction of the prism spectrum (since the agreement of the flux calibration with the NIRCam imaging is better than for the grating, Appendix C). We make the assumption of no dust attenuation to obtain a hydrogen ionising photon production rate of Nion = 8.8 × 1054 photons s−1. This gives an ionising photon production efficiency of 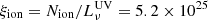ξ ion = N ion / L ν UV =5.2× 10 25 $ \xi_\textrm{ion} = N_\textrm{ion} / L_{\nu}^\mathrm{UV} = 5.2\times 10^{25} $ erg−1Hz. This value log10ξion = 25.7 agrees with that from the BEAGLE SED fitting log10ξion = 25.67 ± 0.02, and has higher ionising efficiency than galaxies at much lower redshifts (e.g., Chevallard et al. 2018 find log10ξion = 25.2 − 25.8 in extreme galaxies at z ∼ 0, whereas Bouwens et al. 2016 find log10ξion = 25.3 in sub-L* galaxies at z = 4 − 5) but is comparable with that seen in z ∼ 7 − 8 galaxies (e.g., Tang et al. 2023 who find log10ξion = 25.7 − 26.0).

Although we have not ruled out an AGN component of GN-z11, we can place upper limits on the star formation rate based on the assumption that the observed line emission is powered solely by star formation. From the rate of ionising photons, we can estimate the star formation rate subject to assumptions about the star formation history and initial mass function (IMF) of stars. Using the Kennicutt (1998) relation, SFR = 1.08 × 10−53(Nion/s−1) M⊙ yr−1 assuming a Salpeter (1955) IMF, gives a star formation rate of 90 M⊙ yr−1. For a Chabrier (2003) IMF the star formation rate is 54 M⊙ yr−1 from the Kennicutt (1998) relation. Using the more recent Hα-based relation from Reddy et al. (2018), which is more representative of the conditions found in galaxies at high redshifts, we obtain a star formation rate of 35 M⊙ yr−1 again assuming Chabrier (2003) IMF with an upper mass cut-off of 100 M⊙. Out BEAGLE fit has a star formation rate of ∼19 M⊙ yr−1 for a Chabrier IMF with a higher upper-mass cut-off of 300 M⊙. Using an upper-mass cut-off of 100 M⊙ reduces the number of ionising photons per unit star formation rate to 62%, bringing the star formation rate to 31 M⊙ yr−1, in agreement with the star formation rate derived using the Reddy et al. (2018) conversion.

We can also potentially use the rest-frame UV continuum to infer the star formation rate (or an upper limit on this, if there is an AGN contribution to the rest-frame UV). Kennicutt (1998) give a relation 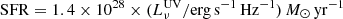SFR = 1.4 × 10 28 × ( L ν UV / erg s − 1 Hz − 1 ) M ⊙ yr − 1 $ \mathrm{SFR}=1.4\times 10^{28} \times (L_{\nu}^{\mathrm{UV}}/ {\mathrm{erg\,s}^{-1}\,\mathrm{Hz}^{-1})\,M_{\odot}\,\mathrm{yr}^{-1}} $ for a Salpeter IMF, which would translate to a star formation rate of 24 M⊙ yr−1 for GN-z11. However, this relation is probably inappropriate since it assumes constant star formation for 100 Myr, and GN-z11 is likely much younger, so the UV luminosity will still be increasing even if star formation is constant, causing the star formation rate to be underestimated.

3.5. ISM ionisation and enrichment

In this section we use line ratio diagnostics to explore the ionisation state and metal enrichment of the ISM, again under the assumption that the emission line fluxes are not dominated by an AGN contribution. We detect a number of collisionally excited metal lines, both of low ionisation ([O II]) and high ionisation (including N III], [Ne III], and C III]), as well as Balmer lines from hydrogen recombination. Our wavelength coverage does not extend to the widely used [O III] λ5007; however, we do have a robust detection of [Ne III] λ3869, which has a similar ionisation potential. Hence, we consider the line flux ratio [Ne III] λ3869 / [O II] λλ3726, 3729 as a probe of ionisation parameter (U) – [Ne III]/[O II] has been shown to track [O III]/[O II] well (e.g., Levesque & Richardson 2014; Witstok et al. 2021), which is the most widely used indicator of U. We measure [Ne III]/[O II] = 1.12 ± 0.13 from the 3-pixel grating extraction ([Ne III] λ3869 is blended in the prism), which is comparable to the redshift z ∼ 5.5 − 9.5 NIRSpec sample presented in Cameron et al. (2023) from our JADES survey, and also z ≳ 7 galaxies observed in the CEERS survey (Tang et al. 2023). Following the calibration set out in Witstok et al. (2021), this corresponds to an ionisation parameter of log10U = −2.03 ± 0.04. We find a similar value of log10U = −2.25 ± 0.97 from our BEAGLE SED fitting.

We report a marginal detection of the [O III] λ 4363 line in our prism spectrum (partially blended with Hγ; Fig. 3), which has already been observed in a number of z > 7 galaxies (e.g., Curti et al. 2023; Katz et al. 2023). Although this line can in theory be used to derive a Te-based (‘direct method’) metallicity, the absence of [O III] λ 5007 from our data means we cannot measure the temperature with the standard approach. The O III] λλ 1660,1666 / [O III] λ 4363 ratio can also be used as a temperature diagnostic, but the low significance of the [O III] λ 4363 coupled with the marginal detection of O III] λλ 1660, 1666 in our grating spectrum means that any derived temperature would be highly uncertain. Thus, we instead considered using strong-line ratios to constrain the metallicity of GN-z11. A widely used metallicity indicator is R23 (the log of the ratio of [O II]+[O III] to Hβ), but since [O III] λ5007 and Hβ fall beyond our spectral coverage, we cannot measure this ratio. We instead considered an analogous ratio of ([Ne III] λ3869 + [O II] λλ3727)/Hδ. All three of these emission lines are well detected in our grating spectra, and conveniently lie at very similar wavelengths, which minimises any uncertainties arising due to wavelength-dependent attenuation. We measure a ratio of log10(([Ne III] + [O II])/Hδ) = 0.50 ± 0.07 from the grating (3-pixel spectral extraction). Following the calibrations from Witstok et al. (2021; which provides [O III]/[Ne III] ≈15 at the derived ionisation parameter) and assuming Hδ/Hβ = 0.268, this would be equivalent to R23 ≈ 0.85. These values place GN-z11 in fairly close alignment with the median values presented in the Cameron et al. (2023) sample; their stacked spectra at z ∼ 6 (z ∼ 8) show R23 = 0.88 (0.86) and log10([Ne III]/[O II]) = 0.05 (0.04). According to the binned average relationships presented in Nakajima et al. (2022), this suggests a metallicity in the range 7.59 < 12 + log10(O/H) < 7.76, which corresponds to 0.08 − 0.12 Z⊙ assuming a solar abundance of 12 + log10(O/H)⊙ = 8.69. Our BEAGLE SED fitting yields a consistent value of Zneb = 0.12 ± 0.02 Z⊙.

In Fig. 8 we compare our [Ne III]/[O II] and ([Ne III]+ [O II])/Hδ measurements from GN-z11 (plotted separately from the prism and the grating data) with measurements from z > 5.5 galaxies from Cameron et al. (2023), z ∼ 0 galaxies from SDSS MPA-JHU catalogues1 (Aihara et al. 2011) and photoionisation model grids from Gutkin et al. (2016). This line-ratio diagram is analogous to the widely used R23-O32 ‘ionisation versus excitation’ diagram since, as described above, [Ne III]/[O II] traces ionisation and ([Ne III]+ [O II])/Hδ traces excitation of both the high- and low-ionisation metal ions.

thumbnail Fig. 8.

Line ratio diagram, showing ([Ne III]+[O II])/Hδ versus [Ne III]/[O II], featuring GN-z11. The yellow diamond denotes the line ratios derived from the medium-dispersion G395M grating, and the cyan diamond uses the low-dispersion prism spectrum (where we have corrected for the blending of [Ne III] λ3869 with He Iλ3889 using the flux ratio from the grating). The background grey 2D probability density function shows the subset of SDSS galaxies with 0.03 < z < 0.1 for which [Ne III] λ3869, [O II] λλ3726, 3729, and Hδ are all detected with S/N > 5. Purple squares show z > 5.5 galaxies from Cameron et al. (2023) after adjusting the reported ratios to be in terms of Hδ by assuming a fixed value of Hδ/Hβ = 0.268. Solid lines show model grids from Gutkin et al. (2016), plotted for nine different values of metallicity (Z/Z⊙ = 0.04, 0.07, 0.15, 0.30, 0.45, 0.60, 0.75, 1.0, 1.5), as indicated by the different colours, and seven values of the ionisation parameter, indicated by marker sizes, in steps of 0.5 from log10U = −4.0 (smallest) to log10U = −1.0 (largest).

The Gutkin et al. (2016) models in Fig. 8 demonstrate the two-valued nature of ([Ne III] λ3869 + [O II] λλ3727)/Hδ with metallicity. Although the S/N requirements significantly cut down the available SDSS sample, one can still see clear evidence of this two-valued relation. The z > 5.5 sample from Cameron et al. (2023) appears to follow an extrapolation of the low-metallicity (high-ionisation) branch of this two-valued sequence. We see that GN-z11 (diamond symbol) lies in good agreement with the sequence formed by these z > 5.5 galaxies. It falls between the Gutkin et al. (2016)Z/Z⊙= 0.07 and Z/Z⊙= 0.15 model lines, suggesting 12 + log10(O/H)≈7.7, and lies proximal to the model values with log10U = −2.0, consistent with the empirical values derived above.

We now consider where GN-z11 might fall on the mass-metallicity relation (see Maiolino & Mannucci 2019 for a review). The stellar mass estimated from BEAGLE of 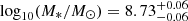log 10 ( M ∗ / M ⊙ ) = 8 . 73 − 0.06 + 0.06 $ \log_{10}(M_*/M_{\odot})=8.73^{+0.06}_{-0.06} $ is consistent with that derived from our NIRCam photometry of 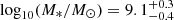log 10 ( M ∗ / M ⊙ ) = 9 . 1 − 0.4 + 0.3 $ \log_{10}(M_*/M_{\odot})=9.1^{+0.3}_{-0.4} $ presented in Tacchella et al. (2023), again assuming that the light is dominated by the stellar population rather than an AGN. Our observed spectrum shows no evidence of a Balmer break, and if the continuum is purely stellar, is dominated by a young stellar population. It is possible a more stochastic star formation history would fit a higher stellar mass. Comparing our metallicity and mass estimates for GN-z11 with the average reported for 8 < z < 10 galaxies in Nakajima et al. (2023) we find GN-z11 is offset to somewhat lower metallicity, albeit within the uncertainty quoted there. We note that the sample presented in that paper is still small and our understanding of the metallicities of galaxies at z > 8 will no doubt continue to evolve significantly over the coming years. We also note that the uncertainties on our derived metallicity are large. In particular, we caution that the set of emission lines used to determine the metallicity presented here has not been robustly calibrated. The systematic uncertainties associated with this quoted metallicity are likely very high, so robust conclusions cannot be drawn from this about the evolution of the mass-metallicity relation. Further work is needed to robustly calibrate shorter-wavelength metallicity diagnostics suitable for the study of z > 10 galaxies with NIRSpec.

What is more puzzling is the strong N III] and N IV] emission observed in the rest-frame UV, especially given the absence of a convincing detection of O III] λλ1660,1666 in our grating spectrum (although the blend with He II is detected in the low-dispersion prism spectrum). The N III] λ1748 emission line complex is not often seen in the spectra of star-forming galaxies, although it is detected in 2 of 44 galaxies in the low-redshift CLASSY survey (Mingozzi et al. 2022), including Mk996 (James et al. 2009). At intermediate redshifts, N III] λ1748 has been observed in stacks of rest-UV galaxy spectra at z ∼ 3 (e.g., Saxena et al. 2022) and is weakly detected in SL2SJ021737-051329, a lensed arc at z = 1.84 with low metallicity and high ionisation (Berg et al. 2018). However, N III] λ1748 is typically observed to be weaker than the nearby [O III] λ1660, 1666 lines.

This ratio of N III] λ1748/O III] λλ1660, 1666 can be used to place constraints on nebular N/O abundance ratios (Garnett et al. 1995). The conversion of N III]/O III] to N++/O++ depends on the electron temperature- and density-sensitive emissivities of these emission lines. However, the temperature and density dependence of these emission lines are remarkably similar. Adopting N III] / O III] ≳ 2.6 (see Table 1), any adopted values of temperature 1 ≤ Te/104 K ≤ 55 and density 2 ≤ log10(ne/cm−3) ≤ 10 results in emissivities that imply 0.72 ≤ N++/O++ ≤ 1.09, significantly higher than the solar N/O value of 0.142

The measured N++/O++ may over-estimate the total N/O if there is a significant fraction of oxygen in other ionisation states. The second and third ionisation energies of nitrogen (29.6 and 47.4 eV) are milder than those of oxygen (35.1 and 54.9 eV). Assuming a simply multi-zone model of the ionisation structure of the ISM, this implies that N++/(O+ + O++) should be a lower limit on the total N/O. However, from detections of [O II] λλ 3727 and [O III] λ 4363 emission for GN-z11, if we assume the [O II] emission arises from gas with density below the critical density of [O II] λλ 3727 (i.e. ne ≲ 104K), we get an approximate lower limit of O++/O+ ≳ 1.5, consistent with the expectation of a highly ionised ISM. Thus, even if we conservatively assume O++/O+ = 1.5, this only lowers the inferred N/O by a factor of 0.6, implying a lower limit on the total nitrogen to oxygen abundance ratio of N/O > 0.43, or log10(N/O) >  − 0.36, more than two times higher than the solar abundance ratio. This would appear quite unusual with respect to z ∼ 0 − 2 galaxies (e.g., Pérez-Montero & Contini 2009; Hayden-Pawson et al. 2022), and strongly inconsistent with canonical chemical evolution models (see Maiolino & Mannucci 2019 or Kobayashi 2022 for reviews).

We note that this simple calculation is independent of the excitation source (i.e. stellar photoionisation or AGN). However, we cannot rule out the scenario in which only a small fraction of the gas in GN-z11 is highly nitrogen enriched, but that this gas is extremely luminous in emission and dominates the global spectrum. More detailed modelling of the ionisation states of nitrogen and oxygen throughout the ISM of GN-z11 would be required to derive a more precise value of N/O, which is beyond the scope of this paper.

We also detect the [C III]λ1907+ C III]λ1909 line in our G235M spectrum. The C III] line has been much more widely observed in star-forming galaxies at high redshifts (e.g., Saxena et al. 2022; Arellano-Córdova et al. 2022; Jones et al. 2023), and its presence does not necessarily point to unusual C/O abundance ratios (Arellano-Córdova et al. 2022; Jones et al. 2023).

In summary, the emission line ratios measured for GN-z11 suggest a very high ionisation parameter and low oxygen abundance in the vicinity of 10% solar, broadly in line with findings from galaxies at z ∼ 6 − 10 (Cameron et al. 2023; Sanders et al. 2023; Mascia et al. 2023; Nakajima et al. 2023; Tang et al. 2023). However, the detection of strong N III] emission suggests unexpected abundance patterns, which may have deeper implications for chemical enrichment histories.

4. Conclusions

We present JWST/NIRSpec spectroscopy of one of the most luminous galaxies at z > 10. GN-z11 is in the GOODS-North field and had previously been identified as a Lyman break galaxy candidate by Oesch et al. (2015), with a tentative redshift of z = 11.1 from a continuum break in slitless HST/WFC3 spectroscopy (Oesch et al. 2016). We see numerous emission lines and a strong Lyman-α break in our NIRSpec spectroscopy, and we unambiguously measure the redshift to be z = 10.603. Our grating spectrum reveals Lyman-α in emission, making it the first object at z > 9 with confirmed Lyman-α emission. The rest-frame equivalent width is W0 = 18 Å. The emission is offset 555 km s−1 redwards of the systemic redshift and spatially extended. These properties are consistent with models of Lyman-α backscattering off the far side of galactic-scale outflows.

The NIRSpec spectrum of GN-z11 is remarkably rich in emission lines, enabling us to study the ISM properties at z > 10. Based on the high [Ne III]/[O II] ratio, we infer a high ionisation parameter (log10(U) >  − 2.0). We report a significant detection of the very rarely seen N III] λ 1748 line, which could suggest unusually high N/O ratios. While some high ionisation lines are detected, the He IIλ1640 and C IV λ1550 lines, which are typically associated with photoionisation due to AGN, are weak. Although we cannot conclusively rule out the contribution of an AGN, if this galaxy is indeed powered by star formation then the Balmer emission lines and UV continuum suggest a current star formation rate of ∼30 M⊙ yr−1 and low dust attenuation.

We have presented a very high signal-to-noise spectrum of a galaxy at z > 10 that shows continuum and line emission. This highlights the power of our JADES observations to not only measure redshifts but allow us to perform detailed studies of the physical and chemical properties of galaxies formed within the first few hundred million years after the Big Bang.

2

Emissivity calculations were performed with PYNEB (Luridiana et al. 2015).

Acknowledgments

AJB, AS, AJC, GCJ, JC, and IEBW acknowledge funding from the “FirstGalaxies” Advanced Grant from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 789056). ECL acknowledges support of an STFC Webb Fellowship (ST/W001438/1). The Cosmic Dawn Center (DAWN) is funded by the Danish National Research Foundation under grant no.140. RS acknowledges support from a STFC Ernest Rutherford Fellowship (ST/S004831/1). RM, JW, MC, FDE, JS, TJL, LS, and WMB acknowledge support by the Science and Technology Facilities Council (STFC) and by the ERC through Advanced Grant 695671 “QUENCH”. RM also acknowledges funding from a research professorship from the Royal Society. JW also acknowledges funding from the Fondation MERAC. This research is supported in part by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. FS, EE, DJE, BDJ, MR, BER, IS, and CNAW acknowledge a JWST/NIRCam contract to the University of Arizona NAS5-02015. DJE is also supported as a Simons Investigator. SC acknowledges support by European Union’s HE ERC Starting Grant No. 101040227 – WINGS. SA, BRDP, and MP acknowledges support from the research project PID2021-127718NB-I00 of the Spanish Ministry of Science and Innovation/State Agency of Research (MICIN/AEI). HÜ gratefully acknowledges support by the Isaac Newton Trust and by the Kavli Foundation through a Newton-Kavli Junior Fellowship. Funding for this research was provided by the Johns Hopkins University, Institute for Data Intensive Engineering and Science (IDIES). RB acknowledges support from an STFC Ernest Rutherford Fellowship [grant number ST/T003596/1]. MP also acknowledges support from the Programa Atracción de Talento de la Comunidad de Madrid via grant 2018-T2/TIC-11715. LW acknowledges support from the National Science Foundation Graduate Research Fellowship under Grant No. DGE-2137419. DP acknowledges support by the Huo Family Foundation through a P.C. Ho PhD Studentship. This work is based [in part] on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with program #1181.

References

  1. Aihara, H., Allende Prieto, C., An, D., et al. 2011, ApJS, 193, 29 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arellano-Córdova, K. Z., Berg, D. A., Chisholm, J., et al. 2022, ApJ, 940, L23 [CrossRef] [Google Scholar]
  3. Berg, D. A., Erb, D. K., Auger, M. W., Pettini, M., & Brammer, G. B. 2018, ApJ, 859, 164 [CrossRef] [Google Scholar]
  4. Bouwens, R. J., Illingworth, G. D., González, V., et al. 2010, ApJ, 725, 1587 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [Google Scholar]
  6. Bouwens, R. J., Smit, R., Labbé, I., et al. 2016, ApJ, 831, 176 [Google Scholar]
  7. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cameron, A. J., Saxena, A., Bunker, A. J., et al. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202346107 [Google Scholar]
  9. Carniani, S., Maiolino, R., Pallottini, A., et al. 2017, A&A, 605, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Caruana, J., Bunker, A. J., Wilkins, S. M., et al. 2014, MNRAS, 443, 2831 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  12. Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [Google Scholar]
  13. Chevallard, J., & Charlot, S. 2016, MNRAS, 462, 1415 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chevallard, J., Charlot, S., Senchyna, P., et al. 2018, MNRAS, 479, 3264 [Google Scholar]
  15. Chisholm, J., Prochaska, J. X., Schaerer, D., Gazagnes, S., & Henry, A. 2020, MNRAS, 498, 2554 [CrossRef] [Google Scholar]
  16. Cuby, J. G., Le Fèvre, O., McCracken, H., et al. 2003, A&A, 405, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Curti, M., D’Eugenio, F., Carniani, S., et al. 2023, MNRAS, 518, 425 [Google Scholar]
  18. Curtis-Lake, E., Carniani, S., Cameron, A., et al. 2023, Nat. Astron., 7, 622 [NASA ADS] [CrossRef] [Google Scholar]
  19. Davies, F. B., Hennawi, J. F., Bañados, E., et al. 2018, ApJ, 864, 142 [NASA ADS] [CrossRef] [Google Scholar]
  20. Dijkstra, M. 2014, PASA, 31, e040 [Google Scholar]
  21. Endsley, R., & Stark, D. P. 2022, MNRAS, 511, 6042 [NASA ADS] [CrossRef] [Google Scholar]
  22. Endsley, R., Stark, D. P., Bouwens, R. J., et al. 2022, MNRAS, 517, 5642 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fan, X., Narayanan, V. K., Lupton, R. H., et al. 2001, AJ, 122, 2833 [Google Scholar]
  24. Feltre, A., Charlot, S., & Gutkin, J. 2016, MNRAS, 456, 3354 [Google Scholar]
  25. Feltre, A., Bacon, R., Tresse, L., et al. 2018, A&A, 617, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Ferruit, P., Jakobsen, P., Giardino, G., et al. 2022, A&A, 661, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Finkelstein, S. L., Papovich, C., Dickinson, M., et al. 2013, Nature, 502, 524 [CrossRef] [Google Scholar]
  28. Finkelstein, S. L., Ryan, Russell E. J., Papovich, C., et al. 2015, ApJ, 810, 71 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fosbury, R. A. E., Villar-Martín, M., Humphrey, A., et al. 2003, ApJ, 596, 797 [NASA ADS] [CrossRef] [Google Scholar]
  30. Furusawa, H., Kashikawa, N., Kobayashi, M. A. R., et al. 2016, ApJ, 822, 46 [NASA ADS] [CrossRef] [Google Scholar]
  31. Garnett, D. R., Skillman, E. D., Dufour, R. J., et al. 1995, ApJ, 443, 64 [Google Scholar]
  32. Greig, B., Mesinger, A., Haiman, Z., & Simcoe, R. A. 2017, MNRAS, 466, 4239 [Google Scholar]
  33. Gunn, J. E., & Peterson, B. A. 1965, ApJ, 142, 1633 [Google Scholar]
  34. Gutkin, J., Charlot, S., & Bruzual, G. 2016, MNRAS, 462, 1757 [Google Scholar]
  35. Hashimoto, T., Inoue, A. K., Mawatari, K., et al. 2019, PASJ, 71, 71 [Google Scholar]
  36. Hayden-Pawson, C., Curti, M., Maiolino, R., et al. 2022, MNRAS, 512, 2867 [NASA ADS] [CrossRef] [Google Scholar]
  37. Henry, A., Berg, D. A., Scarlata, C., Verhamme, A., & Erb, D. 2018, ApJ, 855, 96 [Google Scholar]
  38. Hirschmann, M., Charlot, S., Feltre, A., et al. 2019, MNRAS, 487, 333 [NASA ADS] [CrossRef] [Google Scholar]
  39. Isobe, Y., Ouchi, M., Nakajima, K., et al. 2023, ApJ, submitted [arXiv:2301.06811] [Google Scholar]
  40. Jakobsen, P., Ferruit, P., Alves de Oliveira, C., et al. 2022, A&A, 661, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. James, B. L., Tsamis, Y. G., Barlow, M. J., et al. 2009, MNRAS, 398, 2 [Google Scholar]
  42. Jiang, L., Fan, X., & Vestergaard, M. 2008, ApJ, 679, 962 [NASA ADS] [CrossRef] [Google Scholar]
  43. Jiang, L., Kashikawa, N., Wang, S., et al. 2021, Nat. Astron., 5, 256 [NASA ADS] [CrossRef] [Google Scholar]
  44. Jones, T., Sanders, R., Chen, Y., et al. 2023, ApJ, 951, L17 [CrossRef] [Google Scholar]
  45. Jung, I., Finkelstein, S. L., Dickinson, M., et al. 2019, ApJ, 877, 146 [CrossRef] [Google Scholar]
  46. Jung, I., Finkelstein, S. L., Dickinson, M., et al. 2020, ApJ, 904, 144 [NASA ADS] [CrossRef] [Google Scholar]
  47. Jung, I., Finkelstein, S. L., Larson, R. L., et al. 2022, ApJ, submitted [arXiv:2212.09850] [Google Scholar]
  48. Katz, H., Garel, T., Rosdahl, J., et al. 2022, MNRAS, 515, 4265 [NASA ADS] [CrossRef] [Google Scholar]
  49. Katz, H., Saxena, A., Cameron, A. J., et al. 2023, MNRAS, 518, 592 [Google Scholar]
  50. Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
  51. Knudsen, K. K., Richard, J., Kneib, J.-P., et al. 2016, MNRAS, 462, L6 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kobayashi, C. 2022, in The Origin of Outflows in Evolved Stars, eds. L. Decin, A. Zijlstra, & C. Gielen, 366, 63 [NASA ADS] [Google Scholar]
  53. Kusakabe, H., Verhamme, A., Blaizot, J., et al. 2022, A&A, 660, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Laporte, N., Nakajima, K., Ellis, R. S., et al. 2017, ApJ, 851, 40 [NASA ADS] [CrossRef] [Google Scholar]
  55. Larson, R. L., Finkelstein, S. L., Hutchison, T. A., et al. 2022, ApJ, 930, 104 [NASA ADS] [CrossRef] [Google Scholar]
  56. Leclercq, F., Bacon, R., Wisotzki, L., et al. 2017, A&A, 608, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Levesque, E. M., & Richardson, M. L. A. 2014, ApJ, 780, 100 [Google Scholar]
  58. Luridiana, V., Morisset, C., & Shaw, R. A. 2015, A&A, 573, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Mainali, R., Kollmeier, J. A., Stark, D. P., et al. 2017, ApJ, 836, L14 [Google Scholar]
  60. Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [Google Scholar]
  61. Maiolino, R., Carniani, S., Fontana, A., et al. 2015, MNRAS, 452, 54 [NASA ADS] [CrossRef] [Google Scholar]
  62. Mascia, S., Pentericci, L., Calabrò, A., et al. 2023, A&A, 672, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Mason, C. A., & Gronke, M. 2020, MNRAS, 499, 1395 [Google Scholar]
  64. Mason, C. A., Treu, T., de Barros, S., et al. 2018a, ApJ, 857, L11 [Google Scholar]
  65. Mason, C. A., Treu, T., Dijkstra, M., et al. 2018b, ApJ, 856, 2 [Google Scholar]
  66. McGreer, I. D., Clément, B., Mainali, R., et al. 2018, MNRAS, 479, 435 [Google Scholar]
  67. Mingozzi, M., James, B. L., Arellano-Córdova, K. Z., et al. 2022, ApJ, 939, 110 [NASA ADS] [CrossRef] [Google Scholar]
  68. Nakajima, K., & Maiolino, R. 2022, MNRAS, 513, 5134 [NASA ADS] [CrossRef] [Google Scholar]
  69. Nakajima, K., Schaerer, D., Le Fèvre, O., et al. 2018, A&A, 612, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Nakajima, K., Ouchi, M., Xu, Y., et al. 2022, ApJS, 262, 3 [CrossRef] [Google Scholar]
  71. Nakajima, K., Ouchi, M., Isobe, Y., et al. 2023, ApJS, submitted [arXiv:2301.12825] [Google Scholar]
  72. Oesch, P. A., van Dokkum, P. G., Illingworth, G. D., et al. 2015, ApJ, 804, L30 [Google Scholar]
  73. Oesch, P. A., Brammer, G., van Dokkum, P. G., et al. 2016, ApJ, 819, 129 [NASA ADS] [CrossRef] [Google Scholar]
  74. Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
  75. Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (University Science Books) [Google Scholar]
  76. Park, H., Jung, I., Song, H., et al. 2021, ApJ, 922, 263 [NASA ADS] [CrossRef] [Google Scholar]
  77. Pentericci, L., Fontana, A., Vanzella, E., et al. 2011, ApJ, 743, 132 [NASA ADS] [CrossRef] [Google Scholar]
  78. Pentericci, L., Carniani, S., Castellano, M., et al. 2016, ApJ, 829, L11 [NASA ADS] [CrossRef] [Google Scholar]
  79. Pentericci, L., Vanzella, E., Castellano, M., et al. 2018, A&A, 619, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Pérez-Montero, E., & Contini, T. 2009, MNRAS, 398, 949 [CrossRef] [Google Scholar]
  81. Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Raiter, A., Fosbury, R. A. E., & Teimoorinia, H. 2010, A&A, 510, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Rauch, M., Haehnelt, M., Bunker, A., et al. 2008, ApJ, 681, 856 [NASA ADS] [CrossRef] [Google Scholar]
  84. Reddy, N. A., Shapley, A. E., Sanders, R. L., et al. 2018, ApJ, 869, 92 [NASA ADS] [CrossRef] [Google Scholar]
  85. Roberts-Borsani, G. W., Bouwens, R. J., Oesch, P. A., et al. 2016, ApJ, 823, 143 [NASA ADS] [CrossRef] [Google Scholar]
  86. Robertson, B. E. 2022, ARA&A, 60, 121 [NASA ADS] [CrossRef] [Google Scholar]
  87. Robertson, B. E., Tacchella, S., Johnson, B. D., et al. 2023, Nat. Astron., 7, 611 [NASA ADS] [CrossRef] [Google Scholar]
  88. Sadoun, R., Zheng, Z., & Miralda-Escudé, J. 2017, ApJ, 839, 44 [Google Scholar]
  89. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  90. Sanders, R. L., Shapley, A. E., Topping, M. W., Reddy, N. A., & Brammer, G. B. 2023, ApJ, submitted [arXiv:2301.06696] [Google Scholar]
  91. Santos, M. R. 2004, MNRAS, 349, 1137 [NASA ADS] [CrossRef] [Google Scholar]
  92. Saxena, A., Cryer, E., Ellis, R. S., et al. 2022, MNRAS, 517, 1098 [Google Scholar]
  93. Saxena, A., Robertson, B. E., Bunker, A. J., et al. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202346245 [Google Scholar]
  94. Schenker, M. A., Ellis, R. S., Konidaris, N. P., & Stark, D. P. 2014, ApJ, 795, 20 [NASA ADS] [CrossRef] [Google Scholar]
  95. Smith, A., Kannan, R., Garaldi, E., et al. 2022, MNRAS, 512, 3243 [NASA ADS] [CrossRef] [Google Scholar]
  96. Song, M., Finkelstein, S. L., Livermore, R. C., et al. 2016, ApJ, 826, 113 [NASA ADS] [CrossRef] [Google Scholar]
  97. Stark, D. P., Ellis, R. S., Chiu, K., Ouchi, M., & Bunker, A. 2010, MNRAS, 408, 1628 [Google Scholar]
  98. Stark, D. P., Richard, J., Charlot, S., et al. 2015, MNRAS, 450, 1846 [NASA ADS] [CrossRef] [Google Scholar]
  99. Stark, D. P., Ellis, R. S., Charlot, S., et al. 2017, MNRAS, 464, 469 [NASA ADS] [CrossRef] [Google Scholar]
  100. Tacchella, S., Eisenstein, D. J., Hainline, K., et al. 2023, ApJ, 952, 74 [NASA ADS] [CrossRef] [Google Scholar]
  101. Tang, M., Stark, D. P., Chen, Z., et al. 2023, MNRAS, submitted [arXiv:2301.07072] [Google Scholar]
  102. Übler, H., Maiolino, R., Curtis-Lake, E., et al. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202346137 [Google Scholar]
  103. Vanzella, E., Grazian, A., Hayes, M., et al. 2010, A&A, 513, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Vanzella, E., Pentericci, L., Fontana, A., et al. 2011, ApJ, 730, L35 [NASA ADS] [CrossRef] [Google Scholar]
  105. Vidal-García, A., Charlot, S., Bruzual, G., & Hubeny, I. 2017, MNRAS, 470, 3532 [Google Scholar]
  106. Wang, F., Davies, F. B., Yang, J., et al. 2020, ApJ, 896, 23 [NASA ADS] [CrossRef] [Google Scholar]
  107. Weinberger, L. H., Haehnelt, M. G., & Kulkarni, G. 2019, MNRAS, 485, 1350 [NASA ADS] [CrossRef] [Google Scholar]
  108. Willott, C. J., McLure, R. J., Hibon, P., et al. 2013, AJ, 145, 4 [NASA ADS] [CrossRef] [Google Scholar]
  109. Willott, C. J., Carilli, C. L., Wagg, J., & Wang, R. 2015, ApJ, 807, 180 [NASA ADS] [CrossRef] [Google Scholar]
  110. Wisotzki, L., Bacon, R., Blaizot, J., et al. 2016, A&A, 587, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  111. Witstok, J., Smit, R., Maiolino, R., et al. 2021, MNRAS, 508, 1686 [NASA ADS] [CrossRef] [Google Scholar]
  112. Zackrisson, E., Binggeli, C., Finlator, K., et al. 2017, ApJ, 836, 78 [NASA ADS] [CrossRef] [Google Scholar]
  113. Zitrin, A., Labbé, I., Belli, S., et al. 2015, ApJ, 810, L12 [Google Scholar]

Appendix A: BEAGLE fit to the prism spectrum

The prism spectrum was fitted to with BEAGLE (Chevallard & Charlot 2016) using the updated Bruzual & Charlot (2003) stellar models as described in Vidal-García et al. (2017), with a Chabrier (2003) IMF with upper and lower mass cutoffs of 300M⊙ and 0.1M⊙, respectively. The results are given in Tab. 2. Nebular line+continuum emission is modelled following Gutkin et al. (2016). Treatment of the instrument line spread function is described in Curtis-Lake et al. (2023). We fit varying all stellar and nebular parameters (metallicity, ionisation parameter, dust-to-gas mass ratio), employ a delayed exponential star formation history with recent 10 Myr of constant star formation that can vary independently. Finally, we model attenuation by dust using the Charlot & Fall (2000) two-component dust law. We also allow for a damping wing for the neutral IGM following the prescription described in Curtis-Lake et al. (2023), though we do not report the values here as they will be affected by the Lyα flux, which is unresolved in the PRISM spectrum. The resulting spectral fit and derived parameters are shown in Fig. A.1 and reported in Table 2. The Gutkin et al. (2016) nebular models employ a relation between N/O and O/H abundances, which gives low N/O abundance at low metallicity. As such, our fit does not reproduce the rest-frame UV Nitrogen lines. We therefore mask them to prevent their presence affecting the fit to the rest-frame UV continuum. We also mask the region around C IV, which shows an offset in the emission from the expected wavelength.

thumbnail Fig. A.1.

Triangle plot showing the 2D (1D on the diagonal) posterior probability distributions for the derived stellar mass (M; accounting for mass returned to the ISM through stellar winds and supernova explosions), star formation rate (ψ), maximum age of the stars (t), effective V-band attenuation optical depth ( τ v ̂ $ \hat{\tau_v} $ = AV/1.086), ionisation parameter (log10US), nebular metallicity (Zneb), escape fraction of H-ionising photons (fesc), and ionising photon production efficiency (ξion). The contours in the 2D posterior plots show the 1, 2, and 3σ credible regions in dark, medium, and light blue, respectively. The inset shows the resulting fit to the prism spectrum, with the spectrum and 1σ standard errors shown as the red line and shaded region, respectively, and the 1σ range of fitted model spectra in blue. Regions that are masked in the spectrum are shown as fainter red (data) and fainter blue (model) shaded regions.

Appendix B: R ∼ 1000 grating 1D and 2D spectra

Figure B.1 shows the full NIRSpec medium-resolution grating spectra with detected emission lines marked.

thumbnail Fig. B.1.

Full coverage of the 2D and 1D spectra from the medium resolution G140M (top), G235M (middle), and G395M (bottom) gratings. The main emission lines observed in the spectra have been marked.

Appendix C: Comparison of NIRSpec flux calibration to NIRCam imaging

As a check on our spectroscopic flux calibration, we compare the GN-z11 fluxes derived from the NIRSpec spectroscopy with the NIRCam fluxes across several filters reported in Tacchella et al. (2023). Given the small spatial size of the source, and the narrow (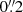 0 . ″ 2 $ 0{{\overset{\prime\prime}{.}}}2 $-wide) NIRSpec microshutters, we use the 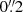0 . ″ 2 $ 0{{\overset{\prime\prime}{.}}}2 $-diameter NIRCam aperture photometry (corrected to total magnitudes assuming a point source) reported in Tacchella et al. (2023) and our 3-pixel ( 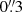0 . ″ 3 $ 0{{\overset{\prime\prime}{.}}}3 $-wide) NIRSpec spectral extraction (again corrected for slit losses to approximate total flux assuming a point source at the location of GN-z11 with the microshutter). Each extracted spectrum was converted to photons per unit wavelength (since NIRCam detects photons, not energy), and the flux density integrated over the bandpass of each filter, weighting by the filter transmission curve. We then computed the brightness (in nJy) of a source with a spectrum uniform in fν (i.e. flat in AB magnitudes) which would produce the same integrated flux, so as to compare with the quoted fluxes for NIRCam on the AB system (see Table C.1).

Table C.1.

Comparison of the NIRCam photometry of GN-z11 with the NIRSpec spectroscopy.

As can be seen from Fig. C.1, the agreement in flux between the low-dispersion prism spectrum and the NIRCam photometry is excellent, with most filters agreeing with the spectral fluxes within the nominal error bars (the agreement is generally within 5%). The flux calibration of the grating spectra is less accurate. The grating spectra show significantly higher fluxes than NIRCam (or the prism spectrum) at 2.5 < λ < 4 μm at the ≈15 − 20% level, greater than the nominal uncertainties in the photon statistics, although at other wavelengths the agreement is better. The exact origin of this is unclear, but the flux calibration of the gratings may be less good, or there may be background subtraction issues affecting the measured flux.

thumbnail Fig. C.1.

NIRSpec low-dispersion prism spectrum of GN-z11 (3-pixel extraction), compared with the NIRCam photometry in different filters (red error bars denote the flux uncertainty and the wavelength span of the filter bandpass). The large diamond symbols denote the flux from the NIRSpec spectrum integrated over the filter response curve, with the small blue error bars within these diamond symbols.

thumbnail Fig. C.2.

NIRSpec medium-dispersion grating spectrum of GN-z11 (3-pixel extraction, smoothed in the spectral direction with a 11-pixel boxcar), compared with the NIRCam photometry in different filters (red error bars denote the flux uncertainty and the wavelength span of the filter bandpass). The light grey spectrum is the G235M, with the G140M and G395M grating spectra in black. The ‘+’ symbols and blue error bars denote the flux from the NIRSpec spectrum integrated over the filter response curve.

All Tables

Table 1.

Emission line fluxes (in units of ×10−19 erg s−1 cm−2) detected in the prism (R ∼ 100) and grating (R ∼ 1000) spectra.

In the text
Table 2.

GN-z11 physical parameters from BEAGLE SED fitting of the prism spectrum.

In the text
Table C.1.

Comparison of the NIRCam photometry of GN-z11 with the NIRSpec spectroscopy.

In the text

All Figures

thumbnail Fig. 1.

NIRCam F200W image of GN-z11 (see Tacchella et al. 2023) with the NIRSpec microshutters overlaid for the four different pointings. The green rectangles denote the illuminated region of each microshutter ( 0 . ″ 2 × 0 . ″ 46 $ 0{{\overset{\prime\prime}{.}}}2 \times 0{{\overset{\prime\prime}{.}}}46 $). North is up and east to the left, and the image is 1.5 arcsec per side. The flux density units on the colour bar are MJy/sr.
In the text
thumbnail Fig. 2.

2D (top) and 1D (bottom) spectra of GN-z11 using the PRISM/CLEAR configuration of NIRSpec. The 1D spectrum has been extracted using a 3-pixel-wide aperture that leads to improved S/N in this highly compact object. Prominent emission lines present in the spectra are marked. The S/N of the continuum is high, and the emission lines are clearly seen in both the 1D and 2D spectra.
In the text
thumbnail Fig. 3.

Gallery of the most prominent emission lines seen in the GN-z11 spectrum from the medium resolution (R1000) gratings using a 3-pixel 1D spectral extraction.
In the text
thumbnail Fig. 4.

Measured C III]/He II versus C III]/C IV ratios for GN-z11 shown along with predictions from photoionisation due to AGN (circles) and star formation (stars) from Feltre et al. (2016) and Gutkin et al. (2016) in the range of Z/Z⊙ = 0.066 − 0.131 and gas densities in the range log10(nH)/cm−3 = 2 − 4. Based on the observed line ratios, neither photoionisation from AGN nor star formation alone can conclusively explain the observations, placing GN-z11 right between the model predictions from the two.
In the text
thumbnail Fig. 5.

Velocity offset of the Lyα emission line (blue solid line) compared with the Hγ line (dashed green line). The Lyα line is redshifted by 555 km s−1 compared to the redshift derived from other emission lines in the spectrum.
In the text
thumbnail Fig. 6.

Zoom in on the Lyα emission line in the G140M 1D (lower) and 2D (upper) spectra. The dashed grey line shows the systemic wavelength of the Lyα transition. The histograms (top left) of the Lyα spatial profile (yellow) and that of the continuum (blue) show the Lyα emission from GN-z11 is more extended towards the south-west (up in the MSA shutter in this view).
In the text
thumbnail Fig. 7.

Lyman-α velocity offset (ΔvLyα) versus MUV for GN-z11 (star) and other high-redshift galaxies, colour-coded by Lyman-α equivalent width. We overplot data of z > 6 galaxies with ground-based observations from the literature (Cuby et al. 2003; Pentericci et al. 2011, 2016, 2018; Vanzella et al. 2011; Willott et al. 2013, 2015; Maiolino et al. 2015; Oesch et al. 2015; Stark et al. 2015, 2017; Furusawa et al. 2016; Knudsen et al. 2016; Carniani et al. 2017; Laporte et al. 2017; Mainali et al. 2017; Hashimoto et al. 2019; see Endsley et al. 2022 and the Table 4 therein) in circles, and Lyα emitting galaxies at z ∼ 7 − 9 from CEERS NIRSpec observations (Tang et al. 2023) in squares. The prediction of the correlation between the Lyα velocity offset and MUV at z = 7 from Mason et al. (2018b) is shown by the dashed grey line. GN-z11 has properties similar to the Lyα-emitting galaxies at z ∼ 7 − 9.
In the text
thumbnail Fig. 8.

Line ratio diagram, showing ([Ne III]+[O II])/Hδ versus [Ne III]/[O II], featuring GN-z11. The yellow diamond denotes the line ratios derived from the medium-dispersion G395M grating, and the cyan diamond uses the low-dispersion prism spectrum (where we have corrected for the blending of [Ne III] λ3869 with He Iλ3889 using the flux ratio from the grating). The background grey 2D probability density function shows the subset of SDSS galaxies with 0.03 < z < 0.1 for which [Ne III] λ3869, [O II] λλ3726, 3729, and Hδ are all detected with S/N > 5. Purple squares show z > 5.5 galaxies from Cameron et al. (2023) after adjusting the reported ratios to be in terms of Hδ by assuming a fixed value of Hδ/Hβ = 0.268. Solid lines show model grids from Gutkin et al. (2016), plotted for nine different values of metallicity (Z/Z⊙ = 0.04, 0.07, 0.15, 0.30, 0.45, 0.60, 0.75, 1.0, 1.5), as indicated by the different colours, and seven values of the ionisation parameter, indicated by marker sizes, in steps of 0.5 from log10U = −4.0 (smallest) to log10U = −1.0 (largest).
In the text
thumbnail Fig. A.1.

Triangle plot showing the 2D (1D on the diagonal) posterior probability distributions for the derived stellar mass (M; accounting for mass returned to the ISM through stellar winds and supernova explosions), star formation rate (ψ), maximum age of the stars (t), effective V-band attenuation optical depth ( τ v ̂ $ \hat{\tau_v} $ = AV/1.086), ionisation parameter (log10US), nebular metallicity (Zneb), escape fraction of H-ionising photons (fesc), and ionising photon production efficiency (ξion). The contours in the 2D posterior plots show the 1, 2, and 3σ credible regions in dark, medium, and light blue, respectively. The inset shows the resulting fit to the prism spectrum, with the spectrum and 1σ standard errors shown as the red line and shaded region, respectively, and the 1σ range of fitted model spectra in blue. Regions that are masked in the spectrum are shown as fainter red (data) and fainter blue (model) shaded regions.
In the text
thumbnail Fig. B.1.

Full coverage of the 2D and 1D spectra from the medium resolution G140M (top), G235M (middle), and G395M (bottom) gratings. The main emission lines observed in the spectra have been marked.
In the text
thumbnail Fig. C.1.

NIRSpec low-dispersion prism spectrum of GN-z11 (3-pixel extraction), compared with the NIRCam photometry in different filters (red error bars denote the flux uncertainty and the wavelength span of the filter bandpass). The large diamond symbols denote the flux from the NIRSpec spectrum integrated over the filter response curve, with the small blue error bars within these diamond symbols.
In the text
thumbnail Fig. C.2.

NIRSpec medium-dispersion grating spectrum of GN-z11 (3-pixel extraction, smoothed in the spectral direction with a 11-pixel boxcar), compared with the NIRCam photometry in different filters (red error bars denote the flux uncertainty and the wavelength span of the filter bandpass). The light grey spectrum is the G235M, with the G140M and G395M grating spectra in black. The ‘+’ symbols and blue error bars denote the flux from the NIRSpec spectrum integrated over the filter response curve.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.