| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346675 | |
| Published online | 23 August 2023 | |
The space weather around the exoplanet GJ 436b
I. The large-scale stellar magnetic field
1
Institut de Recherche en Astrophysique et Planétologie, Université de Toulouse, CNRS, IRAP/UMR 5277, 14 avenue Edouard Belin, 31400 Toulouse, France
e-mail: stefano.bellotti@irap.omp.eu
2
Science Division, Directorate of Science, European Space Research and Technology Centre (ESA/ESTEC), Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
3
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
4
Department of Physics, College of Science, United Arab Emirates University, PO Box 15551 Al Ain, UAE
e-mail: rim.fares@uaeu.ac.ae
5
Laboratoire Univers et Particules de Montpellier, Université de Montpellier, CNRS, 34095 Montpellier, France
6
Observatoire Astronomique de l’Université de Genève, Chemin Pegasi 51b, 1290 Versoix, Switzerland
Received:
17
April
2023
Accepted:
23
June
2023
Context. The space environment in which planets are embedded mainly depends on the host star and impacts the evolution of the planetary atmosphere. The quiet M dwarf GJ 436 hosts a close-in hot Neptune which is known to feature a comet-like tail of hydrogen atoms that escaped from its atmosphere due to energetic stellar irradiation. Understanding such star-planet interactions is essential to shed more light on planet formation and evolution theories, in particular the scarcity of Neptune-sized planets below a 3 d orbital period, also known as the ‘Neptune desert’.
Aims. We aimed to characterise the stellar environment around GJ 436, which requires accurate knowledge of the stellar magnetic field. The latter is studied efficiently with spectropolarimetry, since it is possible to recover the geometry of the large-scale magnetic field by applying tomographic inversion on time series of circularly polarised spectra.
Methods. We used spectropolarimetric data collected in the optical domain with Narval in 2016 to compute the longitudinal magnetic field, examine its periodic content via Lomb-Scargle periodogram and Gaussian process regression analysis, and finally reconstruct the large-scale field configuration by means of Zeeman-Doppler imaging.
Results. We found an average longitudinal field of −12 G and a stellar rotation period of 46.6 d using a Gaussian process model and 40.1 d using Zeeman-Doppler imaging, which are both consistent with the literature. The Lomb-Scargle analysis did not reveal any significant periodicity. The reconstructed large-scale magnetic field is predominantly poloidal, dipolar, and axisymmetric, with a mean strength of 16 G. This is in agreement with magnetic topologies seen for other stars of a similar spectral type and rotation rate.
Key words: stars: activity / stars: magnetic field / stars: individual: GJ 436 / techniques: polarimetric
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The stellar environment in which exoplanets are immersed has a significant impact on their atmospheres. Energetic phenomena associated with intense magnetic activity such as frequent flares can alter the chemical properties of the planetary atmosphere (Segura et al. 2010; Günther et al. 2020; Konings et al. 2022; Louca et al. 2023), with hazardous consequences for habitability (e.g. Tilley et al. 2019). In particular, for planets orbiting closer (< 0.1 au) to the host star, energetic stellar irradiation (X-rays and extreme ultraviolet) heats and expands the upper regions of the atmosphere, resulting in hydrodynamic escape (e.g. Lammer et al. 2003; Vidal-Madjar et al. 2003; Owen & Jackson 2012). In addition to the radiation from the host star, stellar particles from magnetised wind and coronal mass ejections also impact planetary atmospheres, for example by confining and stripping them away (Carolan et al. 2021; Hazra et al. 2022). Evaporation of planetary atmospheres is accentuated in the early stages of a planetary system (Ribas et al. 2005; Allan & Vidotto 2019; Ketzer & Poppenhaeger 2023), and it is one of the mechanisms proposed to explain the Neptune desert, that is to say the paucity of planets with masses between 0.01 and 1 MJup in short-distance orbits (e.g. Lecavelier Des Etangs 2007; Penz et al. 2008; Davis & Wheatley 2009; Ehrenreich & Désert 2011; Beaugé & Nesvorný 2013; Lundkvist et al. 2016; Mazeh et al. 2016). Likewise, photoevaporation can make a mini-Neptune lose a significant amount of hydrogen and helium, morphing it into a potentially habitable super-Earth (Luger et al. 2015).
Characterising the space weather for a specific system and modelling the interaction between the magnetised stellar wind and a close-in planet requires robust knowledge of the stellar magnetic field (Vidotto et al. 2014a,b). Our assumptions on its topology and strength indeed impact the extent of the planetary magnetosphere (Villarreal D’Angelo et al. 2018; Carolan et al. 2021) and predictions of transits’ duration (Llama et al. 2013). Stellar magnetic fields are most effectively studied using spectropolarimetry, with which we can analyse the Zeeman effect, that is the splitting of spectral lines in distinct components characterised by specific polarisation properties (Zeeman 1897). From time series of polarised spectra, we can map the large-scale magnetic field by means of Zeeman-Doppler imaging (ZDI; Semel 1989; Donati & Brown 1997) and obtain a global picture of the magnetic environment. Zeeman-Doppler imaging has been applied extensively in spectropolarimetric studies, and it has revealed a variety of field geometries for low-mass stars (e.g. Petit et al. 2005; Donati et al. 2008; Morin et al. 2008, 2010; Fares et al. 2013, 2017).
GJ 436 is a quiet M2.5 dwarf and hosts a hot-Neptune at 0.0285 AU, corresponding to an orbital period of 2.644 d (Butler et al. 2004; Gillon et al. 2007). The planet mass is 0.07 MJup, which places it at the lower-mass boundary of the Neptune desert. The vicinity of the planet to the host star makes it an excellent laboratory to study interactions between the planetary atmosphere and the impinging stellar wind (Vidotto & Bourrier 2017; Khodachenko et al. 2019; Villarreal D’Angelo et al. 2021). Indeed, because of intense irradiation, the planetary atmosphere is subject to hydrodynamic escape, which forms a comet-like cloud of hydrogen atoms (Kulow et al. 2014; Ehrenreich et al. 2015; Lavie et al. 2017; dos Santos et al. 2019). To explain such observations of the system, Bourrier et al. (2015, 2016) showed that an accurate description of the interactions between the stellar wind and the exospheric cloud, together with radiation pressure, is necessary. For instance, variations occurring locally in the cloud structure can be correlated to changes in stellar wind density. The wind properties of the host star GJ 436 are also important to predict the flux of energetic particles penetrating the atmosphere of GJ 436 b (Mesquita et al. 2021; Rodgers-Lee et al. 2023).
GJ 436 b lies on a polar eccentric orbit (Bourrier et al. 2018, 2022) to which it may have migrated via interactions with an undetected outer companion (Beust et al. 2012; Bourrier et al. 2018). The migration would have occurred late in the life of the planet, implying that the latter would have avoided the strong irradiation of the young star and started evaporating only recently and not substantially. This possibly explains why the planet falls in the Neptune desert even though its atmosphere has not been eroded yet (Attia et al. 2021), and it represents an interesting case to follow up on. Moreover, depending on the topology of the stellar magnetic field, the planet orbit could sweep regions of both open and closed field lines, as well as oscillate in and out of the Alfvén surface, driving intermittent star-planet interactions similar to those modelled for AU Mic (Kavanagh et al. 2021). The imprints of such interactions would be observable at radio wavelengths (e.g. Zarka 1998; Saur et al. 2013; Turnpenney et al. 2018; Kavanagh et al. 2022).
In this first paper, we characterise the large-scale magnetic field of GJ 436 using ZDI on optical spectropolarimetric observations. In a second paper (Vidotto et al. 2023), we will model the stellar wind self-consistently to provide more realistic constraints on the stellar environment at the orbit of GJ 436 b. In Sect. 2 we describe the spectropolarimetric time series collected with Narval, and we outline the longitudinal field computation and its temporal analysis in Sects. 3 and 4. The large-scale magnetic field reconstruction by means of ZDI is presented in Sect. 5. In Sect. 6 we summarise and contextualise our results.
2. Observations
GJ 436 is an M2.5 dwarf at a distance of 9.76 ± 0.01 pc (Gaia Collaboration 2021) and with a V band magnitude of 10.61 (Zacharias et al. 2012). The stellar radius is 0.417 ± 0.008 R⊙ and the mass is 0.441 ± 0.009 M⊙ (Rosenthal et al. 2021), placing it above the fully convective boundary at 0.35 M⊙ (Chabrier & Baraffe 1997). The star is moderately inactive, with a stellar rotation period around 40−44 d (Bourrier et al. 2018; dos Santos et al. 2019; Kumar & Fares 2023) and a chromospheric activity index 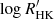 of −5.1 (Boro Saikia et al. 2018; Fuhrmeister et al. 2023).
of −5.1 (Boro Saikia et al. 2018; Fuhrmeister et al. 2023).
For this work, we used sixteen Narval observations of GJ 436 collected between March and June 2016 (PI: E. Hebrard). The time series is provided in Table 1. Narval is the optical spectropolarimeter on the 2 m Télescope Bernard Lyot (TBL) at the Pic du Midi Observatory in France, covering a 360−1050 nm spectral range at a resolving power R of 65 000 (Donati 2003). The data reduction was performed with LIBRE-ESPRIT (Donati et al. 1997), and the reduced spectra were retrieved from PolarBase (Petit et al. 2014).
GJ 436 observations collected in 2016 with Narval.
From the time series of unpolarised and circularly polarised spectra, we computed high signal-to-noise ratio (S/N) Stokes I and V profiles by means of least-square deconvolution (LSD; Donati et al. 1997; Kochukhov et al. 2010). This numerical technique combines the information of thousands of absorption lines in the observed spectrum, which are selected using a theoretical line list with associated properties such as depth, sensitivity to Zeeman effect (Landé factor, geff), and excitation potential.
Considering that GJ 436 is an M2.5 star with an effective temperature of 3586.1 ± 36.4 K (Rosenthal et al. 2021), we adopted a line list corresponding to a MARCS model characterised by log g = 5.0 [cm s−2], vmicro = 1 km s−1, and Teff = 3500 K (Gustafsson et al. 2008). The line list was generated with the Vienna Atomic Line Database1 (VALD, Ryabchikova et al. 2015), and contained 3240 lines in the range 350−1080 nm and with depths larger than 40% the continuum level, similarly to Morin et al. (2008) and Bellotti et al. (2022). The number of lines takes the removal of the following wavelength intervals into account, which may be affected by residuals of telluric correction or are in the vicinity of Hα: [627, 632], [655.5, 657], [686, 697], [716, 734], [759, 770], [813, 835], and [895, 986] nm.
Along with Stokes I and V profiles, we computed the ‘null profile’, which is a powerful diagnostic tool to determine the noise level of the LSD output and whether a spurious polarisation signal is present in the observations (Donati et al. 1997; Bagnulo et al. 2009). As shown in Fig. 1, the null profile contains a positive signal at line centre (∼9.6 km s−1), which is reflected in a vertical offset of Stokes V with respect to a constant null value. Following Folsom et al. (2016), we attributed this signal to an imperfect background subtraction affecting the blue orders of Narval and we removed it by computing LSD profiles using lines in the red part of the spectrum, that is to say larger than 500 nm. Considering a window of ±10 km s−1 from line centre that includes both lobes of the Stokes V profile, the mean and standard deviation of the null profile decrease from 3.2 × 10−4 to 1.5 × 10−4 and from 2.1 × 10−4 to 1.3 × 10−4, respectively. This procedure does not alter the shape of the Stokes V profiles, and it removes the vertical offset (see Fig. 1). The S/N of the final profiles ranges between 1600 and 2600. In the following, the observations are phased according to the ephemeris
 |
Fig. 1. Circular polarisation and null profiles for the 2016 Narval observations. Left: Stokes V (top) and null (bottom) profile computed using the full line list between 360 and 1080 nm. Right: same profiles but obtained using only red (> 500 nm) lines. In the latter case, we note that the spurious signal at line centre has been removed. The red solid lines in all panels indicate the median profile. |
where we used the first collected observation date as reference, Prot is the stellar rotation period found using ZDI (see Sect. 5), and ncyc is the rotation cycle.
3. Longitudinal magnetic field
The longitudinal field (Bl) is sensitive to the appearance of magnetic regions on the visible stellar hemisphere, which is modulated by the stellar rotation period (Prot). As a result, we can generally apply a standard periodogram analysis to Bl time series in order to find Prot (Hébrard et al. 2016; Petit et al. 2021; Carmona et al. 2023).
Previous studies extracted a stellar rotation period of 39.9 ± 0.8 d from chromospheric activity indexes’ time series (Suárez Mascareño et al. 2015; dos Santos et al. 2019) and 44.09 ± 0.08 d from photometric data sets (Bourrier et al. 2018). Recently, Kumar & Fares (2023) analysed GJ 436’s spectra obtained with HARPS and Narval and, by computing time series of activity indexes such as Ca II and Hα, found a significant (the false-alarm probability, i.e. FAP, was less than 0.1%) periodogram peak at 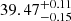 and
and 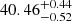 d, respectively. The Narval data set used by Kumar & Fares (2023) was the same one employed in this work.
d, respectively. The Narval data set used by Kumar & Fares (2023) was the same one employed in this work.
We followed Donati et al. (1997) to compute the disk-averaged, line-of-sight-projected stellar magnetic field as the first-order moment of a Stokes V profile
where λ0 (in nanometres) and geff are the normalisation wavelength and Landé factor of the LSD profiles, Ic is the continuum level, v is the radial velocity in the star’s rest frame, and c is the speed of light in vacuum (both in km s−1).
We used a normalisation wavelength and Landé factor of 700 nm and 1.1976, respectively, and performed the integration within ±10 km s−1 from line centre at around 9.6 km s−1. The Bl time series is illustrated in Fig. 2, with all values featuring a negative sign. The mean value is −12 G and both the dispersion and mean error bar are 6 G.
 |
Fig. 2. Analysis of longitudinal field measurements. Top: time series of Bl measurements. All values have a negative sign, and range between −1 and −23 G. Bottom: generalised Lomb-Scargle periodogram of the longitudinal field time series. The analysis does not yield any significant (FAP < 1%) periodicity. The window function of the entire time series has been included and is mirrored with respect to the x axis (VanderPlas 2018), to highlight aliases due to the observation cadence. |
Figure 2 shows the application of a generalised Lomb-Scargle periodogram (Zechmeister & Kürster 2009) to the entire 2016 time series. We do not report any dominant periodicity, with the FAP being systematically higher than 1%. The highest peaks are around 4, 15, and 70 d, but they are probably generated by the sparse sampling of our observations, as illustrated by the window function.
4. Gaussian process regression
We performed a quasi-periodic Gaussian process (GP; Haywood et al. 2014) fit to the longitudinal field curve since this model is more flexible than the standard sine function used in the Lomb-Scargle analysis. In fact, the GP model accounts for the evolution of the magnetic field and its variability (Aigrain & Foreman-Mackey 2022). Formally, we used the quasi-periodic covariance function
where δt, t′ is a Kronecker delta, and θi are the hyperparameters of the model: θ1 is the amplitude of the curve in G, θ2 is the evolution timescale in days (it expresses how rapidly the model evolves), θ3 is the recurrence timescale (i.e. Prot), and θ4 is the smoothness factor (controlling the harmonic structure of the curve). We added an additional hyperparameter to account for the excess of uncorrelated noise (S). In practice, we used the CPNEST package (Del Pozzo & Veitch 2022) which performs Bayesian inference via a nested sampling algorithm (Skilling 2004).
The results are reported in Table 2 and shown in Fig. 3. We applied uniform priors to all five hyperparameters, and allowed the search within realistic boundaries. The model fits the data to a 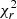 of 0.6, likely indicating that our formal error bars are overestimated. Following Donati et al. (2023), we re-scaled the error bars by a factor of two to fit the data at
of 0.6, likely indicating that our formal error bars are overestimated. Following Donati et al. (2023), we re-scaled the error bars by a factor of two to fit the data at 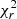 = 1.0, while keeping the excess of uncorrelated noise consistent with zero (see Fig. 3). The GP model is characterised by smooth oscillations (i.e. θ4 = 1.1), with an amplitude of 12 G and a stellar rotation period of 46.6 d, which is in agreement with the value estimated in the literature within error bars (Suárez Mascareño et al. 2015; Bourrier et al. 2018; Kumar & Fares 2023). The dispersion of the residuals is 2.5 G, that is to say slightly lower than the re-scaled error bars.
= 1.0, while keeping the excess of uncorrelated noise consistent with zero (see Fig. 3). The GP model is characterised by smooth oscillations (i.e. θ4 = 1.1), with an amplitude of 12 G and a stellar rotation period of 46.6 d, which is in agreement with the value estimated in the literature within error bars (Suárez Mascareño et al. 2015; Bourrier et al. 2018; Kumar & Fares 2023). The dispersion of the residuals is 2.5 G, that is to say slightly lower than the re-scaled error bars.
 |
Fig. 3. Gaussian process regression applied to the longitudinal field. Top: corner plot display of the 2D posterior distributions of the hyperparameters of the GP model (see Eq. (3)) as well as the 1D marginalised distributions along the diagonal. Vertical solid lines indicate the median of the distribution, while dashed lines indicate the 16th and 84th percentiles. Bottom: GP model overplotted to the time series of Bl values and residuals of the model. The shaded area indicates the 1σ uncertainty region. |
Results of the GP fit carried out on the Bl curve of GJ 436.
For Prot, using a uniform prior between 1 and 100 d results in a marginalised posterior distribution with three peaks, around 20 d, 40 d, and 80 d, with the latter being the highest peak. From the Lomb-Scargle analysis presented in Fig. 2, we observe that the observing window function features a broad peak at 80 d, hence we can exclude it from being the genuine rotation period of the star. If we lower the uniform prior boundary to 60 d, the marginalised posterior distribution exhibits a maximum at 46.6 d.
We also notice that the evolution time scale θ2 is not constrained by the GP. This is not surprising given the short (i.e. 80 d) time span of our observations. We therefore fixed θ2 to either 200 or 300 d, following the results of the starspots’ lifetime analysis carried out by Giles et al. (2017), and we performed a four-hyperparameter GP fit, but the results were only marginally different than those obtained with a five-hyperparameter GP. We also attempted to carry out an analogous test fixing a decay time of 470 d, that is the active regions’ timescale reported by Kumar & Fares (2023), but the results did not differ. Finally, a similar conclusion was obtained when fixing both the decay time scale and the smoothness to the values constrained by Martioli et al. (2022) for TOI-1759, which is an M dwarf of a similar spectral type as GJ 436. We used 400−600 d and 0.7−0.9 for θ2 and θ4, respectively.
Finally, although the GP retrieves the stellar rotation period around the expected value, we note that the error bars of such a time scale are large. An alternative option to extract the stellar rotation period is via ZDI optimisation, as outlined in the next section.
5. Zeeman-Doppler imaging
We reconstructed the large-scale magnetic field at the surface of GJ 436 by means of ZDI. The field is formally described as the sum of a poloidal and toroidal component, which are both expressed via spherical harmonic decomposition (Donati et al. 2006; Lehmann & Donati 2022). With ZDI, we synthesise and adjust Stokes V profiles in an iterative fashion, until a maximum-entropy solution at a fixed reduced χ2 is achieved (Skilling & Bryan 1984; Donati & Brown 1997; Folsom et al. 2018). The iterative process aims to fit the spherical harmonics’ coefficients αℓ, m, βℓ, m, and γℓ, m (with ℓ and m being the degree and order of the mode, respectively).
We optimised the input stellar rotation period following the method described in Petit et al. (2002) and Morin et al. (2008). Basically, we sought for the value that minimises the 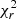 distribution at a fixed entropy (information content) over a grid of possible values between 2 and 100 d. We found Prot = 40.13 ± 1.29 d, which is compatible with the GP model estimate in Sect. 4, as well as with literature estimates (Bourrier et al. 2018; Kumar & Fares 2023). For the other input parameters, we adopted an inclination of 40° and an equatorial projected velocity (vesin(i)) of 0.33 km s−1 (Bourrier et al. 2022). We further assumed solid body rotation, a linear limb darkening law with a V-band coefficient of 0.6964 (Claret & Bloemen 2011), and the maximum degree of harmonic expansion ℓmax = 5, to match the spatial resolution determined by the vesin(i) of the star. The Narval Stokes V time series is shown in Fig. 4.
distribution at a fixed entropy (information content) over a grid of possible values between 2 and 100 d. We found Prot = 40.13 ± 1.29 d, which is compatible with the GP model estimate in Sect. 4, as well as with literature estimates (Bourrier et al. 2018; Kumar & Fares 2023). For the other input parameters, we adopted an inclination of 40° and an equatorial projected velocity (vesin(i)) of 0.33 km s−1 (Bourrier et al. 2022). We further assumed solid body rotation, a linear limb darkening law with a V-band coefficient of 0.6964 (Claret & Bloemen 2011), and the maximum degree of harmonic expansion ℓmax = 5, to match the spatial resolution determined by the vesin(i) of the star. The Narval Stokes V time series is shown in Fig. 4.
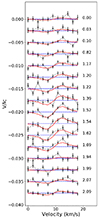 |
Fig. 4. Narval time series of circularly polarised Stokes profiles. Observations are shown as black dots and ZDI models as red lines, and they are offset vertically for better visualisation. The number on the right indicates the rotational cycle (see Eq. (1)). All signatures are antisymmetric, indicating that we are seeing the negative polarity of a dipole, and the moderate variation in amplitude is symbolic of a small tilt of the magnetic axis. |
The model Stokes V profiles were fit down to 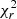 = 1.16, from an initial value of 2.24. The target
= 1.16, from an initial value of 2.24. The target 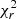 represents the best value that avoids underfitting and overfitting of the Stokes V shape, resulting in a, for example, weaker field or spurious magnetic features, respectively. The magnetic map is illustrated in Fig. 5 and its properties are listed in Table 3. The mean magnetic field strength is Bmean = 16 G, with the poloidal component accounting for 96% of the magnetic energy. The dipolar and quadrupolar modes store 90% and 8% energy, and the field is mostly axisymmetric (79%), with an obliquity of its axis of 15.5°.
represents the best value that avoids underfitting and overfitting of the Stokes V shape, resulting in a, for example, weaker field or spurious magnetic features, respectively. The magnetic map is illustrated in Fig. 5 and its properties are listed in Table 3. The mean magnetic field strength is Bmean = 16 G, with the poloidal component accounting for 96% of the magnetic energy. The dipolar and quadrupolar modes store 90% and 8% energy, and the field is mostly axisymmetric (79%), with an obliquity of its axis of 15.5°.
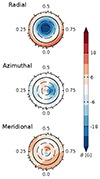 |
Fig. 5. ZDI reconstruction in flattened polar view of the large-scale field of GJ 436. From the top, the radial, azimuthal, and meridional components of the magnetic field vector are displayed. The radial ticks are located at the rotational phases when the observations were collected, while the concentric circles represent different stellar latitudes: −30°, +30°, and +60° (dashed lines), as well as the equator (solid line). The geometry is predominantly poloidal, dipolar, and axisymmetric. The colour bar encapsulates the magnetic field strength, up to a maximum of 31 G. |
Properties of the magnetic map.
Zeeman-Doppler imaging does not provide error bars on the reconstructed maps, and thus nor on field characteristics. We estimated variation bars on the field characteristics following the method of Mengel et al. (2016) and Fares et al. (2017). We reconstructed magnetic maps for the input parameters (inclination, veqsin(i), and Prot) by varying each of them within their error bars. The variation bars reported in Table 3 correspond to the maximum difference of field characteristics between the map with the optimised set of input parameters, and the ones considering the error bars on the input parameters. We also reconstructed the magnetic field topology using Prot = 44.09 d as input (Bourrier et al. 2018). The target 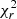 was adjusted to a larger value of 1.18, but the final map is consistent with the one presented in Fig. 5 within variation bars.
was adjusted to a larger value of 1.18, but the final map is consistent with the one presented in Fig. 5 within variation bars.
For illustration purposes, Fig. 6 shows an extrapolation of the surface field of the star. We used a potential field source surface method (e.g. Jardine et al. 2002), adopting a source surface at a distance of 4 stellar radii – beyond this distance, the field lines are fully open and purely radial. Using this extrapolation method, we found that at the orbital distance of GJ 436 b (0.028 au; Butler et al. 2004), the radial magnetic field ranges from 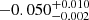 G to
G to 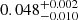 G, with the negative value representing an inward radial field and the positive value an outward radial field. In a follow-up study, we will perform stellar wind modelling and provide more detailed predictions of the characteristics of the wind environment (including its embedded magnetic field) at the orbit of GJ 436 b.
G, with the negative value representing an inward radial field and the positive value an outward radial field. In a follow-up study, we will perform stellar wind modelling and provide more detailed predictions of the characteristics of the wind environment (including its embedded magnetic field) at the orbit of GJ 436 b.
 |
Fig. 6. Three dimensional view of the extrapolated large-scale magnetic field of GJ 436. The colours at the surface of the star represent the radial magnetic field strength, while the blue and red colours along the magnetic field lines represent negative and positive polarities of the radial field. The rotation axis of the star is along the Z axis and the source surface has been set to 4 stellar radii, beyond which the field lines are fully open. |
6. Discussion and conclusions
In this paper, we have presented an analysis of the large-scale magnetic field of the exoplanet host star GJ 436. This will serve as input for the stellar wind and star-planet interaction analysis which will be presented in a future paper (Vidotto et al. 2023). The main goal is to understand stellar environments around M dwarfs, which is relevant for both exoplanet searches and habitability assessment frameworks (Vidotto et al. 2013; O’Malley-James & Kaltenegger 2019; Lingam & Loeb 2019). Ultimately, this will provide insightful feedback on the influence of stellar magnetic fields on planetary atmospheres and habitability, which is of crucial importance for JWST and Ariel, since GJ 436 is in the reference sample of both missions (Edwards & Tinetti 2022).
We used spectropolarimetric data collected with Narval in 2016, and we computed the longitudinal magnetic field from the time series of circularly polarised spectra. To the same time series, we applied tomographic inversion (i.e. ZDI) to reconstruct a map of the large-scale magnetic field topology. Our conclusions are summarised as follows:
-
The longitudinal field (Bl) spans between −0.9 and −23.1 G, with a median error bar of 6 G. Such a field strength is comparable with that of other M dwarfs with similar spectral types and rotation periods.
-
A periodicity analysis by means of a generalised Lomb-Scargle periodogram applied to the Bl time series did not highlight any specific periodicity, similarly to the activity indexes’ analysis of Kumar & Fares (2023). More specifically, we did not retrieve the expected rotation period of about 40 d, but observed different insignificant (FAP > 1%) peaks mostly associated with the observational window. We found TESS (Ricker et al. 2015) observations of GJ 436 collected in 2020 and 2022, but in both cases the observing window is shorter than the expected rotation period of the star, and hence they cannot be used to constrain such a parameter.
-
The GP regression analysis applied to the Bl time series produces a smooth model characterised by a rotation period of
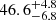 d. From the optimisation of stellar input parameters with ZDI, we were able to infer Prot = 40.13 ± 1.29 d. Both values are in agreement with literature estimates within uncertainties.
d. From the optimisation of stellar input parameters with ZDI, we were able to infer Prot = 40.13 ± 1.29 d. Both values are in agreement with literature estimates within uncertainties. -
The application of ZDI to the Stokes V time series revealed a simple field configuration, characterised by a poloidal, mainly dipolar and axisymmetric topology, with a mean magnetic field strength of 16 G. This simple geometry is in accordance with other stars of a similar spectral type, mass, and rotation period, that is GJ 205 (Hébrard et al. 2016; Cortés-Zuleta et al. 2023) and TOI-1759 (Martioli et al. 2022), as can be seen in Fig. 7.
 |
Fig. 7. Properties of the magnetic topologies for cool, main-sequence stars obtained via ZDI. The label of GJ 436 is highlighted in red. The y and x axes represent the mass and rotation period of the star, and iso-Rossby number curves were overplotted using the empirical relations of Wright et al. (2018). The symbol size, colour, and shape encode the ZDI average field strength, poloidal and toroidal energy fraction, and axisymmetry. Data entering the plot are taken from Donati et al. (2008), Morin et al. (2008, 2010), Phan-Bao et al. (2009), Hébrard et al. (2016), Kochukhov & Lavail (2017), Moutou et al. (2017), Kochukhov & Shulyak (2019), Klein et al. (2021), Martioli et al. (2022), and Cortés-Zuleta et al. (2023). |
GJ 436 is known to have an activity cycle: Lothringer et al. (2018) analysed 14 yr of photometric data (in Strömgren b and y filters) between 2004 and 2018, and reported a 7.4 yr cycle, which was then re-analysed by Loyd et al. (2023) who consistently found a 7.75 yr cycle. Moreover, a similar time scale between 5 and 7 yr was obtained by Kumar & Fares (2023) from time series of chromospheric activity indexes (Hα, Na I, and Ca II H&K), spanning 14 yr. This is in agreement with what is expected for M dwarfs from radial velocity exoplanet searches (Gomes da Silva et al. 2012) and photometric surveys (Suárez Mascareño et al. 2016, 2018) for M dwarfs of a similar spectral type.
In this light, it is interesting to place the magnetic field map we reconstructed along the track of the activity cycle. Our observations were collected in 2016 (see Table 1), meaning that our ZDI map portrays the magnetic field during an ascending phase of the cycle (i.e. towards photometric maximum), as shown in the yellow box in Fig. 8. This advocates for additional spectropolarimetric monitoring of GJ 436, in order to ideally reconstruct a ZDI map during cycle minimum and maximum, and determine whether the magnetic field undergoes polarity reversals as it does for the Sun (Sanderson et al. 2003; Lehmann et al. 2021), and other stars and other cool stars (e.g. τ Boo Fares et al. 2009; Mengel et al. 2016; Jeffers et al. 2018 and 61 Cyg Boro Saikia et al. 2016). If we assume Pcyc = 7.75 yr, we predict the next photometric minimum to be around 2030, whereas the next maximum would be around mid 2026. Monitoring the secular evolution of the large-scale field of GJ 436 would be an essential ingredient to interpret the observed signatures of star-planet interactions. Indeed, magnetic cycles modulate the radiation output of stars (Yeo et al. 2014; Hazra et al. 2020), therefore providing a temporal modulation of planetary atmospheric erosion.
 |
Fig. 8. Photometric cycle reported in Lothringer et al. (2018) and Loyd et al. (2023). Blue data points represent the photometric observations, while the orange line represents the sinusoidal fit at a period of 7.75 yr combined with a linear trend. The yellow box on the right of the plot indicates the time window of our Narval observations in 2016. The figure was adapted from Loyd et al. (2023). |
Acknowledgments
We thank the anonymous referee for the fruitful review of this work. We acknowledge funding from the French National Research Agency (ANR) under contract number ANR-18-CE31-0019 (SPlaSH). S.B. acknowledges funding from the SCI-S department of the European Space Agency (ESA), under the Science Faculty Research fund E/0429-03. R.F. acknowledges support from the United Arab Emirates University (UAEU) startup grant number G00003269. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (projects SPICE DUNE and ASTROFLOW, grant agreements No. 947634 and 817540). This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna; Astropy, 12 a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018); NumPy (van der Walt et al. 2011); Matplotlib: Visualization with Python (Hunter 2007); SciPy (Virtanen et al. 2020) and PyAstronomy (Czesla et al. 2019).
References
- Aigrain, S., & Foreman-Mackey, D. 2022, ArXiv e-prints [arXiv:2209.08940] [Google Scholar]
- Allan, A., & Vidotto, A. A. 2019, MNRAS, 490, 3760 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Attia, O., Bourrier, V., Eggenberger, P., et al. 2021, A&A, 647, A40 [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landolfi, M., Landstreet, J. D., et al. 2009, PASP, 121, 993 [Google Scholar]
- Beaugé, C., & Nesvorný, D. 2013, ApJ, 763, 12 [Google Scholar]
- Bellotti, S., Petit, P., Morin, J., et al. 2022, A&A, 657, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beust, H., Bonfils, X., Montagnier, G., Delfosse, X., & Forveille, T. 2012, A&A, 545, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boro Saikia, S., Jeffers, S. V., Morin, J., et al. 2016, A&A, 594, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boro Saikia, S., Marvin, C. J., Jeffers, S. V., et al. 2018, A&A, 616, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., Ehrenreich, D., & Lecavelier des Etangs, A. 2015, A&A, 582, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., Lecavelier des Etangs, A., Ehrenreich, D., Tanaka, Y. A., & Vidotto, A. A. 2016, A&A, 591, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., Lovis, C., Beust, H., et al. 2018, Nature, 553, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrier, V., Zapatero Osorio, M. R., Allart, R., et al. 2022, A&A, 663, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Carmona, A., Delfosse, X., Bellotti, S., et al. 2023, A&A, 674, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carolan, S., Vidotto, A. A., Villarreal D’Angelo, C., & Hazra, G. 2021, MNRAS, 500, 3382 [Google Scholar]
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortés-Zuleta, P., Boisse, I., Klein, B., et al. 2023, A&A, 673, A14 [CrossRef] [EDP Sciences] [Google Scholar]
- Czesla, S., Schröter, S., Schneider, C. P., et al. 2019, Astrophysics Source Code Library [record ascl:1906.010] [Google Scholar]
- Davis, T. A., & Wheatley, P. J. 2009, MNRAS, 396, 1012 [CrossRef] [Google Scholar]
- Del Pozzo, W., & Veitch, J. 2022, Astrophysics Source Code Library [record ascl:2205.021] [Google Scholar]
- Donati, J. F. 2003, in Solar Polarization, eds. J. Trujillo-Bueno, & J. Sanchez Almeida, ASP Conf. Ser., 307, 41 [Google Scholar]
- Donati, J. F., & Brown, S. F. 1997, A&A, 326, 1135 [Google Scholar]
- Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [Google Scholar]
- Donati, J. F., Howarth, I. D., Jardine, M. M., et al. 2006, MNRAS, 370, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. F., Morin, J., Petit, P., et al. 2008, MNRAS, 390, 545 [Google Scholar]
- Donati, J. F., Cristofari, P. I., Finociety, B., et al. 2023, MNRAS, [arXiv:2304.09642] [Google Scholar]
- dos Santos, L. A., Ehrenreich, D., Bourrier, V., et al. 2019, A&A, 629, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edwards, B., & Tinetti, G. 2022, AJ, 164, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenreich, D., & Désert, J. M. 2011, A&A, 529, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrenreich, D., Bourrier, V., Wheatley, P. J., et al. 2015, Nature, 522, 459 [Google Scholar]
- Fares, R., Donati, J. F., Moutou, C., et al. 2009, MNRAS, 398, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Fares, R., Moutou, C., Donati, J. F., et al. 2013, MNRAS, 435, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Fares, R., Bourrier, V., Vidotto, A. A., et al. 2017, MNRAS, 471, 1246 [Google Scholar]
- Folsom, C. P., Petit, P., Bouvier, J., et al. 2016, MNRAS, 457, 580 [Google Scholar]
- Folsom, C. P., Bouvier, J., Petit, P., et al. 2018, MNRAS, 474, 4956 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmeister, B., Czesla, S., Perdelwitz, V., et al. 2023, A&A, 670, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Smart, R. L., et al.) 2021, A&A, 649, A6 [EDP Sciences] [Google Scholar]
- Giles, H. A. C., Collier Cameron, A., & Haywood, R. D. 2017, MNRAS, 472, 1618 [Google Scholar]
- Gillon, M., Pont, F., Demory, B. O., et al. 2007, A&A, 472, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2012, A&A, 541, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Günther, M. N., Zhan, Z., Seager, S., et al. 2020, AJ, 159, 60 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [Google Scholar]
- Hazra, G., Vidotto, A. A., & D’Angelo, C. V. 2020, MNRAS, 496, 4017 [NASA ADS] [CrossRef] [Google Scholar]
- Hazra, G., Vidotto, A. A., Carolan, S., Villarreal D’Angelo, C., & Manchester, W. 2022, MNRAS, 509, 5858 [Google Scholar]
- Hébrard, É. M., Donati, J. F., Delfosse, X., et al. 2016, MNRAS, 461, 1465 [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jardine, M., Collier Cameron, A., & Donati, J. F. 2002, MNRAS, 333, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffers, S. V., Mengel, M., Moutou, C., et al. 2018, MNRAS, 479, 5266 [NASA ADS] [CrossRef] [Google Scholar]
- Kavanagh, R. D., Vidotto, A. A., Klein, B., et al. 2021, MNRAS, 504, 1511 [Google Scholar]
- Kavanagh, R. D., Vidotto, A. A., Vedantham, H. K., et al. 2022, MNRAS, 514, 675 [CrossRef] [Google Scholar]
- Ketzer, L., & Poppenhaeger, K. 2023, MNRAS, 518, 1683 [Google Scholar]
- Khodachenko, M. L., Shaikhislamov, I. F., Lammer, H., et al. 2019, ApJ, 885, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, B., Donati, J.-F., Moutou, C., et al. 2021, MNRAS, 502, 188 [Google Scholar]
- Kochukhov, O., & Lavail, A. 2017, ApJ, 835, L4 [Google Scholar]
- Kochukhov, O., & Shulyak, D. 2019, ApJ, 873, 69 [Google Scholar]
- Kochukhov, O., Makaganiuk, V., & Piskunov, N. 2010, A&A, 524, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Konings, T., Baeyens, R., & Decin, L. 2022, A&A, 667, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kulow, J. R., France, K., Linsky, J., & Loyd, R. O. P. 2014, ApJ, 786, 132 [Google Scholar]
- Kumar, M., & Fares, R. 2023, MNRAS, 518, 3147 [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [Google Scholar]
- Lavie, B., Ehrenreich, D., Bourrier, V., et al. 2017, A&A, 605, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier Des Etangs, A. 2007, A&A, 461, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehmann, L. T., & Donati, J. F. 2022, MNRAS, 514, 2333 [CrossRef] [Google Scholar]
- Lehmann, L. T., Hussain, G. A. J., Vidotto, A. A., Jardine, M. M., & Mackay, D. H. 2021, MNRAS, 500, 1243 [Google Scholar]
- Lingam, M., & Loeb, A. 2019, Int. J. Astrobiol., 18, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Llama, J., Vidotto, A. A., Jardine, M., et al. 2013, MNRAS, 436, 2179 [NASA ADS] [CrossRef] [Google Scholar]
- Lothringer, J. D., Benneke, B., Crossfield, I. J. M., et al. 2018, AJ, 155, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Louca, A. J., Miguel, Y., Tsai, S.-M., et al. 2023, MNRAS, 521, 3333 [NASA ADS] [CrossRef] [Google Scholar]
- Loyd, R. O. P., Schneider, P. C., Jackman, J. A. G., et al. 2023, AJ, 165, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Luger, R., Barnes, R., Lopez, E., et al. 2015, Astrobiology, 15, 57 [Google Scholar]
- Lundkvist, M. S., Kjeldsen, H., Albrecht, S., et al. 2016, Nat. Commun., 7, 11201 [Google Scholar]
- Martioli, E., Hébrard, G., Fouqué, P., et al. 2022, A&A, 660, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazeh, T., Holczer, T., & Faigler, S. 2016, A&A, 589, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mengel, M. W., Fares, R., Marsden, S. C., et al. 2016, MNRAS, 459, 4325 [NASA ADS] [CrossRef] [Google Scholar]
- Mesquita, A. L., Rodgers-Lee, D., & Vidotto, A. A. 2021, MNRAS, 505, 1817 [NASA ADS] [CrossRef] [Google Scholar]
- Morin, J., Donati, J. F., Petit, P., et al. 2008, MNRAS, 390, 567 [Google Scholar]
- Morin, J., Donati, J. F., Petit, P., et al. 2010, MNRAS, 407, 2269 [Google Scholar]
- Moutou, C., Hébrard, E. M., Morin, J., et al. 2017, MNRAS, 472, 4563 [NASA ADS] [CrossRef] [Google Scholar]
- O’Malley-James, J. T., & Kaltenegger, L. 2019, MNRAS, 485, 5598 [CrossRef] [Google Scholar]
- Owen, J. E., & Jackson, A. P. 2012, MNRAS, 425, 2931 [Google Scholar]
- Penz, T., Micela, G., & Lammer, H. 2008, A&A, 477, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, P., Donati, J. F., & Collier Cameron, A. 2002, MNRAS, 334, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Donati, J. F., Aurière, M., et al. 2005, MNRAS, 361, 837 [Google Scholar]
- Petit, P., Louge, T., Théado, S., et al. 2014, PASP, 126, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Folsom, C. P., Donati, J. F., et al. 2021, A&A, 648, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phan-Bao, N., Lim, J., Donati, J.-F., Johns-Krull, C. M., & Martín, E. L. 2009, ApJ, 704, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Guinan, E. F., Güdel, M., & Audard, M. 2005, ApJ, 622, 680 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Rodgers-Lee, D., Rimmer, P. B., Vidotto, A. A., et al. 2023, MNRAS, 521, 5880 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, L. J., Fulton, B. J., Hirsch, L. A., et al. 2021, ApJS, 255, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr., 90, 054005 [Google Scholar]
- Sanderson, T. R., Appourchaux, T., Hoeksema, J. T., & Harvey, K. L. 2003, J. Geophys. Res.: Space Phys., 108, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Saur, J., Grambusch, T., Duling, S., Neubauer, F. M., & Simon, S. 2013, A&A, 552, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Segura, A., Walkowicz, L. M., Meadows, V., Kasting, J., & Hawley, S. 2010, Astrobiology, 10, 751 [Google Scholar]
- Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
- Skilling, J. 2004, AIP Conf. Ser., 735, 395 [Google Scholar]
- Skilling, J., & Bryan, R. K. 1984, MNRAS, 211, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., & González Hernández, J. I. 2016, A&A, 595, A12 [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., et al. 2018, A&A, 612, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tilley, M. A., Segura, A., Meadows, V., Hawley, S., & Davenport, J. 2019, Astrobiology, 19, 64 [Google Scholar]
- Turnpenney, S., Nichols, J. D., Wynn, G. A., & Burleigh, M. R. 2018, ApJ, 854, 72 [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- VanderPlas, J. T. 2018, ApJS, 236, 16 [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J. M., et al. 2003, Nature, 422, 143 [Google Scholar]
- Vidotto, A. A., & Bourrier, V. 2017, MNRAS, 470, 4026 [NASA ADS] [CrossRef] [Google Scholar]
- Vidotto, A. A., Jardine, M., Morin, J., et al. 2013, A&A, 557, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidotto, A. A., Gregory, S. G., Jardine, M., et al. 2014a, MNRAS, 441, 2361 [Google Scholar]
- Vidotto, A. A., Jardine, M., Morin, J., et al. 2014b, MNRAS, 438, 1162 [Google Scholar]
- Vidotto, A. A., Bourrier, V., Fares, R., et al. 2023, A&A, submitted (Paper II) [Google Scholar]
- Villarreal D’Angelo, C., Esquivel, A., Schneiter, M., & Sgró, M. A. 2018, MNRAS, 479, 3115 [CrossRef] [Google Scholar]
- Villarreal D’Angelo, C., Vidotto, A. A., Esquivel, A., Hazra, G., & Youngblood, A. 2021, MNRAS, 501, 4383 [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Burovski, E., et al. 2020, https://doi.org/10.5281/zenodo.4100507 [Google Scholar]
- Wright, N. J., Newton, E. R., Williams, P. K. G., Drake, J. J., & Yadav, R. K. 2018, MNRAS, 479, 2351 [Google Scholar]
- Yeo, K. L., Krivova, N. A., & Solanki, S. K. 2014, Space Sci. Rev., 186, 137 [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog: I/322A [Google Scholar]
- Zarka, P. 1998, J. Geophys. Res., 103, 20159 [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
- Zeeman, P. 1897, Nature, 55, 347 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Circular polarisation and null profiles for the 2016 Narval observations. Left: Stokes V (top) and null (bottom) profile computed using the full line list between 360 and 1080 nm. Right: same profiles but obtained using only red (> 500 nm) lines. In the latter case, we note that the spurious signal at line centre has been removed. The red solid lines in all panels indicate the median profile. |
| In the text | |
 |
Fig. 2. Analysis of longitudinal field measurements. Top: time series of Bl measurements. All values have a negative sign, and range between −1 and −23 G. Bottom: generalised Lomb-Scargle periodogram of the longitudinal field time series. The analysis does not yield any significant (FAP < 1%) periodicity. The window function of the entire time series has been included and is mirrored with respect to the x axis (VanderPlas 2018), to highlight aliases due to the observation cadence. |
| In the text | |
 |
Fig. 3. Gaussian process regression applied to the longitudinal field. Top: corner plot display of the 2D posterior distributions of the hyperparameters of the GP model (see Eq. (3)) as well as the 1D marginalised distributions along the diagonal. Vertical solid lines indicate the median of the distribution, while dashed lines indicate the 16th and 84th percentiles. Bottom: GP model overplotted to the time series of Bl values and residuals of the model. The shaded area indicates the 1σ uncertainty region. |
| In the text | |
 |
Fig. 4. Narval time series of circularly polarised Stokes profiles. Observations are shown as black dots and ZDI models as red lines, and they are offset vertically for better visualisation. The number on the right indicates the rotational cycle (see Eq. (1)). All signatures are antisymmetric, indicating that we are seeing the negative polarity of a dipole, and the moderate variation in amplitude is symbolic of a small tilt of the magnetic axis. |
| In the text | |
 |
Fig. 5. ZDI reconstruction in flattened polar view of the large-scale field of GJ 436. From the top, the radial, azimuthal, and meridional components of the magnetic field vector are displayed. The radial ticks are located at the rotational phases when the observations were collected, while the concentric circles represent different stellar latitudes: −30°, +30°, and +60° (dashed lines), as well as the equator (solid line). The geometry is predominantly poloidal, dipolar, and axisymmetric. The colour bar encapsulates the magnetic field strength, up to a maximum of 31 G. |
| In the text | |
 |
Fig. 6. Three dimensional view of the extrapolated large-scale magnetic field of GJ 436. The colours at the surface of the star represent the radial magnetic field strength, while the blue and red colours along the magnetic field lines represent negative and positive polarities of the radial field. The rotation axis of the star is along the Z axis and the source surface has been set to 4 stellar radii, beyond which the field lines are fully open. |
| In the text | |
 |
Fig. 7. Properties of the magnetic topologies for cool, main-sequence stars obtained via ZDI. The label of GJ 436 is highlighted in red. The y and x axes represent the mass and rotation period of the star, and iso-Rossby number curves were overplotted using the empirical relations of Wright et al. (2018). The symbol size, colour, and shape encode the ZDI average field strength, poloidal and toroidal energy fraction, and axisymmetry. Data entering the plot are taken from Donati et al. (2008), Morin et al. (2008, 2010), Phan-Bao et al. (2009), Hébrard et al. (2016), Kochukhov & Lavail (2017), Moutou et al. (2017), Kochukhov & Shulyak (2019), Klein et al. (2021), Martioli et al. (2022), and Cortés-Zuleta et al. (2023). |
| In the text | |
 |
Fig. 8. Photometric cycle reported in Lothringer et al. (2018) and Loyd et al. (2023). Blue data points represent the photometric observations, while the orange line represents the sinusoidal fit at a period of 7.75 yr combined with a linear trend. The yellow box on the right of the plot indicates the time window of our Narval observations in 2016. The figure was adapted from Loyd et al. (2023). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



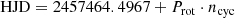
![$$ \begin{aligned} B_{\rm l}\;[G] = \frac{-2.14 \times 10^{11}}{\lambda _0 {g}_{\mathrm{eff} }c}\frac{\int vV(v)\mathrm{d}v}{\int (I_{\rm c}-I)\mathrm{d}v}, \end{aligned} $$](/articles/aa/full_html/2023/08/aa46675-23/aa46675-23-eq5.gif)
![$$ \begin{aligned} k(t,t^\prime ) = \theta _1^2\exp \left[-\frac{(t-t^\prime )^2}{\theta _2^2}-\frac{\sin ^2 \left(\frac{\pi (t-t^\prime )}{\theta _3}\right)}{\theta _4^2} \right] + S^2\delta _{t,t^\prime }, \end{aligned} $$](/articles/aa/full_html/2023/08/aa46675-23/aa46675-23-eq6.gif)