| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A156 | |
| Number of page(s) | 24 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202345843 | |
| Published online | 14 July 2023 | |
Statistics of Magrathea exoplanets beyond the main sequence
Simulating the long-term evolution of circumbinary giant planets with TRES
1
Department of Physics and Astronomy “Galileo Galilei” (DFA), University of Padua,
via Marzolo 8,
35131
Padua, Italy
e-mail: gabriele.columba@phd.unipd.it
2
INAF – Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35142
Padua, Italy
3
Instituto de Astrofísica de Andalucía, CSIC,
Glorieta de la Astronomía s/n,
18008
Granada, Spain
4
Institute of Gravitational Wave Astronomy and School of Physics and Astronomy, University of Birmingham,
Edgbaston, Birmingham
B15 2TT, UK
5
The Anton Pannekoek Institute for Astronomy, University of Amsterdam (UvA),
Science Park 904,
1098 XH
Amsterdam, The Netherlands
Received:
3
January
2023
Accepted:
9
May
2023
Context. Notwithstanding the tremendous growth of the field of exoplanets in the last decade, limited attention has been paid to the planets around binary stars, which represent a small fraction of the total discoveries to date. Circumbinary planets (CBPs) have been discovered primarily with transit and eclipse timing variation methods, mainly around main sequence (MS) stars. No exoplanet has been found orbiting double white dwarf (DWD) binaries yet.
Aims. In the interest of expanding our understanding of the final fate of CBPs, we modelled their long-term evolution, throughout the life stages of their hosts, from the MS to WD. Our goal is to provide the community with theoretical constraints on the evolution of CBPs beyond the MS and with the occurrence rates of planet survival throughout the ageing of the systems.
Methods. We further developed the publicly available Triple Evolution Simulation (TRES) code, to adapt it to the mass range of sub-stellar objects (SSOs). We did so by implementing a variety of physical processes that affect giant planets and brown dwarfs. We used TRES to simulate the evolution, up to one Hubble time, of two synthetic populations of circumbinary giant planets. Each population was generated using different priors for the planetary orbital parameters.
Results. In our simulated populations we identified several evolutionary categories, such as survived, merged, and destabilised systems. Our primary interest is those systems in which the planet survived the WD formation of both stars in the binary. We named these planets Magrathea. We found that a significant fraction of simulated CBPs survive the entire system evolution and become Magratheas, regardless of their mass. In the absence of multi-planet migration mechanisms, this category of CBPs is characterised by long orbital periods.
Conclusions. Magrathea planets are a natural outcome of triple-system evolution, and our study indicates that they should be relatively common in the Galaxy. These gas giants can survive the death of their binary hosts if they orbit far enough away to avoid engulfment and instabilities. Our results can ultimately be a reference to orient future observations of this uncharted class of planets and to compare different theoretical models.
Key words: planets and satellites: dynamical evolution and stability / planets and satellites: gaseous planets / white dwarfs / binaries: general / gravitational waves
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In spite of the diversity of exoplanets uncovered in the last few years, the known sample of planetary bodies does not uniformly cover the stellar Hertzprung–Russell (H–R) diagram. Several H–R regions, which show evidence of the possible existence of planets, show low statistics mostly due to observational bias. For instance, while the majority of planets have been found around main sequence (MS) stars, only one confirmed planet (Blackman et al. 2021) and several candidates (Gänsicke et al. 2019; Vanderburg et al. 2020; Gaia Collaboration 2023a) have been identified orbiting single white dwarfs (WDs). These detections arrived after many years of dedicated research (see Veras 2021 and references therein for a recent review). Another unusual planetary population is the circumbinary planets (CBPs), called P-type systems;1 these planets orbit compact binary stars with typical inner orbital separations of less than ~ 10 au. Over the years, multiple studies have shown that stars in binary and multiple systems are ubiquitous throughout the Milky Way (Raghavan et al. 2010; Duchêne & Kraus 2013; Tokovinin 2014, 2021; Moe & Di Stefano 2017). This physical feature naturally sparked the interest of planet chasers, who sky-hunted planets orbiting multiple-star systems through various methods, such as astrom-etry (e.g. Sahlmann et al. 2015), transit (e.g. Doyle et al. 2011; Kostov et al. 2014, 2020; Martin & Fabrycky 2021), and radial velocities (e.g. Martin et al. 2019; Triaud et al. 2022; Standing et al. 2023), and who also explained the small statistics due to selection bias. For instance, when focusing on the P-type population around double MS binaries, most of the evidence has been collected through the transit method, which highlighted the coplanarity of planetary and binary orbits. However, Armstrong et al. (2014) showed that if planetary orbital inclinations were randomly distributed with respect to the binary orbital plane, then the inferred frequency of planets in circumbinary orbits should be exceptionally high compared to that around single stars. However, if the distribution favoured coplanarity, then the frequency of CBPs would be consistent with what has been observed for planets around single stars. And if CBPs have at least the same occurrence rate of most of the 5300 planets discovered until now, the question is why we cannot see them. The answer most probably lies in the parameter space that this population covers, which makes their detection challenging with the instruments and observational sampling we currently use.
Shifting the attention to the H-R diagram region of evolved stars, very recent works show that the stellar multiplicity percentage is held there too. For instance, thanks to the exceptional Gaia DR3 data (Gaia Collaboration 2023b), a new sample of WDs in binary systems has been established (Gaia Collaboration 2023a). Similarly, a more focused work on the hot WD sample identified a probable binary fraction of ~55% (Gómez-Muñoz et al. 2022). For both studies, the nature of the stellar companion is uncertain.
Very little is known about exoplanets around evolved binary systems. To date, among the S-type systems (Marzari & Thebault 2019 and references therein) planets have only been found orbiting the MS component, never the WD component (e.g. HD 8535, Naef et al. 2010; Mugrauer 2019; WASP-98, Hellier et al. 2014; Southworth et al. 2020; HIP 116454, Vanderburg et al. 2015; TOI-1259, Martin et al. 2021; TOI-3714, Cañas et al. 2022). In these types of systems the stellar binary is usually very wide (e.g. 302 au for TOI-3714 and 3500 au for WASP-98), and therefore the evolution of the stars is not affected by binary interactions. This means that the planet, unless it hopped from the evolved primary star (Kratter & Perets 2012), has not directly suffered the evolution of its host star, which is still in the MS stage.
On the other hand, several P-type exoplanets are known to orbit a binary where one of the stars evolved off the MS. Among the ~45 confirmed circumbinary substellar objects (SSOs) known to date, seven planets orbit one WD star (for a total of five planetary systems: DP Leo, Beuermann et al. 2011; NN Ser, Beuermann et al. 2010; PSR B1620-26, Sigurdsson et al. 2003; RR Cae, Qian et al. 2012; UZ For, Potter et al. 2011) and eight planets have one host that has completed a giant branch phase, but is not yet a WD (for a total of five systems: Kepler-451, Esmer et al. 2022; HW Vir, Beuermann et al. 2012; MXB 1658-298, Jain et al. 2017; NSVS 14256825, Zhu et al. 2019; NY Vir, Song et al. 2019)2. Detecting planets around evolved systems is usually through an indirect method: the direct observation of WDs by optical inspection is known to be quite difficult due to their small radii and faint total luminosity, which inevitably reflects on the hurdle of detecting a possible planetary companion with a high significance. The typical technique used to discover the known evolved P-type systems is the eclipse transit timing variation (ETTV) method, where the significance of a detection increases with the length on the observational baseline. In some cases the relatively short baseline has been a source of discussions on the presence and/or nature of some of these exo-planets (e.g. Bours et al. 2016). This is mostly due to confusion with the Applegate mechanism (Applegate 1992), to questions on the system stability (e.g. Wittenmyer et al. 2013), or to the necessity to refine the ETTV models (Pulley et al. 2022), as alternative interpretations of the data.
When comparing these systems to the S-type siblings, stellar binaries present compact orbits, meaning that any stellar evolution is affected by binary interactions (such as mass transfer episodes). This means that their planetary companions must have experienced, and survived, the consequences of at least one binary evolutionary step.
The evidence of a larger number of planetary systems in evolved binaries than single WDs has been argued not to be a coincidence. A work by Kostov et al. (2016) studied the dynamical evolution of nine Kepler CBPs, with particular focus on the common envelope (CE) phases of the stars. The authors found that CBPs have more chances of survival when orbiting compact binary systems than single stars of similar mass. As an example, a planet orbiting a binary of total mass ≃1.3 M⊙ at the distance of Mercury from the Sun would likely survive the giant phases of its hosts, whereas Mercury (and Earth too) will be completely engulfed as soon as the Sun radius expands along the red giant branch (Schröder & Smith 2008).
The next evolutionary step of these systems is the evolution of the secondary stellar companion, which by definition has a lower mass than the mass of the primary progenitor. By simplifying, this process can either result in the merger of the two stars or in a double degenerate stellar system whose components could be either a double white dwarf (DWD) or a WD and a neutron star. To date, about one hundred double generate systems have been detected, using a variety of methods (see Korol et al. 2022b, for a recent overview). The majority of sources were detected by the Supernova Ia Progenitor surveY (SPY; Napiwotzki et al. 2020, and references therein) and the Extremely Low-Mass (ELM) survey (Brown et al. 2010, 2020) which is based on the Sloan Digital Sky Survey. In addition, the ZTF high-cadence Galactic plane survey (Masci et al. 2019) has been particularly effective in detecting extremely compact DWD systems (Burdge et al. 2019, 2020). All these surveys have helped to increase the number of known short-period binaries, yet the largest improvement in the field will come with the Laser Interferometer Space Antenna (LISA, Amaro-Seoane et al. 2017), which is expected to find around ~104 DWDs (Korol et al. 2017; Lamberts et al. 2019; Breivik et al. 2020; Korol et al. 2022b) and many other types of degenerate short-period binaries (Amaro-Seoane et al. 2023).
The LISA mission will be transformative not only for the stellar physics of binaries, but also for exoplanets, being the only planned mission with the potential to detect giant planets around DWDs anywhere in the Milky Way (Tamanini & Danielski 2019; Danielski et al. 2019) and in the Large Magellanic Cloud (Danielski & Tamanini 2020). At present no exoplanets orbiting DWDs have been found, but the results of Kostov et al. (2016), coupled with the fact that 97% of existing stars will eventually end their lives as WDs (Fontaine et al. 2001), suggest that DWD binaries likely harbour surviving planets. Our work aims to thoroughly explore this possibility via modelling of the long-term evolution of different populations of CBPs.
The focus of this work is to quantify the survival rate of CBPs in the context of the host-binary evolution, from the zero age main sequence (ZAMS) to one Hubble time (i.e. the age of the Universe). For our purposes we exploited the publicly available Triple Evolution Simulation code (TRES;3 Toonen et al. 2016, see also Sect. 2.1) and expanded it into the TRES-Exo code, a TRES option dedicated to the evolution of compact binaries hosting a single giant planet. We then used TRES-Exo to produce two populations of systems with different initial planetary priors to evaluate their impact on the final populations and on the occurrence rates. An important collateral science to our analysis is the exploration of the possibility of using the surviving planets (which we refer to as Magrathea4 planets) to constrain the CE phase of the binary (Ivanova et al. 2013).
Our work is set within the broader context of study for the development of the planetary detection science case of the LISA mission. This development includes the LISA detection prospects of SSOs orbiting DWDs through Bayesian analysis by Katz et al. (2022), the determination of the LISA detection efficiency by Danielski et al., in prep., and the study of second-generation planetary formation around DWD by Ledda et al. (2023).
This paper has the following structure. In Sect. 2, we present the physical models employed to simulate the circumbinary SSOs and implemented in TRES. In Sect. 3, we illustrate the initial properties of our synthetic populations. In Sect. 4, we present our results, divided by category of evolution, and we highlight the most important final properties of the synthetic sample. In Sect. 5, we discuss some implications of our results, and we draw our conclusions in Sect. 6.
2 Methods
2.1 The Triple Evolution Simulation code
The powerhouse of our simulations is the simulation package TRES, which is publicly available on github and described in depth in Toonen et al. (2016). This software was designed to simulate hierarchical triple star systems, and it includes a thorough analytical treatment including secular orbital evolution, and various stellar interactions (e.g. tides, CE evolution, stellar winds, and supernovae and associated natal kicks). The single stellar evolution is modelled by SeBa (Nelemans et al. 2001; Toonen et al. 2012; Toonen & Nelemans 2013), which is a parametrised, fast stellar evolution code. SeBa determines the most important stellar parameters (such as mass, core mass, radius, and luminosity) at a given timestep, using the fitting formula of Hurley et al. (2000). We further developed TRES and SeBa so that we can simulate substellar bodies as well, namely brown dwarfs and gaseous planets. In the following section we illustrate the key physical models that were deemed meaningful for our simulations.
2.2 Developing TRES for planets: TRES–Exo
Given that our main goal is to explore the fate of exoplanets in hierarchical triple systems, we added new features to TRES that reflect the physical processes and properties typical of the giant planet mass range (0.2–16 MJ). We describe each feature in the following paragraphs. It should also be noted that we leave the modelling of the long-term evolution of brown dwarfs for future analysis, and we focus here on the planetary mass range.
2.2.1 Stability criteria
Being interested in the long-term evolution of systems, it is relevant to evaluate the stability of the simulated triples. New stability criteria choices have been added to TRES. For the purpose of generating CBPs, in particular, we decided to adopt the criterion of Holman & Wiegert (1999) for P-type stability, which formulates the critical minimum semi-major axes ratio as
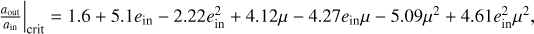 (1)
(1)
where ein is the eccentricity of the inner binary and 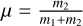 its mass ratio. This criterion, also used in recent N -body literature (see e.g. Ballantyne et al. 2021), results in a minimum planetary semi-major axis of aout = 2.39 ain for the special case of an equal mass inner binary on a circular orbit; higher eccentricity causes the closest stable orbit to move farther away. We note that the critical outer semi-major axis depends on the parameters of the inner binary alone.
its mass ratio. This criterion, also used in recent N -body literature (see e.g. Ballantyne et al. 2021), results in a minimum planetary semi-major axis of aout = 2.39 ain for the special case of an equal mass inner binary on a circular orbit; higher eccentricity causes the closest stable orbit to move farther away. We note that the critical outer semi-major axis depends on the parameters of the inner binary alone.
2.2.2 Tidal interactions
Tidal forces are responsible for several phenomena in binary and close-in systems, including orbit circularisation, synchronisation of rotational periods of the bodies, and shrinking of the orbital distances; specifically for eccentric orbits, they are also known to cause apsidal precession (i.e. a secular change in the position of a body’s periastron). In general, the presence of tides translates to torques that exchange angular momentum between the star and the orbit, together with a dissipation of the energy into the tide itself.
TRES includes a treatment of tidal interaction through the model of Hut (1981), which assumes small tides in their equilibrium shape, in a constant time lag with respect to the line of the centres. The outcome of this tidal interaction is to change the orbital parameters of the stars. Either an equilibrium configuration occurs, where a circular binary of stars rotates synchronously with their orbital period, or there is a fatal decay of the orbits, leading the stars to merge together. Hut’s differential equations for the change in orbital parameters due to tides are all proportional to the k/T factor (the ratio of the apsidal motion constant to the tidal damping timescale).
The particular physical properties of a celestial body correspond to different tidal dissipation mechanisms, influencing the timescales of the tidal effects. For stellar objects, TRES includes damping mechanisms for convective, radiative, or degenerate stars, following Hurley et al. (2002). For giant planets and brown dwarfs, we adopted the tidal timescale used by Fabrycky & Tremaine (2007, see their Eq. (A.9)), plugging in their constant value of the viscous timescale tV = 0.001 yr and using our interpolated value of the apsidal motion constant k2 (described in detail in Sect. 2.2.3).
2.2.3 Stellar and substellar structure constants
We improved the accuracy of our simulations, exploiting the latest results of Claret (2019), to provide more reliable values for two internal structure constants: the gyration radius and the apsi-dal motion constant (k2). We implemented the new tables for both stars and planets, interpolating the parameters as a function of the system age rather than adopting fixed average values. The gyration radius is relevant to the computation of the moment of inertia, while the apsidal motion constant is related to the strength of tidal perturbations (and thus to the effects described in the previous paragraphs). We note that there is a historical ambiguity for the name of the apsidal motion constant, due to different derivations by Sterne (1939) and Love (1911), after whom it was also named ‘the second Love number’, with only a difference of a factor two: k2,AMC = 1/2 k2,Love. However, this terminology, the Love number, is usually employed only in the planetary science field and not in the stellar physics field.
The Claret (2019) results were obtained using the package Modules for Experiments in Stellar Astrophysics (MESA; Paxton et al. 2011, 2015), version R10398, and they include the stellar internal structure constants (k2, k3, and k4), the radius of gyration, and the gravitational potential energy. Based on this work, where those parameters were computed up to the first ascent giant branch, our updated models now cover a larger range of stellar life, from the pre-MS phase up to the WD stage, as required by our simulations. We report in Table 1 a summary of these new models. The mass range covered in our study goes from 0.95 M⊙ to 10 M⊙, for three different metallicities: [Fe/H] = 0.00, −0.50, and −1.00. For the mixing length parameter a solar-calibrated value of αMLT = 1.84 was adopted and microscopic diffusion included. Convective core overshooting was taken into account with the diffusive approximation, using the parameter fov and its relationship with the stellar mass, as illustrated by Claret & Torres (2019). For the opacities we adopted the element mixture used by Asplund et al. (2009), whereas the helium abundance follows the relation Y = 0.249 + 1.67 Z, with ‘Z’ being all elements heavier than He.
Values of the main parameters adopted for the stellar models.
2.2.4 Atmospheric evaporation
Evidence of atmospheric evaporation was revealed not long after the first detections of transiting exoplanets. The main probe (among several) for the existence of outflowing gas is the Lyman-α line absorption during planetary transit (Owen 2019). Traces of neutral hydrogen outside the planet’s Roche lobe show that its atmosphere extends to unbound regions and is thus able to escape.
Many processes can cause the gas to flow out, but in this work we only account for the energy-limited mass loss, which, in the context of close-in gaseous planets, proves to be the prevailing process Owen (2019). It is a thermal evaporation process: the high-energy flux from the star(s) is absorbed by the upper layers of a planetary atmosphere, to the point where their kinetic energy overcomes the planet’s gravitational potential and the gas is free to escape. Therefore, it becomes critical to assess the flux of X-ray and extreme ultraviolet (EUV, together XUV) radiation received by the planet along its orbit, depending on the stellar life stage. For the modelling of atmospheric evaporation, we referred to various works (Flaccomio et al. 2003a; Wright et al. 2011; Sanz-Forcada et al. 2014; Schreiber et al. 2019; Owen 2019). The mass-loss rate due to the high-energy flux FXUV, also known as photoevaporation, can be computed as in Owen (2019)
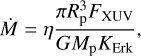 (2)
(2)
where η is an energy-transfer efficiency factor and KErk is a term accounting for the fact that the gas does not need to reach infinity to escape the gravitational well of the planet since it can be considered ‘lost’ as soon as it surpasses its Roche lobe radius (Erkaev et al. 2007). Recent studies have found the η factor to have a value around 0.2 or lower (e.g. Penz et al. 2008; Lammer et al. 2009; Lampón et al. 2023). For our analysis we adopt η = 0.2 as the upper limit (Owen 2019).
To compute the mean XUV flux a planet receives from the binary, we average on one planetary orbital period to be consistent with the secular approximation (and we note that TRES does not keep track of the orbital phases at each time):
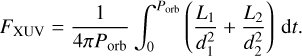 (3)
(3)
Here L1 and L2 are the XUV luminosities of the two host stars and d1, d2 their respective three-dimensional distances from the planet, which are time-dependent variables. Both d1, d2 are dependent on the stellar phase, the planetary phase, and the relative inclination between the two orbital planes. We compute the average distance of a planet from the system’s centre of mass as 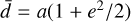 , which is the time-averaged distance in an orbit with semi-major axis a and eccentricity e (e.g. Williams 2003). From trigonometric decomposition, we then compute d1, d2 as a function of
, which is the time-averaged distance in an orbit with semi-major axis a and eccentricity e (e.g. Williams 2003). From trigonometric decomposition, we then compute d1, d2 as a function of 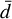 .
.
The luminosity of stars in the high-energy band is not a well-characterised quantity to plug into the equations. Until now in fact, the main focus of most photoevaporation studies has been the high-energy emission of MS or pre-MS stages, but the evidence of planets around evolved stars makes it necessary to extend these studies to all kinds of stars, up to the WD stage. We used different prescriptions to account for the evaporation of planetary atmospheres caused by stars with a range of different masses and varying life stages.
We employed the results of Wright et al. (2011), which deals with the relationship between stellar activity and rotation, to assign the X-ray emission to low-mass stars. The authors performed a fit to observational data and found two regimes of emission, saturated and unsaturated, based on the Rossby number Ro = Prot/τ, where Prot is the rotation period of the star and τ its convective turnover time. Their best fits are
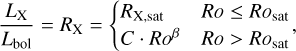 (4)
(4)
with RX,sat = 10−3.13,β = −2.70, and Rosat = 0.13, the threshold of rotational period above which the stars saturate the emission and which is independent of stellar type. The behaviour of stars following this model is generally flat at saturation value at early phases in their life, when they have faster rotational velocities, and then it decays with time proportionally to their rotation. To compute the Rossby number we also took advantage of the analytical fit provided by Wright et al. (2011) for the convective turnover time:
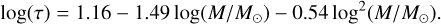
For stars with a mass below 2 M⊙ we used this model to estimate the X-ray emission during their entire life before the WD stage. For stars with 2 < M/M⊙ < 3 we used this model only during the post-MS phases, whereas for their MS we imposed the value of RX ≈ l0−35, taken from Flaccomio et al. (2003a). The extension of the Rossby number approach for the X emission of stars beyond the MS is an approximation necessary to cover the lack of information on this topic. Although far from exact, this approach appears to be a plausible solution; Dixon et al. (2020) conducted a study on red giants and highlighted the remarkable similarity between these evolved stars and M-dwarfs emissions. In their sample they found, in fact, a correlation of the stellar activity, in terms of near-ultraviolet (NUV) excess, to the rotation, suggesting a possibly analogous mechanism for the stellar dynamo, and finding again a regime of saturation.
For intermediate-mass stars, between 3 M⊙ and 10 M⊙, the X-ray luminosity undergoes a sharp decrease, and it is hard to find precise values in the literature, considering both the large scatter of the observations and the different physical processes behind the X emission. For these reasons, we adopted the constant value of LXUV ≈ l0−6 Lbol as the upper bound of the common literature values in this mass range (see e.g. Flaccomio et al. 2003a,b; Nazé 2009; Gorti et al. 2009).
For the EUV component of the high-energy flux, we used the equation of Sanz-Forcada et al. (2011) (without error bars)
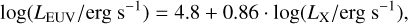 (5)
(5)
which relates LEUV to LX and assumes that X and EUV luminosities have a uniform development in time. If the X-ray emission literature is uncertain on the LX of intermediate to heavy stars, the EUV counterpart is even more obscure because of the sheer lack of available data, due to the severe absorption of these wavelengths in the interstellar space. We then extended the relation of Sanz-Forcada et al. (2011), which was originally calibrated on M-type to late F-type stars, to stars up to 3 M⊙, at any time before the WD stage, to have a rough best estimate of the ultraviolet component.
The photoevaporation can continue even after the death of the stars as they become WDs, and depending on the orbital distance of the planet it can actually have a significant impact on its atmosphere (given the extremely high temperatures of the WD surfaces) right after their formation (Schreiber et al. 2019). We then deemed it worth including the contribution of these compact objects in our high-energy computation for the evaporation. Considering the wide range of possible temperatures of the newborn WDs, up to ~l05 K, the average large distance of the planet from the inner WD, and the lack of published stellar models in this high-energy part of the spectrum, we approximate the WD as a blackbody. Thus, the code integrates the blackbody specific flux, or radiance, Bλ(T), on the wavelength range 10–912 Å and on the star’s surface area to obtain the overall XUV ionising luminosity. In this way a simple temperature-dependent relation is computed for every possible WD, evolving in time as they cool down, regardless of the chemical composition. This approximation represents an overestimate of a real WD’s high-energy flux: real WDs have H- and He-rich atmospheres that re-absorb part of this ionising radiation. However, this approximation is sufficient to serve the purposes of this work, also considering that we deal with generally wide-orbit CBPs, after stars have already expelled their shells.
2.2.5 Stellar winds
Stars considered in this study (i.e. stars with an initial mass range of 0.95 M⊙ ≲ MZAMS ≲ 10 M⊙) lose a significant fraction of their mass in their evolved stage. These stars can lose up to 40% of their initial mass via dust-driven winds during their asymptotic giant branch phase. At this evolutionary phase, the star rapidly expands and their outer layers cool down sufficiently for dust formation. The momentum imparted onto the dust particles by radiation will then drive the mass loss. This mechanism can result in mass-loss rates as high as Ṁ ~ 10−7−10−4 M⊙ yr−1 (see e.g. Höfner 2015). Furthermore, the evolution of O/B stars (roughly corresponding to initial masses MZAMS ≳ 8 M⊙) is also significantly affected by line-driven winds (e.g. Puls et al. 2008). Such massive stars therefore experience significant mass loss from the start of the MS phase.
The mass-loss rates of stellar winds and their effects on stellar evolution are determined by SeBa, while the effects on the orbit of the triple are determined by TRES. How the properties of stars change due to stellar winds in SeBa is explained in Toonen et al. (2012) in detail, which is based on the formalism of Hurley et al. (2002). The stellar wind prescriptions used in SeBa, which provide an estimate on the mass-loss rates based on the properties of the star, are introduced in detail in Toonen et al. (2012), but we also provide a brief summary below.
If the star is on the MS or is a Hertzsprung gap star, and has a luminosity higher than L > 4000 L⊙ and an effective temperature Teff > 8000 K, we assume that line-driven winds are efficient, and we calculate the mass-loss rates according to Vink et al. (2001) if Teff ≤ 50 000 K, or according to Nieuwenhuijzen & de Jager (1990) if Teff > 50 000 K. If the effective temperature of the star is below Teff = 8000 K, we assume line-driven winds are no longer efficient and instead dust-driven winds dominate. In this case we calculate the mass-loss rates according to Nieuwenhuijzen & de Jager (1990) and Reimers (1977) and take the maximum of these two values. However, if the star is on the asymptotic giant branch, in addition to the mass-loss rates of Nieuwenhuijzen & de Jager (1990) and Reimers (1977), we also calculate Vassiliadis & Wood (1993) rates to account for the superwind phase of thermally pulsating asymptotic giant branch stars. The final mass-loss rate is the maximum value given by these three different prescriptions.
In order to compute the change in the orbit due to stellar winds, we assume stellar winds are fast and spherically symmetric. We also neglect accretion by companions. In that case the inner and the outer orbits of the triple widen in an adiabatic fashion as (see e.g. Soberman et al. 1997)
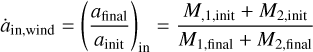 (6)
(6)
where the subscripts ‘init’ and final refer to properties before and after the stellar winds have carried mass away from the inner binary in a given time step. The assumption of adiabatic expansion caused by stellar winds is justified by two arguments. Firstly, the terminal velocities of stellar winds are typically much higher than the stellar orbital velocities, meaning the wind does not interact directly with the orbit (see e.g. Vink et al. 2001). Secondly, the timescale of the orbital change is typically much longer than the mass-loss rate timescale, and therefore the mass loss does not vary within a period (as long as the orbit is not wider than a few thousand au; see discussion in Sect. 5.3). Neglecting wind accretion is justified for line-driven winds; however, the dust-driven winds of asymptotic giant branch stars and supergiants can have velocities as low as υ ≈ 5–30 km s−1. In the latter case, the accretion efficiency could be as high as ~50% (Höfner 2015). We assume that the eccentricity remains unchanged by stellar winds (Huang 1956, 1963).
2.2.6 Inclusion of SSO mass–radius relation
In order to give a spatial dimension to the SSOs under analysis, we implemented an equation to relate the mass of a SSO (i.e. the input to TRES) to its radius. The radius of a planet, and thus its density with a given mass, affects several processes during its dynamical evolution in a triple; for example, both tidal interactions and the photoevaporation are affected, not to mention the moment of inertia and all quantities coupled to it. In the literature there are different kinds of works that use simple analytic relations to determine the size of a SSO. Some have a more theoretical approach and exploit the polytropes (e.g. Chabrier et al. 2009; Guillot & Gautier 2015) and others take an empirical approach (e.g. Chen & Kipping 2017; Bashi et al. 2017; Thorngren et al. 2019). In the end we adopted the simple analytic expression of Chen & Kipping (2017) for their rigorous statistical analysis applied to a large sample of empirical data, spanning the widest mass range (from SSOs of ~10−3 M⊕ to 0.87 M⊙ stars). The authors compiled a table of 316 objects in this range, with well-defined mass and radius values, and employed hierarchical Bayesian modelling to obtain a probabilistic broken power law. They created a Python package, called Forecaster, to easily allow the use of their results. For our purposes we only implemented in SeBa the deterministic power laws in the form
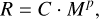
with the radius R, which is a function of the mass M to the power p and coefficient C, where these two coefficients vary in mass sub-intervals, as prescribed by Chen & Kipping (2017).
2.2.7 SSOs spin velocity
The last piece of knowledge needed to properly initialise our giant planets was the rotational velocity, or spin, around their axis at ZAMS. Planets acquire rotation during their formation, when the accreting matter brings its angular momentum to the object; in principle, then, knowing the formation history of a planet provides its initial spin velocity. Unfortunately, planet formation processes are still unclear and have major uncertainties; we did not simulate the earliest phases of stellar and planetary formation, and thus we needed a realistic value of the spin at ZAMS, depending only on the mass of the object and regardless of its specific accretion history.
We decided to use the estimate of Bryan et al. (2018), who compiled a sample of young SSOs up to 20 MJ, with rotation rates constrained by observations (in part by emission line broadening). They found that the spin velocity of the sample is approximately an order of magnitude lower than the break-up velocity, which corresponds to the maximum possible rotation rate to remain gravitationally bound to a body, depending on its mass and radius. Without a process dissipating the angular momentum, the gaseous planets would spin up to nearly the break-up velocity, whereas we observe terminal speeds several times lower that this limit. The main mechanism responsible for this dissipation is thought to be the magneto-hydrodynamical coupling between the gas giant and its circumplanetary accretion disc, expelling angular momentum away (Batygin 2018; Bryan et al. 2020; Dittmann 2021).
Another interesting remark of Bryan et al. (2018) deals with the little evolution of the terminal spin rate. Their sample of young SSOs is aged between 2 and 200 Myr, but they cannot find any time dependence of the spin; considering that Jupiter’s and Saturn’s present-day velocities are compatible with the sample mean, the authors infer that the rotation of these objects is set in the earliest phases of formation, and then does not evolve significantly for billion of years. For the reasons above, we adopted as the rotation velocity of the SSOs at the ZAMS their best-fit mean value:
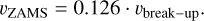
All SSOs are assumed to be spin-orbit aligned and the spin evolves as a scalar quantity.
3 Population synthesis
For the long-term evolution of circumbinary giant planets, we defined a set of priors for the inner stellar binary, and two sets of priors for the planetary companion, which we ran separately. Details of the set-up for the orbital features of inner binaries and planets are described below, including the specifications on the TRES simulations characteristics and population set-up.
3.1 Inner binary priors
To initialise the inner binaries at ZAMS we randomly sample from the following prior distributions for the inner binary separation ain, the mass ratio q = M2/M1, the primary star initial mass M1 and the binary eccentricity ein:
ain: log 10-uniform distribution log 𝒰a for a є (15R⊙; 2200 R⊙) (Abt 1983; Kouwenhoven et al. 2007), (Duchêne & Kraus 2013);
M1: Kroupa’s mass function
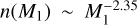 , for M1 є (0.95, 10) M⊙ (Kroupa et al. 1993);
, for M1 є (0.95, 10) M⊙ (Kroupa et al. 1993);q: Uniform distribution 𝒰q for q є (0, 1] (e.g. Raghavan et al. 2010; Sana et al. 2012; Moe & Di Stefano 2017; Duchêne & Kraus 2013) with a lower limit of 0.95 M⊙ on M2;
ein: Thermal distribution f(e) = 2e, for e є (0,0.95) (Heggie 1975).
This set of priors was chosen specifically to generate a population of binary stars that could reproduce the observed Milky Way DWD distributions (Toonen et al. 2012, 2017). The upper limit on ain is influenced by LISA detection limits. The mass boundaries are chosen to maximise our computational efforts specifically on those binary stars evolving on timescales comparable with one Hubble time, and thus to be able to leave WD remnants at their death, for the most part. The initial q of the simulated binaries must always satisfy the given mass boundaries (see the points above), implying that the actual minimum in our simulations is qmin = 0.095.
Common-envelope evolution
CE evolution is an important process in binary evolution (see e.g. Ivanova et al. 2013, 2020; Iaconi & De Marco 2019), thought to be responsible for the formation of the majority of compact star systems (e.g. Izzard et al. 2012). During this process the two stars share a CE (hence the name) that is not in co-rotation with the orbital motion and as a result the stars spiral closer to each other. The end result of a CE-phase is either a merger of the two stars or a successful ejection of the CE material leaving behind a compact binary.
Despite the importance of the phase, and the large effort of the community the CE phase is poorly understood and constrained. Major discussions deal with the nature of the energy source that is responsible for unbinding the CE, such as orbital energy (Paczynski 1976; Webbink 1984), recombination energy (Ivanova et al. 2015; Nandez et al. 2015; Grichener et al. 2018; Kramer et al. 2020; Reichardt et al. 2020; Lau et al. 2022b), ionisation energy (Han et al. 1994, 1995; Sand et al. 2020), radiation energy (Ivanova 2018; Lau et al. 2022a), accretion (Chamandy et al. 2018), convection (Sabach et al. 2017; Ivanova 2018; Wilson & Nordhaus 2019, 2022), jets (Shiber & Soker 2018; Shiber et al. 2019; López-Cámara et al. 2022), and dust (Glanz & Perets 2018; Iaconi et al. 2020). Purely hydrodynamical simulations typically do not unbind the envelope, although some success has been achieved recently by including other energy sources than orbital energy (Ivanova & Nandez 2016; Law-Smith et al. 2020).
In addition to hydrodynamical studies, a few observational constraints exist. These arise from studies of individual post-CE systems whose evolution is modelled backwards in time (Nelemans et al. 2000; van der Sluys et al. 2006; Zorotovic et al. 2010; Zorotovic & Schreiber 2022) or by comparing the observed population demographics to the theoretical models (called population synthesis models; Toonen & Nelemans 2013; Camacho et al. 2014). Specifically for DWDs, this has led to the following insights into their formation (Nelemans et al. 2000; ?; van der Sluys et al. 2006). The first phase of mass transfer leads to a moderate widening of the orbit; the second phase of mass transfer (in which the second WD is formed) leads to a strong shrinkage of the orbit. We follow the suggestion of ? to model the CE-phase with the classical α-prescription with parameters αλ = 2 when the companion is a compact object or when the CE is triggered by a tidal instability (rather than dynamically unstable Roche lobe overflow Darwin 1879), and the γ-prescription with parameter γ = 1.75 otherwise.
3.2 Circumbinary planet priors
To account for different outcomes in the final population that can arise as a consequence of the initial assumptions, we defined two different sets of initial orbital parameters distributions for our simulations. Therefore, we modelled two different populations to study the impact of the planetary orbital priors on the final survival and ejection rates. We note that for both synthetic populations we kept the binary priors (Sect. 3.1) and the CE assumptions (Sect. 3.1) constant. The analysis of the consequence of employing different binary evolution models on the long-term evolution of CBPs will be presented in an upcoming study. As previously mentioned, the low statistics of CBPs does not allow us to robustly trace the typical properties of their orbital parameters, for which we refer to those observed for single-star planetary systems. In particular, for the first population, which we labelled Population A (Pop. A), we employed the distributions reported in Danielski et al. (2019) and references therein. Given our interest for the Magrathea planets, in the framework of the science development of the LISA mission, we adopted their optimistic scenario (B1) distributions for the semi-major axis aout, planetary mass MP, and orbital inclination ip. In addition, we included the eccentricity eout distribution by Bowler et al. (2020), and used in Katz et al. (2022) to study the CBP detection efficiency by LISA. In detail, the distributions used to draw initial parameters for Pop. A are the following:
aout: log10 uniform distribution: log 𝒰a (0.17 au; 200 au);
iP: uniform distribution 𝒰cos(i) (−1; 1);
MP: uniform distribution: 𝒰M(0.2 MJ; 16 MJ);
eout: Beta distribution
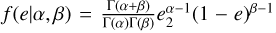 in the range (0; 0.95), where Г is the gamma function, α = 30, and β= 200.
in the range (0; 0.95), where Г is the gamma function, α = 30, and β= 200.
The planetary mass range was chosen to only span the giant planet mass spectra, to focus on those planetary companions that have the chance to be detected by LISA (Danielski et al. 2019; Katz et al. 2022). The upper mass limit was chosen based on Spiegel et al. (2011), instead of the hard deuterium limit. The orbital separation lower boundary a = 0.17 au between the planet and the centre of mass of the binary was defined based on the stability limit by Holman & Wiegert (1999), when computed for a binary with the smallest circular orbit in the binary population (see Sect. 3.1) and equal stellar mass M1 = M2, meaning µ = 0.5 in Eq. (1).
For the second population, Population B (Pop. B), we adopted uniform distributions for all parameters to avoid population biases that might be caused by priors based on observational evidence of single-star planetary systems. Nonetheless, the range spanned by each parameter is the same used for Pop. A.
3.3 Simulations set-up
Once the initial distributions for our stars and planets are chosen, we generate a statistically representative sample of our two populations, simulating 10 500 systems for each population. Each new system is generated by independently sampling two stars and one SSO based on their respective priors. However, since the TRES code can only simulate secularly stable systems, the random draws of initial parameters are checked against stability at zero age. The system is discarded if its random initialisation is unstable, and a new extraction is performed. We imposed an upper limit of 2 h to the CPU time allowed for each evolution phase, to avoid cluttering our population synthesis with few systems requiring an anomalously large amount of computing time. These computationally heavy simulations mostly corresponded to systems lying close to the triple’s stability limit, where the secular approximation time step was pushed to extremely small values, due to fast-evolving three-body dynamics. A quick overview of these systems is given in Sect. 5.2.
Leaving CPU time limits aside, we stopped the simulation of those systems in which any of the components merge, become unbound, or initiate a phase of stable mass transfer, or if the triple became dynamically unstable, in general. It is currently challenging to predict the outcome of a stable phase of mass transfer in the inner binary of a triple system as the orbit tends to be eccentric due to three-body interactions (see also Sect. 4.5). However, systems undergoing CE phases were not stopped, which allowed us to obtain tight inner binaries and remnants. We set the maximum simulation time as one Hubble time, defined as 13.5 Gyr, after the start of the ZAMS. Thus, if a system had not stopped earlier for any of the conditions outlined above, the code would stop the simulation at this moment.
4 Results
To analyse the data, we subdivided the synthetic populations (A and B; see Sect. 3) into categories based on their final fate. The main categories we identified are the following:
Magratheas. CBPs that survive to the full inner binary evolution from ZAMS up to 13.5 Gyr (i.e. one Hubble time), with both stars that turn into WDs;
Collided, systems whose evolution stops once the CBP’s orbit intersects with the inner binary’s orbit. The subsequent fate of these planets cannot be simulated with a secular code;
Destabilised, systems that become dynamically unstable, either due to the three-body dynamics, to disruptive evolution events (e.g. supernovae), or to adiabatic stellar winds.
Merged, systems whose inner binary stars merge before one Hubble time;
Stable-MT. systems whose inner binary initiates a phase of stable mass transfer (which is also a stopping condition in our simulation).
The percentages of simulated systems falling into each of the described categories, for both populations, are reported in Table 2. To avoid cluttering the body of the paper, a complete collection of the plots for all these main categories can be found in the Appendix. For completeness, we mention the presence of two other secondary categories: the CPU-limited systems, introduced in Sect. 3.3 and discussed in Sect. 5.2, and the Ordinaries, a collection of the remaining systems that do not belong to any other of our categories of interest and that basically consist of half-evolved systems with long-lived lower-mass stars (amounting to around 11% of the total sample).
 |
Fig. 1 Population A: overview of the distributions of Magrathea systems in the parameter space. Solid histograms represent the Magrathea parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines, instead, show the initial distributions for the whole population, not restricted to the Magratheas. |
4.1 Magrathea systems
The main interest of our analysis are the Magrathea planets. Our results show that a significant fraction (i.e. between 23% and 32%) of the generated triples survive to become systems with a СВР orbiting a DWD (Table 2).
Population A. ~23% of planets among the total systems become Magratheas by one Hubble time. An overview of the ensemble properties of this population is given in Fig. 1. The giant planets have final orbital parameters that overall preserved their initial distributions shape, but with a larger spread in the final values, particularly for their semi-major axes aout (Fig. 1, top left), and less evident for the eccentricity eout (Fig. 1, top right). The majority of the host stars resulted in tight binaries with circularised orbits (Fig. 1, top right panel). The stellar progenitors of Magrathea systems are biased towards the lighter masses, peaking around 1–2 M⊙ (Fig. 1, bottom right). The pho-toevaporation eroded on average 0.13% of the gas giants starting mass, with the most extreme case losing almost 0.5 MJ during their life. The Magrathea percentage, although not large decreases for the shortest orbital distances, on average. A wide-orbit planet experiences fewer effects of stellar evolution than those on closer orbits. However, we recall that we are assuming both adiabatic stellar winds (see Sect. 5.3) and an isolated gravitational environment; this means that we exclude any external contribution from nearby systems that could likely result in stripping the planets with the widest orbits. In comparison with Pop. A, Pop. B presents a significant difference in the planetary eccentricity distribution, which is mostly a consequence of the initial distributions (Fig. A.1, top right). This may imply that the CBP eccentricity is not by itself a decisive parameter to determine the survival around binaries. In absolute terms, the eccentricities have not been dramatically altered during the systems’ evolution, so that the final distribution shape follows the initial one. Also in this population, the planetary semi-major axes cover a large range of values up to aout = 1100 au, slightly higher than Pop. A. Photoevaporation generated a mean loss of just 0.02% of the initial mass, but with a maximum evaporation of 0.6 MJ similarly to Pop. A. The inner binaries show overall properties similar to those of Pop. A.
Both populations. No appreciable selection effect for the planetary masses is noted for this class of systems. Binary stars have mass ratios peaking at the unit value. The orbital separations of the binary stars range from a few 10−3 au to a few tens of au, with a gap around a few au (Figs. 3 and 4). This gap, as also recently confirmed with Gaia observations (Korol et al. 2022a), separates the post-mass-transfer binaries (with smaller circularised orbits) from the binaries that are too wide to experience a mass transfer phase in any point in their evolution.
From the top two plots in Fig. A.9 it can be seen again (see also the eccentricity panels in Figs. 1 and A.1), how the Magrathea planets at one Hubble time are for the most part orbiting circularised binaries; based on the stability equation described in Sect. 2.2.1, for null eccentricity and equal-mass binaries (which is the case for most Magrathea hosts) the critical semi-major axis ratio assumes the particular value of acrit = 2.39, where most of the CBPs are found. However, the semi-major axes of these giant planets have values reaching up to 105 times the critical semi-major axis. In addition, the CBPs do not seem to pile up in narrow aout stability regions (see top panels of Fig. A.9). When comparing the cumulative distribution of final CBPs semi-major axes across the different categories (Fig. 5), we see that Magrathea planets reside on the largest orbits of all categories, except for a small tail of the Merged category. The stellar hosts, on the other hand, have rather tight orbits, rivalled only by some of the tightest merging DWDs (see Fig. 4). This creates wide and stable hierarchical triples that can survive until one Hubble time.
Finally, we found an asymmetry in the final distribution of relative inclinations of the Magrathea planets: they generally prefer prograde orbits and have a broad peak at around 60° from the stellar orbit plane. In Fig. 6 for Pop. A and Fig. A.7 for Pop. B, it is visible how the final distribution shows an overabundance of prograde planets, which amounts to +12.6% and +7.8%, respectively. In those same figures, we defined as the Destroyed systems those ending with a ‘catastrophic’ event for the triple, consisting of the Merged, Collided, and Destabilised systems collected together for convenience. The Destroyed also registered a gain in the prograde orbits at the end of the evolution, but a factor 2.3 and 4.6 times less than Magratheas, respectively in Pop. A and B, and closer to the 90° inclination. This bias was not present in the initial distribution which was set to uniform in cos(i). This is consistent with recent insights in the Lidov-Kozai mechanism for systems outside the test-particle regime (Anderson et al. 2017; Lei 2019; Hamers 2021). In this model the maximum eccentricity is not reached at a mutual inclination of 90°, but at slightly higher values. As those systems are more likely to interact (e.g. merge), we expect the Magrathea planets to prefer prograde orbits.
Percentages of possible evolution outcomes computed over the total size of Pops. A and В (both with a sample size of 10 500).
 |
Fig. 2 Population A: atmospheric mass loss undergone by Magrathea gas giants, scattered in the mass-distance parameter space. The x-axis corresponds to the final time-averaged orbital distance of the CBPs. We show the planets that lost more mass than the 50% of the category. The colour corresponds to the amount of mass lost (see colour bar). The size of the markers is proportional to the progenitor binary mass, as illustrated in the legend. |
 |
Fig. 3 Comparison of the inner semi-major axis ain distributions for the binaries in Magrathea systems (blue) and the merged-DWDs (orange, ain refers to the timestamp just before merging) of Pop. A and Pop. B (solid and dashed lines, respectively). The grey line denotes a separation of 1R⊙. |
 |
Fig. 4 Complementary cumulative distributions of the final inner binary semi-major axes ain, for all categories (colour-coded in the legend), and for both Pops. A (solid lines) and B (dashed lines). Merged DWDs all resides in orbits smaller than 1R⊙ (vertical grey line) and few of the Magrathea hosts as well. These parameters refer to the last valid simulation step in secular approximation. |
 |
Fig. 5 Complementary cumulative distributions of final semi-major axes aout of CBPs for all categories (colour-coded in the legend), for both Pops. A (solid lines) and B (dashed lines). These parameters refer to the last valid simulation step in secular approximation. |
4.2 Collided systems
The Collided systems, in which the CBP orbit intersects the inner binary orbit, belong to a category with quite distinctive parameters; they are a small but non-negligible fraction. The most characterising feature is the very high eccentricity of all the giant planets in this category, on average higher than for all the other categories, in both populations (see the green lines in Fig. A.6). This category is in some aspects similar to the Destabilised systems (see Sect. 4.3) since the configuration of the triple is severely altered and the assumptions for a hierarchical stability are violated at the ending time. Even so, while the Destabilised category simply accounts for any triple that becomes unstable at some point in its evolution, the Collided category includes specifically those triples where the CBP acquired an orbit eccentric enough to intersect the inner binary orbit, and thus likely goes through phases of fast dynamical re-shaping. The eccentricity of these CBPs orbits reaches high values before they can become unstable, based on the stability criterion described in Sect. 2.2.1. Because of their peculiar properties and their abundance, we present them separately from the Destabilised category. The final parameters of the Collided category are to be carefully interpreted as they refer to the last simulation step, before the stop due to a violation of the secular evolution assumptions. The label of this category should indeed not be confused with a real physical planetary collision scenario.
Population A. ~3.2%. These planets have an entirely different final eccentricity distribution than its initial one, with no overlap between the two, and with the latter always having eout > 0.5, as illustrated in the top right panel of Fig. A.4. Their semi-major axes are relatively small, extending at most to a few tens of au, yet planets are piling up close to the stability limit (see Fig. A.9, second row left). Stellar hosts as well show higher values of eccentricity than Magrathea systems, and their orbits do not circularise. The orbital separation in the inner binaries spans a shorter interval, approximately ain = 0.07–10 au (see Fig. 4). The stellar types of this population mainly consist of MS stars (see central panel of Fig. 7), confirming again the short lifespan.
Population B. 2.1% of the total sample. For this population we see that the progenitors’ planetary eccentricities are skewed towards the highest values possible, peaking right before eout = 0.95, as illustrated in the bottom panel of Fig. A.4. However, the final distribution is devoid of low-eccentricity planets and, interestingly enough, it covers eccentricities eout > 0.5, similarly to Pop. A, notwithstanding the completely different initial distributions. The planetary semi-major axes in this population are spread up to aout = 200 au, and those of the inner binaries up to ain = 10 au, showing larger orbits than in Pop. A (see Fig. A.4). The range of stellar mass covered is the same as that of Pop. A. In Fig. 4, it is remarkable how the inner binary separation of Pop. В covers the whole range to the upper boundary of ~10 au in a more homogeneous way. We found, as well, that in this population there seems to be a dichotomy by age of the Collided systems: the majority have ages that range from 10 to 104 Myr, while another small part of the sample is younger, covering ages down to 10−4 Myr, which is indicative of systems already on the brink of instability and that could realistically never make it to the ZAMS. The statistics of the smaller portion, however, is not sufficient to assess a departure of its features within the Collided category. When the evolution is interrupted, one-quarter of the stars are post-MS stars (see central panel of Fig. A.8), different than in Population A.
Both populations. atmospheric mass loss from the planets is negligible, likely because of the limited lifetime of these systems before the orbital collision. The maximum single mass evaporated is only 10−3 MJ. On the other hand, the lifetime is long enough to alter the eccentricity but not the semi-major axes of planets and the stars.
 |
Fig. 6 Population A: relative inclination distributions for Magrathea and planets in Destroyed systems (which include Merged, Collided, and Destabilised). The population was initialised with an inclination distribution uniform in cos (i); this plot illustrates how at the end of life the systems seem to favour mildly inclined prograde orbits, especially surviving Magratheas. |
 |
Fig. 7 Population A: stellar type of inner binaries, for those planets that do not survive to become Magratheas. From left to right: CBPs around merging binaries, excluded the DWD-mergers, planets in the Collided category, and Destabilised (see Sect. 4 for detailed definitions). For simplicity, the label ‘Post-MS’ includes all stellar types after the MS that are not WDs. We show in Fig. A.8 the same plot for Pop. B. |
4.3 Destabilised systems
The destabilised systems are a tiny fraction of the total, ~0.2% of the simulated triples for both populations, and they reach extremes of the parameter space. This category includes the system that became unstable due to chaotic three-body dynamics, or which are disintegrated by a violent supernovae kick. TRES automatically discards systems that are already unstable at their random initialisation, at t = 0, so the Destabilised category comprises only those triples that became unstable after the ZAMS. We found these systems to be characterised by initial orbital parameters values near the stability limit.
It is estimated that the lowest-mass body, or the outermost, of a hierarchical triple, is most often ejected from the system when it becomes dynamically unstable (Busetti et al. 2018; Toonen et al. 2020, 2022). In our simulations, the circumbinary gas giants satisfy both conditions of lightest and outermost bodies in the triples, and thus they would likely be the ones ejected and transformed into free-floating planets. We provide some number estimates and discussion on the topic in Sect. 5. The meagre statistics of this category did not allow us to produce meaningful plots and histograms, or to disentangle the features of the two populations. However, we note that the majority of the systems become unstable when both stars are in the MS phase (Pop. A, Fig. 7, right panel), or when the primary star has evolved in its post-MS phase, before the WD stage (Pop. B, Fig. A.8, right panel). The common trends we identified in both populations are the following:
1) The planetary semi-major axes are the smallest among all the categories (or are comparable to the Collided planets) and they shrink from ZAMS to instability; Pop. В has a larger semi-major axis lower-bound, while the upper bound is the same (Fig. 5); 2) The inner semi-major axes, on the contrary, are the largest of all the categories, unlike the planetary orbits, setting the conditions for a fragile equilibrium (see Fig. 4); 3) The final planetary eccentricity loosely follows the initial distribution, but it has a heavy tail that reaches eccentricities greater than 1, responsible for unbinding the planet. (Fig. A.6); The stars have several high-mass occurrences, which quickly evolve to disruptive supernovae.
Finally, we note that for Pop. A the Destabilised planets all start closer to the critical stability semi-major axis, whereas Pop. В has a wider spread around it. Atmospheric evaporation is completely negligible in this category, likely due to the short lifetime of these triples.
4.4 Merged stellar systems
The largest fraction of the simulated systems in our parameter space ends with a merger of the inner binary. The mergers are driven by mass transfer events in the inner binary with the corresponding shrinking of their orbits. Given that mergers are not the focus of this work, we did not investigate further the evolution of the merged star and its planet. However, in our isolated environment there is no mechanism to unbind the planet as a consequence of the merger per se, for which we only expect an expansion of the planetary orbit as a response to the mass loss that takes place during the merger itself. Here we present the systems as they were during the last snapshot before the merger moment, to inform on their planetary architecture.
Population A. around 32% of systems had their stars merge within one Hubble time. Figures 5 and A.2 show how these planets underwent scatter to large orbital distances, with a few of them going beyond aout = 1000 au. However, their semi-major axes are for the most part shorter than or comparable to those of Magrathea planets (Fig. 5). The planetary eccentricity distribution is mostly preserved in shape, with some enhancement of the tails, as few planets evolve to cover the whole eccentricity range. Photoevaporation has the highest impact for the giant planets in this category (following the Ordinaries), with an average mass loss of 0.2% and a maximum single loss of 0.9 MJ (Fig. 8). Overall, we identified strong evaporation by heavier progenitors than for Magratheas, but the highest mass loss values are not uniquely related to the shortest final orbital distances.
Population B. 35.1% of the systems merged within one Hubble time. The planet–star separation increases similarly to that in Pop. A (see third row left panel of Fig. A.2). The inner binary eccentricity distribution eout is almost unaltered in time, with mergers happening on the whole range of eccentricities (see third row right panel of Fig. A.2). Photoevaporation for these planets was weak, with a maximum loss of almost 0.3 MJ and a mean relative evaporation of 0.02%.
Both populations. We see that the initial distributions of stellar mass in this category cover the whole range of stellar masses, up to the upper limit of our range (10 M⊙), having larger occurrence rates for the primary stars M1 (see Fig. A.2). The binaries semi-major axes are the shortest of all categories (see Fig. 4) and their distribution even shrunk in time, for Pop. A, compared to that of their progenitors (see Fig. A.2). The Merged category includes hosts at different stellar evolution stages (Fig. 7), mostly beyond the MS.
 |
Fig. 8 Population A: atmospheric mass loss endured by gas giants of Merged binaries, scattered in mass-distance parameter space. The x-axis corresponds to the final time-averaged orbital distance of the CBPs. Shown are the planets that lost more mass than the 50% of the category. The colour corresponds to the amount of mass lost (see colour bar). The size of the markers is proportional to the binary progenitors masses, as illustrated in the legend. |
Merged DWD systems
When analysing the merged systems categories further, we found that a large fraction of Pop. A mergers occur when both stars are WDs.
Population A. 7.5% of all systems (almost one-fourth of the Merged systems) ended up with two WDs merging together within one Hubble time. The CBPs semi-major axes in this category spread up to aout = 1200 au, yet the occurrence of planets decreases at larger planet–binary separations. Other features of these objects are similar to the general Merged category, except for the range of stellar mass, which are usually nearly equal-mass binaries, and present a lack of masses above approximately 5 M⊙ ( Fig. A.3). The inner binary separation before the merger itself is well below 1 R⊙, which is of great relevance for the LISA detectability.
Population B. 10.7% of the simulated systems end with a DWD merger, more than for Pop. A, reflecting the influence of the giant planets on the final destiny of these triples as a whole. Even though the same distributions were used to draw stellar binaries in Pops. A and B, the different distribution of the CBPs slightly altered the dynamical equilibrium of the triples, and thus the configurations actually initialised and simulated, as a selection effect (see Toonen et al. 2020). In this population the CBPs semi-major axes also reach wide separations, up to 1500 au, with a flatter distribution.
4.5 Stable-MT systems
Among the binary evolution a relevant fraction of binaries (Table 2) begin a stable mass transfer process. As previously mentioned, the analytic modelling of this process is not currently included in our software, resulting in a group of systems whose evolution was stopped at an intermediate stage. The difficulty of the simulations lies in the eccentricity of the inner orbit. If an orbit has not circularised upon the onset of the mass transfer, the mass transfer rate will be orbital-phase dependent, and even episodic, leading to a breakdown of the classical prescription of mass transfer (but see Sepinsky et al. 2007, 2009; Dosopoulou & Kalogera 2016a,b; Hamers & Dosopoulou 2019). In circular orbits, stable mass transfer typically leads to the widening of the orbit, when a merger can be avoided (e.g. Soberman et al. 1997; Toonen et al. 2014). In this regard, these systems may enhance the percentage of Magrathea systems (and/or destabilised systems) actually present in the Galaxy, at one Hubble time.
Population A. 16.94% of the binaries in the total systems begin a stable mass transfer. The CBPs of this category retained an orbit close to the initial one, with a limited scatter to larger orbits (Fig. A.5). Their eccentricity follows the initial distribution and is weakly dispersed, in line with planets in most categories, as illustrated in Fig. A.6. The average atmospheric evaporation these gas giant underwent is negligible, with a maximum single loss of 0.25 MJ.
Population B. 17.08% of the inner binaries in the total systems begin a stable mass transfer. As for Pop. A, the semi-major axes of the CBPs are almost the initial ones, as for the eccentricities (see Fig. A.5). The atmospheric evaporation from these planets was, on average, not relevant, with a maximum single loss of 0.13 MJ.
Both populations. This category presents strong similarities in the distributions of both stars and CBPs, and is why we present only one overview panel in Fig. A.5. The binaries of this group are made of stars of all masses within our range, which, up to the onset of mass transfer, are orbiting at distances equal to or smaller than their initial semi-major axes. These stars are split between circular orbits and high-eccentricity orbits, showing a lack of systems in between. As shown in Fig. 5, the semi-major axes of CBPs in this group are basically always smaller than those of Merged and Magratheas systems planets, and always larger than Collided and Destabilised, lying then in a middle region between survival and catastrophe.
5 Discussion
The modelling of two different populations, A and B, of circumbinary planetary systems show that between 23% and 32% (Table 2) of the planets survive the system, and become Magrathea planets. This result confirms that CBPs can survive the evolution of both host stars, and that this possibility is not rare. Our results are in agreement with both the discussion by Kostov et al. (2016), and with the results by Fagginger Auer & Portegies Zwart (2022), whose study showed that planets have a higher probability of surviving one supernova explosion in a binary system than when orbiting a single supernova progenitor. We infer that planet survival is linked to the stellar mass-loss kick, which is lower in the case of compact binary than in the single star case. Nevertheless, increasing the initial planet-to-binary separation beyond 200 au (Sect. 3.2), would reflect in a possible decrease of the fraction of Magrathea planets, due to disruption of the outermost orbits by stellar winds.
In all categories, excluding Collided and Destabilised, we see an expansion of the planetary semi-major axis of a factor ≳ ×4 for both Pops. A and B, reaching the maximum separation of aout = 1500 au. The consequence of such an expansion is due to the fact that the CE wind mass loss in TRES is adiabatic; any change in assumption could be responsible for a different dynamical response on the outer orbit, hindering the planet survival. While we refer to Sect. 5.3 for a discussion on the topic, we leave the investigation into changes in the wind mass loss and its effect on the Magrathea population for a future work.
Overall, when comparing Pop. A and Pop. B (Fig. 5) we see that Pop. B (i.e. the one initialised with fully unconstrained planetary priors) presents larger final separations than Pop. A. Our results also show that there is no selection effect in mass for any of the categories of planets, indicating that the planetary mass does not play a role in the survival of circumbinary gas giants.
5.1 Final fate of unstable CBPs
It is important to note that our simulations were not performed within any Galaxy evolution frame, and thus we did not consider the presence of nearby systems, or the effect of external stellar encounters. This framework justifies the presence and stability of CBPs at very large separations in our results. Any change in these assumptions (together with non-adiabatic winds, see Sect. 5.3) could be responsible for either the capture of weakly gravita-tionally bound planets by external systems or planetary loss to Galactic tides.
Dynamical instabilities in planetary systems can be a source of free-floating planets (or also rogue planets), unbinding the SSO from the host star(s) and leaving it wandering alone in interstellar space. This type of planet was predicted by planet formation models (Veras & Raymond 2012; Ma et al. 2016) and they were first discovered in star-forming regions (Zapatero Osorio et al. 2000; Luhman et al. 2005; Marsh et al. 2010). Their abundance in the Milky Way and the typical mass scale remain uncertain. Consequently, their origin is doubtful, and their formation mechanisms remain an open question. Binary stars, however, could be an efficient source of free-floating planets, as has emerged from the theoretical studies by Sutherland & Fabrycky (2016) and Smullen et al. (2016). These authors simulated the evolution of unstable CBPs, with N-body calculations, covering different parts of the parameter space. They found that in the majority of cases an unstable CBP will be ejected from the system much more often than planets around single stars. In particular, Sutherland & Fabrycky (2016) found ejection rates ranging from ~80% to 93.5% and collision rates on the secondary star from 3.6% to ~8%, depending on the binary properties. The collisions happen less often on the primary star. The consecutive study by Smullen et al. (2016) reported results consistent with Sutherland & Fabrycky. Among our results, we have unstable CBPs in the Collided and Destabilised categories. To provide a rough estimate, assuming that 80% of the unstable planets are indeed ejected, our simulations would generate ~240 free-floating planets over 10500 total (averaged between Pop. A and B).
The collisions are significantly more rare, as reported above, but they deserve a special interest of their own. In general, if a collision occurs in the last stages of the stellar life, when the star is a WD, it should pollute its atmosphere with planetary material. This effect has been widely observed (e.g. Zuckerman et al. 2010; Koester et al. 2014; Wilson et al. 2019; Veras 2021 and references therein). In our Collided category (Pop. B, Fig. A.8) we have only three systems where the primary is a WD, and we cannot extrapolate any meaningful statistics on the occurrence of similar events. With a larger simulation sample we could theoretically start constraining it.
5.2 Systems that hit CPU limit
Having set a maximum computational time for each step in our simulations, a portion of our systems did not run to completion. A total of 12% and 2.5% of systems hit the CPU limit in Pop. A and Pop. B, respectively. These systems appear to be in regions of the parameter space unsuited for the secular approximation, which tries to reduce the integration time to smaller steps until breaking the CPU time limit. Many of these systems are piled up onto the stability limit (Fig. A.9, bottom panels), so that any deviation could lead to wild dynamical evolution and likely phases of instability. The inner binaries show rather high eccentricities and small orbital separations overall, reinforcing the picture of unsuitability to be simulated in the secular regime. Given that their computation stopped, we cannot predict the final parameter space outcome for these systems. However, judging on their proximity to the instability region, it is reasonable to assume that these systems would hardly survive until one Hubble time to become Magratheas; instead, they would probably end up within the Destabilised or Collided categories, the fate of which remain ultimately uncertain. Based on these remarks, we can affirm that the CPU-limited systems have a negligible impact in characterising the features of the surviving CBPs population, which was the ultimate goal of this work. We see that CPU-limited systems share a similar distribution of period ratios with Collided and Destabilised systems; for all these three categories, the great majority of planets orbit with period ratios close to (within ten times) the critical ratio for stability, Pcrit, (defined as the period-equivalent of the critical semi-major axis given by Eq. (1)); Pcrit itself peaks at values from 6 to 8. For comparison, Magrathea planets have period ratios that are a factor of 10–106 times their Pcrit, which instead peaks before the Pcrit = 4 value. From Fig. A.9, we can see the same argument from the critical semi-major axis perspective (which is solely a function of the inner binary parameters, Eq. (1)): while Magrathea planets show a large vertical spread for the semi-major axes ratio (aout/ ain, in units of acrit), in correspondence of acrit ≈ 2.39 (top panels), both the Collided and CPU-limited categories have systems that accumulate at higher values of acrit (≈4) and present a smaller vertical spread (second row and last row of panels, respectively). Moreover, CPU-limited systems mainly consist of MS stars, and do not include any DWD binaries. With regard to this aspect, under the observational point of view we see a pile-up close to the stability boundary of CBPs orbiting MS stars (Martin 2018, 2020), similar to the pile-up and stellar evolutionary types that we see within the CPU-limited category. This result suggests that the known close-in CBPs, detected by transit, will most likely not survive the evolution of the binaries and will end their life by colliding or being ejected from the system. The fact that most of the CBP population known today will not survive, it further justifies the need for dedicated surveys to hunt for long-period circumbinary exoplanets with radial velocities (e.g. BEBOP, Martin et al. 2019), or direct imaging.
All things considered, given that the CPU-limited systems evolution is computationally expensive, we will save for future studies their analysis without a CPU time limit to characterise their nature, as we did here with the rest of our sample.
5.3 The effects of mass loss
In this study, we have assumed that any mass loss from the system affects the orbits in an adiabatic way. Our results (e.g. 23-32% of surviving planets) are therefore strictly only valid under this assumption, and we ask ourselves how good this assumption is.
An example of a process responsible for mass loss in a stellar system is stellar wind. For low- and intermediate-mass stars the wind mass loss predominantly occurs late in the evolution of the star during the giant phases. The assumption that the wind matter is lost from the system in an adiabatic way is a common assumption to make in binary evolutionary calculations (see e.g. Toonen et al. 2014, for a comparison of four binary evolutionary codes); however, it does not mean that the assumption is justified. Toonen et al. (2017) demonstrate that the assumption breaks down in binary orbits larger than a few thousand au. In 2011 the seminal work of Veras et al. (2011) already showed the breakdown of the adiabatic assumption in the planetary context, that is for wide-orbit circumstellar planets or Oort-cloud analogues. They found that up to 20% of Oort cloud planets at 105 au are ejected due to the non-adiabaticity of the stellar winds, and planets at ≈104 au may experience a moderate eccentricity change of a few tenths.
The reason for the breakdown is that the timescale of the mass loss becomes comparable or significantly shorter than the orbital period. In this case the mass-loss rate is no longer constant during a single orbital revolution, but becomes phase-dependent. Whereas adiabatic mass loss merely leads to a widening of the orbit (see e.g. Rahoma et al. 2009), phase-dependent mass loss may lead to the dissolution of the orbit. This can be easily understood by considering the limit of instantaneous wind mass loss as an analogue of supernova explosions, which are well known for their destructive effect on binary orbits (see e.g. Hills 1983).
To estimate the effect of non-adiabatic mass loss on our results, we have to consider the initial orbital configuration of our planetary objects. In the current study, we only consider planetary orbital separations of less than 200 au (see Sect. 3.2). Therefore the adiabatic assumption in our modelling of the stellar winds seems justified, and we do not expect that our planetary orbits will be dissolved (or that the eccentricities will be affected) significantly.
Another process that can lead to mass loss in a binary system is non-conservative mass transfer. Within the context of our simulations set-up, this would be the mass loss during a common-envelope event. As discussed in Sect. 3.1, the physics behind the CE-mass ejection is actively debated. As hydrody-namical simulations typically do not unbind the envelope (with only a handful of exceptions; e.g. Ivanova & Nandez 2016; Law-Smith et al. 2020), the computational constraints on the velocity of the escaping material (or the timescale of ejection) is limited. One may expect ejection on a dynamical timescale; however, observational indications hint at much longer timescales, of the order of ~104 yr (Michaely & Perets 2019; Igoshev et al. 2020). If we assume that a given orbit with orbital period greater than 105 (104) yr is disrupted during a CE-event (i.e. the mass loss occurs during less than 10% of a single revolution), it would mean that CBPs with orbital separations larger than 3000–4000 au (600–1000 au) would be lost from the system. Given our maximum initial orbital separation of 200 au for the planets, our simulated systems are not typically disrupted by CE mass loss, even in the case of non-adiabatic mass loss.
5.4 The LISA framework
The gravitational wave frequency fGW of a stable monochromatic circular binary, consequently valid for DWD, can be approximated to the first order as fGW = 2/PbinЧш (Korol et al. 2020). We note that the timescale on which the orbital period of a typical DWD changes, due to the GW emission, is significantly longer than the LISA nominal mission lifetime. The approximation of fGW excludes the back reaction produced by the GWs, and is hence considered valid for Galactic DWD. The amplitude 𝒜 of the signal is given by
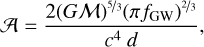 (8)
(8)
where G is the gravitational constant, c is the speed of light, ℳ is the chirp mass of the inner binary ℳ = (M1 M2)3/5/(M1 + M2)1/5, and d is the distance of the binary system from the observer. The characteristic strain of these binaries is defined as 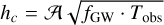 (Korol et al. 2020), where Tobs is is the LISA mission lifetime of 4 yr.
(Korol et al. 2020), where Tobs is is the LISA mission lifetime of 4 yr.
The DWD mergers happening within one Hubble time (Sect. 4.4) are particularly interesting as they will pass through the LISA frequency band. This means that the GW that these compact DWDs usually produce will change its frequency as a function of shrinking of the orbit towards the merging event; when their period falls between 3 to 60 min they can be detected by LISA (Korol et al. 2017). In our Merged-DWDs category the binary period distribution peaks at around 10 min (on the semi-major axis: ain ~ 5 × 10−4 au ~0.1 R⊙, Fig. 3), falling well within the LISA band. Each of the merging DWDs hosts a planet before merging. In the moment the binary is emitting in the LISA band (i.e. when Pbin < 60 min), a planet has the potential to be detected by LISA, depending on the observing time, the planetary mass, and semi-major axis, and depending strongly on the signal-to-noise ratio of the GW (Tamanini & Danielski 2019; Danielski et al. 2019). Moreover, LISA has the potential to detect those giant planets (MP > 0.2 MJ) whose periods are shorter than the LISA observing period Tobs ≈ 4 yr, considering a formal duty cycle of 100% and ignoring maintenance operations and data gaps. A recent Bayesian analysis by Katz et al. (2022), who studied in detail the possibility of detections of planets with eccentric orbits, showed that the posteriors behaviour of these triple systems is highly dependent on both the detectability of the GW source and the period of the third-body orbit. More specifically, CBPs periods shorter than P = Tobs/2 present planetary posteriors that remain fairly Gaussian, increasing the ability to resolve the period of the planetary perturber. This does not prevent some of longer-periods planets (Tobs/2 < P < Tobs) to be detected, but given the lack of Gaussianity of their posterior, due to the failure to meet the Nyquist criterion on the planetary orbit sampling, it is harder to constrain their period.
Looking specifically at the category of Merged-DWDs, we have no systems in both populations with planetary periods shorter than 4 yr. More specifically, the shortest planetary period is 13.8 yr (4.6 au) and 96.6 yr (17.2 au) in Pop. A and B, respectively. Similarly, for the Magrathea systems the shortest planetary period is 43.4 yr (9.6 au) in Pop. A, and 20 yr (6 au) in Pop. B. We note that Pop. B has almost 1000 more Magratheas than Pop. A, highlighting that the lack of planets with LISA-compatible periods might result from statistical biases due to the limited number of systems simulated. The smooth decay of the period distribution, together with the evidence that with a higher number of Magrathea planets we observed shorter periods, suggests that single giant planets on close-in orbits are indeed a possibility, even if rare.
We report in Table 3 the percentages of CBPs with orbital periods shorter than 10 yr (corresponding to the length of a possible extended LISA mission) and 50 yr (as additional reference), for all the categories in both populations. It is important to note that the numbers in Table 3 are the result of the evolution of a single-planet circumbinary population, and do not represent what the dynamics of a multi-planet system could be. In the latter case, destabilisation and dynamical chaos, for instance the dynamics of planet-planet scattering (Rasio & Ford 1996; Weidenschilling & Marzari 1996), might occur as a consequence of binary evolution, and can be responsible for changing the orbit of the planets in the system, migrating them inwards, or pushing them outwards. Furthermore, in our simulations we do not include interactions with the circumbinary disc that form as a consequence of the CE phase (Kashi & Soker 2011; Passy et al. 2012). The presence of a second-generation disc can be in fact responsible for inward migration of the surviving planet (Perets 2010) similarly to what is theorised during planetary formation (e.g. Johansen et al. 2019; Tanaka et al. 2020). The external radius observed for circumbinary discs around evolved binary is usually found between a few dozen au to 500 au (Rafikov 2016; Izzard & Jermyn 2018), which covers mostly all the range of separations of our CBPs. A third possibility for a planet to reach inner orbits, and already described by Perets (2010), is the interaction among first-generation and new generation planets. What was a previously steady planetary configuration may dynamically evolve into a new configuration as a consequence of the formation of new planets in a post-CE disc (Schleicher & Dreizler 2014; Ledda et al. 2023), leading again to several outcomes, such as inward migration and/or ejections and/or collisions with the binary. Dedicated studies will have to be performed to explore the various outcomes of these evolutionary paths, to better constrain the properties of the surviving first generation planets that LISA will be able to detect, in the light of the formation of second-generation planets beyond the MS, for instance around DWD binaries, where different types of planets can form and migrate within 1 au of the inner binary (Ledda et al. 2023).
Percentages of CBPs with periods within 10 yr and 50 yr, divided by category and population.
6 Conclusions
We studied with numerical simulations the long-term evolution of circumbinary planetary systems hosting a single giant planet. To do so we generated two populations of 10 500 systems with different planetary priors. The first population (A) had planets initialised based on the distributions of known planets in single star systems, as reported in the literature; the second population (B) had planets initialised with uniform distributions to serve as unbiased comparison benchmark. The priors for the inner binaries were chosen based on the models yielding the best agreement with the observations of DWDs in the Galaxy (Toonen et al. 2012, 2017), with stellar masses ranging from 0.95 to 10 M⊙. We employed the assumption of adiabatic stellar winds and the model of Nelemans et al. (2001) for the CE phase. We divided the simulated systems based on their evolutive outcome, with the ultimate objective of characterising the Magrathea planets: the planetary survivors orbiting DWDs within one Hubble time. We found a relatively high occurrence of Magratheas in our sample, which gives optimistic hopes for future observations targeted on this category. All our systems were simulated in an isolated environment, outside the framework of any Galactic environment.
The data obtained from our simulations can be analysed from different perspectives and can answer a variety of scientific questions. We focused here on the general evolution of these systems in the orbital parameter space, with particular attention to the CBPs closest to their stars. We summarise below the main takeaways of our data analysis:
23% to 32% of all giants survive for one Hubble time to become Magrathea planets (respectively Pop. A and B) and they tend to reside on wide orbits around light hosts, regardless of their eccentricity;
The largest fraction (~33%) of the systems end up with a merger in the inner binary, which involves DWD mergers for more than one-quarter of them;
The CBP mass in the simulated giant planet range, does not appear to be correlated with its host system category, and does not play a role in the survival;
Photoevaporation has a negligible impact on the majority of our giant planets, due to the adiabatic expansion of their orbits during every stellar wind phase;
CBPs prefer prograde orbits during their evolution, especially the Magratheas;
Unstable systems are short-lived, they can potentially create small percentage of free-floating planets, and set the conditions for WD pollution.
Within the framework of development of the LISA science case for the detection of exoplanets we found that the evolution of single giant planet systems do not produce any systems in the range of sensitivity of LISA. No planet is found with a period smaller than 20 yr among the Magratheas, and smaller than 14 yr in the Merged-DWDs. Our results are a direct reflection of the number of systems we simulated, and much larger simulations need to be performed to check whether they can overcome the statistical bias.
Finally, the variables that play a role in the evolutionary path of a planetary system are many. The study here presented aims at being the first step towards a more comprehensive analysis that accounts for additional physical processes occurring at different stages of the binary life. Dedicated sets of evolutionary studies, that include the presence of multiple planets, the presence of a post-MS disc, and the possible interaction between first-generation and new generation planets (Ledda et al. 2023) need to be developed further to better address the final fate of cir-cumbinary systems, and hence the occurrence rates of the LISA exoplanets.
Acknowledgements
The authors thank Antonio Claret for providing us with the apsidal motion constant models. We also thank Eva Villaver, Valeryia Korol, Diego Turrini and Dimitri Veras for the helpful discussion. G.C. and C.D. acknowledge support from the Ministerio de Ciencia e Innovaciòn, through the project ACERO Ref. PID2019-110689RB-I00/AEI/10.13039/501100011033; C.D. acknowledges financial support from the grant CEX2021-001131-S funded by MCIN/AEI/10.13039/501100011033. S.T. acknowledges support from the Netherlands Research Council NWO (VENI 639.041.645 and VIDI 203.061 grants). Some of the computations described in this paper were performed using the University of Birmingham’s BlueBEAR HPC service, which provides a High Performance Computing service to the University’s research community. See http://www.birmingham.ac.uk/bear for more details.
Appendix A Additional plots
We present in this Appendix additional plots representative of our results. The first block of plots consists of the overview of the distributions for all the categories described in Sect. 4. Then we present plots relative to Pop. B, as counterparts of the ones reported in the main text, for Pop. A: the cumulative CBP eccentricity plot, the inclination distribution comparison plot, and the stellar types of unlucky CBPs. Lastly, we report a series of plots dealing with the critical semi-major axis scatter of CBPs, for the various categories. These are particularly useful for visualising how the CBPs in each category occupy the orbital parameter space with respect to the secular stability limits.
 |
Fig. A.1 Population B: Overview of distributions of Magrathea systems in the parameter space. The solid histograms represent the Magrathea parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Magratheas. |
 |
Fig. A.2 Overview of distributions of Merged systems. The solid histograms represent the Merged parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Merged. Top half : Pop. A, bottom half : Pop. B. For these systems the parameters refer to the last moment preceding the inner binary merger. |
 |
Fig. A.3 Overview of distributions of Merged-DWDs systems. The solid histograms represent the Merged-DWDs parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Merged-DWDs. Top half: Pop. A, bottom half: Pop. B. For these systems the parameters refer to the last moment preceding the inner binary merger. |
 |
Fig. A.4 Overview of distributions of Collided systems (see the detailed definition and caveats of this category in Sect. 4.2). The solid histograms represent the Collided parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Collided. Top half: Pop. A, bottom half: Pop. B. |
 |
Fig. A.5 Overview of distributions of Stable-MT systems. The solid histograms represent the Stable-MT parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Stable-MT. Top half: Pop. A, bottom half: Pop. B. |
 |
Fig. A.6 Cumulative distributions for eccentricity of planets. Solid line: Pop. A, dashed line: Pop. B. The eccentricity of the Destabilised systems with unbound orbits (e > 1) has been artificially set to 1.5 to avoid useless dispersion in the plots. The Collided systems stand out from all the other categories, for both populations. |
 |
Fig. A.7 Population B: Relative inclination distributions for Magrathea and the destroyed systems (Merged, Collided, Destabilised). |
 |
Fig. A.8 Population B. Shown are the stellar types of the inner binaries for those planets that do not become Magratheas. From left to right: CBPs around merging binaries, excluded the DWD-mergers, planets in the Collided and Destabilised categories (see Sect. 4 for the detailed definitions). For simplicity, the label ‘Post-MS’ includes all the stellar types after the MS that are not WDs. |
 |
Fig. A.9 Outer-to-inner binary semi-major axis ratio as a function of critical ratio for each system. acrit depends only on the inner binary, as shown in Sect. 2.2.1. On the left side of each plot is shown a histogram of the ratio distributions; the logarithmic bins do alter the peak’s shape, which in linear scale would always fall towards the lowest values. Left: Pop. A, right: Pop. B. |
References
- Abt, H. A. 1983, ARA&A, 21, 343 [Google Scholar]
- Adams, D. 1979, The Hitchhiker’s Guide to the Galaxy (Pan Books) [Google Scholar]
- Amaro-Seoane, P., Audley, H., Babak, S., et al. 2017, arXiv e-prints, [arXiv:1702.00786] [Google Scholar]
- Amaro-Seoane, P., Andrews, J., Arca Sedda, M., et al. 2023, Liv. Rev. Rel., 26, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, K. R., Lai, D., & Storch, N. I. 2017, MNRAS, 467, 3066 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, J. H. 1992, ApJ, 385, 621 [Google Scholar]
- Armstrong, D. J., Osborn, H. P., Brown, D. J. A., et al. 2014, MNRAS, 444, 1873 [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, H. A., Espaas, T., Norgrove, B. Z., et al. 2021, MNRAS, 507, 4507 [NASA ADS] [CrossRef] [Google Scholar]
- Bashi, D., Helled, R., Zucker, S., & Mordasini, C. 2017, A&A, 604, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batygin, K. 2018, AJ, 155, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Hessman, F. V., Dreizler, S., et al. 2010, A&A, 521, A60 [Google Scholar]
- Beuermann, K., Buhlmann, J., Diese, J., et al. 2011, A&A, 526, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Dreizler, S., Hessman, F. V., & Deller, J. 2012, A&A, 543, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blackman, J. W., Beaulieu, J. P., Bennett, D. P., et al. 2021, Nature, 598, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Bours, M. C. P., Marsh, T. R., Parsons, S. G., et al. 2016, MNRAS, 460, 3873 [Google Scholar]
- Bowler, B. P., Blunt, S. C., & Nielsen, E. L. 2020, ApJ, 159, 63 [CrossRef] [Google Scholar]
- Breivik, K., Coughlin, S., Zevin, M., et al. 2020, ApJ, 898, 71 [Google Scholar]
- Brown, W. R., Kilic, M., Allende Prieto, C., & Kenyon, S. J. 2010, ApJ, 723, 1072 [Google Scholar]
- Brown, W. R., Kilic, M., Kosakowski, A., et al. 2020, ApJ, 889, 49 [Google Scholar]
- Bryan, M. L., Benneke, B., Knutson, H. A., Batygin, K., & Bowler, B. P. 2018, Nat. Astron., 2, 138 [Google Scholar]
- Bryan, M. L., Ginzburg, S., Chiang, E., et al. 2020, ApJ, 905, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Burdge, K. B., Coughlin, M. W., Fuller, J., et al. 2019, Nature, 571, 528 [Google Scholar]
- Burdge, K. B., Prince, T. A., Fuller, J., et al. 2020, ApJ, 905, 32 [Google Scholar]
- Busetti, F., Beust, H., & Harley, C. 2018, A&A, 619, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cañas, C. I., Kanodia, S., Bender, C. F., et al. 2022, AJ, 164, 50 [CrossRef] [Google Scholar]
- Camacho, J., Torres, S., García-Berro, E., et al. 2014, A&A, 566, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., Baraffe, I., Leconte, J., Gallardo, J., & Barman, T. 2009, in 15th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, ed. E. Stempels, American Institute of Physics Conference Series, 1094, 102 [NASA ADS] [Google Scholar]
- Chamandy, L., Frank, A., Blackman, E. G., et al. 2018, MNRAS, 480, 1898 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, J., & Kipping, D. 2017, ApJ, 834, 17 [Google Scholar]
- Claret, A. 2019, A&A, 628, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Torres, G. 2019, ApJ, 876, 134 [Google Scholar]
- Danielski, C., & Tamanini, N. 2020, Int. J. Mod. Phys. D, 29, 2043007 [NASA ADS] [CrossRef] [Google Scholar]
- Danielski, C., Korol, V., Tamanini, N., & Rossi, E. M. 2019, A&A, 632, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Darwin, G. H. 1879, Philos. Trans. Roy. Soc. Lond. Ser. I, 170, 447 [NASA ADS] [Google Scholar]
- Dittmann, A. J. 2021, MNRAS, 508, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Dixon, D., Tayar, J., & Stassun, K. G. 2020, AJ, 160, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Dosopoulou, F., & Kalogera, V. 2016a, ApJ, 825, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Dosopoulou, F., & Kalogera, V. 2016b, ApJ, 825, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, L. R., Carter, J. A., Fabrycky, D. C., et al. 2011, Science, 333, 1602 [NASA ADS] [CrossRef] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Erkaev, N. V., Kulikov, Y. N., Lammer, H., et al. 2007, A&A, 472, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esmer, E. M., Baştürk, Ö., Selam, S. O., & Aliş, S. 2022, MNRAS, 511, 5207 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Fagginger Auer, F., & Portegies Zwart, S. 2022, SciPost Astron., 2, 002 [NASA ADS] [CrossRef] [Google Scholar]
- Flaccomio, E., Damiani, F., Micela, G., et al. 2003a, ApJ, 582, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Flaccomio, E., Damiani, F., Micela, G., et al. 2003b, ApJ, 582, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., & Bergeron, P. 2001, PASP, 113, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Arenou, F., et al.) 2023a, A&A, 674, A34 [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gänsicke, B. T., Schreiber, M. R., Toloza, O., et al. 2019, Nature, 576, 61 [Google Scholar]
- Glanz, H., & Perets, H. B. 2018, MNRAS, 478, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez-Muñoz, M. A., Sabin, L., Raddi, R., & Wells, R. D. 2022, MNRAS, 514, 2434 [CrossRef] [Google Scholar]
- Gorti, U., Dullemond, C. P., & Hollenbach, D. 2009, ApJ, 705, 1237 [Google Scholar]
- Grichener, A., Sabach, E., & Soker, N. 2018, MNRAS, 478, 1818 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., & Gautier, D. 2015, in Treatise on Geophysics, ed. G. Schubert, 529 [CrossRef] [Google Scholar]
- Hamers, A. S. 2021, MNRAS, 500, 3481 [Google Scholar]
- Hamers, A. S., & Dosopoulou, F. 2019, ApJ, 872, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1995, MNRAS, 272, 800 [NASA ADS] [Google Scholar]
- Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2014, MNRAS, 440, 1982 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1983, ApJ, 267, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Höfner, S. 2015, in Why Galaxies Care about AGB Stars III: A Closer Look in Space and Time, eds. F. Kerschbaum, R. F. Wing, & J. Hron, Astronomical Society of the Pacific Conference Series, 497, 333 [Google Scholar]
- Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [Google Scholar]
- Huang, S. S. 1956, AJ, 61, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S.-S. 1963, ApJ, 138, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Iaconi, R., & De Marco, O. 2019, MNRAS, 490, 2550 [Google Scholar]
- Iaconi, R., Maeda, K., Nozawa, T., De Marco, O., & Reichardt, T. 2020, MNRAS, 497, 3166 [NASA ADS] [CrossRef] [Google Scholar]
- Igoshev, A. P., Perets, H. B., & Michaely, E. 2020, MNRAS, 494, 1448 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N. 2018, ApJ, 858, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Ivanova, N., & Nandez, J. L. A. 2016, MNRAS, 462, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., & Podsiadlowski, P. 2015, MNRAS, 447, 2181 [Google Scholar]
- Ivanova, N., Justham, S., & Ricker, P. 2020, Common Envelope Evolution (IOP Publishing) [Google Scholar]
- Izzard, R., & Jermyn, A. 2018, Galaxies, 6, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Hall, P. D., Tauris, T. M., & Tout, C. A. 2012, IAU Symp., 283, 95 [Google Scholar]
- Jain, C., Paul, B., Sharma, R., Jaleel, A., & Dutta, A. 2017, MNRAS, 468, L118 [CrossRef] [Google Scholar]
- Johansen, A., Ida, S., & Brasser, R. 2019, A&A, 622, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashi, A., & Soker, N. 2011, MNRAS, 417, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, M. L., Danielski, C., Karnesis, N., et al. 2022, MNRAS, 517, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, D., Gänsicke, B. T., & Farihi, J. 2014, A&A, 566, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korol, V., Rossi, E. M., Groot, P. J., et al. 2017, MNRAS, 470, 1894 [NASA ADS] [CrossRef] [Google Scholar]
- Korol, V., Toonen, S., Klein, A., et al. 2020, A&A, 638, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korol, V., Belokurov, V., & Toonen, S. 2022a, MNRAS, 515, 1228 [NASA ADS] [CrossRef] [Google Scholar]
- Korol, V., Hallakoun, N., Toonen, S., & Karnesis, N. 2022b, MNRAS, 511, 5936 [NASA ADS] [CrossRef] [Google Scholar]
- Kostov, V. B., McCullough, P. R., Carter, J. A., et al. 2014, ApJ, 784, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Kostov, V. B., Moore, K., Tamayo, D., Jayawardhana, R., & Rinehart, S. A. 2016, ApJ, 832, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Kostov, V. B., Orosz, J. A., Feinstein, A. D., et al. 2020, AJ, 159, 253 [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramer, M., Schneider, F. R. N., Ohlmann, S. T., et al. 2020, A&A, 642, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kratter, K. M., & Perets, H. B. 2012, ApJ, 753, 91 [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Lamberts, A., Blunt, S., Littenberg, T. B., et al. 2019, MNRAS, 490, 5888 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Odert, P., Leitzinger, M., et al. 2009, A&A, 506, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lampón, M., López-Puertas, M., Sanz-Forcada, J., et al. 2023, A&A, 673, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lau, M. Y. M., Hirai, R., González-Bolívar, M., et al. 2022a, MNRAS, 512, 5462 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, M. Y. M., Hirai, R., Price, D. J., & Mandel, I. 2022b, MNRAS, 516, 4669 [NASA ADS] [CrossRef] [Google Scholar]
- Law-Smith, J. A. P., Everson, R. W., Ramirez-Ruiz, E., et al. 2020, arXiv e-prints, [arXiv:2011.06630] [Google Scholar]
- Ledda, S., Danielski, C., & Turrini, D. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202245827 [Google Scholar]
- Lei, H. 2019, MNRAS, 490, 4756 [NASA ADS] [CrossRef] [Google Scholar]
- López-Cámara, D., De Colle, F., Moreno Méndez, E., Shiber, S., & Iaconi, R. 2022, MNRAS, 513, 3634 [CrossRef] [Google Scholar]
- Love, A. E. H. 1911, Some Problems of Geodynamics (Cambridge University Press) [Google Scholar]
- Luhman, K. L., Adame, L., D’Alessio, P., et al. 2005, ApJ, 635, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, S., Mao, S., Ida, S., Zhu, W., & Lin, D. N. C. 2016, MNRAS, 461, L107 [Google Scholar]
- Marsh, K. A., Plavchan, P., Kirkpatrick, J. D., et al. 2010, ApJ, 719, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. V. 2018, in Handbook of Exoplanets, eds. H. J. Deeg, & J. A. Belmonte, 156 [Google Scholar]
- Martin, D. V. 2020, Contrib. Astron. Observ. Skalnate Pleso, 50, 463 [NASA ADS] [Google Scholar]
- Martin, D. V., & Fabrycky, D. C. 2021, AJ, 162, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. V., Triaud, A. H. M. J., Udry, S., et al. 2019, A&A, 624, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, D. V., El-Badry, K., Hodžić, V. K., et al. 2021, MNRAS, 507, 4132 [CrossRef] [Google Scholar]
- Marzari, F., & Thebault, P. 2019, Galaxies, 7, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Masci, F. J., Laher, R. R., Rusholme, B., et al. 2019, PASP, 131, 018003 [Google Scholar]
- Michaely, E., & Perets, H. B. 2019, MNRAS, 484, 4711 [NASA ADS] [CrossRef] [Google Scholar]
- Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
- Mugrauer, M. 2019, MNRAS, 490, 5088 [Google Scholar]
- Naef, D., Mayor, M., Lo Curto, G., et al. 2010, A&A, 523, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nandez, J. L. A., Ivanova, N., & Lombardi, J. C. J. 2015, MNRAS, 450, L39 [Google Scholar]
- Napiwotzki, R., Karl, C. A., Lisker, T., et al. 2020, A&A, 638, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nazé, Y. 2009, A&A, 506, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelemans, G., Verbunt, F., Yungelson, L. R., & Portegies Zwart, S. F. 2000, A&A, 360, 1011 [NASA ADS] [Google Scholar]
- Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
- Owen, J. E. 2019, Annu. Rev. Earth Planet. Sci., 47, 67 [CrossRef] [Google Scholar]
- Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, 73, eds. P. Eggleton, S. Mitton, & J. Whelan, 73, 75 [Google Scholar]
- Passy, J.-C., De Marco, O., Fryer, C. L., et al. 2012, ApJ, 744, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Penz, T., Micela, G., & Lammer, H. 2008, A&A, 477, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perets, H. B. 2010, arXiv e-prints, [arXiv:1001.0581] [Google Scholar]
- Potter, S. B., Romero-Colmenero, E., Ramsay, G., et al. 2011, MNRAS, 416, 2202 [NASA ADS] [CrossRef] [Google Scholar]
- Pulley, D., Sharp, I. D., Mallett, J., & von Harrach, S. 2022, MNRAS, 514, 5725 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S. B., Liu, L., Zhu, L. Y., et al. 2012, MNRAS, 422, L24 [Google Scholar]
- Rafikov, R. R. 2016, ApJ, 830, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190 1 [Google Scholar]
- Rahoma, W. A., Abd El-Salam, F. A., & Ahmed, M. K. 2009, J. Astrophys. Astron., 30, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Rasio, F. A., & Ford, E. B. 1996, Science, 274, 954 [Google Scholar]
- Reichardt, T. A., De Marco, O., Iaconi, R., Chamandy, L., & Price, D. J. 2020, MNRAS, 494, 5333 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1977, A&A, 61, 217 [NASA ADS] [Google Scholar]
- Sabach, E., Hillel, S., Schreier, R., & Soker, N. 2017, MNRAS, 472, 4361 [NASA ADS] [CrossRef] [Google Scholar]
- Sahlmann, J., Triaud, A. H. M. J., & Martin, D. V. 2015, MNRAS, 447, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sand, C., Ohlmann, S. T., Schneider, F. R. N., Pakmor, R., & Röpke, F. K. 2020, A&A, 644, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A&A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanz-Forcada, J., Desidera, S., & Micela, G. 2014, A&A, 570, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., & Dreizler, S. 2014, A&A, 563, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, M. R., Gänsicke, B. T., Toloza, O., Hernandez, M.-S., & Lagos, F. 2019, ApJ, 887, L4 [Google Scholar]
- Schröder, K. P., & Smith, R. C. 2008, MNRAS, 386, 155 [CrossRef] [Google Scholar]
- Sepinsky, J. F., Willems, B., Kalogera, V., & Rasio, F. A. 2007, ApJ, 667, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Sepinsky, J. F., Willems, B., Kalogera, V., & Rasio, F. A. 2009, ApJ, 702, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Shiber, S., & Soker, N. 2018, MNRAS, 477, 2584 [CrossRef] [Google Scholar]
- Shiber, S., Iaconi, R., De Marco, O., & Soker, N. 2019, MNRAS, 488, 5615 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S., Richer, H. B., Hansen, B. M., Stairs, I. H., & Thorsett, S. E. 2003, Science, 301, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Smullen, R. A., Kratter, K. M., & Shannon, A. 2016, MNRAS, 461, 1288 [Google Scholar]
- Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620 [NASA ADS] [Google Scholar]
- Song, S., Mai, X., Mutel, R. L., et al. 2019, AJ, 157, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Tremblay, P.-E., Gänsicke, B. T., Evans, D., & Mocnik, T. 2020, MNRAS, 497, 4416 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, D. S., Burrows, A., & Milsom, J. A. 2011, ApJ, 727, 57 [Google Scholar]
- Standing, M. R., Sairam, L., Martin, D. V., et al. 2023, Nat. Astron., 7, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Sterne, T. E. 1939, MNRAS, 99, 451 [NASA ADS] [Google Scholar]
- Sutherland, A. P., & Fabrycky, D. C. 2016, ApJ, 818, 6 [Google Scholar]
- Tamanini, N., & Danielski, C. 2019, Nat. Astron., 3, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Murase, K., & Tanigawa, T. 2020, ApJ, 891, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Thorngren, D. P., Marley, M. S., & Fortney, J. J. 2019, RNAAS, 3, 128 [NASA ADS] [Google Scholar]
- Tokovinin, A. 2014, AJ, 147, 87 [CrossRef] [Google Scholar]
- Tokovinin, A. 2021, Universe, 7, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., & Nelemans, G. 2013, A&A, 557, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toonen, S., Nelemans, G., & Portegies Zwart, S. 2012, A&A, 546, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toonen, S., Claeys, J. S. W., Mennekens, N., & Ruiter, A. J. 2014, A&A, 562, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toonen, S., Hamers, A., & Portegies Zwart, S. 2016, Comput. Astrophys. Cosmol., 3, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., Hollands, M., Gänsicke, B. T., & Boekholt, T. 2017, A&A, 602, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toonen, S., Portegies Zwart, S., Hamers, A. S., & Bandopadhyay, D. 2020, A&A, 640, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toonen, S., Boekholt, T. C. N., & Portegies Zwart, S. 2022, A&A, 661, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Triaud, A. H. M. J., Standing, M. R., Heidari, N., et al. 2022, MNRAS, 511, 3561 [NASA ADS] [CrossRef] [Google Scholar]
- van der Sluys, M. V., Verbunt, F., & Pols, O. R. 2006, A&A, 460, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanderburg, A., Montet, B. T., Johnson, J. A., et al. 2015, ApJ, 800, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderburg, A., Rappaport, S. A., Xu, S., et al. 2020, Nature, 585, 363 [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [Google Scholar]
- Veras, D. 2021, in Oxford Research Encyclopedia of Planetary Science, 1 [Google Scholar]
- Veras, D., & Raymond, S. N. 2012, MNRAS, 421, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Veras, D., Wyatt, M. C., Mustill, A. J., Bonsor, A., & Eldridge, J. J. 2011, MNRAS, 417, 2104 [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., & Marzari, F. 1996, Nature, 384, 619 [Google Scholar]
- Williams, D. M. 2003, Am. J. Phys., 71, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, E. C., & Nordhaus, J. 2019, MNRAS, 485, 4492 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, E. C., & Nordhaus, J. 2022, MNRAS, 516, 2189 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. G., Farihi, J., Gänsicke, B. T., & Swan, A. 2019, MNRAS, 487, 133 [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Horner, J., & Marshall, J. P. 2013, MNRAS, 431, 2150 [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [Google Scholar]
- Zapatero Osorio, M. R., Béjar, V. J. S., Martín, E. L., et al. 2000, Science, 290, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, L.-Y., Qian, S.-B., Fernández Lajús, E., Wang, Z.-H., & Li, L.-J. 2019, Res. Astron. Astrophys., 19, 134 [Google Scholar]
- Zorotovic, M., & Schreiber, M. 2022, MNRAS, 513, 3587 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zuckerman, B., Melis, C., Klein, B., Koester, D., & Jura, M. 2010, ApJ, 722, 725 [Google Scholar]
We refer to Marzari & Thebault (2019) for a thorough overview of the characteristics of both P-type and S-type populations.
From the book “The Hitchhiker’s Guide to the Galaxy” (Adams 1979). Magrathea is a planet orbiting a binary star burning with ‘white fire’, which we conveniently interpreted to be two white dwarfs since they emit white light instead of yellow, as our Sun does, in the visible band.
All Tables
Percentages of possible evolution outcomes computed over the total size of Pops. A and В (both with a sample size of 10 500).
Percentages of CBPs with periods within 10 yr and 50 yr, divided by category and population.
All Figures
 |
Fig. 1 Population A: overview of the distributions of Magrathea systems in the parameter space. Solid histograms represent the Magrathea parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines, instead, show the initial distributions for the whole population, not restricted to the Magratheas. |
| In the text | |
 |
Fig. 2 Population A: atmospheric mass loss undergone by Magrathea gas giants, scattered in the mass-distance parameter space. The x-axis corresponds to the final time-averaged orbital distance of the CBPs. We show the planets that lost more mass than the 50% of the category. The colour corresponds to the amount of mass lost (see colour bar). The size of the markers is proportional to the progenitor binary mass, as illustrated in the legend. |
| In the text | |
 |
Fig. 3 Comparison of the inner semi-major axis ain distributions for the binaries in Magrathea systems (blue) and the merged-DWDs (orange, ain refers to the timestamp just before merging) of Pop. A and Pop. B (solid and dashed lines, respectively). The grey line denotes a separation of 1R⊙. |
| In the text | |
 |
Fig. 4 Complementary cumulative distributions of the final inner binary semi-major axes ain, for all categories (colour-coded in the legend), and for both Pops. A (solid lines) and B (dashed lines). Merged DWDs all resides in orbits smaller than 1R⊙ (vertical grey line) and few of the Magrathea hosts as well. These parameters refer to the last valid simulation step in secular approximation. |
| In the text | |
 |
Fig. 5 Complementary cumulative distributions of final semi-major axes aout of CBPs for all categories (colour-coded in the legend), for both Pops. A (solid lines) and B (dashed lines). These parameters refer to the last valid simulation step in secular approximation. |
| In the text | |
 |
Fig. 6 Population A: relative inclination distributions for Magrathea and planets in Destroyed systems (which include Merged, Collided, and Destabilised). The population was initialised with an inclination distribution uniform in cos (i); this plot illustrates how at the end of life the systems seem to favour mildly inclined prograde orbits, especially surviving Magratheas. |
| In the text | |
 |
Fig. 7 Population A: stellar type of inner binaries, for those planets that do not survive to become Magratheas. From left to right: CBPs around merging binaries, excluded the DWD-mergers, planets in the Collided category, and Destabilised (see Sect. 4 for detailed definitions). For simplicity, the label ‘Post-MS’ includes all stellar types after the MS that are not WDs. We show in Fig. A.8 the same plot for Pop. B. |
| In the text | |
 |
Fig. 8 Population A: atmospheric mass loss endured by gas giants of Merged binaries, scattered in mass-distance parameter space. The x-axis corresponds to the final time-averaged orbital distance of the CBPs. Shown are the planets that lost more mass than the 50% of the category. The colour corresponds to the amount of mass lost (see colour bar). The size of the markers is proportional to the binary progenitors masses, as illustrated in the legend. |
| In the text | |
 |
Fig. A.1 Population B: Overview of distributions of Magrathea systems in the parameter space. The solid histograms represent the Magrathea parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Magratheas. |
| In the text | |
 |
Fig. A.2 Overview of distributions of Merged systems. The solid histograms represent the Merged parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Merged. Top half : Pop. A, bottom half : Pop. B. For these systems the parameters refer to the last moment preceding the inner binary merger. |
| In the text | |
 |
Fig. A.3 Overview of distributions of Merged-DWDs systems. The solid histograms represent the Merged-DWDs parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Merged-DWDs. Top half: Pop. A, bottom half: Pop. B. For these systems the parameters refer to the last moment preceding the inner binary merger. |
| In the text | |
 |
Fig. A.4 Overview of distributions of Collided systems (see the detailed definition and caveats of this category in Sect. 4.2). The solid histograms represent the Collided parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Collided. Top half: Pop. A, bottom half: Pop. B. |
| In the text | |
 |
Fig. A.5 Overview of distributions of Stable-MT systems. The solid histograms represent the Stable-MT parameters at one Hubble time, while the dashed lines show their initial distributions. The ‘out’ subscript denotes the planetary parameters (blue distributions). The dotted grey lines show the initial distributions for the whole population, not restricted to the Stable-MT. Top half: Pop. A, bottom half: Pop. B. |
| In the text | |
 |
Fig. A.6 Cumulative distributions for eccentricity of planets. Solid line: Pop. A, dashed line: Pop. B. The eccentricity of the Destabilised systems with unbound orbits (e > 1) has been artificially set to 1.5 to avoid useless dispersion in the plots. The Collided systems stand out from all the other categories, for both populations. |
| In the text | |
 |
Fig. A.7 Population B: Relative inclination distributions for Magrathea and the destroyed systems (Merged, Collided, Destabilised). |
| In the text | |
 |
Fig. A.8 Population B. Shown are the stellar types of the inner binaries for those planets that do not become Magratheas. From left to right: CBPs around merging binaries, excluded the DWD-mergers, planets in the Collided and Destabilised categories (see Sect. 4 for the detailed definitions). For simplicity, the label ‘Post-MS’ includes all the stellar types after the MS that are not WDs. |
| In the text | |
 |
Fig. A.9 Outer-to-inner binary semi-major axis ratio as a function of critical ratio for each system. acrit depends only on the inner binary, as shown in Sect. 2.2.1. On the left side of each plot is shown a histogram of the ratio distributions; the logarithmic bins do alter the peak’s shape, which in linear scale would always fall towards the lowest values. Left: Pop. A, right: Pop. B. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.