EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 650 (June 2021) A&A, 650 (2021) A178 Full HTML
Open Access
Issue
A&A
Volume 650, June 2021
Article Number A178
Number of page(s) 10
Section Celestial mechanics and astrometry
DOI https://doi.org/10.1051/0004-6361/202038940
Published online 24 June 2021

© D. E. Graham et al. 2021

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

The discovery of circumbinary planets (CBPs) has opened up the possibility that we may discover some that support liquid surface water and detectable biosignatures. A key driver for sustaining liquid water on Earth’s surface is a nearly stable solar radiation flux that provides enough energy to melt ice, but not so much as to boil water. The incident stellar radiation (instellation) on a CBP necessarily evolves due to the time-varying gravitational interactions of its two host stars, potentially affecting the long-term stability of liquid water on CBPs. While this dynamical feature of CBPs is well known (e.g., Dole 1964; Kane & Hinkel 2013; Forgan 2016; Popp & Eggl 2017), past works have not considered how the long-term tidal evolution of the host binary stars can impact the orbital evolution and habitability of CBPs. In this paper, we perform simulations of a single planet orbiting two stars with a binary orbital period (Porb) less than ~10 days, that is, where tidal forces are expected to strongly impact the binary orbit (Zahn & Bouchet 1989; Meibom & Mathieu 2005; Fleming et al. 2018). We examine the orbital stability and long-term orbital oscillations of potentially habitable CBPs to determine the conditions that permit binary stars to host habitable CBPs, as well as to predict the properties and evolutionary histories of potentially habitable planets in those systems.

The orbits of binary stars span a wide range of both orbital periods and eccentricities (e.g., Duquennoy & Mayor 1991; Raghavan et al. 2010), but nearly all binaries with orbital periods less than about 10 days are on circular orbits (Meibom & Mathieu 2005; Raghavan et al. 2010). This observation is likely due to orbital circularization caused by tidal forces that are strongest during the pre-main sequence phase (Zahn & Bouchet 1989). Low-mass stellar binaries with sufficiently short orbital periods, Porb ≲ 10 days, experience tidal forces that can gravitationally deform the stellar shapes, creating tidal bulges that are maintained by friction within the stellar convective envelopes (Mazeh 2008; Zahn 2008). Under equilibrium tidal theories (see Darwin 1880; Ferraz-Mello et al. 2008), these tidal bulges induce torques that drive secular changes in the binary orbital and stellar rotational angular momenta. Stellar evolution further complicates the story as stars contract and develop a radiative core during the pre-main sequence (Baraffe et al. 2015), changing each star’s angular momentum evolution. Thus, the binary’s orbital semi-major axis abin and eccentricity ebin can change significantly over time due to both stellar evolution and tidal forces.

The coupled stellar–tidal evolution of binaries is complicated and can generate additional observable features beyond the circular orbits of short-period binaries. Fleming et al. (2018) showed that for binary orbits with initial orbital periods less than about 8–10 days, the binary orbit will expand and become more eccentric as tidal torques transfer stellar rotational angular momentum into the binary orbit as the stars, in turn, contract along the pre-main sequence and tides drive the binary toward the tidally locked state. Following the earlier work of Verbunt & Zwaan (1981), Fleming et al. (2018) showed that the binary orbit eventually decays due to the removal of angular momentum via magnetic braking after the stars’ rotational frequencies are synchronized to the orbital frequency. Fleming et al. (2018) demonstrated that, in general, larger initial orbital periods result in less expansion and a slower decay to circular orbits since these larger initial orbits host a larger initial reservoir of angular momentum. They found that the maxima in abin and ebin occurred about 2 Myr after the start of the Baraffe et al. (2015) stellar models. Fleming et al. (2018) dubbed their model the “Stellar-Tidal Evolution Ejection of Planets” (STEEP). We note that Zoppetti et al. (2019) showed that outward-then-inward evolution of the binary orbit can occur even when one ignores the stellar evolution.

Some low-mass binary stars are known to host CBPs and the populations appear to have been sculpted by the process outlined in Fleming et al. (2018). For example, while more than ten transiting CBPs have been detected in the Kepler field, such as Kepler-34 and -35 (Welsh et al. 2012), no CBPs have yet been discovered orbiting binary stars with Porb≲ 7.5 days, the orbital period of Kepler-47 (Orosz et al. 2012; Winn & Fabrycky 2015; Windemuth et al. 2019). This curious lack of CBPs may be due to small number statistics (Windemuth 2020), or it may be real and represent a signature of physical effects that significantly reduces the formation and/or long-term stability of these planets. Muñoz & Lai (2015), Martin et al. (2015) and Hamers et al. (2016) suggested that a third star on a wide orbit could destabilize planets orbiting binary stars with orbital periods in the range 3 days ≲ Porb ≲ 7.5 days. More recent research by Fleming et al. (2018) showed that the outward-then-inward orbital evolution described above can destabilize the innermost planet of a system for all binary periods less than 8 days. They also showed that this process can set off a chain reaction that ejects additional planets. Thus, the coupled stellar–tidal evolution of binary stars can dramatically affect CBP orbits and motivates additional investigations in the role of coupled stellar–tidal evolution of binary stars on the stability, evolution, and habitability of CBPs.

The Fleming et al. (2018) model only employed one tidal model (the “Constant Phase Lag” equilibrium tidal model (CPL; Ferraz-Mello et al. 2008)), and did not include the change in stellar density profile as stars evolve on the pre-main sequence, a property often parameterized as the radius of gyration, rg. Fleming et al. (2019) added this phenomenon in their study of Kepler binary stars and found it significantly impacts the angular momentum evolution of the binary. Thus, a reanalysis of the STEEP method with this “dynamic rg ” model and a quantitative comparison with the “static rg” model would help determine if the STEEP process is still a viable explanation for the lack of CBPs orbiting short-period binaries. Moreover, they did not explore the impact on the circumbinary habitable zone (HZ; Kasting et al. 1993; Kopparapu et al. 2013; Cukier et al. 2019) or systems that are not engulfed by instability, that is to say, the binary orbit evolves, but not significantly enough to eject the planets. In such cases, the tidal evolution of the stars does not remove a planet, but slowly changes its orbit, which can still have a profound affect on the climates and habitability of planets (e.g., Spiegel et al. 2010; Forgan 2016; Popp & Eggl 2017; Haqq-Misra et al. 2019; Deitrick et al. 2018). Thus, a fuller range of models and system parameters must be explored to comprehensively understand the history and properties of CBPs.

The Kepler-47 system is a crucial benchmark for assessing the role of coupled stellar–tidal evolution. The binary orbit is ~ 7.5 days (Orosz et al. 2012), and its inner planet, Kepler-47 b, orbits very close to the critical semi-major axis for stability, acrit (see Holman & Wiegert 1999; Winn & Holman 2005). This system is therefore in the transition region from tidally interacting to non-tidally interacting binaries, yet possesses three planets. Moreover, the Kepler-47 planetary system contains a gas giant (Kepler-47 c) orbiting within the HZ of the binary stars (Orosz et al. 2012), and so may possess a habitable exomoon (Heller & Barnes 2013). Thus, any theory of CBPs orbiting tidally interacting binaries must reproduce this system, preferably without any fine tuning of parameters.

Although Kepler-47 is the only known tidally interacting binary to host a planet, the formation of CBPs in short-period binaries is likely. For example, Alexander (2012) found that circumbinary disks form in a very similar process as single stars’ disks for binary semi-major axes ≾1 au. Moreover, Bromley & Kenyon (2015) show that planetary formation around binary stars is similar to those that form around single stars. They also concluded that circumbinary disks and planets likely form in a similar manner as those hosted by single stars, implying that there should be a sizeable population of short-period CBPs forming during the early stages of binary star evolution, but none have yet been discovered.

To help resolve the outstanding issues, we performed new and more sophisticated simulations of the coupled stellar–tidal–orbital evolution of known and hypothetical systems consisting of two stars orbited by one planet and report the results here. In Sect. 2, we describe our models and the experimental setup of our simulations. In Sect. 3, we present results for (a) the STEEP process with a second tidal model (the Constant Time Lag equilibrium tidal model, CTL; Leconte et al. 2010) and an evolving mass concentration, (b) an extended exploration of the history of the Kepler-47 system, (c) the evolution of the HZ and acrit for equal-mass binary stars, and (d) a reanalysis of the stability of CBPs in the HZ of tidally interacting equal-mass binary stars. In Sect. 4, we discuss our results and conclude. We note that we have made all source code and plotting scripts publicly available, and each figure caption concludes with a link to a GitHub repository for reproducibility.

2 Methods

In this section, we describe our model, implemented in the VPLanet software package (Barnes et al. 2020), which includes validated models for stellar evolution, the equilibrium tidal evolution of binary stars, and the orbital evolution of a single CBP. In the following the subsections, we briefly review VPLanet (Sect. 2.1), the circumbinary HZ in Sect. 2.2, the circumbinary stability limit in Sect. 2.3, and our initial conditions and assumptions in Sect. 2.4. For thorough discussions, derivations, and validations of the numerical methods and physical models used herein, the reader is referred to Barnes et al. (2013); Baraffe et al. (2015); Fleming et al. (2018, 2019) and Barnes et al. (2020).

2.1 VPLanet

VPLanet is a software package designed to connect physical models that can be described by ordinary differential equations or explicit functions of time. (Barnes et al. 2020). Each “module” is a physical process that can be selected at runtime. In our case, we focus on the time evolution of binary stars and their CBPs using the modules STELLAR (stellar evolution), EqTide (tidal evolution), and BINARY (CBP orbital evolution), as described in the next section. During a simulation, each module operates simultaneously to compute time derivatives of each model parameter, advancing the system forward in time and permitting gigayear simulations of common astrophysical phenomena. VPLanet uses a fourth order Runge–Kutta scheme with dynamical timestepping that minimizes computational expense while still resolving all processes, regardless of timescale. A tuneable parameter provides the desired accuracy; here we assume convergence when a change of a factor of 10 in the timestep results in a change of less than 10−4 in the outcome.

The STELLAR module simulates the pre-main sequence and main sequence evolution of stars by interpolating the Baraffe et al. (2015) radius, effective temperature, and radius of gyration (rg, mass concentration) tracks. Angular momentum is conserved during the stellar evolution, so changes to these properties affect the rotational frequency (see Fleming et al. 2018, 2019 for a detailed description of our implementation of this effect). STELLAR also includes several magnetic braking/stellar wind models that also affect the rotational evolution. We use the (Matt et al. 2015) model that is calibrated to Kepler observations of single stars to simulate magnetic braking for our low-mass binary stars.

The EqTide module employs the equilibrium tide model originally described in Darwin (1880), including both the CPL and CTL tidal incarnations (see Ferraz-Mello et al. 2008; Greenberg 2009; Leconte et al. 2010). These two models include ODEs for rotational frequency, obliquity, semi-major axis, and eccentricity for a two-body system (Ferraz-Mello et al. 2008; Leconte et al. 2010) that are appropriate for binary orbital eccentricities ≲   0.3.

The BINARY module is an implementation of the approximate analytic model for the orbital evolution of a CBP derived by Leung & Lee (2013) that is valid for small CBP orbital eccentricities and inclinations. It treats the planet as a massless particle whose motion is completely controlled by the evolving gravitational field of the stars.

The EqTide and STELLAR modules were combined in Fleming et al. (2019) to reproduce the observed distribution of Kepler star rotation periods, including the population of weakly tidally interacting binaries with rotational periods of about 90% the orbital period. These stars’ rotation periods are in a quasi-equilibrium such that the change in rotational frequency due to contraction is about equal to the frequency damping due to the tidal torque. We use the Fleming et al. (2019) models here, with all output produced by VPLanet v1.1.

2.2 The circumbinary habitable zone

We estimatethe circumbinary HZ limits given by Kopparapu et al. (2013) that are defined by the effective stellar flux. The inner edge of the HZ is defined by the runaway greenhouse effect in which the oceans of an Earth-like planet are completely evaporated and lost to space. The outer HZ is defined by the maximum greenhouse effect, where CO2 in an Earth-like atmosphere condenses, reducing the greenhouse effect along with the planet’s surface temperature such that the planet remains permanently and globally ice-covered.

We restrict the investigation to equal-mass binary stars since the HZ model from Kopparapu et al. (2013) focuses on HZs of a single spectral energy distribution (SED). While we could have employed the unequal stellar mass HZ models of Cukier et al. (2019), we only consider equal-mass stars to limit the parameter space and identify first order trends. We assume equal-mass binary stars emit effectively the same SED so we can safely employ the Kopparapu et al. (2013) HZ limits by simply doubling the stellar luminosity term. Our model is functionally identical to that in Eggl (2018). The Kopparapu et al. (2013) HZ limits for single and binary stars are implemented in VPLanet and therefore we can trivially track those limits as a binary system evolves.

We note that the CBP HZ limits vary as a function of the binary’s orbital phase as the stars trace out their orbits (e.g., Haghighipour & Kaltenegger 2013). In this work, we are focused on the evolution of the binary and CBP orbits over billions of years, so we instead neglect those smaller variations by averaging the flux received by the CBP over the binary orbit. Moreover, climate models have found that CBP surface temperatures are generally insensitive to instellation variations that are typical for CBPs (Popp & Eggl 2017).

2.3 The circumbinary stability limit

Both Dvorak (1986) and Holman & Wiegert (1999) characterized the circumbinary stability limit through numerical simulations and found that it lies at approximately 1.6 times the binary’s semi-major axis, but is also a function of both the binary orbital eccentricity and mass ratio. Holman & Wiegert (1999) performed an extensive suite of simulations and developed an accurate analytic fit for this boundary, referred to by those authors as the critical semi-major axis that is given by the following relation 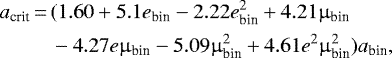(1)

where abin is the binary orbital semi-major axis, ebin the binary orbital eccentricity, and μbin = m2∕(m1 + m2) is the binary mass ratio (with m1 the primary’s mass and m2 the secondary’s mass. This value is calculated by VPLanet so we track its value in our simulations as each binary–planet system evolves.

2.4 Initial conditions and assumptions

With the exception of Kepler-47, we are interested in the evolution of a typical CBP system and therefore must define our parameter space and key model parameters. We limit our studies to stellar masses less than 1.1 M⊙ and ignore the post-main sequence evolution. We consider binaries with Porb ≤ 10 days and ebin < 0.5 to encompass the range of binaries for which tidal evolution is plausible and within the confines of the EqTide module (larger eccentricities can induce effects that are not included). We will use initial rotation periods of 4 days as a fiducial value, but we do change this value in some cases, as noted below. The Baraffe et al. (2015) stellar tracks are uncertain at early ages as the protostars are still coalescing out of the molecular cloud and likely harbor a circumbinary disk that can strongly impact the binary orbital evolution (Fleming & Quinn 2017). Following other investigations (Fleming et al. 2018, 2019), we set the initial age of the systems to be 1 Myr and assume that any planets have formed by this time.

In Fleming et al. (2018), the role of an evolving mass distribution inside the star was not included even though it is a crucial component of accurate stellar evolution models (e.g., Dotter et al. 2008; Baraffe et al. 2015). Assuming that a star is initially a spherical distribution of gas, it eventually collapses and forms a dense H-fusing core, decreasing rg. For this study, we include the rg evolution from the Baraffe et al. (2015) models as implemented by Fleming et al. (2019) in an update to STELLAR.

Tidal parameters in stellar binaries are uncertain. Different investigations have found that tidal parameters can range over several orders of magnitude and still be consistent with observations (e.g., Zahn 1989; Jackson et al. 2009; Fleming et al. 2019). In this study, we use both the CTL and CPL formulations of equilibrium tidal theory. Tidal effects in this model are parameterized by the Love number of degree 2, k2, and the tidal time lag, τ, for the CTL model or the “tidal quality factor,” Q, for the CPL model. The k2 parameter is essentially a measure of the height of the tidal bulge and ranges from [0,1.5]. For our simulations, we assume k2 = 0.5. Both τ and Q are related to frictional forces inside the star that prevent the bulge from aligning perfectly with the centers of mass of the tidal perturber. The tidal Q quantifies the phase offset between the tidal bulges and the line connecting the centers of mass of the tidally interacting bodies (Ferraz-Mello et al. 2008). Smaller values of Q lead to more rapid evolution as tidal effects scale as k2∕Q (Ferraz-Mello et al. 2008). Under the CTL model, τ quantifies the time lag between the passage of the tidal perturber and the tidal bulge (Leconte et al. 2010). Larger values of τ result in faster evolution as the tidal effects scale as k2τ. Therefore, there is a degeneracy between k2 and Q and τ, so we opt to hold k2 fixed and instead vary Q or τ to quantify how the tidal dissipation impacts the evolution.

We adopt τ = 0.1 seconds (Leconte et al. 2010) for our fiducial value for our CTL model. For the CPL model, we use Q = 106 as our fiducial value as it tends to be consistent with observations (e.g., Jackson et al. 2009; Fleming et al. 2019). For simulations that include a CBP, we keep its inclination i ≾ 0.25° to avoid any issues with the approximations made by the Leung & Lee (2013) derivation as implemented in the BINARY module. We also ignore tidal effects on the CBP, as well as any torques on its rotation.

3 Results

In this section, we examine the results of several suites of simulations that elucidated how the coupled stellar–tidal evolution of binary stars can impact the evolution of their planets. In Sect. 3.1, we consider the STEEP process with the CTL model and an evolving internal stellar mass distribution to build on the Fleming et al. (2018) limited exploration. In Sect. 3.2, we perform detailed simulations of Kepler-47 to further understand how its planetary system avoided disruption and in Sect. 3.3 we consider the orbital evolution of a stable CBP orbiting a short-period stellar binary. Finally, in Sect. 3.4 we compare the circumbinary HZ to acrit for equal-mass binary stars to constrain where potentially habitable CBPs can exist.

3.1 Revisiting STEEP

We first simulate STEEP with a dynamic rg over a range of tidal Qs to assess how its inclusion modifies the results from Fleming et al. (2018). We limit our reanalysis to the equal-mass binary case (1 M⊙) shown in their Fig. 6. The top panel of Fig. 1 demonstrates that acrit reaches its largest value when Q = 105. The Q = 105 simulation achieves the highest acrit, max∕acrit, init ratio of roughly 1.69, compared to 1.1 for Q = 107. This behavior is also seen in the middle panel, where once again the Q = 105 stars achieve the longest orbital period. Finally, the bottom panel shows the similar behavior, which shows how the stars reach a peak in eccentricity, followed by a rapid drop due to tidal circularization. We also note that as tidal Q increases, these parameters reach their maximum values at later times: At Q = 104, the maximum acrit occurs at 40 000 yr while at Q = 108, the maximum acrit arrives after about 500 Myr. For 104 ≤ Q ≤ 106, the peaks shift mostly to later times, while for 106 ≤ Q ≤ 108, the peaks occur at about the same time, but are significantly smaller. Q = 106 appears to be a transitional value in which the peak occurs relatively late, but is still relatively high.

We next present results from four simulations designed to quantify the difference between the CPL and CTL models in the STEEP process. Our control is the fiducial example from Fleming et al. (2018), which consists of two solar-mass stars with Q = 106 with an orbital period of 4 days and ebin = 0.15. The four simulations are the four permutations of our tidal models (CPL, CTL) and mass concentrations (dynamic rg, static rg). The results are shown in Fig. 2. The red curves are the fiducial case examined in Fleming et al. (2018).

The top panel of Fig. 2 shows acrit and we clearly see that the dynamic rg cases achieve much larger values than the static cases. The difference between acrit growth between dynamic and static cases for the CPL and CTL models is about 25% and 50%, respectively. We find that larger initial rg produces larger acrit, max∕acrit, init ratios that peak at later times. This result suggests that the analyses and predictions in Fleming et al. (2018) underestimated the impact of pre-main sequence coupled stellar-tidal evolution on CBPs of short-period binary stars because their model omitted stellar rg evolution. Hence, the STEEP process remains a viable explanation for the lack of CBP detections for short-period binaries.

This panel also shows that the two tidal models behave qualitatively differently. The CPL model has an abrupt and discontinuous peak, whereas the CTL model has a smoother peak that arrives much earlier. In many ways, these features are consistent with the assumptions of the tidal models. The CPL model is a discrete function of tidal frequencies whereas the CTL model assumes a continuous distribution (Leconte et al. 2010). As discussed in Fleming et al. (2018), the CPL peak occurs shortly after the stars become tidally locked. The CTL model’s continuous tidal frequency dependence allows acrit, max∕acrit, init to decrease smoothly after the stars tidally lock. The maximum values of acrit, max∕acrit, init are fairly similar between the models, with the differences here likely due to our choices of Q and τ.

thumbnail Fig. 1

Dynamic evolution of the star system from Fleming et al. (2018), influenced by different initial Q factors usingthe CPL model. Redder curves represent low initial Q values, whilebluer curves represent higher Q values. We used the CPL model along with dynamic radius of gyration. Top: binaries’ dynamic stability limit time evolutions, acrit. Middle: orbital period of the secondary star. Bottom: eccentricity of secondary star. The approximate runtime was 15 min. github.com: cbp_dynamic_stability/Qfactors/
thumbnail Fig. 2

Long-term coupled stellar–tidal evolution of two solar-mass stars for various assumptions. Red curves represent stars that experience the CPL tidal model and constant radius of gyration rg ; purple curves are the CPL with evolving rg; orange curves are the CTL tidal model with constant rg; and pale blue curves are the CTL with evolving rg. Top: evolution of the stability limit acrit. Middle: orbital period of the binary star. Bottom: binary’s orbital eccentricity. The approximate runtime was 40 min in total. github.com: cbp_dynamic_stability/STEEP/
Table 1

Initial conditions for the Kepler-47 simulation.

3.2 The Kepler-47 system

In light of the results above that reveal the importance of including rg, we next reevaluate the Kepler-47 system because its inner planet borders the current critical semi-major axis. In Fig. 3, we examine one plausible case in which Kepler-47 b stays safely away from the stability limit. In this simulation, we assumed that Kepler-47 b formed near its observed location, with initial conditions shown in Table 1. Thus, the STEEP model is still consistent with the Kepler-47 system.

To further constrain the history of this system, we also performed simulations that varied the initial binary eccentricity. We first define the critical eccentricity ecrit to be the initial eccentricity in which planet b’s current semi-major axis is equal to acrit. We used Eq. (1) and found ecrit = 0.42. We then performed integrations over a range of initial ebin to identify values that could lead to the ejection of planet b. We find for our fiducial case that if the initial ebin was ≲ 0.24, then the instability zone never engulfed Kepler-47 b. For initial ebin between 0.24 and 0.42, acrit does reach b’s semi-major axis. This result is visualized in Fig. 4 and further supports the STEEP model. Kepler-47 b can avoid an interaction with acrit for initial binary eccentricities between 0.24 and 0.42 if the initial rotation periods of either stars are increased.

3.3 Long-term CBP orbital evolution

Next we consider the evolution of a potentially habitable planet orbiting a low-mass stellar binary to assess how the orbital evolution of the binary affects the CBP’s long-term orbital evolution. To address this possibility, consider the system shown in Table 2, whose evolution is visualized in Fig. 5. In this case, the two stars are M dwarfs and the planet’s semi-major axis remains beyond acrit for the duration of the simulation. As the host stars are M dwarfs, their bolometric luminosity evolves considerably with time (see e.g., Baraffe et al. 2015), so there is some danger the CBP may be rendered uninhabitable during its host stars’ pre-main sequence phases (cf., Luger & Barnes 2015). Should the planet remain habitable after both stars begin fusing hydrogen, itwill settle into a state in which its instellation fluctuates between 50% and 60% of Earth’s current insolation, as shown in the top panel of Fig. 5, which is well within the limits of the HZ (Kopparapu et al. 2013).

The bottom two panels of Fig. 5 show the CBP’s orbital evolution. The semi-major axis oscillates with an amplitude of about 0.02 au, but the limits do evolve over time due to the binary star’s orbit, which is notshown. The eccentricity evolution is considerably more dramatic, with an initial amplitude of ~ 0.04, growing to ~0.1, before damping to a small oscillation at late times. We note also that the “floor” of the eccentricity stays constant at about 0.05 until about 5 Gyr, at which point it also starts to decay. This system is probably evolving to the “fixed point solution” in which one secular frequency decays away and the major axes of the binary and the CBP circulate at constant frequency (Wu & Goldreich 2002; Rodríguez et al. 2011; Van Laerhoven et al. 2014). Thus, while hypothetical, this example demonstrates that the coupled stellar–tidal evolution of a binary star can significantly impact the orbital and instellation evolution of a potentially habitable CBP.

In addition to this case, we performed numerous simulations that we do not show here. The example we do present was chosen because it demonstrated significant evolution – most cases did not show such variations in the orbital evolution. In general, we identified three traits that most correlated with strong variation in the CBP’s dynamics: (1) nonidentical stellar masses, (2) a CBP’s minimum semi-major axis that is close to acrit,max, and (3) a roughly null initial CBP free eccentricity (efree ≲ 0.05, see Leung & Lee 2013).

thumbnail Fig. 3

Orbital evolution of Kepler-47 B and Kepler-47 b. In each plot, we compare the simulated values to their present day observed values. We can also see how the critical semi-major axis affects and raises the amplitude of the CBP’s semi-major axis and eccentricity as the planet approaches the dynamic stability limit. The approximate runtime was 90 min. github.com: cbp_dynamic_stability/kepler47b/
Table 2

Initial conditions for the system shown in Fig. 5.

3.4 Habitable zone stability for equal-mass binaries

Finally, we reconsider the stability of the HZ of equal-mass stellar binaries for which the CBP orbit is approximately coplanar with the binary orbit. We first overlay the location of acrit with the HZ of Kopparapu et al. (2013) in Fig. 6. We assume the initial orbital period is 7.5 days and consider 0 ≤ ebin ≤ 0.5. We note that no stellar and/or tidal evolution is included in this figure, so it represents a conservative treatment of HZ stability since the stellar–tidal evolution almost always results in an expansion of acrit (Fleming et al. 2018). We note for binaries with masses ≲ 0.12M⊙ that the entire HZ is unstable for all values of ebin. On the other hand, we find that for stellar masses larger than 0.47 M⊙, the entire HZ is stable for ebin ≤ 0.5. These threshold stellar masses are listed in Table 3 as a function of initial ebin. The “Unstable HZ” column refers to the maximum stellar mass for which the entire HZ is unstable; “Stable HZ” refers to the minimum stellar mass for which the entire HZ is stable.

Including the stellar–tidal evolution will generally push the stability limits out another 10–50%, depending on the initial eccentricity and stellar rotation periods, as demonstrated above. Rather than simulate this entire parameter space, in Fig. 7 we show three example evolutions, in which ebin is initially 0.3 and the rotation periods are initially 4 days. We note that the HZ moves inward as the stars contract at approximately constant temperature, which causes their luminosities to decrease. (Hayashi 1961; Baraffe et al. 2015). Should any particular binary star become of interest, one can easily modify the script referenced in the caption to Fig. 7 to estimate the evolution and stability of the binary’s HZ.

thumbnail Fig. 4

Dynamic stability and instability behavior of Kepler-47 b depending on the initial binary eccentricity. The top panel represents the maximum difference between acrit and acbp in its entire long-term evolution. If acrit − acbp is less thanzero, the dynamic stability limit never engulfs Kepler-47b. The middle panel shows the time in which acrit crosses into acbp (acrit = acbp) during each simulation’s history. The maximum instability time is 33.6 Myr at ebin = 0.236 and drops as the initial ebin increases. The dashed vertical lines represent transitional values of ebin. The bottom panel shows when each of the binary stars tidally lock during each simulation. Tidal lock time for the secondary star, Kepler-47B, is constant compared to the initial ebin, however the tidal lock time for the more massive primary star, Kepler-47A, jumps from 69.3 Myr at ebin = 0.19 to 3.93 Gyr at ebin = 0.20 and decreases to zero as the initial ebin increases. The approximate runtime was 42 h in total. github.com: cbp_dynamic_stability/K47_Eccentricities
thumbnail Fig. 5

Instellation and the orbital evolution of a potentially habitable CBP with initial conditions listed in Table 2. The initial conditions of the binary stars and the CBP were adjusted so that the CBP can achieve large and variable amplitudes in its semi-major axis and eccentricity evolution due to gravitational perturbations from the central binary. The approximate runtime was 2 h. github.com: cbp_dynamic_stability/HabitableCBP/
Table 3

Stability limits of the HZ for equal-mass binaries.

4 Discussion

We have explored the time evolution of CBPs orbiting low-mass short-period binary stars to further explore how tidal effects and stellar evolution impact the habitability of CBPs. We first revisited the STEEP process with the CTL tidal model and included an evolving mass concentration and discovered that they predict a greater expansion of acrit than in Fleming et al. (2018) found, suggesting their results understated the threat to CBPs posed by coupled stellar-tidal evolution. We reexamined the transitional stellar binary Kepler-47 (Orosz et al. 2012) and found that its planetary system’s stability likely required the initial binary eccentricity to be below 0.2. We presented an example of a stable and potentially habitable CBP orbiting a short-period binary to show that instellation can change dramatically over time in at least some cases due to the tidally driven orbital evolution of the central binary. Finally, we reanalyzed the stability of the equal-mass circumbinary HZ and found that CBPs may be ejected from the HZ for stellar masses < 0.5M⊙. Taken together, these results clarify where habitable CBPs can exist and how they might evolve around short-period stellar binaries.

By considering alternative tidal and structural models of stars, we have improved and clarified the model presented in Fleming et al. (2018). That theory remains the only one that explains the non-detection of CBPs orbiting any binary star with an orbital period less than 7.5 days without a nearby tertiary companion (aside from small number statistics). We find that the Fleming et al. (2018) model is likely to underestimate the effectiveness of the STEEP process. For triple systems, the timescale for the orbital evolution to eject the planet can be arbitrarily long, whereas the STEEP process occurs shortly after formation.

Furthermore, we found that when including the rg evolution, the peak in acrit not only extends to a larger semi-major axis, it occurs ~100 Myr after the stars formed. Fleming et al. (2018) found that acrit, max tended to occur at around 106 yr, or during the tail end of the circumprimary disk’s lifetime, see red curve in Fig. 2. Our updated model now predicts that the peak occurs well after planet formation. We therefore conclude that the coupled stellar–tidal evolution of binaries stars is the likely mechanism that cleared out these planets shortly after they formed, thereby explaining the lack of observed CBPs in the Kepler field for all Porb ≤ 7.5 days.

This conclusion is further supported by our more rigorous analysis of the Kepler-47 system. Although our improvements to the Fleming et al. (2018) model put Kepler-47b at more risk for ejection, we found a large region of parameter space for which planet b remains safely beyond acrit for Gyrs. This parameter space was narrow, and included the initial rotation periods and tidal Qs or τs, but the values we used are broadly consistent with star formation and tidal models (see Fleming et al. 2019, for a review). Future work could identify the boundary in parameter space for Kepler-47b to never cross acrit to derive constraints on the tidal dissipation in the host stars. Kepler-47 remains a valuable laboratory for binary star models, tidal effects, and CBPs.

Our coupled stellar-tidal model improved upon that in Fleming et al. (2018), but more effects should be considered in the future. We did not consider stellar obliquity, which could affect the magnitude of STEEP and the timing of the maximum value of acrit could also be different. Future research should explore this parameter’s role on the CBP evolution and habitability. Dynamical tide models consider friction due to flows often predict more accurate results (e.g., Ogilvie & Lin 2007; Bolmont et al. 2017), and they should be applied to this problem. Future research could also explore how the tidal deformation of stars impacts stellar evolution.

For habitable planets orbiting a short-period binary, a slowly evolving climate is possible. In addition to any changes due solely to stellar evolution, the instellation cycles, in other words, Milankovitch cycles, can change in both frequency and amplitude. We found one case in which the instellation amplitude changes from 20% to 10% over several billion years. Should a potentially habitable CBP be discovered, simulations like those depicted in Fig. 7 could be performed to understand its history, and therefore its likelihood to be habitable.

In some cases, the circumbinary HZ may be unstable and surveys for habitable worlds should avoid them. While this point has been discussed before (e.g., Kane & Hinkel 2013), we have shown quantitatively where the stability limit overlaps with the HZ, at least for a limited parameter space. We find that habitable planets cannot exist around a binary star whose component masses are less than 0.12 M⊙. For stellar masses up to 0.28 M⊙ at least some of the HZ is unstable. For a typical binary eccentricity of 0.3, those values increase to 0.16 M⊙ and 0.42 M⊙. When factoring in stellar–tidal evolution, these limits will increase by 10–50% depending on the initial distribution of angular momentum. Thus, we recommend that surveys for potentially habitable CBPs focus on systems in which the component masses are larger than at least 0.3 M⊙, if the binary’s orbital period is also less than 8 days.

Future research could identify the stable HZ for nonidentical-mass binary stars similar to the analysis in Fig. 6 and further constrain where habitable CBPs may be stable. Although we did not perform that parameter sweep, somegeneral trends emerged from our investigations that are worth noting. We found that the evolution of acrit for nonidentical binaries can achieve a higher acrit, max when compared to their identical mass analogs. The closer a CBP is to acrit, the higher the amplitudes in acbp and ecbp become, therefore the change in their amplitudes can vary more significantly, too. Additional research could also explore the role of inclination, which has can cause deviations from the Holman & Wiegert (1999) stability limit (Pilat-Lohinger et al. 2003; Quarles et al. 2020) and can significantly alter CBP orbital evolution, presumably affecting STEEP and habitability.

Our orbital models are approximate and therefore results at high eccentricity should be treated as preliminary. The gigayear evolution of a CBP system is very challenging for an N-body integrator as the binary orbital period is so short compared to the lifetime of the system. Furthermore, the timescales for the orbital motion are orders of magnitude smaller than the tidal timescales such that properly treating their combined evolution can result in a simulation that will take years to complete. Nonetheless, a first principles approach would provide better insight and confirmation of the results presented here. Switching to an N-body method would also eliminate the uncertainty in Eq. (1), which is a fit to a large number of N-Body simulations (Holman & Wiegert 1999).

We focused our habitability analysis on orbital evolution, but many other factors might be important and could be included in future work. CBP rotation rates may reach a stationary solution analogous to tidal locking (Zoppetti et al. 2019, 2020), which could significantly affect climates (see e.g., Pierrehumbert 2011; Yang et al. 2013; Del Genio et al. 2019). The planets of M dwarf stars, such as those in Figs. 6–7, may spend significant time interior the HZ where XUV photons can desiccate the planet (Luger & Barnes 2015). Colliding winds could exacerbate atmospheric loss on planets orbiting binary stars (Johnstone et al. 2015), although Zuluaga et al. (2016) showed that magnetic field could shield some planets. As with single stars, the habitability of CBPs is complicated and depends on many factors, not all of which could be included in this study (cf. Meadows & Barnes 2018).

The detection of a potentially habitable planet around a binary star would be a landmark achievement. As transit surveys are biased toward detecting planets near acrit in orbit around short-period binaries, the scientific community must understand how the coupled stellar and tidal effects in binary stars impacts the detectability and habitability of such worlds. We have confirmed that habitable CBPs of short-period binary stars must run a gauntlet of dynamical effects that could trigger ejections, dramatic climate change, and possibly sterilization. The results presented here can help guide astronomers toward the discovery of a habitable CBP, as well as provide clues to the history of such fascinating worlds.

thumbnail Fig. 6

Comparison of the equal-mass binary HZ to acrit. The curves correspond to different choices of the binary’s orbital eccentricity, up to 0.5, as shown in the legend. The blue shaded region is the HZ from Kopparapu et al. (2013), but with the stellar luminosity doubled to account for the two stars. The approximate runtime was 15 s. github.com: cbp_dynamic_stability/HZ_CBP/
thumbnail Fig. 7

Evolution of acrit and the HZ for three hypothetical equal-mass binaries. The blue shaded region is the HZ; the black curves are the values of acrit ; the dashed horizontal orange lines are the maximum value of acrit; and the dashed vertical red lines are the time that acrit reached its maximum value. Top: stellar masses are 0.15 M⊙. Middle: stellar masses are 0.3 M⊙. Bottom: stellar masses are 0.45 M⊙. The approximate runtime was 6 min in total. github.com: cbp_dynamic_stability/HZ_Evolution/

Acknowledgements

DPF was supported by NASA Headquarters under the NASA Earth and Space Science Fellowship Program – Grant 80NSSC17K0482. R.B.’s contribution was supported by NASA Virtual Planetary Laboratory Team through grant number 80NSSC18K0829. We thank Siegfried Eggl for valuable input. This work also benefited from participation in the NASA Nexus for Exoplanet Systems Science (NExSS) research coordination network.

References

  1. Alexander, R. 2012, ApJ, 757, L29 [Google Scholar]
  2. Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Barnes, R., Mullins, K., Goldblatt, C., et al. 2013, Astrobiology, 13, 225 [Google Scholar]
  4. Barnes, R., Luger, R., Deitrick, R., et al. 2020, PASP, 132, 024502 [Google Scholar]
  5. Bolmont, E., Selsis, F., Owen, J. E., et al. 2017, MNRAS, 464, 3728 [Google Scholar]
  6. Bromley, B. C., & Kenyon, S. J. 2015, ApJ, 806, 98 [Google Scholar]
  7. Cukier, W., kumar Kopparapu, R., Kane, S. R., et al. 2019, PASP, 131, 124402 [Google Scholar]
  8. Darwin, G. H. 1880, Roy. Soc. Lond. Philos. Trans. Ser. I, 171, 713 [Google Scholar]
  9. Deitrick, R., Barnes, R., Bitz, C., et al. 2018, AJ, 155, 266 [Google Scholar]
  10. Del Genio, A. D., Way, M. J., Amundsen, D. S., et al. 2019, Astrobiology, 19, 99 [Google Scholar]
  11. Dole, S. H. 1964, Habitable planets for man [Google Scholar]
  12. Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [Google Scholar]
  13. Duquennoy, A., & Mayor, M. 1991, A&A, 500, 337 [NASA ADS] [Google Scholar]
  14. Dvorak, R. 1986, A&A, 167, 379 [NASA ADS] [Google Scholar]
  15. Eggl, S. 2018, Habitability of Planets in Binary Star Systems, 61 [Google Scholar]
  16. Ferraz-Mello, S., Rodríguez, A., & Hussmann, H. 2008, Celest. Mech. Dyn. Astron., 101, 171 [Google Scholar]
  17. Fleming, D. P., & Quinn, T. R. 2017, MNRAS, 464, 3343 [Google Scholar]
  18. Fleming, D. P., Barnes, R., Graham, D. E., Luger, R., & Quinn, T. R. 2018, ApJ, 858, 86 [Google Scholar]
  19. Fleming, D. P., Barnes, R., Davenport, J. R. A., & Luger, R. 2019, ApJ, 881, 88 [Google Scholar]
  20. Forgan, D. 2016, MNRAS, 463, 2768 [Google Scholar]
  21. Greenberg, R. 2009, Astrophys. J., 698, L42 [Google Scholar]
  22. Haghighipour, N., & Kaltenegger, L. 2013, ApJ, 777, 166 [Google Scholar]
  23. Hamers, A. S., Perets, H. B., & Portegies Zwart, S. F. 2016, MNRAS, 455, 3180 [Google Scholar]
  24. Haqq-Misra, J., Wolf, E. T., Welsh, W. F., et al. 2019, J. Geophys. Res. (Planets), 124, 3231 [Google Scholar]
  25. Hayashi, C. 1961, PASJ, 13, 450 [NASA ADS] [Google Scholar]
  26. Heller, R., & Barnes, R. 2013, Astrobiology, 13, 18 [Google Scholar]
  27. Holman, M. J., & Wiegert, P. A. 1999, ApJ, 117, 621–8 [Google Scholar]
  28. Jackson, B., Barnes, R., & Greenberg, R. 2009, ApJ, 698, 1357 [Google Scholar]
  29. Johnstone, C. P., Zhilkin, A., Pilat-Lohinger, E., et al. 2015, A&A, 577, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Kane, S. R., & Hinkel, N. R. 2013, ApJ, 762, 7 [Google Scholar]
  31. Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [Google Scholar]
  32. Kopparapu, R. K., Ramirez, R., Kasting, J. F., et al. 2013, ApJ, 765, 131 [Google Scholar]
  33. Leconte, J., Chabrier, G., Baraffe, I., & Levrard, B. 2010, A&A, 516, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Leung, G. C. K., & Lee, M. H. 2013, ApJ, 763, 107 [Google Scholar]
  35. Luger, R., & Barnes, R. 2015, Astrobiology, 15, 119 [Google Scholar]
  36. Martin, D. V., Mazeh, T., & Fabrycky, D. C. 2015, MNRAS, 453, 3554 [Google Scholar]
  37. Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2015, ApJ, 799, L23 [NASA ADS] [CrossRef] [Google Scholar]
  38. Mazeh, T. 2008, in EAS Pub. Ser., 29, eds. M. J. Goupil, & J. P. Zahn, 1–65 [Google Scholar]
  39. Meadows, V. S., & Barnes, R. K. 2018, Factors Affecting Exoplanet Habitability, eds. H. J. Deeg, & J. A. Belmonte, 57 [Google Scholar]
  40. Meibom, S., & Mathieu, R. D. 2005, ApJ, 620, 970 [NASA ADS] [CrossRef] [Google Scholar]
  41. Muñoz, D. J., & Lai, D. 2015, Proc. Natl. Acad. Sci. U.S.A., 112, 9264 [Google Scholar]
  42. Ogilvie, G. I., & Lin, D. N. C. 2007, ApJ, 661, 1180 [NASA ADS] [CrossRef] [Google Scholar]
  43. Orosz, J. A., Welsh, W. F., Carter, J. A., et al. 2012, Science, 337, 1511 [Google Scholar]
  44. Pierrehumbert, R. T. 2011, ApJ, 726, L8 [Google Scholar]
  45. Pilat-Lohinger, E., Funk, B., & Dvorak, R. 2003, A&A, 400, 1085 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Popp, M., & Eggl, S. 2017, Nat. Commun., 8, 14957 [Google Scholar]
  47. Quarles, B., Li, G., Kostov, V., & Haghighipour, N. 2020, AJ, 159, 80 [Google Scholar]
  48. Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Rodríguez, A., Ferraz-Mello, S., Michtchenko, T. A., Beaugé, C., & Miloni, O. 2011, MNRAS, 415, 2349 [Google Scholar]
  50. Spiegel, D. S., Raymond, S. N., Dressing, C. D., Scharf, C. A., & Mitchell, J. L. 2010, ApJ, 721, 1308 [Google Scholar]
  51. Van Laerhoven, C., Barnes, R., & Greenberg, R. 2014, MNRAS, 441, 1888 [Google Scholar]
  52. Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7 [NASA ADS] [Google Scholar]
  53. Welsh, W. F., Orosz, J. A., Carter, J. A., et al. 2012, Nature, 481, 475 [Google Scholar]
  54. Windemuth, D. J. 2020, PhD Thesis, University of Washington [Google Scholar]
  55. Windemuth, D., Agol, E., Carter, J., et al. 2019, MNRAS, 490, 1313 [Google Scholar]
  56. Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [Google Scholar]
  57. Winn, J. N., & Holman, M. J. 2005, ApJ, 628, L159 [Google Scholar]
  58. Wu, Y., & Goldreich, P. 2002, ApJ, 564, 1024 [Google Scholar]
  59. Yang, J., Cowan, N. B., & Abbot, D. S. 2013, ApJ, 771, L45 [NASA ADS] [CrossRef] [Google Scholar]
  60. Zahn, J.-P. 1989, A&A, 220, 112 [NASA ADS] [Google Scholar]
  61. Zahn, J. P. 2008, in EAS Pub. Ser., 29, eds. M. J. Goupil, & J. P. Zahn, 67 [Google Scholar]
  62. Zahn, J.-P., & Bouchet, L. 1989, A&A, 223, 112 [Google Scholar]
  63. Zoppetti, F. A., Beaugé, C., Leiva, A. M., & Folonier, H. 2019, A&A, 627, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Zoppetti, F. A., Leiva, A. M., & Beaugé, C. 2020, A&A, 634, A12 [EDP Sciences] [Google Scholar]
  65. Zuluaga, J. I., Mason, P. A., & Cuartas-Restrepo, P. A. 2016, ApJ, 818, 160 [Google Scholar]

All Tables

Table 1

Initial conditions for the Kepler-47 simulation.

In the text
Table 2

Initial conditions for the system shown in Fig. 5.

In the text
Table 3

Stability limits of the HZ for equal-mass binaries.

In the text

All Figures

thumbnail Fig. 1

Dynamic evolution of the star system from Fleming et al. (2018), influenced by different initial Q factors usingthe CPL model. Redder curves represent low initial Q values, whilebluer curves represent higher Q values. We used the CPL model along with dynamic radius of gyration. Top: binaries’ dynamic stability limit time evolutions, acrit. Middle: orbital period of the secondary star. Bottom: eccentricity of secondary star. The approximate runtime was 15 min. github.com: cbp_dynamic_stability/Qfactors/
In the text
thumbnail Fig. 2

Long-term coupled stellar–tidal evolution of two solar-mass stars for various assumptions. Red curves represent stars that experience the CPL tidal model and constant radius of gyration rg ; purple curves are the CPL with evolving rg; orange curves are the CTL tidal model with constant rg; and pale blue curves are the CTL with evolving rg. Top: evolution of the stability limit acrit. Middle: orbital period of the binary star. Bottom: binary’s orbital eccentricity. The approximate runtime was 40 min in total. github.com: cbp_dynamic_stability/STEEP/
In the text
thumbnail Fig. 3

Orbital evolution of Kepler-47 B and Kepler-47 b. In each plot, we compare the simulated values to their present day observed values. We can also see how the critical semi-major axis affects and raises the amplitude of the CBP’s semi-major axis and eccentricity as the planet approaches the dynamic stability limit. The approximate runtime was 90 min. github.com: cbp_dynamic_stability/kepler47b/
In the text
thumbnail Fig. 4

Dynamic stability and instability behavior of Kepler-47 b depending on the initial binary eccentricity. The top panel represents the maximum difference between acrit and acbp in its entire long-term evolution. If acrit − acbp is less thanzero, the dynamic stability limit never engulfs Kepler-47b. The middle panel shows the time in which acrit crosses into acbp (acrit = acbp) during each simulation’s history. The maximum instability time is 33.6 Myr at ebin = 0.236 and drops as the initial ebin increases. The dashed vertical lines represent transitional values of ebin. The bottom panel shows when each of the binary stars tidally lock during each simulation. Tidal lock time for the secondary star, Kepler-47B, is constant compared to the initial ebin, however the tidal lock time for the more massive primary star, Kepler-47A, jumps from 69.3 Myr at ebin = 0.19 to 3.93 Gyr at ebin = 0.20 and decreases to zero as the initial ebin increases. The approximate runtime was 42 h in total. github.com: cbp_dynamic_stability/K47_Eccentricities
In the text
thumbnail Fig. 5

Instellation and the orbital evolution of a potentially habitable CBP with initial conditions listed in Table 2. The initial conditions of the binary stars and the CBP were adjusted so that the CBP can achieve large and variable amplitudes in its semi-major axis and eccentricity evolution due to gravitational perturbations from the central binary. The approximate runtime was 2 h. github.com: cbp_dynamic_stability/HabitableCBP/
In the text
thumbnail Fig. 6

Comparison of the equal-mass binary HZ to acrit. The curves correspond to different choices of the binary’s orbital eccentricity, up to 0.5, as shown in the legend. The blue shaded region is the HZ from Kopparapu et al. (2013), but with the stellar luminosity doubled to account for the two stars. The approximate runtime was 15 s. github.com: cbp_dynamic_stability/HZ_CBP/
In the text
thumbnail Fig. 7

Evolution of acrit and the HZ for three hypothetical equal-mass binaries. The blue shaded region is the HZ; the black curves are the values of acrit ; the dashed horizontal orange lines are the maximum value of acrit; and the dashed vertical red lines are the time that acrit reached its maximum value. Top: stellar masses are 0.15 M⊙. Middle: stellar masses are 0.3 M⊙. Bottom: stellar masses are 0.45 M⊙. The approximate runtime was 6 min in total. github.com: cbp_dynamic_stability/HZ_Evolution/
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.