| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A182 | |
| Number of page(s) | 16 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202245410 | |
| Published online | 19 July 2023 | |
High-resolution imaging of solar pores⋆
1
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: rkamlah@aip.de
2
Universität Potsdam, Institut für Physik und Astronomie, Karl-Liebknecht-Straße 24/25, 14476 Potsdam, Germany
3
New Jersey Institute of Technology, Space Weather Research Laboratory, University Heights, Newark, New Jersey 07102, USA
Received:
8
November
2022
Accepted:
1
May
2023
Context. Light bridges are bright, long, and narrow features that are typically connected to the formation or decay processes of sunspots and pores.
Aims. The interaction of magnetic fields and plasma flows is investigated in the trailing part of an active region, where pores and magnetic knots evolve into a complex sunspot. The goal is to identify the photospheric and chromospheric processes, which transform the mainly vertical magnetic fields of pores into a sunspot with multiple umbral cores, light bridges, and rudimentary penumbrae.
Methods. Conducting observations with a broad variety of telescopes and instruments provides access to different atmospheric layers and the changing morphology of features connected to strong magnetic fields. While the Helioseismic and Magnetic Imager (HMI) of the Solar Dynamics Observatory (SDO) provides full-disk continuum images and line-of-sight magnetograms, the fine structure and flows around a pore can be deduced from high-resolution observations in various wavelengths as provided by the Goode Solar Telescope (GST) at the Big Bear Solar Observatory (BBSO). Horizontal proper motions are evaluated applying local correlation tracking (LCT) to the available time series, whereas the connectivity of sunspot features can be established using the background-subtracted activity maps (BaSAMs).
Results. Photospheric flow maps indicate radial outflows, where the light bridge connects to the surrounding granulation, whereas inflows are present at the border of the pores. In contrast, the chromospheric flow maps show strong radial outflows at superpenumbral scales, even in the absence of a penumbra in the photosphere. The region in between the two polarities is characterized by expanding granules creating strong divergence centers. Variations in BaSAMs follow locations of significant and persistent changes in and around pores. The resulting maps indicate low variations along the light bridge, as well as thin hairlines connecting the light bridge to the pores and strong variations at the border of pores. Various BaSAMs demonstrate the interaction of pores with the surrounding supergranular cell. The Hα line-of-sight velocity maps provide further insights into the flow structure, with twisted motions along some of the radial filaments around the pore with the light bridge. Furthermore, flows along filaments connecting the two polarities of the active region are pronounced in the line-of-sight velocity maps.
Conclusions. The present observations reveal that even small-scale changes of plasma motions in and around pores are conducive to transform pores into sunspots. In addition, chromospheric counterparts of penumbral filaments appear much earlier than the penumbral filaments in the photosphere. Penumbra formation is aided by a stable magnetic feature that anchors the advection of magnetic flux and provides a connection to the surrounding supergranular cell, whereas continuously emerging flux and strong light bridges are counteragents that affect the appearance and complexity of sunspots and their penumbrae.
Key words: Sun: activity / Sun: photosphere / Sun: chromosphere / line: profiles / methods: observational
Movies are available at https://www.aanda.org.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
High-resolution observations of the solar photosphere facilitate investigating the interaction between magnetic fields and convective processes. Dark features that are formed by a sufficiently strong magnetic field vary in size and lifespan, whereby the critical differentiation between pores and sunspots is based on the absence or presence of a penumbra, respectively (Leka & Skumanich 1998; Rucklidge et al. 1995). The main difference besides size and lifetime is the higher field strength of 1800–3700 G in the darkest parts of sunspot umbra (Livingston 2002), as compared to 600–1800 G (Sütterlin 1998; Verma & Denker 2014) in pores, which is about the same as for the outer parts of penumbrae (Livingston 2002).
The transition of a pore to a sunspot is associated with a variety of flows. For example, the moat flow (Vargas Domínguez et al. 2008) is typically characterized by axially symmetrical flow fields (Löhner-Böttcher & Schlichenmaier 2013). However, Verma et al. (2018) described the formation of significant asymmetries in flows around unipolar axisymmetric sunspots. The asymmetry of the moat flow is due to sunspot motion across the solar disk, which gets further disturbed by the surrounding plasma motion.
Another conspicuous flow feature is the radially outward directed Evershed flow, starting at the umbra-penumbra boundary (Evershed 1909; Murabito et al. 2018; Siu-Tapia et al. 2018) that appears once the penumbra forms. Therefore, the flow pattern around sunspots differs from the flow pattern in the vicinity of pores, which is mostly dominated by inflows towards the pores’ borders and downflows at the pore-surrounding interface (Verma & Denker 2014; Guglielmino & Zuccarello 2011; Hirzberger 2003; Roudier et al. 2002). The Evershed flow is correlated with the inclination angle and horizontal strength of the penumbral magnetic field. Extensions of the penumbral Evershed flow may appear as moving magnetic features in the moat flow (Zuccarello et al. 2009; Criscuoli et al. 2012; Rempel 2015).
Quintero Noda et al. (2016) inferred the temperature, line-of-sight (LOS) velocity, and LOS magnetic field of a pore at photospheric levels (τ = 1) and extended them to higher atmospheric layers (τ = −2). The temperature was coolest inside the pore and hotter in surrounding quiet-Sun region, which is consistent across all evaluated heights. In addition, quiet-Sun temperatures were exceeded in neighboring plage regions. The LOS velocity inside the pores was close to zero, however, with downward motions at the edges, which were only detectable in lower photospheric layers, namely, below τ = −1. The LOS magnetic field was strongest in the central part of the pore, where the canopy effect results in a decrease of field strength with increasing height.
A feature commonly connected to the formation and decay of pores or sunspots are light bridges. These bright, long, and narrow structures, which cross or penetrate the umbra, present a structure different from the surrounding umbra, exhibiting weaker and more inclined fields (Liu & Liu 2015). Light bridges extend in a canopy-like structure to higher atmospheric layers. However, the formation and magnetic properties of light bridges continue to be a key subject of investigations. Studies indicate that the formation of light bridges is a result of intruding umbral dots and relate them to plasma ejections or chromospheric Hα surges along the light bridges (Roy 1973; Bharti et al. 2007). Thus, they may act as a heat source in the chromosphere. According to Louis (2015), the interaction of umbral dots and intruding penumbral filaments, which is generally observable during light bridge formation, further confirms magneto-convection in sunspots and pores. The author emphasizes that the pronounced chromospheric activity, caused by convective disruptions, becomes more vigorous and apparent as compared to the rest of the sunspot. Consequently, light bridges and the surrounding umbra should be treated as two different systems. In recent simulations, Panja et al. (2021) showed that light bridges form at a certain depth by intrusions of plasma that are transported to the surface by upflows.
Using observations and numerical models, Toriumi et al. (2015) presented a physical picture of the formation of light bridges in an emerging region. According to these authors, emerging magnetic fields rising from the convection zone (Zwaan 1985) are split into multiple bundles of two polarities. The local weakly magnetized plasma with upflows is carried along between these flux bundles and shows up as a light bridge in the photosphere. The light bridge has in its center a deep convective upflow, which brings horizontal magnetic flux to the surface. An interaction between this horizontal flux with the vertical field of the neighboring pores leads to the formation of a strong electric current layer at the border of the light bridge. The strong downflows at the borders of the light bridge form concave dips, where the internal horizontal field of the light bridge is connected to external vertical fields. In higher atmospheric layers, these external fields fan out and form a canopy structure. The continuous convection creates upflows that turn into bidirectional flows along the length of the light bridge, transporting plasma and magnetic field towards the connection points of the surrounding granulation.
Small-scale inhomogeneities in the magnetic field and velocity are present in the light bridge, which have opposite polarities to the rest of the light bridge and umbra, and they also exhibit large Doppler shifts (Louis 2015). However, supersonic downflows are also encountered in the more unipolar parts of light bridges (Louis et al. 2009). High-resolution observations of the fine structure at the border of pores reveal downflow rims including filamentary structures near the rims. Positive divergence structures with localized divergence centers are often related to exploding granules (Bonet et al. 2005). Typically, inflows that are not necessarily symmetric are detected in the pores’ interior and the outflows are at their periphery. On the other hand, low velocity and negative divergence are detected inside the pores, and distinct G-band bright points appear in the magnetic flux system in proximity to the border of the pore (Verma & Denker 2014).
In a one-to-one comparison with observations and numerical simulation of pores, Leka & Steiner (2001) confirmed enhanced Stokes-V asymmetry in the encircling magnetic elements including pores and azimuth centers, which are the result of strong downflows at their borders. Intermingled up- and downflows are evident in the interior of magnetic elements. Furthermore, even magnetic features, which are not visible as a dark structure in continuum images harbor a canopy, caused by the same physical effects. In magnetohydrodynamic (MHD) simulations of pores, which include a realistic, predominantly vertical field, adjacent granules present an edge-brightening and the pores are surrounded by downflows (Cameron et al. 2007). Here, the decay is connected to a loss of magnetic flux from the periphery to the adjacent intergranular lanes. Certain differences exist between the leading and trailing polarities of an active region. Rempel & Cheung (2014) identified some of them in simulations covering the whole life cycle of the flux emergence system, namely, from spot formation to decay. In their simulations both leading and trailing spots reach around half their peak flux at the same time. However, the formation of the trailing spot starts before the leading part and extends further. Furthermore, they report delay timescales of the order of a few days, where the decay is mostly driven by convective motions.
This study takes a closer look at a strong light bridge in between two solar pores by combining multi-wavelength observations of the photosphere and chromosphere. Section 2 presents the observations and the data processing. The required techniques are discussed, along with their application to time series of images and data from imaging spectroscopy to investigate flows and magnetic fields in and around pores. The observational results from different instruments are presented in Sect. 3 and discussed in Sect. 4, where the present results are interpreted in context with contemporary literature and standard works on this subject. Section 5 summarizes noteworthy observational findings and highlights their importance for future studies of light bridges in pores.
2. Observations and data reduction
In this section, recording, reduction, and analysis of the high-resolution Goode Solar Telescope (GST, Cao et al. 2010a) and synoptic Solar Dynamics Observatory (SDO, Pesnell et al. 2012) data are described, including relevant details on instruments, observing settings, and methods.
2.1. Observations
The observations were carried out with the 1.6-m aperture GST at the Big Bear Solar Observatory (BBSO) from 18:00 UT to 22:35 UT on 2015 April 1. The local seeing environment at this mountain-lake-site observatory is described in Verdoni & Denker (2007). Recording of flat-field frames interrupted the observations from 18:34–18:56 UT, 20:39–20:49 UT, and 22:01–22:18 UT. The adaptive optics (AO) system AO-308 (Shumko et al. 2014) provided real-time image correction. Continuous records of the seeing quality based on AO measurements were only available for the time period 19:10–20:00 UT (local noon). During this time, the average Fried-parameter r0(550 nm) was (10.5 ± 3.2) cm, where the standard deviation indicates the temporal variation of the 2725 measurements. The Fried-parameter r0 approached 20 cm in three 3–5-min time intervals.
The Nasmyth broadband filter imager (BFI, Cao et al. 2010b) consists of the several filtergraphs that enable high-spatial resolution photometry. Here, only the TiO λ706 nm interference filter with a bandpass of 10 Å was used during the observations. Time series of 14-bit, 2048 × 2048-pixel TiO images were captured using a pco.2000 camera. The exposure time was 1.1 ms, and sets of 100 images were acquired at a cadence of 15 s. After frame selection, only the best 70 images of a set were used for speckle masking image restoration (Wöger et al. 2008). In this process, the original image size is reduced to 1844 × 1844 pixels. An image scale of 0.034″ pixel−1 yields a field of view (FOV) of 63″ × 63″. Thus, the images are oversampled by a factor of 1.6, considering that the diffraction limit of the telescope at the wavelength of TiO is α = 1.22 λ/D = 0.11″ according to the Rayleigh criterion, where D is the diameter of the telescope. The full time series consists of 836 speckle-restored images covering the trailing part of the active region NOAA 12317.
The Visible Imaging Spectrometer (VIS) captured data in the chromospheric Hαλ656.3 nm line (Cao et al. 2010b). Filtergrams with a bandpass of 0.8 Å were taken with a single Fabry-Pérot etalon in telecentric mount. The camera has 2560 × 2160 pixels, and the instrument covers a circular FOV with a diameter of 70″, that is, only about 80% of the detector is illuminated with an image scale of 0.029″ pixel−1. An Hα dataset consists of 5 × 40 = 200 filtergrams covering the line core and four wavelength points in the wings, which are nominally placed at ±0.4 Å and ±0.8 Å from line center. However, the exact locations of the filtergrams in the spectrum may differ from the nominal settings. Frame selection based on the highest image contrast reduces the data volume to 5 × 25 = 125 filtergrams. Exposure times of 9, 15, and 20 ms (line wing to line core) are sufficiently short for image restoration with the speckle masking technique (Wöger et al. 2008). The filtergrams were recorded with a frame rate of 20 Hz and a delay time of 20 s, which results in a cadence of 30 s for 440 speckle-restored datasets of line-core and line-wing images.
The previously described FOV for TiO images and Hα filtergram had to be cropped following the removal of the image rotation. A region of interest (ROI) of 30″ × 30″ was chosen, which enabled the best coverage of the three negative-polarity pores, as indicated by the black square overplotted on HMI data in Fig. 1. This ROI is used in the following to analyze and discuss the GST high-resolution data.
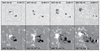 |
Fig. 1. HMI Continuum images (top) and LOS magnetograms (bottom) showing the evolution of active region NOAA 12317 from 17:00 UT on 2015 April 1 (left) to 17:00 UT on 2015 April 3 (right). The FOV covers 150″ × 150″, and the coordinates in the lower left corners refer to the FOV’s center. The black solid squares in the left panels correspond to an ROI of 30″ × 30″, which is used in the analysis of the high-resolution Hα and TiO time series. Dashed squares correspond to an ROI of 95″ × 95″ which is used in the determination of the photometric area and magnetic flux shown in Fig. 6. An arrow in second-lower panel indicates the negative polarity pore belonging to the secondary flux system. Magnetograms are displayed in the range ±400 G. An animated version of this figure is available online. |
The GST data are complemented by observations from the SDO. Full-disk continuum images and LOS magnetograms were provided by the Helioseismic and Magnetic Imager (HMI, Scherrer et al. 2012; Schou et al. 2012). The nominal image scale of HMI is 0.5″ pixel−1, which is increased to 0.6″ pixel−1 in the image registration (rotation, translation, and scaling), that is, in the Level 1 to Level 1.5 data conversion. An ROI with a size of 150″ × 150″ (250 × 250 pixels) was selected, which tracks the active region during its disk passage. Continuum images and magnetograms were both recorded with a cadence of 45 s and four images illustrating the evolution of active region NOAA 12317, from 17:00 UT on 2015 April 1 to 17:00 UT on 2015 April 3, are displayed in Fig. 1 in non-uniform steps. The full time series is provided as online material. Unfortunately, because of technical issues, SDO data are not available for the initial emergence of the region. The processing of continuum images and magnetograms was described in Beauregard et al. (2012) and Verma (2018), which includes correcting solar differential rotation. Here, 20:19:30 UT serves as the reference time for aligning the time series. However, geometrical foreshortening was not corrected due to the small size of the ROI.
The data analysis in the following sections is based on four types of time series data: high-resolution TiO images, high-resolution Hα filtergrams, cutouts from full-disk continuum images, and cutouts from full-disk LOS magnetograms. This nomenclature is subsequently used to uniquely label the data types.
2.2. Data reduction and analysis
The TiO image quality was determined using the Median Filter Laplacian Similarity (MFLS), which is a variant of the Median Filter Gradient Similarity (MFGS, Deng et al. 2015). The MLFS was computed for the full FOV of 63″ × 63″ (1844 × 1844 pixels) and for the central ROI of 30″ × 30″ (878 × 878 pixels) containing only the pores in the solid black square in Fig. 1. The values for both FOVs are comparable throughout the TiO time series, which covers 4.5 hours but with three interruptions. In Fig. 2, TiO images of the central ROI are presented, which have the best image quality within a certain time interval. These images follow the evolution of three pores in active region NOAA 12317. Because of its equatorial mount and coudé feed to the optics laboratory, the GST exhibits an image rotation rate of 15° per hour in the focal plane. Thus, all images of the time series have been rotated, aligned, and matched with sub-pixel accuracy. The Hα images were subsequently aligned to match the 30″ × 30″ ROI of the TiO images. The aligned Hα line-core images are shown in Fig. 3 demonstrating the chromospheric evolution above the three pores. The slight mismatch of the observing time between TiO and Hα images results from applying the image quality metrics independently to the two time series.
 |
Fig. 2. Temporal evolution of pores observed in the TiO λ706 nm bandhead images on 2015 April 1. The best images were selected, hence, they are not equidistant in time. The ROI has a size of 30″ × 30″. In the upper left panel the three major pores are labeled P1, P2, and P3, and the plage region is enclosed within the rectangle. An animated version of this figure is available online. |
 |
Fig. 3. Temporal evolution of pores observed in the Hαλ656.3 nm line-core images on 2015 April 1 (otherwise same as in Fig. 2). An animated version of this figure is available online. |
Observations in Hα blue line wing at −0.535 Å from line-core consistently yields the highest MFLS values during the time series. The values of the other wavelength points are lower and show a larger scatter. In any case, even though metrics such as MFGS and MFLS are less dependent on the structural contents of the images, the different morphology of the Hα contrast features easily explains these differences. Higher MFLS values in the time period 19:00–22:00 UT are indicative of better seeing conditions, which can occur at the mountain-lake site BBSO at any time of the day.
The aligned TiO images are the basis for computing the horizontal proper motions. For this purpose, local correlation tracking (LCT, November & Simon 1988; Verma & Denker 2011) was applied to three datasets covering the time periods (i) 18:00–18:30 UT, (ii) 19:00–20:00 UT, and (iii) 20:50–21:50 UT. Continuous data are available for these three datasets, avoiding the aforementioned data gaps. The focus is on the central ROI 30″ × 30″ (878 × 878 pixels). A subsonic filter is applied with a cut-off velocity vc = 4 km s−1 to remove the intensity variations caused by the five-minute oscillation from the time series. Since the computation of cross-correlations is sensitive to intensity gradients, the images are treated with a high-pass filter. The LCT velocities are computed over image tiles with the size of 2.2″ × 2.2″ (64 × 64 pixels), which corresponds to about 1600 km × 1600 km on the solar surface. A Gaussian kernel with full-width-and-half-maximum (FWHM) of 1200 km is applied to the image tiles to track on granule-size structures. Consecutive image tiles, separated by Δt = 30 s in time, are used for the cross-correlations to compute the local flow vectors. These flow vectors are averaged over the duration of each time series, namely, 30 min for the first time series and 60 min for the other two.
The same LCT algorithm was used to compute the chromospheric horizontal proper motions. Because of artifacts impacting image quality and time gaps, the Hα time series is divided into four datasets of which three are used in the following data analysis. In favor of a compact presentation of the LCT results, especially when comparing them with photospheric flow maps, the fourth Hα time series was excluded from further analysis. The three remaining time series cover the following time periods: (i) 18:01–18:31 UT, (ii) 18:56–20:00 UT, and (iii) 20:03–20:39 UT. The first two datasets are closely matched with those of the TiO time series. However, the third dataset contains only images, which were recorded before the last TiO dataset started. This selection provides data with highest image quality. The Hα datasets comprise (i) 60, (ii) 126, and (iii) 72 filtergrams, respectively. The focus is again in the central part of ROI with a size of 30″ × 30″ (1038 × 1038 pixels). The cut-off velocity for the subsonic filter had to be increased to vc = 20 km s−1 because the chromosphere is rich in dynamic and fast-moving features, which should be preserved. The high-pass filter is also essentially the same, as is the chosen tile size of 2.2″ × 2.2″ (76 × 76 pixels).
Five speckle-restored filtergrams of an Hα line scan are shown in Fig. 4, which were obtained at 18:01 UT. The superimposed white contours are obtained from the time-averaged TiO images of the first time series, where an intensity threshold of Iumbra < 0.8 is used to outline the pores. Visual inspection of the filtergrams suggests that filtergrams acquired in the red line wing are closer to the Hα line core compared to those taken in the blue line wing. Low correlation values for the inner and outer line-wing filtergrams corroborates this observation. An estimate of the wavelength position can be derived using the following procedure: (i) assume that neighboring filtergrams are separated by 0.4 Å, (ii) normalize the filtergrams so that quiet-Sun intensity (i.e., at the corners of the ROI) matches the intensity of an Hα spectrum of the Kitt Peak FTS disk-center spectral atlas (Neckel & Labs 1984; Neckel 1999) at this wavelength position, (iii) compute the linear correlation between the line-wing pairs, (iv) repeat this procedure for various wavelength shifts using linear interpolation, and (v) find the wavelength shift that results in the highest value for the linear correlation. This procedure yields a wavelength shift of 0.135 Å to the blue, which can be reproduced for other Hα line scans of the time series. Thus, the corrected wavelength position of Hα filtergrams are −0.935 Å, −0.535 Å, −0.135 Å, +0.265 Å, and +0.665 Å, when scanning from the blue to the red line wing. We note that in step (ii), the center-to-limb variation of the Hα spectral line was taken into account using interpolated versions of the tabulated profiles by David (1961). The heliocentric angle of the active region was μ = 0.83. The shifted wavelength positions are displayed in the lower left corners of Fig. 4.
 |
Fig. 4. Speckle-restored Hα filtergrams of each wavelength point of the Hα line scan at 18:03 UT on 2015 April 1. The wavelength positions with respect to the Hα line core are given in the lower left corner of each panel. Neighboring wavelength points are separated by 0.4 Å. The ROI has a size of 30″ × 30″. The colored crosses indicate the location of extracted Hα line profiles shown in Fig. 5. The white asterisk within pore P2 indicates the position of the thin, solid black line profile shown in Fig. 5. The white contours outlining the pores are based on the average image of the first time series of TiO images and are computed using an intensity threshold of 0.8. An animated version of this figure is available online. |
The ability to compute Hα Doppler maps is another important result of this procedure. The Doppler shifts are estimated using Gaussian fits to the five-point spectral profiles. The average Doppler velocity in the quiet-Sun region around the pores was (−0.18 ± 1.33) km s−1, whereas the average Doppler velocity inside the pores was (1.00 ± 1.78) km s−1. The standard deviation refers to the variation within the region rather than to a formal error estimate. A sample of Hα line profiles is shown in Fig. 5 for the locations marked by color-coded plus signs, which trace the upward diagonal in Fig. 4. The mean profile of all plotted lines is added as a dashed black line, while the thick, solid black line represents a typical quiet-Sun profile taken from the Kitt Peak FTS disk-center spectral atlas. The thin, solid black line represents a profile within pore P2 at the position marked by a white asterisk in Fig. 4. These sample profiles are derived according to the procedure outlined above and trace different features in the vicinity of major pores, for example, filaments, a small pore, and plage regions.
 |
Fig. 5. Color-coded Hα line profiles, which are marked by matching crosses in Fig. 4. The dashed black line represents the average of the color-coded line profiles. The thin, solid black line refers to an Hα profile of a pore, as indicated by the white asterisk in Fig. 4 inside pore P2. The thick, solid black line denotes the Kitt Peak FTS disk-center spectral atlas, which served as a reference in the wavelength calibration. |
To follow variations in and around the pores and to identify locations where most changes occur, so called background-subtracted solar activity maps (BaSAMs, Denker & Verma 2019) are used. Furthermore, BaSAMs are applied, for the first time, to high-resolution photosphere images and chromosphere images. As explained in Denker & Verma (2019), this technique relies on the computation of an average, 2D map for the entire time series, which is then subtracted from the individual maps, followed by the computation of an average, 2D map of the modulus of these difference maps. The 2D BaSAMs are a good and quantitative visualization tool used to identify locations of significant changes in HMI LOS magnetograms and UV images (e.g., Verma et al. 2012, 2020). However, this is the first application of BaSAMs to images with the high-spatial resolution, namely, a spatial resolution of one-tenth of an arcsecond or better.
3. Results
In this section, the morphology and temporal evolution of the pores are investigated based on high-resolution and synoptic data. The connectivity of the pores to their surroundings is analyzed and photospheric and chromospheric horizontal proper motions are discussed. Furthermore, the evolution of chromospheric Doppler velocities is examined.
3.1. Morphology and temporal evolution
The photospheric and chromospheric morphology and evolution of the pores is very different, which are discussed accordingly based on TiO images, continuum images, and magnetograms for the photosphere and based on Hα line scans for the chromosphere.
3.1.1. Photospheric evolution
Active region NOAA 12317 developed as a typical bipolar region containing pores. Cutouts from full-disk continuum images and magnetograms are shown in Fig. 1 and an animation of the full evolution is provided as online material. The first continuum image and magnetogram show the region one hour before the BBSO high-resolution observations. At 17:00 UT on 2015 April 1, the opposite-polarity region separates along a line, which forms an angle of about 45° with respect to the equator (type B sunspot region according to the Zurich classification). The light bridge’s orientation remains stable over the high-resolution observations while showing a counter-clockwise rotation at later stages. The region between the two polarities is a site of ongoing flux emergence with mixed polarities, which is typical for an emerging region (Verma et al. 2016a). The leading negative-polarity pore has a very dark, elongated core with a smaller, less dark, elongated part extending at a right angle to the west. The trailing positive-polarity region comprises two dominant pores separated by a strong light bridge accompanied by several smaller pores nearby. The light bridge leaves also a clear signature in magnetograms.
The transition from type B to type D region happened on 2015 April 2. This transition is characterized by the continuous separation of the two polarities and an increase in area and magnetic flux caused by the coalescence of same-polarity flux as is evident in continuum images and magnetograms. Another negative-polarity pore appeared in the middle of the bipolar group, which became visible in continuum images at 11:00 UT on 2015 April 2. This pore as indicated by an arrow in the second panel of Fig. 1 belonged to another flux system which developed alongside the primary flux system. The secondary region contributed new flux and interacted with already existing system. This region moved towards the leading negative-polarity and developed a rudimentary penumbra by 23:00 UT on 2015 April 2. The trailing positive-polarity becomes more complex and two sunspots with partial penumbrae and complex light bridges are present at 23:00 UT on 2015 April 2. Both polarities reached the maximum extent in the area and magnetic flux by 23:00 UT on 2015 April 2 (see the third panel in Fig. 1). At 05:00 UT on 2015 April 3, the overall appearance of both polarities had already simplified and the region’s decay started. The two remaining negative-polarity pores shrunk further and almost vanished at 11:00 UT on 2015 April 4 leaving only dispersed magnetic flux in their wake. In contrast, the two major positive-polarity flux concentrations visible at 05:00 UT on 2015 April 2 merged and formed a single sunspot by 23:00 UT on 2015 April 3. The active region NOAA 12317 had an atypical evolution, because the trailing polarity evolved into a mature sunspot, while the leading polarity only produced a small rudimentary penumbra on 2015 April 2.
The high-resolution TiO images are compiled in Fig. 2, with the full time series being provided as online material. They trace the evolution of the trailing positive-polarity pores separated by a light bridge as observed on 2015 April 1 with the GST. The labels P1 and P2 refer to these pores. The label P3 denotes another dark feature caused by the emergence of the magnetic flux next to pore P2.
At 18:03 UT, the pore P1 had a corrugated border with smaller umbral core, namely, compared to pore P2. At the top, P1 showed a curved filamentary extrusion (indicated by an arrow in the top-left panel of Fig. 2), which resembled a rudimentary penumbra at the position highlighted by the arrow. The filamentary extrusion is prominently seen for the first 30 min but disappeared by 19:00 UT. The pore P1 was full of umbral dots and had continuous flux emergence in its bottom part, which was visible as two faint magnetic knots (Beckers & Schröter 1968), as indicated by the rectangle in the top-left panel of Fig. 2. The umbral dots within the pore P1 formed a faint light bridge by 19:45 UT, which remained until the end of the GST observations at 21:17 UT. Out of the two magnetic knots in the bottom one slowly decayed, whereas the other developed further and grew in size by merging with new magnetic knots so that it developed into a pore by 20:50 UT. It is marked in the corresponding panel in Fig. 2.
The largest pore in the ROI is labeled P2. This pore is filled with umbral dots and is separated from pore P1 by a thick light bridge. The borders of pore P2 are also rugged. Thin dark hair-like extrusions are present all around pore P2. A larger extrusion is present at the top, which remains visible until 19:45 UT. However, at the same location, similar features appear and disappear throughout the observations. Over the period of GST observations, pore P2 decreased in area and became more circular in shape. This is quantified by measuring the photometric area of the pore P2 in TiO images, which decreased from 17.8 Mm2 at around 18:00 UT to 15.5 Mm2 at around 21:00 UT. However, P2 is the only pore that survives through the complete evolution of the active region. As seen in the SDO movie, P2 merged with pores from the secondary flux system and pore P1 to form the single sunspot around 23:00 UT on 2015 April 3. Next to pore P2, another elongated pore P3 is situated. At the beginning of the high-resolution observations, pore P3 is closest to pore P2 with a small magnetic knot placed between them (see the first panel in Fig. 2). Over time, pore P3 appeared to move away from P2. The impression of separation between P2 and P3 is further enhanced by the decrease in the size of both pores.
The light bridge between pores P1 and P2 was already present at the start of the GST observations. It contained a few granules, which continuously evolved throughout the next few hours. Its orientation only slightly changed over time. Apart from the smaller pores in the bottom half of FOV, many extending granules were observed. These granules connected the positive-polarity pores and magnetic knots in the ROI to the negative-polarity pores outside the ROI but were covered by the FOV of the SDO continuum images and magnetograms. The lower-right quadrant of the ROI is the site, where flux with mixed polarities emerges as can be seen in the lower-left panels of Fig. 1.
To quantify the growth of the pores, their area and the magnetic flux within the active region were computed over the period 17:00–23:30 UT on 2015 April 1, which correspond to 520 continuum images and magnetograms, also including the observing period at BBSO with a one-hour margin. The FOV was reduced to 95″ × 95″ (160 × 160 pixels, highlighted by the dashed square in Fig. 1) encompassing the trailing pores. A binary template pre-selecting the area covered by the positive-polarity magnetic flux was created by applying a Lee filter (Lee 1986) to the magnetograms. Furthermore, a flux threshold of 100 G was applied, along with morphological erosion using a kernel with a width of 0.5 Mm, followed by dilation using a kernel with a width of 3 Mm. Regions with less than 200 pixels were removed from the binary template. Finally, a threshold of 80% of the normalized continuum intensity and a threshold of 10 G are used for computing the photometric area and the magnetic flux of the pores, respectively. The measured magnetic field strength and area were presented without any additional corrections. The only correction that is carried out concerns the cosine of heliocentric angle μ. The results are compiled in Fig. 6. The photospheric area and magnetic flux decay rates are determined by linear fits after convolution with a smoothing kernel. During the first half of observations, namely, from 17:00 UT to 20:00 UT, both photospheric area and magnetic flux decrease linearly with −2.74 Mm2 h−1 and −0.044 Wb h−1, respectively. This matches with the visual impression of shrinking pores as seen in the TiO images. Between 20:00 UT and 21:00 UT, a slight increase occurs in both photospheric area and magnetic flux before the minimum is reached at 21:00 UT. After 21:00 UT, the photometric area increased, which coincided with newly forming pores in the lower part of the ROI. However, the increase in magnetic flux is not very pronounced.
 |
Fig. 6. Evolution of the magnetic flux (solid) and photometric area (dashed) on 2015 April 1 for a FOV of 95″ × 95″ covering positive-polarity pores in active region NOAA 12317. The two dashed vertical lines demarcate the two time periods 17:00–20:00 UT and 21:00–23:30 UT used for further analysis. |
3.1.2. Chromospheric evolution
The eight line-core Hα filtergrams in Fig. 3 depict snapshots of the region’s chromospheric evolution. In addition, the first Hα scan with five wavelength points shown in Fig. 4 demonstrates different morphology of the region at different chromospheric heights. The complete evolution and dynamics in and around the pores are compiled in an online movie for the Hα line-core filtergrams. In the line core (middle panel in Fig. 4), which traces higher atmospheric layers (Cauzzi et al. 2009), the umbrae of the three pores P1, P2, and P3 are hard to visualize under overlaying chromospheric radial filaments. Contours computed using simultaneous TiO images assist in following the evolution in and around the pores. The light bridge separating the pores P1 and P2 is discernible in all Hα wavelength settings. The region, where new emerging knots can be observed in TiO, is marked by the rectangle in Fig. 3.
The online movie shows a scene with very dynamic pores. In the Hα line core, the pores P1 and P2 are surrounded by radial superpenumbral filaments except for the lower part, which faces the newly emerging pores of opposite polarity. These filaments originate directly at the border of the pores and appear more penumbral in nature than superpenumbral. However, a counterpart of these filaments is absent in the photosphere. Along these penumbral filaments, the running penumbral waves propagate outwards. Furthermore, some of the individual filaments display additional dynamic motions. Filaments in the upper part of pores P1 and P2, namely, at the tip of the light bridge (marked by arrows in Fig. 2), demonstrate twisting motions accompanied by the apparent ejection of material (see online movie). Pore P3 is mostly obscured in Hα line-core filtergrams. The region connecting both polarities of primary and secondary flux systems shows an elongated arch filament system with two major filaments. These arch filaments appear to be stretched out and connect to the bottom of pores P1 and P2. Even though the arch filament system is continuously changing its appearance, it survives until the end of the high-resolution observations.
The time series of the four red- and blue-wing filtergrams also demonstrate the ever-changing appearance of the active region (see online movie corresponding to Fig. 4). Chromospheric fibrils are already significantly suppressed in the outer ling-wing filtergrams at −0.935 Å and +0.665 Å. As mentioned in Sect. 2.2, a slight asymmetry appears in the five wavelength positions with respect to the Hα line core. The features at the third and fourth wavelength position are virtually identical and must be located close to the Hα line core. In any case, in the outer red-wing and both blue-wing filtergrams, small-scale brightenings are present in the vicinity of the pores. Conspicuous bright plage regions are visible in the lower left corner of the filtergrams close to the Hα line core, where one end of the arch filament system is rooted. In this region, continuous interaction between magnetic features can be traced in the time series of the LOS magnetograms. The bright Hα plage region is a persistent feature throughout the high-resolution observations. Furthermore, the presence of the ever-changing chromospheric fibrils is clearly seen in the Hα line-wing filtergrams – and even more so in close vicinity to the pores. These chromospheric fibrils and filaments show much stronger absorption in the Hα line-core filtergrams.
3.2. Background-subtracted Solar Activity Maps – Connectivity
In this section, the application of BaSAMs onto high-resolution TiO and Hα images is presented and discussed.
3.2.1. Background-subtracted Solar Activity Maps – TiO images
The BaSAM of the entire TiO time series is compiled in Fig. 7. The extent of changes in the solar surface within a certain time interval is indicated by changing intensity, whereby blue colors point towards less to almost no changes and strong variations are depicted in red colors. The strongest variations occur at the borders of the three pores and their immediate surroundings. The most extended variations take place at borders of pores P1 and P2, where in later stages of the sunspot evolution a rudimentary penumbra is formed. In addition, variations around pore P3 are less intense. This pore dissolves before the penumbra formation sets in. The interior of the pores shows little to no variation, and the spatial scale of the variations corresponds to that of umbral dots. This is in stark contrast to the borders of the pores, where the strong signals in the BaSAM are seen.
 |
Fig. 7. BaSAM of the entire TiO time series of 836 images covering the time period 18:00–22:34 UT. The ROI has a size of 30″ × 30″. The color bar indicates the variations in intensity on logarithmic scale. |
The variations along the spine of the light bridge are significantly diminished but the interface with the neighboring pores and the ends of the light bridge exhibit strong variations. The region below pores P1 and P2, which is marked by a black rectangle in Fig. 2, also has a strong signal in the BaSAM. This indicates significant variations related to ongoing flux emergence at that location. Although expanding granules are seen in the other half of the region below the pores, no significant signals are recovered in BaSAM. However, a faint magnetic knot ([x = 20, y = 10] in Fig. 7) appeared towards the end of observations left signal in BaSAM. The region in and around all three pores show low to medium signals in the TiO BaSAMs, giving the impression that the main pores are embedded in a web-like structure.
3.2.2. Background-subtracted Solar Activity Maps – Hα filtergrams
The average BaSAMs for the Hα line-core and two outer line-wing positions are compiled in Fig. 8 using the same color scheme as before. In the Hα line-core BaSAM, only minor variations are observed inside the pores. However, it is difficult to visualize the pores beneath the overlaying chromospheric filaments. In contrast, the light bridge causes a strong signal in this BaSAM indicating major changes related to this dynamic feature. The changes along the light bridge differ from those of the photospheric TiO BaSAM, pointing to a distinct chromospheric structure of the light bridge. Along the top and left border of pore P1, variations in form of (super-)penumbral filaments are seen in the Hα line-core BaSAM, which are not as clearly seen around pores P2 and P3. The strongest variations appear in the region below the pores (see the white square in Fig. 3), where the elongated arch filaments are rooted and are visible as bright plages in the Hα line-core filtergrams. The strong variations in the arch filaments are a clear indication of ongoing flux emergence lifting plasma during the ascent of the flux tubes, which subsequently drains towards the footpoints. The dynamics in the bright plage region also points to the interaction of small-scale, mixed-polarity features, which contribute to local heating and lead to the strongest variation in the Hα line-core BaSAM.
 |
Fig. 8. 2D BaSAMs with an ROI of 30″ × 30″ derived from Hα blue line-wing, line-core, and red line-wing filtergrams (left to right). The color bar indicates the variations for the three wavelength settings on logarithmic scale. |
The overall appearance of the outer blue line-wing BaSAM (first panel of Fig. 8) resembles that of the TiO BaSAM. The pores P1, P2, and P3 have a patchy red and blue appearance indicating only small variations, whereas the borders of all three pores are characterized by significant variations, which outlined the pores clearly and formed a ring-like structure encircling the pores. This feature is similar to what is seen in the photospheric TiO BaSAM. The region with flux emergence below the pores that is, the black rectangle marked in Fig. 2 also has high values. The spine of the light bridge shows low values suggesting a rather stable configuration.
The outer red line-wing BaSAM (third panel of Fig. 8) has an appearance drawing from features of Hα line-core, Hα blue line-wing, and TiO BaSAMs. The main difference with respect to the Hα blue-wing BaSAM is the presence of penumbra-like filamentary structure around pores and the arch filament in the region below the pores. Here, the pores have also strong variations encircling them. The periphery of the light bridge also exhibits strong variations at the interface to pores P1 and P2 similar to as seen in Hα blue-wing and TiO BaSAMs. The footpoint region of the arch filaments shows also strong variations in the red line-wing BaSAM. The web-like structure as seen in TiO is also faintly visible in the region below the arch filaments due to the low opacity in the outer Hα line-wing filtergrams.
3.3. Velocity structure in and around pores
The velocity structure in and around the pores P1, P2, and P3 is traced in the photosphere and chromosphere using LCT to derive horizontal proper motions. However, it is only for the chromospheric Hα line scans that the velocity structure can be expanded to three dimensions, based on Doppler velocities. Accordingly, the derived results with respect to the height-dependent horizontal proper motions along with the chromospheric Doppler velocities are presented in the following.
3.3.1. Photospheric horizontal proper motions in TiO images
In Fig. 9, averaged LCT velocities derived from TiO time series are superposed on the corresponding time-averaged TiO image. The rainbow-colored arrows indicate speed and the direction of persistent proper motions. As described in Sect. 2, the three time periods refer to the different stages of the pores’ evolution. The far surroundings of the pores have the usual granulation flow pattern characterized by divergence centers. However, typical inflows are detected at the boundaries of all pores in all three time series. These regions in an 1″-wide envelope around the pores are delineated by pink contours. The inflows on the left side of pore P1 reach a maximum velocity during the third time series. Pore P2 shows inflows during the entire time series, especially at the upper-right side facing P3. The inflows are also present on the upper-right side of pore P3. In general, the inflows around all pores are persistent throughout the observations. The average flow speeds for all time series in the envelope regions of pores P1, P2, and P3 are (0.23 ± 0.10) km s−1, (0.32 ± 0.10) km s−1, and (0.22 ± 0.10) km s−1, respectively. The component of the flow vector towards the center of the pore is typically in the range of 60–85% of the overall flow speed.
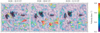 |
Fig. 9. 2D LCT maps with an ROI of 30″ × 30″ show the photospheric horizontal proper motions for the three time periods indicated above each panel. Rainbow-colored arrows refer to magnitude and direction of the average flow vectors, which are superposed on a time-averaged TiO image. The white contours outline the pores in the corresponding TiO images for intensities lower than 0.8, while the pink contours delineate the regions for which the inflow velocities are computed. The black rectangle in the lower right indicates the locations of expanding granules. |
The TiO and Hα BaSAMs help to identify the locations of strong variations, which coincide with the locations of significant proper motions. The most interesting flow features belong to pores P1 and P2. Parallel to the orientation of the light bridge, between pores P1 and P2, diverging motions are present. These appeared in the flow maps as arrows directed towards the interface with the pores on both sides and at the upper and lower ends of the light bridge. This also leaves a strong variation in average BaSAMs. This flow pattern remains present in all three time series, but is most prominent in the first, where it has a mean velocity and standard deviation of (0.40 ± 0.23) km s−1. The corresponding average velocity decreases over the next hours, dropping to (0.27 ± 0.14) km s−1 for the third time series. The standard deviation in these measurements refers to the variation in the observed region, rather than presenting a formal error of the measurement.
Another prominent flow feature is associated with newly emerging flux at the bottom of pores P1, P2, and P3, as indicated by the rectangle in the first panel of Fig. 9. This region also has a strong signal in TiO and Hα BaSAMs. In all three LCT maps, this appears as a large diverging flow pattern. This region expands over time. In the first time series, the region has three divergence centers at coordinates (16.5″, 7.0″), (21.0″, 10.0″), and (26.0″, 7.0″). The largest divergence center, namely, the one at (21.0″, 10.0″) coincides with strong BaSAM signals in TiO and the blue and red wings of Hα. The other divergence centers do not have a one-to-one correspondence in the BaSAMs. However, their expanding motion which contributes to the formation of magnetic knots and flux emergence leaves signal in BaSAMs though slightly displaced. When referring to coordinates, the origin of the coordinate system is always assumed to be at the lower-left corner.
During the second time series, the flow fields become more extended and stronger. It is especially the region that connects both polarities of the active region exhibits considerably large velocities associated with the expanding granules. The average LCT velocity in the region increases from (0.30 ± 0.19) km s−1 to (0.37 ± 0.25) km s−1 from the first to the second time series. By the end of the high-resolution observations, the flow feature is still present, but with a significantly reduced average velocity of (0.27 ± 0.14) km s−1.
3.3.2. Chromospheric horizontal proper motions in Hα filtergrams
The application of LCT and its shortcomings with regard to Hα images are discussed and demonstrated in Chae et al. (2000). The results of applying LCT to Hα line-core images are presented in Fig. 10. The visual appearance of the Hα LCT maps is very different compared to the TiO LCT maps. The ROI is devoid of divergence centers in the surroundings of the pores. For convenience, the same envelope regions (pink contours in Figs. 10 and 11) are used to quantify chromospheric flows, even though they extend well beyond the 1″-wide envelope. The inward motions towards the pores boundary, as seen in the TiO maps, are absent in the chromospheric counterpart. Instead strong radial outflows originate from the center of the pores. The average radial flow speed in the envelope of pores P1 and P2 amounts to (0.98 ± 0.24) km s−1 and (0.88 ± 0.35) km s−1, respectively, in the first time-series. The radial outward flow increases and extends further during the second time series, where the average radial flow speed in the envelope of the pores increases to (1.15 ± 0.29) km s−1 and (0.74 ± 0.17) km s−1, respectively. The radial outward motions persist during the third time series with average values of (1.21 ± 0.18) km s−1 and (1.07 ± 0.22) km s−1, respectively. For both pores, at the location where the outward motion terminates, a second row of outward flow starts, which continues further even extending beyond the edge of the ROI. In contrast, small inward motions are seen at the bottom boundary of pore P3.
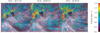 |
Fig. 10. 2D LCT maps with an ROI of 30″ × 30″ show the chromospheric horizontal proper motions for the three time periods indicated above each panel. Rainbow-colored arrows refer to magnitude and direction of the average flow vectors, superposed on a time-averaged Hα line-core filtergram. The white contours outline the pores in the corresponding TiO images for intensities lower than 0.8, while the pink contours delineate the regions for which the inflow velocities are computed. |
The southern part of the ROI, which has large diverging motions in the photosphere, displays a different pattern in the Hα flow maps. The horizontal proper motions are diminished along the lower, dominant arch filament joining the positive and negative polarity of the active region. However, strong proper motions are traced in the region to the left of the arch filament. The overall orientation of the flow pattern above is towards the dominant arch filament. This flow pattern is along the smaller and fast-evolving filaments. In contrast, the region on the left side of the arch filament, which showed brightenings in line-core images, exhibits flows directed toward the newly emerging pores that become more streamlined during the second time series.
3.3.3. Chromospheric Hα Doppler velocity
The Hα Doppler velocities are yet another facet of the dynamic environment encompassing the pores. The average Doppler velocity maps for three time series are displayed in Fig. 11. The exact location of pores is difficult to locate under the veil of the chromospheric filamentary structure. Thus, the contours extracted from the TiO images are added to the Hα Doppler maps to improve the visualization. The detailed changes in the Doppler velocities can be seen in the accompanying online movie. The velocities are scaled between ±3 km s−1. The inner borders of pores P1, P2, and P3 are predominantly characterized by alternating red- and blueshifts mostly corresponding to the running penumbral waves. In all three-time averages, radial redshifts along filamentary structures can be seen, that is, around pore P1, except for the side facing the light bridge, and not so prominent around pores P2 and P3. At the upper end of the light bridge and at pore P1, a twisting filamentary structure is revealed by alternating red- and blueshifts. This feature is associated with a jet that is eventually ejected. A similar jet-like feature is seen at the upper edge of pore P2. However, the velocity pattern along the light bridge appears to be more or less of granular nature.
 |
Fig. 11. 2D maps with an ROI of 30″ × 30″ show the average chromospheric Hα Doppler velocities for the three time periods indicated above each panel. The velocities are clipped at ±3 km s−1. The positions labeled 1–6 refer to Hα Doppler velocities listed in Table 1. The black contours outline the pores in the corresponding TiO images for intensities lower than 0.8, while the pink contours delineate the regions for which the outflow velocities are computed. The region above the black horizontal line is used to compute the average quiet-Sun Doppler velocity. An animated version of this figure is available online. |
The lower part of the ROI is dominated by blueshifts along the arch filaments, which connect the trailing and leading pores of the active region. The footpoints, which coincide with the flux emergence site at the bottom of pores P1 and P2, show strong redshifts in the first and third time series depicted in Fig. 11, respectively. The location of these redshifts match the strong variations in the TiO and Hα BaSAMs.
To demonstrate variations in chromospheric Doppler velocities, Table 1 compiles mean values and standard deviation for six regions. The mean values for the three time series refer to overall up- and downward motions in these regions, while the standard deviation indicates how strongly the flow varies within the region. Thus, a standard deviation larger than the mean flow speed is a clear indication that both up- and downward motions are present at the same time. The numbered plus signs in in Fig. 11 mark regions with a size of 3″ × 3″. Regions 1 and 2 belong to two of the chromospheric penumbral filaments of pore P1. Throughout the observations, the Doppler velocity in both regions remains strongly redshifted.
Hα Doppler velocities for six selected regions with a size of about 3″ × 3″.
In the three time series, the velocity in region 1 changes from (0.89 ± 0.47) km s−1 over (0.35 ± 0.52) km s−1 to (0.82 ± 0.89) km s−1. This trend is even more pronounced in region 2, where the velocity changes from (2.06 ± 1.30) km s−1 over (0.16 ± 0.48) km s−1 to (0.90 ± 0.74) km s−1. This indicates that flows along the superpenumbral filaments are not continuous. Instead, parcels of plasma travel along these filaments. In the absence of such parcels, the standard deviation of the flows is larger than its mean value, that is, both red- and blueshifts are present. Regions 3 and 4 are situated in the region with continuously emerging flux below the pores. Region 3 is located at the apex of one of the arch filaments, whereas region 4 marks the location of the footpoint. As expected from an arch filament system, the Doppler velocity remains blueshifted in region 3, where the rising flux tube is loaded with plasma, which subsequently drains towards the footpoint in region 4 where a redshift is found. The Doppler velocity in region 3 more than doubles from ( − 1.32 ± 0.42) km s−1 to ( − 3.33 ± 0.42) km s−1 from the first to the third time series. This increase in upflow coincides with the rapid increase in downflows at region 4 indicating plasma draining from the flux tube at the footpoint. This reflects the rise of a flux tube loaded with cool material, where plasma rapidly drains from the flux tube when the ascent culminates. Small blue- and redshifts in the foot point region 4 during the first and second time series, along with a large standard deviation, represent the more quiet phase before the vigorous draining of plasma from the ascending flux tube. By the third time series, the Doppler velocity in region 4 reaches up to (6.08 ± 2.21) km s−1. Region 5 is located in the region, where the second layer of outward motions begins in the Hα flow maps. This region starts with a redshift in the first time series (0.70 ± 0.34) km s−1, which drops to almost zero in the second time series, before changing to a blueshifted velocity of ( − 0.56 ± 0.37) km s−1. Region 6 belongs to the inner part of the light bridge and has throughout the observations very low Doppler velocities.
4. Discussion
The data presented in this work display a dynamic interplay of magnetic fields and plasma flows. The region contains dark pores lacking a penumbra during the time of the high-resolution observations. A thick light bridge with a granulation-like pattern separates two dark pores. The FOV of the high-resolution observations covers the trailing part of an active region, which later develops into sunspots surrounded partially by penumbrae as seen in HMI context data. This is an atypical behavior because usually the trailing part decays first. In addition, the light bridge stays in its original location and retains its overall appearance.
The pores did not develop a penumbra over the course of the GST observations. During the three-hour period, TiO images display no obvious indication of penumbral filaments around any of the pores. However, pores P1 and P2 do display corrugated borders. Furthermore, the upper half of both pores P1 and P2 does show extended filamentary extrusions. Sobotka et al. (2013) presented similar observations, but solely for an isolated pore. They concluded based on photospheric and chromospheric data that a photospheric penumbra is not a necessary prerequisite for the formation of a superpenumbra. In the present case, superpenumbral filaments are evident in Hα filtergrams. However, the pores are part of a larger magnetic system with continuous flux emergence.
Apart from continuous flux emergence, the overlaying magnetic canopy also plays a role in the appearance of penumbrae in the photosphere. In Hα filtergrams, superpenumbral filaments or fibrils appear around the pores, which subsequently develop penumbrae. Shimizu et al. (2012) drew their conclusions based on chromospheric Ca II H filtergrams, which show an annular structure even before the appearance of a photospheric penumbra, finding that the magnetic canopy plays an important role in the formation of penumbrae. Jing et al. (2019) found that the flows in these fibrils do not arise from an oscillation or wave phenomenon but are rather similar to the inverse Evershed flow in the chromosphere. Using a 3D potential field model, they concluded that the pore and the encircling fibrils are part of the magnetically confined system, which maintains the dynamics of superpenumbral fibrils. In the present case, the pore is not simple – in fact, two pores with a granular light bridge are involved. The superpenumbral filaments around pores P1 and P2 display inverse Evershed flows, as derived from LOS velocities (see strong redshift regions in Fig. 11), that is, at least on the side that is not facing the leading negative-polarity pores. The inverse Evershed flows are a completely different physical phenomenon as the Evershed flow (e.g., Beck et al. 2020). Murabito et al. (2016) observed that the penumbra is formed by magnetic flux dragged down from the overlaying canopy surrounding the initial pore. In addition, they noticed that the Evershed flow starts when the sinking magnetic field dips below the solar surface and magnetoconvection sets in.
Twisting motions of penumbral filaments are interpreted as overturning convection (Ichimoto et al. 2007; Zakharov et al. 2008; Spruit et al. 2010; Bharti et al. 2010), which is believed to provide sufficient heat to the surface layer to cause the relatively high brightness of the penumbra. Three-dimensional MHD simulations were used to find upflows along the central axes of penumbral filaments and downflows at their edges (Rempel et al. 2009b), which were first measured by Joshi et al. (2011) with velocities up to 2 kms−1 in the body of the penumbra. Despite these upflows potentially being caused by the Evershed flow, the authors interpreted them as strong localized upflows at the filament heads (cf. Rimmele & Marino 2006). The gas moves partially along the filament axis and forms the Evershed flow (Scharmer et al. 2008), while the rest moves to the sides of the filaments and becomes downflows. Additional downflows are located alongside bright filaments in the middle and outer part of the penumbra, as predicted by models (e.g., Rempel et al. 2009a,b; Scharmer & Spruit 2006). In higher atmospheric layers, isolated pores can often be found surrounded by radially elongated fibrils, typically resembling an enlarged version of the photospheric penumbra, called “superpenumbra” (Loughhead 1968), despite the lack of penumbra in the photosphere. Due to the larger area covered by the superpenumbra, it is believed that these fibrils follow magnetic field lines and connect further into the solar surface than a penumbra as seen in the photosphere. These fine-scale fibrils exhibit short-lived mass flows towards and away from the pore with apparent speeds up to 5–14 km s−1. Radially outward propagating concentric wavefronts, namely, running penumbral waves, are commonly observed in chromospheric observation of pores and sunspots, mainly running from the inner to the outer penumbral boundaries (Giovanelli 1972; Zirin & Stein 1972). Another feature observed in the chromospheric superpenumbra is the inverse Evershed flow (Moore & Rabin 1985), which describes a nearly horizontal inflow towards the umbra, turning into a downflow near the umbral border. The driving mechanism of the inverse Evershed flow is attributed to a siphon flow along individual magnetic flux tubes (Meyer & Schmidt 1968). Since the Evershed flow and the inverse Evershed flow are structured on fine scales (see the reviews by Solanki 2003; Thomas & Weiss 2004; and Bellot Rubio 2007), siphon flows are expected along the individual thin flux tubes, which are driven by a pressure gradient along the tube (Meyer & Schmidt 1968).
Light bridges can be broadly categorized into two types: narrow light bridges more akin to penumbral filaments (Louis et al. 2008; Rimmele 2008; Bharti 2015; Hou et al. 2020) and granular light bridges (Sobotka et al. 2013; Lagg et al. 2014). A statistical study of light bridges by Li et al. (2021) based on SDO data summarizes three ways of light bridge formation. Of these three, the one which fits the observed light bridge best is the scenario where the merging of two sunspots results in the formation of a light bridge. Once the pores develop into a sunspot, it never forms a penumbra at the location of the light bridge. This is in very good agreement with the findings of Künzel (1969), who reported that same-polarity sunspots facing each other never develop a penumbra in between, and often the interface between the spots is marked with a thick granular light bridge. The morphology of the present light bridge matches these descriptions. Granular light bridges usually exhibit vigorous convective motions as, for example, described by Lagg et al. (2014). They found that the field-free regions of a granular light bridge are dominated by upflowing plasma with velocities of up to 2 km s−1, whereas the interface with the umbrae was dominated by downflows of up to 10 km s−1.
The formation of a light bridge in an emerging flux region is discussed in Toriumi et al. (2015), based on numerical simulations and observations. The authors constructed a physical picture of light bridge formation (see Fig. 9 in Toriumi et al. 2015). In the present observations, making statements about the convective upflow in the center of the light bridge is difficult due to the lack of photospheric spectropolarimetric data. However, convective motions, which further lead to diverging bi-directional horizontal flows in the light bridge, as suggested by Toriumi et al. (2015), are seen in the high-resolution TiO horizontal flow maps. The diverging motions away from the spine of the light bridge and outward motions at the ends of the light bridge leave also strong variations in TiO BaSAMs. Horizontal velocities of up to 0.89 km s−1 were measured in the first time series. This diverging flow pattern recedes in the next two time series indicating that the convective upflows decrease over time. In chromospheric horizontal flow maps, confirming these motions is difficult due to the chromospheric filamentary structure overshadowing the photospheric light bridge.
Even though the light bridge displays a granular structure, signs of photospheric convection (e.g., Lagg et al. 2014) cannot be confirmed because only chromospheric LOS velocities are available, which show granular patterns to some extent but not as clearly as in slit-reconstructed Doppler maps of photospheric spectral lines. Light bridges are also marked as the location of various types of small-scale energetic activity such as jets (e.g., Tian et al. 2018; Robustini et al. 2016; Louis 2015). In photospheric (as well as in three chromospheric) BaSAMs, various small-scale variations along the observed light bridge are evident. However, jet-like phenomena are absent along the inner interface of the light bridge and pores. Twisted motions are only visible along two superpenumbral filaments, which are located at the intersection of the upper edge of the light bridge and the pores P1 and P2.
The BaSAMs were created to follow the intricate changes in pores and their surroundings. The BaSAMs are computed for the first time for high-resolution images from ground-based telescopes. In earlier applications, they were applied to space mission data namely from Hinode and SDO. The photospheric BaSAMs reveal the location of the strongest variations at the borders of pores, the region along the light bridge, and the region below pores with continuous flux emergence. The horizontal plasma motions and the dynamic interface between the magnetic flux tube and convection contributes to the strong signal in the BaSAM. The usual spoke-like structure seen around pores and sunspots connecting them to surrounding supergranular cells (Verma & Denker 2012; Verma et al. 2018) was absent in the present observations. However, the FOV is small and the supergranular cell, where the pores are situated, is not covered in the observations. Furthermore, the generated BaSAMs cover only four hours of observations rather than the 12 h used to create BaSAMs in previous works. However, the chromospheric BaSAMs show especially the chromospheric fibrils arching out from the borders of pores. The blue and red line-wing BaSAMs are virtually identical to photospheric BaSAMS except for the presence of fibrils. The arch filament system connecting the pores to the leading polarity is conspicuous in the line-core BaSAMs. Comparing the four BaSAMs exposes different features. The changes along the borders of the pores (photospheric BaSAMs) extend as fibrils emanating from the borders (line-wing BaSAMs) further to superpenumbral fibrils (line-core BaSAMs). Changes in BaSAMs also expose the canopy effect. All things considered, the pores are embedded and connected to an extended magnetic flux system, where continuous interactions are driven by plasma motions.
The photospheric horizontal proper motions around pores show inward motions at their borders. Especially, consideration of the flow field within the envelope region indicates that up to 90% of the flows can be directed towards the pore itself. These inflows are seen in numerical models (e.g., Cameron et al. 2007) as well as in observations (e.g., Sankarasubramanian & Rimmele 2003; Sobotka et al. 2012), and they seem to be associated with the downflows at pore borders (e.g., Chae et al. 2015; Roudier et al. 2002). However, in the absence of photospheric LOS velocities, such downflows cannot be confirmed at the borders of the observed pores. Pores are expected to advect flux from the surroundings, which is transported into the pore by horizontal flows (Stein et al. 2011). In photospheric LCT maps, large diverging cells related to expanding granules are present in the light bridge and at the lower-right region within the ROI. In the light bridge, the diverging motion subsides slowly over the course of the observations. In contrast, expanding granules are a common feature in the region connecting the pores to the leading polarity. These diverging motions and expanding granules are closely tied to the region with emerging flux and indicate that new flux rises to the surface (Cheung et al. 2010; Verma et al. 2016a).
In contrast to the inward horizontal proper motions in the photosphere, chromospheric LCT maps exhibit strong radial outflows around pores P1 and P2. These are associated with the running penumbral waves, where contrast changes give the impression of horizontally propagating plasma (Sobotka et al. 2013; Freij et al. 2014). In individual maps, the chromospheric Doppler velocities enable the tracing superpenumbral fibrils around pores. Average Doppler maps (Fig. 11) show the inverse Evershed flow around pores. The average Doppler velocities for all three time series around pores P1, P2, and P3 are predominantly redshifted with (1.10 ± 0.69) km s−1, (0.67 ± 0.38) km s−1, and (0.70 ± 0.58) km s−1 respectively. These values were computed for the envelope regions of the three pores. This agrees with the results of previous works and observations; for instance, Haugen (1969) found inflows and downflows near sunspots with an average velocity of 6.8 km s−1. Using the cloud model (Beckers 1964) to compute the Hα velocities for three different heights, Georgakilas & Christopoulou (2003) found that velocities rise with increasing heights. The average velocities close to the Hα line core (λ0 ± 0.35 Å) are around 5 km s−1. The authors also proposed that the Hα velocities are underestimated because of integrating the velocity values over substantial viewing angles. Chae et al. (2015) also reported downflows around pores on the order of 3 km s−1 based on Hα observations. The average velocities around the pores in the current study are lower than in previous studies. This could be related to the absence of penumbral filaments, which did not form during the high-resolution observations. Another factor affecting the values could be related to the way of estimating Doppler velocities. For example, Chae et al. (2015) used the lambdameter method as discussed in Chae et al. (2014). Finally, the values for the envelope region were averaged in time over all available Doppler maps. Thus, they represent the persistent flows of the inverse Evershed effect, which is very different from Doppler velocities derived from individual spectral profiles. In addition, two locations with penumbral filament-like intrusions at the upper part of pores P1 and P2, where they meet the light bridge, showing twisting motions and even jet-like ejections. Hou et al. (2020) noticed a reconnection jet at the location in the sunspot where the light bridge was intersecting with penumbral filaments. Although the observed pores did not develop penumbral filaments at the time of the observations, the two penumbral filament-like intrusions may have been the site of such reconnection. Furthermore, the lower region, where the pores are connected to leading polarity, has a typical arch filament with the typical LOS flow structure, that is, strong downflows at the footpoints and upflows at the apex of the filament as, for example, described by Bruzek (1969) and González Manrique et al. (2018).
Setting the results of this study in context with the literature offers the following comprehensive description for consideration. This investigation covered a complex active region, where two flux systems interacted with each other. One was a non-Hale active region (Tanaka 1991; López Fuentes et al. 2000) with a highly inclined sunspot group tilt angle, whereby the other smaller region with a much shallower tilt angle emerged. Despite continuous flux emergence in its proximity and advection of flux, pore P2 can be traced throughout the time series of magnetograms. Pore P2 sustained itself by the merging with pore P1 and by accretion of flux from the secondary flux system. This pore seems to anchor the trailing part of the active region, thus providing a sufficiently stable environment for penumbra formation. Furthermore, it attracted much of the positive-polarity flux of the second emerging flux system, while the negative-polarity flux of both flux systems evolved in isolation, assisted by the fast break off of the leading pores and sunspots. The interaction of the two flux systems also explains that a larger, compact umbra could not be formed, namely, the umbral cores maintained their identity and light bridges are a common feature in the evolution of the trailing pores and sunspots. This fragmented appearance is also evident in the rudimentary penumbrae and in the abundance of umbral dots (Watanabe et al. 2012), which are all signs that convection significantly interacts with the flux system.
The penumbra formation is not covered by the high-resolution observations. Nevertheless, the observations provide important clues that penumbra formation is imminent. Photospheric BaSAMs show first indications that the trailing pores begin to interact with the surroundings, which is very similar to the observations of Verma et al. (2018) for axis-symmetric sunspots, where such a connection was clearly established. The chromospheric Hα observations further suggest impending penumbra formation, for instance, curved filamentary extrusions with indications of twist and, more importantly, a semi-circular region with superpenumbral filaments, which already starts at the border of the pores and exhibits the inverse Evershed flow.
Counter-agents of penumbra formation are also present in the trailing part of the active region, namely, continuous flux emergence and strong light bridges. Some studies have found that penumbral formation is being hampered at the flux emergence site (Schlichenmaier et al. 2010, 2012; Rezaei et al. 2012). Once the flux emergence ceases, a penumbra can form (e.g., Verma et al. 2016b), and also the pores P1 and P2 developed a penumbra at later stages of evolution, which was unfortunately not covered by the high-resolution observations. However, other studies have found penumbra formation at the side facing flux emergence (Lim et al. 2013; Murabito et al. 2017). Strong light bridges are characterized by diverging motions perpendicular to the axis of the light bridge and strong horizontal outward motions at their ends. Due to the deep convective upflow in the center of the light bridge (Toriumi et al. 2015), upwelling material is almost squeezed outwards into the surrounding granulation. The two components of horizontal proper motions inside the light bridge become weaker towards the end of the high-resolution time series, so that their impact on penumbra formation is diminished. The time series of LOS magnetograms also imply that the strong light bridge becomes thinner with time. In addition, time series of SDO/HMI vector magnetograms were consulted to validate that the field-free gap between the pores, namely, the strong light bridge, thins out over time. This holds true for both the horizontal and vertical components of the magnetic field. The omnipresent thin hairlines, first mentioned by Scharmer et al. (2002), at the interfaces between light bridge and pores could be considered as an attempt to form a penumbra. However, the extremely limited space within the light bridge makes it impossible to establish flux tubes carrying the Evershed flow. We note that such hairlines were absent at the border between the pores and the surrounding granulation.
5. Summary and conclusions
Combining ground-based high-resolution GST observations with synoptic SDO/HMI data enables us to scrutinize important phases in the evolution of active regions. The bipolar region NOAA 12317 presents a rather atypical behavior, as the leading pore decayed, while the trailing part evolved further into a sunspot. Its evolution in terms of plasma flows and connectivity was followed and analyzed using LCT and BaSAMs, whereby the latter method was applied for the first time to high-resolution observations.
The emergence and evolution of active regions result in very dynamic behavior. In the photosphere, converging and diverging motion can be observed in close proximity. At the boundaries of pores with strong magnetic fields, photospheric inflows can be observed. An asymmetric radial outflow was identified by LCT analysis of chromospheric Hα filtergrams, whereas in chromospheric Doppler velocity maps at the same location, downflows are seen. However, due to the lack of access to photospheric Doppler velocities, it is difficult to construct a complete picture of how the magnetic and flow fields interact at the pores’ borders throughout the photosphere and chromosphere.
The photospheric divergence centers recognized by LCT are evidence of exploding or expanding granules, usually observed in proximity to pores and sunspots with regions of ongoing flux emergence. This is especially evident with respect to the area connecting both polarities exhibits strong structural changes induced by exploding granules. In the chromosphere, where divergence centers are no longer traceable, this region is characterized by upflows. However, horizontal proper motions appear to be the main driver of structural change at this location, as demonstrated in chromospheric BaSAMs.
The current work combines high-resolution photospheric images and chromospheric filtergrams with synoptic continuum images and magnetograms. Their combination addresses important aspects of active region development. However, for a better understanding and a comprehensive description of the 3D flow and velocity structure, more high-resolution observations of newly emerging flux regions are needed – if possible, even well before the formation of stable magnetic features has started. Thus, a detailed analysis of the photospheric and chromospheric response becomes possible, namely, the evolution of velocity and magnetic fields with height in the atmosphere. The question of whether the interaction of pores and subsequently sunspots with the surrounding supergranular cell is indeed a prerequisite for penumbra formation is worthwhile, and warrants future scrutiny in a statistical study based on SDO data. High-resolution case studies offer only an inconclusive picture for this aspect of penumbra formation. Once again, future statistical studies based on SDO data could help to resolve this ambiguity. We note, nonetheless, that the fine structure of strong light bridges evades the scrutiny of full-disk observations with moderate spatial resolution.
Movies
Movie 1 associated with Fig. 1 Access here
Movie 2 associated with Fig. 2 Access here
Movie 3 associated with Fig. 3 Access here
Movie 4 associated with Fig. 4 Access here
Movie 5 associated with Fig. 11 Access here
Acknowledgments
We gratefully acknowledge the use of data from the Goode Solar Telescope (GST) of the Big Bear Solar Observatory (BBSO). BBSO operation is supported by US NSF AGS-1821294 grant and New Jersey Institute of Technology. GST operation is partly supported by the Korea Astronomy and Space Science Institute and the Seoul National University. SDO HMI and AIA data are provided by the Joint Science Operations Center – Science Data Processing. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. This study was supported by grant VE 1112/1-1 of the Deutsche Forschungsgemeinschaft (DFG). HW is supported by NASA under grant 80NSSC19K0257 and NSF under grants AST-2204384 and AGS-1954737. In addition, the support by the European Commission’s Horizon 2020 Program under grant agreements 824064 (ESCAPE – European Science Cluster of Astronomy & Particle physics ESFRI research infrastructures) and 824135 (SOLARNET – Integrating High Resolution Solar Physics) is highly appreciated. We would like to thank the anonymous referee for carefully reading the manuscript and providing ideas, which significantly enhanced the paper.
References
- Beauregard, L., Verma, M., & Denker, C. 2012, AN, 333, 125 [NASA ADS] [Google Scholar]
- Beck, C., Choudhary, D. P., & Ranganathan, M. 2020, ApJ, 902, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Beckers, J. M. 1964, PhD Thesis, University of Utrecht, The Netherlands [Google Scholar]
- Beckers, J. M., & Schröter, E. H. 1968, Sol. Phys., 4, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Bellot Rubio, L. R. 2007, in Highlights of Spanish Astrophysics IV, eds. F. Figueras, J. M. Girart, M. Hernanz, & C. Jordi, 271 [CrossRef] [Google Scholar]
- Bharti, L. 2015, MNRAS, 452, L16 [CrossRef] [Google Scholar]
- Bharti, L., Joshi, C., & Jaaffrey, S. N. A. 2007, ApJ, 669, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Bharti, L., Solanki, S. K., & Hirzberger, J. 2010, ApJ, 722, L194 [NASA ADS] [CrossRef] [Google Scholar]
- Bonet, J. A., Márquez, I., Muller, R., Sobotka, M., & Roudier, T. 2005, A&A, 430, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzek, A. 1969, Sol. Phys., 8, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R., Schüssler, M., Vögler, A., & Zakharov, V. 2007, A&A, 474, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, W., Gorceix, N., Coulter, R., et al. 2010a, AN, 331, 636 [NASA ADS] [Google Scholar]
- Cao, W., Gorceix, N., Coulter, R., et al. 2010b, in Ground-based and Airborne Instrumentation for Astronomy III, eds. I. S. McLean, S. K. Ramsay, & H. Takami, Proc. SPIE, 7735, 77355V [NASA ADS] [Google Scholar]
- Cauzzi, G., Reardon, K., Rutten, R. J., Tritschler, A., & Uitenbroek, H. 2009, A&A, 503, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chae, J., Denker, C., Spirock, T. J., Wang, H., & Goode, P. R. 2000, Sol. Phys., 195, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Yang, H., Park, H., et al. 2014, ApJ, 789, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Song, D., Seo, M., et al. 2015, ApJ, 805, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C. M., Rempel, M., Title, A. M., & Schüssler, M. 2010, ApJ, 720, 233 [Google Scholar]
- Criscuoli, S., Del Moro, D., Giannattasio, F., et al. 2012, A&A, 546, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- David, K.-H. 1961, Z. Astrophys., 53, 37 [NASA ADS] [Google Scholar]
- Deng, H., Zhang, D., Wang, T., et al. 2015, Sol. Phys., 290, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Denker, C., & Verma, M. 2019, Sol. Phys., 294, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Evershed, J. 1909, MNRAS, 69, 454 [Google Scholar]
- Freij, N., Scullion, E. M., Nelson, C. J., et al. 2014, ApJ, 791, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakilas, A. A., & Christopoulou, E. B. 2003, ApJ, 584, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R. G. 1972, Sol. Phys., 27, 71 [NASA ADS] [CrossRef] [Google Scholar]
- González Manrique, S. J., Kuckein, C., Collados, M., et al. 2018, A&A, 617, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guglielmino, S. L., & Zuccarello, F. 2011, ApJ, 743, L9 [CrossRef] [Google Scholar]
- Haugen, E. 1969, Sol. Phys., 9, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Hirzberger, J. 2003, A&A, 405, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hou, Y. J., Li, T., Zhong, S. H., et al. 2020, A&A, 642, A44 [EDP Sciences] [Google Scholar]
- Ichimoto, K., Suematsu, Y., Tsuneta, S., et al. 2007, Science, 318, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, J., Li, Q., Liu, C., et al. 2019, ApJ, 880, 143 [CrossRef] [Google Scholar]
- Joshi, J., Pietarila, A., Hirzberger, J., et al. 2011, ApJ, 734, L18 [Google Scholar]
- Künzel, H. 1969, AN, 291, 265 [Google Scholar]
- Lagg, A., Solanki, S. K., van Noort, M., & Danilovic, S. 2014, A&A, 568, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, J.-S. 1986, Opt. Eng., 25, 636 [NASA ADS] [Google Scholar]
- Leka, K. D., & Skumanich, A. 1998, ApJ, 507, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Leka, K. D., & Steiner, O. 2001, ApJ, 552, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Li, F.-Y., Chen, Y.-H., Song, Y.-L., Hou, Z.-Y., & Tian, H. 2021, Res. Astron. Astrophys., 21, 144 [CrossRef] [Google Scholar]
- Lim, E.-K., Yurchyshyn, V., Goode, P., & Cho, K.-S. 2013, ApJ, 769, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S., & Liu, D. 2015, Adv. Space Res., 55, 2931 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W. 2002, Sol. Phys., 207, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Löhner-Böttcher, J., & Schlichenmaier, R. 2013, A&A, 551, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López Fuentes, M. C., Demoulin, P., Mandrini, C. H., & van Driel-Gesztelyi, L. 2000, ApJ, 544, 540 [CrossRef] [Google Scholar]
- Loughhead, R. E. 1968, Sol. Phys., 5, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Louis, R. E. 2015, Adv. Space Res., 56, 2305 [Google Scholar]
- Louis, R. E., Bayanna, A. R., Mathew, S. K., & Venkatakrishnan, P. 2008, Sol. Phys., 252, 43 [Google Scholar]
- Louis, R. E., Bellot Rubio, L. R., Mathew, S. K., & Venkatakrishnan, P. 2009, ApJL, 704, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, F., & Schmidt, H. U. 1968, Zeitschrift Angewandte Mathematik und Mechanik, 48, 218 [Google Scholar]
- Moore, R., & Rabin, D. 1985, ARA&A, 23, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Murabito, M., Romano, P., Guglielmino, S. L., Zuccarello, F., & Solanki, S. K. 2016, ApJ, 825, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Murabito, M., Romano, P., Guglielmino, S. L., & Zuccarello, F. 2017, ApJ, 834, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Murabito, M., Zuccarello, F., Guglielmino, S. L., & Romano, P. 2018, ApJ, 855, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H. 1999, Sol. Phys., 184, 421 [Google Scholar]
- Neckel, H., & Labs, D. 1984, Sol. Phys., 90, 205 [Google Scholar]
- November, L. J., & Simon, G. W. 1988, ApJ, 333, 427 [Google Scholar]
- Panja, M., Cameron, R. H., & Solanki, S. K. 2021, ApJ, 907, 102 [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Quintero Noda, C., Shimizu, T., Ruiz Cobo, B., et al. 2016, MNRAS, 460, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2015, ApJ, 814, 125 [Google Scholar]
- Rempel, M., & Cheung, M. C. M. 2014, ApJ, 785, 90 [Google Scholar]
- Rempel, M., Schüssler, M., & Knölker, M. 2009a, ApJ, 691, 640 [Google Scholar]
- Rempel, M., Schüssler, M., Cameron, R. H., & Knölker, M. 2009b, Science, 325, 171 [CrossRef] [Google Scholar]
- Rezaei, R., Bello González, N., & Schlichenmaier, R. 2012, A&A, 537, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rimmele, T. 2008, ApJ, 672, 684 [Google Scholar]
- Rimmele, T. R., & Marino, J. 2006, ApJ, 646, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Robustini, C., Leenaarts, J., de la Cruz Rodriguez, J., & Rouppe van der Voort, L. 2016, A&A, 590, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Bonet, J. A., & Sobotka, M. 2002, A&A, 395, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roy, J. R. 1973, Sol. Phys., 28, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Rucklidge, A. M., Schmidt, H. U., & Weiss, N. O. 1995, MNRAS, 273, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Sankarasubramanian, K., & Rimmele, T. 2003, ApJ, 598, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., & Spruit, H. C. 2006, A&A, 460, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Gudiksen, B. V., Kiselman, D., Löfdahl, M. G., & Rouppe van der Voort, L. H. M. 2002, Nature, 420, 151 [CrossRef] [Google Scholar]
- Scharmer, G. B., Narayan, G., Hillberg, T., et al. 2008, ApJ, 689, L69 [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schlichenmaier, R., Rezaei, R., Bello González, N., & Waldmann, T. A. 2010, A&A, 512, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlichenmaier, R., Rezaei, R., & González, N. B. 2012, in 4th Hinode Science Meeting: Unsolved Problems and Recent Insights, eds. L. Bellot Rubio, F. Reale, & M. Carlsson, ASP Conf. Ser., 455, 61 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Shimizu, T., Ichimoto, K., & Suematsu, Y. 2012, ApJ, 747, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Shumko, S., Gorceix, N., Choi, S., et al. 2014, in Adaptive Optics Systems IV, eds. E. Marchetti, L. M. Close, & J. P. Véran, Proc. SPIE, 9148, 1073 [Google Scholar]
- Siu-Tapia, A. L., Rempel, M., Lagg, A., & Solanki, S. K. 2018, ApJ, 852, 66 [Google Scholar]
- Sobotka, M., Del Moro, D., Jurčák, J., & Berrilli, F. 2012, A&A, 537, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sobotka, M., Švanda, M., Jurčák, J., et al. 2013, A&A, 560, A84 [EDP Sciences] [Google Scholar]
- Solanki, S. K. 2003, A&ARev, 11, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., Scharmer, G. B., & Löfdahl, M. G. 2010, A&A, 521, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stein, R. F., Lagerfjärd, A., Nordlund, Å., & Georgobiani, D. 2011, Sol. Phys., 268, 271 [Google Scholar]
- Sütterlin, P. 1998, A&A, 333, 305 [NASA ADS] [Google Scholar]
- Tanaka, K. 1991, Sol. Phys., 136, 133 [Google Scholar]
- Thomas, J. H., & Weiss, N. O. 2004, ARA&A, 42, 517 [Google Scholar]
- Tian, H., Yurchyshyn, V., Peter, H., et al. 2018, ApJ, 854, 92 [Google Scholar]
- Toriumi, S., Cheung, M. C. M., & Katsukawa, Y. 2015, ApJ, 811, 138 [Google Scholar]
- Vargas Domínguez, S., Rouppe van der Voort, L., Bonet, J. A., et al. 2008, ApJ, 679, 900 [Google Scholar]
- Verdoni, A. P., & Denker, C. 2007, PASP, 119, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Verma, M. 2018, A&A, 612, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verma, M., & Denker, C. 2011, A&A, 529, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verma, M., & Denker, C. 2012, A&A, 545, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verma, M., & Denker, C. 2014, A&A, 563, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verma, M., Balthasar, H., Deng, N., et al. 2012, A&A, 538, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verma, M., Denker, C., Balthasar, H., et al. 2016a, A&A, 596, A3 [Google Scholar]
- Verma, M., Denker, C., Böhm, F., et al. 2016b, AN, 337, 1090 [NASA ADS] [Google Scholar]
- Verma, M., Kummerow, P., & Denker, C. 2018, AN, 339, 268 [NASA ADS] [Google Scholar]
- Verma, M., Denker, C., Diercke, A., et al. 2020, A&A, 639, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watanabe, H., Bellot Rubio, L. R., de la Cruz Rodríguez, J., & Rouppe van der Voort, L. 2012, ApJ, 757, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Wöger, F., & von der Lühe, O. 2008, in Advanced Software and Control for Astronomy II, eds. A. Bridger, & N. M. Radziwill, Proc. SPIE, 7019, 70191E [CrossRef] [Google Scholar]
- Zakharov, V., Hirzberger, J., Riethmüller, T. L., Solanki, S. K., & Kobel, P. 2008, A&A, 488, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirin, H., & Stein, A. 1972, ApJ, 178, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Zuccarello, F., Romano, P., Guglielmino, S. L., et al. 2009, A&A, 500, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwaan, C. 1985, Sol. Phys., 100, 397 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. HMI Continuum images (top) and LOS magnetograms (bottom) showing the evolution of active region NOAA 12317 from 17:00 UT on 2015 April 1 (left) to 17:00 UT on 2015 April 3 (right). The FOV covers 150″ × 150″, and the coordinates in the lower left corners refer to the FOV’s center. The black solid squares in the left panels correspond to an ROI of 30″ × 30″, which is used in the analysis of the high-resolution Hα and TiO time series. Dashed squares correspond to an ROI of 95″ × 95″ which is used in the determination of the photometric area and magnetic flux shown in Fig. 6. An arrow in second-lower panel indicates the negative polarity pore belonging to the secondary flux system. Magnetograms are displayed in the range ±400 G. An animated version of this figure is available online. |
| In the text | |
 |
Fig. 2. Temporal evolution of pores observed in the TiO λ706 nm bandhead images on 2015 April 1. The best images were selected, hence, they are not equidistant in time. The ROI has a size of 30″ × 30″. In the upper left panel the three major pores are labeled P1, P2, and P3, and the plage region is enclosed within the rectangle. An animated version of this figure is available online. |
| In the text | |
 |
Fig. 3. Temporal evolution of pores observed in the Hαλ656.3 nm line-core images on 2015 April 1 (otherwise same as in Fig. 2). An animated version of this figure is available online. |
| In the text | |
 |
Fig. 4. Speckle-restored Hα filtergrams of each wavelength point of the Hα line scan at 18:03 UT on 2015 April 1. The wavelength positions with respect to the Hα line core are given in the lower left corner of each panel. Neighboring wavelength points are separated by 0.4 Å. The ROI has a size of 30″ × 30″. The colored crosses indicate the location of extracted Hα line profiles shown in Fig. 5. The white asterisk within pore P2 indicates the position of the thin, solid black line profile shown in Fig. 5. The white contours outlining the pores are based on the average image of the first time series of TiO images and are computed using an intensity threshold of 0.8. An animated version of this figure is available online. |
| In the text | |
 |
Fig. 5. Color-coded Hα line profiles, which are marked by matching crosses in Fig. 4. The dashed black line represents the average of the color-coded line profiles. The thin, solid black line refers to an Hα profile of a pore, as indicated by the white asterisk in Fig. 4 inside pore P2. The thick, solid black line denotes the Kitt Peak FTS disk-center spectral atlas, which served as a reference in the wavelength calibration. |
| In the text | |
 |
Fig. 6. Evolution of the magnetic flux (solid) and photometric area (dashed) on 2015 April 1 for a FOV of 95″ × 95″ covering positive-polarity pores in active region NOAA 12317. The two dashed vertical lines demarcate the two time periods 17:00–20:00 UT and 21:00–23:30 UT used for further analysis. |
| In the text | |
 |
Fig. 7. BaSAM of the entire TiO time series of 836 images covering the time period 18:00–22:34 UT. The ROI has a size of 30″ × 30″. The color bar indicates the variations in intensity on logarithmic scale. |
| In the text | |
 |
Fig. 8. 2D BaSAMs with an ROI of 30″ × 30″ derived from Hα blue line-wing, line-core, and red line-wing filtergrams (left to right). The color bar indicates the variations for the three wavelength settings on logarithmic scale. |
| In the text | |
 |
Fig. 9. 2D LCT maps with an ROI of 30″ × 30″ show the photospheric horizontal proper motions for the three time periods indicated above each panel. Rainbow-colored arrows refer to magnitude and direction of the average flow vectors, which are superposed on a time-averaged TiO image. The white contours outline the pores in the corresponding TiO images for intensities lower than 0.8, while the pink contours delineate the regions for which the inflow velocities are computed. The black rectangle in the lower right indicates the locations of expanding granules. |
| In the text | |
 |
Fig. 10. 2D LCT maps with an ROI of 30″ × 30″ show the chromospheric horizontal proper motions for the three time periods indicated above each panel. Rainbow-colored arrows refer to magnitude and direction of the average flow vectors, superposed on a time-averaged Hα line-core filtergram. The white contours outline the pores in the corresponding TiO images for intensities lower than 0.8, while the pink contours delineate the regions for which the inflow velocities are computed. |
| In the text | |
 |
Fig. 11. 2D maps with an ROI of 30″ × 30″ show the average chromospheric Hα Doppler velocities for the three time periods indicated above each panel. The velocities are clipped at ±3 km s−1. The positions labeled 1–6 refer to Hα Doppler velocities listed in Table 1. The black contours outline the pores in the corresponding TiO images for intensities lower than 0.8, while the pink contours delineate the regions for which the outflow velocities are computed. The region above the black horizontal line is used to compute the average quiet-Sun Doppler velocity. An animated version of this figure is available online. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


