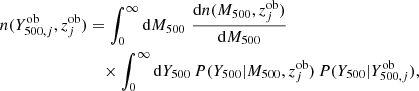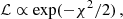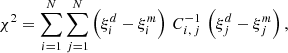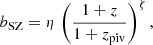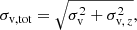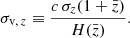| Issue |
A&A
Volume 674, June 2023
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202346261 | |
| Published online | 06 June 2023 | |
Mass bias and cosmological constraints from Planck cluster clustering
1
Dipartimento di Fisica e Astronomia “Augusto Righi” – Alma Mater Studiorum Università di Bologna, Via Piero Gobetti 93/2, 40129 Bologna, Italy
e-mail: giorgio.lesci2@unibo.it
2
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Piero Gobetti 93/3, 40129 Bologna, Italy
3
INAF – Osservatorio Astronomico di Brera, Via Brera 28, 20122 Milan, Via E. Bianchi 46, 20121 Merate, Italy
4
INFN – Sezione di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
Received:
27
February
2023
Accepted:
20
April
2023
Aims. We analysed the 3D clustering of the Planck sample of Sunyaev–Zeldovich (SZ) selected galaxy clusters, focusing on the redshift-space two-point correlation function (2PCF). We compared our measurements to theoretical predictions of the standard Λ cold dark matter (ΛCDM) cosmological model, deriving an estimate of the Planck mass bias, bSZ, and cosmological parameters.
Methods. We measured the 2PCF of the sample in the cluster-centric radial range r ∈ [10, 150] h−1 Mpc, considering 920 galaxy clusters with redshift z ≤ 0.8. A Markov chain Monte Carlo analysis was performed to constrain bSZ, assuming priors on cosmological parameters from Planck cosmic microwave background (CMB) results. We also adopted priors on bSZ from external data sets to constrain the cosmological parameters Ωm and σ8.
Results. We obtained (1−bSZ) = 0.62−0.11+0.14, which agrees with the value required to reconcile primary CMB and cluster count observations. By adopting priors on (1 − bSZ) from external data sets, we derived results on Ωm that fully agree and are competitive, in terms of uncertainties, with those derived from cluster counts. This confirms the importance of including clustering in cosmological studies in order to fully exploit the information from galaxy cluster statistics. On the other hand, we found that σ8 is not constrained.
Key words: cosmological parameters / cosmology: observations / large-scale structure of Universe / galaxies: clusters: general
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Galaxy clusters are excellent tracers of the large-scale matter distribution of the Universe, probing its geometry and evolution through their abundance and clustering (Sereno et al. 2015; Veropalumbo et al. 2016; Costanzi et al. 2019; Marulli et al. 2021; Moresco et al. 2021; To et al. 2021; Lesci et al. 2022a; Euclid Collaboration 2022). In particular, the formation and evolution of galaxy clusters can theoretically be described with high accuracy through numerical simulations. This allows the theoretical calibration of the cluster halo mass and bias functions (Sheth & Tormen 1999; Sheth et al. 2001; Tinker et al. 2008, 2010; Despali et al. 2016; Euclid Collaboration 2023) and the description of the cluster dark matter profiles (Navarro et al. 1997; Baltz et al. 2009), providing the link between cluster local and statistical properties. In addition, cluster masses can be measured with high precision through weak gravitational lensing (Sereno et al. 2017; Bellagamba et al. 2019; Stern et al. 2019) and X-ray observations (Arnaud et al. 2010; Planck Collaboration XX 2014; Sereno & Ettori 2017). Moreover, cluster abundance and clustering are suitable probes for mass calibration if a cosmological model is assumed (Murata et al. 2019; Chiu et al. 2020; Lesci et al. 2022b).
As cosmological parameters are inferred with high precision in current cluster statistical analyses, accurate cluster mass calibrations are of critical importance. An incomplete assessment of systematic uncertainties affecting the derived masses may lead to significant biases in the cosmological constraints (Planck Collaboration XXIV 2016; Abbott et al. 2020). Simulations show that X-ray masses are typically 10–15% underestimated due to the assumption of hydrostatic equilibrium, for which bulk motions and turbulence in the intra-cluster medium are neglected (Nagai et al. 2007; Meneghetti et al. 2010; Rasia et al. 2012; Le Brun et al. 2014). Weak-lensing mass estimates can also be biased by the inaccuracy of density profile models (Oguri & Hamana 2011), baryonic effects influencing the halo concentration (Henson et al. 2017; Shirasaki et al. 2018; Beltz-Mohrmann & Berlind 2021), halo orientation (Becker & Kravtsov 2011; Dietrich et al. 2014; Zhang et al. 2022), and projections (Simet et al. 2017; Melchior et al. 2017). As the biases in the weak-lensing mass estimates are theoretically better understood, weak-lensing observations are exploited for calibrating the main bias affecting X-ray masses, called hydrostatic bias, bh (von der Linden et al. 2014; Hoekstra et al. 2015; Planck Collaboration XXIV 2016; Smith et al. 2016; Sereno & Ettori 2017). In particular, the relation between the X-ray mass, MX, and the true mass, Mtr, is usually expressed as MX = (1 − bh)Mtr.
In this paper, we focus on the mass bias of the Sunyaev–Zeldovich (SZ) selected Planck clusters (Planck Collaboration XXIV 2016; Planck Collaboration XXVII 2016), which is referred to as the Planck mass bias, bSZ. Planck cluster masses are expected to be biased low as they are derived from a scaling relation based on X-ray observations of 20 relaxed clusters at z < 0.2 (Arnaud et al. 2010; Planck Collaboration XX 2014). We obtained an estimate of bSZ that is independent of lensing observations by exploiting the monopole of the 3D two-point correlation function (2PCF) of the galaxy clusters in the sample provided by Planck Collaboration XXVII (2016). In particular, we assumed a standard Λ cold dark matter (ΛCDM) cosmological model, adopting the cosmic microwave background (CMB) constraints on cosmological parameters from Planck Collaboration VI (2020) as priors. In addition, we adopted the same priors on (1 − bSZ) as were used in the Planck cluster count analysis carried out by Planck Collaboration XXIV (2016) in order to constrain the matter density parameter, Ωm, and the amplitude of the matter power spectrum, σ8.
The statistical analyses presented in this paper were performed with the CosmoBolognaLib1 (CBL; Marulli et al. 2016), a set of free software C++/Python numerical libraries for cosmological calculations. Specifically, the measurements and the statistical Bayesian analyses were both performed with the CBL v6.1.
The paper is organised as follows. In Sect. 2 we describe the data set and the methods we used to estimate the 2PCF of the sample. In Sect. 3 we describe the 2PCF model, focusing on the dependence of the effective bias on the mass-observable scaling relation. In Sect. 4 we show our constraints on bSZ and detail the cosmological analysis, and in Sect. 5 we draw our conclusions.
2. Data set and 2PCF measurement
2.1. The Planck cluster sample
Following Planck Collaboration XXIV (2016), we based our analysis on the cosmological sample consisting of detections by the MMF3 matched filter (Melin et al. 2006, 2012) derived from the general Planck full-mission Sunyaev–Zeldovich catalogue (PSZ2; Planck Collaboration XXVII 2016). We considered clusters with a confirmed counterpart in external data sets and an assigned redshift estimate (see Table 9 in Planck Collaboration XXVII 2016), with a redshift limit z ≤ 0.8, for a total of 920 clusters. We applied this redshift cut to exclude 5 clusters that are isolated with respect to the bulk of the redshift distribution because they hindered the derivation of a reliable smoothed redshift distribution, which is necessary for the construction of the random sample (see Sect. 2.2). In addition, differently from Planck Collaboration XXIV (2016), we did not apply any cut in the signal-to-noise ratio (S/N). This does not imply any potential problems due to the reliability of the selection function at low S/N because our model does not rely on assumptions on the sample completeness (see Sect. 3.2).
2.2. Random catalogue
The random catalogue used for the 2PCF measurement is 100 times larger than the Planck cluster sample. We smoothed the observed redshift distribution, n(z), with a Gaussian kernel with an rms equal to 0.02 (see Fig. 1). Then we extracted random redshifts from this distribution. Random RA–Dec pairs were extracted by following the sample angular selection function. It consists of the combination of the MMF3 survey mask2, namely ℳs, the hole mask excluding contaminated regions (e.g., by stars or large galaxies), ℳh, and the error function completeness. Both ℳs and ℳh are equal to 0 if the region is masked, otherwise, they are equal to 1. The error function completeness is defined as (Planck Collaboration XXIX 2014)
 |
Fig. 1. Redshift distribution n(z) of the galaxy clusters considered in the analysis. The blue histogram shows the observed binned n(z), and the black curve represents n(z) smoothed with a Gaussian kernel (with an rms equal to 0.02) that was used to build up the random catalogue. |
where d is the Boolean detection state, erf(x) is the Gauss error function, and Y500 and θ500 are the observed SZ signal and the detection angular scale within a critical radius R500, respectively. The latter is defined as the distance from the cluster centre inside which the mean density is 500 times the critical density of the Universe at the given redshift, z. M500 is defined as the mass enclosed within R500. In Eq. (1), σYi is the standard deviation of pixels for a given patch i, computed by following Melin et al. (2006), and q is the S/N threshold. As we did not apply any S/N cut to the sample, q corresponds to the minimum threshold adopted by Planck Collaboration XXVII (2016) in the detection process, namely q = 4.5. In Eq. (1), we assumed the sample mean values of Y500 and θ500. We verified that using the median values of these quantities does not introduce significant variations in the final results. Then we extracted random angular positions, for each of which we sampled a number in the range [0, 1]. When this number was higher than the product of ℳs, ℳh and P(d|Y500, σYi, q), the random angular position was rejected. As an alternative to the error function completeness in Eq. (1), we weighted the pairs in the 2PCF estimator (described in Sect. 2.3) by 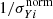 , where
, where 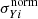 is equal to σYi divided by its minimum value, namely
is equal to σYi divided by its minimum value, namely 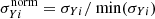 . We verified that this approach provides results that fully agreed with what was derived from the application of the error function completeness.
. We verified that this approach provides results that fully agreed with what was derived from the application of the error function completeness.
2.3. Clustering measurement
We estimated the redshift-space 2PCF monopole using the Landy & Szalay (1993, LS) estimator,
where DD(s), RR(s), and DR(s) are the number of data–data, random–random, and data–random pairs with separation s ± Δs, respectively, while NDD, NRR, and NDR are the total number of data–data, random–random, and data–random pairs, respectively. To convert the observed coordinates into the comoving ones, we assumed the cosmological parameters by Planck Collaboration VI (2020), TT, TE, EE+lowE+lensing (referred to as Planck18 hereafter). The LS estimator is extensively used in clustering analyses as it is unbiased with minimum variance for an infinitely large random sample and when |ξ|≪1 (Hamilton 1992; Kerscher et al. 2000; Labatie et al. 2012; Keihänen et al. 2019).
Specifically, we measured the 2PCF considering two redshift bins, namely z < 0.2 and z ∈ [0.2, 0.8], containing 407 and 513 galaxy clusters, respectively. We considered the cluster-centric radial range s ∈ [10, 150] h−1 Mpc, excluding from the analysis the 2PCF measure at s < 15 h−1 Mpc in the second redshift bin due to the lack of data-data pairs. Moreover, we integrated the 2PCF measurements over larger s bins in z ∈ [0.2, 0.8], compared to those adopted for the lower redshift bin. In this way, we compensated for the reduction of cluster pairs with small s distances, caused by the lower cluster density at high redshifts. We estimated the covariance matrix, including the cross-covariance between radial and redshift bins, through a bootstrap procedure. In particular, we considered 200 angular regions and two redshift regions, corresponding to the redshift bins, and resampled the observed and random catalogues 2000 times. We corrected the inverted covariance matrix following Hartlap et al. (2007). In Fig. 2 we show the measured 2PCF monopole, ξ0. We did not include the other non-zero multipoles in the analysis, as we verified that their contribution is negligible.
 |
Fig. 2. Redshift-space 2PCF monopole (black dots) of the Planck clusters in the spatial range s ∈ [10, 150] h−1 Mpc for z < 0.2 (left plot), and s ∈ [15, 150] h−1 Mpc for z ∈ [0.2, 0.8] (right plot). The blue bands represent the model 68% confidence level derived from the posterior of the free parameters considered in the analysis described in Sect. 4.1. |
3. Modelling
We modelled the 2PCF of Planck clusters by accounting for geometric and redshift-space distortions. In addition, different to what was done in the Planck cluster count analysis by Planck Collaboration XXIV (2016), our model does not rely on assumptions on the sample completeness. We show in Sect. 4 that this approach leads to constraints on bSZ and cosmological parameters that fully agree with those derived by Planck Collaboration XXIV (2016) and Planck Collaboration VI (2020).
3.1. Two-point correlation function model
The lth order 2PCF multipole, ξl(s), can be expressed as follows:
where jl is the spherical Bessel function of order l, and Pl is the redshift-space matter power spectrum multipole of order l,
In Eq. (4), Ll is the Legendre polynomial of order l, and μ is the line of sight cosine. Moreover, in Eq. (4), we accounted for the Alcock & Paczynski (1979, AP) geometric distortions caused by the assumption of a fiducial cosmology used to convert the cluster observed coordinates into comoving ones in Eq. (2). Specifically, k′ and μ′ have the following functional forms (Beutler et al. 2014):
where α⊥ and α∥ are expressed as
Here, Hfid(z) and 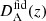 are the fiducial values for the Hubble constant and angular diameter distance, respectively, and
are the fiducial values for the Hubble constant and angular diameter distance, respectively, and 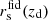 is the fiducial sound horizon at the drag redshift, zd. We stress that the AP correction takes place only in the cosmological analysis described in Sect. 4.3. To derive bSZ, as detailed in Sect. 4.1, we fixed the cosmological parameters to the fiducial ones. In Eq. (4), P(k′,μ′) is the redshift-space dark matter power spectrum expressed as (Taruya et al. 2010)
is the fiducial sound horizon at the drag redshift, zd. We stress that the AP correction takes place only in the cosmological analysis described in Sect. 4.3. To derive bSZ, as detailed in Sect. 4.1, we fixed the cosmological parameters to the fiducial ones. In Eq. (4), P(k′,μ′) is the redshift-space dark matter power spectrum expressed as (Taruya et al. 2010)
where Pδδ, Pθθ, and Pδθ are the real-space auto power spectra of the density and velocity divergence and their cross power spectrum, respectively. These spectra are estimated in the standard perturbation theory (SPT), consisting of expanding the statistics as a sum of infinite terms, corresponding to the n-loop corrections (see e.g., Gil-Marín et al. 2012). Considering corrections up to the first-loop order, the power spectrum can be modelled as follows:
where the leading-order term, PL(k), is the linear matter power spectrum, computed with CAMB3 (Lewis & Challinor 2011), while the one-loop correction terms are computed with the CPT Library 4 (Taruya & Hiramatsu 2008). In Eq. (9), DFoG(k′,μ′,f, σv) is a Gaussian damping function representing the fingers-of-God effect, having the following functional form:
where f is the linear growth rate, and 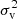 is the linear velocity dispersion, computed as (Taruya et al. 2010)
is the linear velocity dispersion, computed as (Taruya et al. 2010)
In Eqs. (9) and (12), PL(k) is computed at the mean redshift of the cluster sub-sample in the given redshift bin. In addition, in Eq. (9), beff is the effective bias, defined in Sect. 3.2, and the functions A(k′,μ′,f) and B(k′,μ′,f) are correction terms derived from SPT (Taruya et al. 2010; de la Torre & Guzzo 2012; García-Farieta et al. 2020).
3.2. Effective bias
The effective bias, beff, has the following functional form:
where Ncl is the number of clusters in the sample, 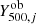 and
and 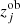 are the observed SZ signal and redshift, respectively, of the jth cluster, and
are the observed SZ signal and redshift, respectively, of the jth cluster, and 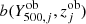 is expressed as
is expressed as
where b(M500, z) is the halo bias, for which the model by Tinker et al. (2010) was assumed, and 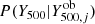 is a Gaussian whose mean is
is a Gaussian whose mean is 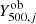 and its root mean square (rms) deviation is given by the error on
and its root mean square (rms) deviation is given by the error on 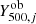 . In addition, P(Y500|M500, z) is a log-normal whose mean is given by the mass-observable scaling relation, and its rms is given by the intrinsic scatter, σlnY,
. In addition, P(Y500|M500, z) is a log-normal whose mean is given by the mass-observable scaling relation, and its rms is given by the intrinsic scatter, σlnY,
Specifically, following Planck Collaboration XXIV (2016), we assumed σlnY to be independent of Y500 and redshift, and the expected value of SZ signal, 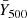 , can be expressed as
, can be expressed as
where E(z)≡H(z)/H0, with H(z) being the Hubble function and H0 the Hubble constant, DA(z) is the angular diameter distance, h ≡ H0/100, bSZ is the Planck mass bias, and Y*, α, and β are the scaling relation parameters. In addition, 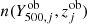 in Eq. (14) is expressed as
in Eq. (14) is expressed as
where dn(M500, z)/dM500 is the halo mass function, for which the model by Tinker et al. (2008) was assumed.
3.3. Likelihood
For the Bayesian analysis performed in this work, a standard Gaussian likelihood was considered,
with
where N is the number of comoving separation bins in which the 2PCF is computed, d and m indicate data and model, respectively, and 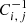 is the inverse of the covariance matrix. As detailed in Sect. 2.3, Ci, j was derived through a bootstrap resampling.
is the inverse of the covariance matrix. As detailed in Sect. 2.3, Ci, j was derived through a bootstrap resampling.
4. Results
Based on the methods outlined in Sects. 2 and 3, we carried out an analysis of the redshift-space 2PCF monopole of the Planck cluster sample (Planck Collaboration XXVII 2016). Specifically, we detail in Sect. 4.1 the derivation of the (1 − bSZ) constraint, performed by assuming the Planck18 cosmological results as priors. In Sect. 4.3 we present the constraints on cosmological parameters, obtained by assuming priors on bSZ from external data sets.
4.1. Constraint on bSZ
In order to derive a constraint on the Planck mass bias, bSZ, we fixed the cosmological parameters to the Planck18 median values. We also assumed the priors on the mass-observable scaling relation parameters in Eq. (16), namely Y*, α, β, and σlnY, adopted by Planck Collaboration XXIV (2016). In particular, this scaling relation was derived from X-ray observations of 20 relaxed clusters at z < 0.2 (Arnaud et al. 2010; Planck Collaboration XX 2014). Finally, we assumed a large flat prior on bSZ. In Table 1 we summarise the priors used for this analysis, along with the result on the mass bias, namely 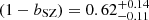 . The corresponding effective bias estimates are
. The corresponding effective bias estimates are 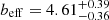 and
and 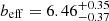 for z < 0.2 and z ∈ [0.2, 0.8], respectively. The constraint on (1 − bSZ) is lower than what was predicted by numerical simulations (Nagai et al. 2007; Piffaretti & Valdarnini 2008; Meneghetti et al. 2010; Rasia et al. 2012; Le Brun et al. 2017; Henson et al. 2017; Gianfagna et al. 2023), but in line with what was found by Planck Collaboration VI (2020). We remark that even though the constraints on beff derived from the two redshift bins have similar associated uncertainties, our result on (1 − bSZ) is dominated by the 2PCF signal measured at low redshift. We obtained
for z < 0.2 and z ∈ [0.2, 0.8], respectively. The constraint on (1 − bSZ) is lower than what was predicted by numerical simulations (Nagai et al. 2007; Piffaretti & Valdarnini 2008; Meneghetti et al. 2010; Rasia et al. 2012; Le Brun et al. 2017; Henson et al. 2017; Gianfagna et al. 2023), but in line with what was found by Planck Collaboration VI (2020). We remark that even though the constraints on beff derived from the two redshift bins have similar associated uncertainties, our result on (1 − bSZ) is dominated by the 2PCF signal measured at low redshift. We obtained 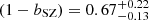 for z < 0.2 and
for z < 0.2 and 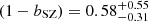 for z ∈ [0.2, 0.8]. This is expected because beff is directly derived from the mass-observable relation, and the number of clusters is comparable in the considered redshift bins. On the other hand, the constraints on (1 − bSZ) depend on the 2PCF measurements, for which we obtained larger uncertainties in the high-redshift bin. In both redshift bins, we found
for z ∈ [0.2, 0.8]. This is expected because beff is directly derived from the mass-observable relation, and the number of clusters is comparable in the considered redshift bins. On the other hand, the constraints on (1 − bSZ) depend on the 2PCF measurements, for which we obtained larger uncertainties in the high-redshift bin. In both redshift bins, we found 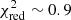 , where
, where 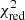 is the reduced χ2. Specifically, we considered three effective free model parameters because the change in the model within the assumed priors on β and σlnY is not statistically significant.
is the reduced χ2. Specifically, we considered three effective free model parameters because the change in the model within the assumed priors on β and σlnY is not statistically significant.
In Fig. 3 we show a comparison between our constraint on (1 − bSZ) and the results obtained from the literature. In presence of systematic uncertainties, we added them in quadrature to the statistical ones. By combining primary CMB likelihood and cluster counts, Planck Collaboration VI (2020) derived (1 − bSZ) = 0.62 ± 0.03 (orange dot in Fig. 3), which fully agrees with our result. Regarding the Planck mass estimates derived from galaxy weak lensing, we found a 1σ agreement with Weighting the Giants (WtG; von der Linden et al. 2014), the Canadian Cluster Comparison Project (CCCP; Hoekstra et al. 2015), the Literature Catalogs of weak Lensing Clusters of galaxies (LC2; Sereno & Ettori 2017), the Cluster Lensing And Supernova survey with Hubble (CLASH; Penna-Lima et al. 2017), and the Subaru Hyper Suprime-Cam (HSC; Medezinski et al. 2018). We found an agreement of only 2σ with the results from the Local Cluster Substructure Survey (LoCuSS; Smith et al. 2016), the Multi Epoch Nearby Cluster Survey (MENeaCS) combined with updated mass weak-lensing estimates in CCCP (MENeaCS+CCCP; Herbonnet et al. 2020), and with the result obtained from CMB lensing by Planck Collaboration XXIV (2016), however. When comparing our results to other analyses based on cluster counts, we found an agreement of 1σ with Zubeldia & Challinor (2019), and Salvati et al. (2019, 2022). Concerning the results derived from the power spectra of the Planck thermal Sunyaev–Zeldovich effect, our constraint agrees within 1σ with Makiya et al. (2018) and Ibitoye et al. (2022). We also found a good agreement with the constraint by Wicker et al. (2022) based on measurements of the cluster gas mass fraction. The hydrostatic bias estimates from dynamical masses by Ferragamo et al. (2021) and Aguado-Barahona et al. (2022) agree with our result within 1σ. In Sect. 4.2 we discuss the impact of the adopted modelling choices on our result, finding that the derived constraint on bSZ is robust with respect to the investigated systematic uncertainties.
 |
Fig. 3. Comparison of the results on (1 − bSZ) with the literature. The median, 16th and 84th percentiles are shown. The black dot shows the constraint derived in this work. Then, in order from top to bottom, the following results are shown: Planck Collaboration VI (2020; orange), von der Linden et al. (2014; blue) Hoekstra et al. (2015; red), Planck Collaboration XXIV (2016; dark green), Smith et al. (2016; grey), Sereno & Ettori (2017; magenta), Penna-Lima et al. (2017; brown), Medezinski et al. (2018; cyan), Herbonnet et al. (2020; pink), Zubeldia & Challinor (2019; purple), Salvati et al. (2019; turquoise), Salvati et al. (2022; green), Makiya et al. (2018; dark blue), Wicker et al. (2022; violet), Ibitoye et al. (2022; indigo), Ferragamo et al. (2021; orange), and Aguado-Barahona et al. (2022; dark brown). |
As many observational studies claimed a redshift dependence of the hydrostatic bias (Smith et al. 2016; Sereno & Ettori 2017; Salvati et al. 2019, 2022; Wicker et al. 2022), we investigated this possibility by expressing bSZ as follows:
where zpiv = 0.25 is the mean redshift of the sample, η is the normalisation, and ζ parametrises the redshift dependence of the mass bias. Our analysis does not constrain ζ, implying that it is not necessary to explain our data. We stress that the redshift dependence of bSZ was derived from cluster statistics only in the case of a strong prior on the total value of bSZ, with a significant dependence on the sample (Salvati et al. 2019, 2022; Wicker et al. 2022).
4.2. Assessment of systematics on bSZ
To assess the robustness of the constraint on bSZ derived in Sect. 4.1, we included the power spectrum damping due to redshift uncertainties in the analysis. No redshift errors are quoted in Planck data products, and therefore, we expressed this damping by means of a free parameter. Specifically, we replaced Eq. (12) by the following expression:
where σv is defined in Eq. (12), while σv, z is the velocity dispersion caused by redshift errors, having the following functional form:
In this equation,  is the mean redshift of the sub-sample in a given redshift bin, c is the speed of light, H(z) is the Hubble function, and σz is the typical redshift uncertainty of the sample. By assuming a flat prior on σz, namely σz ∈ [0, 0.1], we derived
is the mean redshift of the sub-sample in a given redshift bin, c is the speed of light, H(z) is the Hubble function, and σz is the typical redshift uncertainty of the sample. By assuming a flat prior on σz, namely σz ∈ [0, 0.1], we derived 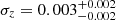 , which is in line with the fact that most of the cluster redshifts are spectroscopic, and
, which is in line with the fact that most of the cluster redshifts are spectroscopic, and 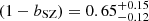 , which fully agrees with our previous result.
, which fully agrees with our previous result.
In addition, we analysed the 2PCF monopole of the Planck union catalogue, containing the clusters detected with the three detection algorithms adopted by Planck Collaboration XXVII (2016). By assuming the same sample selections and bins of redshift and radius described in Sect. 2, we found 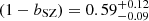 , which is in line with the constraint derived in Sect. 4.1. This implies that our result is independent of the adopted cluster detection algorithm. We also performed the analysis by considering the clusters in the MMF3 sample with S/N > 6, and for which the COSMO entry in the union catalogue is set to ‘T’, meaning that these clusters are part of the cosmological sample, following Planck Collaboration XXIV (2016). Because the statistics are poorer in this case, we analysed the 2PCF in a single redshift bin including clusters with z ≤ 0.8 for a total of 430 objects. As the modelling provides reduced χ2 estimates that are not close to 1, we conclude that in this case, the 2PCF signal does not allow a reliable constraint on bSZ.
, which is in line with the constraint derived in Sect. 4.1. This implies that our result is independent of the adopted cluster detection algorithm. We also performed the analysis by considering the clusters in the MMF3 sample with S/N > 6, and for which the COSMO entry in the union catalogue is set to ‘T’, meaning that these clusters are part of the cosmological sample, following Planck Collaboration XXIV (2016). Because the statistics are poorer in this case, we analysed the 2PCF in a single redshift bin including clusters with z ≤ 0.8 for a total of 430 objects. As the modelling provides reduced χ2 estimates that are not close to 1, we conclude that in this case, the 2PCF signal does not allow a reliable constraint on bSZ.
In order to further assess the robustness of our results on (1 − bSZ), we computed the 2PCF model at the sample median redshifts for each redshift bin, instead of adopting the mean redshift, as discussed in Sect. 3. In this way, we derived a shift of the median (1 − bSZ) of ∼0.006σ. In addition, the reduction of the 2PCF radial range to s ∈ [15, 150] h−1 Mpc or to s ∈ [10, 90] h−1 Mpc implies comparable results, namely shifts of the median (1 − bSZ) lower than ∼0.6σ, and variations in the 1σ interval extension lower than ∼50%. We also checked the impact of a change in the definition of the effective bias, beff, assuming the median of the halo bias distribution instead of considering its mean, as done in Eq. (13). In this case, we obtained a shift of the median (1 − bSZ) corresponding to ∼0.5σ. As the tests described above showed shifts in the median bSZ that are within 1σ of the constraint presented in Sect. 4.1, we can conclude that our results are robust with respect to the investigated modelling choices. Lastly, Salvati et al. (2020) showed that the impact of the halo mass function calibration has a subdominant impact on current cluster count analyses. It will become a relevant source of systematic errors in upcoming surveys, for instance those from Euclid (Laureijs et al. 2011) and the Large Synoptic Survey Telescope (LSST Science Collaboration 2009), because of the larger cluster statistics they will provide. As cluster clustering has a lower constraining power compared to counts, we expect the mass function calibration to provide a negligible impact on the bSZ constraints derived in this work. The same is expected for the halo bias calibration.
4.3. Constraints on cosmological parameters
To further investigate the consistency of our modelling choices with those adopted by Planck Collaboration XXIV (2016), we performed a cosmological analysis aiming at constraining σ8 and Ωm simultaneously by assuming the same Gaussian priors on bSZ as were considered by Planck Collaboration XXIV (2016). Specifically, we assumed large flat priors for σ8 and Ωm, while for the other cosmological parameters, we assumed the same values from Planck18 that were used in the previous section. We also assumed the same Gaussian priors as adopted in Sect. 4.1 on the scaling relation parameters, namely Y*, α, β, and σlnY. We found that σ8 is not constrained through this analysis, while we found 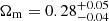 with the WtG bSZ prior,
with the WtG bSZ prior, 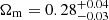 with the CCCP prior, and
with the CCCP prior, and 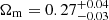 with the CMB lensing prior (see Fig. 4). These results are fully consistent and competitive, in terms of uncertainties, with those derived by Planck Collaboration XXIV (2016). Similar uncertainties on Ωm were obtained by Marulli et al. (2018) and Lindholm et al. (2021), who modelled the 2PCF of 182 and 1892 X-ray selected galaxy clusters, respectively. In addition, Marulli et al. (2018) found that σ8 could not be accurately constrained, in agreement with our results. In general, recent analyses of cluster clustering showed that the constraints on Ωm are significantly more robust than those derived on σ8 (Lindholm et al. 2021; Lesci et al. 2022b). In addition, we note that significant changes in the value of bSZ do not imply significant variations in the Ωm posteriors, similar to what was found by Planck Collaboration XXIV (2016).
with the CMB lensing prior (see Fig. 4). These results are fully consistent and competitive, in terms of uncertainties, with those derived by Planck Collaboration XXIV (2016). Similar uncertainties on Ωm were obtained by Marulli et al. (2018) and Lindholm et al. (2021), who modelled the 2PCF of 182 and 1892 X-ray selected galaxy clusters, respectively. In addition, Marulli et al. (2018) found that σ8 could not be accurately constrained, in agreement with our results. In general, recent analyses of cluster clustering showed that the constraints on Ωm are significantly more robust than those derived on σ8 (Lindholm et al. 2021; Lesci et al. 2022b). In addition, we note that significant changes in the value of bSZ do not imply significant variations in the Ωm posteriors, similar to what was found by Planck Collaboration XXIV (2016).
 |
Fig. 4. Comparison of the results on Ωm obtained by assuming flat priors on Ωm and σ8, along with external priors on bSZ, namely WtG (blue; von der Linden et al. 2014), CCCP (red; Hoekstra et al. 2015) and CMB lensing (green; Planck Collaboration XXIV 2016). For each bSZ prior, the result at the top was derived from the cluster clustering measurements presented in this paper, the middle result refers to the cluster counts analysis by Planck Collaboration XXIV (2016), and the bottom result represents the combination of Planck cluster clustering and counts. The constraint from Planck18 is shown in orange. |
We also derived an estimate of Ωm from the combination of cluster clustering and counts by assuming them to be statistically independent. Hurier & Lacasa (2017) showed that cluster counts and thermal SZ power spectrum are not significantly correlated. The thermal SZ power spectrum mainly depends on massive haloes, while for the number counts, the main contribution comes from lower-mass halos. The differences between the two galaxy cluster populations imply a weak correlation of these probes. As the clustering of SZ selected clusters encloses the same information contained in the SZ power spectrum, we expect a similar behavior for its correlation with counts. With respect to the analysis based on counts only, we found that the uncertainty on Ωm is reduced by a factor of ∼25%−30% if clustering is included in the likelihood. This confirms the importance of including cluster clustering in cosmological analyses (see also Sartoris et al. 2016; Euclid Collaboration 2022; Garrel et al. 2022) in order to fully exploit the cluster statistics information.
5. Summary and discussion
We analysed the 3D 2PCF monopole of the galaxy clusters detected by Planck Collaboration XXVII (2016), focusing on the estimate of the Planck mass bias, bSZ. Following Planck Collaboration XXIV (2016), we based our analysis on the cosmological sample consisting of detections by the MMF3 matched filter (Melin et al. 2006, 2012), considering clusters with a confirmed counterpart in external data sets and having an assigned redshift estimate, with a redshift limit z ≤ 0.8, for a total of 920 clusters. Differently from Planck Collaboration XXIV (2016), we did not apply any cut in S/N to the sample. This does not imply any potential problems due to the reliability of the selection function at low S/N because our model does not rely on assumptions on the sample completeness.
By analysing the 2PCF in the redshift bins z < 0.2 and z ∈ [0.2, 0.8] within the cluster-centric radial range r ∈ [10, 150] h−1 Mpc, we derived 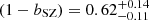 . This result fully agrees with what was found by Planck Collaboration VI (2020) by combining primary CMB likelihood and Planck cluster counts. Thus, we confirmed that Planck cluster statistics provides values of bSZ that are lower than what was predicted by numerical simulations (Nagai et al. 2007; Piffaretti & Valdarnini 2008; Meneghetti et al. 2010; Rasia et al. 2012; Le Brun et al. 2017; Henson et al. 2017; Gianfagna et al. 2023). As redshift errors are not quoted in Planck data products, we also included the power spectrum damping due to redshift uncertainties by means of a free parameter representing the typical redshift error, namely σz. Thus, we simultaneously calibrated σz and bSZ, finding no significant changes in bSZ and
. This result fully agrees with what was found by Planck Collaboration VI (2020) by combining primary CMB likelihood and Planck cluster counts. Thus, we confirmed that Planck cluster statistics provides values of bSZ that are lower than what was predicted by numerical simulations (Nagai et al. 2007; Piffaretti & Valdarnini 2008; Meneghetti et al. 2010; Rasia et al. 2012; Le Brun et al. 2017; Henson et al. 2017; Gianfagna et al. 2023). As redshift errors are not quoted in Planck data products, we also included the power spectrum damping due to redshift uncertainties by means of a free parameter representing the typical redshift error, namely σz. Thus, we simultaneously calibrated σz and bSZ, finding no significant changes in bSZ and 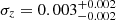 , which is in line with the fact that most of the cluster redshifts are spectroscopic. In addition, from the analysis of the Planck union catalogue of clusters, we showed that our result does not depend on the adopted cluster detection algorithm. We also found that a redshift evolution of bSZ is not necessary to describe our clustering measurements.
, which is in line with the fact that most of the cluster redshifts are spectroscopic. In addition, from the analysis of the Planck union catalogue of clusters, we showed that our result does not depend on the adopted cluster detection algorithm. We also found that a redshift evolution of bSZ is not necessary to describe our clustering measurements.
By adopting priors on bSZ from external data sets, we found results on Ωm that fully agree and are competitive, in terms of uncertainties, with those derived from cluster counts by Planck Collaboration XXIV (2016), while σ8 is not constrained. By assuming cluster clustering and counts to be statistically independent, we found that their combination provides a reduction of up to ∼30% in the Ωm uncertainty derived from counts. Future stage-4 CMB experiments (Abazajian et al. 2016) will detect about 105 galaxy clusters through the SZ effect, which will significantly enhance the cluster statistical analyses. This will improve the calibration of the hydrostatic mass bias from cluster clustering, and might shed light on the degeneracy between σ8 and mass bias. This degeneracy cannot be investigated with current data because σ8 is not constrained, as we detailed in Sect. 4.3. As a consequence, along with cluster abundance, cluster clustering will play a crucial role in the understanding of the current cosmological tensions between early and late Universe observations.
Acknowledgments
We acknowledge support from the grants PRIN-MIUR 2017 WSCC32 and ASI n.2018-23-HH.0. GC thanks the support from INAF theory Grant 2022: Illuminating Dark Matter using Weak Lensing by Cluster Satellites, PI: Carlo Giocoli. MS acknowledges financial contributions from contract ASI-INAF n.2017-14-H.0 and contract INAF mainstream project 1.05.01.86.10.
References
- Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, ArXiv e-prints [arXiv:1610.02743] [Google Scholar]
- Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2020, Phys. Rev. D, 102, 023509P [NASA ADS] [CrossRef] [Google Scholar]
- Aguado-Barahona, A., Rubiño-Martín, J. A., Ferragamo, A., et al. 2022, A&A, 659, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcock, C., & Paczynski, B. 1979, Nature, 281, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Baltz, E. A., Marshall, P., & Oguri, M. 2009, J. Cosmol. Astropart. Phys., 1, 15 [Google Scholar]
- Becker, M. R., & Kravtsov, A. V. 2011, ApJ, 740, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bellagamba, F., Sereno, M., Roncarelli, M., et al. 2019, MNRAS, 484, 1598 [Google Scholar]
- Beltz-Mohrmann, G. D., & Berlind, A. A. 2021, ApJ, 921, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Beutler, F., Saito, S., Seo, H.-J., et al. 2014, MNRAS, 443, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Chiu, I. N., Okumura, T., Oguri, M., et al. 2020, MNRAS, 498, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Costanzi, M., Rozo, E., Simet, M., et al. 2019, MNRAS, 488, 4779 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., & Guzzo, L. 2012, MNRAS, 427, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Despali, G., Giocoli, C., Angulo, R. E., et al. 2016, MNRAS, 456, 2486 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, J. P., Zhang, Y., Song, J., et al. 2014, MNRAS, 443, 1713 [NASA ADS] [CrossRef] [Google Scholar]
- Euclid Collaboration (Fumagalli, A., et al.) 2022, ArXiv e-prints [arXiv:2211.12965] [Google Scholar]
- Euclid Collaboration (Castro, T., et al.) 2023, A&A, 671, A100 [CrossRef] [EDP Sciences] [Google Scholar]
- Ferragamo, A., Barrena, R., Rubiño-Martín, J. A., et al. 2021, A&A, 655, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Farieta, J. E., Marulli, F., Moscardini, L., Veropalumbo, A., & Casas-Miranda, R. A. 2020, MNRAS, 494, 1658 [CrossRef] [Google Scholar]
- Garrel, C., Pierre, M., Valageas, P., et al. 2022, A&A, 663, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gianfagna, G., Rasia, E., Cui, W., et al. 2023, MNRAS, 518, 4238 [Google Scholar]
- Gil-Marín, H., Wagner, C., Verde, L., Porciani, C., & Jimenez, R. 2012, J. Cosmol. Astropart. Phys., 11, 29 [Google Scholar]
- Hamilton, A. J. S. 1992, ApJ, 385, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Hartlap, J., Simon, P., & Schneider, P. 2007, A&A, 464, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henson, M. A., Barnes, D. J., Kay, S. T., McCarthy, I. G., & Schaye, J. 2017, MNRAS, 465, 3361 [NASA ADS] [CrossRef] [Google Scholar]
- Herbonnet, R., Sifón, C., Hoekstra, H., et al. 2020, MNRAS, 497, 4684 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Herbonnet, R., Muzzin, A., et al. 2015, MNRAS, 449, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Hurier, G., & Lacasa, F. 2017, A&A, 604, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ibitoye, A., Tramonte, D., Ma, Y.-Z., & Dai, W.-M. 2022, ApJ, 935, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Keihänen, E., Kurki-Suonio, H., Lindholm, V., et al. 2019, A&A, 631, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerscher, M., Szapudi, I., & Szalay, A. S. 2000, ApJ, 535, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Labatie, A., Starck, J. L., Lachièze-Rey, M., & Arnalte-Mur, P. 2012, Stat. Methodol., 9, 85 [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Le Brun, A. M. C., McCarthy, I. G., Schaye, J., & Ponman, T. J. 2014, MNRAS, 441, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Le Brun, A. M. C., McCarthy, I. G., Schaye, J., & Ponman, T. J. 2017, MNRAS, 466, 4442 [Google Scholar]
- Lesci, G. F., Marulli, F., Moscardini, L., et al. 2022a, A&A, 659, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesci, G. F., Nanni, L., Marulli, F., et al. 2022b, A&A, 665, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, A., & Challinor, A. 2011, Astrophysics Source Code Library [record ascl:1102.026] [Google Scholar]
- Lindholm, V., Finoguenov, A., Comparat, J., et al. 2021, A&A, 646, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- LSST Science Collaboration (Abell, P. A., et al.) 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Makiya, R., Ando, S., & Komatsu, E. 2018, MNRAS, 480, 3928 [Google Scholar]
- Marulli, F., Veropalumbo, A., & Moresco, M. 2016, Astron. Comput., 14, 35 [Google Scholar]
- Marulli, F., Veropalumbo, A., Sereno, M., et al. 2018, A&A, 620, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marulli, F., Veropalumbo, A., García-Farieta, J. E., et al. 2021, ApJ, 920, 13 [Google Scholar]
- Medezinski, E., Battaglia, N., Umetsu, K., et al. 2018, PASJ, 70, S28 [NASA ADS] [Google Scholar]
- Melchior, P., Gruen, D., McClintock, T., et al. 2017, MNRAS, 469, 4899 [CrossRef] [Google Scholar]
- Melin, J. B., Bartlett, J. G., & Delabrouille, J. 2006, A&A, 459, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melin, J. B., Aghanim, N., Bartelmann, M., et al. 2012, A&A, 548, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneghetti, M., Rasia, E., Merten, J., et al. 2010, A&A, 514, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moresco, M., Veropalumbo, A., Marulli, F., Moscardini, L., & Cimatti, A. 2021, ApJ, 919, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Murata, R., Oguri, M., Nishimichi, T., et al. 2019, PASJ, 71, 107 [CrossRef] [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Oguri, M., & Hamana, T. 2011, MNRAS, 414, 1851 [NASA ADS] [CrossRef] [Google Scholar]
- Penna-Lima, M., Bartlett, J. G., Rozo, E., et al. 2017, A&A, 604, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piffaretti, R., & Valdarnini, R. 2008, A&A, 491, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2016, A&A, 594, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVII. 2016, A&A, 594, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasia, E., Meneghetti, M., Martino, R., et al. 2012, New J. Phys., 14, 055018 [Google Scholar]
- Salvati, L., Douspis, M., Ritz, A., Aghanim, N., & Babul, A. 2019, A&A, 626, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvati, L., Douspis, M., & Aghanim, N. 2020, A&A, 643, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvati, L., Saro, A., Bocquet, S., et al. 2022, ApJ, 934, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Sartoris, B., Biviano, A., Fedeli, C., et al. 2016, MNRAS, 459, 1764 [Google Scholar]
- Sereno, M., & Ettori, S. 2017, MNRAS, 468, 3322 [CrossRef] [Google Scholar]
- Sereno, M., Veropalumbo, A., Marulli, F., et al. 2015, MNRAS, 449, 4147 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., Covone, G., Izzo, L., et al. 2017, MNRAS, 472, 1946 [Google Scholar]
- Sheth, R. K., & Tormen, G. 1999, MNRAS, 308, 119 [Google Scholar]
- Sheth, R. K., Mo, H. J., & Tormen, G. 2001, MNRAS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Shirasaki, M., Lau, E. T., & Nagai, D. 2018, MNRAS, 477, 2804 [NASA ADS] [CrossRef] [Google Scholar]
- Simet, M., McClintock, T., Mandelbaum, R., et al. 2017, MNRAS, 466, 3103 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. P., Mazzotta, P., Okabe, N., et al. 2016, MNRAS, 456, L74 [Google Scholar]
- Stern, C., Dietrich, J. P., Bocquet, S., et al. 2019, MNRAS, 485, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Taruya, A., & Hiramatsu, T. 2008, ApJ, 674, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Taruya, A., Nishimichi, T., & Saito, S. 2010, Phys. Rev. D, 82, 063522 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [Google Scholar]
- Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- To, C., Krause, E., Rozo, E., et al. 2021, Phys. Rev. Lett., 126, 141301 [NASA ADS] [CrossRef] [Google Scholar]
- Veropalumbo, A., Marulli, F., Moscardini, L., Moresco, M., & Cimatti, A. 2016, MNRAS, 458, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- von der Linden, A., Mantz, A., Allen, S. W., et al. 2014, MNRAS, 443, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Wicker, R., Douspis, M., Salvati, L., & Aghanim, N. 2022, Eur. Phys. J. Web Conf., 257, 00046 [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Z., Wu, H. Y., Zhang, Y., et al. 2022, ArXiv e-prints [arXiv:2202.08211] [Google Scholar]
- Zubeldia, Í., & Challinor, A. 2019, MNRAS, 489, 401 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Redshift distribution n(z) of the galaxy clusters considered in the analysis. The blue histogram shows the observed binned n(z), and the black curve represents n(z) smoothed with a Gaussian kernel (with an rms equal to 0.02) that was used to build up the random catalogue. |
| In the text | |
 |
Fig. 2. Redshift-space 2PCF monopole (black dots) of the Planck clusters in the spatial range s ∈ [10, 150] h−1 Mpc for z < 0.2 (left plot), and s ∈ [15, 150] h−1 Mpc for z ∈ [0.2, 0.8] (right plot). The blue bands represent the model 68% confidence level derived from the posterior of the free parameters considered in the analysis described in Sect. 4.1. |
| In the text | |
 |
Fig. 3. Comparison of the results on (1 − bSZ) with the literature. The median, 16th and 84th percentiles are shown. The black dot shows the constraint derived in this work. Then, in order from top to bottom, the following results are shown: Planck Collaboration VI (2020; orange), von der Linden et al. (2014; blue) Hoekstra et al. (2015; red), Planck Collaboration XXIV (2016; dark green), Smith et al. (2016; grey), Sereno & Ettori (2017; magenta), Penna-Lima et al. (2017; brown), Medezinski et al. (2018; cyan), Herbonnet et al. (2020; pink), Zubeldia & Challinor (2019; purple), Salvati et al. (2019; turquoise), Salvati et al. (2022; green), Makiya et al. (2018; dark blue), Wicker et al. (2022; violet), Ibitoye et al. (2022; indigo), Ferragamo et al. (2021; orange), and Aguado-Barahona et al. (2022; dark brown). |
| In the text | |
 |
Fig. 4. Comparison of the results on Ωm obtained by assuming flat priors on Ωm and σ8, along with external priors on bSZ, namely WtG (blue; von der Linden et al. 2014), CCCP (red; Hoekstra et al. 2015) and CMB lensing (green; Planck Collaboration XXIV 2016). For each bSZ prior, the result at the top was derived from the cluster clustering measurements presented in this paper, the middle result refers to the cluster counts analysis by Planck Collaboration XXIV (2016), and the bottom result represents the combination of Planck cluster clustering and counts. The constraint from Planck18 is shown in orange. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} P(d|Y_{500},\sigma _{Yi}(\theta _{500}),q) = \frac{1}{2}\left[ 1+\text{ erf}\left(\frac{Y_{500}-q\sigma _{Yi}(\theta _{500})}{\sqrt{2}\sigma _{Yi}(\theta _{500})}\right) \right], \end{aligned} $$](/articles/aa/full_html/2023/06/aa46261-23/aa46261-23-eq2.gif)
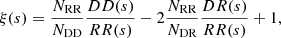
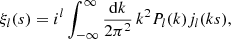
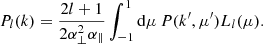
![$$ \begin{aligned} k^\prime = \frac{k}{\alpha _\perp } \left[1 + \mu ^2 \left( \frac{\alpha ^{2}_\perp }{\alpha ^{2}_\parallel } -1 \right)\right]^{1/2} \, , \end{aligned} $$](/articles/aa/full_html/2023/06/aa46261-23/aa46261-23-eq9.gif)
![$$ \begin{aligned} \mu ^\prime = \mu \,\frac{\alpha _\perp }{\alpha _\parallel } \left[1 + \mu ^2 \left( \frac{\alpha ^{2}_\perp }{\alpha ^{2}_\parallel } - 1 \right)\right]^{-1/2}\, , \end{aligned} $$](/articles/aa/full_html/2023/06/aa46261-23/aa46261-23-eq10.gif)
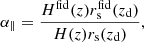
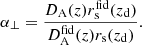
![$$ \begin{aligned} P(k^\prime , \mu^\prime )&= D_{\rm FoG}(k^\prime , \mu^\prime , f, \sigma _{\rm v})\,\biggl [b_{\rm eff}^2P_{\delta \delta }(k^\prime ) + 2fb_{\rm eff}\mu {\prime }^2P_{\delta \theta }(k^\prime )\nonumber \\&\quad + f^2\mu {\prime }^4P_{\theta \theta }(k^\prime ) + b_{\rm eff}^3A(k^\prime , \mu^\prime , f) + b_{\rm eff}^4B(k^\prime , \mu^\prime , f)\biggr ] , \end{aligned} $$](/articles/aa/full_html/2023/06/aa46261-23/aa46261-23-eq15.gif)
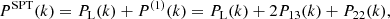
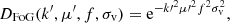
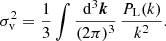
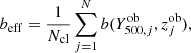
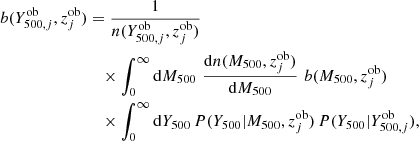
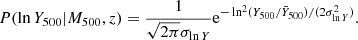
![$$ \begin{aligned} E^{-\beta }(z)\left[\frac{D_{\rm A}^2(z) \bar{Y}_{500}}{\mathrm{10^{-4}\,Mpc^2}}\right] = Y_* \left[ {h \over 0.7} \right]^{-2+\alpha } \left[\frac{(1-b_{\rm SZ})\, M_{500}}{6\times 10^{14}\,{M}_\odot }\right]^{\alpha }, \end{aligned} $$](/articles/aa/full_html/2023/06/aa46261-23/aa46261-23-eq30.gif)