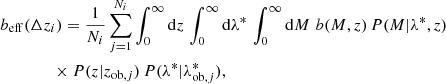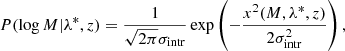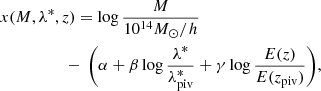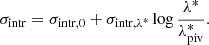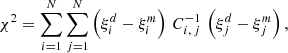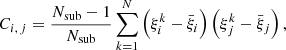| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202243538 | |
| Published online | 14 September 2022 | |
AMICO galaxy clusters in KiDS-DR3: Constraints on cosmological parameters and on the normalisation of the mass-richness relation from clustering⋆
1
Dipartimento di Fisica e Astronomia “Augusto Righi” – Alma Mater Studiorum Università di Bologna, via Piero Gobetti 93/2, 40129 Bologna, Italy
e-mail: giorgio.lesci2@unibo.it
2
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, via Piero Gobetti 93/3, 40129 Bologna, Italy
3
Institute of Cosmology & Gravitation, University of Portsmouth, Dennis Sciama Building, Portsmouth PO1 3FX, UK
4
INFN – Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
5
Dipartimento di Fisica, Università degli Studi Roma Tre, via della Vasca Navale 84, 00146 Roma, Italy
6
Zentrum für Astronomie, Universität Heidelberg, Philosophenweg 12, 69120 Heidelberg, Germany
7
ITP, Universität Heidelberg, Philosophenweg 16, 69120 Heidelberg, Germany
8
INAF – Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
9
Dipartimento di Fisica “E. Pancini”, Università di Napoli Federico II, C.U. di Monte Sant’Angelo, via Cintia, 80126 Napoli, Italy
10
INAF – Osservatorio Astronomico di Capodimonte, Salita Moiariello 16, 80131 Napoli, Italy
11
INFN – Sezione di Napoli, via Cintia, 80126 Napoli, Italy
Received:
14
March
2022
Accepted:
24
June
2022
Aims. We analysed the clustering of a photometric sample of galaxy clusters selected from the Third Data Release of the Kilo-Degree Survey, focusing on the redshift-space two-point correlation function (2PCF). We compared our measurements to theoretical predictions of the standard Λ cold dark matter (ΛCDM) cosmological model.
Methods. We measured the 2PCF of the sample in the cluster-centric radial range r ∈ [5, 80] h−1 Mpc, considering 4934 galaxy clusters with richness λ* ≥ 15 in the redshift range z ∈ [0.1, 0.6]. A Markov chain Monte Carlo analysis has been performed to constrain the cosmological parameters Ωm, σ8, and S8 ≡ σ8(Ωm/0.3)0.5, assuming Gaussian priors on the mass-richness relation given by the posteriors obtained from a joint analysis of cluster counts and weak lensing. In addition, we constrained the normalisation of the mass-richness relation, α, with fixed cosmological parameters.
Results. We obtained Ωm = 0.28+0.05−0.04, σ8 = 0.82+0.14−0.12, and S8 = 0.80+0.08−0.08. The constraint on S8 is consistent within 1σ with the results from WMAP and Planck. Furthermore, by fixing the cosmological parameters to those provided by Planck, we obtained α = 0.12+0.06−0.06, which is fully consistent with the result obtained from the joint analysis of cluster counts and weak lensing performed for this sample.
Key words: galaxies: clusters: general / cosmology: observations / large-scale structure of Universe / surveys
Some supplementary data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/665/A100
© G. F. Lesci et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
According to the standard Λcold dark matter (ΛCDM) cosmological model, galaxy clusters are the largest gravitationally bound systems in the Universe, lying in the highest peaks of the matter density field (Kaiser 1984). Through their abundances and clustering, these objects trace the statistical properties of the matter density field and its growth (Allen et al. 2011), providing stringent constraints on cosmological parameters. However, it is difficult to fully exploit the clustering properties of galaxy clusters because collecting large homogeneous cluster samples is a complex task. Surveys of galaxies, probing increasingly larger volumes of the Universe, have played a primary role in this field (see e.g., Guzzo et al. 2013; de Jong et al. 2015; Aihara et al. 2018). Ongoing and forthcoming wide extra-galactic surveys, from the lowest to the highest frequencies, will provide complete and pure galaxy cluster samples up to high redshifts and down to low masses. These surveys include the Kilo Degree Survey1 (KiDS, de Jong et al. 2017; Kuijken et al. 2019), the Dark Energy Survey2 (The Dark Energy Survey Collaboration 2005; Abbott et al. 2021), the Vera C. Rubin Observatory LSST3 (LSST Dark Energy Science Collaboration 2012, 2021), and Euclid4 (Amendola et al. 2018; Euclid Collaboration 2019, 2020; Scaramella et al. 2022) in the optical and near-infrared, the South Pole Telescope5 (Bayliss et al. 2016; Chown et al. 2018), the Atacama Cosmology Telescope6 (Naess et al. 2020; Orlowski-Scherer et al. 2021), and the Simons Observatory7 (Ade et al. 2019; Xu et al. 2021) surveys at high-radio frequencies, and eROSITA8 (Brunner et al. 2022; Liu et al. 2022) in X-rays.
Although it is observationally expensive to build up complete and pure samples of galaxy clusters covering wide enough ranges of masses and redshifts, there are numerous advantages in exploiting clusters as cosmic tracers. Galaxy clusters are more clustered than galaxies, with a clustering signal that is progressively stronger for richer systems (see e.g., Moscardini et al. 2001, and references therein). Furthermore, clusters are relatively unaffected by nonlinear dynamics at small scales, and the redshift-space anisotropies on large comoving scales have a minor impact on the cluster clustering compared to galaxies because the bias is larger (see e.g., Kaiser 1987; Hamilton 1992). Having smaller theoretical uncertainties over the description of nonlinear dynamics and redshift-space distortions, the modelling of the cluster clustering signal is potentially less affected by systematics than in the galaxy clustering case. Large galaxy cluster samples have been exploited to provide strong cosmological constraints from both second-order and third-order statistics (see e.g., Estrada et al. 2009; Veropalumbo et al. 2014, 2016; Marulli et al. 2018, 2021; Moresco et al. 2021; Lindholm et al. 2021, and references therein). These constraints are even more robust when cluster clustering is combined with cluster number counts (e.g., Mana et al. 2013; Salvati et al. 2018).
Furthermore, measuring cluster masses gives the opportunity of predicting the effective bias of the cluster sample as a function of the cosmological model. It is thus crucial to accurately estimate the cluster masses, possibly with multiple independent probes, such as X-ray emission or the Sunyaev-Zel’dovich effect, and to calibrate mass-observable scaling relations. In view of the ongoing and next-generation large photometric surveys, which explore the Universe in visible and near-infrared wavelengths, it is decisive to estimate the cluster mass-observable scaling relations involving quantities measured in these bands. Currently, the most reliable mass measurements are provided by weak gravitational lensing (e.g., Bardeau et al. 2007; Okabe et al. 2010; Hoekstra et al. 2012; Melchior et al. 2015; Schrabback et al. 2018; Stern et al. 2019; Sereno et al. 2017; Giocoli et al. 2021; Ingoglia et al. 2022). Combining this information with the estimate of some optical cluster properties, such as the richness, it is possible to derive cluster mass-observable scaling relations.
The goal of this paper is to present a cosmological analysis based on the monopole of the redshift-space two-point correlation function (2PCF), measured in the catalogue of galaxy clusters developed by Maturi et al. (2019). This catalogue has been built up through the use of the Adaptive Matched Identifier of Clustered Objects (AMICO) algorithm (Bellagamba et al. 2018) in the Third Data Release of the Kilo Degree Survey (KiDS-DR3, de Jong et al. 2017). In this work, we analyse the AMICO KiDS-DR3 catalogue in two redshift bins, assuming a flat ΛCDM cosmological model, including in the modelling the non-negligible effects of the errors of photometric redshifts (photo-zs) on the 2PCF shape. In particular, our reference cosmological model is given by Planck Collaboration VI (2020, Table 2, TT, TE, and EE+lowE). Through this analysis, we constrain the matter density parameter, Ωm, the amplitude of the density fluctuations, σ8, and the cluster normalisation parameter, S8 ≡ σ8(Ωm/0.3)0.5. Furthermore, by fixing the cosmological parameters, we infer the normalisation of the cluster mass-richness scaling relation, finding results consistent with those derived from the joint analysis of cluster counts and weak lensing by Lesci et al. (2022) in KiDS-DR3.
The statistical analyses presented in this paper are performed with the CosmoBolognaLib9 (CBL; Marulli et al. 2016), a set of free software C++/Python numerical libraries for cosmological calculations. Specifically, both the measurements and the statistical Bayesian analyses are performed with the CBL V5.3.
The paper is organised as follows. In Sect. 2 we present the AMICO KiDS-DR3 cluster catalogue. In Sect. 3 we describe the methods used to measure and model the 2PCF of this sample. The results of our analysis are presented in Sect. 4, leading to our conclusions, which are discussed in Sect. 5.
2. Data
KiDS (de Jong et al. 2013) is an ESO public-imaging survey that will cover 1350 square degrees when it is completed, exploiting the OmegaCAM wide-field camera (Kuijken 2011) on the Very Large Telescope (VLT) survey telescope (Capaccioli et al. 2012, VST) with a resolution of 0.21 arcsec pixel−1. This work is based on the catalogue of galaxy clusters detected in KiDS-DR3 (Maturi et al. 2019) by applying the AMICO algorithm (Bellagamba et al. 2018, discussed in Sect. 2.1). The KiDS-DR3 catalogue provides the 2 arcsec aperture photometry in the bands u, g, r, i, as well as photometric redshifts for all the detected galaxies down to the 5σ magnitude limits of 24.3, 25.1, 24.9, and 23.8 for the aforementioned bands, respectively, over a total area of 438 deg2. The effective area amounts to 377 deg2, obtained by excluding the regions of the sky affected by satellite tracks and haloes produced by bright stars, or falling in the secondary or tertiary halo masks used for the weak-lensing analysis (de Jong et al. 2015; Kuijken et al. 2015).
2.1. AMICO algorithm
AMICO (Bellagamba et al. 2018; Maturi et al. 2019) is an algorithm for the detection of galaxy clusters in photometric surveys, based on the optimal matched-filtering technique (see Maturi et al. 2005, for a detailed discussion). Specifically, AMICO adopts an iterative approach for the extraction of cluster candidates from the observed galaxy distribution, aiming at maximising the signal-to-noise ratio (S/N) of the overdensity detections, exploiting the statistical properties of both field galaxies and member galaxies, which are described by an arbitrary number of observed quantities.
In particular, the detection process adopted in this run of AMICO relies on angular coordinates, r-band magnitudes, and photo-zs of galaxies. The model adopted to describe the clusters is a convolution of a Schechter luminosity function (Schechter 1976) and a Navarro-Frenk-White profile (Navarro et al. 1997). Differently from other cluster-detection algorithms based on the so-called red sequence, colours are not considered by AMICO. This has been done to minimise the dependence of the cluster sample on the colour properties of the cluster members. Therefore, AMICO is expected to be effective also at higher redshifts, where the red sequence may be not prominent yet. AMICO has been applied on realistic mock catalogues reproducing the expected characteristics of the future Euclid photometric survey, achieving remarkable purity and completeness levels compared to other algorithms (Euclid Collaboration 2019). AMICO is one of the two algorithms for cluster identification officially adopted by the Euclid mission.
2.2. AMICO KiDS-DR3 catalogue
We analysed the clustering properties of the AMICO KiDS-DR3 cluster catalogue (Maturi et al. 2019), which contains 7988 galaxy clusters down to S/N = 3.5 that lie in the redshift range z ∈ [0.10, 0.80]. We accounted for the bias described in Maturi et al. (2019) that affects cluster redshifts, that is, we defined the corrected redshift as zcorr = z − 0.02 (1 + z). This bias corresponds to what was found in de Jong et al. (2017) by comparing the KiDS photo-zs to the GAMA spectroscopic redshifts (see their Table 8). In a small redshift range around z ∼ 0.32, the photo-z errors are higher and harder to model because of the shape of the g and r filter transmissions. In the following cosmological analysis (Sect. 4), we also considered the photo-z range z ∈ [0.10, 0.60] because we assumed priors on the mass-richness relation estimated from a weak-lensing analysis performed in this redshift range (see Bellagamba et al. 2019). Consequently, we decided to model the 2PCF in two separate redshift bins: z ∈ [0.10, 0.30] and z ∈ [0.35, 0.60].
In the analysis, we used the intrinsic richness, λ*, as mass proxy. It is defined as
where Pi(j) is the probability assigned by AMICO to the ith galaxy of being a member of a given detection j (see Maturi et al. 2019). The intrinsic richness thus represents the sum of the membership probabilities, that is, the weighted number of visible galaxies belonging to a detection, under the conditions given by Eq. (1). The sum of the membership probabilities is an excellent estimator of the true number of member galaxies, as shown in Bellagamba et al. (2018) by running the AMICO algorithm on mock catalogues (see Fig. 8 in the reference). In particular, in Eq. (1), zj is the redshift of the jth detected cluster, mi is the magnitude of the ith galaxy, and Ri corresponds to the distance of the ith galaxy from the centre of the cluster. The parameter Rmax(zj) represents the radius enclosing a mass M200 = 1014h−1 M⊙, such that the corresponding mean density is 200 times the critical density of the Universe at the given redshift zj. Lastly, m* is the typical magnitude of the Schechter function in the cluster model assumed in the AMICO algorithm. We use the term ’intrinsic richness’ as opposed to ’apparent richness’, both defined in Maturi et al. (2019). In particular, because the threshold in magnitude is always brighter than the survey limit thanks to the redshift dependence of m*, there is no dependence of λ* on the survey limit. Conversely, the apparent richness is a quantity that includes all visible galaxies and therefore is redshift dependent.
We considered only the clusters with λ* > 15, which ensures a purity higher than 97% over the whole sample (see Maturi et al. 2019). Consequently, the sample consists of 1019 clusters for z ∈ [0.10, 0.30] and 3915 clusters for z ∈ [0.35, 0.60]. Fig. 1 shows the redshift and richness distributions of the objects considered in the analysis.
 |
Fig. 1. Redshift and intrinsic richness distributions of the clusters in the sample. Top panel: redshift distribution after the correction for the redshift bias, including only objects with λ* > 15. The grey shaded areas represent the redshift ranges that were not used in the analysis. Bottom panel:λ* distribution of the objects in the redshift ranges z ∈ [0.10, 0.30] (black hatched histogram) and z ∈ [0.35, 0.60] (blue histogram). |
3. Method
3.1. Two-point correlation function estimator
We estimated the redshift-space 2PCF with the Landy & Szalay (1993) (LS) estimator,
where DD(r), RR(r), and DR(r) are the number of data-data, random-random, and data-random pairs with separation r ± Δr, respectively, while NDD, NRR, and NDR are the total number of data-data, random-random, and data-random pairs, respectively. This estimator is widely exploited in clustering studies as it is unbiased and with minimum variance for an infinitely large random sample and when |ξ|≪1 (Hamilton 1992; Kerscher et al. 2000; Labatie et al. 2012; Keihänen et al. 2019).
In order to build up the random catalogue, we extracted random (RA, Dec) cluster positions within the survey tiles by accounting for the same masks as were used by Maturi et al. (2019) for the construction of the cluster catalogue. Regarding the redshifts, we shuffled the observed photo-zs. Namely, to each object of the random sample, we assigned the photo-z randomly extracted from the AMICO KiDS-DR3 catalogue. Hence, the random sample has the same redshift distribution as the real sample by construction. We verified that the observed cluster distribution does not depend on the sky position, which is expected as Maturi et al. (2019) imposed the strict magnitude cut at r = 24, corresponding to the depth of the shallowest tile. The generated random catalogue is 30 times larger than the AMICO KiDS-DR3 cluster sample to limit shot noise effects. The observed coordinates were then converted into comoving ones by assuming the ΛCDM model, with cosmological parameters from Planck18 (Planck Collaboration VI 2020).
3.2. Two-point correlation function model
The observed redshift, zob, can be expressed as
where zc is the cosmological redshift, σz is the error on the redshift measurements, and v∥ is the component of the peculiar velocity along the line of sight. Therefore, using zob to estimate the comoving distance creates distortions in the measures of the 2PCF, not only because of the error on the measurements (σz), but also because zob encodes information on the peculiar motions along the line of sight (v∥). The peculiar motions cause the so-called dynamical distortions, an effect commonly known also as redshift-space distortions (RSD).
Since our whole analysis is performed on a catalogue extracted from photometric data, it is crucial to take the errors on the observed cluster redshifts into account. Following the approach presented in Sereno et al. (2015), we modelled the redshift-space 2D power spectrum as follows:
where PDM(k) is the dark matter power spectrum, 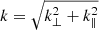 , with k∥ and k⊥ being the wave-vector components parallel and perpendicular to the line of sight, respectively, μ ≡ k∥/k, beff represents the effective bias factor (see Sect. 3.3), f is the growth rate, and the fμ2 term parametrises the coherent motions of large-scale structure, enhancing the clustering signal at all scales (Kaiser 1987). The exponential cut-off term describes the random perturbations affecting redshift measurements, caused by both nonlinear stochastic motions and redshift errors. This is a Gaussian damping term, which causes a scale-dependent effect by removing the signal over a typical scale k ∼ 1/σ, where σ represents the displacement along the line of sight due to random perturbations of cosmological redshifts, defined as
, with k∥ and k⊥ being the wave-vector components parallel and perpendicular to the line of sight, respectively, μ ≡ k∥/k, beff represents the effective bias factor (see Sect. 3.3), f is the growth rate, and the fμ2 term parametrises the coherent motions of large-scale structure, enhancing the clustering signal at all scales (Kaiser 1987). The exponential cut-off term describes the random perturbations affecting redshift measurements, caused by both nonlinear stochastic motions and redshift errors. This is a Gaussian damping term, which causes a scale-dependent effect by removing the signal over a typical scale k ∼ 1/σ, where σ represents the displacement along the line of sight due to random perturbations of cosmological redshifts, defined as
where H(zm) is the Hubble function computed at the mean redshift of the cluster distribution in the bin, zm, and σz is the typical cluster redshift error, expressed as
where σz, 0 is a free parameter in the analysis. We derived σz, 0 from the mock catalogue described in Maturi et al. (2019). In particular, we measured the conditional probability P(zob|ztr), where zob and ztr are the observed and true redshifts, respectively, in several bins of ztr, namely Δztr. We described the standard deviation of P(zob|ztr) through Eq. (6), where zm is the mean value of ztr within Δztr. Given the input galaxy photo-zs, AMICO provides unbiased estimates of redshift (see Maturi et al. 2019). Then we performed a statistical MCMC analysis assuming a common flat prior on σz, 0 in all the Δztr bins, obtaining σz, 0 = 0.02 with an uncertainty of ∼2 × 10−4, namely equal to ∼1%.
To derive the monopole of the correlation function, we integrated Eq. (4) over μ and computed the inverse Fourier transform of the result. The solution can be written as a function of beff as follows:
where ξ′(s) is the inverse Fourier transform of the monopole P′(k), that is,
and ξ″(s) and ξ‴(s) are the inverse Fourier transform of P″(k) and P‴(k), respectively,
We neglected geometric distortions, which appear when a fiducial cosmology is assumed (in our case, Planck Collaboration VI 2020, Table 2, TT, TE, and EE+lowE) to convert observed coordinates into physical ones, because their effect is negligible with respect to dynamic distortions and photo-z errors (see Marulli et al. 2012).
3.3. Effective bias and mass-richness relation
The cosmological model of structure formation and evolution predicts that the dark matter halo bias, b, primarily depends on halo mass and redshift. Specifically, at a fixed redshift, the bias increases with the tracer mass, while for a given mass, the bias is an increasing function of the redshift (e.g., Sheth & Tormen 1999). We derived the effective bias in the ith bin of redshift, namely Δzi, as
where Ni is the number of clusters in the ith redshift bin, j is the cluster index, and b is the halo bias, for which the model by Tinker et al. (2010) is assumed. As discussed in Sect. 4.1, the results do not significantly change when the halo bias model by Sheth et al. (2001) is assumed. In addition, P(M|λ*, z) is a log-normal distribution whose mean is given by the mass-richness scaling relation and the standard deviation (rms) is given by the intrinsic scatter, σintr, set as a free parameter of the model,
where
where E(z)≡H(z)/H0, and we set 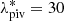 and zpiv = 0.35 following Bellagamba et al. (2019). In addition, the intrinsic scatter is expressed as
and zpiv = 0.35 following Bellagamba et al. (2019). In addition, the intrinsic scatter is expressed as
In Eq. (10), P(z|zob, j) and 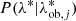 are Gaussian distributions, whose mean is the jth cluster’s observed redshift, zob, j, and richness,
are Gaussian distributions, whose mean is the jth cluster’s observed redshift, zob, j, and richness, 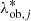 , respectively. The rms of P(z|zob, j) is expressed as σz, 0(1 + zob, j), where σz, 0 was derived from the mock catalogue developed by Maturi et al. (2019) as described in Sect. 3.2. Analogously, we derived an uncertainty on λ* amounting to ∼17% from the mock catalogue.
, respectively. The rms of P(z|zob, j) is expressed as σz, 0(1 + zob, j), where σz, 0 was derived from the mock catalogue developed by Maturi et al. (2019) as described in Sect. 3.2. Analogously, we derived an uncertainty on λ* amounting to ∼17% from the mock catalogue.
3.4. Likelihood
For the cosmological Bayesian analysis performed in this work, a standard Gaussian likelihood was considered,
with
where N is the number of comoving separation bins in which the 2PCF is computed, d and m indicate data and model, respectively, and 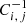 is the inverse of the covariance matrix. The covariance matrix measures the variance and the correlation between the different bins of the 2PCF. It is estimated from the data with the jackknife technique (Norberg et al. 2009),
is the inverse of the covariance matrix. The covariance matrix measures the variance and the correlation between the different bins of the 2PCF. It is estimated from the data with the jackknife technique (Norberg et al. 2009),
where 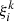 is the value of the correlation function at the ith bin for the kth subsample,
is the value of the correlation function at the ith bin for the kth subsample, 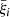 is the mean value of the subsample, and Nsub is the number of resamplings of our cluster catalogue. In particular, the survey tiles are set as the subsample regions for the jackknife.
is the mean value of the subsample, and Nsub is the number of resamplings of our cluster catalogue. In particular, the survey tiles are set as the subsample regions for the jackknife.
4. Results
Based on the methods outlined in Sect. 3, we performed a cosmological analysis of the redshift-space 2PCF of the AMICO KiDS-DR3 cluster sample. Our analysis was based on two fully independent redshift bins, z ∈ [0.10, 0.30] and z ∈ [0.35, 0.60], and we considered galaxy clusters with λ* > 15. The 2PCF of this cluster sample was estimated in the spatial range s ∈ [5, 80] h−1 Mpc. At larger scales, the clustering signal starts to be weak and is dominated by the errors, while at smaller scales, the signal is negligible as the cluster size sets the minimum cluster separation. In Sect. 4.1 we present the clustering measurements and cosmological analysis. The aim of this analysis is to constrain the matter density parameter, Ωm, the square root of the mass variance computed on a scale of 8 h−1 Mpc, σ8, and the cluster normalisation parameter, S8 ≡ σ8(Ωm/0.3)0.5, by assuming Gaussian priors for the parameters of the mass-richness relation. In addition, as described in Sect. 4.2, we investigated a method to infer the normalisation of the cluster mass-observable relation from cluster clustering measurements.
4.1. Constraints on cosmological parameters
We exploited the methods described in Sect. 3 to constrain the main parameters of the ΛCDM model. We assumed large flat priors for σ8 and Ωm, while for the parameters of the mass-richness relation (Eqs. (12) and (13)), α, β, γ, σintr, 0, and σintr, λ*, we considered Gaussian priors with the mean and standard deviation given by the posteriors derived from the joint analysis of cluster counts and weak lensing performed by Lesci et al. (2022). We also assumed a Gaussian prior on σz, 0, entering the damping factor of P(k) accounting for the uncertainties on the photo-zs (Eqs. (5) and (6)), with the mean equal to 0.02 and the standard deviation equal to 2 × 10−4 (see Sect. 3.2). Lastly, we assumed Gaussian priors for the baryon density, Ωb, the primordial spectral index, ns, and the normalised Hubble constant, h, assuming the same mean values derived by Planck Collaboration VI (2020, Table 2, TT, TE, and EE+lowE). With regard to the standard deviation of such priors, for Ωb and ns we imposed a standard deviation equal to five times the 1σ error derived by Planck, while for h we assumed a standard deviation equal to 0.1. We verified that the results do not significantly change if we instead use the 1σ errors derived from Planck as the standard deviations for the priors on Ωb, ns, and h. In Table 1 we show the priors and the posteriors of the free parameters of the model. In Fig. 2 we compare our 2PCF measurements in the two selected redshift ranges to the best-fit model. The statistical analysis was performed by assuming a standard Gaussian likelihood, defined in Eq. (14).
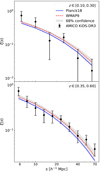 |
Fig. 2. Redshift-space 2PCF (black dots) of the AMICO KiDS-DR3 clusters in the spatial range s ∈ [5, 80] h−1 Mpc, and redshift ranges z ∈ [0.10, 0.30] (top panel) and z ∈ [0.35, 0.60] (bottom panel). In both panels, the grey band represents the 68% confidence level derived from the multivariate posterior of the free parameters considered in the cosmological analysis, described in Sect. 4.1. The model computed by assuming the cosmological parameters derived by Planck (Planck Collaboration VI 2020, Table 2, TT, TE, and EE+lowE; blue lines) and WMAP (Hinshaw et al. 2013, Table 3, WMAP-only Nine-year; red lines) is represented by the solid blue lines and by the dashed red lines, respectively. In both cases, the median values of the scaling relation parameters derived by Lesci et al. (2022) are assumed. |
Parameters considered in the cosmological analysis.
We obtained 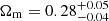 ,
, 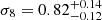 , and S8=
, and S8=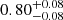 , where we quote the median and 16th and 84th percentiles, as shown in Fig. 3 and Table 1. These constraints agree within 1σ with the WMAP (Hinshaw et al. 2013, Table 3, WMAP-only Nine-year) and Planck results (Planck Collaboration VI 2020, Table 2, TT, TE, and EE+lowE). In addition, Fig. 4 shows that our constraint on S8 agrees within 1σ with the results obtained from the joint analysis of cluster counts and weak lensing performed in KiDS-DR3 by Lesci et al. (2022). The agreement within 1σ also holds for the cluster count analyses performed by Costanzi et al. (2019), based on SDSS-DR8 data, and by Bocquet et al. (2019), based on the 2500 deg2 SPT-SZ survey data, as well as for the results derived from the cosmic shear analyses performed by Amon et al. (2022) and Secco et al. (2022) on DES-Y3 data, Hikage et al. (2019) on HSC-Y1 data, and Asgari et al. (2021) on KiDS-DR4 data. In addition, our result on S8 agrees with the constraint by Lindholm et al. (2021), namely
, where we quote the median and 16th and 84th percentiles, as shown in Fig. 3 and Table 1. These constraints agree within 1σ with the WMAP (Hinshaw et al. 2013, Table 3, WMAP-only Nine-year) and Planck results (Planck Collaboration VI 2020, Table 2, TT, TE, and EE+lowE). In addition, Fig. 4 shows that our constraint on S8 agrees within 1σ with the results obtained from the joint analysis of cluster counts and weak lensing performed in KiDS-DR3 by Lesci et al. (2022). The agreement within 1σ also holds for the cluster count analyses performed by Costanzi et al. (2019), based on SDSS-DR8 data, and by Bocquet et al. (2019), based on the 2500 deg2 SPT-SZ survey data, as well as for the results derived from the cosmic shear analyses performed by Amon et al. (2022) and Secco et al. (2022) on DES-Y3 data, Hikage et al. (2019) on HSC-Y1 data, and Asgari et al. (2021) on KiDS-DR4 data. In addition, our result on S8 agrees with the constraint by Lindholm et al. (2021), namely 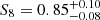 , derived from the autocorrelation of X-ray selected CODEX clusters. We also performed the analysis by assuming the halo bias model by Sheth et al. (2001), obtaining
, derived from the autocorrelation of X-ray selected CODEX clusters. We also performed the analysis by assuming the halo bias model by Sheth et al. (2001), obtaining 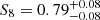 . This result agrees well with the result derived from the previously described analysis.
. This result agrees well with the result derived from the previously described analysis.
 |
Fig. 3. Constraints obtained from the cosmological analysis, compared to WMAP and Planck results. In the left panel, we show the 68% and 95% confidence levels in the Ωm − σ8 parameter space, along with the 1D marginalised posteriors with the relative intervals between the 16th and 84th percentiles, in the case of the cluster clustering analysis of the AMICO KiDS-DR3 catalogue (grey lines). In the same panel, we also display the results from WMAP (Hinshaw et al. 2013, Table 3, WMAP-only Nine-year; red lines) and Planck (Planck Collaboration VI 2020, Table 2, TT, TE, and EE+lowE; blue lines). In the right panel, we show the posteriors for the parameter S8, where the bands show the intervals between 16th and 84th percentiles. The colours are the same as in the left panel. |
4.2. Mass-observable scaling relation
Cluster clustering might provide robust constraints on the normalisation of the mass-observable relation, α, if a cosmological model is assumed (see e.g., Chiu et al. 2020). Based on the 2PCF measures used in the cosmological analysis detailed in the previous section, we also performed the analysis by assuming a flat prior on α and Gaussian priors on β, γ, σintr, 0, and σintr, λ*, given by the posteriors derived by Lesci et al. (2022), and the same prior on σz, 0 assumed in Sect. 4.1. In addition, we fixed the cosmological parameters to the values derived by Planck Collaboration VI (2020, Table 2, TT, TE, and EE+lowE). We obtained 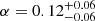 , which agrees within 1σ with the result obtained by Lesci et al. (2022), as shown in Fig. 5. It should be noted that the median value of α corresponds within 2σ to the prior considered in Sect. 4.1. This is due to the adopted prior on S8, whose value is higher than what was predicted by the clustering signal (see Fig. 4). A higher value of α is required to compensate for a higher S8.
, which agrees within 1σ with the result obtained by Lesci et al. (2022), as shown in Fig. 5. It should be noted that the median value of α corresponds within 2σ to the prior considered in Sect. 4.1. This is due to the adopted prior on S8, whose value is higher than what was predicted by the clustering signal (see Fig. 4). A higher value of α is required to compensate for a higher S8.
 |
Fig. 4. Comparison of the constraints on S8 ≡ σ8(Ωm/0.3)0.5 obtained, from top to bottom, from the cluster clustering analysis in the AMICO KiDS-DR3 catalogue (black dot), from the joint analysis of cluster counts and weak lensing in KiDS-DR3 performed by Lesci et al. (2022, pink dot), from the results obtained by Planck Collaboration VI (2020, blue dots), Hinshaw et al. (2013, red dots), Costanzi et al. (2019, green dot), Bocquet et al. (2019, brown dot), Amon et al. (2022) and Secco et al. (2022, magenta dot), Hikage et al. (2019, orange dot), and Asgari et al. (2021, cyan dot). The median and the 16th and 84th percentiles are shown. |
 |
Fig. 5. Constraint on the normalisation of the mass-richness relation, α. The result obtained from the cluster clustering analysis is shown in grey, and the constraint derived from the joint analysis of counts and weak lensing (Lesci et al. 2022) is shown in blue. The bands show the intervals between the 16th and 84th percentiles. |
5. Conclusions
We presented a study of the clustering properties of a photometric sample of galaxy clusters detected by applying the AMICO algorithm on KiDS-DR3 data. The catalogue consists of 4934 clusters in the redshift bins z ∈ [0.1, 0.3], z ∈ [0.35, 0.6], with intrinsic richness λ* > 15. We measured the monopole of the 2PCF and performed a cosmological statistical analysis. The clustering model considered includes a damping of the power spectrum to account for the uncertainties on the photo-zs. In addition, we derived the effective bias in each redshift bin (Eq. (10)) from the mass-richness scaling relation (Eq. (12)).
We performed a cosmological analysis by assuming flat priors on Ωm and σ8, and Gaussian priors on the parameters of the mass-richness relation given by the constraints derived by Lesci et al. (2022), from the joint analysis of cluster counts and weak lensing in KiDS-DR3. In addition, we marginalised our posteriors over the other cosmological parameters and over the damping of the power spectrum caused by the uncertainties on photo-zs. From this modelling, we derived 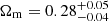 ,
, 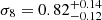 , and
, and 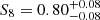 , which are consistent within 1σ with the results obtained from CMB experiments and from the most recent analyses of the evolved Universe. In addition, by fixing the cosmological parameters to the values derived by Planck Collaboration VI (2020, Table 2, TT, TE, and EE+lowE) and assuming Gaussian priors on the parameters β and γ of the mass-richness relation, we derived a robust constraint on the normalisation α. In particular, we obtained
, which are consistent within 1σ with the results obtained from CMB experiments and from the most recent analyses of the evolved Universe. In addition, by fixing the cosmological parameters to the values derived by Planck Collaboration VI (2020, Table 2, TT, TE, and EE+lowE) and assuming Gaussian priors on the parameters β and γ of the mass-richness relation, we derived a robust constraint on the normalisation α. In particular, we obtained 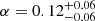 , which agrees within 1σ with the result obtained by Lesci et al. (2022).
, which agrees within 1σ with the result obtained by Lesci et al. (2022).
We expect more accurate constraints on the cosmological parameters and on the mass-richness scaling relation from the analysis of the latest KiDS-DR4 (Kuijken et al. 2019), which covers an area of ∼1000 square degrees (more than two-thirds of the final KiDS area and a factor ∼2.5 larger than DR3). KiDS-DR4 photometry also extends to the near-infrared (ugriZYJHKs), joining the data from KiDS and VIKING (Edge et al. 2013) surveys, which will lead to a better estimate of the photometric redshifts (Wright et al. 2019): this will be of great help for the application of the AMICO code (Maturi et al. in prep.), and will lead to the joint analysis of cluster weak lensing, counts, and clustering (Lesci et al., in prep.).
Acknowledgments
Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme IDs 177.A-3016, 177.A3017 and 177.A-3018, and on data products produced by Target/OmegaCEN, INAF-OACN, INAF-OAPD and the KiDS production team, on behalf of the KiDS consortium. The authors acknowledge the use of computational resources from the parallel computing cluster of the Open Physics Hub (https://site.unibo.it/openphysicshub/en) at the Physics and Astronomy Department in Bologna. F.M. and L.M. acknowledge the grants ASI n.I/023/12/0 and ASI n.2018-23-HH.0. L.M. acknowledges support from the grant PRIN-MIUR 2017 WSCC32. M.S. acknowledges financial contribution from contracts ASI-INAF n.2017-14-H.0 and INAF mainstream project 1.05.01.86.10. We thank Shahab Joudaki for his valuable advice.
References
- Abbott, T. M. C., Adamów, M., Aguena, M., et al. 2021, ApJS, 255, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Ade, P., Aguirre, J., Ahmed, Z., et al. 2019, JCAP, 2019, 056 [Google Scholar]
- Aihara, H., Armstrong, R., Bickerton, S., et al. 2018, PASJ, 70, S8 [NASA ADS] [Google Scholar]
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [Google Scholar]
- Amendola, L., Appleby, S., Avgoustidis, A., et al. 2018, Liv. Rev. Rel., 21, 2 [Google Scholar]
- Amon, A., Gruen, D., Troxel, M. A., et al. 2022, Phys. Rev. D, 105, 023514 [NASA ADS] [CrossRef] [Google Scholar]
- Asgari, M., Lin, C.-A., Joachimi, B., et al. 2021, A&A, 645, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardeau, S., Soucail, G., Kneib, J. P., et al. 2007, A&A, 470, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayliss, M. B., Ruel, J., Stubbs, C. W., et al. 2016, ApJS, 227, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Bellagamba, F., Roncarelli, M., Maturi, M., & Moscardini, L. 2018, MNRAS, 473, 5221 [NASA ADS] [CrossRef] [Google Scholar]
- Bellagamba, F., Sereno, M., Roncarelli, M., et al. 2019, MNRAS, 484, 1598 [Google Scholar]
- Bocquet, S., Dietrich, J. P., Schrabback, T., et al. 2019, ApJ, 878, 55 [Google Scholar]
- Brunner, H., Liu, T., Lamer, G., et al. 2022, A&A, 661, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capaccioli, M., Schipani, P., de Paris, G., et al. 2012, in Science from the Next Generation Imaging and Spectroscopic Surveys, 1 [Google Scholar]
- Chiu, I. N., Okumura, T., Oguri, M., et al. 2020, MNRAS, 498, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Chown, R., Omori, Y., Aylor, K., et al. 2018, ApJS, 239, 10 [Google Scholar]
- Costanzi, M., Rozo, E., Simet, M., et al. 2019, MNRAS, 488, 4779 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, J. T. A., Verdoes Kleijn, G. A., Kuijken, K. H., & Valentijn, E. A. 2013, Exp. Astron., 35, 25 [Google Scholar]
- de Jong, J. T. A., Verdoes Kleijn, G. A., Boxhoorn, D. R., et al. 2015, A&A, 582, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, J. T. A., Verdoes Kleijn, G. A., Erben, T., et al. 2017, A&A, 604, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edge, A., Sutherland, W., Kuijken, K., et al. 2013, The Messenger, 154, 32 [NASA ADS] [Google Scholar]
- Estrada, J., Sefusatti, E., & Frieman, J. A. 2009, ApJ, 692, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Euclid Collaboration (Adam, R., et al.) 2019, A&A, 627, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Euclid Collaboration (Blanchard, A., et al.) 2020, A&A, 642, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giocoli, C., Marulli, F., Moscardini, L., et al. 2021, A&A, 653, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzzo, L., Abbas, U., Adami, C., et al. 2013, The Messenger, 151, 41 [NASA ADS] [Google Scholar]
- Hamilton, A. J. S. 1992, ApJ, 385, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Hikage, C., Oguri, M., Hamana, T., et al. 2019, PASJ, 71, 43 [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [Google Scholar]
- Hoekstra, H., Mahdavi, A., Babul, A., & Bildfell, C. 2012, MNRAS, 427, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Ingoglia, L., Covone, G., Sereno, M., et al. 2022, MNRAS, 511, 1484 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1984, ApJ, 284, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [Google Scholar]
- Keihänen, E., Kurki-Suonio, H., Lindholm, V., et al. 2019, A&A, 631, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerscher, M., Szapudi, I., & Szalay, A. S. 2000, ApJ, 535, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K. 2011, The Messenger, 146, 8 [NASA ADS] [Google Scholar]
- Kuijken, K., Heymans, C., Hildebrandt, H., et al. 2015, MNRAS, 454, 3500 [Google Scholar]
- Kuijken, K., Heymans, C., Dvornik, A., et al. 2019, A&A, 625, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labatie, A., Starck, J. L., Lachièze-Rey, M., & Arnalte-Mur, P. 2012, Statistical Methodology, 9, 85 [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [Google Scholar]
- Lesci, G. F., Marulli, F., Moscardini, L., et al. 2022, A&A, 659, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindholm, V., Finoguenov, A., Comparat, J., et al. 2021, A&A, 646, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, A., Bulbul, E., Ghirardini, V., et al. 2022, A&A, 661, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- LSST Dark Energy Science Collaboration 2012, ArXiv e-prints [arXiv:1211.0310] [Google Scholar]
- LSST Dark Energy Science Collaboration 2021, ArXiv e-prints [arXiv:2101.04855] [Google Scholar]
- Mana, A., Giannantonio, T., Weller, J., et al. 2013, MNRAS, 434, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Bianchi, D., Branchini, E., et al. 2012, MNRAS, 426, 2566 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Veropalumbo, A., & Moresco, M. 2016, Astron. Comput., 14, 35 [Google Scholar]
- Marulli, F., Veropalumbo, A., Sereno, M., et al. 2018, A&A, 620, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marulli, F., Veropalumbo, A., García-Farieta, J. E., et al. 2021, ApJ, 920, 13 [Google Scholar]
- Maturi, M., Meneghetti, M., Bartelmann, M., Dolag, K., & Moscardini, L. 2005, A&A, 442, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maturi, M., Bellagamba, F., Radovich, M., et al. 2019, MNRAS, 485, 498 [Google Scholar]
- Melchior, P., Suchyta, E., Huff, E., et al. 2015, MNRAS, 449, 2219 [NASA ADS] [CrossRef] [Google Scholar]
- Moresco, M., Veropalumbo, A., Marulli, F., Moscardini, L., & Cimatti, A. 2021, ApJ, 919, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Moscardini, L., Matarrese, S., & Mo, H. J. 2001, MNRAS, 327, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Naess, S., Aiola, S., Austermann, J. E., et al. 2020, JCAP, 2020, 046 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Norberg, P., Baugh, C. M., Gaztañaga, E., & Croton, D. J. 2009, MNRAS, 396, 19 [Google Scholar]
- Okabe, N., Zhang, Y. Y., Finoguenov, A., et al. 2010, ApJ, 721, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Orlowski-Scherer, J., Di Mascolo, L., Bhandarkar, T., et al. 2021, A&A, 653, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvati, L., Douspis, M., & Aghanim, N. 2018, A&A, 614, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scaramella, R., Amiaux, J., Mellier, Y., et al. 2022, A&A, 662, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schrabback, T., Applegate, D., Dietrich, J. P., et al. 2018, MNRAS, 474, 2635 [Google Scholar]
- Secco, L. F., Samuroff, S., Krause, E., et al. 2022, Phys. Rev. D, 105, 023515 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., Veropalumbo, A., Marulli, F., et al. 2015, MNRAS, 449, 4147 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., Covone, G., Izzo, L., et al. 2017, MNRAS, 472, 1946 [Google Scholar]
- Sheth, R. K., & Tormen, G. 1999, MNRAS, 308, 119 [Google Scholar]
- Sheth, R. K., Mo, H. J., & Tormen, G. 2001, MNRAS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, C., Dietrich, J. P., Bocquet, S., et al. 2019, MNRAS, 485, 69 [NASA ADS] [CrossRef] [Google Scholar]
- The Dark Energy Survey Collaboration, 2005, ArXiv e-prints [arXiv:astro-ph/0510346] [Google Scholar]
- Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Veropalumbo, A., Marulli, F., Moscardini, L., Moresco, M., & Cimatti, A. 2014, MNRAS, 442, 3275 [NASA ADS] [CrossRef] [Google Scholar]
- Veropalumbo, A., Marulli, F., Moscardini, L., Moresco, M., & Cimatti, A. 2016, MNRAS, 458, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, A. H., Hildebrandt, H., Kuijken, K., et al. 2019, A&A, 632, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, Z., Adachi, S., Ade, P., et al. 2021, Res. Notes Am. Astron. Soc., 5, 100 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Redshift and intrinsic richness distributions of the clusters in the sample. Top panel: redshift distribution after the correction for the redshift bias, including only objects with λ* > 15. The grey shaded areas represent the redshift ranges that were not used in the analysis. Bottom panel:λ* distribution of the objects in the redshift ranges z ∈ [0.10, 0.30] (black hatched histogram) and z ∈ [0.35, 0.60] (blue histogram). |
| In the text | |
 |
Fig. 2. Redshift-space 2PCF (black dots) of the AMICO KiDS-DR3 clusters in the spatial range s ∈ [5, 80] h−1 Mpc, and redshift ranges z ∈ [0.10, 0.30] (top panel) and z ∈ [0.35, 0.60] (bottom panel). In both panels, the grey band represents the 68% confidence level derived from the multivariate posterior of the free parameters considered in the cosmological analysis, described in Sect. 4.1. The model computed by assuming the cosmological parameters derived by Planck (Planck Collaboration VI 2020, Table 2, TT, TE, and EE+lowE; blue lines) and WMAP (Hinshaw et al. 2013, Table 3, WMAP-only Nine-year; red lines) is represented by the solid blue lines and by the dashed red lines, respectively. In both cases, the median values of the scaling relation parameters derived by Lesci et al. (2022) are assumed. |
| In the text | |
 |
Fig. 3. Constraints obtained from the cosmological analysis, compared to WMAP and Planck results. In the left panel, we show the 68% and 95% confidence levels in the Ωm − σ8 parameter space, along with the 1D marginalised posteriors with the relative intervals between the 16th and 84th percentiles, in the case of the cluster clustering analysis of the AMICO KiDS-DR3 catalogue (grey lines). In the same panel, we also display the results from WMAP (Hinshaw et al. 2013, Table 3, WMAP-only Nine-year; red lines) and Planck (Planck Collaboration VI 2020, Table 2, TT, TE, and EE+lowE; blue lines). In the right panel, we show the posteriors for the parameter S8, where the bands show the intervals between 16th and 84th percentiles. The colours are the same as in the left panel. |
| In the text | |
 |
Fig. 4. Comparison of the constraints on S8 ≡ σ8(Ωm/0.3)0.5 obtained, from top to bottom, from the cluster clustering analysis in the AMICO KiDS-DR3 catalogue (black dot), from the joint analysis of cluster counts and weak lensing in KiDS-DR3 performed by Lesci et al. (2022, pink dot), from the results obtained by Planck Collaboration VI (2020, blue dots), Hinshaw et al. (2013, red dots), Costanzi et al. (2019, green dot), Bocquet et al. (2019, brown dot), Amon et al. (2022) and Secco et al. (2022, magenta dot), Hikage et al. (2019, orange dot), and Asgari et al. (2021, cyan dot). The median and the 16th and 84th percentiles are shown. |
| In the text | |
 |
Fig. 5. Constraint on the normalisation of the mass-richness relation, α. The result obtained from the cluster clustering analysis is shown in grey, and the constraint derived from the joint analysis of counts and weak lensing (Lesci et al. 2022) is shown in blue. The bands show the intervals between the 16th and 84th percentiles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



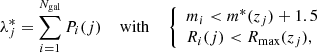
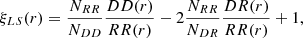
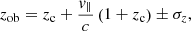
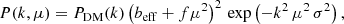
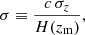
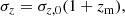
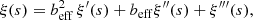
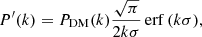
![$$ \begin{aligned}&P^{\prime \prime }(k)= \frac{f}{\left( k \sigma \right)^3}P_{\rm DM}(k) \left[\frac{\sqrt{\pi }}{2}{{\,\mathrm{erf}\,}}(k\sigma ) - k\sigma \exp (-k^2 \sigma ^2) \right] \nonumber ,\\&P^{\prime \prime \prime }(k)= \frac{f^2}{\left( k \sigma \right)^5}P_{\rm DM}(k) \frac{3\sqrt{\pi }}{8}{{\,\mathrm{erf}\,}}(k\sigma ) -\\&\qquad \quad -\frac{k \sigma }{4} \left[ 2 \left(k\sigma \right)^2+3\right]\exp (-k^2 \sigma ^2) \nonumber . \end{aligned} $$](/articles/aa/full_html/2022/09/aa43538-22/aa43538-22-eq14.gif)