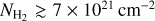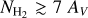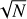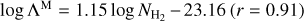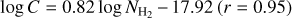EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 674 (June 2023) A&A, 674 (2023) A225 Full HTML
Open Access
Issue
A&A
Volume 674, June 2023
Article Number A225
Number of page(s) 15
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202345846
Published online 26 June 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Star formation takes place within molecular clouds (André et al. 2014; Heyer & Dame 2015) that generally appear as blends of (round) sources, filamentary structures, large-scale background, and small-scale fluctuations. Separations of the structural components, measurements, and analyses of the sources and filaments are thought to improve our understanding of the initial conditions of star formation (cf. Bergin & Tafalla 2007; André et al. 2010).

Photometric surveys of the nearby (≲500pc) molecular clouds and Galactic plane with Herschel, covering thermal far-IR and submillimeter continuum in five bands between 70 and 500 μm, probe the peak of the dust spectral energy distribution (SED), and allow the determination of the temperature and mass of the clouds (André et al. 2010; Molinari et al. 2010; Zhang et al. 2022). Multiband images from the Herschel telescope probe molecular clouds on a wide range of spatial scales. The orbital telescope has revolutionized our understanding of the link between the structure of the cold interstellar medium (ISM) and the process of star formation. In particular, it has revealed filamentary structures with a wide range of sizes, densities, and morphologies that are indeed widespread in the molecular clouds (Men’shchikov et al. 2010; Li & Goldsmith 2012; Schisano et al. 2020). Most dense cores are located on the supercritical filaments, which suggests that the filaments can fragment into the cores that eventually collapse into stars (Könyves et al. 2015). The detailed fragmentation manner may be controlled by the linear density, geometrical bending, continued accretion of gas, and magnetic fields in the filaments (Zhang et al. 2020). The mass distribution of stars at their birth is known as the stellar initial mass function (IMF; Salpeter 1955; Kroupa 2001; Chabrier 2005; Kroupa et al. 2013). Since stars are born in dense cores, studies of the core mass function (CMF) might help understand the IMF (Andre et al. 2000; Ward-Thompson et al. 2007). A great deal of observational evidence supports the idea that CMFs are similar to the IMF in shape (e.g., Motte et al. 1998; Alves et al. 2007; Könyves et al. 2015). A mass conversion efficiency (from the cores to the stars) of approximately 1/3 was proposed by Alves et al. (2007).

The Vela molecular ridge (Galactic longitudes l ≈ 260 to 275° and latitudes b ≈ ±3°) was initially identified from low-resolution (5°) CO emissions in the direction of Vela, and roughly outlined as four molecular clouds named as Vela A, B, C, and D (May et al. 1988; Murphy & May 1991). Vela A, C, and D have a kinematic distance of 0.7–1 kpc, whereas Vela B has a kinematic distance of 2 kpc (Murphy & May 1991). Vela C, the most massive of the four molecular clouds, spans roughly 3.5 degrees (south to north), and there are nest structures dispersed throughout a large amount of low-density gas in which low-mass stars form, and tight linear ridges in which massive or intermediate-mass stars form (Liseau et al. 1992; Lorenzetti et al. 1993; Yamaguchi et al. 1999; Massi et al. 2003; Baba et al. 2006; Netterfield et al. 2009; Hill et al. 2011). In previous studies (Molinari et al. 2011; Giannini et al. 2012; Minier et al. 2013; Massi et al. 2019), a distance of ~700pc to Vela C was adopted (Murphy & May 1991). The mean distance of Vela C, estimated by Zucker et al. (2020) from Gaia DR2 (Gaia Collaboration 2018) stellar parallaxes, is 905 ± 45 pc. The different distance measurements bring deviations of about 20% in the size and 60% in the mass of Vela C. Considering that Gaia measured distances with unprecedented precision, we adopted the distance of 905 pc in this work.

A decade ago, Giannini et al. (2012) detected dense cores in Herschel multiband images of Vela C with the CuTeX source extraction algorithm (Molinari et al. 2011), and Hill et al. (2011) traced skeletons of filaments with the DisPerSE algorithm (Sousbie 2011). For this work we chose to apply the multiscale source and filament extraction method getsf (Men’shchikov 2021a), which separates the structural components of sources, filamentary structures, and their backgrounds before applying a consistent approach to extracting both sources and filaments. The method has no free (unconstrained) parameters, which is a property that sets getsf apart from other extraction methods. Its single user-definable parameter, the maximum size of the sources or filaments of interest, is constrained from the observed images and is used to place a reasonable upper limit on the range of scales in a spatial decomposition of the observed images. Interested readers are referred to Men’shchikov (2021a) for a full description of getsf and to Men’shchikov (2021b) for its benchmarking that showed improved detection completeness and measurement accuracy with respect to the older getsources and getfilaments extraction methods (Men’shchikov et al. 2012; Men’shchikov 2013).

The outline of the present paper is as follows. In Sect. 2 we describe the Herschel submillimeter dust emission data. The data analysis and results are presented in Sect. 3. In Sect. 4 we discuss the extracted sources at different resolutions, their core mass function, and the filamentary structures. We summarize our conclusions in Sect. 5.

2 The Herschel images

The Vela C molecular cloud was observed on May 18, 2010, within the frame of the HOBYS imaging survey (PI: F. Motte, observation IDs: 1342196657, 1342196658; Motte et al. 2010). Using the PACS/SPIRE parallel mode (Poglitsch et al. 2010; Griffin et al. 2010) with a scanning speed of 20″ s−1, an area of ~1.4 × 3.2 deg2 was imaged simultaneously at 70, 160, 250, 350, and 500 μm, with angular resolutions of 5.9, 11.7, 18.2, 24.9, and 36.3″, respectively. We retrieved the images from the Herschel Science Archive (HSA)1. The SPIRE extended-source calibrated map and PACS Unimap (Piazzo et al. 2015) products at level 2.5 were used, because the level 3 images did not undergo quality control at the Herschel Science Centre.

3 Data analysis and results

3.1 The high-resolution surface density image

To properly compute the surface densities, it was necessary to derive zero-level offsets for the five Herschel images. We assume that the images probe the optically thin dust emission following the empirical fit (e.g., Planck Collaboration XI 2014), 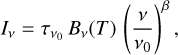Iv=τv0 Bv(T)  (vv0)β,${I_v} = {\tau _{{v_0}}}\,{B_v}\left( T \right)\,\,{\left( {{v \over {{v_0}}}} \right)^\beta },$(1)

where ν0 is the reference frequency at which the optical depth 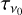τν0${\tau _{{\nu _0}}}$ is estimated, Iν is the specific intensity, and Bv(T) is the Planck function for the emission of dust at temperature T and frequency υ. Using a modified blackbody fit to the Planck 353, 545, and 857 GHz images, and IRAS 100 μm data, Planck Collaboration XI (2014) presented all-sky maps of the dust optical depth at v0 = 353 GHz (850 μm) and the dust temperature map with a resolution of 5′. Using β = 2, adopting v0 = 353 GHz as the reference frequency, and substituting the optical depth at 353 GHz in Eq. (1), we used the Planck dust temperature map to derive the images at 70, 160, 250, 350, and 500 μm of Vela C, corresponding to the Herschel images. Convolving each Herschel image to the Planck resolution, we obtained the offsets of each Herschel image by a comparison with the derived intensity maps (Bernard et al. 2010). They were found to be 23, 320, 146, 59.8, and 18.7 MJy sr−1 at 70, 160, 250, 350, and 500 μm respectively.

We used prepobs from getsf to reproject the Herschel images to the same size and number of pixels (3″, 2820 × 4050) and the hires method (Men’shchikov 2021a) to compute the temperature and surface density images at the Herschel resolutions. An advantage of the hires algorithm over other similar methods is that it can use the shortest-wavelength highest-resolution images, assuming that their emission is dominated by the normal dust grains in radiative equilibrium. Such high-resolution surface density images are helpful in our detailed study of the complex structural diversity in Vela C. The pixel-to-pixel SED fitting was performed by the fitfluxes utility (Men’shchikov 2016). The images at 160, 250, 350, and 500 μm were used to derive the temperature and surface density maps at 36.3″ resolution, the images at 160, 250, and 350 μm were used to obtain those maps at 24.9″ resolution, and the images at 160 and 250 μm were used to compute the maps at 18.2″ resolution. These three sets of temperatures and observed images (from 70 to 500 μm) were used to compute the surface density and temperature images (Fig. 1) with the improved resolutions of 5.9, 11.7, and 18.2″ (Men’shchikov 2021a). To reduce the noisiness of the 5.9″ surface densities induced by the Herschel 70 μm image, we smoothed the map to an 8.5″ resolution and used this in our work.

3.2 Source and filament extraction

We applied the multiscale multiwavelength extraction method getsf (Men’shchikov 2021a) to extract sources and filaments from the Herschel multiwavelength dust continuum images. The only constrained parameter that it requires is the maximum sizes of the structures to be extracted, determined from the observed images as the footprint radii of the largest source and widest filament (Sect. 3.1.3 in Men’shchikov 2021a). The footprint of a source or filament is defined as the full extent of the structures at zero (background) level (i.e., the area beyond which their contribution becomes negligible).

In our multiwavelength extraction of the sources and filaments with getsf in Vela C, we used the five Herschel images at 70-500 μm and three surface density images with the angular resolutions of 8.5, 11.7, and 18.2″. To extract sources the detection images combined information from all the images, whereas to extract filaments the 70 μm image was not used. After inspecting the images, we chose the following sets of maximum sizes: 40, 60, 80, 100, and 120″ for the Herschel wavebands and 25, 60, and 80″ for the surface densities.

thumbnail Fig. 1

High-resolution (11.7″) surface density map of Vela C, obtained from the Herschel images.

3.3 Mass distribution in Vela C

Molecular clouds are complex structures that consist of various components (Bergin & Tafalla 2007). Sources are the round intensity peaks, corresponding to the individual fragments within molecular clouds. Filaments are the significantly elongated structures, often significantly curved, whose properties depend on the position along their crests. Both types of structure are characterized by a local overdensity and minimum in the gravitational potential of their parent cloud.

The hierarchical structure of Vela C (Figs. 1 and 2) includes the filamentary network, sources, and their backgrounds, all of them are separated from each other by getsf in the extraction process (Men’shchikov 2021a; Zhang et al. 2020). Assuming the cloud is optically thin at the observed wavelengths, the molecular cloud mass can be derived from its surface densities, 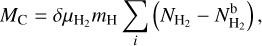MC=δμH2mH ∑i (NH2−NH2b),${M_{\rm{C}}} = \delta {\mu _{{{\rm{H}}_2}}}{m_{\rm{H}}}\,\sum\limits_i {\,\left( {{N_{{{\rm{H}}_2}}} - N_{{{\rm{H}}_2}}^{\rm{b}}} \right)} ,$(2)

where δ is the pixel area, 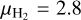μH2=2.8${\mu _{{{\rm{H}}_2}}} = 2.8$ the mean molecular weight per hydrogen molecule, mH the mass of the hydrogen atom, 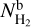NH2b$N_{{{\rm{H}}_{\rm{2}}}}^{\rm{b}}$ the global background of the image, and the summation is done over all pixels. In Eq. (2), we adopted the value 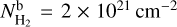NH2b=2×1021 cm−2$N_{{{\rm{H}}_{\rm{2}}}}^{\rm{b}} = 2 \times {10^{21}}\,{\rm{c}}{{\rm{m}}^{ - {\rm{2}}}}$ as the image background, corresponding to an integrated mass of 3.7 × 104 Μ⊙.

Comparisons with a simulated star-forming region (Fig. A.1 in Men’shchikov 2021a) suggest that the highest-resolution surface densities are expected to be more accurate for the structural components than the standard maps at a 36.3″ resolution. One exception is the unresolved protostellar peaks (which can be strongly overestimated because of the steep temperature gradients in the protostellar cores) created by the accretion luminosity. To give a sense of possible uncertainties in the derived masses of the structural components, Table 1 presents the estimates obtained from the surface densities at each of the three angular resolutions used in the extraction, along with the total masses at the lower resolutions. The bulk of the cloud is the low-density background with 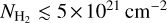NH2≲5×1021cm−2${N_{{{\rm{H}}_2}}} \mathbin{\lower.3ex\hbox{$\buildrel<\over {\smash{\scriptstyle\sim}\vphantom{_x}}$}} 5 \times {10^{21}}{\rm{c}}{{\rm{m}}^{ - 2}}$, accounting for 60% of the total mass MC, whereas the components of filaments and sources constitute 35 and 3% of MC, respectively.

A surface density probability distribution function (PDFN) is useful for obtaining insights into the physical processes acting in the molecular cloud (Vazquez-Semadeni 1994; Passot & Vázquez-Semadeni 1998; Federrath et al. 2008; Kainulainen et al. 2009, 2011; Tassis et al. 2010; Kritsuk et al. 2011; Ballesteros-Paredes et al. 2011). Figure 3 shows the PDFN of the Vela C surface densities at 11.7″ resolution. At high surface densities (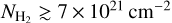NH2≳ 7×1021cm−2${N_{{{\rm{H}}_2}}} \mathbin{\lower.3ex\hbox{$\buildrel>\over {\smash{\scriptstyle\sim}\vphantom{_x}}$}} 7 \times {10^{21}}{\rm{c}}{{\rm{m}}^{ - 2}}$), PDFN can be well fitted by a power law: 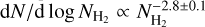dN/d log NH2∝NH2−2.8±0.1${{{\rm{d}}N} \mathord{\left/{\vphantom {{{\rm{d}}N} {{\rm{d}}\,{\rm{log}}\,{N_{{{\rm{H}}_{\rm{2}}}}} \propto N_{{{\rm{H}}_{\rm{2}}}}^{ - 2.8 \pm 0.1}}}} \right.\kern-\nulldelimiterspace} {{\rm{d}}\,{\rm{log}}\,{N_{{{\rm{H}}_{\rm{2}}}}} \propto N_{{{\rm{H}}_{\rm{2}}}}^{ - 2.8 \pm 0.1}}}$. Surface densities are convertible to visual extinction, assuming 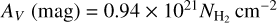AV(mag)=0.94×1021NH2cm−2${A_V}\left( {{\rm{mag}}} \right) = 0.94 \times {10^{21}}{N_{{{\rm{H}}_{\rm{2}}}}}{\rm{c}}{{\rm{m}}^{ - 2}}$ (Bohlin et al. 1978). The high-density tail corresponds to 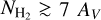NH2≳7 AV${N_{{{\rm{H}}_{\rm{2}}}}} \mathbin{\lower.3ex\hbox{$\buildrel>\over{\smash{\scriptstyle\sim}\vphantom{_x}}$}} 7\,{A_V}$. The PDFN of the interstellar medium, and in particular of the molecular clouds, is also a rapidly decreasing function, unless a special arrangement of masses occurs. Most of the space in the molecular cloud is filled with a low-density background and only a small fraction of the dense structures, as can be inferred from the rapid decline in PDFN (Kainulainen et al. 2009).

3.4 Selection of reliable cores

After applying getsf for source extraction, we adopted its definition of sources (cf. Sects. 1 and 3.2.2 in Men’shchikov 2021a). The sources are the relatively round emission peaks that are significantly stronger than the local surrounding fluctuations (of background and noise), suggesting the presence of the physical objects in space that produced the observed emission. In total, 3711 sources were detected by getsf.

Only sources that were good enough were then selected by getsf at each wavelength λ, using the following conditions (Sect. 3.4.6 in Men’shchikov 2021a): (1) Ξλ > 1, where Ξλ is the monochromatic goodness (combining detection significance and signal-to-noise ratio); (2) Γλ > 1, where Γλ is the detection significance from monochromatic single scales; (3) FPλ/σPλ > 2, where FPλ is the peak intensity and σPλ the peak intensity error; (4) FTλ/σTλ > 2, where FTλ is the total flux and σTλ the total flux error; (5) Αλ/Βλ < 2, where Αλ and Βλ are the major and minor widths at half maximum; (6) ΑFλ/Αλ > 1.15, where AFλ is the full major axis of the elliptical footprint of a source.

The above criteria clean up the extraction catalog, removing spurious detections and selecting for further analysis only reliable and well-measurable sources, as verified by Men’shchikov (2021b). Conditions (1)–(4) ensure that the detected source peaks are sufficiently strong to be distinguished from the background and noise fluctuations. Condition (5) ensures that sources are circular or elliptical, excluding too elongated structures that are unlikely to be sources. Condition (6) is used to discard the sources with unrealistically low ratios of their footprint to half maximum sizes. The criteria excluded a substantial number of detected peaks that are likely spurious and removed the sources with unreliable (inaccurate) measurements, leaving 1755 selected good sources.

Extragalactic sources are physically different from the starless cores or YSOs of our interest and must be excluded. Based on their peak positions, we cross-matched the sources with the SIMBAD database2 (Wenger et al. 2000) and the NASA/IPAC Extragalactic Database3 (NED) within a 6″ radius. As a result, we removed one source based on SIMBAD and nine sources based on NED, which left us with 1745 acceptable sources.

Conditions (1)–(6) are necessary for a source to be acceptable in a single image or in a surface density map. In order to improve the reliability, we further selected as starless cores only those sources that are acceptable in at least two of the four wavebands of 160, 250, 350, and 500 μm and also in the surface density map at the 11.7″ resolution, but not detectable in the 70 μm map. Figure 4 illustrates the selection process that resulted in 421 acceptable starless cores.

The protostellar cores differ from the starless cores in that they produce accretion luminosity at their centers, which creates a strong unresolved peak at short wavelengths (λ≲ 100 μm), where the prestellar cores do not radiate a noticeable amount of energy. Following the standard approach, we identified as protostellar cores those sources that are detected and acceptable at 70 μm, not very resolved with a 5.9″ beam, and not too elongated, meaning that their major and minor half maximum sizes A and B obey the relations (AB)1/2 < 1.5 × 5.9″ and A/Β < 1.3. In addition, the protostellar cores must be acceptable in at least two of the four images at 160, 250, 350, and 500 μm and in the surface density image at 11.7″ resolution. Figure 5 illustrates the selection process that resulted in 149 acceptable protostellar cores.

thumbnail Fig. 2

Extracted cores and filaments in the Vela C molecular cloud on the 11.7″-resolution surface density image. The locations and sizes of the cores are measured from the surface density map. The black, green, and blue ellipses represent the 329 prestellar cores, 84 unbound starless cores, and 149 protostellar cores, respectively. The full axis of the ellipses is two times the Gaussian full width at half maximum (FWHM). Filamentary networks are shown by the global scale-independent skeletons of the filamentary structure. The filament linear density ΛW in each point along the skeletons was estimated from Eq. (7) assuming a width of W = 0.3 pc (Fig. 11).
Table 1

Masses of the structural components of the Vela C molecular cloud, separated by getsf in the surface density images with different angular resolutions.

thumbnail Fig. 3

Probability density function PDFN for Vela C. The vertical axis gives the actual number of pixels per bin in the 11.7″ resolution surface density image. At NH2≳2×1021cm−2${N_{{{\rm{H}}_2}}} \mathbin{\lower.3ex\hbox{$\buildrel>\over{\smash{\scriptstyle\sim}\vphantom{_x}}$}} 2 \times {10^{21}}{\rm{c}}{{\rm{m}}^{ - 2}}$, corresponding to NH2≳7AV${N_{{{\rm{H}}_{\rm{2}}}}} \mathbin{\lower.3ex\hbox{$\buildrel>\over {\smash{\scriptstyle\sim}\vphantom{_x}}$}} 7{A_V}$, it can be fit well with a power law.

3.5 Classification of extracted cores

Stars form in the process of the gravitational collapse of dense prestellar cores of a typical size of ~0.1 pc that represent the local density maxima of the parent molecular cloud, producing the local minima of the gravitational potential (e.g., Bergin & Tafalla 2007; André et al. 2014; Zhang et al. 2020). Prestellar cores are the gravitationally bound starless cores with the potential to give birth to stars (Ward-Thompson et al. 2007; Bergin & Tafalla 2007; André et al. 2014; Könyves et al. 2015). The prestellar cores, supported by the pressure of the ambient gas of the parental cloud (e.g., Alves et al. 2001; Kirk et al. 2005), can be approximated by the equilibrium self-gravitational, isothermal Bonnor-Ebert (BE) spheres (Ebert 1955; Bonnor 1956). The BE model is useful even if the real core is not strictly isothermal or not in the hydrostatic equilibrium (e.g., Galli et al. 2002; Ballesteros-Paredes et al. 2003). The mass of the critical BE sphere can be expressed as (Bonnor 1956) 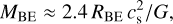MBE≈2.4 RBE cs2/G,${M_{{\rm{BE}}}} \approx 2.4\,{R_{{\rm{BE}}}}\,{{c_{\rm{s}}^2} \mathord{\left/ {\vphantom {{c_{\rm{s}}^2} G}} \right. \kern-\nulldelimiterspace} G}, $(3)

where G is the gravitational constant, cs the isothermal sound speed, and RBE is the radius of the BE sphere, approximated in our work by the deconvolved radius, 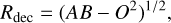Rdec=(AB−O2)1/2,${R_{{\rm{dec}}}} = {\left( {AB - {O^2}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}, $(4)

where A and B are the major and minor half maximum sizes, measured in the surface densities with the angular resolution of Ο = 11.7″. The sound speed in Eq. (3) was computed for the actual SED temperature TF of each extracted core. Only the partially resolved and unresolved sources (resolvedness (AB)112 O−1 > 1.1) were used in Eq. (4) to avoid unacceptably large deconvolution errors (Men’shchikov 2023), and hence eight unresolved starless cores were ignored. The starless cores are deemed self-gravitating (bound) and classified as prestellar cores, when the ratio αBE = MBE/Mcore ⩽ 2, where the core masses (and luminosities) are estimated by fitting the spectral energy distribution of the total fluxes Fλ of the sources over the Herschel wavebands. The resulting total number of prestellar cores is 329 and the number of the unbound starless cores is 84 (Fig. 2). The distributions of the source radii measured from the surface density maps at the angular resolutions of 8.5, 11.7, and 18.2″ are shown in Fig. 6.

Table A.1 presents a template of the online catalog of our multiwavelength source extraction and Table A.2 is a template of the online catalog of the derived parameters for the 570 reliable cores from Table A.1, which includes their dust temperatures TF, masses MF, and luminosities LF (Fig. 7), obtained from fitting the spectral energy distribution (SED) of each core.

Figure 8 presents the mass-size diagram for the reliable cores in Vela C, where the deconvolved sizes were obtained from Eq. (4) using the measured sizes from the surface density image at 11.7″ resolution. The prestellar cores with αBE ≤ 2 are more massive than the starless cores not bound by gravity (αBE > 2). Kauffmann et al. (2010) proposed an empirical formula M ∝ 870 Μ⊙ (R/pc)1.33 that provides a lower limit for the mass of massive stars that can form in molecular clouds, derived from observations of the distribution of masses of young stars in different environments. The presence of prestellar and protostellar cores above this line suggests that they likely form massive stars.

thumbnail Fig. 4

Illustration of the selection criteria for starless cores in five Herschel images and in high-resolution surface density maps at resolutions of 8.5, 11.7, and 18.2″ (Sect. 3.4). The black ellipses represent the measured major and minor FWHM sizes.
thumbnail Fig. 5

Illustration of the selection criteria for protostellar cores in five Herschel images and in high-resolution surface density maps at resolutions of 8.5, 11.7, and 18.2″ (Sect. 3.4). The black ellipses represent the measured major and minor FWHM sizes.

3.6 Core mass function

A fundamental property of molecular clouds is their mass distribution (Ballesteros-Paredes et al. 2020). Investigations of their CO emission (Sanders et al. 1985; Stutzki & Guesten 1990; Williams et al. 1994; Heyer & Terebey 1998; Kramer et al. 1998) and later studies of their dust continuum emission (Motte et al. 1998; Johnstone et al. 2000; Alves et al. 2007), have shown that the molecular clouds and their substructures do not have characteristic masses. Typically, they display a power-law distribution over mass: 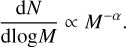dNdlogM∝M−α.${{{\rm{d}}N} \over {{\rm{d}}\log M}} \propto {M^{ - \alpha }}.$(5)

Using the masses derived from the SED fitting, we obtained the mass functions for the 421 starless, 329 prestellar cores, and 149 protostellar cores (Fig. 9). The CMFs for the starless and prestellar cores are indistinguishable at M > 2 M⊙ (all starless cores are bound) and they can be fitted well with dN/dlogM ∝ M−135±016 between 20 and 200 M⊙. The power-law exponent is the same as that of the stellar IMF (α = 1.35; Salpeter 1955). The CMFs also reveal that the population of protostellar cores has a deficit of massive cores with respect to the prestellar cores.

3.7 Physical properties of filaments

Molecular filaments are the strongly elongated structures in molecular clouds (e.g., Men’shchikov et al. 2010; André et al. 2014). The omnipresent filaments are usually blended with each other, and sources, and fluctuating background clouds, and the degree of blending becomes more severe at lower angular resolutions (Men’shchikov 2021a). Unfortunately, there are no reliable methods to accurately subtract backgrounds and deblend filaments from other structures in order to properly measure their physical parameters. Therefore, it is preferable to choose clear examples of the isolated (not blended) relatively straight filaments on simple backgrounds, which would enable more accurate measurements of their properties and more reliable conclusions.

In practice, we used the simple (nonbranching) global skeletons, produced by getsf and measured the 11.7″-resolution surface densities of the component of filaments, separated from the sources and backgrounds. The contrast C of a source- and background-subtracted filament can be defined as 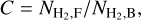C=NH2,F/NH2,B,${{C = {N_{{{\rm{H}}_2},{\rm{F}}}}} \mathord{\left/ {\vphantom {{C = {N_{{{\rm{H}}_2},{\rm{F}}}}} {{N_{{{\rm{H}}_2},{\rm{B}}}}}}} \right. \kern-\nulldelimiterspace} {{N_{{{\rm{H}}_2},{\rm{B}}}}}}, $(6)

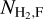where NH2,F${N_{\rm{H}}}_{_{\rm{2}},{\rm{F}}}$ is the median value of the surface densities along the filament crest (skeleton) and 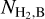NH2,B${N_{\rm{H}}}_{_{\rm{2}},B}$ the background surface density. After a visual inspection (Fig. 10), only the prominent filaments with C ≳ 0.5 and length L ≳ 0.4pc were used in the measurements of their profiles. We selected 68 filaments in which at least one side does not blend with the adjacent structures. A histogram of the physical parameters of the 68 selected filamentary filaments is shown in Fig. 11 and correlations of some parameters are displayed in Fig. 12.

We denote as W the median half maximum width of the surface density profiles of a filament along its length, and WB the width measured on the broader side and WN the width measured on the narrower side. When the two one-sided estimates are only moderately different (by less than 50%), we choose their arithmetic mean as the filament width W, otherwise we set the filament width W = WN. The widths are in the range from 0.15 to 0.63 pc (median of 0.3 ± 0.11 pc) and they have no correlation with the filament temperature and surface density (Fig. 12). The filament lengths L, defined as the length of the skeletons, are in the range from 0.35 to 2.14 pc (median of 0.7 pc). The median filament dust temperatures are in the range from 12.6 to 26.6 K (median of 15.5 K), measured on the crest in the temperature map.

Three estimates of the linear density Λ of each filament can be computed from the average integrated profile along the crest (ΛΡ), from the average width (ΛW), and from the filament mass (ΛΜ): 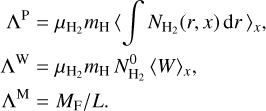ΛP=μH2mH  〈   ∫ NH2(r,x) dr 〉x,ΛW=μH2mH NH20 〈 W 〉x,ΛM=MF/L.$\matrix{ {{{\rm{\Lambda }}^{\rm{P}}} = {\mu _{{{\rm{H}}_2}}}{m_{\rm{H}}}\,\,{{\left\langle {\,\,\int {\,{N_{{{\rm{H}}_2}}}\left( {r,x} \right)\,{\rm{d}}r} } \right\rangle }_x},} \hfill \cr {{{\rm{\Lambda }}^{\rm{W}}} = {\mu _{{{\rm{H}}_2}}}{m_{\rm{H}}}\,N_{{{\rm{H}}_2}}^0\,{{\left\langle W \right\rangle }_x},} \hfill \cr {{{\rm{\Lambda }}^{\rm{M}}} = {{{M_{\rm{F}}}} \mathord{\left/ {\vphantom {{{M_{\rm{F}}}} {L.}}} \right. \kern-\nulldelimiterspace} {L.}}} \hfill \cr } $(7)

Here the averaging is done over the coordinate x along the filament crest, 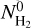NH20$N_{{{\rm{H}}_{\rm{2}}}}^{\rm{0}}$ is the crest surface density, and the filament mass MF is obtained by integrating the surface densities over the filament footprint. The linear densities span more than an order of magnitude and are clearly correlated with some other parameters (Fig. 12). Table A.3 summarizes the derived physical parameters of the filaments that include their lengths, masses, linear densities, and widths.

With the assumption that filaments can be described by the infinitely-long linear isothermal hydrostatic nonmagnetic cylinders (Stodólkiewicz 1963; Ostriker 1964), their critical linear density has a very simple expression 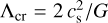Λcr=2cs2/G${{\rm{\Lambda }}_{{\rm{cr}}}} = 2c_{\rm{s}}^2/G$ that depends on the sound speed (gas temperature) in the filament. Observed filaments with linear densities above the critical value are usually considered unstable, fragmenting into cores under their own gravity (e.g., André et al. 2014; Zhang et al. 2020).

Applicability of the above instability criterion to the real observations is, however, completely unclear because the properties of the complex filaments observed with Herschel (e.g., Figs. 1, 2, and 10) show that the assumptions of the highly idealized model are invalid. The filaments do not resemble a linear cylinder, they are finite in length (actually relatively short) and nonisothermal, they have nonnegligible magnetic fields, and there is no clear indication that they are in a hydrostatic equilibrium. The observed filamentary structures appear embedded in very complex, inhomogeneous environments (backgrounds), they are quite substantially curved, overlap with other nearby structures (filaments and sources), and have temperature gradients toward their centers as well as significantly variable radial profiles and widths (hence linear densities) along their crests (e.g., Figs. 6, 13, 19-23 in Men’shchikov 2021a). It is quite reasonable to conclude, therefore, that the critical linear density Λcr, based on the simplistic model assumptions, must be considered only a rough (order-of-magnitude) indicator that perhaps they might be unstable.

In the absence of a more realistic criterion, we analyzed the linear densities of the extracted filaments in Vela C, calculating the critical linear density using the median value of the dust temperature along each filament crest and assuming that Λcr is uncertain within a factor of 3. The linear densities are shown in Fig. 2 for each point along the crests of the entire network of the filamentary structures. A distribution of filaments over the stability parameter ΛΜ/Λcr is also shown in Fig. 11. The peak of the distribution is contained within the uncertainties 0.33 < ΛΜ/Λcr < 3, which means that most of the filaments (39 of 68) may be both supercritical and subcritical. There is also a tail of 29 filaments with the parameter value above 3 that can definitely be considered supercritical, in which are found 94 prestellar cores, 83 protostellar cores, and only 1 unbound starless core. On the other hand, the filaments with the stability parameter above 1 contain 210 prestellar cores, 127 protostellar cores, and 8 unbound starless cores. In other words, taking into account the uncertainties, the supercritical filaments contain only prestellar and protostellar cores.

thumbnail Fig. 6

Histograms of the sizes of isolated cores, not blended with any other source in any waveband. The core radius is the arithmetic mean of the major and minor half maximum sizes, measured in the surface density images with three different resolutions (indicated by the vertical dashed lines). Panel a: distribution of source radii at 8.5″ resolution. Panel b: distribution of source radii at 11.7″ resolution. Panel c: distribution of source radii at 18.2″ resolution.
thumbnail Fig. 7

Histograms of the physical parameters of the 570 reliable cores obtained from fitting SEDs of the extracted sources. Panel a: distribution of their average temperatures (median of 11.7 K). Panel b: distribution of their masses (median of 4.8 M⊙). Panel c: distribution of their luminosities (median of 0.9 L⊙). The red dashed lines indicate the median values.
thumbnail Fig. 8

Mass-size diagram for Vela C for the unbound cores (green squares), prestellar cores (blue circles), and protostellar cores (red stars). Only the partially resolved and resolved cores are shown (with sizes 10% larger than the 11.7″ beam) to ensure acceptably accurate decon-volution results using Eq. (4). The critical Bonnor-Ebert spheres with temperatures of 6, 10, and 20 Κ are displayed by the dashed black, dashed green, and solid red lines, respectively. The dashed cyan line is the radius-mass relation for open star clusters (Marks & Kroupa 2012, Eq. (7)) and the gray envelope represents its uncertainty range. The dashed magenta line indicates an empirical relationship proposed by Kauffmann et al. (2010). The physical scale of 0.05 pc at the 11.7″ resolution is indicated by the vertical line.
thumbnail Fig. 9

Differential core mass function (dN/dlogM) for the 329 prestellar cores (green) 421 starless cores (orange), and 149 protostellar cores (magenta). The error bars correspond to the N$\sqrt N $ statistical uncertainties.
thumbnail Fig. 10

Illustration of a detected and measured filament in a high-resolution surface density image at 11.7″. Left: skeletons of the detected filaments with a contrast C > 0.5 is shown by the white curves and the black curve is the skeleton of a filament whose measured radial profile is shown in the right panel. Right: median one-sided surface density profiles measured on the two sides of the filament (blue and purple solid lines). The black dashed curve shows the beam profile. The median half maximum width of the filament is 0.33 ± 0.19 pc.
thumbnail Fig. 11

Histograms of physical parameters of 68 selected filaments in Vela C. (a): filament contrasts; (b): filament widths; (c): logarithmic slope of profile; (d): dust temperatures along the filament crests; (e): surface densities along the crest; (f): ratio of linear density to the critical value. The red dashed line indicates the median value, and the error is the rms of the data.
thumbnail Fig. 12

Correlations of physical parameters of 68 filaments in Vela C. The red dashed lines indicate the median values and the red solid lines represent fits to the data: log ΛΡ = 0.86 log ΛΜ + 0.13 (r = 0.96), logΛM=1.15logNH2−23.16(r=0.91)$\log {\Lambda ^{\rm{M}}} = 1.15\log {N_{{{\rm{H}}_{\rm{2}}}}} - 23.16\left( {r = 0.91} \right)$, logC=0.82logNH2−17.92(r=0.95)$\log C = 0.82\log {N_{{{\rm{H}}_{\rm{2}}}}} - 17.92\left( {r = 0.95} \right)$, T = −2.20 log ΛΜ + 19.38 (r = 0.77), where r is the Pearson product moment correlation coefficient.

4 Discussion

4.1 Extracted sources at different resolutions

Insufficient angular resolutions are known to make extracted sources artificially wider and more massive (Louvet et al. 2021; Men’shchikov 2023), because of the heavier blending with the structured backgrounds and incorporation of the background into the extracted source, caused by the errors in background determination. Convergence tests at lower angular resolutions might indicate whether a given resolution is sufficiently high to produce accurate measurements (Louvet et al. 2021). To check for possible resolution effects, we measured properties of the extracted cores in the available surface densities at the resolutions of 8.5, 11.7, and 18.2″, selecting only isolated sources for the distributions of source sizes in Fig. 6 to avoid the considerable inaccuracies associated with deblending overlapping sources.

The starless (prestellar) cores are consistently well resolved at all three resolutions (Fig. 4), whereas the protostellar cores appear partially resolved at 18.2″, and become progressively less resolved toward the highest 8.5″ resolution (Fig. 5). The differences are caused by the fact that the protostellar cores are the accreting envelopes around protostars, generating accretion luminosity that heats up the inner opaque area of the envelopes to T ≳ 1000 K at radii θ ≪ 1″ (cf. Fig. 3 in Men’shchikov 2016), making the compact hot zone appear as an unresolved peak at 70 μm and a weaker peak at 160 μm (Fig. 5). The strong temperature gradients around the unresolved protostellar peaks make their derived surface densities inaccurate, especially the highest-resolution images (Appendix A in Men’shchikov 2021a).

The significantly overestimated unresolved peaks of the protostellar cores in the 11.7 and 8.5″ resolution surface densities provide a likely explanation of why their size distributions in Fig. 6 become increasingly unresolved at higher resolutions. We note, however, that protostellar envelopes have power-law volume densities ρ ∝ r−2 (surface densities σ ∝ θ−1), and therefore their sizes A must be proportional to the angular resolution O, if their outer boundaries are sufficiently distant (O ≪ Θ). Simple numerical convolutions with Gaussian kernels confirm that the surface density image of such a power-law structure obeys the relationship A = 1.6 × O. The size distribution of protostellar cores in Fig. 6 in the 18.2″ resolution surface densities (much less affected by the inaccuracies of pixel SED fitting) is indeed centered at sizes of approximately 1.3 × 18.2″.

4.2 Star formation and the CMF

Our analysis of the source extraction in Vela C resulted in the massive CMF that peaks at 5 M⊙ and extends to 200 M⊙, with a slope of −1.35 ± 0.16 above 20 M⊙, which happened to have the same value as that proposed by Salpeter (1955) for an initial mass function (IMF) of stars (from 0.4 to 10 M⊙). The cores extracted in this work are much more massive than the low-mass stars analyzed in the more abundant studies of the nearby regions of low-mass star formation. We constructed mass functions for the starless, prestellar, and protostellar cores. The CMF of protostellar cores can have a more complex shape, with a peak or plateau at intermediate masses, and a steep drop-off at high masses. This occurs because the protostar formation process tends to concentrate mass in a smaller range of core masses, and can also be affected by feedback mechanisms from the newly formed protostar, such as outflows and radiation (McKee & Tan 2002; Bate et al. 2003; Enoch et al. 2008).

There is a debate in the literature of whether the IMF and CMF have the same distribution. Some observations from the ground-based single-aperture telescopes (e.g., Motte et al. 1998; Alves et al. 2007) and Herschel (e.g., Könyves et al. 2015) have shown that there are similar mass distributions in the CMF and IMF in star-forming regions. There are also cases within the Galaxy where the CMF and IMF are dissimilar (e.g., Li et al. 2007; Motte et al. 2018; Zhang et al. 2018). The similarity of the two is often interpreted as indicating that there may be a constant core-to-star conversion efficiency (Alves et al. 2007). A recent ALMA study of the MM2 and MM3 clouds in W43 (Pouteau et al. 2022) found an excess of high-mass cores and a significantly shallower CMF slope. There are also indications that the CMF peak may shift to the lower masses with increasing angular resolution of the images (Louvet et al. 2021).

The mechanisms of high-mass star formation are not very clear yet. One scenario is that the massive dense cores collapse gravitationally and form high-mass stars because of their larger mass reservoirs and stronger gravitational potentials (McKee & Tan 2003; Tan et al. 2014). Other scenarios include disk fragmentation, competitive accretion, and mergers of the lower-mass protostars (e.g., Bonnell et al. 2004; Bate 2009; Kruijssen et al. 2012). The similarity of the CMF and IMF slopes at the highmass end may be suggestive of a possible link between the formation of high-mass stars and the formation of their progenitors, the dense cores. More studies are necessary to reach a reliable understanding of the CMFs and their relationship with the IMF, including independent source and filament extractions and re-evaluation of the existing dataset of the Herschel observations of low-mass and high-mass star-forming regions.

4.3 Filamentary structures

Herschel discovered widespread networks of filamentary structures within the molecular clouds (Men’shchikov et al. 2010), proposed as the key actors in the formation of stars (André et al. 2014). The dense cores, formed by the gravitational fragmentation of the supercritical filaments are thought to be the progenitors of the next generations of stars (e.g., Zhang et al. 2020).

The filamentary structures in Vela C have crest temperatures of 15.5 K with a dispersion of roughly 2 K (Fig. 11). Radial dust temperature profiles, created from the dust temperature map, reveal shapes similar to an inverted surface density profile (Zhang et al. 2020) wherever the filament does not contain a hot source. The higher the surface or linear densities, the lower the crest temperature (Fig. 12) because of the increased shielding from the interstellar radiation field (Arzoumanian et al. 2019). The very common filament pattern is a main filament or a ridge and a network of stripes or subfilaments (e.g., Kirk et al. 2013; Men’shchikov 2021a). To facilitate more accurate measurements, getsf separated all branches of the skeleton network. The length of the 68 well-shaped filaments is approximately 0.5 pc, which is comparable to the lengths of the 599 filaments measured by Arzoumanian et al. (2019). Filamentary structures are interconnected with various nearby branches, and variations along the crest introduce uncertainties in the width, mass, and profile measurements (Fig. 10).

Studies of the nearby molecular clouds observed with Herschel suggested that the widths of the filaments are independent of the surface density and have a typical values of ~0.1 pc (Arzoumanian et al. 2011, 2019). Whether such a typical width actually exists or whether it is also applicable to the high-mass star-forming regions is still debated (Panopoulou et al. 2022; André et al. 2022). The widths of the filamentary structures that we selected in this work range from 0.15 to 0.63 pc, with a median value of 0.3 ± 0.11 pc. The angular resolution of the surface density map (11.7″) corresponds to ~0.05 pc at the distance of 905 pc adopted for Vela C, which means that all the filaments appear resolved. The widths and linear masses of the filaments in our study are similar to those found in the Cygnus X high-mass star-forming region, located at 1.4 kpc (Hennemann et al. 2012).

5 Conclusions

Using the hires algorithm to create high-resolution surface densities from the Herschel observations and the getsf method to extract sources and filaments (Men’shchikov 2021a), we detected the sources and filamentary structures in the Vela C molecular cloud and analyzed their physical properties. Our systematic study of the individual molecular cloud led to the following main results.

The PDFN of the surface density map with a resolution of 11.7″ shows a prominent power-law tail at AV ≳ 7 mag with the power exponent of −2.8 ± 0.1. The steep power law indicates that a major part of the molecular cloud space is the low-density background, with the source and filamentary components comprising 40% of the mass of the entire cloud (4.6 × 104 Μ⊙).

We extracted 570 reliable sources that were classified as 176 protostellar cores and 394 starless cores, which were further interpreted as 291 self-gravitating prestellar cores and 103 unbound cores. The median values of the core masses and dust temperatures, estimated from fitting the SEDs are 4.8 Μ⊙ and 11.7 K, respectively. The starless and prestellar CMF can be well fitted with dN/d log Μ ∝ μ−1.35±0.16 between 20 and 200 Μ⊙, with an exponent identical to that of the Salpeter’s IMF. The masses and radii of the star-forming Vela cores are in a broad agreement with the birth radii deduced for open stars clusters by Marks & Kroupa (2012), which suggests that the prestellar cores more massive than 100 Μ⊙ analyzed in this paper may be forming embedded star clusters.

We measured isolated sources on the surface density maps with angular resolutions of 8.5, 11.7 and 18.2″ and found that the prestellar and unbound starless cores are well resolved, especially at the highest resolutions. Their distributions are centered on a half maximum size of 30″ (0.13 pc). The proportionality of the sizes of the protostellar cores to the angular resolution is likely caused by both overestimated peaks in the derived surface densities and the power-law radial density distribution of the collapsing envelopes.

We measured the 68 well-behaved isolated filaments with contrasts C ≳ 0.5 and lengths L ≳ 0.4 pc, extracted in the surface density map of Vela C at 11.7″ resolution. The filament widths are in the range from 0.15 to 0.63 pc, with a median of 0.3 ± 0.11 pc. The filament instability criterion Λ > Λcr, based on the critical surface density of the highly simplified model of an infinite isothermal hydrostatic cylinder, is considered in this work to be only a rough uncertain indicator. We analyzed the linear densities of the extracted filaments, assuming that the critical value is uncertain within a factor of 3.

A majority of the filaments (39) may be supercritical or subcritical, within the large uncertainties. Only 29 filaments (with ΛΜ > 3 Λcr) may be definitely considered supercritical, in which we found 94 prestellar cores, 83 protostellar cores, and only 1 unbound starless core. Thus, the supercritical filaments contain only prestellar and protostellar cores. We found that 64% of the prestellar cores and 85% of the protostellar cores are associated with the filamentary structures of ΛΜ > Λcr, whereas only 1 % of the unbound starless cores are located on such filaments. The observed close connection between the cores and filaments is consistent with the idea that dense filamentary structures provide the most favorable local environment for the formation of stars in molecular clouds.

Acknowledgements

We carried out this work at the China-Argentina Cooperation Station of NAOC/CAS. This work was supported by the Key Project of International Cooperation of Ministry of Science and Technology of China through grant 2010DFA02710, and by the National Natural Science Foundation of China through grants 11503035, 11573036, 11373009, 11433008, 11403040 and 11403041. G.Z. acknowledges support from the Postdoctoral Science Foundation of China (No. 2021T140672), and the National Natural Science Foundation of China (No. U2031118). Z.W. acknowledges support from the National Natural Science foundation of China (No. U1931203). The authors thank the anonymous referee for constructive comments that prompted improvements of this paper.

Appendix A Catalogs of dense cores and filaments identified with Herschel in Vela C

Our extraction in the Herschel SPIRE and PACS images of the Vela C molecular cloud identified a total of 570 dense cores, including 421 starless cores and 149 protostellar cores. A template of our online catalog, listing the observed properties of the extracted Herschel cores, is given in Table A.1. A template of our online catalog of the derived properties for each core (e.g., physical radius, mass, SED dust temperature) is given in Table A.2. A template of our online catalog of the physical parameters of 68 filaments (e.g., lengths, masses, linear densities, widths) is given in Table A.3.

Table A.1

Catalog of 570 reliable cores identified in the multiwavelength Herschel maps of the Vela C molecular cloud (template; full catalog provided online).

Table A.2

Derived properties of 570 reliable cores identified in the multiwavelength Herschel maps of the Vela C molecular cloud (template; full table provided online).

Table A.3

Catalog of the 68 selected filaments identified in the multiwavelength Herschel maps of the Vela C molecular cloud (template, full catalog only provided online).

References

  1. Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Andre, P., Ward-Thompson, D., & Barsony, M. 2000, in Protostars and Planets IV, eds. V. Mannings, A. P. Boss, & S. S. Russell (Tucson: Univeristy of Arizona Press), 59 [Google Scholar]
  4. André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, A102 [Google Scholar]
  5. André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: Univeristy of Arizona Press), 27 [Google Scholar]
  6. André, P. J., Palmeirim, P., & Arzoumanian, D. 2022, A&A, 667, A1 [Google Scholar]
  7. Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Arzoumanian, D., André, P., Könyves, V., et al. 2019, A&A, 621, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Baba, D., Sato, S., Nagashima, C., et al. 2006, AJ, 132, 1692 [NASA ADS] [CrossRef] [Google Scholar]
  10. Ballesteros-Paredes, J., Klessen, R. S., & Vázquez-Semadeni, E. 2003, ApJ, 592, 188 [NASA ADS] [CrossRef] [Google Scholar]
  11. Ballesteros-Paredes, J., Vázquez-Semadeni, E., Gazol, A., et al. 2011, MNRAS, 416, 1436 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ballesteros-Paredes, J., André, P., Hennebelle, P., et al. 2020, Space Sci. Rev., 216, 76 [Google Scholar]
  13. Bate, M. R. 2009, MNRAS, 392, 590 [Google Scholar]
  14. Bate, M. R., Bonnell, I. A., & Bromm, V. 2003, MNRAS, 339, 577 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [Google Scholar]
  16. Bernard, J. P., Paradis, D., Marshall, D. J., et al. 2010, A&A, 518, A88 [Google Scholar]
  17. Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [Google Scholar]
  18. Bonnell, I. A., Vine, S. G., & Bate, M. R. 2004, MNRAS, 349, 735 [Google Scholar]
  19. Bonnor, W. B. 1956, MNRAS, 116, 351 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chabrier, G. 2005, Astrophys. Space Sci. Lib., 327, 41 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ebert, R. 1955, ZAp, 37, 217 [Google Scholar]
  22. Enoch, M. L., Evans, I., Neal, J., Sargent, A. I., et al. 2008, ApJ, 684, 1240 [NASA ADS] [CrossRef] [Google Scholar]
  23. Federrath, C., Klessen, R. S., & Schmidt, W. 2008, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Giannini, T., Elia, D., Lorenzetti, D., et al. 2012, A&A, 539, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, A3 [Google Scholar]
  28. Hennemann, M., Motte, F., Schneider, N., et al. 2012, A&A, 543, A3 [Google Scholar]
  29. Heyer, M., & Dame, T. M. 2015, ARA&A, 53, 583 [Google Scholar]
  30. Heyer, M. H., & Terebey, S. 1998, ApJ, 502, 265 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Johnstone, D., Wilson, C. D., Moriarty-Schieven, G., et al. 2000, ApJ, 545, 327 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Kainulainen, J., Beuther, H., Banerjee, R., Federrath, C., & Henning, T. 2011, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Kauffmann, J., Pillai, T., Shetty, R., Myers, P. C., & Goodman, A. A. 2010, ApJ, 716, 433 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kirk, J. M., Ward-Thompson, D., & André, P. 2005, MNRAS, 360, 1506 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kirk, H., Myers, P. C., Bourke, T. L., et al. 2013, ApJ, 766, 115 [Google Scholar]
  38. Könyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [Google Scholar]
  39. Kramer, C., Stutzki, J., Rohrig, R., & Corneliussen, U. 1998, A&A, 329, 249 [NASA ADS] [Google Scholar]
  40. Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, in Planets, Stars and Stellar Systems, Vol. 5: Galactic Structure and Stellar Populations, eds. T. D. Oswalt, & G. Gilmore (Dordrecht: Springer), 115 [Google Scholar]
  43. Kruijssen, J. M. D., Pelupessy, F. I., Lamers, H. J. G. L. M., et al. 2012, MNRAS, 421, 1927 [NASA ADS] [CrossRef] [Google Scholar]
  44. Li, D., & Goldsmith, P. F. 2012, ApJ, 756, 12 [NASA ADS] [CrossRef] [Google Scholar]
  45. Li, D., Velusamy, T., Goldsmith, P. F., & Langer, W. D. 2007, ApJ, 655, 351 [NASA ADS] [CrossRef] [Google Scholar]
  46. Liseau, R., Lorenzetti, D., Nisini, B., Spinoglio, L., & Moneti, A. 1992, A&A, 265, 577 [NASA ADS] [Google Scholar]
  47. Lorenzetti, D., Spinoglio, L., & Liseau, R. 1993, A&A, 275, 489 [NASA ADS] [Google Scholar]
  48. Louvet, F., Hennebelle, P., Men’shchikov, A., et al. 2021, A&A, 653, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Marks, M., & Kroupa, P. 2012, A&A, 543, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Massi, F., Lorenzetti, D., & Giannini, T. 2003, A&A, 399, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Massi, F., Weiss, A., Elia, D., et al. 2019, A&A, 628, A110 [EDP Sciences] [Google Scholar]
  52. May, J., Murphy, D. C., & Thaddeus, P. 1988, A&AS, 73, 51 [NASA ADS] [Google Scholar]
  53. McKee, C. F., & Tan, J. C. 2002, Nature, 416, 59 [CrossRef] [Google Scholar]
  54. McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [Google Scholar]
  55. Men’shchikov, A. 2013, A&A, 560, A63 [Google Scholar]
  56. Men’shchikov, A. 2016, A&A, 593, A71 [Google Scholar]
  57. Men’shchikov, A. 2021a, A&A, 649, A89 [EDP Sciences] [Google Scholar]
  58. Men’shchikov, A. 2021b, A&A, 654, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Men’shchikov, A. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202346152 [Google Scholar]
  60. Men’shchikov, A., André, P., Didelon, P., et al. 2010, A&A, 518, A103 [Google Scholar]
  61. Men’shchikov, A., André, P., Didelon, P., et al. 2012, A&A, 542, A81 [Google Scholar]
  62. Minier, V., Tremblin, P., Hill, T., et al. 2013, A&A, 550, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Molinari, S., Swinyard, B., Bally, J., et al. 2010, PASP, 122, 314 [Google Scholar]
  64. Molinari, S., Schisano, E., Faustini, F., et al. 2011, A&A, 530, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
  66. Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, A77 [Google Scholar]
  67. Motte, F., Nony, T., Louvet, F., et al. 2018, Nat. Astron., 2, 478 [Google Scholar]
  68. Murphy, D. C., & May, J. 1991, A&A, 247, 202 [NASA ADS] [Google Scholar]
  69. Netterfield, C. B., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1824 [NASA ADS] [CrossRef] [Google Scholar]
  70. Ostriker, J. 1964, ApJ, 140, 1056 [Google Scholar]
  71. Panopoulou, G. V., Clark, S. E., Hacar, A., et al. 2022, A&A, 657, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Passot, T., & Vázquez-Semadeni, E. 1998, Phys. Rev. E, 58, 4501 [Google Scholar]
  73. Piazzo, L., Calzoletti, L., Faustini, F., et al. 2015, MNRAS, 447, 1471 [NASA ADS] [CrossRef] [Google Scholar]
  74. Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, A2 [Google Scholar]
  76. Pouteau, Y., Motte, F., Nony, T., et al. 2022, A&A, 664, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  78. Sanders, D. B., Scoville, N. Z., & Solomon, P. M. 1985, ApJ, 289, 373 [NASA ADS] [CrossRef] [Google Scholar]
  79. Schisano, E., Molinari, S., Elia, D., et al. 2020, MNRAS, 492, 5420 [Google Scholar]
  80. Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
  81. Stodólkiewicz, J. S. 1963, Acta Astron., 13, 30 [NASA ADS] [Google Scholar]
  82. Stutzki, J., & Guesten, R. 1990, ApJ, 356, 513 [Google Scholar]
  83. Tan, J. C., Beltrán, M. T., Caselli, P., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: Univeristy of Arizona Press), 149 [Google Scholar]
  84. Tassis, K., Christie, D. A., Urban, A., et al. 2010, MNRAS, 408, 1089 [NASA ADS] [CrossRef] [Google Scholar]
  85. Vazquez-Semadeni, E. 1994, ApJ, 423, 681 [Google Scholar]
  86. Ward-Thompson, D., André, P., Crutcher, R., et al. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: Univeristy of Arizona Press), 33 [Google Scholar]
  87. Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&As, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [Google Scholar]
  89. Yamaguchi, N., Mizuno, N., Saito, H., et al. 1999, PASJ, 51, 775 [NASA ADS] [Google Scholar]
  90. Zhang, G.-Y., Xu, J.-L., Vasyunin, A. I., et al. 2018, A&A, 620, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Zhang, G.-Y., André, P., Men’shchikov, A., & Wang, K. 2020, A&A, 642, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Zhang, C., Zhang, G.-Y., Li, J.-Z., & Li, X.-M. 2022, Res. Astron. Astrophys., 22, 055012 [CrossRef] [Google Scholar]
  93. Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2020, A&A, 633, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Masses of the structural components of the Vela C molecular cloud, separated by getsf in the surface density images with different angular resolutions.

In the text
Table A.1

Catalog of 570 reliable cores identified in the multiwavelength Herschel maps of the Vela C molecular cloud (template; full catalog provided online).

In the text
Table A.2

Derived properties of 570 reliable cores identified in the multiwavelength Herschel maps of the Vela C molecular cloud (template; full table provided online).

In the text
Table A.3

Catalog of the 68 selected filaments identified in the multiwavelength Herschel maps of the Vela C molecular cloud (template, full catalog only provided online).

In the text

All Figures

thumbnail Fig. 1

High-resolution (11.7″) surface density map of Vela C, obtained from the Herschel images.
In the text
thumbnail Fig. 2

Extracted cores and filaments in the Vela C molecular cloud on the 11.7″-resolution surface density image. The locations and sizes of the cores are measured from the surface density map. The black, green, and blue ellipses represent the 329 prestellar cores, 84 unbound starless cores, and 149 protostellar cores, respectively. The full axis of the ellipses is two times the Gaussian full width at half maximum (FWHM). Filamentary networks are shown by the global scale-independent skeletons of the filamentary structure. The filament linear density ΛW in each point along the skeletons was estimated from Eq. (7) assuming a width of W = 0.3 pc (Fig. 11).
In the text
thumbnail Fig. 3

Probability density function PDFN for Vela C. The vertical axis gives the actual number of pixels per bin in the 11.7″ resolution surface density image. At NH2≳2×1021cm−2${N_{{{\rm{H}}_2}}} \mathbin{\lower.3ex\hbox{$\buildrel>\over{\smash{\scriptstyle\sim}\vphantom{_x}}$}} 2 \times {10^{21}}{\rm{c}}{{\rm{m}}^{ - 2}}$, corresponding to NH2≳7AV${N_{{{\rm{H}}_{\rm{2}}}}} \mathbin{\lower.3ex\hbox{$\buildrel>\over {\smash{\scriptstyle\sim}\vphantom{_x}}$}} 7{A_V}$, it can be fit well with a power law.
In the text
thumbnail Fig. 4

Illustration of the selection criteria for starless cores in five Herschel images and in high-resolution surface density maps at resolutions of 8.5, 11.7, and 18.2″ (Sect. 3.4). The black ellipses represent the measured major and minor FWHM sizes.
In the text
thumbnail Fig. 5

Illustration of the selection criteria for protostellar cores in five Herschel images and in high-resolution surface density maps at resolutions of 8.5, 11.7, and 18.2″ (Sect. 3.4). The black ellipses represent the measured major and minor FWHM sizes.
In the text
thumbnail Fig. 6

Histograms of the sizes of isolated cores, not blended with any other source in any waveband. The core radius is the arithmetic mean of the major and minor half maximum sizes, measured in the surface density images with three different resolutions (indicated by the vertical dashed lines). Panel a: distribution of source radii at 8.5″ resolution. Panel b: distribution of source radii at 11.7″ resolution. Panel c: distribution of source radii at 18.2″ resolution.
In the text
thumbnail Fig. 7

Histograms of the physical parameters of the 570 reliable cores obtained from fitting SEDs of the extracted sources. Panel a: distribution of their average temperatures (median of 11.7 K). Panel b: distribution of their masses (median of 4.8 M⊙). Panel c: distribution of their luminosities (median of 0.9 L⊙). The red dashed lines indicate the median values.
In the text
thumbnail Fig. 8

Mass-size diagram for Vela C for the unbound cores (green squares), prestellar cores (blue circles), and protostellar cores (red stars). Only the partially resolved and resolved cores are shown (with sizes 10% larger than the 11.7″ beam) to ensure acceptably accurate decon-volution results using Eq. (4). The critical Bonnor-Ebert spheres with temperatures of 6, 10, and 20 Κ are displayed by the dashed black, dashed green, and solid red lines, respectively. The dashed cyan line is the radius-mass relation for open star clusters (Marks & Kroupa 2012, Eq. (7)) and the gray envelope represents its uncertainty range. The dashed magenta line indicates an empirical relationship proposed by Kauffmann et al. (2010). The physical scale of 0.05 pc at the 11.7″ resolution is indicated by the vertical line.
In the text
thumbnail Fig. 9

Differential core mass function (dN/dlogM) for the 329 prestellar cores (green) 421 starless cores (orange), and 149 protostellar cores (magenta). The error bars correspond to the N$\sqrt N $ statistical uncertainties.
In the text
thumbnail Fig. 10

Illustration of a detected and measured filament in a high-resolution surface density image at 11.7″. Left: skeletons of the detected filaments with a contrast C > 0.5 is shown by the white curves and the black curve is the skeleton of a filament whose measured radial profile is shown in the right panel. Right: median one-sided surface density profiles measured on the two sides of the filament (blue and purple solid lines). The black dashed curve shows the beam profile. The median half maximum width of the filament is 0.33 ± 0.19 pc.
In the text
thumbnail Fig. 11

Histograms of physical parameters of 68 selected filaments in Vela C. (a): filament contrasts; (b): filament widths; (c): logarithmic slope of profile; (d): dust temperatures along the filament crests; (e): surface densities along the crest; (f): ratio of linear density to the critical value. The red dashed line indicates the median value, and the error is the rms of the data.
In the text
thumbnail Fig. 12

Correlations of physical parameters of 68 filaments in Vela C. The red dashed lines indicate the median values and the red solid lines represent fits to the data: log ΛΡ = 0.86 log ΛΜ + 0.13 (r = 0.96), logΛM=1.15logNH2−23.16(r=0.91)$\log {\Lambda ^{\rm{M}}} = 1.15\log {N_{{{\rm{H}}_{\rm{2}}}}} - 23.16\left( {r = 0.91} \right)$, logC=0.82logNH2−17.92(r=0.95)$\log C = 0.82\log {N_{{{\rm{H}}_{\rm{2}}}}} - 17.92\left( {r = 0.95} \right)$, T = −2.20 log ΛΜ + 19.38 (r = 0.77), where r is the Pearson product moment correlation coefficient.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.