EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 671 (March 2023) A&A, 671 (2023) A171 Full HTML
Open Access
Issue
A&A
Volume 671, March 2023
Article Number A171
Number of page(s) 20
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/202244482
Published online 23 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Determining the fundamental stellar properties is important in many different fields of astronomy, from galactic archaeology to exoplanet studies. High-resolution spectroscopy is one of the most reliable ways to determine these parameters, as it analyzes the absorption features of the spectrum based on first principles. With the ever-increasing sizes of surveys it becomes especially necessary to have analysis tools that can be applied to a large number of targets as well. Here we present the most recent evolution in the popular Spectroscopy Made Easy package (SME, Valenti & Piskunov 1996; Piskunov & Valenti 2017), called PySME. Previous iterations of SME were limited by the closed source IDL (Interactive Data Language1) language in its application to large samples; this has been solved here by transitioning to Python2. This allowed us to improve on some other aspects of the software as well.

PySME is one of only a few stellar spectral analysis tools available; others include Turbospectrum (Plez et al. 1993; Plez 2012b; Gerber et al. 2022), MOOG (Sneden 1973; Sneden et al. 2012), Korg (Wheeler et al. 2023), SYNSPEC (Hubeny & Lanz 2011, 2017; Hubeny et al. 2021), SYNTHE (Kurucz 1993d; Sbordone et al. 2004), and SPECTRUM (Gray & Corbally 1994).

In this paper, we focus our analysis on a relatively small sample of target stars to illustrate the changes, assess the performance, and discuss some improved practical aspects of installation, use, and support of this new incarnation of SME. The target stars selected here are all exoplanet host stars as those are of particular interest to exoplanet studies, but this new version of SME can be applied to a wide variety of stars, just as the earlier SME. It should be noted that exoplanet host stars have statistically higher metallicities than their non-exoplanet hosting counterparts (Heiter & Luck 2003; Fischer & Valenti 2005).

The paper is divided into four parts. We start by introducing PySME, highlighting the changes and the differences from the original IDL implementation (Sect. 2). Then we perform a comparison between the new PySME and the IDL SME implementation (Sect. 3) to test both the accuracy of the spectral synthesis and the stability of the stellar parameter fitting. After this, we present a spectroscopic analysis carried out for a sample of planet-hosting FGK stars (Sect. 4) and compare the results to those of other studies (Sect. 5). Finally, we analyze trends in the derived parameters and their uncertainties in relation to the stellar effective temperature (Sect. 6), as a proxy for the stellar type.

2 PySME

Spectroscopy Made Easy is a spectral synthesis and fitting tool for the interpretation of stellar spectra. We focus here on exoplanet host stars exclusively; however, PySME is applicable to a wide variety of stars. In synthesis mode it generates a spectrum for a given set of stellar parameters (Teff, log g, abundances, macro- and microturbulence υmac and υmic, and projected equatorial rotation velocity υ sin i) for specified spectral intervals and spectral resolution (instrumental profile). In analysis mode SME finds the optimal values for selected stellar parameters that result in the best fit to the provided observations given the uncertainties of the data. The free parameters may include one or several (or even all) of the stellar parameters from the list above, including specific elemental abundances as well as some atomic line parameters of any transition in the line list.

The original SME package was written in IDL with the radiative transfer solver inherited from the antique FORTRAN code Synth by Piskunov (Piskunov 1992) accessed in the form of an external dynamic library. Throughout the years more and more improved and updated parts of spectral synthesis were incorporated into the library, which was later named the SME library3. It currently includes the molecular-ionization equilibrium solver EOS (Piskunov & Valenti 2017), the continuous opacity package CONTOP, the line opacity package LINOP (Barklem & Piskunov 2015), and a plane-parallel and spherical radiative transfer solver based on the Bezier-spline approximation to the source functions (De la Cruz Rodríguez & Piskunov 2013).

The whole package is divided into two parts: the graphical user interface (GUI) that handles data input and output and the presentation and/or inspection of the results, and the actual solver that either generates the synthetic spectrum or performs fitting of the observations. These two parts communicate with each other through a data structure, known as the SME structure, which contains all the information necessary for the calculations. To initiate a process the user needs to create this structure either using the GUI or any other method. The calculation part then uses the input structure to initiate its work, and upon completion packages the results into a similar output structure, which can explored with the GUI.

At the time of the initial development of SME, IDL was widely used in astronomy for data reduction and data analysis. Therefore, only the performance-critical parts of SME were written in C and FORTRAN. However, new developments since then, such as the recent marketing policy of IDL, motivated us to move SME to Python, an open and free platform. This has the benefit that PySME no longer relies on commercial software, simplifies parallelization, and opens additional functionality through the use of existing Python libraries. This also simplifies the use of PySME for large surveys, as was done for example for the GALactic Archaeology with HERMES (GALAH) survey (Buder et al. 2021) with IDL SME. Additionally, the switch to Python offers us an opportunity to improve and modernize several components of SME. In the following sections we discuss in greater detail the specific changes that were made to PySME.

2.1 Optimization algorithm

One of the most useful capabilities of PySME is its ability to determine the best fit stellar parameters from comparison with the observations. In PySME this is done by solving the least-squares problem, 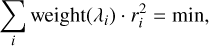∑iweight(λi)⋅ri2=min,$\sum\limits_i {{\rm{weight}}\left( {{\lambda _i}} \right) \cdot r_i^2 = \min ,}$(1)

where the residuals ri ≡ synth(λi, p0, p1, …) – obs(λi); synth is the synthetic spectrum generated by PySME; obs is the observed spectrum; p0, p1, … are the fitting parameters (e.g., effective temperature Teff); λi is the wavelength of point i; and ‘weight’ is the weight of each point conventionally set to the inverse of data uncertainties σ. In IDL SME the weights were modified to include the residual intensity of observations: 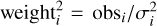weighti2=obsi/σi2${\rm{weight}}_i^{\rm{2}} = {{{\rm{ob}}{{\rm{s}}_i}} \mathord{\left/ {\vphantom {{{\rm{ob}}{{\rm{s}}_i}} {\sigma _i^2}}} \right. \kern-\nulldelimiterspace} {\sigma _i^2}}$. In this way the optimization algorithm is discouraged from improving the fit to the line cores at the expense of the continuum points. We find this scheme useful, in particular when fitting a short spectral interval with a comparable amount of continuum and line points, and so we kept this weighing scheme in the PySME.

Instead of the Levenberg-Marquardt (LM) algorithm employed in the IDL SME, PySME uses the dogbox algorithm, as described in Voglis & Lagaris (2004) and implemented in SciPy (Virtanen et al. 2020). This method is similar to the LM algorithm in that it uses the Gauss–Newton step and the steepest decent, but it also uses an explicit rectangular trust region. At each iteration it calculates the Gauss–Newton step and the steepest decent; the next step is then one of three options: if the Gauss–Newton step is within the trust region, the Gauss–Newton step is used; if the Gauss–Newton step is outside the trust region, but the steepest decent step is inside it, a combination of the two is used (as shown in Fig. 1); if both are outside the trust region, the steepest decent direction to the edge of the trust region is followed. The size of the trust region ∆ is adjusted between iterations depending on the improvement of the residuals. The size of the trust region is kept constant unless the changes stop matching the linear estimate for the convergence. If the improvement is greater than expected, the trust region is increased. If it is marginal, the trust region is decreased.

Of all the methods implemented in SciPy, in our experience this method results in the smallest number of function evaluations needed to reach convergence. It also allows us to set limits on the stellar parameters without confusing the fitting process. This is occasionally required to prevent SME from extrapolating outside the grid of stellar atmospheres and keep the interpolated model physical.

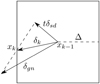thumbnail Fig. 1

Sketch of the dogbox algorithm in two dimensions for step k. The previous point is xk−i, the next point is xk. The rectangle gives the trust region with size ∆, δgn is the Gauss–Newton step, and tδsd is the steepest decent step. Here the Gauss–Newton step falls outside the trust region, so the new step δk is a combination of the Gauss–Newton step and the steepest decent, cut off at the boundary of the trust region.

2.2 Continuum fitting

Correct continuum normalization is very important for the accurate determination of stellar parameters. In PySME, we achieve this by changing the continuum of the synthetic spectrum to match the observed spectrum, similar to IDL SME. Since every spectrum is different, there is no good solution that fits all situations. We therefore implement several continuum correction alternatives in PySME. A list of the methods is presented in Table 1 and a longer explanation can be found in the PySME documentation4. Each continuum fitting method has an associated degrees of freedom parameter, whose meaning depends on the selected method. Examples of some options are given in Fig. 2 for the F7 dwarf HD 148816 (Houk & Swift 1999) with Teff = 5908 K, log g = 4.32 log g, and [M/H] = −0.7l dex (Costa Silva et al. 2020).

In the mask method a user-defined mask is adopted to specify continuum points. Then a polynomial fit to those points is used as the continuum of the spectrum. The degree of the polynomial is a user-defined parameter. The benefit of this method is that it allows good control over the continuum placing, and it works reliably if continuum points are present in selected wavelength regions. Moreover, it does not rely on the synthetic spectrum, so the continuum stays the same throughout the SME iterations. The downside is the need for interactive setting of the mask, and the requirement of having continuum points may be impossible to meet, for example for TiO molecular bands in M dwarfs or for regions around strong lines with very broad wings.

An alternative approach is to match the relative depth of various lines to the spectral synthesis. This is implemented as match option, which uses the fact that line depth is affected nonlinearly by the selected continuum level: spectral points in the center of strong lines are much less affected by a change in continuum placing than points in weak lines. Thus, the idea is to fit the continuum such that ∑i[ obs(λi)−syn(λi)⋅f(λi) ]2=min,${\sum\limits_i {\left[ {{\rm{obs}}\left( {{\lambda _i}} \right) - {\rm{syn}}\left( {{\lambda _i}} \right) \cdot f\left( {{\lambda _i}} \right)} \right]} ^2} = \min ,$(2)

where f is an analytical continuum function. We choose f to be a polynomial and determine the coefficients using a least-squares fit. The degree of the polynomial is a user-defined parameter. To match the concept of continuum, PySME sets the weights for spectral points proportional to their residual intensity so that a good continuum is found even if some lines are missing in the synthesis. This method has the advantage that it does not require the continuum points to be present in observations. On the other hand, it needs the observations to represent a good range of line depths and a reasonable match to the synthetic spectrum. This frequently means fitting a relatively large spectral range, and works best for observations with a high signal-to-noise ratio (S/N). We note that this option requires re-evaluation of the continuum on every SME iteration. The other methods listed in Table 1 are various combinations of the mask and the match methods.

Finally, PySME can also rely on continuum normalization done before the import of observations making no continuum adjustments. Figure 2 shows some of the more successful fits to a spectral fragment for HD 148816.

Table 1

Continuum normalization options.

2.3 Radial velocity fitting

Just as important as the continuum is the radial velocity shift between the observed spectrum and the synthetic spectrum. The radial velocity determination can be done for each wavelength segment separately or for the entire spectrum. In PySME, we determine the radial velocity in two steps. First we perform a wide-range search using the cross-correlation between the observed spectrum and the synthetic spectrum to get a rough estimate of the radial velocity value and avoid shallow local minima. The accuracy of this first guess is limited by the wavelength resolution of the observation as we avoid interpolation and perform cross-correlation of data pixels. By default, we limit the range of this search to ±500 km s−1, but this value can be adjusted by the user. In the second step, we refine the radial velocity value in a least-squares sense, starting from the previous estimate. We shift the synthetic spectrum wavelength using the relativistic Doppler shift formula (Eq. (3)) in each iteration until it matches the observed spectrum: 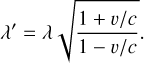λ′=λ1+υ/c1−υ/c.$\lambda ' = \lambda \sqrt {{{1 + {\upsilon \mathord{\left/ {\vphantom {\upsilon c}} \right. \kern-\nulldelimiterspace} c}} \over {1 - {\upsilon \mathord{\left/ {\vphantom {\upsilon c}} \right. \kern-\nulldelimiterspace} c}}}} .$(3)

Here, λ′ is the wavelength shifted into the rest frame of the star, λ is the wavelength in the rest frame of the observer, υ is the radial velocity (positive for a star moving away from the observer), and c is the speed of light.

2.4 Auxiliary data

The radiative transfer calculations at the core of SME require additional data with atomic and molecular line properties (line lists), as well as stellar model atmosphere(s). Additionally, to correct for non-local thermodynamic equilibrium (NLTE) effects, PySME requires NLTE departure coefficients matching the selected atmospheric model, all of which are discussed in this section.

The line data for each transition must at least include the species name, ionization stage, excitation energy of the lower level, and the transition oscillator strength. These can be complemented by the line broadening parameters for the natural, Stark, and van der Waals broadening mechanisms. If they are not known, PySME will use approximations as described in Valenti & Piskunov (1996) and Piskunov & Valenti (2017). Finally for NLTE corrections (see below), the line list should also include the term designation for the lower and upper energy levels, as well as their angular momentum quantum numbers J. Conveniently, PySME supports the line list format returned by VALD3 (Ryabchikova et al. 2015, 1997; Kupka et al. 2000, 1999; Piskunov et al. 1995) for the extract stellar query, which includes all the required information. Both short and long formats are supported, but the long format is required for NLTE corrections.

Spectral synthesis in PySME also needs a stellar atmosphere model that describes the temperature and pressure profiles as functions of “depth,” where depth could be an optical depth at a standard wavelength or a column mass. When the effective temperature, surface gravity, or metallicity of the synthesis does not match that of a pre-computed model, PySME interpolates in a three-dimensional grid (Teff, log g, and [M/H]). Grids for use with PySME are provided by several authors. These include the MARCS models (Gustafsson et al. 2008) for cool dwarf and giant stars, and the ATLAS (Kurucz 2017; Heiter et al. 2002) and LL models (Shulyak et al. 2004) for hotter main sequence objects. Each model grid is packed in rather large data files (on the order of GB), and multiple grids are often available for different microturbulence parameters and alpha-element abundances, for example.

To account for NLTE effects, PySME uses departure coefficient tables. The departure coefficient is the ratio of the NLTE to the LTE population of an energy level involved in radiative transition (see Piskunov & Valenti 2017, who describe the source function and the impact on absorption coefficient). The departure coefficient depends on the local physical conditions described by the model atmosphere and the abundance of the species responsible for absorption or emission. Thus, fitting specific abundance and/or atmospheric parameters may require interpolation. To this end, departure coefficients need to be computed for each layer of every atmospheric model in a grid, and for several elemental abundances around the model metallicity. The resulting data files are even larger than the model grids, and notably they can only be used with the model atmosphere grid they were calculated for.

In the original IDL SME, all these files were included with the distribution package, bringing its size to over 1 TB, even though most users only need a subset of this data. In PySME, atmosphere model grids and departure coefficient files are instead stored on a data server until requested by the user, at which point they are automatically downloaded. This significantly reduces the installation footprint of PySME in comparison to IDL SME; in addition, this allows PySME to provide updates for these data files when available. It is still possible to add custom grids.

The new default atmosphere grid is the marcs2014 grid, which is essentially the marcs2012 grid with some holes filled and with an improved spherical models (T. Nordlander, priv. comm.). Additionally, PySME also supports the latest NLTE departure coefficient grids by Amarsi et al. (2020), which have been calculated for the 2014 MARCS atmospheric grids.

thumbnail Fig. 2

Comparison of the different continuum normalization options on a small segment of the spectrum of HD 148816. Each plot shows the original observation (blue), the corrected synthetic spectrum (dotted orange), and the continuum detected by the method (purple). The shaded regions show the selected pixels used as the mask (green).

2.5 Elemental abundances

In addition to the overall metallicity, PySME also allows the individual elemental abundances to be set manually for the first 100 elements (up to Einsteinium) or to be set as a free parameter in the fitting. PySME supports abundance input following different conventions. These include the H = 12 convention with elemental abundances set relative to hydrogen and the SME convention where abundances are set relative to the total number of atoms in a volume. Internally they are all converted to the H = 12 format in the Python part of PySME; however, the SME library uses the SME format, which was the only format used in IDL SME. For convenience PySME supports three alternatives for default solar abundances, as described in Table 2. These replace the solar abundance values of IDL SME, which was evolving with time.

Table 2

Solar abundance sets included in PySME.

Table 3

Initial parameters for the convergence test.

2.6 Convergence

We tested the PySME convergence to ensure the robustness of the new optimization algorithm; in other words, we tested whether we get similar results for different initial sets of parameters. For this test we used a segment of the solar spectrum (4489–4603 Å) provided by the National Solar Observatory Atlas 1 (Kurucz et al. 1984), which is an optical flux spectrum for a relatively inactive Sun. We then determined the best fit Teff, log g, and [M/H], starting with different initial parameters on a 3 × 3 × 3 grid (see Table 3). The derived parameters of these 27 runs are all within the uncertainties of the fit. In Fig. 3, we show the distribution of the points in the parameter space. The standard deviation of the final values are 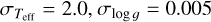σTeff=2.0,σlog g=0.005${\sigma _{{T_{{\rm{eff}}}}}} = 2.0,{\sigma _{\log \,g}} = 0.005$, and σ[м/н] = 0.001.

2.7 Parameter uncertainties

As in all parameter determinations, there are two different types of uncertainties to measure. The first is the statistical uncertainty, which depends on the S/N of the observations and is easily determined from the least-squares fit in PySME using the covariance matrix. We corrected these uncertainties in PySME using the final χ2, by multiplying the covariance matrix with √χ2. This normalized the initial uncertainties on the data points to those expected for this fit.

The second uncertainty is the systematic uncertainty, which is due to inherent deficiencies of the atomic and molecular data as well as observational defects (e.g., due to incorrect parameters in the line list). These uncertainties are much more difficult to constrain as there is no reference for PySME to use. Instead, PySME uses the uncertainty method described in Ryabchikova et al. (2016) and Piskunov & Valenti (2017). This method uses the fit residuals, derivatives, and uncertainties of the observed spectrum to determine the cumulative probability distribution under the assumption that the entire residual can be explained by the variation in one parameter. Ignoring the sensitivity to other free parameters leads to an overestimation of the uncertainties. This approach works reasonably well for free parameters that explicitly affect the majority of spectral points (e.g., Teff, [M/H]), but the estimate becomes unrealistically exaggerated for parameters affecting spectra locally (log g, individual abundances). We also note here that this method is invariant to the absolute scale of the input uncertainties of the spectrum.

In Fig. 4, we show the distribution for uncertainties for Teff for ϵ Eri (details of the analysis are discussed in Sect. 4) as cumulative probability and as probability density5. We note that the central part looks reasonably close to a Gaussian distribution, which explains why we get a realistic estimate for the uncertainty of Teff. For other more local parameters, such as individual abundances, the central part is often very asymmetric and quite different from a Gaussian.

To evaluate the accuracy of these uncertainty estimates we ran a simple Monte Carlo test. For this we created a synthetic spectrum for a single wavelength segment between 6400 Å to 6500 Å with stellar parameters Teff = 6000 K, log g = 4.4 log(cm s−2), [M/H] = 0dex. Then we applied white noise with a S/N of 100 to this spectrum and extracted the stellar parameters Teff, log g, and [M/H] using PySME with the initial parameters disturbed around the true values. Repeating this process for 1000 runs we were able to estimate the uncertainty of the parameters from the scatter of the values. This scatter is shown in Fig. 5 for Teff, the other parameters show a similar behavior. A comparison between the values is given in Table 4. This process does not include the systematic uncertainties of the input data as we create a synthetic spectrum for comparison, and thus the uncertainties derived from the scatter match those derived by the least-squares fit.

A final way to estimate the uncertainties is by comparing the results obtained here with those from previous studies (see Sect. 6). Using the scatter of the differences we can then infer an estimate for the systematic uncertainties. The systematic uncertainties obtained in this way are 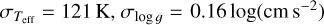σTeff=121 K,σlog g=0.16 log(cm s−2)${\sigma _{{T_{{\rm{eff}}}}}} = 121\,{\rm{K}},{\sigma _{\log \,g}} = 0.16\,\log \left( {{\rm{cm}}\,{{\rm{s}}^{ - 2}}} \right)$, and σ[M/H] = 0.07 dex.

thumbnail Fig. 3

Distribution of the best fit stellar parameters Teff, log g, and [M/H] for different initial parameters. Initial values are shown in blue and final values in orange. The cutout in the upper left corner shows the entire parameter space spanned by the initial parameters, while the rest is zoomed in on the closely clustered final distribution.
thumbnail Fig. 4

Cumulative probability (top) and probability density (bottom) distribution of Teff for a spectrum of ϵ Eri derived from the fit results (blue). For comparison, also shown is the distribution of a Gaussian with the same median and σ as derived from the cumulative probability (orange). The median is marked by a dashed line (bottom), and the 1er range is shown as dash dotted lines and a shaded region (bottom). The distributions for the other fitted stellar parameters are shown Fig. C.1.

2.8 Graphical user interface

For PySME an entirely new graphical user interface (GUI) was developed6. For improved usability it relies on established web technologies using the Electron7 framework. The interface is divided into a number of sections, each managing one part of the SME structure. The spectrum section allows the user to zoom and pan on the spectra, both observed and synthetic, together with the positions of the lines in the line list. Furthermore, it is possible to manually set and manipulate the bad pixel and continuum normalization mask.

The other sections can be used to change the parameters of the SME structure, including the entirety of the line list, the elemental abundances, and the NLTE settings. However, it does not offer some of the functionality that the IDL SME GUI included. For example, it is not possible to select lines directly in the spectrum to inspect or modify their parameters nor is it possible to measure the equivalent width of lines directly in the interface.

thumbnail Fig. 5

Scatter of the recovered Teff around the true value for a synthetic spectra with random noise of S/N 100.
Table 4

Comparison between the uncertainty estimates based on a synthetic spectrum.

2.9 Interoperability between IDL SME and PySME

PySME was designed to provide an easy transition for existing IDL SME users. It is therefore capable of importing existing IDL SME input (. inp) and output (. out) structures for use with PySME or its GUI. PySME itself however uses a new file format to store those structures (. sme), which can currently not be used by IDL SME. It is possible though to create IDL readable files if an IDL installation is available on the machine using the save_as_idl function.

2.10 Parallelization

In some circumstances users may be interested in analyzing a large number of stellar spectra (e.g., in surveys). Previously this required an individual IDL license for each process running at the same time. This was expensive (IDL cluster license) and complicated. PySME solves both of these problems at once. Even so, care should be taken; it is recommended that each synthesis or fitting be run in a separate process since the SME library should not be shared between them. Many tools exist for different systems, for example the GNU parallel tool (Tange 2011). PySME includes an easy example of such a script.

thumbnail Fig. 6

Comparison between the IDL SME stellar synthesis (dashed green) and the PySME stellar synthesis (orange) for a small section of the stellar spectrum. All lines in the line list are indicated and accordingly labeled by vertical lines. The zoom-in on the Ca line highlights the small numerical difference between the two codes.

2.11 Open source

In addition to replacing IDL with Python, an open-source language, we also made the SME library available under the BSD 3-Clause license, which is an open-source license. This means that you can use PySME in your projects which specify open source requirements as part of your funding, which is in line with the European Commission’s Open Science guidelines.

3 Comparison between IDL SME and PySME

With the new version of SME it is interesting to compare PySME to IDL SME, which we split into two parts. First we ensure that both versions reach the same set of free parameters (within the estimated uncertainties) given the same spectral synthesis as the observations. In the second step we compare the performance (i.e., the runtimes) of the two versions.

3.1 Comparison of spectral synthesis

The results of the stellar synthesis are plotted in Fig. 6. At first glance the two codes seem to create identical synthetic spectra; however, upon closer inspection there are small numerical differences, as shown in the zoomed-in panel for the Ca line in Fig. 6. These differences are on the order of 0.01 %, which matches the declared precision of the radiative transfer solver included in the library. That these spectra differ by this amount is not trivial, as the Python/IDL layer of SME performs significant calculations, including the interpolation in the stellar atmosphere grid, wavelength re-sampling, the application of the instrumental profile, and disk integration using the macroturbulence and rotational broadening. We believe that the two implementations are sufficiently close so as not to cause any additional change that exceeds the precision of the radiative transfer solving.

To further convince ourselves that the new incarnation of SME performs spectral fitting at least as well as the IDL SME, we performed a blind comparison between the two. To this end, we used HARPS spectra of a K dwarf, 55 Cnc. The IDL SME analysis was carried out by Ryabchikova (TR) while PySME fitting was done by Wehrhahn (AW). The only common parts between the two were the observations, the spectral range, and the SME library. More details on the comparison and the results are presented in Sect. 4.3.

Table 5

Minimum and average runtime of PySME and IDL SME on the same machine over 1000 runs.

3.2 Comparison of performance

The second test dealt with the speed of the calculation. For this purpose we compared the execution time for the same short stellar spectral interval shown in Fig. 6 for both PySME and IDL SME. Even on the same machine the execution time varied due to input–output (I/O) performance, and so we recorded the minimum time and average time of the 1000 runs presented in Table 5. This shows that the execution times between PySME and IDL SME are similar. Further analysis shows that the vast majority of CPU time is spent in radiative transfer calculation in the SME library, which is shared between the two versions of SME.

4 Analysis

Finally we applied PySME to a small selection of targets. The target selection is discussed in Sect. 4.1, followed by discussions on the chosen settings (Sect. 4.2) and a short discussion of each target (Sect. 4.3). The final parameters are given in Table 6. The results are compared to each other in Sect. 6.

4.1 Target selection

Determination of accurate stellar parameters for a small number of exoplanet host stars is important for the interpretation of transit spectroscopy, but it also gives us an opportunity to assess the PySME performance for a range of spectral types. Close proximity to the Sun and the presence of planets makes these stars interesting, and so we expected to find additional data, such as accurate parallaxes and interferometry, to help us set independent constraints on some of the stellar parameters. The selection of targets includes eight stars, six of which have transiting planets. High-quality spectra for these targets are available from ESO archive (3.6m HARPS), while interferometric radii were taken from Yee et al. (2017) and von Braun et al. (2014). Table 7 summarizes the data we used for the analysis.

4.2 Preparation of our test sample

4.2.1 Continuum

The standard HARPS pipeline does not do continuum normalization (which is not required for radial velocity measurements), and thus our first task was to correct for the spectrometer blaze function and rely on PySME correction for the fine-tuning as described earlier in Sect. 2.2. We determine the upper envelope of the spectrum by selecting the local maxima and fitting a smooth function. The maxima are found by comparing neighboring points, and then only keeping the largest local maximum in a given interval (step size). The step size should be larger than the width of absorption features, but small enough to follow the continuum. For our data we choose a step size of i000 pixels. Then we connect the selected points with straight lines and smooth the resulting curve using a Gaussian of the same width as the step size. This creates a continuous and smooth fit that is good enough for further analysis. The observations are then split into segments corresponding to 100 000 pixels each. This number is arbitrary, mostly set by the ease of inspecting the results. When running PySME the selected linear correction of the continuum was based on the best match to the synthetic spectrum.

Table 6

Stellar parameters of all stars investigated in this paper.

Table 7

Stars analyzed with PySME including the ESO program and archive IDs, average signal-to-noise ratio, and the availability of reliable interferometric measurements.

thumbnail Fig. 7

Observation (blue) and synthesis (orange) flux of one wavelength section for all target stars.

4.2.2 Radial velocities

For the radial velocities, we could rely on the HARPS wavelength calibration. We thus used a single radial velocity value for all spectral intervals.

4.2.3 Uncertainties

The PySME package uses the uncertainties of spectral points to compute the weights for the fitting procedure. The HARPS data do not contain an independent estimate of uncertainties. Only the flux value in each pixel is available. We therefore assume that the Poissonian shot noise is the only source of noise. The data have a S/N on the order of 100 (or higher) making this a good assumption. We additionally add weight to the line centers by multiplying these uncertainties by the flux values. The final uncertainties are then 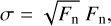σ=FnFn,$\sigma = \sqrt {{F_{\rm{n}}}} {F_{\rm{n}}},$(4)

where Fn is the normalized flux of the observation.

thumbnail Fig. 8

Comparison of the least-squares fit results for 55 Cnc between the IDL SME and the PySME analysis. Both analyses used the same continuum normalization, mask, line list, atmosphere grid, and NLTE departure coefficients. The difference between PySME and IDL SME is small, but noticeable in the derived parameters.

4.2.4 Tellurics

As with any ground-based observation, our spectra also contain telluric absorption features. We therefore provide PySME with a telluric spectrum generated with TAPAS (Bertaux et al. 2014), ignoring the Rayleigh scattering as it affects the continuum on much larger wavelength scales and will therefore be removed as part of the continuum correction. We also remove slow variations in the tellurics using the same method for the spectrum as described in Sect. 4.2.1. The telluric spectrum is used to mask any significant telluric lines in the observation. To this end, any points in the spectrum are marked as bad pixels if the tellurics are larger than 0.5% of the normalized spectrum.

4.2.5 Instrumental broadening

La Silla HARPS has a slightly asymmetric instrumental profile, but for our purposes deviations from Gaussian are small. We use Gaussian broadening with a resolution of 105 000 to match the spectral synthesis with HARPS spectra.

4.2.6 Stellar disk Integration

Disk integration combines the rotational broadening and broadening due to radial-tangential macroturbulence. As described in Sect. 3.3 of the original paper (Valenti & Piskunov 1996), disk integration is carried out using quadratures. For the calculations described here stellar flux spectra are computed using specific intensity at seven nodes (limb distances) allowing us to reach a precision better than 0.1 %, typically 3 × 10−4. Both SME implementations allow us to adjust the number of nodes for better precision or faster computations, while the nodes and weights are generated automatically.

Table 8

Stellar parameters derived from the same HARPS spectrum of 55 Cnc, in two independent analyses, one using PySME and one using IDL SME.

4.2.7 Line list

We generated the line lists for all stars using VALD (Piskunov et al. 1995), covering the wavelength range from 3781.22 Å to 6912.21 Å. We used the same list for all stars, which includes 52496 individual lines with an expected depth of at least 1% at Teff 5770 K, log g 4.4 log(cm s−2), [M/H] 0 dex, and 1 km s−1. All lines are given in the long format necessary for NLTE corrections. The line list wavelengths are in air, even though the HARPS instrument works inside a vacuum chamber, since the data reduction pipeline converts the wavelength scale of the reduced spectra to air. All references for the line parameters in each element are given in Appendix D.

4.2.8 Model atmosphere

For the model atmosphere grid we chose the marcs2012 grid (Gustafsson et al. 2008), which is included in the PySME distribution (see Sect. 2.4). We chose this grid since it spans the parameter space of our target stars and supports the NLTE departure coefficient grids.

4.2.9 Elemental abundances

While we do fit the overall metallicity of our stars, we do not fit abundances of individual elements (even though PySME is capable of doing so). The relative abundances are instead assumed to be solar, as defined by Asplund et al. (2009).

4.2.10 NLTE departure coefficients

We allow PySME to apply NLTE corrections for 13 elements (H, Li, C, N, O, Na, Mg, Al, Si, K, Ca, Mn, Ba) using the departure coefficient grids described in Amarsi et al. (2020). In addition, we use the Fe NLTE departure coefficients for Fe described in Amarsi et al. (2016). All references for the NLTE grids are given in Appendix E.

4.2.11 Initial stellar parameters

The least-squares fit requires an initial guess of the stellar parameters. The better the guess is, the fewer iterations needed to determine the optimal fit parameters. The results may vary slightly depending on the initial guess, but, as was shown in Sect. 2.6, our algorithm is quite robust and the space we explore does not contain important local minima. Thus, we opted to select the stellar parameters from previous studies given in the NASA Exoplanet Archive (NEXA, NASA Exoplanet Science Institute 2020) as the initial guess. The comparison of our results with the NEXA parameters and alternative estimates based on interferometric data is presented in Table 6, together with the references.

4.3 Individual targets

We ran PySME on all our targets and compared the results with IDL SME (see 55 Cnc below) and with other techniques (Sect. 5). The free parameters were Teff, log g, [M/H], υ sin i, υmic, υmac, and υrv. Figure 7 shows the final fit to the observations for a small but representative fragment of the spectrum.

ϵ Eri is a nearby sun-like star of spectral type K2 (Keenan & McNeil 1989), with at least one planet (Mawet et al. 2019; Benedict et al. 2006; Hatzes et al. 2000) and a proposed second planet (Quillen & Thorndike 2002). ϵ Eri is one of the Gaia FGK benchmark stars (Jofré et al. 2018), and results in the following parameters: Teff = 5076K, log g =4.61, and [M/H] = −0.09. These are to be compared with PySME results: 4949 K, 4.21, and −0.22 (see Table 8). The HARPS data have the highest S/N in our sample so we used the example of ϵ Eri to illustrate the uncertainty estimation by PySME in Sect. 2.7.

HN Peg

is a star of spectral type G0 (Gray et al. 2001), with one known exoplanet (Luhman et al. 2007). Of the stars in this paper it is the most similar to the Sun.

HD 102195

is a K0 star (Houk & Swift 1999), with one known exoplanet (Ge et al. 2006).

HD 130322

is another K0 star (Houk & Swift 1999), with one known exoplanet (Udry et al. 2000).

HD 179949

is an F8 star (Houk & Smith-Moore 1988), with one known exoplanet (Tinney et al. 2001).

HD 189733

is a K2 star (Gray et al. 2003) in a binary system, with one known exoplanet (Bouchy et al. 2005).

WASP 18

is an F6 star (Houk 1978) in a binary system, with two known exoplanets (Hellier et al. 2009; Pearson 2019). This star has the lowest S/N in the sample: S/N of 81.

55 Cnc

is a binary system consisting of a G8-K0 dwarf (55 Cnc A, Gray et al. 2003) and an M4 dwarf (55 Cnc B, Alonso-Floriano et al. 2015). Here we investigate 55 Cnc A, which is host to a complex system of five planets (Bourrier et al. 2018). This star was independently analyzed with IDL SME and so we used it in the comparison between the two implementations of SME.

Observational data included several spectra of 55 Cnc obtained with the La Silla HARPS instrument in January 2012. The raw data were reduced using the standard ESO HARPS pipeline and combined to produce a single spectrum with mean S/N of 135. We (TR) started the IDL SME analysis by manually adjusting the continuum and selecting five spectral intervals: 4900–5500Å, 5500–5700Å, 5700–6000Å, 6000–6300Å, and 6300–6700 Å. After computing a spectral synthesis based on stellar parameters taken from the literature (Udry et al. 2000) and the VALD3 line data we adjusted the “bad” pixels mask and let IDL SME perform the final linear correction of the continuum level in each interval. We then solved for Teff, log g, [M/H], υ sin i, and υrv. We assumed fixed υmic and a Gaussian instrumental profile corresponding to the resolving power of HARPS.

After this step we revisited the mask to remove poorly fitted spectral lines with obviously erroneous line data. The decision was based on a comparison with the average fit quality for lines of the same species. The final step was to re-fit the parameters listed above enabling NLTE correction for Fe, Mg, Mn, Na, Si, Ba, and Ca.

The PySME analysis for the comparison used the same observational data, spectral intervals, continuum normalization, mask, line list, atmosphere grid, and NLTE departure coefficients; it thus uses the same input parameters, and only compares the results of the fitting procedure. The resulting parameters are given in Table 8, and Fig. 8 shows the comparison for a fragment of spectral data included in the analysis. The difference between the best fit spectra is small and the derived parameters are consistent with each other, though not identical.

The values given in Table 6 are taken from an independent PySME analysis that follows the same steps as all other stars; it uses a different continuum normalization, line list, mask, and NLTE departure coefficients than the comparison analysis.

thumbnail Fig. 9

Differences between the literature values and the parameter values derived in this paper. For stars represented by filled blue circles, Teff and log g literature values are derived from interferometry, while for stars represented by unfilled orange circles the literature values are derived from spectroscopy or photometry instead. Sources for all values are given in Table 6.
thumbnail Fig. 10

Uncertainty trends with the stellar temperature. Each star is indicated (blue solid circle) with its name. It also shows the best fit linear relationship (orange). HN Peg and 55 Cnc are ignored in the surface gravity fit.

5 Comparison with other studies

It is useful to compare the stellar parameters we derived in this study with the parameters derived in other studies. Where possible we used values derived from interferometric measurements, as they are independent from spectroscopic or photometric methods. However, this was only possible for Teff and log g, but not for metallicity. The numerical values of our results and that of other studies are given in Table 6, while we plot the differences in Fig. 9. We can see that our values agree mostly with the other studies, but there appears to be some dependence on Teff, especially for Teff itself. We also see a notable offset between our [M/H] and log g values and those from other studies.

6 Trends

Finally, it is interesting to investigate how the uncertainties of the different parameters depend on the Teff of the star. We therefore plot this relationship in Fig. 10 for all stars. The uncertainty of the temperature depends only weakly on the temperature. Similarly, the uncertainty of the surface gravity decreases slightly with temperature, while the uncertainty of the metallicity shows a stronger negative correlation. The uncertainty of the microturbulence parameter shows no visible correlation with temperature, while the uncertainty of the macroturbulence shows a clear upward trend. The uncertainty of the rotation velocity decreases with increasing temperature. However there is a degeneracy with the resolution of the instrument as below ≈2 km s−1 the rotational broadening is smaller than the instrumental broadening. This increases the uncertainties of υ sin i significantly for those cases.

Additionally, we compare the values of the turbulence parameters and the stellar rotation as a function of the stellar temperature in Fig. 11. As expected, the micro- and macroturbulence increase with stellar temperature. The rotational velocity also increases with stellar temperature since the rotational velocity increases along the main sequence toward earlier spectral types (Gray 2005).

thumbnail Fig. 11

Micro- and macroturbulence parameters, as well as the rotational velocity of the star, as a function of the stellar temperature. The orange dashed line shows the linear regression fit to those values.

7 Conclusion

We have shown that PySME is a suitable successor for IDL SME. We have additionally derived stellar parameters with PySME for a number of exoplanet host stars and see that their values agree both with values derived from spectroscopy and with independent interferometric values from other studies.

Acknowledgements

This research has made use of the services of the ESO Science Archive Facility. Based on observations collected at the European Southern Observatory under ESO programs 60.A-9036(A), 192.C-0224(A), 083.C-0794(A), 072.C-0488(E), 288.C-5010(A), 0104.C-0849(A), and 098.C-0739(A). This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. Software: PySME relies on a number of Python packages to function, these are NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020), Astropy (Astropy Collaboration 2013, 2018), Matplotlib (Hunter 2007), and pandas (McKinney 2010).

Appendix A Data access

The input spectra are available from the ESO Archive Science Portal http://archive.eso.org/scienceportal/ with the program IDs and archive IDs given in Table 7. All generated spectra are available as SME files from Zenodo servers using DOI 10.5281/zenodo.6701350

Appendix B Installation

PySME was developed with usability in mind. We therefore decided to make the installation process as convenient as possible. For this purpose we provide compiled versions of the SME libraries for the most common environments: windows, mac osx, and linux (using the manylinux2010 specification). Additionally, we prepared the installation via PyPi so that PySME can be installed using pip using the following command:

pip install pysme-astro

The distribution on PyPi is automatically updated with any changes made to the open-source Github repository.

In the case that the pre-compiled libraries are not compatible with your system, it is also easy to compile the SME library from the source code:

git clone https://github.com/AWehrhahn/SMElib.git
cd SMElib
./bootstrap
./configure --prefix=$PWD
make install

This will download and compile the code on your system. Afterward you should find the library in the lib (or bin for windows) directory. Simply copy it into your installation of PySME.

Appendix C Uncertainties

Here we give the probability distributions for the stellar parameters derived for ϵ Eri, as discussed in Section 2.7.

thumbnail Fig. C.1

Cumulative probability (left) and probability density (right) distribution of the fitting parameters for the ϵ Eri spectrum derived from the fit results (blue). For comparison, also shown is the distribution of a Gaussian with the same median and σ as derived from the cumulative probability. The median is indicated by a dashed line (in density plots only), and the 1σ range is shown as a shaded region and dash dotted lines.

Appendix D Line list references

Table D.1

References for the input parameters of the line list used, sorted by element

Appendix E NLTE Grid References

Table E.1

NLTE departure coefficient grid references

References

  1. Alonso-Floriano, F.J., Morales, J.C., Caballero, J.A., et al. 2015, A&A, 577, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Amarsi, A.M., & Asplund, M. 2017, MNRAS, 464, 264 [NASA ADS] [CrossRef] [Google Scholar]
  3. Amarsi, A.M., Lind, K., Asplund, M., Barklem, P.S., & Collet, R. 2016, MNRAS, 463, 1518 [NASA ADS] [CrossRef] [Google Scholar]
  4. Amarsi, A.M., Barklem, P.S., Asplund, M., Collet, R., & Zatsarinny, O. 2018a, A&A, 616, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Amarsi, A.M., Nordlander, T., Barklem, P.S., et al. 2018b, A&A, 615, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Amarsi, A.M., Barklem, P.S., Collet, R., Grevesse, N., & Asplund, M. 2019, A&A, 624, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Amarsi, A.M., Lind, K., Osorio, Y., et al. 2020, A&A, 642, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Andersen, T., & Soerensen, G. 1973, J. Quant. Spec. Radiat. Transf., 13, 369 [NASA ADS] [CrossRef] [Google Scholar]
  9. Anderson, E.M., Zilitis, V.A., & Sorokina, E.S. 1967, Opt. Spectrosc., 23, 102 [NASA ADS] [Google Scholar]
  10. Asplund, M., Grevesse, N., Sauval, A.J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  11. Astropy Collaboration (Price-Whelan, A.M., et al.) 2018, AJ, 156, 123 [NASA ADS] [CrossRef] [Google Scholar]
  12. Astropy Collaboration (Robitaille, T.P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Barklem, P.S., & Piskunov, N. 2015, HLINOP: Hydrogen LINe OPacity in stellar atmospheres, Astrophysics Source Code Library, [record ascl:1507.008] [Google Scholar]
  14. Barklem, P.S., Piskunov, N., & O’Mara, B.J. 2000, A&AS, 142, 467 [CrossRef] [EDP Sciences] [Google Scholar]
  15. Benedict, G.F., McArthur, B.E., Gatewood, G., et al. 2006, AJ, 132, 2206 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bergemann, M., Gallagher, A.J., Eitner, P., et al. 2019, A&A, 631, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Bertaux, J.L., Lallement, R., Ferron, S., Boonne, C., & Bodichon, R. 2014, A&A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Biémont, É., Grevesse, N., Hannaford, P., & Lowe, R.M. 1981, ApJ, 248, 867 [CrossRef] [Google Scholar]
  19. Biémont, É., Grevesse, N., Faires, L.M., Marsden, G., & Lawler, J.E. 1989, A&A, 209, 391 [Google Scholar]
  20. Biémont, É., Quinet, P., & Zeippen, C.J. 1993, A&AS, 102, 435 [Google Scholar]
  21. Biémont, É., Lefèbvre, P., Quinet, P., Svanberg, S., & Xu, H.L. 2003, Eur. Phys. J. D, 27, 33 [CrossRef] [Google Scholar]
  22. Biémont, É., Blagoev, K., Engström, L., et al. 2011, MNRAS, 414, 3350 [Google Scholar]
  23. Blackwell-Whitehead, R.J., Xu, H.L., Pickering, J.C., Nave, G., & Lundberg, H. 2005, MNRAS, 361, 1281 [NASA ADS] [CrossRef] [Google Scholar]
  24. Bonomo, A.S., Desidera, S., Benatti, S., et al. 2017, A&A, 602, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Bouchy, F., Udry, S., Mayor, M., et al. 2005, A&A, 444, L15 [EDP Sciences] [Google Scholar]
  26. Bourrier, V., Dumusque, X., Dorn, C., et al. 2018, A&A, 619, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Brooke, J.S.A., Bernath, P.F., Schmidt, T.W., & Bacskay, G.B. 2013, J. Quant. Spec. Radiat. Transf., 124, 11 [NASA ADS] [CrossRef] [Google Scholar]
  28. Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
  29. Corliss, C.H., & Bozman, W.R. 1962, NBS Monograph, 53, Experimental tran- sition probabilities for spectral lines of seventy elements; derived from the NBS Tables of spectral-line intensities (US Government Printing Office) [CrossRef] [Google Scholar]
  30. Costa Silva, A.R., Delgado Mena, E., & Tsantaki, M. 2020, A&A, 634, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Cowley, C.R., & Corliss, C.H. 1983, MNRAS, 203, 651 [Google Scholar]
  32. De la Cruz Rodríguez, J., & Piskunov, N. 2013, ApJ, 764, 33 [NASA ADS] [CrossRef] [Google Scholar]
  33. Den Hartog, E.A., Curry, J.J., Wickliffe, M.E., & Lawler, J.E. 1998, Sol. Phys., 178, 239 [NASA ADS] [CrossRef] [Google Scholar]
  34. Den Hartog, E.A., Wickliffe, M.E., & Lawler, J.E. 2002, ApJS, 141, 255 [NASA ADS] [CrossRef] [Google Scholar]
  35. Den Hartog, E.A., Lawler, J.E., Sneden, C., & Cowan, J.J. 2003, ApJS, 148, 543 [NASA ADS] [CrossRef] [Google Scholar]
  36. Den Hartog, E.A., Herd, M.T., Lawler, J.E., et al. 2005, ApJ, 619, 639 [NASA ADS] [CrossRef] [Google Scholar]
  37. Den Hartog, E.A., Lawler, J.E., Sneden, C., & Cowan, J.J. 2006, ApJS, 167, 292 [NASA ADS] [CrossRef] [Google Scholar]
  38. Den Hartog, E.A., Lawler, J.E., Sobeck, J.S., Sneden, C., & Cowan, J.J. 2011, ApJS, 194, 35 [NASA ADS] [CrossRef] [Google Scholar]
  39. Drozdowski, R., Ignaciuk, M., Kwela, J., & Heldt, J. 1997, Z. Phys. D, 41, 125 [CrossRef] [Google Scholar]
  40. Duquette, D.W., & Lawler, J.E. 1982, Phys. Rev. A, 26, 330 [Google Scholar]
  41. Duquette, D.W., Salih, S., & Lawler, J.E. 1982a, Phys. Rev. A, 26, 2623 [Google Scholar]
  42. Duquette, D.W., Salih, S., & Lawler, J.E. 1982b, J. Phys. B Atom. Mol. Phys., 15, L897 [NASA ADS] [CrossRef] [Google Scholar]
  43. Fedchak, J.A., Den Hartog, E.A., Lawler, J.E., et al. 2000, ApJ, 542, 1109 [NASA ADS] [CrossRef] [Google Scholar]
  44. Fischer, D.A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
  45. Fuhr, J.R., Martin, G.A., & Wiese, W.L. 1988, J. Phys. Chem. Ref. Data Suppl., 17, 4 [Google Scholar]
  46. Gaia Collaboration (Brown, A.G.A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Gallagher, A.J., Bergemann, M., Collet, R., et al. 2020, A&A, 634, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. García, G., & Campos, J. 1988, J. Quant. Spec. Radiat. Transf., 39, 477 [CrossRef] [Google Scholar]
  49. Garz, T. 1973, A&A, 26, 471 [NASA ADS] [Google Scholar]
  50. Ge, J., van Eyken, J., Mahadevan, S., et al. 2006, ApJ, 648, 683 [NASA ADS] [CrossRef] [Google Scholar]
  51. Gerber, J.M., Magg, E., Plez, B., et al. 2022, A&A, 669, A43 [Google Scholar]
  52. Gray, D.F. 2005, The Observation and Analysis of Stellar Photospheres (Cambridge University Press) [CrossRef] [Google Scholar]
  53. Gray, R.O., & Corbally, C.J. 1994, AJ, 107, 742 [NASA ADS] [CrossRef] [Google Scholar]
  54. Gray, R.O., Napier, M.G., & Winkler, L.I. 2001, AJ, 121, 2148 [NASA ADS] [CrossRef] [Google Scholar]
  55. Gray, R.O., Corbally, C.J., Garrison, R.F., McFadden, M.T., & Robinson, P.E. 2003, AJ, 126, 2048 [NASA ADS] [CrossRef] [Google Scholar]
  56. Grevesse, N., Asplund, M., & Sauval, A.J. 2007, Space Sci. Rev., 130, 105 [NASA ADS] [CrossRef] [Google Scholar]
  57. Gurell, J., Nilsson, H., Engström, L., et al. 2010, A&A, 511, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Harris, C.R., Millman, K.J., van der Walt, S.J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
  60. Hatzes, A.P., Cochran, W.D., McArthur, B., et al. 2000, ApJ, 544, L145 [NASA ADS] [CrossRef] [Google Scholar]
  61. Heiter, U., & Luck, R.E. 2003, AJ, 126, 2015 [CrossRef] [Google Scholar]
  62. Heiter, U., Kupka, F., van’t Veer-Menneret, C., et al. 2002, A&A, 392, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Hellier, C., Anderson, D.R., Collier Cameron, A., et al. 2009, Nature, 460, 1098 [NASA ADS] [CrossRef] [Google Scholar]
  64. Hinkel, N.R., Kane, S.R., Henry, G.W., et al. 2015, ApJ, 803, 8 [NASA ADS] [CrossRef] [Google Scholar]
  65. Houk, N. 1978, Michigan catalogue of two-dimensional spectral types for the HD stars [Google Scholar]
  66. Houk, N., & Smith-Moore, M. 1988, Michigan Catalogue of Two-dimensional Spectral Types for the HD Stars. 4, Declinations -26°.0 to -12°.0 [Google Scholar]
  67. Houk, N., & Swift, C. 1999, Michigan Spectral Survey, 5 [Google Scholar]
  68. Hubeny, I., & Lanz, T. 2011, Synspec: General Spectrum Synthesis Program, Astrophysics Source Code Library, [record ascl:1109.022] [Google Scholar]
  69. Hubeny, I., & Lanz, T. 2017, ArXiv e-prints [arXiv:1706.01859] [Google Scholar]
  70. Hubeny, I., Allende Prieto, C., Osorio, Y., & Lanz, T. 2021, ArXiv e-prints [arXiv:2104.02829] [Google Scholar]
  71. Hunter, J.D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  72. Ivarsson, S., Litzén, U., & Wahlgren, G.M. 2001, Physica Scripta, 64, 455 [NASA ADS] [CrossRef] [Google Scholar]
  73. Jofré, P., Heiter, U., Tucci Maia, M., et al. 2018, Res. Notes Am. Astron. Soc., 2, 152 [Google Scholar]
  74. Jorgensen, U.G., Larsson, M., Iwamae, A., & Yu, B. 1996, A&A, 315, 204 [NASA ADS] [Google Scholar]
  75. Karlsson, H., & Litzén, U. 2000, J. Phys. B At. Mol. Phys., 33, 2929 [NASA ADS] [CrossRef] [Google Scholar]
  76. Keenan, P.C., & McNeil, R.C. 1989, ApJS, 71, 245 [NASA ADS] [CrossRef] [Google Scholar]
  77. Kupka, F., Piskunov, N., Ryabchikova, T.A., Stempels, H.C., & Weiss, W.W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Kupka, F.G., Ryabchikova, T.A., Piskunov, N.E., Stempels, H.C., & Weiss, W.W. 2000, Baltic Astron., 9, 590 [NASA ADS] [Google Scholar]
  79. Kurucz, R.L. 1975, unpublished [Google Scholar]
  80. Kurucz, R.L. 1993a, CDROM 18 (Cambridge: SAO) [Google Scholar]
  81. Kurucz, R.L. 1993b, Based on multiplet tables [Google Scholar]
  82. Kurucz, R.L. 1993c, Oscillator strengths estimated by Kurucz from multiplet table intensities for Zr I and Zr II lines [Google Scholar]
  83. Kurucz, R.L. 1993d, SYNTHE spectrum synthesis programs and line data [Google Scholar]
  84. Kurucz, R.L. 1995, Robert L. Kurucz on-line database of molecular line lists, MgH A-X and B’-X transitions [Google Scholar]
  85. Kurucz, R.L. 2004, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  86. Kurucz, R.L. 2006, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  87. Kurucz, R.L. 2007, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  88. Kurucz, R.L. 2008, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  89. Kurucz, R.L. 2009, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  90. Kurucz, R.L. 2010, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  91. Kurucz, R.L. 2011, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  92. Kurucz, R.L. 2012, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  93. Kurucz, R.L. 2013, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  94. Kurucz, R.L. 2014, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  95. Kurucz, R.L. 2016, Robert L. Kurucz on-line database of observed and predicted atomic transitions [Google Scholar]
  96. Kurucz, R.L. 2017, ATLAS9: Model atmosphere program with opacity distribu- tion functions [Google Scholar]
  97. Kurucz, R.L., & Peytremann, E. 1975, SAO Special Rep., 362, 1 [Google Scholar]
  98. Kurucz, R.L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm [Google Scholar]
  99. Lambert, D.L., & Warner, B. 1968, MNRAS, 138, 181 [NASA ADS] [CrossRef] [Google Scholar]
  100. Lambert, D.L., Mallia, E.A., & Warner, B. 1969, MNRAS, 142, 71 [NASA ADS] [CrossRef] [Google Scholar]
  101. Laughlin, C., & Victor, G.A. 1974, ApJ, 192, 551, (LV) [NASA ADS] [CrossRef] [Google Scholar]
  102. Lawler, J.E., & Dakin, J.T. 1989, J. Opt. Soc. Am. B Opt. Phys., 6, 1457 [NASA ADS] [CrossRef] [Google Scholar]
  103. Lawler, J.E., Whaling, W., & Grevesse, N. 1990, Nature, 346, 635 [NASA ADS] [CrossRef] [Google Scholar]
  104. Lawler, J.E., Bonvallet, G., & Sneden, C. 2001a, ApJ, 556, 452 [NASA ADS] [CrossRef] [Google Scholar]
  105. Lawler, J.E., Wickliffe, M.E., Cowley, C.R., & Sneden, C. 2001b, ApJS, 137, 341 [NASA ADS] [CrossRef] [Google Scholar]
  106. Lawler, J.E., Wickliffe, M.E., den Hartog, E.A., & Sneden, C. 2001c, ApJ, 563, 1075 [CrossRef] [Google Scholar]
  107. Lawler, J.E., Sneden, C., Cowan, J.J., et al. 2008, ApJS, 178, 71 [NASA ADS] [CrossRef] [Google Scholar]
  108. Lawler, J.E., Sneden, C., Cowan, J.J., Ivans, I.I., & Den Hartog, E.A. 2009, ApJS, 182, 51 [NASA ADS] [CrossRef] [Google Scholar]
  109. Lawler, J.E., Wood, M.P., Den Hartog, E.A., et al. 2014, ApJS, 215, 20 [CrossRef] [Google Scholar]
  110. Lawler, J.E., Hala, Sneden, C., et al. 2019, ApJS, 241, 21 [NASA ADS] [CrossRef] [Google Scholar]
  111. Lincke, R., & Ziegenbein, B. 1971, Z. Phys., 241, 369 [NASA ADS] [CrossRef] [Google Scholar]
  112. Lind, K., Asplund, M., Barklem, P.S., & Belyaev, A.K. 2011, A&A, 528, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Ljung, G., Nilsson, H., Asplund, M., & Johansson, S. 2006, A&A, 456, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Lodders, K. 2003, ApJ, 591, 1220 [Google Scholar]
  115. Lotrian, J., Cariou, J., Guern, Y., & Johannin-Gilles, A. 1978, J. Phys. B At. Mol. Phys., 11, 2273 [NASA ADS] [CrossRef] [Google Scholar]
  116. Luhman, K.L., Patten, B.M., Marengo, M., et al. 2007, ApJ, 654, 570 [NASA ADS] [CrossRef] [Google Scholar]
  117. Martin, G., Fuhr, J., & Wiese, W. 1988, J. Phys. Chem. Ref. Data Suppl., 17 [Google Scholar]
  118. Martioli, E., Hébrard, G., Correia, A.C.M., Laskar, J., & Lecavelier des Etangs, A. 2021, A&A, 649, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Mawet, D., Hirsch, L., Lee, E.J., et al. 2019, AJ, 157, 33 [NASA ADS] [CrossRef] [Google Scholar]
  120. McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 56 [Google Scholar]
  121. Meggers, W.F., Corliss, C.H., & Scribner, B.F. 1975, Tables of Spectral- line Intensities. Part I, II_- Arranged by Elements (Washington DC: US Government Printing Office) [Google Scholar]
  122. Melo, C., Santos, N.C., Gieren, W., et al. 2007, A&A, 467, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. Miles, B.M., & Wiese, W.L. 1969, Atomic Data, 1, 1 [NASA ADS] [CrossRef] [Google Scholar]
  124. NASA Exoplanet Science Institute 2020, Planetary Systems Composite Table [Google Scholar]
  125. Nilsson, H., Ljung, G., Lundberg, H., & Nielsen, K.E. 2006, A&A, 445, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  126. Nordlander, T., & Lind, K. 2017, A&A, 607, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. O’Brian, T.R., Wickliffe, M.E., Lawler, J.E., Whaling, W., & Brault, J.W. 1991, J. Opt. Soc. Am. B Opt. Phys., 8, 1185 [CrossRef] [Google Scholar]
  128. Obbarius, H.U., & Kock, M. 1982, J. Phys. B At. Mol. Phys., 15, 527 [NASA ADS] [CrossRef] [Google Scholar]
  129. Osorio, Y., Barklem, P.S., Lind, K., et al. 2015, A&A, 579, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Osorio, Y., Lind, K., Barklem, P.S., Allende Prieto, C., & Zatsarinny, O. 2019, A&A, 623, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Palmeri, P., Quinet, P., Wyart, J., & Biémont, E. 2000, Physica Scripta, 61, 323 [NASA ADS] [CrossRef] [Google Scholar]
  132. Parkinson, W.H., Reeves, E.M., & Tomkins, F.S. 1976, Roy. Soc. Lond. Proc. A, 351, 569 [NASA ADS] [CrossRef] [Google Scholar]
  133. Pearson, K.A. 2019, AJ, 158, 243 [NASA ADS] [CrossRef] [Google Scholar]
  134. Penkin, N.P., & Shabanova, L.N. 1963, Opt. Spectrosc., 14, 5 [NASA ADS] [Google Scholar]
  135. Pinnington, E.H., Ji, Q., Guo, B., et al. 1993, Can. J. Phys., 71, 470 [NASA ADS] [CrossRef] [Google Scholar]
  136. Piskunov, N.E. 1992, in Physics and Evolution of Stars: Stellar Magnetism, 92 [Google Scholar]
  137. Piskunov, N.E., & Valenti, J.A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  138. Piskunov, N.E., Kupka, F., Ryabchikova, T.A., Weiss, W.W., & Jeffery, C.S. 1995, A&AS, 112, 525 [Google Scholar]
  139. Plavchan, P., Barclay, T., Gagné, J., et al. 2020, Nature, 582, 497 [Google Scholar]
  140. Plez, B. 2012a, https://www.astro.uu.se/valdwiki/linelistRefs#P2012 [Google Scholar]
  141. Plez, B. 2012b, Turbospectrum: Code for spectral synthesis, Astrophysics Source Code Library, [record ascl:1205.004] [Google Scholar]
  142. Plez, B., Smith, V.V., & Lambert, D.L. 1993, ApJ, 418, 812 [CrossRef] [Google Scholar]
  143. Quillen, A.C., & Thorndike, S. 2002, ApJ, 578, L149 [NASA ADS] [CrossRef] [Google Scholar]
  144. Quinet, P., Palmeri, P., Biémont, E., et al. 1999, MNRAS, 307, 934 [NASA ADS] [CrossRef] [Google Scholar]
  145. Ralchenko, Y., Kramida, A., Reader, J., & NIST ASD Team 2010, NIST Atomic Spectra Database (ver. 4.0.0) [Online] [Google Scholar]
  146. Reggiani, H., Amarsi, A.M., Lind, K., et al. 2019, A&A, 627, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  147. Ryabchikova, T.A., Piskunov, N.E., Kupka, F., & Weiss, W.W. 1997, Baltic Astron., 6, 244 [NASA ADS] [Google Scholar]
  148. Ryabchikova, T., Piskunov, N., Kurucz, R.L., et al. 2015, Physica Scripta, 90, 054005 [NASA ADS] [CrossRef] [Google Scholar]
  149. Ryabchikova, T., Piskunov, N., Pakhomov, Y., et al. 2016, MNRAS, 456, 1221 [CrossRef] [Google Scholar]
  150. Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R.L. 2004, Mem. Soc. Astron. Ital. Suppl., 5, 93 [Google Scholar]
  151. Seaton, M.J., Yan, Y., Mihalas, D., & Pradhan, A.K. 1994, MNRAS, 266, 805 [Google Scholar]
  152. Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz, C., & Weiss, W.W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  153. Sigut, T.A.A., & Landstreet, J.D. 1990, MNRAS, 247, 611 [NASA ADS] [Google Scholar]
  154. Smith, G. 1988, J. Phys. B At. Mol. Phys., 21, 2827 [NASA ADS] [CrossRef] [Google Scholar]
  155. Smith, G., & O’Neill, J.A. 1975, A&A, 38, 1 [NASA ADS] [Google Scholar]
  156. Smith, G., & Raggett, D.S.J. 1981, J. Phys. B At. Mol. Phys., 14, 4015 [NASA ADS] [CrossRef] [Google Scholar]
  157. Sneden, C. 1973, ApJ, 184, 839 [Google Scholar]
  158. Sneden, C., Bean, J., Ivans, I., Lucatello, S., & Sobeck, J. 2012, MOOG: LTE line analysis and spectrum synthesis, Astrophysics Source Code Library, [record ascl:1202.009] [Google Scholar]
  159. Sobeck, J.S., Lawler, J.E., & Sneden, C. 2007, ApJ, 667, 1267 [NASA ADS] [CrossRef] [Google Scholar]
  160. Stassun, K.G., Oelkers, R.J., Paegert, M., et al. 2019, AJ, 158, 138 [NASA ADS] [CrossRef] [Google Scholar]
  161. Swastik, C., Banyal, R.K., Narang, M., et al. 2021, AJ, 161, 114 [NASA ADS] [CrossRef] [Google Scholar]
  162. Tange, O. 2011, login: The USENIX Magazine, 42 [Google Scholar]
  163. Tinney, C.G., Butler, R.P., Marcy, G.W., et al. 2001, ApJ, 551, 507 [NASA ADS] [CrossRef] [Google Scholar]
  164. Tsantaki, M., Sousa, S.G., Santos, N.C., et al. 2014, A&A, 570, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  165. Udry, S., Mayor, M., Naef, D., et al. 2000, A&A, 356, 590 [NASA ADS] [Google Scholar]
  166. Vaeck, N., Godefroid, M., & Hansen, J.E. 1988, Phys. Rev. A, 38, 2830 [CrossRef] [PubMed] [Google Scholar]
  167. Valenti, J.A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  168. Valenti, J.A., & Fischer, D.A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [Google Scholar]
  169. Virtanen, P., Gommers, R., Oliphant, T.E., et al. 2020, Nat. Methods, 17, 261 [NASA ADS] [CrossRef] [Google Scholar]
  170. Voglis, C., & Lagaris, I.E. 2004, in WSEAS International Conference on Applied Mathematics [Google Scholar]
  171. von Braun, K., Boyajian, T.S., van Belle, G.T., et al. 2014, MNRAS, 438, 2413 [NASA ADS] [CrossRef] [Google Scholar]
  172. Wallace, L., & Hinkle, K. 2009, ApJ, 700, 720 [NASA ADS] [CrossRef] [Google Scholar]
  173. Wang, E.X., Nordlander, T., Asplund, M., et al. 2021, MNRAS, 500, 2159 [Google Scholar]
  174. Warner, B. 1968, MNRAS, 140, 53 [NASA ADS] [Google Scholar]
  175. Whaling, W., & Brault, J.W. 1988, Phys. Scr, 38, 707 [CrossRef] [Google Scholar]
  176. Wheeler, A.J., Abruzzo, M.W., Casey, A.R., & Ness, M.K. 2023, AJ, 165, 68 [NASA ADS] [CrossRef] [Google Scholar]
  177. Wickliffe, M.E., & Lawler, J.E. 1997, ApJS, 110, 163 [CrossRef] [Google Scholar]
  178. Wickliffe, M.E., Salih, S., & Lawler, J.E. 1994, J. Quant. Spec. Radiat. Transf., 51, 545 [NASA ADS] [CrossRef] [Google Scholar]
  179. Wickliffe, M.E., Lawler, J.E., & Nave, G. 2000, JQSRT, 66, 363 [NASA ADS] [CrossRef] [Google Scholar]
  180. Wiese, W.L., Smith, M.W., & Glennon, B.M. 1966, Atomic Transition Probabilities. 1: Hydrogen through Neon. A Critical Data Compilation (US Government Printing Office) [Google Scholar]
  181. Wiese, W.L., Smith, M.W., & Miles, B.M. 1969, Atomic Transition Prob- abilities. 2: Sodium through Calcium. A Critical Data Compilation (US Government Printing Office) [Google Scholar]
  182. Wood, M.P., Lawler, J.E., Den Hartog, E.A., Sneden, C., & Cowan, J.J. 2014a, ApJS, 214, 18 [NASA ADS] [CrossRef] [Google Scholar]
  183. Wood, M.P., Lawler, J.E., Sneden, C., & Cowan, J.J. 2014b, ApJS, 211, 20 [NASA ADS] [CrossRef] [Google Scholar]
  184. Xu, H.L., Svanberg, S., Cowan, R.D., et al. 2003, MNRAS, 346, 433 [CrossRef] [Google Scholar]
  185. Yan, Z.-C., & Drake, G.W.F. 1995, Phys. Rev. A, 52, 4316 [Google Scholar]
  186. Yee, S.W., Petigura, E.A., & von Braun, K. 2017, ApJ, 836, 77 [NASA ADS] [CrossRef] [Google Scholar]
  187. Zhiguo, Z., Zhongshan, L., & Zhankui, J. 1999, Eur. Phys. J. D, 7, 499 [CrossRef] [Google Scholar]
5

Distributions for the other parameters can be found in Appendix C

All Tables

Table 1

Continuum normalization options.

In the text
Table 2

Solar abundance sets included in PySME.

In the text
Table 3

Initial parameters for the convergence test.

In the text
Table 4

Comparison between the uncertainty estimates based on a synthetic spectrum.

In the text
Table 5

Minimum and average runtime of PySME and IDL SME on the same machine over 1000 runs.

In the text
Table 6

Stellar parameters of all stars investigated in this paper.

In the text
Table 7

Stars analyzed with PySME including the ESO program and archive IDs, average signal-to-noise ratio, and the availability of reliable interferometric measurements.

In the text
Table 8

Stellar parameters derived from the same HARPS spectrum of 55 Cnc, in two independent analyses, one using PySME and one using IDL SME.

In the text
Table D.1

References for the input parameters of the line list used, sorted by element

In the text
Table E.1

NLTE departure coefficient grid references

In the text

All Figures

thumbnail Fig. 1

Sketch of the dogbox algorithm in two dimensions for step k. The previous point is xk−i, the next point is xk. The rectangle gives the trust region with size ∆, δgn is the Gauss–Newton step, and tδsd is the steepest decent step. Here the Gauss–Newton step falls outside the trust region, so the new step δk is a combination of the Gauss–Newton step and the steepest decent, cut off at the boundary of the trust region.
In the text
thumbnail Fig. 2

Comparison of the different continuum normalization options on a small segment of the spectrum of HD 148816. Each plot shows the original observation (blue), the corrected synthetic spectrum (dotted orange), and the continuum detected by the method (purple). The shaded regions show the selected pixels used as the mask (green).
In the text
thumbnail Fig. 3

Distribution of the best fit stellar parameters Teff, log g, and [M/H] for different initial parameters. Initial values are shown in blue and final values in orange. The cutout in the upper left corner shows the entire parameter space spanned by the initial parameters, while the rest is zoomed in on the closely clustered final distribution.
In the text
thumbnail Fig. 4

Cumulative probability (top) and probability density (bottom) distribution of Teff for a spectrum of ϵ Eri derived from the fit results (blue). For comparison, also shown is the distribution of a Gaussian with the same median and σ as derived from the cumulative probability (orange). The median is marked by a dashed line (bottom), and the 1er range is shown as dash dotted lines and a shaded region (bottom). The distributions for the other fitted stellar parameters are shown Fig. C.1.
In the text
thumbnail Fig. 5

Scatter of the recovered Teff around the true value for a synthetic spectra with random noise of S/N 100.
In the text
thumbnail Fig. 6

Comparison between the IDL SME stellar synthesis (dashed green) and the PySME stellar synthesis (orange) for a small section of the stellar spectrum. All lines in the line list are indicated and accordingly labeled by vertical lines. The zoom-in on the Ca line highlights the small numerical difference between the two codes.
In the text
thumbnail Fig. 7

Observation (blue) and synthesis (orange) flux of one wavelength section for all target stars.
In the text
thumbnail Fig. 8

Comparison of the least-squares fit results for 55 Cnc between the IDL SME and the PySME analysis. Both analyses used the same continuum normalization, mask, line list, atmosphere grid, and NLTE departure coefficients. The difference between PySME and IDL SME is small, but noticeable in the derived parameters.
In the text
thumbnail Fig. 9

Differences between the literature values and the parameter values derived in this paper. For stars represented by filled blue circles, Teff and log g literature values are derived from interferometry, while for stars represented by unfilled orange circles the literature values are derived from spectroscopy or photometry instead. Sources for all values are given in Table 6.
In the text
thumbnail Fig. 10

Uncertainty trends with the stellar temperature. Each star is indicated (blue solid circle) with its name. It also shows the best fit linear relationship (orange). HN Peg and 55 Cnc are ignored in the surface gravity fit.
In the text
thumbnail Fig. 11

Micro- and macroturbulence parameters, as well as the rotational velocity of the star, as a function of the stellar temperature. The orange dashed line shows the linear regression fit to those values.
In the text
thumbnail Fig. C.1

Cumulative probability (left) and probability density (right) distribution of the fitting parameters for the ϵ Eri spectrum derived from the fit results (blue). For comparison, also shown is the distribution of a Gaussian with the same median and σ as derived from the cumulative probability. The median is indicated by a dashed line (in density plots only), and the 1σ range is shown as a shaded region and dash dotted lines.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.