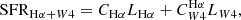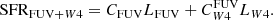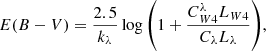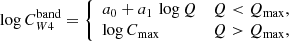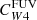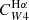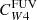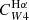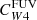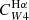| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244863 | |
| Published online | 06 February 2023 | |
Calibration of hybrid resolved star formation rate recipes based on PHANGS–MUSE Hα and Hβ maps
1
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Florence, Italy
e-mail: francesco.belfiore@inaf.it
2
Department of Astronomy, The Ohio State University, 140 West 18th Avenue, Columbus, OH 43210, USA
3
Department of Physics and Astronomy, McMaster University, 1280 Main St. West, Hamilton, ON L8S 4M1, Canada
4
Canadian Institute for Theoretical Astrophysics (CITA), University of Toronto, 60 St George Street, Toronto, ON M5S 3H8, Canada
5
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
6
Centro de Astronomía (CITEVA), Universidad de Antofagasta, Avenida Angamos 601, Antofagasta, Chile
7
Max-Planck-Institut für extraterrestrische Physik (MPE), Giessenbachstrasse 1, 85748 Garching, Germany
8
Departamento de Astronomía, Universidad de Chile, Camino del Observatorio 1515, Las Condes, Santiago, Chile
9
Department of Physics and Astronomy, University of Wyoming, Laramie, WY 82071, USA
10
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
11
Universität Heidelberg, Zentrum für Astronomie, Institut für theoretische Astrophysik, Albert-Ueberle-Straße 2, 69120 Heidelberg, Germany
12
Research School of Astronomy and Astrophysics, Australian National University, Canberra, ACT 2611, Australia
13
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), Stromlo Mount, Australia
14
International Centre for Radio Astronomy Research, University of Western Australia, 7 Fairway, Crawley, 6009 WA, Australia
15
Universität Heidelberg, Interdisziplinäres Zentrum für Wissenschaftliches Rechnen, Im Neuenheimer Feld 205, 69120 Heidelberg, Germany
16
Observatorio Astronómico Nacional (IGN), C/Alfonso XII, 3, 28014 Madrid, Spain
17
Departamento de Física de la Tierra y Astrofísica, Universidad Complutense de Madrid, 28040, Madrid, Spain
18
Instituto de Física de Partículas y del Cosmos IPARCOS, Facultad de CC Físicas, UCM, 28040, Madrid, Spain
19
Max-Planck-Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
Received:
1
September
2022
Accepted:
10
November
2022
Mapping star-formation rates (SFR) within galaxies is key to unveiling their assembly and evolution. Calibrations exist for computing the SFR from a combination of ultraviolet and infrared bands for galaxies as integrated systems, but their applicability to sub-galactic (kiloparsec) scales remains largely untested. We used integral field spectroscopy of 19 nearby (D < 20 Mpc) galaxies obtained by PHANGS–MUSE to derive accurate Balmer decrements (Hα/Hβ) and attenuation-corrected Hα maps. We combined this information with mid-infrared maps from WISE at 22 μm and ultraviolet maps from GALEX in the far-UV band to derive SFR surface densities in nearby galaxies on resolved (kiloparsec) scales. Using the Hα attenuation-corrected SFR as a reference, we find that hybrid recipes from the literature overestimate the SFR in regions of low SFR surface density, low specific star-formation rate (sSFR), low attenuation, and old stellar ages. We attribute these trends to heating of the dust by old stellar populations (IR cirrus). We calibrated this effect by proposing functional forms for the coefficients in front of the IR term that depend on band ratios sensitive to the sSFR. These recipes return SFR estimates that agree with those in the literature at high sSFR (log(sSFR/yr−1) > − 9.9). Moreover, they lead to negligible bias and < 0.16 dex scatter when compared to our reference attenuation-corrected SFR from Hα. These calibrations prove reliable as a function of physical scale. In particular, they agree within 10% with the attenuation corrections computed from the Balmer decrement on 100 pc scales. Despite small quantitative differences, our calibrations are also applicable to integrated galaxy scales probed by the MaNGA survey, but with a larger scatter (up to 0.22 dex). Observations with JWST open up the possibility to calibrate these relations in nearby galaxies with cloud-scale (∼100 pc) resolution mid-IR imaging.
Key words: techniques: spectroscopic / galaxies: fundamental parameters / galaxies: star formation / galaxies: ISM / galaxies: evolution
The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Estimates of the recent star-formation rate (SFR) play a central role in studies of galaxy evolution, chemical enrichment, stellar feedback, and the physics of stellar birth. Estimating the SFR in distant galaxies entails measuring light from young massive stars, either directly (e.g., in the ultraviolet, UV), or indirectly, via recombination line emission (e.g., Hα) or the radiation re-emitted by dust in the infrared (IR).
From the cosmological perspective, for example, knowledge of how the dust attenuation affects UV emission is fundamental to correctly reconstruct the peak and decline of the cosmic star formation history at z < 4 (Lilly et al. 1996; Gruppioni et al. 2013; Madau & Dickinson 2014; Koprowski et al. 2017), and to interpret the properties of the first galaxies, which may already be subject to substantial dust obscuration (Casey & Zavala 2018; Gruppioni et al. 2020; Algera et al. 2022). The physics of the star formation process, on the other hand, can be probed in the extragalactic context by studying the so-called star formation laws, relating gas content with SFR for entire galaxies or sub-galactic regions (Kennicutt 1998; Bigiel et al. 2008; Bacchini et al. 2019). Accurate dust corrections have been instrumental in reducing the systematic uncertainties in the measurement of slope of these relations (Kennicutt & De Los Reyes 2021), and therefore in distinguishing between competing physical models.
Unfortunately, both UV and IR emission can arise from sources other than young stars, and different SFR tracers are dependent on the age of the stellar population and other physical properties of the interstellar medium (ISM) in complex ways. As a result, calibrating SFR estimates and linking between different systems remains an important open topic (Kennicutt 1998; Murphy et al. 2011; Wuyts et al. 2011; Kennicutt & Evans 2012; Calzetti 2013; Boquien et al. 2016).
In this paper, we focus on measurements of the SFR per unit area (ΣSFR) on kiloparsec (kpc) scales, and attempt to link three of the most commonly used calibration methods: (1) Hα emission corrected for dust attenuation by using the Balmer decrement (e.g., Groves et al. 2012a, and posited as early as Berman 1936); (2) Hα emission corrected using an empirically calibrated combination with Wide-field Infrared Survey Explorer (WISE) 22 μm, Spitzer Space Telescope 24 μm, or Infrared Astronomical Satellite (IRAS) 25 μm emission (e.g., Kennicutt et al. 2007; Calzetti et al. 2007); and (3) UV emission combined with WISE 22 μm emission (e.g., Meurer et al. 1999; Leroy et al. 2008; Hao et al. 2011; Boquien et al. 2016).
The first technique contrasts the expected ratio of Hα to Hβ line emission for case B recombination with the observed ratio to calculate the ratio of attenuations. Combined with an adopted attenuation curve, the paired measurement of Hα and Hβ line emission yields the attenuation affecting Hα, AHα, and the attenuation-corrected Hα flux, 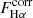 . Although this method has a long pedigree, it has been used more widely in recent years because optical integral field spectroscopy (IFS) from surveys such as CALIFA (Calar Alto Legacy Integral Field Area, Sánchez et al. 2012), SAMI (Sydney – Australian Astronomical Observatory Multi-Object Integral Field Spectrograph, Croom et al. 2012), and MaNGA (Mapping Nearby Galaxies at Apache Point Observatory, Bundy et al. 2015) has become available.
. Although this method has a long pedigree, it has been used more widely in recent years because optical integral field spectroscopy (IFS) from surveys such as CALIFA (Calar Alto Legacy Integral Field Area, Sánchez et al. 2012), SAMI (Sydney – Australian Astronomical Observatory Multi-Object Integral Field Spectrograph, Croom et al. 2012), and MaNGA (Mapping Nearby Galaxies at Apache Point Observatory, Bundy et al. 2015) has become available.
The second method consists of combining Hα with mid-IR maps, generally (but not always) via a linear combination. The ratio of mid-IR to Hα emission is treated as an indicator of AHα or, put another way, the mid-IR emission is used to trace the portion of Hα emission absorbed by dust. Although this approach can be theoretically motivated, its calibration is fundamentally empirical: the mid-IR flux is scaled by a (pre)factor set by benchmarking against some gold standard reference SFR tracer, most commonly attenuation-corrected hydrogen recombination lines as described in the previous paragraph (e.g., Calzetti et al. 2007; Kennicutt et al. 2009).
The third approach combines UV and IR emission. We consider linear combinations of individual bands (e.g., Thilker et al. 2007; Leroy et al. 2008, 2012, 2019; Hao et al. 2011; Boquien et al. 2016), but previous versions of this approach also include multi-band or higher-order calibrations, and summing full bolometric estimates of the IR and UV emission (e.g., Meurer et al. 1999). In a broad sense, this approach represents a simplified adaptation of the increasingly common practice of fitting population synthesis models to the spectral energy distribution (SED) of galaxies in the UV, optical, and IR bands (e.g., Da Cunha et al. 2008; Conroy et al. 2013; Salim et al. 2016, 2018; Nersesian et al. 2019; Hunt et al. 2019).
We focus here on the linear combination of UV and the 22 μm mid-IR band. The mid-IR offers several advantages with respect to the far-IR. Physically, the mid-IR continuum is expected to be directly sensitive to the incident radiation field. Empirically, the warm mid-IR dust appears to be physically associated with regions of massive star formation (e.g., Helou et al. 2004; Relaño 2010), with a smaller contribution from cool dust heated by older stellar populations than the far-IR. Crucially, Spitzer had excellent performance at 24 μm, and more recently, WISE (Wright et al. 2010) provided mid-IR data at sufficient resolution (θFWHM ≈ 12″ at 22 μm) to map nearby star-forming galaxies (Jarrett et al. 2013). Further emphasizing the importance of the mid-IR, JWST is providing maps of the mid-IR emission at even higher resolution and sensitivity for both local and distant galaxies.
Despite the utility of the mid-IR based methods, their calibration remains exclusively empirical. Fortunately, studies of nearby galaxies have established self-consistent calibrations for the mid-IR in combination with UV or Hα to estimate the SFR for whole galaxies (Kennicutt et al. 2009; Hao et al. 2011; Catalán-Torrecilla et al. 2015; Leroy et al. 2019). Another line of studies has established calibrations that can be applied to individual star-forming regions inside of galaxies (including Kennicutt et al. 2007; Calzetti et al. 2007; Murphy et al. 2011; Boquien et al. 2016). These calibrations are generally found to be accurate to ∼0.1–0.15 dex (Kennicutt et al. 2009; Leroy et al. 2012), but systematically differ from each other at the level of ∼0.2 dex.
Physically, mid-IR emission reflects the combined effect of dust abundance, relative geometry of dust and stars, and dust heating by the surrounding stellar populations. While young stars may provide the bulk of the heating in individual star-forming regions, in more quiescent regions, older stars also play a substantial role in heating the dust and powering the emission in the IR (e.g., Groves et al. 2012b; Li et al. 2013). High-resolution studies (≲100 pc) can isolate individual regions and effectively avoid or filter out this diffuse background, or IR cirrus (e.g., Calzetti et al. 2007). However, on the larger scales of kpcs or whole galaxies, this IR cirrus will be an unavoidable part of the measurement (Boquien et al. 2016). This fact leads to a non-linear relation between total IR luminosity and the SFR that is dependent on the specific SFR (sSFR = SFR/M⋆; e.g., Cortese et al. 2008; Boquien & Salim 2021). The contribution of the IR cirrus may be physically modelled and subtracted (e.g., Leroy et al. 2012). Alternatively, the calibration of the IR term may take the contribution of this diffuse dust component into account (Boquien et al. 2016).
So far, the lack of quality reference maps has been a major obstacle in calibrating the IR term in SFR prescriptions to apply at sub-galactic scales. In this work, we revisit these questions, prompted by a unique combination of new data. The PHANGS–MUSE survey (Emsellem et al. 2022) has recently obtained comprehensive integral field spectroscopy (IFS) mapping of the star-forming discs of 19 nearby galaxies (distance < 20 Mpc), using the MUSE (Multi-unit Spectroscopic Explorer) instrument (Bacon et al. 2010) on the ESO Very Large Telescope. These observations give us access to maps of Hα and Hβ with a high signal-to-noise ratio (S/N), free from the continuum-subtraction systematics associated with narrow-band images. Because PHANGS–MUSE targets nearby galaxies, the relatively coarse ∼5 − 15″ resolution of mid-IR maps from WISE or Spitzer translates into ≲1 kpc. This scale is fortuitously set because it allows us to define regions with significant numbers of the relatively rare massive stars, but is not so large as to merge multiple adjacent star-forming regions.
Extensive, homogenised multi-wavelength imaging is available for the PHANGS–MUSE targets from GALEX far-UV (FUV; λ ∼ 154 nm) and near-UV (NUV; λ ∼ 231 nm) as well as WISE Band 1, 2, 3, and 4 imaging (λ = 3.4, 4.5, 12, and 22 μm) with 15″ or ∼1 kpc resolution (Leroy et al. 2019). This data set allows us to check for consistency among the three methods of estimating SFR discussed above, to quantify systematic uncertainties, and to derive new empirical coefficients appropriate for this scale and sample, using the attenuation-corrected Hα maps from MUSE as a reference.
A key motivation for this new calibration effort is the desire to derive SFR maps that are anchored in the Balmer-corrected MUSE data and combine WISE IR maps with new narrow-band Hα observations of nearby galaxies (Razza et al., in prep.). Moreover, we wish to integrate the UV+IR-based SFR maps that are widely available for the nearest galaxies (D ≲ 50 Mpc; e.g., Jarrett et al. 2013; Leroy et al. 2019) into a common framework with the attenuation-corrected Hα derived from optical IFS mapping that has been obtained for large samples of more distant (D ∼ 20 − 150 Mpc) galaxies (Belfiore et al. 2018; Medling et al. 2018; Sánchez 2020). Finally, observations in the mid-IR with JWST now provide us with a high-resolution view of embedded star formation in the nearby Universe, therefore making it urgent to verify the validity of SFR calibrations across a range of physical scales.
With these goals in mind, Sect. 2 presents our compilation of 15″ resolution MUSE, UV, and IR measurements, and describes our methods and assumptions. Section 3 compares results for ΣSFR and AHα calculated using previous calibrations and presents updated recipes for kpc-scale SFR calibrations using Hα+IR and UV+IR. In Sect. 4 we discuss the impact on our new calibrations together with their limitations. We summarise our results in Sect. 5.
2. Data and methods
The starting point of this work is the sample of 19 galaxies targeted by the PHANGS-MUSE survey. These objects were selected to be nearby (D < 20 Mpc), close to the star formation main sequence, and moderately inclined (i < 57.3°). The main properties of the sample, which spans the stellar mass range log(M⋆/M⊙) = 9.4 − 11.0, are presented in Emsellem et al. (2022) and are summarised in Table 1.
Key properties of the PHANGS–MUSE sample of galaxies.
We compiled and analysed a data set that includes intensities and associated uncertainties at a 15″ common resolution from MUSE, GALEX, and WISE. The limiting resolution was set by WISE W4 band centred at 22 μm. For the distances of our galaxy sample (D = 5.2 − 19.6 Mpc), this angular resolution corresponds to a median physical resolution of 1.1 kpc. It varies across our sample from 400 pc to 1.4 kpc (see Table 1).
2.1. PHANGS–MUSE, optical IFS
Each galaxy in the PHANGS–MUSE sample was observed with several (3–15) MUSE pointings, each 1′×1′. Observing strategy, data reduction, and analysis of this data set are described in detail in Emsellem et al. (2022). The data reduction was carried out via PYMUSEPIPE, a Python wrapper to the ESOREX MUSE reduction recipes (Weilbacher et al. 2020). The point spread function (PSF) and sky background of each MUSE pointing were determined by comparison with wide-field R-band imaging (Razza et al., in prep.). Reconstructed photometry from MUSE is consistent with Sloan Digital Sky Survey (SDSS) imaging with a typical scatter of 0.04 mag. In this work, we mostly use datacubes where the native-resolution mosaicked cube was convolved with a suitable kernel in order to deliver a common Gaussian resolution of 15″ full width at half maximum (FWHM) and spaxels 2 4 in size. In Sect. 3.3.1 we study the effect of spatial resolution on our results, and we therefore use the optimally convolved (copt) datacubes described in Emsellem et al. (2022). In these data products, the PSF was homogenised across each individual mosaic and as a function of wavelength using the PYPHER tool (Boucaud et al. 2016) to obtain the best possible common Gaussian PSF for each galaxy. The median PSF FWHM of the copt data is 0
4 in size. In Sect. 3.3.1 we study the effect of spatial resolution on our results, and we therefore use the optimally convolved (copt) datacubes described in Emsellem et al. (2022). In these data products, the PSF was homogenised across each individual mosaic and as a function of wavelength using the PYPHER tool (Boucaud et al. 2016) to obtain the best possible common Gaussian PSF for each galaxy. The median PSF FWHM of the copt data is 0 95.
95.
Emission-line fluxes and other stellar population properties were obtained by using the PHANGS data analysis pipeline (DAP), as described in Emsellem et al. (2022). The DAP was used to perform three full spectral fitting steps: the first optimised for the recovery of the stellar kinematics, the second aimed at determining the stellar population properties, and the final step optimised for the extraction of fluxes and kinematics of gas emission lines. The core of all three spectral fitting modules is the pPXF Python module (Cappellari & Emsellem 2004; Cappellari 2017). The stellar continuum was fitted using a set of simple stellar population models from the E-MILES library (Vazdekis et al. 2012). From the DAP output, we used maps of Hα and Hβ line emission (corrected for Galactic extinction), and also consider the mean light-weighted age of the stellar population in Sect. 3.1.1. We applied a set of custom-designed masks to the output MUSE maps. In particular, for the 15″ resolution data, we masked foreground stars brighter than 16.5 mag in Gaia G-band from Gaia Data Release 2 (Gaia Collaboration 2018) and applied a few additional masks to stars that were missed and the central regions of galaxies hosting active galactic nuclei (AGN).
2.2. Mid-IR and UV maps
IR and UV imaging was obtained from z0MGS (z = 0 multi-wavelength galaxy synthesis; Leroy et al. 2019), an atlas of WISE and GALEX (Martin 2005) images of nearby (D < 50 Mpc) galaxies. z0MGS is based on the unWISE reprocessing by Lang (2014) and draws heavily on HyperLEDA (Makarov et al. 2014) for the atlas construction.
Images used in this work were taken from the publicly available atlas, and were convolved to a common 15″ FWHM resolution, with a pixel size of 5 5. Masking based on Gaia DR2, 2MASS (Skrutskie et al. 2006), and HyperLEDA was carried out to remove foreground stars or other galaxies in the field, and a local background subtraction was performed for each object. GALEX imaging was corrected for Galactic extinction following Peek & Schiminovich (2013) and the Schlegel et al. (1998) dust maps. Stellar mass surface density maps were derived according to the prescription of Leroy et al. (2019), who used the WISE 3.4 μm W1 band in combination with a mass-to-light ratio that scales with SFR to obtain masses in agreement with Salim et al. (2018). As already noted in Leroy et al. (2021), this mass estimate agrees well with the masses derived from full spectral fitting of the MUSE data, up to a roughly constant multiplicative offset, which makes the MUSE masses higher by 0.09 dex.
5. Masking based on Gaia DR2, 2MASS (Skrutskie et al. 2006), and HyperLEDA was carried out to remove foreground stars or other galaxies in the field, and a local background subtraction was performed for each object. GALEX imaging was corrected for Galactic extinction following Peek & Schiminovich (2013) and the Schlegel et al. (1998) dust maps. Stellar mass surface density maps were derived according to the prescription of Leroy et al. (2019), who used the WISE 3.4 μm W1 band in combination with a mass-to-light ratio that scales with SFR to obtain masses in agreement with Salim et al. (2018). As already noted in Leroy et al. (2021), this mass estimate agrees well with the masses derived from full spectral fitting of the MUSE data, up to a roughly constant multiplicative offset, which makes the MUSE masses higher by 0.09 dex.
Since much of the work on SFR calibration in the literature is based on the Spitzer MIPS 24 μm band, we have compared the WISE W4 maps from z0MGS with Spitzer MIPS 24 μm mosaics for a subset of eight galaxies with available Spitzer images from either the SINGS (Kennicutt et al. 2003) or LVL (Dale et al. 2009) programs (NGC 0628, NGC 1512, NGC 1566, NGC 3351, NGC 3627, NGC 4254, NGC 4321, and NGC 5068). The Spitzer MIPS 24 μm images were convolved to the same common 15″ FWHM resolution. While the Spitzer maps are substantially deeper than those of WISE (by a factor of 6 on average), the fluxes in regions that are detected in both maps (S/N> 5 in the WISE maps) are in excellent agreement. In particular, we find a small multiplicative offset, which goes in the direction of making the MIPS flux densities lower by 11% (0.05 dex), in line with the previous comparisons (Jarrett et al. 2011, 2013; Brown et al. 2014)1. In energy units, which are used in the next section to define the SFR calibration, log(νMIPSFν, MIPS) = log(νW4Fν, W4) − 0.08, with an uncertainty due to galaxy-to-galaxy scatter of 0.03 dex.
2.3. Data processing
In order to generate a catalogue of distinct regions at our working resolution, the Hα and Hβ 15″-resolution maps were resampled with pixels of 14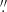 4 (comparable to the 15″ FWHM). The z0MGS data were reprojected (using the REPROJECT Python module) onto the same world coordinate system, and their pixel size was matched to that of the MUSE data. A cut on S/N of 5 was applied to the Hα and Hβ lines, but this only affects a negligible fraction of our data set (< 3% of the regions). This procedure led to a sample of 1759 regions, covering a total area of ∼100 arcmin2 or 104 kpc2 across our 19 targets. Stellar and SFR surface density measurements were corrected for the effect of inclination by multiplication by cosine of the inclination angles compiled in Leroy et al. (2021).
4 (comparable to the 15″ FWHM). The z0MGS data were reprojected (using the REPROJECT Python module) onto the same world coordinate system, and their pixel size was matched to that of the MUSE data. A cut on S/N of 5 was applied to the Hα and Hβ lines, but this only affects a negligible fraction of our data set (< 3% of the regions). This procedure led to a sample of 1759 regions, covering a total area of ∼100 arcmin2 or 104 kpc2 across our 19 targets. Stellar and SFR surface density measurements were corrected for the effect of inclination by multiplication by cosine of the inclination angles compiled in Leroy et al. (2021).
2.4. Formalism for computing SFR
The attenuation-corrected Hα flux was obtained as
where kHα is the value of the reddening curve at the Hα wavelength. We quote all luminosities in energy units (erg s−1), that is, L ≡ νLν, where ν is the (effective) frequency of the band considered.
We measured E(B − V) from the Balmer decrement (BD) assuming case B recombination, temperature T = 104 K, and density ne = 102 cm−2, leading to LHα, corr/LHβ, corr = 2.86. This ratio is almost independent of density for the range of densities relevant to H II regions, and it depends only weakly on temperature (Osterbrock & Ferland 2006). Under these assumptions,
On the scales probed by our observations, dust will be mixed with the gas, leading to the need of considering an effective attenuation law, and not just the effect of dust extinction along the line of sight. We nonetheless used a foreground screen attenuation model with a total-to-selective extinction RV = 3.1 equivalent to the Milky Way extinction law of O’Donnell (1994), which represents a small modification to the law proposed by Cardelli et al. (1989). There is some observational support for the use of this simplified foreground screen model as applied to the nebular lines in galaxies (Calzetti et al. 1996; Wild et al. 2011). Moreover, the use of a Milky Way-like extinction law follows the conventions of the field, making our results directly comparable with the literature (Calzetti et al. 2000; Kennicutt et al. 2009; Boquien et al. 2019). We discuss the effect of making different assumptions regarding the attenuation curve for the nebular component in Sect. 4.
The conversion factors C for different monochromatic SFR estimators (e.g., Hαcorr) are defined by
For Hα and the FUV, the values of the parameter C can be derived from stellar population synthesis models by making some suitable simplifying assumption for the star formation history, the metallicity, and the initial mass function (IMF). This is particularly important for the FUV, which traces longer timescales (∼100 Myr) than Hα (∼5 Myr; Kennicutt & Evans 2012). We adopted the CHα value presented by Calzetti et al. (2007), computed using Starburst99 (Leitherer et al. 1999), a constant star formation history, an age of 100 Myr, solar metallicity, and a Kroupa (2001) IMF. Using a Chabrier (2003) IMF changes this factor by less than 5%, while a Salpeter (1955) IMF requires dividing by a factor of ∼0.66 (Madau & Dickinson 2014). For reference, this value is within ≈2% of the value of CHα suggested by Murphy et al. (2011) and endorsed by Kennicutt & Evans (2012). For the FUV emission, we adopted the value of CFUV recommended by Leroy et al. (2019), based on the SED fitting results of Salim et al. (2018), using a Chabrier (2003) IMF. The CFUV factor has a stronger dependence on the star formation history, and consequently, on the position of galaxies in the SFR-M⋆ plane (see Leroy et al. 2019, their Fig. 25), than CHα. The value adopted here is 0.07 dex higher than that recommended by Kennicutt & Evans (2012).
For hybridised SFR estimators (e.g., W4 22 μm + Hαobs), we defined the conversion factors C in a similar fashion as
where by definition, CHα was taken to be the same value as the monochromatic estimator (Eq. (3)), so that the sum in Eq. (4) may be interpreted as the combination of an unobscured and an obscured SFR term. The conversion factor of the W4 22 μm emission is written as 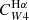 to emphasize that it multiplies the W4 22 μm luminosity when hybridised with Hα. In all cases, the conversion factors C have units of M⊙ yr−1/(erg s−1), which we omit for clarity from now on. We adopted the same approach as Leroy et al. (2019) to construct the UV+IR hybrid SFR calibration, given by
to emphasize that it multiplies the W4 22 μm luminosity when hybridised with Hα. In all cases, the conversion factors C have units of M⊙ yr−1/(erg s−1), which we omit for clarity from now on. We adopted the same approach as Leroy et al. (2019) to construct the UV+IR hybrid SFR calibration, given by
We express 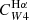 in this form because our main goal is to infer SFRs, but the drawback of this formalism is that it makes the IR-coefficient dependent upon the assumed SFR conversion factor for Hα (CHα). Because by equating Eqs. (3) and (4),
in this form because our main goal is to infer SFRs, but the drawback of this formalism is that it makes the IR-coefficient dependent upon the assumed SFR conversion factor for Hα (CHα). Because by equating Eqs. (3) and (4), 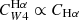 , our inferred value of
, our inferred value of 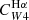 can be directly rescaled to a different assumed CHα.
can be directly rescaled to a different assumed CHα.
We summarise the values for coefficients of monochromatic and hybridised SFR estimators from the literature in Table 2. Where relevant, coefficients derived using Spitzer MIPS 24 μm were revised downward by 0.08 dex to account for the bandpass difference with WISE W4 (Sect. 2.2).
Summary of coefficients to convert the luminosity in different bands into SFR.
3. Results
3.1. Comparisons of the results for existing prescriptions
In this section, we focus on comparing the SFR obtained from the Balmer decrement-corrected Hα against the FUV+W4 prescription of Leroy et al. (2019). In Fig. 1 we show SFR maps for three example galaxies from the PHANGS–MUSE sample. NGC 5068 is a low-mass galaxy, and the closest object in our sample (15″ = 400 pc). NGC 628 is an archetypal grand-design spiral galaxy, and finally, NGC 1566 is a massive barred Seyfert 1 galaxy.
 |
Fig. 1. Comparison between ΣSFR/(M⊙ kpc−2 yr−1) estimates at 15″ resolution from extinction-corrected Hα emission and UV+IR (FUV + W4) using the Leroy et al. (2019) prescription for three example galaxies. The maps are shown on the original pixel size of 5 |
The comparison between Hα and FUV+W4 SFR shows that deviations from equality are spatially correlated with the intensity of the star formation activity. In particular, the FUV+W4 SFR is biased high in regions of low ΣSFR, while the trend is inverted for regions of high ΣSFR. This trend is evident in all three galaxies shown in Fig. 1, despite clear differences in the ΣSFR distributions, and it is also seen in the other PHANGS–MUSE galaxies in our sample. The AGN in NGC 1566 shows excess IR emission, but the region is masked in the further analysis, as already discussed in Sect. 2.1.
3.1.1. Secondary dependences
In this section, we study how well the SFR estimated from FUV+W4 agrees with the SFR estimated from attenuation-corrected Hα as a function of several physical properties (Fig. 2). The strongest observed trend is that the ratio log(SFRFUV + W4/SFRHα, corr) decreases as a function of both ΣSFR and sSFR = ΣSFR/Σ⋆. On average, our data demonstrate that most regions have a higher SFRFUV + W4 than SFRHα, corr, but the two estimates agree well at the highest sSFR and ΣSFR values in our sample, log(sSFR/yr−1)≳ − 10 and log(ΣSFR/M⊙ yr−1 kpc−2) > − 2.
 |
Fig. 2. Dependence of the ratio of the SFR measured from FUV+W4 (and the Leroy et al. 2019 coefficient) and that measured from attenuation-corrected Hα on various physical properties for a sample of 1759 ∼ kpc sized regions taken from the 19 galaxies of the PHANGS-MUSE sample: (a) sSFR, (b) SFR surface density (both measured from attenuation-corrected Hα), (c) E(B − V) of the ionised gas measured from the Balmer decrement, (d) stellar mass surface density, (e) deprojected galactocentric radius normalised to Reff, (f) light-weighted mean age of the stellar population, derived from fits to the MUSE stellar continuum. The grey points represent individual ∼15″ regions, and the red hexagons and dashed red lines represent the median and scatter (16th − 84th percentiles) of the distribution. In panel c, we also show the result of calculating the SFR from the FUV flux, without considering the IR term (blue lines). This demonstrates that the inclusion of the IR term correctly reproduces the Hα-based SFR for highly attenuated regions, but it overestimates the attenuation level for regions with a low Balmer decrement. These trends are consistent with an increasing contamination from old stellar population to the dust heating at lower SFR levels. |
In panel c, we show the dependence of log(SFRFUV + W4/SFRHα, corr) on E(B − V) measured from the Balmer decrement. The vertical scale in this panel was extended to show in blue the median relation obtained by calculating the SFR using the FUV alone, without any IR correction. Using FUV+IR, we obtain an overestimate of the SFR at low E(B − V), which is driven by an overestimate of the attenuation from the IR term. At higher values of E(B − V), the IR term provides a correction to the FUV flux that brings the inferred SFR in agreement with the Hα SFR estimate.
No trend is evident between log(SFRFUV + W4/SFRHα, corr) and stellar mass surface density or deprojected galactocentric radius (Fig. 2, panels d and e). Considering the light-weighted age of the stellar population (panel f), the log(SFRFUV + W4/SFRHα, corr) ratio increases for older ages, in agreement with the sSFR trend noted above.
We find no dependence on distance or on the physical scale corresponding to our 15″ resolution (≈400 − 1400 pc). In particular, the median trends are consistent within the scatter when considering two sub-samples of galaxies divided according to the median distance of the sample (15.85 Mpc). We verified that the scatter within individual galaxies is comparable to the sample-wide scatter, indicating small galaxy-to-galaxy variations.
Trends associated with the Hα+W4 calibration using the Calzetti et al. (2007) coefficient are similar and are presented in Fig. 3. The main difference is the substantially smaller scatter, as expected because in this case, both SFR estimates rely on Hα for the un-attenuated portion.
 |
Fig. 3. Same as Fig. 2, but using Hα+W4 instead of FUV+W4. The coefficient |
3.1.2. Comparison of the implied E(B – V)
By equating Eq. (4) (or equivalently, Eq. (5) for the FUV) and (1), we can write E(B − V) as a function of the W4/Hα or the W4/FUV ratio. In calculating E(B − V), we need to assume both the hybridisation coefficients (we use Table 2) and an attenuation law to determine kλ. In particular,
where λ refers to either Hα or the FUV band. As discussed in Sect. 2.4, we assumed a Milky Way-like foreground screen as parametrised by O’Donnell (1994) for the Hα line, and the Calzetti (2001) law for the FUV.
In Fig. 4 we plot the resulting E(B − V), inferred from FUV + W4 and Hα + W4, versus the E(B − V)BD inferred from the Balmer decrement for the ∼15″ regions, colour-coded by sSFR. On kiloparsec scales, the attenuation of the stars in the FUV is expected to be lower than that of the ionised gas because nebular emission is more closely linked to the most recent star formation, and therefore to dust. Calzetti et al. (2000) report the differential reddening between the stars and the gas to be a factor of 0.44, which we show as a dashed line in the left panel of Fig. 4 (equivalent to the relation AFUV = 1.78 AHα). More recent work on nearby galaxies based on MaNGA (Greener et al. 2020) supports a somewhat lower ratio, between 0.25 and 0.44. The subset of our regions with the largest sSFR lies close to the latter value, with an average ratio of E(B − V)FUV + W4/E(B − V)BD = 0.52 for log(sSFR/yr−1) > −10. On the other hand, regions of low sSFR, with log(sSFR/yr−1) < − 10.8, show E(B − V)FUV + W4 > E(B − V)BD.
 |
Fig. 4. Comparison between E(B − V) estimated via the Balmer decrement and the same quantity calculated via FUV+W4 (left) and Hα+W4 (right), colour-coded by sSFR. In the left panel, we show as a dashed line the ratio of the differential reddening of gas and stars inferred by Calzetti et al. (2000), E(B − V)stars = 0.44 E(B − V)gas. Solid black lines in both panels represent the one-to-one line. In both panels, attenuation is overestimated in regions of low sSFR because of IR cirrus. |
The right panel of Fig. 4 compares E(B − V)Hα + W4 with E(B − V)BD and confirms our findings. For regions with log(sSFR/yr−1) > − 10, the two estimates of the E(B − V) of the nebular emission agree to within 10%. At low sSFR, however, E(B − V)Hα + W4 is significantly larger, indicating a likely contribution from IR cirrus (see Sect. 4).
3.2. Multi-wavelength calibration scheme for SFR at kiloparsec scales
In order to bring the FUV+W4 and Hα+W4 SFR into agreement with the star formation rates obtained from attenuation-corrected Hα, we calibrated the hybridisation coefficients 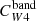 as a function of physical quantities that trace the ratio of young to old stars (e.g., Boquien et al. 2016). From Sect. 3.1 we determined that sSFR, ΣSFR, and stellar population light-weighted age show well-defined trends, all potentially attributable to IR cirrus. We focused on sSFR as well as Hα/W1 and FUV/W1 as empirical proxies for sSFR because they are intensive quantities (unlike ΣSFR), less model dependent than the light-weighted age derived from full spectral fitting, and are widely available for nearby galaxies through the combination of GALEX and WISE.
as a function of physical quantities that trace the ratio of young to old stars (e.g., Boquien et al. 2016). From Sect. 3.1 we determined that sSFR, ΣSFR, and stellar population light-weighted age show well-defined trends, all potentially attributable to IR cirrus. We focused on sSFR as well as Hα/W1 and FUV/W1 as empirical proxies for sSFR because they are intensive quantities (unlike ΣSFR), less model dependent than the light-weighted age derived from full spectral fitting, and are widely available for nearby galaxies through the combination of GALEX and WISE.
Assuming the attenuation correction from the Balmer decrement, we used Eqs. (4) and (3) to determine 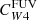 and
and 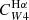 , and plot these coefficients as a function of sSFR (Fig. 5, a and d). Both coefficients show a strong positive correlation with sSFR (Spearman r = 0.71–0.72). We fit the median relation with a broken power law of the form
, and plot these coefficients as a function of sSFR (Fig. 5, a and d). Both coefficients show a strong positive correlation with sSFR (Spearman r = 0.71–0.72). We fit the median relation with a broken power law of the form
 |
Fig. 5. Hybridisation coefficients of W4 with either FUV ( |
where Q refers to the quantity of interest (e.g., sSFR) and a0 = log Cmax − a1 log Qmax for the function to be continuous at log Qmax. The best-fit broken power-law relations are shown in Fig. 5 as dashed blue lines, and the values of the best-fit parameters (Cmax, Qmax and a1) are given in Table 3. These relations should not be extrapolated past the range populated by our data. We therefore also show in Table 3 the fifth percentile of the distribution of the quantity of interest, log(Qmin). We do not recommend using the best fits for values lower than log(Qmin).
Best-fit broken power law coefficients for computing 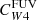 and
and 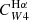 as a function of the quantity Q.
as a function of the quantity Q.
A broken power law of this form was chosen in order to allow for a constant coefficient at high sSFR. The choice reflects the expectation that the contribution to emission at 22 μm from dust heated by old stellar populations becomes negligible in regions dominated by young stars, and therefore, the hybridisation coefficients should approach a constant value. This flattening is evident in Fig. 5 (panels a and d) for both 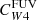 and
and 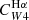 and logsSFR/yr−1 ≳ −9.9. The best-fit value of the coefficients for high sSFR are
and logsSFR/yr−1 ≳ −9.9. The best-fit value of the coefficients for high sSFR are 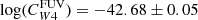 and
and 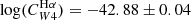 . We consider these values to be our best estimates for the hybridisation coefficients in star-forming regions. The value of log Cmax for
. We consider these values to be our best estimates for the hybridisation coefficients in star-forming regions. The value of log Cmax for 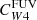 agrees within the error with the estimate by Leroy et al. (2019), based on galaxy-integrated fluxes log(
agrees within the error with the estimate by Leroy et al. (2019), based on galaxy-integrated fluxes log(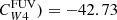 . Regarding the
. Regarding the 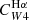 coefficient, our inferred value of log Cmax is virtually identical to the value preferred by Calzetti et al. (2007) log(
coefficient, our inferred value of log Cmax is virtually identical to the value preferred by Calzetti et al. (2007) log(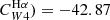 , based on star-forming regions and higher than that of Kennicutt et al. (2009) log(
, based on star-forming regions and higher than that of Kennicutt et al. (2009) log(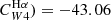 , based on galaxy-integrated photometry.
, based on galaxy-integrated photometry.
The parametrisation of 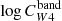 in terms of sSFR is instructive, but cannot be used directly to infer the SFR. If a stellar mass measurement is available, however, an iterative approach can be used to determine the SFR. Nonetheless, we also investigated alternative parametrisations in terms of band ratios that can be used as proxies for sSFR. In particular, we considered the luminosity ratios of Hα/W1 and FUV/W1 (Fig. 5 middle and right columns). We find that a broken power law of the form of Eq. (7) is a good description for the relation between
in terms of sSFR is instructive, but cannot be used directly to infer the SFR. If a stellar mass measurement is available, however, an iterative approach can be used to determine the SFR. Nonetheless, we also investigated alternative parametrisations in terms of band ratios that can be used as proxies for sSFR. In particular, we considered the luminosity ratios of Hα/W1 and FUV/W1 (Fig. 5 middle and right columns). We find that a broken power law of the form of Eq. (7) is a good description for the relation between 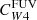 and
and 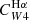 and the Hα/W1 luminosity ratio. The scatter between the data and the best-fit models (0.25 dex in the case of
and the Hα/W1 luminosity ratio. The scatter between the data and the best-fit models (0.25 dex in the case of 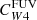 and 0.20 dex for
and 0.20 dex for 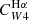 ) is comparable to that obtained for the sSFR parametrisation discussed above. Therefore, we consider these fits our recommended approach for calculating SFR when Hα fluxes are available.
) is comparable to that obtained for the sSFR parametrisation discussed above. Therefore, we consider these fits our recommended approach for calculating SFR when Hα fluxes are available.
The use of FUV/W1 instead of Hα/W1 leads to larger scatter, and the resulting median relation between the hybridisation coefficients and FUV/W1 is less well described by a broken power law. We therefore only recommend the use of FUV/W1 when Hα data are not available (i.e. only for 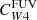 coefficient). The scatter in the parametrisation in this case increases to 0.3 dex (Fig. 5, panel c).
coefficient). The scatter in the parametrisation in this case increases to 0.3 dex (Fig. 5, panel c).
Finally, we checked the effect of our suggested calibrations on the inferred E(B − V). In particular, we focused on the case for which W1, W4 and Hα data are available because it is relevant to the galaxies observed by the PHANGS-Hα narrow-band survey. We calculated E(B − V) via Eq. (6), using the calibration of 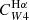 as a function of Hα/W1 given by Eq. (7). Comparing the E(B − V) computed in this fashion with those obtained from the Balmer decrement, we find that they agree very well on average (median offset of < 0.01 mag), with a scatter of 0.08 mag. This represents a substantial improvement over the situation shown in Fig. 4, where the E(B − V) obtained using a constant Hα+W4 was on average 0.14 mag larger than the one obtained from the Balmer decrement. An evaluation of the performance of our calibrations is delayed to Sect. 4.1.
as a function of Hα/W1 given by Eq. (7). Comparing the E(B − V) computed in this fashion with those obtained from the Balmer decrement, we find that they agree very well on average (median offset of < 0.01 mag), with a scatter of 0.08 mag. This represents a substantial improvement over the situation shown in Fig. 4, where the E(B − V) obtained using a constant Hα+W4 was on average 0.14 mag larger than the one obtained from the Balmer decrement. An evaluation of the performance of our calibrations is delayed to Sect. 4.1.
3.3. Validity of calibrations as a function of physical scale
In this section, we study the validity of our proposed calibrations as a function of physical scale. In particular, we address the question of whether the ΣSFR estimates obtained at kpc scales are consistent with those measured at 100 pc scales, accessible in MUSE surveys of nearby galaxies such as PHANGS-MUSE (Emsellem et al. 2022; Pessa et al. 2021) or the MUSE Atlas of Discs (Erroz-Ferrer et al. 2019). We then explore whether the calibrations can be applied to spatially integrated (galaxy-wide) scales, in order to connect to the SFR measurements obtained by large spectroscopic surveys in the nearby Universe.
3.3.1. Dust extinction from kpc to 100 pc scales
The mixing of regions with different physical conditions within the same resolution element leads to an underestimate of the overall attenuation correction because the more attenuated regions contribute less to the integrated light in the larger aperture. Vale Asari et al. (2020) showed analytically that, assuming the attenuation law does not vary across a galaxy, a low-resolution measurement of the attenuation-corrected Hα luminosity always underestimates the result obtained at high spatial resolution. The magnitude of this underestimation depends in a complex fashion on the spatial distribution of the dust emission and the strength of the correlation between dust attenuation and Hα surface brightness. Vale Asari et al. (2020) used MaNGA data to demonstrate that this effect is negligible in practice (3% on average) when comparing measurements taken on kpc scale resolution elements to entire galaxies, but they cautioned against extending this result to smaller scales.
We reconsidered the effect of spatial sampling on the attenuation corrections based on the Balmer decrement, focusing on the spatial scales of interest in this work (1–15″, or from ∼70 to 1100 pc at the average distance of our targets). To do this, we resampled the MUSE Hα and Hβ copt maps with pixels of 5″, 10″, 15″ (the sampling adopted in the previous sections to match WISE W4), 20″, and 30″. For simplicity, we did not convolve the data before resampling, but the effect of the convolution process does not significantly change the outcome of our results. Using these resampled maps, we computed the Balmer decrement and the attenuation-corrected Hα luminosity (Llow res) in each coarser pixel. We then compared this estimate with that obtained by correcting individual pixels in the original high-resolution maps and summing the attenuation-corrected Hα flux (Lhigh res). We followed this procedure for each galaxy in the sample and computed the average ratio of Llow res/Lhigh res as a function of aperture size.
Figure 6 demonstrates that the ratio Llow res/Lhigh res varies across the galaxies in our sample, presumably due to differences in the overall dust morphology. At 15″ resolution, the underestimation in the attenuation correction with respect to the estimate obtained at the copt (arcsec resolution) data is 10% on average, with a 0.1 dex scatter within different regions of individual galaxies. This is a small source of uncertainty in the overall uncertainty budget of the attenuation-corrected Hα.
 |
Fig. 6. Mean ratio of the attenuation-corrected Hα luminosity computed in low-resolution apertures of varying size to the luminosity derived at the highest spatial scales accessible with the PHANGS-MUSE data (∼1″) as a function of the low-resolution aperture size. Trends are shown for each of the 19 galaxies in the PHANGS-MUSE sample, colour-coded by total stellar mass. The data for each galaxy were resampled on apertures of 5, 10, 15, 20, and 30″. The alternative x-axis at the top of the plot shows the equivalent physical size in kpc at the median distance of the sample. At 15″ resolution, the resolution of the WISE W4 data, the median difference is 10% (⟨Llow res/Lhigh res⟩ = 0.92). |
We checked for a correlation between the slope of the Llow res/Lhigh res versus aperture size and other quantities of galaxies. In particular, we considered the effect of inclination, distance, M⋆, SFR, and sSFR. The strongest correlation manifests itself with stellar mass (Spearman r = −0.6), indicating that low-mass galaxies tend to have flatter trends in this space (as already evident in the colour-coding in Fig. 6). A mild inverse correlation is also seen with inclination (Spearman r = −0.32), where more inclined galaxies have flatter slopes in this space. We determined the effect of distance on these correlations by rerunning the analysis using apertures of fixed physical size in kpc. We find that the trend with mass persists (Spearman r = −0.51), but the trend with inclination is considerably weaker (Spearman r = −0.09).
The result of this exercise is dependent on our approach to the low-S/N area in the arcsec resolution copt maps. In particular, while Hα is detected in nearly 100% of the pixels of our maps, Hβ is only detected with S/N > 3 in 85% of the pixels in each map on average (in some galaxies, up to 50% of their pixels is undetected in Hβ at the 3 σ level). These spaxels contain 3% of the total Hα flux on average, but in some galaxies, this fraction can increase to 10%. It is important, therefore, to exclude the possibility that the undetected Hβ hides large amounts of attenuated star formation.
In order to estimate the importance of dust attenuation in regions where Hβ is undetected, we used the adaptive binning procedure described in Belfiore et al. (2022) to detect Hβ in the low surface brightness regions via binning. This binning procedure was optimised for recovery of emission line fluxes in the diffuse ionised gas, and therefore generates larger bins in regions of faint Hα emission (e.g., inter-arm regions). We find that low-surface-brightness pixels lie on the extrapolation of the power-law relation between Hα and E(B − V) observed at high surface brightness. At Hβ surface brightness corresponding to a 3σ detection limit in the individual spaxels of our copt maps (log LHβ/erg s−1 kpc−2 = 37.5), the median E(B − V) is ∼0.1 mag (−0.1/+0.15). Given this modest level of average attenuation. The relative contribution of Hβ undetected regions to the attenuation-corrected Hα would remain small, and we therefore treated spaxels with an S/N in Hβ lower than 3 as having zero attenuation for the purposes of our test. We tested the effect of assigning to all the Hβ undetected spaxel an E(B − V) = 0.1 mag, and the results do not change substantially.
We conclude that attenuation corrections calculated via Hα + W4 (Sect. 3.2) on kpc scales agree with those derived from arcsec resolution (∼100 pc physical resolution) Balmer decrement maps.
3.3.2. SFR calibration for whole galaxies from integrated UV, IR, and Hα fluxes
We tested the validity of our approach for whole galaxies using integrated fluxes for a sample of galaxies from the MaNGA IFS survey. MaNGA is the largest optical IFS survey of the local Universe (0.01 < z < 0.15), offering measurements of the Hα and Hβ fluxes out to at least 1.5 r-band effective radii. Aperture corrections in calculating the SFR are negligible, as demonstrated by Belfiore et al. (2018). In order to test our hybrid SFR estimator on MaNGA data, we cross-matched the MaNGA catalogue from the SDSS Data Release 17 (Abdurro’uf 2022), and in particular, the summary DAPALL catalogue file generated by the MaNGA Data Analysis Pipeline (Westfall et al. 2019; Belfiore et al. 2019), with the integrated GALEX and WISE photometry derived by Salim et al. (2018) as part of GSWLC22 (GALEX-SDSS-WISE legacy catalogue). We considered the version of the GSWLC2 catalogue that contains the deepest available GALEX data, denoted as GSWLC2-X2. The MaNGA DR17 catalogue contains 10248 galaxies, 86% of which have a match in GSLWC-X2. We further restricted the sample to galaxies that are star forming according to the Kewley et al. (2001) criteria in the [SII]λ6717,31/Hα versus [OIII]λ5007/Hβ Baldwin-Phillips-Terlevich (Baldwin et al. 1981; Phillips et al. 1986) diagnostic diagram, have S/N > 3 in GALEX FUV, WISE W1, and W4 bands, and have a semi-axis ratio b/a > 0.4 (inclination ∼66°), to exclude highly inclined systems. These cuts led to a final sample of 1955 galaxies. We also tested the criterion of Stern et al. (2012) for selecting AGN using the WISE bands, and find that this leads to the exclusion of only 13 additional galaxies. The results do not depend on whether this additional cut is performed.
We first compared the SFR derived by Salim et al. (2018) with those obtained using the attenuation-corrected Hα data from MaNGA. Salim et al. (2018) computed SFRs using the CIGALE SED-fitting code applied on UV-optical (GALEX-SDSS) data, and constraining the total IR luminosity via the 22 μm WISE W4 flux (or 12 μm WISE W3, if the object is not detected in WISE W4). This approach allowed Salim et al. (2018) to also fit for the slope of the attenuation curve without having access to data in the far-IR. The SFR estimates from Salim et al. (2018) agree well with those we obtain from attenuation-corrected Hα, with a relative scatter of 0.16 dex and an offset of 0.09 dex. The CIGALE-derived SFR estimates are larger than those obtained from attenuation-corrected Hα, and the offset is independent of the sSFR. The reason for the discrepancy is unclear, but may include differences in the treatment of the attenuation law.
To test the applicability of our derived hybrid calibrations, we repeat the analysis in Sect. 3.2 using the MaNGA/GSWLC data. In Fig. 7 we show the dependences of 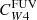 and
and 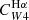 on sSFR, LHα/LW1, and LFUV/LW1 for the MaNGA data (grey points). All the physical quantities involved were computed in the same way as for the PHANGS/z0MGS data to allow for a direct comparison. We find that the trends present in the MaNGA data go in the same direction as those observed in PHANGS: galaxies with lower sSFRs show lower values of the C coefficients. At high sSFR, however, the MaNGA data tend to lie below the best-fit model from PHANGS (shown in blue in Fig. 7). This discrepancy is more evident for the Hα+IR calibration than for the FUV+IR one.
on sSFR, LHα/LW1, and LFUV/LW1 for the MaNGA data (grey points). All the physical quantities involved were computed in the same way as for the PHANGS/z0MGS data to allow for a direct comparison. We find that the trends present in the MaNGA data go in the same direction as those observed in PHANGS: galaxies with lower sSFRs show lower values of the C coefficients. At high sSFR, however, the MaNGA data tend to lie below the best-fit model from PHANGS (shown in blue in Fig. 7). This discrepancy is more evident for the Hα+IR calibration than for the FUV+IR one.
 |
Fig. 7. Hybridisation coefficients of W4 with either FUV (panels a, b, and c) or Hα (panels d and e) as a function of sSFR (left), LHα/LW1 (middle), and LFUV/LW1 (right) for the MaNGA sample (using galaxy-integrated fluxes). Best-fit relations obtained for the PHANGS 15″ data (Fig. 5) are shown in blue. Blue diamonds show the results obtained considering the integrated fluxes from the 19 PHANGS galaxies. Values of |
The results from MaNGA are consistent with the value given by Kennicutt et al. (2009), who also used integrated measurements of galaxies for their calibration, but lower than the best estimate from Calzetti et al. (2007), who used data on smaller spatial scales. Depending on a proxy for the sSFR, Boquien et al. (2016) find an amplitude of the variation of 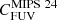 of a factor 2–3 on kpc sized regions in nearby galaxies. This value is very similar to what is found for integrated MaNGA galaxies here. Leroy et al. (2019) find a similar sSFR-dependent trend for
of a factor 2–3 on kpc sized regions in nearby galaxies. This value is very similar to what is found for integrated MaNGA galaxies here. Leroy et al. (2019) find a similar sSFR-dependent trend for 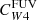 using the SFR from Salim et al. (2018). In Fig. 7 we show the median sSFR-dependent trend obtained by Leroy et al. (2019; from their Table 5), scaled by the 0.09 dex offset discussed above to bring the Salim et al. (2018) and Hα attenuation-corrected SFR in agreement. After performing this correction, our results agree very well with those of Leroy et al. (2019).
using the SFR from Salim et al. (2018). In Fig. 7 we show the median sSFR-dependent trend obtained by Leroy et al. (2019; from their Table 5), scaled by the 0.09 dex offset discussed above to bring the Salim et al. (2018) and Hα attenuation-corrected SFR in agreement. After performing this correction, our results agree very well with those of Leroy et al. (2019).
The trends in Fig. 7 show that the contribution of old stellar populations to the heating of the dust is significant even at high sSFR because of the unavoidable mixing of emission from a variety of regions (e.g., arm and interarm) when considering galaxies as a whole. This mixing implies a lower C coefficient than that measured for kpc scale regions of high sSFR. The slope of the trend at lower sSFR is also shallower for MaNGA than for PHANGS, which can also be qualitatively explained by an averaging effect. Finally, we show as blue diamonds the results obtained on integrated scales for the 19 galaxies in the PHANGS-MUSE sample. In particular, for each galaxy, we integrated the relevant fluxes within the MUSE mosaic coverage, taking the masks into account. We find that the PHANGS sample agrees within the scatter with the general population of local galaxies from MaNGA.
The MaNGA sample leads to relations that show a larger scatter than for PHANGS regions, highlighting the wider range of conditions found in the overall galaxy population. The trends do not change making a more aggressive inclination cut, for example, b/a > 0.6 (i < 53°), although a stricter cut decreases the number of systems with low FUV/W1 ratios. The larger sampling of low FUV/W1 values in MaNGA with respect to PHANGS is primarily due to inclination effects. Because of the larger scatter, we do not provide new fits to the median relations based on the MaNGA data. We evaluate the effect on the estimated SFR of using the PHANGS-based corrections on the MaNGA data in the next section.
4. Discussion
4.1. Recommendations on estimating the SFR from hybrid indicators
We evaluated the success of our kpc scale calibrations based on PHANGS data (Eq. (7)) by comparing the median offset and scatter between the hybrid estimators and the SFR inferred from attenuation-corrected Hα. In Fig. 8 we show the median log ratio and the scatter of the hybrid SFR estimators considered in Sect. 3.2 as a function of sSFR for kpc scale regions in PHANGS and for galaxy-integrated fluxes from MaNGA. We also considered the usage of constant C coefficients taken from the literature. For the case of the Hα+W4 calibration, we used the Calzetti et al. (2007) value for PHANGS and the Kennicutt et al. (2009) value for MaNGA, in order to match each coefficient to the range of spatial scales it was computed for. Our results confirm that both coefficients are accurate and their difference is due to the different level of cirrus contamination affecting typical galaxies as a function of spatial scale. The median value of the offset and scatter for each data set and calibration strategy are provided in Table 4.
 |
Fig. 8. Comparison of the SFR estimated from hybrid tracers (FUV+W4 and Hα+W4) and from attenuation-corrected Hα as a function of sSFR. We consider different calibrations, including the use of constant C coefficients (red points, Leroy et al. 2019, L19 for the FUV+W4 and Calzetti et al. 2007, C07, and Kennicutt et al. 2009, K09, for Hα+W4, see Table 2), and PHANGS-based calibrations with C(FUV/W1) (blue points) and C(Hα/W1) (green points) derived in this work. The left panels show the results for PHANGS (kpc scale) 15″ regions, and the right panel shows the result for MaNGA galaxies. Dashed lines show the 1σ scatter, and hexagons show the median relations. The mean offset and scatter for each calibration for both PHANGS and MaNGA is presented in Table 4. |
Quality assessment of the SFR recipes discussed in this work in terms of their median offset and scatter with respect to Hα attenuation-corrected SFR.
For both calibrations and both data sets, the use of constant coefficients (red points in Fig. 8) leads to an overestimation of the SFR using the hybrid calibrations at low sSFR levels. We therefore recommend against the use of constant coefficients, especially when investigators are interested in comparing regions or galaxies of different sSFRs. We find, however, that the coefficient are roughly constant for log(sSFR/yr−1) > −9.9.
The Hα + W4 calibration using a C coefficient scaling with Hα/W1 (green points in the bottom panel, Fig. 8) leads to the least scatter in both PHANGS and MaNGA (0.08 and 0.14 dex, respectively). This calibration performs extremely well for PHANGS regions because its residual dependence on sSFR is negligible. In case of the integrated galaxies from MaNGA, it shows a slight sSFR-dependent tilt, underestimating the SFR at low sSFR and overestimating at high sSFR. This tilt is the result of a flatter slope in the 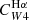 versus Hα/W1 plane shown by the MaNGA data with respect to PHANGS shown in panel e of Fig. 7.
versus Hα/W1 plane shown by the MaNGA data with respect to PHANGS shown in panel e of Fig. 7.
When Hα data are not available, we recommend using the FUV+W4 calibration with a C coefficient depending on FUV/W1 (blue points in Fig. 8). This calibration also successfully removes the mean offset between the hybrid SFR and the Hα-based SFR in both MaNGA and PHANGS. Despite being calibrated on the PHANGS data, it performs better on MaNGA, where it more successfully removes the residual sSFR dependence.
In summary, our best-effort SFR indicators require the use of WISE W1 band in addition to the canonical bands used for hybridisation: FUV (or Hα) and W4. When compared to Balmer-decrement corrected Hα SFR, our calibrations using WISE W4 lead to a scatter smaller than 0.2 dex. Since WISE is an all-sky survey, our prescriptions can be readily applied to a large sample of local galaxies (e.g., z0MGS; Leroy et al. 2019).
The use of closely related bands, including the IRAC1, J, H, K band instead of W1 and MIPS24 or JWST MIRI F2100W (21 μm) band instead of W4, is expected to lead to comparable results if appropriate conversion factors are applied. In anticipation of a comparison with upcoming results from JWST, we note the mean ratio log(LF2100W/LW4) = −0.10 obtained by Leroy et al. (2022) for four galaxies in the PHANGS-MUSE sample (NGC 0628, NGC 1365, NGC 7496, and IC 5332). The use of the WISE W3 band (centred at 11.6 μm) would lead to additional systematic uncertainty in the SFR estimation because this band includes strong features from polycyclic aromatic hydrocarbon (PAH). The flux ratio of PAH-tracing bands and 24 μm emission is not constant, and may depend systematically on metallicity and the intensity of the radiation field (Calzetti et al. 2007; Lee et al. 2013). We nonetheless calculated the ratio of the W3 and W4 fluxes in our data to allow a first-order correction and obtained a mean ratio of log(LW3/LW4) = 0.08 for our PHANGS kpc scale regions. As already shown in Leroy et al. (2019), however, the 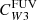 factor shows significant changes across the M⋆-SFR plane (their Fig. 21), therefore pointing to the importance of additional physics in addition to the cirrus contamination we aim to correct for in this work.
factor shows significant changes across the M⋆-SFR plane (their Fig. 21), therefore pointing to the importance of additional physics in addition to the cirrus contamination we aim to correct for in this work.
4.2. Caveats and future prospects
Our calibrations derived from the small PHANGS galaxy sample can be well generalised to the larger population of main-sequence galaxies probed on integrated scales by the MaNGA survey. However, our sample does not contain dwarf galaxies or ultra-luminous IR galaxies. PHANGS-MUSE data are also limited to the inner star-forming disc and have limited coverage of the H I-dominated outer parts (rgal ≳ 0.5 r25) of disc galaxies. In particular, PHANGS-MUSE does not cover extended UV discs (Thilker et al. 2007) outside the optical radius at all. Tomicic et al. (2019), for example, studied regions in the H I-dominated disc of M31 with IFS and found conversion factors for the IR term (both 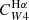 and
and 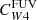 ) that were a factor of 5-8 times larger than those we obtain here. They attributed this difference to the high inclination of M31 (∼77°; Walterbos & Kennicutt 1988) and the flaring of the H I disc. Within the limits of our data, we do not find any hint of such a radial trend, but it is reasonable to expect an increased mid-IR cirrus contribution in the presence of a large diffuse ISM component. We highlight future extension of this analysis to the H I-dominated outer parts of galaxies as an important future direction.
) that were a factor of 5-8 times larger than those we obtain here. They attributed this difference to the high inclination of M31 (∼77°; Walterbos & Kennicutt 1988) and the flaring of the H I disc. Within the limits of our data, we do not find any hint of such a radial trend, but it is reasonable to expect an increased mid-IR cirrus contribution in the presence of a large diffuse ISM component. We highlight future extension of this analysis to the H I-dominated outer parts of galaxies as an important future direction.
The impact of the old stellar populations on the calibration of hybrid SFR calibrators on a resolved scale has previously been discussed by Boquien et al. (2016). They studied a sample of eight nearby galaxies and used SED fitting based on UV-to-FIR imaging to derive the attenuation in the FUV, and therefore attenuation-corrected SFR. In agreement with our work, they find a trend between 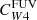 and sSFR and other band ratios used as sSFR proxies (including FUV – 3.6 μm). In particular, they find a flattening in the relation between
and sSFR and other band ratios used as sSFR proxies (including FUV – 3.6 μm). In particular, they find a flattening in the relation between 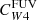 and sSFR at sSFR ∼ −9.75, comparable to what is found here. However, their conversion factors are systematically higher than those derived here by ∼0.3 dex, perhaps due to differing assumptions on the attenuation curve as they allowed for curves steeper than a bona fide starburst curve. This shows the dependence of hybrid estimators on indirect but necessary assumptions on the attenuation curve, as we discuss below.
and sSFR at sSFR ∼ −9.75, comparable to what is found here. However, their conversion factors are systematically higher than those derived here by ∼0.3 dex, perhaps due to differing assumptions on the attenuation curve as they allowed for curves steeper than a bona fide starburst curve. This shows the dependence of hybrid estimators on indirect but necessary assumptions on the attenuation curve, as we discuss below.
The calibrations presented in this paper are consistent with the large body of literature presenting SFR calibrations that are based, directly or indirectly, on attenuation-corrected recombination line fluxes (Calzetti et al. 2007; Kennicutt et al. 2009; Hao et al. 2011; Catalán-Torrecilla et al. 2015). They represent an update, extending the validity of the calibrations to smaller physical scales with respect to the recipes presented in the review of Kennicutt & Evans (2012). Our calibrations also agree with the SFRs measured based on radio continuum by Murphy et al. (2012) for a sample of nuclear and extra-nuclear star-forming regions.
The calibrations presented in this work are subject to the systematic uncertainties associated with attenuation corrections via the Balmer decrement and with using Hα as a tracer of star formation. Regarding the dust correction, uncertainties are related to the temperature (and density) dependence of the intrinsic Hα/Hβ ratio and to the use of a Milky Way-like extinction law to model attenuation of the nebular lines. The intrinsic Balmer decrement changes only weakly with temperature, increasing from 2.76 for 5000 K to 3.05 at 20 000 K, therefore causing changes of less than 0.02 mag in the derived E(B − V). The attenuation law (and in particular, the assumed value of RV) for the nebular component represents a more significant systematic uncertainty. Assuming a Calzetti et al. (2000) attenuation law for the nebular continuum does not substantially change our conclusions. However, radiative transfer models predict a change in the slope of the attenuation law with dust optical depth (Chevallard et al. 2013; Salim & Narayanan 2020; Tacchella et al. 2022), and dust attenuation curves have been shown to vary within and between galaxies at all redshifts (e.g., Salmon et al. 2016; Buat et al. 2018; Salim et al. 2018; Decleir et al. 2019; Reddy et al. 2020; Boquien et al. 2022, and many others). For example, implementing the attenuation and slope of the curve presented by Tacchella et al. (2022) implies substantially higher values of AHα than using a Milky Way law, especially for the more attenuated regions, and would therefore lead a substantial recalibration of the IR coefficients presented here. More detailed observational work is required in order to confirm changes in the slope of the nebular attenuation law as a function of optical depth.
The conversion between attenuation-corrected Hα flux and SFR is affected by additional systematic uncertainties, including the escape of ionising radiation from galaxies, the absorption of ionising photons from dust, the stochastic sampling of the IMF in low-mass clusters (Da Silva et al. 2014), and to some extent, the variability of star formation at low SFR. The fraction of Lyman continuum photons absorbed by dust is found to be significant in nearby galaxies and clusters, between 30-50% (Inoue et al. 2001; Iglesias-Páramo et al. 2004), in agreement with some theoretical models of radiatative transfer (Kado-Fong et al. 2020; Tacchella et al. 2022). However, substantial uncertainty affects these estimates, and in detailed models of dusty H II regions, dust competes with hydrogen only for high values of the ionisation parameter (the ratio of ionising photons to hydrogen atoms), a regime only relevant to young, compact H II regions. Potential dust absorption of ionising photons is not taken into account by our calibration, and would imply a change in the CHα factor. For example, if the fraction of Lyman continuum photons that are directly absorbed by dust were 30%, CHα would need to be increased by 0.23 dex. Stochastic sampling of the IMF in low-mass clusters, on the other hand, will cause a bias (and increased scatter) at the lowest SFR levels, but should only have a limited effect on our kpc scale data of the inner regions of discs.
At kpc resolution, it is not possible to distinguish individual H II regions from the diffuse emission surrounding them. The nature of the diffuse emission at Hα and 22 μm, however, represents one of the main systematic uncertainties to the determination of SFR on even smaller spatial scales. The diffuse Hα emission (also known as diffuse ionised gas) is directly powered by ionising radiation leaking from H II regions (Ferguson et al. 1996; Zurita et al. 2000; Haffner et al. 2009; Belfiore et al. 2022). In particular, Belfiore et al. (2022) studied the same sample of galaxies used in this work and showed that the DIG is consistent with being powered by leaking radiation, with a mean free path of ∼2 kpc. This therefore affects the SFR estimates on kpc scales only very little.
Diffuse emission at 22 μm results from the convolution of the dust distribution with the local radiation field. Therefore it is potentially sensitive to both heating due to the radiation field from old stars (Leroy et al. 2008, 2012; Verley et al. 2009; Kennicutt et al. 2009) and the presence of an extended dust-bearing gas reservoir, especially atomic gas, mixed with the old stellar population (e.g., Leroy et al. 2012).
The calibrations we present in this work effectively model this spatially unresolved background emission by making the IR calibration coefficient dependent on an sSFR-like quantity. Higher-resolution IR maps, capable of resolving dust heated by H II regions from the diffuse component, are needed to directly test this interpretation. While Spitzer 24 μm offers cloud-scale ∼100 pc resolution in the Local Group and in galaxies ≲4 Mpc (e.g., Helou et al. 2004; Verley et al. 2009; Faesi et al. 2014), these targets probe only a limited set of environments. The PHANGS-JWST program will address this shortcoming by providing sub-arcsec-resolution 21 μm mapping of the 19 PHANGS-MUSE galaxies using the MIRI instrument on board JWST. In combination with arcsec-resolution mapping of Hα and Hβ from MUSE and FUV maps at ∼2″ resolution from AstroSat (Hassani et al., in prep.), this combined data set will shed new light on the nature of diffuse IR emission, small-scale behaviour of dust attenuation in star-forming discs, and the statistics of fully embedded regions (Prescott et al. 2007).
As discussed of above, a complementary future direction will be to extend this analysis to the outer parts of galaxies that are dominated by atomic gas. In these regions, we might expect much of the dust (i.e. the dust mixed with diffuse atomic gas) to reside in an extended distribution rather than being concentrated towards the peaks of star formation. This situation could produce increased IR cirrus emission even when the average sSFR remains high, and so will represent an important test of the generality of our prescriptions.
5. Summary and conclusions
We used Hα maps corrected for attenuation using the Balmer decrement to calibrate multi-wavelength hybrid SFR recipes for use in nearby galaxies at kpc scale resolution. We used a sample of 19 galaxies observed with optical IFS as part of the PHANGS-MUSE program, and combined these data with FUV imaging from GALEX and mid-IR imaging at 22 μm from WISE W4. We focused on calibrating two commonly used hybrid recipes: FUV+W4 and Hα+W4. We further assessed the reliability of the resulting calibrations as a function of physical scale. We summarise our main results below.
-
Calibrations of FUV+W4 and Hα+W4 from the literature overestimate the SFR obtained from attenuation-corrected Hα in regions of low sSFR, or equivalently, low ΣSFR, old light-weighed stellar age or low E(B − V). We attribute this trend to the presence of IR cirrus: diffuse IR emission originating from dust heated by the interstellar radiation field and not associated with star formation.
-
In order to correct for IR cirrus, we propose to modify the calibration term in front of the IR term in the hybrid SFR recipes and make it a function of band ratios that correlate with sSFR. We present broken power-law fits (Eq. (7)) for the dependence of
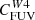 on Hα/W1 and FUV/W1 and of
on Hα/W1 and FUV/W1 and of 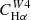 on Hα/W1 in Table 3. These calibrations lead to an SFR that agrees with those obtained from attenuation-corrected Hα with negligible bias and scatter of less than 0.16 dex.
on Hα/W1 in Table 3. These calibrations lead to an SFR that agrees with those obtained from attenuation-corrected Hα with negligible bias and scatter of less than 0.16 dex. -
The SFR obtained on kpc scales with these recipes agrees well with the estimates from attenuation-corrected Hα calculated on scales of 100 pc using the MUSE IFS data at their native resolution. In particular, we find that based on our sample of 19 star-forming galaxies, the lower-resolution SFR is underestimated by less than 10% on average.
-
We tested the validity of our calibration on the scales of entire galaxies by using attenuation-corrected Hα data for star-forming galaxies from the MaNGA IFS survey. We observe comparable trends in terms of the sSFR dependence of the IR coefficient, albeit with quantitative differences compatible with the inevitable mixing of regions with various levels of star formation activity when considering galaxies as whole. Nonetheless, we find that the calibrations derived from PHANGS kpc scale data perform well with MaNGA, leading to a scatter smaller than 0.2 dex when comparing hybrid and Hα attenuation-corrected SFRs.
-
At high sSFR, our calibrations agree well with the coefficients recommended by the Kennicutt & Evans (2012) review. In particular, for the Hα+W4 calibration, the kpc scale analysis of the PHANGS-MUSE data is comparable with the results of Calzetti et al. (2007) at high sSFR, and the MaNGA analysis of flux-integrated galaxies is compatible with the coefficient derived by Kennicutt et al. (2009). However, our calibrations will lead to more accurate SFR measurements than obtained using constant coefficients from the literature when considering samples of regions or galaxies sampling a wide range of sSFR.
The WISE data used here are calibrated to MJy sr−1 units following the WISE documentation Sect. 4.4h, and Wright et al. (2010) assuming a ∝ν−2 reference spectrum without colour corrections. Brown et al. (2014) showed that the W4 colour correction, which depends on the spectral index of the source, can be significant. However, we did not perform such a correction because because we wished to directly compare with Leroy et al. (2019) and Salim et al. (2018), who did not perform such a correction to their W4 fluxes, and because we wished to derive prescriptions that can be applied to the WISE data without this preprocessing. In any case, the SED fitting necessary to determine it is beyond the scope of this work.
Acknowledgments
This work has been carried out as part of the PHANGS collaboration. Based on observations collected at the European Southern Observatory under ESO programmes 094.C-0623 (PI: Kreckel), 095.C-0473, 098.C-0484 (PI: Blanc), 1100.B-0651 (PHANGS-MUSE; PI: Schinnerer), as well as 094.B-0321 (MAGNUM; PI: Marconi), 099.B-0242, 0100.B-0116, 098.B-0551 (MAD; PI: Carollo) and 097.B-0640 (TIMER; PI: Gadotti). Science-level MUSE mosaicked datacubes and high-level analysis products are provided via the ESO archive phase 3 interface (https://archive.eso.org/scienceportal/home?data_collection=PHANGS). A full description of the first PHANGS data release is presented in Emsellem et al. (2022). The work of AKL was partially supported by the National Science Foundation (NSF) under Grants No. 1615105, 1615109, and 1653300. The work of JS is partially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) through a Canadian Institute for Theoretical Astrophysics (CITA) National Fellowship. ATB would like to acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No.726384/Empire, PI Bigiel). MB gratefully acknowledges support by the ANID BASAL project FB210003 and from the FONDECYT regular grant 1211000. EC acknowledge support from ANID Basal projects ACE210002 and FB210003. OE and KK gratefully acknowledge funding from the German Research Foundation (DFG) in the form of an Emmy Noether Research Group (Grant No. KR4598/2-1, PI Kreckel). CE gratefully acknowledges funding from the Deutsche Forschungsgemeinschaft (DFG) Sachbeihilfe, Grant number BI1546/3-1. SCOG and RSK thank for funding from the Heidelberg Cluster of Excellence EXC 2181 (Project-ID 390900948) ‘STRUCTURES’, supported by the German Excellence Strategy, from the ERC in the Synergy Drant ‘ECOGAL’ (project ID 855130), from DFG via the Collaborative Research Center (SFB 881, Project-ID 138713538) ‘The Milky Way System’ (subprojects A1, B1, B2, B8), and from the German Ministry for Economic Affairs and Climate Action for funding in project ‘MAINN’ (funding ID 50OO2206). KG is supported by the Australian Research Council through the Discovery Early Career Researcher Award (DECRA) Fellowship DE220100766 funded by the Australian Government. MQ acknowledges support from the Spanish grant PID2019-106027GA-C44, funded by MCIN/AEI/10.13039/501100011033. PSB acknowledges financial support from the Spanish Ministry of Science, Innovation and Universities under Grant number PID2019-107427GB-C31. ES and TGW acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 694343, PI Schinnerer).
References
- Abdurro’uf, Accetta K., Aerts, C., et al. 2022, ApJS, 259, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Algera, H., Inami, H., Oesch, P., et al. 2022, MNRAS, 16, 1 [Google Scholar]
- Anand, G. S., Lee, J. C., Van Dyk, S. D., et al. 2021, MNRAS, 501, 3621 [Google Scholar]
- Bacchini, C., Fraternali, F., Pezzulli, G., et al. 2019, A&A, 632, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, Proc. SPIE, 7735, 773508 [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Belfiore, F., Maiolino, R., Bundy, K., et al. 2018, MNRAS, 477, 3014 [Google Scholar]
- Belfiore, F., Westfall, K. B., Schaefer, A., et al. 2019, AJ, 158, 160 [CrossRef] [Google Scholar]
- Belfiore, F., Santoro, F., Groves, B., et al. 2022, A&A, 659, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berman, L. 1936, MNRAS, 96, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., & Salim, S. 2021, A&A, 653, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Kennicutt, R., Calzetti, D., et al. 2016, A&A, 591, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Buat, V., Burgarella, D., et al. 2022, A&A, 663, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boucaud, A., Bocchio, M., Abergel, A., et al. 2016, A&A, 596, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M., Tumlinson, J., Geha, M., et al. 2014, ApJ, 796, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Boquien, M., Małek, K., et al. 2018, A&A, 619, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [Google Scholar]
- Calzetti, D. 2013, Secul. Evol. Galaxies (Cambridge, UK: Cambridge University Press), 419 [CrossRef] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1996, ApJ, 458, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Casey, C. M., Zavala, A. J., Spilker, J., et al. 2018, ApJ, 862, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Catalán-Torrecilla, C., Gil de Paz, A., Castillo-Morales, A., et al. 2015, A&A, 584, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chevallard, J., Charlot, S., Wandelt, B., & Wild, V. 2013, MNRAS, 432, 2061 [CrossRef] [Google Scholar]
- Conroy, C., Van Dokkum, P. G., & Graves, G. J. 2013, ApJ, 763, 2 [Google Scholar]
- Cortese, L., Boselli, A., Franzetti, P., et al. 2008, MNRAS, 386, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Lawrence, J. S., Bland-Hawthorn, J., et al. 2012, MNRAS, 421, 872 [NASA ADS] [Google Scholar]
- Da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Da Silva, R. L., Fumagalli, M., & Krumholz, M. R. 2014, MNRAS, 444, 3275 [CrossRef] [Google Scholar]
- Dale, D. A., Cohen, S. A., Johnson, L. C., et al. 2009, ApJ, 703, 517 [Google Scholar]
- Decleir, M., De Looze, I., Boquien, M., et al. 2019, MNRAS, 486, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Schinnerer, E., Santoro, F., et al. 2022, A&A, 659, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erroz-Ferrer, S., Carollo, C. M., Den Brok, M., et al. 2019, MNRAS, 484, 5009 [NASA ADS] [CrossRef] [Google Scholar]
- Faesi, C. M., Lada, C. J., Forbrich, J., Menten, K. M., & Bouy, H. 2014, ApJ, 789, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, A. M. N., Wyse, R. F. G., & Gallagher, J. S. 1996, AJ, 112, 2567 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greener, M. J., Aragón-Salamanca, A., Merrifield, M. R., et al. 2020, MNRAS, 495, 2305 [CrossRef] [Google Scholar]
- Groves, B., Brinchmann, J., & Walcher, C. J. 2012a, MNRAS, 419, 1402 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B., Krause, O., Sandstrom, K., et al. 2012b, MNRAS, 426, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Pozzi, F., Rodighiero, G., et al. 2013, MNRAS, 432, 23 [Google Scholar]
- Gruppioni, C., Béthermin, M., Loiacono, F., et al. 2020, A&A, 643, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haffner, L., Dettmar, R.-J., Beckman, J., et al. 2009, Rev. Mod. Phys., 81, 969 [CrossRef] [Google Scholar]
- Hao, C. N., Kennicutt, R. C., Johnson, B. D., et al. 2011, ApJ, 741, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., Roussel, H., Appleton, P., et al. 2004, ApJS, 154, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., De Looze, I., Boquien, M., et al. 2019, A&A, 621, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglesias-Páramo, J., Boselli, A., Gavazzi, G., & Zaccardo, A. 2004, A&A, 421, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, A. K., Hirashita, H., & Kamaya, H. 2001, ApJ, 555, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735 [Google Scholar]
- Jarrett, T. H., Masci, F., Tsai, C. W., et al. 2013, AJ, 145, 6 [Google Scholar]
- Kado-Fong, E., Kim, J.-G., Ostriker, E. C., & Kim, C.-G. 2020, ApJ, 897, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Walter, F., et al. 2007, ApJ, 671, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Hao, C. N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & De Los Reyes, M. A. C. 2021, ApJ, 908, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Koprowski, M. P., Dunlop, J. S., Michalowski, M. J., et al. 2017, MNRAS, 471, 4155 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, D. 2014, AJ, 147, 108 [Google Scholar]
- Lang, P., Meidt, S. E., Rosolowsky, E., et al. 2020, ApJ, 897, 122 [CrossRef] [Google Scholar]
- Lee, J. C., Hwang, H. S., & Ko, J. 2013, ApJ, 774, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [Google Scholar]
- Leroy, A. K., Bigiel, F., de Blok, W. J. G., et al. 2012, AJ, 144, 3 [Google Scholar]
- Leroy, A. K., Sandstrom, K. M., Lang, D., et al. 2019, ApJS, 244, 24 [Google Scholar]
- Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2021, ApJS, 257, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A., Sandstrom, K., Rosolowsky, E., et al. 2022, ApJ, submitted [arXiv:2212.10574] [Google Scholar]
- Li, Y., Crocker, A. F., Calzetti, D., et al. 2013, ApJ, 768, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S., Le Fevre, O., Hammer, F., & Crampton, D. 1996, ApJ, 460, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, C. L. 2005, ApJ, 621, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Medling, A. M., Cortese, L., Croom, S. M., et al. 2018, MNRAS, 475, 5194 [Google Scholar]
- Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [Google Scholar]
- Murphy, E. J., Bremseth, J., Mason, B. S., et al. 2012, ApJ, 761, 97 [Google Scholar]
- Nersesian, A., Xilouris, E. M., Bianchi, S., et al. 2019, A&A, 624, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei (Mill Valley, CA: University Science Books) [Google Scholar]
- Peek, J. E., & Schiminovich, D. 2013, ApJ, 771, 1 [Google Scholar]
- Pessa, I., Schinnerer, E., Belfiore, F., et al. 2021, A&A, 650, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, M. M., Jenkins, E. B., Dopita, M. A., Sadler, E. M., & Binette, L. 1986, AJ, 91, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Prescott, M. K. M., Kennicutt, R. C., Jr, Bendo, G. J., et al. 2007, ApJ, 668, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Shapley, A. E., Kriek, M., et al. 2020, ApJ, 902, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Relaño, M., & Monreal-Ibero, a., Vílchez, J. M., & Kennicutt, R. C., 2010, MNRAS, 402, 1635 [CrossRef] [Google Scholar]
- Salim, S., & Narayanan, D. 2020, ARA&A, 58, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Lee, J. C., Janowiecki, S., et al. 2016, ApJS, 227, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Boquien, M., & Lee, J. C. 2018, ApJ, 859, 11 [Google Scholar]
- Salmon, B., Papovich, C., Long, J., et al. 2016, ApJ, 827, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sánchez, S. F. 2020, ARA&A, 58, 99 [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Marino, R. A., et al. 2012, A&A, 546, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J. D., Finkbeiner, D. P. D., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., Assef, R. J., Benford, D. J., et al. 2012, ApJ, 753, 18 [Google Scholar]
- Tacchella, S., Smith, A., Kannan, R., et al. 2022, MNRAS, 513, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Bianchi, L., Meurer, G., et al. 2007, ApJS, 173, 538 [Google Scholar]
- Tomicic, N., Ho, I. T., Kreckel, K., et al. 2019, ApJ, 873, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Vale Asari, N., Wild, V., De Amorim, A. L., et al. 2020, MNRAS, 498, 4205 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Ricciardelli, E., Cenarro, A. J., et al. 2012, MNRAS, 424, 157 [Google Scholar]
- Verley, S., Corbelli, E., Giovanardi, C., & Hunt, L. K. 2009, A&A, 493, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walterbos, R. A., & Kennicutt, R. 1988, A&A, 198, 61 [NASA ADS] [Google Scholar]
- Weilbacher, P. M., Palsa, R., Streicher, O., et al. 2020, A&A, 641, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westfall, K. B., Cappellari, M., Bershady, M. A., et al. 2019, AJ, 158, 57 [Google Scholar]
- Wild, V., Groves, B., Heckman, T., et al. 2011, MNRAS, 410, 1593 [NASA ADS] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., van der Wel, A., et al. 2011, ApJ, 742, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Zurita, A., Rozas, M., & Beckman, J. E. 2000, A&A, 363, 9 [Google Scholar]
All Tables
Best-fit broken power law coefficients for computing 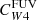 and
and 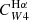 as a function of the quantity Q.
as a function of the quantity Q.
Quality assessment of the SFR recipes discussed in this work in terms of their median offset and scatter with respect to Hα attenuation-corrected SFR.
All Figures
 |
Fig. 1. Comparison between ΣSFR/(M⊙ kpc−2 yr−1) estimates at 15″ resolution from extinction-corrected Hα emission and UV+IR (FUV + W4) using the Leroy et al. (2019) prescription for three example galaxies. The maps are shown on the original pixel size of 5 |
| In the text | |
 |
Fig. 2. Dependence of the ratio of the SFR measured from FUV+W4 (and the Leroy et al. 2019 coefficient) and that measured from attenuation-corrected Hα on various physical properties for a sample of 1759 ∼ kpc sized regions taken from the 19 galaxies of the PHANGS-MUSE sample: (a) sSFR, (b) SFR surface density (both measured from attenuation-corrected Hα), (c) E(B − V) of the ionised gas measured from the Balmer decrement, (d) stellar mass surface density, (e) deprojected galactocentric radius normalised to Reff, (f) light-weighted mean age of the stellar population, derived from fits to the MUSE stellar continuum. The grey points represent individual ∼15″ regions, and the red hexagons and dashed red lines represent the median and scatter (16th − 84th percentiles) of the distribution. In panel c, we also show the result of calculating the SFR from the FUV flux, without considering the IR term (blue lines). This demonstrates that the inclusion of the IR term correctly reproduces the Hα-based SFR for highly attenuated regions, but it overestimates the attenuation level for regions with a low Balmer decrement. These trends are consistent with an increasing contamination from old stellar population to the dust heating at lower SFR levels. |
| In the text | |
 |
Fig. 3. Same as Fig. 2, but using Hα+W4 instead of FUV+W4. The coefficient |
| In the text | |
 |
Fig. 4. Comparison between E(B − V) estimated via the Balmer decrement and the same quantity calculated via FUV+W4 (left) and Hα+W4 (right), colour-coded by sSFR. In the left panel, we show as a dashed line the ratio of the differential reddening of gas and stars inferred by Calzetti et al. (2000), E(B − V)stars = 0.44 E(B − V)gas. Solid black lines in both panels represent the one-to-one line. In both panels, attenuation is overestimated in regions of low sSFR because of IR cirrus. |
| In the text | |
 |
Fig. 5. Hybridisation coefficients of W4 with either FUV ( |
| In the text | |
 |
Fig. 6. Mean ratio of the attenuation-corrected Hα luminosity computed in low-resolution apertures of varying size to the luminosity derived at the highest spatial scales accessible with the PHANGS-MUSE data (∼1″) as a function of the low-resolution aperture size. Trends are shown for each of the 19 galaxies in the PHANGS-MUSE sample, colour-coded by total stellar mass. The data for each galaxy were resampled on apertures of 5, 10, 15, 20, and 30″. The alternative x-axis at the top of the plot shows the equivalent physical size in kpc at the median distance of the sample. At 15″ resolution, the resolution of the WISE W4 data, the median difference is 10% (⟨Llow res/Lhigh res⟩ = 0.92). |
| In the text | |
 |
Fig. 7. Hybridisation coefficients of W4 with either FUV (panels a, b, and c) or Hα (panels d and e) as a function of sSFR (left), LHα/LW1 (middle), and LFUV/LW1 (right) for the MaNGA sample (using galaxy-integrated fluxes). Best-fit relations obtained for the PHANGS 15″ data (Fig. 5) are shown in blue. Blue diamonds show the results obtained considering the integrated fluxes from the 19 PHANGS galaxies. Values of |
| In the text | |
 |
Fig. 8. Comparison of the SFR estimated from hybrid tracers (FUV+W4 and Hα+W4) and from attenuation-corrected Hα as a function of sSFR. We consider different calibrations, including the use of constant C coefficients (red points, Leroy et al. 2019, L19 for the FUV+W4 and Calzetti et al. 2007, C07, and Kennicutt et al. 2009, K09, for Hα+W4, see Table 2), and PHANGS-based calibrations with C(FUV/W1) (blue points) and C(Hα/W1) (green points) derived in this work. The left panels show the results for PHANGS (kpc scale) 15″ regions, and the right panel shows the result for MaNGA galaxies. Dashed lines show the 1σ scatter, and hexagons show the median relations. The mean offset and scatter for each calibration for both PHANGS and MaNGA is presented in Table 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



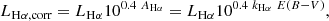
![$$ \begin{aligned} E(B-V)_{\rm BD} = \frac{2.5}{k_{\mathrm{H}\beta } - k_{\mathrm{H}\alpha }} \log _{10} \left[ \frac{ L_{\mathrm{H}\alpha }/L_{\mathrm{H}\beta } }{2.86} \right]. \end{aligned} $$](/articles/aa/full_html/2023/02/aa44863-22/aa44863-22-eq7.gif)
![$$ \begin{aligned} \mathrm{SFR} [{M_{\odot }\, \mathrm{yr}^{-1}}] = C_{\rm H\alpha } L_{\rm H\alpha , corr }\ [\mathrm{erg\, s}^{-1}]. \end{aligned} $$](/articles/aa/full_html/2023/02/aa44863-22/aa44863-22-eq8.gif)