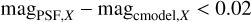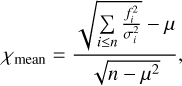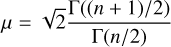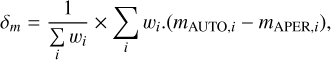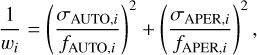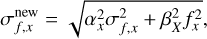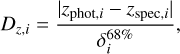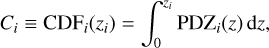| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 25 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202243363 | |
| Published online | 16 February 2023 | |
Combining the CLAUDS and HSC-SSP surveys
U + grizy(+YJHKs) photometry and photometric redshifts for 18M galaxies in the 20 deg2 of the HSC-SSP Deep and ultraDeep fields★
1
Department of Astronomy, University of Geneva,
ch. d'Écogia 16,
1290
Versoix, Switzerland
2
Institute for Computational Astrophysics and Department of Astronomy and Physics, Saint Mary's University,
Halifax,
Nova Scotia
B3H 3C3, Canada
e-mail: guillaume.desprez@smu.ca
3
Aix Marseille Univ, CNRS, CNES, LAM,
Marseille, France
4
Department of Astronomy, Columbia University,
550 W. 120th Street,
New York, NY
10027, USA
5
NRC-Herzberg,
5071 West Saanich Road, Victoria,
British Columbia
V9E 2E7, Canada
6
Chinese Academy of Sciences South America Center for Astronomy, National Astronomical Observatories, CAS,
Beijing
100101, PR China
7
National Astronomical Observatory of Japan,
2-21-1 Osawa, Mitaka,
Tokyo
181-8588, Japan
8
National Institute of Technology, Wakayama College,
77 Noshima, Nada-cho, Gobo,
Wakayama
644-0023, Japan
9
Institute of Astronomy & Astrophysics,
Academia Sinica,
Taipei
10617, Taiwan
10
Institut d'Astrophysique de Paris,
UMR 7095, CNRS, et Sorbonne Université, 98 bis boulevard Arago,
75014
Paris, France
11
Cosmic Dawn Center (DAWN),
Denmark
12
Niels Bohr Institute, University of Copenhagen,
Jagtvej 128,
2200
Copenhagen, Denmark
Received:
18
February
2022
Accepted:
29
November
2022
We present the combination of the Canada-France-Hawaii Telescope (CHFT) Large Area U-bands Deep Survey (CLAUDS) and the Hyper-Suprime-Cam (HSC) Subaru Strategic Program (HSC-SSP) data over their four deep fields. We provide photometric catalogs for u, u* (CFHT-MegaCam), g, r, i, z, and y (Subaru-HSC) bands over ~20 deg2, complemented in two fields by data from the Visible and Infrared Survey Telescope for Astronomy (VISTA) Deep Extragalactic Observations (VIDEO) survey and the UltraVISTA survey, thus extending the wavelength coverage toward near-infrared with VIRCAM Y, J, H, and Ks observations over 5.5 deg2. The extraction of the photometry was performed with two different softwares: the HSC pipeline hscPipe and the standard and robust SExtractor software. Photometric redshifts were computed with template-fitting methods using the new Phosphoros code for the hscPipe photometry and the well-known Le Phare code for the SExtractor photometry. The products of these methods were compared with each other in detail. We assessed their quality using the large spectroscopic sample available in those regions, together with photometry and photometric redshifts from COSMOS2020, the latest version of the Cosmic Evolution Survey catalogs. We find that both photometric data sets are in good agreement in Ugrizy down to magnitude ~26, and to magnitude ~24.5 in the YJHKs bands. We achieve good performance for the photometric redshifts, reaching precisions of σNMAD ≲ 0.04 down to mi ~ 25, even using only the CLAUDS and HSC bands. At the same magnitude limit, we measured an outlier fraction of η ≲ 10% when using the Ugrizy bands, and down to η ≲ 6% when considering near-infrared data. The hscPipe plus Phosphoros pipeline performs slightly worse in terms of photometric-redshifts precision and outlier fraction than its SExtractor plus Le Phare counterpart, which has essentially been tracked down to differences in the photometry. Thus, this work is also a validation of the Phosphoros code. The photometric catalogs with the data and photometric redshifts from the two pipelines are presented and made publicly available.
Key words: galaxies: photometry / galaxies: distances and redshifts / surveys / catalogs
The catalogs are also available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/670/A82
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Deep, wide-area multiband imaging surveys play a pivotal role in our studies of the Universe and of the formation and evolution of its content (e.g., CANDELS, Grogin et al. 2011; COSMOS, Scoville et al. 2007; CFHTLS, Hudelot et al. 2012; DES, Abbott et al. 2018). They are expected to continue to do so for the foreseeable future given the large investment of resources into projects such as LSST on the Rubin Observatory (Ivezic et al. 2019), Euclid (Laureijs et al. 2011), and Roman Space Telescope (Akeson et al. 2019). While spectroscopy – particularly when highly multiplexed – can yield detailed physical information on samples of distant galaxies, it is expensive in telescope time, which makes it difficult to assemble very large samples of faint objects. In contrast to spectroscopy, photometry is relatively inexpensive, extremely multiplexed when done with modern, large-area mosaic imagers, and is also significantly less affected by selection biases.
Much can be learned from photometry, particularly when samples are large and contain many faint objects. In particular, photometry can be used to estimate redshifts of vast samples of distant galaxies (e.g., Beck et al. 2016; Tanaka et al. 2018; Moutard et al. 2020), to characterize key physical properties such as their stellar masses and star formation rates (SFRs; e.g., Sawicki & Yee 1998; Papovich et al. 2001; Laigle et al. 2016), and even constrain star formation histories (e.g., Pacifici et al. 2016; Iyer et al. 2019). These measurements are key ingredients in studies of how galaxies form and evolve over cosmic time and motivate many of the modern photometric surveys.
The Hyper Suprime-Cam Strategic Survey Program (HSC-SSP, Aihara et al. 2018a), which recently completed observations on the Subaru telescope, represents the current state of the art in deep, wide-area imaging surveys. Of particular interest here are HSC-SSP’s Deep and ultraDeep layers, which cover 26 and 3.5 deg2, respectively, in the grizy filters to depths of ~25–28 AB (signal to noise ratio S/N = 5σ in 2″ apertures). This is an unprecedented combination of area and depth that allows studies of galaxy evolution as a function of redshift and environment that are largely insensitive to cosmic variance and that will be unsurpassed until several years into LSST’s science operations.
However, the HSC-SSP grizy photometry spans only the optical and lacks both the shorter and the longer wavelengths that are critical for a number of science applications. In particular, complementing grizy imaging with U-band photometry provides better measurements of SFRs at all redshifts and significantly improves photometric redshift performance at z < 0.7 and at z ~ 2–3 because it allows the combined filter set to span the Balmer and Lyman breaks, respectively, at these redshifts (see Fig. 9 and Sect. 4.2 of Sawicki et al. 2019 for more discussion on the U-band benefits for photo-zs). The SFR and photometric redshift measurements in the HSC-SSP Deep and ultraDeep layers were indeed key motivators for the Canada–France–Hawaii Telescope (CFHT) Large Area U-band Deep Survey (CLAUDS; Sawicki et al. 2019), a major (68 dedicated nights plus archival data) imaging survey that complements, with U-band, the grizy imaging in the Deep and ultraDeep layers of HSC-SSP with an overlap of ~20 deg2 between both surveys. Meanwhile, at longer wavelengths, complementing the CLAUDS+HSC-SSP U+grizy photometry with near-infrared data would make measurements of galaxy stellar masses beyond z ~ 1 possible and further improve photometric redshift performance by adding coverage of the Balmer break at higher redshifts.
These ingredients – uniform photometry, photometric redshifts, and galaxy physical parameters – are key elements needed for many studies of distant galaxy populations and their evolution. For this reason, in this paper, we present our latest multiband catalogs that combine CLAUDS, HSC-SSP, and – where available – VIDEO (VISTA Deep Extragalactic Observations; Jarvis et al. 2013) and UltraVISTA (McCracken et al. 2012) data in the HSC-SSP Deep and ultraDeep fields. In previous papers (Sawicki et al. 2019; Moutard et al. 2020), we presented CLAUDS+HSC-SSP catalogs for these fields based on shallower HSC-SSP photometry and less sophisticated technical treatment. These earlier catalogs have already been used for several science applications: for example, Halevi et al. (2019) used this earlier CLAUDS+HSC-SSP photometry to characterize the properties of an active galaxy nucleus (AGN) containing low-mass galaxy; Moutard et al. (2020) and Harikane et al. (2021) constrained ultra-violet luminosity functions; and Iwata et al. (2022) used them to constrain the Lyman continuum escape fraction from AGNs. Additionally, the data were used for star-galaxy classification (Golob et al. 2021), selection of low-luminosity galaxies (Cheng et al. 2021), photometric redshift estimation (Sawicki et al. 2019; Moutard et al. 2020; Huang et al. 2020), and constraining galaxy-galaxy merger fraction evolution (Thibert et al. 2021).
These earlier CLAUDS+HSC-SSP catalogs already demonstrated the usefulness of a deep, U-band-enhanced wide-area photometric dataset in the HSC-SSP Deep and ultraDeep fields. However, because of their developmental nature, we did not make these earlier catalogs publicly available to the community. Moreover, the depth of grizy imaging used in their creation was significantly shallower than what has become available as the HSC-SSP survey accumulated data over time. Finally, for simplicity, our earlier catalogs did not include any NIR information even though deep NIR imaging.
The goal of the present paper is then to provide well-characterized catalogs that contain U + grizy (+NIR, where available) photometry, photometric redshifts in the Deep and ultraDeep areas of the CLAUDS+HSC-SSP surveys. To build these catalogs, we use two sets of codes. We use recently developed photometry and photo-z methods, namely a modified version of the HSC-SSP photometric pipeline (hscPipe, Bosch et al. 2018) for photometry extraction and Phosphoros (Paltani et al., in prep.; Euclid Collaboration 2020) for photo-z computation. We also provide photometry and photometric redshifts measured with widely used and long-established codes, namely SExtractor (Bertin & Arnouts 1996) and Le Phare (Arnouts et al. 2002; Ilbert et al. 2006). The comparison of the results is allowing the validation of the different methods.With the present paper, we are making both catalogs publicly available for the community. This work shows the overall agreement between both catalogs in terms of photometry and photometric redshifts. The availability of the two catalogs allows the users to select the one most suitable for their own interests or to use them in tandem to assess the reliability of results as advocated by Weaver et al. (2022) for COSMOS2020.
Throughout the paper, magnitudes are provided in the AB system. CLAUDS u and u* bands are referred to as U bands when no distinction is made between them (see Sect. 2.1 of this paper or Sect. 2.1 of Sawicki et al. 2019). We also assume the Planck Collaboration XIII (2016) cosmology with H0 = 67.74 km s−1 Mpc−1, ΩM = 0.3089, and ΩΛ = 0.6911.
2 Data
2.1 Overview of photometric data
The data consist of four fields (E-COSMOS, DEEP2-3, ELAIS-N1, and XMM-LSS; see Tables 1 and 2) and come from four different surveys. All the fields are covered by CLAUDS (Sawicki et al. 2019) and the HSC-SSP (Aihara et al. 2018a), but E-COSMOS and XMM-LSS are also partly covered by two near-infrared (NIR) surveys, UltraVISTA (McCracken et al. 2012) and VIDEO (Jarvis et al. 2013), respectively. The transmissions of the photometric bands of these data are shown in Fig. 1, while their coverage and depth are presented in Fig. 2 and Table 2.
CLAUDS is a deep survey using the Canada–France–Hawaii-Telescope (CFHT) MegaCam imager (Boulade et al. 2003) in the u and u* bands1. This program combines observing time from Canada, France, and China and consists of a total of 462 h of observations, including dedicated CLAUDS observations plus archival u*-band data in the COSMOS and XMM-LSS fields. The full survey covers a total area of 18.60 deg2 over the four fields down to a median depth of mU = 27.1 (deep survey) and two smaller but ultradeep areas covering regions of the E-COSMOS and XMM-LSS fields, reaching a median depth of mU = 27.7 over 1.36 deg2. The ELAIS-N1 and DEEP2-3 fields are exclusively covered in the u band, whereas the XMM-LSS is covered in the u* band. Only the central region of the E-COSMOS field has been observed in both u* and u bands with a large overlap in the deep region, however only the u* observations have a distinct ultradeep region. All the details of the CLAUDS survey and data are presented in Sawicki et al. (2019).
The HSC-SSP survey is a recently completed survey conducted with the Hyper Suprime-Cam camera (Miyazaki et al. 2018) on the Subaru telescope in Hawaii. In this work, we consider the public data release 2 (PDR2) Deep and ultraDeep layers of the survey presented in Aihara et al. (2019). The four fields have been observed in the g, r, i, z, and y bands (Kawanomoto et al. 2018) with median depths ranging from mg = 27.3 to my = 25.3 for point sources detected at 5 σ (all the depths are presented in Aihara et al. 2019, Table 2).
The UltraVISTA survey is a NIR survey covering 1.5 deg2 in the central region of the E-COSMOS field. We use the publicly available data release three images in the Y, J, H, and Ks bands2. The images were acquired by the VISTA Telescope (Emerson et al. 2004) with the VIRCAM instrument (Dalton et al. 2006). The data reach depths of mY ~ 25 and 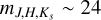 for 2″-diameter apertures at 5 σ (McCracken et al. 2012).
for 2″-diameter apertures at 5 σ (McCracken et al. 2012).
For the XMM-LSS field, we use the public VIDEO survey data release 4 images in the NIR Y, J, H, and Ks bands3. As for UltraVISTA, the images were produced using the VIRCAM instrument on the VISTA Telescope. The VIDEO data cover around 4.5 deg2, down to depths ranging from mY = 24.6 to 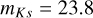 for 5 σ in 2″ apertures (Jarvis et al. 2013).
for 5 σ in 2″ apertures (Jarvis et al. 2013).
A summary of the data available in the different fields is presented in Table 2. The depths shown in the table are the medians of the 5σ scatter measured by us in 2″ apertures thrown in the background of the images in all the patches (see Sect. 2.3 for patches definition). We note that our reported depths can differ from the ones announced by other teams, depending on the adopted definition. Indeed, the depths computed from point sources are deeper than those computed from the standard deviations of background fluxes in 2″ apertures.
Right ascension and declination coordinates (J2000) of the four deep field centers.
 |
Fig. 1 Transmission curves of the photometric bands accounting for instrument throughputs and typical atmospheric absorption. All curves are scaled to 1. The horizontal lines indicate the 5σ depths in 2″ aperture measured for each band in the ultradeep regions for the E-COSMOS field. |
2.2 Spectroscopic data
The spectroscopic-redshift sample is a compilation of released spectroscopic surveys, including: the SDSS-BOSS surveys (Data Release 16, Ahumada et al. 2020); the GAMA survey (Data release 3, Baldry et al. 2018); the WiggleZ survey (final release, Drinkwater et al. 2018); the VVDS Wide and Deep surveys (Le Fèvre et al. 2013); the VUDS survey (Le Fèvre et al. 2015); the DEEP2 survey (Data Release 4, Newman et al. 2013); the VIPERS survey (Data Release 2, Scodeggio et al. 2018); the VANDELS survey (Data Release 4, Garilli et al. 2021); the CLAMATO survey (Data Release 1, Lee et al. 2018); the UDSz survey (McLure et al. 2013; Bradshaw et al. 2013).
We also include private spectroscopic observations from the spectroscopic follow-up of faint low redshift galaxies (r ≤ 22 and z ≤ 0.5) in three of the HSC fields with the Hectospec spectrograph on the MMT telescope (Cheng et al. 2021); and from the spectroscopic redshift catalog from the COSMOS team (M. Salvato, private communication), which consists of several optical and NIR spectroscopic follow-ups of X-ray to far-IR/radio sources, high-redshift star-forming and passive galaxies, as well as poorly represented galaxies in multidimensional color space (C3R2, Masters et al. 2019). We also include the low-resolution spectroscopic redshifts from slitless spectroscopy with the near-infrared grism from the 3DHST survey data release v4.1.5 using only those classified as secure grism redshift measurements (Momcheva et al. 2016; Skelton et al. 2014).
For all the above redshift surveys, we compare our photometric redshifts with the most secure spectroscopic redshifts only, identified with high signal-to-noise and with several spectral features (i.e., equivalent to VVDS or VIPERS redshift flags 3 and 4).
2.3 Data preparation
The PDR2 of HSC-SSP has been processed with version 6 of the HSC/LSST pipeline (Bosch et al. 2018; Aihara et al. 2019). We process the U and NIR bands using the same version of the pipeline, which has been modified in order to process non-HSC data.
The first step is to project the images onto the HSC reference pixel grid. As presented in Bosch et al. (2018), the hscPipe divides the sky into tracts, themselves divided in patches. A patch has a resolution of 4200 × 4100 pixels, with a pixel scale of 0.168″ pixel−1. A tract is composed of 9 × 9 patches, all having a 100-pixel overlap with the adjacent patches and sharing the same tract coordinate system. The tracts form a mosaic on the sky, with some overlaps varying depending on the declination. The U-band data reduction uses the same HSC data format (i.e., tract patch and pixel grid) for the final products. The full details of U-band image processing are given in Sawicki et al. (2019), but we review the key steps below. The detrended Mega-Cam images were processed using the MEGAPIPE data pipeline (Gwyn 2008) for astrometric and photometric calibration and for the stacking of the images. Two versions of the CLAUDS images are produced, one using the Pan-STARRS astrometry and another one using the more recent Gaia astrometry (Gaia Collaboration 2016a,b). The processing done with the hscPipe described in Sect. 3.1 uses the Pan-STARRS calibration for the U band and the processing done with SExtractor described in Sect. 3.2 uses the images calibrated with Gaia. Individual images underwent photometric calibration before the production of stacks, generated directly on the HSC pixel grid. The images were resampled using Swarp (Bertin et al. 2002), the background subtracted using a 128 × 128 pixel mesh grid done with Swarp, and stacked to produce the images and weight maps matching the HSC patches. In the case of the NIR data, the fully calibrated public mosaics (image and weight maps) are projected onto the HSC pixel grid with Swarp for all the patches covered by the NIR data. For the VIDEO data, some tiles are duplicated due to the layout and overlap of the different observations. The duplicated tiles are combined by averaging them over the overlaps to obtain a single tile per patch.
The U and NIR band processed data are formatted into coadd files that can be handled by hscPipe (see Bosch et al. 2018). This is performed with a module developed for hscPipe4. For each patch and band, the corresponding coadd file is gathering the images, and the variance map is computed from the weight map. A mask of the bright stars found in the patch is created using the prescription of Coupon et al. (2018). The point spread function (PSF) of the patch image is estimated. Finally, the coadd file is provided to the hscPipe for source detection and photometry extraction.
Summary of the characteristics of the survey in the different fields: filter coverage, 5σ, 2″ depth and area.
 |
Fig. 2 Detection images in the four CLAUDS-HSC fields. The footprints of the different observations are over-plotted in different colors: The CLAUDS Deep layer u and u⋆ bands in blue; the HSC-SSP grizy data in green; the VIDEO Near Infrared data in red (except in the XMM-LSS field where only two J band pointings are available, colored in pink). The footprints of the ultraDeep areas are shown with dashed lines. |
 |
Fig. 3 Flow chart and illustration of the process of mask creation. Images are smoothed and converted into binary masks with a threshold to identify bright extended objects. To avoid the masking of bright extragalactic objects, the masks are eroded (the pixels at the edges are set to 0), which removes small-scale objects. The masks are then dilated to recover the full size of the original masks for bright stars. Contours are created around masked areas (plotted in green) and we compare our new masks with the Coupon et al. (2018) ones (displayed as white circles and rectangles). |
2.4 Masking
2.4.1 Bright-star masks
Aihara et al. (2019) identified some issues in the bright-star masks in the HSC PDR2, due to the change in the sky subtraction algorithm from HSC PDR1 (Aihara et al. 2018b). An outcome of this change is that the bright-star masks based on Gaia and Tycho-2 catalogs presented in Coupon et al. (2018) are not conservative enough for PDR2. Moreover, stars in the NIR bands suffer more diffusion, implying that their halos are not completely covered by the masks. In addition to this problem, some bright stars are missing from the masks used by hscPipe5, requiring some improvements in the masking procedure. To solve these two issues, we combine the original masks with new masks derived using a simple image-based approach that follows the flowchart described in Fig. 3. Swarp is used to smooth the images suffering the most scattering (H-band if available, HSC y-band otherwise) using the LANCZOS3 method down to ~5″ pixel scale (Bertin et al. 2002). Then a threshold is applied to the pixel flux values to identify very bright objects and the images are converted onto binary masks (1 for masked and 0 otherwise) matching approximately the HSC ones. Finally, we apply to the binned masks a 5 × 5 erosion-dilation process. This process removes small masked areas and smooths the edges of the larger ones. Contours are converted into DS9 polygon regions that can be handled by the VENICE code6 (Coupon et al. 2018) and applied to the source catalogs.
As shown in the comparison with the masks of Coupon et al. (2018; bottom left plot of Fig. 3), our image-based approach does not mask all stars, but manages to mask the missing bright (mg < 16.5) stars and increases the size of the mask that were undersized compared to the observations. The final bright-star masks are built by combining the Coupon et al. (2018) masks with those we generated.
2.4.2 Satellite trails
Despite the update of HSC-Pipe that identifies and clips transient artifacts before coaddition, PDR2 images (as well as CLAUDS images) still exhibit an important number of satellite trails (≫10 deg−2). These trails could be easily handled via median-type stacking, but this would lead to a depth loss of 0.3 mag. An alternative is to use artifact rejection, but it misses a significant number of trails, which affects both source detection and photometry estimation. Indeed, SExtractor often fails at detecting sources close to bright satellite trails or generates spurious detections in those cases. This creates a bias in the number of counts per surface element. In addition, even when objects are detected around satellite trails, the photometry in the band with the satellite trail can be biased. This bias will propagate in the redshift estimation accuracy by generating catastrophic failures.
We decided to flag the regions possibly affected by these trails. We used the convolutional neural network (CNN) Maxi-Mask (Paillassa et al. 2020) to detect satellite trails in astronomical images. We used 0.6% prior for satellite detections and thresholded the probability mapping to the minimum to get most of the trails. On 4200 × 4200 images, 0.6% corresponds to approximately two satellite trails of 10 pixels width crossing the image diagonally. Maxi-Mask can mismatch edge-on galaxies with track and generate false satellite detections that are significantly smaller than the satellite trails. We get rid of these false detections by removing any detection shorter than 1′.
We only applied the code to the detection images, as most bright satellite trails can be detected from them. To avoid galaxies with photometry contaminated by the trails, we perform a 2″ binary dilation on the satellite mask images and use VENICE to convert these binary images into the ST_TRAILS flag in the released catalogs.
3 Source detection and photometry
Source extraction and photometric analyses are two crucial steps to optimize the detection of faint sources in deep and crowded regions and to estimate the colors required for the photometric redshifts. As mentioned by Weaver et al. (2022), photometric redshift estimates are more sensitive to the input flux catalogs than to the photo-z codes themselves. Hereafter we perform these two steps with two different codes: the one implemented in hscPipe (Bosch et al. 2018), which has been adapted to handle images from other facilities (e.g., U and NIR images), and the well tested and widely used SExtractor software (Bertin & Arnouts 1996). In the following part we describe the main steps followed by each software to generate the multiband catalogs and we compare the photometry obtained by the two catalogs as well as with the external catalog from COSMOS2020 (Weaver et al. 2022).
3.1 HSC pipeline
The source detection process using the hscPipe is described in detail in Bosch et al. (2018). It consists first of source detection in all individual bands. The configuration to run the detection on both U-band images is the same as that used in Aihara et al. (2019) on the HSC PDR2. However, for the NIR-data, a custom detection threshold was required to perform efficiently7, as the default configuration led to an important number of false detections of background fluctuations in these bands. Then, the lists of detected objects are merged and the photometry of all sources is extracted in all bands. Two measurements of the photometry are produced for the detected sources: one independent in all the bands, and one forced photometry across all the bands; we use the latter in the following sections. The full raw hscPipe data products, divided in tracts, patches (see Sect. 2.3), and bands, are available through the HSC data access portal (see Sect. 5). However, those data contain redundant sources due to the overlap between tracts and between patches that need to be cleaned to construct the final catalogs. In the E-COSMOS field, both U-bands were treated as two different sets of images, with detection and flux measurements made in both bands.
For each field, we include several photometric flux measurements: 2″ and 3″ aperture photometry, PSF photometry, Kron photometry (Kron 1980), and cmodel photometry (Abazajian et al. 2004). Among these measurements both cmodel and PSF photometries take into account the PSF variation across patches and bands. Quality flags from the output data are also included for each band to ensure the quality of the photometry. Sources identified by the hscPipe as duplicated are removed. The masks for bright stars used by the pipeline are the same as those used in Aihara et al. (2019) and thus suffer from the same issues as discussed in Sect. 2.4.1. We thus apply the updated star masks presented in Sect. 2.4 as well as the satellite trail masks using the VENICE code (Coupon et al. 2018).
We check the consistency of our photometry with that obtained in Aihara et al. (2019) for the HSC PDR2 release. Fig. A.1 shows the comparison for 2 arcsec aperture photometry. This comparison is done in the center of the E-COSMOS field where all the bands are available and where pipeline issues are most likely to happen, in particular in the processing of non-HSC data. The photometry of the hscPipe is in excellent agreement with the HSC PDR2 one. No bias is observed with magnitudes, and the scatter remains below ~0.011 mag in all the HSC bands. This is also true for the cmodel magnitudes, where the scatter never exceeds 0.04 mag.
A compactness flag is computed in each band by comparing the PSF photometry to the cmodel one. A source that meets the following criterion:
is considered as compact in band X. If this criterion applies to all HSC bands, the source is considered as compact and flagged accordingly.
3.2 SExtractor
We also produce a version of the HSC-CLAUDS catalogs with the detection and photometry based on the SExtractor software (Bertin & Arnouts 1996).
The source detection is performed on a detection image constructed by a nonlinear combination of the U + grizy bands. When near-infrared observations are available, the detection image also includes the Ks band. To compute the detection image we adopt the χmean combination proposed by Drlica-Wagner et al. (2018) as an alternative to the standard χ2 image (Szalay et al. 1999), because it minimizes the discontinuities between regions with a different number of input images.
The detection image, χmean, is defined as:
with
and fi is the image in the band i, 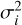 its variance and n the number of input images used in the combination. The χmean detection images are shown in Fig. 2.
its variance and n the number of input images used in the combination. The χmean detection images are shown in Fig. 2.
Before constructing the χmean images, we first checked the homogenization of the variance maps, as the procedures used to generate the images and their associated weight maps are different for the different datasets (CLAUDS, HSC, VIDEO or UltraVISTA). To ensure that the weight map properly scales as a variance map, we measured the standard deviation, σ(Im), of 5000 randomly thrown 2″ apertures in the background of the image, Im, and compared with the median value, median(Var), obtained in its associated variance map, Var. For each patch and passband, we rescaled the variance map by the factor: σ2(Im) /median(Var).
For CLAUDS and HSC bands, the scaling factors are around ~2.5–3, which means that without the rescaling we would underestimate the photometric errors by a factor ~1.5. For the NIR data, the variance maps are rescaled by a factor ~4 in the deepest areas and up to ~10 in the shallowest areas, implying an underestimation of the photometric errors by a factor ~2–3.
The source detection is performed on the χmean images convolved with a Gaussian with a 4 × 4 pixel kernel. A source is detected if a minimum of 10 contiguous pixels is above a signal-to-noise ratio of 0.8σ per pixel. The source deblending is controlled by the DEBLEND_MINCONT parameter, setting the fraction of the total intensity to be considered as a separated source, while the number of deblending thresholds is set by the DEBLEND_NTHRESH parameter. We found that the values of 0.0003 and 64 for the two parameters provide efficient deblending.
The detections and flux measurements are performed using the SExtractor dual mode. The χmean image is used to detect and measure the shape parameters, while flux measurements are performed in individual images. For each object, we provide two fixed aperture magnitudes (MAG_APER) with 2″ and 3″ diameters and the Kron magnitude (MAG_AUTO Kron 1980). The Kron magnitude automatically adapts to the first-order moment of the light distribution, and its elliptical aperture is scaled to provide a pseudo-total magnitude (Bertin & Arnouts 1996). However, fixed-aperture magnitudes are expected to be less noisy for faint sources and less impacted by blended sources, offering less noisy colors, a key input ingredient for the photometric redshift estimates (Sawicki et al. 1997; Hildebrandt et al. 2012; Moutard et al. 2016). As proposed by Moutard et al. (2016), for each object, we compute a single offset (the same for all the bands) that allows us to convert from aperture to total magnitudes, that are required for physical parameters measurements: mi = mAPER,i + δm, with the offset defined as:
where i runs through the Ugrizy and J, Ks filters and wi, the weight, defined as
where fAUTO and fAPER are the fluxes associated to the Kron and aperture magnitudes respectively and σAUTO and σAPER are their respective uncertainties. Being defined as a weighted average over all bands, the offset is more robust than if it were estimated for each band individually. However, some objects can have an unrealistic error in one band, which then accounts for more than 99% of the total weight. To prevent this situation, we iteratively set to 0 the individual weights representing more than 95% of the total weight. The offsets for the 2 and 3″ aperture magnitudes are given in the final catalog. All the magnitudes provided in the catalog are corrected for galactic extinction based on the Schlegel extinction maps (Schlegel et al. 1998).
3.3 Comparison and quality assessment
The HSC-CLAUDS photometry is assessed by comparing the measurements of our hscPipe and SExtractor catalogs. We also compare to a third and distinct method, delivered in the COSMOS2020 catalog (Weaver et al. 2022), based on Farmer software (Weaver et al., in prep.) which uses The Tractor (Lang et al. 2016) to measure the photometry. Farmer performs model photometry of individual sources with a simultaneous optimization of a group of nearby sources with additional constraints from the multi-channels. The COSMOS2020 catalog uses, among others, the same CLAUDS, HSC and UltraVISTA data as we did. The comparison is thus performed in the central E-COSMOS field, which is also the only region where all filters are available.
In Figs. 4, 5 and 6, we compare the magnitudes. The cmodel from the hscPipe with the SExtractor aperture corrected magnitudes (Fig. 4); the cmodel with Farmer magnitudes (Fig. 5) and the SExtractor corrected aperture with the Farmer magnitudes (Fig. 6). The panels show for each filter the magnitude differences as a function of magnitude for the matched sources and the median of the distributions (solid lines) and their ±34% intervals around the median (dashed lines) down to the 5σ depth measured in the ultraDeep region of E-COSMOS. Several points are noteworthy. First, in the optical bands (bluer than y band), we observe small offsets (≤−0.1 mag) in the bright end, with SExtractor magnitudes being systematically brighter than hscPipe and Farmer photometry, while almost no offset is observed between hscPipe and Farmer. The two latter magnitudes are based on modeled magnitudes and are not sensitive to seeing variations between bands, in contrast to the SExtractor aperture corrected magnitudes (see Eq. (3)), where no PSF homogenization has been applied, and the mean offset can be slightly over-estimated due to the worse seeing images.
In the optical bands also, hscPipe magnitudes are getting gradually brighter than SExtractor and Farmer magnitudes for the faint objects (m ≳ 25.5). The effect is much less pronounced between SExtractor and Farmer photometry. This faint-end trend could arise if the background correction in hscPipe is underestimated. This can be seen as well, although less pronounced, when comparing 2″ aperture magnitudes between SExtractor and hscPipe optical magnitudes (Fig. C.1). In contrast to the optical bands, in the near-infrared bands (redder than the Y band), the three different sets of magnitudes are consistent with only small systematic biases (≤0.05) with no trend with magnitude.
Finally, for all the bands, the distribution of the difference between the cmodel and SExtractor magnitudes shows a skewness with a large negative tail for the brighter SExtractor magnitudes. As a modeled photometry, the hscPipe may better handle the contribution of neighbors than the SExtractor aperture-corrected magnitudes. Consistently with this interpretation, the distributions for the two modeled magnitudes, Farmer and hscPipe (Fig. 5), are almost symmetrical around the median, while the distributions between Farmer and SExtractor also show a slight asymmetry in the same direction.
Since the photo-z computation is made using 2″ aperture photometry with both catalogs (see Sects. 4.1 and 4.2), we make a comparison of the color apertures in Fig. 7. We show the color differences between SExtractor and hscPipe photometry for six colors, namely u – g, u* – g, g – r, i – y, z – Ks, and J – Ks. We note the good agreement between the colors provided by both catalogs up to magnitude ~24 in all the tested colors with no bias and a scatter ≲ 0.1. For fainter objects, a bias appears in colors involving optical and NIR bands, accompanied by a strong increase of the scatter. This can be due to the difference in background treatment, but also to the differences in depths. For i – y and z – Ks colors, this difference is ≳1 mag. The large scatter observed would be due to strong noise in the NIR band magnitudes of the faint objects compared to the optical ones.
To check the consistency of the photometric calibration between the four different regions of HSC-CLAUDS, we selected the stellar population and compare their stellar loci in color diagrams. We perform this test only with the hscPipe catalog, where a PSF magnitude is provided to get optimal stellar colors. Figure 8 displays the contours encompassing 68% of the stars in four color–color diagrams for all the fields (color coded) available in a given color combination. The stellar loci for the different fields show an excellent overlap between each other in the optical bands. Combined with NIR color (bottom right panel, z – Ks vs. i – z), the stellar locus in the XMM-LSS field shows a larger scatter and a shift of ~0.05) compared to the E-COSMOS field. The figure shows that the observed loci are not properly aligned with the main-sequence star colors computed from the Pickles template library (Pickles 1998). This indicates a need for zero-point calibration to correct colors. From the diagrams, it appears that the U bands and the NIR bands require the largest corrections. Although, for the bluest bands, the shift can also be due to Milky-Way extinction which is not accounted for because of the difficulty of computing it for objects (stars) inside the Galaxy. We conclude that the photometry in the optical bands is consistent across the four fields but requires further correction in the form of zero-points calibration. The NIR band photometry might present some differences between E-COSMOS and XMM-LSS fields, which can be taken into account in the analysis by adjusting the zero-points on a field-to-field basis.
Figure 9 shows the number counts in all bands for the SExtractor and hscPipe catalogs. The number counts in the two ultraDeep regions (COSMOS-UD and XMM-LSS-UD) are presented separately, while those from the deep regions are the averages of the four fields. The comparison of the ultraDeep region of E-COSMOS and COSMOS2020 shows a good agreement, especially in the HSC bands, which is expected as the data used to build the catalogs are the same in the three cases. More differences arise in the NIR bands, first due to the difference in data, as COSMOS2020 uses the DR4 of UltraVISTA and our catalogs are built with the DR3, which is shallower. The number counts in Fig. 9 show the counts after applying a cut at S/N > 3 in the concerned bands, which peak at brighter magnitudes than the COSMOS2020 counts. This could be explained by the rescaling of the errors, which affects strongly the NIR bands, leading to larger errors and hence pushing some objects below the S/N cut. The ultraDeep uncut counts match rather well with the COSMOS2020 ones, which is further evidence that the discrepancy is due to the cut in S/N.
For the bluest bands, there is a shift between the COSMOS2020 counts and ours. This shift could indicate some uncertainties in the estimation of the area that would produce a vertical shift, or systematic overestimation of the flux that would cause a horizontal shift, but it could also be explained by the differences in detection schemes used in the different pipelines. The hscPipe performs source detection in all the bands, while SExtractor uses a χ2 image constructed with bands from U to z, with the addition of the Ks band when available. The detection in COSMOS2020 uses only the reddest bands from i to Ks. This difference makes our catalog more sensitive to blue objects, which explains why the discrepancy between the curves in Fig. 9 is stronger in the blue bands at faint magnitudes.
 |
Fig. 4 Comparison of hscPipe cmodel magnitudes with SExtractor total magnitudes. The color shades show the density of sources. The solid lines are the median of the distributions and the dashed lines are the ±34% intervals around the medians. These values are computed down to the 5σ depth in each band in the E-COSMOS ultraDeep region (vertical dotted line). |
 |
Fig. 5 Same as Fig. 4, but comparing hscPipe cmodel magnitudes with COSMOS2020 Farmer total magnitudes. |
 |
Fig. 7 Comparison of hscPipe and SExtractor colors computed from 2″ aperture photometry. In all the plots, the x-axis shows the SExtractor 2″ aperture magnitudes of the second term in the colors. The solid line is the median of the distribution, and the dashed lines are the ±34% confidence interval around the median. The vertical dotted lines mark the 5σ depth in the reference band (x-axis one). |
 |
Fig. 8 Color-color density contours of stars in the different fields computed from the hscPipe PSF photometry. The contours enclose 68% of the stellar loci. The crosses show the positions of main sequence stars from the Pickles library in these color–color diagrams. The offset between templates and observed loci indicates the need of proper extinction and zero-point corrections, which are applied in Sect. 4. |
 |
Fig. 9 Number counts for SExtractor and hscPipe catalogs compared to COSMOS 2020 Farmer number counts. The number counts in the deep area combine the four fields. A cut at S/N > 3 in all bands is made for SExtractor and hscPipe data displayed as points. The solid black line shows the number counts for COSMOS2020 Farmer photometry. The dashed lines show the hscPipe (dark blue) and SExtractor (light blue) number counts in the ultraDeep region of COSMOS without the cut in S/N. |
Compilation of the zero-point corrections computed by Phosphoros and Le Phare.
4 Photometric redshifts
The photometric redshifts (photo-zs) are estimated with two template-fitting codes for the two photometric catalogs based on the 2″ aperture flux in all bands. The hscPipe catalog is processed with the Phosphoros code, created to be part of the Euclid photo-z pipeline (Paltani et al., in prep.; Euclid Collaboration 2020), while the SExtractor catalog is processed with the well-tested code, Le Phare (Arnouts et al. 2002; Ilbert et al. 2006). As this is the first application of Phosphoros on deep imaging surveys destined to be released, we also run Phosphoros on SExtractor photometry to distinguish the differences related to photometry issues from template-fitting code issues; this is detailed in Appendix D.
For both codes, several configurations were considered and tested. We explored using different templates, prior information, photometry, and errors. The configuration presented in this section is the result of this exploration. We make the choice to use similar configurations, most of the differences being due to differences in the parameters both codes can adjust.
Both code use the templates library of Ilbert et al. (2013) for galaxies, consisting of a total of 33 spectral energy distributions (SED): seven elliptical galaxies, twelve spiral galaxies (Polletta et al. 2007; Ilbert et al. 2009), twelve starburst galaxies, and two elliptical SEDs generated with the Bruzual & Charlot (2003) stellar population synthesis models. Intrinsic extinction is also configured in a similar manner in both codes. Extinction was added as a free parameter for a reddening excess E(B–V) = 0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5 and by considering four attenuation laws: starburst-like Calzetti et al. (2000) and two dusty versions of the Calzetti law (with a bump at 2175 Å) for templates bluer than SB3, SMC-like Prevot et al. (1984) for templates redder than SB3 and no extinction for templates redder than Sb.
Emission lines are added to the templates by assuming an empirical relation between the UV light and Hα line flux (Kennicutt 1998) and ratios between the different hydrogen lines and oxygen lines as measured from high redshift spectroscopic surveys (Ilbert et al. 2009) or SDSS survey (Paltani et al., in prep.).
As proposed by Ilbert et al. (2006), to account for photometric variations in the four HSC-CLAUDS fields, the spectroscopic redshifts of bright sources (19 ≤ i ≤ 21.5) are used to apply a band-per-band zero-point correction in each field separately. These corrections are given in Table 3 for each field and combination of bands used. A small difference between the two configurations is that Phosphoros computed the zero points for both the Ugrizy and Ugrizy+NIR configurations in the E-COSMOS and XMM-LSS fields. Also, for both codes, the photo-zs computed in the central part of the E-COSMOS field use both u and u* data separately when available.
4.1 Phosphoros
Phosphoros is a template-fitting code that implements all the main functionalities of other template-fitting implementations. The focus on Phosphoros is the fully Bayesian treatment of the multi-dimensional likelihoods, with the possibility to apply complex priors and to marginalize over any parameters. Phosphoros uses the configuration provided in Sect. 4.
Phosphoros uses fluxes uncorrected for the Milky Way extinction, as the Galactic extinction is handled internally by Phosphoros by applying it directly on the fitted SED, following the prescription of Galametz et al. (2017). Photometric errors in the different bands x, σf,x, are modified using the following equation:
where f is the flux, x the band and α is the uncertainty rescaling factor and is 2 for Ugrizy bands and 4 for NIR bands, and β corresponds to a systematic uncertainty (which could come from the photometry or from the models) and is set to 0.03 for all the bands.
We also consider several prior information. When computing photo-zs using the NIR bands, a top-hat prior in absolute magnitude is applied, allowing only results with −24 < Mg < −8, as well as a volume prior to take into account that the probability of a source to be in a slice of redshift increases with the volume of the slice. When the number of available bands is restricted to the optical wavelengths, we apply a more informative prior based on luminosity functions from Zucca et al. (2006). The rest-frame templates are sorted into four types according to their B – I colors. For each type, we construct a prior assuming a Schechter function (Schechter 1976), with the a, the index of the power law at low luminosity, and ϕ*, the source density, parameters given by Zucca et al. (2006) in the rest-frame B-band for galaxies between redshift z = 0.4–0.9. However, the M* values are modified, setting them 3 magnitudes brighter, to avoid an overly strong suppression of luminous galaxies at high redshift. We introduce this modification because the strong evolution of M* makes the values determined by Zucca et al. (2006), which are essentially obtained at low redshift, not applicable even at moderately high redshifts. Any small variation of this shift value (±0.5 mag) only has a small impact on the results. We prefer this prior to that on the magnitude-redshift distribution from Benítez (2000) because its shape is physically better justified, which is especially important at high redshifts.
For each object, the probability distribution function of the redshift (PDZ) is obtained by marginalizing the posterior on the redshift dimension. The PDZs are defined with a fixed redshift grid (z = 0–6) with a step δz = 0.01. The photo-zs point estimates are defined as the median values of the PDZs. To deliver a consistent dataset across the entire HSC-CLAUDS survey, we provide a complete set of photo-zs with their PDZs based on the Ugrizy photometry alone, and an additional set based on Ugrizy YJHKs in the regions where near-infrared bands are available.
We also provide a star/galaxy separation by fitting the sources with stellar templates from the Pickles (1998) library. In the catalog, all object with; 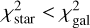 are flagged as potential stars. Objects that are both potential stars and compact according to Eq. (1) are flagged as stars.
are flagged as potential stars. Objects that are both potential stars and compact according to Eq. (1) are flagged as stars.
4.2 Le Phare
Le Phare (Arnouts et al. 2002; Ilbert et al. 2006) is a well known and standard template-fitting method. With Le Phare, we adopted the same configuration as with Phosphoros, in terms of the SED library, attenuation laws and reddening excess, emission lines and zero-point calibrations (see above, Sect. 4).
The SED fitting is run on SExtractor 2″ aperture photometry, corrected for the Galactic extinction. Photometric errors are amplified by a factor 1.5, on top of which systematic magnitude errors of 0.02 mag and 0.05 mag are added in quadrature for optical and NIR bands respectively. Depending on whether NIR photometry is used, a different prior set is adopted. In the case of Ugrizy+NIR, a g-band absolute magnitude is applied to reject solutions with Mg < −24. When only the optical bands are used, a fine-tuned prior similar to the Benítez (2000) prior is used (Ilbert et al. 2006).
The redshift output of Le Phare is the median of the PDZ as point estimate, or, when the PDZ is not defined, the redshift is associated to the lowest χ2 value in the grid (the redshift grid is the same as the Phosphoros one, see Sect. 4.1). The photo-zs errors are computed from the 68% confidence interval of the PDZ.
In addition to the galaxy template library, we also run the SED fitting with stellar and quasar template libraries. The stellar library includes normal spectral types at solar abundance, metal-weak and metal-rich F-K dwarfs and G-K giants (Pickles 1998), low mass stars with different effective temperatures, gravity, and types (Chabrier & Baraffe 2000) and white dwarfs (Bohlin et al. 1995). The quasar library is a compilation of observed quasar templates (Polletta et al. 2007) and templates with different contribution of galaxy and AGN spectra (Salvato et al. 2009, 2011). A first star/QSO/galaxy classification is provided, where compact objects with best fit obtained for a star or QSO template are flagged as such (see Appendix E).
4.3 Comparisons
In this section, we compare our photometric redshift estimates with spectroscopic redshifts (described in Sect. 2.2) and the latest 30-band photometric redshifts in the COSMOS field (COSMOS2020, Weaver et al. 2022). As mentioned in Weaver et al. (2022), more than the differences in the photometric redshift codes, the main differences in the photo-z vs. spec-z comparisons are due to the input photometric catalogs. This is especially true in our work where we use two SED fitting codes with similar approaches but two quite different photometry codes. For this reason in the following we perform the comparisons using the photometric redshifts derived with the combinations hscPipe+Phosphoros (hereafter HPH) and SExtractor+Le Phare (hereafter SLP). In Appendix D, we show that the results from the two photo-z codes are similar when run on the same SExtractor catalog (see Fig. D.1).
4.3.1 Metrics
The performance of the photometric redshifts is evaluated using the following metrics: the residuals, Δz = (zphot − zspec)/(1 + zspec), following the definition of Cohen et al. (2000); the normalized MAD, σMAD = 1.4826 × MAD, where MAD (Median Absolute Deviation) is the median of |Δz − Median(Δz)| (Hoaglin et al. 1983); and the fraction of outliers η with |Δz| ≥ 0.15.
The photometric redshift point estimates are delivered with an uncertainty based on the 68% confidence interval. To assess the relevance of the errors, for each galaxy i, we compute the absolute scaled residuals:
where 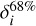 is the 68% confidence interval for the galaxy i. The cumulative distribution, Dz, should reach 0.68 for Dz = 1.
is the 68% confidence interval for the galaxy i. The cumulative distribution, Dz, should reach 0.68 for Dz = 1.
We also assess the quality of the PDZs with the Probability Integral Transform (PIT) statistic (PIT plot, Dawid 1984; D’Isanto & Polsterer 2018). It is based on the shape of the distribution of the cumulative probabilities (CDF) at the true value:
for galaxy i with spectroscopic redshift zi and probability distribution function PDZi. If the spec-z’s can be randomly drawn from the PDZs then a flat PIT distribution is expected, suggesting that the PDZs are statistically correct, whereas convex or concave PIT distributions point to under- or over-dispersed PDZs, respectively (Polsterer et al. 2016).
 |
Fig. 10 Comparisons of the photo-zs based on the Ugrizy photometry with spectroscopic redshifts down to i ≤ 22.5 in the four HSC-CLAUDS deep fields. Top panels show the photo-zs computed by Phosphoros code and the hscPipe catalogs, while the bottom panels show the photo-zs computed with Le Phare and SExtractor catalogs. The solid gray lines show the 1:1 line and the dashed lines show the zphoto = zspec ± 0.15(1 + zspec) corresponding to the limits for catastrophic failure. |
4.3.2 Comparisons with spectroscopic redshifts
Figure 10 presents density plots comparing the photo-zs from the HPH (top panels) and SLP (bottom panels) runs to spec-z’s for sources with mi < 22.5 in the four fields separately and based only on the Ugrizy photometry. A zero-point calibration has been applied to each field separately. The performance appears similar in the two configurations, with a precision varying between σ = 0.02–0.04 and outlier fractions η = 2–3% across the four fields. However, we note a systematically higher scatter for the HPH results compared to the SLP ones by ~0.01.
In Fig. 11, the four HSC-CLAUDS fields are combined together and the Ugrizy photo-zs are compared with spectro-scopic redshifts in faint magnitude bins. However, we note that the ELAIS-N1 field has almost no spectroscopic redshift with mi ≥ 22.5 and the DEEP-23 field only down to mi ≤ 24. The vast majority of the faint spectroscopic sources come from the XMM-LSS and E-COSMOS fields.
The precision of the photometric redshifts gradually deteriorates with magnitude, passing from σ ~ 0.03 at mi ≤ 22.5 to σ ~ 0.09 at mi ≤ 26, with slightly worse results for the HPH implementation. Similarly, the fraction of catastrophic failures gradually increases from η ~ 4% to η ~ 29%.
Although the fraction is similar between the two implementations, there are differences in the location of the outliers. Due to the Balmer and Lyman break confusion, two approximately symmetric clouds of outliers are generally produced, one for low spec-z sources with a zphot ≥ 2, and the other one for high spec-z galaxies with a low photo-zs (zphot ≤ 0.3). The SLP implementation presents a visible cloud for sources with high spec-z’s and low photo-zs, while the HPH one leads to fewer sources in this cloud, but presents a higher population at low spec-z’s and high photo-zs than the SLP implementation. This difference is due to the application of a volume prior in the Phosphoros code since this volume prior favors the high redshift values for poorly constrained photometric sources.
A striking feature is present with spectroscopic sources around zspec ~ 1, to which higher photometric redshifts zphot ~ 1.5–2 are assigned. The vast majority of those sources show a red z – y color that can be interpreted either as caused by the 4000 Å break at z ~ 1.5, or by the contribution of emission lines (e.g., H β and [O III] lines) at z ~ 0.9 (putting the 4000 Å break in the r – i color). Without the near-infrared, this double solution cannot easily be broken by the N(z) prior and occasionally leads to favor the wrong solution.
In Fig. 12, we show the comparisons of photometric redshifts measured by taking into account the NIR data. All the performance metrics are improved and we still observe slightly better results for the SLP implementation compared to the HPH one. For the faint galaxy population, the scatter and the catastrophic rate are improved by almost a factor of two. Including NIR data also alleviates the degeneracy observed around zspec ~ 0.9 with zphot ~ 1.5–2. This illustrates the benefit of the NIR observations to provide robust photometric redshifts over the entire redshift range.
The point estimate photometric redshifts are given with an uncertainty based on the 68% confidence level interval derived from the individual redshift probability distribution function (PDZ). To assess the relevance of the errors, for each source we compute the absolute scaled residual, Dz (Eq. (6), Sect. 4.3.1). Figure 13 presents the cumulative distribution of Dz for the two implementations (HPH and SLP) and the two imaging datasets (optical, optical+NIR). If the photo-z uncertainties are correct we expect the cumulative curves to reach the 68% level at D(z) = 1. Indeed, all the cumulative distributions cross the 68% level at higher D(z), suggesting that the estimated photo-z uncertainties are underestimated. In both configurations, the effect seems even worse when the near-infrared photometry is included, probably because of the additional constraints it provides on the PDZs. Despite the fact that scaling factors have been applied to enlarge the photometric errors (see Sects. 4.1 and 4.2), they seem insufficient to provide realistic photo-z uncertainties. We note that SLP configuration seems to provide more reliable error estimates than HPH. As it is still the case when Phosphoros is run on SExtractor photometry, this difference is probably due to the code configurations, and in particular the rescaling of the errors, and not only to the photometry. We, therefore, caution that the current photometric-redshift uncertainties are on average underestimated.
Alternatively, instead of the 68% confidence interval, we can directly estimate the quality of the PDZs with a PIT plot (see Sect. 4.3.1). In Fig. 14, we show the histogram of the HPH Ci values.The concave shape of the histograms shows that the PDZs are too narrow, leading to an underestimation of the errors. Such behavior has already been reported with several template-fitting methods on similar data sets (Tanaka et al. 2018; Euclid Collaboration 2020). We also see that using the NIR data has the effect of constraining the PDZs even more. These observations are in agreement with the conclusions drawn from Fig. 13.
 |
Fig. 11 Same as Fig. 10 but for all the HSC-CLAUDS fields combined and split by i-band magnitudes. The comparison is extended to faint magnitude bins, as indicated in each panel, with faint spectroscopic sources coming from the DEEP-23 (mi ≤ 24), XMM-LSS, and E-COSMOS (mi ≤ 26) fields. |
 |
Fig. 12 Same as Fig. 11, but for the XMM-LSS and COSMOS fields only and including the near-infrared photometry. |
 |
Fig. 13 Absolute scaled residuals (Dz) cumulative distributions for the two implementations (HPH: blue lines and SLP: green lines) with the optical (light lines) and optical+NIR (dark lines) catalogs. The horizontal dashed gray lines show the 68% level that all the distributions should cross at Dz = 1 (vertical dashed line). |
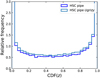 |
Fig. 14 PIT plots for Phosphoros PDZs computed from the hscPipe photometry with (dark blue) and without (light blue) the infrared bands. |
4.3.3 Comparison with 3DHST and COSMOS2020 surveys
At faint magnitudes, the spectroscopic samples are often selected with specific photometric criteria and are therefore not a representative sample of the overall photometric population (Masters et al. 2015). To address this issue, we compare our results to the 3DHST (Skelton et al. 2014) and COSMOS2020 (Weaver et al. 2022) surveys. The 3DHST is a slitless low-resolution grism survey that provides spectroscopic redshifts of near-infrared sources down to mH ≤ 24. However, 3DHST is still impacted by a selection bias due to the success rate of reliable redshift identifications, which is strongly dependent on the galaxy type, and in particular on the strength of the emission lines. COSMOS2020 provides robust photometric redshifts over the entire color-space thanks to its 30 photometric bands, but these redshifts are less precise than the spectroscopic ones. These two samples are used to assess the quality of our photometric redshifts for the faint population.
In Fig. 15, we compare the photometric redshifts from the HPH and SLP catalogs with the 3DHST redshifts, down to mH ~24. Two 3DHST fields overlap with the HSC-CLAUDS observations in the E-COSMOS and XMM-LSS fields and the sources are matched with a 1″ tolerance. A small fraction of spectroscopic redshifts, especially when determined using slit-less grisms, can be wrongly assigned; however, the impact should be negligible on the estimated scatter, as the median absolute deviation (MAD) is robust against outliers. The results are consistent with the trends observed in Sect. 4.3.2 with optically selected spectroscopic sources. HPH photo-zs have slightly higher scatter and outlier fractions in the two adopted sets of filters. The catastrophic-failure fraction is reduced by a factor of two when including the NIR bands and the mismatch in the redshift domain 1 ≤ z ≤ 2 is noticeably reduced. On the code side, the implementation of priors used in Phosphoros for the optical configuration reduces the number of low photo-z outliers compared to those from the Le Phare code.
In Fig. 16, we show the comparisons with the COSMOS2020 photometric redshifts. As described in Weaver et al. (2022), four versions of photometric redshifts are available based on two photometric extraction softwares (Farmer and SExtractor) and two photometric redshift codes (Le Phare and EAzY; Brammer et al. 2008). In an attempt to be as independent as possible from source extraction and photometric redshift methods, in Fig. 16 (top 2 rows) we first compare our measurements based on the optical+NIR bands with the COSMOS2020 Farmer/EAzY catalog. However we point out that we use the same deep images (HSC, CLAUDS, and UltraVISTA) as COSMOS2020; these images provide the strongest constraints on the photo-zs at faint magnitudes. But COSMOS2020 benefits from the ultradeep IRAC images and the narrow and intermediate Suprime-Cam bands (Taniguchi et al. 2007, 2015). The former will reduce the number of catastrophic failures, while the latter will improve the scatter at bright magnitudes. In Fig. 16, the sources are restricted to cleaned flags (FLAG_COMB INED=0) and sorted according to the Farmer i-band magnitude (Weaver et al. 2022) to get the same number of sources in each magnitude bin. The comparisons show similar trends in the metrics to those in Figs. 12 and 15, with slightly better results for the SLP implementation. No systematic bias is observed up to redshift z ~ 6 and down to mi ~ 26 with a catastrophic-failure fraction below 15%. In the faintest magnitude bin, 26 ≤ mi ≤ 27, the scatter almost doubles and the catastrophic-failure rate becomes significant, reaching 30%; but those numbers are comparable to the level of consistency between the different photometric redshifts in the COSMOS2020 catalogs (Weaver et al. 2022, see their Fig. 14). The metrics are in good agreement with the values reported for the spectroscopic redshifts up to mi ~ 26 (see Fig. 12) and confirm that we do not expect major photometric-redshift issues for the whole galaxy population up to this depth. However two noticeable features are observed: first, a larger catastrophic-failure fraction at bright magnitudes with COSMOS2020 with respect to the comparison with spectroscopic redshifts; second, a mismatched photo-z population at low redshift (zFARMER/EAzY < 0.5) for which our two HSC-CLAUDS configurations estimate higher redshifts (above the 1:1 line). These two points are due to the fact that we are comparing our photo-zs with other photo-zs from COSMOS2020 that have their own inaccuracies.
To mitigate this effect, we make another comparison with the COSMOS2020 results by considering the four different versions of the photometric redshifts provided by Weaver et al. (2022). For all the sources with four photo-zs, we compute the mean redshift (〈z〉) and its standard deviation, σ(z). We then select the COSMOS2020 self-consistent photo-zs by imposing a cut in the standard deviation σ(z) < 0.1(1 + 〈z〉). Strictly speaking, this does not constitute a guarantee to select secure redshifts, but rather it reduces issues related to either photometric extraction in problematic sources or sources with degenerate solutions, which may not be apprehended the same way by the two codes used in Weaver et al. (2022).
The comparisons with the mean COSMOS2020 photo-zs are shown in Fig. 16 (two bottom rows). With respect to the whole COSMOS2020 catalog, more than 85% and 70% of COSMOS2020 photo-zs are consistent with each other up to mi ~ 25 and 26 respectively. Our own photo-zs also appear consistent with the mean COSMOS2020 photo-zs with a scatter lower than σ = 0.03 and a small fraction of catastrophic failures (η ≤ 5%). In the faintest magnitude bin, 26 ≤ mi ≤ 27, only 40% of the COSMOS2020 redshifts are consistent with each other (Weaver et al. 2022). For this population, our photo-zs are still in good agreement with a scatter σ ~ 0.05 and a catastrophic-failure fraction not exceeding η = 10%. As already noted, we observed with the COSMOS2020 photo-zs that the distribution of catastrophic failures for the SLP and HPH catalogs are different. For the former, most of the catastrophic sources are high-z COSMOS2020 photo-zs which are assigned to low redshifts, while the latter mainly assign high redshifts to low-z COSMOS2020 photo-zs.
In Table 4, we report the scatter and the catastrophic-failure fractions for the different configurations for different i-band cuts tested against the spectroscopic sample and COSMOS2020. In the former case, the scatter and outlier fraction values are misleading, because the spec-z sample is strongly biased toward brighter magnitudes compared to the whole photometric catalog. Therefore we provide scatter σ and outlier fraction η values weighted by the number of photometric objects in each magnitude bin, which provides a much more realistic view of the performance on the full photometric sample (Euclid Collaboration 2020; Hartley et al. 2022). There is no such problem when comparing with COSMOS2020 since it contains essentially all photometric sources. The weighted σ and η for the spec-z sample are thus computed as follows:
and:
where j represents the magnitude bins (mi < 22.5, 22.5 ≤ mi < 24, 24 ≤ mi < 25, etc.), nj is the number of sources in the photometric catalog in the magnitude bin j, and σj and ηj are the metrics for bin j. The weighting scheme doubles the outlier fractions measured in the spectroscopic sample with a mi < 25 cut and triples it at mi < 26. We note that the scatter values with the weighted scheme are consistent with those of COSMOS2020 FARMER/EAzY. For the outlier fractions, we note some differences especially for the bright cuts, as by construction the results in the first magnitude bin do not change. It is with a cut at mi < 25 that we have the most consistent results. With this cut, we have a scatter σ ≲ 0.04, even when using only Ugrizy data and after weighting the spectroscopic sample results or using the COSMOS2020 data as a reference. With the same cut, we obtain an outlier fraction η < 0.05 for the spectroscopic sample, regardless of the photometry used. At mi < 25, the catastrophic-failure rate remains below 10%, both when compared with the spec-z sample and with COSMOS2020.
 |
Fig. 15 Photo-z comparison with 3DHST redshifts for galaxies down to mH ~ 24 for HPH (top panels) and SLP (bottom panels) catalogs, with the optical+NIR (left panels) and optical only (right panels) bands. The metrics are reported in each panel. |
 |
Fig. 16 Comparison of HPH and SLP photo-zs to COSMOS2020 results. Top panels present the comparison with Farmer/EAzY results. The bottom ones show the comparison with the mean photo-zs computed from the four COSMOS2020 configurations clipped to only include photo-zs with standard deviation lower than 0.1[1 + mean(z)] between the four-point estimates. photo-zs have been computed using optical and NIR bands. The bins in i-band magnitude are based on the FARMER photometry. |
Summary of the results in the different configurations tested in this work depending on i-band cuts.
4.3.4 Redshift distributions
In Fig. 17 we show the galaxy redshift distributions (N(z)) for the HSC-CLAUDS catalogs with three different magnitude limits (mU ≤ 26.5, mi ≤ 25.5, and 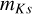 ≤ 24.5). The distributions are obtained with the photometric redshifts based on the optical bands only and the optical+NIR bands and with the two configurations (HPH and SLP). In addition to the point estimate photo-zs, for the HPH configuration we also include the redshift distributions by summing up the individual PDZs. The figure also shows the distribution obtained with Farmer/EAzY photo-zs and the same cuts in the photometry. The COSMOS2020 results are weighted such as the integral of the distributions match the average total number of sources between HPH and SLP results.
≤ 24.5). The distributions are obtained with the photometric redshifts based on the optical bands only and the optical+NIR bands and with the two configurations (HPH and SLP). In addition to the point estimate photo-zs, for the HPH configuration we also include the redshift distributions by summing up the individual PDZs. The figure also shows the distribution obtained with Farmer/EAzY photo-zs and the same cuts in the photometry. The COSMOS2020 results are weighted such as the integral of the distributions match the average total number of sources between HPH and SLP results.
The different estimates lead to reasonably consistent redshift distributions, and are in agreement with the COSMOS2020 redshift distributions. The selection band impacts the overall shape of the distributions, with a bounded N(z) below z ~ 2.5–3 with the u band selection and an increasing population at high redshift when adopting a redder selection band.
We also observe some specific differences. With the NIR selection, a bump at z ~ 3.5 is visible for the point estimates in the HPH configuration. This bump might be due to poorly informative PDZs (nearly flat) skewed toward high redshift because of the priors, putting the median point estimate of the PDZ in this redshift range. This effect vanishes when adopting the sum of the PDZs.
With the U-band selection, we observe a significant difference in the shape of the N(z) between the photo-zs based on the optical bands and those using all bands, the former showing a higher fraction of sources between 1.3 ≤ z ≤ 2. This reflects the biased population seen in Fig. 11 (Ugrizy plots) and discussed in Sect. 4.3.2. It means that these features are due to the lack of constraints in the absence of NIR data. However, the use of the stacked PDZ helps to reduce this effect.
Finally, we also observe differences between the SLP and HPH redshift distributions in the case of the all-band based photo-zs. At low redshift, the SLP distributions increase more rapidly while at high redshift they tend to decrease faster. While the Le Phare code does not apply the Benítez (2000) prior on the redshift likelihood when the NIR bands are included in the computation, Phosphoros always uses the volume prior which penalizes low redshift solutions and favors higher redshift ones. This is the same effect we observe in Fig. 16 for the faintest sources.
 |
Fig. 17 Galaxy redshift distributions (N(z)) in the CLAUDS-HSC regions for three selections, as indicated in the top of each panel. The three panels in the top row show the results based on estimates with all the bands and are thus limited to E-COSMOS and XMM-LSS fields. The two panels in the bottom row show those computed with Ugrizy photometry for the four deep fields. For HPH, the N(z) is either based on the redshift point estimates (median of each PDZ; light red lines) or based on the stack of the individual PDZs (dark red line). For SLP, the N(z) is obtained with the redshift point estimate (blue lines). A comparison is made with COSMOS2020 Farmer/EAzY photo-zs (black lines) in the top panels. The COSMOS2020 curves are weighted to match the CLAUDS-HSC ones. The distributions are constructed in bins of δz = 0.05. |
5 Data access/catalogs
Two catalogs are presented in this work. They correspond to two different processing methods applied to the same data, providing overall similar data products of equivalent quality as demonstrated in the previous sections. However, the two catalogs also present differences in the data products (e.g., types of photometry, PDZs, or classification) which can be suited for different purposes. We discuss here these differences that can lead to the selection of a particular catalog for different science cases, though, we recommend the use of both catalogs.
The SLP catalog is extremely similar to the Classic/Le Phare version of the COSMOS2020 catalogs in its production. Therefore, for applications where a close comparison with COSMOS2020 results is desired, this catalog is the most suited. This catalog will also benefit from source physical parameters computed in a similar way as for the COSMOS2020 catalogs (Picouet et al., in prep.).
The HPH catalog provides different types of photometry, not present in the SLP one. For instance, it includes cmodel photometry and PSF photometry, that take into account PSF variation across the fields. On the photo-z side, it includes individual PDZ for each object in the catalog. Another interesting feature it the similarities between the HSC pipeline and the LSST pipeline. With its depth and wavelength coverage, the CLAUDS+HSC combination is close to the expected LSST ten-year dataset (Ivezic et al. 2019). Thus, the HPH catalog is most similar to the future LSST data.
The catalogs presented in this work will be publicly released and available for download on several sites8. For the SExtractor photometry, several catalogs are provided with photometric redshifts estimated with Le Phare run with the 6 optical bands and all-bands configurations.
For the hscPipe photometry, all the catalogs are provided with the photometric redshifts estimated with the Phosphoros code. When run with the Phosphoros code, all the catalogs have their full PDZ available in separate files.
The full description of the columns for the SLP and HPH configurations are given in Appendix E together with some practical information not detailed in the core of the paper.
This release is expected to evolve over time and other catalogs will be available. Additional information such as physical parameters derived with the Le Phare code (Picouet et al., in prep.) and photometric redshifts based on convolutional neural network (Pasquet et al. 2019; Ait-Ouahmed et al., in prep.) will also be delivered.
6 Summary
In this work, we presented the first public data release of the combined data over the 20 deg2 of the CLAUDS and HSC surveys. For the four deep and ultraDeep fields of the HSC survey, we processed the CLAUDS data along with the HSC data. For the E-COSMOS and XMM-LSS fields, we also added NIR data parts of the UltraVISTA and VIDEO surveys to extend the wavelength coverage of our catalogs, especially in the ultraDeep regions.
We produced catalogs containing the photometry extracted in two ways. One uses the well-known SExtractor code. The other uses a modified version of the hscPipe that allows the handling of the non-HSC data. CLAUDS and NIR data are pre-processed to match the HSC data format, then are treated by both codes to detect sources and extract their photometry across all bands. We then test the obtained photometry against one another and compare it to the COSMOS2020 photometry. Overall, we find that the photometry from the different methods is in good agreement down to mag ~ 26 for Ugrizy bands, and down to mag ~ 24.5 for the NIR ones. For fainter sources, the agreement declines, with increased bias and scatter for the photometry of both codes. For the hscPipe photometry, we found that the obtained photometry in the grizy bands is extremely consistent with that of HSC PDR2. However, the comparisons with our SExtractor photometry and the COSMOS2020 Farmer photometry show some differences probably related to the background determination and subtraction. hscPipe seems to systematically over-subtract the background, leading to flux loss for all the sources. We also found good agreement when comparing our galaxy number counts with those from Weaver et al. (2022) Farmer catalog. The strongest differences are found in the U and NIR bands, which are mainly due to the difference in detection strategy and error computation.
We computed photo-zs from both our photometry catalogs. Two template-fitting codes were used: Phosphoros was used to produce photo-zs from both hscPipe and SExtractor photometry, and Le Phare was used to process SExtractor photometry. The comparison of the different results shows that the major factor for the differences found between the photo-z catalogs is the photometry, which is similar to the observation made by Weaver et al. (2022) with their four different versions of COSMOS2020 photo-zs. Here, we found that the photo-zs from hscPipe and SExtractor photometry are in good agreement. Whatever the reference redshift they are compared to, we find a scatter σ ≲ 0.05 down to mi ~ 25 or  ~ 24. However, we find that photo-zs derived from hscPipe photometry present a systematically higher scatter, of around 0.01, probably due to the difference in the photometry, as both codes perform very similarly on the SExtractor photometry. Another difference in the results, this time attributed to the photo-z code configurations, is the systematic lack of low photo-z solutions from Phosphoros for faint galaxies, due to the priors used in its configuration, which for badly constrained PDZ is favoring higher redshift solutions. All the photo-z comparisons made show that Phosphoros is as efficient as Le Phare and ready to be used as a stand-alone photo-z code.
~ 24. However, we find that photo-zs derived from hscPipe photometry present a systematically higher scatter, of around 0.01, probably due to the difference in the photometry, as both codes perform very similarly on the SExtractor photometry. Another difference in the results, this time attributed to the photo-z code configurations, is the systematic lack of low photo-z solutions from Phosphoros for faint galaxies, due to the priors used in its configuration, which for badly constrained PDZ is favoring higher redshift solutions. All the photo-z comparisons made show that Phosphoros is as efficient as Le Phare and ready to be used as a stand-alone photo-z code.
The catalogs presented in this work have been publicly released. For the hscPipe photometry, all the data from the images to the fluxes can be fully retrieved in the HSC data access portal. Otherwise, all the CLAUDS images and data product catalogs are accessible on the CLAUDS and DEEPDIP websites and will be updated with upcoming works on photometric redshift and physical parameter estimates.
Acknowledgements
We thank the anonymous referee for providing helpful comments and suggestions that improved the quality of this work. GD acknowledges the support from the Sinergia program of the Swiss National Science Foundation. This work was supported by the Spin(e) ANR project (ANR-13-BS05-0005), the DEEPDIP ANR project (ANR-19-CE31-0023), and by the Programme National Cosmology et Galaxies (PNCG) of CNRS/INSU with INP and IN2P3, co-funded by CEA and CNES. M.S. acknowledges funding support from the Natural Sciences and Engineering Research Council (NSERC) of Canada Discovery Grant and Discovery Accelerator programs, and from the Canada Research Chairs program. C.C. is supported by the National Natural Science Foundation of China, Nos. 11803044, 11933003, 12173045, and in part by the National Key R&D Program of China grant 2017YFA0402704. C.C. acknowledges the science research grants from the China Manned Space Project with No. CMS-CSST-2021-A05. This work is sponsored (in part) by the Chinese Academy of Sciences (CAS), through a grant to the CAS South America Center for Astronomy (CASSACA). The Cosmic Dawn Center is funded by the Danish National Research Foundation under Grant No. 140. JRW and ST acknowledge support from the European Research Council (ERC) Consolidator Grant funding scheme (project ConTExt, Grant No. 648179). These data were obtained and processed as part of the CFHT Large Area U-band Deep Survey (CLAUDS), which is a collaboration between astronomers from Canada, France, and China described in Sawicki et al. (2019). CLAUDS is based on observations obtained with MegaPrime/ MegaCam, a joint project of CFHT and CEA/DAPNIA, at the CFHT which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. CLAUDS uses data obtained in part through the Telescope Access Program (TAP), which has been funded by the National Astronomical Observatories, Chinese Academy of Sciences, and the Special Fund for Astronomy from the Ministry of Finance of China. CLAUDS uses data products from CALET and the Canadian Astronomy Data Centre (CADC) and was processed using resources from Compute Canada and Canadian Advanced Network For Astrophysical Research (CANFAR) and the CANDIDE cluster at IAP maintained by Stephane Rouberol. The Hyper Suprime-Cam (HSC) collaboration includes the astronomical communities of Japan and Taiwan, and Princeton University. The HSC instrumentation and software were developed by the National Astronomical Observatory of Japan (NAOJ), the Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU), the University of Tokyo, the High Energy Accelerator Research Organization (KEK), the Academia Sinica Institute for Astronomy and Astrophysics in Taiwan (ASIAA), and Princeton University. Funding was contributed by the FIRST program from Japanese Cabinet Office, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), the Japan Society for the Promotion of Science (JSPS), Japan Science and Technology Agency (JST), the Toray Science Foundation, NAOJ, Kavli IPMU, KEK, ASIAA, and Princeton University. This paper makes use of software developed for the Large Synoptic Survey Telescope. We thank the LSST Project for making their code available as free software at http://dm.lsst.org. The Pan-STARRS1 Surveys (PS1) have been made possible through contributions of the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, The Johns Hopkins University, Durham University, the University of Edinburgh, Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration under Grant No. NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the National Science Foundation under Grant No. AST-1238877, the University of Maryland, and Eotvos Lorand University (ELTE), and the Los Alamos National Laboratory. This work is based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under ESO program ID 179.A-2005 and on data products produced by CALET and the Cambridge Astronomy Survey Unit on behalf of the Ultra VISTA consortium. Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory as part of the VISTA Deep Extragalactic Observations (VIDEO) survey, under program ID 179.A-2006 (PI: Jarvis).
Appendix A HSC-SSP PDR2 photometry
We compare here the photometry we obtain with the hscPipe on the HSC bands to the HSC PDR2 photometry. The comparison is made in the ultraDeep region of the E-COSMOS field. This field is one of the deepest in the U-band and is the only field observed across all bands. Thus it could be the most sensitive to any problem caused by considering the extra bands in the hscPipe source detection phase and the forced extraction.
Figure A.1 shows the comparison of the magnitudes in the grizy bands. The distributions show nearly no deviations and an extremely tight scatter between our photometry and the HSC PDR2 one, down to the faintest magnitudes. As the data from which the photometry is extracted are exactly the same in both cases, the few differences can only be due to the addition of the CLAUDS and NIR bands in the source detection process. The effect can be the new detection of close-by sources or deblending of new sources, resulting in a slightly different allocation of the flux in the two versions of the photometry.
 |
Fig. A.1 Comparison between our hscPipe photometry and that of HSC PDR2. The dashed lines encompass 68% of the distributions. |
Appendix B COSMOS2020 SExtractor photometry
The Classic configuration of COSMOS2020 photometry extraction is extremely similar to our SExtractor configuration. Indeed, the same code is applied to the same data. However, there are a few differences in the settings of the two extractions, for instance, the bands on which the detection is made. SExtracor uses mostly the bluest bands, Ugrizy (+Ks when available), for the detection, whereas Classic uses the reddest bands, izY JHKs, to build its detection map. Another difference is the step of PSF homogenization of the images that is made with the COSMOS2020 Classic methods but not our SExtractor one.
 |
Fig. B.1 Comparison of COSMOS2020 Classic and SExtractor 2″ aperture magnitudes. |
A comparison of the obtained photometry in both cases, like the one presented in Fig. B.1, shows the differences induced by these configuration choices. The figure presents the comparison of the 2″ photometry between Classic and SExtractor. As expected, the relation between the two photometry catalogs is tight. However, we can observe strong biases, as large as ~0.07mag (e.g., for the z or the Y bands). This effect is due to PSF homogenization.
Appendix C SExtractor-hscPipe 2″ photometry
The 2″ aperture photometry is the one used in both configurations to compute photometric redshifts. In Fig. C.1, we present the direct comparison of the 2″ aperture photometry from SExtractor and hscPipe. We note a tight relation between the measurements obtained with these two codes; however, an asymmetric scatter is present. This asymmetry seems to indicate that the hscPipe fluxes are lower than the SExtractor ones, and this effect is stronger for fainter sources. As these sources are more sensitive to background noise, we interpret the increase in asymmetry toward fainter magnitudes as a sign of stronger subtraction of the background by hscPipe compared to SExtractor. The same conclusion was reached when analyzing Fig. 5, 4 and 7 in Sect. 3.3.
 |
Fig. C.1 Comparison of SExtractor and the hscPipe 2″ aperture magnitudes. |
Appendix D Phosphoros results on SExtractor photometry
Throughout the paper, the results that are presented are those of Phosphoros/hscPipe and Le Phare/SExtractor. This choice makes it difficult to attribute the differences observed in the photo-zs to the codes or to the photometry. To address this problem, we apply here Phosphoros to the SExtractor photometry to create a version of the photo-zs for which only the photo-z codes differ. The configuration used to compute these photo-zs is the same as that presented in Sect. 4.1. We use SExtractor 2″ aperture photometry uncorrected for galactic extinction, that we fit with the templates, extinction law, and priors described in Sect. 4.1. As a result, PDZs are produced, from which the point estimates (median) are computed.
Figure D.1 presents a comparison of the results of SExtractor/Phosphoros (middle panels) with both hscPipe/Phosphoros (top panels) and SExtractor/Le Phare (bottom panels). In all three cases, Ugrizy photo-zs are compared with the spectroscopic sample. In these plots, we can see that the two sets of photo-zs computed from the SExtractor photometry have the same quality when comparing the scatter and the outlier fractions. The scatter from the Phosphoros results is still larger in the bright bins, whereas for the fainter sources the Phosphoros results present a better scatter and outlier fraction than Le Phare photo-zs. This is probably due to the choices in the priors applied by both codes.
These results show that the majority of the differences observed between the photo-zs presented in this work are due to the differences in photometry. Outside of the effect of the priors, there are a few differences between Phosphoros and Le Phare photo-zs, which is expected due to the strong similarities between the two template-fitting codes. All these comparisons thus validate that Phosphoros is able to provide sensible results and is ready to be used by the community.
 |
Fig. D.1 Comparison of Phosphoros results when computing photo-zs on hscPipe (Top) and SExtractor (Middle) photometry. The results are also compared to those of Le Phare and SExtractor (Bottom). The comparison is made using photo-zs computed using only the Ugrizy bands in all three cases. |
Appendix E Description of the released catalogs
The current release (Sect. 5) consists of a set of catalogs for the four HSC-CLAUDS regions. Several versions are available depending on the adopted photometry (based on the HSC pipeline (Sect. 3.1) or SExtractor run (Sect. 3.2)), the photometric code used (Phosphoros (Sect. 4.1) or Le Phare (Sect. 4.2)) and the number of photometric bands considered for the photometric redshift runs (Ugrizy and all-bands). Only sub-regions in the XMM-LSS and E-COSMOS fields are covered with the near-infrared VISTA imaging.
The description of the catalog outputs is given in Tab E.1 for the SExtractor -Le Phare catalogs and in Tab E.2 for the hscPipe -Phosphoros catalogs9.
As the footprints of the different surveys are different, the keyword FLAG_FIELD_B INARY allows the user to restrict the data to a specific dataset by combining its 7 boolean elements (described in Tab E.1). A version defined with a single integer is also available (FLAG_FIELD for Le Phare catalogs). To guarantee the selection of clean objects, the flags MASK and ST_TRAIL must be set to 0 (for SExtractor catalogs) or ISOUTSIDEMASK to “True” (for hscPipe catalogs).
All the catalogs include a stellar classification based on χ2 estimates between the Pickles stellar templates (Pickles 1998) and the galaxy templates. If the sources are compact and better fitted by a stellar template they are flagged as stars (OBJ_TYPE=2 or ISSTAR=True). In addition the Le Phare code also performs a classification using a QSO library (Salvato et al. 2011). If the sources are compact and better fitted by a QSO template, they are flagged as QSO (OBJ_TYPE=1).
For the catalogs based on the Phosphoros code, the PDZs of all sources are provided in separate catalogs for each tract of the HSC data system. They only contain the source IDs and the PDZ values within the redshift range 0 ≤ z ≤ 6 in steps of δz = 0.01. For the catalogs based on the Le Phare code, we also provide the measurement of the physical parameters (Picouet et al., in prep.) derived with synthetic SEDs from the Bruzual & Charlot (2003) library.
Summary of the SExtractor/Le Phare catalog.
Summary of the hscPipe/Phosphoros catalog.
References
- Abazajian, K., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2004, AJ, 128, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, T. M. C., Abdalla, F. B., Allam, S., et al. 2018, ApJS, 239, 18 [Google Scholar]
- Ahumada, R., Prieto, C. A., Almeida, A., et al. 2020, ApJS, 249, 3 [Google Scholar]
- Aihara, H., Arimoto, N., Armstrong, R., et al. 2018a, PASJ, 70, S4 [NASA ADS] [Google Scholar]
- Aihara, H., Armstrong, R., Bickerton, S., et al. 2018b, PASJ, 70, S8 [NASA ADS] [Google Scholar]
- Aihara, H., AlSayyad, Y., Ando, M., et al. 2019, PASJ, 71, 114 [Google Scholar]
- Akeson, R., Armus, L., Bachelet, E., et al. 2019, ArXiv e-prints [arXiv:1902.05569] [Google Scholar]
- Arnouts, S., Moscardini, L., Vanzella, E., et al. 2002, MNRAS, 329, 355 [Google Scholar]
- Baldry, I. K., Liske, J., Brown, M. J. I., et al. 2018, MNRAS, 474, 3875 [Google Scholar]
- Beck, R., Dobos, L., Budavári, T., Szalay, A. S., & Csabai, I. 2016, MNRAS, 460, 1371 [Google Scholar]
- Benítez, N. 2000, ApJ, 536, 571 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, ASP Conf. Ser., 281, 228 [Google Scholar]
- Bohlin, R. C., Colina, L., & Finley, D. S. 1995, AJ, 110, 1316 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch, J., Armstrong, R., Bickerton, S., et al. 2018, PASJ, 70, S5 [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, SPIE Conf. Ser., 4841, 72 [Google Scholar]
- Bradshaw, E. J., Almaini, O., Hartley, W. G., et al. 2013, MNRAS, 433, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [Google Scholar]
- Cheng, C., Huang, J.-S., Willmer, C. N. A., et al. 2021, ApJS, 256, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Hogg, D. W., Blandford, R., et al. 2000, ApJ, 538, 29 [Google Scholar]
- Coupon, J., Czakon, N., Bosch, J., et al. 2018, PASJ, 70, S7 [Google Scholar]
- Dalton, G. B., Caldwell, M., Ward, A. K., et al. 2006, SPIE Conf. Ser., 6269, 62690X [Google Scholar]
- Dawid, A. P. 1984, J. Roy. Stat. Soc. Ser. A (General), 147, 278 [CrossRef] [Google Scholar]
- D’Isanto, A., & Polsterer, K. L. 2018, A&A, 609, A111 [Google Scholar]
- Drinkwater, M. J., Byrne, Z. J., Blake, C., et al. 2018, MNRAS, 474, 4151 [Google Scholar]
- Drlica-Wagner, A., Sevilla-Noarbe, I., Rykoff, E. S., et al. 2018, ApJS, 235, 33 [Google Scholar]
- Emerson, J. P., Sutherland, W. J., McPherson, A. M., et al. 2004, The Messenger, 117, 27 [NASA ADS] [Google Scholar]
- Euclid Collaboration (Desprez, G., et al.) 2020, A&A, 644, A31 [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, et al.) 2016a, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, A., Saglia, R., Paltani, S., Apostolakos, N., & Dubath, P. 2017, A&A, 598, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garilli, B., McLure, R., Pentericci, L., et al. 2021, A&A, 647, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Golob, A., Sawicki, M., Goulding, A. D., & Coupon, J. 2021, MNRAS, 503, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Gwyn, S. D. J. 2008, PASP, 120, 212 [Google Scholar]
- Halevi, G., Goulding, A., Greene, J., et al. 2019, ApJ, 885, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Harikane, Y., Ono, Y., Ouchi, M., et al. 2022, ApJS, 259, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Hartley, W. G., Choi, A., Amon, A., et al. 2022, MNRAS, 509, 3547 [Google Scholar]
- Hildebrandt, H., Erben, T., Kuijken, K., et al. 2012, MNRAS, 421, 2355 [Google Scholar]
- Hoaglin, D. C., Mosteller, F., & Tukey, J. W. 1983, Understanding Robust and Exploratory Data Anlysis (New York: Wiley) [Google Scholar]
- Huang, Y.-J., Urata, Y., Huang, K., et al. 2020, ApJ, 897, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Hudelot, P., Cuillandre, J. C., Withington, K., et al. 2012, VizieR Online Data Catalog: II/317 [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezic, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Iwata, I., Sawicki, M., Inoue, A. K., et al. 2022, MNRAS, 509, 1820 [Google Scholar]
- Iyer, K. G., Gawiser, E., Faber, S. M., et al. 2019, ApJ, 879, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Jarvis, M. J., Bonfield, D. G., Bruce, V. A., et al. 2013, MNRAS, 428, 1281 [Google Scholar]
- Kawanomoto, S., Uraguchi, F., Komiyama, Y., et al. 2018, PASJ, 70, 66 [Google Scholar]
- Kennicutt, J. Robert, C., 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Kron, R. G. 1980, ApJS, 43, 305 [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [Google Scholar]
- Lang, D., Hogg, D. W., & Mykytyn, D. 2016, The Tractor: Probabilistic Astronomical Source Detection and Measurement Astrophysics Source Code Library, [record ascl:1604.008] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [Google Scholar]
- Le Fèvre, O., Tasca, L. A. M., Cassata, P., et al. 2015, A&A, 576, A79 [Google Scholar]
- Lee, K.-G., Krolewski, A., White, M., et al. 2018, ApJS, 237, 31 [Google Scholar]
- Masters, D. C., Capak, P., Stern, D., et al. 2015, ApJ, 813, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Masters, D. C., Stern, D. K., Cohen, J. G., et al. 2019, ApJ, 877, 81 [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLure, R. J., Pearce, H. J., Dunlop, J. S., et al. 2013, MNRAS, 428, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Miyazaki, S., Komiyama, Y., Kawanomoto, S., et al. 2018, PASJ, 70, S1 [NASA ADS] [Google Scholar]
- Momcheva, I. G., Brammer, G. B., van Dokkum, P. G., et al. 2016, ApJS, 225, 27 [Google Scholar]
- Moutard, T., Arnouts, S., Ilbert, O., et al. 2016, A&A, 590, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutard, T., Sawicki, M., Arnouts, S., et al. 2020, MNRAS, 494, 1894 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, J. A., Cooper, M. C., Davis, M., et al. 2013, ApJS, 208, 5 [Google Scholar]
- Pacifici, C., Kassin, S. A., Weiner, B. J., et al. 2016, ApJ, 832, 79 [Google Scholar]
- Paillassa, M., Bertin, E., & Bouy, H. 2020, A&A, 634, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papovich, C., Dickinson, M., & Ferguson, H. C. 2001, ApJ, 559, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquet, J., Bertin, E., Treyer, M., Arnouts, S., & Fouchez, D. 2019, A&A, 621, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Polsterer, K. L., D’Isanto, A., & Gieseke, F. 2016, ArXiv e-prints [arXiv:1608.08016] [Google Scholar]
- Prevot, M. L., Lequeux, J., Maurice, E., Prevot, L., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [Google Scholar]
- Salvato, M., Hasinger, G., Ilbert, O., et al. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
- Salvato, M., Ilbert, O., Hasinger, G., et al. 2011, ApJ, 742, 61 [Google Scholar]
- Sawicki, M., & Yee, H. K. C. 1998, AJ, 115, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Sawicki, M. J., Lin, H., & Yee, H. K. C. 1997, AJ, 113, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sawicki, M., Arnouts, S., Huang, J., et al. 2019, MNRAS, 489, 5202 [NASA ADS] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Scodeggio, M., Guzzo, L., Garilli, B., et al. 2018, A&A, 609, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [Google Scholar]
- Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
- Szalay, A. S., Connolly, A. J., & Szokoly, G. P. 1999, AJ, 117, 68 [Google Scholar]
- Tanaka, M., Coupon, J., Hsieh, B.-C., et al. 2018, PASJ, 70, S9 [Google Scholar]
- Taniguchi, Y., Scoville, N., Murayama, T., et al. 2007, ApJS, 172, 9 [Google Scholar]
- Taniguchi, Y., Kajisawa, M., Kobayashi, M. A. R., et al. 2015, PASJ, 67, 104 [NASA ADS] [Google Scholar]
- Thibert, N., Sawicki, M., Goulding, A., et al. 2021, RNAAS, 5, 144 [NASA ADS] [Google Scholar]
- Weaver, J. R., Kauffmann, O. B., Ilbert, O., et al. 2022, ApJS, 258, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [CrossRef] [EDP Sciences] [Google Scholar]
The associated passband is simply noted U when no distinction is made between the filters, following Sawicki et al. (2019).
Details on the detection configuration can be found here: https://github.com/jcoupon/importExtData/blob/master/config/detectCoaddSources_fixedThreshold.py
CLAUDS website: https://clauds.net; DEEPDIP website: https://deepdip.iap.fr
the catalogs do not contain all the information produced by the hscPipe output, but the raw photometry file are available through the HSC collaboration distribution portal. https://hsc-release.mtk.nao.ac.jp/doc/index.php/data-access__pdr3/
All Tables
Right ascension and declination coordinates (J2000) of the four deep field centers.
Summary of the characteristics of the survey in the different fields: filter coverage, 5σ, 2″ depth and area.
Summary of the results in the different configurations tested in this work depending on i-band cuts.
All Figures
 |
Fig. 1 Transmission curves of the photometric bands accounting for instrument throughputs and typical atmospheric absorption. All curves are scaled to 1. The horizontal lines indicate the 5σ depths in 2″ aperture measured for each band in the ultradeep regions for the E-COSMOS field. |
| In the text | |
 |
Fig. 2 Detection images in the four CLAUDS-HSC fields. The footprints of the different observations are over-plotted in different colors: The CLAUDS Deep layer u and u⋆ bands in blue; the HSC-SSP grizy data in green; the VIDEO Near Infrared data in red (except in the XMM-LSS field where only two J band pointings are available, colored in pink). The footprints of the ultraDeep areas are shown with dashed lines. |
| In the text | |
 |
Fig. 3 Flow chart and illustration of the process of mask creation. Images are smoothed and converted into binary masks with a threshold to identify bright extended objects. To avoid the masking of bright extragalactic objects, the masks are eroded (the pixels at the edges are set to 0), which removes small-scale objects. The masks are then dilated to recover the full size of the original masks for bright stars. Contours are created around masked areas (plotted in green) and we compare our new masks with the Coupon et al. (2018) ones (displayed as white circles and rectangles). |
| In the text | |
 |
Fig. 4 Comparison of hscPipe cmodel magnitudes with SExtractor total magnitudes. The color shades show the density of sources. The solid lines are the median of the distributions and the dashed lines are the ±34% intervals around the medians. These values are computed down to the 5σ depth in each band in the E-COSMOS ultraDeep region (vertical dotted line). |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but comparing hscPipe cmodel magnitudes with COSMOS2020 Farmer total magnitudes. |
| In the text | |
 |
Fig. 6 Same as Fig. 4, but comparing SExtractor with COSMOS2020 Farmer total magnitudes. |
| In the text | |
 |
Fig. 7 Comparison of hscPipe and SExtractor colors computed from 2″ aperture photometry. In all the plots, the x-axis shows the SExtractor 2″ aperture magnitudes of the second term in the colors. The solid line is the median of the distribution, and the dashed lines are the ±34% confidence interval around the median. The vertical dotted lines mark the 5σ depth in the reference band (x-axis one). |
| In the text | |
 |
Fig. 8 Color-color density contours of stars in the different fields computed from the hscPipe PSF photometry. The contours enclose 68% of the stellar loci. The crosses show the positions of main sequence stars from the Pickles library in these color–color diagrams. The offset between templates and observed loci indicates the need of proper extinction and zero-point corrections, which are applied in Sect. 4. |
| In the text | |
 |
Fig. 9 Number counts for SExtractor and hscPipe catalogs compared to COSMOS 2020 Farmer number counts. The number counts in the deep area combine the four fields. A cut at S/N > 3 in all bands is made for SExtractor and hscPipe data displayed as points. The solid black line shows the number counts for COSMOS2020 Farmer photometry. The dashed lines show the hscPipe (dark blue) and SExtractor (light blue) number counts in the ultraDeep region of COSMOS without the cut in S/N. |
| In the text | |
 |
Fig. 10 Comparisons of the photo-zs based on the Ugrizy photometry with spectroscopic redshifts down to i ≤ 22.5 in the four HSC-CLAUDS deep fields. Top panels show the photo-zs computed by Phosphoros code and the hscPipe catalogs, while the bottom panels show the photo-zs computed with Le Phare and SExtractor catalogs. The solid gray lines show the 1:1 line and the dashed lines show the zphoto = zspec ± 0.15(1 + zspec) corresponding to the limits for catastrophic failure. |
| In the text | |
 |
Fig. 11 Same as Fig. 10 but for all the HSC-CLAUDS fields combined and split by i-band magnitudes. The comparison is extended to faint magnitude bins, as indicated in each panel, with faint spectroscopic sources coming from the DEEP-23 (mi ≤ 24), XMM-LSS, and E-COSMOS (mi ≤ 26) fields. |
| In the text | |
 |
Fig. 12 Same as Fig. 11, but for the XMM-LSS and COSMOS fields only and including the near-infrared photometry. |
| In the text | |
 |
Fig. 13 Absolute scaled residuals (Dz) cumulative distributions for the two implementations (HPH: blue lines and SLP: green lines) with the optical (light lines) and optical+NIR (dark lines) catalogs. The horizontal dashed gray lines show the 68% level that all the distributions should cross at Dz = 1 (vertical dashed line). |
| In the text | |
 |
Fig. 14 PIT plots for Phosphoros PDZs computed from the hscPipe photometry with (dark blue) and without (light blue) the infrared bands. |
| In the text | |
 |
Fig. 15 Photo-z comparison with 3DHST redshifts for galaxies down to mH ~ 24 for HPH (top panels) and SLP (bottom panels) catalogs, with the optical+NIR (left panels) and optical only (right panels) bands. The metrics are reported in each panel. |
| In the text | |
 |
Fig. 16 Comparison of HPH and SLP photo-zs to COSMOS2020 results. Top panels present the comparison with Farmer/EAzY results. The bottom ones show the comparison with the mean photo-zs computed from the four COSMOS2020 configurations clipped to only include photo-zs with standard deviation lower than 0.1[1 + mean(z)] between the four-point estimates. photo-zs have been computed using optical and NIR bands. The bins in i-band magnitude are based on the FARMER photometry. |
| In the text | |
 |
Fig. 17 Galaxy redshift distributions (N(z)) in the CLAUDS-HSC regions for three selections, as indicated in the top of each panel. The three panels in the top row show the results based on estimates with all the bands and are thus limited to E-COSMOS and XMM-LSS fields. The two panels in the bottom row show those computed with Ugrizy photometry for the four deep fields. For HPH, the N(z) is either based on the redshift point estimates (median of each PDZ; light red lines) or based on the stack of the individual PDZs (dark red line). For SLP, the N(z) is obtained with the redshift point estimate (blue lines). A comparison is made with COSMOS2020 Farmer/EAzY photo-zs (black lines) in the top panels. The COSMOS2020 curves are weighted to match the CLAUDS-HSC ones. The distributions are constructed in bins of δz = 0.05. |
| In the text | |
 |
Fig. A.1 Comparison between our hscPipe photometry and that of HSC PDR2. The dashed lines encompass 68% of the distributions. |
| In the text | |
 |
Fig. B.1 Comparison of COSMOS2020 Classic and SExtractor 2″ aperture magnitudes. |
| In the text | |
 |
Fig. C.1 Comparison of SExtractor and the hscPipe 2″ aperture magnitudes. |
| In the text | |
 |
Fig. D.1 Comparison of Phosphoros results when computing photo-zs on hscPipe (Top) and SExtractor (Middle) photometry. The results are also compared to those of Le Phare and SExtractor (Bottom). The comparison is made using photo-zs computed using only the Ugrizy bands in all three cases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.