EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 669 (January 2023) A&A, 669 (2023) A43 Full HTML
Open Access
Issue
A&A
Volume 669, January 2023
Article Number A43
Number of page(s) 14
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/202243673
Published online 06 January 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model.

Open Access funding provided by Max Planck Society.

1 Introduction

Diagnostic stellar spectroscopy is one of the major instruments in modern astrophysical research. With the advent of large-scale stellar surveys, such as Gaia-ESO, Apache Point Observatory Galactic Evolution Experiment (APOGEE), Sloan Digital Sky Survey (SDSS), Galactic Archaeology with HERMES (GALAH), Gaia, 4-metre Multi-Object Spectrograph Telescope (4MOST), and WHT Enhanced Area Velocity Explorer (WEAVE), we are entering a new era of precision stellar physics. Large sets of high-quality stellar spectra can be exploited to derive direct observational constraints on stellar chemical composition, and therefore on the detailed chemical evolution of stellar populations and the Milky Way galaxy.

In this study, we focus on the role of physical processes in stellar spectroscopy, in particular on the physics of non-local thermodynamic equilibrium (NLTE) in the determination of stellar metallicities and detailed abundances. Much of the previous work in the field has been carried out under the assumption of local thermodynamic equilibrium (LTE), in which the atomic number densities have been computed using the Saha-Boltzmann formulae from statistical mechanics. However, in the atmospheres of FGKM-type stars, the complex interaction of strong, highly non-local radiation fields and the gas particles leads to deviations from LTE. Nowadays, this detailed microphysics can be modeled using the concept of statistical equilibrium (e.g., Asplund 2005; Mashonkina et al. 2007; Lind et al. 2011; Bergemann et al. 2012b; Amarsi et al. 2016; Semenova et al. 2020; Masseron et al. 2021), in which chemical elements are modeled under the assumption of a trace element that includes the NLTE effects in the line formation and spectrum synthesis, but ignores their influence on the energy balance, and thus the thermodynamic structure of stellar atmospheres. This assumption has, so far, been used in all studies, in which NLTE modeling is used to determine abundances for large stellar samples (Kovalev et al. 2019; Buder et al. 2020; Amarsi et al. 2020).

Another concept in classical stellar spectroscopy is the assumption of 1D geometry and hydrostatic equilibrium (HE). Different families of 1D HE LTE atmospheric models have been computed, including Phoenix (Hauschildt et al. 1999), ATLAS (Kurucz 1979, 2005), MARCS (Gustafsson et al. 2008), and MAFAGS-OS (Grupp 2004a,b). However, despite their general utility and low computational cost, the models offer only an approximate description of stellar atmospheres, as convection and turbulence – critical physical processes in stars with convective envelopes – are replaced by highly simplified parametrizations (e.g., Nordlund et al. 2009; Freytag et al. 2012). Convective energy transport is typically modeled using the mixing-length theory (Böhm-Vitense 1958), and turbulence is represented using the “macroturbulence” and “microturbulence” parameters. The classical 1D HE models have the advantage of including a very detailed account of opacities, although the opacities are still computed in LTE.

The main goal of this paper is to introduce an open-source NLTE version of the widely used Turbospectrum synthesis code (TS, Alvarez & Plez 1998; Plez 2012)1. Our main motivation is to provide a public software that allows the user to generate realistic wide-band synthetic stellar spectra of FGKM-type stars, relying on state-of-the-art NLTE model atoms for multiple chemical elements simultaneously and at low computational cost, comparable to standard 1D LTE codes such as MOOG (Sneden 1973) or Synthe (Kurucz 1970). The code can self-consistently handle complex blends, hyperfine structure, isotopic shifts, and enables the treatment of very large – several million – linelists, including all atoms and tens of molecules. We also provide associated ready-to-use 1D and average 3D model atmospheres in the appropriate format, and the grids of NLTE departure coefficients. The code is conceptually similar to the SIU (Reetz 1991, 1999), SME (Valenti & Piskunov 1996; Piskunov & Valenti 2017), and SYNSPEC (Hubeny et al. 2021) codes, which operate, in the NLTE case, with precomputed grids of NLTE departure coefficients2,3. However, the NLTE versions of these other codes in the literature are not open-source. Also, different from SIU, the NLTE TS code feeds on a more comprehensive and up-to-date set of background bound-free and bound-bound opacities. Furthermore, it is superior to SME in terms of computational efficiency, as a detailed high-resolutio spectrum from 400 to 900 nm of a typical G-type solar-metallicity star can be computed on timescales of a few minutes. For example, we were able to generate a 1D NLTE spectrum of the Sun with this wavelength range and a sampling of 0.05 Å on a 2.5 GHz processor, computing roughly 35 million atomic and molecular lines in 12 min. This model also included NLTE computations for all 13 elements for which we have pre-computed departure coefficient grids. The most recent version of SYNSPEC also offers a capability to calculate NLTE synthetic spectra, but NLTE is included in lines of H, Ca, and Mg (Hubeny et al. 2021) only.

The paper is organized as follows. Section 2 describes Turbospectrum (hereafter, TS) and the model atmospheres used. We then outline the updates to TS in Sect. 3, comment on the comparison with another radiative transfer code (Sect. 3.1), demonstrate the capability to compute NLTE calculations for multiple elements simultaneously (Sect. 3.2), and the ability to compute 1D and 〈3D〉 NLTE H line profiles (Sect. 3.3). In Sect. 4, we provide an example of the type of abundance analysis that can be done with TS using observations of Gaia benchmark stars as a sample. Finally, we present the results of our example analysis for Fe and Ca in Sect. 5, and we discuss our findings in the context of previous studies in the literature in Sect. 6.

2 Methodology

2.1 Model atmospheres

We make use of two grids of stellar model atmospheres computed for low-mass late-type (FGKM) stars. We use the 1D line-blanketed hydrostatic MARCS models (Gustafsson et al. 2008) and average 3D Stagger models (hereafter, 〈3D〉) from Magic et al. (2013a,b). We briefly describe the models below.

The MARCS4 models were computed in LTE, solving the equation of radiative transfer in plane-parallel geometry for dwarf models (surface gravity log g[cm s−2] ≥ 3.0) and in spherical symmetry for giants (log g ≤ 3.5). Convective energy transport is computed in the framework of the mixing-length theory (Henyey et al. 1965), with the mixing-length coefficient α set to 1.5. Very comprehensive treatment of radiative bound-bound and bound-free opacities, including all atoms in the first and second ionization stages, as well as 519 di- and tri-atomic molecules, are included in the code. The grid relies on the solar abundance mixture by Grevesse et al. (2007), but the abundances of oxygen and α-capture-elements are enhanced for models with metallicity [Fe/H] ≤ −0.25, reflecting the typical elemental abundance ratios in stars as a function of metallicity in the solar neighborhood5. The parameter space of the MARCS grid is shown in Fig. 1. The grids cover the following range of stellar parameters: Teff = 2500, 8000 K with a step of 100 K from 2500 to 4000 K and 250 K from 4000 to 8000 K, log g = 0, 5.5 dex with a step of 0.5 dex, [Fe/H] = −5.0, 1.0 with a step of 1 dex from −5 to −3, 0.5 dex from −3 to −1, and 0.25 dex from −1 to 1 dex. The grids also include three different values for microturbulence at 1, 2, and 5 km s−1.

The 〈3D〉 Stagger models were adopted from Magic et al. (2013a,b)6. These models were constructed by spatial and temporal averaging of 3D radiation-hydrodynamics (RHD) simulations of stellar surface convection. Specifically, averages were carried out on surfaces of equal optical depth (log τ5000). The Stagger code relies on the modified version of the equation of state (EoS) from Mihalas et al. (1988) and abundances were taken from Asplund et al. (2009). For a more detailed description of the input physics and technical aspects, we refer the reader to Magic et al. (2013a,b). Since in these simulations, convection and turbulence are the natural consequences of solving the equations of fluid dynamics coupled with the equation of radiative transfer, there is no need to introduce ad hoc free parameters, such as the mixing length or “microturbulence” ξt, which directly affect the line opacity. Therefore, we include a depth-dependent velocity profile computed from the original 3D velocity field in the simulation cubes in the form of a microturbulence with a depth-dependent value of one standard deviation of the 3D components, as suggested in Uitenbroek & Criscuoli (2011).

It has not yet been extensively tested whether this approximation provides the most realistic description of turbulent flows in stellar atmospheres. For some elements such as Mg (Bergemann et al. 2017), the 〈3D〉 NLTE approach works well, whereas for the other species such as Fe (Amarsi et al. 2016), the differences between 〈3D〉 NLTE and full 3D NLTE are somewhat larger. Nonetheless, the 〈3D〉 model atmosphere approach has an important advantage over standard 1D hydrostatic model atmospheres, in that it eliminates two important free parameters (mixing length and ξt) from the modeling. Therefore, and most crucially, our 〈3D〉 spectral models are predictive. In particular, numerically the classical ξt is defined as a simple correction to the line opacity, which is commonly either set by hand, or is optimized using some recipes defined by each user. Thus, it is partially degenerate with the abundances of chemical elements. This implies, strictly speaking, that the user has the freedom to influence the resulting chemical abundance estimate obtained by fitting standard 1D LTE synthetic spectra to the observed data.

Figure 2 compares the structures of the MARCS and 〈3D〉 Stagger models by showing temperature as a function of optical depth at 5000 Å (log τ5000Å) for several model atmospheres representative of low-mass dwarfs (effective temperature Teff = 6000 K, log g = 4.5) and giants (Teff = 4500 K, log g = 2.0) at low and solar metallicity ([Fe/H] = −2 and 0, respectively). As can be seen, the differences between the 1D and 〈3D〉 models are generally largest in the interior. In the case of the low-metallicity dwarf, the outer layers of the atmosphere also show significant differences almost reaching 1000 K.

thumbnail Fig. 1

MARCS model atmosphere grid used in this work. PARSEC isochrones (Bressan et al. 2012) calculated for [M/H] = −2 and 0 are overplotted as dashed and solid black lines, respectively.
thumbnail Fig. 2

Comparison between the structures of the MARCS to 〈3D〉 Stagger models. The top two panels show temperature as a function of optical depth at 5000 Å for model atmospheres of four types of stars. The open (giant stars) and solid (dwarf stars) black circles and squares show the MARCS model atmospheres for the parameters given in the legend (low metallicity to the left, solar metallicity to the right). The corresponding 〈3D〉 Stagger models are shown as cyan dots. The bottom two panels show the difference between the MARCS model and the 〈3D〉 Stagger model for each case, following the same convention for open and solid circles or squares as in the top panels.

2.2 Turbospectrum

Turbospectrum (Alvarez & Plez 1998; Plez 2012) is an LTE radiative transfer code based on the same methods and input physics as the MARCS model atmosphere code. It uses the Feautrier scheme (Feautrier 1964; Nordlund 1984) to solve the radiative transfer equation including scattering, and works in plane-parallel and spherically symmetric geometry for flux and intensities at various angles. Rayleigh and electron scattering in the continuum is fully taken into account, although we note that this effect is mostly relevant in the atmospheres of extremely metal-poor red giants and it influences only the spectra in the near-UV (Gustafsson et al. 1975; Cayrel et al. 2004; Sobeck et al. 2011). TS uses exactly the same EoS as MARCS, with up to four ions of all 92 natural elements, and hundreds of molecules and radicals. Continuous opacities are identical in both codes, and they include bound-free transitions for all major species (H I, H−, He I, C I, C II, N I, N II, O I, O II, Mg I, Mg II, Al I, Al II, Si I, Si II, Cal, Ca II, Fe I, and Fell, and an approximation for the remaining metals, and CH and OH), free-free transitions for H I, H−, He I, He−, C I, C II, C−, N−, O−, Mg I, Si I, , CO−, and H2O−, collision induced absorption for H I+H I, H I+He I, H2+H I, H2+H2, and H2+He I, scattering by electrons, as well as Rayleigh scattering by H I, H2, and He I. References to all the data used are provided in Gustafsson et al. (2008). The H− opacity was improved in the present version from the original Wishart (1979) to the more recent McLaughlin et al. (2017a,b). For the solar model, the difference in the optical and near infrared is less than 0.5%. Bound-free opacity for NH was also added following Shen et al. (2014; P.C. Stancil, priv. comm.). Hydrogen bound-free and line opacity is treated using the code of Barklem & Piskunov (2015). Line broadening is included through a Voigt profile resulting from the convolution of the Gaussian microturbulence and thermal broadening profile with the natural and collisional broadening Lorentz profile. Broadening caused by elastic hydrogen collisions is treated with the so-called “ABO” (Anstee, Barklem, O’Mara) theory (Anstee & O’Mara 1995; Barklem & O’Mara 1997; Barklem et al. 2000). Electron (linear Stark) collisional broadening has also been added in the present version.

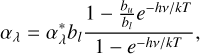The NLTE version of TS uses grids of NLTE departure coefficients to compute NLTE line profiles. This is done by correcting the line opacity and the line source functions of all lines, similar to other spectrum synthesis and abundance analyses codes, such as SIU and SME. The NLTE extinction coefficient is obtained from the LTE value using (1)

where bu and bl are the departure coefficients for the upper and lower levels, respectively. The other symbols having their usual meaning. The emissivity of a line is given by (2)

where Bλ is the Planck function, and the source function at a given wavelength is obtained by summing the emissivity from the continuum and all contributing lines: (3)

For the elements that are computed in LTE, the standard Saha-Boltzmann distribution functions are used.

TS can compute large chunks of spectra, including lines from all species, with some elements in LTE and others in NLTE, enabling the treatment of blends. The elements to be calculated in NLTE are handled by the user via a dedicated input file. A new feature allows the user to specify a list of spectral windows to be calculated, reducing computing time and the size of the output. There is not yet any provision for taking into account departures from LTE for the continuum opacities, but we do not expect any significant differences associated with this approximation in the optical and near-IR wavelength ranges, which are typically used as diagnostics in stellar spectroscopy. Haberreiter et al. (2008) showed that using NLTE opacity distribution functions in the calculations of the solar model atmosphere has a significant effect only at wavelengths shorter than 260 nm (UV). Young & Short (2014) investigated NLTE model atmospheres for red giants. Also, their work shows that NLTE effects influence the spectral energy distribution in stars with Teff ≳ 4000 K only below 400 nm.

2.3 Line list

Concerning atomic and molecular data, we make use of the Gaia-ESO line list (Heiter et al. 2021), which covers the wavelength ranges from 475 to 685 nm and from 850 to 895 nm. The atomic part of the line list is mainly based on experimental data supplemented by the most reliable theoretical data (see Heiter et al. 2021 for a detailed description of the data sources). For the wavelength ranges not covered by the Gaia-ESO line list, we use data from the VALD database7 (Piskunov et al. 1995; Ryabchikova et al. 2015). It is important to note that the line list was not calibrated on any observational data, which is sometimes done in the literature (e.g., Smith et al. 2021), and therefore it is not tied to any particular type of star or stellar model, which makes it universally applicable to any object in the entire parameter space of cool stars.

Table 1

Literature studies containing the NLTE model atoms.

2.4 Statistical equilibrium

The grids of departure coefficients were computed using the 1D NLTE radiative transfer solver MULTI (Carlsson 1986), updated as described in Bergemann et al. (2019) and Gallagher et al. (2020). Statistical equilibrium of an NLTE element in MULTI is computed under the standard assumption of a trace element that assumes that deviations from LTE do not influence the structure of the input model atmosphere.

The departure grids were computed for 13 chemical elements, namely H, O, Na, Mg, Si, Ca, Ti, Mn, Fe, Co, Ni, Sr, and Ba. The NLTE model atoms were taken from the studies listed in Table 1.

For Fe, we solved the radiative transfer and statistical equilibrium equations for each metallicity ([Fe/H]) point in the MARCS and STAGGER model grids. For all other chemical elements, we solved the same equations by varying the element abundance within [−2, +1] dex in abundance steps of 0.1 dex relative to the corresponding solar ratio [X/Fe] (which is always zero by definition). The grid of NLTE departure coefficients is available for each of the 12 chemical elements, described in Table 18.

The NLTE grids of departures were computed for each model atmosphere in the MARCS and STAGGER grids (as described in Sect. 2.1) and are supplied with the public release of the code. We recommend using the model atmosphere grids supplied with the grids of departure coefficients, because we also provide a dedicated interpolating function (based on the Fortran code by Thomas Masseron, see also Gustafsson et al. 2008) that takes the rectangular grids of model atmosphere and the corresponding grids of departures coefficients, and produces an interpolated atmosphere structure and departure file for any desired combination of stellar parameters. We adjusted this module to also interpolate the grid of departure coefficients in four dimensions: Teff, log g, [Fe/H], and elemental abundances. We have also created a new module that provides the same function for model atmospheres formatted for use with MULTI to handle the interpolation of the 〈3D〉 models from STAGGER9.

thumbnail Fig. 3

Synthetic spectrum computed with a 〈3D〉 Stagger model atmosphere in NLTE, compared with a spectrum calculated in 1D LTE. The stellar parameters used in the calculations are indicated in the figure inset.

3 New capabilities of Turbospectrum

3.1 Comparison with NLTE calculations from MULTI

We tested our method for calculating NLTE line profiles using TS by generating NLTE model spectra using the MULTI code, and by comparing the equivalent widths (EWs) of various Ca lines. MULTI is the code that we use to calculate the NLTE statistical equilibrium and NLTE grids of departures, and so it provides the most self-consistent anchor point for our TS results. The same four sets of atmospheric parameters as in Fig. 2 were taken from grid points of the MARCS model atmosphere grid and chosen as test cases to represent giant and dwarf stars at solar and low metallicity. As mentioned previously, the giant stars were given an effective temperature of 4000 K and a surface gravity of log g = 2.0, and the dwarfs were given an effective temperature of 6000 K and a surface gravity of log g = 4.5. Our low-metallicity model used an [Fe/H] of −2.0 dex.

The results of this test for each of the model spectra are shown in Table 2. Direct comparisons of NLTE EWs are not useful, because small discrepancies may arise due to other differences between the two codes in quantities such as EoS, background opacities, or radiative transfer solvers and angle quadrature. We therefore calculated with each code the ratio of NLTE to LTE EWs for a given set of Ca lines. Ca was chosen as the element, for which the NLTE abundance corrections show a large dynamic range, as it is positive for some lines and negative for the others. The average percent difference of the ratio of EWs (EWNLTE/EWLTE) computed with MULTI and TS is given in the final column of the table. All lines show a difference below 0.5%, with the average being below 0.1%, showing that the TS predicts correct NLTE effects in spectral lines.

We do not detect any systematic bias against the atomic properties of the transition, the lower- and upper-level excitation potential, oscillator strength, or wavelength. Also, there is no evidence that either of the codes systematically over-or underestimates the line EWs. A similar test was performed for the Fe lines, confirming our results for Ca. Therefore, we conclude that our method for calculating NLTE line profiles with TS is robust.

Table 2

Average percent difference between TS and MULTI calculations of the ratio of NLTE to LTE equivalent width of nine Ca lines computed for four different sets of parameters.

3.2 NLTE calculations with multiple elements

The main novelty of the new TS is that it can compute NLTE spectra, treating multiple elements in NLTE at the same time. Computing multiple elements in NLTE is crucial for studies that want to consider blended lines for abundance determination or study large regions of spectra where NLTE contributions to multiple elements are important.

To test and showcase this capability, we generated spectra with 〈3D〉 NLTE line profiles for H, O, Mg, Ca, Mn, and Fe for all four test cases that we used to compare our NLTE calculations with MULTI, and compared them to spectra generated using 1D LTE. The model spectra were then convolved to a resolution of R = λ/∆λ ~ 20 000 to demonstrate how the differences between the two models would appear at a resolution similar to the resolutions used for future surveys such as WEAVE and 4MOST. Figure 3 shows these two spectra for comparison in a window centered on 5190 Å. There are several areas where the 1D LTE model differs significantly from the 〈3D〉 NLTE model.

thumbnail Fig. 4

Hα line profiles of the Sun, Procyon, HD 84937, and HD 140283. The black lines are observations made by UVES. The red and cyan lines are the 1D LTE and 〈3D〉 NLTE model profiles, respectively, generated with Turbospectrum. Inset in the lower right corner of each panel is a zoomed-in look at the core of each line.

3.3 H line profiles

The new version of TS also has the ability to calculate H line profiles using NLTE. The wings of Hα are arguably the most sensitive and powerful spectroscopic diagnostics of effective temperature for dwarf stars (e.g., Fuhrmann et al. 1993, 1994; Grupp 2004a,b). It is therefore important to compare the H line profiles generated with NLTE physics with LTE profiles and observations.

Figure 4 shows the simulated 〈3D〉 NLTE and 1D LTE Hα lines compared to the observed spectra for the Sun, Procyon, HD 84937, and HD 140283.The model lines were calculated using independent stellar parameters for these targets, obtained using non-spectroscopic diagnostics (see Sect. 4.1).

Clearly, the 〈3D〉 NLTE models provide an excellent fit to the Hα wings, supporting previous studies of H lines in the literature (Amarsi et al. 2018). In contrast, the 1D LTE models fail to reproduce the wings, leading to a systematic underestimation when using the line to derive Teff. The line cores cannot be described even in 〈3D〉 NLTE. This is not a concern in this work because it is well known that the Balmer line cores are formed in chromospheres, and so require magneto-hydrodynamical modeling and NLTE for a self-consistent description (Leenaarts et al. 2012; Bergemann et al. 2016).

4 Example abundance analysis with NLTE Turbospectrum

4.1 Observational data

Our observational sample is drawn from the Gaia FGK benchmark star sample (Jofré et al. 2018), and we refer the reader to Jofré et al. (2014) and Heiter et al. (2015) for the details on the methods used for the determination of the atmospheric parameters and abundances. In short, the sample comprises 31 FGK-type stars covering a broad range of Teff, log g, and [Fe/H], and it includes main-sequence dwarfs, turn-off stars, subgiants, and red giants. For all of these stars, spectra collected with the Ultraviolet and Visual Echelle Spectrograph (UVES) and High Accuracy Radial velocity Planet Searcher (HARPS) spectrographs at the ESO Very Large Telescope (VLT) and the La Silla 3.6 m telescope are available, and we make use of these data in this work. The typical signal-to-noise ratio of the data exceeds 1000, and the resolving power is R = 47 000 for UVES and R = 115 000 for the HARPS data. The spectra cover a broad wavelength range of 480–680 nm (UVES) and 378–691 nm (HARPS). For more details on the spectra and their reduction, including the continuum normalization, we refer the reader to Blanco-Cuaresma et al. (2014).

We adopt the reference stellar parameters for these stars from Jofré et al. (2018), with a few updates as described in Gent et al. (2022). The Teff estimates for the majority of the stars are based on angular diameters determined from interferometric data collected with several different facilities, such as Center for High Angular Resolution Astronomy (CHARA) or the Very Large Telescope Interferometer (VLTI), together with bolometric flux estimates. For a few stars, the angular diameters were determined from surface-brightness relations using (B − K) and (V − K) color indices, or from infrared photometry (Heiter et al. 2015, Sect. 3). The surface gravities were determined using angular diameters, HIPPARCOS parallaxes10, and masses estimated from evolutionary tracks (Heiter et al. 2015, Sect. 4). For the stars in the sample that have asteroseismic data, it was verified that the surface gravities determined from the angular diameters agree with those calculated from the frequency of maximum power and the Teff values (Heiter et al. 2015, Sect. 5.3). Metallicities and microturbulence estimates were determined by fitting Fe line profiles or equivalent widths in LTE using MARCS models and several different radiative transfer codes, and applying NLTE corrections to the resulting Fe line abundances (Jofré et al. 2014). For some of the stars (Procyon, HD 122563, HD 140283), more accurate metallicities computed using a full 3D NLTE approach became available recently (Amarsi et al. 2016). Therefore, we also use 3D NLTE [Fe/H] values, where possible.

thumbnail Fig. 5

Normalized flux vs. wavelength for four sample Fe I lines in an observed solar spectrum, together with model fits. Observations are shown as black circles, 1D LTE model fits are shown as red lines, and 〈3D〉 NLTE model fits are shown as cyan lines. Residuals for the 1D LTE and 〈3D〉 NLTE model fits are shown as red and cyan points, respectively. The points have been shifted by 0.1 and are plotted above each spectrum with a dashed line to indicate the zero point at 1.1.

4.2 Fitting stellar parameters with Turbospectrum

For this work, we developed a Python module that wraps NLTE TS, which can be used to directly determine stellar parameters, including, for example, Teff, log g, [Fe/H], ξt, Vmac, and abundances from the observed stellar spectrum. In other words, TS can be used to not only generate synthetic grids, but also as a standalone code to perform spectrum synthesis and stellar parameter diagnostics. This method allows us to instantly update the macro- and microphysics (atomic and molecular data) of our models, and seamlessly switch between 1D NLTE, 1D LTE, 〈3D〉 LTE, or 〈3D〉 NLTE between runs without any overhead. This also allows us to directly investigate the quality of the spectral line fits and enhance the flexibility of the analysis, as the abundance of any chemical element in the periodic table can be determined directly, provided a suitable line list exists.

We use the Nelder-Mead numerical method (also known as the simplex method) to fit a set of observed lines within a predefined spectral range with a model spectrum. The line choice is controlled by a set of user-defined line and continuum masks. The Nelder-Mead method uses a simplex to test n + 1 points in an n-dimensional space until the minimum of a function consisting of n dimensions is found. We apply this method to a given set of spectral windows centered on spectral features of the element under consideration. The element abundance, a radial velocity shift, and - if needed - other parameters (such as micro-turbulence) are simultaneously adjusted until the χ2 value is minimized and a solution to both parameters is determined. The selection of diagnostic lines is described in Sect. 2.3.

For fitting multiple lines at a time in a single spectrum, we find that the precision of our abundances is improved by setting the microturbulence based on an empirical relation from Gaia-ESO related to the stellar parameters of the star being fit (see Bergemann et al. in prep and references therein for a description of the relation used)11. We also adopt a macroturbulence value of 3.5 km s−1 for all stars in the sample and apply a broadening correction to the synthetic spectra to get line profiles that better match the observed spectra. Our Python module used to conduct the fitting handles the convolution of synthetic spectra automatically.

In Fig. 5, we show 〈3D〉 NLTE and 1D LTE profiles of selected Fe I lines. Both models use the same input parameters and input Fe abundance, the fit being optimized for the NLTE case. The quality of the fit is very good, suggesting that the new approach can be used for a robust spectrum synthesis in the parameter space described by our input models.

Our Python wrapper used for the fitting can be found at the following Github page12. It makes use of the model interpolator mentioned in Sect. 2.4 and the latest version of TS, both of which can be found on the main TS Github page. In addition to our fitting module, we also include a script that can be used to run the model interpolator and generate a synthetic spectrum with TS for a given set of stellar parameters.

thumbnail Fig. 6

The difference between the line abundances derived from an NLTE and an LTE fit for both 〈3D〉 (Stagger) and MARCS model atmospheres for various Fe I lines, for HD 84937 and HD 140283, as a function of excitation potential of the line. Fits using MARCS model atmospheres are shown as red squares and those using 〈3D〉 model atmospheres are shown as black circles. The differences are given in units of dex.

5 Abundance results

5.1 Metallicity

Figure 6 shows the differences between NLTE and LTE abundances of Fe I lines for two example stars in the sample. The atomic parameters of Fe I lines used for these fits are given in Table 3. The abundances were computed using 1D LTE, 1D NLTE, 〈3D〉 LTE, and 〈3D〉 NLTE. These figures confirm that the 1D LTE and 〈3D〉 LTE models generally underestimate the abundances derived from the lines of neutral species, similar to other findings in the literature (Bergemann et al. 2012b, 2019; Amarsi et al. 2016; Sitnova et al. 2016; Lind et al. 2017). We find no trend with the line EW, other than the fact that weak lines (especially those with EW < 5 mA) show a higher spread in abundance for the same star than strong lines, as expected. Similarly, there is no clear trend in abundance with lines arising from different energy levels. However, there does appear to be a trend in the difference between NLTE and LTE abundance with the excitation potential for 〈3D〉 models. As seen in Fig. 6, lines with higher excitation potential tend to have a lower ∆(NLTE − LTE). This is consistent with the results by Bergemann et al. (2012b) and Amarsi et al. (2016), who found the same trends in their analyses of Fe lines in FGK-type stars.

Figure 7 shows the differences between 1D NLTE and 〈3D〉 NLTE abundances and the 1D LTE results. We note that the available 〈3D〉 model atmosphere grid is limited in terms of the Teff-log g coverage, and therefore, in an attempt to avoid extrapolation, we could not determine Fe abundances for selected types of stars (very cool red giants and red supergiants). The differences are systematic, which simply reflects the smooth and regular behavior of NLTE effects with the Teff, log g, and [Fe/H] of the star. As shown in previous works (Bergemann et al. 2012b; Bergemann & Nordlander 2014), NLTE effects on Fel lines grow with increasing Teff, and decreasing surface gravity and metallicity. In hotter or more metal-poor stars, the more intense UV radiation field enhances over-ionization, which is the main driver of NLTE effects in neutral species with large photo-ionization cross-sections and low ionization potentials. In lower-log g stars (lower densities), larger NLTE effects are rather caused by less efficient collisional thermalization. For most stars we find an average difference of about +0.05 dex between the [Fe/H] determined using 1D NLTE and 1D LTE. When 〈3D〉 model atmospheres are used (Fig. 7, bottom panel), the differences for the stars in our sample fall between 0.00 and +0.15 dex, with lower-metallicity stars showing the largest differences. This value for the overall difference and slight trend with metallicity agrees well with differences expected by model calculations (Bergemann et al. 2012b; Amarsi et al. 2016; Semenova et al. 2020).

Figure 8 shows the final 〈3D〉 NLTE or 1D NLTE metallicities determined by minimizing the total χ2 of all Fe lines. The values are compared to the 1D NLTE values from Jofré et al. (2018). Generally, we find that the metallicities are in good agreement with those in the literature within the uncertainties, with no systematic offsets between stars observed with either instrument (HARPS or UVES). We emphasize, however, that there is no direct model-independent method to derive abundances, which is why accuracy cannot be tested this way. Our approach, using 〈3D〉 model atmospheres, is physically more realistic compared to Jofré et al. (2018), and therefore differences in results are expected. For the Sun, we obtain a 〈3D〉 NLTE iron abundance of log A(Fe) = 7.50, which is consistent within the uncertainty with the 3D NLTE estimate by Lind et al. (2017) and Magg et al. (2022). Minor differences are expected, not only because of methodological differences (〈3D〉 NLTE vs. 3D NLTE, different line selection), but also because solar intensities, rather than fluxes, were used in Lind et al. (2017). The Fe results are given in Table 4, and the differences between 1D LTE, 1D NLTE, and 〈3D〉 NLTE are given in Table 5.

Table 3

Fe I lines used for fitting.

thumbnail Fig. 7

Difference in the [Fe/H] value determined using 1D NLTE (top) and 〈3D〉 NLTE (bottom) and 1D LTE, as a function of [Fe/H]. Symbols are color coded based on the effective temperature of the star. Fits to spectra of the Sun are indicated as stars.
Table 4

Results for Fe I ([Fe/H] using a solar abundance of log A(Fe) = 7.50).

5.2 Ca abundances

In addition to Fe, we derived Ca abundances using the new TS to compare our results with what has been observed in the literature. Ca was chosen because, in contrast to Fe, the lines of Ca I show pronounced negative NLTE effects. We studied abundances for each individual line given in Table 6 of the same stars for which we conducted an individual line analysis for Fe by minimizing the χ2 value for each line individually in our fitting procedure. Figure 9 shows the difference between the NLTE and LTE abundances as a function of EW of a given line for the Sun and Procyon, for both MARCS and average Stagger model atmospheres. We chose to present the abundances as a function of EW instead of excitation potential as done in the previous section, because these lines all had excitation potentials between 1.8 and 3 eV, with most lines having an excitation potential of ~2.5 eV. In general, we find that NLTE abundances are lower than LTE abundances for both 1D and 〈3D〉 model atmospheres. This result is similar to what was observed by Mashonkina et al. (2017) for the same lines as the ones we used. We also find a correlation with EW for the LTE abundance fits as the abundances of lines with EW > 75 mÅ increase with increasing EW. We do not find the same correlation in the NLTE fits. The same correlation for LTE fits was also observed by Mashonkina et al. (2017) in their measurements of Procyon. This behavior explains the trend observed in the ∆(NLTE − LTE) versus EW diagram for Procyon (Fig. 9, right panel), where the difference becomes more negative with increasing EW, especially for EW ≳ 100 mÅ.

For the remaining stars in the sample, we calculated Ca abundances by minimizing the χ2 for all Ca lines simultaneously, similar to what was done for Fe. We used the effective temperature and surface gravity from the literature (and given in Table 4), and our final [Fe/H] value from the previous section. For simplicity, we used the 〈3D〉 NLTE [Fe/H] value for all Ca fits where available, and the 1D NLTE [Fe/H] value for the cases where we were not able to interpolate a 〈3D〉 model as described in the previous section. Our Ca abundance results for the sample of Gaia benchmark stars are shown in Table 7. We also analyzed the difference between NLTE and LTE fits to compare with what has been modeled and determined in the literature. We find that the NLTE Ca abundance for both 1D and 〈3D〉 is ~0.1 dex less than the LTE 1D fit with differences ranging from 0.0 dex to roughly −0.2 dex, as shown in Fig. 10. For stars with low metallicity ([Fe/H] ~ −2.0), the difference is very small and close to zero for most stars in the sample. The smaller difference in these stars is likely due to the previously mentioned LTE abundance trend with EW. Since the low-metallicity stars do not have lines stronger than 100 mÅ, the LTE Ca abundances are not skewed toward stronger values by these lines, which means the results are closer to the NLTE abundances. Our differences between the 1D LTE, 〈3D〉 LTE, 1D NLTE, and 〈3D〉 NLTE Ca abundance determinations are shown fully in Table 8.

thumbnail Fig. 8

[Fe/H] determined from the Turbospectrum fit versus values from the literature (see text). For the TS fit, the adopted value is the 〈3D〉 NLTE fit, or the 1D NLTE fit in cases where a 〈3D〉 NLTE fit was not available.
thumbnail Fig. 9

The difference between the line abundances derived from an NLTE and an LTE fit for both 〈3D〉 (Stagger) and MARCS model atmospheres for each Caí line fit, for the Sun and Procyon, as a function of equivalent width of the line. Fits using MARCS model atmospheres are shown as red squares and those using 〈3D〉 model atmospheres are shown as black circles.
Table 5

Abundance corrections for Fe I lines (relative to 1D LTE).

Table 6

Ca I lines used for the fitting.

Table 7

Results for Ca I ([Ca/Fe] using a solar abundance of log A(Ca) = 6.37).

Table 8

Abundance corrections for Caí lines (relative to 1D LTE).

6 Discussion and conclusions

We have presented a new version of Turbospectrum capable of handling computations of synthetic spectra using NLTE physics. This new capability, plus the existing capability for Turbospectrum to handle 〈3D〉 model atmospheres, means that Turbospectrum can now be used to compute model spectra in 1D LTE, 1D NLTE, 〈3D〉 LTE, and 〈3D〉 NLTE. We compared the calculation of EWs of Ca line profiles in NLTE using Turbospectrum to a similar calculation using MULTI (a code well established in the literature for its ability to handle NLTE calculations), and found that the EWs using NLTE profiles agreed within 1% for all test cases. This result indicates that the computations by Turbospectrum using NLTE physics are correct, or at least, match well with those from a previous verified source in the literature that has been used to successfully model various observed stellar spectral features in NLTE.

As part of this update, the new version of Turbospectrum is able to compute H line profiles in NLTE, as well as line profiles of multiple elements in NLTE at the same time. Our tests with H line computations also show the importance of 〈3D〉 NLTE calculations when evaluating the temperature of a star using the wings of H lines in the Balmer series. We further provide an example of a spectrum computed using departure coefficient grids for H, O, Mg, Ca, and Fe at the same time, to show how multiple elements can be computed in NLTE simultaneously. This capability will be extremely important in future studies that want to model blends of lines from two elements in NLTE, or to model NLTE lines in a crowded spectral region.

Finally, we provide an example of how the new version of Turbospectrum can be used to determine elemental abundances in observations of stellar spectra by fitting Fe and Ca lines in a number of Gaia FGK benchmark stars. As part of this example, we provide a code that involves a Python wrapper that can be used to automate generating spectra with the Fortran based Turbospectrum code, and automates the fitting procedure of spectral features. Our code also includes a script that cross matches information in an LTE Turbospectrum line list with a model atom to create an NLTE formatted Turbospectrum line list. Our abundance values from the example fits agree well with literature values, and show some of the 1D NLTE and 〈3D〉 NLTE effects on abundances determined through spectral fitting as a function of metallicity.

thumbnail Fig. 10

Difference in the [Ca/Fe] value determined using 1D NLTE (top) and 〈3D〉 NLTE (bottom), and 1D LTE as a function of [Fe/H]. Symbols are color coded based on the effective temperature of the star. Fits to spectra of the Sun are indicated as stars.

Acknowledgements

E.M. and M.B. acknowledge support by the Collaborative Research centre SFB 881 (projects A5, A10), Heidelberg University, of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation). B.P. is supported in part by the Centre National d’Etudes Spatiales (CNES) in the frame of a PLATO grant. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 949173). T.O. and U.H. acknowledge support from the Swedish National Space Agency (SNSA/Rymdstyrelsen). This work benefitted from support by the National Science Foundation under Grant No. OISE-1927130 (IReNA).

References

  1. Aldenius, M., Lundberg, H., & Blackwell-Whitehead, R. 2009, A&A, 502, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
  3. Amarsi, A. M., Lind, K., Asplund, M., Barklem, P. S., & Collet, R. 2016, MNRAS, 463, 1518 [NASA ADS] [CrossRef] [Google Scholar]
  4. Amarsi, A. M., Barklem, P. S., Asplund, M., Collet, R., & Zatsarinny, O. 2018, A&A, 616, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Amarsi, A. M., Lind, K., Osorio, Y., et al. 2020, A&A, 642, A62 [EDP Sciences] [Google Scholar]
  6. Anstee, S. D., & O’Mara, B. J. 1991, MNRAS, 253, 549 [NASA ADS] [CrossRef] [Google Scholar]
  7. Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [Google Scholar]
  8. Asplund, M. 2005, ARA&A, 43, 481 [Google Scholar]
  9. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bard, A., Kock, A., & Kock, M. 1991, A&A, 248, 315 [NASA ADS] [Google Scholar]
  11. Bard, A., & Kock, M. 1994, A&A, 282, 1014 [NASA ADS] [Google Scholar]
  12. Barklem, P. S., & O’Mara, B. J. 1997, MNRAS, 290, 102 [Google Scholar]
  13. Barklem, P. S. & Piskunov, N. 2015, Astrophysics Source Code Library [record ascl:1507.008] [Google Scholar]
  14. Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Belyaev, A. K., Yakovleva, S. A., & Barklem, P. S. 2014, A&A, 572, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bergemann, M. 2011, MNRAS, 413, 2184 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bergemann, M., & Nordlander, T. 2014, ArXiv e-prints [arXiv: 1403.3088] [Google Scholar]
  18. Bergemann, M., Pickering, J. C., & Gehren, T. 2010, MNRAS, 401, 1334 [CrossRef] [Google Scholar]
  19. Bergemann, M., Hansen, C. J., Bautista, M., & Ruchti, G. 2012a, A&A, 546, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012b, MNRAS, 427, 27 [Google Scholar]
  21. Bergemann, M., Kudritzki, R.-P., Würl, M., et al. 2013, ApJ, 764, 115 [NASA ADS] [CrossRef] [Google Scholar]
  22. Bergemann, M., Serenelli, A., Schönrich, R., et al. 2016, A&A, 594, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Bergemann, M., Collet, R., Amarsi, A. M., et al. 2017, ApJ, 847, 15 [NASA ADS] [CrossRef] [Google Scholar]
  24. Bergemann, M., Gallagher, A. J., Eitner, P., et al. 2019, A&A, 631, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Bergemann, M., Hoppe, R., Semenova, E., et al. 2021, MNRAS, 508, 2236 [NASA ADS] [CrossRef] [Google Scholar]
  26. Blackwell, D. E., Petford, A. D., & Shallis, M. J. 1979, MNRAS, 186, 657 [NASA ADS] [CrossRef] [Google Scholar]
  27. Blackwell, D. E., Petford, A. D., Shallis, M. J., & Simmons, G. J. 1982a, MNRAS, 199, 43 [NASA ADS] [CrossRef] [Google Scholar]
  28. Blackwell, D. E., Petford, A. D., & Simmons, G. J. 1982b, MNRAS, 201, 595 [NASA ADS] [CrossRef] [Google Scholar]
  29. Blackwell, D. E., Booth, A. J., Menon, S. L. R., & Petford, A. D. 1986, MNRAS, 220, 289 [NASA ADS] [CrossRef] [Google Scholar]
  30. Blanco-Cuaresma, S., Soubiran, C., Jofré, P., & Heiter, U. 2014, A&A, 566, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
  32. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [Google Scholar]
  33. Buder, S., Sharma, S., Kos, J., et al. 2020, MNRAS, 506, 150 [Google Scholar]
  34. Carlsson, M. 1986, Uppsala Astronomical Observatory Reports, 33 [Google Scholar]
  35. Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Den Hartog, E. A., Ruffoni, M. P., Lawler, J. E., et al. 2014, ApJS, 215, 23 [NASA ADS] [CrossRef] [Google Scholar]
  37. Feautrier, P. 1964, Compt. Rendus Acad. Sci., 258, 3189 [NASA ADS] [Google Scholar]
  38. Freytag, B., Steffen, M., Ludwig, H. G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
  39. Froese Fischer, C., & Tachiev, G. 2012, Multiconfiguration Hartree-Fock and Multiconfiguration Dirac-Hartree-Fock Collection, Version 2, available online at http://physics.nist.gov/mchf/ [Google Scholar]
  40. Fuhr, J. R., Martin, G. A., & Wiese, W. L. 1988, J. Phys. Chem. Ref. Data, 17, 4 [Google Scholar]
  41. Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
  42. Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 [NASA ADS] [Google Scholar]
  43. Gallagher, A. J., Bergemann, M., Collet, R., et al. 2020, A&A, 634, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Gent, M. R., Bergemann, M., Serenelli, A., et al. 2022, A&A, 658, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
  46. Grupp, F. 2004a, A&A, 420, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Grupp, F. 2004b, A&A, 426, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Gustafsson, B., Bell, R. A., Eriksson, K., & Nordlund, A. 1975, A&A, 42, 407 [NASA ADS] [Google Scholar]
  49. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Haberreiter, M., Schmutz, W., & Hubeny, I. 2008, A&A, 492, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [Google Scholar]
  52. Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
  54. Henyey, L., Vardya, M. S., & Bodenheimer, P. 1965, ApJ, 142, 841 [Google Scholar]
  55. Hubeny, I., Allende Prieto, C., Osorio, Y., & Lanz, T. 2021, ArXiv e-prints [arXiv:2104.02829] [Google Scholar]
  56. Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Jofré, P., Heiter, U., Tucci Maia, M., et al. 2018, Res. Notes Am. Astron. Soc., 2, 152 [Google Scholar]
  58. Kovalev, M., Bergemann, M., Ting, Y.-S., & Rix, H.-W. 2019, A&A, 628, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Kurucz, R. L. 1970, SAO Sp. Rep., 309 [Google Scholar]
  60. Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
  61. Kurucz, R. L. 2005, Memorie della Soc. Astron. It. Suppl., 8, 14 [Google Scholar]
  62. Larsen, S. S., Eitner, P., Magg, E., et al. 2022, A&A, 660, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2012, ApJ, 749, 136 [NASA ADS] [CrossRef] [Google Scholar]
  64. Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Lind, K., Amarsi, A. M., Asplund, M., et al. 2017, MNRAS, 468, 4311 [NASA ADS] [CrossRef] [Google Scholar]
  66. Magg, E., Bergemann, M., Serenelli, A., et al. 2022, A&A, 661, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Magic, Z., Collet, R., Asplund, M., et al. 2013a, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Magic, Z., Collet, R., Hayek, W., & Asplund, M. 2013b, A&A, 560, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Mashonkina, L., Korn, A. J., & Przybilla, N. 2007, A&A, 461, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Mashonkina, L., Zhao, G., Gehren, T., et al. 2008, A&A, 478, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Mashonkina, L., Sitnova, T., & Belyaev, A. K. 2017, A&A, 605, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Masseron, T., Osorio, Y., García-Hernández, D. A., et al. 2021, A&A, 647, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. May, M., Richter, J., & Wichelmann, J. 1974, A&AS, 18, 405 [NASA ADS] [Google Scholar]
  74. McLaughlin, B. M., Stancil, P. C., Sadeghpour, H. R., & Forrey, R. C. 2017a, J. Phys. B Atm. Mol. Phys., 50, 209501 [NASA ADS] [CrossRef] [Google Scholar]
  75. McLaughlin, B. M., Stancil, P. C., Sadeghpour, H. R., & Forrey, R. C. 2017b, J. Phys. B Atm. Mol. Phys., 50, 114001 [NASA ADS] [CrossRef] [Google Scholar]
  76. Mihalas, D., Dappen, W., & Hummer, D. G. 1988, ApJ, 331, 815 [NASA ADS] [CrossRef] [Google Scholar]
  77. Nordlund, Å. 1984, in Methods in Radiative Transfer, ed. W. Kalkofen (Cambridge: Cambridge University Press), 211 [Google Scholar]
  78. Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
  79. O’Brian, T. R., Wickliffe, M. E., Lawler, J. E., Whaling, W., & Brault, J. W. 1991, J. Opt. Soc. Am. B Opt. Phys., 8, 1185 [Google Scholar]
  80. Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
  82. Plez, B. 2012, Astrophysics Source Code Library [record ascl:1205.004] [Google Scholar]
  83. Reetz, J. 1991, Diplomarbeit, Universität München, Germany [Google Scholar]
  84. Reetz, J. 1999, Ap&SS, 265, 171 [NASA ADS] [CrossRef] [Google Scholar]
  85. Ruffoni, M. P., Den Hartog, E. A., Lawler, J. E., et al. 2014, MNRAS, 441, 3127 [NASA ADS] [CrossRef] [Google Scholar]
  86. Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr., 90, 054005 [Google Scholar]
  87. Semenova, E., Bergemann, M., Deal, M., et al. 2020, A&A, 643, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Shen, G., Kuri, A., Fontenla, J. M., Stancil, P. C., & Wang, J. G. 2014, APS Meeting Abstracts, D1.122 [Google Scholar]
  89. Sitnova, T. M., Mashonkina, L. I., & Ryabchikova, T. A. 2016, MNRAS, 461, 1000 [Google Scholar]
  90. Smith, G. 1988, J. Phys. B Atm. Mol. Phys., 21, 2827 [NASA ADS] [CrossRef] [Google Scholar]
  91. Smith, G., & Raggett, D. S. J. 1981, J. Phys. B Atm. Mol. Phys., 14, 4015 [NASA ADS] [CrossRef] [Google Scholar]
  92. Smith, V. V., Bizyaev, D., Cunha, K., et al. 2021, AJ, 161, 254 [NASA ADS] [CrossRef] [Google Scholar]
  93. Sneden, C. 1973, ApJ, 184, 839 [Google Scholar]
  94. Sobeck, J. S., Kraft, R. P., Sneden, C., et al. 2011, AJ, 141, 175 [NASA ADS] [CrossRef] [Google Scholar]
  95. Uitenbroek, H., & Criscuoli, S. 2011, ApJ, 736, 69 [NASA ADS] [CrossRef] [Google Scholar]
  96. Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Voronov, Y. V., Yakovleva, S. A., & Belyaev, A. K. 2022, ApJ, 926, 173 [NASA ADS] [CrossRef] [Google Scholar]
  98. Wishart, A. W. 1979, MNRAS, 187, 59P [NASA ADS] [CrossRef] [Google Scholar]
  99. Wolnik, S. J., Berthel, R. O., & Wares, G. W. 1970, ApJ, 162, 1037 [NASA ADS] [CrossRef] [Google Scholar]
  100. Wolnik, S. J., Berthel, R. O., & Wares, G. W. 1971, ApJ, 166, L31 [NASA ADS] [CrossRef] [Google Scholar]
  101. Yakovleva, S. A., Belyaev, A. K., & Bergemann, M. 2020, Atoms, 8, 34 [NASA ADS] [CrossRef] [Google Scholar]
  102. Young, M. E., & Short, C. I. 2014, ApJ, 787, 43 [NASA ADS] [CrossRef] [Google Scholar]
1

The new NLTE version is presented at: https://github.com/bertrandplez/Turbospectrum2020. The previous LTE release 19.1.4 is available at: https://github.com/bertrandplez/Turbospectrum2019

2

A departure coefficient describes the ratio of the number density of an atom at a given energy level computed in NLTE to that computed in LTE, i.e., using the Saha-Boltzmann equilibrium relations.

3

SYNSPEC can also work with NLTE populations.

5

The enhancement is +0.1 for [Fe/H] = −0.25, +0.2 for [Fe/H] = −0.5, +0.3 for [Fe/H] = −0.75, and +0.4 for [Fe/H] ≤ −1.0.

8

The current grids of departure coefficients can be found at https://keeper.mpdl.mpg.de/d/6eaecbf95b88448f98a4/

9

The code to simultaneously interpolate model atmospheres and departure coefficient grids is included on the TS Github.

10

The HIPPARCOS parallaxes are consistent with Gaia DR2 and Gaia eDR3 values for these stars.

11

For the full relationship used, see the function “calculate_vturb” in the script “TSFitPy.py” in the folder “scripts” on the TSFitPy Github page.

All Tables

Table 1

Literature studies containing the NLTE model atoms.

In the text
Table 2

Average percent difference between TS and MULTI calculations of the ratio of NLTE to LTE equivalent width of nine Ca lines computed for four different sets of parameters.

In the text
Table 3

Fe I lines used for fitting.

In the text
Table 4

Results for Fe I ([Fe/H] using a solar abundance of log A(Fe) = 7.50).

In the text
Table 5

Abundance corrections for Fe I lines (relative to 1D LTE).

In the text
Table 6

Ca I lines used for the fitting.

In the text
Table 7

Results for Ca I ([Ca/Fe] using a solar abundance of log A(Ca) = 6.37).

In the text
Table 8

Abundance corrections for Caí lines (relative to 1D LTE).

In the text

All Figures

thumbnail Fig. 1

MARCS model atmosphere grid used in this work. PARSEC isochrones (Bressan et al. 2012) calculated for [M/H] = −2 and 0 are overplotted as dashed and solid black lines, respectively.
In the text
thumbnail Fig. 2

Comparison between the structures of the MARCS to 〈3D〉 Stagger models. The top two panels show temperature as a function of optical depth at 5000 Å for model atmospheres of four types of stars. The open (giant stars) and solid (dwarf stars) black circles and squares show the MARCS model atmospheres for the parameters given in the legend (low metallicity to the left, solar metallicity to the right). The corresponding 〈3D〉 Stagger models are shown as cyan dots. The bottom two panels show the difference between the MARCS model and the 〈3D〉 Stagger model for each case, following the same convention for open and solid circles or squares as in the top panels.
In the text
thumbnail Fig. 3

Synthetic spectrum computed with a 〈3D〉 Stagger model atmosphere in NLTE, compared with a spectrum calculated in 1D LTE. The stellar parameters used in the calculations are indicated in the figure inset.
In the text
thumbnail Fig. 4

Hα line profiles of the Sun, Procyon, HD 84937, and HD 140283. The black lines are observations made by UVES. The red and cyan lines are the 1D LTE and 〈3D〉 NLTE model profiles, respectively, generated with Turbospectrum. Inset in the lower right corner of each panel is a zoomed-in look at the core of each line.
In the text
thumbnail Fig. 5

Normalized flux vs. wavelength for four sample Fe I lines in an observed solar spectrum, together with model fits. Observations are shown as black circles, 1D LTE model fits are shown as red lines, and 〈3D〉 NLTE model fits are shown as cyan lines. Residuals for the 1D LTE and 〈3D〉 NLTE model fits are shown as red and cyan points, respectively. The points have been shifted by 0.1 and are plotted above each spectrum with a dashed line to indicate the zero point at 1.1.
In the text
thumbnail Fig. 6

The difference between the line abundances derived from an NLTE and an LTE fit for both 〈3D〉 (Stagger) and MARCS model atmospheres for various Fe I lines, for HD 84937 and HD 140283, as a function of excitation potential of the line. Fits using MARCS model atmospheres are shown as red squares and those using 〈3D〉 model atmospheres are shown as black circles. The differences are given in units of dex.
In the text
thumbnail Fig. 7

Difference in the [Fe/H] value determined using 1D NLTE (top) and 〈3D〉 NLTE (bottom) and 1D LTE, as a function of [Fe/H]. Symbols are color coded based on the effective temperature of the star. Fits to spectra of the Sun are indicated as stars.
In the text
thumbnail Fig. 8

[Fe/H] determined from the Turbospectrum fit versus values from the literature (see text). For the TS fit, the adopted value is the 〈3D〉 NLTE fit, or the 1D NLTE fit in cases where a 〈3D〉 NLTE fit was not available.
In the text
thumbnail Fig. 9

The difference between the line abundances derived from an NLTE and an LTE fit for both 〈3D〉 (Stagger) and MARCS model atmospheres for each Caí line fit, for the Sun and Procyon, as a function of equivalent width of the line. Fits using MARCS model atmospheres are shown as red squares and those using 〈3D〉 model atmospheres are shown as black circles.
In the text
thumbnail Fig. 10

Difference in the [Ca/Fe] value determined using 1D NLTE (top) and 〈3D〉 NLTE (bottom), and 1D LTE as a function of [Fe/H]. Symbols are color coded based on the effective temperature of the star. Fits to spectra of the Sun are indicated as stars.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.