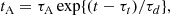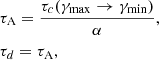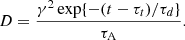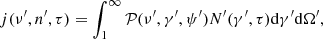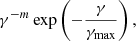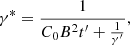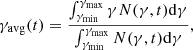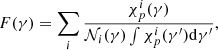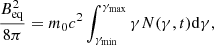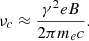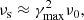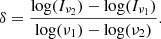| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244251 | |
| Published online | 17 November 2022 | |
A numerical study of the interplay between Fermi acceleration mechanisms in radio lobes of FR-II radio galaxies
1
Discipline of Astronomy, Astrophysics and Space Engineering, Indian Institute of Technology, Indore, Madhya Pradesh 452020, India
e-mail: sayan.astronomy@gmail.com
2
Dipartimento di Fisica Generale, Universita degli Studi di Torino, Via Pietro Giuria 1, 10125 Torino, Italy
3
Center for Astrophysics Research, Department of Physics, Astronomy and Mathematics, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK
Received:
11
June
2022
Accepted:
21
August
2022
Context. Radio-loud active galactic nuclei (AGNs) are thought to possess various sites of particle acceleration, which gives rise to the observed nonthermal spectra. Stochastic turbulent acceleration (STA) and diffusive shock acceleration (DSA) are commonly cited as potential sources of high-energy particles in weakly magnetized environments. Together, these acceleration processes and various radiative losses determine the emission characteristics of these extragalactic radio sources.
Aims. The purpose of this research is to investigate the dynamical interplay between the STA and DSA in the radio lobes of FR-II radio galaxies, as well as the manner in which these acceleration mechanisms, along with a variety of radiative losses, collectively shape the emission features seen in these extragalactic sources.
Methods. A phenomenologically motivated model of STA is considered and subsequently employed on a magnetohydrodynamically simulated radio lobe through a novel hybrid Eulerian-Lagrangian framework.
Results. STA gives rise to a curved particle spectrum that is morphologically different from the usual shock-accelerated spectrum. As a consequence of this structural difference in the underlying particle energy spectrum, various multiwavelength features arise in the spectral energy distribution of the radio lobe. Additionally, we observe enhanced diffuse X-ray emission from radio lobes for cases where STA is taken into account in addition to DSA.
Key words: magnetohydrodynamics (MHD) / methods: numerical / acceleration of particles / radio continuum: galaxies / X-rays: galaxies / turbulence
© S. Kundu et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Radio galaxies are thought to be among the most energetic systems in the Universe. These extragalactic objects are observed to possess a huge reservoir of relativistic nonthermal particles, which collectively shape their emission features (Blandford et al. 2019). Furthermore, due to the abundance of highly energetic particles, these galaxies are generally considered favorable sites to study various high-energy phenomena (Meisenheimer 2003). In recent years, thanks to the advent of multi-messenger astronomy, different observations have uncovered various features and are helping us understand the different microphysical processes occurring in these systems (Marcowith et al. 2020).
Low-frequency radio observations of these radio galaxies provide insights about their morphological structures (see Hardcastle & Croston 2020, for more details), their magnetic field strength (Croston et al. 2005), and their age (Alexander & Leahy 1987; Carilli et al. 1991; Mahatma et al. 2019). Based on the brightness of these sources at 178 MHz, they are classified as Fanaroff-Riley (FR) class I (low power) or II (high power) (Fanaroff & Riley 1974). These two classes of radio galaxies are observed to manifest different morphological structures. While FR-II sources exhibit a one-sided smooth spine-like structure with a bright termination point, FR-I sources show a two-sided plume-like structure. Additionally, FR-II sources show prominent signs of turbulent cocoons that have an extent of a few hundred kiloparsecs, and are often partly visible as lobes (Mullin et al. 2008; Hardcastle & Croston 2020). These lobes are believed to be highly magnetized cavities of rarefied plasma where most of the jet kinetic power is deposited. Radio lobes also have a hotspot region near the jet termination region, responsible for accelerating particles to high energies via diffusive shock acceleration (DSA; Brunetti et al. 2001; Prieto et al. 2002; Araudo et al. 2018). These freshly shock-accelerated particles further mix with the older plasma particles already residing in the lobe, which makes the lobe a turbulent playground for various plasma waves to interact with the particles and then accelerate them via stochastic turbulent acceleration (STA). This mechanism has also been invoked to explain the particle acceleration in various astrophysical systems such as solar flares (Petrosian 2012), the corona above the accretion disk of compact objects (Dermer et al. 1996; Liu et al. 2004; Belmont et al. 2008; Vurm & Poutanen 2009), supernova remnants (Bykov & Fleishman 1992; Kirk et al. 1996; Marcowith & Casse 2010; Ferrand & Marcowith 2010), gamma-ray bursts (Schlickeiser & Dermer 2000), emission from blazars (see Asano & Hayashida 2018; Tavecchio et al. 2022, and references therein), Fermi bubbles (Mertsch & Petrosian 2019), and galaxy clusters (Brunetti & Lazarian 2007; Donnert & Brunetti 2014; Vazza et al. 2021). STA has been invoked as a possible mechanism for producing ultra-high-energy cosmic rays (UHECRs) from the radio lobe of Pictor A (Fan et al. 2008) and Cen A (Hardcastle et al. 2009; O’Sullivan et al. 2009). Recently, it has also been invoked as a plausible candidate in explaining the spectral curvature usually observed in FR-II radio lobes (Harris et al. 2019).
In addition to the radio observations, X-ray observations of these radio-loud active galactic nuclei (AGNs) have become popular due to the minimal contamination of the X-ray radiation by non-AGN sources. Several components of these sources, such as radio lobes, hotspots, and collimated radio jet spines, are observed to radiate in the X-ray band (de Vries et al. 2018; Massaro et al. 2018). Additionally, these lobes are often observed to give rise to diffuse X-ray emission from the region between the host galaxy and the radio hotspot, which is usually ascribed to the inverse-Compton emission off the cosmic microwave background radiation (IC-CMB; Hardcastle et al. 2002; Croston et al. 2005; Blundell et al. 2006). Recent observations reveal that the nonthermal X-ray emission from the radio lobe increases with redshift, further supporting the IC-CMB origin (Gill et al. 2021). Diffuse X-ray emission has also been reported in the jets of the FR-I class of radio galaxies and has been ascribed to a distributed particle acceleration mechanism (Hardcastle et al. 2007; Worrall et al. 2008; Worrall 2009). An IC-CMB model is sometimes invoked to explain X-ray emission from the jets of FR-II radio galaxies and quasars; however, such models require the jet to be highly relativistic and well aligned with the line of sight, and consequently tend to imply very large physical jet lengths, sometimes in excess of several megaparsecs (Tavecchio et al. 2000; Celotti et al. 2001; Ghisellini et al. 2005). Furthermore, recent polarimetric studies and high-energy gamma-ray constraints provide evidence supporting the synchrotron emission model as the origin of diffuse X-ray emission from AGN jets (see Perlman et al. 2020, for a recent review). This consequently requires particles with very high energies to be present in the jet, and also favors a distributed particle acceleration mechanism due to the short synchrotron lifetime of the radiating particles.
The present work explores, for the first time, the interplay of vital particle acceleration mechanisms in a weakly magnetised plasma environment such as the radio lobes of FR-II radio galaxies and studies their effect on the emission properties of these systems. Due to the complicated evolution of the dynamical quantities as a result of a nonlinear plasma flow pattern inside these lobes, we adopt a numerical approach for this work. In particular, we employed magnetohydrodynamic (MHD) simulations to produce radio lobes and analyze the emission features caused by particle energization in the presence of shocks and underlying turbulence. We adopted our recently developed second-order accurate STA framework (Kundu et al. 2021) for this purpose. Owing to the increased computational complexity of the developed framework, this paper focuses on a 2D axisymmetric MHD jet model only, while leaving the more computationally expensive 3D case to forthcoming works.
The paper is organised in the following way. We describe our numerical setup for simulating a 2D axisymmetric AGN jet in Sect. 2.1. Section 2.2 describes the numerical model to compute the emission properties. In Sect. 3 we present the results of the simulations. In Sect. 4 we summarize our findings and discuss the limitations of our model.
2. Numerical setup
In this section we describe the numerical setup adopted for the present work. The radio lobes are typically associated with the termination point of the AGN jet, where the velocity of the jet material reduces considerably such that relativistic effects become negligible (Huarte-Espinosa et al. 2011). Furthermore, as shown by Hardcastle & Krause (2013), numerical simulations of realistic radio lobes require high Mach number flows as well as very high-resolution meshes in order to have radio lobes in pressure equilibrium with the surrounding medium and to resolve the transverse radial equilibrium. Therefore, to investigate the emission profile of the radio lobes, we focus on a nonrelativistic scenario and perform a two-dimensional axisymmetric ideal MHD simulation using the PLUTO code (Mignone et al. 2007). In particular, we solve the following set of conservation equations
where the quantities ρ, P, v, and B represents density, pressure, velocity, and magnetic field, respectively; the magnetic field B further satisfies the constraint ∇ ⋅ B = 0; and Γ represents the ratio of specific heats and its value is taken to be 5/3, which is typically considered for supersonic nonrelativistic jets (Massaglia et al. 2016). Equations (1)–(4) are solved with the Harten-Lax-van Leer contact (HLLC) Riemann solver using piece-wise linear reconstruction, the van Leer flux limiter (van Leer 1977) and second-order Runge-Kutta time-stepping. Additionally, we consider divergence cleaning (Dedner et al. 2002) to satisfy the solenoidal constraint of magnetic field.
2.1. Dynamical setup
The two-dimensional axisymmetric simulations are carried out in a cylindrical geometry {r, z} such that the radial and vertical extents range from {0, 0} to {65L0, 195L0} with a resolution of 780 × 2340. The physical quantities defined in our simulations are appropriately scaled by defining length, velocity, and density scales. For the length we define the jet radius rj = L0 = 2 kpc as the scale length. The core density is adopted as the scale for density such that ρ0 = 5 × 10−26 gm cc−1. Finally, for an ambient temperature Ta = 2 keV, we define the sound speed ca = v0 = 730 km s−1 as the scale velocity.
The ambient medium density is initialized with an isothermal King profile (King 1972)
where ρa is the ambient density that consists of a core with radius Rc = 40L0, and 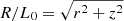 is the spherical radius. The value of the power-law index is kept constant at β = 0.35. Initially, the ambient medium is set to hydrostatic equilibrium using a gravitational potential (Φk) (Krause 2005)
is the spherical radius. The value of the power-law index is kept constant at β = 0.35. Initially, the ambient medium is set to hydrostatic equilibrium using a gravitational potential (Φk) (Krause 2005)
where kB, μ, and mH are the Boltzmann constant, mean molecular weight, and hydrogen atom mass, respectively. The ambient pressure (Pa) is computed as
The ambient medium is set to be nonmagnetized initially, with the expectation that the magnetic field in the environment will have minimal impact on the nonthermal particle transport and the subsequent emission features within the lobe.
An underdense beam of density ρj = ηρ0 with velocity vj is continuously injected in the medium from a circular nozzle of radius rj, along the vertical direction (ẑ) at t = 0, with η = 0.1 being the density contrast. The nozzle is placed within the numerical domain with a height of 0.5L0. The adopted resolution samples the jet nozzle radius with 12 computational cells. The injection velocity (vj) is obtained by choosing the sonic Mach number M such that
with M = 25.0. The injected beam includes a toroidal magnetic field (Bj) with the following radial profile (Lind et al. 1989)
where the value of Bm is governed by the plasma-beta parameter and rm is the magnetization radius. This magnetic field profile corresponds to a uniform current density within the radius rm, the zero current density between rm and r, and a return current at r. Furthermore, this configuration also respects the symmetry condition on the z-axis (Bj = 0 at r = 0) (Komissarov et al. 2007). Additionally, a suitable gas pressure is provided inside the jet to ensure radial balance between the hoop stress and pressure gradient force
where 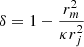 and
and 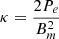 , and Pe is the pressure in units of
, and Pe is the pressure in units of 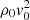 at the nozzle radius computed from the ambient medium (Pe = Pa at r = rj). Owing to the constraint imposed by the 2D axisymmetric geometry, the induction equation (Eq. (4)) does not enable conversion of the toroidal magnetic field (Bϕ) to a poloidal one. As a result, we consider a minimum value of Bm ∼ 100 μG to avoid significant amplification of the Bϕ due to its continuous injection into the computational domain over time. Furthermore, the initial kinetic power of the jet is calculated from the quantities defined at the jet nozzle (Massaglia et al. 2016)
at the nozzle radius computed from the ambient medium (Pe = Pa at r = rj). Owing to the constraint imposed by the 2D axisymmetric geometry, the induction equation (Eq. (4)) does not enable conversion of the toroidal magnetic field (Bϕ) to a poloidal one. As a result, we consider a minimum value of Bm ∼ 100 μG to avoid significant amplification of the Bϕ due to its continuous injection into the computational domain over time. Furthermore, the initial kinetic power of the jet is calculated from the quantities defined at the jet nozzle (Massaglia et al. 2016)
where NA is Avogadro’s number. For the choices adopted in the present work, we obtain W ≃ 1045 erg s−1 corresponding to the FR-II class of radio galaxies (Fanaroff & Riley 1974).
For the boundaries we employ axisymmetric boundary conditions about the axis for the inner r boundary and free flow boundary conditions for all the other boundaries in the computational domain.
2.2. Numerical setup to compute emission
The nonthermal emission from the radio lobe is modeled using the Eulerian-Lagrangian hybrid framework of the PLUTO code (Vaidya et al. 2018; Mukherjee et al. 2021). It employs passive Lagrangian (or macro-) particles whose dynamics is governed by the underlying fluid motion. Physically, these macro-particles represent an ensemble of nonthermal particles (typically leptons) residing very closely together in physical space with a finite energy distribution.
The energy distribution of these macro-particles is evolved by solving the transport equation
where τ is the proper time; γ ≈ p/m0c is the Lorentz factor of the electrons, with m0 being the rest mass of the electron; and c is the speed of light in vacuum. The dimensionless quantity χp = N/n, with N(p, τ) being the number density of the nonthermal particles with momentum between p and p + dp and n being the number density of the fluid at the position of the macro-particle. The quantity S represents various radiative and adiabatic losses. The acceleration due to the Fermi second-order mechanism is given as DA = 2D/γ, with D being the momentum diffusion coefficient. For simplicity, we neglect the source and sink terms in the transport equation.
Equation (12) is solved using a second-order accurate finite-volume conservative implicit-explicit (IMEX) scheme (Kundu et al. 2021). The radiative losses considered include synchrotron, IC-CMB, and adiabatic expansion to model the cooling processes of relativistic electrons. Additionally, as the particle spectra in the high-energy region falls off rapidly due to various cooling processes, we follow Winner et al. (2019) and set the values of χp = 0 beyond a threshold χcut = 10−21. We note that Eq. (12) does not include shock acceleration; instead, a separate sub-grid prescription is employed to account for DSA (Vaidya et al. 2018; Mukherjee et al. 2021).
The microphysics of turbulent acceleration is encapsulated in the diffusion coefficient D. Typically, the empirical form of D is given as an input in numerical simulations (Donnert & Brunetti 2014; Vazza et al. 2021) as its quantification from first principles is complex, particularly when applied to study large-scale astrophysical environments. In this work we opt for a phenomenologically motivated ansatz of exponentially decaying hard-sphere turbulence as a model of STA inside the radio lobe. We consider the acceleration timescale (tA) as (Kundu & Vaidya 2022)
where τd is the turbulence decay timescale, τA represents the acceleration timescale when turbulence decay is absent (or τd → ∞), t is the simulation time, and τt is the injection time of the macro-particle in a turbulent region. For a macro-particle that encounters a shock, its value is set to the time at which the last shock is encountered, while for those macro-particles that never undergo a shock the value of τt is set to the initial injection time in the computational domain.
This acceleration timescale has the capability to mimic the decay of turbulence, generally observed in various astrophysical sources. The decay is a consequence of the finite lifetime of the turbulence and prevents particles from being continuously accelerated. For this work we model τA and τd as
where τc(γmax → γmin) represents the radiative loss time for a particle to cool from γmax to γmin, and α is the ratio of synchrotron cooling time to acceleration time, which also controls the efficiency of STA. A higher value of α corresponds to smaller τA (STA timescale) and τd (turbulence damping timescale). Hence higher α indicates faster stochastic acceleration and faster damping. In addition, with lower values of α the effect of STA asymptotically diminishes. It is a parametric representation that models the turbulence that actually occurs in realistic radio lobes of FR-II radio galaxies, which is unresolved in our simulation. In this work we vary its value and study how this affects the emission signatures. The diffusion coefficient can subsequently be written as
The γ2 dependency of the diffusion coefficient is a characteristic of the hard-sphere turbulence. Furthermore, instead of a γ2 dependent diffusion coefficient, alternative diffusion models can also be explored. For example, adopting Bohm diffusion (∝γ) could influence the results; however, a study of varying dependence of the diffusion coefficient on γ is beyond the scope of this paper. To explore the ramifications of STA with varying efficiency on the emission of the simulated radio lobe structure, we use two alternative values for α = 104 and 105 in this study. Furthermore, to sample the jet cocoon uniformly, we inject enough (∼20) macro-particles at every time step in the computational domain. Initially, the normalized particle spectrum for each macro-particle is assumed to be a power law, defined as χp(γ) = χ0γ−9, ranging from γmin = 1 to γmax = 105. The value of χ0 is set by prescribing the energy density of the macro-particles to be a fraction (≈10−4) of the initial magnetic energy density. We note that the initial spectral index has a negligible effect on the emission of the system at later times as long as we consider a steep power law.
To compute the emissivity, we convolve the instantaneous energy spectrum of each macro-particle with the corresponding single-particle radiative power and extrapolate it to the nearest grid cells. In particular we solve the following integral to compute the emissivity
where 𝒫(ν′,γ′,ψ′) is the power emitted by a nonthermal particle per unit frequency (ν′) and unit solid angle (Ω′) with Lorentz factor γ′, and whose velocity makes an angle of ψ′ with the direction n′, and N′(γ′,τ) is the number of micro-particles between Lorentz factor γ′ and γ′+dγ′ at time τ′. In the case of an axisymmetric simulation, the magnetic field becomes independent of the polar angle, and therefore to consider the line-of-sight (LOS) effect in the synchrotron emissivity, an appropriate coordinate transformation is required (Meyer et al. 2021). We transform the magnetic field from cylindrical to Cartesian coordinates and compute the LOS effect by rotating the simulated structure explicitly. The entire rotation (of 360°) is performed with an interval of 5°. Subsequently, the intensity maps of the structure are computed by doing a LOS integration of the calculated emissivity. We note that all the emissivity calculations are performed by considering a viewing angle of θ = 90° (i.e., along the z = 0 plane in Cartesian coordinates).
3. Results
We categorize the major results from our simulations in two parts. The first part gives an overview of dynamical aspects of radio lobes and the second part provides a detailed analysis of multiwavelength emission signatures and particle acceleration processes within these lobes.
3.1. Dynamics
We carried out axisymmetric MHD simulations following the initial conditions described in Sect. 2 using the relevant jet and ambient medium parameters. The simulation was carried out up to a physical time of ∼120 Myr. In Fig. 1 we show the density evolution of the injected jets at different times: t = 37, 64, 91, and 117 Myr. The density structure at every time snapshot shows an expanding bi-directional underdense region, which at a later time (t = 117 Myr) can be identified as lobes (English et al. 2016). Similarly to Hardcastle & Krause (2013), we found the formation of a long, thin lobe initially and a transverse expansion afterward. This subsequent expansion in the transverse direction is attributed to the thermalization of the jet material by the shocks present in the lobe. Furthermore, we observe the formation of vortices at the lobe boundary, which are typically attributed to Kelvin-Helmholtz instabilities originated from the velocity shear between the lobe material and shocked ambient material. Moreover, the entire structure is encapsulated within a forward-moving shock that can be seen to propagate through the ambient medium. This shock remains in the computational domain throughout the simulation time, preventing any mass, energy, and momentum from escaping the domain.
 |
Fig. 1. Normalized density ρ/ρ0 evolution of the simulated radio lobe structure. The images depict a slice through the mid-plane of the notional 3D volume; all images are reflection-symmetric around the jet axis and the z = 0 plane since the simulations are axisymmetric. The color bar shows a logarithmic scale of density. |
In Fig. 2 we show the temperature (left panel), thermal pressure (second panel), absolute velocity |v| (third panel), and plasma-beta (right panel) maps of the bi-directional jet at time t = 117 Myr. The temperature of the lobe (average value of ∼70 keV) is higher than the ambient medium (Ta = 2 keV). This is expected given the presence of a strong shock at the jet termination region, which is responsible for heating the jet material in the cocoon. The existence of the strong shock can be seen from the pressure map, as shown in the second panel of the figure. The pressure map also provides evidence of multiple re-collimation shocks along the jet axis. These shocks are expected to be favorable sites for accelerating particles via shock acceleration, and are known to be a source of localised high-energy emissions. Furthermore, we observe that the velocity of the jet is within the nonrelativistic limit, with an average value of ∼0.02c. The plasma-beta map, as depicted in the right panel of the figure, shows that the lobes are thermally dominated with an average lobe plasma-beta value of ∼32.
 |
Fig. 2. Temperature, pressure, absolute velocity, and plasma-beta maps of the simulated jet structure for time t = 117 Myr. Temperature and pressure are shown in physical units, velocity is shown in units of c, and the color bars are shown in logarithmic scale. The average temperature of the radio lobe is on the order of ∼70 keV, average plasma-beta is ∼32, and average velocity is ∼0.02c. |
The underdense lobes observed in 2D simulations resemble the radio galaxies in a more consistent manner at later times (Hardcastle & Krause 2013), in particular when the expansion results in the length of the underdense region being comparable to the core radius of the galaxy. Therefore, in this work, for the emission studies, we adopt the dynamical results at time t = 117 Myr.
3.2. Emission
We now look at the emission signatures of our model. The discussion is based on the comparison of synthetic emission signatures from different runs considered in our study. The parametric study focuses mainly on the properties of the stochastic turbulent acceleration mechanism. The details of these simulation runs are listed in Table 1; various acceleration scenarios are considered, corresponding to different turbulent acceleration timescales tA, while the background thermal fluid evolution remains exactly the same.
Properties of the different cases considered in the present study for calculating emission from the radio lobe.
The results obtained from cases (a) and (b) are useful in comprehending the impact of STA and its interplay with DSA. Cases (b) and (c) highlight the implications of having different turbulent decay timescales (see Eqs. (13) and (14)). For cases (d) and (e), the turbulent decay is turned off by setting τd → ∞ in Eq. (13). Comparing results from these cases demonstrate the effect of the turbulent decay process in our simulations. In realistic astrophysical environments, we expect the turbulence to decay on a timescale that is governed by the micro-physical properties of the wave–particle interaction in that system. As the current work incorporates turbulence via a sub-grid model, we explored the implications of different parameters through these five cases. All the results presented in this section are for a dynamical time of 117 Myr, unless specified otherwise. Logarithmic binning has been adopted for all the histograms.
3.2.1. Effect of turbulent acceleration on individual macro-particle energy spectra
In Fig. 3 we show the evolution of the energy spectra for all the cases listed in Table 1 for a randomly chosen macro-particle that encountered final shock at a dynamical time t = 25 Myr. In the simulations presented in this work the majority of the Lagrangian macro-particles are observed to encounter more than one shock. We selected one particular particle that had experienced multiple shocks only at earlier times as a representative candidate to demonstrate the effects of turbulent acceleration on the particle energy distribution in the downstream of the shock for all the case scenarios. The effect of multiple shocks on the energy spectrum of a Lagrangian macro-particle without STA has already been investigated in the context of AGN jet simulation (see, e.g., Mukherjee et al. 2021; Giri et al. 2022).
 |
Fig. 3. Evolution of the energy spectrum for a randomly chosen macro-particle for all the cases described in Table 1. The macro-particle encountered shock at a dynamical time of t = 25 Myr. The color bar shows how much time has elapsed since the simulation began. The value of the lower end of the color bar is set to the time when the macro-particle encountered the final shock. |
The spectral evolution of the macro-particle of case (a) is shown in the top left panel. The spectrum exhibits a power law with a high-energy cutoff which gradually shifts to lower energy with time owing to various energy losses. Additionally, a small hump can be seen in the low-energy part of the spectrum, caused by an excess of lower energy electrons arising from their higher energy counterparts due to radiative cooling.
The shape of the spectrum changes considerably when STA is considered in addition to DSA. For cases (d) and (e) (right plot of the middle panel and left plot of the bottom panel, respectively) the spectrum exhibits an ultra-relativistic Maxwellian distribution at later times. This is a consequence of a steady competition between stochastic acceleration and radiative losses resulting in the acceleration of low-energy electrons toward higher energies (Kundu et al. 2021). Moreover, the peak of the distribution corresponds to the value of γ at which acceleration and loss timescales match (i.e., τc = tA). We find that the peak corresponds to γ ≈ α and depends on the choice of the turbulent acceleration timescale (see Eq. (13)).
When turbulent decay is included (cases b and c) we observe flatness of the spectrum in the lower energy regime, compared to the power-law behavior observed in case (a), along with a high-energy cutoff. The flattening of the lower energy component of the spectrum is a consequence of the fact that STA provides a continuous acceleration to all the micro-particles, resulting in their acceleration to higher energies, depopulating the low-energy regime.
We also note that for the macro-particles that have encountered a shock, STA starts acting in the downstream and modifies the energy spectra on a timescale that depends on tA (Eq. (13)), which in turn is regulated by the turbulent decay timescale τd, and consequently develops a cutoff that moves toward lower energies.
In summary, the spectral evolution of a macro-particle, presented in Fig. 3 for different cases, clearly indicates that the presence of turbulent acceleration significantly affects the spectral energy distribution and its evolution. Our results indicate, in the absence of turbulent decay, that spectral evolution eventually relaxes toward a steady-state configuration in which energy losses are balanced by turbulent acceleration, while, when accounting for the decay of turbulence, the energy spectrum exhibits a nonstationary behavior in time and the cutoff is governed by the radiative loss timescale subsequent to the decay of turbulence. Furthermore, the spectrum shows flattening in the lower energy regime owing to the energization of low-energy micro-particles to higher energy by STA.
3.2.2. Effect of turbulent acceleration on particle population
This section focuses on the effects of turbulent acceleration on the entire macro-particle population in the lobe. In particular, we compute the effect of the STA with turbulence decay on the cutoff energy (γmax) for the macro-particle population. To compute the cutoff energy of a macro-particle we consider a generic form of its energy spectrum
where m can be positive or negative depending on the macro-particle and γmax is the cutoff energy. The exponential decay term takes care of the effects on the spectrum due to various radiative losses (see Sect. 3.2.1). The value of γmax is calculated by multiplying Eq. (17) by a power-law profile, γ10, and calculating the maximum point of the resultant curve.
In Fig. 4 we show the probability distribution function (PDF) of the maximum (or cutoff) energy (γmax) attained by individual macro-particles for cases (a) (left panel), (b) (middle panel), and (c) (right panel). For case (a) the distribution peaks around γmax ≈ 102, followed by a broken power-law-like tail beyond that. The origin of this peak can be attributed to the presence of various radiative losses in the system. The peak is also observed to gradually move toward lower values of γmax with time. To support this argument, we undertake the following exercise: for a particle undergoing synchrotron cooling only, the initial Lorentz factor γ′ after a time period of t′ becomes
where C0 = 1.28 × 10−9 is the synchrotron constant for the electron and B is the magnetic field. For our case, considering an averaged magnetic field of B = 19.70 μG and t′=117 Myr, we obtain γ* ≈ 5.4 × 102 for a range of γ′ values, which correlates with the position of the peak. The break in the power law around γmax ∼ 105 is attributed to the continuous injection of the macro-particles in the computational domain with γmax = 105 (see Sect. 2.2). The presence of an additional smaller peak around γmax ∼ 109 can also be observed. This smaller peak is a transient feature, which arises from recently shocked macro-particles and is a manifestation of the continuous injection of jet material along with the Lagrangian macro-particles inside the computational domain. The presence of this transient peak has been reported in earlier works as well (see, e.g., Borse et al. 2021). Furthermore, the power-law trend of the tail of the PDF is typically ascribed to the interplay between the continuous injection of macro-particles in the computational domain and the shock acceleration of these freshly injected particles. This power-law-like behavior of the distribution in an AGN jet cocoon is also reported in Mukherjee et al. (2021).
 |
Fig. 4. Probability distribution function of the cutoff energy for the entire macro-particle population. The left, middle, and right panels show the PDF for cases (a), (b), and (c), respectively. |
The PDFs for cases (b) and (c) show some additional peaks compared to case (a). The origin of the peak at γmax ∼ 102 is similar to case (a), while the high-energy peak (γmax ∼ 109) is again due to recently shocked macro-particles. In addition, humps are observed at γmax ∼ 104 (for case b) and at γmax ∼ 105 (for case c). Their presence is caused by particles undergoing turbulent acceleration downstream of the shock, resulting in freezing the evolution of the cutoff at γmax ≈ α for some time, due to the competition between STA and radiative losses, and afterward, due to the decay of turbulence, the cutoff continues to decrease toward lower energy, as dictated by loss processes.
To understand the distribution of electron energy within macro-particles, we also estimate the average value of γ (at the final simulation time, t = 117 Myr) denoted by γavg as
where γmax and γmin are given in Sect. 2.2. In Fig. 5, we plot the PDF of γavg for the entire macro-particle population. In the left panel of the figure we show the PDF for γavg for case (a). The distribution exhibits a power-law tail (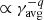 , with q ≈ 2.54) beyond γavg ∼ 102. For cases (b) and (c) in the middle and right panels of the figure the PDFs exhibit a power-law distribution starting from γavg ∼ 103 with a small hump and an exponential cutoff. The hump feature arises due to competition between STA and radiative losses (see above). It is interesting to note that the slope of the power law for cases (b) and (c) (q = 0.29, 0.38, respectively) are both flatter than for case (a). This is a consequence of the fact that STA continuously supplies energy to the macro-particles by accelerating the low-energy micro-particles to the higher energy, thus compensating for the radiative losses, as opposed to the case with only DSA. Finally, in the presence of both DSA and STA, the γavg PDFs exhibit a low-energy break around γavg ∼ 103 because STA boosts low-energy particles to higher energies. This process is absent if only DSA is present since there is no selective mechanism to accelerate only the low-energy particles during shock acceleration (which involves convolution of the entire upstream spectrum of each macro-particles to downstream; Mukherjee et al. 2021), and hence γavg PDF cannot form a low-energy break.
, with q ≈ 2.54) beyond γavg ∼ 102. For cases (b) and (c) in the middle and right panels of the figure the PDFs exhibit a power-law distribution starting from γavg ∼ 103 with a small hump and an exponential cutoff. The hump feature arises due to competition between STA and radiative losses (see above). It is interesting to note that the slope of the power law for cases (b) and (c) (q = 0.29, 0.38, respectively) are both flatter than for case (a). This is a consequence of the fact that STA continuously supplies energy to the macro-particles by accelerating the low-energy micro-particles to the higher energy, thus compensating for the radiative losses, as opposed to the case with only DSA. Finally, in the presence of both DSA and STA, the γavg PDFs exhibit a low-energy break around γavg ∼ 103 because STA boosts low-energy particles to higher energies. This process is absent if only DSA is present since there is no selective mechanism to accelerate only the low-energy particles during shock acceleration (which involves convolution of the entire upstream spectrum of each macro-particles to downstream; Mukherjee et al. 2021), and hence γavg PDF cannot form a low-energy break.
 |
Fig. 5. PDF of the γavg (see Eq. (19)) for the entire macro-particle population. The left, middle, and right panels show the PDF for cases (a), (b), and (c) respectively. |
In Fig. 6 we present the integrated particle spectrum considering the whole macro-particle population for each of the three case scenarios. The integrated particle spectrum is calculated as
 |
Fig. 6. Integrated spectrum of the entire macro-particle population for the three cases. The portion of the spectrum highlighted in orange corresponds to the low-energy break. The highlighted portions of the spectrum in blue and green correspond to the high-energy cutoff for case (b) and (c), respectively. |
where i corresponds to individual macro-particles inside the computational domain, 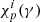 is the distribution function of the ith macro-particle, and 𝒩i(γ) represents the number of macro-particles with Lorentz factor γ. The DSA spectrum (case (a)) is in the form of a broken power law with the break at γ ≈ 5 × 102 (region highlighted in orange in the figure). This behavior is expected when computing a resultant distribution comprising all the macro-particles, where the spectral evolution is mediated by shock acceleration and radiative losses (Heavens & Meisenheimer 1987). The position of the break has a direct correspondence with the peak in the γmax PDF for case (a) and can be explained by the same reasoning (see Eq. (18)). When STA is taken into account (cases (b) and (c)), the spectrum exhibits an inverse power-law behavior for γ ≲ 4 × 102, followed by a low-energy break and a power-law trend with a high-energy cutoff (highlighted in blue and green for cases (b) and (c), respectively). The spectral behavior in the region γ ≲ 4 × 102 is a manifestation of the low-energy flattening in the individual macro-particle spectrum (see Sect. 3.2.1) due to turbulent acceleration. The origin of the low-energy break bears a similar explanation to case (a). However, for cases where STA is taken into account the cutoff is accompanied by piled up micro-particles (see case (c) in Fig. 3) as opposed to case (a), which is why the break appears more prominent in cases (b) and (c). The high-energy cutoff in the integrated particle spectrum (at γ ≈ 104 for case (b) and ≈105 for case (c)) is governed by the formation of the quasi-stationary cutoff in the individual macro-particle spectrum due to the interplay of DSA and STA. As a result, the position of these high-energy cutoffs has an exact correspondence with the peaks observed in Fig. 4 for the cases where STA is taken into account. The power-law trend beyond γ ≳ 106 for all the case scenarios is a consequence of the continuous macro-particle injection in the computational domain and a fraction of them subsequently undergoing shock acceleration.
is the distribution function of the ith macro-particle, and 𝒩i(γ) represents the number of macro-particles with Lorentz factor γ. The DSA spectrum (case (a)) is in the form of a broken power law with the break at γ ≈ 5 × 102 (region highlighted in orange in the figure). This behavior is expected when computing a resultant distribution comprising all the macro-particles, where the spectral evolution is mediated by shock acceleration and radiative losses (Heavens & Meisenheimer 1987). The position of the break has a direct correspondence with the peak in the γmax PDF for case (a) and can be explained by the same reasoning (see Eq. (18)). When STA is taken into account (cases (b) and (c)), the spectrum exhibits an inverse power-law behavior for γ ≲ 4 × 102, followed by a low-energy break and a power-law trend with a high-energy cutoff (highlighted in blue and green for cases (b) and (c), respectively). The spectral behavior in the region γ ≲ 4 × 102 is a manifestation of the low-energy flattening in the individual macro-particle spectrum (see Sect. 3.2.1) due to turbulent acceleration. The origin of the low-energy break bears a similar explanation to case (a). However, for cases where STA is taken into account the cutoff is accompanied by piled up micro-particles (see case (c) in Fig. 3) as opposed to case (a), which is why the break appears more prominent in cases (b) and (c). The high-energy cutoff in the integrated particle spectrum (at γ ≈ 104 for case (b) and ≈105 for case (c)) is governed by the formation of the quasi-stationary cutoff in the individual macro-particle spectrum due to the interplay of DSA and STA. As a result, the position of these high-energy cutoffs has an exact correspondence with the peaks observed in Fig. 4 for the cases where STA is taken into account. The power-law trend beyond γ ≳ 106 for all the case scenarios is a consequence of the continuous macro-particle injection in the computational domain and a fraction of them subsequently undergoing shock acceleration.
In summary, turbulent acceleration with exponential decay modifies the macro-particles’ maximum energy (γmax) distribution by presenting an additional hump to the PDFs. The location of the each hump is closely connected to the γ of individual macro-particles, where τc = tA. The PDF of γavg for cases (b) and (c) exhibits a power-law trend with an exponential cutoff and a low-energy break. The integrated spectrum with only DSA exhibits a low-energy break, whereas with STA an additional cutoff at high energy is also seen.
3.2.3. Turbulent acceleration as a sustained acceleration process
In this section we examine how STA supports the macro-particles to sustain their energy from extreme radiative losses. To properly characterize this behavior we consider an equivalent magnetic field for each macro-particle and compare it with the dynamical magnetic field at the position of the macro-particle. This is computed from the instantaneous single macro-particle energy distribution as
where Beq is the corresponding equivalent magnetic field.
Following Eq. (21), we compute Beq for cases (a), (b), and (c) and compare it with the corresponding dynamical magnetic field Bdyn computed at the local macro-particle position at each instant. We plot the time evolution of the histogram of the quantity Beq/Bdyn on a logarithmic scale for all three cases in the top panel of Fig. 7, where orange, blue, green, and black curves in each panel depict the histogram at times 5 Myr, 29 Myr, 58 Myr, and 117 Myr, respectively. All the histograms are normalized so that the maximum peak value is unity.
 |
Fig. 7. Histogram of macro-particles with respect to Beq/Bdyn to further study the effect of STA on the macro-particle population. The histograms are normalized and then scaled with the maximum value. Top panel: histograms for three different cases at four different times (color-coded, see inset at right). The top left, middle, and right panels show the histogram for cases (a), (b), and (c), respectively. Bottom panel: two-dimensional histograms showing τt vs. Beq/Bdyn at the final time t = 117 Myr for three cases. The bottom left, middle, and right panels show the histogram for cases (a), (b), and (c), respectively. The color bar at the bottom panel shows the number of macro-particles. |
As shown in the top left panel, for case (a) the histogram gradually shifts toward a state with Bdyn ∼ Beq as time progresses. Cases (b) and (c) exhibit a similar pattern, and a broadening of the histogram is observed as well. For case (a) the shape of the PDF can be observed to evolve to a negatively skewed distribution on a logarithmic scale. To analyze the reason for this evolution, we show a 2D histogram (bottom left panel) depicting the value of τt with respect to the magnetic field ratio, which indicates that the macro-particle population with a larger magnetic field ratio has recently been shocked. This should not be surprising since the shock acceleration energizes particles, thereby increasing Beq. The 2D histogram also shows that a relatively small fraction of macro-particles has magnetic field ratios higher than unity, due to the absence of any further acceleration process. As a result these particles undergo strong cooling and quickly lose their energy, hence featuring an exponential fall in the histogram beyond Beq ∼ Bdyn (top left plot of Fig. 7).
On the contrary, for cases (b) and (c) (top middle and right panels) the 1D histogram evolves to a more extended structure, which closely resembles the log-normal shape. This extended form of the histograms is ascribed to the presence of STA which provides a continuous acceleration to the macro-particles and helps them maintain their energy even in the presence of radiative cooling. This is further confirmed by observing the corresponding 2D histograms in the bottom panels (middle and right, respectively). In contrast to case (a), both figures show more macro-particles in the region Beq/Bdyn ≳ 1. We can also infer that even macro-particles that were shocked earlier (smaller τt) feature a higher value of Beq/Bdyn as a result of the fact that with STA macro-particles can sustain their energy for a longer amount of time.
In summary, for all the cases, we observe that the distribution gradually evolves toward a state where Beq ∼ Bdyn. Furthermore, due to the presence of STA, compared to only DSA, the histogram manifests a more extended structure that is evenly spread due to the macro-particles that were shocked at earlier time, but could sustain their energy from radiative losses because of STA.
3.2.4. Synthetic spectral energy distribution of radio lobe
In Fig. 8 we present the spectral energy distribution (SED) for cases (a), (b), and (c). The SED is calculated by integrating the emissivity (Eq. (16)) along the line of sight (Vaidya et al. 2018) with two different radiation mechanisms: synchrotron and IC-CMB. The synchrotron SED shows, for case (a), enhanced emission in the X-ray band with multiple peaks at ν ∼ 1018 and ν ∼ 1021 Hz. These peaks originate from freshly shocked macro-particles (Borse et al. 2021; Mukherjee et al. 2021). This can be further verified analytically using the relation between the critical (or cutoff) frequency (νc) of synchrotron radiation and the corresponding γ (see, e.g., Eqs. (5.80) from Condon & Ransom 2016):
 |
Fig. 8. Synthetic spectral energy distribution for case (a) (in green), case (b) (in red), and case (c) (in blue). The SED due to the synchrotron mechanism is shown in solid lines and the IC-CMB part is shown in dashed lines. The vertical axis shows the value of νFν in arbitrary units. |
For instance, with an averaged magnetic field of the lobe B = 19.70 μG and νc ∼ 1021 Hz, we obtain a corresponding value for γ ∼ 109, which is consistent with the peak in the PDF of γmax seen in Fig. 4.
For case (b), in addition to similar shock-induced transient signatures, the synchrotron emission shows a distinct peak in the low-energy GHz radio band (ν ∼ 1010 Hz). The origin of such a low-energy peak is direct evidence of turbulent acceleration, and corresponds to the hump in the PDF at γmax ∼ 104 (see middle panel of Fig. 4). Likewise, the synchrotron peak can also be observed for case (c) at a slightly higher energy, ν ∼ 1013 Hz. The macro-particles that are accelerated via STA and give rise to the peak in PDF around γmax ∼ 105 (right panel of Fig. 4) are mainly contributing to the emission at this frequency band. The macro-particle population that is stochastically accelerated in cases (b) and (c) is not only responsible for synchroton emission, but also contributes to the distinct peaks in the IC-CMB spectral energy distribution (ν ∼ 1019 Hz for case b, ν ∼ 1021 Hz for case c). We verified that these values correspond to the frequency of the photons scattered of a population of electrons with energy γmax ∼ 104 and γmax ∼ 105 for case (b) and (c), respectively. The post-scattering frequency of the photons νs is related to the electron energy as
where ν0 is the frequency at which the cosmic microwave background (CMB) radiates. Using ν0 = 160 GHz in Eq. (23), we find that an electron population at γmax ∼ 104 would scatter the CMB photons at a frequency of ∼1019 Hz. A similar inference can be drawn for the origin of the IC-CMB peak around ∼1021 Hz for case (c). Additionally, the peaks in the γ-ray band (ν ∼ 1027 Hz) for all cases corresponds to the particles with γmax ∼ 109.
After observing the SED and identifying the particle populations responsible for the various peaks, we proceed to show the spatial distributions of these particle populations in order to understand the resulting emission structure. In Fig. 9 we show the spatial distribution of the particle populations responsible for these peaks. The top panels depict the particle distributions with γmax ∼ 104 for case (a) (left plot), case (b) (middle plot), and case (c) (right plot). These particles are correlated to the peak in the SED caused by IC-CMB at ν ∼ 1019 Hz, as explained earlier in this section. The macro-particles in case (a) can be seen to be more confined around the shocks in the beam and, to a lesser extent, to the cocoon region. The reason is that, after the shock acceleration, the macro-particles’ energy evolution is governed by loss mechanisms alone, and as a result they lose a considerable amount of energy in a short distance. On the contrary, when turbulent acceleration is included, the particle distribution corresponding to γmax ∼ 104 stretches over a wider area (see the upper middle and right plot) since macro-particles can be reaccelerated via turbulence, sustaining high energy for a longer distance before losing a substantial portion of their energy. In comparison to case (a), this extended spatial distribution implies a more diffuse structure of X-ray radiation attributable to IC-CMB. In the lower panel of Fig. 9 we show the spatial distribution of the macro-particles with γmax ∼ 105, responsible for the peak in the IC-CMB SED at ∼1021 Hz. Similar to the former scenario, the particle distribution shows an extended morphology for case (c) compared to the other two cases for the same reasons discussed before. Interestingly, the spatial distributions for case (a) (left panel) and case (b) (middle panel) have a very similar structure. The reason for this can be investigated by comparing the γmax histograms for case (a) and (b) (left and middle panels in Fig. 4), showing a similar behavior (after the peak at γmax ∼ 104 for the latter).
 |
Fig. 9. Spatial distribution of the particles responsible for the peaks in SED. Top panel: position of the particle population with γmax ∼ 104 for case (a) (left), case (b) (middle), and case (c) (right). Bottom panel: position of the particle population with γmax ∼ 105 for case (a) (left), case (b) (middle), and case (c) (right). |
In summary, we showed that in the presence of stochastic acceleration the emission from the radio lobe changes significantly compared to the case where STA is neglected. With the inclusion of STA, the spatial distribution of the X-ray emitting particles through IC-CMB exhibit a wider extent (see Fig. 9) compared to the DSA-only case, indicating an emission structure that is diffusive.
3.2.5. Spectral index distribution
In this section we focus on the effect of STA on the radio frequency regime (≤15 GHz). With the advent of several high-resolution low-frequency telescope arrays it is possible to quantify the distribution of the spectral index in extended lobes (Alexander & Leahy 1987; Harwood et al. 2013). In this regime the emission from astrophysical systems are dominated by synchrotron radiation, which follows a power-law relation with the frequency Iν ∝ ν−δ, with δ being the spectral index. In our simulation we compute the intensity from the macro-particle energy distribution (see Sect. 2.2) and further calculate the spectral index δ using the equation
In the top panel of Fig. 10 we show the Gaussian-filtered spectral index maps of the radio lobe considering two frequencies, ν1 = 1.5 GHz and ν2 = 15 GHz, for cases (a), (b), and (c). All the spectral maps show signs of spectral steepening from the outer regions of the lobe (near the bow-shock) toward the inner part. This spatial distribution can be further analyzed by observing the bottom panel of the figure, where we plot the vertical distribution of the spectral index value on the path depicted by the black dashed line shown in the corresponding top panel, from the inner region of the lobe to the outer region. The spectral index distribution behaves similarly for all three cases, showing a rapid increase followed by a softer (or almost constant) increase. By analyzing the slope of this second part, we obtain an average value for case (a) of −1.01, while for cases (b) and (c) it is −0.80 and −0.49, respectively. This implies that the radiation spectrum becomes harder with increasing α in the lobe. The spatial extent of the region with constant spectral index is larger for case (b) compared to cases (a) and (c). For case (a) this directly follows from the absence of any continuous acceleration mechanism other than shocks, and the ensuing radiative cooling of the macro-particles in the back flow over a short timescale. In contrast, for cases (b) and (c), STA provides additional continuous acceleration to the macro-particles. For this reason, the macro-particles could radiate for a longer amount of time and the value of the spectral index could be maintained for a longer distance. Additionally, due to faster turbulence decay, case (c) maintains the spectral index for a shorter spatial extent compared to case (b).
 |
Fig. 10. Spectral index map and spectral index distribution of the radio lobe for cases (a), (b), and (c). The spectral index maps are drawn considering two radio frequencies, 1.5 GHz and 15 GHz. Top left panel: spectral index map for case (a). Top middle panel: for case (b). Top right panel: for case (c). Bottom panel: spectral index distribution for all three cases. |
Our results have shown that the signature of the continuous acceleration of particles is due to the stochastic turbulence impact on several observables, including the spectral index variation along the lobe. We also observed that while with increasing α the spectral index value inside the lobe increases owing to the shorter acceleration timescale, the extent of the region with constant spectral index decreases due to turbulence decay. We discuss the implications of the synthetic measures quantified in Sect. 3 with multiwavelength observational signatures in the next section.
4. Summary and discussion
In this work we presented 2D axisymmetric large-scale numerical simulations of AGN jets using a fluid-particle hybrid approach, in order to focus on particle acceleration processes and emissions from radio lobes. In spite of their limitations, and owing to the prohibitive cost of 3D computations, 2D models still provide fundamental insights into the interplay between different acceleration mechanisms and their influence on emission signatures.
Owing to the multiscale nature of the system, the underlying turbulence is considered in a sub-grid manner and its effect on the cosmic ray transport is modeled with a phenomenologically motivated ansatz for the turbulent acceleration timescale that can mimic the turbulence decay process usually observed in various astrophysical sources. By introducing this timescale, we solve the cosmic ray transport equation to evolve their energy distribution, accounting for diffusive shock acceleration (DSA), stochastic turbulent acceleration (STA), and for radiative losses (synchrotron and inverse-Compton), as implemented in the PLUTO code by Vaidya et al. (2018). We explore different scenarios by selectively including or excluding these acceleration mechanisms, and study their effects on the emission signatures of the radio lobes.
We summarize the primary results from this work as follows:
-
We observe significant modification of the energy spectra of macro-particles when turbulent acceleration is included in addition to DSA compared to the shock acceleration-only case. The interplay of DSA, STA, and turbulent decay results in features such as flattening of the spectrum in the low-energy region and a dynamically evolving high-energy cutoff. These features produce curvature in the particle spectrum which can further manifest in the emission properties of the radio lobe (Duffy & Blundell 2012).
-
The analysis of the maximum attainable energy results in a unimodal PDF with a broken power-law tail when only shock acceleration is accounted for; instead, when both DSA and STA are included the PDF exhibits a bimodal structure. Furthermore, the PDF of the average energy (γavg) for each macro-particle shows a power-law profile with an exponential cutoff on inclusion of STA. These distributions closely resemble the case in which STA is mediated by continuous particle injection and escape (see Fig. 2b of Katarzyński et al. 2006). Here particle injection due to shocks act as a source, while the escape is due to turbulence decay. The lobe integrated spectrum exhibits a broken power-law structure for DSA, whereas with STA it displays a high-energy cutoff in addition to the low-energy break. The position of the low-energy break corresponds to the γ where radiative loss time becomes equal to the dynamical time. The integrated spectrum generated by including STA can be utilized as a consistent input for one-zone radio lobe modeling that accounts for particle acceleration due to turbulence.
-
Further analysis of STA and its effect on sustaining the particle’s energy against radiative cooling is performed through the evolution of Beq/Bdyn histograms, showing for all three cases that the system evolves to a state where Beq ∼ Bdyn. However, with STA the corresponding distributions become wider when compared to the shock-only scenario as a result of the additional energization.
-
The study of the synthetic SED of the simulated source demonstrates the existence of additional peaks in the radio band due to synchrotron emission, and in the X-ray band through the IC-CMB mechanism when STA is taken into account. Further analysis of the spatial distribution of the macro-particles corresponding to these additional peaks implies a more extended and diffuse emission in the X-ray band owing to the interplay of the two acceleration mechanisms. The extent of the spatial distribution is further observed to be modulated by changing the value of α (see Eq. (13)). This implies that with an appropriate choice of α one might achieve diffuse emission around localized regions inside the radio lobe (e.g., diffuse synchrotron emission around the hotspot of 3C445, see Prieto et al. 2002).
-
The radio frequency spectral maps along with the spectral index profile inside the lobe indicate a harder emission spectrum due to STA compared to the DSA case. The spectral index is observed to remain constant over a distance inside the radio lobe whose length is modulated with the efficiency of the turbulent acceleration. The value of the spectral index in this region is ∼ − 0.49 for case (c), for case (b) it is ∼ − 0.8, and for case (a) it is ∼ − 1.01. This behavior has also been found in various observations of radio lobes (Parma et al. 1999). Radio lobes of parsec-scale AGN jets have been observed to exhibit similar characteristics (Hovatta et al. 2014). However, it should be noted that from observation of radio lobes there is no evidence of a spectral index ≈ − 0.5 or higher. This, consequently, may impose a limit to the extent and the effectiveness of STA in the actual radio lobes.
4.1. Present limitations and future extension
The results shown in the present study represent a first step toward a more realistic description of the complex interaction between the turbulent radio lobe material and the nonthermal particles, and it is certainly limited by a number of considerations.
Two-dimensional axisymmetric models, for instance, are similar to 3D models only in the case of stable jets and homogeneous media. Time-dependent jet propagation is known to be prone to 3D instabilities (e.g., Kelvin-Helmholtz and current-driven modes) that cannot be captured by axisymmetric models (see, e.g., Mignone et al. 2010; Bodo et al. 2013, 2016). These instabilities are known to have an effect on the jet emission (Acharya et al. 2021; Borse et al. 2021) and can induce a range of non-axisymmetric structures, such as filaments and shocks along jets and in the back-flowing zone (see, e.g., Tregillis et al. 2001; Matthews et al. 2019). These non-axisymmetric structures are known to enhance the turbulence inside the back-flowing region, and hence would strongly influence particle mixing (Jones et al. 1999).
Another potential issue with 2D axisymmetric simulations is that, because of the ∂ϕ = 0 condition, the induction equation (Eq. (4)) does not allow conversion of a toroidal magnetic field (Bϕ) to a poloidal field (Porth 2013). This leads to the continuous amplification of the injected Bϕ component in the computational domain over time, eventually affecting the jet dynamics. However, for this work we consider a very small Bϕ value to lessen any substantial impact on the dynamics. Nevertheless, 2D computations still allow our method to be tested with finer grid spacing providing better resolution across shocked structures. This would be computationally expensive in the fully 3D case. Additionally, we also consider an un-magnetized ambient medium in the expectation that the magnetic field in the ambient medium will have minimal impact on the nonthermal particle transport within the lobe.
Our simulations describe the interaction between cosmic ray particles and jet materials although the former behave essentially as passive scalars without back-reaction on the fluid. A future extension of our work will consider more exhaustive two-fluid approaches by also taking into account energy and momentum transfer between the two components in a self-consistent way (Girichidis et al. 2020; Ogrodnik et al. 2021). It should be emphasized that the employment of parameters in our model is an unwanted, albeit necessary, consequence of the fact that large-scale simulations cannot possibly resolve (and therefore sample) the small-scale turbulence regions. Sub-scale micro-physical processes (such as turbulent acceleration timescales or MHD turbulence damping rates) must therefore be encoded through a sub-grid recipe. In this work, in fact, we consider a one-parameter exponentially decaying hard-sphere turbulence as a model of STA inside the radio lobe, with certain values for the parameter (α = 104, 105) and compute the emission signatures from the radio lobes via synchrotron and IC-CMB processes.
Future extensions of this work will hopefully consider fully 3D investigations, where the impact of non-axisymmetric plasma instabilities may deeply affect the morphology. Additionally, the sub-grid prescription of turbulence decay plays a crucial role in governing some of the essential properties of emission.
Acknowledgments
The authors thank the referee for the comments and suggestions on the work. S.K. and B.V. appreciate the financial assistance provided by the Max Planck partner group award at the Indian Institute of Technology, Indore. All the simulations have been carried out using the computing facility at the Indian Institute of Technology, Indore and Max Planck Gesellschaft (MPG) super-computing resources. S.K. would also like to thank Arghyadeep Paul, Gaurab Giri, Sriyasriti Acharya and Suchismita Banerjee for the valuable discussion sessions during the course of this work.
References
- Acharya, S., Borse, N. S., & Vaidya, B. 2021, MNRAS, 506, 1862 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, P., & Leahy, J. P. 1987, MNRAS, 225, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Araudo, A. T., Bell, A. R., & Blundell, K. M. 2018, Nucl. Part. Phys. Proc., 297-299, 242 [CrossRef] [Google Scholar]
- Asano, K., & Hayashida, M. 2018, ApJ, 861, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Belmont, R., Malzac, J., & Marcowith, A. 2008, A&A, 491, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., Fabian, A. C., Crawford, C. S., Erlund, M. C., & Celotti, A. 2006, ApJ, 644, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Mamatsashvili, G., Rossi, P., & Mignone, A. 2013, MNRAS, 434, 3030 [Google Scholar]
- Bodo, G., Mamatsashvili, G., Rossi, P., & Mignone, A. 2016, MNRAS, 462, 3031 [Google Scholar]
- Borse, N., Acharya, S., Vaidya, B., et al. 2021, A&A, 649, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunetti, G., & Lazarian, A. 2007, MNRAS, 378, 245 [Google Scholar]
- Brunetti, G., Bondi, M., Comastri, A., et al. 2001, ApJ, 561, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., & Fleishman, G. D. 1992, MNRAS, 255, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., Perley, R. A., Dreher, J. W., & Leahy, J. P. 1991, ApJ, 383, 554 [Google Scholar]
- Celotti, A., Ghisellini, G., & Chiaberge, M. 2001, MNRAS, 321, L1 [Google Scholar]
- Condon, J. J., & Ransom, S. M. 2016, Essential Radio Astronomy (Princeton: Princeton University Press) [Google Scholar]
- Croston, J. H., Hardcastle, M. J., Harris, D. E., et al. 2005, ApJ, 626, 733 [NASA ADS] [CrossRef] [Google Scholar]
- de Vries, M. N., Wise, M. W., Huppenkothen, D., et al. 2018, MNRAS, 478, 4010 [NASA ADS] [CrossRef] [Google Scholar]
- Dedner, A., Kemm, F., Kröner, D., et al. 2002, J. Comput. Phys., 175, 645 [Google Scholar]
- Dermer, C. D., Miller, J. A., & Li, H. 1996, ApJ, 456, 106 [Google Scholar]
- Donnert, J., & Brunetti, G. 2014, MNRAS, 443, 3564 [NASA ADS] [CrossRef] [Google Scholar]
- Duffy, P., & Blundell, K. M. 2012, MNRAS, 421, 108 [NASA ADS] [Google Scholar]
- English, W., Hardcastle, M. J., & Krause, M. G. H. 2016, MNRAS, 461, 2025 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Z.-H., Liu, S., Wang, J.-M., Fryer, C. L., & Li, H. 2008, ApJ, 673, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Ferrand, G., & Marcowith, A. 2010, A&A, 510, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [CrossRef] [EDP Sciences] [Google Scholar]
- Gill, A., Boyce, M. M., O’Dea, C. P., et al. 2021, ApJ, 912, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Giri, G., Vaidya, B., Rossi, P., et al. 2022, A&A, 662, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girichidis, P., Pfrommer, C., Hanasz, M., & Naab, T. 2020, MNRAS, 491, 993 [Google Scholar]
- Hardcastle, M. J., Birkinshaw, M., Cameron, R. A., et al. 2002, ApJ, 581, 948 [Google Scholar]
- Hardcastle, M. J., Kraft, R. P., Sivakoff, G. R., et al. 2007, ApJ, 670, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Cheung, C. C., Feain, I. J., & Stawarz, Ł. 2009, MNRAS, 393, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., & Krause, M. G. H. 2013, MNRAS, 430, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., & Croston, J. H. 2020, New A Rev., 88, 101539 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. E., Moldón, J., Oonk, J. R. R., et al. 2019, ApJ, 873, 21 [Google Scholar]
- Harwood, J. J., Hardcastle, M. J., Croston, J. H., & Goodger, J. L. 2013, MNRAS, 435, 3353 [NASA ADS] [CrossRef] [Google Scholar]
- Heavens, A. F., & Meisenheimer, K. 1987, MNRAS, 225, 335 [NASA ADS] [Google Scholar]
- Hovatta, T., Aller, M. F., Aller, H. D., et al. 2014, AJ, 147, 143 [Google Scholar]
- Huarte-Espinosa, M., Krause, M., & Alexander, P. 2011, MNRAS, 417, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T. W., Ryu, D., & Engel, A. 1999, ApJ, 512, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Katarzyński, K., Ghisellini, G., Mastichiadis, A., Tavecchio, F., & Maraschi, L. 2006, A&A, 453, 47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, I. R. 1972, ApJ, 174, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Duffy, P., & Gallant, Y. A. 1996, A&A, 314, 1010 [NASA ADS] [Google Scholar]
- Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51 [Google Scholar]
- Krause, M. 2005, A&A, 431, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kundu, S., & Vaidya, B. 2022, Proceedings of the International Astronomical Union (IAU) [Google Scholar]
- Kundu, S., Vaidya, B., & Mignone, A. 2021, ApJ, 921, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K. R., Payne, D. G., Meier, D. L., & Blandford, R. D. 1989, ApJ, 344, 89 [Google Scholar]
- Liu, S., Petrosian, V., & Melia, F. 2004, ApJ, 611, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Mahatma, V. H., Hardcastle, M. J., Croston, J. H., et al. 2019, MNRAS, 491, 5015 [Google Scholar]
- Marcowith, A., & Casse, F. 2010, A&A, 515, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcowith, A., Ferrand, G., Grech, M., et al. 2020, Liv. Rev. Comput. Astrophys., 6, 1 [Google Scholar]
- Massaglia, S., Bodo, G., Rossi, P., Capetti, S., & Mignone, A. 2016, A&A, 596, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, F., Missaglia, V., Stuardi, C., et al. 2018, ApJS, 234, 7 [Google Scholar]
- Matthews, J. H., Bell, A. R., Blundell, K. M., & Araudo, A. T. 2019, MNRAS, 482, 4303 [NASA ADS] [CrossRef] [Google Scholar]
- Meisenheimer, K. 2003, New Astron. Rev., 47, 495 [CrossRef] [Google Scholar]
- Mertsch, P., & Petrosian, V. 2019, A&A, 622, A203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, D. M. A., Pohl, M., Petrov, M., & Oskinova, L. 2021, MNRAS, 502, 5340 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Rossi, P., Bodo, G., Ferrari, A., & Massaglia, S. 2010, MNRAS, 402, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Mukherjee, D., Bodo, G., Rossi, P., Mignone, A., & Vaidya, B. 2021, MNRAS, 505, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Mullin, L. M., Riley, J. M., & Hardcastle, M. J. 2008, MNRAS, 390, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Ogrodnik, M. A., Hanasz, M., & Wóltański, D. 2021, ApJS, 253, 18 [CrossRef] [Google Scholar]
- O’Sullivan, S., Reville, B., & Taylor, A. M. 2009, MNRAS, 400, 248 [CrossRef] [Google Scholar]
- Parma, P., Murgia, M., Morganti, R., et al. 1999, A&A, 344, 7 [NASA ADS] [Google Scholar]
- Perlman, E. S., Clautice, D., Avachat, S., et al. 2020, Galaxies, 8, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V. 2012, Space Sci. Rev., 173, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Porth, O. 2013, MNRAS, 429, 2482 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto, M. A., Brunetti, G., & Mack, K.-H. 2002, Science, 298, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R., & Dermer, C. D. 2000, A&A, 360, 789 [NASA ADS] [Google Scholar]
- Tavecchio, F., Maraschi, L., Sambruna, R. M., & Urry, C. M. 2000, ApJ, 544, L23 [Google Scholar]
- Tavecchio, F., Costa, A., & Sciaccaluga, A. 2022, MNRAS, 517, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Tregillis, I. L., Jones, T. W., & Ryu, D. 2001, ApJ, 557, 475 [Google Scholar]
- Vaidya, B., Mignone, A., Bodo, G., Rossi, P., & Massaglia, S. 2018, ApJ, 865, 144 [Google Scholar]
- van Leer, B. 1977, J. Comput. Phys., 23, 276 [Google Scholar]
- Vazza, F., Wittor, D., Brunetti, G., & Brüggen, M. 2021, A&A, 653, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vurm, I., & Poutanen, J. 2009, ApJ, 698, 293 [Google Scholar]
- Winner, G., Pfrommer, C., Girichidis, P., & Pakmor, R. 2019, MNRAS, 488, 2235 [Google Scholar]
- Worrall, D. M. 2009, A&ARv, 17, 1 [Google Scholar]
- Worrall, D. M., Birkinshaw, M., Kraft, R. P., et al. 2008, ApJ, 673, L135 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Properties of the different cases considered in the present study for calculating emission from the radio lobe.
All Figures
 |
Fig. 1. Normalized density ρ/ρ0 evolution of the simulated radio lobe structure. The images depict a slice through the mid-plane of the notional 3D volume; all images are reflection-symmetric around the jet axis and the z = 0 plane since the simulations are axisymmetric. The color bar shows a logarithmic scale of density. |
| In the text | |
 |
Fig. 2. Temperature, pressure, absolute velocity, and plasma-beta maps of the simulated jet structure for time t = 117 Myr. Temperature and pressure are shown in physical units, velocity is shown in units of c, and the color bars are shown in logarithmic scale. The average temperature of the radio lobe is on the order of ∼70 keV, average plasma-beta is ∼32, and average velocity is ∼0.02c. |
| In the text | |
 |
Fig. 3. Evolution of the energy spectrum for a randomly chosen macro-particle for all the cases described in Table 1. The macro-particle encountered shock at a dynamical time of t = 25 Myr. The color bar shows how much time has elapsed since the simulation began. The value of the lower end of the color bar is set to the time when the macro-particle encountered the final shock. |
| In the text | |
 |
Fig. 4. Probability distribution function of the cutoff energy for the entire macro-particle population. The left, middle, and right panels show the PDF for cases (a), (b), and (c), respectively. |
| In the text | |
 |
Fig. 5. PDF of the γavg (see Eq. (19)) for the entire macro-particle population. The left, middle, and right panels show the PDF for cases (a), (b), and (c) respectively. |
| In the text | |
 |
Fig. 6. Integrated spectrum of the entire macro-particle population for the three cases. The portion of the spectrum highlighted in orange corresponds to the low-energy break. The highlighted portions of the spectrum in blue and green correspond to the high-energy cutoff for case (b) and (c), respectively. |
| In the text | |
 |
Fig. 7. Histogram of macro-particles with respect to Beq/Bdyn to further study the effect of STA on the macro-particle population. The histograms are normalized and then scaled with the maximum value. Top panel: histograms for three different cases at four different times (color-coded, see inset at right). The top left, middle, and right panels show the histogram for cases (a), (b), and (c), respectively. Bottom panel: two-dimensional histograms showing τt vs. Beq/Bdyn at the final time t = 117 Myr for three cases. The bottom left, middle, and right panels show the histogram for cases (a), (b), and (c), respectively. The color bar at the bottom panel shows the number of macro-particles. |
| In the text | |
 |
Fig. 8. Synthetic spectral energy distribution for case (a) (in green), case (b) (in red), and case (c) (in blue). The SED due to the synchrotron mechanism is shown in solid lines and the IC-CMB part is shown in dashed lines. The vertical axis shows the value of νFν in arbitrary units. |
| In the text | |
 |
Fig. 9. Spatial distribution of the particles responsible for the peaks in SED. Top panel: position of the particle population with γmax ∼ 104 for case (a) (left), case (b) (middle), and case (c) (right). Bottom panel: position of the particle population with γmax ∼ 105 for case (a) (left), case (b) (middle), and case (c) (right). |
| In the text | |
 |
Fig. 10. Spectral index map and spectral index distribution of the radio lobe for cases (a), (b), and (c). The spectral index maps are drawn considering two radio frequencies, 1.5 GHz and 15 GHz. Top left panel: spectral index map for case (a). Top middle panel: for case (b). Top right panel: for case (c). Bottom panel: spectral index distribution for all three cases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



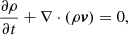
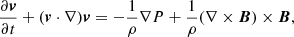
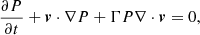
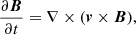
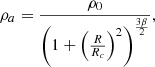
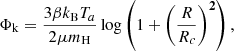
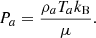
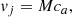
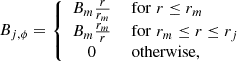
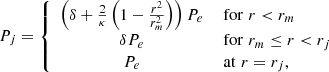
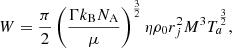
![$$ \begin{aligned} \displaystyle \frac{\partial \chi _p}{\partial \tau } + \frac{\partial }{\partial \gamma }\left[(S+D_{A})\chi _{p}\right] = \frac{\partial }{\partial \gamma }\left(D\frac{\partial \chi _p}{\partial \gamma }\right) ,\end{aligned} $$](/articles/aa/full_html/2022/11/aa44251-22/aa44251-22-eq16.gif)