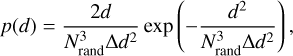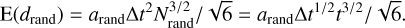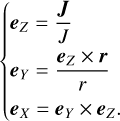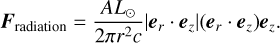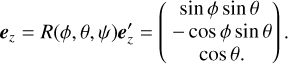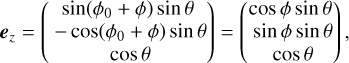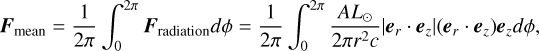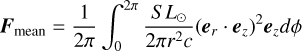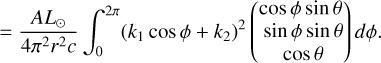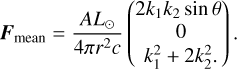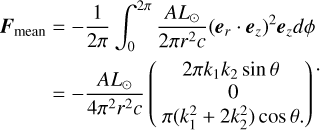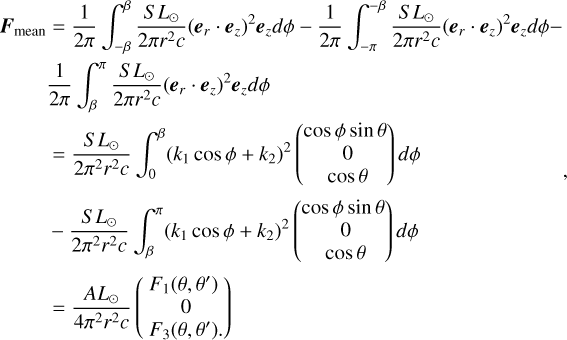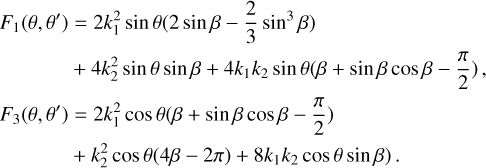| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202244119 | |
| Published online | 15 November 2022 | |
Observable tests for the light-sail scenario of interstellar objects
1
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange,
06304
Nice, France
e-mail: wenhan.zhou@oca.eu
2
Origin Space Technology Co. Ltd.,
Apartment D4, Hongfeng Science Park,
Nanjing, Jiangsu
212415, PR China
e-mail: liushangfei@mail.sysu.edu.cn
3
School of Physics and Astronomy, Sun Yat-sen University,
2 Daxue Road,
Zhuhai
519082, Guangdong Province, PR China
4
CSST Science Center for the Guangdong-Hong Kong-Macau Greater Bay Area, Sun Yat-sen University,
2 Daxue Road,
Zhuhai
519082, Guangdong Province, PR China
5
Department of Aerospace Engineering, University of Maryland,
College Park, MD
20742, USA
6
Department of Astronomy and Astrophysics, University of California,
Santa Cruz, CA
95064, USA
7
Institute for Advanced Studies, Tsinghua University,
Beijing
100086, PR China
Received:
25
May
2022
Accepted:
24
August
2022
Context. Enigmatic dynamical and spectral properties of the first interstellar object (ISO), 1I/2017 U1 (Oumuamua), led to many hypotheses, including a suggestion that it may be an “artificial” spacecraft with a thin radiation-pressure-driven light sail. Since similar discoveries by forthcoming instruments, such as the Vera C. Rubin telescope and the Chinese Space Station Telescope (CSST), are anticipated, a critical identification of key observable tests is warranted for the quantitative distinctions between various scenarios.
Aims. We scrutinize the light-sail scenario by making comparisons between physical models and observational constraints. These analyses can be generalized for future surveys of ‘Oumuamua-like objects.
Methods. The light sail goes through a drift in interstellar space due to the magnetic field and gas atoms, which poses challenges to the navigation system. When the light sail enters the inner Solar System, the sideways radiation pressure leads to a considerable non-radial displacement. The immensely high dimensional ratio and the tumbling motion could cause a light curve with an extremely large amplitude and could even make the light sail invisible from time to time. These observational features allow us to examine the light-sail scenario of interstellar objects.
Results. The drift of the freely rotating light sail in the interstellar medium is ~100 au even if the travel distance is only 1 pc. The probability of the expected brightness modulation of the light sail matching with ‘Oumuamua’s observed variation amplitude (~2.5–3) is <1.5%. In addition, the probability of the tumbling light sail being visible (brighter than V = 27) in all 55 observations spread over two months after discovery is 0.4%. Radiation pressure could cause a larger displacement normal to the orbital plane for a light sail than that for ‘Oumuamua. Also, the ratio of antisolar to sideways acceleration of ‘Oumuamua deviates from that of the light sail by ~1.5 σ.
Conclusions. We suggest that ‘Oumuamua is unlikely to be a light sail. The dynamics of an intruding light sail, if it exists, has distinct observational signatures, which can be quantitatively identified and analyzed with our methods in future surveys.
Key words: minor planets / asteroids: individual: interstellar objects
© W.-H. Zhou et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The unprecedented trajectory and unique spectral properties (Meech et al. 2017) exhibited during a brief visit of the first interstellar object (ISO), 1I/2017 U1 (‘Oumuamua), gave rise to a protracted controversy regarding its origin (Raymond et al. 2018b,a; Cuk 2018; Moro-Martín 2019; Zhang & Lin 2020; Jackson & Desch 2021). According to one particularly bold assumption, it is an “artificial” spacecraft with a thin light sail driven by radiation pressure on an intentional mission to our Solar System (Bialy & Loeb 2018; Loeb 2021). Based on the sensitivity limitation of the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS), the interplanetary density of ‘Oumuamua-like ISOs is estimated to be nISO ≲ 0.2 au−3 in the proximity of the Earth orbit (Do et al. 2018; Trilling et al. 2017; Bannister et al. 2019). If their parent bodies randomly came across the Solar System, the inferred mass of ejected objects per star, Mej, would exceed a few M⊕ in the solar neighborhood (Do et al. 2018; Portegies Zwart et al. 2018). Prior to its entry into the Sun’s domain of gravitational influence, ‘Oumuamua’s velocity relative to the local standard of rest (LSR) was vO ~ 10 km s−1. At a heliocentric distance r ~ 1.5 au, its large-amplitude, irregularly varying light curve (Meech et al. 2017; Drahus et al. 2018; Bolin et al. 2017; Bannister et al. 2017; Knight et al. 2017; Jewitt et al. 2017) suggests that ‘Oumuamua is either a prolate or oblate object, freely tumbling with the period of its light curve increasing at a rate PO ~ 0.3 h day−1 from PO ~ 8 h (Flekkøy et al. 2019). In the absence of any detectable trace of outgassing, its orbital path has an observationally inferred perihelion distance of pO ~ 0.26 au and departs from a parabolic Keplerian trajectory with a component of nongravitational acceleration predominantly in the radial direction away from the Sun (Micheli et al. 2018), although the validity of the fitting procedure has been questioned by Katz (2019). Its surface albedo resembles that of asteroids rather than comets (Trilling et al. 2018). Shortly after ‘Oumuamua was discovered, data taken with multiple telescopes provided a high-cadence light curve (from October 25, 2017, to October 27,2017) with an irregular brightness variation over an amplitude range ~2.5–3. This high-cadence light curve has been used to deduce ‘Oumuamua’s tumbling motion (Meech et al. 2017). In addition, ‘Oumuamua was detected (Micheli et al. 2018) with magnitudes brighter than 27 in all 55 follow-up trackings (over 49 days starting on November 15, 2017).
A rationale for the spacecraft hypothesis is that it circumvents the large Mej inferred for the parent bodies of randomly distributed ISOs. It also attributes ‘Oumuamua’s nongravitational acceleration to the Sun’s radiation pressure to a light sail under the assumption that it has a thin oblate shape with a length l1 ~ 102 m, width l2 ≃ l1, surface area A, mass mO, and surface density (Bialy & Loeb 2018) mO/A = ρOl3 ≈ 1 kg m−2. If ‘Oumuamua’s density, ρO, is comparable to that of refractory asteroids (≃2–3 × 103 kg m−3), its effective thickness, l3(~ 3–5 × 10−4m ≪ l1) would be comparable to that of an eggshell, two orders of magnitude smaller than that of the International Space Station; although, a much thinner light sail (~ 7 × 10−6 m) has been deployed, without tumbling, on the spacecraft Interplanetary Kite-craft Accelerated by Radiation Of the Sun (IKAROS; Tsuda et al. 2011).
However, the turbulent interstellar medium (ISM) poses challenges to the navigation of the light sail. Hydrogen atoms exert a drag force that is normal to the surface of the light sail, leading to a sideways acceleration of the tumbling light sail. Moreover, in the disorderly magnetic field, B, of interstellar space, a Lorentz force in the direction (B · vmagB − |B|2vmag)/|B|2|vmag| is induced, which contains a drag and a sideways force component with a magnitude amag ~ B2vmag/2ρOl3µ0vA, where vA is the Alfvén speed in the ISM. As ‘Oumuamua passes through randomly oriented B in eddies of all sizes, Ltur, the magnitude and direction of the magnetic drag change on a timescale τtur ~ Ltur/vO. On timescales t ⩾ τtur, the value of ‘Oumuamua’s path deviation from its initial target goes through a random walk.
Even if the light sail manages to arrive at the Solar System, the unique configuration (i.e., the extremely high dimensional ratio) of the light sail would give rise to recognizable observational features. The radiation pressure would cause a sideways acceleration due to the imperfect alignment of the surface normal vector with heliocentric position vector, which would result in a considerable non-radial deviation from Kepler motion. In addition, the tumbling of the extremely thin light sail would lead to a light curve with an immense amplitude. The light sail can even be invisible when the sunlight is edge-on to the light sail. Stringent probability assessments for the spaceship scenario can be made using ‘Oumuamua’s observed light curve and detected magnitude as well as a prefect recurrence rate.
Previous studies (e.g., Katz 2021; Curran 2021) have questioned the light-sail scenario based on the unlikely coincidence between the advancement of extraterrestrial technology and the advent of the observational capability of Pan-STARRS, though a quantitative and comprehensive analysis of observation data has not yet been performed. In this paper, we revisit the light-sail scenario with its model parameters and estimate the ram-pressure and magnetic drag and the torque on the light sail during ‘Oumuamua’s voyage through the turbulent ISM (Sect. 2). In Sect. 3, we model ‘Oumuamua’s dynamics as a tumbling light sail cruising the Solar System, and in particular we study the implications of its nongravitational acceleration due to the sideways radiation force and the observable features due to its tumbling motion and high dimensional ratio. We summarize our results and compare them with observations in Sect. 4. Lastly, we discuss our results and propose observable tests for future surveys in Sect. 5.
2 Dynamics of a tumbling light sail in interstellar space
In the solar neighborhood, the ISM contains (Draine 2010): (1) a diffuse warm neutral medium (WNM) with number density nISM ~ 106 m−3 and sound speed cs ~ 9 km s−1; (2) a cold neutral medium (CNM) with nISM ~ 108m−3, cs ~ 1.3 km s−1; and (3) giant molecular clouds (GMCs) with nISM ~ 1010–1012 m−3, cs ~ 0.5 km s−1. The local volume filling factor for the WNM, the CNM, and GMCs is 0.5, 5 × 10−3, and 2 × 10−3, respectively (Draine 2010), although ‘Oumuamua may have recently traveled through some GMCs (Pfalzner et al. 2020; Hsieh et al. 2021). Due to the perturbation of GMCs, the velocity dispersion of ‘Oumuamua and nearby stars relative to the LSR vd(τ„)  increases as they advance in age, τ*. Their corresponding rate of kinetic energy gain, per unit mass, is
increases as they advance in age, τ*. Their corresponding rate of kinetic energy gain, per unit mass, is 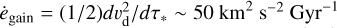 .
.
With a relative velocity v, atoms in the volume-filling WNM bombard the tumbling light sail. Their momentum impulse on its bumpy surface introduces a residual torque and modulates its rotation frequency (Zhou 2020) with a chaotic reorientation of its spin axis (Fig. 1) on a timescale τrot. The efficiency of this effect can be extrapolated (Mashchenko 2019) from PO due to a similar torque induced by the solar radiation on the light sail, though the required surface roughness is ~102l3 (i.e., much larger than its thickness). Readers are referred to Appendix A for our detailed analysis on the ISM’s torque on the light sail’s asymmetric surface and its application to ‘Oumuamua’s spin.
Collectively, atoms in the streaming WNM exert a drag on the hypothetical tumbling light sail with an energy dissipation rate ėdiss. ‘Oumuamua accelerates with agas ≃ nISMmpv2/ρOl3 until a terminal speed vterm,gas ~ vO, with which ėgain ≃ ėdiss, after it has traveled on a timescale t ≳ τterm,gas ~ 1 Gyr. In Sect. 2.1, we analyze the ISM gas drag effect and how it determines the terminal speed and causes the light sail to deviate from the intended course.
The ISM’s turbulent motion is also associated with disorderly magnetic fields, B. An electric potential drop is induced across the light sail, and an Alfvén wing (Drell et al. 1965) is launched when ‘Oumuamua moves with a velocity vmag relative to these fields. In Sect. 2.2, we show that the dissipation along the Alfvén wings also leads to a Lorentz force, which includes a drag and sideways acceleration. Similarly, as ‘Oumuamua passes through randomly oriented B in turbulent eddies of all sizes, Ltur, the magnitude and direction of the magnetic drag change over time, and one can derive the expected value of ‘Oumuamua’s path deviation from its initial target.
Although ‘Oumuamua’s initial velocity does not change significantly over shorter time intervals τterm,gas > t > τrot (or travel distance L < Lterm,gas ~ 10 kpc), it endures a fluctuating sideways acceleration due to both the ISM’s ram pressure normal to the randomly oriented surface and magnetic drag. Accumulation of this random-walk acceleration prompts ‘Oumuamua to drift off course from its intended destination. The expectation value of the path deviation (or impact parameter), E(d) ~ (t)3/2, increases with t and L (Appendix C).
2.1 Terminal speed and off-course deviation caused by ISM gas drag
The hypothetical tumbling light sail moving with velocity v through the ISM also experiences a drag force (Laibe & Price 2012):
This Epstein limit is appropriate for l1 ≪ the molecular mean free path such that gas particles, with a mass mp, can be treated as a dilute medium. We applied the heat capacity ratio γ0 = 5/3 for the ideal gas. The area correction factor fA = A/l1l2 has a magnitude 1 ≳ fA ≫ l3/l1. For a light sail with v ~ vO ≳ cs, Fgas ≃ nISMmpfAl1l2v2 with an acceleration
and an energy dissipated rate
On the timescale
the light sail attains an energy equilibrium with a terminal speed
which ~vO due to the drag by the volume-filling WNM on it over a travel distance
Nevertheless, the spaceship hypothesis is based on the conjecture that the Solar System has always been ‘Oumuamua’s intended destination and that it has maintained its original course with its initial and current v ~ vO rather than vtermgas despite their coincidentally similar magnitude. Its corollary implies a traveled distance L ≤ Lterm,gas and duration t ≤ τterm,gas.
The ram-pressure force is primarily applied in the direction normal to the surface of a smooth thin light sail rather than the direction of its motion relative to the ISM, and it does not sensitively depend on the ISM’s turbulent speed, vtur, or eddy size, Ltur, in the limit v ~ vO > vtur > cs. Moreover, due to the finite net torque exerted by the turbulent ISM on the light sail’s asymmetric and uneven surface, which is revealed by the radiative torque measured in the case of ‘Oumuamua (see details in Appendix A), the spin orientation and frequency, ω, of its tumbling motion evolve on a timescale (see Eq. (B.2))
Consequently, the ram-pressure-driven acceleration adrift ~ agas is redirected on a timescale τrot, which is generally smaller than the eddy turnover timescale τtur ~ Ltur/vtur over a wide range of Ltur (Eq. (14)). Over a brief travel time, t < τrot, or distance, L = vt, the light sail’s spin vector does not change significantly and as such drifts with a dispersion velocity σdrift ≃ adriftt in some random directions. Over a longer travel time, τrot ≤ t < τterm,gas, the light sail’s evolving spin vector and sideways acceleration, adrift, lead to a random walk in its accumulative σdrift ≃ (t/τrot)1/2agasτrot ≪ v, the detail of which is shown in Appendix C. The expected value of the deviation from the light sail’s initial course for these two limiting timescales (see Eq. (C.7)) are
 |
Fig. 1 Schematic illustration of the hydrodynamic (left panel) and magnetic (right panel) drag on a moving light sail in a turbulent ISM with a magnetic field, B (green). The tumbling sail is represented by a thin gray sheet with a bumpy surface and a spin axis in the Z direction that precesses around its angular momentum, J, axis. The bombardment of atoms (with open and solid yellow dots representing pre- and post-collision trajectories) and photons (wavy arrows) leads to a force, Fgas (red), which can be decomposed into a drag, Fdrag, in the direction of the sail’s velocity, v (gray), and a sideways force, Fdrift. The induced currents (blue arrows) conducted away by surrounding charged particles lead to a Lorentz force, Fmag, with components perpendicular to both v and B. |
2.2 Alfvén-wing drag by turbulent WNM
The ISM also contains magnetic fields with B ≈ 10 µG = 1 nT in the neutral medium and a few times larger in the molecular clouds (Draine 2011). As a light sail traverses the magnetic field with a relative velocity vmag, an electric field vmag×B is induced with a potential drop U ≃ 〈l〉vmagB across the time-averaged length, 〈l〉, of the tumbling light sail. An Alfvén wave is emitted along a wing (Drell et al. 1965), leading to a drag against vmag with an acceleration
in the direction (B · vmagB − |B|2vmag)/|B|2|vmag|, where fD ≃ 〈l〉/l1, with 1 ≳ fD >> l3/l1, μ0(= 4π × 10−7N A−2), 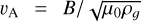 is the Alfvèn speed,
is the Alfvèn speed, 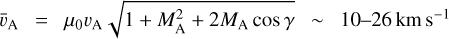 in the diffuse ISM, MA = vmag/vA is the magnetic Mach number, and the angle cos γ = vmag · B/(|vmag| · |B|). When the rate of energy dissipation per unit mass in the Alfvén wing,
in the diffuse ISM, MA = vmag/vA is the magnetic Mach number, and the angle cos γ = vmag · B/(|vmag| · |B|). When the rate of energy dissipation per unit mass in the Alfvén wing,
is balanced by 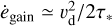 , a terminal speed is established with
, a terminal speed is established with
which ~vO with fD ~ O(1) The timescale to reach vterrm,mag is
over a travel distance
Based on the same assumption that the light sail has preserved its original course, we only considered the limit L ≤ Lterm,mag and v ≃ vO.
The magnetic fields in the diffuse ISM are characterized by chaotic structure, although they are more orderly in star-forming GMCs (Crutcher 2012). We assume they are coupled to the large eddies in the WNM, which has a turbulent speed vtur ~ (Ltur/pc)0.38 km s−1 that persists on the timescale (Choudhuri & Roy 2019)
on size scale 10−2pc ≲ Ltur ≲ 102pc. The orientation between ‘Oumuamua vmag and the background B (or equivalently γ) evolves on its travel timescale across eddies on scales with measured turbulent fields (Ltur ≲ 1 pc), τtur ~ Ltur/vO ~ 0.1 Myr. This revision leads to greater variations, over a shorter timescale but on the same turbulent-eddy length scale, in the direction of the drag force on ‘Oumuamua than those due to the limited modification in the amplitude vmag (Eq. (9) and Fig. 1).
For the spacecraft hypothesis, the initial value of v is preserved (~vO) over a travel distance L ≤ Lterm,mag. Over a brief travel time interval, t < τtur, the direction and magnitude of the drag by the turbulent fields on the light sail is sustained such that adnft ≃ amag and dispersion velocity σdrift ≃ amagt. Over a longer duration with τtur ≤ t ≤ τterm,mag, the light sail encounters a new turbulent eddy with different vtur, γ, and Ltur. While the magnitude of its adrift ~ amag, random walk in the direction of relative motion leads to accumulative σdrift ≃ (t/τtur)1/2αmagτtur. The expected values of the deviation from the light sail’s initial course for these two limiting timescales are
Since the magnitude of vtur and τtur are increasing functions of Ltur, that of amag and E(dmag) also increases with Ltur (Eqs. (9) and (15)). In the present context, we estimated a lower limit for E(dmag) by assuming the small Ltur ≤ 1 pc, where turbulent fields can be resolved. We also neglected the Ltur dependence in B.
The total trajectory deflection has an expected value 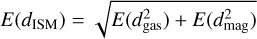 with a Rayleigh distribution (see Eq. (C.6)). In the diffuse WNM, E(dgas) < E(dmag), τtur ~ 0.1 Myr such that E(dISM) ~ E(dmag) and the light sail’s sideways motion undergo Levy walk over a travel length scale L ≳ 1 pc. In more dense CNM, E(dISM) ~ E(dgas) ~ E(dmag), τrot ~ 0.1 Myr and the sideways drift also follows a Levy walk path over travel length scale L ≳ 1 pc. Although E(dISM) ~ E(dgas) > E(dmag) in relatively dense (nISM > 1010 cm−3) GMCs, their hydrodynamic drag may lead to limited drift, despite their short τrot and τterm,gas, due to their sparse volume filling factor.
with a Rayleigh distribution (see Eq. (C.6)). In the diffuse WNM, E(dgas) < E(dmag), τtur ~ 0.1 Myr such that E(dISM) ~ E(dmag) and the light sail’s sideways motion undergo Levy walk over a travel length scale L ≳ 1 pc. In more dense CNM, E(dISM) ~ E(dgas) ~ E(dmag), τrot ~ 0.1 Myr and the sideways drift also follows a Levy walk path over travel length scale L ≳ 1 pc. Although E(dISM) ~ E(dgas) > E(dmag) in relatively dense (nISM > 1010 cm−3) GMCs, their hydrodynamic drag may lead to limited drift, despite their short τrot and τterm,gas, due to their sparse volume filling factor.
In the evaluation of amag, we neglected the light sail’s spin because vO >> 2πl1/P. Nevertheless, this motion also leads to the excitation of Alfvén waves at both ends and dissipation of its spin energy Erot = Iω2/2 (Zhang & Lin 2020) with a power
The damping timescale of rotation is
if the Alfvén speed is assumed to be 1 kms-1 in interstellar space. We see that this damping timescale is much longer than that due to the ISM’s ram pressure, τrot (Eq. (B.2)), and eddy turnover timescale, τtur. In the determination of relative velocity between it and the magnetic field, the light sail’s rotational damping due to magnetic torque can be neglected. Overall, we show that the rotational evolution timescale is inversely proportional to the gas number density and τtur ≈ 0.1 τrot ≈ 0.1 Myr for nISM ~ 106m−3. The deflections induced by the magnetic field and the gas pressure are comparable (E(dmag) ≈ E(dgas)).
Under the assumption that a light sail’s original v is preserved before it enters the Solar System, there is no a priori reason for its v to be correlated with its l1 or l2. In contrast, the distance traveled, L, by freely floating interstellar asteroids and comets (with l3 not much smaller than l1 or l2) is likely to be greater than min(Lterm,gas, Lterm,mag), and as such their motion will be gravitationally accelerated, dragged by the interstellar gas, and retarded by the interstellar magnetic field through Alfvén-wing drag (Zhang & Lin 2020). When a dynamical equilibrium is established by the balance of these effects, the ISOs attain a terminal speed relative to the LSR, vd(l1) ≃ min(vterm,gas, vterm,mag), which depends on their sizes.
3 Dynamics of a tumbling light sail in the Solar System
3.1 Sideways radiation force
During its sojourn through the Solar System, ‘Oumuamua endures intense heating near its perihelion. The surface temperature of the light sail increases rapidly, resulting in an increased average atomic kinetic energy of material. The atoms oscillate with anharmonic potentials in greater amplitudes, and therefore the material tends to expand with a larger separation between atoms. The fractional change in the light sail’s surface area can be estimated as ∆S/S = αA∆T × 100%, where αA is the thermal expansion coefficient. Molaro et al. (2020) estimate αA = 8 × 10−6 for boulders and αA = 2.4 × 10−4 for regolith. The thermal expansion coefficient, α, changes over the temperature as
The thermal equilibrium temperature at pO is ~800 K, so the thermal expansion coefficient, α, is nearly constant. The expansion ratio of the area is ∆S/S ≈ 16% for regolith material and ∆S/S ≈ 0.6% for boulder material. Such thermal stress would not significantly alter the shape or surface roughness of the light sail.
However, the solar radiation pressure exerts a sideways force on ‘Oumuamua analogous to that due to ram-pressure drag (Fig. 1). When photons hit the surface, some are reflected immediately while some get absorbed and reradiated with a time lag. The latter effect is negligible since the thickness we consider here is so thin that it could be smaller than the penetration depth of the thermal wave, which leads to a nearly equal temperature all over the surface. The immediately reflected photons cause a recoil force F ≃ ΦA/c in the direction perpendicular to the surface. Reflection on its rough surface also leads to a torque Trad (Eq. (A.3)), which cause ‘Oumuamua’s spin period, PO, and orientation to evolve on a timescale τrad >> PO (Eq. (A.4)).
The direction of this mean radiative force (integrated over a precession period) is about the wobble angle, θ, of ‘Oumuamua and the angle between the incident light and ‘Oumuamua’s angular momentum, θ. The heliocentric radial and sideways forces (in the antisolar and transverse directions) are
The deflection angle of the force can be defined as
The values of the angle, α, for different θ and θ′ are shown in Fig. 8. In the trajectory of ‘Oumuamua, the value of θ′ varies. Since information on ‘Oumuamua’s spin (e.g., the directions of its spin angular momentum vector, principle axis, and precession angle) is not available, we used the mean value of α as an approximation. The mean value is α ≈ 26°, which gives the ratio of the sideways force to the radial force
We can simply use this value to estimate the sideways deflection of ‘Oumuamua’s orbital paths through the Solar System.
Since the position of ‘Oumuamua is poorly constrained, we applied a Monte Carlo simulation to ‘Oumuamua’s orbital evolution over 80 days by testing 105 cases with random initial orientations of angular momentum. Since the observation timescale of de-spin is ~24 days, we reset the angular momentum to a random orientation every 24 days. For each case, we calculated the mean ratio of the sideways force to the radial force along the way. The sideways force will lead to a displacement that is normal to the Keplerian orbital plane. The comparison of the result of the light sail and ‘Oumuamua is shown in Sect. 4.3.
In addition, the nongravitational model that fits the observation data best indicates that the radial force is A1r−2, with A1 being constant. However, the tumbling motion of the light sail also leads to a variation in the magnitude of the force due to the time-varying orientation of the thin sheet. The timescale of the de-spin is ~24 days, which results in considerable changes in the angular momentum vector. We have already shown that the radiation force relies on the angular momentum (Eq. (D.11)), so we would expect a large variation range of the radiation force during 80 days of observation instead of a constant coefficient A1. At the very least, even if the angular momentum does not change a lot during the orbit, the light angle (θ′) changes due to the orbital motion, which also leads to a time-varying radiative radial force. During the observational period (80 days), the mean-ratio changes of the radial force, ∆A1/A1, estimated from 104 randomly generated test particles, show a normal distribution. The standard deviation is ~0.3, which indicates that the coefficient of the nongravitational force is expected to fluctuate by ~30%, while its reported value of A1 = 4.92 ± 0.16 × 10−6 m/s2 is inferred (Micheli et al. 2018) under the assumption of no change (i.e., ∆A1 = 0).
Since the light curve and the radiation force components highly depend on the orientation of the light sail, they build a correlation with each other that can be examined for ISOs in the future. The correlation can be described quantitatively by the circular cross-correlation function:
where 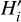 and
and 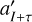 are the ith and (i + τ)th elements in the time-sequence absolute magnitude signal, H′, and the acceleration, a′, during a rotation cycle, which is centralized by
are the ith and (i + τ)th elements in the time-sequence absolute magnitude signal, H′, and the acceleration, a′, during a rotation cycle, which is centralized by
Here, H and ā are the mean values of H and a. Considering the periodicity of the light curve and the radiation force, we made a periodic extension of H′ and a′, which leads to a modified correlation function:
Therefore, the correlation function is a periodic function with the same period as H′ and a′ and we only need to pay attention to its behavior in one period. The correlation function reveals the similarity of the two signals at a time delay τ. The value range of R′H,a(τ) is [−1, 1], and a larger value of |R′H,a(τ)| implies a higher correlation between H and a.
 |
Fig. 2 Illustration of the light sails in the one-facet illumination state and two-facet illumination (left panels) and their light curves (right panels). The rotation angular momentum is J, and the spin vector is along the major principal axis, z. The position vector r is pointing ‘Oumuamua away from the Sun. The solid lines denote the absolute magnitude, while the dashed line denotes the areas of projection along the sunlight direction. The imperfect consistency results from the nonzero phase angle ~20° (Fraser et al. 2018). |
3.2 Light curve and visibility
The light curve of a tumbling light sail can exhibit a very large amplitude due to the large dimensional ratio. For a light sail with three axes of 60 m × 60 m × 0.3 mm, the amplitude could reach as large as 2.5 log (60 m/0.3 mm) ~ 13.25 in the case that the phase angle of the light sail is equal to 0°, which means the light sail is on the opposite side of the Sun relative to Earth. With a nonzero phase angle, the amplitude is even larger (Fraser et al. 2018). We used a symmetric ellipsoid (l1 = l2) model with an an isotropic-scattering surface for the calculation of the absolute magnitude of the light sail. The absolute magnitude is expressed as (Mashchenko 2019; Muinonen & Lumme 2015)
where
Here S = (S1, S2, S3) and E = (E1, E2, E3) are the position vectors of the Sun and Earth in the corotating coordinate system. The parameter l′3 is defined as l′3 = l3/l1. The angle α′ is the angle between T⊙ and T⊕, and λ′ is the angle between T⊙ and T. The parameter ∆V is the offset between the model and the observed light curve.
As already mentioned, the light curve can show an extremely large amplitude, which is shown in Fig. 2. Whether the amplitude is exotically large depends on the rotation state of the light sail and its orientation to the Sun, which can be categorized into two types. The first is the one-facet illumination state (OIS), where the light sail is in such a rotation that only one facet is exposed to sunlight. In this case, the projected area of the sunlight direction cannot reach the minimum value (l1 × l3) except when the sunlight comes from the edge of the light sail. Therefore, in the OIS the amplitude is usually not exotically large.
The second is the two-facet illumination state (TIS), where two facets of the light sail are successively exposed to sunlight due to rotation. In this case, the projected area of the sunlight direction reaches the lowest point the moment when the illuminated facet transfers from one to the other. In the TIS, the light curve of the light sail exhibits an extremely large amplitude, and the light sail becomes invisible for some time in its rotational cycle.
Figure 2 shows two examples of the light curve of the light sail, one for the OIS and the other for the TIS. Due to the symmetry of the square light sail, the periodical variation in the orientation of the light sail can be described by one parameter, the wobble angle (θ), as Fig. 2 shows. Another variable that affects the light curve is the direction of the position vector of the light sail relative to the Sun, which is equally translated to the illumination angle, θ′. The light sail is in the OIS when θ′ + θ ≤ 90° and is otherwise in the TIS.
Figure 3 shows the amplitude ∆H maps over a (θ, θ′) parameter space for the oblate shape, the prolate shape, and the light sail. We can see a clear boundary between the OIS and the TIS of the light sail in the amplitude map, although it does not strictly follows θ′ + θ ≤ 90° due to the nonzero phase angle.
 |
Fig. 3 Amplitude map for the light curves of an oblate shape (left), prolate shape (middle), and light sail (right). The fractions of area where the amplitude ∆H is between 2.5 and 3 are 0.34, 0.1, and 0.015 for the oblate shape, prolate shape, and light sail, respectively. |
4 Comparison between a free-floating light sail and ‘Oumuamua
4.1 Probability of close perihelion passage and occurrence timescale
In Sects. 2.1 and 2.2, we model the dynamics of ‘Oumuamua as a free-floating light sail traveling through a turbulent magnetized ISM under the influences of gas and magnetic drags on an intended journey to the Solar System. Together, these drag forces lead to a deviation with a Rayleigh distribution around an expected value  , which is equivalent to an impact parameter in the gravitational domain of the Sun. The corresponding expected value of the perihelion distance
, which is equivalent to an impact parameter in the gravitational domain of the Sun. The corresponding expected value of the perihelion distance 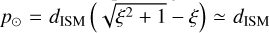 , where ξ = GM/v2dISM << 1 and p⊙ is generally much larger than ‘Oumuamua’s observed pO (Fig. 4).
, where ξ = GM/v2dISM << 1 and p⊙ is generally much larger than ‘Oumuamua’s observed pO (Fig. 4).
The probability of ‘Oumuamua attaining p⊙ smaller than ‘Oumuamua’s observed perihelion pO(0.26 au) is
where 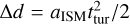 . For various values of nISM, P(p⊙ < pO) is smaller than 10−3 over a travel distance L ≳ 1 pc, and it scales as P ∝ L−3 for larger L, which is shown in Fig. 4.
. For various values of nISM, P(p⊙ < pO) is smaller than 10−3 over a travel distance L ≳ 1 pc, and it scales as P ∝ L−3 for larger L, which is shown in Fig. 4.
One possible solution for reconciling the low close-encounter probability with the expeditious discovery of ‘Oumuamua is the assumption that it was dispatched at one time with a population of Ntot cohorts, among which it had the smallest p⊙. Based on the Nobs = 1 observation of ‘Oumuamua with pO = 0.255 au, we infer Ntot = Nobs/P(p⊙ < pO) as a function of d. If they were launched concurrently at the same location, they would diffuse with a nearly uniform density 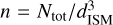 within a patch with a size ~dISM (Fig. 4). This dispersion would lead to a spread in the arrival time near the Sun τoccurrence = 2dISM/vO(n − 1), where n is the number per unit distance to the Sun (#/au) given by Ntotp(d). Figure 5 shows that ‘Oumuamua-like objects would occur more frequently in the outer Solar System. A shorter distance for ‘Oumuamua’s birthplace leads to a shorter occurrence timescale. However, none of ‘Oumuamua’s hypothetical cohorts has been discovered yet, implying that ‘Oumuamua comes from a distant place where it has a much lower probability of reaching the Solar System (Fig. 4).
within a patch with a size ~dISM (Fig. 4). This dispersion would lead to a spread in the arrival time near the Sun τoccurrence = 2dISM/vO(n − 1), where n is the number per unit distance to the Sun (#/au) given by Ntotp(d). Figure 5 shows that ‘Oumuamua-like objects would occur more frequently in the outer Solar System. A shorter distance for ‘Oumuamua’s birthplace leads to a shorter occurrence timescale. However, none of ‘Oumuamua’s hypothetical cohorts has been discovered yet, implying that ‘Oumuamua comes from a distant place where it has a much lower probability of reaching the Solar System (Fig. 4).
With its limiting sensitivity (24 magnitude), the Vera C. Rubin telescope can detect an ‘Oumuamua-like object out to ~1.6 au, and the number of cohorts passing through this distance is extrapolated to occur over time at intervals ∆τoccur ~ 2–3 yr, which are insensitive to the distance they have traveled through the ISM (Fig. 5). The accumulated discoveries over the telescope’s first 10 yr of operation (Abell et al. 2009) correspond to a significant fraction of N(d ≤ 1.6 au) ~ 3–5 independent cohorts, from the same direction in interstellar space, which is smaller than that estimated for freely floating ISOs (~ 10)1. Although this random drift may be rectified with a sophisticated guiding system, such a remote-control prowess during its arduous journey would be difficult to reconcile with ‘Oumuamua’s apparently freely tumbling motion, inferred from its evolving light curve (with PO) and small sideways displacement, relative to that in the antisolar direction (Sect. 4.3) without introducing an additional assumption regarding an accidental guiding-system failure during its most recent Solar System passage.
4.2 Variability and visibility of ‘Oumuamua’s light curve
After an initial flurry of high-cadence observations (mostly provided by discretionary-time allocation), regular follow-up monitoring of ‘Oumuamua continued for another two months. Based on this limited data set, the following useful information can be extracted.
First, the amplitude of ‘Oumuamua’s light curve on October 25, 2017, from the Very Large Telescope (VLT) data is ∆H ~ 2.5 magnitudes, and the that on October 27,2017, from the Canada-France-Hawaii Telescope (CFHT) and the United Kingdom Infra-Red Telescope (UKIRT) data is ∆H ~ 3 magnitudes (Meech et al. 2017). The true amplitude could be larger due to the large error on the faintest point in the light curve, and thus it is safe to conclude that the amplitude was in range ∆H ≃ (2.5, 3) from October 25, 2017, to October 27, 2017.
Second, ‘Oumuamua is visible in later observations, from November 15, 2017, to January 2,2018, which means it is at least brighter than 27 magnitudes (Micheli et al. 2018).
Based on the above data, we investigated the probability of ‘Oumuamua being a light sail by considering the probabilities of the following two independent characteristics. (1) Regarding the variability, the light curve amplitude of ‘Oumuamua as a light sail is in the range ΔH ≃ (2.5, 3), based on the first fact. (2) Regarding the visibility, ‘Oumuamua as a light sail is brighter than 27 magnitudes and so is visible on each observational attempt, based on the second fact.
To calculate the probability of event A, we tested 104 models, with the variable parameters wobble angle, θ, and the illumination angle, θ′, each sampled with 102 values uniformly distributed over (0◦, 90◦). Therefore, each of the 104 models has an equal probability. Counting the number of models where the amplitude is in range ∆H ≃ (2.5,3) and dividing this number by 104, we obtain the probability of event A. The likelihood function of the dimension ratio fi given event A is expressed as
Therefore, applying the maximum likelihood estimation (MLE), we find that the most likely shape of Oumuamua is the oblate shape with fl = l1/l3 ~ 7. The results for other fl are shown in the embedded panel in Fig. 6. We confirm that the probability of reproducing the observed variation amplitude (Mashchenko 2019) peaks at 10% with a 1:1:7 prolate axis ratio; at 34% with a 7:7:1 oblate axis ratio; and is ≲ 1.5% with a 1:1:5 × 10−6 thin-solar-sail axis ratio. This indicates that the most likely shape of Oumuamua is an oblate shape with an axis ratio of 7:7:1. Early studies favor a prolate shape according to the estimation of the density (Meech et al. 2017; Drahus et al. 2018), while Belton et al. (2018) suggest an oblate shape in the case that ‘Oumuamua’s rotational state is close to its highest energy state. By computing the possibilities of the best fitting prolate and oblate shape models, Mashchenko (2019) proposes that Oumuamua is more like an oblate spheroid with some torque exerted. Here our result supports the argument that Oumuamua is more likely to be oblate, making use of a different method, which compares the possibilities of various shapes inducing the observed amplitude of the light curve. This low probability of a light sail (~1.5%) is due to the common occurrence of a TIS, expected for thin freely tumbling light sails, which leads to very low surface exposure and reflection when they are nearly edge-on in the direction of the Sun (see Sect. 3.2), analogous to Saturn’s ring-plane crossing. In contrast, the tumbling motion in an OIS generally does not produce sufficiently large-amplitude modulations except under some special circumstances: θ + θ’′~ π/2, where θ and θ′ are the angles between the rotation axis relative to the normal vector of the light sail and to the direction of the Sun, respectively.
For event B, we generated 104 test light sails with initial amplitudes in the range (2.5, 3) and added random torques with the magnitude given by Eq. (A.4) and a random direction. The magnitude of the torque decreases with the distance from the Sun, and the direction is assumed constant in the corotating reference frame over time. With a lack of information about the torque, we made the assumption of a constant torque in the corotating frame as previous work obtained a good fit to the light curve by applying this assumption (Mashchenko 2019). Due to the torque, the light sail can switch from the OIS to the TIS and therefore become invisible for part of its rotation cycle. For each model, we ran a 70-day simulation, covering from October 25, 2017 January 2, 2018. Since the timescale of spin evolution due to the torque is ~24 days, the rotation state of ‘Oumuamua since November 15, 2017, is considered to be random and uncorrelated to that on October 25, 2017, when the light curve is derived. We can thus calculate the visible fraction for each case and obtain the distribution of the whole sample set, which contains 104 test particles. We deduce an expectation probability of 86.1 ± 3.2% of the entire 49-day monitoring interval that a freely tumbling light sail’s brightness is above the detection threshold (i.e., brighter than 27 magnitude), assuming a uniform sampling (gray distribution in Fig. 6). If the sampling is taken at epochs when ground-based and Hubble Space Telescope (HST) astrometry was obtained, the probability would be 84.8 ± 6.1% (blue distribution in Fig. 6).
The likelihood of the ISO as a light sail is revealed by comparing the distribution of the visible fraction of the tested 104 cases with that purely inferred from observations between November 15, 2017, and to January 2, 2018 (49 days). The latter can be derived by statistic methods. For the simplest guess, one could use the MLE, which yields a 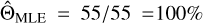 probability of visibility. However, such an estimation only generates a single fixed value. To calculate the posterior probability distribution f(Θ|B) – that is, the probability distribution function of ‘Oumuamua’s being visible given the fact that it was successfully detected in all 55 observations (event B) – we refer to Bayesian inference for a continuous probability variable Θ ∈ [0, 1]:
probability of visibility. However, such an estimation only generates a single fixed value. To calculate the posterior probability distribution f(Θ|B) – that is, the probability distribution function of ‘Oumuamua’s being visible given the fact that it was successfully detected in all 55 observations (event B) – we refer to Bayesian inference for a continuous probability variable Θ ∈ [0, 1]:
where B(n, k) is a statistical model describing a particular event of k times positive results out of n independent tests, and here we have n = k = 55 for event B. The f(Θ) is the prior probability distribution. Since we have no prior knowledge of ‘Oumuamua’s visible probability, it is reasonable to assume f(Θ) = 1; in other words, any visible probability, Θ, is equally likely. The f(B|Θ) is the probability of B(n, k) when the probability parameter Θ is given, and it can be written as
Thus, we can calculate the posterior probability distribution using
We show ‘Oumuamua’s posterior visible probability density distribution f(Θ|B(55,55) in Fig. 6. The expected a posteriori (EAP) of ‘Oumuamua’s visibility is
This 3σ (or 2.2σ) discrepancy between the uniform (or nonuniform) sampling model and observational detection probability poses another challenge to the freely tumbling light-sail scenario. In fact, only 8 out of 104 models report a 100% visible fraction.
The above analysis could be strengthened by additional observational results, such as the Minor Planet Center (MPC) astrometric database, after taking into account their limitations intrinsic to all photometric measurements obtained with astrometric purposes.
 |
Fig. 4 Schematic illustration of the diverse pathways of a constellation of Ntot tumbling solar sails traveling over a distance L through the turbulent magnetized ISM (left panel) and the expected value of the perihelion distance as a function of travel distance (right panel). As shown in the left panel, dispersive hydrodynamic and magnetic drag lead to a sideways drift, 4SM, and a dispersion in time of arrival, δt, at the Sun. The expected value E(dISM) (dashed gray circle) is generally much larger than the targeted Oumuamua’s perihelion distance, po. In the right panel, the expected value of the perihelion distance, E(p⊙) (solid lines), is shown as a consequence of deflection after traveling over a distance L through the ISM with a number density nISM. The probability of a single light sail striking the Solar System at a distance p⊙ ≤ pO (represented by a solid dot) from the Sun is shown with dashed lines. |
 |
Fig. 5 Fig. 5. Occurrence timescale (solid lines) and cumulative number (dashed lines) of ‘Oumuamua’s cohorts within d of the Sun for travel distances in the ISM L = 1 pc, 10 pc, 100 pc (increasing line widths). The timescale of occurrence of a light sail grows with increasing traveling distance, L, as a result of diffusion in the interstellar space. The timescale of occurrence within 100 au is insensitive to the travel distance, L, when L > 10 pc. The unshaded region is the observational domain of the first ∼10 yr of the Vera C. Rubin telescope. |
 |
Fig. 6 Fig. 6 – Histogram of 104 simulations of visible probability of a light sail versus posterior visible probability density distribution of Oumuamua over 49 days. The gray histogram represents the statistical result from a uniform random sampling, whereas the blue histogram is the statistical outcome from a nonuniform sampling that mimics ground-based and HST astrometry of Oumuamua. The dot-dashed gray and blue lines denote the mean values of these two statistical visibility simulations of a light sail, respectively. The dot-dashed and solid red lines represent the expected a posteriori estimation and the posterior probability distribution of Oumuamua’s visible probability (see Eq. (35)), respectively, based on the fact that Oumuamua was visible in all 55 observations. The embedded panel shows the likelihood that the amplitude of the light curve varies within the ranges ΔH ≃ (2.5,3) (Meech et al. 2017) and (2.5, 3.5) during the period October 25 = −27, 2017, for the light-sail, oblate shape, and prolate shape models. |
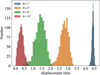 |
Fig. 7 Distribution of the ratios of the sideways displacement to the radial displacement for different tumbling angles, θ, during observation (80 days). The initial rotation states of 103 test particles are constrained by the fact that the light curve amplitude is between 2.5 and 3. The sideways-to-radial displacement is 4.4 ± 0.1, 2.8 ± 0.2, 1.4 ± 0.3, and 0.3 ± 0.1 for the initial wobble angles θ ≤ Io, ≤ 3°, ≤ 5°, and ≤ 10°, respectively. |
 |
Fig. 8 Fig. 8 – Ratio of the sideways radiation force (Fmean,s) to the radial radiation force (Fmean,r) for a tumbling light sail suffering radiation pressure. (a) Distribution of the deflection angle, α, with tan α = Fmean,s/Fmean,r for the whole value range of the wobble angle, θ, and the photon incident angle, θ′. (b) Distribution of Fmean,s/Fmean,r for 105 light sails with random θ and θ′ after an 80-day motion. The mean value of the sideways-to-radial force ratio is 0.7 ± 0.4 for light sails, while this ratio for Oumuamua is ~0.08 (Micheli et al. 2018), which is a discrepancy (Micheli et al. 2018) of ~1.5σ. The embedded panel shows the distribution of ∆A1/A1 for 104 generated pseudo ‘Oumuamuas during 80-day movements, where A1 and ΔA1 denote the coefficient of the radiation pressure and its variation over 55 days, from November 15, 2017, to January 2, 2018 (see Sect. 3). The standard deviation, denoted by the dash lines, is 0.3. |
 |
Fig. 9 Fig. 9 – Histogram of the ratio between the parallel deviation and the normal deviation. The radiation-pressure-induced deviation from a Keplerian trajectory during Oumuamua’s sojourns through the inner Solar System are shown with the dashed green line. The red star represents the Sun, and solid black, cyan, blue, and red arcs indicate the orbits of Mercury, Venus, Earth, and Mars, respectively. The purple cross indicates the position of Oumuamua at the last record. In total, 5 × 104 light-sail models with randomized initial spin orientations are integrated from Oumuamua’s discovery position for the same period of time. An additional Keplerian trajectory without radiation force is integrated, with which an orbital plane is defined. The circular inset panel zooms in to show Oumuamua’s last position (purple cross) surrounded by all light-sail models at the end of integration. And deviations from the Keplerian orbit (green square in the plane) are measured in the parallel and perpendicular directions to the orbital plane (indicated by two red arrows). The distribution of the ratio of the parallel displacement to the normal displacement peaks at ~3, while Oumuamua lies at ~17, which is obtained by applying the nongravitational acceleration suggested by Micheli et al. (2018). |
 |
Fig. 10 Light curve (upper panels), radiation acceleration (middle panels), and correlation within one day between them (bottom panels) for the light sail in the OIS (left panels) and in the TIS (right panels). |
4.3 Displacement normal to the orbit plane
‘Oumuamua’s “persistently visible” magnitude may be maintained under a highly unlikely scenario, that its tumbling motion is marginally kept in a protracted OIS near its current (θ + θ′ ≃ π/2) configuration. This probability can be constrained by the observationally inferred nongravitational force and acceleration in the radial (Fr away from the Sun) and sideways (Fs orthogonal to the radial) directions, due to the reflective torque on the light sail s surface (Micheli et al. 2018). Figure 7 shows that for θ < 5° – 10°, ∆rmean,s > ∆rmean,r. For a randomly distributed value of θ, the most likely mean ratio of these components Fmean,s/Fmean,r ~ 0.7 ± 0.4 (Eq. (22), Figs. 8 and 9), while it is 0.08 for the observed trajectory of ‘Oumuamua (Micheli et al. 2018), deviating from the light-sail model by 1.5σ. Since these forces correlate with the light curve (Fig. 10), which evolves due to changes in ‘Oumuamua’s tumbling motion (PO) and orbit, a ~30% revision in the radiation-pressure-driven acceleration is expected during its 80 days observational window. Observation data (Micheli et al. 2018) show that their ratio is only ~0.08, while in our simulation the fraction of the ratios equal to or smaller than 0.08 is only 2%.
As a result of the sideways force, an observable non-radial displacement is introduced to ‘Oumuamua’s trajectory. The sideways force causes a displacement normal to the orbital plane. The normal displacement is a good indication of the sideways force since the radial displacement and the transverse displacement are not well defined due to their changes of direction in the orbital motion. We used the REBOUND code (Rein & Liu 2012) and the REBOUNDx extension (Tamayo et al. 2019) to compute the ratio of the parallel displacement (in-plane displacement) to the normal displacement for 5 × 104 randomly generated models. The distribution of the ratio is shown in Fig. 9. The peak of the ratio distribution is at ~3, implying that the most likely parallel-to-normal ratio is ~3 for the light sail. However, the parallel-displacement ratio of ‘Oumuamua was found to be ~17 by applying the nongravitational acceleration reported by Micheli et al. (2018). Although existing data do not have adequate accuracy to firmly establish any discriminating constraints on the light-sail hypothesis, they highlight the requirement of low-probability coincidences for ‘Oumuamua.
Since both the radiation force and the light curve highly depend on the orientation and rotation of the light sail, there is a strong correlation between the acceleration and light curve. Figure 10 shows an example of the correlation functions between the absolute magnitude, H′, and the radiation force, a′, for the light sail. The correlation functions exhibit a regular mode, and the maximum value reaches 0.4 for both OIS and TIS, implying a high correlation between the absolute magnitude and the radiation force. However, for tumbling comets with nongravitational acceleration due to outgassing, the correlation is expected to be much weaker due to the chaotic tumbling motion and thermal delay. This correlation for a light sail declines within several rotational cycles (~2 days), which is shown in Fig. 11; this allows us to place a requirement on the high-cadence observational data. Therefore, with help of a huge amount of highly accurate observation data in the future, we will be able to identify the light sail by investigating the correlation between the light curve and the force curve.
 |
Fig. 11 Correlation between the light curve and the acceleration as a function of the delay time for a light sail. The correlation declines quickly within two days, which indicates that high-cadence time series data are required for the diagnosis of a light sail. |
5 Summary and discussions
We have analyzed the dynamics of light sails in the interstellar space and Solar System and show that their signatures, if they exist, are observable and can be quantitatively analyzed with some forthcoming instruments, such as the Vera C. Rubin telescope and the Chinese Space Station Telescope (CSST). In the forthcoming observations, our methods can function as a pipeline to test the probability of an ISO being a light sail.
After applying these analyses in the context of the first-discovered ISO ‘Oumuamua, we find its observed properties to be incompatible with those expected from the light-sail hypothesis. Based on inferences from ‘Oumuamua’s data, we suggest additional stringent tests for any potential interstellar light sails:
Freely floating light sails endure drifts due to the magnetic and gas drag by the ISM. The drift of freely rotating light sails in the ISM can reach ~100 au over a travel distance of 1 pc. It increases with the travel distance as ~L3. In order for any light sail to venture into ‘Oumuamua’s intended closest approach to the Sun, a constellation of light-sail probes is needed. Some members of this flotilla should be detectable over the next few years;
The solar radiation would cause a sideways pressure if the net flux of incident solar light is not parallel or antiparallel to the light sails orbital trajectories. Consequently, any tumbling motion would impose a non-negligible sideways radiation force on light sails and provoke sideways displacements. In reality, the sideways force experienced by ‘Oumuamua as inferred from its observed orbit is one order of magnitude smaller than the radial force, whereas these forces are expected to be comparable for a typical tumbling light sail. Quantitatively, the observed ‘Oumuamua ratio deviates from the value expected for a light sail by ~1.5 σ. Moreover, the probability distribution of the ratio between the displacement in the orbital plane to that in the normal direction for light sails peaks at 3, while the observationally inferred ratio is 17 for ‘Oumuamua. The displacement normal to the orbital plane is expected to be correlated with the light curve of light sails. This test can be applied with future high-cadence observations;
The amplitude of the light curve can also be used to assess the likelihood of the axis ratio of ISOs. Our analysis of ‘Oumuamua s observed light curve suggests it is most likely to have an oblate shape with an axis ratio of ~7:7: 1, while the probability for such a light curve to be due to a light sail is ~1.5%. The large amplitudes in the light-curve variation and the prospect of undetectable phases during their tumbling motion can be used to quantify the light-sail probability for future observations of ISOs. The probability for a light sail to be persistently brighter than the 27th magnitude in all 55 ‘Oumuamua s monitoring attempts during the two months after its discovery is estimated to be 0.4%. We find a 3σ discrepancy between ‘Oumuamua’s perfect-detection record and the expectation based on the light-sail hypothesis.
We suggest that ‘Oumuamua is unlikely to be a light sail. The dynamics of an intruding light sail would give rise to observational features such as the occurrence of its cohorts, a remarkable sideways radiation force and normal displacement from the Kepler orbit, a light curve with an extremely high amplitude, and irregular invisibility in the sky. These features can be quantitatively identified and analyzed with our methods in future surveys.
Acknowledgements
We thank Greg Laughlin and Scott Tremaine, as well as Tingtao Zhou, Patrick Michel, Meng Su, Xiaojia Zhang, Wenchao Wang, Yue Wang, Quanzhi Ye, Shoucun Hu, and Bo Ma for useful discussions. This work is supported by the National Natural Science Foundation of China under grant No. 11903089, the Guangdong Basic and Applied Basic Research Foundation under grant Nos. 2021B1515020090 and 2019B030302001, the Fundamental Research Funds for the Central Universities, Sun Yat-sen University under grant No. 22lgqb33, and the China Manned Space Project under grant nos. CMS-CSST-2021-A11 and CMS-CSST-2021-B09.
Appendix A ISM’s torque on the light sail’s asymmetric surface and ‘Oumuamua’s spin
The large-amplitude variations in ‘Oumuamua’s light curve suggest it has an asymmetry surface. Such a feature may be inherent in its original architecture, be bestowed by micro-meteorite and cosmic-ray bombardments during its passage through the ISM, or be deformed by the thermal stress due to a nonuniform albedo. Although the light sail may also have encountered an air mass comparable to mO after traveling L ≳ Lterm,gas (Bialy & Loeb 2018), the ISM’s condensation on its surface is unlikely to significantly modify its thickness, l3, especially in the limit L ≲ Lterm,gas.
With an asymmetric shape, the light sail endures a torque due to the gas ram pressure and dust bombardment. Over time, this torque changes the light sail’s spin orientation and frequency (Zhou 2020). We approximate the torque due to gas pressure by
where Cz,ISM measures the efficiency of the gas torque, depending on light sail’s shape and surface topology. Similarly, torque due to dust bombardment (Stern 1986) is
where μgr is the mean mass density of the interstellar grains, h1 and h2 are the ratios of evaporated mass and the ejected mass of the object to the mass of incident grain, respectively, and vej is the velocity of the ejection. The dust torque, Tdust, does not make much difference unless ‘Oumuamua moves very fast (e.g., > 20 km/s).
In order to infer the magnitude of Cz,ISM, we note that the irregular roughness and/or curvatures on the light sail’s surface also lead to a finite radiative torque, and the torque coefficient Cz,ISM ≃ Cz,rad (Zhou 2020). The finite magnitude of the radiative torque arises from a residual radiation pressure exerted by the incident photons on an asymmetric surface that does not cancel out during any spin period (Rubincam 2000; Vokrouhlicky & Capek 2002; Bottke Jr et al. 2006). Averaged over time, the radiative torque is approximately
where the efficiency of the radiative torque Cz,rad ≃ Cz,ISM, c is the light speed, A = fAl1l2, and Φ = L⊙/4πr2 is the solar flux at the object’s heliocentric distance, r. Subject to this torque, the light sails spin to evolve on a timescale
where its moment of inertia  .
.
‘Oumuamua’s observed de-spin timescale (PO/PO ~ 24 days) during its passage through the inner Solar System has been explained in terms of this radiative torque (Mashchenko 2019). Applying our model parameters to Eq. (A.4), we infer Cz,rad (as well as Cz,ISM) ~ 4 × 10−4. From this value of both Cz,rad and Cz,ISM, we place constraints on the surface roughness of the light sail with a set of Monte Carlo simulations. For our numerical model of the light sail shape, we constructed hundreds of surfaces with ~1500 vertexes and ~3000 facets in each generated surface (as shown in Fig. 1). The roughness can be measured by the standard deviation of departures, ∆h, from vertexes to a hypothetical perfectly flat sheet. We tested different cases where the deviations are ∆h ≃ (0.1,1,10,102)l3. For each case, we processed 10000 runs with random surfaces and random orientations. Figure A.1 shows a typical example of the distribution of the departures of vertexes from the plane with the standard deviation of 50 mm. The results show that the surface cannot introduce a sufficiently large torque efficiency (Cz,ISM = 4 × 10−4) unless it has a roughness such that the deviation of the vertexes is hundreds of times greater than the light sail thickness (l3 ~ 3–5 × 10−4m). The results are shown in Fig. A.1.
Appendix B Spin evolution during passage through the ISM
During its passage through the ISM with v ≤ 20 km s−1, the light sail s spin evolution is mostly determined by the gas torque (Zhou 2020), Tgas (Eq. A.1). The maximum moment of inertia, 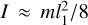 , of a solar sail (with a large dimension ratio l1 /l3 >> 1) dominates over that of its command module with sizes ≲ 0.1l1. (The actual integrated moment of inertia of the spacecraft is likely to be slightly smaller than this value since part of the mass is contained in the command module located near the center of the spacecraft.) The angular acceleration of the space craft is
, of a solar sail (with a large dimension ratio l1 /l3 >> 1) dominates over that of its command module with sizes ≲ 0.1l1. (The actual integrated moment of inertia of the spacecraft is likely to be slightly smaller than this value since part of the mass is contained in the command module located near the center of the spacecraft.) The angular acceleration of the space craft is
The light sail s spin angular momentum and its direction of acceleration, agas, change on the timescale of
Since the coefficient of the gas torque, Cz,ISM, has the same order of magnitude of that of the radiative torque, Cz,rad (Zhou 2020), we estimate Cz,ISM ≃ Cz,rad ≃ 4 × 10−4 from ‘Oumuamua’s observed de-spin rate during its passage through the Solar System (Appendix A).
It is possible for the Tgas torque to spin down the light sail, deplete its spin angular momentum, and restart a subsequent rotational cycle with a different orientation. It is also possible for the torque to transfer positive angular momentum to the object until it reaches a breakup spin limit. A creative epilogue (Bialy & Loeb 2018; Loeb 2021) of the spacecraft hypothesis is the suggestion that ‘Oumuamua’s tumbling motion may have been intentionally instated to enable the spacecraft to emit and receive signals in and from all directions. Since any initial spin state can only be preserved over τrot ~ 1(ρOl3/1 kg m−2)(106m−3/ng)(l1/60m)Myr, such an assumption would require that ‘Oumuamua s interstellar odyssey, with its observed vO, be limited to a maximum traveled distance Lmax ≈ 10 pc. The total population of stars, including white dwarfs and brown dwarfs, in this domain is ~400.
Appendix C Accumulative drift
In the limit t ≥ trot and t ≥ ttur, E(dgas) and E(dmag) (in Eqs. 8 and 15) are derived for randomly evolving acceleration agas and amag. For the convenience of a general discussion, we use variables {E(drand), ∆t, arand} to represent both {E(dgas), τrot, adrflt) and {E(dmag), τtur, amag}. The motion of the object follows Langevin’s equation:
where the drag coefficient λ = 0 in our case. We started with the simplest 1D model, where the acceleration arand,i∙ is reset, after each time step ∆t, to be ±arand with a 50% probability for each value. The velocity gains a random increment arand time interval ∆t. The velocity at time t is the sum of the independent random variable arand,i∙ for i = 0,1, …Nrand with Nrand = t/∆t. According to the central limit theorem, the probability distribution of velocity, vrand, obeys a Gaussian distribution: 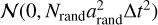 . The displacement is
. The displacement is
 |
Fig. A.1 Example of the rough surface with ∆h ~ 0.05 m (left panel) and the distribution of the values of Cz for 104 runs on random surfaces with ∆h ≈ 0.05 m. The mean value of Cz is (4 ± 4) × 10−4. |
The distribution of drand can be solved by determining the distribution of the limit of the right-hand sums:
Since only the acceleration is the independent variable, we needed to unfold Eq C.3 in terms of arand.i:
Due to the central limit theorem, the sum of independent random variables arand,i (with the variance of arand) exhibits a Gaussian distribution, with the variance
Therefore, the displacement 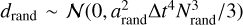 . The expected value
. The expected value 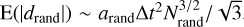 . The displacement in higher dimensions obeys a chi distribution. In particular in a 2D case, the probability distribution of the displacement, d, is given by a Rayleigh distribution:
. The displacement in higher dimensions obeys a chi distribution. In particular in a 2D case, the probability distribution of the displacement, d, is given by a Rayleigh distribution:
with 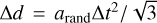 . This analytic approximation of p(d) was verified with a Monte Carlo simulation for the random-walk process (Fig. C.1). The expected value is expressed as
. This analytic approximation of p(d) was verified with a Monte Carlo simulation for the random-walk process (Fig. C.1). The expected value is expressed as
Appendix D Radiation force for a tumbling light sail
D.1 Coordinate system
In order to reconstruct ‘Oumuamua’s equation of motion in the Solar System, we approximated it as an object with a non-principal axis rotation analogous to that of a symmetric top. In this case, the spin axis rotates around the angular momentum vector, J. At a heliocentric position, r, the force components along the direction r × J cancel each other out. The resulting net force by radiation pressure lies on the (r, J) plane. The mean force can be considered in a coordinate system described by three basis vectors, eX, eY, and eZ, with
 |
Fig. C.1 Normalized distribution of dISM for 1000 test particles that feel a random magnetic force when the travel distance is 100 pc. The orange curve is the Rayleigh distribution given by Eq. C.6. |
Since ‘Oumuamua’s spin frequency, ωO, is much faster than its heliocentric orbital angular frequency, we can approximate er to be a constant within a rotational period. We also need a rotating coordinate frame, described by the three unit vectors ex, ey, and ez along the three principal axes of ‘Oumuamua. Here ez points in the positive direction of the principal axis of the maximum moment of inertia. The orientation of the rotating coordinate frame can be described by three Euler angles, ϕ, θ, and ψ (in x − z − x sequence). For an arbitrary vector k, the transformation between the nonrotating reference frame (XYZ) and the rotating reference frame (xyz) is k = R(ϕ, θ, ψ)k′. Here k denotes the vector in the nonrotating reference frame while k′ denotes the vector in the rotating frame. Here R(ϕ, θ, ψ) is the rotation matrix.
In the spaceship hypothesis, ‘Oumuamua is considered as an extremely thin solar sail (Fig. 1). To simplify the problem, we made two main assumptions in this context. First, the radiation pressure mainly exerts on the maximum face, whose normal vector is along the z axis, and the forces felt by other faces are ignored. Second, we assume the extremely thin ‘Oumuamua is a near-symmetric top that has a moment of inertia I = (I1, I2, I3) with I1 = I2 < I3. Under the first assumption, the radiation pressure on the a perfectly reflecting light sail is
Here A|er · ez| is the face area that is normal to the solar light and L⊙ is the solar luminosity. The unit vector ez is
Without the loss of generality, we set the initial ϕ0 = π/2 so that the initial ez lies on the plane (X, Z) and ez becomes
where θ is the nutation angle. The unit vector of the position in the nonrotating reference frame (XYZ) can be assigned as er = (sin θ′, 0, cos θ′), where θ′ is in the range (0, π). The solution for a symmetric top is
D.2 Averaging over a spin period
With a constant θ, Fradiation is a periodic force that is modulated on the timescale of the precession period 2π/ϕ. The mean force, integrating over its period, is
where er · ez = k1 cos ϕ + k2 = k1(cos ϕ + k2/k1), where k1 = sin θ sin θ′ and k2 = cos θ cos θ′.
In the limit k2/k1 ≥ 1, equivalently θ′ ≤ π/2 − θ, we have er · ez ≥ 0, and the mean force can be expressed as
With a constant θ,
In the limit k2/k1 ≤ −1, or equivalently θ′ ≥ π/2 + θ, er · ez ≤ 0, and the mean force reduces to
In the intermediate region with −1 < k2/k1 < 1, or equivalently π/2 − θ < θ′ < π/2 + θ, we find that the condition for er · ez > 0 is −β < ϕ < β where β is defined as 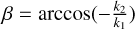 . The mean force becomes
. The mean force becomes
where
References
- Abell, P. A., Allison, J., Anderson, S. F., et al. 2009, arXiv preprint [arXiv:0912.0201] [Google Scholar]
- Bannister, M. T., Schwamb, M. E., Fraser, W. C., et al. 2017, ApJ, 851, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Bannister, M. T., Bhandare, A., Dybczynski, P., et al. 2019, Nat. Astron., 3, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J., Hainaut, O. R., Meech, K. J., et al. 2018, ApJ, 856, L21Bialy, S., & Loeb, A. 2018, ApJ, 868, L1 [NASA ADS] [Google Scholar]
- Bolin, B. T., Weaver, H. A., Fernandez, Y. R., et al. 2017, ApJ, 852, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke Jr, W. F., Vokrouhlicky, D., Rubincam, D. P., & Nesvorny, D. 2006, Annu. Rev. Earth Planet. Sci., 34, 157 [CrossRef] [Google Scholar]
- Choudhuri, S., & Roy, N. 2019, MNRAS, 483, 3437 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 2012 [Google Scholar]
- Cuk, M. 2018, ApJ, 852, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, S. 2021, A&A, 649, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Do, A., Tucker, M. A., & Tonry, J. 2018, ApJ, 855, L10 [Google Scholar]
- Drahus, M., Guzik, P., Waniak, W., et al. 2018, Nat. Astron., 2, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2010, Physics of the Interstellar and Intergalactic Medium, 19 (Princeton University Press) [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Drell, S. D., Foley, H. M., & Ruderman, M. A. 1965, J. Geophys. Res., 70, 3131 [Google Scholar]
- Flekkøy, E. G., Luu, J., & Toussaint, R. 2019, ApJ, 885, L41 [CrossRef] [Google Scholar]
- Fraser, W. C., Pravec, P., Fitzsimmons, A., et al. 2018, Nat. Astron., 2, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, C.-H., Laughlin, G., & Arce, H. G. 2021, ApJ, 917, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, A. P., & Desch, S. J. 2021, J. Geophys. Res.: Planets, 126, e2020JE006706 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D., Luu, J., Rajagopal, J., et al. 2017, ApJ, 850, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, J. 2019, Astrophys. Space Sci., 364, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, J. 2021, ArXiv preprint [arXiv:21S2.07871] [Google Scholar]
- Knight, M. M., Protopapa, S., Kelley, M. S., et al. 2017, ApJ, 851, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Laibe, G., & Price, D. J. 2012, MNRAS, 420, 2345 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A. 2021, Extraterrestrial: The First Sign of Intelligent Life Beyond Earth (Houghton Mifflin) [Google Scholar]
- Mashchenko, S. 2019, MNRAS, 489, 3003 [NASA ADS] [CrossRef] [Google Scholar]
- Meech, K. J., Weryk, R., Micheli, M., et al. 2017, Nature, 552, 378 [Google Scholar]
- Micheli, M., Farnocchia, D., Meech, K. J., et al. 2018, Nature, 559, 223 [Google Scholar]
- Molaro, J. L., Hergenrother, C. W., Chesley, S. R., et al. 2020, J. Geophys. Res.: Planets, 125, e2019JE006325 [Google Scholar]
- Moro-Martín, A. 2019, ApJ, 872, L32 [CrossRef] [Google Scholar]
- Muinonen, K., & Lumme, K. 2015, A&A, 584, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfalzner, S., Davies, M. B., Kokaia, G., & Bannister, M. T. 2020, ApJ, 903, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S., Torres, S., Pelupessy, I., Bédorf, J., & Cai, M. X. 2018, MNRAS, 479, L17 [Google Scholar]
- Raymond, S. N., Armitage, P. J., & Veras, D. 2018a, ApJ, 856, L7 [Google Scholar]
- Raymond, S. N., Armitage, P. J., Veras, D., Quintana, E. V., & Barclay, T. 2018b, MNRAS, 476, 3031 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Liu, S.-F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubincam, D. P. 2000, Icarus, 148, 2 [Google Scholar]
- Stern, S. A. 1986, Icarus, 68, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Tamayo, D., Rein, H., Shi, P., & Hernandez, D. M. 2019, MNRAS, 491, 2885 [Google Scholar]
- Trilling, D. E., Robinson, T., Roegge, A., et al. 2017, ApJ, 850, L38 [Google Scholar]
- Trilling, D. E., Mommert, M., Hora, J. L., et al. 2018, AJ, 156, 261 [Google Scholar]
- Tsuda, Y., Mori, O., Funase, R., et al. 2011, Acta Astronaut., 69, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlicky, D., & Capek, D. 2002, Icarus, 159, 449 [CrossRef] [Google Scholar]
- Zhang, Y., & Lin, D. N. 2020, Nat. Astron., 4, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, W. H. 2020, ApJ, 899, 42 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Schematic illustration of the hydrodynamic (left panel) and magnetic (right panel) drag on a moving light sail in a turbulent ISM with a magnetic field, B (green). The tumbling sail is represented by a thin gray sheet with a bumpy surface and a spin axis in the Z direction that precesses around its angular momentum, J, axis. The bombardment of atoms (with open and solid yellow dots representing pre- and post-collision trajectories) and photons (wavy arrows) leads to a force, Fgas (red), which can be decomposed into a drag, Fdrag, in the direction of the sail’s velocity, v (gray), and a sideways force, Fdrift. The induced currents (blue arrows) conducted away by surrounding charged particles lead to a Lorentz force, Fmag, with components perpendicular to both v and B. |
| In the text | |
 |
Fig. 2 Illustration of the light sails in the one-facet illumination state and two-facet illumination (left panels) and their light curves (right panels). The rotation angular momentum is J, and the spin vector is along the major principal axis, z. The position vector r is pointing ‘Oumuamua away from the Sun. The solid lines denote the absolute magnitude, while the dashed line denotes the areas of projection along the sunlight direction. The imperfect consistency results from the nonzero phase angle ~20° (Fraser et al. 2018). |
| In the text | |
 |
Fig. 3 Amplitude map for the light curves of an oblate shape (left), prolate shape (middle), and light sail (right). The fractions of area where the amplitude ∆H is between 2.5 and 3 are 0.34, 0.1, and 0.015 for the oblate shape, prolate shape, and light sail, respectively. |
| In the text | |
 |
Fig. 4 Schematic illustration of the diverse pathways of a constellation of Ntot tumbling solar sails traveling over a distance L through the turbulent magnetized ISM (left panel) and the expected value of the perihelion distance as a function of travel distance (right panel). As shown in the left panel, dispersive hydrodynamic and magnetic drag lead to a sideways drift, 4SM, and a dispersion in time of arrival, δt, at the Sun. The expected value E(dISM) (dashed gray circle) is generally much larger than the targeted Oumuamua’s perihelion distance, po. In the right panel, the expected value of the perihelion distance, E(p⊙) (solid lines), is shown as a consequence of deflection after traveling over a distance L through the ISM with a number density nISM. The probability of a single light sail striking the Solar System at a distance p⊙ ≤ pO (represented by a solid dot) from the Sun is shown with dashed lines. |
| In the text | |
 |
Fig. 5 Fig. 5. Occurrence timescale (solid lines) and cumulative number (dashed lines) of ‘Oumuamua’s cohorts within d of the Sun for travel distances in the ISM L = 1 pc, 10 pc, 100 pc (increasing line widths). The timescale of occurrence of a light sail grows with increasing traveling distance, L, as a result of diffusion in the interstellar space. The timescale of occurrence within 100 au is insensitive to the travel distance, L, when L > 10 pc. The unshaded region is the observational domain of the first ∼10 yr of the Vera C. Rubin telescope. |
| In the text | |
 |
Fig. 6 Fig. 6 – Histogram of 104 simulations of visible probability of a light sail versus posterior visible probability density distribution of Oumuamua over 49 days. The gray histogram represents the statistical result from a uniform random sampling, whereas the blue histogram is the statistical outcome from a nonuniform sampling that mimics ground-based and HST astrometry of Oumuamua. The dot-dashed gray and blue lines denote the mean values of these two statistical visibility simulations of a light sail, respectively. The dot-dashed and solid red lines represent the expected a posteriori estimation and the posterior probability distribution of Oumuamua’s visible probability (see Eq. (35)), respectively, based on the fact that Oumuamua was visible in all 55 observations. The embedded panel shows the likelihood that the amplitude of the light curve varies within the ranges ΔH ≃ (2.5,3) (Meech et al. 2017) and (2.5, 3.5) during the period October 25 = −27, 2017, for the light-sail, oblate shape, and prolate shape models. |
| In the text | |
 |
Fig. 7 Distribution of the ratios of the sideways displacement to the radial displacement for different tumbling angles, θ, during observation (80 days). The initial rotation states of 103 test particles are constrained by the fact that the light curve amplitude is between 2.5 and 3. The sideways-to-radial displacement is 4.4 ± 0.1, 2.8 ± 0.2, 1.4 ± 0.3, and 0.3 ± 0.1 for the initial wobble angles θ ≤ Io, ≤ 3°, ≤ 5°, and ≤ 10°, respectively. |
| In the text | |
 |
Fig. 8 Fig. 8 – Ratio of the sideways radiation force (Fmean,s) to the radial radiation force (Fmean,r) for a tumbling light sail suffering radiation pressure. (a) Distribution of the deflection angle, α, with tan α = Fmean,s/Fmean,r for the whole value range of the wobble angle, θ, and the photon incident angle, θ′. (b) Distribution of Fmean,s/Fmean,r for 105 light sails with random θ and θ′ after an 80-day motion. The mean value of the sideways-to-radial force ratio is 0.7 ± 0.4 for light sails, while this ratio for Oumuamua is ~0.08 (Micheli et al. 2018), which is a discrepancy (Micheli et al. 2018) of ~1.5σ. The embedded panel shows the distribution of ∆A1/A1 for 104 generated pseudo ‘Oumuamuas during 80-day movements, where A1 and ΔA1 denote the coefficient of the radiation pressure and its variation over 55 days, from November 15, 2017, to January 2, 2018 (see Sect. 3). The standard deviation, denoted by the dash lines, is 0.3. |
| In the text | |
 |
Fig. 9 Fig. 9 – Histogram of the ratio between the parallel deviation and the normal deviation. The radiation-pressure-induced deviation from a Keplerian trajectory during Oumuamua’s sojourns through the inner Solar System are shown with the dashed green line. The red star represents the Sun, and solid black, cyan, blue, and red arcs indicate the orbits of Mercury, Venus, Earth, and Mars, respectively. The purple cross indicates the position of Oumuamua at the last record. In total, 5 × 104 light-sail models with randomized initial spin orientations are integrated from Oumuamua’s discovery position for the same period of time. An additional Keplerian trajectory without radiation force is integrated, with which an orbital plane is defined. The circular inset panel zooms in to show Oumuamua’s last position (purple cross) surrounded by all light-sail models at the end of integration. And deviations from the Keplerian orbit (green square in the plane) are measured in the parallel and perpendicular directions to the orbital plane (indicated by two red arrows). The distribution of the ratio of the parallel displacement to the normal displacement peaks at ~3, while Oumuamua lies at ~17, which is obtained by applying the nongravitational acceleration suggested by Micheli et al. (2018). |
| In the text | |
 |
Fig. 10 Light curve (upper panels), radiation acceleration (middle panels), and correlation within one day between them (bottom panels) for the light sail in the OIS (left panels) and in the TIS (right panels). |
| In the text | |
 |
Fig. 11 Correlation between the light curve and the acceleration as a function of the delay time for a light sail. The correlation declines quickly within two days, which indicates that high-cadence time series data are required for the diagnosis of a light sail. |
| In the text | |
 |
Fig. A.1 Example of the rough surface with ∆h ~ 0.05 m (left panel) and the distribution of the values of Cz for 104 runs on random surfaces with ∆h ≈ 0.05 m. The mean value of Cz is (4 ± 4) × 10−4. |
| In the text | |
 |
Fig. C.1 Normalized distribution of dISM for 1000 test particles that feel a random magnetic force when the travel distance is 100 pc. The orange curve is the Rayleigh distribution given by Eq. C.6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



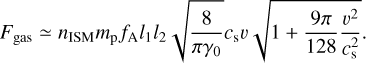
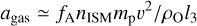
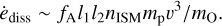
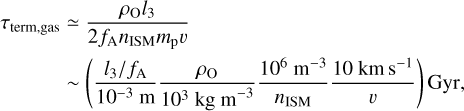
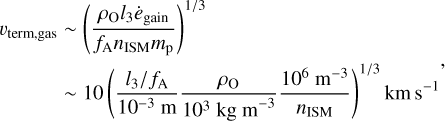
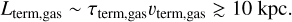
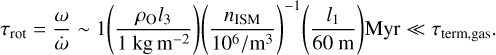
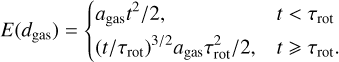
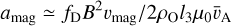
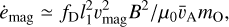


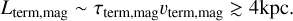
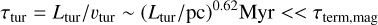
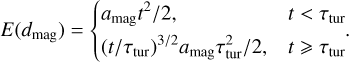
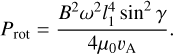
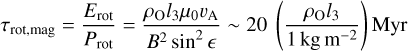
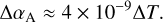
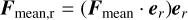

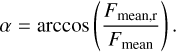
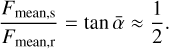
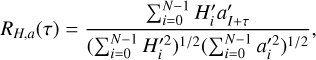
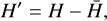
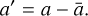
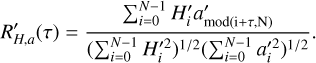
![$\matrix{H \hfill & { = {\rm{\Delta }}V - 2.5\log {{l'}_3}{{{T_ \oplus }{T_ \odot }} \over T} - 2.5\log \left[ {\cos \left( {\lambda ' - \alpha '} \right)} \right.} \hfill & {} \hfill \cr {} \hfill & {\left. { + \cos \lambda ' + \sin \lambda '\sin \left( {\lambda ' - \alpha '} \right)\ln \left( {\cot {{\lambda '} \over 2}\cot {1 \over 2}\left( {\alpha ' - \lambda '} \right)} \right)} \right],} \hfill & {} \hfill \cr} $](/articles/aa/full_html/2022/11/aa44119-22/aa44119-22-eq35.png)
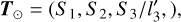
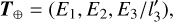
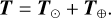
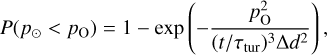
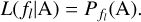
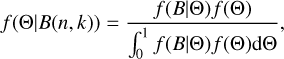
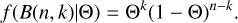
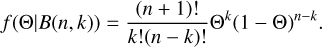
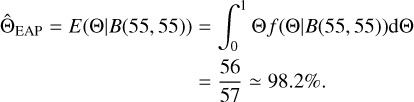
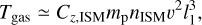
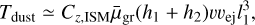
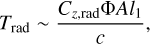
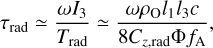
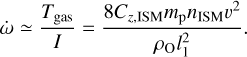
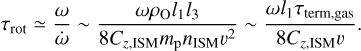

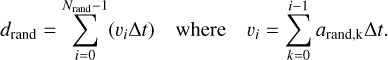
![$\matrix{{{d_{{\rm{rand}}}}} \hfill & = \hfill & {{\rm{\Delta }}t\left( {{v_{{\rm{rand,0}}}} + {v_{{\rm{rand,1}}}} + \ldots + {v_{{N_{{\rm{rand}}}} - 1}}} \right)} \hfill \cr {} \hfill & = \hfill & {{\rm{\Delta }}{t^2}\left[ {{a_{{\rm{rand}},0}} + {a_{{\rm{rand,1}}}} + \ldots + {a_{{N_{{\rm{rand}}}} - 2}}} \right.} \hfill \cr {} \hfill & {} \hfill & {\left. { + \left( {{a_{{\rm{rand,0}}}} + {a_{{\rm{rand,1}}}} + \ldots + {a_{{N_{{\rm{rand}}}} - 2}}} \right)} \right]} \hfill \cr {} \hfill & = \hfill & {{\rm{\Delta }}{t^2}\left( {{N_{{\rm{rand}}}} - 1} \right){a_{{\rm{rand,0}}}} + \left( {{N_{{\rm{rand}}}} - 2} \right){a_{{\rm{rand,1}}}} + \ldots + {a_{{N_{{\rm{rand}}}} - 2}}} \hfill \cr {} \hfill & = \hfill & {\Delta {t^2}\sum\limits_{i = 0}^{{N_{{\rm{rand}}}} - 2} {\left( {{N_{{\rm{rand}}}} - 1 - i} \right){a_i}} } \hfill \cr} .$](/articles/aa/full_html/2022/11/aa44119-22/aa44119-22-eq62.png)
![$\matrix{{{\rm{Var}}\left( {{d_{{\rm{rand}}}}} \right)} \hfill & = \hfill & {{\rm{Var}}\left( {\sum\limits_{i = 0}^{{N_{{\rm{rand}}}} - 2} {\left( {{N_{{\rm{rand}}}} - 1 - i} \right){a_{{\rm{rand,}}i}}{\rm{\Delta }}{t^2}} } \right)} \hfill \cr {} \hfill & = \hfill & {\sum\limits_{i = 0}^{{N_{{\rm{rand}}}} - 2} {{{\left[ {\left. {\left( {{N_{{\rm{rand}}}} - 1 - i} \right){a_{{\rm{rand}}}}{\rm{\Delta }}{t^2}} \right)} \right]}^2}} } \hfill \cr {} \hfill & = \hfill & {a_{{\rm{rand}}}^2{\rm{\Delta }}{t^4}\left[ {1 + {2^2} + \ldots + {{\left( {{N_{{\rm{rand}}}} - 1} \right)}^2}} \right]} \hfill \cr {} \hfill & \simeq \hfill & {{1 \over 3}a_{{\rm{rand}}}^2{\rm{\Delta }}{t^4}N_{{\rm{rand}}}^3} \hfill \cr} .$](/articles/aa/full_html/2022/11/aa44119-22/aa44119-22-eq63.png)