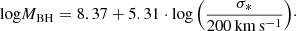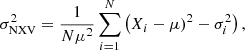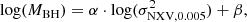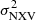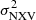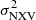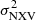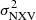| Issue |
A&A
Volume 666, October 2022
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244162 | |
| Published online | 14 October 2022 | |
Black hole mass estimation using X-ray variability measurements in Seyfert galaxies
1
Institute for Astronomy Astrophysics Space Applications and Remote Sensing (IAASARS), National Observatory of Athens, I. Metaxa & V. Pavlou, Penteli 15236, Greece
e-mail: aakylas@noa.gr
2
Department of Physics and Institute of Theoretical and Computational Physics, University of Crete, 71003 Heraklion, Greece
3
Institute of Astrophysics – FORTH, N. Plastira 100, 70013 Vassilika Vouton, Greece
Received:
1
June
2022
Accepted:
4
August
2022
Aims. Our objective is to critically assess the X-ray flux variability as a tool for measuring the black hole (BH) mass in active galactic nuclei (AGN). We aim to establish a prescription for estimating BH masses based on measurements of the normalised excess variance from X-ray data. We discuss the minimum requirements in terms of the light-curve duration and X-ray signal-to-noise ratio (S/N) to enable a reliable determination that is comparable to what can be derived from the continuum and emission line reverberation studies.
Methods. We used the light curves of local Seyfert from the Nuclear Spectroscopic Telescope Array hard X-ray mission (NuSTAR), to compute the normalised excess variance (σNXV2) in the 3–10 and 10–20 keV bands, thus extending the analysis to an energy band higher than 10 keV. The excess variance measurements were then combined with independent BH mass estimates from the literature to establish the MBH vs. σNXV2 relation for different samples and weigh its accuracy in terms of the light-curve duration and X-ray S/N.
Results. We find that it is possible to accurately measure the BH mass in AGN using excess variance measurements in the 3–10 and the 10–20 keV bands, however, strong quality requirements should be applied. The minimum necessary S/N and duration of the light curves used to compute the excess variance ought to be ∼3 and ∼80 − 100 ks, respectively. We provide a linear relationship between the normalised excess variance and the black hole mass that can be used to estimate the latter, with an average uncertainty of the order of 0.4 − 0.25 dex (depending on the adopted light-curve segment duration). In general, BH mass estimates from 3–10 keV and 10–20 keV band light curves are expected to be similar. The 10–20 keV band is preferred for sources that are heavily absorbed and the 3–10 keV band is preferred for sources that may be dominated by the X-ray reflection component at energies above 10 keV.
Key words: black hole physics / X-rays: galaxies / galaxies: active / galaxies: Seyfert / accretion, accretion disks / quasars: supermassive black holes
© A. Akylas et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Super-massive black holes (SMBHs) reside in the centre of most (if not all) galaxies and are responsible for their most energetic face, namely, of active galactic nuclei (AGN). According to the current paradigm, the incredibly high luminosity of these objects is powered by the accretion of matter in the vicinity of the SMBHs. As matter spirals inward, copious amounts of energy are released, over a wide range of wavelengths (from radio to gamma rays) due to the conversion of gravitational potential energy into radiation. The emitted power in AGN depends on the black hole (BH) mass and the accretion rate. Their luminosity can reach 1015 times that of the Sun, while the accretion of matter may significantly contribute to the growth of the BH mass.
Studies have made it clear that SMBHs play a major role in regulating star formation in galaxies and, thus, affect their surroundings. One of the strongest pieces of empirical evidence of the mutual interaction between AGN and its host galaxy is demonstrated by the strong correlation between the mass of SMBHs and the bulge stellar velocity dispersion, σ*, (e.g. Ferrarese & Merritt 2000; Gebhardt et al. 2000). This relation can be established through the interaction between the energy and radiation generated by accretion and the gas in the host galaxy, known as AGN feedback (e.g. Fabian 2012).
In order to understand and investigate the role of SMBHs in galaxy formation and evolution processes, we need to monitor the growth of the SMBHs across the cosmic timescale. Therefore, it is not surprising that a lot of effort has been focussed on finding ways of measuring the mass of SMBHs in galaxies–overall, and, in particular, in the case of AGN.
Direct mass measurements of SMBHs are possible with stellar kinematics and gas dynamics, although these methods require good spatial resolution and are presently only feasible for a small number of nearby galaxies. These methods can be used for weak AGN, such as low-luminosity AGNs, LINERs, and Seyfert-2s; this is because for more luminous AGNs, the strong nuclear emission weakens the stellar features in the spectrum.
Based on the assumption that the motion of the gas in the broad line region (BLR) of AGNs is dominated by the gravitational influence of the SMBH, we can use the virial equation MBH = (fRBLRΔV2)/G to estimate SMBHs. Here, RBLR is the average radius of the emitting gas in the broad line region, usually determined with reverberation mapping (e.g. Peterson et al. 2004), while the velocity dispersion of the gas (ΔV) is measured from the width of the broad emission lines. The dimensionless factor, f, is referred to as a virial coefficient and encapsulates the unknown geometry and dynamics of the broad line region gas. Its true value for each AGN is unknown and, in most cases, an average value is used, based on the assumption that AGNs follow the MBH–σ* relation observed in quiescent galaxies (e.g. Grier et al. 2013).
Black hole masses can also be inferred indirectly from observable quantities that are correlated with the mass of the SMBHs, such as the velocity dispersion of bulge stars, that is, the value of the MBH–σ* scaling relationship (mentioned above) or the bulge luminosity (e.g. Gültekin et al. 2009).
In this work, we focus on the flux variability of AGN as a means of measuring SMBHs. Stochastic variations of the radiated energy is one of the main observational characteristics of the accretion flows onto compact objects and SMBHs in particular. The origin of these variations is still not well understood and could be related to accretion flow instabilities, a flaring corona, or hot-spots orbiting the central compact object (e.g. Gravity Collaboration 2018, 2020).
Although the AGN flux variability is observed across the entire electromagnetic spectrum, analysing light curves at X-ray wavelengths offers several advantages. Stellar processes emit (very) little X-ray radiation and, therefore, observations at these energies arguably provide the cleanest diagnostic of active SMBHs at the centres of galaxies over a broad redshift range and accretion luminosity baselines (e.g. Brandt & Alexander 2015). The X-ray photons can also penetrate relatively dense gas clouds and be virtually unaffected, thereby providing a representative sampling of the obscured AGN in the Universe. Therefore, X-ray observations enable flux variation measurements across a broad range of AGN (including low-luminosity and obscured objects) that are challenging or even impossible to perform at other wavebands, where the host galaxy emission is dominant. The proximity of the X-ray emitting region to the active black hole implies the possibility of a direct connection between the X–ray flux variations and the physical properties of the system (e.g. black-hole mass or accretion rate).
Past observations have indicated that such a relation exists in AGN. The X-ray power spectral density (PSD) of AGN has been modelled using a bending power-law with a slope of −1 at low frequencies and then a slope of −2 (e.g. McHardy et al. 2004). Various studies have indicated that the PSD bend frequency may be aptly correlated with BH mass and (potentially) with the bolometric luminosity (e.g. Czerny et al. 2001; McHardy et al. 2006; Körding et al. 2007; González-Martín & Vaughan 2012). However, it is difficult to estimate the PSD in AGN (and, even more so, detect the bending frequency) as this requires long, high signal-to-noise ratios (S/N) and uninterrupted light curves. Therefore, it is not practical to use the bending-frequency versus BH mass relation to measure the BH mass in AGN.
Using the normalised excess variance, 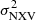 , (e.g. Nandra et al. 1997) as an estimator of the intrinsic ’band-variance’ of the source, a tight anti-correlation between
, (e.g. Nandra et al. 1997) as an estimator of the intrinsic ’band-variance’ of the source, a tight anti-correlation between 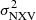 and MBH has also been found in the local universe (e.g. Papadakis 2004; O’Neill et al. 2005; Zhou et al. 2010; Ponti et al. 2012) as well as the high-redshift universe (e.g. Lanzuisi et al. 2014). In particular, the value of
and MBH has also been found in the local universe (e.g. Papadakis 2004; O’Neill et al. 2005; Zhou et al. 2010; Ponti et al. 2012) as well as the high-redshift universe (e.g. Lanzuisi et al. 2014). In particular, the value of 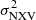 can be estimated much more easily with the available data sets for many types of AGN, both at low and high redshifts. It is for this reason that most of the SMBH mass measurements in AGN are based on the use of the
can be estimated much more easily with the available data sets for many types of AGN, both at low and high redshifts. It is for this reason that most of the SMBH mass measurements in AGN are based on the use of the 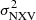 vs. MBH relation (e.g. Ponti et al. 2012).
vs. MBH relation (e.g. Ponti et al. 2012).
Our objective is to critically assess the X-ray flux variability as a tool for measuring AGN SMBHs. We used the light curves of local Seyfert from the NuSTAR observatory to compute 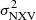 in the energy bands 3–10 and 10–20 keV. The use of NuSTAR data has allowed us to extend our analysis to an energy band higher than 10 keV, which may be important for obscured AGN. The excess variance measurements are then combined with independent BH mass estimates from the literature to establish the MBH vs.
in the energy bands 3–10 and 10–20 keV. The use of NuSTAR data has allowed us to extend our analysis to an energy band higher than 10 keV, which may be important for obscured AGN. The excess variance measurements are then combined with independent BH mass estimates from the literature to establish the MBH vs. 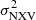 relation in AGN. All studies in the past have focused on the reverse relation (i.e.
relation in AGN. All studies in the past have focused on the reverse relation (i.e. 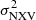 vs. MBH) as the main goal was the study of the X-ray variability, while our focus here is the estimation of the BH mass in AGN from the excess variance measurements.
vs. MBH) as the main goal was the study of the X-ray variability, while our focus here is the estimation of the BH mass in AGN from the excess variance measurements.
We present a prescription to measure SMBH masses using the excess variance measurements and we discuss, for the first time, the minimum requirements in terms of light-curve duration and X-ray S/N values that enable a reliable determination, similar to those derived from the continuum and emission line reverberation studies or the MBH–σ* relation.
2. The sample
Our sample consists of the Seyfert galaxies detected in the 105-month survey of the Burst Alert Telescope, (BAT; Barthelmy et al. 2004) on board the Gehrels Swift Gamma-Ray Burst observatory (Gehrels et al. 2004), along with archival observations from the NuSTAR mission (Harrison et al. 2013).
The BAT 105 month catalogue (Oh et al. 2018) contains 379 Seyfert-1s and 448 Seyfert-2s galaxies. There are 161 Seyfert-1s and 253 Seyfert-2s (414 in total) that have been observed by NuSTAR until September 2020, with a duration greater than 10 ks. We found 664 independent, archival NuSTAR observations for these sources. In these NuSTAR observations, a total of 114 are flagged as having been affected by increased solar activity and these have been removed from further analysis. Moreover, we restricted our analysis to the low-redshift regime. This is meant to minimise the inconsistencies on the excess variance estimation when using intervals with a fixed length in the observers frame. Therefore, sources with redshift greater than 0.07 (i.e. the maximum redshift for the sources in the reverberation sample; see Sect. 2.1 below for details) are not included in the sample. Our final sample consists of 473 independent observation of 300 local AGN–of which 108 are Seyfert-1s and 192 are Seyfert-2s galaxies.
In order to provide a recipe for the MBH estimation, we need to study sources with known BH mass. Thus, we kept sources with BH measurements, which are based either on the so-called reverberation mapping technique or on the use of good-quality, host galaxy velocity dispersion measurements, as we explain below.
2.1. The reverberation sample
Reverberation mapping (e.g. Blandford & McKee 1982) is one of the most direct ways to obtain BH masses in AGNs. It provides an estimate of the size of the BLR from the lag between the variability in the photo-ionising continuum and the broad emission lines. On this basis, it is possible to infer a virial mass for the SMBH in the central region of the AGN.
We cross-correlated the original sample with the sources included in the AGN BH mass database (Bentz & Katz 2015) to obtain a sample with BH mass measurements based on reverberation mapping technique (hereafter, the ‘rev sample’). We adopt the weighted average of the individual BH mass estimates determined from all the emission lines, assuming that ⟨f⟩ = 4.3, as suggested by Grier et al. (2013). The rev sample consists of 26 AGN with 86 NuSTAR observations. The average duration per NuSTAR observation in the rev sample is ∼80 ks. The rev sample log is presented in Table B.1.
2.2. The velocity dispersion sample
Reverberation mapping data are currently available only for a small number of AGN, but the empirical scaling relation between black hole mass and host-galaxy properties, namely, the MBH–σ* relation (e.g. Grier et al. 2013) offers an alternative way to obtain BH mass estimates. To this end, we used the central velocity dispersion measurements (σ*) presented in the first catalogue of the Swift-BAT AGN Spectroscopic Survey (BASS, Koss et al. 2017). These authors provided measurements of σ* for many AGN in the 70-month Swift BAT all-sky catalogue. We considered only secure velocity dispersion measurements by selecting the data with spectral fitting quality flag value of 1 or 2. Dual AGN systems, as reported in Koss et al. (2012) are excluded from the analysis. There are 84 sources fulfilling these criteria, with 111 NuSTAR observations.
We also searched the Hyperleda database (Paturel et al. 2003) to obtain additional central velocity dispersion measurements and increase our sample. We find σ* measurements for 24 new sources (i.e without σ* measurements in the BASS survey sample) with 49 NuSTAR observations. Before merging the targets from both the BASS project and the Hyperleda database, we checked whether there are any systematic differences in the velocity dispersion estimates between the two samples. We then identified the common sources, that is, sources with σ* measurements in both the Hyperleda and the BASS databases and compare the corresponding σ* values. There are 15 common sources in these samples. Figure 1 shows a plot of σ*, Hyperleda vs. σ*, BASS. The plot clearly shows that the BASS and the Hyperleda σ* measurements are very well correlated. There are no large amplitude or systematic deviations from the one-to-one relation and, therefore, we chose to merge the two samples.
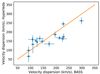 |
Fig. 1. Comparison of the velocity dispersion measurements of the common sources from the Hyperleda database and the BASS catalogue. The error-bars correspond to 1σ confidence interval. The solid line show the one-to-one (y = x) relation. |
In the last step, we cross-correlated the data with Ricci et al. (2017) in order to obtain information on the X-ray column density (NH) of each source. We excluded from the sample the Compton thick (CT) sources, namely, the sources with NH > 1024 cm−2. The final velocity dispersion sample (hereafter, the VD sample) is comprised of 84 AGN with reliable measurements of σ* and 107 NuSTAR observations. The VD sample log is presented in Table B.2.
For each source in the VD sample, we can estimate the BH mass using the MBH–σ* relation of Woo et al. (2013):
As shown by Grier et al. (2013), BH mass estimates using Eq. (1) are fully compatible with the masses obtained from the reverberation technique, when assuming a mean virial factor ⟨f⟨ of 4.3. The mass estimates for the VD sample are also listed in Table B.2.
2.3. The Compton-thick sample
The sources that have been excluded from the VD sample, due to being CT in nature, make up our CT sample. There are in total 24 CT sources with 53 NuSTAR observations available. These sources are treated separately since their continuum emission, particularly in the 3–10 keV band is severely suppressed, due to heavy absorption, and their spectrum may be dominated by reflected emission (e.g. Baloković et al. 2014). The log of the CT sample is presented in Table B.3.
3. X-ray data reduction
The observations were processed with the NuSTAR data analysis pipeline (NUPIPELINE) in order to produce cleaned, calibrated event list files. For this standard pipeline processing, we used NuSTAR data analysis software NUSTARDAS v2.0.0 and CALDB version 201702221. From the cleaned event files, we extracted source and background light curves for each of the two NuSTAR focal plane modules (FPMA & FPMB) using the NUPRODUCTS script. We adopted a source radius of 60 arcsec for the source light curve extraction, for both FPMA & FPMB observations and applied the live-time, point spread function (PSF), and vignetting corrections. The background light curves are extracted from a four times larger (120 arcsec radius) source-free region of the image at an off-axis angle similar to the source position. We extracted light curves in the 3–10 and 10–20 keV bands, using a bin size of 250 s.
The light curves obtained for the FMPA and FMPB modules were first background subtracted and then summed using the LCMATH tool within FTOOLS. For the subtraction of the background from the source light curves, the proper scaling factors, accounting for the differences in extraction radius for the source and background light curves, have been taken into account. The combined error in the count rate during subtraction or addition of the light curves is always calculated as: 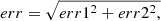 where err1 and err2 are the uncertainties in the count rate in each light curve bin obtained during the NuSTAR data reduction process.
where err1 and err2 are the uncertainties in the count rate in each light curve bin obtained during the NuSTAR data reduction process.
4. The normalised excess variance
To measure the variability power of the sources in our sample we compute the normalised excess variance (e.g. Nandra et al. 1997) using:
where N is the number of bins in the light curve, Xi and σi are the count rates and their uncertainties, respectively, and μ is the unweighted mean count rate.
The 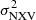 has been measured using light curve segments with a duration of Δt = 10, 20, 40, and 80 ks. When more than one valid segments are available for a source (for a given timescale, Δt), we compute the mean of the individual excess variances. This approach should reduce the uncertainty due to the stochastic nature of the X-ray variations (see e.g. Allevato et al. 2013). Following Ponti et al. (2012), all time bins in the light curve segments with fractional exposure lower than 0.35 have been excluded. We note that due to the restriction of our analysis in the local universe (the median redshift of the sample equals 0.02 and the maximum redshift equals 0.07), the impact of the source redshift in the estimation of
has been measured using light curve segments with a duration of Δt = 10, 20, 40, and 80 ks. When more than one valid segments are available for a source (for a given timescale, Δt), we compute the mean of the individual excess variances. This approach should reduce the uncertainty due to the stochastic nature of the X-ray variations (see e.g. Allevato et al. 2013). Following Ponti et al. (2012), all time bins in the light curve segments with fractional exposure lower than 0.35 have been excluded. We note that due to the restriction of our analysis in the local universe (the median redshift of the sample equals 0.02 and the maximum redshift equals 0.07), the impact of the source redshift in the estimation of 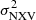 in fixed length intervals is negligible and it is also very similar for all the samples.
in fixed length intervals is negligible and it is also very similar for all the samples.
5. Measuring MBH using 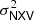
Previous studies have explored the dependence of the normalised excess variance on the BH mass, ultimately suggesting a linear correlation in the log-log space between the two quantities. We aim to establish a prescription to estimate BH masses given the measurements of the normalised excess variance from X-ray data, therefore, we chose to establish the reverse relation, that is, the relation of MBH vs. 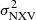 . Our objective is to investigate what are the requirements for the light curves that will be used to compute
. Our objective is to investigate what are the requirements for the light curves that will be used to compute 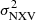 , so that the resulting BH mass estimates will be as unbiased as possible and of known variance.
, so that the resulting BH mass estimates will be as unbiased as possible and of known variance.
Instead of applying, a priory, a certain cut to the S/N value, we simply consider only the sources where the AGN variability is well detected, namely, the computed 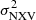 is positive (either the mean or a single value, if there is only one light curve segment available). In this way, observations where the S/Ns is low or the intrinsic amplitude is weak were excluded from further analysis. Then we carried out a separate study of the MBH vs.
is positive (either the mean or a single value, if there is only one light curve segment available). In this way, observations where the S/Ns is low or the intrinsic amplitude is weak were excluded from further analysis. Then we carried out a separate study of the MBH vs. 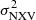 relation for the rev and VD samples in four timescales (Δt = 10, 20, 40, and 80 ks) and we investigate how the MBH vs.
relation for the rev and VD samples in four timescales (Δt = 10, 20, 40, and 80 ks) and we investigate how the MBH vs. 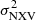 relation changes with respect to the total duration of the light curves used to compute
relation changes with respect to the total duration of the light curves used to compute 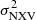 . In this way (as we show in the following), we are able to establish the minimum requirements for the light curves (i.e. the necessary number of segments and S/N values) in order to acquire a reliable MBH estimate.
. In this way (as we show in the following), we are able to establish the minimum requirements for the light curves (i.e. the necessary number of segments and S/N values) in order to acquire a reliable MBH estimate.
5.1. MBH–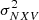 relation for the rev and VD samples
relation for the rev and VD samples
The four panels of Fig. 2 show the MBH vs. 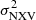 plots for the rev and the VD samples (filled-blue circles and open-red squares respectively) in the 3–10 keV band, when using segments with durations of 10, 20, 40 and 80 ks. The four panels of Fig. 3 present the same results in the 10–20 keV band.
plots for the rev and the VD samples (filled-blue circles and open-red squares respectively) in the 3–10 keV band, when using segments with durations of 10, 20, 40 and 80 ks. The four panels of Fig. 3 present the same results in the 10–20 keV band.
 |
Fig. 2. MBH vs. |
A strong anti-correlation between MBH and 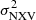 is observed in all timescales for the rev sample. Smaller BH masses show the largest variability amplitude, as has been observed many times in the past. However, this is not the case for the VD sample, especially at timescales shorter than 40 ks (top panels in both figures).
is observed in all timescales for the rev sample. Smaller BH masses show the largest variability amplitude, as has been observed many times in the past. However, this is not the case for the VD sample, especially at timescales shorter than 40 ks (top panels in both figures).
We fit a straight line to each plot, in log-log scale, of the following form,
to model the observed behaviour. The 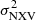 values have been normalised to the value of 0.005 in order to minimise the error on the line parameters, α and β. Since our objective is to predict MBH from
values have been normalised to the value of 0.005 in order to minimise the error on the line parameters, α and β. Since our objective is to predict MBH from 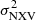 we used the ordinary least-squares regression of Y on X, OLS(Y|X), where Y is the variable to be predicted (i.e. MBH) and X is the measured variable (
we used the ordinary least-squares regression of Y on X, OLS(Y|X), where Y is the variable to be predicted (i.e. MBH) and X is the measured variable (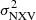 ), following the prescription of Isobe et al. (1990).
), following the prescription of Isobe et al. (1990).
Table 1 lists the best-fit results and the corresponding 1σ uncertainties to the MBH–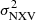 plots, both for the rev and the VD samples, at all timescales, in both bands. The best-fit slope for the rev sample remains roughly constant, within the errors, in both bands, while the intercept constantly increases as we move to higher timescales. This is fully consistent with the expectations, as the variance provides a measure of the (intrinsic) PSD integral from the shortest to the longest sampled timescale. In the case of red-noise PSDs, this integral should increase with increasing segment duration, hence, the positive correlation of the best-fit line normalisation with the segment duration (Δt).
plots, both for the rev and the VD samples, at all timescales, in both bands. The best-fit slope for the rev sample remains roughly constant, within the errors, in both bands, while the intercept constantly increases as we move to higher timescales. This is fully consistent with the expectations, as the variance provides a measure of the (intrinsic) PSD integral from the shortest to the longest sampled timescale. In the case of red-noise PSDs, this integral should increase with increasing segment duration, hence, the positive correlation of the best-fit line normalisation with the segment duration (Δt).
Best-fit results for the rev and VD MBH vs. 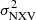 relations.
relations.
The VD data points shown in Figs. 2 and 3 and the best-fit results show that the situation is more complicated in the VD sample. There is almost a complete lack of correlation between MBH and 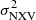 on the shortest timescales (Δt = 10 & 20 ks), in both energy bands. The situation improves progressively as we move to longer timescales where the intrinsic variability is higher. A clear and strong anti-correlation between MBH and
on the shortest timescales (Δt = 10 & 20 ks), in both energy bands. The situation improves progressively as we move to longer timescales where the intrinsic variability is higher. A clear and strong anti-correlation between MBH and 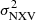 is present only in the Δt = 80 ks plots. In fact, the best-fit results to the rev and VD plots are remarkably similar in the case of Δt = 80 ks.
is present only in the Δt = 80 ks plots. In fact, the best-fit results to the rev and VD plots are remarkably similar in the case of Δt = 80 ks.
 |
Fig. 3. MBH vs. |
The inconsistency of the MBH vs. 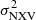 relations between the rev and the VD samples at Δt ≲ 40 ks could not be attributed to any differences in the accuracy of the BH mass measurements between the two cases. After all, the rev BH mass measurements are based on relations that are ‘forced’ to agree with the MBH − σ* relation. Therefore, the difference between the MBH vs.
relations between the rev and the VD samples at Δt ≲ 40 ks could not be attributed to any differences in the accuracy of the BH mass measurements between the two cases. After all, the rev BH mass measurements are based on relations that are ‘forced’ to agree with the MBH − σ* relation. Therefore, the difference between the MBH vs. 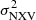 plots for the rev and VD samples when the light curve segments are short is expected to be related to limitations in accurately measuring the X-ray variability of the sources in the VD sample. In the following section, we quantify this limitation and present a prescription for the use of
plots for the rev and VD samples when the light curve segments are short is expected to be related to limitations in accurately measuring the X-ray variability of the sources in the VD sample. In the following section, we quantify this limitation and present a prescription for the use of 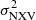 in the BH mass determination.
in the BH mass determination.
5.2. Significance of the observation duration
The main difference between the rev and VD samples is the average number of observations per target and their duration. There are, on average, 3.3 observations per source in the rev sample, with a mean duration of 80 ks each. On the contrary, there are only 1.3 observations per target in the VD sample, with a mean duration of 60 ks each. In order to quantify the impact of the available exposure time of a source in the estimation of the 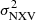 , we performed the following experiment.
, we performed the following experiment.
For each timescale, we progressively increased the minimum number of light curve segments required in order to keep a target in the sample. Effectively, this leads to smaller and smaller sub-samples, with an increased average duration for the observations. For example, when we request a minimum of at least two time segments of 20 ks for the estimation of 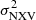 , then only sources with one observation of at least Δt = 40 ks or two observations of at least 20 ks each are considered. When, for instance, we increase the minimum number of 20 ks segments to five, then it is only those sources with at least a Δt = 100 ks observation or five observations of 20 ks each are considered. We repeated this exercise, namely, increasing the minimum number of segments for both the rev and the VD samples, until there were less than six sources left in the sample and we stopped.
, then only sources with one observation of at least Δt = 40 ks or two observations of at least 20 ks each are considered. When, for instance, we increase the minimum number of 20 ks segments to five, then it is only those sources with at least a Δt = 100 ks observation or five observations of 20 ks each are considered. We repeated this exercise, namely, increasing the minimum number of segments for both the rev and the VD samples, until there were less than six sources left in the sample and we stopped.
For each new sub-sample, we again fit a straight line to obtain the best fit slope and intercept of the MBH vs. 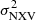 relation. Figures A.1 and A.2 show the resulted best-fit parameters plotted as a function of the average duration of the observations for each sub-sample. The numbers next to each point indicate the number of sources left in each sub-sample after increasing the minimum number of segments.
relation. Figures A.1 and A.2 show the resulted best-fit parameters plotted as a function of the average duration of the observations for each sub-sample. The numbers next to each point indicate the number of sources left in each sub-sample after increasing the minimum number of segments.
The best-fit parameters remain roughly constant for the rev sample, irrespective of the number of segments required to compute 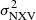 . An increase in that number does not affect the fitting results. However, this is not the case with the VD sample. The VD sample includes many sources with observations with a significantly shorter average duration than the average duration of the rev sample. The best-fit line parameters change as we increase the number of segments we use to compute
. An increase in that number does not affect the fitting results. However, this is not the case with the VD sample. The VD sample includes many sources with observations with a significantly shorter average duration than the average duration of the rev sample. The best-fit line parameters change as we increase the number of segments we use to compute 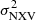 . When the average duration of the observations in the VD sub-sample is similar to that of the rev sample, then the best-fit slopes and intercepts become consistent.
. When the average duration of the observations in the VD sub-sample is similar to that of the rev sample, then the best-fit slopes and intercepts become consistent.
We also note, as explained in Isobe et al. (1990), that the best-fit parameter errors may be underestimated for the smaller-sized samples (i.e. for the best-fit parameters determined by fitting the objects with the longest observations). This actually makes the agreement between the rev and VD best-fit parameters even more impressive. It also shows that the systematic bias present in the best-fit parameters when we consider all the VD sample sources is much greater than the statistical uncertainty of the best-fit parameters.
The black circles in Figs. A.1 and A.2 indicate the first VD and rev sub-samples (i.e. those with a shorter average duration and, therefore, a larger size) for which the best-fit line slope and intercept are consistent (within errors). For all subsequent sub-samples, the best-fit results remain roughly constant.
Our results indicate that an average of ∼250 ks in the duration of the observations per source is necessary for the best-fit results, from both samples, to agree when using 10 ks segments. This number decreases to ∼180 − 200 ks when the estimation of the 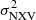 is based on 40 ks and 80 ks segments. This is probably due to the fact that as the segment duration increases, the intrinsic variance increases as well; therefore, it is easier (for a given S/N) to measure it accurately using slightly shorter average duration of observations. The results are similar for both the 3–10 and the 10–20 keV bands.
is based on 40 ks and 80 ks segments. This is probably due to the fact that as the segment duration increases, the intrinsic variance increases as well; therefore, it is easier (for a given S/N) to measure it accurately using slightly shorter average duration of observations. The results are similar for both the 3–10 and the 10–20 keV bands.
6. A prescription for measuring MBH in Seyfert galaxies.
Figures 4 and 5 show the MBH vs. 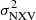 data for the largest rev and VD samples, where the best-fit line slope and intercept are consistent with each other (see the encircled points in Figs. A.1 and A.2). The blue-dotted and red-dashed lines indicate these best-fit models to the rev and VD samples, respectively (for the same Δt value and energy band).
data for the largest rev and VD samples, where the best-fit line slope and intercept are consistent with each other (see the encircled points in Figs. A.1 and A.2). The blue-dotted and red-dashed lines indicate these best-fit models to the rev and VD samples, respectively (for the same Δt value and energy band).
 |
Fig. 4. MBH vs. |
 |
Fig. 5. MBH vs. |
Our rev sample is comprised of Type I AGN only, since the mass estimation is obtained by the reverberation method. On the other hand, the VD sample, where the mass is estimated using stellar velocity dispersion measurements from high-quality spectra, contains both Type I and Type II AGNs. We note, however, that we do not expect any systematic difference in the MBH–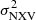 relation for Type I and Type II AGNs. For example, Rani et al. (2017) presented their results on the flux variability on hourly timescales for a large sample of AGN using NuSTAR and suggested no difference in the variability behaviour between Seyfert 1 and 2 galaxies in all X-ray bands.
relation for Type I and Type II AGNs. For example, Rani et al. (2017) presented their results on the flux variability on hourly timescales for a large sample of AGN using NuSTAR and suggested no difference in the variability behaviour between Seyfert 1 and 2 galaxies in all X-ray bands.
To further explore this notion, in Figs. 4 and 5, we plot Type I AGN separately from the rev sample (filled-blue circles), Type I AGN from the VD sample (open-red squares), and Type II AGN from the VD sample (filled-red squares). The small number statistics in the individual VD sub-samples does not allow for a separate line fitting analysis. However, the plots clearly show that there are no systematic differences or inconsistencies between the different populations. We therefore chose to combine the samples and fit all the data simultaneously.
The solid green lines in Figs. 4 and 5 show the best-fit lines obtained from the combined (rev+VD) sample. The best-fit results are listed in Table 2 (Cols. 5 and 6 for the 3–10 keV band, Cols. 11 and 12 for the 10–20 keV band). We propose for these best fit-line models to be used to measure the BH mass in Seyfert galaxies.
Best-fit results of the MBH vs. 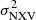 relation for the combined rev and VD samples.
relation for the combined rev and VD samples.
Columns 2 and 8 in the same table present a list of the total number of sources in the combined (rev+VD) sample for each band. The samples are smaller in the 10–20 keV band, mainly because the S/N of the light curves in this band is significantly smaller; hence, there are fewer objects with positive excess variance measurements. Columns 3 and 9 list the average duration of the observations (Δta) as well as the average (NA) and the minimum (Nm) number of segments for the objects in each sample, rounded to the lower integer. Here, Nm corresponds to the number of segments of the target with the shortest duration for the observations in the combined sample. Columns 4 and 10 list the average and the minimum S/N of the light curves that we used to compute the excess variance in the combined sample. Lastly, Cols. 7 and 13 list the average scatter of the points around the best-fit line.
6.1. The prescription
Based on the results presented in the previous section, we propose the following prescription for the measurement of the BH mass in AGN excess variance measurements.
First, the light curve(s) should be divided into a number of segments, the average 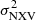 should be computed, and then Eq. (3) can be used to derive MBH, with α and β listed in Table 2, depending on the duration of the segment that was chosen and the energy band.
should be computed, and then Eq. (3) can be used to derive MBH, with α and β listed in Table 2, depending on the duration of the segment that was chosen and the energy band.
Second, the number of light curve segments that will be used to compute the excess variance should ideally be comparable to the average number of segments listed in Table 2 and (at least) larger than the minimum number of segments listed in the same table. Since the scatter of the points around the best-fit lines decreases with increasing segment duration, we propose the use of the longest possible segment to estimate the BH mass.
Finally, the average S/N of the light curves should be comparable to the average S/N and (at least) greater than the minimum S/N listed in Table 2 (see Cols. 4 and 10 in Table 2). The smallest S/N values suggest that S/Ns at least equal to ∼3 are necessary to achieve a reliable estimate of the BH mass.
6.2. Compton-thick sources
We used the prescription mentioned above to measure the BH mass of the CT sources. Therefore, we apply the same minimum duration and S/N criteria for the measurement of 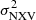 presented above for the sources in the CT sample. Due to the small size of the CT sample and the reduced photon statistics due to the absorption, we were able to measure
presented above for the sources in the CT sample. Due to the small size of the CT sample and the reduced photon statistics due to the absorption, we were able to measure 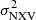 in only four sources when using the 80 ks segments. The number of sources with positive
in only four sources when using the 80 ks segments. The number of sources with positive 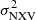 measurements on shorter timescales is very small (only one or two).
measurements on shorter timescales is very small (only one or two).
Black cross-marks in Fig. 6 show the MBH vs. 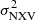 for the CT sources, in the 3–10 keV (upper panel) and the 10–20 keV band (lower panel) for the 80 ks segments. The solid green line shows the best-fit relation to the combined rev+VD sources. An inspection of Fig. 6 suggests that the
for the CT sources, in the 3–10 keV (upper panel) and the 10–20 keV band (lower panel) for the 80 ks segments. The solid green line shows the best-fit relation to the combined rev+VD sources. An inspection of Fig. 6 suggests that the 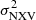 measurements in the 10–20 keV band are in good agreement with the model. Although the number of the CT sources is small, this result suggests that we could use the variability method to measure the BH mass in CT sources, when we use data in the 10–20 keV band.
measurements in the 10–20 keV band are in good agreement with the model. Although the number of the CT sources is small, this result suggests that we could use the variability method to measure the BH mass in CT sources, when we use data in the 10–20 keV band.
 |
Fig. 6. MBH vs. |
On the other hand, the scatter of the BH-mass versus excess variance CT points around the best-fit line in the 3–10 keV is significantly greater. The CT data in the top panel of Fig. 6 may even indicate a lack of correlation between BH mass and variability for the CT sources in the 3–10 keV band. This could be due to the fact that most of the observed flux in the 3–10 keV band may be due to scattered radiation rather than the primary continuum in CT sources, although the limited number of CT measurements do not allow us to reach a firm conclusion in this regard.
7. Application of the proposed prescription
We applied the proposed prescription to obtain BH mass estimates for AGN that are not part of either the rev, VD, or CT samples and that have NuSTAR archival observations which fulfill the minimum number of segments and S/N criteria (as presented in Sect. 6.1). There are 22 such sources, which are listed in Table 3 and these constitute our ’prediction’ sample (prd sample, hereafter). The observation log of these sources is presented in Table B.4. We followed the same steps as detailed in Sects. 3 and 4 to compute 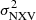 in the 3–10 and the 10–20 keV bands, using Δt = 10, 20, 40, and 80 ks segments. Then we used the best-fit models listed in Table 2 to estimate the BH mass for each source. Our BH mass predictions are listed in Table 3.
in the 3–10 and the 10–20 keV bands, using Δt = 10, 20, 40, and 80 ks segments. Then we used the best-fit models listed in Table 2 to estimate the BH mass for each source. Our BH mass predictions are listed in Table 3.
Black hole mass estimates for the prediction sample.
There are two sources (i.e. ESO511-30 and 2MASXJ19301380) where the excess variance is negative, at all timescales and in both energy bands. This is despite the fact that the light curves have a S/N value greater than 3 in both bands and are relatively long, specially in the case of ESO511-30 (BAT ID = 719)m where the observation is ∼320 ks long. Since all the sources in the rev+VD sample have a positive excess variance measurement and their BH mass is (mostly) smaller than 108 M⊙, we suspect that the mass of the BH in these objects is significantly larger than 108 M⊙.
Within each energy band, the BH mass estimates from the various light curve segments agree with each other within 1 − 2σ (where σ is equal to the average scatter of the points around the best-fit line, as listed in Table 2). This is not surprising, as the various light curve segments are all part of the same observations for each source.
The 3–10 keV and the 10–20 keV band BH mass estimates agree within 1 − 2σ, at all timescales, in all sources, except IRAS09149-6206. In this case, we are able to measure the BH mass using segments with durations of 10, 20, 40m and 80 ks in the 3–10 keV band and the log(MBH) estimates ranging between 7.35 and 7.55. On the other hand, we cannot measure the BH mass using 10 and 20 ks long segments in the 10–20 keV band, because the resulting excess variance is negative. Moreover, the 10–20 keV excess variance using the 40 and 80 ks segments implies a much larger BH mass. The reason for this discrepancy is the fact that a (relatively) large amplitude variation appears in one of the 3–10 keV band light curves, while it is absent in the respective 10–20 keV light curves (see also Walton et al. 2020).
For two more sources (i.e. Pictor A and HE1143-1810), the excess variance is positive in the 3–10 keV band, but negative in the 10–20 keV band. There are low-amplitude variations in the 3–10 keV band light curves, which do not appear in the 10–20 keV light curves. In both cases, log(MBH) is greater than ∼7.6 − 7.7. It is possible that the variability detection in the 3–10 keV band only is a statistical effect: due to the high BH mass, it just might happen that the variability is detected only in the 3–10 keV band, where the S/N is greater anyway. Another possibility may be that these sources are dominated by the reflection component at energies above 10 keV; hence, the continuum variations are better sampled at lower energies.
There are also two cases (i.e 3C111 and Mrk 926) where the 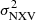 was measured only in the 10–20 keV band. Mrk 926 is the source with the largest BH mass estimate in the prd sample. We believe that the detection of variability in the 10–20 keV and not in the 3–10 keV band is purely statistical in nature. It just happens to measure a positive excess variance in this source at energies above 10 keV; and this is probably the case for 3C111 as well.
was measured only in the 10–20 keV band. Mrk 926 is the source with the largest BH mass estimate in the prd sample. We believe that the detection of variability in the 10–20 keV and not in the 3–10 keV band is purely statistical in nature. It just happens to measure a positive excess variance in this source at energies above 10 keV; and this is probably the case for 3C111 as well.
Finally, we note that BH mass estimates should always be treated with care. For example, NGC6240, is a galaxy that is known to harbour two active nuclei, each with a mass in excess of 9 × 107 M⊙ (e.g. Kollatschny et al. 2020). Such galaxies are excluded from both the rev and the VD samples. We estimate a log(MBH) of 7.5–8.2 (for Δt = 40 ks, in the 10–20 and 3–10 keV bands, respectively), in agreement with the previous estimates. However, we have not explored how the presence of two active nuclei may affect the accuracy of our method.
8. Summary and guidelines
Here, we present a prescription for measuring the mass of the central BH in AGN using excess variance measurements. We emphasise that we did not study the variability versus BH mass relation in AGN, as this has been widely considered in previous studies. Our objective is to select a well-defined sample of sources with available BH mass measurements and then to identify the minimum duration and S/N of the light curves that are necessary for the MBH vs. 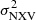 , relation to be well defined, that is, for the scatter of the points around the best-fit lines to be similar to the average uncertainty of BH mass estimates computed with other methods. If the X-ray variability mechanism is the same for all AGN, we can measure BH mass in any AGN following the prescription we outlined in Sect. 6.1, as long as the duration and S/N of the available light curves satisfy the ’quality’ criteria discussed there.
, relation to be well defined, that is, for the scatter of the points around the best-fit lines to be similar to the average uncertainty of BH mass estimates computed with other methods. If the X-ray variability mechanism is the same for all AGN, we can measure BH mass in any AGN following the prescription we outlined in Sect. 6.1, as long as the duration and S/N of the available light curves satisfy the ’quality’ criteria discussed there.
We emphasise that the prescription to measure AGN that we present in this work is only applicable to the case of light curves with a bin size of 250 s that can be divided in segments of 80, 40, 20, and 10 ks. Such light curves can be obtained from observations taken by NuSTAR and XMM-Newton, as well as from past X–ray observatories, such as Suzaku and ASCA. There are many AGN observations in the RXTE and Swift/XRT archive, however, their mean bin size is significantly larger than 250 s and, hence, they cannot be used to estimate BH mass using the prescription in Sect. 6.1. Nevertheless, there are already quite a few AGN whose NuSTAR and XMM-Newton archival light curves can meet the criteria described in Sect. 6.1. We already applied our prescription to archival light curves of 22 AGN with NuSTAR light curves that fulfill the necessary criteria and we computed BH mass estimates for them. In the near future, we plan to search the XMM-Newton archive for AGN with light curves that can satisfy the necessary criteria and estimate their BH mass.
The average scatter of the rev+VD sources around the best-fit line, 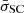 , is 0.25, 0.35, and 0.4, for the segments with Δt = 80 ks, 40 and 20 ks, and 10 ks, respectively (these numbers are equal to the mean of σSC, 3 − 10 keV and σSC, 10 − 20 keV values, listed in Table 2). On average, the error of log(MBH) should be comparable to
, is 0.25, 0.35, and 0.4, for the segments with Δt = 80 ks, 40 and 20 ks, and 10 ks, respectively (these numbers are equal to the mean of σSC, 3 − 10 keV and σSC, 10 − 20 keV values, listed in Table 2). On average, the error of log(MBH) should be comparable to 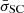 . We stress that
. We stress that 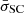 is not the formal error on the BH mass estimate of an individual source. Instead, it should be considered as representative of the expected standard deviation of these estimates. It is possible to compute the error of log(MBH) for an individual source, but only if the available light curves are long enough (see below).
is not the formal error on the BH mass estimate of an individual source. Instead, it should be considered as representative of the expected standard deviation of these estimates. It is possible to compute the error of log(MBH) for an individual source, but only if the available light curves are long enough (see below).
Our results demonstrate that it is possible to measure the BH mass in AGN using excess variance measurements if the available light curves are long enough and have the necessary S/N values. The resulting BH mass estimates will be as reliable as the estimates which are based on other techniques (e.g. the continuum and emission line reverberation and velocity dispersion measurements). The ‘quality’ requirements on the light-curve duration and S/N are quite strong. They are mainly imposed by the statistical properties of 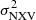 . The normalised excess variance is a statistic which follows a highly asymmetric distribution function, with a broad variance (see Allevato et al. 2013). We strongly advise against the use of light curves that do not follow the duration and S/N criteria that we list in Sect. 6.1. If such light curves are used to compute
. The normalised excess variance is a statistic which follows a highly asymmetric distribution function, with a broad variance (see Allevato et al. 2013). We strongly advise against the use of light curves that do not follow the duration and S/N criteria that we list in Sect. 6.1. If such light curves are used to compute 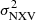 and then log(MBH) using the best-fit results listed in Table 2, the resulting estimate may be heavily biased. Due to the
and then log(MBH) using the best-fit results listed in Table 2, the resulting estimate may be heavily biased. Due to the 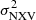 statistical properties, the MBH vs.
statistical properties, the MBH vs. 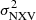 relation may actually depend on the characteristics of the light curves we use (for the same segment duration). For example, the difference between the slope of the best-fit line to the VD data plotted in the top left and bottom right panels in Fig. 2 is 1.09 ± 0.19, which is significant at the 5.7σ level. This result clearly shows that it will be inappropriate to use the best-fit results listed in Table 2 to compute the BH mass for sources with low-quality light curves.
relation may actually depend on the characteristics of the light curves we use (for the same segment duration). For example, the difference between the slope of the best-fit line to the VD data plotted in the top left and bottom right panels in Fig. 2 is 1.09 ± 0.19, which is significant at the 5.7σ level. This result clearly shows that it will be inappropriate to use the best-fit results listed in Table 2 to compute the BH mass for sources with low-quality light curves.
It may be worth investigating the relation between BH mass and excess variance for shorter light curves or light curves with lower S/N and to establish a prescription for estimating their MBH values as well. In this way, BH masses could be measured for many more sources. This aspect, however, is beyond the scope of this work and, in any case, we suspect that the resulting estimates will have significantly larger uncertainties, hence, they may be of limited applicability.
Table 2 lists the best-fit parameters of the lines we fitted to the data of the combined (rev+VD) sample, when the excess variance is computed using light curve segments which are Δt = 10, 20, 40 and 80 ks long (Figs. 4 and 5). We expect that the BH mass estimates should be independent of the segment duration. However, whenever possible, it would be advisable to compute MBH using all four different light-curve segment durations to verify that there are no unexpected complications with the observations. Since the average error of the BH estimates should decrease with increasing segment duration, we propose to adopt BH mass estimates based on the longest Δt.
The accuracy of the BH mass estimate will not increase even if the duration of the light curves is longer than the longest light curves among the sources in the rev+VD sample. This is because the uncertainty on MBH mainly depends on the uncertainty of the best-fit line parameters, which should be representative of the typical scatter of the points plotted in Figs. 4 and 5. On the other hand, if there are more than 50 segments, with an average S/Ns greater than 3, then it is possible to compute the error on the mean 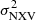 (see Allevato et al. 2013). In this case, an error on the BH mass measurement of the individual source can be measured, using the error of the best-fit line parameters (listed in Table 2) and the commonly used rule of error propagation.
(see Allevato et al. 2013). In this case, an error on the BH mass measurement of the individual source can be measured, using the error of the best-fit line parameters (listed in Table 2) and the commonly used rule of error propagation.
The best-fit results and the scatter of the rev and VD points around the best-fit lines are comparable for the 3–10 and the 10–20 keV bands (see Figs. 4 and 5). Black hole mass estimates should be similar when using light curves in both bands to compute the excess variance. Nevertheless, we suggest computing the BH mass in both bands when there are light curves in both bands (i.e. from NuSTAR observations). The 10–20 keV band should be preferred for sources which are heavily absorbed (as our results, from a limited number of CT sources, indicate). On the other hand, the 3–10 keV band should be preferred for sources which may be dominated by the X-ray reflection component at energies above 10 keV.
The MBH–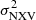 relations studied here are well calibrated for sources with BH mass between 106 − 108 M⊙. We caution against the use of the proposed method for sources with MBH ≤106 M⊙. In this regime, the relation between MBH and
relations studied here are well calibrated for sources with BH mass between 106 − 108 M⊙. We caution against the use of the proposed method for sources with MBH ≤106 M⊙. In this regime, the relation between MBH and 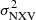 could significantly deviate from the linear assumption adopted in this paper. On the other hand, the method we present should be valid for AGN with larger BH masses, although the available data sets for such sources may not be sufficient. The best-fit line in Figs. 4 and 5 show that the normalised excess variance in sources with BH mass larger than 108 M⊙ should be smaller than ∼10−3, even when Δt = 80 ks (the limit is smaller for shorter segments). This is a small excess variance limit and light curves with the minimum S/N and duration requirements will probably result in a negative
could significantly deviate from the linear assumption adopted in this paper. On the other hand, the method we present should be valid for AGN with larger BH masses, although the available data sets for such sources may not be sufficient. The best-fit line in Figs. 4 and 5 show that the normalised excess variance in sources with BH mass larger than 108 M⊙ should be smaller than ∼10−3, even when Δt = 80 ks (the limit is smaller for shorter segments). This is a small excess variance limit and light curves with the minimum S/N and duration requirements will probably result in a negative 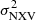 . It will be necessary to use light curves with a much higher S/N or many light curve segments in order to measure such a low intrinsic excess variance.
. It will be necessary to use light curves with a much higher S/N or many light curve segments in order to measure such a low intrinsic excess variance.
The proposed prescription should be valid both for Type I and Type II objects. Although all AGN in the rev sample are Type I, the VD sample contains a mixture of Type I and Type II sources. Our plots show no difference in the MBH–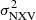 relation for these two classes and, moreover, the best-fit lines to the rev and VD log(MBH)–
relation for these two classes and, moreover, the best-fit lines to the rev and VD log(MBH)–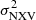 plots are almost identical. Therefore we expect the method to perform equally well for objects in either class.
plots are almost identical. Therefore we expect the method to perform equally well for objects in either class.
In this work, we study mainly radio-quiet AGN, although a limited number of objects from the 3C (and one for the 4C) catalogue are included in our sample. Emission from the jet is not supposed to be dominant in the bands we study for any of these sources and we therefore expect the proposed prescription to be valid for these sources as well. In any case, we strongly advise against the use of the proposed prescription to blazars. In this class of sources, in constrast to their radio-quiet counterparts, the X-ray emission could be dominated by radiative processes in the relativistic jet. In agreement to this scenario, Rani et al. (2017) suggested that blazars show much greater X-ray flux variation amplitudes as compared to Seyfert galaxies.
In order to compare or combine BH mass measurements using the prescription presented here with those derived using different methods, it is necessary to take into account (when relevant) that our estimators are normalised to the MBH–σ* relation of Woo et al. (2013). We note that our results are applicable for AGN in the nearby Universe (i.e. sources with z ≤ 0.07). Our prescription should also be applicable to AGN further away, as long as rest-frame light curves satisfy the necessary quality-criteria. Obviously, the reliability of the BH mass estimates in this case will also depend on the assumption that the AGN variability properties do not change with redshift.
It would be interesting to see if a similar method can be established for the AGN light curves resulting from e-ROSITA sky survey data. The method will have to be calibrated appropriately, as the light curve sampling properties will be entirely different to the light curves that are currently delivered by the pointed observations of XMM-Newton and NuSTAR. It is not certain that it will be possible to measure AGN using variability measurements with the e-ROSITA light curves, but given the large amount of sources that will be identified, it may be worth investigating this possibility.
Acknowledgments
We have made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory, and funded by the National Aeronautics and Space Administration. We thank the NuSTAR Operations, Software and Calibration teams for support with the execution and analysis of these observations. This research has made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the Space Science Data Center (SSDC; ASI, Italy) and the California Institute of Technology (USA). This work is based on archival data, software or online services provided by the SSDC. This research has made use of the High Energy Astrophysics Science Archive Research Centre Online Service, provided by the NASA/Goddard Space Flight Centre and NASA’s Astrophysics Data System.
References
- Allevato, V., Paolillo, M., Papadakis, I., & Pinto, C. 2013, ApJ, 771, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Baloković, M., Comastri, A., Harrison, F. A., et al. 2014, ApJ, 794, 111 [CrossRef] [Google Scholar]
- Barth, A. J., Pancoast, A., Bennert, V. N., et al. 2013, ApJ, 769, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D. 2004, in X-Ray and Gamma-Ray Instrumentation for Astronomy XIII, eds. K. A. Flanagan, & O. H. W. Siegmund, SPIE Conf. Ser., 5165, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C. 2021, ApJ, 908, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., & Katz, S. 2015, PASP, 127, 67 [Google Scholar]
- Bentz, M. C., Denney, K. D., Cackett, E. M., et al. 2006, ApJ, 651, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Walsh, J. L., Barth, A. J., et al. 2008, ApJ, 689, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Walsh, J. L., Barth, A. J., et al. 2009, ApJ, 705, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Walsh, J. L., Barth, A. J., et al. 2010, ApJ, 716, 993 [Google Scholar]
- Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [Google Scholar]
- Bentz, M. C., Horenstein, D., Bazhaw, C., et al. 2014, ApJ, 796, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Batiste, M., Seals, J., et al. 2016a, ApJ, 831, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Cackett, E. M., Crenshaw, D. M., et al. 2016b, ApJ, 830, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Street, R., Onken, C. A., & Valluri, M. 2021, ApJ, 906, 50 [Google Scholar]
- Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [Google Scholar]
- Brandt, W. N., & Alexander, D. M. 2015, A&ARv, 23, 1 [Google Scholar]
- Clavel, J., Boksenberg, A., Bromage, G. E., et al. 1990, MNRAS, 246, 668 [NASA ADS] [Google Scholar]
- Clavel, J., Reichert, G. A., Alloin, D., et al. 1991, ApJ, 366, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Collier, S. J., Horne, K., Kaspi, S., et al. 1998, ApJ, 500, 162 [Google Scholar]
- Czerny, B., Nikołajuk, M., Piasecki, M., & Kuraszkiewicz, J. 2001, MNRAS, 325, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Dalla Bontà, E., Peterson, B. M., Bentz, M. C., et al. 2020, ApJ, 903, 112 [CrossRef] [Google Scholar]
- De Rosa, G., Peterson, B. M., Ely, J., et al. 2015, ApJ, 806, 128 [NASA ADS] [CrossRef] [Google Scholar]
- De Rosa, G., Fausnaugh, M. M., Grier, C. J., et al. 2018, ApJ, 866, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Denney, K. D., Bentz, M. C., Peterson, B. M., et al. 2006, ApJ, 653, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Denney, K. D., Watson, L. C., Peterson, B. M., et al. 2009, ApJ, 702, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Denney, K. D., Peterson, B. M., Pogge, R. W., et al. 2010, ApJ, 721, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, M., Kollatschny, W., Peterson, B. M., et al. 1993, ApJ, 408, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, M., Peterson, B. M., Albrecht, P., et al. 1998, ApJS, 115, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, M., Peterson, B. M., Grier, C. J., et al. 2012, ApJ, 757, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Du, P., Hu, C., Lu, K.-X., et al. 2014, ApJ, 782, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [Google Scholar]
- Fausnaugh, M. M., Grier, C. J., Bentz, M. C., et al. 2017, ApJ, 840, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [Google Scholar]
- González-Martín, O., & Vaughan, S. 2012, A&A, 544, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gravity Collaboration (Abuter, R., et al.) 2018, A&A, 618, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gravity Collaboration (Abuter, R., et al.) 2020, A&A, 636, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grier, C. J., Peterson, B. M., Pogge, R. W., et al. 2012a, ApJ, 755, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Grier, C. J., Peterson, B. M., Pogge, R. W., et al. 2012b, ApJ, 744, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Grier, C. J., Martini, P., Watson, L. C., et al. 2013, ApJ, 773, 90 [CrossRef] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
- Hu, C., Du, P., Lu, K.-X., et al. 2015, ApJ, 804, 138 [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [Google Scholar]
- Kollatschny, W., Bischoff, K., Robinson, E. L., Welsh, W. F., & Hill, G. J. 2001, A&A, 379, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kollatschny, W., Weilbacher, P. M., Ochmann, M. W., et al. 2020, A&A, 633, A79 [EDP Sciences] [Google Scholar]
- Körding, E. G., Migliari, S., Fender, R., et al. 2007, MNRAS, 380, 301 [Google Scholar]
- Korista, K. T., Alloin, D., Barr, P., et al. 1995, ApJS, 97, 285 [Google Scholar]
- Koss, M., Mushotzky, R., Treister, E., et al. 2012, ApJ, 746, L22 [Google Scholar]
- Koss, M., Trakhtenbrot, B., Ricci, C., et al. 2017, ApJ, 850, 74 [Google Scholar]
- Kovačević, A., Popović, L. Č., Shapovalova, A. I., et al. 2014, Adv. Space Res., 54, 1414 [CrossRef] [Google Scholar]
- Lanzuisi, G., Ponti, G., Salvato, M., et al. 2014, ApJ, 781, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Netzer, H., Leibowitz, E., et al. 1990, ApJ, 351, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Netzer, H., Mazeh, T., et al. 1991, ApJ, 367, 493 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Papadakis, I. E., Uttley, P., Page, M. J., & Mason, K. O. 2004, MNRAS, 348, 783 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Koerding, E., Knigge, C., Uttley, P., & Fender, R. P. 2006, Nature, 444, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Metzroth, K. G., Onken, C. A., & Peterson, B. M. 2006, ApJ, 647, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., George, I. M., Mushotzky, R. F., Turner, T. J., & Yaqoob, T. 1997, ApJ, 476, 70 [Google Scholar]
- O’Brien, P. T., Dietrich, M., Leighly, K., et al. 1998, ApJ, 509, 163 [CrossRef] [Google Scholar]
- Oh, K., Koss, M., Markwardt, C. B., et al. 2018, ApJS, 235, 4 [Google Scholar]
- O’Neill, P. M., Nandra, K., Papadakis, I. E., & Turner, T. J. 2005, MNRAS, 358, 1405 [CrossRef] [Google Scholar]
- Onken, C. A., & Peterson, B. M. 2002, ApJ, 572, 746 [CrossRef] [Google Scholar]
- Papadakis, I. E. 2004, MNRAS, 348, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Paturel, G., Theureau, G., Bottinelli, L., et al. 2003, A&A, 412, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pei, L., Fausnaugh, M. M., Barth, A. J., et al. 2017, ApJ, 837, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Wanders, I., Bertram, R., et al. 1998, ApJ, 501, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Berlind, P., Bertram, R., et al. 2002, ApJ, 581, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [Google Scholar]
- Peterson, B. M., Bentz, M. C., Desroches, L.-B., et al. 2005, ApJ, 632, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Denney, K. D., De Rosa, G., et al. 2013, ApJ, 779, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Grier, C. J., Horne, K., et al. 2014, ApJ, 795, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Papadakis, I., Bianchi, S., et al. 2012, A&A, 542, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rani, P., Stalin, C. S., & Rakshit, S. 2017, MNRAS, 466, 3309 [NASA ADS] [CrossRef] [Google Scholar]
- Reichert, G. A., Rodriguez-Pascual, P. M., Alloin, D., et al. 1994, ApJ, 425, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017, ApJS, 233, 17 [Google Scholar]
- Rodríguez-Pascual, P. M., Alloin, D., Clavel, J., et al. 1997, ApJS, 110, 9 [CrossRef] [Google Scholar]
- Santos-Lleó, M., Chatzichristou, E., de Oliveira, C. M., et al. 1997, ApJS, 112, 271 [CrossRef] [Google Scholar]
- Santos-Lleó, M., Clavel, J., Schulz, B., et al. 2001, A&A, 369, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sergeev, S. G., Klimanov, S. A., Doroshenko, V. T., et al. 2011, MNRAS, 410, 1877 [NASA ADS] [Google Scholar]
- Sergeev, S. G., Nazarov, S. V., & Borman, G. A. 2017, MNRAS, 465, 1898 [NASA ADS] [CrossRef] [Google Scholar]
- Shapovalova, A. I., Popović, L. Č., Burenkov, A. N., et al. 2010, A&A, 517, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stirpe, G. M., Winge, C., Altieri, B., et al. 1994, ApJ, 425, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, M.-H., & Horne, K. 1996, MNRAS, 283, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, S., Sand, D. J., Barth, A. J., et al. 2015, ApJ, 813, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Alston, W. N., Kosec, P., et al. 2020, MNRAS, 499, 1480 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., Schulze, A., Park, D., et al. 2013, ApJ, 772, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, X.-L., Zhang, S.-N., Wang, D.-X., & Zhu, L. 2010, ApJ, 710, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Zu, Y., Kochanek, C. S., & Peterson, B. M. 2011, ApJ, 735, 80 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Plots of the best-fit results as function of observation durations
 |
Fig. A.1. Best-fit slope and intercept in the 3–10 keV band for the rev sub-samples (filled-blue circles) and the VD sub-samples (open-red squares) as a function of the average duration of their sources. The circles indicate the first rev and VD sub-samples (i.e those with a shorter duration) for which the best-fit results are in agreement (within errors). The horizontal lines indicates the best fit value when we fit the combined data from the two sub-samples in agreement (rev and VD). |
 |
Fig. A.2. Best-fit slope and intercept in the 10–20 keV band for the rev sub-samples (filled-blue circles) and the VD sub-samples (open-red squares) as a function of the average duration of their sources. The circles indicate the first rev and VD sub-samples (i.e those with a shorter duration) for which the best-fit results are in agreement (within errors). The horizontal lines indicates the best fit value when we fit the combined data from the two sub-samples in agreement (rev and VD). |
Appendix B: Observation logs
Log of the rev sample
Log of VD sample
Log of CT sample
Log of the prediction sample
All Tables
All Figures
 |
Fig. 1. Comparison of the velocity dispersion measurements of the common sources from the Hyperleda database and the BASS catalogue. The error-bars correspond to 1σ confidence interval. The solid line show the one-to-one (y = x) relation. |
| In the text | |
 |
Fig. 2. MBH vs. |
| In the text | |
 |
Fig. 3. MBH vs. |
| In the text | |
 |
Fig. 4. MBH vs. |
| In the text | |
 |
Fig. 5. MBH vs. |
| In the text | |
 |
Fig. 6. MBH vs. |
| In the text | |
 |
Fig. A.1. Best-fit slope and intercept in the 3–10 keV band for the rev sub-samples (filled-blue circles) and the VD sub-samples (open-red squares) as a function of the average duration of their sources. The circles indicate the first rev and VD sub-samples (i.e those with a shorter duration) for which the best-fit results are in agreement (within errors). The horizontal lines indicates the best fit value when we fit the combined data from the two sub-samples in agreement (rev and VD). |
| In the text | |
 |
Fig. A.2. Best-fit slope and intercept in the 10–20 keV band for the rev sub-samples (filled-blue circles) and the VD sub-samples (open-red squares) as a function of the average duration of their sources. The circles indicate the first rev and VD sub-samples (i.e those with a shorter duration) for which the best-fit results are in agreement (within errors). The horizontal lines indicates the best fit value when we fit the combined data from the two sub-samples in agreement (rev and VD). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.