| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202245291 | |
| Published online | 08 May 2023 | |
The universal shape of the X-ray variability power spectrum of AGN up to z ∼ 3
1
Dipartimento di Fisica “Ettore Pancini”, Università di Napoli Federico II, Via Cintia 80126, Italy
2
INAF – Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Naples, Italy
3
INFN – Unità di Napoli, Via Cintia 9, 80126 Napoli, Italy
e-mail: paolillo@na.infn.it
4
Department of Physics and Institute of Theoretical and Computational Physics, University of Crete, Voutes University Campus, 71003 Heraklion, Greece
5
Institute of Astrophysics–FORTH, N. Plastira 100, 70013 Vassilika Vouton, Greece
6
Department of Astronomy and Astrophysics, 525 Davey Lab., The Pennsylvania State University, University Park, PA 16802, USA
7
Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA
8
Department of Physics, The Pennsylvania State University, University Park, PA 16802, USA
9
Instituto de Astrofísica and Centro de Astroingeniería, Facultad de Física, Pontificia Universidad Católica de Chile, Casilla 306, Santiago 22, Chile
10
Millennium Institute of Astrophysics, Nuncio Monseñor Sótero Sanz 100, Of 104, Providencia Santiago, Chile
11
Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, CO 80301, USA
12
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
13
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
14
Department of Physics, University of North Texas, Denton, TX 76203, USA
15
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
16
School of Astronomy and Space Science, Nanjing University, Nanjing, Jiangsu 210093, PR China
17
Key Laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, Nanjing 210093, PR China
18
INAF – Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, Firenze, Italy
19
CAS Key Laboratory for Research in Galaxies and Cosmology, Department of Astronomy, University of Science and Technology of China, Hefei 230026, PR China
20
School of Astronomy and Space Sciences, University of Science and Technology of China, Hefei 230026, PR China
Received:
25
October
2022
Accepted:
15
February
2023
Aims. We study the ensemble X-ray variability properties of active galactic nuclei (AGN) over large ranges of timescale (20 ks ≤ T ≤ 14 yr), redshift (0 ≤ z ≲ 3), luminosity (1040 erg s−1 ≤ LX ≤ 1046 erg s−1), and black hole (BH) mass (106 ≤ M⊙ ≤ 109).
Methods. We propose the use of the variance-frequency diagram as a viable alternative to the study of the power spectral density (PSD), which is not yet accessible for distant, faint, and/or sparsely sampled AGN.
Results. We show that the data collected from archival observations and previous literature studies are fully consistent with a universal PSD form, which does not show any evidence for systematic evolution of shape or amplitude with redshift or luminosity, even if there may be differences between individual AGN at a given redshift or luminosity. We find new evidence that the PSD bend frequency depends on BH mass and possibly on accretion rate. We finally discuss the implications for current and future AGN population and cosmological studies.
Key words: galaxies: active / black hole physics / quasars: supermassive black holes / X-rays: galaxies / surveys / methods: statistical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Flux variability is a defining characteristic of active galactic nuclei (AGN) and has been observed in these objects on all timescales, and across the whole electromagnetic spectrum. The fastest variations, as well as those of the greatest amplitude, are observed at the highest energies (X-rays and γ-rays), strongly suggesting that such radiation is mainly generated in relatively small regions, close to the central engine.
One of the most frequently used tools to study the observed variations is the power spectral density (PSD) function (or power spectrum for simplicity). Early studies of the X-ray variability of AGN with EXOSAT showed that the PSD has a power-law shape with a slope of ∼ − 1.5, and an amplitude that scales with the source luminosity (Green et al. 1993; Lawrence & Papadakis 1993). Long observing campaigns with the Rossi X-ray Timing Explorer (RXTE) over many years, combined with shorter XMM-Newton observations (mainly) have allowed the detailed study of AGN X-ray PSDs over a large frequency range, revealing at least one – and in some cases two – breaks in the PSD of nearby AGN (e.g., Uttley et al. 2002; Papadakis et al. 2002; Markowitz et al. 2003; McHardy et al. 2004; González-Martín & Vaughan 2012). These should represent characteristic timescales linked to the physical process producing the observed emission.
Most of our knowledge about AGN power spectra in the X-ray band is derived from extensive observations of relatively nearby and mostly low-luminosity AGN. It is not yet possible to estimate the PSD of AGN at larger redshifts because the available light curves have few points and are sparsely sampled. For this reason, our knowledge of the variability properties of the overall AGN population is mainly based on studies of the excess variance as a function of redshift and luminosity, using light curves from large samples of X-ray-detected AGN in various surveys (e.g., Paolillo et al. 2004; Papadakis et al. 2008; Young et al. 2012; Shemmer et al. 2014; Lanzuisi et al. 2014; Yang et al. 2016; Middei et al. 2017; Zheng et al. 2017; Ding et al. 2018; Thomas et al. 2021).
Recently, Paolillo et al. (2017, P17 hereafter) studied the X-ray-variability properties of distant AGN in the Chandra Deep Field-South region (CDF-S) over 17 years. These authors used the normalised excess variance 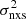 (i.e., the average light-curve variance corrected for noise; see Eq. (1) in P17) as a measure of the amplitude of the X-ray variability of the sources, and they studied the dependence of
(i.e., the average light-curve variance corrected for noise; see Eq. (1) in P17) as a measure of the amplitude of the X-ray variability of the sources, and they studied the dependence of 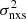 on X-ray luminosity in various redshift bins. P17 assumed power-spectrum models based on PSD analysis of relatively nearby, bright X-ray Seyferts, and found that the variability properties of high-z AGN are consistent with a PSD described by a bending power law, where the bend frequency (and perhaps also the PSD amplitude) depends on the accretion rate expressed in terms of the Eddington ratio λE = Ṁ/ṀEdd, where Ṁ is the mass accretion rate and ṀEdd is the Eddington accretion rate.
on X-ray luminosity in various redshift bins. P17 assumed power-spectrum models based on PSD analysis of relatively nearby, bright X-ray Seyferts, and found that the variability properties of high-z AGN are consistent with a PSD described by a bending power law, where the bend frequency (and perhaps also the PSD amplitude) depends on the accretion rate expressed in terms of the Eddington ratio λE = Ṁ/ṀEdd, where Ṁ is the mass accretion rate and ṀEdd is the Eddington accretion rate.
In this work, we expand this study, collecting several complementary AGN samples with available excess-variance measurements, including the CDF-S (P17), COSMOS (Lanzuisi et al. 2014), CAIXA (Ponti et al. 2012), TARTARUS (O’Neill et al. 2005), and RXTE (Zhang 2011), in order to cover a wide range of timescales, redshifts, luminosities, and black-hole (BH) masses. We also estimated the excess variance of numerous additional local AGN using Swift/XRT and RXTE light curves in order to cover timescales in between the shortest and the longest ones probed by the 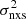 data from the literature.
data from the literature.
Our objective is to study the PSD itself using excess-variance measurements. In most previous works, 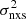 was used to investigate the dependence of AGN variability amplitude on X-ray luminosity, BH mass, and redshift. However, the dependence of
was used to investigate the dependence of AGN variability amplitude on X-ray luminosity, BH mass, and redshift. However, the dependence of 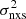 on total light-curve duration T itself is also important, because the excess variance is (approximately) equal to the integral of the intrinsic power spectrum in the range of frequencies 1/T ≤ ν ≤ 1/(2Δtmin), where Δtmin is the minimum time difference between successive points in the light curve1 (see Sect. 2). Due to the close relation between the PSD and
on total light-curve duration T itself is also important, because the excess variance is (approximately) equal to the integral of the intrinsic power spectrum in the range of frequencies 1/T ≤ ν ≤ 1/(2Δtmin), where Δtmin is the minimum time difference between successive points in the light curve1 (see Sect. 2). Due to the close relation between the PSD and 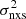 , we can compute
, we can compute 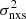 from light curves with different duration T, and then plot
from light curves with different duration T, and then plot 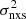 as a function of νT (≡1/T)2. This variance–frequency plot (VFP) provides information closely related to the PSD, with the advantage that it can be directly derived for large samples of faint and/or distant AGN, and can therefore be studied with the aim of constraining the intrinsic PSD properties.
as a function of νT (≡1/T)2. This variance–frequency plot (VFP) provides information closely related to the PSD, with the advantage that it can be directly derived for large samples of faint and/or distant AGN, and can therefore be studied with the aim of constraining the intrinsic PSD properties.
Although 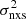 is easy to compute, so that we can create a VFP even from sparsely sampled light curves (which are not sufficient to measure the PSD), the use of the VFP is difficult on an individual AGN basis. In fact, given the statistical properties of the
is easy to compute, so that we can create a VFP even from sparsely sampled light curves (which are not sufficient to measure the PSD), the use of the VFP is difficult on an individual AGN basis. In fact, given the statistical properties of the 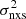 , in the case of a single object we would need many light curves in order to reliably estimate the intrinsic variance on various timescales (see Allevato et al. 2013, and references therein).
, in the case of a single object we would need many light curves in order to reliably estimate the intrinsic variance on various timescales (see Allevato et al. 2013, and references therein).
On the other hand, we could consider samples of AGN that have been monitored in the same way (i.e., where T and Δtmin are the same for all sources) in order to compute the mean excess variance, and use it to create the VFP. However, in the case where we use light curves of many AGN, one has to consider the dependence of 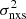 on BH mass (MBH) as well: for a given light-curve duration, the variance decreases with increasing BH mass (e.g., Papadakis 2004; O’Neill et al. 2005; Ponti et al. 2012). Therefore, assuming we know the BH masses for all AGN in the sample, we must first model the dependence of the excess variance on MBH to create VFP for AGN at a fixed mass.
on BH mass (MBH) as well: for a given light-curve duration, the variance decreases with increasing BH mass (e.g., Papadakis 2004; O’Neill et al. 2005; Ponti et al. 2012). Therefore, assuming we know the BH masses for all AGN in the sample, we must first model the dependence of the excess variance on MBH to create VFP for AGN at a fixed mass.
Following this approach, we aim to investigate whether or not the measured VFP is consistent with the hypothesis that the X-ray PSD has the same form in all AGN, implying that the X-ray variability mechanism is the same in all of them and, if this is indeed found to be the case, we intend to identify the characteristics of this ‘universal’ X-ray PSD of AGN.
The paper is organized as follows. In Sect. 2 we explain the relation between the VFP and the PSD, and how we can measure the VFP for sparsely sampled, low-S/N AGN. In Sect. 3 we present the BH mass and variability measurements for high-redshift sources in CDF-S and COSMOS samples, and the best-fit results to their 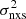 –MBH relations. In Sect. 4 we present the best-fit results for low-redshift sources from literature or archival data. In Sects. 5 and 6 we present the VFP of AGN up to redshift ∼3, the method we use to fit the observed VFP, and the best-fit results. Finally, in Sect. 7, we summarise our work and discuss the implications of our study. Throughout the paper, we adopt values of H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7.
–MBH relations. In Sect. 4 we present the best-fit results for low-redshift sources from literature or archival data. In Sects. 5 and 6 we present the VFP of AGN up to redshift ∼3, the method we use to fit the observed VFP, and the best-fit results. Finally, in Sect. 7, we summarise our work and discuss the implications of our study. Throughout the paper, we adopt values of H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7.
2. The variance–frequency plot: a substitute for the PSD
2.1. The PSD versus the VFP
Let us assume that the AGN X-ray PSD follows a relation of the form:
where A is the PSD normalisation (A = PSD(νb)×2νb), and νb is the bend frequency3. The PSD defined in this way has a logarithmic slope of −1 at low frequencies (ν ≪ νb), which steepens to −(1 + s) at higher frequencies (ν ≫ νb). This model PSD is based on the results from PSD studies of relatively nearby, low-luminosity (but X-ray bright) AGN (e.g., McHardy et al. 2004). Let us also assume that νb depends on the BH mass as follows (e.g., McHardy et al. 2006; González-Martín & Vaughan 2012):
where B is a constant. According to Eq. (4) in Allevato et al. 2013, the excess variance of a light curve of duration T will be a measure of the normalised ‘band’ variance, defined as follows4:
where νT = 1/Tmax and νmax = 1/(2Δtmin). In the case of equally sampled light curves with a few missing points (as in the RXTE, Swift, ASCA, and XMM-Newton light curves we use; see below) the shortest frequency sampled by the data is well defined, with Δtmin = 2Δt, where Δt is the bin size of the light curves. However, in the case of the unevenly sampled light curves (like CDF-S and COSMOS), the choice of Δtmin is not as clear (see e.g., the discussion in Appendix D in Scargle 1982). For these light curves, we decided to take Δtmin to be the shortest time difference between successive observations. For a fixed Δtmin, we expect a negative correlation between σ2 and νT, that is, the variability amplitude should increase with increasing light curve duration in AGN (due to the red-noise nature of the AGN PSD).
Equation (3) shows that σ2(νT, νmax) depends on the shape (and normalisation) of the PSD. Consequently, a plot of σ2 as a function of νT holds similar information to the PSD. As mentioned in Sect. 1, we refer to the plot of σ2(νT, νmax) versus νT as the VFP of an AGN5.
Figure 1 shows the PSD and the VFP plot (upper and lower panels, respectively) for an AGN with a BH mass of 108 M⊙. The PSD is computed using Eq. (1), while σ2(νT, νmax) is computed using Eq. (3), for various PSD parameters. The variance plotted in this figure should be equal to the (intrinsic) variance of light-curve segments with a duration of T = 1/ν and Δt = 250 s, so that νmax = 4 × 10−3 Hz.
 |
Fig. 1. PSD and VFP (upper and lower panels, respectively) of an AGN with a BH mass of 108 M⊙. The PSD model parameters are: A = 0.02 Hz−1, s = 1, and νb = 3 ⋅ 10−6 Hz (black solid lines). Black dashed lines indicate the PSD and VFP when we increase the PSD amplitude by a factor of 2. Red lines show the PSD and VFP when we increase the bend frequency (by a factor of 10), while the blue lines show the changes when we increase the high-frequency PSD slope from −2 to −3 (all the other parameters in this case are like those of the red lines). For the computation of the variance, we assumed νmax = (1/250 s). |
The figure shows that all the major features of the PSD are apparent in the VFP plot as well. For example, both the PSD and VFP have a power-law-like shape at high frequencies, with the VFP being flatter than the PSD (we highlight the different scale of the y-axis of the two panels in Fig. 1). At frequencies lower than νb, both the PSD and VFP flatten to a slope of −1 in the case of the PSD, while σ2 ∝ −ln(νT) below νb. The various lines in the same figure also show that when varying the PSD parameters, the PSD and the VFP shapes also vary in similar ways.
It is always better to estimate the power spectrum itself, even from a statistical point of view. The statistical properties of the periodogram (the estimator of the PSD) are far superior to the statistical properties of the excess variance as a measure of the intrinsic variance of a single source (see Allevato et al. 2013 for the statistical properties of the latter). However, as we already mentioned in Sect. 1, we cannot use the available light curves of the high-z AGN to estimate their PSD. On the other hand, we can measure their excess variance on different timescales (i.e., different νT), and therefore we can compute the VFP and, as Fig. 1 shows, infer the intrinsic PSD of the sources.
2.2. Measuring the VFP of active galaxies
Ideally, we would need long and short, well-sampled light curves of an AGN to reliably measure variance on a large range of timescales and construct the VFP. However, this is not possible with the currently available data, especially for high-z sources. The available light curves are insufficient (because they are too sparse and/or their signal-to-noise ratio is too low) to measure the VFP of a single AGN. For this reason, we follow a different approach to construct the VFP of active galaxies, as we describe below.
We can consider samples of AGN with known BH mass, and light curves with the same duration (Tobs) and bin size (Δt) for all AGN in each sample. We can use the light curves to measure the excess variance 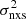 for each AGN in the sample. One way to study the VFP would be to choose objects with the same BH mass in each sample, and then plot
for each AGN in the sample. One way to study the VFP would be to choose objects with the same BH mass in each sample, and then plot 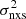 versus 1/Tobs for all of them. However, as the excess variance measurements do not follow a Gaussian distribution and their error is unknown (see Allevato et al. 2013), we cannot fit the resulting VFP and compare it with model predictions. In order to overcome this serious problem, we have to average the measured excess variances in some way.
versus 1/Tobs for all of them. However, as the excess variance measurements do not follow a Gaussian distribution and their error is unknown (see Allevato et al. 2013), we cannot fit the resulting VFP and compare it with model predictions. In order to overcome this serious problem, we have to average the measured excess variances in some way.
On the other hand, we cannot simply compute the mean excess variance of all the objects in the sample if they host BHs of different masses, because the excess variance will depend on the BH mass. However, we can take advantage of this property, and produce a 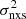 –MBH plot for all sources in each sample. The excess variance is a measure of the band variance, σ2(νT, νmax), defined by Eq. (3). This equation, together with Eq. (2), shows how
–MBH plot for all sources in each sample. The excess variance is a measure of the band variance, σ2(νT, νmax), defined by Eq. (3). This equation, together with Eq. (2), shows how 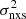 should depend on BH mass, depending on the sampled frequencies: if neither νmax nor νT are much smaller than νb,
should depend on BH mass, depending on the sampled frequencies: if neither νmax nor νT are much smaller than νb, 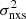 should decrease with increasing BH mass in a roughly linear way in log–log space; if instead νmax and νT ≪ νb,
should decrease with increasing BH mass in a roughly linear way in log–log space; if instead νmax and νT ≪ νb, 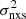 will not depend on BH mass (it will depend on νT and νmax only; see Eq. (3)) and the
will not depend on BH mass (it will depend on νT and νmax only; see Eq. (3)) and the 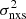 vs. MBH plot will be flat. This behaviour is illustrated by the models plotted as dotted lines, in all the figures of Sects. 3 and 4..
vs. MBH plot will be flat. This behaviour is illustrated by the models plotted as dotted lines, in all the figures of Sects. 3 and 4..
We can fit the 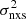 vs. MBH plot with a linear function of the form:
vs. MBH plot with a linear function of the form:
where 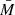 is the mean BH mass of the sample, and α(Tobs) is the variance of an AGN with a mass of
is the mean BH mass of the sample, and α(Tobs) is the variance of an AGN with a mass of 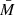 , computed using a light curve of duration Tobs. The key point here is that, as α(Tobs) is computed by fitting all the data in the
, computed using a light curve of duration Tobs. The key point here is that, as α(Tobs) is computed by fitting all the data in the 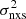 vs. MBH plot, its distribution will be much closer to the Gaussian distribution, and its error will be known (from the fitting procedure).
vs. MBH plot, its distribution will be much closer to the Gaussian distribution, and its error will be known (from the fitting procedure).
We can therefore consider AGN (with known BH mass) that have been observed by various satellites, over different timescales, Tobs, in order to compute 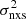 , plot
, plot 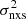 vs. MBH, and fit the data with Eq. (4). If
vs. MBH, and fit the data with Eq. (4). If 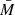 is the same for all samples, then the plot of α(Tobs) vs. 1/Tobs will be representative of the VFP plot for the AGN with a mass of
is the same for all samples, then the plot of α(Tobs) vs. 1/Tobs will be representative of the VFP plot for the AGN with a mass of 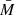 . In this way, we can also take advantage of the study of the β(Tobs) vs. 1/Tobs plot as well. As shown in Sect. 2, for a given MBH (and hence νb), the VFP shape, and therefore β(Tobs), should vary with Tobs. The way the VFP shape varies depends on the relation between νb and MBH. In other words, the study of the β(Tobs) vs. 1/Tobs plot will constrain the parameter B in Eq. (2).
. In this way, we can also take advantage of the study of the β(Tobs) vs. 1/Tobs plot as well. As shown in Sect. 2, for a given MBH (and hence νb), the VFP shape, and therefore β(Tobs), should vary with Tobs. The way the VFP shape varies depends on the relation between νb and MBH. In other words, the study of the β(Tobs) vs. 1/Tobs plot will constrain the parameter B in Eq. (2).
We plan to follow the approach we outline above in order to study the VFP of AGN, as we describe in detail in the following sections. We use data from various X-ray surveys for high-z objects and light curves from pointed observations of relatively nearby objects in order to construct the VFP of AGN, both at high and low redshift. In this way, we are able to directly compare the low and high-z objects, and investigate whether or not their PSDs are the same.
3. The variance–BH mass relation of high-redshift AGN
3.1. Black-hole mass measurements for the CDF-S sources
The first AGN sample we considered is derived from the CDF-S X-ray catalog of Luo et al. (2017), and the CDF-S variability measurements used in this work are described in P17; we refer to those works for specific details. Black hole mass measurements for CDF-S sources are primarily based on the measurements published by Suh et al. (2015). These are derived from optical/near-infrared spectroscopic measurements of Hα, Hβ, and Mg-II line widths of X-ray sources in the E-CDF-S region. Black hole masses were obtained from scaling relations of MBH with the FWHM and the luminosity of the broad-line components in the spectra. We refer to the original paper for details of the method and the assessment of the reliability of the masses. The authors claim a median uncertainty of ∼0.1 dex with an additional 0.3 dex due to calibration uncertainties in the scaling relations. This data set was integrated with Hα BH mass measurements from Schulze et al. (2018), after recalibrating the scaling relation to that adopted in Suh et al. (2015, their Eq. (1)), and with Mg-II BH mass measurements from Schramm & Silverman (2013). In total, we collected masses for 40 sources: 35 from Suh et al. (2015), 3 from Schulze et al. (2018), and 2 from Schramm & Silverman (2013). In the case of multiple BH mass measurements for the same source, we used the average value; however, our results do not change if we adopt individual BH mass measurements instead (giving priority to Hα measurements). For the subsequent analysis, we define a ‘robust sample’ of 15 sources with available MBH measurements, an average S/N > 0.8 per point, and more than 90 points in their X-ray light curves in order to have reliable 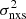 measurements. In fact, we verified that including more sources with lower quality light curves does not yield significant improvements in the final analysis and increases the uncertainties on the measured variability (see P17 for further details).
measurements. In fact, we verified that including more sources with lower quality light curves does not yield significant improvements in the final analysis and increases the uncertainties on the measured variability (see P17 for further details).
In Fig. 2, we plot the luminosity–redshift distribution of CDF-S sources with available MBH measurements and those in the robust samples. The sources in the robust sample are within the following ranges: ∼0.5–1.7 in redshift, ∼5 × 1042–2 × 1044 erg s−1 in (2–8 keV rest-frame) X-ray luminosity, and 107–109 M⊙ in BH mass, and have low absorption NH < 2 × 1022 cm−2 as expected from their type 1 spectra.
 |
Fig. 2. Luminosity–redshift distribution of CDF-S and COSMOS sources. Solid symbols represent sources with available BH mass measurements, while empty ones highlight the final samples used in this work (see text for details). |
3.2. The CDF-S 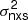 –MBH relation
–MBH relation
We created 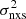 –MBH plots for the CDF-S data using the excess variance measurements of P17 and the BH mass measurements for the sources in the ‘robust sample’ discussed in the previous section. P17 calculated the excess variance of the CDF-S AGN using light curves with Tobs = 45, 128, 654, and 6005 days (observer’s frame; see the discussion in their Sect. 4.2). Here we used only their excess variance measurements from the 128 and 654 day light-curve segments; that is, the segments plotted in the two rightmost panels in Fig. 1 of P17. These are separated by almost 5 years, and the excess-variance measurements based on them should be uncorrelated. On the contrary, the
–MBH plots for the CDF-S data using the excess variance measurements of P17 and the BH mass measurements for the sources in the ‘robust sample’ discussed in the previous section. P17 calculated the excess variance of the CDF-S AGN using light curves with Tobs = 45, 128, 654, and 6005 days (observer’s frame; see the discussion in their Sect. 4.2). Here we used only their excess variance measurements from the 128 and 654 day light-curve segments; that is, the segments plotted in the two rightmost panels in Fig. 1 of P17. These are separated by almost 5 years, and the excess-variance measurements based on them should be uncorrelated. On the contrary, the 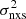 measurements from the longest and shortest timescales use light-curve parts that overlap with each other (see Fig. 1 in P17), and therefore the resulting
measurements from the longest and shortest timescales use light-curve parts that overlap with each other (see Fig. 1 in P17), and therefore the resulting 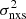 will be correlated. We note that, given that the AGN PSD is known to depend on the energy (e.g., McHardy et al. 2004), and to minimise the effect of absorption, the light curves are extracted in the 2–8 keV rest-frame band.
will be correlated. We note that, given that the AGN PSD is known to depend on the energy (e.g., McHardy et al. 2004), and to minimise the effect of absorption, the light curves are extracted in the 2–8 keV rest-frame band.
The panels in Fig. 3 show the 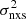 –MBH plots for the two different timescales. A weak anti-correlation between
–MBH plots for the two different timescales. A weak anti-correlation between 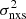 and MBH can be observed, although the scatter is considerable. This is due to several reasons. First, the error on MBH and, more importantly, on the individual
and MBH can be observed, although the scatter is considerable. This is due to several reasons. First, the error on MBH and, more importantly, on the individual 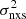 measurements (Allevato et al. 2013) will introduce considerable scatter around the intrinsic relation. In addition, although Tobs is the same for all objects, the light-curve variance depends on the duration in rest-frame, Trest, which is not the same for all objects, as their redshifts differ.
measurements (Allevato et al. 2013) will introduce considerable scatter around the intrinsic relation. In addition, although Tobs is the same for all objects, the light-curve variance depends on the duration in rest-frame, Trest, which is not the same for all objects, as their redshifts differ.
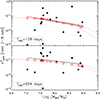 |
Fig. 3.
|
We note that, as we explained in Sect. 2, if both the duration and bin size of the light curve are much longer than the bend timescale, then the 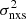 –MBH relation will be flat (unless the PSD amplitude depends on MBH). In other words, a lack of correlation between excess variance and BH mass provides important information regarding the intrinsic shape of the VFP and the PSD at low frequencies.
–MBH relation will be flat (unless the PSD amplitude depends on MBH). In other words, a lack of correlation between excess variance and BH mass provides important information regarding the intrinsic shape of the VFP and the PSD at low frequencies.
We cannot use χ2 to fit the data plotted in Fig. 3 (as well as in all figures which show 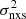 –MBH relations) and then test whether or not the model fits the data well because the excess-variance measurements are not Gaussian (and in any case their error is unknown). For that reason, we assumed that a straight line provides a good fit to the data, and we used the ordinary least-squares regression of Y on X (OLS(Y|X)) method of Isobe et al. (1990) to fit the data in Fig. 3 (in log–log space), with the linear model defined by Eq. (4), with
–MBH relations) and then test whether or not the model fits the data well because the excess-variance measurements are not Gaussian (and in any case their error is unknown). For that reason, we assumed that a straight line provides a good fit to the data, and we used the ordinary least-squares regression of Y on X (OLS(Y|X)) method of Isobe et al. (1990) to fit the data in Fig. 3 (in log–log space), with the linear model defined by Eq. (4), with 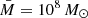 , which is similar to the average MBH in the CDF-S sample. As such, the line normalisation will be best determined at this mass. In this case, α(Tobs) corresponds to the intrinsic variance of an AGN with MBH = 108 M⊙, when measured from a light curve of duration Tobs.
, which is similar to the average MBH in the CDF-S sample. As such, the line normalisation will be best determined at this mass. In this case, α(Tobs) corresponds to the intrinsic variance of an AGN with MBH = 108 M⊙, when measured from a light curve of duration Tobs.
Best-fit results are listed in Table 1 and black solid lines in Fig. 3 show the best-fit linear models. Unsurprisingly, given the large scatter of the points around the best-fit lines, the error on the slope is large; however, the error on the normalisation is small. This is due to the fact that, given the rather flat best-fit slope, α(Tobs) is representative of the mean excess variance of all the points in each plot, which is reasonably well determined from the 15 measurements at each timescale.
Results of the linear fits to the 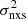 –MBH relation (in log–log space), for the different datasets used in this work.
–MBH relation (in log–log space), for the different datasets used in this work.
3.3. The COSMOS 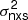 –MBH relation
–MBH relation
Lanzuisi et al. (2014) used XMM observations in the COSMOS field over a period of ∼3.5 years to study the long-term X-ray variability of a large sample of AGN. We used the data plotted in their Fig. 5 to fit the 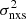 –MBH relation. To improve the accuracy of the measured variances, we selected only objects with at least three points in their light curves and with a total rest-frame duration between 100 and 560 days (see their Fig. 1). As the final sample spans a wide range in Tobs, we further divided it into two bins based on the rest-frame light-curve length: 100 days ≤ Trest < 330 days and 330 days ≤ Trest < 560 days, with a median duration
–MBH relation. To improve the accuracy of the measured variances, we selected only objects with at least three points in their light curves and with a total rest-frame duration between 100 and 560 days (see their Fig. 1). As the final sample spans a wide range in Tobs, we further divided it into two bins based on the rest-frame light-curve length: 100 days ≤ Trest < 330 days and 330 days ≤ Trest < 560 days, with a median duration 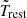 of 240 and 413 days, respectively. There are 82 AGN in both groups, with a median redshift of 1.5 and 1.0 in the first and second group, respectively (see Fig. 2). Their X-ray luminosity ranges from 6 × 1042 to 3 × 1045 erg s−1 in the 2–10 keV band. We fitted both
of 240 and 413 days, respectively. There are 82 AGN in both groups, with a median redshift of 1.5 and 1.0 in the first and second group, respectively (see Fig. 2). Their X-ray luminosity ranges from 6 × 1042 to 3 × 1045 erg s−1 in the 2–10 keV band. We fitted both 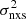 –MBH plots with the model defined by Eq. (4), and the same OLS(Y|X) routine as above (Fig. 4). The timescales and best-fit results for the COSMOS data are listed in Table 1.
–MBH plots with the model defined by Eq. (4), and the same OLS(Y|X) routine as above (Fig. 4). The timescales and best-fit results for the COSMOS data are listed in Table 1.
 |
Fig. 4.
|
4. The variance–BH mass relation of low-redshift AGN
4.1. Compilation of 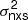 –MBH relations from literature
–MBH relations from literature
In order to sample shorter and longer timescales, which are not accessible for high-redshift AGN, we used both published and archival data. We first considered the 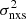 –MBH data from the CAIXA sample (Ponti et al. 2012). These authors presented the results from a systematic study of the excess variance of a large sample of AGN using XMM-Newton light curves. We used their
–MBH data from the CAIXA sample (Ponti et al. 2012). These authors presented the results from a systematic study of the excess variance of a large sample of AGN using XMM-Newton light curves. We used their 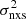 measurements (2–10 keV) from the light curves with Tobs = 80 ks. Ponti et al. (2012) measured the excess variance on three shorter time timescales as well, but the use of the same light curves when measuring
measurements (2–10 keV) from the light curves with Tobs = 80 ks. Ponti et al. (2012) measured the excess variance on three shorter time timescales as well, but the use of the same light curves when measuring 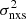 on different timescales would imply that their
on different timescales would imply that their 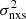 measurements would be heavily correlated (for the same source). We constructed the respective
measurements would be heavily correlated (for the same source). We constructed the respective 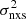 –MBH plot (see the bottom panel of Fig. 5) using the data from their ‘Rev’ AGN sample6. In doing so, we updated their BH mass estimates with the measurements listed in the AGN BH mass database (Bentz & Katz 2015). There are 11 radio-quiet AGN in this sample with excess variance measurements based on light curves of 80 ks in duration. For consistency, we fitted the CAIXA
–MBH plot (see the bottom panel of Fig. 5) using the data from their ‘Rev’ AGN sample6. In doing so, we updated their BH mass estimates with the measurements listed in the AGN BH mass database (Bentz & Katz 2015). There are 11 radio-quiet AGN in this sample with excess variance measurements based on light curves of 80 ks in duration. For consistency, we fitted the CAIXA 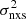 –MBH plot using Eq. (4), with
–MBH plot using Eq. (4), with 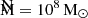 , and the same OLS(Y|X) routine that we used to fit the respective CDF-S plots. The best-fit results are listed in Table 1, and the black solid line in the lower panel of Fig. 5 shows the best-fit line.
, and the same OLS(Y|X) routine that we used to fit the respective CDF-S plots. The best-fit results are listed in Table 1, and the black solid line in the lower panel of Fig. 5 shows the best-fit line.
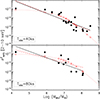 |
Fig. 5.
|
In order to get information on shorter timescales, we considered the excess-variance measurements from the TARTARUS sample of O’Neill et al. (2005). These latter authors used ASCA light curves of 40 ks in duration, and measured the excess variance of nearby X-ray-bright Seyferts (in the 2–10 keV band). We chose 16 (radio-quiet) AGN from their sample with BH mass measurements based on the reverberation mapping technique, as listed in the database of Bentz & Katz (2015). We added six sources from the CAIXA sample for which Ponti et al. (2012) provide 40 ks 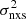 measurements (namely NGC 4151, Mrk 110, Mrk 279, Mrk 590, NGC 4593, and PG 1211+143); these are not part of the 80 ks sample and have BH mass estimates based on reverberation mapping. The respective
measurements (namely NGC 4151, Mrk 110, Mrk 279, Mrk 590, NGC 4593, and PG 1211+143); these are not part of the 80 ks sample and have BH mass estimates based on reverberation mapping. The respective 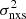 –MBH plot is shown in the top panel of Fig. 5. As above, we fitted the data using Eq. (4) and the same OLS(Y|X) routine that we used to fit the respective CDF-S plots. Best-fit results are listed in Table 1, and the solid line in the upper panel of Fig. 5 indicates the best-fit line.
–MBH plot is shown in the top panel of Fig. 5. As above, we fitted the data using Eq. (4) and the same OLS(Y|X) routine that we used to fit the respective CDF-S plots. Best-fit results are listed in Table 1, and the solid line in the upper panel of Fig. 5 indicates the best-fit line.
We also considered the 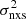 –MBH data from the RXTE light curves of Zhang (2011) in order to obtain information on longer timescales. These authors used data from the ASM on board RXTE to study the X-ray variability amplitude of 27 AGN over a period of Tobs = 14 years. Using their
–MBH data from the RXTE light curves of Zhang (2011) in order to obtain information on longer timescales. These authors used data from the ASM on board RXTE to study the X-ray variability amplitude of 27 AGN over a period of Tobs = 14 years. Using their 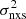 and MBH measurements, we fitted the resulting variability–MBH relation with the same model and fitting routine as above. The
and MBH measurements, we fitted the resulting variability–MBH relation with the same model and fitting routine as above. The 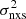 –MBH relation is shown in Fig. 6 together with the best-fit line, while the best-fit results are listed in Table 1. The AGN in the O’Neill et al. (2005), Ponti et al. (2012), and the Zhang (2011) samples are all relatively nearby, and their X-ray luminosity span the range 1040 − 1046 erg s−1.
–MBH relation is shown in Fig. 6 together with the best-fit line, while the best-fit results are listed in Table 1. The AGN in the O’Neill et al. (2005), Ponti et al. (2012), and the Zhang (2011) samples are all relatively nearby, and their X-ray luminosity span the range 1040 − 1046 erg s−1.
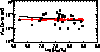 |
Fig. 6.
|
4.2. Medium-term 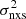 measurements from archival observations
measurements from archival observations
There is a considerable gap between the duration of the shortest CDF-S light curves (128 days) and the CAIXA light curves, which have a duration of ∼1 day. In order to measure the excess variance on intermediate timescales, we used RXTE/PCA and Swift/XRT data for relatively nearby AGN, and we computed their excess variance using light curves that are 9.45 days in duration (rest-frame). This timescale is ten times longer than the CAIXA light curves and about ten times shorter than the CDF-S. The sources are listed in Table 2, together with information on the light curves we used and the resulting excess variance.
RXTE and Swift light curves used in the present study to measure the excess variance of AGN on timescales of ∼10 days.
Columns (2) and (3) list the starting/ending time of the light curves we used (in MJD), and the (minimum) light curve bin size Δtmin in days. We did not reduce the Swift data ourselves; instead we used the light curves from Edelson et al. (2019) for all sources and from Cackett et al. (2020) for Mrk 142. The Swift light curves are in the 1.5–10 keV band, except for Mrk 142, where the published light curve is in the 0.3–10 keV band. All the other light curves were taken from the RXTE AGN Timing and Spectral Database7 (Rivers et al. 2013) and are in the 2–10 keV band. BH mass estimates (from Bentz & Katz 2015) are listed in Col. (3).
We divided the light curves into segments with a (rest-frame) duration of 9.45 days (as determined by the shortest light curve in the sample). We computed the excess variance of each segment in the usual way (i.e., using Eq. (1) in P17). We then computed the mean of the individual 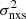 measurements for each source, which is listed in the last column of Table 2. As for all the other samples, we fitted the
measurements for each source, which is listed in the last column of Table 2. As for all the other samples, we fitted the 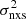 –MBH relation using Eq. (4) and the OLS(Y|X) routine. The result is shown in Fig. 7, together with the best-fit model, while the best-fit results are listed in Table 1.
–MBH relation using Eq. (4) and the OLS(Y|X) routine. The result is shown in Fig. 7, together with the best-fit model, while the best-fit results are listed in Table 1.
5. The observed VFP of AGN
As explained above, the best-fit α(T) values listed in Table 1 are representative of the variance of a 108 M⊙ AGN on the timescales that are listed in the second column of the same table. We therefore used the α(T) values listed in this table and constructed the VFP for the 108 M⊙ AGN.
Figure 8 shows the best-fit α(T) and β(T) values plotted as a function of νT (top and bottom panels, respectively). The two timescales probed by the CAIXA+TARTARUS data (filled squares) constrain the high-frequency part of the VFP, and the Swift+RXTE data (filled stars) allow us to sample intermediate timescales. The results from CDF-S (filled circles) provide information on long timescales, while the COSMOS and the RXTE points (filled diamonds and filled triangle, respectively) further improve the accuracy of the VFP at low frequencies.
 |
Fig. 8. Variance– and slope–frequency plots of our AGN sample. Upper panel: observed VFP of a 108 M⊙ AGN as a function of the rest-frame frequency νT using our measurements from Table 1 (filled symbols). The red empty symbols indicate the best-fit model values (α(Tmax) in Eq. (4)). For reference, we also show the theoretically expected trends for a 108 M⊙ BH monitored with an average Δtmin = 250 s (dashed line) and Δtmin = 300 days (dotted line), but we stress that the comparison should be made between the filled and empty points. Lower panel: measured and best-fit model slope of the |
The limits of the PSD integral in Eq. (3) depend on rest-frame Tmax and Δtmin. All AGN in the CAIXA, TARTARUS, RXTE, and Swift samples are at low-redshift and all light curves are of the same duration, which means Tobs = Trest (and Δtmin, obs = Δtmin, rest). The situation is more complicated in the CDF-S and COSMOS samples. Tobs is the same for all AGN in the CDF-S; however, Trest is not, because they do not have the same redshift. In the case of the COSMOS AGN, even Tobs differ for different sources because of the survey strategy (see Lanzuisi et al. 2014). Given the differences in Trest in these samples, in Fig. 8 we plot all quantities as a function of νT = 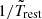 , where
, where 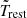 is the median light-curve duration in the AGN rest-frame (
is the median light-curve duration in the AGN rest-frame (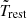 values are listed in the fourth column of Table 1). We note that this choice is for visualisation purposes only, because in the fitting procedure we properly take into account the actual rest-frame timescales sampled for each individual source (see Sect. 6).
values are listed in the fourth column of Table 1). We note that this choice is for visualisation purposes only, because in the fitting procedure we properly take into account the actual rest-frame timescales sampled for each individual source (see Sect. 6).
The overall VFP (upper panel in Fig. 8) appears to be very well described by a single function, from the lowest to the highest sampled frequencies. We can see the logarithmic rise of the variance with decreasing frequency (i.e. increasing timescale), with a slope roughly equal to −1 from the CAIXA+TARTARUS to the high-frequency CDF-S point. This implies a PSD slope of ∼ − 2 at high frequencies. The variance–frequency slope flattens at lower frequencies, indicating the presence of a bend frequency analogous to that of the PSD, νb, that is, somewhere between 1 and 20 days−1. The low- and high-frequency parts of the observed VFP are determined by the high-z and low-z AGN samples, respectively, but the important observational result is that the low-frequency VFP appears to be the continuation of the high-frequency VFP, without any hints of a normalisation mismatch between the two parts.
At low frequencies, the RXTE variance may appear to underestimate the value expected from a simple extrapolation of the CDF-S and the COSMOS measurements in the VFP, although Trest of the RXTE light curves is longer than the rest-frame duration of the longest CDF-S light curves. In principle, this could suggest that the PSD normalisation at low frequencies is not the same in the distant and local AGN. However, Δtmin in the RXTE light curves is also significantly larger than the (rest-frame) minimum timescale in all other light curves. Indeed, it is almost certainly much longer than the PSD bend frequency of a 108 M⊙ AGN. This implies that we are missing a significant part of the intrinsic variance in the RXTE light curves, hence the smaller α(T) value.
The bottom panel of Fig. 8 shows how the slope of the 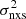 –MBH relation varies with frequency. Similar to the case for the VFP plot, the best-fit slopes at high frequencies appear to connect smoothly, without any normalisation discontinuities, with the best-fit β(T) values at lower frequencies. The slope of the
–MBH relation varies with frequency. Similar to the case for the VFP plot, the best-fit slopes at high frequencies appear to connect smoothly, without any normalisation discontinuities, with the best-fit β(T) values at lower frequencies. The slope of the 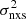 –MBH plots at low frequencies (long timescales) approaches zero, that is, the bending frequency of the 108 M⊙ AGN is probably higher than both the mean bin size and the duration of the available light curves in the RXTE sample and, to some extent, also those in the CDF-S and the COSMOS sample.
–MBH plots at low frequencies (long timescales) approaches zero, that is, the bending frequency of the 108 M⊙ AGN is probably higher than both the mean bin size and the duration of the available light curves in the RXTE sample and, to some extent, also those in the CDF-S and the COSMOS sample.
6. Model fitting procedure and best-fit results
We considered a grid of A, B, and s values, and for each (A, B, s) combination we used Eqs. (2) and (3) to compute the variance σ2 for the AGN in the CDF-S, COSMOS, CAIXA+TARTARUS, RXTE, and Swift+RXTE samples. To this end, we derived νT, νmax, and νb using the MBH and z values of each source, and the timescales Tobs and Δtmin, obs in Table 1 (we assumed z = 0 for the AGN in the CAIXA+TARTARUS, RXTE, and the Swift+RXTE samples, which only contain relatively nearby AGN).
In order to properly fit the data, we must take into account the biases due to a sparse and/or irregular sampling of the light curves. To this end, we used Eq. (11) in Allevato et al. (2013) to compute the bias affecting the measured 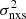 and we include the same factor in the model variance σ2. The bias correction depends on the PSD slope itself, and so we used the ‘average’ slope (from Eq. (1)) over the range of sampled rest-frame timescales for each source. Furthermore, we assumed a sparse sampling for the COSMOS sources, and a continuous sampling pattern for the remaining samples.
and we include the same factor in the model variance σ2. The bias correction depends on the PSD slope itself, and so we used the ‘average’ slope (from Eq. (1)) over the range of sampled rest-frame timescales for each source. Furthermore, we assumed a sparse sampling for the COSMOS sources, and a continuous sampling pattern for the remaining samples.
For each model-parameter combination, we therefore ended up with a pair of model (σ2, MBH) values for each source and timescale in the CDF-S, COSMOS, CAIXA+TARTARUS, and Swift+RXTE samples. If the observed 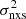 measurements were Gaussian variables with known errors, then we would be able to use χ2 statistics to fit all the observed
measurements were Gaussian variables with known errors, then we would be able to use χ2 statistics to fit all the observed 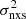 vs. MBH data plotted in Figs. 3–7 with the model (σ2, MBH) curves. However, this is not the case, and so we cannot directly fit the model to the observed
vs. MBH data plotted in Figs. 3–7 with the model (σ2, MBH) curves. However, this is not the case, and so we cannot directly fit the model to the observed 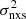 –MBH plots. Instead, we used a different approach to fit the model to the data.
–MBH plots. Instead, we used a different approach to fit the model to the data.
For each parameter combination, we fit the resulting σ2–MBH points with Eq. (4), with 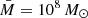 , using the same OLS(Y|X) routine that we used to fit the data. In the end, each set of model parameters (A, B, s) would result in two best-fit values, αmod(A, B, s, Tobs) and βmod(A, B, s, Tobs), for each σ2–MBH relation.
, using the same OLS(Y|X) routine that we used to fit the data. In the end, each set of model parameters (A, B, s) would result in two best-fit values, αmod(A, B, s, Tobs) and βmod(A, B, s, Tobs), for each σ2–MBH relation.
The overall model fit: Based on the discussion above, each set of model parameters (A, B, s) would result in eight αmod(A, s, B, Tobs) and βmod(A, s, B, Tobs) values, that is, one for each of the observed 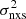 –MBH relations plotted in Figs. 3–7. To get the best-fit model, we minimised the χ2, which is defined as follows:
–MBH relations plotted in Figs. 3–7. To get the best-fit model, we minimised the χ2, which is defined as follows:
where δ[α(Tobs, i)] and δ[β(Tobs, i)] are the errors on the best-fit normalisation and slope values, α(Tobs) and β(Tobs), listed in Table 1. Defined in this way, the best-fit model is the one that minimises the differences between the model and the observed VFP (i.e., the points plotted in the upper panel of Fig. 8), as well as the model and the observed slope of the 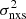 –MBH relations (bottom panel of Fig. 8).
–MBH relations (bottom panel of Fig. 8).
The best-fit results are: 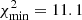 for μ = 13 degrees of freedom, corresponding to P(< χ2, μ) = 0.6, at
for μ = 13 degrees of freedom, corresponding to P(< χ2, μ) = 0.6, at 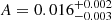 Hz−1,
Hz−1, 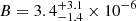 Hz, and
Hz, and 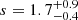 . Here, the errors are the 90% uncertainties for two interesting parameters. The errors of the best-fit parameter values are both asymmetric and correlated as shown in Fig. 9. Open diamonds in Figs. 3–7 show the best-fit model (σ2, MBH) predictions for each source in these plots. The dashed red lines show the best linear fit to the model points. In some cases (e.g., Figs. 5 and 7), the model clearly predicts a curved
. Here, the errors are the 90% uncertainties for two interesting parameters. The errors of the best-fit parameter values are both asymmetric and correlated as shown in Fig. 9. Open diamonds in Figs. 3–7 show the best-fit model (σ2, MBH) predictions for each source in these plots. The dashed red lines show the best linear fit to the model points. In some cases (e.g., Figs. 5 and 7), the model clearly predicts a curved 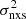 –MBH relation (dotted curve), which may indeed be closer to the observed one. However, even in these cases, a straight line can provide a reasonably good fit to the data (and the model predictions). As we fit a straight line to both the observed and the model relations, we can compare the best-fit line parameters, and search for the values that provide the best agreement between the data and the model predictions. The open symbols in Fig. 8 show the normalisation and slope of the best-fit lines to the model
–MBH relation (dotted curve), which may indeed be closer to the observed one. However, even in these cases, a straight line can provide a reasonably good fit to the data (and the model predictions). As we fit a straight line to both the observed and the model relations, we can compare the best-fit line parameters, and search for the values that provide the best agreement between the data and the model predictions. The open symbols in Fig. 8 show the normalisation and slope of the best-fit lines to the model 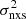 –MBH relations that are closest to the data.
–MBH relations that are closest to the data.
 |
Fig. 9. Best-fit values (crosses) and 68%, 90%, and 99% uncertainty contours for each combination of two of the fitted interesting parameters A (i.e., the PSD normalisation), B (i.e., νb for a 108 M⊙ BH) and s (the high-frequency PSD slope). |
Strictly speaking, the VFP plotted in the upper panel of Fig. 8 is representative of the average VFP of an AGN with a mass of 108 M⊙. The best-fit parameters also refer to such an object. For example, if we had normalised the 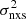 vs. MBH relation at a different MBH, then the expected VFP would be different (see the black and red lines in Fig. 1) and the best-fit bending frequency would be different if νb depended on BH mass. However, the fact that we consider the VFP of an AGN at 108 M⊙ is merely a ‘technicality’ as this mass is close to the mean BH mass of the sources in the samples we considered. In reality, the best-fit αmod(A, B, s, Tobs) and βmod(A, B, s, Tobs) model parameters are computed by fitting a straight line to all the model points (i.e., open red points in Figs. 3–7). Therefore, the best-fit model VFP plotted in Fig. 8 holds information about the PSD of all AGN in each sample, and the same would be true if we had normalised the best-fit lines to another BH mass.
vs. MBH relation at a different MBH, then the expected VFP would be different (see the black and red lines in Fig. 1) and the best-fit bending frequency would be different if νb depended on BH mass. However, the fact that we consider the VFP of an AGN at 108 M⊙ is merely a ‘technicality’ as this mass is close to the mean BH mass of the sources in the samples we considered. In reality, the best-fit αmod(A, B, s, Tobs) and βmod(A, B, s, Tobs) model parameters are computed by fitting a straight line to all the model points (i.e., open red points in Figs. 3–7). Therefore, the best-fit model VFP plotted in Fig. 8 holds information about the PSD of all AGN in each sample, and the same would be true if we had normalised the best-fit lines to another BH mass.
We find it impressive that a single PSD model can fit the observed VFP so well, given that we constructed 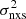 –MBH plots using light curves of 160 AGN, both nearby and distant, observed with different satellites, and with different sampling and light curve duration. This result strongly suggests that, on average, the X-ray PSD over five orders of magnitude in frequency (i.e., from timescales of ∼40 ks up to ∼10 − 15 years) is described by the same form for all AGN at z ≤ 2 − 3. If there were significant differences in amplitude, bend frequency, or high-frequency slope between the high-z and low-z PSDs, then the low- and high-frequency parts of the VFP plotted in the top panel of Fig. 8, which are determined by the high-z and low-z AGN, respectively, would differ significantly (see e.g., the various curves in Fig. 1).
–MBH plots using light curves of 160 AGN, both nearby and distant, observed with different satellites, and with different sampling and light curve duration. This result strongly suggests that, on average, the X-ray PSD over five orders of magnitude in frequency (i.e., from timescales of ∼40 ks up to ∼10 − 15 years) is described by the same form for all AGN at z ≤ 2 − 3. If there were significant differences in amplitude, bend frequency, or high-frequency slope between the high-z and low-z PSDs, then the low- and high-frequency parts of the VFP plotted in the top panel of Fig. 8, which are determined by the high-z and low-z AGN, respectively, would differ significantly (see e.g., the various curves in Fig. 1).
7. Summary and discussion
We used excess-variance measurements computed using light curves of short (CAIXA+TARTARUS, Ponti et al. 2012; O’Neill et al. 2005), intermediate (Swift+RXTE, this work), and long (RXTE, Zhang 2011) duration, as well as light curves from the COSMOS and the CDF-S surveys (Lanzuisi et al. 2014, P17), to construct 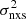 –MBH plots on various timescales. We fitted them with a simple linear model (in the log–log space), and studied the resulting VFP, together with the slope of the variance–BH mass relations as a function of frequency. Our main result is that the hypothesis of a common X-ray PSD form in all AGN, which remains the same irrespective of redshift or luminosity, is fully consistent with the observed VFP.
–MBH plots on various timescales. We fitted them with a simple linear model (in the log–log space), and studied the resulting VFP, together with the slope of the variance–BH mass relations as a function of frequency. Our main result is that the hypothesis of a common X-ray PSD form in all AGN, which remains the same irrespective of redshift or luminosity, is fully consistent with the observed VFP.
The variance versus timescale relation of the CDF-S sources was used in P17 as well (see their Fig. 7) to show that the excess-variance measurements were indeed consistent with the assumption of a bending power-law PSD, and in Zheng et al. (2017) to study the low-frequency PSD slope. In the present work, we consider a much larger data set to create a more detailed VFP, and we use it together with the slope of the variance–BH mass plots to constrain the X-ray PSD.
Indeed, detailed PSDs have only been determined (and fitted with models) for nearby AGN. We used excess-variance measurements from over 100 AGN with a wide range of BH mass (∼106 − 109 M⊙) and X-ray luminosity (∼1040 − 1046 erg s−1) to determine the VFP over timescales from a few hours up to 5–14 years. Based on the fact that the VFP and the PSD hold the same information, we were able to determine the average PSD of the AGN in our sample. To the best of our knowledge, this is the first time that the average X-ray PSD of a representative sample of (X-ray selected) AGN has been accurately determined up to a redshift of ∼3.
The fact that the observed VFP is well fitted by a single function is remarkable. We measured the average variance, α(T), using light curves of different objects and obtained from different instruments, at different times, and over entirely different timescales. Our results therefore strongly suggest that the shape of the average PSD (defined by Eq. (1)) is the same in all AGN, irrespective of luminosity and/or redshift, and is consistent with almost all relatively nearby AGN. We note that the PSD shape of least one nearby AGN, namely Ark 564, is different. It has a power-law shape and shows two breaks, at high and low frequency, respectively (Papadakis et al. 2002; McHardy et al. 2007). This shape implies that Ark 564 may be in a state equivalent to the so-called ‘high/intermediate’ state in BH X-ray binaries. Our results suggest that such a state should be rare among AGN.
We assumed a fixed value for the low-frequency slope. If we consider a more general extension of Eq. (1), that is, ![$ \mathrm{PSD}(\nu)=A\nu^{-l}\left [ 1+\left(\frac{\nu}{\nu_{\mathrm{b}}}\right)^{(s+l)} \right ]^{-1} $](/articles/aa/full_html/2023/05/aa45291-22/aa45291-22-eq97.gif) , this means fixing l = −1. On the other hand, Zheng et al. (2017) suggested that a steeper low-frequency slope l ≃ −1.2 is more appropriate to fit the CDF-S data. In order to test this possibility, we repeated all our fits using the more general expression above; we find that our data are better fit by the canonical slope of −1, and while we cannot rule out a marginally steeper low-frequency slope, a value as steep as −1.2 is excluded at the 99% significance level.
, this means fixing l = −1. On the other hand, Zheng et al. (2017) suggested that a steeper low-frequency slope l ≃ −1.2 is more appropriate to fit the CDF-S data. In order to test this possibility, we repeated all our fits using the more general expression above; we find that our data are better fit by the canonical slope of −1, and while we cannot rule out a marginally steeper low-frequency slope, a value as steep as −1.2 is excluded at the 99% significance level.
Our results are not meant to imply that all AGN should have the same high-frequency slope and PSD amplitude. Most likely, both the PSD amplitude and high-frequency slope will be distributed over a range of values, and the best-fit values we report should be indicative of the means of these distributions. For example, González-Martín & Vaughan (2012) studied the X-ray PSD in X-ray bright, local AGN in detail and their results do show a rather broad range of high-frequency slopes (between 1.8 and 4.6; see their Table 4). Similarly, their best-fit PSD amplitude values (also listed in their Table 4) span a broad range, from 0.001 to 0.04. What is interesting is that the means of these distributions are the same as our results.
Indeed, the best-fit high-frequency PSD slope from the modelling of the mean VFP is 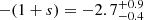 (90% confidence limits). Although the PSD slope may depend on the energy band (e.g., McHardy et al. 2004), we point out that in our case we used the hard X-ray band (i.e., E ≳ 2 keV) whenever possible and even in the COSMOS sample the large median redshift of the sources implies that we tend to sample energies ≳1 keV. The median of the high-frequency PSD slopes reported by González-Martín & Vaughan (2012) in their Table 4 is −2.57 for sources where a bend frequency has been detected8. This is consistent with our results.
(90% confidence limits). Although the PSD slope may depend on the energy band (e.g., McHardy et al. 2004), we point out that in our case we used the hard X-ray band (i.e., E ≳ 2 keV) whenever possible and even in the COSMOS sample the large median redshift of the sources implies that we tend to sample energies ≳1 keV. The median of the high-frequency PSD slopes reported by González-Martín & Vaughan (2012) in their Table 4 is −2.57 for sources where a bend frequency has been detected8. This is consistent with our results.
In addition, our best-fit PSD normalisation of 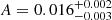 Hz−1 is also consistent with the mean PSD normalisation as determined by the PSD modeling of local AGN. According to Eq. (1), the PSD amplitude at the bend frequency, in terms of νb × PSD(νb), is equal to A/2. Based on our best-fit results, this is 0.008 ± 0.001, which is fully consistent with the mean PSD amplitude of ∼0.009 reported by González-Martín & Vaughan (2012)9.
Hz−1 is also consistent with the mean PSD normalisation as determined by the PSD modeling of local AGN. According to Eq. (1), the PSD amplitude at the bend frequency, in terms of νb × PSD(νb), is equal to A/2. Based on our best-fit results, this is 0.008 ± 0.001, which is fully consistent with the mean PSD amplitude of ∼0.009 reported by González-Martín & Vaughan (2012)9.
The broad-band VFP plotted in the upper panel of Fig. 8 shows a clear flattening below ∼10−6 Hz, which implies (from our best-fit result) a low-frequency bend in the PSD at 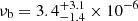 Hz. This corresponds to a bend timescale of (1.8 − 5.8) days (90% confidence). According to González-Martín & Vaughan (2012), log(Tb)≃log(MBH)−1.7, where Tb is in days and MBH is the BH mass in units of 106 M⊙10. For a 108 M⊙ AGN, this relation predicts Tb = 2 days, which is consistent with our results. On the other hand, according to McHardy et al. (2006), the bend timescale should also depend on the source luminosity. These authors find that log(Tb) = 2 × log(MBH)−log(Lbol)−2.33, where Tb is in days, MBH is the BH mass in units of 106 M⊙, and Lbol is the bolometric luminosity in units of 1044 erg s−111. We assumed that the constants A and B in the McHardy et al. (2006) equation are equal to 2 and 1, respectively, which means that the bend timescale is proportional to the BH mass and inversely proportional to accretion rate (in units of the Eddington limit). For Tb = 3.5 days, as derived in this work, and MBH = 108 M⊙, then Lbol = 1.3 × 1045 erg s−1, which is 10% of LEdd. The VFP analysis therefore allows for a dependence of the PSD bend frequency on the AGN accretion rate as well.
Hz. This corresponds to a bend timescale of (1.8 − 5.8) days (90% confidence). According to González-Martín & Vaughan (2012), log(Tb)≃log(MBH)−1.7, where Tb is in days and MBH is the BH mass in units of 106 M⊙10. For a 108 M⊙ AGN, this relation predicts Tb = 2 days, which is consistent with our results. On the other hand, according to McHardy et al. (2006), the bend timescale should also depend on the source luminosity. These authors find that log(Tb) = 2 × log(MBH)−log(Lbol)−2.33, where Tb is in days, MBH is the BH mass in units of 106 M⊙, and Lbol is the bolometric luminosity in units of 1044 erg s−111. We assumed that the constants A and B in the McHardy et al. (2006) equation are equal to 2 and 1, respectively, which means that the bend timescale is proportional to the BH mass and inversely proportional to accretion rate (in units of the Eddington limit). For Tb = 3.5 days, as derived in this work, and MBH = 108 M⊙, then Lbol = 1.3 × 1045 erg s−1, which is 10% of LEdd. The VFP analysis therefore allows for a dependence of the PSD bend frequency on the AGN accretion rate as well.
We note that our results suggest that the average bend frequency and PSD amplitude are the same for the high- and low-z sources. This implies that either these two PSD parameters do not depend on accretion rate, or the accretion rate is the same for both the nearby and the distant AGN in our sample. P17 found that the average accretion rate of the CDF-S sources is ∼0.05 − 0.1 of the Eddington limit. Regarding the low-z objects, if we use the data listed in Table 1 of Zhang (2011) for the RXTE sample (which are representative of all our low-z AGN) we find an average accretion rate of ∼0.06 of the Eddington limit, which is comparable with the accretion rate of the CDF-S sources. We will need to study the VFP of AGN with significantly different accretion rates in order to investigate the dependence of the PSD amplitude and bending frequency on the accretion rate.
Our results should be useful in future variability studies of large AGN samples using X-ray light curves from the eROSITA all-sky survey for example, and future surveys that may be conducted with the eXTP (in’t Zand et al. 2019), Einstein probe Yuan et al. (2018, 2022), and Star-X (Saha et al. 2017) proposed missions, as well as Athena (Nandra et al. 2013), Lynx (Gaskin et al. 2018), or AXIS (Mushotzky 2018), provided that deep surveys are properly planned to probe the time domain as well (see e.g., Paolillo et al. 2012). In previous studies, such as P17, it was assumed that the shape of the X-ray PSD is the same in both nearby and distant luminous AGN. We show in this work that this is indeed the case. Therefore, our result can be useful to any study that involves the modelling of the ensemble X-ray variability of AGN in order to, for example, use them as cosmological probes (La Franca et al. 2014; Lusso et al. 2019, 2020; Demianski et al. 2020), or to constrain the AGN demographics through their ensemble X-ray variability properties (Sartori et al. 2019; Georgakakis et al. 2021). From a more physical point of view, a common X-ray PSD shape implies that the same variability mechanism operates in all luminous AGN, and that the mechanism does not evolve with time until up to at least z ∼ 2 − 3. This result is also in agreement with the lack of evolution observed in the spectral features of AGN, such as the UV vs. LX ratio αox (e.g., Lusso et al. 2010, 2020) or the X-ray spectral slope Γ (e.g., Young et al. 2009), and indicates that it is the underlying X-ray emission mechanism in general that does not evolve with time. Although we do not have a well-developed physical model for the X-ray emission or variability in AGN, the present findings provide further observational constraints for any future attempts.
Although the excess variance is a biased estimate of the PSD integral, in the case of red-noise PSDs and sparsely sampled light curves, it is possible to correct 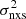 for this effect, as discussed in Sect. 5 of Allevato et al. (2013).
for this effect, as discussed in Sect. 5 of Allevato et al. (2013).
We note that, for simplicity, here we use σ2 instead of 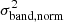 as in Allevato et al. (2013).
as in Allevato et al. (2013).
In case of multiple entries, we adopted the best-fit results of González-Martín & Vaughan (2012), except from Ark 564 and PKS0558-504. We adopted the results of McHardy et al. (2007) and Papadakis et al. (2010) for these sources, because these authors used more data sets and on various timescales, to compute the PSDs.
We note that the amplitude reported in González-Martín & Vaughan (2012) is 0.009 ± 0.011 where the uncertainty represents the standard deviation of their sample; using the proper error on the mean their measurements yield 0.009 ± 0.003 which is still consistent with our result. Even removing from their sample the three NLSy1 with very high normalisation, they would obtain 0.0044 ± 0.0013, consistent within 2σ with our value.
Acknowledgments
I.E.P. thanks the University of Naples Federico II for the financial support provided by the International Mobility program. M.P. acknowledges financial support received through the agreement ASI-INAF n.2017-14-H.O. W.N.B. acknowledges support from Chandra X-ray Center grant GO9-20099X and the V.M. Willaman Endowment. F.E.B. acknowledges support from ANID-Chile BASAL AFB-170002 and FB210003, FONDECYT Regular 1200495 and 1190818, and Millennium Science Initiative Program – ICN12_009. Y.Q.X. acknowledges support from NSFC grants (12025303 and 11890693), the K.C. Wong Education Foundation, and the National Key R&D Program of China No. 2022YFF0503401. B.L. acknowledges financial support from the National Natural Science Foundation of China grant 11991053. D.D. acknowledges support from PON R&I 2021, CUP E65F21002880003. This work has made use of lightcurves provided by the University of California, San Diego Center for Astrophysics and Space Sciences, X-ray Group (R.E. Rothschild, A.G. Markowitz, E.S. Rivers, and B.A. McKim), obtained at https://cass.ucsd.edu/~rxteagn/.
References
- Allevato, V., Paolillo, M., Papadakis, I., & Pinto, C. 2013, ApJ, 771, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., & Katz, S. 2015, PASP, 127, 67 [Google Scholar]
- Cackett, E. M., Gelbord, J., Li, Y.-R., et al. 2020, ApJ, 896, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Demianski, M., Lusso, E., Paolillo, M., Piedipalumbo, E., & Risaliti, G. 2020, Front. Astron. Space Sci., 7, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Ding, N., Luo, B., Brandt, W. N., et al. 2018, ApJ, 868, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Gelbord, J., Cackett, E., et al. 2019, ApJ, 870, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskin, J. A., Dominguez, A., & Gelmis, K. 2018, SPIE Conf. Ser., 10699, 106990N [Google Scholar]
- Georgakakis, A., Papadakis, I., & Paolillo, M. 2021, MNRAS, 508, 3463 [NASA ADS] [CrossRef] [Google Scholar]
- González-Martín, O., & Vaughan, S. 2012, A&A, 544, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, A. R., McHardy, I. M., & Lehto, H. J. 1993, MNRAS, 265, 664 [NASA ADS] [Google Scholar]
- in’t Zand, J. J. M., Bozzo, E., Qu, J., et al. 2019, Sci. China Phys. Mech. Astron., 62, 29506 [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [Google Scholar]
- La Franca, F., Bianchi, S., Ponti, G., Branchini, E., & Matt, G. 2014, ApJ, 787, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzuisi, G., Ponti, G., Salvato, M., et al. 2014, ApJ, 781, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A., & Papadakis, I. 1993, ApJ, 414, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Brandt, W. N., Xue, Y. Q., et al. 2017, ApJS, 228, 2 [Google Scholar]
- Lusso, E., Comastri, A., Vignali, C., et al. 2010, A&A, 512, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lusso, E., Piedipalumbo, E., Risaliti, G., et al. 2019, A&A, 628, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lusso, E., Risaliti, G., Nardini, E., et al. 2020, A&A, 642, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markowitz, A., Edelson, R., Vaughan, S., et al. 2003, ApJ, 593, 96 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Papadakis, I. E., Uttley, P., Page, M. J., & Mason, K. O. 2004, MNRAS, 348, 783 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Koerding, E., Knigge, C., Uttley, P., & Fender, R. P. 2006, Nature, 444, 730 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Arévalo, P., Uttley, P., et al. 2007, MNRAS, 382, 985 [Google Scholar]
- Middei, R., Vagnetti, F., Bianchi, S., et al. 2017, A&A, 599, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mushotzky, R. 2018, SPIE Conf. Ser., 10699, 1069929 [Google Scholar]
- Nandra, K., Barret, D., Barcons, X., et al. 2013, ArXiv e-prints [arXiv:1306.2307] [Google Scholar]
- O’Neill, P. M., Nandra, K., Papadakis, I. E., & Turner, T. J. 2005, MNRAS, 358, 1405 [CrossRef] [Google Scholar]
- Paolillo, M., Schreier, E. J., Giacconi, R., Koekemoer, A. M., & Grogin, N. A. 2004, ApJ, 611, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Paolillo, M., Pinto, C., Allevato, V., et al. 2012, Mem. Soc. Astron. Ital., 19, 264 [Google Scholar]
- Paolillo, M., Papadakis, I., Brandt, W. N., et al. 2017, MNRAS, 471, 4398 [Google Scholar]
- Papadakis, I. E. 2004, MNRAS, 348, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Papadakis, I. E., Brinkmann, W., Negoro, H., & Gliozzi, M. 2002, A&A, 382, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papadakis, I. E., Chatzopoulos, E., Athanasiadis, D., Markowitz, A., & Georgantopoulos, I. 2008, A&A, 487, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papadakis, I. E., Brinkmann, W., Gliozzi, M., & Raeth, C. 2010, A&A, 518, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponti, G., Papadakis, I., Bianchi, S., et al. 2012, A&A, 542, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivers, E., Markowitz, A., & Rothschild, R. 2013, ApJ, 772, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, T. T., Zhang, W. W., & McClelland, R. S. 2017, SPIE Conf. Ser., 10399, 103990I [NASA ADS] [Google Scholar]
- Sartori, L. F., Trakhtenbrot, B., Schawinski, K., et al. 2019, ApJ, 883, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Schramm, M., & Silverman, J. D. 2013, ApJ, 767, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, A., Silverman, J. D., Kashino, D., et al. 2018, ApJS, 239, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W. N., Paolillo, M., et al. 2014, ApJ, 783, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Suh, H., Hasinger, G., Steinhardt, C., Silverman, J. D., & Schramm, M. 2015, ApJ, 815, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, M. O., Shemmer, O., Brandt, W. N., et al. 2021, ApJ, 923, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., McHardy, I. M., & Papadakis, I. E. 2002, MNRAS, 332, 231 [Google Scholar]
- Yang, G., Brandt, W. N., Luo, B., et al. 2016, ApJ, 831, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2009, ApJS, 183, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M., Brandt, W. N., Xue, Y. Q., et al. 2012, ApJ, 748, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Zhang, C., Ling, Z., et al. 2018, SPIE Conf. Ser., 10699, 1069925 [Google Scholar]
- Yuan, W., Zhang, C., Chen, Y., & Ling, Z. 2022, The Einstein Probe Mission, in Handbook of X-ray and Gamma-ray Astrophysics, eds. C. Bambi, & A. Santangelo (Singapore: Springer) [Google Scholar]
- Zhang, Y.-H. 2011, ApJ, 726, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, X. C., Xue, Y. Q., Brandt, W. N., et al. 2017, ApJ, 849, 127 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Results of the linear fits to the 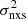 –MBH relation (in log–log space), for the different datasets used in this work.
–MBH relation (in log–log space), for the different datasets used in this work.
RXTE and Swift light curves used in the present study to measure the excess variance of AGN on timescales of ∼10 days.
All Figures
 |
Fig. 1. PSD and VFP (upper and lower panels, respectively) of an AGN with a BH mass of 108 M⊙. The PSD model parameters are: A = 0.02 Hz−1, s = 1, and νb = 3 ⋅ 10−6 Hz (black solid lines). Black dashed lines indicate the PSD and VFP when we increase the PSD amplitude by a factor of 2. Red lines show the PSD and VFP when we increase the bend frequency (by a factor of 10), while the blue lines show the changes when we increase the high-frequency PSD slope from −2 to −3 (all the other parameters in this case are like those of the red lines). For the computation of the variance, we assumed νmax = (1/250 s). |
| In the text | |
 |
Fig. 2. Luminosity–redshift distribution of CDF-S and COSMOS sources. Solid symbols represent sources with available BH mass measurements, while empty ones highlight the final samples used in this work (see text for details). |
| In the text | |
 |
Fig. 3.
|
| In the text | |
 |
Fig. 4.
|
| In the text | |
 |
Fig. 5.
|
| In the text | |
 |
Fig. 6.
|
| In the text | |
 |
Fig. 7.
|
| In the text | |
 |
Fig. 8. Variance– and slope–frequency plots of our AGN sample. Upper panel: observed VFP of a 108 M⊙ AGN as a function of the rest-frame frequency νT using our measurements from Table 1 (filled symbols). The red empty symbols indicate the best-fit model values (α(Tmax) in Eq. (4)). For reference, we also show the theoretically expected trends for a 108 M⊙ BH monitored with an average Δtmin = 250 s (dashed line) and Δtmin = 300 days (dotted line), but we stress that the comparison should be made between the filled and empty points. Lower panel: measured and best-fit model slope of the |
| In the text | |
 |
Fig. 9. Best-fit values (crosses) and 68%, 90%, and 99% uncertainty contours for each combination of two of the fitted interesting parameters A (i.e., the PSD normalisation), B (i.e., νb for a 108 M⊙ BH) and s (the high-frequency PSD slope). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \mathrm{PSD}(\nu )=A\nu ^{-1}\left[ 1+\left(\frac{\nu }{\nu _{\rm b}}\right)^{s} \right] ^{-1}, \end{aligned} $$](/articles/aa/full_html/2023/05/aa45291-22/aa45291-22-eq13.gif)
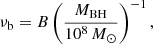
![$$ \begin{aligned} \sigma ^2 (\nu _T,\nu _{\rm max})&= \int ^{\nu _{\rm max}}_{\nu _{\rm T}}\mathrm{PSD}(\nu )\ \mathrm{d}\nu \nonumber \\&= A\left[ \ln \left(\frac{\nu _{\rm max}}{\nu _{\rm T}}\right)-\frac{1}{s}\ln \left(\frac{\nu _{\rm b}^s+\nu _{\rm max}^s}{\nu _{\rm b}^s+\nu _{T}^s}\right) \right], \end{aligned} $$](/articles/aa/full_html/2023/05/aa45291-22/aa45291-22-eq15.gif)
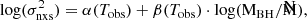
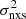
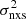
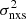
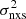
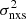
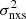
![$$ \begin{aligned} \chi ^2&=\sum _{i=1}^N \ \Biggl \{\left[\frac{\alpha _{\rm mod}(A,B,s, T_{\rm obs, i}) - \alpha (T_{\rm obs,i})}{\delta [\alpha (T_{\rm obs,i})]}\right]^2 \nonumber \\&+ \left[\frac{\beta _{\rm mod}(A,B,s, T_{\rm obs, i}) - \beta (T_{\rm obs,i})}{\delta [\beta (T_{\rm obs,i})]}\right]^2\Biggr \}, \end{aligned} $$](/articles/aa/full_html/2023/05/aa45291-22/aa45291-22-eq86.gif)