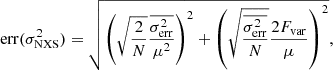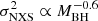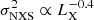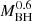| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A145 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202450777 | |
| Published online | 04 October 2024 | |
Investigating the interplay between the coronal properties and the hard X-ray variability of active galactic nuclei with NuSTAR
1
INAF - Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monte Porzio Catone (Roma), Italy
2
INAF - Istituto di Astrofisica e Planetologia Spaziali, Via del Fosso del Cavaliere 100, 00133 Roma, Italy
3
Dipartimento di Fisica, Università degli Studi di Roma “Tor Vergata”, via della Ricerca Scientifica 1, 00133 Roma, Italy
4
Dipartimento di Matematica e Fisica, Università degli Studi Roma Tre, Via della Vasca Navale 84, 00146 Roma, Italy
5
Instituto de Estudios Astrofísicos, Facultad de Ingeniería y Ciencias, Universidad Diego Portales, Avenida Ejercito Libertador 441, Santiago, Chile
6
Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing 100871, PR China
7
INAF - Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
8
CNRS, IPAG, Université Grenoble Alpes, 38000 Grenoble, France
9
Space Science Data Center, Agenzia Spaziale Italiana, Via del Politecnico snc, 00133 Roma, Italy
10
INAF - Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti, 93/3, 40129 Bologna, Italy
11
ASI - Agenzia Spaziale Italiana, Via del Politecnico snc, 00133 Roma, Italy
Received:
18
May
2024
Accepted:
9
July
2024
Active galactic nuclei (AGN) are extremely variable in the X-ray band down to very short timescales. However, the driver behind the X-ray variability is still poorly understood. Previous results suggest that the hot corona responsible for the primary Comptonized emission observed in AGN is expected to play an important role in driving the X-ray variability. In this work, we investigate the connection between the X-ray amplitude variability and the coronal physical parameters; namely, the temperature (kT) and optical depth (τ). We present the spectral and timing analysis of 46 NuSTAR observations corresponding to a sample of 20 AGN. For each source, we derived the coronal temperature and optical depth through X-ray spectroscopy and computed the normalized excess variance for different energy bands on a timescale of 10 ks. We find a strong inverse correlation between kT and τ, with correlation coefficient of r < −0.9 and negligible null probability. No clear dependence was found among the temperature and physical properties, such as the black hole mass or the Eddington ratio. We also see that the observed X-ray variability is not correlated with either the coronal temperature or optical depth under the thermal equilibrium assumption, whereas it is anticorrelated with the black hole mass. These results can be interpreted through a scenario where the observed X-ray variability could primarily be driven by variations in the coronal physical properties on a timescale of less than 10 ks; whereas we assume thermal equilibrium on such timescales in this work, given the capability of the currently available hard X-ray telescopes. Alternatively, it is also possible that the X-ray variability is mostly driven by the absolute size of the corona, which depends on the supermassive black hole mass, rather than resulting from any of its physical properties.
Key words: black hole physics / galaxies: active / galaxies: Seyfert / X-rays: galaxies
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Active galactic nuclei (AGN) are bright extragalactic sources powered by the accretion of matter onto a supermassive black hole (SMBH). In brief, AGN emit light at all wavelengths and they are characterized by a significantly loud X-ray emission (e.g., Padovani et al. 2017). The X-ray emission of AGN is produced by inverse Compton scattering of UV seed photons, emitted by the accretion disk, off a hot relativistic electron plasma known as the corona (e.g., Haardt & Maraschi 1991, 1993). The typical shape of the X-ray spectrum of an AGN is that of a power law, characterized by a photon index Γ, up to a characteristic energy, Ec, known as the cut-off energy where the power law breaks. The relation between the cut-off energy and the temperature can be approximated with Ec ∼ 2 − 3 kT (e.g., Petrucci et al. 2001), depending on the geometry of the corona and the optical depth, while the photon index is dependent on both the coronal temperature and the optical depth. However, more complex relations with both the temperature and optical depth are needed when considering broader ranges of temperatures and optical depths (Middei et al. 2019).
Many models have been proposed for the coronal geometry, including slab (e.g., Haardt & Maraschi 1991), spherical (e.g., Frontera et al. 2003) or lamp-post coronal geometry (e.g., Miniutti & Fabian 2004). Details of its shape, location and size are yet largely unknown, though, since spectroscopy alone is not able to distinguish among different geometries, which can be probed with polarimetry measurements (e.g., Ursini et al. 2022). Indeed, recent results with Imaging X-ray Polarimetry Explorer (e.g., Weisskopf et al. 2016) are starting to unveil the geometrical properties of the AGN corona. Gianolli et al. (2023) measured the coronal X-ray polarization for the first time in the Seyfert galaxy NGC 4151, strongly suggesting a wedge or a slab above the accretion disk (e.g., Poutanen et al. 2018). For IC4329A (Ingram et al. 2023), a marginal detection for the X-ray polarimetry also suggests a wedge coronal geometry. Only upper limits were found for MCG-5-23-16 (Marinucci et al. 2022; Tagliacozzo et al. 2023), although the results, combined with the inclination measurement obtained with XMM-Newton and NuSTAR (Serafinelli et al. 2023a), tentatively favors a wedge geometry as well.
Several measurements of the cut-off energy have been undertaken using many hard X-ray instruments, like BeppoSAX (e.g., Dadina 2007), INTEGRAL (e.g., Molina et al. 2009; De Rosa et al. 2012), Swift-BAT (e.g., Ricci et al. 2018) and NuSTAR (e.g., Fabian et al. 2015, 2017; Tortosa et al. 2018a), including obscured sources (e.g., Baloković et al. 2020; Serafinelli et al. 2023b). This task is far from trivial, since the hard X-ray spectrum is also characterized by a reflection component, due to X-ray photons interacting with the surrounding environment, such as the accretion disk, the broad line region or the torus, whose parameters are often degenerate with those of the continuum (see e.g. the review in Reynolds 2021. The cut-off energy is found in a large energy range, from Ec ∼ 23 keV (Kammoun et al. 2023) to Ec ∼ 750 keV (Matt et al. 2015), with average values around ∼100 − 200 keV (e.g., Ricci et al. 2018; Kamraj et al. 2022). Direct measurements of the coronal parameters such as the electron temperature kT and the optical depth τ have also been extensively performed on many AGN, finding a tight correlation between the temperature and the optical depth (e.g., Tortosa et al. 2018a; Kamraj et al. 2022).
The X-ray emission of AGN is well-known to be variable on several timescales, both in amplitude (e.g., Markowitz & Edelson 2004; Ponti et al. 2012; Vagnetti et al. 2016; Middei et al. 2017; Serafinelli et al. 2020) and spectral shape (e.g., Sobolewska & Papadakis 2009; Serafinelli et al. 2017). Variability is found on very short timescales down to a few hours (e.g., Ponti et al. 2012), and this suggests that the X-ray emitting region is compact (e.g., Mushotzky et al. 1993; De Marco et al. 2013), with a typical radius of Rc ∼ 10Rg (Ursini et al. 2020a), also supported by microlensing results (e.g., Chartas et al. 2009; Morgan et al. 2012. Moreover, the X-ray emission is variable in a wide range of energies, including very hard X-rays (E > 10 keV) on both long (e.g., years, Soldi et al. 2014; Akylas et al. 2022; Papadakis & Binas-Valavanis 2024) and shorter timescales (e.g., hours, Rani et al. 2019; Akylas et al. 2022).
The X-ray variability of AGN provides crucial insight on the size of the central source, but its main driver is still poorly understood. We aim here to investigate the possible relation between the variability of the X-ray emission coming from the corona and the physical properties of the corona itself with NuSTAR, which is able to study both coronal parameters and variability because of its high sensitivity at hard X-rays (E = 3 − 79 keV). We present a study of a sample of 20 nearby (z < 0.2) Seyfert galaxies for which we study the coronal parameters using NuSTAR, in order to investigate possible relations with the X-ray variability. In Sect. 2, we describe our sample, made up of sources with a wide range of coronal temperatures and optical depths, and the data reduction of the available X-ray data. In Sect. 3 we describe the spectral analysis we performed. In Sect. 4 we investigate the X-ray variability through the computation of the excess variance in different bands with NuSTAR. Finally our results are discussed in Sect. 5 and present a summary in Sect. 6. Throughout the paper, we adopt a standard ΛCDM cosmology, with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7.
2. Sample selection and data reduction
We selected our sample of AGN from the 70-Month Swift-BAT catalogue (Baumgartner et al. 2013). Ricci et al. (2017) computed many X-ray properties of the AGN in the catalog, such as the X-ray flux in several bands, the photon index, and the cut-off energy. We select all sources where the cut-off has been measured, namely, excluding the ones with only lower limits. Out of 836 AGN of the whole Swift-BAT sample, 165 satisfy this first condition. Among those AGN, we selected the ones with public NuSTAR observations as of 10th October 2021, for a total of 229 observations of 110 AGN. Not all NuSTAR observations have sufficient statistics to compute the coronal parameters; therefore, we selected only those with enough NuSTAR counts. To this end, we considered the value of the X-ray flux in the 20–50 keV, as reported by Ricci et al. (2017), and we converted such a flux to NuSTAR count rate in the same band using WebPimms1, adopting an unabsorbed power law with Γ = 1.8, which is typical for Seyfert galaxies (e.g., Serafinelli et al. 2017). This count rate was multiplied by the sum of the exposures of each observation of every source and we selected all sources with at least 1500 counts per FPM module. We note that this selection might exclude very variable sources in which the NuSTAR count rate may exceed the expected count rate from the BAT flux, not easily spotted with this criterion. A total of 34 sources are selected with these criteria. Six of these sources (IC4329A, MCG-5-23-16, MCG+8-11-11, NGC 5506, NGC 6814, and SWIFT J2127.4+5654) were already present in the sample analyzed by Tortosa et al. (2018a). Out of completeness, we decided to include two more sources from Tortosa et al. (2018a) that are not included in our selection, Ark 564 (not detected in BAT) and GRS 1734-292, to consider all non-jetted nearby (z ≤ 0.2) AGN from their sample. This resulted in a total of 36 AGN.
Sources analyzed in this paper.
Even though our sample might possibly be biased towards the low tail of the high energy cut-off distributions, this selection provides the best spectral signal-to-noise ratio (S/N) needed to derive coronal physical properties with high confidence level. Furthermore, excluding the sources with only lower limits for the cut-off energy also excludes AGN with additional spectral complexities, such as multiple ionized absorption gas layers, which could introduce systematic errors in the measure of kT and τ due to an inaccurate continuum fit. For these sources, a simultaneous spectroscopy with a low energy (E < 3 keV) bandpass is recommended.
We reduced the NuSTAR observations with NUPIPELINE, available through HEASOFT v6.30, which is part of the NUSTARDAS software package, calibration files (CALDB), updated as recently as March 31, 2022. We extracted the FPMA and FPMB source spectra and light curves from a circular region with 60″ radius, centered on the source, using the NUPRODUCTS command. The background spectra are extracted using two source-free regions of 40″ each.
3. Spectral analysis
We performed a quick analysis of 36 selected AGN to verify whether the coronal temperature is also constrained with NuSTAR. All fits included Galactic absorption extracted from HI4PI Collaboration (2016) (see Appendix B for all details). We considered three models. Model A consists of a continuum plus ionized reflection model, using XILLVERCP, which is the combination of the reflection model XILLVER (García & Kallman 2010; García et al. 2011) and the continuum model NTHCOMP (Zdziarski et al. 1996). The XSPEC equation is:
For simplicity, the inclination and iron abundance are fixed to ι = 30°, and AFe = 1, respectively. The reflection fraction ℛ is left free to vary, as XILLVERCP models both continuum and reflection. Model B is adopted when the Fe Kα region is not properly modeled by model A because of the presence of a broad emission line, interpreted as due to the presence of a relativistic reflection component (e.g., Reynolds 2021). In such cases, we also included a second reflector, using RELXILLCP, which is the convolution of RELLINE (Dauser et al. 2014) and XILLVERCP for the reflection component, and NTHCOMP for the continuum. In this scenario XILLVERCP models reflection from material located farther out from the black hole, while RELLXILLCP models reflection from the innermost parts of the accretion disk (e.g., Serafinelli et al. 2023a). The XSPEC equation is:
We assumed a single emissivity index of −3 for the accretion disk and we assumed that RELXILLCP only models reflection (ℛ = −1). Unless otherwise specified (see Appendix B), we fixed an inner radius of Rin = 10 Rg and outer radius of Rout = 400 Rg. We assumed a Schwarzschild black hole (a = 0), while the XILLVERCP parameters are the same as model A, including a free-to-vary reflection fraction. Finally, model C was adopted when the reflection component was due to a single neutral reflector, and the model with one or two ionized reflection components does not fit the data satisfactorily. In this case, the reflection component was modeled with BORUS, which models the reflection from spherical distribution of neutral material with polar cutouts2 (see Baloković et al. 2018, for details). Thus, we added a NTHCOMP component for the continuum, since BORUS does not have an in-built continuum one and we tied all the reflection parameters in BORUS that describe the continuum to that of the NTHCOMP. The XSPEC equation is:
Since the physical properties of the neutral reflector are not the main goal of this paper, we always assumed a Compton thick reflector (log NH, refl/cm−2 = 24.5), with a covering factor Cf = 0.5 and reflector assumed on the line of sight. All three models include a neutral absorption component modeled with ZTBABS whenever required (see Appendix B for details).
We did not find any relevant variability of the coronal parameters kT or Γ, when considering different observation epochs of the same source. This is consistent with the recent results obtained by Pal & Stalin (2023), where evidence of variations in the coronal parameters was found in less than 5% of their AGN sample. Therefore, during the fit, we kept kT and τ tied between different observations of the same AGN. We were able to constrain the coronal parameters in 20 sources; however, we excluded the 16 sources for which we only obtained lower limits for either the coronal temperature or the optical depth. The final sample is shown in Table 1, where black hole masses (MBH), bolometric luminosities (Lbol), and Eddington ratios (λEdd) have been taken from the catalog presented in Koss et al. (2022); the only exception is Ark 564, which is absent from their list. Koss et al. (2022) selected masses preferably from reverberation mapping (when available) followed by single-epoch measurements from Hα or Hβ lines and, ultimately, from the host galaxy velocity dispersion. For Ark 564, we considered the reverberation mapping measurement in Peterson et al. (2004), MBH = 3.2 × 106 M⊙, with a bolometric luminosity computed by applying the bolometric correction proposed by Marconi et al. (2004) to the unabsorbed X-ray luminosity in the 2–10 keV energy band, along with an Eddington ratio computed as λEdd = Lbol/LEdd, where LEdd = 1.26 × 1038 M/M⊙ erg s−1 is the Eddington luminosity. All the values are reported in Table 1.
As we are interested in exploring different coronal geometries and the interplay between temperature and optical depth, we separated the continuum and the reflection by including a Comptonization model as continuum, COMPTT (Magdziarz & Zdziarski 1995), which is capable of assuming slab-shaped and spherical-shaped coronae. In models A and B, we simply replaced NTHCOMPT with COMPTT by setting the reflection parameter to a fixed value of −13; whereas in model C, we explicitly removed the external NTHCOMP component and replaced it with COMPTT. We started with the baseline models used for the first round of fits. All the parameters of the reflection, with the exception of the normalization, are frozen to the results of the first round of fits, as we are mainly interested in the coronal parameters. We fix the parameter approx in COMPTT to 0.5 to model a slab geometry, and to 1.5 to model a spherical coronal shape. We checked the consistency between the two continuum models by comparing the best-fit values of the temperature obtained before the addition of COMPTT and those obtained after, assuming a spherical geometry, the only one allowed by NTHCOMP. We find consistent kT results at 90% confidence level in all cases. Furthermore, we also simulated spectra in a large range of temperatures and exposures with NTHCOMP. We fit the simulated spectra with COMPTT, assuming a spherical geometry, such as the one considered in NTHCOMP model, also finding good agreement at least 90% confidence level.
We report the values obtained for kT and τ for both geometries in Table 2, while details on the fits are available in Appendix B.
4. Variability analysis
 |
Fig. 1. Excess variance in the soft (3–10 keV) versus the excess variance in the full (3–79 keV) NuSTAR bands (left). All excess variances are normalized at 10 ks. The best-fit line is fully consistent with the bisector at 90% confidence level, with an angular coefficient of 0.96 ± 0.05. The correlation coefficient is r = 0.95 with a negligible or null probability. Excess variance in the soft band vs. excess variance in the hard (10–40 keV) X-ray band (right). The best-fit angular coefficient is 0.7 ± 0.1 with a correlation coefficient r = 0.90 and a negligible probability of finding the correlation by chance. |
A straightforward estimator of the X-ray variability is the normalized excess variance (e.g., Vaughan et al. 2003), defined as:
where xi are the values of the X-ray amplitude of every time bin, μ is the mean value of the amplitude, N is the number of points, and σi is the photometric error on the X-ray amplitude. The excess variance of a random process is the integral of the power spectral density (PSD) over all frequencies between 0 and infinity. However, with real data it is limited by fmin = 1/tmax and fmax = 1/tmin, where tmin = 2Δt, with Δt being the time bin of the light curves we use (in our case 1 ks), and tmax is the length of the observation segment (10 ks, see below). We note that the excess variance is not a good estimator when a large range of redshifts is considered, since same-length light curves in the observer frame represent different rest-frame lengths at different redshifts (Vagnetti et al. 2016); at the same time, we would be looking at a different energy range. However, our sample is limited at z < 0.2, hence, we were able to avoid these biases among the excess variance.
NuSTAR excess variances in the energy bands 3–79, 3–10, and 10–40 keV.
Since the excess variance is a quadratic sum over the number of points of a light curve, two conditions should be satisfied in order to properly compare these quantities over different sources. First of all, they must have the same binning, which is ensured in our case by how the light curves were prepared. Indeed, every NuSTAR light curve is binned at 1 ks. The other condition is that the light curves should be equally long, which is not satisfied in our sample as the exposures are different in the observations of different sources. To avoid this bias, we normalize every excess variance to the same length. Given that the smallest NuSTAR exposure in our sample is Δt ∼ 17 ks, we decide to study the variability on a timescale lower than that, namely: 10 ks. In order to normalize the excess variance, we divided the light curve in intervals of 10 ks and discarded the leftover points up to a maximum of 9 ks. We computed σNXS2 for each interval and we adopted the average value between all intervals as the excess variance of the whole light curve.
Every excess variance value computed for each interval is associated with an error given by Vaughan et al. (2003):
where σerr2 = ∑iσi2/Nμ2 and 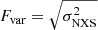 is the fractional variability.
is the fractional variability.
Following Ponti et al. (2012), we considered the following three cases. When only one interval was present for the considered light curve (Δt < 20 ks, one observation in our sample), the error associated with the excess variance is given by Eq. (2), computed in the single interval available. If the number of intervals is between 2 and 9 (i.e. 20 ≤ Δt < 100 ks, 33 observations), we calculated Eq. (2) for each interval and took its average value as the global error on the whole light curve. Finally, when the number of intervals exceeded 10 (i.e., Δt ≥ 100 ks, 12 observations), the standard deviation of the excess variance is adopted as error. We caution that the distribution of σNXS2 is Gaussian for an ideal number of intervals n ≳ 20 (e.g., Allevato et al. 2013). However, given that this condition is only satisfied for a total of four observations of two sources, we opted for the less conservative approach described above.
We computed the excess variance in the full (3–79 keV), soft (3–10 keV) and hard (10–40 keV) NuSTAR bands, which are listed in Table 3. As shown in Fig. 1, as expected, the broadband variability in the full band is dominated by the soft band variability, as most of the signal is detected in this energy band. Nearly all the points are located in the bisector line. Indeed, we fit the σNXS2 in the two bands in the logarithmic scale, we obtain a very tight correlation (r = 0.95 with negligible or null probability) and we find a slope of 0.96 ± 0.05, indicating that the variability of the continuum in the 3–10 keV band is dominant. We also find a tight correlation (r = 0.90) between the excess variance between the soft 3–10 keV and the hard 10–40 keV bands, which is however not consistent with the bisector at 90% confidence level, as we find an angular coefficient of 0.7 ± 0.1 and an intercept of −0.7 ± 0.2.
Since all three bands are so tightly correlated, in the following sections, we only used the excess variance derived from the light curves extracted in the full NuSTAR energy band (E = 3 − 79 keV). Full band light curves of every observation for each AGN of the sample here presented are shown in Appendix D.
5. Discussion
5.1. Physics of the corona
We considered the best-fit values of the temperature, kT, and the optical depth, τ, for each source, as listed in Table 2. We find a strong correlation between the coronal temperature and the optical depth, as reported in Fig. 2. Indeed, the τ − kT relations have a correlation coefficient of r = −0.96 for the slab geometry, and r = −0.97 for the sphere geometry, both with a negligible probability of finding such correlations by chance. We fit the linear relation log kT = alog τ + b and found best-fit parameters of a = −0.76 ± 0.08 and b = 1.54 ± 0.05, assuming a slab geometry. For the spherical corona, we obtained a = −0.90 ± 0.09 and b = 1.91 ± 0.07. These results are consistent at 90% confidence level with those obtained by Tortosa et al. (2018a) with a smaller sample.
 |
Fig. 2. Temperature versus optical depth plot. The kT − τ points obtained assuming a slab geometry are shown in blue, with the blue line indicating the best-fit line. The red points and line denote the points obtained with a sphere geometry and their best-fit line, respectively. Confidence intervals are shown at 90% level. |
It is very important to exclude any possible systematic effect when two quantities are found to be tightly correlated. To do that, we built a simple spectrum for an AGN, which is made of neutral absorption modeled with TBABS, a comptonizing continuum modeled with the physical model COMPTT and a ionized reflection component modeled with XILLVER, a mock version of model A. We simulate 1000 NuSTAR spectra assuming random parameters in predetermined ranges. We assume that the column density may take any value between NH = 1020 cm−2 to NH = 1023 cm−2. We allowed for a wide range of photon indices in the reflection spectrum, from a flat spectrum with Γ = 1.45 to a very steep one with Γ = 2.5. The iron abundance is taken in the range AFe = [0.5 5], while the ionization describes a nearly neutral (log ξ/(erg cm s−1) = 0) to a highly ionized reflector (log ξ/(erg cm s−1) = 4.7). For simplicity, we tie the reflection normalization to the one of the continuum, assuming a reflection parameter in the range ℛ = [−0.1 −1], where the negative values have been adopted in order to simulate pure reflection spectra. The adopted ranges of coronal temperature (kTe < 500 keV) and optical depth (τ < 10) are roughly based on the values of Table 2. Finally, the normalization of the continuum is chosen between 10−4 counts cm−2 s−1 keV−1 and 5 × 10−2 counts cm−2 s−1 keV−1, which corresponds to fluxes in the range FX = 5 × 10−14 − 10−10 erg cm−2 s−1. Each simulation was run assuming different exposures, between a minimum of 10 ks to a maximum of 100 ks, using simulated background spectra and the latest NuSTAR response and effective area. As shown in Fig. 3, in the adopted large range of parameters, the average value of the best-fit parameters, kT, and τ (right) are not much different than the simulated ones (left); the exception is the last bin (kT > 450 keV), where the optical depth tends to be slightly overestimated, due to the lower sensitivity of NuSTAR to high-temperature coronae. The simulations were designed with uncorrelated kT − τ; therefore, if a spurious correlation was indeed present, it would also be expected to be present in the right panel of Fig. 3. This suggests that from a statistical point of view, the correlation found in the data is not spurious. It is worth noting that the sample has been selected to be not strongly contaminated from complex, ionized, and multiple soft X-ray absorbers (see Sect. 2); thus, we did not expect for the model systematics to contribute to affecting the continuum best-fit parameters.
 |
Fig. 3. Temperature and optical depth of the simulated spectra used to validate the correlation found in the NuSTAR data. A thousand NuSTAR spectra were simulated with random values of kT and τ (see details in Sect. 5). The left panel show the values used to simulate the data with average values in bins of temperature (red), while the right panel shows the temperature and optical depth found when fitting the simulated spectra, with the average values in temperature bins. |
As discussed by Tortosa et al. (2018a), the observed kT − τ anticorrelation is not consistent with a global disk-corona configuration in radiative balance, which would imply the same heating-to-cooling ratio (HCR) for the coronae of all the AGN in the sample. One possibility to explain this anticorrelation is that colder coronae are more compact. In this case, a more compact corona would imply a larger optical depth, where the number of scatterings is larger. This will lead to a more efficient cooling (smaller HCR), and vice versa, a less compact corona would imply a smaller number of scattering, resulting in a larger HCR. Another possibility is that the disk-corona configuration is the same for all sources, but the sources might show different thermal emission due to viscous dissipation over the whole disk emission, which would also result in a larger cooling efficiency.
We also investigate a possible dependence of the coronal temperature from the physical properties of the AGN, such as the black hole mass, MBH, and the Eddington ratio, λ = Lbol/LEdd. As described in Sect. 2, the masses and bolometric luminosities were retrieved from the catalog published by Koss et al. (2022), with the sole exception of Ark 564, whose mass and bolometric luminosity were retrieved from Peterson et al. (2004) and adopting the bolometric correction from Marconi et al. (2004) to the X-ray luminosity obtained from the present data, respectively. As shown in Fig. 4, there is no indication of a possible correlation between kT or τ with either the black hole mass or the Eddington ratio. This is consistent with past studies of coronal parameters (e.g., Tortosa et al. 2018a; Kamraj et al. 2022). However, we note that Ricci et al. (2018) found a trend between λEdd and the cut-off energy, Ec, when considering a very large sample of sources.
 |
Fig. 4. We report here the coronal parameters (kT and τ) vs the black hole mass (left panels) and the Eddington ratio (right panels) for the sources in our sample (see Table 1). The blue dots are the temperatures obtained assuming a slab corona, while the red dots are those obtained assuming a spherical one. |
 |
Fig. 5. Excess variance in the E = 3 − 79 keV energy band versus the black hole mass of the AGN (left). The excess variances shown here are averaged among the different epochs. A clear trend |
5.2. X-ray variability and coronal properties
We investigate a possible correlation between the excess variance in the full NuSTAR band (E = 3 − 79 keV) and the mass of the black hole (Fig. 5, left panel). For this purpose, we exclude the sources for which Koss et al. (2022) report the mass value from the velocity dispersion of the stars in the host galaxy, as they are affected by large uncertainties. We find that the two quantities are well correlated with a correlation coefficient of r = −0.7 and a null probability of pnull ≃ 10−5. If we perform a linear fit on the logarithmic quantities, namely, log σNXS2 = alog(MBH/105 M⊙)+b, we obtain a = −0.6 ± 0.2 and b = −1.2 ± 0.7. An anticorrelation was also found in previous variability analyses with XMM-Newton (e.g., Ponti et al. 2012; Tortosa et al. 2023). We tested whether the excess variance is dependent on the X-ray luminosity, LX, and we found a moderate anticorrelation r = −0.5 (pnull ≃ 0.02), with the two quantities related as σNXS2 ∝ LXa (Fig. 5, middle panel) with a = −0.4 ± 0.3. Despite not being highly significant, this relation is also found in other analyses with a much larger number of sources (e.g., Vagnetti et al. 2016; Prokhorenko et al. 2024). We also report an anticorrelation (r ∼ −0.7 and pnull ∼ 10−5) with the bolometric luminosity (σNXS2 ∝ Lbola with a = −0.6 ± 0.3). As shown in Fig. 6, though, both LX and Lbol are correlated with the black hole mass, scaling as 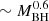 , with correlation coefficient r ∼ 0.5 (pnull ∼ 0.02) and r ∼ 0.7 (pnull ∼ 10−5), respectively. Therefore it is likely that the two luminosity relations are degenerate with the black hole mass relation. Alternatively, the variability-luminosity relation has often been attributed to a superposition of small flares (e.g., Nandra et al. 1997; Almaini et al. 2000).
, with correlation coefficient r ∼ 0.5 (pnull ∼ 0.02) and r ∼ 0.7 (pnull ∼ 10−5), respectively. Therefore it is likely that the two luminosity relations are degenerate with the black hole mass relation. Alternatively, the variability-luminosity relation has often been attributed to a superposition of small flares (e.g., Nandra et al. 1997; Almaini et al. 2000).
 |
Fig. 6. Bolometric (upper panel) and X-ray (lower panel) luminosities vs. black hole mass of the sources considered in this work. Both luminosities scale with mass as |
We also test the possible relation between the excess variance and the Eddington ratio derived in Sect. 5.1 (see Fig. 5, right panel), finding a correlation coefficient r = −0.03, with a probability of finding such correlation by chance pnull = 0.3. This suggests a lack of correlation between the Eddington ratio and the X-ray variability. We also tried to remove the previously described dependency from the mass, checking a possible correlation between the quantity 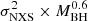 , but this quantity is also uncorrelated with the Eddington ratio values.
, but this quantity is also uncorrelated with the Eddington ratio values.
We analyzed the possible correlation between the excess variance and the coronal parameters of the 20 sources analyzed here. We do not find a relevant dependence between the temperature obtained with both geometries and the excess variance in the 3–79 keV energy band, as the correlation coefficient is r = −0.02, with null probability pnull = 0.3, and the angular coefficient is consistent with a flat line (see Fig. 7, left panel). For completeness, we also show that the excess variance and the optical depth are not correlated (r = 0.01, pnull = 0.35, see Fig. 7, right panel). This result was expected once the σ − kT relation is found to be absent, given the tight kT − τ correlations found in Sect. 5.1.
 |
Fig. 7. Excess variance in the E = 3 − 79 keV energy band versus the coronal temperature (left panel) and the optical depth (right panel) of the sample analyzed in this work. Blue circles identify temperature and optical depth values obtained assuming a slab geometry, while the red triangles indicate the values obtained assuming a spherical geometry. |
These results suggest that the X-ray variability on timescales of 10 ks is not dependent on the coronal temperature nor the optical depth, raising questions about the origin of the X-ray variability. Indeed, the corona must introduce variability at timescales shorter than the ones observed for the UV radiation, which provides the seed photons for the Comptonization. Additionally, the corona must be responsible for the X-ray variability, because the UV light curves lag behind the X-ray ones (e.g., Kammoun et al. 2021).
We note that, so far, we have considered the corona to be in thermal equilibrium, meaning that we have computed average values of the temperature and optical depth over the whole observation, which is indeed larger than the timescale for which we have probed the variability. Therefore, one possibility is that the X-ray variability could be driven by changes of the temperature and optical depth at timescales that are consistent with the observed flux variations (i.e., below 10 ks). However, measuring time-resolved temperatures is not yet possible with the currently most advanced hard X-ray telescope NuSTAR. Moreover, the physical environment could be much more complex than its simplification above. For instance, geometry is undoubtedly a parameter that could play a major role in driving the X-ray variability. In fact, variations in the intrinsic geometry or disk-corona geometry, such as the ones observed in X-ray binaries (e.g., Kara et al. 2019), could also drive the X-ray variability. It would be expected that, following a geometry variation, the temperature and optical depth would change accordingly, but these variations may also happen at shorter timescales than the ones probed by the spectral fits, possibly even shorter than 10 ks.
An additional complexity to take into account is a possible spatial (likely radial) distribution of the temperature of the corona, while we have assumed an average single value for the whole electron plasma. The spatial and temporal average values of the temperature may spread out the link between the best-fit results and the calculations of the variability.
Another possibility is that the variability is mainly driven by the observed anticorrelation with the black hole mass, which is likely proportional to the absolute size of the corona. If we consider, for instance, that all coronae of the AGN in the sample have a typical coronal radius of Rc = 10 Rg (e.g., Dovčiak & Done 2016; Ursini et al. 2020a), where Rg = GMBH/c2 is the gravitational radius, the coronal size in physical units would be directly proportional to the supermassive black hole mass. However, we note that the size of the coronae in Rg units could differ from source to source, as discussed in the previous section; furthermore, the relation between coronal size and black hole mass, although still increasing, it may be far from trivial to derive. In any case, even considering more complex relations between the coronal size and the black hole mass, more massive black holes correspond to larger coronae, which would imply a larger number of random scattering of the seed photons in the corona, resulting in a smaller X-ray variability amplitude.
6. Summary and conclusions
We have presented a spectral and timing study of 20 bright AGN with the best signal-to-noise ratio available based on NuSTAR data. We measured the temperature, kTe, and optical depth, τ, of the X-ray emitting corona under two different geometries (sphere and slab) by modeling the spectrum continuum with the Comptonization model COMPTT. Additionally, we have studied the NuSTAR variability in the time range between 1 and 10 ks by means of the excess variance σNXS2. We note that the results of this paper are related to the sample at hand, which is the highest quality data to date. We summarize our results in the following
-
We report that there is no correlation found between the X-ray variability and the electron temperature or the optical depth of the corona. This may imply that the X-ray variability is dependent on kT and τ variations on timescales below 10 ks, which is the timescale probed by the variability in this paper.
-
We did find a strong anticorrelation between kT and τ adopting both slab and spherical geometries. In particular, we find that the optical depth is related to the temperature by a relation kT ∝ (τ)−a with a ∼ −0.7 ÷ −1 (Fig. 2), depending on the assumed geometry. Therefore, we confirm the trend found by Tortosa et al. (2018a) with our AGN sample size increased by a factor of 2 with respect to the cited work.
-
We did not find any dependence of kTe and τ with either the black hole mass or Eddington ratio. This is also consistent with previous results on other samples of AGN (e.g., Tortosa et al. 2018a; Kamraj et al. 2022).
-
There is a strong correlation between the 3–10 keV and 3–79 keV, which implies that the variability of the X-ray emission below 10 keV is dominant over the rest of the spectrum. We also find a strong correlation between the variability of the 10–40 keV band and the one in 3–10 keV.
-
We found a strong anticorrelation between the X-ray variability and the mass, following σNXS2 ∝ M−0.6. This correlation is consistent to the one found by past variability studies with XMM-Newton (e.g., Ponti et al. 2012; Tortosa et al. 2023). We also report a moderate correlation with the X-ray luminosity
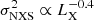 , as well as no correlation seen with the Eddington ratio.
, as well as no correlation seen with the Eddington ratio.
The results of our study show that the main driver of the X-ray continuum variability produced in the hot-corona remains elusive; furthermore, it is not even clear whether there is a main driver for the observed variability at all and it may instead be the product of the superposition of several effects at work. We have shown here that the variability at 10 ks does not depend on the physical properties of the corona, namely, electron temperature and optical depth. This then raises the question of what drives the X-ray variability. One possibility is that we might be probing different timescales, since we are studying relatively fast variability within 10 ks; on the other hand, we have averaged the coronal temperature over days, months, and even years to reach a sufficient signal-to-noise ratio that would allow for an accurate measurement of the coronal temperature. Variations in the coronal geometry may also play an important role in producing the observed variability. In the future, detectors sensitive in a broadband energy range with much larger effective area, such as the Large Area Detector (LAD; e.g., Feroci et al. 2022) proposed for the future enhanced X-ray Timing and Polarimetry mission (eXTP; Zhang et al. 2019) and the Spectroscopic Time-Resolving Observatory for Broadband Energy X-rays (STROBE-X; Ray et al. 2018), will allow us to measure AGN coronal temperatures with high precision for exposures as short as 10 ks (De Rosa et al. 2019). This would open up the possibility to probe both the coronal parameters and variability on the same timescale. Moreover, thanks to the extremely broadband E = 0.2 − 80 keV, now only available with joint NuSTAR observations with other facilities such as XMM-Newton, the future X-ray telescope HEX-P (Kammoun et al. 2024) will be able to measure optical depth and temperatures with much more accuracy than NuSTAR, with much shorter exposures.
Data availability
Appendices C and D are available at https://doi.org/10.5281/zenodo.12807347
The BORUS grids are available at https://sites.astro.caltech.edu/~mislavb/download
We recall that XILLVERCP models both continuum and reflection, by fitting the reflection fraction ℛ > 0 and assuming NTHCOMP as continuum. When the reflection fraction is assumed to be frozen to ℛ = −1, XILLVERCP will only model a pure reflection spectrum, which means that we then need a second component to model the continuum.
Acknowledgments
We thank the referee for their comments, which improved the quality of this paper. The authors thank Iossif Papadakis and Julien Malzac for useful discussions on the results of this paper. RS and ADR acknowledge support from the agreements ASI-INAF n.2017-14-H.0 “Science case study and scientific simulations for the enhanced X-ray Timing Polarimetry mission, eXTP”, ASI-INAF eXTP Fase B-2020-3-HH.1-2021, Bando Ricerca Fondamentale INAF 2022 Large Grant “Dual and binary supermassive black holes in the multi-messenger era: from galaxy mergers to gravitational waves” and the INAF-PRIN grant “A Systematic Study of the largest reservoir of baryons and metals in the Universe: the circumgalactic medium of galaxies” (No. 1.05.01.85.10). AT acknowledges financial support from the Bando Ricerca Fondamentale INAF 2022 Large Grant “Toward an holistic view of the Titans: multi-band observations of z > 6 QSOs powered by greedy supermassive black holes”. SB acknowledges funding from PRIN MUR 2022 SEAWIND 2022Y2T94C, supported by European Union - Next Generation EU, from INAF LG 2023 BLOSSOM, and from the EU grant AHEAD-2020 (GA no. 871158). CR acknowledges support from the Fondecyt Regular grant 1230345 and ANID BASAL project FB210003. POP acknowledges financial support from the French space agency (CNES) and the National High Energy Programme (PNHE) of CNRS. This research has made use of data and software provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC and the High Energy Astrophysics Division of the Smithsonian Astrophysical Observatory. This research has made use of the NuSTAR Data Analysis Software (NUSTARDAS) jointly developed by the ASI Space Science Data Center (SSDC, Italy) and the California Institute of Technology (Caltech, USA).
References
- Agís-González, B., Miniutti, G., Kara, E., et al. 2014, MNRAS, 443, 2862 [CrossRef] [Google Scholar]
- Akylas, A., Papadakis, I., & Georgakakis, A. 2022, A&A, 666, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allevato, V., Paolillo, M., Papadakis, I., & Pinto, C. 2013, ApJ, 771, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Almaini, O., Lawrence, A., Shanks, T., et al. 2000, MNRAS, 315, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Baloković, M., Matt, G., Harrison, F. A., et al. 2015, ApJ, 800, 62 [CrossRef] [Google Scholar]
- Baloković, M., Brightman, M., Harrison, F. A., et al. 2018, ApJ, 854, 42 [Google Scholar]
- Baloković, M., Harrison, F. A., Madejski, G., et al. 2020, ApJ, 905, 41 [Google Scholar]
- Baumgartner, W. H., Tueller, J., Markwardt, C. B., et al. 2013, ApJS, 207, 19 [Google Scholar]
- Brenneman, L. W., Madejski, G., Fuerst, F., et al. 2014, ApJ, 788, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Buisson, D. J. K., Fabian, A. C., & Lohfink, A. M. 2018, MNRAS, 481, 4419 [Google Scholar]
- Chartas, G., Kochanek, C. S., Dai, X., Poindexter, S., & Garmire, G. 2009, ApJ, 693, 174 [Google Scholar]
- Dadina, M. 2007, A&A, 461, 1209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dauser, T., Garcia, J., Parker, M. L., Fabian, A. C., & Wilms, J. 2014, MNRAS, 444, L100 [Google Scholar]
- De Marco, B., Ponti, G., Cappi, M., et al. 2013, MNRAS, 431, 2441 [Google Scholar]
- De Rosa, A., Panessa, F., Bassani, L., et al. 2012, MNRAS, 420, 2087 [NASA ADS] [CrossRef] [Google Scholar]
- De Rosa, A., Uttley, P., Gou, L., et al. 2019, Sci. China: Phys. Mech. Astron., 62, 29504 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 420, 1848 [Google Scholar]
- Dovčiak, M., & Done, C. 2016, Astron. Nachr., 337, 441 [CrossRef] [Google Scholar]
- Fabian, A. C., Lohfink, A., Kara, E., et al. 2015, MNRAS, 451, 4375 [Google Scholar]
- Fabian, A. C., Lohfink, A., Belmont, R., Malzac, J., & Coppi, P. 2017, MNRAS, 467, 2566 [Google Scholar]
- Feroci, M., Ambrosi, G., Ambrosino, F., et al. 2022, SPIE Conf. Ser., 12181, 121811X [NASA ADS] [Google Scholar]
- Frontera, F., Amati, L., Zdziarski, A. A., et al. 2003, ApJ, 592, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., & Kallman, T. R. 2010, ApJ, 718, 695 [CrossRef] [Google Scholar]
- García, J., Kallman, T. R., & Mushotzky, R. F. 2011, ApJ, 731, 131 [CrossRef] [Google Scholar]
- Gianolli, V. E., Kim, D. E., Bianchi, S., et al. 2023, MNRAS, 523, 4468 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ingram, A., Ewing, M., Marinucci, A., et al. 2023, MNRAS, 525, 5437 [CrossRef] [Google Scholar]
- Kammoun, E. S., Papadakis, I. E., & Dovčiak, M. 2021, MNRAS, 503, 4163 [CrossRef] [Google Scholar]
- Kammoun, E. S., Igo, Z., Miller, J. M., et al. 2023, MNRAS, 522, 5217 [NASA ADS] [CrossRef] [Google Scholar]
- Kammoun, E., Lohfink, A. M., Masterson, M., et al. 2024, Front. Astron. Space Sci., 10, 1308056 [NASA ADS] [CrossRef] [Google Scholar]
- Kamraj, N., Brightman, M., Harrison, F. A., et al. 2022, ApJ, 927, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Kara, E., García, J. A., Lohfink, A., et al. 2017, MNRAS, 468, 3489 [NASA ADS] [CrossRef] [Google Scholar]
- Kara, E., Steiner, J. F., Fabian, A. C., et al. 2019, Nature, 565, 198 [Google Scholar]
- Kayanoki, T., Mao, J., & Fukazawa, Y. 2024, MNRAS, 528, 4504 [CrossRef] [Google Scholar]
- Koss, M. J., Ricci, C., Trakhtenbrot, B., et al. 2022, ApJS, 261, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [Google Scholar]
- Marinucci, A., Matt, G., Kara, E., et al. 2014, MNRAS, 440, 2347 [NASA ADS] [CrossRef] [Google Scholar]
- Marinucci, A., Muleri, F., Dovciak, M., et al. 2022, MNRAS, 516, 5907 [NASA ADS] [CrossRef] [Google Scholar]
- Markowitz, A., & Edelson, R. 2004, ApJ, 617, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Baloković, M., Marinucci, A., et al. 2015, MNRAS, 447, 3029 [NASA ADS] [CrossRef] [Google Scholar]
- Middei, R., Vagnetti, F., Bianchi, S., et al. 2017, A&A, 599, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Middei, R., Bianchi, S., Marinucci, A., et al. 2019, A&A, 630, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miniutti, G., & Fabian, A. C. 2004, MNRAS, 349, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Molina, M., Bassani, L., Malizia, A., et al. 2009, MNRAS, 399, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Molina, M., Malizia, A., Bassani, L., et al. 2019, MNRAS, 484, 2735 [CrossRef] [Google Scholar]
- Morgan, C. W., Hainline, L. J., Chen, B., et al. 2012, ApJ, 756, 52 [Google Scholar]
- Mushotzky, R. F., Done, C., & Pounds, K. A. 1993, ARA&A, 31, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., George, I. M., Mushotzky, R. F., Turner, T. J., & Yaqoob, T. 1997, ApJ, 476, 70 [Google Scholar]
- Padovani, P., Alexander, D. M., Assef, R. J., et al. 2017, A&ARv, 25, 2 [Google Scholar]
- Pal, I., & Stalin, C. S. 2023, MNRAS, 518, 2529 [Google Scholar]
- Papadakis, I. E., & Binas-Valavanis, V. 2024, A&A, 685, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [Google Scholar]
- Petrucci, P. O., Haardt, F., Maraschi, L., et al. 2001, ApJ, 556, 716 [Google Scholar]
- Ponti, G., Papadakis, I., Bianchi, S., et al. 2012, A&A, 542, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porquet, D., Reeves, J. N., Grosso, N., Braito, V., & Lobban, A. 2021, A&A, 654, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poutanen, J., Veledina, A., & Zdziarski, A. A. 2018, A&A, 614, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prokhorenko, S. A., Sazonov, S. Y., Gilfanov, M. R., et al. 2024, MNRAS, 528, 5972 [NASA ADS] [CrossRef] [Google Scholar]
- Rani, P., Stalin, C. S., & Goswami, K. D. 2019, MNRAS, 484, 5113 [NASA ADS] [CrossRef] [Google Scholar]
- Ray, P. S., Arzoumanian, Z., Brandt, S., et al. 2018, SPIE Conf. Ser., 10699, 1069919 [NASA ADS] [Google Scholar]
- Reeves, J. N., Porquet, D., Braito, V., Grosso, N., & Lobban, A. 2021, A&A, 649, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, C. S. 2021, ARA&A, 59, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017, ApJS, 233, 17 [Google Scholar]
- Ricci, C., Ho, L. C., Fabian, A. C., et al. 2018, MNRAS, 480, 1819 [NASA ADS] [CrossRef] [Google Scholar]
- Serafinelli, R., Vagnetti, F., & Middei, R. 2017, A&A, 600, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serafinelli, R., Severgnini, P., Braito, V., et al. 2020, ApJ, 902, 10 [Google Scholar]
- Serafinelli, R., Marinucci, A., De Rosa, A., et al. 2023a, MNRAS, 526, 3540 [NASA ADS] [CrossRef] [Google Scholar]
- Serafinelli, R., Braito, V., Reeves, J. N., et al. 2023b, A&A, 672, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Soldi, S., Beckmann, V., Baumgartner, W. H., et al. 2014, A&A, 563, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tagliacozzo, D., Marinucci, A., Ursini, F., et al. 2023, MNRAS, 525, 4735 [CrossRef] [Google Scholar]
- Tazaki, F., Ueda, Y., Ishino, Y., et al. 2010, ApJ, 721, 1340 [NASA ADS] [CrossRef] [Google Scholar]
- Tortosa, A., Marinucci, A., Matt, G., et al. 2017, MNRAS, 466, 4193 [NASA ADS] [Google Scholar]
- Tortosa, A., Bianchi, S., Marinucci, A., Matt, G., & Petrucci, P. O. 2018a, A&A, 614, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tortosa, A., Bianchi, S., Marinucci, A., et al. 2018b, MNRAS, 473, 3104 [CrossRef] [Google Scholar]
- Tortosa, A., Ricci, C., Arévalo, P., et al. 2023, MNRAS, 526, 1687 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, T. J., Reeves, J. N., Braito, V., & Costa, M. 2018, MNRAS, 476, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Ursini, F., Dovčiak, M., Zhang, W., et al. 2020a, A&A, 644, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ursini, F., Petrucci, P. O., Bianchi, S., et al. 2020b, A&A, 634, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ursini, F., Matt, G., Bianchi, S., et al. 2022, MNRAS, 510, 3674 [NASA ADS] [CrossRef] [Google Scholar]
- Vagnetti, F., Middei, R., Antonucci, M., Paolillo, M., & Serafinelli, R. 2016, A&A, 593, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [Google Scholar]
- Weisskopf, M. C., Ramsey, B., O’Dell, S. L., et al. 2016, Results Phys., 6, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S., Santangelo, A., Feroci, M., et al. 2019, Sci. China: Phys. Mech. Astron., 62, 29502 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Data
NuSTAR spectra analyzed in this work.
Appendix B: Spectral fits
1H0419-577
This is a Seyfert 1 galaxy at z = 0.104, with a black hole mass of MBH = 3.8 × 108 M⊙. We binned the spectra at a minimum of 100 counts per energy bin over the whole 3 − 79 keV energy range. A Galactic absorption with column density NH, Gal = 1.14 × 1020 cm−2 is adopted. The spectra are well fitted by an absorbed continuum plus non-relativistic reflection (model A, ztbabs*(comptt+xillvercp)). We let the intrinsic absorption column density NH to vary between observations. We find NH = (6 ± 4)×1021 cm−2 for the 2015 observation and NH = (1.0 ± 0.5)×1022 cm−2 for both the 2018 observations. When we assume a slab geometry (parameter approx = 0.5) we obtain 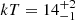 keV and an optical depth
keV and an optical depth 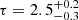 , while when a sphere geometry (approx = 1.5) is adopted we find the same temperature and an optical depth of
, while when a sphere geometry (approx = 1.5) is adopted we find the same temperature and an optical depth of 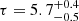 . We find a goodness of fit χ2/dof = 1566/1588. The results are consistent with the broadband analysis performed by Turner et al. (2018), although we note that in that work the OPTXAGNF model (Done et al. 2012) was used.
. We find a goodness of fit χ2/dof = 1566/1588. The results are consistent with the broadband analysis performed by Turner et al. (2018), although we note that in that work the OPTXAGNF model (Done et al. 2012) was used.
4C 50.55
4C 50.55 is a radio-loud Seyfert 1 galaxy at redshift z = 0.02, yielding a black hole mass of 6.4 × 107 M⊙. We bin the NuSTAR spectra at a minimum of 100 counts per energy bin and consider the full E = 3 − 79 keV energy band. We note that Tazaki et al. (2010) ruled out a significant role of the jet in the X-ray spectrum of this source using Suzaku. We consider a Galactic column of NH, Gal = 9.45 × 1021 cm−2. The source is well fitted by an absorbed continuum plus a single disk reflector, i.e. ztbabs*(comptt+xillvercp) (model A). The column densities of the two observations are NH = (3.0 ± 0.4)×1022 cm−2 and NH = (2.0 ± 0.3)×1022 cm−2 for the 2014 and 2018 observations, respectively. We find a temperature of 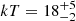 keV (
keV (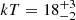 keV) and optical depth of
keV) and optical depth of 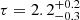 (
(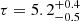 ) assuming a slab (sphere) geometry. The statistic is χ2/dof = 1325/1243. These results are consistent with the analysis of Buisson et al. (2018).
) assuming a slab (sphere) geometry. The statistic is χ2/dof = 1325/1243. These results are consistent with the analysis of Buisson et al. (2018).
Ark 564
Ark 564 is a Narrow-Line Seyfert 1, with mass MBH = 3.2 × 106 M⊙ (Peterson et al. 2004). The NuSTAR spectra have been binned at a minimum of 100 counts per energy bin and only considered in the E = 3 − 30 keV energy range. A Galactic column of NH, Gal = 5 × 1020 cm−2 is assumed. A simple power law model unveils a single narrow Fe Kα component and a reflection component in the residual spectra. Therefore, the reflection is modeled with model A (compTT+xillvercp), with no absorption needed. Assuming a slab (sphere) geometry we obtain kT = 15 ± 2 keV (16 ± 1 keV) and an optical depth of τ = 1.4 ± 0.1 (3.3 ± 0.3). The statistic is χ2/dof = 1267/1127. A detailed broadband spectral analysis, which is consistent with the results presented here, can be found in Kara et al. (2017).
ESO 103-G35
ESO 103-G35 is a Seyfert 2 galaxy at redshift z = 0.00914 with a black hole mass of MBH = 1.3 × 107 M⊙. The four FPM spectra were binned at a minimum of 100 counts per energy bin in the E = 3 − 50 keV energy band. We consider a Galactic absorption of NH, Gal = 5.8 × 1020 cm−2. The source X-ray spectra appear reflection-dominated due to a heavy obscuration, therefore we adopt a model consisting of a distant absorber plus continuum, with intrinsic absorption on the line of sight, i.e. ztbabs*(comptt+borus12) (model C). The two observations are characterized by nearly the same Compton-thin absorbing column density, which is consequently kept tied between epochs, of NH = (1.65 ± 0.08)×1023 cm−2. The temperature and optical depth assuming a slab geometry are 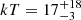 keV and
keV and 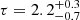 , respectively, while the two parameters assuming a sphere geometry are
, respectively, while the two parameters assuming a sphere geometry are 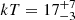 keV and τ = 5.2 ± 0.7. The goodness of fit is χ2/dof = 1320/1302. The results are consistent with the analysis of Buisson et al. (2018), in which a different reflection model was used.
keV and τ = 5.2 ± 0.7. The goodness of fit is χ2/dof = 1320/1302. The results are consistent with the analysis of Buisson et al. (2018), in which a different reflection model was used.
ESO 362-G18
ESO 362-G18 is a Seyfert 1.5 galaxy at redshift z = 0.01244 with a black hole mass MBH = 4.5 × 107 M⊙. The spectra were binned at a minimum of 50 photon counts per energy bin in the full E = 3 − 79 keV NuSTAR energy band. We consider a Galactic absorption of NH, Gal = 1.35 × 1020 cm−2. The X-ray spectrum has a typical Seyfert 1 shape with no evident intrinsic absorption. Following Agís-González et al. (2014) we model the spectrum with two reflection components, i.e. comptt+xillvercp+relxillcp (model B). For a slab (sphere) coronal geometry we obtain a temperature of 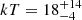 keV (
keV (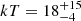 keV) and an optical depth of
keV) and an optical depth of 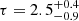 (τ = 5.2 ± 0.7). The goodness of fit is given by χ2/dof = 464/641.
(τ = 5.2 ± 0.7). The goodness of fit is given by χ2/dof = 464/641.
ESO 383-G18
ESO 383-G18 is a Seyfert 2 galaxy with z = 0.01241, with MBH = 3 × 105 M⊙. We bin the spectra of OBSID 60061243002 at a minimum of 50 counts per energy bin and the spectra of OBSID 60261002002 at a minimum of 100 counts per energy bin. We consider the E = 3 − 50 keV energy band for both observations. We assume a Galactic absorption of NH, Gal = 3.8 × 1020 cm−2. The X-ray spectrum appears severely absorbed by a intervening cold material, which suggests that the reflector is best modeled by distant cold material, i.e. ztbabs*(comptt+borus12) (model C). The absorbing column density of the two observations is consistent within the error at 90% confidence level, therefore we decided to keep them tied and obtain NH = (1.2 ± 0.2)×1023 cm−2. The temperature is identical assuming both assuming a slab or a spherical corona, i.e. 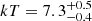 keV, while instead we find τ = 4.7 ± 0.3 for a slab geometry and τ = 10.1 ± 0.6 for a spherical one. The goodness of fit is χ2/dof = 1035/1054.
keV, while instead we find τ = 4.7 ± 0.3 for a slab geometry and τ = 10.1 ± 0.6 for a spherical one. The goodness of fit is χ2/dof = 1035/1054.
GRS 1734-292
GRS 1734-292 is a Seyfert 1 galaxy, having mass MBH = 2.5 × 108 M⊙. We binned each FPM module of the two NuSTAR epochs at a minimum of 100 counts per energy bin, and considered the full E = 3 − 79 keV energy band. We adopt a Galactic absorption of NH, Gal = 6.5 × 1021 cm−2. The source is also intrinsically moderately absorbed, with 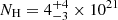 cm−2 for OBSID 60061279002 and NH = (15 ± 4)×1021 cm−2 for OBSID 60301010002. An absorbed powerlaw only show narrow Fe Kα residuals, therefore we adopt model A plus absorption (ztbabs(compTT+xillvercp)). We obtain a coronal temperature of
cm−2 for OBSID 60061279002 and NH = (15 ± 4)×1021 cm−2 for OBSID 60301010002. An absorbed powerlaw only show narrow Fe Kα residuals, therefore we adopt model A plus absorption (ztbabs(compTT+xillvercp)). We obtain a coronal temperature of 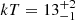 keV for both slab and sphere geometries. An optical depth of τ = 2.9 ± 0.2 (6.5 ± 0.4) is recovered in a slab (sphere) geometry. We obtain a statistic of χ2/dof = 1103/983. These results are consistent with the broadband analysis presented in Tortosa et al. (2017), in which OBSID 60061279002 was studied.
keV for both slab and sphere geometries. An optical depth of τ = 2.9 ± 0.2 (6.5 ± 0.4) is recovered in a slab (sphere) geometry. We obtain a statistic of χ2/dof = 1103/983. These results are consistent with the broadband analysis presented in Tortosa et al. (2017), in which OBSID 60061279002 was studied.
HE 1143-1810
HE 1143-1810 is a Seyfert 1 galaxy at redshift z = 0.0329 with an estimated black hole mass MBH = 4 × 107 M⊙. The 10 FPM spectra were all binned at a minimum of 100 photon counts per energy bin in the E = 3 − 79 keV energy band. The Galactic absorption is fixed at NH, Gal = 3 × 1020 cm−2. The spectrum has a typical unabsorbed shape, therefore no neutral absorption is needed. The source is nicely modeled by a single reflector plus continuum, i.e. comptt+xillvercp (model A). Assuming a slab (spherical) coronal geometry we find a temperature of 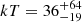 keV (
keV (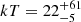 keV) and an optical depth of
keV) and an optical depth of 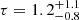 (
(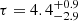 ). The goodness of fit is χ2/dof = 2639/2665. These values are largely in agreement with the broadband analysis presented in Ursini et al. (2020b).
). The goodness of fit is χ2/dof = 2639/2665. These values are largely in agreement with the broadband analysis presented in Ursini et al. (2020b).
IC 4329A
IC 4329A is a Seyfert 1 galaxy with mass MBH = 1.3 × 108. We bin both FPM modules of the analyzed observation (OBSID 60001045002) at a minimum of 100 counts per energy bin. We consider the full NuSTAR band, i.e. E = 3 − 79 keV. The Galactic absorption is NH, Gal = 4 × 1020 cm−2. A modest absorption of NH = (5 ± 2)×1021 cm−2 is included. A single distant reflector is needed, therefore we adopt model A. The coronal temperature for a slab (sphere) coronal geometry is 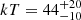 keV (
keV (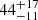 keV) and the optical depth is τ = 1.1 ± 0.3 (2.8 ± 0.7). The goodness of fit is χ2/dof = 1411/1298. A broadband spectral analysis is presented in Brenneman et al. (2014) and Ingram et al. (2023), with consistent results with our NuSTAR fits.
keV) and the optical depth is τ = 1.1 ± 0.3 (2.8 ± 0.7). The goodness of fit is χ2/dof = 1411/1298. A broadband spectral analysis is presented in Brenneman et al. (2014) and Ingram et al. (2023), with consistent results with our NuSTAR fits.
MCG-5-23-16
MCG-5-23-16 is a Seyfert 1.9 galaxy with a mass of MBH = 1.8 × 107 M⊙. All FPMA and FPMB spectra of the five available observations are binned at 100 counts per energy bin and the 3 − 79 keV energy range is considered. We assume a Galactic absorption of NH, Gal = 8 × 1020 cm−2 and we include cold intrinsic absorption with the model ztbabs, finding a column density NH = (1.4 ± 0.1)×1022 cm−2. We the source is modeled with a single reflector plus continuum with xillvercp, we find significant residuals on the Fe Kα region, strongly hinting at the presence of a broad component, likely a reflection component from the accretion disk. Therefore, we adopt the absorbed model B, ztbabs(compTT+xillvercp+relxillcp). Following Serafinelli et al. (2023a), we assume an emissivity index of −3, an inner radius Rin = 40Rg, inclination 45°, and a non-spinning black hole. Assuming a slab geometry, we find a coronal temperature kT = 44 ± 11 keV and an optical depth τ = 0.9 ± 0.2, while 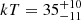 keV and τ = 2.7 ± 0.3 are found if a spherical coronal geometry is assumed. The goodness of fit is χ2/dof = 6995/5776. These values are consistent at 99% confidence level with the broadband analyses of Baloković et al. (2015) and Serafinelli et al. (2023a) performed on this source.
keV and τ = 2.7 ± 0.3 are found if a spherical coronal geometry is assumed. The goodness of fit is χ2/dof = 6995/5776. These values are consistent at 99% confidence level with the broadband analyses of Baloković et al. (2015) and Serafinelli et al. (2023a) performed on this source.
MCG+8-11-11
MCG+8-11-11 is a Seyfert 1 galaxy with mass MBH = 1.6 × 107 M⊙. The FPMA and FPMB spectra were binned at 100 counts per energy bin over the whole energy range (E = 3 − 79 keV), and a Galactic column density of NH = 1.75 × 1021 cm−2 is assumed. No intrinsic cold absorption is present. Two reflection components are required in the model, as the Fe Kα emission line is not adequately fitted by a single narrow component. We adopt therefore model B, compTT+xillvercp+relxillcp. We assume a non-spinning black hole and a disk with inner radius Rin = 2Rg, where Rg = GM/c2 is the gravitational radius, and emissivity index −3. We find a coronal temperature of 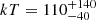 keV and an optical depth τ = 0.3 ± 0.2 when assuming a slab coronal geometry. When a spherical geometry is assumed for the corona, we obtain
keV and an optical depth τ = 0.3 ± 0.2 when assuming a slab coronal geometry. When a spherical geometry is assumed for the corona, we obtain 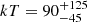 keV and
keV and 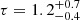 . The goodness of fit is χ2/dof = 873/851. These values are consistent with the results of Tortosa et al. (2018b), where this data was analyzed with contemporaneous Swift-XRT data.
. The goodness of fit is χ2/dof = 873/851. These values are consistent with the results of Tortosa et al. (2018b), where this data was analyzed with contemporaneous Swift-XRT data.
Mrk 6
Mrk 6 is a Seyfert 1.5 galaxy at z = 0.01951 with mass MBH = 1.9 × 107 M⊙. All four FPM spectra were binned at a minimum of 100 counts per energy bin. We consider the E = 3 − 50 keV energy band. The X-ray spectrum appear severely absorbed as in previous analyses of this source (e.g., Molina et al. 2019). Therefore, once the Galactic absorption is modeled with a fixed NH, Gal = 7.6 × 1020 cm−2, we model the spectra with an absorbed continua and a distant neutral reflector, i.e. ztbabs*(comptt+borus12) (model C). For OBSID 60102044002 and 60102044004 we find an intrinsic column density NH = (1.2 ± 0.1)×1023 cm−2 and NH = (1.0 ± 0.1)×1023 cm−2, respectively. The temperature is 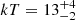 keV both assuming a slab or a spherical coronal geometry, while the optical depth is
keV both assuming a slab or a spherical coronal geometry, while the optical depth is 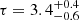 and
and 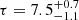 , respectively. The statistic is χ2/dof = 1283/1335. A few moderate residuals are present below 5 keV, possibly due to the presence of a warm absorber (Kayanoki et al. 2024), but given the low energy resolution of NuSTAR in the 3 − 5 keV energy range, we did not model such a component.
, respectively. The statistic is χ2/dof = 1283/1335. A few moderate residuals are present below 5 keV, possibly due to the presence of a warm absorber (Kayanoki et al. 2024), but given the low energy resolution of NuSTAR in the 3 − 5 keV energy range, we did not model such a component.
Mrk 110
Mrk 110 is a Seyfert 1 galaxy with redshift z = 0.03552 and mass MBH = 1.8 × 107 M⊙. The FPM spectra are all binned at a minimum of 100 counts per energy bin in the full E = 3 − 65 keV energy range. We adopt a Galactic absorption of NH, Gal = 1.3 × 1020 cm−2, while no intrinsic absorption is present confirming its nature as a "bare" AGN (Reeves et al. 2021; Porquet et al. 2021). We model the X-ray spectra with two reflectors, i.e. comptt+xillvercp+relxillcp (model B) finding 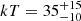 keV (
keV (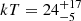 keV) and
keV) and 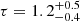 (
(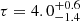 ) when assuming a slab (sphere) coronal geometry. The goodness of fit is χ2/dof = 2600/2305. The results agree with the broadband analysis presented in Porquet et al. (2021).
) when assuming a slab (sphere) coronal geometry. The goodness of fit is χ2/dof = 2600/2305. The results agree with the broadband analysis presented in Porquet et al. (2021).
Mrk 509
Mrk 509 is a Seyfert 1 galaxy at z = 0.01951 with a black hole mass of MBH = 2 × 108 M⊙. The FPMA and FPMB spectra for the two epochs were binned at a minimum of 100 photon counts per energy bin in E = 3 − 65 keV. The Galactic absorption is fixed at NH, Gal = 3.9 × 1020 cm−2. We model the X-ray spectra with an unabsorbed continuum with a single ionized reflector, i.e. comptt*xillvercp (model A). We find a temperature of 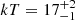 keV for both slab and sphere geometries, while the optical depth is τ = 2.2 ± 0.1 (
keV for both slab and sphere geometries, while the optical depth is τ = 2.2 ± 0.1 (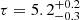 ) when assuming a slab (sphere) geometry. The statistic is χ2/dof = 1949/1647.
) when assuming a slab (sphere) geometry. The statistic is χ2/dof = 1949/1647.
NGC 3281
NGC 3281 is a Seyfert 2 galaxy with redshift z = 0.01073, with mass MBH = 1.7 × 108 M⊙. We bin the FPM spectra with a minimum of 50 counts per energy bin in the energy band E = 3 − 60 keV. We assume a Galactic absorption of NH, Gal = 6.6 × 1020 cm−2. The shape of the X-ray spectrum is that of a severely absorbed source, therefore we model the spectra with an absorbed continuum plus neutral reflection, i.e. ztbabs*(comptt+borus12) (model C). We find that the intrinsic column density is moderately variable, by a factor of ∼4, since we find 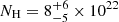 cm−2 for OBSID 60061201002 and NH = (3.1 ± 0.5)×1023 cm−2 for OBSID 60662003002. Assuming either a slab or a spherical geometry we find a temperature
cm−2 for OBSID 60061201002 and NH = (3.1 ± 0.5)×1023 cm−2 for OBSID 60662003002. Assuming either a slab or a spherical geometry we find a temperature 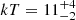 keV, with optical depth
keV, with optical depth 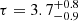 and τ = 8 ± 2, respectively. The goodness of fit is χ2/dof = 693/612.
and τ = 8 ± 2, respectively. The goodness of fit is χ2/dof = 693/612.
NGC 5506
NGC 5506 is a Seyfert 1 galaxy with mass M = 8.8 × 107 M⊙. The NuSTAR Focal Plane Modules were both binned at a minimum of 100 counts per energy bin in the full NuSTAR band E = 3 − 79 keV. The Galactic cold absorption is NH, Gal = 4.2 × 1020 cm−2, and we recover an intrinsic absorption of NH = (2.4 ± 0.3)×1022 cm−2. A single reflector is able to model the hard X-ray spectrum of this AGN, therefore we adopt model A with neutral absorption (ztbabs(compTT+xillvercp)). When a slab geometry is assumed, we obtain 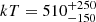 keV and τ = 0.02 ± 0.01, while assuming a sphere geometry the best-fit parameters are kT = 550 ± 250 keV and
keV and τ = 0.02 ± 0.01, while assuming a sphere geometry the best-fit parameters are kT = 550 ± 250 keV and 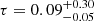 . The goodness of fit is χ2/dof = 819/738 and the best-fit values are largely in agreement with the broadband analysis performed in Matt et al. (2015).
. The goodness of fit is χ2/dof = 819/738 and the best-fit values are largely in agreement with the broadband analysis performed in Matt et al. (2015).
NGC 5728
NGC 5728 is a Seyfert 2 galaxy at z = 0.00947 with an estimated black hole mass of MBH = 3.4 × 107 M⊙. We bin all the X-ray spectra at a minimum of 50 counts per energy bin. We consider We adopt a fixed Galactic absorption column density of NH, Gal = 7.5 × 1020 cm−2. The spectrum appears as that of a typical absorbed source, therefore we model it with an absorbed continuum plus neutral reflection, i.e. ztbabs*(comptt+borus12) (model C). The intrinsic absorption is not variable and therefore we keep it tied between the two epochs, finding 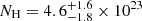 cm−2. We find a coronal temperature of kT = 13 ± 1 keV for both slab and spherical geometry and an optical depth of
cm−2. We find a coronal temperature of kT = 13 ± 1 keV for both slab and spherical geometry and an optical depth of 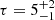 (
(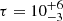 ) for a slab (spherical) coronal geometry. The statistic is given by χ2/dof = 480/524.
) for a slab (spherical) coronal geometry. The statistic is given by χ2/dof = 480/524.
NGC 6814
NGC 6814 is a Seyfert 1 galaxy with mass M = 2.7 × 106 M⊙. We bin both FPMA and FPMB detectors at a minimum of 100 counts per energy bin in the E = 3 − 60 keV energy band. We assume a Galactic absorption with column density NH, Gal = 8 × 1020 cm−2, while no intrinsic cold absorption is found in this source. The spectra need to be modeled with model B (comptt+xillvercp+relxillcp), having two reflection components, since the Fe Kα emission line is broadened. For simplicity, we assume a non-spinning black hole, and a disk with emissivity index −3 from a disk with inner radius Rin = 2Rg. The coronal temperature for a slab (spherical) coronal geometry is 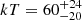 keV (
keV (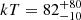 keV) and the optical depth is
keV) and the optical depth is 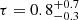 (
(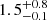 ). The goodness of fit is χ2/dof = 897/846. Though with larger errors due to the sole use of NuSTAR, the values are consistent with those found by Tortosa et al. (2018b) in the broad (E = 0.5 − 60 keV) band.
). The goodness of fit is χ2/dof = 897/846. Though with larger errors due to the sole use of NuSTAR, the values are consistent with those found by Tortosa et al. (2018b) in the broad (E = 0.5 − 60 keV) band.
SWIFT J2127.4+5654
The Narrow-line Seyfert 1 galaxy SWIFT J2127.4+5654 is characterized by a mass of M = 1.5 × 107 M⊙ at redshift z = 0.014. Both FPM spectra A and B are binned at 100 min counts per energy bin in the whole NuSTAR band E = 3 − 79 keV. The Galactic absorption column density is NH, Gal = 7 × 1020 cm−2 and negligible intrinsic absorption. The source is well modeled by model A with a single non-relativistic reflector, i.e. compTT+xillvercp, we obtain for a slab (spherical) coronal geometry a temperature of 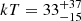 keV (
keV (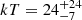 keV) and an optical depth of
keV) and an optical depth of 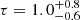 (
(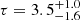 ). The statistic is χ2/dof = 1751/1775, with values consistent at 99% confidence level with those of the broadband study by Marinucci et al. (2014).
). The statistic is χ2/dof = 1751/1775, with values consistent at 99% confidence level with those of the broadband study by Marinucci et al. (2014).
UGC 6728
UGC 6728 is a Seyfert 1 galaxy with redshift z = 0.00652 with a black hole mass of MBH = 7.1 × 105 M⊙. The four FPM spectra were binned at a minimum of 50 photon counts per energy bin. We consider data in the E = 3 − 40 keV energy band. We assume a Galactic absorption of NH = 4.5 × 1020 cm−2. No evident intrinsic absorption is present. The spectra are best modeled with continuum and two reflectors, i.e. comptt+xillvercp+relxillcp (model B). We find a temperature of 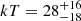 keV (
keV (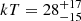 keV) and an optical depth of τ = 2.0 ± 1.2 (τ = 5.0 ± 2.0) when assuming a slab (sphere) coronal geometry. The goodness of fit is χ2/dof = 1321/1183.
keV) and an optical depth of τ = 2.0 ± 1.2 (τ = 5.0 ± 2.0) when assuming a slab (sphere) coronal geometry. The goodness of fit is χ2/dof = 1321/1183.
All Tables
All Figures
 |
Fig. 1. Excess variance in the soft (3–10 keV) versus the excess variance in the full (3–79 keV) NuSTAR bands (left). All excess variances are normalized at 10 ks. The best-fit line is fully consistent with the bisector at 90% confidence level, with an angular coefficient of 0.96 ± 0.05. The correlation coefficient is r = 0.95 with a negligible or null probability. Excess variance in the soft band vs. excess variance in the hard (10–40 keV) X-ray band (right). The best-fit angular coefficient is 0.7 ± 0.1 with a correlation coefficient r = 0.90 and a negligible probability of finding the correlation by chance. |
| In the text | |
 |
Fig. 2. Temperature versus optical depth plot. The kT − τ points obtained assuming a slab geometry are shown in blue, with the blue line indicating the best-fit line. The red points and line denote the points obtained with a sphere geometry and their best-fit line, respectively. Confidence intervals are shown at 90% level. |
| In the text | |
 |
Fig. 3. Temperature and optical depth of the simulated spectra used to validate the correlation found in the NuSTAR data. A thousand NuSTAR spectra were simulated with random values of kT and τ (see details in Sect. 5). The left panel show the values used to simulate the data with average values in bins of temperature (red), while the right panel shows the temperature and optical depth found when fitting the simulated spectra, with the average values in temperature bins. |
| In the text | |
 |
Fig. 4. We report here the coronal parameters (kT and τ) vs the black hole mass (left panels) and the Eddington ratio (right panels) for the sources in our sample (see Table 1). The blue dots are the temperatures obtained assuming a slab corona, while the red dots are those obtained assuming a spherical one. |
| In the text | |
 |
Fig. 5. Excess variance in the E = 3 − 79 keV energy band versus the black hole mass of the AGN (left). The excess variances shown here are averaged among the different epochs. A clear trend |
| In the text | |
 |
Fig. 6. Bolometric (upper panel) and X-ray (lower panel) luminosities vs. black hole mass of the sources considered in this work. Both luminosities scale with mass as |
| In the text | |
 |
Fig. 7. Excess variance in the E = 3 − 79 keV energy band versus the coronal temperature (left panel) and the optical depth (right panel) of the sample analyzed in this work. Blue circles identify temperature and optical depth values obtained assuming a slab geometry, while the red triangles indicate the values obtained assuming a spherical geometry. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



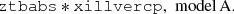
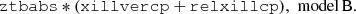
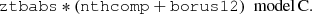
![$$ \begin{aligned} \sigma ^2_{\rm NXS}=\frac{1}{N\mu ^2}\sum _{i = 1}^{N}\left[ \left( x_i-\mu \right)^2 - \sigma _i^2 \right], \end{aligned} $$](/articles/aa/full_html/2024/10/aa50777-24/aa50777-24-eq61.gif)