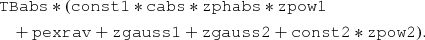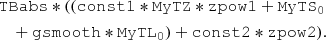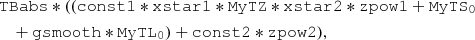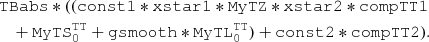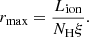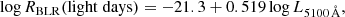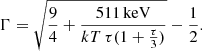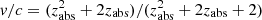| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202245224 | |
| Published online | 24 March 2023 | |
The NuSTAR view of the changing-look AGN ESO 323-G77
1
INAF – Istituto di Astrofisica e Planetologia Spaziali, Via del Fosso del Cavaliere 100, 00133 Roma, Italy
e-mail: roberto.serafinelli@inaf.it
2
INAF – Osservatorio Astronomico di Brera, Via Brera 28, 20121, Milano, Italy & Via Bianchi 46, Merate, (LC), Italy
3
Department of Physics, Institute for Astrophysics and Computational Sciences, The Catholic University of America, Washington, DC 20064, USA
4
Eureka Scientific, Inc, 2452 Delmer St. Suite 100, Oakland, CA 94602, USA
Received:
16
October
2022
Accepted:
28
January
2023
The presence of an obscuring torus at parsec-scale distances from the central black hole is the main ingredient for the Unified Model of active galactic nuclei (AGN), as obscured sources are thought to be seen through this structure. However, the Unified Model fails to describe a class of sources that undergo dramatic spectral changes, transitioning from obscured to unobscured and vice versa through time. The variability in these sources, which are known as changing-look AGN (CLAGN), is thought to be produced by a clumpy medium at much smaller distances than the conventional obscuring torus. ESO 323-G77 is a CLAGN that was observed in various states through the years with Chandra, Suzaku, Swift-XRT, and XMM-Newton, from unobscured (NH < 3 × 1022 cm−2) to Compton-thin (NH ∼ 1 − 6 × 1023 cm−2) and even Compton-thick (NH > 1 × 1024 cm−2), on timescales as short as one month. We present an analysis of the first NuSTAR monitoring of ESO 323-G77, consisting of five observations taken at different timescales (1, 2, 4, and 8 weeks from the first one) in 2016–2017, in which the AGN was caught in a persistent Compton-thin obscured state (NH ∼ 2 − 4 × 1023 cm−2). We find that a Compton-thick reflector is present (NH, refl = 5 × 1024 cm−2), most likely associated with the presence of the putative torus. Two ionized absorbers are unequivocally present, located within maximum radii of rmax, 1 = 1.5 pc and rmax, 2 = 0.01 pc. In one of the observations, the inner ionized absorber is blueshifted, indicating the presence of a possible faster (vout = 0.2c) ionized absorber, marginally detected at 3σ. Finally, we are able to constrain the coronal temperature and the optical depth of ESO 323-G77, obtaining kTe = 38 keV or kTe = 36 keV, and τ = 1.4 or τ = 2.8, depending on the coronal geometry assumed.
Key words: X-rays: galaxies / galaxies: active / galaxies: individual: ESO 323-G77
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Observations of active galactic nuclei (AGN) reveal the presence of two main classes of sources. Type 1 AGN are sources for which the optical spectra show both narrow (FWHM ≤ 1000 km s−1) and broad (FWHM > 1000 km s−1) lines, while type 2 AGN are objects whose spectra only manifest narrow lines. This suggests that in type 1 AGN, the broad line region (BLR) is visible, while type 2 AGN have the BLR covered by obscuring material. The dichotomy between type 1 and type 2 objects led to a unification scheme based on the orientation of the AGN (e.g., Antonucci 1993; Urry & Padovani 1995), where the central engine is surrounded by an axisymmetric absorber, called the torus, and the amount of obscuration is entirely due to the angle of the line of sight with respect to the AGN axis.
According to the unification model, the column density NH measured in X-ray spectra should follow this simple physical scheme. However, in many AGN, the amount of obscuration in the X-rays is variable on a wide range of timescales (e.g., Risaliti et al. 2002; Markowitz et al. 2014; Laha et al. 2020), suggesting that the unification model is too simplistic to properly describe the whole phenomenon in detail. In particular, in some cases, the X-ray absorbing medium is variable on relatively very short timescales (days to weeks), which implies that the obscuring medium is clumpy and located at much smaller distances than the torus, possibly consistent with the BLR (e.g., Risaliti et al. 2007; Bianchi et al. 2009; Maiolino et al. 2010; Sanfrutos et al. 2013; Marinucci et al. 2013; Walton et al. 2014). In other cases, the X-ray absorption variability timescale is of the order of months or years (e.g., Piconcelli et al. 2007; Rivers et al. 2011, 2015; Coffey et al. 2014; Ricci et al. 2016; Pizzetti et al. 2022), suggesting an origin from the putative circumnuclear torus. However, these results strongly depend on the observation sampling time; frequently adopted monthly observational monitoring may lose the variations at lower timescales. These findings suggest that the X-ray obscurer is not a single homogeneous entity, but rather the observational product of multiple layers of absorbing material from the BLR and the torus.
Moreover, there is mounting evidence for a clumpiness of the circumnuclear torus (e.g., Tristram et al. 2007), which would imply that the probability of observing the central engine is always nonzero (e.g., Elitzur 2008, 2012). The X-ray obscuration can therefore occur because of individual clumps passing through the line of sight, either in the BLR or in the circumnuclear torus.
ESO 323-G77 is a nearby Seyfert 1 galaxy at redshift z = 0.015, with a complex and highly variable absorber. A ∼20 ks observation by XMM-Newton in 2006 unveiled complex absorption and emission features that revealed the presence of outflowing material (Jiménez-Bailón et al. 2008). Subsequent observations with XMM-Newton (2013), Chandra (2011), Swift-XRT (2006), and Suzaku (2011) revealed a wide range of spectral shapes, mainly driven by variations of the column density of a neutral absorber at several timescales (Miniutti et al. 2014; Sanfrutos et al. 2016).
The spectral shape of the source ranges from an unobscured state (NH < 1022 cm−2) in four Chandra observations taken in 2010, a moderately absorbed state (NH ∼ 3 × 1022 − 1023 cm−2) for the 2006 XMM-Newton observation and two 2006 Swift-XRT snapshots, a Compton-thin obscured state (NH ∼ 1 − 6 × 1023 cm−2) observed by XMM-Newton in 2013 and in one Swift-XRT pointing in 2006, and finally a Compton-thick obscured state (NH > 1024 cm−2) in the Suzaku observation taken in 2011. Miniutti et al. (2014) argued that low-column-density states (NH ≲ 1023 cm−2) are due to the presence of a clumpy obscuring torus, while the states with larger column densities are produced by obscuration by clumps of a closer medium, likely co-spatial with the BLR. This is reminiscent of other changing-look sources such as NGC 1365 (e.g., Risaliti et al. 2007).
Here we report the spectral analysis of the first Nuclear Spectroscopic Telescope Array (NuSTAR, Harrison et al. 2013) observations of ESO 323-G77. The paper is organized as follows. In Sect. 2, we describe the data used for this work and the data-reduction pipeline. Section 3 describes the spectral analysis and all the models tested for the data. In Sect. 4, we discuss the spectral models adopted, and in Sect. 5 we summarize our results. We adopt a standard flat cosmology with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7.
2. Data reduction
We analyze here a campaign of five NuSTAR observations performed between December 2016 and March 2017 for a total of ∼200 ks. Each observation has an exposure of approximately 40 ks, taken at 1, 2, 4, and 8 weeks from the first one (see Table 1 for details). The observations were coordinated with ∼2 ks of Neil Gehrels Swift Observatory (Gehrels et al. 2004) snapshots taken with the X-ray Telescope (XRT). The NuSTAR spectra were reduced using the standard HEASOFT v6.28 command NUPIPELINE from the NUSTARDAS software package using the most recent CALDB version. We filtered passages through the South Atlantic Anomaly by setting the task NUCALSAA “optimized” mode. The two Focal Plane Module (FPM) source spectra A and B were extracted from a circular region with a radius of 40″ centered on the source, while the background spectra were extracted from two circular regions with a radius of 45″ each on the same chip. The two FPMA and FPMB spectra were combined and the resulting spectrum was binned to a minimum of 50 counts per bin. The energy band considered for our fits is in the range E = 3 − 65 keV. The spectra of the Swift-XRT observations were extracted with the HEASOFT command XSELECT, selecting a circular region with a 30″ radius. Background spectra were also extracted with the same procedure, but selecting a source-free circular region of 70″ radius. The XRTMKARF task was used to produce ancillary files, and the response was provided by the CALDB repository. Given the negligible variability, the XRT spectra were all combined, and grouped at a minimum of ten counts per energy bin. The energy range 0.5 − 10 keV was considered for the spectral fits. The unfolded spectra, adopting a simple power law with photon index Γ = 2, are shown in Fig. 1.
 |
Fig. 1. Unfolded spectrum of the data analyzed here, adopting a simple model with an absorbed continuum power law with Γ = 2. Red, blue, cyan, black, and magenta spectra mark the NuSTAR spectra of Epochs 1 to 5, respectively. The grey spectrum is the Swift-XRT one. |
NuSTAR observations considered in this work.
3. Spectral analysis
All spectral fits are performed using the software XSPEC v12.12.0 (Arnaud 1996). We adopt a constant Galactic absorption described by a column density of NH = 7.75 × 1020 cm−2 (HI4PI Collaboration 2016) – which is modeled with TBABS – in all our models. In all models, a cross-correlation constant between XRT and NuSTAR (CXRT/NuSTAR) is adopted. In every model, the best fit for this constant is CXRT/NuSTAR = 0.8 ± 0.1. All errors on the best-fit parameters are given with a 90% confidence level, corresponding to Δχ2 = 2.71.
3.1. Slab-reflection model
We first tested a simple absorbed continuum power law plus a scattered power law, with tied photon index. Fe Kα at E = 6.4 keV and Fe Kβ at E = 7.06 keV emission lines are also included, with fixed centroid energies and width (σ = 0.03 keV). The Fe Kβ line normalization is fixed at 13% of the Kα line (e.g., Palmeri et al. 2003). However, this simple model does not properly describe the current data set. As a very flat photon index (Γ ∼ 1.35) and an unacceptable statistic (χ2/d.o.f. = 1751/907) are obtained, it is clear that this model does not properly fit the data. Moreover, an equivalent width of EW > 250 eV is obtained for the Fe Kα line, which is a signature of the presence of a reflection component in obscured sources (e.g., Krolik et al. 1994). Therefore, we test a model that includes an absorbed power law and a neutral reflector. The slab-reflection model PEXRAV (Magdziarz & Zdziarski 1995) is used with Fe Kα and Fe Kβ emission lines modeled by two ZGAUSS components, plus an absorbed main power law ZPHABS*CABS*ZPOW, and a soft-scattered power law ZPOW. The overall model is
The five NuSTAR spectra are fitted together, keeping all parameters tied among different epochs to those of Epoch 4, which is the brightest observation, with the exception of the column density NH of the absorber and the normalizations of the main power law and the reflection component, in order to take their variability into account. The Swift-XRT spectrum has all parameters tied to Epoch 4, as in all models considered in this work. We assume that the Fe K lines do not vary, as in most absorbed AGN (e.g., Fukazawa et al. 2016), and we keep the Fe Kβ normalization fixed at 13% of the value of the Fe Kα. All parameters of the scattered power law are kept tied to those of the main one, whereas CONST1 is kept fixed to a value of 1 at all epochs, while CONST2 is fitted for Epoch 4 and not allowed to vary, in order to take their ratio into account.
The continuum is characterized by a photon index Γ = 1.75 ± 0.03 and a normalization that varies from 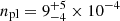 to npl = (2.0 ± 0.3)×10−3 photons cm−2 s−1 keV−1, while the second constant is kept free and is ∼10−2. PEXRAV models a pure reflection component from an infinite slab, meaning that the reflection constant is fixed to ℛ = −1. The photon index of the reflection component is tied to that of the main continuum, while the cut-off energy is fixed to Ecut = 500 keV. The line of sight absorption is given by NH ∼ (7 − 11)×1023 cm−2, depending on the observation, and therefore the model CABS is included to take into account the suppression of the continuum due to electron scattering, which is non-negligible at column densities larger than 5 × 1023 cm−2 (e.g., Yaqoob 2012), with column density fixed to the value of ZPHABS.
to npl = (2.0 ± 0.3)×10−3 photons cm−2 s−1 keV−1, while the second constant is kept free and is ∼10−2. PEXRAV models a pure reflection component from an infinite slab, meaning that the reflection constant is fixed to ℛ = −1. The photon index of the reflection component is tied to that of the main continuum, while the cut-off energy is fixed to Ecut = 500 keV. The line of sight absorption is given by NH ∼ (7 − 11)×1023 cm−2, depending on the observation, and therefore the model CABS is included to take into account the suppression of the continuum due to electron scattering, which is non-negligible at column densities larger than 5 × 1023 cm−2 (e.g., Yaqoob 2012), with column density fixed to the value of ZPHABS.
The Fe Kα emission line centroid is found at 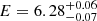 keV, with width σ = 0.2 ± 0.1 keV and normalization nFeKα = (1.3 ± 0.4)×10−5 photons cm−2 s−1 keV−1. The range of the equivalent width of the Fe Kα emission line is EW ∼ 0.2 − 0.4 keV. The cut-off energy in the reflection spectrum is fixed at Ecut = 500 keV, while the photon index is tied to that of the continuum component. The abundances are fixed to solar ones, and the reflector normalizations vary in the range nrefl ∼ (4 − 5)×10−3 photons cm−2 s−1 keV−1. The model has an overall goodness of fit of χ2/d.o.f. = 978/909 = 1.07.
keV, with width σ = 0.2 ± 0.1 keV and normalization nFeKα = (1.3 ± 0.4)×10−5 photons cm−2 s−1 keV−1. The range of the equivalent width of the Fe Kα emission line is EW ∼ 0.2 − 0.4 keV. The cut-off energy in the reflection spectrum is fixed at Ecut = 500 keV, while the photon index is tied to that of the continuum component. The abundances are fixed to solar ones, and the reflector normalizations vary in the range nrefl ∼ (4 − 5)×10−3 photons cm−2 s−1 keV−1. The model has an overall goodness of fit of χ2/d.o.f. = 978/909 = 1.07.
3.2. Toroidal model MYTORUS
The disk-reflection model provides an acceptable goodness of fit. However, as pointed out by Yaqoob (2012), the model is inadequate to describe the reflector in detail. Indeed, the reflection spectrum assumes an infinite line-of-sight column density and does not consider the finite nature of the reflector, as it was created assuming a point source illuminating an infinite slab.
Therefore, in the following, we adopt a detailed toroidal reflection model, MYTORUS (Murphy & Yaqoob 2009). This model assumes a toroidal geometry characterized by a column density NH and a fixed covering factor of 0.5, corresponding to a torus opening angle of 60°. As the column density of ESO 323-G77 is variable, we adopt the decoupled standard model, in which the column density of the absorber NH, abs is different from the column density of the reflector NH, refl (Yaqoob 2012). As a first step, we multiply the continuum power law by the zeroth-order component of the model, namely the XSPEC table MYTZ1. This table allows us to evaluate the line-of-sight column density NH of the absorber. We consider the angle θ, which is the inclination angle between the polar axis of the absorber and the line of sight. For the MYTZ, we fix θ = 90°, which corresponds to a line-of-sight direction for the absorber. We model the Compton hump continuum due to neutral reflection with the additive table MyTS02. We fix θ = 0° to assume that this reflected component does not come from the line of sight. The column density of this component is independent from that of the line of sight (decoupled model), and the normalization and photon index are kept fixed to those of the continuum. The Fe Kα and Fe Kβ emission lines of the line-of-sight reflection are included with the additive table MyTL03, with fixed value θ = 0°, and the normalization and Γ tied to the absorbed continuum values. We multiply MyTL0 by the convolution model GSMOOTH in order to take into account the broadening of the iron line. We fix the line width in the model to σ = 0.03 keV, following the upper limit found by Sanfrutos et al. (2016) with Chandra HETG. The fit has a global statistic of χ2/d.o.f. = 1129/915 = 1.23.
We also allow for a forward scattering component on the line of sight, namely another Compton-reflected continuum with fixed θ = 90° (hereafter MyTS90). We assume that the column density (NH, 90) of this component coincides with the line-of-sight NH. This additional reflection component is also accompanied by a table with iron lines MyTL90, where the column density is tied to NH, 90. MyTL90 is also multiplied by a GSMOOTH model with fixed σ = 0.03 keV. The normalizations and photon indices of MyTS90 and MyTL90 are also tied to that of the main power law. The goodness of fit is given by χ2/d.o.f. = 1162/915 = 1.25. This means that the reflection due to the absorbing material on the line of sight is not required in our model. In all models from here on, we only consider the reflection component out of the line of sight.
The model is therefore
We find a line-of-sight NH, abs ranging from (3.2 ± 0.3)×1023 cm−2 in Epoch 4 up to (5.5 ± 0.5)×1023 cm−2 at Epoch 2. The column density of the reflector outside of the line of sight is 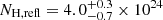 cm−2. We also obtain a flatter photon index (Γ = 1.61 ± 0.03) with respect to the one obtained with the slab-reflection model.
cm−2. We also obtain a flatter photon index (Γ = 1.61 ± 0.03) with respect to the one obtained with the slab-reflection model.
3.3. Ionized absorbers
Figure 2 shows the residuals of the model in Eq. (2). There are significant residuals in the E ∼ 5 − 10 keV energy range and above E ∼ 20 keV, showing that it does not properly fit the curvature of the spectrum, which means that additional components might be needed. As past observations of this source reported the presence of ionized absorbers (Jiménez-Bailón et al. 2008; Miniutti et al. 2014; Sanfrutos et al. 2016), we consider the addition of one such feature. We denote this absorber Zone 1. We adopt a grid of photoionized absorbers produced with the XSTAR (Kallman & Bautista 2001) photoionization code. The grid spans a relatively wide ionization (log(ξ/erg cm s−1)∼2 − 6) and column density (NH ∼ 5 × 1022 − 5 × 1024 cm−2) range. The turbulent velocity adopted to generate the grid is vturb = 3000 km s−1. We first allow the ionization and the column density to vary among different observations; however, we do not find significant changes in either parameter, and therefore we fix both parameters to those of Epoch 4. The addition of this component improves the fit by Δχ2/Δd.o.f. = 159/2, with the overall goodness of fit being χ2/d.o.f. = 970/913. The photon index is 1.74 ± 0.06. The column density of this absorber is given by NH, z1 = (5.8 ± 0.5)×1023 cm−2 and the ionization is log ξz1/(erg cm s−1) = 2.6 ± 0.1.
 |
Fig. 2. Data-to-model ratio for the model in Eq. (2), where the reflector is modeled with MYTS0, and only the neutral absorber is considered. There are still significant ratios in the whole analyzed band, in particular the curvature is not well modeled by a single neutral absorber. |
The addition of the Zone 1 absorber significantly reduces the curvature residuals in Fig. 2. The residuals with the new model in the E = 4 − 13 keV band are shown in Fig. 3, where the data still show significant residuals in the Fe Kα spectral region (E = 6 − 10 keV) in almost all observations. Most observations show an absorbing structure around 6.5 − 7 keV, which may be due to absorbing material. This is particularly noticeable near 7 keV in epochs 3 and 4 (see Fig. 3, panels 3 and 4). Moreover, a second more ionized absorber was reported in Jiménez-Bailón et al. (2008), Miniutti et al. (2014) and Sanfrutos et al. (2016), which could be responsible for this absorbing feature. We therefore add a second absorber, which we label Zone 2, using the same XSTAR grid used for the first one. We initially assumed that this more ionized absorber also did not vary between the five epochs. The addition of this absorber improves the statistic by Δχ2/Δd.o.f. = 26/2 to χ2/d.o.f. = 944/911. We obtain a photon index of 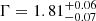 , a column density of
, a column density of 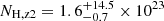 cm−2, and an ionization parameter of
cm−2, and an ionization parameter of 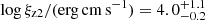 . Given its higher ionization, we assume that Zone 2 is closer to the black hole with respect to Zone 1. As NH and log ξ are notoriously degenerate, we keep the ionization at all epochs fixed to that of Epoch 4, while all column densities are allowed to vary independently. The goodness of fit slightly improves to χ2/d.o.f. = 938/907.
. Given its higher ionization, we assume that Zone 2 is closer to the black hole with respect to Zone 1. As NH and log ξ are notoriously degenerate, we keep the ionization at all epochs fixed to that of Epoch 4, while all column densities are allowed to vary independently. The goodness of fit slightly improves to χ2/d.o.f. = 938/907.
 |
Fig. 3. Residuals when the model with only one ionized absorber is fitted. The observations are ordered top to bottom from the first to the last taken. An absorption complex at ∼7 keV is observed in Epochs 1, 3, and 4. At Epoch 5, the absorption complex is observed at ∼8.5 keV, suggesting a possible outflowing velocity of v ∼ 0.2c. |
Finally, as shown in Fig. 3, the absorber in Epoch 5 appears as a blueshifted absorption line at Erest ∼ 8.5 keV, which is a clear signature of a nonzero velocity. Hence, we free the velocity of the Zone 2 absorber in Epoch 5 in order to take this blueshift into account. We obtain zobs = −0.18 ± 0.02, which corresponds4 to a velocity 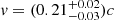 . The goodness of fit further improves by Δχ2/Δd.o.f. = 11/1 to a final value of χ2/d.o.f. = 927/906 = 1.02. The column density of the absorber in Zone 2 is constrained in four out of five observations, ranging from
. The goodness of fit further improves by Δχ2/Δd.o.f. = 11/1 to a final value of χ2/d.o.f. = 927/906 = 1.02. The column density of the absorber in Zone 2 is constrained in four out of five observations, ranging from 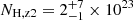 cm−2 (Epoch 1) to
cm−2 (Epoch 1) to 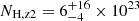 cm−2 (Epoch 3). We note that, in Epoch 2, we can place only an upper limit on the column density. Indeed, Epoch 2 does not show a clear absorption signature in Fig. 3 (blue curve). The ionization parameter is
cm−2 (Epoch 3). We note that, in Epoch 2, we can place only an upper limit on the column density. Indeed, Epoch 2 does not show a clear absorption signature in Fig. 3 (blue curve). The ionization parameter is 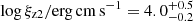 .
.
The final model is therefore
where XSTAR1 and XSTAR2 are the ionized absorbers in Zones 1 and 2, respectively. Following the addition of these two ionized absorbers, the photon index of the spectrum is 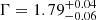 . Figure 4 shows the contour plot of Γ with the MyTZ column density NH for the brightest observation of the campaign, namely Epoch 4. The contour plot shows that both the photon index Γ and the absorbing column density NH, abs are well constrained at 3σ confidence level. The best-fit parameters obtained with this model are summarized in Table 2. The normalized spectrum with data-to-model ratios and the unfolded spectrum are shown in Figs. 5 and 6.
. Figure 4 shows the contour plot of Γ with the MyTZ column density NH for the brightest observation of the campaign, namely Epoch 4. The contour plot shows that both the photon index Γ and the absorbing column density NH, abs are well constrained at 3σ confidence level. The best-fit parameters obtained with this model are summarized in Table 2. The normalized spectrum with data-to-model ratios and the unfolded spectrum are shown in Figs. 5 and 6.
 |
Fig. 4. Contour plot of the spectral slope Γ and the line-of-sight column density NH obtained for Epoch 4, as obtained from the zero-order MYTORUS model. The red, green, and blue lines represent 68% (1σ), 95% (2σ), and 99.7% (3σ) contours. |
 |
Fig. 5. Normalized spectra and data-to-model ratio of ESO 323-G77. The MYTORUS model is shown here. The same color code as that used in Fig. 3 is adopted, with the addition of the Swift-XRT spectrum, shown in gray. |
 |
Fig. 6. Unfolded spectra of ESO 323-G77 determined from the Swift-XRT and NuSTAR data based on the MYTORUS model. |
We also tested an alternative approach in which the absorber column density NH, abs is kept tied among the observations, while the photon index Γ is allowed to vary. Unsurprisingly, the column density is NH = (2.6 ± 0.5)×1023 cm−2, which is the mean value of the NH found independently when the parameter is allowed to vary between observations. We find various values of the photon index, ranging from Γ = 1.51 ± 0.06 for Epoch 3 to 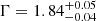 for Epoch 4. However, we obtain a poorer fit statistic of χ2/d.o.f. = 983/906, which means that an absorber variation is favored. Notably, the smaller photon indices are also the ones with greater absorption and vice versa, resulting in an apparent steeper-when-brighter effect. This effect is driven by the absorption variability, as the source has historically experienced in the past, and should not be confused with the continuum softer when brighter effect, driven by intrinsic Γ variations (e.g., Sobolewska & Papadakis 2009; Serafinelli et al. 2017).
for Epoch 4. However, we obtain a poorer fit statistic of χ2/d.o.f. = 983/906, which means that an absorber variation is favored. Notably, the smaller photon indices are also the ones with greater absorption and vice versa, resulting in an apparent steeper-when-brighter effect. This effect is driven by the absorption variability, as the source has historically experienced in the past, and should not be confused with the continuum softer when brighter effect, driven by intrinsic Γ variations (e.g., Sobolewska & Papadakis 2009; Serafinelli et al. 2017).
3.4. Alternative model for the reflector: BORUS
We also tested for a spherical reprocessor using the model BORUS (Baloković et al. 2018). We consider a continuum described by a cut-off power law, ZCUTOFFPL, with a line-of-sight absorption modeled by ZPHABS, and reflector described by the table BORUS025. We also include the two ionized absorbers located in Zones 1 and 2. In this model, we again allow the column density of the Zone 2 high-ionization absorber NH to vary between observations, while we assume the ionization parameter to remain constant between the observations of the campaign. The model used is
We obtain a photon index 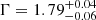 , which is consistent with the value obtained with the MYTORUS model. As the cut-off energy Ecut is unconstrained, we fix it to a fiducial Ecut = 500 keV. The neutral column density varies from NH, abs = (2.7 ± 0.3)×1023 cm−2 (Epochs 1 and 2) to (3.4 ± 0.3)×1023 cm−2 (Epoch 5), which is roughly consistent with those found with the MYTORUS model. The column density of the reprocessor is
, which is consistent with the value obtained with the MYTORUS model. As the cut-off energy Ecut is unconstrained, we fix it to a fiducial Ecut = 500 keV. The neutral column density varies from NH, abs = (2.7 ± 0.3)×1023 cm−2 (Epochs 1 and 2) to (3.4 ± 0.3)×1023 cm−2 (Epoch 5), which is roughly consistent with those found with the MYTORUS model. The column density of the reprocessor is 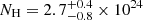 cm−2, which is consistent with the value found in the MYTORUS model. The covering factor of the reprocessor is given by
cm−2, which is consistent with the value found in the MYTORUS model. The covering factor of the reprocessor is given by 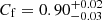 . Finally, we obtain consistent values for the column density and the ionization parameter of the ionized absorber in Zone 1. The ionization parameter of the absorber in Zone 2 is also consistent with the one obtained with the MYTORUS model. The column density of the absorber in Zone 2 is also consistent, although with large uncertainties. The goodness of fit of this model is given by χ2/d.o.f. = 923/901.
. Finally, we obtain consistent values for the column density and the ionization parameter of the ionized absorber in Zone 1. The ionization parameter of the absorber in Zone 2 is also consistent with the one obtained with the MYTORUS model. The column density of the absorber in Zone 2 is also consistent, although with large uncertainties. The goodness of fit of this model is given by χ2/d.o.f. = 923/901.
3.5. Comptonizing plasma continuum
It is also interesting to investigate the coronal parameters of this source, as these are often elusive for obscured sources. Therefore, we investigated physical Comptonization models for the continuum with both the MYTORUS and BORUS models. Starting from the MYTORUS model in Eq. (3), we adopted the same configuration and free parameters, but we replaced the power-law continuum with COMPTT (Titarchuk 1994). We also adopted the appropriate MYTORUS table, namely we adopt the tables MYTS 6 and MyTL
6 and MyTL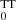 7, and we use them in the same way as we used MYTS0 and MYTL0 in Sect. 3.2. The model is then
7, and we use them in the same way as we used MYTS0 and MYTL0 in Sect. 3.2. The model is then
We first explored the slab coronal geometry by fixing the value of the parameter approx to 0.5. We do not find significant differences in any other parameter obtained in the previous section. The coronal temperature with this fit is kT = 38 ± 2 keV, while the optical depth is τ = 1.4 ± 0.1. The goodness of fit of this model is given by χ2/d.o.f. = 920/906. Typically, assuming a spherical geometry in COMPTT, the best-fit coronal parameters would be a similar temperature, but a larger optical depth (e.g., Tortosa et al. 2018). However, the MYTS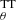 tables do not include larger values of τ, and therefore it is not possible to explore the parameters of a spherical geometry.
tables do not include larger values of τ, and therefore it is not possible to explore the parameters of a spherical geometry.
However, the spherical geometry might be explored within the BORUS model shown in Eq. (4). BORUS12 is produced with the thermal comptonization continuum model NTHCOMP (Magdziarz & Zdziarski 1995), which assumes a spherical geometry for the corona. Hence, we also use this model for the continuum, and the overall model is therefore:
with a goodness of fit of χ2/d.o.f. = 915/901. We obtain 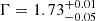 and a coronal temperature of
and a coronal temperature of 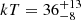 keV. Remarkably, this value is consistent with the COMPTT temperature obtained assuming a slab geometry in the MYTORUS model, even though we adopted a different continuum model.
keV. Remarkably, this value is consistent with the COMPTT temperature obtained assuming a slab geometry in the MYTORUS model, even though we adopted a different continuum model.
3.6. Relativistic reflection
The presence of a possible relativistic iron line in the X-ray spectra of this AGN was inferred by Jiménez-Bailón et al. (2008) during an unabsorbed state. Therefore, we tested the possibility that such component could also be detected in an absorbed state, and we added the relativistic reflection component RELXILL (García et al. 2014; Dauser et al. 2014) to the model in Eq. (3). The global fit improves by Δχ2/Δd.o.f. = 38/7. All parameters with the exception of the normalization are kept tied between observations. We assume a frozen cut-off energy Ecut = 500 keV, a disk external radius of Rout = 400Rg, where Rg = GM/c2 is the gravitational radius, a 45° inclination (Schmid et al. 2003), a solar iron abundance, and an emissivity index of −3. The spin of the black hole is unconstrained, for which we therefore freeze a = 0, and we obtain a disk internal radius Rin < 12Rg, which is consistent with the findings of Miniutti et al. (2014). The disk ionization parameter is log(ξ/erg cm s−1) > 3. A steeper photon index 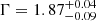 is found, although this is consistent with the one found with the model in Eq. (3) at 90% confidence level. The normalization of the relativistic component is unconstrained in Epoch 4, normrelx, 4 < 8 × 10−6 photons cm−2 s−1 keV−1, while in Epochs 2, 3, and 5, it is roughly constant (
is found, although this is consistent with the one found with the model in Eq. (3) at 90% confidence level. The normalization of the relativistic component is unconstrained in Epoch 4, normrelx, 4 < 8 × 10−6 photons cm−2 s−1 keV−1, while in Epochs 2, 3, and 5, it is roughly constant (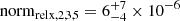 photons cm−2 s−1 keV−1), and in Epoch 1 it is
photons cm−2 s−1 keV−1), and in Epoch 1 it is 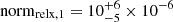 photons cm−2 s−1 keV−1. We do not find significant differences in the absorbing column density from Table 2. However, the two reflectors are degenerate, and therefore we find a lower limit for the neutral reflector column density, NH, refl > 4 × 1024 cm−2, even though it is consistent with the value of Table 2.
photons cm−2 s−1 keV−1. We do not find significant differences in the absorbing column density from Table 2. However, the two reflectors are degenerate, and therefore we find a lower limit for the neutral reflector column density, NH, refl > 4 × 1024 cm−2, even though it is consistent with the value of Table 2.
We also tested RELXILL as an additional reflection component in the model where we assume a comptonizing continuum COMPTT (Eq. (5)) to test the possible influence on the measurements of kT and τ. The temperature of the corona is kT = 26 ± 9 keV, and 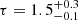 , which is consistent within the 3σ contour plot of these two parameters for the model without a disk-reflection component (see Fig. 7). Very similar results are obtained by testing RELXILL on the two models that use BORUS for the neutral reflection.
, which is consistent within the 3σ contour plot of these two parameters for the model without a disk-reflection component (see Fig. 7). Very similar results are obtained by testing RELXILL on the two models that use BORUS for the neutral reflection.
 |
Fig. 7. Contour plot of the optical depth τ versus the coronal temperature kTe, assuming a slab coronal geometry with the COMPTT Comptonization model. The red, green, and blue lines represent 68% (1σ), 95% (2σ), and 99.7% (3σ) confidence levels, respectively. |
We stress that the RELXILL component contributes to ≲10% of the 2 − 10 keV observed flux, and the main changes in this model are in the spectral region between 3 and 5 keV, where NuSTAR is less sensitive. Also, many parameters of the relativistic reflection model are unconstrained because of the complex model and numerous degeneracies with the neutral reflector. We point out that, in order to accurately measure the parameters of the ionized relativistic reflection within the framework of such a complex spectral model, a broad band spectrum and an improved energy resolution would be needed. For instance, a simultaneous XMM-Newton and NuSTAR observation would be ideal to observe the Fe Kα spectral region in detail.
4. Discussion
4.1. Comparison between MYTORUS and BORUS models
The MYTORUS model has been built assuming a toroidal shape that is asymmetric on the azimuthal axis. The covering factor in this model is kept fixed by assuming that the torus opening angle is θOA = 60°, which means that its value is Cf = cos(θOA) = 0.5 (Murphy & Yaqoob 2009). Conversely, BORUS has a spherical geometry for the reprocessor, with polar cutouts corresponding to a variable opening angle θOA, and therefore is able to fit a value for the Cf, ranging from Cf = 0.1 to Cf = 1 (Baloković et al. 2018). The two best-fit values of the average column density of the reflector are slightly different, 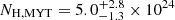 cm−2 and
cm−2 and 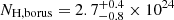 cm−2. Moreover, the covering factor found with the BORUS model is not consistent with the value of Cf = 0.5 assumed in the MYTORUS one, and this might explain the difference in the column density estimate.
cm−2. Moreover, the covering factor found with the BORUS model is not consistent with the value of Cf = 0.5 assumed in the MYTORUS one, and this might explain the difference in the column density estimate.
In order to properly compare the two models, we construct a BORUS version of the MYTORUS decoupled model. We consider an out of line of sight reflector by setting the torus inclination to cos θ = 0.95, which is the maximum value allowed by the BORUS model. This corresponds to an inclination angle of θ = 18°, differently from the MYTORUS value θ = 0. The covering factor is fixed to the MYTORUS value Cf = 0.5. As expected, the inclination discrepancy is not crucial (see also Marchesi et al. 2019) and we obtain 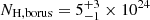 cm−2 ≃ NH, MYT. We stress that this model has been built with the sole purpose of comparing the column density of the torus for the MYTORUS to the one obtained with BORUS, as the goodness of fit is χ2/d.o.f. = 944/902, which is marginally worse than the model presented in Eq. (4).
cm−2 ≃ NH, MYT. We stress that this model has been built with the sole purpose of comparing the column density of the torus for the MYTORUS to the one obtained with BORUS, as the goodness of fit is χ2/d.o.f. = 944/902, which is marginally worse than the model presented in Eq. (4).
However, this configuration is more realistic than the one with a covering factor of Cf ∼ 0.9, as the latter would imply that ∼90% of the sightline intercepts a Compton-thick column density. As a consequence, a Compton-thick state would be observed far more frequently. In fact, while this source has been observed several times, it has been caught in a Compton-thick state only once in 2011 by Suzaku. This would be possible if we were looking at this Seyfert galaxy with an exceptional, extremely polar line of sight, whereas Schmid et al. (2003) estimated a 45° angle for the inclination. Therefore a lower covering factor is likely a more realistic scenario for this source.
4.2. Compton-thin absorber and Compton-thick reflector
Both models indicate that the absorbing material is Compton-thin, with column density ranging from NH, abs ∼ 2 × 1023 cm−2 up to NH, abs ∼ 4 × 1023 cm−2. This AGN was already caught in this state by one Swift-XRT snapshot in 2006 and by XMM-Newton in 2013. However, as shown by Miniutti et al. (2014), the source is able to change from a relatively unobscured state (NH, abs ∼ 2 − 4 × 1022 cm−2) up to a Compton-thick state.
Previous analyses of ESO 323-G77 suggested that low obscuration states (NH ≲ 1023 cm−2) might be caused by the presence of the obscuring torus, while higher obscuration states are likely due to absorption by cold intra-clump material located in the broad line region (Miniutti et al. 2014; Sanfrutos et al. 2016). However, given that we do not observe a change of state during the campaign analyzed in this work, but only moderate changes in the absorber column density NH, abs, we are not able to argue in favor of or against this hypothesis.
The unprecedented effective area of NuSTAR in the E > 10 keV band allows us to properly study the reflection component of the X-ray spectrum of this source. In particular, both the MYTORUS and BORUS models clearly point to the presence of a Compton-thick reflector with 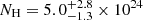 cm−2 or
cm−2 or 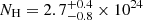 , depending on the model. If the absorption is indeed produced by BLR clumps or intra-clump cold material, this result indicates that the constant Compton-thick reflector is located farther away from the central X-ray source, and it should be associated with the classic torus.
, depending on the model. If the absorption is indeed produced by BLR clumps or intra-clump cold material, this result indicates that the constant Compton-thick reflector is located farther away from the central X-ray source, and it should be associated with the classic torus.
4.3. Ionized absorbers
Similar to the results presented in Jiménez-Bailón et al. (2008), Miniutti et al. (2014), and Sanfrutos et al. (2016), our data show the presence of two ionized absorbers. We can estimate the location of these ionized absorbers using standard arguments. For instance, the maximum distance from the black hole can be estimated by considering that the size of the absorbing clump Rclump cannot be larger than the distance, that is Rclump = NH/n < rmax, where n is the density of the clump (e.g., Crenshaw & Kraemer 2012; Serafinelli et al. 2021). From the ionization parameter definition, the maximum distance from the black hole can be written as
The first absorber, located in what we denote Zone 1, is characterized by an ionization parameter of ξ ∼ 250 erg cm s−1. The ionizing luminosity in the E = 13.6 eV–13.6 keV energy band is Lion ≃ (2.6 ± 0.2)×1044 erg s−1 and the column density is NH ≃ 3 × 1023 cm−2. Therefore, using Eq. (7), we obtain 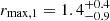 pc.
pc.
The second ionized absorber, located in Zone 2, is characterized by a larger ionization parameter, ξ ≃ 104 erg cm s−1. The average column density is given by NH ≃ 6 × 1023 cm−2. Therefore, using Eq. (7) we obtain a maximum distance of 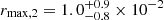 pc.
pc.
We consider an Eddington ratio of log λEdd = −0.56 and a black hole mass of MBH = 2.5 × 107 M⊙ (Wang & Zhang 2007), from which we can compute log Lbol ≃ 44.93. Assuming that Lbol/L5100 Å ∼ 10 (e.g., Collin et al. 2002), this means an optical luminosity of log L5100&Å ≃ 43.93. We consider the relation between the size of the BLR and the optical luminosity introduced by Bentz et al. (2009):
and we obtain a radius for the BLR of RBLR ≃ 0.02 pc. We therefore obtain that the moderately ionized absorber in Zone 1 could be located outside the BLR at r1 ≲ 1.5 pc, while the more ionized absorber in Zone 2 is likely co-spatial or within the BLR.
In the scenario in which the cold absorber is either co-spatial with one of the two ionized absorbers or sandwiched between them (Sanfrutos et al. 2016), the cold absorber would be located between the outer BLR – which would be consistent with the model proposed by Miniutti et al. (2014) – and parsec-scale distances. In the latter case, a possible scenario would be the presence of an inner thick reflecting ring surrounded by a thinner absorbing layer at parsec scales (e.g., Buchner et al. 2019). Recent mid-infrared results (Leftley et al. 2021) provide evidence of the presence of polar warm dust at a distance r ≳ 1.5 pc, which is consistent with this scenario. The outer layer would also be clumpy, allowing the observed long-term variability, which is a similar scenario to the one proposed for NGC 7479 by Pizzetti et al. (2022).
4.4. Ultra-fast outflow
The velocity of the absorber in Zone 2 is v ≲ 9000 km s−1, which is consistent with the values measured by Jiménez-Bailón et al. (2008) and Sanfrutos et al. (2016) of v ≃ 2000 km s−1 in Epochs 1–4. However, in Epoch 5, we notice a moderately relativistic velocity v ∼ 0.21c, with a level of Δχ2/d.o.f. = 11/1. This is a tentative indication that we are observing an absorber outflowing at high velocity, a phenomenon that is commonly known as ultra-fast outflow (UFO) and is fairly common (∼40%) in Seyfert galaxies and quasars (e.g., Pounds et al. 2003; Braito et al. 2007; Tombesi et al. 2010, 2015; Gofford et al. 2013; Nardini et al. 2015; Serafinelli et al. 2019). Moreover, UFOs are known to be extremely variable (e.g., Reeves et al. 2014; Matzeu et al. 2017; Braito et al. 2018, 2022), therefore it is not surprising that the UFO appears within a relatively short timescale in an AGN that never showed signs of its presence before. However, given its modest (∼3σ) detection here, further observations would be required to confirm the detection of the UFO feature or its variability.
4.5. Coronal parameters
The X-ray continuum is well known to be produced by inverse Compton on UV seed photons gaining energy by a very hot electron corona (e.g., Haardt & Maraschi 1991, 1993). The electron temperature therefore plays a crucial role in regulating the Comptonization of UV seed photons. Indeed, the main continuum breaks at the so-called cut-off energy Ecut, which is tied to the temperature by the relation Ecut = 2 − 3 kTe, depending on the geometry of the corona (e.g., Petrucci et al. 2001).
When the COMPTT model is adopted to model the continuum, assuming a slab geometry for the corona in the MYTORUS model shown in Eq. (5), we find that the temperature of the corona is kTe = 38 ± 2 keV, with an optical depth τ = 1.4 ± 0.1. The τ − Γ contour plot is shown in Fig. 7. As the grids do not allow much larger values of τ, the only way to study the spherical geometry is to use the NTHCOMP Comptonization continuum with the BORUS model (Eq. (6)), and we find a consistent temperature, albeit with larger errors: 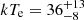 keV. We can estimate the optical depth using the following equation, which is valid for a spherical optically thick (τ > 1) corona (Zdziarski et al. 1996):
keV. We can estimate the optical depth using the following equation, which is valid for a spherical optically thick (τ > 1) corona (Zdziarski et al. 1996):
Using the best-fit values of the BORUS model summarized in Table 3, we obtain τ ≃ 2.8.
These are fairly standard values, as the coronal temperature is known to span from kT ∼ 3 keV up to kT ∼ 450 keV (e.g., Matt et al. 2015; Tortosa et al. 2018, 2022; Serafinelli et al., in prep.). However, even though some authors recently unveiled coronal temperatures in isolated obscured sources (e.g., Middei et al. 2021) and samples of Seyfert 2 galaxies (e.g., Baloković et al. 2020), they are not easily constrained, because they are often degenerate with the reflection spectrum cut-off.
5. Summary and conclusions
We presented the spectral analysis of a campaign of five NuSTAR observations of the Seyfert 1.2 galaxy ESO 323-G77. Our results can be summarized as follows.
-
The source has been observed in a persistently obscured but Compton-thin state due to the presence of neutral obscuring material on the line of sight, with column densities in the range NH ∼ 2 − 4 × 1023 cm−2.
-
We find a Compton-thick reflector when modeling it with MYTORUS or BORUS. The two NH, refl values are not consistent, but this result is dependent on the covering factor of the reflector, which is assumed as Cf = 0.5 in MYTORUS and fitted (
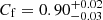 ) in BORUS. By fixing a more realistic Cf = 0.5 in BORUS, the two results are consistent.
) in BORUS. By fixing a more realistic Cf = 0.5 in BORUS, the two results are consistent. -
Two ionized absorbers are needed in our models, which is consistent with the findings of Jiménez-Bailón et al. (2008), Miniutti et al. (2014), and Sanfrutos et al. (2016). The ionized absorber identified with Zone 1 is located at a distance of about r1 ∼ 1.5 pc from the black hole, most likely outside the broad line region, whose size is estimated as RBLR ≃ 0.02 pc. The ionized absorber in Zone 2 is instead located at r2 ≃ 10−2 pc, either co-spatial with or within the BLR.
-
Assuming that the cold absorber is either at the same distance of one of the two ionized absorbers or at an intermediate one, its location can be placed between the outer BLR and at parsec-scale distances. In the first case, this would be consistent with the model proposed by Miniutti et al. (2014), consisting of cold absorbing intra-clump material in the BLR. In the second case, the most likely scenario is parsec-scale Compton-thin absorbing material surrounding a Compton-thick reflector (Buchner et al. 2019), which is supported by recent mid-infrared detection of polar dust at r ≳ 1.5 pc (Leftley et al. 2021).
-
The ionized absorber in Zone 2 is blueshifted at Epoch 5 to the value zobs ≃ −0.18, which suggests an outflowing velocity of vout ≃ 0.2c.
-
The coronal temperature is constrained in both models, finding kTe ≃ 36 − 38 keV, assuming spherical and slab geometry, respectively. The optical depth is τ ≃ 1.4 when the slab coronal geometry is assumed, and τ ≃ 2.8 for a spherical corona.
-
We find hints of the possible presence of a relativistic reflection component from the accretion disk. However, this component contributes to ≲10% of the observed 2 − 10 keV flux, and it mostly affects the 3 − 5 keV energy band. Hence, the parameters of the disk reflection component are very difficult to constrain, and data with better energy resolution are needed to study this feature further.
Although the source has undergone changes of state (e.g., obscured to unobscured) several times in the past (Miniutti et al. 2014), no such significant change was observed during this campaign. However, longer campaigns should be able to observe the source passing from obscured to unobscured or vice versa, setting an upper limit on the location of the obscurer. Future high-resolution instruments such as the microcalorimeter Resolve on board XRISM (XRISM Science Team 2020) will be able to measure the properties of the absorbers with much more detail, particularly on their location and outflowing velocity. Moreover, future hard X-ray (E = 2 − 200 keV) instruments such as the High Energy X-ray Probe (HEX-P, Madsen et al. 2018) will allow us to measure the reflection parameters with unprecedented accuracy.
All MYTORUS tables are available at http://mytorus.com/model-files-mytorus-downloads.html. The MYTZ model can be downloaded with the table mytorus_Ezero_v00.fits
All BORUS tables can be downloaded from the website https://sites.astro.caltech.edu/~mislavb/download
Acknowledgments
The authors thank the referee for useful comments that improved the quality of this paper. RS, VB, PS, ADR, and RDC acknowledge financial contribution from the agreements ASI-INAF n.2017-14-H.0 and n.I/037/12/0. This research has made use of data and software provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC and the High Energy Astrophysics Division of the Smithsonian Astrophysical Observatory. This research has made use of the NuSTAR Data Analysis Software (NUSTARDAS) jointly developed by the ASI Space Science Data Center (SSDC, Italy) and the California Institute of Technology (Caltech, USA). We acknowledge the use of public data from the Swift data archive.
References
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Baloković, M., Brightman, M., Harrison, F. A., et al. 2018, ApJ, 854, 42 [Google Scholar]
- Baloković, M., Harrison, F. A., Madejski, G., et al. 2020, ApJ, 905, 41 [Google Scholar]
- Bentz, M. C., Peterson, B. M., Netzer, H., Pogge, R. W., & Vestergaard, M. 2009, ApJ, 697, 160 [Google Scholar]
- Bianchi, S., Piconcelli, E., Chiaberge, M., et al. 2009, ApJ, 695, 781 [Google Scholar]
- Braito, V., Reeves, J. N., Dewangan, G. C., et al. 2007, ApJ, 670, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Braito, V., Reeves, J. N., Matzeu, G. A., et al. 2018, MNRAS, 479, 3592 [Google Scholar]
- Braito, V., Reeves, J. N., Matzeu, G., et al. 2022, ApJ, 926, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Brightman, M., Nandra, K., Nikutta, R., & Bauer, F. E. 2019, A&A, 629, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coffey, D., Longinotti, A. L., Rodríguez-Ardila, A., et al. 2014, MNRAS, 443, 1788 [NASA ADS] [CrossRef] [Google Scholar]
- Collin, S., Boisson, C., Mouchet, M., et al. 2002, A&A, 388, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crenshaw, D. M., & Kraemer, S. B. 2012, ApJ, 753, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., Garcia, J., Parker, M. L., Fabian, A. C., & Wilms, J. 2014, MNRAS, 444, L100 [Google Scholar]
- Elitzur, M. 2008, New Astron. Rev., 52, 274 [CrossRef] [Google Scholar]
- Elitzur, M. 2012, ApJ, 747, L33 [Google Scholar]
- Fukazawa, Y., Furui, S., Hayashi, K., et al. 2016, ApJ, 821, 15 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [Google Scholar]
- Gofford, J., Reeves, J. N., Tombesi, F., et al. 2013, MNRAS, 430, 60 [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiménez-Bailón, E., Krongold, Y., Bianchi, S., et al. 2008, MNRAS, 391, 1359 [CrossRef] [Google Scholar]
- Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [Google Scholar]
- Krolik, J. H., Madau, P., & Zycki, P. T. 1994, ApJ, 420, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Laha, S., Markowitz, A. G., Krumpe, M., et al. 2020, ApJ, 897, 66 [Google Scholar]
- Leftley, J. H., Tristram, K. R. W., Hönig, S. F., et al. 2021, ApJ, 912, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, K. K., Harrison, F., Broadway, D., et al. 2018, in Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, eds. J.-W. A. den Herder, S. Nikzad, & K. Nakazawa, International Society for Optics and Photonics (SPIE), 10699, 1566 [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [Google Scholar]
- Maiolino, R., Risaliti, G., Salvati, M., et al. 2010, A&A, 517, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchesi, S., Ajello, M., Zhao, X., et al. 2019, ApJ, 872, 8 [Google Scholar]
- Marinucci, A., Risaliti, G., Wang, J., et al. 2013, MNRAS, 429, 2581 [NASA ADS] [CrossRef] [Google Scholar]
- Markowitz, A. G., Krumpe, M., & Nikutta, R. 2014, MNRAS, 439, 1403 [Google Scholar]
- Matt, G., Baloković, M., Marinucci, A., et al. 2015, MNRAS, 447, 3029 [NASA ADS] [CrossRef] [Google Scholar]
- Matzeu, G. A., Reeves, J. N., Braito, V., et al. 2017, MNRAS, 472, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Middei, R., Matzeu, G. A., Bianchi, S., et al. 2021, A&A, 647, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miniutti, G., Sanfrutos, M., Beuchert, T., et al. 2014, MNRAS, 437, 1776 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, K. D., & Yaqoob, T. 2009, MNRAS, 397, 1549 [Google Scholar]
- Nardini, E., Reeves, J. N., Gofford, J., et al. 2015, Science, 347, 860 [Google Scholar]
- Palmeri, P., Mendoza, C., Kallman, T. R., Bautista, M. A., & Meléndez, M. 2003, A&A, 410, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrucci, P. O., Haardt, F., Maraschi, L., et al. 2001, ApJ, 556, 716 [Google Scholar]
- Piconcelli, E., Bianchi, S., Guainazzi, M., Fiore, F., & Chiaberge, M. 2007, A&A, 466, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pizzetti, A., Torres-Alba, N., Marchesi, S., et al. 2022, ApJ, 936, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., Reeves, J. N., King, A. R., et al. 2003, MNRAS, 345, 705 [Google Scholar]
- Reeves, J. N., Braito, V., Gofford, J., et al. 2014, ApJ, 780, 45 [Google Scholar]
- Ricci, C., Bauer, F. E., Arevalo, P., et al. 2016, ApJ, 820, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Elvis, M., & Nicastro, F. 2002, ApJ, 571, 234 [Google Scholar]
- Risaliti, G., Elvis, M., Fabbiano, G., et al. 2007, ApJ, 659, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Rivers, E., Markowitz, A., & Rothschild, R. 2011, ApJ, 742, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Rivers, E., Baloković, M., Arévalo, P., et al. 2015, ApJ, 815, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Sanfrutos, M., Miniutti, G., Agís-González, B., et al. 2013, MNRAS, 436, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Sanfrutos, M., Miniutti, G., Krongold, Y., Agís-González, B., & Longinotti, A. L. 2016, MNRAS, 457, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, H. M., Appenzeller, I., & Burch, U. 2003, A&A, 404, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serafinelli, R., Vagnetti, F., & Middei, R. 2017, A&A, 600, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serafinelli, R., Tombesi, F., Vagnetti, F., et al. 2019, A&A, 627, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serafinelli, R., Braito, V., Severgnini, P., et al. 2021, A&A, 654, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., et al. 2010, A&A, 521, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tombesi, F., Meléndez, M., Veilleux, S., et al. 2015, Nature, 519, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Tortosa, A., Bianchi, S., Marinucci, A., Matt, G., & Petrucci, P. O. 2018, A&A, 614, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tortosa, A., Ricci, C., Tombesi, F., et al. 2022, MNRAS, 509, 3599 [Google Scholar]
- Tristram, K. R. W., Meisenheimer, K., Jaffe, W., et al. 2007, A&A, 474, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Risaliti, G., Harrison, F. A., et al. 2014, ApJ, 788, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.-M., & Zhang, E.-P. 2007, ApJ, 660, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- XRISM Science Team 2020, ArXiv e-prints [arXiv:2003.04962] [Google Scholar]
- Yaqoob, T. 2012, MNRAS, 423, 3360 [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Unfolded spectrum of the data analyzed here, adopting a simple model with an absorbed continuum power law with Γ = 2. Red, blue, cyan, black, and magenta spectra mark the NuSTAR spectra of Epochs 1 to 5, respectively. The grey spectrum is the Swift-XRT one. |
| In the text | |
 |
Fig. 2. Data-to-model ratio for the model in Eq. (2), where the reflector is modeled with MYTS0, and only the neutral absorber is considered. There are still significant ratios in the whole analyzed band, in particular the curvature is not well modeled by a single neutral absorber. |
| In the text | |
 |
Fig. 3. Residuals when the model with only one ionized absorber is fitted. The observations are ordered top to bottom from the first to the last taken. An absorption complex at ∼7 keV is observed in Epochs 1, 3, and 4. At Epoch 5, the absorption complex is observed at ∼8.5 keV, suggesting a possible outflowing velocity of v ∼ 0.2c. |
| In the text | |
 |
Fig. 4. Contour plot of the spectral slope Γ and the line-of-sight column density NH obtained for Epoch 4, as obtained from the zero-order MYTORUS model. The red, green, and blue lines represent 68% (1σ), 95% (2σ), and 99.7% (3σ) contours. |
| In the text | |
 |
Fig. 5. Normalized spectra and data-to-model ratio of ESO 323-G77. The MYTORUS model is shown here. The same color code as that used in Fig. 3 is adopted, with the addition of the Swift-XRT spectrum, shown in gray. |
| In the text | |
 |
Fig. 6. Unfolded spectra of ESO 323-G77 determined from the Swift-XRT and NuSTAR data based on the MYTORUS model. |
| In the text | |
 |
Fig. 7. Contour plot of the optical depth τ versus the coronal temperature kTe, assuming a slab coronal geometry with the COMPTT Comptonization model. The red, green, and blue lines represent 68% (1σ), 95% (2σ), and 99.7% (3σ) confidence levels, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.