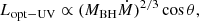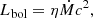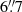| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834448 | |
| Published online | 25 February 2019 | |
A deep X-ray view of the bare AGN Ark 120
V. Spin determination from disc-Comptonisation efficiency method
1
Aix-Marseille Univ., CNRS, CNES, LAM, Marseille, France
e-mail: delphine.porquet@lam.fr
2
Department of Physics, University of Durham, South Road, Durham DH1 3LE, UK
3
Center for Space Science and Technology, University of Maryland Baltimore County, 1000 Hilltop Circle, Baltimore, MD 21250, USA
4
Dipartimento di Matematica e Fisica, Università degli Studi Roma Tre, Via della Vasca Navale 84, Roma 00146, Italy
5
Astrophysics Group, School of Physical and Geographical Sciences, Keele University, Keele, Staffordshire ST5 5BG, UK
6
INAF – Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, Firenze 50125, Italy
7
INAF – Osservatorio Astronomico di Brera, Via Bianchi 46, Merate 23807, LC, Italy
8
Université de Strasbourg, CNRS, Observatoire Astronomique de Strasbourg, UMR 7550, Strasbourg 67000, France
9
Department of Electronic Information Systems, Shibaura Institute of Technology, 307 Fukasaku, Minuma-ku, Saitama-shi, Saitam 337-8570, Japan
10
Núcleo de Astronomía de la Facultad de Ingeniería, Universidad Diego Portales, Av. Ejército Libertador 441, Santiago, Chile
11
Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing 100871, PR China
12
Institute for Particle Physics and Astrophysics, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zürich, Switzerland
13
Eureka Scientific Inc., 2452 Delmer Street, Suite 100, Oakland, CA 94602, USA
14
Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Mail Stop 169-221, Pasadena, CA 91109, USA
15
Center for Relativistic Astrophysics, School of Physics, Georgia Institute of Technology, 837 State Street, Atlanta, GA 30332-0430, USA
16
Department of Physics, Virginia Tech, Blacksburg, VA 24061, USA
Received:
17
October
2018
Accepted:
18
December
2018
Context. The spin of supermassive black holes (SMBH) in active galactic nuclei (AGN) can be determined from spectral signature(s) of relativistic reflection such as the X-ray iron Kα line profile, but this can be rather uncertain when the line of sight intersects the so-called warm absorber and/or other wind components as these distort the continuum shape. Therefore, AGN showing no (or very weak) intrinsic absorption along the line-of-sight such as Ark 120, a so-called bare AGN, are the ideal targets for SMBH spin measurements. However, in our previous work on Ark 120, we found that its 2014 X-ray spectrum is dominated by Comptonisation, while the relativistic reflection emission only originates at tens of gravitational radii from the SMBH. As a result, we could not constrain the SMBH spin from disc reflection alone.
Aims. Our aim is to determine the SMBH spin in Ark 120 from an alternative technique based on the global energetics of the disc-corona system. Indeed, the mass accretion rate (Ṁ) through the outer disc can be measured from the optical-UV emission, while the bolometric luminosity (Lbol) can be fairly well constrained from the optical to hard X-rays spectral energy distribution, giving access to the accretion efficiency η = Lbol/(Ṁc2) which depends on the SMBH spin.
Methods. The spectral analysis uses simultaneous XMM-Newton (OM and pn) and NuSTAR observations on 2014 March 22 and 2013 February 18. We applied the OPTXCONV model (based on OPTXAGNF) to self consistently reproduce the emission from the inner corona (warm and hot thermal Comptonisation) and the outer disc (colour temperature corrected black body), taking into account both the disc inclination angle and relativistic effects. For self-consistency, we modelled the mild relativistic reflection of the incident Comptonisation components using the XILCONV convolution model.
Results. We infer a SMBH spin of 0.83+0.05−0.03, adopting the SMBH reverberation mass of 1.50 × 108 M⊙. In addition, we find that the coronal radius decreases with increasing flux (by about a factor of two), from 85+13−10Rg in 2013 to 14 ± 3 Rg in 2014.
Conclusions. This is the first time that such a constraint is obtained for a SMBH spin from this technique, thanks to the bare properties of Ark 120, its well determined SMBH reverberation mass, and the presence of a mild relativistic reflection component in 2014 which allows us to constrain the disc inclination angle. We caution that these results depend on the detailed disc-corona structure, which is not yet fully established. However, the realistic parameter values (e.g. Lbol/LEdd, disc inclination angle) found suggest that this is a promising method to determine spin in moderate-Ṁ AGN.
Key words: X-rays: individuals: Ark 120 / galaxies: active / quasars: general / radiation mechanisms: general / accretion, accretion disks
© ESO 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In the standard paradigm (the so-called no hair theorem), astrophysical black holes (BH) are described by their mass and their angular momentum commonly called spin. The spin is usually expressed in terms of the dimensionless parameter 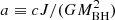 , where c, J, G and MBH are the speed of light, the angular momentum, the Gravitational constant and the black hole mass, respectively. In stellar-mass BHs (black hole X-ray binaries, BHXBs), the spin is expected to be native (King & Kolb 1999, but see Fragos & McClintock 2015); while, in SMBHs (with masses spanning from a few millions to several billions solar masses), the spin is related to the accretion-ejection history of SMBHs, for example chaotic versus coherent accretion, relativistic jets, and to the galaxy merger history (e.g. Blandford & Znajek 1977; Berti & Volonteri 2008; King et al. 2008).
, where c, J, G and MBH are the speed of light, the angular momentum, the Gravitational constant and the black hole mass, respectively. In stellar-mass BHs (black hole X-ray binaries, BHXBs), the spin is expected to be native (King & Kolb 1999, but see Fragos & McClintock 2015); while, in SMBHs (with masses spanning from a few millions to several billions solar masses), the spin is related to the accretion-ejection history of SMBHs, for example chaotic versus coherent accretion, relativistic jets, and to the galaxy merger history (e.g. Blandford & Znajek 1977; Berti & Volonteri 2008; King et al. 2008).
For BHXBs, there are up-to-now four main methods that can be applied to X-ray data to determine their spin (e.g. Remillard & McClintock 2006; Miller et al. 2009; McClintock et al. 2011; Reynolds 2014, and references therein): Spectral fitting of the relativistic reflection iron Kα line profile, spectral fitting of the thermal continuum emission (also called “disc continuum fitting” method), quasi periodic oscillations (QPO), and polarimetry. The first two are the most used and depend on the accretion disc extending down to the innermost stable circular orbit (ISCO) radius, RISCO, which is spin dependent. Determining the spin from the QPO depends on the assumed model – even with current data favouring Lense-Thirring precession for low frequency QPOs (Ingram et al. 2009, 2016). Indeed, the constraints on the spin are not tight unless combined with models for the high frequency QPOs (Motta 2016) whose origin is more uncertain. The last technique, X-ray polarimetry (e.g. Dovčiak et al. 2004; Schnittman & Krolik 2009) is waiting for the launch of the next generation of X-ray polarimeters, such as the Imaging X-ray Polarimetry Explorer (IXPE, a NASA Small Explorer planned for launch in 2021; Weisskopf et al. 2016).
In the case of SMBHs in AGN, the method based on X-ray spectral analysis of the relativistic reflection signature(s) was the only one used until recently (e.g. Reynolds 2014, and references therein). Indeed, disc continuum fitting is more difficult in local AGN for two reasons. Firstly, whereas the disc radiates in the X-rays for BHXBs, the disc models predict a peak temperature for typical broad-line Seyfert 1 s (BLS1s) AGN (with a BH mass of 108 M⊙ accreting at Lbol/LEdd = 0.2) in the extreme UV (∼20 eV) that is unobservable due to Galactic absorption. Secondly, the observed emission in typical AGN is not generally as disc-dominated as observed in BHXBs at similar Lbol/LEdd = 0.2. Instead, the optically-thick, geometrically-thin disc emission appears to turn over in the far UV, connecting to an upturn in the observed soft X-ray flux. This can be fit by an additional warm Comptonisation component with kTe ∼ 0.1 − 0.5 keV, which is optically-thick with τ ∼ 10 − 20 (e.g. Porquet et al. 2004; Piconcelli et al. 2005; Bianchi et al. 2009; Scott et al. 2012; Petrucci et al. 2018), very different from the standard hot X-ray corona which has τ ∼ 1, and kTe ∼ 30–150 keV (e.g. Brenneman et al. 2014; Baloković et al. 2015; Fabian et al. 2015, 2017; Marinucci et al. 2014; Marinucci & Tortosa 2016; Tortosa et al. 2018, but see for some exceptions, Matt et al. 2015; Tortosa et al. 2017; Kara et al. 2017; Turner et al. 2018). However, as pointed out by Done et al. (2012), one exception can be AGN with much lower BH masses and higher Lbol/LEdd such as the narrow-line Seyfert 1 s (NLS1s) for which the disc emission is predicted to extend to the soft X-rays and peak near 0.1 keV, and where such disc-dominated spectra are often seen. However, even here the disc models drop much more sharply than the observed soft X-ray shape, these also require a small additional warm Compton component as well as the dominant disc emission and weak (and steep) X-ray coronal emission typically seen in BHXBs at high Eddington ratio (Done et al. 2012; Jin et al. 2012).
Done et al. (2012) developed a radially stratified two-zone Comptonisation disc model (see their Fig. 5), called OPTXAGNF. This model conserves energy, assuming that the emissivity is set by the standard geometrically thin disc Novikov & Thorne (1973)’s relation, but the energy generated by mass accretion between Rcorona and RISCO is dissipated as both warm and hot coronal Comptonisation emission, while the outer disc (R > Rcorona) emits in the optical-UV as expected for a multi-colour black-body disc. This model has been applied to some disc-dominated NLS1s (that is, those where Rcorona is close to RISCO) to constrain spin and mass (Done et al. 2012, 2013; Jin et al. 2012; Done & Jin 2016); but typically the spin value was either fixed or almost unconstrained due to large uncertainties in the BH mass. For disc-dominated objects, pure disc models can also be used for spin measurements but, until now, have only provided weak constraints due to large uncertainties on the BH mass of the considered AGN, for example SDSS J094533.99+100950.1, NGC 3783, and H1821+643 (Czerny et al. 2011; Capellupo et al. 2017). This latter technique is similar to the disc-continuum fitting method (which also depends on BH mass, distance and disc inclination) used for BHXBs.
The OPTXAGNF model can also fit the BLS1s for which the soft X-ray excess is found to produce mainly by warm Comptonisation (Done et al. 2012; Jin et al. 2012; Mehdipour et al. 2011, 2015; Porquet et al. 2018) rather than by relativistic reflection (Crummy et al. 2006). Indeed, in case the X-ray spectrum is mainly due to warm and hot Comptonisation the spin can still be constrained from the global energetics of the flow (Done et al. 2012). This was first explored by Davis & Laor (2011), who assumed that the optical-UV emission was produced in the outer disc, so that the mass accretion rate for a standard disc could be constrained simply from the optical-UV luminosity as:
where MBH is the SMBH mass, Ṁ the absolute accretion rate and θ the accretion disc inclination angle. If MBH is known, for example from reverberation mapping, and θ is constrained or already known, then this relation determines the mass accretion rate through the outer disc. The bolometric luminosity is:
where η is the accretion radiative efficiency that indicates how much binding energy at the ISCO is radiated away. Since the ISCO radius varies monotonically with the black hole spin value (Bardeen et al. 1972), η is directly related to the black hole spin, assuming that the inner radius of the accretion disc corresponds to the ISCO. Davis & Laor (2011) applied this disc-Comptonisation efficiency method to a sample of bright QSOs. They find that η increased with MBH, being consistent with low spin for lower mass SMBH but requiring higher spin for the most massive objects in their sample. This is consistent with the results of Jin et al. (2012), where their sample of nearby, fairly low mass SMBH could all be fit with zero spin (that is, η = 0.057) models.
Ark 120 (z = 0.03271; Theureau et al. 2005) is the brightest and cleanest bare AGN known. Indeed, its UV and X-ray spectra are “contaminated” neither by line of sight warm absorption signatures (Crenshaw et al. 1999; Vaughan et al. 2004; Reeves et al. 2016) nor by a neutral intrinsic absorber (Reeves et al. 2016). Ark 120 is also free from intrinsic reddening in its infrared-optical-UV continuum (Ward et al. 1987; Vasudevan et al. 2009), though there are non-negligible UV reddening and X-ray absorption from our own Galaxy in its direction. Moreover, the SMBH mass of Ark 120 is well constrained thanks to reverberation mapping measurement performed by Peterson et al. (2004) who assumed the virial factor1 from Onken et al. (2004), and obtained 1.50 ± 0.19 × 108 M⊙. In Porquet et al. (2018), using a deep X-ray observation performed in March 2014 with XMM-Newton and NuSTAR, we show that the X-ray spectra of Ark 120 is dominated by warm and hot Comptonisation components. A mild reflection component is still required above about 10 keV, but with a low degree of relativistic smearing indicating that the relativistic reflection only occurs beyond several 10 s of Rg (see also Nardini et al. 2016), and therefore does not enable us to infer any constraint on the SMBH spin from disc reflection alone.
In this work, we report on the Ark 120 spectral energy distribution (SED) fitting using the disc-Comptonisation efficiency method combining simultaneous optical–UV (XMM-Newton/OM), and X-rays (XMM-Newton/pn and NuSTAR) observations performed on 2014 March 22 and 2013 February 18. In Sect. 2, we describe the data reduction procedure, while the spectral modelling is described in Sect. 3. The simultaneous optical to hard X-ray data analysis for the 2014 March 22 and the 2013 February 18 observations is reported in Sect. 4. In Sect. 5 our main results are discussed, followed by our conclusions in Sect. 6.
2. Observation, data reduction
Ark 120 was observed by XMM-Newton (Jansen et al. 2001) over four consecutive orbits between 2014 March 18 and March 24 (PI: D. Porquet). Here, we used the 2014 March 22 observation, which was the only one that was simultaneous with a NuSTAR observation (PI: NuSTAR AGN team). We also analysed an earlier joint XMM-Newton and NuSTAR observation, which was performed in a single XMM-Newton orbit on 2013 February 18 (PI: G. Matt). During this 2013 observation, the X-ray flux of Ark 120 was about a factor of two lower than in 2014 (Matt et al. 2014; Marinucci et al. 2019), while the optical-UV flux was also lower (Lobban et al. 2018). Figure 1 shows the six-month Swift UVOT and XRT light curves (Lobban et al. 2018). We note that the shaded areas show the equivalent XRT rates, corresponding to the flux levels measured from the 2013 and 2014 XMM-Newton observations described above. This illustrates that during the 2013 and 2014 XMM-Newton observations, the source was observed very close to its lowest and highest flux state levels, respectively. The log of the observations of Ark 120 used in this work is reported in Table 1.
 |
Fig. 1. The Swift UVOT light curve of Ark 120 showing the corrected count rates in the U (red) and UVM2 (blue) bands (adapted from Lobban et al. 2018). Each point corresponds to a single image observation. The 0.3–10 keV XRT light curve (black) is overlaid with an additional y-axis scale. The lower and upper grey shaded areas correspond to the XRT count rates at the 2013 and 2014 XMM-Newton 0.3–10 keV fluxes, respectively. The horizontal dashed lines correspond to the mean flux for each dataset. |
Observation log of the data analysed in this work for Ark 120.
2.1. XMM-Newton data reduction
For the data reduction we used the Science Analysis System (SAS) v16.1.0, applying the latest calibrations available on 2018 February 2. This updated calibration, compared to Porquet et al. (2018), results in a better 7–10 keV cross-calibration between pn and NuSTAR data with a slight steepening of the 2–10 keV photon indices by about +0.03, in other words, by about 1.6%.
2.1.1. pn data
Due to the high source brightness, the EPIC-pn camera (Strüder et al. 2001) was operated in Small Window mode to prevent any pile-up. The 2013 and 2014 pn spectra were extracted from circular regions centred on Ark 120, with radii of 30″. We selected the event patterns 0–4, that is, single and double pixels, while we also applied FLAG==0 in order that all events at the edge of a CCD and at the edge of a bad pixel were excluded. The background spectra were extracted from a rectangular region in the lower part of the small window that contains no (or negligible) source photons. After the correction for dead time and background flaring, the total net pn exposures were about 82 ks for the 2014 observation and about 88 ks for the 2013 observation. Redistribution matrices and ancillary response files for the two pn spectra were generated with the SAS tasks RMFGEN and ARFGEN. We used the time-averaged pn spectra since, as shown in Lobban et al. (2018), the spectral variability within a single orbit is slow and moderate. The 0.3–10 keV pn spectra were binned to give 100 counts per bin.
A gain shift was applied to take into account the known inaccuracy of the EPIC-pn energy scale likely due to inaccuracies in the long-term charge transfer inefficiency (CTI) calibration2. The GAIN xspec command allows us to modify accordingly the response file gain and is characterised by two parameters: SLOPE and INTERCEPT (in units of keV). The new energy is calculated by E′ = E/⟨SLOPE⟩ − ⟨INTERCEPT⟩. For the 2014 observations, we fit simultaneously the four available pn spectra tying the GAIN parameters values using the following baseline model: TBNEW×(COMPTT+ZPO+ZGA(BROAD)+3×ZGA(BLR)). Indeed, such modelling is adequate for the 2014 observation as shown in Porquet et al. (2018). The parameters of the broad Gaussian and of the three BLR Gaussian lines were tied between the four observations. We allowed to vary between each observation: kTe, τ, normalisation(comptt), Γ and normalisation(zpo). We infered SLOPE = 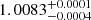 and INTERCEPT =
and INTERCEPT = 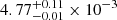 keV. We performed the same modelling for the 2013 pn spectrum but without the need of a broad Gaussian line, and we infered SLOPE =
keV. We performed the same modelling for the 2013 pn spectrum but without the need of a broad Gaussian line, and we infered SLOPE = 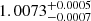 and INTERCEPT =
and INTERCEPT = 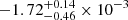 keV.
keV.
2.1.2. OM data
We used the XMM-Newton optical-UV Monitor telescope (hereafter OM; Mason et al. 2001). For the March 2014 observation, we acquired about about five ∼1.2 ks exposures in default imaging and fast mode consecutively through the V (effective wavelength = 5430 Å), B (4500 Å), U (3440 Å), UVW1 (2910 Å) and UVM2 (2310 Å) filters before spending the rest of the observation acquiring exposures with the UVW2 (2120 Å) filter. We did not use the (redundant) fast mode data reported in Lobban et al. (2018). For the 2013 observation, a series of snapshots were consecutively acquired with the UVW1 (ten ∼3.4 ks exposures), UVM2 (ten ∼4.4 ks exposures) and UVW2 (ten ∼4.4 ks exposures) filters.
The imaging mode data were processed using the SAS script omichain which takes into account all necessary calibration processes (e.g. flat-fielding), and runs a source detection algorithm before performing aperture photometry on each detected source, and combines the source lists from separate exposures into a single master list to compute mean corrected count rates. The optical and UV counterparts of Ark 120 detected with the OM is point-like. The FWHM is 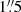 and 3″ with the V and UV filters, respectively (Mason et al. 2001). The aperture radius is 12 unbinned pixels (corresponding to
and 3″ with the V and UV filters, respectively (Mason et al. 2001). The aperture radius is 12 unbinned pixels (corresponding to 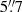 for
for 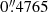 square pixels) and the background is estimated within an annulus region: for the optical filters the inner and outer radii of the annulus are 14.0 and 25.1 unbinned pixels, respectively (corresponding to
square pixels) and the background is estimated within an annulus region: for the optical filters the inner and outer radii of the annulus are 14.0 and 25.1 unbinned pixels, respectively (corresponding to 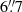 and
and 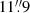 , respectively); for the UV filters the inner and outer radius of the annulus are 37.0 and 42.4 unbinned pixels, respectively (corresponding to
, respectively); for the UV filters the inner and outer radius of the annulus are 37.0 and 42.4 unbinned pixels, respectively (corresponding to 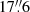 and
and 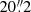 , respectively).
, respectively).
For comparison we show in Fig. 2 the omichain apertures for the V-filter overlaid on the Pan-STARRS-1 g-filter image3 (Chambers et al. 2016). As the omichain background apertures for the optical filter are located on the galaxy disc, we recomputed the OM optical photometry with the SAS task omsource from the unbinned central images in the detector plane, corrected for the modulo-8 pattern (*OM*IMAGE_0000.FIT) using a background aperture of ∼12″-radius located ∼43″ SW of Ark 120.
 |
Fig. 2. Pan-STARRS-1 g-filter image of Ark 120. North is up and east is left. The intensity is non-linearly scaled using an asinh transformation. The circle and the dashed annulus are the OM source and background apertures, respectively. The dashed circle is the custom background aperture that we used for the optical photometry. |
Figure 3 illustrates the wavelength coverage with the OM broad-band UV-filters of the UV emission of Ark 120 by comparison with the observed UV spectrum obtained with the Hubble Space Telescope Faint Object Spectrograph (HST/FOS) on 1995 July 29 (post-COSTAR with a science aperture of 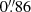 in diameter) by Kuraszkiewicz et al. (2004)4. The green data are the UVW2 and UVM2 synthetised photometry from the HST/FOS spectrum using the OM filter profiles. The OM broad-band UV photometry is little affected by the bright broad emission lines and is a measure of the continuum emission. The red and blue data, respectively, are the observed OM UV photometry on 2014 March 22 and on 2013 February 18 (Lobban et al. 2018).
in diameter) by Kuraszkiewicz et al. (2004)4. The green data are the UVW2 and UVM2 synthetised photometry from the HST/FOS spectrum using the OM filter profiles. The OM broad-band UV photometry is little affected by the bright broad emission lines and is a measure of the continuum emission. The red and blue data, respectively, are the observed OM UV photometry on 2014 March 22 and on 2013 February 18 (Lobban et al. 2018).
 |
Fig. 3. Wavelength coverage of the UV emission of Ark 120 with the OM broad-band UV-filters. The continuous line is the observed UV spectrum of Ark 120 obtained with the Hubble Space Telescope Faint Object Spectrograph (HST/FOS) on 1995 July 29 (Kuraszkiewicz et al. 2004), where the main broad emission lines are labelled. The faint absorption lines are galactic in origin (Crenshaw et al. 1999). The dashed lines are the OM filter areas. The green data are the synthetised photometry that we computed from this HST/FOS spectrum using the OM broad-band UV-filter profiles. The red and blue data are the observed mean UVW2, UVM2, and UVW1 fluxes from the corrected observed mean count rates on 2014 March 22 and on 2013 February 18, respectively (Lobban et al. 2018). |
We estimated the contribution of the host galaxy to the OM optical photometry by using the flux variation gradient method proposed by Choloniewski (1981). In this method, the combined fluxes of the galaxy and the AGN are obtained in two broad-band filters within an aperture centred on the galactic nucleus and plotted in a flux-flux diagram. The observed flux-flux variation produced by the AGN activity follows a linear trend, characterised by a slope determined by the host-free AGN continuum in the filter pair, and independent of the aperture size as the AGN is spatially unresolved (e.g. Choloniewski 1981; Doroshenko et al. 2008; Winkler et al. 1992; Haas et al. 2011). Therefore, the AGN colour index in the filter pair is independent of the AGN flux. In this flux-flux diagram, the galaxy locus is a line going through the origin with a slope given by the galaxy colour index in the filter pair. The intersection of these two lines provides the estimate of the galaxy flux in the aperture.
We selected near-simultaneous OM photometry in V-U and U-B filters obtained in subsequent exposures5. To convert the OM count rates to fluxes we used the conversion factors obtained from observations of standard white dwarf stars6 to be consistent with the canned OM response matrices used for the spectral modelling in Sect. 3. We dereddened these observed fluxes using E(B − V) = 0.113 (Schlafly & Finkbeiner 2011) and the extinction law of Cardelli et al. (1989) using RV = 3.1, leading to AV, OM = 0.355 mag, AB, OM = 0.451 mag, and AU, OM = 0.563 mag. We obtain: FV = 17.68 ± 0.09 mJy, FB = 13.32 ± 0.05 mJy, and FU = 14.63 ± 0.05 mJy.
We used the AGN and galaxy colour indices obtained by Doroshenko et al. (2008) for Ark 120 in 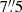 -radius aperture and
-radius aperture and 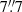 –
–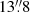 –radius annulus, respectively, neglecting possible variations of the galaxy colour indices with distance from the nucleus. Following Doroshenko et al. (2008), we used U − V and U − B filter pairs to minimise the impact of the colour-index errors on the intersection, as the differences between the colour indices of the AGN and galaxy is largest for these filter pairs. From the AGN colour indices U − B = −1.015 ± 0.018 and B − V = +0.021 ± 0.009 (see Table 3 of Doroshenko et al. 2008) and after dereddening7 we computed8 the galaxy+AGN flux-flux slopes of 1.48 ± 0.03 and 1.21 ± 0.02 for the UV and UB flux-flux plot, respectively. From the galaxy colour indices (U − B)g = −0.13 ± 0.24 and (B − V)g = +0.80 ± 0.03 (Doroshenko et al. 2008) and after dereddening, we computed the galaxy flux-flux slopes of 0.32 ± 0.07 and 0.54 ± 0.12 for the UV and UB flux-flux plot, respectively.
–radius annulus, respectively, neglecting possible variations of the galaxy colour indices with distance from the nucleus. Following Doroshenko et al. (2008), we used U − V and U − B filter pairs to minimise the impact of the colour-index errors on the intersection, as the differences between the colour indices of the AGN and galaxy is largest for these filter pairs. From the AGN colour indices U − B = −1.015 ± 0.018 and B − V = +0.021 ± 0.009 (see Table 3 of Doroshenko et al. 2008) and after dereddening7 we computed8 the galaxy+AGN flux-flux slopes of 1.48 ± 0.03 and 1.21 ± 0.02 for the UV and UB flux-flux plot, respectively. From the galaxy colour indices (U − B)g = −0.13 ± 0.24 and (B − V)g = +0.80 ± 0.03 (Doroshenko et al. 2008) and after dereddening, we computed the galaxy flux-flux slopes of 0.32 ± 0.07 and 0.54 ± 0.12 for the UV and UB flux-flux plot, respectively.
Figures 4 and 5 show the UV and UB flux-flux plots, respectively. Taking into account the slope uncertainties, we obtain the following dereddened fluxes of the galaxy in the central aperture: 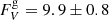 mJy,
mJy, 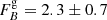 mJy, and
mJy, and 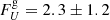 mJy (average value of the UV and UB flux-flux plots), corresponding to 56 ± 4%, 17 ± 5%, and 15 ± 7%, respectively, of the dereddened flux inside the central aperture. Since the V data are strongly dominated by the host galaxy emission, we did not use them for the SED fitting, and used the B value from the UB flux-flux plot. Therefore, we subtracted the following estimate of the galaxy contributions inside the central aperture to the observed (reddened) count rates: 9.8 ± 3.1, and 16.7 ± 8.6 counts s−1 in the B, and U filters, respectively.
mJy (average value of the UV and UB flux-flux plots), corresponding to 56 ± 4%, 17 ± 5%, and 15 ± 7%, respectively, of the dereddened flux inside the central aperture. Since the V data are strongly dominated by the host galaxy emission, we did not use them for the SED fitting, and used the B value from the UB flux-flux plot. Therefore, we subtracted the following estimate of the galaxy contributions inside the central aperture to the observed (reddened) count rates: 9.8 ± 3.1, and 16.7 ± 8.6 counts s−1 in the B, and U filters, respectively.
 |
Fig. 4. U versus V dereddened fluxes of Ark 120, measured in a |
 |
Fig. 5. U versus B dereddened fluxes of Ark 120, measured in a |
For each optical and UV filters, we took the average (without weighting) of count rates in the unbinned central image (by contrast to omichain, we did not include the redundant count rate of the binned central image) with corresponding Gaussian propagated errors. We subtracted the above contribution of the galaxy only for the optical count rates, as the host contribution is negligible in the UV.
In order to take into account the OM calibration uncertainty of the conversion factor between the count rate and the flux, we added quadratically to the statistical error of the count rate a representative systematic error of 1.5%9. The final OM reddened count rates and associated errors are reported in Table 2. We used OM canned response matrices10 to fit this OM photometry with XSPEC.
OM average reddened count rates (expressed in s−1) of the AGN and associated errors for optical and UV filters used for the SED fitting.
2.2. NuSTAR data reduction
NuSTAR (Harrison et al. 2013) observed Ark 120 with its two co-aligned X-ray telescopes with corresponding focal planes: Focal Plane Module A (FPMA) and B (FPMB) starting on 2013 February 18 and 2014 March 22 for a total of ∼166 ks and ∼131 ks of elapsed time, respectively. The Level 1 data products were processed with the NuSTAR Data Analysis Software (NuSTARDAS) package (v. 1.6.0). Cleaned event files (level 2 data products) were produced and calibrated using standard filtering criteria with the NUPIPELINE task and the calibration files available in the NuSTAR calibration database (CALDB: 20170222). Extraction radii for both the source and background spectra were 1.25 arcmin. After this process, the net exposure times for the two observations were about 79 ks (2013) and 65 ks (2014). The two pairs of NuSTAR spectra were binned in order to over-sample the instrumental resolution by at least a factor of 2.5 and to have a signal-to-noise ratio (S/N) greater than five in each spectral channel. We allowed for cross-calibration uncertainties between the two NuSTAR spectra and the simultaneous XMM-Newton/pn spectrum by including in the fit a cross-normalisation constant – which are let free to vary – corresponding to CNuSTAR A and CNuSTAR B for NuSTAR FPMA and FPMB spectra, respectively.
3. Spectral modelling
3.1. Galactic hydrogen column density and extinction correction
The Galactic Hydrogen column density (NH) is assumed to be 9.78 × 1020 cm−2 as inferred from the weighted average NH value of the Leiden/Argentine/Bonn Survey of Galactic H I (Kalberla et al. 2005). Since there can be some additional contribution associated with molecular hydrogen (Willingale et al. 2013), we allowed the value of Galactic NH to slightly vary. However, we did not allow for any intrinsic absorption in the rest frame of Ark 120, since, as found in Reeves et al. (2016) from the 2014 deep RGS spectrum, none is present. We used the X-ray absorption model TBNEW (V2.3.2) from Wilms et al. (2000), assuming throughout their ISM elemental abundances and the cross-sections from Verner et al. (1996).
The REDDEN component allows us to take into account the IR-optical-UV extinction from our Galaxy (Cardelli et al. 1989). The extinction at V is A(V) = E(B − V)×RV, with the standard value of RV being 3.1 for the Milky Way. We fixed E(B − V) to 0.113 that corresponds to Galactic Extinction from the Schlafly & Finkbeiner (2011) recalibration of the Schlegel et al. (1998) infrared-based dust map. As mentioned previously, Ark 120 does not show any intrinsic reddening in its infrared-optical continuum (Ward et al. 1987; Vasudevan et al. 2009).
3.2. Disc-Comptonisation modelling: optxconv
The broad X-ray spectrum of Ark 120 is dominated by warm and hot Comptonisation in both March 2014 (Porquet et al. 2018, see their Fig. 9), and February 2013 observations (Matt et al. 2014), though a mild relativistic reflection contribution is observed beyond tens of Rg in 2014. As described in the introduction, the baseline model used in this work, OPTXAGNF (Done et al. 2012), allows us to infer the global energetics of the flow (Davis & Laor 2011), and then the SMBH spin. Since the OPTXAGNF model includes the colour temperature corrected black body of the outer accretion disc, we were able to use the corresponding OM data (see Sect. 2.1.2).
3.2.1. Description of the optxagnf model parameters
The OPTXAGNF model is characterised by the following parameters:
-
The SMBH mass (MBH) in solar masses.
-
The co-moving distance (D) in Mpc.
-
The log(Lbol/LEdd) ratio, which is equal to log(Ṁ/ṀEdd), where Ṁ is the absolute accretion rate (see Eq. (1)) and ṀEdd is the Eddington accretion rate.
-
The dimensionless BH spin (a): 0≤ a ≤ 0.998.
-
The coronal radius (Rcorona) in units of Rg where the transition from a colour temperature corrected black body emission to a Comptonised spectrum occurs (the latter extending down to RISCO).
-
The log of the outer radius of the disc in units of Rg: here, we used the option allowing to fix it to the self-gravity radius as calculated from Laor & Netzer (1989). However, fixing it to a specific value, such as for example five, has only a marginal impact of the fit results.
-
The electron temperature (kTe) of the warm Comptonisation component in keV.
-
The optical depth (τ) of the warm Comptonisation component.
-
The spectral index (Γ) of the hot Comptonisation component (power-law shape) which has a (fixed) temperature set internally at 100 keV (based on the NTHCOMP model; Zdziarski et al. 1996; Życki et al. 1999).
-
The fraction (fpl) of the power below Rcorona which is emitted in the hot Comptonisation component.
3.2.2. Taking into account inclination effects
The OPTXAGNF model is by default calculated for a disc inclination angle (θ) of 60° (that is, for a normalisation value tied to unity). Therefore in order to take into account inclination effects on the OPTXAGNF component emission, we linked its normalisation to the disc inclination angle of the relativistic reflection component (REFLCOMP, see Sect. 3.3) using a cos(θ)/cos(60 ° ) relationship.
3.2.3. Taking into account relativistic effects: the optxconv model
The OPTXAGNF model does not include any relativistic effects on the propagation of light from the disc to the observer, but the combination of Doppler and gravitational shifts may impact the results. We included these relativistic effects using the OPTXCONV model detailed in Done et al. (2013), which effectively convolves the broad-band emission from OPTXAGNF with the relativistic blurring calculated by the RELCONV convolution model (v0.4c; Dauser et al. 2010). The RELCONV model is characterised by the following parameters:
-
the radius (Rbr expressed in Rg) where the broken power-law emissivity index changes from q1 (for R < Rbr) to q2 (for R > Rbr). Throughout this work, q1 and q2 are tied together and fixed to the typical value of 3.0.
-
the dimensionless BH spin (a);
-
the disc inclination angle (θ, expressed in degrees);
-
the inner and outer radii of the disc where the relativistic reflection is observed: Rin and Rout (expressed in Rg), respectively;
-
The limb-darkening/-brightening laws (0, 1 and 2 correspond to isotropic, darkening and brightening law, respectively). Here, we assumed an isotropic value but we checked that this has a negligible impact on the fit results.
The soft excess (warm Comptonisation) and the hard energy tail (hot Comptonisation) were convolved with the RELCONV relativistic kernel between RISCO and Rcorona where the coronal emission occurs. Outside Rcorona, that is, the colour temperature corrected black body spectrum (here called the outer disc emission) at each radius could be in principle convolved with RELCONV at that radius, and integrated from Rcorona to Rout. However, this would be extremely time-consuming to calculate. Therefore, we used the fact that most of the outer disc emission arises from radii less than twice that of its innermost radius, that is, from Rcorona to 2 Rcorona (see Done et al. 2013). Indeed, at much larger disc radii far from the black hole, the relativistic correction to OPTXAGNF are largely negligible.
The OPTXCONV model can be summarised as: RELCONV [Rin=Rcorona;Rout=2Rcorona]⊗OPTXAGNF(outer disc) + RELCONV[Rin=RISCO;Rout=Rcorona]⊗OPTXAGNF(warm and hot Comptonisation).
3.3. Relativistic reflection modelling: the REFLCOMP model
The 2013 and 2014 X-ray broad-band spectra are dominated by warm and hot Comptonisation (Matt et al. 2014; Porquet et al. 2018), nonetheless in 2014 an additionnal mild relativistic reflection component is still required (Nardini et al. 2016; Porquet et al. 2018). Its low degree of relativistic smearing indicates that this emission only arises from a few tens of gravitational radii rather than closer to the ISCO. However, this reflection component becomes non negligible above about 10 keV and must be included in the spectral fits for an accurate determination of the bolometric luminosity (Eq. (2)). Even if no significant relativistic reflection component is reported for the 2013 February 18 observation (Matt et al. 2014), we included one for self-consistency, and checked for any possible contribution.
The relativistic reflection component, hereafter called REFLCOMP, was calculated using the following model: RELCONV⊗XILCONV⊗OPTXAGNF.
The XILCONV convolution model (Done & Gierliński 2006; Kolehmainen et al. 2011) combines an ionised disc table model from the XILLVER model (Garcia & Kallman 2010) with the Magdziarz & Zdziarski (1995) Compton reflection code. Therefore, it allows us to use the optxagnf (Comptonisation) emission as the incident spectrum for the reflection component, that is, xilconv⊗optxagnf. In order to account for relativistic effects, we also convolved it with the RELCONV model.
The XILCONV model is characterised by the following parameters:
-
the reflection fraction: ℛ;
-
the iron abundance relative to the solar value (Grevesse & Sauval 1998): AFe. Here, we fixed it to unity, but if let free to vary it has only a marginal impact on the fit results;
-
the ionisation parameter (erg cm s−1, in log units) at the surface of the disc (that is, the ratio of the X-ray flux to the gas density): log ξ;
-
the high-energy cut-off: Ecut (expressed in keV). Here, its value was fixed to 300 keV to be consistent with the temperature internally set at 100 keV in OPTXAGNF (Sect. 3.2) – which is taken as the incident spectrum for the relativistic reflection model – as for a thermal distribution of electrons Ecut ∼ 3 kT (e.g. Fabian et al. 2015).
The parameters of the RELCONV and OPTXAGNF models have been already described in Sect. 3.2.
In this work, we assumed that the warm optically-thick corona has a full coverage. Therefore, unless otherwise mentioned we fixed Rin (inner radius of the observed relativistic reflection) to Rcorona (corona radius) meaning that below Rcorona any reflection is hidden to the observer by the warm optically-thick corona.
3.4. Modelling of the Fe K complex components from the broad line region (BLR)
In Nardini et al. (2016), from modelling the 2014 Chandra HETG observation of Ark 120, we resolved the core of the Fe Kα line, where its velocity width (FWHM ∼ 4700 km s−1) was found to be consistent with the broad Hβ line in the optical spectrum. Thus, the narrow neutral core of the Fe Kα emission is assumed to be associated with the optical BLR rather than the torus, which may also be the case for any ionised emission from Fe XXVI Lyα. Therefore, throughout this work we took into account the contribution from the BLR emission to the Fe K complex using three Gaussian lines (as in Porquet et al. 2018): the Fe KαBLR (E fixed at 6.40 keV) plus its associated Fe KβBLR line (E fixed at 7.05 keV), and the H-like iron line (E fixed at 6.97 keV). The normalisation of Fe KβBLR was set to 0.135 times that of Fe KαBLR (Palmeri et al. 2003). The widths of these three lines were fixed to the value inferred for the Fe Kα narrow core, that is, 43 eV as determined from the simultaneous Chandra/HETG spectrum Nardini et al. (2016). These three BLR emission lines are called hereafter “3× ZGAUSSIAN(BLR)”.
4. Spectral analysis
The XSPEC V12.9.1p software package (Arnaud 1996) was used for spectral analysis. We used throughout the χ2 minimisation, quoting confidence levels of 90 percent for one interesting parameter (Δχ2 = 2.71). Unless stated otherwise, we assumed a reverberation SMBH mass value of 1.50 × 108 M⊙ (Peterson et al. 2004). We adopted a distance11 of 143.5 Mpc inferred from the cosmological constants from Planck Collaboration XIII (2016), that is, H0 = 67.8 km s−1 Mpc−1, Ωm = 0.308, and ΩΛ0 = 0.692. All spectra are displayed in the AGN rest-frame. Hereafter, the energy range over which the models are calculated has been extended up to 500 keV and down to 1 eV (B filter band).
Throughout this work, we used the following model (where the components have been described in Sect. 3) simultaneously to the SED of both the 2014 March 22 and the 2013 February 18 XMM-Newton (OM + pn) and NuSTAR observations: REDDEN×TBNEW×{OPTXCONV + REFLCOMP +3×ZGAUSSIAN(BLR)}.
Since the Galactic column density (NH), the disc inclination angle (θ), and the BH spin (a) are not supposed to vary in a year time-scale, they were tied between both datasets. Moreover, the disc ionisation parameter was also tied between both datasets since its value is similar for 2013 and 2014 observations.
We find a good fit statistic (χ2/d.o.f. = 3824.4/3517, 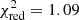 ), the best fit parameters of this model are listed in Table 3 (left-hand column). However, some deviations are found in the hardest energy part of both X-ray spectra (Fig. 6, top panel). In OPTXAGNF the temperature of the hot component is not a free parameter since internally fixed to 100 keV (see Sect. 3.2). The best-fit temperature may vary from this value during these 2014 and 2013 observations. Indeed, Marinucci et al. (2019), using a NTHCOMP component (as used in OPTXAGNF and OPTXCONV models) for the hot corona find kTe ≥ 40 keV for the 2013 dataset and
), the best fit parameters of this model are listed in Table 3 (left-hand column). However, some deviations are found in the hardest energy part of both X-ray spectra (Fig. 6, top panel). In OPTXAGNF the temperature of the hot component is not a free parameter since internally fixed to 100 keV (see Sect. 3.2). The best-fit temperature may vary from this value during these 2014 and 2013 observations. Indeed, Marinucci et al. (2019), using a NTHCOMP component (as used in OPTXAGNF and OPTXCONV models) for the hot corona find kTe ≥ 40 keV for the 2013 dataset and 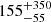 keV for the 2014 dataset. However, these deviations have a very marginal impact on the determination of the bolometric luminosity and then on the inferred spin value found in this work. There is also a deviation of the B band flux for 2014 that may be due to an overestimation of the true galaxy host contribution at this wavelength.
keV for the 2014 dataset. However, these deviations have a very marginal impact on the determination of the bolometric luminosity and then on the inferred spin value found in this work. There is also a deviation of the B band flux for 2014 that may be due to an overestimation of the true galaxy host contribution at this wavelength.
 |
Fig. 6. Simultaneous fit of the Ark 120 SED (XMM-Newton/OM/pn and NuSTAR) spectra of Ark 120 (AGN rest-frame) obtained on 2014 March 22 and on 2013 February 18. The 2014 and 2013 observations are displayed in black and red, respectively. Top panel: spectra and data/model. Bottom panel: intrinsic (that is, corrected for reddening and Galactic absorption) SED and the corresponding model components. Continuous curves: total SED. Dotted curves: outer disc emission. Dashed curved: warm optically-thick Comptonisation component (soft excess). Dotted-dashed curves: hot Comptonisation component (hard energy tail). 3-dotted-dashed curves: relativistic reflection component. For clarity purposes, the three BLR Gaussian line components are not displayed. |
For the 2014 observation, we infer temperature and optical depth values for the warm Comptonisation (producing part of the soft excess) that are similar to those found in Porquet et al. (2018), where a simplified modelling with the COMPTT model has been used. It is worth pointing out, that during this 2014 observation, both the flux and photon index correspond to the “high-flux spectrum” found for Ark 120 from a Swift monitoring (Gliozzi et al. 2017; Lobban et al. 2018), as illustrated in Fig. 1. The optically-thick corona extension is rather moderate with Rcorona of about 14 Rg. We infer an accretion rate consistent with the one inferred from the ∼ six-month Swift monitoring data of Ark 120 (Buisson et al. 2017).
We find the overall observed luminosity requires a spin value of 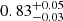 which is remarkably well constrained. Since relativistic reflection component (REFLCOMP) is only observed beyond about 14 Rg in 2014, the spin constraint is driven by the OPTXCONV SED modelling, however the disc inclination – that is an important variable to determine the accretion rate (see Eq. (1)) – is well constrained thanks to the mildly relativistic reflection component present during the 2014 observation. Therefore, this shows that in order to obtain via this method a good constraint on the spin value, the presence of a relativistic reflection component is needed in order to measure the disc inclination. Hence, if we consider the 2013 data in isolation, we are unable to constrain the spin value, due to the lack of any disc relativistic reflection component (also see Matt et al. 2014). We notice that the inferred value of the accretion disc inclination (θ ∼ 30°) is similar to that of the host galaxy (that is, 26°; Nordgren et al. 1995). Figure 7 displays the 2D contour plots of the spin versus the disc inclination angle (top panel).
which is remarkably well constrained. Since relativistic reflection component (REFLCOMP) is only observed beyond about 14 Rg in 2014, the spin constraint is driven by the OPTXCONV SED modelling, however the disc inclination – that is an important variable to determine the accretion rate (see Eq. (1)) – is well constrained thanks to the mildly relativistic reflection component present during the 2014 observation. Therefore, this shows that in order to obtain via this method a good constraint on the spin value, the presence of a relativistic reflection component is needed in order to measure the disc inclination. Hence, if we consider the 2013 data in isolation, we are unable to constrain the spin value, due to the lack of any disc relativistic reflection component (also see Matt et al. 2014). We notice that the inferred value of the accretion disc inclination (θ ∼ 30°) is similar to that of the host galaxy (that is, 26°; Nordgren et al. 1995). Figure 7 displays the 2D contour plots of the spin versus the disc inclination angle (top panel).
 |
Fig. 7. 2D contour plots (at the 68%, 90% and 99% confidence levels) from the simultaneous fit of the 2013 and 2014 observations. Top panel: disc inclination angle versus spin. Bottom panel: log(Lbol/LEdd) versus Rcorona (expressed in Rg) found for the 2014 observation (high-flux state, in black) and for the 2013 observation (low-flux state, in red). |
We find that the temperature of the warm optically-thick corona has slightly increased with statistical significance of about 1.8σ between 2013 and 2014 (see Table 3, Col. 1), corresponding to unabsorbed 0.3–2 keV fluxes of 2.58 × 10−11 erg cm−2 s−1 and 5.42 × 10−11 erg cm−2 s−1, respectively. Moreover, the photon index of the hot optically-thin corona has softened (by about 3.9σ) between the 2013 (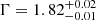 ) and 2014 (Γ = 1.93 ± 0.02) observations, corresponding to 2–79 keV flux of 7.28×10−11 erg cm−2 s−1 and 1.03×10−10 erg cm−2 s−1, respectively. This again confirms previous results (Matt et al. 2014; Gliozzi et al. 2017; Lobban et al. 2018) where a “softer when brighter” behaviour for Ark 120 was reported.
) and 2014 (Γ = 1.93 ± 0.02) observations, corresponding to 2–79 keV flux of 7.28×10−11 erg cm−2 s−1 and 1.03×10−10 erg cm−2 s−1, respectively. This again confirms previous results (Matt et al. 2014; Gliozzi et al. 2017; Lobban et al. 2018) where a “softer when brighter” behaviour for Ark 120 was reported.
This disc-corona model implies that the radius of the (warm and hot) corona (Rcorona) has significantly decreased (with a statistical significance of about 5.5σ) between the 2013 and 2014 observations, from 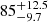 to 14 ± 3 Rg. Figure 7 (bottom panel) displays the 2D contour plots of Lbol/LEdd versus Rcorona (expressed in Rg) found for the 2014 observation (high-flux state, in black) and for the 2013 observation (low-flux state, in red). Consequently, the decreasing inner radius of the observed relativistic reflection can explain the broader Fe K profile in 2014, while in 2013 the more extended warm optically-thick corona hid most of the relativistic reflection from the accretion disc, implying a smaller and narrower Fe K line. However, in contradiction with the expected viscous disc time-scale, we infer from the fit a significant increase in mass accretion rate through the disc from Lbol/LEdd ∼ 0.03 (2013) to 0.07 (2014) in only one year. This issue is discussed in Sect. 5.2.
to 14 ± 3 Rg. Figure 7 (bottom panel) displays the 2D contour plots of Lbol/LEdd versus Rcorona (expressed in Rg) found for the 2014 observation (high-flux state, in black) and for the 2013 observation (low-flux state, in red). Consequently, the decreasing inner radius of the observed relativistic reflection can explain the broader Fe K profile in 2014, while in 2013 the more extended warm optically-thick corona hid most of the relativistic reflection from the accretion disc, implying a smaller and narrower Fe K line. However, in contradiction with the expected viscous disc time-scale, we infer from the fit a significant increase in mass accretion rate through the disc from Lbol/LEdd ∼ 0.03 (2013) to 0.07 (2014) in only one year. This issue is discussed in Sect. 5.2.
Figure 6 (bottom panel) displays the different intrinsic (corrected for both Galactic reddenning and absorption) SED for both the 2013 (in red) and 2014 (in black) observations. The intrinsic luminosities from optical to hard X-rays are 1.07 × 1045 erg s−1 and 2.42 × 1045 erg s−1, respectively. The outer disc emission (dotted curves) in 2014 (in black) is much stronger and peaks at a higher energy than in 2013 (in red) due to a much smaller inner radius (that is, 14 Rg and 85 Rg in 2014 and 2013, respectively). The UV band flux is significantly higher in 2014 than in 2013, as for example by a factor of about 50% for the UVW2 filter (Lobban et al. 2018; see also Table 2). This higher UV flux likely drives the requirement in the SED model for a lower inner disc radius (Rcorona) in 2014. The warm optically-thick Comptonisation components (dashed curves) also differ significantly between the two observations with different peak energies, but nonetheless are the dominant process in both observations in the soft X-ray band below 1 keV. The hot Comptonisation component is much steeper in 2014 when the source is brighter as mentioned above, but becomes similar to the 2013 one above about 100 keV.
In order to assess the impact on the spin value of the hypothesis of a full covering optically-thick corona, we relaxed the assumption where Rin is tied to Rcorona. The inferred spin value of 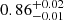 is slightly higher than the spin value found assuming a full covering warm optically-thick corona (that is, Rin tied to Rcorona), but still compatible within the error bars. For the 2014 observation, Rcorona and Rin are found to be similar with
is slightly higher than the spin value found assuming a full covering warm optically-thick corona (that is, Rin tied to Rcorona), but still compatible within the error bars. For the 2014 observation, Rcorona and Rin are found to be similar with 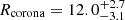 Rg and
Rg and 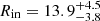 Rg, while for the 2013 observation the two values differ significantly with
Rg, while for the 2013 observation the two values differ significantly with 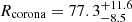 Rg and
Rg and 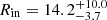 Rg (χ2/d.o.f. = 3809.6/3515). For the 2013 observation, this suggests that beyond 14 Rg some contribution of the reflection off the disc is observed and that the optically-thick corona may be patchy above this radius. This would be consistent with the rapid variability of the FeK emission complex, as discussed in Nardini et al. (2016). Alternatively, the reflection continuum from more distant material (e.g. the outer disc, dense BLR clouds or the inner torus) may also become more important in the lower flux 2013 observation.
Rg (χ2/d.o.f. = 3809.6/3515). For the 2013 observation, this suggests that beyond 14 Rg some contribution of the reflection off the disc is observed and that the optically-thick corona may be patchy above this radius. This would be consistent with the rapid variability of the FeK emission complex, as discussed in Nardini et al. (2016). Alternatively, the reflection continuum from more distant material (e.g. the outer disc, dense BLR clouds or the inner torus) may also become more important in the lower flux 2013 observation.
5. Discussion
5.1. Impacts of the assumed fixed parameter values
The disc-Comptonisation efficiency method using OPTXAGNF/OPTXCONV has been applied to some other AGN (Done et al. 2012, 2013; Done & Jin 2016) but the spin value was either fixed or almost unconstrained. Indeed, this method requires a rather precise knowledge of: the BH mass, the AGN distance and the accretion disc inclination angle along the line of sight. Therefore, in practice, the uncertainties in the spin estimates are dominated by their systematic uncertainties. As previously mentioned in Sect. 4, the disc inclination angle (θ ∼30°) is well determined here thanks to the mildly relativistic reflection component observed in the 2014 observation, and is found to be similar to that of the host galaxy (that is, 26°; Nordgren et al. 1995). Therefore, we now investigate in this section the impact of the assumed values of the fixed parameters: E(B − V), the AGN distance, and the BH mass.
5.1.1. Impact of the assumed E(B − V) and of the AGN distance values
We first investigated how the fit measurement depends on the assumption on the values of the Galactic extinction (E(B − V)), and of the AGN distance. We allowed each of these to be free sequentially, and compared the inferred spin value with that found in the previous section.
We assumed E(B − V)=0.128 (instead of 0.113) which corresponds to the original value from Schlegel et al. (1998) without the recalibration performed by Schlafly & Finkbeiner (2011). We find a slightly lower value of the spin (0.79 ± 0.05, Table 3, Col. 2) compared to that found previously with E(B − V)=0.113 (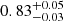 , Table 3, Col. 1), but still compatible within the error bars. Indeed, for a given observed optical-UV luminosity a higher reddening along the line of sight implies a higher intrinsic luminosity, then a larger accretion rate (Eq. (1)) and at last a smaller accretion efficiency (Eq. (2)).
, Table 3, Col. 1), but still compatible within the error bars. Indeed, for a given observed optical-UV luminosity a higher reddening along the line of sight implies a higher intrinsic luminosity, then a larger accretion rate (Eq. (1)) and at last a smaller accretion efficiency (Eq. (2)).
We then evaluated the impact on the fit results with a different AGN distance of D = 137.2 Mpc (instead of 143.5 Mpc) corresponding to the distance assuming the older cosmological constants from the five-year WMAP (Spergel et al. 2003) where the corresponding cosmological constants are H0 = 71 km s−1 Mpc−1, and ΩΛ0 = 0.73. We find a negligible impact on the parameters fit compared to the reference model (Table 3, Col. 3).
5.1.2. Black hole mass value
Ark 120 is one of the about 60 AGN (Bentz & Katz 2015) for which the BH mass has been determined via reverberation mapping (Blandford & McKee 1982; Peterson 1993), which is one of the most reliable and direct methods to measure it in AGN (e.g. Peterson et al. 2004; Peterson 2014, and references therein).
This method is based on the response of the broad emission lines of the BLR to changes in the continuum. The virial BH mass is then estimated as f (ΔV2RBLR/G), where ΔV is the line width, RBLR is the reverberation radius, and G is the Gravitational constant. The quantity in brackets is called the “virial product” and is determined by two directly observable parameters (ΔV and RBLR). f is a dimensionless factor – often called the “virial factor” – to take into account the unknown BLR properties (structure, geometry, kinematics and inclination with respect to the observer) and can be different from object to object. A mean f, ⟨f⟩, value is currently determined via the MBH–σ* relationship assuming that it is the same for quiescent and active galaxies (Ferrarese & Merritt 2000; Gebhardt et al. 2000; Woo et al. 2013), and by normalising the reverberation mapped AGN to this relation (see Peterson et al. 2004 for a detailed explanation). However, this ⟨f⟩ quantity is not straightforward to infer since it may, for example, depend on the bulge classification and/or on the presence of bars (e.g. Ho & Kim 2014; Graham et al. 2011), but see Graham (2014) on caveats about bulge classification. The estimated values of ⟨f⟩ broadly range from about 4 and 6 (e.g. Onken et al. 2004; Shen et al. 2008; Woo et al. 2010, 2013; Park et al. 2012; Grier et al. 2013; McConnell & Ma 2013; Ho & Kim 2014; Batiste et al. 2017). So we now consider the minimum and maximum values of ⟨f⟩ reported in the literature since the last few years. Ho & Kim (2014) find ⟨f⟩=6.3 ± 1.5 for classical bulge galaxies such as Ark 120, though Batiste et al. (2017) find that their best-fit relationship is insensitive to galaxy morphology. Alternatively, Grier et al. (2013) find a smaller mean virial factor with ⟨f⟩=4.31 ± 1.05. This is the default value taken for the calculation of the BH mass in “The AGN Black Hole Mass Database” (Bentz & Katz 2015)12, using the calibration of the MBH–σ⋆ relation for AGNs based on high-luminosity quasars hosts.
The commonly used BH mass in the literature for Ark 120 is 1.50 × 108 M⊙. This is calculated from the virial product of 2.72 × 107 M⊙ determined by Peterson et al. (2004), and assuming the viral factor of 5.5 ± 1.8 from Onken et al. (2004; see Table 6 in Peterson et al. 2004). So we now appraise the impact on the inferred spin value still based on the virial product value from Peterson et al. (2004) but using the lowest and highest virial product values as discussed above, that is, ⟨f⟩=4.31 ± 1.05 (Grier et al. 2013) and ⟨f⟩=6.3 ± 1.5 (Ho & Kim 2014). These values would correspond to BH masses of 1.17 × 108 M⊙ and 1.71 × 108 M⊙, respectively.
As reported in Table 3, the value of the BH mass has the most important impact on the inferred spin value, compared to the E(B − V) and AGN distance values for which the impact is much less or even marginal. We find a spin value of 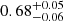 and
and 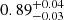 for ⟨f⟩=4.31 ± 1.05 and ⟨f⟩=6.3 ± 1.5, respectively. The higher the BH mass, the higher the BH spin value. Indeed, for a given observed Lopt − UV, increasing/decreasing MBH leads to a lower/higher Ṁ value (Eq. (1)). Therefore, to reproduce the overall Lbol a higher/lower efficiency (η) is required (Eq. (2)) which corresponds to a higher/smaller BH spin value.
for ⟨f⟩=4.31 ± 1.05 and ⟨f⟩=6.3 ± 1.5, respectively. The higher the BH mass, the higher the BH spin value. Indeed, for a given observed Lopt − UV, increasing/decreasing MBH leads to a lower/higher Ṁ value (Eq. (1)). Therefore, to reproduce the overall Lbol a higher/lower efficiency (η) is required (Eq. (2)) which corresponds to a higher/smaller BH spin value.
It is noteworthy that applying a general relativistic accretion disc corona model – but excluding the soft X-ray data (soft X-ray excess) – to five higher accretion rate AGN (0.3 ≲ Ṁ ≲ 0.5), You et al. (2016) show that the spin can be well constrained if the mass measurement is known to within 50% accuracy (see also Czerny et al. 2011; Done et al. 2013). Here, considering the lowest and highest BH masses for Ark 120 as determined above, this correspond to an accuracy of the BH value compared to the reference one of 22% and 14%, respectively.
Other direct methods to determine the mass exist and have been applied to Ark 120. Recently, Denissyuk et al. (2015) used the radial velocities of emission features to infer a BH mass for Ark 120 of 1.675 ± 0.028 × 108 M⊙, similar to that found by Peterson et al. (2004) and Ho & Kim (2015). Another method is based on polarisation of the broad emission lines (e.g. Afanasiev & Popović 2015; Songsheng & Wang 2018; Savić et al. 2018), and has been applied to Ark 120 by Afanasiev & Popović (2015). The inferred a BH mass of 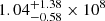 M⊙ that is compatible within its error bars with the values used in this work.
M⊙ that is compatible within its error bars with the values used in this work.
Finally, we estimate from the SED shape the required BH mass that would correspond to a non-rotating BH (a = 0) or a maximally rotating BH (a = 0.998). We find 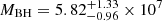 M⊙ ( χ2/d.o.f. = 3820.3/3517), and
M⊙ ( χ2/d.o.f. = 3820.3/3517), and 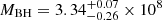 M⊙ ( χ2/d.o.f. = 3850.7/3517), respectively. These would correspond, respectively, to mean virial factors of about 2.1 and 12.3 which are very discrepant from the mean values published during the last few years. So, unless the individual virial factor for Ark 120 strongly differs from the mean value reported for AGN, these two “extreme” solutions appear unlikely. Therefore, an intermediate spin value of about 0.7–0.9 is strongly favoured for Ark 120.
M⊙ ( χ2/d.o.f. = 3850.7/3517), respectively. These would correspond, respectively, to mean virial factors of about 2.1 and 12.3 which are very discrepant from the mean values published during the last few years. So, unless the individual virial factor for Ark 120 strongly differs from the mean value reported for AGN, these two “extreme” solutions appear unlikely. Therefore, an intermediate spin value of about 0.7–0.9 is strongly favoured for Ark 120.
5.2. Deviations from Novikov-Thorne thin disc?
As shown by general relativistic magnetohydrodynamic (GRMHD) simulations of accretion onto stellar BHs, contrary to the basic assumptions of the thin disc model of Novikov & Thorne (1973, hereafter NT), there can be significant magnetic stress throughout the plunging region. This means that additional dissipation and radiation can be expected. However, as shown by Kulkarni et al. (2011) for an accretion rate of 0.1 times Eddington and an accretion disc inclination angle of 30°, that is, similar to the values found for Ark 120, the discrepancies on the inferred spin values between calculations from GRMHD simulations and a NT disc assumption are only about 0.007 and 0.02 for spin values of 0.9 and 0.7, respectively (see also, Penna et al. 2010; Noble et al. 2011; Penna et al. 2012; Zhu et al. 2012; Sąowski 2016). This would mean that for objects with both low-to-moderate accretion rates and inclination angles, as Ark 120, such systematic error is marginal (and much smaller than the error bars from spectral measurements), and that the NT disc theory is adequate and can be safely applied.
However, for the Ark 120 the warm and hot Comptonisation components are dominant in the SED. Therefore, the hot corona in particular may well have significant scale height, especially during the 2013 low-flux state observation that would correspond to a low accretion rate (L/LEdd) of about 0.03 and may be in form of a hot inner flow with large scale height (Kubota & Done 2018, see their Fig. 2 for the disc-corona scheme). This could mean that the flow has some pressure support so is sub-Keplerian, and then that advection is important as a cooling mechanism, which acts to suppress η below that expected from a thin disc (Narayan & Yi 1995). Therefore, dedicated calculations are required to determine possible deviations from the NT model (and then ultimately on spin measurements) for moderate accretion rate AGN for which warm and hot Comptonisation are the dominant processes. However, it is noteworthy that You et al. (2016) from their general relativistic accretion disc-corona model find that for a BH mass of 108 M⊙ and spin of 0.9 the disc thickness (H/R) is much less than 0.1 (see their Fig. 13) for an accretion rate value of about 0.08 of Eddington, that is, similar to that of Ark 120 in 2014.
Another clear difference for Ark 120 with the NT thin disc predictions is the variability. From the best simultaneous fit of the 2013 and 2014 observations, we infer a significant increase in mass accretion rate through the disc from 0.03 to 0.07 Lbol/LEdd in only one year, but a standard thin disc around a SMBH cannot vary on such timescale. Indeed, the radial mass accretion rate change via viscous processes has a time-scale of torb(R)/[α(H/R)2]. For Ark,120, assuming an orbital time-scale at R = 100 Rg, a viscosity parameter of 0.1 and a H/R (H is the height scale of the disc) value of 0.1, this corresponds to ∼150 years. Moreover, the optical-UV flux significantly changes in less than a year, varying for example by a factor of 50% in the UVW2 band between 2013 and 2014 (e.g. see Fig. 1, Lobban et al. 2018). Similar rapid changes in the optical-UV flux are typically seen in other BLS1s, especially those at low Lbol/LEdd (e.g. MacLeod et al. 2010; Kozłowski 2016; Simm et al. 2016; Rakshit & Stalin 2017). These are generally assumed to be from reprocessing, where the X-ray flux illuminates the outer disc (e.g. Buisson et al. 2017), and adds to the intrinsic emission. An additional reprocessed component in the optical-UV would lead us to overestimate the value of the intrinsic Ṁ, so to an underestimate of BH spin via the efficiency argument (Kubota & Done 2018). Nonetheless, changes as large as about 50% in the UV flux are unlikely to be driven by X-ray reprocessing, as the UV flux in Ark 120 is much higher than in the X-ray band. Besides, detailed models of the expected optical-UV variability from X-ray reprocessing fail to fit the excellent long term simultaneous optical-UV-X-ray datasets, and would imply a larger disc size than expected by standard thin disc (e.g. NGC 5548: McHardy et al. 2014; Edelson et al. 2015; Gardner & Done 2017; NGC 4151: Edelson et al. 2017; Ark 120: Gliozzi et al. 2017; Fairall 9: Pal et al. 2017; NGC 4593: Cackett et al. 2018; Pal & Naik 2018; Microlensing studies: Morgan et al. 2010; Dai et al. 2010). Such large discs should be significantly brighter than observed and this discrepancy may be explained for example by a flatter temperature profile than in NT discs, from scattering of a significant part of the optical flux on larger scales, by electron scattering in the disc atmosphere (Dai et al. 2010; Morgan et al. 2010; Hall et al. 2018).
To resolve this issue, Gardner & Done (2017) propose an alternative scenario where the observed optical-UV lags do not arise from hard X-ray reprocessing of the accretion disc emission from the hot corona, because it is shielded by the soft X-ray excess region, but instead arise from reprocessing of the far-UV emission by optically thick clouds in the inner regions of the BLR (see their Fig. 14). In addition, Lawrence (2018) argue that reprocessing by “clouds lifted out of the disc” might solve this “viscosity crisis”. Moreover, as suggested by Cackett et al. (2018) studying NGC 4593, diffuse emission from the BLR must also contribute significantly to the interband lags (see also, McHardy et al. 2018; Lawther et al. 2018).
It has been also proposed by Noda & Done (2018) that this faster than expected disc emission variability may be connected to the propation of heating-cooling waves across the disc which can change the accretion rate locally on faster timescale than the viscous one. Such changes mean that the flow is non-stationary with the accretion rate, not always constant with radius as assumed in the NT model. In addition, magnetically elevated discs, which are thicker than NT disc, would lead to much shorter inflow times (Dexter & Begelman 2019).
All these proposed scenarios show the importance for intensive multi-wavelength monitorings (from short to long timescales) of accretion disc emissions to better understand their origin(s) and check for genuine possible departure(s) from the NT model in AGN. However, the optical-UV to X-ray timing analysis of Ark 120 showed that the time lag between X-rays and the U band is only about two days and the time lag between UVW2 is compatible with zero within the uncertainties (Lobban et al. 2018). Therefore, these timescales are similar to duration of the multi-wavelength simultaneous observations used in this work. Moreover on such short timescales, the variability of the optical and UV bands is within only a few percent, with a maximum of six percent for the UVW2 band. Therefore, this restrained optical-UV variability should prevent from too large a departure from energy conservation in a steady state accretion disc as used in the optxagnf model.
In conclusion, we caution that our results on BH spin depend on the detailed disc-corona structure, which is not yet fully constrained. However, the realistic parameter values (e.g. log(Lbol/LEdd) range, disc inclination angle) found from this analysis for Ark 120 seem to show that this is a promising method to determine spin in BLS1s.
5.3. Other spin measurement methods from X-rays
One way to check the disc-Comptonisation efficiency method used in this work and then the disc-corona structure assumed, is to compare the inferred spin value with those derived from other methods, when applicable.
5.3.1. X-ray relativistic reflection fitting
A promising way to strengthen the spin determination would be to compare the spin determination for the same AGN from the disc-Comptonisation efficiency method and from relativistic reflection modelling. For this, finding AGN – with well constrained BH mass – displaying at different periods spectra dominated by either Comptonisation or relativistic reflection would be of great interest. This could be the case for Ark 120. Indeed, the 2007 Suzaku spectrum – with an X-ray flux between the ones observed in 2013 and 2014 – displayed an apparently broader FeKα line compared to that observed in 2014 with XMM-Newton (Nardini et al. 2016), and the X-ray Suzaku spectrum has been interpreted as due to relativistic reflection emission (Nardini et al. 2011). However, the lack of good S/N data above 30 keV from this 2007 Suzaku observation precludes for a discrimination between Comptonisation versus relativistic reflection as the dominant process (as shown in Porquet et al. 2018).
In the case where the spin values inferred from the two methods do not agree, this will give us an indication that one or both models have to be improved until both inferred spin values match each other. Indeed, there are a lot of caveats in the determination of AGN spin, such as the presence of a strong warm absorber and/or wind component(s). For example, such a comparison between X-ray relativistic reflection fitting and the disc-Comptonisation efficiency method has been applied to the “complex” NLS1 1H 0707–495 by Done & Jin (2016). Fixing the parameters inferred from relativistic reflection models (that is high spin, moderate inclination and low-mass BH) to the efficiency method, Done & Jin (2016) infer a non physical extreme accretion rate value of 140–260 times the Eddington limit for this object. Therefore, they argue that strong winds expected for such type of objects could bias the spin measurement in relativistic reflections models. Indeed, a strong wind could alter the determination of the spin if the sharp drop usually interpreted as the blue wing of a relativistic FeK line is actually due (at least in part) to a blueshifted absorption feature(s) (Kosec et al. 2018; Parker et al. 2018a; Jiang et al. 2018). This could also suggest that for high-accretion rate AGN like 1H 0707–495 pure relativistic reflection modelling is not adequate. Indeed, as shown in Kammoun et al. (2018) the spin can be recovered even if complex warm and cold absorptions are present (provided that both reflection is strong and the spin is high, assuming a lamp-post geometry), but leaving such effects unmodelled can introduce significant and poorly controlled systematics.
Moreover, before applying one of these fitting methods the origin of the soft excess must be robustly determined to avoid biased determination of the spin value (Patrick et al. 2011; Boissay et al. 2016; Porquet et al. 2018). For example, Walton et al. (2013) applying a pure relativistic reflection model to the NLS1 Ton S180 spectrum infer a high spin value of about 0.9 and a very high emissivity index (q > 8) to be able to reproduce the extremely smooth soft X-ray excess. This was contradicted recently by Parker et al. (2018b; see also discussion in Nardini et al. 2012) who – applying a state-of-the-art relativistic reflection model (RELXILL_LP; Dauser et al. 2010) to a higher S/N X-ray spectrum – ascertain that the soft X-ray excess in Ton S180 cannot be accounted for by reflection and inferred from the 3–10 keV energy band a low spin value (a < 0.4). As for Ark 120 (Porquet et al. 2018), they find for the broad-band spectrum of Ton S180 can be modelled by a two-component Comptonisation continuum plus mildly relativistic disc reflection component. This emphasises the need to describe the broad band continuum correctly in order to reliably estimate the black hole spin.
5.3.2. X-ray QPOs and X-ray polarisation
As discussed in the introduction section there are two other methods to determine spin from X-ray data: high-frequency QPOs and polarisation.
High-frequency QPO are primarily dependent on the BH mass and spin (Abramowicz & Kluźniak 2001; Remillard & McClintock 2006). However, these have only recently been detected in AGN as for example in RE J1034+396 (Gierliński et al. 2008; Alston et al. 2014), in MS 2254.9–3712 (Alston et al. 2015), in 2XMM J123103.2+110648 (Lin et al. 2013), and possibly in 1H 0707–495 (Pan et al. 2016). These are all high accretion rate objects, with Lbol/LEdd ≳ 1, which are in a very different accretion regime compared to Ark 120. Additionally, transient QPOs have been detected in tidal disruption events as in Swift J164449.3+573451 (Reis et al. 2012; Wang et al. 2014). So far, the only results from all these detections are a single upper limit of about 0.08 for the BH spin for RE J1034+396 (Mohan & Mangalam 2014), though again it depends on a good BH mass estimate which is lacking in this AGN (Czerny et al. 2016).
Special and general relativistic effects strongly modify the polarisation properties of the radiation observed at infinity. For instance, a spin-dependent rotation of the polarisation angle with energy is expected for the disc thermal emission (e.g. Stark & Connors 1977; Dovčiak et al. 2008; Li et al. 2009; Schnittman & Krolik 2009). For a stellar-mass accreting black hole in the soft state, this rotation happens mostly above 1 keV, and can therefore be searched for by the X-ray polarimetry missions already approved (IXPE, Weisskopf et al. 2016) or under study (eXTP, Zhang et al. 2016), which work in the 2−8 keV band. In AGN, this energy band is dominated by coronal emission and reflection, and the use of polarimetry to derive the black hole spin is still possible but less straightforward (Schnittman & Krolik 2010; Dovčiak et al. 2011; Beheshtipour et al. 2017; Marin et al. 2018a,b), not mentioning further complications arising from the contribution of reflection from parsec-scale AGN components such as the molecular torus. Effects in different coronal geometries, like the one adopted in this paper, are yet to be investigated to predict whether the spin and mass of the central SMBH can be robustly extracted from the polarimetric signal of AGN in the IXPE band.
6. Conclusion
We performed optical to hard X-ray SED fitting of Ark 120, using XMM-Newton and NuSTAR data obtained in March 2014 and February 2013 applying the disc-Comptonisation efficiency method. We used the OPTXCONV model (based on the OPTXAGNF model, Done et al. 2013) to self consistently model the outer disc emission and the inner (warm and hot) Comptonisation components, taking into account both inclination and relativistic effects. For the relativistic reflection we used as incident spectrum the Comptonisation spectral shape for self-consistency. Assuming a full covering optically-thick corona for the warm Comptonisation component, meaning that any relativistic reflection below the optically-thick corona radius Rcorona is hidden to the observer, we find a good fit for both datasets, though some excess at high energy indicates that the hot Comptonisation component has a temperature larger than 100 keV.
We find that the warm optically-thick corona (τ ∼ 9–12) has a temperature (kTe ∼ 0.4–0.5 keV) that slightly increases when the source is brighter (2014 March 22). We also confirm the softer when brighter behaviour for Ark 120 reported previously (Matt et al. 2014; Gliozzi et al. 2017; Lobban et al. 2018).
We infer a receding coronal radius (at a statistical significance of about 5.5σ) with increasing flux (by about a factor of two) from about 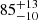 Rg to about 14 ± 3 Rg from February 2013 to March 2014. However, there is some indication that for the 2013 observation the optically-thick corona may be patchy above about 14 Rg. We find a well constrained spin value of
Rg to about 14 ± 3 Rg from February 2013 to March 2014. However, there is some indication that for the 2013 observation the optically-thick corona may be patchy above about 14 Rg. We find a well constrained spin value of 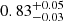 assuming a reverberation BH mass of 1.50 × 108 M⊙. We investigated the impact of assumption of the E(B − V) values as well as the SMBH properties (distance, mass). We find that the most important impact on the spin value is due to the BH mass. However, we are able to infer that the likely SMBH spin is located between
assuming a reverberation BH mass of 1.50 × 108 M⊙. We investigated the impact of assumption of the E(B − V) values as well as the SMBH properties (distance, mass). We find that the most important impact on the spin value is due to the BH mass. However, we are able to infer that the likely SMBH spin is located between 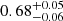 and
and 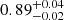 even if we assumed the minimum and maximum mean virial factor (⟨f⟩) values reported in the literature.
even if we assumed the minimum and maximum mean virial factor (⟨f⟩) values reported in the literature.
In conclusion, for the first time we are able to infer tight constraints on the spin of a SMBH using the disc efficiency method, via modelling the optical-UV to X-ray emission from the Comptonised disc spectrum. This was possible thanks to the properties of Ark 120, namely that it is a bare AGN devoid of intrinsic absorption, its reliable black hole mass determined via reverberation mapping, as well as the presence of a mild relativistic reflection in the 2014 observation. The latter allows us to obtain a good constraint on the inclination angle, another important parameter to constrain the spin.
However, this method crucially depends upon the assumption that the emissivity is given by the expected thin disc Novikov-Thorne relation. Indeed, it is possible that the accretion flow in Ark 120 does not comply with the predictions of a thin disc, firstly as its X-ray spectrum is dominated by warm and hot Comptonisation components rather than by the disc emission, and secondly as the optical-UV varies on much faster time-scales than expected, as well as the accretion rate. Therefore, a much better understanding of the accretion flow is required before this technique to measure the spin can be deemed as robust. In this framework, a comparison of BH spin measurements using different methods in X-rays (e.g. relativistic reflection modelling, high-frequency QPO, and polarisation properties that will be accessible in the near future) will be of great interest. However, the realistic parameter values, such as the Eddington ratio and the accretion disc inclination angle, found from this method for Ark 120 suggest that this is a promising technique to determine spin in BLS1s.
A definition of the virial factor is given in Sect. 5.
The Pan-STARRS-1 image cutout server is available at http://ps1images.stsci.edu
The merged calibrated spectrum of Ark 120 was downloaded from http://hea-www.harvard.edu/~pgreen/HRCULES.html, and smoothed with a four-bin window for better visibility.
Available at https://www.cosmos.esa.int/web/xmm-newton/om-response-files
This distance value is calculated via the NED Cosmology Calculator (Wright 2006), assuming a flat Universe: http://www.astro.ucla.edu/~wright/CosmoCalc.html
Acknowledgments
We thank the anonymous referee for her/his comments. Based on observations obtained with the XMM-Newton, and ESA science mission with instruments and contributions directly funded by ESA member states and the USA (NASA). This work made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory, and funded by NASA. This research has made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center and the California Institute of Technology. J. N. Reeves acknowledges support through NASA grant NNX15AF12G. A. L. acknowledges support from the UK STFC under grant ST/M001040/1. E. N. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 664931. F. M. is grateful to the Centre national d’études spatiales (CNES) and its post-doctoral grant “Probing the geometry and physics of active galactic nuclei with ultraviolet and X-ray polarized radiative transfer”. C. R. acknowledges support from the CONICYT+PAI Convocatoria Nacional subvencion a instalacion en la academia convocatoria año 2017 PAI77170080 (C.R.).
References
- Abramowicz, M. A., & Kluźniak, W. 2001, A&A, 374, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Afanasiev, V. L., & Popović, L. Č. 2015, ApJ, 800, L35 [Google Scholar]
- Alston, W. N., Markeviĉiūtė, J., Kara, E., Fabian, A. C., & Middleton, M. 2014, MNRAS, 445, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Alston, W. N., Parker, M. L., Markeviĉiūtė, J., et al. 2015, MNRAS, 449, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Baloković, M., Matt, G., Harrison, F. A., et al. 2015, ApJ, 800, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Batiste, M., Bentz, M. C., Raimundo, S. I., Vestergaard, M., & Onken, C. A. 2017, ApJ, 838, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Beheshtipour, B., Krawczynski, H., & Malzac, J. 2017, ApJ, 850, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., & Katz, S. 2015, PASP, 127, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Berti, E., & Volonteri, M. 2008, ApJ, 684, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Guainazzi, M., Matt, G., Fonseca Bonilla, N., & Ponti, G. 2009, A&A, 495, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Boissay, R., Ricci, C., & Paltani, S. 2016, A&A, 588, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brenneman, L. W., Madejski, G., Fuerst, F., et al. 2014, ApJ, 781, 83 [CrossRef] [Google Scholar]
- Buisson, D. J. K., Lohfink, A. M., Alston, W. N., & Fabian, A. C. 2017, MNRAS, 464, 3194 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Chiang, C.-Y., McHardy, I., et al. 2018, ApJ, 857, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Capellupo, D. M., Wafflard-Fernandez, G., & Haggard, D. 2017, ApJ, 836, L8 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arxiv:1612.05560] [Google Scholar]
- Choloniewski, J. 1981, Acta Astron., 31, 293 [NASA ADS] [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., Boggess, A., et al. 1999, ApJ, 516, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Crummy, J., Fabian, A. C., Gallo, L., & Ross, R. R. 2006, MNRAS, 365, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B., Hryniewicz, K., Nikołajuk, M., & Sąowski, A. 2011, MNRAS, 415, 2942 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B., You, B., Kurcz, A., et al. 2016, A&A, 594, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dai, X., Kochanek, C. S., Chartas, G., et al. 2010, ApJ, 709, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., Wilms, J., Reynolds, C. S., & Brenneman, L. W. 2010, MNRAS, 409, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, S. W., & Laor, A. 2011, ApJ, 728, 98 [CrossRef] [Google Scholar]
- Denissyuk, E. K., Valiullin, R. R., & Gaisina, V. N. 2015, Astron. Rep., 59, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., & Begelman, M. C. 2019, MNRAS, 483, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., & Gierliński, M. 2006, MNRAS, 367, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., & Jin, C. 2016, MNRAS, 460, 1716 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 2196 [Google Scholar]
- Done, C., Jin, C., Middleton, M., & Ward, M. 2013, MNRAS, 434, 1955 [NASA ADS] [CrossRef] [Google Scholar]
- Doroshenko, V. T., Sergeev, S. G., & Pronik, V. I. 2008, Astron. Rep., 52, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Dovčiak, M., Karas, V., & Matt, G. 2004, MNRAS, 355, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Dovčiak, M., Muleri, F., Goosmann, R. W., Karas, V., & Matt, G. 2008, MNRAS, 391, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Dovčiak, M., Muleri, F., Goosmann, R. W., Karas, V., & Matt, G. 2011, ApJ, 731, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Gelbord, J. M., Horne, K., et al. 2015, ApJ, 806, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Gelbord, J., Cackett, E., et al. 2017, ApJ, 840, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Lohfink, A., Kara, E., et al. 2015, MNRAS, 451, 4375 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Lohfink, A., Belmont, R., Malzac, J., & Coppi, P. 2017, MNRAS, 467, 2566 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Fragos, T., & McClintock, J. E. 2015, ApJ, 800, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia, J., & Kallman, T. R. 2010, ApJ, 718, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Gardner, E., & Done, C. 2017, MNRAS, 470, 3591 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Gierliński, M., Nikołajuk, M., & Czerny, B. 2008, MNRAS, 383, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Gliozzi, M., Papadakis, I. E., Grupe, D., Brinkmann, W. P., & Räth, C. 2017, MNRAS, 464, 3955 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W. 2014, in Structure and Dynamics of Disk Galaxies, eds. M. S. Seigar, & P. Treuthardt, ASP Conf. Ser., 480, 185 [NASA ADS] [Google Scholar]
- Graham, A. W., Onken, C. A., Athanassoula, E., & Combes, F. 2011, MNRAS, 412, 2211 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
- Grier, C. J., Martini, P., Watson, L. C., et al. 2013, ApJ, 773, 90 [CrossRef] [Google Scholar]
- Haas, M., Chini, R., Ramolla, M., et al. 2011, A&A, 535, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, P. B., Sarrouh, G. T., & Horne, K. 2018, ApJ, 854, 93 [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., & Kim, M. 2014, ApJ, 789, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., & Kim, M. 2015, ApJ, 809, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A., Done, C., & Fragile, P. C. 2009, MNRAS, 397, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A., van der Klis, M., Middleton, M., et al. 2016, MNRAS, 461, 1967 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, J., Walton, D. J., Parker, M. L., & Fabian, A. C. 2018, MNRAS, 481, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jin, C., Ward, M., & Done, C. 2012, MNRAS, 425, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kammoun, E. S., Nardini, E., & Risaliti, G. 2018, A&A, 614, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kara, E., García, J. A., Lohfink, A., et al. 2017, MNRAS, 468, 3489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, A. R., & Kolb, U. 1999, MNRAS, 305, 654 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Pringle, J. E., & Hofmann, J. A. 2008, MNRAS, 385, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Kolehmainen, M., Done, C., & Díaz Trigo, M. 2011, MNRAS, 416, 311 [NASA ADS] [Google Scholar]
- Kosec, P., Buisson, D. J. K., Parker, M. L., et al. 2018, MNRAS, 481, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Kozłowski, S. 2016, ApJ, 826, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Kubota, A., & Done, C. 2018, MNRAS, 480, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, A. K., Penna, R. F., Shcherbakov, R. V., et al. 2011, MNRAS, 414, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kuraszkiewicz, J. K., Green, P. J., Crenshaw, D. M., et al. 2004, ApJS, 150, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., & Netzer, H. 1989, MNRAS, 238, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A. 2018, Nat. Astron., 2, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Lawther, D., Goad, M. R., Korista, K. T., Ulrich, O., & Vestergaard, M. 2018, MNRAS, 481, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X., Narayan, R., & McClintock, J. E. 2009, ApJ, 691, 847 [CrossRef] [Google Scholar]
- Lin, D., Irwin, J. A., Godet, O., Webb, N. A., & Barret, D. 2013, ApJ, 776, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Lobban, A. P., Porquet, D., Reeves, J. N., et al. 2018, MNRAS, 474, 3237 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, C. L., Ivezić, Ž., Kochanek, C. S., et al. 2010, ApJ, 721, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F., Dovčiak, M., Muleri, F., Kislat, F. F., & Krawczynski, H. S. 2018a, MNRAS, 473, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F., Dovčiak, M., & Kammoun, E. S. 2018b, MNRAS, 478, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Marinucci, A., Matt, G., Kara, E., et al. 2014, MNRAS, 440, 2347 [NASA ADS] [CrossRef] [Google Scholar]
- Marinucci, A., Tortosa, A., & NuSTAR AGN Physics Working Group 2016, Astron. Nachr., 337, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Marinucci, A., Porquet, D., Tamborra, F., et al. 2019, A&A, 623, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, K. O., Breeveld, A., Much, R., et al. 2001, A&A, 365, L36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, G., Marinucci, A., Guainazzi, M., et al. 2014, MNRAS, 439, 3016 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Baloković, M., Marinucci, A., et al. 2015, MNRAS, 447, 3029 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., Narayan, R., Davis, S. W., et al. 2011, Classical and Quantum Gravity, 28, 114009 [NASA ADS] [CrossRef] [Google Scholar]
- McConnell, N. J., & Ma, C.-P. 2013, ApJ, 764, 184 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Cameron, D. T., Dwelly, T., et al. 2014, MNRAS, 444, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Connolly, S. D., Horne, K., et al. 2018, MNRAS, 480, 2881 [NASA ADS] [CrossRef] [Google Scholar]
- Mehdipour, M., Branduardi-Raymont, G., Kaastra, J. S., et al. 2011, A&A, 534, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mehdipour, M., Kaastra, J. S., Kriss, G. A., et al. 2015, A&A, 575, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, J. M., Reynolds, C. S., Fabian, A. C., Miniutti, G., & Gallo, L. C. 2009, ApJ, 697, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Mohan, P., & Mangalam, A. 2014, ApJ, 791, 74 [CrossRef] [Google Scholar]
- Morgan, C. W., Kochanek, C. S., Morgan, N. D., & Falco, E. E. 2010, ApJ, 712, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Motta, S. E. 2016, Astron. Nachr., 337, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Fabian, A. C., Reis, R. C., & Walton, D. J. 2011, MNRAS, 410, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Fabian, A. C., & Walton, D. J. 2012, MNRAS, 423, 3299 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Porquet, D., Reeves, J. N., et al. 2016, ApJ, 832, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, S. C., Krolik, J. H., Schnittman, J. D., & Hawley, J. F. 2011, ApJ, 743, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Noda, H., & Done, C. 2018, MNRAS, 480, 3898 [NASA ADS] [CrossRef] [Google Scholar]
- Nordgren, T. E., Helou, G., Chengalur, J. N., Terzian, Y., & Khachikian, E. 1995, ApJS, 99, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, in Black Holes (Les Astres Occlus), eds. C. Dewitt, & B. S. Dewitt, 343 [Google Scholar]
- Onken, C. A., Ferrarese, L., Merritt, D., et al. 2004, ApJ, 615, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Pal, M., & Naik, S. 2018, MNRAS, 474, 5351 [NASA ADS] [CrossRef] [Google Scholar]
- Pal, M., Dewangan, G. C., Connolly, S. D., & Misra, R. 2017, MNRAS, 466, 1777 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeri, P., Mendoza, C., Kallman, T. R., Bautista, M. A., & Meléndez, M. 2003, A&A, 410, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pan, H.-W., Yuan, W., Yao, S., et al. 2016, ApJ, 819, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Park, D., Woo, J.-H., Treu, T., et al. 2012, ApJ, 747, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, M. L., Alston, W. N., Buisson, D. J. K., et al. 2018a, Proceedings of Science, PoS(NLS1-2018)031 [Google Scholar]
- Parker, M. L., Miller, J. M., & Fabian, A. C. 2018b, MNRAS, 474, 1538 [NASA ADS] [CrossRef] [Google Scholar]
- Patrick, A. R., Reeves, J. N., Porquet, D., et al. 2011, MNRAS, 411, 2353 [NASA ADS] [CrossRef] [Google Scholar]
- Penna, R. F., McKinney, J. C., Narayan, R., et al. 2010, MNRAS, 408, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Penna, R. F., Sąowski, A., & McKinney, J. C. 2012, MNRAS, 420, 684 [Google Scholar]
- Peterson, B. M. 1993, PASP, 105, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M. 2014, Space Sci. Rev., 183, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P.-O., Ursini, F., De Rosa, A., et al. 2018, A&A, 611, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porquet, D., Reeves, J. N., O’Brien, P., & Brinkmann, W. 2004, A&A, 422, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porquet, D., Reeves, J. N., Matt, G., et al. 2018, A&A, 609, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rakshit, S., & Stalin, C. S. 2017, ApJ, 842, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., Porquet, D., Braito, V., et al. 2016, ApJ, 828, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Reis, R. C., Miller, J. M., Reynolds, M. T., et al. 2012, Science, 337, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S. 2014, Space Sci. Rev., 183, 277 [Google Scholar]
- Sąowski, A. 2016, MNRAS, 459, 4397 [NASA ADS] [CrossRef] [Google Scholar]
- Savić, D., Goosmann, R., Popović, L. Č., Marin, F., & Afanasiev, V. L. 2018, A&A, 614, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schnittman, J. D., & Krolik, J. H. 2009, ApJ, 701, 1175 [CrossRef] [Google Scholar]
- Schnittman, J. D., & Krolik, J. H. 2010, ApJ, 712, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, A. E., Stewart, G. C., & Mateos, S. 2012, MNRAS, 423, 2633 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, J., Vanden Berk, D. E., Schneider, D. P., & Hall, P. B. 2008, AJ, 135, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Simm, T., Salvato, M., Saglia, R., et al. 2016, A&A, 585, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Songsheng, Y.-Y., & Wang, J.-M. 2018, MNRAS, 473, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, R. F., & Connors, P. A. 1977, Nature, 266, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Theureau, G., Coudreau, N., Hallet, N., et al. 2005, A&A, 430, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tortosa, A., Marinucci, A., Matt, G., et al. 2017, MNRAS, 466, 4193 [NASA ADS] [Google Scholar]
- Tortosa, A., Bianchi, S., Marinucci, A., et al. 2018, MNRAS, 473, 3104 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Turner, T. J., Reeves, J. N., Braito, V., & Costa, M. 2018, MNRAS, 476, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Mushotzky, R. F., Winter, L. M., & Fabian, A. C. 2009, MNRAS, 399, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Fabian, A. C., Ballantyne, D. R., et al. 2004, MNRAS, 351, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Nardini, E., Fabian, A. C., Gallo, L. C., & Reis, R. C. 2013, MNRAS, 428, 2901 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.-Z., Lei, W.-H., Wang, D.-X., et al. 2014, ApJ, 788, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, M., Elvis, M., Fabbiano, G., et al. 1987, ApJ, 315, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Ramsey, B., O’Dell, S., et al. 2016, in Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, Proc. SPIE, 9905, 990517 [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, H., Glass, I. S., van Wyk, F., et al. 1992, MNRAS, 257, 659 [NASA ADS] [Google Scholar]
- Woo, J.-H., Treu, T., Barth, A. J., et al. 2010, ApJ, 716, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., Schulze, A., Park, D., et al. 2013, ApJ, 772, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L. 2006, PASP, 118, 1711 [NASA ADS] [CrossRef] [Google Scholar]
- You, B., Cao, X.-W., & Yuan, Y.-F. 2016, Res. Astron. Astrophys., 16, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S. N., Feroci, M., Santangelo, A., et al. 2016, in Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, Proc. SPIE, 9905, 99051Q [CrossRef] [Google Scholar]
- Zhu, Y., Davis, S. W., Narayan, R., et al. 2012, MNRAS, 424, 2504 [NASA ADS] [CrossRef] [Google Scholar]
- Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
OM average reddened count rates (expressed in s−1) of the AGN and associated errors for optical and UV filters used for the SED fitting.
All Figures
 |
Fig. 1. The Swift UVOT light curve of Ark 120 showing the corrected count rates in the U (red) and UVM2 (blue) bands (adapted from Lobban et al. 2018). Each point corresponds to a single image observation. The 0.3–10 keV XRT light curve (black) is overlaid with an additional y-axis scale. The lower and upper grey shaded areas correspond to the XRT count rates at the 2013 and 2014 XMM-Newton 0.3–10 keV fluxes, respectively. The horizontal dashed lines correspond to the mean flux for each dataset. |
| In the text | |
 |
Fig. 2. Pan-STARRS-1 g-filter image of Ark 120. North is up and east is left. The intensity is non-linearly scaled using an asinh transformation. The circle and the dashed annulus are the OM source and background apertures, respectively. The dashed circle is the custom background aperture that we used for the optical photometry. |
| In the text | |
 |
Fig. 3. Wavelength coverage of the UV emission of Ark 120 with the OM broad-band UV-filters. The continuous line is the observed UV spectrum of Ark 120 obtained with the Hubble Space Telescope Faint Object Spectrograph (HST/FOS) on 1995 July 29 (Kuraszkiewicz et al. 2004), where the main broad emission lines are labelled. The faint absorption lines are galactic in origin (Crenshaw et al. 1999). The dashed lines are the OM filter areas. The green data are the synthetised photometry that we computed from this HST/FOS spectrum using the OM broad-band UV-filter profiles. The red and blue data are the observed mean UVW2, UVM2, and UVW1 fluxes from the corrected observed mean count rates on 2014 March 22 and on 2013 February 18, respectively (Lobban et al. 2018). |
| In the text | |
 |
Fig. 4. U versus V dereddened fluxes of Ark 120, measured in a |
| In the text | |
 |
Fig. 5. U versus B dereddened fluxes of Ark 120, measured in a |
| In the text | |
 |
Fig. 6. Simultaneous fit of the Ark 120 SED (XMM-Newton/OM/pn and NuSTAR) spectra of Ark 120 (AGN rest-frame) obtained on 2014 March 22 and on 2013 February 18. The 2014 and 2013 observations are displayed in black and red, respectively. Top panel: spectra and data/model. Bottom panel: intrinsic (that is, corrected for reddening and Galactic absorption) SED and the corresponding model components. Continuous curves: total SED. Dotted curves: outer disc emission. Dashed curved: warm optically-thick Comptonisation component (soft excess). Dotted-dashed curves: hot Comptonisation component (hard energy tail). 3-dotted-dashed curves: relativistic reflection component. For clarity purposes, the three BLR Gaussian line components are not displayed. |
| In the text | |
 |
Fig. 7. 2D contour plots (at the 68%, 90% and 99% confidence levels) from the simultaneous fit of the 2013 and 2014 observations. Top panel: disc inclination angle versus spin. Bottom panel: log(Lbol/LEdd) versus Rcorona (expressed in Rg) found for the 2014 observation (high-flux state, in black) and for the 2013 observation (low-flux state, in red). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.