EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A89 Full HTML
Open Access
Issue
A&A
Volume 654, October 2021
Article Number A89
Number of page(s) 11
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202141577
Published online 19 October 2021

© D. Porquet et al. 2021

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

In the standard picture, the emission of an active galactic nucleus (AGN) stems from an accretion disc around a supermassive black hole (SMBH) with mass spanning from a few million to billions of solar masses. X-ray spectra offer a unique potential to probe matter very close to the black hole, such as the disc-corona system. The X-ray spectra of AGN usually exhibit, in addition to a power-law continuum between ∼2 and 10 keV, one or more of the following components: a soft X-ray excess below 2 keV, a Fe Kα line complex near 6.4 keV, and a Compton scattering hump peaking near 20−30 keV. However, the geometry of the disc-corona system is still highly debated, as is the dominant emission process at work: either relativistic reflection resulting from the illumination of the accretion disc by a hot corona or the Comptonisation of seed photons from the accretion disc by a warm-hot corona (e.g. Magdziarz et al. 1998; Porquet et al. 2004; Crummy et al. 2006; Bianchi et al. 2009; Fabian et al. 2012; Done et al. 2012; Gliozzi et al. 2013; Petrucci et al. 2018; Gliozzi & Williams 2020; Waddell & Gallo 2020). Moreover, some AGN exhibit warm absorbers along the line-of-sight that can severely complicate the X-ray data analysis. Therefore, bare AGN that show no (or very weak) X-ray warm absorbers are the best targets for directly investigating the process(es) at work in the vicinity of SMBHs (Porquet et al. 2018).

The bright bare AGN Mrk 110 (z = 0.035291) has been classified as a narrow-line Seyfert 1 (NLS1) due to the relatively narrow optical emission lines (< 2000 km s−1 FWHM) emitted by its broad-line region (BLR; Osterbrock & Pogge 1985; Goodrich 1989). However, two much broader and more redshifted line components are also observed (∼5000−6000 km s−1 and ∼3340 km s−1; Bischoff & Kollatschny 1999; Véron-Cetty et al. 2007). In addition, and contrary to NLS1s, Mrk 110 displays an unusually large [O III]λ5007/Hβ ratio and very weak Fe II emission, which is more consistent with a broad-line Seyfert 1 (BLS1) and indicates a low Eddington ratio (Boroson & Green 1992; Grupe 2004; Véron-Cetty et al. 2007). Its X-ray photon index, soft X-ray excess strength, and X-ray variability are similar to that found for BLS1s (Porquet et al. 2004; Boller et al. 2007; Piconcelli et al. 2005; Zhou & Zhang 2010; Ponti et al. 2012; Gliozzi & Williams 2020). It hosts a SMBH with a mean mass value of Mgrav = 1.4 ± 0.3 × 108 M⊙ measured from the detection of gravitational redshifted emission in the variable component of all of the broad optical lines (Kollatschny 2003; Liu et al. 2017). In contrast to the virial method, for which a much lower black hole mass has been estimated, this gravitational method is independent of any assumption on the BLR geometry, such as its inclination angle. Indeed, as argued by Liu et al. (2017), the large discrepancy between Mvir and Mgrav for Mrk 110 is explained by the use of a virial factor of fFWHM ∼ 1 to infer Mvir, which is equivalent to a geometrically thin disc-like BLR with an inclination angle θ = 30° (fFWHM = 1/(4 sin2θ), the squared of Eq. (4) of Decarli et al. 2008). Therefore, the ∼8 times lower virial mass of Mrk 110 compared to its gravitational mass is explained by fFWHM ≈ 8−16 (Liu et al. 2017), that is to say, a BLR-disc system seen almost face-on with an inclination of 7−10° (see also Bian & Zhao 2002; Kollatschny 2003). Black hole mass values consistent with Mgrav have been inferred for Mrk 110 from different independent methods, such as optical spectro-polarimetric observations (Afanasiev et al. 2019), X-ray excess variance (Ponti et al. 2012), and X-ray scaling methods (Gliozzi et al. 2011; Williams et al. 2018). Judging from its optical and X-ray properties, black hole mass, and accretion rate, Mrk 110 is a BLS1.

Reeves et al. (2021a) found that the XMM-Newton-RGS (Reflection Grating Spectrometer; den Herder et al. 2001) spectra of Mrk 110 obtained between 2004 and 2020 exhibit no significant intrinsic X-ray warm absorption, with an upper limit for its column density of only 2.6 × 1020 cm−2. This indicates that Mrk 110 is a bare AGN whatever its flux level is. Moreover, they confirm the presence of a broad O VII soft X-ray emission line, first identified by Boller et al. (2007). For the first time, Reeves et al. (2021a) report that the O VII line flux varies significantly with the soft X-ray continuum flux level, being brightest when the continuum flux is highest, similar to the reported behaviour of the optical He II line (Véron-Cetty et al. 2007). This O VII line originates from the accretion disc at a distance of a few tens of gravitational radii. From the spectral analysis, a very stringent constraint on the inclination angle of the accretion disc has been measured, 9.9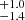 degrees, which is consistent with an almost face-on view, as also inferred from the optical emission lines emitted by the disc-like BLR (Bian & Zhao 2002; Kollatschny 2003; Liu et al. 2017).

In this paper we report the X-ray broadband spectral analysis of the first two simultaneous XMM-Newton and NuSTAR observations of Mrk 110, performed on November 16−17, 2019, and April 5−6, 2020. In Sect. 2 the data reduction and analysis method of the dataset are presented. The data analysis above 3 keV also uses a deep NuSTAR observation performed in January 2017 (Sect. 4). The X-ray broadband spectra analysis using a combination of Comptonisation and relativistic reflection models is reported (Sect. 5). Finally, the main results are summarised and discussed in Sect. 6.

2. Observations, data reduction, and analysis method

2.1. XMM-Newton and NuSTAR data reduction

The log of the XMM-Newton and NuSTAR simultaneous observations of Mrk 110 (NuSTAR cycle-5; PI: D. Porquet) used in this work is reported in Table 1. For the data analysis above 3 keV (Sect. 4), we also used the deep NuSTAR observation performed in January 2017.

Table 1.

Observation log of the XMM-Newton and NuSTAR dataset analysed in this work.

The XMM-Newton/EPIC (European Photon Imaging Camera) event files were reprocessed with the Science Analysis System (SAS; version 18.0.0), applying the latest calibration available on February 24, 2021. Due to the high source brightness, the EPIC-pn instrument was operated in the Small Window mode. We notice that only the EPIC-pn (Strüder et al. 2001) data were used (selecting the event patterns 0−4, that is to say, single and double events) since they do not suffer from pileup (contrary to the EPIC-MOS data; Turner et al. 2001) and they have a much better sensitivity above ∼6 keV. The pn spectra were extracted from a circular region centred on Mrk 110, with a radius of 35″ to avoid the edge of the chip. The background spectra were extracted from a rectangular region in the lower part of the small window that contains no (or negligible) source photons. The total net exposure times, obtained after the correction for dead time and background flaring, are reported in Table 1. Redistribution matrix files (rmf) and ancillary response files (arf) were generated with the SAS tasks RMFGEN and ARFGEN, and were binned in order to over-sample the instrumental resolution by at least a factor of three, with no impact on the fit results. As shown in Lobban et al. (in prep.), there is some flux variability during each XMM-Newton observation and between them. However, the spectral variability within any single observation is slow and moderate, and therefore we used the pn time-averaged spectra for each epoch. Finally, the background-corrected pn spectra were binned in order to have a signal-to-noise ratio greater than four in each spectral channel.

NuSTAR (Harrison et al. 2013) observed Mrk 110 with its two co-aligned X-ray telescopes with corresponding focal plane modules A (FPMA) and B (FPMB). The level 1 data products were processed with the NuSTAR Data Analysis Software (NuSTARDAS) package (version 2.0.0; June 19, 2020). Cleaned event files (level 2 data products) were produced and calibrated using standard filtering criteria with the NUPIPELINE task and the calibration files available in the NuSTAR calibration database (CALDB: 20210210). Extraction radii for both the source and the background spectra were 75 arcsec. The corresponding net exposure time for the observations with FPMA are reported in Table 1. The processed rmf and arf files are provided on a linear grid of 40 eV steps. As the FWHM energy resolution of NuSTAR is 400 eV below ∼50 keV and increases to 1 keV at 86 keV (Harrison et al. 2013), we re-binned the rmf and arf files in energy and channel space by a factor of 4 to over-sample the instrumental energy resolution by at least a factor of 2.5. The background-corrected NuSTAR spectra were finally binned in order to have a signal-to-noise ratio greater than five in each spectral channel.

2.2. Spectral analysis method

The XSPEC v12.11.1 software package (Arnaud 1996) was used for the spectral analysis. Since Reeves et al. (2021a) find that there is no additional absorption compared to the Galactic one, we fixed it in all forthcoming modelling at 1.27 × 1020 cm−2 (HI4PI Collaboration 2016). We used the X-ray absorption model TBNEW (VERSION 2.3.2) from Wilms et al. (2000), applying their interstellar medium (ISM) elemental abundances and the cross-sections from Verner et al. (1996). We allowed for cross-calibration uncertainties between the two NuSTAR spectra and the XMM-Newton/pn spectra by including in the fit a cross-normalisation factor for the pair of NuSTAR FPMA and FPMB spectra, with respect to the pn spectra. Except in Sect. 3, the inclination angle of the accretion disc was fixed at 9.9° (Reeves et al. 2021a). We used χ2 minimisation throughout, quoting errors with 90% confidence intervals for one interesting parameter (Δχ2 = 2.71). Default values of H0 = 67.66 km s−1 Mpc−1, Ωm = 0.3111, and ΩΛ = 0.6889 were assumed (Planck Collaboration VI 2020).

3. Main X-ray spectral components of the 2019 and 2020 XMM-Newton and NuSTAR observations

In order to characterise the main X-ray components of the spectra, we fit the two simultaneous XMM-Newton/pn and NuSTAR spectra between 3−5 keV (AGN rest-frame) using a power-law model with Galactic absorption. We find photon indices of 1.70 ± 0.07 and 1.69 ± 0.07 for November 2019 and April 2010, respectively. As illustrated in Fig. 1 (top panel), the extrapolation of this fit over the full energy range shows a prominent and absorption-free smooth soft X-ray excess below 2 keV, which is variable between the two epochs, with the highest flux observation (2019) exhibiting the largest soft X-ray excess. Mrk 110 does not display any Compton hump, which suggests a weak (or even a lack of) relativistic reflection component; Mrk 110 has a flat hard X-ray shape with a notable deficit above ∼30 keV that indicates a low high-energy cutoff, that is to say, a low hot corona temperature.

thumbnail Fig. 1.

Data-to-model ratio of the two simultaneous XMM-Newton/pn and NuSTAR spectra of Mrk 110 fit with a power-law model (with Galactic absorption) over the 3−5 keV energy range. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. Top panel: extrapolation over the full broadband X-ray energy range. Bottom panel: zoom-in on the Fe Kα line. Only the pn spectra (using here a 75 eV spectral binning) are reported for purposes of clarity. The vertical dashed red line corresponds to 6.4 keV.

The Fe Kα line profile is found to be consistent between these two epochs, though the flux of the latter observation is lower (Fig. 1, bottom panel). Aiming to characterise this Fe Kα complex, we first fit the two pn spectra between 3 and 10 keV with a power-law model with Galactic absorption and a Gaussian line. The energy and width (σ) of the line were tied between both observations. We find a good fit with E = 6.36 ± 0.03 keV and σ ≤ 0.106 keV (χ2/d.o.f. = 585.1/669). The equivalent widths (EWs) are 58 ± 16 eV and 41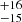 eV for 2019 and 2020, respectively. The mean value of the line energy is slightly lower than that expected from the neutral Fe Kα fluorescence line in the AGN rest-frame. We checked that this is not due to a gain issue by analysing other AGN observed at similar periods using the small window mode. Even if the line width is not constrained, its high upper limit and the slightly lower line energy might indicate that a mild relativistic reflection component is present. The upper limit to the line width corresponds to a FWHM velocity width, of < 12 000 km s−1, that is compatible with the widths of the accretion disc O VII emission line in the high resolution RGS spectra, for which the inner radius of the line emission is inferred to lie between about 20−100 Rg from the black hole (Reeves et al. 2021a). We note that since the accretion disc is seen almost face-on, the width of lines emitted above a few tens of Rg appears much narrower than for systems viewed at higher inclination angles, such as found in the bare AGN Ark 120 for which the system is observed with an inclination angle of ∼30° (Porquet et al. 2018, 2019). This explains the moderate value of the width upper limit for Mrk 110. Moreover, the ionisation parameter of the medium from which the O VII emission line originates, log ξ ∼ 1.2, is expected to also give rise to a neutral Fe K emission line.

Therefore, we now fit the two pn spectra between 3 and 10 keV using a power-law model with Galactic absorption, a narrow neutral Fe Kα core (En = 6.4 keV and σn = 0 eV), and a disc line model (RELLINE; Dauser et al. 2010, 2013) to account for the mildly broad line. For the third component, the energy was fixed at 6.4 keV and the spin at zero (since it is not constrained). All parameters of the Fe Kα narrow component and the emissivity index for the mild relativistic Fe K line component were tied between the two epochs. From this modelling (χ2/d.o.f. = 585.4/668), we infer an accretion disc emissivity index lower than 2.1 and a disc inclination lower than 24.6°, which is consistent with the inclination angle inferred from the variable O VII soft X-ray emission line (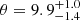) arising from the accretion disc too (Reeves et al. 2021a). For the narrow core of the Fe Kα line, we measure a EWn ≲ 20 eV, which is in the lower range of the values found for type-1 AGN (∼30−200 eV; Liu & Wang 2010; Shu et al. 2010; Fukazawa et al. 2011; Ricci et al. 2014). This is consistent with the very weak covering factor of 0.06 for the putative torus, which is inferred from the ratio of the infrared to the bolometric luminosity of the source (Ezhikode et al. 2017). Moreover, the torus covering factor measured for Mrk 110 is one of the lowest reported in the Ezhikode et al. (2017) sample; this is also in agreement with the lack of Compton hump. The equivalent widths of the moderately broad Fe Kα line are EWb = 61 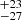eV and EWb = 43 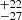eV for 2019 and 2020, respectively. Likewise, if we allow the inner disc radius to be free to vary and assume a standard value of three for the disc emissivity index, as well as fixing the inclination angle at 9.9° (χ2/d.o.f. = 585.1/668), we infer Rin = 120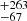Rg. This strengthens that the moderately broad Fe line could originate from the accretion disc but not too close to the inner stable circular orbit (ISCO), as was found for the O VII soft X-ray emission line (Reeves et al. 2021a). Its origin from the outer accretion disc is also consistent with the timing analysis reported in Lobban et al. (in prep.) where a hint of an extra variability is found at the Fe Kα complex energy range in the fractional variability spectra.

4. Spectral analysis above 3 keV at three epochs: 2017, 2019, and 2020

In this section we focus on the hard X-ray shape of Mrk 110 using the simultaneous XMM-Newton and NuSTAR data above 3 keV to prevent the fit from being driven by the soft X-ray emission. We also include here the deep NuSTAR observation of Mrk 110 performed in January 2017 (Ezhikode et al. 2020; Panagiotou & Walter 2020).

We first fit the data of these three epochs with a phenomenological model combining a power-law (Γ) continuum with an exponential cutoff at high energy (Ecut) and a Gaussian line. The line energy and its width were assumed to be constant between the three epochs, while its normalisation was allowed to vary. A very good fit is found as reported in Table 2. Thanks to the use of both XMM-Newton and NuSTAR data over the 3−79 keV and the deep 2017 NuSTAR data, both the energy and width of the Fe Kα line are well constrained, as illustrated by the 2D contour plot displayed in Fig. 2. The AGN rest-frame line energy is slightly redshifted towards 6.4 keV as previously found with the pn data, and line width corresponds to a FWHM of 22 000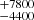 km s−1. This confirms that a mild relativistic reflection component is present.

thumbnail Fig. 2.

Contour plot of the Fe Kα Gaussian line width (keV) versus its energy (keV), assuming an underlying cutoff power-law continuum over the 3−79 keV energy range (see Sect. 4). The red, green, and blues curves show the confidence levels at 68% (Δχ2 = 2.3), 90% (Δχ2 = 4.61), and 99% (Δχ2 = 9.21), respectively.

Table 2.

Simultaneous fits above 3 keV of the 2019 and 2020 XMM-Newton/NuSTAR and 2017 NuSTAR observations of Mrk 110.

Now, we consider more physical models in order to determine both the hot corona properties and the disc reflection contribution. For this purpose, we use models that combine the primary continuum shape (hot corona) and the relativistic reflection contribution: RELXILL/RELXILLCP1 (version 1.4.3; Dauser et al. 2010; García et al. 2016) and REFLKERR2 (version 2019; Niedźwiecki et al. 2019).

Since the lamppost geometry does not allow us to obtain satisfactory fits, we only report below the results for a coronal geometry. The single power-law disc emissivity index (q; with emissivity ∝R−q) was fixed at the standard value of three, while the inner radius of the reflection component (Rin, expressed in units of Rg) was allowed to vary. The inclination of the accretion disc was fixed at 9.9° and the iron abundance was set to unity. Since the spin value is not constrained, we fixed it at zero.

The RELXILL model allows for relativistic reflection assuming a primary power-law (Γ) continuum with an exponential cutoff at high energy (Ecut). A good fit is found (Table 2). The inner radii, where the reflection occurs, are inferred to be a few tens of Rg. Moreover, the inferred very small reflection fraction values (ratio of intensity emitted towards the disc compared to that escaping to infinity) of ℛ ≃ 0.1−0.2, and the high-energy cutoff values of Ecut ∼ 110−130 keV for the three epochs indicate that the lack of Compton hump is due to the weak reflection strength combined with the presence of a moderately low high-energy cutoff value.

We now investigate relativistic reflection models with a primary Comptonisation continuum shape, which is more physical and has a sharper high-energy rollover compared to an exponential cutoff power law. In addition, such models have the advantage of having the hot corona temperature (kThot) as a physical parameter rather than a phenomenological exponential cutoff energy. We first apply the RELXILLCP model, which uses the NTHCOMP Comptonisation model (Zdziarski et al. 1996; Życki et al. 1999) as the incident spectrum. The other physical parameters are the same as those in the RELXILL model presented above. We find a good fit and infer similar hot corona temperatures of kThot ∼ 26 keV for all three epochs (Table 2). Then, we consider the REFLKERR where the hard X-ray Comptonisation spectrum is computed with the COMPPS model (Poutanen & Svensson 1996), which appears to be a better description of thermal Comptonisation when compared to Monte Carlo simulations (Zdziarski et al. 2020). Moreover, REFLKERR has, as physical parameter, either the Compton parameter (y) or the optical depth (τ). We choose to perform the fit with the optical depth as the direct inferred parameter. The temperature of the thermal seed photons (kTbb) Comptonised by the hot corona is an explicit physical parameter of this model. Here, we assume that the seed photons are provided by the cold disc, then kTbb was fixed at 10 eV corresponding to the expected maximum temperature of the accretion disc around a black hole mass of 1.4 × 108 M⊙ accreting at a ∼10% Eddington rate. In addition, REFLKERR allows us to choose either a slab or a spherical geometry for the hot corona. The latter corresponds to numerous active sphere regions above the disc surface. The hard X-ray shape of the reflected component is calculated using IREFLECT convolved with COMPPS rather than using XILLVERCP (see Niedźwiecki et al. 2019 for detailed explanations). Both models give good fits (Table 2, Fig. 3), though a larger χ2 value for the spherical geometry. Similar values of the hot corona temperature are measured for the three epochs: kThot ∼ 30−31 keV and kThot ∼ 21−22 keV for the slab and spherical geometries, respectively. From τ, we can infer the corresponding Compton-parameter of the hot corona (yhot) using the relation y = 4τ(kT/511 keV) (Beloborodov 1999). This correspond to yhot ∼ 0.5 and yhot ∼ 1.1 for the slab and spherical geometries, respectively.

thumbnail Fig. 3.

Data-to-model ratio of the fit above 3 keV with the REFLKERR relativistic reflection model, using a primary Comptonisation continuum shape and assuming a slab geometry for the hot corona. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR; orange: 2017 NuSTAR.

The extrapolation of the fits down to 0.3 keV for the 2019 and 2020 observations shows that the soft excess is not accounted for by any of these models, leaving a huge positive residual below 2 keV. Figure 4 (top panel) displays the extrapolation of the fit with the RELXILL model for illustration purposes. We notice that over the 0.3−10 keV energy range, the RELXILL model provides a good fit (Table A.1, Fig. A.1), while when this model is applied to the whole 0.3−79 keV X-ray broadband range, it fails to both reproduce the soft and hard X-ray shapes (Fig. 4, bottom panel). Similar results are found for other relativistic models (see Appendix A for more details).

thumbnail Fig. 4.

Fits of the two 2019 and 2020 simultaneous XMM-Newton/pn and NuSTAR spectra with the RELXILL relativistic reflection model that assumes a coronal geometry for the disc emissivity. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. Top panel: fit above 3 keV, which has been extrapolated down to 0.3 keV. The fit parameters are reported in Table 2. Bottom panel: fit over the full 0.3−79 keV energy range. The fit parameters are reported in Table A.1.

5. The X-ray broadband analysis of the 2019 and 2020 observations: A mixed Comptonisation and mild relativistic reflection modelling

We now aim to reproduce the X-ray broadband spectra of Mrk 110 with a model where Comptonisation is the dominant process combined with a moderate relativistic reflection component (Sect. 3; Reeves et al. 2021a). Indeed, as shown above, relativistic reflection alone is not able to explain the soft X-ray excess, thereby we investigate the alternative scenario where it (mainly) originates from a warm corona.

We apply to the two simultaneous XMM-Newton and NuSTAR spectra the following model: TBNEW(GAL) × [COMPTT(WARM) + REFLKERR(HOT) + REFLKERR(REFL)]. Since the COMPPS model cannot be used for coronal temperature value of a few hundred eV, we instead make use of the COMPTT model to take for the warm corona contribution and infer its temperature, kTwarm, and optical depth, τwarm (Titarchuk 1994). The REFLKERR model is split into two components in order to disentangle and display the contributions of the hot corona and of the moderate relativistic reflection. For the former, the reflection strength is set to zero to only calculate the emission from the hot corona, while for the latter it is set to a negative value (here set to −0.2; Sect. 4) in order to only return the reflection component due to the illumination of the accretion disc by the hot corona. As in Sect. 4, we fixed the seed photon temperature (kTbb) at 10 eV corresponding to the maximum temperature expected from the cold disc. A slab geometry for the hot corona was assumed. The other parameters of the two REFLKERR components were tied together for each epoch; we also set the emissivity index to the standard value of three and allowed the inner radius, where the relativistic reflection occurs, to be free to vary. The hot corona temperature values were fixed at those found in Sect. 4. The disc inclination degree was still set to 9.9°. The spin value is not constrained and then fixed at zero, but we checked that taking other values has no significant impact on other inferred parameter values. Since we previously found that the contribution of the molecular torus is negligible, we do not include it. We obtain an overall very good fit for the full X-ray broadband energy range for both epochs (Fig. 5 top panel; Table 3). The inferred ionisation parameter, log ξ = 1.1 ± 0.1, for the accretion disc agrees very well with that found for the O VII soft X-ray emission line (log ξ ∼ 1.2; Reeves et al. 2021a), and is also consistent with the emission of the moderately broad neutral Fe Kα emission line too (Fig. 5, bottom panel, magenta curves). We derive warm corona temperature values of kTwarm ∼ 0.3 keV and high optical depth values of τwarm ∼ 13 for the two epochs (Table 3). The variability of the soft X-ray excess between both epochs appears to be driven by its flux variability, being stronger when brighter (at a 5.5σ confidence level for the normalisation) rather than by any statistical change of its physical parameters.

thumbnail Fig. 5.

Fit of the two simultaneous 2019 and 2020 XMM-Newton/pn and NuSTAR spectra with the TBNEW(GAL) × [COMPTT(WARM) + REFLKERR(HOT) + REFLKERR(REFL)] model. The fit parameters are reported in Table 3. Top panel: data-to-model ratio. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. The Y-axis range is identical to that of Fig. 4 to allow for a direct comparison. Bottom panel: unfolded unabsorbed spectra (black: 2019; blue: 2020), where the separate contributions of the model components are displayed (solid and dotted curves for 2019 and 2020, respectively): Orange: soft Comptonisation (warm corona); green: hard Comptonisation (hot corona); magenta: disc reflection component.

Table 3.

Simultaneous fits over the broadband energy range of the two simultaneous XMM-Newton/pn and NuSTAR spectra with TBNEW(GAL) × [COMPTT(WARM) + REFLKERR(HOT) + REFLKERR(REFL)].

Since there is a significant soft X-ray excess mainly due to the warm corona, these soft X-ray photons may be Comptonised by the hot corona too, as was found for PKS 0558–504 (Gliozzi et al. 2013). Therefore, we allowed the input seed photon temperature, kTbb, to vary, but noting that it was tied between the 2019 and 2020 epochs due to the lack of significant variability of the temperature of the soft excess (Fig. 6). The ionisation parameter of the accretion disc was fixed at log ξ = 1.1, as was found above. The resulting seed photon temperature is kTbb = 75 ± 4 eV, which is much higher than the maximum temperature of an accretion disc around a SMBH of mass ∼108 M⊙ and instead corresponds to a black hole mass of about three decades lower and accreting near Eddington. This value could instead represent an intermediate temperature between the seed photons from the cold disc and from the warm corona. Therefore, the seed photons Comptonised by the electrons of the hot corona may be provided by a combination of both the cold disc and the warm corona. This is strengthened by the correlation between both the hard and soft X-ray fluxes and the X-ray and UV fluxes inferred from the long-term Swift monitoring of Mrk 110 (Lobban et al., in prep.).

thumbnail Fig. 6.

Same as Fig. 5 (top panel) but with the seed photon temperature allowed to be free to vary.

6. Summary and discussion

This paper presents the X-ray spectral analysis of two first simultaneous XMM-Newton and NuSTAR observations of Mrk 110 performed within about a half-year interval, on November 16−17, 2019, and April 5−6, 2020.

A prominent and absorption-free smooth soft X-ray excess is observed in both observations, with the strongest one seen during the brightest observation (2019). This confirms the presence of such a feature, as reported in the 2004 XMM-Newton observation, which caught the source in a slightly higher-flux state (Boller et al. 2007; Boissay et al. 2016; Jiang et al. 2019; Gliozzi & Williams 2020). A very similar spectral shape is found above 2−3 keV for both the continuum and the Fe Kα emission line.

The AGN rest-frame peak energy of the Fe Kα line is slightly redshifted towards 6.4 keV (E = 6.37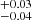 keV), and its width ( 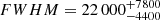km s−1) indicates that the Fe Kα line could originate from the accretion disc, as inferred for the O VII soft X-ray emission line with the RGS data analysis (Reeves et al. 2021a). The Fe Kα profile is mainly produced by moderately broadened reflection arising from an almost face-on accretion disc. Indeed, only a very weak possible additional contribution from the molecular torus (EWn ≲ 20 eV) is found, as expected from the very small total luminosity of the torus measured by Ezhikode et al. (2017), which is one of the lowest found in their sample. Only a much higher spectral resolution near 6.4 keV – as targeted by the future calorimeter-resolution X-ray missions XRISM (X-ray Imaging and Spectroscopy Mission; XRISM Science Team 2020) and Athena (Advanced Telescope for High-ENergy Astrophysics; Barret et al. 2018) – will provide an accurate determination of the genuine possible contributions of the BLR and torus regions.

The photon indices are found to be ∼1.7−1.8, confirming previous measurements found with the 2004 XMM-Newton (Boller et al. 2007), the 2007 Suzaku (Patrick et al. 2012; Walton et al. 2013; Mantovani et al. 2016; Waddell & Gallo 2020), and the 2017 NuSTAR (Ezhikode et al. 2020; Panagiotou & Walter 2020) observations. Such values are much flatter than what are commonly observed in NLS1s but are consistent with BLS1s (e.g. Porquet et al. 2004; Zhou & Zhang 2010; Waddell & Gallo 2020; Gliozzi & Williams 2020). This is in agreement with the BLS1 classification of Mrk 110 (see Sect. 1) rather than an NLS1 one, the latter of which is still commonly assumed in the literature. Moreover, no Compton hump is observed in the NuSTAR spectra, which instead has a flat spectrum and a hard X-ray deficit above ∼30 keV; this is in line with what was found previously for the deep January 2017 NuSTAR observation, which caught the source in a slightly higher flux level (Panagiotou & Walter 2020; Ezhikode et al. 2020).

The spectral analysis above 3 keV allows us to characterise the hot corona and the relativistic reflection emission properties. The deep January 2017 NuSTAR observation was also included in the simultaneous fit (Ezhikode et al. 2020; Panagiotou & Walter 2020). From the RELXILL reflection model, and assuming a primary exponential cutoff power-law continuum, we find moderate reflection strengths, ℛ ∼ 0.1−0.2, and high cutoff energies, Ecut ∼ 110−120 keV. These values are in very good agreement with those measured from the average long-term Swift/BAT (Burst Alert Telescope) spectrum (Vincentelli et al. 2021). Applying relativistic reflection models that assume a primary Comptonisation continuum, we infer the hot corona temperature to be kThot ∼ 26−31 keV (kThot ∼ 21−22 keV) and the optical depth to be τhot ∼ 2 (τhot ∼ 6−7) for the slab (or spherical) geometry. From the spectral analysis, it is not possible to discriminate between either of the hot corona geometries, although the slab geometry provides a better fit. In the near future, X-ray polarimetry is expected to play an important role within such a framework (e.g. Schnittman & Krolik 2010; Beheshtipour et al. 2017; Tamborra et al. 2018; Marinucci et al. 2019) thanks to, for example, IXPE (Imaging X-Ray Polarimetry Explorer; Weisskopf et al. 2016) and eXTP (Enhanced X-ray Timing and Polarimetry observatory; Zhang et al. 2016). While the corona temperatures found for Mrk 110 are broadly consistent with the average ones found by Middei et al. (2019) from a sample of 26 AGN (with ⟨kThot⟩ = 50 ± 21 keV and ⟨kThot⟩ = 53 ± 23 keV for the slab and spherical geometry, respectively), it is likely to be located in the lower range of this distribution. However, its hot coronal temperature is not as low as the temperatures inferred for some AGN with much lower high-energy cutoffs, such as GRS 1734–292 (Tortosa et al. 2017), Ark 564 (Kara et al. 2017), and PDS 456 (Reeves et al. 2021b), where kT could be as low as 15 keV.

The lack of variability in the cutoff energy and in the hot corona temperature may be due to the fact that during the 2017, 2019, and 2020 NuSTAR observations the source was caught in a very similar hard X-ray flux state with a 3−79 keV flux variability of only 1.5 between the 2017 and 2020 observations. Therefore, any possible ‘hotter-when-brighter’ or ‘cooler-when-brighter’ behaviour cannot be confirmed here (Keek & Ballantyne 2016; Ursini et al. 2016; Zhang et al. 2018; Middei et al. 2019; Kang et al. 2021). Further broadband X-ray monitoring of this bright source, using the unique synergy of XMM-Newton and NuSTAR, will be needed before any definitive statement about the physical and/or geometrical changes of the hot corona can be made. In particular, the observations would need to sample a larger flux range, as is observed in the long-term Swift monitoring of Mrk 110 (Vincentelli et al. 2021; Lobban et al., in prep.).

The X-ray broadband analysis shows that relativistic reflection models due to illumination on a constant density accretion disc alone cannot explain the X-ray broadband XMM-Newton/NuSTAR spectra of Mrk 110 (Appendix A), and data below 10 keV do not allow us to rule out pure relativistic reflection models (Fig. A.1). This confirms that X-ray broadband spectra are needed to determine the physical processes at work in disc-corona systems in AGN and their relative contributions (Matt et al. 2014; Porquet et al. 2018; Middei et al. 2020; Ursini et al. 2020; Walton et al. 2020). Instead, the broadband energy analysis demonstrates that soft Comptonisation and hard Comptonisation are the dominant processes, though a moderate relativistic reflection component is also present. The latter occurs at a distance of a few tens of Rg (see Sect. 4 and Reeves et al. 2021a) and is responsible for both the moderately broad O VII and Fe Kα emission lines. We also find that both the cold disc and the warm corona can provide seed photons to the hot corona. Such a model, combining Comptonisation and relativistic reflection, has been proven to explain the X-ray broadband spectra of several other AGN, such as: Ark 120 (Porquet et al. 2018), Fairall 9 (Lohfink et al. 2016), Ton S180 (Matzeu et al. 2020), and ESO 362-G18 (Xu et al. 2021). In a forthcoming article, we will study the spectral energy distribution of Mrk 110 from optical-UV to hard X-ray excess, as done previously for the bare AGN Ark 120 (Porquet et al. 2019). This will allow us to take both the geometry and the global energetics of the warm-hot corona and the outer disc into account, to determine the accretion rate, and to measure the black hole spin (e.g. Done et al. 2012; Kubota & Done 2018).

The physical properties of the warm corona (kTwarm ∼ 0.3 keV, τwarm ∼ 13) are compatible in both the 2019 and 2020 XMM-Newton/NuSTAR observations of Mrk 110, with only the warm corona flux found to be significantly different (at a ∼5.5σ confidence level). They are also consistent with those measured in XMM-Newton AGN samples (kTwarm ∼ 0.3−1 keV, τwarm ∼ 10−20; e.g. Porquet et al. 2004; Bianchi et al. 2009) and in several individual X-ray broadband spectral analyses of AGN, such as: Mrk 509 (Petrucci et al. 2013; Mehdipour et al. 2015), Ark 120 (Matt et al. 2014; Porquet et al. 2018), HE 1143−1810 (Ursini et al. 2020), NGC 4593 (Middei et al. 2019), Mrk 359 (Middei et al. 2020), TON S180 (Matzeu et al. 2020), and ESO 511-G030 (Ghosh & Laha 2021). Very recent state-of-the-art simulations have been performed that show that a warm corona with such properties can indeed exist, until sufficient internal mechanical heating is present, and that warm and hot coronae can co-exist (Petrucci et al. 2018, 2020; Ballantyne 2020; Ballantyne & Xiang 2020). Moreover, these authors found that neither strong absorption nor emission lines are formed, which can explain the absorption-free smooth soft X-ray shape observed in bare AGN or in most other AGN when the warm absorber and any moderate relativistic reflection contributions have been removed.

2

The usage notes as well as the full description of the models and their associated parameters are reported at https://users.camk.edu.pl/mitsza/reflkerr/reflkerr.pdf.

Acknowledgments

D. Porquet dedicates this paper to her friend and colleague, Cécile Renault, who has sadly passed away on April 2021. The authors thank the anonymous referee for useful and constructive comments. The paper is based on observations obtained with the XMM-Newton, and ESA science mission with instruments and contributions directly funded by ESA member states and the USA (NASA). This work made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory, and funded by NASA. This research has made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center and the California Institute of Technology. This work was supported by CNES.

References

  1. Afanasiev, V. L., Popović, L. Č., & Shapovalova, A. I. 2019, MNRAS, 482, 4985 [Google Scholar]
  2. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
  3. Ballantyne, D. R. 2020, MNRAS, 491, 3553 [NASA ADS] [CrossRef] [Google Scholar]
  4. Ballantyne, D. R., & Xiang, X. 2020, MNRAS, 496, 4255 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baloković, M., Brightman, M., Harrison, F. A., et al. 2018, ApJ, 854, 42 [Google Scholar]
  6. Baloković, M., García, J. A., & Cabral, S. E. 2019, Res. Notes Am. Astron. Soc., 3, 173 [Google Scholar]
  7. Barret, D., Lam Trong, T., den Herder, J. W., et al. 2018, in Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, S. Nikzad, & K. Nakazawa, SPIE Conf. Ser., 10699, 106991G [NASA ADS] [Google Scholar]
  8. Beheshtipour, B., Krawczynski, H., & Malzac, J. 2017, ApJ, 850, 14 [NASA ADS] [CrossRef] [Google Scholar]
  9. Beloborodov, A. M. 1999, in High Energy Processes in Accreting Black Holes, eds. J. Poutanen, & R. Svensson, ASP Conf. Ser., 161, 295 [Google Scholar]
  10. Bian, W., & Zhao, Y. 2002, A&A, 395, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bianchi, S., Guainazzi, M., Matt, G., Fonseca Bonilla, N., & Ponti, G. 2009, A&A, 495, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bischoff, K., & Kollatschny, W. 1999, A&A, 345, 49 [NASA ADS] [Google Scholar]
  13. Boissay, R., Ricci, C., & Paltani, S. 2016, A&A, 588, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Boller, T., Balestra, I., & Kollatschny, W. 2007, A&A, 465, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [Google Scholar]
  16. Crummy, J., Fabian, A. C., Gallo, L., & Ross, R. R. 2006, MNRAS, 365, 1067 [Google Scholar]
  17. Dauser, T., Wilms, J., Reynolds, C. S., & Brenneman, L. W. 2010, MNRAS, 409, 1534 [Google Scholar]
  18. Dauser, T., Garcia, J., Wilms, J., et al. 2013, MNRAS, 430, 1694 [Google Scholar]
  19. Decarli, R., Dotti, M., Fontana, M., & Haardt, F. 2008, MNRAS, 386, L15 [NASA ADS] [Google Scholar]
  20. den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 420, 1848 [Google Scholar]
  22. Ezhikode, S. H., Gandhi, P., Done, C., et al. 2017, MNRAS, 472, 3492 [NASA ADS] [CrossRef] [Google Scholar]
  23. Ezhikode, S. H., Dewangan, G. C., Misra, R., & Philip, N. S. 2020, MNRAS, 495, 3373 [CrossRef] [Google Scholar]
  24. Fabian, A. C., Zoghbi, A., Wilkins, D., et al. 2012, MNRAS, 419, 116 [Google Scholar]
  25. Fukazawa, Y., Hiragi, K., Mizuno, M., et al. 2011, ApJ, 727, 19 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fürst, F., Nowak, M. A., Tomsick, J. A., et al. 2015, ApJ, 808, 122 [Google Scholar]
  27. García, J. A., Fabian, A. C., Kallman, T. R., et al. 2016, MNRAS, 462, 751 [Google Scholar]
  28. Ghosh, R., & Laha, S. 2021, ApJ, 908, 198 [NASA ADS] [CrossRef] [Google Scholar]
  29. Gliozzi, M., & Williams, J. K. 2020, MNRAS, 491, 532 [Google Scholar]
  30. Gliozzi, M., Titarchuk, L., Satyapal, S., Price, D., & Jang, I. 2011, ApJ, 735, 16 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gliozzi, M., Papadakis, I. E., Grupe, D., Brinkmann, W. P., & Räth, C. 2013, MNRAS, 433, 1709 [NASA ADS] [CrossRef] [Google Scholar]
  32. Goodrich, R. W. 1989, ApJ, 342, 224 [Google Scholar]
  33. Grupe, D. 2004, AJ, 127, 1799 [NASA ADS] [CrossRef] [Google Scholar]
  34. Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
  35. HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Jiang, J., Fabian, A. C., Dauser, T., et al. 2019, MNRAS, 489, 3436 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kang, J.-L., Wang, J.-X., & Kang, W.-Y. 2021, MNRAS, 502, 80 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kara, E., García, J. A., Lohfink, A., et al. 2017, MNRAS, 468, 3489 [NASA ADS] [CrossRef] [Google Scholar]
  39. Keek, L., & Ballantyne, D. R. 2016, MNRAS, 456, 2722 [CrossRef] [Google Scholar]
  40. Kollatschny, W. 2003, A&A, 412, L61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Kubota, A., & Done, C. 2018, MNRAS, 480, 1247 [Google Scholar]
  42. Liu, T., & Wang, J.-X. 2010, ApJ, 725, 2381 [NASA ADS] [CrossRef] [Google Scholar]
  43. Liu, H. T., Feng, H. C., & Bai, J. M. 2017, MNRAS, 466, 3323 [NASA ADS] [CrossRef] [Google Scholar]
  44. Lohfink, A. M., Reynolds, C. S., Pinto, C., et al. 2016, ApJ, 821, 11 [CrossRef] [Google Scholar]
  45. Magdziarz, P., Blaes, O. M., Zdziarski, A. A., Johnson, W. N., & Smith, D. A. 1998, MNRAS, 301, 179 [NASA ADS] [CrossRef] [Google Scholar]
  46. Mantovani, G., Nandra, K., & Ponti, G. 2016, MNRAS, 458, 4198 [NASA ADS] [CrossRef] [Google Scholar]
  47. Marinucci, A., Porquet, D., Tamborra, F., et al. 2019, A&A, 623, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Matt, G., Marinucci, A., Guainazzi, M., et al. 2014, MNRAS, 439, 3016 [NASA ADS] [CrossRef] [Google Scholar]
  49. Matzeu, G. A., Nardini, E., Parker, M. L., et al. 2020, MNRAS, 497, 2352 [CrossRef] [Google Scholar]
  50. Mehdipour, M., Kaastra, J. S., Kriss, G. A., et al. 2015, A&A, 575, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Middei, R., Bianchi, S., Petrucci, P. O., et al. 2019, MNRAS, 483, 4695 [NASA ADS] [CrossRef] [Google Scholar]
  52. Middei, R., Petrucci, P. O., Bianchi, S., et al. 2020, A&A, 640, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Murphy, K. D., & Yaqoob, T. 2009, MNRAS, 397, 1549 [Google Scholar]
  54. Niedźwiecki, A., Szanecki, M., & Zdziarski, A. A. 2019, MNRAS, 485, 2942 [CrossRef] [Google Scholar]
  55. Osterbrock, D. E., & Pogge, R. W. 1985, ApJ, 297, 166 [Google Scholar]
  56. Panagiotou, C., & Walter, R. 2020, A&A, 640, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Patrick, A. R., Reeves, J. N., Porquet, D., et al. 2012, MNRAS, 426, 2522 [NASA ADS] [CrossRef] [Google Scholar]
  58. Petrucci, P.-O., Paltani, S., Malzac, J., et al. 2013, A&A, 549, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Petrucci, P.-O., Ursini, F., De Rosa, A., et al. 2018, A&A, 611, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Petrucci, P. O., Gronkiewicz, D., Rozanska, A., et al. 2020, A&A, 634, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Ponti, G., Papadakis, I., Bianchi, S., et al. 2012, A&A, 542, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Porquet, D., Reeves, J. N., O’Brien, P., & Brinkmann, W. 2004, A&A, 422, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Porquet, D., Reeves, J. N., Matt, G., et al. 2018, A&A, 609, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Porquet, D., Done, C., Reeves, J. N., et al. 2019, A&A, 623, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Poutanen, J., & Svensson, R. 1996, ApJ, 470, 249 [CrossRef] [Google Scholar]
  68. Reeves, J. N., Porquet, D., Braito, V., Grosso, N., & Lobban, A. 2021a, A&A, 649, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Reeves, J. N., Braito, V., Porquet, D., et al. 2021b, MNRAS, 500, 1974 [Google Scholar]
  70. Ricci, C., Ueda, Y., Ichikawa, K., et al. 2014, A&A, 567, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Schnittman, J. D., & Krolik, J. H. 2010, ApJ, 712, 908 [NASA ADS] [CrossRef] [Google Scholar]
  72. Shu, X. W., Yaqoob, T., & Wang, J. X. 2010, ApJS, 187, 581 [NASA ADS] [CrossRef] [Google Scholar]
  73. Steiner, J. F., García, J. A., Eikmann, W., et al. 2017, ApJ, 836, 119 [NASA ADS] [CrossRef] [Google Scholar]
  74. Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [Google Scholar]
  75. Tamborra, F., Matt, G., Bianchi, S., & Dovčiak, M. 2018, A&A, 619, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
  77. Tortosa, A., Marinucci, A., Matt, G., et al. 2017, MNRAS, 466, 4193 [NASA ADS] [Google Scholar]
  78. Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [CrossRef] [EDP Sciences] [Google Scholar]
  79. Ursini, F., Petrucci, P.-O., Matt, G., et al. 2016, MNRAS, 463, 382 [NASA ADS] [CrossRef] [Google Scholar]
  80. Ursini, F., Petrucci, P. O., Bianchi, S., et al. 2020, A&A, 634, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
  82. Véron-Cetty, M. P., Véron, P., Joly, M., & Kollatschny, W. 2007, A&A, 475, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Vincentelli, F. M., McHardy, I., Cackett, E. M., et al. 2021, MNRAS, 504, 4337 [CrossRef] [Google Scholar]
  84. Waddell, S. G. H., & Gallo, L. C. 2020, MNRAS, 498, 5207 [NASA ADS] [CrossRef] [Google Scholar]
  85. Walton, D. J., Nardini, E., Fabian, A. C., Gallo, L. C., & Reis, R. C. 2013, MNRAS, 428, 2901 [NASA ADS] [CrossRef] [Google Scholar]
  86. Walton, D. J., Alston, W. N., Kosec, P., et al. 2020, MNRAS, 499, 1480 [NASA ADS] [CrossRef] [Google Scholar]
  87. Weisskopf, M. C., Ramsey, B., O’Dell, S., et al. 2016, Proc. SPIE, 9905, 990517 [NASA ADS] [CrossRef] [Google Scholar]
  88. Williams, J. K., Gliozzi, M., & Rudzinsky, R. V. 2018, MNRAS, 480, 96 [NASA ADS] [CrossRef] [Google Scholar]
  89. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
  90. XRISM Science Team 2020, ArXiv e-prints [arXiv:2003.04962] [Google Scholar]
  91. Xu, Y., García, J. A., Walton, D. J., et al. 2021, ApJ, 913, 13 [NASA ADS] [CrossRef] [Google Scholar]
  92. Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
  93. Zdziarski, A. A., Szanecki, M., Poutanen, J., Gierliński, M., & Biernacki, P. 2020, MNRAS, 492, 5234 [NASA ADS] [CrossRef] [Google Scholar]
  94. Zhang, S. N., Feroci, M., Santangelo, A., et al. 2016, in Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, T. Takahashi, & M. Bautz, SPIE Conf. Ser., 9905, 99051Q [NASA ADS] [CrossRef] [Google Scholar]
  95. Zhang, J.-X., Wang, J.-X., & Zhu, F.-F. 2018, ApJ, 863, 71 [CrossRef] [Google Scholar]
  96. Zhou, X.-L., & Zhang, S.-N. 2010, ApJ, 713, L11 [NASA ADS] [CrossRef] [Google Scholar]
  97. Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [Google Scholar]

Appendix A: Results of relativistic reflection modelling over the full X-ray broadband range

Table A.1.

Simultaneous fits of the two XMM-Newton and NuSTAR spectra with a relativistic reflection model with a coronal geometry for the accretion disc emissivity (RELXILL). The column density along the line-of-sight has been fixed at the Galactic value (1.27×1020 cm−2), and the accretion disc inclination angle at 9.9 degrees. (a) The breaking radius Rbr of the emissivity shape is expressed in ISCO units. ‘(f)’ means that the cutoff value was fixed at that found from the fit above 3 keV (see Table 2).

In this appendix, we report the spectral analysis of the two simultaneous XMM-Newton and NuSTAR observations, considering only relativistic reflection models.

The fit using the RELXILL model between 0.3 and 10 keV provides a good statistical fit (Table A.1, Fig. A.1). However, it fails to reproduce the hard X-ray shape when data above 10 keV are included in the fit (Fig. 4, bottom panel), with very significant positive hard X-ray residuals for both observations above ∼30 keV (χ2/d.o.f. = 1954.8/1617, 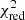= 1.21). Since the fit is driven by the smooth soft X-ray emission, high values for the disc emissivity index, the photon power-law index and the reflection strength are required to reproduce it (Table A.1, third column), at odds with the low values required to explain the data above 3 keV (Table 2).

We then investigate the scenario whereby the incident continuum of the relativistic component can be different from the direct observed one, as was proposed by Fürst et al. (2015) (though see also Steiner et al. 2017) to explain the X-ray spectrum of the X-ray binary GX 339-4 in low-luminosity, hard states. However, this requires a very significant divergence between the incident and observed spectral indices with ΔΓ = 0.7 (at 22σ confidence level) and ΔΓ = 0.9 (at 14σ confidence level) for the 2019 and 2020 observations, respectively. This means that this scenario appears highly unlikely to explain these observations of Mrk 110.

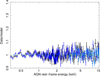thumbnail Fig. A.1.

Data-to-model ratio of the two simultaneous 2019 and 2020 XMM-Newton/pn and NuSTAR spectra over the 0.3−10 keV energy range fit with the RELXILL model. The Y-axis range is identical to that of Fig. 4 for a direct comparison. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. See Table A.1 for the corresponding inferred parameter values.

Alternatively, we investigate whether the broadband X-ray spectra can be explained by a lamppost geometry for the corona, different disc properties (disc ionisation gradient, density) and/or a different continuum shape (Comptonisation). Even relativistic reflection from two different medium properties, allowing for different ionisation parameters, have been investigated. The modelling is performed thanks to the various available relxill model flavours. However, none of them is able to simultaneously account for the soft X-ray excess and the hard X-ray emission shape in both the 2019 and 2020 XMM-Newton and NuSTAR observations. Similar results are found using the relativistic modelling package REFLKERR (Niedźwiecki et al. 2019) assuming either a coronal geometry (REFLKERR) or a lamppost geometry (REFLKERR_LP). We note that even upon using an unblurred reflection component to take into account the very weak molecular torus contribution – using XILLVER, MYTORUS (Murphy & Yaqoob 2009), or BORUS12 (Baloković et al. 2018, 2019) – does not help to remove these huge hard X-ray residuals.

Three examples of the above models are described below for illustration purposes (Table A.2, Fig. A.2).

The first is higher disc density. As demonstrated by García et al. (2016) (see also Jiang et al. 2019) high-density accretion disc models can lead to a larger soft excess compared to those in lower-density discs. Therefore, we investigate whether the strong soft X-ray excess found in Mrk 110 can be explained by a higher accretion-disc density compared to the RELXILL model, which assumes a fixed constant disc density of 1015 cm−3. We use the RELXILLD model, which allows the density to be free to vary between 1015 cm−3 and 1019 cm−3. For this model the cutoff energy value is fixed at 300 keV and cannot be allowed to vary.

The second is lamppost geometry. The RELXILL model assumes a coronal geometry for the disc emissivity. Here, we test the alternative disc emissivity, that is to say, the lamppost geometry using RELXILLLPION, with the X-ray point source being located at height h above the black hole and outflowing at a velocity β=v/c. Moreover, this model allows for a disc ionisation gradient along the radial distance with a power-law shape, R−index.

Table A.2.

Simultaneous fits of the two XMM-Newton and NuSTAR spectra with three different relativistic reflection models. The column density along the line-of-sight was fixed at the Galactic one, i.e. 1.27×1020 cm−2, and the inclination angle at 9.9 degrees. (a) Velocity of primary source. (b) Index of the ionisation gradient with a power-law shape. (c) The breaking radius Rbr and the height of the primary source are both expressed in ISCO units, except for the REFLKERR model for which Rbr is expressed in gravitational radius units. The data-to-model ratio for each model is reported in Fig. A.2.

The third is the REFLKERR code: We also use the alternative relativistic reflection model (Niedźwiecki et al. 2019). We apply the REFLKERRD model where the incident continuum is due to Comptonisation and a corona disc geometry is assumed. The disc density can vary between 1015 cm−3 and 1019 cm−3.

None of the above models provides a satisfactory account of both the soft and hard X-ray spectra of Mrk 110. Indeed large hard X-ray excess are found (as per Fig. A.2) for all the cases considered and the models cannot simultaneously fit the soft excess, while at the same time correctly account for the hard X-ray spectral shape. Thus, it appears most likely that the broadband X-ray spectra of Mrk 110 require the presence of both soft and hard Comptonisation to explain the spectral curvature, as is discussed in the main text.

thumbnail Fig. A.2.

Data-to-model ratio of the two simultaneous 2019 and 2020 XMM-Newton/pn and NuSTAR spectra fitted with relativistic models. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. Top panel: RELXILLD model. Middle panel: RELXILLLPION model. Bottom panel: REFLKERRD model. See text for explanations and Table A.2 for their corresponding inferred parameter values.

All Tables

Table 1.

Observation log of the XMM-Newton and NuSTAR dataset analysed in this work.

In the text
Table 2.

Simultaneous fits above 3 keV of the 2019 and 2020 XMM-Newton/NuSTAR and 2017 NuSTAR observations of Mrk 110.

In the text
Table 3.

Simultaneous fits over the broadband energy range of the two simultaneous XMM-Newton/pn and NuSTAR spectra with TBNEW(GAL) × [COMPTT(WARM) + REFLKERR(HOT) + REFLKERR(REFL)].

In the text
Table A.1.

Simultaneous fits of the two XMM-Newton and NuSTAR spectra with a relativistic reflection model with a coronal geometry for the accretion disc emissivity (RELXILL). The column density along the line-of-sight has been fixed at the Galactic value (1.27×1020 cm−2), and the accretion disc inclination angle at 9.9 degrees. (a) The breaking radius Rbr of the emissivity shape is expressed in ISCO units. ‘(f)’ means that the cutoff value was fixed at that found from the fit above 3 keV (see Table 2).

In the text
Table A.2.

Simultaneous fits of the two XMM-Newton and NuSTAR spectra with three different relativistic reflection models. The column density along the line-of-sight was fixed at the Galactic one, i.e. 1.27×1020 cm−2, and the inclination angle at 9.9 degrees. (a) Velocity of primary source. (b) Index of the ionisation gradient with a power-law shape. (c) The breaking radius Rbr and the height of the primary source are both expressed in ISCO units, except for the REFLKERR model for which Rbr is expressed in gravitational radius units. The data-to-model ratio for each model is reported in Fig. A.2.

In the text

All Figures

thumbnail Fig. 1.

Data-to-model ratio of the two simultaneous XMM-Newton/pn and NuSTAR spectra of Mrk 110 fit with a power-law model (with Galactic absorption) over the 3−5 keV energy range. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. Top panel: extrapolation over the full broadband X-ray energy range. Bottom panel: zoom-in on the Fe Kα line. Only the pn spectra (using here a 75 eV spectral binning) are reported for purposes of clarity. The vertical dashed red line corresponds to 6.4 keV.
In the text
thumbnail Fig. 2.

Contour plot of the Fe Kα Gaussian line width (keV) versus its energy (keV), assuming an underlying cutoff power-law continuum over the 3−79 keV energy range (see Sect. 4). The red, green, and blues curves show the confidence levels at 68% (Δχ2 = 2.3), 90% (Δχ2 = 4.61), and 99% (Δχ2 = 9.21), respectively.
In the text
thumbnail Fig. 3.

Data-to-model ratio of the fit above 3 keV with the REFLKERR relativistic reflection model, using a primary Comptonisation continuum shape and assuming a slab geometry for the hot corona. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR; orange: 2017 NuSTAR.
In the text
thumbnail Fig. 4.

Fits of the two 2019 and 2020 simultaneous XMM-Newton/pn and NuSTAR spectra with the RELXILL relativistic reflection model that assumes a coronal geometry for the disc emissivity. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. Top panel: fit above 3 keV, which has been extrapolated down to 0.3 keV. The fit parameters are reported in Table 2. Bottom panel: fit over the full 0.3−79 keV energy range. The fit parameters are reported in Table A.1.
In the text
thumbnail Fig. 5.

Fit of the two simultaneous 2019 and 2020 XMM-Newton/pn and NuSTAR spectra with the TBNEW(GAL) × [COMPTT(WARM) + REFLKERR(HOT) + REFLKERR(REFL)] model. The fit parameters are reported in Table 3. Top panel: data-to-model ratio. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. The Y-axis range is identical to that of Fig. 4 to allow for a direct comparison. Bottom panel: unfolded unabsorbed spectra (black: 2019; blue: 2020), where the separate contributions of the model components are displayed (solid and dotted curves for 2019 and 2020, respectively): Orange: soft Comptonisation (warm corona); green: hard Comptonisation (hot corona); magenta: disc reflection component.
In the text
thumbnail Fig. 6.

Same as Fig. 5 (top panel) but with the seed photon temperature allowed to be free to vary.
In the text
thumbnail Fig. A.1.

Data-to-model ratio of the two simultaneous 2019 and 2020 XMM-Newton/pn and NuSTAR spectra over the 0.3−10 keV energy range fit with the RELXILL model. The Y-axis range is identical to that of Fig. 4 for a direct comparison. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. See Table A.1 for the corresponding inferred parameter values.
In the text
thumbnail Fig. A.2.

Data-to-model ratio of the two simultaneous 2019 and 2020 XMM-Newton/pn and NuSTAR spectra fitted with relativistic models. Black: 2019 XMM-Newton/pn; dark grey: 2019 NuSTAR; blue: 2020 XMM-Newton/pn; light blue: 2020 NuSTAR. Top panel: RELXILLD model. Middle panel: RELXILLLPION model. Bottom panel: REFLKERRD model. See text for explanations and Table A.2 for their corresponding inferred parameter values.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.