EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) A101 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number A101
Number of page(s) 17
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202244022
Published online 05 April 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The broadband emission in active galactic nuclei (AGNs) can be interpreted as an interplay between thermal and non-thermal processes taking place in the close surroundings of a central supermassive black hole (SMBH; see Padovani et al. 2017, for an overview on AGNs). Accretion onto the SMBH is responsible for the optical-UV emission, and a fraction of the thermal photons from the emission is intercepted and Comptonised up to the X-rays by the so-called hot corona (e.g. Galeev et al. 1979; Haardt & Maraschi 1991, 1993). Our understanding of this plasma is still lacking, though timing and micro-lensing arguments (e.g. Chartas et al. 2009; Morgan et al. 2012; De Marco et al. 2013; Kara et al. 2016) support the hypothesis of this component being compact and located in the inner regions of the accretion flow.

The presence of this hot plasma well explains the cut-off power-law-like continuum of AGNs, with the high-energy rollover being interpreted as a further signature of the inverse-Compton of the seed photons from the thermal plasma of electrons with Ec, depending on the temperature of the relativistic electrons (kT; Rybicki & Lightman 1979). The characterisation of the primary X-ray continuum has been the focus of several studies (e.g. Perola et al. 2000; Dadina 2007; Molina et al. 2009, 2013; Malizia et al. 2014; Ricci et al. 2018), and research in this area has been further boosted since the launch of NuSTAR (Harrison et al. 2013), as demonstrated by the increasing number of high-energy cut-off measurements (e.g. Baloković et al. 2020; Reeves et al. 2021; Kamraj et al. 2022).

Reflection off Compton-thin and Compton-thick matter imprints additional features onto the emerging X-ray spectrum. This is the case of the fluorescence Fe Kα emission line at 6.4 keV (e.g. Bianchi et al. 2009) and the Compton-hump (George & Fabian 1991; Matt et al. 1993; García et al. 2014). Noticeably, the analysis of the Fe Kα profile carries a wealth of information on the location of the reflecting materials. In fact, its intrinsically narrow profile can undergo distortions, resulting in a broader shape due to relativistic effects (e.g. Fabian et al. 1989, 2000; Tanaka et al. 1995; Nandra et al. 2007; de La Calle Pérez et al. 2010).

Finally, the soft X-ray band of AGNs ubiquitously shows a bump of counts below ∼2 keV that is not accounted by the high-energy power-law continuum (e.g Piconcelli et al. 2005; Bianchi et al. 2009; Gliozzi & Williams 2020). The origin of this component, the so-called soft excess, is still debated, and two possible scenarios have been tested using various datasets: blurred ionised reflection and warm Comptonisation (e.g. Crummy et al. 2006; Magdziarz et al. 1998; Jin et al. 2012; Done et al. 2012). The two models have been found to reproduce the data. Walton et al. (2013) tested the relativistic reflection origin of the soft excess on a broad number of Seyfert galaxies using Suzaku data (see also Crummy et al. 2006), while the two-coronae model was found to be the best-fit for the broadband emission spectrum of an increasing number of AGNs (e.g. Petrucci et al. 2018; Porquet et al. 2018; Kubota & Done 2018; Ursini et al. 2018, 2020; Mahmoud & Done 2020; Matzeu et al. 2020; Middei et al. 2020).

Variability is another key feature of AGN emission (Bregman 1990; Mushotzky et al. 1993; Wagner & Witzel 1995; Ulrich et al. 1997). Spectral variations are characterised by a softer-when-brighter behaviour that is commonly observed in nearby Seyfert galaxies and unobscured quasars (e.g. Sobolewska & Papadakis 2009; Serafinelli et al. 2017, respectively). X-ray amplitude variations have been witnessed over different time intervals, from hourly (Ponti et al. 2012) up to yearly changes (Vagnetti et al. 2016; Paolillo et al. 2017; Middei et al. 2017; Falocco et al. 2017; Gallo et al. 2018; Timlin et al. 2020). X-ray variability has been found to anti-correlate with the source luminosity; however, this can be naturally explained if changes result from the superposition of N randomly emitting sub-units. This scenario, already considered in optical studies (e.g. Pica & Smith 1983; Aretxaga et al. 1997), predicts a variability amplitude ∝N−0.5 ∝ L−0.5 and accounts for the sub-units being identical and the flare being independent (e.g. Green et al. 1993; Almaini et al. 2000). Interestingly, this behaviour has been reported by many authors for both local and high-redshift AGNs also in the X-rays (e.g. Barr & Mushotzky 1986; Lawrence & Papadakis 1993; Papadakis et al. 2008; Vagnetti et al. 2011, 2016).

In this context, we report on the X-ray spectral properties of ESO 511-G030, a nearby (z = 0.02239 ± 0.00001, Theureau et al. 1998) spiral galaxy (de Vaucouleurs et al. 1991) hosting an unobscured Type 1 AGN (Véron-Cetty & Véron 2010). One of the first X-ray spectra of ESO 511-G030 was taken with ASCA (Advanced Satellite for Cosmology and Astrophysics) in 1998 (Turner et al. 2001b), and the source spectrum was best-fitted using an absorbed power-law. A subsequent INTEGRAL-based analysis allowed for measurement of a high-energy cut-off 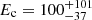E c = 100 − 37 + 101 $ E_{\mathrm{c}}=100^{+101}_{-37} $ keV (Malizia et al. 2014). The AGN ESO 511-G030 is reported in the 105-month BAT catalogue (Oh et al. 2018) with a flux of ∼4×10−11 erg s−1 cm−2 (14–195 keV), and it is one of the 13 objects in the FERO sample, an XMM-Newton-based collection of AGNs with a > 5σ detection of a relativistic iron line (details in de La Calle Pérez et al. 2010). In a recent paper by Ghosh & Laha (2021), who studied a 2007 XMM-Newton exposure, the source flux was consistent with F2 − 10 keV ∼ 2 × 10−11 erg s−1 cm−2. In the same paper, two Suzaku observations five years apart from the XMM-Newton one are also discussed. In those observations, the source flux was compatible with the XMM-Newton 2007 observation, and the second observation was about 50% higher. Moreover, ESO 511-G030 does not show the presence of cold and/or warm absorption components (e.g. Laha et al. 2014), leaving the soft X-ray band free from complex absorption features and with only a modest attenuation of the UV emission.

This paper is organised as follows: Sect. 2 reports on data reduction, and in Sect. 3 the timing properties of the observations are discussed. In Sect. 4, we describe the spectral analyses of the XMM-Newton-NuSTAR 2019 monitoring campaign, and we test the same spectral model on the archival data in Sect. 5. Then in Sects. 6 and 7, we describe the broadband Swift data analysis, including XRT (Swift’s X-Ray Telescope) and UVOT (Swift’s Ultraviolet/Optical Telescope) data. In Sect. 8, we test a self-consistent model on the 2019 and the 2007 XMM-Newton exposures also considering optical monitor (OM) data. Our conclusions and comments are reported in Sect. 9.

2. Data reduction

In this section, we present the analysis of our multi-wavelength XMM-Newton/NuSTAR observational campaign from 2019, and we compare it with data taken using different facilities across a time interval of more than 20 years. In Table 1, the log of the observations is reported, while in Fig. 1 we show a snapshot of all spectra simply folded with a power-law (Γ = 2), from which it is possible to witness the variations of ESO 511-G030 in both the X-ray and optical-UV bands.

thumbnail Fig. 1.

Unfolded spectra of ESO 511-G030 corresponding to the observations listed in Table 1. Variability is observed both in terms of spectral and amplitude changes. In the optical-UV band, the source faded by a factor of approximately ten. The underlying model folding the data is a power-law with Γ = 2 and a unitary normalisation.

Table 1.

Log of the observations.

ASCA: We retrieved the already reduced data products of ESO 511-G030 from the Tartarus ASCA AGN database (Turner et al. 2001b).

Suzaku: ESO 511-G030 was observed with Suzaku (Mitsuda et al. 2007) on July 20 (OBSID: 707023010), July 22 (707023020), and August 6 (707023030), 2012, through the X-ray Imaging Spectrometer (XIS; Koyama et al. 2007) with net exposure times of 5.7 ks, 224 ks, and 51 ks, respectively. Following the processes described in the Suzaku data reduction guide1, the XIS (X-ray Imaging Spectrometer) 0, 1, and 3 CCD spectra were extracted with HEASOFT (v6.29.1) and the latest version of the CALDB (November 2021). The cleaned event files were selected from the 3×3 and 5×5 edit modes and subsequently processed according to the suggested screening criteria. Both XIS source and background spectra were extracted from circular regions with radii of 3.0 arcmin. Care was also taken to avoid the chip corners containing Fe55 calibration sources. The corresponding spectra and light curves were subsequently extracted using XSELECT for the second and third observations, as the first pointing was too short. For each detector, response matrices and ancillary response files were generated by running the XISRMFGEN and XISSIMARFGEN tasks. After verifying their consistency, we combined the front illuminated (XIS-FI) 0 and 3 spectra into a single XIS03-FI spectrum for observations 707023020 and 707023030. We used a cross-calibration constant to account for the inter-calibration between the XIS and Pin detectors. In the fits, the constant has its expected value of k ∼ 1.16 for the 707023030 data only, and it increases to a value of k ∼ 1.50 in the 707023020 observation. Such a particularly high value for this constant is explained by the non-simultaneity of the XIS-PIN exposures, which caused telemetry issues to occur and led to a shortening of the actual PIN exposure to about one-fifth of what was scheduled. Thus, the high value of the cross-correlation constant is straightforwardly explained by the intra-observation variability that the source had undergone.

XMM-Newton: We reduced and analysed both a 120 ks 2007 XMM-Newton orbit and five exposures of about 30 ksec, all of which were obtained simultaneously with NuSTAR in 2019. The exposures were made with the EPIC camera (European Photon Imaging Camera, Strüder et al. 2001; Turner et al. 2001a) operating in the Small Window mode. Data were processed using the XMM-Newton Science Analysis System (SAS; Version 19.0.0). Because of its larger effective area with respect to the MOS (Metal Oxide Semi-conductor) cameras, we only report the results for the pn instrument. Source spectra were derived using a circular region with a 40 arcsec radius centred on the source, while the background was extracted from a blank 50-arcsec radius area near the source. The extraction regions were selected using an iterative process that maximises the S/N, similar to what is described in Piconcelli et al. (2004). The spectra were re-binned in order to have at least 30 counts for each bin and to not over sample the spectral resolution by a factor greater than three. Finally, from ‘epatplot’, pile up issues were found to not affect this dataset.

NuSTAR: We calibrated and cleaned raw NuSTAR (Harrison et al. 2013) data using the NuSTAR Data Analysis Software (NuSTARDAS; Perri et al., 20132) package (v. 1.8.0). Level 2 cleaned products were obtained with the standard ‘nupipeline’ task, while third level science products were computed with the ‘nuproducts’ pipeline and the calibration database 20191219. A circular region with a radius of 50 arcsec was used to extract the source spectrum. The background was calculated using the same circular region but centred on a blank area near the source. To account for the inter-calibration of the two modules carried on the NuSTAR focal plane, we used a cross-normalisation constant in all the fits. The calibration constant was always found to be within 3%, indicating the FPMA/B spectra to be in good agreement. Spectra were binned so that each bin had at least 50 counts so as to not over sample the instrumental resolution by a factor greater than 2.5.

Swift: The Swift satellite observed ES0511-G030 from 2018 to 2021, and we reduced the data acquired with XRT and UVOT. The XRT observed the source in photon counting mode, and we derived the corresponding scientific products using the facilities provided by the Space Science Data Center (SSDC3) of the Italian Space Agency. In particular, spectra were extracted adopting a circular region of ∼60 arcsec centred on the source, and a concentric annulus was used for the background. The spectra were binned in order to have at least five counts in each bin. The UVOT aperture photometry was used to obtain the monochromatic fluxes for all the available filters. A source extraction region of 5 arcsec radius was adopted, and an appropriate blank annular region concentric with the source was adopted for the background.

All the errors quoted in our tables and text account for 90% uncertainties, while 68% errors are shown in the figures. Fits were performed using XSPEC (Arnaud 1996) and assuming the standard cosmological framework given by H0 = 70 Km s−1 Mpc−1, ΩΛ = 0.73, and Ωm = 0.27.

3. Timing properties

We extracted the background-subtracted light curves for all the observations. In the top panels of Fig. 2, we show the soft and hard X-ray light curves of the 2019 monitoring campaign time series, while those of archival observations (XMM-Newton and Suzaku) are shown in the bottom panels. From Fig. 2, both short- and long-term variability characterises the ESO 511-G030 light curves. During 2019, ESO 511-G030 had a quite stable behaviour, with both the soft and hard X-rays being fairly constant within each exposure and amongst the different pointings. This constancy, apart from a small fraction in the fifth exposure, can be observed through the ratios of the panels. This behaviour suggests that the balance between soft and hard X-rays did not change during the campaign. The flat shape of the 2019 hardness ratios can be quantitatively (qualitatively) compared with those computed from XMM-Newton (Suzaku) archival exposures. The ratios between the 0.5–2 and 2–10 keV bands were more variable in the 2007 XMM-Newton exposure, with changes of about 25%. Hardness ratios from Suzaku show moderate variations within the same exposure, fluctuating by approximately 10% on daily rather than monthly timescales.

thumbnail Fig. 2.

ESO511-G030 light curves. Top panels: Background-subtracted light curves from the 2019 multi-wavelength campaign. The first and second row refer to the XMM-Newton 0.5–2 and 2–10 keV bands, respectively, while the last row shows the ratios between the two bands. The NuSTAR light curves extracted in the 10–79 keV band are also shown. Bottom panels: Background-subtracted time series for ASCA (black), the 2007 XMM-Newton orbit (red) and the Suzaku visits two and three (in blue).

Short-term X-ray variations are related to the intrinsic properties of the AGN, such as its SMBH mass or its luminosity (e.g. Vaughan et al. 2003; Papadakis 2004; McHardy et al. 2006). Ponti et al. (2012) computed the normalised excess variance of ESO 511-G030 using the 2007 XMM-Newton light curves, and the authors derived the black hole mass of ESO 511-G030 to be 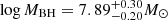log M BH = 7 . 89 − 0.20 + 0.30 M ⊙ $ \log M_{\mathrm{BH}}=7.89_{-0.20}^{+0.30} M_\odot $.

Another commonly adopted estimator suitable for X-ray variability characterisation is the fractional root mean square variability amplitude (Fvar; e.g. Edelson et al. 2002; Vaughan et al. 2003; Ponti et al. 2004). The Fvar tool calculates the square root of the normalised excess variance, and it has been widely used to characterise the variability properties of AGN in X-rays (e.g. Vaughan et al. 2004; Ponti et al. 2006; Matzeu et al. 2016, 2017; Alston et al. 2019; Parker et al. 2020; De Marco et al. 2020; Igo et al. 2020; Middei et al. 2020). We studied the variability properties of ESO 511-G030 by computing the Fvar spectra for each of the 2019 XMM-Newton observations. This spectral sample contained variability on timescales ranging between ∼1 − 40 ks. We used the background-subtracted light curves calculated in different energy intervals and adopted a temporal bin of 1000 sec. Following the same procedure, we also computed the Fvar spectrum of the 2007 XMM-Newton observation. These samples had longer timescales ranging between ∼1 − 120 ks and enabled us to identify variable spectral components contributing to the time-averaged spectrum. The resulting Fvar spectra of each observation are shown in Fig. 3. The errors were computed using Eq. (B2) of Vaughan et al. (2003) and account only for the uncertainty caused by Poisson noise. Aside from some excess towards the high-energy region of the spectra (e.g., due to residual background variability), all the observations from the 2019 monitoring campaign show a rather flat Fvar spectrum, therefore implying a similar variability power across different energy bands. In contrast, the 2007 Fvar spectrum clearly shows a divergence from the 2019 observations in the soft X-rays, which is consistent with the presence of an additional variability component. To better highlight this difference, we overlayed the 2007 Fvar spectrum with the grouped Fvar spectra from the 2019 campaign (see Fig. 4). We used publicly available table models4 to describe the 2007 Fvar spectrum in terms of combined contribution from flux variability of a power-law-like continuum and a soft excess. While the model well reproduces the 2007 Fvar spectrum and the high-energy part of the 2019 data, it clearly overestimates the soft band part of the 2019 Fvar spectrum. One possible explanation for this is the presence of an additional soft variability component in the 2007 data that is not present in the 2019 data.

thumbnail Fig. 3.

Fvar spectra for the XMM-Newton observations in Table 1. Spectra from the 2019 monitoring campaign are all characterised by a fairly flat shape, while data from 2007 clearly show a variability bump in the soft X-rays.

thumbnail Fig. 4.

Comparison between the Fvar spectrum of the 2007 and 2019 data. The 2019 observations (magenta) were obtained by grouping together the five exposures via the standard command SETPLOTGROUP within XSPEC. The spectrum derived from 2007 data is in black. The magenta curve represents a theoretical Fvar spectrum, which depicts the combined contribution from a variable power-law-like continuum and a variable soft excess.

4. Spectral properties: The XMM-Newton/NuSTAR 2019 campaign

4.1. The Fe Kα complex

We begun our investigation by focusing on the 2019 EPIC-pn spectra (between 4 and 8 keV) and the properties of the Fe Kα emission line. We adopted two components, a power-law and a Gaussian line that were assumed to be narrow (σ = 0 eV) and centred at 6.4 keV. We simultaneously fitted all the spectra, computing the photon index (we assumed its value to be the same amongst the pointings) and the power-law normalisation. For the Gaussian component, we calculated its normalisation in all the exposures. This simple fit returned a Fe Kα flux consistent with being constant, NormFeKα = (6.8 ± 0.8)×10−6 photons cm−2 s−1. We then considered the 2007 XMM-Newton data on the 4–8 keV energy range. We tested the data with the same model and further assumed the Fe Kα to have the same normalisation from 2007 to 2019. In other words, we only fitted the photon index and the normalisation of the continuum for the newly added data (see top panel of Fig. 5). The narrow emission line only reproduced the 2019 spectra, and an additional broader component was required for the 2007 data. We thus froze the narrow Gaussian component to its best-fit value and added a new broad Gaussian emission line. In this fit, the line energy centroid and width were computed, and we assumed these values to be the same among the all observations. We only allowed the line’s normalisation to vary between the 2019 dataset and the 2007 exposure. This new model resulted in the fit shown in the bottom panel of Fig. 5 with χ2/d.o.f. = 400/310. We subsequently re-fit the data, also allowing the narrow Gaussian normalisation to vary between the datasets. This test resulted in a slight benefit in terms of statistic, with Δχ2/Δd.o.f. = −10/−1. In this case, however, only an upper limit was returned for the flux of the narrow Gaussian components.

thumbnail Fig. 5.

Zoom of the Fe Kα complex. Top panels: EPIC-pn data in the 4–8 keV energy band fitted using a power-law and a narrow Gaussian emission line assumed to be constant among the exposures. Residuals in the Fe K energy range are present. Bottom panels: Same as above but with the addition of a broad Fe Kα emission line for which the line normalisation was assumed to be constant among the 2019 pointings but free to vary in 2007.

We further tested the origin of the Fe Kα emission line by computing the fit once again but only including a broad Gaussian component. Again, we assumed the line’s energy centroid and width to be the same across the years, and only its normalisation was calculated separately for the 2019 and 2007 data. Interestingly, this step led to a statistically equivalent fit χ2/d.o.f. = 400/310, which suggests the Fe Kα in ESO 511-G030 to be consistent either with a superposition of a narrow and constant core plus a broad and variable component or with a single and moderately broad Gaussian that varies in time and becomes stronger at a higher continuum flux. This result is illustrated in Fig. 6, whereby the line normalisation for a single broadened Gaussian significantly decreases between the high flux (2007) and low flux (2019) observations. This behaviour, which is quite at odds with what is commonly observed in AGNs, was also seen in NGC 2992 (Marinucci et al. 2020).

thumbnail Fig. 6.

Confidence regions at 99%, 90%, and 68% for the line’s width and normalisation. The contours were obtained assuming the model power-law+zGaussbroad and using a single broad Gaussian component.

4.2. Spectral modelling

We investigated the broadband spectral properties of ESO 511-G030 by testing a purely phenomenological model. We modelled the XMM-Newton/NuSTAR data with a cut-off power-law absorbed for the Galaxy (NH = 4.33 × 1020 cm−2, HI4PI Collaboration 2016), a moderately broad Gaussian component for the Fe Kα, and a thermal component to account for curvature in the soft band (Model A). We fitted each observation separately. We report the inferred best-fit values and the statistic associated to each fit in Table 2. This procedure revealed that no significant spectral variations occurred during the campaign. The Fe Kα was constant in terms of normalisation, and in all observations except two and four, the line profile was consistent with being broad. The high-energy cut-off was constrained in observations one and five, while only lower limits were obtained in the remaining exposures. At lower energies, a weak and constant black-body-like component did not vary amongst the different observations. Given the little variability amongst the parameters, we fitted all the observations simultaneously, tying the photon index, the cut-off energy for the primary continuum, the energy centroid and width of the Gaussian component, and the temperature and normalisation of the black body. This resulted in a fit with χ2 = 1470 for 1416 d.o.f and an associated null probability of 0.1. Moreover we found a Γ = 1.62 ± 0.02, while the high-energy rollover was Ec > 160 keV. For the Fe Kα, we obtained EFeKα = 6.39 ± 0.02, σFeKα = 70 ± 30, and a normalisation of NormFeKα = 7.2 ± 1.8 × 10−6 photons cm−2 s−1, which is in full agreement with the results reported in Sect 4.1.

Table 2.

Best-fit parameters obtained using models A and B (see Sect. 4.2 for details).

We subsequently tested a more reliable physical framework for the ESO 511-G030 2019 spectra. We started by considering two scenarios: (i) one accounting for a narrow Fe Kα, signature of distant reflecting material and (ii) another in which this emission feature is a blend of a relativistically broadened component plus a narrow one. The model Borus (e.g. Baloković et al. 2018) was used to account for the distant reflection and the relxill model (e.g. García et al. 2013, 2014) for the relativistic component. Within Borus, the toroidal X-ray reprocessor was assumed to have a spherical shape with conical cutouts at both poles, and the X-ray source was assumed to be at its centre. We used the table borus01_v161215a.ftz. Relxill (e.g. Dauser et al. 2016) is part of a model suite that accounts for ionised reflection from an accretion disc illuminated by a hot corona. In XSPEC notation, we thus tested the following models: tbabsG × (cutoffpl + Borus), referred to as Model B, and tbabsG × (cutoffpl + relxill + Borus), referred to as Model C, for cases (i) and (ii), respectively. These models were applied to each XMM-Newton and NuSTAR dataset, and we fitted the Γ, the high-energy cut-off, and the normalisation of the primary continuum, tying these values with those of the Borus table. The column density and the normalisation of the Borus table were also computed in each exposure. We proceeded similarly when testing Model C, but in this case, we assumed the iron abundance to be solar (AFe = 1) and computed the ionisation parameter ξ and the inner radius rin. Model C better reproduces the data, and Fig. 7 reports the corresponding best-fit values.

thumbnail Fig. 7.

Model C fitting to the 2019 spectra. Borus and relxill account for the cold and hot reflection components, respectively.

The ESO 511-G030 spectra are well described by a primary continuum with Γ = 1.73 ± 0.02. Lower limits for the high-energy cut-off were inferred in all observations but observation five, for which Ec = 75 ± 20 keV was obtained. Then, the narrow core of the Fe Kα emerges from a Compton-thin medium with an averaged column density NH ∼ 1.8 × 1023 cm−2, which is also responsible for the moderate high-energy curvature of the spectra. A relativistic reflection component likely originates from the mildly ionised matter, as the ionisation parameter is consistent amongst the exposures. However, the inner radius of this component is poorly constrained in this model. The best-fit quantities inferred from the fits are shown in Table 2.

As a final test, we added a black body component in each observation to account for any weak underlying soft X-ray spectral features. The addition of this soft component did not provide any significant improvement to the fit. This test accords with the scenario of an absent or weak soft X-ray excess in the source.

5. Archival X-ray observations of ESO 511-G030

Thus far, ESO 511-G030 AGN has been observed by different facilities. Detailed studies on ASCA, Suzaku as well as the 2007 XMM-Newton exposure have already been published (e.g. Turner et al. 2001b; Ghosh & Laha 2021). Thus, we performed straightforward fits on these data to extract information on the spectral properties of ESO 511-G030 in previous years.

We tested our Model C by adopting the same fitting procedure described in Sect. 4.2 but also slightly modifying the model when necessary. As clearly shown in Fig. 1, all archival exposures have larger fluxes than the data in 2019 and different spectral shapes, especially in the soft band. For this reason, we fitted separately the ASCA data, all the Suzaku observations, and XMM-Newton data. Concerning Suzaku, the additional cross-calibration constant (k) was used for the XIS and PIN data.

Interestingly, our baseline Model C failed to reproduce all the archival spectra, and thus additional components to this model were needed. In particular, a neutral absorption was required by ASCA data for which no relativistic reflection was necessary. For the Suzaku data, we added a single black body component to account for the soft excess observed below ∼1 keV, while two black body components were added to fit the 2007 XMM-Newton exposure (see also Ghosh & Laha 2021). These steps yielded the fits in Fig. 8, and in Table 3 we report the corresponding best-fit values.

thumbnail Fig. 8.

Fit to the ASCA, 2007 XMM-Newton, and Suzaku data. We show these spectra in black, magenta and blue, respectively. Bottom panels report on the data-model ratios.

Table 3.

Parameters derived by adapting the baseline Model C to the archival data.

Apart from the 1999 absorption event observed in the ASCA data, due to matter with constant NH = 1.2 ± 0.3 × 1021 cm−2, ESO 511-G030 archival spectra are consistent with a variable power-law that is, on average, softer than the power-law in the 2019 data (ΔΓ ∼ 0.2). The continuum flux in the 2–10 keV energy range is up to a factor of six larger than in 2019, while the soft X-ray flux in the 0.5–2 keV range is even larger, by up to a factor of ten. The large changes in the soft flux can be ascribed to the presence(absence) of the soft excess component. The soft excess clearly plays a major role in shaping the soft band in the 2007 XMM-Newton and 2011 Suzaku observations.

The relativistic reflection observed in the archival observations is about ten times larger than the one inferred in 2019, which is in agreement with the hot reflection responding to the primary changes. On the other hand, the reflected spectrum due to cold matter and that also contributes to the Fe Kα has a more constant behaviour across the years. Values derived for the normalisation of the Borus table are, in fact, rather constant across the epochs. Thus, a lower (higher) primary flux would correspond to a larger (smaller) reflection fraction. Finally, the Compton-thin nature of the reprocessor in ESO 511-G030 is further confirmed by this data.

6. The Swift Monitoring campaign

We present in this section the Swift X-ray and UV data that were taken in the context of two different observational campaigns, one of which is still ongoing, performed between 2020 and 2022. The objective of the campaigns is to keep track of the broadband properties of ESO 511-G030 and, possibly, observe a revenant soft excess. Up to fall 2021, however, the source flux state had been consistent with the state observed in 2019 with XMM-Newton and NuSTAR. In Fig. 9, we show the light curves derived for different X-ray bands (0.3–0.5, 0.5–0.8, 0.8–1.2, 1.2-2, 2–5, and 5–10 keV) and optical-UV filters (which are possibly dominated by the host galaxy). The Swift-XRT data show a min-to-max variability of about a factor of five across the light curve. Once converted into fluxes, both X-rays and UVs were about a factor of approximately 10 fainter than in the XMM-Newton observation of 2007. Thus ESO 511-G030 as observed with Swift appears to be an extension of the quiescent state of ESO 511-G030 observed during 2019. By analysing the Swift spectra, our main objective was to establish whether a simple power-law component (plus Galactic absorption) was enough to explain the data. Our test confirmed that a simple power-law well represents the 0.3–10 keV energy range of our source and no additional components are required. In Table A.1, the inferred best-fit quantities are listed, and the corresponding best-fit values are shown as a function of the observing time in Fig. 10. The Swift data are consistent with a fairly flat spectral shape of Γ = 1.62 ± 0.09, and only small variability was observed in the power-law normalisation. This may suggest the source still remains in a quiescent state with no soft excess awakening.

thumbnail Fig. 9.

Multi-filter light curves derived from 2018 up to 2022 for ESO 511-G030 using Swift-XRT and -UVOT. Until the end of 2021 (MJD < 59580), after which a moderate increase of ultraviolet emission can be observed, the optical-UV curves could be highly affected by the host emission. We noticed that to quantify the actual amplitude of the optical-UV emission, an estimate of the contribution of the host galaxy is required (see Sect. 6).

thumbnail Fig. 10.

Best-fit parameters and fluxes in the 0.3–2 (Soft) and 2–10 keV (hard) bands derived from Swift. Straight solid lines show the mean value of the parameter, while dotted lines represent the corresponding standard deviation. Fluxes are in units of 10−12 erg cm−2 s−1.

To test whether the soft excess was or was not present in XRT spectra, we used all the observations cited in Table A.1 to produce a stacked spectrum of ESO 511-G030. The obtained spectrum has no signature of this component. A simple power-law absorbed by the Galaxy (Γ = 1.62 ± 0.02) is in fact enough to account for the data (χ2 = 337 for 339 d.o.f.), thus ruling out any additional component. The Swift fluxes in the 0.5–2 and 2–10 keV bands are compatible with what was observed during the 2019 XMM-Newton and NuSTAR monitoring campaigns, with F0.5 − 2 keV = (2.18 ± 0.02)×10−12 erg cm−2 s−1 and F2 − 10 keV = (5.1 ± 0.1)×10−12 erg cm−2 s−1. Moreover, the stacked spectrum does not show any evidence of a Fe Kα emission line. The lack of this feature can be likely explained by the coupled effects of the source low flux and the small effective area of the Swift-XRT telescope in the hard X-rays. Finally, we note that the last four Swift exposures of ESO 511-G030 were consistent with a flux increase of the source in both the X-ray and UV energy bands.

7. Relation between X-rays and UVs

A viable way to quantify the actual relation between X-rays and UVs band is provided by the αOX parameter. The non-linear relation between the UV and X-ray luminosity in AGNs was discovered in late 1970s by Tananbaum et al. (1979), and several other authors have investigated the physical meaning of such a relation (e.g. Tananbaum et al. 1986; Zamorani et al. 1981; Vagnetti et al. 2010; Martocchia et al. 2017; Chiaraluce et al. 2018) and its implication in a cosmological framework (e.g. Risaliti & Lusso 2015; Lusso & Risaliti 2016, 2017; Lusso et al. 2020; Bisogni et al. 2021). Optical and UV data simultaneous with X-ray information are available for both XMM-Newton and Swift. For the 2007 XMM-Newton observation, only four OM filters are available (B, UVW1, UVM2, UVW2), and all of them were used in the 2019 monitoring campaign (V, B, U, UVW1, UVM2, and UVW2 at 5235 Å, 4050 Å, 3275 Å, 2675 Å, 2205 Å, and 1894 Å, respectively). Swift-XRT observations are accompanied by one to six UVOT filters (V, B, U, UVW1, UVM2, and UVW2 at 5468 Å, 4392 Å, 3465 Å, 2600 Å, 2246 Å, and 1928 Å, respectively), providing rich information on the UV continuum slope. We therefore derived the X-ray luminosity at 2 keV in order to compute the αOX values. We relied on our best-fit to the EPIC-pn spectra discussed in Sects. 4 and 5, while the XRT spectra were modelled with a simple power-law with Galactic absorption (see Appendix A).

The total AGN plus Galaxy luminosity at logν* = 15.08 corresponding to λ = 2500 Å was estimated at each epoch as an interpolation between the data in the closest filters, which for these observations are UVW1 and UVM2. We computed the optical-UV spectral energy distributions (SEDs) to get an estimate of the host galaxy fraction at ν*, which may be significant, and of the AGN luminosity, LUV, following the prescriptions by Vagnetti et al. (2013). We assumed each optical-UV SED to be the sum of an AGN spectrum proportional to the average SED by Richards et al. (2006) with a typical slope of αAGN = −0.57 (with Fν ∼ ναAGN) and a host galaxy contribution whose spectrum was modelled with a typical slope αgalaxy = −3 (see e.g., Lusso et al. 2010; Vagnetti et al. 2013). The host galaxy fraction fg at ν* was then derived at each epoch as a function of the sole spectral index. Indeed, expressing the total luminosity as L = L*[fg(ν/ν*)−3 + (1 − fg)(ν/ν*)−0.57], the spectral index in ν* was then equal to α = [d log L/dlogν]ν = ν* = −3fg − 0.57(1 − fg). The fraction fg was thus estimated by inverting the previous relation as fg = −(0.57 + α)/2.43. Therefore, when fg tends to zero, then the slope α tends to −0.57, as per the Richards et al. (2006) AGN SED. However, when fg = 1, α tends to −3, which is consistent with a pure host galaxy spectrum.

The monochromatic fluxes for the optical and UV filters were computed by converting the observed rates using the appropriate conversion factors. The spectral index was derived by applying least squares on these data. Figure 11 shows the optical-UV SEDs for the XMM-Newton and Swift observations. From 2007 to 2022 pointings, the ESO511-G030 SEDs underwent dramatic spectral changes. The optical-UV ESO 511-G030 SEDs appear quite steep, with the exception of the 2007 exposure and those from Swift in 2022. The corresponding spectral index lies in the range between −2.7 and −3. These values are far steeper than the more typical slope of −0.57 derived from the average spectral energy distribution of a statistically significant number of AGNs by Richards et al. (2006) around ν*. The variation in the SEDs suggests that the nuclear emission changes, while a substantial constant contribution from the host galaxy is also present. In particular, the steep slopes derived for the observations taken after 2019 but before 2022 can be ascribed to the dominant shape of the host galaxy.

thumbnail Fig. 11.

ESO 511-G030 optical-UV SEDs derived using XMM-Newton and Swift data (dark green). The corresponding least squares fits are shown as straight dashed lines. XMM-Newton and Swift data are in blue and dark green, respectively. The solid, thick black line is the average SED by Richards et al. (2006) for Type 1 objects in the SDSS. The vertical dashed line is at logν* = 15.08, corresponding to 2500 Å. We noticed a remarkable change in spectral shape from the 2007 observation compared to the later ones.

The host galaxy luminosity at 2500 Å was defined as the average value of its estimates at different epochs, which was found to be log Lgalaxy = 27.68 (erg s−1 Hz−1) with a small dispersion, σ = 0.05. This average value was subtracted from the total luminosity at 2500 Å to obtain the AGN luminosity, LUV, at each epoch. This luminosity was often smaller than the host galaxy luminosity, as shown in the top panel of Fig. 12. For most observations, the ratio between the AGN and the total monochromatic luminosity (AGN+host) is in the range of 0–50%. In many cases, the SED slope is ≲ − 3, and the AGN fraction is negligible and thus not plotted in Figs. 12 and 13. Regarding the SED of the 2007 archival observation, it is flatter than the one reported by Richards et al. (2006), with α = −0.44. Thus, for this 2007 observation, we assumed the total monochromatic luminosity at 2500 Å to be due to the AGN only.

thumbnail Fig. 12.

Light curves for the AGN luminosity at 2500 Å, at 2 keV, and the inferred αOX. Blue dots identify values derived using XMM-Newton observations while in green the same quantities were estimated using Swift. The dashed horizontal line accounts for the adopted host galaxy luminosity at 2500 Å. Finally, both LUV and L2 keV are in units of erg s−1 Hz−1.

The αOX derived for our source can be also compared with the well-known LUV − αOX anti-correlation (Vignali et al. 2003; Just et al. 2007; Vagnetti et al. 2010). Figure 13 shows the track of ESO 511-G030 in the log LUV − αOX plane.

thumbnail Fig. 13.

ESO 511-G030 αOX estimates compared with the sample by Chiaraluce et al. (2018). The solid black line represents logLUV − αox linear relation as derived in the same work. The αOX computed of ESO 511-G030 shows significant variability in agreement with the drop in the OM data shown in Fig. 1.

8. Ultraviolet to X-ray modelling

In accordance with Sect. 6, the multi-wavelength properties of ESO 511-G030 varied dramatically with time. In 2007, in fact, the source UV-to-X-rays were consistent with that of a bare Type 1 AGN. Later, once re-observed in 2019, neither the UVs nor the X-rays where compatible with their historical fluxes. Moreover, the UV emission, which in 2007 was fully ascribable to the accretion process, turned out to be Galaxy dominated, with only a few percent of the flux being due to the AGN.

To better understand the interplay amongst the different emission components in ESO 511-G030 across the years, we modelled the XMM-Newton spectrum taken in 2007 and those obtained in 2019. At this stage, we included the corresponding OM data and tested AGNSED (Kubota & Done 2018). This model allowed us to self-consistently reproduce the UV-to-X-ray spectra of ESO 511-G030. In accordance with Done et al. (2012), AGNSED accounts for three distinct emitting regions: an outer standard disc region, a warm Comptonising corona, and an inner hot Comptonising plasma. The flow is radially stratified and emits as a standard black-body-like disc from Rout to Rwarm, as warm Comptonisation from Rwarm to Rhot (adopting the passive disc scenario by Petrucci et al. 2018), and as the typical hot Comptonisation component below Rhot down to RISCO. We thus tested the model5:

tbabs G × redden × ( galaxy + AGNSED + relxillcp + Borus ) . $$ \begin{aligned} \mathrm{tbabs}_G \times \mathrm{redden}\times (\mathrm{galaxy+AGNSED+relxillcp+Borus}).\\ \end{aligned} $$(1)

The tbabsG was fixed to the value NH = 4.33 × 1020 cm−2 (HI4PI Collaboration 2016), while the ‘redden’ component was fixed to a value of E(B − V) = 0.056, in agreement with Schlafly & Finkbeiner (2011). We tested this model by fitting each observation separately, and within AGNSED, we allowed the photon indices of the warm and hot coronae to vary as well as the Rhot and Rwarm parameters. The hot coronal temperature was fixed to 100 keV to fit the 2007 data because there is no constraint above 10 keV, while it was left free to vary in the 2019 data. The warm coronal temperature was computed in both datasets. We used a co-moving distance of 96 Mpc (derived from the redshift)6 and adopted the mass for the SMBH in ESO 511-G030 by Ponti et al. (2012). The models Relxillcp and Borus (borus11_v190815a.fits), both accounting for a Comptonised continuum, were set similarly to what we described in Sect. 4.2. These different flavours of relxill and Borus were used in order to tie the model parameters accounting for a Comptonised continuum (e.g. kTe instead of Ecut) with the corresponding parameters in AGNSED, which assumes an underlying Comptonised continuum and not simply a cut-off power-law. In the fit procedure, we assumed the spin of the central SMBH to be maximally rotating in both relxillcp and AGNSED, and the same disc inclination of 30° was also assumed. Within AGNSED, the upper limit of the scale height for the hot Comptonisation component was set to be 10 Rg, which mimics a spherical Comptonisation region of similar radius. In relxillcp, we set the emissivity profile to its default value of three. The inner radius for the relxillcp reflection was fixed to Rhot. This assumption is discussed later. Then the outer disc radius was set to be the same (Rout = 400Rg) between the model component AGNSED and relxillcp. After preliminary tests, we fixed the relxillcp parameter Rin to 100 Rg, as it could not be constrained in the 2019 data. Finally, we added a galaxy template accounting for the host galaxy (matching the morphological type of ESO 511-G030; i.e. Sc; Lauberts 1982) contributing to the UV flux. The table was computed following Ezhikode et al. (2017) and included within XSPEC as a template named ‘hostpol’ (Polletta et al. 2007). We note that our galaxy model has a spectral shape between 3–10 eV of ∼Γ = 4. This shape is fully consistent with our assumption in Sect. 7 for the host galaxy. We tied the normalisation of hostpol across the five spectra.

This procedure led us to the best-fit and model for data ratios, shown in Fig. 14. The fit information as well as the corresponding yielded quantities are shown in Table 4.

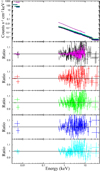thumbnail Fig. 14.

AGNSED reproducing the 2019 campaign and the archival XMM-Newton exposure. In the bottom panels, the data-model ratios for each dataset are shown. Magenta is used for the 2007 data.

Table 4.

Best-fit parameters derived adopting AGNSED on the XMM-Newton 2007 exposure and data from the 2019 monitoring campaign.

According to these fits, the SED of ESO 511-G030 varied dramatically from 2007 to 2019. As for the Eddington ratio, it varied from a value of L/LEdd ∼ 2% (in the 2007 spectrum soft excess+power-law) to a rather low and radiatively inefficient value of ∼0.2% in 2019. The standard configuration assumed within AGNSED, that is, the presence of a hot plasma (for R between Risco and Rhot ∼ 27Rg), a warm plasma (from Rhot to Rwarm ∼ 150Rg), and an accretion disc radially segregated, agrees with the 2007 XMM-Newton observation. As stated before, the reflection in our model is produced beyond Rhot. However, in AGNSED a warm corona is present between Rhot and Rwarm, and the standard disc starts only beyond Rwarm. Though we believe that the impact on our best-fit results should be limited, we note that our modelling does not take into account the presence of the warm corona in the reflection computation and thus does not provide a fully self-consistent physical picture of the emission emerging from ESO511-G030. To our knowledge, the model REXCOR (Xiang et al. 2022) is the sole publicly available model that self-consistently computes the reflection spectrum from the combination of an outer standard disc and inner warm corona. However, this model cannot be extended to the UV energy range and cannot be used to simultaneously fit the OM data.

The lack of a substantial soft excess during the 2019 campaign leads towards a different layout where the hot corona is now more extended than before and no clear indication of a warm Comptonising region is found. This warm region has shrunk, and the disc already extends from ≲50Rg, close to the hot component. The relativistic reflection component is less prominent, and no constraints on the inner radius were obtained. The cold reflection component is compatible amongst the 2007 and 2019 data, in agreement with its distant origin from the central engine. Finally, the change of the hot corona is also accompanied by the spectra evolving from a softer to a harder state, from Γ = 1.91 ± 0.03 to an average value of Γ = 1.75 ± 0.02.

9. Discussion and conclusions

We reported on the spectral and temporal properties of ESO 511-G030 that showed significant variability in both the optical-UV and X-ray bands. Our analysis revealed the ESO 511-G030 spectrum to be consistent with a primary power-law Γ = 1.73 ± 0.02 and accompanied by a poorly constrained high-energy rollover. The reflected flux we observed in the X-rays of ESO 511-G030 emerges from regions of different densities (Compton-thin and Compton-thick). In Fig. 7, we find the high-energy spectrum of the source to be dominated by reflection off a Compton-thin medium NH ∼ 1.8 × 1023 cm−2 that does not produce a relevant Compton-hump but accounts for a narrow Fe Kα line. The relativistic reflection component reproduces the moderate broad shape of the same emission line and contributes to the overall spectral curvature.

Testing our Model C on archival data (see Sect. 5 and the work by Ghosh & Laha 2021) revealed the primary component to be harder in 2019 than in past observations. We found these harder states to correspond to lower flux levels, suggesting the commonly observed softer-when-brighter trend. The reflected flux also varied. In particular, the relativistic reflection was found to follow the variations of the primary emission (in agreement with this flux being released in the close surroundings of the central engine), while a less variable behaviour was observed for the cold reflection.

One of the main features of the 2019 observational campaign is a lack of substantial soft excess. A simple power-law, in fact, dominates the soft-to-hard X-ray spectrum of ESO 511-G030, at least from 2019. The lack of a soft excess, or its negligible contribution to the overall emission spectrum, is further supported by the analysis of the 2007 and 2019 excess variance spectra. Two different components are in fact needed to account for the 2007 Fvar spectrum: one responsible for the changes in the X-ray continuum and a second accounting for the soft excess. In contrast, the Fvar computed for the 2019 XMM-Newton exposures only requires a single component accounting for variance due to the nuclear continuum. It is worth noting that while the Fvar spectra of the Fig. 4 sample has slightly different timescales (see Sect. 3), we verified that when cutting the 2007 observation into shorter segments (so as to sample similar timescales as for the 2019 Fvar spectra), a soft excess component still appears in the Fvar of the lowest flux segment.

The absence of a strong soft excess is quite unusual since it is ubiquitously observed in AGNs (e.g. Piconcelli et al. 2005; Bianchi et al. 2009; Gliozzi & Williams 2020). We note that ESO 511-G030 data do not require any absorbing component, as also discussed in Laha et al. (2014), thus the lack of the soft excess in this source cannot be explained with an absorption process.

The case of ESO 511-G030 is peculiar, and we can only compare its behaviour with that of Mrk 1018. This AGN had been studied in depth by Noda & Done (2018), who observed very different spectral shapes corresponding to different Eddington ratios. From a typical Type 1 spectrum with a strong soft excess, the source dimmed down, became harder, and showed a weaker soft excess. This spectral transition corresponded to a change in the Eddington ratio from L/LEdd∼2% to L/LEdd∼0.4%, which is very similar to what is observed here for ESO 511-G030. As the soft excess is responsible for most of the ionising photons, the dramatic drop in the X-rays also led to the disappearance of the Broad Line Region, producing the ‘changing-look’ phenomenon. In other words, the presence (lack) of the soft excess corresponded to a general softening (hardening) of the X-ray continuum emission with an accompanying dramatic change in the disc emission and a disappearance of the optical broad lines.

Similar to Mrk 1018, ESO 511-G030 had a dramatic change in its accretion rate, passing from L/LEdd ∼ 2% in 2007 down to L/LEdd ∼ 0.2% in 2019. This dimming was also accompanied by a dramatic change in the UV SEDs (see Figs. 11 and 14), though it did not lead to a ‘complete’ changing-look process. An optical FLOYDS spectrum was in fact taken quasi-simultaneously with the XMM-Newton-NuSTAR campaign to check whether broad lines were present or not. From a quick comparison between the FLOYDS spectrum and an 6dF archival one taken in 2000, the Hβ line does not disappear in 2019, and its velocity width was similar between the spectra (FWHMHβ ∼ 4500 km s−1, private communications with Keith Horne and Juan V. Hernández Santisteban).

The strong decrease of the accretion rate between 2007 and 2019 seems to be the crucial element for explaining the observed spectral UV-X-ray behaviour. Indeed this decrease naturally explains the strong decrease of the UV emission (see Figs. 12 and 13). To the 0th order, the decrease of the UV flux would also mean a reduction of the soft photons flux entering and cooling the hot corona. So we would expect an increase of the hot plasma temperature and a hardening of the X-ray spectrum with respect to the observation from 2007. Spectral hardening was observed, and the absence of a stringent high-energy cut-off signature in 2019 agrees with a high corona temperature, much higher than the usual values observed in Seyfert galaxies (e.g. Fabian et al. 2015, 2017; Tamborra et al. 2018; Middei et al. 2019). The absence of high signal-high energy observations in the archives prevents any comparison with past observations that would help to support this scenario. But the strong decrease of the accretion rate could also explain the absence of the soft X-ray excess in 2019, at least in the case of the warm corona model. The observations agree with the warm corona being the upper layers of the accretion disc (Petrucci et al. 2018, and references therein). More importantly, to reproduce the soft X-ray spectral shape, simulations show that a large enough accretion power has to be released inside this warm corona and not in the accretion disc underneath (Różańska et al. 2015; Petrucci et al. 2020; Ballantyne 2020). So if the accretion power becomes too low, the warm corona cannot be energetically sustained. It is less obvious to understand why the soft X-ray excess would disappear if it is due to relativistically blurred ionised reflection. It is possible, however, that at a low accretion rate, the disc becomes more optically thin (or even recedes) and produces less reflection, as is indeed observed in 2019. However, other possible explanations for the lack of the soft excess in ESO 511-G030 may be viable, and new exposures, possibly performed during the awakening of this component, are needed in order to shed light onto the engine of this Seyfert galaxy. The increasing UV and X-ray fluxes observed by Swift in the first quarter of 2022 encourage us to ask for more observing time to, possibly, observe the revenant soft excess of ESO 511-G030.

5

We did not include the Balmer continuum nor the Fe II emission lines in the fit. In fact, the UV emission of ESO511-G030 in 2019 can likely be ascribed only to the host.

Acknowledgments

RM thanks Francesco Saturni, Mauro Dadina and Emanuele Nardini for useful discussions and insights. Fondazione Angelo Della Riccia for financial support and Université Grenoble Alpes and the high energy SHERPAS group for welcoming him at IPAG. Part of this work is based on archival data, software or online services provided by the Space Science Data Center - ASI. This work has been partially supported by the ASI-INAF programme I/004/11/5. RM acknowledges financial contribution from the agreement ASI-INAF n.2017-14-H.0. SB and EP acknowledge financial support from ASI under grants ASI-INAF I/037/12/0 and n. 2017-14-H.O. POP acknowledges financial support from the CNES, the French spatial agency, and from the PNHE, High energy programme of CNRS. ADR acknowledges financial contribution from the agreement ASI-INAF n.2017-14-H.O. BDM acknowledges support from a Ramón y Cajal Fellowship (RYC2018-025950-I) and the Spanish MINECO grant PID2020-117252GB-I00. This work is based on observations obtained with: the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory and funded by NASA; XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA).

References

  1. Almaini, O., Lawrence, A., Shanks, T., et al. 2000, MNRAS, 315, 325 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alston, W. N., Fabian, A. C., Buisson, D. J. K., et al. 2019, MNRAS, 482, 2088 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aretxaga, I., Cid Fernandes, R., & Terlevich, R. J. 1997, MNRAS, 286, 271 [NASA ADS] [CrossRef] [Google Scholar]
  4. Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
  5. Ballantyne, D. R. 2020, MNRAS, 491, 3553 [NASA ADS] [CrossRef] [Google Scholar]
  6. Baloković, M., Brightman, M., Harrison, F. A., et al. 2018, ApJ, 854, 42 [Google Scholar]
  7. Baloković, M., Harrison, F. A., Madejski, G., et al. 2020, ApJ, 905, 41 [Google Scholar]
  8. Barr, P., & Mushotzky, R. F. 1986, Nature, 320, 421 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bianchi, S., Guainazzi, M., Matt, G., Fonseca Bonilla, N., & Ponti, G. 2009, A&A, 495, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bisogni, S., Lusso, E., Civano, F., et al. 2021, A&A, 655, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bregman, J. N. 1990, A&A Rv., 2, 125 [NASA ADS] [Google Scholar]
  12. Chartas, G., Kochanek, C. S., Dai, X., Poindexter, S., & Garmire, G. 2009, ApJ, 693, 174 [Google Scholar]
  13. Chiaraluce, E., Vagnetti, F., Tombesi, F., & Paolillo, M. 2018, A&A, 619, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Crummy, J., Fabian, A. C., Gallo, L., & Ross, R. R. 2006, MNRAS, 365, 1067 [Google Scholar]
  15. Dadina, M. 2007, A&A, 461, 1209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Dauser, T., García, J., Walton, D. J., et al. 2016, A&A, 590, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. de La Calle Pérez, I., Longinotti, A. L., Guainazzi, M., et al. 2010, A&A, 524, A50 [CrossRef] [EDP Sciences] [Google Scholar]
  18. De Marco, B., Ponti, G., Cappi, M., et al. 2013, MNRAS, 431, 2441 [Google Scholar]
  19. De Marco, B., Adhikari, T. P., Ponti, G., et al. 2020, A&A, 634, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. de Vaucouleurs, G., de Vaucouleurs, A., Corwin Herold G. J., et al. 1991, Third Reference Catalogue of Bright Galaxies [Google Scholar]
  21. Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 420, 1848 [Google Scholar]
  22. Edelson, R., Turner, T. J., Pounds, K., et al. 2002, ApJ, 568, 610 [CrossRef] [Google Scholar]
  23. Ezhikode, S. H., Gandhi, P., Done, C., et al. 2017, MNRAS, 472, 3492 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [Google Scholar]
  25. Fabian, A. C., Iwasawa, K., Reynolds, C. S., & Young, A. J. 2000, PASP, 112, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fabian, A. C., Lohfink, A., Kara, E., et al. 2015, MNRAS, 451, 4375 [Google Scholar]
  27. Fabian, A. C., Lohfink, A., Belmont, R., Malzac, J., & Coppi, P. 2017, MNRAS, 467, 2566 [Google Scholar]
  28. Falocco, S., Paolillo, M., Comastri, A., et al. 2017, A&A, 608, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Galeev, A. A., Rosner, R., & Vaiana, G. S. 1979, ApJ, 229, 318 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gallo, L. C., Blue, D. M., Grupe, D., Komossa, S., & Wilkins, D. R. 2018, MNRAS, 478, 2557 [NASA ADS] [CrossRef] [Google Scholar]
  31. García, J., Dauser, T., Reynolds, C. S., et al. 2013, ApJ, 768, 146 [Google Scholar]
  32. García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [Google Scholar]
  33. George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [Google Scholar]
  34. Ghosh, R., & Laha, S. 2021, ApJ, 908, 198 [NASA ADS] [CrossRef] [Google Scholar]
  35. Gliozzi, M., & Williams, J. K. 2020, MNRAS, 491, 532 [Google Scholar]
  36. Green, A. R., McHardy, I. M., & Lehto, H. J. 1993, MNRAS, 265, 664 [NASA ADS] [Google Scholar]
  37. Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [Google Scholar]
  38. Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [Google Scholar]
  39. Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
  40. HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Igo, Z., Parker, M. L., Matzeu, G. A., et al. 2020, MNRAS, 493, 1088 [NASA ADS] [CrossRef] [Google Scholar]
  42. Jin, C., Ward, M., & Done, C. 2012, MNRAS, 425, 907 [NASA ADS] [CrossRef] [Google Scholar]
  43. Just, D. W., Brandt, W. N., Shemmer, O., et al. 2007, ApJ, 665, 1004 [Google Scholar]
  44. Kamraj, N., Brightman, M., Harrison, F. A., et al. 2022, ApJ, 927, 42 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kara, E., Alston, W., & Fabian, A. 2016, Astron. Nachr., 337, 473 [Google Scholar]
  46. Koyama, K., Tsunemi, H., Dotani, T., et al. 2007, PASJ, 59, 23 [Google Scholar]
  47. Kubota, A., & Done, C. 2018, MNRAS, 480, 1247 [Google Scholar]
  48. Laha, S., Guainazzi, M., Dewangan, G. C., Chakravorty, S., & Kembhavi, A. K. 2014, MNRAS, 441, 2613 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lauberts, A. 1982, ESO/Uppsala Survey of the ESO(B) Atlas [Google Scholar]
  50. Lawrence, A., & Papadakis, I. 1993, ApJ, 414, L85 [NASA ADS] [CrossRef] [Google Scholar]
  51. Lusso, E., & Risaliti, G. 2016, ApJ, 819, 154 [Google Scholar]
  52. Lusso, E., & Risaliti, G. 2017, A&A, 602, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Lusso, E., Comastri, A., Vignali, C., et al. 2010, A&A, 512, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Lusso, E., Risaliti, G., Nardini, E., et al. 2020, A&A, 642, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Magdziarz, P., Blaes, O. M., Zdziarski, A. A., Johnson, W. N., & Smith, D. A. 1998, MNRAS, 301, 179 [NASA ADS] [CrossRef] [Google Scholar]
  56. Mahmoud, R. D., & Done, C. 2020, MNRAS, 491, 5126 [NASA ADS] [Google Scholar]
  57. Malizia, A., Molina, M., Bassani, L., et al. 2014, ApJ, 782, L25 [NASA ADS] [CrossRef] [Google Scholar]
  58. Marinucci, A., Bianchi, S., Braito, V., et al. 2020, MNRAS, 496, 3412 [NASA ADS] [CrossRef] [Google Scholar]
  59. Martocchia, S., Piconcelli, E., Zappacosta, L., et al. 2017, A&A, 608, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Matt, G., Fabian, A. C., & Ross, R. R. 1993, MNRAS, 262, 179 [NASA ADS] [CrossRef] [Google Scholar]
  61. Matzeu, G. A., Reeves, J. N., Nardini, E., et al. 2016, MNRAS, 458, 1311 [Google Scholar]
  62. Matzeu, G. A., Reeves, J. N., Nardini, E., et al. 2017, MNRAS, 465, 2804 [NASA ADS] [CrossRef] [Google Scholar]
  63. Matzeu, G. A., Nardini, E., Parker, M. L., et al. 2020, MNRAS, 497, 2352 [CrossRef] [Google Scholar]
  64. McHardy, I. M., Koerding, E., Knigge, C., Uttley, P., & Fender, R. P. 2006, Nature, 444, 730 [NASA ADS] [CrossRef] [Google Scholar]
  65. Middei, R., Vagnetti, F., Bianchi, S., et al. 2017, A&A, 599, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Middei, R., Bianchi, S., Marinucci, A., et al. 2019, A&A, 630, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Middei, R., Petrucci, P. O., Bianchi, S., et al. 2020, A&A, 640, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Mitsuda, K., Bautz, M., Inoue, H., et al. 2007, PASJ, 59, S1 [NASA ADS] [CrossRef] [Google Scholar]
  69. Molina, M., Bassani, L., Malizia, A., et al. 2009, MNRAS, 399, 1293 [NASA ADS] [CrossRef] [Google Scholar]
  70. Molina, M., Bassani, L., Malizia, A., et al. 2013, MNRAS, 433, 1687 [NASA ADS] [CrossRef] [Google Scholar]
  71. Morgan, C. W., Hainline, L. J., Chen, B., et al. 2012, ApJ, 756, 52 [Google Scholar]
  72. Mushotzky, R. F., Done, C., & Pounds, K. A. 1993, ARAA, 31, 717 [NASA ADS] [CrossRef] [Google Scholar]
  73. Nandra, K., O’Neill, P. M., George, I. M., & Reeves, J. N. 2007, MNRAS, 382, 194 [NASA ADS] [CrossRef] [Google Scholar]
  74. Noda, H., & Done, C. 2018, MNRAS, 480, 3898 [Google Scholar]
  75. Oh, K., Koss, M., Markwardt, C. B., et al. 2018, ApJS, 235, 4 [Google Scholar]
  76. Padovani, P., Alexander, D. M., Assef, R. J., et al. 2017, A&ARv., 25, 2 [NASA ADS] [CrossRef] [Google Scholar]
  77. Paolillo, M., Papadakis, I., Brandt, W. N., et al. 2017, MNRAS, 471, 4398 [Google Scholar]
  78. Papadakis, I. E. 2004, MNRAS, 348, 207 [NASA ADS] [CrossRef] [Google Scholar]
  79. Papadakis, I. E., Chatzopoulos, E., Athanasiadis, D., Markowitz, A., & Georgantopoulos, I. 2008, A&A, 487, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Parker, M. L., Alston, W. N., Igo, Z., & Fabian, A. C. 2020, MNRAS, 492, 1363 [NASA ADS] [CrossRef] [Google Scholar]
  81. Perola, G. C., Matt, G., Fiore, F., et al. 2000, A&A, 358, 117 [NASA ADS] [Google Scholar]
  82. Petrucci, P. O., Ursini, F., De Rosa, A., et al. 2018, A&A, 611, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Petrucci, P. O., Gronkiewicz, D., Rozanska, A., et al. 2020, A&A, 634, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Pica, A. J., & Smith, A. G. 1983, ApJ, 272, 11 [NASA ADS] [CrossRef] [Google Scholar]
  85. Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2004, MNRAS, 351, 161 [Google Scholar]
  86. Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
  88. Ponti, G., Cappi, M., Dadina, M., & Malaguti, G. 2004, A&A, 417, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Ponti, G., Miniutti, G., Cappi, M., et al. 2006, MNRAS, 368, 903 [CrossRef] [Google Scholar]
  90. Ponti, G., Papadakis, I., Bianchi, S., et al. 2012, A&A, 542, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Porquet, D., Reeves, J. N., Matt, G., et al. 2018, A&A, 609, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Reeves, J. N., Braito, V., Porquet, D., et al. 2021, MNRAS, 500, 1974 [Google Scholar]
  93. Ricci, C., Ho, L. C., Fabian, A. C., et al. 2018, MNRAS, 480, 1819 [NASA ADS] [CrossRef] [Google Scholar]
  94. Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [Google Scholar]
  95. Risaliti, G., & Lusso, E. 2015, ApJ, 815, 33 [NASA ADS] [CrossRef] [Google Scholar]
  96. Różańska, A., Malzac, J., Belmont, R., Czerny, B., & Petrucci, P. O. 2015, A&A, 580, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics [Google Scholar]
  98. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  99. Serafinelli, R., Vagnetti, F., & Middei, R. 2017, A&A, 600, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1597 [NASA ADS] [CrossRef] [Google Scholar]
  101. Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [Google Scholar]
  102. Tamborra, F., Matt, G., Bianchi, S., & Dovčiak, M. 2018, A&A, 619, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Tanaka, Y., Nandra, K., Fabian, A. C., et al. 1995, Nature, 375, 659 [NASA ADS] [CrossRef] [Google Scholar]
  104. Tananbaum, H., Avni, Y., Branduardi, G., et al. 1979, ApJ, 234, L9 [Google Scholar]
  105. Tananbaum, H., Avni, Y., Green, R. F., Schmidt, M., & Zamorani, G. 1986, ApJ, 305, 57 [NASA ADS] [CrossRef] [Google Scholar]
  106. Theureau, G., Bottinelli, L., Coudreau-Durand, N., et al. 1998, A&AS, 130, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Timlin, J. D. I., Brandt, W. N., Zhu, S., et al. 2020, MNRAS, 498, 4033 [Google Scholar]
  108. Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001a, A&A, 365, L27 [CrossRef] [EDP Sciences] [Google Scholar]
  109. Turner, T. J., Nandra, K., Turcan, D., & George, I. M. 2001b, Am. Inst. Phys. Conf. Ser., 599, 991 [NASA ADS] [Google Scholar]
  110. Ulrich, M.-H., Maraschi, L., & Urry, C. M. 1997, ARA&A, 35, 445 [NASA ADS] [CrossRef] [Google Scholar]
  111. Ursini, F., Petrucci, P. O., Matt, G., et al. 2018, MNRAS, 478, 2663 [NASA ADS] [CrossRef] [Google Scholar]
  112. Ursini, F., Petrucci, P. O., Bianchi, S., et al. 2020, A&A, 634, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Vagnetti, F., Turriziani, S., Trevese, D., & Antonucci, M. 2010, A&A, 519, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Vagnetti, F., Turriziani, S., & Trevese, D. 2011, A&A, 536, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Vagnetti, F., Antonucci, M., & Trevese, D. 2013, A&A, 550, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Vagnetti, F., Middei, R., Antonucci, M., Paolillo, M., & Serafinelli, R. 2016, A&A, 593, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [Google Scholar]
  118. Vaughan, S., Fabian, A. C., Ballantyne, D. R., et al. 2004, MNRAS, 351, 193 [NASA ADS] [CrossRef] [Google Scholar]
  119. Véron-Cetty, M. P., & Véron, P. 2010, A&A, 518, A10 [Google Scholar]
  120. Vignali, C., Brandt, W. N., & Schneider, D. P. 2003, AJ, 125, 433 [Google Scholar]
  121. Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS] [CrossRef] [Google Scholar]
  122. Walton, D. J., Nardini, E., Fabian, A. C., Gallo, L. C., & Reis, R. C. 2013, MNRAS, 428, 2901 [NASA ADS] [CrossRef] [Google Scholar]
  123. Xiang, X., Ballantyne, D. R., Bianchi, S., et al. 2022, MNRAS, 515, 353 [NASA ADS] [CrossRef] [Google Scholar]
  124. Zamorani, G., Henry, J. P., Maccacaro, T., et al. 1981, ApJ, 245, 357 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: The Swift-XRT observations

Results of the spectral analysis performed on the Swift-XRT observations belonging to our monitoring campaigns. Details are provided in Sect. 6.

Table A.1.

Best-fitted parameters as inferred from a spectral analysis of Swift-XRT spectra. Soft (0.3-2 keV) and hard (2-10 keV) fluxes are given in units of × 10−12 erg cm−2 s−1.

All Tables

Table 1.

Log of the observations.

In the text
Table 2.

Best-fit parameters obtained using models A and B (see Sect. 4.2 for details).

In the text
Table 3.

Parameters derived by adapting the baseline Model C to the archival data.

In the text
Table 4.

Best-fit parameters derived adopting AGNSED on the XMM-Newton 2007 exposure and data from the 2019 monitoring campaign.

In the text
Table A.1.

Best-fitted parameters as inferred from a spectral analysis of Swift-XRT spectra. Soft (0.3-2 keV) and hard (2-10 keV) fluxes are given in units of × 10−12 erg cm−2 s−1.

In the text

All Figures

thumbnail Fig. 1.

Unfolded spectra of ESO 511-G030 corresponding to the observations listed in Table 1. Variability is observed both in terms of spectral and amplitude changes. In the optical-UV band, the source faded by a factor of approximately ten. The underlying model folding the data is a power-law with Γ = 2 and a unitary normalisation.
In the text
thumbnail Fig. 2.

ESO511-G030 light curves. Top panels: Background-subtracted light curves from the 2019 multi-wavelength campaign. The first and second row refer to the XMM-Newton 0.5–2 and 2–10 keV bands, respectively, while the last row shows the ratios between the two bands. The NuSTAR light curves extracted in the 10–79 keV band are also shown. Bottom panels: Background-subtracted time series for ASCA (black), the 2007 XMM-Newton orbit (red) and the Suzaku visits two and three (in blue).
In the text
thumbnail Fig. 3.

Fvar spectra for the XMM-Newton observations in Table 1. Spectra from the 2019 monitoring campaign are all characterised by a fairly flat shape, while data from 2007 clearly show a variability bump in the soft X-rays.
In the text
thumbnail Fig. 4.

Comparison between the Fvar spectrum of the 2007 and 2019 data. The 2019 observations (magenta) were obtained by grouping together the five exposures via the standard command SETPLOTGROUP within XSPEC. The spectrum derived from 2007 data is in black. The magenta curve represents a theoretical Fvar spectrum, which depicts the combined contribution from a variable power-law-like continuum and a variable soft excess.
In the text
thumbnail Fig. 5.

Zoom of the Fe Kα complex. Top panels: EPIC-pn data in the 4–8 keV energy band fitted using a power-law and a narrow Gaussian emission line assumed to be constant among the exposures. Residuals in the Fe K energy range are present. Bottom panels: Same as above but with the addition of a broad Fe Kα emission line for which the line normalisation was assumed to be constant among the 2019 pointings but free to vary in 2007.
In the text
thumbnail Fig. 6.

Confidence regions at 99%, 90%, and 68% for the line’s width and normalisation. The contours were obtained assuming the model power-law+zGaussbroad and using a single broad Gaussian component.
In the text
thumbnail Fig. 7.

Model C fitting to the 2019 spectra. Borus and relxill account for the cold and hot reflection components, respectively.
In the text
thumbnail Fig. 8.

Fit to the ASCA, 2007 XMM-Newton, and Suzaku data. We show these spectra in black, magenta and blue, respectively. Bottom panels report on the data-model ratios.
In the text
thumbnail Fig. 9.

Multi-filter light curves derived from 2018 up to 2022 for ESO 511-G030 using Swift-XRT and -UVOT. Until the end of 2021 (MJD < 59580), after which a moderate increase of ultraviolet emission can be observed, the optical-UV curves could be highly affected by the host emission. We noticed that to quantify the actual amplitude of the optical-UV emission, an estimate of the contribution of the host galaxy is required (see Sect. 6).
In the text
thumbnail Fig. 10.

Best-fit parameters and fluxes in the 0.3–2 (Soft) and 2–10 keV (hard) bands derived from Swift. Straight solid lines show the mean value of the parameter, while dotted lines represent the corresponding standard deviation. Fluxes are in units of 10−12 erg cm−2 s−1.
In the text
thumbnail Fig. 11.

ESO 511-G030 optical-UV SEDs derived using XMM-Newton and Swift data (dark green). The corresponding least squares fits are shown as straight dashed lines. XMM-Newton and Swift data are in blue and dark green, respectively. The solid, thick black line is the average SED by Richards et al. (2006) for Type 1 objects in the SDSS. The vertical dashed line is at logν* = 15.08, corresponding to 2500 Å. We noticed a remarkable change in spectral shape from the 2007 observation compared to the later ones.
In the text
thumbnail Fig. 12.

Light curves for the AGN luminosity at 2500 Å, at 2 keV, and the inferred αOX. Blue dots identify values derived using XMM-Newton observations while in green the same quantities were estimated using Swift. The dashed horizontal line accounts for the adopted host galaxy luminosity at 2500 Å. Finally, both LUV and L2 keV are in units of erg s−1 Hz−1.
In the text
thumbnail Fig. 13.

ESO 511-G030 αOX estimates compared with the sample by Chiaraluce et al. (2018). The solid black line represents logLUV − αox linear relation as derived in the same work. The αOX computed of ESO 511-G030 shows significant variability in agreement with the drop in the OM data shown in Fig. 1.
In the text
thumbnail Fig. 14.

AGNSED reproducing the 2019 campaign and the archival XMM-Newton exposure. In the bottom panels, the data-model ratios for each dataset are shown. Magenta is used for the 2007 data.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.